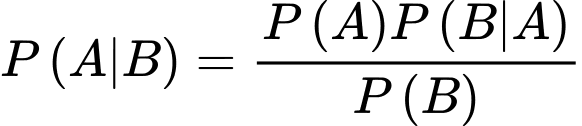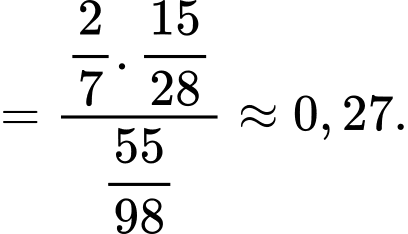PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [512858]: Cho hàm số 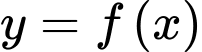 có bảng biến thiên như bên dưới.
có bảng biến thiên như bên dưới.
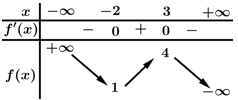
Hàm số đã cho đạt cực đại tại
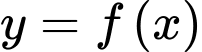 có bảng biến thiên như bên dưới.
có bảng biến thiên như bên dưới.
Hàm số đã cho đạt cực đại tại
A, 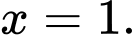
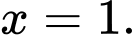
B, 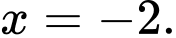
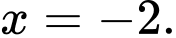
C, 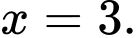
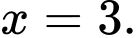
D, 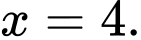
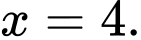
Chọn đáp án C.
Hàm số đạt cực tiểu tại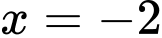 và đạt cực đại tại
và đạt cực đại tại 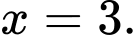 Đáp án: C
Đáp án: C
Hàm số đạt cực tiểu tại
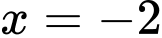 và đạt cực đại tại
và đạt cực đại tại 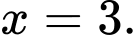 Đáp án: C
Đáp án: C
Câu 2 [316351]: Trong không gian 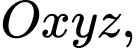 cho đường thẳng
cho đường thẳng 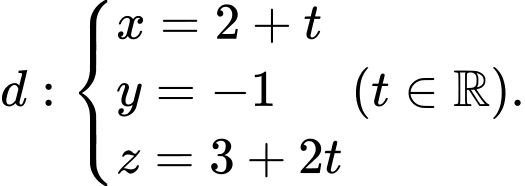 Vectơ nào dưới đây là một vectơ chỉ phương của
Vectơ nào dưới đây là một vectơ chỉ phương của 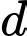 ?
?
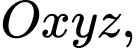 cho đường thẳng
cho đường thẳng 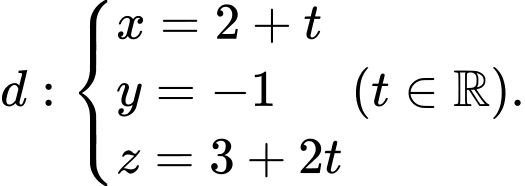 Vectơ nào dưới đây là một vectơ chỉ phương của
Vectơ nào dưới đây là một vectơ chỉ phương của 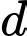 ?
? A, 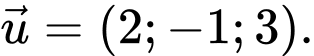
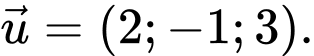
B, 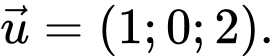
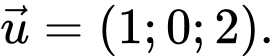
C, 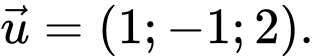
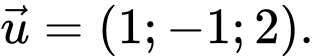
D, 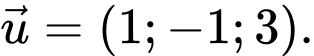
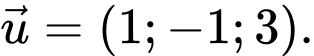
Chọn đáp án B.
Đường thẳng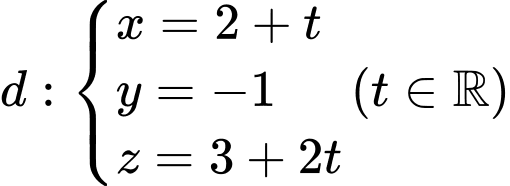 có một VTCP là
có một VTCP là 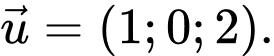 Đáp án: B
Đáp án: B
Đường thẳng
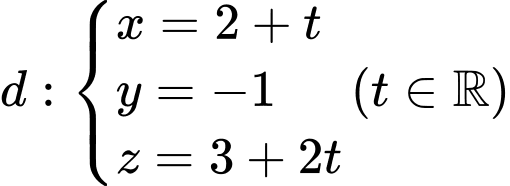 có một VTCP là
có một VTCP là 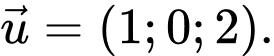 Đáp án: B
Đáp án: B
Câu 3 [801230]: 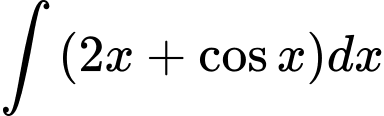 bằng
bằng
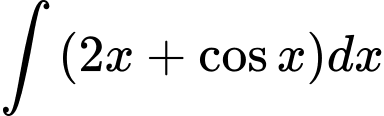 bằng
bằng A, 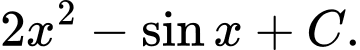
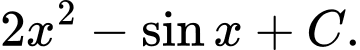
B, 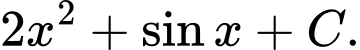
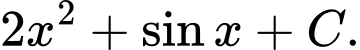
C, 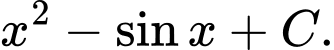
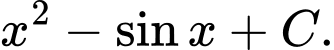
D, 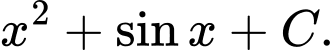
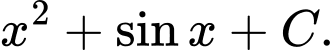
Chọn đáp án D.
Ta có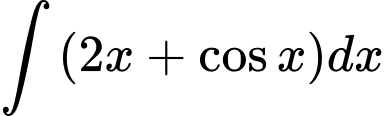
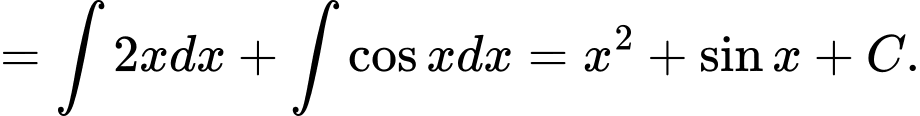 Đáp án: D
Đáp án: D
Ta có
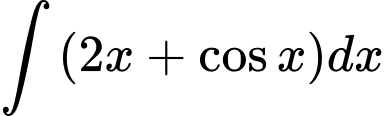
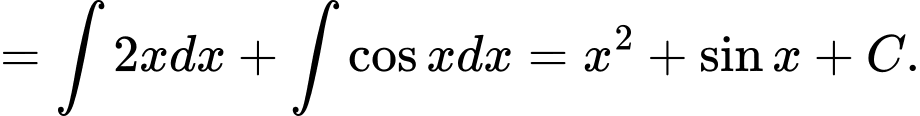 Đáp án: D
Đáp án: D
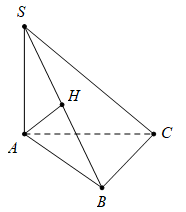
Câu 4 [975554]: Cho hình chóp 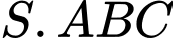 có đáy
có đáy 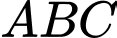 là tam giác vuông tại
là tam giác vuông tại 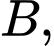
 Gọi
Gọi 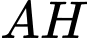 là đường cao kẻ từ
là đường cao kẻ từ 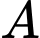 của tam giác
của tam giác 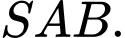 Khẳng định nào dưới đây sai?
Khẳng định nào dưới đây sai?
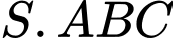 có đáy
có đáy 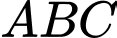 là tam giác vuông tại
là tam giác vuông tại 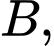
 Gọi
Gọi 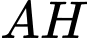 là đường cao kẻ từ
là đường cao kẻ từ 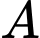 của tam giác
của tam giác  Khẳng định nào dưới đây sai?
Khẳng định nào dưới đây sai? A, 

B, 

C, 

D, 

Chọn đáp án C.
Ta có: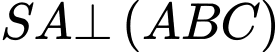

Mặt khác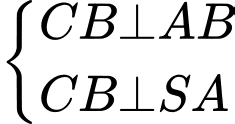
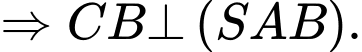
Khi đó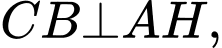 do
do 
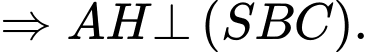
Vậy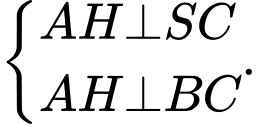 Đáp án: C
Đáp án: C

Ta có:
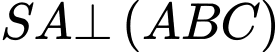

Mặt khác
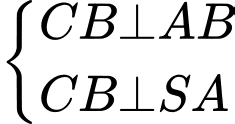
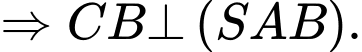
Khi đó
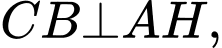 do
do 
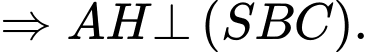
Vậy
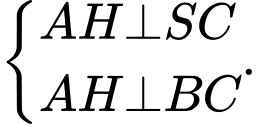 Đáp án: C
Đáp án: C
Câu 5 [517965]: Cấp số cộng 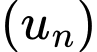 có
có 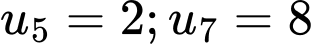 thì
thì 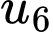 bằng
bằng
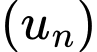 có
có 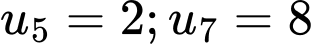 thì
thì 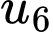 bằng
bằng A, 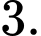
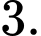
B, 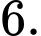
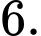
C, 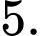
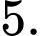
D, 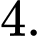
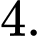
Chọn đáp án C.
Ta có: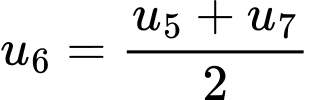
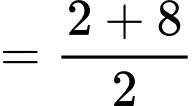
 Đáp án: C
Đáp án: C
Ta có:
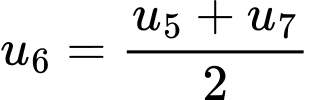
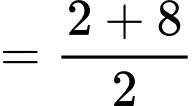
 Đáp án: C
Đáp án: C
Câu 6 [328516]: Tìm tập xác định của hàm số: 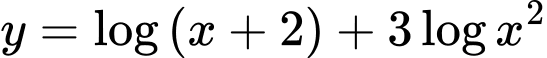
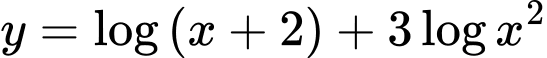
A, 

B, 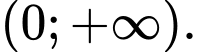
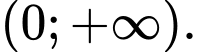
C, 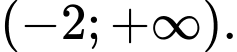
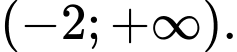
D, 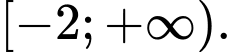
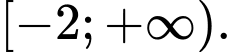
Chọn đáp án A.
Điều kiện xác định: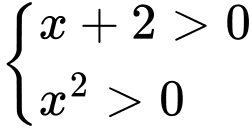
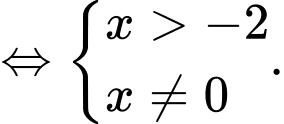
Vậy tập xác định của hàm số là Đáp án: A
Đáp án: A
Điều kiện xác định:
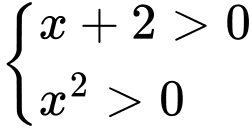
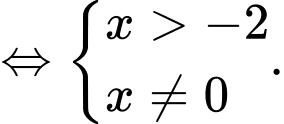
Vậy tập xác định của hàm số là
 Đáp án: A
Đáp án: A
Câu 7 [807215]: Trong không gian 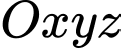 , cho mặt phẳng
, cho mặt phẳng 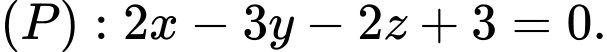 Điểm nào dưới đây thuộc mặt phẳng
Điểm nào dưới đây thuộc mặt phẳng 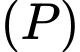 ?
?
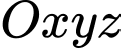 , cho mặt phẳng
, cho mặt phẳng 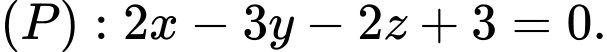 Điểm nào dưới đây thuộc mặt phẳng
Điểm nào dưới đây thuộc mặt phẳng 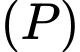 ?
? A, 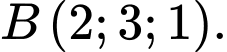
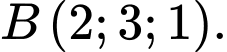
B, 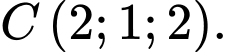
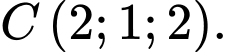
C, 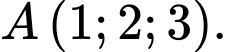
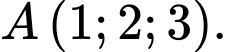
D, 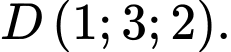
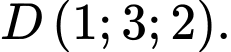
Chọn đáp án B.
Ta có: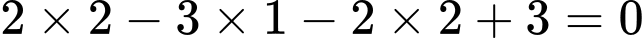 đúng.
đúng.
Vậy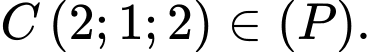 Đáp án: B
Đáp án: B
Ta có:
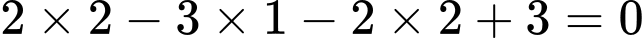 đúng.
đúng. Vậy
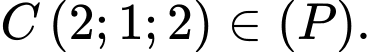 Đáp án: B
Đáp án: B
Câu 8 [977411]: Cho hàm số 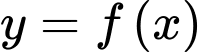 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ. 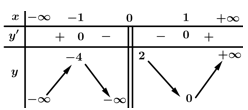
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
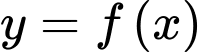 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ. 
A, 1.
B, 2.
C, 3.
D, 4.
Chọn đáp án A.
Đồ thị hàm số không có tiệm cận ngang vì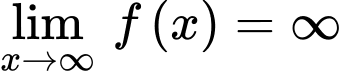
Mặt khác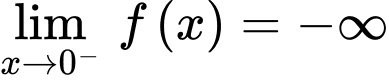 nên đồ thị hàm số có tiệm cận đứng
nên đồ thị hàm số có tiệm cận đứng 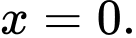 Đáp án: A
Đáp án: A
Đồ thị hàm số không có tiệm cận ngang vì
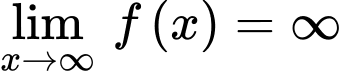
Mặt khác
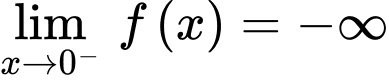 nên đồ thị hàm số có tiệm cận đứng
nên đồ thị hàm số có tiệm cận đứng 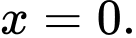 Đáp án: A
Đáp án: A
Câu 9 [801233]: Cho 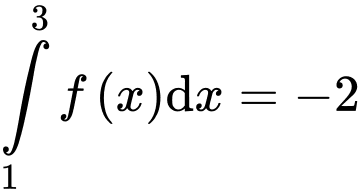 và
và 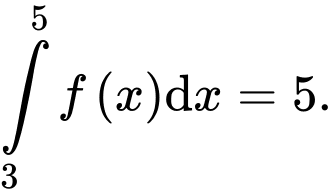 Tích phân
Tích phân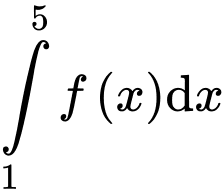 bằng
bằng
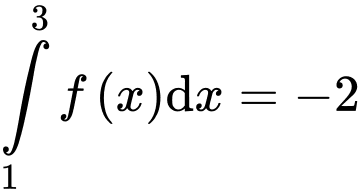 và
và 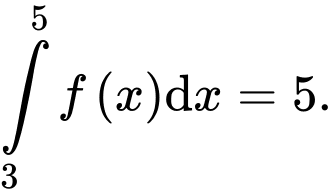 Tích phân
Tích phân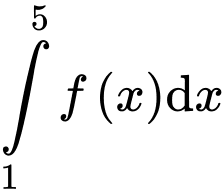 bằng
bằng A, 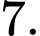
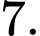
B, 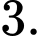
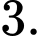
C, 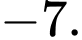
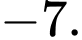
D, 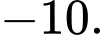
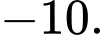
Chọn đáp án B.
Ta có: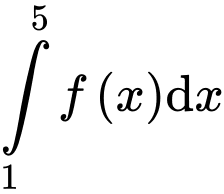
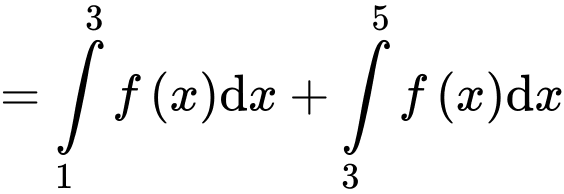
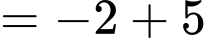
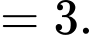 Đáp án: B
Đáp án: B
Ta có:
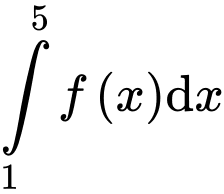
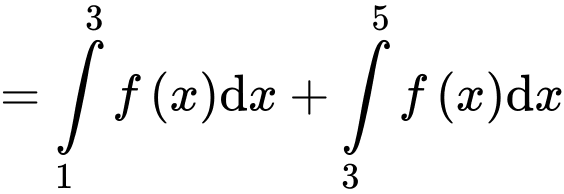
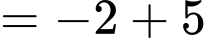
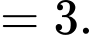 Đáp án: B
Đáp án: B
Câu 10 [601704]: Tập nghiệm của bất phương trình 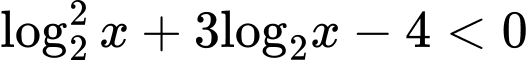
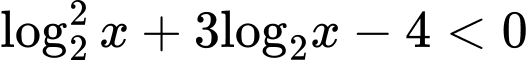
A, 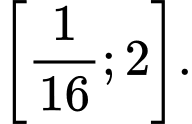
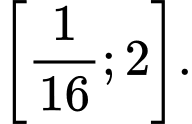
B, 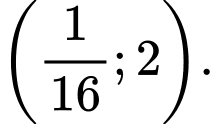
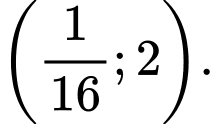
C, 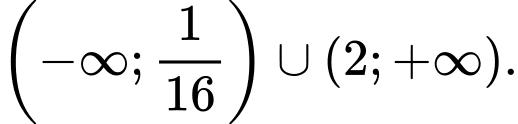
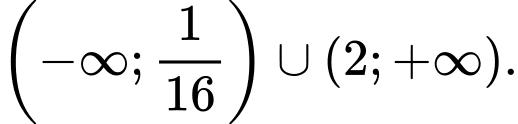
D, 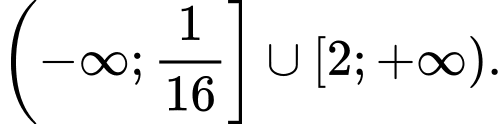
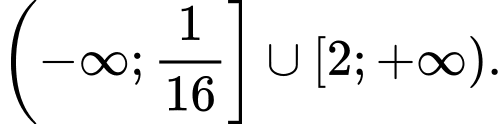
Chọn đáp án B.
Xét Điều kiện:
Điều kiện: 
Ta có: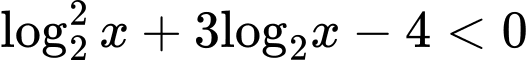
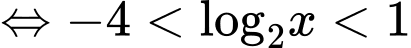
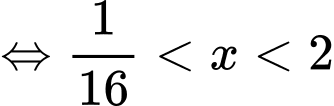 (thỏa đk). Đáp án: B
(thỏa đk). Đáp án: B
Xét
 Điều kiện:
Điều kiện: 
Ta có:
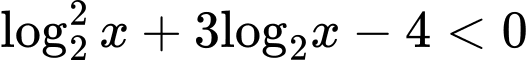
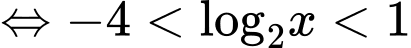
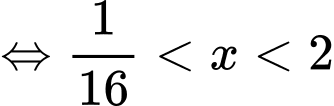 (thỏa đk). Đáp án: B
(thỏa đk). Đáp án: B
Câu 11 [599922]: Cho hình lăng trụ tam giác 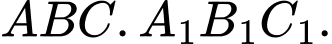 Đặt
Đặt 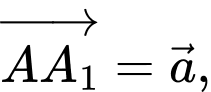
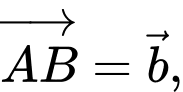
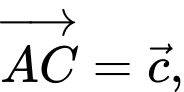
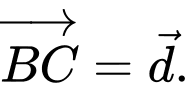 Trong các đẳng thức sau đẳng thức nào đúng?
Trong các đẳng thức sau đẳng thức nào đúng?
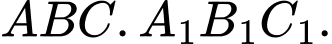 Đặt
Đặt 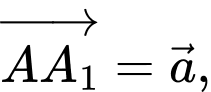
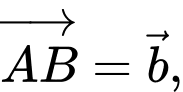
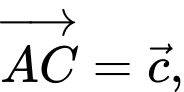
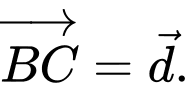 Trong các đẳng thức sau đẳng thức nào đúng?
Trong các đẳng thức sau đẳng thức nào đúng? A, 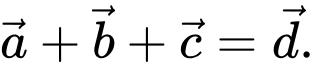
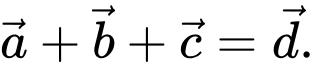
B, 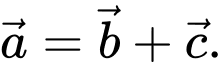
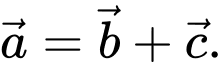
C, 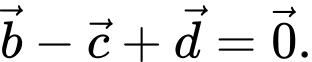
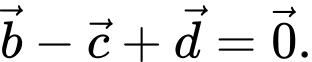
D, 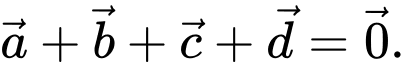
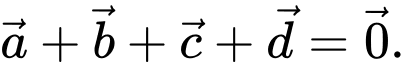
Chọn đáp án C.
Ta có:
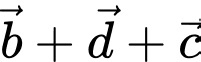
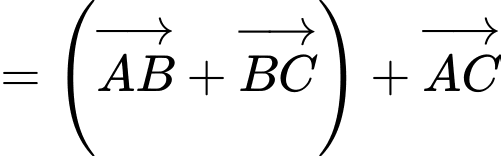
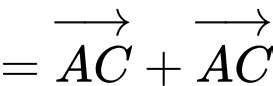
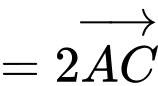
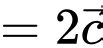
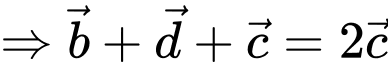
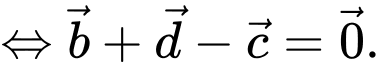 Đáp án: C
Đáp án: C
Ta có:
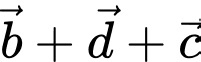
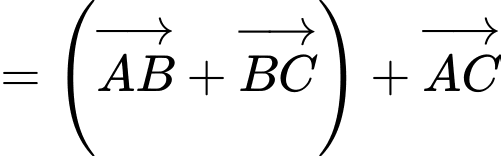
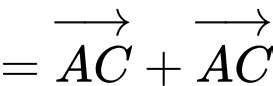
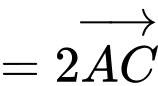
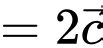
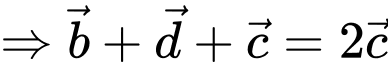
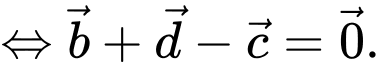 Đáp án: C
Đáp án: C
Câu 12 [695534]: Kết quả đo chiều cao của 100 cây dừa trồng sau 10 năm tại một vườn trái cây ở Bến Tre cho ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần bằng giá trị nào dưới đây nhất?

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần bằng giá trị nào dưới đây nhất?
A, 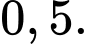
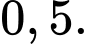
B, 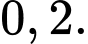
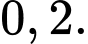
C, 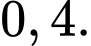
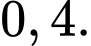
D, 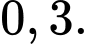
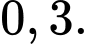
Chọn đáp án D.
Cỡ mẫu
Gọi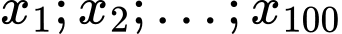 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có:




Tứ phân vị thứ nhất của mẫu số liệu gốc là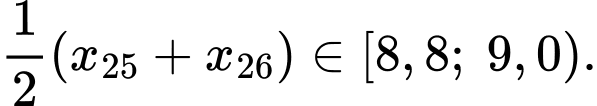 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
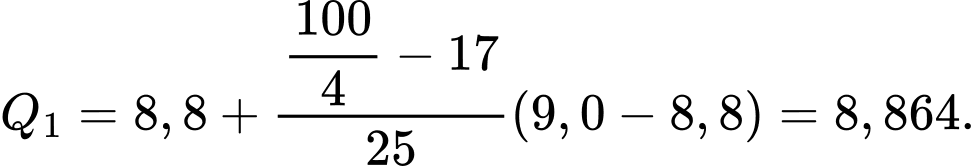
Tứ phân vị thứ ba của mẫu số liệu gốc là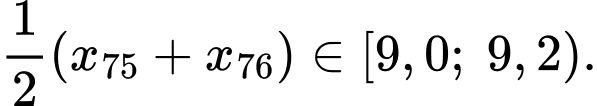 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
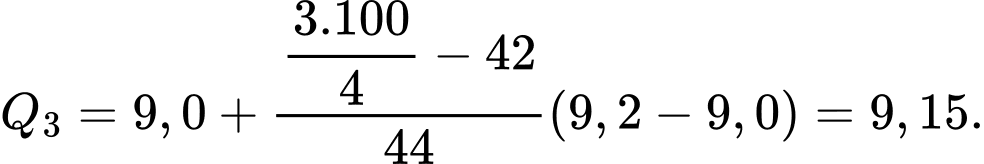
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
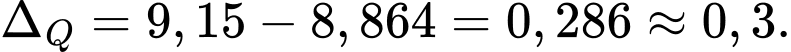 Đáp án: D
Đáp án: D
Cỡ mẫu

Gọi
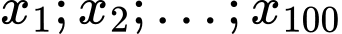 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm. Ta có:





Tứ phân vị thứ nhất của mẫu số liệu gốc là
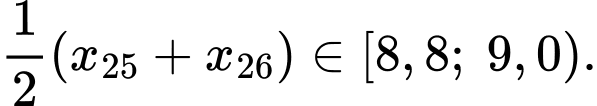 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 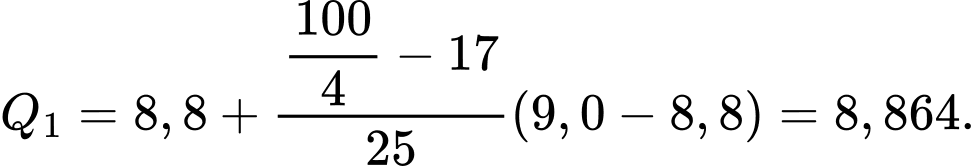
Tứ phân vị thứ ba của mẫu số liệu gốc là
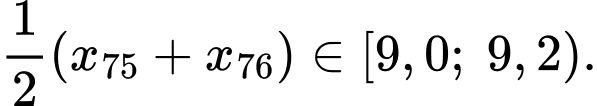 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 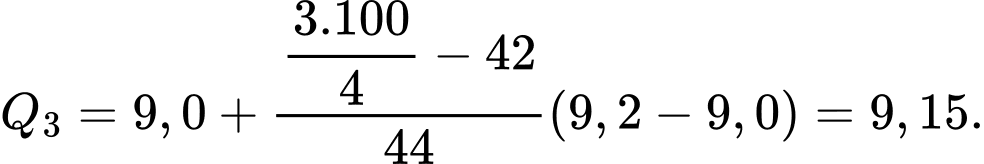
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
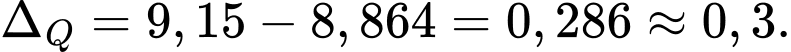 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695535]: Trong không gian với hệ tọa độ 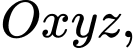 cho đường thẳng
cho đường thẳng 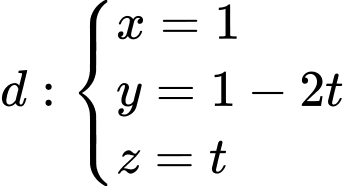 và hai điểm
và hai điểm 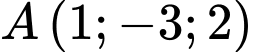 và
và 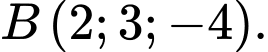 Gọi
Gọi 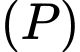 là mặt phẳng qua
là mặt phẳng qua 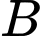 và chứa đường thẳng
và chứa đường thẳng 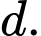
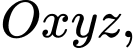 cho đường thẳng
cho đường thẳng 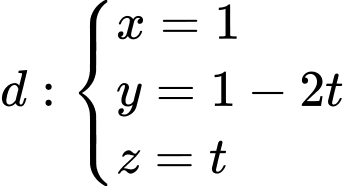 và hai điểm
và hai điểm 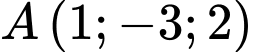 và
và 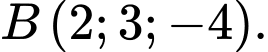 Gọi
Gọi 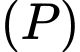 là mặt phẳng qua
là mặt phẳng qua 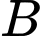 và chứa đường thẳng
và chứa đường thẳng 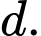
a) Sai.
Vectơ chỉ phương của đường thẳng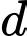 là
là 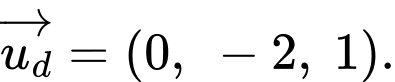
b) Đúng.
Thay tọa độ điểm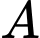 vào phương trình đường thẳng
vào phương trình đường thẳng 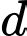 ta thấy hệ phương trình có nghiệm:
ta thấy hệ phương trình có nghiệm: 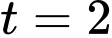
c) Sai.
Ta có: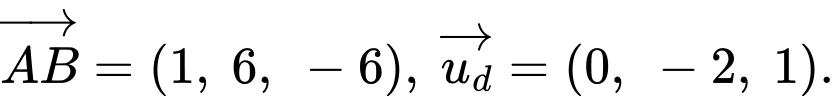
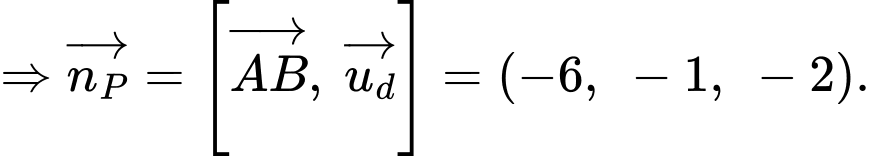
d) Đúng.
Phương trình mặt phẳng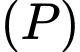 là
là
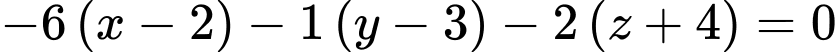

Khoảng cách từ đến mặt phẳng
đến mặt phẳng 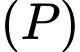 là
là
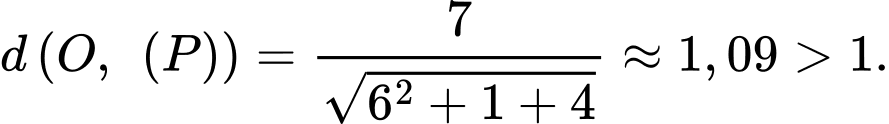
Vectơ chỉ phương của đường thẳng
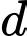 là
là 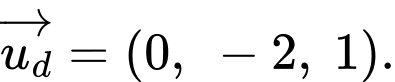
b) Đúng.
Thay tọa độ điểm
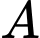 vào phương trình đường thẳng
vào phương trình đường thẳng 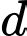 ta thấy hệ phương trình có nghiệm:
ta thấy hệ phương trình có nghiệm: 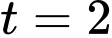
c) Sai.
Ta có:
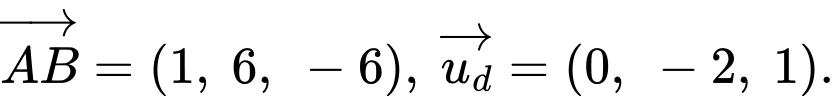
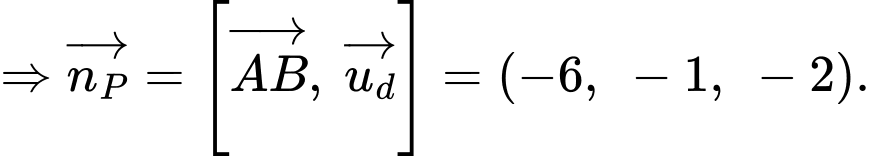
d) Đúng.
Phương trình mặt phẳng
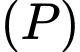 là
là 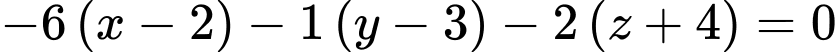

Khoảng cách từ
 đến mặt phẳng
đến mặt phẳng 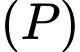 là
là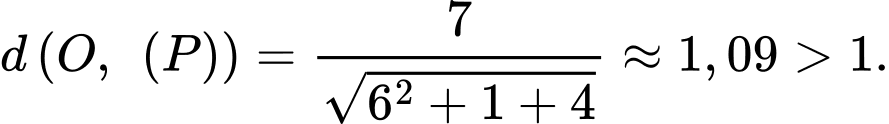
Câu 14 [695536]: Bảng sau đây tóm tắt kết quả phân tích quá trình tự phân hủy (sự phá hủy tế bào sau khi tế bảo chết do hoạt động của các enzym của chính tế bào) và sự thối rữa (sự phân hủy chất hữu cơ, đặc biệt là protein, bởi vi sinh vật dẫn đến tạo ra mùi hôi thối) của các con bọ cánh cứng chết

Chọn ngẫu nhiên một con bọ cánh cứng trong các mẫu phân tích trên.

Chọn ngẫu nhiên một con bọ cánh cứng trong các mẫu phân tích trên.

a) Sai.
Xác suất để mẫu chọn ra có quá trình tự phân hủy cao là
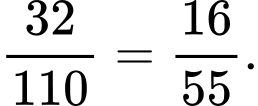
b) Sai.
Xác suất để mẫu chọn ra có quá trình tự phân hủy cao và độ thối rữa thấp là
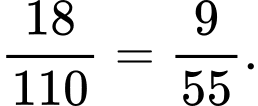
c) Đúng.
Nếu quá trình tự phân hủy của một mẫu chọn ra là cao thì xác suất để thối rữathấp là
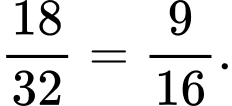
d) Đúng.
Nếu độ thối rữa một mẫu chọn ra là cao thì xác suất để quá trình tự phân hủy cao bằng
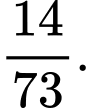
Câu 15 [695537]: Một người nông dân có một mảnh đất hình vuông 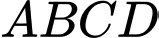 cạnh bằng 8 m. Ông ta định chia mảnh đất thành ba phần, bởi các parabol đi qua các đỉnh của hình vuông như hình vẽ, biết rằng đỉnh của parabol cách cạnh hình vuông 2 m. Ông dự định trồng hoa trên phần diện tích giới hạn bởi các parabol và cạnh hình vuông (phần tô đậm), trồng cỏ trên phần diện tích còn lại. Chọn hệ trục
cạnh bằng 8 m. Ông ta định chia mảnh đất thành ba phần, bởi các parabol đi qua các đỉnh của hình vuông như hình vẽ, biết rằng đỉnh của parabol cách cạnh hình vuông 2 m. Ông dự định trồng hoa trên phần diện tích giới hạn bởi các parabol và cạnh hình vuông (phần tô đậm), trồng cỏ trên phần diện tích còn lại. Chọn hệ trục 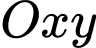 sao cho
sao cho 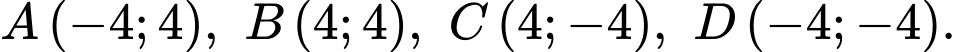
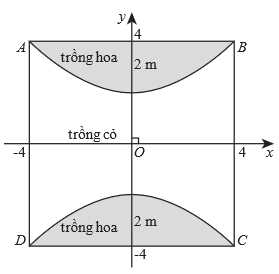
 cạnh bằng 8 m. Ông ta định chia mảnh đất thành ba phần, bởi các parabol đi qua các đỉnh của hình vuông như hình vẽ, biết rằng đỉnh của parabol cách cạnh hình vuông 2 m. Ông dự định trồng hoa trên phần diện tích giới hạn bởi các parabol và cạnh hình vuông (phần tô đậm), trồng cỏ trên phần diện tích còn lại. Chọn hệ trục
cạnh bằng 8 m. Ông ta định chia mảnh đất thành ba phần, bởi các parabol đi qua các đỉnh của hình vuông như hình vẽ, biết rằng đỉnh của parabol cách cạnh hình vuông 2 m. Ông dự định trồng hoa trên phần diện tích giới hạn bởi các parabol và cạnh hình vuông (phần tô đậm), trồng cỏ trên phần diện tích còn lại. Chọn hệ trục 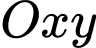 sao cho
sao cho 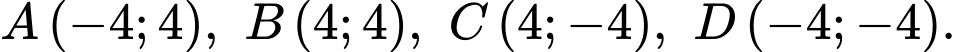

a) Sai.
Diện tích mảnh vườn là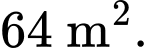
b) Sai.
Phương trình parabol có dạng: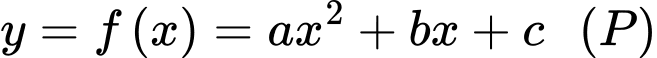
Ta có: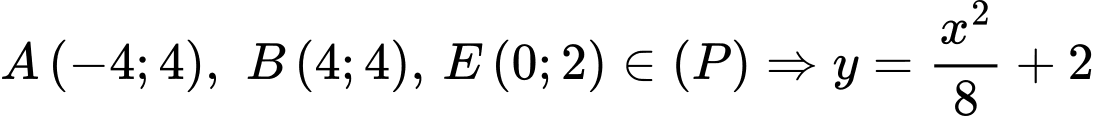 .
.
Tương tự, phương trình parabol thứ hai là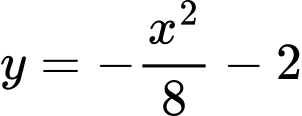 .
.
c) Sai.
Gọi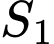 là diện tích hình phẳng giới hạn bởi parabol
là diện tích hình phẳng giới hạn bởi parabol 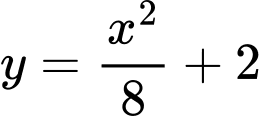 , đường thẳng
, đường thẳng 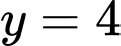 và hai đường thẳng
và hai đường thẳng 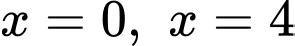 .
.
Diện tích đất trồng hoa là
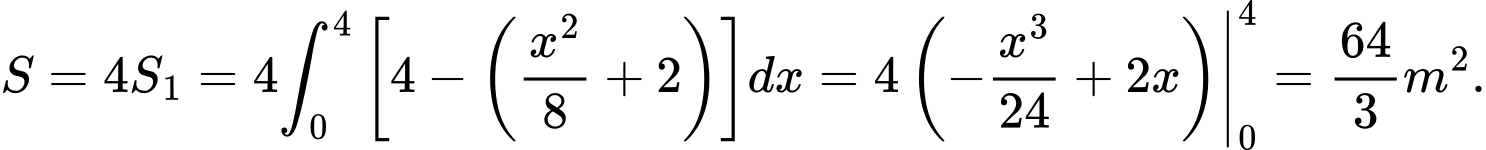
Diện tích đất trồng cỏ: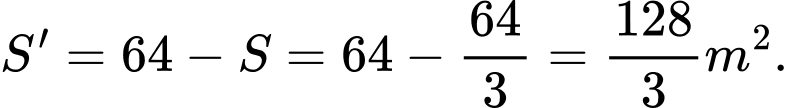
Tỉ số diện tích đất trồng hoa và trồng cỏ: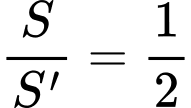 .
.
d) Sai.
Tổng chi phí cần thiết cho cả khu vườn là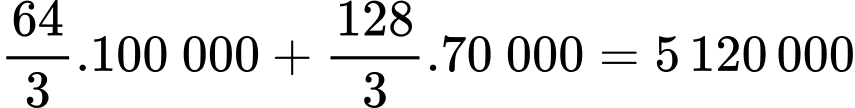 đồng.
đồng.
Diện tích mảnh vườn là
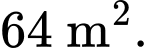
b) Sai.
Phương trình parabol có dạng:
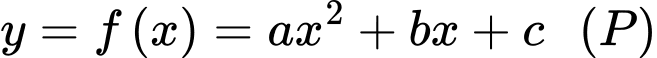
Ta có:
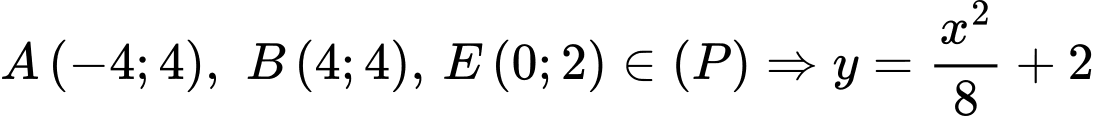 .
.
Tương tự, phương trình parabol thứ hai là
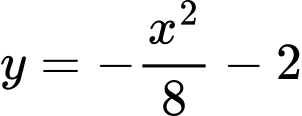 .
.
c) Sai.
Gọi
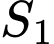 là diện tích hình phẳng giới hạn bởi parabol
là diện tích hình phẳng giới hạn bởi parabol 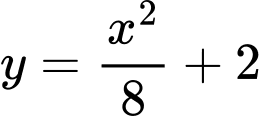 , đường thẳng
, đường thẳng 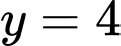 và hai đường thẳng
và hai đường thẳng 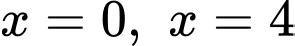 .
.
Diện tích đất trồng hoa là
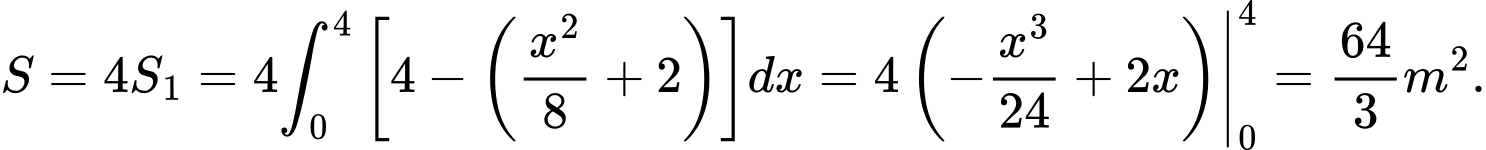
Diện tích đất trồng cỏ:
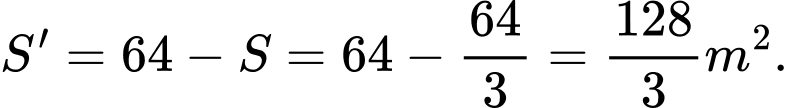
Tỉ số diện tích đất trồng hoa và trồng cỏ:
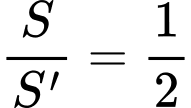 .
.
d) Sai.
Tổng chi phí cần thiết cho cả khu vườn là
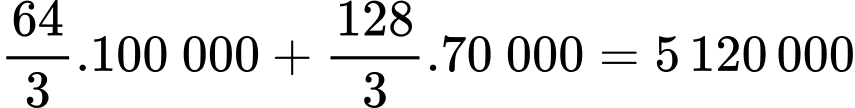 đồng.
đồng.
Câu 16 [695037]: Một con tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 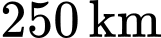 so với bề mặt của Mặt Trăng. Trong khoảng thời gian
so với bề mặt của Mặt Trăng. Trong khoảng thời gian 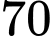 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao
giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao 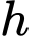 của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm
của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm 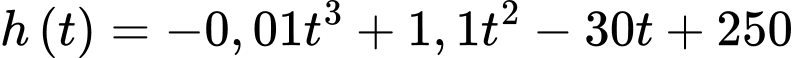 , trong đó
, trong đó 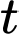 là khoảng thời gian tính bằng giây và
là khoảng thời gian tính bằng giây và 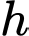 là độ cao tính bằng kílômét.
là độ cao tính bằng kílômét.

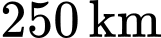 so với bề mặt của Mặt Trăng. Trong khoảng thời gian
so với bề mặt của Mặt Trăng. Trong khoảng thời gian 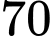 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao
giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao 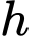 của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm
của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm 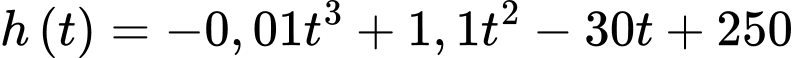 , trong đó
, trong đó 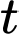 là khoảng thời gian tính bằng giây và
là khoảng thời gian tính bằng giây và 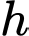 là độ cao tính bằng kílômét.
là độ cao tính bằng kílômét.
a) Đúng.
Ta có: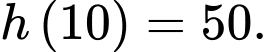
b) Đúng.
Ta có: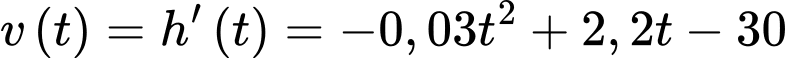
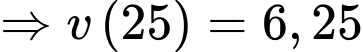
c) Sai.
Ta có: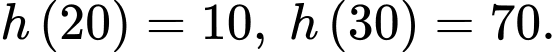
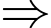 Con tàu ngày càng tiến ra xa Mặt trăng.
Con tàu ngày càng tiến ra xa Mặt trăng.
d) Sai.
Xét hàm số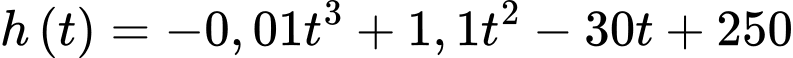
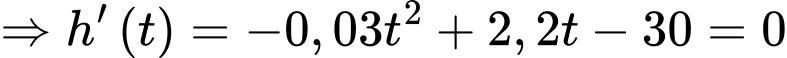
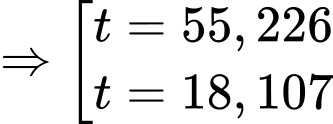
Bảng biến thiên:
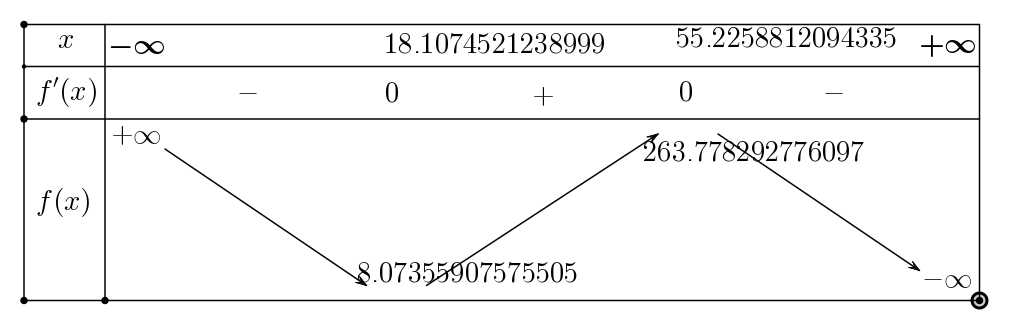 Theo bảng biến thiên ta thấy khoảng cách con tàu gần với Mặt trăng nhất là
Theo bảng biến thiên ta thấy khoảng cách con tàu gần với Mặt trăng nhất là 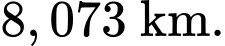
Ta có:
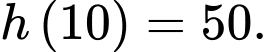
b) Đúng.
Ta có:
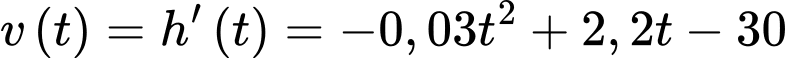
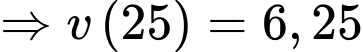
c) Sai.
Ta có:
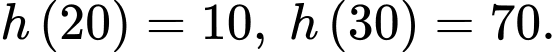
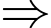 Con tàu ngày càng tiến ra xa Mặt trăng.
Con tàu ngày càng tiến ra xa Mặt trăng.
d) Sai.
Xét hàm số
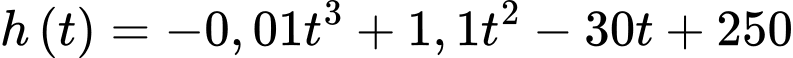
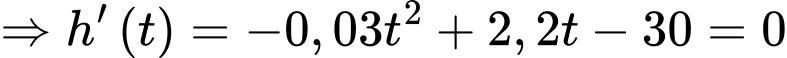
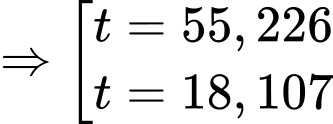
Bảng biến thiên:

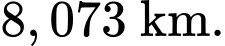
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
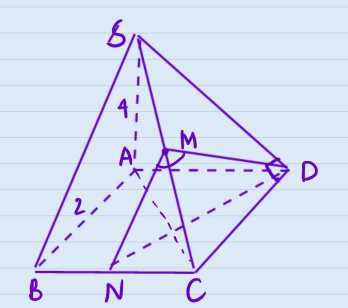
Câu 17 [695539]: Cho hình chóp 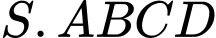 có đáy
có đáy 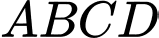 là hình vuông,
là hình vuông, 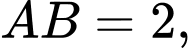
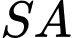 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 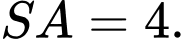 Gọi
Gọi 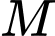 là trung điểm
là trung điểm  Gọi
Gọi 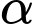 là góc giữa hai vectơ
là góc giữa hai vectơ 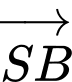 và
và  Giá trị của
Giá trị của 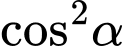 bằng bao nhiêu?
bằng bao nhiêu?
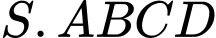 có đáy
có đáy 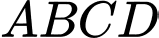 là hình vuông,
là hình vuông, 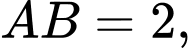
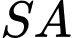 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 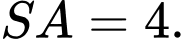 Gọi
Gọi 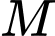 là trung điểm
là trung điểm  Gọi
Gọi 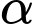 là góc giữa hai vectơ
là góc giữa hai vectơ 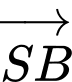 và
và  Giá trị của
Giá trị của 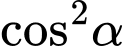 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 0,3.
![]()
Gọi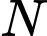 là trung điểm của
là trung điểm của 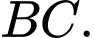 Lại có
Lại có 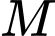 là trung điểm của
là trung điểm của 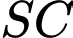 suy ra
suy ra 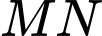 là đường trung bình của tam giác
là đường trung bình của tam giác 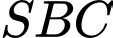
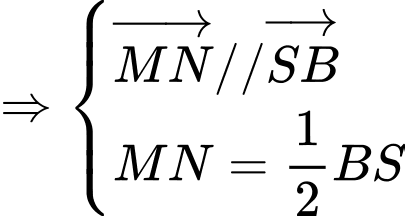
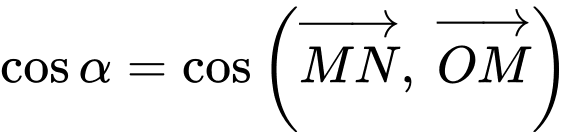

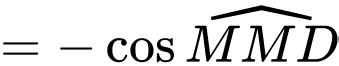
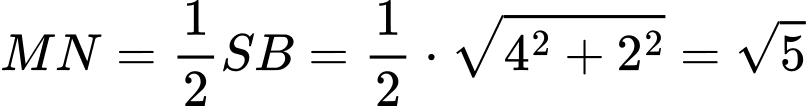
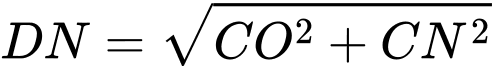
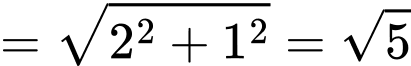
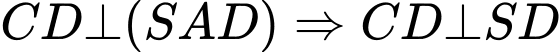
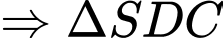 vuông tại
vuông tại 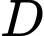
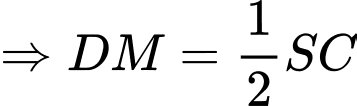
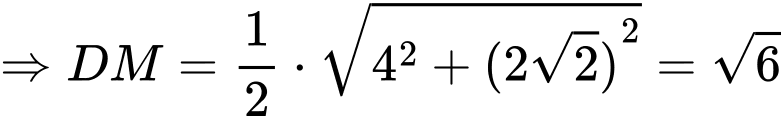
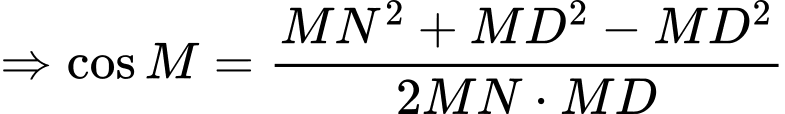
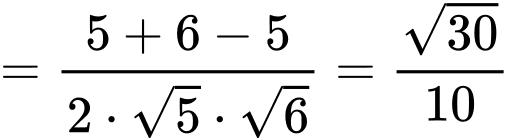
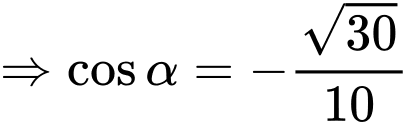
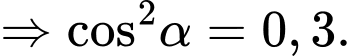

Gọi
 là trung điểm của
là trung điểm của 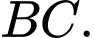 Lại có
Lại có 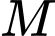 là trung điểm của
là trung điểm của 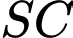 suy ra
suy ra 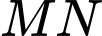 là đường trung bình của tam giác
là đường trung bình của tam giác 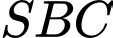
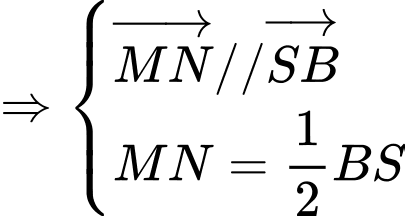
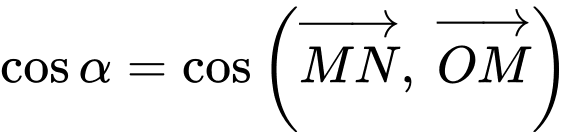

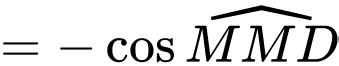
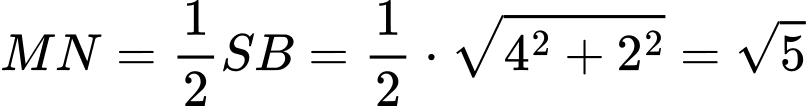
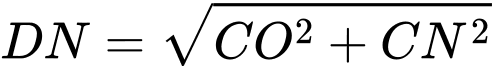
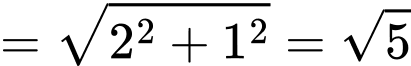
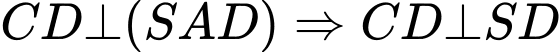
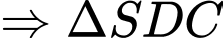 vuông tại
vuông tại 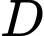
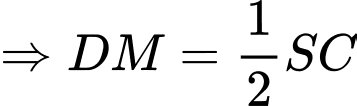
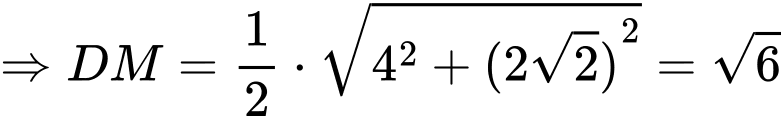
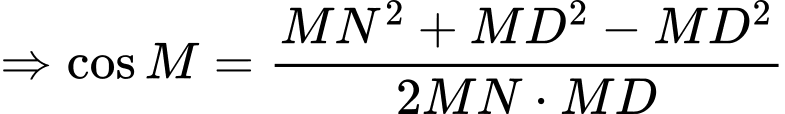
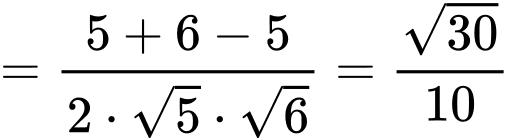
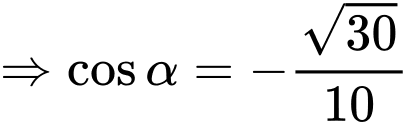
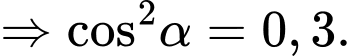
Câu 18 [695540]: Trong một khoảng thời gian nhất định, tại một địa phương. Đài khí tượng thủy văn đã thống kê được: số ngày có mưa: 10 ngày; số ngày có gió to: 8 ngày; số ngày lạnh: 6 ngày; số ngày có mưa và gió to: 5 ngày; số ngày có mưa và lạnh: 4 ngày; số ngày lạnh và có gió to: 3 ngày; số ngày có mưa, lạnh và có gió to: 1 ngày. Hỏi trong khoảng thời gian đó, địa phương trên có bao nhiêu ngày có thời tiết xấu? Giả sử rằng ngày thời tiết xấu là ngày có mưa hoặc có gió hoặc lạnh.
Điền đáp án: 
Ký hiệu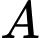 là tập hợp những ngày có mưa,
là tập hợp những ngày có mưa, 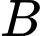 là tập hợp những ngày có gió to,
là tập hợp những ngày có gió to,  là tập hợp những ngày lạnh.
là tập hợp những ngày lạnh.
Theo giả thiết ta có:
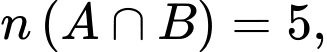
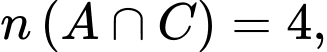
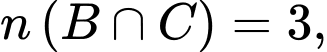
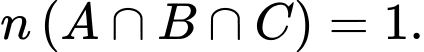
Để tìm số những ngày có thời tiết xấu ta tính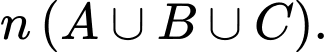
Ta có :
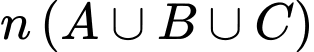
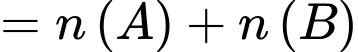
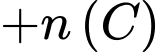
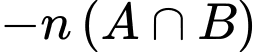
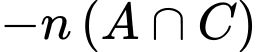
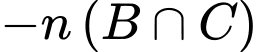
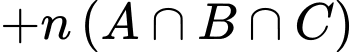
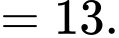
Vậy số ngày thời tiết xấu là 13 ngày.
Ký hiệu
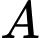 là tập hợp những ngày có mưa,
là tập hợp những ngày có mưa, 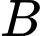 là tập hợp những ngày có gió to,
là tập hợp những ngày có gió to,  là tập hợp những ngày lạnh.
là tập hợp những ngày lạnh.Theo giả thiết ta có:

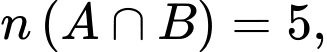
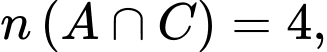
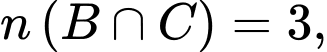
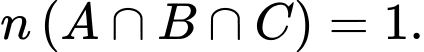
Để tìm số những ngày có thời tiết xấu ta tính
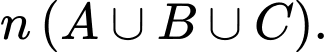
Ta có :
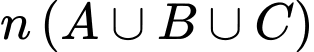
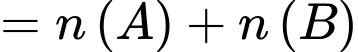
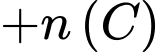
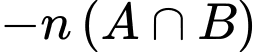
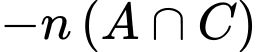
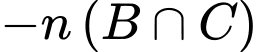
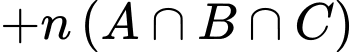
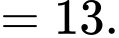
Vậy số ngày thời tiết xấu là 13 ngày.
Câu 19 [695543]: Khối nón 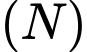 có chiều cao
có chiều cao 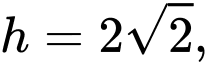 bán kính đáy
bán kính đáy 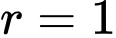 được đặt trên mặt phẳng
được đặt trên mặt phẳng  như hình vẽ. Mặt phẳng
như hình vẽ. Mặt phẳng  song song với
song song với  và
và  qua điểm
qua điểm  là tâm đáy của
là tâm đáy của 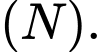 Thiết diện tạo bởi
Thiết diện tạo bởi  và
và  (phần tô đậm trong hình vẽ) có diện tích bằng bao nhiêu? (biết giao tuyến của
(phần tô đậm trong hình vẽ) có diện tích bằng bao nhiêu? (biết giao tuyến của  và
và  là một đường Parabol).
là một đường Parabol).
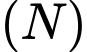 có chiều cao
có chiều cao 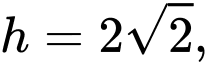 bán kính đáy
bán kính đáy 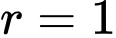 được đặt trên mặt phẳng
được đặt trên mặt phẳng  như hình vẽ. Mặt phẳng
như hình vẽ. Mặt phẳng  song song với
song song với  và
và  qua điểm
qua điểm  là tâm đáy của
là tâm đáy của 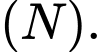 Thiết diện tạo bởi
Thiết diện tạo bởi  và
và 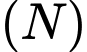 (phần tô đậm trong hình vẽ) có diện tích bằng bao nhiêu? (biết giao tuyến của
(phần tô đậm trong hình vẽ) có diện tích bằng bao nhiêu? (biết giao tuyến của  và
và 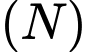 là một đường Parabol).
là một đường Parabol).
Điền đáp án: 2.
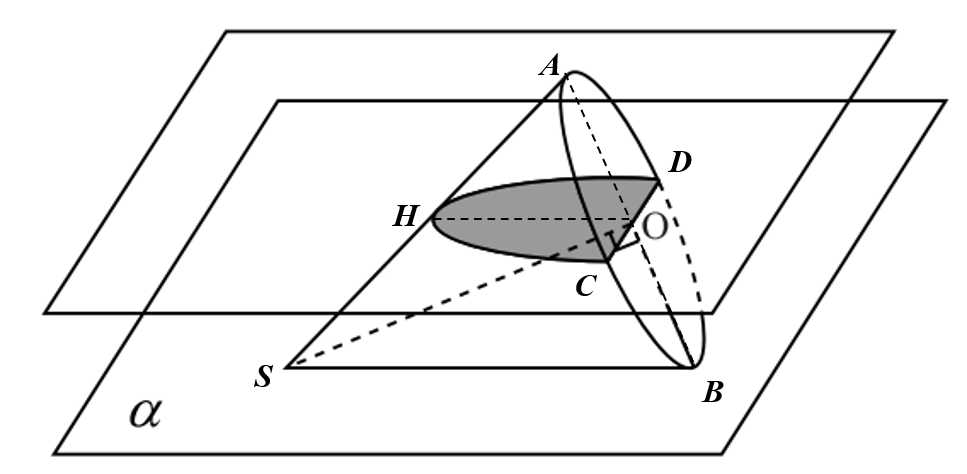
Xét 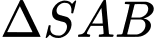 có:
có: 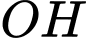 là đường trung bình
là đường trung bình
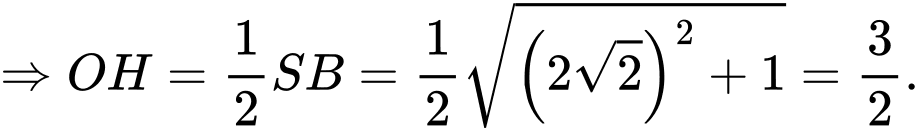
Vì diện tích thiết diện cần tìm có hình parabol nên ta có diện tích đó là
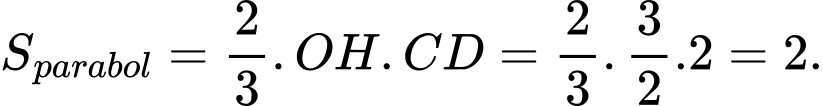

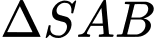 có:
có: 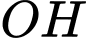 là đường trung bình
là đường trung bình 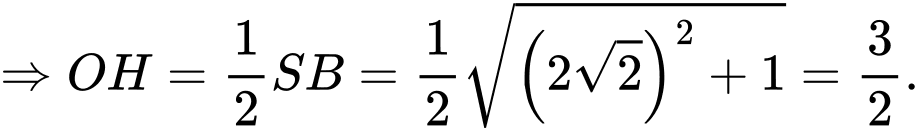
Vì diện tích thiết diện cần tìm có hình parabol nên ta có diện tích đó là
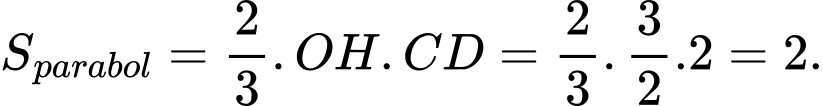
Câu 20 [702528]: Trong không gian với hệ tọa độ cho 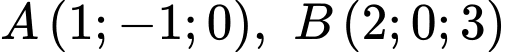 và mặt phẳng
và mặt phẳng 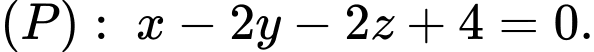 Điểm
Điểm 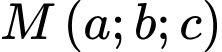 có hoành độ dương thuộc mặt phẳng
có hoành độ dương thuộc mặt phẳng 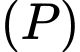 sao cho
sao cho  và
và 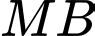 vuông góc với
vuông góc với 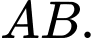 Khi đó giá trị của
Khi đó giá trị của 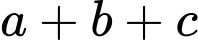 bằng bao nhiêu?
bằng bao nhiêu?
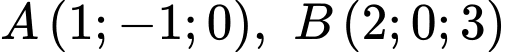 và mặt phẳng
và mặt phẳng 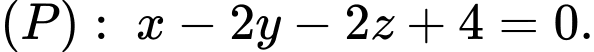 Điểm
Điểm 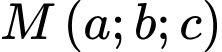 có hoành độ dương thuộc mặt phẳng
có hoành độ dương thuộc mặt phẳng 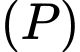 sao cho
sao cho  và
và 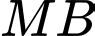 vuông góc với
vuông góc với 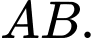 Khi đó giá trị của
Khi đó giá trị của 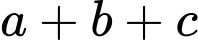 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 11.
C1: Ta có: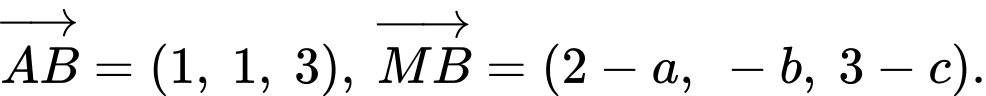
Vì
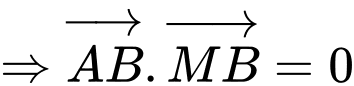


Vì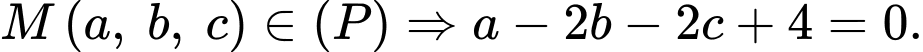
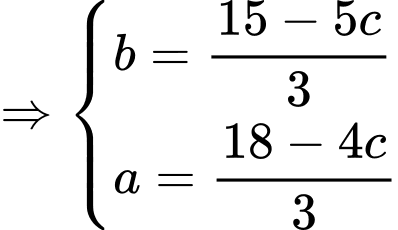
Vì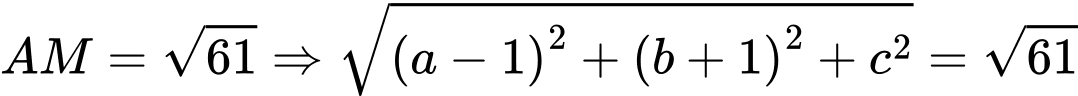
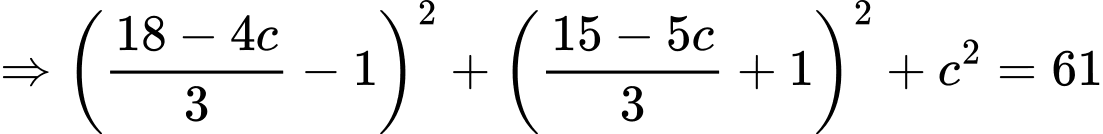
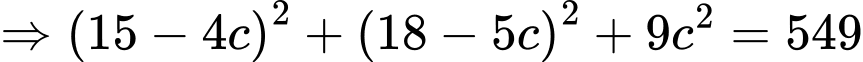
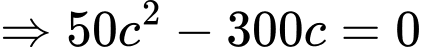
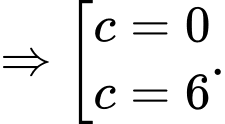
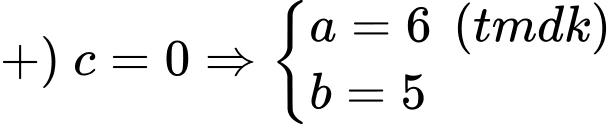


C2: + Nhận xét:
+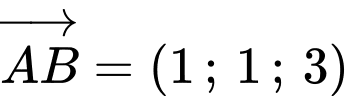
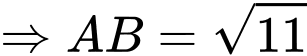
+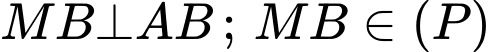
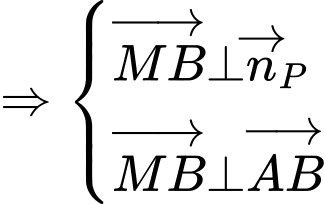
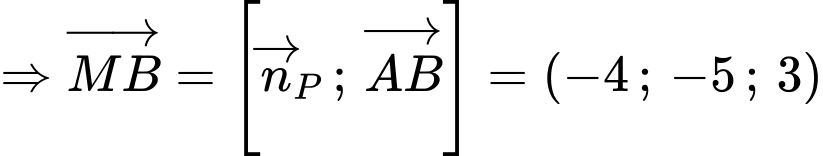
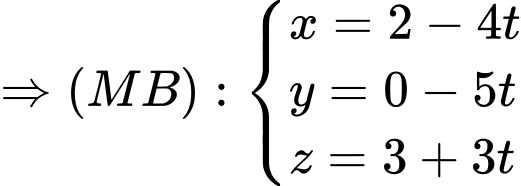
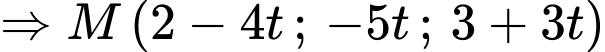
+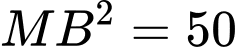
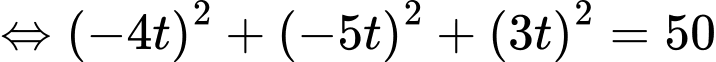
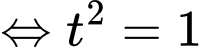
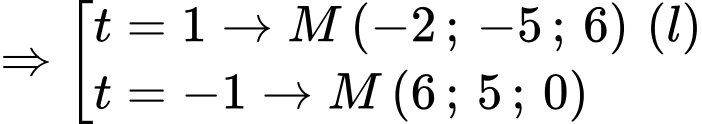

C1: Ta có:
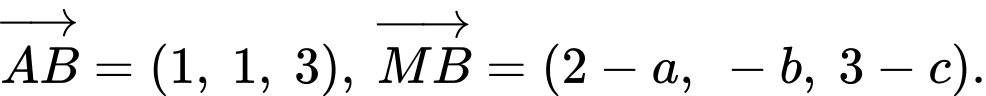
Vì

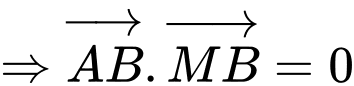


Vì
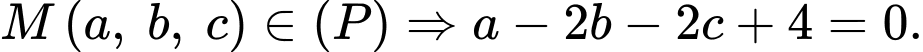
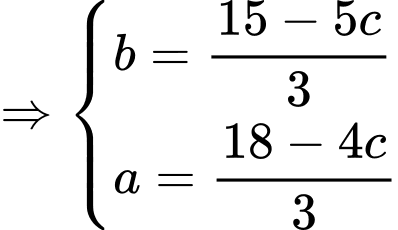
Vì
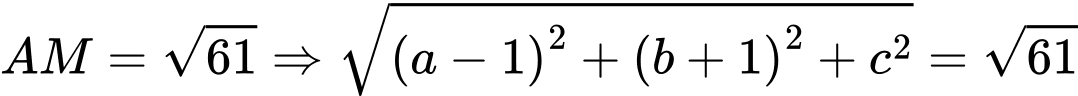
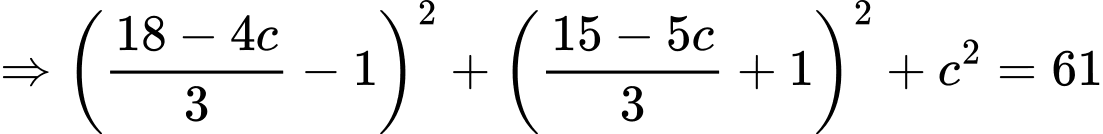
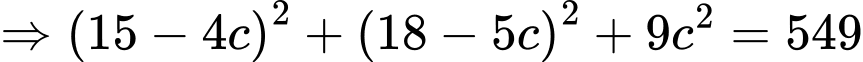
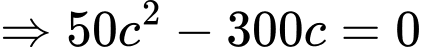
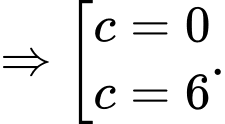
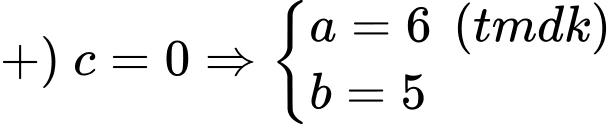


C2: + Nhận xét:

+
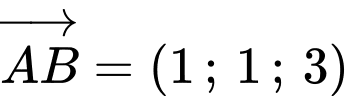
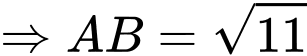
+
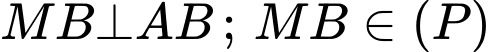
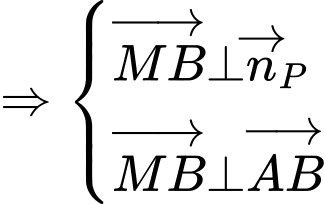
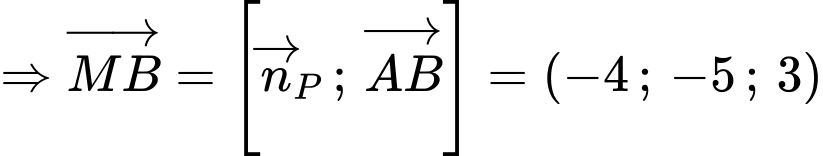
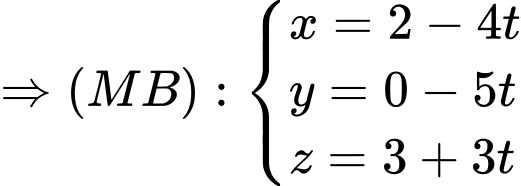
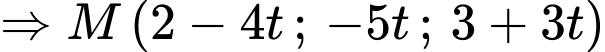
+
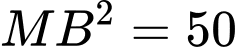
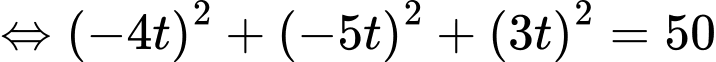
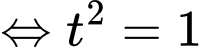
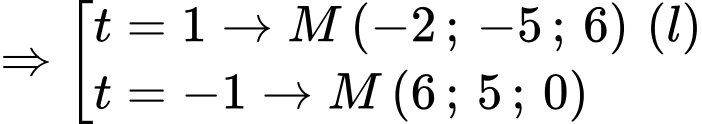

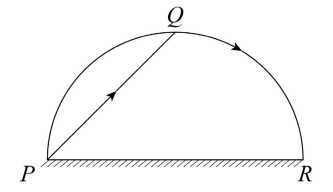
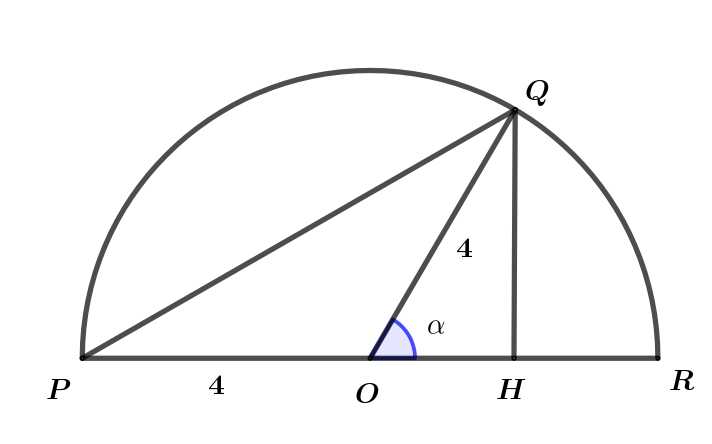
Câu 21 [693195]: Cho một bờ hồ hình bán nguyệt có bán kính bằng  đường kính
đường kính 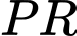 như hình vẽ. Từ điểm
như hình vẽ. Từ điểm 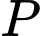 anh Tuấn có thể đi thuyền máy đến điểm
anh Tuấn có thể đi thuyền máy đến điểm  nằm trên bờ hồ với vận tốc
nằm trên bờ hồ với vận tốc  rồi đi xe máy dọc theo thành hồ đến vị trí
rồi đi xe máy dọc theo thành hồ đến vị trí  với vận tốc
với vận tốc  Thời gian ngắn nhất mà anh Tuấn di chuyển từ
Thời gian ngắn nhất mà anh Tuấn di chuyển từ  đến
đến  là bao nhiêu phút?. Viết kết quả làm tròn đến hàng đơn vị.
là bao nhiêu phút?. Viết kết quả làm tròn đến hàng đơn vị.
 đường kính
đường kính 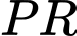 như hình vẽ. Từ điểm
như hình vẽ. Từ điểm 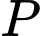 anh Tuấn có thể đi thuyền máy đến điểm
anh Tuấn có thể đi thuyền máy đến điểm  nằm trên bờ hồ với vận tốc
nằm trên bờ hồ với vận tốc  rồi đi xe máy dọc theo thành hồ đến vị trí
rồi đi xe máy dọc theo thành hồ đến vị trí 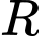 với vận tốc
với vận tốc  Thời gian ngắn nhất mà anh Tuấn di chuyển từ
Thời gian ngắn nhất mà anh Tuấn di chuyển từ 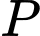 đến
đến  là bao nhiêu phút?. Viết kết quả làm tròn đến hàng đơn vị.
là bao nhiêu phút?. Viết kết quả làm tròn đến hàng đơn vị.
Điền đáp án: 27.
Đặt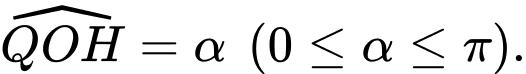
Xét có:
có:
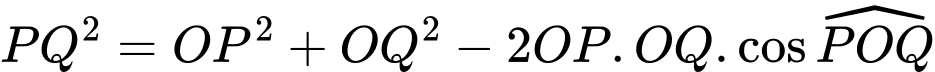
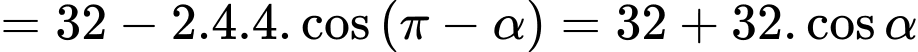
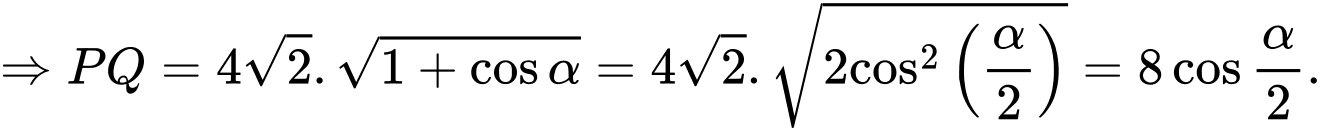
Độ dài cung tròn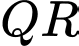 là
là 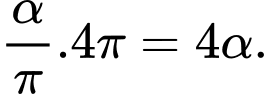
Thời gian anh Tuấn di chuyển từ P đến R là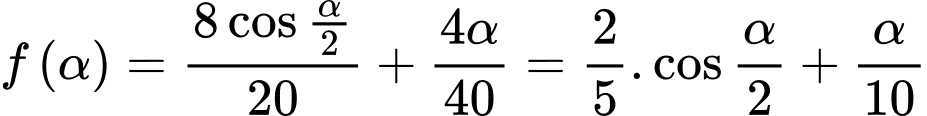 (giờ)
(giờ)
Xét hàm số
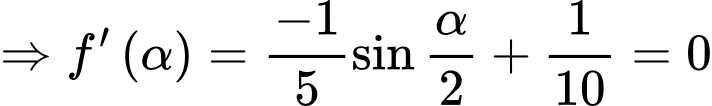
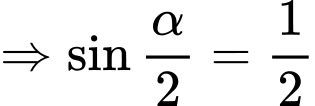
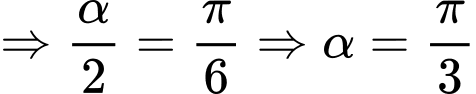 là điểm cực đại của đồ thị hàm số đã cho.
là điểm cực đại của đồ thị hàm số đã cho.
Ta có: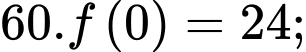
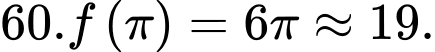
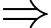 Thời gian ngắn nhất cần tìm là
Thời gian ngắn nhất cần tìm là 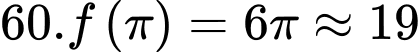 phút.
phút.

Đặt
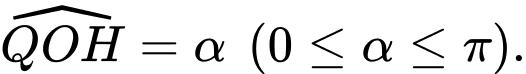
Xét
 có:
có:
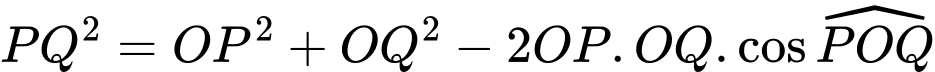
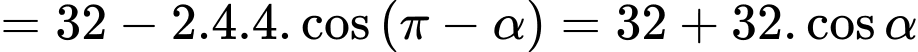
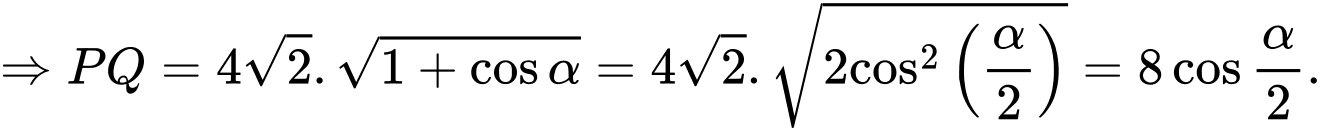
Độ dài cung tròn
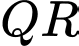 là
là 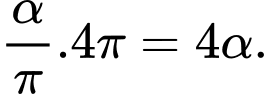
Thời gian anh Tuấn di chuyển từ P đến R là
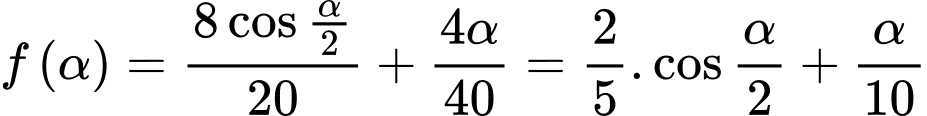 (giờ)
(giờ)
Xét hàm số

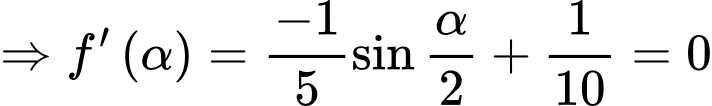
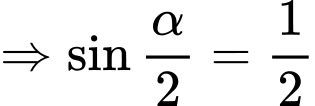
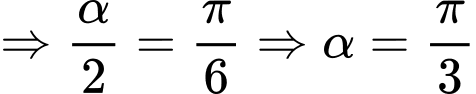 là điểm cực đại của đồ thị hàm số đã cho.
là điểm cực đại của đồ thị hàm số đã cho.
Ta có:
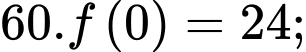
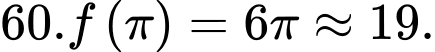
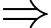 Thời gian ngắn nhất cần tìm là
Thời gian ngắn nhất cần tìm là 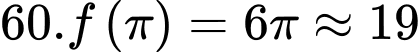 phút.
phút.
Câu 22 [702531]: Hai bạn Hưng và Nhâm tham gia một trò chơi, quản trò đưa ra thử thách như sau: Mỗi người bốc 2 quả trong một hộp đựng 10 quả bóng được đánh số từ 1 đến 10. Người chơi có quyền lựa chọn cách chiến thắng trước khi bốc: Hưng chọn cách bốc được 2 quả có tổng là một số lẻ và Nhâm chọn bốc được 2 quả có tích là một số chẵn. Do đã có lợi thế ở vòng trước, Nhâm được bốc trước và bước vào vòng trong. Tính xác suất để Nhâm bốc được 2 quả có tổng là số chẵn, biết rằng Hưng cũng bước vào vòng trong, và quả bóng được bốc ra sẽ không hoàn lại (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,27.
Số cách bốc 2 số có tích chẵn là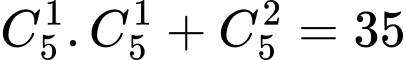 (vì có 2 TH xảy ra: chọn được 2 quả bóng có số chẵn hoặc bốc được 1 quả mang số chẵn và 1 quả mang số lẻ)
(vì có 2 TH xảy ra: chọn được 2 quả bóng có số chẵn hoặc bốc được 1 quả mang số chẵn và 1 quả mang số lẻ)
Số cách bốc 2 số có tổng là số lẻ (tích chẵn) là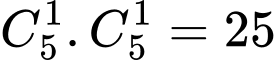 (xảy ra khi bốc được 1 quả bóng mang số lẻ và 1 quả bóng mang số chẵn)
(xảy ra khi bốc được 1 quả bóng mang số lẻ và 1 quả bóng mang số chẵn)
Số cách bốc 2 số có tích chẵn và tổng chẵn là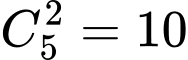 (xảy ra khi bốc được 2 quả bóng mang số chẵn)
(xảy ra khi bốc được 2 quả bóng mang số chẵn)
Do Nhâm đã thắng nên Nhâm đã bốc được 2 quả có tích chẵn, nên
Gọi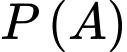 là biến cố Nhâm bốc tổng chẵn
là biến cố Nhâm bốc tổng chẵn 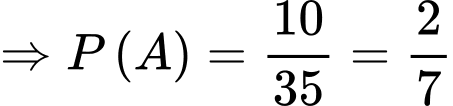
Gọi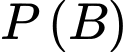 là biến cố “Hưng thắng”
là biến cố “Hưng thắng”
YCBT Tính
Tính 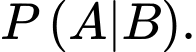
Xác suất Hưng thắng khi Nhâm bốc được tổng lẻ (tức Nhâm bốc được 1 chẵn và 1 lẻ nên còn lại 4 bi chẵn, 4 bi lẻ) là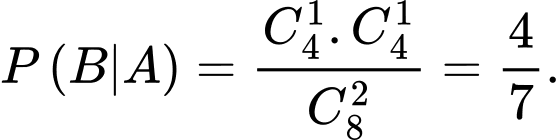
Tương tự, xác suất Hưng thắng khi Nhâm bốc được tổng chẵn (còn lại 3 chẵn, 5 lẻ) là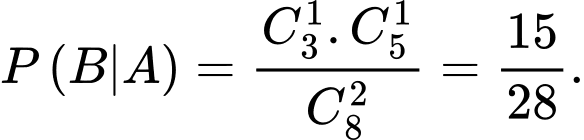
Ta có sơ đồ cây sau:
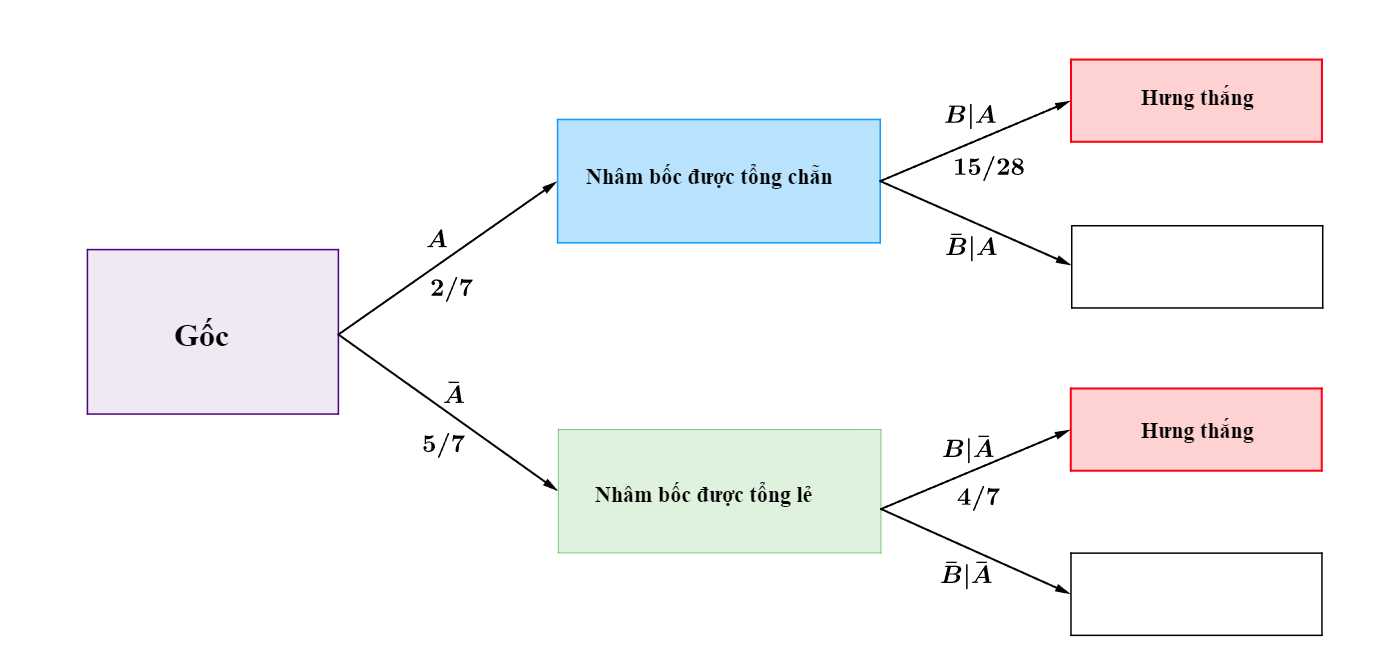
Áp dụng công thức xác suất toàn phần, ta có
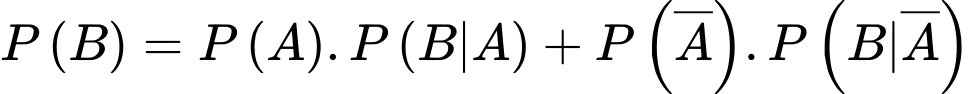
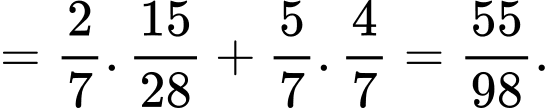
Suy ra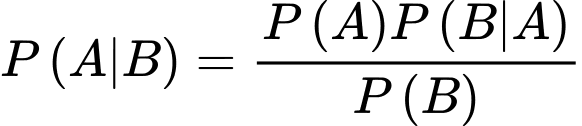
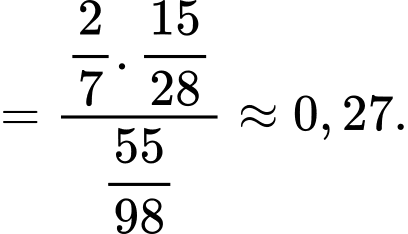
Số cách bốc 2 số có tích chẵn là
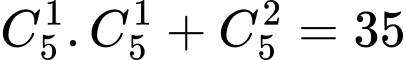 (vì có 2 TH xảy ra: chọn được 2 quả bóng có số chẵn hoặc bốc được 1 quả mang số chẵn và 1 quả mang số lẻ)
(vì có 2 TH xảy ra: chọn được 2 quả bóng có số chẵn hoặc bốc được 1 quả mang số chẵn và 1 quả mang số lẻ)Số cách bốc 2 số có tổng là số lẻ (tích chẵn) là
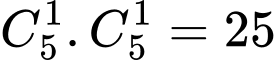 (xảy ra khi bốc được 1 quả bóng mang số lẻ và 1 quả bóng mang số chẵn)
(xảy ra khi bốc được 1 quả bóng mang số lẻ và 1 quả bóng mang số chẵn)Số cách bốc 2 số có tích chẵn và tổng chẵn là
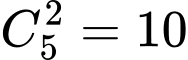 (xảy ra khi bốc được 2 quả bóng mang số chẵn)
(xảy ra khi bốc được 2 quả bóng mang số chẵn)Do Nhâm đã thắng nên Nhâm đã bốc được 2 quả có tích chẵn, nên
Gọi
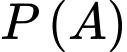 là biến cố Nhâm bốc tổng chẵn
là biến cố Nhâm bốc tổng chẵn 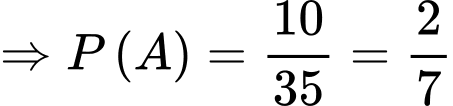
Gọi
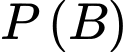 là biến cố “Hưng thắng”
là biến cố “Hưng thắng”YCBT
 Tính
Tính 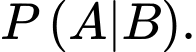
Xác suất Hưng thắng khi Nhâm bốc được tổng lẻ (tức Nhâm bốc được 1 chẵn và 1 lẻ nên còn lại 4 bi chẵn, 4 bi lẻ) là
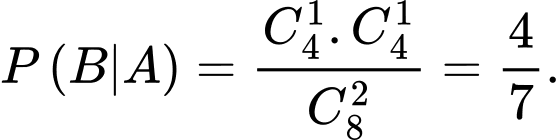
Tương tự, xác suất Hưng thắng khi Nhâm bốc được tổng chẵn (còn lại 3 chẵn, 5 lẻ) là
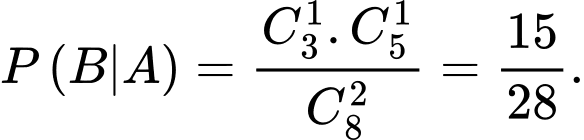
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
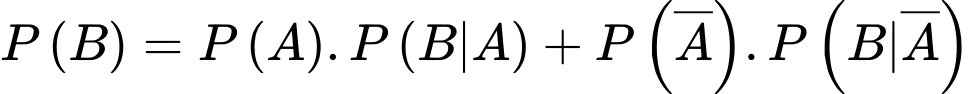
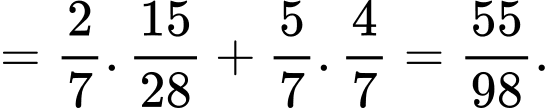
Suy ra