PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [257286]: Cho hàm số 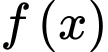 có bảng biến thiên như sau:
có bảng biến thiên như sau:
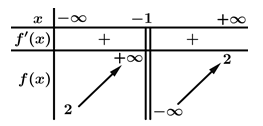
Tiệm cận ngang của đồ thị hàm số đã cho có phương trình là
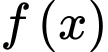 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tiệm cận ngang của đồ thị hàm số đã cho có phương trình là
A, 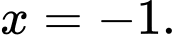
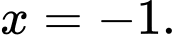
B, 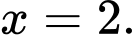
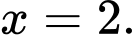
C, 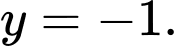
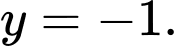
D, 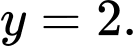
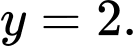
Chọn đáp án D.
Dựa vào bảng biến thiên, ta có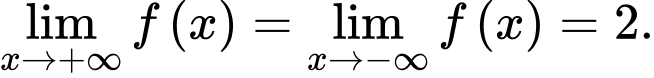
Suy ra đồ thị hàm số có 1 đường TCN là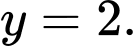 Đáp án: D
Đáp án: D
Dựa vào bảng biến thiên, ta có
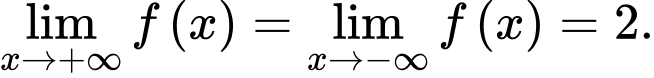
Suy ra đồ thị hàm số có 1 đường TCN là
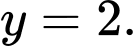 Đáp án: D
Đáp án: D
Câu 2 [256994]: Nghiệm của phương trình 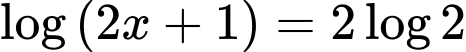 là
là
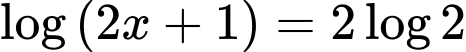 là
là A, 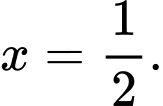
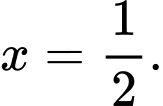
B, 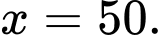
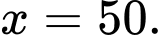
C, 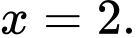
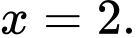
D, 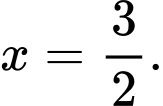
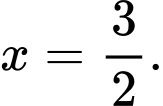
Chọn đáp án D.
Điều kiện xác định: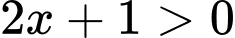
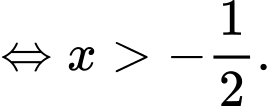
Ta có phương trình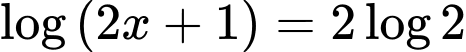
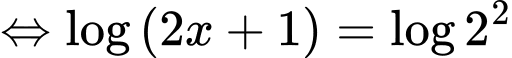

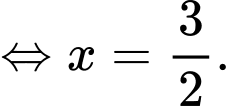 Đáp án: D
Đáp án: D
Điều kiện xác định:
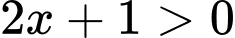
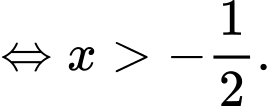
Ta có phương trình
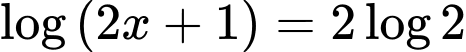
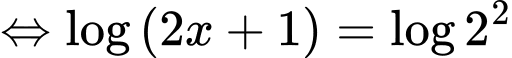

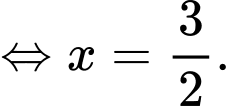 Đáp án: D
Đáp án: D
Câu 3 [257596]: Trên 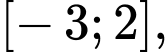 hàm số
hàm số 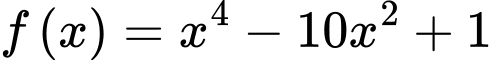 đạt giá trị nhỏ nhất tại điểm
đạt giá trị nhỏ nhất tại điểm
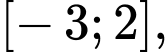 hàm số
hàm số 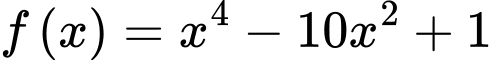 đạt giá trị nhỏ nhất tại điểm
đạt giá trị nhỏ nhất tại điểm A, 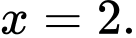
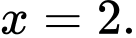
B, 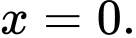
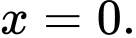
C, 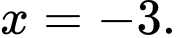
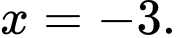
D, 

Chọn đáp án D.
Ta có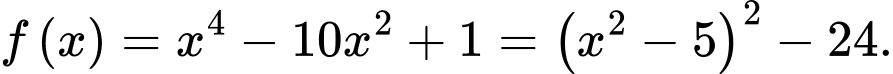
Do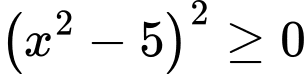 nên
nên 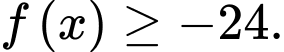
Đẳng thức xảy ra khi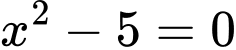
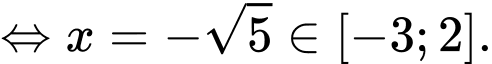
Vậy giá trị nhỏ nhất của hàm số trên đoạn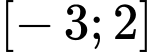 bằng
bằng 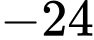 khi
khi  Đáp án: D
Đáp án: D
Ta có
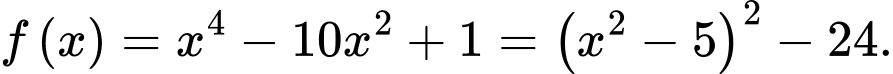
Do
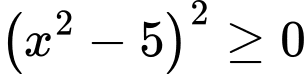 nên
nên 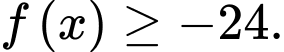
Đẳng thức xảy ra khi
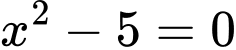
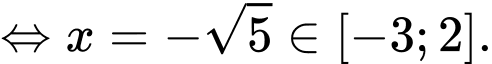
Vậy giá trị nhỏ nhất của hàm số trên đoạn
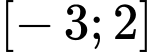 bằng
bằng 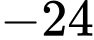 khi
khi  Đáp án: D
Đáp án: D
Câu 4 [255908]: Trong không gian 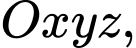 đường thẳng song song với mặt phẳng
đường thẳng song song với mặt phẳng 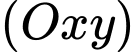 có một vectơ chỉ phương là
có một vectơ chỉ phương là
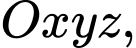 đường thẳng song song với mặt phẳng
đường thẳng song song với mặt phẳng 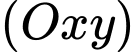 có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 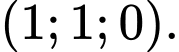
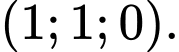
B, 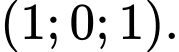
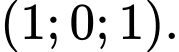
C, 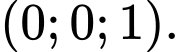
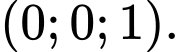
D, 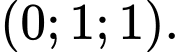
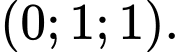
Chọn đáp án A.
Mặt phẳng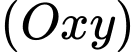 có một vecto pháp tuyến là
có một vecto pháp tuyến là 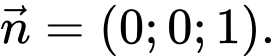
Gọi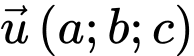 là một vecto chỉ phương của đường thẳng
là một vecto chỉ phương của đường thẳng 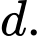
Đường thẳng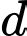 song song mặt phẳng
song song mặt phẳng 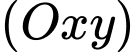
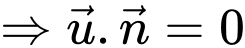
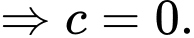 Đáp án: A
Đáp án: A
Mặt phẳng
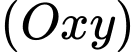 có một vecto pháp tuyến là
có một vecto pháp tuyến là 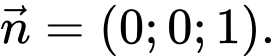
Gọi
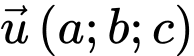 là một vecto chỉ phương của đường thẳng
là một vecto chỉ phương của đường thẳng 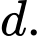
Đường thẳng
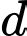 song song mặt phẳng
song song mặt phẳng 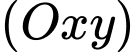
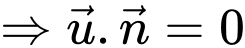
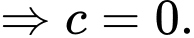 Đáp án: A
Đáp án: A
Câu 5 [257284]: Cho 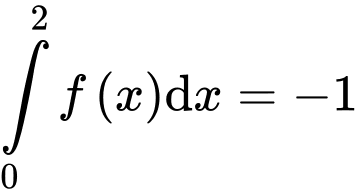 và
và 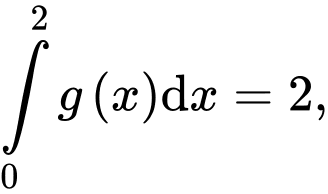 khi đó
khi đó 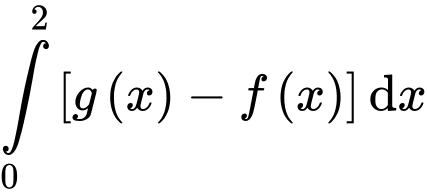 bằng
bằng
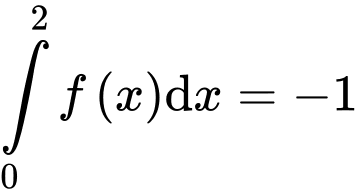 và
và 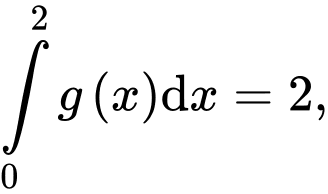 khi đó
khi đó 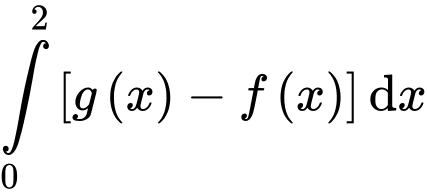 bằng
bằng A, 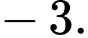
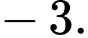
B, 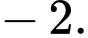
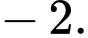
C, 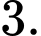
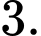
D, 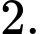
Chọn đáp án C.
Ta có
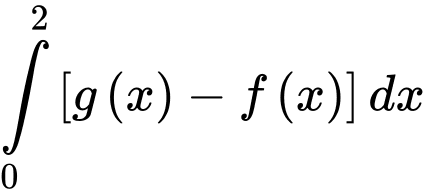
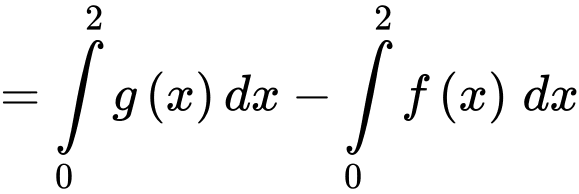
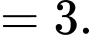 Đáp án: C
Đáp án: C
Ta có
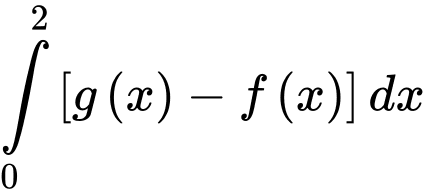
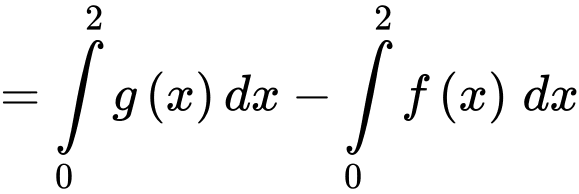
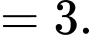 Đáp án: C
Đáp án: C
Câu 6 [695585]: Cho cấp số nhân 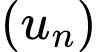 với số hạng tổng quát
với số hạng tổng quát 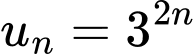
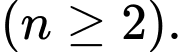 Công bội của cấp số nhân đã cho là
Công bội của cấp số nhân đã cho là
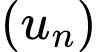 với số hạng tổng quát
với số hạng tổng quát 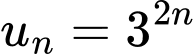
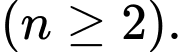 Công bội của cấp số nhân đã cho là
Công bội của cấp số nhân đã cho là A, 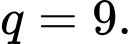
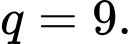
B, 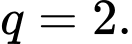
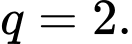
C, 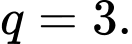
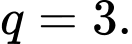
D, 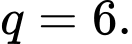
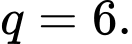
Chọn đáp án A.
Cấp số nhân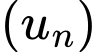 với số hạng tổng quát
với số hạng tổng quát 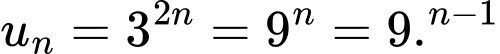
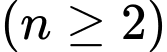 nên công bội của cấp số nhân này là
nên công bội của cấp số nhân này là 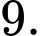 Đáp án: A
Đáp án: A
Cấp số nhân
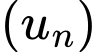 với số hạng tổng quát
với số hạng tổng quát 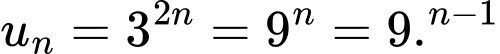
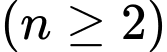 nên công bội của cấp số nhân này là
nên công bội của cấp số nhân này là 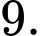 Đáp án: A
Đáp án: A
Câu 7 [695586]: Cho hình chóp 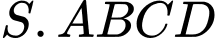 có đáy
có đáy 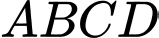 là hình chữ nhật và
là hình chữ nhật và  Phát biểu nào sau đây đúng?
Phát biểu nào sau đây đúng?
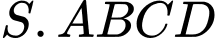 có đáy
có đáy 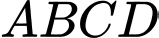 là hình chữ nhật và
là hình chữ nhật và  Phát biểu nào sau đây đúng?
Phát biểu nào sau đây đúng? A, 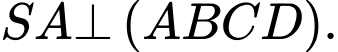
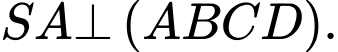
B, 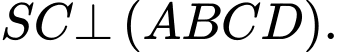
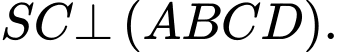
C, 

D, 

Chọn đáp án D.
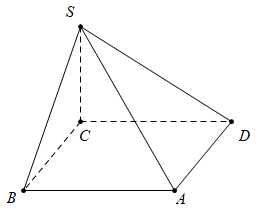
Ta có: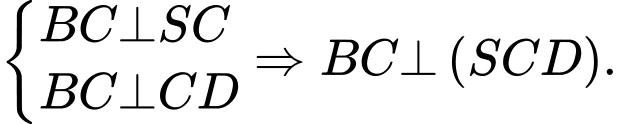 Đáp án: D
Đáp án: D

Ta có:
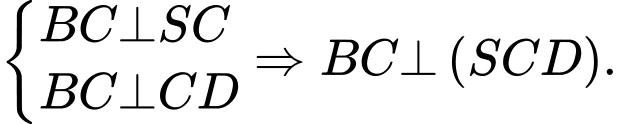 Đáp án: D
Đáp án: D
Câu 8 [695587]: Biết đồ thị hàm số 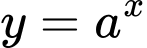
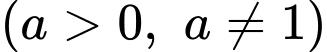 đi qua điểm
đi qua điểm 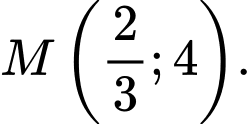 Giá trị của
Giá trị của 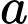 bằng
bằng
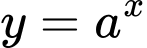
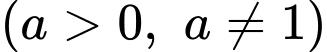 đi qua điểm
đi qua điểm 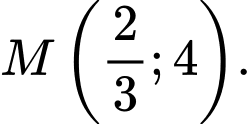 Giá trị của
Giá trị của 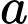 bằng
bằng A, 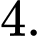
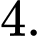
B, 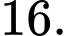
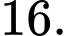
C, 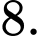
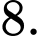
D, 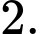
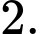
Chọn đáp án C.
Ta có: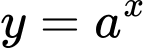
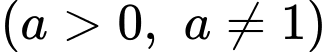 đi qua điểm
đi qua điểm 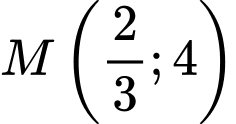 nên
nên 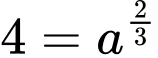
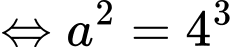
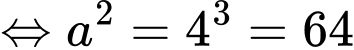
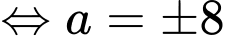
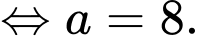 Đáp án: C
Đáp án: C
Ta có:
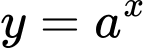
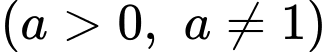 đi qua điểm
đi qua điểm 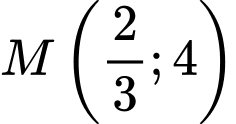 nên
nên 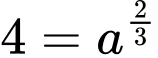
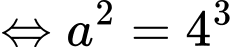
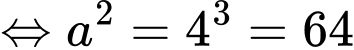
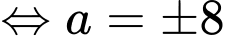
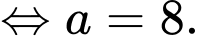 Đáp án: C
Đáp án: C
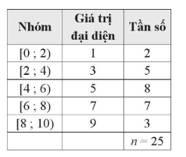
Câu 9 [695588]: Cho mẫu số liệu ghép nhóm trong bảng ở hình vẽ bên. Số trung bình của mẫu số liệu đã cho là

A, 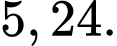
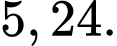
B, 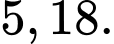
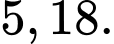
C, 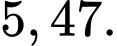
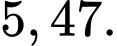
D, 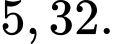
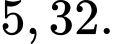
Chọn đáp án D.
Số trung bình của mẫu số liệu đã cho là:
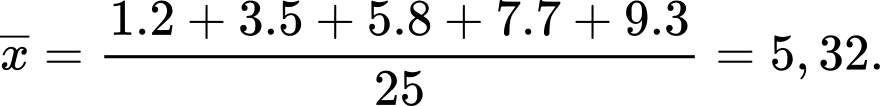 Đáp án: D
Đáp án: D
Số trung bình của mẫu số liệu đã cho là:
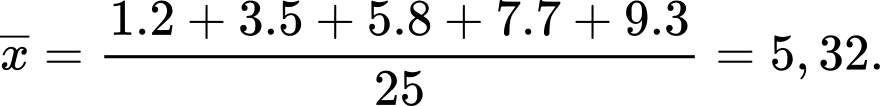 Đáp án: D
Đáp án: D
Câu 10 [695589]: Trong không gian 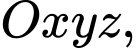 cho hai mặt phẳng
cho hai mặt phẳng 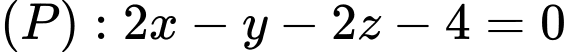 và
và 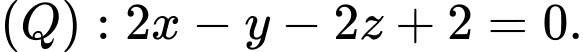 Khoảng cách giữa hai mặt phẳng đã cho bằng
Khoảng cách giữa hai mặt phẳng đã cho bằng
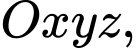 cho hai mặt phẳng
cho hai mặt phẳng 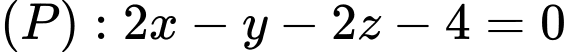 và
và 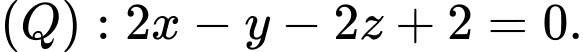 Khoảng cách giữa hai mặt phẳng đã cho bằng
Khoảng cách giữa hai mặt phẳng đã cho bằng A, 
B, 
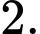
C, 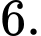
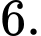
D, 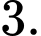
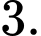
Chọn đáp án B.
Khoảng cách giữa hai mặt phẳng là
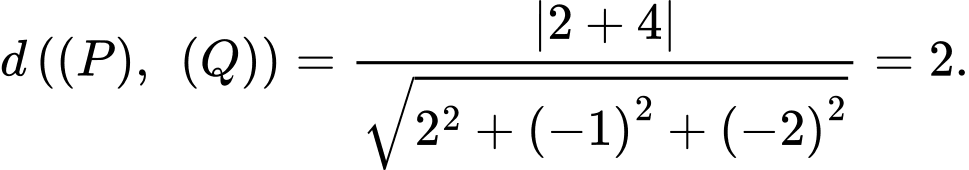 Đáp án: B
Đáp án: B
Khoảng cách giữa hai mặt phẳng là
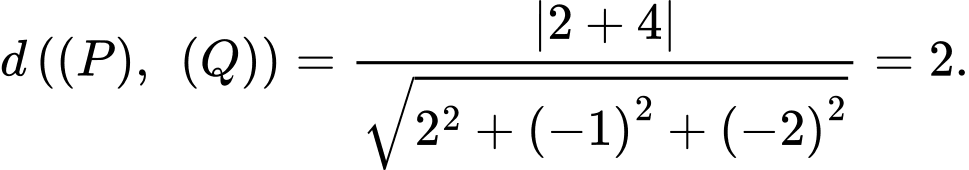 Đáp án: B
Đáp án: B
Câu 11 [289706]: Cho 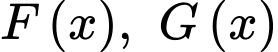 là các nguyên hàm của hàm số
là các nguyên hàm của hàm số 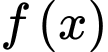 trên
trên 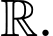 Biết
Biết 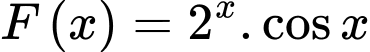 và
và 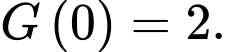 Khi đó
Khi đó 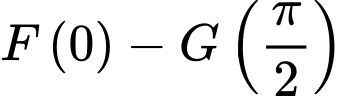 bằng
bằng
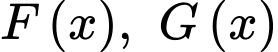 là các nguyên hàm của hàm số
là các nguyên hàm của hàm số 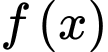 trên
trên 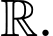 Biết
Biết 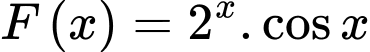 và
và 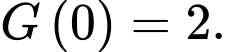 Khi đó
Khi đó 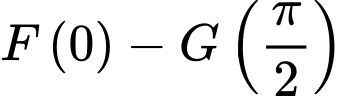 bằng
bằng A, 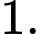
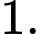
B, 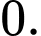
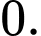
C, 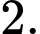
D, 

Chọn đáp án B.
Vì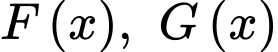 là các nguyên hàm của hàm số
là các nguyên hàm của hàm số 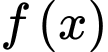 trên
trên  nên
nên 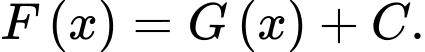
Ta có: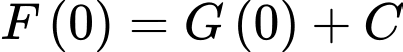
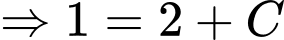
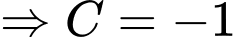

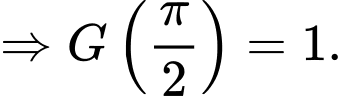
Suy ra: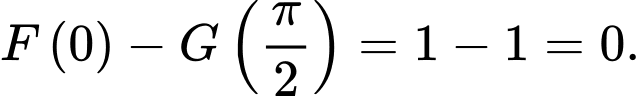 Đáp án: B
Đáp án: B
Vì
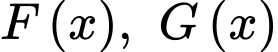 là các nguyên hàm của hàm số
là các nguyên hàm của hàm số 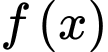 trên
trên 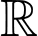 nên
nên 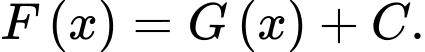
Ta có:
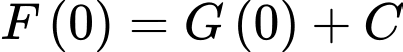
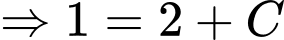
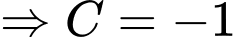

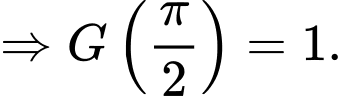
Suy ra:
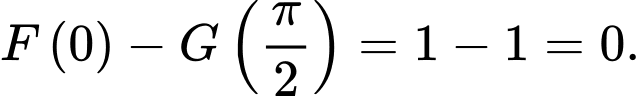 Đáp án: B
Đáp án: B
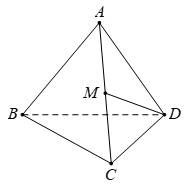
Câu 12 [695590]: Cho tứ diện đều  cạnh bằng
cạnh bằng 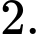 Gọi
Gọi 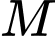 là trung điểm của
là trung điểm của 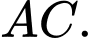 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ  và
và  bằng
bằng
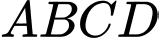 cạnh bằng
cạnh bằng 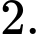 Gọi
Gọi 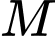 là trung điểm của
là trung điểm của 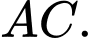 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ  và
và  bằng
bằng
A, 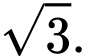
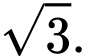
B, 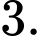
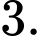
C, 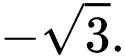
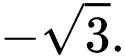
D, 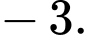
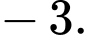

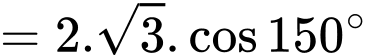
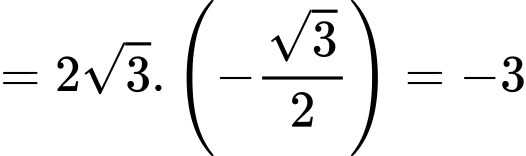
Chọn đáp án D. Đáp án: B
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695591]: Cho hai biến cố 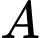 và
và 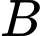 có
có 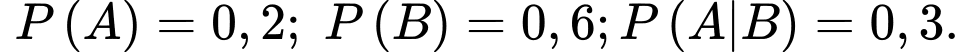
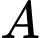 và
và 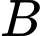 có
có 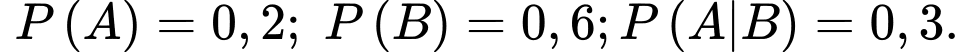
a) Sai.
Ta có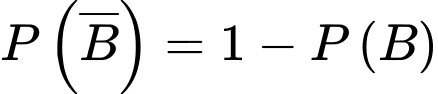
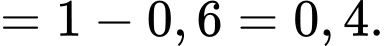
b) Sai.
Ta có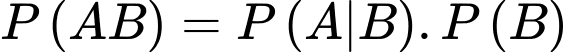
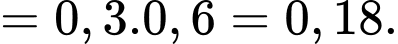
c) Đúng.
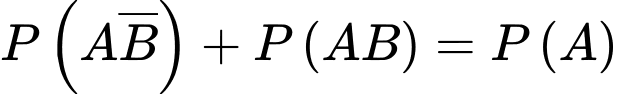
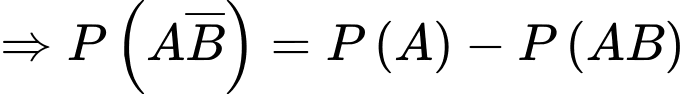
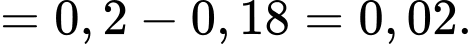
d) Sai.
Theo công thức xác suất điều kiện, ta có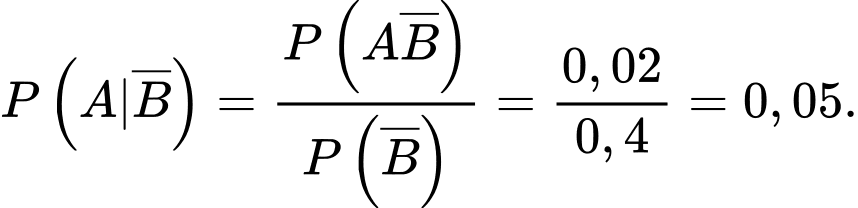
Ta có
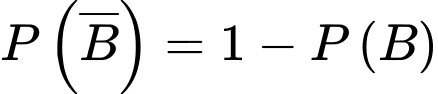
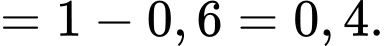
b) Sai.
Ta có
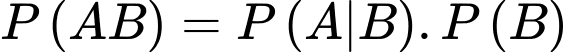
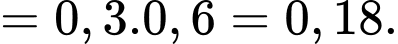
c) Đúng.
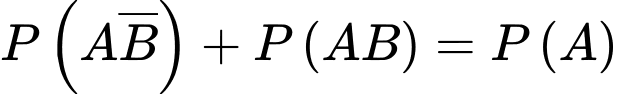
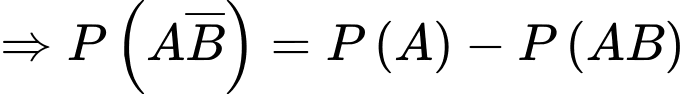
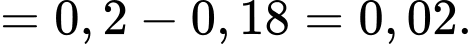
d) Sai.
Theo công thức xác suất điều kiện, ta có
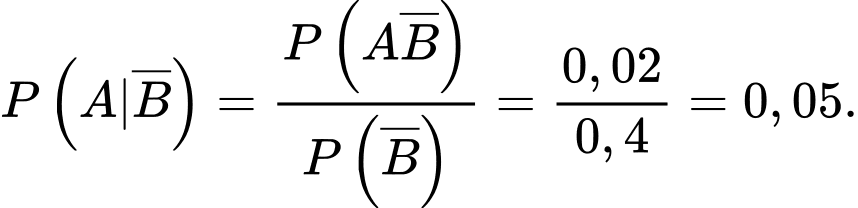
Câu 14 [695516]: Hình bên dưới minh họa hình ảnh hai mái nhà hình bình hành của một nhà kho trong không gian với hệ tọa độ (đơn vị trên mỗi trục tọa độ là mét, mặt đất là mặt phẳng ). Các bức tường của nhà kho đều được xây vuông góc với mặt đất (xem hình vẽ). Gọi 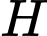 là trung điểm của
là trung điểm của 
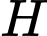 là trung điểm của
là trung điểm của 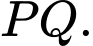

a) Sai.
Vì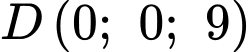 nên
nên 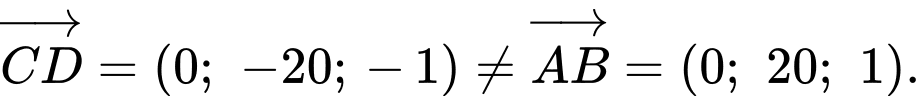
b) Đúng.
Gọi lần lượt là trung điểm của
lần lượt là trung điểm của 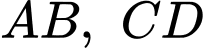
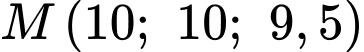 và
và 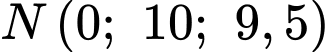
K sẽ là trung điểm của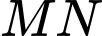 và
và 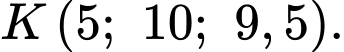
c) Đúng.
Độ dài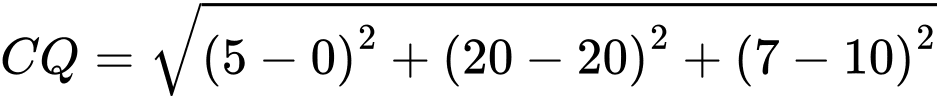
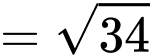
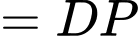
Ta có: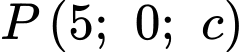 nên
nên 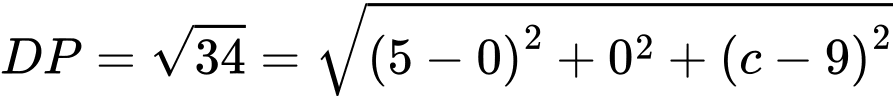
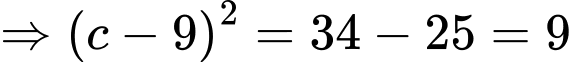
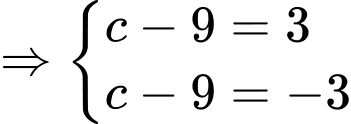
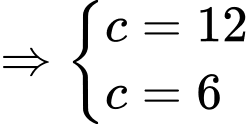
Mà có cao độ lớn hơn
có cao độ lớn hơn 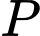 nên
nên 
Nên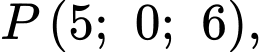 tọa độ trung điểm
tọa độ trung điểm  của
của  là
là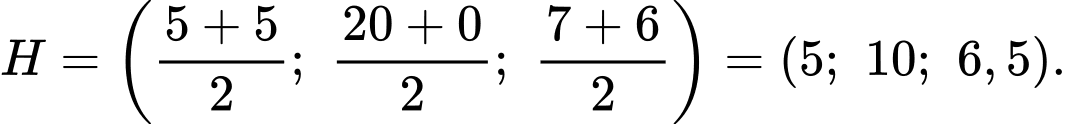
d) Sai.
Điểm cách đều các điểm
cách đều các điểm  nên nó sẽ nằm trên đường thẳng đi qua tâm hình chữ nhật
nên nó sẽ nằm trên đường thẳng đi qua tâm hình chữ nhật  và đi qua điểm
và đi qua điểm 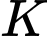 và nó cũng cách điểm
và nó cũng cách điểm 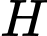 khoảng cách tương tự.
khoảng cách tương tự.
Phương trình mặt phẳng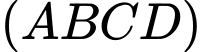 với
với 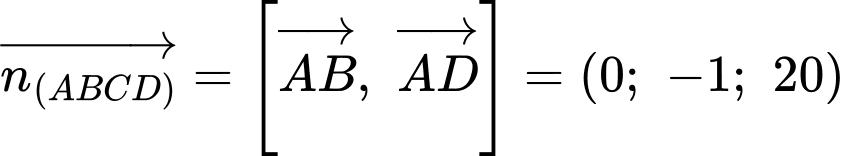 và đi qua điểm
và đi qua điểm 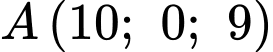 có phương trình là
có phương trình là 
Gọi đường thẳng đi qua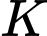 và vuông góc với
và vuông góc với 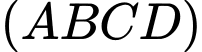 là
là 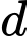
Ta có: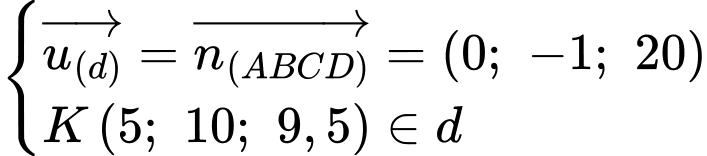
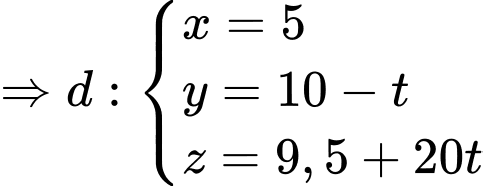
Tham số điểm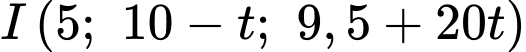 và
và 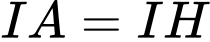
Ta có: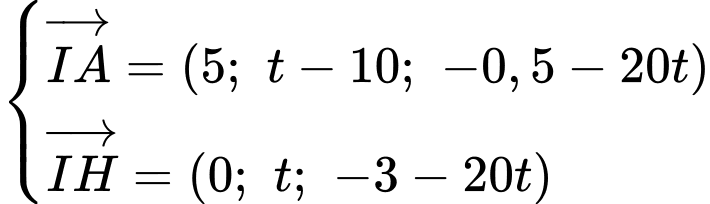
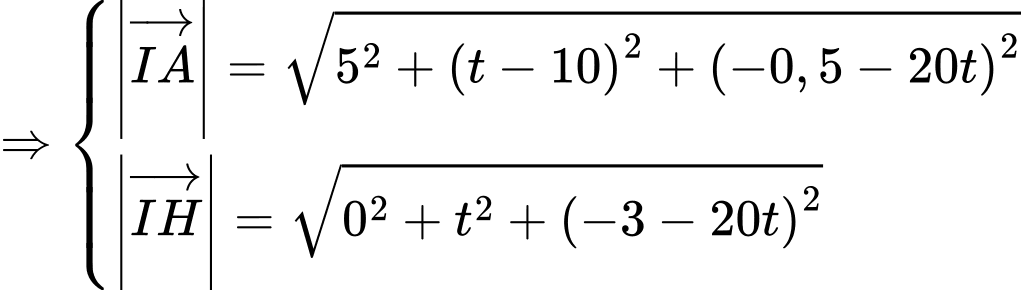
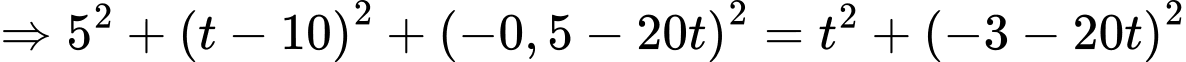
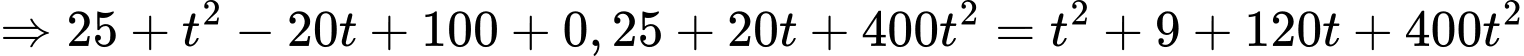
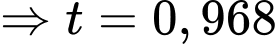
Vậy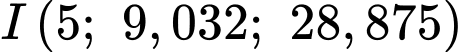 cách mặt đất 28,875 mét.
cách mặt đất 28,875 mét.
Vì
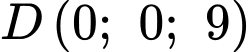 nên
nên 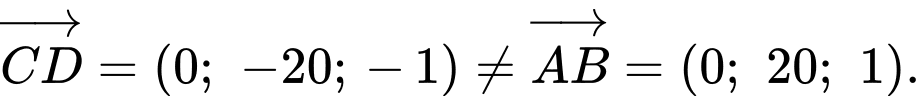
b) Đúng.
Gọi
 lần lượt là trung điểm của
lần lượt là trung điểm của 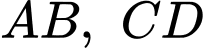
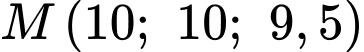 và
và 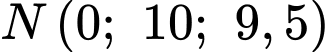
K sẽ là trung điểm của
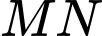 và
và 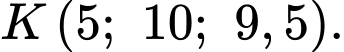
c) Đúng.
Độ dài
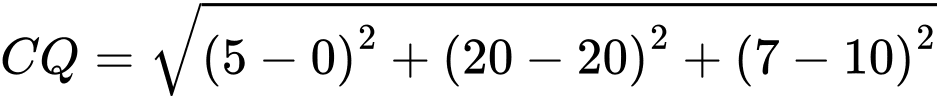
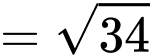
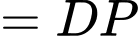
Ta có:
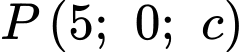 nên
nên 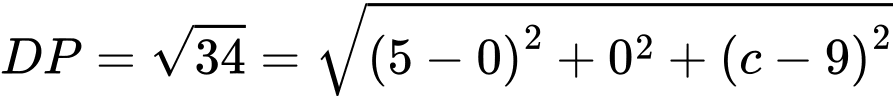
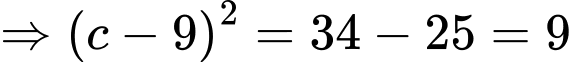
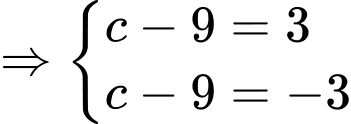
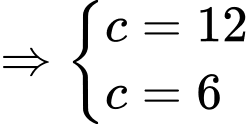
Mà
 có cao độ lớn hơn
có cao độ lớn hơn 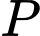 nên
nên 
Nên
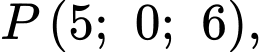 tọa độ trung điểm
tọa độ trung điểm  của
của 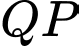 là
là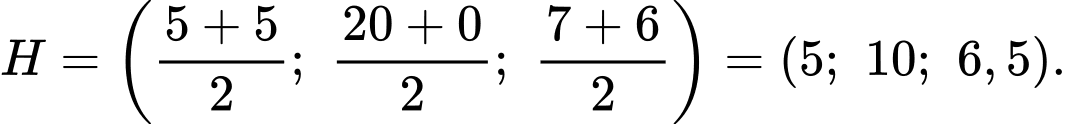
d) Sai.
Điểm
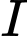 cách đều các điểm
cách đều các điểm 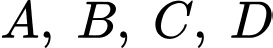 nên nó sẽ nằm trên đường thẳng đi qua tâm hình chữ nhật
nên nó sẽ nằm trên đường thẳng đi qua tâm hình chữ nhật 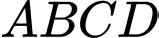 và đi qua điểm
và đi qua điểm 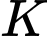 và nó cũng cách điểm
và nó cũng cách điểm 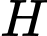 khoảng cách tương tự.
khoảng cách tương tự. Phương trình mặt phẳng
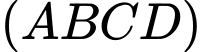 với
với 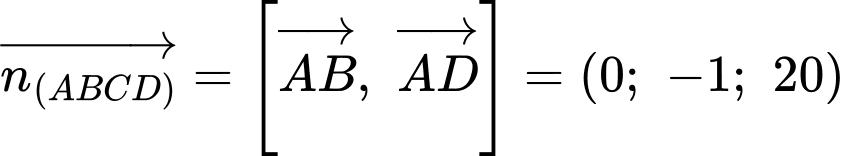 và đi qua điểm
và đi qua điểm 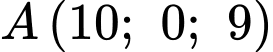 có phương trình là
có phương trình là 
Gọi đường thẳng đi qua
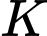 và vuông góc với
và vuông góc với 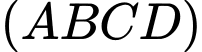 là
là 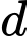
Ta có:
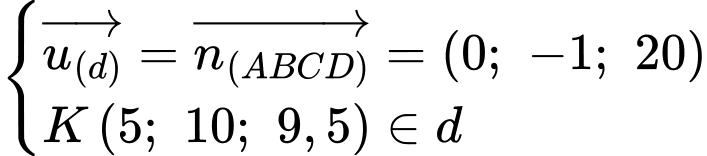
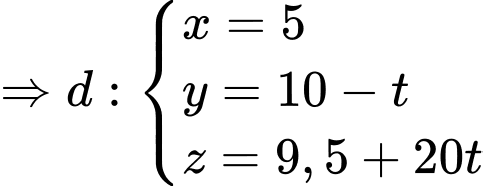
Tham số điểm
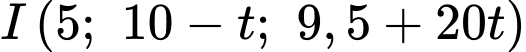 và
và 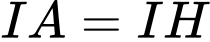
Ta có:
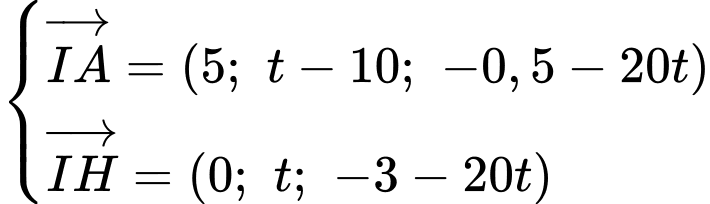
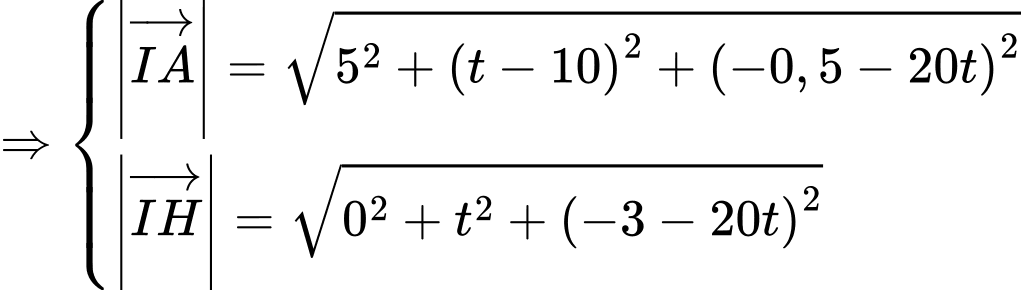
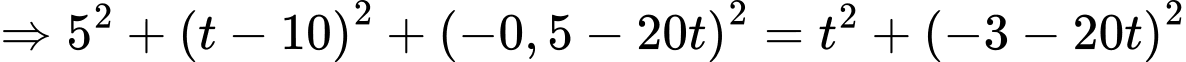
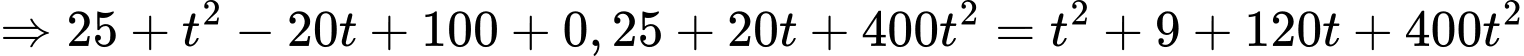
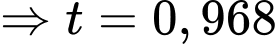
Vậy
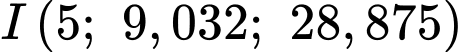 cách mặt đất 28,875 mét.
cách mặt đất 28,875 mét.
Câu 15 [695068]: Trong khoảng thời gian một năm tính từ ngày 01/01/2024, một nhóm nghiên cứu đã quan sát sự phát triển của một quần thể sinh vật X. Kết quả nghiên cứu chỉ ra rằng, tại ngày thứ 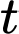 của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số
của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số 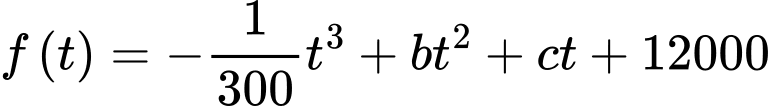 (con),
(con), 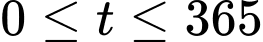 và ngày thứ 270 của năm 2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với 55740 con.
và ngày thứ 270 của năm 2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với 55740 con.
 của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số
của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số 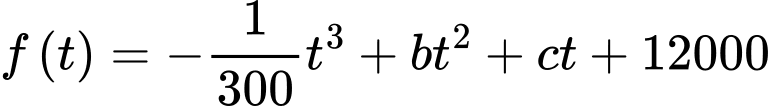 (con),
(con), 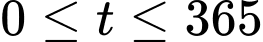 và ngày thứ 270 của năm 2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với 55740 con.
và ngày thứ 270 của năm 2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với 55740 con.
a) Đúng.
Thay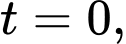 ta có:
ta có: 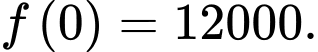
b) Đúng.
Đạo hàm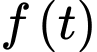 :
: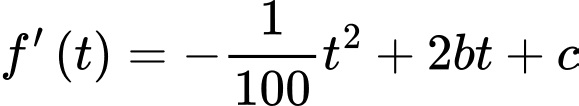
Vì ngày thứ 270 có số lượng cá thể lớn nhất, nên: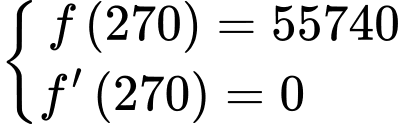
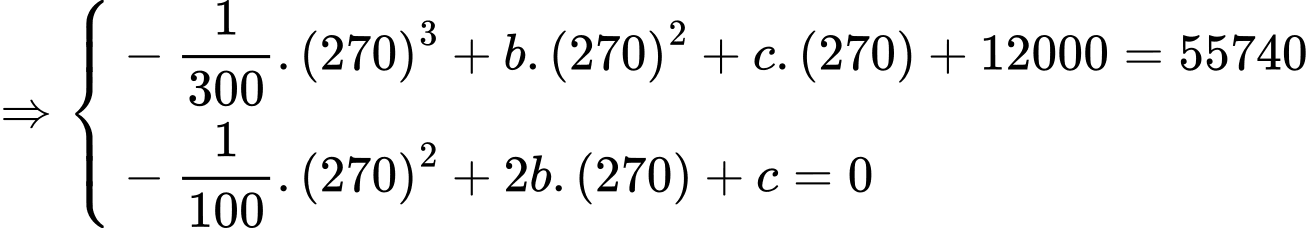
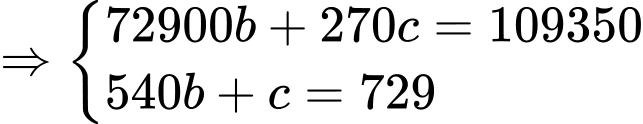
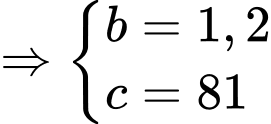
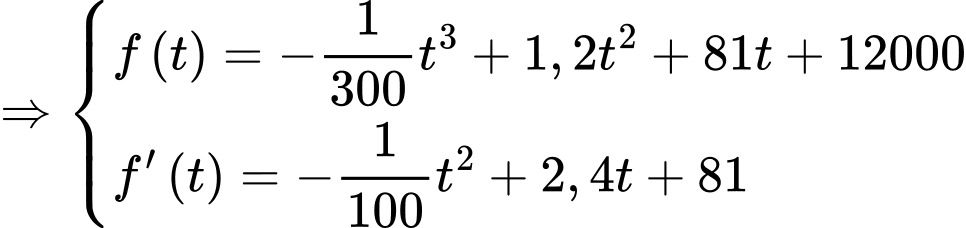
Với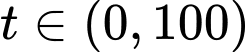 thì
thì 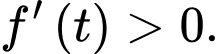
Nên trong 100 ngày đầu tiên của năm 2024, số lượng cá thể sinh vật X luôn tăng.
c) Sai.
Theo câu b),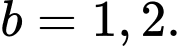
d) Sai.
Vào ngày thứ 300, ta có :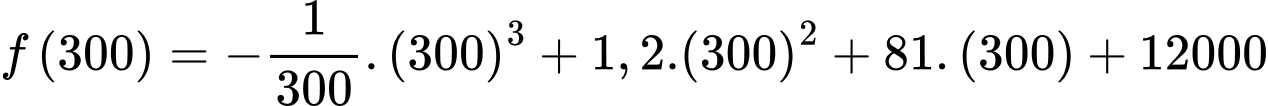
 con.
con.
Thay
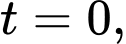 ta có:
ta có: 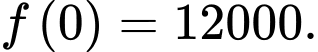
b) Đúng.
Đạo hàm
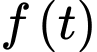 :
: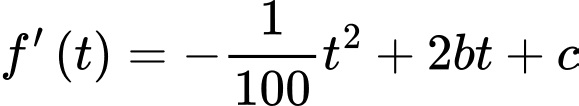
Vì ngày thứ 270 có số lượng cá thể lớn nhất, nên:
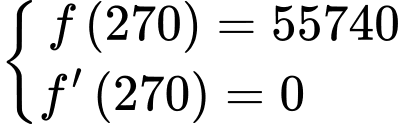
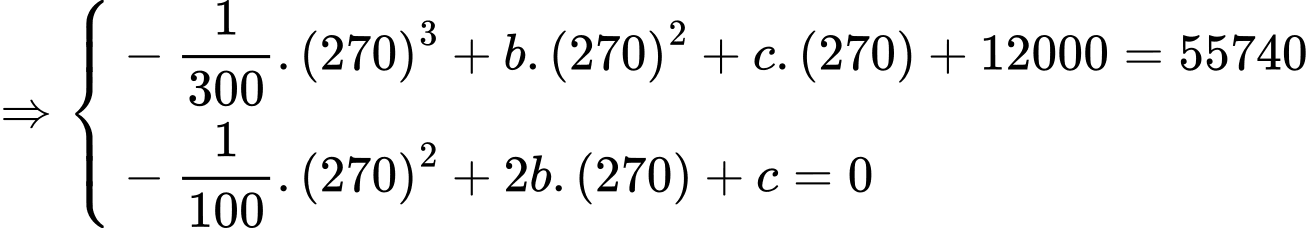
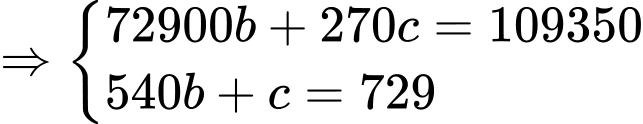
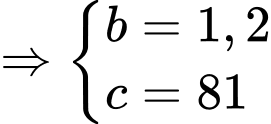
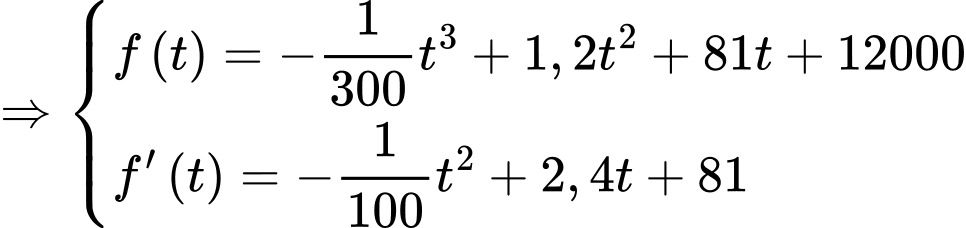
Với
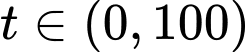 thì
thì 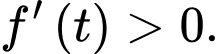
Nên trong 100 ngày đầu tiên của năm 2024, số lượng cá thể sinh vật X luôn tăng.
c) Sai.
Theo câu b),
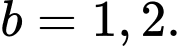
d) Sai.
Vào ngày thứ 300, ta có :
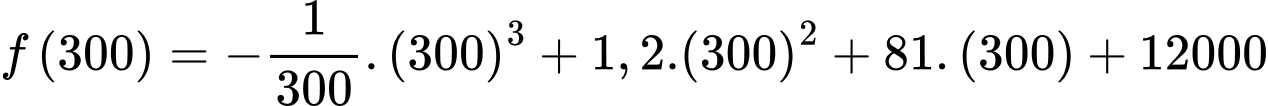
 con.
con.
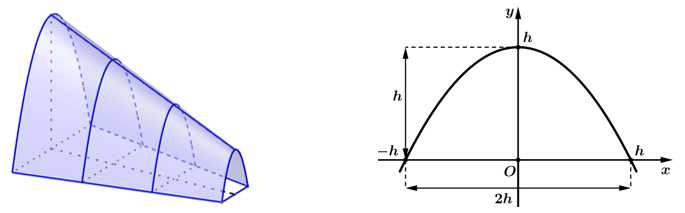
Câu 16 [695594]: Một kỹ sư thiết kế một mô hình đường hầm như bên dưới. Biết rằng đường hầm mô hình có chiều dài 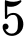
 Khi cắt mô hình này bởi các mặt phẳng vuông góc với đáy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao của parabol (như hình vẽ). Diện tích của thiết diện là
Khi cắt mô hình này bởi các mặt phẳng vuông góc với đáy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao của parabol (như hình vẽ). Diện tích của thiết diện là 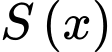 và chiều cao của mỗi thiết diện parabol cho bởi công thức
và chiều cao của mỗi thiết diện parabol cho bởi công thức 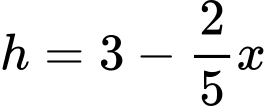 với
với 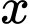
 là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình đến mặt phẳng chứa thiết diện.
là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình đến mặt phẳng chứa thiết diện.
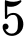
 Khi cắt mô hình này bởi các mặt phẳng vuông góc với đáy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao của parabol (như hình vẽ). Diện tích của thiết diện là
Khi cắt mô hình này bởi các mặt phẳng vuông góc với đáy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao của parabol (như hình vẽ). Diện tích của thiết diện là 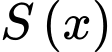 và chiều cao của mỗi thiết diện parabol cho bởi công thức
và chiều cao của mỗi thiết diện parabol cho bởi công thức 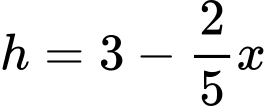 với
với 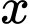
 là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình đến mặt phẳng chứa thiết diện.
là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình đến mặt phẳng chứa thiết diện.
a) Sai.
Vì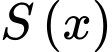 là diện tích thiết diện nên thể tích của hầm phải là
là diện tích thiết diện nên thể tích của hầm phải là 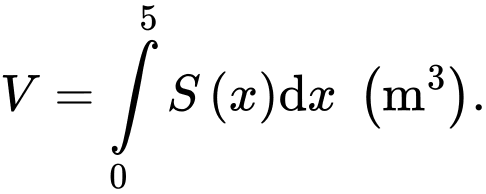
b) Đúng.
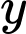 đi qua
đi qua 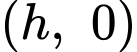 và
và 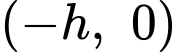
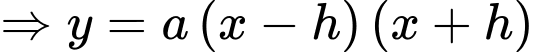
Tại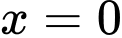 thì
thì 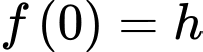
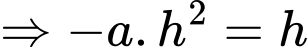
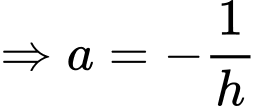
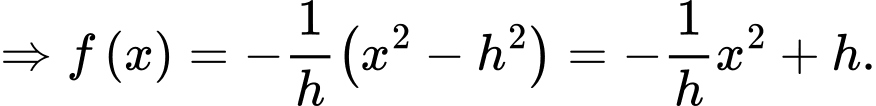
c) Đúng.
Diện tích của thiết diện là :
của thiết diện là : 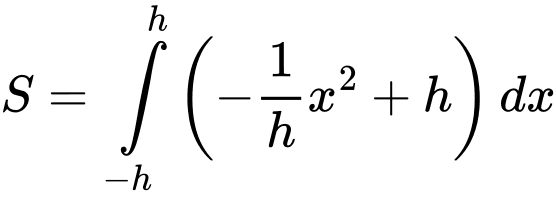
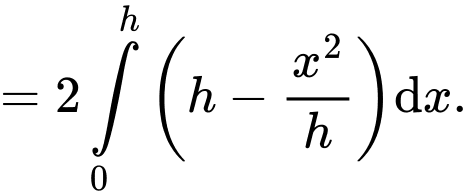
d) Sai.
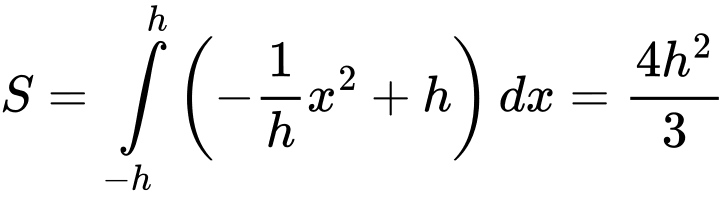
Với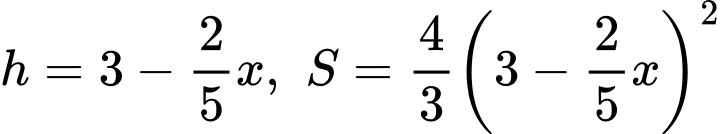
Thể tích của hầm là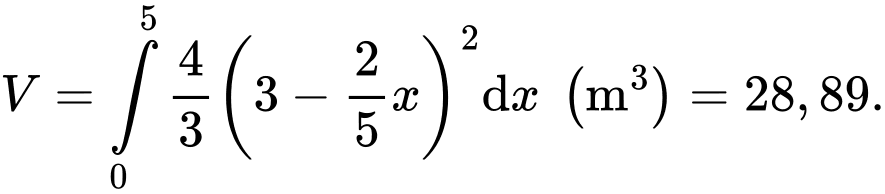
Vì
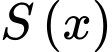 là diện tích thiết diện nên thể tích của hầm phải là
là diện tích thiết diện nên thể tích của hầm phải là 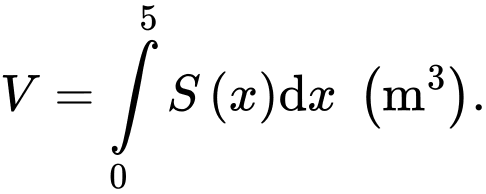
b) Đúng.
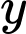 đi qua
đi qua 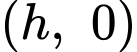 và
và 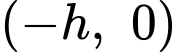
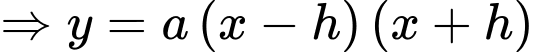
Tại
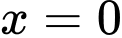 thì
thì 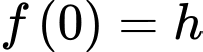
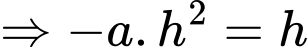
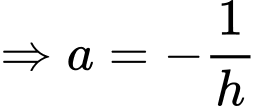
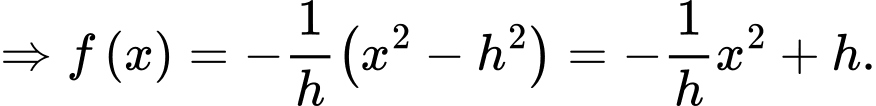
c) Đúng.
Diện tích
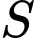 của thiết diện là :
của thiết diện là : 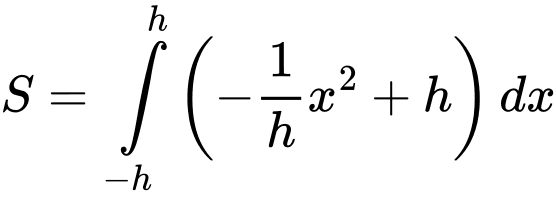
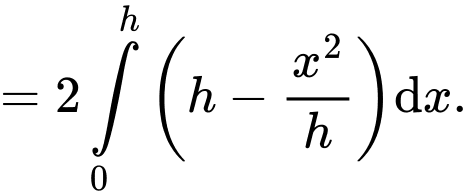
d) Sai.
Với
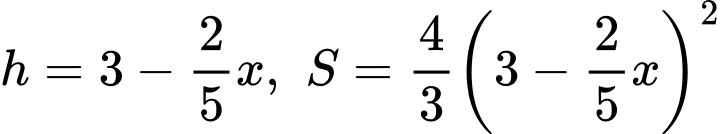
Thể tích của hầm là
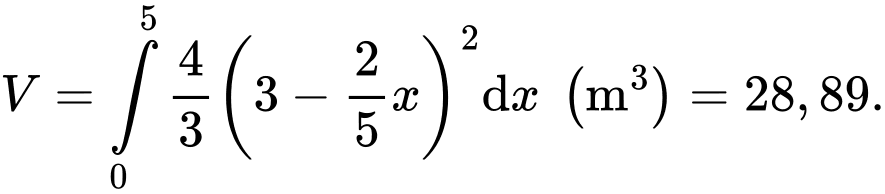
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695595]: Cho hình lăng trụ  có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 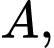
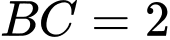 và
và 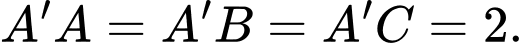 Góc giữa đường thẳng
Góc giữa đường thẳng 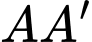 và mặt phẳng
và mặt phẳng 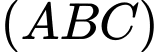 bằng bao nhiêu độ?
bằng bao nhiêu độ?
 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 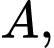
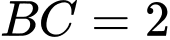 và
và 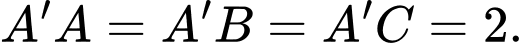 Góc giữa đường thẳng
Góc giữa đường thẳng 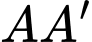 và mặt phẳng
và mặt phẳng 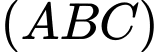 bằng bao nhiêu độ?
bằng bao nhiêu độ?
Điền đáp án: 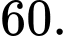
Gọi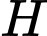 là trung điểm
là trung điểm 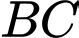
Ta có :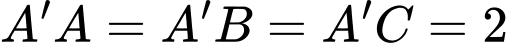 nên hình chiếu của đỉnh
nên hình chiếu của đỉnh 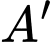 xuống
xuống 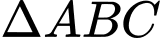 chính là tâm đường tròn ngoại tiếp tam giác.
chính là tâm đường tròn ngoại tiếp tam giác.
Mà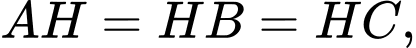 nên
nên 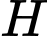 là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 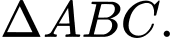
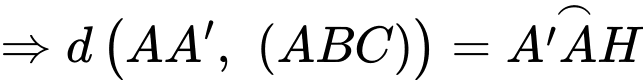
Xét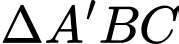 là tam giác đều :
là tam giác đều : 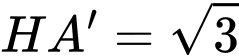 (đường trung tuyến tam giác đều)
(đường trung tuyến tam giác đều)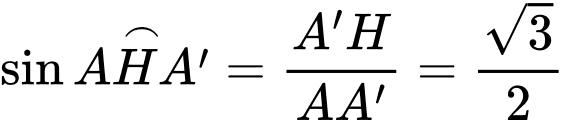
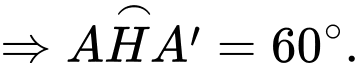
Gọi
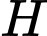 là trung điểm
là trung điểm 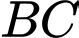
Ta có :
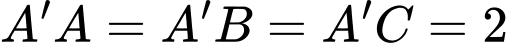 nên hình chiếu của đỉnh
nên hình chiếu của đỉnh  xuống
xuống  chính là tâm đường tròn ngoại tiếp tam giác.
chính là tâm đường tròn ngoại tiếp tam giác. Mà
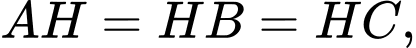 nên
nên 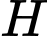 là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 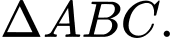
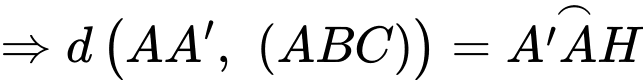
Xét
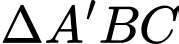 là tam giác đều :
là tam giác đều : 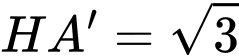 (đường trung tuyến tam giác đều)
(đường trung tuyến tam giác đều)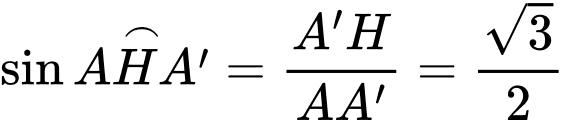
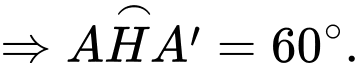
Câu 18 [695596]: Thẻ tín dụng ngân hàng cho phép người dùng chi tiêu trước và thanh toán sau. Giả sử vào ngày 15/8, chị Lan sử dụng thẻ tín dụng để thanh toán hóa đơn mua sắm quần áo tổng giá trị 8 triệu đồng. Chu kỳ thanh toán là từ ngày 15/8 đến ngày 15/9 với mức lãi suất 22%/năm và phí giao dịch mua sắm qua thẻ là 1,5%. Chị Lan chỉ thanh toán toàn bộ số tiền này vào ngày 20/9. Tính tổng chi phí mà chị Lan phải trả cho ngân hàng sau khi thanh toán hóa đơn mua sắm là bao nhiêu nghìn đồng? (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 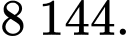
Số ngày chịu lãi suất là 5 ngày.
Lãi suất hàng ngày là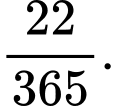
Số tiền chưa thanh toán: 8 000 000 đồng.
Phí giao dịch là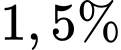 trên tổng giá trị hóa đơn là:
trên tổng giá trị hóa đơn là:
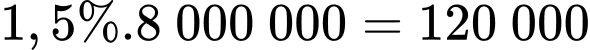 ( đồng).
( đồng).
Số tiền chị Lan phải thanh toán đến ngày 20/9 là
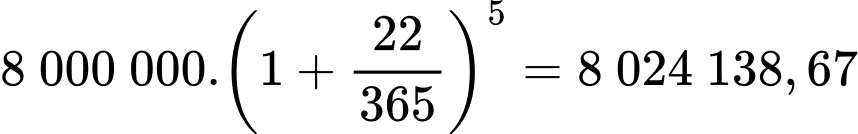 (đồng).
(đồng).
Tổng số tiền mà chị Lan phải trả là
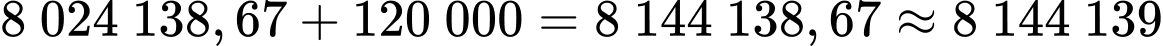 (đồng).
(đồng).
Số ngày chịu lãi suất là 5 ngày.
Lãi suất hàng ngày là
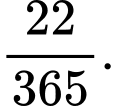
Số tiền chưa thanh toán: 8 000 000 đồng.
Phí giao dịch là
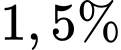 trên tổng giá trị hóa đơn là:
trên tổng giá trị hóa đơn là: 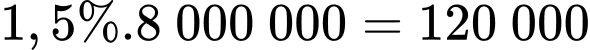 ( đồng).
( đồng).Số tiền chị Lan phải thanh toán đến ngày 20/9 là
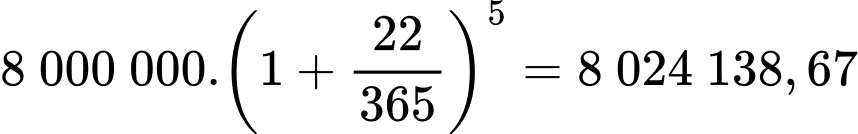 (đồng).
(đồng).Tổng số tiền mà chị Lan phải trả là
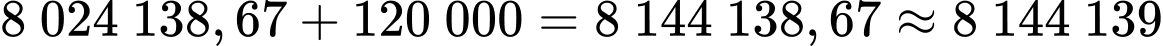 (đồng).
(đồng).
Câu 19 [686984]: Trong một quá trình sản xuất hóa chất nhất định, trọng lượng hàng ngày 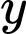 của sản phẩm hóa chất bị lỗi phụ thuộc vào tổng trọng lượng
của sản phẩm hóa chất bị lỗi phụ thuộc vào tổng trọng lượng 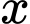 của tất cả sản phẩm theo công thức thực nghiệm
của tất cả sản phẩm theo công thức thực nghiệm 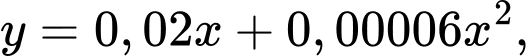 trong đó,
trong đó, 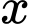 và
và 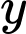 tính bằng kilogram. Nếu lợi nhuận là 50 triệu đồng cho mỗi kilogram hóa chất không bị lỗi và tổn thất là 10 triệu đồng cho mỗi kilogram hóa chất bị lỗi, vậy thì nên sản xuất bao nhiêu kilogram hóa chất mỗi ngày để tối đa hóa tổng lợi nhuận hàng ngày? (làm tròn kết quả đến hàng đơn vị).
tính bằng kilogram. Nếu lợi nhuận là 50 triệu đồng cho mỗi kilogram hóa chất không bị lỗi và tổn thất là 10 triệu đồng cho mỗi kilogram hóa chất bị lỗi, vậy thì nên sản xuất bao nhiêu kilogram hóa chất mỗi ngày để tối đa hóa tổng lợi nhuận hàng ngày? (làm tròn kết quả đến hàng đơn vị).
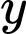 của sản phẩm hóa chất bị lỗi phụ thuộc vào tổng trọng lượng
của sản phẩm hóa chất bị lỗi phụ thuộc vào tổng trọng lượng 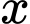 của tất cả sản phẩm theo công thức thực nghiệm
của tất cả sản phẩm theo công thức thực nghiệm 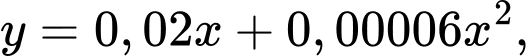 trong đó,
trong đó, 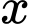 và
và 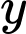 tính bằng kilogram. Nếu lợi nhuận là 50 triệu đồng cho mỗi kilogram hóa chất không bị lỗi và tổn thất là 10 triệu đồng cho mỗi kilogram hóa chất bị lỗi, vậy thì nên sản xuất bao nhiêu kilogram hóa chất mỗi ngày để tối đa hóa tổng lợi nhuận hàng ngày? (làm tròn kết quả đến hàng đơn vị).
tính bằng kilogram. Nếu lợi nhuận là 50 triệu đồng cho mỗi kilogram hóa chất không bị lỗi và tổn thất là 10 triệu đồng cho mỗi kilogram hóa chất bị lỗi, vậy thì nên sản xuất bao nhiêu kilogram hóa chất mỗi ngày để tối đa hóa tổng lợi nhuận hàng ngày? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 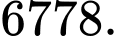
Số sản phẩm không bị lỗi là
Tổng lợi nhuận hằng ngày là: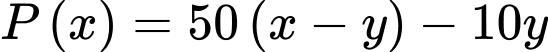
Thay vào phương trình lợi nhuận, ta được:
vào phương trình lợi nhuận, ta được:
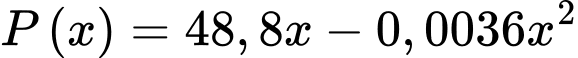
Lợi nhuận mỗi ngày được tối đa hóa khi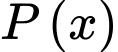 lớn nhất và
lớn nhất và 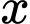 là điểm cực đại.
là điểm cực đại.
Ta có: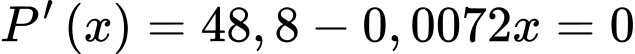
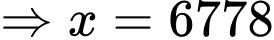
Vậy nên sản suất 6778 kilogram để tối đa hóa lợi nhuận.
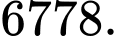
Số sản phẩm không bị lỗi là

Tổng lợi nhuận hằng ngày là:
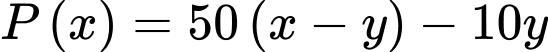
Thay
 vào phương trình lợi nhuận, ta được:
vào phương trình lợi nhuận, ta được:
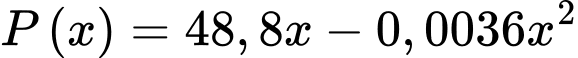
Lợi nhuận mỗi ngày được tối đa hóa khi
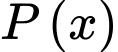 lớn nhất và
lớn nhất và 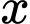 là điểm cực đại.
là điểm cực đại. Ta có:
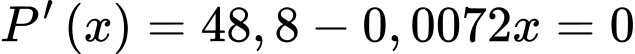
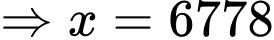
Vậy nên sản suất 6778 kilogram để tối đa hóa lợi nhuận.
Câu 20 [695541]: Một chuỗi của hàng sơn kinh doanh sơn mủ và sơn nước. Dựa trên doanh số bán hàng trong một thời gian dài họ nhận thấy rằng: Trong số những người đến mua sơn mủ, 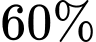 cũng mua con lăn, nhưng chỉ có
cũng mua con lăn, nhưng chỉ có 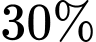 những người mua sơn nước mua con lăn. Trong những người mua con lăn có 14% người mua sơn mủ. Một người vào cửa hàng đó để mua hàng, tính xác suất người đó mua sơn mủ? Làm tròn đến hàng phần trăm.
những người mua sơn nước mua con lăn. Trong những người mua con lăn có 14% người mua sơn mủ. Một người vào cửa hàng đó để mua hàng, tính xác suất người đó mua sơn mủ? Làm tròn đến hàng phần trăm.
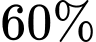 cũng mua con lăn, nhưng chỉ có
cũng mua con lăn, nhưng chỉ có 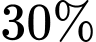 những người mua sơn nước mua con lăn. Trong những người mua con lăn có 14% người mua sơn mủ. Một người vào cửa hàng đó để mua hàng, tính xác suất người đó mua sơn mủ? Làm tròn đến hàng phần trăm.
những người mua sơn nước mua con lăn. Trong những người mua con lăn có 14% người mua sơn mủ. Một người vào cửa hàng đó để mua hàng, tính xác suất người đó mua sơn mủ? Làm tròn đến hàng phần trăm.
Điền đáp án: 0,08.
Xác suất để khách hàng mua sơn mủ là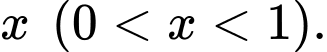
Gọi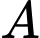 là biến cố “Người đó mua con lăn”.
là biến cố “Người đó mua con lăn”.
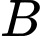 là biến cố “Người đó mua hộp sơn mủ”.
là biến cố “Người đó mua hộp sơn mủ”.
Khi đó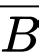 là biến cố “Người đó mua hộp sơn nước”.
là biến cố “Người đó mua hộp sơn nước”.
YCBT Tính
Tính 
Giả sử
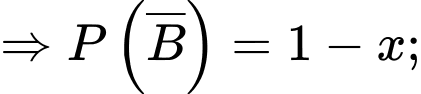
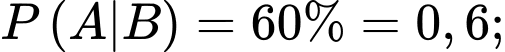
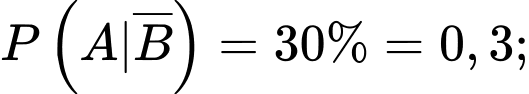
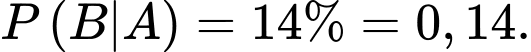
Ta có sơ đồ cây sau:
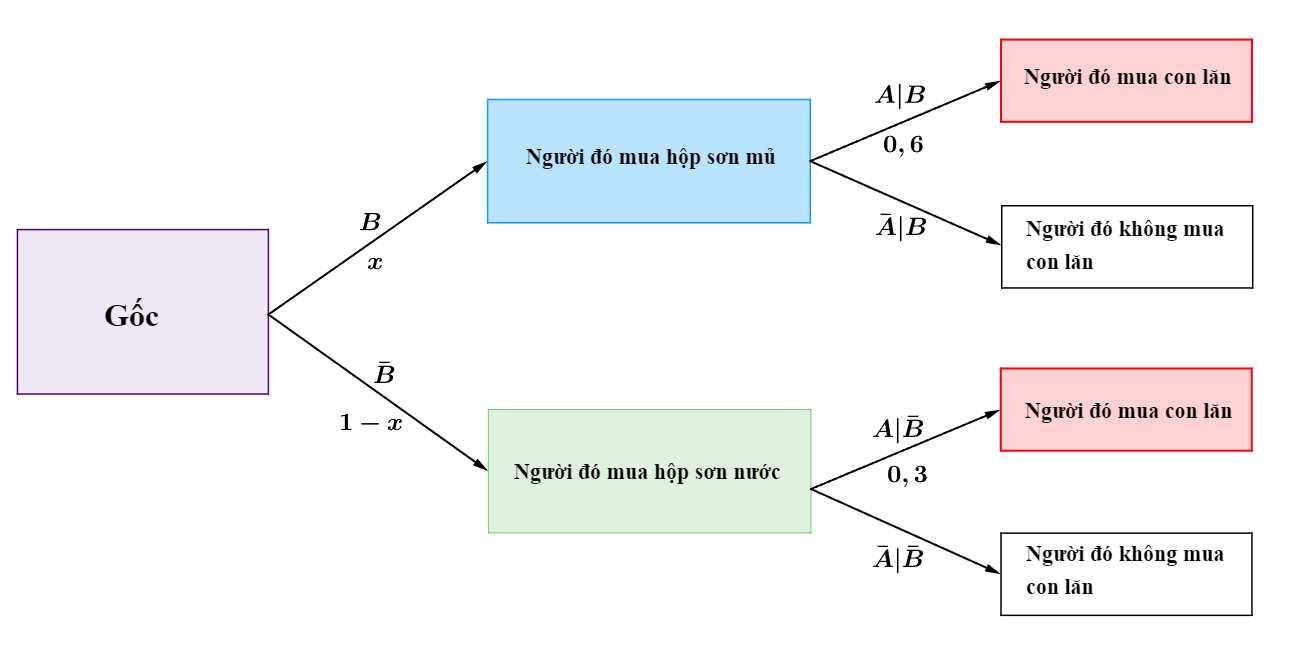
Áp dụng công thức xác suất toàn phần ta có xác suất người đó mua con lăn là
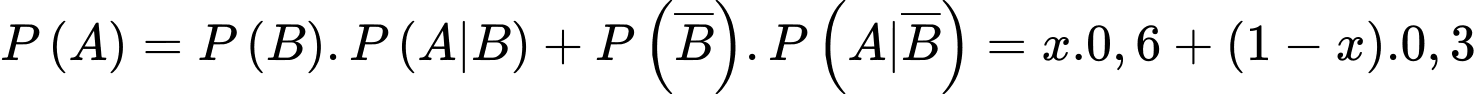
Suy ra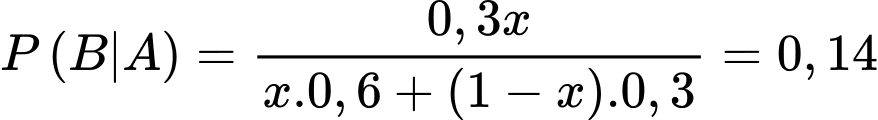
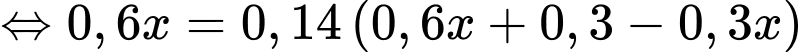
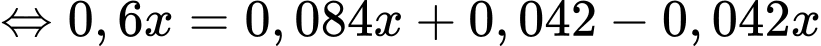
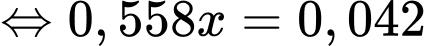
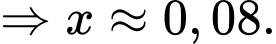
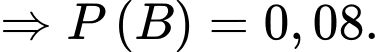
Vậy xác suất người đó mua sơn mủ bằng 0,08.
Xác suất để khách hàng mua sơn mủ là
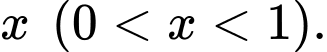
Gọi
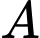 là biến cố “Người đó mua con lăn”.
là biến cố “Người đó mua con lăn”.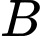 là biến cố “Người đó mua hộp sơn mủ”.
là biến cố “Người đó mua hộp sơn mủ”.Khi đó
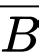 là biến cố “Người đó mua hộp sơn nước”.
là biến cố “Người đó mua hộp sơn nước”.YCBT
 Tính
Tính 
Giả sử

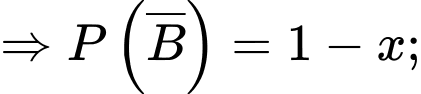
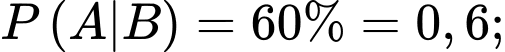
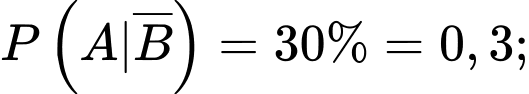
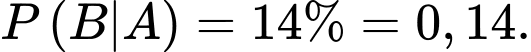
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần ta có xác suất người đó mua con lăn là
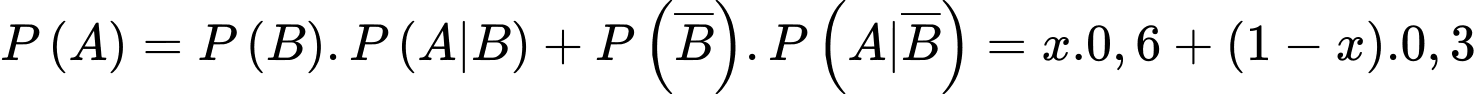
Suy ra
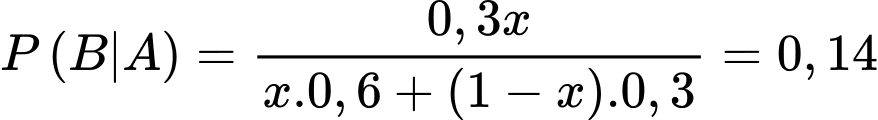
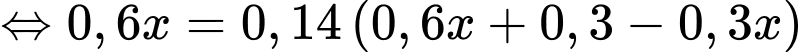
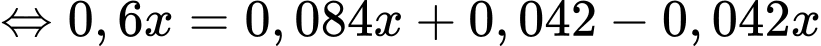
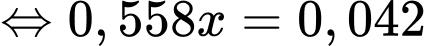
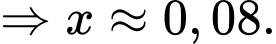
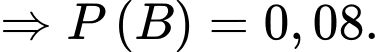
Vậy xác suất người đó mua sơn mủ bằng 0,08.
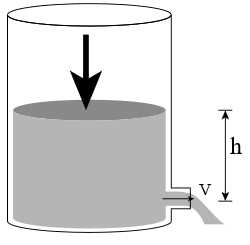
Câu 21 [696436]: Theo định luật Torricelli tốc độ mà một bể chứa nước thoát nước tỷ lệ thuận với căn bậc hai độ sâu của chất lỏng trong bể trên mức của cống thoát nước: nếu 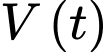 là thể tích chất lỏng đã thoát ra tại thời điểm
là thể tích chất lỏng đã thoát ra tại thời điểm 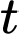 và
và 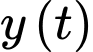 là chiều cao của mặt chất lỏng trên cống thoát nước, thì
là chiều cao của mặt chất lỏng trên cống thoát nước, thì 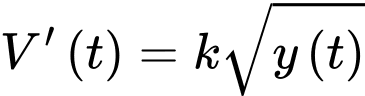 . Đối với một bể hình trụ có chiều cao bằng 9 m và bán kính bằng 2 m. Giả sử ống thoát nước nằm ở đáy bể và bể ban đầu đầy nước. Sau 15 phút độ sâu của nước bằng 4 m. Sau 42 phút, thể tích chất lỏng còn lại trong bể bằng bao nhiêu lít? (làm tròn kết quả đến đơn vị).
. Đối với một bể hình trụ có chiều cao bằng 9 m và bán kính bằng 2 m. Giả sử ống thoát nước nằm ở đáy bể và bể ban đầu đầy nước. Sau 15 phút độ sâu của nước bằng 4 m. Sau 42 phút, thể tích chất lỏng còn lại trong bể bằng bao nhiêu lít? (làm tròn kết quả đến đơn vị).
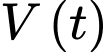 là thể tích chất lỏng đã thoát ra tại thời điểm
là thể tích chất lỏng đã thoát ra tại thời điểm 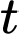 và
và 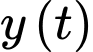 là chiều cao của mặt chất lỏng trên cống thoát nước, thì
là chiều cao của mặt chất lỏng trên cống thoát nước, thì 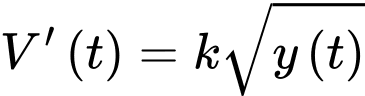 . Đối với một bể hình trụ có chiều cao bằng 9 m và bán kính bằng 2 m. Giả sử ống thoát nước nằm ở đáy bể và bể ban đầu đầy nước. Sau 15 phút độ sâu của nước bằng 4 m. Sau 42 phút, thể tích chất lỏng còn lại trong bể bằng bao nhiêu lít? (làm tròn kết quả đến đơn vị).
. Đối với một bể hình trụ có chiều cao bằng 9 m và bán kính bằng 2 m. Giả sử ống thoát nước nằm ở đáy bể và bể ban đầu đầy nước. Sau 15 phút độ sâu của nước bằng 4 m. Sau 42 phút, thể tích chất lỏng còn lại trong bể bằng bao nhiêu lít? (làm tròn kết quả đến đơn vị).
Điền đáp án: 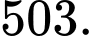
Ta có bán kính hình trụ (bán kính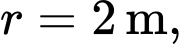 chiều cao
chiều cao 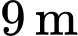 ), ban đầu mực nước cao bằng miệng bể (tức
), ban đầu mực nước cao bằng miệng bể (tức 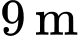 so với lỗ thoát ở đáy).
so với lỗ thoát ở đáy).
Định luật Torricelli dạng thể tích thoát ra là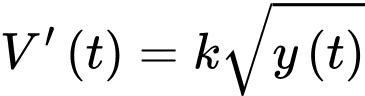
Thể tích nước còn lại là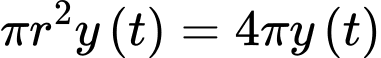
Thể tích đã chảy ra: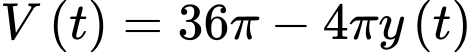
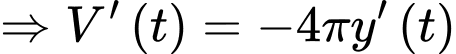
Suy ra: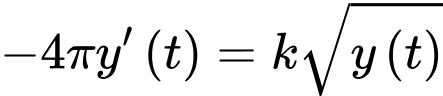
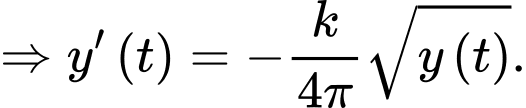
Đặt hằng số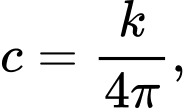 ta được
ta được 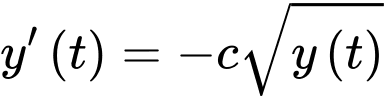
Ta có phương trình :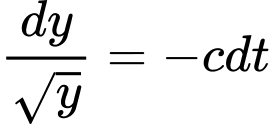 (vì
(vì 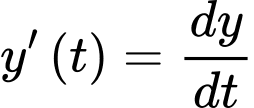 )
)
Tích phân 2 vế ta được: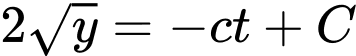
Ban đầu,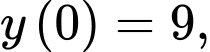 thay vào phương trình trên ta được:
thay vào phương trình trên ta được: 
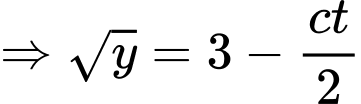 x
x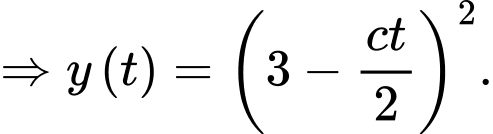
Sau 15 phút, mực nước còn 4m: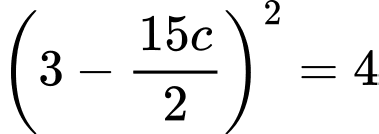
Ta giải được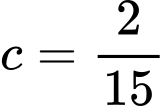
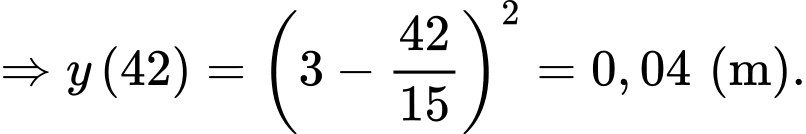
Vậy thể tích chất lỏng còn lại trong bể là :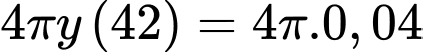
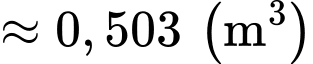
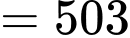 lít.
lít.
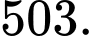
Ta có bán kính hình trụ (bán kính
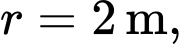 chiều cao
chiều cao 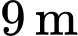 ), ban đầu mực nước cao bằng miệng bể (tức
), ban đầu mực nước cao bằng miệng bể (tức 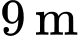 so với lỗ thoát ở đáy).
so với lỗ thoát ở đáy). Định luật Torricelli dạng thể tích thoát ra là
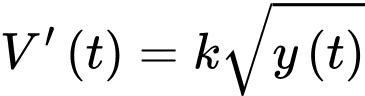
Thể tích nước còn lại là
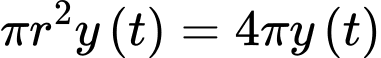
Thể tích đã chảy ra:
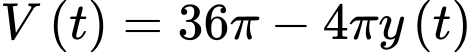
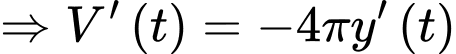
Suy ra:
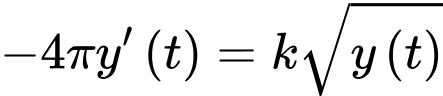
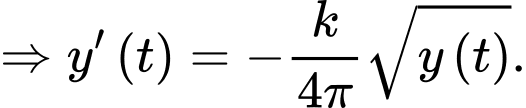
Đặt hằng số
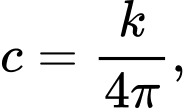 ta được
ta được 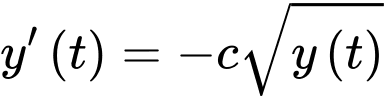
Ta có phương trình :
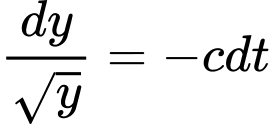 (vì
(vì 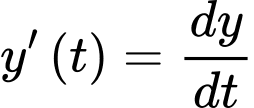 )
)Tích phân 2 vế ta được:
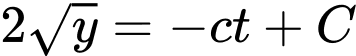
Ban đầu,
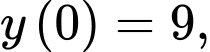 thay vào phương trình trên ta được:
thay vào phương trình trên ta được: 
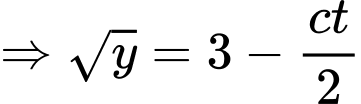 x
x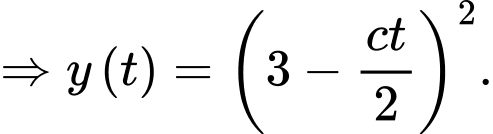
Sau 15 phút, mực nước còn 4m:
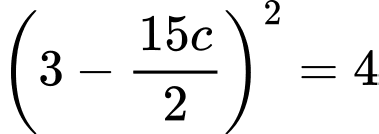
Ta giải được
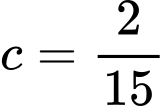
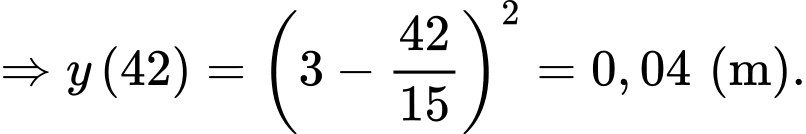
Vậy thể tích chất lỏng còn lại trong bể là :
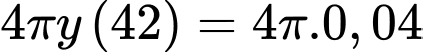
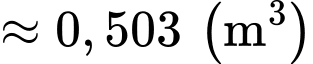
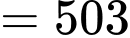 lít.
lít.
Câu 22 [695600]: Trong không gian với hệ tọa độ 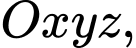 cho điểm
cho điểm 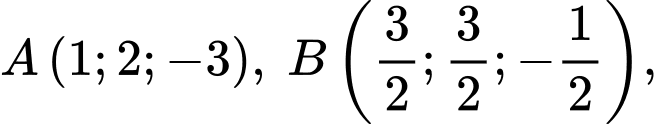
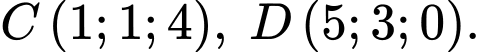 Gọi
Gọi 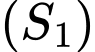 là mặt cầu tâm
là mặt cầu tâm 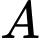 bán kính bằng
bán kính bằng 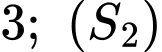 là mặt cầu tâm
là mặt cầu tâm 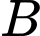 bán kính bằng
bán kính bằng 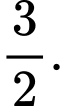 Mặt phẳng tiếp xúc với hai mặt cầu
Mặt phẳng tiếp xúc với hai mặt cầu 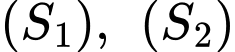 đồng thời song song với đường thẳng qua
đồng thời song song với đường thẳng qua  và
và 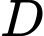 có phương trình là
có phương trình là 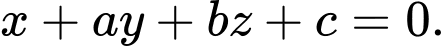 Giá trị của
Giá trị của 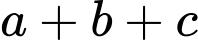 bằng bao nhiêu?
bằng bao nhiêu?
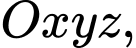 cho điểm
cho điểm 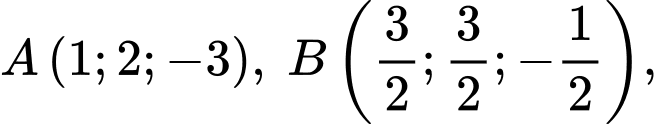
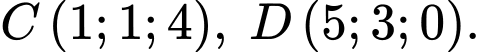 Gọi
Gọi 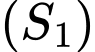 là mặt cầu tâm
là mặt cầu tâm 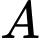 bán kính bằng
bán kính bằng 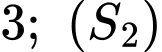 là mặt cầu tâm
là mặt cầu tâm 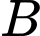 bán kính bằng
bán kính bằng 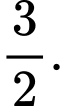 Mặt phẳng tiếp xúc với hai mặt cầu
Mặt phẳng tiếp xúc với hai mặt cầu 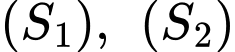 đồng thời song song với đường thẳng qua
đồng thời song song với đường thẳng qua  và
và 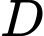 có phương trình là
có phương trình là 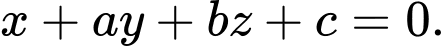 Giá trị của
Giá trị của 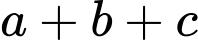 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 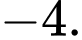
Gọi phương trình mặt phẳng cần tìm là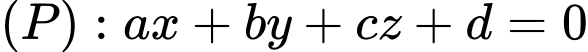
Vì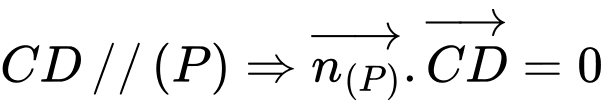
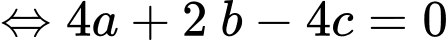
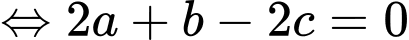
Khoảng cách từ điểm A đến mặt phẳng là
là
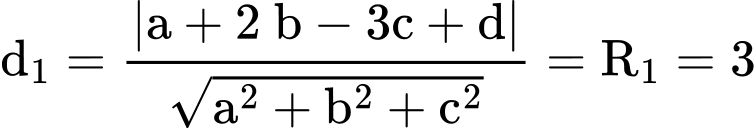
Khoảng cách từ điểm đến mặt phẳng
đến mặt phẳng  là
là
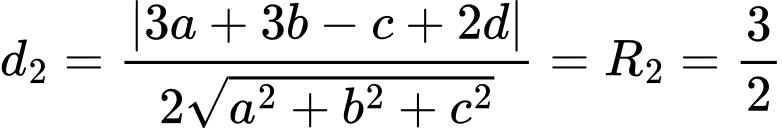
Từ (1), (2), (3) suy ra: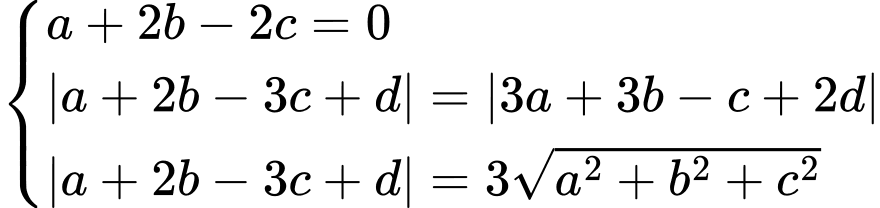
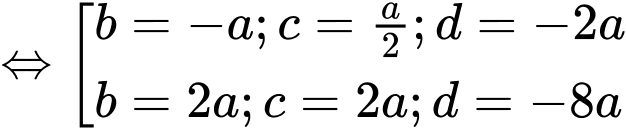
Với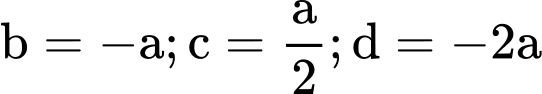 suy ra phương trình
suy ra phương trình 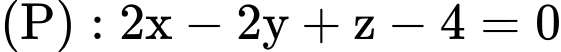 loại vì chứa
loại vì chứa 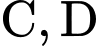
Với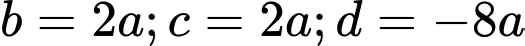 suy ra phương trình
suy ra phương trình 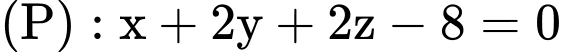
Vậy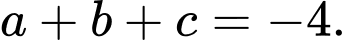 .
.
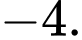
Gọi phương trình mặt phẳng cần tìm là
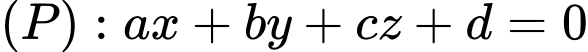
Vì
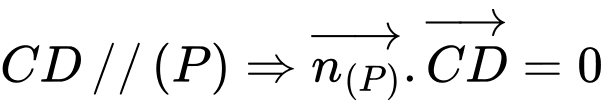
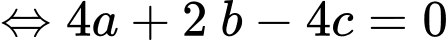
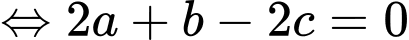
Khoảng cách từ điểm A đến mặt phẳng
 là
là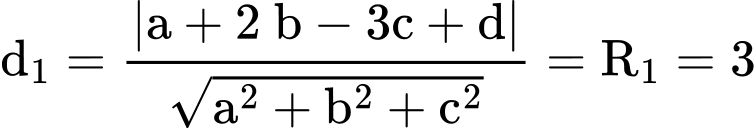
Khoảng cách từ điểm
 đến mặt phẳng
đến mặt phẳng  là
là 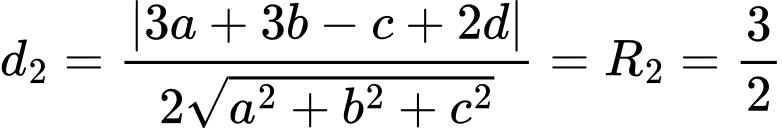
Từ (1), (2), (3) suy ra:
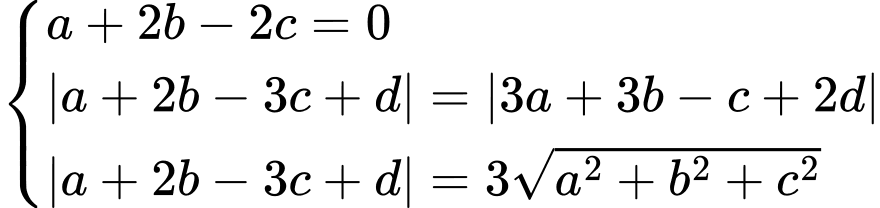
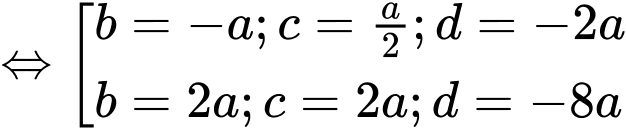
Với
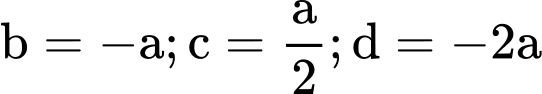 suy ra phương trình
suy ra phương trình 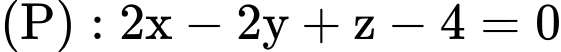 loại vì chứa
loại vì chứa 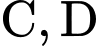
Với
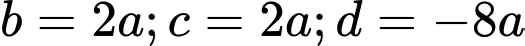 suy ra phương trình
suy ra phương trình 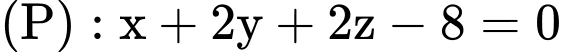
Vậy
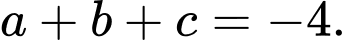 .
.