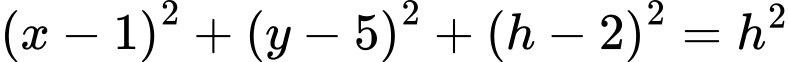PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [696292]: Trong không gian 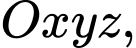 cho mặt phẳng
cho mặt phẳng 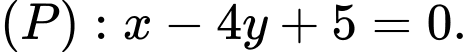 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 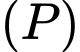 có toạ độ là
có toạ độ là
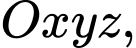 cho mặt phẳng
cho mặt phẳng 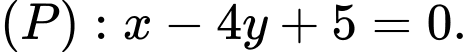 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 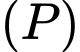 có toạ độ là
có toạ độ là A, 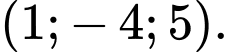
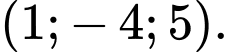
B, 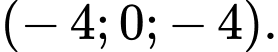
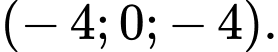
C, 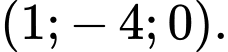
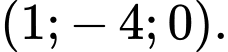
D, 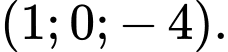
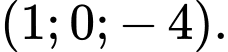
Chọn đáp án C. Đáp án: C
Câu 2 [696293]: Cho hàm số 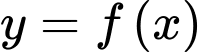 có đạo hàm
có đạo hàm 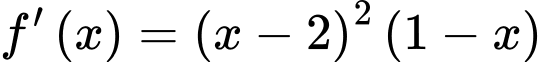 với mọi
với mọi 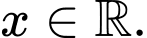 Hàm số đã cho đồng biến trên khoảng nào sau đây?
Hàm số đã cho đồng biến trên khoảng nào sau đây?
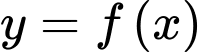 có đạo hàm
có đạo hàm 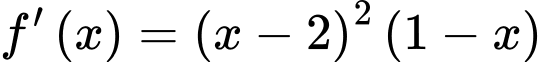 với mọi
với mọi 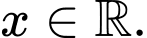 Hàm số đã cho đồng biến trên khoảng nào sau đây?
Hàm số đã cho đồng biến trên khoảng nào sau đây? A, 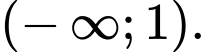
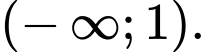
B, 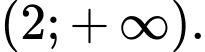
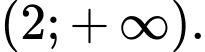
C, 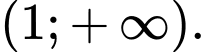
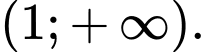
D, 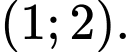
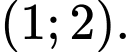
Chọn đáp án A.
Ta có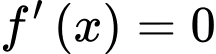
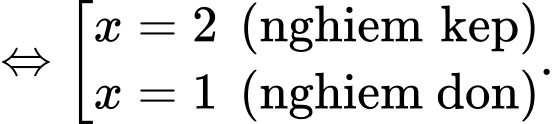
Suy ra trục xét dấu của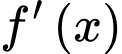 như sau:
như sau:
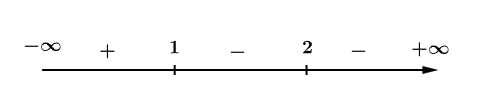
Vậy hàm số đồng biến trên khoảng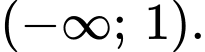 Đáp án: A
Đáp án: A
Ta có
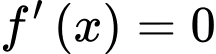
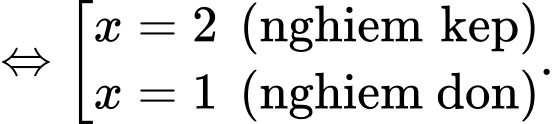
Suy ra trục xét dấu của
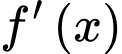 như sau:
như sau: 
Vậy hàm số đồng biến trên khoảng
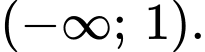 Đáp án: A
Đáp án: A
Câu 3 [696294]: Cho bốn số 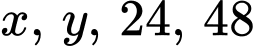 theo thứ tự lập thành cấp số nhân. Tính
theo thứ tự lập thành cấp số nhân. Tính 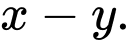
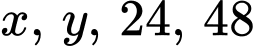 theo thứ tự lập thành cấp số nhân. Tính
theo thứ tự lập thành cấp số nhân. Tính 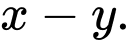
A, 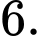
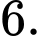
B, 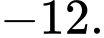
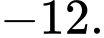
C, 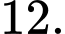
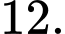
D, 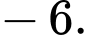
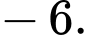
Chọn đáp án D.
Vì 4 số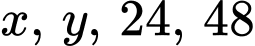 lập thành một cấp số nhân, nên ta có
lập thành một cấp số nhân, nên ta có 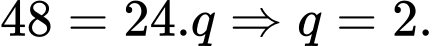
Suy ra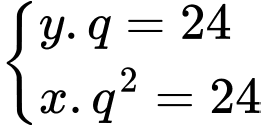
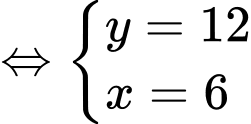
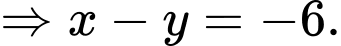 Đáp án: D
Đáp án: D
Vì 4 số
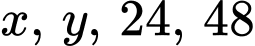 lập thành một cấp số nhân, nên ta có
lập thành một cấp số nhân, nên ta có 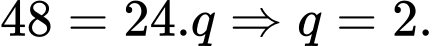
Suy ra
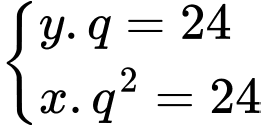
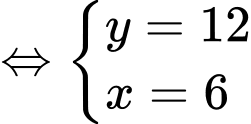
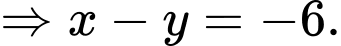 Đáp án: D
Đáp án: D
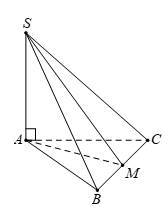
Câu 4 [696296]: Cho hình chóp 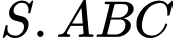 có đáy
có đáy 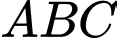 là tam giác đều,
là tam giác đều, 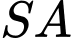 vuông góc với mặt phẳng đáy. Gọi
vuông góc với mặt phẳng đáy. Gọi 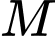 là trung điểm của
là trung điểm của 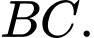 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
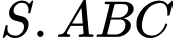 có đáy
có đáy 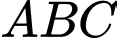 là tam giác đều,
là tam giác đều, 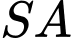 vuông góc với mặt phẳng đáy. Gọi
vuông góc với mặt phẳng đáy. Gọi 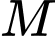 là trung điểm của
là trung điểm của 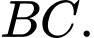 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
A, 

B, 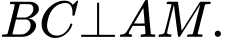
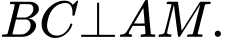
C, 

D, 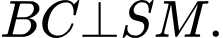
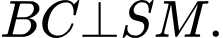
Chọn đáp án C.
A. Đúng. Vì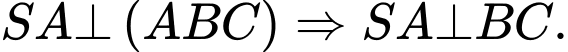
B. Đúng. Vì là trung tuyến của tam giác đều nên
là trung tuyến của tam giác đều nên  cũng là đường cao của tam giác
cũng là đường cao của tam giác 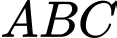 hay
hay 
C. Sai.
D. Đúng. Vì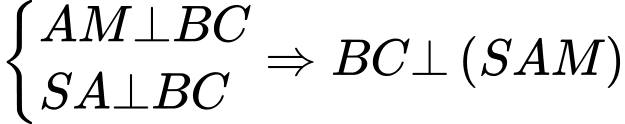
 Đáp án: C
Đáp án: C
A. Đúng. Vì
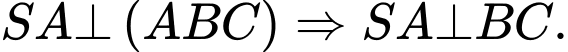
B. Đúng. Vì
 là trung tuyến của tam giác đều nên
là trung tuyến của tam giác đều nên  cũng là đường cao của tam giác
cũng là đường cao của tam giác 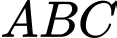 hay
hay 
C. Sai.
D. Đúng. Vì
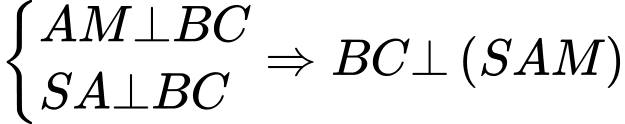
 Đáp án: C
Đáp án: C
Câu 5 [696297]: Tập xác định của hàm số 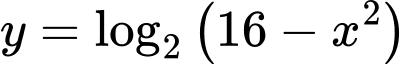 chứa bao nhiêu số nguyên?
chứa bao nhiêu số nguyên?
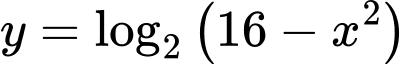 chứa bao nhiêu số nguyên?
chứa bao nhiêu số nguyên? A, 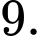
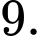
B, 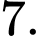
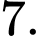
C, 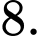
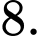
D, 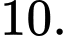
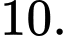
Chọn đáp án B.
Điều kiện xác định của hàm số là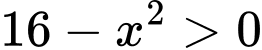
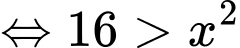

Vậy tập xác định của hàm số chứa 7 số nguyên.
Đáp án: B
Điều kiện xác định của hàm số là
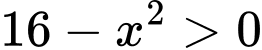
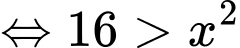

Sử dụng thông tin dưới đây để trả lời câu 6 và câu 7
Câu 6 [702661]: Họ tất cả các nguyên hàm của hàm 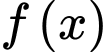 trên khoảng
trên khoảng 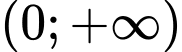 là
là
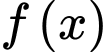 trên khoảng
trên khoảng 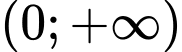 là
là A, 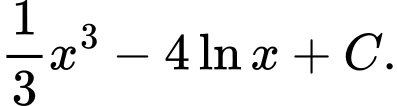
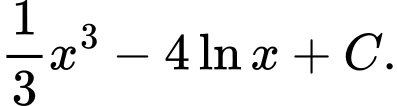
B, 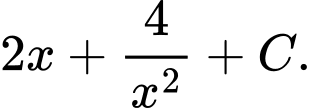
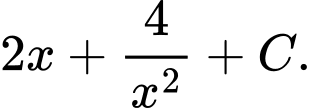
C, 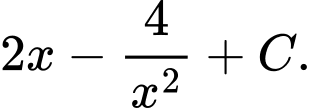
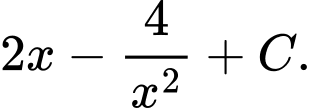
D, 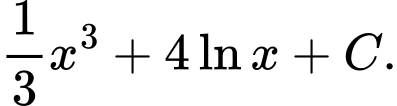
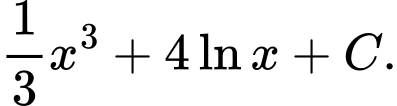
Chọn đáp án A.
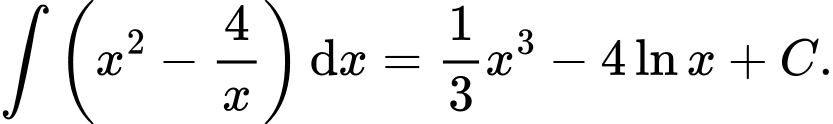 Đáp án: A
Đáp án: A
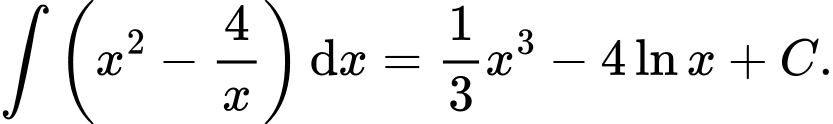 Đáp án: A
Đáp án: A
Câu 7 [702662]: Giá trị của 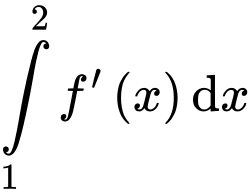 bằng
bằng
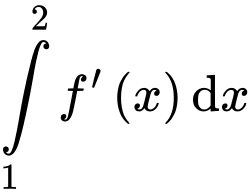 bằng
bằng A, 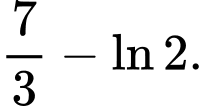
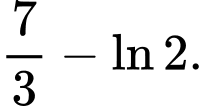
B, 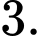
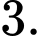
C, 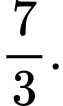
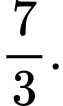
D, 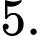
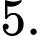
Chọn đáp án D.
Cách 1: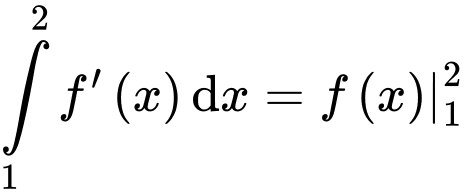
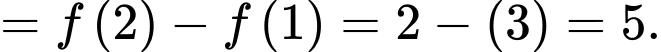
Cách 2: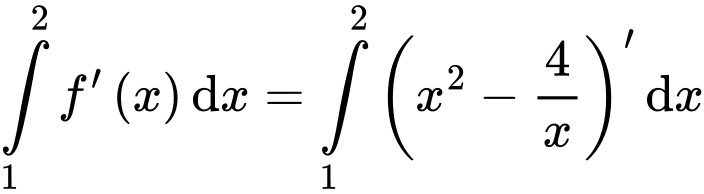
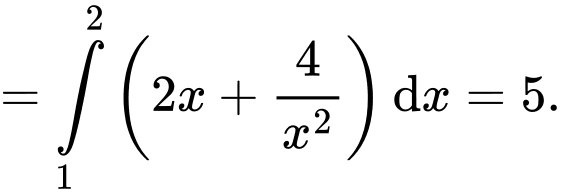 Đáp án: D
Đáp án: D
Cách 1:
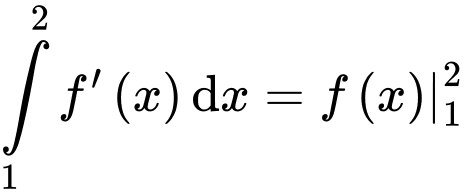
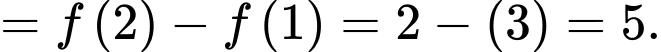
Cách 2:
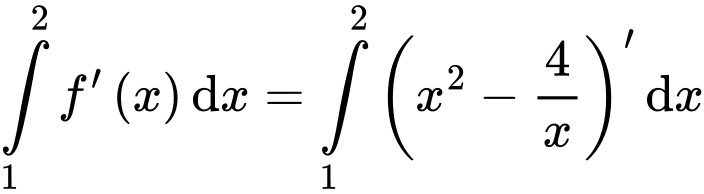
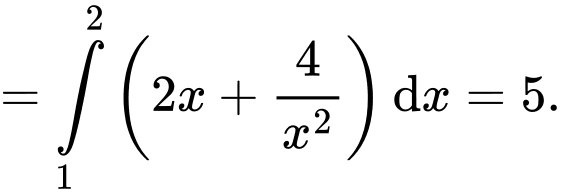 Đáp án: D
Đáp án: D
Câu 8 [696299]: Trong không gian 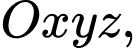 cho điểm
cho điểm 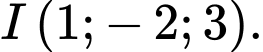 Mặt cầu tâm
Mặt cầu tâm 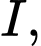 tiếp xúc với trục
tiếp xúc với trục 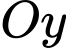 có phương trình là
có phương trình là
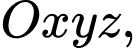 cho điểm
cho điểm 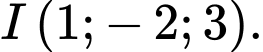 Mặt cầu tâm
Mặt cầu tâm 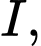 tiếp xúc với trục
tiếp xúc với trục 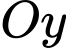 có phương trình là
có phương trình là A, 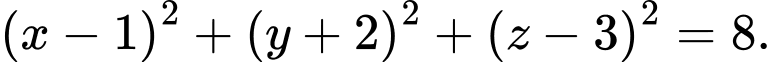
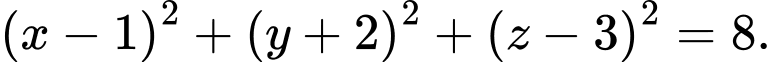
B, 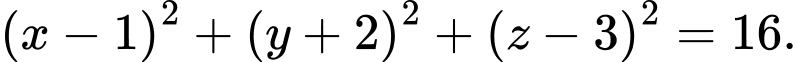
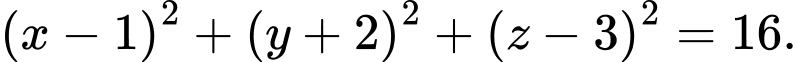
C, 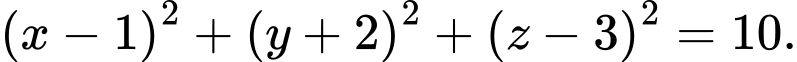
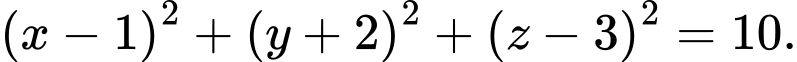
D, 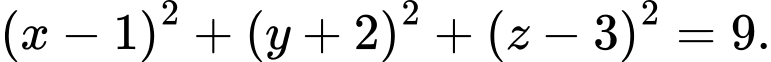
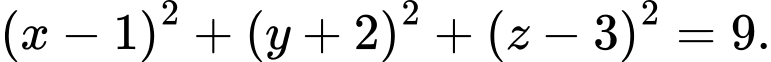
Chọn đáp án C.
Mặt cầu tâm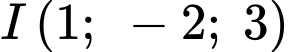 tiếp xúc với
tiếp xúc với 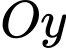 có bán kính
có bán kính 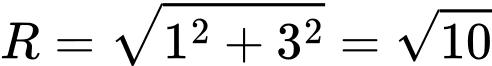 có phương trình là
có phương trình là 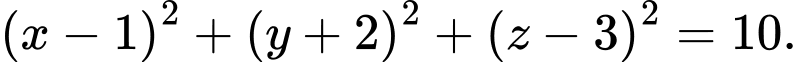 Đáp án: C
Đáp án: C
Mặt cầu tâm
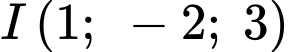 tiếp xúc với
tiếp xúc với 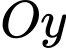 có bán kính
có bán kính 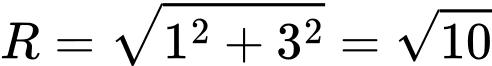 có phương trình là
có phương trình là 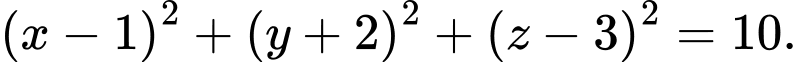 Đáp án: C
Đáp án: C
Câu 9 [696300]: Cho hàm số 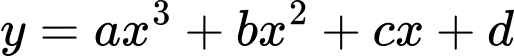
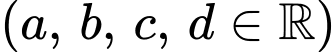 có đồ thị là đường cong trong hình bên. Giá trị của
có đồ thị là đường cong trong hình bên. Giá trị của  bằng
bằng
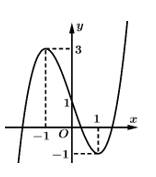
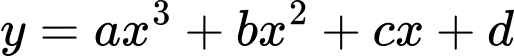
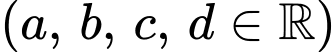 có đồ thị là đường cong trong hình bên. Giá trị của
có đồ thị là đường cong trong hình bên. Giá trị của  bằng
bằng
A, 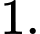
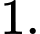
B, 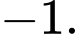
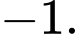
C, 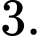
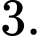
D, 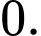
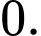
Chọn đáp án B.
Dựa vào đồ thị hàm số ta có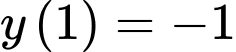 hay
hay 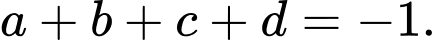 Đáp án: B
Đáp án: B
Dựa vào đồ thị hàm số ta có
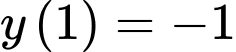 hay
hay 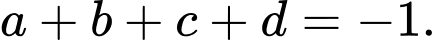 Đáp án: B
Đáp án: B
Câu 10 [696301]: Nếu đặt 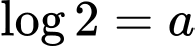 và
và 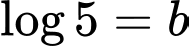 thì
thì 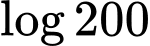 bằng
bằng
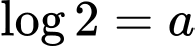 và
và 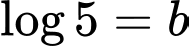 thì
thì 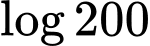 bằng
bằng A, 

B, 

C, 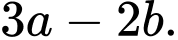
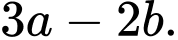
D, 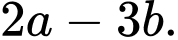
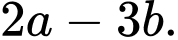
Chọn đáp án A.
Ta có:
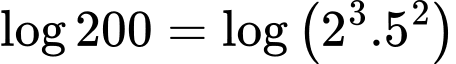
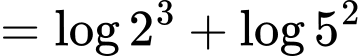
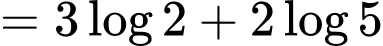
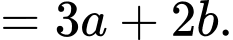 Đáp án: A
Đáp án: A
Ta có:
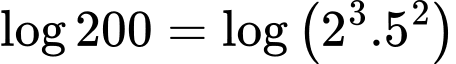
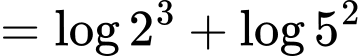
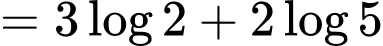
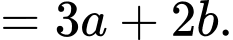 Đáp án: A
Đáp án: A
Câu 11 [696302]: Thời gian đàm thoại của một số cuộc gọi bởi một nhân viên sale được cho kết quả như bảng sau:
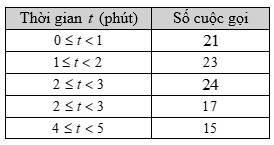
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên? (làm tròn đến hàng phần trăm).

Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên? (làm tròn đến hàng phần trăm).
A, 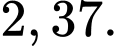
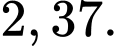
B, 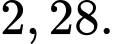
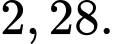
C, 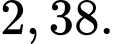
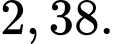
D, 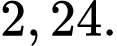
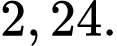
Chọn đáp án D.
Cỡ mẫu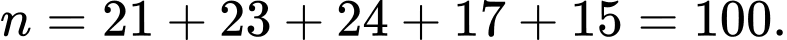
Gọi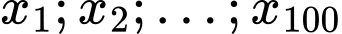 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có: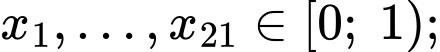
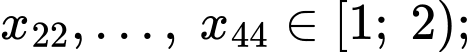
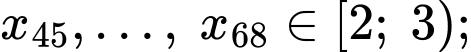
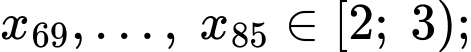
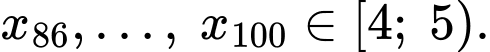
Tứ phân vị thứ nhất của mẫu số liệu gốc là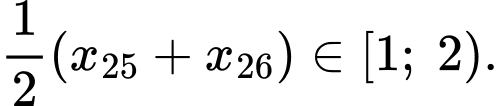 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
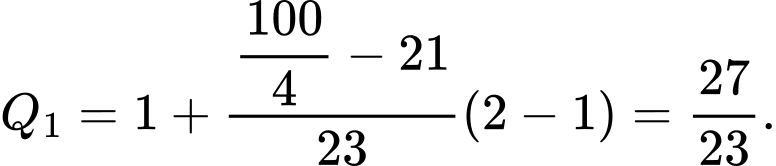
Tứ phân vị thứ ba của mẫu số liệu gốc là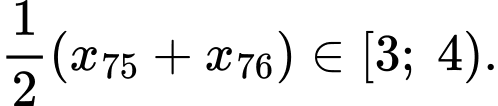 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
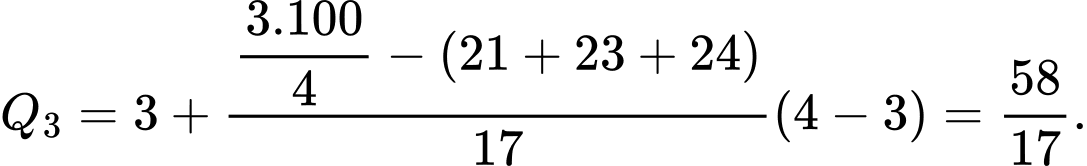
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
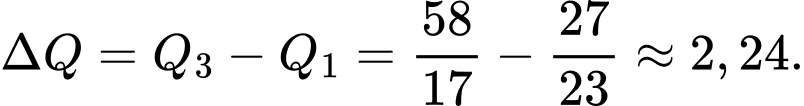 Đáp án: D
Đáp án: D
Cỡ mẫu
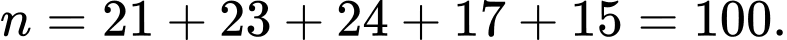
Gọi
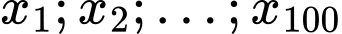 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.Ta có:
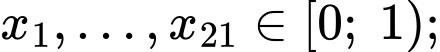
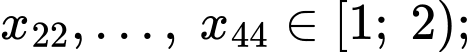
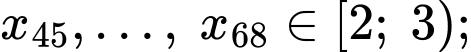
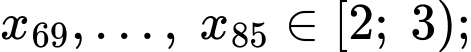
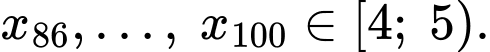
Tứ phân vị thứ nhất của mẫu số liệu gốc là
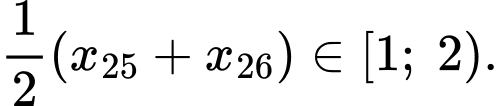 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 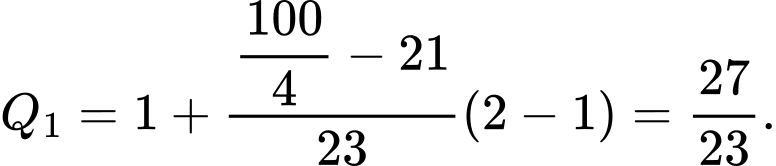
Tứ phân vị thứ ba của mẫu số liệu gốc là
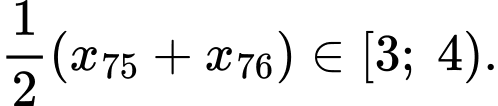 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 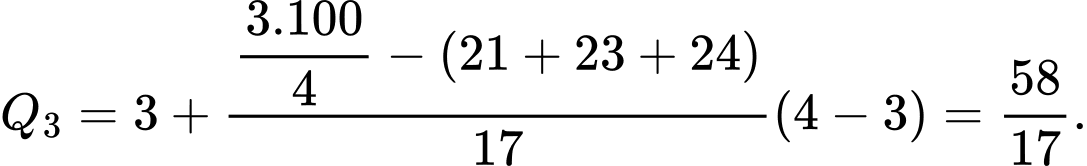
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
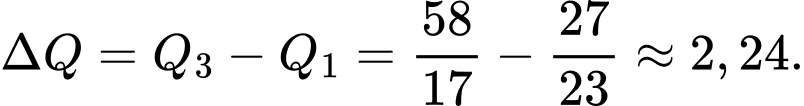 Đáp án: D
Đáp án: D
Câu 12 [696303]: Cho hình lập phương 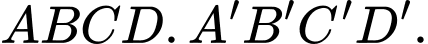 Đặt
Đặt 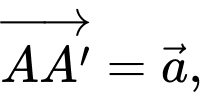
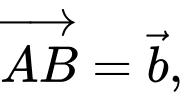
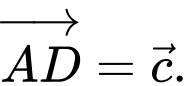 Gọi
Gọi  lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 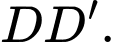 Phát biểu nào sau đây đúng?
Phát biểu nào sau đây đúng?
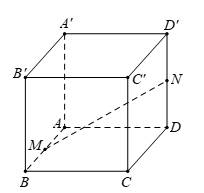
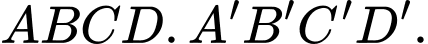 Đặt
Đặt 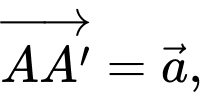
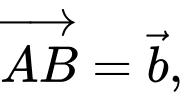
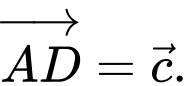 Gọi
Gọi  lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 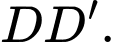 Phát biểu nào sau đây đúng?
Phát biểu nào sau đây đúng?
A, 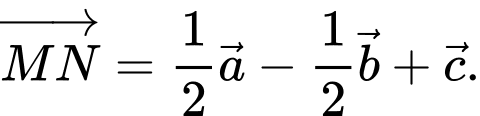
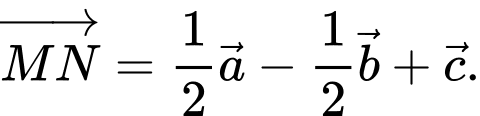
B, 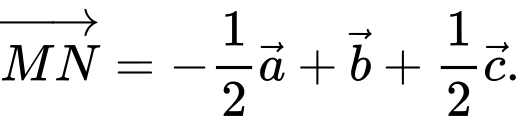
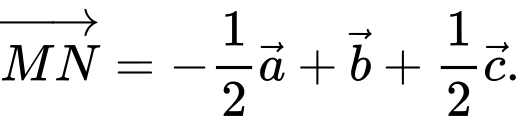
C, 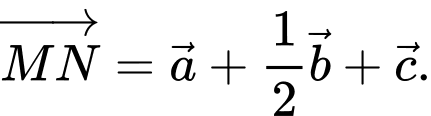
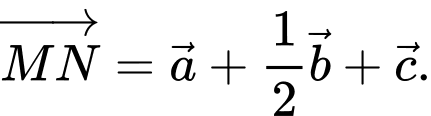
D, 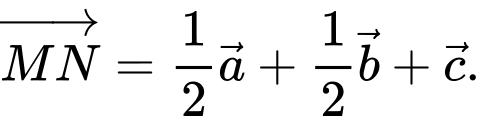
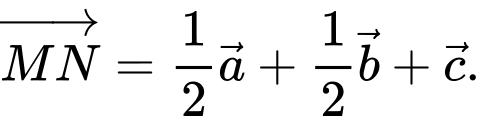
Chọn đáp án A.
Ta có:
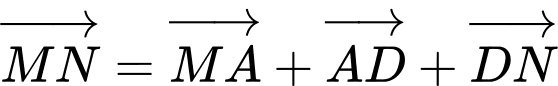
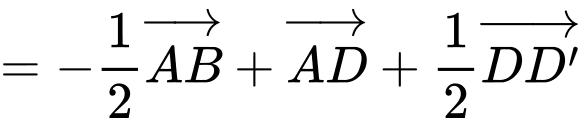
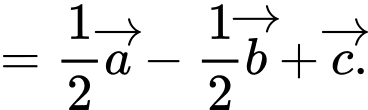 Đáp án: A
Đáp án: A
Ta có:
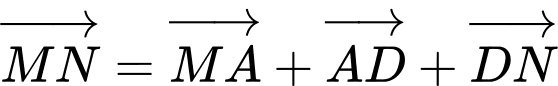
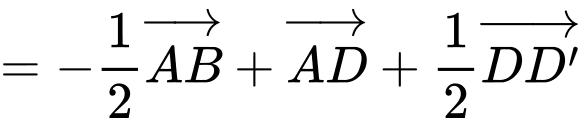
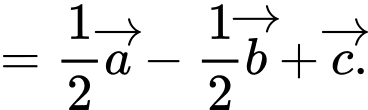 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696304]: Cho hàm số 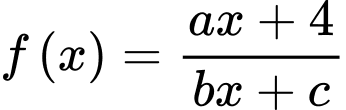
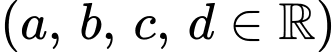 có bảng biến thiên như sau:
có bảng biến thiên như sau:
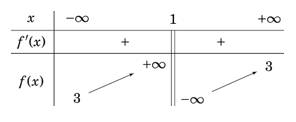
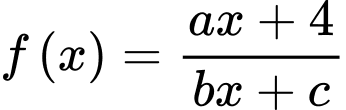
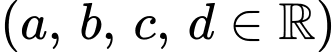 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Thứ tự đáp án: Đúng, Đúng, Sai, Đúng.
a) Sử dụng định nghĩa tiệm cận đứng của đồ thị hàm số, nếu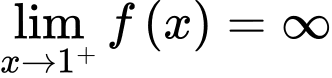 hoặc
hoặc 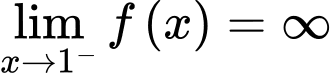 thì
thì 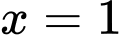 là tiệm cận đứng của đồ thị đã cho.
là tiệm cận đứng của đồ thị đã cho.
b) Sử dụng định nghĩa tiệm cận ngang của đồ thị hàm số, ta thấy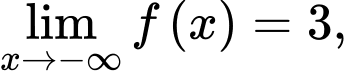
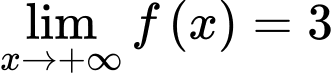 nên
nên 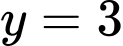 là tiệm cận ngang của đồ thị đã cho.
là tiệm cận ngang của đồ thị đã cho.
c) Vì tiệm cận đứng của đồ thị hàm số là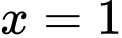 nên
nên 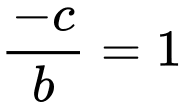
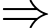
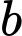 trái dấu
trái dấu 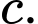
Vì tiệm cận ngang của đồ thị hàm số là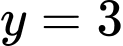 nên
nên 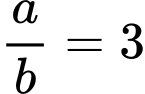
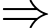
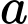 cùng dấu
cùng dấu 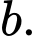
Ta có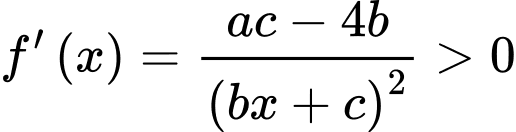 với mọi
với mọi 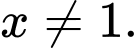
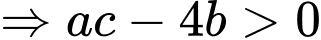
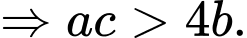
Vì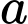 trái dấu
trái dấu  nên
nên  Do đó,
Do đó, 
Vậy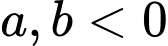 và
và 
d) Từ câu c) ta có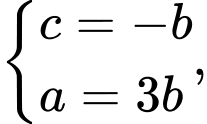 thay vào bất phương trình
thay vào bất phương trình  ta được
ta được
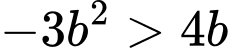

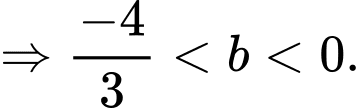
Do đó, có duy nhất số nguyên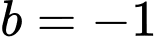 thỏa mãn bài toán.
thỏa mãn bài toán.
a) Sử dụng định nghĩa tiệm cận đứng của đồ thị hàm số, nếu
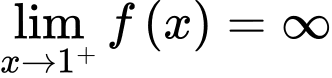 hoặc
hoặc 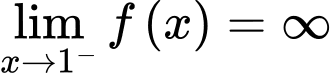 thì
thì 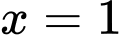 là tiệm cận đứng của đồ thị đã cho.
là tiệm cận đứng của đồ thị đã cho.
b) Sử dụng định nghĩa tiệm cận ngang của đồ thị hàm số, ta thấy
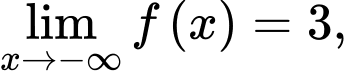
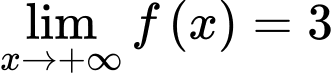 nên
nên 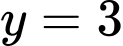 là tiệm cận ngang của đồ thị đã cho.
là tiệm cận ngang của đồ thị đã cho.
c) Vì tiệm cận đứng của đồ thị hàm số là
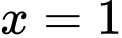 nên
nên 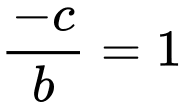
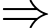
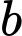 trái dấu
trái dấu 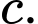
Vì tiệm cận ngang của đồ thị hàm số là
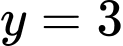 nên
nên 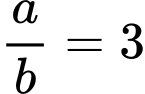
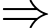
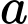 cùng dấu
cùng dấu 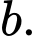
Ta có
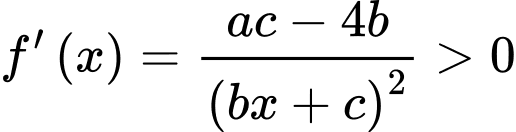 với mọi
với mọi 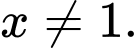
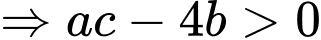
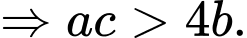
Vì
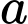 trái dấu
trái dấu  nên
nên  Do đó,
Do đó, 
Vậy
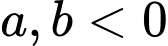 và
và 
d) Từ câu c) ta có
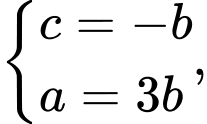 thay vào bất phương trình
thay vào bất phương trình  ta được
ta được
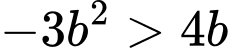

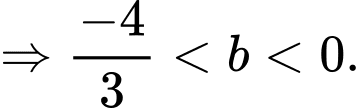
Do đó, có duy nhất số nguyên
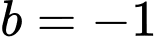 thỏa mãn bài toán.
thỏa mãn bài toán.
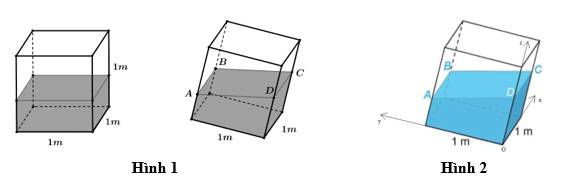
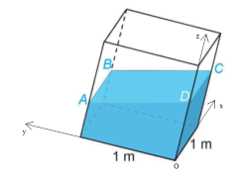
Câu 14 [696305]: Trong một bể hình lập phương cạnh 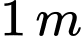 có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành
có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành  và khoảng cách từ các điểm hoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40 cm, 44 cm, 48 cm. Chọn hệ trục toạ độ như hình 2 (đơn vị mỗi trục là cm).
và khoảng cách từ các điểm hoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40 cm, 44 cm, 48 cm. Chọn hệ trục toạ độ như hình 2 (đơn vị mỗi trục là cm).
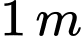 có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành
có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành  và khoảng cách từ các điểm hoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40 cm, 44 cm, 48 cm. Chọn hệ trục toạ độ như hình 2 (đơn vị mỗi trục là cm).
và khoảng cách từ các điểm hoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40 cm, 44 cm, 48 cm. Chọn hệ trục toạ độ như hình 2 (đơn vị mỗi trục là cm).
Thứ tự đáp án: Đúng, Sai, Sai, Đúng.
Chọn hệ trục tọa độ như hình vẽ.
Khi đó ta có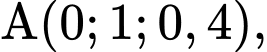
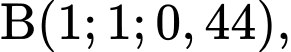
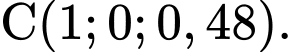
Ta có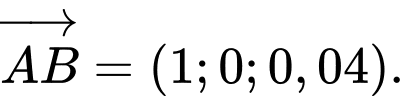
Vì ABCD là hình bình hành nên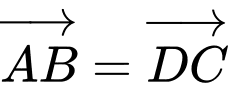
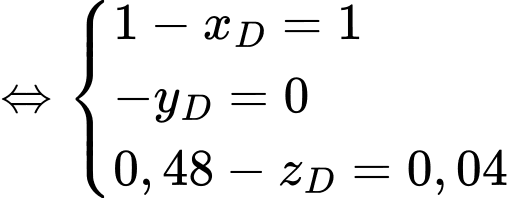
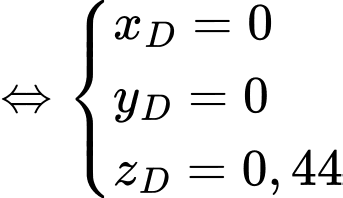
Suy ra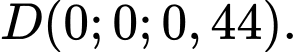
Vậy khoảng cách từ điểm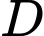 đến đáy bể là 44cm.
đến đáy bể là 44cm.
Ta có đáy bể nằm trong mặt phẳng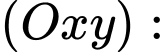
 có vectơ pháp tuyến
có vectơ pháp tuyến 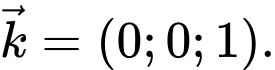
Ta có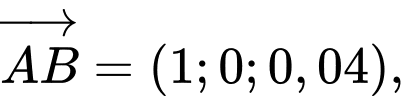
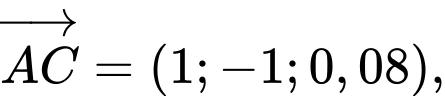
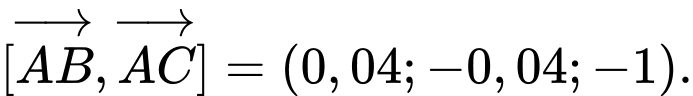
Mặt phẳng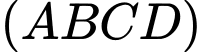 đi qua
đi qua 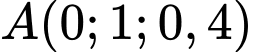 và có vectơ pháp tuyến
và có vectơ pháp tuyến 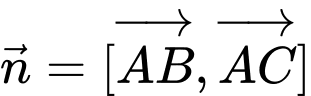
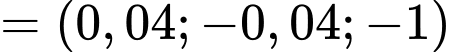 có phương trình là:
có phương trình là:
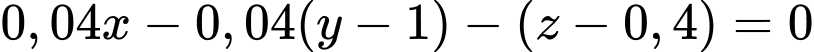
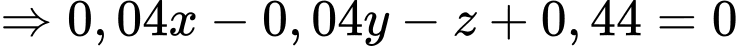
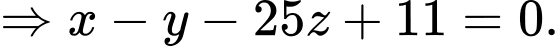
Do đó, góc giữa đáy bể và mặt phẳng nằm ngang là góc giữa mặt phẳng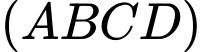 và mặt đáy
và mặt đáy 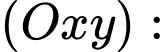
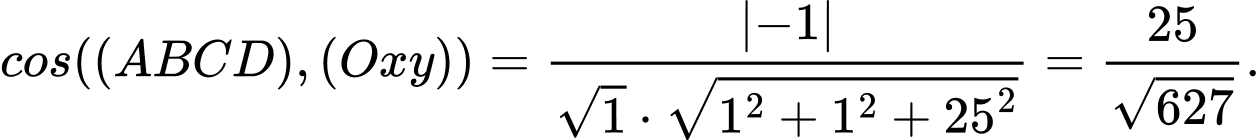
Suy ra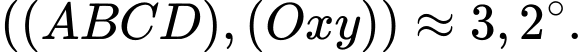

Chọn hệ trục tọa độ như hình vẽ.
Khi đó ta có
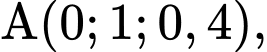
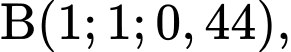
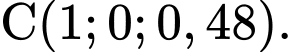
Ta có
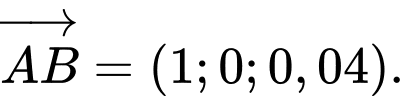
Vì ABCD là hình bình hành nên
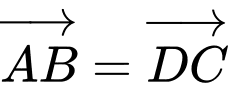
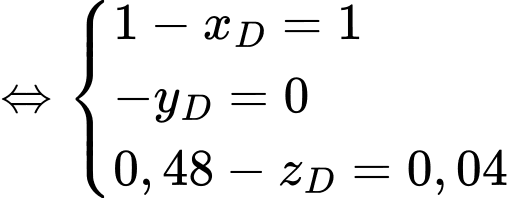
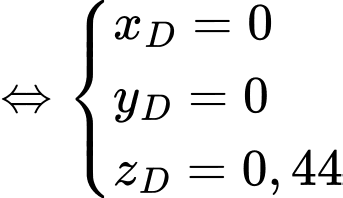
Suy ra
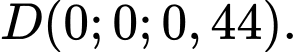
Vậy khoảng cách từ điểm
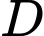 đến đáy bể là 44cm.
đến đáy bể là 44cm.Ta có đáy bể nằm trong mặt phẳng
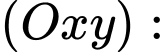
 có vectơ pháp tuyến
có vectơ pháp tuyến 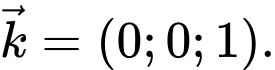
Ta có
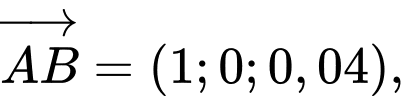
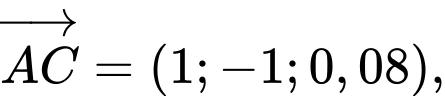
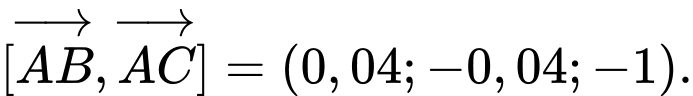
Mặt phẳng
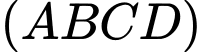 đi qua
đi qua 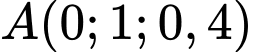 và có vectơ pháp tuyến
và có vectơ pháp tuyến 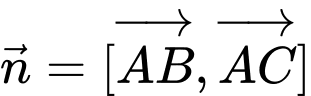
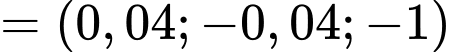 có phương trình là:
có phương trình là: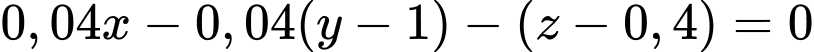
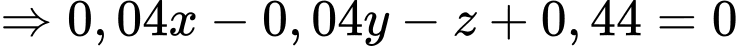
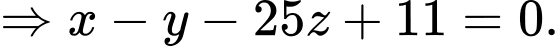
Do đó, góc giữa đáy bể và mặt phẳng nằm ngang là góc giữa mặt phẳng
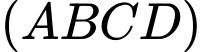 và mặt đáy
và mặt đáy 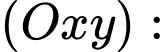
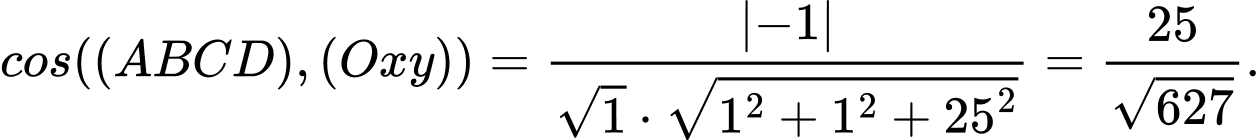
Suy ra
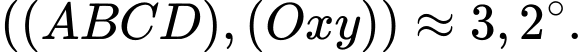
Câu 15 [702663]: Một đoàn tàu đang đứng yên trong sân ga, ngay trước đầu tàu có một cái cây. Đoàn tàu khởi hành từ trạng thái đứng yên với gia tốc 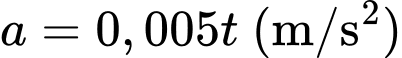 và đi qua cái cây trong thời gian
và đi qua cái cây trong thời gian 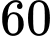 giây. Sau
giây. Sau 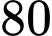 giây đoàn tàu chuyển sang trạng thái chuyển động đều.
giây đoàn tàu chuyển sang trạng thái chuyển động đều.
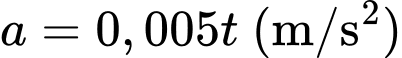 và đi qua cái cây trong thời gian
và đi qua cái cây trong thời gian 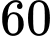 giây. Sau
giây. Sau 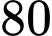 giây đoàn tàu chuyển sang trạng thái chuyển động đều.
giây đoàn tàu chuyển sang trạng thái chuyển động đều.
Thứ tự đáp án: Sai, Đúng, Đúng, Sai.
a) Vận tốc của đoàn tàu là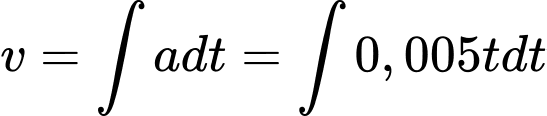
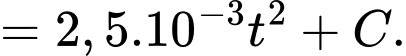
Vì ban đầu tàu đứng yên nên
Vậy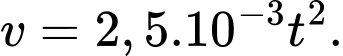
b) Quãng đường đoàn tàu đi được là
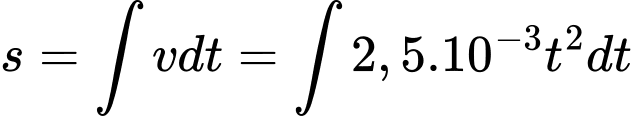
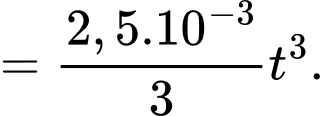
Chiều dài của đoàn tàu là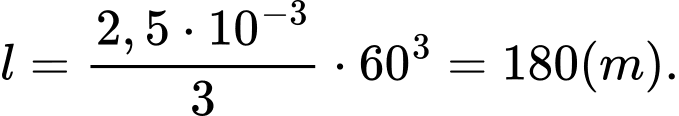
c) Sau 80 giây vận tốc của đoàn tàu là
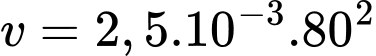
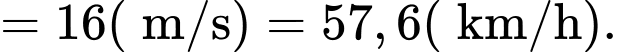
d) Khi bắt đầu chuyển động đều, vận tốc của đoàn tàu là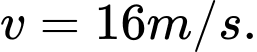
Tổng quãng đường đoàn tàu đi để vượt qua cây cầu là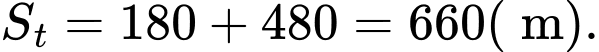
Vậy thời gian đoàn tàu qua cầu là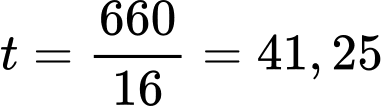 (giây).
(giây).
a) Vận tốc của đoàn tàu là
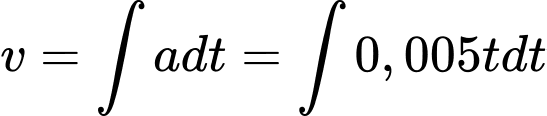
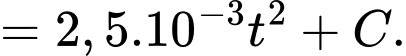
Vì ban đầu tàu đứng yên nên

Vậy
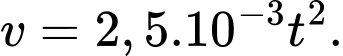
b) Quãng đường đoàn tàu đi được là
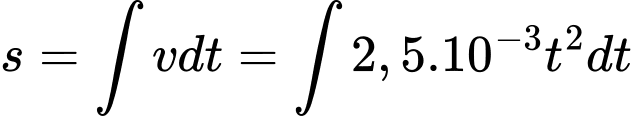
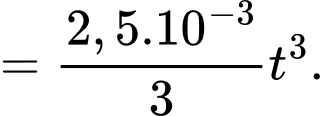
Chiều dài của đoàn tàu là
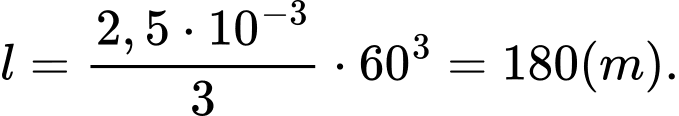
c) Sau 80 giây vận tốc của đoàn tàu là
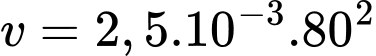
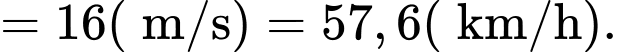
d) Khi bắt đầu chuyển động đều, vận tốc của đoàn tàu là
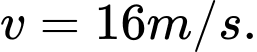
Tổng quãng đường đoàn tàu đi để vượt qua cây cầu là
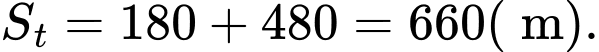
Vậy thời gian đoàn tàu qua cầu là
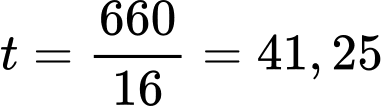 (giây).
(giây).
Câu 16 [696306]: Một căn bệnh có 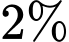 dân số mắc phải. Với những người bị bệnh, phương án này sẽ đưa ra kết quả dương tính
dân số mắc phải. Với những người bị bệnh, phương án này sẽ đưa ra kết quả dương tính 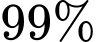 số trường hợp. Với những người không mắc bệnh, phương pháp này chẩn đoán đúng 99 trong 100 trường hợp.
số trường hợp. Với những người không mắc bệnh, phương pháp này chẩn đoán đúng 99 trong 100 trường hợp.
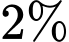 dân số mắc phải. Với những người bị bệnh, phương án này sẽ đưa ra kết quả dương tính
dân số mắc phải. Với những người bị bệnh, phương án này sẽ đưa ra kết quả dương tính 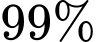 số trường hợp. Với những người không mắc bệnh, phương pháp này chẩn đoán đúng 99 trong 100 trường hợp.
số trường hợp. Với những người không mắc bệnh, phương pháp này chẩn đoán đúng 99 trong 100 trường hợp.
a) Sai.
Vì có 2% dân số mắc phải căn bệnh này nên xác suất người đó mắc bệnh khi chưa kiểm tra là 0,02.
b) Đúng.
Vì giả thiết cho: “Với những người bị bệnh, phương án này sẽ đưa ra kết quả dương tính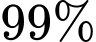 số trường hợp” nên xác suất kết quả dương tính nếu có người đó mắc bệnh là 0,99.
số trường hợp” nên xác suất kết quả dương tính nếu có người đó mắc bệnh là 0,99.
c) Sai.
Gọi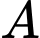 là biến cố “Người đó mắc bệnh”. Suy ra
là biến cố “Người đó mắc bệnh”. Suy ra 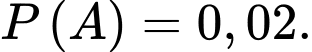
Gọi là biến cố “Người đó không mắc bệnh”.
là biến cố “Người đó không mắc bệnh”. 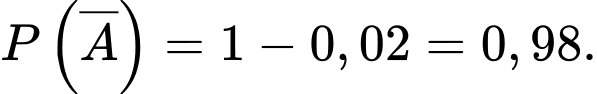
Gọi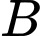 là biến cố “Kết quả kiểm tra người đó là dương tính”.
là biến cố “Kết quả kiểm tra người đó là dương tính”.
Khi đó xác suất kết quả dương tính nếu người đó mắc bệnh là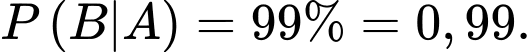
Xác xuất kết quả dương tính nếu người đó không mắc bệnh là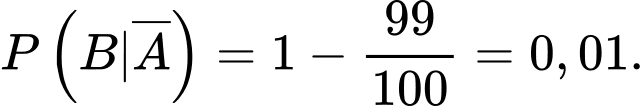
Ta có sơ đồ cây sau:
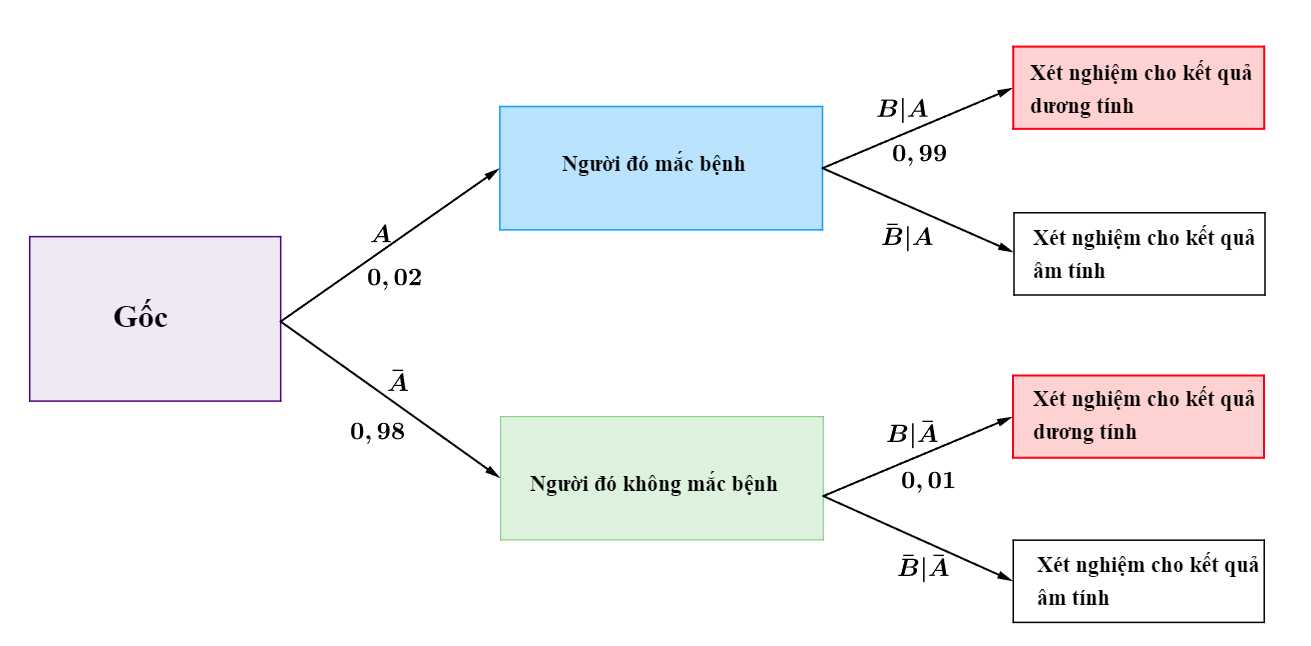
Áp dụng công thức xác suất toàn ta được xác suất của biến cố “Kết quả kiểm tra người đó là dương tính (bị bệnh)” là: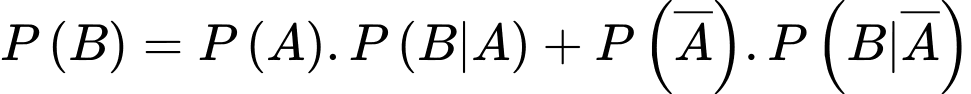
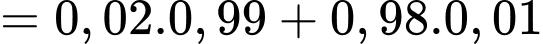
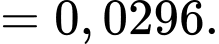
d) Sai.
Áp dụng công thức Bayes, xác suất người đó bị mắc bệnh thực khi kiểm tra là dương tính là: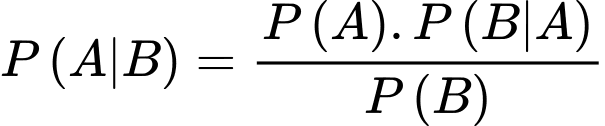
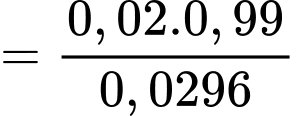
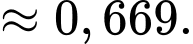
Vì có 2% dân số mắc phải căn bệnh này nên xác suất người đó mắc bệnh khi chưa kiểm tra là 0,02.
b) Đúng.
Vì giả thiết cho: “Với những người bị bệnh, phương án này sẽ đưa ra kết quả dương tính
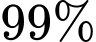 số trường hợp” nên xác suất kết quả dương tính nếu có người đó mắc bệnh là 0,99.
số trường hợp” nên xác suất kết quả dương tính nếu có người đó mắc bệnh là 0,99.c) Sai.
Gọi
 là biến cố “Người đó mắc bệnh”. Suy ra
là biến cố “Người đó mắc bệnh”. Suy ra 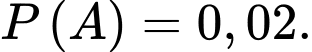
Gọi
 là biến cố “Người đó không mắc bệnh”.
là biến cố “Người đó không mắc bệnh”. 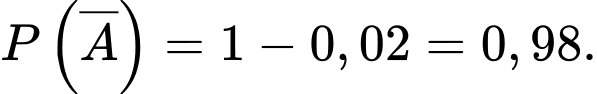
Gọi
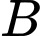 là biến cố “Kết quả kiểm tra người đó là dương tính”.
là biến cố “Kết quả kiểm tra người đó là dương tính”.Khi đó xác suất kết quả dương tính nếu người đó mắc bệnh là
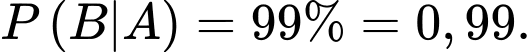
Xác xuất kết quả dương tính nếu người đó không mắc bệnh là
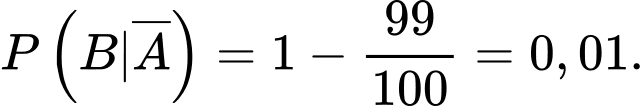
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn ta được xác suất của biến cố “Kết quả kiểm tra người đó là dương tính (bị bệnh)” là:
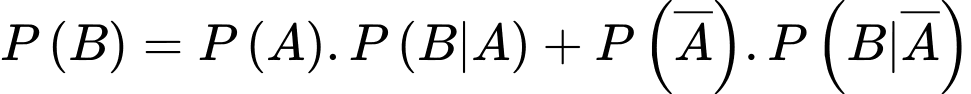
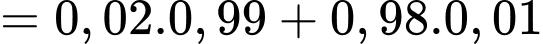
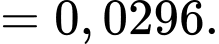
d) Sai.
Áp dụng công thức Bayes, xác suất người đó bị mắc bệnh thực khi kiểm tra là dương tính là:
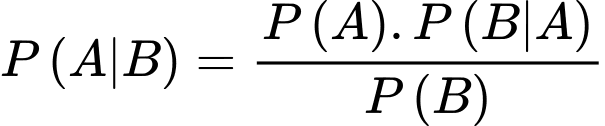
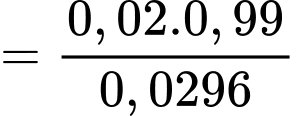
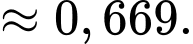
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696307]: Cho hình chóp  có đáy
có đáy 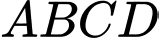 là hình vuông tâm
là hình vuông tâm 
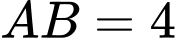 và
và 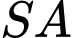 vuông góc với mặt phẳng đáy. Gọi
vuông góc với mặt phẳng đáy. Gọi 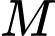 là trung điểm của
là trung điểm của 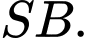 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 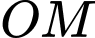 và
và 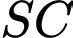 bằng
bằng 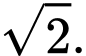 Thể tích của khối chóp đã cho bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
Thể tích của khối chóp đã cho bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
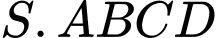 có đáy
có đáy 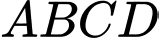 là hình vuông tâm
là hình vuông tâm 
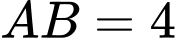 và
và 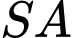 vuông góc với mặt phẳng đáy. Gọi
vuông góc với mặt phẳng đáy. Gọi 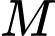 là trung điểm của
là trung điểm của 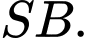 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 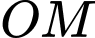 và
và 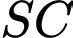 bằng
bằng 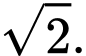 Thể tích của khối chóp đã cho bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
Thể tích của khối chóp đã cho bằng bao nhiêu (làm tròn kết quả đến hàng phần mười). 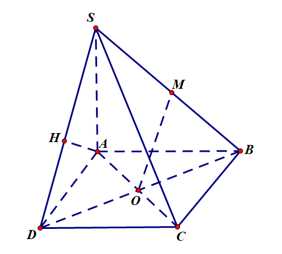
Vì O và M lần lượt là trung điểm của DB và SB nên OM là đường trung bình của
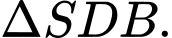
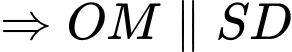
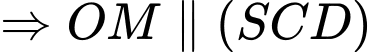
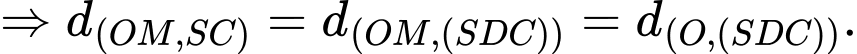
Mặt khác, ta thấy AC=2OC nên
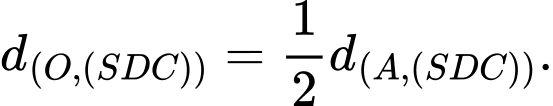
Ta có
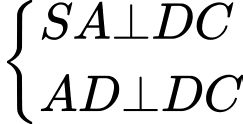 nên
nên 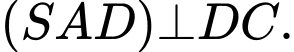
Kẻ

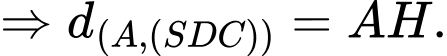
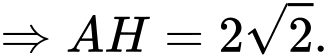
Áp dụng hệ thức lượng trong
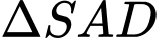 vuông tại A:
vuông tại A:
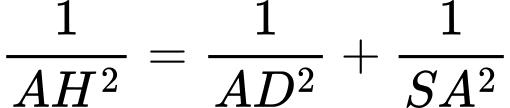
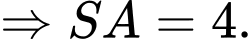
Vậy, thể tích khối chóp là
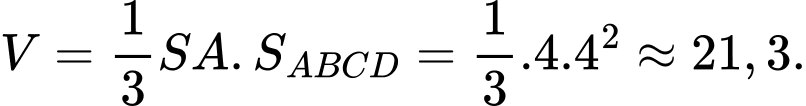
Câu 18 [696308]: Các cầu thủ trong một đội bóng rổ đã thực hiện một số cú ném ba điểm, một số cú ném hai điểm và một số cú ném phạt một điểm. Họ ghi được số điểm bằng nhau từ các cú ném hai điểm và các cú ném ba điểm. Số lần ném phạt thành công của họ nhiều hơn một lần so với số cú ném hai điểm thành công. Tổng điểm của cả đội là 61 điểm. Vậy họ đã thực hiện bao nhiêu cú ném phạt?
Điền đáp án: 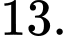
Cách 1:
Gọi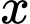 là số cú ném phạt 3 điểm,
là số cú ném phạt 3 điểm, 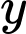 là số cú ném phạt 3 điểm,
là số cú ném phạt 3 điểm, 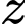 là số quả ném phạt.
là số quả ném phạt.
Theo đề bài ta có: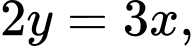
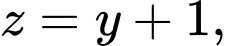
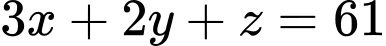
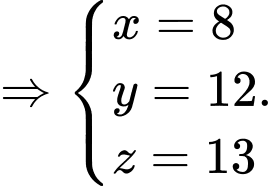
Do đó số quả ném phạt mà họ thực hiện là 13 quả.
Cách 2:
Để số điểm được ghi từ cú ném hai điểm và từ cú ném ba điểm bằng nhau, số cú ném thành công sẽ theo tỷ lệ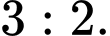
Do đó, giả sử họ thực hiện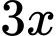 và
và 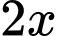 ném hai điểm và ném ba điểm tương ứng, do đó có
ném hai điểm và ném ba điểm tương ứng, do đó có 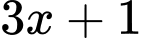 cú ném phạt.
cú ném phạt.
Tổng số điểm là: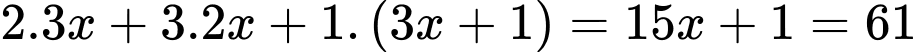
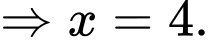
Vậy số quả ném phạt mà họ thực hiện là: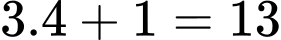 quả.
quả.
Cách 3:
Giả sử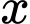 là số lần ném phạt.
là số lần ném phạt.
Khi đó, số điểm ghi được của cú ném hai điểm là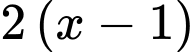 và tương tự với ba điểm vì chúng ghi được cùng số điểm với hai điểm và ba điểm.
và tương tự với ba điểm vì chúng ghi được cùng số điểm với hai điểm và ba điểm.
Do đó, ta có phương trình là:
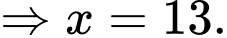
Vậy số quả ném phạt mà họ thực hiện là quả.
quả.
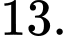
Cách 1:
Gọi
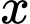 là số cú ném phạt 3 điểm,
là số cú ném phạt 3 điểm, 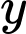 là số cú ném phạt 3 điểm,
là số cú ném phạt 3 điểm, 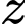 là số quả ném phạt.
là số quả ném phạt. Theo đề bài ta có:
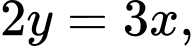
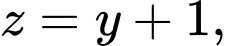
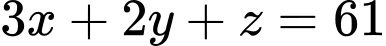
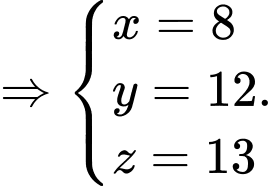
Do đó số quả ném phạt mà họ thực hiện là 13 quả.
Cách 2:
Để số điểm được ghi từ cú ném hai điểm và từ cú ném ba điểm bằng nhau, số cú ném thành công sẽ theo tỷ lệ
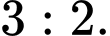
Do đó, giả sử họ thực hiện
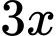 và
và 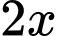 ném hai điểm và ném ba điểm tương ứng, do đó có
ném hai điểm và ném ba điểm tương ứng, do đó có 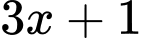 cú ném phạt.
cú ném phạt. Tổng số điểm là:
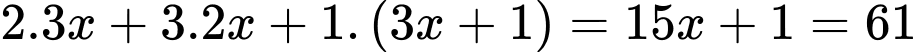
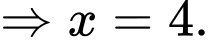
Vậy số quả ném phạt mà họ thực hiện là:
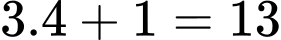 quả.
quả.
Cách 3:
Giả sử
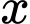 là số lần ném phạt.
là số lần ném phạt.
Khi đó, số điểm ghi được của cú ném hai điểm là
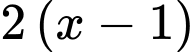 và tương tự với ba điểm vì chúng ghi được cùng số điểm với hai điểm và ba điểm.
và tương tự với ba điểm vì chúng ghi được cùng số điểm với hai điểm và ba điểm. Do đó, ta có phương trình là:

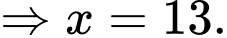
Vậy số quả ném phạt mà họ thực hiện là
 quả.
quả.
Câu 19 [696311]: Có hai loại kiện hàng I và II ở trong kho, kiện hàng loại I chiếm 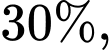 kiện hàng loại II chiếm 70%, trong mỗi kiện hàng có 20 sản phẩm. Mỗi kiện hàng loại I có 18 sản phẩm tốt, còn mỗi kiện loại II có 16 sản phẩm tốt. Lấy ngẫu nhiên một kiện hàng ở kho, rồi từ đó lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Trả sản phẩm này lại kiện hàng vừa lấy, sau đó lại lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Tính xác suất để các sản phẩm tốt đó được lấy từ kiện hàng thứ nhất. Làm tròn kết quả đến hàng phần trăm.
kiện hàng loại II chiếm 70%, trong mỗi kiện hàng có 20 sản phẩm. Mỗi kiện hàng loại I có 18 sản phẩm tốt, còn mỗi kiện loại II có 16 sản phẩm tốt. Lấy ngẫu nhiên một kiện hàng ở kho, rồi từ đó lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Trả sản phẩm này lại kiện hàng vừa lấy, sau đó lại lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Tính xác suất để các sản phẩm tốt đó được lấy từ kiện hàng thứ nhất. Làm tròn kết quả đến hàng phần trăm.
 kiện hàng loại II chiếm 70%, trong mỗi kiện hàng có 20 sản phẩm. Mỗi kiện hàng loại I có 18 sản phẩm tốt, còn mỗi kiện loại II có 16 sản phẩm tốt. Lấy ngẫu nhiên một kiện hàng ở kho, rồi từ đó lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Trả sản phẩm này lại kiện hàng vừa lấy, sau đó lại lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Tính xác suất để các sản phẩm tốt đó được lấy từ kiện hàng thứ nhất. Làm tròn kết quả đến hàng phần trăm.
kiện hàng loại II chiếm 70%, trong mỗi kiện hàng có 20 sản phẩm. Mỗi kiện hàng loại I có 18 sản phẩm tốt, còn mỗi kiện loại II có 16 sản phẩm tốt. Lấy ngẫu nhiên một kiện hàng ở kho, rồi từ đó lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Trả sản phẩm này lại kiện hàng vừa lấy, sau đó lại lấy ngẫu nhiên một sản phẩm thì được sản phẩm tốt. Tính xác suất để các sản phẩm tốt đó được lấy từ kiện hàng thứ nhất. Làm tròn kết quả đến hàng phần trăm.
Điền đáp án: 0,35.
Gọi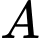 là biến cố “Lấy được một kiện hàng I”
là biến cố “Lấy được một kiện hàng I”
Khi đó là biến cố “Lấy được một kiện hàng II”
là biến cố “Lấy được một kiện hàng II”
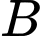 là biến cố “2 lần lấy được sản phẩm tốt”
là biến cố “2 lần lấy được sản phẩm tốt”
YCBT Tính
Tính 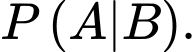
Từ dữ kiện đề bài, ta có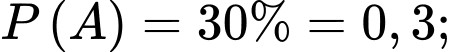
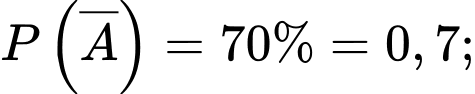
Vì trong mỗi kiện hàng có 20 sản phẩm và trong kiện hàng loại I có 18 sản phẩm tốt nên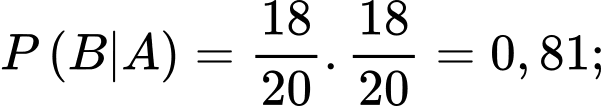 còn kiện hàng loại II có 16 sản phẩm tốt nên
còn kiện hàng loại II có 16 sản phẩm tốt nên 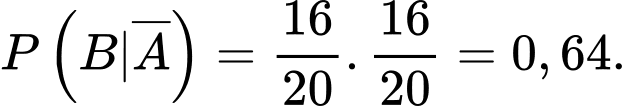
Ta có sơ đồ cây sau:
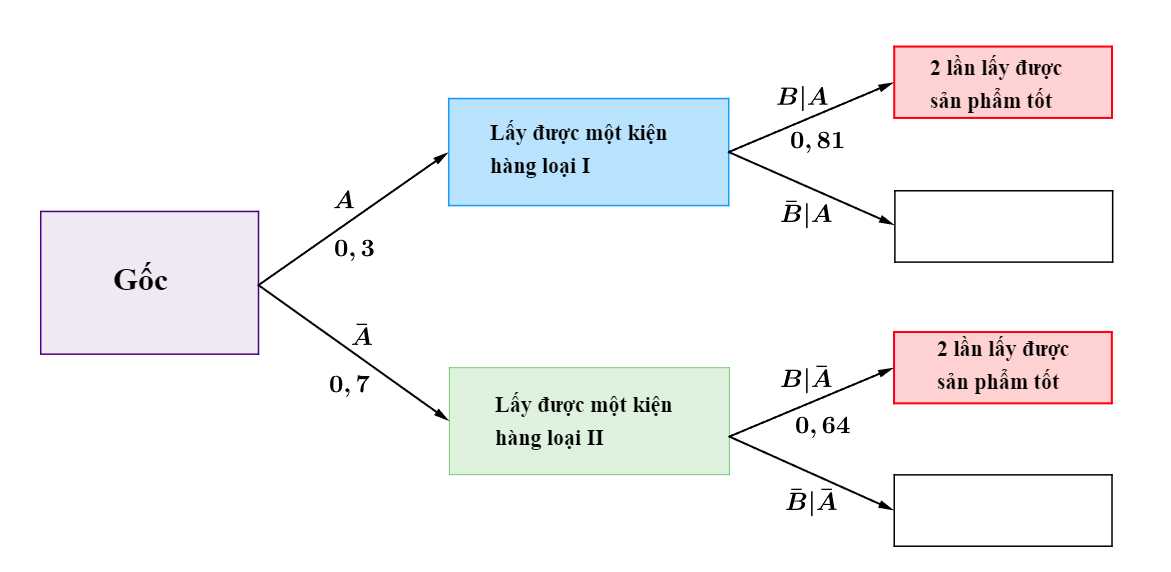
Áp dụng công thức xác suất toàn phần, ta có
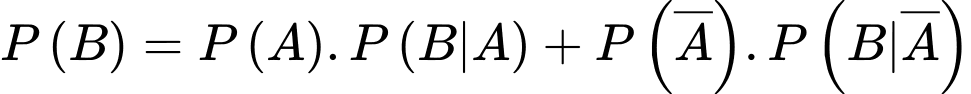
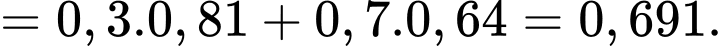
Khi đó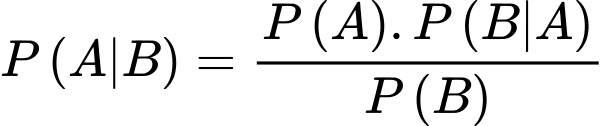
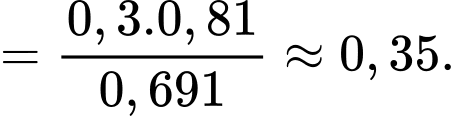
Gọi
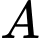 là biến cố “Lấy được một kiện hàng I”
là biến cố “Lấy được một kiện hàng I”Khi đó
 là biến cố “Lấy được một kiện hàng II”
là biến cố “Lấy được một kiện hàng II”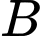 là biến cố “2 lần lấy được sản phẩm tốt”
là biến cố “2 lần lấy được sản phẩm tốt”YCBT
 Tính
Tính 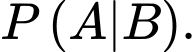
Từ dữ kiện đề bài, ta có
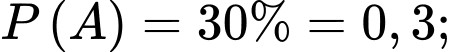
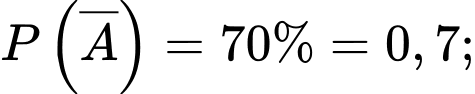
Vì trong mỗi kiện hàng có 20 sản phẩm và trong kiện hàng loại I có 18 sản phẩm tốt nên
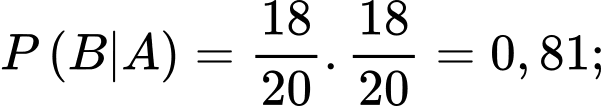 còn kiện hàng loại II có 16 sản phẩm tốt nên
còn kiện hàng loại II có 16 sản phẩm tốt nên 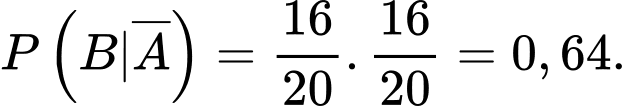
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
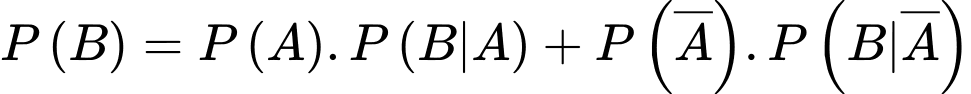
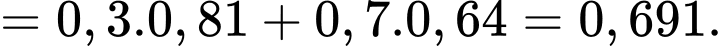
Khi đó
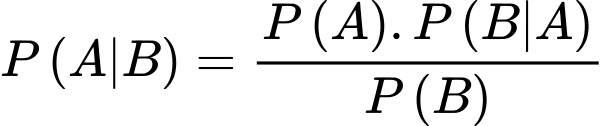
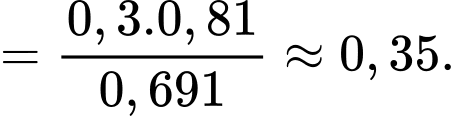
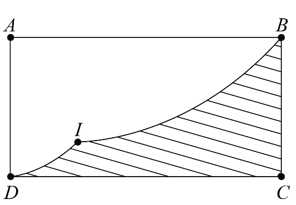
Câu 20 [695259]: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền  (miền gạch chéo trong hình vẽ) quanh trục
(miền gạch chéo trong hình vẽ) quanh trục 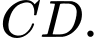 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh 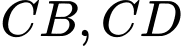 của hình chữ nhật
của hình chữ nhật 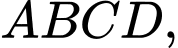
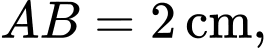
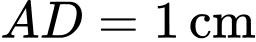 và một phần của các đường parabol
và một phần của các đường parabol 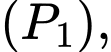
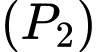 với
với 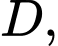
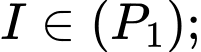
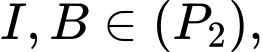
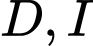 lần lượt là đỉnh của
lần lượt là đỉnh của 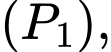
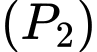 trong đó
trong đó 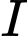 nằm miền trong hình chữ nhật
nằm miền trong hình chữ nhật 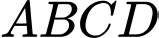 sao cho khoang cách từ
sao cho khoang cách từ 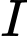 đến các cạnh
đến các cạnh 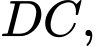
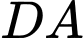 lần lượt bằng
lần lượt bằng 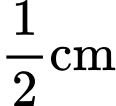 và
và 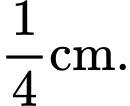 Tính thể tích của vật trang trí đó (đơn vị centimet khối), làm tròn kết quả đến hàng phần trăm.
Tính thể tích của vật trang trí đó (đơn vị centimet khối), làm tròn kết quả đến hàng phần trăm.
 (miền gạch chéo trong hình vẽ) quanh trục
(miền gạch chéo trong hình vẽ) quanh trục 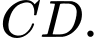 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh 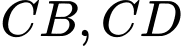 của hình chữ nhật
của hình chữ nhật 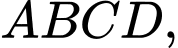
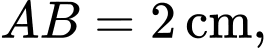
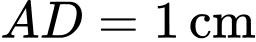 và một phần của các đường parabol
và một phần của các đường parabol 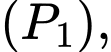
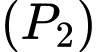 với
với 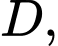
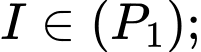
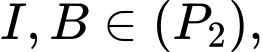
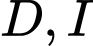 lần lượt là đỉnh của
lần lượt là đỉnh của 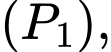
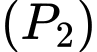 trong đó
trong đó 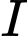 nằm miền trong hình chữ nhật
nằm miền trong hình chữ nhật 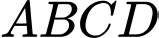 sao cho khoang cách từ
sao cho khoang cách từ 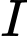 đến các cạnh
đến các cạnh 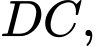
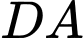 lần lượt bằng
lần lượt bằng 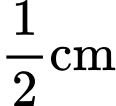 và
và 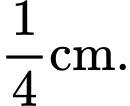 Tính thể tích của vật trang trí đó (đơn vị centimet khối), làm tròn kết quả đến hàng phần trăm.
Tính thể tích của vật trang trí đó (đơn vị centimet khối), làm tròn kết quả đến hàng phần trăm.
Điền đáp án: 2,60
Chọn hệ trục D là gốc toạ độ, DC là trục Ox, DA là Oy
Từ đề bài ta có tọa độ điểm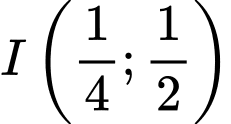 và
và 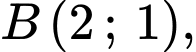
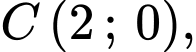
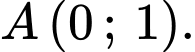
Parabol có tâm là
có tâm là  có dạng
có dạng 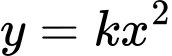 và đi qua điểm
và đi qua điểm 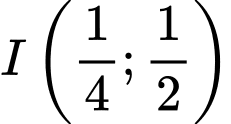 nên ta có:
nên ta có:
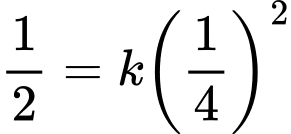
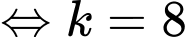
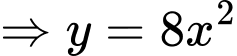
Parabol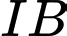 có tâm là
có tâm là 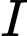 có dạng
có dạng 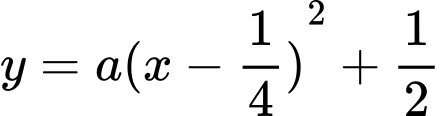 đi qua điểm
đi qua điểm 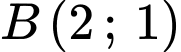 nên ta có:
nên ta có:
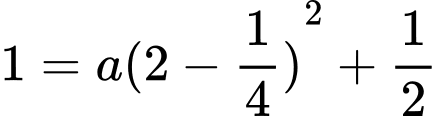
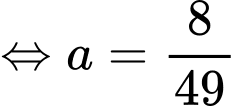
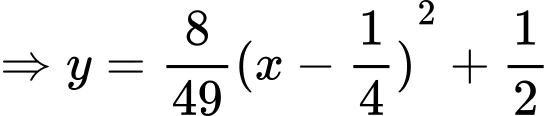
Thể tích của vật trang trí đó là:
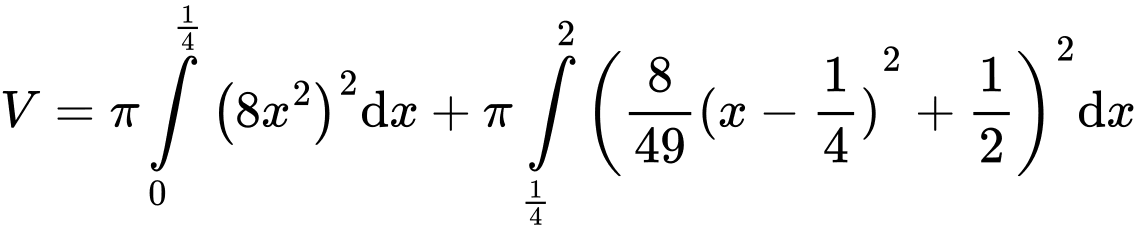
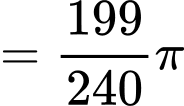
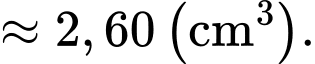
Chọn hệ trục D là gốc toạ độ, DC là trục Ox, DA là Oy
Từ đề bài ta có tọa độ điểm
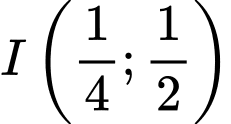 và
và 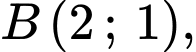
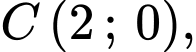
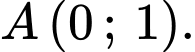
Parabol
 có tâm là
có tâm là  có dạng
có dạng 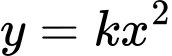 và đi qua điểm
và đi qua điểm 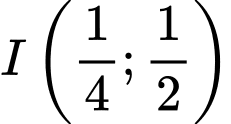 nên ta có:
nên ta có:
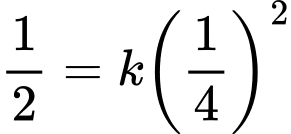
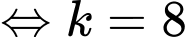
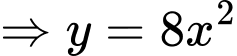
Parabol
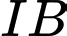 có tâm là
có tâm là 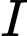 có dạng
có dạng 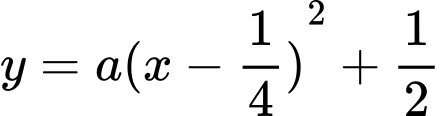 đi qua điểm
đi qua điểm 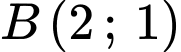 nên ta có:
nên ta có:
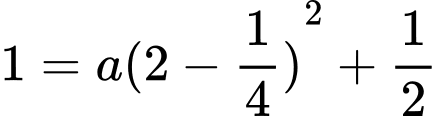
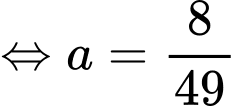
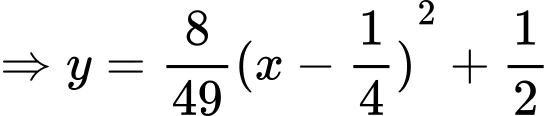
Thể tích của vật trang trí đó là:
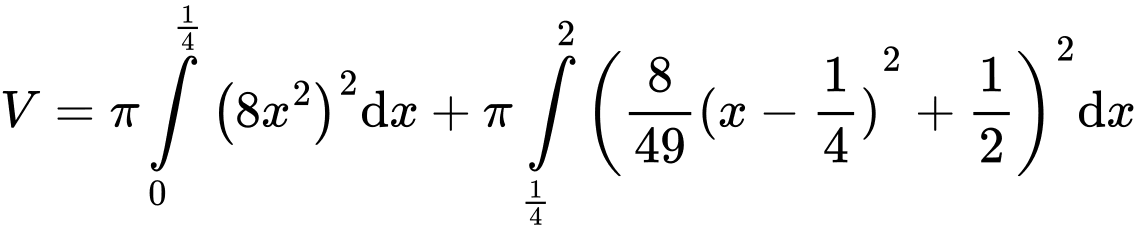
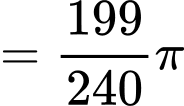
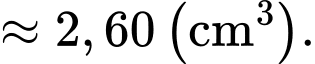
Câu 21 [693691]: Giám đốc của show diễn ca nhạc “ATSH” đang xác định mức vé vào cửa cho đêm biểu diễn dự kiến vào tháng 12/2024 tại Hà Nội. Theo kinh nghiệm nhiều năm tổ chức show diễn của mình, giám đốc đã xác định được rằng: Nếu giá vé vào cửa là 85 USD/vé thì trung bình có 15 000 khán giả đến xem. Mỗi lần tăng giá vé thêm 10 USD/vé thì số khán giả đến xem sẽ giảm đi 1 000 người. Mỗi lần giảm giá vé đi 10 USD/vé thì số khán giả đến xem sẽ tăng lên 1 000 người. Biết rằng, trung bình mỗi khán giả đến xem còn giúp show diễn có thêm 5 USD từ các dịch vụ đi kèm và mỗi khá giả vào xem phải có 1 vé vào cửa. Hỏi giám đốc chọn giá vé vào cửa cho show diễn này là bao nhiêu USD/vé để tổng số tiền thu được sau đêm diễn (gồm tổng tiền bán vé và tiền thu từ các dịch vụ đi kèm) là lớn nhất?
Đáp án: 115 USD/vé.
Gọi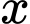 là số lần tăng giá vé (
là số lần tăng giá vé (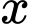 có thể là số âm nếu giảm giá).
có thể là số âm nếu giảm giá).
Giá vé là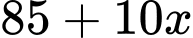 USD/vé.
USD/vé.
Số khán giả là (người).
(người).
Doanh thu từ vé là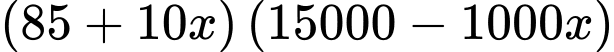 USD.
USD.
Doanh thu từ dịch vụ đi kèm là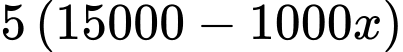 USD.
USD.
Tổng doanh thu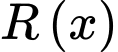 là:
là:
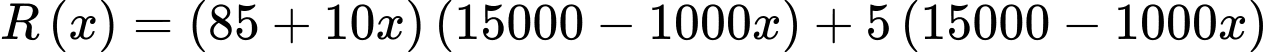
Để tìm giá trị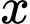 làm cho
làm cho 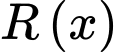 lớn nhất, ta tính đạo hàm của
lớn nhất, ta tính đạo hàm của 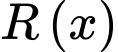 theo
theo 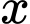 và cho đạo hàm bằng 0:
và cho đạo hàm bằng 0:
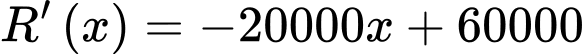
Cho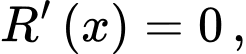 ta được:
ta được:

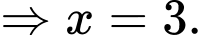
Ta tính đạo hàm cấp hai: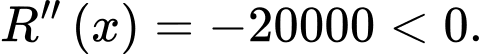
Vì đạo hàm cấp hai âm, nên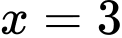 là điểm cực đại.
là điểm cực đại.
Khi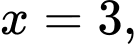 giá vé là
giá vé là 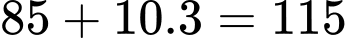 USD/vé.
USD/vé.
Gọi
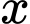 là số lần tăng giá vé (
là số lần tăng giá vé (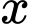 có thể là số âm nếu giảm giá).
có thể là số âm nếu giảm giá).
Giá vé là
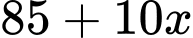 USD/vé.
USD/vé.
Số khán giả là
 (người).
(người).
Doanh thu từ vé là
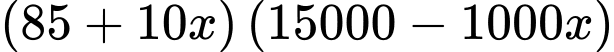 USD.
USD.
Doanh thu từ dịch vụ đi kèm là
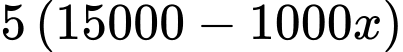 USD.
USD.
Tổng doanh thu
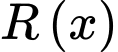 là:
là:
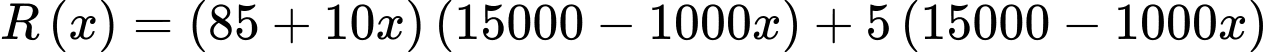
Để tìm giá trị
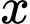 làm cho
làm cho 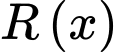 lớn nhất, ta tính đạo hàm của
lớn nhất, ta tính đạo hàm của 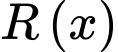 theo
theo 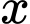 và cho đạo hàm bằng 0:
và cho đạo hàm bằng 0:
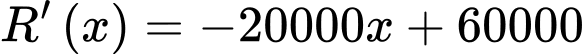
Cho
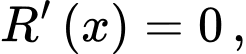 ta được:
ta được:

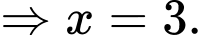
Ta tính đạo hàm cấp hai:
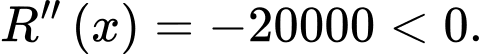
Vì đạo hàm cấp hai âm, nên
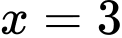 là điểm cực đại.
là điểm cực đại.
Khi
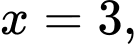 giá vé là
giá vé là 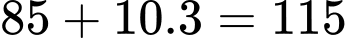 USD/vé.
USD/vé.
Câu 22 [696312]: Trong một thành phố kỹ sư muốn xây dựng một trung tâm quan sát tại vị trí 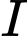 để có thể theo dõi tòa nhà
để có thể theo dõi tòa nhà 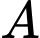 và tòa nhà
và tòa nhà 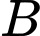 (minh hoạ như hình vẽ), kỹ sư thấy rằng để thuận tiện thì vị trí của trung tâm quan sát phải cách đều đỉnh của hai tòa nhà, và độ cao của trung tâm quan sát chính bằng khoảng cách từ trung tâm đến đỉnh mỗi tòa nhà.
(minh hoạ như hình vẽ), kỹ sư thấy rằng để thuận tiện thì vị trí của trung tâm quan sát phải cách đều đỉnh của hai tòa nhà, và độ cao của trung tâm quan sát chính bằng khoảng cách từ trung tâm đến đỉnh mỗi tòa nhà.
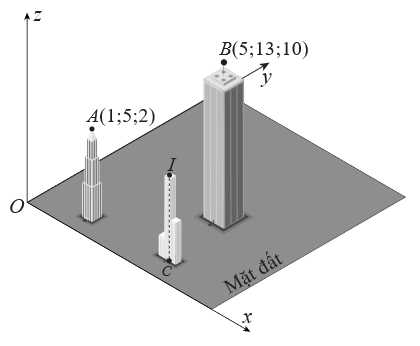
Xét trong hệ tọa độ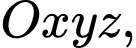 coi mặt đất là mặt phẳng
coi mặt đất là mặt phẳng 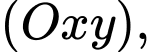 tòa nhà
tòa nhà 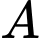 có tọa độ đỉnh là
có tọa độ đỉnh là 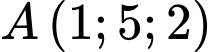 và tòa nhà
và tòa nhà 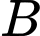 có tọa độ đỉnh là
có tọa độ đỉnh là 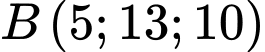 (đơn vị trên mỗi trục tọa độ tính bằng 10 mét). Biết rằng trung tâm quan sát được đặt tại vị trí có tọa độ là các số nguyên. Trung tâm quan sát có chiều cao tối thiểu bằng bao nhiêu mét thỏa mãn các yêu cầu trên?
(đơn vị trên mỗi trục tọa độ tính bằng 10 mét). Biết rằng trung tâm quan sát được đặt tại vị trí có tọa độ là các số nguyên. Trung tâm quan sát có chiều cao tối thiểu bằng bao nhiêu mét thỏa mãn các yêu cầu trên?
 để có thể theo dõi tòa nhà
để có thể theo dõi tòa nhà  và tòa nhà
và tòa nhà  (minh hoạ như hình vẽ), kỹ sư thấy rằng để thuận tiện thì vị trí của trung tâm quan sát phải cách đều đỉnh của hai tòa nhà, và độ cao của trung tâm quan sát chính bằng khoảng cách từ trung tâm đến đỉnh mỗi tòa nhà.
(minh hoạ như hình vẽ), kỹ sư thấy rằng để thuận tiện thì vị trí của trung tâm quan sát phải cách đều đỉnh của hai tòa nhà, và độ cao của trung tâm quan sát chính bằng khoảng cách từ trung tâm đến đỉnh mỗi tòa nhà. 
Xét trong hệ tọa độ
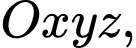 coi mặt đất là mặt phẳng
coi mặt đất là mặt phẳng 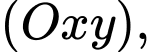 tòa nhà
tòa nhà 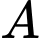 có tọa độ đỉnh là
có tọa độ đỉnh là 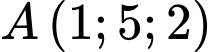 và tòa nhà
và tòa nhà 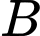 có tọa độ đỉnh là
có tọa độ đỉnh là 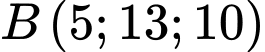 (đơn vị trên mỗi trục tọa độ tính bằng 10 mét). Biết rằng trung tâm quan sát được đặt tại vị trí có tọa độ là các số nguyên. Trung tâm quan sát có chiều cao tối thiểu bằng bao nhiêu mét thỏa mãn các yêu cầu trên?
(đơn vị trên mỗi trục tọa độ tính bằng 10 mét). Biết rằng trung tâm quan sát được đặt tại vị trí có tọa độ là các số nguyên. Trung tâm quan sát có chiều cao tối thiểu bằng bao nhiêu mét thỏa mãn các yêu cầu trên?
Giả sử tọa độ của trung tâm quan sát là 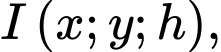 với
với 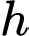 là chiều cao cần tìm.
là chiều cao cần tìm.
Ta có:
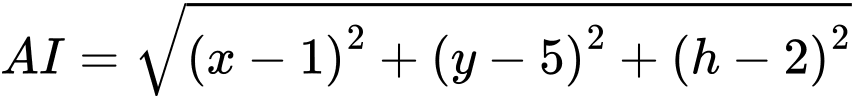
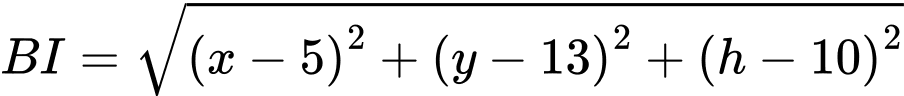
Để vị trí của trung tâm quan sát phải cách đều đỉnh của hai tòa nhà, hay
hay 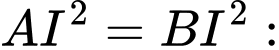
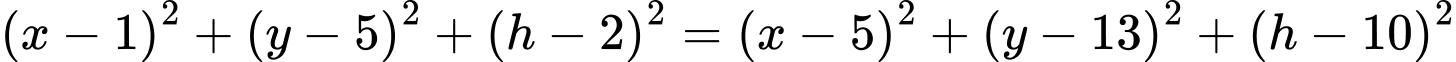
Vì độ cao của trung tâm quan sát chính bằng khoảng cách từ trung tâm đến đỉnh mỗi tòa nhà nên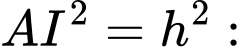
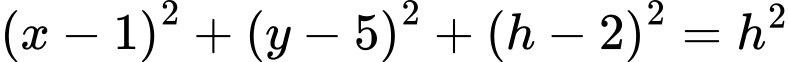
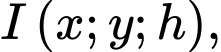 với
với 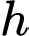 là chiều cao cần tìm.
là chiều cao cần tìm.
Ta có:
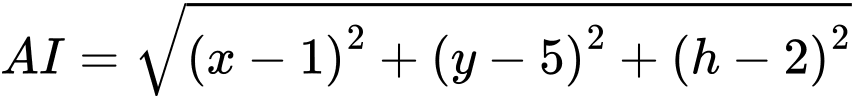
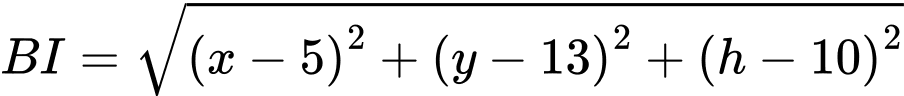
Để vị trí của trung tâm quan sát phải cách đều đỉnh của hai tòa nhà,
 hay
hay 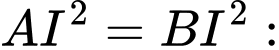
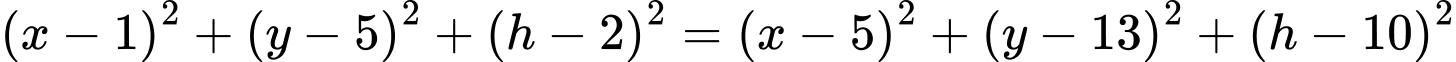
Vì độ cao của trung tâm quan sát chính bằng khoảng cách từ trung tâm đến đỉnh mỗi tòa nhà nên