PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [890648]: Thể tích của khối lập phương cạnh 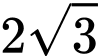 bằng
bằng
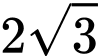 bằng
bằng A, 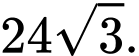
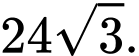
B, 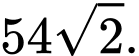
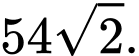
C, 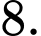
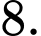
D, 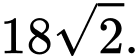
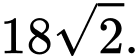
Chọn đáp án A.
Thể tích hình lập phương là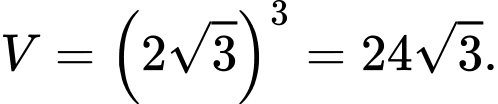 Đáp án: A
Đáp án: A
Thể tích hình lập phương là
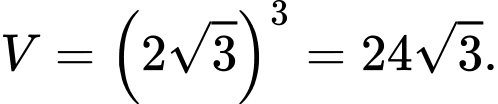 Đáp án: A
Đáp án: A
Câu 2 [502999]: Phương trình 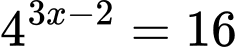 có nghiệm là
có nghiệm là
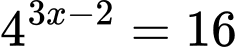 có nghiệm là
có nghiệm là A, 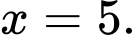
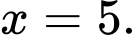
B, 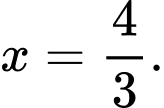
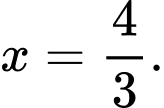
C, 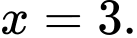
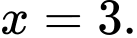
D, 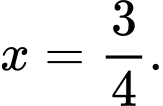
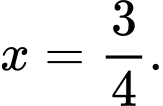
Chọn đáp án B.
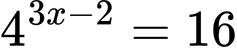
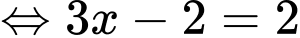
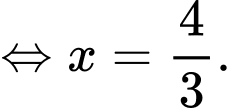 Đáp án: B
Đáp án: B
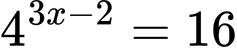
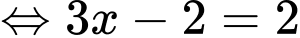
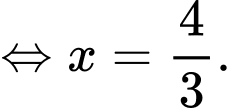 Đáp án: B
Đáp án: B
Câu 3 [806524]: Hàm số 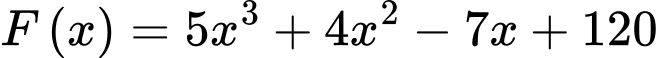 là nguyên hàm của hàm số nào sau đây?
là nguyên hàm của hàm số nào sau đây?
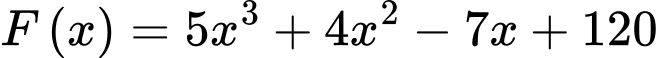 là nguyên hàm của hàm số nào sau đây?
là nguyên hàm của hàm số nào sau đây? A, 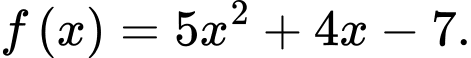
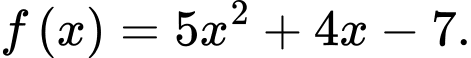
B, 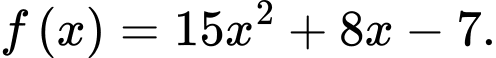
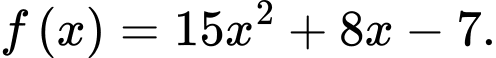
C, 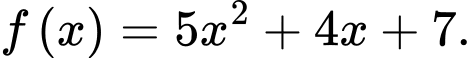
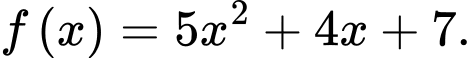
D, 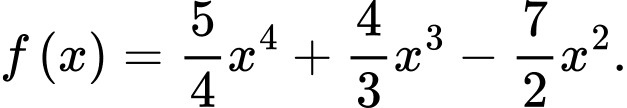
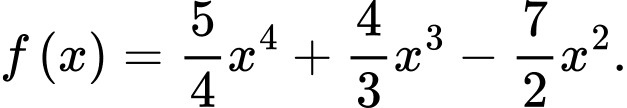
Chọn đáp án B.
Ta có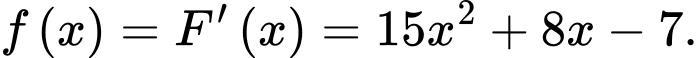 Đáp án: B
Đáp án: B
Ta có
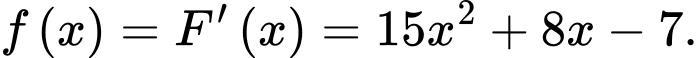 Đáp án: B
Đáp án: B
Câu 4 [330093]: Cho cấp số cộng 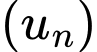 có số hạng đầu
có số hạng đầu 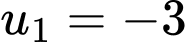 và
và 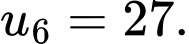 Tìm công sai
Tìm công sai 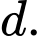
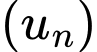 có số hạng đầu
có số hạng đầu 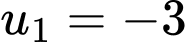 và
và 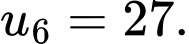 Tìm công sai
Tìm công sai 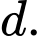
A, 

B, 

C, 

D, 

Chọn đáp án D.
Ta có: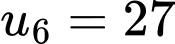
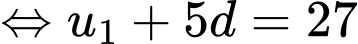
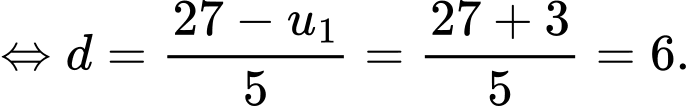 Đáp án: D
Đáp án: D
Ta có:
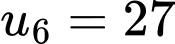
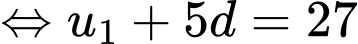
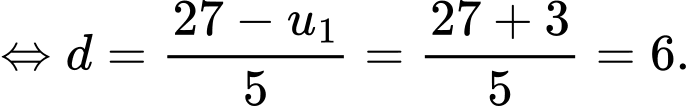 Đáp án: D
Đáp án: D
Câu 5 [803796]: Trong không gian với hệ trục tọa độ 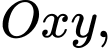 phương trình của mặt phẳng đi qua ba điểm
phương trình của mặt phẳng đi qua ba điểm 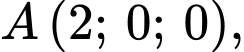
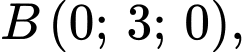
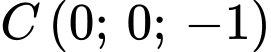 là
là
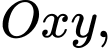 phương trình của mặt phẳng đi qua ba điểm
phương trình của mặt phẳng đi qua ba điểm 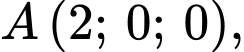
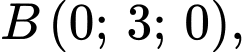
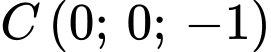 là
là A, 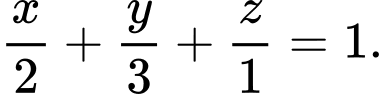
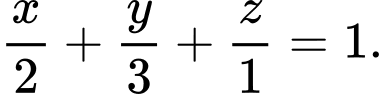
B, 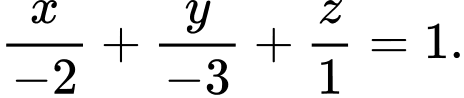
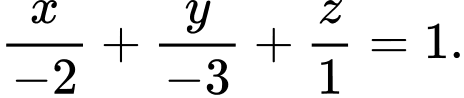
C, 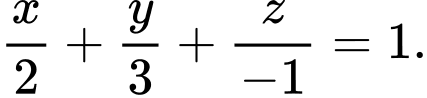
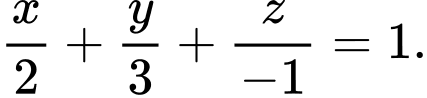
D, 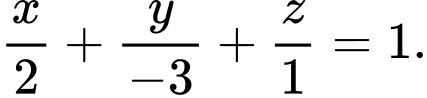
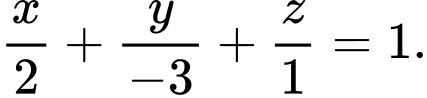
Chọn đáp án C.
Phương trình mặt phẳng qua các điểm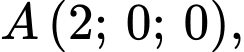
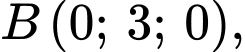
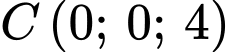 là:
là: 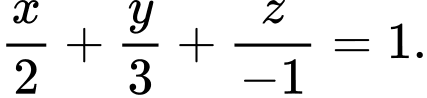 Đáp án: C
Đáp án: C
Phương trình mặt phẳng qua các điểm
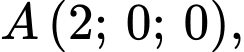
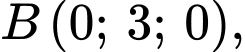
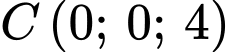 là:
là: 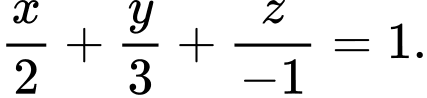 Đáp án: C
Đáp án: C
Câu 6 [503780]: Đạo hàm hàm số 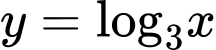 là
là
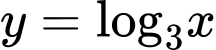 là
là A, 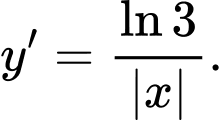
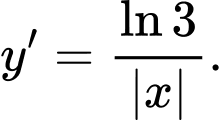
B, 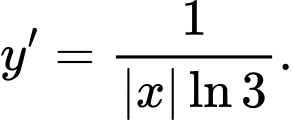
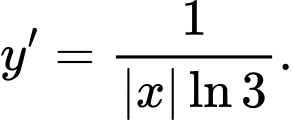
C, 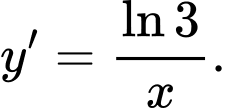
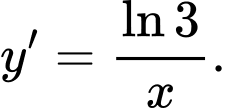
D, 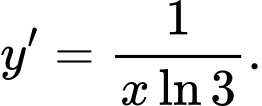
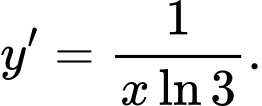
Chọn đáp án D.
Ta có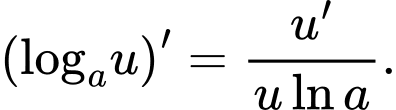 Đáp án: D
Đáp án: D
Ta có
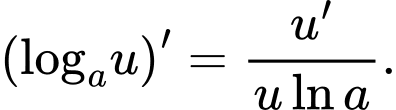 Đáp án: D
Đáp án: D
Câu 7 [239602]: Cho hai vectơ 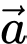 và
và 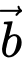 thỏa mãn
thỏa mãn 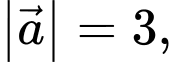
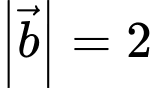 và
và  Xác định góc
Xác định góc 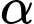 giữa hai vectơ
giữa hai vectơ 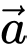 và
và 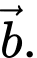
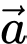 và
và 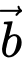 thỏa mãn
thỏa mãn 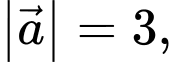
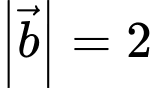 và
và  Xác định góc
Xác định góc 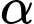 giữa hai vectơ
giữa hai vectơ 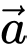 và
và 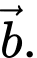
A, 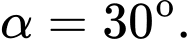
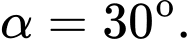
B, 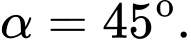
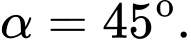
C, 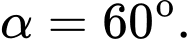
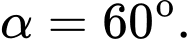
D, 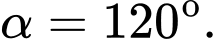
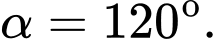
Chọn đáp án D.
Ta có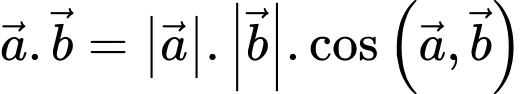
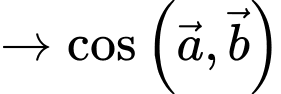
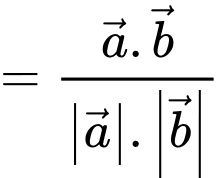
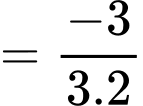
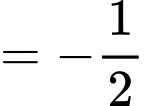
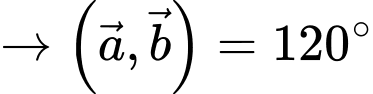 Đáp án: D
Đáp án: D
Ta có
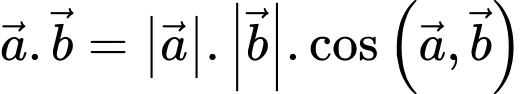
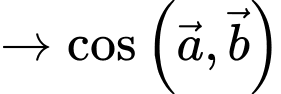
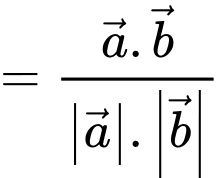
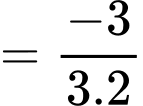
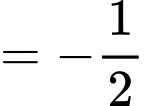
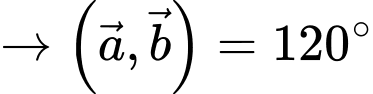 Đáp án: D
Đáp án: D
Câu 8 [599920]: Cho hàm số 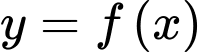 liên tục trên
liên tục trên 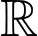 và có đạo hàm là
và có đạo hàm là 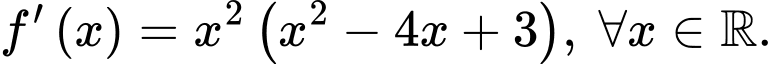 Hàm số
Hàm số 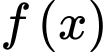 có bao nhiêu điểm cực tiểu?
có bao nhiêu điểm cực tiểu?
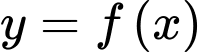 liên tục trên
liên tục trên 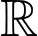 và có đạo hàm là
và có đạo hàm là 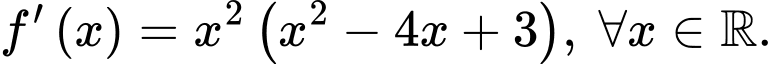 Hàm số
Hàm số 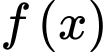 có bao nhiêu điểm cực tiểu?
có bao nhiêu điểm cực tiểu? A, 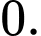
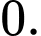
B, 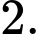
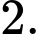
C, 
D, 
Chọn đáp án C.
Ta có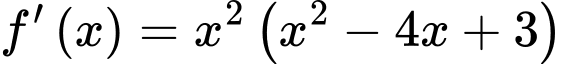
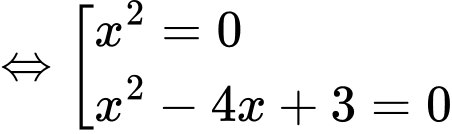
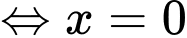 (nghiệm kép) hoặc
(nghiệm kép) hoặc 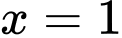 hoặc
hoặc 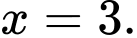
Bảng biến thiên của hàm số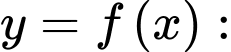
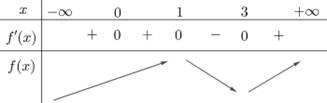
Quan sát bảng biến thiên, ta thấy hàm số đã cho có 1 điểm cực tiểu là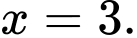 Đáp án: C
Đáp án: C
Ta có
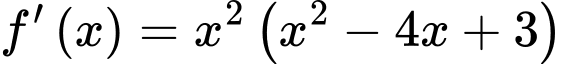
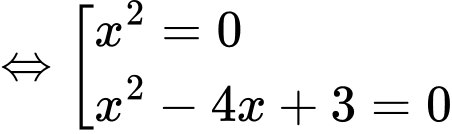
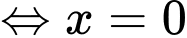 (nghiệm kép) hoặc
(nghiệm kép) hoặc 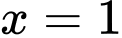 hoặc
hoặc 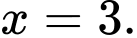
Bảng biến thiên của hàm số
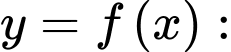

Quan sát bảng biến thiên, ta thấy hàm số đã cho có 1 điểm cực tiểu là
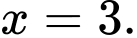 Đáp án: C
Đáp án: C
Câu 9 [806810]: Gọi 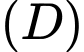 là hình phẳng giới hạn bởi các đường thẳng
là hình phẳng giới hạn bởi các đường thẳng 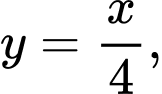
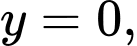
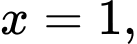
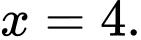 Thể tích vật thể tròn xoay tạo thành khi quay
Thể tích vật thể tròn xoay tạo thành khi quay 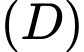 quanh trục
quanh trục 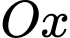 được tính theo công thức nào dưới đây?
được tính theo công thức nào dưới đây?
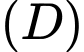 là hình phẳng giới hạn bởi các đường thẳng
là hình phẳng giới hạn bởi các đường thẳng 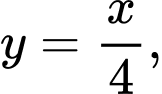
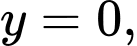
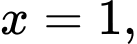
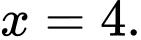 Thể tích vật thể tròn xoay tạo thành khi quay
Thể tích vật thể tròn xoay tạo thành khi quay 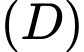 quanh trục
quanh trục 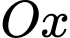 được tính theo công thức nào dưới đây?
được tính theo công thức nào dưới đây? A, 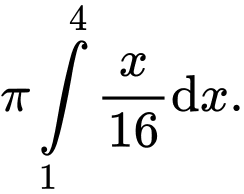
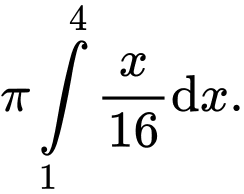
B, 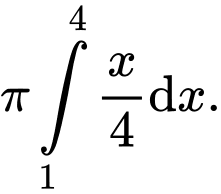
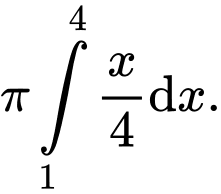
C, 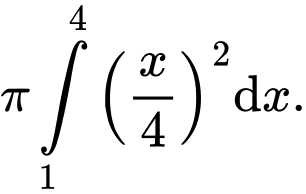
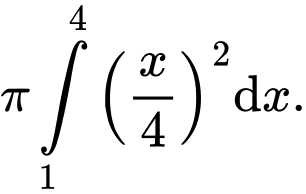
D, 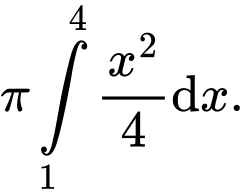
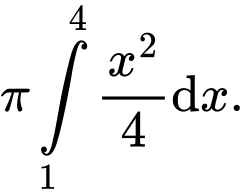
Chọn đáp án C.
Thể tích vật thể tròn xoay tạo thành khi quay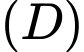 quanh trục
quanh trục 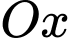 được tính theo công thức
được tính theo công thức 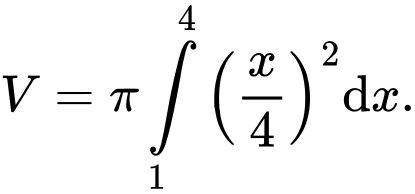 Đáp án: C
Đáp án: C
Thể tích vật thể tròn xoay tạo thành khi quay
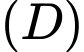 quanh trục
quanh trục 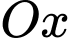 được tính theo công thức
được tính theo công thức 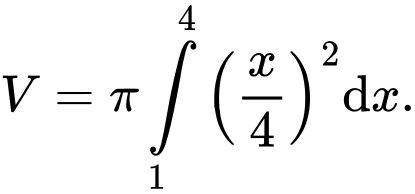 Đáp án: C
Đáp án: C
Câu 10 [501907]: Cho hàm số 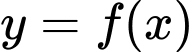 có bảng biến thiên như hình vẽ dưới đây.
có bảng biến thiên như hình vẽ dưới đây.
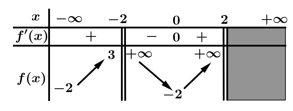
Tổng số đường tiệm cận đứng và tiệm cận ngang là
 có bảng biến thiên như hình vẽ dưới đây.
có bảng biến thiên như hình vẽ dưới đây. 
Tổng số đường tiệm cận đứng và tiệm cận ngang là
A,
B,
C,
D,
Tập xác định của hàm số : 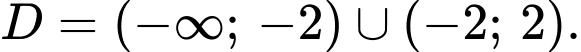
Ta có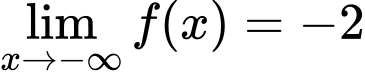
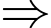 Đường thẳng có phương trình:
Đường thẳng có phương trình: 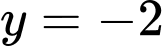 là tiệm cận ngang.
là tiệm cận ngang.
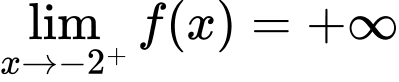
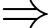 Đường thẳng có phương trình:
Đường thẳng có phương trình: 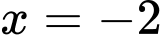 là tiệm cận đứng.
là tiệm cận đứng.
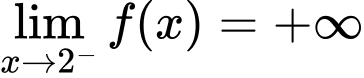
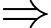 Đường thẳng có phương trình:
Đường thẳng có phương trình: 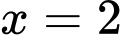 là tiệm cận đứng.
là tiệm cận đứng.
Vậy đồ thị hàm số có 3 đường tiệm cận. Đáp án: D
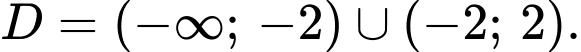
Ta có
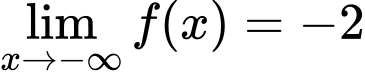
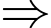 Đường thẳng có phương trình:
Đường thẳng có phương trình: 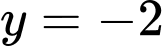 là tiệm cận ngang.
là tiệm cận ngang.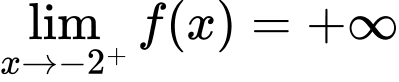
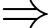 Đường thẳng có phương trình:
Đường thẳng có phương trình: 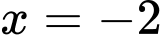 là tiệm cận đứng.
là tiệm cận đứng.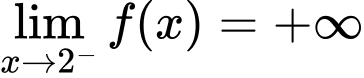
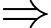 Đường thẳng có phương trình:
Đường thẳng có phương trình: 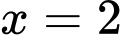 là tiệm cận đứng.
là tiệm cận đứng.Vậy đồ thị hàm số có 3 đường tiệm cận. Đáp án: D
Câu 11 [806825]: Trong không gian 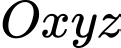 , phương trình đường thẳng đi qua hai điểm
, phương trình đường thẳng đi qua hai điểm 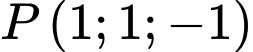 và
và 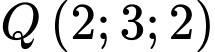 là
là
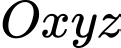 , phương trình đường thẳng đi qua hai điểm
, phương trình đường thẳng đi qua hai điểm 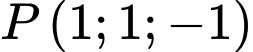 và
và 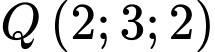 là
là A, 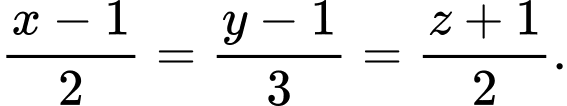
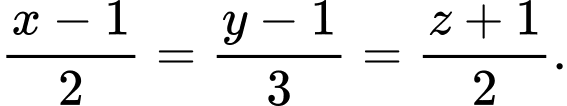
B, 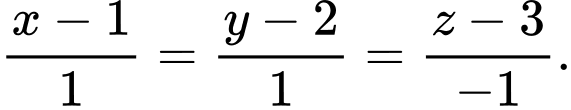
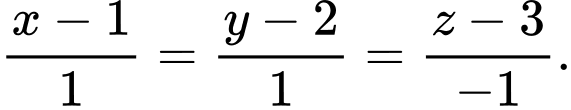
C, 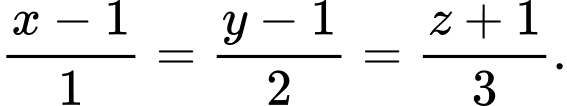
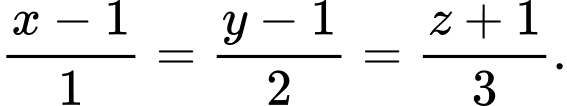
D, 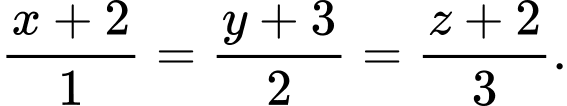
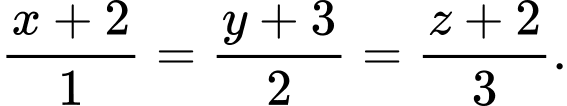
Chọn đáp án C.
* Ta có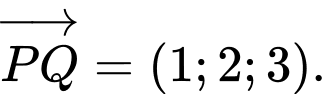
* Khi đó đường thẳng đi qua hai điểm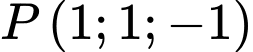 và
và 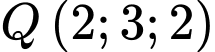 nhận véc tơ
nhận véc tơ 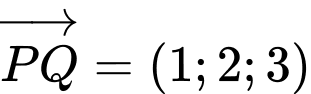 làm véc tơ chỉ phương có phương trình:
làm véc tơ chỉ phương có phương trình: 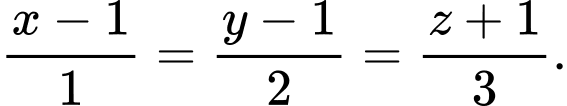 Đáp án: C
Đáp án: C
* Ta có
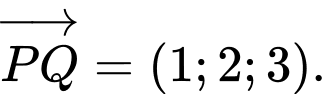
* Khi đó đường thẳng đi qua hai điểm
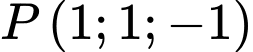 và
và 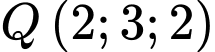 nhận véc tơ
nhận véc tơ 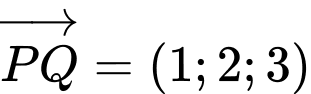 làm véc tơ chỉ phương có phương trình:
làm véc tơ chỉ phương có phương trình: 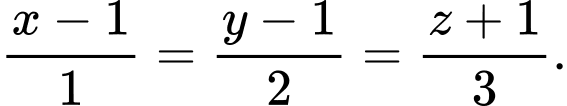 Đáp án: C
Đáp án: C
Câu 12 [696313]: Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 12 khách hàng mua sách ở một cửa hàng trong một ngày.

Xác định khoảng tứ phân vị của mẫu số liệu ghép nhóm trên

Xác định khoảng tứ phân vị của mẫu số liệu ghép nhóm trên
A, 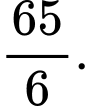
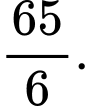
B, 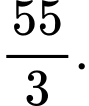
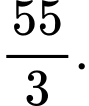
C, 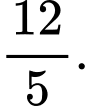
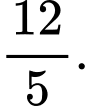
D, 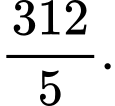
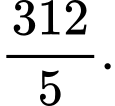
Chọn đáp án A.
Cỡ mẫu
Gọi là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có: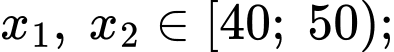

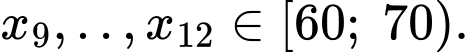
Tứ phân vị thứ nhất của mẫu số liệu là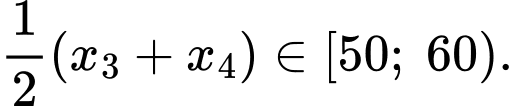 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
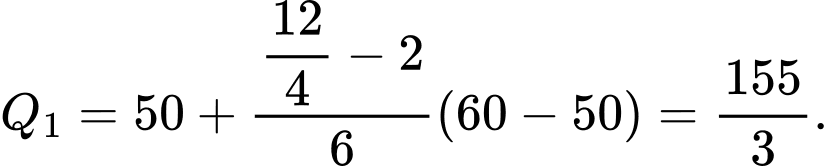
Tứ phân vị thứ ba của mẫu số liệu là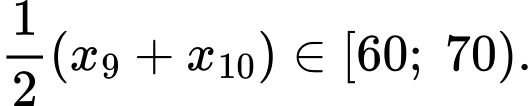 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
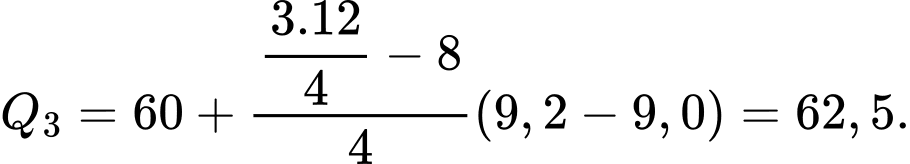
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
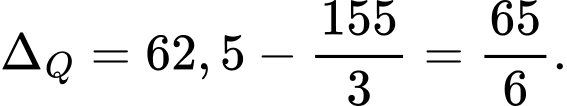 Đáp án: A
Đáp án: A
Cỡ mẫu

Gọi
 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có:
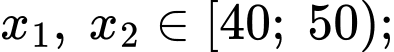

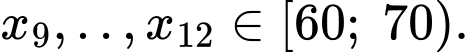
Tứ phân vị thứ nhất của mẫu số liệu là
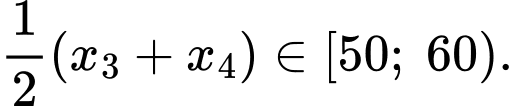 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 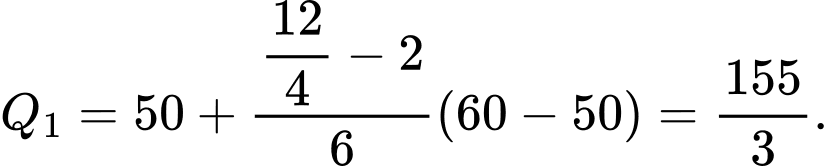
Tứ phân vị thứ ba của mẫu số liệu là
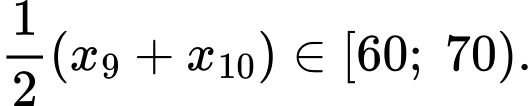 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 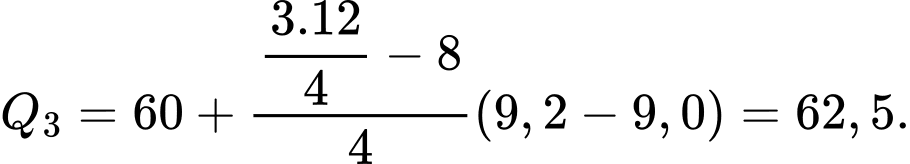
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
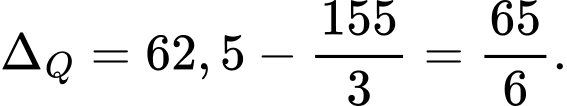 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696314]: Cho hai biến cố 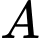 và
và 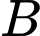 biết
biết 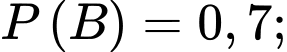

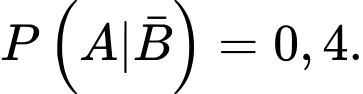
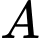 và
và 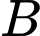 biết
biết 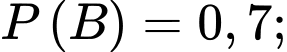

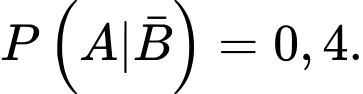
a) Sai.
Ta có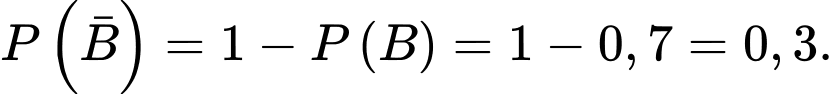
b) Đúng.
Ta có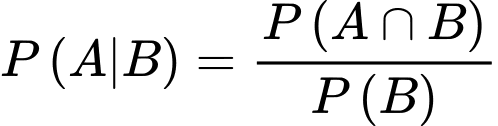
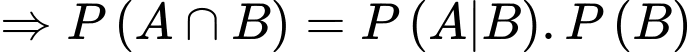
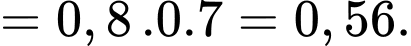
c) Sai.
Áp dụng công thức xác suất toàn phần, ta có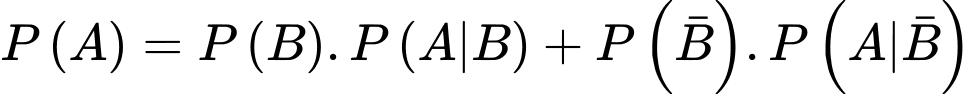
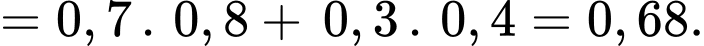
d) Sai.
Áp dụng công thức Bayes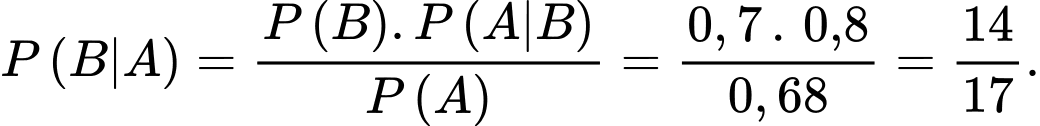
Ta có
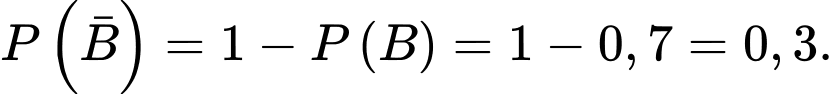
b) Đúng.
Ta có
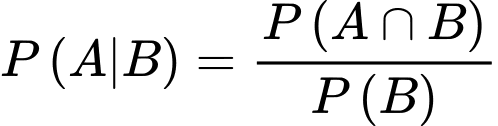
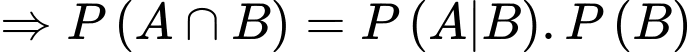
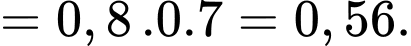
c) Sai.
Áp dụng công thức xác suất toàn phần, ta có
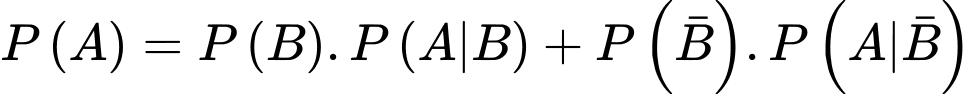
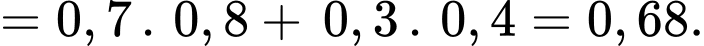
d) Sai.
Áp dụng công thức Bayes
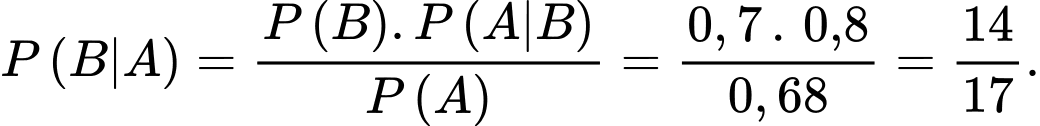
Câu 14 [595597]: Người ta bơm xăng vào bình xăng của một xe ô tô. Biết rằng thể tích  (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng
(lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng 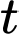 (phút) được cho bởi công thức
(phút) được cho bởi công thức 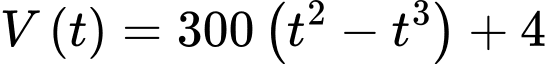 với
với 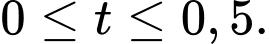 Gọi
Gọi 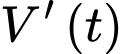 là tốc độ tăng thể tích tại thời điểm
là tốc độ tăng thể tích tại thời điểm 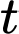 với
với 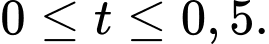
a) Lượng xăng trong bình ban đầu là 1 lít.
b)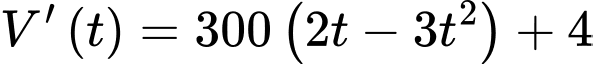 với
với 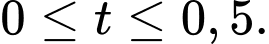
c) Lượng xăng lớn nhất bơm vào bình xăng là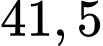 lít.
lít.
d) Xăng chảy vào bình xăng vào thời điểm ở giây thứ 30 thì tốc độ tăng thể tích là lớn nhất.
 (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng
(lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng 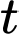 (phút) được cho bởi công thức
(phút) được cho bởi công thức 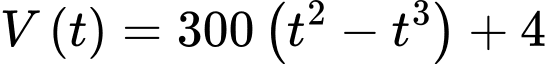 với
với 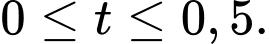 Gọi
Gọi 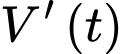 là tốc độ tăng thể tích tại thời điểm
là tốc độ tăng thể tích tại thời điểm 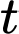 với
với 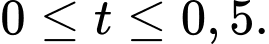
a) Lượng xăng trong bình ban đầu là 1 lít.
b)
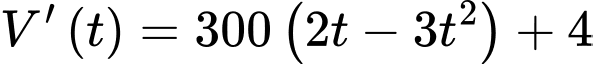 với
với 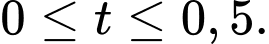
c) Lượng xăng lớn nhất bơm vào bình xăng là
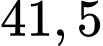 lít.
lít. d) Xăng chảy vào bình xăng vào thời điểm ở giây thứ 30 thì tốc độ tăng thể tích là lớn nhất.
Thứ tự đáp án: Sai, Sai, Đúng, Sai.
Lượng xăng ban đầu là: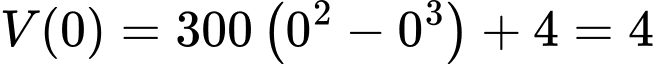 (l).
(l).
Ta có: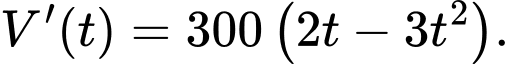
Xét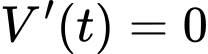
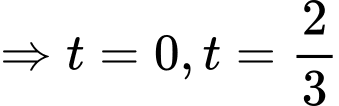 (loại).
(loại).
Ta tính được: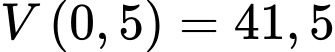 (l).
(l).
Vì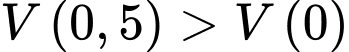 nên lượng xăng lớn nhất bơm vào bình xăng là
nên lượng xăng lớn nhất bơm vào bình xăng là 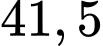 lít.
lít.
Xét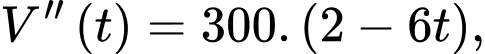
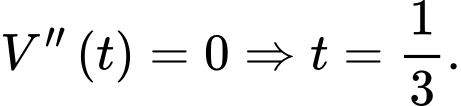
Ta tính được:
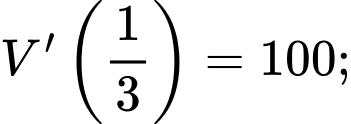
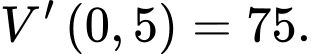
Do đó, tốc độ tăng thể tích là lớn nhất khi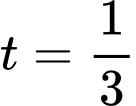 (phút).
(phút).
Lượng xăng ban đầu là:
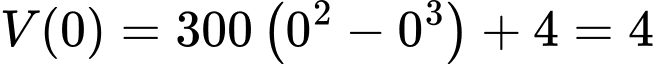 (l).
(l).Ta có:
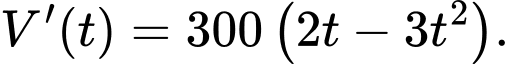
Xét
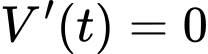
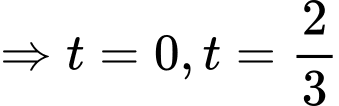 (loại).
(loại).Ta tính được:
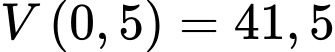 (l).
(l).Vì
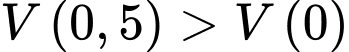 nên lượng xăng lớn nhất bơm vào bình xăng là
nên lượng xăng lớn nhất bơm vào bình xăng là 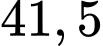 lít.
lít.Xét
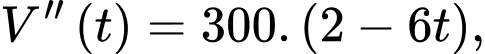
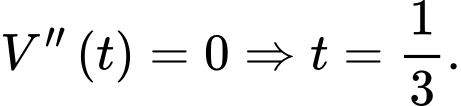
Ta tính được:

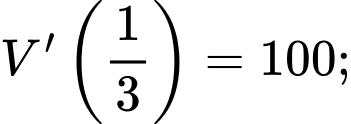
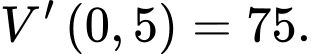
Do đó, tốc độ tăng thể tích là lớn nhất khi
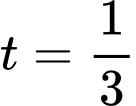 (phút).
(phút).
Câu 15 [696316]: Một điệp viên đang có ý định chạy chốn khỏi sự theo dõi của cảnh sát, điệp viên lái một chiếc xe thể thao tới vùng ngoại ô. Để không gây nhiều chú ý tới cảnh sát, anh ta di chuyển với tốc độ hợp pháp 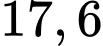 m/s. Đột nhiên trên đường xuất hiện một con lạc đà trên đường cách anh ấy 60 mét. Điệp viên không phản ứng gì khi nhìn thấy lạc đà trong 1 giây, sau đó anh ấy đạp phanh và chiếc xe giảm tốc với gia tốc không đổi là
m/s. Đột nhiên trên đường xuất hiện một con lạc đà trên đường cách anh ấy 60 mét. Điệp viên không phản ứng gì khi nhìn thấy lạc đà trong 1 giây, sau đó anh ấy đạp phanh và chiếc xe giảm tốc với gia tốc không đổi là 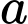 (m/s2). Khi dừng xe hẳn con lạc đà còn cách xe 7,2 mét.
(m/s2). Khi dừng xe hẳn con lạc đà còn cách xe 7,2 mét.
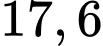 m/s. Đột nhiên trên đường xuất hiện một con lạc đà trên đường cách anh ấy 60 mét. Điệp viên không phản ứng gì khi nhìn thấy lạc đà trong 1 giây, sau đó anh ấy đạp phanh và chiếc xe giảm tốc với gia tốc không đổi là
m/s. Đột nhiên trên đường xuất hiện một con lạc đà trên đường cách anh ấy 60 mét. Điệp viên không phản ứng gì khi nhìn thấy lạc đà trong 1 giây, sau đó anh ấy đạp phanh và chiếc xe giảm tốc với gia tốc không đổi là 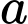 (m/s2). Khi dừng xe hẳn con lạc đà còn cách xe 7,2 mét.
(m/s2). Khi dừng xe hẳn con lạc đà còn cách xe 7,2 mét.
Thứ tự đáp án: Đúng, Đúng, Sai, Sai.
Khoảng cách từ lúc anh ta bắt đầu có phản ứng đến khi dừng hẳn là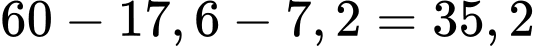 m.
m.
Áp dụng công thức của chuyển động thẳng biến đổi đều khi bắt đầu đạp phanh ta có:
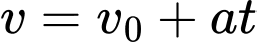
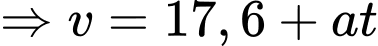 (m/s).
(m/s).
Đến khi dừng hẳn,
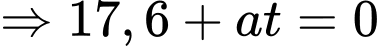
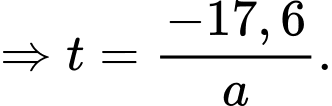
Do đó,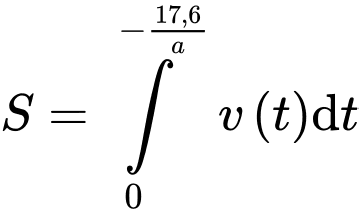 (m).
(m).
Suy ra,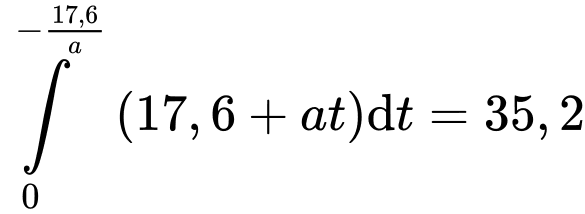
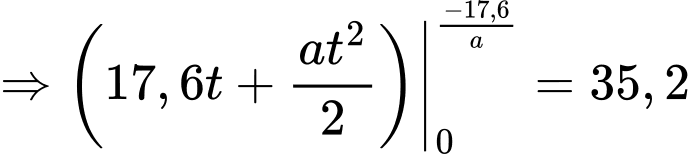
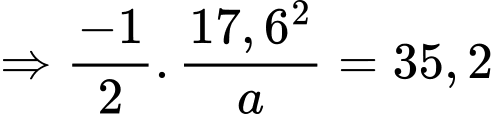
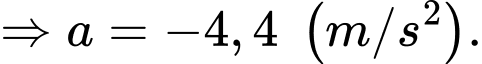
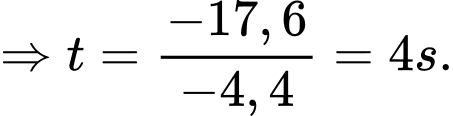
Vậy, vận tốc trung bình mà người đó di chuyển từ khi thấy con lạc đà đến khi dừng hẳn là
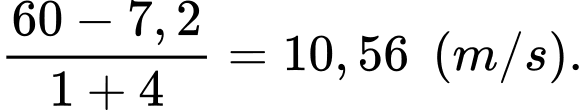
Khoảng cách từ lúc anh ta bắt đầu có phản ứng đến khi dừng hẳn là
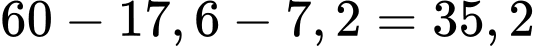 m.
m.Áp dụng công thức của chuyển động thẳng biến đổi đều khi bắt đầu đạp phanh ta có:
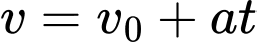
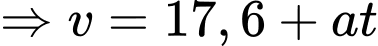 (m/s).
(m/s).Đến khi dừng hẳn,

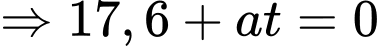
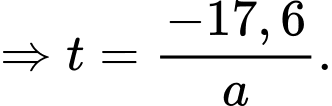
Do đó,
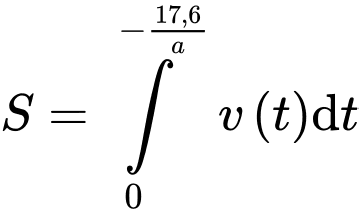 (m).
(m).Suy ra,
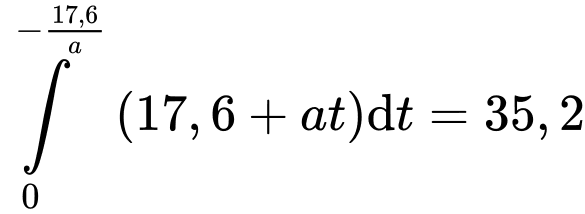
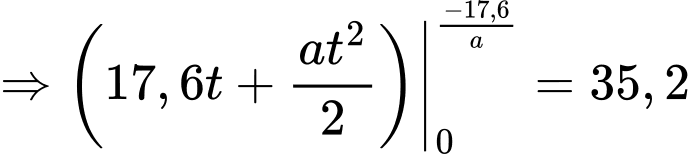
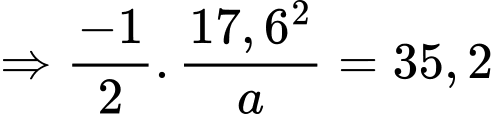
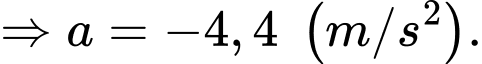
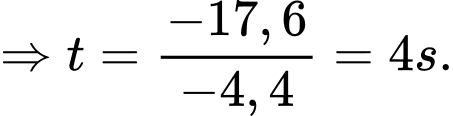
Vậy, vận tốc trung bình mà người đó di chuyển từ khi thấy con lạc đà đến khi dừng hẳn là
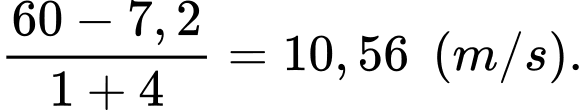
Câu 16 [687489]: Các thiên thạch có đường kính lớn hơn 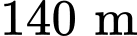 và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn
và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 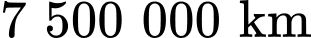 được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, các nhà nghiên cứu của trung tâm Vũ Trụ Nasa đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất.
được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, các nhà nghiên cứu của trung tâm Vũ Trụ Nasa đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất.
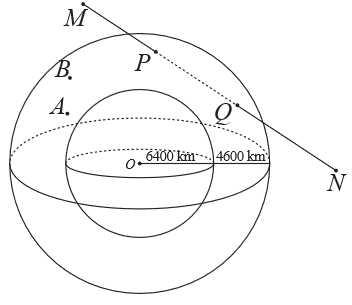
Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá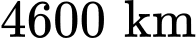 so với mực nước biển. Coi Trái Đất là khối cầu có bán kính
so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 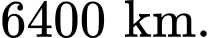 Chọn hệ trục tọa độ
Chọn hệ trục tọa độ 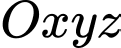 trong không gian có gốc
trong không gian có gốc  tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là
tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là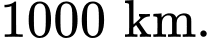 Một thiên thạch (coi như một hạt) chuyển động với tốc độ
Một thiên thạch (coi như một hạt) chuyển động với tốc độ 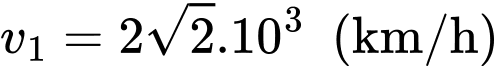 không đổi theo đường thẳng xuất phát từ điểm
không đổi theo đường thẳng xuất phát từ điểm 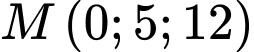 đến
đến 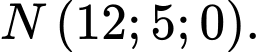
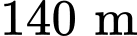 và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn
và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 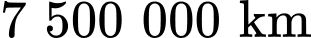 được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, các nhà nghiên cứu của trung tâm Vũ Trụ Nasa đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất.
được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, các nhà nghiên cứu của trung tâm Vũ Trụ Nasa đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. 
Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá
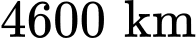 so với mực nước biển. Coi Trái Đất là khối cầu có bán kính
so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 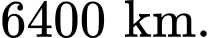 Chọn hệ trục tọa độ
Chọn hệ trục tọa độ 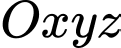 trong không gian có gốc
trong không gian có gốc  tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là
tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là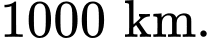 Một thiên thạch (coi như một hạt) chuyển động với tốc độ
Một thiên thạch (coi như một hạt) chuyển động với tốc độ 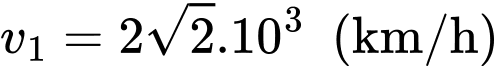 không đổi theo đường thẳng xuất phát từ điểm
không đổi theo đường thẳng xuất phát từ điểm 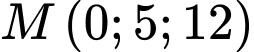 đến
đến 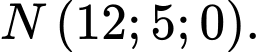
Thứ tự đáp án: Đúng, Đúng, Sai, Đúng.
a) Đúng.
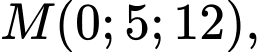
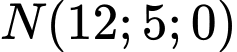 nên
nên 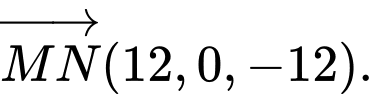
Đường thẳng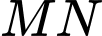 có VTCP là
có VTCP là 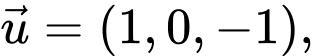 qua
qua 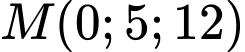 có phương trình
có phương trình
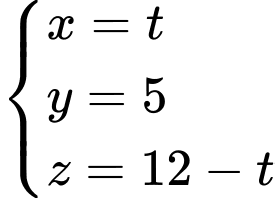
Gọi tại
tại 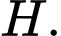 Khi đó
Khi đó 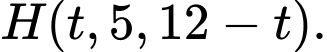
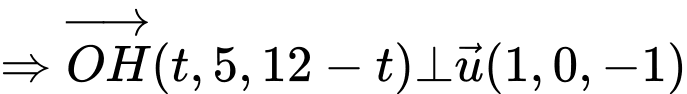
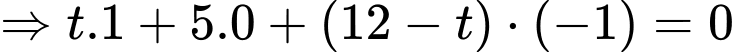
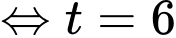
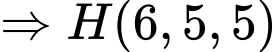
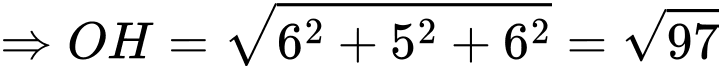
Suy ra khoảng cách ngắn nhất từ tâm trái đất đến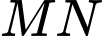 là
là 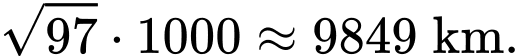
Khoảng cách thiên thạch gần với trái đất nhất có độ dài bằng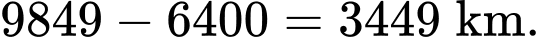
b) Đúng.
Gọi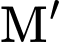 là điểm va chạm của
là điểm va chạm của 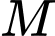 với Trái Đất.
với Trái Đất.
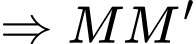 lớn nhất khi
lớn nhất khi 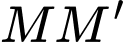 là tiếp tuyến kẻ từ M tới mặt cầu - là bề mặt trái đất.
là tiếp tuyến kẻ từ M tới mặt cầu - là bề mặt trái đất.

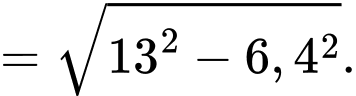
Hay quãng đường dài nhất là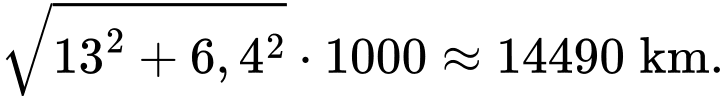
c) Sai.
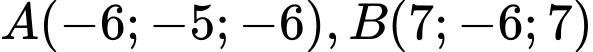
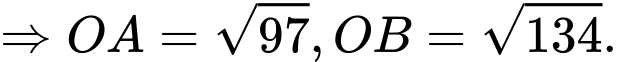

Vậy lớn nhất bằng 21425 km khi
lớn nhất bằng 21425 km khi 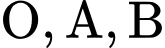 thẳng hàng.
thẳng hàng.
d) Đúng.
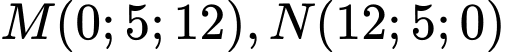 nên trung điểm
nên trung điểm 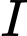 của MN có tọa độ
của MN có tọa độ 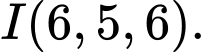
Do không đổi nên A luôn thuộc mặt cầu có tâm O, bán kính
không đổi nên A luôn thuộc mặt cầu có tâm O, bán kính 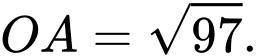
Để vệ tinh va chạm với thiên thạch thì chỉ có thể va chạm tại I
Khi đó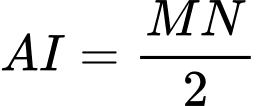
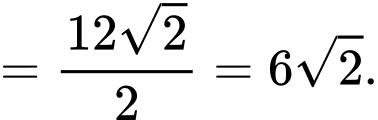
Thời gian để thiên thạch di chuyển từ M đến I là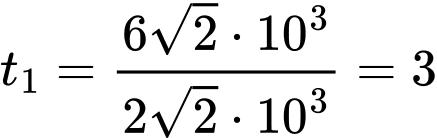 (giờ).
(giờ).
Nhận thấy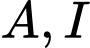 đối xứng nhau qua O nên quãng đường để vệ tinh di chuyển từ A đến I là một đường cong có độ dài bằng nửa chu vi đường tròn bán kính OA và bằng
đối xứng nhau qua O nên quãng đường để vệ tinh di chuyển từ A đến I là một đường cong có độ dài bằng nửa chu vi đường tròn bán kính OA và bằng 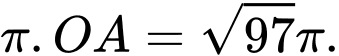
Vậy thời gian để vệ tinh đi từ A đến I là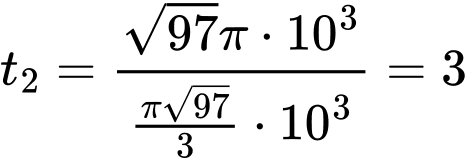 (giờ).
(giờ).
Vậy vệ tinh và thiên thạch có va chạm.
a) Đúng.
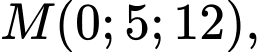
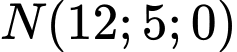 nên
nên 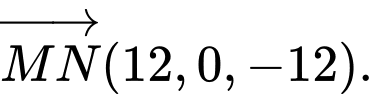
Đường thẳng
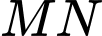 có VTCP là
có VTCP là 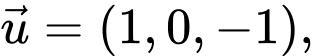 qua
qua 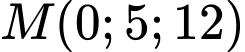 có phương trình
có phương trình 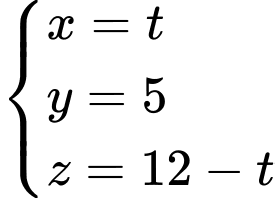
Gọi
 tại
tại 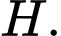 Khi đó
Khi đó 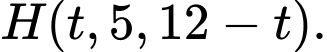
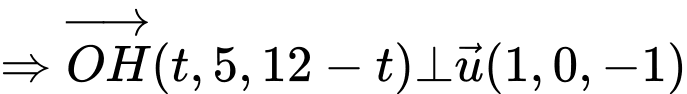
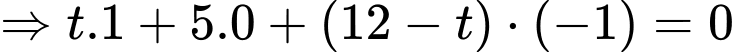
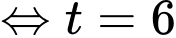
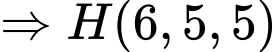
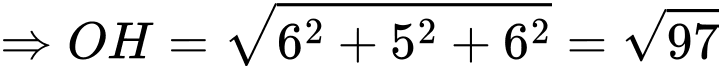
Suy ra khoảng cách ngắn nhất từ tâm trái đất đến
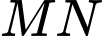 là
là 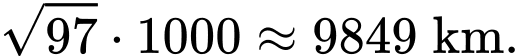
Khoảng cách thiên thạch gần với trái đất nhất có độ dài bằng
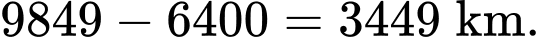
b) Đúng.
Gọi
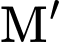 là điểm va chạm của
là điểm va chạm của 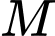 với Trái Đất.
với Trái Đất.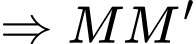 lớn nhất khi
lớn nhất khi 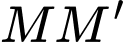 là tiếp tuyến kẻ từ M tới mặt cầu - là bề mặt trái đất.
là tiếp tuyến kẻ từ M tới mặt cầu - là bề mặt trái đất.
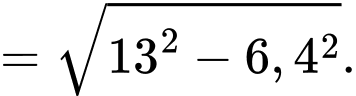
Hay quãng đường dài nhất là
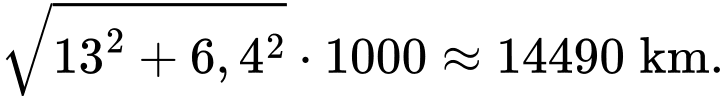
c) Sai.
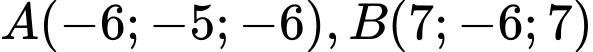
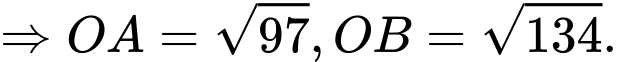

Vậy
 lớn nhất bằng 21425 km khi
lớn nhất bằng 21425 km khi 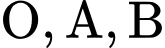 thẳng hàng.
thẳng hàng.d) Đúng.
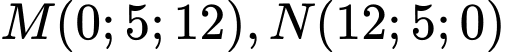 nên trung điểm
nên trung điểm 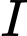 của MN có tọa độ
của MN có tọa độ 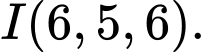
Do
 không đổi nên A luôn thuộc mặt cầu có tâm O, bán kính
không đổi nên A luôn thuộc mặt cầu có tâm O, bán kính 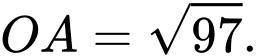
Để vệ tinh va chạm với thiên thạch thì chỉ có thể va chạm tại I
Khi đó
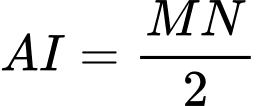
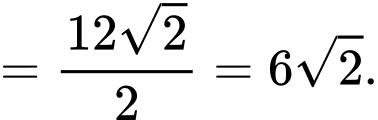
Thời gian để thiên thạch di chuyển từ M đến I là
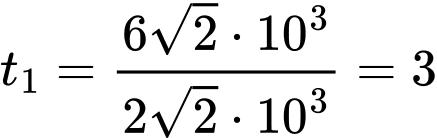 (giờ).
(giờ).Nhận thấy
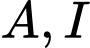 đối xứng nhau qua O nên quãng đường để vệ tinh di chuyển từ A đến I là một đường cong có độ dài bằng nửa chu vi đường tròn bán kính OA và bằng
đối xứng nhau qua O nên quãng đường để vệ tinh di chuyển từ A đến I là một đường cong có độ dài bằng nửa chu vi đường tròn bán kính OA và bằng 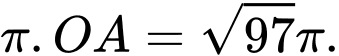
Vậy thời gian để vệ tinh đi từ A đến I là
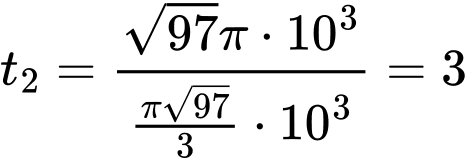 (giờ).
(giờ).Vậy vệ tinh và thiên thạch có va chạm.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696317]: Người ta mài một phiến đá để được một khối chóp cụt tam giác đều có đáy lớn cạnh bằng 30 cm, đáy nhỏ cạnh bằng 10 cm và cạnh bên bằng 25 cm. Thể tích của khối chóp cụt tạo thành bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
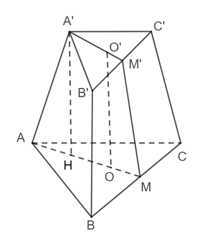
Gọi khối chóp cụt tam giác đều
 có đáy lớn
có đáy lớn 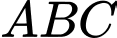 và đáy bé
và đáy bé 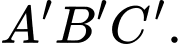
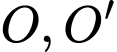 lần lượt là tâm của đáy lớn và đáy bé.
lần lượt là tâm của đáy lớn và đáy bé.Kẻ chiều cao
 của khối chóp cụt.
của khối chóp cụt.Ta có:
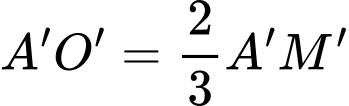
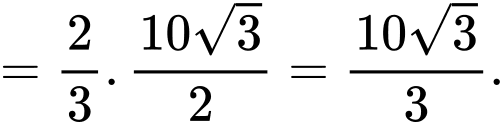
Tương tự,
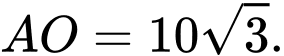
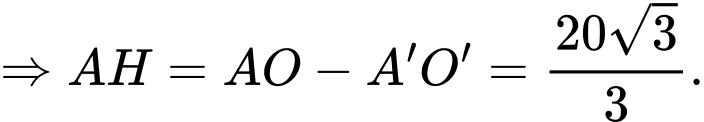
Do đó, chiều cao

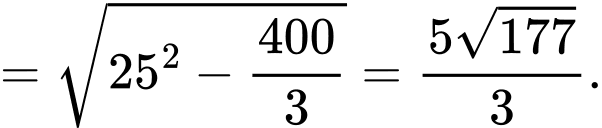
Ta có:
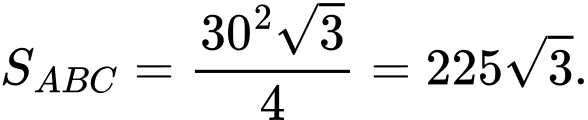
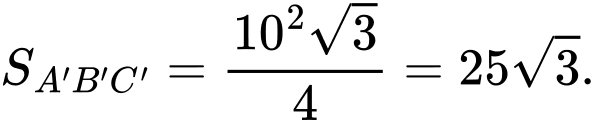
Vậy thể tích khối chóp cụt là
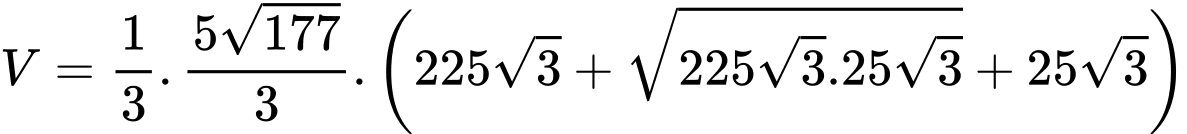
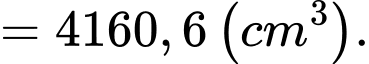
Câu 18 [693321]: Trong một ngày, tổng chi phí để một xưởng sản xuất 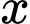 (kg) thành phẩm được cho bởi hàm số
(kg) thành phẩm được cho bởi hàm số 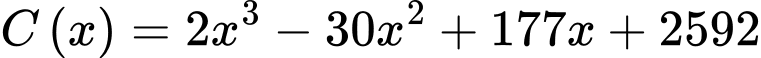 (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng là 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
(nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng là 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
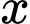 (kg) thành phẩm được cho bởi hàm số
(kg) thành phẩm được cho bởi hàm số 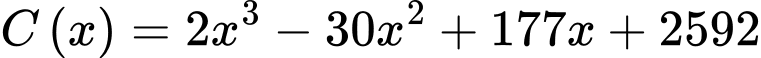 (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng là 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
(nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng là 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
Lợi nhuận xưởng thu được trong một ngày khi sản xuất x (kg) thành phẩm là:
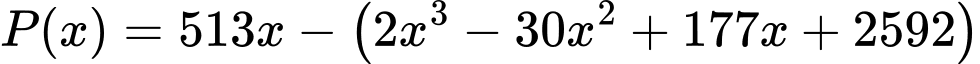
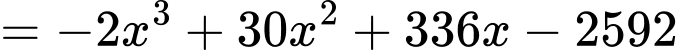 với
với 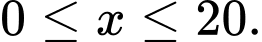
Ta có: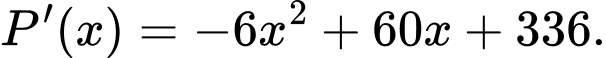
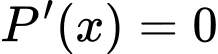
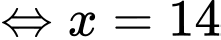 hoặc
hoặc 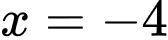 (loại).
(loại).
Ta có bảng biến thiên:
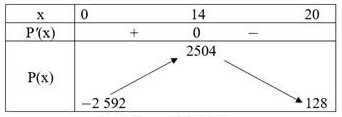
Do đó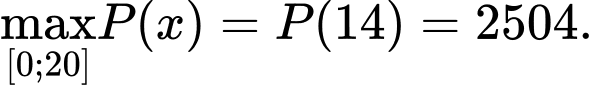
Vậy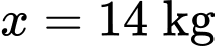 thì lợi nhuận thu được của xưởng trong một ngày là cao nhất.
thì lợi nhuận thu được của xưởng trong một ngày là cao nhất.
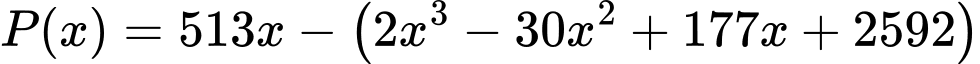
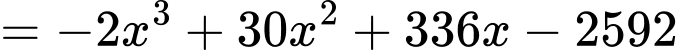 với
với 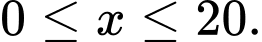
Ta có:
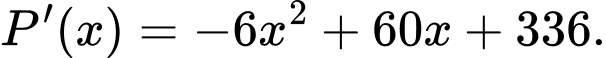
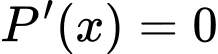
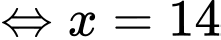 hoặc
hoặc 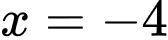 (loại).
(loại).
Ta có bảng biến thiên:

Do đó
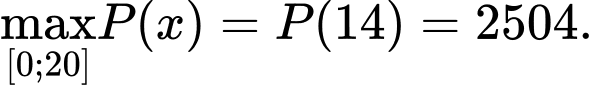
Vậy
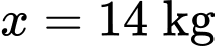 thì lợi nhuận thu được của xưởng trong một ngày là cao nhất.
thì lợi nhuận thu được của xưởng trong một ngày là cao nhất.
Câu 19 [696318]: Một xe vận tải đang ở kho hàng và cần giao cho 4 khách hàng tại các địa điểm khác nhau. Các khoảng cách giữa các địa điểm được ghi lại như sau:
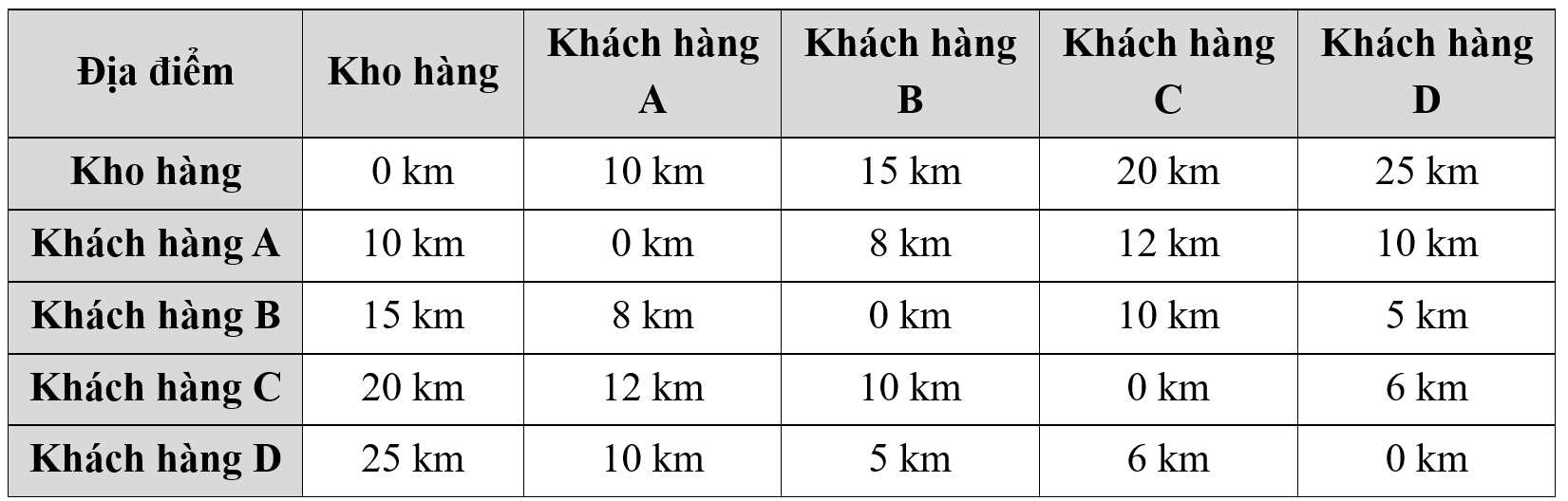
Vậy khoảng cách tối thiểu để hoàn thành lộ trình giao hàng cho tất cả các khách hàng và quay lại kho hàng là bao nhiêu kilômét?

Vậy khoảng cách tối thiểu để hoàn thành lộ trình giao hàng cho tất cả các khách hàng và quay lại kho hàng là bao nhiêu kilômét?
Dựa vào dữ kiện: “Một xe vận tải đang ở kho hàng và cần giao cho 4 khách hàng tại các địa điểm khác nhau”.
Kết hợp với dữ kiện câu hỏi: “khoảng cách tối thiểu để hoàn thành lộ trình giao hàng cho tất cả các khách hàng và quay lại kho hàng”.
Từ bảng số liệu, ta vẽ được đồ thị
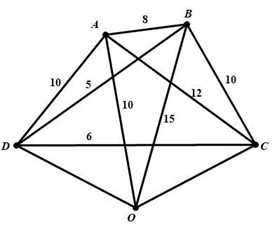
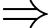 Đồ thị có 5 đỉnh, các đỉnh đều có bậc
Đồ thị có 5 đỉnh, các đỉnh đều có bậc 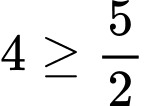 nên đồ thị có chu trình Hamilton.Ta có các chu trình xuất phát từ O:
nên đồ thị có chu trình Hamilton.Ta có các chu trình xuất phát từ O:
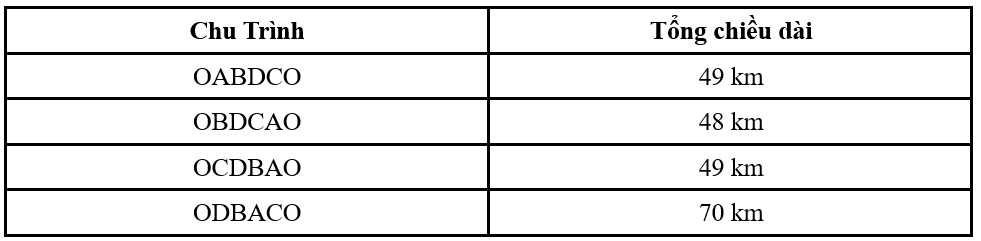
Vậy khoảng cách tối thiểu để hoàn thành lộ trình giao hàng cho tất cả các khách hàng và quay lại kho hàng là 48 km với chu trình OBDCAO.
Kết hợp với dữ kiện câu hỏi: “khoảng cách tối thiểu để hoàn thành lộ trình giao hàng cho tất cả các khách hàng và quay lại kho hàng”.
Từ bảng số liệu, ta vẽ được đồ thị

 Đồ thị có 5 đỉnh, các đỉnh đều có bậc
Đồ thị có 5 đỉnh, các đỉnh đều có bậc 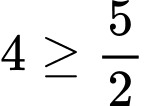 nên đồ thị có chu trình Hamilton.Ta có các chu trình xuất phát từ O:
nên đồ thị có chu trình Hamilton.Ta có các chu trình xuất phát từ O:
Vậy khoảng cách tối thiểu để hoàn thành lộ trình giao hàng cho tất cả các khách hàng và quay lại kho hàng là 48 km với chu trình OBDCAO.
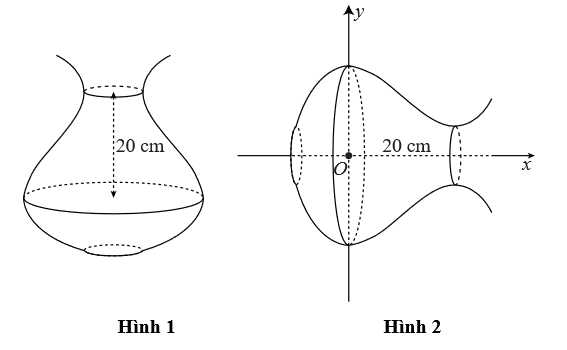
Câu 20 [702800]: Một con quạ khát nước, nó tìm thấy một cái lọ có nước nhưng cổ lọ lại cao nó không thò mỏ uống được nên đã gắp từng viên bi (hình cầu) bỏ vào trong lọ để nước dâng lên. Hỏi con quạ cần bỏ vào lọ ít nhất bao nhiêu viên bi để có thể uống nước? Biết rằng viên bi có bán kính là  và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất
và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất 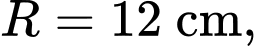 mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất
mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất 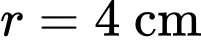 và khoảng cách giữa hai mặt này bằng
và khoảng cách giữa hai mặt này bằng  được minh họa ở hình vẽ bên dưới.
được minh họa ở hình vẽ bên dưới.
 và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất
và không thấm nước, khi đặt nằm ngang cái lọ có hình dáng là một khối tròn xoay với đường sinh là đồ thị của một hàm bậc 3 (hình 2), mực nước trong lọ ban đầu ở vị trí mà hình tròn có bán kính lớn nhất 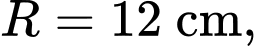 mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất
mực nước mà quạ có thể uống được là vị trí mà hình tròn có bán kính nhỏ nhất 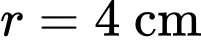 và khoảng cách giữa hai mặt này bằng
và khoảng cách giữa hai mặt này bằng  được minh họa ở hình vẽ bên dưới.
được minh họa ở hình vẽ bên dưới.
Gọi phương trình của đường sinh là 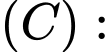
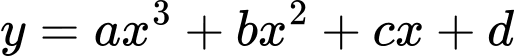
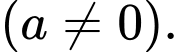
Theo đề bài, ta có: có điểm cực đại
có điểm cực đại 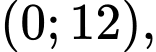 điểm cực tiểu là
điểm cực tiểu là 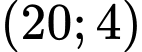
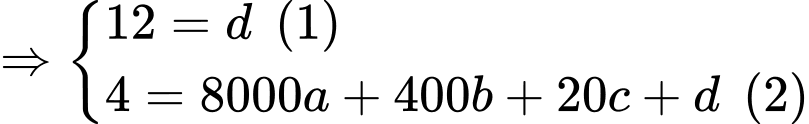
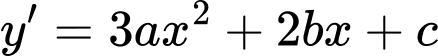
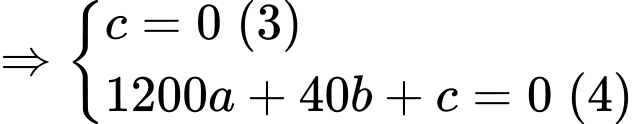
Từ (1), (2), (3) và (4)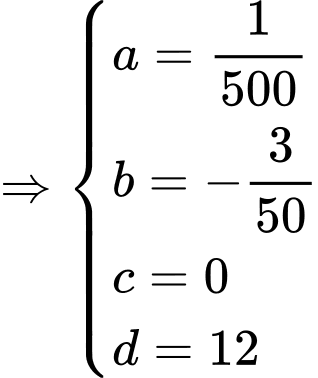

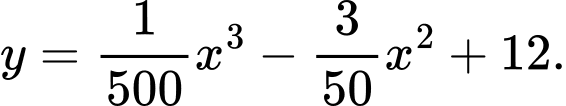
Thể tích đã cho vào:
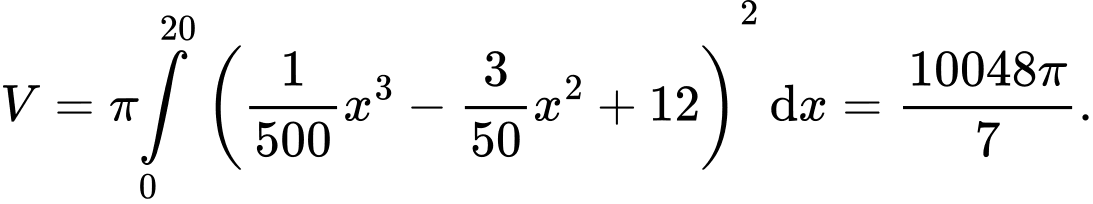
Thể tích 1 viên bi là
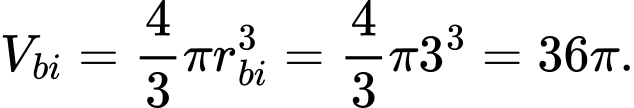
Cần số viên bi: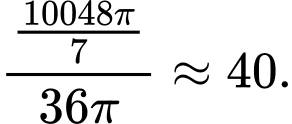 (viên).
(viên).
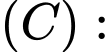
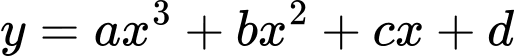
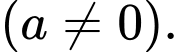
Theo đề bài, ta có:
 có điểm cực đại
có điểm cực đại 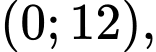 điểm cực tiểu là
điểm cực tiểu là 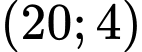
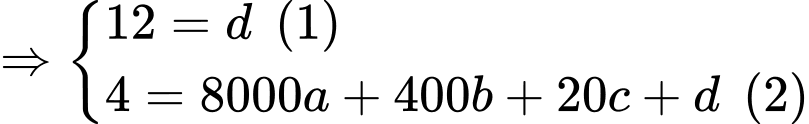
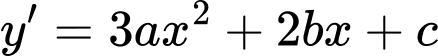
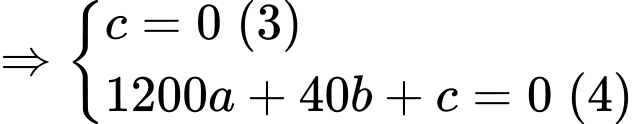
Từ (1), (2), (3) và (4)
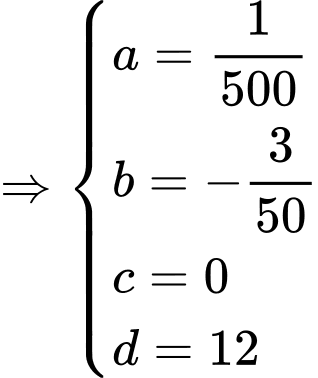

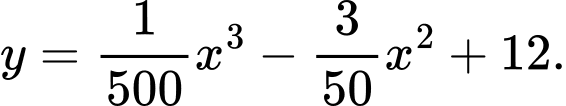
Thể tích đã cho vào:
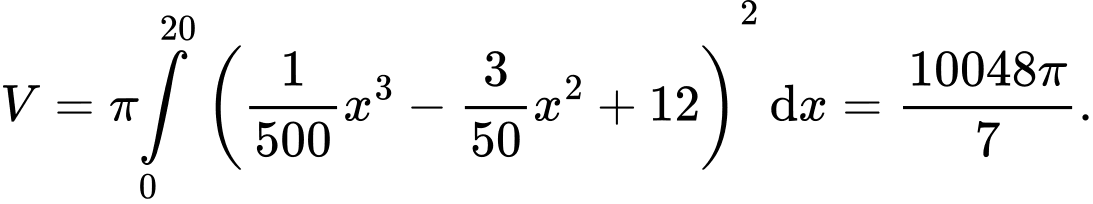
Thể tích 1 viên bi là
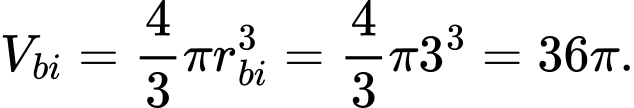
Cần số viên bi:
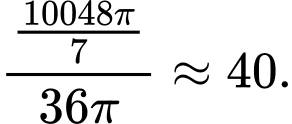 (viên).
(viên).
Câu 21 [696320]: Trong không gian 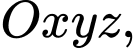 cho mặt phẳng
cho mặt phẳng 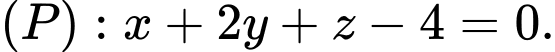 Có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng
Có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng 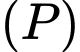 và tiếp xúc với ba trục toạ độ
và tiếp xúc với ba trục toạ độ 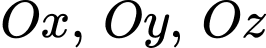 ?
?
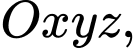 cho mặt phẳng
cho mặt phẳng 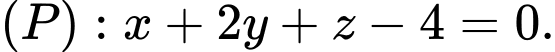 Có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng
Có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng 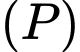 và tiếp xúc với ba trục toạ độ
và tiếp xúc với ba trục toạ độ 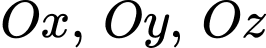 ?
?
Giả sử 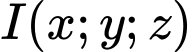 là tâm mặt cầu cần tìm.
là tâm mặt cầu cần tìm.
Ta có hình chiếu vuông góc của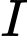 lên các trục tọa độ lần lượt là
lên các trục tọa độ lần lượt là 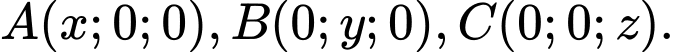
Theo giả thiết, ta có:
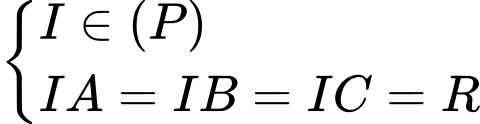
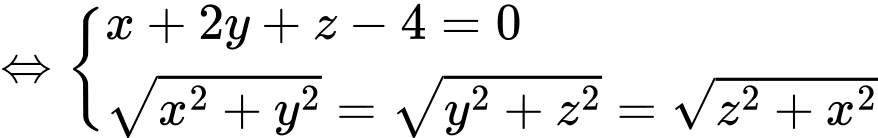
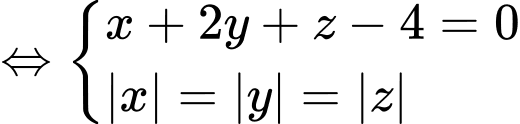
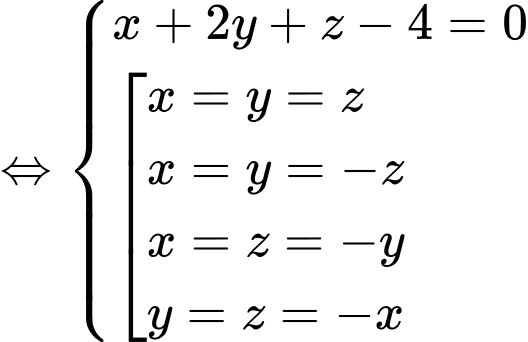
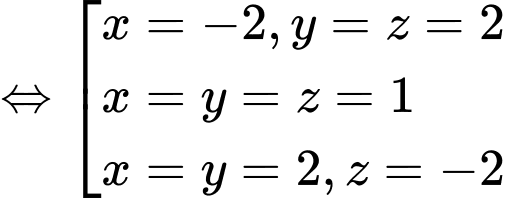
Vậy có tất cả 3 mặt cầu thoả mãn.
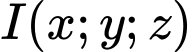 là tâm mặt cầu cần tìm.
là tâm mặt cầu cần tìm.Ta có hình chiếu vuông góc của
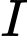 lên các trục tọa độ lần lượt là
lên các trục tọa độ lần lượt là 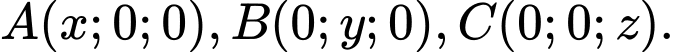
Theo giả thiết, ta có:
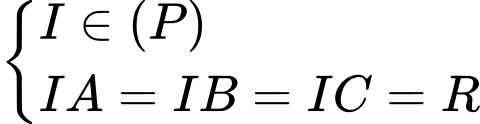
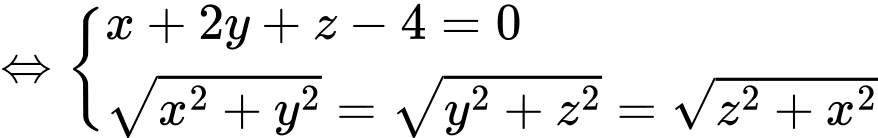
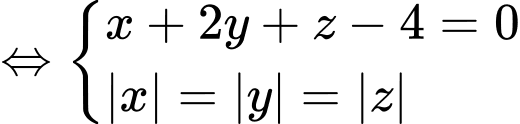
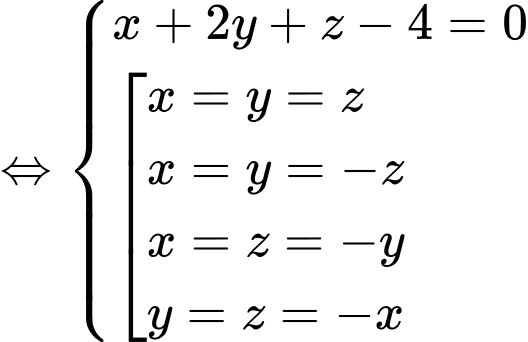
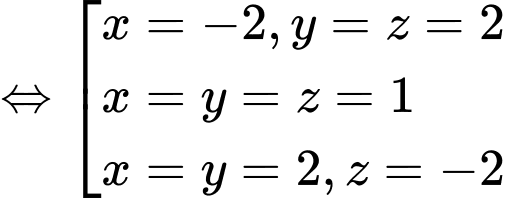
Vậy có tất cả 3 mặt cầu thoả mãn.
Câu 22 [696321]: Một trạm chỉ phát hai loại tín hiệu 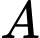 và
và 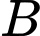 với xác suất phát đi tương ứng là 0,84 và 0,16. Do có nhiễu trên đường truyền nên một phần tín hiệu A bị méo và được thu như là tín hiệu
với xác suất phát đi tương ứng là 0,84 và 0,16. Do có nhiễu trên đường truyền nên một phần tín hiệu A bị méo và được thu như là tín hiệu 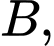 còn một phần tín hiệu
còn một phần tín hiệu 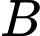 bị méo và được thu như là tín hiệu
bị méo và được thu như là tín hiệu 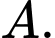 Thống kê cho thấy xác suất thu được tín hiệu đúng là
Thống kê cho thấy xác suất thu được tín hiệu đúng là 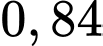 và xác suất thu được tín hiệu
và xác suất thu được tín hiệu 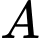 là
là 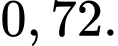 Hỏi có bao nhiêu % tín hiệu
Hỏi có bao nhiêu % tín hiệu 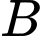 bị méo thành tín hiệu
bị méo thành tín hiệu 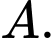
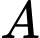 và
và 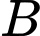 với xác suất phát đi tương ứng là 0,84 và 0,16. Do có nhiễu trên đường truyền nên một phần tín hiệu A bị méo và được thu như là tín hiệu
với xác suất phát đi tương ứng là 0,84 và 0,16. Do có nhiễu trên đường truyền nên một phần tín hiệu A bị méo và được thu như là tín hiệu 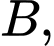 còn một phần tín hiệu
còn một phần tín hiệu 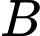 bị méo và được thu như là tín hiệu
bị méo và được thu như là tín hiệu 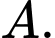 Thống kê cho thấy xác suất thu được tín hiệu đúng là
Thống kê cho thấy xác suất thu được tín hiệu đúng là 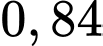 và xác suất thu được tín hiệu
và xác suất thu được tín hiệu 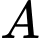 là
là 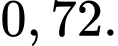 Hỏi có bao nhiêu % tín hiệu
Hỏi có bao nhiêu % tín hiệu 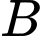 bị méo thành tín hiệu
bị méo thành tín hiệu 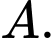
Điền đáp án: 12,5.
Gọi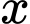 là xác suất tín hiệu A thu được tín hiệu đúng;
là xác suất tín hiệu A thu được tín hiệu đúng;
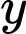 là xác suất tín hiệu B thu được tín hiệu đúng;
là xác suất tín hiệu B thu được tín hiệu đúng;
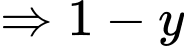 là xác suất tín hiệu B bị méo thành tín hiệu A.
là xác suất tín hiệu B bị méo thành tín hiệu A.
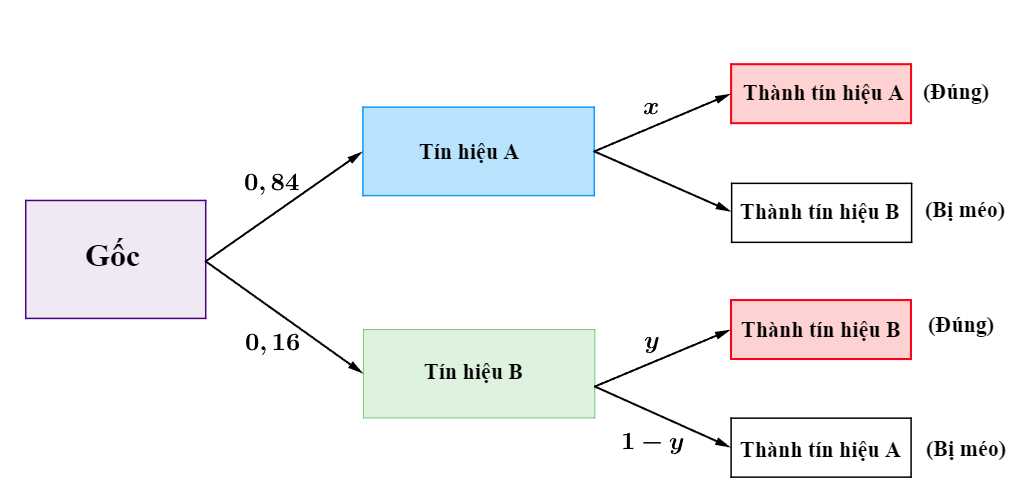
Ta có sơ đồ cây sau:
Giả thiết cho:
+) Xác suất thu được tín hiệu đúng là 0,84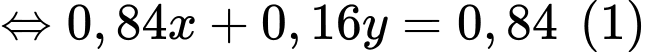
+) Xác suất thu được tín hiệu A là 0,72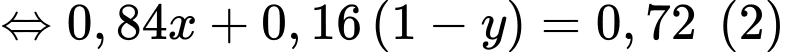
Từ (1) và (2) ta có hệ phương trình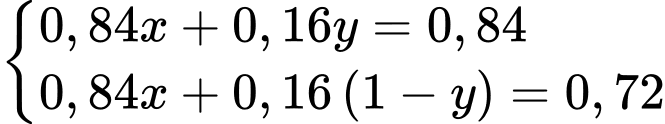
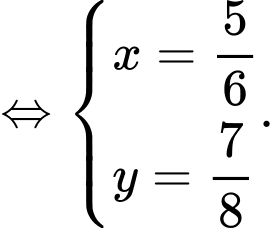
Suy ra xác suất tín hiệu B bị méo thành tín hiệu A bằng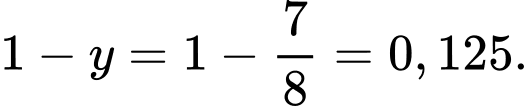
Vậy phần trăm tín hiệu B bị méo thành tín hiệu A là 12,5%.
Gọi
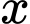 là xác suất tín hiệu A thu được tín hiệu đúng;
là xác suất tín hiệu A thu được tín hiệu đúng;
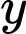 là xác suất tín hiệu B thu được tín hiệu đúng;
là xác suất tín hiệu B thu được tín hiệu đúng;
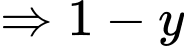 là xác suất tín hiệu B bị méo thành tín hiệu A.
là xác suất tín hiệu B bị méo thành tín hiệu A.
Ta có sơ đồ cây sau:
Giả thiết cho:

+) Xác suất thu được tín hiệu đúng là 0,84
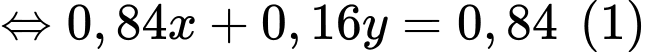
+) Xác suất thu được tín hiệu A là 0,72
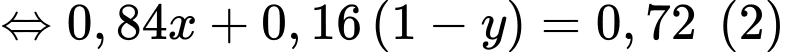
Từ (1) và (2) ta có hệ phương trình
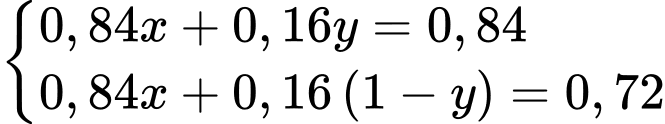
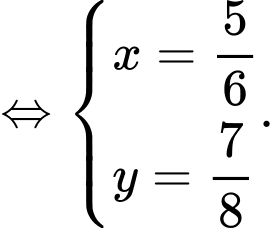
Suy ra xác suất tín hiệu B bị méo thành tín hiệu A bằng
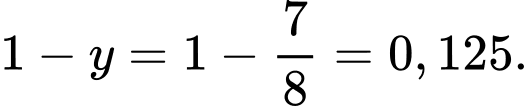
Vậy phần trăm tín hiệu B bị méo thành tín hiệu A là 12,5%.