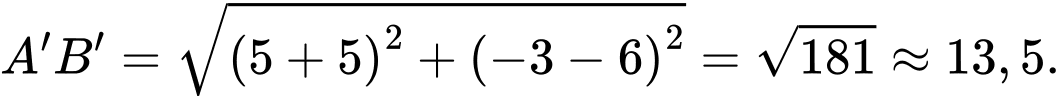PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [513167]: Cho hàm số 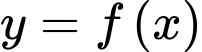 có bảng biến thiên như sau:
có bảng biến thiên như sau:
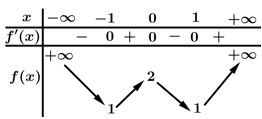
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
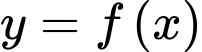 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A, 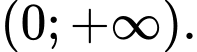
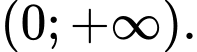
B, 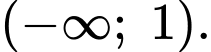
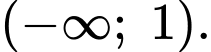
C, 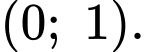
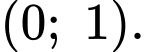
D, 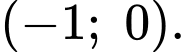
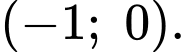
Chọn đáp án C.
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên từng khoảng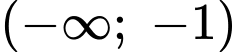 và
và 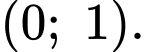 Đáp án: C
Đáp án: C
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên từng khoảng
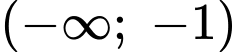 và
và 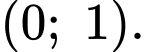 Đáp án: C
Đáp án: C
Câu 2 [313359]: Họ tất cả các nguyên hàm của hàm số 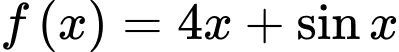 là
là
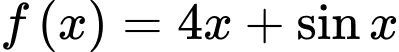 là
là A, 

B, 

C, 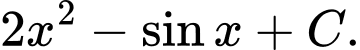
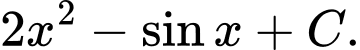
D, 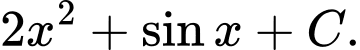
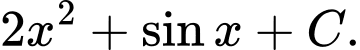
Chọn đáp án A.
Ta có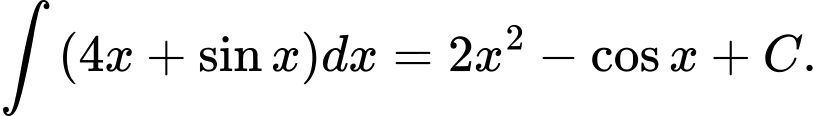 Đáp án: A
Đáp án: A
Ta có
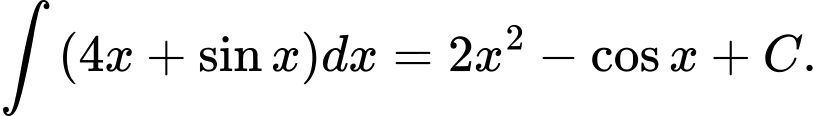 Đáp án: A
Đáp án: A
Câu 3 [547598]: Kết quả khảo sát cân nặng số táo ở lô hàng B được cho ở bảng sau:

Số táo được khảo sát trong bảng số liệu là

Số táo được khảo sát trong bảng số liệu là
A, 
B, 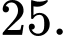
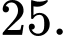
C, 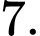
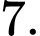
D, 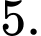
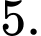
Chọn đáp án B.
Số táo được khảo sát trong bảng số liệu là: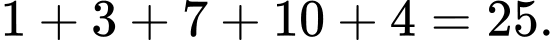 Đáp án: B
Đáp án: B
Số táo được khảo sát trong bảng số liệu là:
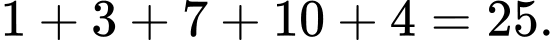 Đáp án: B
Đáp án: B Sử dụng thông tin dưới đây để trả lời câu 4 và câu 5
Trong không gian Oxyz, cho mặt phẳng (P):2x - 3y + 6z - 5 = 0 và điểm A(2; - 3;1).
Câu 4 [697545]: Một vectơ pháp tuyến của mặt phẳng 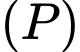 là
là
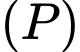 là
là A, 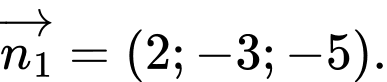
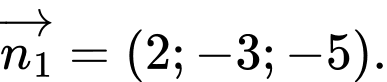
B, 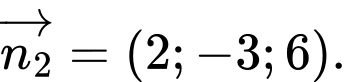
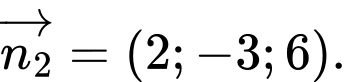
C, 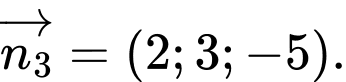
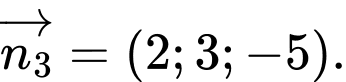
D, 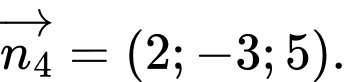
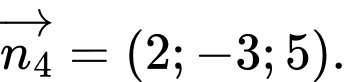
Chọn đáp án B.
Một vectơ pháp tuyến của mặt phẳng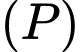 là
là 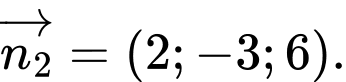 Đáp án: B
Đáp án: B
Một vectơ pháp tuyến của mặt phẳng
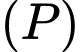 là
là 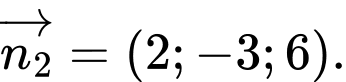 Đáp án: B
Đáp án: B
Câu 5 [697546]: Đường thẳng 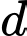 đi qua điểm
đi qua điểm 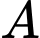 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 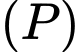 có phương trình tham số là:
có phương trình tham số là:
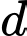 đi qua điểm
đi qua điểm 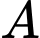 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 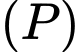 có phương trình tham số là:
có phương trình tham số là: A, 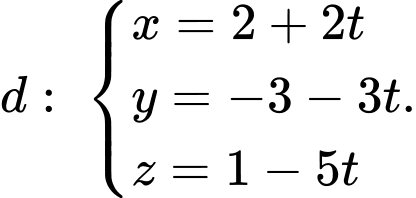
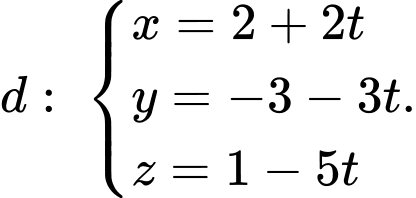
B, 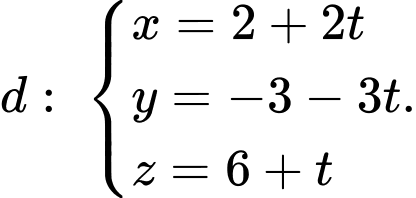
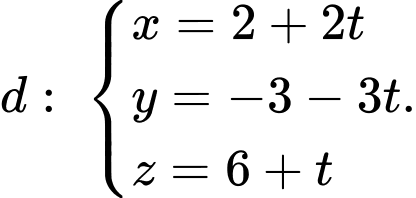
C, 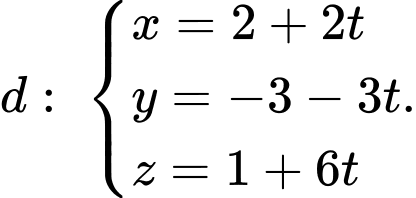
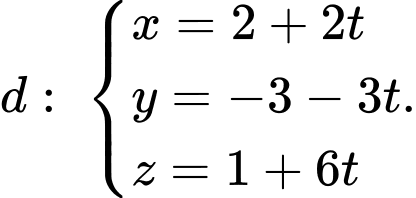
D, 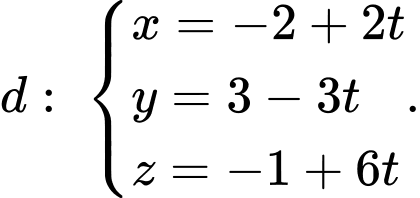
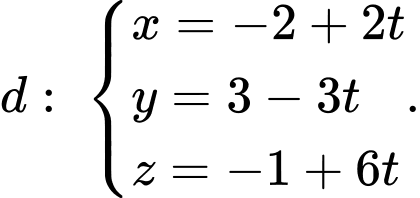
Chọn đáp án C.
Đường thẳng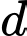 vuông góc với mặt phẳng
vuông góc với mặt phẳng 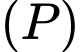 nên có vtcp là
nên có vtcp là 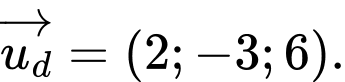
Đường thẳng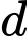 đi qua
đi qua  và có vtcp
và có vtcp 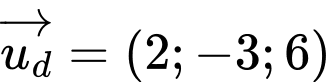 có phương trình tham số là:
có phương trình tham số là: 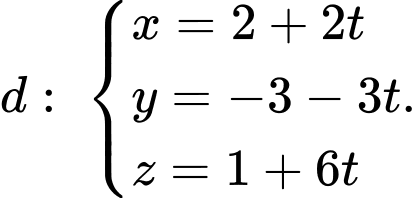 Đáp án: C
Đáp án: C
Đường thẳng
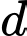 vuông góc với mặt phẳng
vuông góc với mặt phẳng 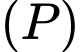 nên có vtcp là
nên có vtcp là 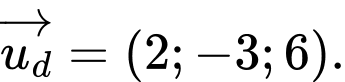
Đường thẳng
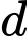 đi qua
đi qua  và có vtcp
và có vtcp 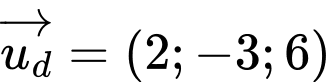 có phương trình tham số là:
có phương trình tham số là: 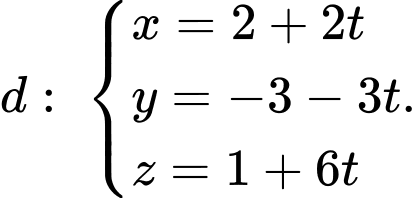 Đáp án: C
Đáp án: C
Câu 6 [677708]: 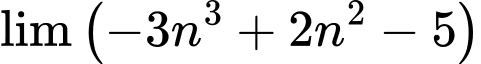 bằng
bằng
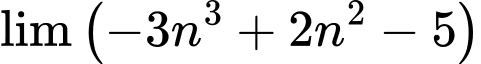 bằng
bằng A, 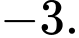
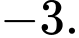
B, 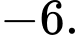
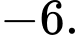
C, 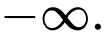
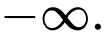
D, 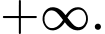
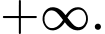
Chọn đáp án C.
Ta có:
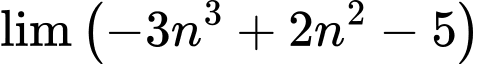
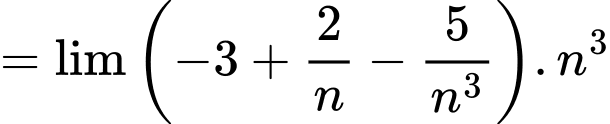
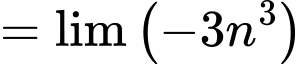
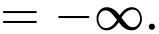 Đáp án: C
Đáp án: C
Ta có:
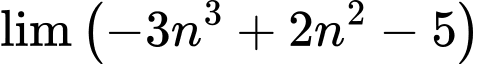
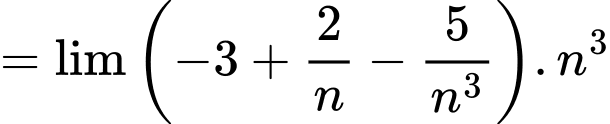
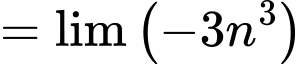
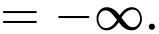 Đáp án: C
Đáp án: C
Câu 7 [693099]: Diện tích hình thang cong ở hình vẽ bên là 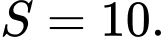 Tích phân
Tích phân 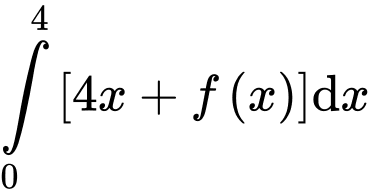 bằng
bằng
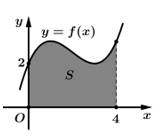
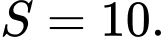 Tích phân
Tích phân 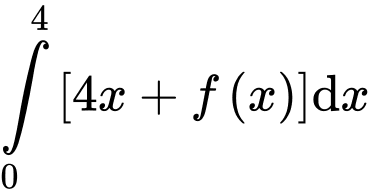 bằng
bằng
A, 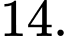
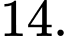
B, 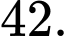
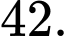
C, 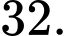
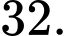
D, 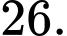
Chọn đáp án B.
Ta có:
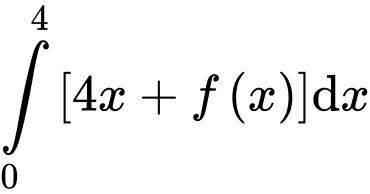

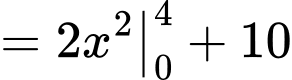
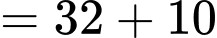
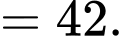 Đáp án: B
Đáp án: B
Ta có:
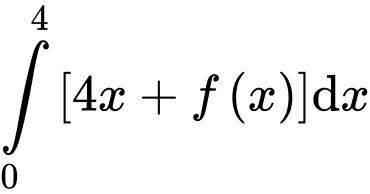

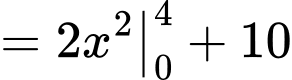
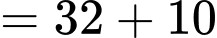
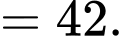 Đáp án: B
Đáp án: B
Câu 8 [528708]: Cho các số thực dương 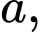
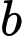 thỏa mãn
thỏa mãn 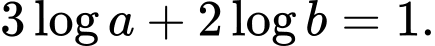 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
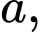
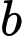 thỏa mãn
thỏa mãn 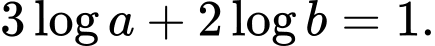 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng? A, 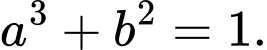
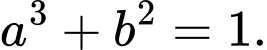
B, 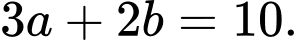
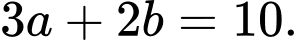
C, 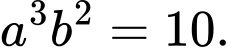
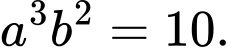
D, 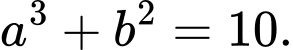
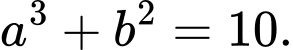
Chọn đáp án C.
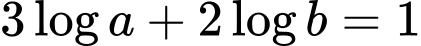
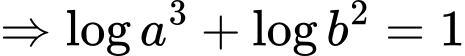
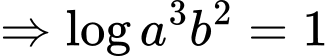
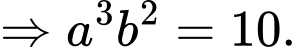 Đáp án: C
Đáp án: C
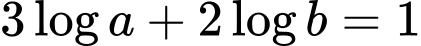
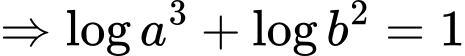
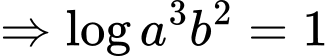
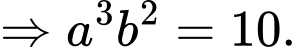 Đáp án: C
Đáp án: C
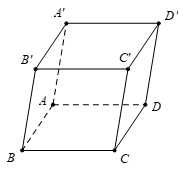
Câu 9 [597371]: Cho hình hộp 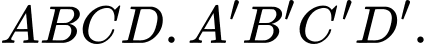 Tính tổng
Tính tổng 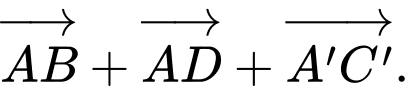
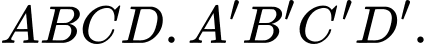 Tính tổng
Tính tổng 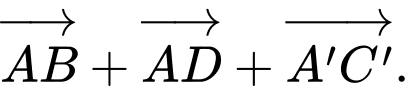

A, 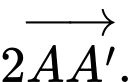
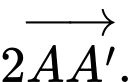
B, 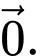
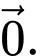
C, 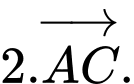
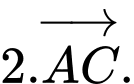
D, 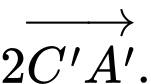
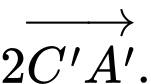
Chọn đáp án C
Theo quy tắc hình bình hành ta có,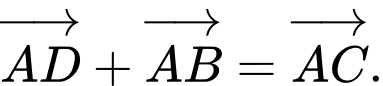
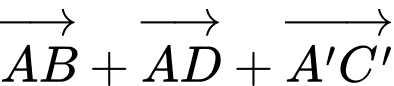
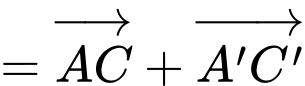
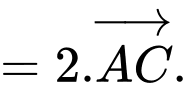 Đáp án: C
Đáp án: C
Theo quy tắc hình bình hành ta có,
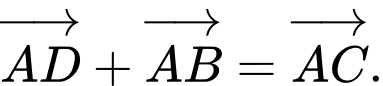
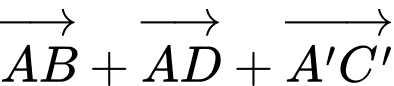
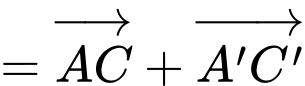
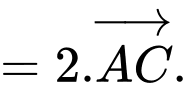 Đáp án: C
Đáp án: C
Câu 10 [216368]: Đồ thị hàm số 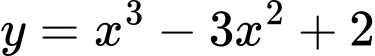 là đường cong trong hình nào dưới đây?
là đường cong trong hình nào dưới đây?
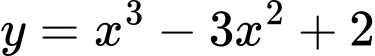 là đường cong trong hình nào dưới đây?
là đường cong trong hình nào dưới đây? A, 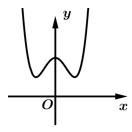

B, 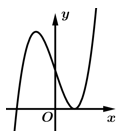

C, 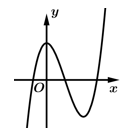

D, 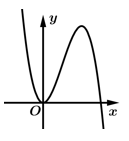

Chọn đáp án C.
+)Vì hàm số đã cho là hàm bậc 3 nên sẽ có nhiều nhất 2 điểm cực trị, suy ra Loại A.
+)Vì hệ số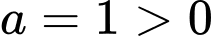 nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
+)Ấn máy tính tìm nghiệm của phương trình giao điểm hoành độ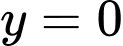 thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
+)Vì hàm số đã cho là hàm bậc 3 nên sẽ có nhiều nhất 2 điểm cực trị, suy ra Loại A.
+)Vì hệ số
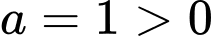 nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
nên phần cuối cùng của đồ thị phải đi lên, suy ra Loại D.
+)Ấn máy tính tìm nghiệm của phương trình giao điểm hoành độ
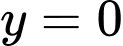 thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
thì được 3 nghiệm đơn. Suy ra Loại B. Vì đồ thị ở hình B có 1 nghiệm kép.
Đáp án: C
Câu 11 [693100]: Cho hình chóp 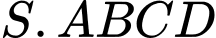 có đáy
có đáy 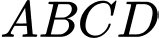 là hình thoi tâm
là hình thoi tâm  Biết rẳng
Biết rẳng  và
và 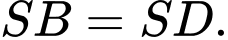 Khẳng định nào sau đây là sai?
Khẳng định nào sau đây là sai?
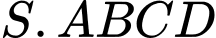 có đáy
có đáy 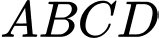 là hình thoi tâm
là hình thoi tâm  Biết rẳng
Biết rẳng  và
và 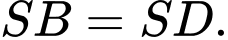 Khẳng định nào sau đây là sai?
Khẳng định nào sau đây là sai? A, 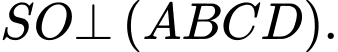
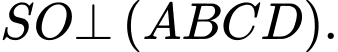
B, 

C, 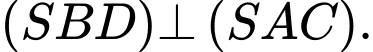
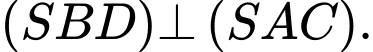
D, 

Chọn đáp án D.
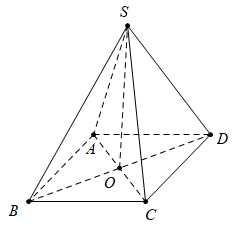
Ta có:
 (do
(do  nên tam
nên tam 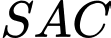 cân tại
cân tại 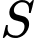 )
)
 (do
(do  nên tam giác
nên tam giác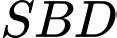 cân tại
cân tại 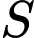 )
)
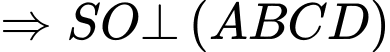
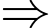 Đáp án A đúng.
Đáp án A đúng.
Ta có: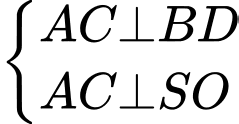
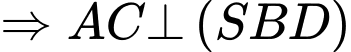

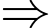 Đáp án B đúng
Đáp án B đúng
Tương tự: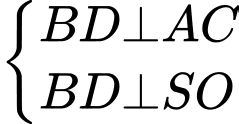
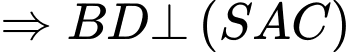
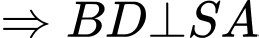
Mà
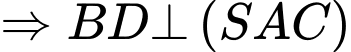

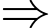 Đáp án C đúng. Đáp án: D
Đáp án C đúng. Đáp án: D

Ta có:
 (do
(do  nên tam
nên tam 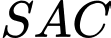 cân tại
cân tại 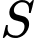 )
) (do
(do  nên tam giác
nên tam giác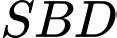 cân tại
cân tại 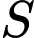 )
)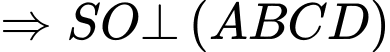
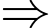 Đáp án A đúng.
Đáp án A đúng.Ta có:
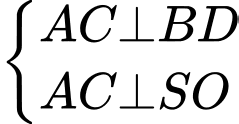
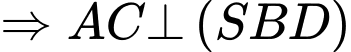

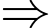 Đáp án B đúng
Đáp án B đúngTương tự:
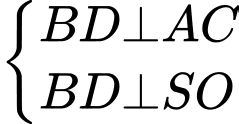
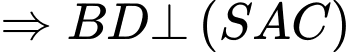
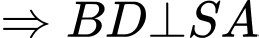
Mà

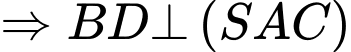

 Đáp án C đúng. Đáp án: D
Đáp án C đúng. Đáp án: D
Câu 12 [807055]: Tìm tập nghiệm 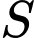 của bất phương trình
của bất phương trình 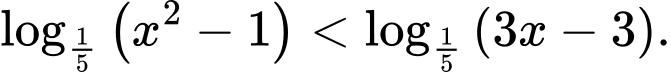
 của bất phương trình
của bất phương trình 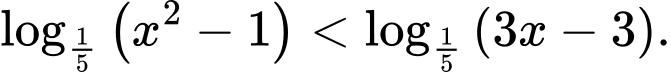
A, 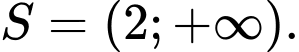
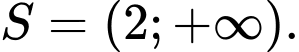
B, 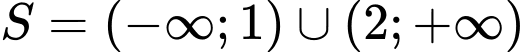 .
.
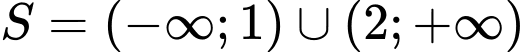 .
.C, 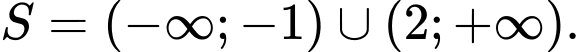
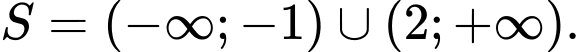
D, 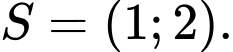
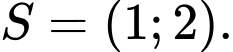
Chọn đáp án A.
Điều kiện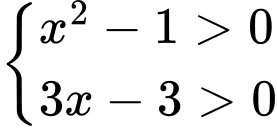
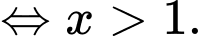
Bất phương trình đưa về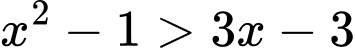
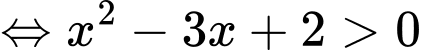
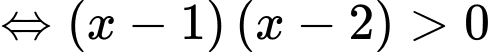
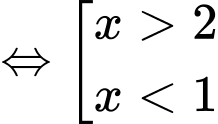
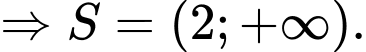 Đáp án: A
Đáp án: A
Điều kiện
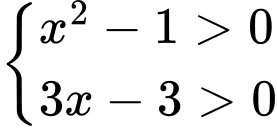
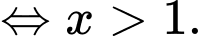
Bất phương trình đưa về
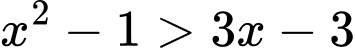
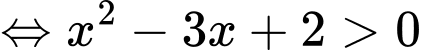
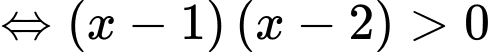
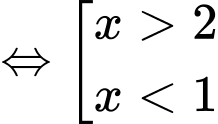
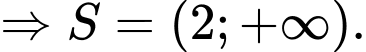 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693102]: Trong không gian với hệ trục tọa độ 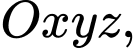 cho các điểm
cho các điểm 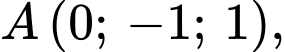
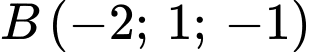 và
và 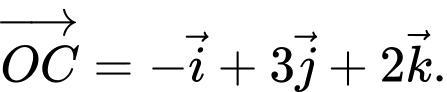
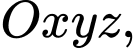 cho các điểm
cho các điểm 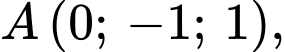
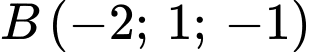 và
và 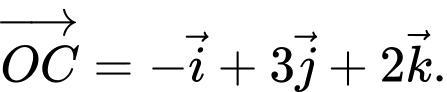
a) Sai.
Ta có: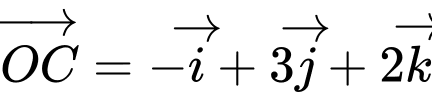
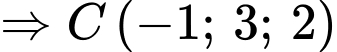
b) Đúng.
Ta có: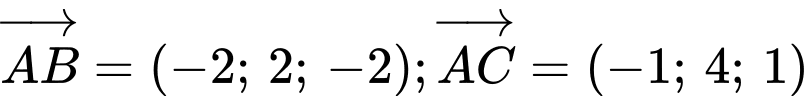
c) Sai.
Ta có: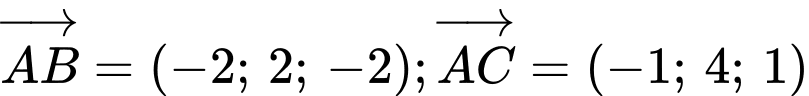
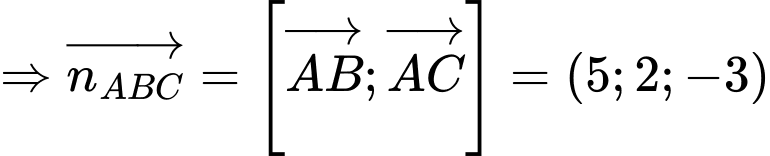
d) Sai.
Phương trình (ABC) khi đó là: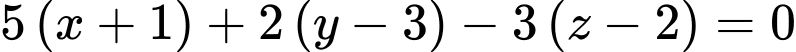
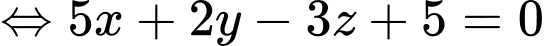
Khoảng cách từ O đến (ABC) là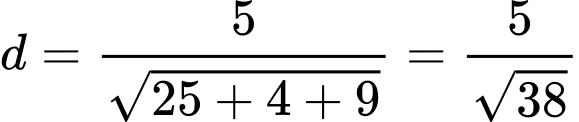
Ta có:
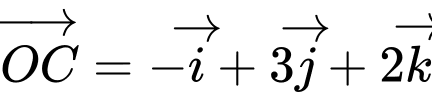
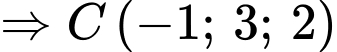
b) Đúng.
Ta có:
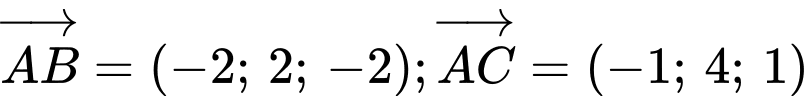
c) Sai.
Ta có:
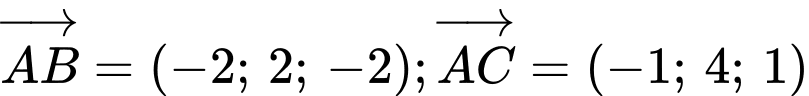
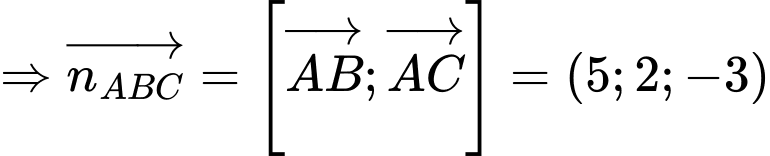
d) Sai.
Phương trình (ABC) khi đó là:
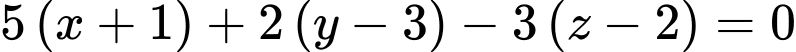
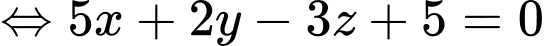
Khoảng cách từ O đến (ABC) là
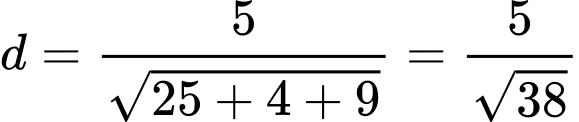
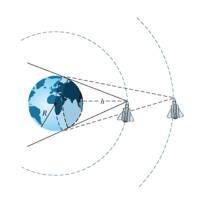
Câu 14 [695176]: Ta coi Trái Đất là hình cầu hoàn hảo với bán kính 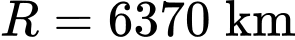 và diện tích toàn phần là
và diện tích toàn phần là 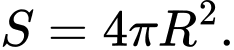 Các phi hành gia từ tàu vũ trụ chỉ có thể nhìn thấy một phần bề mặt Trái Đất. Ở độ cao
Các phi hành gia từ tàu vũ trụ chỉ có thể nhìn thấy một phần bề mặt Trái Đất. Ở độ cao 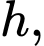 phần diện tích Trái Đất các phi hành gia có thể nhìn thấy sẽ được tính theo công thức
phần diện tích Trái Đất các phi hành gia có thể nhìn thấy sẽ được tính theo công thức 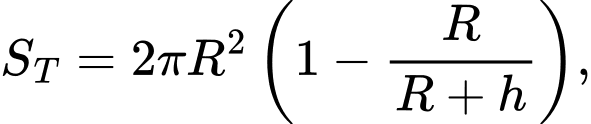 trong đó
trong đó 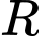 là bán kính Trái Đất. Gọi
là bán kính Trái Đất. Gọi 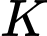 là tỷ số diện tích bề mặt Trái Đất nhìn thấy được ở độ cao
là tỷ số diện tích bề mặt Trái Đất nhìn thấy được ở độ cao 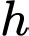 với diện tích toàn phần của Trái Đất.
với diện tích toàn phần của Trái Đất.
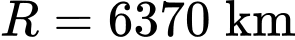 và diện tích toàn phần là
và diện tích toàn phần là 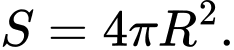 Các phi hành gia từ tàu vũ trụ chỉ có thể nhìn thấy một phần bề mặt Trái Đất. Ở độ cao
Các phi hành gia từ tàu vũ trụ chỉ có thể nhìn thấy một phần bề mặt Trái Đất. Ở độ cao 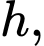 phần diện tích Trái Đất các phi hành gia có thể nhìn thấy sẽ được tính theo công thức
phần diện tích Trái Đất các phi hành gia có thể nhìn thấy sẽ được tính theo công thức 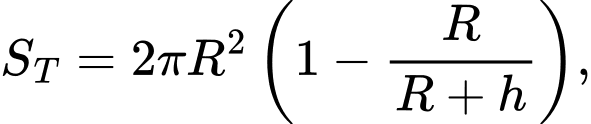 trong đó
trong đó 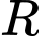 là bán kính Trái Đất. Gọi
là bán kính Trái Đất. Gọi 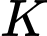 là tỷ số diện tích bề mặt Trái Đất nhìn thấy được ở độ cao
là tỷ số diện tích bề mặt Trái Đất nhìn thấy được ở độ cao 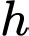 với diện tích toàn phần của Trái Đất.
với diện tích toàn phần của Trái Đất. 
a) Sai.
Ta có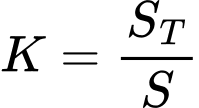
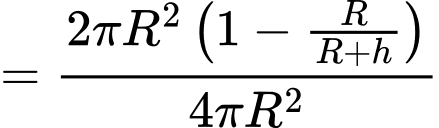
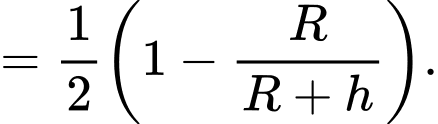
b) Sai.
Ở độ cao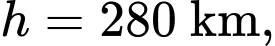 tỉ lệ diện tích bề mặt Trái Đất có thể nhìn thấy là
tỉ lệ diện tích bề mặt Trái Đất có thể nhìn thấy là
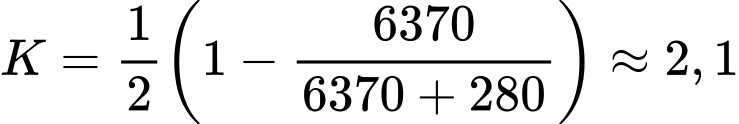
c) Sai.
Muốn nhìn thấy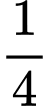 diện tích bề mặt Trái Đất thì
diện tích bề mặt Trái Đất thì 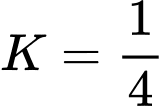
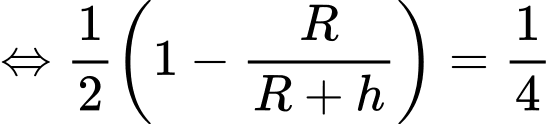
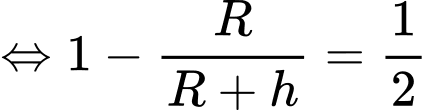
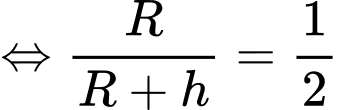
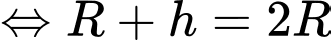
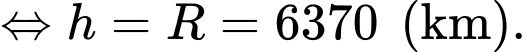
d) Đúng.
+) Ta có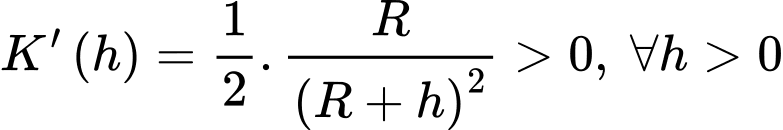
Suy ra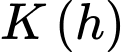 là đồng biến trên khoảng
là đồng biến trên khoảng 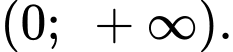
Nên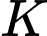 luôn tăng khi
luôn tăng khi 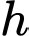 tăng.
tăng.
+) Ta có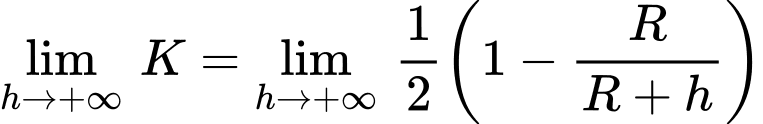
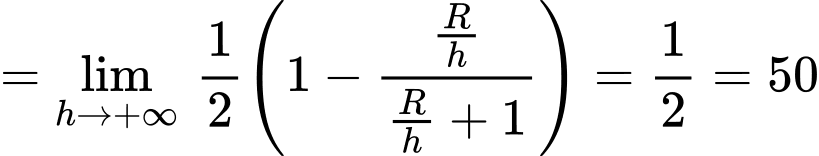
Vậy khi độ cao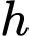 càng tăng lên thì
càng tăng lên thì 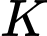 càng tăng nhưng không vượt quá
càng tăng nhưng không vượt quá 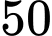
Ta có
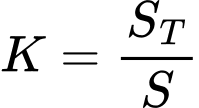
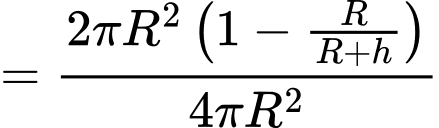
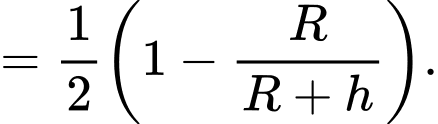
b) Sai.
Ở độ cao
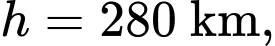 tỉ lệ diện tích bề mặt Trái Đất có thể nhìn thấy là
tỉ lệ diện tích bề mặt Trái Đất có thể nhìn thấy là 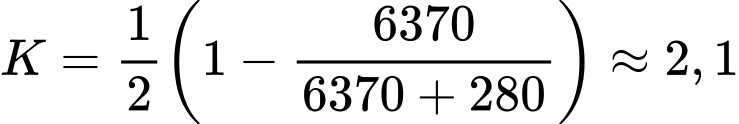
c) Sai.
Muốn nhìn thấy
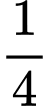 diện tích bề mặt Trái Đất thì
diện tích bề mặt Trái Đất thì 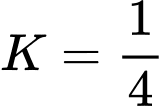
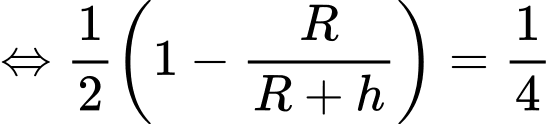
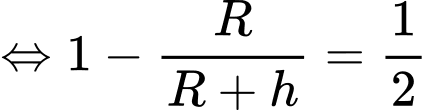
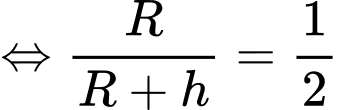
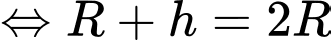
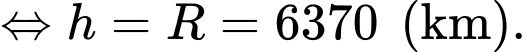
d) Đúng.
+) Ta có
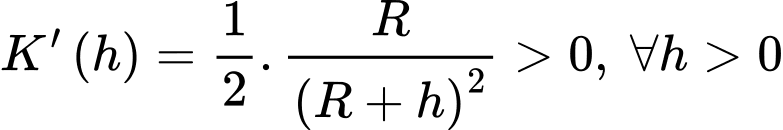
Suy ra
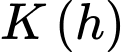 là đồng biến trên khoảng
là đồng biến trên khoảng 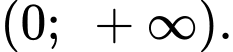
Nên
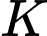 luôn tăng khi
luôn tăng khi 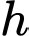 tăng.
tăng.+) Ta có
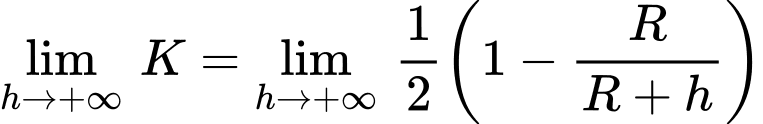
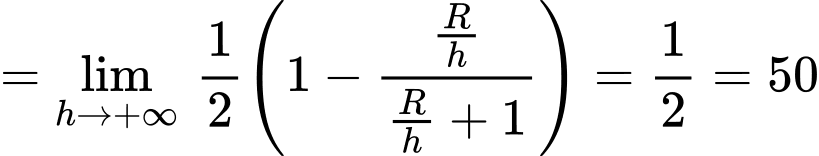
Vậy khi độ cao
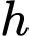 càng tăng lên thì
càng tăng lên thì 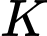 càng tăng nhưng không vượt quá
càng tăng nhưng không vượt quá 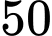
Câu 15 [693103]: Tốc độ trao đổi chất cơ bản của sinh vật có thể tăng hoặc giảm tùy thuộc vào hoạt động của sinh vật. Cụ thể, sau khi hấp thụ chất dinh dưỡng, sinh vật thường trải qua một sự tăng đột biến trong tốc độ trao đổi chất của nó, sau đó dần dần trở lại mức cơ bản.
Linh vừa kết thúc bữa tối trong buổi sinh nhật của mình với năng lượng nạp vào là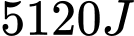 và tốc độ trao đổi chất của cô đã tăng đột biến từ mức cơ bản
và tốc độ trao đổi chất của cô đã tăng đột biến từ mức cơ bản 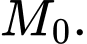 Sau đó cô đã tiêu hao hết năng lượng đó trong 12 giờ tiếp theo. Giả sử
Sau đó cô đã tiêu hao hết năng lượng đó trong 12 giờ tiếp theo. Giả sử 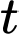 giờ sau bữa ăn Linh tiêu hao được
giờ sau bữa ăn Linh tiêu hao được 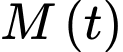
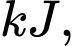 tốc độ trao đổi chất của cô được cho bởi hàm số
tốc độ trao đổi chất của cô được cho bởi hàm số 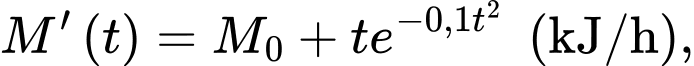
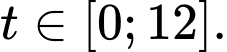
Linh vừa kết thúc bữa tối trong buổi sinh nhật của mình với năng lượng nạp vào là
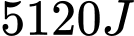 và tốc độ trao đổi chất của cô đã tăng đột biến từ mức cơ bản
và tốc độ trao đổi chất của cô đã tăng đột biến từ mức cơ bản 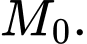 Sau đó cô đã tiêu hao hết năng lượng đó trong 12 giờ tiếp theo. Giả sử
Sau đó cô đã tiêu hao hết năng lượng đó trong 12 giờ tiếp theo. Giả sử 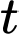 giờ sau bữa ăn Linh tiêu hao được
giờ sau bữa ăn Linh tiêu hao được 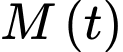
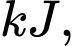 tốc độ trao đổi chất của cô được cho bởi hàm số
tốc độ trao đổi chất của cô được cho bởi hàm số 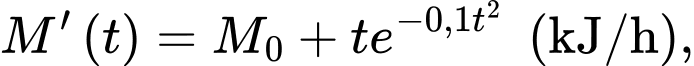
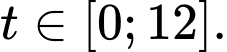
a) Đúng.
Ta có công thức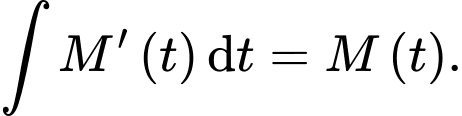
Nên để kiểm tra tính đúng sai của phần a), thay vì nguyên hàm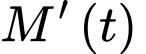 ta sẽ đạo hàm
ta sẽ đạo hàm 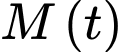 và
và
kiểm tra xem nó có đúng bằng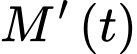 đã được cho ở đề bài không.
đã được cho ở đề bài không.
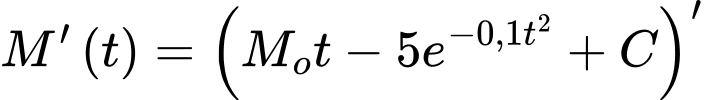
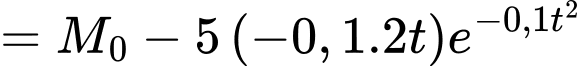
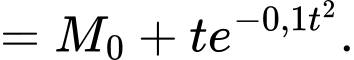
Vậy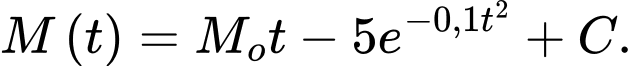
b) Đúng.
Vì sau 0 giờ thì Linh tiêu hao được 0 kJ nên a có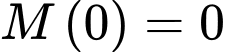
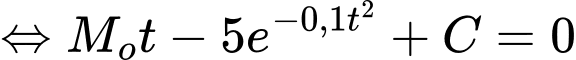
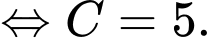
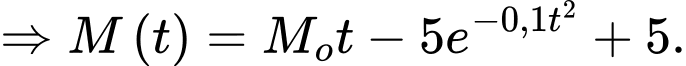
Theo giả thiết, ta có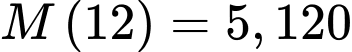
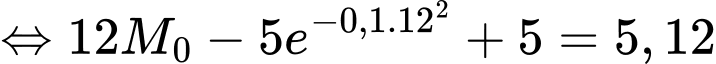
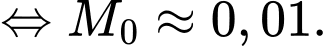
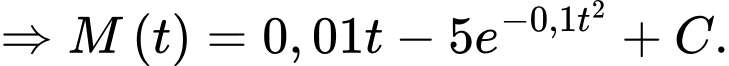
c) Đúng.
Năng lượng Linh tiêu hao sau 6 giờ đầu là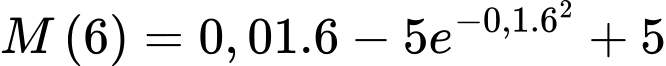
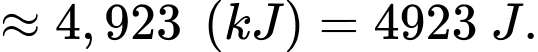
Vậy năng lượng còn lại sau 6 giờ đầu bằng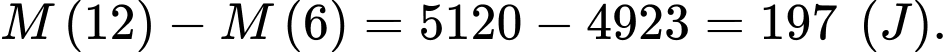
d) Sai.
Tốc độ tiêu hao năng lượng trung bình từ 6 giờ đến 12 giờ của Linh là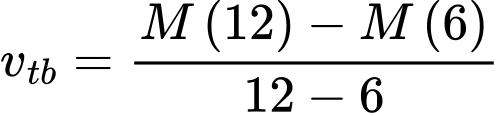
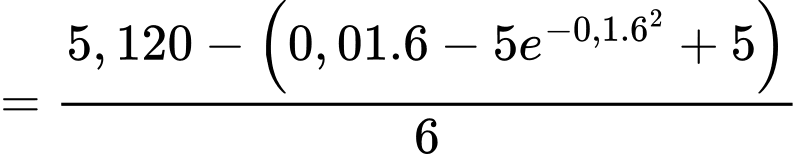
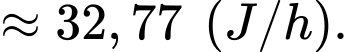
Ta có công thức
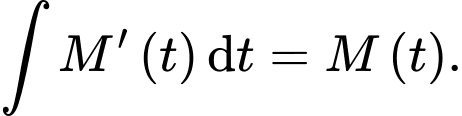
Nên để kiểm tra tính đúng sai của phần a), thay vì nguyên hàm
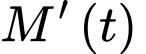 ta sẽ đạo hàm
ta sẽ đạo hàm 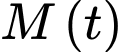 và
và kiểm tra xem nó có đúng bằng
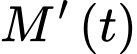 đã được cho ở đề bài không.
đã được cho ở đề bài không.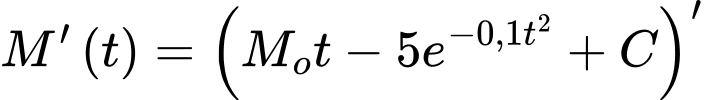
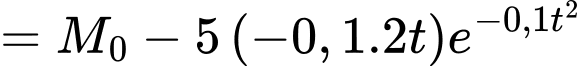
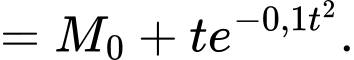
Vậy
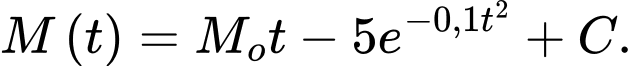
b) Đúng.
Vì sau 0 giờ thì Linh tiêu hao được 0 kJ nên a có
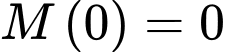
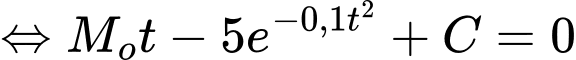
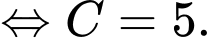
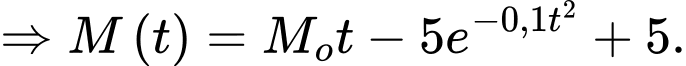
Theo giả thiết, ta có
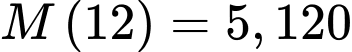
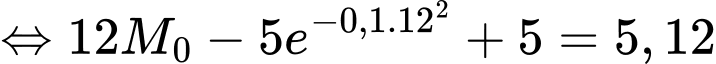
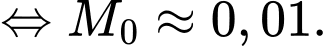
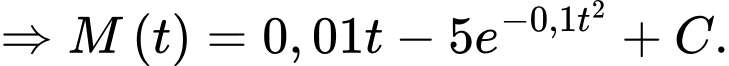
c) Đúng.
Năng lượng Linh tiêu hao sau 6 giờ đầu là
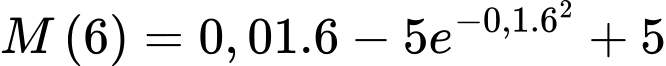
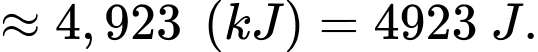
Vậy năng lượng còn lại sau 6 giờ đầu bằng
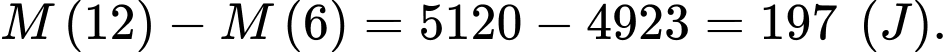
d) Sai.
Tốc độ tiêu hao năng lượng trung bình từ 6 giờ đến 12 giờ của Linh là
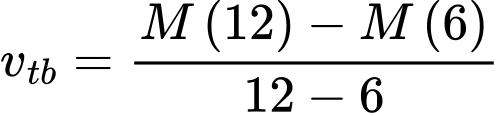
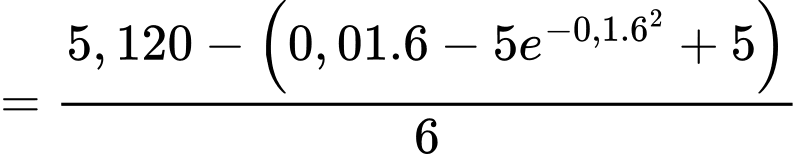
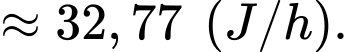
Câu 16 [693105]: Ở một khu rừng nọ có 7 chú lùn, trong đó có 5 chú luôn nói thật, 2 chú còn lại nói thật với xác suất 0,5. Một nàng Bạch Tuyết lạc vào trong rừng và gặp một chú lùn
Gọi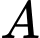 là biến cố: “Chú lùn gặp được luôn nói thật”
là biến cố: “Chú lùn gặp được luôn nói thật”
Gọi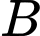 là biến cố: “Chú lùn đó tự nhận mình luôn nói thật”
là biến cố: “Chú lùn đó tự nhận mình luôn nói thật”
Gọi
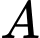 là biến cố: “Chú lùn gặp được luôn nói thật”
là biến cố: “Chú lùn gặp được luôn nói thật”Gọi
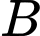 là biến cố: “Chú lùn đó tự nhận mình luôn nói thật”
là biến cố: “Chú lùn đó tự nhận mình luôn nói thật”
a) Đúng.
Ta có: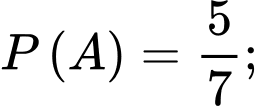
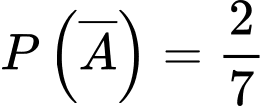
b) Sai.
Xác xuất có điều kiện
Ta có sơ đồ cây sau:
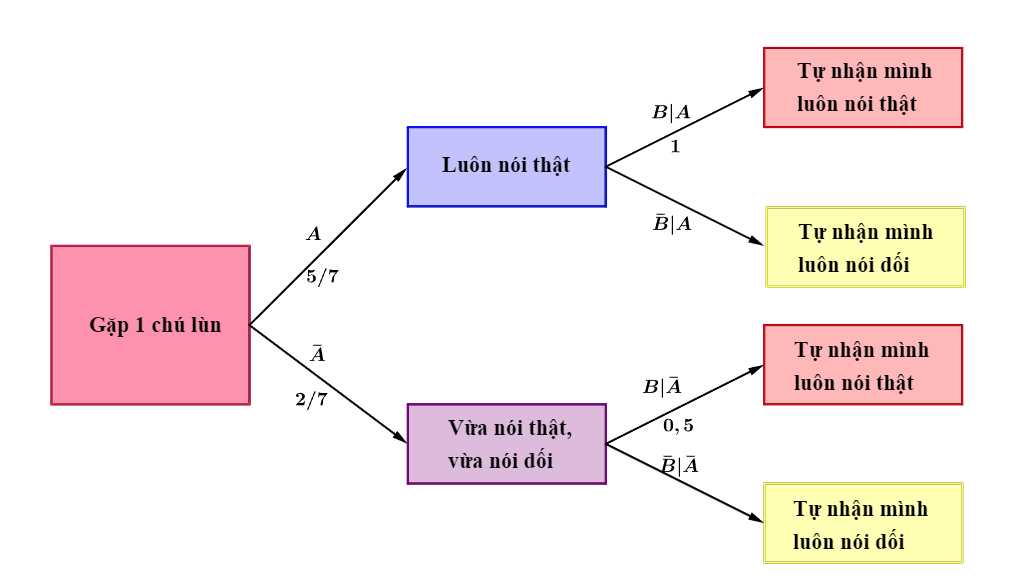
c) Đúng.
Ta có: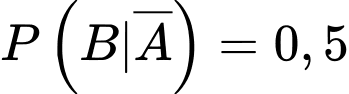
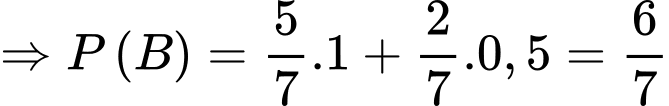
d) Đúng.
Áp dụng Bayes, ta có:
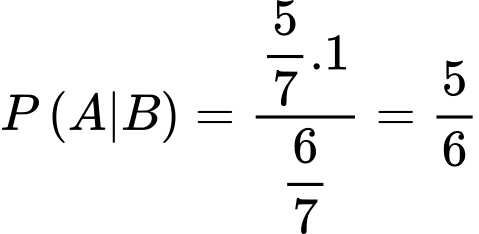
Ta có:
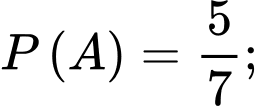
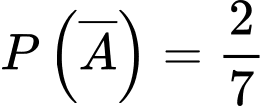
b) Sai.
Xác xuất có điều kiện

Ta có sơ đồ cây sau:

c) Đúng.
Ta có:
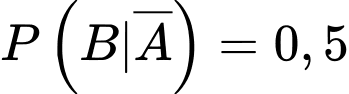
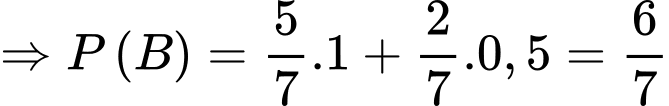
d) Đúng.
Áp dụng Bayes, ta có:
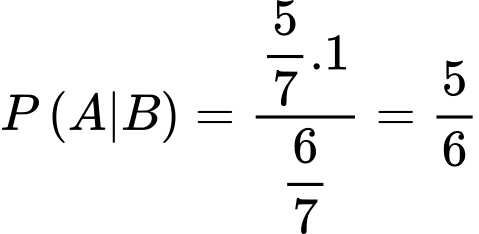
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693106]: Cho hình chóp đều 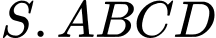 có cạnh đáy bằng
có cạnh đáy bằng 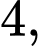 khoảng cách giữa hai đường thẳng
khoảng cách giữa hai đường thẳng 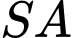 và
và 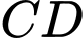 bằng
bằng 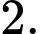 Thể tích của khối chóp
Thể tích của khối chóp 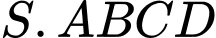 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
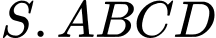 có cạnh đáy bằng
có cạnh đáy bằng 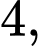 khoảng cách giữa hai đường thẳng
khoảng cách giữa hai đường thẳng 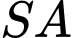 và
và 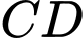 bằng
bằng 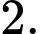 Thể tích của khối chóp
Thể tích của khối chóp 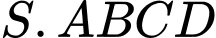 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 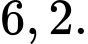
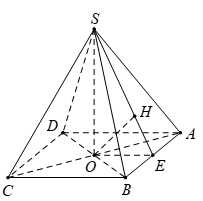
Gọi là tâm hình vuông
là tâm hình vuông 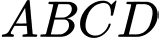
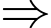
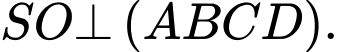
Ta có
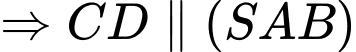
Suy ra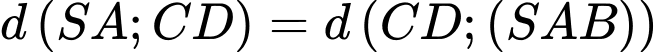
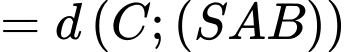
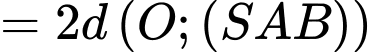
Mà
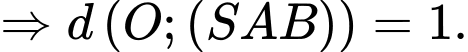
Từ kẻ
kẻ  (
(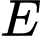 là trung điểm
là trung điểm  ),
),  (tham khảo hình vẽ)
(tham khảo hình vẽ)
Suy ra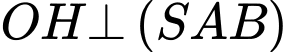
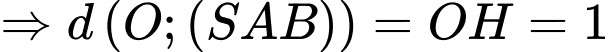
Tam giác vuông tại
vuông tại  có
có 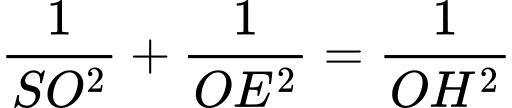
Do đó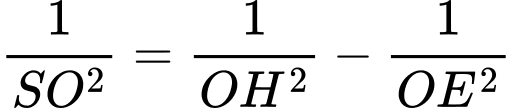
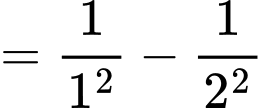
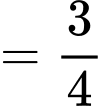
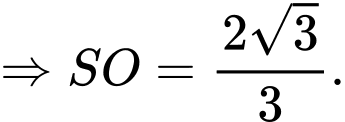
Vậy thể tích khối chóp đã cho là
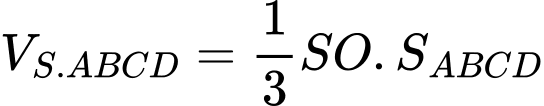
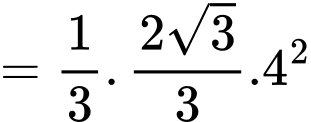
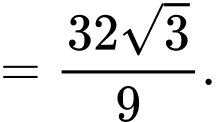
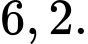

Gọi
 là tâm hình vuông
là tâm hình vuông 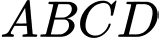
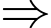
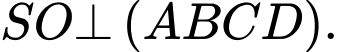
Ta có

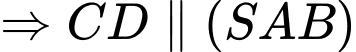
Suy ra
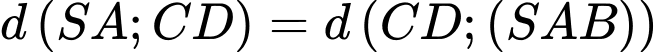
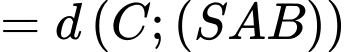
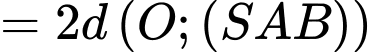
Mà

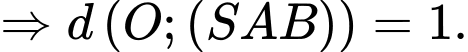
Từ
 kẻ
kẻ  (
(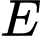 là trung điểm
là trung điểm  ),
),  (tham khảo hình vẽ)
(tham khảo hình vẽ)Suy ra
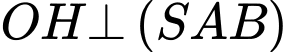
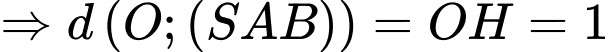
Tam giác
 vuông tại
vuông tại  có
có 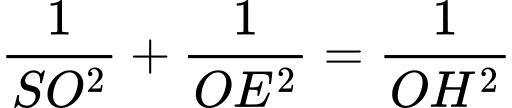
Do đó
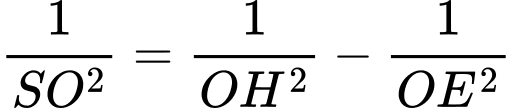
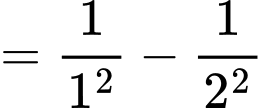
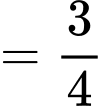
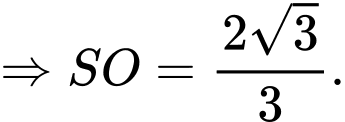
Vậy thể tích khối chóp đã cho là
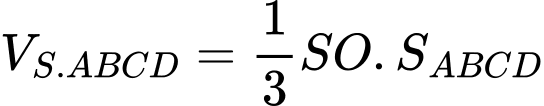
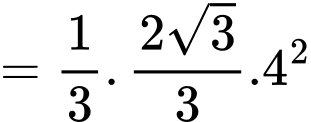
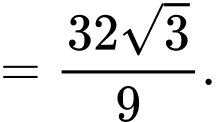
Câu 18 [693110]: Một xạ thủ bắn hai viên đạn vào một bia. Xác suất bắn trúng viên thứ nhất là 0,7. Nếu bắn trúng viên thứ nhất thì khả năng bắn trúng viên thứ hai là 0,8, nhưng nếu bắn trượt viên thứ nhất thì sẽ bị tâm lí dẫn đến khả năng bắn trúng viên thứ hai chỉ còn 0,3. Biết rằng viên thứ hai xạ thủ bắn trúng, xác suất xạ thủ bắn trúng viên thứ nhất là bao nhiêu % (làm tròn kết quả đến hàng phần chục).


Điền đáp án: 
Gọi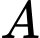 là biến cố bắn viên thứ nhất trúng
là biến cố bắn viên thứ nhất trúng
Ta có: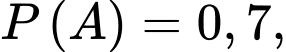
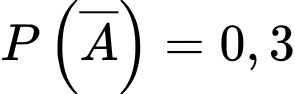
Gọi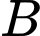 là biến cố bắn viên thứ hai trúng:
là biến cố bắn viên thứ hai trúng: 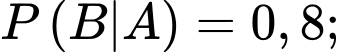
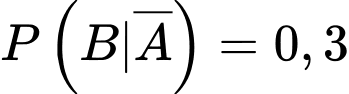
Ta có sơ đồ cây sau:
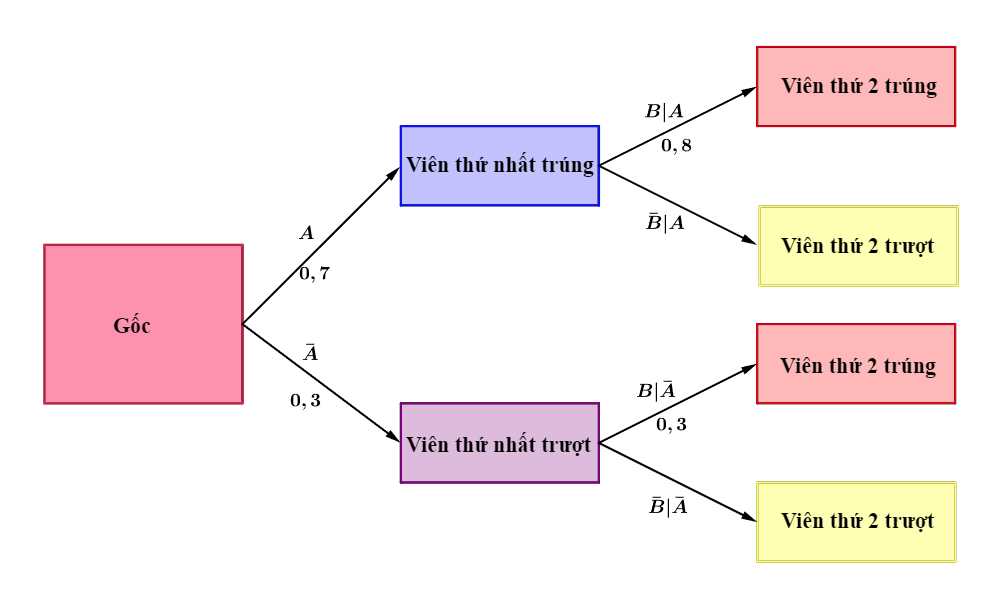
Áp dụng công thức xác suất toàn phần ta có:
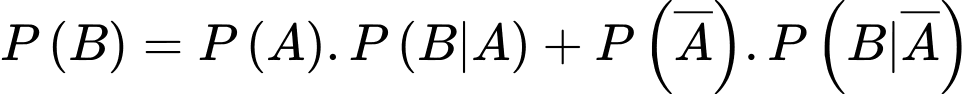
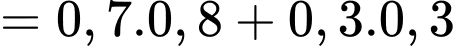
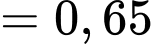
Xác suất viên thứ nhất trúng khi viên thứ hai bắn trúng là
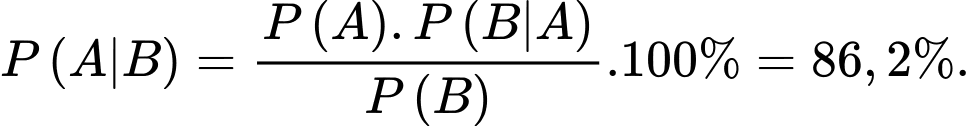
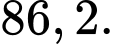
Gọi
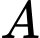 là biến cố bắn viên thứ nhất trúng
là biến cố bắn viên thứ nhất trúng Ta có:
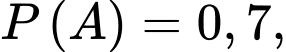
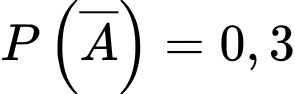
Gọi
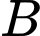 là biến cố bắn viên thứ hai trúng:
là biến cố bắn viên thứ hai trúng: 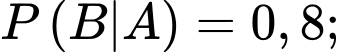
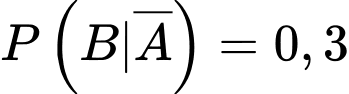
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần ta có:
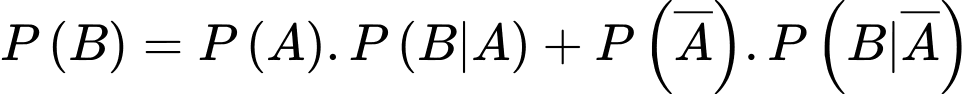
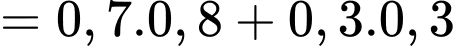
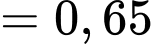
Xác suất viên thứ nhất trúng khi viên thứ hai bắn trúng là
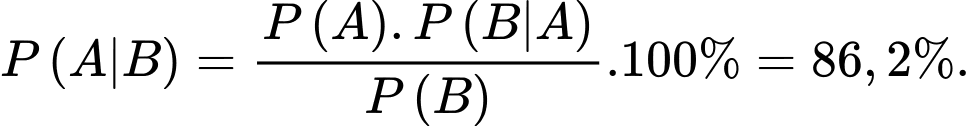
Câu 19 [694291]: Một con bọ di chuyển từ điểm A đến điểm B dọc theo các đoạn thẳng trong mạng lưới lục giác như hình bên dưới.
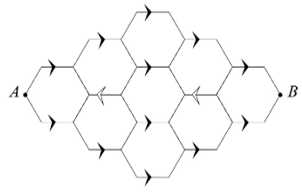
Các đoạn thẳng có dấu mũi tên chỉ được di chuyển theo hướng của mũi tên và con bọ không bao giờ di chuyển trên cùng một đoạn thẳng quá một lần. Vậy con bọ có bao nhiêu con đường khác nhau từ A đến B?

Các đoạn thẳng có dấu mũi tên chỉ được di chuyển theo hướng của mũi tên và con bọ không bao giờ di chuyển trên cùng một đoạn thẳng quá một lần. Vậy con bọ có bao nhiêu con đường khác nhau từ A đến B?
Điền đáp án : 
Cách 1:
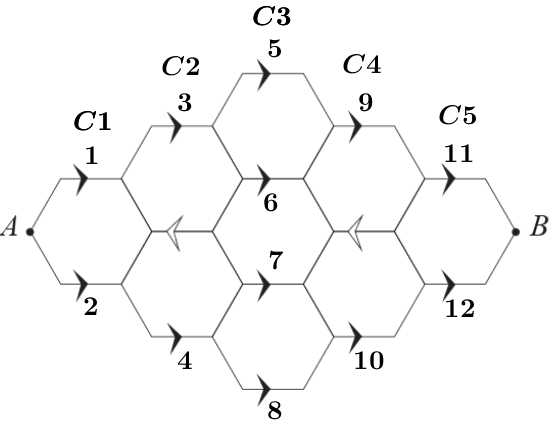
Từ A có 2 cách đến C1:
• Từ A có 1 cách đến mũi tên số 1.
• Từ A có 1 cách đến mũi tên số 2.
Từ C1 có 5 cách đến C3:
Không mất tính tổng quát giả sử đi từ C1 mũi tên số 1 đến C3 mũi tên số 6 hoặc mũi tên số 7.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6.
• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7.
 Từ C1 có 5 cách đến C3.
Từ C1 có 5 cách đến C3.
Từ C3 có 5 cách đến C5:
Không mất tính tổng quát giả sử đi từ C3 mũi tên số 5 đến C5 mũi tên số 11 hoặc mũi tên số 12.
• Từ mũi tên số 5 có 2 cách để đi đến mũi tên số 11.
• Từ mũi tên số 5 có 3 cách để đi đến mũi tên số 11.
 Từ C3 có 5 cách đến C5.
Từ C3 có 5 cách đến C5.
Từ C5 có 2 cách đến B:
• Từ mũi tên số 11 có 1 cách đến B.
• Từ mũi tên số 12 có 1 cách đến B.
Vậy có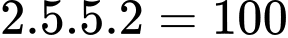 cách đi từ A đến B.
cách đi từ A đến B.
Cách 2:
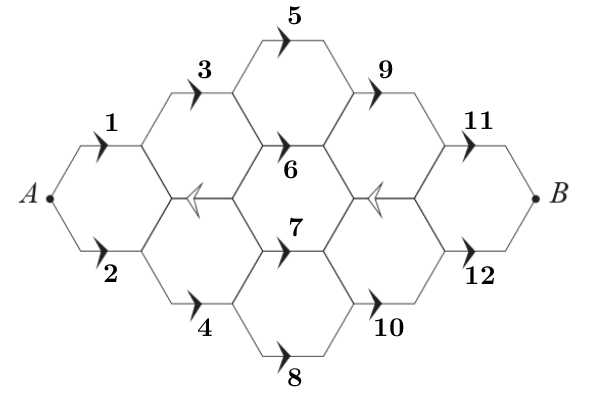
Từ A có 1 cách đi đến mũi tên 1.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 5, từ mũi tên số 5 có 2 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B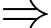 Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 11 và B có 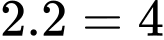 cách.
cách.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6, từ mũi tên số 6 có 2 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B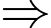 Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 11 và B có 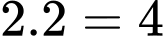 cách.
cách.
• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7, từ mũi tên số 7 có 3 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B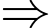 Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 11 và B có 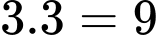 cách.
cách.
• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 8, từ mũi tên số 8 có 3 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B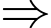 Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 11 và B có 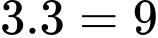 cách.
cách.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 5, từ mũi tên số 5 có 3 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B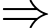 Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 12 và B có 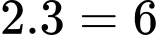 cách.
cách.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6, từ mũi tên số 6 có 3 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B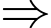 Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 12 và B có 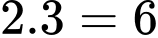 cách.
cách.
• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7, từ mũi tên số 7 có 2 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B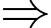 Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 12 và B có 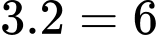 cách.
cách.
• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 8, từ mũi tên số 8 có 2 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B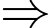 Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 12 và B có 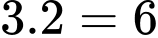 cách.
cách.
Do đó, từ mũi tên 1 có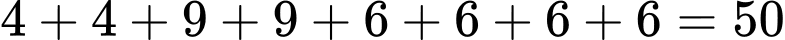 cách đi đến B.
cách đi đến B.
Tương tự, từ A có 1 cách đi đến mũi tên 2 và từ mũi tên 2 có 50 cách đi đến B.
Vậy từ A có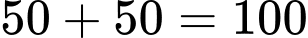 cách đi đến B.
cách đi đến B.
Cách 1:

Từ A có 2 cách đến C1:
• Từ A có 1 cách đến mũi tên số 1.
• Từ A có 1 cách đến mũi tên số 2.
Từ C1 có 5 cách đến C3:
Không mất tính tổng quát giả sử đi từ C1 mũi tên số 1 đến C3 mũi tên số 6 hoặc mũi tên số 7.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6.
• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7.
 Từ C1 có 5 cách đến C3.
Từ C1 có 5 cách đến C3. Từ C3 có 5 cách đến C5:
Không mất tính tổng quát giả sử đi từ C3 mũi tên số 5 đến C5 mũi tên số 11 hoặc mũi tên số 12.
• Từ mũi tên số 5 có 2 cách để đi đến mũi tên số 11.
• Từ mũi tên số 5 có 3 cách để đi đến mũi tên số 11.
 Từ C3 có 5 cách đến C5.
Từ C3 có 5 cách đến C5.Từ C5 có 2 cách đến B:
• Từ mũi tên số 11 có 1 cách đến B.
• Từ mũi tên số 12 có 1 cách đến B.
Vậy có
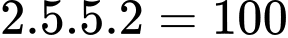 cách đi từ A đến B.
cách đi từ A đến B. Cách 2:

Từ A có 1 cách đi đến mũi tên 1.
• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 5, từ mũi tên số 5 có 2 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
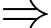 Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 11 và B có 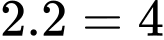 cách.
cách.• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6, từ mũi tên số 6 có 2 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
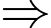 Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 11 và B có 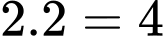 cách.
cách.• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7, từ mũi tên số 7 có 3 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
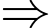 Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 11 và B có 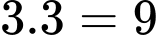 cách.
cách.• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 8, từ mũi tên số 8 có 3 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
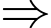 Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 11 và B có
Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 11 và B có 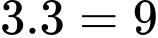 cách.
cách.• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 5, từ mũi tên số 5 có 3 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
 Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 12 và B có 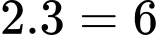 cách.
cách.• Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6, từ mũi tên số 6 có 3 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
 Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 12 và B có 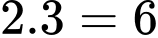 cách.
cách.• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7, từ mũi tên số 7 có 2 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
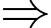 Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 12 và B có 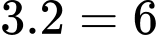 cách.
cách.• Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 8, từ mũi tên số 8 có 2 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
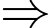 Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 12 và B có
Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 12 và B có 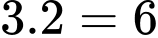 cách.
cách.Do đó, từ mũi tên 1 có
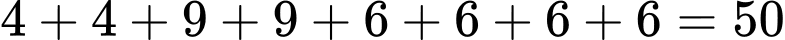 cách đi đến B.
cách đi đến B. Tương tự, từ A có 1 cách đi đến mũi tên 2 và từ mũi tên 2 có 50 cách đi đến B.
Vậy từ A có
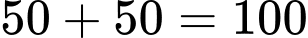 cách đi đến B.
cách đi đến B.
Câu 20 [696446]: Một tấm ván gỗ chỉ được hỗ trợ ở hai đầu  và
và 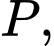 cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục
cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục 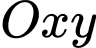 như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình
như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình 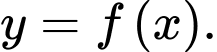
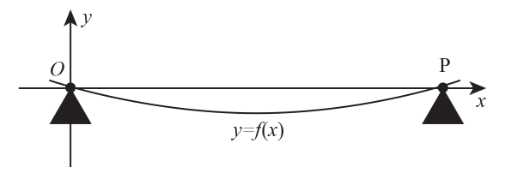
Người ta chứng minh được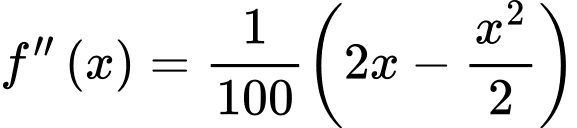 với
với 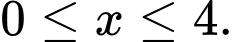 Tại điểm cách điểm
Tại điểm cách điểm 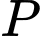 một khoảng 1 mét, tấm ván bị võng xuống bao nhiêu cm? (làm tròn kết quả đến hàng phần trăm).
một khoảng 1 mét, tấm ván bị võng xuống bao nhiêu cm? (làm tròn kết quả đến hàng phần trăm).
 và
và 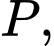 cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục
cách nhau 4 m. Tấm ván võng xuống dưới do trọng lượng của nó tạo thành một đường cong. Xét trên hệ trục 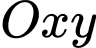 như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình
như hình vẽ dưới, đơn vị mỗi trục là mét, đường cong trong hình vẽ có phương trình 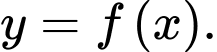

Người ta chứng minh được
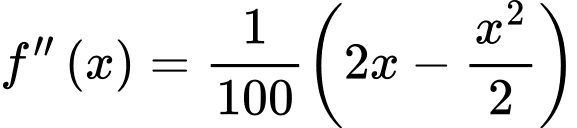 với
với 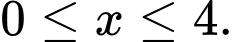 Tại điểm cách điểm
Tại điểm cách điểm 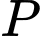 một khoảng 1 mét, tấm ván bị võng xuống bao nhiêu cm? (làm tròn kết quả đến hàng phần trăm).
một khoảng 1 mét, tấm ván bị võng xuống bao nhiêu cm? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 2,38.
Ta có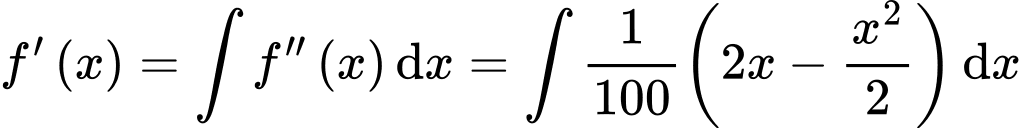
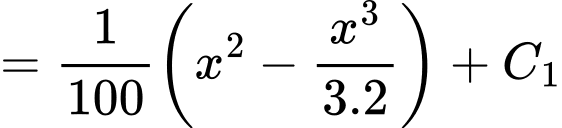
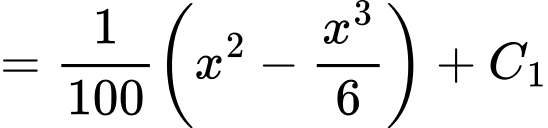
Suy ra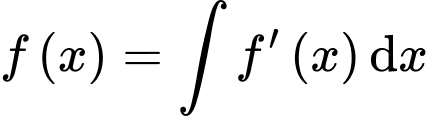
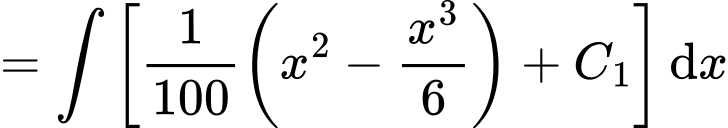
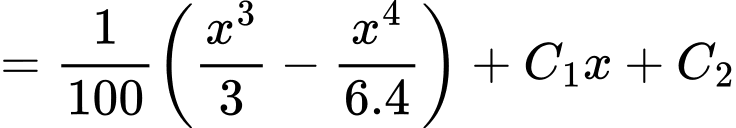
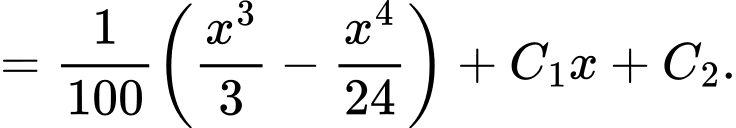
Dựa vào hình vẽ ta có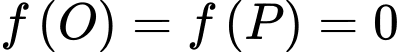
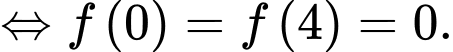
Từ đó ta có hệ phương trình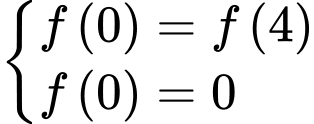
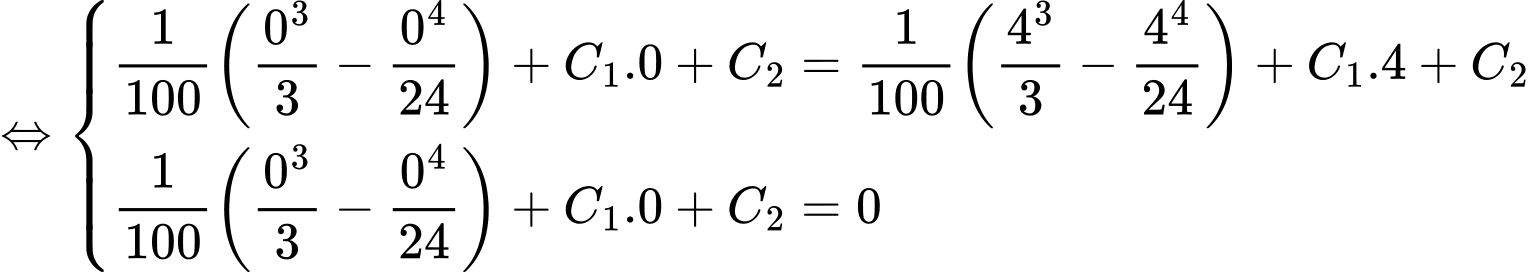
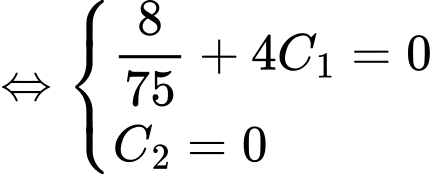
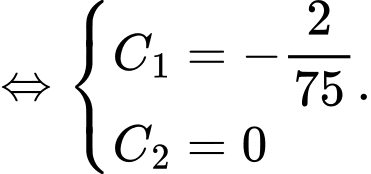
Suy ra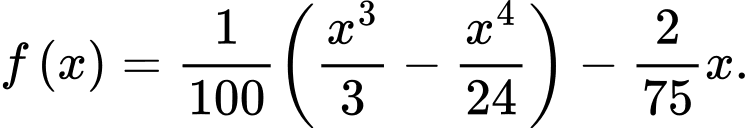
Tại điểm cách điểm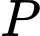 một khoảng 1 mét tức
một khoảng 1 mét tức 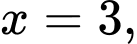 ta có tấm ván bị võng xuống số mét là
ta có tấm ván bị võng xuống số mét là 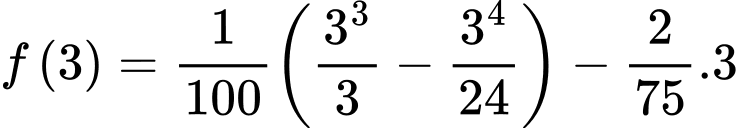
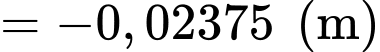
Vậy tấm ván vị võng xuống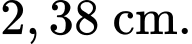
Ta có
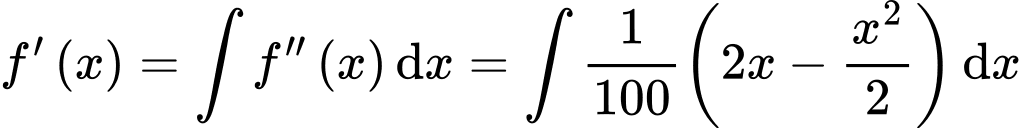
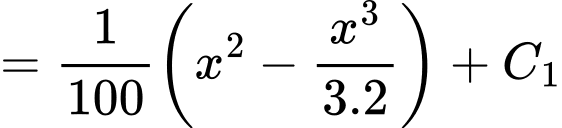
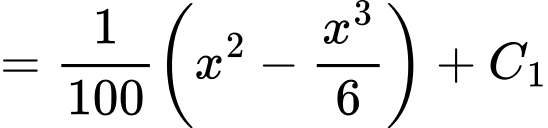
Suy ra
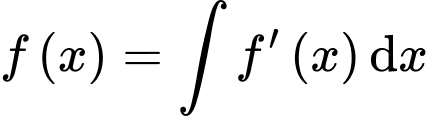
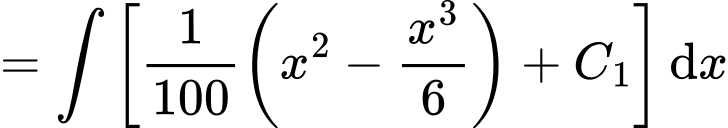
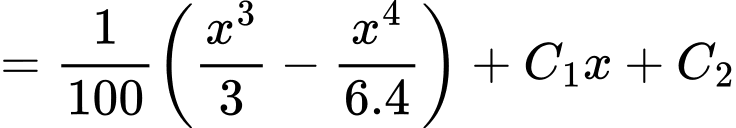
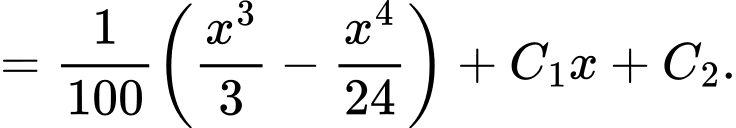
Dựa vào hình vẽ ta có
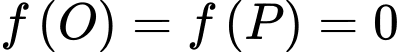
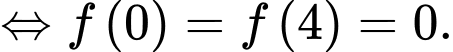
Từ đó ta có hệ phương trình
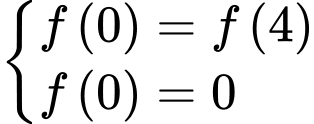
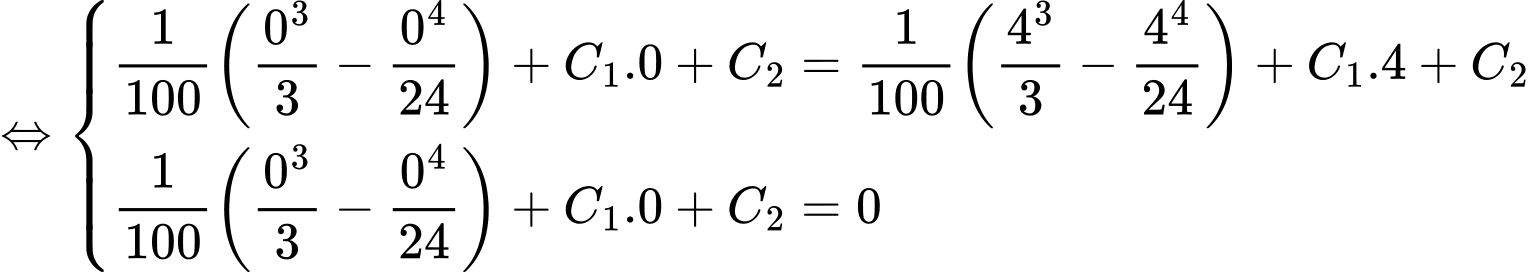
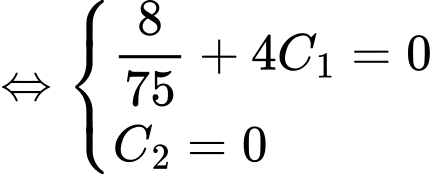
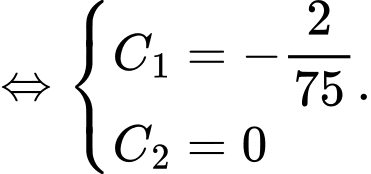
Suy ra
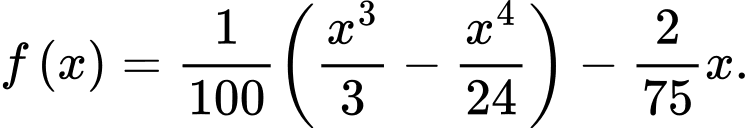
Tại điểm cách điểm
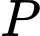 một khoảng 1 mét tức
một khoảng 1 mét tức 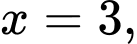 ta có tấm ván bị võng xuống số mét là
ta có tấm ván bị võng xuống số mét là 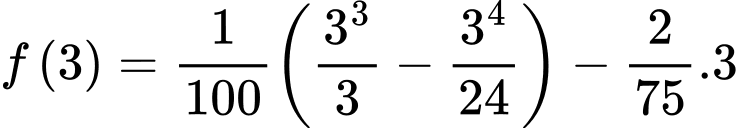
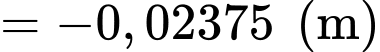
Vậy tấm ván vị võng xuống
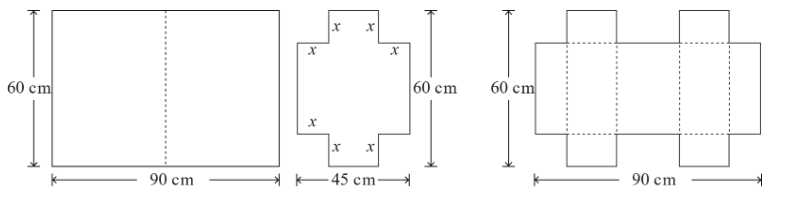
Câu 21 [699672]: Một tấm bìa cứng có kích thước  được gấp đôi thành một hình chữ nhật
được gấp đôi thành một hình chữ nhật  như hình vẽ. Sau đó, cắt ra từ các góc của hình chữ nhật vừa gấp bốn hình vuông bằng nhau có cạnh
như hình vẽ. Sau đó, cắt ra từ các góc của hình chữ nhật vừa gấp bốn hình vuông bằng nhau có cạnh 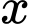 (cm). Tấm bìa được mở ra và sáu mép được gấp lên để tạo thành một hộp chữ nhật (H) có nắp và đáy (như hình vẽ). Thể tích lớn nhất của khối (H) bằng bao nhiêu lít? Làm tròn đến hàng phần mười.
(cm). Tấm bìa được mở ra và sáu mép được gấp lên để tạo thành một hộp chữ nhật (H) có nắp và đáy (như hình vẽ). Thể tích lớn nhất của khối (H) bằng bao nhiêu lít? Làm tròn đến hàng phần mười.
 được gấp đôi thành một hình chữ nhật
được gấp đôi thành một hình chữ nhật  như hình vẽ. Sau đó, cắt ra từ các góc của hình chữ nhật vừa gấp bốn hình vuông bằng nhau có cạnh
như hình vẽ. Sau đó, cắt ra từ các góc của hình chữ nhật vừa gấp bốn hình vuông bằng nhau có cạnh 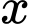 (cm). Tấm bìa được mở ra và sáu mép được gấp lên để tạo thành một hộp chữ nhật (H) có nắp và đáy (như hình vẽ). Thể tích lớn nhất của khối (H) bằng bao nhiêu lít? Làm tròn đến hàng phần mười.
(cm). Tấm bìa được mở ra và sáu mép được gấp lên để tạo thành một hộp chữ nhật (H) có nắp và đáy (như hình vẽ). Thể tích lớn nhất của khối (H) bằng bao nhiêu lít? Làm tròn đến hàng phần mười.
Điền đáp án: 20,5.
Dựa vào hình vẽ, ta có hộp chữ nhật có chiều cao là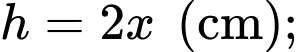 chiều rộng của đáy là
chiều rộng của đáy là 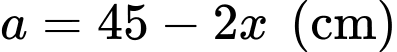 và chiều dài đáy là
và chiều dài đáy là 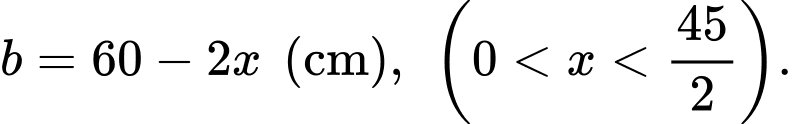
Suy ra thể tích của hình hộp là 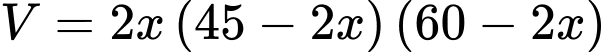
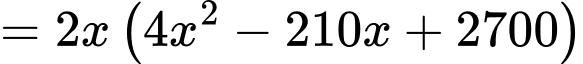

Xét hàm số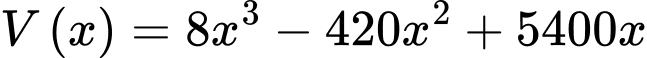 trên khoảng
trên khoảng 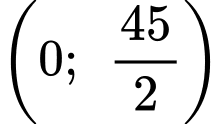
Ta có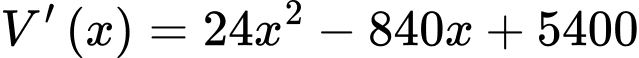
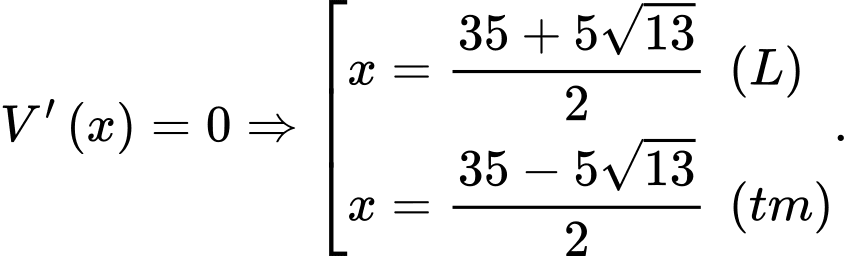
Bảng biến thiên
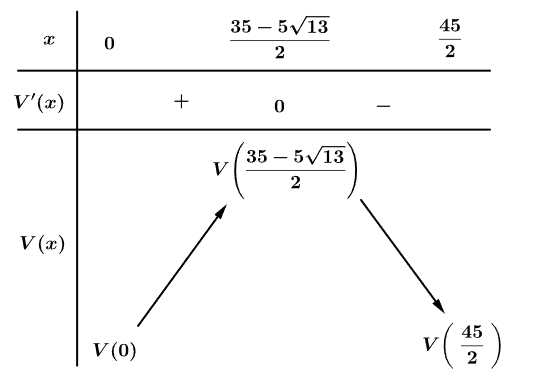
Vậy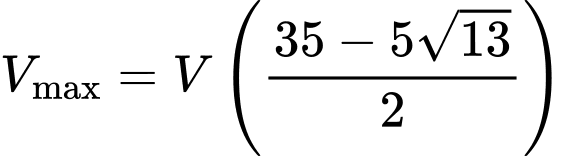

Dựa vào hình vẽ, ta có hộp chữ nhật có chiều cao là
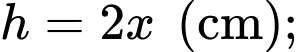 chiều rộng của đáy là
chiều rộng của đáy là 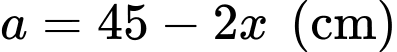 và chiều dài đáy là
và chiều dài đáy là 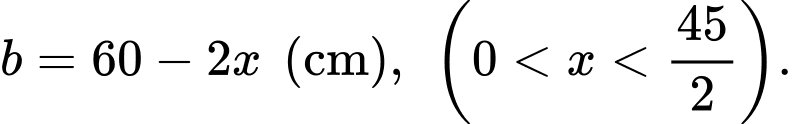
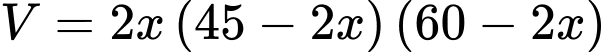
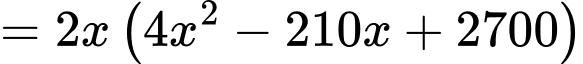

Xét hàm số
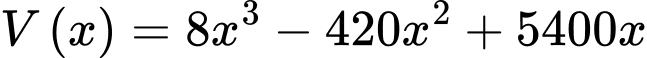 trên khoảng
trên khoảng 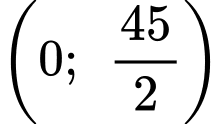
Ta có
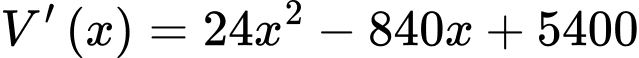
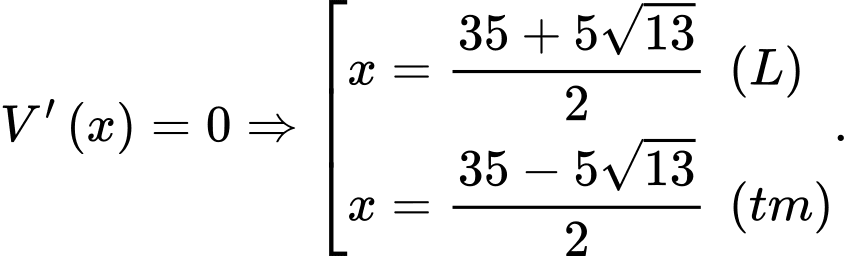
Bảng biến thiên

Vậy
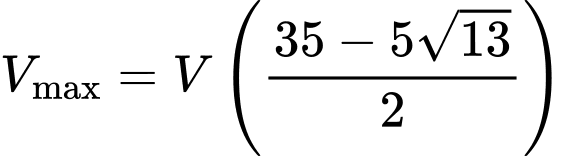

Câu 22 [694727]: Trong không gian 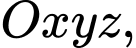 cho hai điểm
cho hai điểm 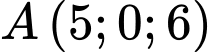 và
và 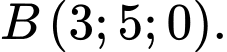 Điểm
Điểm 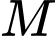 di động trên trục
di động trên trục 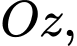 điểm
điểm 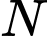 di động trên trục
di động trên trục 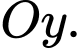 Độ dài đường gấp khúc
Độ dài đường gấp khúc 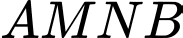 có độ dài nhỏ nhất bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).
có độ dài nhỏ nhất bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).
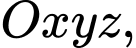 cho hai điểm
cho hai điểm 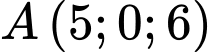 và
và 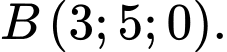 Điểm
Điểm 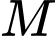 di động trên trục
di động trên trục 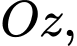 điểm
điểm 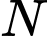 di động trên trục
di động trên trục 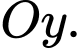 Độ dài đường gấp khúc
Độ dài đường gấp khúc  có độ dài nhỏ nhất bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).
có độ dài nhỏ nhất bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 13,5.
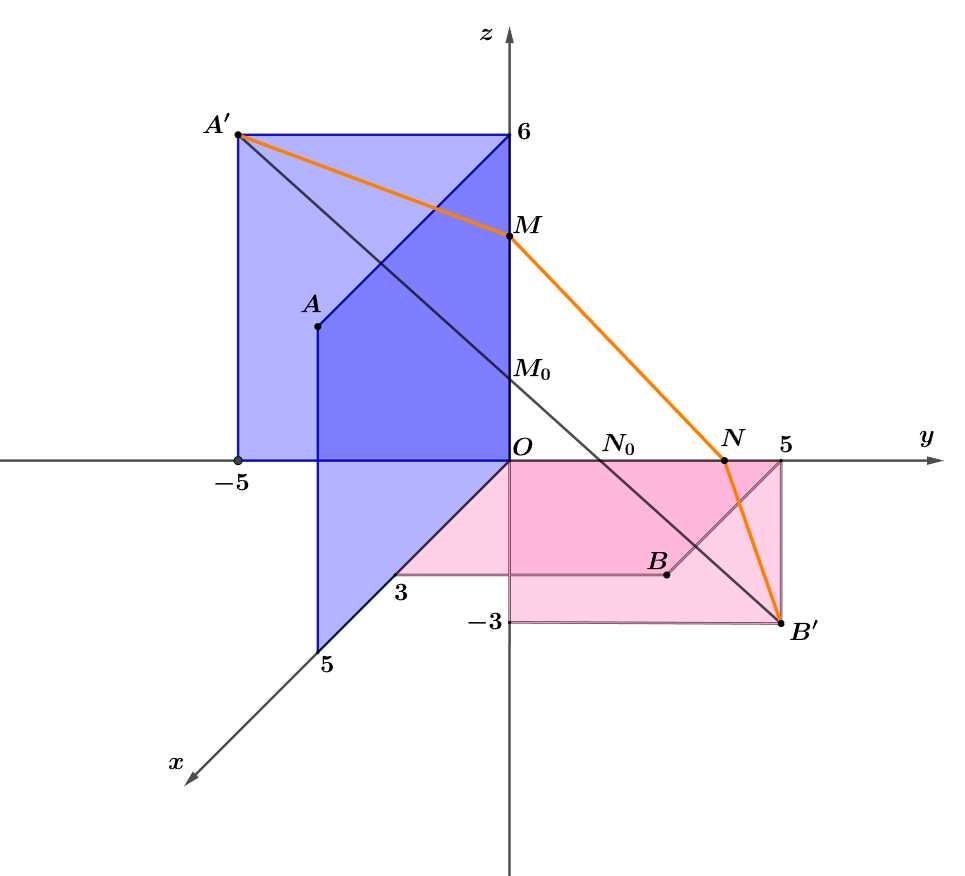
Để tìm độ dài ngắn nhất của đường gấp khúc ta sẽ “trải” các điểm
ta sẽ “trải” các điểm  về cùng 1 mặt phẳng
về cùng 1 mặt phẳng 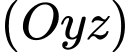 với các điểm
với các điểm 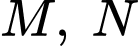 và thoả mãn đoạn thẳng mới bằng với đoạn thẳng ban đầu (tức
và thoả mãn đoạn thẳng mới bằng với đoạn thẳng ban đầu (tức 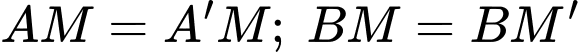 ) và đoạn gấp khúc ngắn nhất khi 4 điểm trên thẳng hàng.
) và đoạn gấp khúc ngắn nhất khi 4 điểm trên thẳng hàng.
Ta quay vuông góc mặt phẳng chứa điểm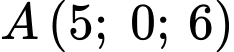 (tức mặt phẳng màu xanh) xuống mặt phẳng
(tức mặt phẳng màu xanh) xuống mặt phẳng 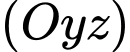 ta được điểm
ta được điểm 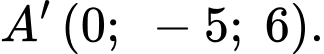
Giả sử điểm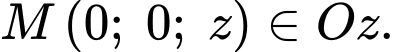
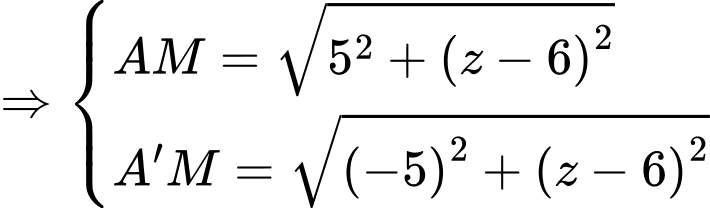
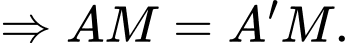
Tương tự, ta quay vuông góc mặt phẳng chứa điểm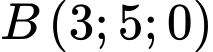 (tức mặt phẳng màu hồng) xuống mặt phẳng
(tức mặt phẳng màu hồng) xuống mặt phẳng 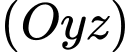 ta được điểm
ta được điểm 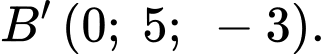
Giả sử điểm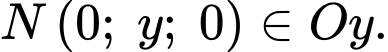
Suy ra được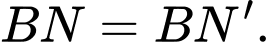
Ta có độ dài đường gấp khúc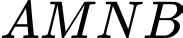
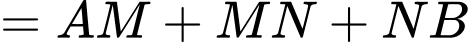
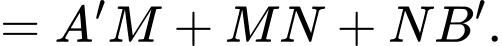
Suy ra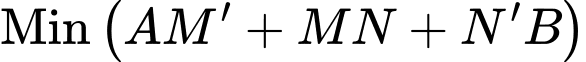 xảy ra khi
xảy ra khi 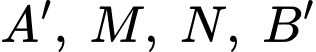 thẳng hàng và bằng đường thẳng
thẳng hàng và bằng đường thẳng 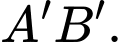 Và có độ dài là
Và có độ dài là 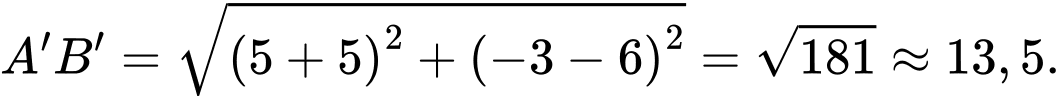

Để tìm độ dài ngắn nhất của đường gấp khúc
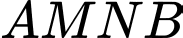 ta sẽ “trải” các điểm
ta sẽ “trải” các điểm 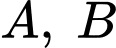 về cùng 1 mặt phẳng
về cùng 1 mặt phẳng 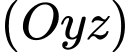 với các điểm
với các điểm 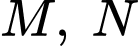 và thoả mãn đoạn thẳng mới bằng với đoạn thẳng ban đầu (tức
và thoả mãn đoạn thẳng mới bằng với đoạn thẳng ban đầu (tức 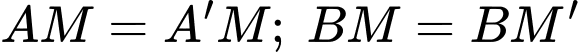 ) và đoạn gấp khúc ngắn nhất khi 4 điểm trên thẳng hàng.
) và đoạn gấp khúc ngắn nhất khi 4 điểm trên thẳng hàng.Ta quay vuông góc mặt phẳng chứa điểm
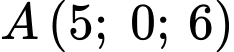 (tức mặt phẳng màu xanh) xuống mặt phẳng
(tức mặt phẳng màu xanh) xuống mặt phẳng 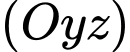 ta được điểm
ta được điểm 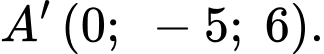
Giả sử điểm
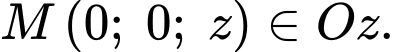
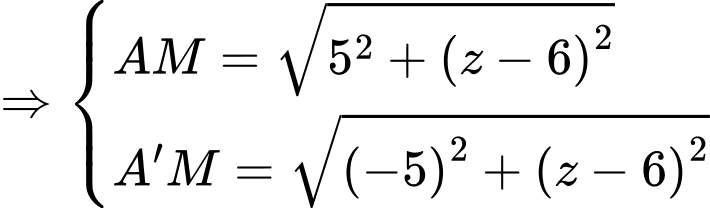
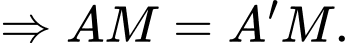
Tương tự, ta quay vuông góc mặt phẳng chứa điểm
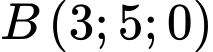 (tức mặt phẳng màu hồng) xuống mặt phẳng
(tức mặt phẳng màu hồng) xuống mặt phẳng 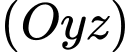 ta được điểm
ta được điểm 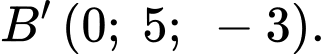
Giả sử điểm
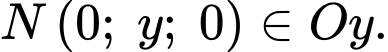
Suy ra được
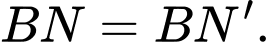
Ta có độ dài đường gấp khúc
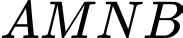
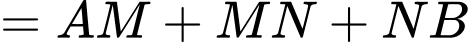
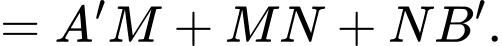
Suy ra
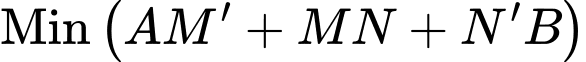 xảy ra khi
xảy ra khi 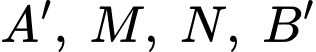 thẳng hàng và bằng đường thẳng
thẳng hàng và bằng đường thẳng 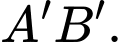 Và có độ dài là
Và có độ dài là