PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [256789]: Trong không gian 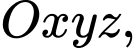 mặt phẳng
mặt phẳng 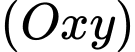 có phương trình là
có phương trình là
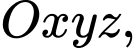 mặt phẳng
mặt phẳng 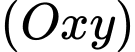 có phương trình là
có phương trình là A, 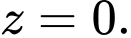
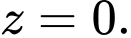
B, 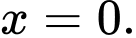
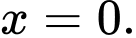
C, 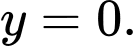
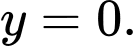
D, 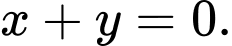
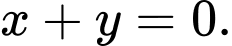
Chọn đáp án A.
Mặt phẳng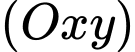 đi qua điểm
đi qua điểm 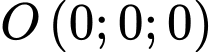 và nhận
và nhận 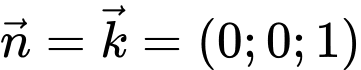 là một vecto pháp tuyến có phương trình là
là một vecto pháp tuyến có phương trình là 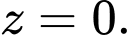 Đáp án: A
Đáp án: A
Mặt phẳng
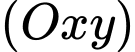 đi qua điểm
đi qua điểm 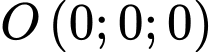 và nhận
và nhận 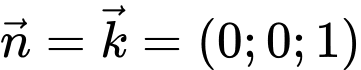 là một vecto pháp tuyến có phương trình là
là một vecto pháp tuyến có phương trình là 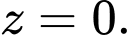 Đáp án: A
Đáp án: A
Câu 2 [256161]: Cho hàm số 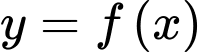 liên tục trên
liên tục trên 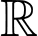 và có đồ thị như hình vẽ bên.
và có đồ thị như hình vẽ bên.

Hàm số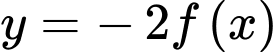 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
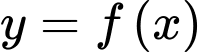 liên tục trên
liên tục trên  và có đồ thị như hình vẽ bên.
và có đồ thị như hình vẽ bên. 
Hàm số
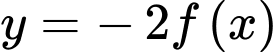 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 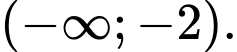
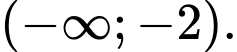
B, 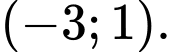
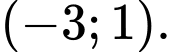
C, 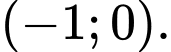
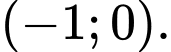
D, 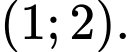
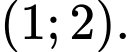
Chọn đáp án C.
Hàm số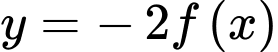 đồng biến
đồng biến 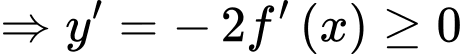
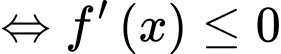
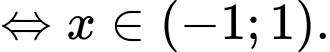 Đáp án: C
Đáp án: C
Hàm số
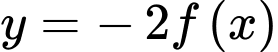 đồng biến
đồng biến 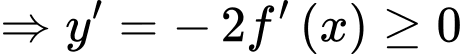
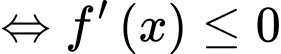
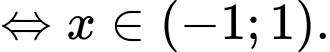 Đáp án: C
Đáp án: C
Câu 3 [696324]: Cho hai vectơ 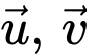 có
có 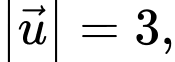
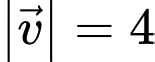 và góc giữa hai vectơ
và góc giữa hai vectơ 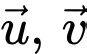 bằng
bằng 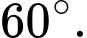 Tích vô hướng của hai vectơ đã cho bằng
Tích vô hướng của hai vectơ đã cho bằng
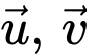 có
có 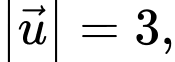
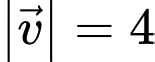 và góc giữa hai vectơ
và góc giữa hai vectơ 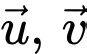 bằng
bằng 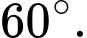 Tích vô hướng của hai vectơ đã cho bằng
Tích vô hướng của hai vectơ đã cho bằng A, 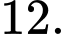
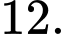
B, 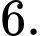
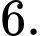
C, 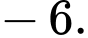
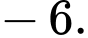
D, 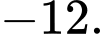
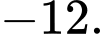
Chọn đáp án B.
Tích vô hướng của hai vectơ đã cho bằng
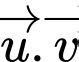
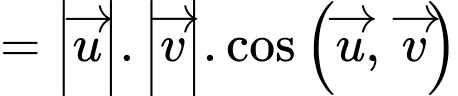
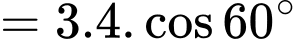
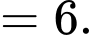 Đáp án: B
Đáp án: B
Tích vô hướng của hai vectơ đã cho bằng
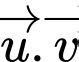
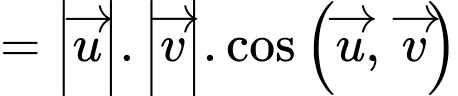
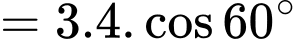
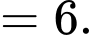 Đáp án: B
Đáp án: B
Câu 4 [696323]: Cho cấp số cộng 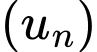 với
với 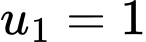 và công sai
và công sai  Tính
Tính 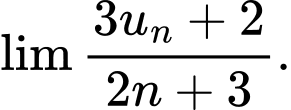
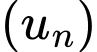 với
với 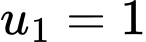 và công sai
và công sai  Tính
Tính 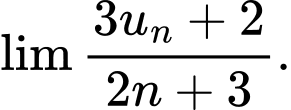
A, 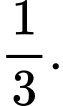
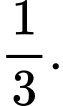
B, 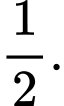
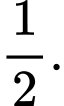
C, 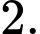
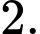
D, 
Chọn đáp án D.
Ta có:
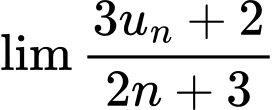
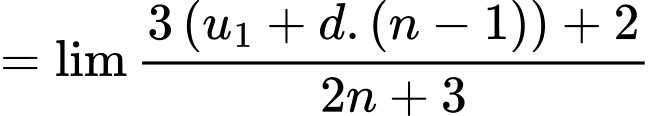
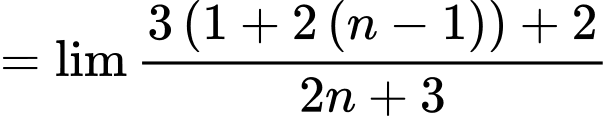
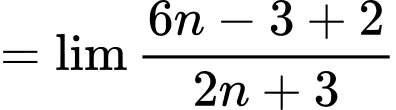
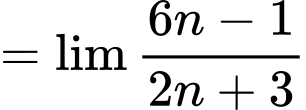
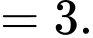 Đáp án: D
Đáp án: D
Ta có:
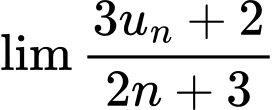
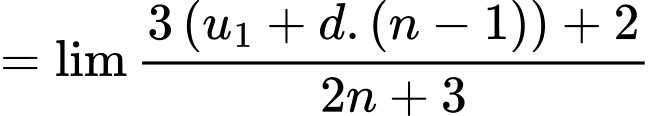
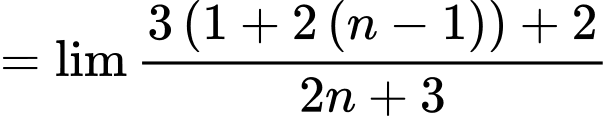
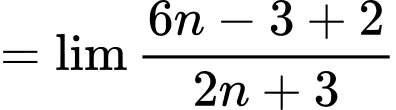
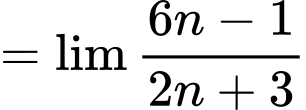
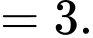 Đáp án: D
Đáp án: D
Câu 5 [257399]: Nghiệm của phương trình 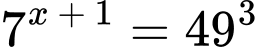 là
là
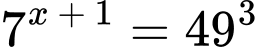 là
là A, 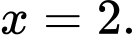
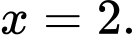
B, 

C, 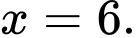
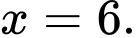
D, 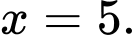
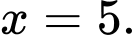
Chọn đáp án D.
Xét phương trình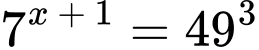
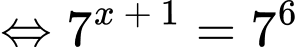

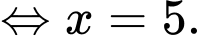 Đáp án: D
Đáp án: D
Xét phương trình
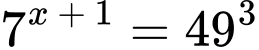
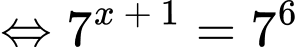

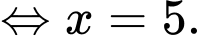 Đáp án: D
Đáp án: D
Câu 6 [257437]: Họ các nguyên hàm của hàm số 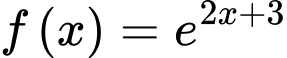 là
là
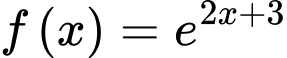 là
là A, 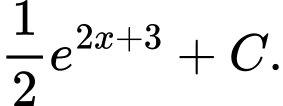
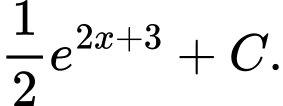
B, 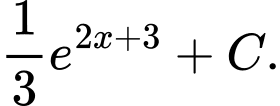
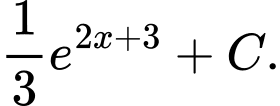
C, 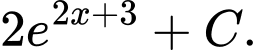
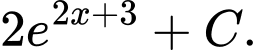
D, 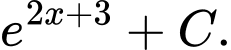
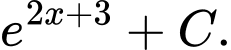
Chọn đáp án A.
Ta có họ các nguyên hàm của hàm số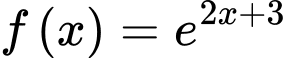 là:
là:
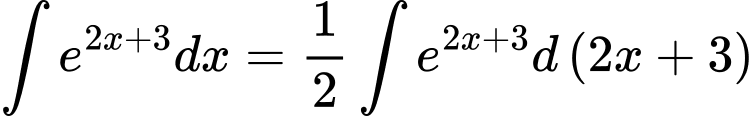
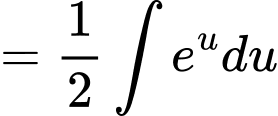
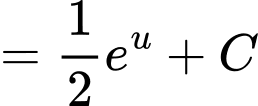
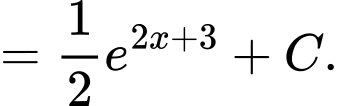 Đáp án: A
Đáp án: A
Ta có họ các nguyên hàm của hàm số
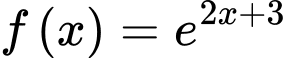 là:
là: 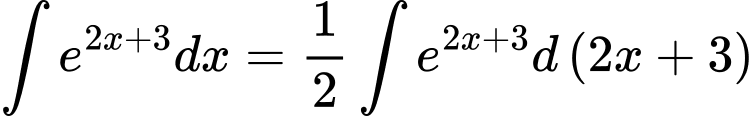
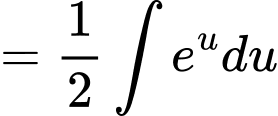
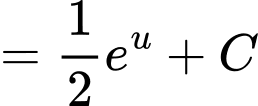
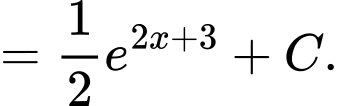 Đáp án: A
Đáp án: A
Câu 7 [256792]: Cho hàm số 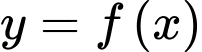 có đạo hàm
có đạo hàm 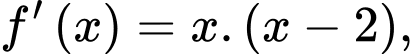 với mọi
với mọi 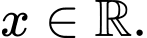 Giá trị nhỏ nhất của hàm số
Giá trị nhỏ nhất của hàm số 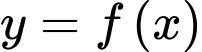 trên đoạn
trên đoạn 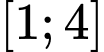 bằng
bằng
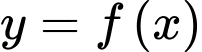 có đạo hàm
có đạo hàm 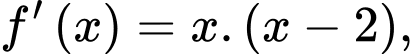 với mọi
với mọi 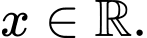 Giá trị nhỏ nhất của hàm số
Giá trị nhỏ nhất của hàm số 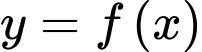 trên đoạn
trên đoạn 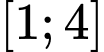 bằng
bằng A, 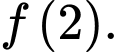
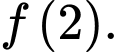
B, 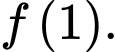
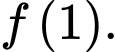
C, 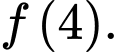
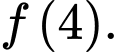
D, 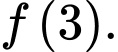
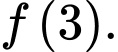
Chọn đáp án A.
Ta có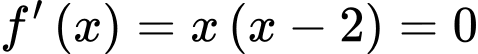
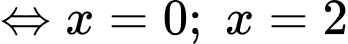
Bảng biến thiên của hàm số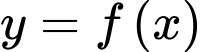 trên đoạn
trên đoạn 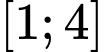 :
:
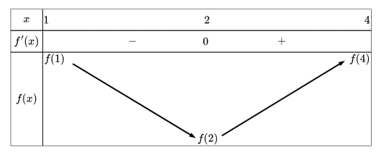
Khi đó ta thấy giá trị nhỏ nhất của hàm số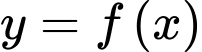 trên đoạn
trên đoạn 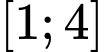 bằng
bằng 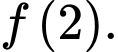 Đáp án: A
Đáp án: A
Ta có
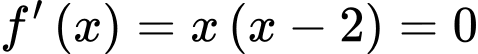
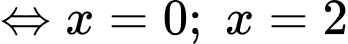
Bảng biến thiên của hàm số
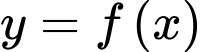 trên đoạn
trên đoạn 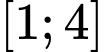 :
:
Khi đó ta thấy giá trị nhỏ nhất của hàm số
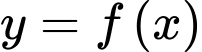 trên đoạn
trên đoạn 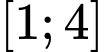 bằng
bằng 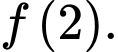 Đáp án: A
Đáp án: A
Câu 8 [256801]: Với mọi số thực dương 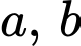 thỏa mãn
thỏa mãn 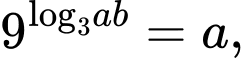 khẳng định nào dưới đây đúng?
khẳng định nào dưới đây đúng?
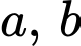 thỏa mãn
thỏa mãn 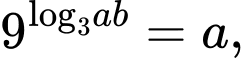 khẳng định nào dưới đây đúng?
khẳng định nào dưới đây đúng? A, 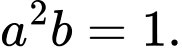
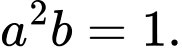
B, 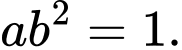
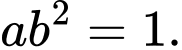
C, 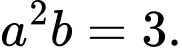
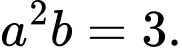
D, 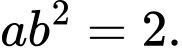
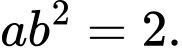
Chọn đáp án B.
Ta có: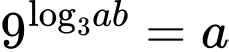
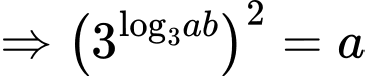
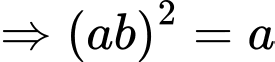
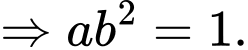 Đáp án: B
Đáp án: B
Ta có:
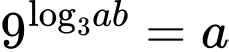
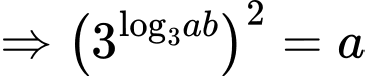
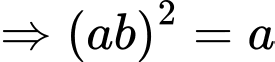
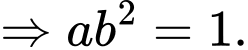 Đáp án: B
Đáp án: B
Câu 9 [256790]: Nếu 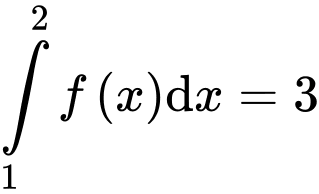 và
và 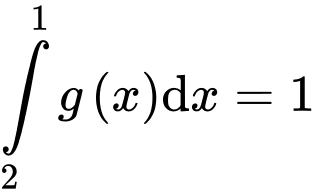 thì
thì 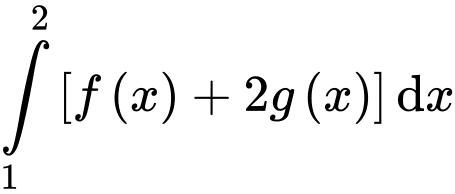 bằng
bằng
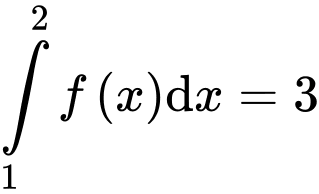 và
và 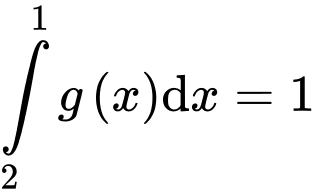 thì
thì 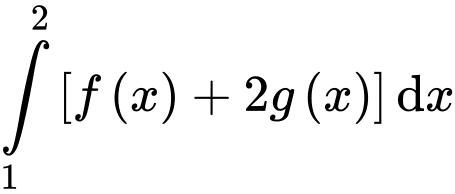 bằng
bằng A, 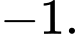
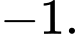
B, 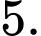
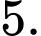
C, 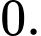
D, 
Chọn đáp án D.
Ta có:
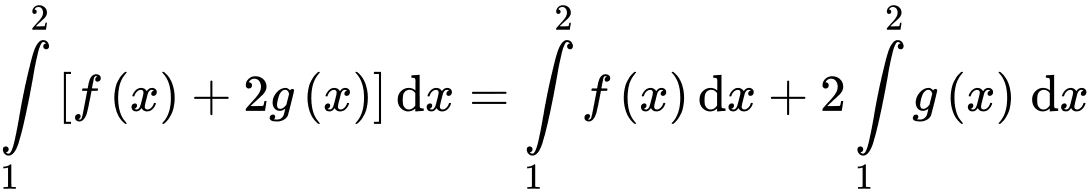
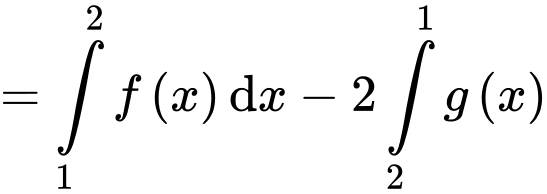
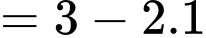
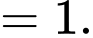 Đáp án: D
Đáp án: D
Ta có:
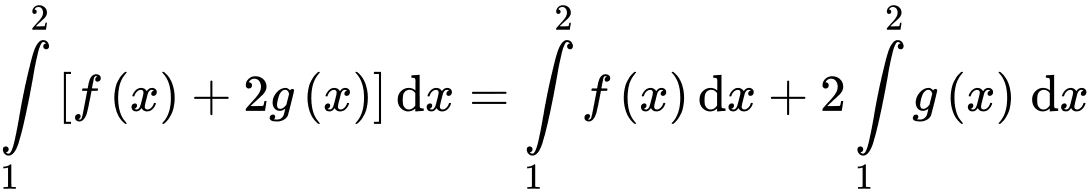
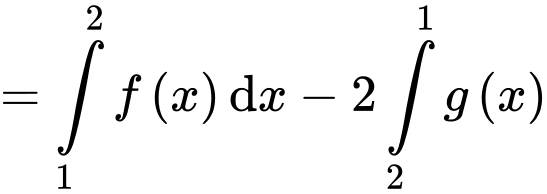
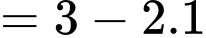
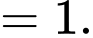 Đáp án: D
Đáp án: D
Câu 10 [696325]: Trong không gian 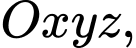 mặt cầu
mặt cầu 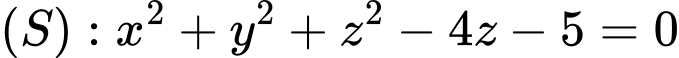 có diện tích bằng
có diện tích bằng
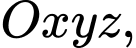 mặt cầu
mặt cầu 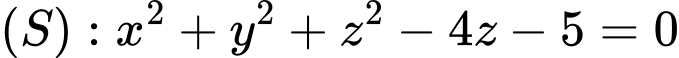 có diện tích bằng
có diện tích bằng A, 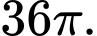
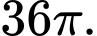
B, 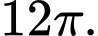
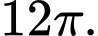
C, 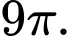
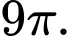
D, 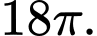
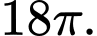
Chọn dáp án A.
Mặt cầu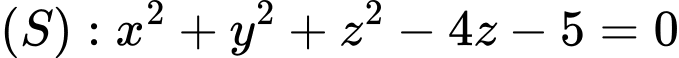 có tâm
có tâm 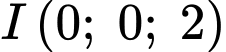 và bán kính
và bán kính 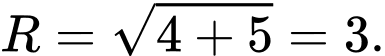
Diện tích mặt cầu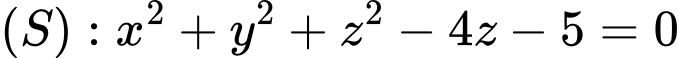 có diện tích bằng
có diện tích bằng 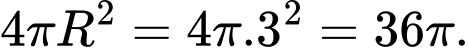 Đáp án: A
Đáp án: A
Mặt cầu
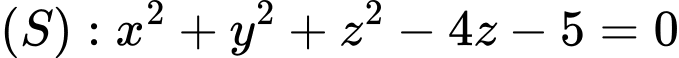 có tâm
có tâm 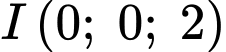 và bán kính
và bán kính 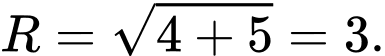
Diện tích mặt cầu
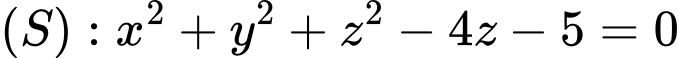 có diện tích bằng
có diện tích bằng 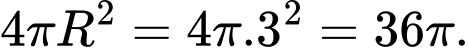 Đáp án: A
Đáp án: A
Câu 11 [696326]: Kết quả khảo sát cân nặng của 25 quả táo được cho trong bảng sau:

Tứ phân vị thứ ba của mẫu số liệu trên thuộc nhóm nào sau đây?

Tứ phân vị thứ ba của mẫu số liệu trên thuộc nhóm nào sau đây?
A, 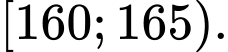
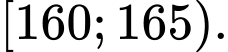
B, 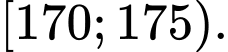
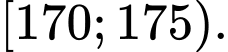
C, 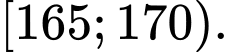
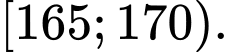
D, 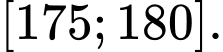
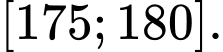
Chọn đáp án C.
Cỡ mẫu: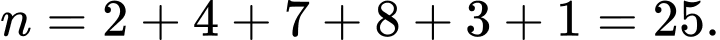
Gọi là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có:
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có: 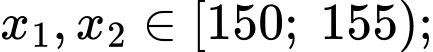
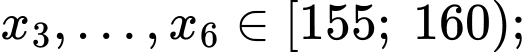



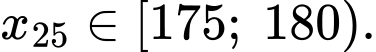
Tứ phân vị thứ ba của mẫu số liệu là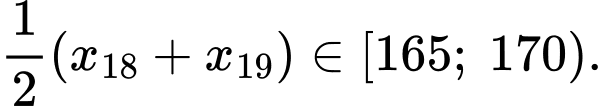 Đáp án: C
Đáp án: C
Cỡ mẫu:
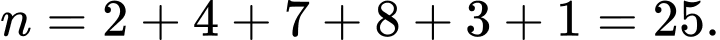
Gọi
 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có:
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có: 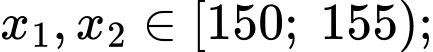
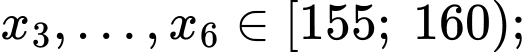



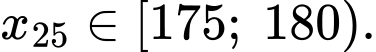
Tứ phân vị thứ ba của mẫu số liệu là
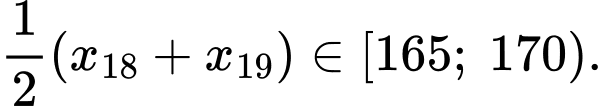 Đáp án: C
Đáp án: C
Câu 12 [696327]: Cho hình chóp 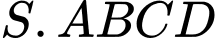 có đáy
có đáy 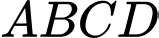 là hình bình hành. Đường thẳng nối trọng tâm của hai tam giác
là hình bình hành. Đường thẳng nối trọng tâm của hai tam giác 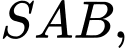
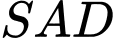 song song với đường thẳng nào sau đây?
song song với đường thẳng nào sau đây?
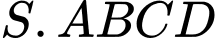 có đáy
có đáy 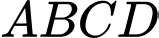 là hình bình hành. Đường thẳng nối trọng tâm của hai tam giác
là hình bình hành. Đường thẳng nối trọng tâm của hai tam giác 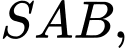
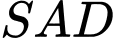 song song với đường thẳng nào sau đây?
song song với đường thẳng nào sau đây? A, 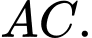
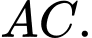
B, 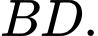
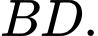
C, 

D, 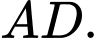
Chọn đáp án B.
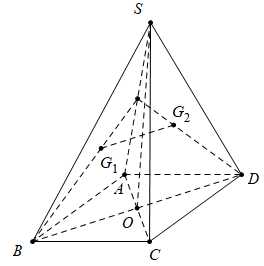
Lấy là trung điểm của
là trung điểm của  ta có:
ta có:
 là trọng tâm của tam giác
là trọng tâm của tam giác 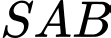 nên
nên 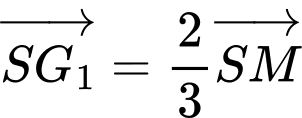
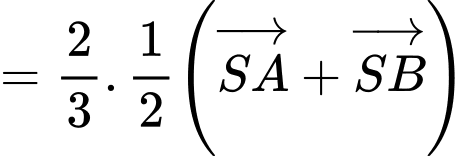
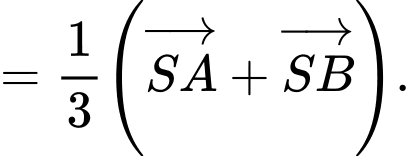
Tương tự,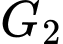 là trọng tâm của tam giác
là trọng tâm của tam giác 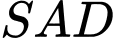 nên
nên 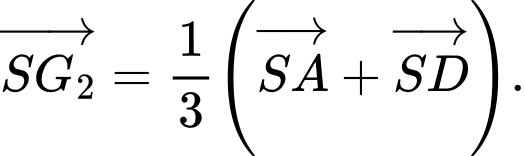
Do đó,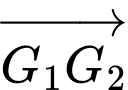
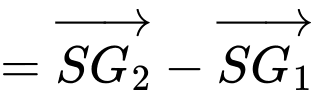
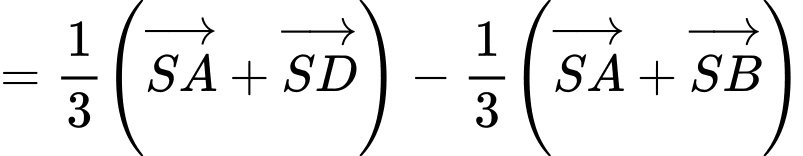
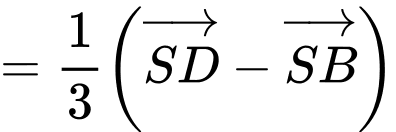
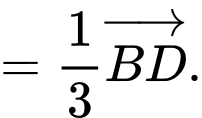
Vậy đường thẳng nối trọng tâm của hai tam giác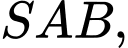
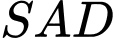 song song với đường thẳng
song song với đường thẳng 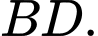 Đáp án: B
Đáp án: B

Lấy
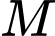 là trung điểm của
là trung điểm của  ta có:
ta có:
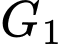 là trọng tâm của tam giác
là trọng tâm của tam giác 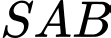 nên
nên 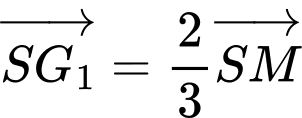
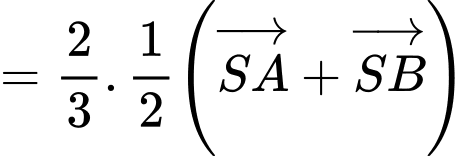
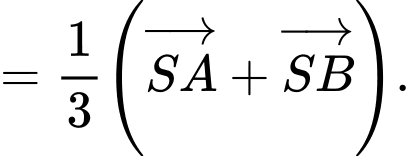
Tương tự,
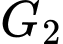 là trọng tâm của tam giác
là trọng tâm của tam giác 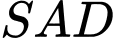 nên
nên 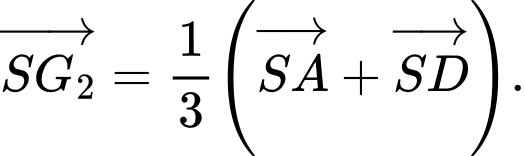
Do đó,
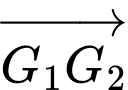
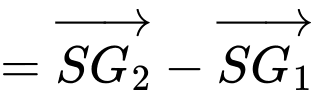
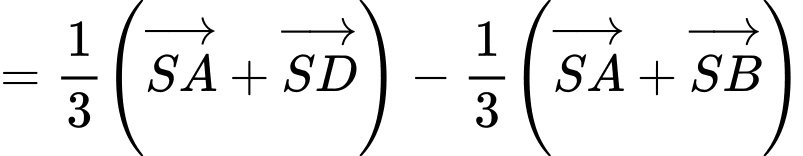
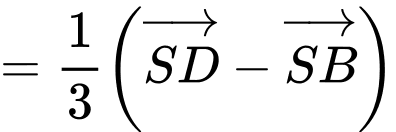
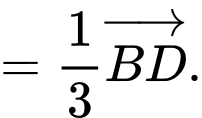
Vậy đường thẳng nối trọng tâm của hai tam giác
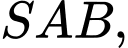
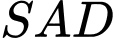 song song với đường thẳng
song song với đường thẳng 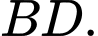 Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693308]: Cho hàm số 

Thứ tự đáp án: Đúng, Sai, Đúng, Đúng.
a) Ta có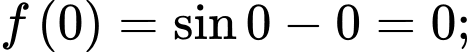
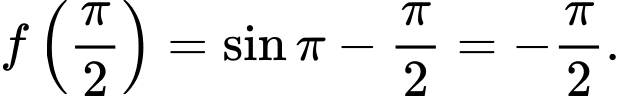
b) Ta có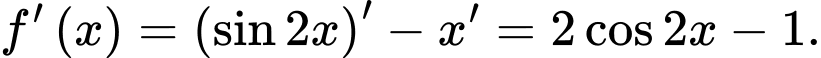
c)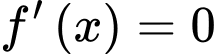

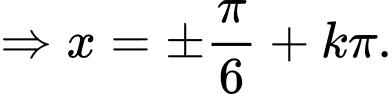
Do đó, nghiệm của phương trình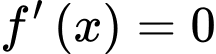 trên đoạn
trên đoạn 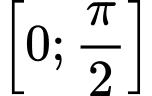 là
là 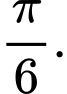
d) Ta có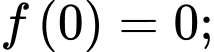
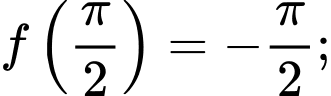
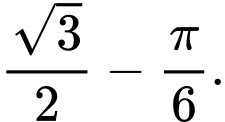
Do đó, giá trị lớn nhất của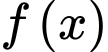 trên đoạn
trên đoạn 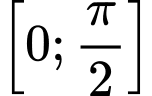 là
là 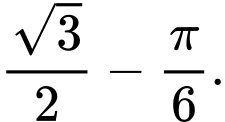
a) Ta có
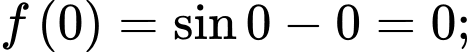
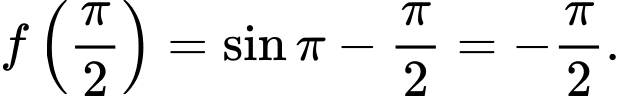
b) Ta có
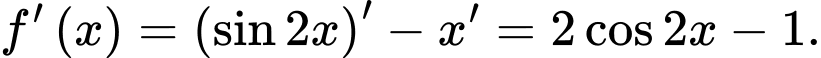
c)
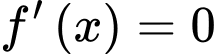

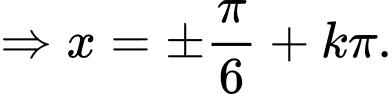
Do đó, nghiệm của phương trình
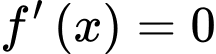 trên đoạn
trên đoạn 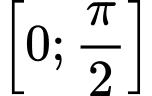 là
là 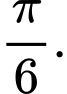
d) Ta có
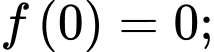
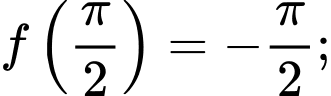
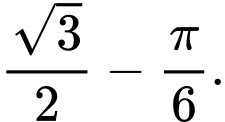
Do đó, giá trị lớn nhất của
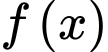 trên đoạn
trên đoạn 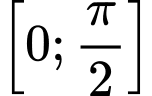 là
là 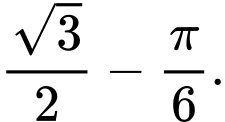
Câu 14 [696329]: Hệ thống phòng không “Vòm sắt” là một trong những hệ thống đánh chặn tên lửa từ xa rất nổi tiếng của Israel. Để “Vòm sắt” hoạt động được chính xác người ta trang bị một Radar có khả năng phát hiện tên lửa với bán kính 417 km. Giả sử, trong hệ trục tọa độ Oxyz một hệ thống “Vòm sắt” đang ở vị trí 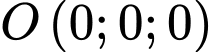 và một quả tên lửa đang ở vị trí
và một quả tên lửa đang ở vị trí 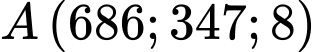 được phóng lên và bay theo một quỹ đạo là đường thẳng có vectơ chỉ phương là
được phóng lên và bay theo một quỹ đạo là đường thẳng có vectơ chỉ phương là 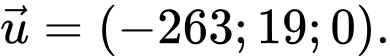 Đơn vị trên các hệ trục toạ độ tính bằng kilomet.
Đơn vị trên các hệ trục toạ độ tính bằng kilomet.
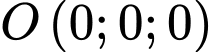 và một quả tên lửa đang ở vị trí
và một quả tên lửa đang ở vị trí 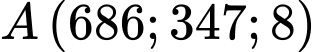 được phóng lên và bay theo một quỹ đạo là đường thẳng có vectơ chỉ phương là
được phóng lên và bay theo một quỹ đạo là đường thẳng có vectơ chỉ phương là 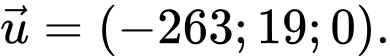 Đơn vị trên các hệ trục toạ độ tính bằng kilomet.
Đơn vị trên các hệ trục toạ độ tính bằng kilomet.
Thứ tự đáp án: Sai, Sai, Sai, Sai.
a) Phương trình mặt cầu tâm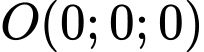 bán kính
bán kính 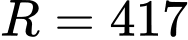 là
là 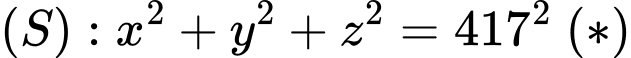
b) Thay tọa độ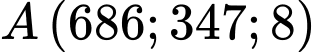 vào
vào  ta được:
ta được:
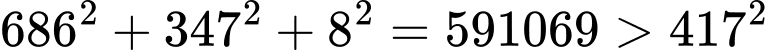 suy ra điểm
suy ra điểm 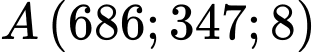 nằm ngoài mặt cầu.
nằm ngoài mặt cầu.
Suy ra radar không thể phát hiện quả tên lửa tại vị trí được phóng lên.
c) Quỹ đạo của tên lửa là đường thẳng có phương trình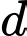 :
: 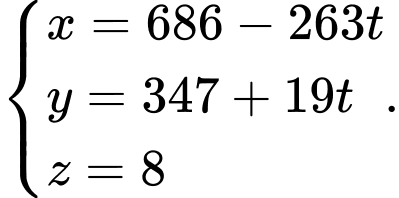
Giả sử điểm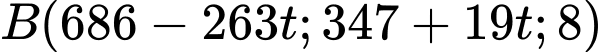 là điểm đầu tiênn trên màn hình radar phát hiện ra quả tên lửa khi đó điểm
là điểm đầu tiênn trên màn hình radar phát hiện ra quả tên lửa khi đó điểm 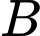 nằm trên mặt cầu
nằm trên mặt cầu 
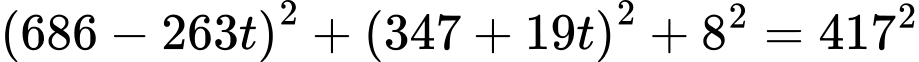
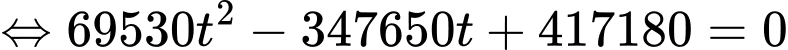
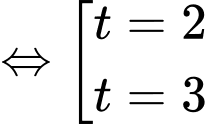
Với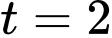 suy rа
suy rа 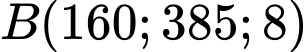 , khi đó
, khi đó 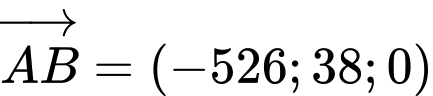 suy rа
suy rа 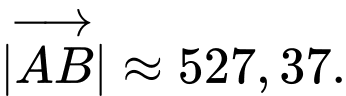
Với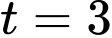 suy ra
suy ra 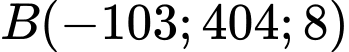 , khi đó
, khi đó 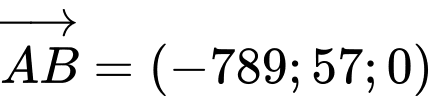 suy ra
suy ra 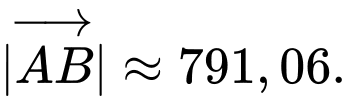
Rõ ràng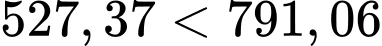 do đó vị cuối cùng quả tên lửa xuất hiện trên Radar là
do đó vị cuối cùng quả tên lửa xuất hiện trên Radar là 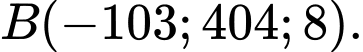
d) Gọi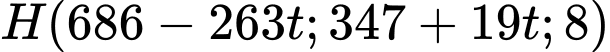 là vị trị hệ thống "Vòm sắt" gần quả tên lửa.
là vị trị hệ thống "Vòm sắt" gần quả tên lửa.
Khi đó để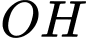 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi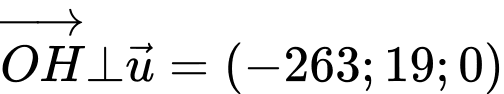
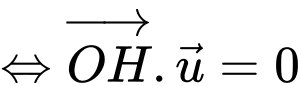

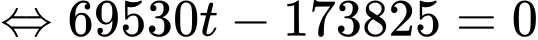
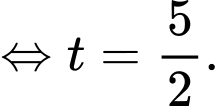
Suy ra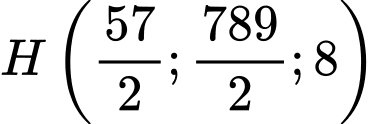
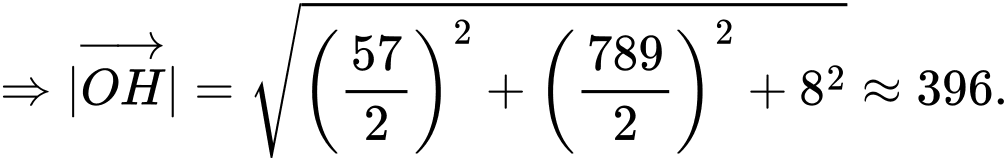
a) Phương trình mặt cầu tâm
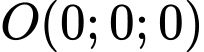 bán kính
bán kính 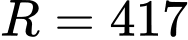 là
là 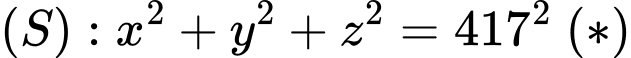
b) Thay tọa độ
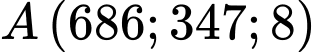 vào
vào  ta được:
ta được: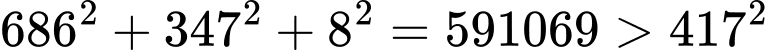 suy ra điểm
suy ra điểm 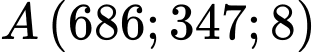 nằm ngoài mặt cầu.
nằm ngoài mặt cầu.Suy ra radar không thể phát hiện quả tên lửa tại vị trí được phóng lên.
c) Quỹ đạo của tên lửa là đường thẳng có phương trình
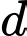 :
: 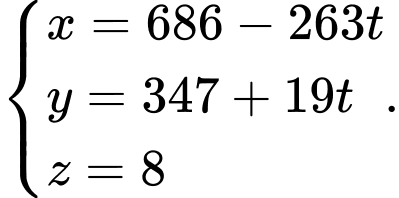
Giả sử điểm
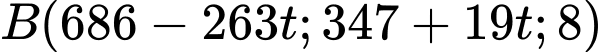 là điểm đầu tiênn trên màn hình radar phát hiện ra quả tên lửa khi đó điểm
là điểm đầu tiênn trên màn hình radar phát hiện ra quả tên lửa khi đó điểm 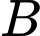 nằm trên mặt cầu
nằm trên mặt cầu 
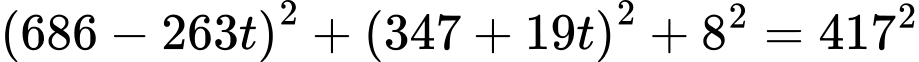
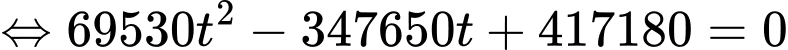
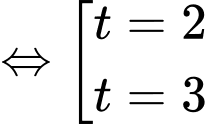
Với
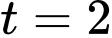 suy rа
suy rа 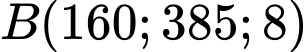 , khi đó
, khi đó 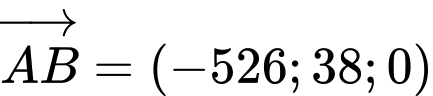 suy rа
suy rа 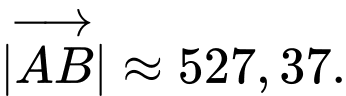
Với
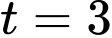 suy ra
suy ra 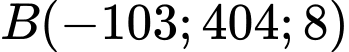 , khi đó
, khi đó 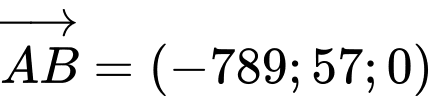 suy ra
suy ra 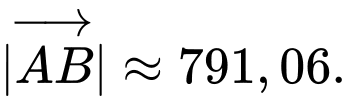
Rõ ràng
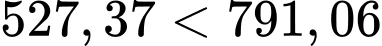 do đó vị cuối cùng quả tên lửa xuất hiện trên Radar là
do đó vị cuối cùng quả tên lửa xuất hiện trên Radar là 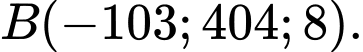
d) Gọi
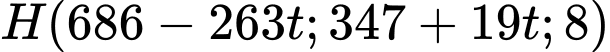 là vị trị hệ thống "Vòm sắt" gần quả tên lửa.
là vị trị hệ thống "Vòm sắt" gần quả tên lửa. Khi đó để
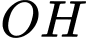 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi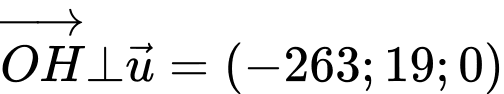
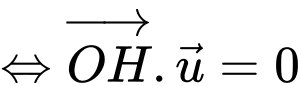

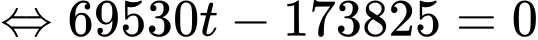
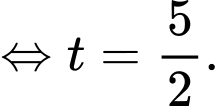
Suy ra
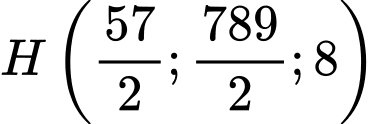
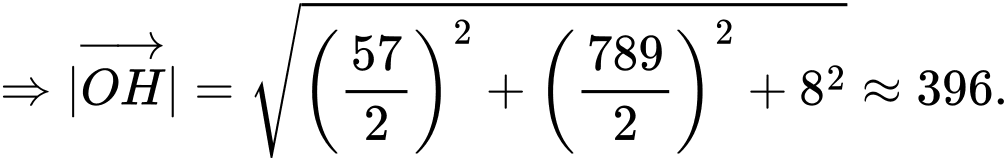
Câu 15 [702827]: Một người có 5 con gà mái, 2 con gà trống nhốt chung trong một cái lồng. Một người đến mua, người bán gà bắt ngẫu nhiên 1 con. Người mua chấp nhận mua con gà đó, người bán gà quên mất rằng con gà bán cho người thứ nhất là gà trống hay gà mái.
a) Đúng.
Xác suất để người thứ nhất mua được con gà mái là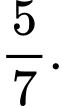
b) Đúng.
Một người thứ hai lại đến mua gà, người bán gà lại bắt ngẫu nhiên ra 1 con, xác suất để người thứ hai mua được con gà trống là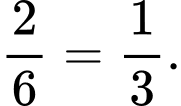
c) Sai.
Gọi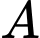 là biến cố: “Người thứ hai mua được gà trống”
là biến cố: “Người thứ hai mua được gà trống”
B là biến cố “Người thứ nhất mua được gà mái”
Khi đó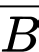 là biến cố “Người thứ nhất mua được gà trống”
là biến cố “Người thứ nhất mua được gà trống”
YCBT Tính
Tính 
Ta có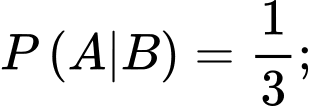
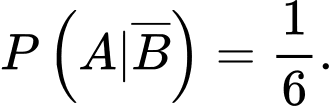
Ta có sơ đồ cây sau:
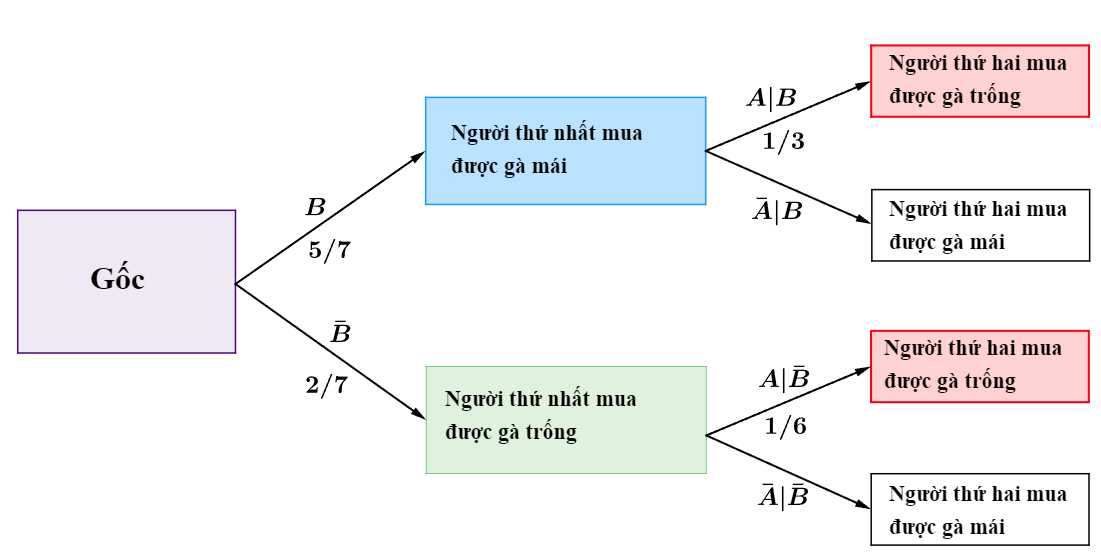
Áp dụng công thức xác suất toàn phần, ta có
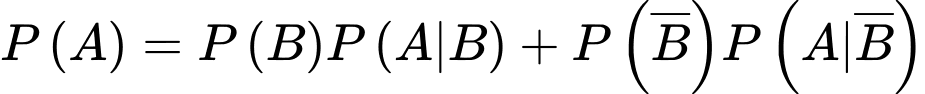
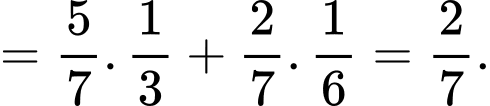
d) Đúng.
YCBT Tính
Tính 
Theo công thức Bayes, ta có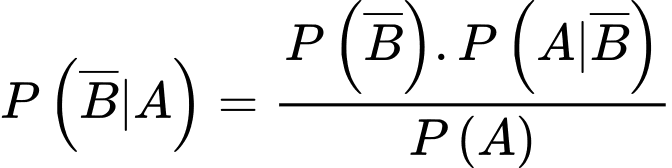
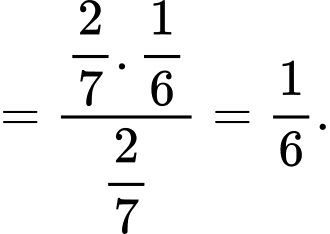
Xác suất để người thứ nhất mua được con gà mái là
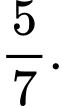
b) Đúng.
Một người thứ hai lại đến mua gà, người bán gà lại bắt ngẫu nhiên ra 1 con, xác suất để người thứ hai mua được con gà trống là
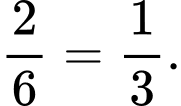
c) Sai.
Gọi
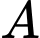 là biến cố: “Người thứ hai mua được gà trống”
là biến cố: “Người thứ hai mua được gà trống”B là biến cố “Người thứ nhất mua được gà mái”
Khi đó
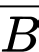 là biến cố “Người thứ nhất mua được gà trống”
là biến cố “Người thứ nhất mua được gà trống” YCBT
 Tính
Tính 
Ta có
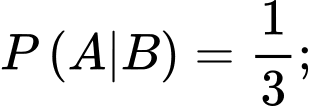
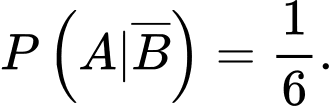
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
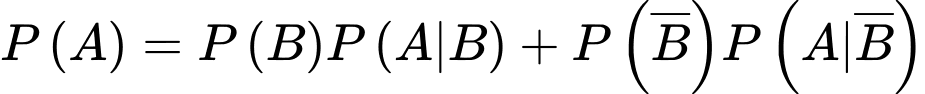
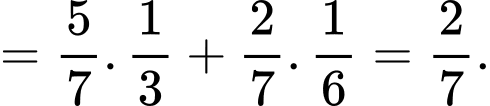
d) Đúng.
YCBT
 Tính
Tính 
Theo công thức Bayes, ta có
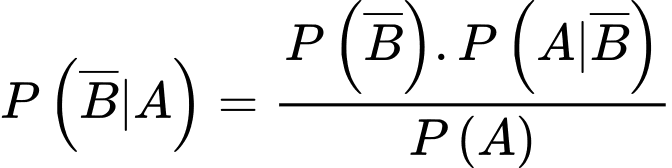
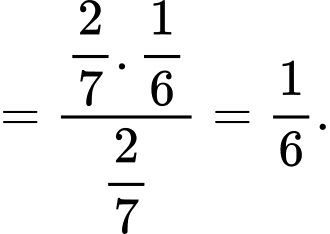
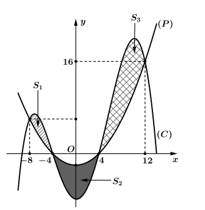
Câu 16 [696330]: Cho hàm số 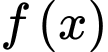 xác định và liên tục trên đoạn
xác định và liên tục trên đoạn 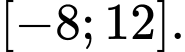 Biết rằng diện tích hình phẳng
Biết rằng diện tích hình phẳng 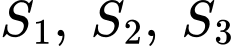 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 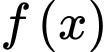 và đường parabol
và đường parabol 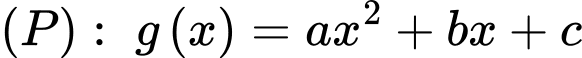 lần lượt bằng
lần lượt bằng 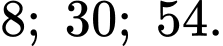
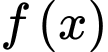 xác định và liên tục trên đoạn
xác định và liên tục trên đoạn 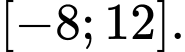 Biết rằng diện tích hình phẳng
Biết rằng diện tích hình phẳng 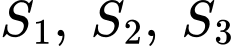 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 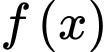 và đường parabol
và đường parabol 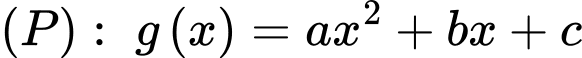 lần lượt bằng
lần lượt bằng 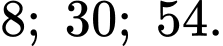

Thứ tự đáp án: Đúng, Đúng, Sai, Sai.
a) Quan sát đồ thị ta thấy trên đoạn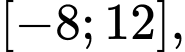
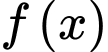 có 4 giao điểm với
có 4 giao điểm với 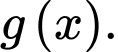
Do đó, phương trình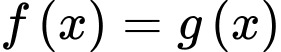 có 4 nghiệm.
có 4 nghiệm.
b) Ta có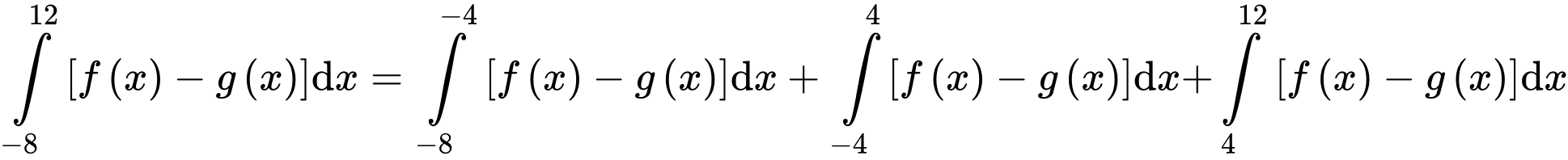
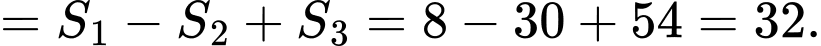
c) Từ đồ thị hàm số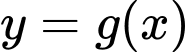 ta thấy nó đi qua các điểm
ta thấy nó đi qua các điểm 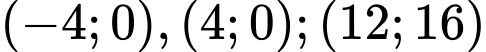 nên:
nên:
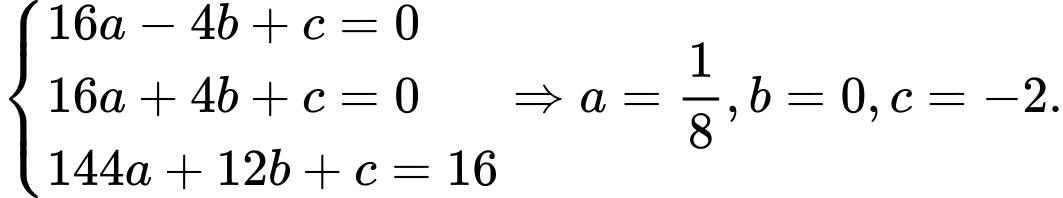
Do đó: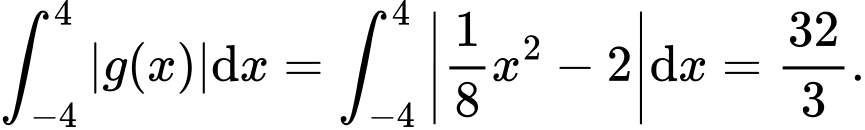
d) Vì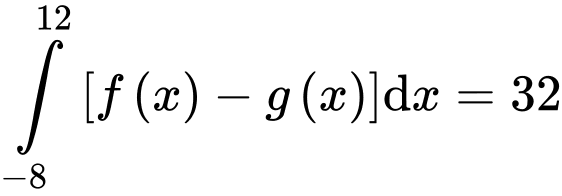 nên
nên 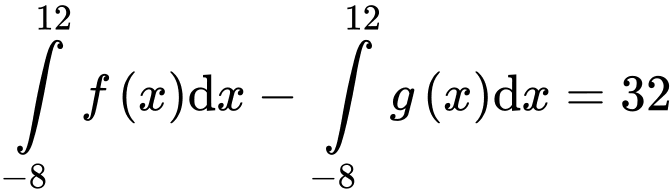
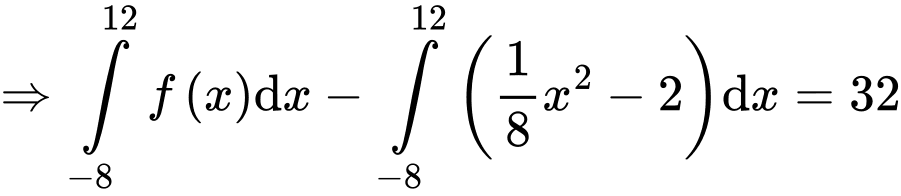
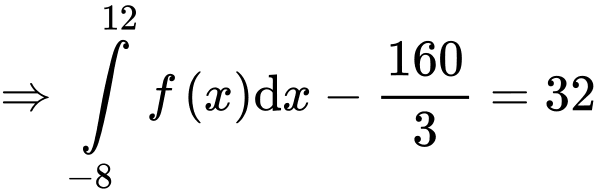
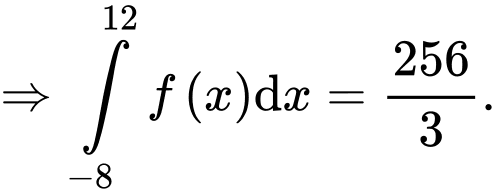
a) Quan sát đồ thị ta thấy trên đoạn
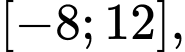
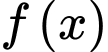 có 4 giao điểm với
có 4 giao điểm với 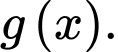
Do đó, phương trình
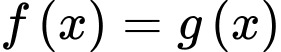 có 4 nghiệm.
có 4 nghiệm.b) Ta có
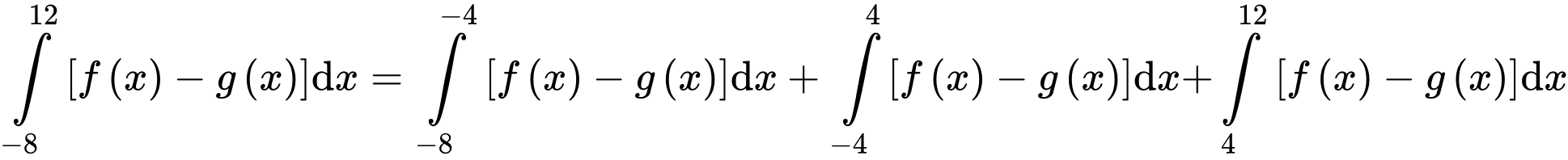
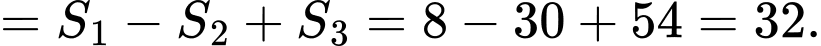
c) Từ đồ thị hàm số
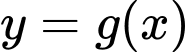 ta thấy nó đi qua các điểm
ta thấy nó đi qua các điểm 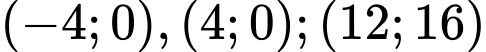 nên:
nên: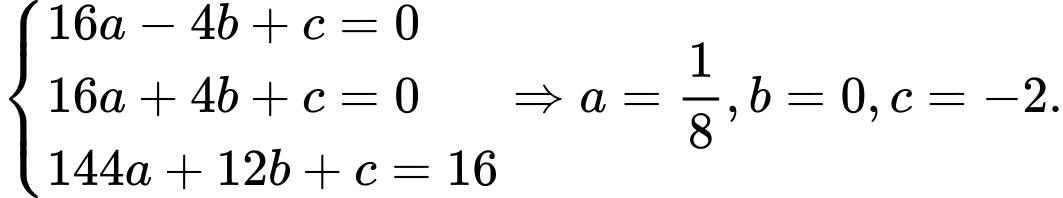
Do đó:
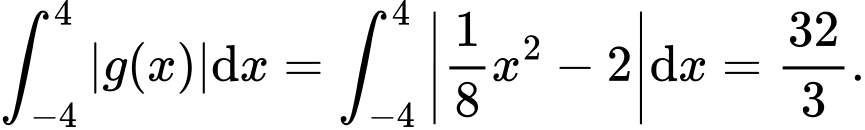
d) Vì
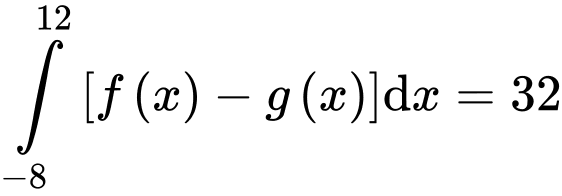 nên
nên 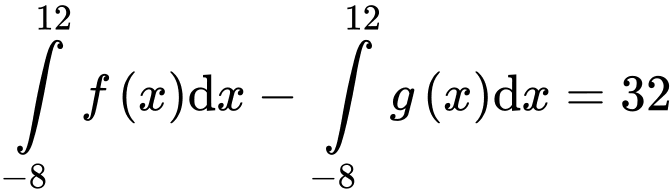
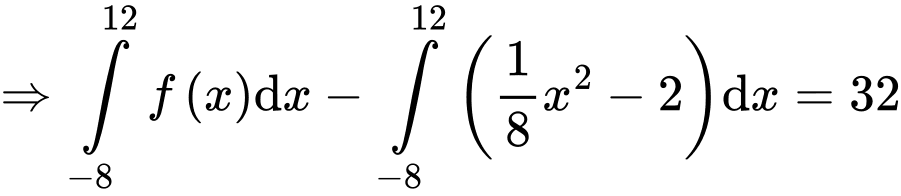
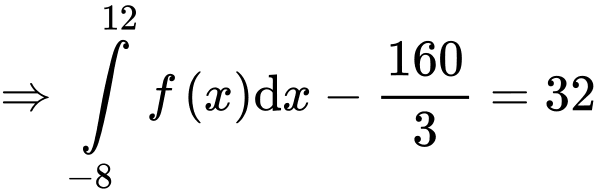
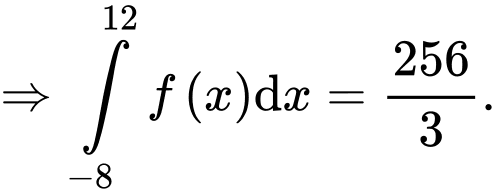
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696331]: Cho hình chóp tứ giác đều 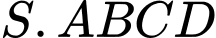 có độ dài cạnh đáy bằng
có độ dài cạnh đáy bằng 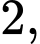
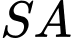 tạo với mặt đáy một góc
tạo với mặt đáy một góc 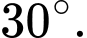 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 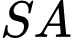 và
và 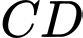 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
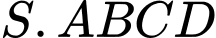 có độ dài cạnh đáy bằng
có độ dài cạnh đáy bằng 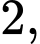
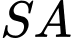 tạo với mặt đáy một góc
tạo với mặt đáy một góc 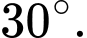 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 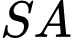 và
và 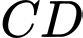 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 1,3.
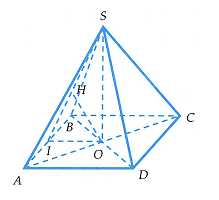
Gọi là trung điểm của
là trung điểm của 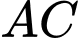 và
và 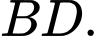
Ta có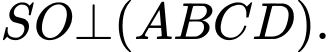
Do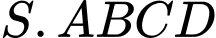 là hình chóp tứ giác đều nên
là hình chóp tứ giác đều nên 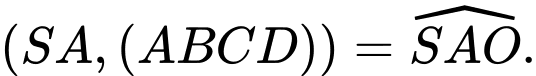
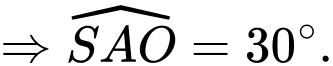
Vì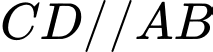 nên
nên 
Do đó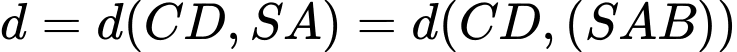
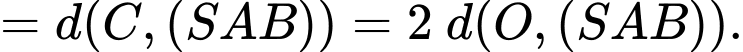
Gọi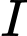 là trung điểm của
là trung điểm của 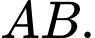
Ta có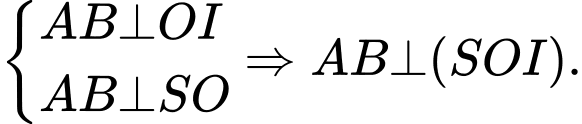
Dựng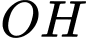 vuông góc với
vuông góc với 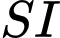 tại
tại 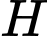 thì
thì 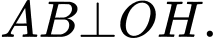
Ta có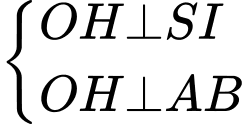
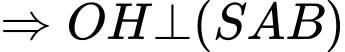
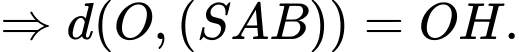
Ta có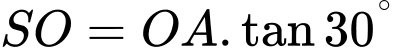
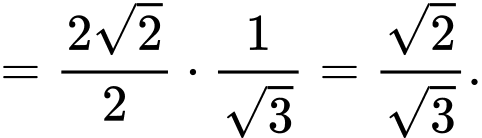
Ta có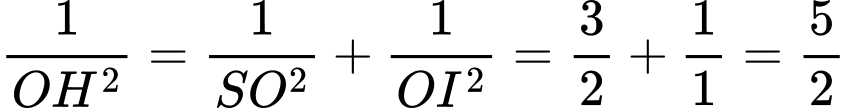
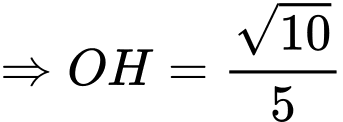
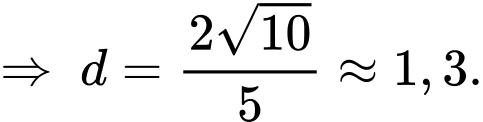

Gọi
 là trung điểm của
là trung điểm của 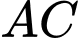 và
và 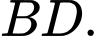
Ta có
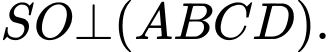
Do
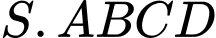 là hình chóp tứ giác đều nên
là hình chóp tứ giác đều nên 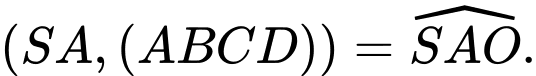
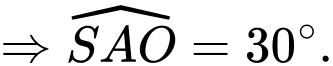
Vì
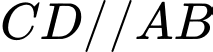 nên
nên 
Do đó
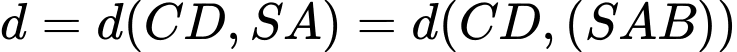
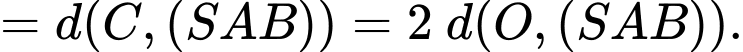
Gọi
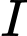 là trung điểm của
là trung điểm của 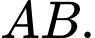
Ta có
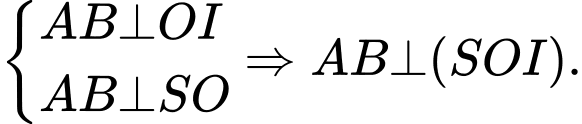
Dựng
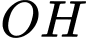 vuông góc với
vuông góc với 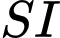 tại
tại 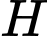 thì
thì 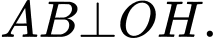
Ta có
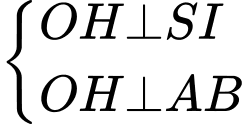
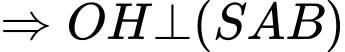
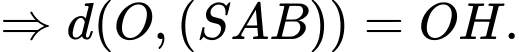
Ta có
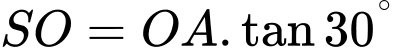
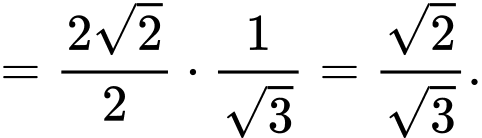
Ta có
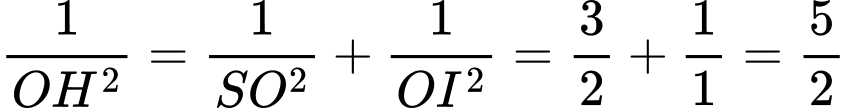
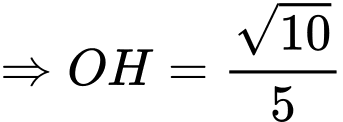
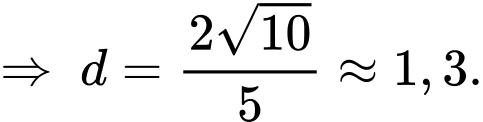
Câu 18 [696332]: Bạn Hưng về nghỉ hè ở quê một số ngày, trong đó có 10 ngày mưa. Biết rằng có 11 buổi sáng không mưa, có 9 buổi chiều không mưa và không bao giờ trời mưa cả sáng lẫn chiều. Hỏi bạn Hưng về quê có bao nhiêu ngày mưa buổi sáng?
Điền đáp án: 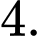
Đặt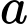 là số ngày chỉ mưa buổi sáng.
là số ngày chỉ mưa buổi sáng.
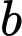 là số ngày chỉ mưa buổi chiều.
là số ngày chỉ mưa buổi chiều.
 là số ngày không mưa.
là số ngày không mưa.
Theo đề bài, ta có hệ phương trình: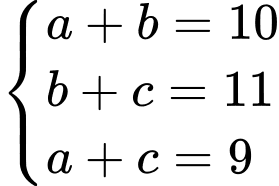
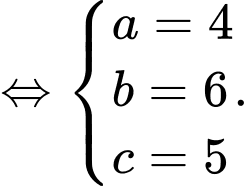
Vậy bạn Hưng về quê có 4 ngày mưa buổi sáng.
Cách khác:
Theo giả thiết: 10 ngày mưa mà không bao giờ trời mưa cả sáng lẫn chiều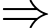 Bạn Hưng về quê nghỉ hè có 10 buổi mưa.
Bạn Hưng về quê nghỉ hè có 10 buổi mưa.
Mà có 11 buổi sáng không mưa, có 9 buổi chiều không mưa Bạn Hưng về quê số buổi là:
Bạn Hưng về quê số buổi là:  buổi.
buổi.
Do 1 ngày có 2 buổi sáng và chiều Bạn Hưng về quê số ngày là:
Bạn Hưng về quê số ngày là: 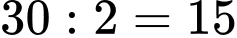 ngày.
ngày.
Mà bạn Hưng về quê có 11 buổi sáng không mưa Bạn Hưng về quê có số ngày mưa buổi sáng là:
Bạn Hưng về quê có số ngày mưa buổi sáng là:  ngày.
ngày.
Đặt
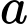 là số ngày chỉ mưa buổi sáng.
là số ngày chỉ mưa buổi sáng.
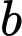 là số ngày chỉ mưa buổi chiều.
là số ngày chỉ mưa buổi chiều.
 là số ngày không mưa.
là số ngày không mưa.
Theo đề bài, ta có hệ phương trình:
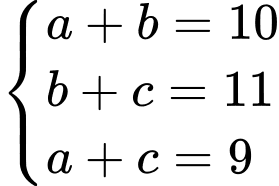
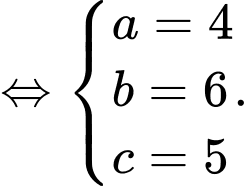
Vậy bạn Hưng về quê có 4 ngày mưa buổi sáng.
Cách khác:
Theo giả thiết: 10 ngày mưa mà không bao giờ trời mưa cả sáng lẫn chiều
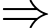 Bạn Hưng về quê nghỉ hè có 10 buổi mưa.
Bạn Hưng về quê nghỉ hè có 10 buổi mưa.
Mà có 11 buổi sáng không mưa, có 9 buổi chiều không mưa
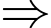 Bạn Hưng về quê số buổi là:
Bạn Hưng về quê số buổi là:  buổi.
buổi.
Do 1 ngày có 2 buổi sáng và chiều
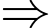 Bạn Hưng về quê số ngày là:
Bạn Hưng về quê số ngày là: 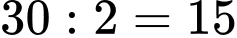 ngày.
ngày.
Mà bạn Hưng về quê có 11 buổi sáng không mưa
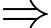 Bạn Hưng về quê có số ngày mưa buổi sáng là:
Bạn Hưng về quê có số ngày mưa buổi sáng là:  ngày.
ngày.
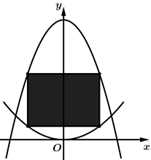
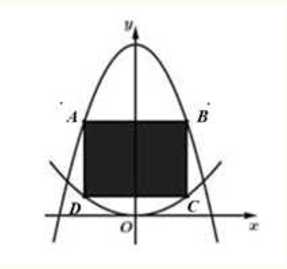
Câu 19 [696335]: Cho một hình chữ nhật có hai điểm nằm trên đồ thị hàm số 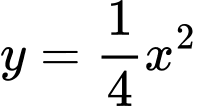 và hai điểm còn lại nằm trên đồ thị hàm số
và hai điểm còn lại nằm trên đồ thị hàm số 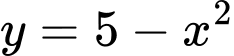 trên khoảng
trên khoảng 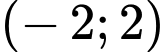 như hình vẽ bên. Hình chữ nhật đó có diện tích lớn nhất là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
như hình vẽ bên. Hình chữ nhật đó có diện tích lớn nhất là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
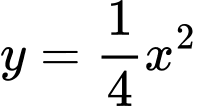 và hai điểm còn lại nằm trên đồ thị hàm số
và hai điểm còn lại nằm trên đồ thị hàm số 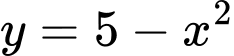 trên khoảng
trên khoảng  như hình vẽ bên. Hình chữ nhật đó có diện tích lớn nhất là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
như hình vẽ bên. Hình chữ nhật đó có diện tích lớn nhất là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 7,7.
Gọi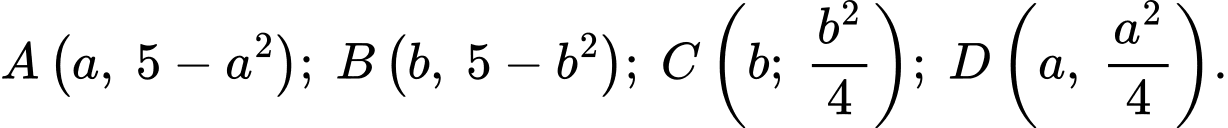
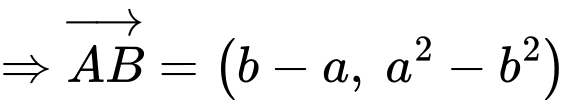 ,
, 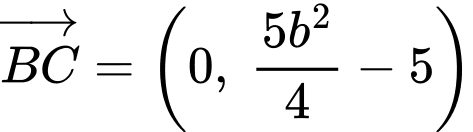
Vì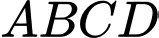 là hình chữ nhật
là hình chữ nhật
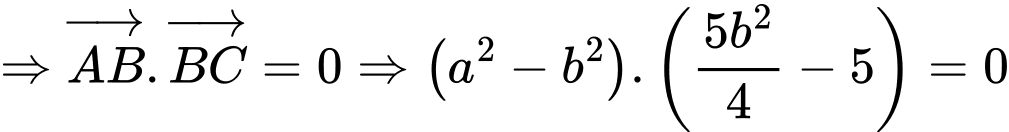
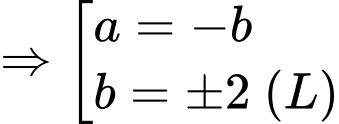
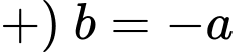
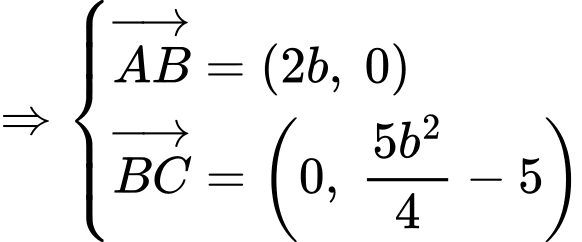
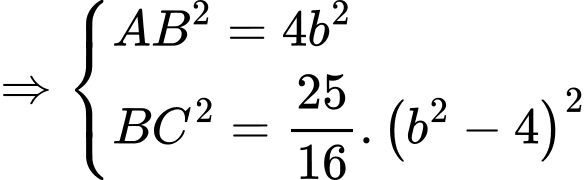
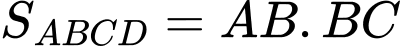
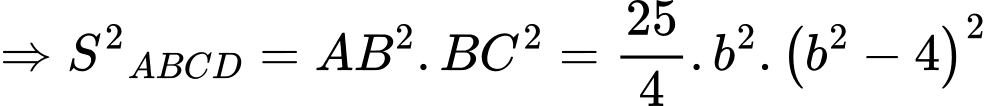
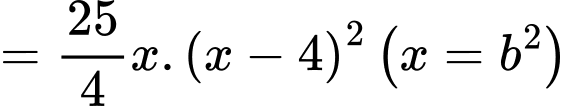
Xét hàm số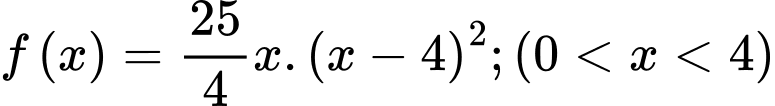
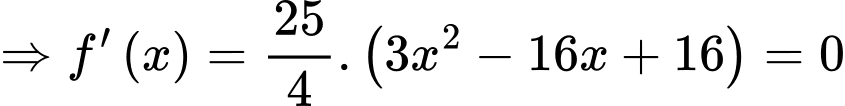
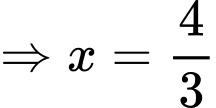
BBT:
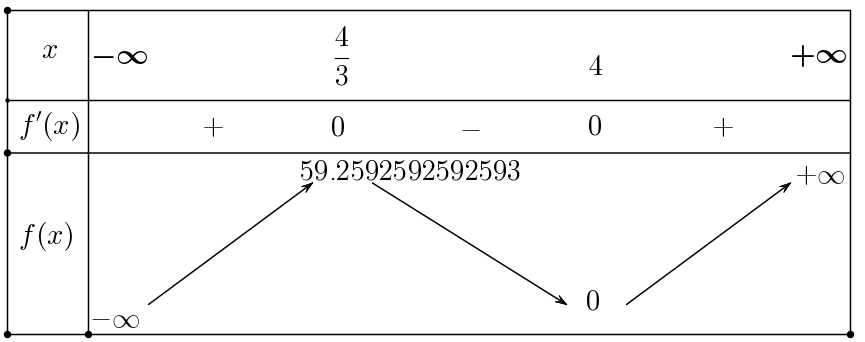
Dựa theo bảng biến thiên ta thấy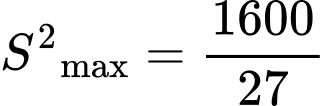 tại
tại 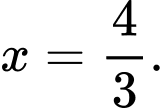
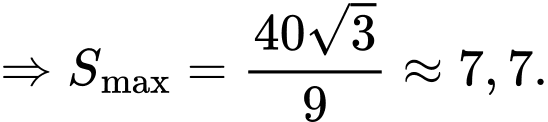

Gọi
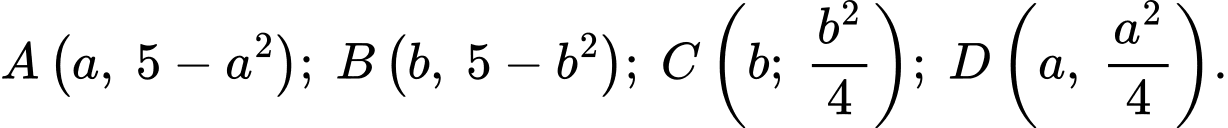
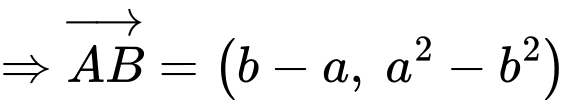 ,
, 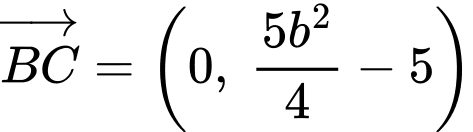
Vì
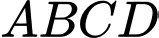 là hình chữ nhật
là hình chữ nhật
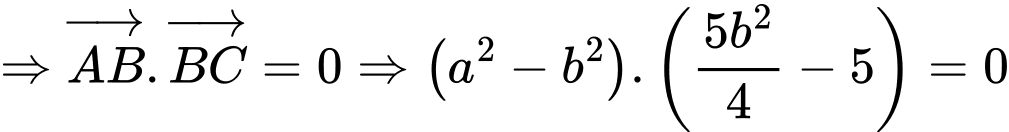
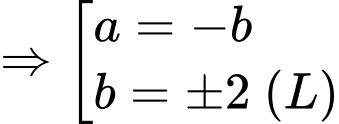
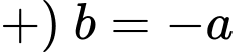
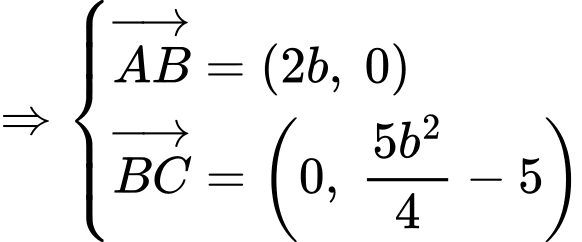
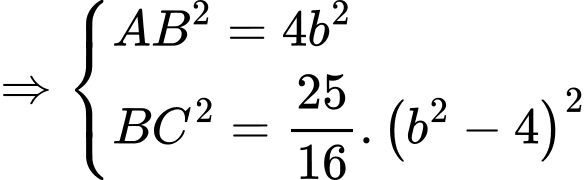
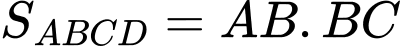
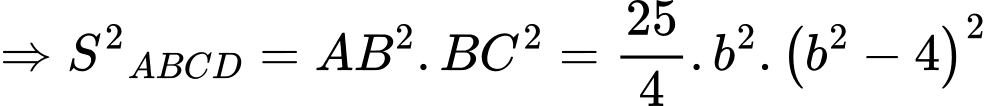
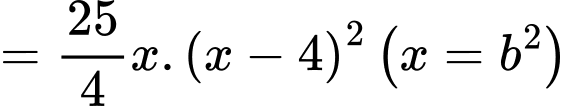
Xét hàm số
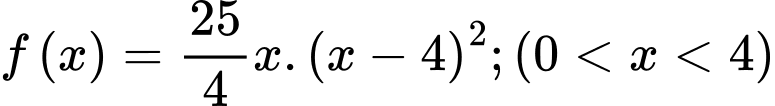
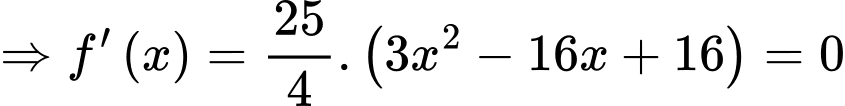
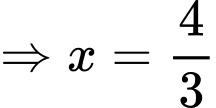
BBT:

Dựa theo bảng biến thiên ta thấy
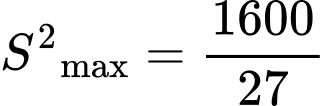 tại
tại 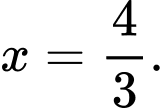
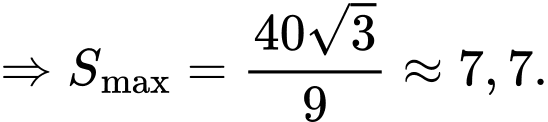
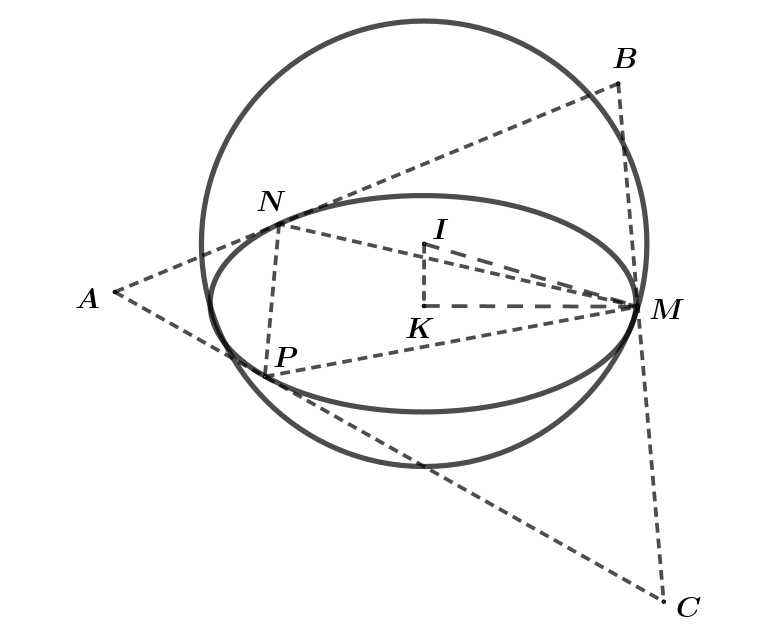
Câu 20 [696336]: Trong không gian 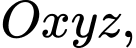 cho tam giác ABC có
cho tam giác ABC có 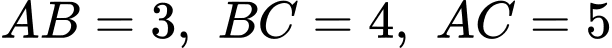 và mặt phẳng
và mặt phẳng 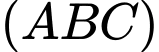 song song với mặt phẳng
song song với mặt phẳng 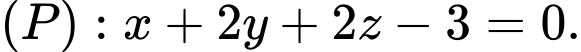 Biết ba cạnh của tam giác
Biết ba cạnh của tam giác 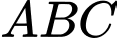 tiếp xúc với mặt cầu
tiếp xúc với mặt cầu 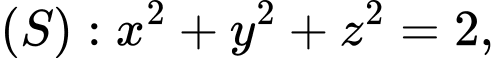 khi đó mặt phẳng
khi đó mặt phẳng 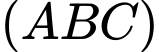 cắt trục
cắt trục 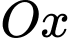 tại điểm có hoành độ là bao nhiêu?
tại điểm có hoành độ là bao nhiêu?
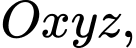 cho tam giác ABC có
cho tam giác ABC có 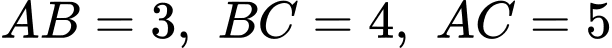 và mặt phẳng
và mặt phẳng 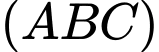 song song với mặt phẳng
song song với mặt phẳng 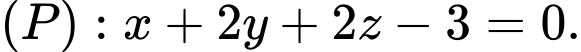 Biết ba cạnh của tam giác
Biết ba cạnh của tam giác 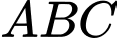 tiếp xúc với mặt cầu
tiếp xúc với mặt cầu 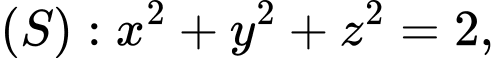 khi đó mặt phẳng
khi đó mặt phẳng 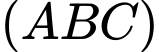 cắt trục
cắt trục 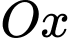 tại điểm có hoành độ là bao nhiêu?
tại điểm có hoành độ là bao nhiêu?
Điền đáp án: -3.
 +) Tam giác
+) Tam giác 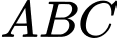 vuông tại
vuông tại 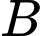 .
.
+) Mặt cầu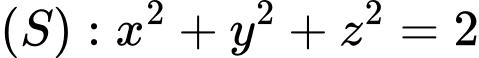 có tâm
có tâm 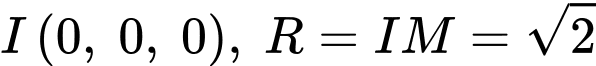 .
.
Ta có: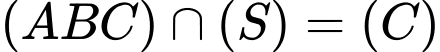 , 3 cạnh của
, 3 cạnh của 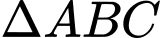 tiếp xúc với mặt cầu
tiếp xúc với mặt cầu 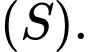
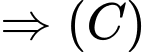 là đường tròn nội tiếp
là đường tròn nội tiếp 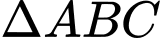 .
.
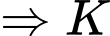 là tâm đường tròn nội tiếp
là tâm đường tròn nội tiếp 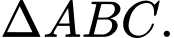
Ta có: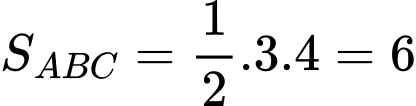
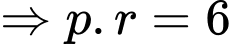
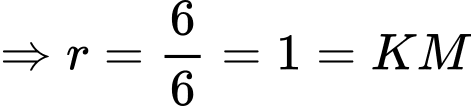 .
.
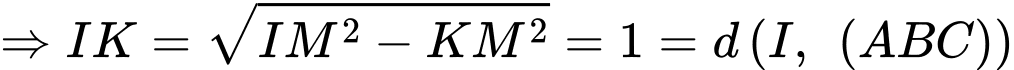 .
.
+) Vì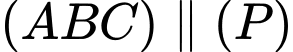
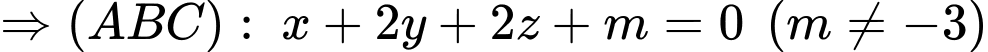
Có: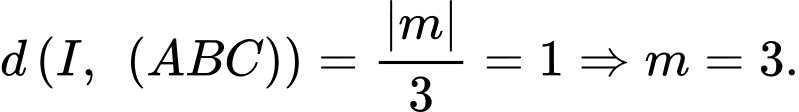
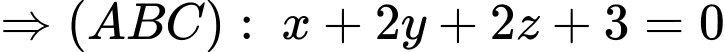
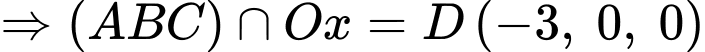
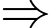 Mặt phẳng
Mặt phẳng 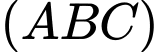 cắt trục
cắt trục 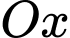 tại điểm có hoành độ bằng -3.
tại điểm có hoành độ bằng -3.

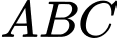 vuông tại
vuông tại 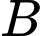 .
.
+) Mặt cầu
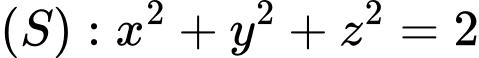 có tâm
có tâm 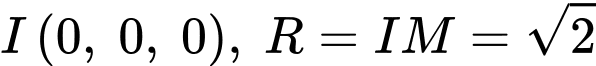 .
.
Ta có:
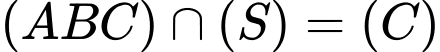 , 3 cạnh của
, 3 cạnh của 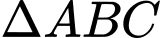 tiếp xúc với mặt cầu
tiếp xúc với mặt cầu 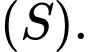
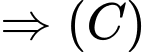 là đường tròn nội tiếp
là đường tròn nội tiếp 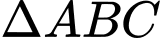 .
. 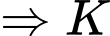 là tâm đường tròn nội tiếp
là tâm đường tròn nội tiếp 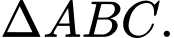
Ta có:
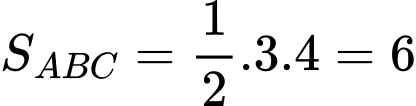
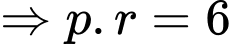
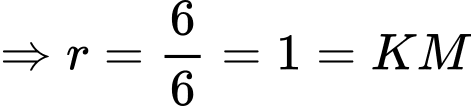 .
.
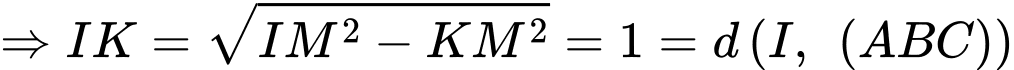 .
.
+) Vì
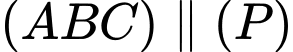
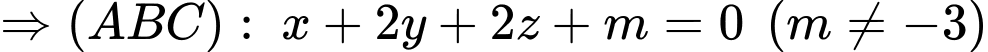
Có:
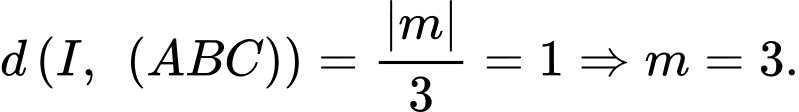
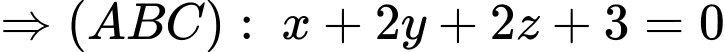
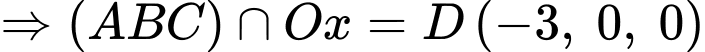
 Mặt phẳng
Mặt phẳng 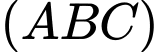 cắt trục
cắt trục 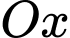 tại điểm có hoành độ bằng -3.
tại điểm có hoành độ bằng -3.
Câu 21 [696334]: Một bệnh viện sử dụng một xét nghiệm để phát hiện một loại bệnh X với độ chính xác là 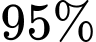 (nghĩa là
(nghĩa là 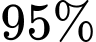 bệnh nhân mắc bệnh sẽ có kết quả dương tính). Xét nghiệm này cũng có tỷ lệ dương tính giả là
bệnh nhân mắc bệnh sẽ có kết quả dương tính). Xét nghiệm này cũng có tỷ lệ dương tính giả là 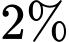 (nghĩa là
(nghĩa là 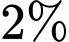 bệnh nhân không mắc bệnh cũng có kết quả dương tính). Biết rằng, nếu một người nhận kết quả xét nghiệm dương tính thì xác suất thực sự người đó mắc bệnh X là
bệnh nhân không mắc bệnh cũng có kết quả dương tính). Biết rằng, nếu một người nhận kết quả xét nghiệm dương tính thì xác suất thực sự người đó mắc bệnh X là 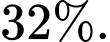 Tính tỷ lệ mắc bệnh X trong dân số theo đơn vị %. (làm tròn kết quả đến hàng phần trăm).
Tính tỷ lệ mắc bệnh X trong dân số theo đơn vị %. (làm tròn kết quả đến hàng phần trăm).
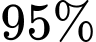 (nghĩa là
(nghĩa là 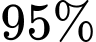 bệnh nhân mắc bệnh sẽ có kết quả dương tính). Xét nghiệm này cũng có tỷ lệ dương tính giả là
bệnh nhân mắc bệnh sẽ có kết quả dương tính). Xét nghiệm này cũng có tỷ lệ dương tính giả là 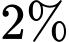 (nghĩa là
(nghĩa là 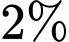 bệnh nhân không mắc bệnh cũng có kết quả dương tính). Biết rằng, nếu một người nhận kết quả xét nghiệm dương tính thì xác suất thực sự người đó mắc bệnh X là
bệnh nhân không mắc bệnh cũng có kết quả dương tính). Biết rằng, nếu một người nhận kết quả xét nghiệm dương tính thì xác suất thực sự người đó mắc bệnh X là 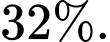 Tính tỷ lệ mắc bệnh X trong dân số theo đơn vị %. (làm tròn kết quả đến hàng phần trăm).
Tính tỷ lệ mắc bệnh X trong dân số theo đơn vị %. (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,98.
Giả sử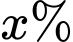 dân số thực sự mắc bệnh này.
dân số thực sự mắc bệnh này.
Để giải câu hỏi này, chúng ta sẽ sử dụng công thức Bayes.
Gọi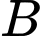 là biến cố “Người mắc bệnh”, có
là biến cố “Người mắc bệnh”, có 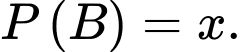
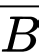 là biến cố “Người không mắc bệnh”, có
là biến cố “Người không mắc bệnh”, có 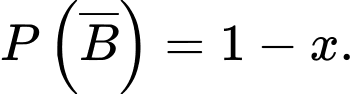
Gọi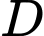 là biến cố “Người đó được xét nghiệm có kết quả dương tính”. Khi đó,
là biến cố “Người đó được xét nghiệm có kết quả dương tính”. Khi đó,
Xác suất xét nghiệm dương tính nếu mắc bệnh là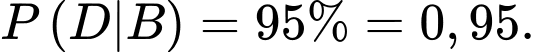
Xác suất xét nghiệm dương tính nếu không mắc bệnh là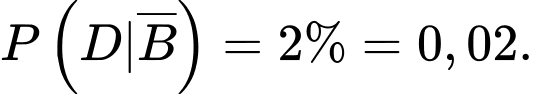
YCBT

Ta có sơ đồ cây sau:
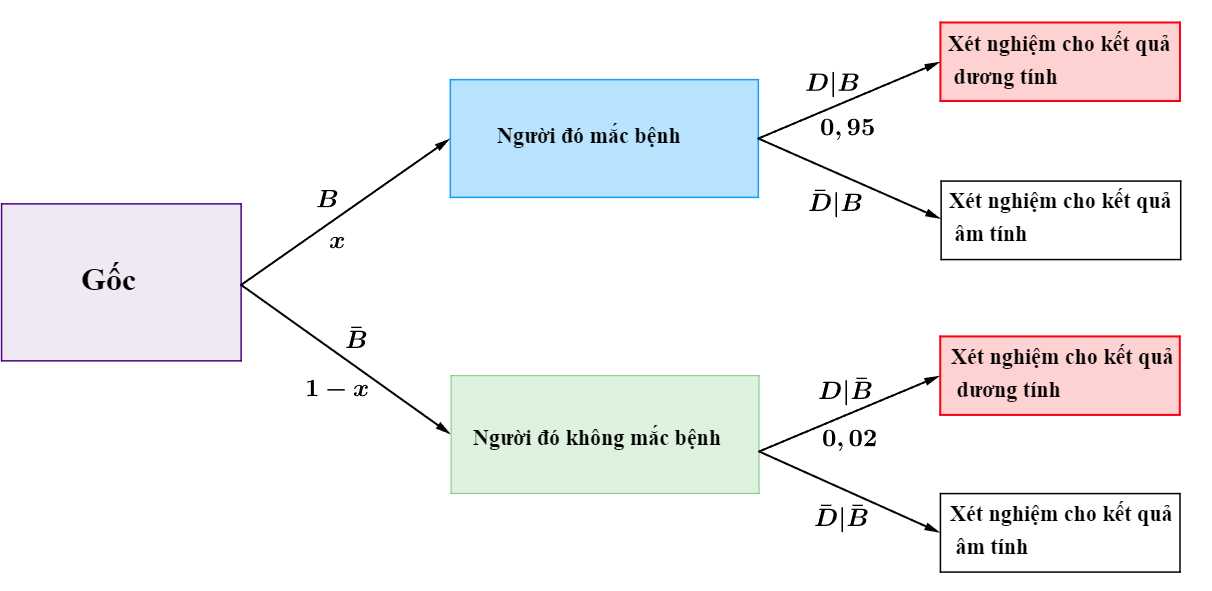
Suy ra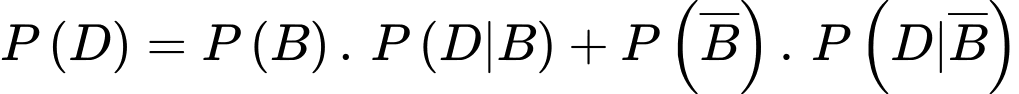
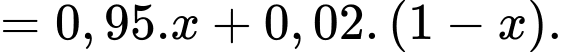
Theo giả thiết, ta có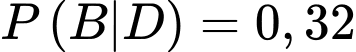
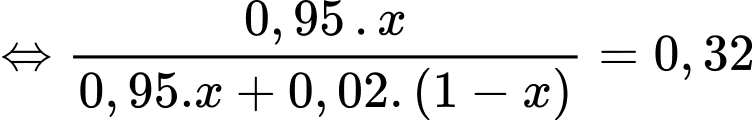
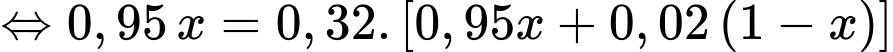
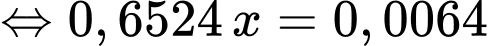
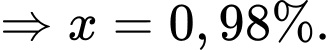
Vậy tỷ lệ mắc bệnh X trong dân số là 0,98%.
Giả sử
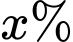 dân số thực sự mắc bệnh này.
dân số thực sự mắc bệnh này.
Để giải câu hỏi này, chúng ta sẽ sử dụng công thức Bayes.
Gọi
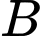 là biến cố “Người mắc bệnh”, có
là biến cố “Người mắc bệnh”, có 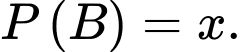
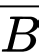 là biến cố “Người không mắc bệnh”, có
là biến cố “Người không mắc bệnh”, có 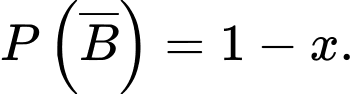
Gọi
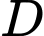 là biến cố “Người đó được xét nghiệm có kết quả dương tính”. Khi đó,
là biến cố “Người đó được xét nghiệm có kết quả dương tính”. Khi đó,
Xác suất xét nghiệm dương tính nếu mắc bệnh là
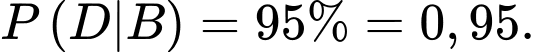
Xác suất xét nghiệm dương tính nếu không mắc bệnh là
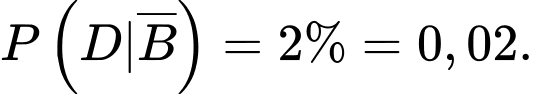
YCBT


Ta có sơ đồ cây sau:

Suy ra
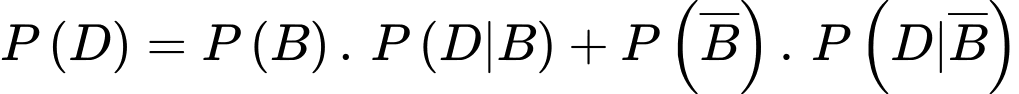
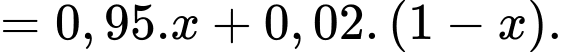
Theo giả thiết, ta có
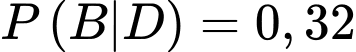
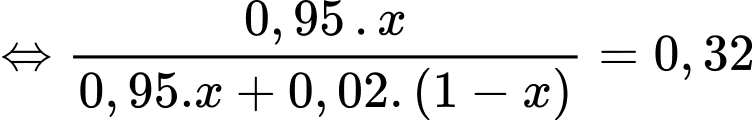
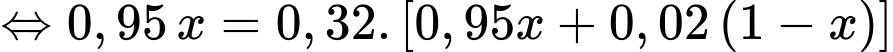
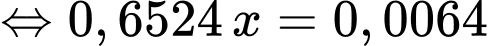
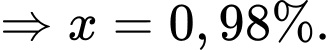
Vậy tỷ lệ mắc bệnh X trong dân số là 0,98%.
Câu 22 [696488]: Định luật làm mát của Newton phát biểu rằng tốc độ làm mát của một vật tỉ lệ thuận với chênh lệch nhiệt độ giữa vật đó và môi trường xung quanh, với điều kiện là chênh lệch này không quá lớn. Giả sử 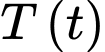 là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm
là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm 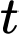 (đơn vị: giờ) và
(đơn vị: giờ) và 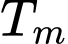 là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là
là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là 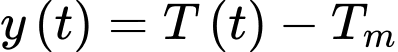 thì
thì 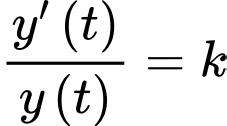 với
với 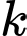 là hằng số. Lúc 8 giờ sáng, nhiệt độ của một xác chết là 13°C. Đến 11 giờ sáng, nhiệt độ đã giảm xuống còn 9°C. Biết rằng nhiệt độ của một cơ thể sống là 37°C và nhiệt độ môi trường xung quanh không đổi ở mức 5°C. Hỏi lúc 11 giờ sáng, nạn nhân đã tử vong được bao nhiêu giờ? (Kết quả làm tròn đến hàng phần mười).
là hằng số. Lúc 8 giờ sáng, nhiệt độ của một xác chết là 13°C. Đến 11 giờ sáng, nhiệt độ đã giảm xuống còn 9°C. Biết rằng nhiệt độ của một cơ thể sống là 37°C và nhiệt độ môi trường xung quanh không đổi ở mức 5°C. Hỏi lúc 11 giờ sáng, nạn nhân đã tử vong được bao nhiêu giờ? (Kết quả làm tròn đến hàng phần mười).
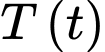 là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm
là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm 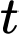 (đơn vị: giờ) và
(đơn vị: giờ) và 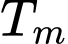 là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là
là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là 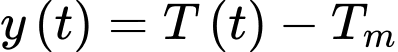 thì
thì 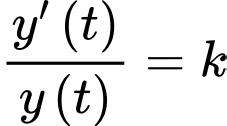 với
với 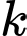 là hằng số. Lúc 8 giờ sáng, nhiệt độ của một xác chết là 13°C. Đến 11 giờ sáng, nhiệt độ đã giảm xuống còn 9°C. Biết rằng nhiệt độ của một cơ thể sống là 37°C và nhiệt độ môi trường xung quanh không đổi ở mức 5°C. Hỏi lúc 11 giờ sáng, nạn nhân đã tử vong được bao nhiêu giờ? (Kết quả làm tròn đến hàng phần mười).
là hằng số. Lúc 8 giờ sáng, nhiệt độ của một xác chết là 13°C. Đến 11 giờ sáng, nhiệt độ đã giảm xuống còn 9°C. Biết rằng nhiệt độ của một cơ thể sống là 37°C và nhiệt độ môi trường xung quanh không đổi ở mức 5°C. Hỏi lúc 11 giờ sáng, nạn nhân đã tử vong được bao nhiêu giờ? (Kết quả làm tròn đến hàng phần mười).
Điền đáp án: 9.
Do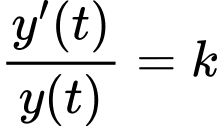 với
với 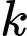 là hằng số, lấy tích phân với cận từ 0 đến
là hằng số, lấy tích phân với cận từ 0 đến 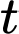 hai vế ta được
hai vế ta được 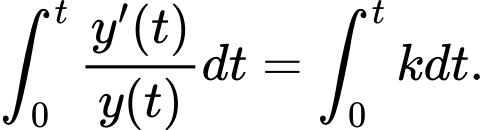
Do đó,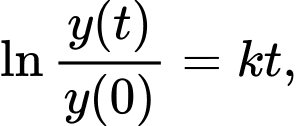 hay
hay 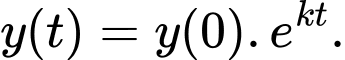
Theo đề bài ta có: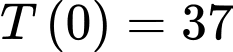
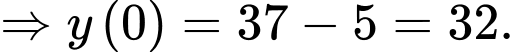
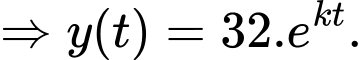
Ta gọi là khoảng thời gian từ lúc người đó chết đến 11h.
là khoảng thời gian từ lúc người đó chết đến 11h.
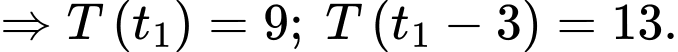
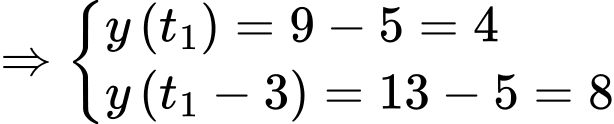
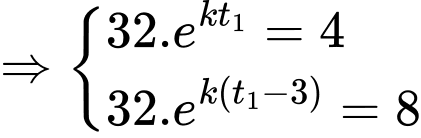
Chia vế cho vế ta được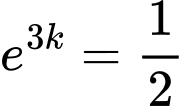
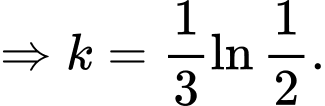
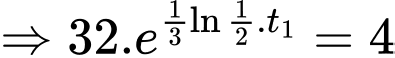
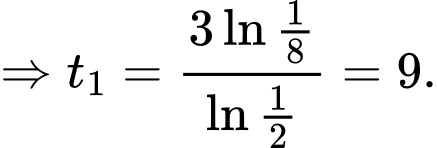
Vậy lúc 11 giờ sáng, nạn nhân đã tử vong được 9 giờ.
Do
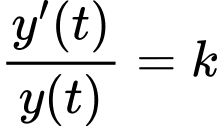 với
với 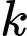 là hằng số, lấy tích phân với cận từ 0 đến
là hằng số, lấy tích phân với cận từ 0 đến 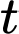 hai vế ta được
hai vế ta được 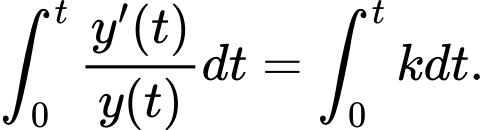
Do đó,
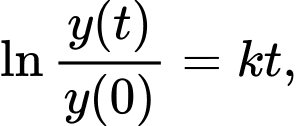 hay
hay 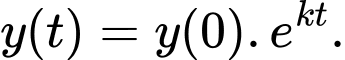
Theo đề bài ta có:
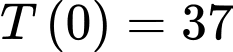
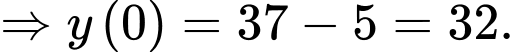
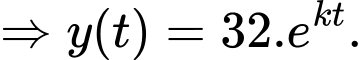
Ta gọi
 là khoảng thời gian từ lúc người đó chết đến 11h.
là khoảng thời gian từ lúc người đó chết đến 11h.
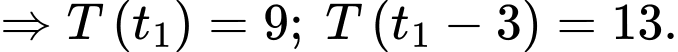
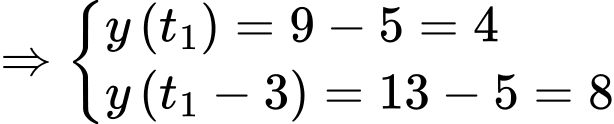
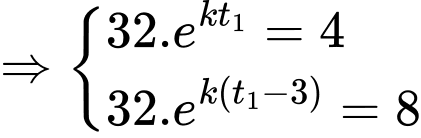
Chia vế cho vế ta được
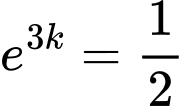
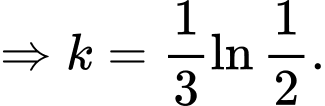
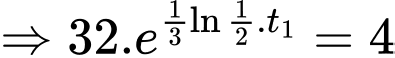
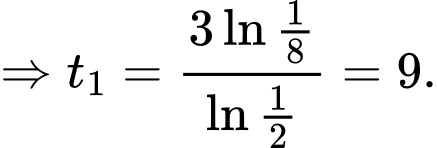
Vậy lúc 11 giờ sáng, nạn nhân đã tử vong được 9 giờ.