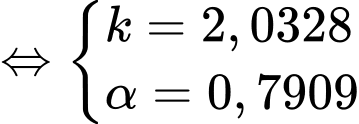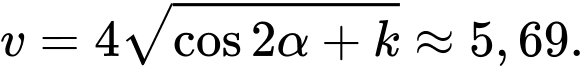PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [626660]: Trong không gian 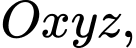 cho mặt phẳng
cho mặt phẳng 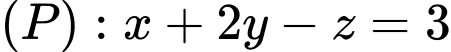 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây?
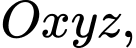 cho mặt phẳng
cho mặt phẳng 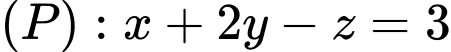 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây? A, 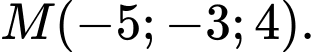
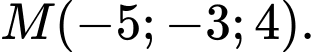
B, 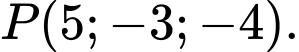
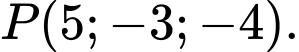
C, 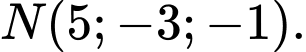
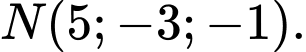
D, 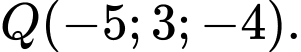
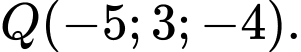
Chọn đáp án B.
Thế lần lượt tọa độ các điểm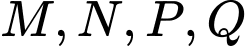 vào phương trình mặt phẳng
vào phương trình mặt phẳng 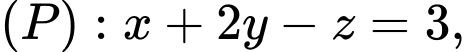 ta thấy chỉ có
ta thấy chỉ có 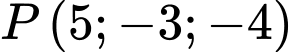 thỏa:
thỏa: 
Từ đó suy ra mặt phẳng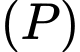 đi qua điểm
đi qua điểm 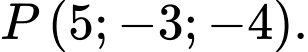 Đáp án: B
Đáp án: B
Thế lần lượt tọa độ các điểm
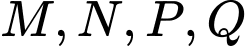 vào phương trình mặt phẳng
vào phương trình mặt phẳng 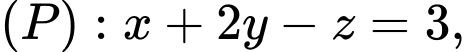 ta thấy chỉ có
ta thấy chỉ có 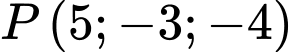 thỏa:
thỏa: 
Từ đó suy ra mặt phẳng
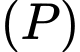 đi qua điểm
đi qua điểm 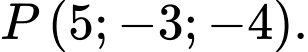 Đáp án: B
Đáp án: B
Câu 2 [328881]: Toạ độ giao điểm hai đường tiệm cận của đồ thị hàm số 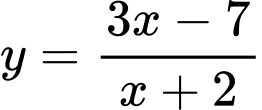 là
là
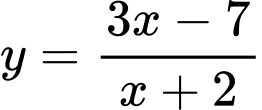 là
là A, 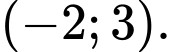
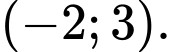
B, 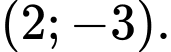
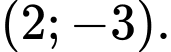
C, 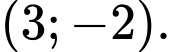
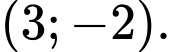
D, 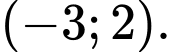
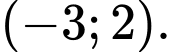
Chọn đáp án A.
Đồ thị có tiệm cận đứng, tiệm cận ngang tương ứng là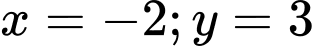
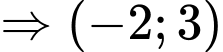 là giao điểm hai tiệm cận. Đáp án: A
là giao điểm hai tiệm cận. Đáp án: A
Đồ thị có tiệm cận đứng, tiệm cận ngang tương ứng là
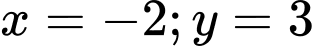
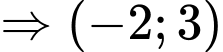 là giao điểm hai tiệm cận. Đáp án: A
là giao điểm hai tiệm cận. Đáp án: A
Câu 3 [696337]: Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường cao tốc trong một khoảng thời gian ở bảng sau.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
A, 75 km/h.
B, 25 km/h.
C, 100 km/h.
D, 5 km/h.
Chọn đáp án B.
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: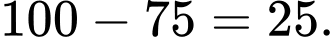 Đáp án: B
Đáp án: B
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
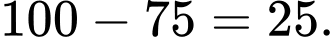 Đáp án: B
Đáp án: B
Câu 4 [146618]: Trong không gian 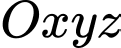 , cho hai điểm
, cho hai điểm 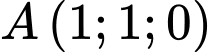 và
và 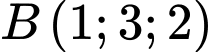 . Phương trình của mặt cầu đường kính
. Phương trình của mặt cầu đường kính  là
là
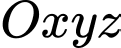 , cho hai điểm
, cho hai điểm 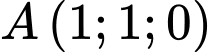 và
và 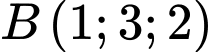 . Phương trình của mặt cầu đường kính
. Phương trình của mặt cầu đường kính  là
là A, 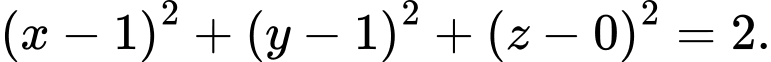
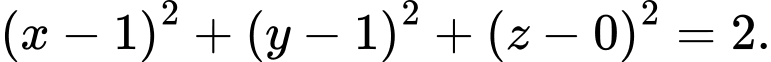
B, 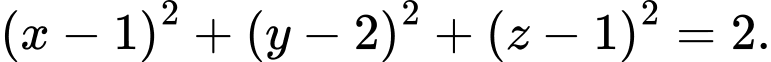
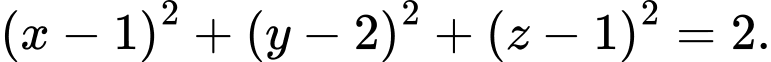
C, 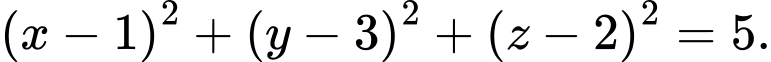
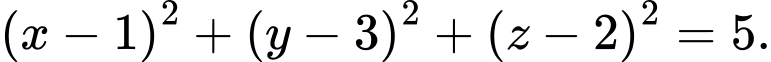
D, 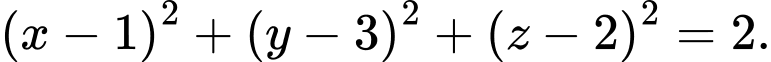
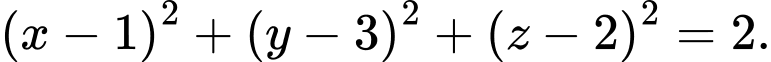
Chọn đáp án B.
Do đường kính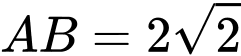 nên tâm
nên tâm 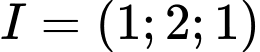 (
( trung điểm
trung điểm 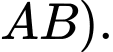
Nên phương trình mặt cầu là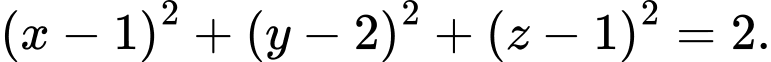 Đáp án: B
Đáp án: B
Do đường kính
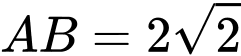 nên tâm
nên tâm 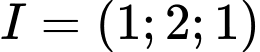 (
(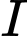 trung điểm
trung điểm 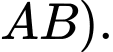
Nên phương trình mặt cầu là
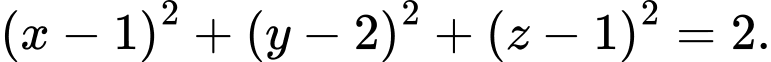 Đáp án: B
Đáp án: B
Câu 5 [803795]: Họ tất cả các nguyên hàm của hàm số 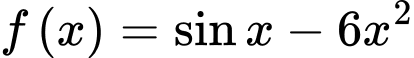 là
là
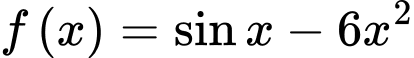 là
là A, 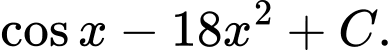
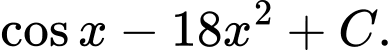
B, 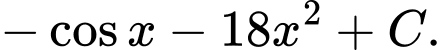
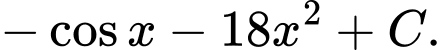
C, 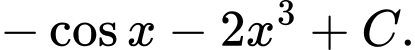
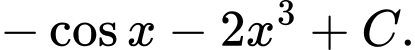
D, 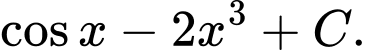
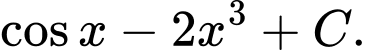
Chọn đáp án C.
Ta có: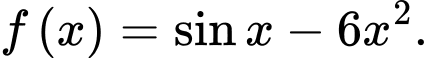
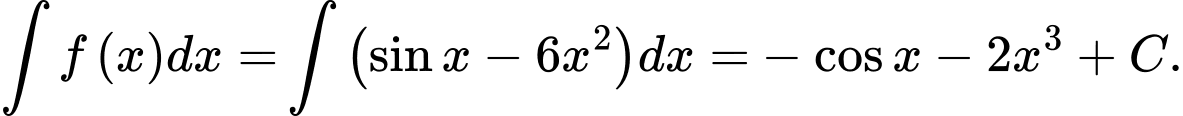 Đáp án: C
Đáp án: C
Ta có:
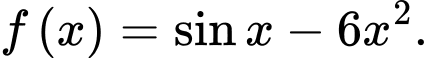
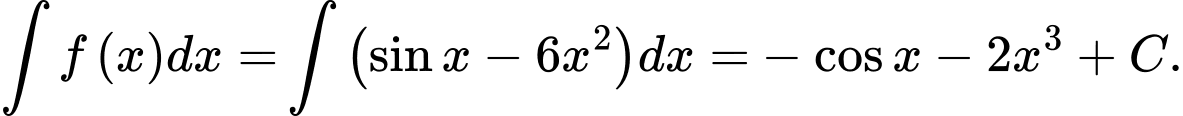 Đáp án: C
Đáp án: C
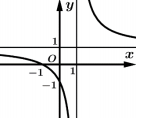
Câu 6 [30672]: Đồ thị ở bên dưới là của hàm số nào?

A, 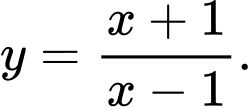
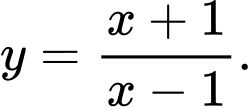
B, 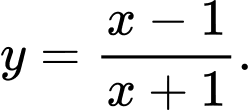
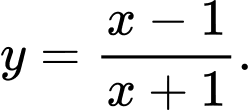
C, 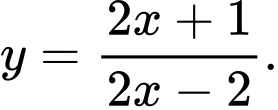
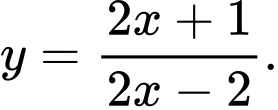
D, 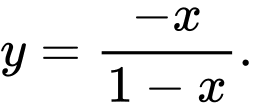
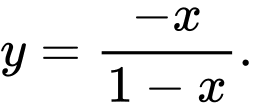
Chọn đáp án A.
Đồ thị hàm số có tiệm cận đứng là nên loại B.
Đồ thị hàm số có tiệm cận đứng là nên loại B.
Mặt khác đồ thị đi qua điểm 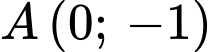 nên chọn đáp án A.
nên chọn đáp án A.
Đáp án: A 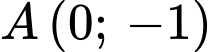 nên chọn đáp án A.
nên chọn đáp án A.
Câu 7 [306856]: Cho 10 điểm phân biệt. Hỏi có thể lập được bao nhiêu vectơ khác  mà điểm đầu và điểm cuối thuộc 10 điểm đã cho
mà điểm đầu và điểm cuối thuộc 10 điểm đã cho
 mà điểm đầu và điểm cuối thuộc 10 điểm đã cho
mà điểm đầu và điểm cuối thuộc 10 điểm đã cho A, 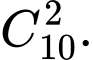
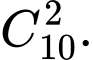
B, 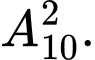
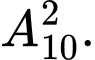
C, 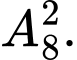
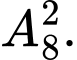
D, 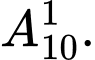
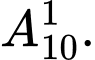
Chọn đáp án B.
Mỗi một vectơ khác mà điểm đầu và điểm cuối thuộc 10 điểm đã cho là một chỉnh hợp chập 2 của 10 phần tử.
mà điểm đầu và điểm cuối thuộc 10 điểm đã cho là một chỉnh hợp chập 2 của 10 phần tử.
Vậy số vectơ cần tìm là: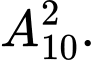 Đáp án: B
Đáp án: B
Mỗi một vectơ khác
 mà điểm đầu và điểm cuối thuộc 10 điểm đã cho là một chỉnh hợp chập 2 của 10 phần tử.
mà điểm đầu và điểm cuối thuộc 10 điểm đã cho là một chỉnh hợp chập 2 của 10 phần tử. Vậy số vectơ cần tìm là:
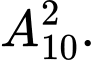 Đáp án: B
Đáp án: B
Câu 8 [599604]: Cho hai vectơ 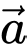 và
và 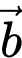 thỏa mãn
thỏa mãn 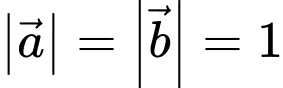 và hai vectơ
và hai vectơ 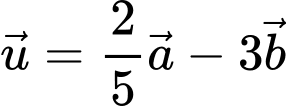 và
và 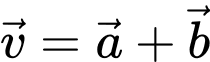 vuông góc với nhau. Xác định góc
vuông góc với nhau. Xác định góc 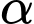 giữa hai vectơ
giữa hai vectơ 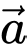 và
và 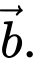
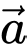 và
và 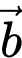 thỏa mãn
thỏa mãn 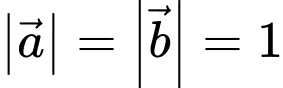 và hai vectơ
và hai vectơ 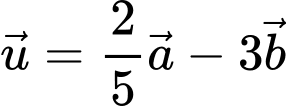 và
và 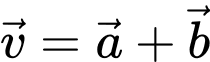 vuông góc với nhau. Xác định góc
vuông góc với nhau. Xác định góc 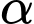 giữa hai vectơ
giữa hai vectơ 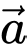 và
và 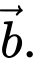
A, 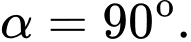
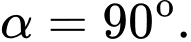
B, 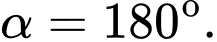
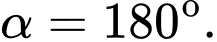
C, 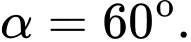
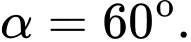
D, 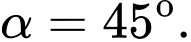
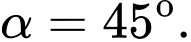
Chọn đáp án B.
Ta có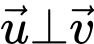
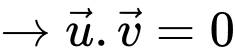
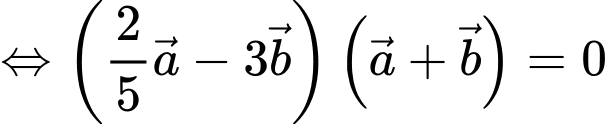
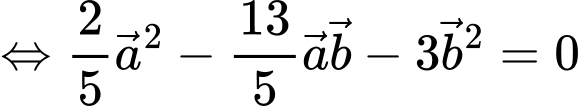
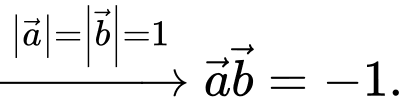
Suy ra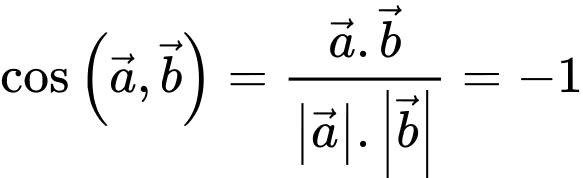
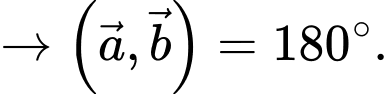 Đáp án: B
Đáp án: B
Ta có
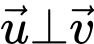
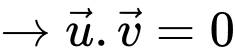
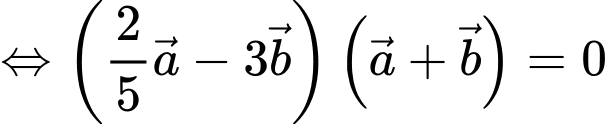
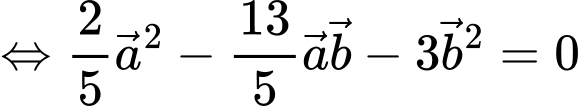
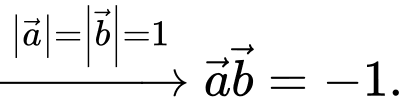
Suy ra
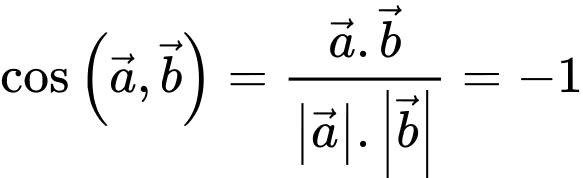
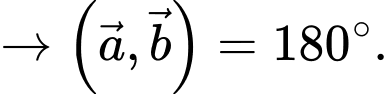 Đáp án: B
Đáp án: B
Câu 9 [306807]: Cho các số thực dương a, b với 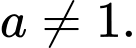 Tìm mệnh đề đúng trong các mệnh đề dưới đây
Tìm mệnh đề đúng trong các mệnh đề dưới đây
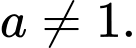 Tìm mệnh đề đúng trong các mệnh đề dưới đây
Tìm mệnh đề đúng trong các mệnh đề dưới đây A, 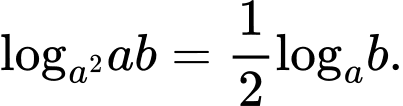
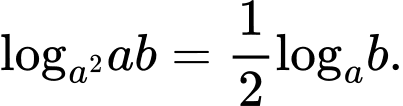
B, 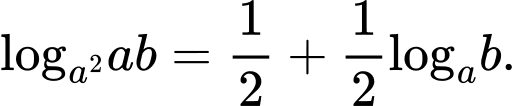
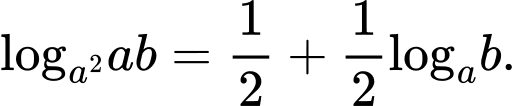
C, 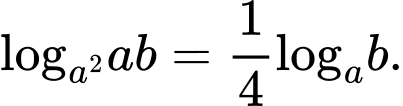
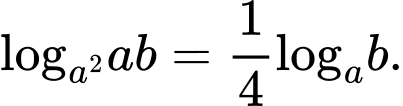
D, 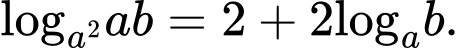
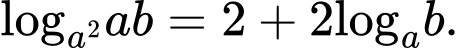
Chọn đáp án B.
Theo công thức logarit ta có:
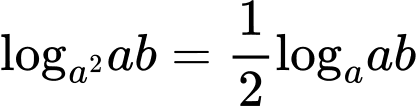
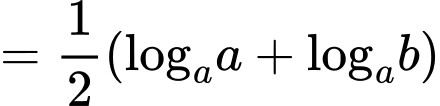
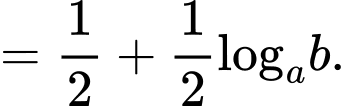 Đáp án: B
Đáp án: B
Theo công thức logarit ta có:
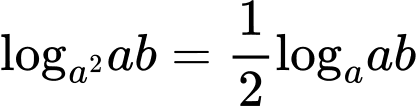
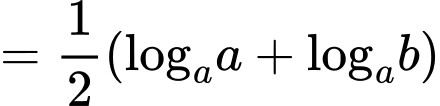
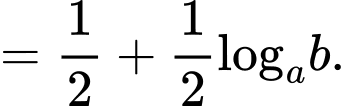 Đáp án: B
Đáp án: B
Câu 10 [522589]: Nếu 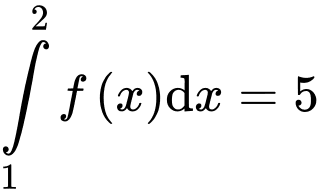 và
và 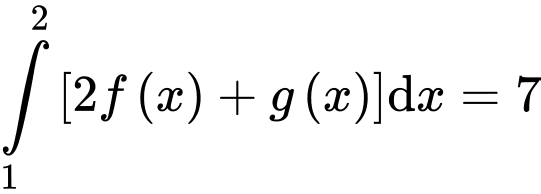 thì
thì 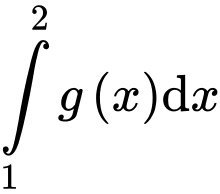 bằng
bằng
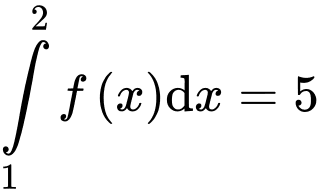 và
và 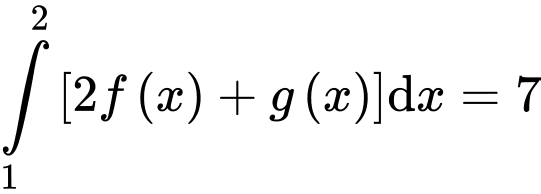 thì
thì 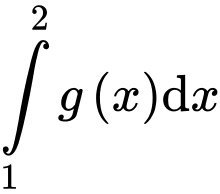 bằng
bằng A, 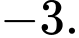
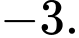
B, 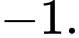
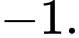
C, 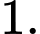
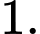
D, 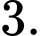
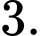
Chọn đáp án A.
Ta có: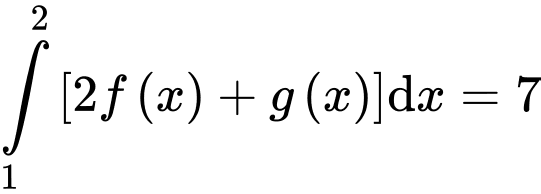
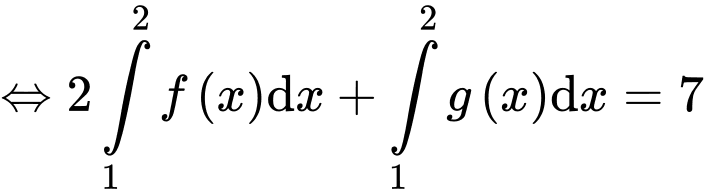 .
.
Do đó: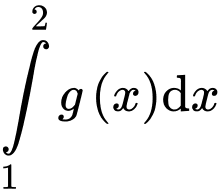
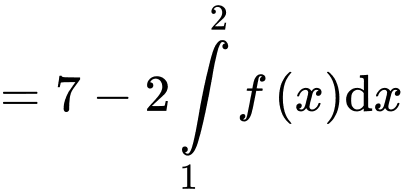
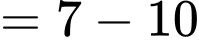
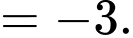 Đáp án: A
Đáp án: A
Ta có:
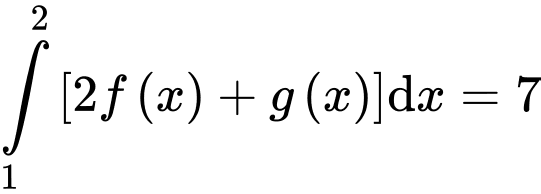
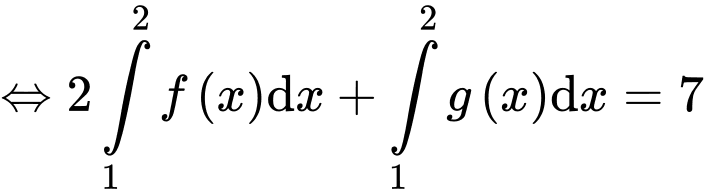 .
. Do đó:
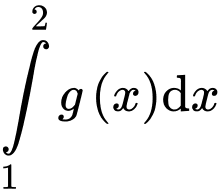
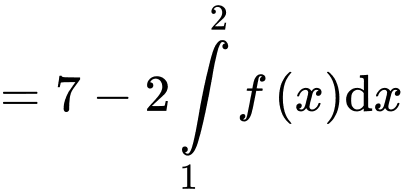
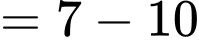
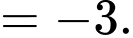 Đáp án: A
Đáp án: A
Câu 11 [502690]: Tập nghiệm của bất phương trình 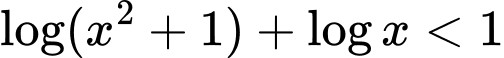 là
là
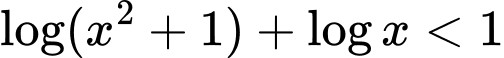 là
là A, 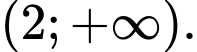
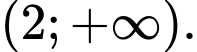
B, 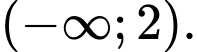
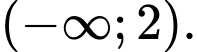
C, 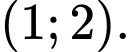
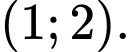
D, 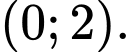
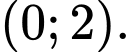
Chọn đáp án D.
Điều kiện
Bất phương trình đã cho tương đương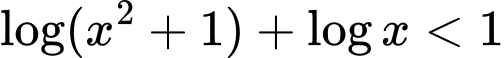
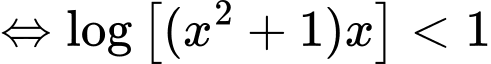
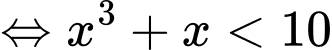
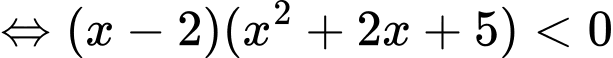
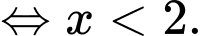
Tập nghiệm bất phương trình là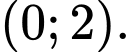 Đáp án: D
Đáp án: D
Điều kiện

Bất phương trình đã cho tương đương
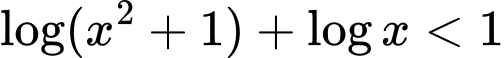
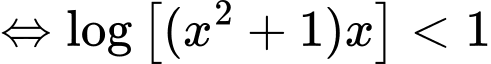
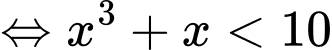
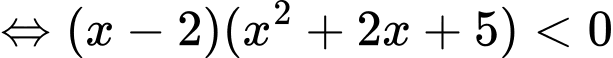
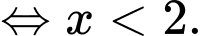
Tập nghiệm bất phương trình là
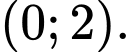 Đáp án: D
Đáp án: D
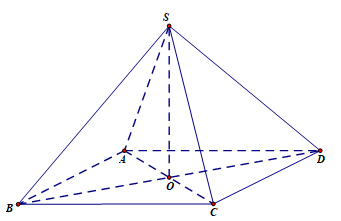
Câu 12 [26351]: Cho hình chóp tứ giác đều 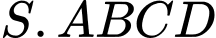 có cạnh đáy bằng
có cạnh đáy bằng 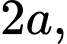 cạnh bên bằng
cạnh bên bằng 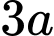 (tham khảo hình vẽ). Tính thể tích
(tham khảo hình vẽ). Tính thể tích  của khối chóp đã cho.
của khối chóp đã cho.
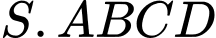 có cạnh đáy bằng
có cạnh đáy bằng 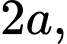 cạnh bên bằng
cạnh bên bằng 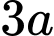 (tham khảo hình vẽ). Tính thể tích
(tham khảo hình vẽ). Tính thể tích  của khối chóp đã cho.
của khối chóp đã cho.
A, 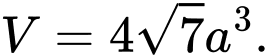
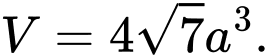
B, 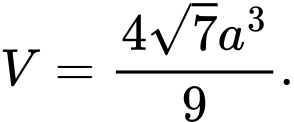
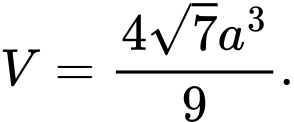
C, 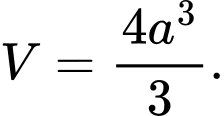
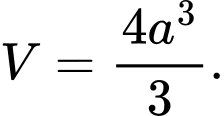
D, 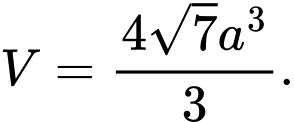
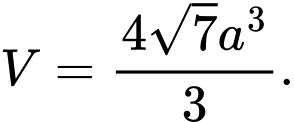
Chọn đáp án D.
Ta có:
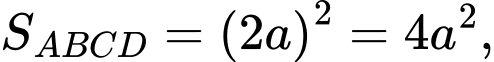

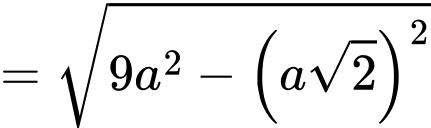
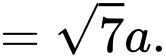
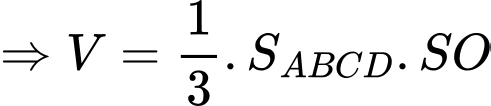
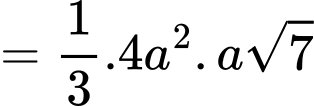
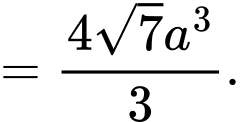 Đáp án: D
Đáp án: D
Ta có:
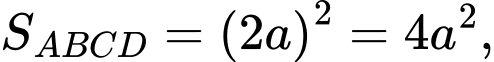

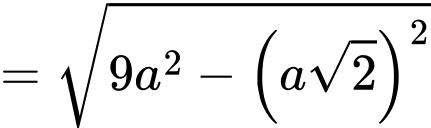
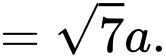
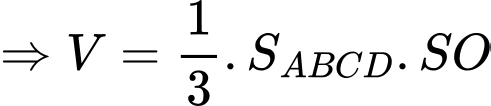
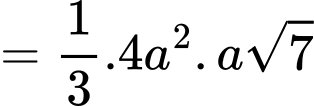
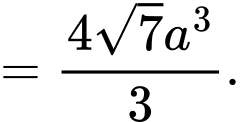 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696338]: Trong không gian 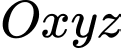 cho măt phẳng
cho măt phẳng 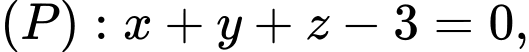 đường thẳng
đường thẳng 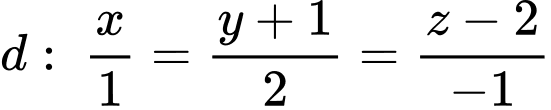 và điểm
và điểm 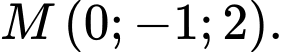
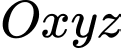 cho măt phẳng
cho măt phẳng 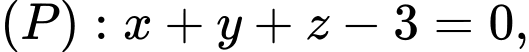 đường thẳng
đường thẳng 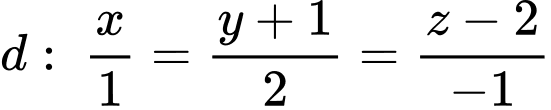 và điểm
và điểm 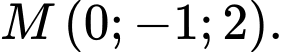
a) Đúng.
Thay tọa độ điểm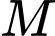 vào phương trình đường thẳng
vào phương trình đường thẳng 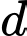 ta thấy thỏa mãn.
ta thấy thỏa mãn.
b) Sai.
Phương trình tham số của đường thẳng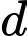 là
là 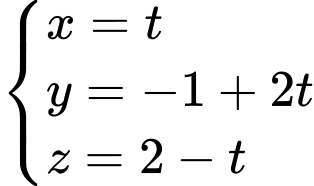 .
.
Thay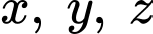 theo
theo 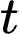 vào phương trình mặt phẳng
vào phương trình mặt phẳng 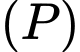 ta được:
ta được:
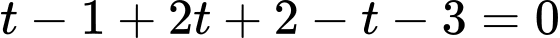
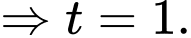
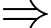 Giao điểm của đường thẳng
Giao điểm của đường thẳng 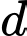 và mặt phẳng
và mặt phẳng 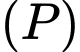 là
là 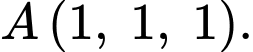
c) Đúng.
Vì là đường thẳng đi qua
là đường thẳng đi qua 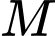 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 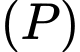 .
.
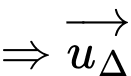
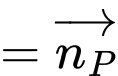
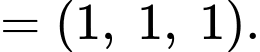
Khi đó có phương trình tham số là
có phương trình tham số là 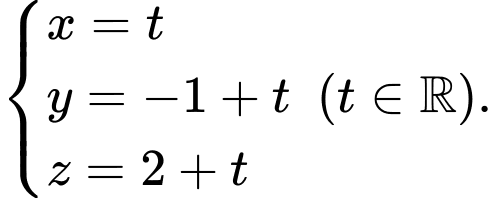
d) Đúng.
Ta có :
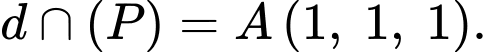
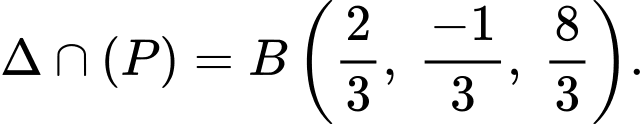
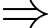
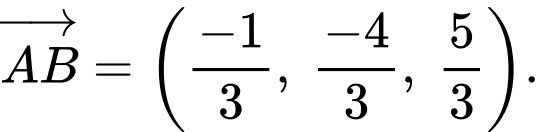
 Hình chiếu vuông góc của
Hình chiếu vuông góc của 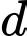 trên
trên 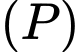 có một vectơ chỉ phương là
có một vectơ chỉ phương là 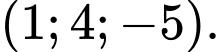
Thay tọa độ điểm
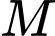 vào phương trình đường thẳng
vào phương trình đường thẳng 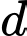 ta thấy thỏa mãn.
ta thấy thỏa mãn.
b) Sai.
Phương trình tham số của đường thẳng
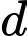 là
là 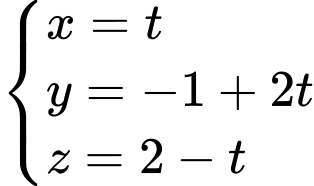 .
.
Thay
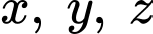 theo
theo 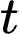 vào phương trình mặt phẳng
vào phương trình mặt phẳng 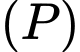 ta được:
ta được:
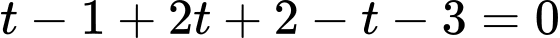
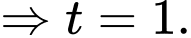
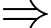 Giao điểm của đường thẳng
Giao điểm của đường thẳng 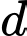 và mặt phẳng
và mặt phẳng 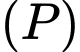 là
là 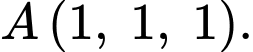
c) Đúng.
Vì
 là đường thẳng đi qua
là đường thẳng đi qua 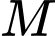 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 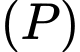 .
.
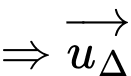
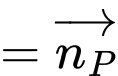
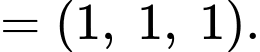
Khi đó
 có phương trình tham số là
có phương trình tham số là 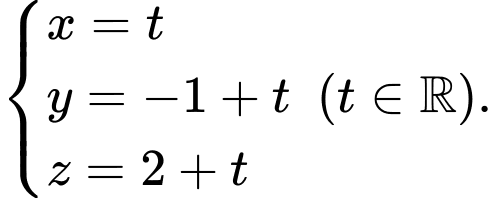
d) Đúng.
Ta có :
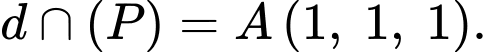
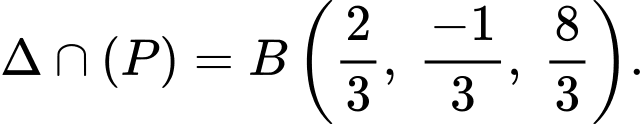
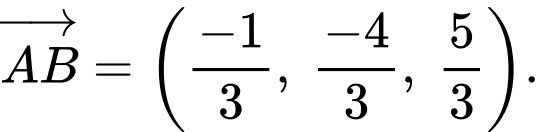
 Hình chiếu vuông góc của
Hình chiếu vuông góc của 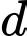 trên
trên 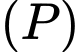 có một vectơ chỉ phương là
có một vectơ chỉ phương là 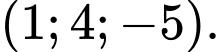
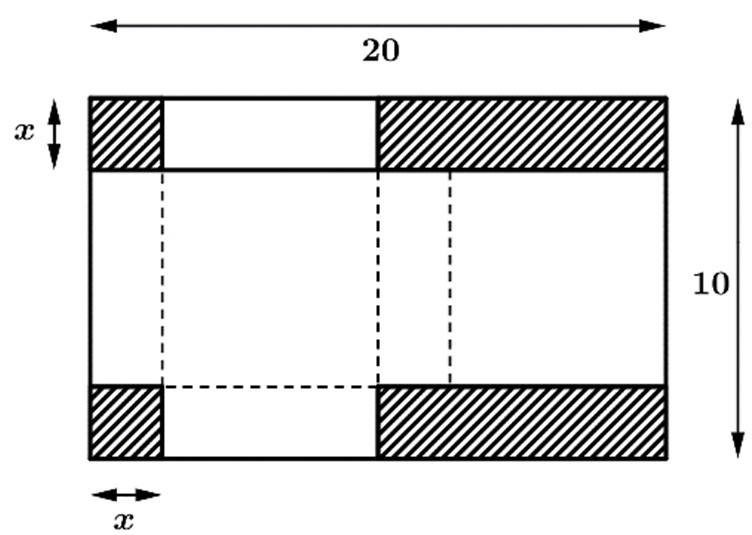
Câu 14 [693208]: Cho miếng bìa hình chữ nhật với kích thước  . Bạn Huy cắt bỏ hai hình vuông nhỏ có cạnh là
. Bạn Huy cắt bỏ hai hình vuông nhỏ có cạnh là  và hai hình chữ nhật (phần gạch sọc như hình vẽ) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp. Gọi
và hai hình chữ nhật (phần gạch sọc như hình vẽ) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp. Gọi  là chiều cao của cái hộp đó.
là chiều cao của cái hộp đó.
 . Bạn Huy cắt bỏ hai hình vuông nhỏ có cạnh là
. Bạn Huy cắt bỏ hai hình vuông nhỏ có cạnh là  và hai hình chữ nhật (phần gạch sọc như hình vẽ) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp. Gọi
và hai hình chữ nhật (phần gạch sọc như hình vẽ) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp. Gọi  là chiều cao của cái hộp đó.
là chiều cao của cái hộp đó.
a) Sai.
Đáy của hộp lần lượt có kích thước là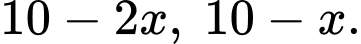
b) Đúng.
Biểu thức thể tích của hộp là
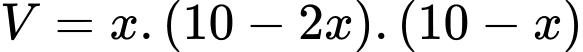

c) Sai.
Xét hàm số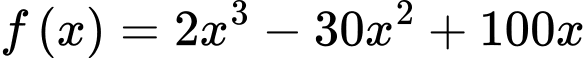
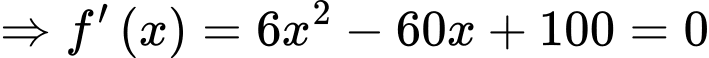
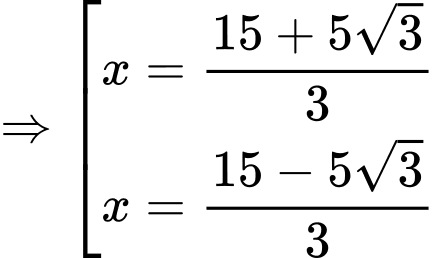
BBT:
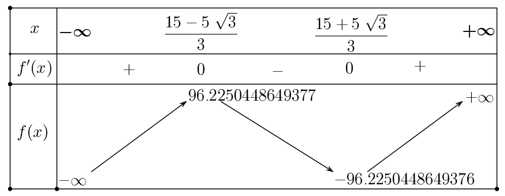
Theo BBT ta thấy thể tích lớn nhất của cái hộp bằng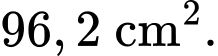
d) Đúng.
Diện tích miếng bìa bạn Huy cần phải cắt là
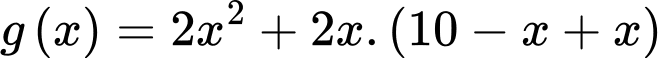
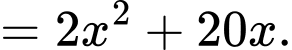
Để thể tích hộp lớn nhất thì bạn Huy cần phải cắt miếng bìa có diện tích
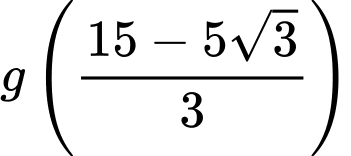
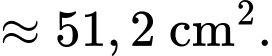
Đáy của hộp lần lượt có kích thước là
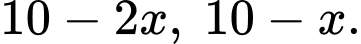
b) Đúng.
Biểu thức thể tích của hộp là
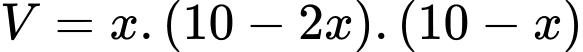

c) Sai.
Xét hàm số
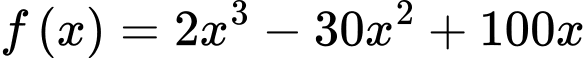
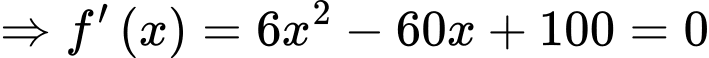
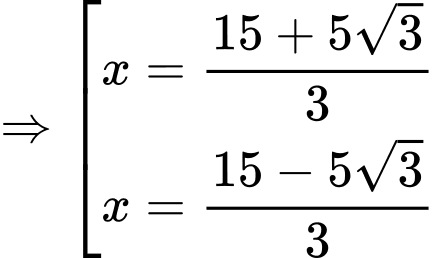
BBT:

Theo BBT ta thấy thể tích lớn nhất của cái hộp bằng
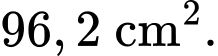
d) Đúng.
Diện tích miếng bìa bạn Huy cần phải cắt là
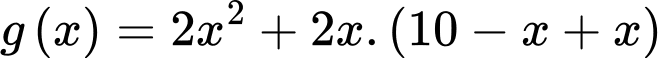
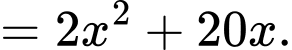
Để thể tích hộp lớn nhất thì bạn Huy cần phải cắt miếng bìa có diện tích
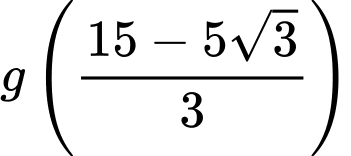
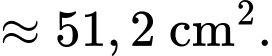
Câu 15 [696341]: Chạy Marathon là môn thể thao mà tại đó, người chơi sẽ hoàn thành quãng đường 42,195 km trong khoảng thời gian nhất định. FM sub 4 là thành tích dành cho những người chơi hoàn thành quãng đường Marathon dưới 4 giờ.
Trong CLB AKR, tỷ lệ thành viên nam là 72%, tỷ lệ thành viên nữ là 28%. Đối với nam, tỷ lệ VĐV hoàn thành Marathon sub 4 là 32%; đối với nữ tỷ lệ VĐV hoàn thành sub 4 là 3%. Chọn ngẫu nhiên 1 thành viên từ CLB AKR:
Trong CLB AKR, tỷ lệ thành viên nam là 72%, tỷ lệ thành viên nữ là 28%. Đối với nam, tỷ lệ VĐV hoàn thành Marathon sub 4 là 32%; đối với nữ tỷ lệ VĐV hoàn thành sub 4 là 3%. Chọn ngẫu nhiên 1 thành viên từ CLB AKR:
Gọi 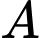 là biến cố “VĐV được chọn là nam”.
là biến cố “VĐV được chọn là nam”.
Gọi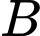 là biến cố “VĐV được chọn đã hoàn thành cự ly Marathon sub 4”.
là biến cố “VĐV được chọn đã hoàn thành cự ly Marathon sub 4”.
Từ giả thiết, ta có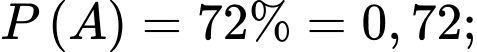
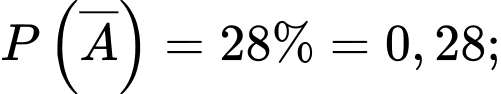
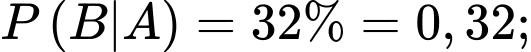
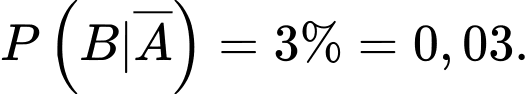
a) Đúng.
Khi VĐV được chọn là nam, xác suất để VĐV này chưa hoàn thành sub 4 cự ly Marathon là
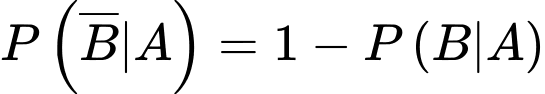
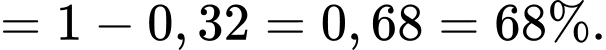
b) Sai.
Xác suất để VĐV được chọn là nữ và đã hoàn thành sub 4 là
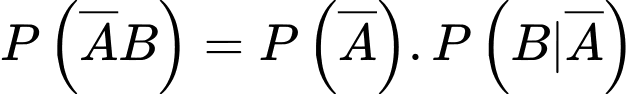
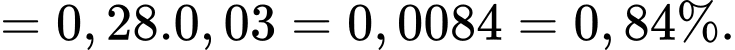
c) Sai.
Ta có sơ đồ cây sau:
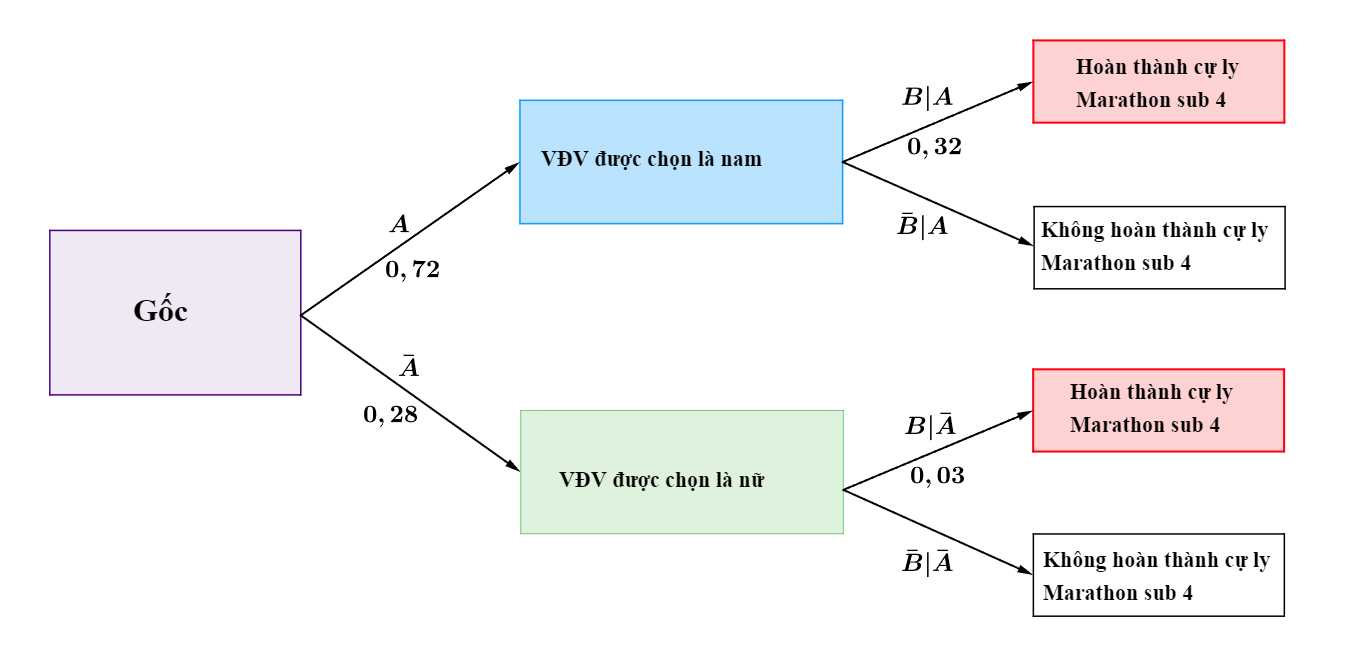
Áp dụng công thức xác suất toàn phần, xác suất để VĐV được chọn đã hoàn thành sub 4 là
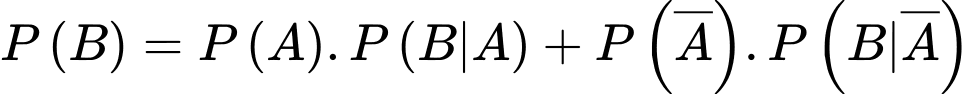
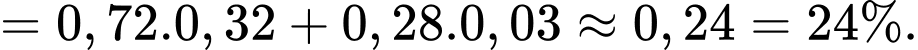
d) Đúng.
Biết VĐV đã hoàn thành sub 4, xác suất để VĐV đó là nam là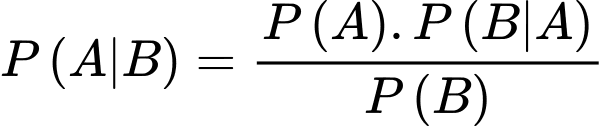
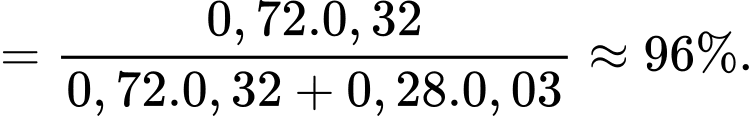
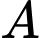 là biến cố “VĐV được chọn là nam”.
là biến cố “VĐV được chọn là nam”.
Gọi
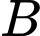 là biến cố “VĐV được chọn đã hoàn thành cự ly Marathon sub 4”.
là biến cố “VĐV được chọn đã hoàn thành cự ly Marathon sub 4”.
Từ giả thiết, ta có
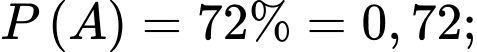
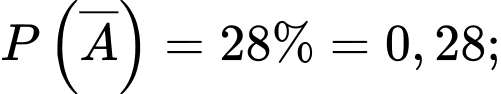
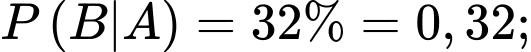
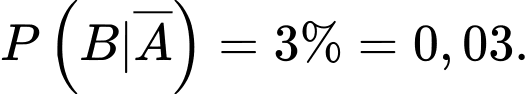
a) Đúng.
Khi VĐV được chọn là nam, xác suất để VĐV này chưa hoàn thành sub 4 cự ly Marathon là
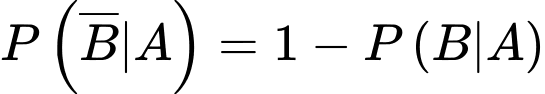
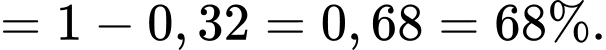
b) Sai.
Xác suất để VĐV được chọn là nữ và đã hoàn thành sub 4 là
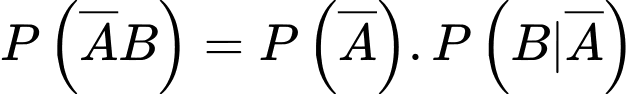
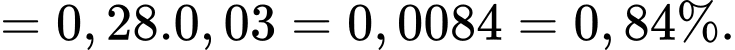
c) Sai.
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, xác suất để VĐV được chọn đã hoàn thành sub 4 là
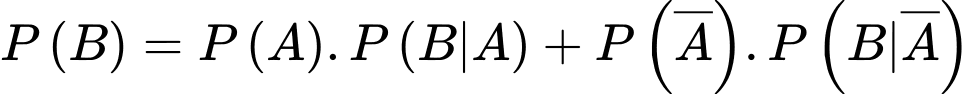
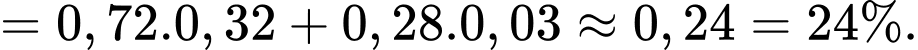
d) Đúng.
Biết VĐV đã hoàn thành sub 4, xác suất để VĐV đó là nam là
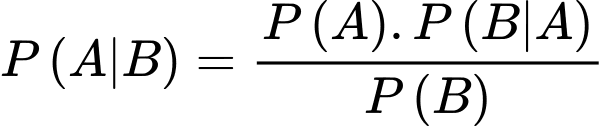
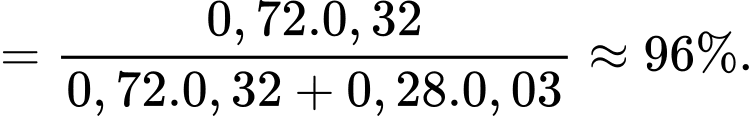
Câu 16 [694661]: Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức  Ở đây
Ở đây 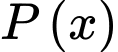 là lợi nhuận (tính bằng triệu đồng) khi bán được
là lợi nhuận (tính bằng triệu đồng) khi bán được 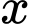 đơn vị sản phẩm. Biết lợi nhuận khi bán được
đơn vị sản phẩm. Biết lợi nhuận khi bán được 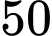 sản phẩm đầu tiên là
sản phẩm đầu tiên là 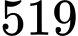 triệu đồng và ta coi rằng khi chưa bán được đơn vị sản phẩm nào thì lợi nhuận bằng 0.
triệu đồng và ta coi rằng khi chưa bán được đơn vị sản phẩm nào thì lợi nhuận bằng 0.
 Ở đây
Ở đây 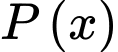 là lợi nhuận (tính bằng triệu đồng) khi bán được
là lợi nhuận (tính bằng triệu đồng) khi bán được 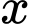 đơn vị sản phẩm. Biết lợi nhuận khi bán được
đơn vị sản phẩm. Biết lợi nhuận khi bán được 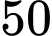 sản phẩm đầu tiên là
sản phẩm đầu tiên là 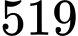 triệu đồng và ta coi rằng khi chưa bán được đơn vị sản phẩm nào thì lợi nhuận bằng 0.
triệu đồng và ta coi rằng khi chưa bán được đơn vị sản phẩm nào thì lợi nhuận bằng 0.
a) Sai.
Lợi nhuận khi bán được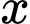 đơn vị sản phẩm được tính bằng công thức
đơn vị sản phẩm được tính bằng công thức 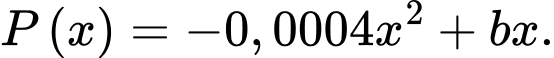
b) Đúng.
Ta có :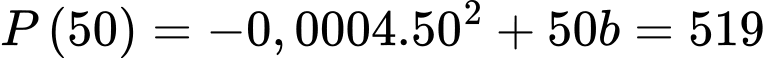
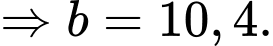
c) Sai.
Lợi nhuận khi bán được 55 sản phẩm là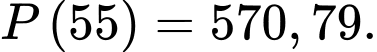
Lợi nhuận tăng thêm khi doanh số tăng từ 50 lên 55 sản phẩm là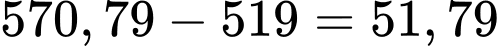 triệu đồng.
triệu đồng.
d) Sai.
Lợi nhuận tăng thêm khi doanh số tăng từ 50 lên đến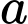 đơn vị sản phẩm là
đơn vị sản phẩm là 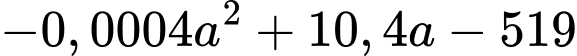
Lợi nhuận tăng lên một lượng lớn hơn 517 triệu đồng nên ta có: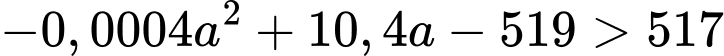

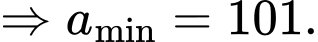
Lợi nhuận khi bán được
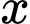 đơn vị sản phẩm được tính bằng công thức
đơn vị sản phẩm được tính bằng công thức 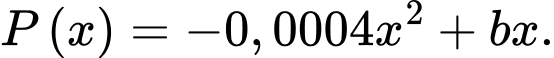
b) Đúng.
Ta có :
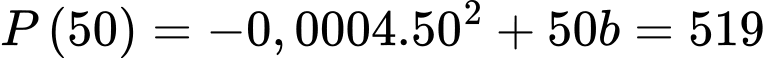
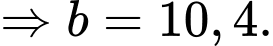
c) Sai.
Lợi nhuận khi bán được 55 sản phẩm là
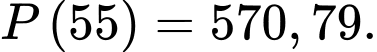
Lợi nhuận tăng thêm khi doanh số tăng từ 50 lên 55 sản phẩm là
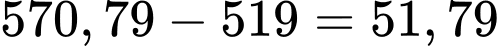 triệu đồng.
triệu đồng.d) Sai.
Lợi nhuận tăng thêm khi doanh số tăng từ 50 lên đến
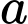 đơn vị sản phẩm là
đơn vị sản phẩm là 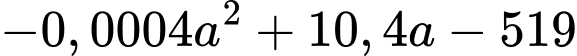
Lợi nhuận tăng lên một lượng lớn hơn 517 triệu đồng nên ta có:
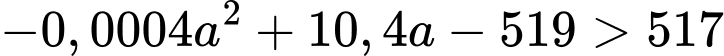

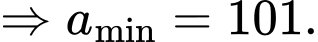
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696342]: Cho hình hộp chữ nhật  có
có 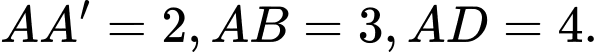 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng  và
và 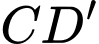 bằng bao nhiêu độ? (kết quả làm tròn đến độ).
bằng bao nhiêu độ? (kết quả làm tròn đến độ).
 có
có 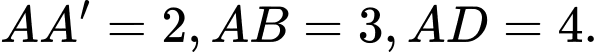 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng  và
và 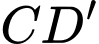 bằng bao nhiêu độ? (kết quả làm tròn đến độ).
bằng bao nhiêu độ? (kết quả làm tròn đến độ).
Điền đáp án: 75.
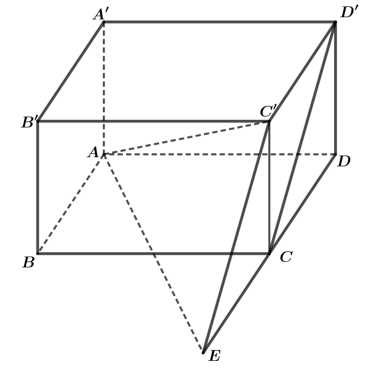
Kẻ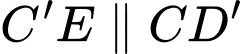
Ta có :
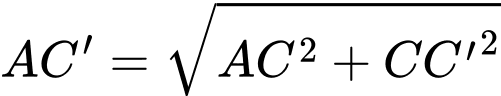
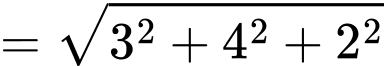
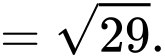

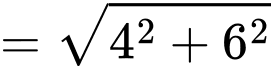
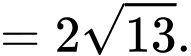
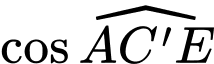
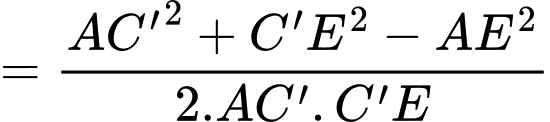
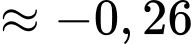
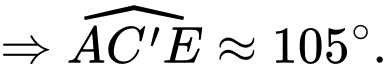
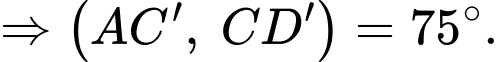

Kẻ
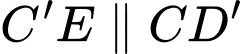
Ta có :

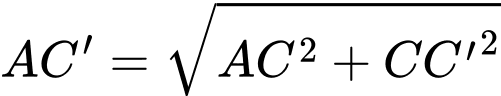
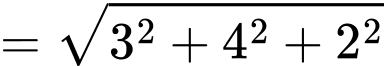
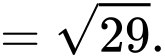

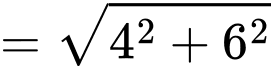
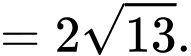
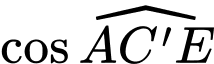
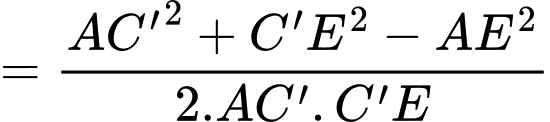
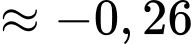
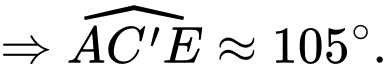
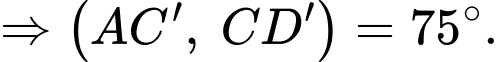
Câu 18 [696343]: Nhân dịp lễ Noel sắp đến, người ta tạo điểm nhấn trong khuôn viên nhà thờ bằng cách xây dựng một cây thông có dạng hình nón có kích thước như sau: đường sinh 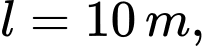 bán kính đáy
bán kính đáy 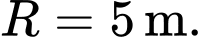 Biết rằng tam giác
Biết rằng tam giác 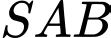 là thiết diện qua trục của hình nón đỉnh S và
là thiết diện qua trục của hình nón đỉnh S và  là trung điểm của
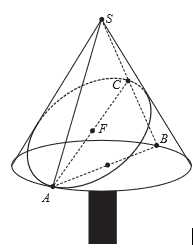
là trung điểm của 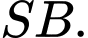 Trang trí một hệ thống đèn điện tử chạy từ
Trang trí một hệ thống đèn điện tử chạy từ 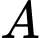 đến
đến  trên mặt nón (tham khảo hình vẽ). Vậy chiều dài dây đèn điện tử ngắn nhất có thể là bao nhiêu mét? (kết quả làm tròn đến hàng phần chục).
trên mặt nón (tham khảo hình vẽ). Vậy chiều dài dây đèn điện tử ngắn nhất có thể là bao nhiêu mét? (kết quả làm tròn đến hàng phần chục).
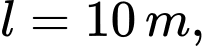 bán kính đáy
bán kính đáy 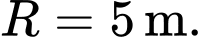 Biết rằng tam giác
Biết rằng tam giác 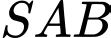 là thiết diện qua trục của hình nón đỉnh S và
là thiết diện qua trục của hình nón đỉnh S và  là trung điểm của
là trung điểm của 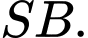 Trang trí một hệ thống đèn điện tử chạy từ
Trang trí một hệ thống đèn điện tử chạy từ 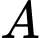 đến
đến  trên mặt nón (tham khảo hình vẽ). Vậy chiều dài dây đèn điện tử ngắn nhất có thể là bao nhiêu mét? (kết quả làm tròn đến hàng phần chục).
trên mặt nón (tham khảo hình vẽ). Vậy chiều dài dây đèn điện tử ngắn nhất có thể là bao nhiêu mét? (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 11,2.
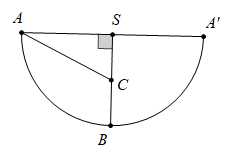
Cố định cạnh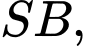 ta trải phẳng hình nón ra theo trục
ta trải phẳng hình nón ra theo trục 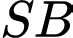 ta được hình vẽ như trên.
ta được hình vẽ như trên.
Ta có chiều dài của dây cung AA’ chính là chu vi của đường tròn đáy trước khi trải của hình nón và bằng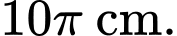
Vì hĩnh vẽ trên là hình quạt tròn có bán kính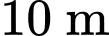 nên ta có
nên ta có 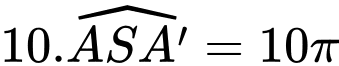
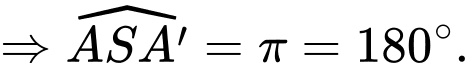
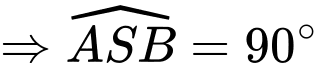
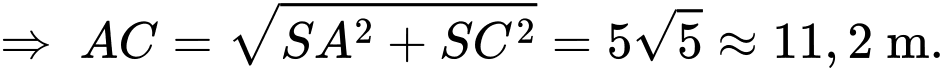
Giá trị ngắn nhất của chiều dài dây đèn là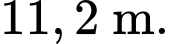

Cố định cạnh
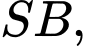 ta trải phẳng hình nón ra theo trục
ta trải phẳng hình nón ra theo trục 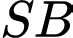 ta được hình vẽ như trên.
ta được hình vẽ như trên.Ta có chiều dài của dây cung AA’ chính là chu vi của đường tròn đáy trước khi trải của hình nón và bằng
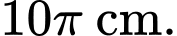
Vì hĩnh vẽ trên là hình quạt tròn có bán kính
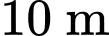 nên ta có
nên ta có 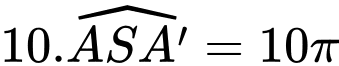
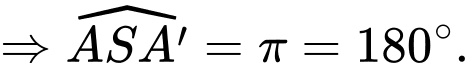
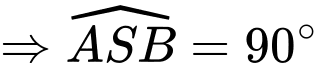
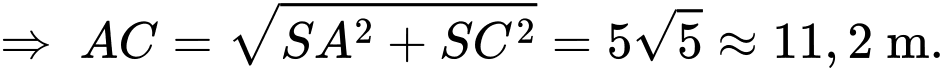
Giá trị ngắn nhất của chiều dài dây đèn là
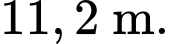
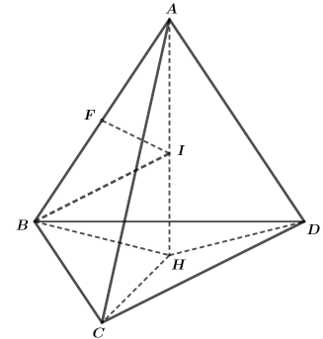
Câu 19 [696344]: Trong không gian 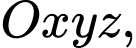 cho tứ diện đều
cho tứ diện đều 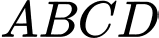 có
có 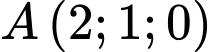 và hình chiếu vuông góc của A trên mặt phẳng
và hình chiếu vuông góc của A trên mặt phẳng 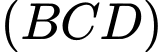 là
là 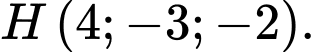 Tọa độ tâm
Tọa độ tâm 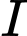 của mặt cầu ngoại tiếp tứ diện
của mặt cầu ngoại tiếp tứ diện 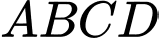 là
là 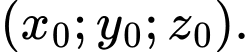 Giá trị của
Giá trị của 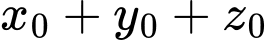 bằng bao nhiêu?
bằng bao nhiêu?
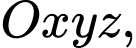 cho tứ diện đều
cho tứ diện đều 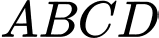 có
có 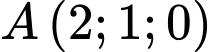 và hình chiếu vuông góc của A trên mặt phẳng
và hình chiếu vuông góc của A trên mặt phẳng 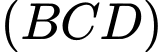 là
là 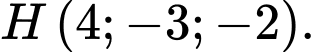 Tọa độ tâm
Tọa độ tâm 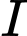 của mặt cầu ngoại tiếp tứ diện
của mặt cầu ngoại tiếp tứ diện 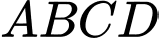 là
là 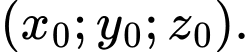 Giá trị của
Giá trị của 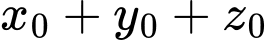 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 0.
Vì tứ diện đều có
có  là chân đường cao kẻ từ
là chân đường cao kẻ từ  xuống mặt phẳng
xuống mặt phẳng  .
.
 là trọng tâm của tam giác
là trọng tâm của tam giác  .
.
Gọi là trung điểm của
là trung điểm của  .
.
Từ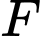 kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với  và cắt
và cắt 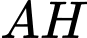 tại
tại 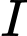 .
.
Đặt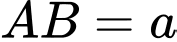 .
.
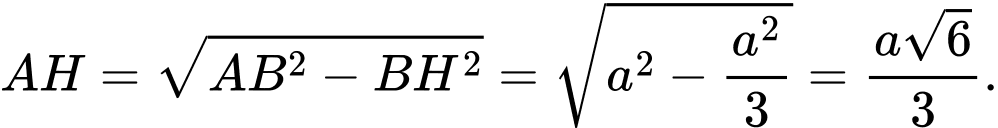
Xét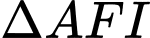 và
và 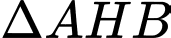 có:
có:
 ,
,  chung
chung

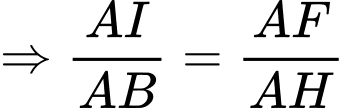
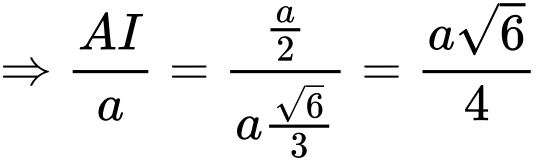
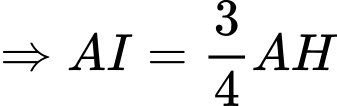
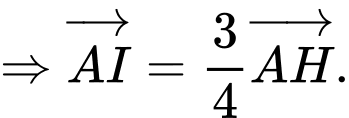
Ta có :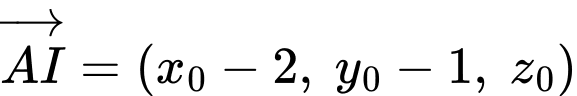 ,
, 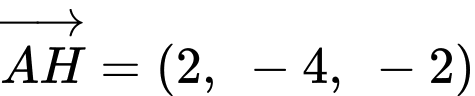
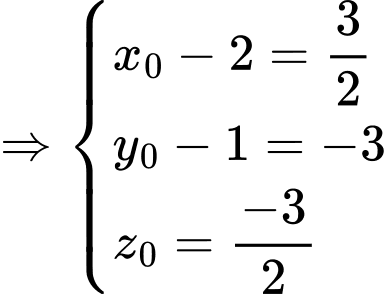
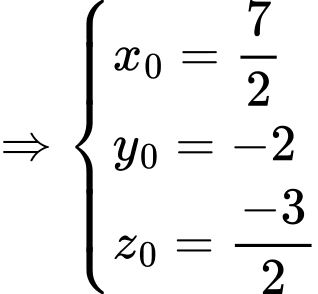
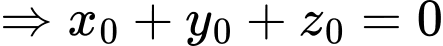 .
.

Vì tứ diện đều
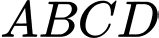 có
có 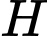 là chân đường cao kẻ từ
là chân đường cao kẻ từ 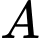 xuống mặt phẳng
xuống mặt phẳng 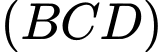 .
.
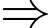
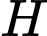 là trọng tâm của tam giác
là trọng tâm của tam giác  .
.
Gọi
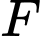 là trung điểm của
là trung điểm của  .
.
Từ
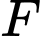 kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với  và cắt
và cắt 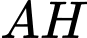 tại
tại 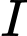 .
.
Đặt
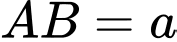 .
.
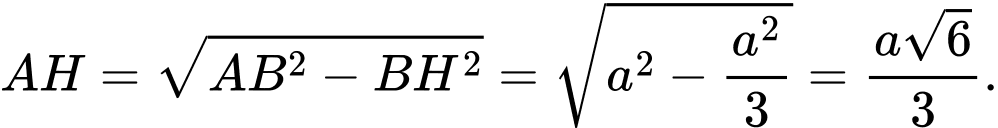
Xét
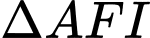 và
và 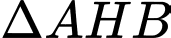 có:
có:
 ,
,  chung
chung

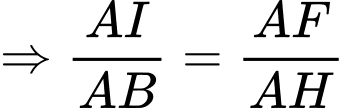
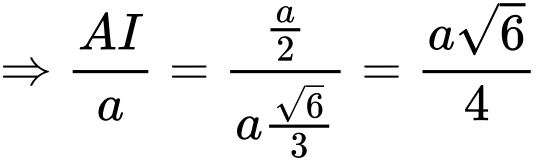
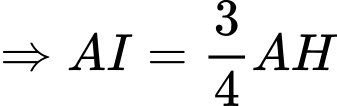
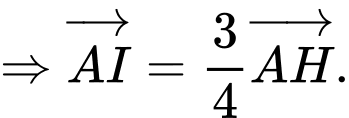
Ta có :
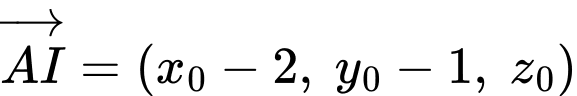 ,
, 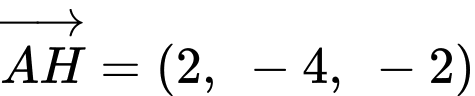
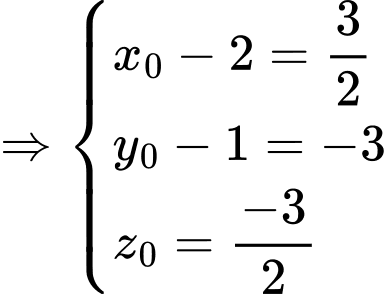
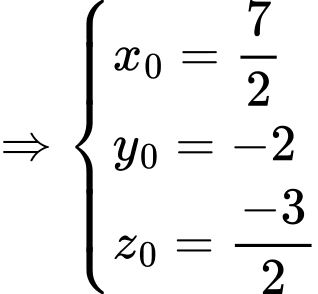
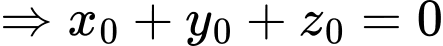 .
.
Câu 20 [696347]: Có 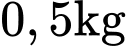 thóc giống ST24 bị trộn lẫn với
thóc giống ST24 bị trộn lẫn với 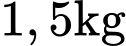 thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là
thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là 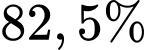 và số hạt thóc trên
và số hạt thóc trên 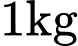 của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
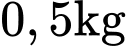 thóc giống ST24 bị trộn lẫn với
thóc giống ST24 bị trộn lẫn với 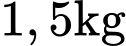 thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là
thóc giống ST25 và được gieo trên một thửa ruộng, xác suất hạt nảy mầm của thóc giống ST24 gấp 1,125 lần xác suất hạt nảy mầm của thóc giống ST25. Biết rằng, xác suất nảy mầm của các hạt thóc trên thửa ruộng này là 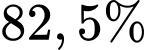 và số hạt thóc trên
và số hạt thóc trên 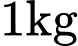 của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
của các giống là bằng nhau. Chọn ngẫu nhiên một hạt nảy mầm, tính xác suất hạt này thuộc giống ST24. Kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,27.
Gọi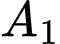 là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra 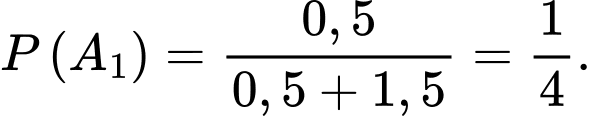
Gọi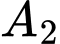 là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra 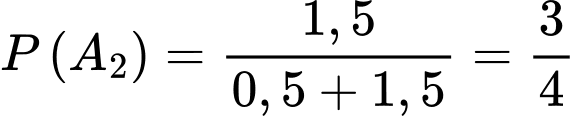 .
.
Gọi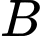 là biến cố “Lấy được một hạt nảy mầm”.
là biến cố “Lấy được một hạt nảy mầm”.
YCBT Tính
Tính 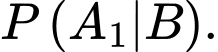
Giả sử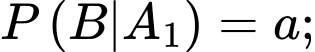
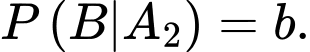
Ta có sơ đồ cây sau:
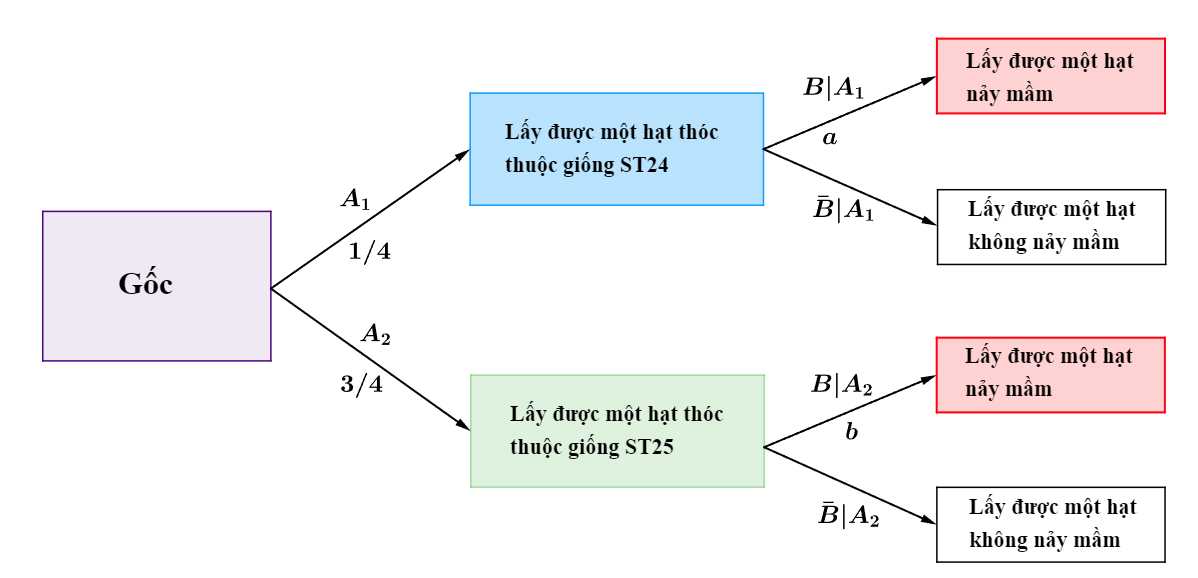
Áp dụng công thức xác suất toàn phần, ta có xác suất nảy mầm của các hạt thóc trên thửa ruộng là
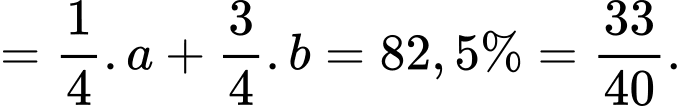
Lại có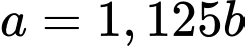 suy ra
suy ra 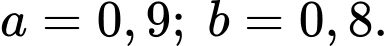
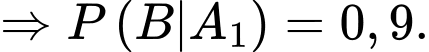
Khi đó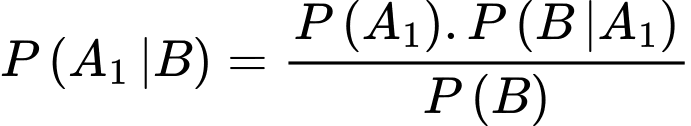
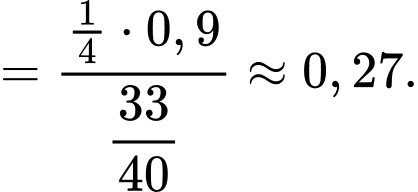
Gọi
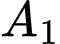 là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST24”. Suy ra 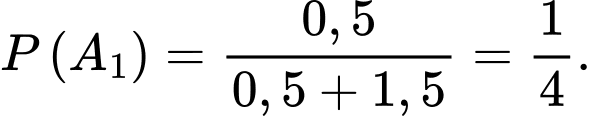
Gọi
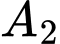 là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra
là biến cố “Lấy được một hạt thóc thuộc giống ST25”. Suy ra 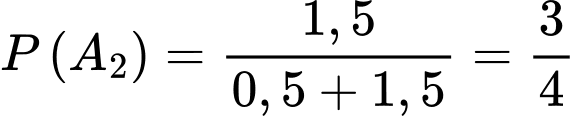 .
.Gọi
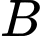 là biến cố “Lấy được một hạt nảy mầm”.
là biến cố “Lấy được một hạt nảy mầm”. YCBT
 Tính
Tính 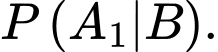
Giả sử
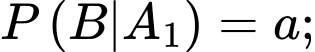
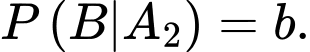
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có xác suất nảy mầm của các hạt thóc trên thửa ruộng là

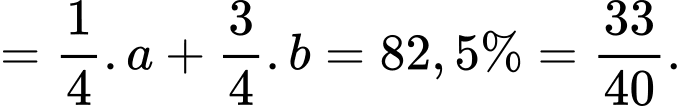
Lại có
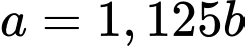 suy ra
suy ra 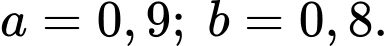
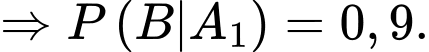
Khi đó
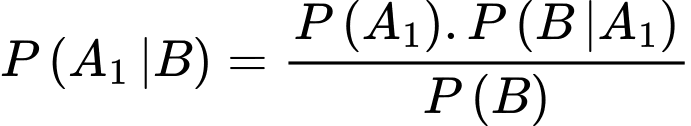
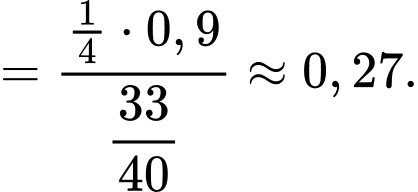
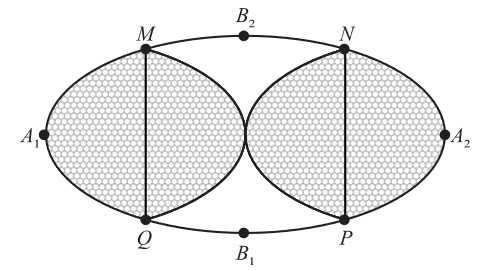
Câu 21 [696333]: Mảnh vườn nhà ông An có dạng hình elip với bốn đỉnh 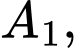
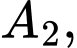
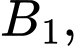
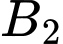 như hình vẽ bên. Ông dùng 2 đường Parabol có đỉnh là tâm đối xứng của elip cắt elip tại 4 điểm
như hình vẽ bên. Ông dùng 2 đường Parabol có đỉnh là tâm đối xứng của elip cắt elip tại 4 điểm 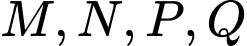 như hình vẽ sao cho tứ giác
như hình vẽ sao cho tứ giác 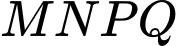 là hình chữ nhật có
là hình chữ nhật có 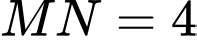 để chia vườn. Phần tô đậm dùng để trồng hoa và phần còn lại để trồng rau. Biết chi phí trồng hoa là
để chia vườn. Phần tô đậm dùng để trồng hoa và phần còn lại để trồng rau. Biết chi phí trồng hoa là  nghìn đồng/
nghìn đồng/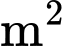 và trồng rau là
và trồng rau là 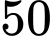 nghìn đồng/
nghìn đồng/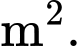 Hỏi số tiền phải chi bằng bao nhiêu nghìn đồng, biết
Hỏi số tiền phải chi bằng bao nhiêu nghìn đồng, biết 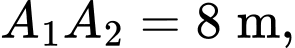
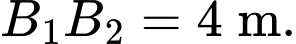 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.
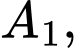
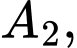
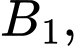
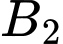 như hình vẽ bên. Ông dùng 2 đường Parabol có đỉnh là tâm đối xứng của elip cắt elip tại 4 điểm
như hình vẽ bên. Ông dùng 2 đường Parabol có đỉnh là tâm đối xứng của elip cắt elip tại 4 điểm 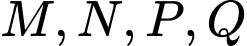 như hình vẽ sao cho tứ giác
như hình vẽ sao cho tứ giác 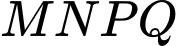 là hình chữ nhật có
là hình chữ nhật có 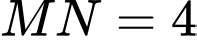 để chia vườn. Phần tô đậm dùng để trồng hoa và phần còn lại để trồng rau. Biết chi phí trồng hoa là
để chia vườn. Phần tô đậm dùng để trồng hoa và phần còn lại để trồng rau. Biết chi phí trồng hoa là  nghìn đồng/
nghìn đồng/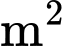 và trồng rau là
và trồng rau là 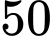 nghìn đồng/
nghìn đồng/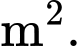 Hỏi số tiền phải chi bằng bao nhiêu nghìn đồng, biết
Hỏi số tiền phải chi bằng bao nhiêu nghìn đồng, biết 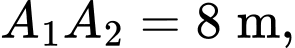
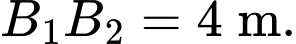 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.
Điền đáp án: 11 742.
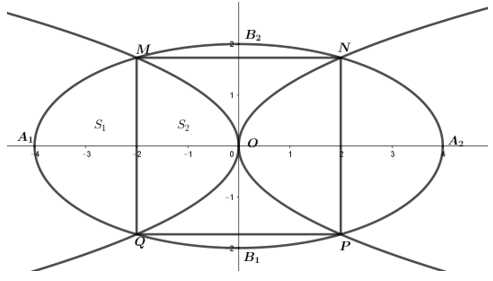
Ta có: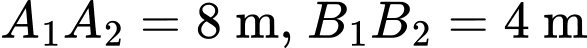
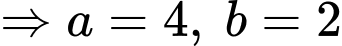 .
.
 Phương trình elip có dạng
Phương trình elip có dạng 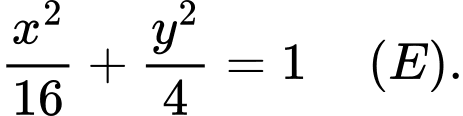
Vì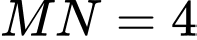
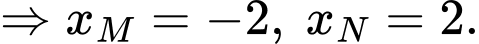
Thay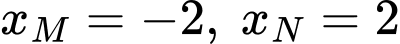 vào phương trình
vào phương trình  ta được:
ta được: 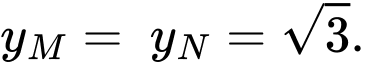
Gọi phương trình parabol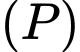 đi qua 3 điểm
đi qua 3 điểm  có dạng
có dạng 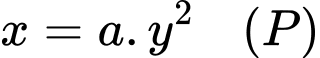
Thay tọa độ điểm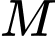 vào phương trình parabol
vào phương trình parabol 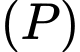 ta được:
ta được: 
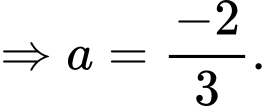
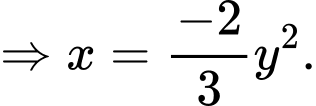
Gọi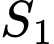 là diện tích hình phẳng giới hạn bởi elip
là diện tích hình phẳng giới hạn bởi elip  , đường thẳng
, đường thẳng 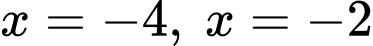 .
.
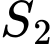 là diện tích hình phẳng giới hạn bởi parabol
là diện tích hình phẳng giới hạn bởi parabol 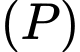 , đường thẳng
, đường thẳng 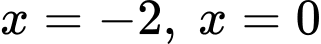 .
.
Ta có: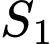
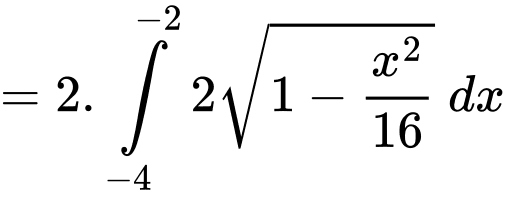
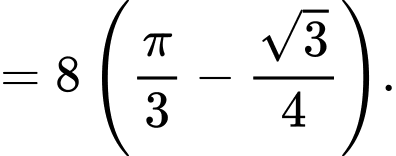
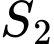
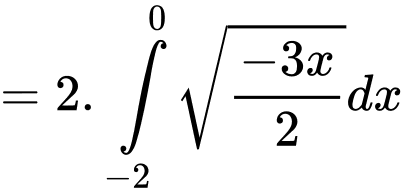
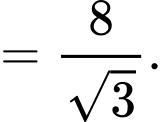
Diện tích hình elip là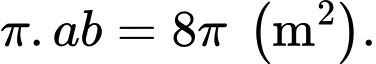
Diện tích dùng để trồng hoa là
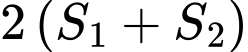
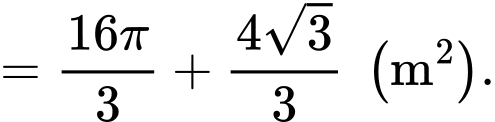
Diện tích dùng để trồng rau là
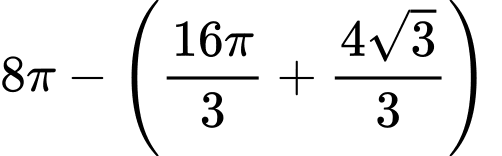
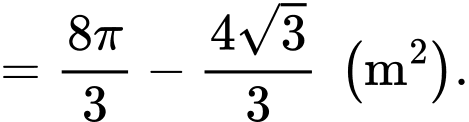
Số tiền phải chi là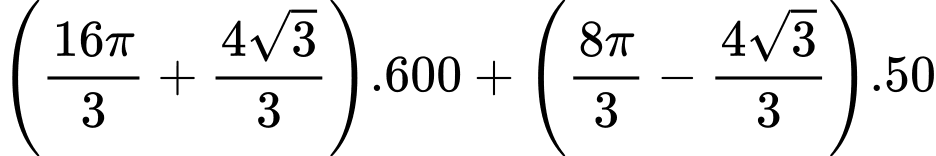
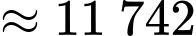 nghìn đồng.
nghìn đồng.

Ta có:
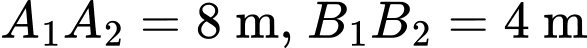
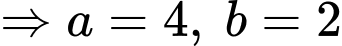 .
. Phương trình elip có dạng
Phương trình elip có dạng 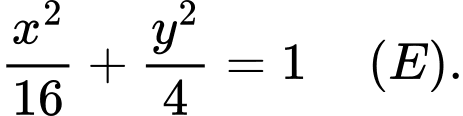
Vì
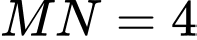
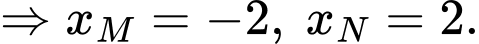
Thay
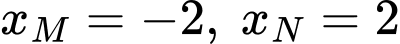 vào phương trình
vào phương trình  ta được:
ta được: 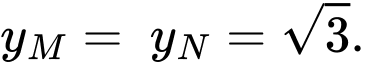
Gọi phương trình parabol
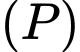 đi qua 3 điểm
đi qua 3 điểm  có dạng
có dạng 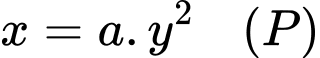
Thay tọa độ điểm
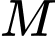 vào phương trình parabol
vào phương trình parabol 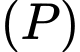 ta được:
ta được: 
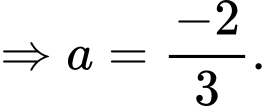
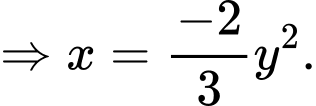
Gọi
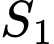 là diện tích hình phẳng giới hạn bởi elip
là diện tích hình phẳng giới hạn bởi elip  , đường thẳng
, đường thẳng 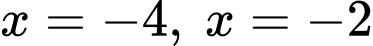 .
.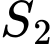 là diện tích hình phẳng giới hạn bởi parabol
là diện tích hình phẳng giới hạn bởi parabol 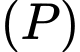 , đường thẳng
, đường thẳng 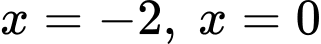 .
.Ta có:
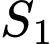
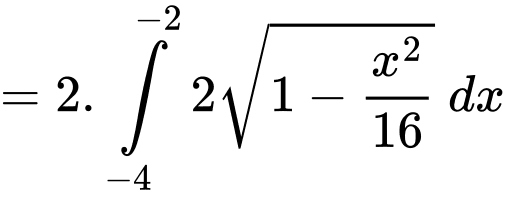
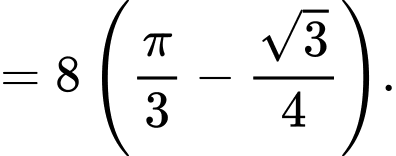
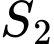
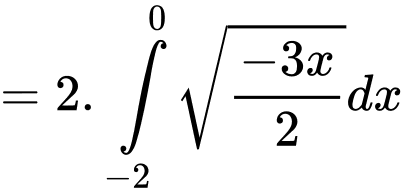
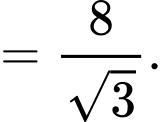
Diện tích hình elip là
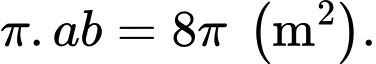
Diện tích dùng để trồng hoa là
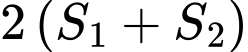
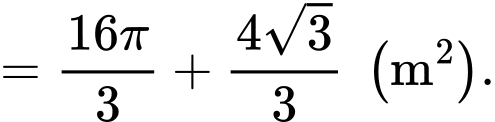
Diện tích dùng để trồng rau là
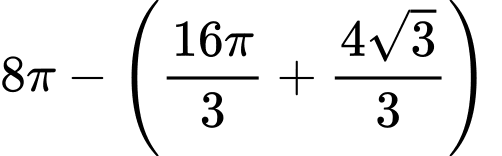
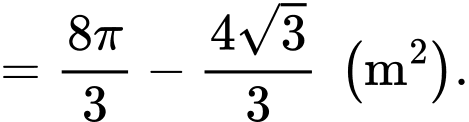
Số tiền phải chi là
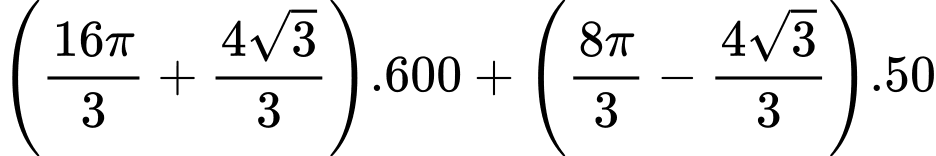
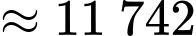 nghìn đồng.
nghìn đồng.
Câu 22 [696345]: Độ xa  mà một quả bóng bầu dục có thể bay từ khi rời tay người ném đến khi chạm đất được được mô hình hóa bởi phương trình
mà một quả bóng bầu dục có thể bay từ khi rời tay người ném đến khi chạm đất được được mô hình hóa bởi phương trình 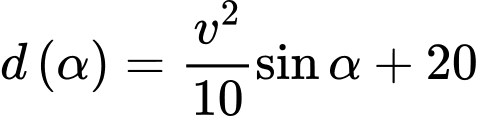 trong đó
trong đó 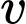 (m/s) là vận tốc của quả bóng tính bằng mét trên giây và
(m/s) là vận tốc của quả bóng tính bằng mét trên giây và 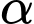 (
(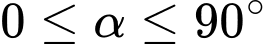 ) là góc so với phương ngang mà quả bóng rời khỏi tay người ném. Biết người đó ném với vận tốc
) là góc so với phương ngang mà quả bóng rời khỏi tay người ném. Biết người đó ném với vận tốc  (m/s) (
(m/s) (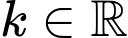 ) và khoảng cách xa nhất đo được là
) và khoảng cách xa nhất đo được là 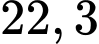 mét. Vận tốc khi ném của người đó bằng bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
mét. Vận tốc khi ném của người đó bằng bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
 mà một quả bóng bầu dục có thể bay từ khi rời tay người ném đến khi chạm đất được được mô hình hóa bởi phương trình
mà một quả bóng bầu dục có thể bay từ khi rời tay người ném đến khi chạm đất được được mô hình hóa bởi phương trình 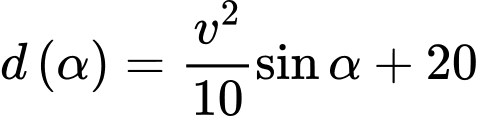 trong đó
trong đó 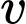 (m/s) là vận tốc của quả bóng tính bằng mét trên giây và
(m/s) là vận tốc của quả bóng tính bằng mét trên giây và 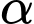 (
(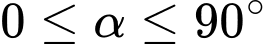 ) là góc so với phương ngang mà quả bóng rời khỏi tay người ném. Biết người đó ném với vận tốc
) là góc so với phương ngang mà quả bóng rời khỏi tay người ném. Biết người đó ném với vận tốc  (m/s) (
(m/s) (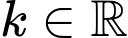 ) và khoảng cách xa nhất đo được là
) và khoảng cách xa nhất đo được là 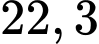 mét. Vận tốc khi ném của người đó bằng bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
mét. Vận tốc khi ném của người đó bằng bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 5,69.
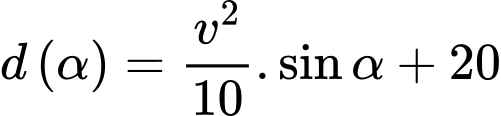
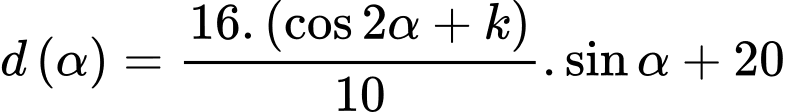

*ĐN: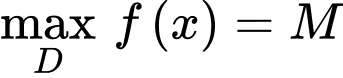
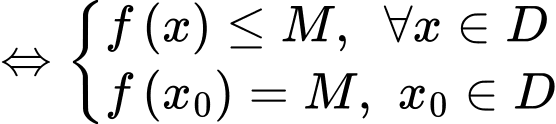
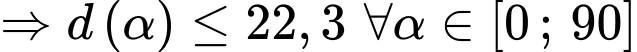
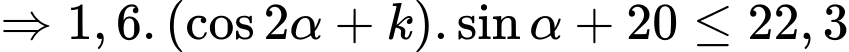
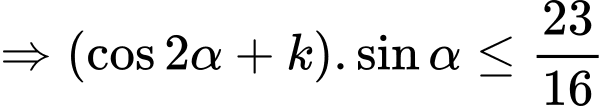
+)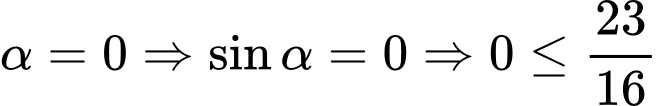 (luôn đúng)
(luôn đúng)
+)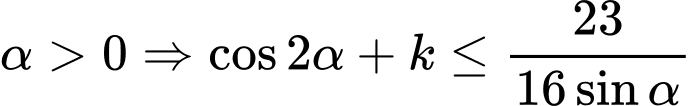

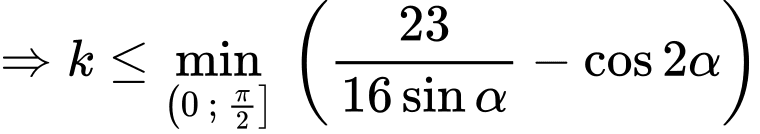
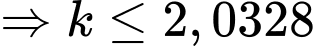
Dấu “=” xảy ra khi và chỉ khi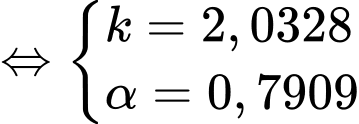
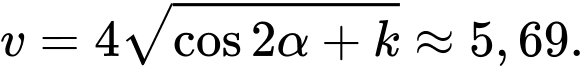
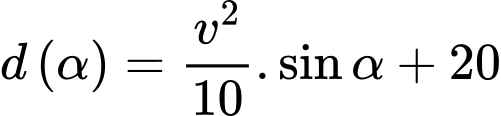
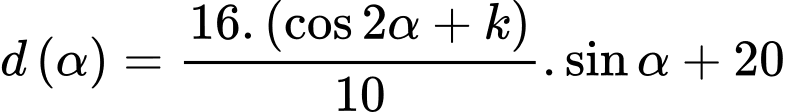

*ĐN:
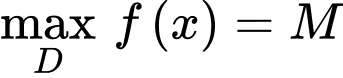
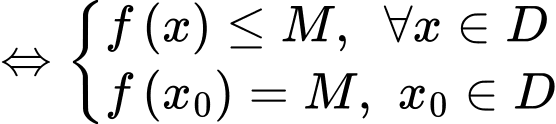
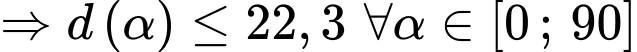
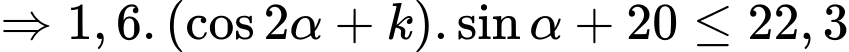
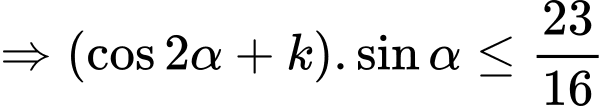
+)
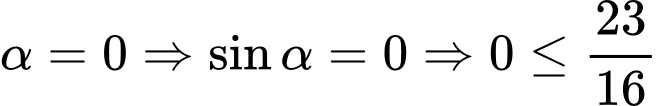 (luôn đúng)
(luôn đúng)+)
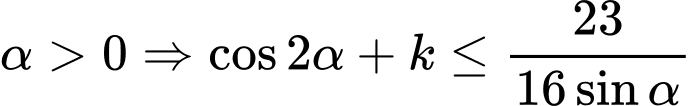

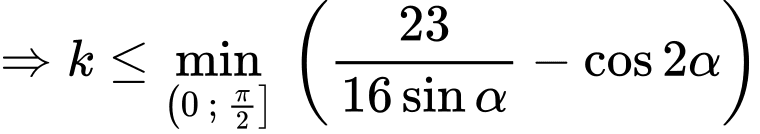
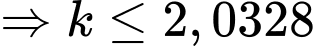
Dấu “=” xảy ra khi và chỉ khi