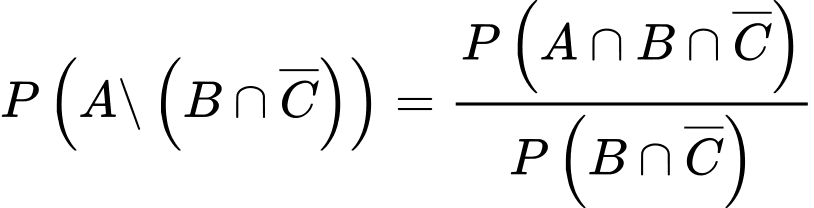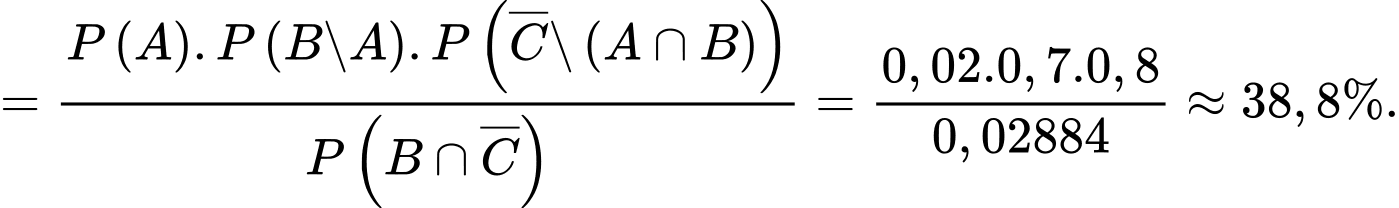PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [256775]: Tiệm cận ngang của đồ thị hàm số 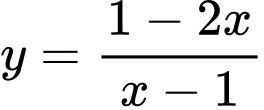 là
là
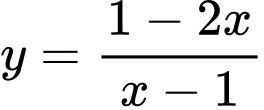 là
là A, 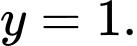
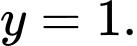
B, 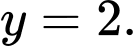
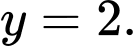
C, 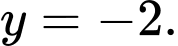
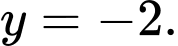
D, 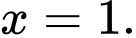
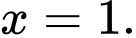
Chọn đáp án C.
Ta có:
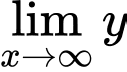
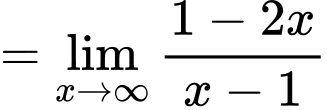
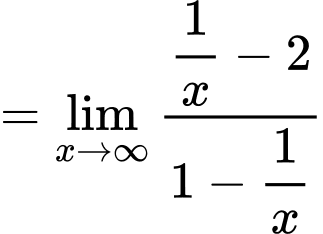
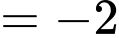 nên đồ thị hàm số có đường tiệm cận ngang là
nên đồ thị hàm số có đường tiệm cận ngang là 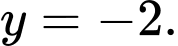 Đáp án: C
Đáp án: C
Ta có:
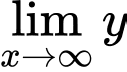
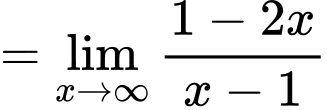
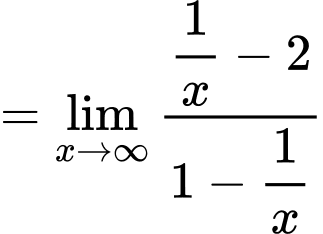
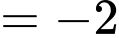 nên đồ thị hàm số có đường tiệm cận ngang là
nên đồ thị hàm số có đường tiệm cận ngang là 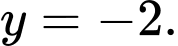 Đáp án: C
Đáp án: C
Câu 2 [695641]: Cho 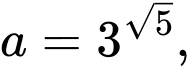
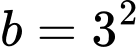 và
và 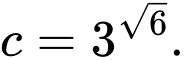 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
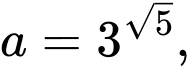
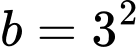 và
và 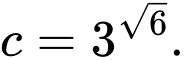 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 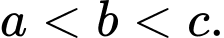
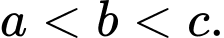
B, 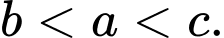
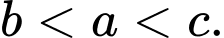
C, 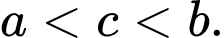
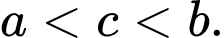
D, 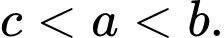
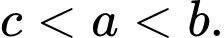
Chọn đáp án B.
Ta có: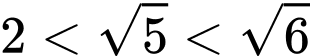 nên
nên 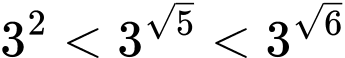 hay
hay 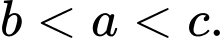 Đáp án: B
Đáp án: B
Ta có:
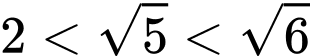 nên
nên 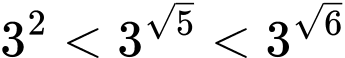 hay
hay 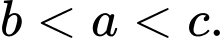 Đáp án: B
Đáp án: B
Câu 3 [695642]: Cho hình lập phương  (tham khảo hình vẽ bên). Mặt phẳng
(tham khảo hình vẽ bên). Mặt phẳng 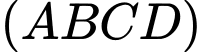 vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây?
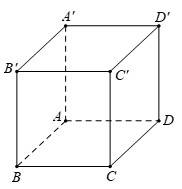
 (tham khảo hình vẽ bên). Mặt phẳng
(tham khảo hình vẽ bên). Mặt phẳng 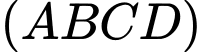 vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây?
A, 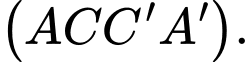
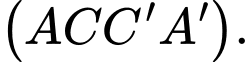
B, 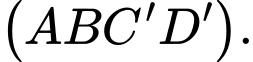
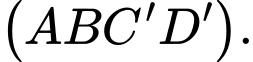
C, 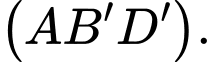
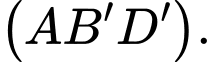
D, 

Chọn đáp án A. Đáp án: A
Câu 4 [349068]: Trong không gian 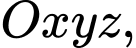 cho
cho 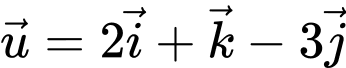 và
và 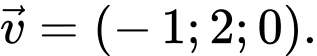 Toạ độ của vectơ
Toạ độ của vectơ  là
là
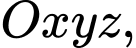 cho
cho 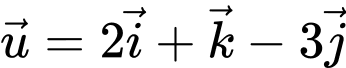 và
và 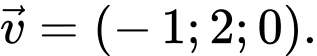 Toạ độ của vectơ
Toạ độ của vectơ  là
là A, 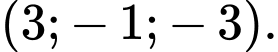
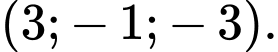
B, 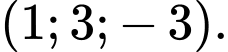
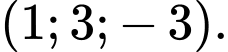
C, 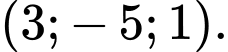
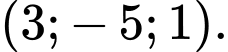
D, 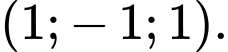
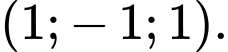
Chọn đáp án C.
Ta có: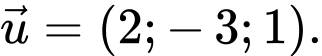

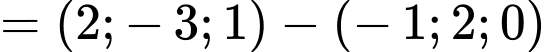
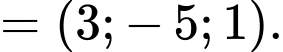 Đáp án: C
Đáp án: C
Ta có:
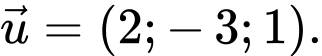

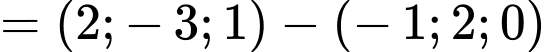
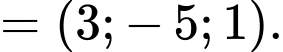 Đáp án: C
Đáp án: C
Câu 5 [695643]: Cho cấp số nhân 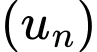 với
với 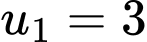 và công bội
và công bội 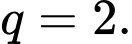 Số hạng tổng quát
Số hạng tổng quát 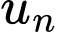
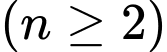 bằng
bằng
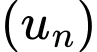 với
với 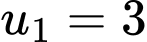 và công bội
và công bội 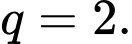 Số hạng tổng quát
Số hạng tổng quát 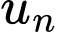
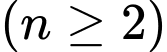 bằng
bằng A, 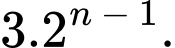
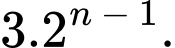
B, 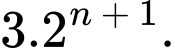
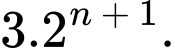
C, 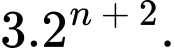
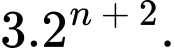
D, 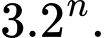
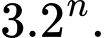
Chọn đáp án A.
Số hạng tổng quát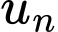
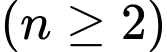 bằng
bằng 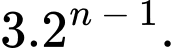 Đáp án: A
Đáp án: A
Số hạng tổng quát
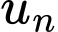
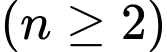 bằng
bằng 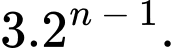 Đáp án: A
Đáp án: A
Câu 6 [695644]: Khảo sát thời gian (đơn vị: phút) tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:

Trung bình mỗi học sinh tập bao nhiêu phút mỗi ngày? (làm tròn đến hàng phần mười).

Trung bình mỗi học sinh tập bao nhiêu phút mỗi ngày? (làm tròn đến hàng phần mười).
A, 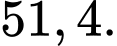
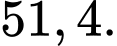
B, 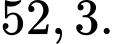
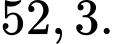
C, 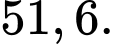
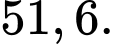
D, 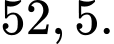
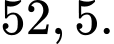
Nhóm 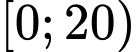 có giá trị đại diện
có giá trị đại diện 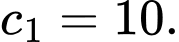
Nhóm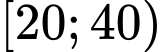 có giá trị đại diện
có giá trị đại diện 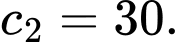
Nhóm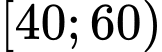 có giá trị đại diện
có giá trị đại diện 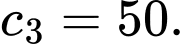
Nhóm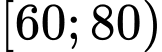 có giá trị đại diện
có giá trị đại diện 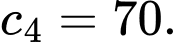
Nhóm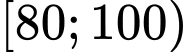 có giá trị đại diện
có giá trị đại diện 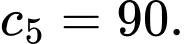
Vậy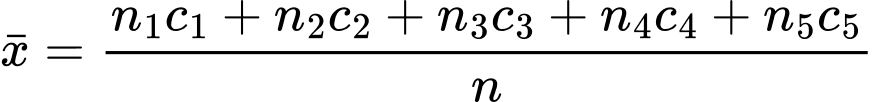
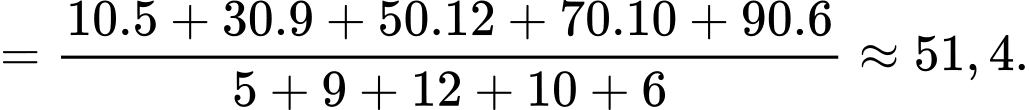 Đáp án: A
Đáp án: A
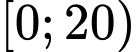 có giá trị đại diện
có giá trị đại diện 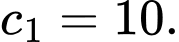
Nhóm
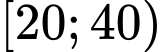 có giá trị đại diện
có giá trị đại diện 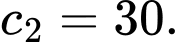
Nhóm
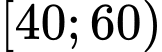 có giá trị đại diện
có giá trị đại diện 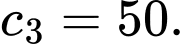
Nhóm
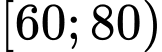 có giá trị đại diện
có giá trị đại diện 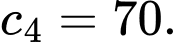
Nhóm
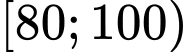 có giá trị đại diện
có giá trị đại diện 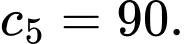
Vậy
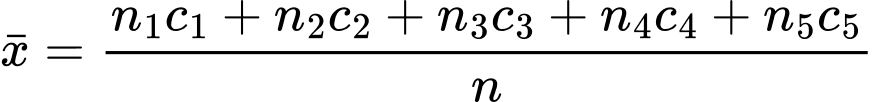
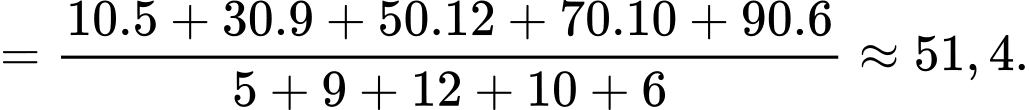 Đáp án: A
Đáp án: A
Câu 7 [256956]: Cho hàm số 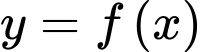 có đạo hàm trên
có đạo hàm trên 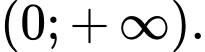 Biết
Biết 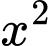 là một nguyên hàm của
là một nguyên hàm của 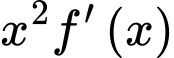 trên
trên 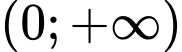 và
và 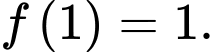 Tính
Tính 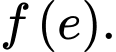
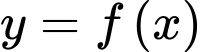 có đạo hàm trên
có đạo hàm trên 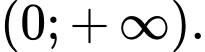 Biết
Biết 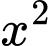 là một nguyên hàm của
là một nguyên hàm của 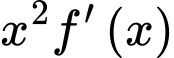 trên
trên 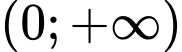 và
và 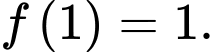 Tính
Tính 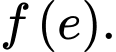
A, 

B, 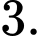
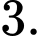
C, 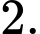
D, 
Chọn đáp án B.
Ta có: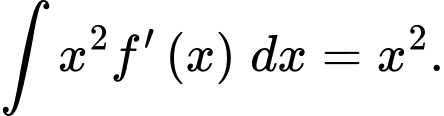
Suy ra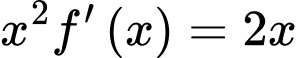
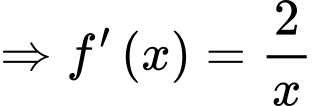
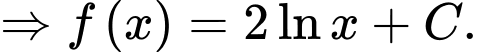
Lại có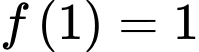
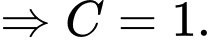
Khi đó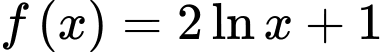 và
và 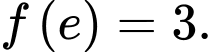 Đáp án: B
Đáp án: B
Ta có:
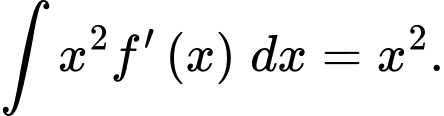
Suy ra
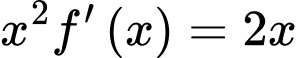
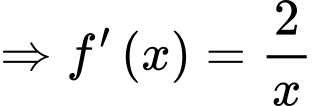
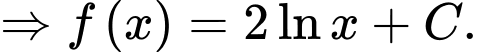
Lại có
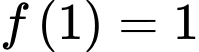
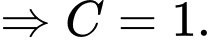
Khi đó
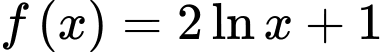 và
và 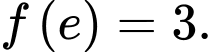 Đáp án: B
Đáp án: B
Câu 8 [702592]: Cho hàm số đa thức 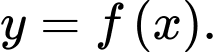 Hàm số
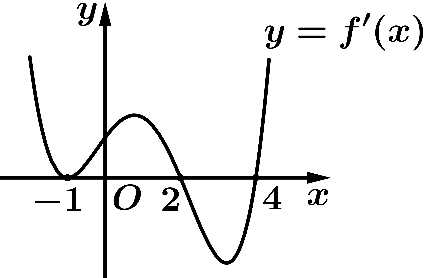
Hàm số 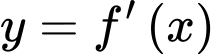 có đồ thị là đường cong trong hình vẽ bên. Hàm số
có đồ thị là đường cong trong hình vẽ bên. Hàm số 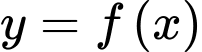 nghịch biến trên khoảng nào sau đây?
nghịch biến trên khoảng nào sau đây?
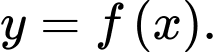 Hàm số
Hàm số 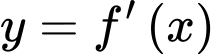 có đồ thị là đường cong trong hình vẽ bên. Hàm số
có đồ thị là đường cong trong hình vẽ bên. Hàm số 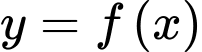 nghịch biến trên khoảng nào sau đây?
nghịch biến trên khoảng nào sau đây?
A, 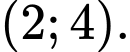
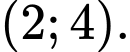
B, 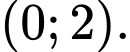
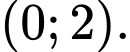
C, 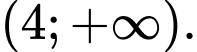
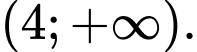
D, 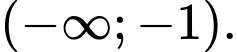
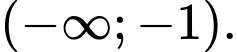
Chọn đáp án A.
Dựa vào đồ thị hàm số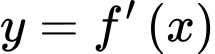 ta có: Hàm số
ta có: Hàm số 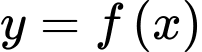 nghịch biến trên khoảng
nghịch biến trên khoảng 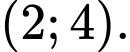 Đáp án: A
Đáp án: A
Dựa vào đồ thị hàm số
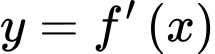 ta có: Hàm số
ta có: Hàm số 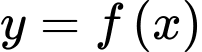 nghịch biến trên khoảng
nghịch biến trên khoảng 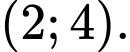 Đáp án: A
Đáp án: A
Câu 9 [256971]: Cho 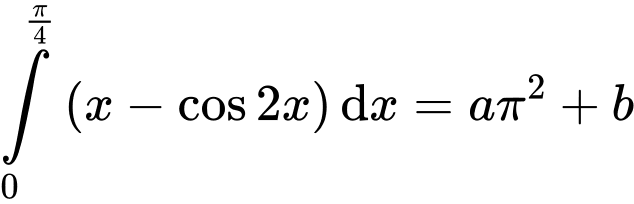 với
với 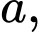
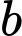 là các số hữu tỉ. Tính
là các số hữu tỉ. Tính 
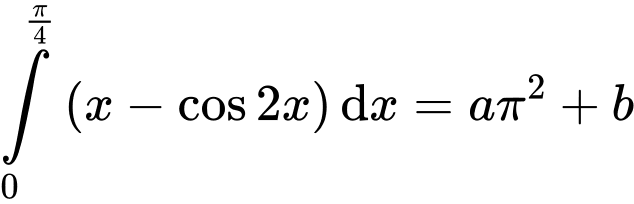 với
với 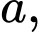
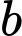 là các số hữu tỉ. Tính
là các số hữu tỉ. Tính 
A, 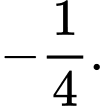
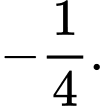
B, 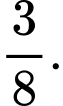
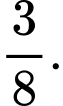
C, 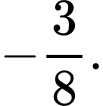
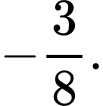
D, 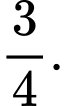
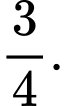
Chọn đáp án C.
Ta có: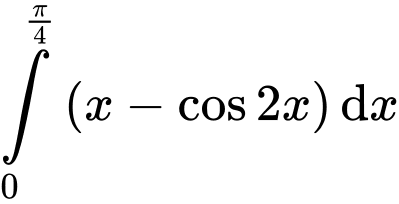
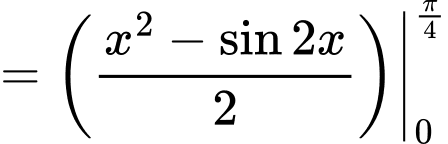
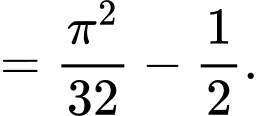
Suy ra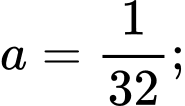
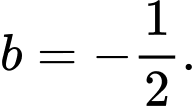
Khi đó ta có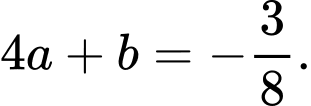 Đáp án: C
Đáp án: C
Ta có:
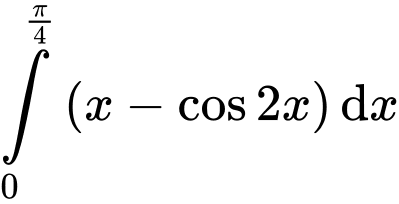
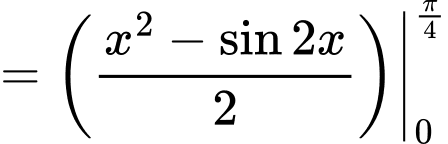
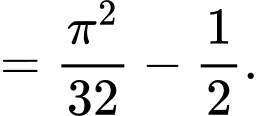
Suy ra
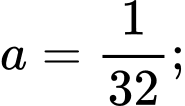
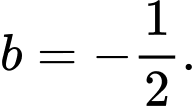
Khi đó ta có
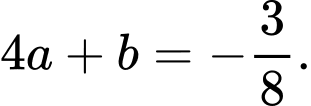 Đáp án: C
Đáp án: C
Câu 10 [695645]: Cho tứ diện 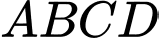 (tham khảo hình vẽ bên).
(tham khảo hình vẽ bên).
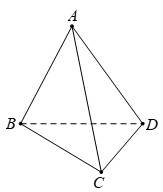
Khẳng định nào sau đây đúng?
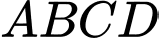 (tham khảo hình vẽ bên).
(tham khảo hình vẽ bên).
Khẳng định nào sau đây đúng?
A, 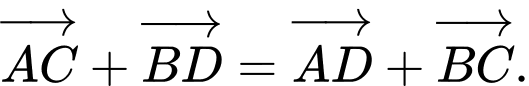
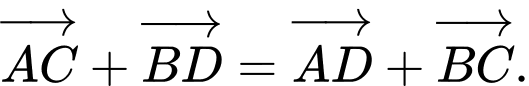
B, 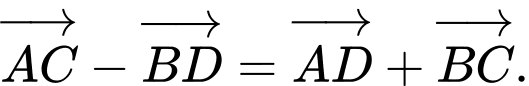
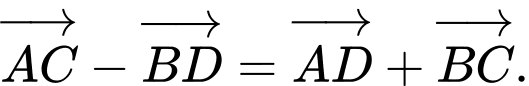
C, 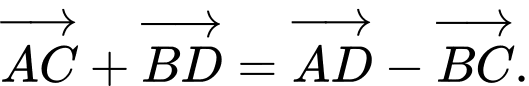
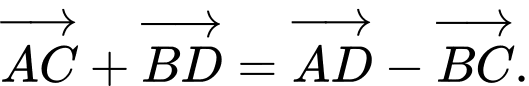
D, 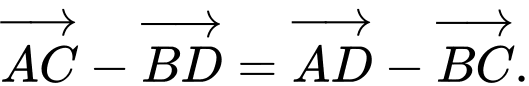
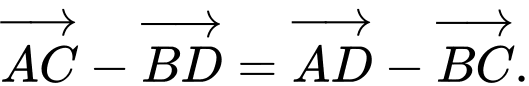
Chọn đáp án A.
Ta có:
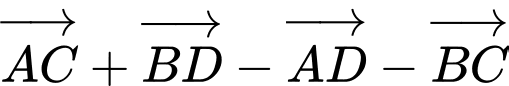
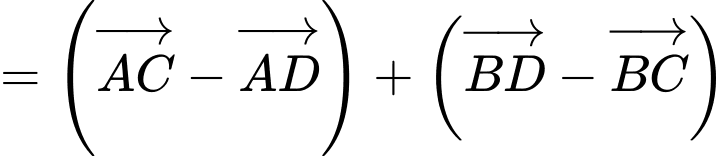
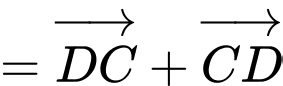
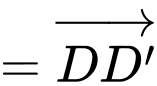
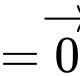
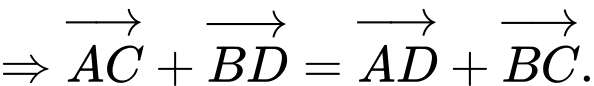 Đáp án: A
Đáp án: A
Ta có:
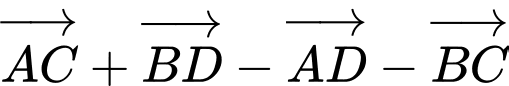
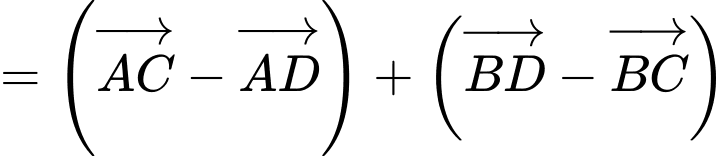
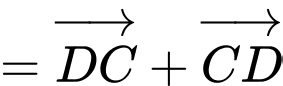
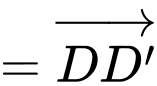
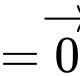
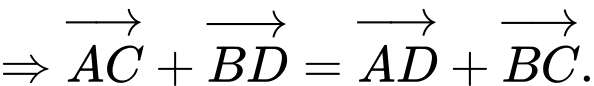 Đáp án: A
Đáp án: A
Câu 11 [256807]: Biết rằng phương trình 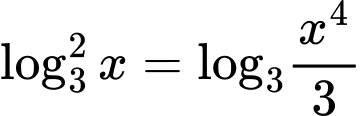 có hai nghiệm là
có hai nghiệm là 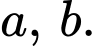 Khi đó
Khi đó 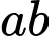 bằng
bằng
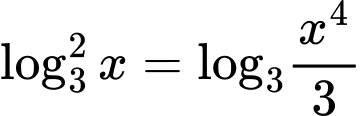 có hai nghiệm là
có hai nghiệm là 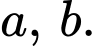 Khi đó
Khi đó 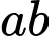 bằng
bằng A, 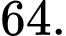
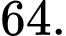
B, 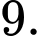
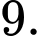
C, 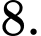
D, 
Chọn đáp án D.
Điều kiện xác định:
Ta có phương trình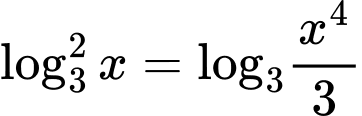
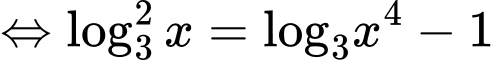

Đặt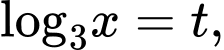 phương trình được viết lại thành:
phương trình được viết lại thành: 
Theo hệ thức Vi – ét, ta có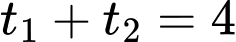

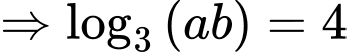
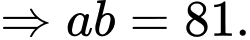 Đáp án: D
Đáp án: D
Điều kiện xác định:

Ta có phương trình
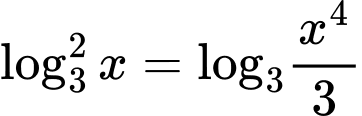
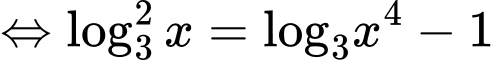

Đặt
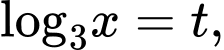 phương trình được viết lại thành:
phương trình được viết lại thành: 
Theo hệ thức Vi – ét, ta có
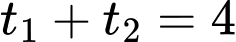

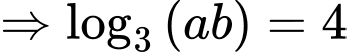
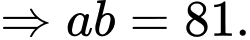 Đáp án: D
Đáp án: D
Câu 12 [257300]: Trong không gian 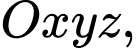 mặt phẳng
mặt phẳng  cắt các trục
cắt các trục 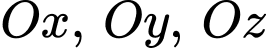 lần lượt tại ba điểm
lần lượt tại ba điểm 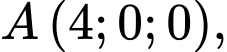
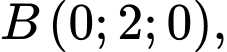
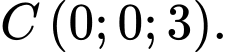 Khoảng cách từ gốc toạ độ
Khoảng cách từ gốc toạ độ  đến
đến  bằng
bằng
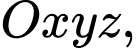 mặt phẳng
mặt phẳng  cắt các trục
cắt các trục 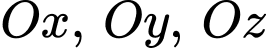 lần lượt tại ba điểm
lần lượt tại ba điểm 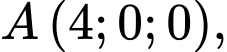
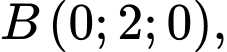
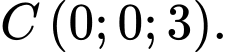 Khoảng cách từ gốc toạ độ
Khoảng cách từ gốc toạ độ  đến
đến  bằng
bằng A, 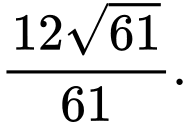
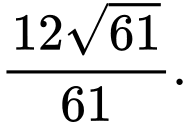
B, 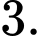
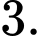
C, 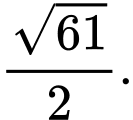
D, 
Chọn đáp án A.
Ta có phương trình mặt phẳng cắt các trục
cắt các trục 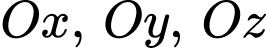 lần lượt tại ba điểm
lần lượt tại ba điểm 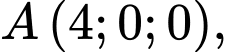
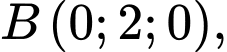
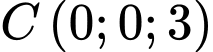 là
là 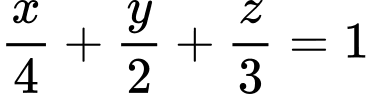
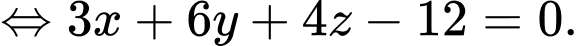
Khoảng cách từ đến
đến  bằng
bằng
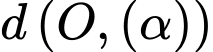
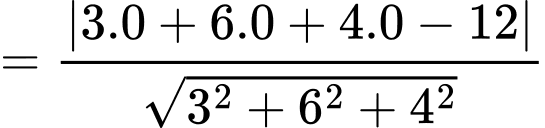
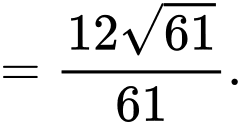 Đáp án: A
Đáp án: A
Ta có phương trình mặt phẳng
 cắt các trục
cắt các trục 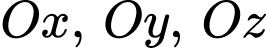 lần lượt tại ba điểm
lần lượt tại ba điểm 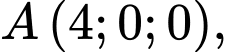
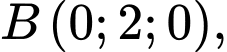
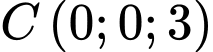 là
là 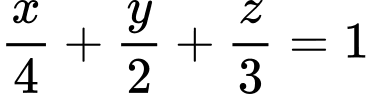
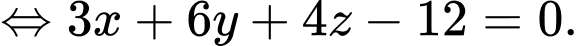
Khoảng cách từ
 đến
đến  bằng
bằng 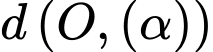
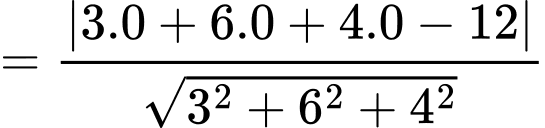
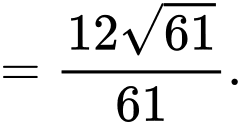 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695647]: Trong không gian với hệ trục tọa độ 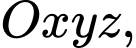 cho hai điểm
cho hai điểm 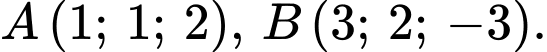 Mặt cầu
Mặt cầu 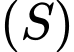 có tâm
có tâm 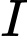 thuộc trục
thuộc trục  có hoành độ bằng
có hoành độ bằng 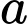 và đi qua hai điểm
và đi qua hai điểm 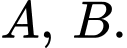
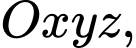 cho hai điểm
cho hai điểm 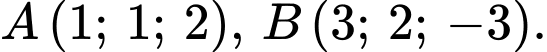 Mặt cầu
Mặt cầu 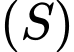 có tâm
có tâm 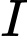 thuộc trục
thuộc trục  có hoành độ bằng
có hoành độ bằng 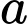 và đi qua hai điểm
và đi qua hai điểm 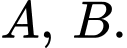
a) Sai.
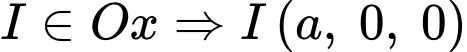
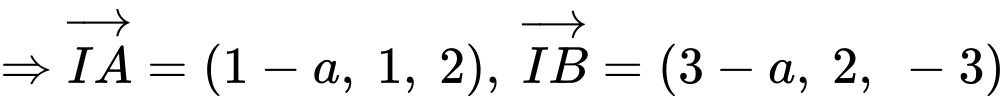
b) Sai.
Ta có:
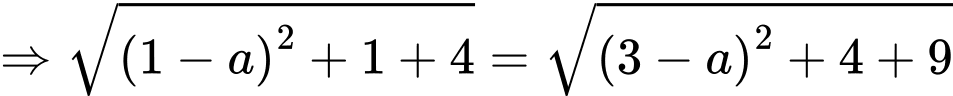
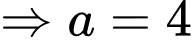
c) Sai.
Bán kính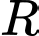 của mặt cầu
của mặt cầu 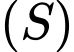 là
là 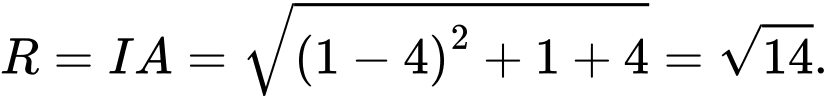
d) Sai.
Ta có: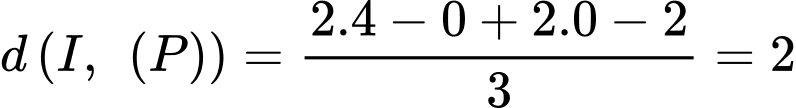
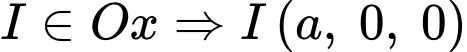
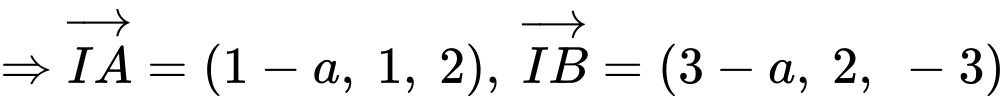
b) Sai.
Ta có:

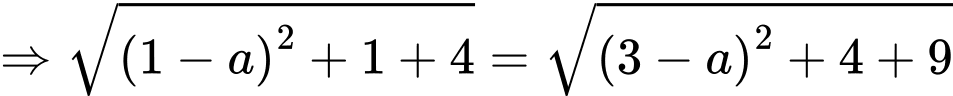
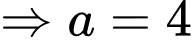
c) Sai.
Bán kính
 của mặt cầu
của mặt cầu 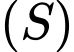 là
là 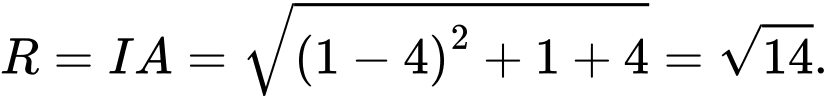
d) Sai.
Ta có:
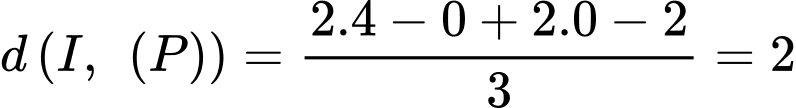
Câu 14 [695646]: Trong một khu bảo tồn động vật hoang dã, người ta đang nghiên cứu  con vật, trong đó có
con vật, trong đó có  con báo đốm và
con báo đốm và 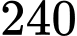 con sư tử. Sau khi thống kê, người ta thấy: có
con sư tử. Sau khi thống kê, người ta thấy: có 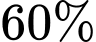 số báo đốm đã được tiêm phòng và
số báo đốm đã được tiêm phòng và 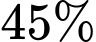 số sư tử đã được tiêm phòng.
số sư tử đã được tiêm phòng.
 con vật, trong đó có
con vật, trong đó có 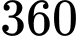 con báo đốm và
con báo đốm và 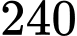 con sư tử. Sau khi thống kê, người ta thấy: có
con sư tử. Sau khi thống kê, người ta thấy: có 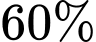 số báo đốm đã được tiêm phòng và
số báo đốm đã được tiêm phòng và 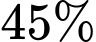 số sư tử đã được tiêm phòng.
số sư tử đã được tiêm phòng.
a) Đúng.
Số con báo đốm đã được tiêm phòng là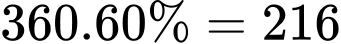 (con).
(con).
b) Sai.
Số con sư tử chưa được tiêm phòng là: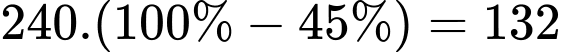 (con).
(con).
c) Sai.
Xét các biến cố:
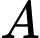 : “Chọn được 1 con sư tử”
: “Chọn được 1 con sư tử”
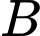 : “Chọn được 1 con vật đã tiêm phòng”.
: “Chọn được 1 con vật đã tiêm phòng”.
Số con sư tử đã được tiêm phòng là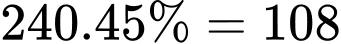 (con).
(con).
Tổng số con vật đã được tiêm phòng là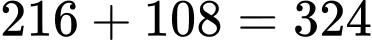 (con).
(con).
Xác suất để chọn ra được một con sư tử đã được tiêm phòng là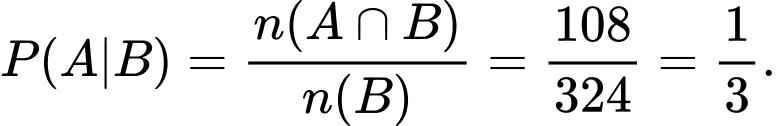
d) Đúng.
Dễ dàng tính được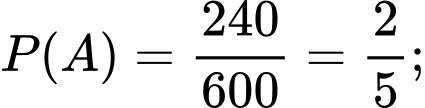
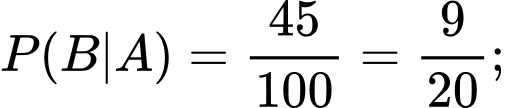
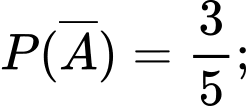
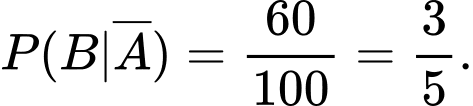
Ta có sơ đồ cây sau:
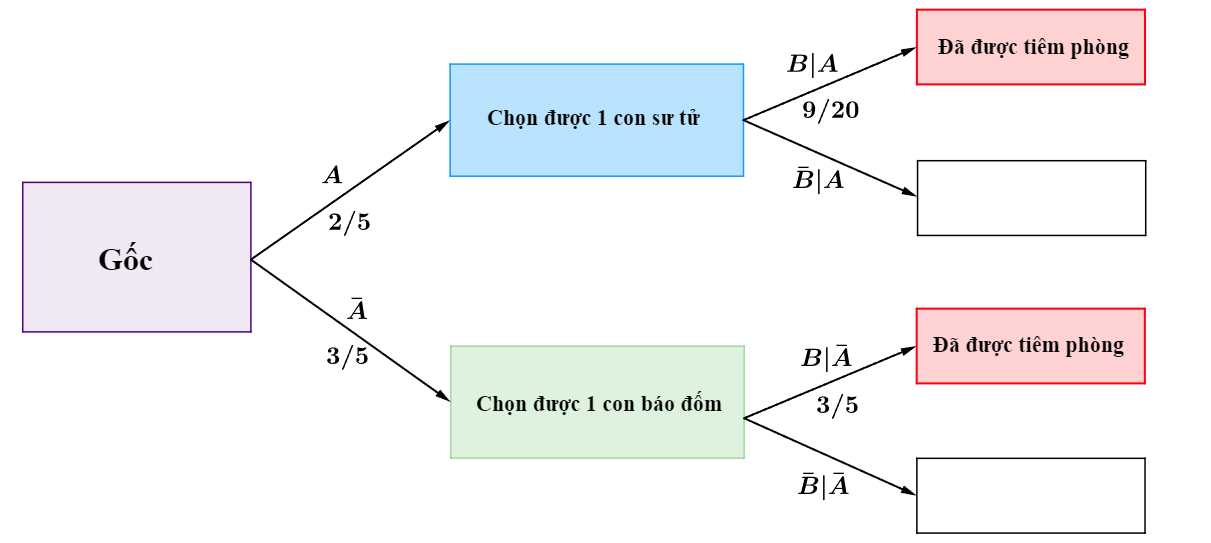
Theo công thức xác suất toàn phần, ta có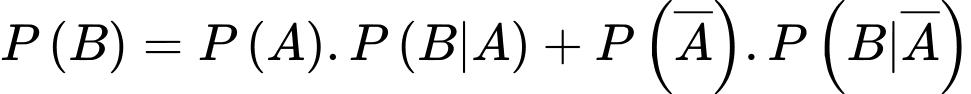
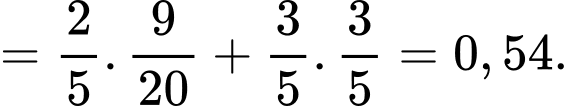
Vậy xác suất để chọn được một con vật chưa tiêm phòng là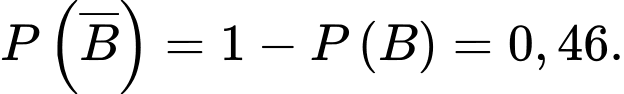
Số con báo đốm đã được tiêm phòng là
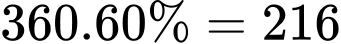 (con).
(con).
b) Sai.
Số con sư tử chưa được tiêm phòng là:
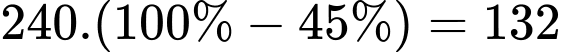 (con).
(con).
c) Sai.
Xét các biến cố:
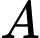 : “Chọn được 1 con sư tử”
: “Chọn được 1 con sư tử”
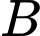 : “Chọn được 1 con vật đã tiêm phòng”.
: “Chọn được 1 con vật đã tiêm phòng”.
Số con sư tử đã được tiêm phòng là
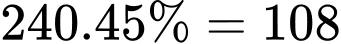 (con).
(con).
Tổng số con vật đã được tiêm phòng là
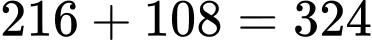 (con).
(con).
Xác suất để chọn ra được một con sư tử đã được tiêm phòng là
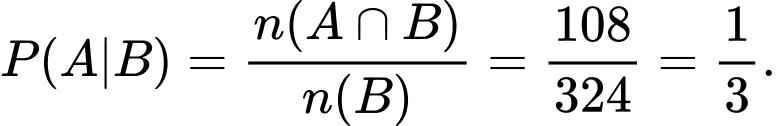
d) Đúng.
Dễ dàng tính được
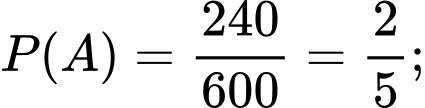
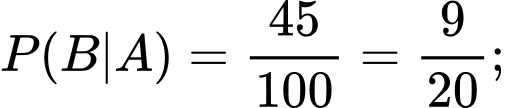
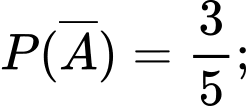
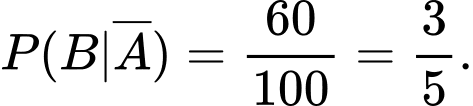
Ta có sơ đồ cây sau:

Theo công thức xác suất toàn phần, ta có
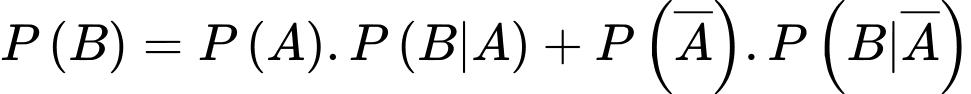
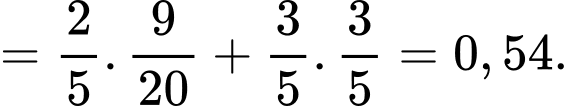
Vậy xác suất để chọn được một con vật chưa tiêm phòng là
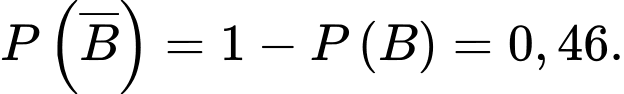
Câu 15 [695648]: Một cơ sở đóng giày sản xuất mỗi ngày được 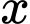 đôi giầy với
đôi giầy với 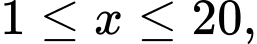 chi phí sản xuất bình quân cho một sản phẩm là
chi phí sản xuất bình quân cho một sản phẩm là 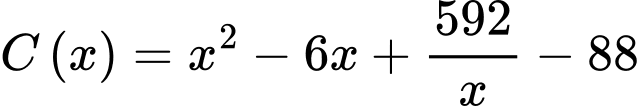 (đơn vị nghìn đồng). Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá
(đơn vị nghìn đồng). Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá 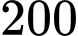 nghìn đồng /một đôi. Gọi
nghìn đồng /một đôi. Gọi 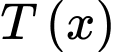 là số tiền bán được và
là số tiền bán được và 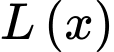 là lợi nhuận thu được sau khi bán hết
là lợi nhuận thu được sau khi bán hết 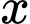 đôi giày.
đôi giày.
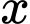 đôi giầy với
đôi giầy với 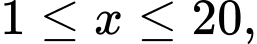 chi phí sản xuất bình quân cho một sản phẩm là
chi phí sản xuất bình quân cho một sản phẩm là 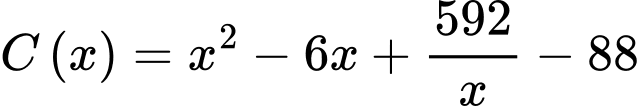 (đơn vị nghìn đồng). Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá
(đơn vị nghìn đồng). Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá 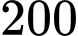 nghìn đồng /một đôi. Gọi
nghìn đồng /một đôi. Gọi 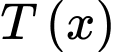 là số tiền bán được và
là số tiền bán được và 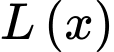 là lợi nhuận thu được sau khi bán hết
là lợi nhuận thu được sau khi bán hết 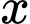 đôi giày.
đôi giày.
a) Đúng.
Ta có: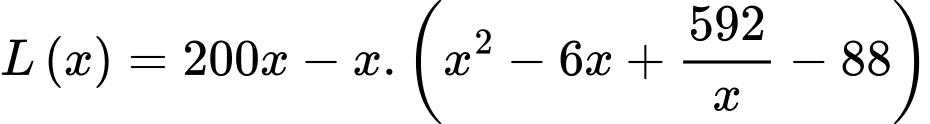
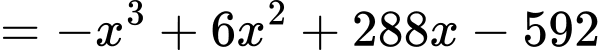
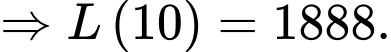
b) Sai.
Ta có: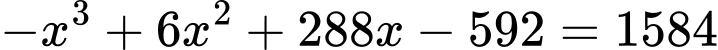
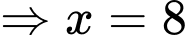
c) Đúng.
Xét hàm số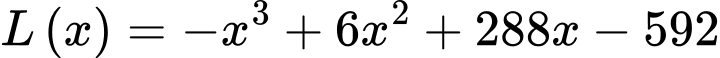
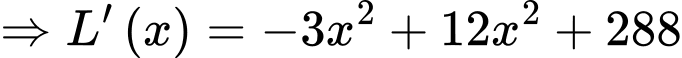
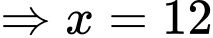
BBT:
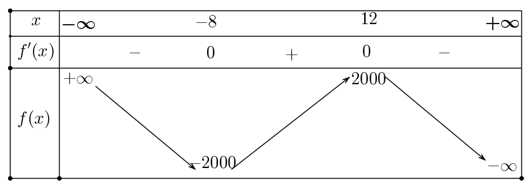
Dựa theo BBT ta thấy cơ sở này sản xuất được 12 đôi giày thì lợi nhuận thu được là nhiều nhất.
d) Sai.
Chi phí sản suất bình quân cho 1 đôi giày là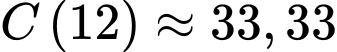 nghìn đồng.
nghìn đồng.
Ta có:
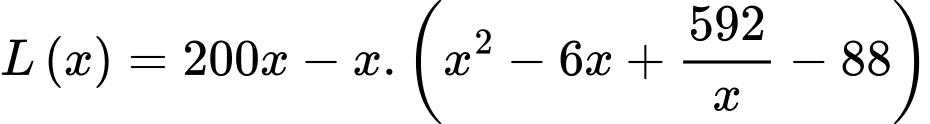
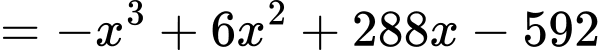
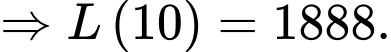
b) Sai.
Ta có:
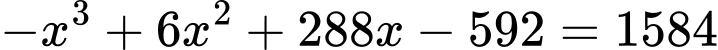
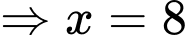
c) Đúng.
Xét hàm số
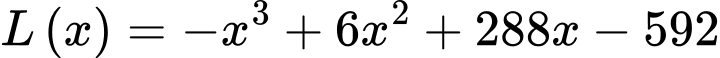
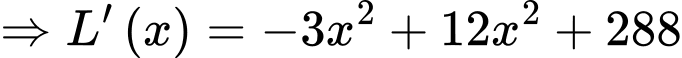
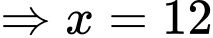
BBT:

Dựa theo BBT ta thấy cơ sở này sản xuất được 12 đôi giày thì lợi nhuận thu được là nhiều nhất.
d) Sai.
Chi phí sản suất bình quân cho 1 đôi giày là
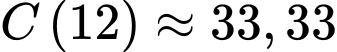 nghìn đồng.
nghìn đồng.
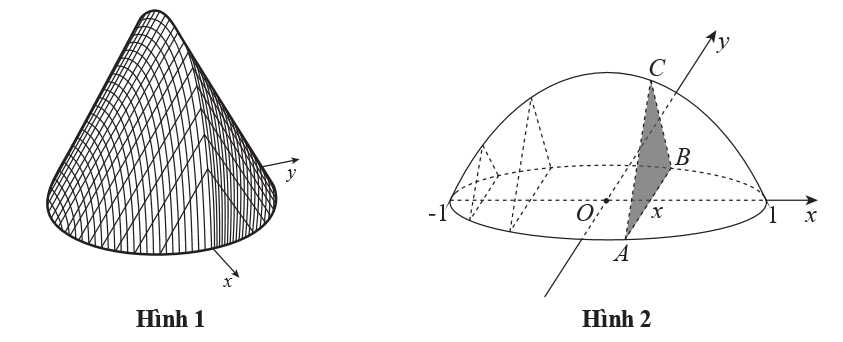
Câu 16 [695649]: Hình 1 sau thể hiện một vật rắn  có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ
có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ 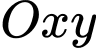 sao cho
sao cho  là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với
là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với 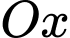 tại
tại 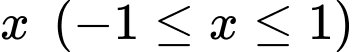 cắt vật thể đó theo hình phẳng là tam giác đều
cắt vật thể đó theo hình phẳng là tam giác đều 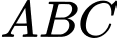 (Hình 2) có diện tích là
(Hình 2) có diện tích là 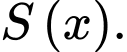
 có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ
có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Trên mặt phẳng đáy của vật rắn, chọn hệ trục toạ độ 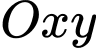 sao cho
sao cho  là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với
là tâm đường tròn đáy. Một mặt phăng tuỳ ý vuông góc với 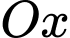 tại
tại 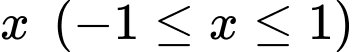 cắt vật thể đó theo hình phẳng là tam giác đều
cắt vật thể đó theo hình phẳng là tam giác đều 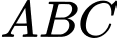 (Hình 2) có diện tích là
(Hình 2) có diện tích là 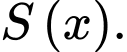

a) Đúng.
Vì đáy là hình tròn tâm bán kính bằng 1.
bán kính bằng 1.
b) Sai.
Ta có: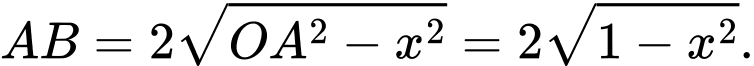
c) Sai.
Ta có: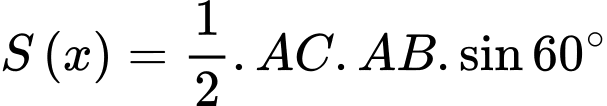
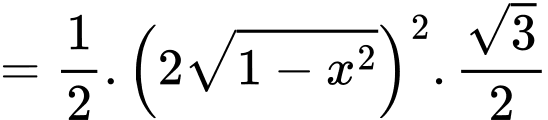
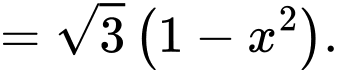
d) Đúng.
Ta có :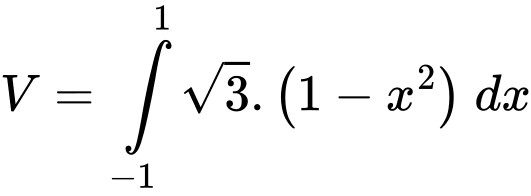
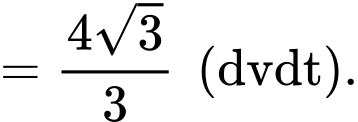
Vì đáy là hình tròn tâm
 bán kính bằng 1.
bán kính bằng 1.b) Sai.
Ta có:
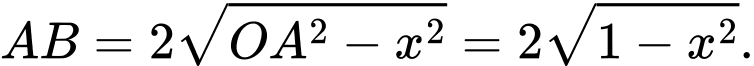
c) Sai.
Ta có:
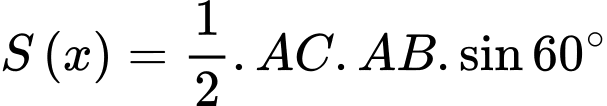
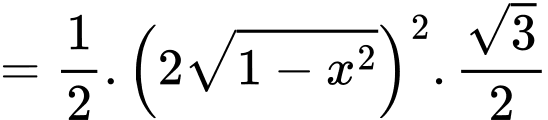
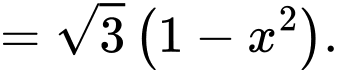
d) Đúng.
Ta có :
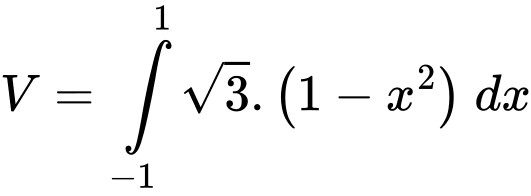
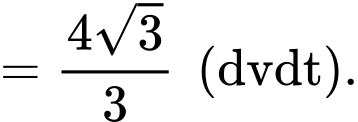
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695650]: Cho hai tam giác  và
và  nằm trên hai mặt phẳng vuông góc với nhau và
nằm trên hai mặt phẳng vuông góc với nhau và 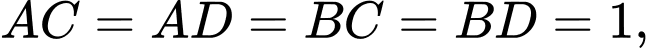
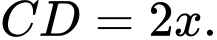 Với giá trị nào của
Với giá trị nào của 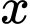 thì mặt phẳng
thì mặt phẳng 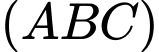 vuông góc với mặt phẳng
vuông góc với mặt phẳng 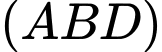 ? (làm tròn kết quả đến hàng phần mười).
? (làm tròn kết quả đến hàng phần mười).
 và
và  nằm trên hai mặt phẳng vuông góc với nhau và
nằm trên hai mặt phẳng vuông góc với nhau và 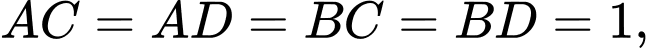
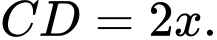 Với giá trị nào của
Với giá trị nào của 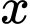 thì mặt phẳng
thì mặt phẳng 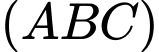 vuông góc với mặt phẳng
vuông góc với mặt phẳng 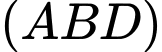 ? (làm tròn kết quả đến hàng phần mười).
? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 0,6.
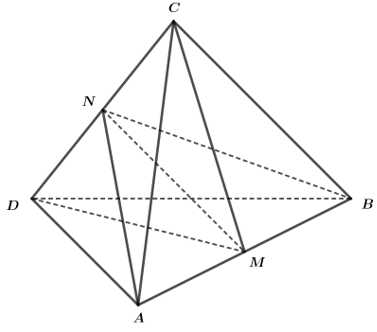
Gọi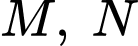 lần lượt là trung điểm của
lần lượt là trung điểm của 
Xét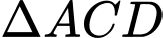 cận tại
cận tại 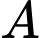 có:
có: 
Xét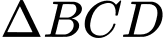 cận tại
cận tại 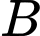 có:
có: 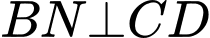
Mà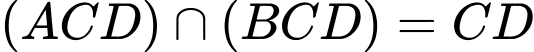

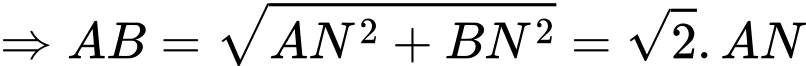

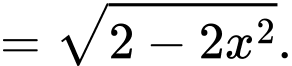
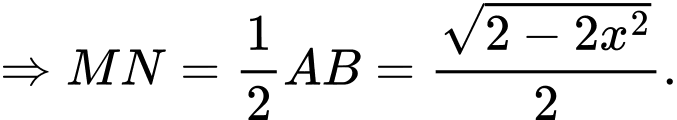
Xét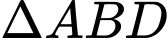 cận tại
cận tại 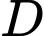 có:
có: 
Xét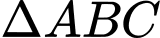 cận tại
cận tại  có:
có: 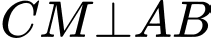
Mà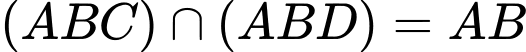
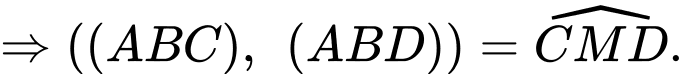
Để mặt phẳng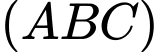 vuông góc với mặt phẳng
vuông góc với mặt phẳng 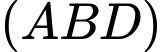 thì
thì 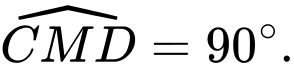
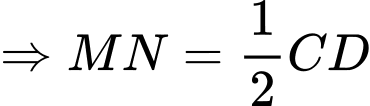
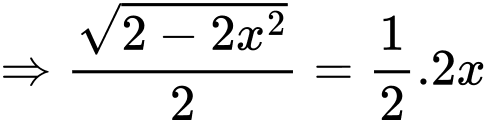
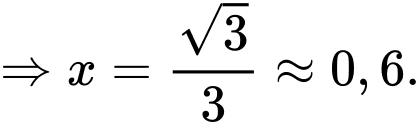

Gọi
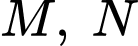 lần lượt là trung điểm của
lần lượt là trung điểm của 
Xét
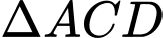 cận tại
cận tại 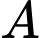 có:
có: 
Xét
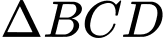 cận tại
cận tại 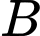 có:
có: 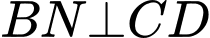
Mà
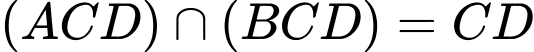

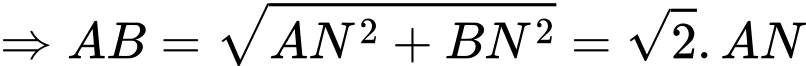

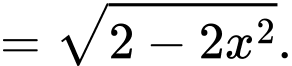
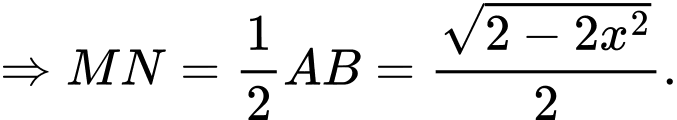
Xét
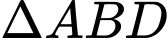 cận tại
cận tại 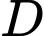 có:
có: 
Xét
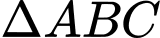 cận tại
cận tại  có:
có: 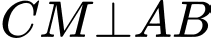
Mà
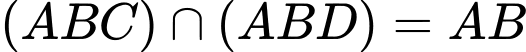
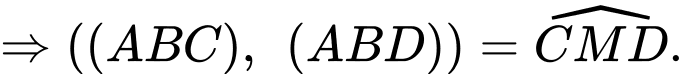
Để mặt phẳng
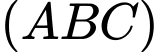 vuông góc với mặt phẳng
vuông góc với mặt phẳng 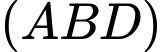 thì
thì 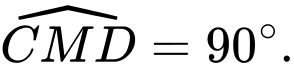
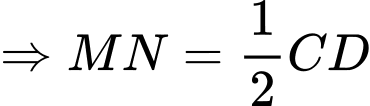
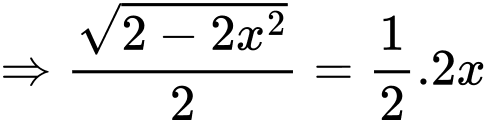
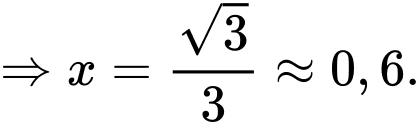
Câu 18 [695651]: Mặc dù Bún bò Huế là một đặc sản của ẩm thực Huế nhưng lại là món ăn rất được yêu thích của người dân TP. Hồ Chí Minh. Hương vị đặc biệt của món ăn này chủ yếu là ở vị cay nồng, mùi sả đặc trưng của nước lèo. Vốn là một hương vị Huế không lẫn vào đâu được và chính điều đó khiến người ăn cứ nhớ mãi về món ăn này. Quán nhà bạn An dùng 2 chiếc nồi hình trụ có bán kính đáy nồi là 0,3 m; chiều cao nồi là 0,8 m để nấu nước lèo bún bò Huế. Sau khi vớt xương và các gia vị thì lượng nước lèo trong nồi chiếm 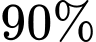 thể tích nồi. Để bán bún bò, mỗi lần bán một tô bún, mẹ bạn An dùng cái muôi (hoặc cái muỗng) có dạng nửa hình cầu bán kính
thể tích nồi. Để bán bún bò, mỗi lần bán một tô bún, mẹ bạn An dùng cái muôi (hoặc cái muỗng) có dạng nửa hình cầu bán kính 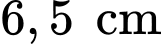 và múc đúng một muôi đầy cho mỗi tô. Giả sử mẹ bạn An múc hết sạch lượng nước lèo đã nấu, hỏi sau khi bán hết bún bò thì quán nhà bạn An thu được bao nhiêu triệu đồng với giá một tô bún bò là 35 000 đồng? (kết quả làm tròn đến hàng phần chục).
và múc đúng một muôi đầy cho mỗi tô. Giả sử mẹ bạn An múc hết sạch lượng nước lèo đã nấu, hỏi sau khi bán hết bún bò thì quán nhà bạn An thu được bao nhiêu triệu đồng với giá một tô bún bò là 35 000 đồng? (kết quả làm tròn đến hàng phần chục).

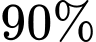 thể tích nồi. Để bán bún bò, mỗi lần bán một tô bún, mẹ bạn An dùng cái muôi (hoặc cái muỗng) có dạng nửa hình cầu bán kính
thể tích nồi. Để bán bún bò, mỗi lần bán một tô bún, mẹ bạn An dùng cái muôi (hoặc cái muỗng) có dạng nửa hình cầu bán kính 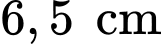 và múc đúng một muôi đầy cho mỗi tô. Giả sử mẹ bạn An múc hết sạch lượng nước lèo đã nấu, hỏi sau khi bán hết bún bò thì quán nhà bạn An thu được bao nhiêu triệu đồng với giá một tô bún bò là 35 000 đồng? (kết quả làm tròn đến hàng phần chục).
và múc đúng một muôi đầy cho mỗi tô. Giả sử mẹ bạn An múc hết sạch lượng nước lèo đã nấu, hỏi sau khi bán hết bún bò thì quán nhà bạn An thu được bao nhiêu triệu đồng với giá một tô bún bò là 35 000 đồng? (kết quả làm tròn đến hàng phần chục). 
Điền đáp án: 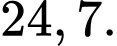
Đổi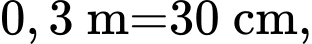
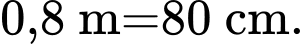
Thể tích 2 nồi nước lèo nhà bạn An nấu là: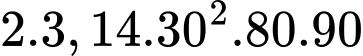
Thể tích của vá nước lèo là: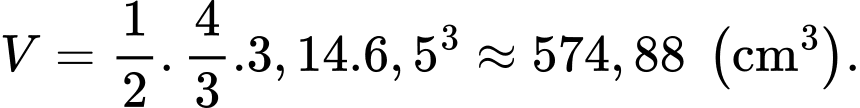
Số bát bún mà mẹ bạn An múc được là: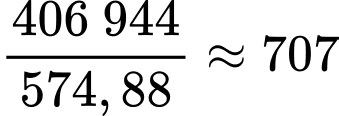 ( bát ).
( bát ).
Số tiền quán nhà bạn An thu được là: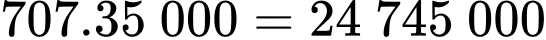 (đồng).
(đồng).
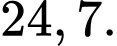
Đổi
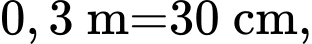
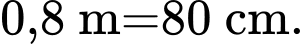
Thể tích 2 nồi nước lèo nhà bạn An nấu là:
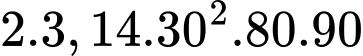
Thể tích của vá nước lèo là:
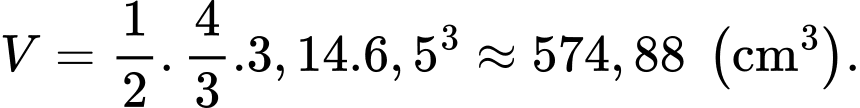
Số bát bún mà mẹ bạn An múc được là:
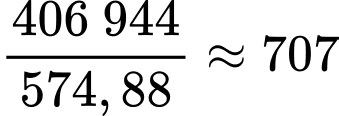 ( bát ).
( bát ).Số tiền quán nhà bạn An thu được là:
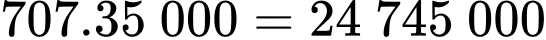 (đồng).
(đồng).
Câu 19 [695652]: Trong không gian tọa độ 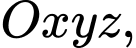 cho hai điểm
cho hai điểm 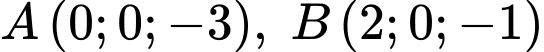 và mặt phẳng
và mặt phẳng 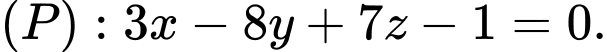 Điểm
Điểm 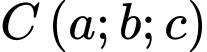 là điểm nằm trên mặt phẳng
là điểm nằm trên mặt phẳng 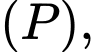 có hoành độ dương sao cho tam giác
có hoành độ dương sao cho tam giác 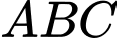 đều. Tính
đều. Tính 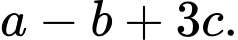
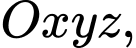 cho hai điểm
cho hai điểm 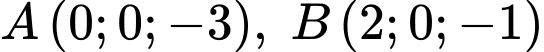 và mặt phẳng
và mặt phẳng 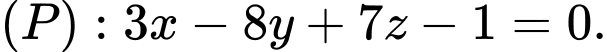 Điểm
Điểm 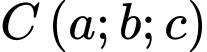 là điểm nằm trên mặt phẳng
là điểm nằm trên mặt phẳng 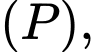 có hoành độ dương sao cho tam giác
có hoành độ dương sao cho tam giác 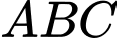 đều. Tính
đều. Tính 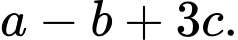
Điền đáp án: -5.
Gọi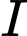 là trung điểm của
là trung điểm của 
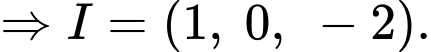
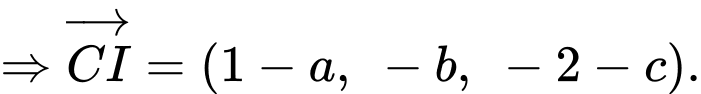
Vì tam giác đều có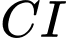 là đường trung tuyến
là đường trung tuyến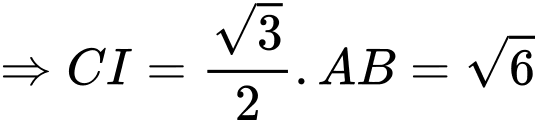
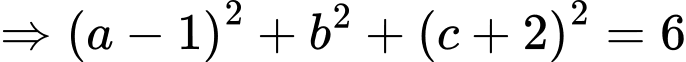 (1)
(1)
Vì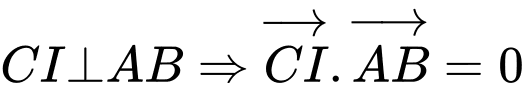
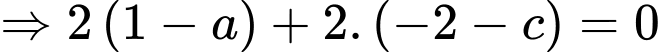
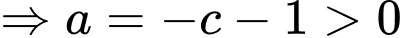

Vì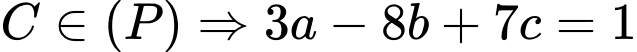
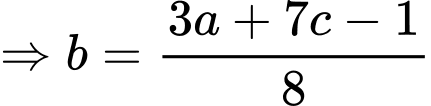
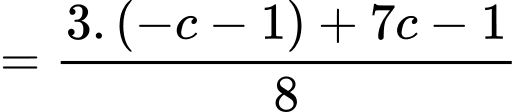
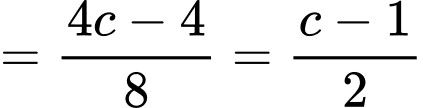
Thay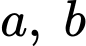 vào (1) ta được:
vào (1) ta được: 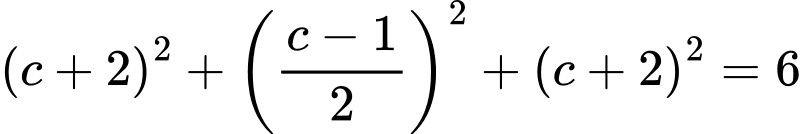
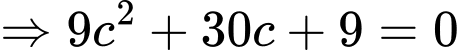
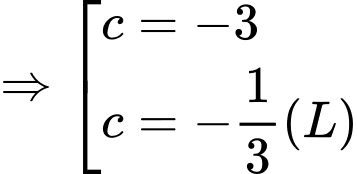
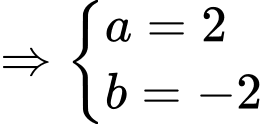

Gọi
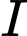 là trung điểm của
là trung điểm của 
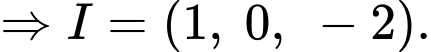
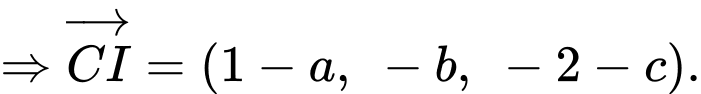
Vì tam giác đều có
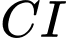 là đường trung tuyến
là đường trung tuyến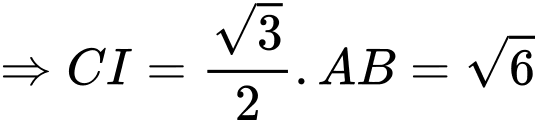
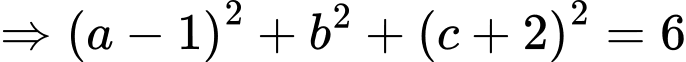 (1)
(1)
Vì
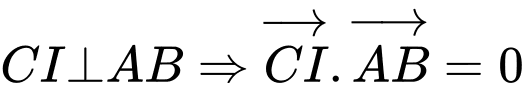
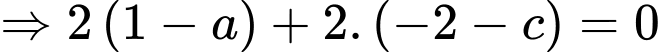
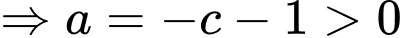

Vì
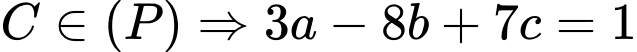
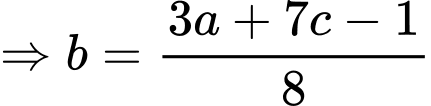
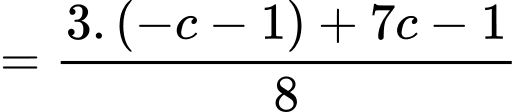
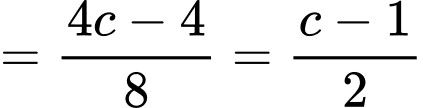
Thay
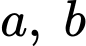 vào (1) ta được:
vào (1) ta được: 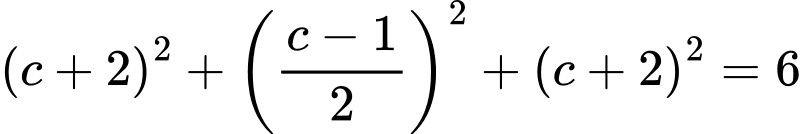
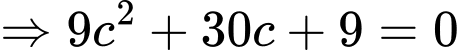
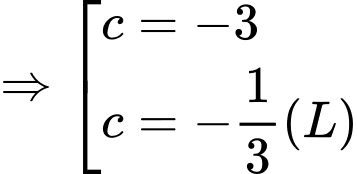
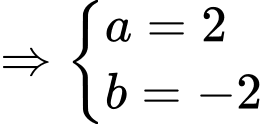

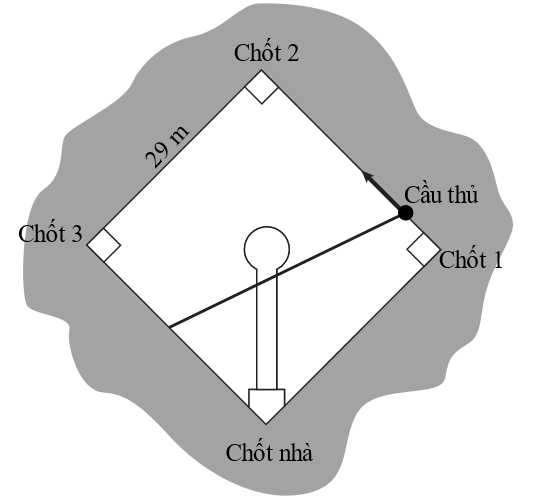
Câu 20 [702908]: Một sân bóng chày là một hình vuông có cạnh 29 mét, một người chơi chạy xung quanh các cạnh của hình vuông từ chốt thứ nhất, đến chốt thứ 2 rồi đến chốt thứ 3 sau đó chạy về chốt nhà như hình vẽ. Một người chơi đang cách chốt thứ nhất 9 mét, chạy đến chốt thứ hai với vận tốc 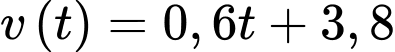 (m/s). Tại thời điểm vận động viên đến chốt thứ 2 thì khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
(m/s). Tại thời điểm vận động viên đến chốt thứ 2 thì khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
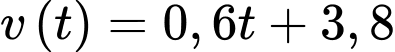 (m/s). Tại thời điểm vận động viên đến chốt thứ 2 thì khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
(m/s). Tại thời điểm vận động viên đến chốt thứ 2 thì khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ bao nhiêu m/s? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 2,77.
Giả sử chốt nhà trùng với gốc tọa độ trong mặt phẳng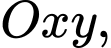 chốt 3 trùng với điểm
chốt 3 trùng với điểm 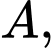 chốt 2 trùng với điểm
chốt 2 trùng với điểm 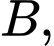 chốt 1 trùng với điểm
chốt 1 trùng với điểm 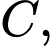 vận động viên trùng với điểm
vận động viên trùng với điểm 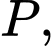 đoạn
đoạn 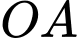 nằm trên trục
nằm trên trục  đoạn
đoạn 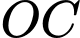 nằm trên trục
nằm trên trục 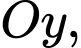 là trung điểm của
là trung điểm của 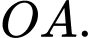
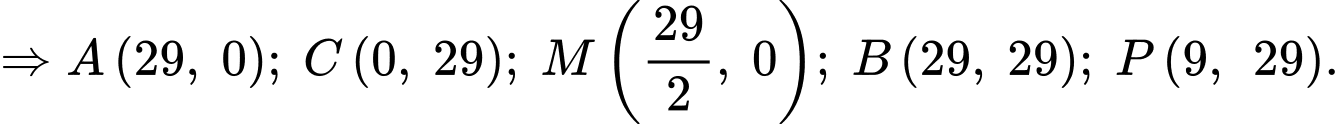
Vị trí của vận động viên tại thời điểm là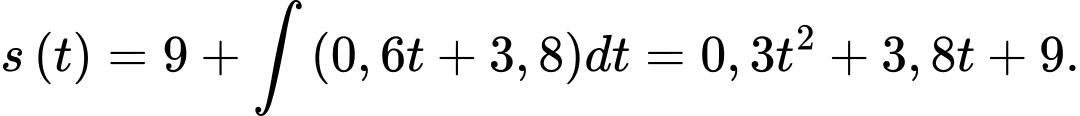
Thời gian để chạy đến chốt 2 ( điểm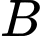 ) là
) là 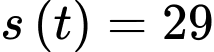
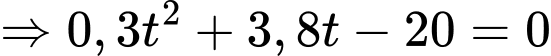
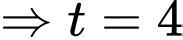
Khi vận động viên đến chốt 2 thì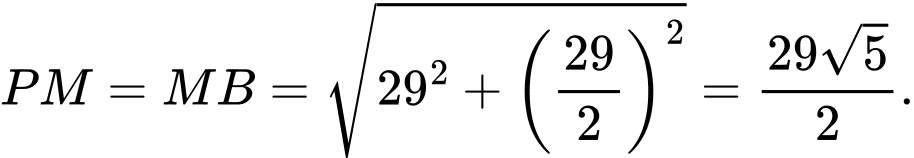
Ta có tọa độ quả điểm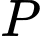 thay đổi theo thời gian
thay đổi theo thời gian 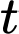 là
là 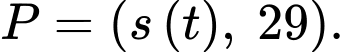
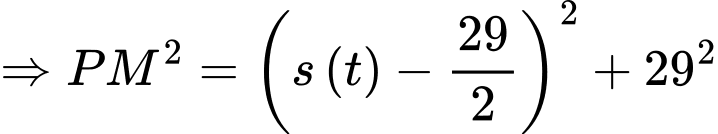
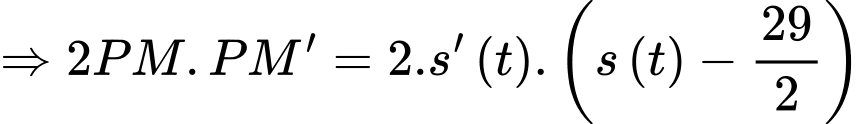
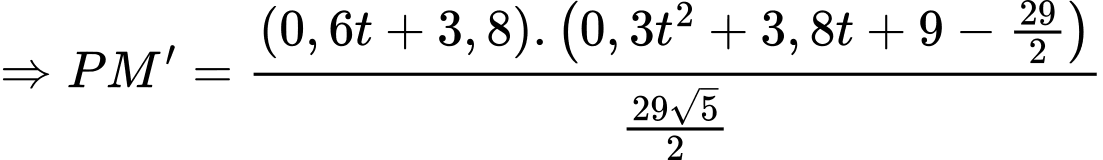
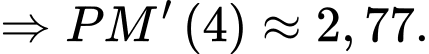
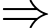 Khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ
Khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ 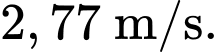

Giả sử chốt nhà trùng với gốc tọa độ trong mặt phẳng
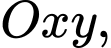 chốt 3 trùng với điểm
chốt 3 trùng với điểm 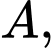 chốt 2 trùng với điểm
chốt 2 trùng với điểm 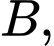 chốt 1 trùng với điểm
chốt 1 trùng với điểm 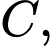 vận động viên trùng với điểm
vận động viên trùng với điểm 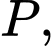 đoạn
đoạn 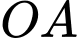 nằm trên trục
nằm trên trục  đoạn
đoạn 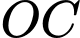 nằm trên trục
nằm trên trục 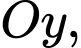 là trung điểm của
là trung điểm của 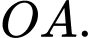
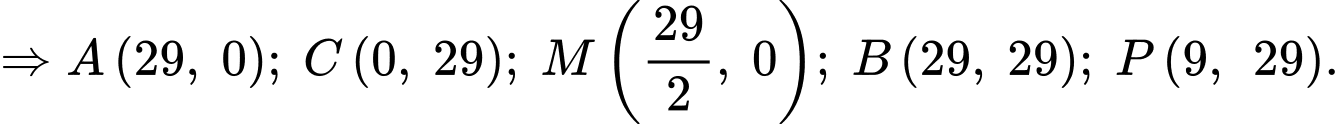
Vị trí của vận động viên tại thời điểm là
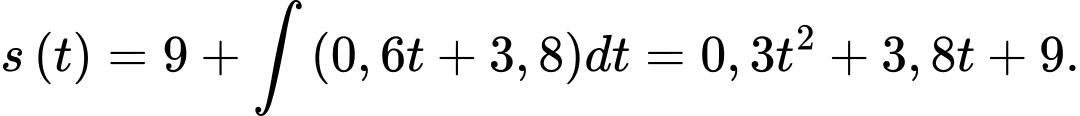
Thời gian để chạy đến chốt 2 ( điểm
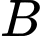 ) là
) là 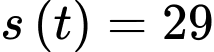
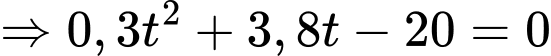
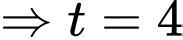
Khi vận động viên đến chốt 2 thì
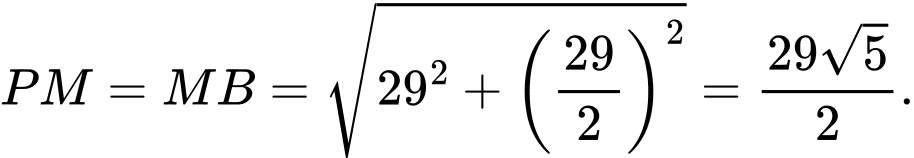
Ta có tọa độ quả điểm
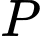 thay đổi theo thời gian
thay đổi theo thời gian 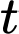 là
là 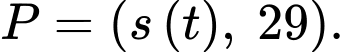
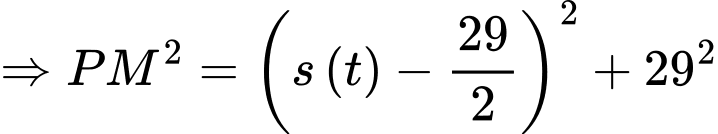
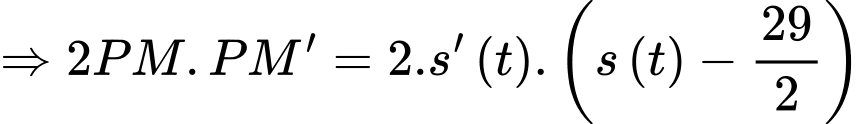
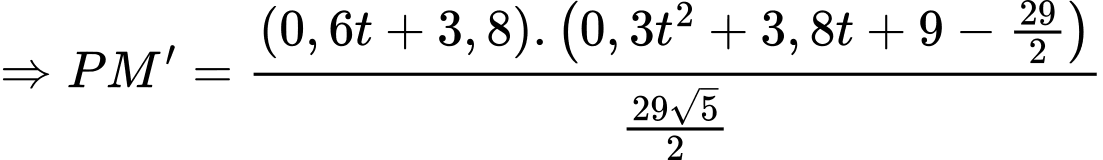
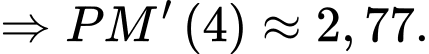
 Khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ
Khoảng cách từ người chơi đến điểm chính giữa chốt thứ ba và chốt nhà thay đổi với tốc độ 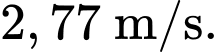
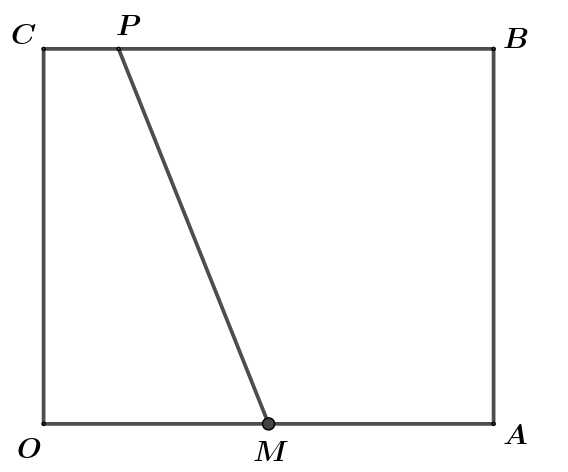
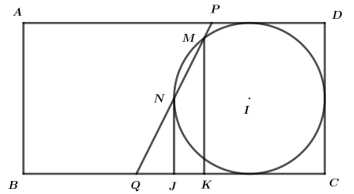
Câu 21 [695654]: Từ một tấm bìa giấy hình chữ nhật 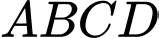 có
có 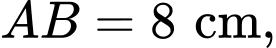
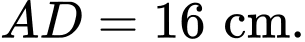 Người ta vẽ một đường tròn tiếp xúc với ba cạnh
Người ta vẽ một đường tròn tiếp xúc với ba cạnh 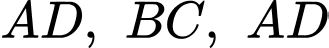 và kẻ một đường thẳng
và kẻ một đường thẳng 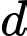 cắt đường tròn theo dây
cắt đường tròn theo dây 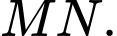 Biết
Biết 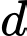 cắt cạnh
cắt cạnh 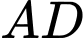 tại
tại 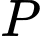 sao cho
sao cho  và
và 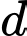 chia tấm bìa thành hai miền có diện tích bằng nhau. Quay tấm bìa quanh cạnh
chia tấm bìa thành hai miền có diện tích bằng nhau. Quay tấm bìa quanh cạnh 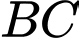 thì miền phẳng được tô đậm tạo thành một khối tròn xoay có thể tích bằng bao nhiêu
thì miền phẳng được tô đậm tạo thành một khối tròn xoay có thể tích bằng bao nhiêu  ? (làm tròn kết quả đến hàng phần mười).
? (làm tròn kết quả đến hàng phần mười).
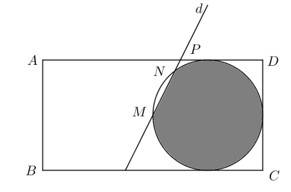
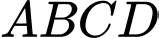 có
có 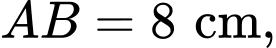
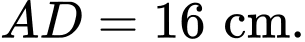 Người ta vẽ một đường tròn tiếp xúc với ba cạnh
Người ta vẽ một đường tròn tiếp xúc với ba cạnh 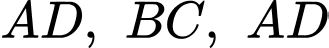 và kẻ một đường thẳng
và kẻ một đường thẳng 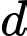 cắt đường tròn theo dây
cắt đường tròn theo dây 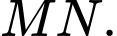 Biết
Biết 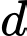 cắt cạnh
cắt cạnh 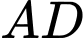 tại
tại 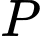 sao cho
sao cho  và
và 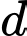 chia tấm bìa thành hai miền có diện tích bằng nhau. Quay tấm bìa quanh cạnh
chia tấm bìa thành hai miền có diện tích bằng nhau. Quay tấm bìa quanh cạnh 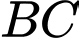 thì miền phẳng được tô đậm tạo thành một khối tròn xoay có thể tích bằng bao nhiêu
thì miền phẳng được tô đậm tạo thành một khối tròn xoay có thể tích bằng bao nhiêu  ? (làm tròn kết quả đến hàng phần mười).
? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 1,2.
Giả sử trùng với gốc tọa độ
trùng với gốc tọa độ  trong mặt phẳng
trong mặt phẳng 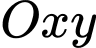 ,
,  nằm trên trục
nằm trên trục 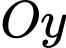 ,
, 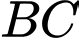 nằm trên trục
nằm trên trục 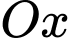 .
.
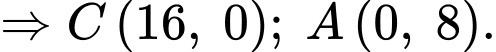
Đặt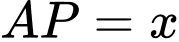

Ta có:
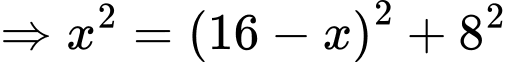
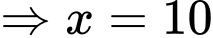
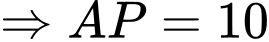
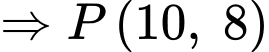
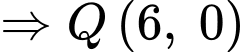 ( do
( do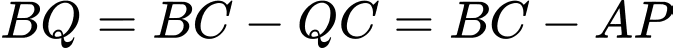 ).
).
Gọi phương trình đường thẳng đi qua 2 điểm
đi qua 2 điểm 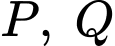 có dạng
có dạng 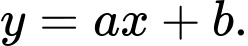
Thay tọa độ 2 điểm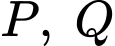 vào phương trình đường thẳng
vào phương trình đường thẳng  ta được:
ta được: 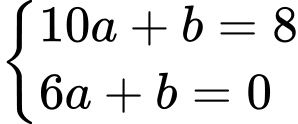
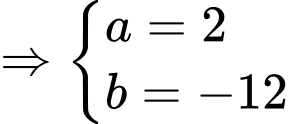
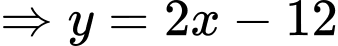 .
.
Vì đường tròn tâm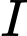 tiếp xúc với ba cạnh
tiếp xúc với ba cạnh 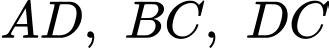
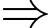 Bán kính của hình tròn tâm
Bán kính của hình tròn tâm 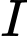 là
là 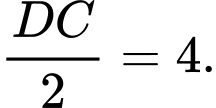
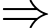 Phương trình đường tròn tâm
Phương trình đường tròn tâm 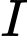 là
là 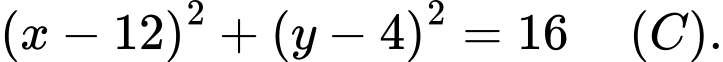
Thay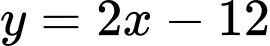 vào phương trình đường tròn tâm
vào phương trình đường tròn tâm 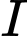 ta được:
ta được: 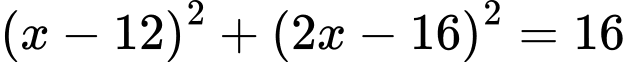
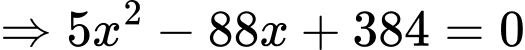
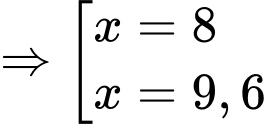
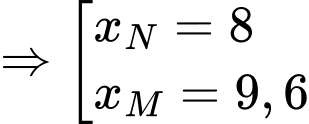
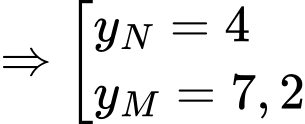
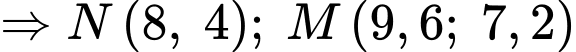
Gọi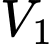 là thể tích khối tròn xoay giới hạn bởi đường thẳng
là thể tích khối tròn xoay giới hạn bởi đường thẳng  ; đường tròn
; đường tròn  ; các đường thẳng
; các đường thẳng 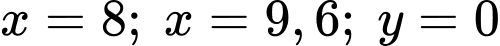 khi quay quanh cạnh
khi quay quanh cạnh 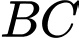 .
.
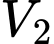 là thể tích khối tròn xoay giới hạn bởi đường tròn
là thể tích khối tròn xoay giới hạn bởi đường tròn  ; các đường thẳng
; các đường thẳng 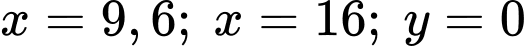 khi quay quanh cạnh
khi quay quanh cạnh 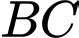 .
.
Ta có: phương trình nửa đường tròn tâm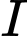 nằm trên đường thẳng
nằm trên đường thẳng 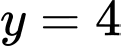 có dạng
có dạng 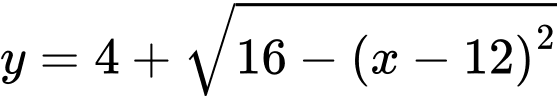 , phương trình nửa đường tròn tâm
, phương trình nửa đường tròn tâm 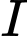 nằm dưới đường thẳng
nằm dưới đường thẳng 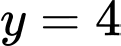 có dạng
có dạng 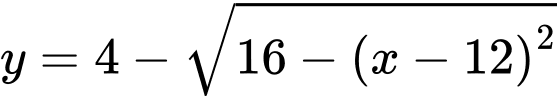 .
.
Ta có :
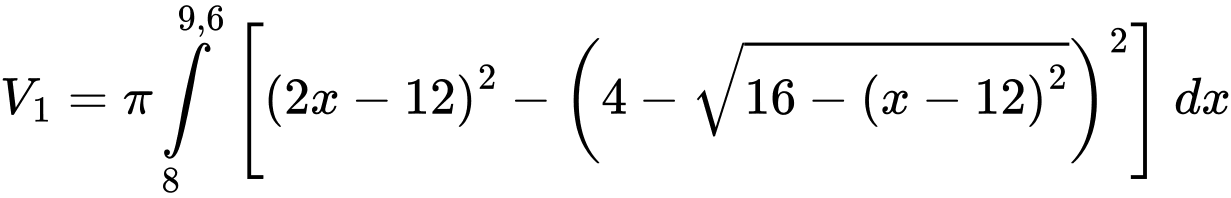
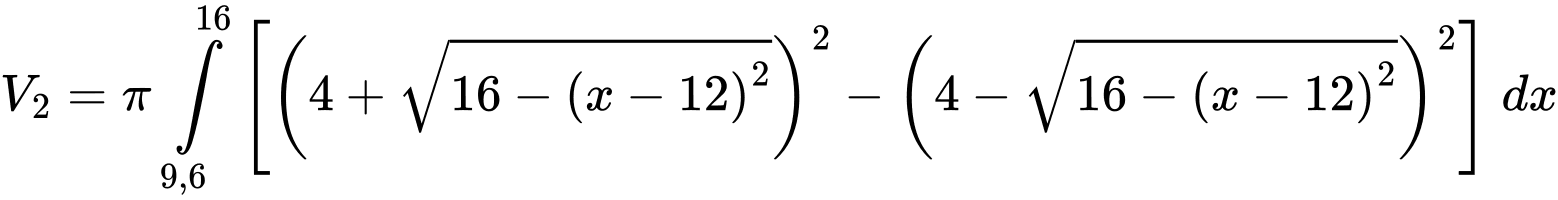
 Thể tích phần tô đậm khi quay quanh cạnh
Thể tích phần tô đậm khi quay quanh cạnh 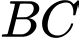 là
là 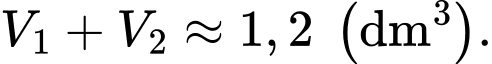

Giả sử
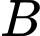 trùng với gốc tọa độ
trùng với gốc tọa độ  trong mặt phẳng
trong mặt phẳng 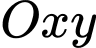 ,
,  nằm trên trục
nằm trên trục 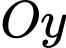 ,
, 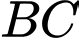 nằm trên trục
nằm trên trục 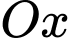 .
.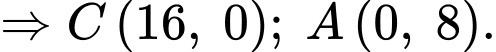
Đặt
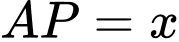

Ta có:

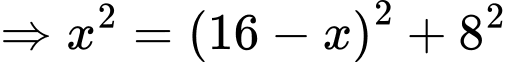
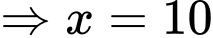
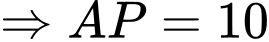
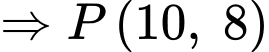
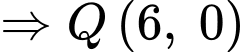 ( do
( do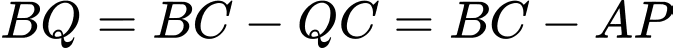 ).
).Gọi phương trình đường thẳng
 đi qua 2 điểm
đi qua 2 điểm 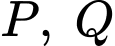 có dạng
có dạng 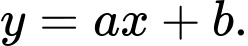
Thay tọa độ 2 điểm
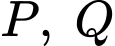 vào phương trình đường thẳng
vào phương trình đường thẳng  ta được:
ta được: 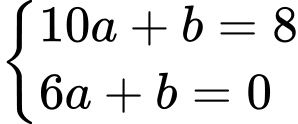
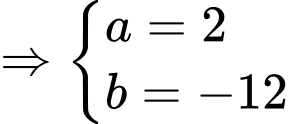
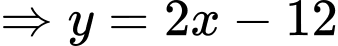 .
.Vì đường tròn tâm
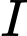 tiếp xúc với ba cạnh
tiếp xúc với ba cạnh 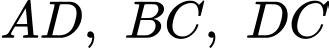
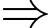 Bán kính của hình tròn tâm
Bán kính của hình tròn tâm 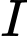 là
là 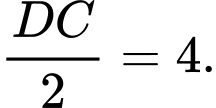
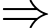 Phương trình đường tròn tâm
Phương trình đường tròn tâm 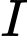 là
là 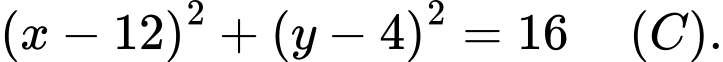
Thay
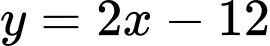 vào phương trình đường tròn tâm
vào phương trình đường tròn tâm 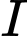 ta được:
ta được: 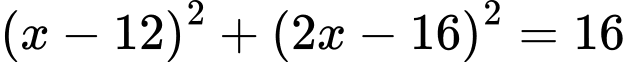
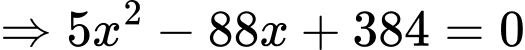
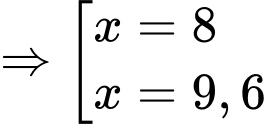
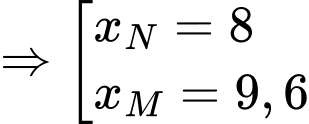
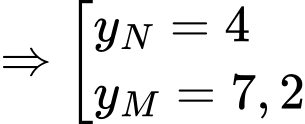
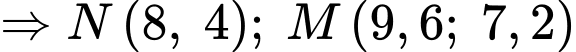
Gọi
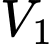 là thể tích khối tròn xoay giới hạn bởi đường thẳng
là thể tích khối tròn xoay giới hạn bởi đường thẳng  ; đường tròn
; đường tròn  ; các đường thẳng
; các đường thẳng 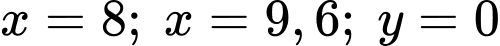 khi quay quanh cạnh
khi quay quanh cạnh 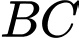 .
.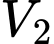 là thể tích khối tròn xoay giới hạn bởi đường tròn
là thể tích khối tròn xoay giới hạn bởi đường tròn  ; các đường thẳng
; các đường thẳng 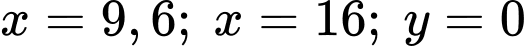 khi quay quanh cạnh
khi quay quanh cạnh 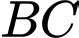 .
.Ta có: phương trình nửa đường tròn tâm
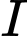 nằm trên đường thẳng
nằm trên đường thẳng 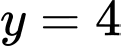 có dạng
có dạng 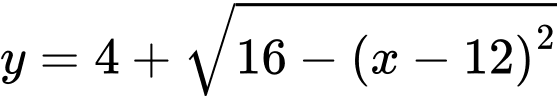 , phương trình nửa đường tròn tâm
, phương trình nửa đường tròn tâm 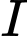 nằm dưới đường thẳng
nằm dưới đường thẳng 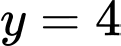 có dạng
có dạng 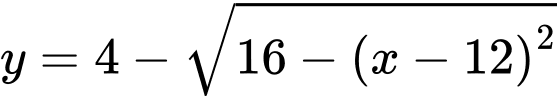 .
.Ta có :
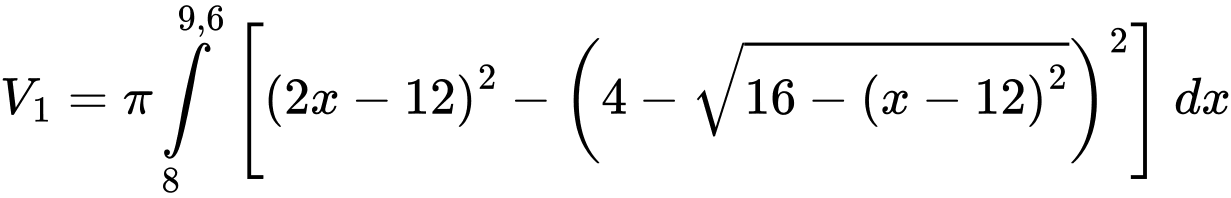
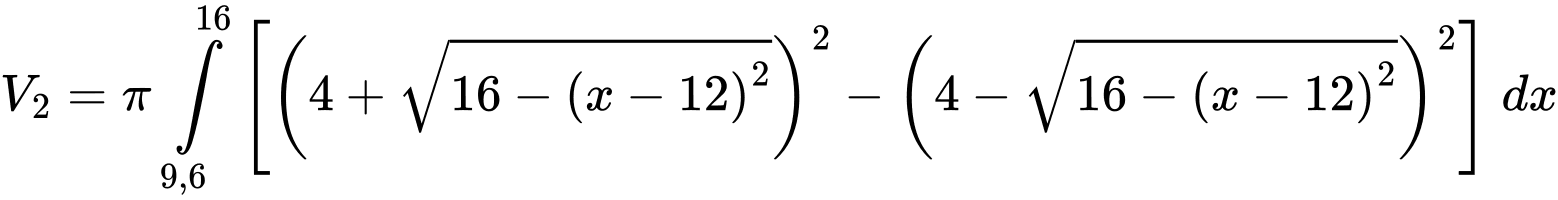
 Thể tích phần tô đậm khi quay quanh cạnh
Thể tích phần tô đậm khi quay quanh cạnh 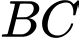 là
là 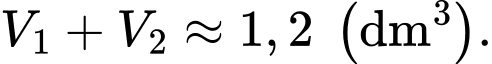
Câu 22 [695655]: Một đợt nghiên cứu về bệnh sốt xuất huyết ở tỉnh X phát hiện số người mắc bệnh chiếm 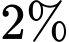 , trong số người mắc bệnh có
, trong số người mắc bệnh có 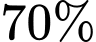 người lá lách to và
người lá lách to và 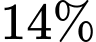 vừa gan to vừa lá lách to. Thống kê tất cả mẫu nghiên cứu có
vừa gan to vừa lá lách to. Thống kê tất cả mẫu nghiên cứu có 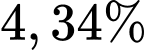 người có lá lách to và
người có lá lách to và 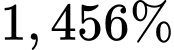 người vừa gan to vừa lá lách to. Chọn ngẫu nhiên một người lá lách to nhưng gan bình thường, xác suất người đó bị bệnh sốt xuất huyết bằng bao nhiêu phần trăm? (làm tròn đến hàng phần mười).
người vừa gan to vừa lá lách to. Chọn ngẫu nhiên một người lá lách to nhưng gan bình thường, xác suất người đó bị bệnh sốt xuất huyết bằng bao nhiêu phần trăm? (làm tròn đến hàng phần mười).
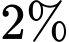 , trong số người mắc bệnh có
, trong số người mắc bệnh có 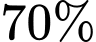 người lá lách to và
người lá lách to và 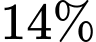 vừa gan to vừa lá lách to. Thống kê tất cả mẫu nghiên cứu có
vừa gan to vừa lá lách to. Thống kê tất cả mẫu nghiên cứu có 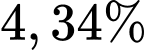 người có lá lách to và
người có lá lách to và 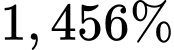 người vừa gan to vừa lá lách to. Chọn ngẫu nhiên một người lá lách to nhưng gan bình thường, xác suất người đó bị bệnh sốt xuất huyết bằng bao nhiêu phần trăm? (làm tròn đến hàng phần mười).
người vừa gan to vừa lá lách to. Chọn ngẫu nhiên một người lá lách to nhưng gan bình thường, xác suất người đó bị bệnh sốt xuất huyết bằng bao nhiêu phần trăm? (làm tròn đến hàng phần mười).
Điền đáp án: 38,8.
Gọi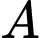 là biến cố “Người đó bị bệnh”
là biến cố “Người đó bị bệnh” 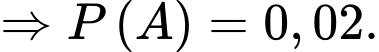
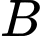 là biến cố “ Lách to”
là biến cố “ Lách to” 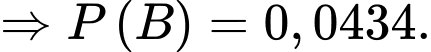
 là biến cố “ Gan to”.
là biến cố “ Gan to”.
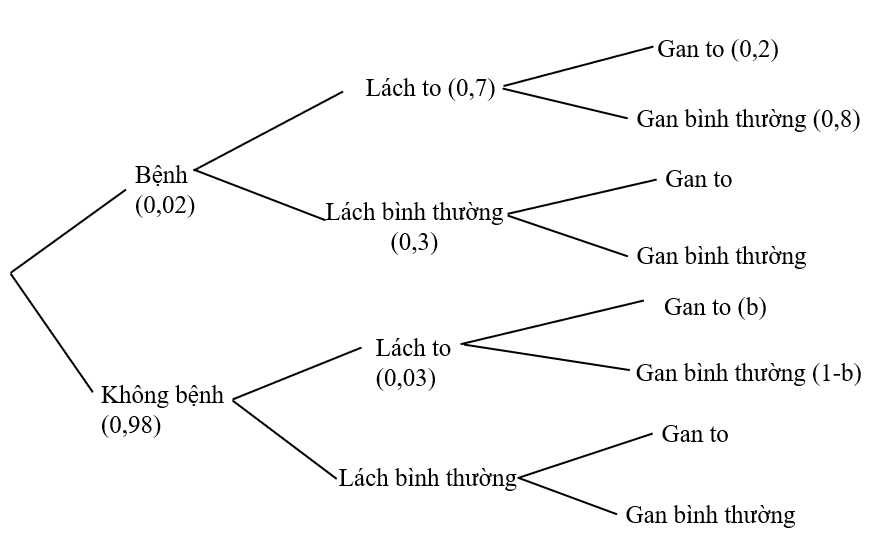 Ta có sơ đồ hình cây như hình vẽ trên:
Ta có sơ đồ hình cây như hình vẽ trên:
Theo công thức xác suất toàn phần ta có:
+)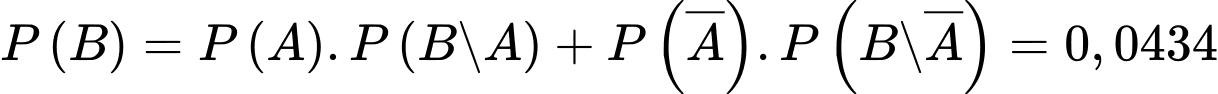
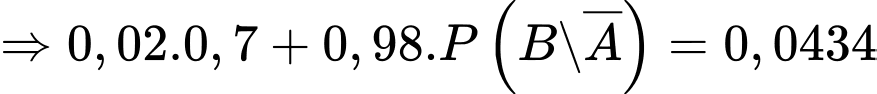
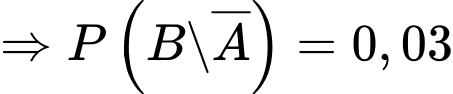
+)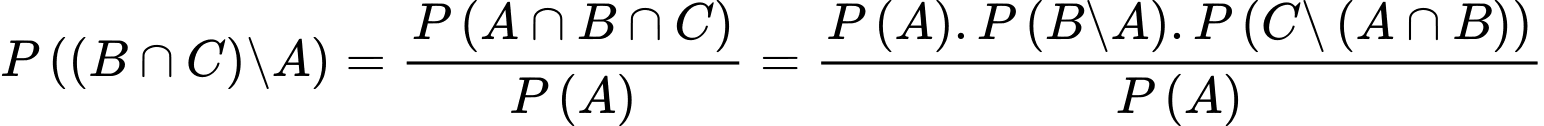
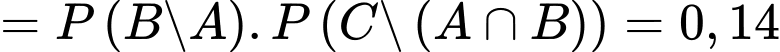
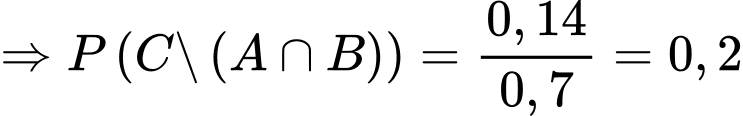
+)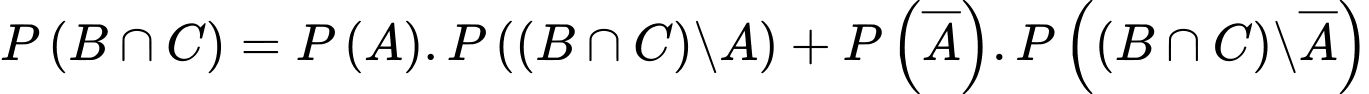

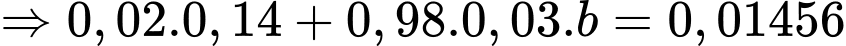
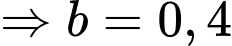
+)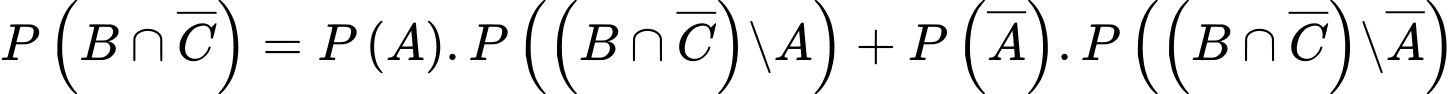
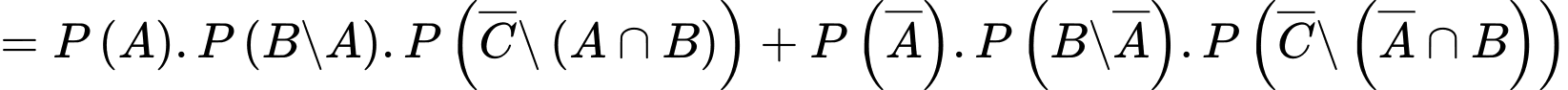
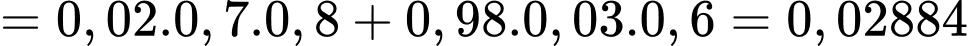
+) Xác suất cần tìm là
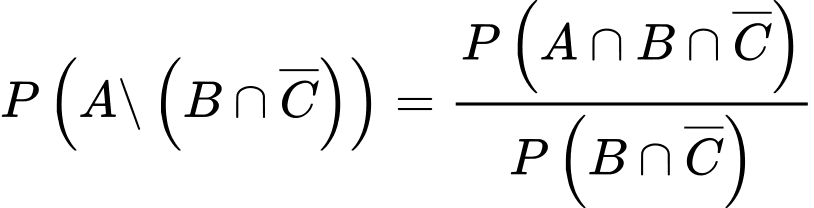
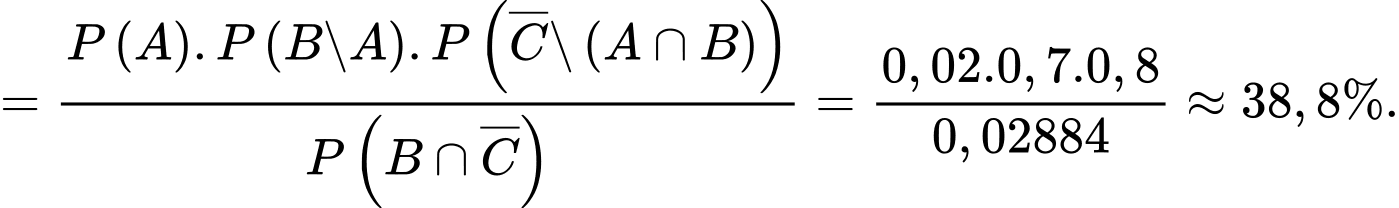
Gọi
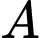 là biến cố “Người đó bị bệnh”
là biến cố “Người đó bị bệnh” 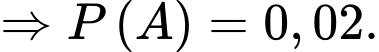
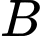 là biến cố “ Lách to”
là biến cố “ Lách to” 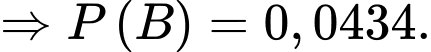
 là biến cố “ Gan to”.
là biến cố “ Gan to”.
Theo công thức xác suất toàn phần ta có:
+)
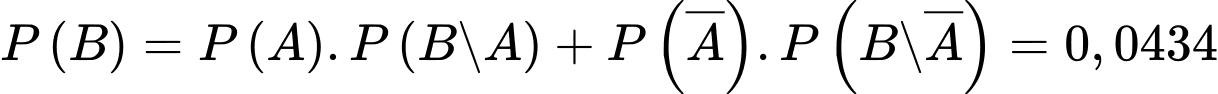
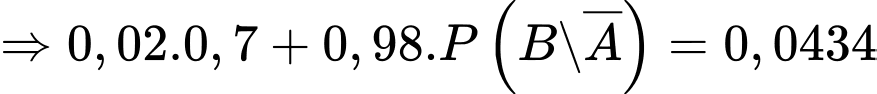
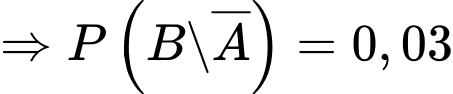
+)
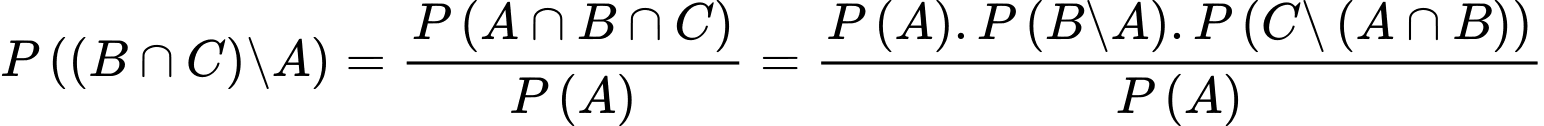
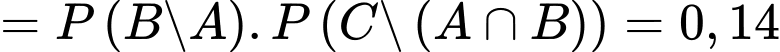
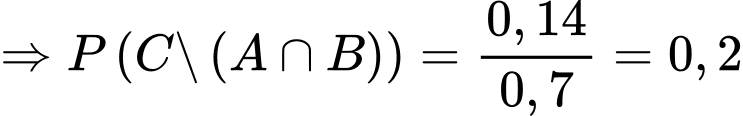
+)
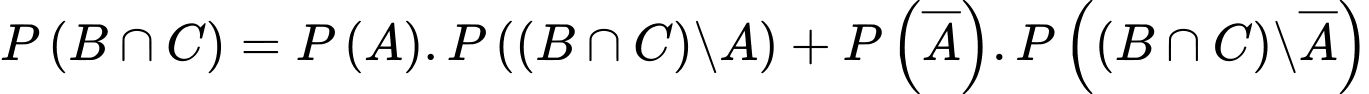

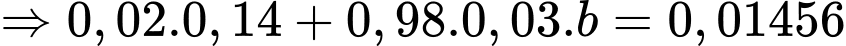
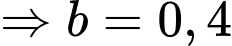
+)
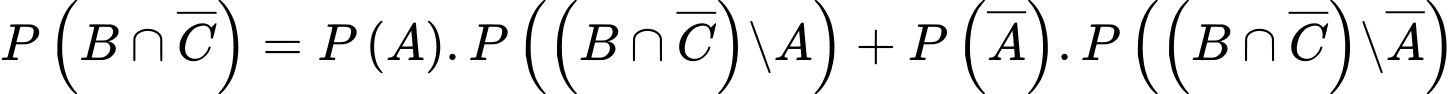
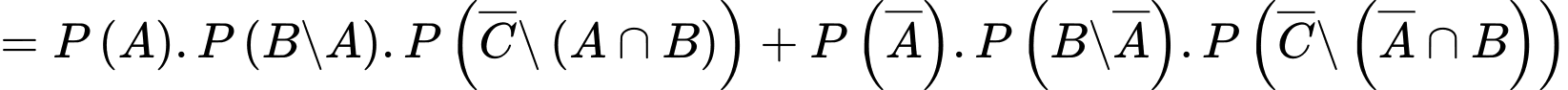
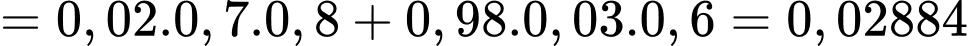
+) Xác suất cần tìm là