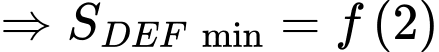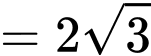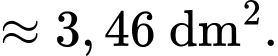PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [522969]: Tập nghiệm của bất phương trình 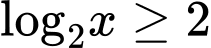 là
là
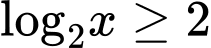 là
là A, 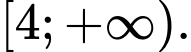
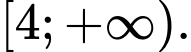
B, 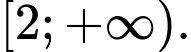
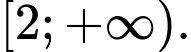
C, 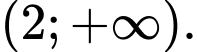
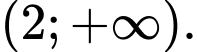
D, 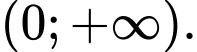
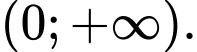
Chọn đáp án A.
Ta có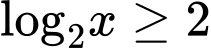
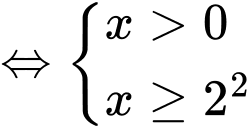
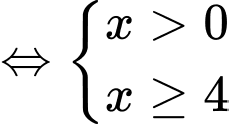
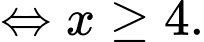
Vậy tập nghiệm của bất phương trình đã cho là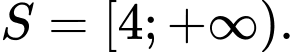 Đáp án: A
Đáp án: A
Ta có
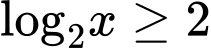
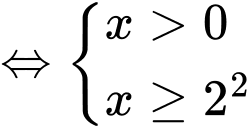
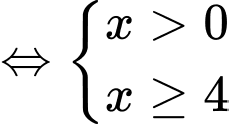
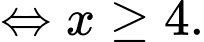
Vậy tập nghiệm của bất phương trình đã cho là
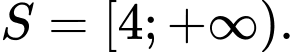 Đáp án: A
Đáp án: A
Câu 2 [333994]: Cho cấp số cộng 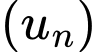 có số hạng đầu
có số hạng đầu 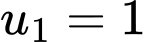 và công sai
và công sai  Giá trị của
Giá trị của 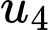 bằng
bằng
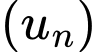 có số hạng đầu
có số hạng đầu 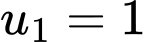 và công sai
và công sai  Giá trị của
Giá trị của 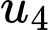 bằng
bằng A, 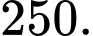
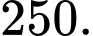
B, 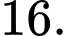
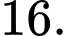
C, 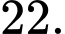
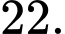
D, 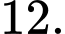
Chọn đáp án B.
Ta có: Đáp án: B
Đáp án: B
Ta có:
 Đáp án: B
Đáp án: B
Câu 3 [808425]: Trong không gian 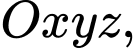 cho đường thẳng
cho đường thẳng 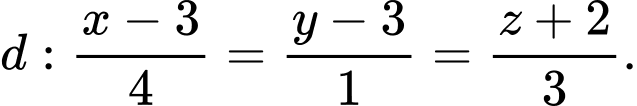 Vectơ nào dưới đây là một vectơ chỉ phương của
Vectơ nào dưới đây là một vectơ chỉ phương của 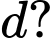
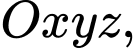 cho đường thẳng
cho đường thẳng 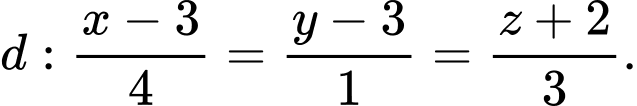 Vectơ nào dưới đây là một vectơ chỉ phương của
Vectơ nào dưới đây là một vectơ chỉ phương của 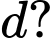
A, 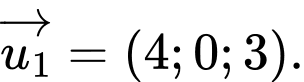
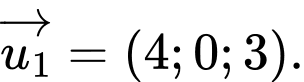
B, 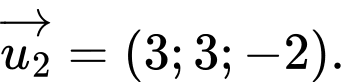
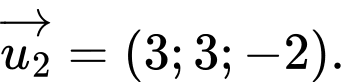
C, 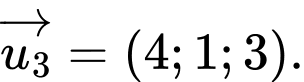
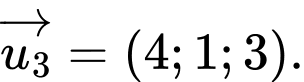
D, 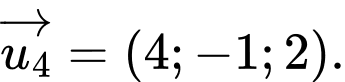
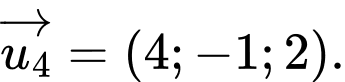
Chọn đáp án C.
Đường thẳng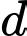 có một véc-tơ chỉ phương là
có một véc-tơ chỉ phương là 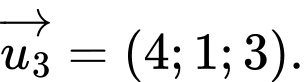 Đáp án: C
Đáp án: C
Đường thẳng
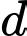 có một véc-tơ chỉ phương là
có một véc-tơ chỉ phương là 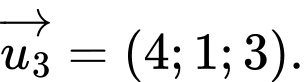 Đáp án: C
Đáp án: C
Câu 4 [806529]: Một nguyên hàm của hàm số 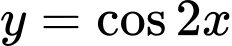 là
là
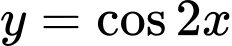 là
là A, 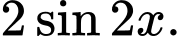
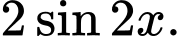
B, 

C, 

D, 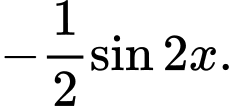
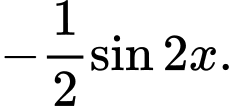
Chọn đáp án C.
Ta có:

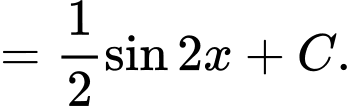
Một nguyên hàm của hàm số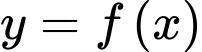
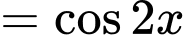 là
là 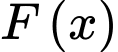
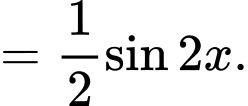 Đáp án: C
Đáp án: C
Ta có:


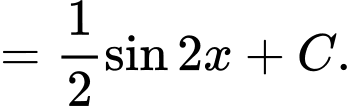
Một nguyên hàm của hàm số
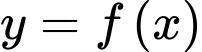
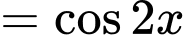 là
là 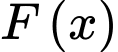
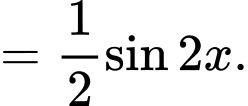 Đáp án: C
Đáp án: C
Câu 5 [330110]: Tính thể tích của khối hộp chữ nhật  có
có 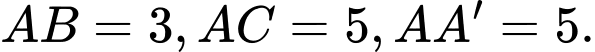
 có
có 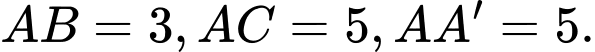
A, 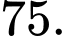
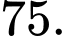
B, 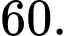
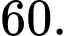
C, 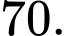
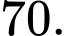
D, 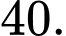
Chọn đáp án B.
Do
Khi đó thể tích của khối hộp chữ nhật bằng
bằng 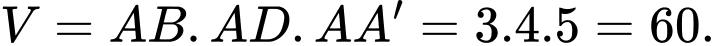 Đáp án: B
Đáp án: B
Do

Khi đó thể tích của khối hộp chữ nhật
 bằng
bằng 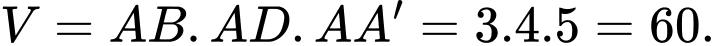 Đáp án: B
Đáp án: B
Câu 6 [512601]: Cho hàm số 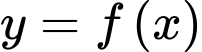 liên tục trên
liên tục trên 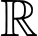 và có bảng xét dấu của đạo hàm như hình vẽ. Số điểm cực tiểu của hàm số đã cho là
và có bảng xét dấu của đạo hàm như hình vẽ. Số điểm cực tiểu của hàm số đã cho là
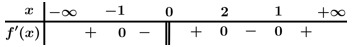
 liên tục trên
liên tục trên 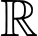 và có bảng xét dấu của đạo hàm như hình vẽ. Số điểm cực tiểu của hàm số đã cho là
và có bảng xét dấu của đạo hàm như hình vẽ. Số điểm cực tiểu của hàm số đã cho là A, 
B, 
C, 
D, 
Chọn đáp án A.
Từ bảng xét dấu của đạo hàm của hàm số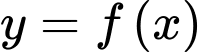 ta có hàm số
ta có hàm số 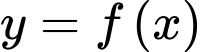 có 2 điểm cực tiểu. Đáp án: A
có 2 điểm cực tiểu. Đáp án: A
Từ bảng xét dấu của đạo hàm của hàm số
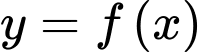 ta có hàm số
ta có hàm số 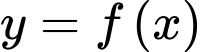 có 2 điểm cực tiểu. Đáp án: A
có 2 điểm cực tiểu. Đáp án: A
Câu 7 [511065]: Nghiệm của phương trình 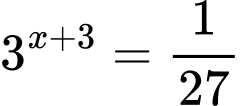 là
là
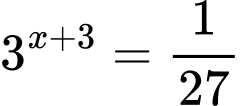 là
là A, 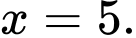
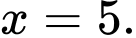
B, 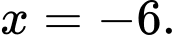
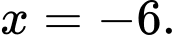
C, 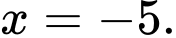
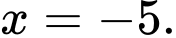
D, 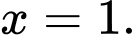
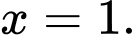
Chọn đáp án B.
Ta có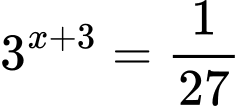
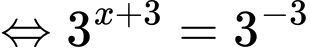
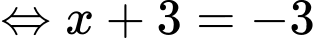
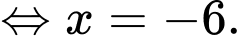
Vậy nghiệm của phương trình đã cho là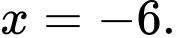 Đáp án: B
Đáp án: B
Ta có
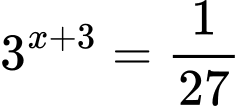
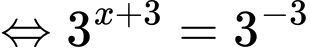
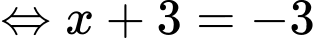
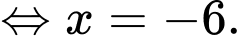
Vậy nghiệm của phương trình đã cho là
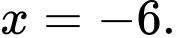 Đáp án: B
Đáp án: B
Câu 8 [890667]: Trong không gian 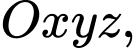 mặt cầu
mặt cầu 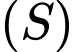 có tâm
có tâm 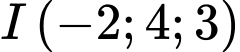 và đi qua
và đi qua 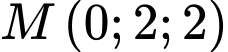 có phương trình là
có phương trình là
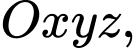 mặt cầu
mặt cầu 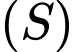 có tâm
có tâm 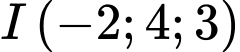 và đi qua
và đi qua 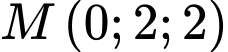 có phương trình là
có phương trình là A, 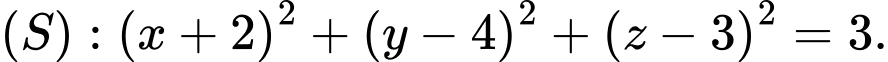
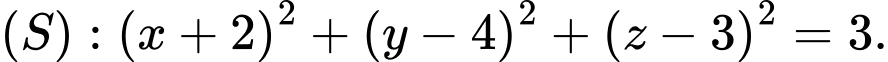
B, 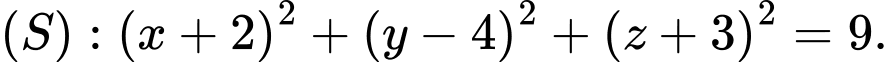
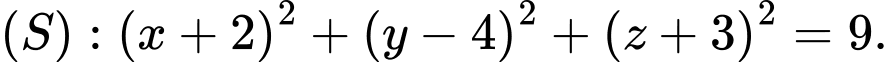
C, 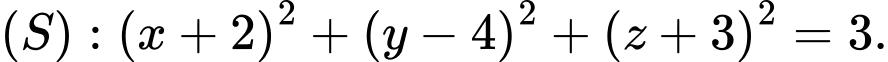
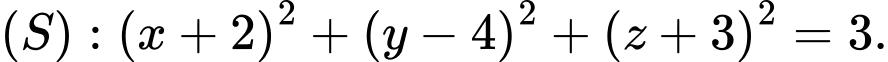
D, 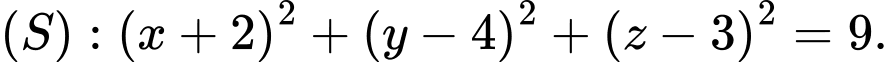
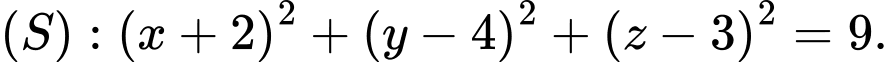
Chọn đáp án D.
Bán kính mặt cầu là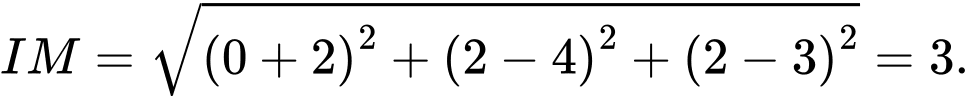
Phương trình mặt cầu là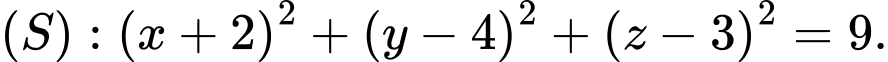 Đáp án: D
Đáp án: D
Bán kính mặt cầu là
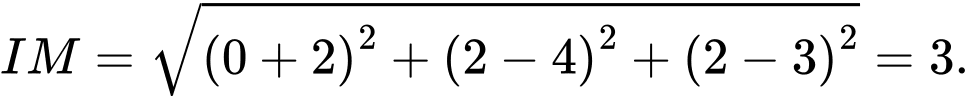
Phương trình mặt cầu là
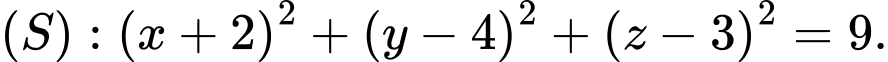 Đáp án: D
Đáp án: D
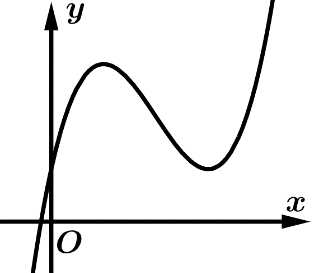
Câu 9 [801985]: Đường cong trong hình bên là là đồ thị của hàm số nào trong các hàm số dưới đây?

A, 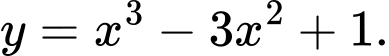
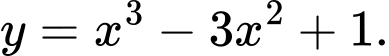
B, 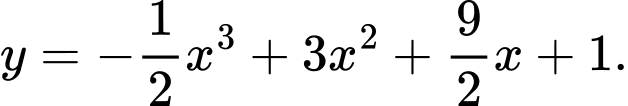
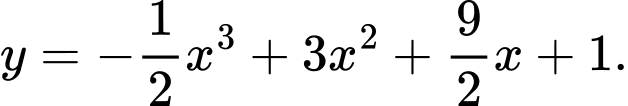
C, 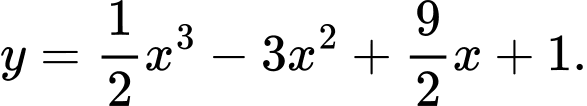
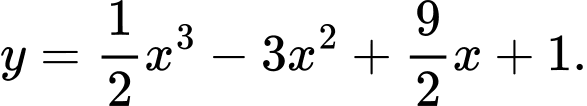
D, 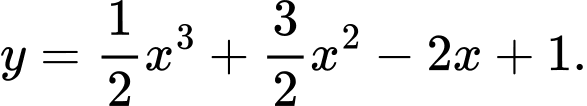
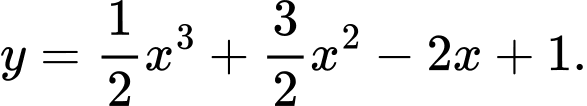
Chọn đáp án C.
Đường cong trên là dạng đồ thị hàm bậc ba nên hàm số có dạng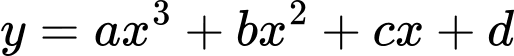
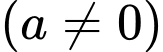
Vì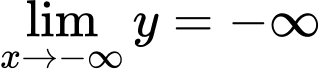
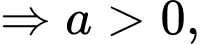 do đó loại đáp án B.
do đó loại đáp án B.
Mặt khác đồ thị hàm số có 2 điểm cực trị là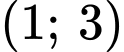 và
và 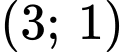 nên phương trình
nên phương trình 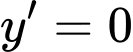 có hai nghiệm phân biệt
có hai nghiệm phân biệt 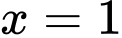 hoặc
hoặc 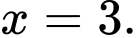
Thử phương trình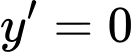 trong các đáp án A, B, C ta thấy đáp án C thỏa mãn. Đáp án: C
trong các đáp án A, B, C ta thấy đáp án C thỏa mãn. Đáp án: C
Đường cong trên là dạng đồ thị hàm bậc ba nên hàm số có dạng
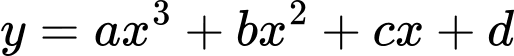
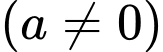
Vì
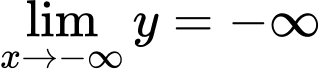
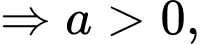 do đó loại đáp án B.
do đó loại đáp án B. Mặt khác đồ thị hàm số có 2 điểm cực trị là
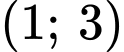 và
và 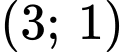 nên phương trình
nên phương trình 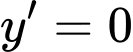 có hai nghiệm phân biệt
có hai nghiệm phân biệt 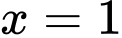 hoặc
hoặc 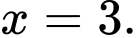
Thử phương trình
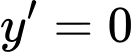 trong các đáp án A, B, C ta thấy đáp án C thỏa mãn. Đáp án: C
trong các đáp án A, B, C ta thấy đáp án C thỏa mãn. Đáp án: C
Câu 10 [681553]: Cho tứ diện đều 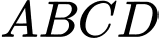 có cạnh bằng 1. Gọi M là trung điểm cạnh AB. Giá trị của
có cạnh bằng 1. Gọi M là trung điểm cạnh AB. Giá trị của 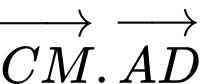 bằng
bằng
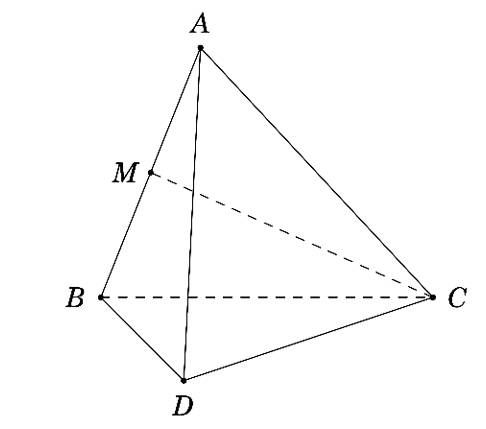
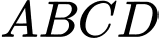 có cạnh bằng 1. Gọi M là trung điểm cạnh AB. Giá trị của
có cạnh bằng 1. Gọi M là trung điểm cạnh AB. Giá trị của 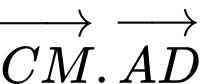 bằng
bằng
A, 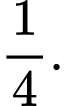
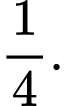
B, 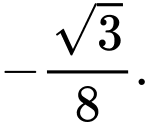
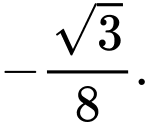
C, 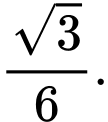
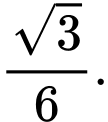
D, 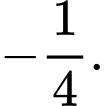
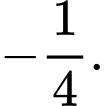
Chọn đáp án D.
Gọi N là trung điểm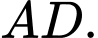 Suy ra:
Suy ra: 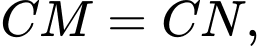
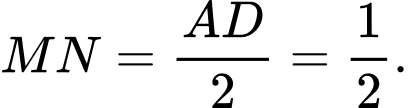
Khi đó, ta có: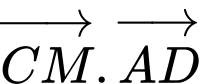
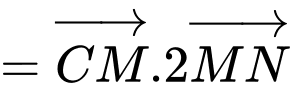
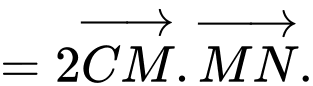
Xét biểu thức: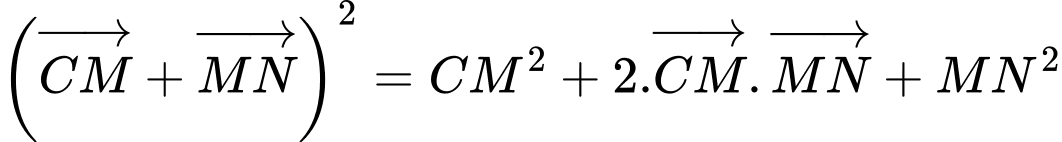
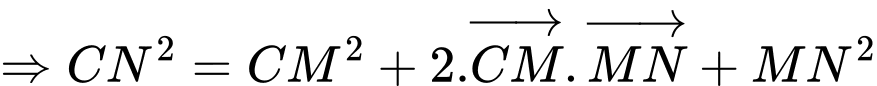 .
.
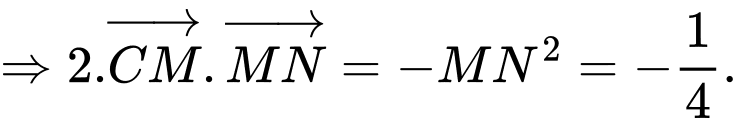 Đáp án: D
Đáp án: D
Gọi N là trung điểm
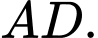 Suy ra:
Suy ra: 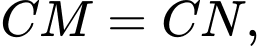
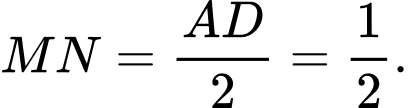
Khi đó, ta có:
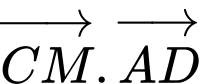
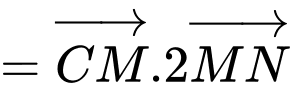
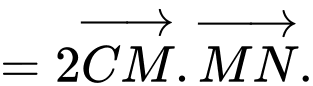
Xét biểu thức:
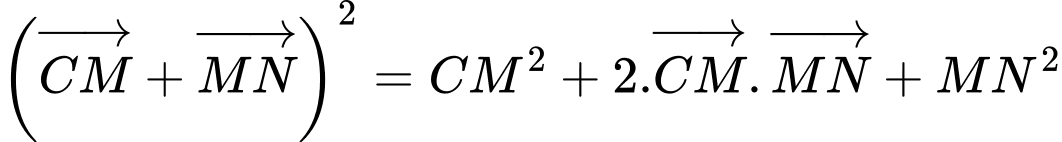
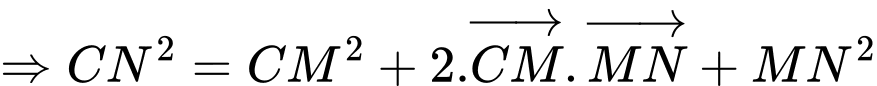 .
.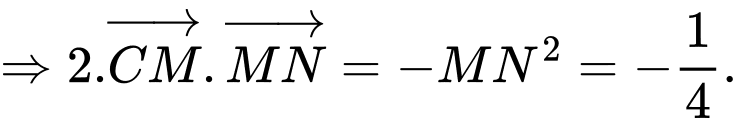 Đáp án: D
Đáp án: D
Câu 11 [696348]: Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên bằng bao nhiêu chục nghìn đồng? (làm tròn kết quả đến hàng đơn vị).

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên bằng bao nhiêu chục nghìn đồng? (làm tròn kết quả đến hàng đơn vị).
A, 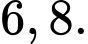
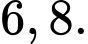
B, 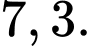
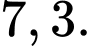
C, 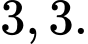
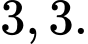
D, 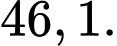
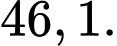
Chọn đáp án A.
Số trung bình của mấu số liệu ghép nhóm là
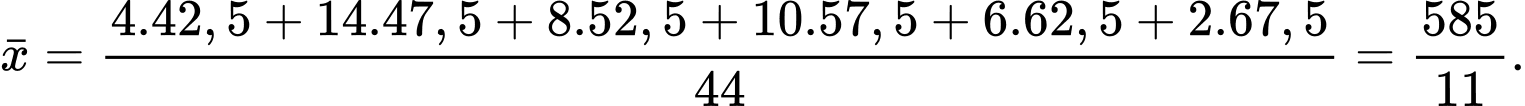
Phương sai của mẫu số liệu ghép nhóm là
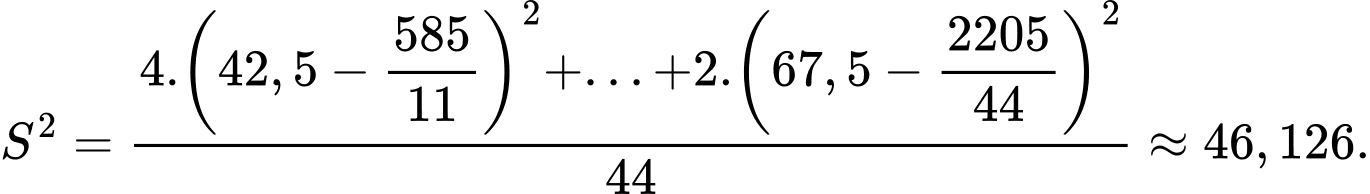
Độ lệch chuẩn của mẫu số liệu ghép nhóm là
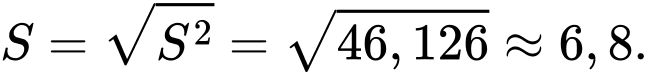 Đáp án: A
Đáp án: A
Số trung bình của mấu số liệu ghép nhóm là
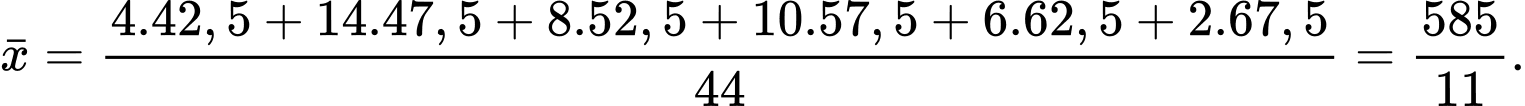
Phương sai của mẫu số liệu ghép nhóm là
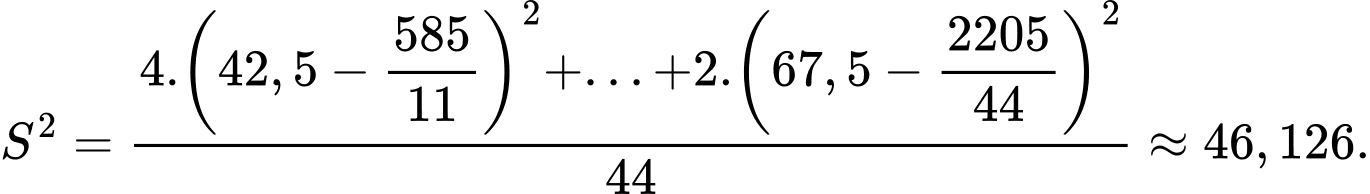
Độ lệch chuẩn của mẫu số liệu ghép nhóm là
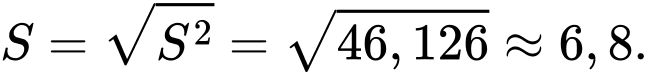 Đáp án: A
Đáp án: A
Câu 12 [807235]: Diện tích hình phẳng giới hạn bởi các đường 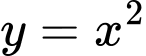 và
và 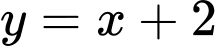 là
là
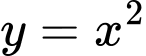 và
và 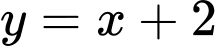 là
là A, 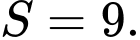
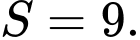
B, 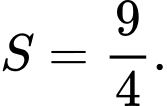
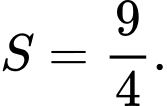
C, 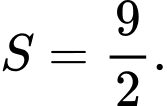
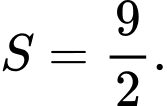
D, 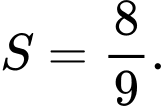
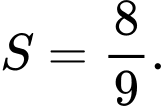
Chọn đáp án C.
* Phương trình hoành độ giao điểm của đồ thị hàm số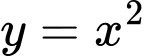 và đường thẳng
và đường thẳng 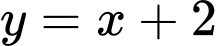 là:
là:
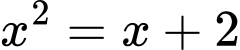
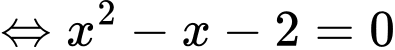
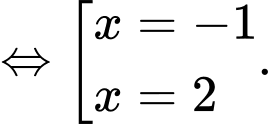
* Diện tích hình phẳng giới hạn bởi các đường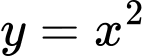 và
và 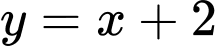 là:
là:
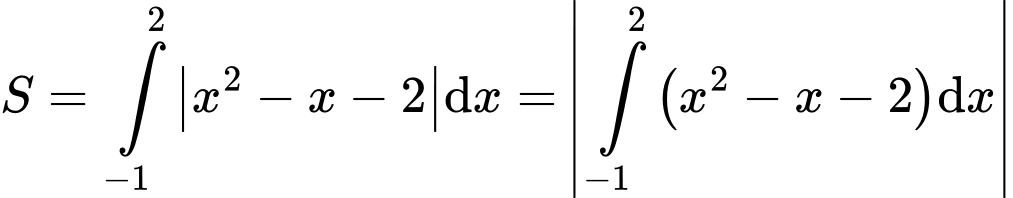
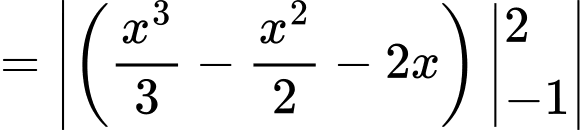
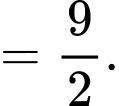 Đáp án: C
Đáp án: C
* Phương trình hoành độ giao điểm của đồ thị hàm số
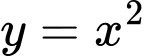 và đường thẳng
và đường thẳng 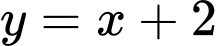 là:
là: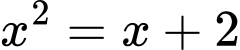
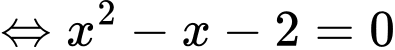
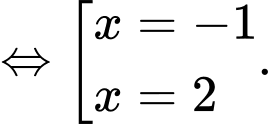
* Diện tích hình phẳng giới hạn bởi các đường
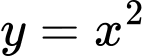 và
và 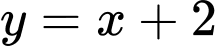 là:
là: 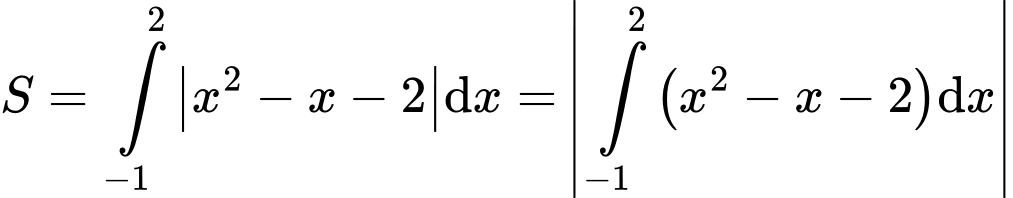
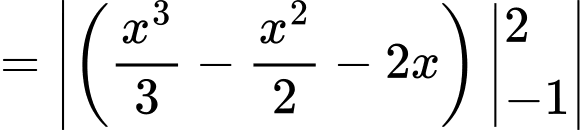
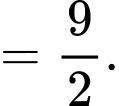 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696349]: Cho hàm số 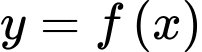 liên tục trên
liên tục trên 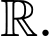 Hàm số
Hàm số 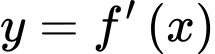 là hàm bậc bốn có đồ thị như hình vẽ bên. Xét hàm số
là hàm bậc bốn có đồ thị như hình vẽ bên. Xét hàm số 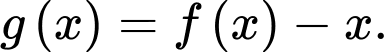
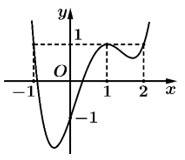
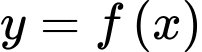 liên tục trên
liên tục trên 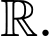 Hàm số
Hàm số 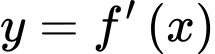 là hàm bậc bốn có đồ thị như hình vẽ bên. Xét hàm số
là hàm bậc bốn có đồ thị như hình vẽ bên. Xét hàm số 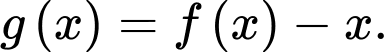

a) Đúng.
Vì hàm số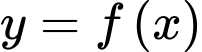 và
và 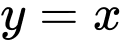 liên tục trên
liên tục trên 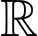
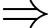 Hàm số
Hàm số 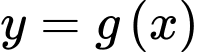 liên tục trên
liên tục trên 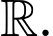
b) Đúng.
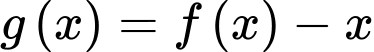
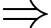
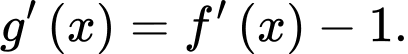
c) Sai.
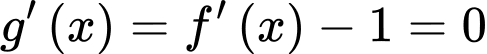
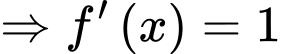
Dựa theo hình vẽ đồ thị ta thấy đường thẳng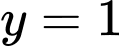 cắt đồ thị hàm số
cắt đồ thị hàm số 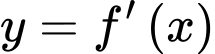 tại 3 điểm (trong đó có tiếp xúc tại điểm có hoành độ
tại 3 điểm (trong đó có tiếp xúc tại điểm có hoành độ 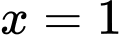 )
)
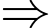 Đồ thị hàm số
Đồ thị hàm số 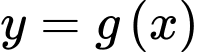 có 2 điểm cực trị.
có 2 điểm cực trị.
d) Sai.
Dựa theo đồ thị ta có: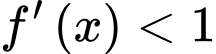 trên đoạn
trên đoạn 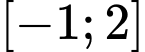
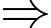 Hàm số
Hàm số 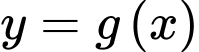 luôn nghịch biến trên đoạn
luôn nghịch biến trên đoạn 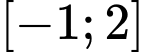
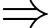 Giá trị lớn nhất của hàm số
Giá trị lớn nhất của hàm số 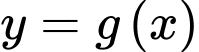 trên đoạn
trên đoạn 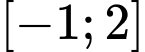 là
là 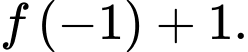
Vì hàm số
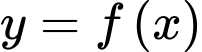 và
và 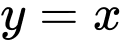 liên tục trên
liên tục trên 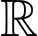
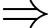 Hàm số
Hàm số 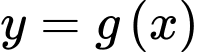 liên tục trên
liên tục trên 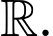
b) Đúng.
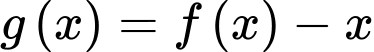
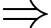
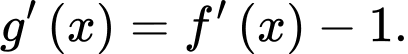
c) Sai.
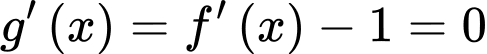
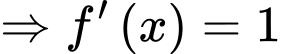
Dựa theo hình vẽ đồ thị ta thấy đường thẳng
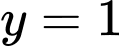 cắt đồ thị hàm số
cắt đồ thị hàm số 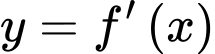 tại 3 điểm (trong đó có tiếp xúc tại điểm có hoành độ
tại 3 điểm (trong đó có tiếp xúc tại điểm có hoành độ 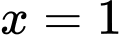 )
) 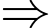 Đồ thị hàm số
Đồ thị hàm số 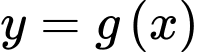 có 2 điểm cực trị.
có 2 điểm cực trị. d) Sai.
Dựa theo đồ thị ta có:
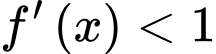 trên đoạn
trên đoạn 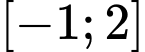
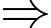 Hàm số
Hàm số 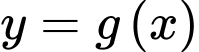 luôn nghịch biến trên đoạn
luôn nghịch biến trên đoạn 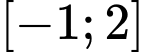
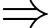 Giá trị lớn nhất của hàm số
Giá trị lớn nhất của hàm số 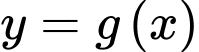 trên đoạn
trên đoạn 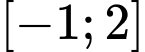 là
là 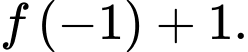
Câu 14 [693086]: Một nhà bán lẻ nhận được một lô hàng gạo nặng 10 000 kg, sẽ được sử dụng hết trong vòng 5 tháng với tốc độ tiêu thụ đều đặn là 2 000 kg mỗi tháng. Biết rằng chi phí lưu trữ là 1 000 đồng cho mỗi kg mỗi tháng.
a) Đúng. Số  còn lại sau
còn lại sau 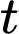 (tháng) là
(tháng) là 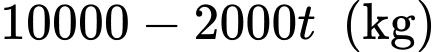
b) Đúng. là tổng chi phí lưu trữ
Chi phí lưu trữ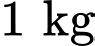 gạo:
gạo: 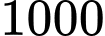 đồng/tháng.
đồng/tháng.
Suy ra, chi phí lưu trữ sau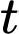 (tháng) là
(tháng) là 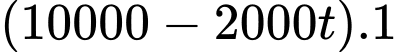 tức là
tức là 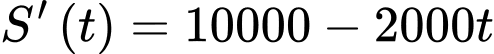 (nghìn đồng/tháng).
(nghìn đồng/tháng).
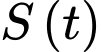 là tổng, ta sẽ tính toán giống bài toán tích phân nghĩa là
là tổng, ta sẽ tính toán giống bài toán tích phân nghĩa là
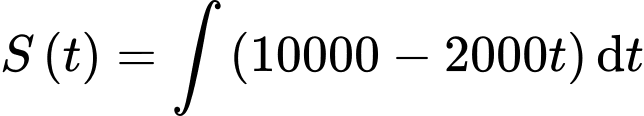
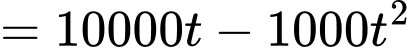 (nghìn đồng)
(nghìn đồng)
c) Đúng.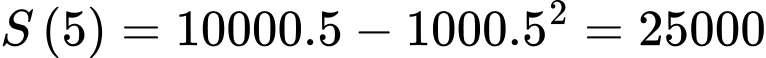 (nghìn đồng)
(nghìn đồng) 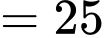 triệu đồng .
triệu đồng .
d) Sai. Do giá gạo luôn lưu động, và là hàm phụ thuộc thời gian.
Nên ta không thể tính giá gạo mỗi tháng nhân số kg mà ta sẽ tính giá gạo trung bình mỗi tháng ta bán được đều đặn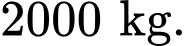
Suy ra, tiền thu về sau bán gạo bằng giá gạo trung bình: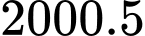
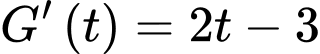 (nghìn đồng/t)
(nghìn đồng/t) 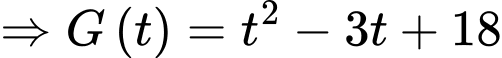 (nghìn đồng)
(nghìn đồng)
Giá gạo trung bình trong 5 tháng được tính bởi công thức:
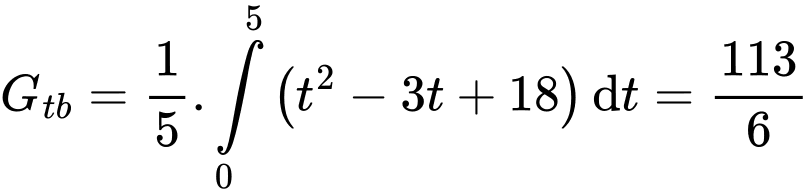 (nghìn đồng)
(nghìn đồng)
Suy ra tiền thu về là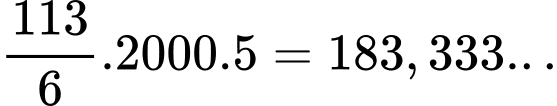 (triệu đồng)
(triệu đồng)
Chi phí lưu kho là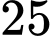 triệu đồng.
triệu đồng.
Suy ra, lợi nhuận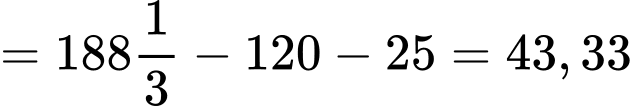 (triệu đồng).
(triệu đồng).
 còn lại sau
còn lại sau 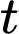 (tháng) là
(tháng) là 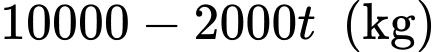
b) Đúng. là tổng chi phí lưu trữ
Chi phí lưu trữ
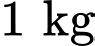 gạo:
gạo: 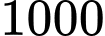 đồng/tháng.
đồng/tháng.Suy ra, chi phí lưu trữ sau
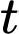 (tháng) là
(tháng) là 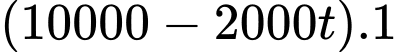 tức là
tức là 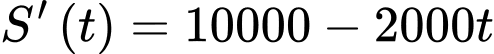 (nghìn đồng/tháng).
(nghìn đồng/tháng).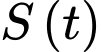 là tổng, ta sẽ tính toán giống bài toán tích phân nghĩa là
là tổng, ta sẽ tính toán giống bài toán tích phân nghĩa là 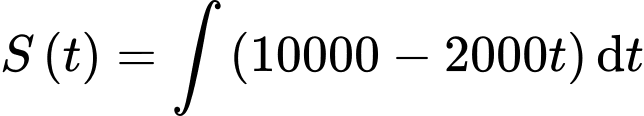
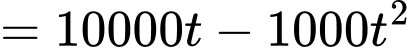 (nghìn đồng)
(nghìn đồng)c) Đúng.
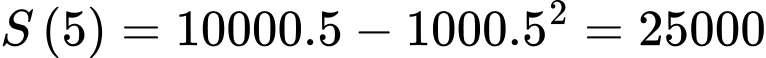 (nghìn đồng)
(nghìn đồng) 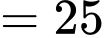 triệu đồng .
triệu đồng .d) Sai. Do giá gạo luôn lưu động, và là hàm phụ thuộc thời gian.
Nên ta không thể tính giá gạo mỗi tháng nhân số kg mà ta sẽ tính giá gạo trung bình mỗi tháng ta bán được đều đặn
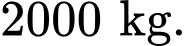
Suy ra, tiền thu về sau bán gạo bằng giá gạo trung bình:
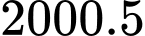
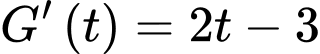 (nghìn đồng/t)
(nghìn đồng/t) 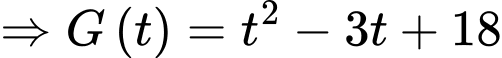 (nghìn đồng)
(nghìn đồng)Giá gạo trung bình trong 5 tháng được tính bởi công thức:
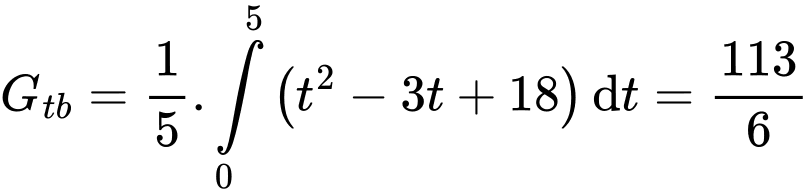 (nghìn đồng)
(nghìn đồng)Suy ra tiền thu về là
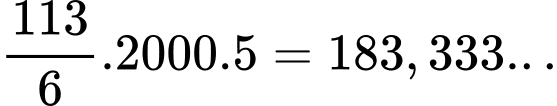 (triệu đồng)
(triệu đồng)Chi phí lưu kho là
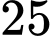 triệu đồng.
triệu đồng.Suy ra, lợi nhuận
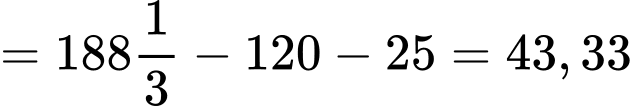 (triệu đồng).
(triệu đồng).
Câu 15 [696351]: Có hai đội thi đấu môn Bóng bàn. Đội 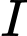 có 6 vận động viên, đội
có 6 vận động viên, đội 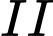 có 8 vận động viên. Xác suất đạt huy chương đồng của mỗi vận động viên đội
có 8 vận động viên. Xác suất đạt huy chương đồng của mỗi vận động viên đội 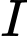 và đội
và đội 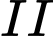 tương ứng là
tương ứng là 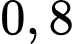 và
và 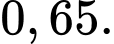 Chọn ngẫu nhiên một vận động viên.
Chọn ngẫu nhiên một vận động viên.
Gọi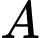 là biến cố: “Vận động viên được chọn thuộc đội I”.
là biến cố: “Vận động viên được chọn thuộc đội I”.
Gọi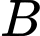 là biến cố: “Vận động viên được chọn đạt huy chương đồng”.
là biến cố: “Vận động viên được chọn đạt huy chương đồng”.
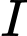 có 6 vận động viên, đội
có 6 vận động viên, đội 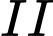 có 8 vận động viên. Xác suất đạt huy chương đồng của mỗi vận động viên đội
có 8 vận động viên. Xác suất đạt huy chương đồng của mỗi vận động viên đội 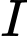 và đội
và đội 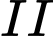 tương ứng là
tương ứng là 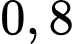 và
và 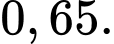 Chọn ngẫu nhiên một vận động viên.
Chọn ngẫu nhiên một vận động viên.Gọi
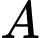 là biến cố: “Vận động viên được chọn thuộc đội I”.
là biến cố: “Vận động viên được chọn thuộc đội I”. Gọi
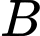 là biến cố: “Vận động viên được chọn đạt huy chương đồng”.
là biến cố: “Vận động viên được chọn đạt huy chương đồng”.
a) Sai.
Ta có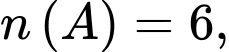
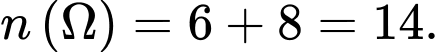
Do đó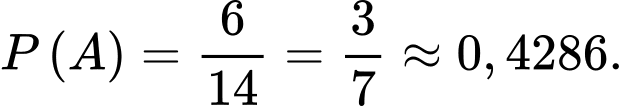
b) Đúng.
YCBT Tính
Tính 
Ta có là biến cố “Vận động viên được chọn thuộc đội II”.
là biến cố “Vận động viên được chọn thuộc đội II”.
Suy ra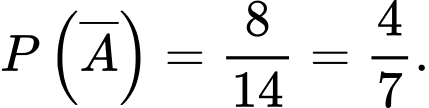
Lại có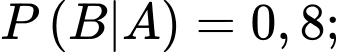
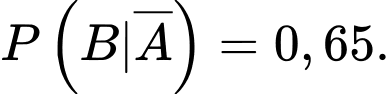
c) Đúng.
Ta có sơ đồ cây sau:
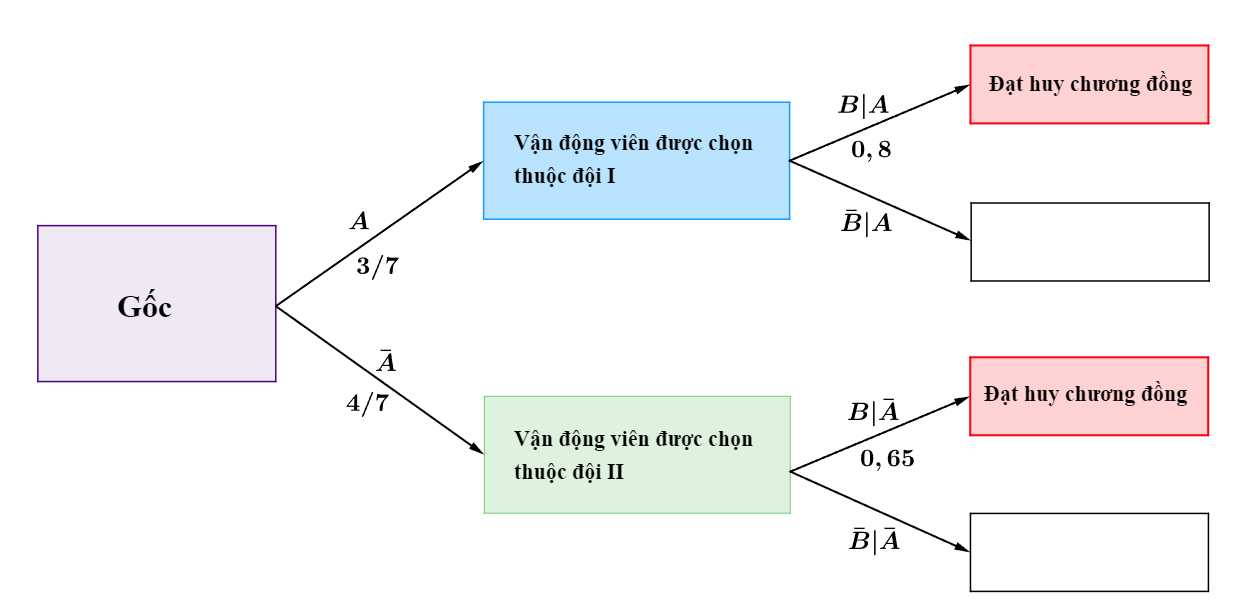
Áp dụng công thức xác suất toàn phần, xác suất để vận động viên được chọn đạt huy chương đồng là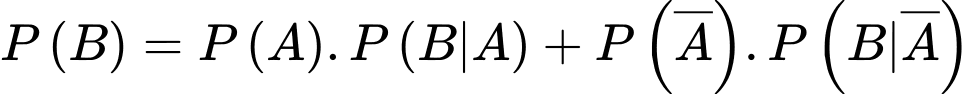
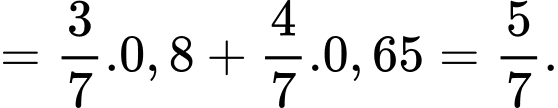
d) Sai.
YCBT Tính
Tính 
Áp dụng công thức Bayes, ta có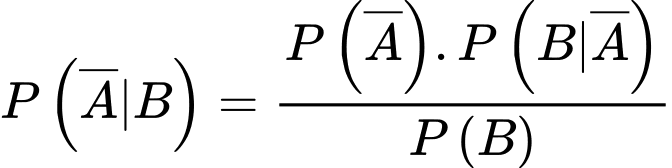
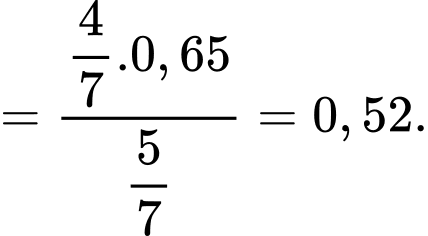
Ta có
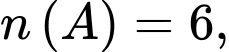
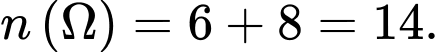
Do đó
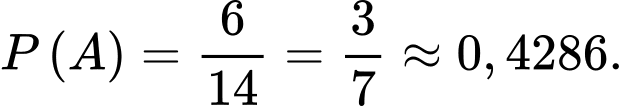
b) Đúng.
YCBT
 Tính
Tính 
Ta có
 là biến cố “Vận động viên được chọn thuộc đội II”.
là biến cố “Vận động viên được chọn thuộc đội II”.
Suy ra
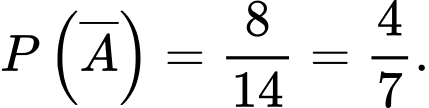
Lại có
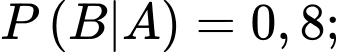
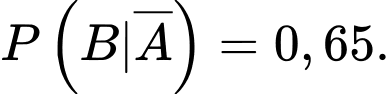
c) Đúng.
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, xác suất để vận động viên được chọn đạt huy chương đồng là
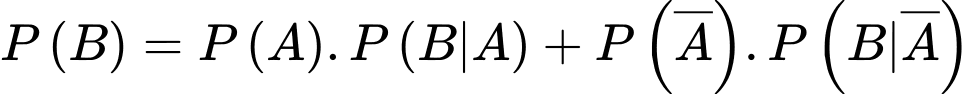
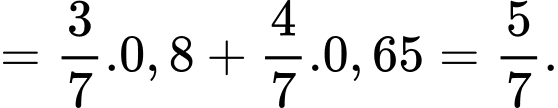
d) Sai.
YCBT
 Tính
Tính 
Áp dụng công thức Bayes, ta có
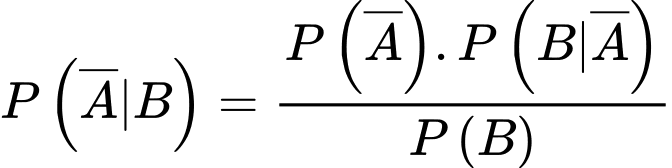
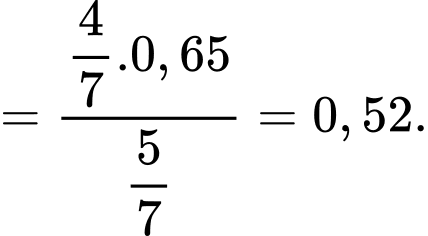
Câu 16 [696352]: Có một chiếc lồng bằng sắt dạng hình hộp chữ nhật  có
có 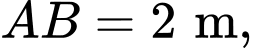
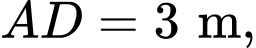
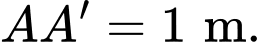 Người thợ hàn muốn hàn một thanh sắt
Người thợ hàn muốn hàn một thanh sắt 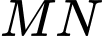 nối hai đoạn
nối hai đoạn 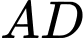 và
và 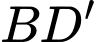 (minhh hoạ như hình vẽ). Chọn hệ trục toạ độ như hình vẽ, với gốc toạ độ
(minhh hoạ như hình vẽ). Chọn hệ trục toạ độ như hình vẽ, với gốc toạ độ  trùng với điểm
trùng với điểm 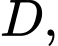 điểm
điểm 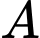 thuộc tia
thuộc tia  điểm
điểm  thuộc tia
thuộc tia 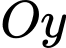 và điểm
và điểm 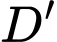 thuộc tia
thuộc tia  (đơn vị mỗi trục là mét).
(đơn vị mỗi trục là mét).
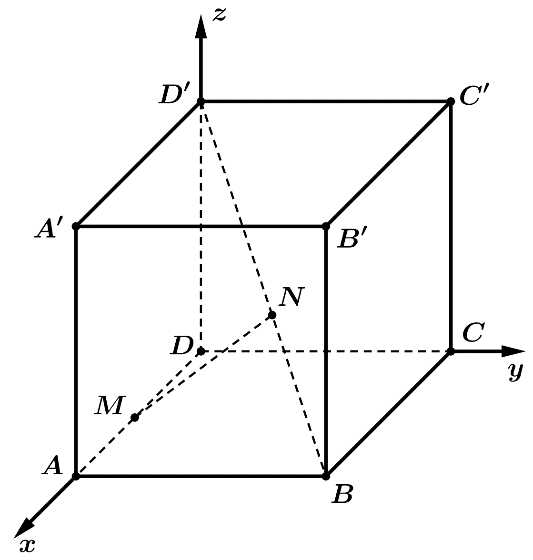
 có
có 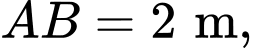
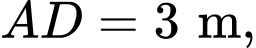
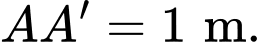 Người thợ hàn muốn hàn một thanh sắt
Người thợ hàn muốn hàn một thanh sắt 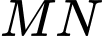 nối hai đoạn
nối hai đoạn 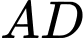 và
và 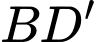 (minhh hoạ như hình vẽ). Chọn hệ trục toạ độ như hình vẽ, với gốc toạ độ
(minhh hoạ như hình vẽ). Chọn hệ trục toạ độ như hình vẽ, với gốc toạ độ  trùng với điểm
trùng với điểm 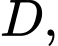 điểm
điểm 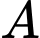 thuộc tia
thuộc tia  điểm
điểm  thuộc tia
thuộc tia 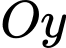 và điểm
và điểm 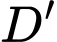 thuộc tia
thuộc tia  (đơn vị mỗi trục là mét).
(đơn vị mỗi trục là mét). 
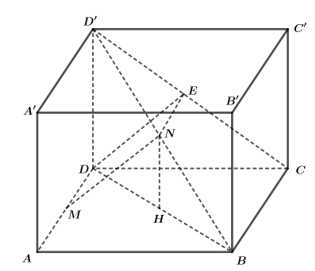
a) Đúng.
Ta có:
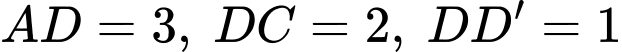
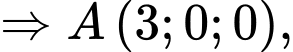
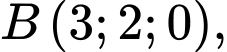
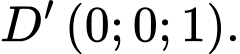
b) Sai.
Ta có:
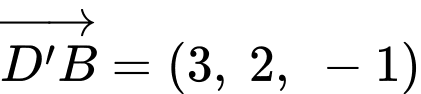
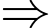 Phương trình đường thẳng
Phương trình đường thẳng 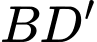 là
là 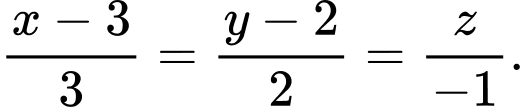
c) Đúng.
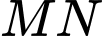 ngắn nhất
ngắn nhất 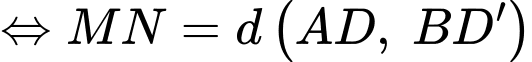
Có
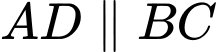
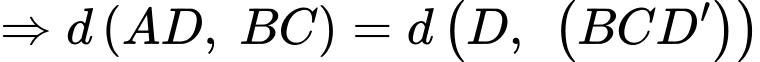
Kẻ

Có:
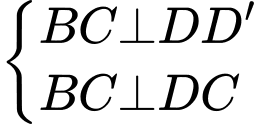
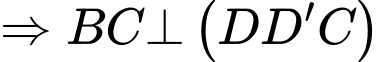

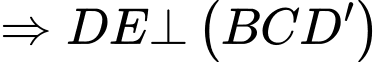

Xét
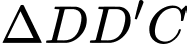 vuông tại
vuông tại 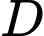 có:
có: 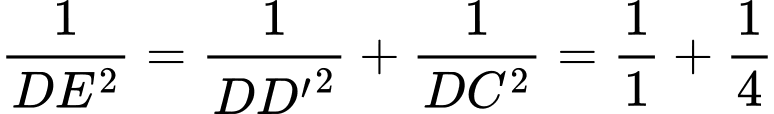
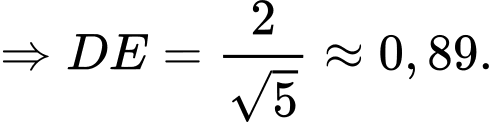
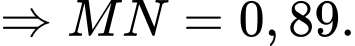
d) Sai.
Kẻ
 .Lấy điểm
.Lấy điểm 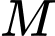 trên
trên 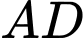 sao cho
sao cho 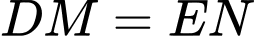 .
.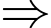 Tứ giác
Tứ giác 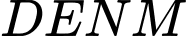 là hình bình hành
là hình bình hành 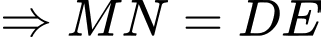
Kẻ
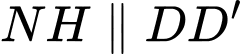 cắt
cắt 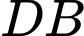 tại
tại 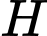 .
.Do

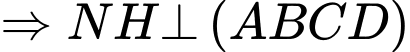
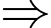 Cao độ của điểm
Cao độ của điểm 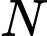 là
là 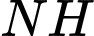 .
.Ta có:
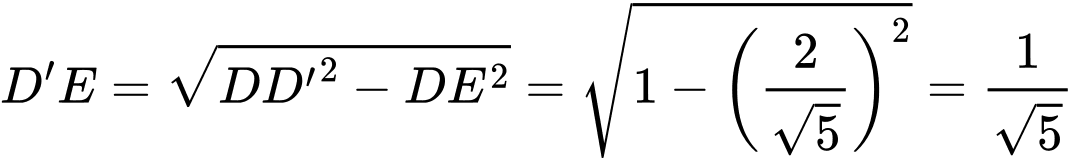
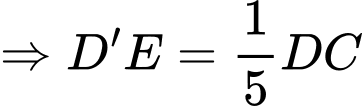 .
.Xét
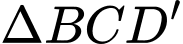 có:
có: 
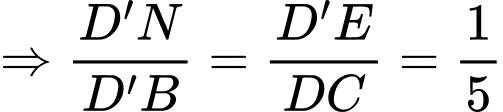
Xét
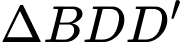 có:
có: 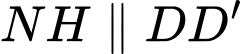
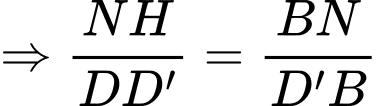
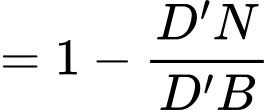
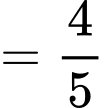
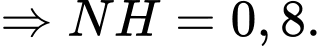
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696353]: Cho hình chóp 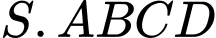 có đáy
có đáy 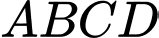 là hình thoi cạnh
là hình thoi cạnh 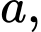
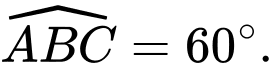 Gọi
Gọi  là giao điểm của
là giao điểm của 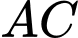 và
và 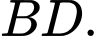 Biết rằng
Biết rằng 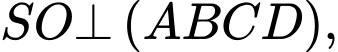
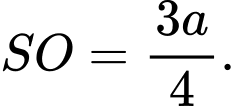 Khoảng cách từ
Khoảng cách từ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 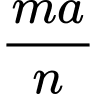 với
với 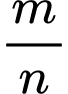 là phân số tối giản,
là phân số tối giản, 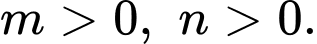 Giá trị của
Giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
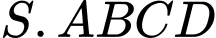 có đáy
có đáy 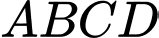 là hình thoi cạnh
là hình thoi cạnh 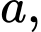
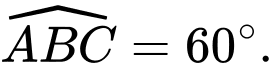 Gọi
Gọi  là giao điểm của
là giao điểm của 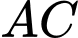 và
và 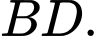 Biết rằng
Biết rằng 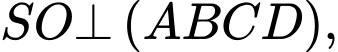
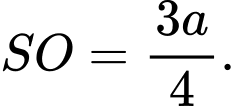 Khoảng cách từ
Khoảng cách từ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 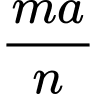 với
với 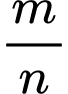 là phân số tối giản,
là phân số tối giản, 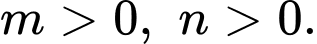 Giá trị của
Giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 11
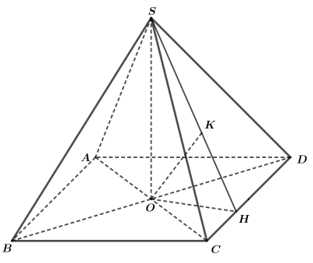
Kẻ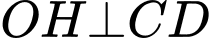 , mà
, mà 
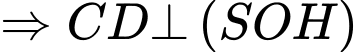
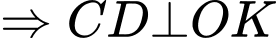
Kẻ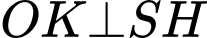
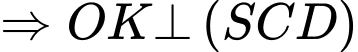
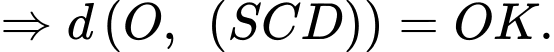
Ta có: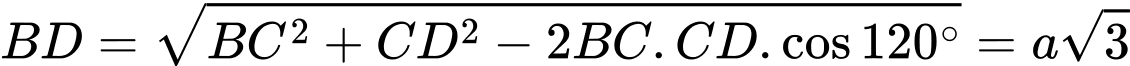
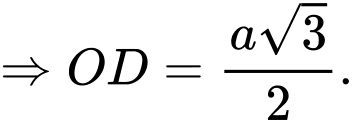
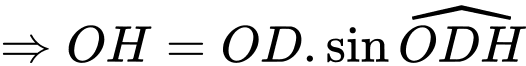
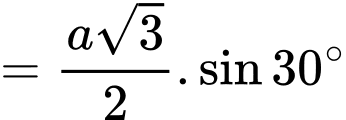
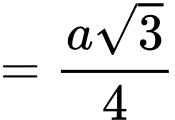
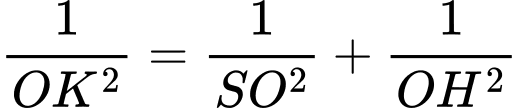
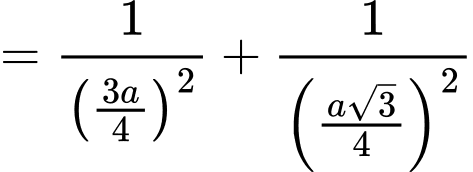
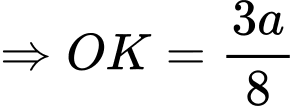
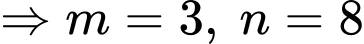
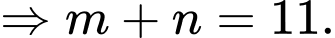

Kẻ
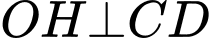 , mà
, mà 
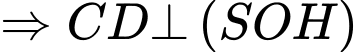
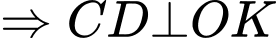
Kẻ
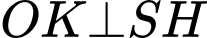
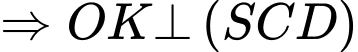
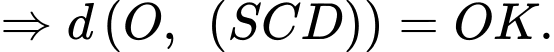
Ta có:
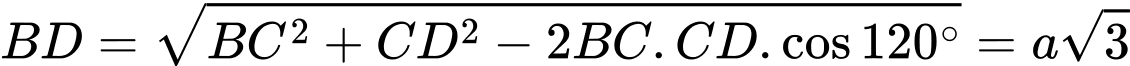
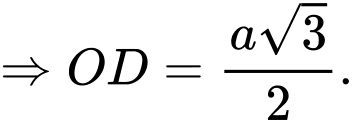
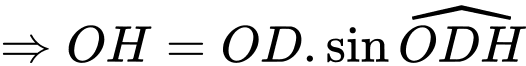
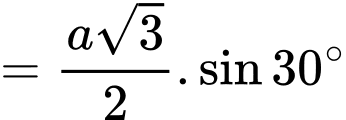
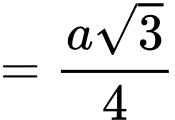
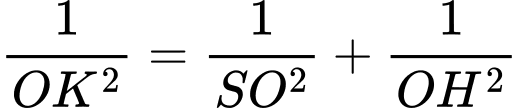
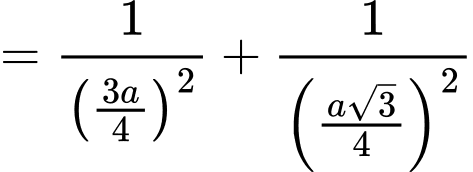
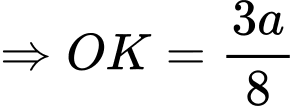
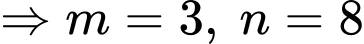
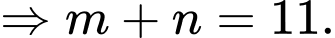
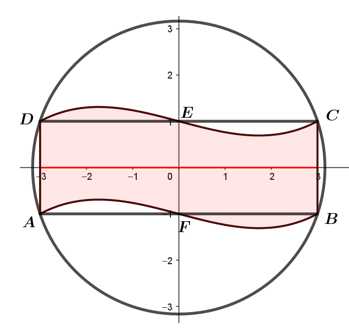
Câu 18 [694840]: Anh Kiên đổ bê tông một đường đi sân vườn hình tròn bán kính 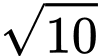 m (phần được tô đậm) trong hình bên dưới.
m (phần được tô đậm) trong hình bên dưới.
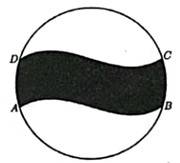
Biết rằng đường cong là một phần đồ thị của một hàm số liên tục, đường cong
là một phần đồ thị của một hàm số liên tục, đường cong 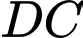 nhận được bằng cách tịnh tiến đường cong
nhận được bằng cách tịnh tiến đường cong  theo phương thẳng đứng, lên phía trên 2 m. Ngoài ra con đường được đổ lớp bê tông dày 15 cm và giá tiền
theo phương thẳng đứng, lên phía trên 2 m. Ngoài ra con đường được đổ lớp bê tông dày 15 cm và giá tiền 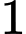
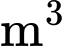 bê tông là 1 200 000 đồng. Số tiền anh Kiên cần dùng để đổ bê tông con đường đó bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
bê tông là 1 200 000 đồng. Số tiền anh Kiên cần dùng để đổ bê tông con đường đó bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
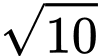 m (phần được tô đậm) trong hình bên dưới.
m (phần được tô đậm) trong hình bên dưới. 
Biết rằng đường cong
 là một phần đồ thị của một hàm số liên tục, đường cong
là một phần đồ thị của một hàm số liên tục, đường cong  nhận được bằng cách tịnh tiến đường cong
nhận được bằng cách tịnh tiến đường cong  theo phương thẳng đứng, lên phía trên 2 m. Ngoài ra con đường được đổ lớp bê tông dày 15 cm và giá tiền
theo phương thẳng đứng, lên phía trên 2 m. Ngoài ra con đường được đổ lớp bê tông dày 15 cm và giá tiền 
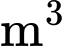 bê tông là 1 200 000 đồng. Số tiền anh Kiên cần dùng để đổ bê tông con đường đó bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
bê tông là 1 200 000 đồng. Số tiền anh Kiên cần dùng để đổ bê tông con đường đó bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 2,2.
Đường tròn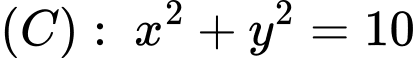 .
.
Ta có: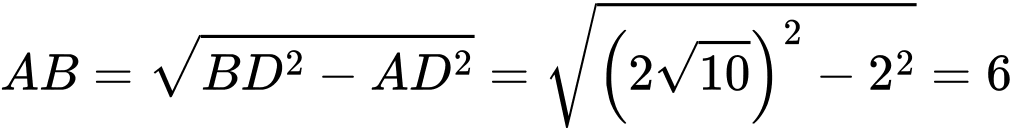
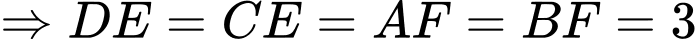 .
.
Dựa theo hình vẽ ta thấy diện tích giới hạn bởi đường cong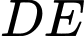 và đoạn thẳng
và đoạn thẳng 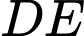 bằng diện tích giới hạn bởi đường cong
bằng diện tích giới hạn bởi đường cong 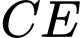 và đoạn thẳng
và đoạn thẳng 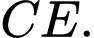
Tương tự diện tích giới hạn bởi đường cong và đoạn thẳng
và đoạn thẳng  bằng diện tích giới hạn bởi đường cong
bằng diện tích giới hạn bởi đường cong 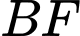 và đoạn thẳng
và đoạn thẳng 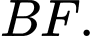
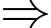 Diện tích đường đi bằng diện tích hình chữ nhật
Diện tích đường đi bằng diện tích hình chữ nhật 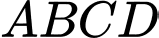 cộng với 2 lần diện tích giới hạn bởi đường tròn
cộng với 2 lần diện tích giới hạn bởi đường tròn  , đường thẳng
, đường thẳng 
Diện tích giới hạn bởi đường tròn , đường thẳng
, đường thẳng 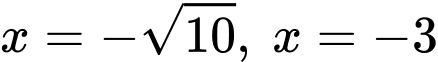 là
là
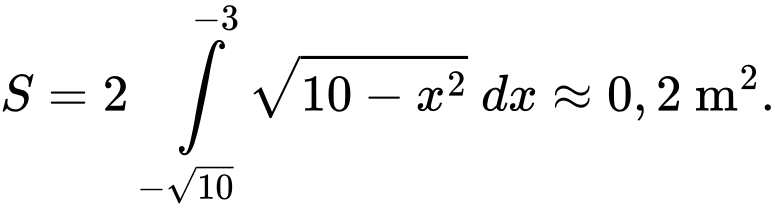
Số tiền anh Kiên cần dùng để đổ bê tông con đường đó là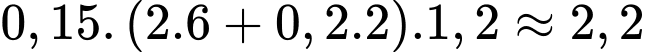 (triệu đồng).
(triệu đồng).

Đường tròn
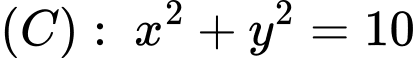 .
.
Ta có:
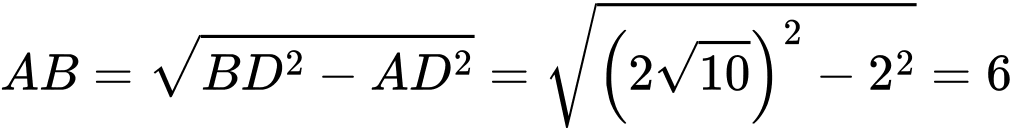
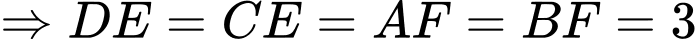 .
.
Dựa theo hình vẽ ta thấy diện tích giới hạn bởi đường cong
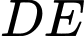 và đoạn thẳng
và đoạn thẳng 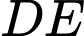 bằng diện tích giới hạn bởi đường cong
bằng diện tích giới hạn bởi đường cong 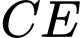 và đoạn thẳng
và đoạn thẳng 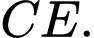
Tương tự diện tích giới hạn bởi đường cong
 và đoạn thẳng
và đoạn thẳng  bằng diện tích giới hạn bởi đường cong
bằng diện tích giới hạn bởi đường cong 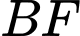 và đoạn thẳng
và đoạn thẳng 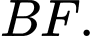
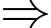 Diện tích đường đi bằng diện tích hình chữ nhật
Diện tích đường đi bằng diện tích hình chữ nhật 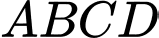 cộng với 2 lần diện tích giới hạn bởi đường tròn
cộng với 2 lần diện tích giới hạn bởi đường tròn  , đường thẳng
, đường thẳng 
Diện tích giới hạn bởi đường tròn
 , đường thẳng
, đường thẳng 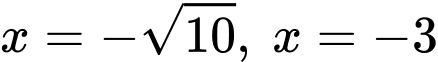 là
là
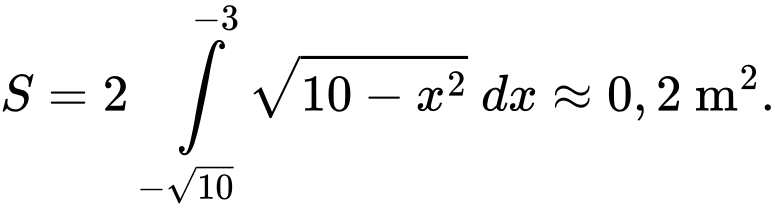
Số tiền anh Kiên cần dùng để đổ bê tông con đường đó là
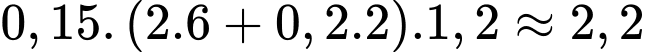 (triệu đồng).
(triệu đồng).
Câu 19 [696354]: Một xưởng có máy cắt và máy tiện dùng để sản xuất trục sắt và đinh ốc. Sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ với tiền lãi là 2 triệu. Sản xuất 1 tấn đinh ốc thì máy cắt chạy trong 1 giờ và máy tiện chạy trong 1 giờ với tiền lãi là 1 triệu. Một máy không thể sản xuất cả 2 loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Số tiền lãi nhiều nhất của xưởng trong một ngày là bao nhiêu triệu đồng?
Điền đáp án: 
Gọi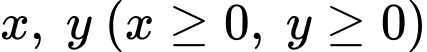 là số tấn trục sắt và đỉnh ốc sản xuất trong ngày.
là số tấn trục sắt và đỉnh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày: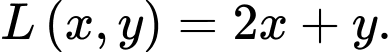
Số giờ làm việc mỗi ngày của máy cắt: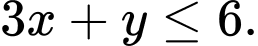
Số giờ làm việc mỗi ngày của máy tiện: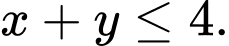
Ta có bài toán tìm giá trị lớn nhất của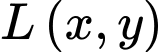 biết
biết 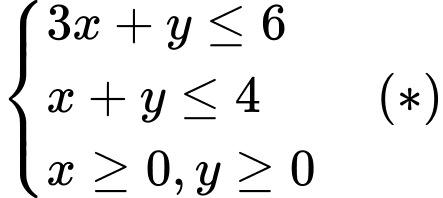
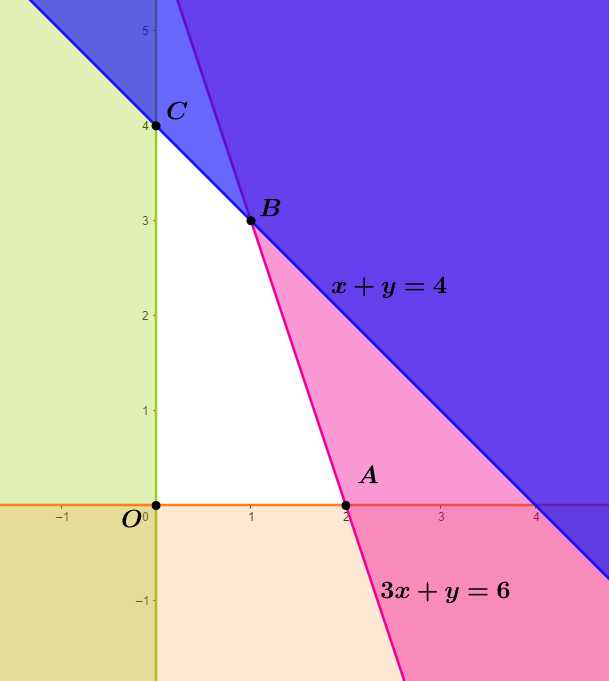
Miền nghiệm của hệ là tứ giác
là tứ giác 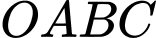 như hình vẽ với
như hình vẽ với 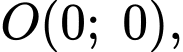
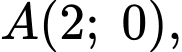
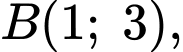
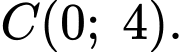
Ta có: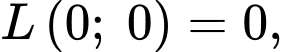
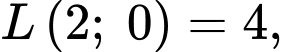
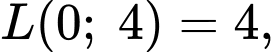
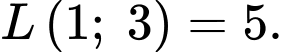
Vậy mỗi ngày sản xuất 1 tấn trục sắt và 3 tấn đỉnh ốc thì thu được tiền lãi cao nhất là 5 triệu đồng.
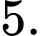
Gọi
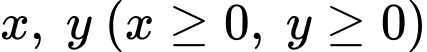 là số tấn trục sắt và đỉnh ốc sản xuất trong ngày.
là số tấn trục sắt và đỉnh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày:
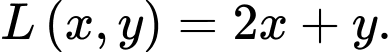
Số giờ làm việc mỗi ngày của máy cắt:
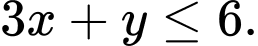
Số giờ làm việc mỗi ngày của máy tiện:
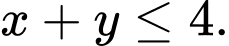
Ta có bài toán tìm giá trị lớn nhất của
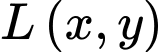 biết
biết 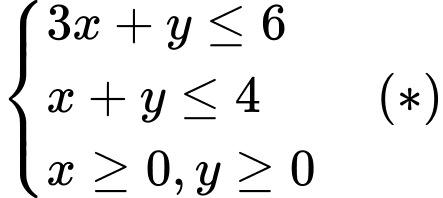

Miền nghiệm của hệ
 là tứ giác
là tứ giác 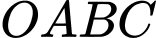 như hình vẽ với
như hình vẽ với 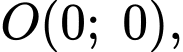
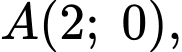
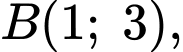
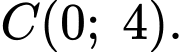
Ta có:
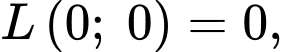
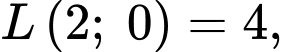
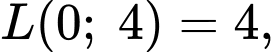
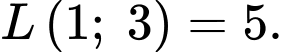
Vậy mỗi ngày sản xuất 1 tấn trục sắt và 3 tấn đỉnh ốc thì thu được tiền lãi cao nhất là 5 triệu đồng.
Câu 20 [687495]: Có hai hộp bi, hộp I có 5 viên bi trắng và 7 viên bi đỏ, hộp II có 10 viên bi trắng và 15 viên bi đỏ. Lấy ngẫu nhiên hai viên bi từ hộp I chuyển sang hộp II. Sau đó, từ hộp II lấy ngẫu nhiên một viên bi thì được bi trắng. Xác suất để hai viên bi chuyển từ hộp I sang hộp II không cùng màu là 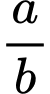 (
(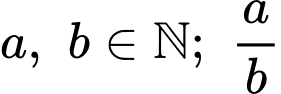 là phân số tối giản). Tính
là phân số tối giản). Tính 
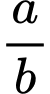 (
(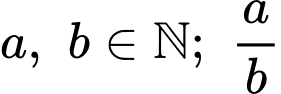 là phân số tối giản). Tính
là phân số tối giản). Tính 
Điền đáp án: 20.
Gọi là biến cố “2 bi lấy từ I không cùng màu”
là biến cố “Lấy từ hộp II được một bi trắng”
YCBT Tính
Tính 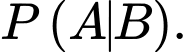
Ta có: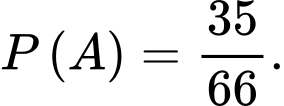
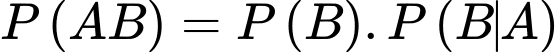
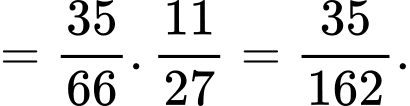
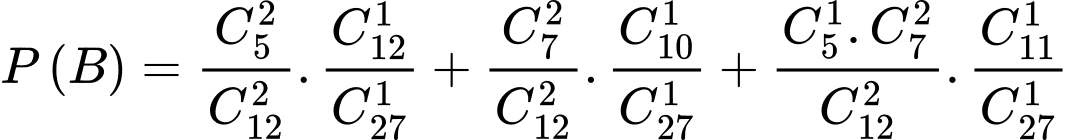
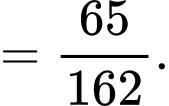
Suy ra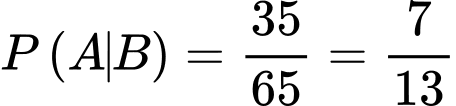
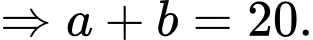
Gọi là biến cố “2 bi lấy từ I không cùng màu”
là biến cố “Lấy từ hộp II được một bi trắng”
YCBT
 Tính
Tính 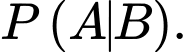
Ta có:
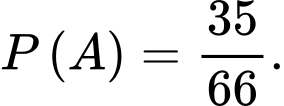
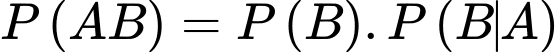
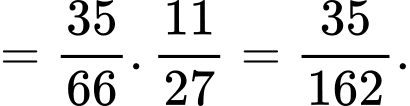
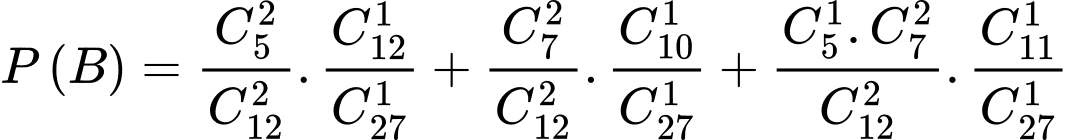
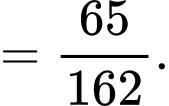
Suy ra
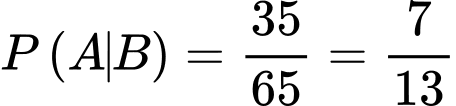
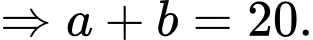
Câu 21 [696356]: Trong không gian 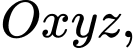 cho hình chóp
cho hình chóp 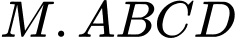 có đỉnh
có đỉnh 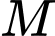 thay đổi luôn nằm trên mặt cầu
thay đổi luôn nằm trên mặt cầu 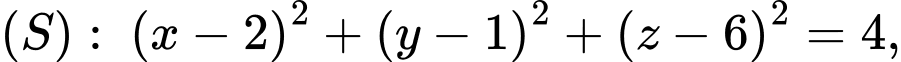 đáy
đáy 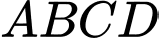 là hình vuông có tâm
là hình vuông có tâm 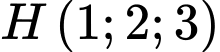 và điểm
và điểm 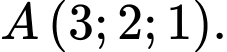 Khi đó thể tích lớn nhất của khối chóp
Khi đó thể tích lớn nhất của khối chóp 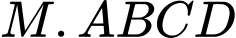 bằng bao nhiêu? (Làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (Làm tròn kết quả đến hàng phần mười).
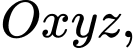 cho hình chóp
cho hình chóp 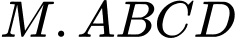 có đỉnh
có đỉnh 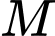 thay đổi luôn nằm trên mặt cầu
thay đổi luôn nằm trên mặt cầu 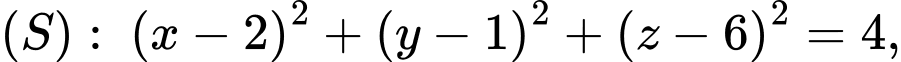 đáy
đáy 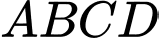 là hình vuông có tâm
là hình vuông có tâm 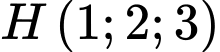 và điểm
và điểm 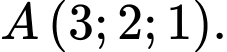 Khi đó thể tích lớn nhất của khối chóp
Khi đó thể tích lớn nhất của khối chóp 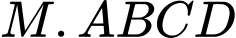 bằng bao nhiêu? (Làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (Làm tròn kết quả đến hàng phần mười).
Điền đáp án: 26,7
Hình chóp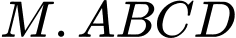 có đỉnh
có đỉnh 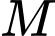 thay đổi luôn năm trên mặt cầu
thay đổi luôn năm trên mặt cầu 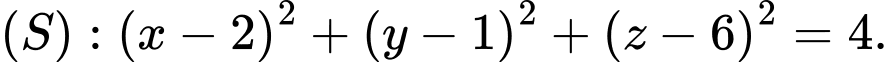
Đáy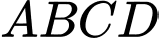 là hình vuông có tâm
là hình vuông có tâm 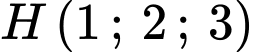 và điểm
và điểm 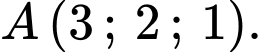
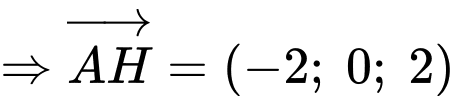
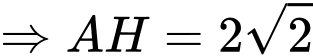
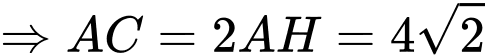
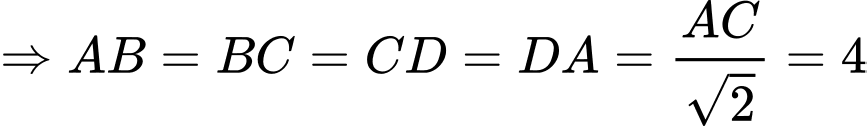
Diện tích hình vuông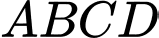 là
là 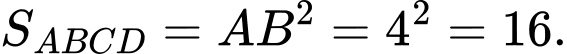
Ta có: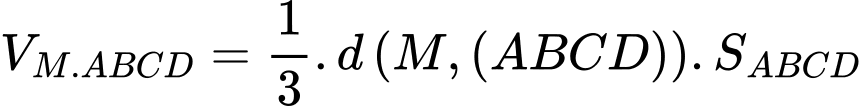
Suy ra, để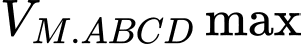 thì
thì 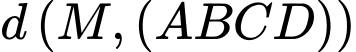 phải đạt giá trị lớn nhất.
phải đạt giá trị lớn nhất.
Suy ra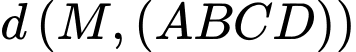 phải đi qua
phải đi qua 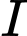 và có hình chiếu
và có hình chiếu 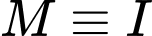 tại
tại 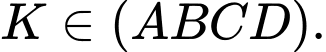
Giả sử, hình chiếu của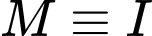 nằm trên
nằm trên 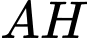 hay
hay 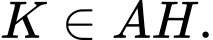
Phương trình đường thẳng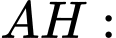
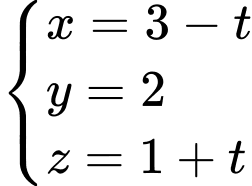
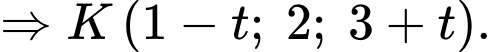
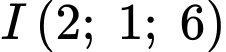
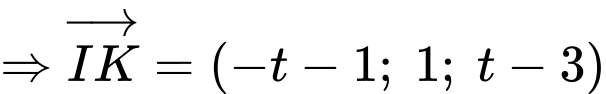
Ta có: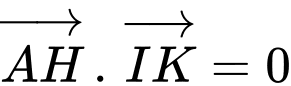
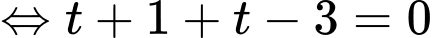
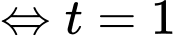
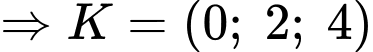
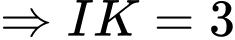
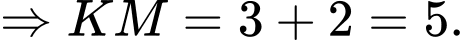
Vậy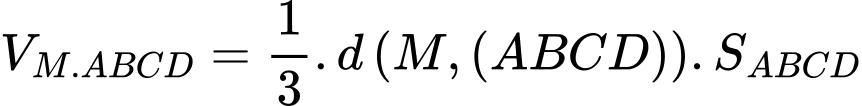
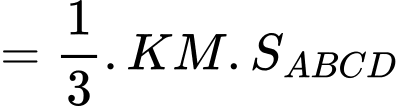
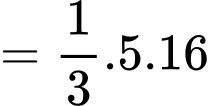
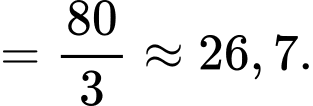
Hình chóp
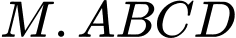 có đỉnh
có đỉnh 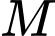 thay đổi luôn năm trên mặt cầu
thay đổi luôn năm trên mặt cầu 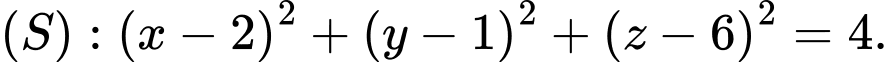
Đáy
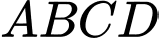 là hình vuông có tâm
là hình vuông có tâm 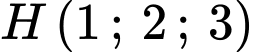 và điểm
và điểm 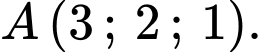
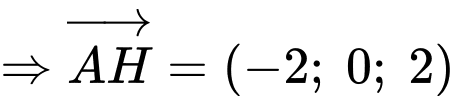
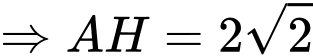
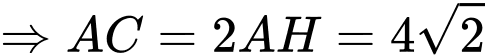
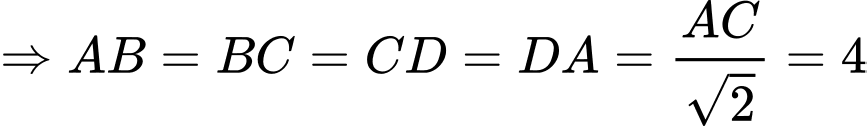
Diện tích hình vuông
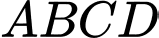 là
là 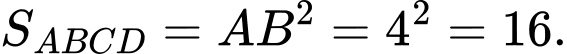
Ta có:
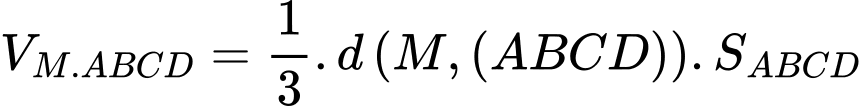
Suy ra, để
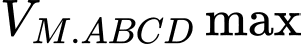 thì
thì 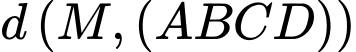 phải đạt giá trị lớn nhất.
phải đạt giá trị lớn nhất. Suy ra
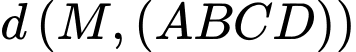 phải đi qua
phải đi qua 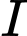 và có hình chiếu
và có hình chiếu 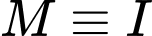 tại
tại 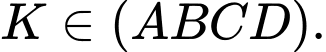
Giả sử, hình chiếu của
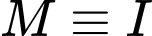 nằm trên
nằm trên 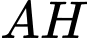 hay
hay 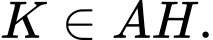
Phương trình đường thẳng
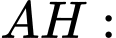
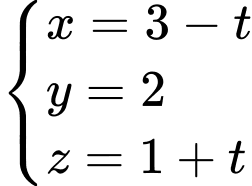
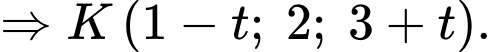
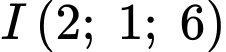
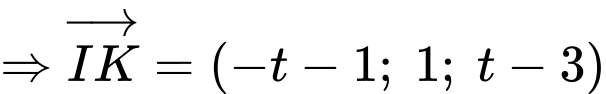
Ta có:
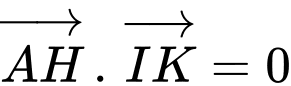
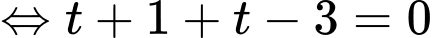
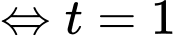
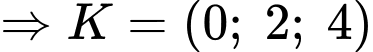
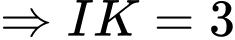
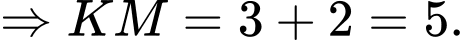
Vậy
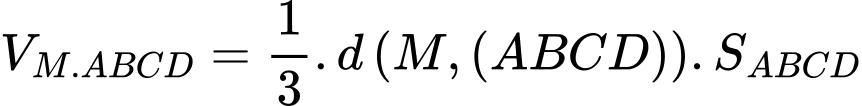
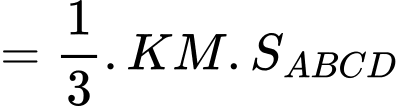
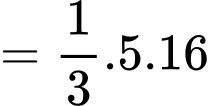
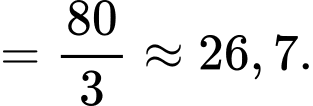
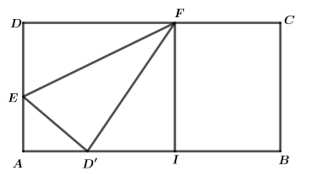
Câu 22 [696357]: Trong một trò chơi gấp giấy. Người ta muốn từ một tờ giấy hình chữ nhật 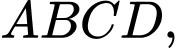 gấp theo đường thẳng
gấp theo đường thẳng 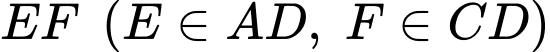 sao cho
sao cho 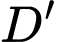 rơi vào mép cạnh
rơi vào mép cạnh  (như hình vẽ).
(như hình vẽ).
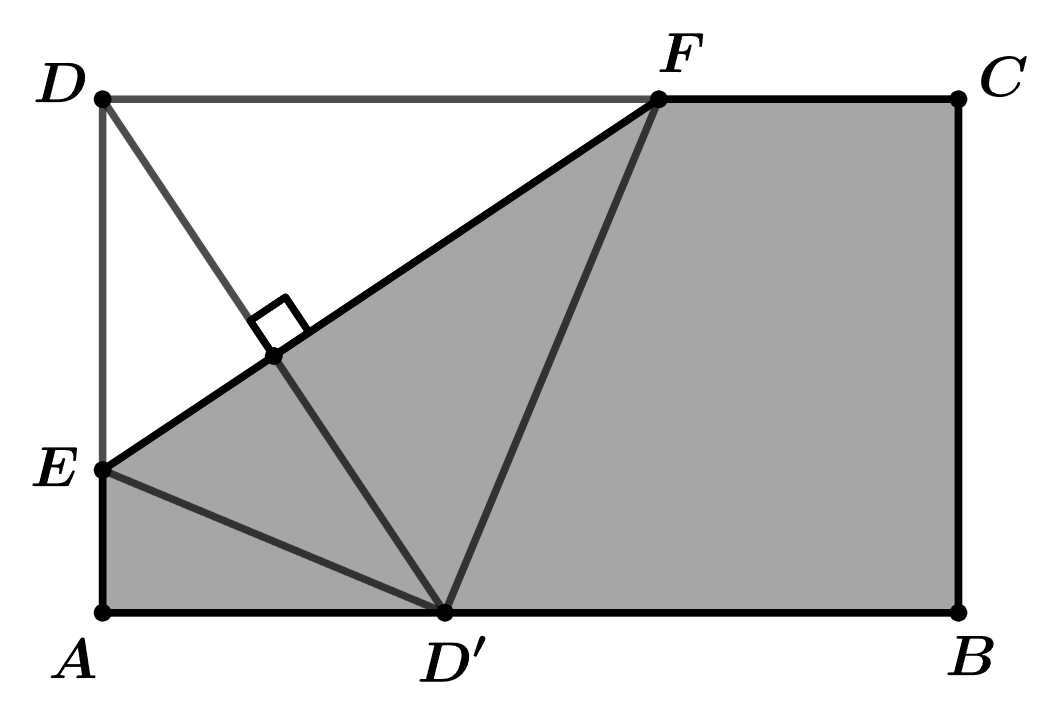
Biết chiều rộng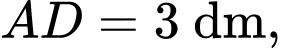 diện tích nhỏ nhất có thể của phần gấp là bao nhiêu
diện tích nhỏ nhất có thể của phần gấp là bao nhiêu  ? (làm tròn đến hàng phần trăm).
? (làm tròn đến hàng phần trăm).
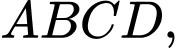 gấp theo đường thẳng
gấp theo đường thẳng 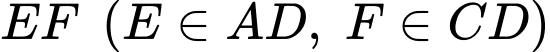 sao cho
sao cho 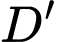 rơi vào mép cạnh
rơi vào mép cạnh  (như hình vẽ).
(như hình vẽ).
Biết chiều rộng
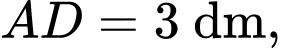 diện tích nhỏ nhất có thể của phần gấp là bao nhiêu
diện tích nhỏ nhất có thể của phần gấp là bao nhiêu  ? (làm tròn đến hàng phần trăm).
? (làm tròn đến hàng phần trăm).
Điền đáp án: 3,46.
Đặt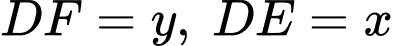
Có: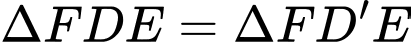
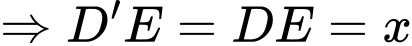
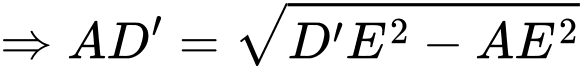
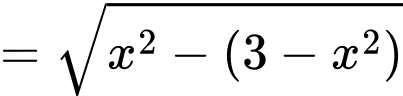
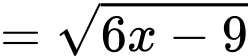
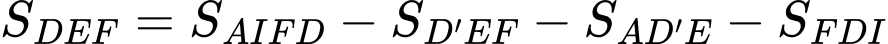
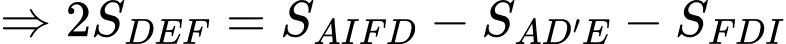
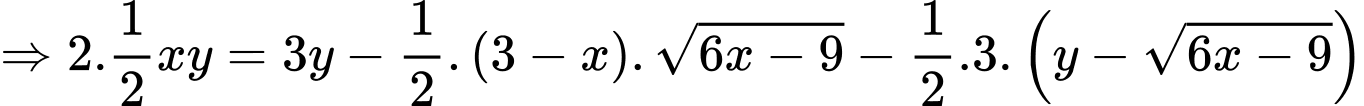
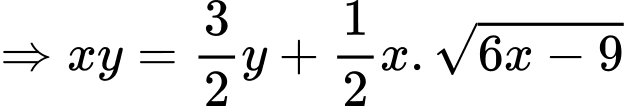
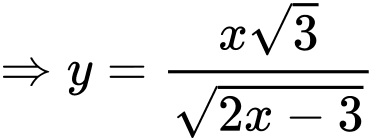
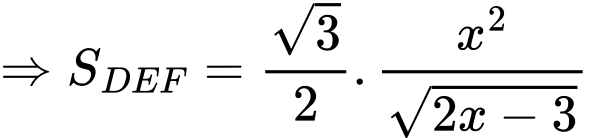
Xét hàm số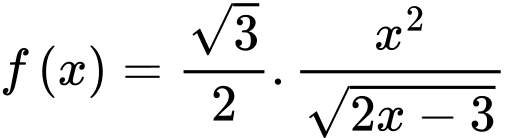
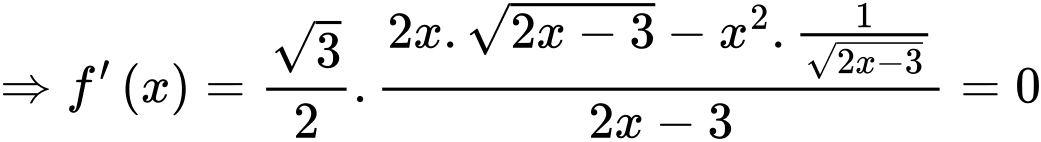
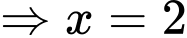 là điểm cực tiểu của đồ thị hàm số
là điểm cực tiểu của đồ thị hàm số 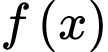 .
.
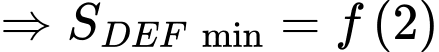
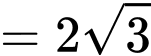
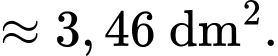

Đặt
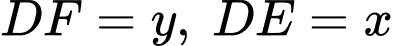
Có:
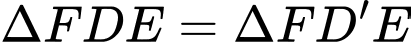
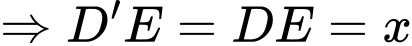
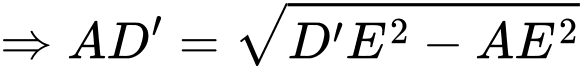
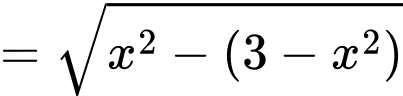
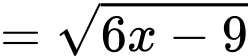
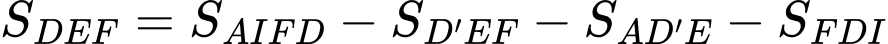
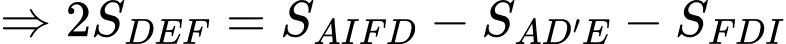
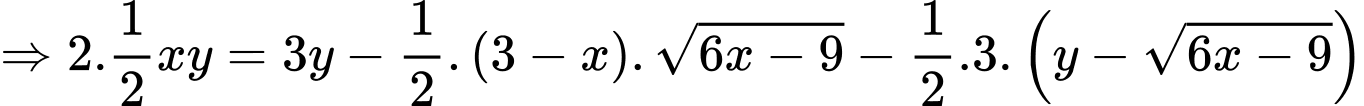
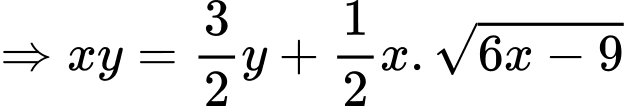
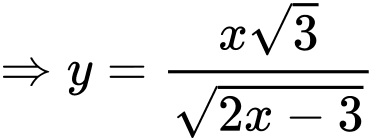
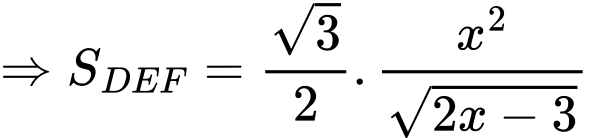
Xét hàm số
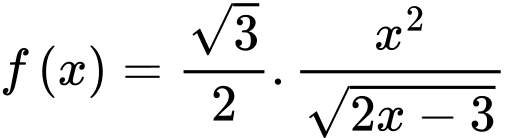
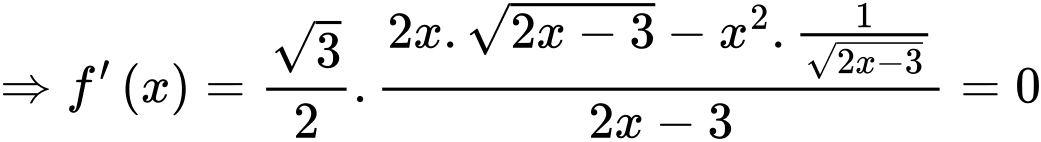
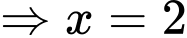 là điểm cực tiểu của đồ thị hàm số
là điểm cực tiểu của đồ thị hàm số 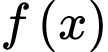 .
.