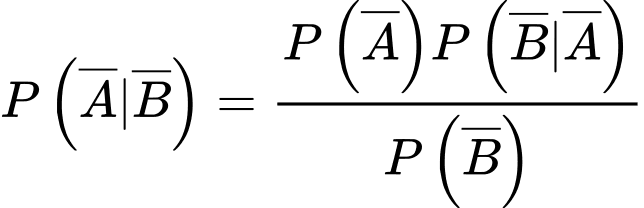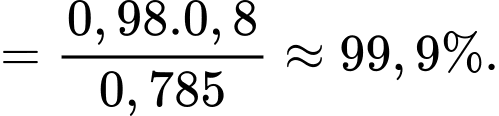PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [696397]: Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 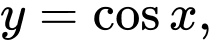 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 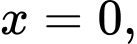
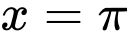 là
là
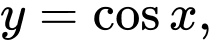 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 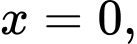
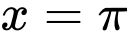 là
là A, 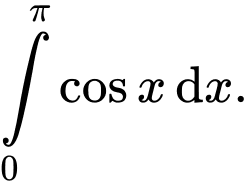
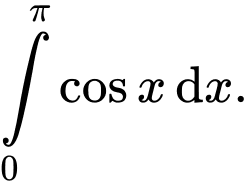
B, 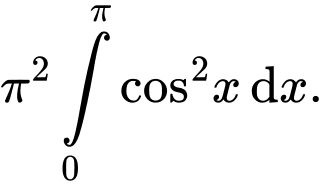
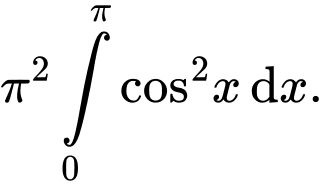
C, 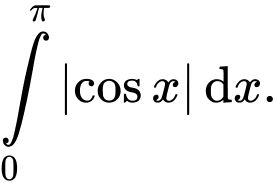
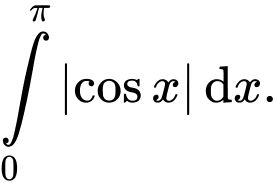
D, 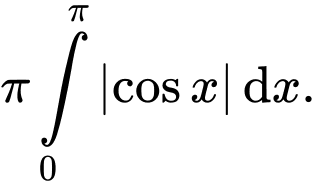
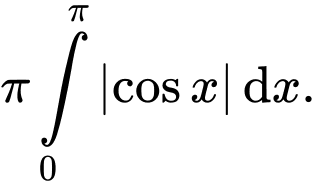
Chọn đáp án C.
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số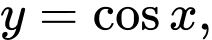 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 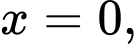
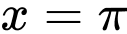 là
là 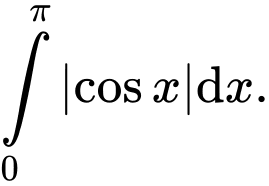 Đáp án: C
Đáp án: C
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
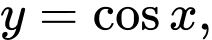 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 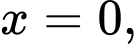
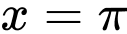 là
là 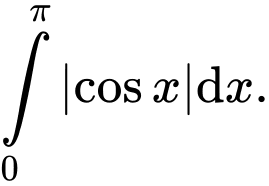 Đáp án: C
Đáp án: C
Câu 2 [696395]: Cho cấp số cộng 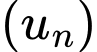 với
với 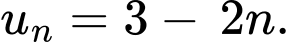 Công sai của
Công sai của 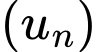 bằng
bằng
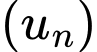 với
với 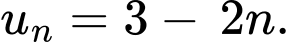 Công sai của
Công sai của 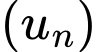 bằng
bằng A, 

B, 

C, 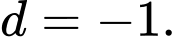
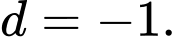
D, 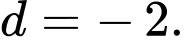
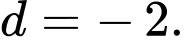
Chọn đáp án D.
Ta có: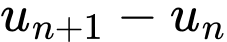
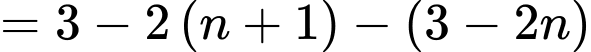
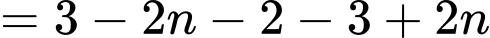
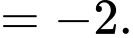
Vậy công sai của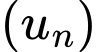 bằng
bằng 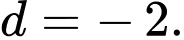 Đáp án: D
Đáp án: D
Ta có:
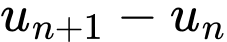
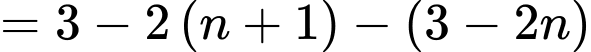
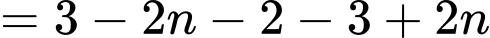
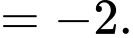
Vậy công sai của
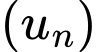 bằng
bằng 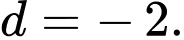 Đáp án: D
Đáp án: D
Câu 3 [801231]: Nghiệm của phương trình 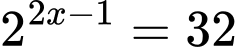 là
là
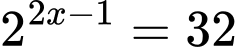 là
là A, 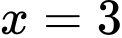 .
.
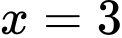 .
.B, 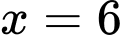 .
.
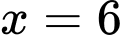 .
.C, 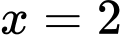 .
.
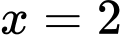 .
.D,  .
.
 .
.
Chọn đáp án A.
Ta có: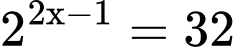


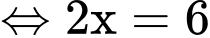
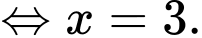 Đáp án: A
Đáp án: A
Ta có:
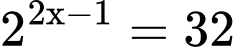


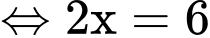
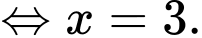 Đáp án: A
Đáp án: A
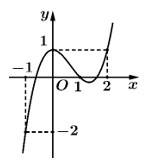
Câu 4 [696394]: Cho hàm số 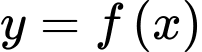 có đồ thị là đường cong trong hình bên dưới.
có đồ thị là đường cong trong hình bên dưới.
Giá trị nhỏ nhất của hàm số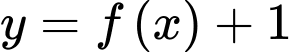 trên
trên 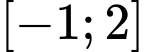 bằng
bằng
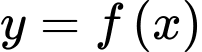 có đồ thị là đường cong trong hình bên dưới.
có đồ thị là đường cong trong hình bên dưới. 
Giá trị nhỏ nhất của hàm số
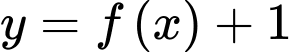 trên
trên 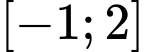 bằng
bằng A, 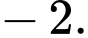
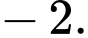
B, 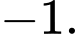
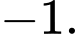
C, 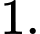
D, 
Chọn đáp án B.
Dựa vào đồ thị hàm số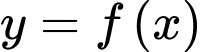 ta có: Giá trị nhỏ nhất của hàm số
ta có: Giá trị nhỏ nhất của hàm số 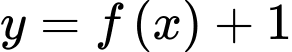 trên
trên 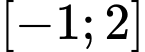 bằng
bằng 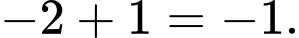 Đáp án: B
Đáp án: B
Dựa vào đồ thị hàm số
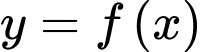 ta có: Giá trị nhỏ nhất của hàm số
ta có: Giá trị nhỏ nhất của hàm số 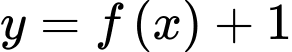 trên
trên 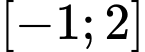 bằng
bằng 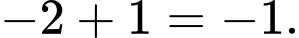 Đáp án: B
Đáp án: B
Câu 5 [256946]: Trong không gian 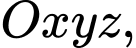 cho mặt phẳng
cho mặt phẳng 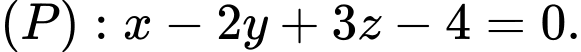 Đường thẳng
Đường thẳng 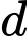 đi qua gốc toạ độ
đi qua gốc toạ độ  và vuông góc với
và vuông góc với 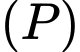 có một vectơ chỉ phương là
có một vectơ chỉ phương là
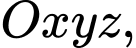 cho mặt phẳng
cho mặt phẳng 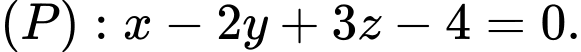 Đường thẳng
Đường thẳng  đi qua gốc toạ độ
đi qua gốc toạ độ  và vuông góc với
và vuông góc với 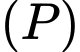 có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 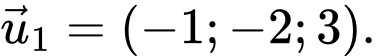
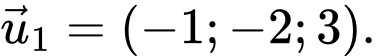
B, 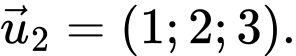
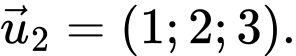
C, 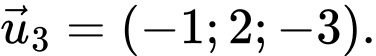
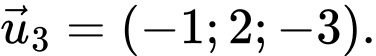
D, 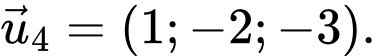
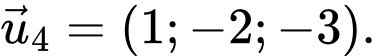
Chọn đáp án C.
Đường thẳng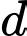 đi qua
đi qua  và vuông góc với
và vuông góc với 
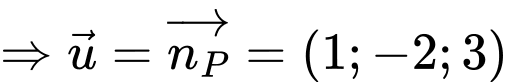 cùng phương với vecto
cùng phương với vecto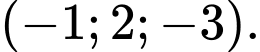
Vậy một vecto chỉ phương của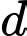 là
là 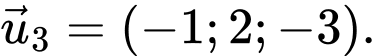 Đáp án: C
Đáp án: C
Đường thẳng
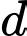 đi qua
đi qua  và vuông góc với
và vuông góc với 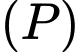
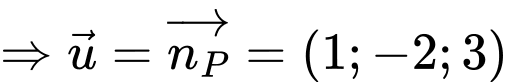 cùng phương với vecto
cùng phương với vecto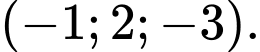
Vậy một vecto chỉ phương của
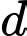 là
là 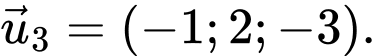 Đáp án: C
Đáp án: C
Câu 6 [257441]: Với 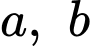 là hai số thực dương bất kỳ,
là hai số thực dương bất kỳ, 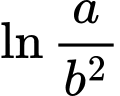 bằng
bằng
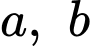 là hai số thực dương bất kỳ,
là hai số thực dương bất kỳ, 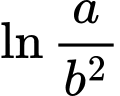 bằng
bằng A, 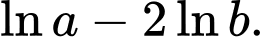
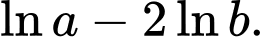
B, 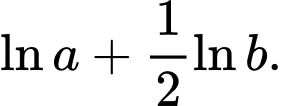
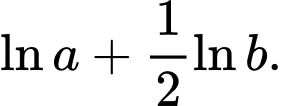
C, 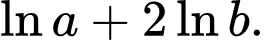
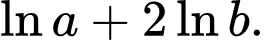
D, 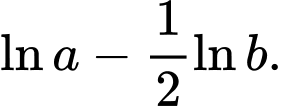
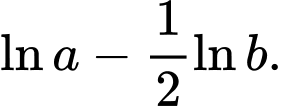
Chọn đáp án A.
Ta có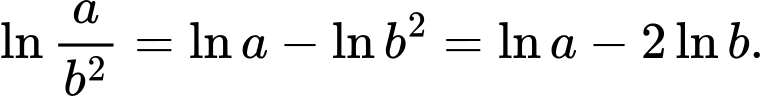 Đáp án: A
Đáp án: A
Ta có
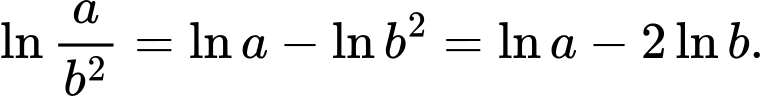 Đáp án: A
Đáp án: A
Câu 7 [349420]: Khẳng định nào dưới đây đúng?
A, 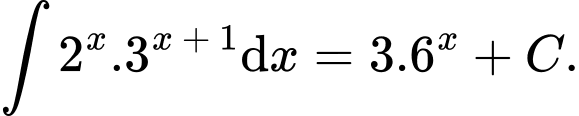
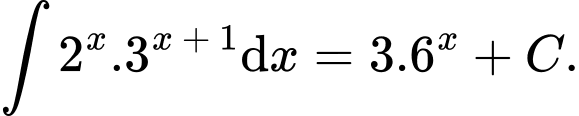
B, 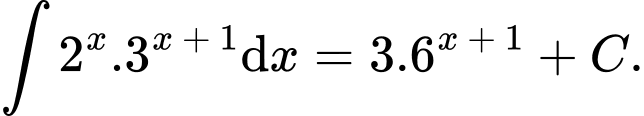
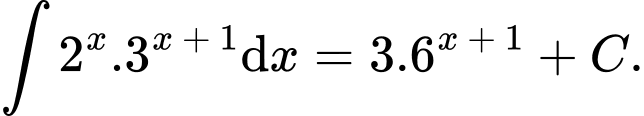
C, 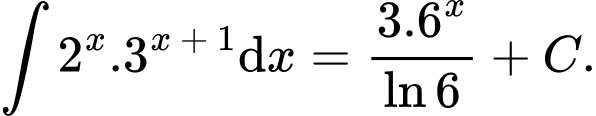
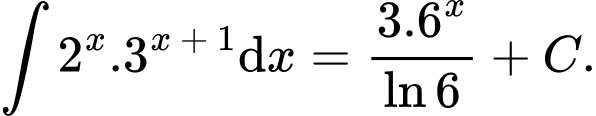
D, 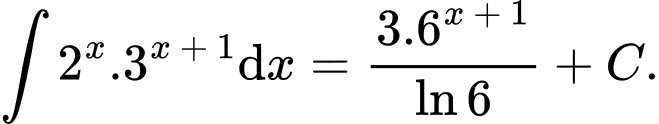
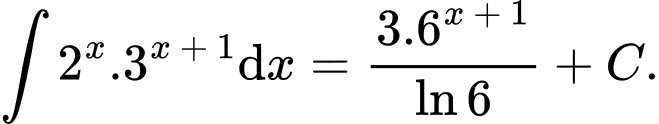
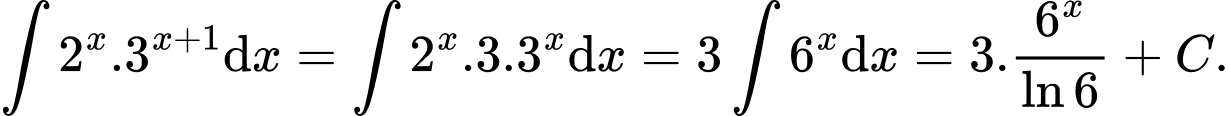
Chọn đáp án C.
Đáp án: C
Câu 8 [696396]: Tiệm cận xiên của đồ thị hàm số 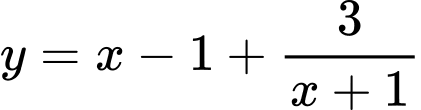 đi qua điểm nào sau đây?
đi qua điểm nào sau đây?
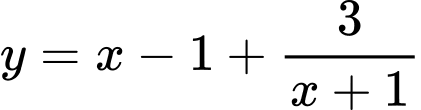 đi qua điểm nào sau đây?
đi qua điểm nào sau đây? A, Điểm 

B, Điểm 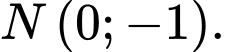
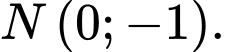
C, Điểm 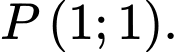
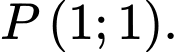
D, Điểm 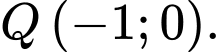
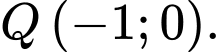
Tiệm cận xiên của đồ thị hàm số đã cho là 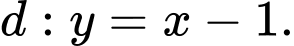
Do đó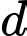 đi qua điểm
đi qua điểm 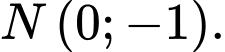 Đáp án: B
Đáp án: B
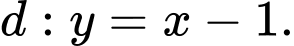
Do đó
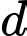 đi qua điểm
đi qua điểm 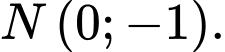 Đáp án: B
Đáp án: B
Câu 9 [810115]: Trong không gian 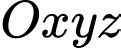 , cho điểm
, cho điểm 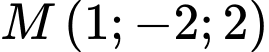 và mặt phẳng
và mặt phẳng 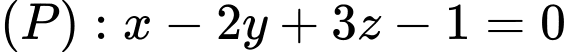 . Mặt phẳng đi qua
. Mặt phẳng đi qua 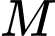 và song song với
và song song với 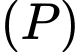 có phương trình là
có phương trình là
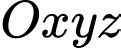 , cho điểm
, cho điểm 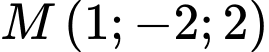 và mặt phẳng
và mặt phẳng 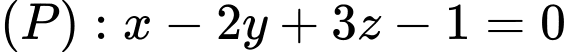 . Mặt phẳng đi qua
. Mặt phẳng đi qua 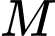 và song song với
và song song với 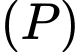 có phương trình là
có phương trình là A, 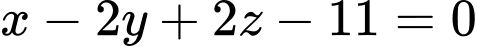 .
.
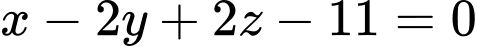 .
.B, 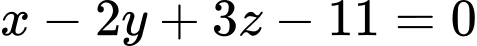 .
.
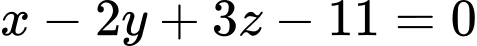 .
.C, 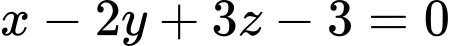 .
.
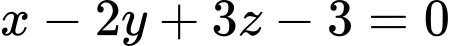 .
.D, 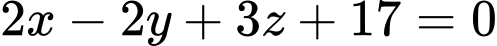 .
.
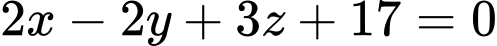 .
.
Chọn đáp án B.
Gọi là mặt phẳng cần tìm.
là mặt phẳng cần tìm.

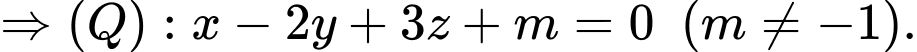
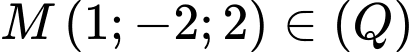
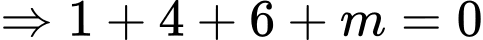
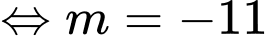
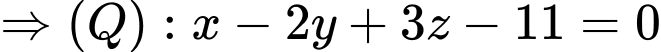 . Đáp án: B
. Đáp án: B
Gọi
 là mặt phẳng cần tìm.
là mặt phẳng cần tìm. 
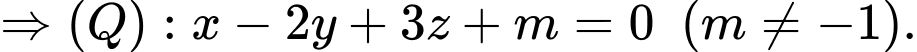
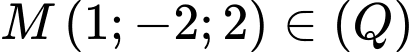
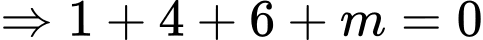
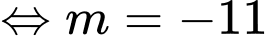
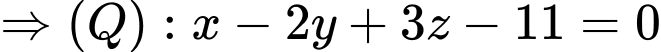 . Đáp án: B
. Đáp án: B Sử dụng thông tin dưới đây để trả lời câu 10 và câu 11
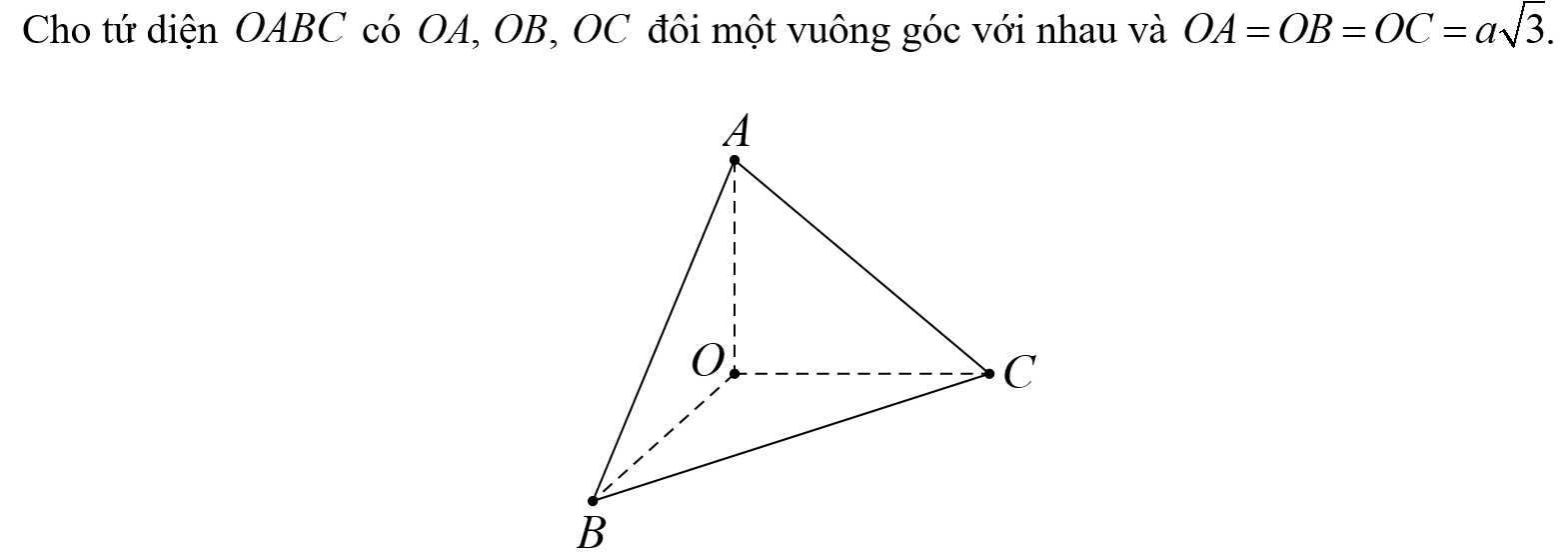
Câu 10 [702910]: Góc giữa hai vectơ 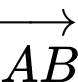 và
và 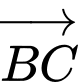 bằng
bằng
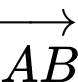 và
và 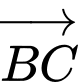 bằng
bằng A, 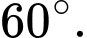
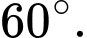
B, 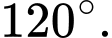
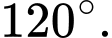
C, 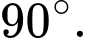
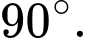
D, 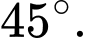
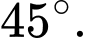
Chọn đáp án B.
Góc giữa hai vectơ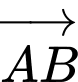 và
và 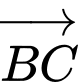 là
là 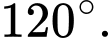 Đáp án: B
Đáp án: B
Góc giữa hai vectơ
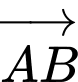 và
và 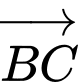 là
là 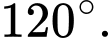 Đáp án: B
Đáp án: B
Câu 11 [702911]: Khoảng cách từ  đến mặt phẳng
đến mặt phẳng 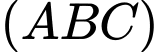 bằng
bằng
 đến mặt phẳng
đến mặt phẳng 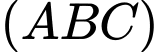 bằng
bằng A, 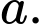
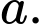
B, 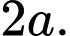
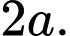
C, 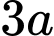
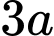
D, 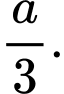
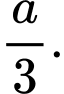
Chọn đáp án A.
Ta có:
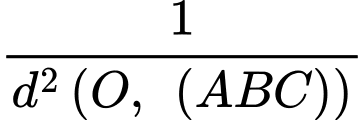
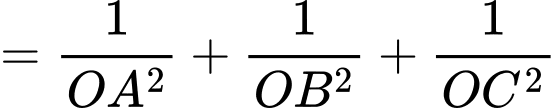
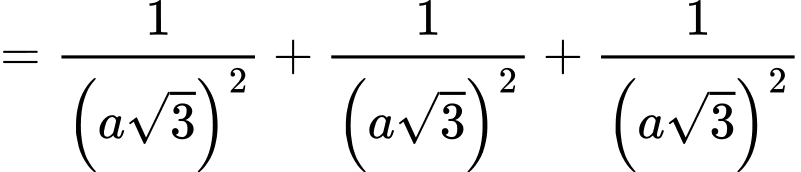
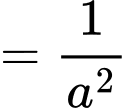
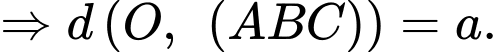 Đáp án: A
Đáp án: A
Ta có:
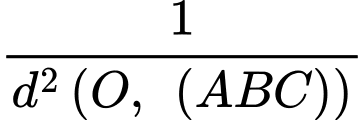
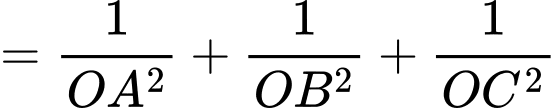
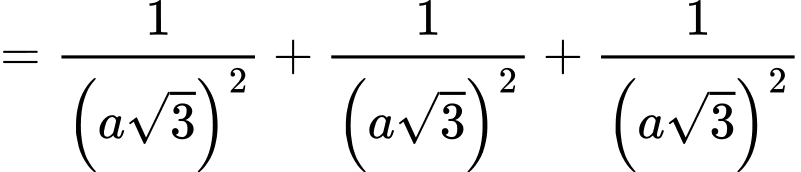
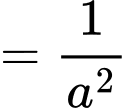
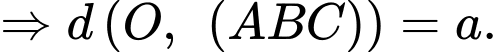 Đáp án: A
Đáp án: A
Câu 12 [257301]: Chọn ngẫu nhiên  số từ
số từ 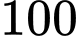 số tự nhiên đầu tiên, xác suất để số chọn được là một số chia hết cho
số tự nhiên đầu tiên, xác suất để số chọn được là một số chia hết cho  bằng
bằng
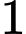 số từ
số từ 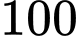 số tự nhiên đầu tiên, xác suất để số chọn được là một số chia hết cho
số tự nhiên đầu tiên, xác suất để số chọn được là một số chia hết cho  bằng
bằng A, 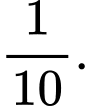
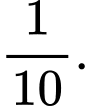
B, 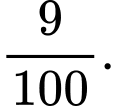
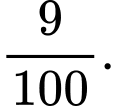
C, 

D, 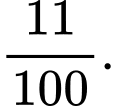
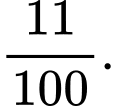
Chọn đáp án A.
Gọi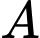 là biến cố “chọn được là một số chia hết cho
là biến cố “chọn được là một số chia hết cho  trong 100 số tự nhiên đầu tiên”.
trong 100 số tự nhiên đầu tiên”.
Số phần tử của không gian mẫu là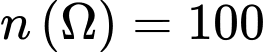 .
.
Ta có các số chia hết cho 11 trong 100 số tự nhiên đầu tiên (từ 0 đến 99) là: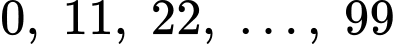 , tổng cộng là 10 số.
, tổng cộng là 10 số.
Suy ra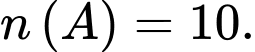
Khi đó, xác suất của biến cố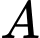 là
là

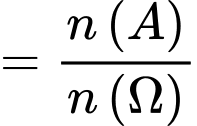
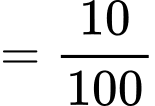
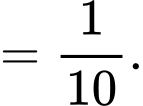 Đáp án: A
Đáp án: A
Gọi
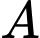 là biến cố “chọn được là một số chia hết cho
là biến cố “chọn được là một số chia hết cho  trong 100 số tự nhiên đầu tiên”.
trong 100 số tự nhiên đầu tiên”.Số phần tử của không gian mẫu là
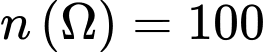 .
.Ta có các số chia hết cho 11 trong 100 số tự nhiên đầu tiên (từ 0 đến 99) là:
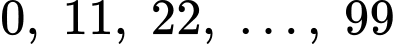 , tổng cộng là 10 số.
, tổng cộng là 10 số. Suy ra
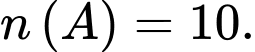
Khi đó, xác suất của biến cố
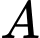 là
là 
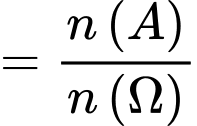
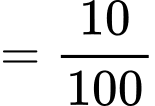
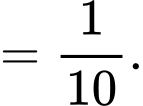 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696401]: Trong không gian với hệ tọa độ 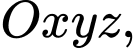 cho đường thẳng
cho đường thẳng 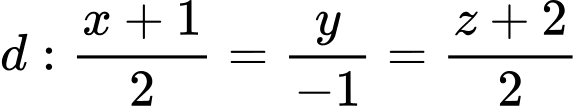 và mặt phẳng
và mặt phẳng 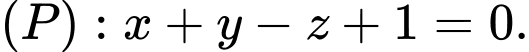
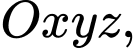 cho đường thẳng
cho đường thẳng 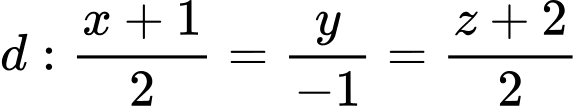 và mặt phẳng
và mặt phẳng 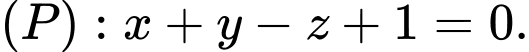
a) Đúng.
Một vectơ chỉ phương của đường thẳng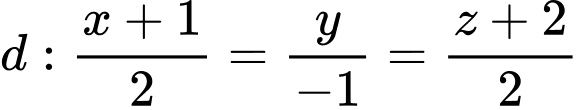 là
là 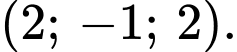
b) Đúng.
Ta có: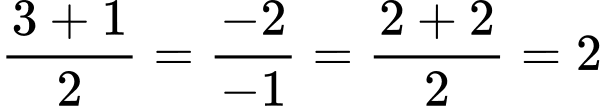 nên đường thẳng
nên đường thẳng 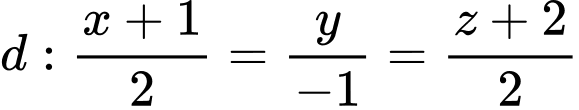 đi qua điểm
đi qua điểm 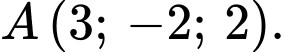
c) Sai.
Ta có: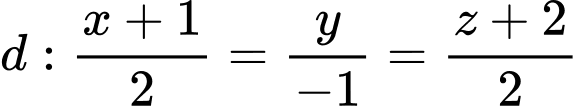 hay
hay 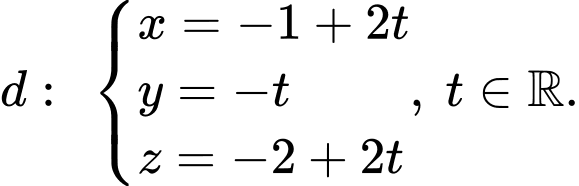
Gọi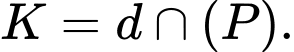 Khi đó:
Khi đó: 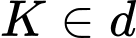 nên
nên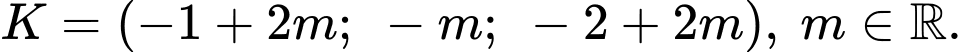
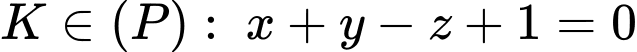 nên
nên  hay
hay 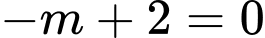 hay
hay 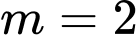
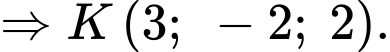
d) Sai.
Gọi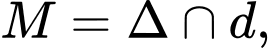 mà
mà  nằm trong mặt phẳng
nằm trong mặt phẳng  nên
nên 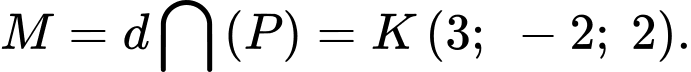
Đường thẳng nằm trong mặt phẳng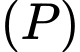 đồng thời cắt và vuông góc với d nên có vectơ chỉ phương là
đồng thời cắt và vuông góc với d nên có vectơ chỉ phương là 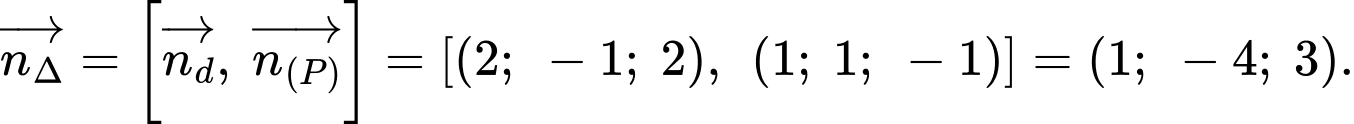
Phương trình đường thẳng đi qua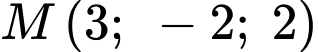 và VTCP
và VTCP 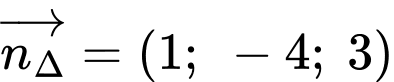 là
là 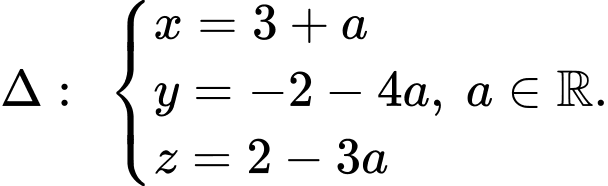
Giao điểm giữa và mặt phẳng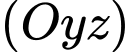 là
là 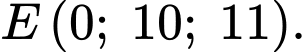
Một vectơ chỉ phương của đường thẳng
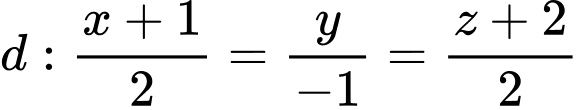 là
là 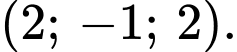
b) Đúng.
Ta có:
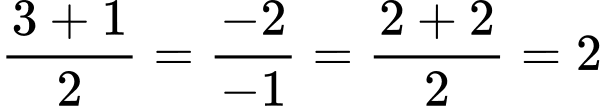 nên đường thẳng
nên đường thẳng 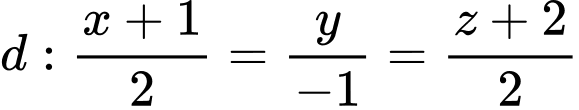 đi qua điểm
đi qua điểm 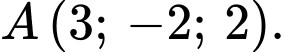
c) Sai.
Ta có:
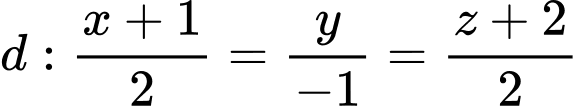 hay
hay 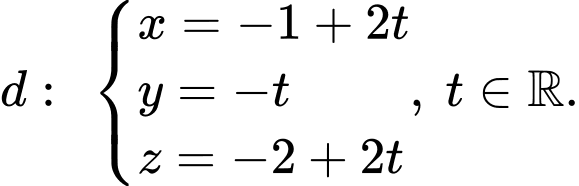
Gọi
 Khi đó:
Khi đó:  nên
nên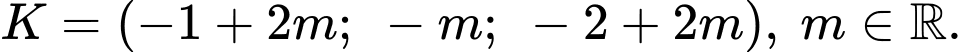
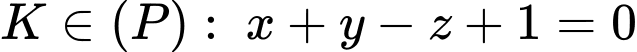 nên
nên  hay
hay 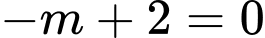 hay
hay 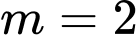
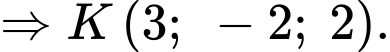
d) Sai.
Gọi
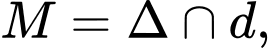 mà
mà  nằm trong mặt phẳng
nằm trong mặt phẳng  nên
nên 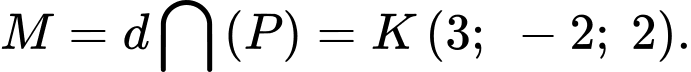
Đường thẳng nằm trong mặt phẳng
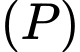 đồng thời cắt và vuông góc với d nên có vectơ chỉ phương là
đồng thời cắt và vuông góc với d nên có vectơ chỉ phương là 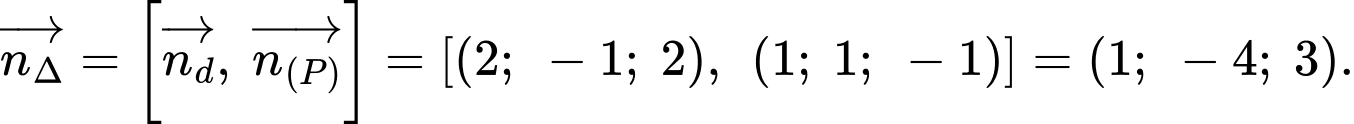
Phương trình đường thẳng đi qua
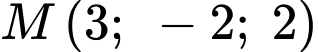 và VTCP
và VTCP 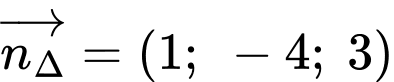 là
là 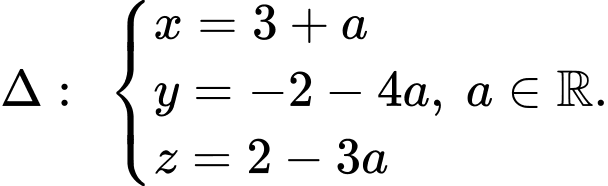
Giao điểm giữa và mặt phẳng
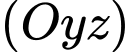 là
là 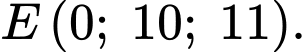
Câu 14 [693318]: Một bể chứa ban đầu có 300 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 60 lít nước và 20 gam chất khử trùng (hoà tan).
a) Sai.
Thể tích nước sau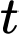 phút bơm là
phút bơm là 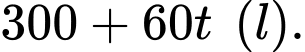
Thể tích nước sau 1 giờ bơm bằng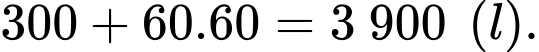
b) Sai.
Khối lượng chất khử sau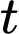 phút là
phút là 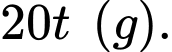
Nồng độ chất khử sau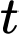 phút bằng
phút bằng 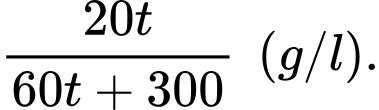
c) Đúng.
Xét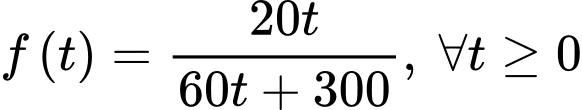
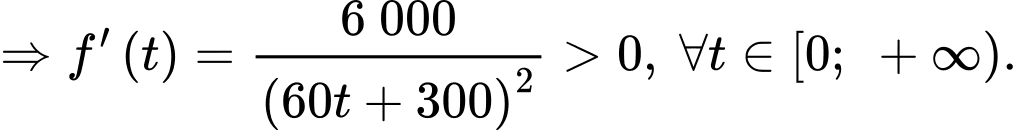
Do đó hàm số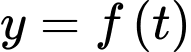 luôn đồng biến trên tập xác định của nó.
luôn đồng biến trên tập xác định của nó.
d) Đúng.
Ta có: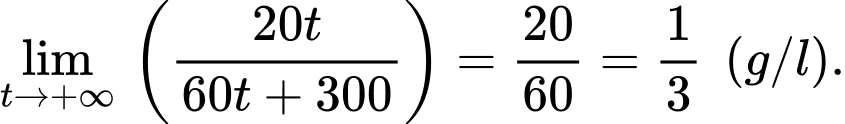
Thể tích nước sau
 phút bơm là
phút bơm là 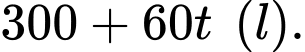
Thể tích nước sau 1 giờ bơm bằng
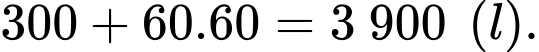
b) Sai.
Khối lượng chất khử sau
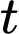 phút là
phút là 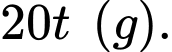
Nồng độ chất khử sau
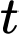 phút bằng
phút bằng 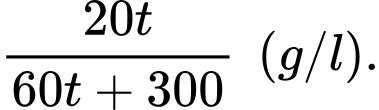
c) Đúng.
Xét
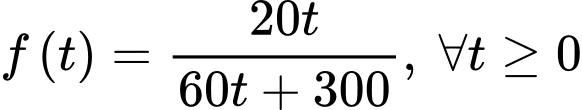
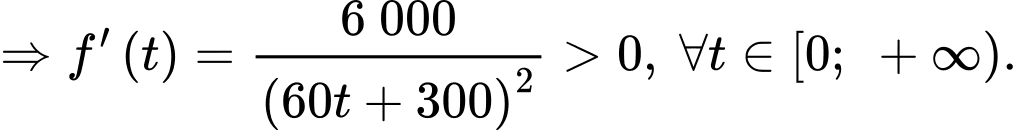
Do đó hàm số
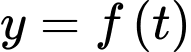 luôn đồng biến trên tập xác định của nó.
luôn đồng biến trên tập xác định của nó.
d) Đúng.
Ta có:
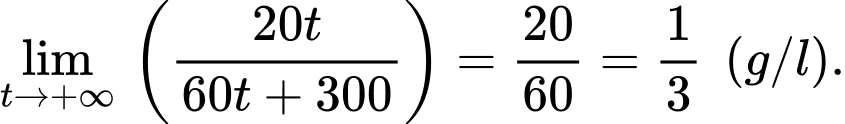
Câu 15 [702913]: Theo thống kê ở các gia đình có hai con thì xác suất để con thứ nhất và con thứ hai đều là trai là 0,27 và hai con đều là gái là 0,23, còn xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau. Chọn ngẫu nhiên một gia đình có hai con.
Gọi là biến cố: “con thứ nhất là con gái”.
là biến cố: “con thứ nhất là con gái”.
Gọi là biến cố: “con thứ hai là con trai”.
là biến cố: “con thứ hai là con trai”.
Gọi
 là biến cố: “con thứ nhất là con gái”.
là biến cố: “con thứ nhất là con gái”.Gọi
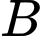 là biến cố: “con thứ hai là con trai”.
là biến cố: “con thứ hai là con trai”.
a) Đúng.
 là xác suất con thứ nhất là con gái và con thứ hai là con gái.
là xác suất con thứ nhất là con gái và con thứ hai là con gái.
Theo giả thiết: Xác suất để hai con đều là gái là 0,23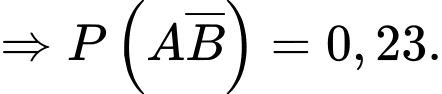
b) Sai.
Theo giả thiết: Xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau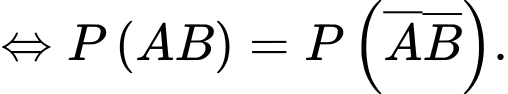
Lại có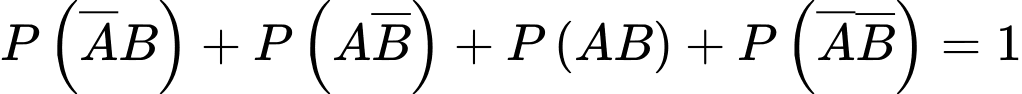
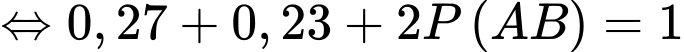
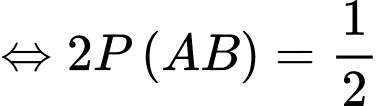

c) Đúng.
Ta có xác suất gặp gia đình có con thứ nhất là gái là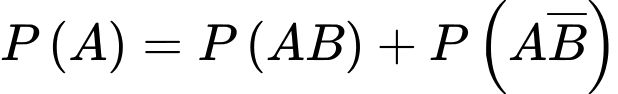
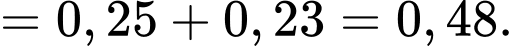
d) Đúng.
YCBT Tính
Tính 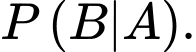
Theo công thức xác suất có điều kiện, ta có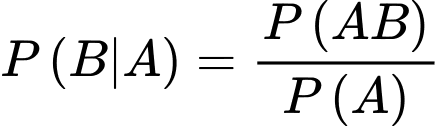
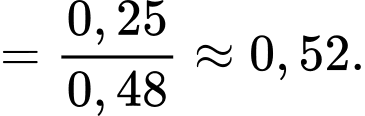
 là xác suất con thứ nhất là con gái và con thứ hai là con gái.
là xác suất con thứ nhất là con gái và con thứ hai là con gái.
Theo giả thiết: Xác suất để hai con đều là gái là 0,23
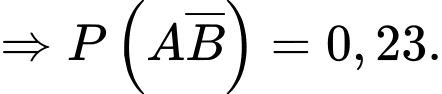
b) Sai.
Theo giả thiết: Xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau
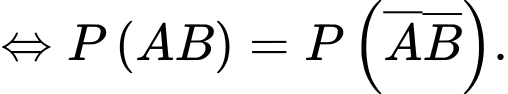
Lại có
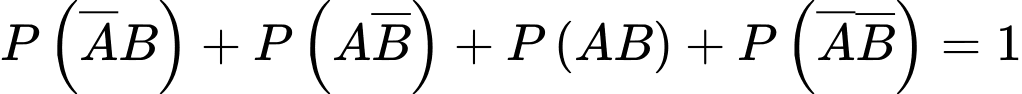
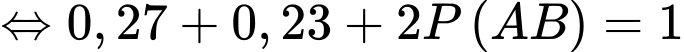
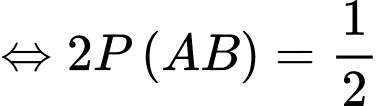

c) Đúng.
Ta có xác suất gặp gia đình có con thứ nhất là gái là
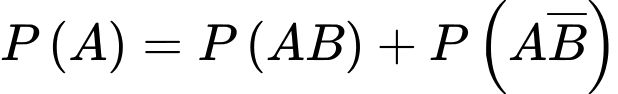
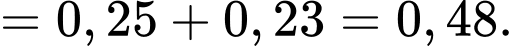
d) Đúng.
YCBT
 Tính
Tính 
Theo công thức xác suất có điều kiện, ta có
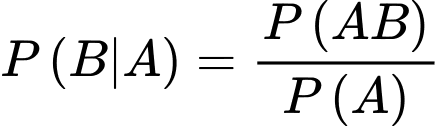
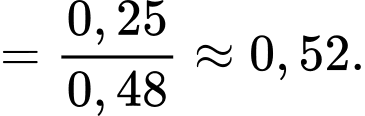
Câu 16 [696404]: Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng 1. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc 30o ta thu được khối gỗ hình nêm  và đặt khối
và đặt khối  vào hệ trục tọa độ như hình vẽ.
vào hệ trục tọa độ như hình vẽ.
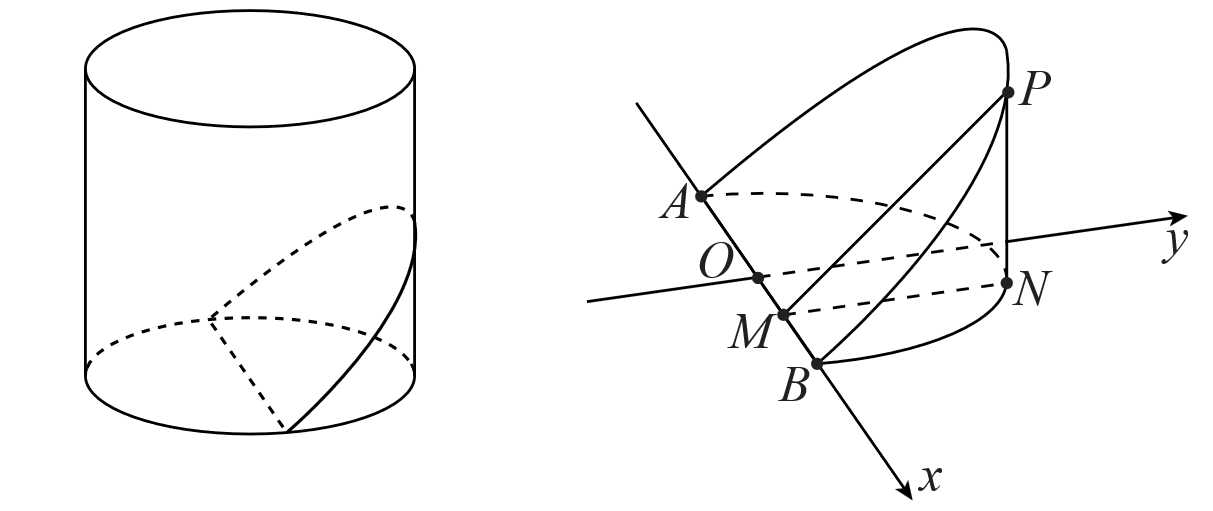
 và đặt khối
và đặt khối  vào hệ trục tọa độ như hình vẽ.
vào hệ trục tọa độ như hình vẽ.
a) Sai.
Nửa đường tròn đáy của khối gỗ hình trụ (đường kính ) có phương trình là
) có phương trình là 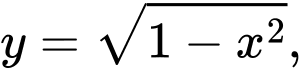

b) Đúng.
Một mặt phẳng vuông góc với trục tại điểm
tại điểm 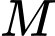 có hoành độ
có hoành độ 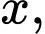 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 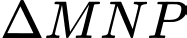 vuông tại
vuông tại 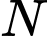 và độ dài
và độ dài 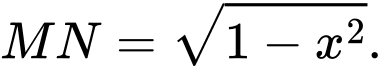
c) Sai.
Một mặt phẳng vuông góc với trục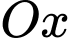 tại điểm
tại điểm 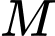 có hoành độ
có hoành độ 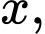 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 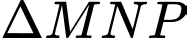 vuông tại
vuông tại 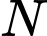 và
và 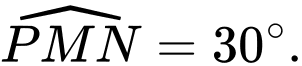
Ta có: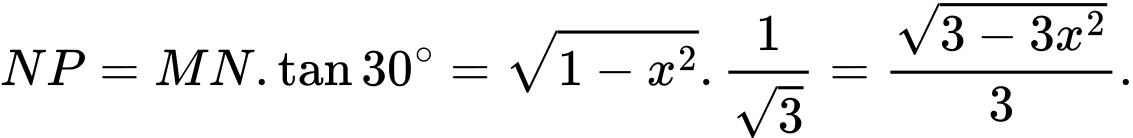
Diện tích tam giác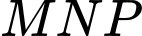 bằng
bằng
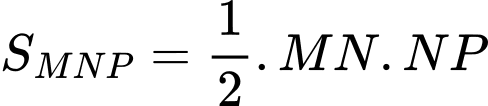
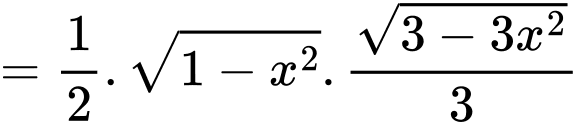
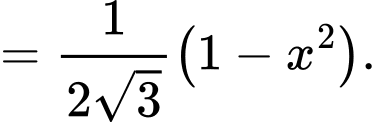
d) Đúng.
Thể tích hình nêm là:
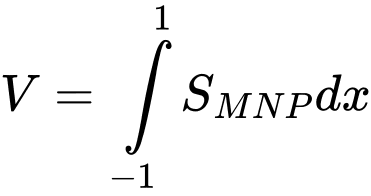
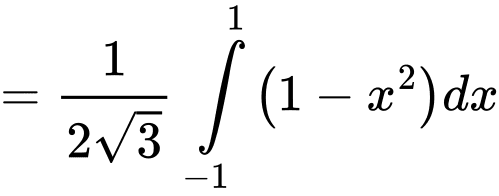
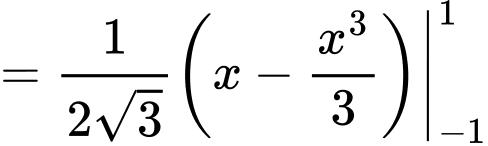
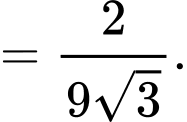
Nửa đường tròn đáy của khối gỗ hình trụ (đường kính
 ) có phương trình là
) có phương trình là 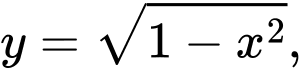

b) Đúng.
Một mặt phẳng vuông góc với trục
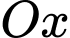 tại điểm
tại điểm 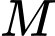 có hoành độ
có hoành độ 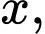 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 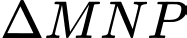 vuông tại
vuông tại 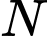 và độ dài
và độ dài 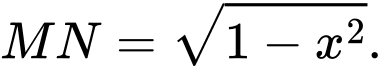
c) Sai.
Một mặt phẳng vuông góc với trục
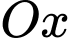 tại điểm
tại điểm 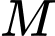 có hoành độ
có hoành độ 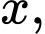 cắt hình nêm theo thiết diện là
cắt hình nêm theo thiết diện là 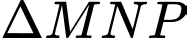 vuông tại
vuông tại 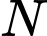 và
và 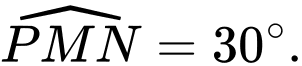
Ta có:
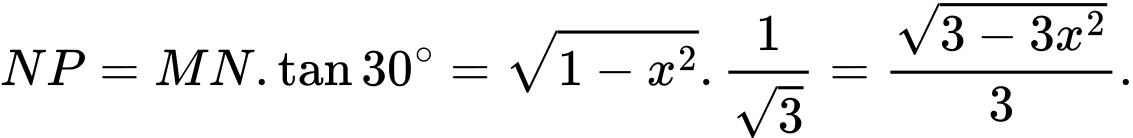
Diện tích tam giác
 bằng
bằng 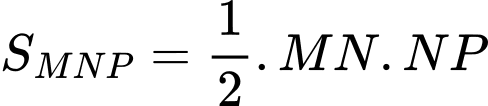
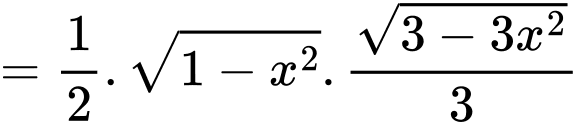
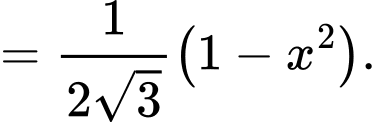
d) Đúng.
Thể tích hình nêm là:
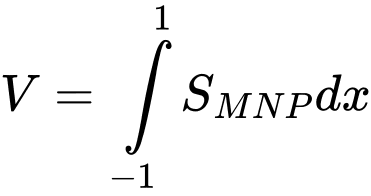
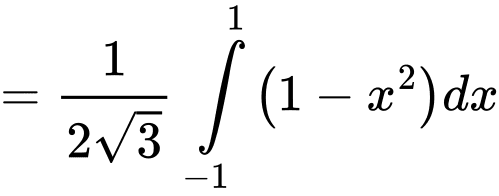
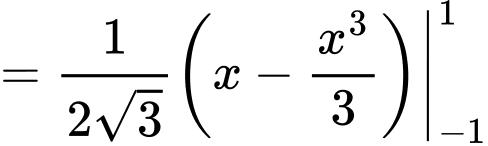
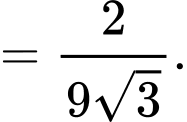
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696405]: Cho hình chóp  có đáy
có đáy  là hình vuông cạnh
là hình vuông cạnh 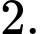 Cạnh bên
Cạnh bên 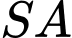 vuông góc với đáy và
vuông góc với đáy và 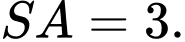 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 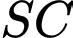 và
và 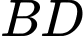 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
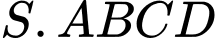 có đáy
có đáy 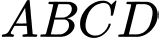 là hình vuông cạnh
là hình vuông cạnh  Cạnh bên
Cạnh bên 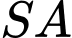 vuông góc với đáy và
vuông góc với đáy và 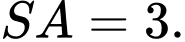 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 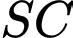 và
và 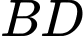 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 1.
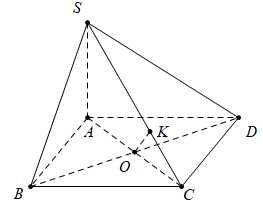
Gọi là tâm hình vuông
là tâm hình vuông 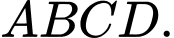
Ta có: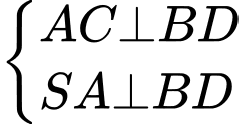
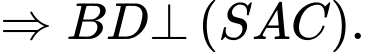
Ta có: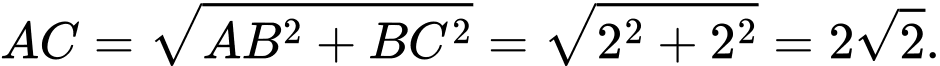
Dựng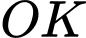 là đoạn vuông góc chung của
là đoạn vuông góc chung của 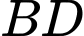 và
và 
Khi đó,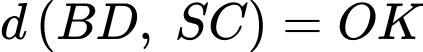
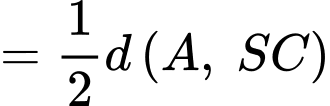
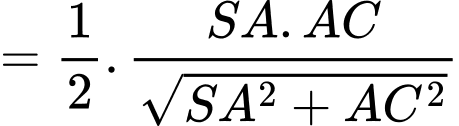
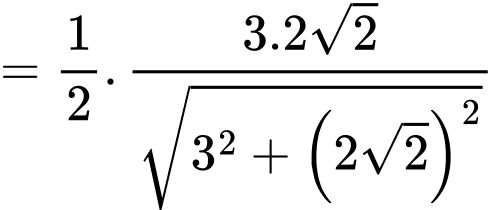
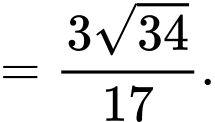
Vậy khoảng cách giữa hai đường thẳng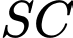 và
và 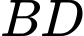 bằng
bằng 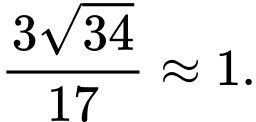

Gọi
 là tâm hình vuông
là tâm hình vuông 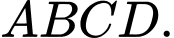
Ta có:
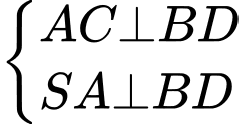
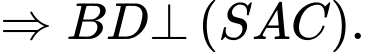
Ta có:
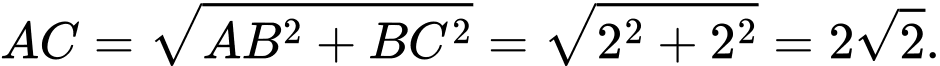
Dựng
 là đoạn vuông góc chung của
là đoạn vuông góc chung của 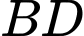 và
và 
Khi đó,
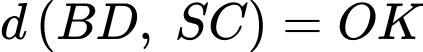
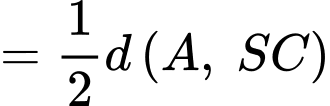
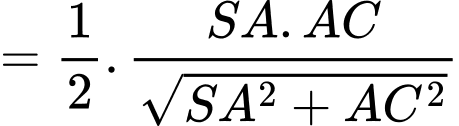
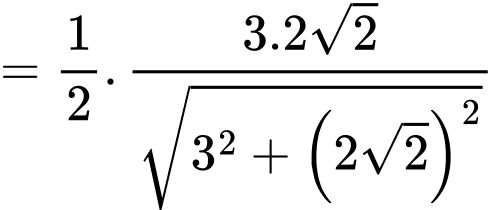
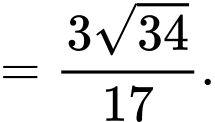
Vậy khoảng cách giữa hai đường thẳng
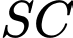 và
và 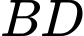 bằng
bằng 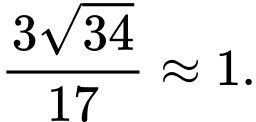
Câu 18 [696406]: Công ty TNHH Moon sản xuất 4 mặt hàng là P, Q, R và S. Giá của 4 mặt hàng P, Q, R và S lần lượt là 12 USD, 15 USD, 10 USD và 20 USD trên một kg vào năm 2008. Giá của mỗi mặt hàng tăng 10\% mỗi năm. Biểu đồ cột sau đây cho biết khối lượng các mặt hàng được bán (tính theo kg) từ năm 2008 đến năm 2011.
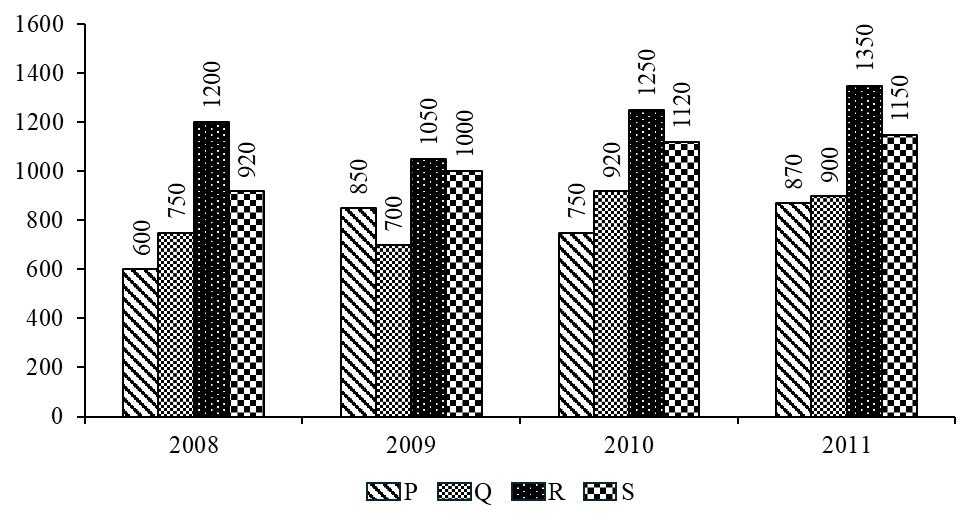
Tỉ lệ phần trăm tăng trưởng doanh số bán hàng của công ty từ năm 2010 đến năm 2011 xấp xỉ bao nhiêu? (kết quả làm tròn đến hàng phần chục).

Tỉ lệ phần trăm tăng trưởng doanh số bán hàng của công ty từ năm 2010 đến năm 2011 xấp xỉ bao nhiêu? (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 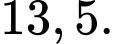
Doanh số bán hàng của công ty năm 2010 là:
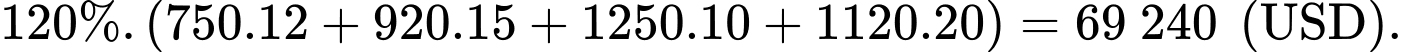
Doanh số bán hàng của công ty năm 2011 là:
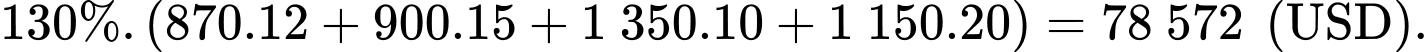
Tỷ lệ phần trăm tăng trưởng doanh số bán hàng của công ty từ năm 2010 đến năm 2011 là:
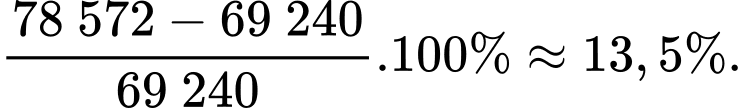
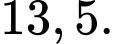
Doanh số bán hàng của công ty năm 2010 là:
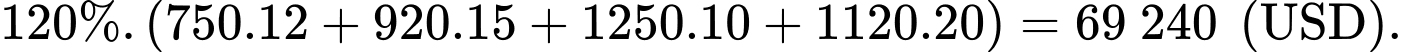
Doanh số bán hàng của công ty năm 2011 là:
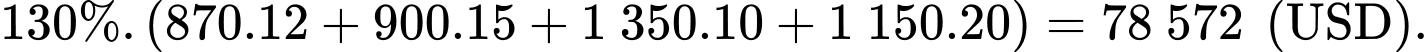
Tỷ lệ phần trăm tăng trưởng doanh số bán hàng của công ty từ năm 2010 đến năm 2011 là:
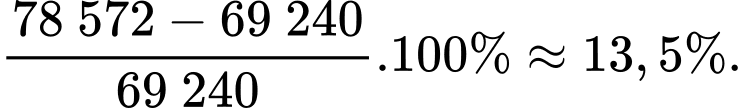
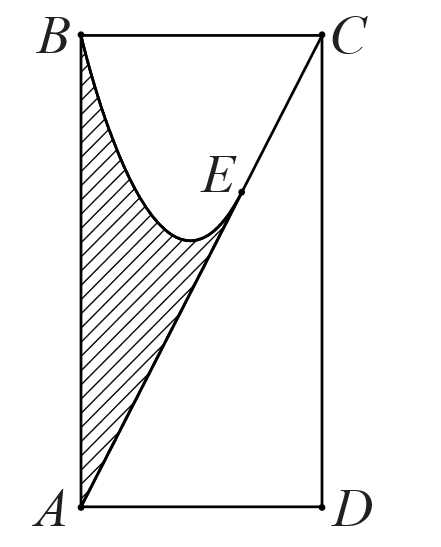
Câu 19 [696408]: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền  (phần gạch chéo trong hình vẽ bên) quanh trục
(phần gạch chéo trong hình vẽ bên) quanh trục  Miền
Miền  được giới hạn bởi cạnh
được giới hạn bởi cạnh  đường chéo
đường chéo  của hình chữ nhật
của hình chữ nhật 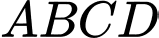 và parabol qua điểm
và parabol qua điểm 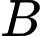 tiếp xúc với
tiếp xúc với 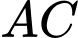 tại điểm
tại điểm 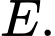 Biết
Biết 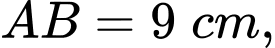
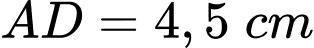 và
và 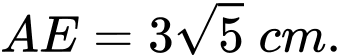 Thể tích của vật trang trí đó bằng bao nhiêu
Thể tích của vật trang trí đó bằng bao nhiêu 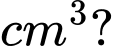 (kết quả làm tròn đến hàng phần mười).
(kết quả làm tròn đến hàng phần mười).
 (phần gạch chéo trong hình vẽ bên) quanh trục
(phần gạch chéo trong hình vẽ bên) quanh trục  Miền
Miền  được giới hạn bởi cạnh
được giới hạn bởi cạnh  đường chéo
đường chéo  của hình chữ nhật
của hình chữ nhật  và parabol qua điểm
và parabol qua điểm 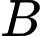 tiếp xúc với
tiếp xúc với 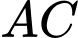 tại điểm
tại điểm 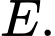 Biết
Biết 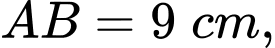
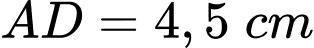 và
và 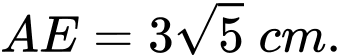 Thể tích của vật trang trí đó bằng bao nhiêu
Thể tích của vật trang trí đó bằng bao nhiêu 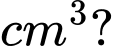 (kết quả làm tròn đến hàng phần mười).
(kết quả làm tròn đến hàng phần mười).
Điền đáp án: 42,4
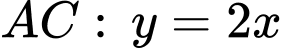
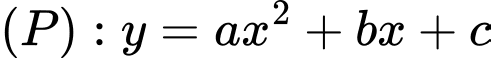 đi qua
đi qua 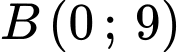
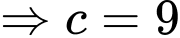
Mặt phẳng đi qua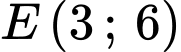
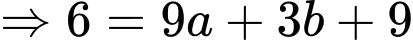
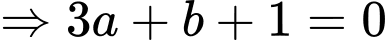
Mặt phẳng tiếp xúc tại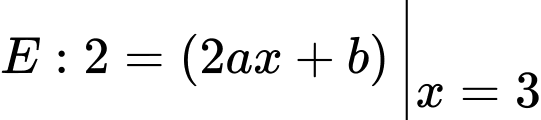
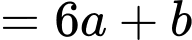
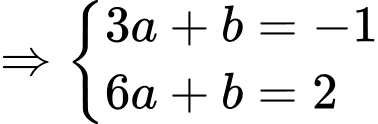
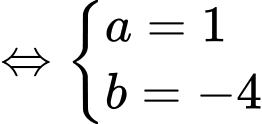
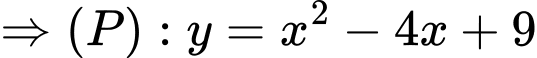
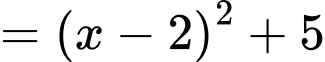
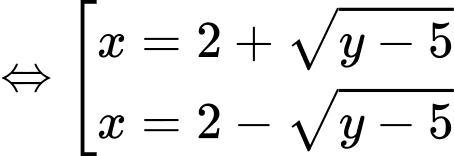
Có: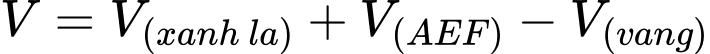
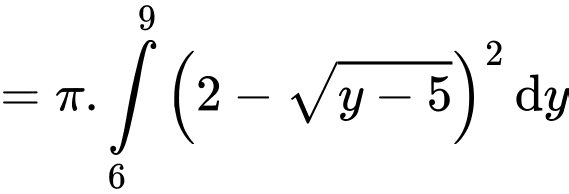
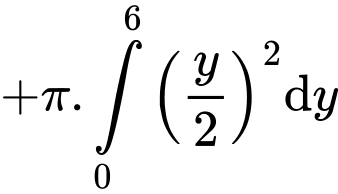
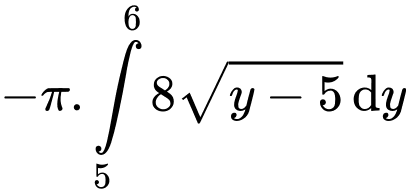
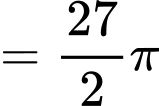
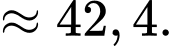
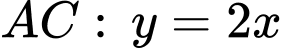
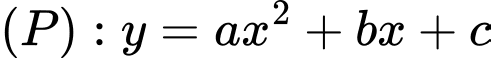 đi qua
đi qua 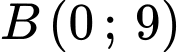
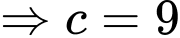
Mặt phẳng đi qua
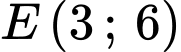
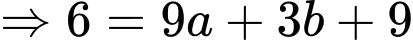
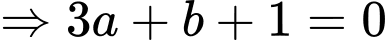
Mặt phẳng tiếp xúc tại
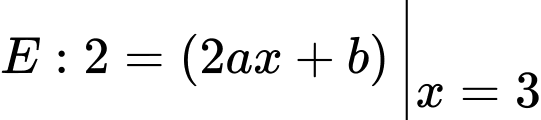
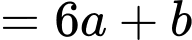
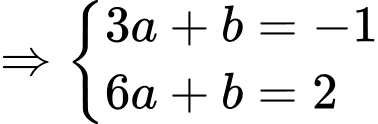
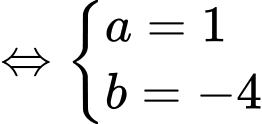
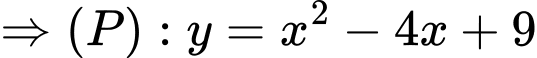
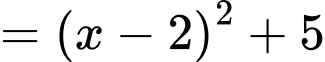
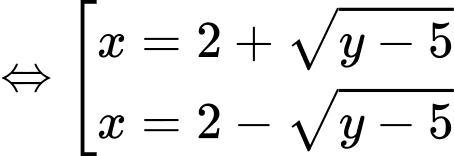
Có:
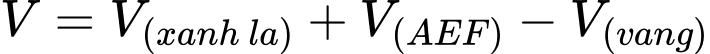
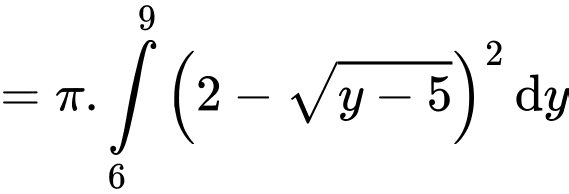
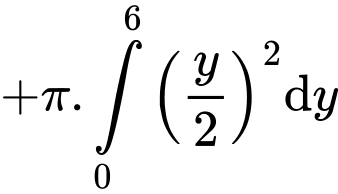
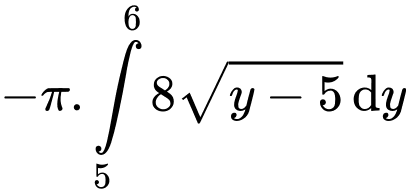
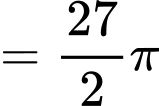
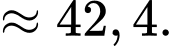
Câu 20 [693315]: Trong công viên, có một hồ nước hình bán nguyệt đường kính AB bằng 100 (m). Tại A và B người ta dựng hai bức tượng lần lượt cao 8 m và 10 m. Một người đứng trên phần cung tròn của bờ hồ muốn đặt máy ảnh cao 1,6 m để chụp toàn cảnh hai bức tượng. Gọi góc quan sát là góc tạo bởi hai tia nối vị trí đặt máy ảnh với hai đỉnh của các bức tượng. Khi người đó di chuyển trên phần cung tròn của bờ hồ thì góc quan sát lớn nhất bằng bao nhiêu độ? (làm tròn hàng đơn vị).
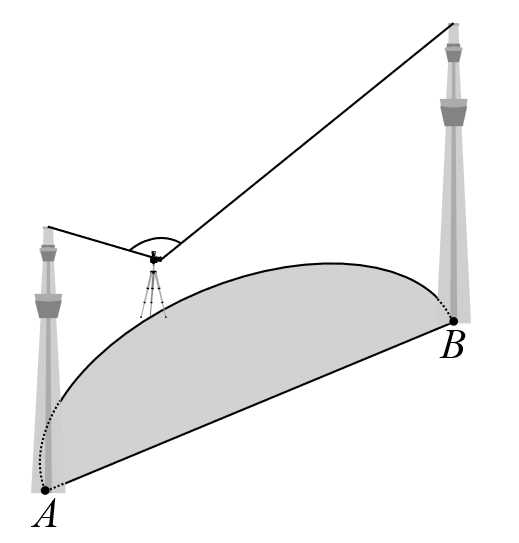

Điền đáp án: 89.
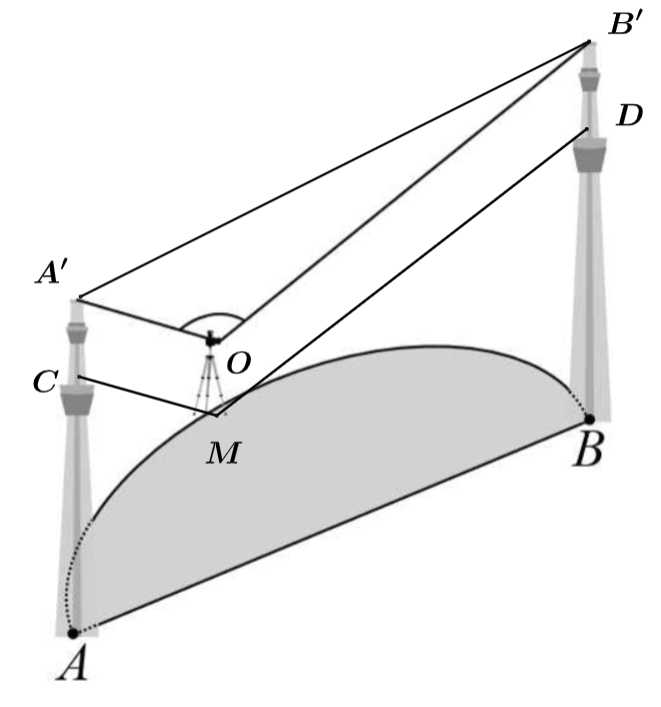
+) Kẻ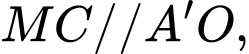
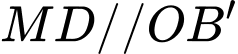
 và
và 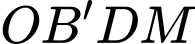 là hình bình hành.
là hình bình hành.
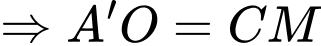 và
và 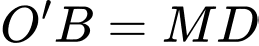
+)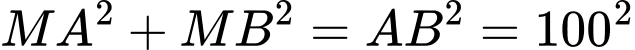
Đặt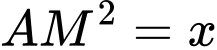
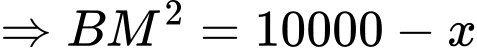
Có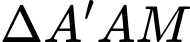 vuông tại
vuông tại 
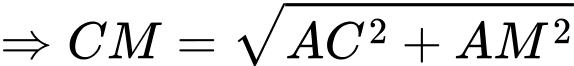
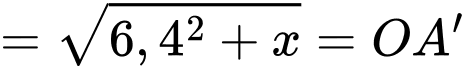
Ta chứng minh tương tự:

Kẻ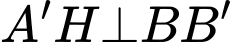
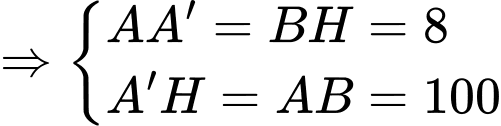
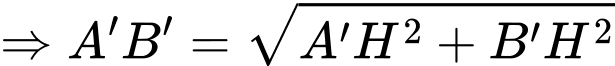
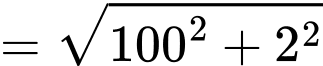
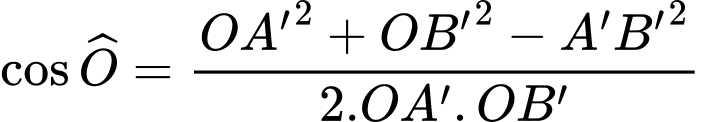
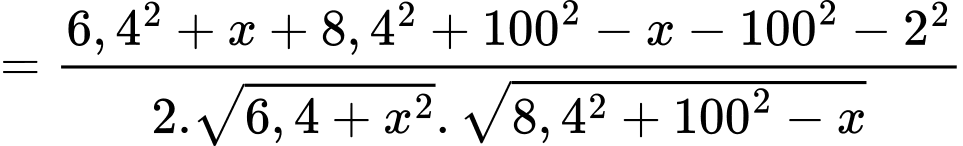
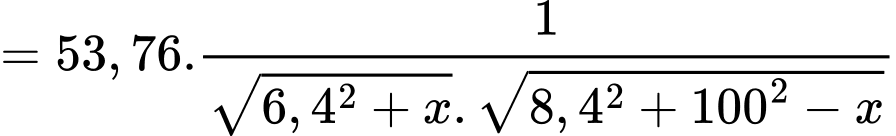
Ta có: tại
tại 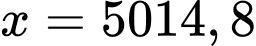
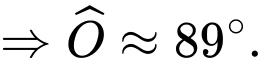

+) Kẻ
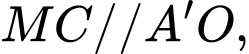
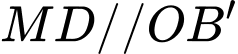
 và
và 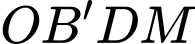 là hình bình hành.
là hình bình hành.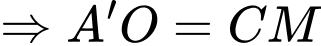 và
và 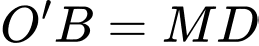
+)
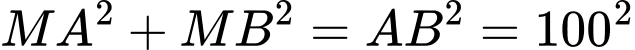
Đặt
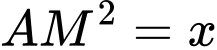
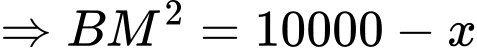
Có
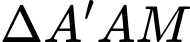 vuông tại
vuông tại 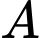
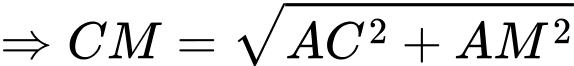
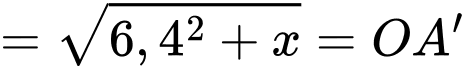
Ta chứng minh tương tự:


Kẻ
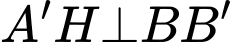
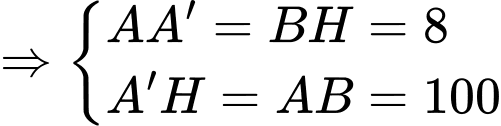
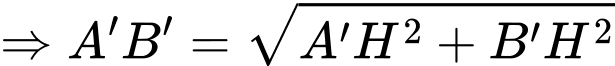
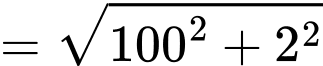
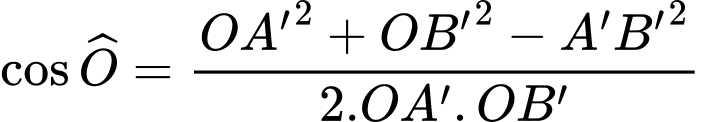
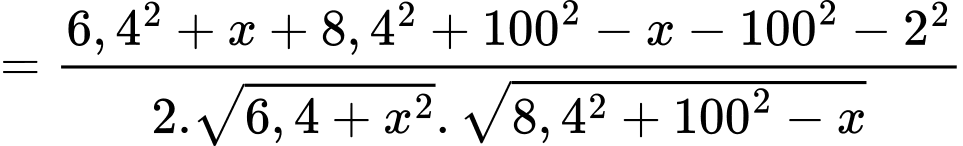
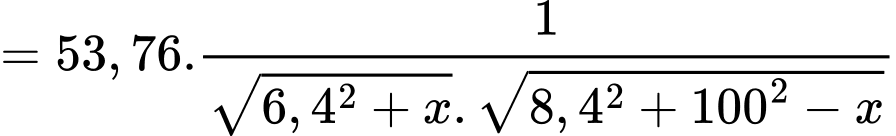
Ta có:
 tại
tại 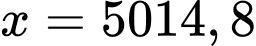
Câu 21 [703219]: Trong không gian với hệ trục toạ độ  , cho ba điểm
, cho ba điểm 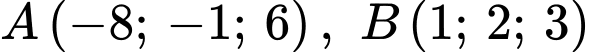 và
và 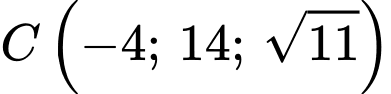 . Điểm
. Điểm 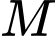 di động trên mặt cầu
di động trên mặt cầu 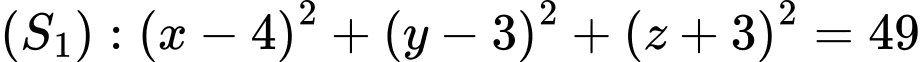 sao cho tam giác
sao cho tam giác 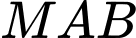 có
có 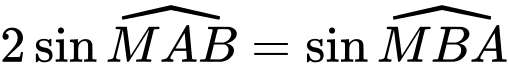 . Giá trị nhỏ nhất của đoạn thẳng
. Giá trị nhỏ nhất của đoạn thẳng 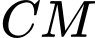 bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
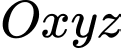 , cho ba điểm
, cho ba điểm 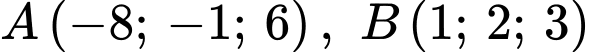 và
và 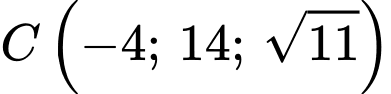 . Điểm
. Điểm 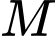 di động trên mặt cầu
di động trên mặt cầu 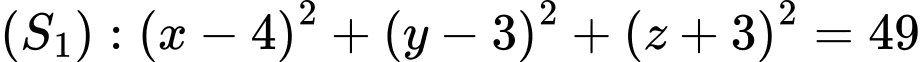 sao cho tam giác
sao cho tam giác 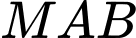 có
có 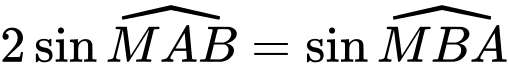 . Giá trị nhỏ nhất của đoạn thẳng
. Giá trị nhỏ nhất của đoạn thẳng 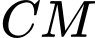 bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu (làm tròn kết quả đến hàng phần mười).
Ta có: 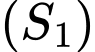 có tâm
có tâm 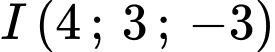 , bán kính
, bán kính 
+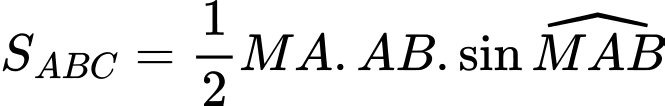
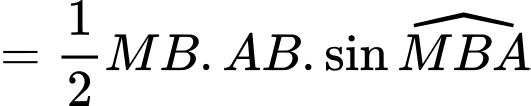
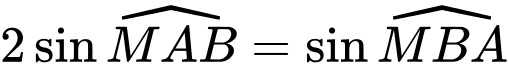
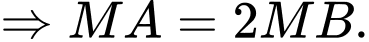
Gọi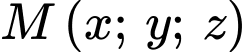 , từ
, từ 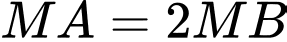
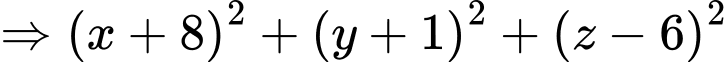
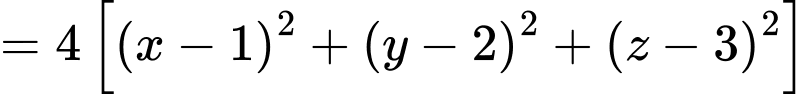
 điểm
điểm 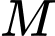 di động trên mặt cầu
di động trên mặt cầu 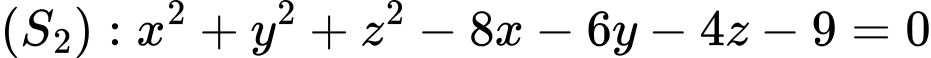 .
.
Từ đó suy ra điểm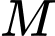 di động trên đường tròn
di động trên đường tròn 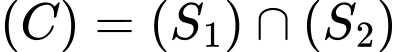 , nằm trên
, nằm trên 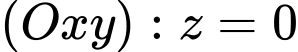 và có tâm
và có tâm 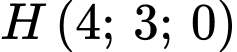 , bán kính
, bán kính 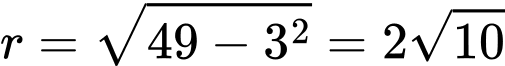 .
.

Gọi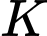 là hình chiếu vuông góc của
là hình chiếu vuông góc của 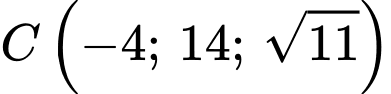 lên
lên 
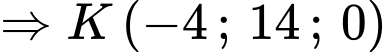 và
và 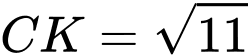 .
.
Ta có: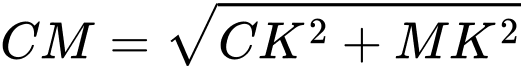
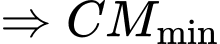
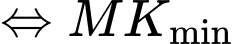 và
và 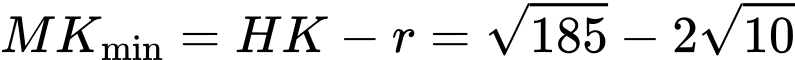 .
.
Vậy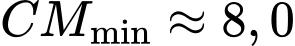
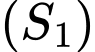 có tâm
có tâm 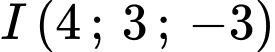 , bán kính
, bán kính 
+
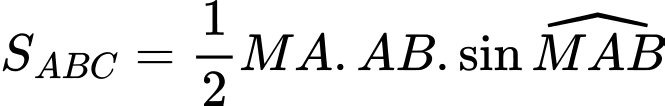
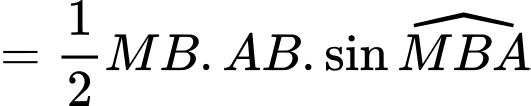
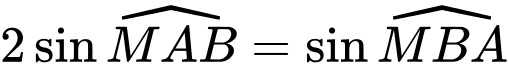
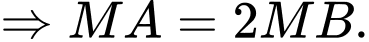
Gọi
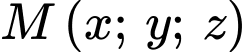 , từ
, từ 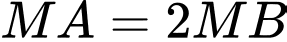
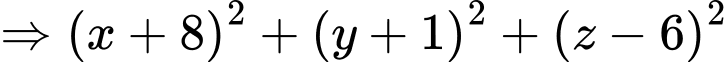
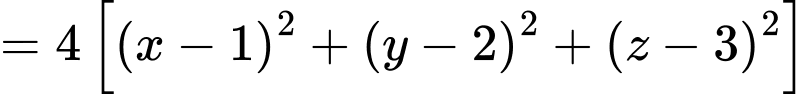
 điểm
điểm 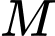 di động trên mặt cầu
di động trên mặt cầu 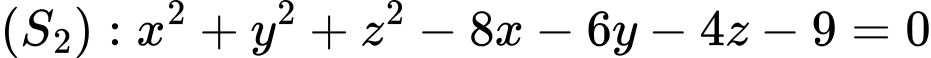 .
.Từ đó suy ra điểm
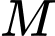 di động trên đường tròn
di động trên đường tròn 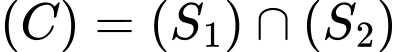 , nằm trên
, nằm trên 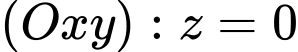 và có tâm
và có tâm 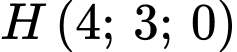 , bán kính
, bán kính 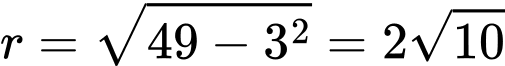 .
.
Gọi
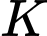 là hình chiếu vuông góc của
là hình chiếu vuông góc của 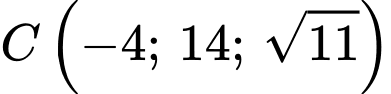 lên
lên 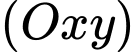
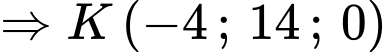 và
và 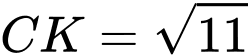 .
.Ta có:
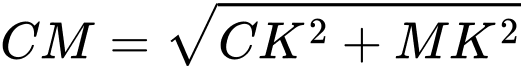
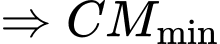
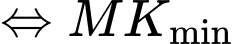 và
và 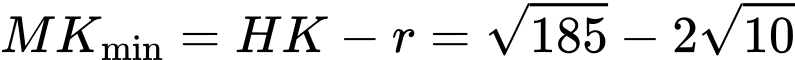 .
.Vậy
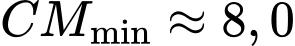
Câu 22 [696407]: Một nhóm sinh viên tham gia hồi cứu năm 2020 về bệnh Covid 19 ở tỉnh X. Tỉ lệ bị bệnh Covid của tỉnh X là 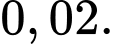 Tại thời điểm đó người ta đã sử dụng một phản ứng (hay còn gọi là test nhanh) để chẩn đoán bệnh, phản ứng trên có tỉ lệ chẩn đoán sai bằng
Tại thời điểm đó người ta đã sử dụng một phản ứng (hay còn gọi là test nhanh) để chẩn đoán bệnh, phản ứng trên có tỉ lệ chẩn đoán sai bằng 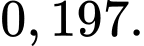 Dân số của toàn bộ tỉnh X năm 2020 đều bắt buộc tham gia test nhanh và người ta nhận thấy số người có kết quả dương tính chiếm
Dân số của toàn bộ tỉnh X năm 2020 đều bắt buộc tham gia test nhanh và người ta nhận thấy số người có kết quả dương tính chiếm 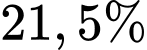 . Chọn ngẫu nhiên một mẫu phản ứng có kết quả âm tính, xác suất để người này không bị bệnh bằng bao nhiêu? (làm tròn đến hàng phần mười).
. Chọn ngẫu nhiên một mẫu phản ứng có kết quả âm tính, xác suất để người này không bị bệnh bằng bao nhiêu? (làm tròn đến hàng phần mười).
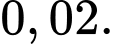 Tại thời điểm đó người ta đã sử dụng một phản ứng (hay còn gọi là test nhanh) để chẩn đoán bệnh, phản ứng trên có tỉ lệ chẩn đoán sai bằng
Tại thời điểm đó người ta đã sử dụng một phản ứng (hay còn gọi là test nhanh) để chẩn đoán bệnh, phản ứng trên có tỉ lệ chẩn đoán sai bằng 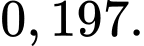 Dân số của toàn bộ tỉnh X năm 2020 đều bắt buộc tham gia test nhanh và người ta nhận thấy số người có kết quả dương tính chiếm
Dân số của toàn bộ tỉnh X năm 2020 đều bắt buộc tham gia test nhanh và người ta nhận thấy số người có kết quả dương tính chiếm 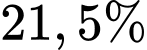 . Chọn ngẫu nhiên một mẫu phản ứng có kết quả âm tính, xác suất để người này không bị bệnh bằng bao nhiêu? (làm tròn đến hàng phần mười).
. Chọn ngẫu nhiên một mẫu phản ứng có kết quả âm tính, xác suất để người này không bị bệnh bằng bao nhiêu? (làm tròn đến hàng phần mười).
Điền đáp án: 99,9.
Gọi là biến cố “Người đó bị bệnh”
là biến cố “Người đó bị bệnh”
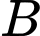 là biến cố “Xét nghiệm cho kết quả dương tính”
là biến cố “Xét nghiệm cho kết quả dương tính”
Khi đó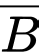 là biến cố “Xét nghiệm cho kết quả âm tính”
là biến cố “Xét nghiệm cho kết quả âm tính”
YCBT Tính
Tính  (dùng công thức Bayes để tính)
(dùng công thức Bayes để tính)
Từ dữ kiện đề bài, ta có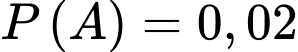
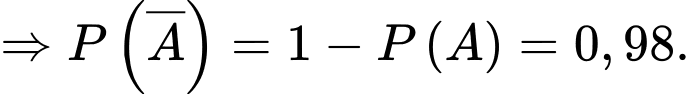
Giả sử
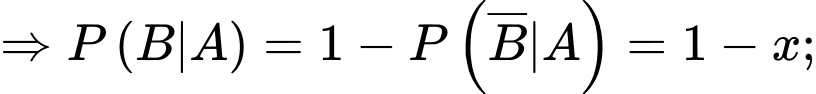

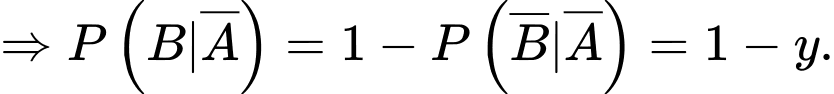
Ta có sơ đồ cây sau:
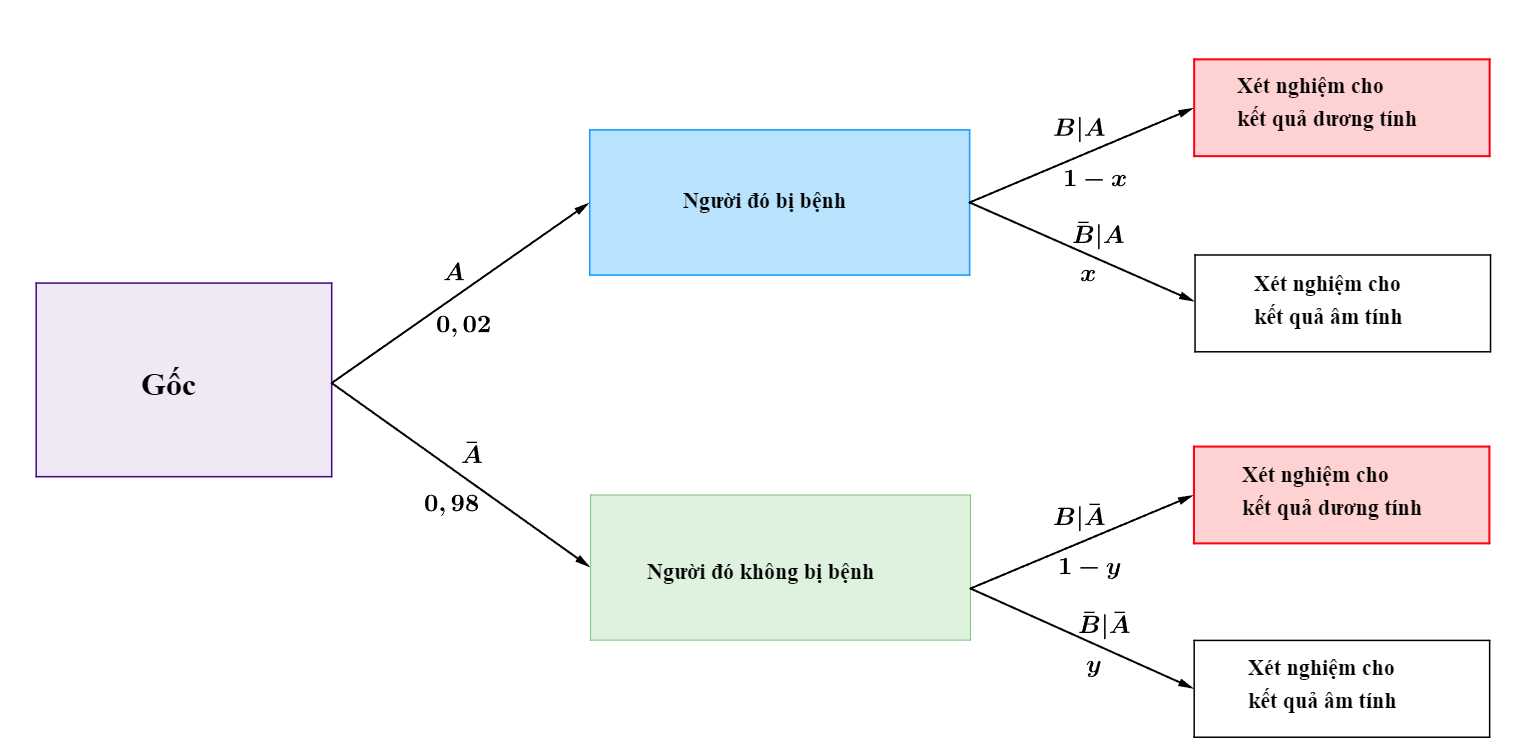
Từ giả thiết, ta có
+) Tỉ lệ chẩn đoán sai (tức người đó bị bệnh và xét nghiệm cho kết quả dương tính hoặc người đó không bị bệnh và xét nghiệm cho kết quả dương tính) bằng 0,197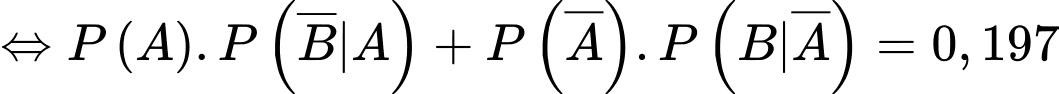
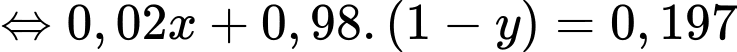
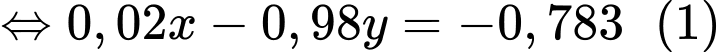
+) Số người có kết quả dương tính chiếm 21,5%
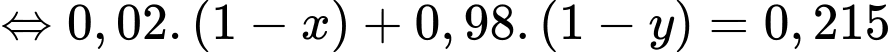
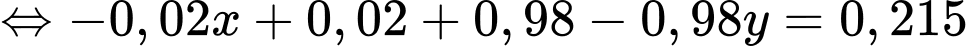
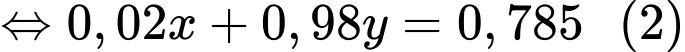
Từ (1) và (2) ta có hệ phương trình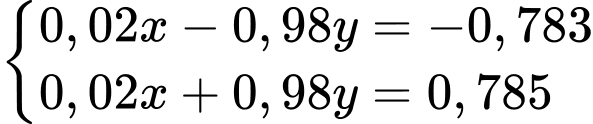
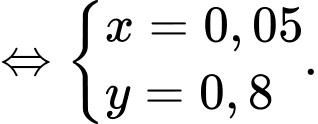
Suy ra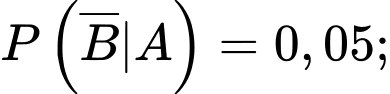
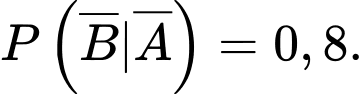
Áp dụng công thức xác suất toàn phần, ta có

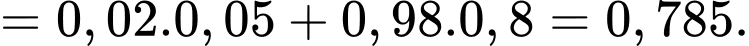
Áp dụng công thức Bayes, suy ra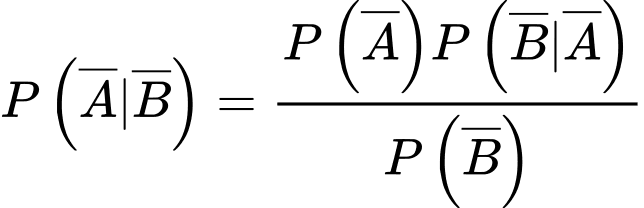
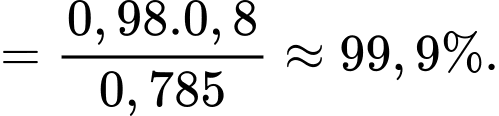
Gọi
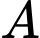 là biến cố “Người đó bị bệnh”
là biến cố “Người đó bị bệnh”
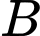 là biến cố “Xét nghiệm cho kết quả dương tính”
là biến cố “Xét nghiệm cho kết quả dương tính”
Khi đó
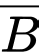 là biến cố “Xét nghiệm cho kết quả âm tính”
là biến cố “Xét nghiệm cho kết quả âm tính”
YCBT
 Tính
Tính  (dùng công thức Bayes để tính)
(dùng công thức Bayes để tính)
Từ dữ kiện đề bài, ta có
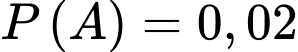
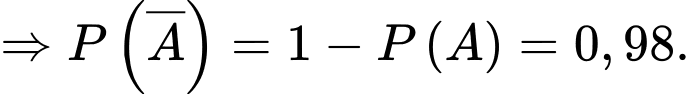
Giả sử

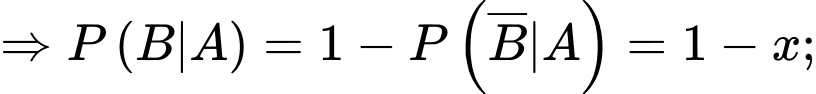

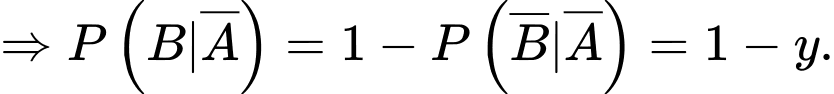
Ta có sơ đồ cây sau:

Từ giả thiết, ta có
+) Tỉ lệ chẩn đoán sai (tức người đó bị bệnh và xét nghiệm cho kết quả dương tính hoặc người đó không bị bệnh và xét nghiệm cho kết quả dương tính) bằng 0,197
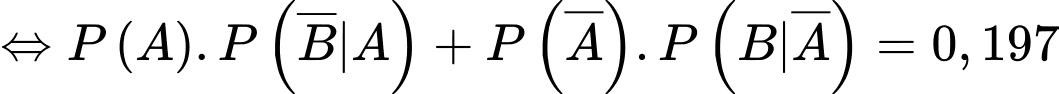
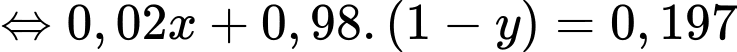
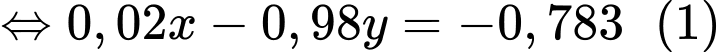
+) Số người có kết quả dương tính chiếm 21,5%

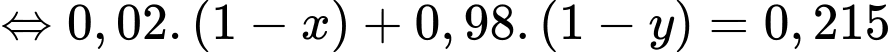
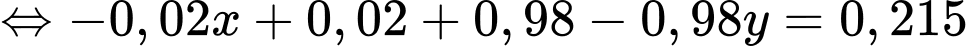
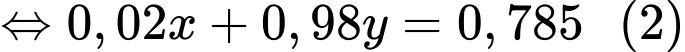
Từ (1) và (2) ta có hệ phương trình
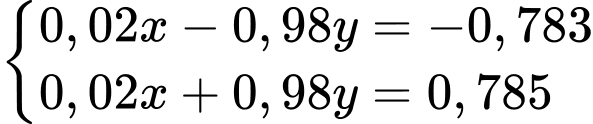
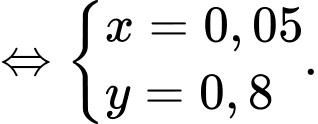
Suy ra
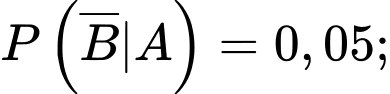
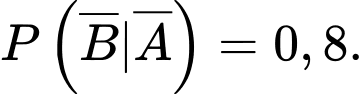
Áp dụng công thức xác suất toàn phần, ta có

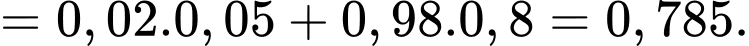
Áp dụng công thức Bayes, suy ra