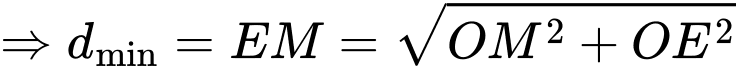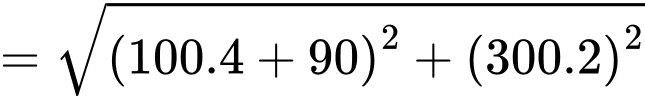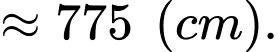PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [257842]: Cho hàm số 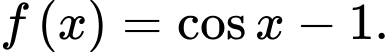 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
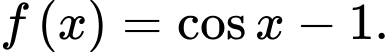 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 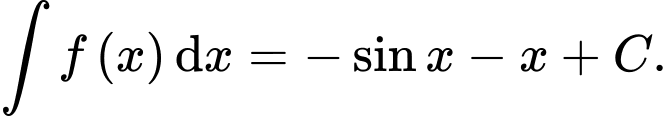
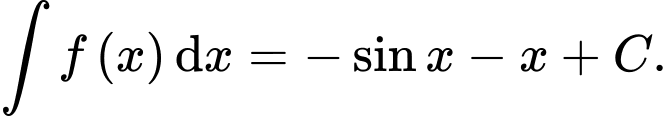
B, 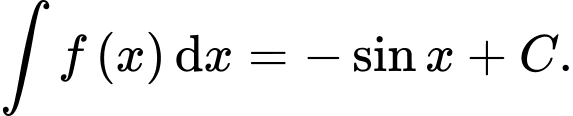
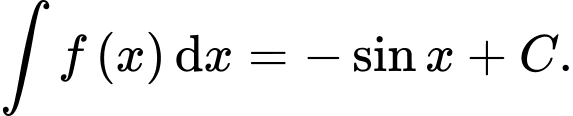
C, 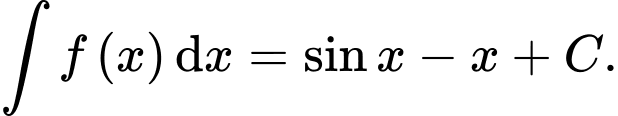
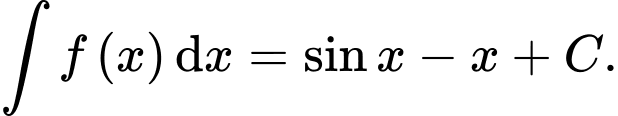
D, 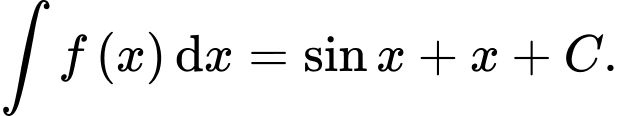
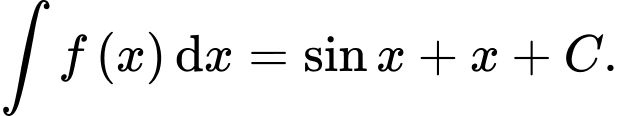
Chọn đáp án C.
Ta có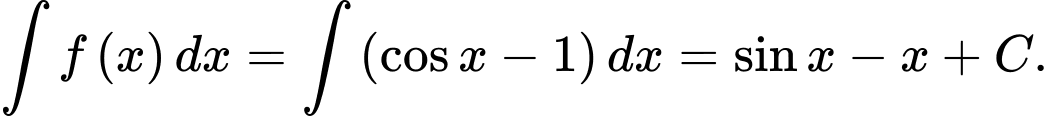 Đáp án: C
Đáp án: C
Ta có
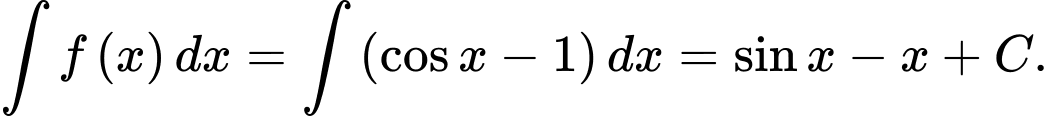 Đáp án: C
Đáp án: C
Câu 2 [696421]: Trong không gian 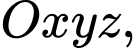 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 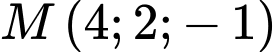 trên trục
trên trục 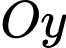 là
là
 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 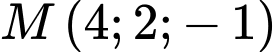 trên trục
trên trục  là
là A, 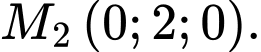
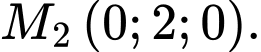
B, 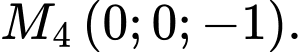
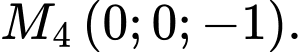
C, 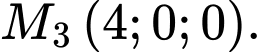
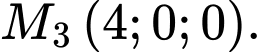
D, 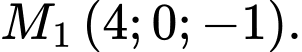
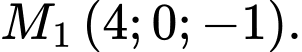
Chọn đáp án A.
Trong không gian hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 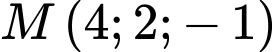 trên trục
trên trục  là
là 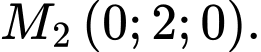 Đáp án: A
Đáp án: A
Trong không gian
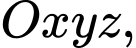 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 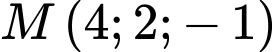 trên trục
trên trục 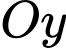 là
là 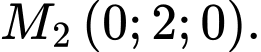 Đáp án: A
Đáp án: A
Câu 3 [616551]: Tiệm cận đứng của đồ thị hàm số 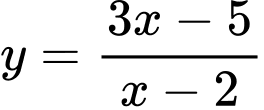 là
là
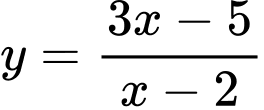 là
là A, 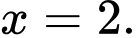
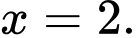
B, 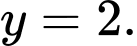
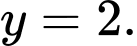
C, 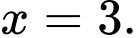
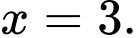
D, 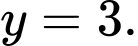
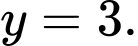
Chọn đáp án A.
Hàm số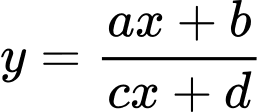 có tiệm cận đứng là
có tiệm cận đứng là 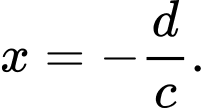
Áp dụng ta được: Tiệm cận đứng của đồ thị hàm số là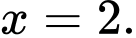 Đáp án: A
Đáp án: A
Hàm số
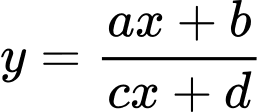 có tiệm cận đứng là
có tiệm cận đứng là 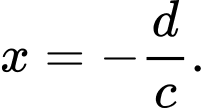
Áp dụng ta được: Tiệm cận đứng của đồ thị hàm số là
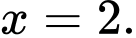 Đáp án: A
Đáp án: A
Câu 4 [696423]: Cho 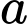 là số thực dương tuỳ ý,
là số thực dương tuỳ ý, 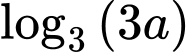 bằng
bằng
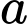 là số thực dương tuỳ ý,
là số thực dương tuỳ ý, 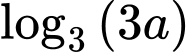 bằng
bằng A, 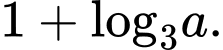
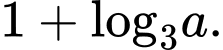
B, 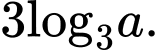
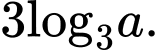
C, 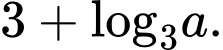
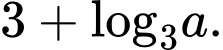
D, 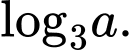
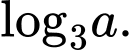
Chọn đáp án A.
Ta có: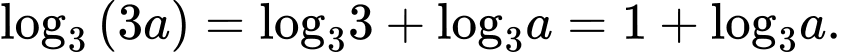 Đáp án: A
Đáp án: A
Ta có:
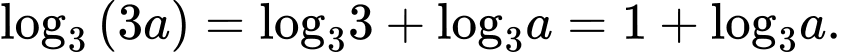 Đáp án: A
Đáp án: A
Câu 5 [696424]: Cho mẫu số liệu ghép nhóm có bảng tần số ghép nhóm như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
A, 2.
B, 6.
C, 8.
D, 4.
Chọn đáp án C.
Khoảng biến thiên của mẫu số liệu ghép nhóm là: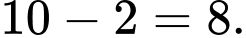 Đáp án: C
Đáp án: C
Khoảng biến thiên của mẫu số liệu ghép nhóm là:
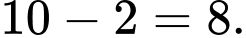 Đáp án: C
Đáp án: C
Câu 6 [696425]: Trong không gian 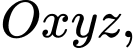 cho mặt phẳng
cho mặt phẳng 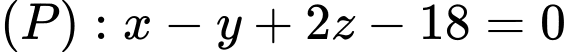 và điểm
và điểm 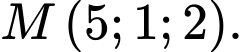 Đường thẳng đi qua
Đường thẳng đi qua 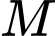 và vuông góc với
và vuông góc với 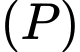 có phương trình tham số là
có phương trình tham số là
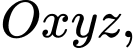 cho mặt phẳng
cho mặt phẳng 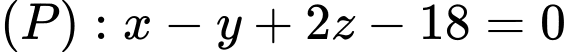 và điểm
và điểm 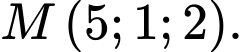 Đường thẳng đi qua
Đường thẳng đi qua 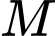 và vuông góc với
và vuông góc với 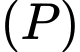 có phương trình tham số là
có phương trình tham số là A, 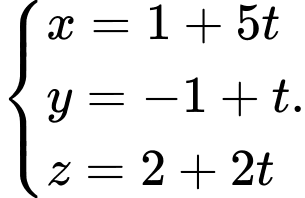
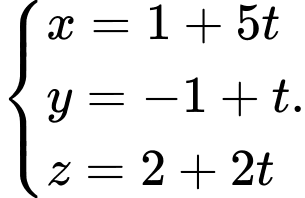
B, 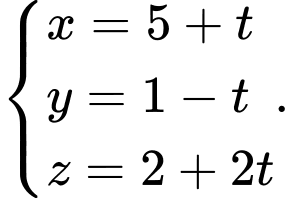
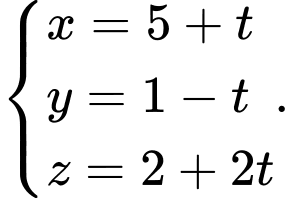
C, 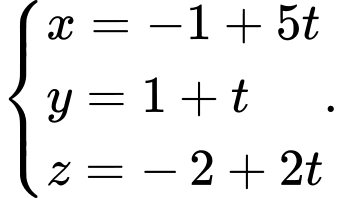
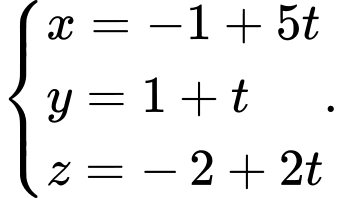
D, 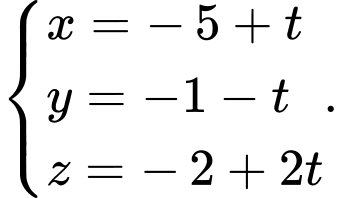
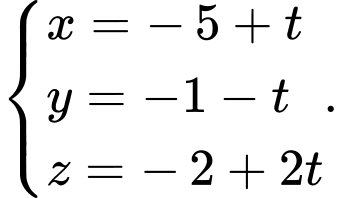
Chọn đáp án B.
Đường thẳng đi qua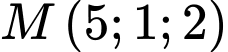 và vuông góc với
và vuông góc với 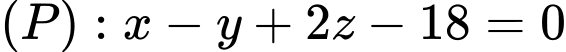 có phương trình tham số là
có phương trình tham số là 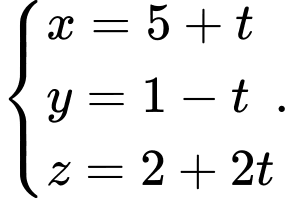 Đáp án: B
Đáp án: B
Đường thẳng đi qua
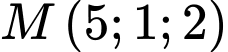 và vuông góc với
và vuông góc với 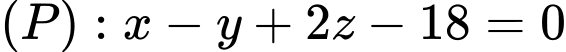 có phương trình tham số là
có phương trình tham số là 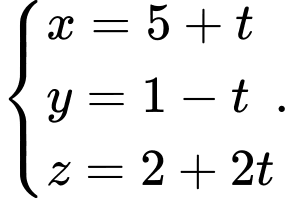 Đáp án: B
Đáp án: B
Câu 7 [696426]: Cho tứ diện  có
có  đôi một vuông góc. Khẳng định nào sau đây sai?
đôi một vuông góc. Khẳng định nào sau đây sai?
 có
có  đôi một vuông góc. Khẳng định nào sau đây sai?
đôi một vuông góc. Khẳng định nào sau đây sai? A, 

B, 

C, 

D, 

Chọn đáp án B.
Ta có: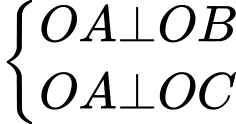
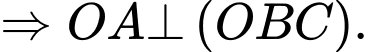
Tương tự,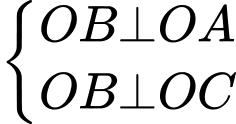
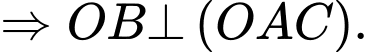
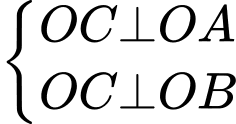
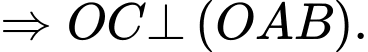 Đáp án: B
Đáp án: B
Ta có:
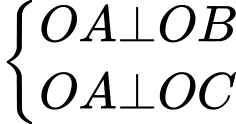
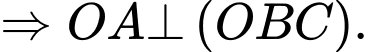
Tương tự,
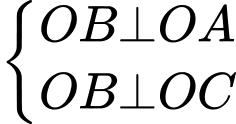
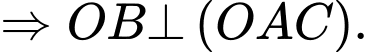
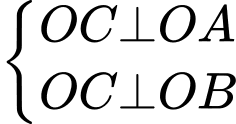
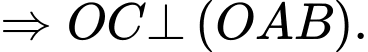 Đáp án: B
Đáp án: B Sử dụng thông tin dưới đây để trả lời câu 8 và câu 9
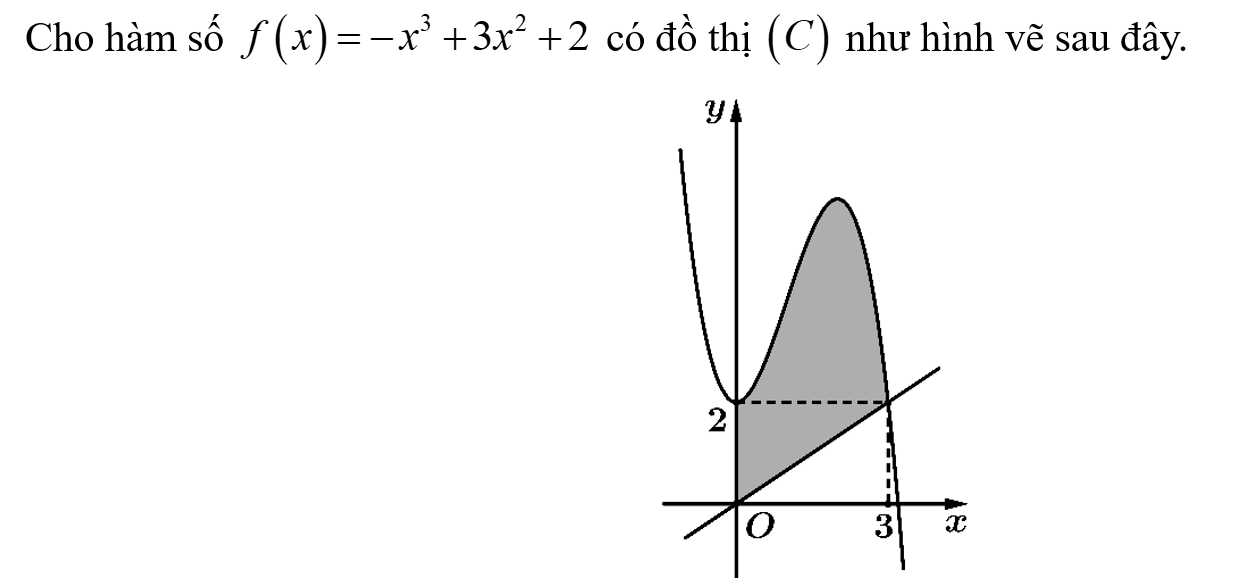
Câu 8 [702912]: Giá trị cực đại của hàm số 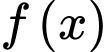 bằng
bằng
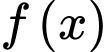 bằng
bằng A, 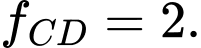
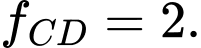
B, 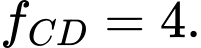
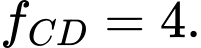
C, 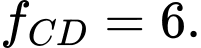
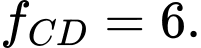
D, 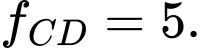
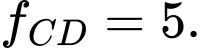
Chọn đáp án C.
Ta có: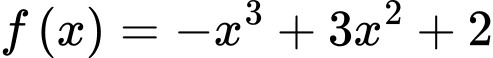
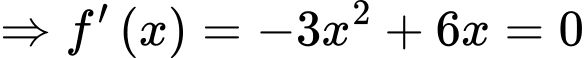
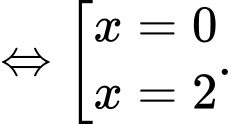
Dựa vào đồ thị hàm số ta có: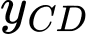
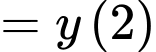
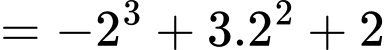
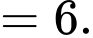 Đáp án: C
Đáp án: C
Ta có:
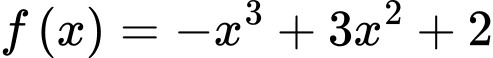
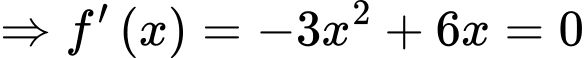
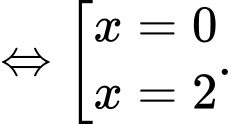
Dựa vào đồ thị hàm số ta có:
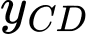
 Đáp án: C
Đáp án: C
Câu 9 [702972]: Diện tích 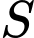 của phần tô đậm trong hình vẽ bằng
của phần tô đậm trong hình vẽ bằng
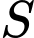 của phần tô đậm trong hình vẽ bằng
của phần tô đậm trong hình vẽ bằng A, 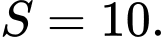
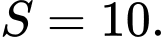
B, 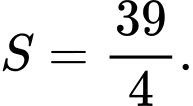
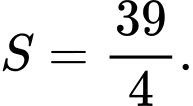
C, 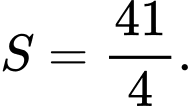
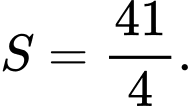
D, 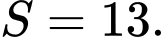
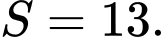
Chọn đáp án B.
Phương trình đường thẳng đi qua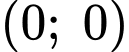 và
và 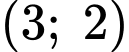 là
là 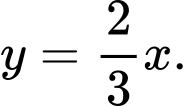
Diện tích của phần tô đậm trong hình vẽ bằng
của phần tô đậm trong hình vẽ bằng
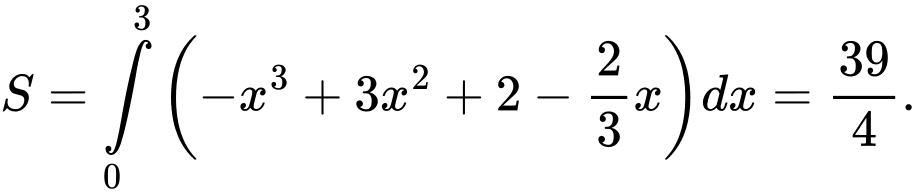 Đáp án: B
Đáp án: B
Phương trình đường thẳng đi qua
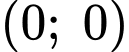 và
và 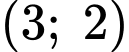 là
là 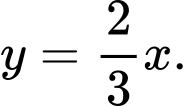
Diện tích
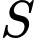 của phần tô đậm trong hình vẽ bằng
của phần tô đậm trong hình vẽ bằng 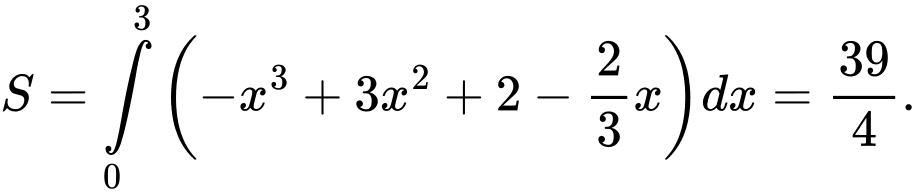 Đáp án: B
Đáp án: B
Câu 10 [696427]: Cho hình chóp 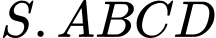 có đáy
có đáy 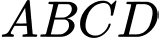 là hình bình hành và mặt bên
là hình bình hành và mặt bên 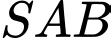 là tam giác đều. Tính góc giữa hai vectơ
là tam giác đều. Tính góc giữa hai vectơ  và
và 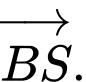
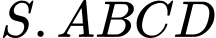 có đáy
có đáy 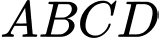 là hình bình hành và mặt bên
là hình bình hành và mặt bên 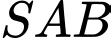 là tam giác đều. Tính góc giữa hai vectơ
là tam giác đều. Tính góc giữa hai vectơ 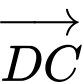 và
và 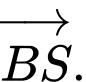
A, 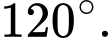
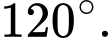
B, 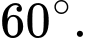
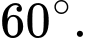
C, 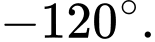
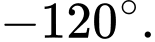
D, 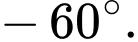
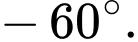
Chọn đáp án A.
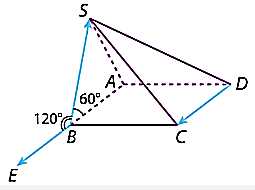
Vì ABCD là hình bình hành nên .
.
Trên tia AB lấy điểm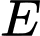 sao cho
sao cho 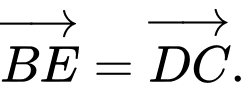 .
.
Ta có: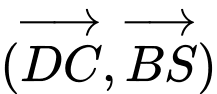
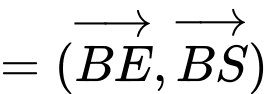
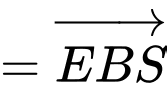

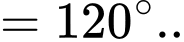
Vậy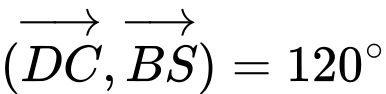 . Đáp án: A
. Đáp án: A

Vì ABCD là hình bình hành nên
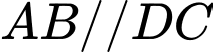 .
.
Trên tia AB lấy điểm
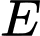 sao cho
sao cho 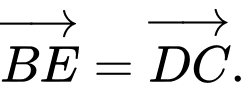 .
.
Ta có:
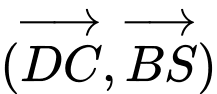
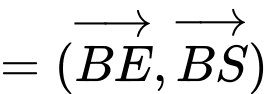
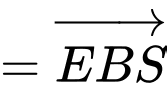

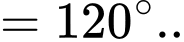
Vậy
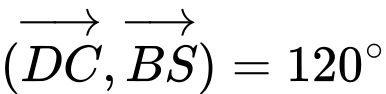 . Đáp án: A
. Đáp án: A
Câu 11 [696428]: Cho cấp số nhân 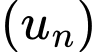 với
với 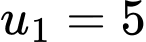 và
và 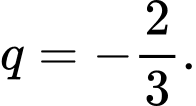 Gọi
Gọi 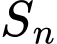 là tổng của
là tổng của 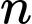 số hạng đầu tiên của
số hạng đầu tiên của 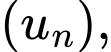 khi đó
khi đó 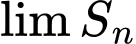 bằng
bằng
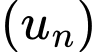 với
với 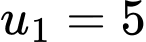 và
và 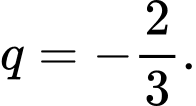 Gọi
Gọi 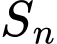 là tổng của
là tổng của 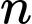 số hạng đầu tiên của
số hạng đầu tiên của 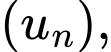 khi đó
khi đó 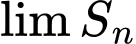 bằng
bằng A, 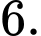
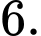
B, 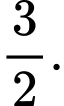
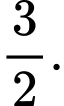
C, 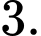
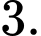
D, 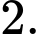
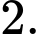
Chọn đáp án C.
Ta có:
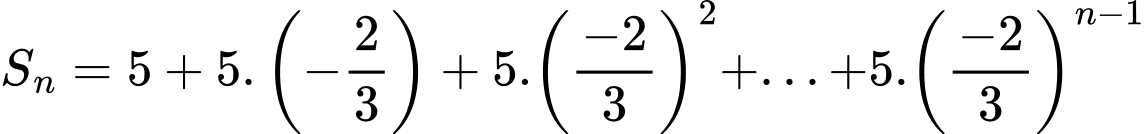
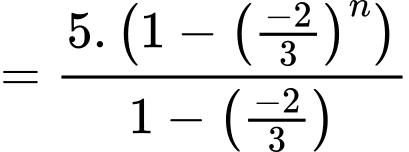
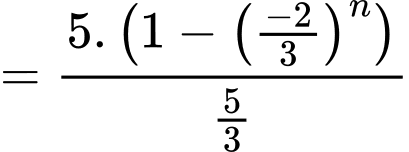
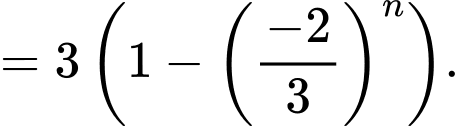
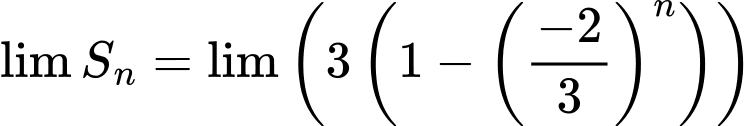
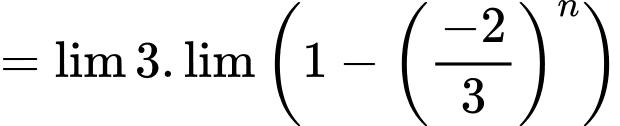
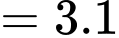
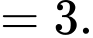 Đáp án: C
Đáp án: C
Ta có:
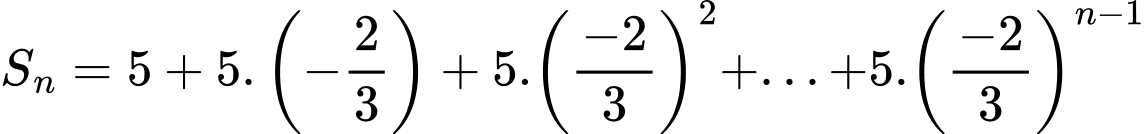
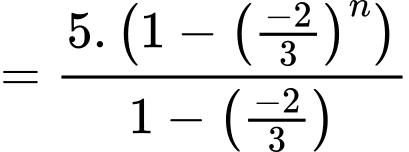
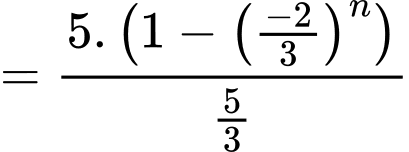
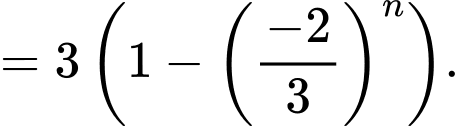
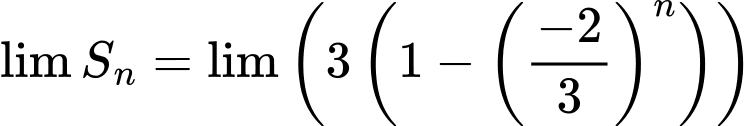
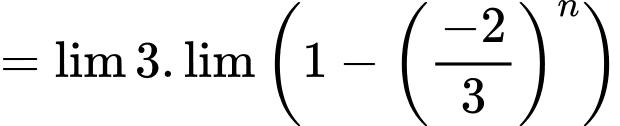
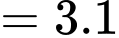
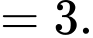 Đáp án: C
Đáp án: C
Câu 12 [257666]: Tập nghiệm của bất phương trình 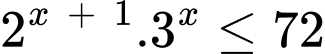 là
là
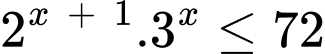 là
là A, 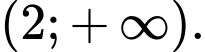
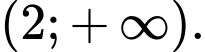
B, 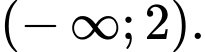
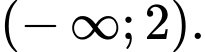
C, 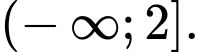
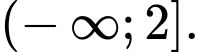
D, 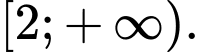
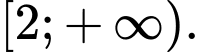
Chọn đáp án C.
Ta có bất phương trình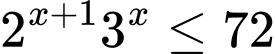
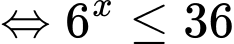
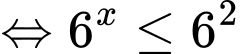
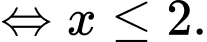
Vậy tập nghiệm của bất phương trình là Đáp án: C
Đáp án: C
Ta có bất phương trình
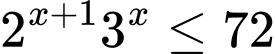
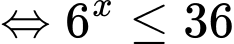
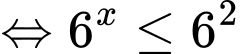
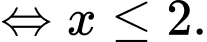
Vậy tập nghiệm của bất phương trình là
 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
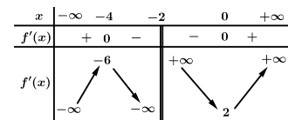
Câu 13 [696429]: Cho hàm số 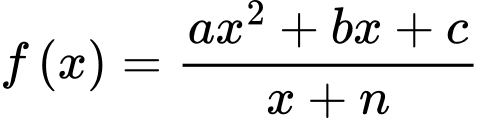 xác định trên
xác định trên 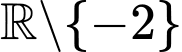 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
 xác định trên
xác định trên 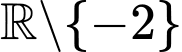 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
a) Sai.
Dựa theo bảng biến thiên ta thấy đồ thị hàm số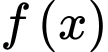 có tiệm cận đứng là
có tiệm cận đứng là 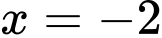
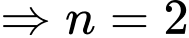 .
.
b) Sai.
Dựa theo bảng biến thiên ta thấy đồ thị hàm số có 2 điểm cực trị là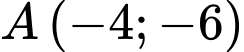 và
và 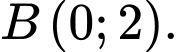
c) Đúng.
Phương trình đường thẳng đi qua 2 điểm cực trị có dạng
đi qua 2 điểm cực trị có dạng 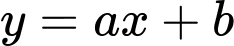 .
.
Thay tọa độ 2 điểm cực trị vào phương trình đường thẳng ta được:
ta được:
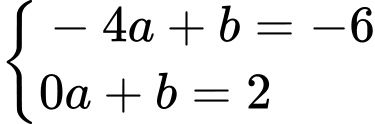
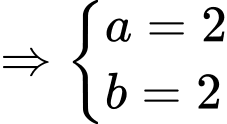
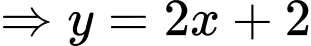
d) Đúng.
Tâm đối xứng của đồ thị hàm số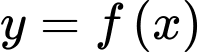 là giao điểm của đường tiệm đứng và tiệm cận xiên của đồ thị.
là giao điểm của đường tiệm đứng và tiệm cận xiên của đồ thị.
Ta có: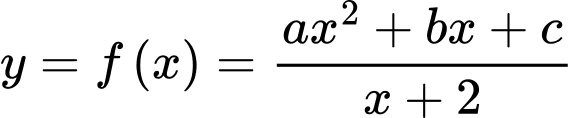
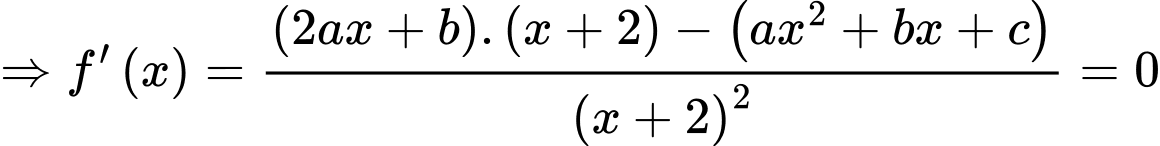
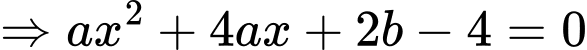 (1)
(1)
Thay hoành độ 2 điểm cực trị vào (1) ta được: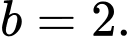
Thay tọa độ 2 điểm cực trị vào đồ thị hàm số ta được:
ta được:
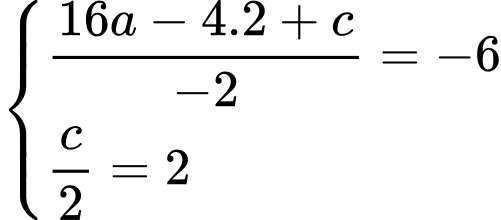
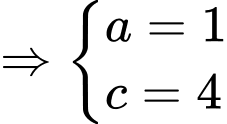
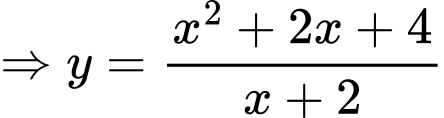 .
.
Đường tiệm cận xiên của đồ thị hàm số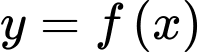 có dạng
có dạng 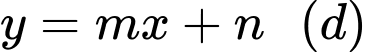 , trong đó:
, trong đó:
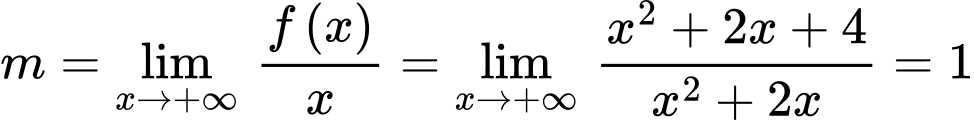
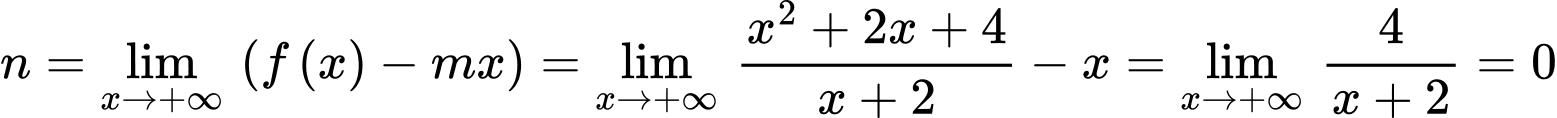
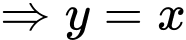

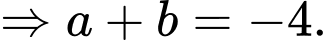
Dựa theo bảng biến thiên ta thấy đồ thị hàm số
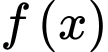 có tiệm cận đứng là
có tiệm cận đứng là 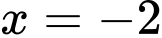
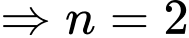 .
.b) Sai.
Dựa theo bảng biến thiên ta thấy đồ thị hàm số có 2 điểm cực trị là
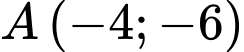 và
và 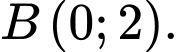
c) Đúng.
Phương trình đường thẳng
 đi qua 2 điểm cực trị có dạng
đi qua 2 điểm cực trị có dạng 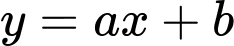 .
.Thay tọa độ 2 điểm cực trị vào phương trình đường thẳng
 ta được:
ta được: 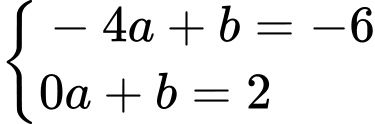
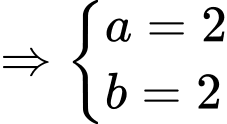
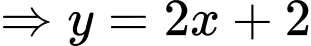
d) Đúng.
Tâm đối xứng của đồ thị hàm số
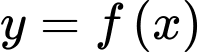 là giao điểm của đường tiệm đứng và tiệm cận xiên của đồ thị.
là giao điểm của đường tiệm đứng và tiệm cận xiên của đồ thị.Ta có:
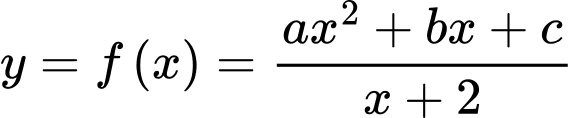
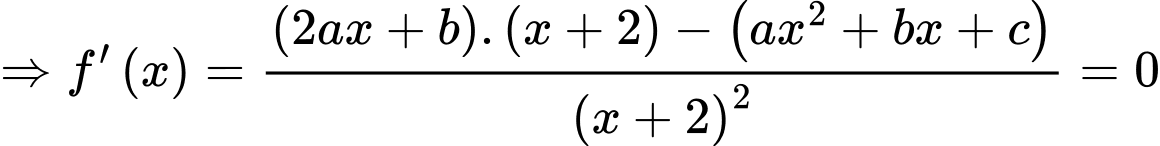
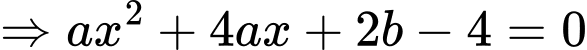 (1)
(1)Thay hoành độ 2 điểm cực trị vào (1) ta được:
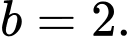
Thay tọa độ 2 điểm cực trị vào đồ thị hàm số
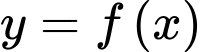 ta được:
ta được: 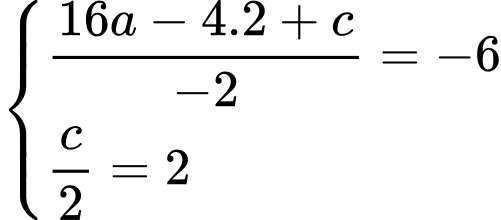
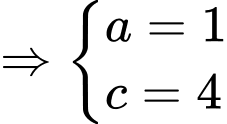
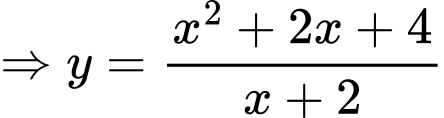 .
.Đường tiệm cận xiên của đồ thị hàm số
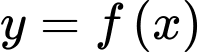 có dạng
có dạng 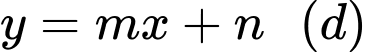 , trong đó:
, trong đó: 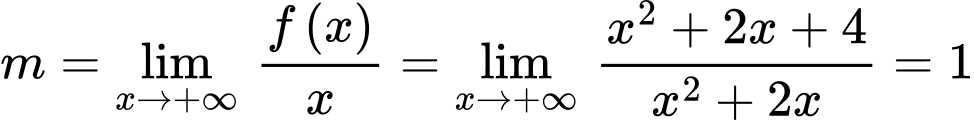
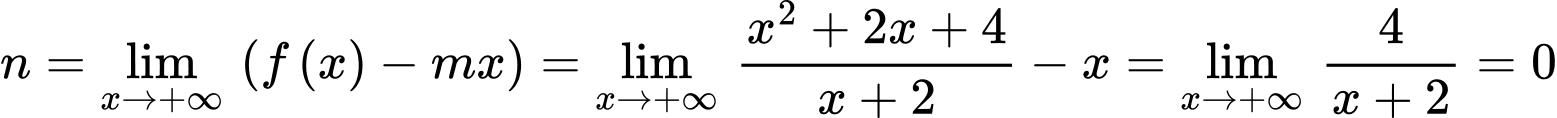
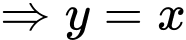

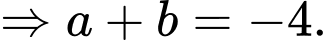
Câu 14 [696430]: Một thùng hàng có 20 sản phẩm, trong đó có 3 sản phẩm loại I và 17 sản phẩm loại II. Trong quá trình vận chuyển, một sản phẩm bị thất lạc không rõ chất lượng. Lấy ngẫu nhiên 1 sản phẩm từ 19 sản phẩm còn lại.
Gọi 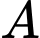 là biến cố “Sản phẩm thất lạc là sản phẩm loại II”.
là biến cố “Sản phẩm thất lạc là sản phẩm loại II”.
Gọi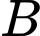 là biến cố “Sản phẩm lấy được là sản phẩm loại I”.
là biến cố “Sản phẩm lấy được là sản phẩm loại I”.
a) Sai.
Xác suất sản phẩm bị thất lạc là sản phẩm loại II là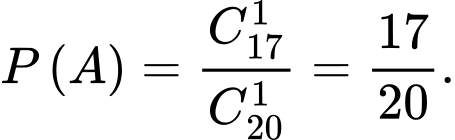
b) Sai.
Xác suất lấy được sản phẩm loại I nếu sản phẩm bị thất lạc là sản phẩm loại II là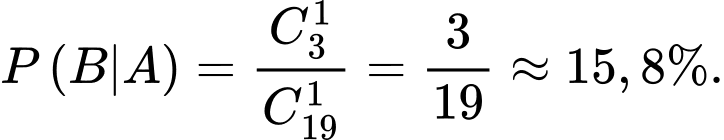
c) Đúng.
Ta có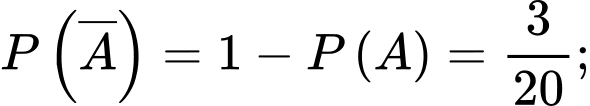
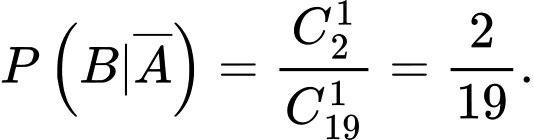
Ta có sơ đồ cây sau:
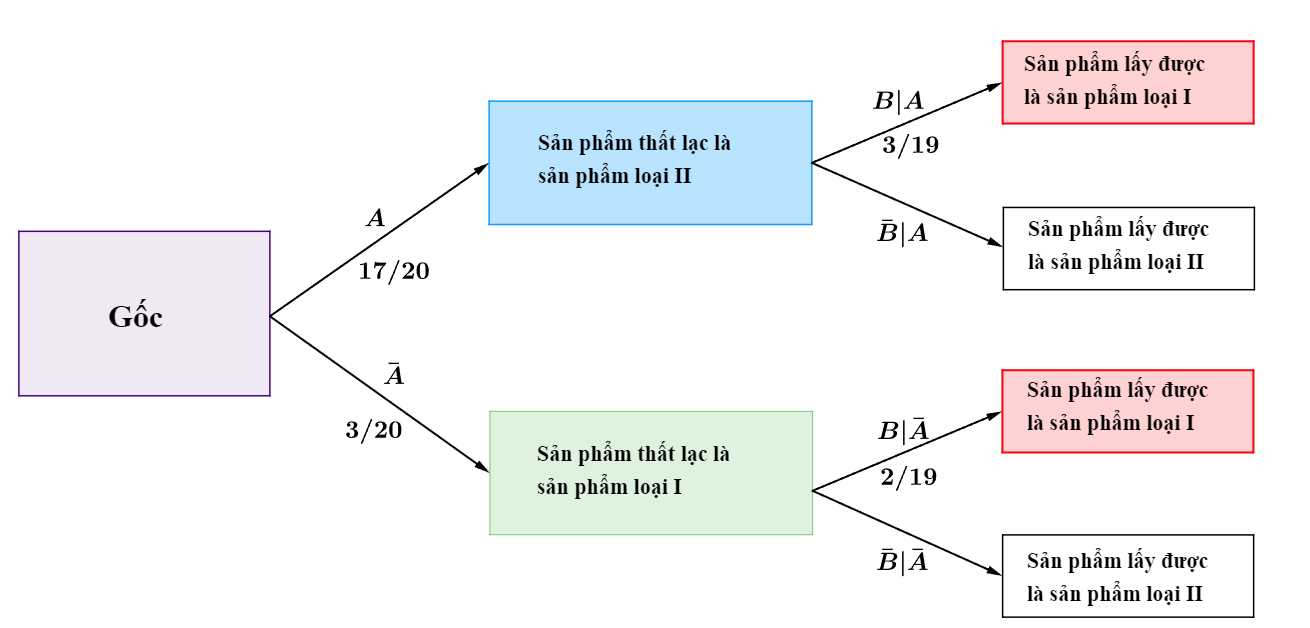
Suy ra xác suất lấy được sản phẩm loại I là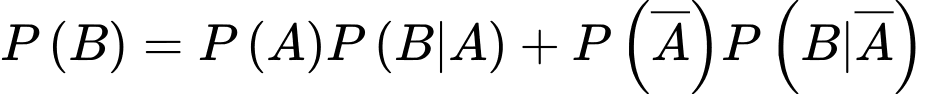
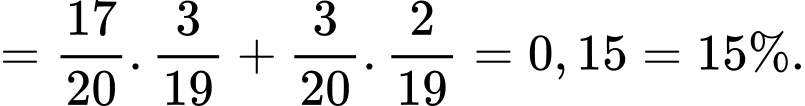
d) Sai.
Ta cần tính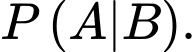
Áp dụng công thức Bayes, ta có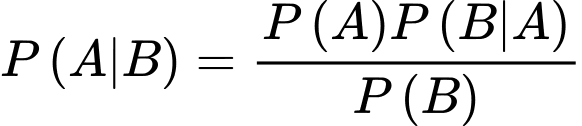
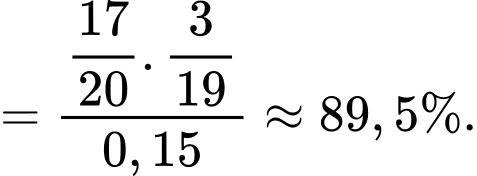
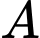 là biến cố “Sản phẩm thất lạc là sản phẩm loại II”.
là biến cố “Sản phẩm thất lạc là sản phẩm loại II”. Gọi
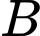 là biến cố “Sản phẩm lấy được là sản phẩm loại I”.
là biến cố “Sản phẩm lấy được là sản phẩm loại I”.a) Sai.
Xác suất sản phẩm bị thất lạc là sản phẩm loại II là
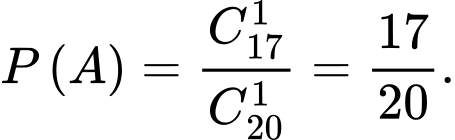
b) Sai.
Xác suất lấy được sản phẩm loại I nếu sản phẩm bị thất lạc là sản phẩm loại II là
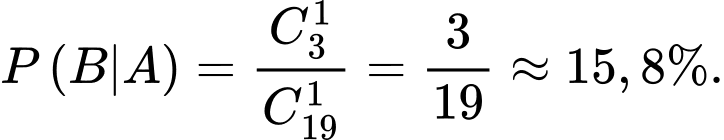
c) Đúng.
Ta có
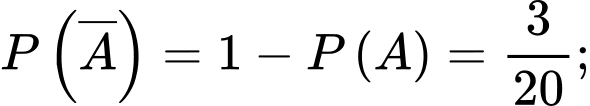
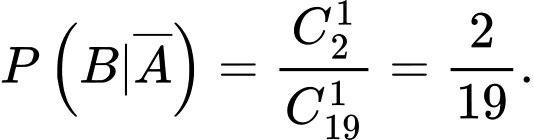
Ta có sơ đồ cây sau:

Suy ra xác suất lấy được sản phẩm loại I là
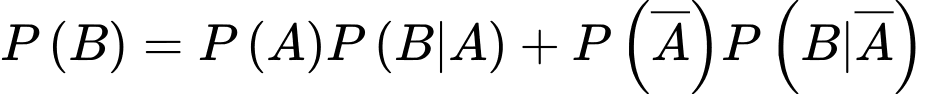
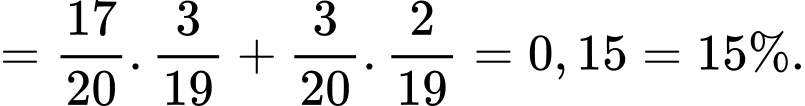
d) Sai.
Ta cần tính
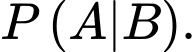
Áp dụng công thức Bayes, ta có
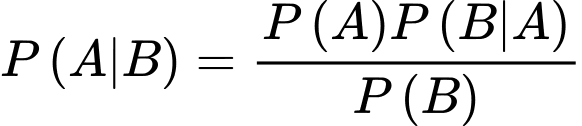
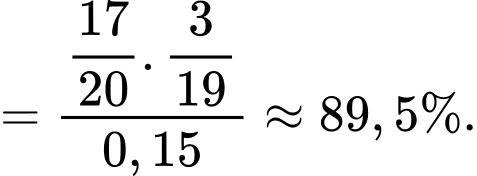
Câu 15 [696431]: Hải đăng là một ngọn tháp (nhà hoặc khung) được thiết kế để chiếu sáng từ một hệ thống đèn và thấu kính, hoặc thời xưa là chiếu sáng bằng lửa, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Vào năm 293 trước Công nguyên, ngọn hải đăng đầu tiên đã được người Phoenicia xây dựng trên hòn đảo Pharos tại Alexandria. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là một mét), coi một phần mặt biển được khảo sát là mặt phẳng 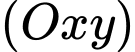 , trục
, trục  hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao
hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 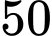 mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí
mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí 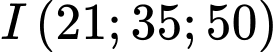 , biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
, biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.

 , trục
, trục  hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao
hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 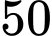 mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí
mét so với mực nước biển (hình vẽ bên dưới) biết đỉnh ở vị trí 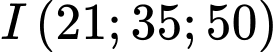 , biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
, biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km. 
a) Sai.
Vì đỉnh là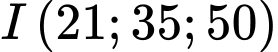 và có bán kính phủ sóng
và có bán kính phủ sóng 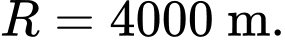
 Phương trình mặt cầu tâm
Phương trình mặt cầu tâm 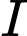 bán kính
bán kính 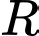 là
là 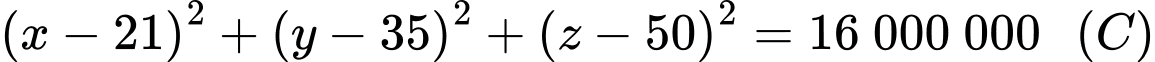 .
.
b) Sai.
Thay tọa độ điểm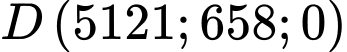 vào phương trình mặt cầu
vào phương trình mặt cầu  ta được:
ta được: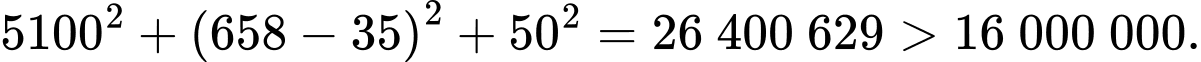
c) Đúng.
Bán kính vùng sáng này là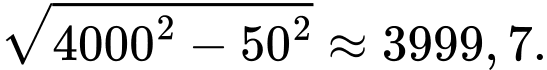
d) Đúng.
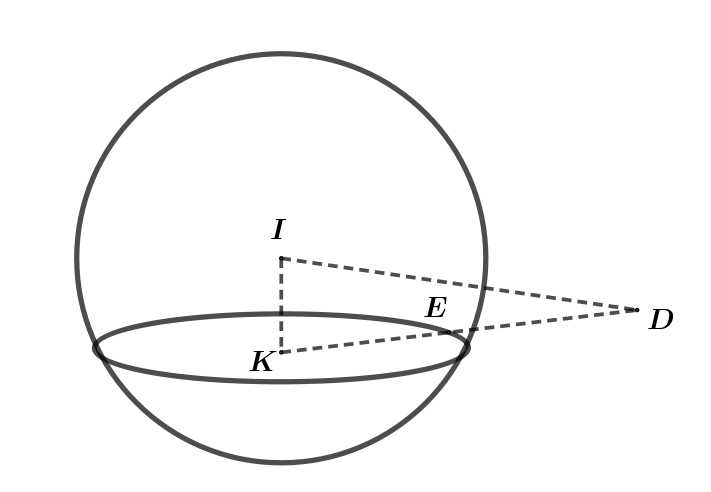
Chân ngọn hải đăng là hình chiếu của điểm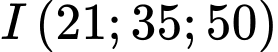 lên mặt phẳng
lên mặt phẳng 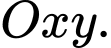
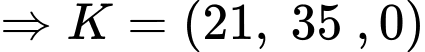
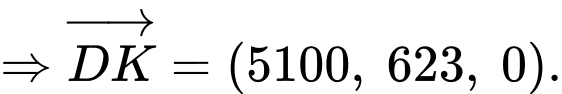
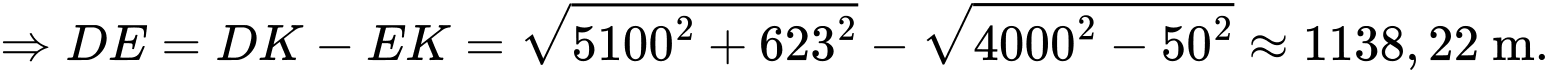
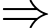 Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là
Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là 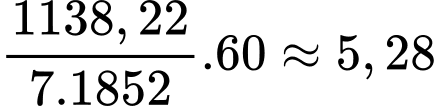 phút.
phút.
Vì đỉnh là
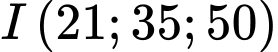 và có bán kính phủ sóng
và có bán kính phủ sóng 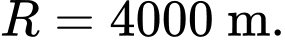
 Phương trình mặt cầu tâm
Phương trình mặt cầu tâm 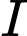 bán kính
bán kính 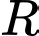 là
là 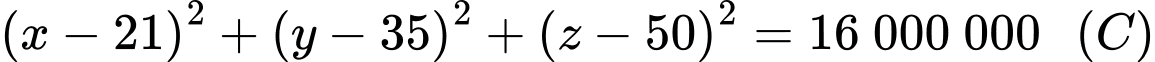 .
.b) Sai.
Thay tọa độ điểm
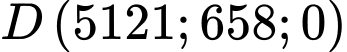 vào phương trình mặt cầu
vào phương trình mặt cầu  ta được:
ta được: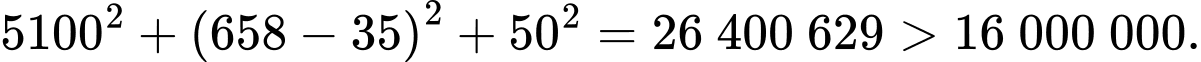
c) Đúng.
Bán kính vùng sáng này là
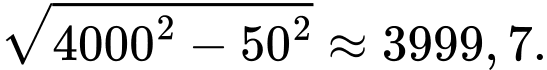
d) Đúng.

Chân ngọn hải đăng là hình chiếu của điểm
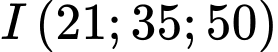 lên mặt phẳng
lên mặt phẳng 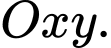
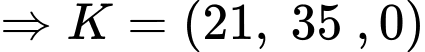
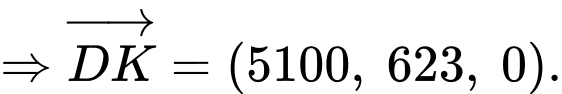
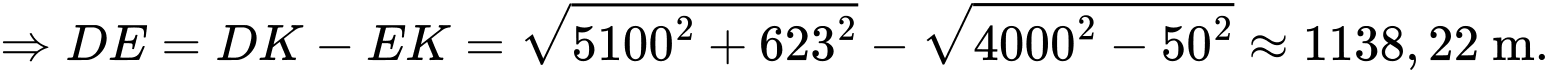
 Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là
Thời gian để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên là 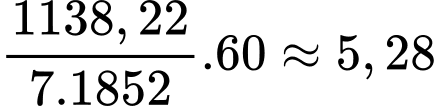 phút.
phút.
Câu 16 [696432]: Chất béo di chuyển qua dòng máu gắn kết với protein trong một tổ hợp được gọi là lipoprotein. Lipoprotein mật độ thấp (LDL) lấy cholesterol từ gan và chuyển đến các tế bào, thả bất kỳ cholesterol dư thừa nào trên thành động mạch. Quá nhiều LDL trong máu làm tăng nguy cơ mắc bệnh tim và đột quỵ. Một bệnh nhân có mức LDL ban đầu là 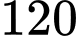 nhận được một loại thuốc được phát hiện có thể giảm mức LDL theo tốc độ được cho bởi
nhận được một loại thuốc được phát hiện có thể giảm mức LDL theo tốc độ được cho bởi
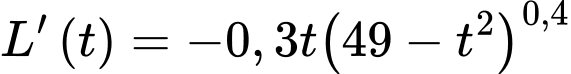 đơn vị/ngày
đơn vị/ngày
trong đó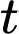 là số ngày sau khi thuốc được dùng, với
là số ngày sau khi thuốc được dùng, với 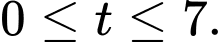
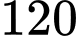 nhận được một loại thuốc được phát hiện có thể giảm mức LDL theo tốc độ được cho bởi
nhận được một loại thuốc được phát hiện có thể giảm mức LDL theo tốc độ được cho bởi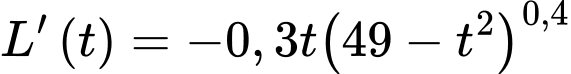 đơn vị/ngày
đơn vị/ngàytrong đó
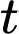 là số ngày sau khi thuốc được dùng, với
là số ngày sau khi thuốc được dùng, với 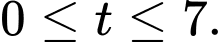
a) Sai.
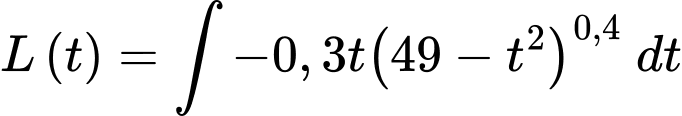
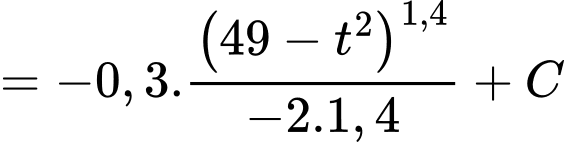
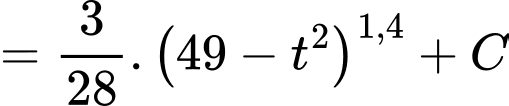
b) Đúng.
Ta có: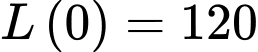
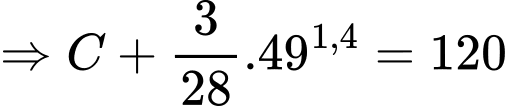
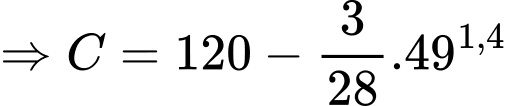
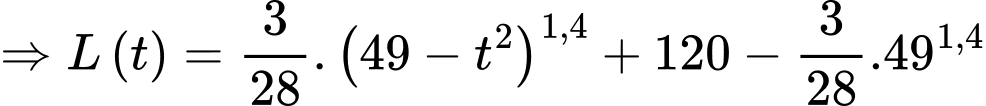
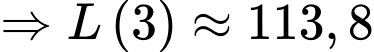 .
.
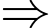 Mức LDL của bệnh nhân giảm được
Mức LDL của bệnh nhân giảm được 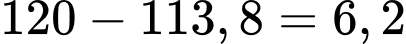 đơn vị trong 3 ngày đầu sau khi dùng thuốc.
đơn vị trong 3 ngày đầu sau khi dùng thuốc.
c) Đúng.
LDL tại thời điểm dùng thuốc lần cuối cùng bằng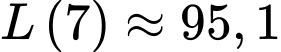 đơn vị.
đơn vị.
d) Sai.
Ta có: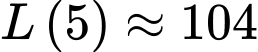 đơn vị
đơn vị
 Sau 5 ngày mức LDL của bệnh nhân chưa trở về mức “an toàn”.
Sau 5 ngày mức LDL của bệnh nhân chưa trở về mức “an toàn”.
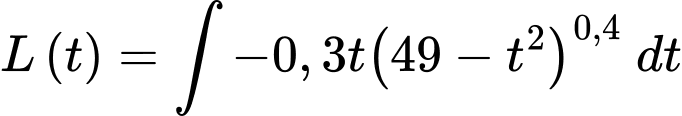
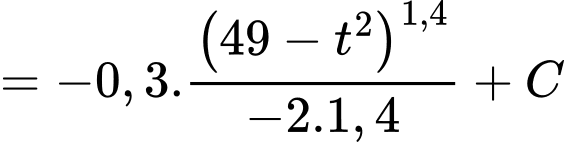
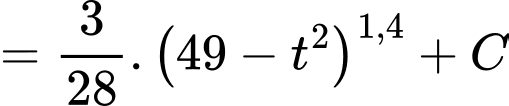
b) Đúng.
Ta có:
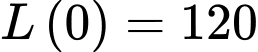
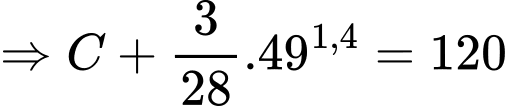
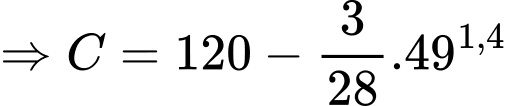
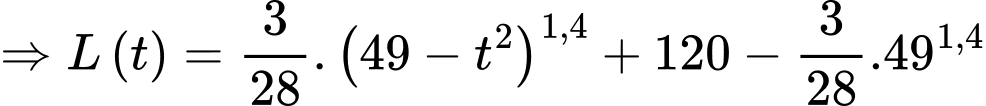
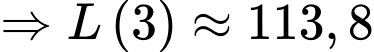 .
. Mức LDL của bệnh nhân giảm được
Mức LDL của bệnh nhân giảm được 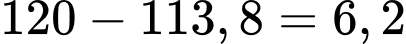 đơn vị trong 3 ngày đầu sau khi dùng thuốc.
đơn vị trong 3 ngày đầu sau khi dùng thuốc.c) Đúng.
LDL tại thời điểm dùng thuốc lần cuối cùng bằng
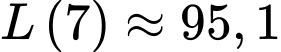 đơn vị.
đơn vị.d) Sai.
Ta có:
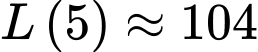 đơn vị
đơn vị Sau 5 ngày mức LDL của bệnh nhân chưa trở về mức “an toàn”.
Sau 5 ngày mức LDL của bệnh nhân chưa trở về mức “an toàn”. PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696433]: Cho hình chóp 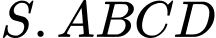 có đáy
có đáy 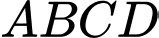 là hình thang vuông tại
là hình thang vuông tại 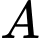 và
và 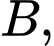
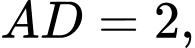
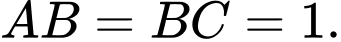 Cạnh bên
Cạnh bên 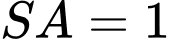 và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng 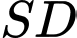 và mặt phẳng
và mặt phẳng 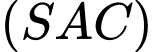 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
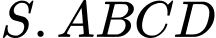 có đáy
có đáy 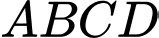 là hình thang vuông tại
là hình thang vuông tại 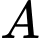 và
và 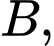
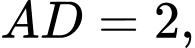
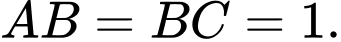 Cạnh bên
Cạnh bên 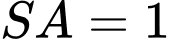 và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng
và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng 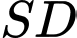 và mặt phẳng
và mặt phẳng 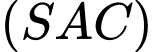 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 0,8.
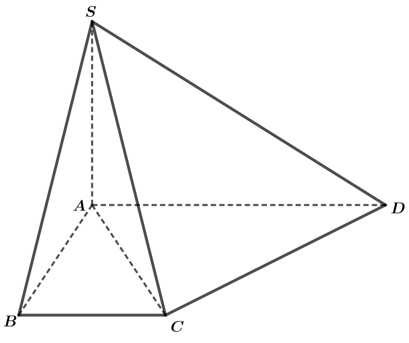
Ta có:
+)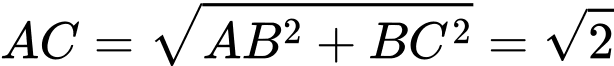
+)
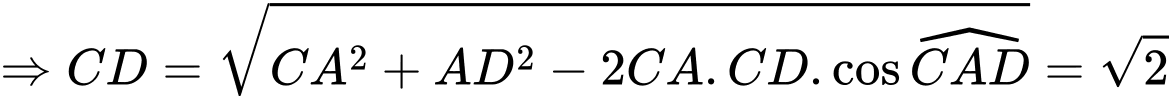

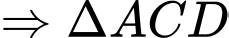 vuông tại
vuông tại 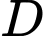
 , mà
, mà 
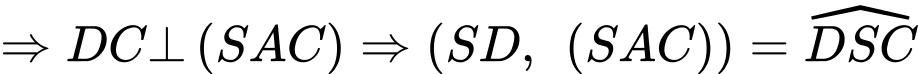
+)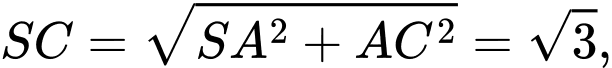
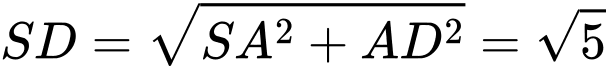
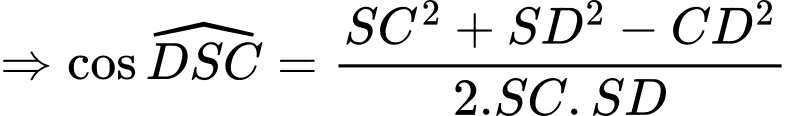
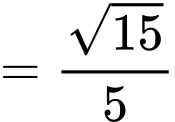
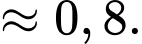

Ta có:
+)
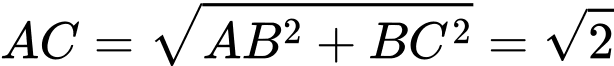
+)

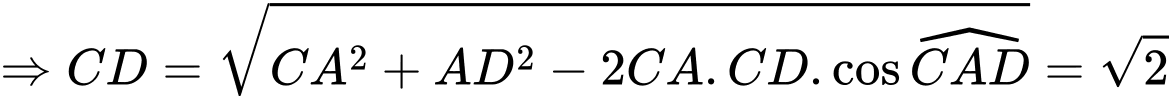

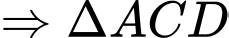 vuông tại
vuông tại 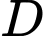
 , mà
, mà 
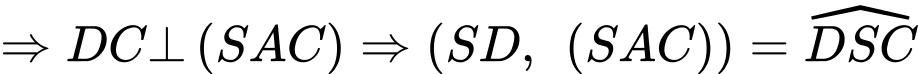
+)
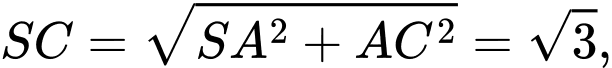
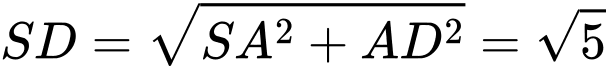
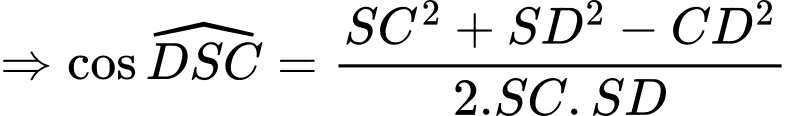
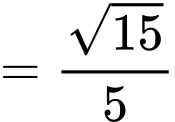
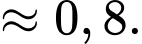
Câu 18 [696435]: Để nghiên cứu xác suất của một loại cây trồng mới phát triển bình thường, người ta trồng hạt giống của loại cây đó trên hai ô đất thí nghiệm  khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất
khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất 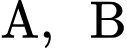 lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
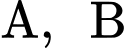 khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất
khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất 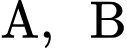 lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
lần lượt là 0,61 và 0,7. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng thì thấy hạt giống chỉ phát triển bình thường được trên duy nhất một ô đất. Tính xác suất hạt giống chỉ phát triển bình thường trên ô đất A. (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,18.
Gọi: A: Biến cố "Hạt giống phát triển bình thường trên ô đất A"
B: Biến cố "Hạt giống phát triển bình thường trên ô đất B"
Biết: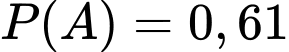 ,
,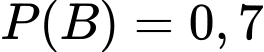
Ta cần tính xác suất để hạt giống chỉ phát triển bình thường trên ô đất A , tức là biến cố
Do các ô đất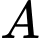 và
và 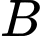 là độc lập, nên:
là độc lập, nên:
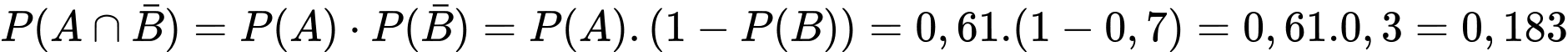
Vậy xác suất hạt giống chỉ phát triển bình thường trên ô đất A là: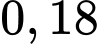
Gọi: A: Biến cố "Hạt giống phát triển bình thường trên ô đất A"
B: Biến cố "Hạt giống phát triển bình thường trên ô đất B"
Biết:
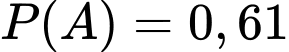 ,
,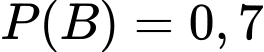
Ta cần tính xác suất để hạt giống chỉ phát triển bình thường trên ô đất A , tức là biến cố

Do các ô đất
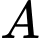 và
và  là độc lập, nên:
là độc lập, nên:
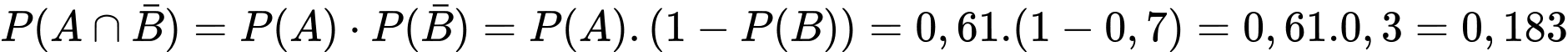
Vậy xác suất hạt giống chỉ phát triển bình thường trên ô đất A là:
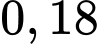
Câu 19 [693129]: Người ta thiết kế một mẫu gạch lát nền nhà có dạng hình vuông cạnh 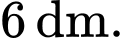 Bốn góc viên gạch màu trắng, phần ở giữa màu đen (xem hình vẽ). Đường viền của phần màu đen bao gồm bốn đoạn thẳng nằm trên các cạnh hình vuông và bốn đường cong có tính chất: Tích khoảng cách từ một điểm bất kì thuộc đường cong đó đến hai trục đối xứng của viên gạch (hai đường thẳng đi qua tâm viên gạch và lần lượt song song với hai cạnh vuông góc) bằng
Bốn góc viên gạch màu trắng, phần ở giữa màu đen (xem hình vẽ). Đường viền của phần màu đen bao gồm bốn đoạn thẳng nằm trên các cạnh hình vuông và bốn đường cong có tính chất: Tích khoảng cách từ một điểm bất kì thuộc đường cong đó đến hai trục đối xứng của viên gạch (hai đường thẳng đi qua tâm viên gạch và lần lượt song song với hai cạnh vuông góc) bằng  Hãy cho biết phần màu đen có diện tích bằng bao nhiêu decimét vuông? (làm tròn kết quả đến hàng phần mười).
Hãy cho biết phần màu đen có diện tích bằng bao nhiêu decimét vuông? (làm tròn kết quả đến hàng phần mười).
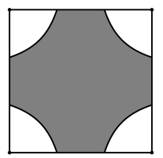
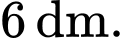 Bốn góc viên gạch màu trắng, phần ở giữa màu đen (xem hình vẽ). Đường viền của phần màu đen bao gồm bốn đoạn thẳng nằm trên các cạnh hình vuông và bốn đường cong có tính chất: Tích khoảng cách từ một điểm bất kì thuộc đường cong đó đến hai trục đối xứng của viên gạch (hai đường thẳng đi qua tâm viên gạch và lần lượt song song với hai cạnh vuông góc) bằng
Bốn góc viên gạch màu trắng, phần ở giữa màu đen (xem hình vẽ). Đường viền của phần màu đen bao gồm bốn đoạn thẳng nằm trên các cạnh hình vuông và bốn đường cong có tính chất: Tích khoảng cách từ một điểm bất kì thuộc đường cong đó đến hai trục đối xứng của viên gạch (hai đường thẳng đi qua tâm viên gạch và lần lượt song song với hai cạnh vuông góc) bằng  Hãy cho biết phần màu đen có diện tích bằng bao nhiêu decimét vuông? (làm tròn kết quả đến hàng phần mười).
Hãy cho biết phần màu đen có diện tích bằng bao nhiêu decimét vuông? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 25,2.
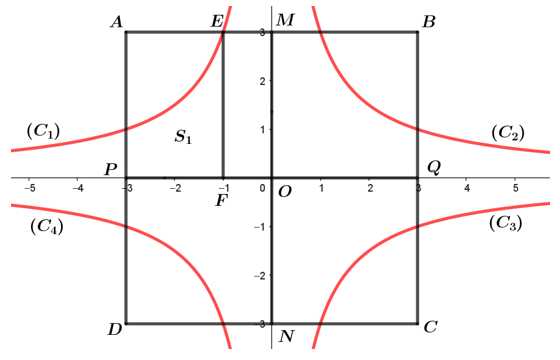
Vì tích khoảng cách từ một điểm bất kì thuộc đường cong đó đến hai trục đối xứng của viên gạch bằng .
.
 Theo hình vẽ ta có: đường cong
Theo hình vẽ ta có: đường cong 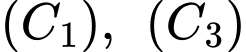 thuộc đồ thị hàm số
thuộc đồ thị hàm số 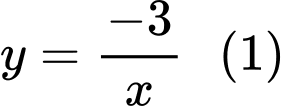 ; đường cong
; đường cong 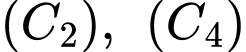 thuộc đồ thị hàm số
thuộc đồ thị hàm số 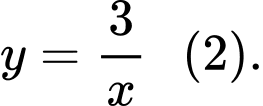
Gọi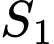 diện tích giới hạn bởi đường cong
diện tích giới hạn bởi đường cong 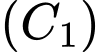 , các đường thẳng
, các đường thẳng 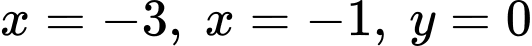 .
.
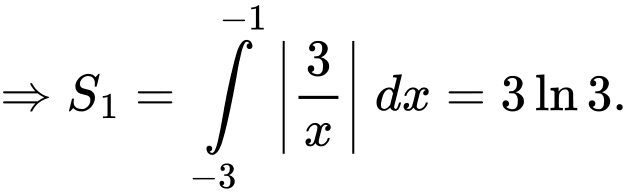
Có: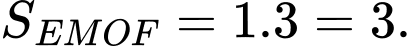
Diện tích phần tô đậm là
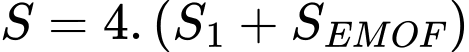
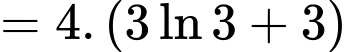
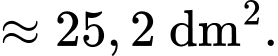

Vì tích khoảng cách từ một điểm bất kì thuộc đường cong đó đến hai trục đối xứng của viên gạch bằng
 .
. Theo hình vẽ ta có: đường cong
Theo hình vẽ ta có: đường cong 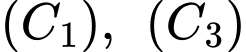 thuộc đồ thị hàm số
thuộc đồ thị hàm số 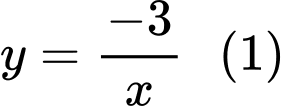 ; đường cong
; đường cong 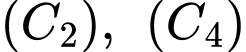 thuộc đồ thị hàm số
thuộc đồ thị hàm số 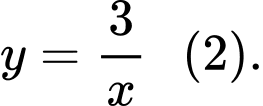
Gọi
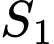 diện tích giới hạn bởi đường cong
diện tích giới hạn bởi đường cong 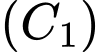 , các đường thẳng
, các đường thẳng 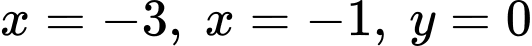 .
.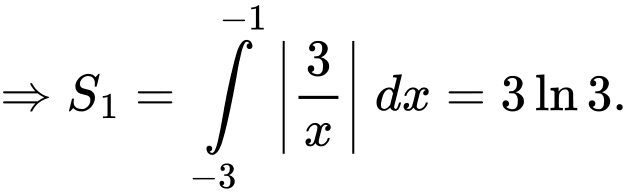
Có:
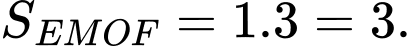
Diện tích phần tô đậm là
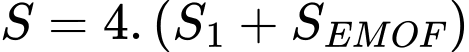
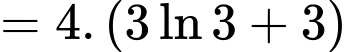
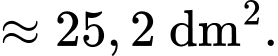
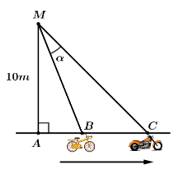
Câu 20 [693651]: Một người quan sát đang đứng ở điểm 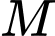 cách con đường một khoảng
cách con đường một khoảng 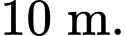 Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp ba lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn
Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp ba lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn 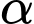 (đơn vị rad) của người quan sát với hai chiếc xe đó (kết quả làm tròn đến hàng phần trăm).
(đơn vị rad) của người quan sát với hai chiếc xe đó (kết quả làm tròn đến hàng phần trăm).
 cách con đường một khoảng
cách con đường một khoảng 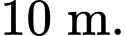 Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp ba lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn
Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp ba lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn 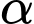 (đơn vị rad) của người quan sát với hai chiếc xe đó (kết quả làm tròn đến hàng phần trăm).
(đơn vị rad) của người quan sát với hai chiếc xe đó (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,52.
Đặt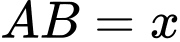
 ( do vận tốc của xe máy gấp ba lần vận tốc xe đạp)
( do vận tốc của xe máy gấp ba lần vận tốc xe đạp)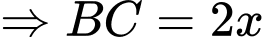 .
.
Ta có: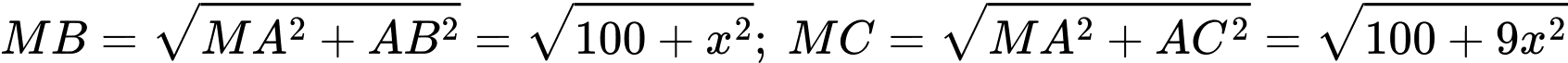
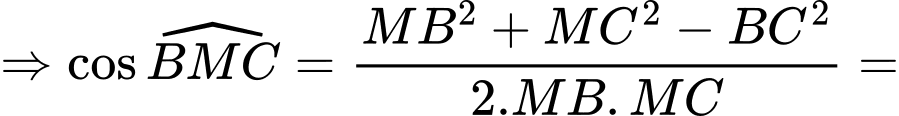
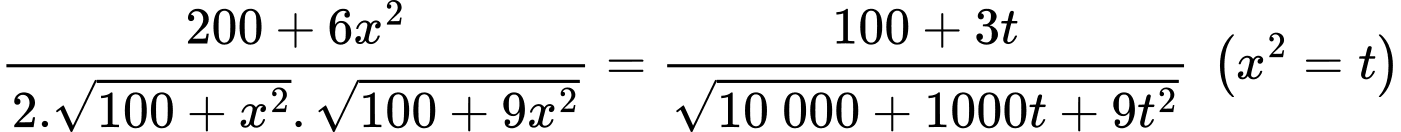
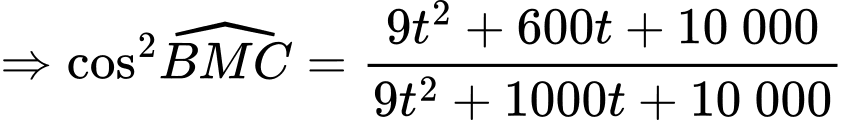
Xét hàm số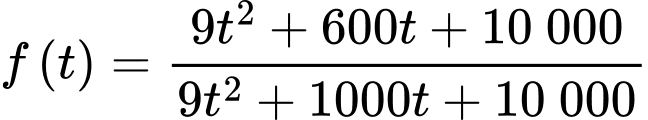
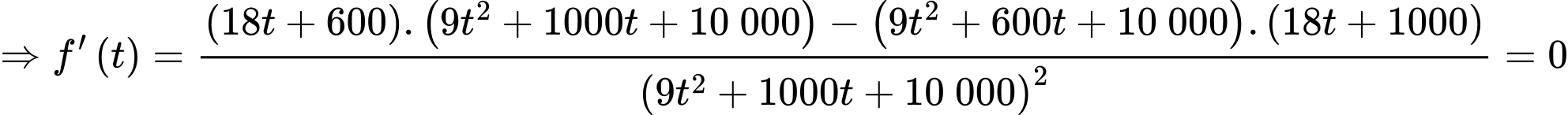
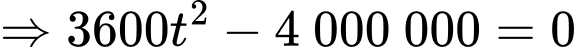
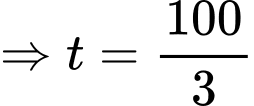 là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm số 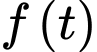 .
.
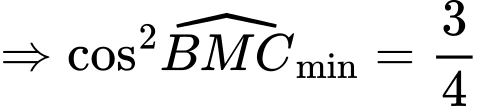
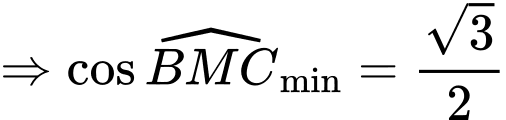
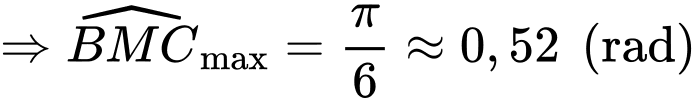 .
.
Đặt
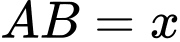
 ( do vận tốc của xe máy gấp ba lần vận tốc xe đạp)
( do vận tốc của xe máy gấp ba lần vận tốc xe đạp)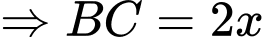 .
.Ta có:
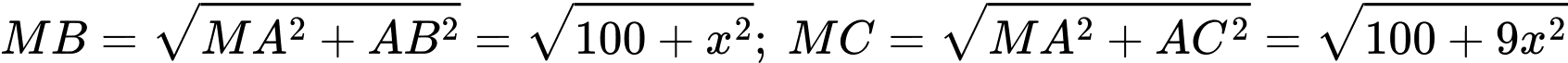
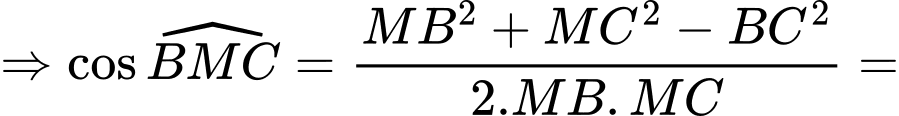
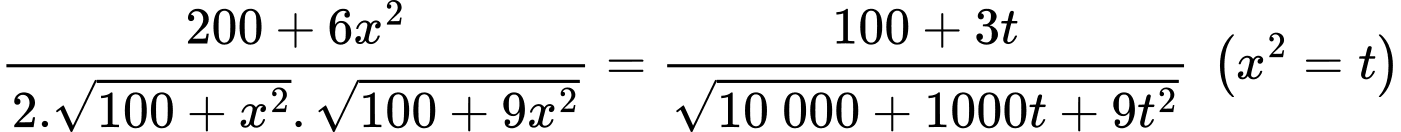
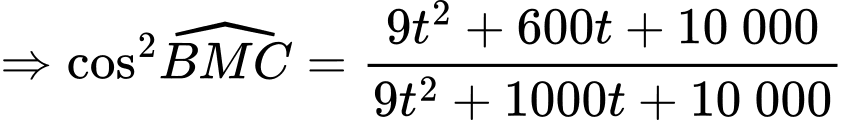
Xét hàm số
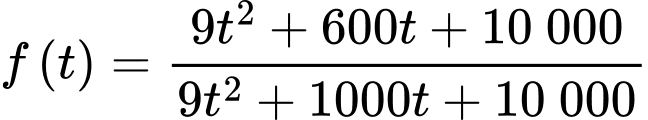
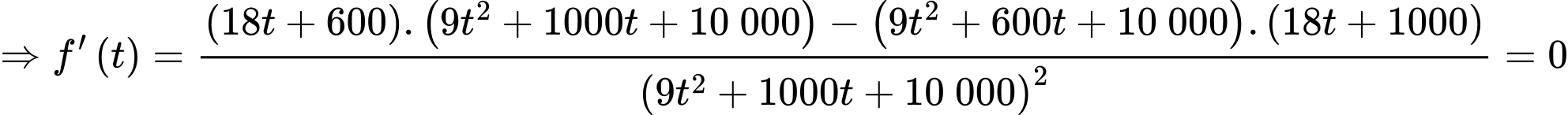
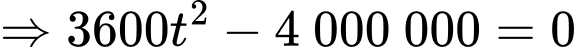
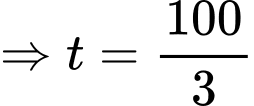 là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm số 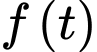 .
.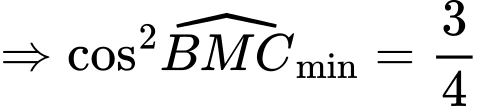
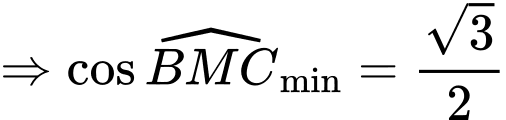
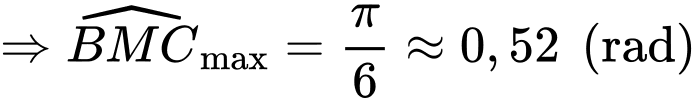 .
.
Câu 21 [696438]: Trong không gian 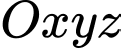 cho các điểm
cho các điểm 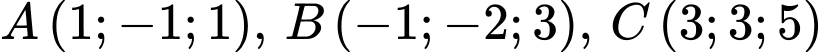 và mặt cầu
và mặt cầu 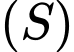 có tâm
có tâm 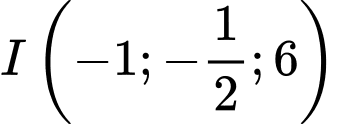 bán kính
bán kính  Gọi
Gọi 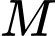 là điểm thuộc mặt cầu
là điểm thuộc mặt cầu 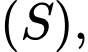
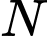 là điểm thỏa mãn
là điểm thỏa mãn 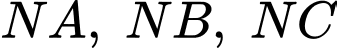 hợp với mặt phẳng
hợp với mặt phẳng 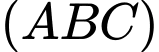 các góc bằng nhau. Tìm giá trị nhỏ nhất của
các góc bằng nhau. Tìm giá trị nhỏ nhất của 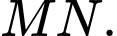
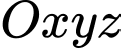 cho các điểm
cho các điểm 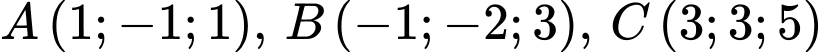 và mặt cầu
và mặt cầu 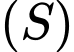 có tâm
có tâm 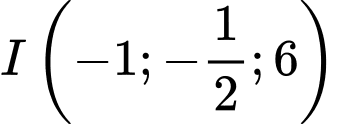 bán kính
bán kính  Gọi
Gọi 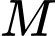 là điểm thuộc mặt cầu
là điểm thuộc mặt cầu 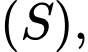
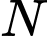 là điểm thỏa mãn
là điểm thỏa mãn 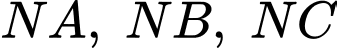 hợp với mặt phẳng
hợp với mặt phẳng 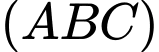 các góc bằng nhau. Tìm giá trị nhỏ nhất của
các góc bằng nhau. Tìm giá trị nhỏ nhất của 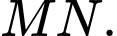
Điền đáp án: 0.
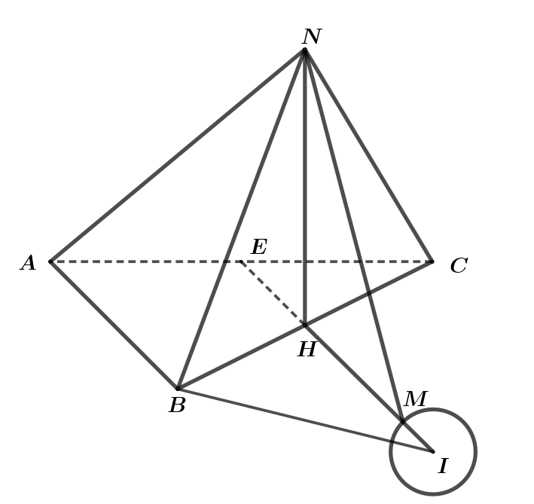
Ta có: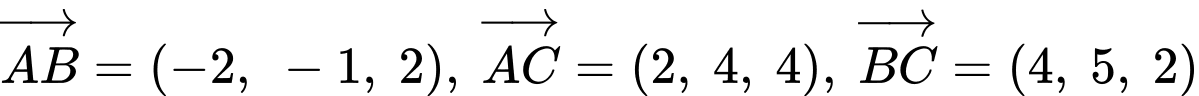
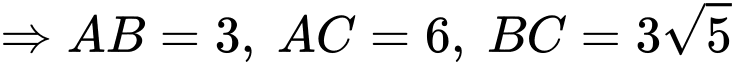
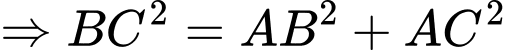
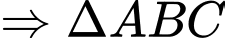 vuông tại
vuông tại 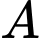
Vậy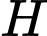 là trung điểm của
là trung điểm của 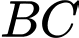 và
và 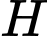 là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 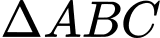
Qua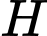 kẻ đường thẳng
kẻ đường thẳng 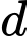 vuông góc với
vuông góc với 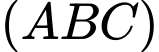
 là trục đường tròn ngoại tiếp
là trục đường tròn ngoại tiếp 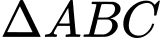
Phương trình mặt phẳng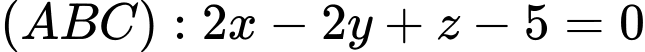
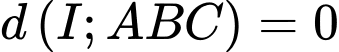

TH1: hợp với mặt phẳng
hợp với mặt phẳng 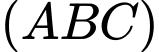 một góc
một góc 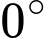
 là điểm bất kì thuộc
là điểm bất kì thuộc 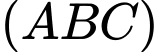
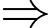
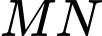 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi  .
.
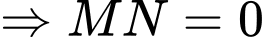
TH2: hợp với mặt phẳng
hợp với mặt phẳng 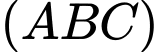 một góc
một góc 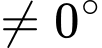
Vì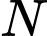 là điểm thỏa mãn
là điểm thỏa mãn  hợp với mặt phẳng
hợp với mặt phẳng 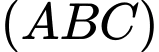 các góc bằng nhau.
các góc bằng nhau.
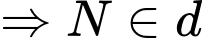
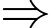
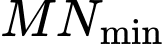 khi và chỉ khi
khi và chỉ khi 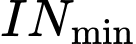
Từ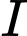 dựng vuông góc
dựng vuông góc 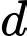 tại
tại 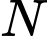 .Khi đó:
.Khi đó: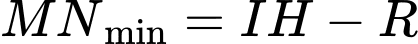
Dấu bằng xảy ra khi hay
hay 
Vậy hợp với mặt phẳng
hợp với mặt phẳng 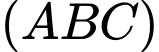 một góc
một góc 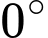 (loại vì không thỏa trường hợp)
(loại vì không thỏa trường hợp)
Vậy giá trị nhỏ nhất của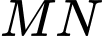 bằng 0.
bằng 0.

Ta có:
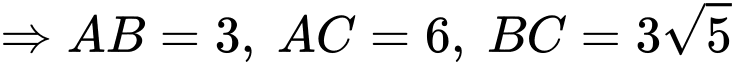
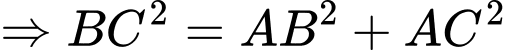
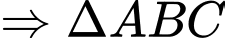 vuông tại
vuông tại 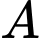
Vậy
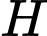 là trung điểm của
là trung điểm của 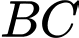 và
và 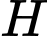 là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 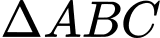
Qua
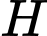 kẻ đường thẳng
kẻ đường thẳng 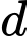 vuông góc với
vuông góc với 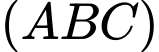
 là trục đường tròn ngoại tiếp
là trục đường tròn ngoại tiếp 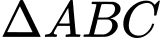
Phương trình mặt phẳng
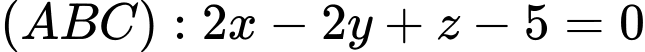
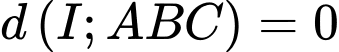

TH1:
 hợp với mặt phẳng
hợp với mặt phẳng 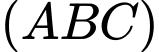 một góc
một góc 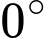
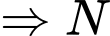 là điểm bất kì thuộc
là điểm bất kì thuộc 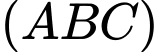
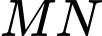 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi  .
.
TH2:
 hợp với mặt phẳng
hợp với mặt phẳng 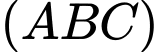 một góc
một góc 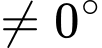
Vì
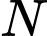 là điểm thỏa mãn
là điểm thỏa mãn  hợp với mặt phẳng
hợp với mặt phẳng 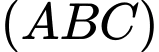 các góc bằng nhau.
các góc bằng nhau.
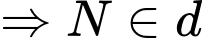
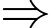
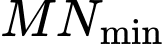 khi và chỉ khi
khi và chỉ khi 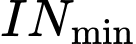
Từ
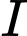 dựng vuông góc
dựng vuông góc 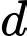 tại
tại 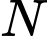 .Khi đó:
.Khi đó: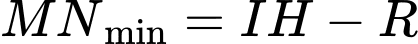
Dấu bằng xảy ra khi
 hay
hay 
Vậy
 hợp với mặt phẳng
hợp với mặt phẳng 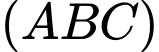 một góc
một góc 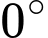 (loại vì không thỏa trường hợp)
(loại vì không thỏa trường hợp)
Vậy giá trị nhỏ nhất của
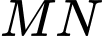 bằng 0.
bằng 0.
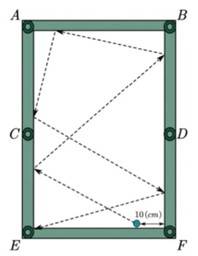
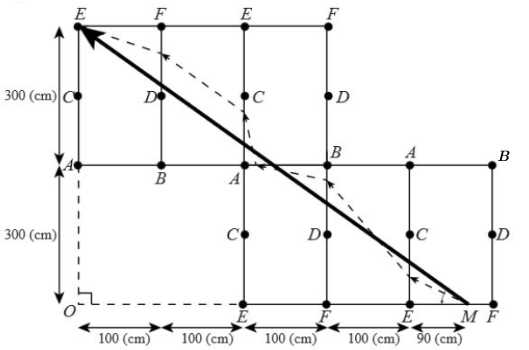
Câu 22 [694764]: Trong một trận chơi Bi-a có 6 lỗ 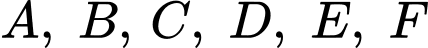 và có kích thước
và có kích thước 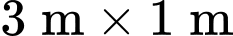 như hình vẽ, bạn Minh đánh mạnh một viên bi từ điểm sát thành cạnh
như hình vẽ, bạn Minh đánh mạnh một viên bi từ điểm sát thành cạnh 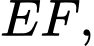 cách lỗ
cách lỗ 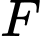 một đoạn
một đoạn 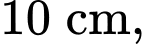 bật vào thành cạnh
bật vào thành cạnh 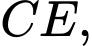 rồi bật lần lượt vào các cạnh
rồi bật lần lượt vào các cạnh 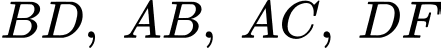 và cuối cùng rơi vào lỗ
và cuối cùng rơi vào lỗ 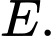 Biết rằng viên bi không rơi vào lỗ nào trước khi đến điểm kết thúc. Quãng đường ngắn nhất mà viên bi có thể di chuyển là bao nhiêu cm? (kết quả được làm tròn đến hàng phần đơn vị).
Biết rằng viên bi không rơi vào lỗ nào trước khi đến điểm kết thúc. Quãng đường ngắn nhất mà viên bi có thể di chuyển là bao nhiêu cm? (kết quả được làm tròn đến hàng phần đơn vị).
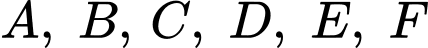 và có kích thước
và có kích thước 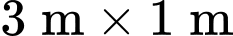 như hình vẽ, bạn Minh đánh mạnh một viên bi từ điểm sát thành cạnh
như hình vẽ, bạn Minh đánh mạnh một viên bi từ điểm sát thành cạnh 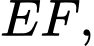 cách lỗ
cách lỗ 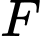 một đoạn
một đoạn 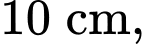 bật vào thành cạnh
bật vào thành cạnh 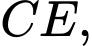 rồi bật lần lượt vào các cạnh
rồi bật lần lượt vào các cạnh 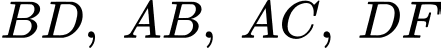 và cuối cùng rơi vào lỗ
và cuối cùng rơi vào lỗ 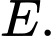 Biết rằng viên bi không rơi vào lỗ nào trước khi đến điểm kết thúc. Quãng đường ngắn nhất mà viên bi có thể di chuyển là bao nhiêu cm? (kết quả được làm tròn đến hàng phần đơn vị).
Biết rằng viên bi không rơi vào lỗ nào trước khi đến điểm kết thúc. Quãng đường ngắn nhất mà viên bi có thể di chuyển là bao nhiêu cm? (kết quả được làm tròn đến hàng phần đơn vị).
Điền đáp án: 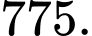
Gọi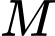 là điểm bắt đầu, quãng đường ngắn nhất là
là điểm bắt đầu, quãng đường ngắn nhất là 
Lật hình cho từng đoạn di chuyển, ta được:
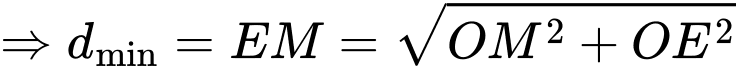
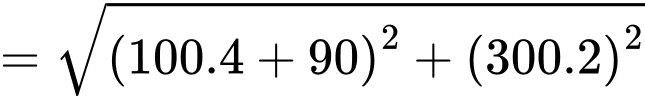
Gọi
 là điểm bắt đầu, quãng đường ngắn nhất là
là điểm bắt đầu, quãng đường ngắn nhất là 
Lật hình cho từng đoạn di chuyển, ta được: