PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
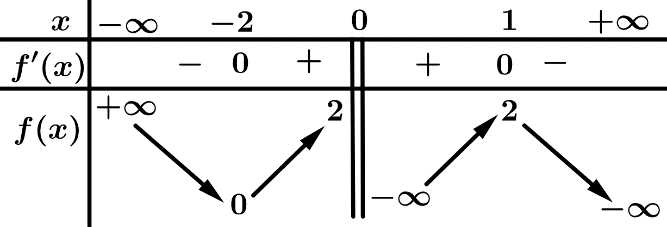
Câu 1 [333811]: Cho hàm số 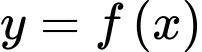 có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
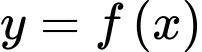 có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
A, Hàm số 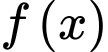 đạt cực đại tại
đạt cực đại tại 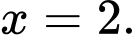
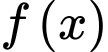 đạt cực đại tại
đạt cực đại tại 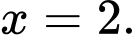
B, Hàm số 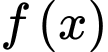 đạt cực tiểu tại
đạt cực tiểu tại 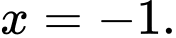
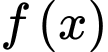 đạt cực tiểu tại
đạt cực tiểu tại 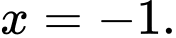
C, Hàm số 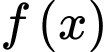 đạt cực tiểu tại
đạt cực tiểu tại 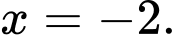
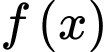 đạt cực tiểu tại
đạt cực tiểu tại 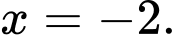
D, Hàm số 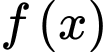 đạt cực đại tại
đạt cực đại tại 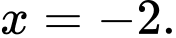
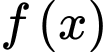 đạt cực đại tại
đạt cực đại tại 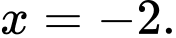
Chọn đáp án C.
Dựa vào bảng biến thiên ta có hàm số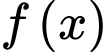 đạt cực tiểu tại
đạt cực tiểu tại 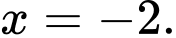 Đáp án: C
Đáp án: C
Dựa vào bảng biến thiên ta có hàm số
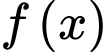 đạt cực tiểu tại
đạt cực tiểu tại 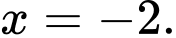 Đáp án: C
Đáp án: C
Câu 2 [809333]: Trong không gian 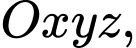 khoảng cách từ gốc tọa độ
khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 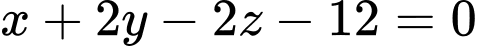 bằng
bằng
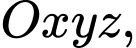 khoảng cách từ gốc tọa độ
khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 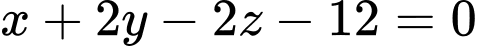 bằng
bằng A, 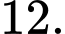
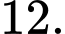
B, 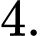
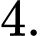
C, 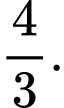
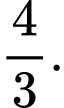
D, 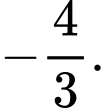
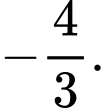
Chọn đáp án B.
Khoảng cách từ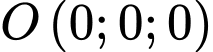 đến mặt phẳng
đến mặt phẳng 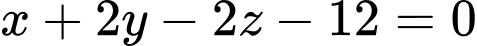 bằng
bằng 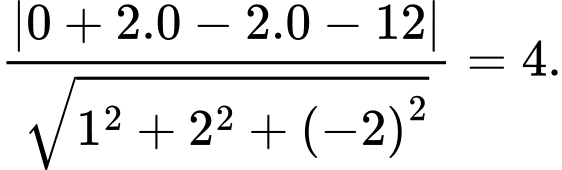 Đáp án: B
Đáp án: B
Khoảng cách từ
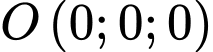 đến mặt phẳng
đến mặt phẳng 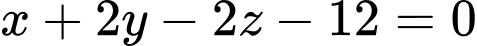 bằng
bằng 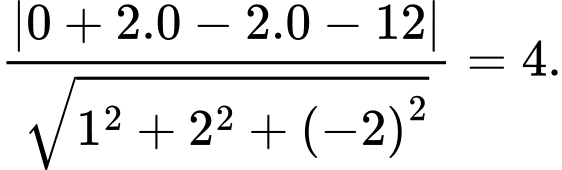 Đáp án: B
Đáp án: B
Câu 3 [516425]: Cho khối chóp tứ giác đều có cạnh đáy bằng 4 và thể tích bằng 32. Chiều cao của khối chóp bằng
A, 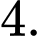
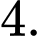
B, 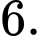
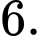
C, 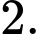
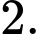
D, 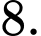
Chọn đáp án B.
Diện tích mặt đáy :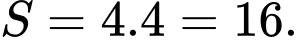
Thể tích khối chóp là :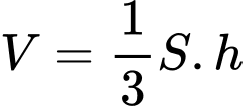
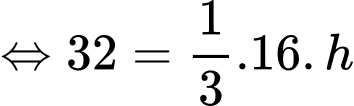
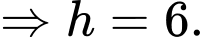 Đáp án: B
Đáp án: B
Diện tích mặt đáy :
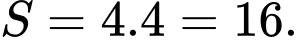
Thể tích khối chóp là :
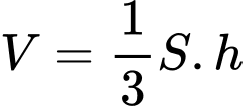
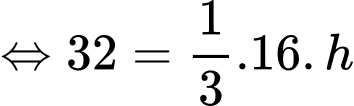
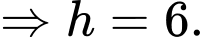 Đáp án: B
Đáp án: B
Câu 4 [808148]: Giả sử các biểu thức sau đều có nghĩa, khi đó công thức nào sau đây sai?
A, 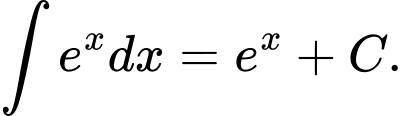
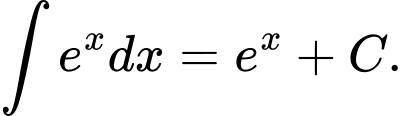
B, 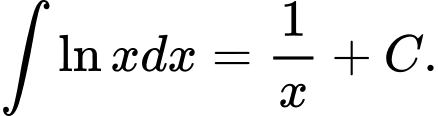
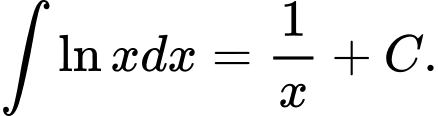
C, 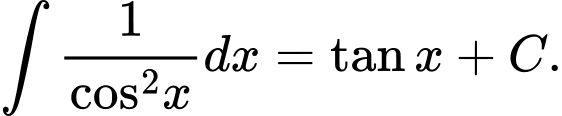
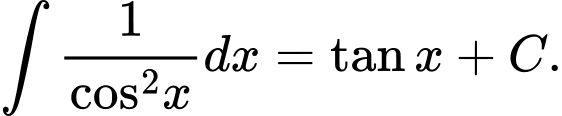
D, 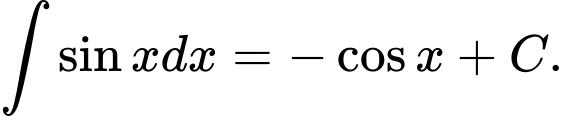
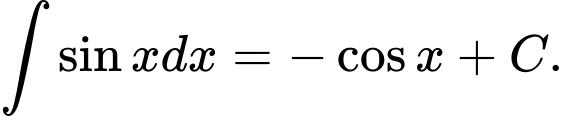
Chọn đáp án B.
Ta có: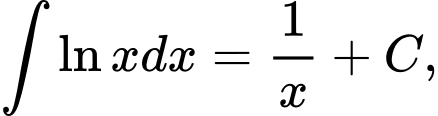 với
với  Đáp án: B
Đáp án: B
Ta có:
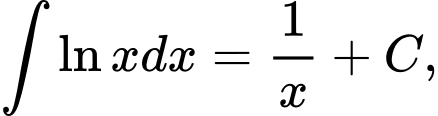 với
với  Đáp án: B
Đáp án: B
Câu 5 [522584]: Cho cấp số cộng 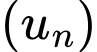 với
với 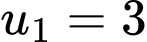 và
và 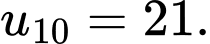 Tính giá trị của
Tính giá trị của 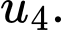
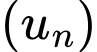 với
với 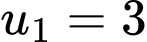 và
và 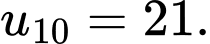 Tính giá trị của
Tính giá trị của 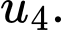
A, 9.
B, 3.
C, 18.
D, 10.
Chọn đáp án A.
Ta có: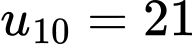
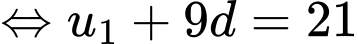
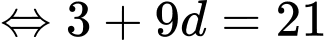
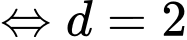
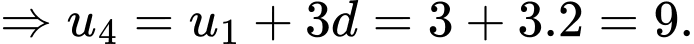 Đáp án: A
Đáp án: A
Ta có:
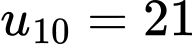
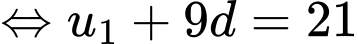
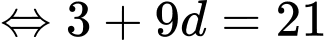
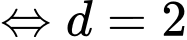
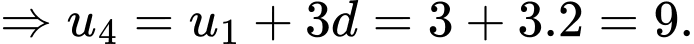 Đáp án: A
Đáp án: A
Câu 6 [327433]: Cho 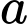 và
và 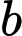 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 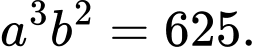 Giá trị của
Giá trị của  bằng
bằng
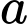 và
và 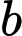 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 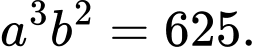 Giá trị của
Giá trị của  bằng
bằng A, 8.
B, 12.
C, 5.
D, 4.
Chọn đáp án D.
Ta có:

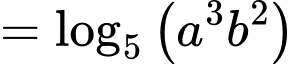
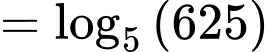
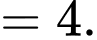 Đáp án: D
Đáp án: D
Ta có:

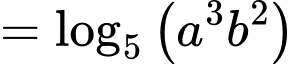
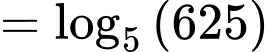
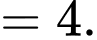 Đáp án: D
Đáp án: D
Câu 7 [522551]: Trong không gian 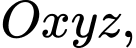 đường thẳng đi qua hai điểm
đường thẳng đi qua hai điểm 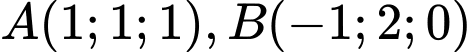 có phương trình là
có phương trình là
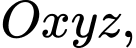 đường thẳng đi qua hai điểm
đường thẳng đi qua hai điểm 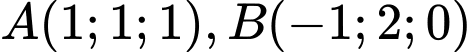 có phương trình là
có phương trình là A, 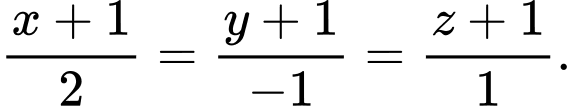
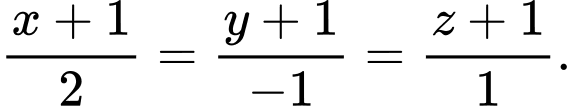
B, 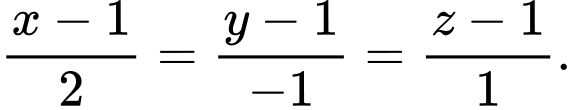
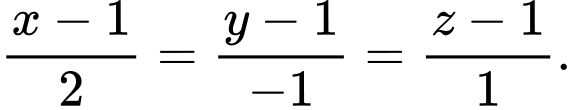
C, 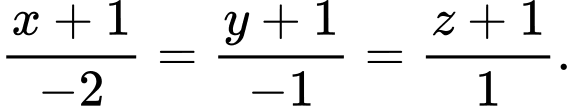
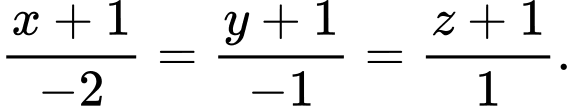
D, 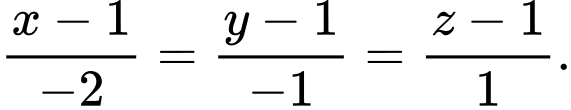
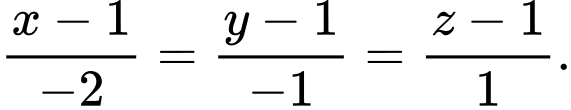
Chọn đáp án B.
Vecto chỉ phương của đường thẳng là
là 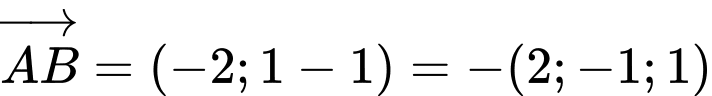
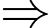 loại đáp án C và D.
loại đáp án C và D.
Điểm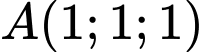 thuộc đường thẳng
thuộc đường thẳng 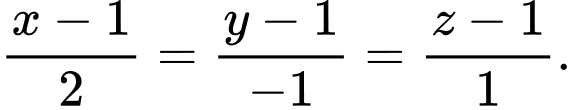
Vậy đáp án B đúng. Đáp án: B
Vecto chỉ phương của đường thẳng
 là
là 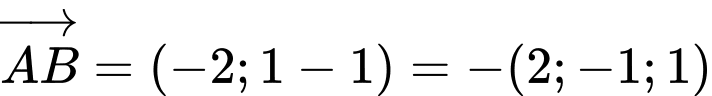
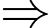 loại đáp án C và D.
loại đáp án C và D. Điểm
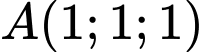 thuộc đường thẳng
thuộc đường thẳng 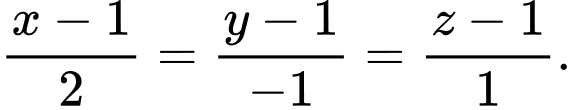
Vậy đáp án B đúng. Đáp án: B
Câu 8 [808125]: Biết 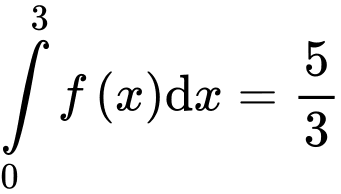 và
và 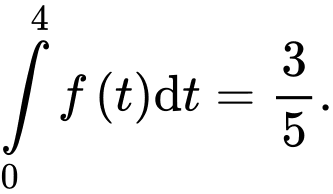 Tính
Tính 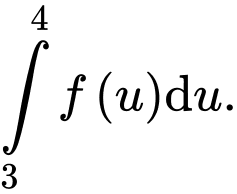
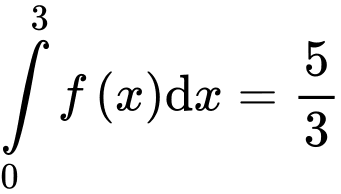 và
và 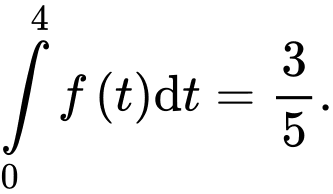 Tính
Tính 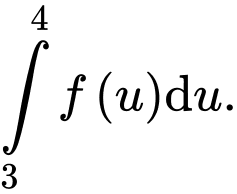
A, 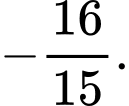
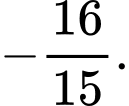
B, 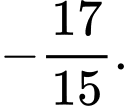
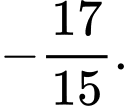
C, 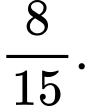
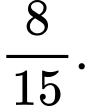
D, 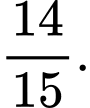
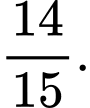
Chọn đáp án A.
Vì tích phân không phụ thuộc vào đối số nên ta có:
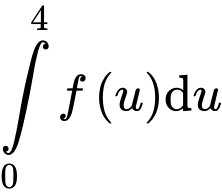
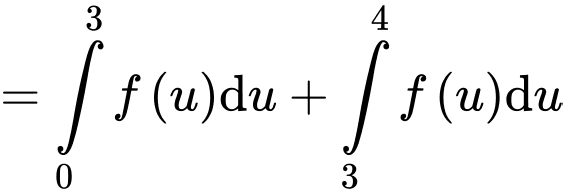
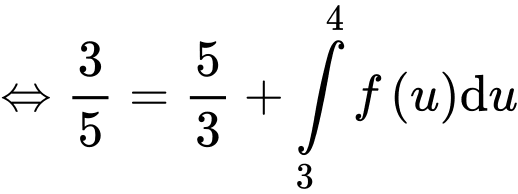
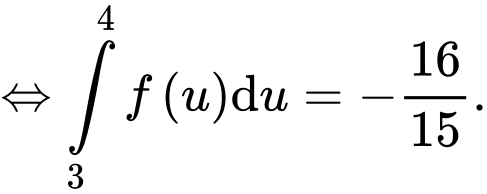 Đáp án: A
Đáp án: A
Vì tích phân không phụ thuộc vào đối số nên ta có:
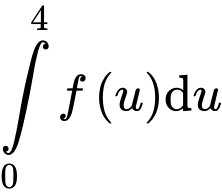
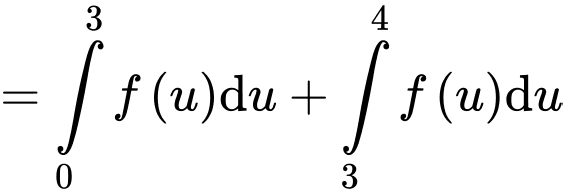
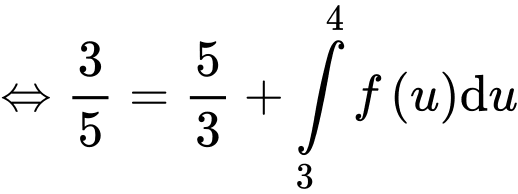
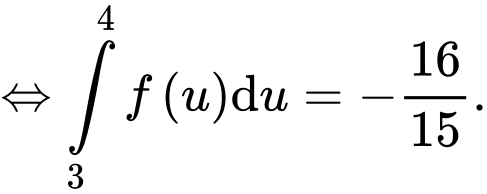 Đáp án: A
Đáp án: A
Câu 9 [696439]: Một vận động viên luyện tập chạy cự li 100 m đã ghi lại kết quả luyện tập như sau.

Tìm phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến chữ số thập phân thứ 2).

Tìm phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến chữ số thập phân thứ 2).
A, 1,03.
B, 0,03.
C, 2,90.
D, 1,86.
Chọn đáp án B.
Số trung bình của mẫu số liệu ghép nhóm là:
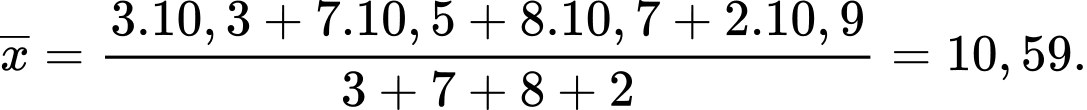
Phương sai của mẫu số liệu ghép nhóm là:
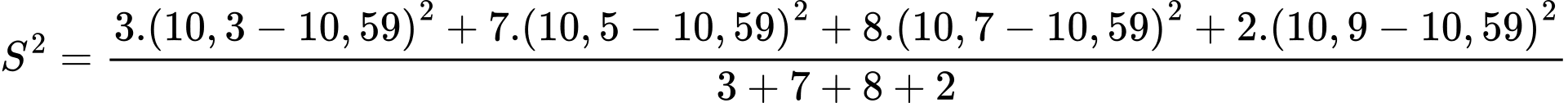
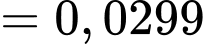
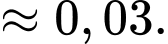 Đáp án: B
Đáp án: B
Số trung bình của mẫu số liệu ghép nhóm là:
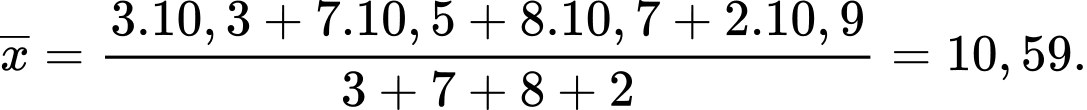
Phương sai của mẫu số liệu ghép nhóm là:
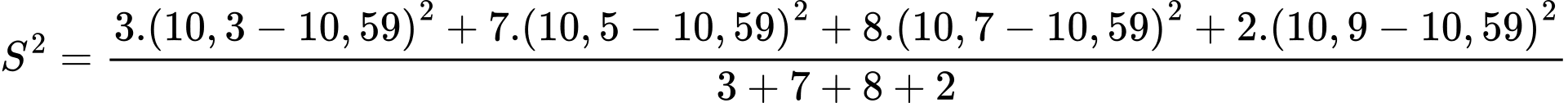
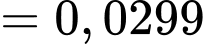
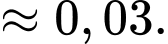 Đáp án: B
Đáp án: B
Câu 10 [681569]: Tiệm cận xiên của đồ thị hàm số 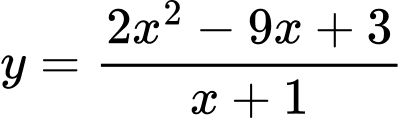 là đường thẳng:
là đường thẳng:
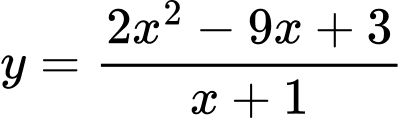 là đường thẳng:
là đường thẳng: A, 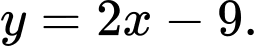
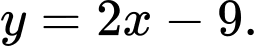
B, 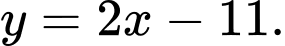
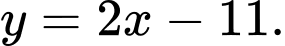
C, 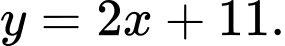
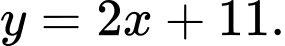
D, 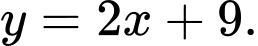
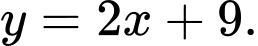
Chọn đáp án B.
Tập xác định của hàm số là
Ta có:
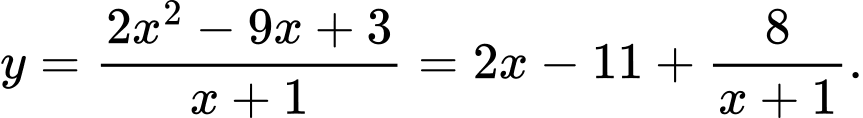
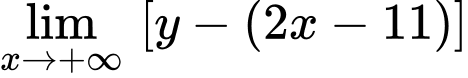
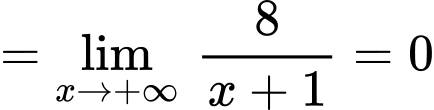 ;
;
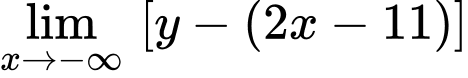
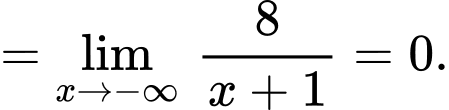
Vậy đường thẳng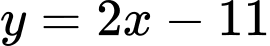 là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: B
là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: B
Tập xác định của hàm số là

Ta có:
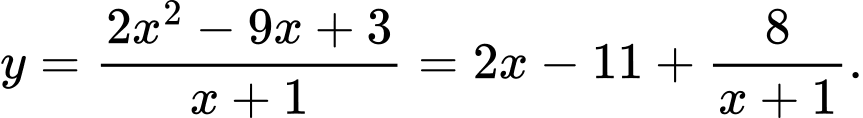
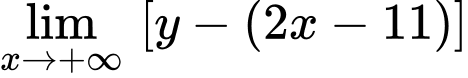
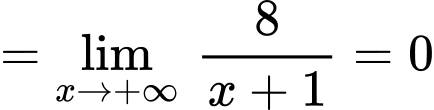 ;
; 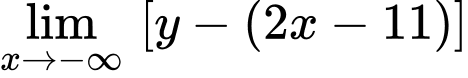
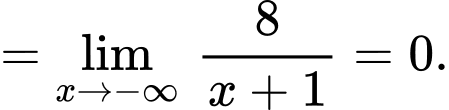
Vậy đường thẳng
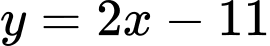 là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: B
là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: B
Câu 11 [512215]: Tập nghiệm của bất phương trình 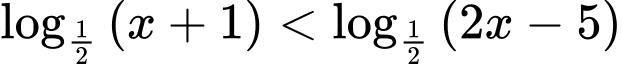 là
là
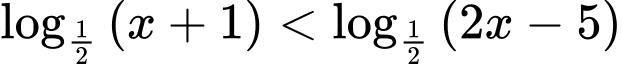 là
là A, 

B, 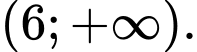
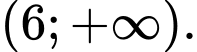
C, 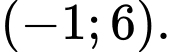
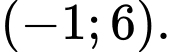
D, 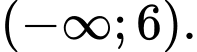
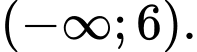
Chọn đáp án A.
Ta có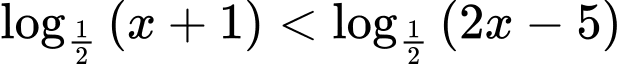
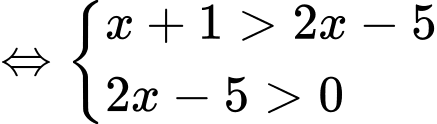
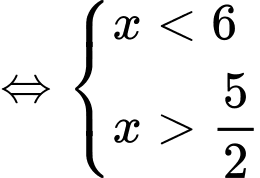
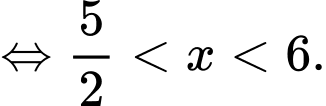
Vậy tập nghiệm của bất phương trình là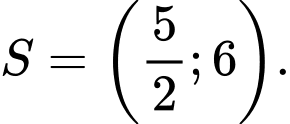 Đáp án: A
Đáp án: A
Ta có
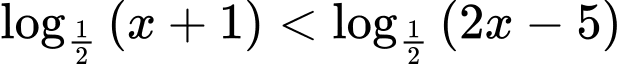
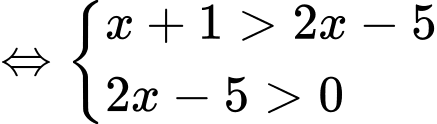
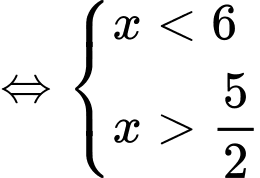
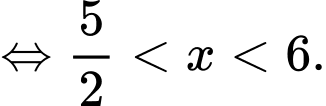
Vậy tập nghiệm của bất phương trình là
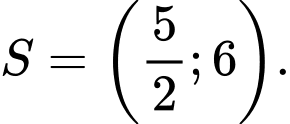 Đáp án: A
Đáp án: A
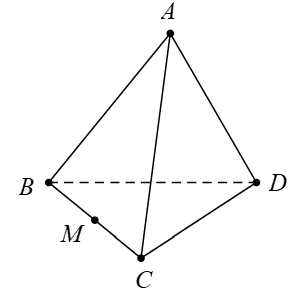
Câu 12 [379535]: Cho tứ diện đều 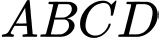 có các cạnh bằng
có các cạnh bằng 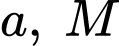 là trung điểm của cạnh
là trung điểm của cạnh 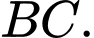 Tính
Tính 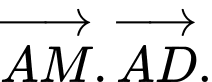
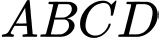 có các cạnh bằng
có các cạnh bằng 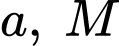 là trung điểm của cạnh
là trung điểm của cạnh 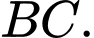 Tính
Tính 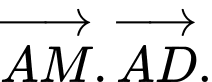
A, 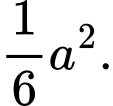
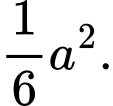
B, 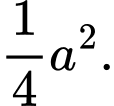
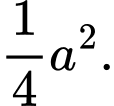
C, 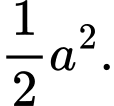
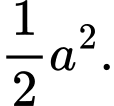
D, 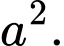
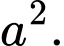
Chọn đáp án C.
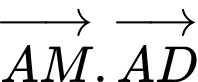
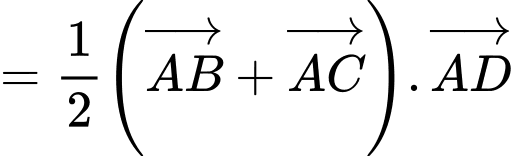
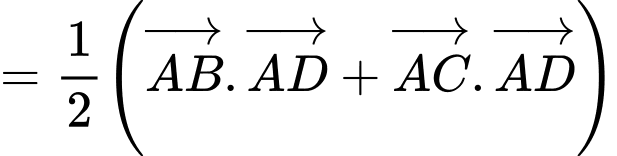
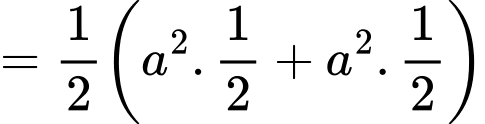
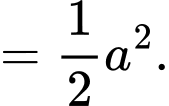 Đáp án: C
Đáp án: C

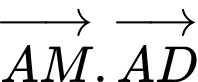
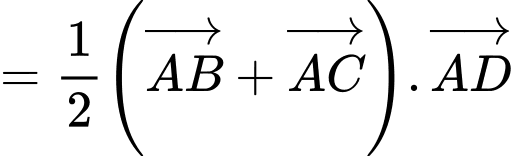
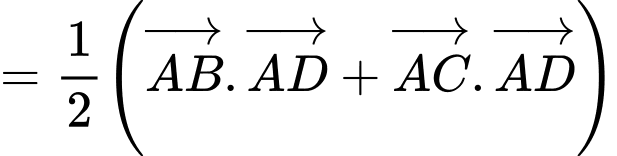
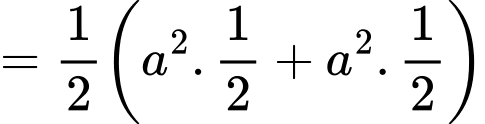
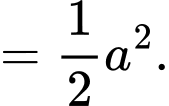 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
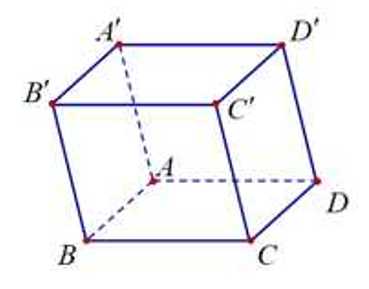
Câu 13 [696440]: Trong không gian với hệ trục tọa độ 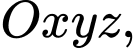 cho hình hộp
cho hình hộp  biết tọa độ các điểm
biết tọa độ các điểm 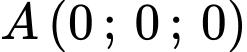 ;
; 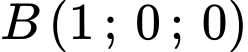 ;
; 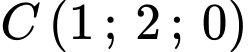 ;
; 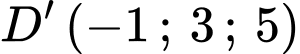 .
.
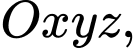 cho hình hộp
cho hình hộp  biết tọa độ các điểm
biết tọa độ các điểm 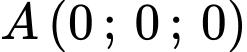 ;
; 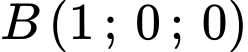 ;
; 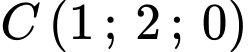 ;
; 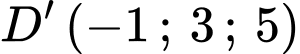 .
. 
Từ giả thiết ta dễ có
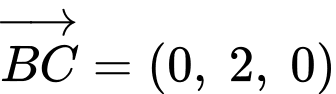
b) Đúng.
 là hình hộp nên
là hình hộp nên 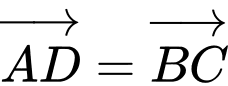 .
.c) Sai.
Gọi tọa độ của điểm
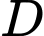 và
và 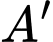 lần lượt là:
lần lượt là: 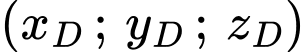 và
và 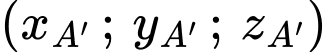 .
.Ta có:
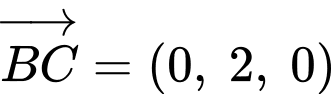 ;
;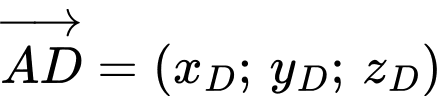
 là hình hộp nên:
là hình hộp nên: 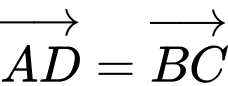
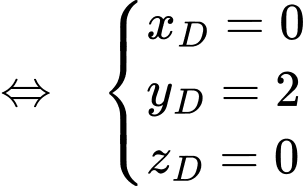
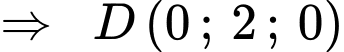
d) Đúng.
Ta có
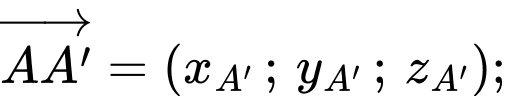
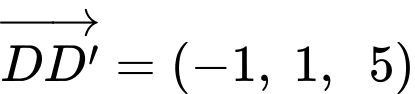
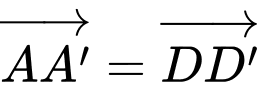
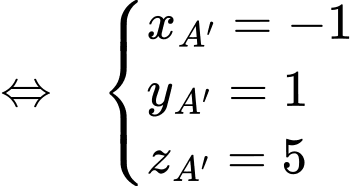
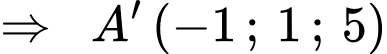
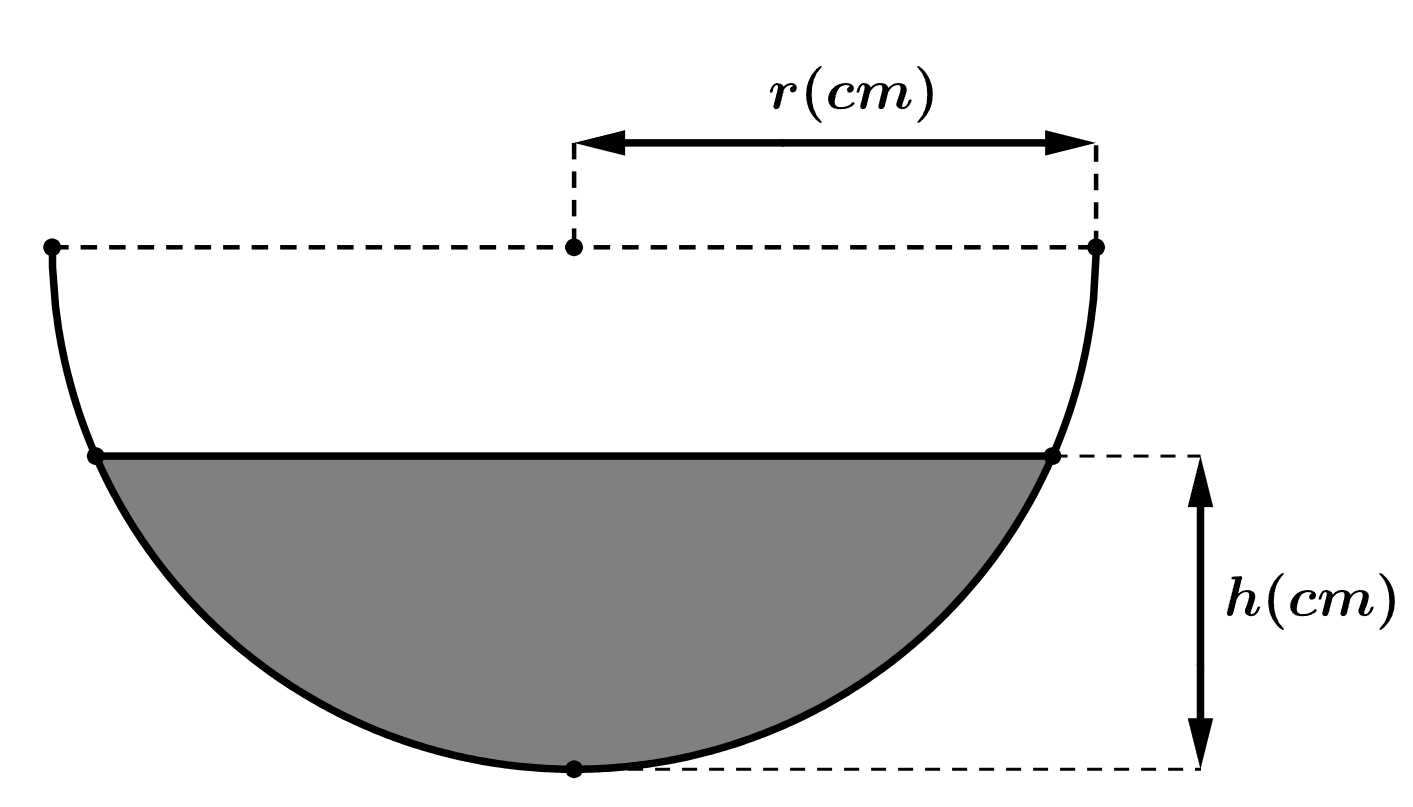
Câu 14 [696442]: Nước bốc hơi từ một bát hình bán cầu có bán kính r (cm) với tốc độ 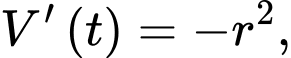 trong đó
trong đó 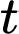 là thời gian tính bằng giờ. Thể tích nước có độ cao
là thời gian tính bằng giờ. Thể tích nước có độ cao 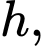 trong một bát hình bán cầu có bán kính
trong một bát hình bán cầu có bán kính 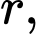 được biểu thị bằng
được biểu thị bằng 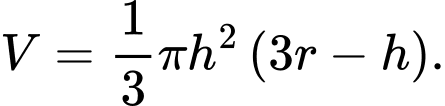 Giả sử bán kính của bát là
Giả sử bán kính của bát là 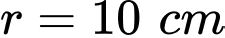 và ban đầu (lúc
và ban đầu (lúc 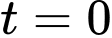 ) bát chứa đầy nước.
) bát chứa đầy nước.
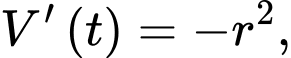 trong đó
trong đó 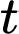 là thời gian tính bằng giờ. Thể tích nước có độ cao
là thời gian tính bằng giờ. Thể tích nước có độ cao 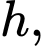 trong một bát hình bán cầu có bán kính
trong một bát hình bán cầu có bán kính 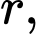 được biểu thị bằng
được biểu thị bằng 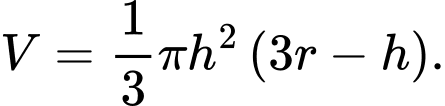 Giả sử bán kính của bát là
Giả sử bán kính của bát là 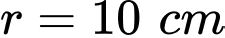 và ban đầu (lúc
và ban đầu (lúc 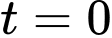 ) bát chứa đầy nước.
) bát chứa đầy nước.
a) Sai.
Lượng nước trong bát ban đầu là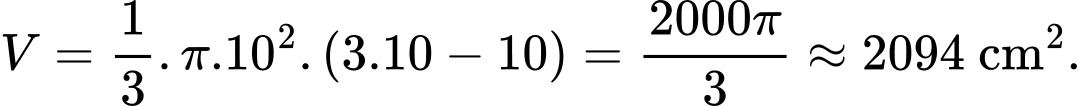
b) Sai.
Ta có: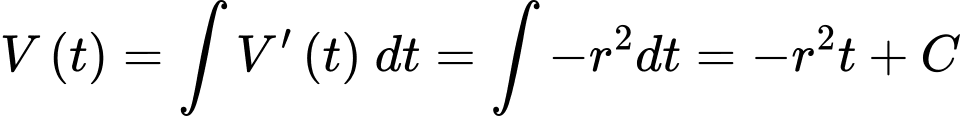
Mà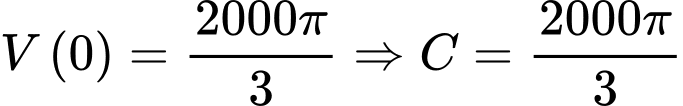
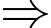 Lượng nước còn lại sau
Lượng nước còn lại sau 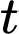 giờ là
giờ là 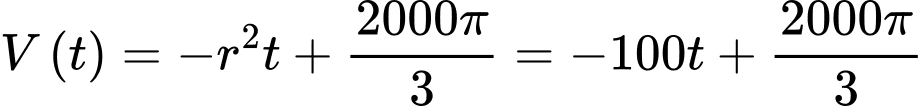
c) Đúng.
Khi bát cạn nước thì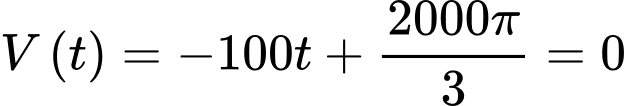
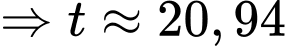 giờ.
giờ.
d) Đúng.
Ta có: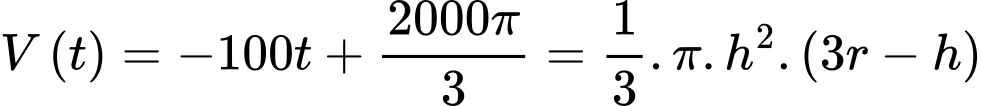
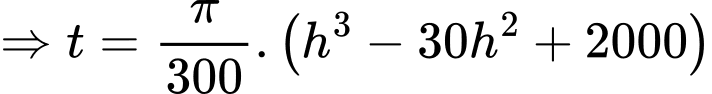
Lượng nước trong bát ban đầu là
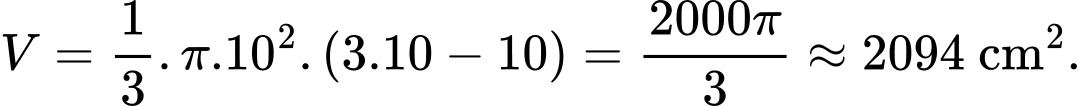
b) Sai.
Ta có:
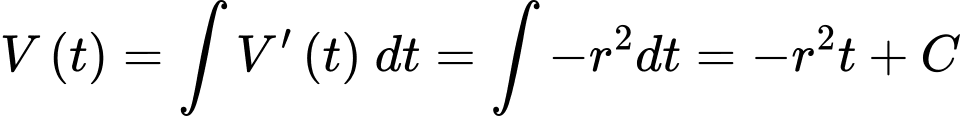
Mà
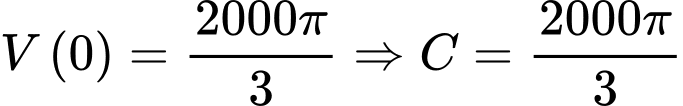
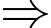 Lượng nước còn lại sau
Lượng nước còn lại sau 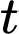 giờ là
giờ là 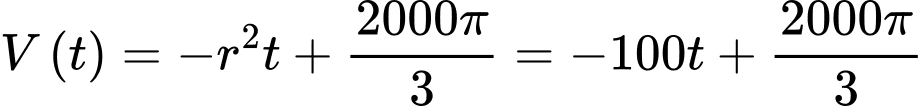
c) Đúng.
Khi bát cạn nước thì
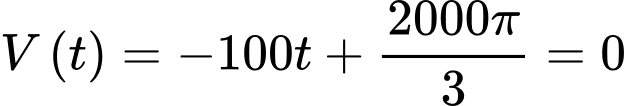
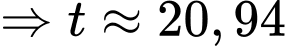 giờ.
giờ.d) Đúng.
Ta có:
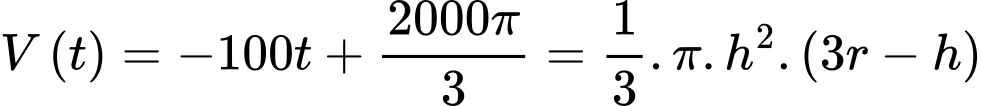
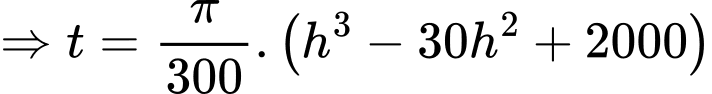
Câu 15 [696443]: Một công ty sản xuất bóng đèn huỳnh quang có hai phân xưởng I và II. Phân xưởng I sản xuất 30% số bóng đèn của công ty và phân xưởng II sản xuất 70% bóng đèn của công ty. Tỉ lệ bóng đèn bị lỗi của phân xưởng I là 3% và của phân xưởng II là 2%. Chọn ngẫu nhiên một bóng đèn của công ty để kiểm tra.
Gọi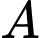 là biến cố: “Bóng đèn kiểm tra bị lỗi”.
là biến cố: “Bóng đèn kiểm tra bị lỗi”.
Gọi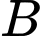 là biến cố: “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
là biến cố: “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
Gọi
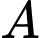 là biến cố: “Bóng đèn kiểm tra bị lỗi”.
là biến cố: “Bóng đèn kiểm tra bị lỗi”.Gọi
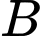 là biến cố: “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
là biến cố: “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
Gọi 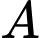 là biến cố “ Bóng đèn kiểm tra bị lỗi”
là biến cố “ Bóng đèn kiểm tra bị lỗi”
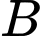 là biến cố “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
là biến cố “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
a) Đúng.
Do phân xưởng I sản xuất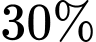 số bóng đèn và phân xưởng II sản xuất
số bóng đèn và phân xưởng II sản xuất 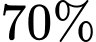 số bóng đèn nên
số bóng đèn nên 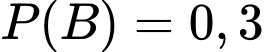 và
và 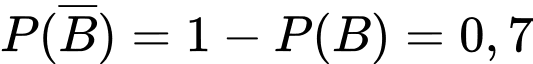
b) Sai.
Do tỉ lệ bóng đèn bị lỗi của phân xưởng I là 3% và của phân xưởng II là 2% nên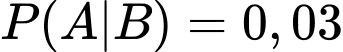 và
và 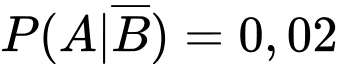
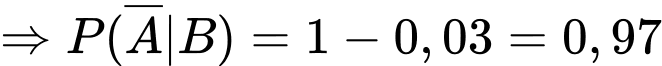
c) Sai.
Xác suất để bóng đèn kiểm tra bị lỗi là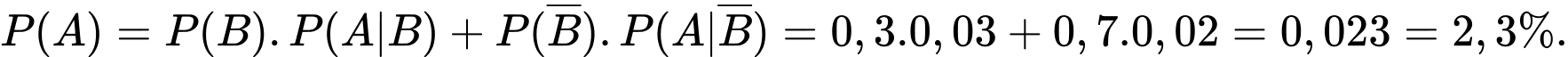
d) Sai.
Xác suất bóng đèn kiểm tra bị lỗi do phân xưởng I sản xuất là
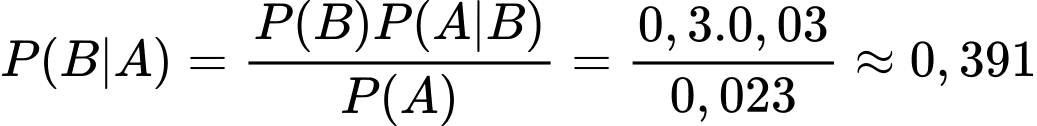
Xác suất bóng đèn kiểm tra bị lỗi do phân xưởng II sản xuất là
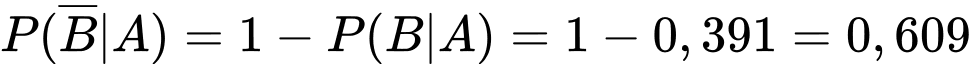
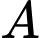 là biến cố “ Bóng đèn kiểm tra bị lỗi”
là biến cố “ Bóng đèn kiểm tra bị lỗi”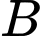 là biến cố “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.
là biến cố “Bóng đèn được kiểm tra do phân xưởng I sản xuất”.a) Đúng.
Do phân xưởng I sản xuất
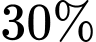 số bóng đèn và phân xưởng II sản xuất
số bóng đèn và phân xưởng II sản xuất 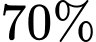 số bóng đèn nên
số bóng đèn nên 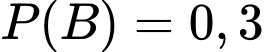 và
và 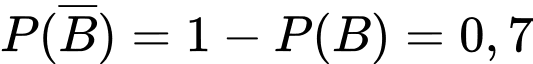
b) Sai.
Do tỉ lệ bóng đèn bị lỗi của phân xưởng I là 3% và của phân xưởng II là 2% nên
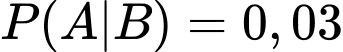 và
và 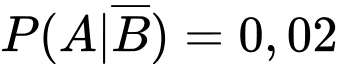
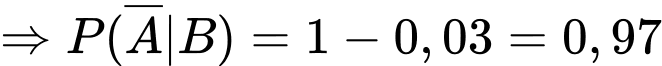
c) Sai.
Xác suất để bóng đèn kiểm tra bị lỗi là
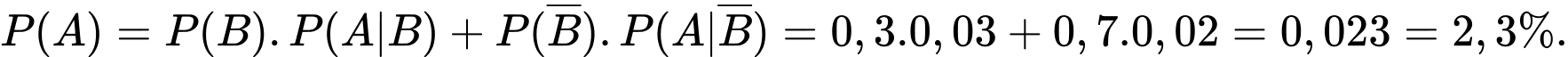
d) Sai.
Xác suất bóng đèn kiểm tra bị lỗi do phân xưởng I sản xuất là
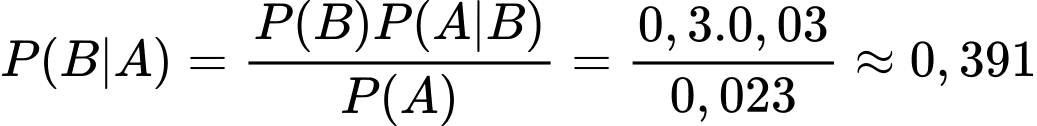
Xác suất bóng đèn kiểm tra bị lỗi do phân xưởng II sản xuất là
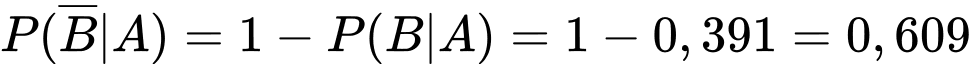
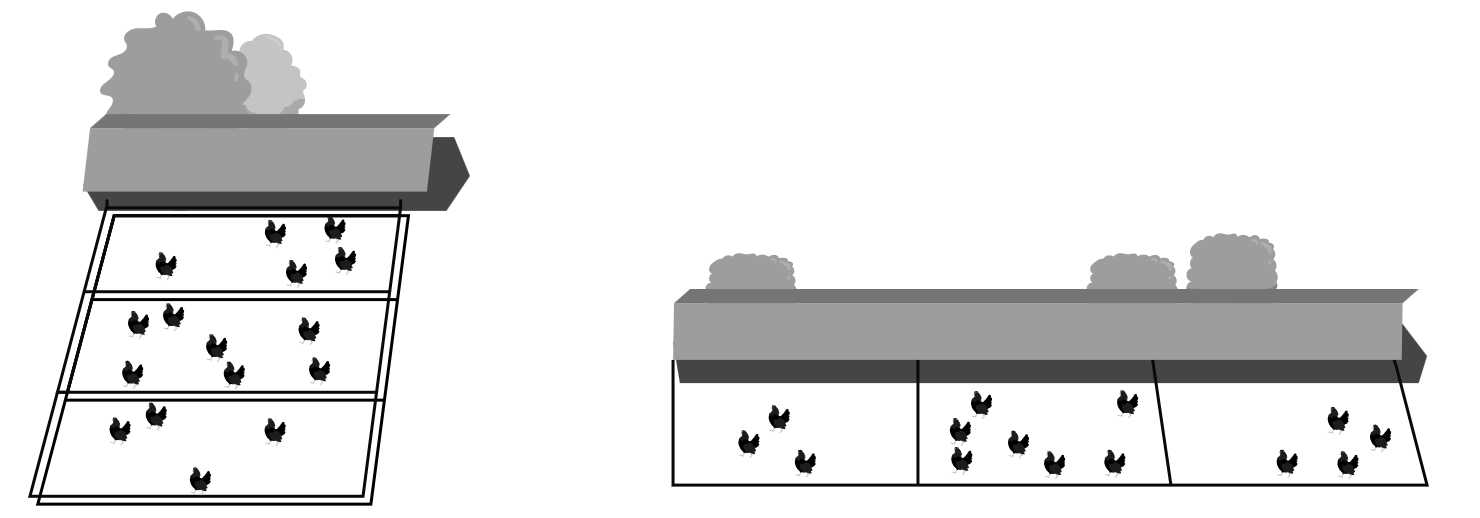
Câu 16 [696403]: Trang trại Grayson dự định xây dựng ba chuồng trại hình chữ nhật song song bên trong một khu vực hình chữ nhật lớn để nuôi gà, sử dụng 180 mét hàng rào. Một cạnh của khu vực này là một bức tường đá sẵn có. Người chủ trang trại có 2 kế hoạch để xây dựng và chọn ra phương án có diện tích lớn nhất: phương án 1 là ba chuồng trại hình chữ nhật có các cạnh dài song song với bức tường đá, phương án 2 là ba chuồng hình chữ nhật có các cạnh ngắn hơn vuông góc với bức tường đá (như hình vẽ).

a) Đúng.
Ta có: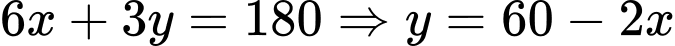
b) Đúng.
Ta có: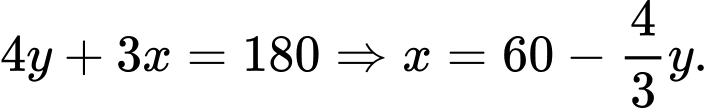
c) Sai.
Diện tích nuôi gà theo phương án 1 là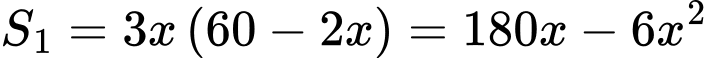
Diện tích nuôi gà theo phương án 2 là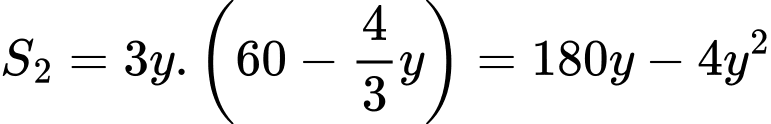
d) Đúng.
Ta có: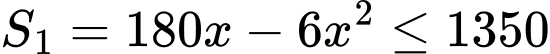 ,
, 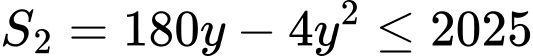
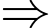 Diện tích nuôi gà lớn nhất là
Diện tích nuôi gà lớn nhất là 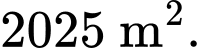
Ta có:
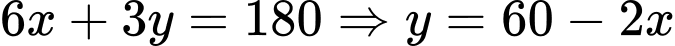
b) Đúng.
Ta có:
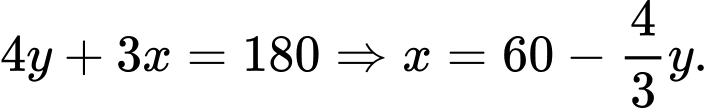
c) Sai.
Diện tích nuôi gà theo phương án 1 là
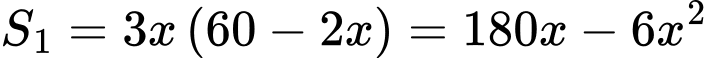
Diện tích nuôi gà theo phương án 2 là
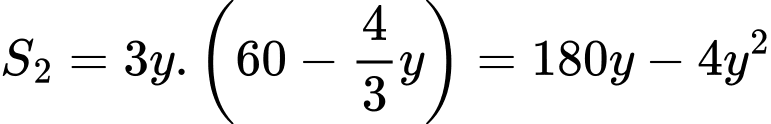
d) Đúng.
Ta có:
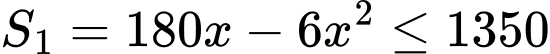 ,
, 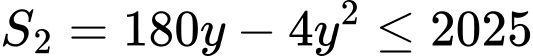
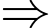 Diện tích nuôi gà lớn nhất là
Diện tích nuôi gà lớn nhất là 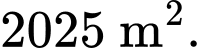
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [255888]: Cho khối trụ có bán kính đáy bằng 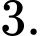 Gọi
Gọi 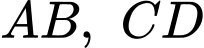 lần lượt là đường kính của hai đường tròn đáy. Biết
lần lượt là đường kính của hai đường tròn đáy. Biết 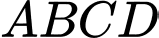 là tứ diện đều. Thể tích của khối trụ đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
là tứ diện đều. Thể tích của khối trụ đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 Gọi
Gọi 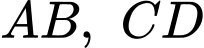 lần lượt là đường kính của hai đường tròn đáy. Biết
lần lượt là đường kính của hai đường tròn đáy. Biết 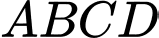 là tứ diện đều. Thể tích của khối trụ đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
là tứ diện đều. Thể tích của khối trụ đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 120.
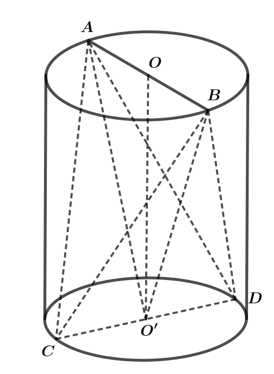
Gọi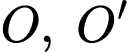 là tâm của 2 đường tròn đáy.
là tâm của 2 đường tròn đáy. là đường cao của hình trụ
là đường cao của hình trụ
Xét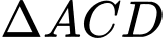 cân tại
cân tại 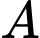 có:
có: 
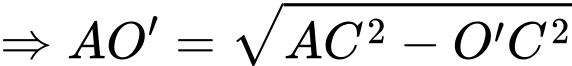
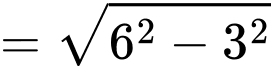
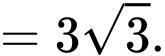
Xét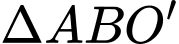 cân tại
cân tại  có:
có: 
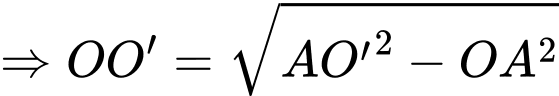
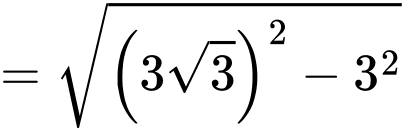
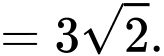
Thể tích của khối trụ đã cho bằng
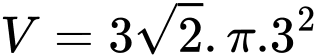
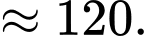

Gọi
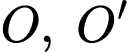 là tâm của 2 đường tròn đáy.
là tâm của 2 đường tròn đáy. là đường cao của hình trụ
là đường cao của hình trụXét
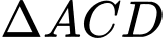 cân tại
cân tại 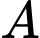 có:
có: 
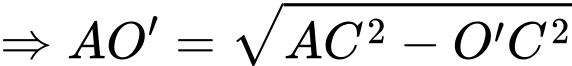
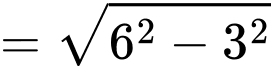
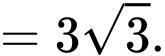
Xét
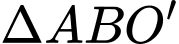 cân tại
cân tại  có:
có: 
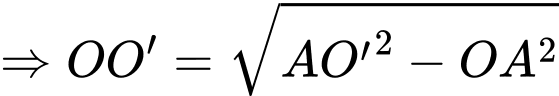
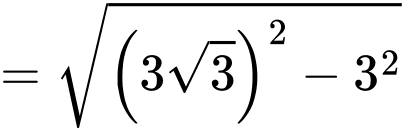
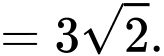
Thể tích của khối trụ đã cho bằng
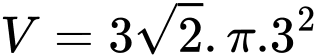
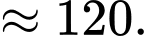
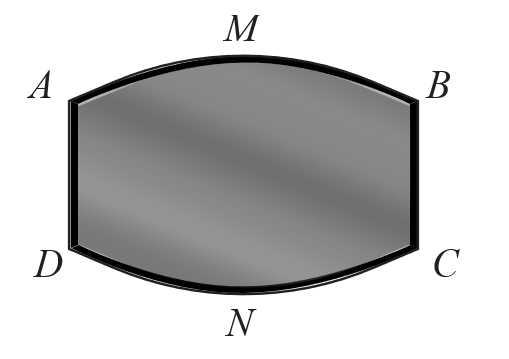
Câu 18 [693091]: Ông Duy mua cho phòng ngủ của nhà mình một tấm gương phẳng có dạng như hình vẽ. Biết 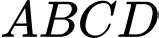 là hình chữ nhật nhận
là hình chữ nhật nhận 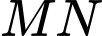 là trục đối xứng với
là trục đối xứng với 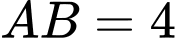 m;
m; 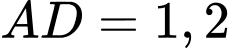 m;
m; 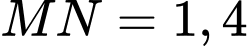 m; hai cạnh cong
m; hai cạnh cong 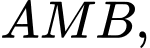
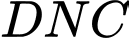 là các đường parabol với đỉnh tương ứng là
là các đường parabol với đỉnh tương ứng là 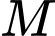 và
và  giá của
giá của 
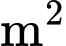 kính dùng để làm gương như trên là 300 000 đồng. Số tiền ông Duy mua tấm gương trên là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
kính dùng để làm gương như trên là 300 000 đồng. Số tiền ông Duy mua tấm gương trên là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
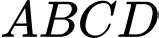 là hình chữ nhật nhận
là hình chữ nhật nhận 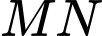 là trục đối xứng với
là trục đối xứng với 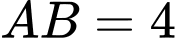 m;
m; 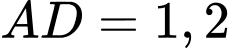 m;
m; 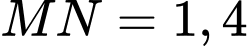 m; hai cạnh cong
m; hai cạnh cong 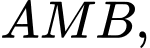
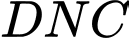 là các đường parabol với đỉnh tương ứng là
là các đường parabol với đỉnh tương ứng là 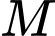 và
và 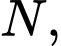 giá của
giá của 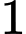
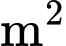 kính dùng để làm gương như trên là 300 000 đồng. Số tiền ông Duy mua tấm gương trên là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
kính dùng để làm gương như trên là 300 000 đồng. Số tiền ông Duy mua tấm gương trên là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 1,6.
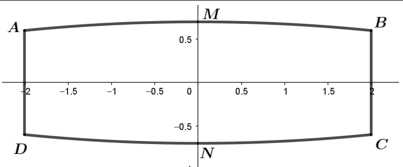
Theo hình vẽ ta có: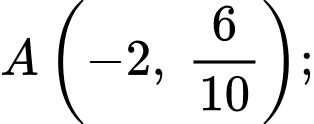
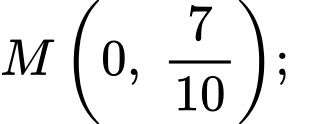
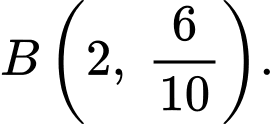
Phương trình parabol đi qua 3 điểm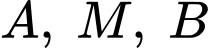 có dạng
có dạng 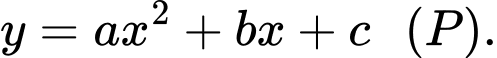
Thay tọa độ 3 điểm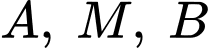 vào phương trình parabol
vào phương trình parabol 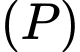 ta được:
ta được:
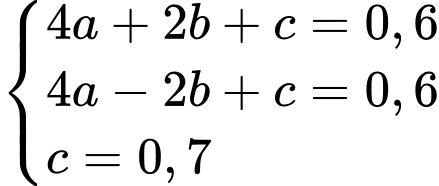
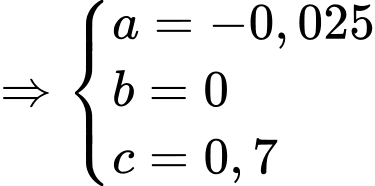
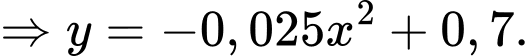
Diện tích tấm gương trên là
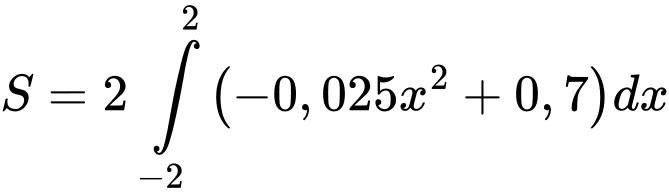
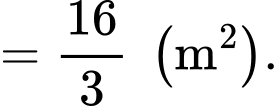
Số tiền ông Duy mua tấm gương trên là
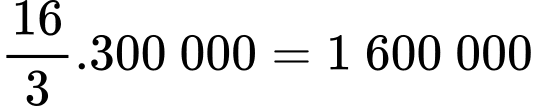 đồng = 1,6 triệu đồng.
đồng = 1,6 triệu đồng.

Theo hình vẽ ta có:
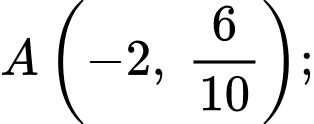
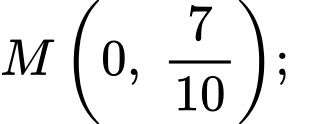
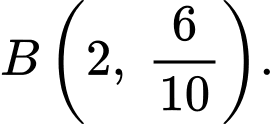
Phương trình parabol đi qua 3 điểm
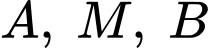 có dạng
có dạng 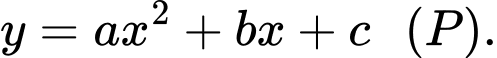
Thay tọa độ 3 điểm
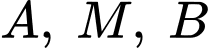 vào phương trình parabol
vào phương trình parabol 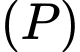 ta được:
ta được: 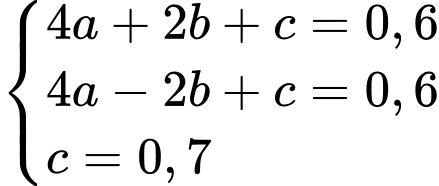
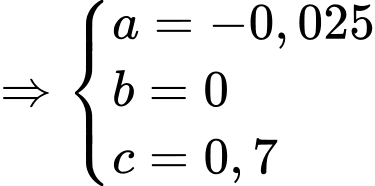
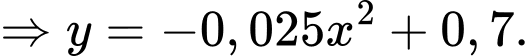
Diện tích tấm gương trên là
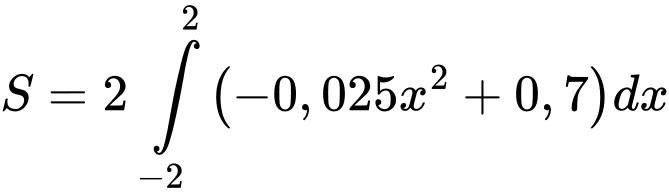
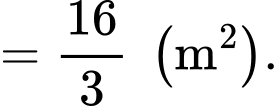
Số tiền ông Duy mua tấm gương trên là
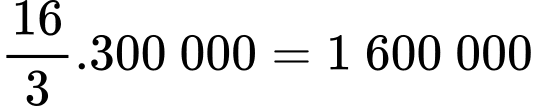 đồng = 1,6 triệu đồng.
đồng = 1,6 triệu đồng.
Câu 19 [696445]: Cho hình elip  tâm
tâm  có độ dài trục bé bằng 10, độ dài trục lớn bằng 16. Một tam giác
có độ dài trục bé bằng 10, độ dài trục lớn bằng 16. Một tam giác 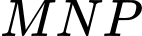 được xây dựng bằng cách vẽ 3 đường tiếp tuyến của elip
được xây dựng bằng cách vẽ 3 đường tiếp tuyến của elip  tại
tại 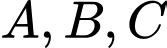 (trong đó
(trong đó 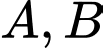 có cùng tung độ và tung độ dương,
có cùng tung độ và tung độ dương, 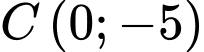 ) và cho ba đường thẳng đó cắt nhau tại
) và cho ba đường thẳng đó cắt nhau tại 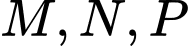 (như hình vẽ). Diện tích tam giác
(như hình vẽ). Diện tích tam giác 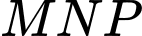 nhỏ nhất bằng bao nhiêu?
nhỏ nhất bằng bao nhiêu?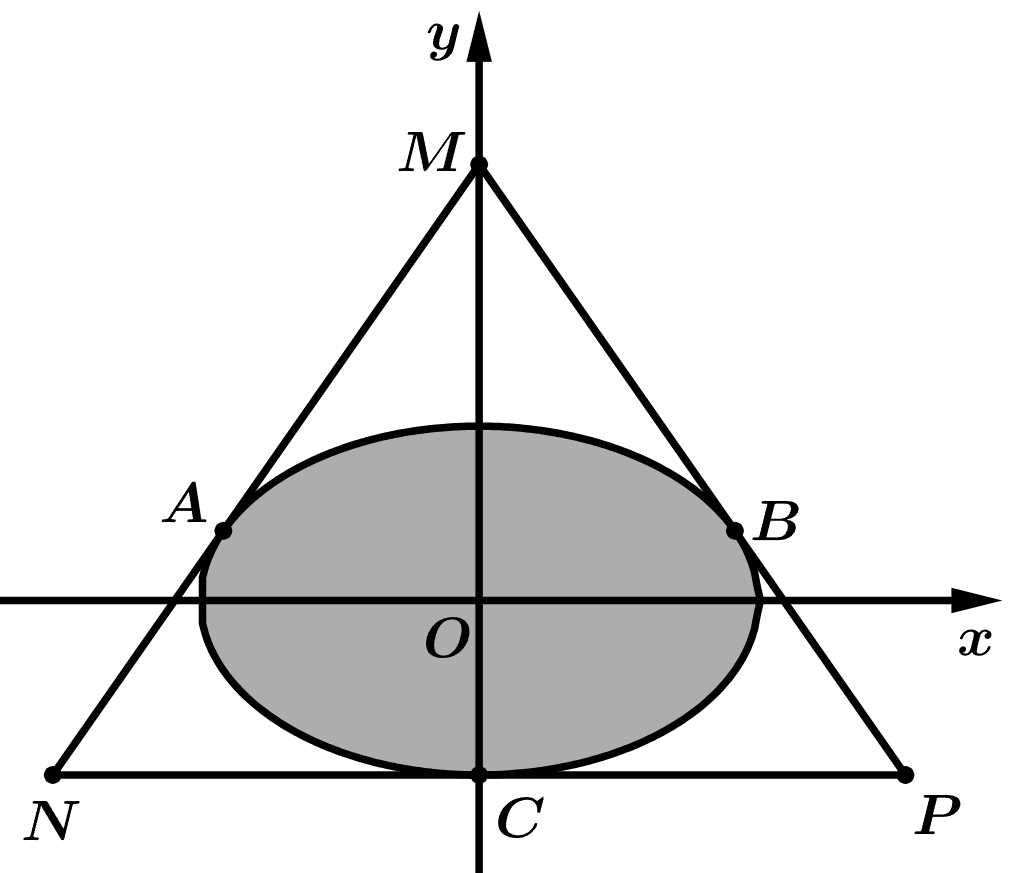
 tâm
tâm  có độ dài trục bé bằng 10, độ dài trục lớn bằng 16. Một tam giác
có độ dài trục bé bằng 10, độ dài trục lớn bằng 16. Một tam giác 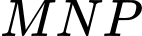 được xây dựng bằng cách vẽ 3 đường tiếp tuyến của elip
được xây dựng bằng cách vẽ 3 đường tiếp tuyến của elip  tại
tại 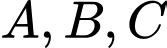 (trong đó
(trong đó 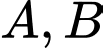 có cùng tung độ và tung độ dương,
có cùng tung độ và tung độ dương, 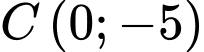 ) và cho ba đường thẳng đó cắt nhau tại
) và cho ba đường thẳng đó cắt nhau tại 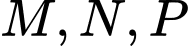 (như hình vẽ). Diện tích tam giác
(như hình vẽ). Diện tích tam giác 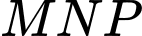 nhỏ nhất bằng bao nhiêu?
nhỏ nhất bằng bao nhiêu?
Điền đáp án: 208.
Phương trình elip có dạng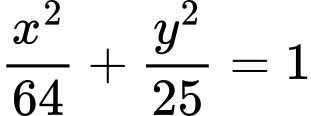
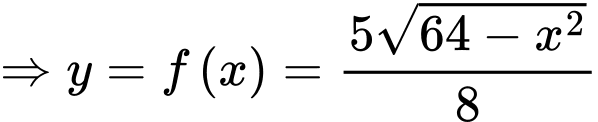
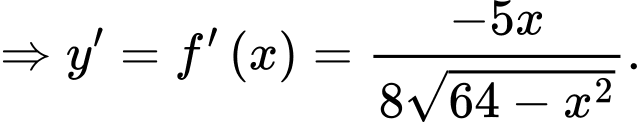
Phương trình tiếp tuyến của elip (E) tại điểm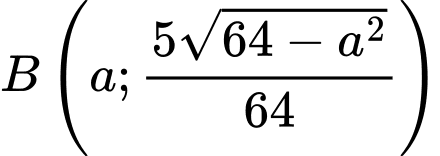 là
là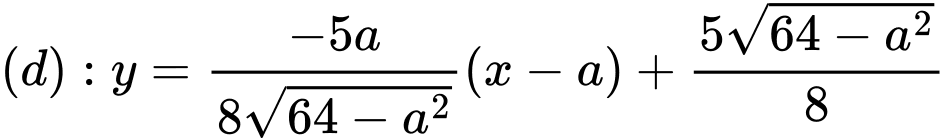
Đường thẳng cắt trục
cắt trục 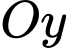 tại điểm
tại điểm 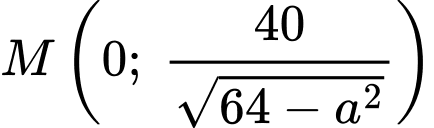 , cắt đường thẳng
, cắt đường thẳng 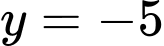 tại điểm
tại điểm 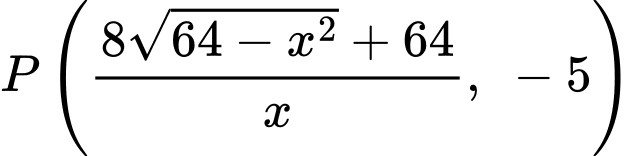 .
.
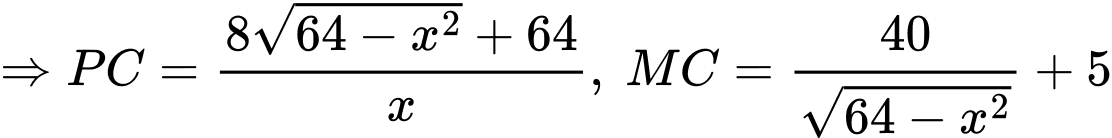
Diện tích tam giác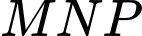 là
là
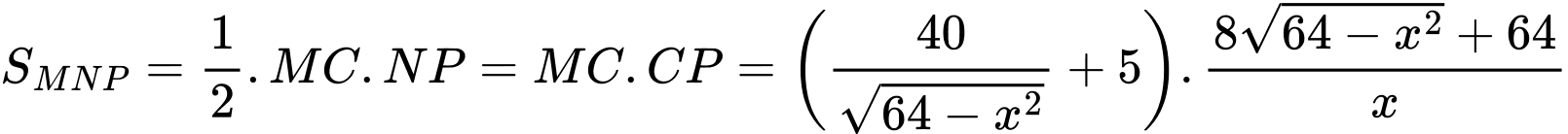
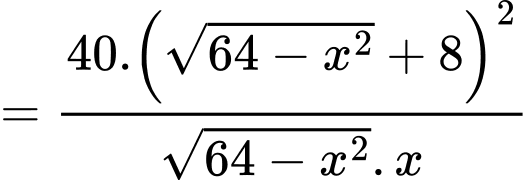
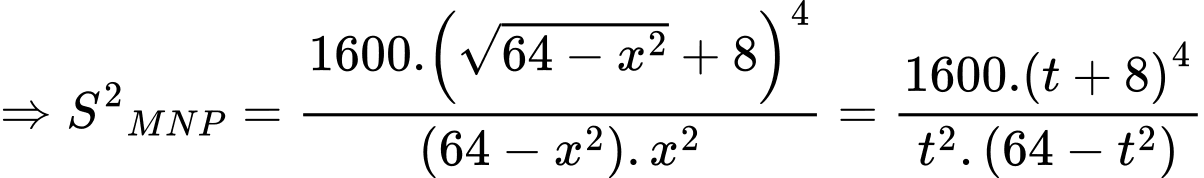
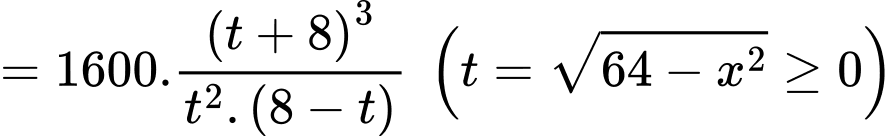
Xét hàm số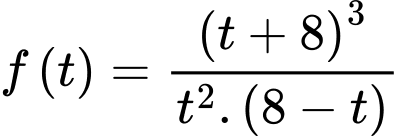
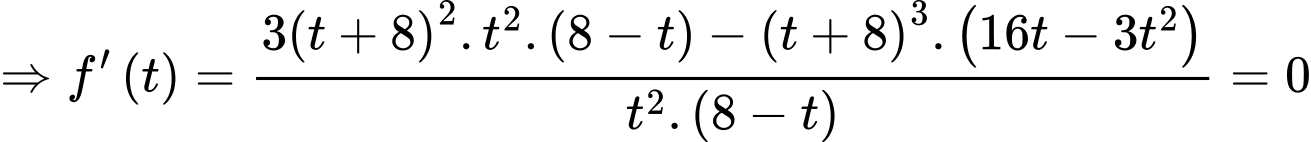
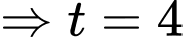 là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm số 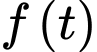 .
.
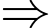
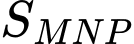 đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là 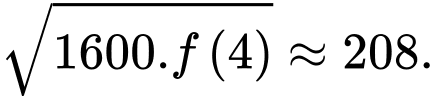
Phương trình elip có dạng
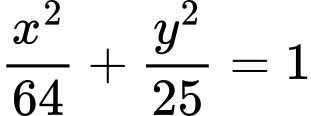
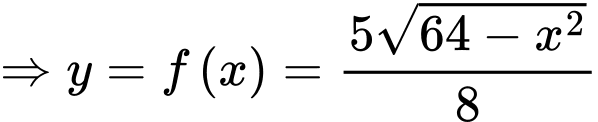
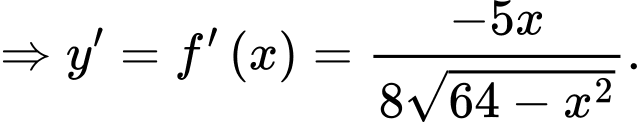
Phương trình tiếp tuyến của elip (E) tại điểm
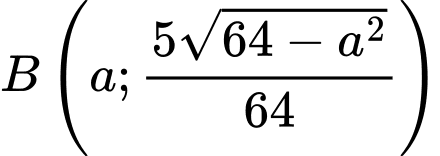 là
là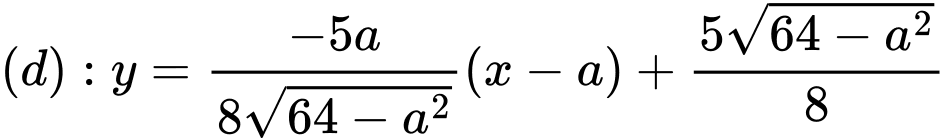
Đường thẳng
 cắt trục
cắt trục 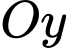 tại điểm
tại điểm 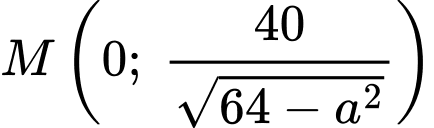 , cắt đường thẳng
, cắt đường thẳng 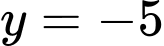 tại điểm
tại điểm 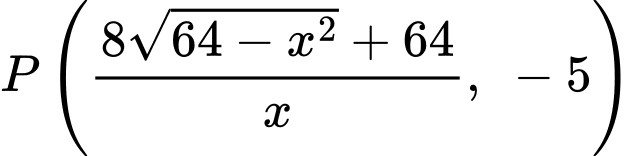 .
.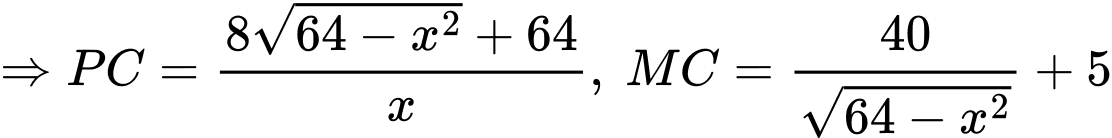
Diện tích tam giác
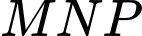 là
là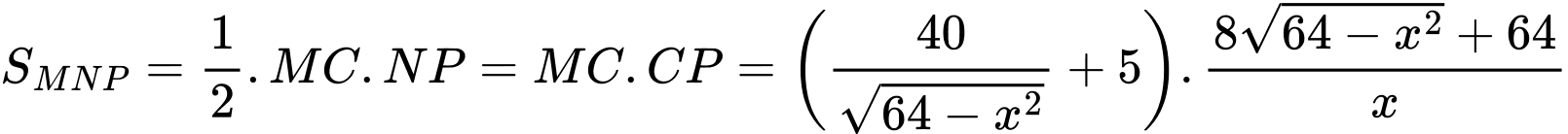
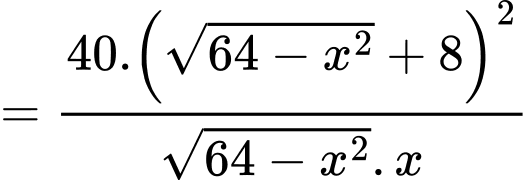
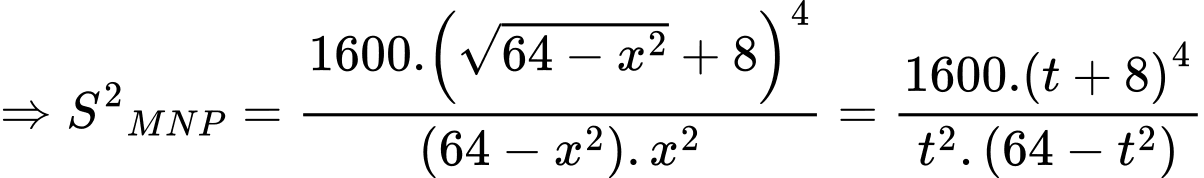
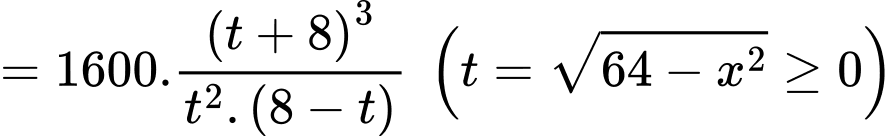
Xét hàm số
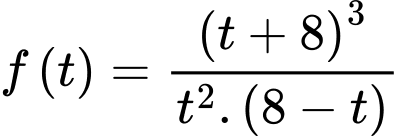
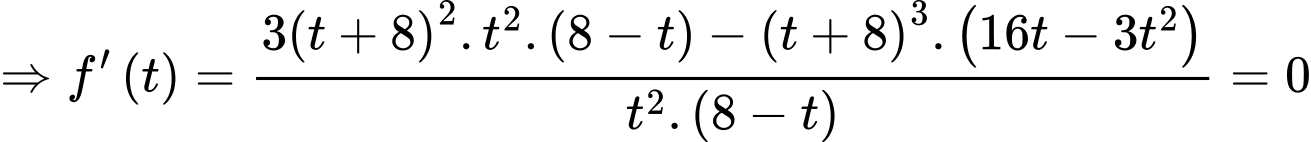
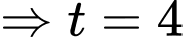 là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm số 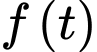 .
.
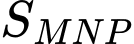 đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là 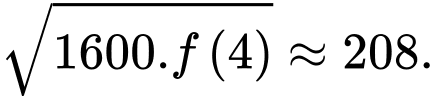
Câu 20 [696447]: Trong không gian 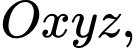 cho tam giác
cho tam giác 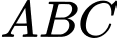 có
có 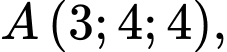
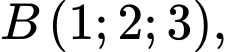
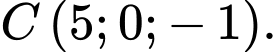 Điểm
Điểm 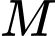 thay đổi trong không gian thoả mãn
thay đổi trong không gian thoả mãn  Mặt phẳng
Mặt phẳng  đi qua
đi qua 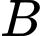 và vuông góc với
và vuông góc với 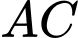 cắt
cắt  tại
tại 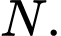 Khoảng cách từ
Khoảng cách từ 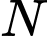 đến
đến 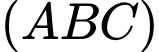 có giá trị lớn nhất bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
có giá trị lớn nhất bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
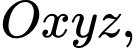 cho tam giác
cho tam giác 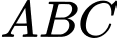 có
có 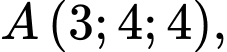
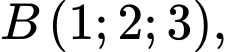
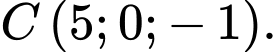 Điểm
Điểm 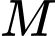 thay đổi trong không gian thoả mãn
thay đổi trong không gian thoả mãn  Mặt phẳng
Mặt phẳng  đi qua
đi qua 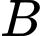 và vuông góc với
và vuông góc với 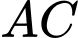 cắt
cắt  tại
tại 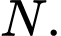 Khoảng cách từ
Khoảng cách từ 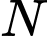 đến
đến 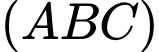 có giá trị lớn nhất bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
có giá trị lớn nhất bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 1,3.
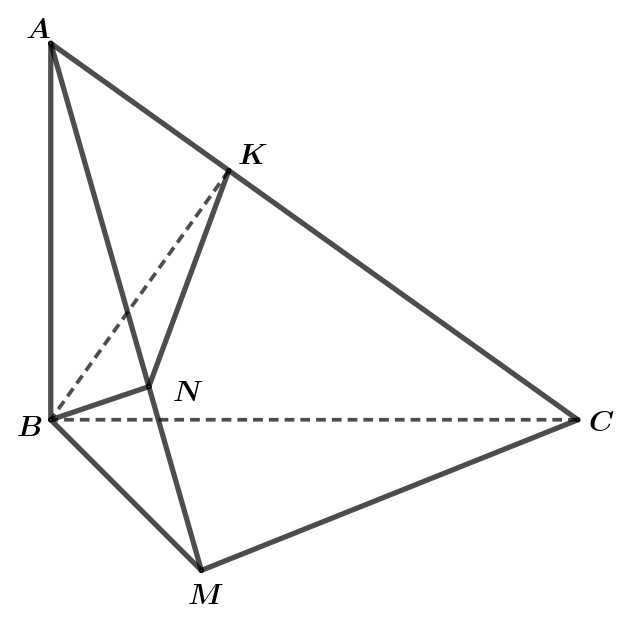
Ta có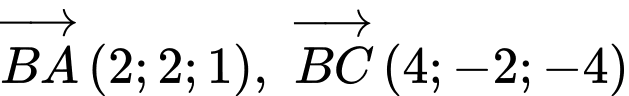
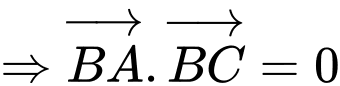
Do đó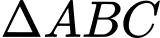 vuông tại
vuông tại 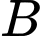
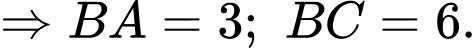
Từ giả thiết suy ra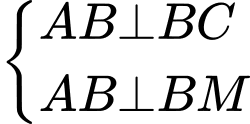
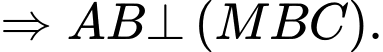
Gọi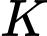 là hình chiếu của
là hình chiếu của 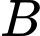 lên
lên 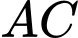 .
.
Xét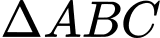 vuông tại
vuông tại 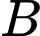 có đường cao
có đường cao 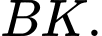
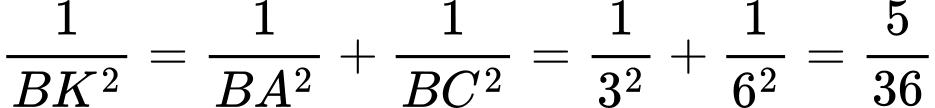
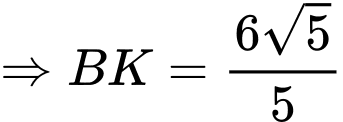
Ta có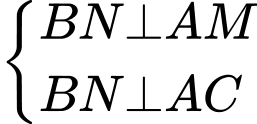
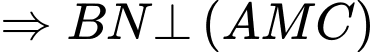
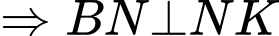
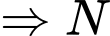 chạy trên đường tròn đường kính
chạy trên đường tròn đường kính 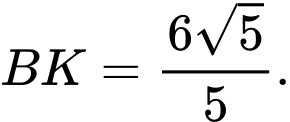
Trong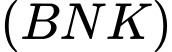 kẻ
kẻ 
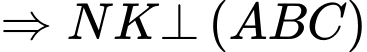
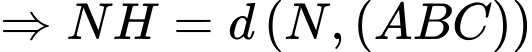
Trong tam giác vuông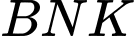 có
có 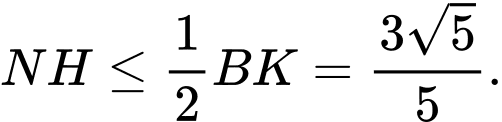
Vậy giá trị lớn nhất cần tìm là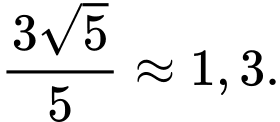

Ta có
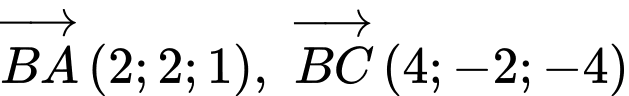
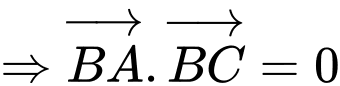
Do đó
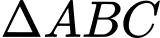 vuông tại
vuông tại 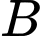
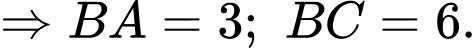
Từ giả thiết suy ra
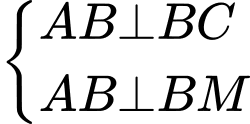
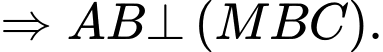
Gọi
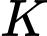 là hình chiếu của
là hình chiếu của 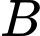 lên
lên 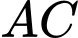 .
.Xét
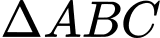 vuông tại
vuông tại 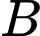 có đường cao
có đường cao 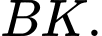
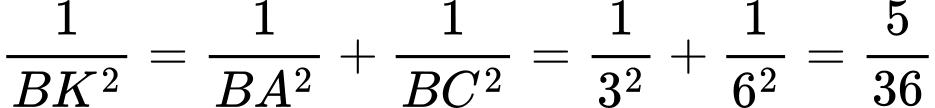
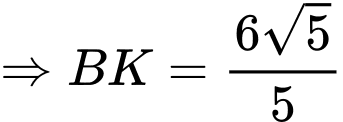
Ta có
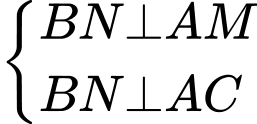
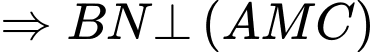
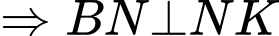
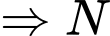 chạy trên đường tròn đường kính
chạy trên đường tròn đường kính 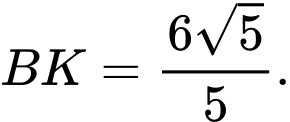
Trong
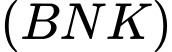 kẻ
kẻ 
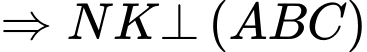
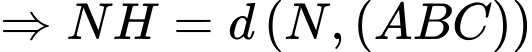
Trong tam giác vuông
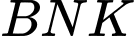 có
có 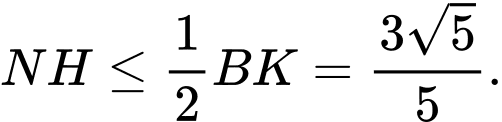
Vậy giá trị lớn nhất cần tìm là
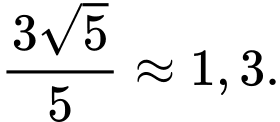
Câu 21 [696448]: Có hai chiếc hộp, hộp I có 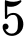 viên bi màu trắng và
viên bi màu trắng và 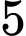 viên bi màu đen; hộp II có
viên bi màu đen; hộp II có 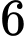 viên bi màu trắng và
viên bi màu trắng và 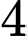 viên bi màu đen. Các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên đồng thời hai viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II. Lấy ra ngẫu nhiên một viên bi, giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I (làm tròn kết quả hai chữ số thập phân).
viên bi màu đen. Các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên đồng thời hai viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II. Lấy ra ngẫu nhiên một viên bi, giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I (làm tròn kết quả hai chữ số thập phân).
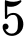 viên bi màu trắng và
viên bi màu trắng và 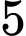 viên bi màu đen; hộp II có
viên bi màu đen; hộp II có 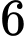 viên bi màu trắng và
viên bi màu trắng và 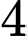 viên bi màu đen. Các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên đồng thời hai viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II. Lấy ra ngẫu nhiên một viên bi, giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I (làm tròn kết quả hai chữ số thập phân).
viên bi màu đen. Các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên đồng thời hai viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II. Lấy ra ngẫu nhiên một viên bi, giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I (làm tròn kết quả hai chữ số thập phân).
Điền đáp án: 0,14.
Xét các biến cố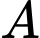 : “Viên bi lấy ra là viên màu trắng”.
: “Viên bi lấy ra là viên màu trắng”.
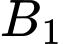 : “2 viên bi lấy ra từ hộp I có màu trắng”.
: “2 viên bi lấy ra từ hộp I có màu trắng”.
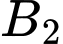 : “2 viên bi lấy ra từ hộp I có màu đen”.
: “2 viên bi lấy ra từ hộp I có màu đen”.
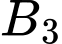 : “2 viên bi lấy ra từ hộp I có cả hai màu đen trắng”.
: “2 viên bi lấy ra từ hộp I có cả hai màu đen trắng”.
 : “Viên bi màu trắng thuộc hộp I”.
: “Viên bi màu trắng thuộc hộp I”.
Ta có:
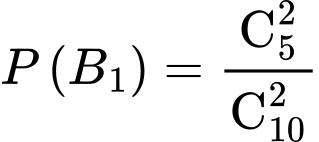
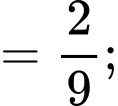
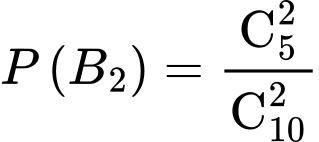
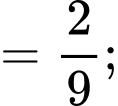
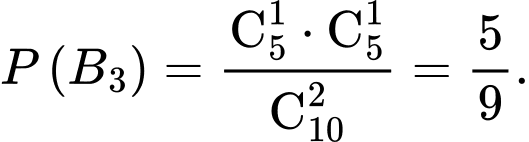
Áp dụng công thức xác suất toàn phần, ta có:

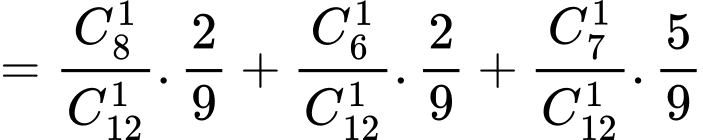
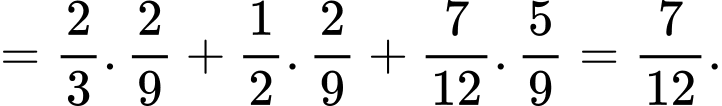
Xác suất lấy được viên bi màu trắng trong từng trường hợp:
+) Hộp II có 8 bi trắng và 4 bi đen: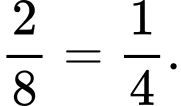
+) Hộp II có 6 bi trắng và 6 bi đen: 0.
+) Hộp II có 7 bi trắng và 7 bi đen: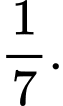
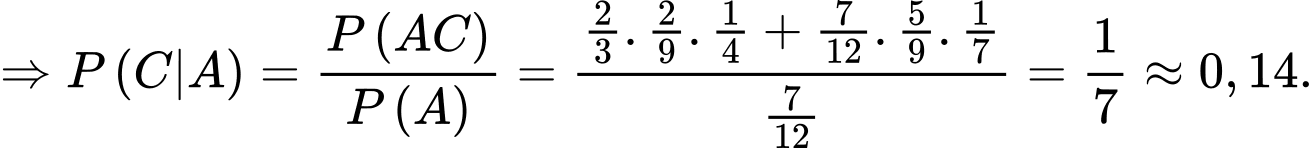
Xét các biến cố
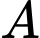 : “Viên bi lấy ra là viên màu trắng”.
: “Viên bi lấy ra là viên màu trắng”.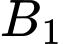 : “2 viên bi lấy ra từ hộp I có màu trắng”.
: “2 viên bi lấy ra từ hộp I có màu trắng”.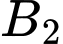 : “2 viên bi lấy ra từ hộp I có màu đen”.
: “2 viên bi lấy ra từ hộp I có màu đen”.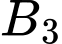 : “2 viên bi lấy ra từ hộp I có cả hai màu đen trắng”.
: “2 viên bi lấy ra từ hộp I có cả hai màu đen trắng”. : “Viên bi màu trắng thuộc hộp I”.
: “Viên bi màu trắng thuộc hộp I”.Ta có:
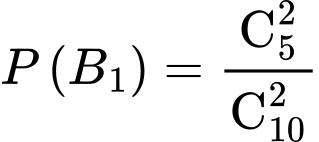
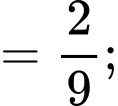
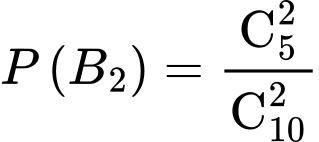
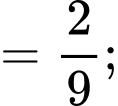
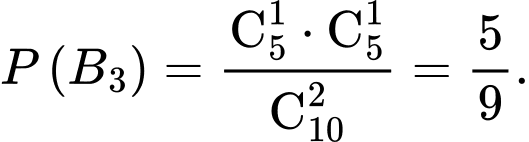
Áp dụng công thức xác suất toàn phần, ta có:

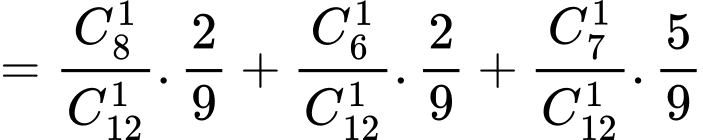
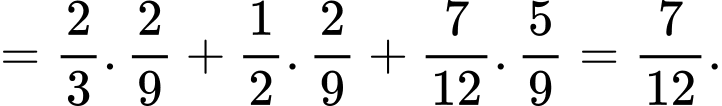
Xác suất lấy được viên bi màu trắng trong từng trường hợp:
+) Hộp II có 8 bi trắng và 4 bi đen:
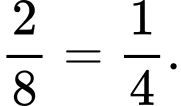
+) Hộp II có 6 bi trắng và 6 bi đen: 0.
+) Hộp II có 7 bi trắng và 7 bi đen:
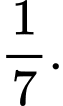
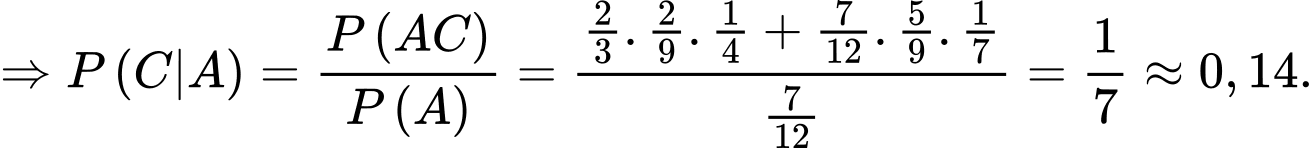
Câu 22 [696444]: Một con mèo bắt được 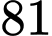 con chuột, sắp xếp chúng thành một vòng tròn và đánh số từ
con chuột, sắp xếp chúng thành một vòng tròn và đánh số từ 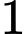 đến
đến 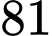 theo chiều kim đồng hồ. Con mèo đếm “Một, Hai, Ba!” theo chiều kim đồng hồ. Khi đếm đến ba, con mèo ăn con chuột xấu số đó và lại bắt đầu đếm “Một, Hai, Ba!” từ con chuột kế tiếp. Cứ như vậy, vòng tròn ngày càng nhỏ đi, cho đến khi chỉ còn lại
theo chiều kim đồng hồ. Con mèo đếm “Một, Hai, Ba!” theo chiều kim đồng hồ. Khi đếm đến ba, con mèo ăn con chuột xấu số đó và lại bắt đầu đếm “Một, Hai, Ba!” từ con chuột kế tiếp. Cứ như vậy, vòng tròn ngày càng nhỏ đi, cho đến khi chỉ còn lại 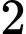 con chuột. Nếu biết một trong hai con chuột này được đánh số lớn hơn
con chuột. Nếu biết một trong hai con chuột này được đánh số lớn hơn 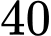 thì con chuột đầu tiên mà con mèo bắt đầu đếm có số bao nhiêu?
thì con chuột đầu tiên mà con mèo bắt đầu đếm có số bao nhiêu?
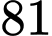 con chuột, sắp xếp chúng thành một vòng tròn và đánh số từ
con chuột, sắp xếp chúng thành một vòng tròn và đánh số từ 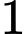 đến
đến 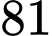 theo chiều kim đồng hồ. Con mèo đếm “Một, Hai, Ba!” theo chiều kim đồng hồ. Khi đếm đến ba, con mèo ăn con chuột xấu số đó và lại bắt đầu đếm “Một, Hai, Ba!” từ con chuột kế tiếp. Cứ như vậy, vòng tròn ngày càng nhỏ đi, cho đến khi chỉ còn lại
theo chiều kim đồng hồ. Con mèo đếm “Một, Hai, Ba!” theo chiều kim đồng hồ. Khi đếm đến ba, con mèo ăn con chuột xấu số đó và lại bắt đầu đếm “Một, Hai, Ba!” từ con chuột kế tiếp. Cứ như vậy, vòng tròn ngày càng nhỏ đi, cho đến khi chỉ còn lại 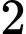 con chuột. Nếu biết một trong hai con chuột này được đánh số lớn hơn
con chuột. Nếu biết một trong hai con chuột này được đánh số lớn hơn 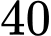 thì con chuột đầu tiên mà con mèo bắt đầu đếm có số bao nhiêu?
thì con chuột đầu tiên mà con mèo bắt đầu đếm có số bao nhiêu?
Điền đáp án: 7.
Để đơn giản hóa bài toán ta sẽ viết số thứ tự của con chuột từ 1 đến 81 như trong bảng sau:
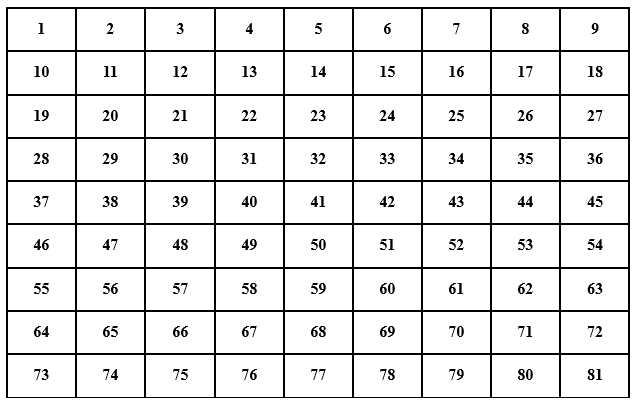
Giả sử con mèo bắt đầu đếm từ số 1.
Vòng 1, các con chuột ở các cột 3, 6, 9 bị con mèo ăn.
Vòng 2, các con chuột ở các cột 4, 8 bị con mèo ăn.
Vì còn 4 cột, ta tiếp tục viết số của các con chuột còn lại theo 9 cột như bảng bên dưới.
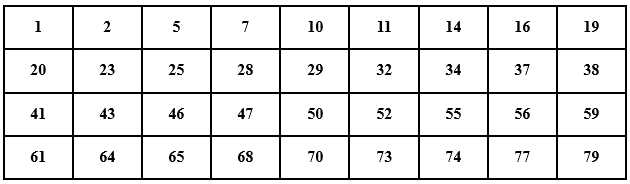
Sau vòng 3 và 4, các con chuột có số thứ tự ở cột thứ 3, 4, 6, 8, 9 sẽ bị con mèo ăn.
Tiếp tục đếm và loại bỏ các số cho tới khi chỉ còn 2 con chuột, ta thấy còn 2 số 1 và 34 .
Tuy nhiên đây là kết quả khi chúng ta đã giả sử mèo bắt đầu đếm từ con chuột số 1 .
Theo đề bài trong 2 con chuột còn lại con có số lớn hơn là 40.
Từ đó suy ra con mèo đã bắt đầu đếm từ con chuột số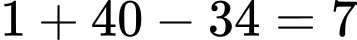 .
.
Để đơn giản hóa bài toán ta sẽ viết số thứ tự của con chuột từ 1 đến 81 như trong bảng sau:

Giả sử con mèo bắt đầu đếm từ số 1.
Vòng 1, các con chuột ở các cột 3, 6, 9 bị con mèo ăn.
Vòng 2, các con chuột ở các cột 4, 8 bị con mèo ăn.
Vì còn 4 cột, ta tiếp tục viết số của các con chuột còn lại theo 9 cột như bảng bên dưới.

Sau vòng 3 và 4, các con chuột có số thứ tự ở cột thứ 3, 4, 6, 8, 9 sẽ bị con mèo ăn.
Tiếp tục đếm và loại bỏ các số cho tới khi chỉ còn 2 con chuột, ta thấy còn 2 số 1 và 34 .
Tuy nhiên đây là kết quả khi chúng ta đã giả sử mèo bắt đầu đếm từ con chuột số 1 .
Theo đề bài trong 2 con chuột còn lại con có số lớn hơn là 40.
Từ đó suy ra con mèo đã bắt đầu đếm từ con chuột số
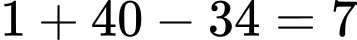 .
.