PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [696449]: Cho hình chóp  có đáy
có đáy 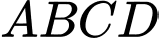 là hình vuông và
là hình vuông và 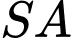 vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
vuông góc với mặt phẳng đáy. Góc giữa đường thẳng 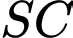 và mặt phẳng
và mặt phẳng 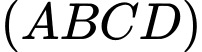 là
là
 có đáy
có đáy 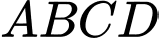 là hình vuông và
là hình vuông và 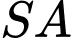 vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
vuông góc với mặt phẳng đáy. Góc giữa đường thẳng 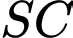 và mặt phẳng
và mặt phẳng 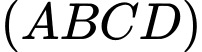 là
là A, 

B, 

C, 

D, 

Chọn đáp án C.
Góc giữa đường thẳng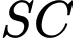 và mặt phẳng
và mặt phẳng 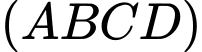 là
là  Đáp án: C
Đáp án: C
Góc giữa đường thẳng
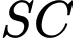 và mặt phẳng
và mặt phẳng 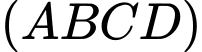 là
là  Đáp án: C
Đáp án: C
Câu 2 [256684]: Cho hàm số 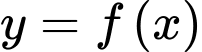 có bảng biến thiên như hình sau:
có bảng biến thiên như hình sau:
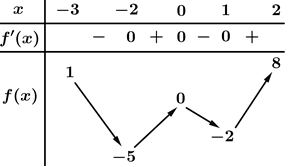
Giá trị nhỏ nhất của hàm số đã cho trên đoạn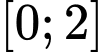 bằng
bằng
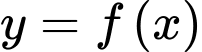 có bảng biến thiên như hình sau:
có bảng biến thiên như hình sau: 
Giá trị nhỏ nhất của hàm số đã cho trên đoạn
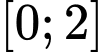 bằng
bằng A, 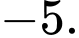
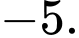
B, 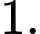
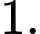
C, 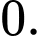
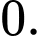
D, 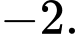
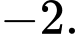
Chọn đáp án D.
Dựa vào bảng biến thiên ta có: Giá trị nhỏ nhất của hàm số đã cho trên đoạn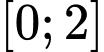 bằng
bằng 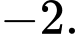 Đáp án: D
Đáp án: D
Dựa vào bảng biến thiên ta có: Giá trị nhỏ nhất của hàm số đã cho trên đoạn
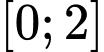 bằng
bằng 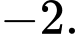 Đáp án: D
Đáp án: D
Câu 3 [696450]: Cho ba số 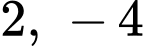 và
và 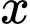 theo thứ tự lập thành cấp số nhân. Giá trị của
theo thứ tự lập thành cấp số nhân. Giá trị của 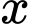 bằng
bằng
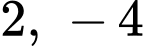 và
và 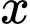 theo thứ tự lập thành cấp số nhân. Giá trị của
theo thứ tự lập thành cấp số nhân. Giá trị của 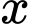 bằng
bằng A, 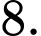
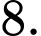
B, 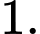
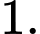
C, 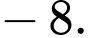
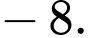
D, 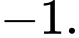
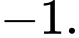
Chọn đáp án A.
Ta có: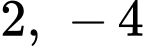 và
và 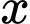 theo thứ tự lập thành cấp số nhân nên
theo thứ tự lập thành cấp số nhân nên 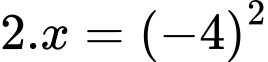
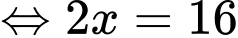
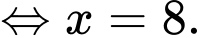 Đáp án: A
Đáp án: A
Ta có:
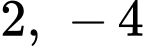 và
và 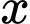 theo thứ tự lập thành cấp số nhân nên
theo thứ tự lập thành cấp số nhân nên 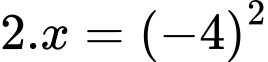
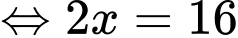
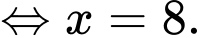 Đáp án: A
Đáp án: A
Câu 4 [696451]: Trong không gian 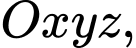 vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ
vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ  và điểm
và điểm 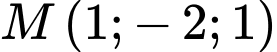 ?
?
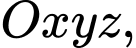 vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ
vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ  và điểm
và điểm 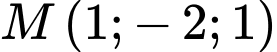 ?
? A, 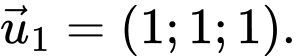
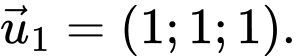
B, 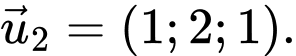
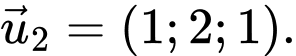
C, 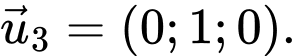
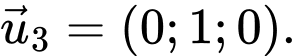
D, 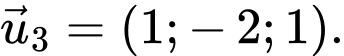
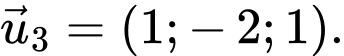
Chọn đáp án D.
Đường thẩng đi qua gốc tọa dộ và điểm
và điểm 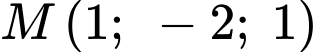 có vectơ chỉ phương
có vectơ chỉ phương 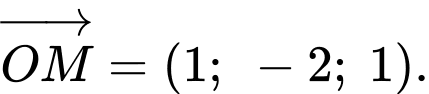
Vậy trong không gian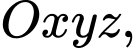 vectơ
vectơ 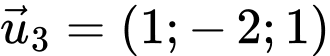 là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ
là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ  và điểm
và điểm 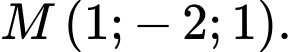 Đáp án: D
Đáp án: D
Đường thẩng đi qua gốc tọa dộ
 và điểm
và điểm 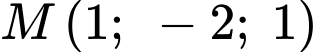 có vectơ chỉ phương
có vectơ chỉ phương 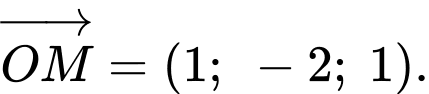
Vậy trong không gian
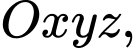 vectơ
vectơ 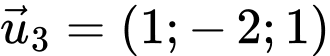 là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ
là một vectơ chỉ phương của đường thẳng đi qua gốc toạ độ  và điểm
và điểm 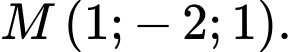 Đáp án: D
Đáp án: D
Câu 5 [258434]: Tập nghiệm của bất phương trình 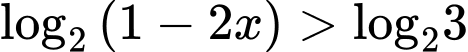 là
là
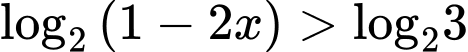 là
là A, 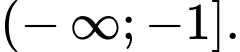
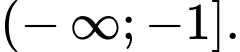
B, 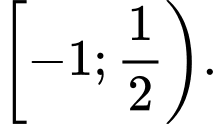
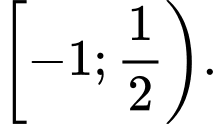
C, 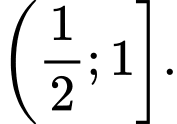
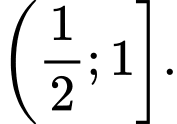
D, 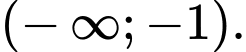
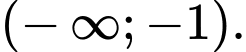
Chọn đáp án D.
Điều kiện xác định: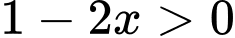
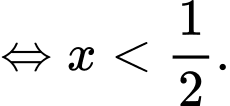
Ta có bất phương trình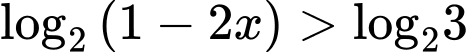
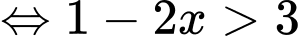
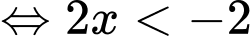

Vậy tập nghiệm của bất phương trình là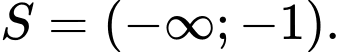 Đáp án: D
Đáp án: D
Điều kiện xác định:
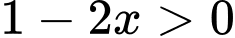
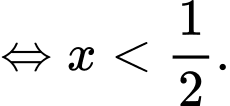
Ta có bất phương trình
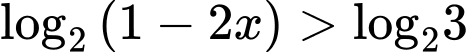
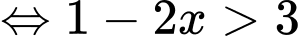
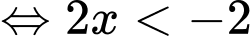

Vậy tập nghiệm của bất phương trình là
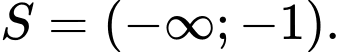 Đáp án: D
Đáp án: D
Câu 6 [696452]: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 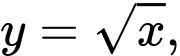 trục
trục 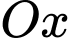 và hai đường thẳng
và hai đường thẳng 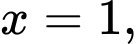
 quanh trục hoành được tính bởi công thức nào sau đây?
quanh trục hoành được tính bởi công thức nào sau đây?
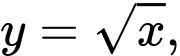 trục
trục 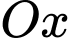 và hai đường thẳng
và hai đường thẳng 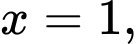
 quanh trục hoành được tính bởi công thức nào sau đây?
quanh trục hoành được tính bởi công thức nào sau đây? A, 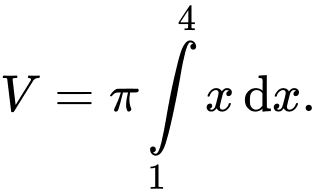
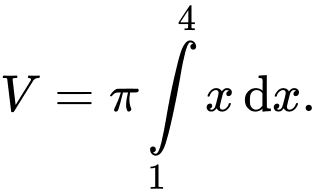
B, 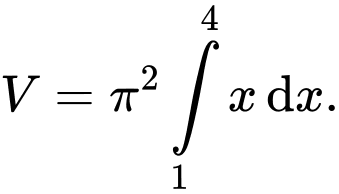
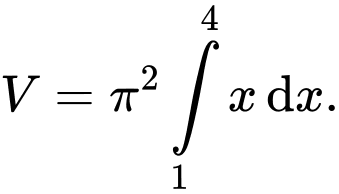
C, 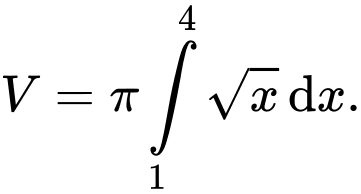
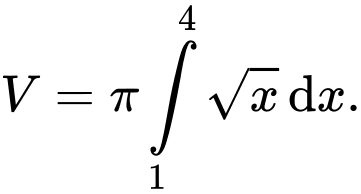
D, 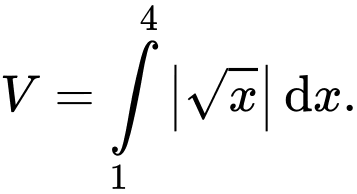
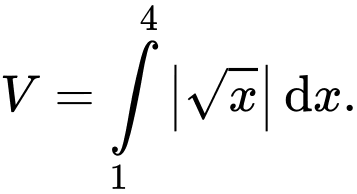
Chọn đáp án A.
Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường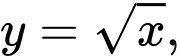 trục
trục 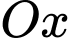 và hai đường thẳng
và hai đường thẳng 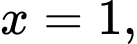
 quanh trục hoành là
quanh trục hoành là 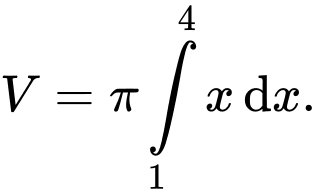 Đáp án: A
Đáp án: A
Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
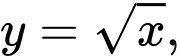 trục
trục 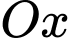 và hai đường thẳng
và hai đường thẳng 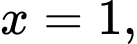
 quanh trục hoành là
quanh trục hoành là 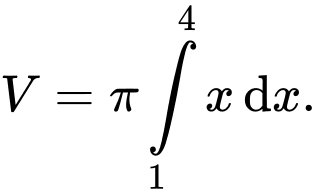 Đáp án: A
Đáp án: A
Câu 7 [696453]: Cho tứ diện đều 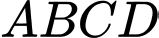 cạnh bằng
cạnh bằng 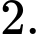 Độ dài của vectơ
Độ dài của vectơ 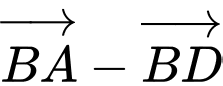 là
là
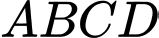 cạnh bằng
cạnh bằng  Độ dài của vectơ
Độ dài của vectơ 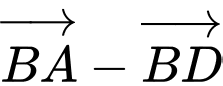 là
là A, 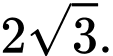
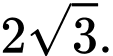
B, 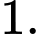
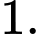
C, 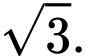
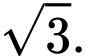
D, 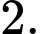
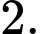
Chọn đáp án D.
Ta có: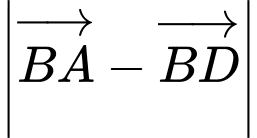
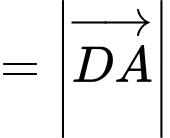
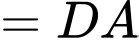
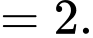 Đáp án: D
Đáp án: D
Ta có:
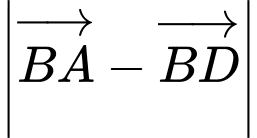
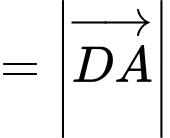
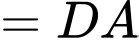
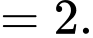 Đáp án: D
Đáp án: D
Câu 8 [696454]: Tìm 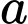 để
để 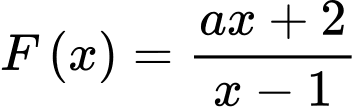 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 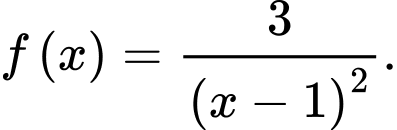
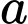 để
để 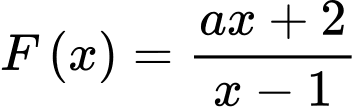 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 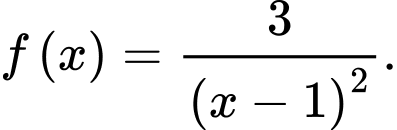
A, 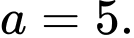
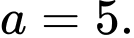
B, 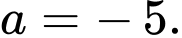
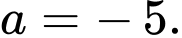
C, 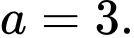
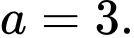
D, 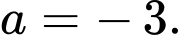
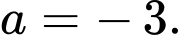
Chọn đáp án B.
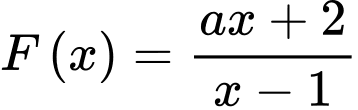 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 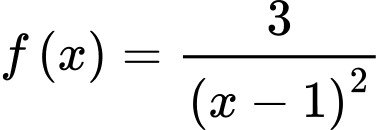 nên
nên 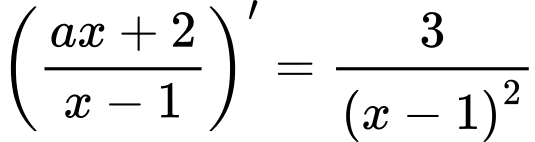
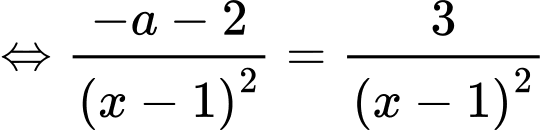
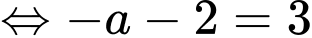
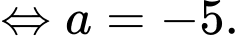 Đáp án: B
Đáp án: B
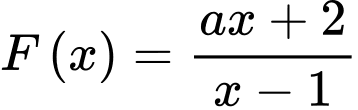 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 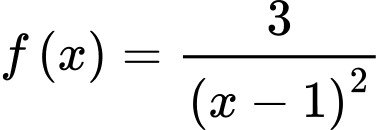 nên
nên 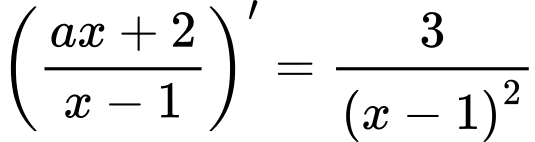
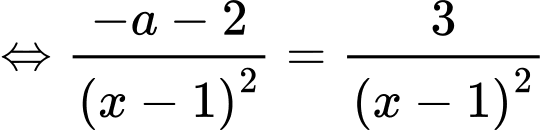
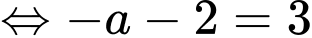
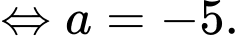 Đáp án: B
Đáp án: B
Câu 9 [258459]: Trong không gian 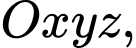 cho mặt phẳng
cho mặt phẳng 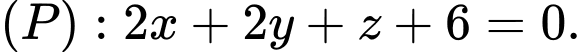 Tìm tọa độ điểm
Tìm tọa độ điểm 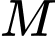 thuộc tia
thuộc tia  sao cho khoảng cách từ
sao cho khoảng cách từ 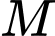 đến
đến 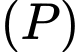 bằng
bằng 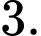
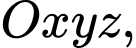 cho mặt phẳng
cho mặt phẳng 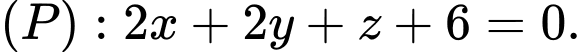 Tìm tọa độ điểm
Tìm tọa độ điểm 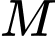 thuộc tia
thuộc tia  sao cho khoảng cách từ
sao cho khoảng cách từ 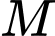 đến
đến 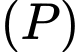 bằng
bằng 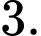
A, 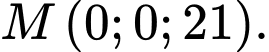
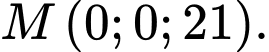
B, 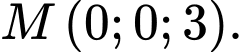
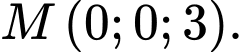
C, 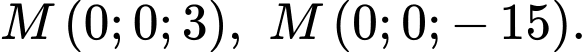
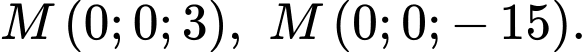
D, 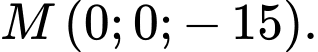
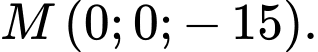
Chọn đáp án B.
Gọi tọa độ điểm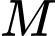 là
là 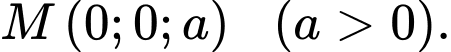
Ta có: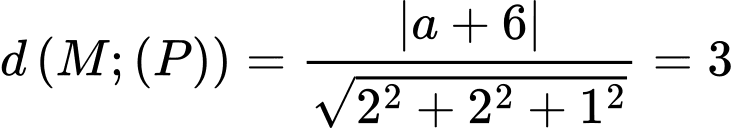
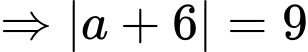
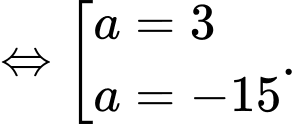
Vậy ta có các điểm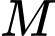 thỏa mãn là:
thỏa mãn là: 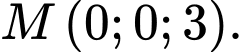 Đáp án: B
Đáp án: B
Gọi tọa độ điểm
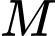 là
là 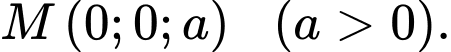
Ta có:
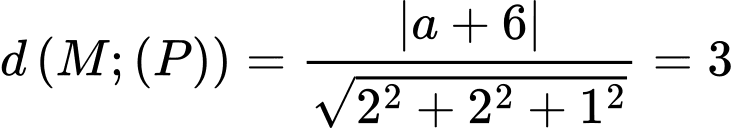
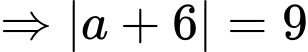
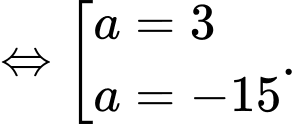
Vậy ta có các điểm
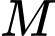 thỏa mãn là:
thỏa mãn là: 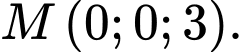 Đáp án: B
Đáp án: B
Câu 10 [258449]: Cho số thực 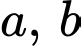 thoả mãn
thoả mãn 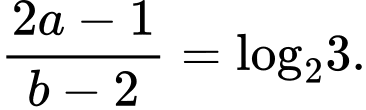 Giá trị của
Giá trị của 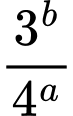 bằng
bằng
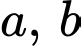 thoả mãn
thoả mãn 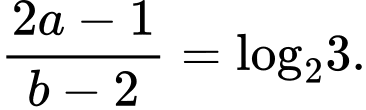 Giá trị của
Giá trị của 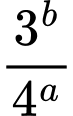 bằng
bằng A, 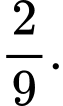
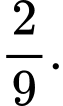
B, 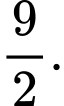
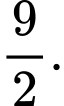
C, 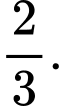
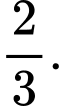
D, 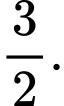
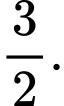
Chọn đáp án B.
Ta có: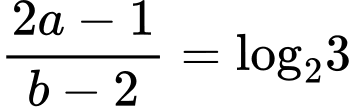
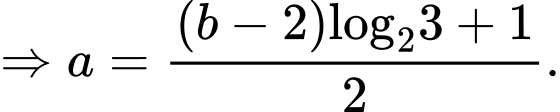
Khi đó: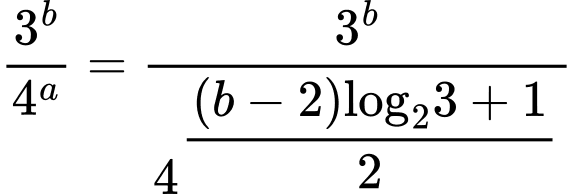
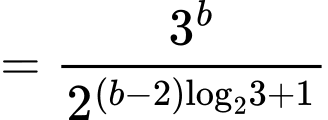
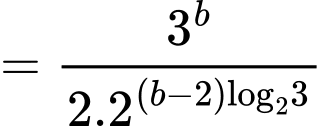
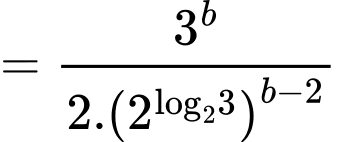
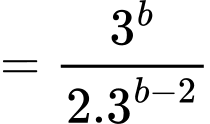
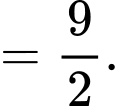 Đáp án: B
Đáp án: B
Ta có:
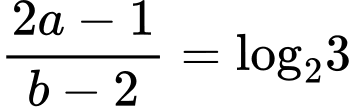
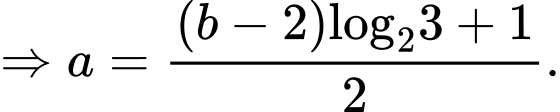
Khi đó:
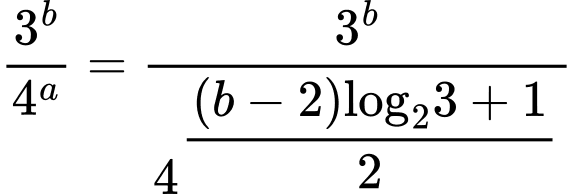
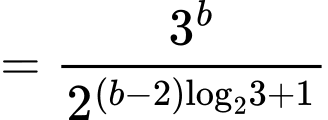
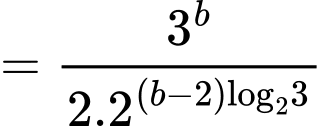
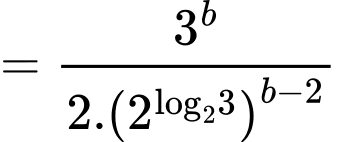
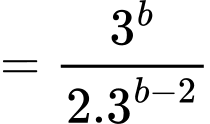
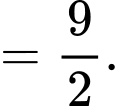 Đáp án: B
Đáp án: B
Câu 11 [696455]: Bảng bên dưới biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
A, 13,9.
B, 14,2.
C, 15,1.
D, 14,6.
Chọn đáp án B.
Gọi là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có:
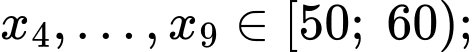
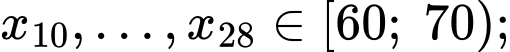
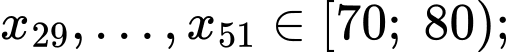
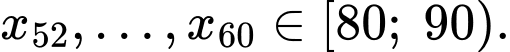
Tứ phân vị thứ nhất của mẫu số liệu gốc là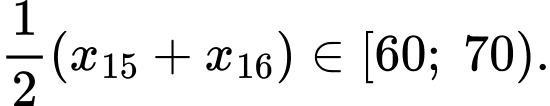 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
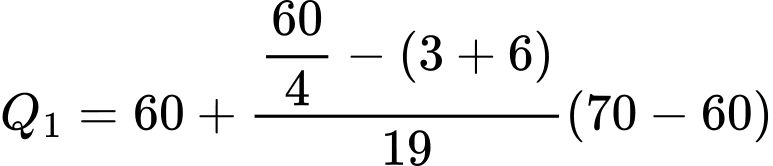
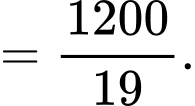
Tứ phân vị thứ ba của mẫu số liệu gốc là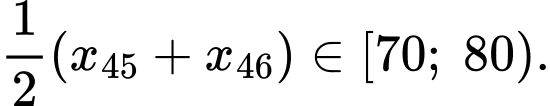 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
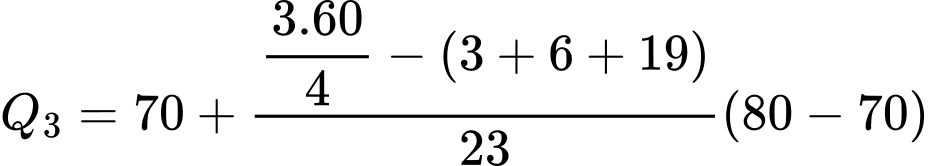
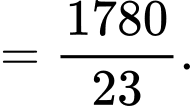
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
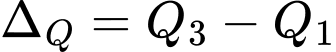
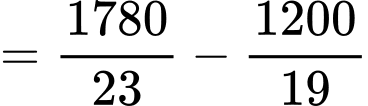
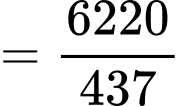
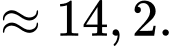 Đáp án: B
Đáp án: B
Gọi
 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.Ta có:

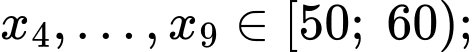
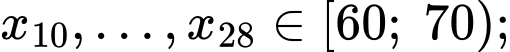
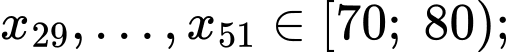
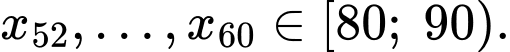
Tứ phân vị thứ nhất của mẫu số liệu gốc là
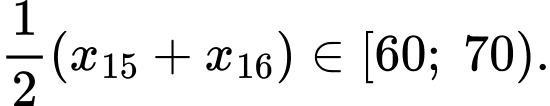 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 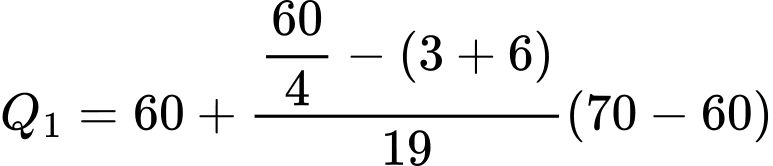
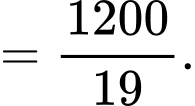
Tứ phân vị thứ ba của mẫu số liệu gốc là
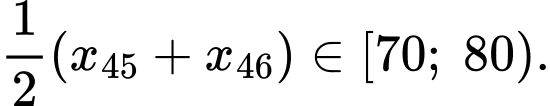 Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 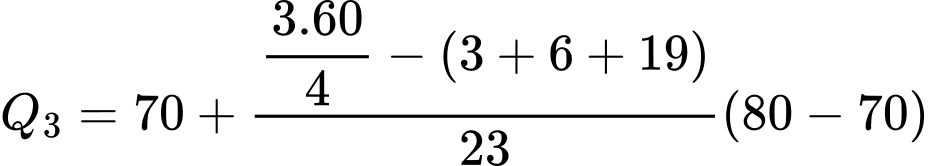
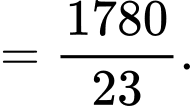
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
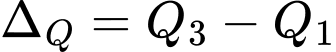
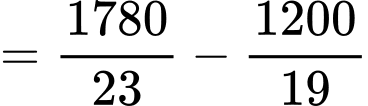
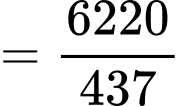
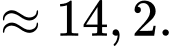 Đáp án: B
Đáp án: B
Câu 12 [256900]: Đồ thị hàm số 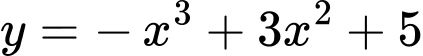 có hai điểm cực trị là
có hai điểm cực trị là 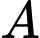 và
và 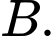 Tính diện tích của tam giác
Tính diện tích của tam giác 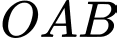 với
với  là gốc tọa độ.
là gốc tọa độ.
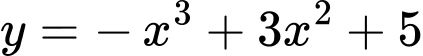 có hai điểm cực trị là
có hai điểm cực trị là 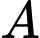 và
và 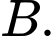 Tính diện tích của tam giác
Tính diện tích của tam giác 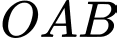 với
với  là gốc tọa độ.
là gốc tọa độ. A, 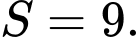
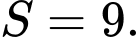
B, 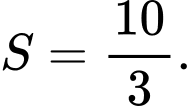
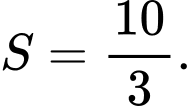
C, 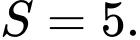
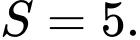
D, 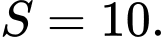
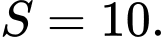
Chọn đáp án C.
Hàm số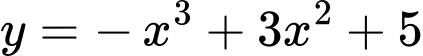 có
có 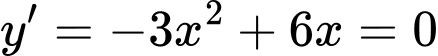
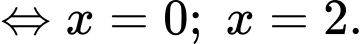
Suy ra đồ thị hàm số có hai điểm cực trị là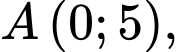
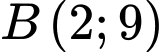 và
và 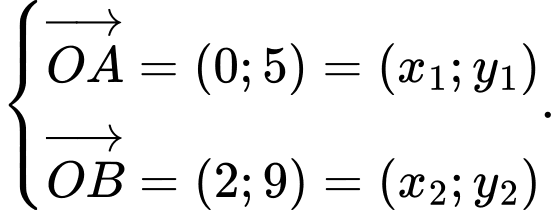
Diện tích của tam giác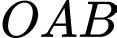 là
là 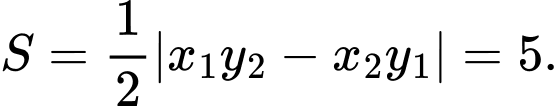 Đáp án: C
Đáp án: C
Hàm số
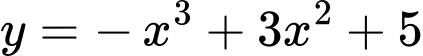 có
có 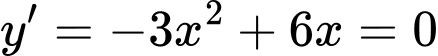
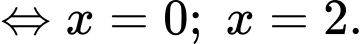
Suy ra đồ thị hàm số có hai điểm cực trị là
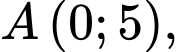
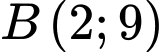 và
và 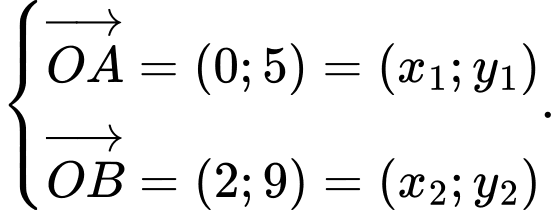
Diện tích của tam giác
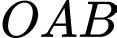 là
là 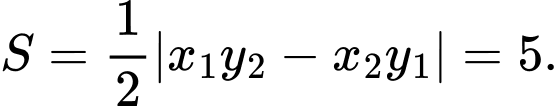 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696456]: Cho hàm số 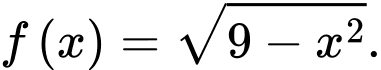
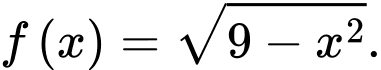
a) Đúng.
Điều kiện xác định là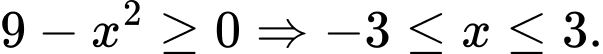
b) Sai.
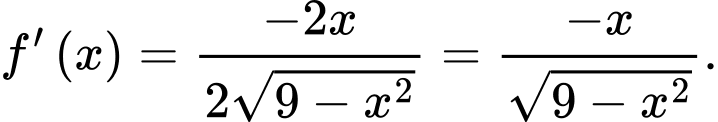
c) Đúng.
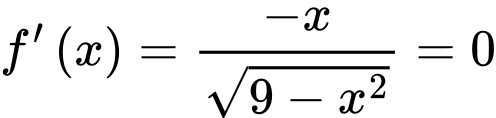
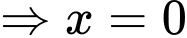
BBT:
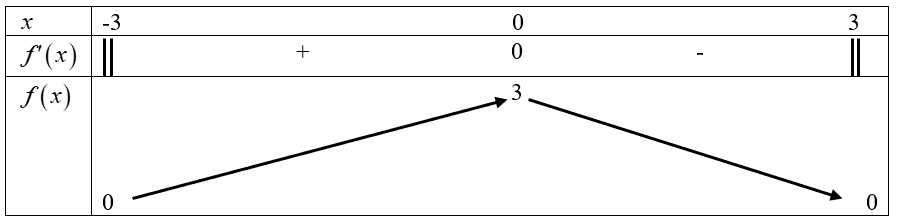 d) Sai.
d) Sai.
Ta có:
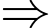 Tập giá trị của hàm số chứa đúng 4 số nguyên.
Tập giá trị của hàm số chứa đúng 4 số nguyên.
Điều kiện xác định là
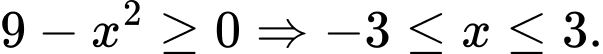
b) Sai.
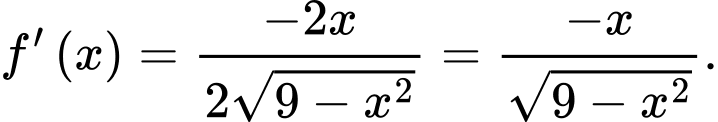
c) Đúng.
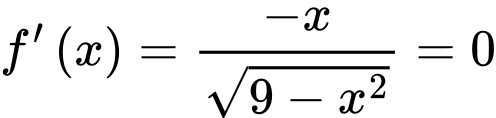
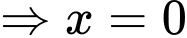
BBT:

Ta có:

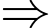 Tập giá trị của hàm số chứa đúng 4 số nguyên.
Tập giá trị của hàm số chứa đúng 4 số nguyên.
Câu 14 [696457]: Trong không gian tọa độ 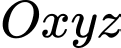 cho điểm
cho điểm 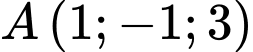 và hai đường thẳng
và hai đường thẳng 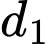 :
: 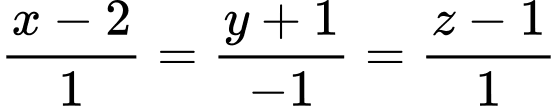 và
và 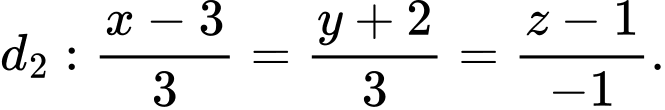 Gọi
Gọi 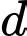 là đường thẳng đi qua
là đường thẳng đi qua 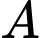 , cắt đường thẳng
, cắt đường thẳng 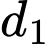 và vuông góc với đường thẳng
và vuông góc với đường thẳng 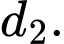
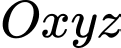 cho điểm
cho điểm 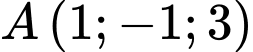 và hai đường thẳng
và hai đường thẳng 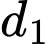 :
: 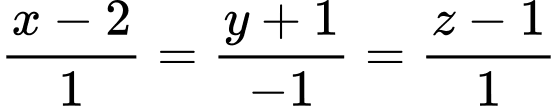 và
và 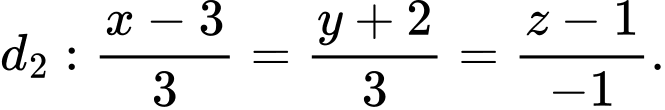 Gọi
Gọi 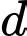 là đường thẳng đi qua
là đường thẳng đi qua 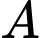 , cắt đường thẳng
, cắt đường thẳng 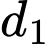 và vuông góc với đường thẳng
và vuông góc với đường thẳng 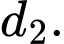
a) Đúng.
b) Sai.
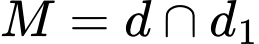
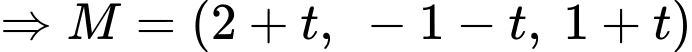
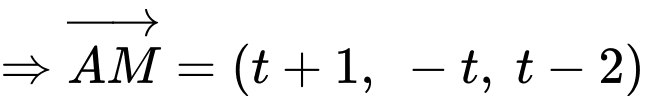
Có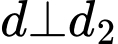
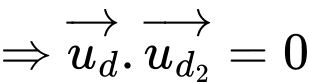
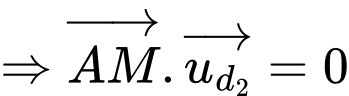
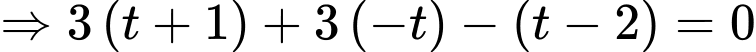
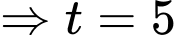
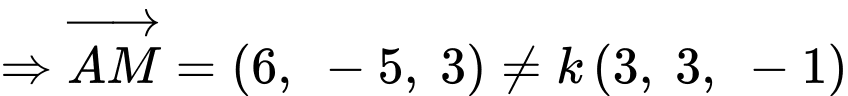
c) Sai.
Theo câu b) ta có: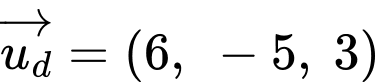 .
.
d) Sai.
Phương trình tham số của đường thẳng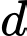 là
là 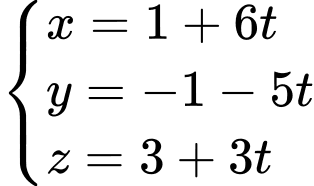
Thay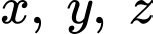 theo
theo 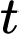 vào phương trình mặt phẳng
vào phương trình mặt phẳng 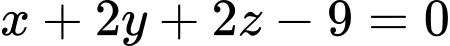 ta được:
ta được:
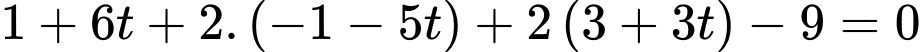
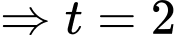
 Tung độ của giao điểm là
Tung độ của giao điểm là 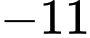 .
.
b) Sai.
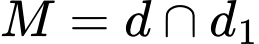
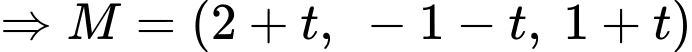
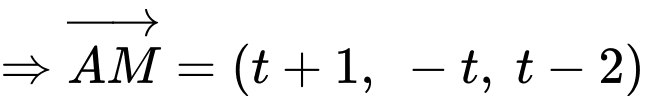
Có
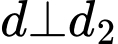
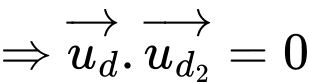
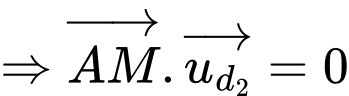
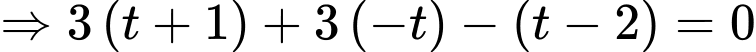
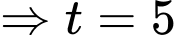
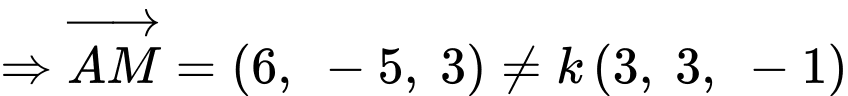
c) Sai.
Theo câu b) ta có:
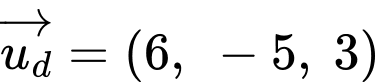 .
.d) Sai.
Phương trình tham số của đường thẳng
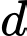 là
là 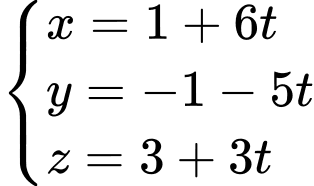
Thay
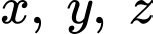 theo
theo 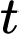 vào phương trình mặt phẳng
vào phương trình mặt phẳng 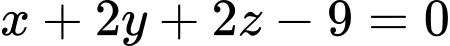 ta được:
ta được: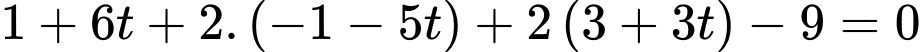
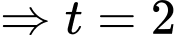
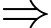 Tung độ của giao điểm là
Tung độ của giao điểm là 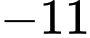 .
.
Câu 15 [697014]: Một nghiên cứu cho thấy có 5% các tin nhắn trên một mạng viễn thông X là tin nhắn quảng cáo. Trong các tin nhắn quảng cáo, 80% tin nhắn có chứa chữ “sale”. Trong các tin nhắn không quảng cáo, 2% tin nhắn có chữ “sale”. Chọn ngẫu nhiên 1 tin nhắn trên mạng viễn thông X.
Gọi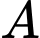 là biến cố: “tin nhắn là tin nhắn quảng cáo”.
là biến cố: “tin nhắn là tin nhắn quảng cáo”.
Gọi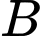 là biến cố: “tin nhắn chứa chữ “sale”.
là biến cố: “tin nhắn chứa chữ “sale”.
Gọi
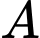 là biến cố: “tin nhắn là tin nhắn quảng cáo”.
là biến cố: “tin nhắn là tin nhắn quảng cáo”. Gọi
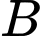 là biến cố: “tin nhắn chứa chữ “sale”.
là biến cố: “tin nhắn chứa chữ “sale”.
Gọi 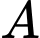 là biến cố “ Tin nhắn là tin nhắn quảng cáo”
là biến cố “ Tin nhắn là tin nhắn quảng cáo”
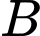 là biến cố “ Tin nhắn chứa chữ sale”
là biến cố “ Tin nhắn chứa chữ sale”
a) Đúng.
Theo đề bài ta có: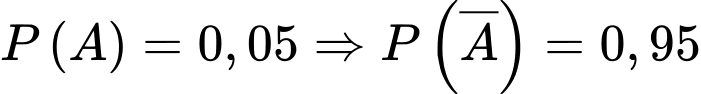
b) Sai.
Vì trong các tin nhắn quảng cáo, 80% tin nhắn có chứa chữ “sale”
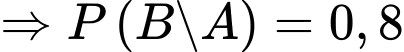 .
.
c) Sai.
Theo công thức xác suất toàn phần ta có:
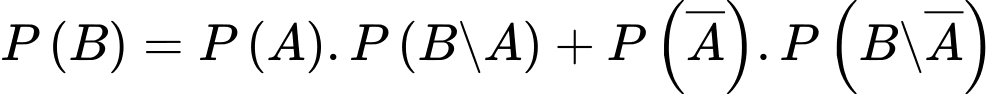
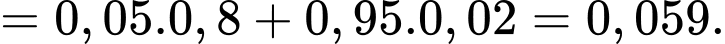
d) Đúng.
Theo công thức Bayes ta có: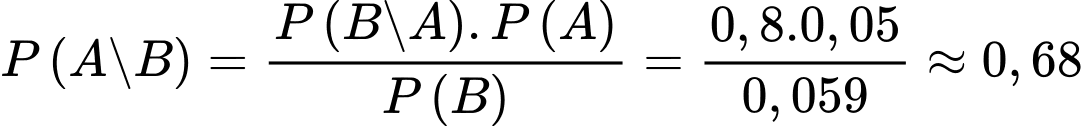
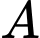 là biến cố “ Tin nhắn là tin nhắn quảng cáo”
là biến cố “ Tin nhắn là tin nhắn quảng cáo”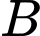 là biến cố “ Tin nhắn chứa chữ sale”
là biến cố “ Tin nhắn chứa chữ sale”a) Đúng.
Theo đề bài ta có:
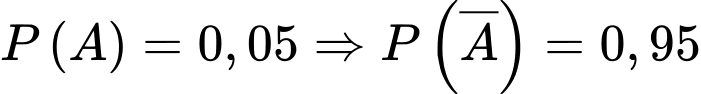
b) Sai.
Vì trong các tin nhắn quảng cáo, 80% tin nhắn có chứa chữ “sale”
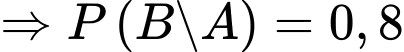 .
.c) Sai.
Theo công thức xác suất toàn phần ta có:
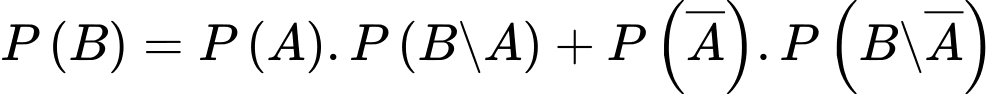
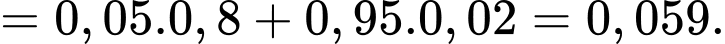
d) Đúng.
Theo công thức Bayes ta có:
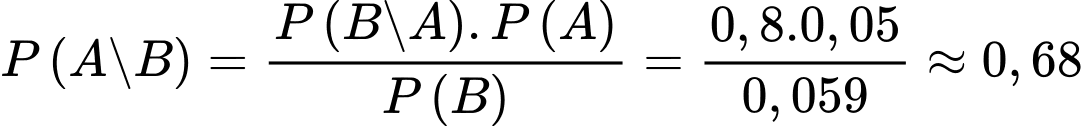
Câu 16 [696460]: Cho hàm số 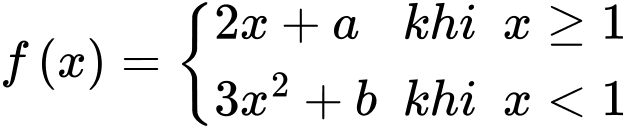 liên tục trên
liên tục trên 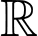 thoả mãn
thoả mãn 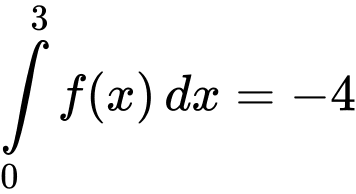 với
với 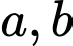 là các số thực. Gọi
là các số thực. Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 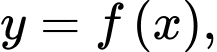 trục hoành và các đường thẳng
trục hoành và các đường thẳng 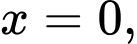
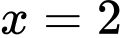 .
.
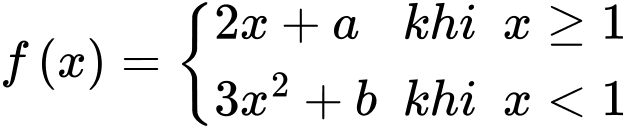 liên tục trên
liên tục trên 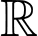 thoả mãn
thoả mãn 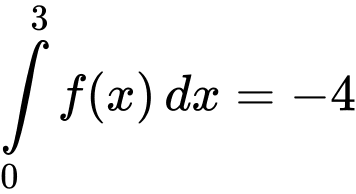 với
với 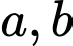 là các số thực. Gọi
là các số thực. Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 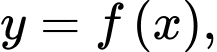 trục hoành và các đường thẳng
trục hoành và các đường thẳng 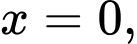
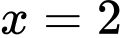 .
.
a) Đúng.
Vì hàm số liên tục tại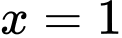
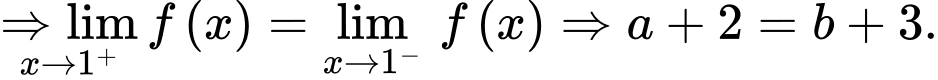
b) Sai.
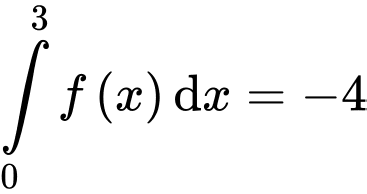
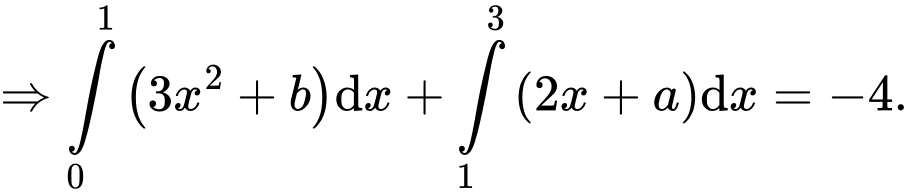
c) Sai.
Từ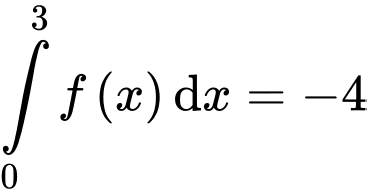
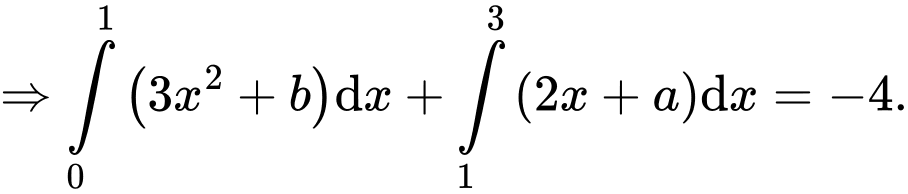
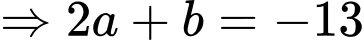
Mà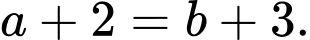
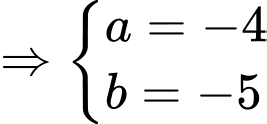
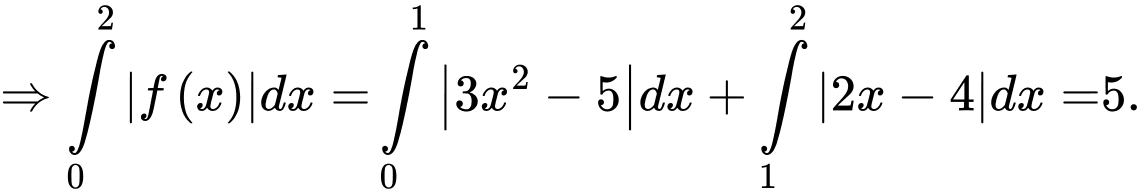
d) Sai.
Thể tích khối tròn xoay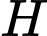 khi quay quanh trục hoành là
khi quay quanh trục hoành là
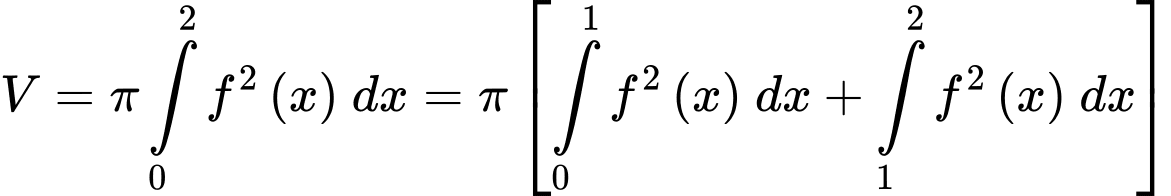
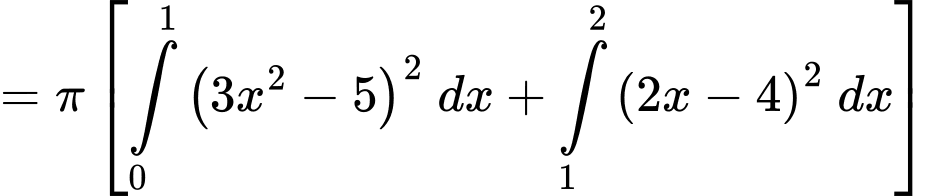
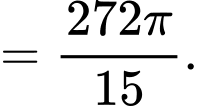
Vì hàm số liên tục tại
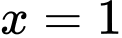
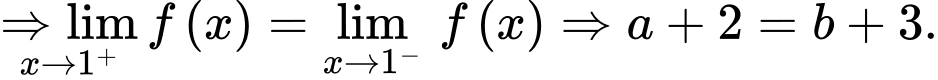
b) Sai.
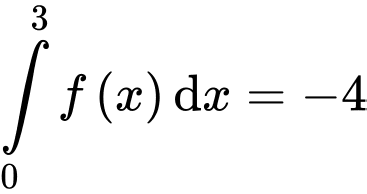
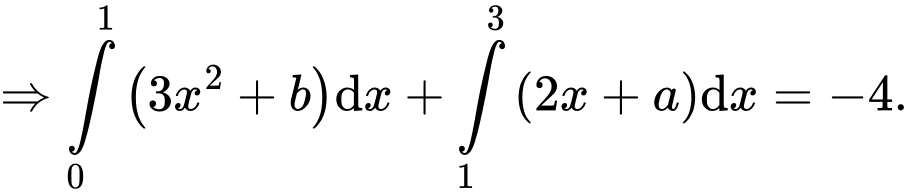
c) Sai.
Từ
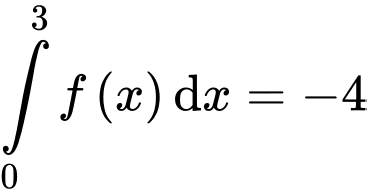
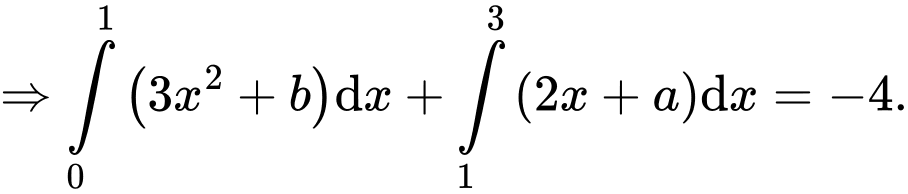
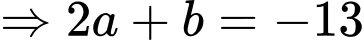
Mà
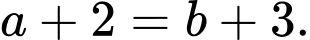
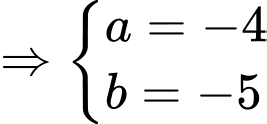
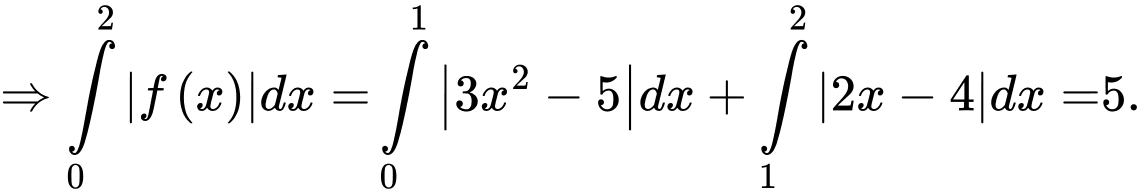
d) Sai.
Thể tích khối tròn xoay
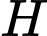 khi quay quanh trục hoành là
khi quay quanh trục hoành là 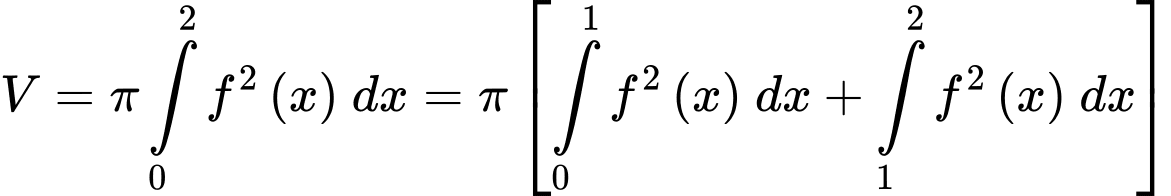
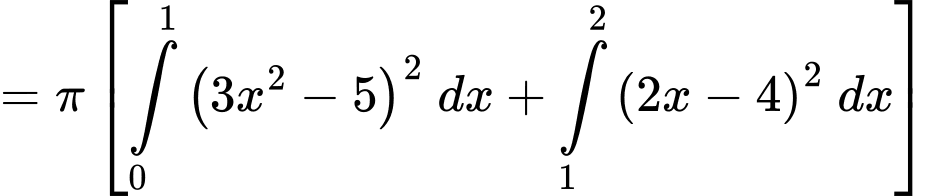
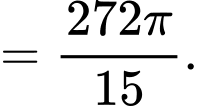
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696461]: Cho hình hộp đứng  có đáy
có đáy 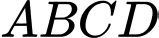 là hình thoi cạnh bằng
là hình thoi cạnh bằng 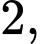 tam giác
tam giác 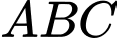 đều,
đều, 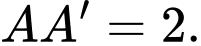 Gọi
Gọi 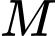 là trung điểm của cạnh
là trung điểm của cạnh 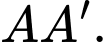 Khoảng cách từ
Khoảng cách từ 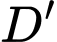 đến mặt phẳng
đến mặt phẳng 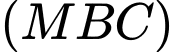 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 có đáy
có đáy 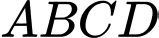 là hình thoi cạnh bằng
là hình thoi cạnh bằng 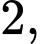 tam giác
tam giác 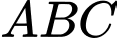 đều,
đều, 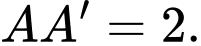 Gọi
Gọi 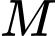 là trung điểm của cạnh
là trung điểm của cạnh 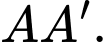 Khoảng cách từ
Khoảng cách từ 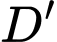 đến mặt phẳng
đến mặt phẳng 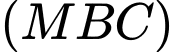 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 0,9.
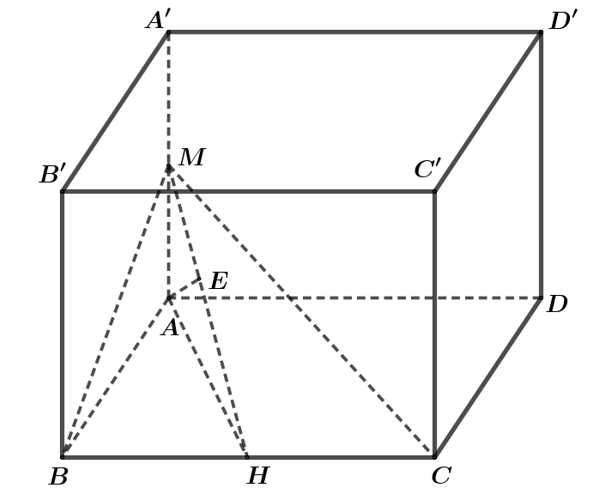 Vì
Vì 
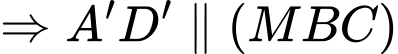
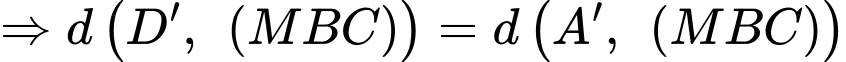
Vì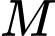 là trung điểm của
là trung điểm của 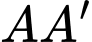
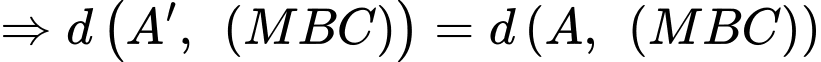
Kẻ
Mà
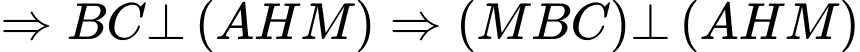
Kẻ
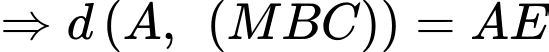
Xét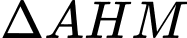 vuông tại
vuông tại 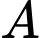 có:
có:
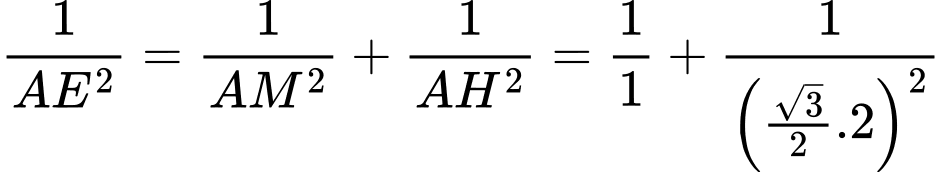
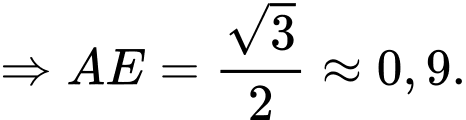


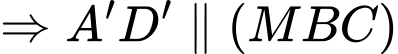
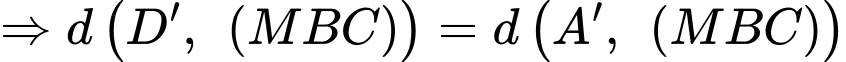
Vì
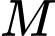 là trung điểm của
là trung điểm của 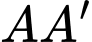
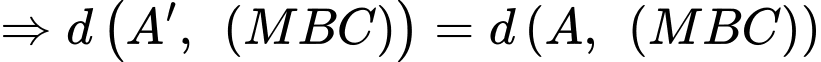
Kẻ

Mà

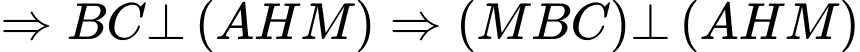
Kẻ

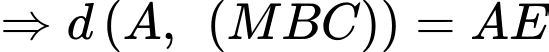
Xét
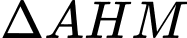 vuông tại
vuông tại 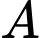 có:
có: 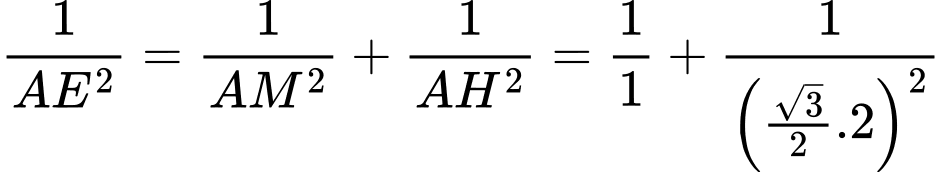
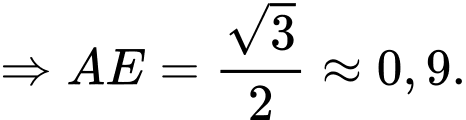
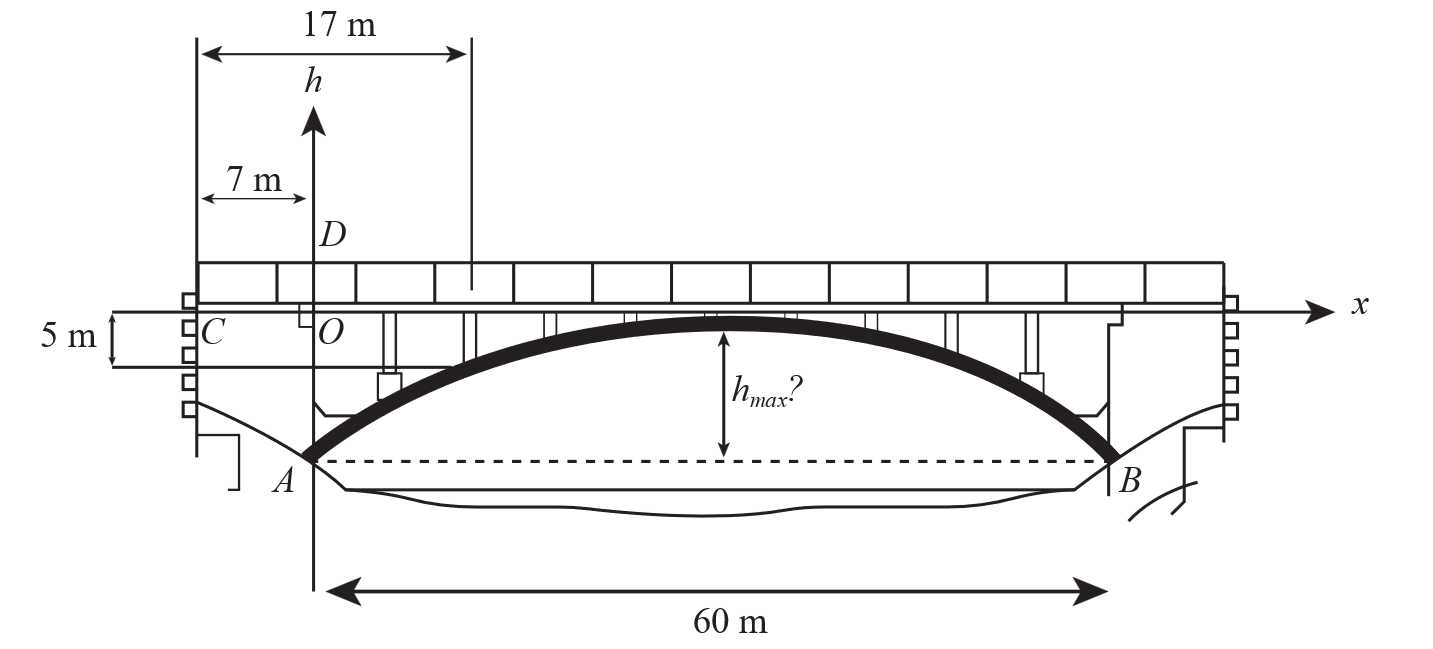
Câu 18 [696462]: Một chiếc cầu được bắc qua sông. Để trợ lực cho cây cầu, người ta làm một vòm đỡ cong hình parabol. Với hệ trục toạ độ  được gắn vào như hình vẽ, khoảng cách giữa 2 chân của vòm đỡ là
được gắn vào như hình vẽ, khoảng cách giữa 2 chân của vòm đỡ là 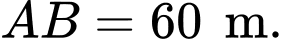 Khoảng cách từ chân cầu (điểm
Khoảng cách từ chân cầu (điểm  ) tới điểm
) tới điểm  là
là 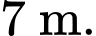 Tại một điểm cách chân cầu (điểm
Tại một điểm cách chân cầu (điểm  )
) 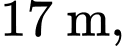 người ta đo được khoảng cách từ mặt cầu xuống vòm đỡ là
người ta đo được khoảng cách từ mặt cầu xuống vòm đỡ là 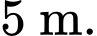 Nếu kết quả làm tròn đến hàng đơn vị thì chiều cao tối đa
Nếu kết quả làm tròn đến hàng đơn vị thì chiều cao tối đa 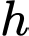 của vòm đỡ là bao nhiêu mét? (khoảng cách từ đỉnh vòm đến đường thẳng
của vòm đỡ là bao nhiêu mét? (khoảng cách từ đỉnh vòm đến đường thẳng  ).
).
 được gắn vào như hình vẽ, khoảng cách giữa 2 chân của vòm đỡ là
được gắn vào như hình vẽ, khoảng cách giữa 2 chân của vòm đỡ là 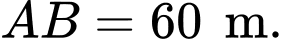 Khoảng cách từ chân cầu (điểm
Khoảng cách từ chân cầu (điểm  ) tới điểm
) tới điểm  là
là 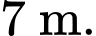 Tại một điểm cách chân cầu (điểm
Tại một điểm cách chân cầu (điểm  )
) 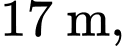 người ta đo được khoảng cách từ mặt cầu xuống vòm đỡ là
người ta đo được khoảng cách từ mặt cầu xuống vòm đỡ là 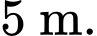 Nếu kết quả làm tròn đến hàng đơn vị thì chiều cao tối đa
Nếu kết quả làm tròn đến hàng đơn vị thì chiều cao tối đa 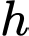 của vòm đỡ là bao nhiêu mét? (khoảng cách từ đỉnh vòm đến đường thẳng
của vòm đỡ là bao nhiêu mét? (khoảng cách từ đỉnh vòm đến đường thẳng  ).
).
Điền đáp án: 
Parabol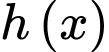 có đỉnh nằm trên trục
có đỉnh nằm trên trục 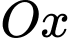 và nằm hoàn toàn dưới trục
và nằm hoàn toàn dưới trục 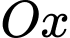 với hệ tọa độ như hình vẽ nên suy ra phương trình của
với hệ tọa độ như hình vẽ nên suy ra phương trình của 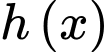 có dạng
có dạng 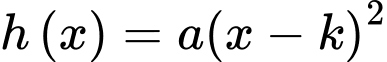 với
với 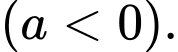
Do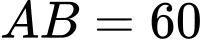 nên hoành độ của đỉnh parabol là 30.
nên hoành độ của đỉnh parabol là 30.
Do đó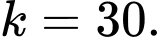
Ta có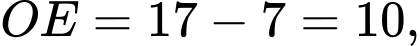 suy ra tọa độ của điểm
suy ra tọa độ của điểm 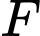 nằm trên parabol là điểm
nằm trên parabol là điểm 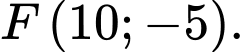
Thay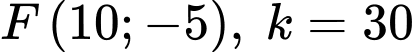 tọa độ vào phương trình parabol ta có:
tọa độ vào phương trình parabol ta có: 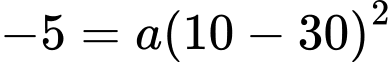
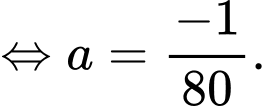
Ta có phương trình parabol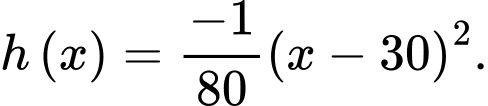
Độ dài của vòm đỡ cũng chính là độ dài đoạn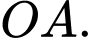
Ta có :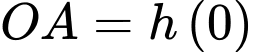
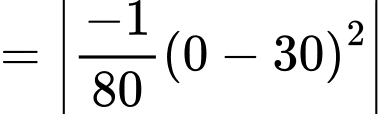
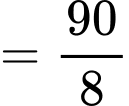
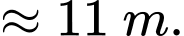

Parabol
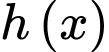 có đỉnh nằm trên trục
có đỉnh nằm trên trục 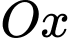 và nằm hoàn toàn dưới trục
và nằm hoàn toàn dưới trục 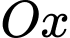 với hệ tọa độ như hình vẽ nên suy ra phương trình của
với hệ tọa độ như hình vẽ nên suy ra phương trình của 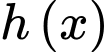 có dạng
có dạng 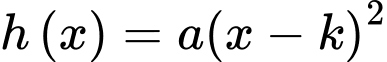 với
với 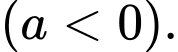
Do
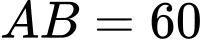 nên hoành độ của đỉnh parabol là 30.
nên hoành độ của đỉnh parabol là 30. Do đó
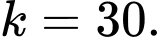
Ta có
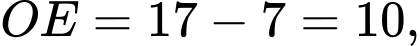 suy ra tọa độ của điểm
suy ra tọa độ của điểm 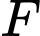 nằm trên parabol là điểm
nằm trên parabol là điểm 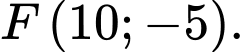
Thay
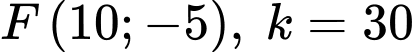 tọa độ vào phương trình parabol ta có:
tọa độ vào phương trình parabol ta có: 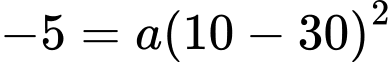
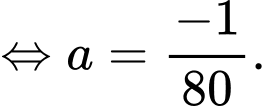
Ta có phương trình parabol
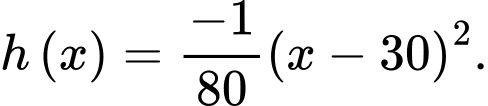
Độ dài của vòm đỡ cũng chính là độ dài đoạn
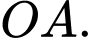
Ta có :
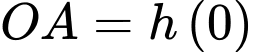
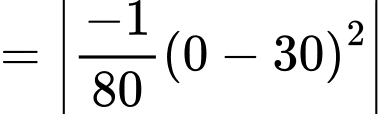
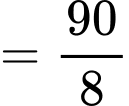
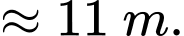
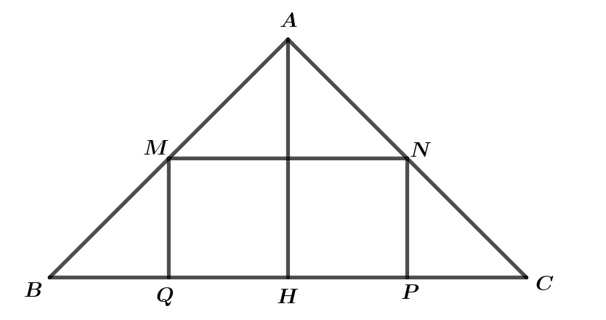
Câu 19 [693214]: Nhân dịp ngày Nhà giáo Việt Nam 20/11, thầy Duy tổ chức một trò chơi và phần thưởng dành cho các bạn học sinh trong lớp 12A khi có kết quả đúng là một cuốn Sách ID. Trò chơi như sau: thầy Duy phát cho mỗi bạn một cây kéo và một tấm vải hình tam giác có độ dài ba cạnh là 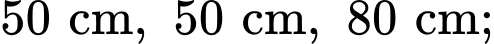 từ tấm vải đó mỗi bạn phải cắt một hình chữ nhật với hai đỉnh nằm trên hai cạnh bên và hai đỉnh còn lại nằm trên cạnh đáy sao cho hình chữ nhật cắt ra có diện tích lớn nhất bằng
từ tấm vải đó mỗi bạn phải cắt một hình chữ nhật với hai đỉnh nằm trên hai cạnh bên và hai đỉnh còn lại nằm trên cạnh đáy sao cho hình chữ nhật cắt ra có diện tích lớn nhất bằng 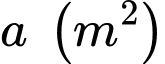 (xem hình minh hoạ).
(xem hình minh hoạ).
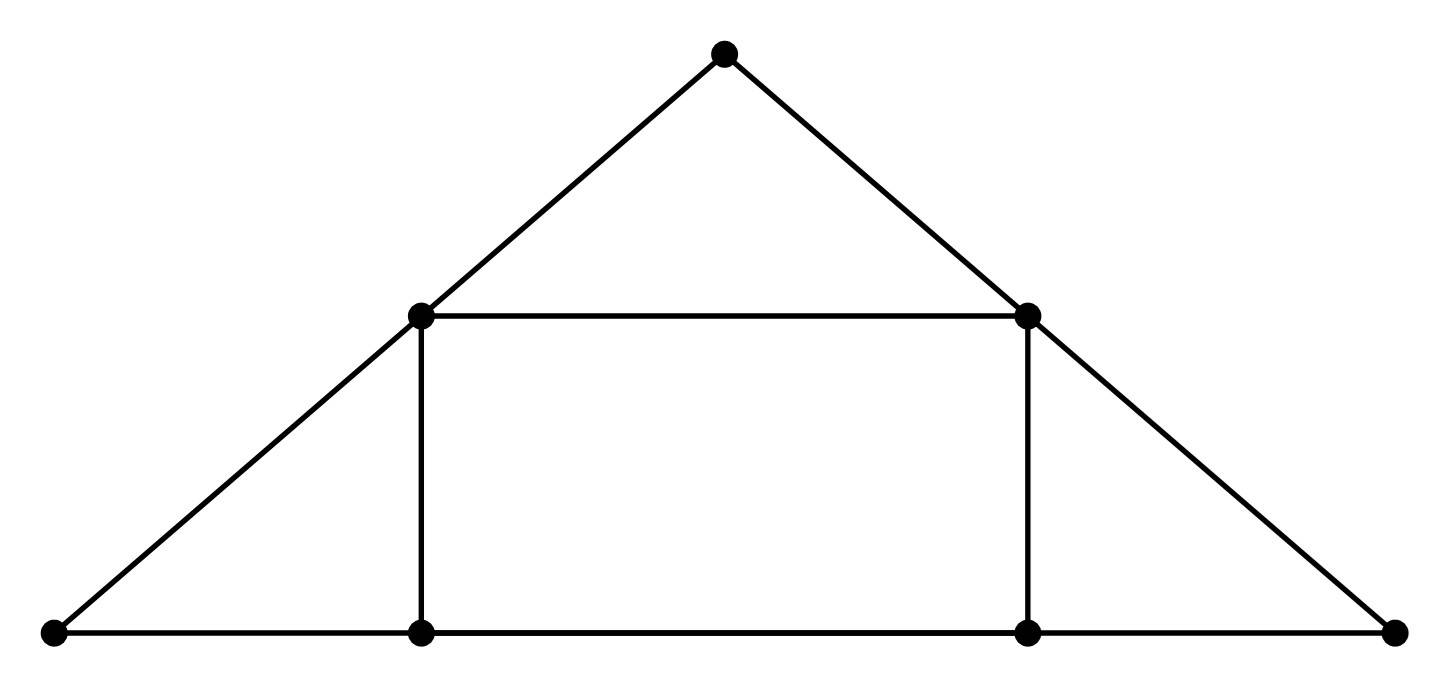
Vậy để nhận được thưởng thì giá trị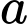 mà các bạn cần tính bằng bao nhiêu?
mà các bạn cần tính bằng bao nhiêu?
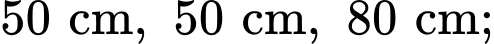 từ tấm vải đó mỗi bạn phải cắt một hình chữ nhật với hai đỉnh nằm trên hai cạnh bên và hai đỉnh còn lại nằm trên cạnh đáy sao cho hình chữ nhật cắt ra có diện tích lớn nhất bằng
từ tấm vải đó mỗi bạn phải cắt một hình chữ nhật với hai đỉnh nằm trên hai cạnh bên và hai đỉnh còn lại nằm trên cạnh đáy sao cho hình chữ nhật cắt ra có diện tích lớn nhất bằng 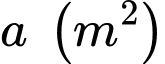 (xem hình minh hoạ).
(xem hình minh hoạ). 
Vậy để nhận được thưởng thì giá trị
 mà các bạn cần tính bằng bao nhiêu?
mà các bạn cần tính bằng bao nhiêu?
Điền đáp án: 0,06.
 Đặt
Đặt 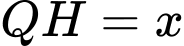
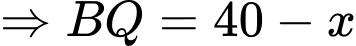
Vì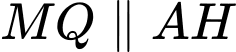
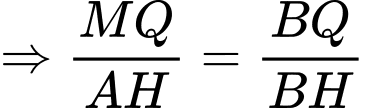
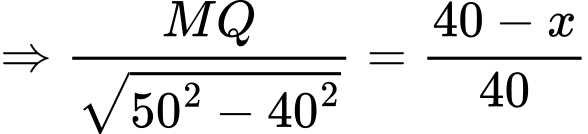
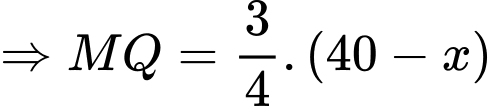
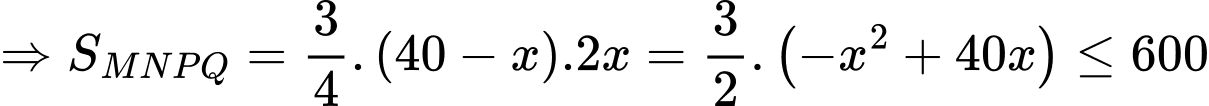
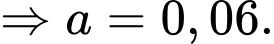

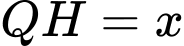
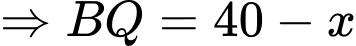
Vì
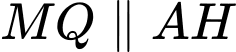
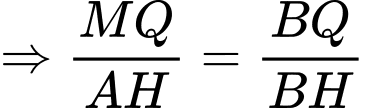
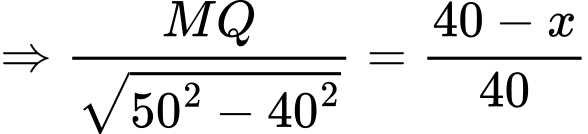
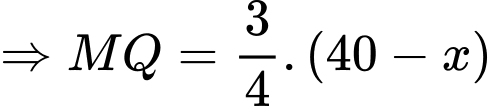
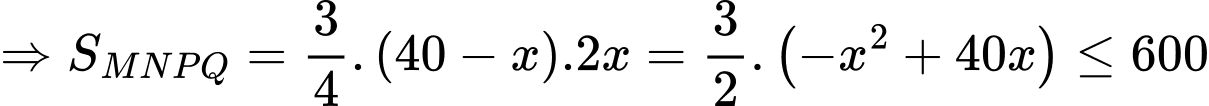
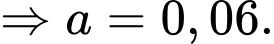
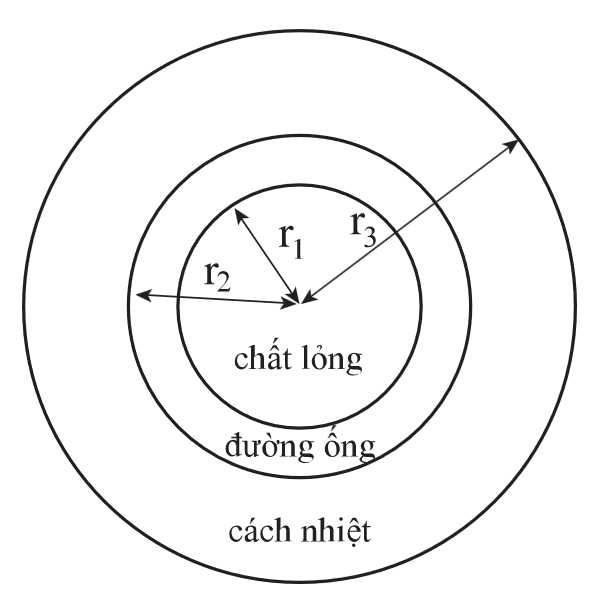
Câu 20 [696463]: Chất lỏng chảy qua một ống thép không gỉ có độ dẫn nhiệt  Ống có bán kính trong
Ống có bán kính trong 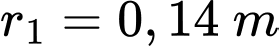 và bán kính ngoài
và bán kính ngoài 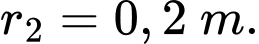 Nhiệt độ của thành bên trong được duy trì ở mức 400°C. Ống thép không gỉ cần được cách nhiệt bằng bọt urethane với
Nhiệt độ của thành bên trong được duy trì ở mức 400°C. Ống thép không gỉ cần được cách nhiệt bằng bọt urethane với 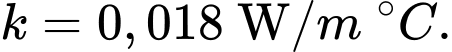 Nhiệt lượng mất mát
Nhiệt lượng mất mát 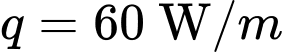 là hằng số trong toàn bộ đường ống và lớp cách nhiệt. Theo định luật Fourier ta có
là hằng số trong toàn bộ đường ống và lớp cách nhiệt. Theo định luật Fourier ta có 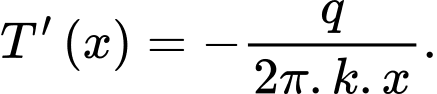 (trong đó
(trong đó 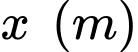 là khoảng cách từ điểm A đến tâm mặt cắt). Độ dày của lớp cách nhiệt cần thiết là bao nhiêu centimét để nhiệt độ ở bên ngoài của bọt không quá 50°C? (làm tròn đến hàng đơn vị).
là khoảng cách từ điểm A đến tâm mặt cắt). Độ dày của lớp cách nhiệt cần thiết là bao nhiêu centimét để nhiệt độ ở bên ngoài của bọt không quá 50°C? (làm tròn đến hàng đơn vị).
 Ống có bán kính trong
Ống có bán kính trong 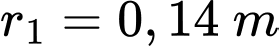 và bán kính ngoài
và bán kính ngoài 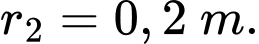 Nhiệt độ của thành bên trong được duy trì ở mức 400°C. Ống thép không gỉ cần được cách nhiệt bằng bọt urethane với
Nhiệt độ của thành bên trong được duy trì ở mức 400°C. Ống thép không gỉ cần được cách nhiệt bằng bọt urethane với 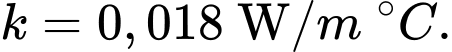 Nhiệt lượng mất mát
Nhiệt lượng mất mát 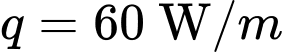 là hằng số trong toàn bộ đường ống và lớp cách nhiệt. Theo định luật Fourier ta có
là hằng số trong toàn bộ đường ống và lớp cách nhiệt. Theo định luật Fourier ta có 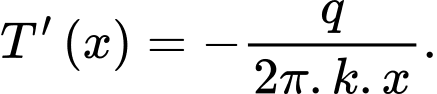 (trong đó
(trong đó 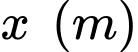 là khoảng cách từ điểm A đến tâm mặt cắt). Độ dày của lớp cách nhiệt cần thiết là bao nhiêu centimét để nhiệt độ ở bên ngoài của bọt không quá 50°C? (làm tròn đến hàng đơn vị).
là khoảng cách từ điểm A đến tâm mặt cắt). Độ dày của lớp cách nhiệt cần thiết là bao nhiêu centimét để nhiệt độ ở bên ngoài của bọt không quá 50°C? (làm tròn đến hàng đơn vị).
Điền đáp án: 19
Từ đề bài ra, ta có:
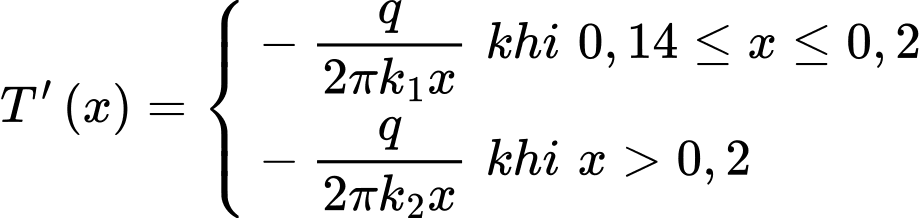 và có
và có 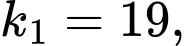
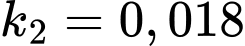
Nhiệt độ của thành bên trong được duy trì ở mức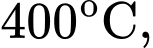 nhiệt độ thành ngoài là
nhiệt độ thành ngoài là  nên ta có:
nên ta có:
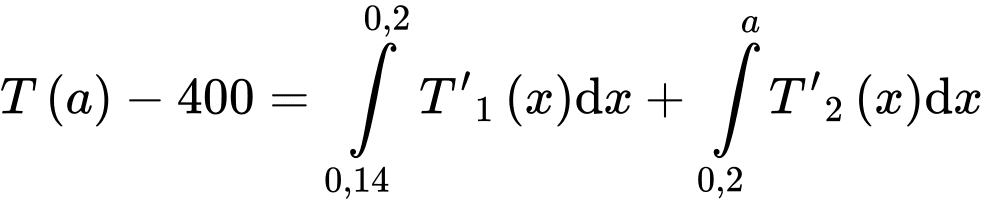
Nhiệt độ ở bên ngoài của bọt không quá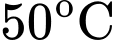 nên ta có:
nên ta có:
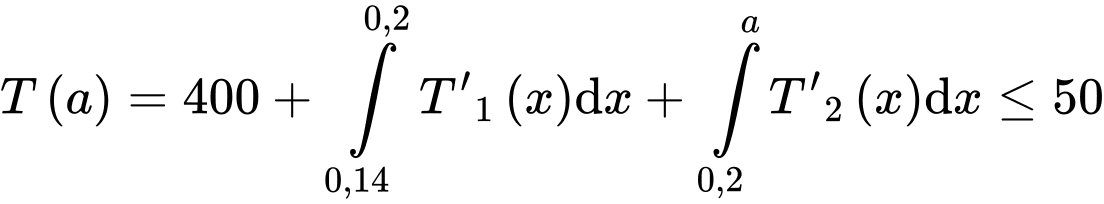
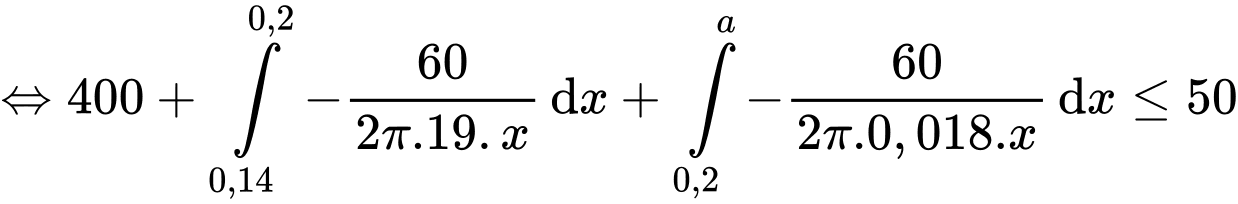
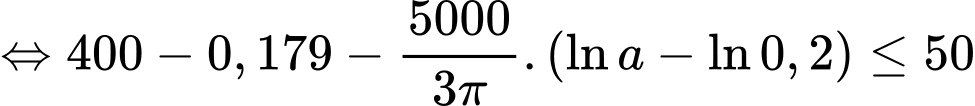
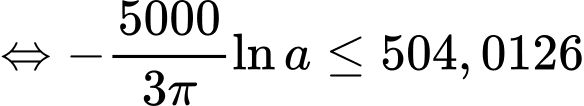
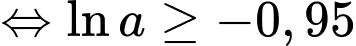
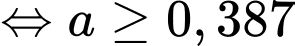
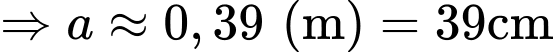
Vậy độ dày của lớp cách nhiệt cần thiết là: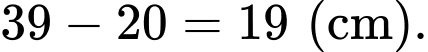
Từ đề bài ra, ta có:
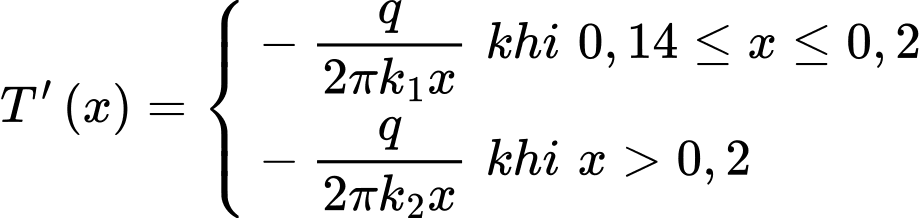 và có
và có 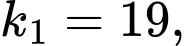
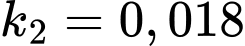
Nhiệt độ của thành bên trong được duy trì ở mức
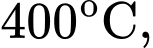 nhiệt độ thành ngoài là
nhiệt độ thành ngoài là  nên ta có:
nên ta có: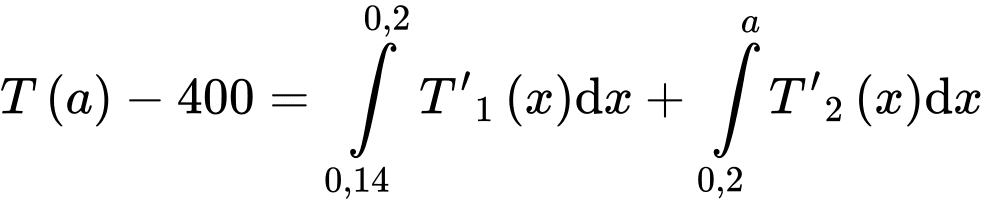
Nhiệt độ ở bên ngoài của bọt không quá
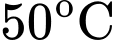 nên ta có:
nên ta có: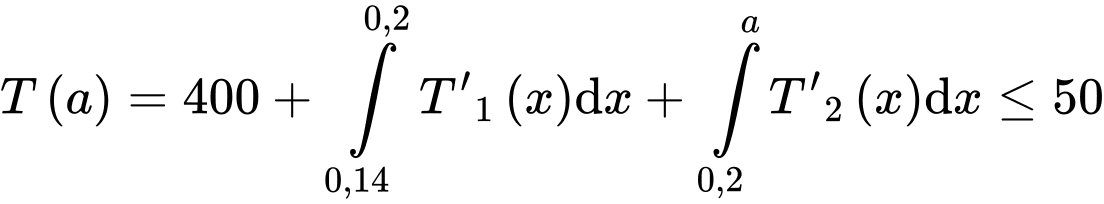
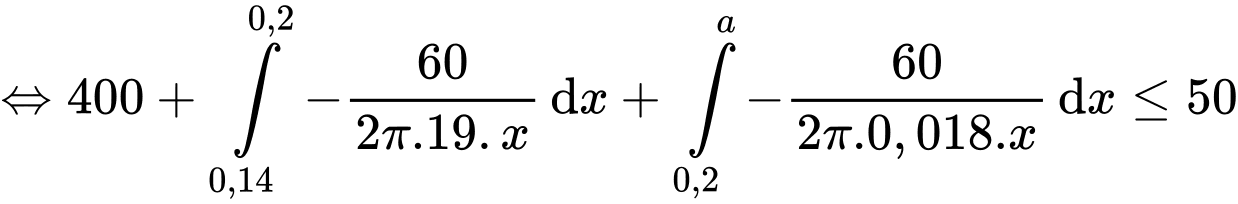
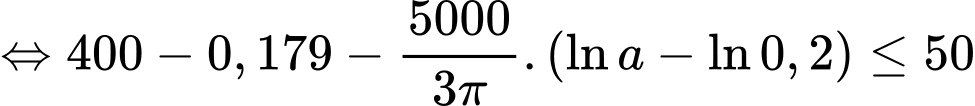
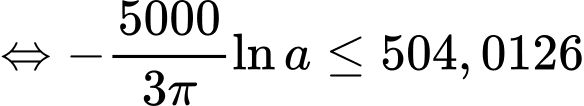
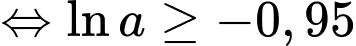
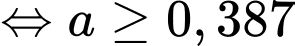
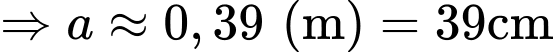
Vậy độ dày của lớp cách nhiệt cần thiết là:
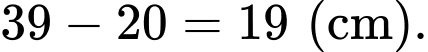
Câu 21 [703026]: Cho một lưới ô vuông kích thước  với các kí hiệu như hình vẽ. Với
với các kí hiệu như hình vẽ. Với 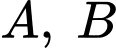 là 2 điểm nằm ở các nút giao (như hình vẽ).
là 2 điểm nằm ở các nút giao (như hình vẽ).
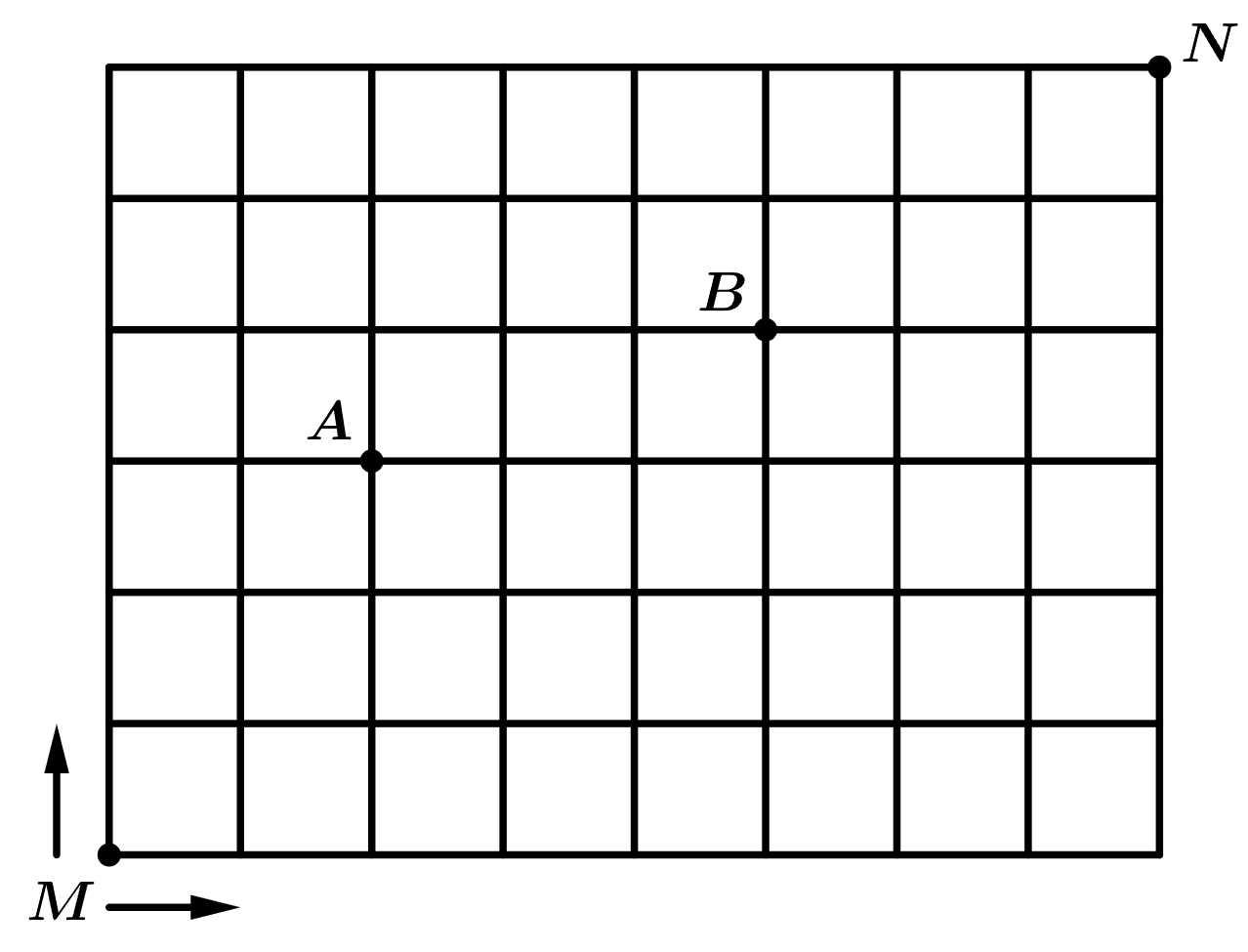
Để đi từ điểm đến
đến  một con kiến di chuyển ngẫu nhiên sang phải hoặc đi lên theo các đoạn thẳng là cạnh của hình vuông đơn vị.
một con kiến di chuyển ngẫu nhiên sang phải hoặc đi lên theo các đoạn thẳng là cạnh của hình vuông đơn vị.
Gọi là biến cố: “Con kiến đi từ
là biến cố: “Con kiến đi từ 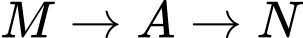 ”.
”.
Gọi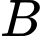 là biến cố: “Con kiến đi từ
là biến cố: “Con kiến đi từ 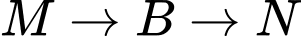 ”.
”.
Tính xác suất có điều kiện (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
 với các kí hiệu như hình vẽ. Với
với các kí hiệu như hình vẽ. Với 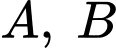 là 2 điểm nằm ở các nút giao (như hình vẽ).
là 2 điểm nằm ở các nút giao (như hình vẽ).
Để đi từ điểm
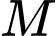 đến
đến 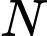 một con kiến di chuyển ngẫu nhiên sang phải hoặc đi lên theo các đoạn thẳng là cạnh của hình vuông đơn vị.
một con kiến di chuyển ngẫu nhiên sang phải hoặc đi lên theo các đoạn thẳng là cạnh của hình vuông đơn vị.Gọi
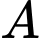 là biến cố: “Con kiến đi từ
là biến cố: “Con kiến đi từ 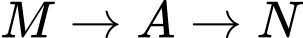 ”.
”.Gọi
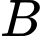 là biến cố: “Con kiến đi từ
là biến cố: “Con kiến đi từ 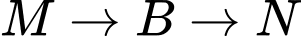 ”.
”. Tính xác suất có điều kiện
 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,32.
Ta đặt hệ trục tọa độ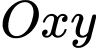 tại điểm
tại điểm 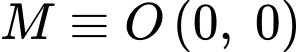 .
.
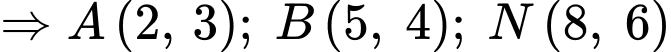 .
.
Ta có bài toán tổng quát sau:
Nếu di chuyển sang phải hoặc đi lên từ điểm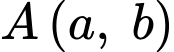 đến điểm
đến điểm 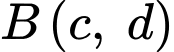 thì số cách di chuyển sẽ là
thì số cách di chuyển sẽ là 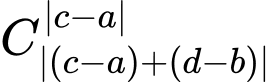 cách .
cách .
Số cách con kiến đi từ điểm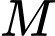 đến
đến 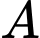 là
là 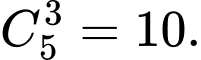
Số cách con kiến đi từ điểm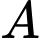 đến
đến 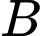 là
là 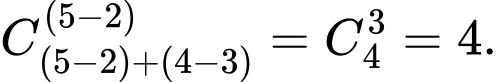
Số cách con kiến đi từ điểm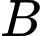 đến
đến 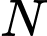 là
là 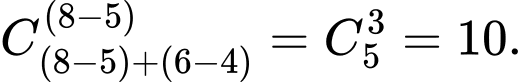
Số cách con kiến đi từ điểm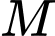 đến
đến 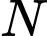 là
là 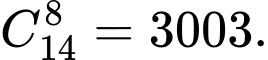
Số cách con kiến đi từ điểm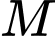 đến
đến 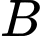 là
là 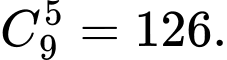
Ta có: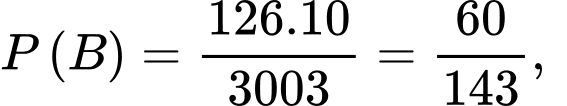
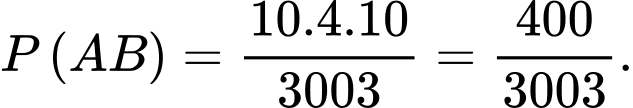
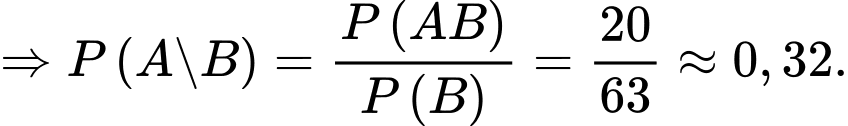
Ta đặt hệ trục tọa độ
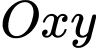 tại điểm
tại điểm 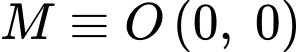 .
.
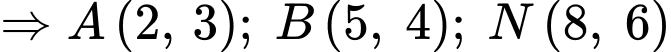 .
.
Ta có bài toán tổng quát sau:
Nếu di chuyển sang phải hoặc đi lên từ điểm
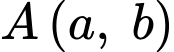 đến điểm
đến điểm 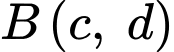 thì số cách di chuyển sẽ là
thì số cách di chuyển sẽ là 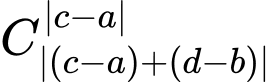 cách .
cách .
Số cách con kiến đi từ điểm
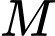 đến
đến 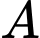 là
là 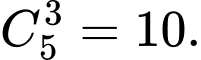
Số cách con kiến đi từ điểm
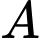 đến
đến 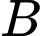 là
là 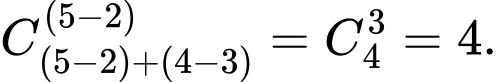
Số cách con kiến đi từ điểm
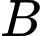 đến
đến 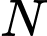 là
là 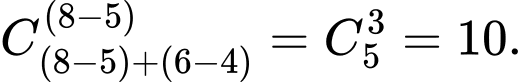
Số cách con kiến đi từ điểm
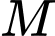 đến
đến 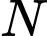 là
là 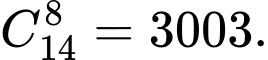
Số cách con kiến đi từ điểm
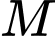 đến
đến 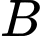 là
là 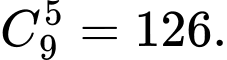
Ta có:
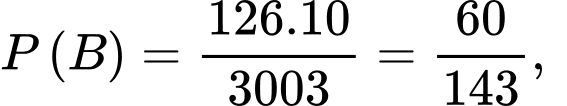
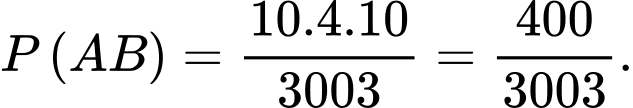
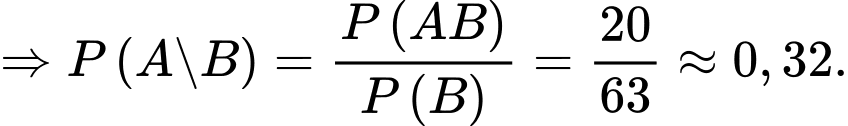
Câu 22 [696503]: Trong không gian 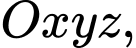 cho mặt cầu
cho mặt cầu 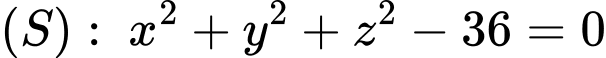 và mặt phẳng
và mặt phẳng 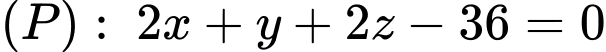 và điểm
và điểm 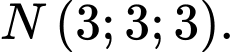 Từ một điểm
Từ một điểm 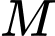 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 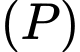 kẻ các tiếp tuyến phân biệt
kẻ các tiếp tuyến phân biệt 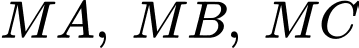 đến
đến 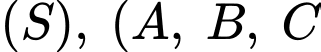 là các tiếp điểm). Khi khoảng cách từ
là các tiếp điểm). Khi khoảng cách từ 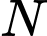 đến mặt phẳng
đến mặt phẳng 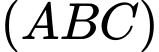 lớn nhất thì phương trình mặt phẳng
lớn nhất thì phương trình mặt phẳng 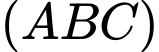 là
là 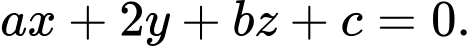 Giá trị của biểu thức
Giá trị của biểu thức 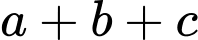 bằng bao nhiêu?
bằng bao nhiêu?
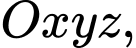 cho mặt cầu
cho mặt cầu 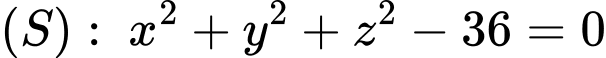 và mặt phẳng
và mặt phẳng 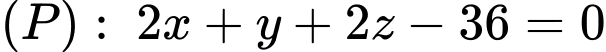 và điểm
và điểm 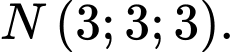 Từ một điểm
Từ một điểm 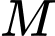 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 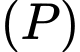 kẻ các tiếp tuyến phân biệt
kẻ các tiếp tuyến phân biệt 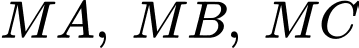 đến
đến 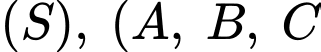 là các tiếp điểm). Khi khoảng cách từ
là các tiếp điểm). Khi khoảng cách từ 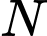 đến mặt phẳng
đến mặt phẳng 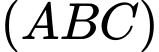 lớn nhất thì phương trình mặt phẳng
lớn nhất thì phương trình mặt phẳng 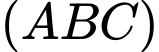 là
là 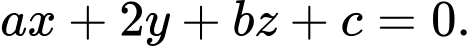 Giá trị của biểu thức
Giá trị của biểu thức 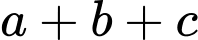 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: -4.
Mặt cầu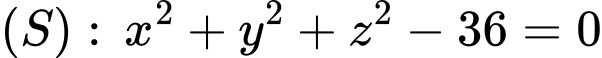 có
có 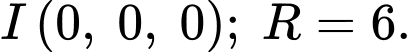
Giả sử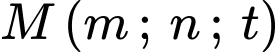 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 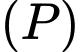

Vì các tiếp tuyến phân biệt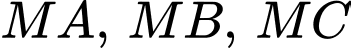 đến
đến 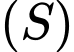
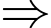
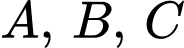 luôn nhìn
luôn nhìn 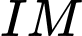 dưới một góc vuông.
dưới một góc vuông.
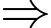 Luôn tồn tại mặt cầu ngoại tiếp
Luôn tồn tại mặt cầu ngoại tiếp  tâm là trung điểm
tâm là trung điểm 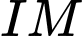 .
.
Gọi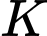 là trung điểm
là trung điểm 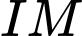
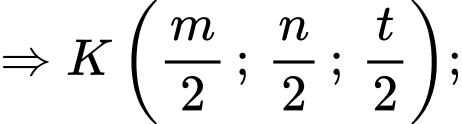
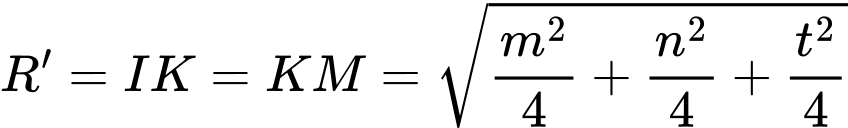
Phương trình mặt cầu: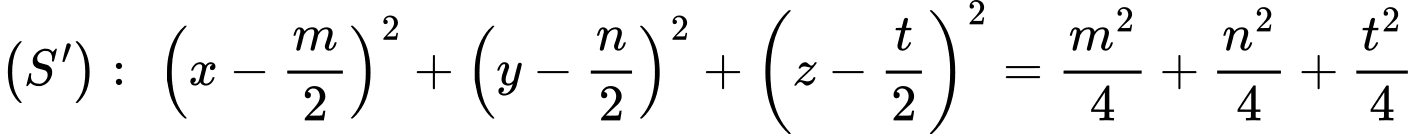
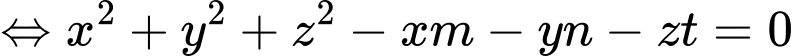
Dễ dàng thấy được mặt cầu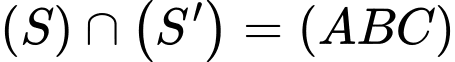
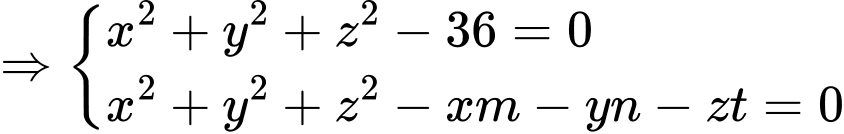
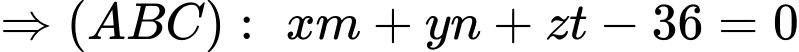
Ta có mặt phẳng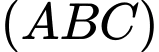 luôn đi qua điểm cố định
luôn đi qua điểm cố định 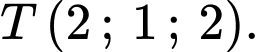
Gọi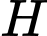 là hình chiếu của
là hình chiếu của 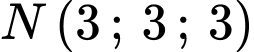 trên mặt phẳng
trên mặt phẳng 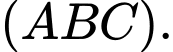
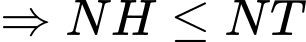
Vậy khoảng cách từ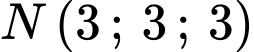 đến mặt phẳng
đến mặt phẳng 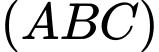 lớn nhất
lớn nhất
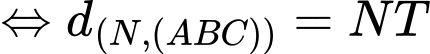
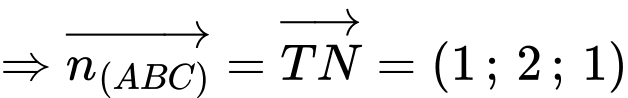
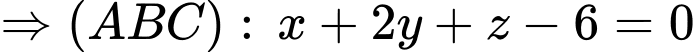
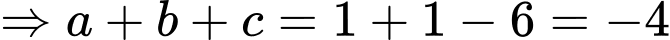
Mặt cầu
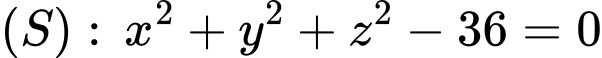 có
có 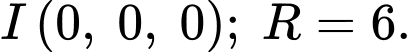
Giả sử
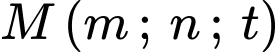 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 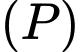

Vì các tiếp tuyến phân biệt
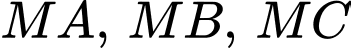 đến
đến 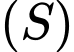
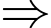
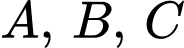 luôn nhìn
luôn nhìn 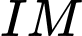 dưới một góc vuông.
dưới một góc vuông.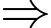 Luôn tồn tại mặt cầu ngoại tiếp
Luôn tồn tại mặt cầu ngoại tiếp  tâm là trung điểm
tâm là trung điểm 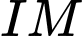 .
.Gọi
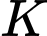 là trung điểm
là trung điểm 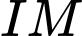
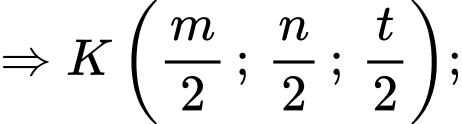
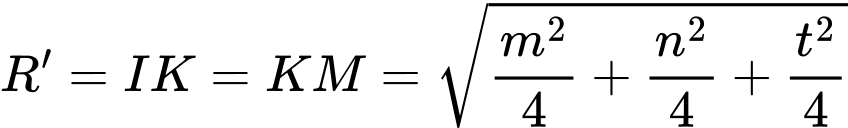
Phương trình mặt cầu:
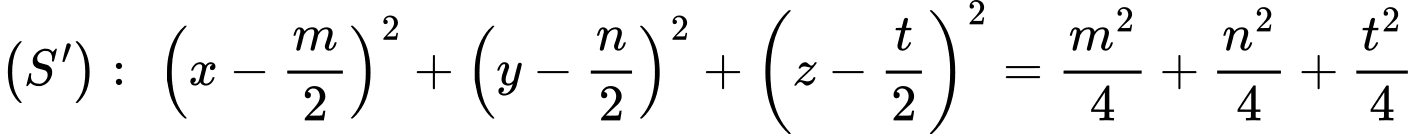
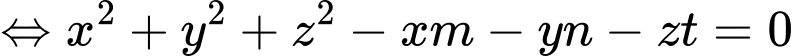
Dễ dàng thấy được mặt cầu
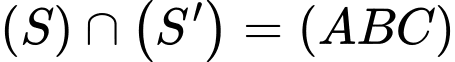
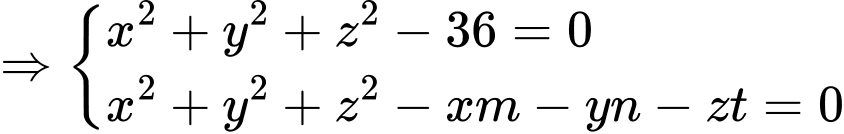
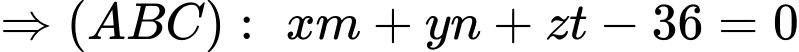
Ta có mặt phẳng
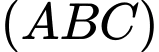 luôn đi qua điểm cố định
luôn đi qua điểm cố định 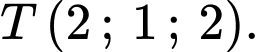
Gọi
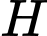 là hình chiếu của
là hình chiếu của 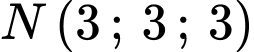 trên mặt phẳng
trên mặt phẳng 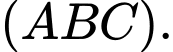
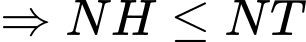
Vậy khoảng cách từ
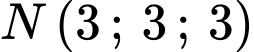 đến mặt phẳng
đến mặt phẳng 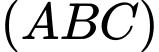 lớn nhất
lớn nhất