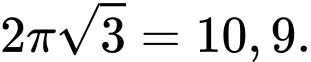PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [322649]: Cho 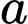 là số thực dương tùy ý,
là số thực dương tùy ý,  bằng
bằng
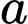 là số thực dương tùy ý,
là số thực dương tùy ý,  bằng
bằng A, 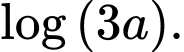
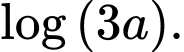
B, 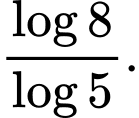
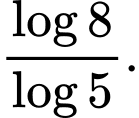
C, 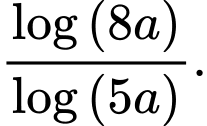
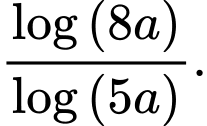
D, 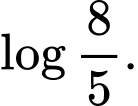
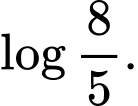
Chọn đáp án D.
Ta có:
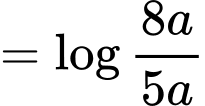
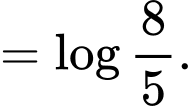 Đáp án: D
Đáp án: D
Ta có:

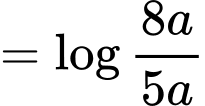
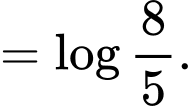 Đáp án: D
Đáp án: D
Câu 2 [502678]: Họ nguyên hàm của hàm số 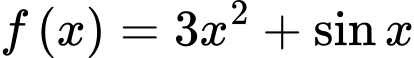 là
là
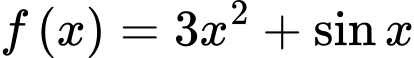 là
là A, 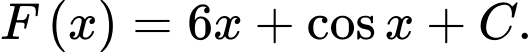
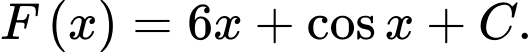
B, 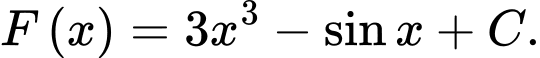
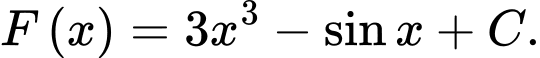
C, 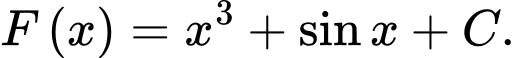
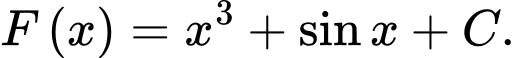
D, 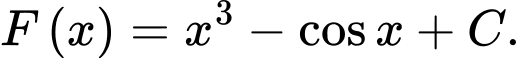
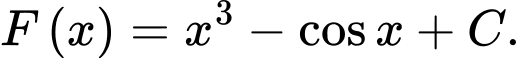
Chọn đáp án D.
Ta có: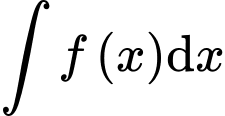
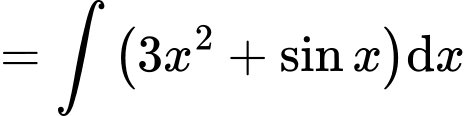
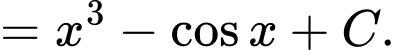 Đáp án: D
Đáp án: D
Ta có:
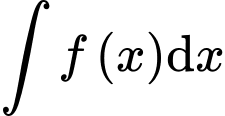
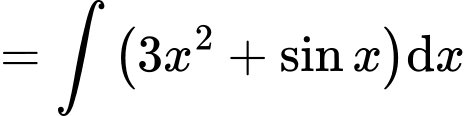
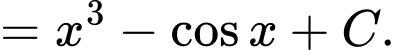 Đáp án: D
Đáp án: D
Câu 3 [522549]: Trong không gian 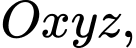 mặt cầu
mặt cầu 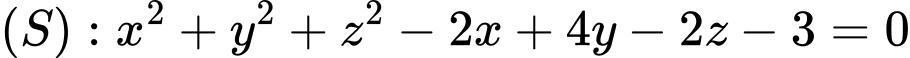 có tọa độ tâm là
có tọa độ tâm là
 mặt cầu
mặt cầu 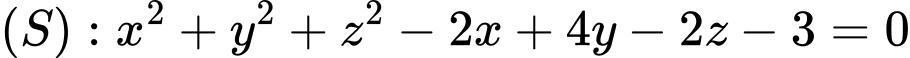 có tọa độ tâm là
có tọa độ tâm là A, 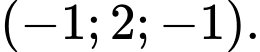
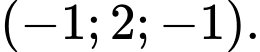
B, 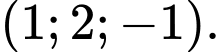
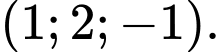
C, 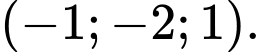
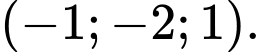
D, 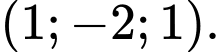
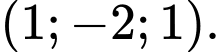
Chọn đáp án D.
Trong không gian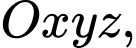 mặt cầu
mặt cầu 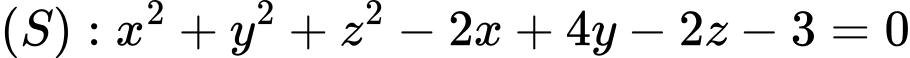 có tọa độ tâm là
có tọa độ tâm là 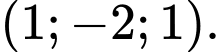 Đáp án: D
Đáp án: D
Trong không gian
 mặt cầu
mặt cầu 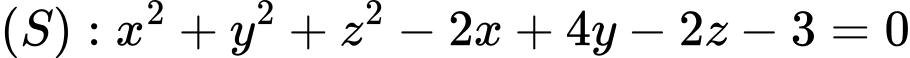 có tọa độ tâm là
có tọa độ tâm là 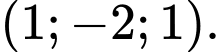 Đáp án: D
Đáp án: D Sử dụng thông tin dưới đây để trả lời câu 4 và câu 5
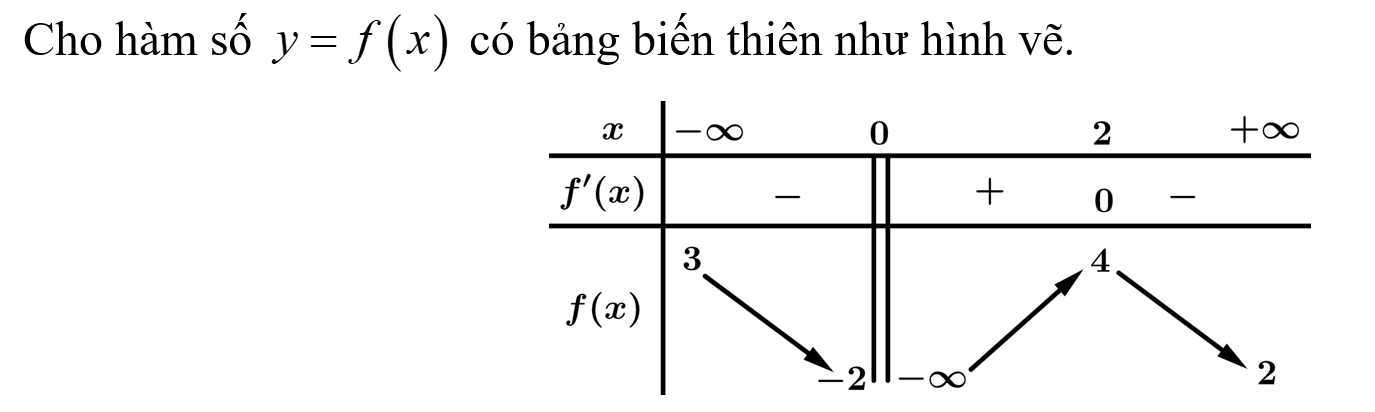
Câu 4 [703043]: Hàm số đã cho có bao nhiêu điểm cực trị?
A, 2.
B, 4.
C, 3.
D, 1.
Chọn đáp án B.
Dựa vào bảng biến thiên ta có: Hàm số đã cho có 1 điểm cực trị Đáp án: B
Đáp án: B
Dựa vào bảng biến thiên ta có: Hàm số đã cho có 1 điểm cực trị
 Đáp án: B
Đáp án: B
Câu 5 [703044]: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là bao nhiêu?
A, 2.
B, 4.
C, 3.
D, 1.
Chọn đáp án C.
Dựa vào bảng biến thiên ta có:
Đồ thị hàm số có 2 tiệm cận ngang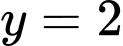 và
và 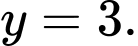
Đồ thị có 1 tiệm cận đứng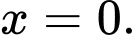
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 3. Đáp án: C
Dựa vào bảng biến thiên ta có:
Đồ thị hàm số có 2 tiệm cận ngang
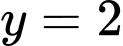 và
và 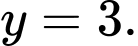
Đồ thị có 1 tiệm cận đứng
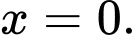
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 3. Đáp án: C
Câu 6 [522616]: Trong không gian 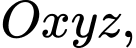 mặt phẳng
mặt phẳng 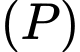 đi qua
đi qua 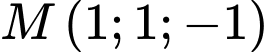 và vuông góc với đường thẳng
và vuông góc với đường thẳng 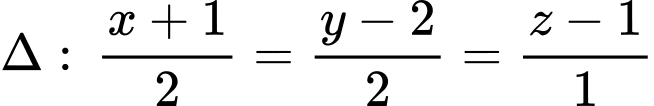 có phương trình là
có phương trình là
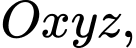 mặt phẳng
mặt phẳng 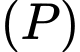 đi qua
đi qua 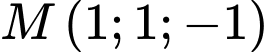 và vuông góc với đường thẳng
và vuông góc với đường thẳng 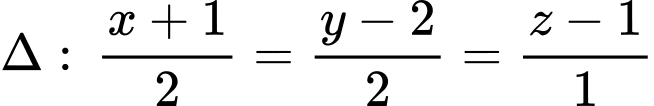 có phương trình là
có phương trình là A, 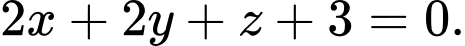
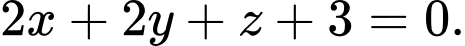
B, 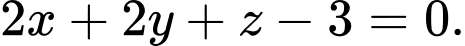
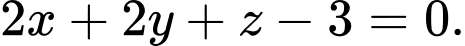
C, 

D, 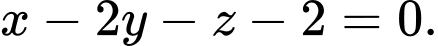
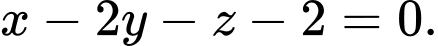
Chọn đáp án B.
Ta có một VTPT của mặt phẳng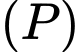 là
là 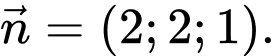
Vậy phương trình mặt phẳng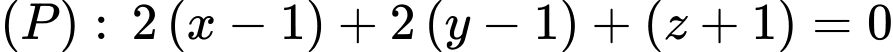
 Đáp án: B
Đáp án: B
Ta có một VTPT của mặt phẳng
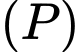 là
là 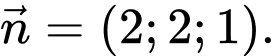
Vậy phương trình mặt phẳng
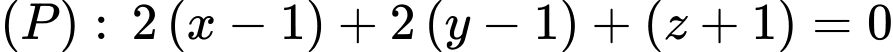
 Đáp án: B
Đáp án: B
Câu 7 [626659]: Số nghiệm nguyên âm của bất phương trình 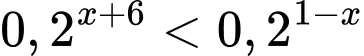 là
là
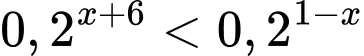 là
là A, vô số.
B, 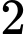 .
.
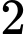 .
.C, 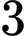 .
.
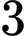 .
.D, 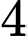 .
.
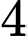 .
.
Chọn đáp án B.
Ta có: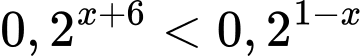
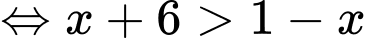
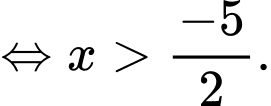
Do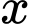 là nghiệm nguyên âm nên
là nghiệm nguyên âm nên 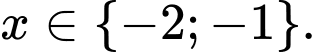
Vậy số nghiệm nguyên âm của bất phương trình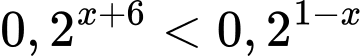 là 2. Đáp án: B
là 2. Đáp án: B
Ta có:
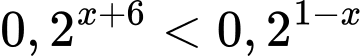
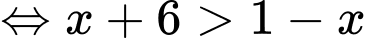
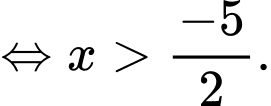
Do
 là nghiệm nguyên âm nên
là nghiệm nguyên âm nên 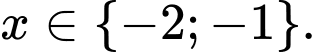
Vậy số nghiệm nguyên âm của bất phương trình
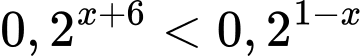 là 2. Đáp án: B
là 2. Đáp án: B
Câu 8 [502682]: Cho cấp số cộng 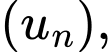 biết
biết 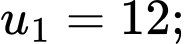
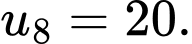 Tìm công sai
Tìm công sai 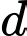 của cấp số cộng đã cho.
của cấp số cộng đã cho.
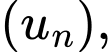 biết
biết 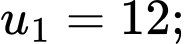
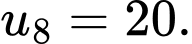 Tìm công sai
Tìm công sai 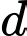 của cấp số cộng đã cho.
của cấp số cộng đã cho. A, 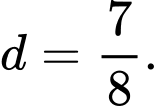
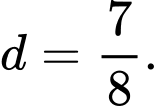
B, 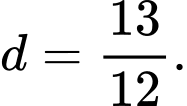
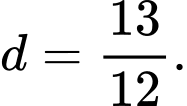
C, 

D, 

Chọn đáp án D.
Ta có: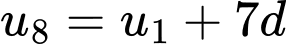
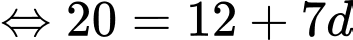
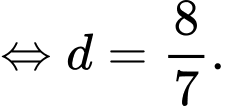
Vậy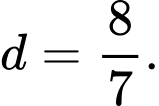 Đáp án: D
Đáp án: D
Ta có:
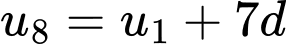
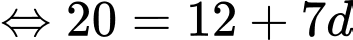
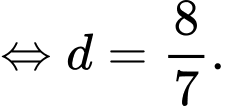
Vậy
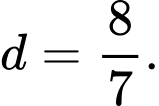 Đáp án: D
Đáp án: D
Câu 9 [527784]: Cho 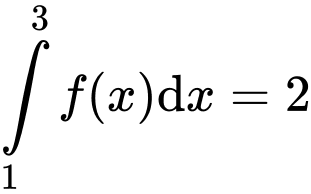 và
và 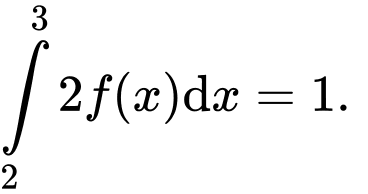 Tính
Tính 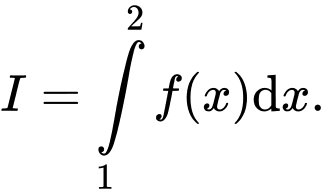
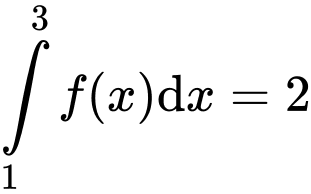 và
và 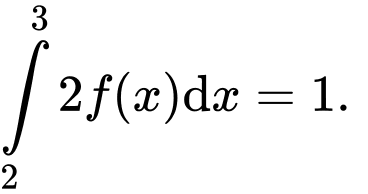 Tính
Tính 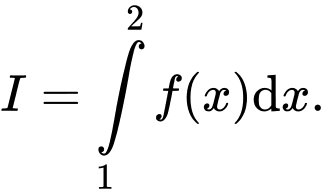
A,  .
.
 .
.B, 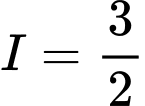 .
.
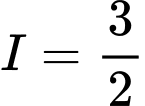 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn đáp án B.
Ta có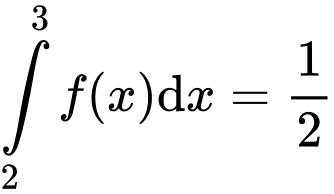
Suy ra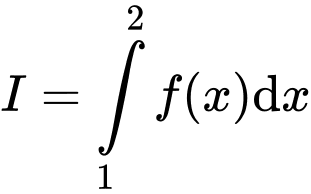
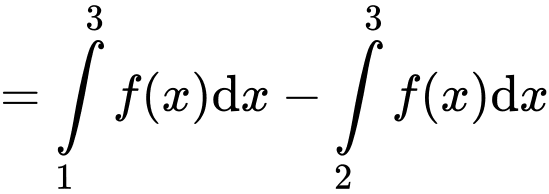
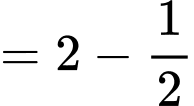
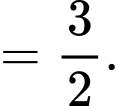 Đáp án: B
Đáp án: B
Ta có
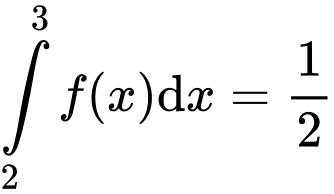
Suy ra
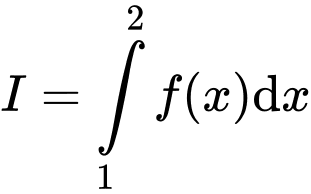
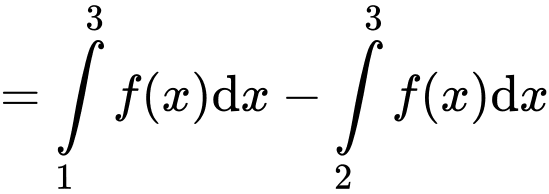
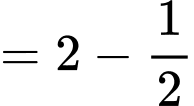
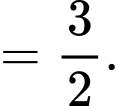 Đáp án: B
Đáp án: B
Câu 10 [280727]: Cho hình chóp 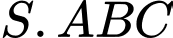 có đáy
có đáy 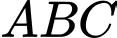 là tam giác vuông tại
là tam giác vuông tại 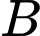 ,
, 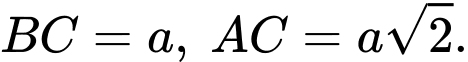 Cạnh bên
Cạnh bên  vuông góc với mặt phẳng đáy. Tính số đo của góc nhị diện
vuông góc với mặt phẳng đáy. Tính số đo của góc nhị diện 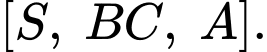
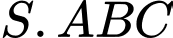 có đáy
có đáy 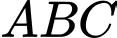 là tam giác vuông tại
là tam giác vuông tại 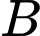 ,
, 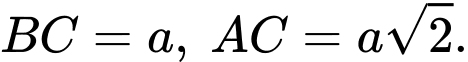 Cạnh bên
Cạnh bên  vuông góc với mặt phẳng đáy. Tính số đo của góc nhị diện
vuông góc với mặt phẳng đáy. Tính số đo của góc nhị diện 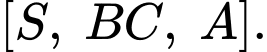
A, 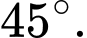
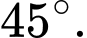
B, 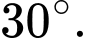
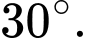
C, 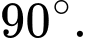
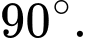
D, 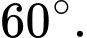
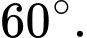
Chọn đáp án A.
Ta có:

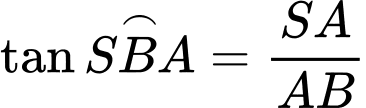
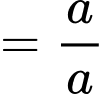
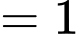
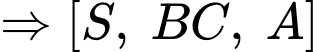

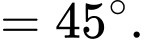
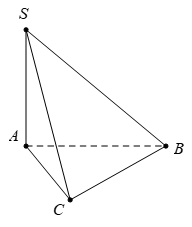 Đáp án: A
Đáp án: A
Ta có:

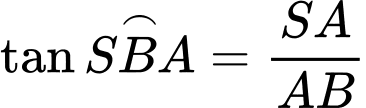
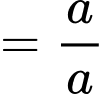
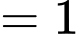
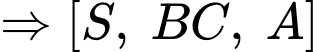

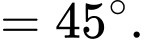
 Đáp án: A
Đáp án: A
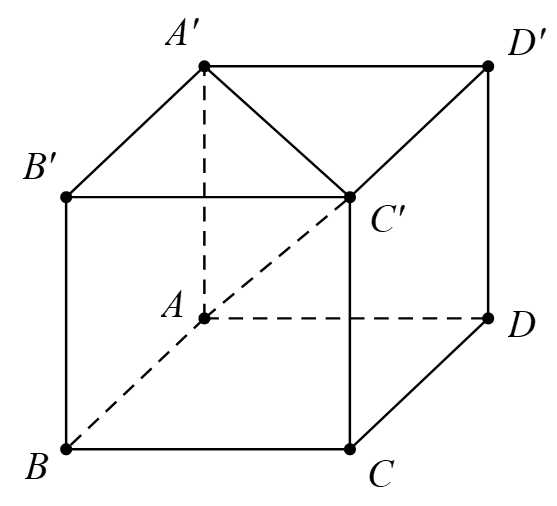
Câu 11 [597382]: Cho hình hộp đứng  có đáy
có đáy 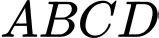 là hình bình hành với
là hình bình hành với  Biết độ dài các cạnh
Biết độ dài các cạnh 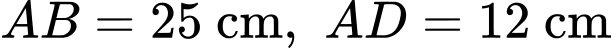 và
và 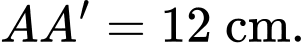 Tính
Tính 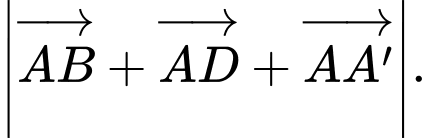
 có đáy
có đáy 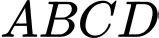 là hình bình hành với
là hình bình hành với  Biết độ dài các cạnh
Biết độ dài các cạnh 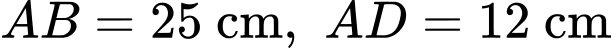 và
và 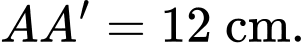 Tính
Tính 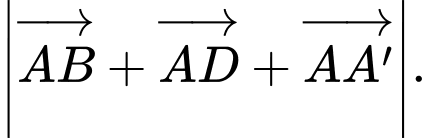

A, 12 cm.
B, 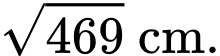
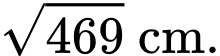
C, 

D, 25 cm.
Chọn đáp án C.
Theo quy tắc hình hộp, ta có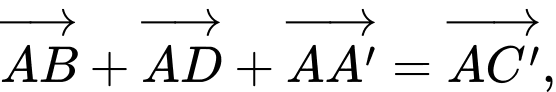
Vậy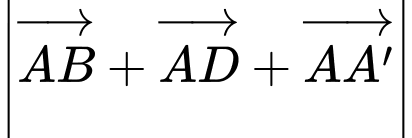
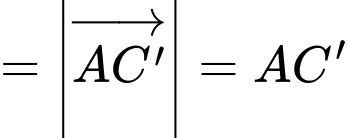
Với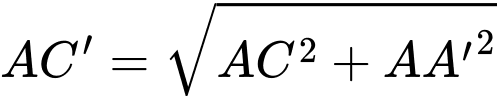
Trong đó: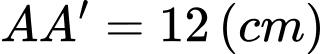
Do tổng hai góc kề của một hình bình hành là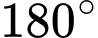 nên ta có góc
nên ta có góc 
Áp dụng định lý cosin trong tam giác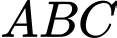 , ta có
, ta có
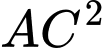
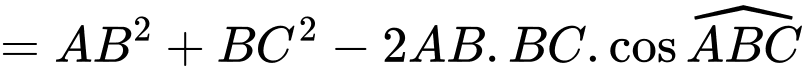
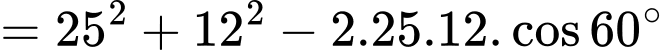
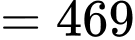 .
.
Vậy
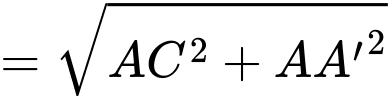
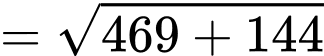
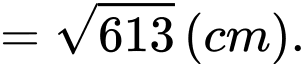 Đáp án: C
Đáp án: C
Theo quy tắc hình hộp, ta có
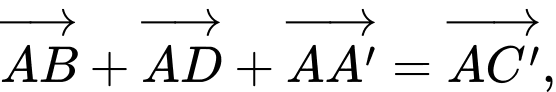
Vậy
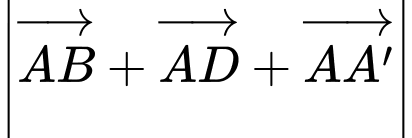
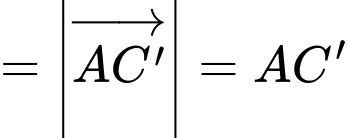
Với
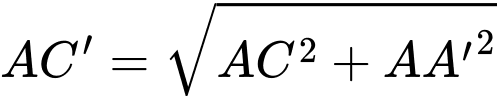
Trong đó:
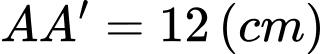
Do tổng hai góc kề của một hình bình hành là
 nên ta có góc
nên ta có góc 
Áp dụng định lý cosin trong tam giác
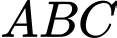 , ta có
, ta có 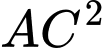
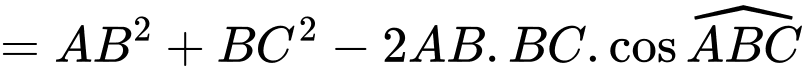
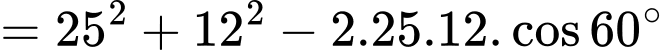
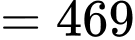 .
. Vậy

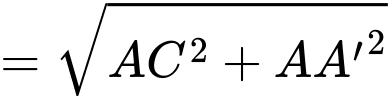
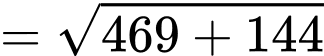
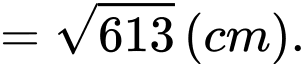 Đáp án: C
Đáp án: C
Câu 12 [696466]: Một cửa hàng cho thuê truyện đã thống kê số lượng truyện được thuê mỗi ngày trong ba tháng ở bảng sau. Hãy tính phương sai của mẫu số liệu ghép nhóm.


A, 40,7.
B, 42.
C, 41,5.
D, 45,1.
Chọn đáp án A.
Cỡ mẫu: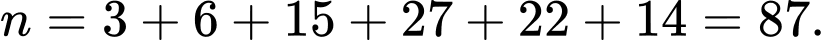
Số trung bình của mẫu số liệu ghép nhóm là:
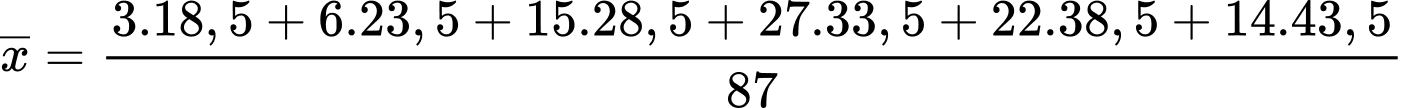
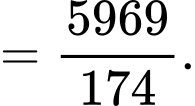
Phương sai của mẫu số liệu ghép nhóm là:
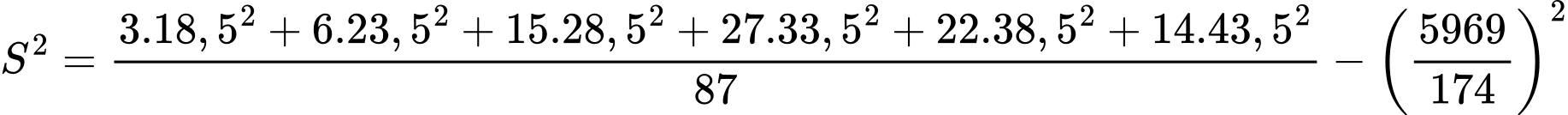
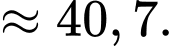 Đáp án: A
Đáp án: A
Cỡ mẫu:
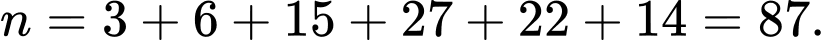
Số trung bình của mẫu số liệu ghép nhóm là:
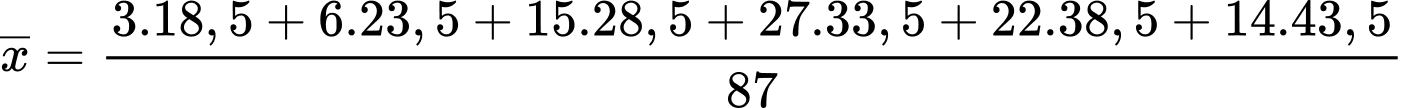
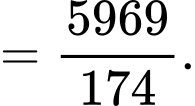
Phương sai của mẫu số liệu ghép nhóm là:
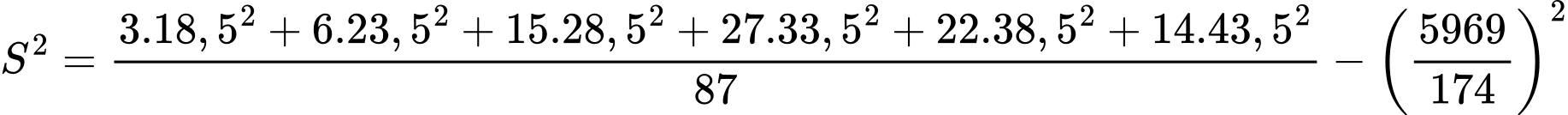
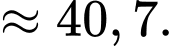 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696467]: Cho hàm số 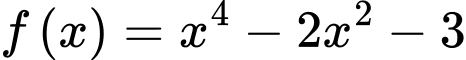 có đồ thị
có đồ thị 
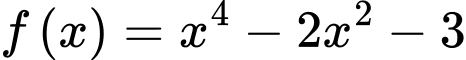 có đồ thị
có đồ thị 
a) Đúng.
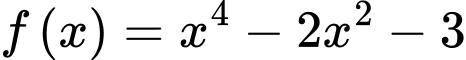
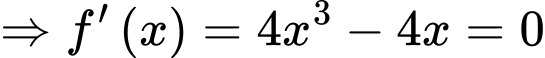
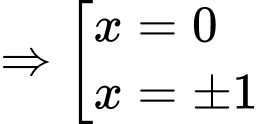
b) Sai.
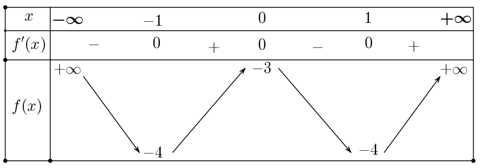
Ta có bảng biến thiên: >
c) Sai.
Khoảng cách giữa điểm cực đại và điểm cực tiểu của đồ thị hàm số là
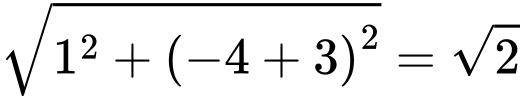
d) Đúng.
Giả sử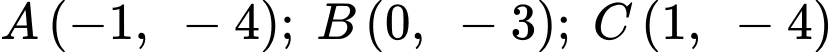
Gọi là trung điểm
là trung điểm 
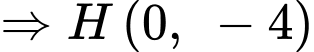
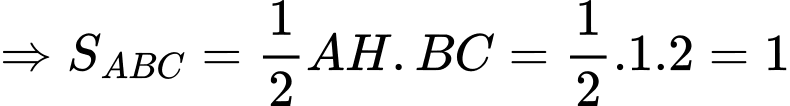
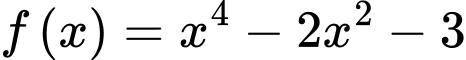
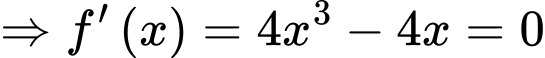
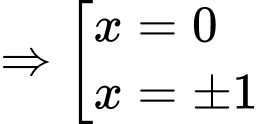
b) Sai.
Ta có bảng biến thiên: >

c) Sai.
Khoảng cách giữa điểm cực đại và điểm cực tiểu của đồ thị hàm số là
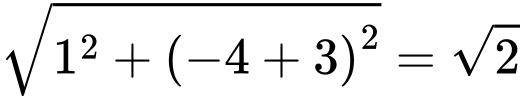
d) Đúng.
Giả sử
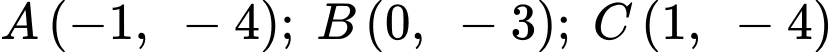
Gọi
 là trung điểm
là trung điểm 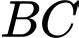
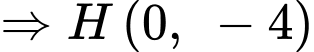
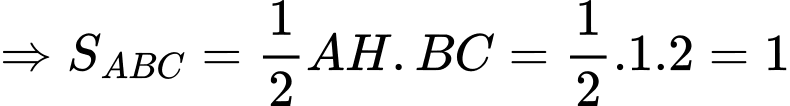
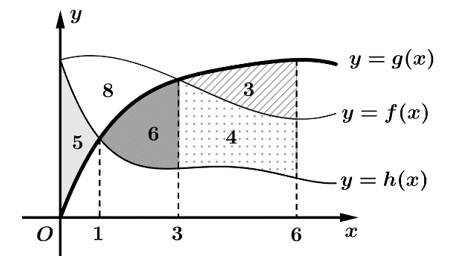
Câu 14 [696468]: Cho ba hàm số 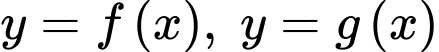 và
và 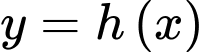 liên tục trên đoạn
liên tục trên đoạn  có đồ thị và diện tích mỗi miền được ghi bằng số tương ứng trong hình vẽ dưới đây.
có đồ thị và diện tích mỗi miền được ghi bằng số tương ứng trong hình vẽ dưới đây.
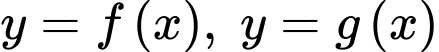 và
và 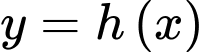 liên tục trên đoạn
liên tục trên đoạn 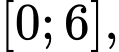 có đồ thị và diện tích mỗi miền được ghi bằng số tương ứng trong hình vẽ dưới đây.
có đồ thị và diện tích mỗi miền được ghi bằng số tương ứng trong hình vẽ dưới đây.
a) Sai.
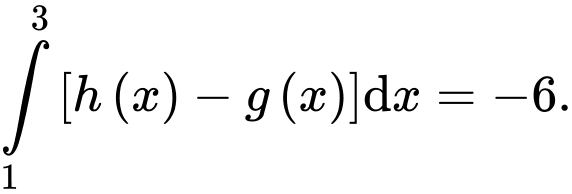
b) Đúng.
c) Sai.
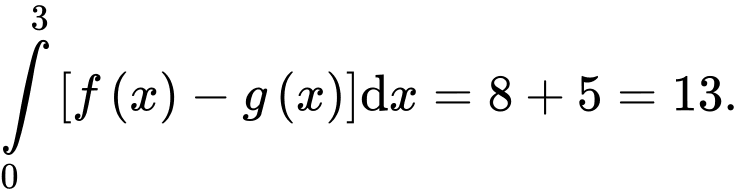
d) Đúng.
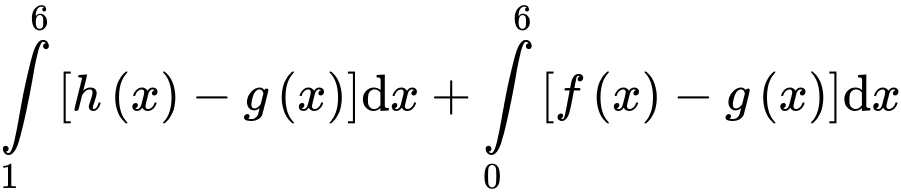
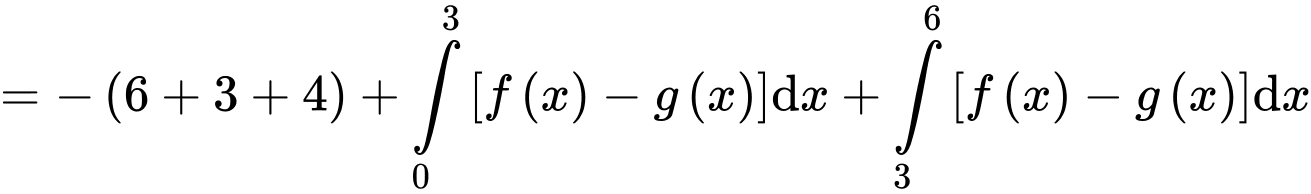
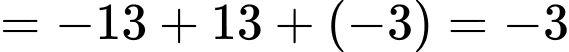
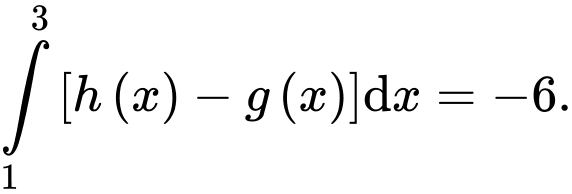
b) Đúng.
c) Sai.
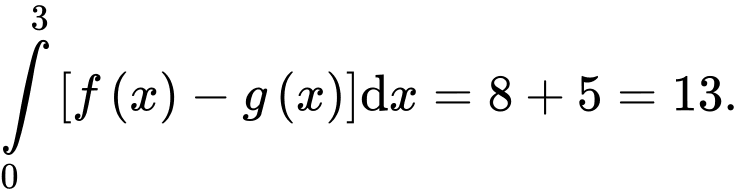
d) Đúng.
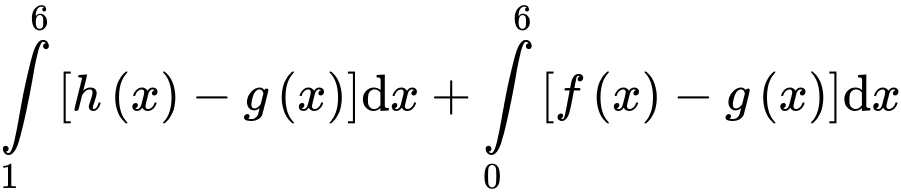
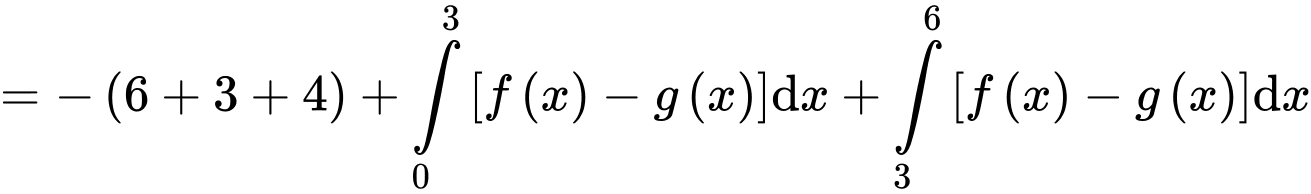
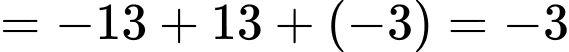
Câu 15 [687488]: Trước 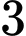 tiếng khi diễn ra trận Derby thành Manchester giữa MU và MC. Người ta phỏng vấn ngẫu nhiên
tiếng khi diễn ra trận Derby thành Manchester giữa MU và MC. Người ta phỏng vấn ngẫu nhiên 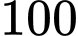 người hâm mộ của MU (có 20 người đang mặc áo của đội bóng) về việc có nên xem trận đấu đó hay không. Kết quả cho thấy rằng
người hâm mộ của MU (có 20 người đang mặc áo của đội bóng) về việc có nên xem trận đấu đó hay không. Kết quả cho thấy rằng 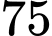 người trả lời sẽ xem,
người trả lời sẽ xem, 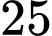 người trả lời sẽ không xem. Nhưng thực tế cho thấy rằng tỉ lệ người hâm mộ MU thực sự xem trận đấu tương ứng với những cách trả lời “ có xem” và “ không xem” là 80% và 20% .
người trả lời sẽ không xem. Nhưng thực tế cho thấy rằng tỉ lệ người hâm mộ MU thực sự xem trận đấu tương ứng với những cách trả lời “ có xem” và “ không xem” là 80% và 20% .
Gọi A là biến cố “ Người được phóng vấn thực sự sẽ xem trận đấu”.
Gọi B là biến cố “ Người được phóng vấn trả lời sẽ xem trận đấu”.
a)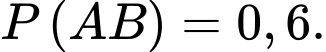
b) Tỉ lệ người được phỏng vấn thực sự sẽ xem trận đấu là 72,5%.
c) Trong số người được phỏng vấn thực sự sẽ xem có 17% người trả lời không xem khi được phỏng vấn.
d) Trong số những người mặc áo đội bóng có 30% người phỏng vấn thực sự sẽ không xem trận đấu biết rằng số người được phỏng vấn thực sự sẽ xem trận đấu mặc áo đội bóng là 14 người.
 tiếng khi diễn ra trận Derby thành Manchester giữa MU và MC. Người ta phỏng vấn ngẫu nhiên
tiếng khi diễn ra trận Derby thành Manchester giữa MU và MC. Người ta phỏng vấn ngẫu nhiên 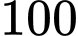 người hâm mộ của MU (có 20 người đang mặc áo của đội bóng) về việc có nên xem trận đấu đó hay không. Kết quả cho thấy rằng
người hâm mộ của MU (có 20 người đang mặc áo của đội bóng) về việc có nên xem trận đấu đó hay không. Kết quả cho thấy rằng 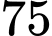 người trả lời sẽ xem,
người trả lời sẽ xem, 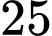 người trả lời sẽ không xem. Nhưng thực tế cho thấy rằng tỉ lệ người hâm mộ MU thực sự xem trận đấu tương ứng với những cách trả lời “ có xem” và “ không xem” là 80% và 20% .
người trả lời sẽ không xem. Nhưng thực tế cho thấy rằng tỉ lệ người hâm mộ MU thực sự xem trận đấu tương ứng với những cách trả lời “ có xem” và “ không xem” là 80% và 20% . Gọi A là biến cố “ Người được phóng vấn thực sự sẽ xem trận đấu”.
Gọi B là biến cố “ Người được phóng vấn trả lời sẽ xem trận đấu”.
a)
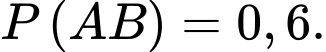
b) Tỉ lệ người được phỏng vấn thực sự sẽ xem trận đấu là 72,5%.
c) Trong số người được phỏng vấn thực sự sẽ xem có 17% người trả lời không xem khi được phỏng vấn.
d) Trong số những người mặc áo đội bóng có 30% người phỏng vấn thực sự sẽ không xem trận đấu biết rằng số người được phỏng vấn thực sự sẽ xem trận đấu mặc áo đội bóng là 14 người.
a) Đúng.
Theo đề bài ta có: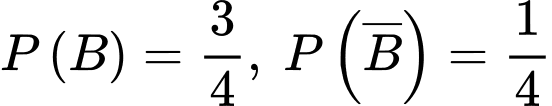 ,
,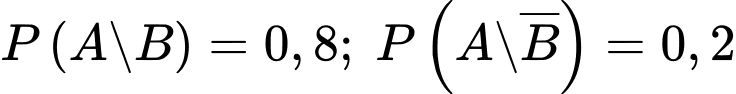
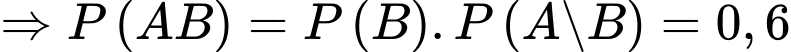
b) Sai.
Theo công thức xác suất toàn phần ta có:
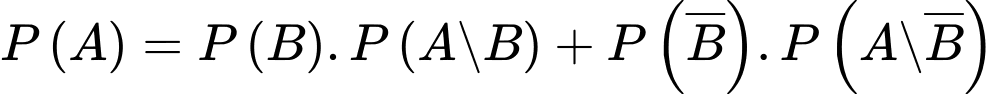
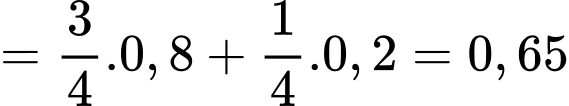
c) Sai.
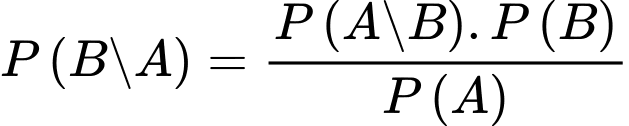
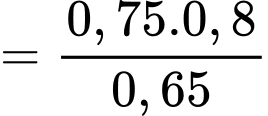
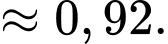
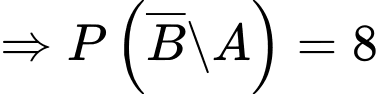
d) Đúng.
Gọi là biến cố “Những người mặc áo đội bóng”
là biến cố “Những người mặc áo đội bóng”
Theo đề bài ta có: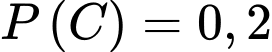
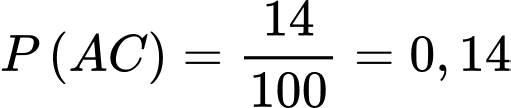
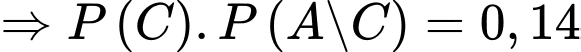

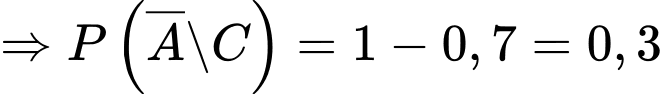
Theo đề bài ta có:
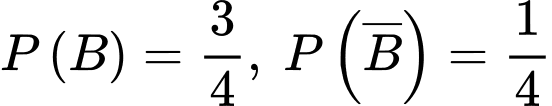 ,
,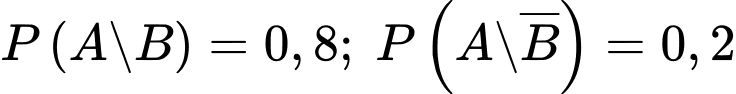
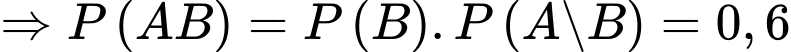
b) Sai.
Theo công thức xác suất toàn phần ta có:
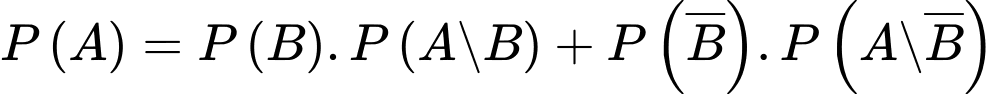
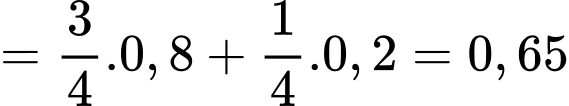
c) Sai.
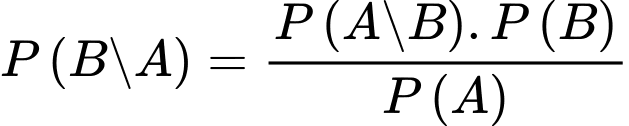
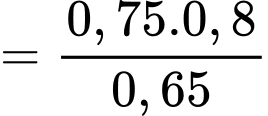
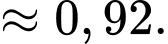
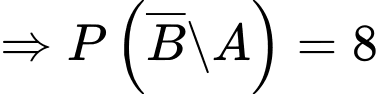
d) Đúng.
Gọi
 là biến cố “Những người mặc áo đội bóng”
là biến cố “Những người mặc áo đội bóng”
Theo đề bài ta có:
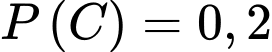
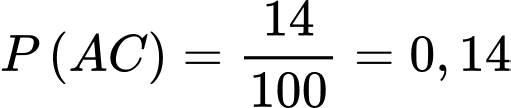
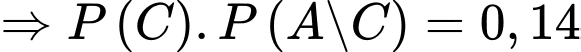

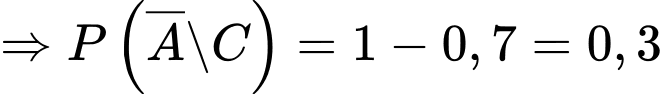
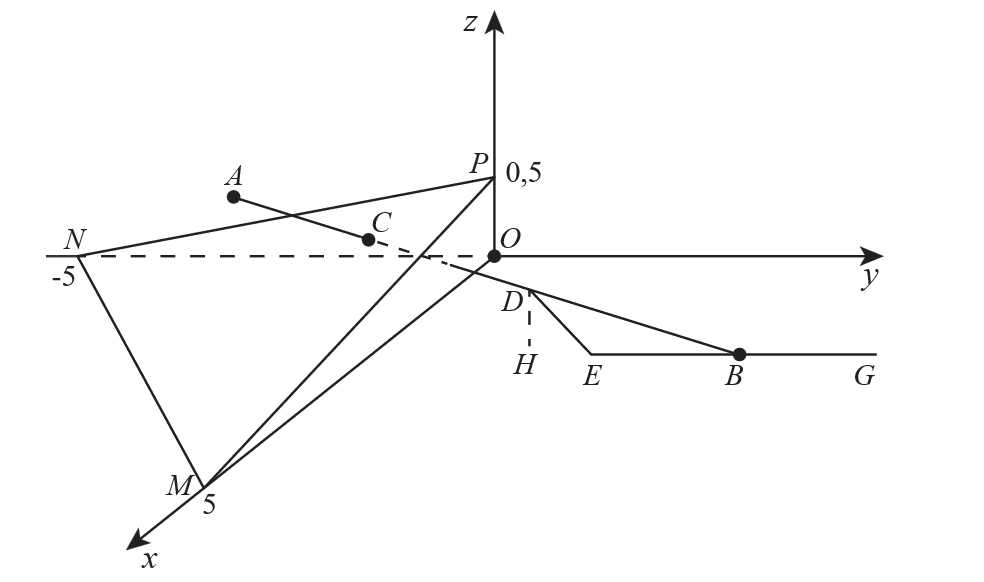
Câu 16 [696470]: Trong không gian với hệ tọa độ 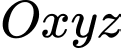 (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí
(đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí 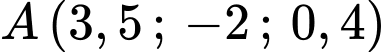 và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí 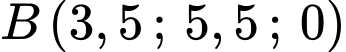 trên đường băng
trên đường băng 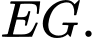 Có một lớp mây được mô phỏng bởi một mặt phẳng
Có một lớp mây được mô phỏng bởi một mặt phẳng  đi qua ba điểm
đi qua ba điểm 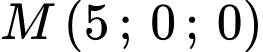 ,
, 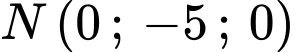 ,
, 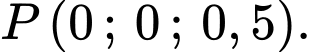
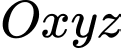 (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí
(đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trị trí 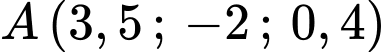 và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí 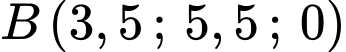 trên đường băng
trên đường băng 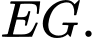 Có một lớp mây được mô phỏng bởi một mặt phẳng
Có một lớp mây được mô phỏng bởi một mặt phẳng  đi qua ba điểm
đi qua ba điểm 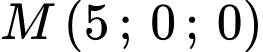 ,
, 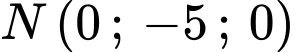 ,
, 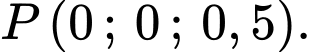

a) Sai.
Phương trình mặt phẳng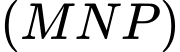 là
là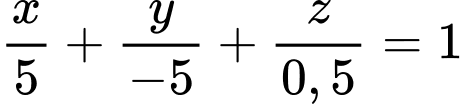
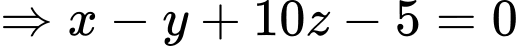
b) Đúng.
Phương trình đường thẳng là
là 
Thay theo
theo  vào phương trình mặt phẳng
vào phương trình mặt phẳng 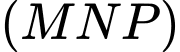 ta được:
ta được:
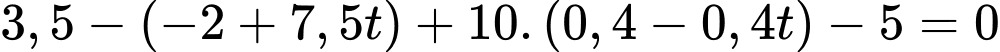
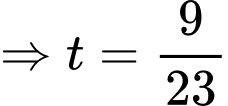
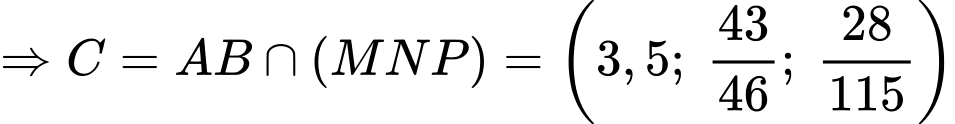
 cách mặt đất một khoảng là
cách mặt đất một khoảng là 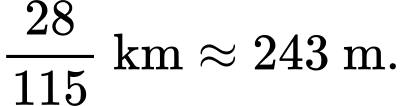
c) Đúng.
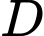 ở độ cao 120 m
ở độ cao 120 m 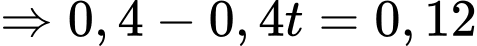
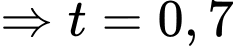
 Tung độ của điểm
Tung độ của điểm 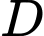 là
là 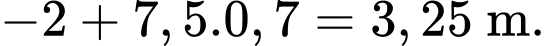
d) Sai.
Theo câu c) ta có: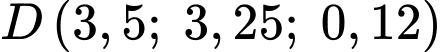
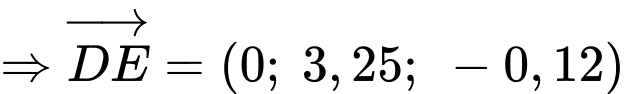
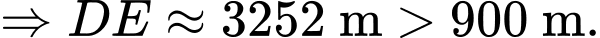
 Sau khi ra khỏi đám mây, người phi công không đạt được quy định an toàn bay.
Sau khi ra khỏi đám mây, người phi công không đạt được quy định an toàn bay.
Phương trình mặt phẳng
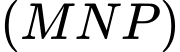 là
là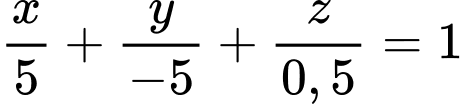
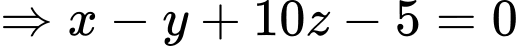
b) Đúng.
Phương trình đường thẳng
 là
là 
Thay
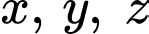 theo
theo 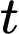 vào phương trình mặt phẳng
vào phương trình mặt phẳng 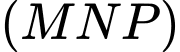 ta được:
ta được: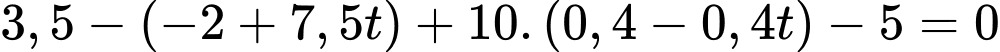
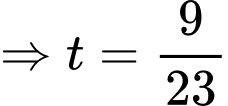
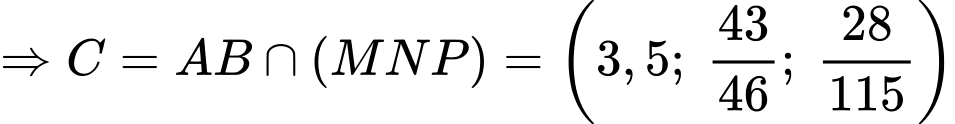
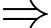
 cách mặt đất một khoảng là
cách mặt đất một khoảng là 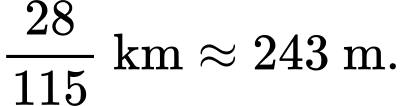
c) Đúng.
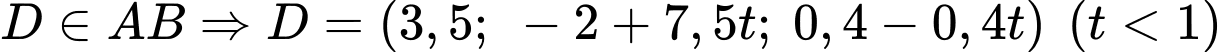
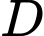 ở độ cao 120 m
ở độ cao 120 m 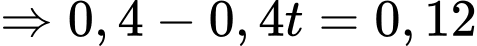
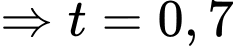
 Tung độ của điểm
Tung độ của điểm 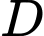 là
là 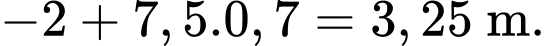
d) Sai.
Theo câu c) ta có:
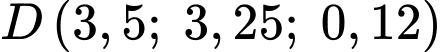
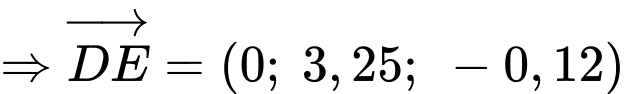
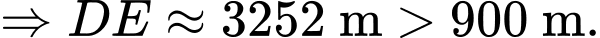
 Sau khi ra khỏi đám mây, người phi công không đạt được quy định an toàn bay.
Sau khi ra khỏi đám mây, người phi công không đạt được quy định an toàn bay. PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
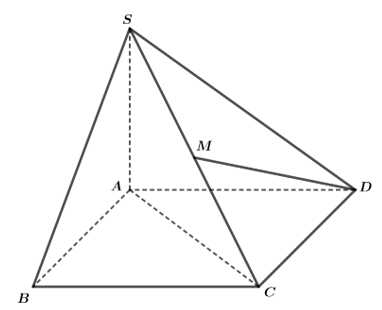
Câu 17 [696471]: Cho hình chóp  có đáy
có đáy 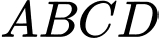 là hình thoi cạnh
là hình thoi cạnh 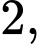
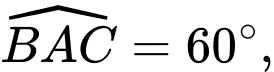
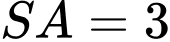 và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 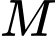 là trung điểm của
là trung điểm của  Côsin của góc giữa hai đường thẳng
Côsin của góc giữa hai đường thẳng 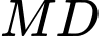 và
và  bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
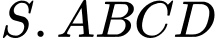 có đáy
có đáy 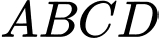 là hình thoi cạnh
là hình thoi cạnh 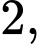
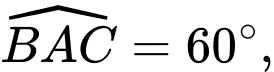
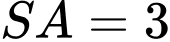 và vuông góc với mặt phẳng đáy. Gọi
và vuông góc với mặt phẳng đáy. Gọi 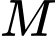 là trung điểm của
là trung điểm của  Côsin của góc giữa hai đường thẳng
Côsin của góc giữa hai đường thẳng 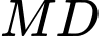 và
và  bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 0,7.
Vì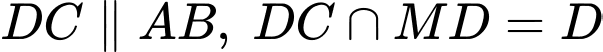
Vì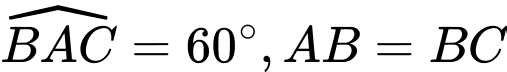
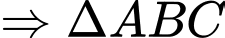 đều
đều 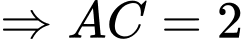
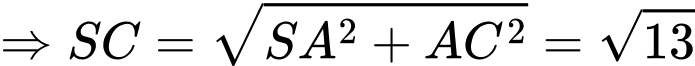
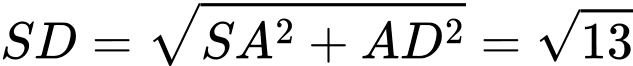
Xét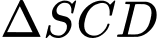 có:
có: 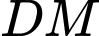 là đường trung tuyến
là đường trung tuyến 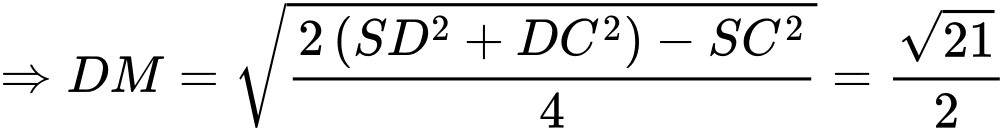
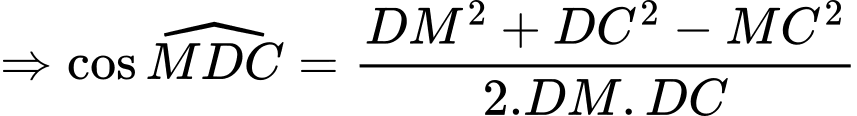
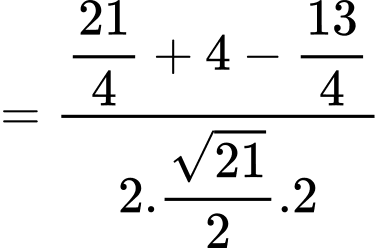
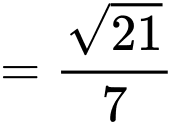
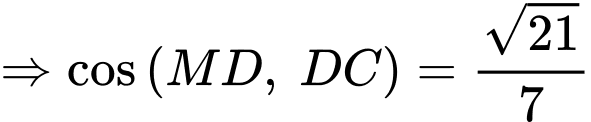
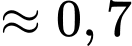 .
.

Vì
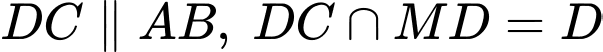
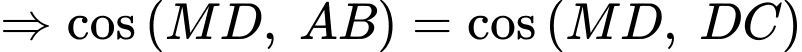
Vì
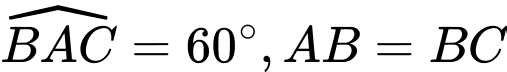
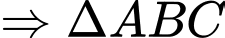 đều
đều 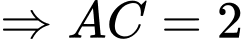
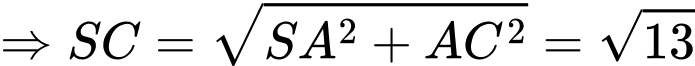
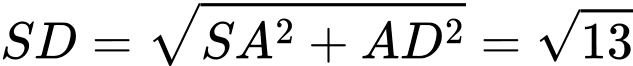
Xét
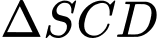 có:
có: 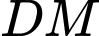 là đường trung tuyến
là đường trung tuyến 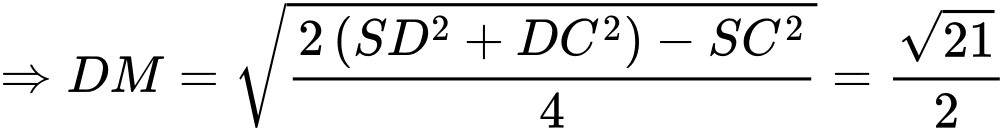
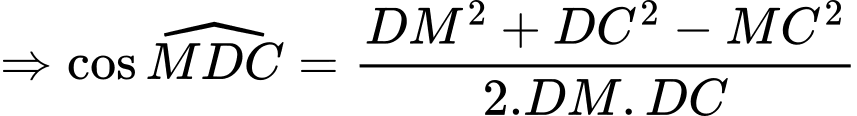
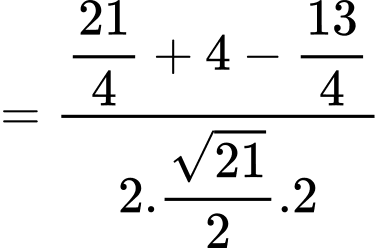
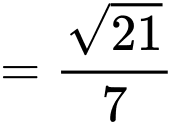
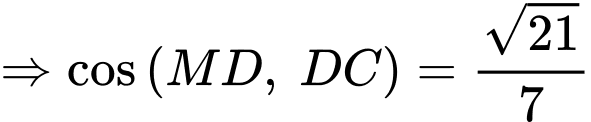
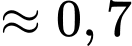 .
.
Câu 18 [696472]: Cho tứ diện ABCD, một con bọ đang đậu ở đỉnh A của tứ diện. Mỗi lần nghe một tiếng trống thì nó nhảy sang một đỉnh bất kì của tứ diện ABCD mà kề với đỉnh nó đang đậu. Hỏi sau 4 tiếng trống nó có bao nhiêu cách trở về đỉnh A?
Điền đáp án: 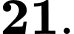
TH1: với
với  là các đỉnh khác nhau khác
là các đỉnh khác nhau khác 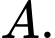
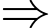 Có
Có 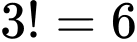 cách chọn
cách chọn
TH2: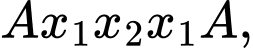 với
với 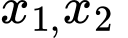 là các đỉnh khác nhau khác
là các đỉnh khác nhau khác 
 Có 3 cách chọn
Có 3 cách chọn 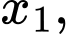 2 cách chọn
2 cách chọn 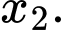
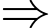 Có 6 cách thỏa mãn.
Có 6 cách thỏa mãn.
TH3: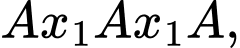 với
với 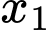 là đỉnh bất kỳ khác
là đỉnh bất kỳ khác 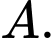
 Có 3 cách thỏa mãn.
Có 3 cách thỏa mãn.
TH4: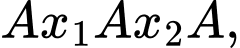 với
với 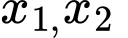 là các đỉnh khác nhau khác
là các đỉnh khác nhau khác 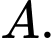
 Có 3 cách chọn
Có 3 cách chọn 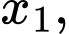 2 cách chọn
2 cách chọn 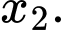
 Có 6 cách thỏa mãn.
Có 6 cách thỏa mãn.
Vậy có tất cả 21 cách thỏa mãn.

TH1:
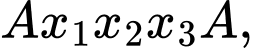 với
với 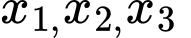 là các đỉnh khác nhau khác
là các đỉnh khác nhau khác 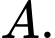
 Có
Có 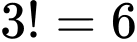 cách chọn
cách chọn
TH2:
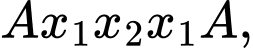 với
với 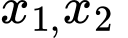 là các đỉnh khác nhau khác
là các đỉnh khác nhau khác 
 Có 3 cách chọn
Có 3 cách chọn 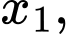 2 cách chọn
2 cách chọn 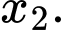
 Có 6 cách thỏa mãn.
Có 6 cách thỏa mãn.
TH3:
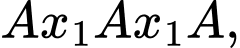 với
với  là đỉnh bất kỳ khác
là đỉnh bất kỳ khác 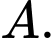
 Có 3 cách thỏa mãn.
Có 3 cách thỏa mãn.
TH4:
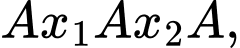 với
với 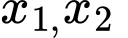 là các đỉnh khác nhau khác
là các đỉnh khác nhau khác 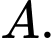
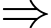 Có 3 cách chọn
Có 3 cách chọn 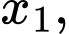 2 cách chọn
2 cách chọn 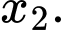
 Có 6 cách thỏa mãn.
Có 6 cách thỏa mãn.
Vậy có tất cả 21 cách thỏa mãn.
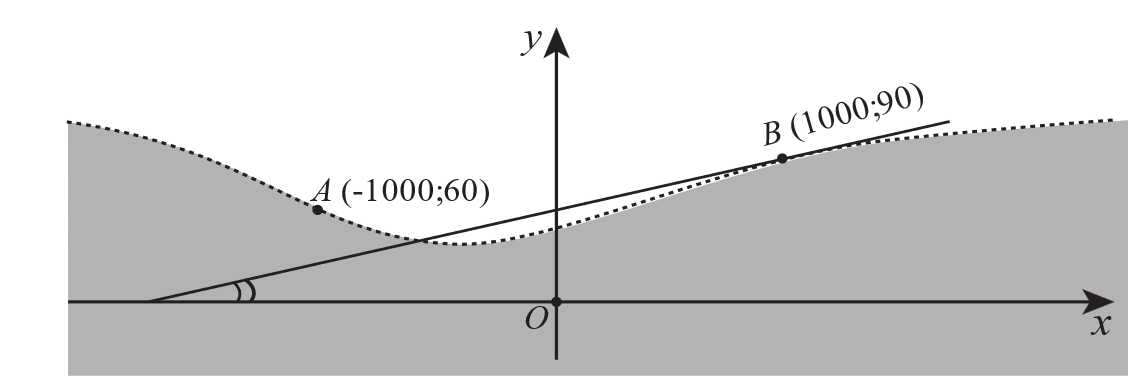
Câu 19 [703069]: Thiết kế đường cao tốc một đoạn đường cao tốc nối hai sườn đồi có độ dốc 6% và 4% sẽ được xây dựng giữa hai điểm cách nhau theo chiều ngang là 2000 feet (xem hình vẽ). Trong hệ toạ độ 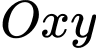 (đơn vị mỗi trục là feet (ft)) quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có chọn hàm số bậc ba
(đơn vị mỗi trục là feet (ft)) quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có chọn hàm số bậc ba 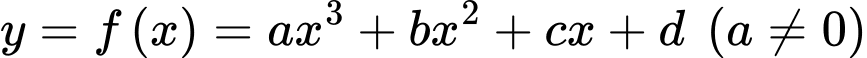 sao cho trong hệ trục toạ độ
sao cho trong hệ trục toạ độ 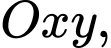 đồ thị hàm số đó trên đoạn
đồ thị hàm số đó trên đoạn 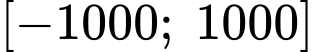 mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại
mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại 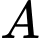 và tại
và tại 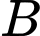 của đồ thị hàm số đó lần lượt bằng
của đồ thị hàm số đó lần lượt bằng 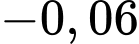 và
và 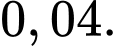 Giả sử bằng cách đo đạc ta có
Giả sử bằng cách đo đạc ta có 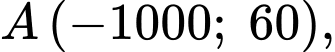
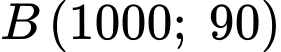 (hình vẽ). Hỏi giao điểm của đường cao tốc với trục
(hình vẽ). Hỏi giao điểm của đường cao tốc với trục  cách trục
cách trục  bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị) (biết feet là đơn vị đo độ dài và 1 feet = 0,3408 mét).
bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị) (biết feet là đơn vị đo độ dài và 1 feet = 0,3408 mét).
 (đơn vị mỗi trục là feet (ft)) quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có chọn hàm số bậc ba
(đơn vị mỗi trục là feet (ft)) quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có chọn hàm số bậc ba 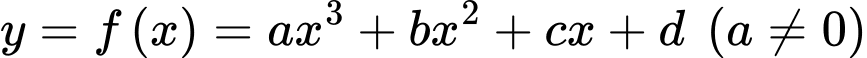 sao cho trong hệ trục toạ độ
sao cho trong hệ trục toạ độ 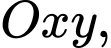 đồ thị hàm số đó trên đoạn
đồ thị hàm số đó trên đoạn 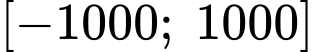 mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại
mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại 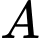 và tại
và tại 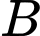 của đồ thị hàm số đó lần lượt bằng
của đồ thị hàm số đó lần lượt bằng 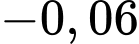 và
và 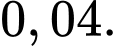 Giả sử bằng cách đo đạc ta có
Giả sử bằng cách đo đạc ta có 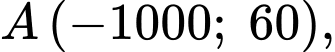
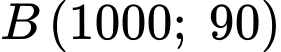 (hình vẽ). Hỏi giao điểm của đường cao tốc với trục
(hình vẽ). Hỏi giao điểm của đường cao tốc với trục 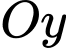 cách trục
cách trục 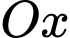 bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị) (biết feet là đơn vị đo độ dài và 1 feet = 0,3408 mét).
bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị) (biết feet là đơn vị đo độ dài và 1 feet = 0,3408 mét).
Điền đáp án: 17.
Ta có: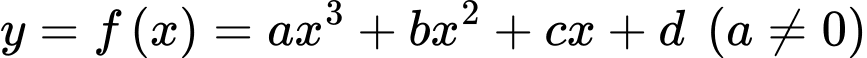

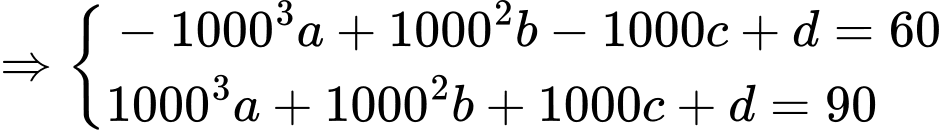 (1)
(1)
Có: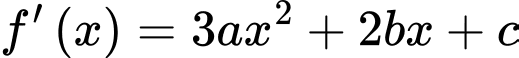
Vì hệ số góc của tiếp tuyến tại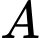 và tại
và tại 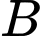 của đồ thị hàm số đó lần lượt bằng
của đồ thị hàm số đó lần lượt bằng 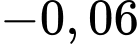 và
và 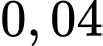 nên
nên 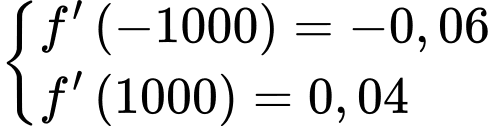
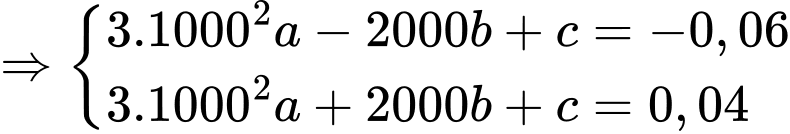 (2)
(2)
Từ (1) và (2)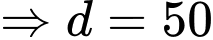
 Giao điểm của đường cao tốc với trục
Giao điểm của đường cao tốc với trục 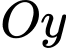 cách trục
cách trục 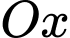 là
là
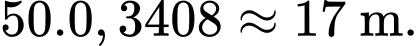
Ta có:
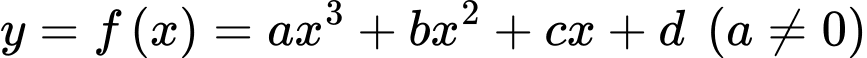

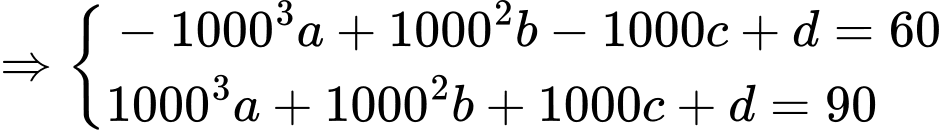 (1)
(1)
Có:
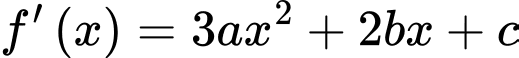
Vì hệ số góc của tiếp tuyến tại
 và tại
và tại 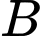 của đồ thị hàm số đó lần lượt bằng
của đồ thị hàm số đó lần lượt bằng  và
và 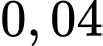 nên
nên 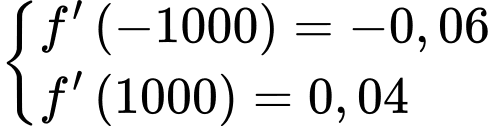
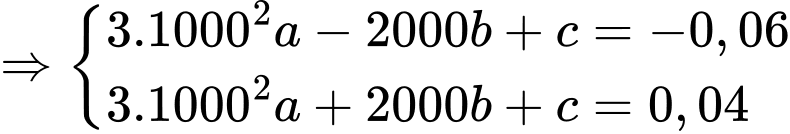 (2)
(2)
Từ (1) và (2)
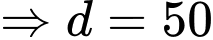
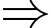 Giao điểm của đường cao tốc với trục
Giao điểm của đường cao tốc với trục  cách trục
cách trục 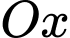 là
là 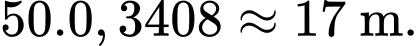
Câu 20 [696490]: Có hai chiếc hộp, hộp I có 6 bi đỏ và 4 bi trắng, hộp II có 7 bi đỏ và 3 bi trắng, các bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên từ mỗi hộp ra hai bi. Tính xác suất để lấy được ít nhất một bi đỏ từ hộp I, biết rằng trong bốn bi lấy ra số bi đỏ bằng số bi trắng.
Điền đáp án: 0,81.
Gọi A là biến cố “Lấy được ít nhất một bi đỏ từ hộp I”.
B là biến cố “Bốn bi lấy ra số bi đỏ bằng số bi trắng”.
Ta có xác suất cần tính là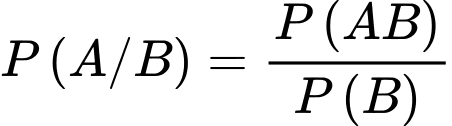 .
.
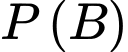
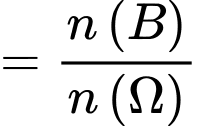
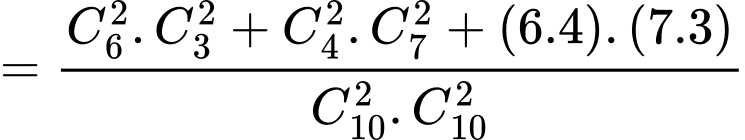
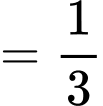 .
.
TH1. Lấy được mỗi hộp một bi đỏ và một bi trắng ta có
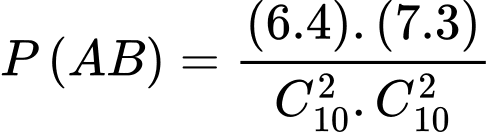
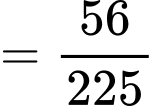 .
.
TH2. Lấy đươc 2 bi đỏ từ hộp I và 2 bi trắng từ hộp II ta có
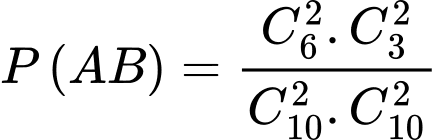
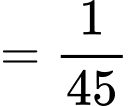 .
.
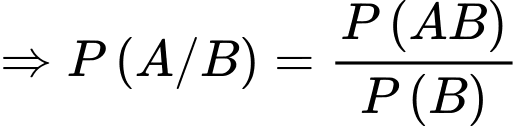
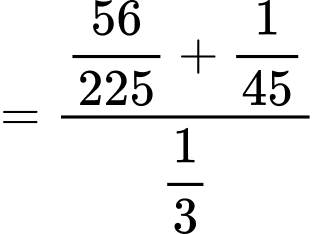
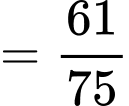
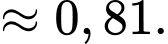
Gọi A là biến cố “Lấy được ít nhất một bi đỏ từ hộp I”.
B là biến cố “Bốn bi lấy ra số bi đỏ bằng số bi trắng”.
Ta có xác suất cần tính là
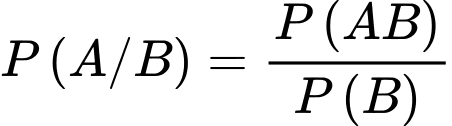 .
.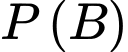
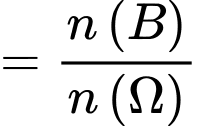
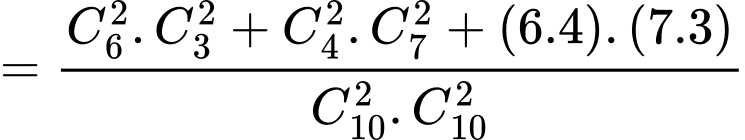
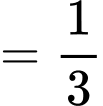 .
.TH1. Lấy được mỗi hộp một bi đỏ và một bi trắng ta có
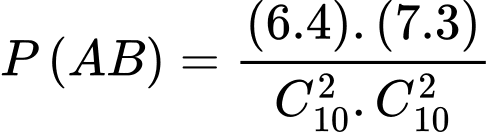
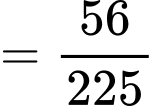 .
.TH2. Lấy đươc 2 bi đỏ từ hộp I và 2 bi trắng từ hộp II ta có
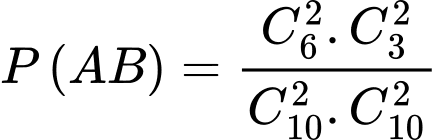
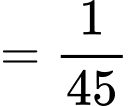 .
.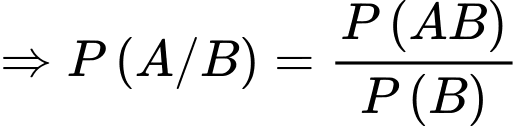
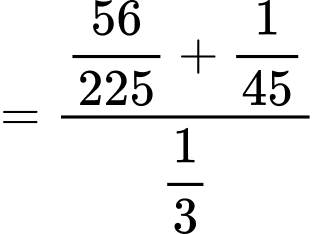
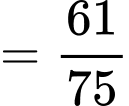
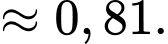
Câu 21 [700841]: Trong thực tế, người ta muốn chế tác một cái bình bằng cách cho quay hình vẽ dưới đây quanh trục 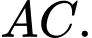
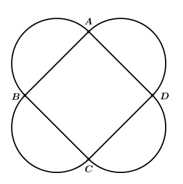
Biết rằng hình vuông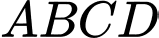 đường chéo
đường chéo 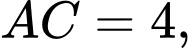 phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính. Thể tích của cái bình đó bằng bao nhiêu? (Làm tròn đến hàng đơn vị).
phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính. Thể tích của cái bình đó bằng bao nhiêu? (Làm tròn đến hàng đơn vị).
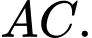

Biết rằng hình vuông
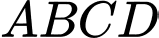 đường chéo
đường chéo 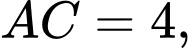 phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính. Thể tích của cái bình đó bằng bao nhiêu? (Làm tròn đến hàng đơn vị).
phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính. Thể tích của cái bình đó bằng bao nhiêu? (Làm tròn đến hàng đơn vị).
Điền đáp án: 73.
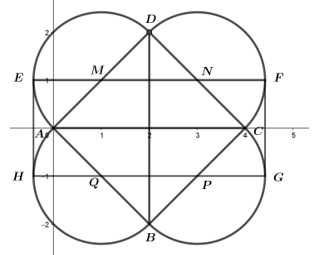
Ta đặt hệ trục tọa độ như hình vẽ.
Vì hình vuông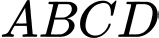 đường chéo
đường chéo 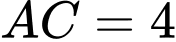
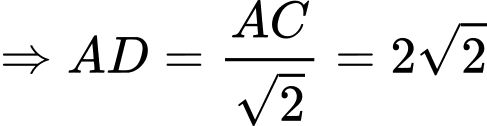 .
.
Phương trình đường tròn tâm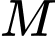 , bán kính bằng
, bán kính bằng 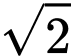 là
là
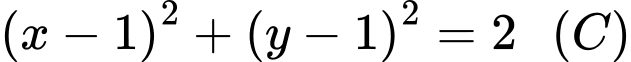
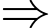 Phần đường tròn nằm phía trên đường thẳng
Phần đường tròn nằm phía trên đường thẳng 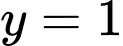 có phương trình là
có phương trình là 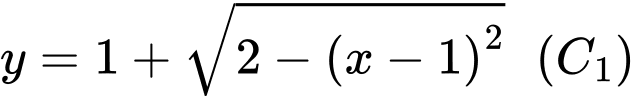 , phần đường tròn nằm phía dưới đường thẳng
, phần đường tròn nằm phía dưới đường thẳng 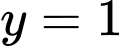 có phương trình là
có phương trình là 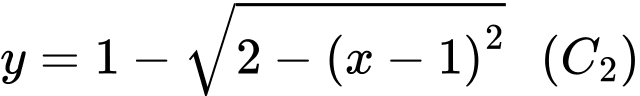 .
.
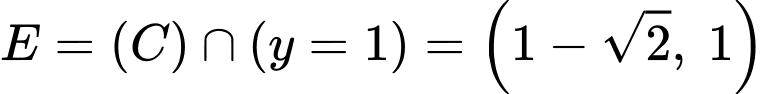
Gọi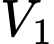 là phần thể tích giới hạn bởi đường cong
là phần thể tích giới hạn bởi đường cong 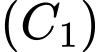 , các đường thẳng
, các đường thẳng 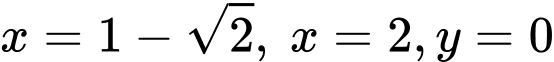 khi quay quanh trục
khi quay quanh trục 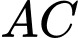 .
.
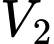 là phần thể tích giới hạn bởi đường cong
là phần thể tích giới hạn bởi đường cong 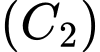 , các đường thẳng
, các đường thẳng 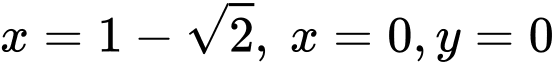 khi quay quanh trục
khi quay quanh trục 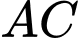 .
.
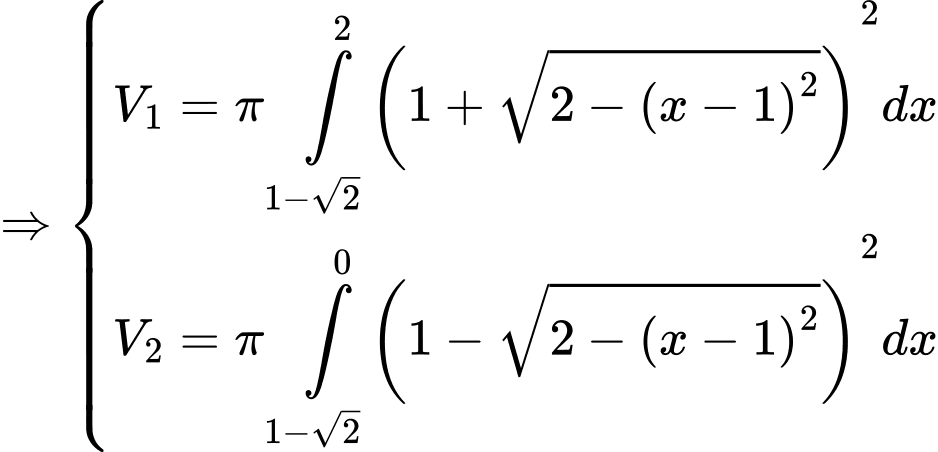
Thể tích của cái bình đó là

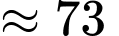 .
.

Ta đặt hệ trục tọa độ như hình vẽ.
Vì hình vuông
 đường chéo
đường chéo 
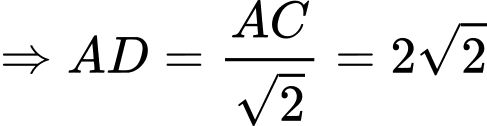 .
.
Phương trình đường tròn tâm
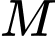 , bán kính bằng
, bán kính bằng 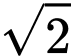 là
là
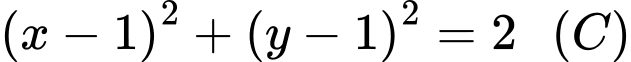
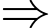 Phần đường tròn nằm phía trên đường thẳng
Phần đường tròn nằm phía trên đường thẳng 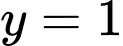 có phương trình là
có phương trình là 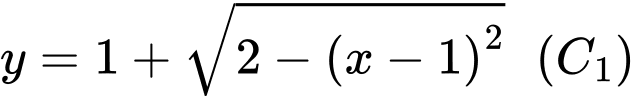 , phần đường tròn nằm phía dưới đường thẳng
, phần đường tròn nằm phía dưới đường thẳng 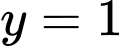 có phương trình là
có phương trình là 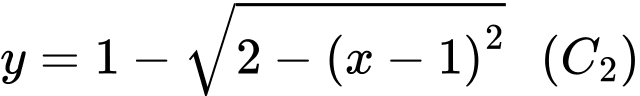 .
.
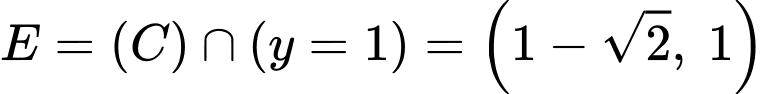
Gọi
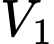 là phần thể tích giới hạn bởi đường cong
là phần thể tích giới hạn bởi đường cong 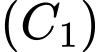 , các đường thẳng
, các đường thẳng 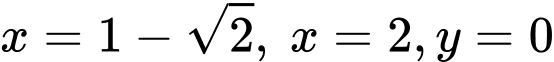 khi quay quanh trục
khi quay quanh trục 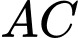 .
.
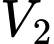 là phần thể tích giới hạn bởi đường cong
là phần thể tích giới hạn bởi đường cong 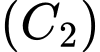 , các đường thẳng
, các đường thẳng 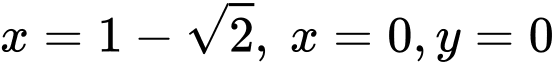 khi quay quanh trục
khi quay quanh trục  .
.
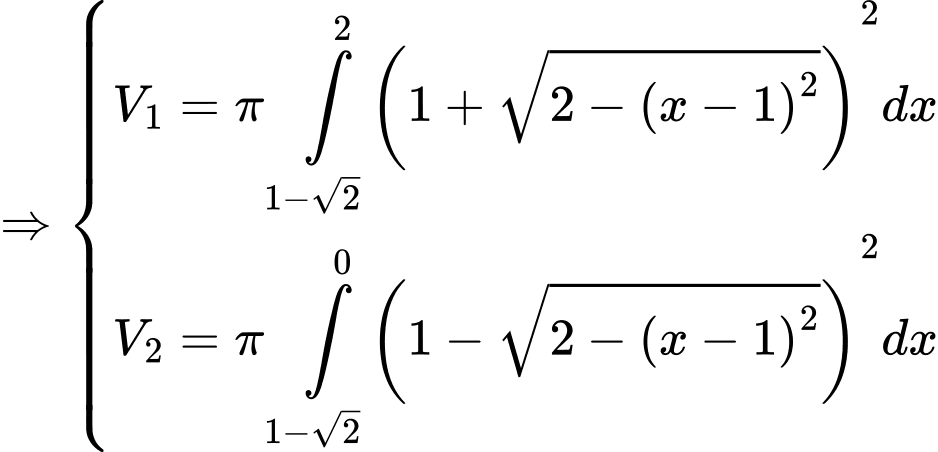
Thể tích của cái bình đó là

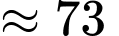 .
.
Câu 22 [695074]: Trong không gian với hệ tọa độ 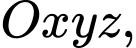 cho hai mặt phẳng là
cho hai mặt phẳng là 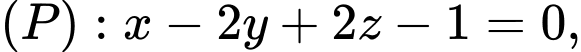
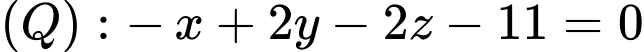 và điểm
và điểm 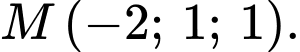 Một mặt cầu
Một mặt cầu 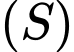 di động đi qua A đồng thời tiếp xúc với cả hai mặt phẳng
di động đi qua A đồng thời tiếp xúc với cả hai mặt phẳng 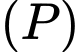 và
và  Tâm của mặt cầu
Tâm của mặt cầu 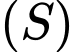 luôn nằm trên một đường cong cố định. Đường cong đó có độ dài bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
luôn nằm trên một đường cong cố định. Đường cong đó có độ dài bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
 cho hai mặt phẳng là
cho hai mặt phẳng là 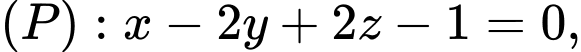
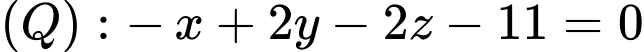 và điểm
và điểm 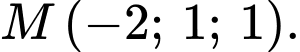 Một mặt cầu
Một mặt cầu 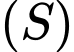 di động đi qua A đồng thời tiếp xúc với cả hai mặt phẳng
di động đi qua A đồng thời tiếp xúc với cả hai mặt phẳng  và
và  Tâm của mặt cầu
Tâm của mặt cầu  luôn nằm trên một đường cong cố định. Đường cong đó có độ dài bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
luôn nằm trên một đường cong cố định. Đường cong đó có độ dài bằng bao nhiêu (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 10,9.
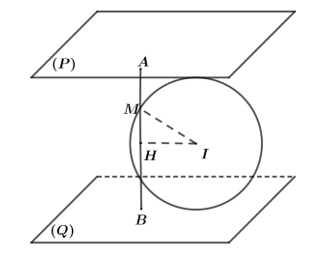
Ta có:
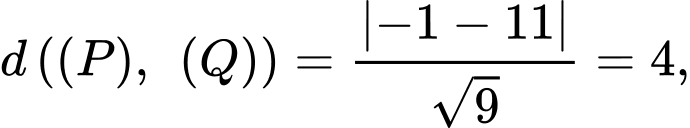
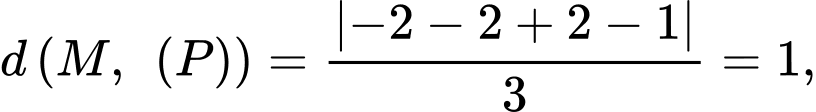
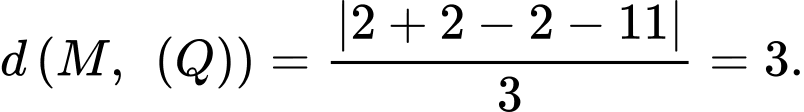
Mặt cầu tâm
tâm  tiếp xúc với cả hai mặt phẳng
tiếp xúc với cả hai mặt phẳng 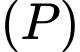 và
và 
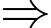 Bán kính của mặt cầu
Bán kính của mặt cầu 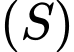 tâm
tâm 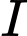 bằng 2.
bằng 2.
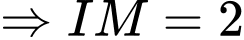
Kẻ
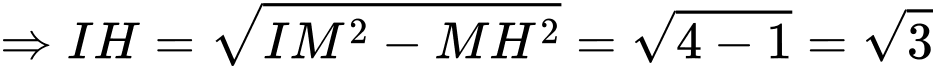
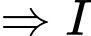 chạy trên đường tròn tâm
chạy trên đường tròn tâm  , bán kính bằng
, bán kính bằng 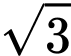 .
.
 Đường cong có độ dài là
Đường cong có độ dài là 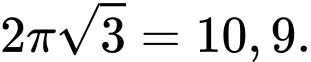

Ta có:
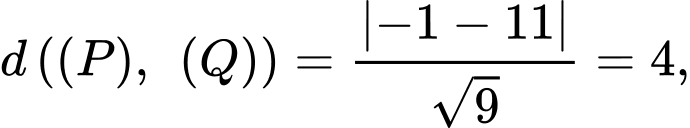
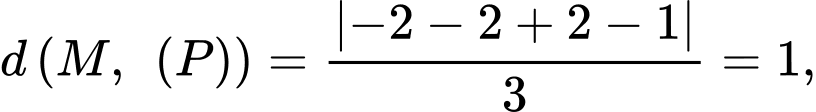
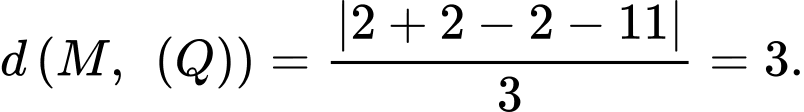
Mặt cầu
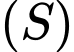 tâm
tâm  tiếp xúc với cả hai mặt phẳng
tiếp xúc với cả hai mặt phẳng 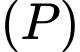 và
và 
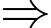 Bán kính của mặt cầu
Bán kính của mặt cầu 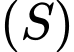 tâm
tâm 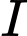 bằng 2.
bằng 2.
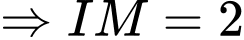
Kẻ

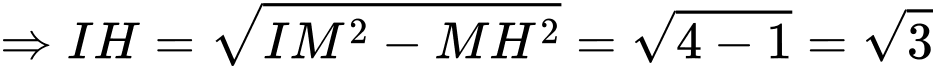
 chạy trên đường tròn tâm
chạy trên đường tròn tâm  , bán kính bằng
, bán kính bằng 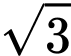 .
.
 Đường cong có độ dài là
Đường cong có độ dài là