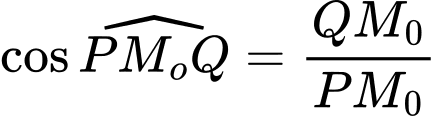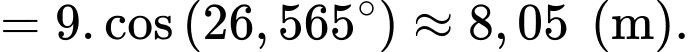PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [697647]: Cho dãy số 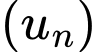 với
với 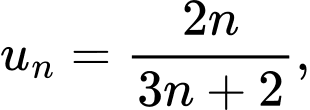
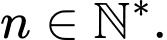 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
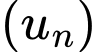 với
với 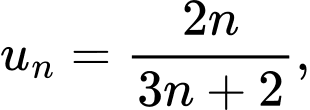
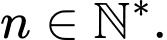 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 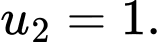
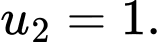
B, 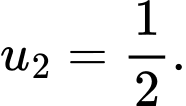
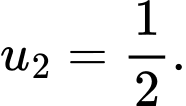
C, 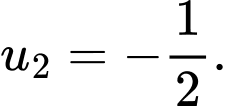
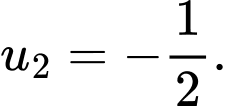
D, 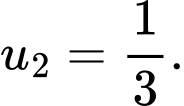
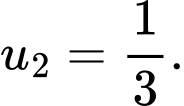
Chọn đáp án B.
Ta có: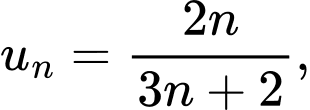
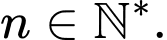
Suy ra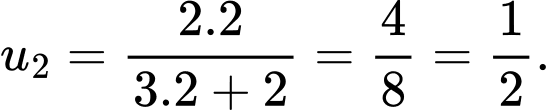 Đáp án: B
Đáp án: B
Ta có:
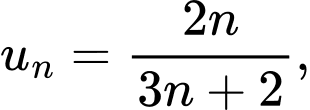
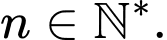
Suy ra
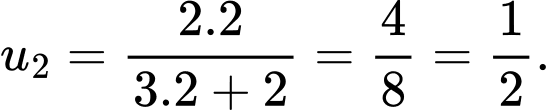 Đáp án: B
Đáp án: B
Câu 2 [697648]: Trong không gian  cho đường thẳng
cho đường thẳng 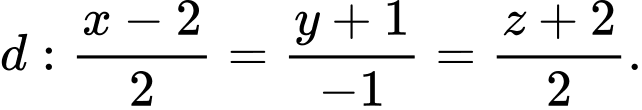 Đường thẳng
Đường thẳng 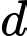 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây?
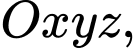 cho đường thẳng
cho đường thẳng 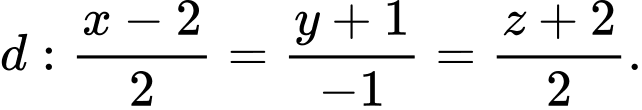 Đường thẳng
Đường thẳng 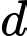 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây? A, 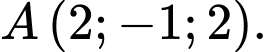
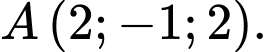
B, 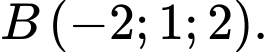
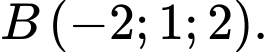
C, 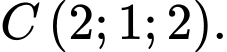
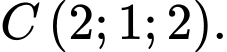
D, 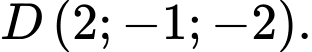
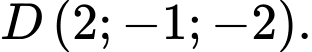
Chọn đáp án D.
Cho đường thẳng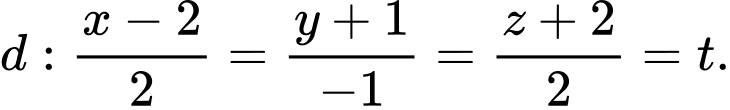
Ta có phương trình tham số của đường thẳng là: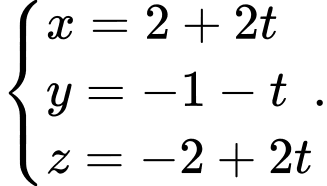
Suy ra đường thẳng đi qua điểm
đi qua điểm 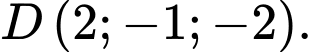 Đáp án: D
Đáp án: D
Cho đường thẳng
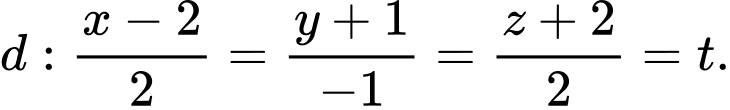
Ta có phương trình tham số của đường thẳng là:
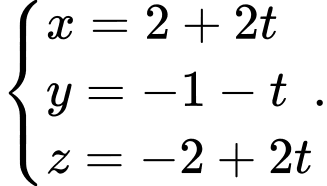
Suy ra đường thẳng
 đi qua điểm
đi qua điểm 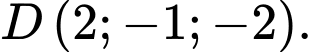 Đáp án: D
Đáp án: D
Câu 3 [697649]: Với 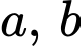 là các số thực dương khác
là các số thực dương khác 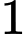 thoả mãn
thoả mãn 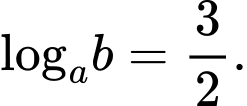 Giá trị của biểu thức
Giá trị của biểu thức 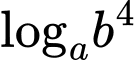 bằng
bằng
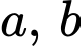 là các số thực dương khác
là các số thực dương khác 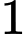 thoả mãn
thoả mãn 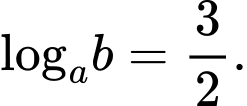 Giá trị của biểu thức
Giá trị của biểu thức 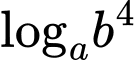 bằng
bằng A, 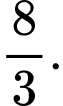
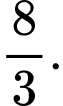
B, 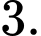
C, 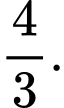
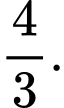
D, 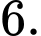
Chọn đáp án D.
Ta có: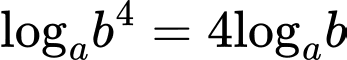
Mặt khác bài cho: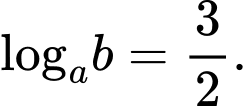
Suy ra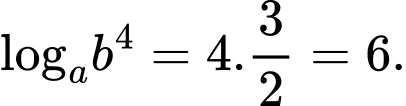 Đáp án: D
Đáp án: D
Ta có:
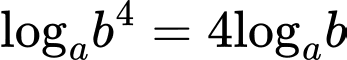
Mặt khác bài cho:
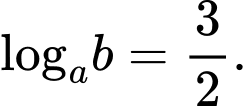
Suy ra
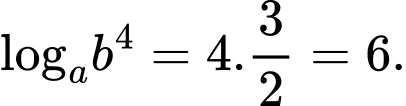 Đáp án: D
Đáp án: D
Câu 4 [255909]: Cho khối chóp 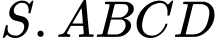 có chiều cao bằng
có chiều cao bằng 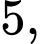 đáy
đáy 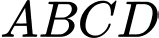 là hình bình hành có diện tích bằng
là hình bình hành có diện tích bằng  Thể tích khối chóp
Thể tích khối chóp  bằng
bằng
 có chiều cao bằng
có chiều cao bằng 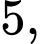 đáy
đáy 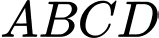 là hình bình hành có diện tích bằng
là hình bình hành có diện tích bằng 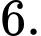 Thể tích khối chóp
Thể tích khối chóp 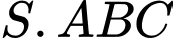 bằng
bằng A, 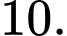
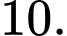
B, 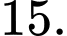
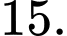
C, 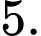
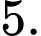
D, 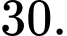
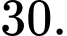
Chọn đáp án C.
Ta có công thức tính thể tích: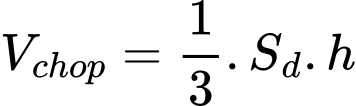
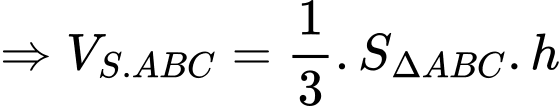
Mặt khác ta có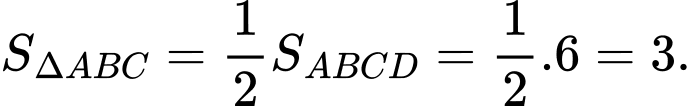
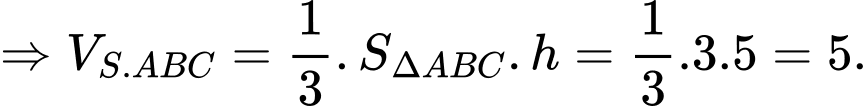 Đáp án: C
Đáp án: C
Ta có công thức tính thể tích:
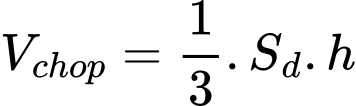
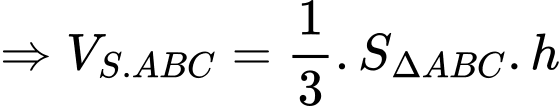
Mặt khác ta có
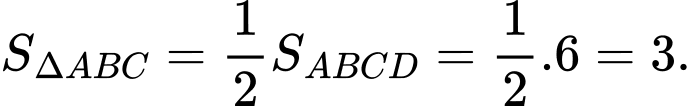
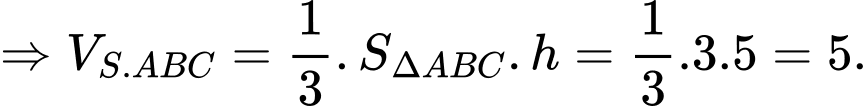 Đáp án: C
Đáp án: C
Câu 5 [693113]: Trong không gian  mặt phẳng
mặt phẳng 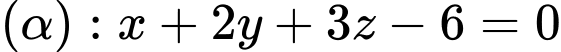 cắt trục tung tại điểm có tung độ bằng
cắt trục tung tại điểm có tung độ bằng
 mặt phẳng
mặt phẳng 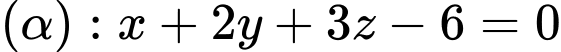 cắt trục tung tại điểm có tung độ bằng
cắt trục tung tại điểm có tung độ bằng A, 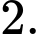
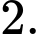
B, 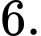
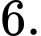
C, 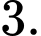
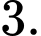
D, 

Chọn đáp án C.
Trong không gian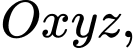 mặt phẳng
mặt phẳng 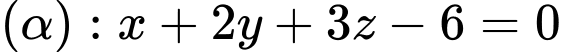 cắt trục tung, suy ra mặt phẳng
cắt trục tung, suy ra mặt phẳng  sẽ cắt trục tung tại điểm
sẽ cắt trục tung tại điểm 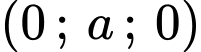

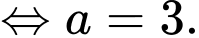
Vậy mặt phẳng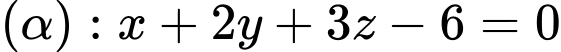 cắt trục tung tại điểm có tung độ bằng 3. Đáp án: C
cắt trục tung tại điểm có tung độ bằng 3. Đáp án: C
Trong không gian
 mặt phẳng
mặt phẳng 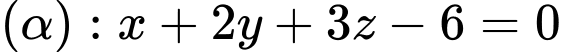 cắt trục tung, suy ra mặt phẳng
cắt trục tung, suy ra mặt phẳng  sẽ cắt trục tung tại điểm
sẽ cắt trục tung tại điểm 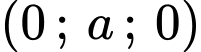

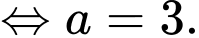
Vậy mặt phẳng
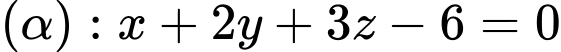 cắt trục tung tại điểm có tung độ bằng 3. Đáp án: C
cắt trục tung tại điểm có tung độ bằng 3. Đáp án: C Sử dụng thông tin dưới đây để trả lời câu 6 và câu 7
Cho hàm số y=f(x) có bảng biến thiên như sau:
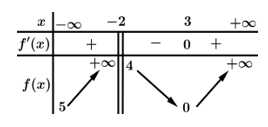

Câu 6 [697650]: Giá trị nhỏ nhất của hàm số 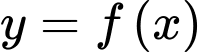 trên đoạn
trên đoạn 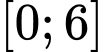 bằng
bằng
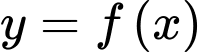 trên đoạn
trên đoạn 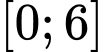 bằng
bằng A, 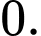
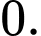
B, 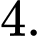
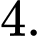
C, 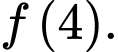
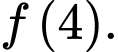
D, 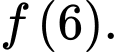
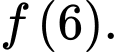
Chọn đáp án A.
Từ bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số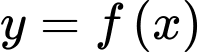 trên đoạn
trên đoạn 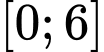 bằng 0.
Đáp án: A
bằng 0.
Đáp án: A
Từ bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số
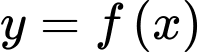 trên đoạn
trên đoạn 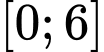 bằng 0.
Đáp án: A
bằng 0.
Đáp án: A
Câu 7 [697651]: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 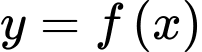 là
là
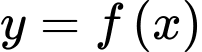 là
là A, 
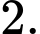
B, 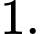
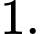
C, 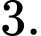
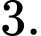
D, 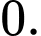
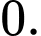
Chọn đáp án A.
Từ bảng biến thiên, ta có:
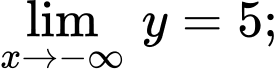
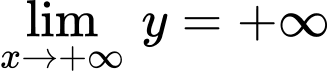 nên đồ thị hàm số
nên đồ thị hàm số 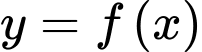 có một tiệm cận ngang.
có một tiệm cận ngang.
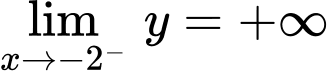 nên đồ thị hàm số
nên đồ thị hàm số 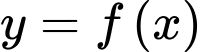 có một tiệm cận đứng.
có một tiệm cận đứng.
Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số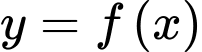 là 2.
Đáp án: A
là 2.
Đáp án: A
Từ bảng biến thiên, ta có:
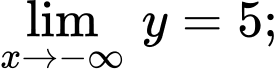
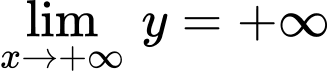 nên đồ thị hàm số
nên đồ thị hàm số 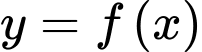 có một tiệm cận ngang.
có một tiệm cận ngang.
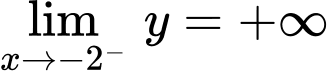 nên đồ thị hàm số
nên đồ thị hàm số 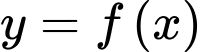 có một tiệm cận đứng.
có một tiệm cận đứng.
Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
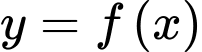 là 2.
Đáp án: A
là 2.
Đáp án: A
Câu 8 [693115]: Tập nghiệm của bất phương trình 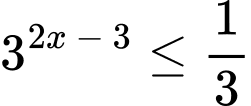 là
là
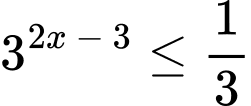 là
là A, 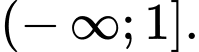
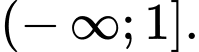
B, 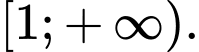
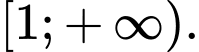
C, 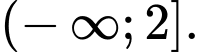
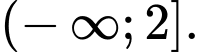
D, 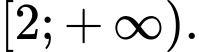
Chọn đáp án A.
Ta có: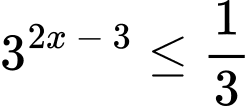
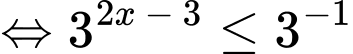
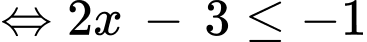
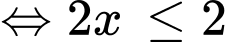
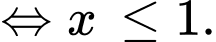
Vậy tập nghiệm của bất phương trình là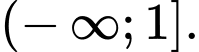 Đáp án: A
Đáp án: A
Ta có:
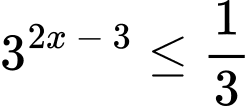
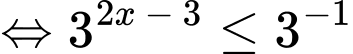
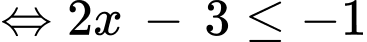
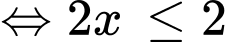
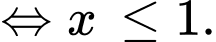
Vậy tập nghiệm của bất phương trình là
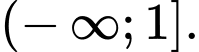 Đáp án: A
Đáp án: A
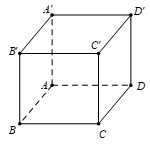
Câu 9 [693116]: Cho hình lập phương  có cạnh bằng
có cạnh bằng  Độ dài của vectơ
Độ dài của vectơ 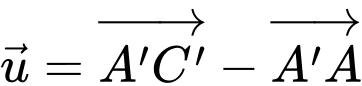 bằng
bằng
 có cạnh bằng
có cạnh bằng 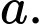 Độ dài của vectơ
Độ dài của vectơ 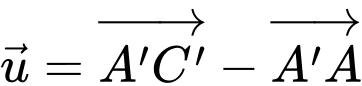 bằng
bằng
A, 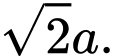
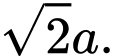
B, 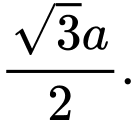
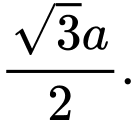
C, 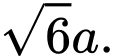
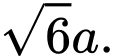
D, 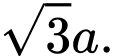
Chọn đáp án D.
Từ hình vẽ ta có: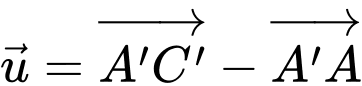
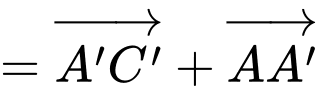
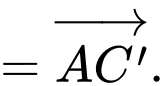
Suy ra độ dài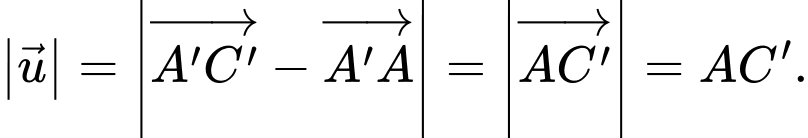
Có là hình lập phương cạnh
là hình lập phương cạnh  và có
và có  là đường chéo của hình lập phương nên ta suy ra:
là đường chéo của hình lập phương nên ta suy ra:
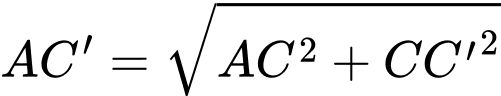
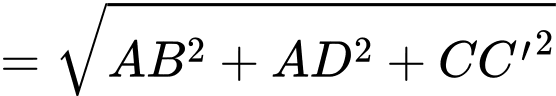
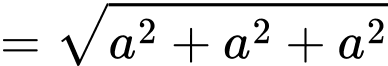
 Đáp án: D
Đáp án: D
Từ hình vẽ ta có:
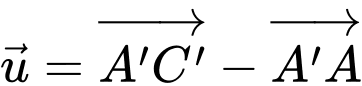
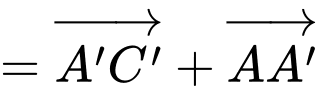
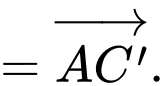
Suy ra độ dài
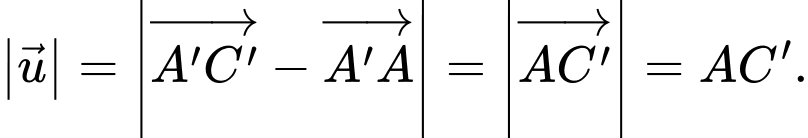
Có
 là hình lập phương cạnh
là hình lập phương cạnh 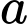 và có
và có  là đường chéo của hình lập phương nên ta suy ra:
là đường chéo của hình lập phương nên ta suy ra:
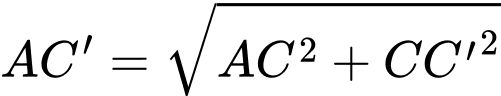
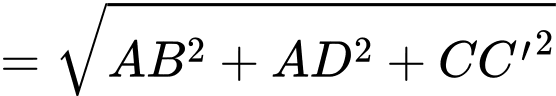
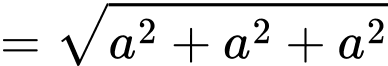
 Đáp án: D
Đáp án: D
Câu 10 [693117]: Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Nhóm chứa tứ phân vị thứ nhất là

Nhóm chứa tứ phân vị thứ nhất là
A, 
B, 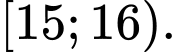
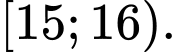
C, 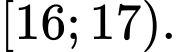
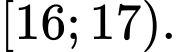
D, 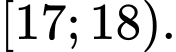
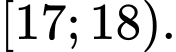
Chọn đáp án C.
Số con hổ được khảo sát là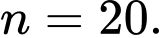
Gọi là tuổi thọ của 20 con hổ được sắp xếp theo thứ tự không giảm.
là tuổi thọ của 20 con hổ được sắp xếp theo thứ tự không giảm.
Ta có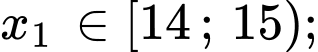
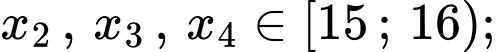
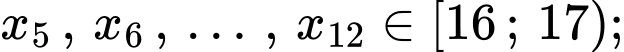
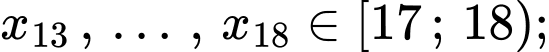
 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu  thì
thì
Tứ phân vị thứ nhất của dãy số liệu là
là 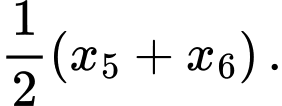 Do
Do 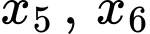 thuộc nhóm
thuộc nhóm 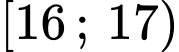 nên tứ phân vị thứ nhất thuộc nhóm
nên tứ phân vị thứ nhất thuộc nhóm 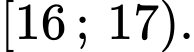 Đáp án: C
Đáp án: C
Số con hổ được khảo sát là
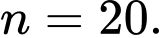
Gọi
 là tuổi thọ của 20 con hổ được sắp xếp theo thứ tự không giảm.
là tuổi thọ của 20 con hổ được sắp xếp theo thứ tự không giảm.
Ta có
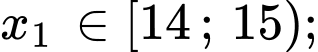
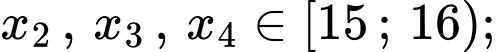
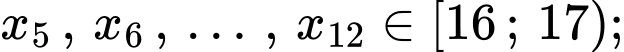
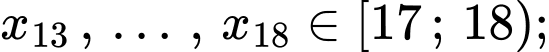
 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu  thì
thì
Tứ phân vị thứ nhất của dãy số liệu
 là
là 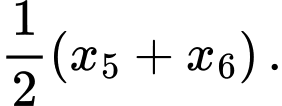 Do
Do 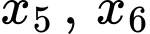 thuộc nhóm
thuộc nhóm 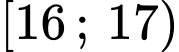 nên tứ phân vị thứ nhất thuộc nhóm
nên tứ phân vị thứ nhất thuộc nhóm 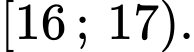 Đáp án: C
Đáp án: C
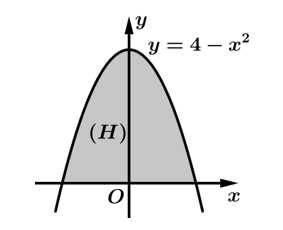
Câu 11 [693119]: Cho hình phẳng  giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 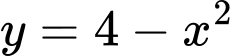 và trục hoành. Thể tích khối tròn xoay được tạo thành khi quay
và trục hoành. Thể tích khối tròn xoay được tạo thành khi quay  xung quanh trục
xung quanh trục 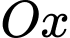 bằng
bằng
 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 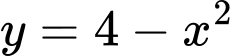 và trục hoành. Thể tích khối tròn xoay được tạo thành khi quay
và trục hoành. Thể tích khối tròn xoay được tạo thành khi quay  xung quanh trục
xung quanh trục  bằng
bằng
A, 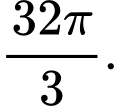
B, 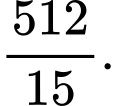
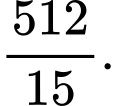
C, 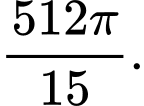
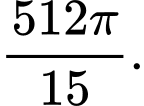
D, 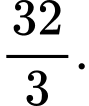
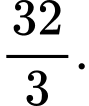
Chọn đáp án C.
Ta có phương trình hoành độ giao điểm của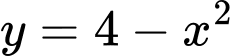 và trục hoành:
và trục hoành: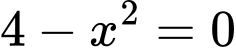
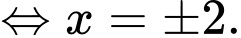
Thể tích khối tròn xoay được tạo thành khi quay xung quanh trục
xung quanh trục 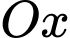 là:
là:
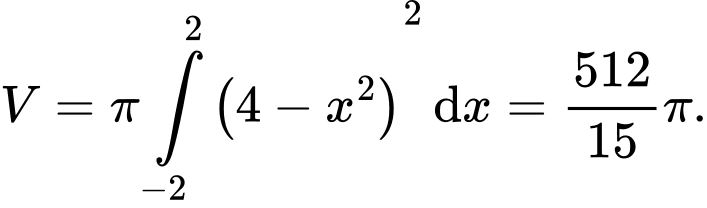 Đáp án: C
Đáp án: C
Ta có phương trình hoành độ giao điểm của
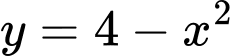 và trục hoành:
và trục hoành: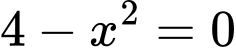
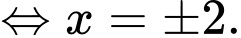
Thể tích khối tròn xoay được tạo thành khi quay
 xung quanh trục
xung quanh trục 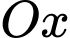 là:
là: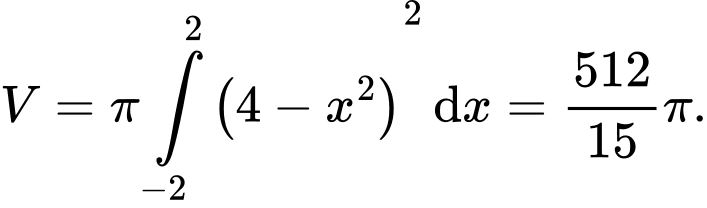 Đáp án: C
Đáp án: C
Câu 12 [693122]: Cho hàm số 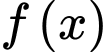 liên tục trên
liên tục trên 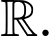 Biết
Biết 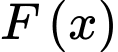 là nguyên hàm của
là nguyên hàm của 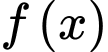 thoả mãn
thoả mãn 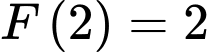 và
và 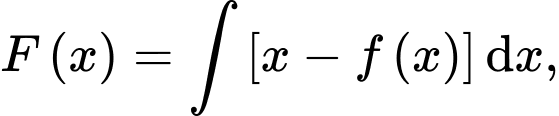
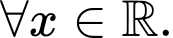 Giá trị của
Giá trị của 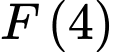 bằng
bằng
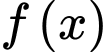 liên tục trên
liên tục trên 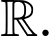 Biết
Biết 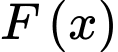 là nguyên hàm của
là nguyên hàm của 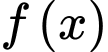 thoả mãn
thoả mãn 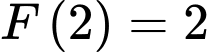 và
và 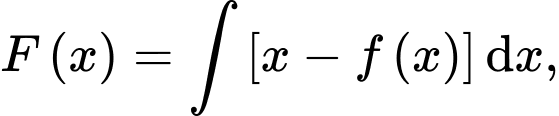
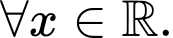 Giá trị của
Giá trị của 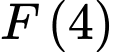 bằng
bằng A, 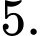
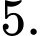
B, 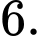
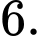
C, 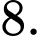
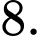
D, 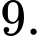
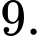
Chọn đáp án A.
Ta có: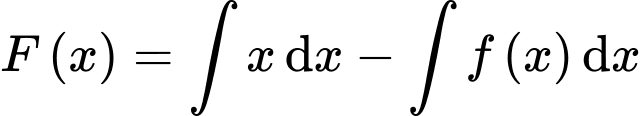
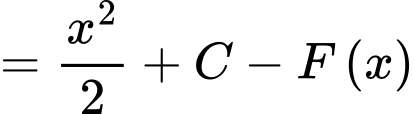
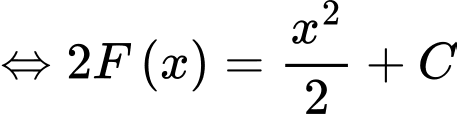
Tại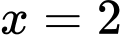 ta có:
ta có: 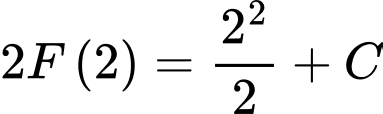

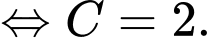
Suy ra với ta được:
ta được: 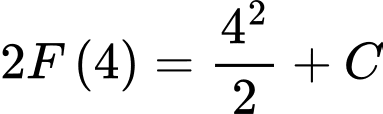
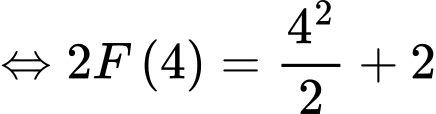
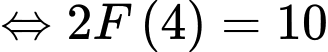
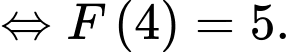 Đáp án: A
Đáp án: A
Ta có:
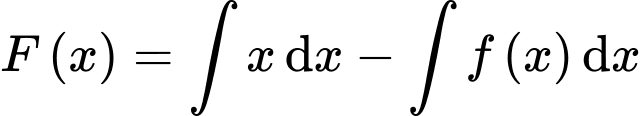
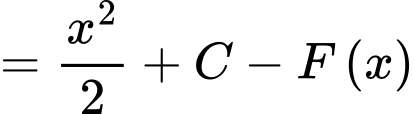
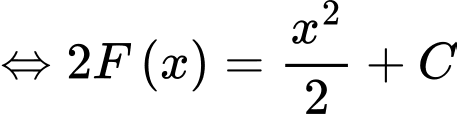
Tại
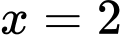 ta có:
ta có: 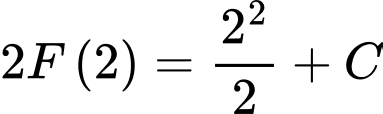

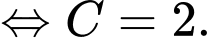
Suy ra với
 ta được:
ta được: 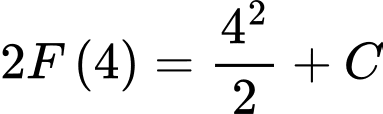
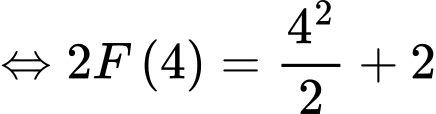
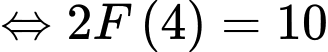
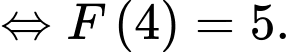 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693123]: Cho hàm số 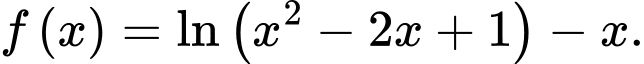
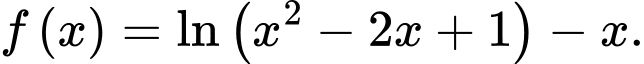
a) Sai.
Điều kiện: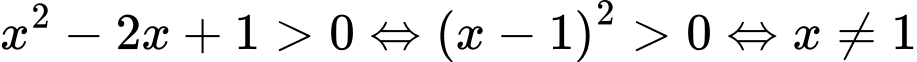
Suy ra tập xác định của hàm số là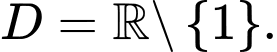
b) Đúng.
Áp dụng công thức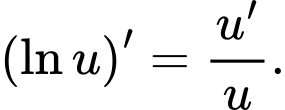
Ta có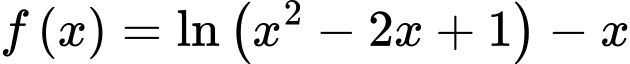
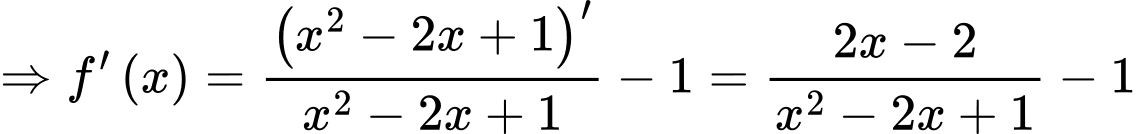
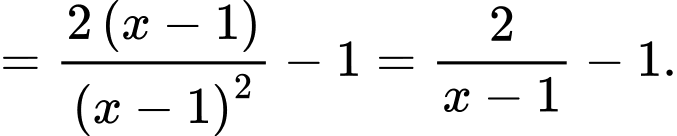
c) Đúng.
Ta có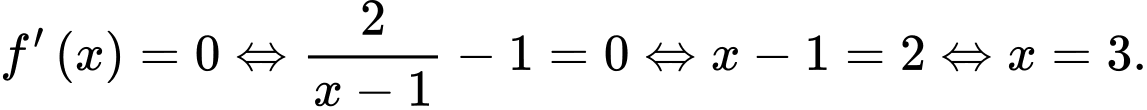
Suy ra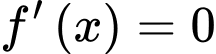 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Sai.
Lập bảng biến thiên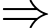
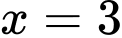 là điểm cực đại của hàm số
là điểm cực đại của hàm số
Do đó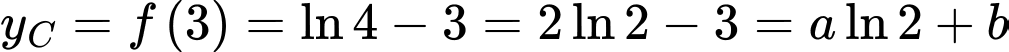
Suy ra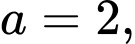
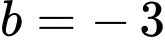 nên
nên 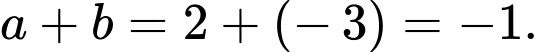
Điều kiện:
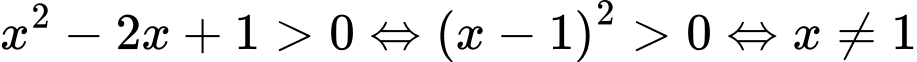
Suy ra tập xác định của hàm số là
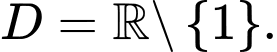
b) Đúng.
Áp dụng công thức
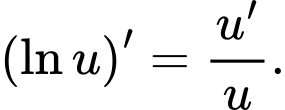
Ta có
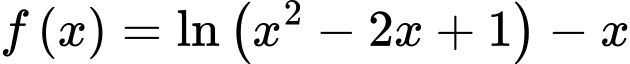
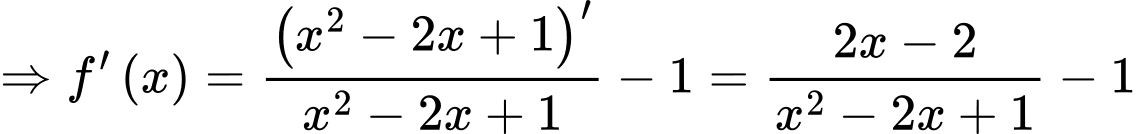
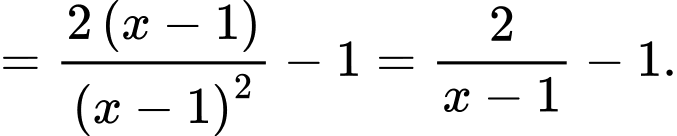
c) Đúng.
Ta có
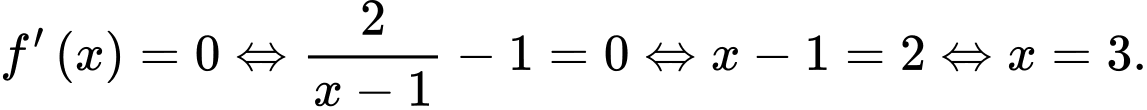
Suy ra
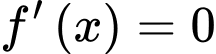 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Sai.
Lập bảng biến thiên
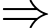
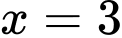 là điểm cực đại của hàm số
là điểm cực đại của hàm số
Do đó
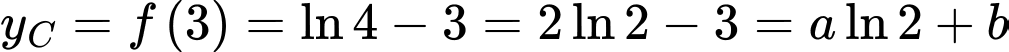
Suy ra
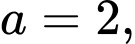
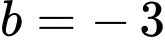 nên
nên 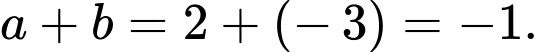
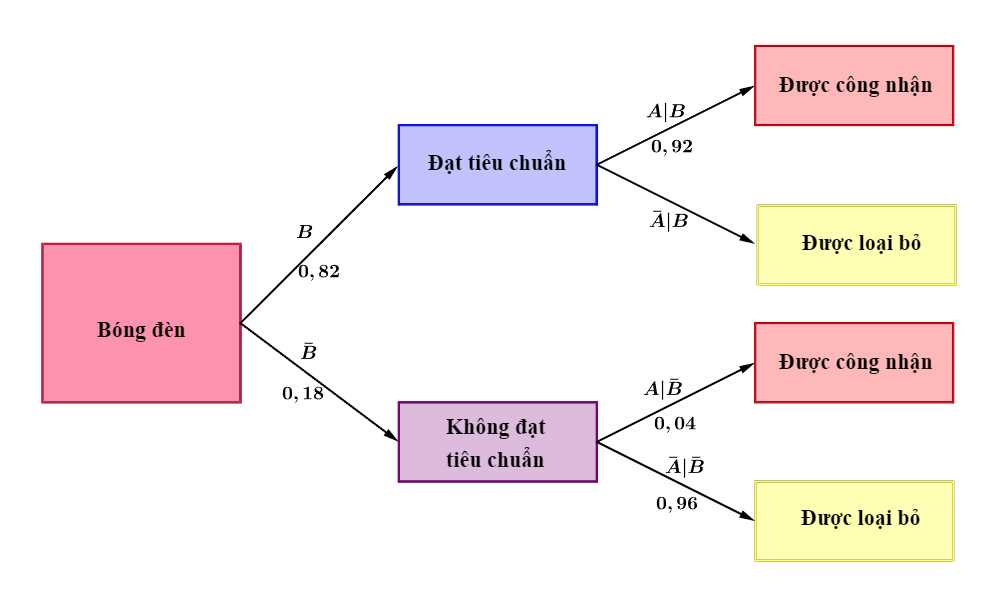
Câu 14 [693124]: Một nhà máy sản xuất bóng đèn có tỷ lệ bóng đèn đạt tiêu chuẩn là 82%. Trước khi xuất ra thị trường, mỗi bóng đèn được sản xuất ra đều phải qua một khâu kiểm tra chất lượng tự động. Vì sự kiểm tra này không chính xác tuyệt đối nên một bóng đèn tốt chỉ có xác suất 92% được công nhận, và một bóng đèn hỏng có xác suất 96% được loại bỏ.
Gọi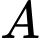 là biến cố “bóng được công nhận đạt tiêu chuẩn sau khi qua kiểm tra chất lượng”
là biến cố “bóng được công nhận đạt tiêu chuẩn sau khi qua kiểm tra chất lượng”
Gọi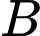 là biến cố “Sản phẩm đạt tiêu chuẩn”.
là biến cố “Sản phẩm đạt tiêu chuẩn”.
Gọi
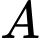 là biến cố “bóng được công nhận đạt tiêu chuẩn sau khi qua kiểm tra chất lượng”
là biến cố “bóng được công nhận đạt tiêu chuẩn sau khi qua kiểm tra chất lượng”Gọi
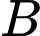 là biến cố “Sản phẩm đạt tiêu chuẩn”.
là biến cố “Sản phẩm đạt tiêu chuẩn”.
Chú thích: Bóng đèn đạt tiểu chuẩn là bóng đèn tốt và bóng đèn không đạt tiêu chuẩn là bóng đèn hỏng.
a) Sai.
Theo bài ra ta có: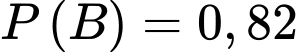 ;
; 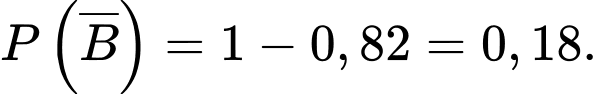
b) Sai.
Do tỉ lệ công nhận một bóng đèn đạt tiêu chuẩn là 0,92 nên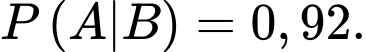
Tỉ lệ loại bỏ một bóng hỏng là 0,96 nên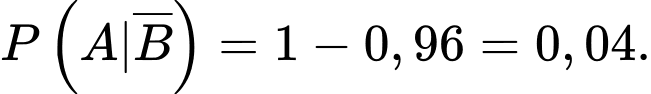
Ta có sơ đồ cây sau:
c) Đúng.
Theo công thức xác suất toàn phần ta có: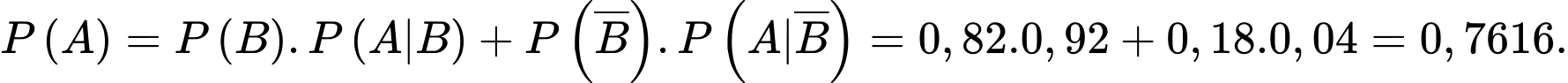
d) Sai.
Tỷ lệ bóng đèn tốt trong số những bóng đèn được công nhận là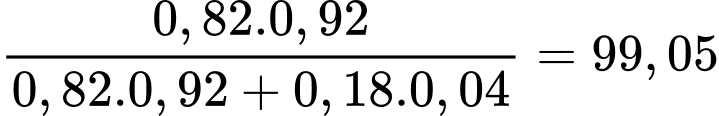
a) Sai.
Theo bài ra ta có:
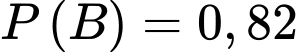 ;
; 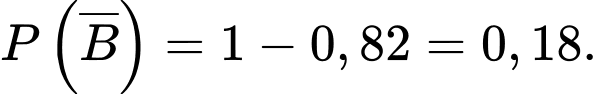
b) Sai.
Do tỉ lệ công nhận một bóng đèn đạt tiêu chuẩn là 0,92 nên
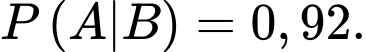
Tỉ lệ loại bỏ một bóng hỏng là 0,96 nên
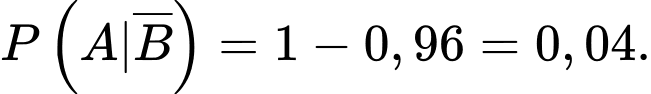
Ta có sơ đồ cây sau:

c) Đúng.
Theo công thức xác suất toàn phần ta có:
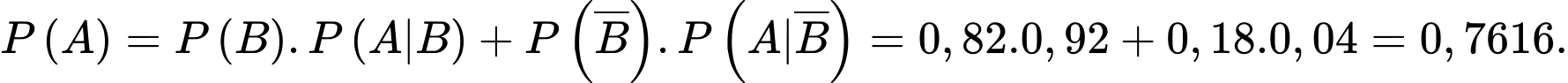
d) Sai.
Tỷ lệ bóng đèn tốt trong số những bóng đèn được công nhận là
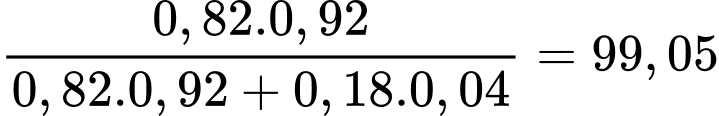
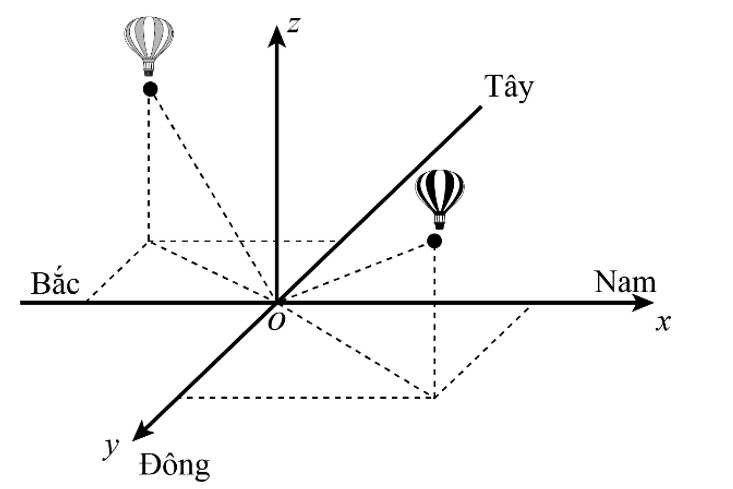
Câu 15 [693125]: Xét hai chiếc khinh khí cầu bay lên từ cùng một điểm trong cùng một ngày. Lúc 9h sáng, chiếc thứ nhất đang ở vị trí  cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai đang ở vị trí
cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai đang ở vị trí  nằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây đồng thời cách mặt đất 0,8 km. Chọn hệ trục tọa độ
nằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây đồng thời cách mặt đất 0,8 km. Chọn hệ trục tọa độ 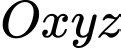 với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng
với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng 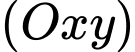 trùng với mặt đất, trục
trùng với mặt đất, trục 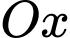 hướng về phía nam, trục
hướng về phía nam, trục 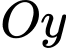 hướng về phía đông và trục
hướng về phía đông và trục  hướng thẳng đứng lên trời (như hình vẽ). Lấy đơn vị đo trên mỗi trục là km.
hướng thẳng đứng lên trời (như hình vẽ). Lấy đơn vị đo trên mỗi trục là km.
 cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai đang ở vị trí
cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai đang ở vị trí  nằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây đồng thời cách mặt đất 0,8 km. Chọn hệ trục tọa độ
nằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây đồng thời cách mặt đất 0,8 km. Chọn hệ trục tọa độ  với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng
với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng 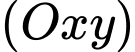 trùng với mặt đất, trục
trùng với mặt đất, trục 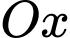 hướng về phía nam, trục
hướng về phía nam, trục 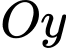 hướng về phía đông và trục
hướng về phía đông và trục  hướng thẳng đứng lên trời (như hình vẽ). Lấy đơn vị đo trên mỗi trục là km.
hướng thẳng đứng lên trời (như hình vẽ). Lấy đơn vị đo trên mỗi trục là km.
a) Đúng.
Vị trí của khinh khí cầu thứ nhất lúc 9 giờ sáng là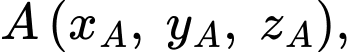 biết:
biết:
+)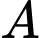 cách điểm xuất phát 2 km về phía Nam
cách điểm xuất phát 2 km về phía Nam 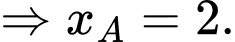
+) 1 km về phía Đông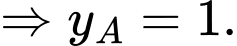
+) cách mặt đất 0,5 km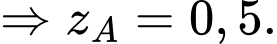
Vậy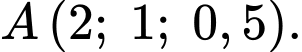
b) Sai.
Dựa vào giả thiết, ta có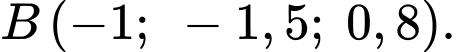
Suy ra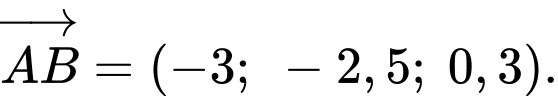
Đường thẳng đi qua điểm
đi qua điểm 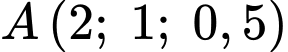 và có vectơ chỉ phương
và có vectơ chỉ phương 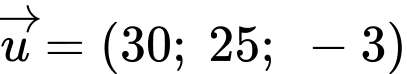 có phương trình chính tắc là
có phương trình chính tắc là 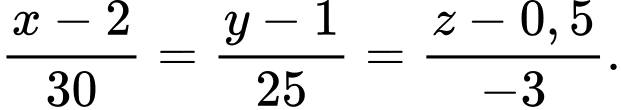
c) Đúng.
Lúc 9 giờ sáng, khoảng cách giữa hai kinh khí cầu bằng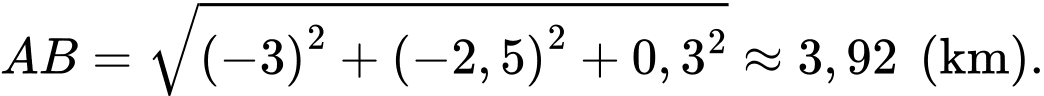
d) Sai.
Để tính được khoảng cách ta cần tìm được toạ độ của điểm
ta cần tìm được toạ độ của điểm  và
và  lúc 9 giờ 10 phút sáng.
lúc 9 giờ 10 phút sáng.
+) Tìm điểm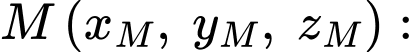
Ta có khinh khí cầu thứ nhất di chuyển thẳng đều về phía Nam (tức hoành độ của khinh khí cầu không đổi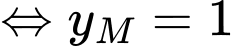 ) với vận tốc
) với vận tốc  suy ra từ 9 giờ sáng đến 9 giờ 10 phút sáng, khinh khí cầu đi được
suy ra từ 9 giờ sáng đến 9 giờ 10 phút sáng, khinh khí cầu đi được 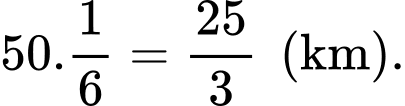
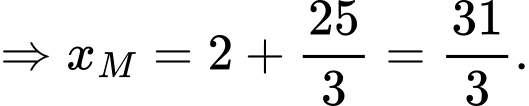
Và cao đội không đổi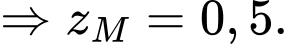
Vậy điểm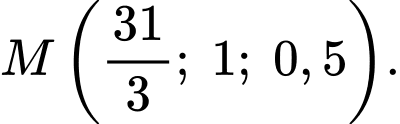
+) Tìm điểm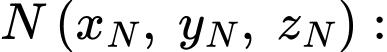
Vì vectơ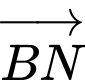 cùng hướng với vectơ
cùng hướng với vectơ 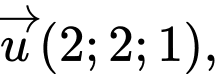 nên suy ra
nên suy ra 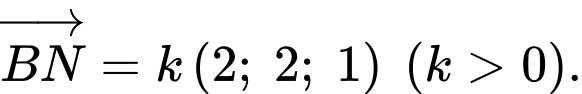
Khinh khí cầu thứ hai chuyển động thẳng đều đến điểm với vận tốc
với vận tốc  nên trong khoảng thời gian từ 9 giờ sáng đến 9 giờ 10 phút sáng khinh khí cầu đi được 1 đoạn
nên trong khoảng thời gian từ 9 giờ sáng đến 9 giờ 10 phút sáng khinh khí cầu đi được 1 đoạn 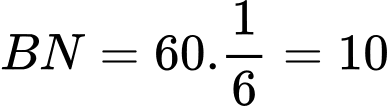
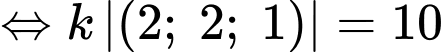
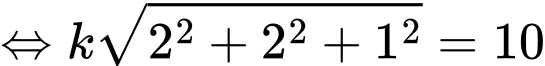
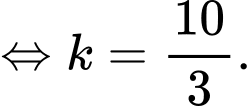
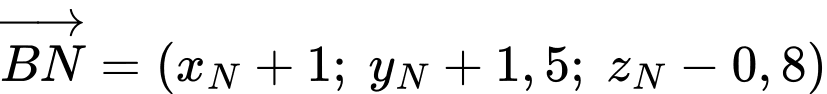
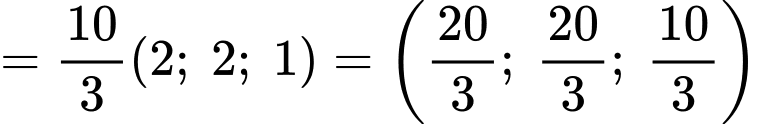
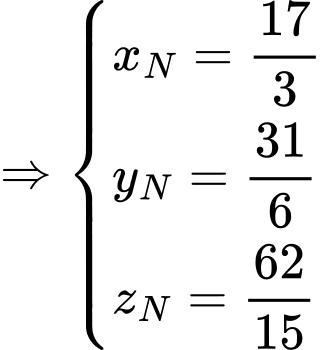
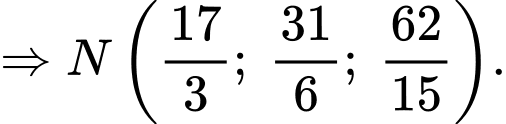
Suy ra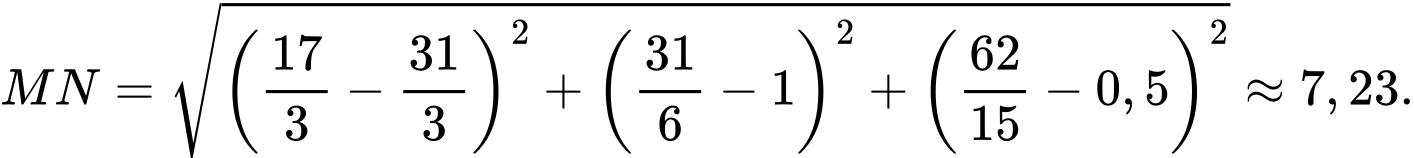
Vị trí của khinh khí cầu thứ nhất lúc 9 giờ sáng là
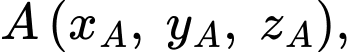 biết:
biết:+)
 cách điểm xuất phát 2 km về phía Nam
cách điểm xuất phát 2 km về phía Nam 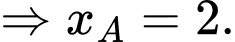
+) 1 km về phía Đông
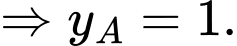
+) cách mặt đất 0,5 km
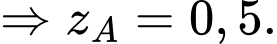
Vậy
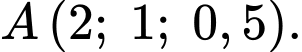
b) Sai.
Dựa vào giả thiết, ta có
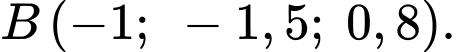
Suy ra
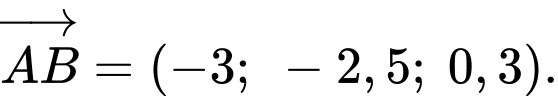
Đường thẳng
 đi qua điểm
đi qua điểm 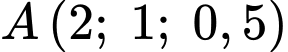 và có vectơ chỉ phương
và có vectơ chỉ phương 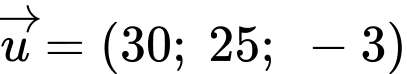 có phương trình chính tắc là
có phương trình chính tắc là 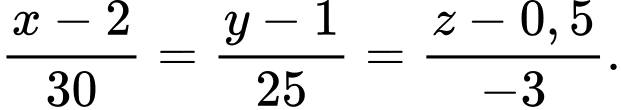
c) Đúng.
Lúc 9 giờ sáng, khoảng cách giữa hai kinh khí cầu bằng
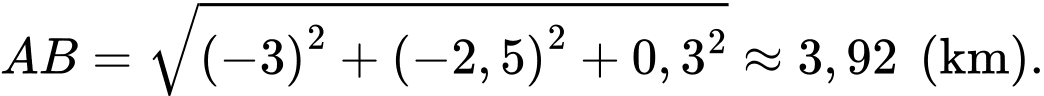
d) Sai.
Để tính được khoảng cách
 ta cần tìm được toạ độ của điểm
ta cần tìm được toạ độ của điểm  và
và 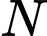 lúc 9 giờ 10 phút sáng.
lúc 9 giờ 10 phút sáng.+) Tìm điểm
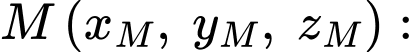
Ta có khinh khí cầu thứ nhất di chuyển thẳng đều về phía Nam (tức hoành độ của khinh khí cầu không đổi
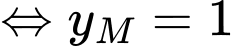 ) với vận tốc
) với vận tốc  suy ra từ 9 giờ sáng đến 9 giờ 10 phút sáng, khinh khí cầu đi được
suy ra từ 9 giờ sáng đến 9 giờ 10 phút sáng, khinh khí cầu đi được 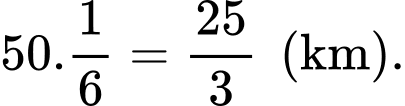
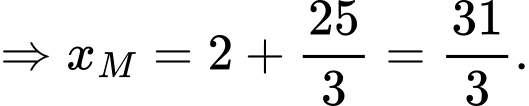
Và cao đội không đổi
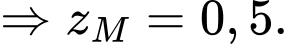
Vậy điểm
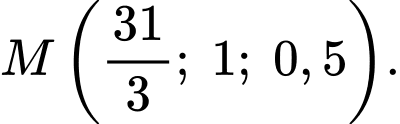
+) Tìm điểm
Vì vectơ
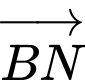 cùng hướng với vectơ
cùng hướng với vectơ 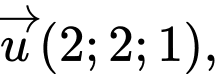 nên suy ra
nên suy ra 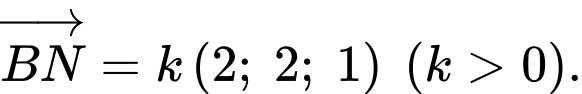
Khinh khí cầu thứ hai chuyển động thẳng đều đến điểm
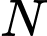 với vận tốc
với vận tốc  nên trong khoảng thời gian từ 9 giờ sáng đến 9 giờ 10 phút sáng khinh khí cầu đi được 1 đoạn
nên trong khoảng thời gian từ 9 giờ sáng đến 9 giờ 10 phút sáng khinh khí cầu đi được 1 đoạn 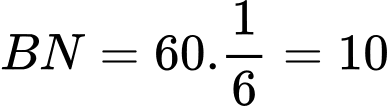
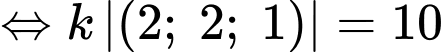
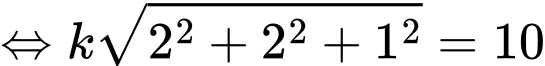
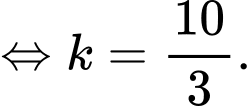
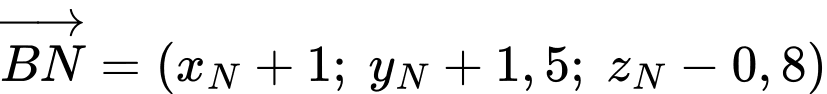
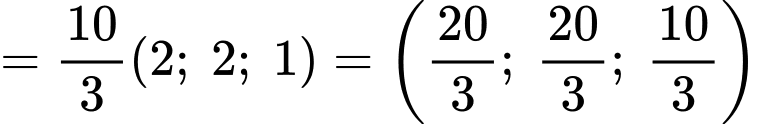
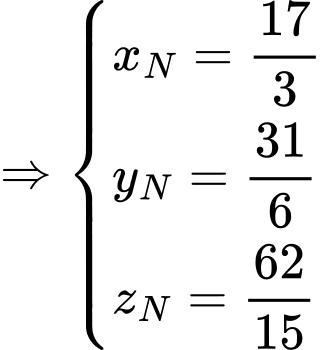
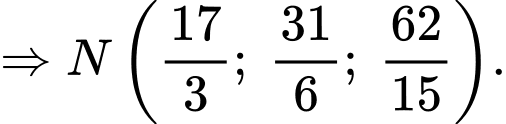
Suy ra
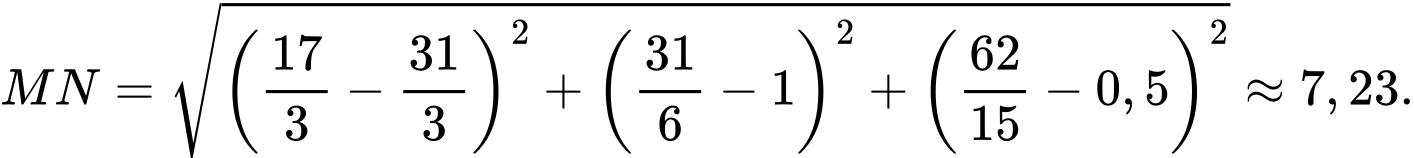
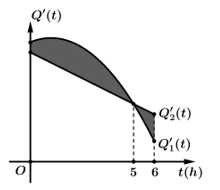
Câu 16 [693126]: Hình vẽ bên mô tả hiệu suất làm việc của hai công nhân trong một nhà máy trong thời gian 6 giờ. Công nhân  đang sản xuất với hiệu suất
đang sản xuất với hiệu suất 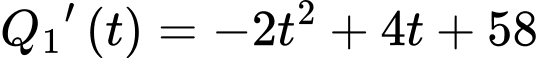 sản phẩm mỗi giờ, trong khi công nhân
sản phẩm mỗi giờ, trong khi công nhân  đang sản xuất với hiệu suất
đang sản xuất với hiệu suất 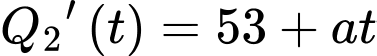 sản phẩm mỗi giờ
sản phẩm mỗi giờ 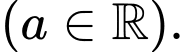 Biết rằng hàm
Biết rằng hàm 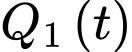 và
và 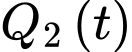 mô phỏng số lượng sản phẩm mới làm được của công nhân
mô phỏng số lượng sản phẩm mới làm được của công nhân 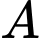 và công nhân
và công nhân 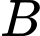 sau
sau 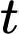 giờ.
giờ.
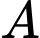 đang sản xuất với hiệu suất
đang sản xuất với hiệu suất 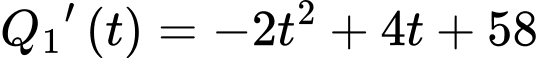 sản phẩm mỗi giờ, trong khi công nhân
sản phẩm mỗi giờ, trong khi công nhân 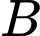 đang sản xuất với hiệu suất
đang sản xuất với hiệu suất 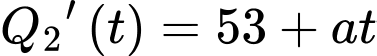 sản phẩm mỗi giờ
sản phẩm mỗi giờ 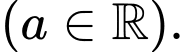 Biết rằng hàm
Biết rằng hàm 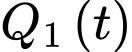 và
và 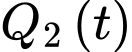 mô phỏng số lượng sản phẩm mới làm được của công nhân
mô phỏng số lượng sản phẩm mới làm được của công nhân 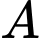 và công nhân
và công nhân  sau
sau  giờ.
giờ.
a) Đúng.
Ta có hiệu suất của công nhân là
là 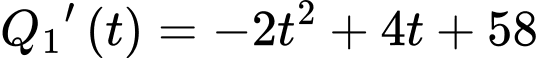
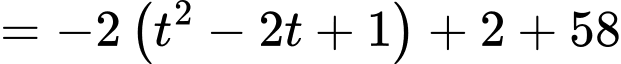
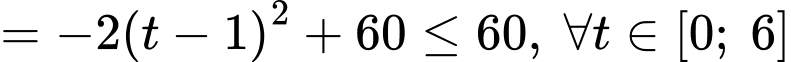
Dấu "=" xảy ra khi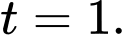
Vậy hiệu suất cực đại của công nhân A là 60 sản phẩm mỗi giờ.
b) Sai.
Diện tích tô đậm bằng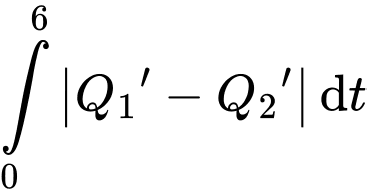 nên nó không biểu diễn cho tổng số lượng sản phẩm mới mà 2 công nhân làm được trong 6 giờ.
nên nó không biểu diễn cho tổng số lượng sản phẩm mới mà 2 công nhân làm được trong 6 giờ.
c) Đúng.
Dựa vào biểu đồ, ta có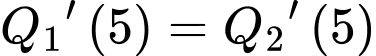
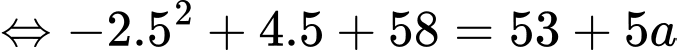
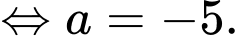
Suy ra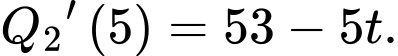
Sau 5 giờ, số lượng sản phẩm mới của công nhân A hoàn thành nhiều hơn số lượng sản phẩm mới của công nhân B bằng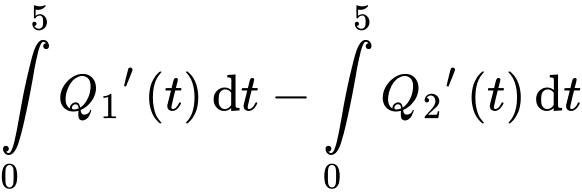
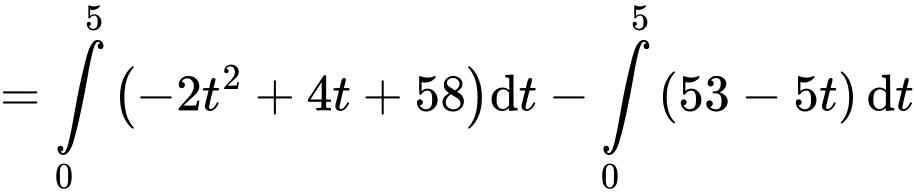
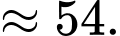
d) Sai.
Sau 6 giờ làm việc tổng số lượng sản phẩm mới mà 2 công nhân hoàn thành bằng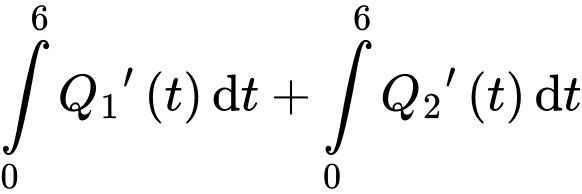
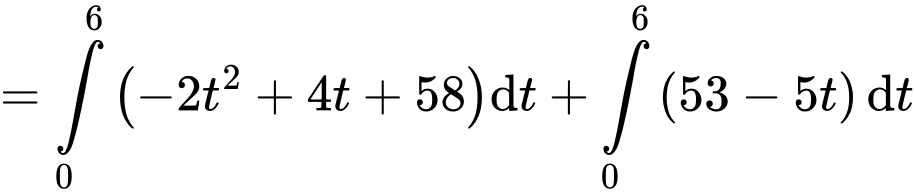
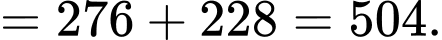
Ta có hiệu suất của công nhân
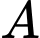 là
là 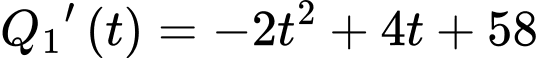
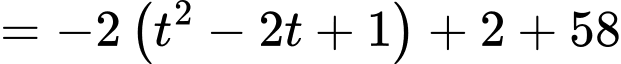
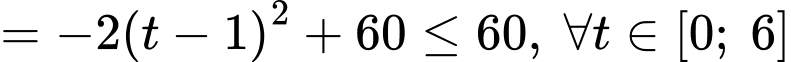
Dấu "=" xảy ra khi
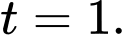
Vậy hiệu suất cực đại của công nhân A là 60 sản phẩm mỗi giờ.
b) Sai.
Diện tích tô đậm bằng
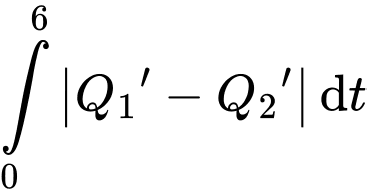 nên nó không biểu diễn cho tổng số lượng sản phẩm mới mà 2 công nhân làm được trong 6 giờ.
nên nó không biểu diễn cho tổng số lượng sản phẩm mới mà 2 công nhân làm được trong 6 giờ.c) Đúng.
Dựa vào biểu đồ, ta có
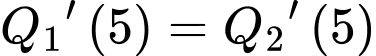
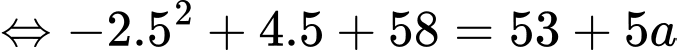
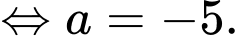
Suy ra
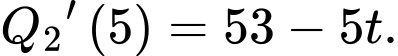
Sau 5 giờ, số lượng sản phẩm mới của công nhân A hoàn thành nhiều hơn số lượng sản phẩm mới của công nhân B bằng
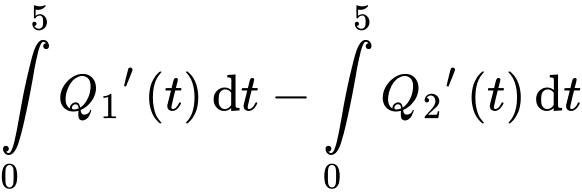
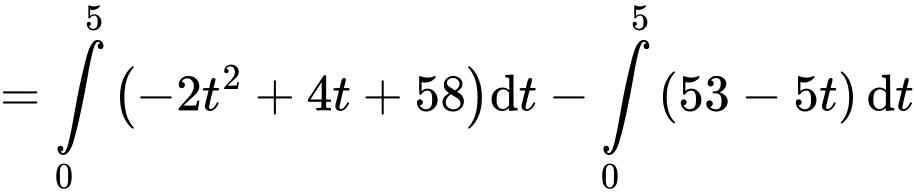
d) Sai.
Sau 6 giờ làm việc tổng số lượng sản phẩm mới mà 2 công nhân hoàn thành bằng
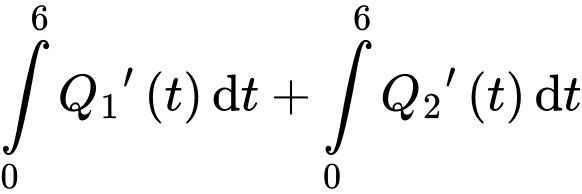
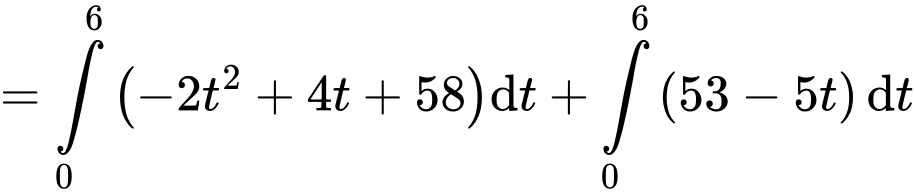
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693127]: Cho hình chóp tam giác đều 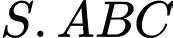 có
có 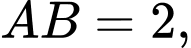
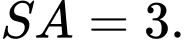 Gọi
Gọi 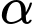 là số đo của góc nhị diện
là số đo của góc nhị diện 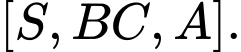 Giá trị
Giá trị 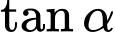 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 có
có 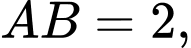
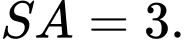 Gọi
Gọi 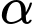 là số đo của góc nhị diện
là số đo của góc nhị diện 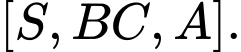 Giá trị
Giá trị 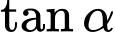 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 4,8.
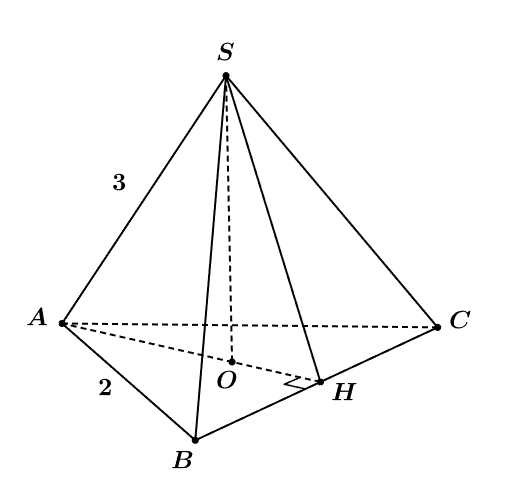
Kẻ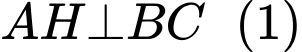
Gọi là tâm của tam giác
là tâm của tam giác 
Suy ra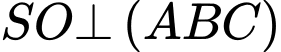 (theo tính chất của hình chóp đều).
(theo tính chất của hình chóp đều).
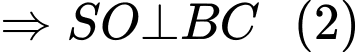
Từ (1) và (2) suy ra
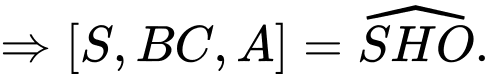
Vì tam giác đều nên ta có
đều nên ta có 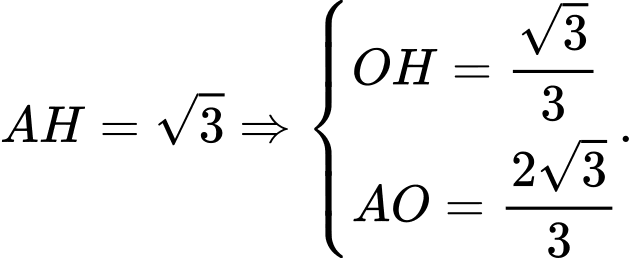
Suy ra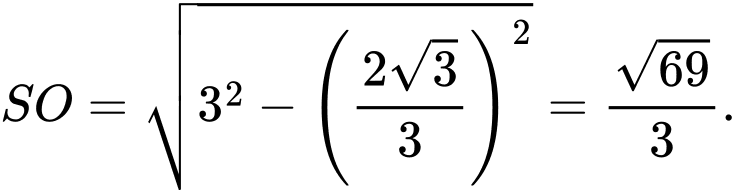

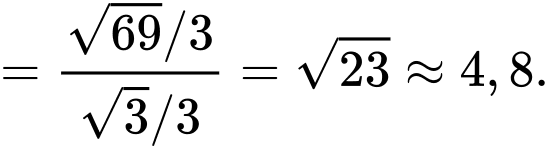

Kẻ
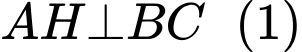
Gọi
 là tâm của tam giác
là tâm của tam giác 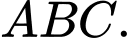
Suy ra
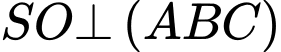 (theo tính chất của hình chóp đều).
(theo tính chất của hình chóp đều).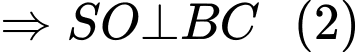
Từ (1) và (2) suy ra

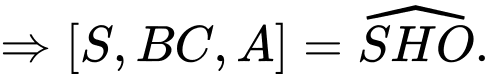
Vì tam giác
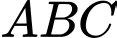 đều nên ta có
đều nên ta có 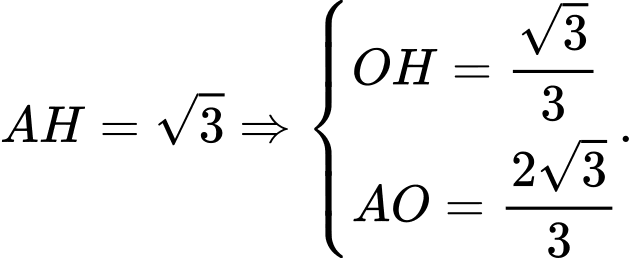
Suy ra
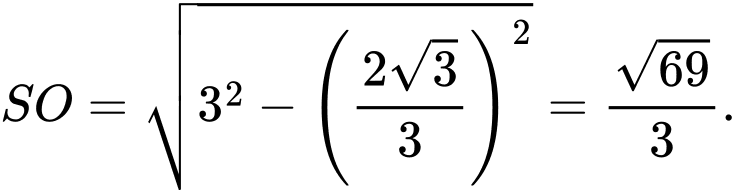

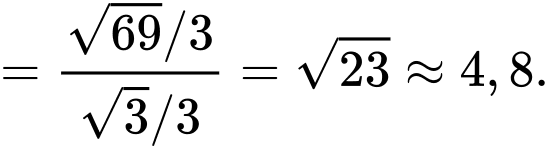
Câu 18 [694292]: Mỗi hộp đựng 12 bóng đèn, các bóng đèn trong cùng hộp thì cùng màu. Số hộp đựng bóng đèn màu xanh nhiều gấp 9 lần số hộp đựng bóng đèn màu vàng. Trong mỗi hộp đựng bóng đèn màu xanh có 3 bóng bị hỏng, mỗi hộp đựng bóng đèn màu vàng có 2 bóng bị hỏng Tính xác xuất để lấy ra hai bóng đèn màu xanh ở cùng một hộp, biết cả hai bóng đều bị hỏng. Viết kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,96.
Gọi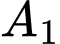 là biến cố lấy được một hộp đựng bóng đèn màu vàng.
là biến cố lấy được một hộp đựng bóng đèn màu vàng.
Suy ra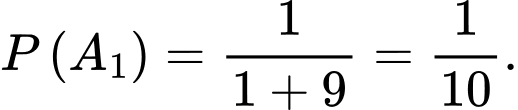
Gọi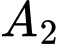 là biến cố lấy được một hộp đựng bóng đèn màu xanh.
là biến cố lấy được một hộp đựng bóng đèn màu xanh.
Suy ra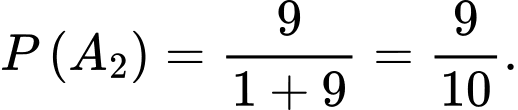
Gọi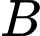 là biến cố lấy được hai bóng đèn hỏng ở cùng 1 hộp.
là biến cố lấy được hai bóng đèn hỏng ở cùng 1 hộp.
Ta có xác suất lấy được 2 bóng đèn hỏng từ một hộp đựng bóng đèn vàng là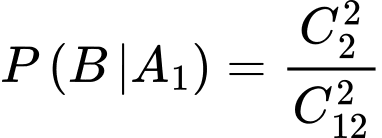 (vì trong mỗi hộp đựng bóng đèn vàng có 2 bóng bị hỏng).
(vì trong mỗi hộp đựng bóng đèn vàng có 2 bóng bị hỏng).
Tương tự, vì trong mỗi hộp đựng bóng đèn màu xanh có 3 bóng bị hỏng nên xác suất lấy được 2 bóng đèn hỏng từ một hộp đựng bóng đèn xanh là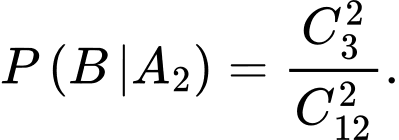
Ta có sơ đồ cây sau:
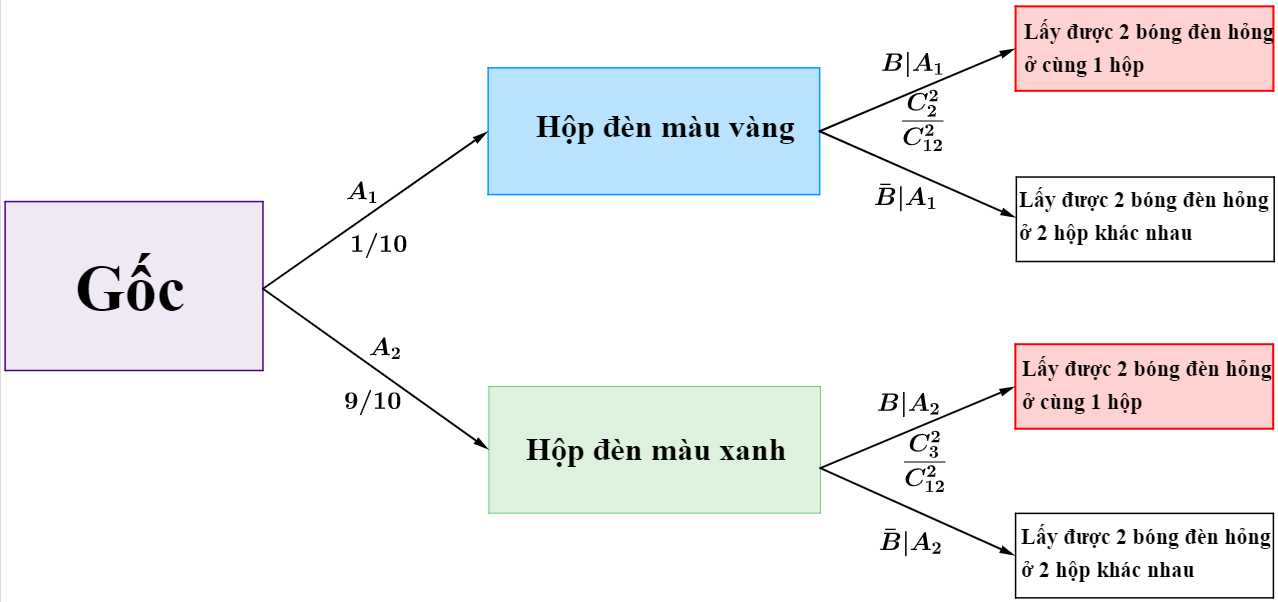
Ta có
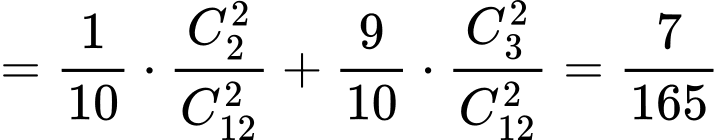
Suy ra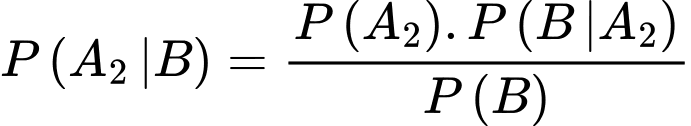
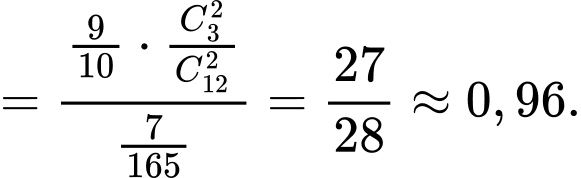
Gọi
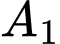 là biến cố lấy được một hộp đựng bóng đèn màu vàng.
là biến cố lấy được một hộp đựng bóng đèn màu vàng. Suy ra
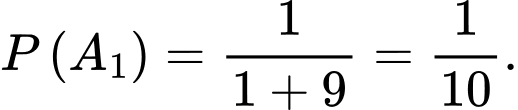
Gọi
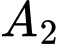 là biến cố lấy được một hộp đựng bóng đèn màu xanh.
là biến cố lấy được một hộp đựng bóng đèn màu xanh. Suy ra
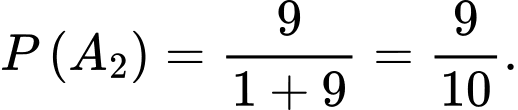
Gọi
 là biến cố lấy được hai bóng đèn hỏng ở cùng 1 hộp.
là biến cố lấy được hai bóng đèn hỏng ở cùng 1 hộp.Ta có xác suất lấy được 2 bóng đèn hỏng từ một hộp đựng bóng đèn vàng là
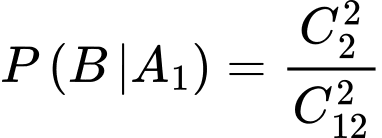 (vì trong mỗi hộp đựng bóng đèn vàng có 2 bóng bị hỏng).
(vì trong mỗi hộp đựng bóng đèn vàng có 2 bóng bị hỏng).Tương tự, vì trong mỗi hộp đựng bóng đèn màu xanh có 3 bóng bị hỏng nên xác suất lấy được 2 bóng đèn hỏng từ một hộp đựng bóng đèn xanh là
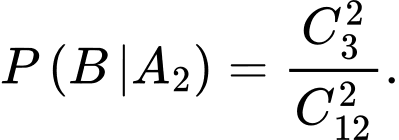
Ta có sơ đồ cây sau:

Ta có

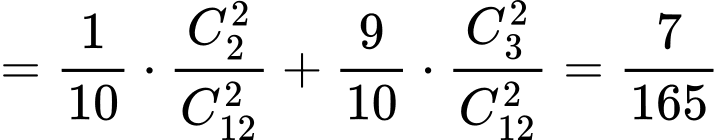
Suy ra
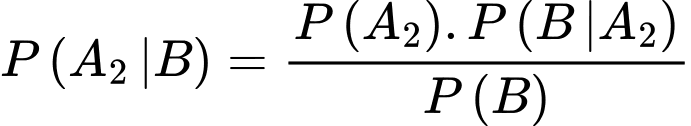
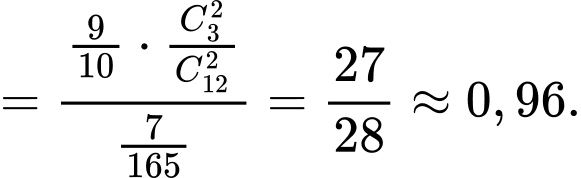
Câu 19 [693128]: Trên đường Mạnh đi từ nhà (M) đến công ty (C) có điểm A người ta đang thi công sửa chữa đường nên không thể đi qua A. Biết rằng toàn bộ cung đường theo bản đồ từ dưới lên trên và từ trái qua phải là đường một chiều vì vậy Mạnh chỉ được phép đi lên hoặc đi sang phải. Vậy Mạnh có bao nhiêu cách đến công ty?
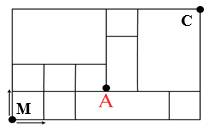

Điền đáp án: 
Số cách Mạnh đến công ty là: 15 cách.
Minh họa:
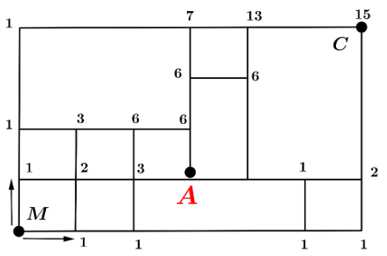
Số cách Mạnh đến công ty là: 15 cách.
Minh họa:

Câu 20 [703003]: Bên trong hình vuông cạnh  dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình bên). Tính thể tích
dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình bên). Tính thể tích  của khối tròn xoay sinh ra khi quay hình sao đó quanh trục
của khối tròn xoay sinh ra khi quay hình sao đó quanh trục  (làm tròn kết quả đến hàng phần mười).
(làm tròn kết quả đến hàng phần mười).
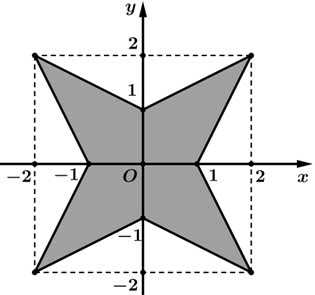
 dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình bên). Tính thể tích
dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình bên). Tính thể tích  của khối tròn xoay sinh ra khi quay hình sao đó quanh trục
của khối tròn xoay sinh ra khi quay hình sao đó quanh trục  (làm tròn kết quả đến hàng phần mười).
(làm tròn kết quả đến hàng phần mười).
Điền đáp án: 20,9.
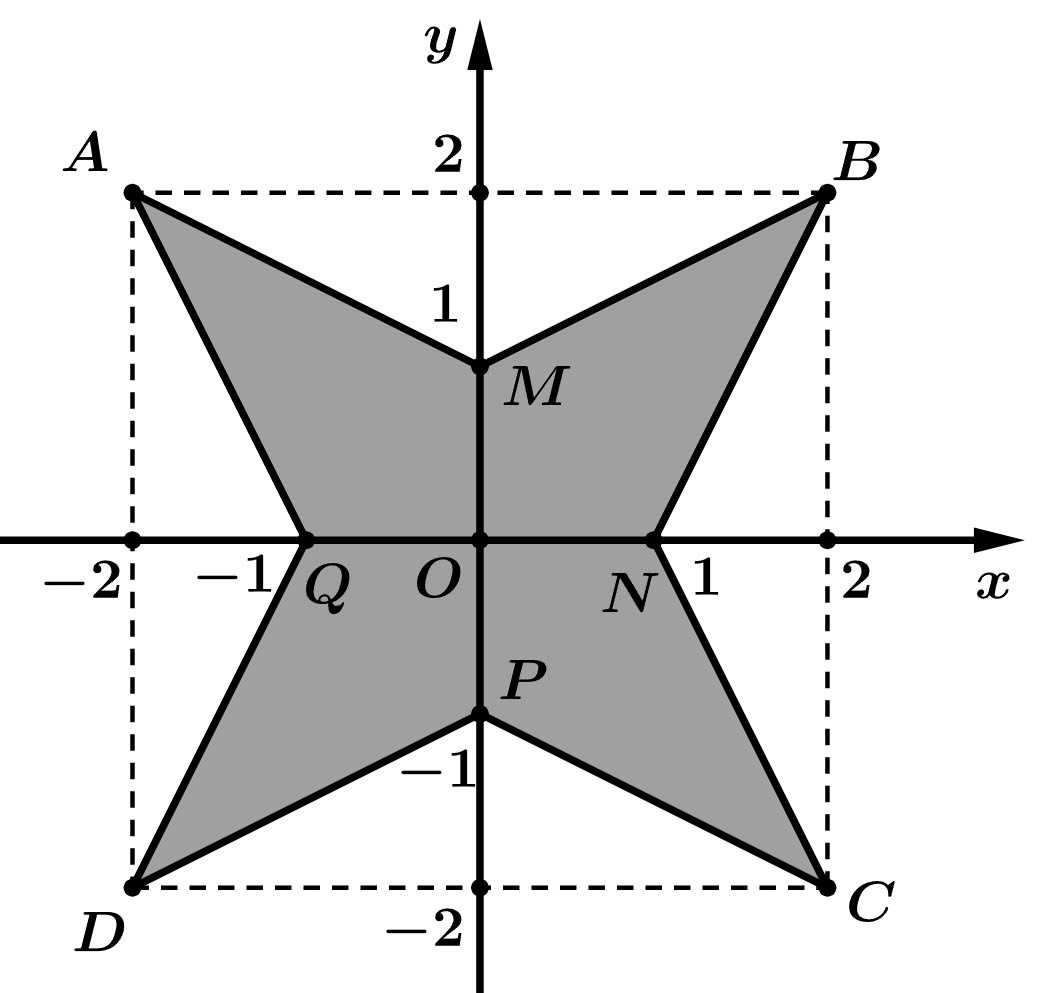
Ta kí hiệu các điểm như hình vẽ.
Ta có khối tròn xoay đó được tạo thành khi quay hình phẳng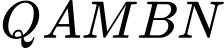 quanh trục
quanh trục 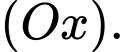
Mà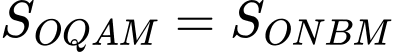 nên thể tích của khối tròn xoay đó sẽ = 2 lần thể tích của khối tròn xoay khi quay hình phẳng
nên thể tích của khối tròn xoay đó sẽ = 2 lần thể tích của khối tròn xoay khi quay hình phẳng 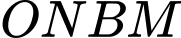 quanh trục
quanh trục 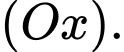
Suy ra ta có thể tích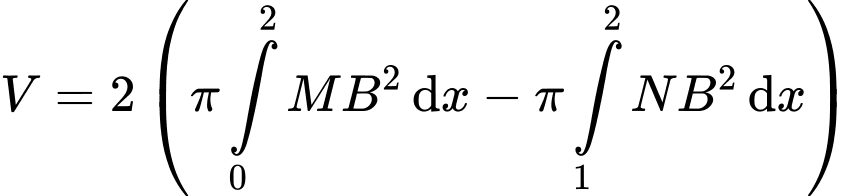
+) Viết phương trình đường thẳng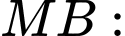
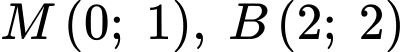
Có vectơ chỉ phương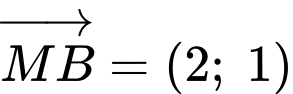 suy ra một vectơ pháp tuyến của đường thẳng là
suy ra một vectơ pháp tuyến của đường thẳng là 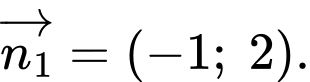
Suy ra
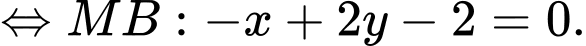
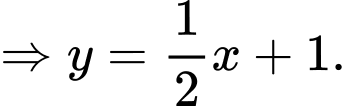
+) Tương tự, ta viết được phương trình đường thẳng là
là
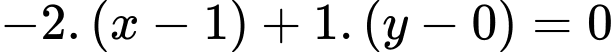
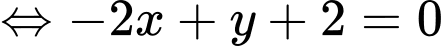
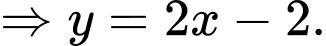
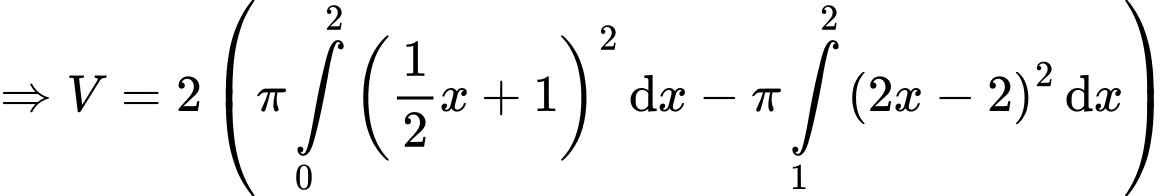
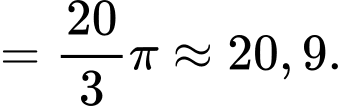

Ta kí hiệu các điểm như hình vẽ.
Ta có khối tròn xoay đó được tạo thành khi quay hình phẳng
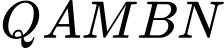 quanh trục
quanh trục 
Mà
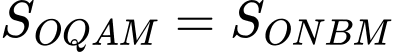 nên thể tích của khối tròn xoay đó sẽ = 2 lần thể tích của khối tròn xoay khi quay hình phẳng
nên thể tích của khối tròn xoay đó sẽ = 2 lần thể tích của khối tròn xoay khi quay hình phẳng 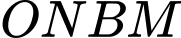 quanh trục
quanh trục 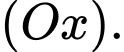
Suy ra ta có thể tích
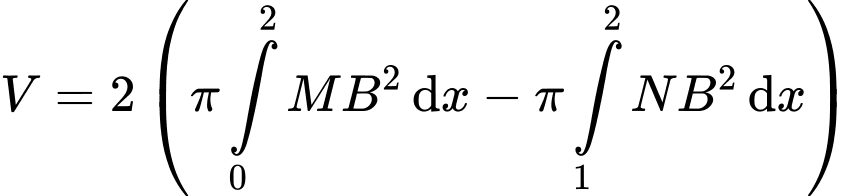
+) Viết phương trình đường thẳng
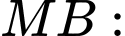
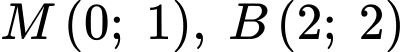
Có vectơ chỉ phương
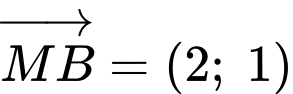 suy ra một vectơ pháp tuyến của đường thẳng là
suy ra một vectơ pháp tuyến của đường thẳng là 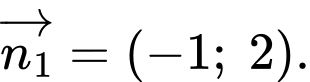
Suy ra

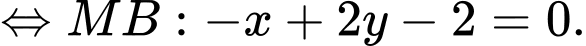
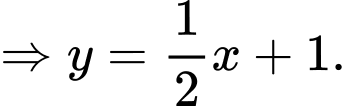
+) Tương tự, ta viết được phương trình đường thẳng
 là
là
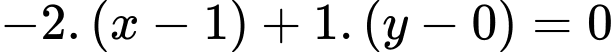
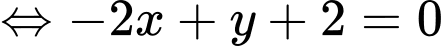
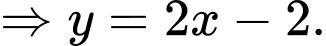
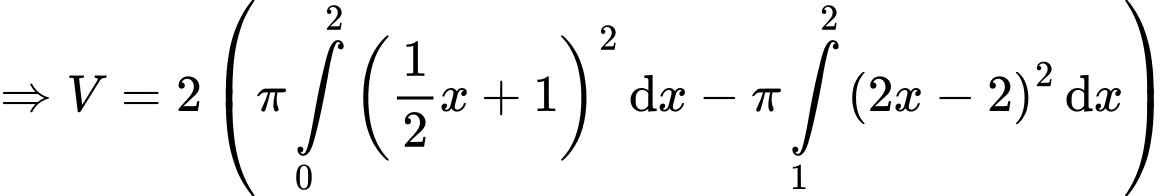
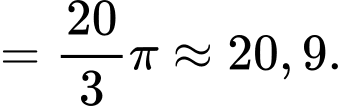
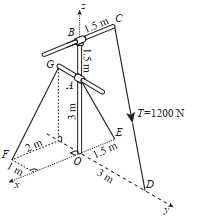
Câu 21 [693092]: Một ống phun nước có hình dạng như hình vẽ dưới. Để giữ cho ống nước được cân bằng không bị nghiêng kỹ sư sử dụng ba đoạn thép để nối các điểm 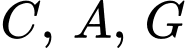 với mặt đất, các đoạn thép
với mặt đất, các đoạn thép 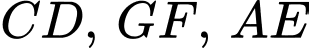 có độ lớn lực căng lần lượt bằng
có độ lớn lực căng lần lượt bằng 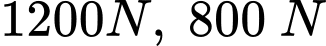 và
và 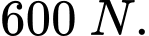 Trong hệ tọa độ
Trong hệ tọa độ 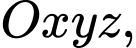 coi gốc tọa độ là chân ống nước, trục
coi gốc tọa độ là chân ống nước, trục  hướng lên trời, mặt đất là mặt phẳng
hướng lên trời, mặt đất là mặt phẳng 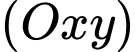 các thông số được cho như hình vẽ, đơn vị trên các hệ trục tọa độ tính bằng mét. Coi đường kính ống không đáng kể, độ lớn vectơ hợp lực của ba sợi thép tác động lên ông nước là bao nhiêu Niutơn (làm tròn kết quả đến hàng đơn vị).
các thông số được cho như hình vẽ, đơn vị trên các hệ trục tọa độ tính bằng mét. Coi đường kính ống không đáng kể, độ lớn vectơ hợp lực của ba sợi thép tác động lên ông nước là bao nhiêu Niutơn (làm tròn kết quả đến hàng đơn vị).
 với mặt đất, các đoạn thép
với mặt đất, các đoạn thép 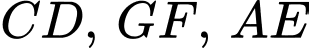 có độ lớn lực căng lần lượt bằng
có độ lớn lực căng lần lượt bằng 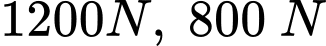 và
và 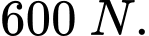 Trong hệ tọa độ
Trong hệ tọa độ 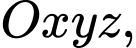 coi gốc tọa độ là chân ống nước, trục
coi gốc tọa độ là chân ống nước, trục  hướng lên trời, mặt đất là mặt phẳng
hướng lên trời, mặt đất là mặt phẳng  các thông số được cho như hình vẽ, đơn vị trên các hệ trục tọa độ tính bằng mét. Coi đường kính ống không đáng kể, độ lớn vectơ hợp lực của ba sợi thép tác động lên ông nước là bao nhiêu Niutơn (làm tròn kết quả đến hàng đơn vị).
các thông số được cho như hình vẽ, đơn vị trên các hệ trục tọa độ tính bằng mét. Coi đường kính ống không đáng kể, độ lớn vectơ hợp lực của ba sợi thép tác động lên ông nước là bao nhiêu Niutơn (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 2311.
Giả sử lực tác dụng lên 3 đoạn dây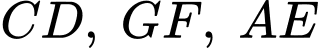 lần lượt là
lần lượt là 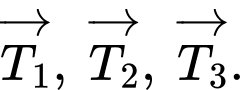
Suy ra hợp lực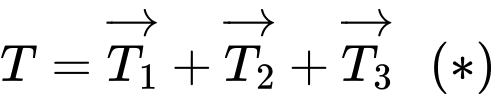
(Áp dụng công thức: Cho 2 vectơ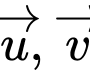 cùng hướng, ta có
cùng hướng, ta có 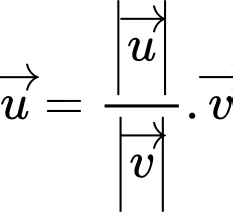 )
)
+) Vì và
và  cùng hướng nên ta suy ra
cùng hướng nên ta suy ra 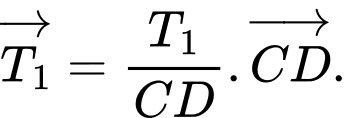
Tương tự, ta sẽ thấy
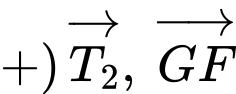 cùng hướng
cùng hướng 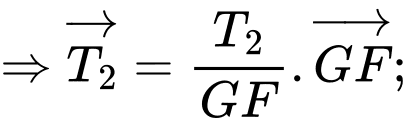
 cùng hướng
cùng hướng 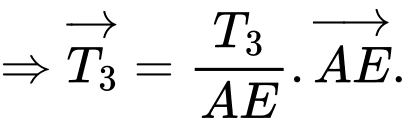
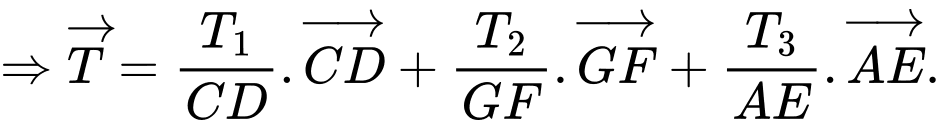
+) Ta có
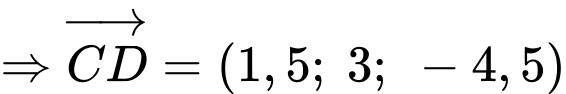
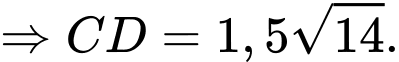
+) Ta có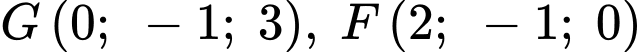
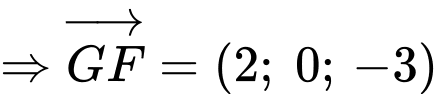
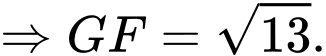
+) Ta có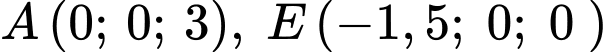
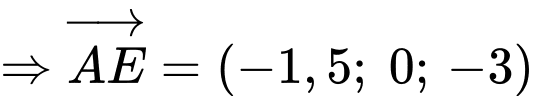
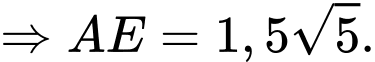
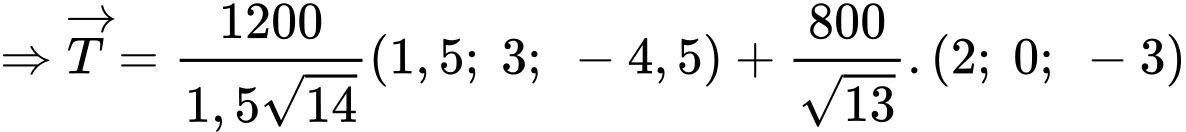
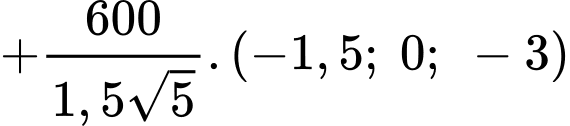
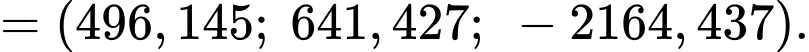
Suy ra độ lớn của vectơ hợp lực là
Giả sử lực tác dụng lên 3 đoạn dây
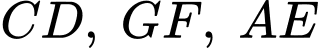 lần lượt là
lần lượt là 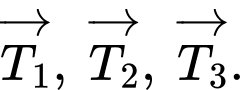
Suy ra hợp lực
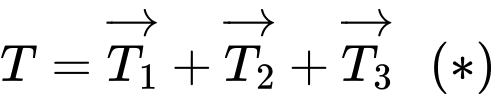
(Áp dụng công thức: Cho 2 vectơ
 cùng hướng, ta có
cùng hướng, ta có 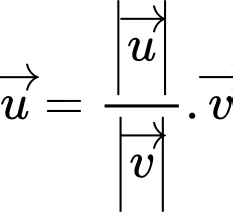 )
)+) Vì
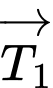 và
và 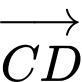 cùng hướng nên ta suy ra
cùng hướng nên ta suy ra 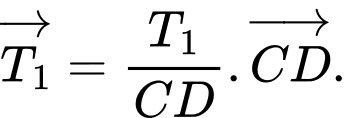
Tương tự, ta sẽ thấy
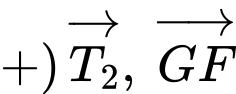 cùng hướng
cùng hướng 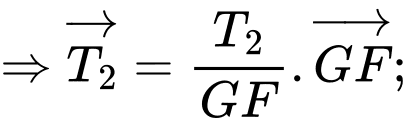
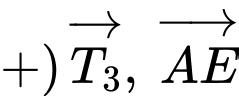 cùng hướng
cùng hướng 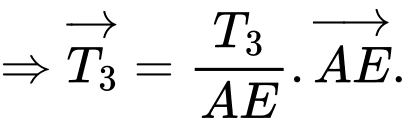
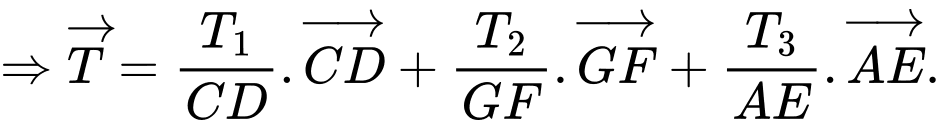
+) Ta có
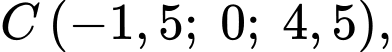
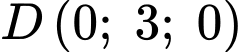
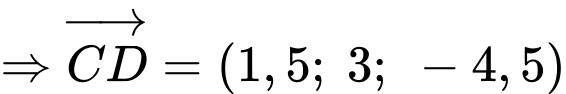
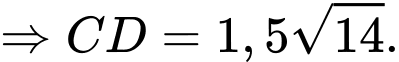
+) Ta có
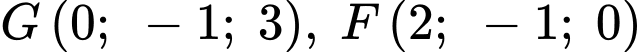
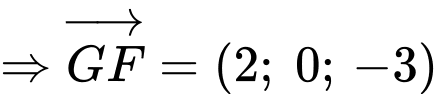
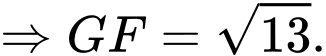
+) Ta có
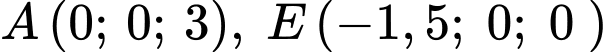
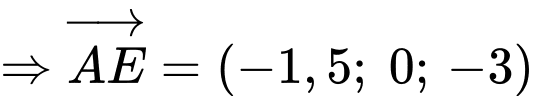
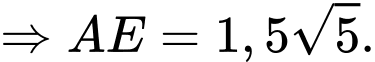
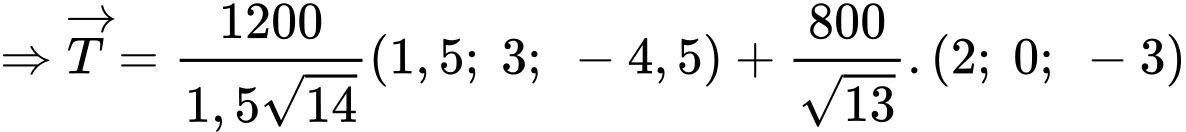
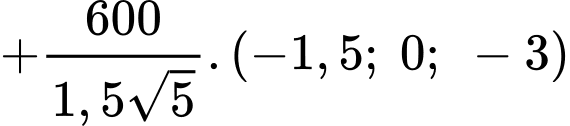
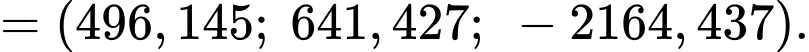
Suy ra độ lớn của vectơ hợp lực là

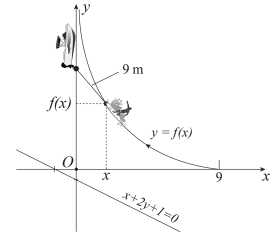
Câu 22 [702350]: Hình vẽ sau mô tả một con thuyền đang kéo một người đàn ông trượt ván bằng một đoạn dây dài 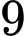 mét. Xét trên hệ trục
mét. Xét trên hệ trục 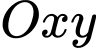 (đơn vị trên các hệ trục bằng mét), ban đầu con thuyền đang ở gốc tọa độ và di chuyển trên tia
(đơn vị trên các hệ trục bằng mét), ban đầu con thuyền đang ở gốc tọa độ và di chuyển trên tia 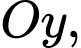 người đàn ông xuất phát từ điểm có tọa độ
người đàn ông xuất phát từ điểm có tọa độ 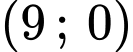 bị kéo theo và quãng đường di chuyển tạo thành một đường cong
bị kéo theo và quãng đường di chuyển tạo thành một đường cong 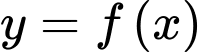 (tham khảo hình vẽ bên), bờ biển là đường thẳng
(tham khảo hình vẽ bên), bờ biển là đường thẳng  Khi người đàn ông đến gần bờ biển nhất thì khoảng cách giữa người đàn ông và trục
Khi người đàn ông đến gần bờ biển nhất thì khoảng cách giữa người đàn ông và trục 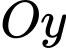 bằng bao nhiêu mét (làm tròn đến hàng phần trăm)? Biết rằng trong quá trình di chuyển, người đàn ông luôn hướng về phía thuyền, đoạn dây luôn căng và nằm trên tiếp tuyến của đường cong
bằng bao nhiêu mét (làm tròn đến hàng phần trăm)? Biết rằng trong quá trình di chuyển, người đàn ông luôn hướng về phía thuyền, đoạn dây luôn căng và nằm trên tiếp tuyến của đường cong 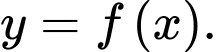
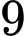 mét. Xét trên hệ trục
mét. Xét trên hệ trục 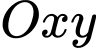 (đơn vị trên các hệ trục bằng mét), ban đầu con thuyền đang ở gốc tọa độ và di chuyển trên tia
(đơn vị trên các hệ trục bằng mét), ban đầu con thuyền đang ở gốc tọa độ và di chuyển trên tia 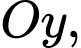 người đàn ông xuất phát từ điểm có tọa độ
người đàn ông xuất phát từ điểm có tọa độ 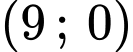 bị kéo theo và quãng đường di chuyển tạo thành một đường cong
bị kéo theo và quãng đường di chuyển tạo thành một đường cong 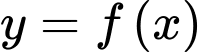 (tham khảo hình vẽ bên), bờ biển là đường thẳng
(tham khảo hình vẽ bên), bờ biển là đường thẳng  Khi người đàn ông đến gần bờ biển nhất thì khoảng cách giữa người đàn ông và trục
Khi người đàn ông đến gần bờ biển nhất thì khoảng cách giữa người đàn ông và trục 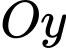 bằng bao nhiêu mét (làm tròn đến hàng phần trăm)? Biết rằng trong quá trình di chuyển, người đàn ông luôn hướng về phía thuyền, đoạn dây luôn căng và nằm trên tiếp tuyến của đường cong
bằng bao nhiêu mét (làm tròn đến hàng phần trăm)? Biết rằng trong quá trình di chuyển, người đàn ông luôn hướng về phía thuyền, đoạn dây luôn căng và nằm trên tiếp tuyến của đường cong 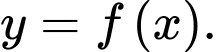

Điền đáp án: 8,05.
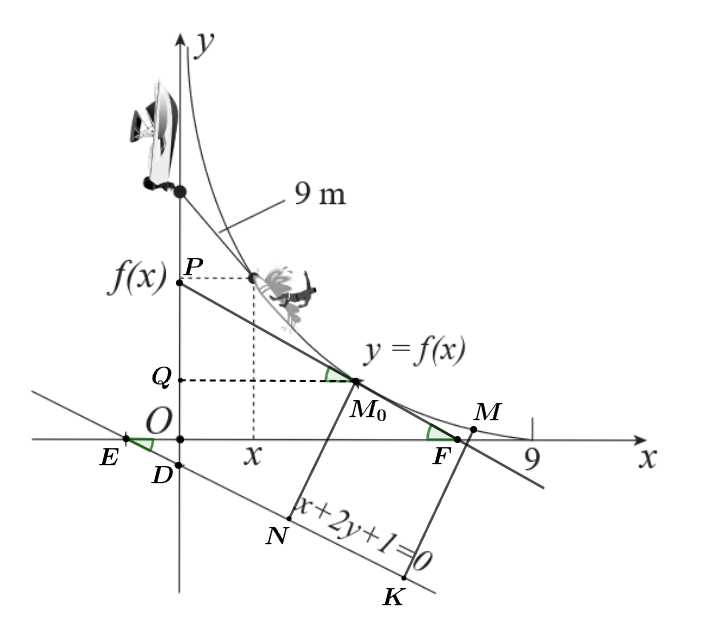
Giả sử người đó ở vị trí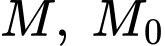 là điểm mà tiếp tuyến tại
là điểm mà tiếp tuyến tại 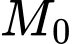 song song với đường thẳng
song song với đường thẳng 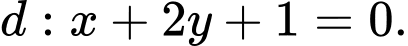
Dựng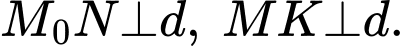
Dựa vào hình vẽ, ta có nên khoảng cách từ người đến bờ biển ngắn nhất khi tiếp tuyến tại
nên khoảng cách từ người đến bờ biển ngắn nhất khi tiếp tuyến tại 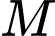 song song với đường thẳng
song song với đường thẳng 
Dựa vào hình, ta có:
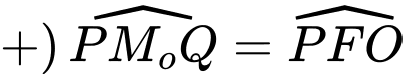 (2 góc đồng vị)
(2 góc đồng vị)
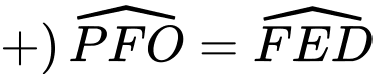 (2 góc so le trong)
(2 góc so le trong)
Suy ra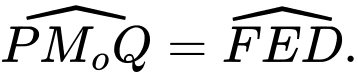
Thay lần lượt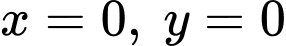 vào đường thẳng
vào đường thẳng  ta có
ta có 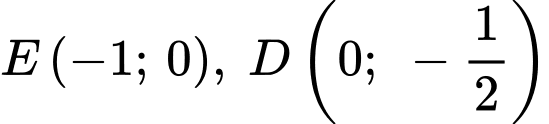
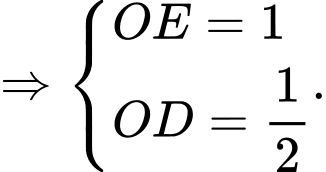
Xét tam giác vuông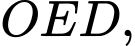 ta có
ta có 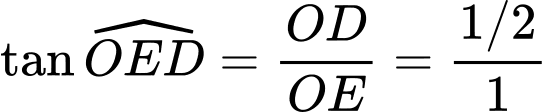
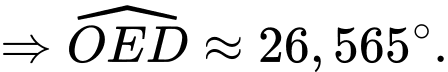
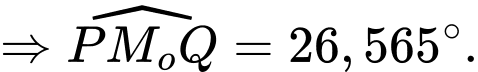
Xét tam giác vuông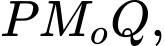 ta có
ta có 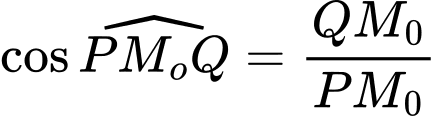

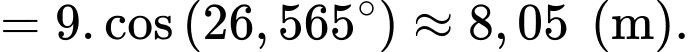

Giả sử người đó ở vị trí
 là điểm mà tiếp tuyến tại
là điểm mà tiếp tuyến tại 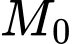 song song với đường thẳng
song song với đường thẳng 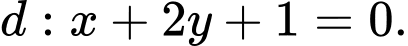
Dựng
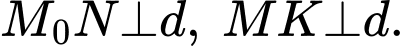
Dựa vào hình vẽ, ta có
 nên khoảng cách từ người đến bờ biển ngắn nhất khi tiếp tuyến tại
nên khoảng cách từ người đến bờ biển ngắn nhất khi tiếp tuyến tại 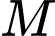 song song với đường thẳng
song song với đường thẳng 
Dựa vào hình, ta có:
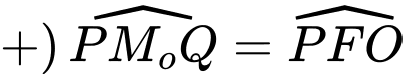 (2 góc đồng vị)
(2 góc đồng vị)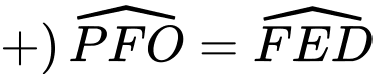 (2 góc so le trong)
(2 góc so le trong)Suy ra
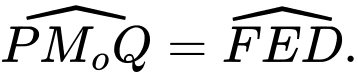
Thay lần lượt
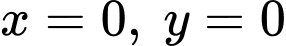 vào đường thẳng
vào đường thẳng  ta có
ta có 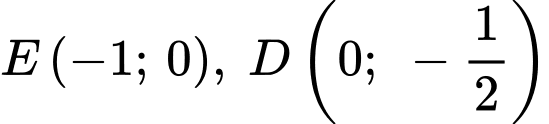
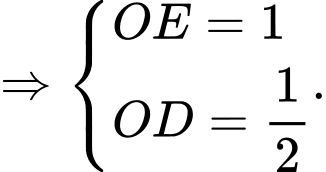
Xét tam giác vuông
 ta có
ta có 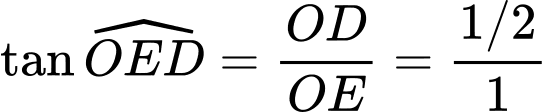
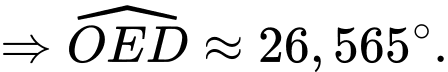
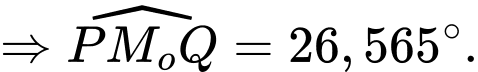
Xét tam giác vuông
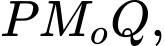 ta có
ta có