PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
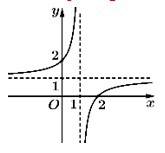
Câu 1 [696477]: Cho hàm số 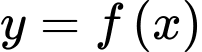 có đồ thị là đường cong trong hình vẽ bên. Tiệm cận đứng của đồ thị hàm số đã cho là
có đồ thị là đường cong trong hình vẽ bên. Tiệm cận đứng của đồ thị hàm số đã cho là
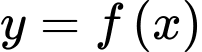 có đồ thị là đường cong trong hình vẽ bên. Tiệm cận đứng của đồ thị hàm số đã cho là
có đồ thị là đường cong trong hình vẽ bên. Tiệm cận đứng của đồ thị hàm số đã cho là
A, 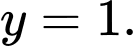
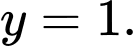
B, 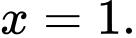
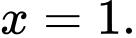
C, 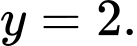
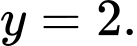
D, 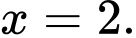
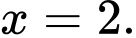
Chọn đáp án B.
Dựa vào đò thị ta có: Tiệm cận đứng của đồ thị hàm số đã cho là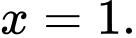 Đáp án: B
Đáp án: B
Dựa vào đò thị ta có: Tiệm cận đứng của đồ thị hàm số đã cho là
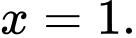 Đáp án: B
Đáp án: B
Câu 2 [258427]: Cho hàm số  Đạo hàm
Đạo hàm 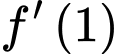 bằng
bằng
 Đạo hàm
Đạo hàm 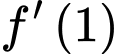 bằng
bằng A, 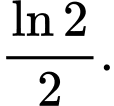
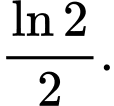
B, 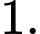
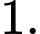
C, 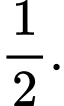
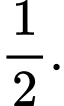
D, 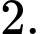
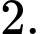
Chọn đáp án D.
Xét hàm số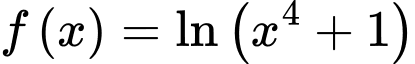 có đạo hàm
có đạo hàm 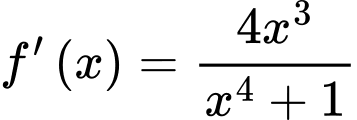
 Đáp án: D
Đáp án: D
Xét hàm số
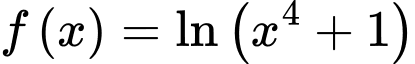 có đạo hàm
có đạo hàm 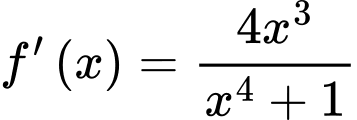
 Đáp án: D
Đáp án: D
Câu 3 [696478]: Bảng bên dưới biểu diễn mẫu số liệu ghép nhóm vể độ tuổi của cư dân trong một khu phố. Tần số tích luỹ của nhóm 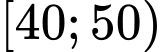 là
là

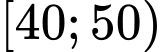 là
là
A, 20.
B, 65.
C, 45.
D, 80.
Chọ đáp án B.
Tần số tích luỹ của nhóm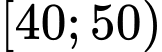 là 25+20+20=65. Đáp án: B
là 25+20+20=65. Đáp án: B
Tần số tích luỹ của nhóm
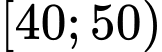 là 25+20+20=65. Đáp án: B
là 25+20+20=65. Đáp án: B
Câu 4 [696479]: Cho hai vectơ 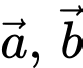 cùng hướng và
cùng hướng và 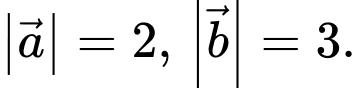 Tính
Tính 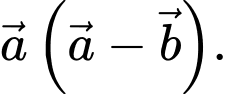
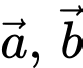 cùng hướng và
cùng hướng và 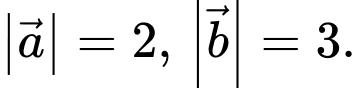 Tính
Tính 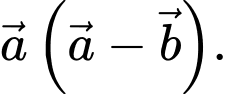
A, 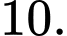
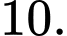
B, 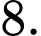
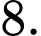
C, 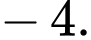
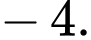
D, 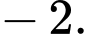
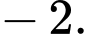
Chọn đáp án D.
Ta có:
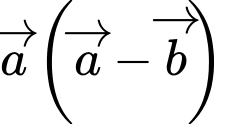
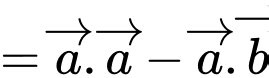
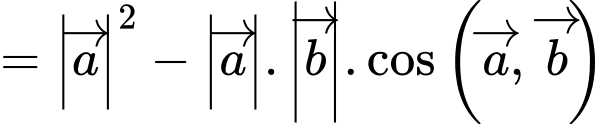

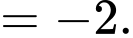 Đáp án: D
Đáp án: D
Ta có:
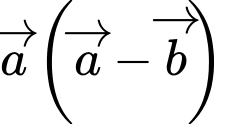
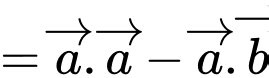
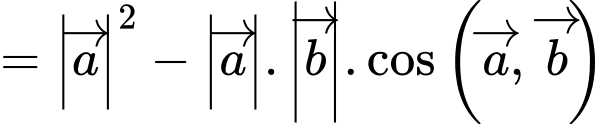

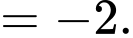 Đáp án: D
Đáp án: D
Câu 5 [256732]: Cho hàm số 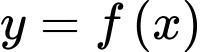 có bảng biến thiên như sau
có bảng biến thiên như sau
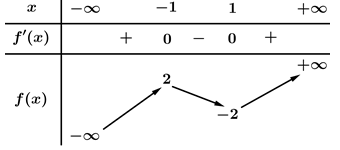
Giá trị cực tiểu của hàm số đã cho bằng
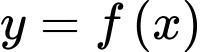 có bảng biến thiên như sau
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A, 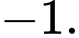
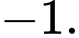
B, 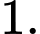
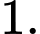
C, 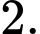
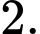
D, 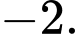
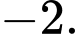
Chọn đáp án D.
Dựa vào bảng biến thiên, ta thấy hàm số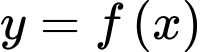 đạt cực tiểu tại
đạt cực tiểu tại 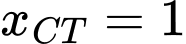 và có giá trị cực tiểu là
và có giá trị cực tiểu là 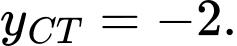 Đáp án: D
Đáp án: D
Dựa vào bảng biến thiên, ta thấy hàm số
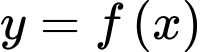 đạt cực tiểu tại
đạt cực tiểu tại 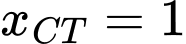 và có giá trị cực tiểu là
và có giá trị cực tiểu là 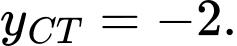 Đáp án: D
Đáp án: D
Câu 6 [696480]: Cho 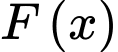 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 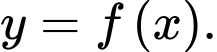 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
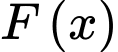 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 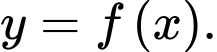 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 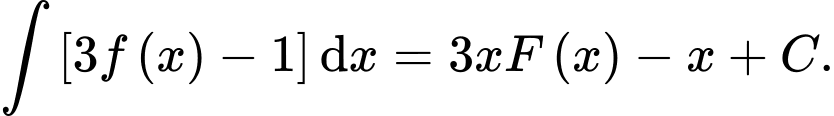
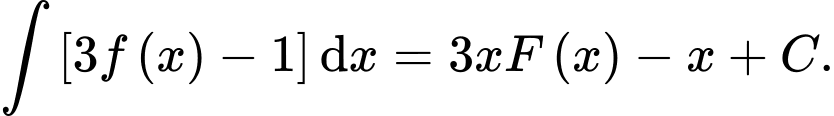
B, 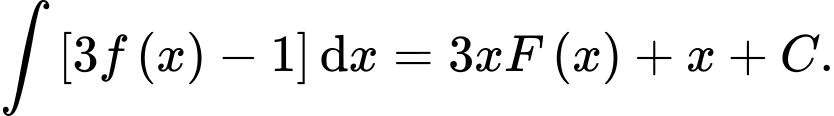
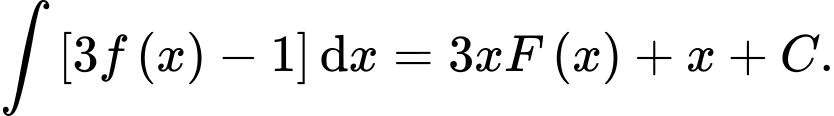
C, 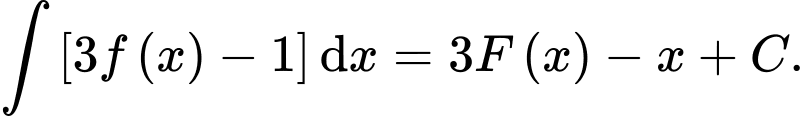
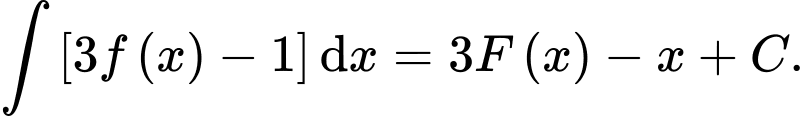
D, 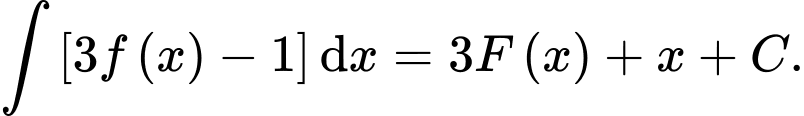
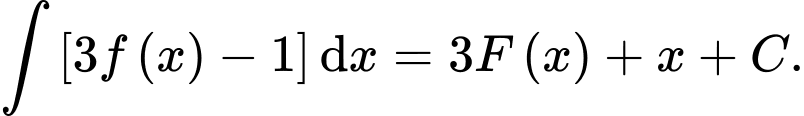
Chọn đáp án C.
Ta có: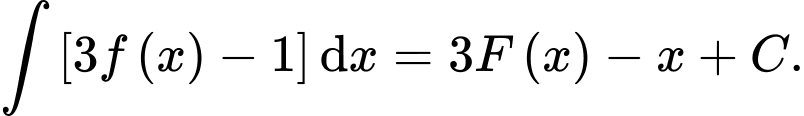 Đáp án: C
Đáp án: C
Ta có:
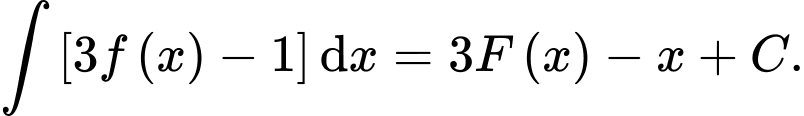 Đáp án: C
Đáp án: C Sử dụng thông tin dưới đây để trả lời câu 7 và câu 8

Câu 7 [703071]: Phương trình mặt phẳng đi qua 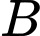 và vuông góc với
và vuông góc với 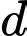 là
là
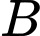 và vuông góc với
và vuông góc với 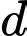 là
là A, 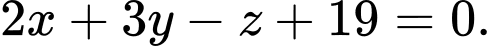
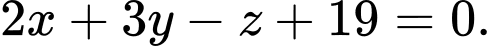
B, 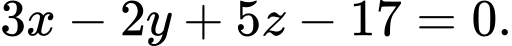
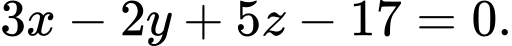
C, 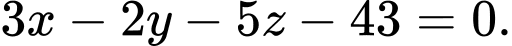
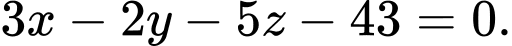
D, 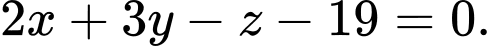
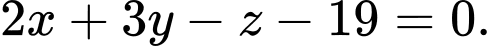
Chọn đáp án D.
Phương trình mặt phẳng vuông góc với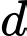 có dạng
có dạng 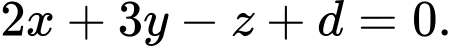
Phương trình mặt phẳng này đi qua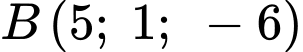 nên
nên 
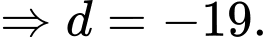
Vậy phương trình mặt phẳng đi qua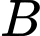 và vuông góc với
và vuông góc với 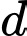 là
là 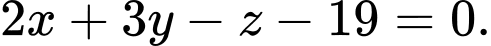 Đáp án: D
Đáp án: D
Phương trình mặt phẳng vuông góc với
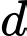 có dạng
có dạng 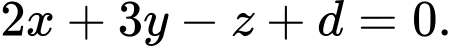
Phương trình mặt phẳng này đi qua
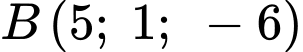 nên
nên 
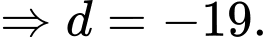
Vậy phương trình mặt phẳng đi qua
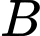 và vuông góc với
và vuông góc với 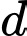 là
là 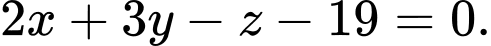 Đáp án: D
Đáp án: D
Câu 8 [703072]: Giá trị của 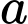 bằng
bằng
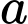 bằng
bằng A, 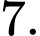
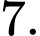
B, 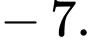
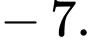
C, 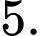
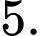
D, 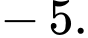
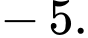
Chọn đáp án D.
Đường thẳng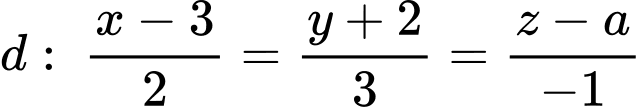 đi qua điểm
đi qua điểm 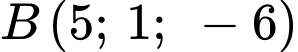 nên
nên 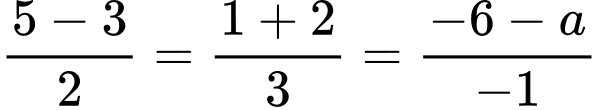
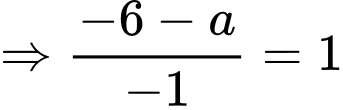
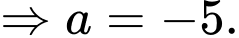 Đáp án: D
Đáp án: D
Đường thẳng
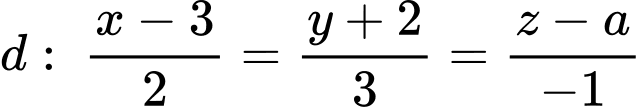 đi qua điểm
đi qua điểm 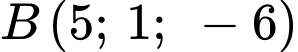 nên
nên 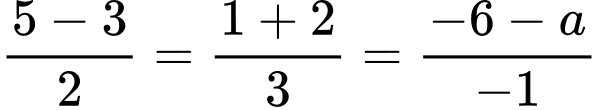
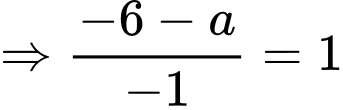
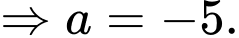 Đáp án: D
Đáp án: D
Câu 9 [258356]: Cho hai số thực 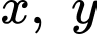 thỏa mãn
thỏa mãn 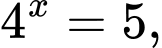
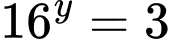 thì
thì 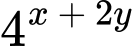 bằng
bằng
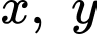 thỏa mãn
thỏa mãn 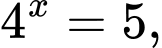
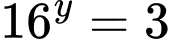 thì
thì 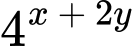 bằng
bằng A, 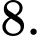
B, 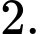
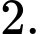
C, 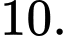
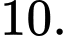
D, 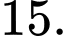
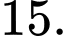
Chọn đáp án D.
Ta có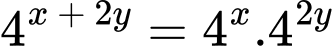
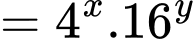
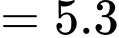
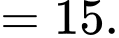 Đáp án: D
Đáp án: D
Ta có
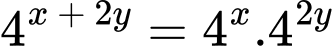
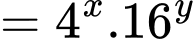
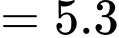
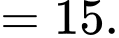 Đáp án: D
Đáp án: D
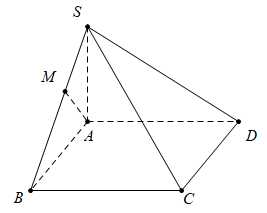
Câu 10 [696481]: Cho hình chóp 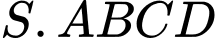 có đáy
có đáy 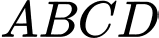 là hình chữ nhật và
là hình chữ nhật và 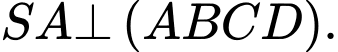 Gọi
Gọi 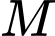 là hình chiếu vuông góc của
là hình chiếu vuông góc của 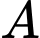 trên
trên 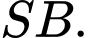 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
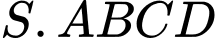 có đáy
có đáy 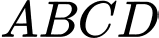 là hình chữ nhật và
là hình chữ nhật và 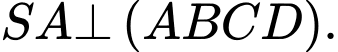 Gọi
Gọi 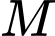 là hình chiếu vuông góc của
là hình chiếu vuông góc của 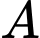 trên
trên 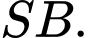 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 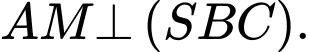
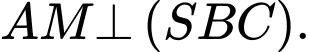
B, 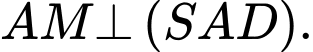
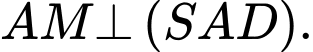
C, 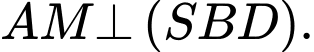
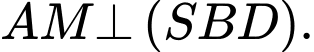
D, 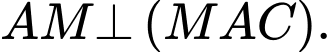
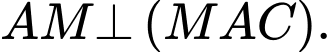
Chọn đáp án A.
Ta có: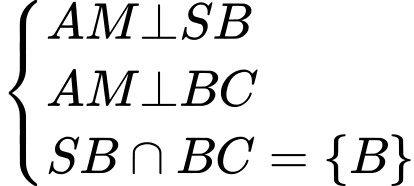
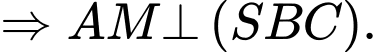 Đáp án: A
Đáp án: A

Ta có:
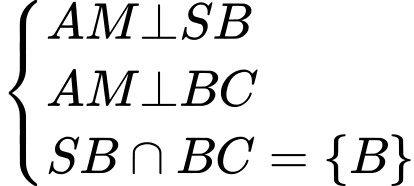
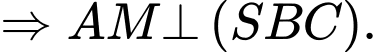 Đáp án: A
Đáp án: A
Câu 11 [258446]: Cho cấp số cộng 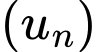 với
với 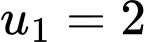 và công sai
và công sai  . Hỏi có bao nhiêu số hạng của cấo số cộng nhỏ hơn
. Hỏi có bao nhiêu số hạng của cấo số cộng nhỏ hơn  ?
?
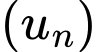 với
với 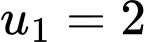 và công sai
và công sai  . Hỏi có bao nhiêu số hạng của cấo số cộng nhỏ hơn
. Hỏi có bao nhiêu số hạng của cấo số cộng nhỏ hơn  ?
? A, 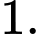
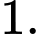
B, 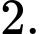
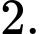
C, 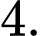
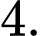
D, 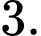
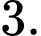
Chọn đáp án D.
Ta có cấp số cộng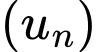 với
với 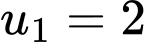 và công sai
và công sai 
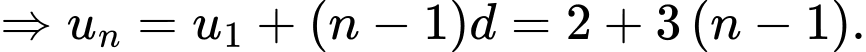
Xét
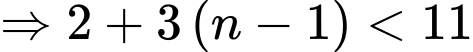
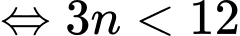
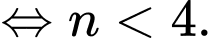
Vậy có tất cả 3 số hạng. Đáp án: D
Ta có cấp số cộng
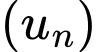 với
với 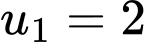 và công sai
và công sai 
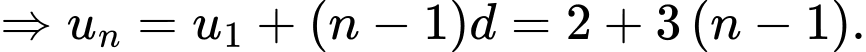
Xét

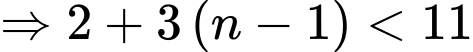
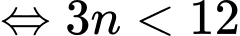
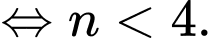
Vậy có tất cả 3 số hạng. Đáp án: D
Câu 12 [352582]: Cho hàm số 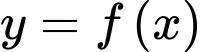 có đạo hàm liên tục trên
có đạo hàm liên tục trên 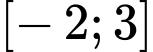 và
và 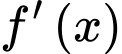 có đồ thị như hình vẽ bên dưới.
có đồ thị như hình vẽ bên dưới.
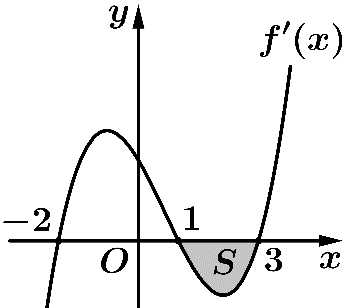
Biết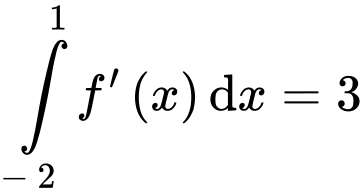 và diện tích
và diện tích 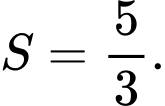 Giá trị của
Giá trị của 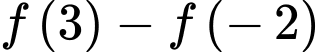 bằng
bằng
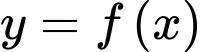 có đạo hàm liên tục trên
có đạo hàm liên tục trên 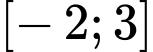 và
và 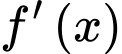 có đồ thị như hình vẽ bên dưới.
có đồ thị như hình vẽ bên dưới.
Biết
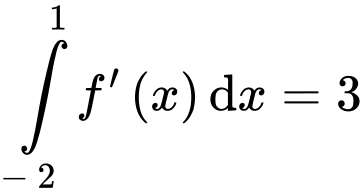 và diện tích
và diện tích 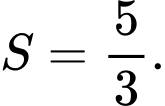 Giá trị của
Giá trị của 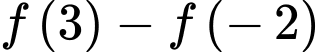 bằng
bằng A, 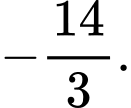
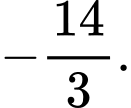
B, 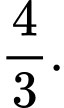
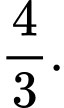
C, 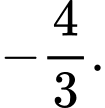
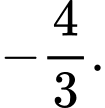
D, 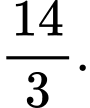
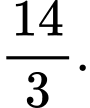
Chọn đáp án B.
Ta có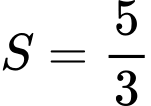
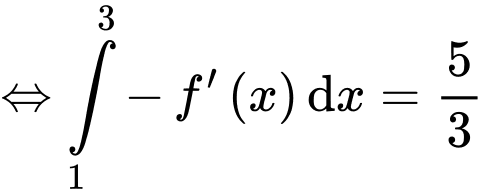
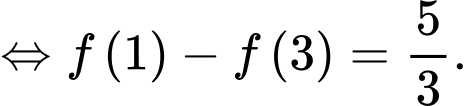
Lại có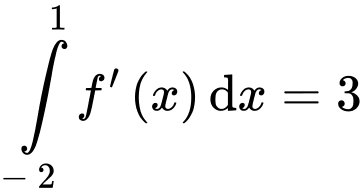
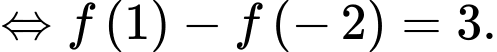
Do đó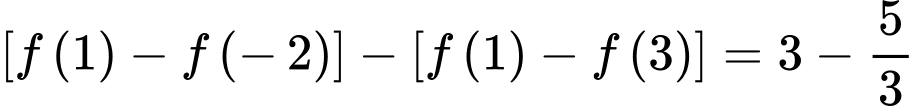
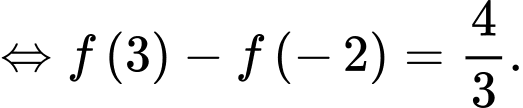 Đáp án: B
Đáp án: B
Ta có
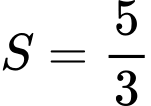
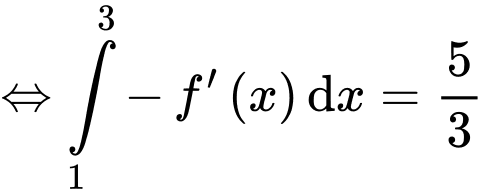
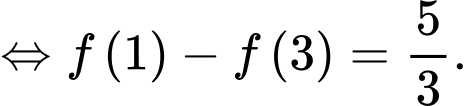
Lại có
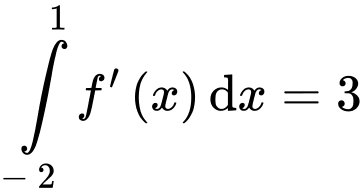
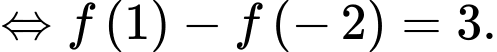
Do đó
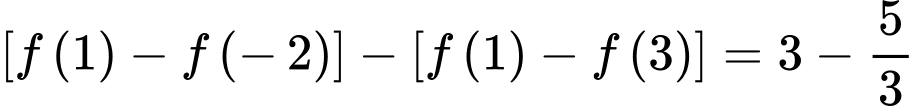
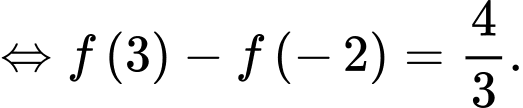 Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696494]: Trong không gian toạ độ 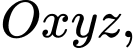 cho mặt phẳng
cho mặt phẳng 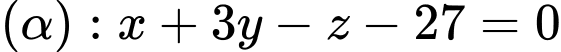 và điểm
và điểm 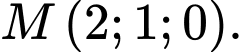
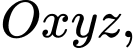 cho mặt phẳng
cho mặt phẳng 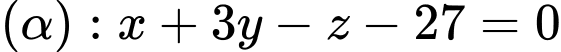 và điểm
và điểm 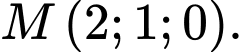
a) Sai.
Một vectơ pháp tuyến của mặt phẳng là
là 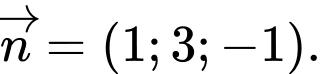
b) Đúng.
Phương trình đường thẳng qua M vuông góc với là:
là:
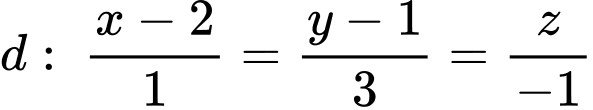
c) Sai.
Hình chiếu vuông góc của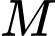 lên mặt phẳng
lên mặt phẳng  là
là 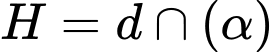
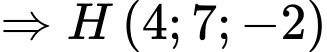
d) Đúng.
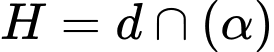
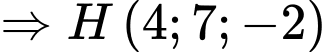 là trung điểm của
là trung điểm của 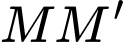
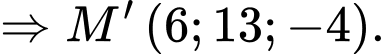
Một vectơ pháp tuyến của mặt phẳng
 là
là 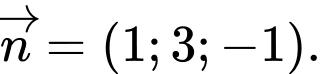
b) Đúng.
Phương trình đường thẳng qua M vuông góc với
 là:
là: 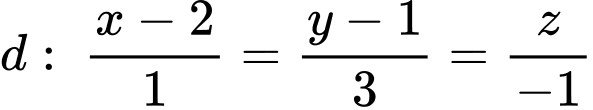
c) Sai.
Hình chiếu vuông góc của
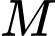 lên mặt phẳng
lên mặt phẳng  là
là 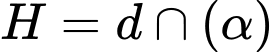
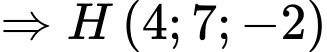
d) Đúng.
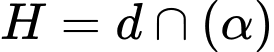
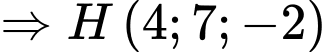 là trung điểm của
là trung điểm của 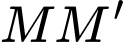
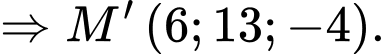
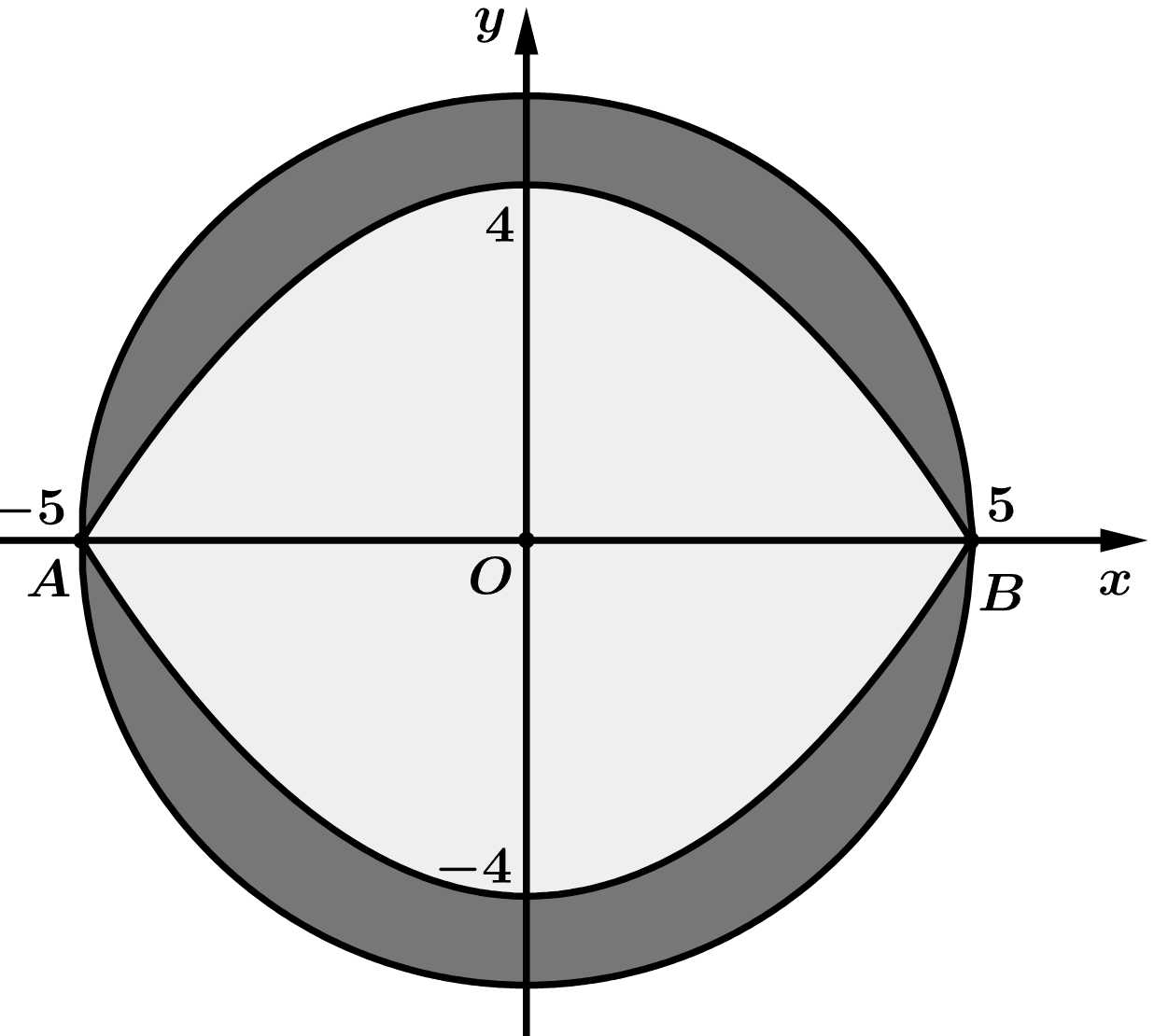
Câu 14 [696483]: Khu vực trung tâm một quảng trường có dạng hình tròn đường kính AB bằng 10 m. Người ta trang trí khu vực này bằng hai đường Parabol đối xứng nhau qua AB, nằm trong một hình tròn, hai parabol đi qua các điểm A, B và có đỉnh cách mép hình tròn 1m. Phần giới hạn bởi 2 parabol được trồng hoa với chi phí 200 nghìn đồng 1 mét vuông, phần còn lại được lát gốm sứ với chi phí 800 nghìn đồng 1 mét vuông. Để tính toán chi phí người ta gắn vườn hoa vào hệ trục tọa độ 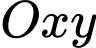 như hình vẽ.
như hình vẽ.
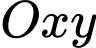 như hình vẽ.
như hình vẽ.
a) Sai.
Đường tròn nằm ngoài 2 parabol có phương trình là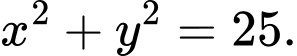
b) Sai.
Phương trình parabol có dạng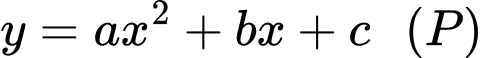
Thay tọa độ các điểm vào phương trình parabol ta được:
vào phương trình parabol ta được:
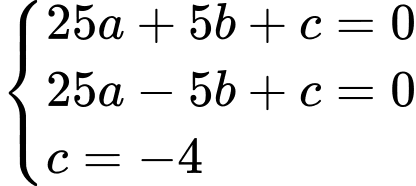
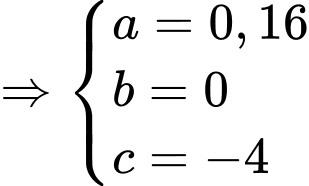
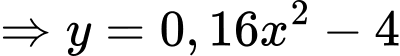
c) Đúng.
d) Đúng.
Diện tích phần trồng hoa giới hạn bới 2 parabol là:
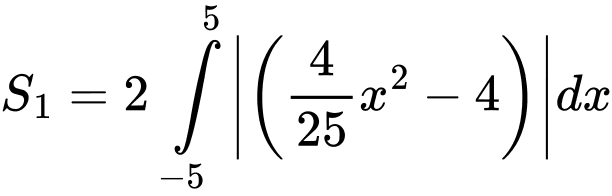
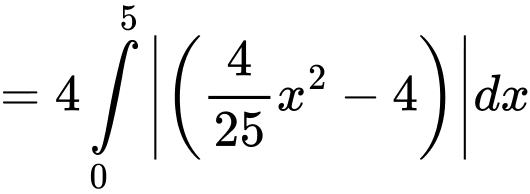
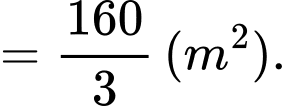
Diện tích toàn bộ phần hình tròn là: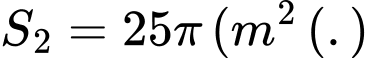
Diện tích phần còn lại để trang trí gốm sứ là:
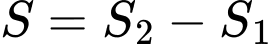
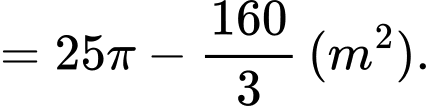
Vậy tổng chi phí để làm khu vực trung tâm quảng trường là
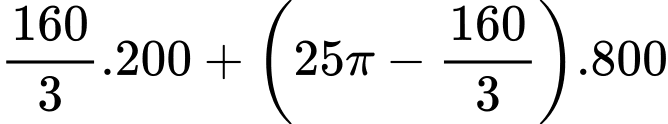
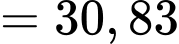 (triệu đồng).
(triệu đồng).
Đường tròn nằm ngoài 2 parabol có phương trình là
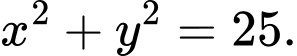
b) Sai.
Phương trình parabol có dạng
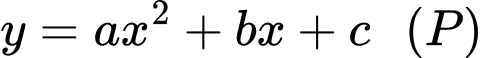
Thay tọa độ các điểm
 vào phương trình parabol ta được:
vào phương trình parabol ta được: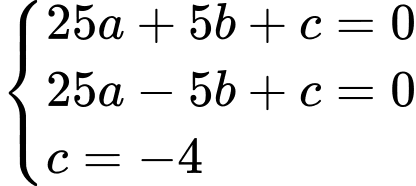
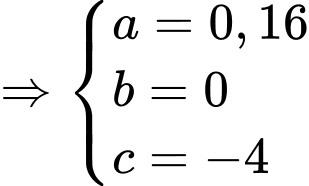
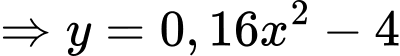
c) Đúng.
d) Đúng.
Diện tích phần trồng hoa giới hạn bới 2 parabol là:
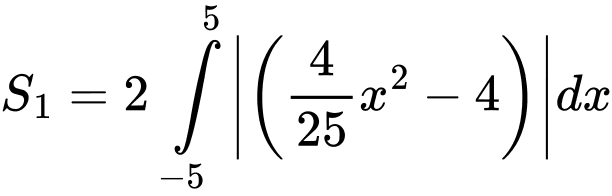
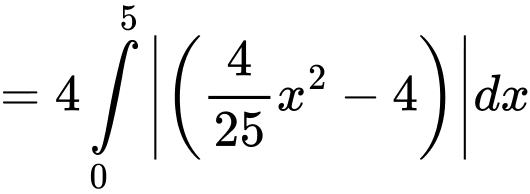
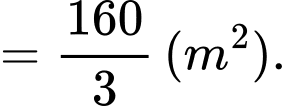
Diện tích toàn bộ phần hình tròn là:
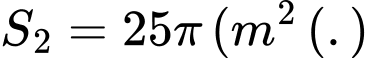
Diện tích phần còn lại để trang trí gốm sứ là:
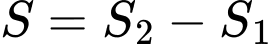
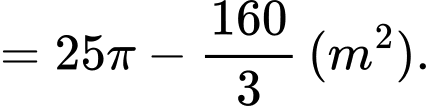
Vậy tổng chi phí để làm khu vực trung tâm quảng trường là
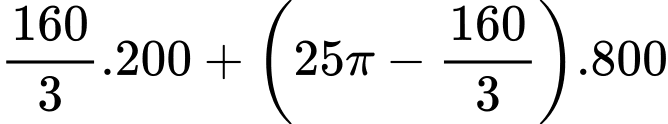
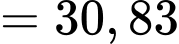 (triệu đồng).
(triệu đồng).
Câu 15 [696458]: Xác suất để cơ quan  thuê 1 trong các công ty
thuê 1 trong các công ty  và
và 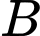 tư vấn lần lượt là
tư vấn lần lượt là 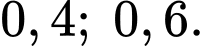 Theo kinh nghiệm khả năng
Theo kinh nghiệm khả năng  phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty
phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty 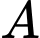 và
và 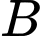 lần lượt là
lần lượt là 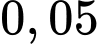 và
và 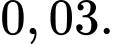
 thuê 1 trong các công ty
thuê 1 trong các công ty 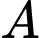 và
và 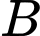 tư vấn lần lượt là
tư vấn lần lượt là 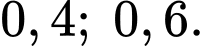 Theo kinh nghiệm khả năng
Theo kinh nghiệm khả năng  phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty
phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty 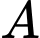 và
và 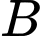 lần lượt là
lần lượt là 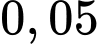 và
và 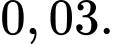
Gọi 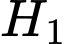 là biến cố “cơ quan
là biến cố “cơ quan  thuê công ty
thuê công ty 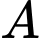 tư vấn”
tư vấn”
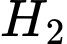 là biến cố “cơ quan
là biến cố “cơ quan  thuê công ty
thuê công ty 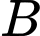 tư vấn”
tư vấn”
a) Sai.
Gọi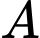 là biến cố “cơ quan
là biến cố “cơ quan  có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”
Theo đề bài ta có:
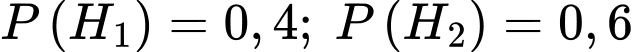
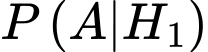 là xác xuất để
là xác xuất để  có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện  thuê công ty
thuê công ty 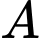 do đó
do đó 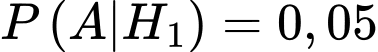
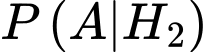 là xác xuất để
là xác xuất để  có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện  thuê công ty
thuê công ty 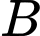 do đó
do đó 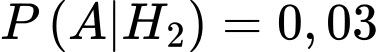
b) Đúng.
Theo công thức toàn phần ta có:

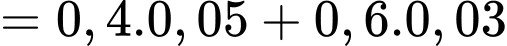
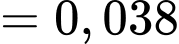
c) Sai.
Theo công thức Bayes ta có:
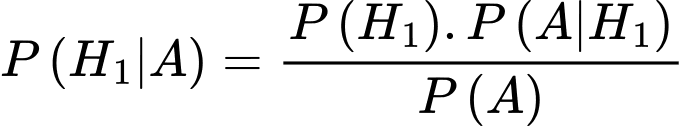
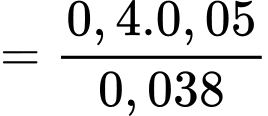
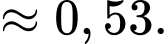
d) Đúng.
Theo công thức Bayes ta có:
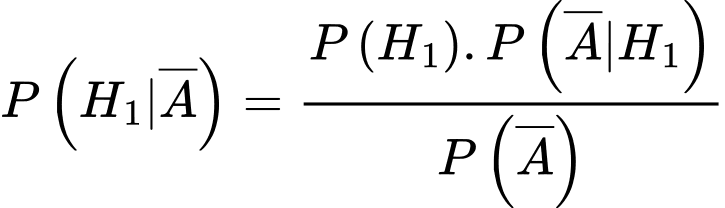
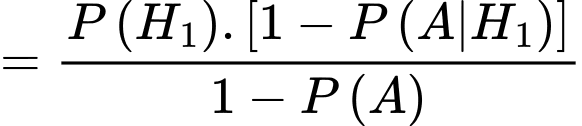
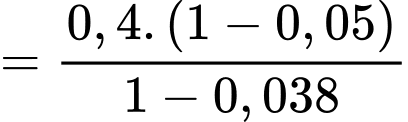
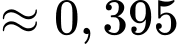
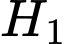 là biến cố “cơ quan
là biến cố “cơ quan  thuê công ty
thuê công ty 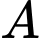 tư vấn”
tư vấn”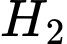 là biến cố “cơ quan
là biến cố “cơ quan  thuê công ty
thuê công ty 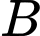 tư vấn”
tư vấn”a) Sai.
Gọi
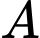 là biến cố “cơ quan
là biến cố “cơ quan  có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”Theo đề bài ta có:
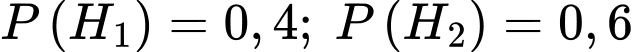
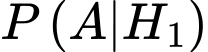 là xác xuất để
là xác xuất để  có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện  thuê công ty
thuê công ty 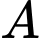 do đó
do đó 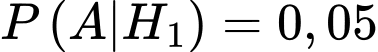
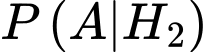 là xác xuất để
là xác xuất để  có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn với điều kiện  thuê công ty
thuê công ty 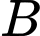 do đó
do đó 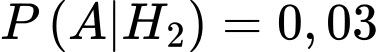
b) Đúng.
Theo công thức toàn phần ta có:

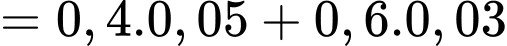
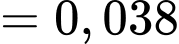
c) Sai.
Theo công thức Bayes ta có:
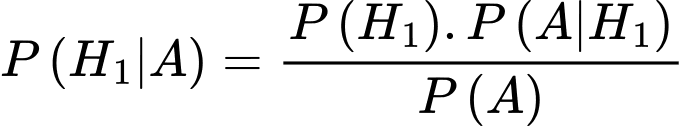
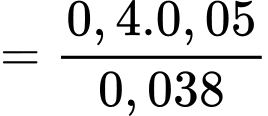
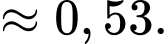
d) Đúng.
Theo công thức Bayes ta có:
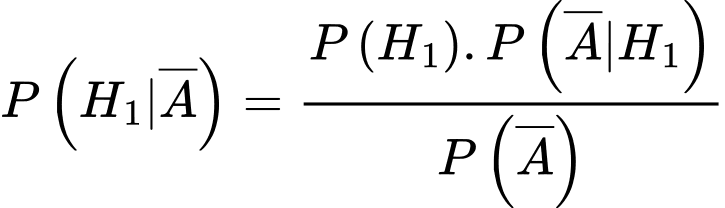
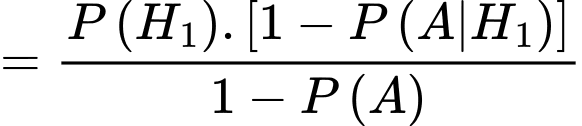
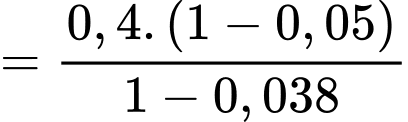
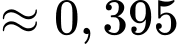
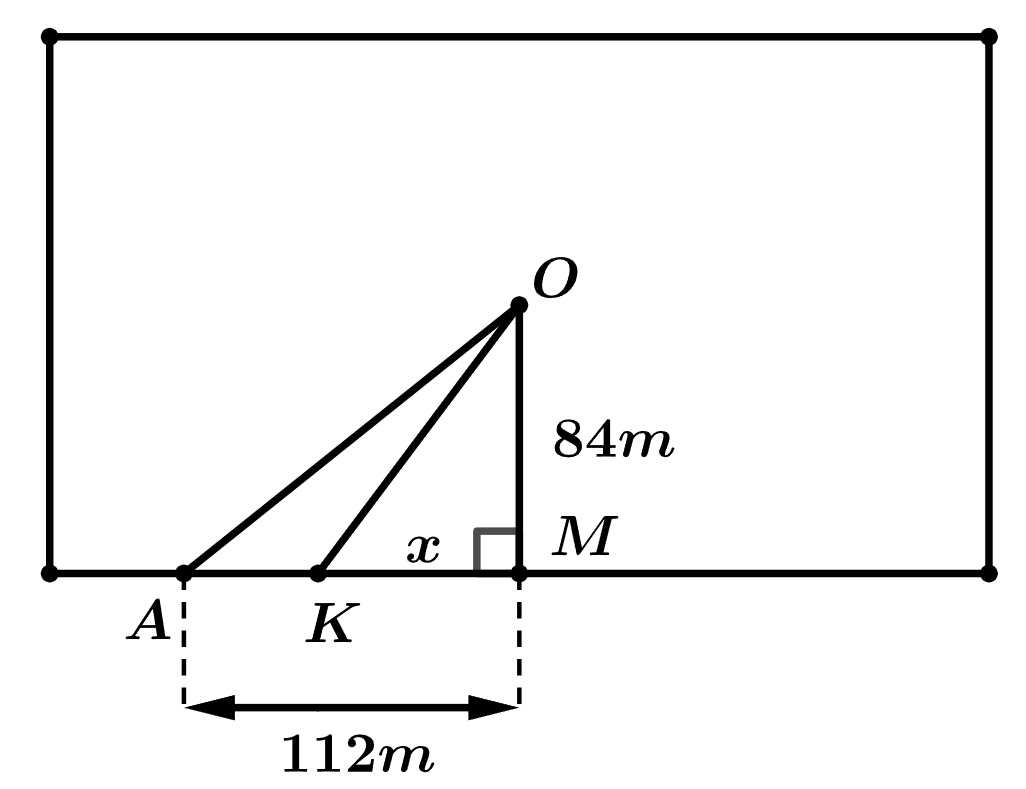
Câu 16 [696496]: Gia đình bác Hùng có một ao cá hình chữ nhật. Để lắp đặt một hệ thống điện ra vị trí  ở giữa hồ bác dự định nối một đường dây điện từ vị trí
ở giữa hồ bác dự định nối một đường dây điện từ vị trí 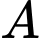 trên bờ hồ đến vị trí
trên bờ hồ đến vị trí  ở giữa hồ (như hình vẽ). Biết khoảng cách ngắn nhất từ
ở giữa hồ (như hình vẽ). Biết khoảng cách ngắn nhất từ  đến bờ hồ là
đến bờ hồ là 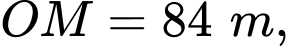 khoảng cách từ
khoảng cách từ 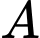 đến
đến 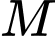 là
là 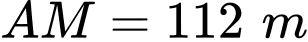 . Mỗi mét dây điện lắp đặt ở trên bờ có chi phí cả tiền công và tiền vật liệu là 25 200 đồng và mỗi mét dây điện lắp đặt ở dưới nước có chi phí cả tiền công và tiền vật liệu là 42 000 đồng.
. Mỗi mét dây điện lắp đặt ở trên bờ có chi phí cả tiền công và tiền vật liệu là 25 200 đồng và mỗi mét dây điện lắp đặt ở dưới nước có chi phí cả tiền công và tiền vật liệu là 42 000 đồng.
 ở giữa hồ bác dự định nối một đường dây điện từ vị trí
ở giữa hồ bác dự định nối một đường dây điện từ vị trí 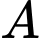 trên bờ hồ đến vị trí
trên bờ hồ đến vị trí  ở giữa hồ (như hình vẽ). Biết khoảng cách ngắn nhất từ
ở giữa hồ (như hình vẽ). Biết khoảng cách ngắn nhất từ  đến bờ hồ là
đến bờ hồ là 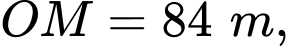 khoảng cách từ
khoảng cách từ 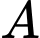 đến
đến 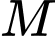 là
là 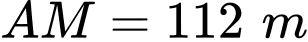 . Mỗi mét dây điện lắp đặt ở trên bờ có chi phí cả tiền công và tiền vật liệu là 25 200 đồng và mỗi mét dây điện lắp đặt ở dưới nước có chi phí cả tiền công và tiền vật liệu là 42 000 đồng.
. Mỗi mét dây điện lắp đặt ở trên bờ có chi phí cả tiền công và tiền vật liệu là 25 200 đồng và mỗi mét dây điện lắp đặt ở dưới nước có chi phí cả tiền công và tiền vật liệu là 42 000 đồng.
a) Sai.
Nếu nối đường dây điện theo đường gấp khúc thì chi phí lắp đặt đường dây điện là
thì chi phí lắp đặt đường dây điện là
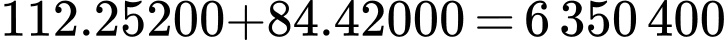 .
.
b) Đúng.
Ta có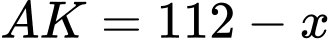 và
và 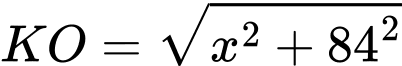
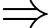 Chi phí lắp đặt đường dây điện theo đường gấp khúc
Chi phí lắp đặt đường dây điện theo đường gấp khúc  là
là 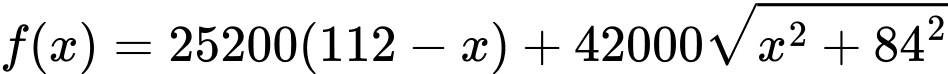
c) Sai.
Xét hàm số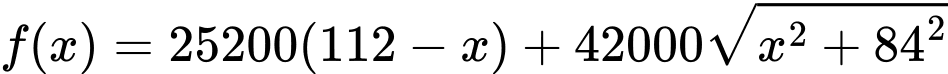
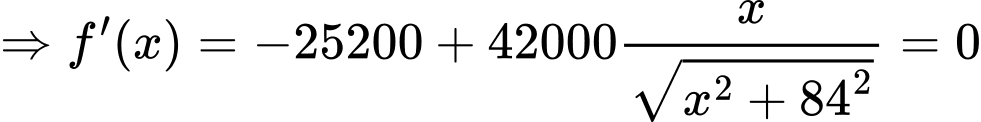
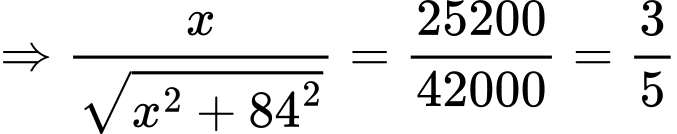
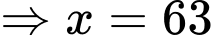 là điểm cực tiếu của hàm số trên.
là điểm cực tiếu của hàm số trên.
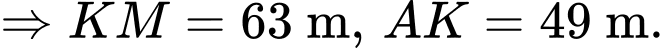
d) Đúng.
Chi phí lắp đặt thấp nhất là
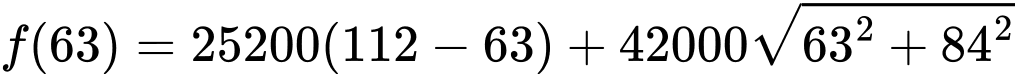
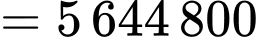
Nếu nối đường dây điện theo đường gấp khúc
 thì chi phí lắp đặt đường dây điện là
thì chi phí lắp đặt đường dây điện là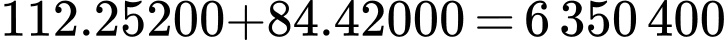 .
.
b) Đúng.
Ta có
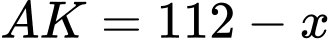 và
và 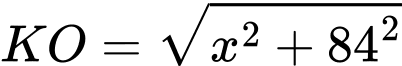
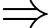 Chi phí lắp đặt đường dây điện theo đường gấp khúc
Chi phí lắp đặt đường dây điện theo đường gấp khúc  là
là 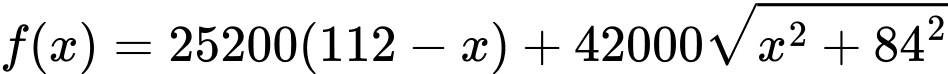
c) Sai.
Xét hàm số
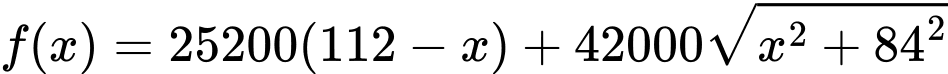
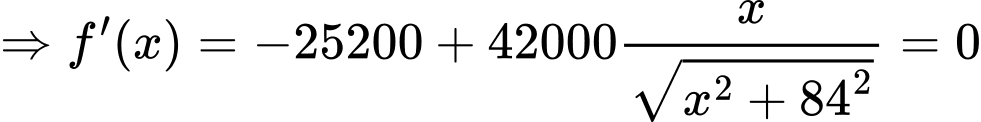
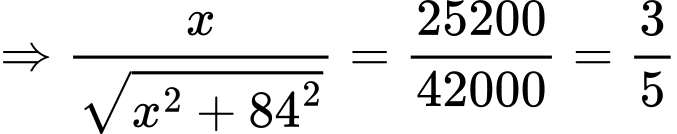
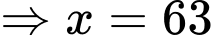 là điểm cực tiếu của hàm số trên.
là điểm cực tiếu của hàm số trên.
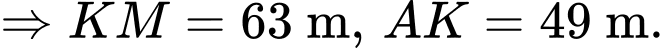
d) Đúng.
Chi phí lắp đặt thấp nhất là
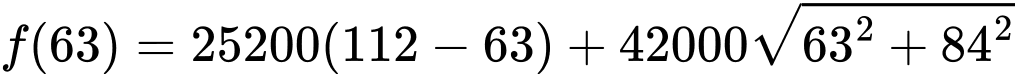
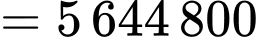
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696486]: Cho hình chóp 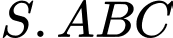 có đáy
có đáy 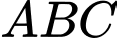 là tam giác đều, cạnh bên
là tam giác đều, cạnh bên 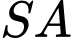 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 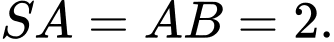 Góc giữa đường thẳng
Góc giữa đường thẳng 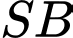 và mặt phẳng
và mặt phẳng 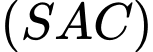 bằng bao nhiêu độ? (kết quả làm tròn đến độ).
bằng bao nhiêu độ? (kết quả làm tròn đến độ).
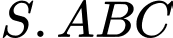 có đáy
có đáy 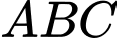 là tam giác đều, cạnh bên
là tam giác đều, cạnh bên 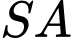 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 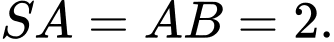 Góc giữa đường thẳng
Góc giữa đường thẳng 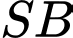 và mặt phẳng
và mặt phẳng 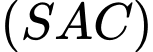 bằng bao nhiêu độ? (kết quả làm tròn đến độ).
bằng bao nhiêu độ? (kết quả làm tròn đến độ).
Điền đáp án: 38.
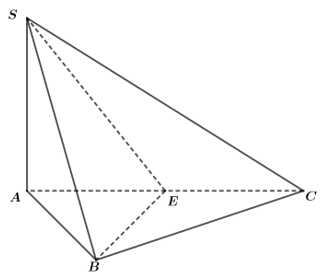
Gọi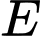 là trung điểm của
là trung điểm của 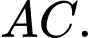
Do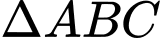 đều
đều 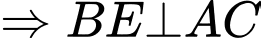
Mà
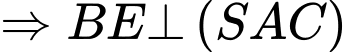
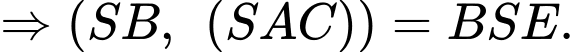
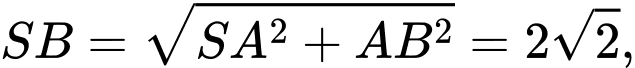
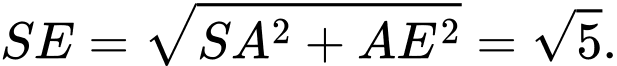
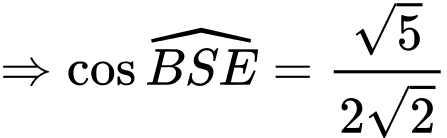
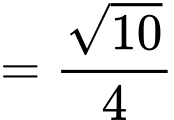
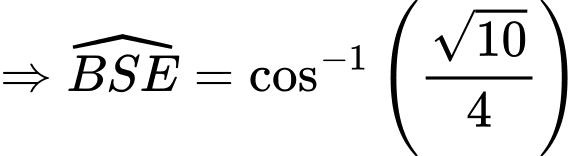
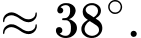

Gọi
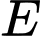 là trung điểm của
là trung điểm của 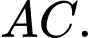
Do
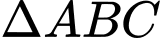 đều
đều 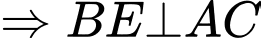
Mà

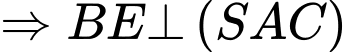
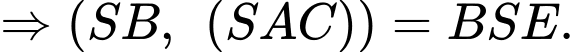
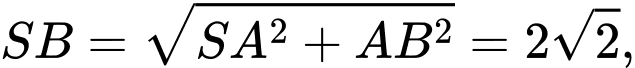
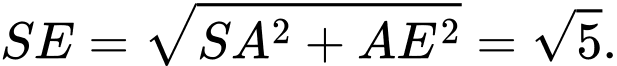
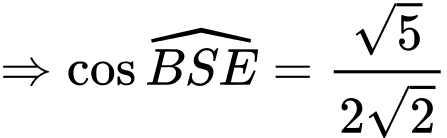
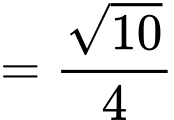
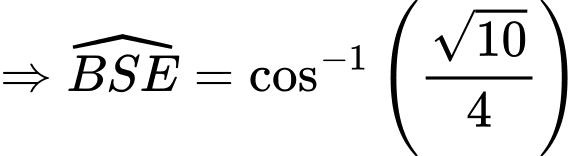
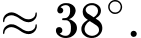
Câu 18 [696487]: Một công ty sản xuất nước giải khát có hợp đồng yêu cầu mỗi chai nước phải chứa ít nhất 80 đơn vị hóa chất A và 60 đơn vị hóa chất B. Các hóa chất này được cung cấp dưới dạng các gói hỗn hợp từ hai nhà cung cấp khác nhau. Nhà cung cấp S cung cấp gói hỗn hợp gồm 4 đơn vị A và 2 đơn vị B với giá 10 000 nghìn/gói. Nhà cung cấp T cung cấp gói hỗn hợp gồm 1 đơn vị A và 1 đơn vị B với giá 4 000 đồng/gói. Công ty nên mua 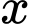 gói hỗ trợ từ nhà cung cấp S và
gói hỗ trợ từ nhà cung cấp S và 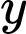 gói hỗ trợ từ nhà cung cấp T để thực hiện đúng yêu cầu hợp đồng và đồng thời giảm thiểu chi phí. Vậy tổng
gói hỗ trợ từ nhà cung cấp T để thực hiện đúng yêu cầu hợp đồng và đồng thời giảm thiểu chi phí. Vậy tổng  bằng bao nhiêu?
bằng bao nhiêu?
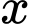 gói hỗ trợ từ nhà cung cấp S và
gói hỗ trợ từ nhà cung cấp S và 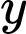 gói hỗ trợ từ nhà cung cấp T để thực hiện đúng yêu cầu hợp đồng và đồng thời giảm thiểu chi phí. Vậy tổng
gói hỗ trợ từ nhà cung cấp T để thực hiện đúng yêu cầu hợp đồng và đồng thời giảm thiểu chi phí. Vậy tổng  bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 50.
Chi phí của công ty là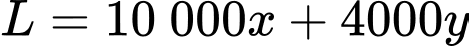 (đồng)
(đồng)
Theo đề bài ta có hệ bất phương trình:
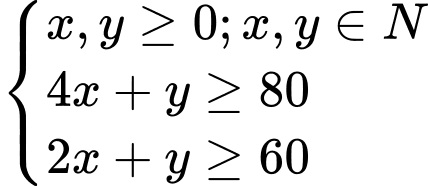
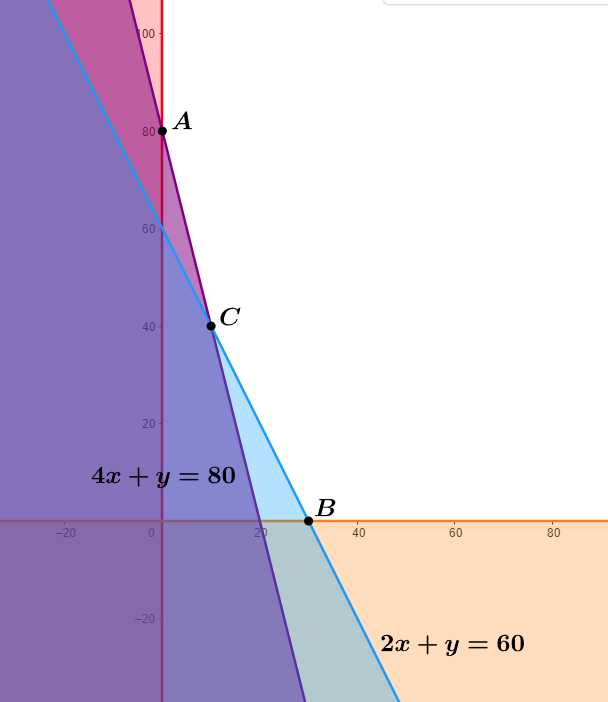
Ta có miền nghiệm của hệ bất phương trình trên là phần không tô đậm trong hình vẽ trên.
Hàm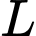 đạt giá trị nhỏ nhất tại điểm 3 điểm
đạt giá trị nhỏ nhất tại điểm 3 điểm 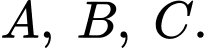
Tại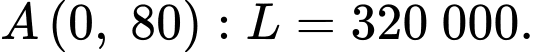
Tại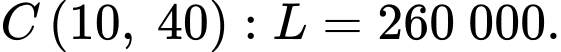
Tại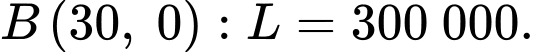
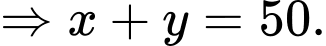
Chi phí của công ty là
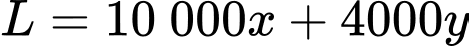 (đồng)
(đồng)
Theo đề bài ta có hệ bất phương trình:
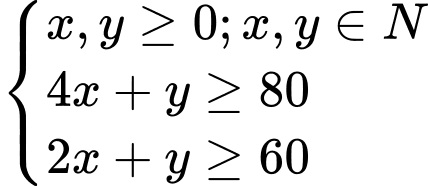

Ta có miền nghiệm của hệ bất phương trình trên là phần không tô đậm trong hình vẽ trên.
Hàm
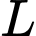 đạt giá trị nhỏ nhất tại điểm 3 điểm
đạt giá trị nhỏ nhất tại điểm 3 điểm 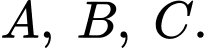
Tại
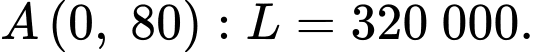
Tại
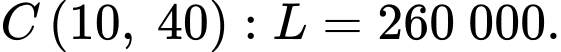
Tại
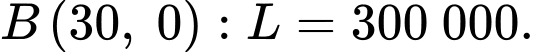
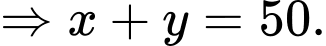
Câu 19 [696465]: Trong không gian với hệ tọa độ 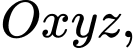 cho hai mặt cầu
cho hai mặt cầu 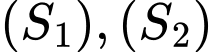 lần lượt có phương trình là
lần lượt có phương trình là 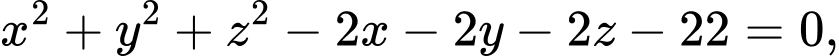
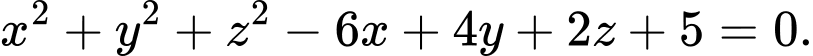 Xét các mặt phẳng
Xét các mặt phẳng 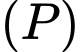 thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Biết rằng mặt phẳng
thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Biết rằng mặt phẳng 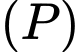 luôn đi qua điểm
luôn đi qua điểm 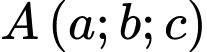 . Tính tổng
. Tính tổng 
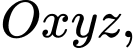 cho hai mặt cầu
cho hai mặt cầu 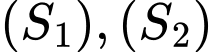 lần lượt có phương trình là
lần lượt có phương trình là 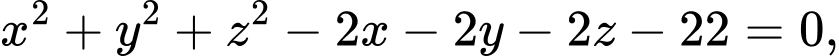
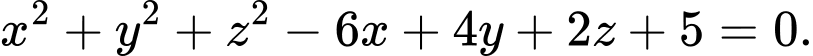 Xét các mặt phẳng
Xét các mặt phẳng 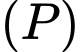 thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Biết rằng mặt phẳng
thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Biết rằng mặt phẳng 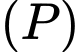 luôn đi qua điểm
luôn đi qua điểm 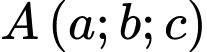 . Tính tổng
. Tính tổng 
Điền đáp án: -4,5.
Mặt cầu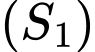 có
có 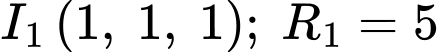 .
.
Mặt cầu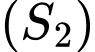 có
có 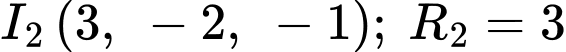 .
.
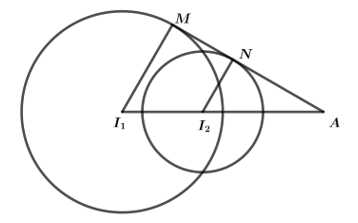
Gọi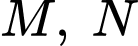 lần lượt là tiếp điểm của mặt phẳng
lần lượt là tiếp điểm của mặt phẳng 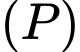 với mặt cầu
với mặt cầu 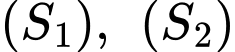
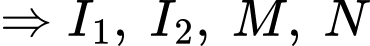 đồng phẳng.
đồng phẳng.
Gọi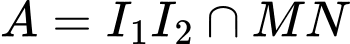 .
.
Vì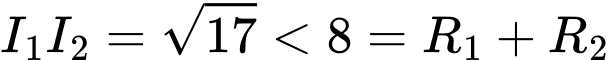
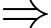 Điểm
Điểm 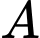 nằm ngoài đoạn
nằm ngoài đoạn 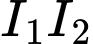 .
.
Ta có: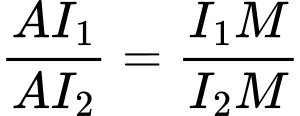
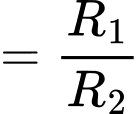
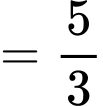
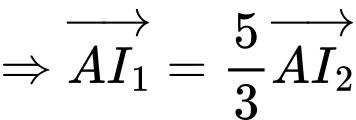
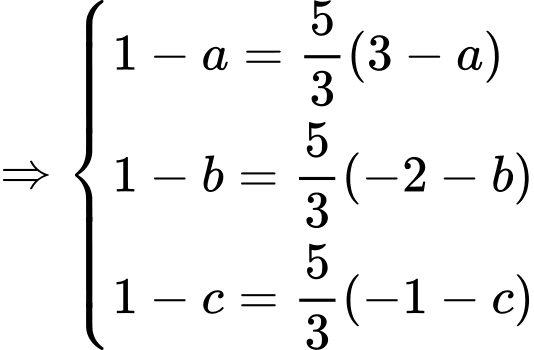
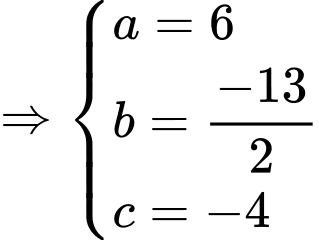
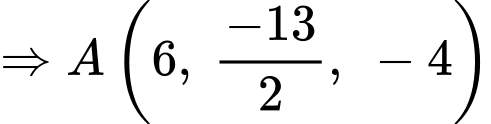 là điểm cố định mà mặt phẳng
là điểm cố định mà mặt phẳng 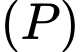 luôn đi qua.
luôn đi qua.
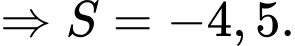

Mặt cầu
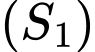 có
có 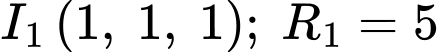 .
.Mặt cầu
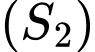 có
có 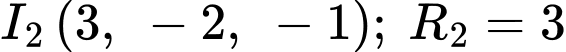 .
.Gọi
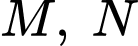 lần lượt là tiếp điểm của mặt phẳng
lần lượt là tiếp điểm của mặt phẳng 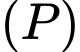 với mặt cầu
với mặt cầu 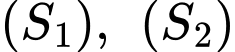
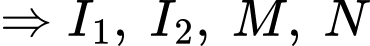 đồng phẳng.
đồng phẳng.Gọi
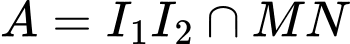 .
.Vì
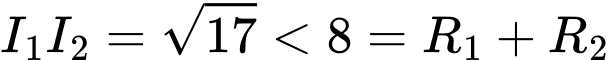
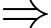 Điểm
Điểm 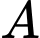 nằm ngoài đoạn
nằm ngoài đoạn 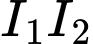 .
.Ta có:
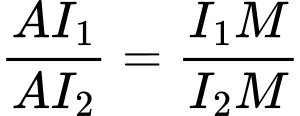
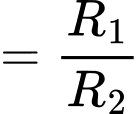
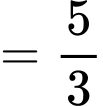
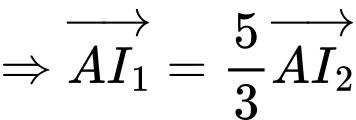
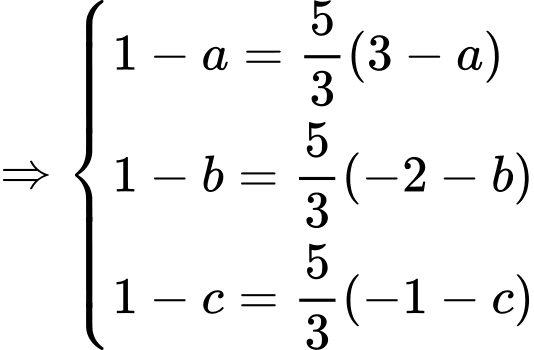
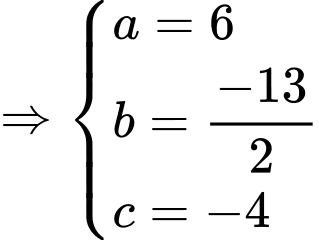
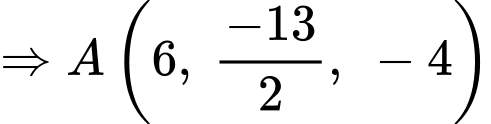 là điểm cố định mà mặt phẳng
là điểm cố định mà mặt phẳng 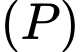 luôn đi qua.
luôn đi qua.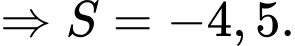
Câu 20 [694667]: Một phụ nữ trên 50 tuổi có khối u ở một vú lo ngại bị ung thư vú nên đã đi khám bệnh. Trong báo cáo, xét nghiệm Mammography người mắc bệnh ung thư vú cho kết quả dương tính với xác suất là 93%, người không mắc bệnh ung thư vú cho kết quả âm tính với xác suất 92%. Biết rằng trong số phụ nữ trên 50 tuổi có khối u ở một vú thì có 40,3% xét nghiệm cho kết quả dương tính. Xét nghiệm người phụ nữ này có kết quả dương tính, xác suất người này bị bệnh là bao nhiêu %? (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 88.
Gọi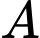 là biến cố “ Xét nghiệm người phụ nữ có kết quả dương tính”,
là biến cố “ Xét nghiệm người phụ nữ có kết quả dương tính”, 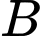 là biến cố “ Người đó bị bệnh”
là biến cố “ Người đó bị bệnh”
Theo đề bài ta có:
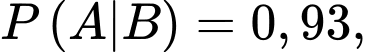

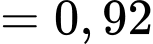
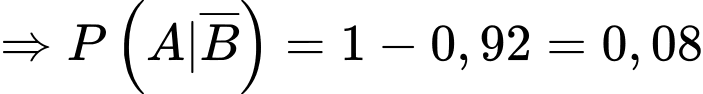
Theo công thức xác suất toàn phần ta có:
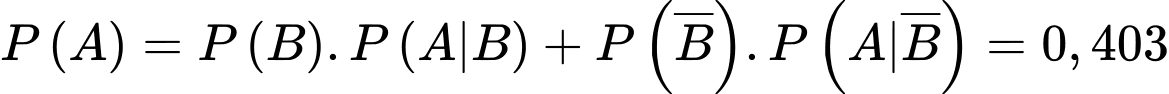
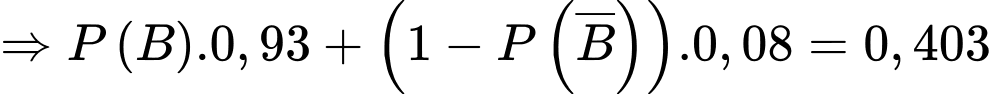

Theo công thức Bayes ta có:
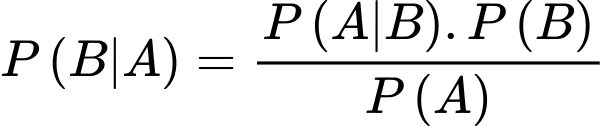
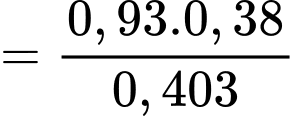
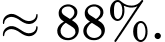
Gọi
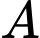 là biến cố “ Xét nghiệm người phụ nữ có kết quả dương tính”,
là biến cố “ Xét nghiệm người phụ nữ có kết quả dương tính”, 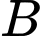 là biến cố “ Người đó bị bệnh”
là biến cố “ Người đó bị bệnh”
Theo đề bài ta có:
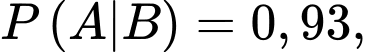

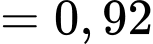
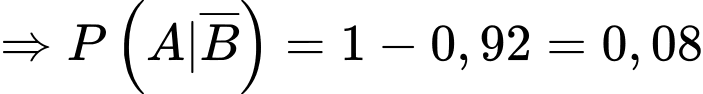
Theo công thức xác suất toàn phần ta có:
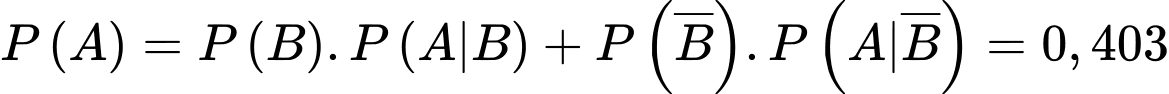
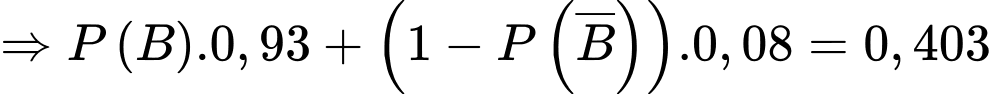

Theo công thức Bayes ta có:
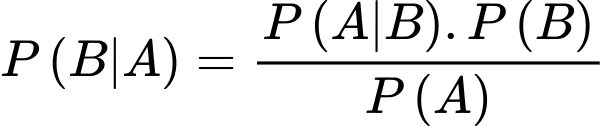
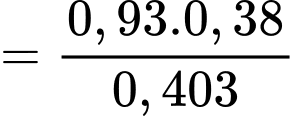
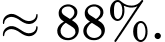
Câu 21 [703097]: Khi kim loại thiếc được giữ ở nhiệt độ dưới 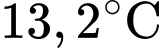 nó dần trở nên giòn và vỡ vụn thành bột màu xám. Các vật thể bằng thiếc cuối cùng sẽ tự vỡ vụn thành bột màu xám này nếu được giữ trong khí hậu lạnh trong nhiều năm. Người châu Âu, khi nhìn thấy các ống organ bằng thiếc trong nhà thờ của họ bị vỡ vụn cách đây nhiều năm, đã gọi hiện tượng này là bệnh dịch thiếc vì nó dường như lây lan, và quả thật là như vậy, vì bột màu xám là chất xúc tác cho sự hình thành của chính nó. Chất xúc tác cho một phản ứng hóa học là một chất điều khiển tốc độ phản ứng mà không trải qua bất kỳ sự thay đổi vĩnh viễn nào trong chính nó. Một phản ứng tự xúc tác là phản ứng có sản phẩm là chất xúc tác cho sự hình thành của chính nó. Phản ứng như vậy có thể diễn ra chậm ban đầu nếu lượng chất xúc tác hiện diện nhỏ và lại chậm dần vào cuối, khi hầu hết chất ban đầu đã được sử dụng hết. Nhưng ở giữa, khi cả chất và sản phẩm xúc tác của nó đều dồi dào, phản ứng diễn ra với tốc độ nhanh hơn.
nó dần trở nên giòn và vỡ vụn thành bột màu xám. Các vật thể bằng thiếc cuối cùng sẽ tự vỡ vụn thành bột màu xám này nếu được giữ trong khí hậu lạnh trong nhiều năm. Người châu Âu, khi nhìn thấy các ống organ bằng thiếc trong nhà thờ của họ bị vỡ vụn cách đây nhiều năm, đã gọi hiện tượng này là bệnh dịch thiếc vì nó dường như lây lan, và quả thật là như vậy, vì bột màu xám là chất xúc tác cho sự hình thành của chính nó. Chất xúc tác cho một phản ứng hóa học là một chất điều khiển tốc độ phản ứng mà không trải qua bất kỳ sự thay đổi vĩnh viễn nào trong chính nó. Một phản ứng tự xúc tác là phản ứng có sản phẩm là chất xúc tác cho sự hình thành của chính nó. Phản ứng như vậy có thể diễn ra chậm ban đầu nếu lượng chất xúc tác hiện diện nhỏ và lại chậm dần vào cuối, khi hầu hết chất ban đầu đã được sử dụng hết. Nhưng ở giữa, khi cả chất và sản phẩm xúc tác của nó đều dồi dào, phản ứng diễn ra với tốc độ nhanh hơn.
Trong một số trường hợp, thực nghiệm nghiên cứu tốc độ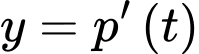 của phản ứng phân rã một miếng thiếc
của phản ứng phân rã một miếng thiếc  (kg) tỷ lệ thuận với tích của lượng chất đã mất
(kg) tỷ lệ thuận với tích của lượng chất đã mất 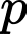 (kg) và lượng chất còn lại sau
(kg) và lượng chất còn lại sau 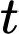 năm, tức là
năm, tức là 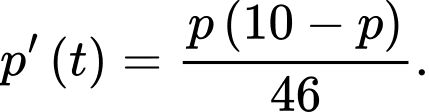 Hiện tại miếng thiếc đó có khối lượng
Hiện tại miếng thiếc đó có khối lượng 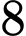 (kg), sau bao nhiêu năm nữa miếng thiếc đó còn
(kg), sau bao nhiêu năm nữa miếng thiếc đó còn 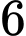 (kg)? (làm tròn kết quả đến hàng phần trăm).
(kg)? (làm tròn kết quả đến hàng phần trăm).
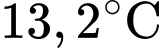 nó dần trở nên giòn và vỡ vụn thành bột màu xám. Các vật thể bằng thiếc cuối cùng sẽ tự vỡ vụn thành bột màu xám này nếu được giữ trong khí hậu lạnh trong nhiều năm. Người châu Âu, khi nhìn thấy các ống organ bằng thiếc trong nhà thờ của họ bị vỡ vụn cách đây nhiều năm, đã gọi hiện tượng này là bệnh dịch thiếc vì nó dường như lây lan, và quả thật là như vậy, vì bột màu xám là chất xúc tác cho sự hình thành của chính nó. Chất xúc tác cho một phản ứng hóa học là một chất điều khiển tốc độ phản ứng mà không trải qua bất kỳ sự thay đổi vĩnh viễn nào trong chính nó. Một phản ứng tự xúc tác là phản ứng có sản phẩm là chất xúc tác cho sự hình thành của chính nó. Phản ứng như vậy có thể diễn ra chậm ban đầu nếu lượng chất xúc tác hiện diện nhỏ và lại chậm dần vào cuối, khi hầu hết chất ban đầu đã được sử dụng hết. Nhưng ở giữa, khi cả chất và sản phẩm xúc tác của nó đều dồi dào, phản ứng diễn ra với tốc độ nhanh hơn.
nó dần trở nên giòn và vỡ vụn thành bột màu xám. Các vật thể bằng thiếc cuối cùng sẽ tự vỡ vụn thành bột màu xám này nếu được giữ trong khí hậu lạnh trong nhiều năm. Người châu Âu, khi nhìn thấy các ống organ bằng thiếc trong nhà thờ của họ bị vỡ vụn cách đây nhiều năm, đã gọi hiện tượng này là bệnh dịch thiếc vì nó dường như lây lan, và quả thật là như vậy, vì bột màu xám là chất xúc tác cho sự hình thành của chính nó. Chất xúc tác cho một phản ứng hóa học là một chất điều khiển tốc độ phản ứng mà không trải qua bất kỳ sự thay đổi vĩnh viễn nào trong chính nó. Một phản ứng tự xúc tác là phản ứng có sản phẩm là chất xúc tác cho sự hình thành của chính nó. Phản ứng như vậy có thể diễn ra chậm ban đầu nếu lượng chất xúc tác hiện diện nhỏ và lại chậm dần vào cuối, khi hầu hết chất ban đầu đã được sử dụng hết. Nhưng ở giữa, khi cả chất và sản phẩm xúc tác của nó đều dồi dào, phản ứng diễn ra với tốc độ nhanh hơn.Trong một số trường hợp, thực nghiệm nghiên cứu tốc độ
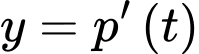 của phản ứng phân rã một miếng thiếc
của phản ứng phân rã một miếng thiếc  (kg) tỷ lệ thuận với tích của lượng chất đã mất
(kg) tỷ lệ thuận với tích của lượng chất đã mất 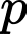 (kg) và lượng chất còn lại sau
(kg) và lượng chất còn lại sau 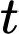 năm, tức là
năm, tức là 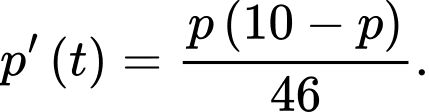 Hiện tại miếng thiếc đó có khối lượng
Hiện tại miếng thiếc đó có khối lượng 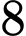 (kg), sau bao nhiêu năm nữa miếng thiếc đó còn
(kg), sau bao nhiêu năm nữa miếng thiếc đó còn 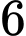 (kg)? (làm tròn kết quả đến hàng phần trăm).
(kg)? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 4,51.
Ta có: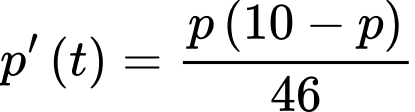
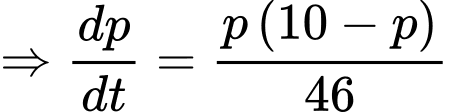
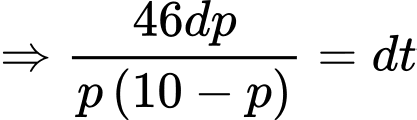
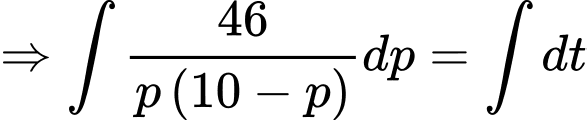
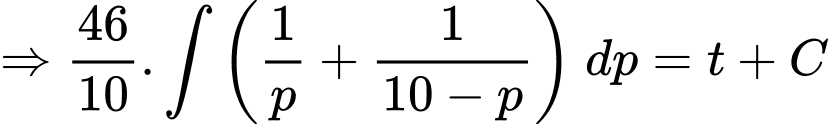
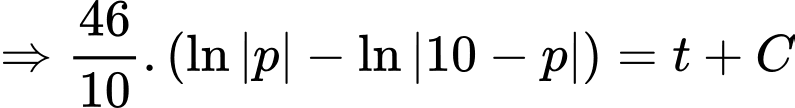
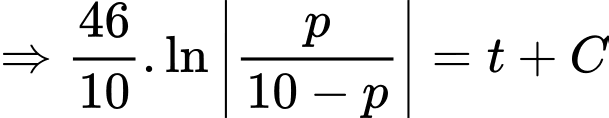
Vì tại thời điểm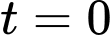 , miếng thiếc đó có khối lượng
, miếng thiếc đó có khối lượng 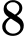 kg
kg
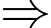 Miếng thiếc đã mất 2 kg
Miếng thiếc đã mất 2 kg
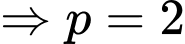
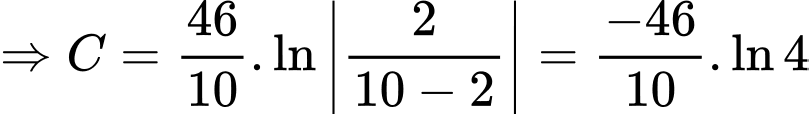
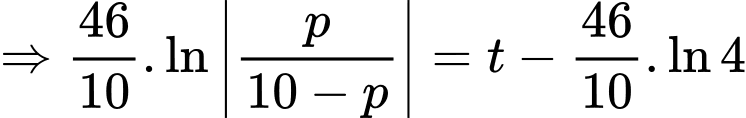
Khi miếng thiếc còn 6 kg thì miếng thiếc đó đã mất đi 4 kg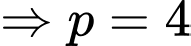
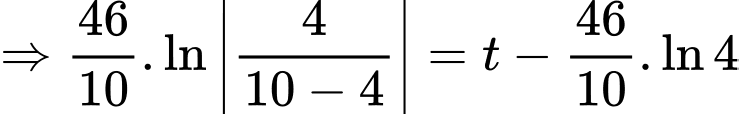
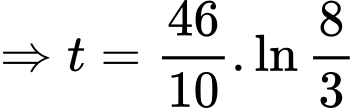
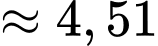 năm.
năm.
Ta có:
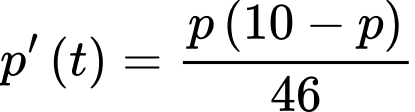
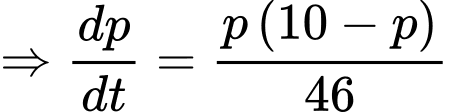
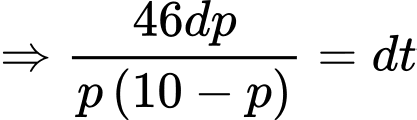
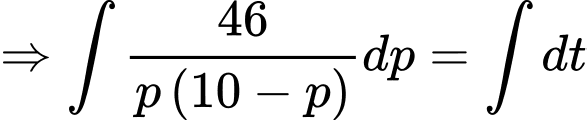
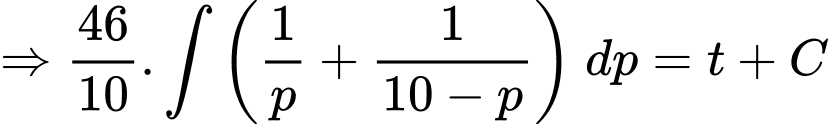
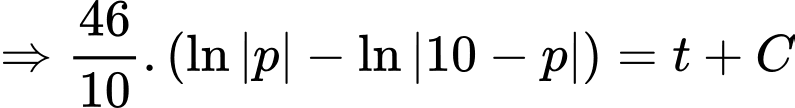
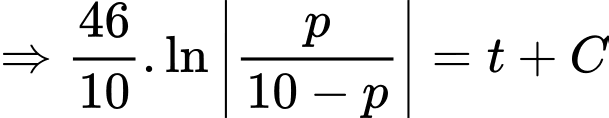
Vì tại thời điểm
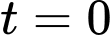 , miếng thiếc đó có khối lượng
, miếng thiếc đó có khối lượng 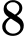 kg
kg 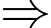 Miếng thiếc đã mất 2 kg
Miếng thiếc đã mất 2 kg 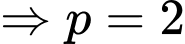
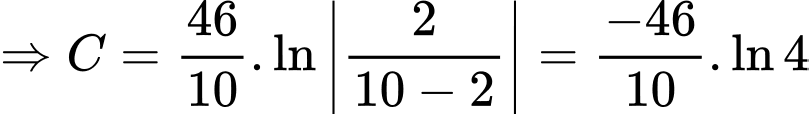
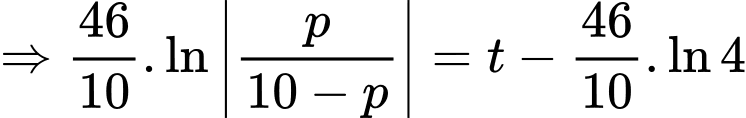
Khi miếng thiếc còn 6 kg thì miếng thiếc đó đã mất đi 4 kg
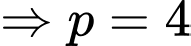
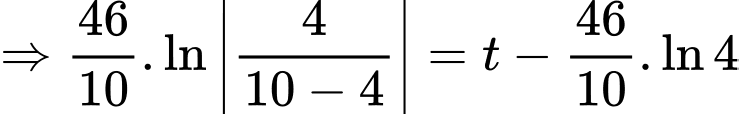
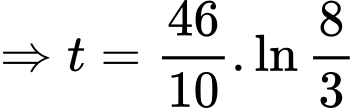
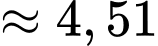 năm.
năm.
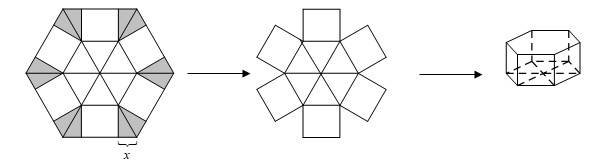
Câu 22 [696491]: Cho một tấm nhôm hình lục giác đều cạnh 90 cm. Người ta cắt ở mỗi đỉnh của tấm nhôm hai hình tam giác vuông bằng nhau, biết cạnh góc vuông nhỏ bằng  (cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm
(cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm 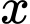 để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (đơn vị cm).
để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (đơn vị cm).
 (cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm
(cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm 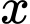 để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (đơn vị cm).
để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (đơn vị cm).
Điền đáp án: 15.
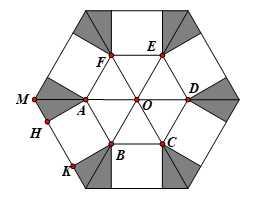
Điều kiện: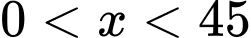
Cạnh đáy của lăng trụ lục giác đều là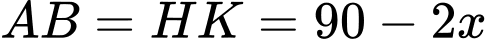
Chiều cao của lăng trụ lục giác đều là

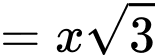
Diện tích đáy của lăng trụ lục giác đề là
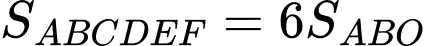
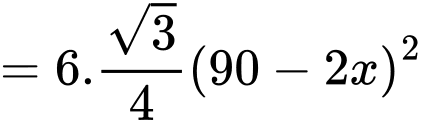
Thể tích của khối lăng trụ lục giác đều là
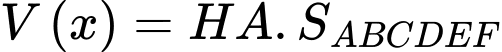
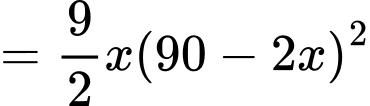
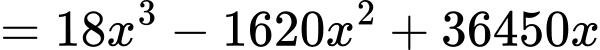
Xét hàm số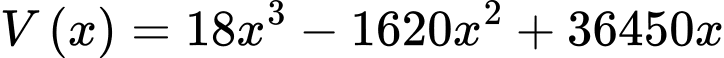 trên khoảng
trên khoảng 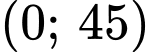 .
.
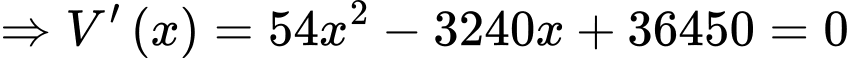
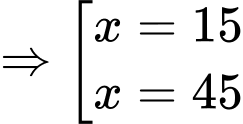
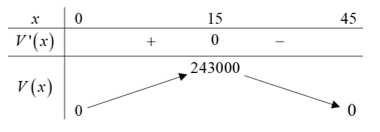
Bảng biến thiên:
Từ bảng biến thiên ta có: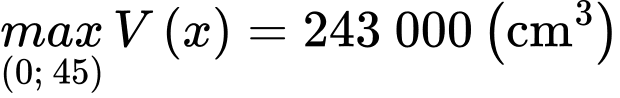 tại
tại 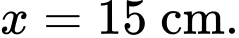 .
.

Điều kiện:
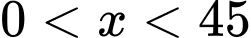
Cạnh đáy của lăng trụ lục giác đều là
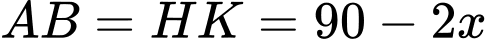
Chiều cao của lăng trụ lục giác đều là

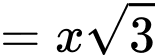
Diện tích đáy của lăng trụ lục giác đề là
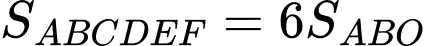
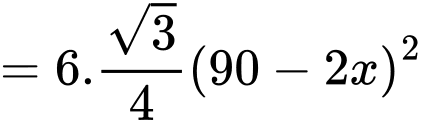
Thể tích của khối lăng trụ lục giác đều là
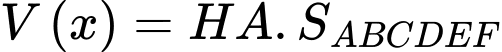
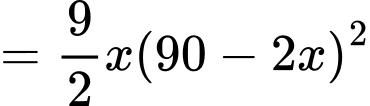
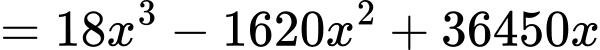
Xét hàm số
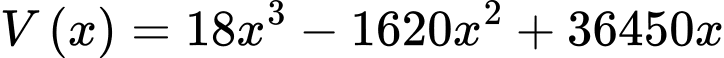 trên khoảng
trên khoảng 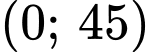 .
.
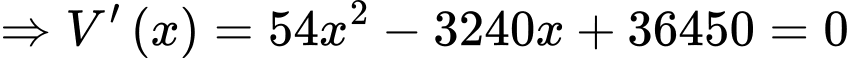
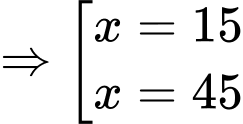
Bảng biến thiên:

Từ bảng biến thiên ta có:
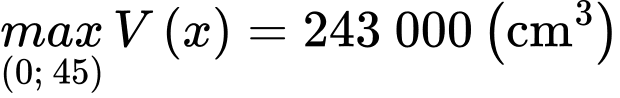 tại
tại 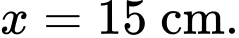 .
.