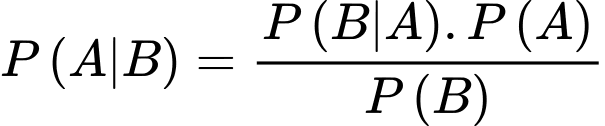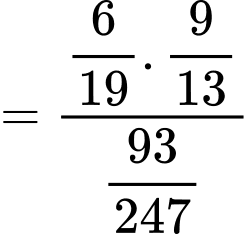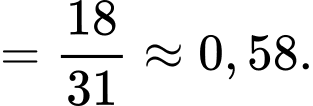PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [527797]: Trong không gian 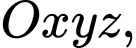 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 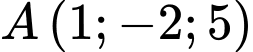 trên trục
trên trục 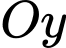 có tọa độ là
có tọa độ là
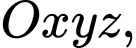 hình chiếu vuông góc của điểm
hình chiếu vuông góc của điểm 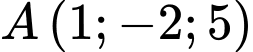 trên trục
trên trục 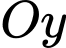 có tọa độ là
có tọa độ là A, 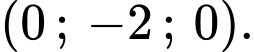
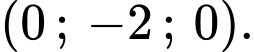
B, 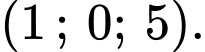
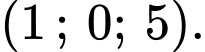
C, 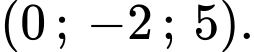
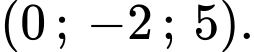
D, 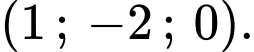
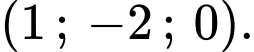
Chọn đáp án A.
Hình chiếu vuông góc của điểm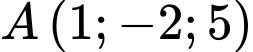 trên trục
trên trục 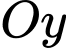 là
là 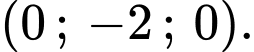 Đáp án: A
Đáp án: A
Hình chiếu vuông góc của điểm
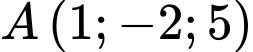 trên trục
trên trục 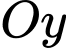 là
là 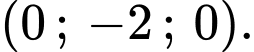 Đáp án: A
Đáp án: A
Câu 2 [307984]: Cho hình chóp 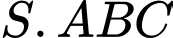 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 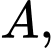
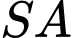 vuông góc với đáy,
vuông góc với đáy, 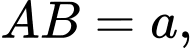
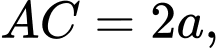
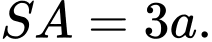 Tính thể tích khối chóp
Tính thể tích khối chóp 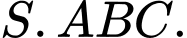
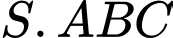 có đáy là tam giác vuông tại
có đáy là tam giác vuông tại 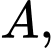
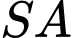 vuông góc với đáy,
vuông góc với đáy, 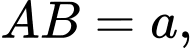
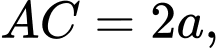
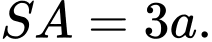 Tính thể tích khối chóp
Tính thể tích khối chóp 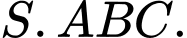
A, 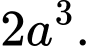
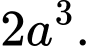
B, 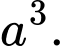
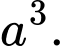
C, 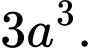
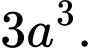
D, 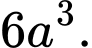
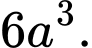
Chọn đáp án B.
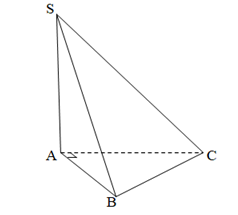
Diện tích đáy :
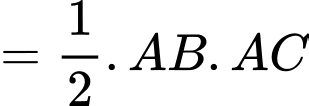
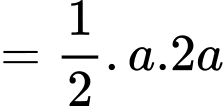
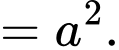
Do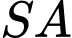 vuông góc với đáy nên
vuông góc với đáy nên 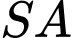 là chiều cao hình chóp.
là chiều cao hình chóp.
Vậy: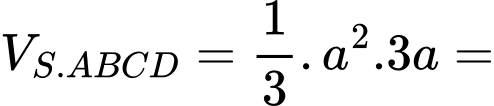
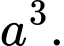 Đáp án: B
Đáp án: B

Diện tích đáy :

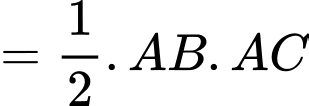
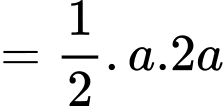
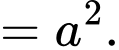
Do
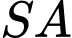 vuông góc với đáy nên
vuông góc với đáy nên 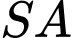 là chiều cao hình chóp.
là chiều cao hình chóp.Vậy:
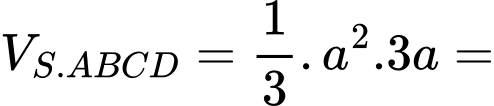
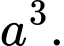 Đáp án: B
Đáp án: B
Câu 3 [527796]: Đồ thị của hàm số nào sau đây không có tiệm cận ngang?
A, 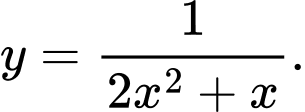
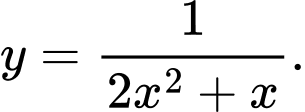
B, 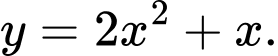
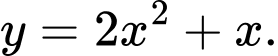
C, 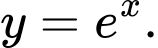
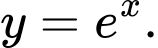
D, 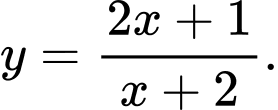
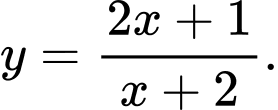
Chọn đáp án B.
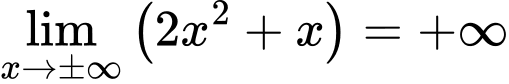
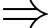 đồ thị của hàm số
đồ thị của hàm số 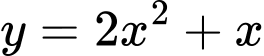 không có tiệm cận ngang. Đáp án: B
không có tiệm cận ngang. Đáp án: B
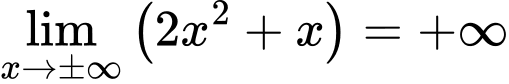
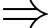 đồ thị của hàm số
đồ thị của hàm số 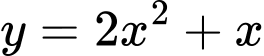 không có tiệm cận ngang. Đáp án: B
không có tiệm cận ngang. Đáp án: B
Câu 4 [677095]: Cho cấp số cộng 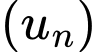 có số hạng đầu
có số hạng đầu 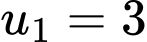 và công sai
và công sai  Tính
Tính 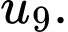
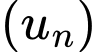 có số hạng đầu
có số hạng đầu 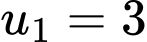 và công sai
và công sai  Tính
Tính 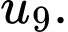
A, 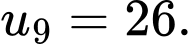
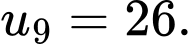
B, 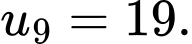
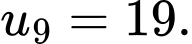
C, 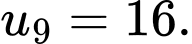
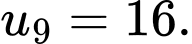
D, 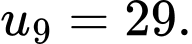
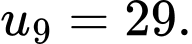
Chọn đáp án B.
Ta có: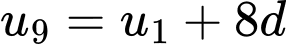

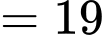 Đáp án: B
Đáp án: B
Ta có:
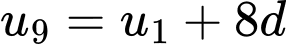

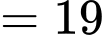 Đáp án: B
Đáp án: B
Câu 5 [326635]: Hàm số 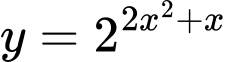 có đạo hàm là
có đạo hàm là
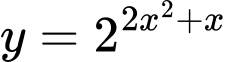 có đạo hàm là
có đạo hàm là A, 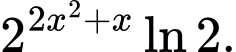
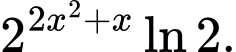
B, 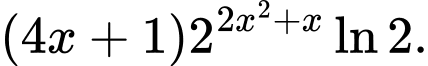
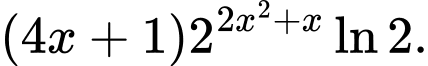
C, 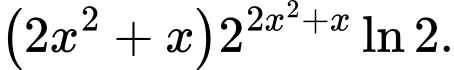
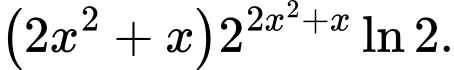
D, 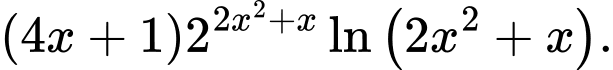
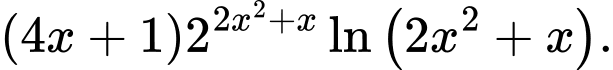
Chọn đáp án B.
Ta có: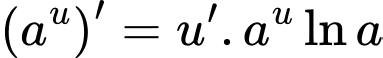 nên
nên 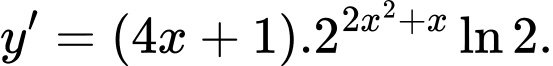 Đáp án: B
Đáp án: B
Ta có:
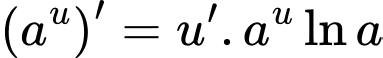 nên
nên 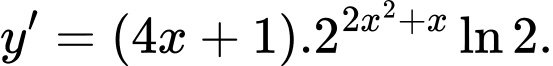 Đáp án: B
Đáp án: B
Câu 6 [256645]: Tập nghiệm của bất phương trình 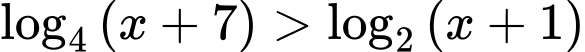 là khoảng
là khoảng 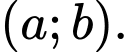 Khi đó tổng
Khi đó tổng 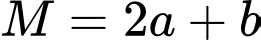 bằng
bằng
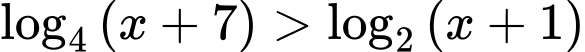 là khoảng
là khoảng 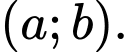 Khi đó tổng
Khi đó tổng 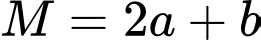 bằng
bằng A, 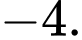
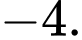
B, 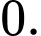
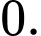
C, 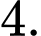
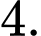
D, 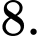
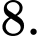
Chọn đáp án B.
Điều kiện xác định: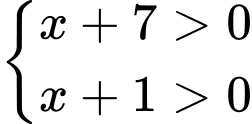

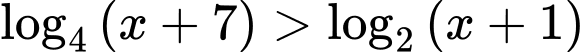
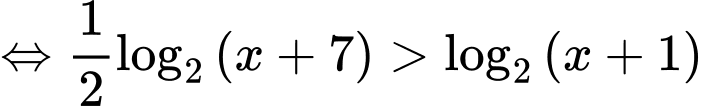
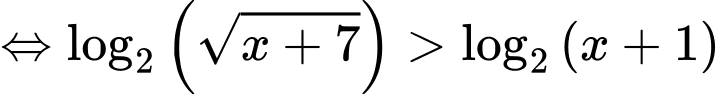
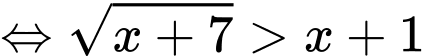
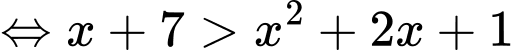
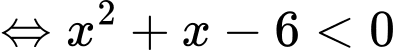

Kết hợp với ĐKXĐ, bất phương trình có tập nghiệm là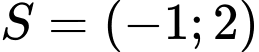
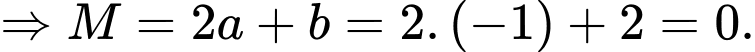 Đáp án: B
Đáp án: B
Điều kiện xác định:
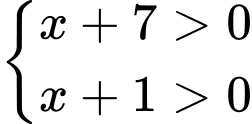

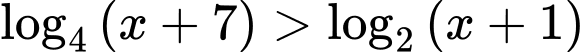
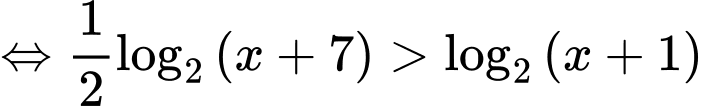
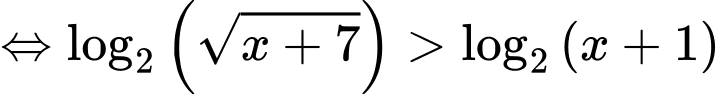
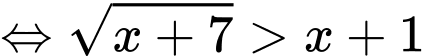
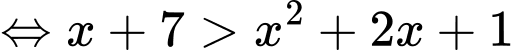
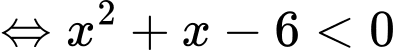

Kết hợp với ĐKXĐ, bất phương trình có tập nghiệm là
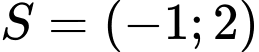
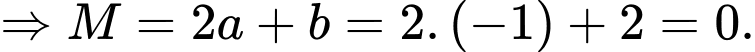 Đáp án: B
Đáp án: B
Câu 7 [527800]: Cho hàm số 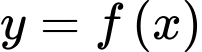 có đạo hàm
có đạo hàm 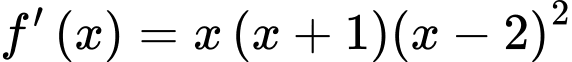 với mọi
với mọi 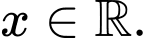 Giá trị nhỏ nhất của hàm số trên đoạn
Giá trị nhỏ nhất của hàm số trên đoạn 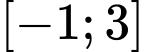 là
là
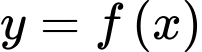 có đạo hàm
có đạo hàm 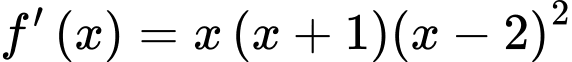 với mọi
với mọi 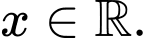 Giá trị nhỏ nhất của hàm số trên đoạn
Giá trị nhỏ nhất của hàm số trên đoạn 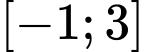 là
là A, 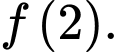
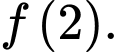
B, 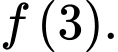
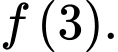
C, 

D, 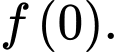
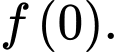
Chọn đáp án D.
Trên đoạn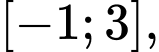 ta xét
ta xét 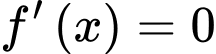
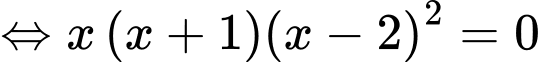
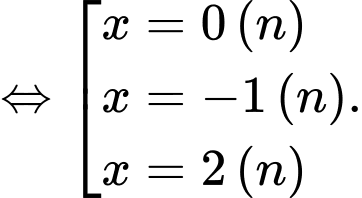
Ta có bảng biến thiên:
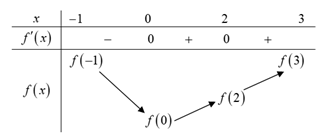
Vậy Đáp án: D
Đáp án: D
Trên đoạn
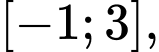 ta xét
ta xét 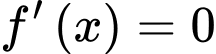
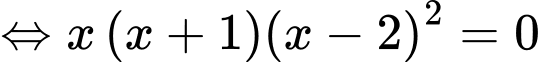
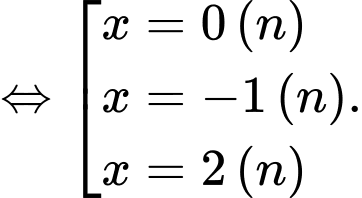
Ta có bảng biến thiên:

Vậy
 Đáp án: D
Đáp án: D
Câu 8 [696493]: Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu 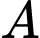 trong 50 ngày giao dịch liên tiếp.
trong 50 ngày giao dịch liên tiếp.

Số trung bình của mẫu số liệu ghép nhóm (đơn vị: nghìn đồng) là
 trong 50 ngày giao dịch liên tiếp.
trong 50 ngày giao dịch liên tiếp.
Số trung bình của mẫu số liệu ghép nhóm (đơn vị: nghìn đồng) là
A, 50.
B, 12528.
C, 125,28.
D, 10.
Chọn đáp án C.
Số trung bình của mẫu số liệu ghép nhóm là:
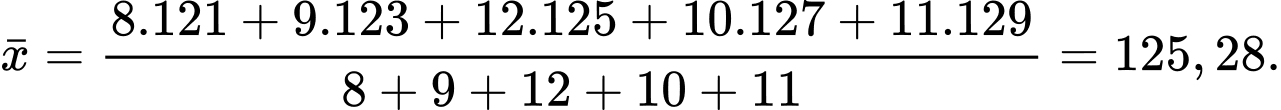 Đáp án: C
Đáp án: C
Số trung bình của mẫu số liệu ghép nhóm là:
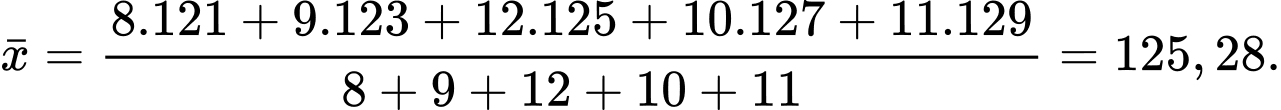 Đáp án: C
Đáp án: C
Câu 9 [379534]: Cho hình lập phương 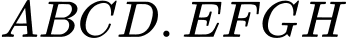 có cạnh bằng
có cạnh bằng 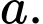 Tính
Tính 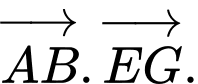
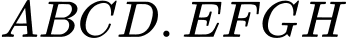 có cạnh bằng
có cạnh bằng 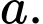 Tính
Tính 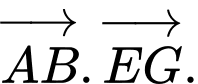
A, 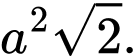
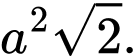
B, 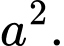
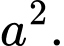
C, 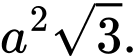
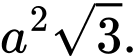
D, 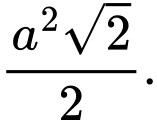
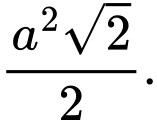
Chọn dáp án B.
Ta có: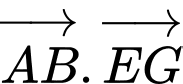
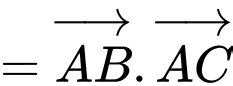
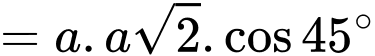
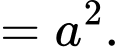 Đáp án: B
Đáp án: B
Ta có:
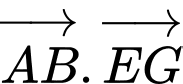
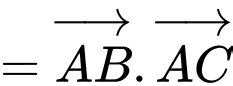
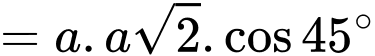
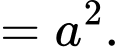 Đáp án: B
Đáp án: B
Câu 10 [322584]: Trong không gian 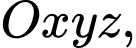 khoảng cách giữa hai mặt phẳng
khoảng cách giữa hai mặt phẳng  và
và 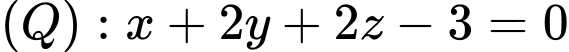 bằng
bằng
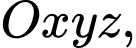 khoảng cách giữa hai mặt phẳng
khoảng cách giữa hai mặt phẳng  và
và 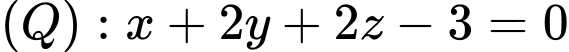 bằng
bằng A, 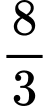
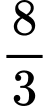
B, 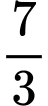
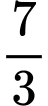
C, 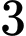
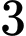
D, 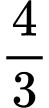
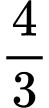
Chọn đáp án B.
Ta có: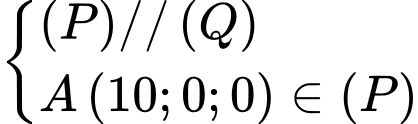
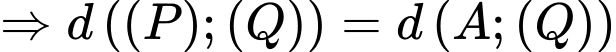
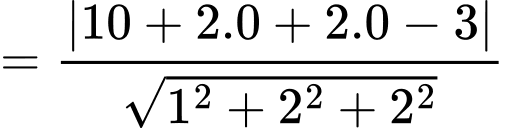
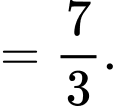 Đáp án: B
Đáp án: B
Ta có:
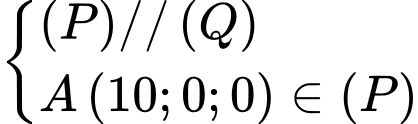
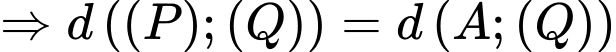
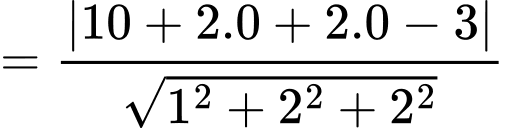
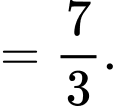 Đáp án: B
Đáp án: B Sử dụng thông tin dưới đây để trả lời câu 11 và câu 12

Câu 11 [703155]: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 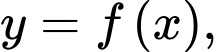 trục
trục 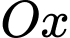 và các đường thẳng
và các đường thẳng 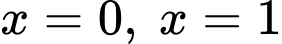 bằng
bằng
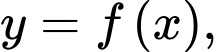 trục
trục 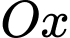 và các đường thẳng
và các đường thẳng 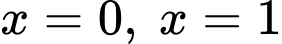 bằng
bằng A, 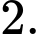
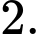
B, 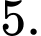
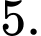
C, 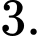
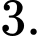
D, 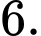
Chọn đáp án D.
Ta có: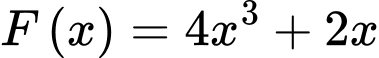 là một nguyên hàm của
là một nguyên hàm của 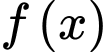 nên
nên 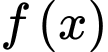
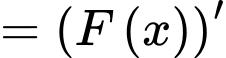
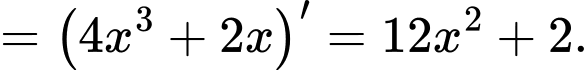
Diện tích hình phẳng giới hạn bởi đồ thị hàm số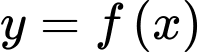 và các đường thẳng
và các đường thẳng 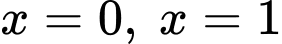 bằng
bằng
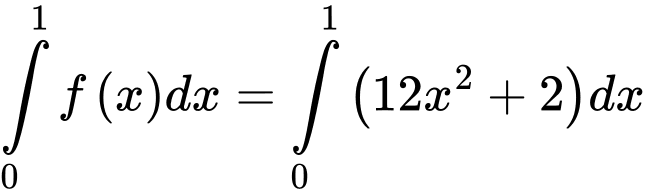
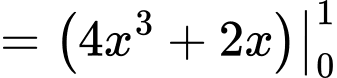
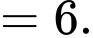 Đáp án: D
Đáp án: D
Ta có:
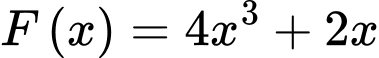 là một nguyên hàm của
là một nguyên hàm của 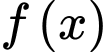 nên
nên 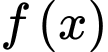
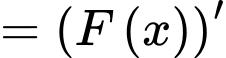
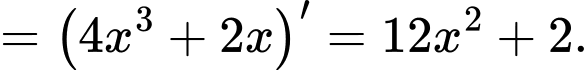
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
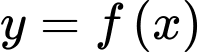 và các đường thẳng
và các đường thẳng 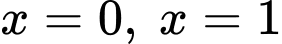 bằng
bằng 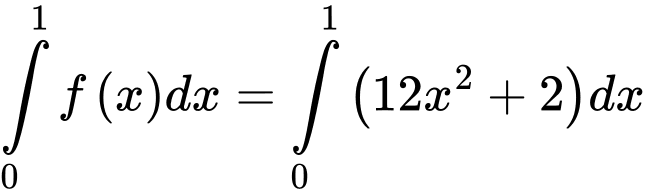
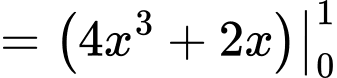
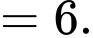 Đáp án: D
Đáp án: D
Câu 12 [703156]: Gọi 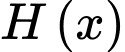 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 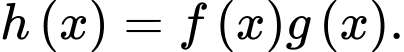 Phương án nào dưới đây đúng?
Phương án nào dưới đây đúng?
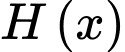 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 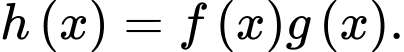 Phương án nào dưới đây đúng?
Phương án nào dưới đây đúng? A, 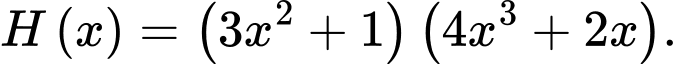
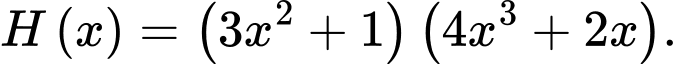
B, 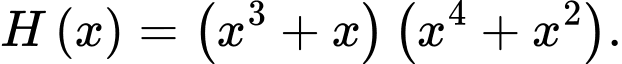
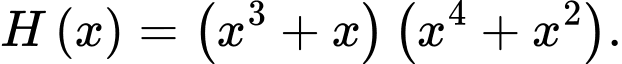
C, 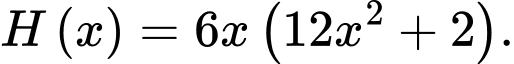
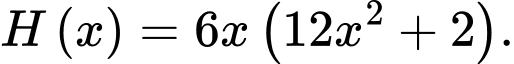
D, 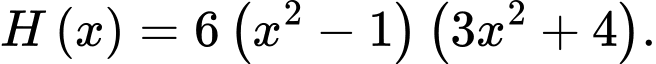
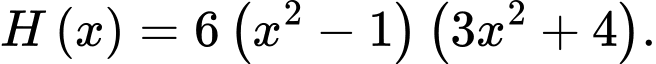
Chọn đáp án D.
Ta có:
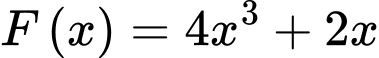 là một nguyên hàm của
là một nguyên hàm của 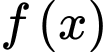 nên
nên 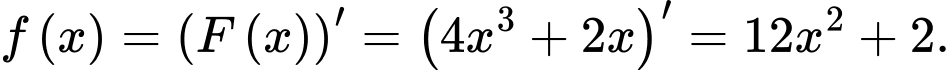
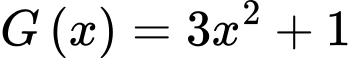 là một nguyên hàm của
là một nguyên hàm của 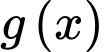 nên
nên 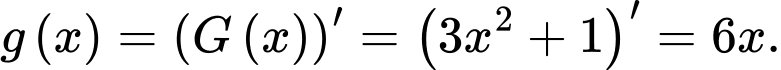
Khi đó: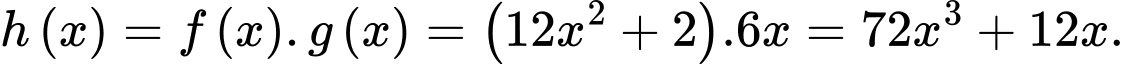
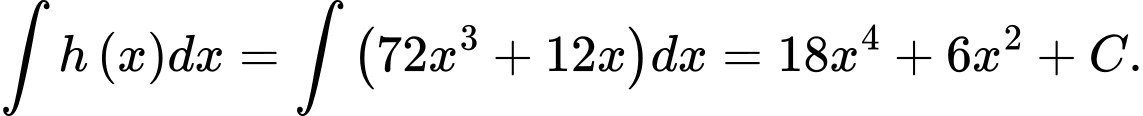
Vậy một nguyên hàm của hàm số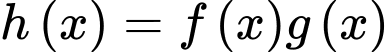 là
là 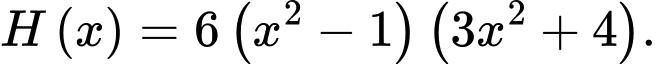 Đáp án: D
Đáp án: D
Ta có:
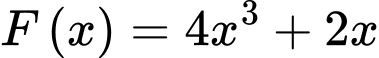 là một nguyên hàm của
là một nguyên hàm của 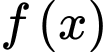 nên
nên 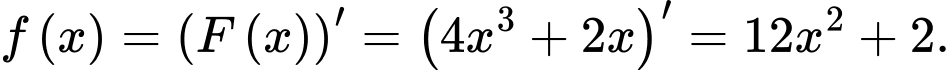
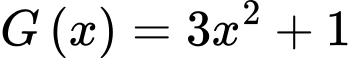 là một nguyên hàm của
là một nguyên hàm của 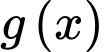 nên
nên 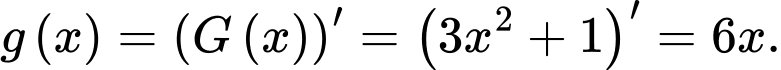
Khi đó:
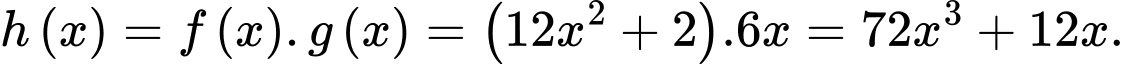
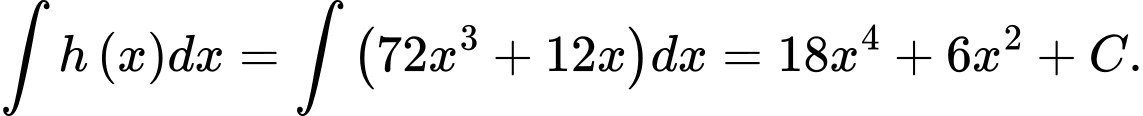
Vậy một nguyên hàm của hàm số
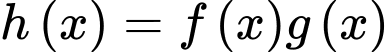 là
là 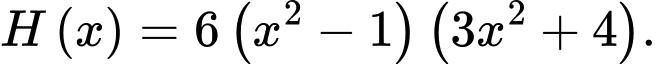 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [703157]: Cho hàm số 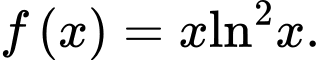
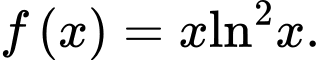
a) Đúng.
b) Đúng.
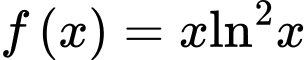
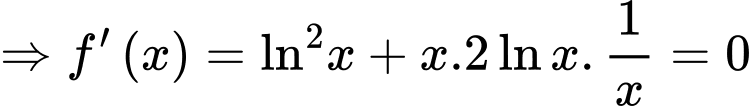
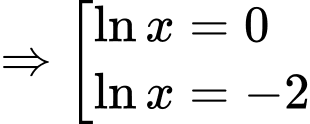
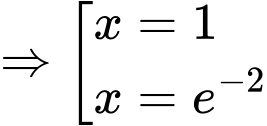
 Phương trình
Phương trình 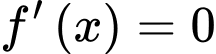 có đúng một nghiệm nguyên.
có đúng một nghiệm nguyên.
c) Sai.
Ta có: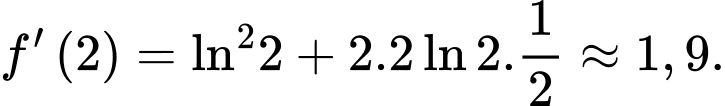
d) Đúng.
Hàm số trên đạt cực đại tại điểm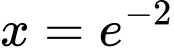
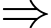 Giá trị cực của hàm số là
Giá trị cực của hàm số là 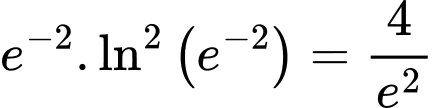
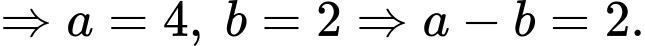
b) Đúng.
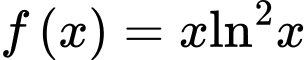
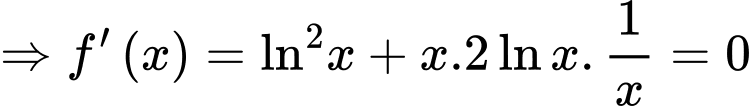
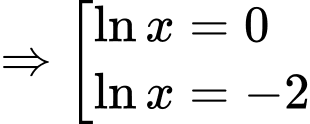
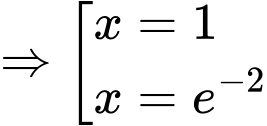
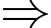 Phương trình
Phương trình 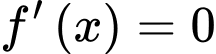 có đúng một nghiệm nguyên.
có đúng một nghiệm nguyên.c) Sai.
Ta có:
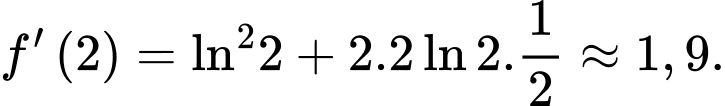
d) Đúng.
Hàm số trên đạt cực đại tại điểm
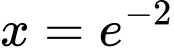
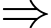 Giá trị cực của hàm số là
Giá trị cực của hàm số là 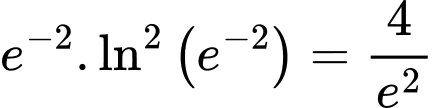
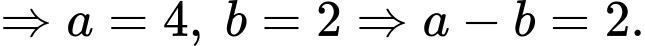
Câu 14 [696497]: Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai.
Gọi A là biến cố “Viên bi được chuyển từ hộp thứ nhất sang hộp thứ hai là viên bi xanh”.
Gọi B là biến cố “Hai viên bi được lấy ngẫu nhiên đồng thời từ hộp thứ hai là bi xanh”.
Gọi A là biến cố “Viên bi được chuyển từ hộp thứ nhất sang hộp thứ hai là viên bi xanh”.
Gọi B là biến cố “Hai viên bi được lấy ngẫu nhiên đồng thời từ hộp thứ hai là bi xanh”.
Thứ tự đáp án: Đúng, Đúng, Sai, Sai.
a) là xác suất lấy được hai viên bi từ hộp thứ hai khi biết viên bi được chuyển từ hộp thứ nhất sang hộp thứ hai là viên bi xanh. Khi đó, hộp thứ hai có tổng cộng 11 viên bi, trong đó có
là xác suất lấy được hai viên bi từ hộp thứ hai khi biết viên bi được chuyển từ hộp thứ nhất sang hộp thứ hai là viên bi xanh. Khi đó, hộp thứ hai có tổng cộng 11 viên bi, trong đó có 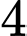 viên bi xanh, nên
viên bi xanh, nên 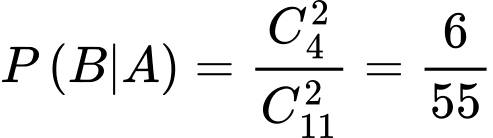 .
.
 Mệnh đề Đúng.
Mệnh đề Đúng.
b) YCBT Tính
Tính 
Ta có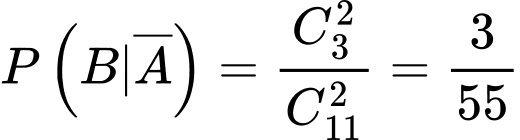 (Vì ta sẽ chuyển 1 viên bi đỏ từ hộp thứ nhất sang hộp thứ hai nên hộp thứ hai có tổng cộng 11 viên với 3 viên bi xanh)
(Vì ta sẽ chuyển 1 viên bi đỏ từ hộp thứ nhất sang hộp thứ hai nên hộp thứ hai có tổng cộng 11 viên với 3 viên bi xanh)
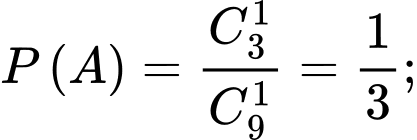
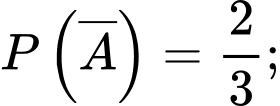
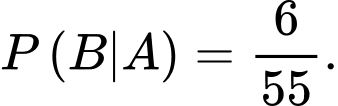
Từ đó, ta có sơ đồ cây sau:
Áp dụng công thức xác suất toàn phần, suy ra xác suất để hai viên bi lấy ra từ hộp thứ hai là bi xanh là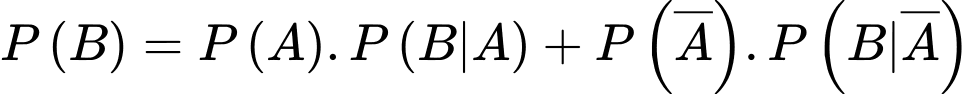
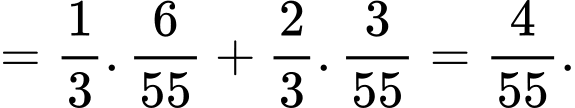
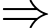 Mệnh đề Đúng.
Mệnh đề Đúng.
c) YCBT Tính
Tính 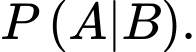
Áp dụng công thức Bayes, ta có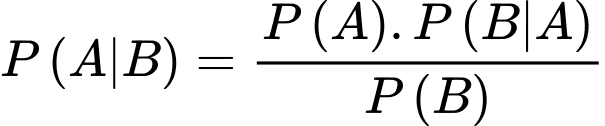
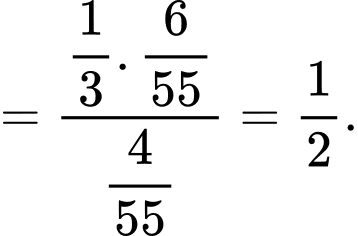
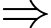 Mệnh đề Sai.
Mệnh đề Sai.
d) YCBT Tính
Tính 
Theo công thức Bayes, ta có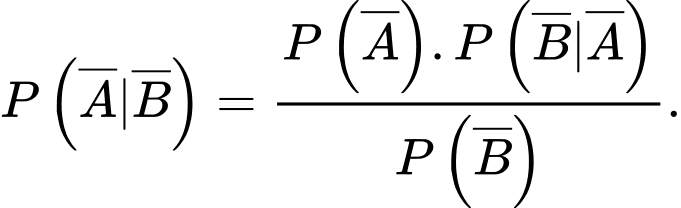 Do đó, ta cần đi tìm các dữ kiện còn thiếu ở đây là
Do đó, ta cần đi tìm các dữ kiện còn thiếu ở đây là  và
và 
Ta có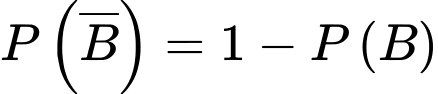
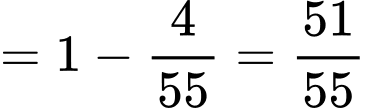 (theo tính chất của xác suất)
(theo tính chất của xác suất)
Lại có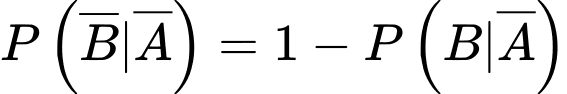
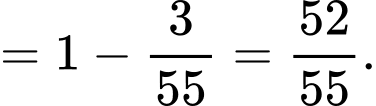
Suy ra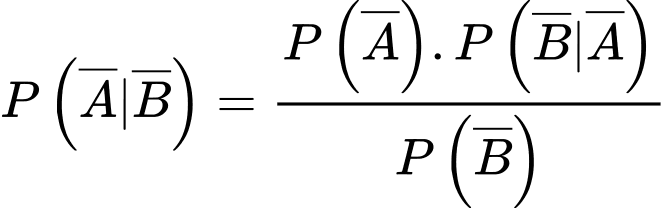
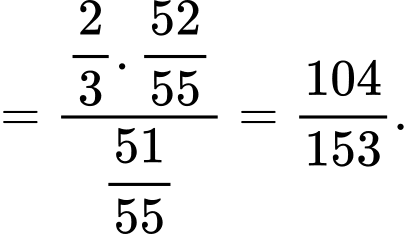
 Mệnh đề Sai.
Mệnh đề Sai.
a)
 là xác suất lấy được hai viên bi từ hộp thứ hai khi biết viên bi được chuyển từ hộp thứ nhất sang hộp thứ hai là viên bi xanh. Khi đó, hộp thứ hai có tổng cộng 11 viên bi, trong đó có
là xác suất lấy được hai viên bi từ hộp thứ hai khi biết viên bi được chuyển từ hộp thứ nhất sang hộp thứ hai là viên bi xanh. Khi đó, hộp thứ hai có tổng cộng 11 viên bi, trong đó có 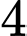 viên bi xanh, nên
viên bi xanh, nên 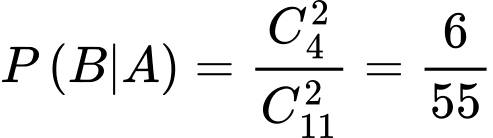 .
.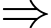 Mệnh đề Đúng.
Mệnh đề Đúng.b) YCBT
 Tính
Tính 
Ta có
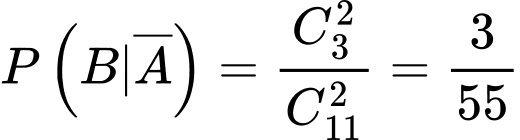 (Vì ta sẽ chuyển 1 viên bi đỏ từ hộp thứ nhất sang hộp thứ hai nên hộp thứ hai có tổng cộng 11 viên với 3 viên bi xanh)
(Vì ta sẽ chuyển 1 viên bi đỏ từ hộp thứ nhất sang hộp thứ hai nên hộp thứ hai có tổng cộng 11 viên với 3 viên bi xanh)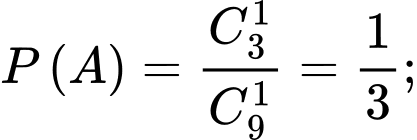
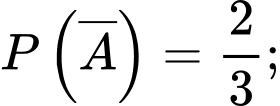
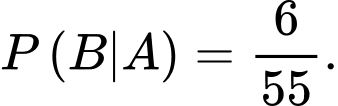
Từ đó, ta có sơ đồ cây sau:
Áp dụng công thức xác suất toàn phần, suy ra xác suất để hai viên bi lấy ra từ hộp thứ hai là bi xanh là
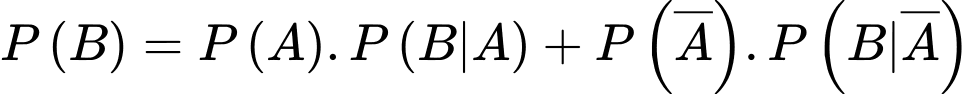
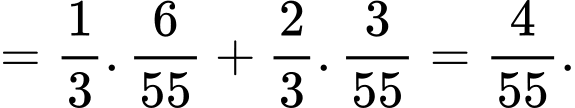
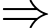 Mệnh đề Đúng.
Mệnh đề Đúng.c) YCBT
 Tính
Tính 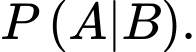
Áp dụng công thức Bayes, ta có
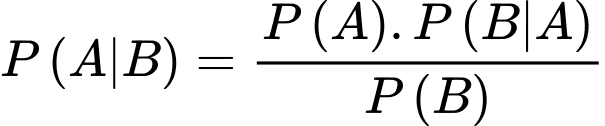
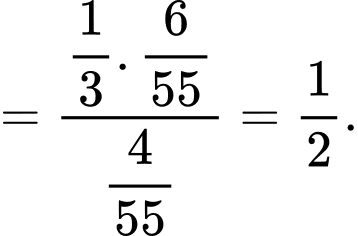
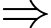 Mệnh đề Sai.
Mệnh đề Sai.d) YCBT
 Tính
Tính 
Theo công thức Bayes, ta có
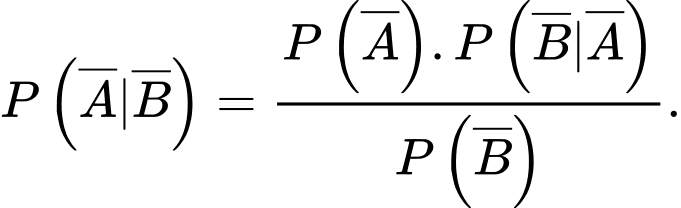 Do đó, ta cần đi tìm các dữ kiện còn thiếu ở đây là
Do đó, ta cần đi tìm các dữ kiện còn thiếu ở đây là  và
và 
Ta có
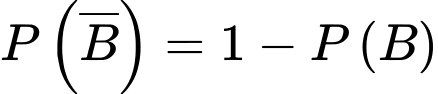
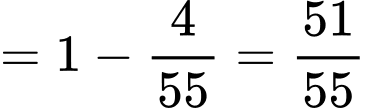 (theo tính chất của xác suất)
(theo tính chất của xác suất)Lại có
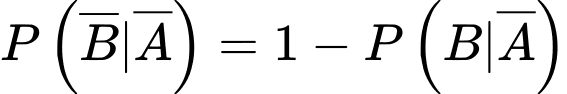
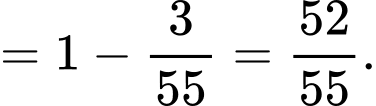
Suy ra
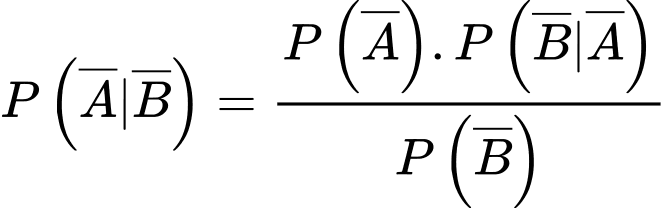
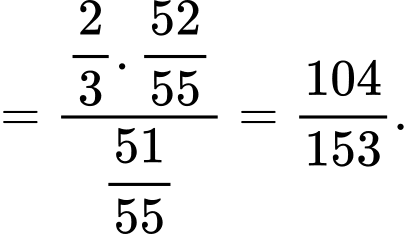
 Mệnh đề Sai.
Mệnh đề Sai.
Câu 15 [693835]: Đồ thị hàm số 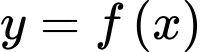 liên tục trên đoạn
liên tục trên đoạn 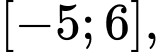 đi qua các điểm
đi qua các điểm 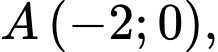
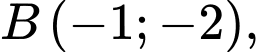
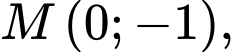
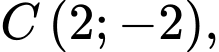
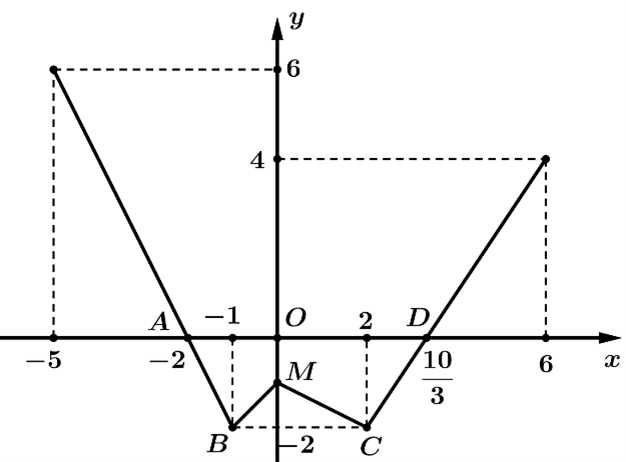
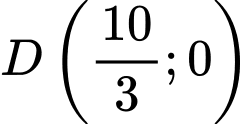 và được cho dưới dạng đường gấp khúc như hình vẽ bên. Gọi
và được cho dưới dạng đường gấp khúc như hình vẽ bên. Gọi 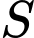 là diện tích hình phẳng giới hạn bởi đồ thị hàm số
là diện tích hình phẳng giới hạn bởi đồ thị hàm số 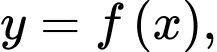 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 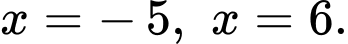
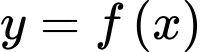 liên tục trên đoạn
liên tục trên đoạn 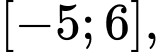 đi qua các điểm
đi qua các điểm 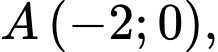
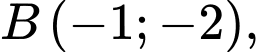
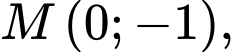
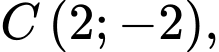
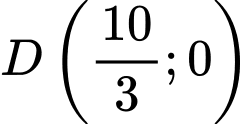 và được cho dưới dạng đường gấp khúc như hình vẽ bên. Gọi
và được cho dưới dạng đường gấp khúc như hình vẽ bên. Gọi 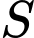 là diện tích hình phẳng giới hạn bởi đồ thị hàm số
là diện tích hình phẳng giới hạn bởi đồ thị hàm số 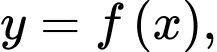 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 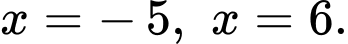

a) Đúng.
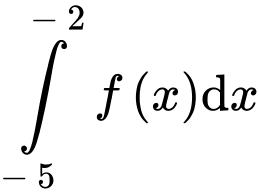
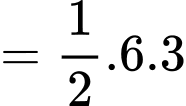
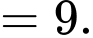
b) Đúng.
Vì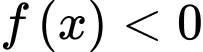 trên
trên 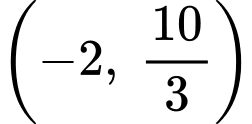
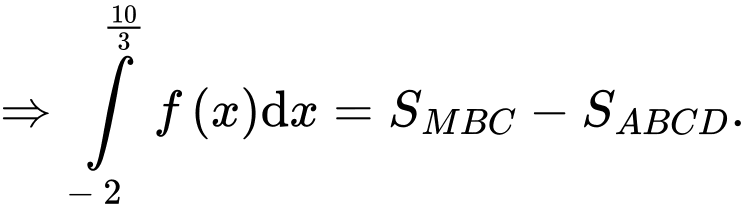
c) Đúng.
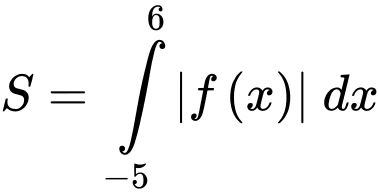
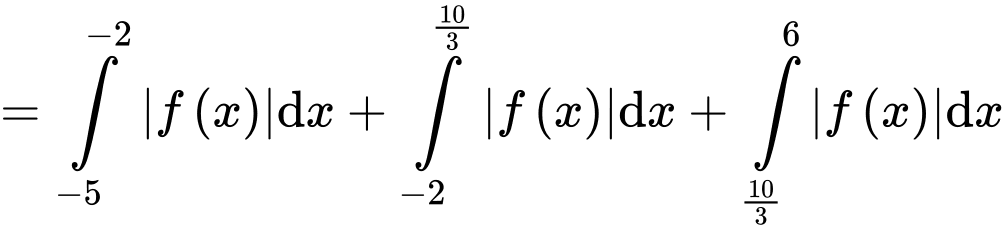
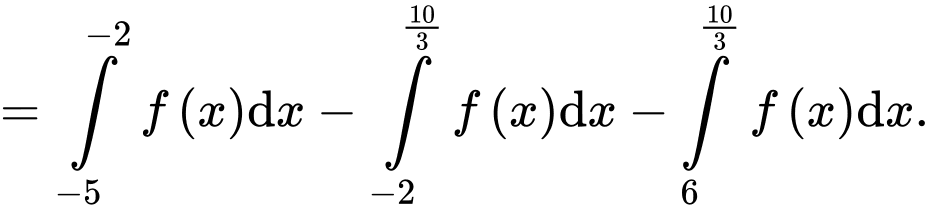
d) Sai.
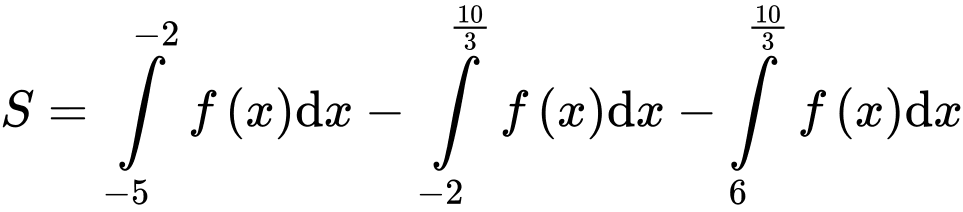
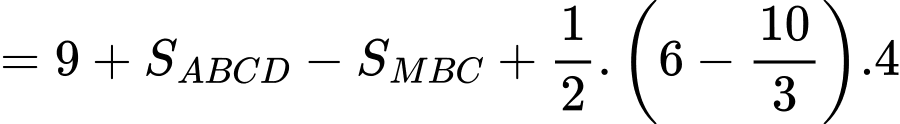
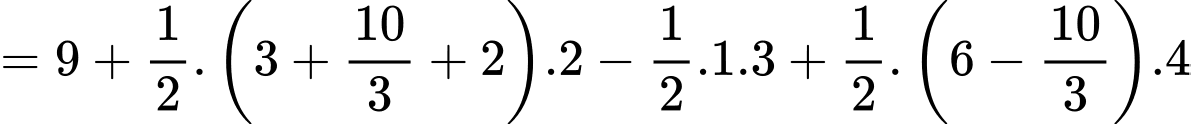
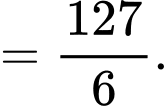
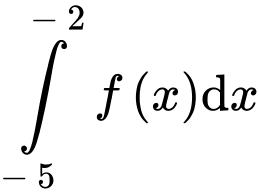
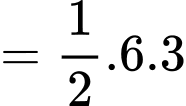
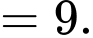
b) Đúng.
Vì
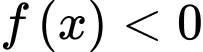 trên
trên 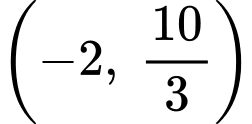
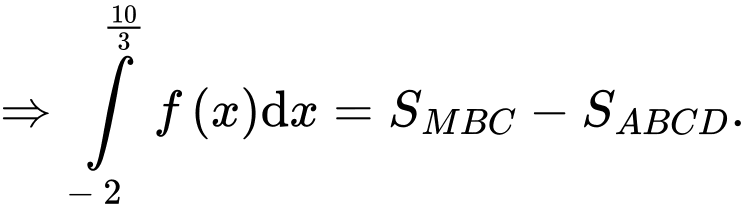
c) Đúng.
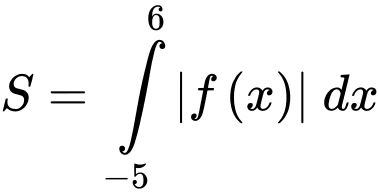
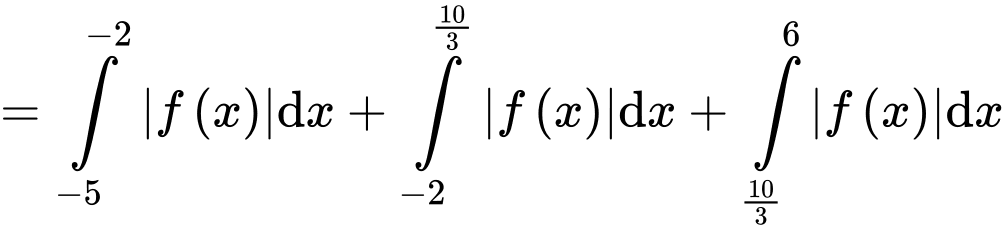
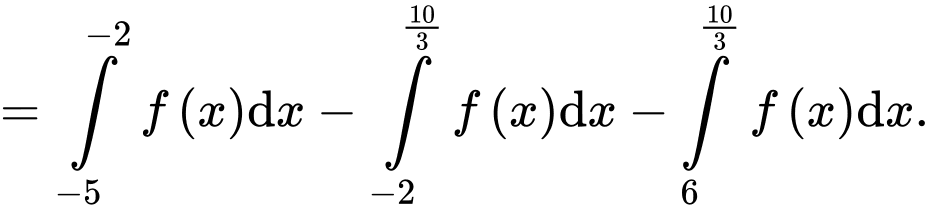
d) Sai.
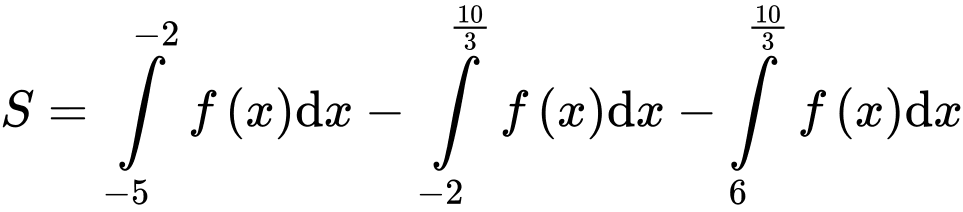
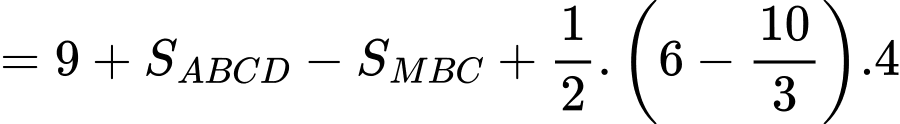
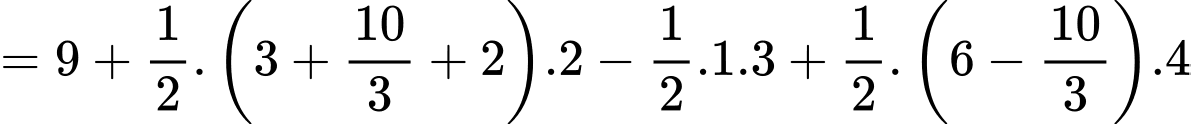
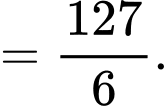
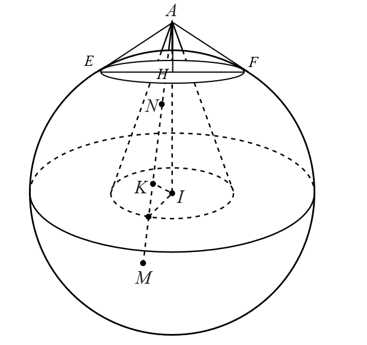
Câu 16 [703159]: Trong không gian 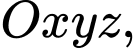 cho hình nón
cho hình nón  có đỉnh
có đỉnh 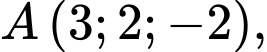 nhận
nhận 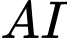 làm trục đối xứng với
làm trục đối xứng với 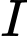 là tâm mặt cầu mặt cầu
là tâm mặt cầu mặt cầu 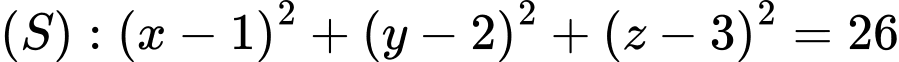 . Một đường sinh của hình nón
. Một đường sinh của hình nón  cắt mặt cầu
cắt mặt cầu 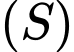 tại
tại 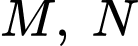 sao cho
sao cho 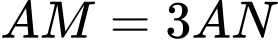 (tham khảo hình vẽ).
(tham khảo hình vẽ).
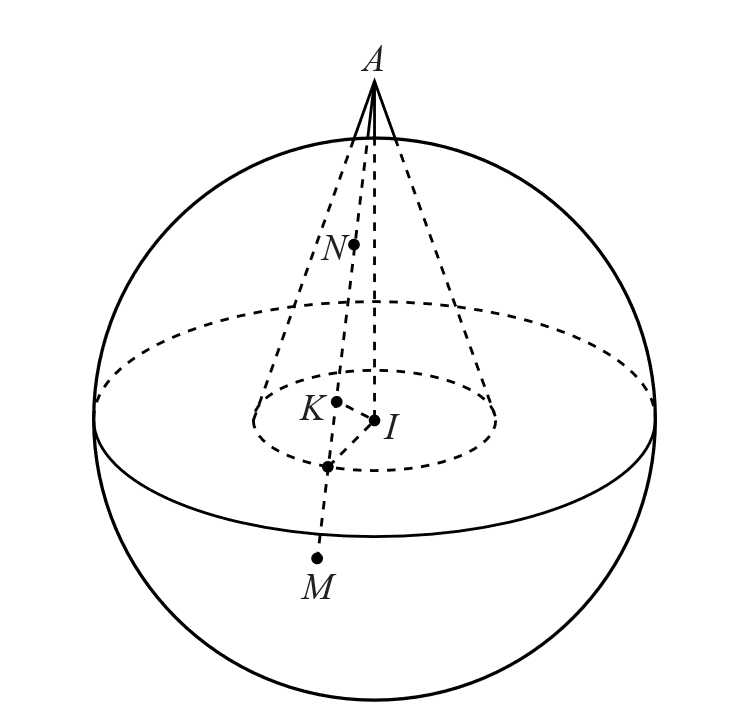
Biết rằng điểm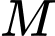 thuộc mặt phẳng
thuộc mặt phẳng 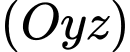 . Gọi
. Gọi 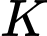 là hình chiếu vuông góc của
là hình chiếu vuông góc của 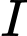 lên
lên 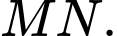
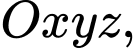 cho hình nón
cho hình nón  có đỉnh
có đỉnh 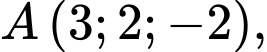 nhận
nhận 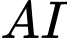 làm trục đối xứng với
làm trục đối xứng với 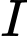 là tâm mặt cầu mặt cầu
là tâm mặt cầu mặt cầu 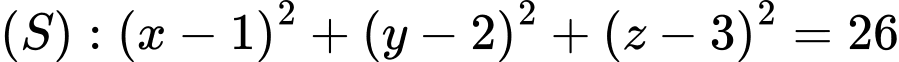 . Một đường sinh của hình nón
. Một đường sinh của hình nón  cắt mặt cầu
cắt mặt cầu 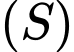 tại
tại 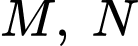 sao cho
sao cho 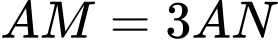 (tham khảo hình vẽ).
(tham khảo hình vẽ).
Biết rằng điểm
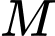 thuộc mặt phẳng
thuộc mặt phẳng 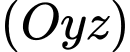 . Gọi
. Gọi 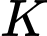 là hình chiếu vuông góc của
là hình chiếu vuông góc của 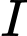 lên
lên 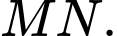
a) Đúng.
Vì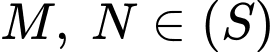
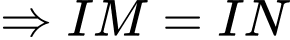
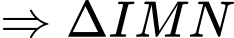 cân tại
cân tại 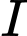
Mà
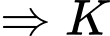 là trung điểm
là trung điểm 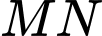
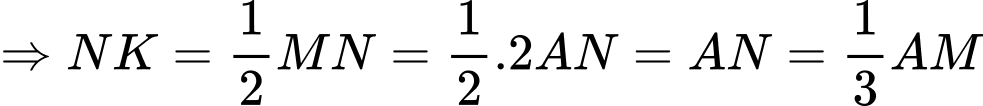 .
.
b) Đúng.
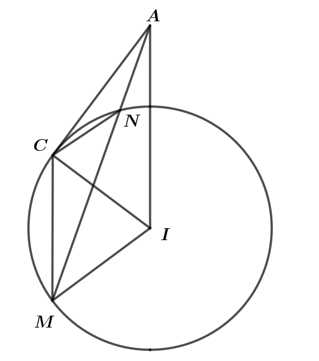
Từ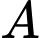 kẻ
kẻ 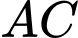 là tiếp tuyến tại
là tiếp tuyến tại  của đường tròn tâm
của đường tròn tâm 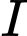 .
.
Ta có:
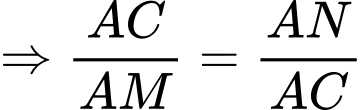
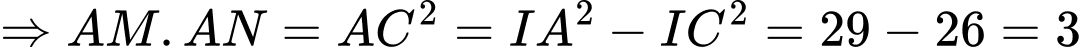
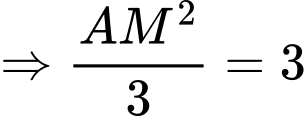
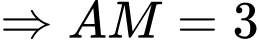
Vì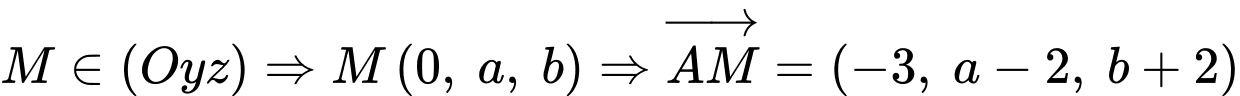
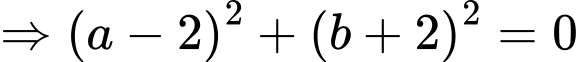
Mà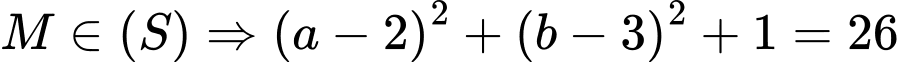
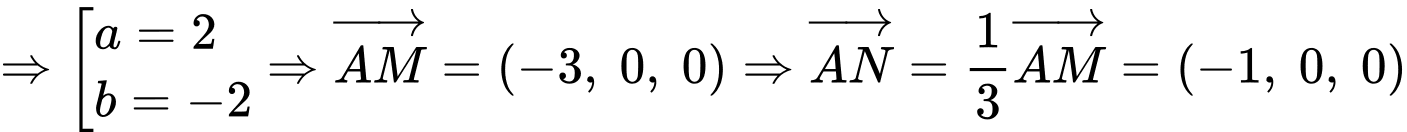
Gọi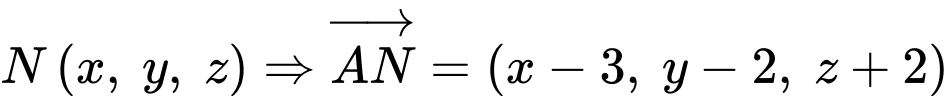
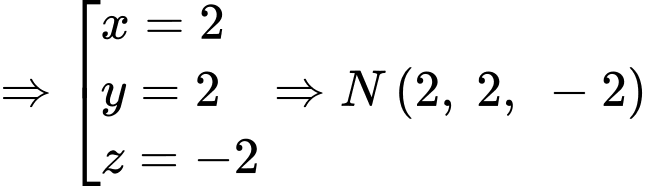
c) Đúng.
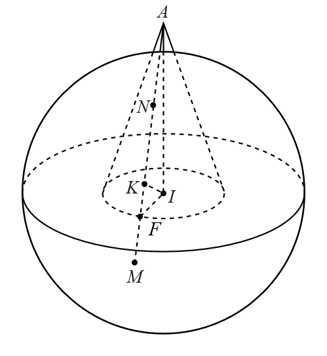
Ta có:

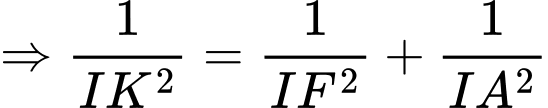
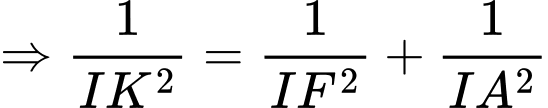
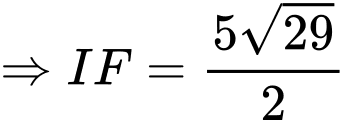 .
.
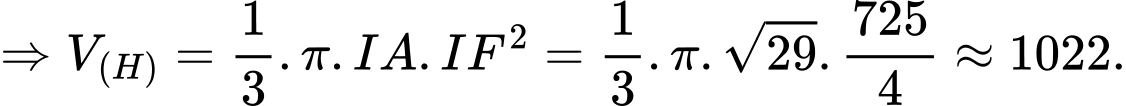
d) Sai.
Theo hình vẽ ta có đường tròn tâm
tâm 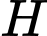 , bán kính bằng
, bán kính bằng 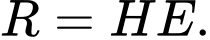
Ta có: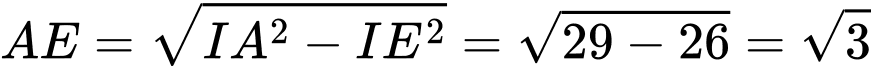
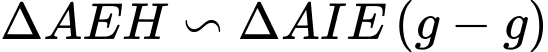
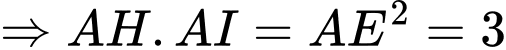
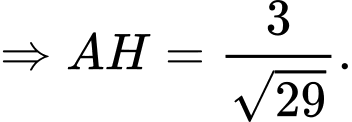
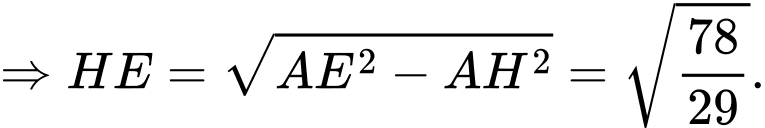
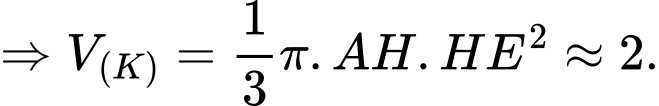
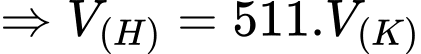
Vì
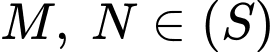
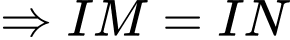
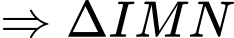 cân tại
cân tại 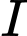
Mà

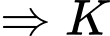 là trung điểm
là trung điểm 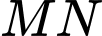
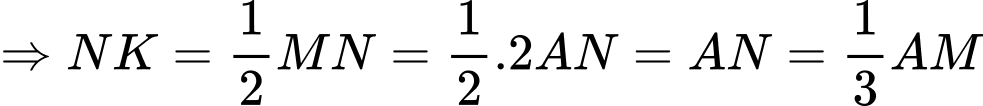 .
.b) Đúng.

Từ
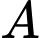 kẻ
kẻ 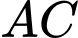 là tiếp tuyến tại
là tiếp tuyến tại  của đường tròn tâm
của đường tròn tâm 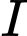 .
.Ta có:

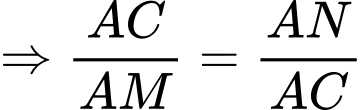
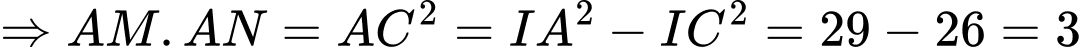
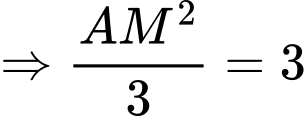
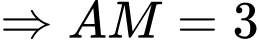
Vì
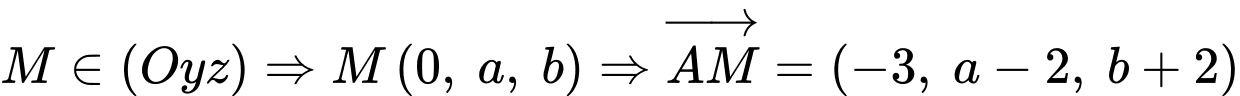
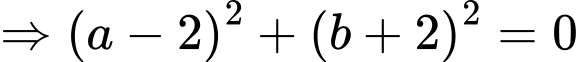
Mà
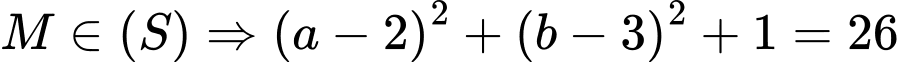
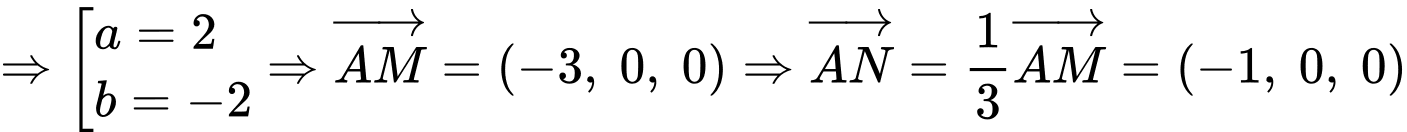
Gọi
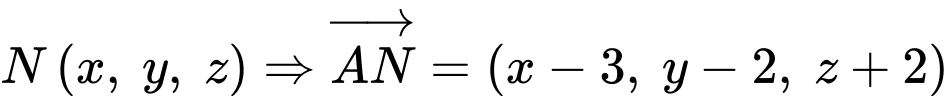
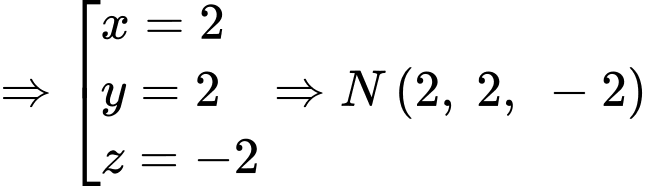
c) Đúng.

Ta có:


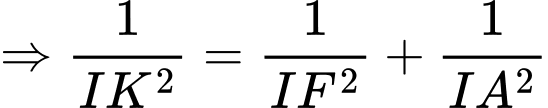
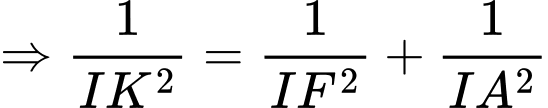
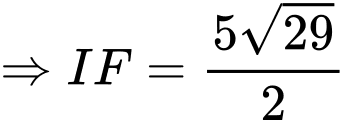 .
.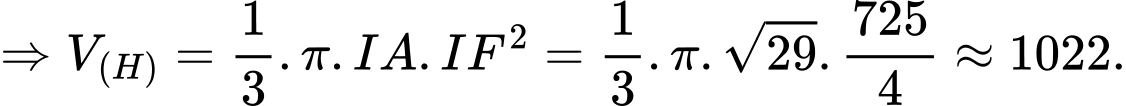
d) Sai.

Theo hình vẽ ta có đường tròn
 tâm
tâm 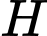 , bán kính bằng
, bán kính bằng 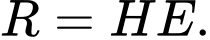
Ta có:
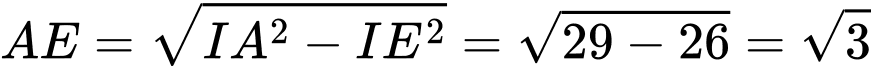
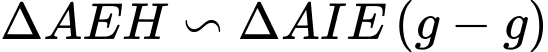
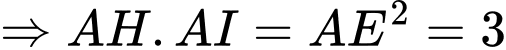
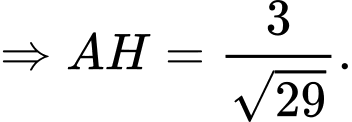
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [696287]: Cho hình chóp 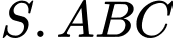 có đáy
có đáy 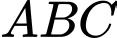 là tam giác vuông cân tại
là tam giác vuông cân tại 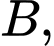
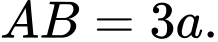 Biết
Biết  và khoảng cách từ
và khoảng cách từ 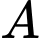 đến mặt phẳng
đến mặt phẳng 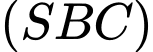 bằng
bằng  Tang của góc giữa hai đường thẳng
Tang của góc giữa hai đường thẳng  và
và 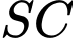 bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
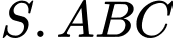 có đáy
có đáy 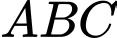 là tam giác vuông cân tại
là tam giác vuông cân tại 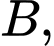
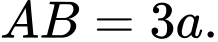 Biết
Biết  và khoảng cách từ
và khoảng cách từ 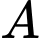 đến mặt phẳng
đến mặt phẳng 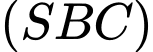 bằng
bằng  Tang của góc giữa hai đường thẳng
Tang của góc giữa hai đường thẳng  và
và 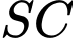 bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 1,12.
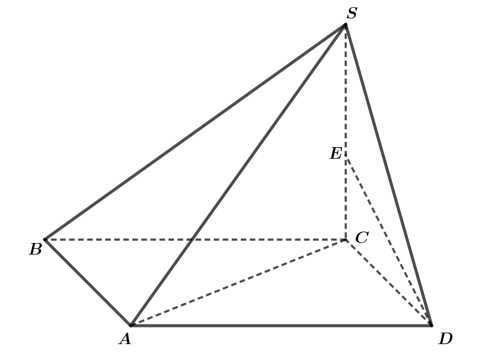
Kẻ
Mà
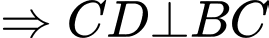
Có
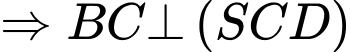
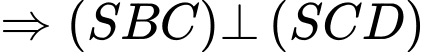
Kẻ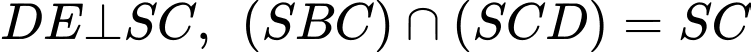

Có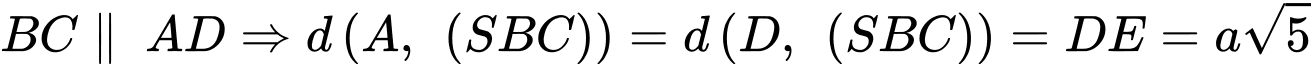
Có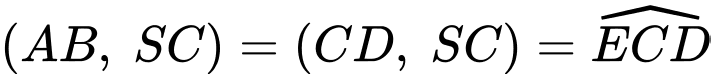
Xét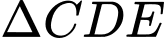 vuông tại
vuông tại 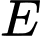 có:
có: 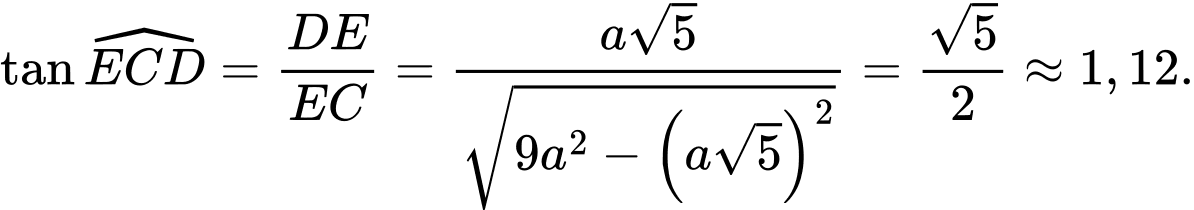

Kẻ

Mà

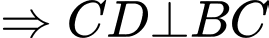
Có

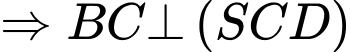
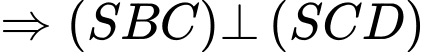
Kẻ
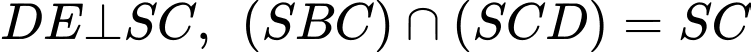

Có
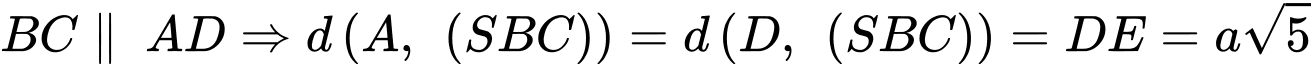
Có
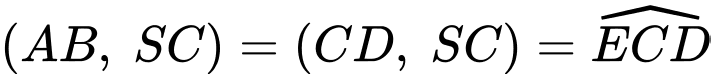
Xét
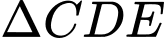 vuông tại
vuông tại 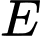 có:
có: 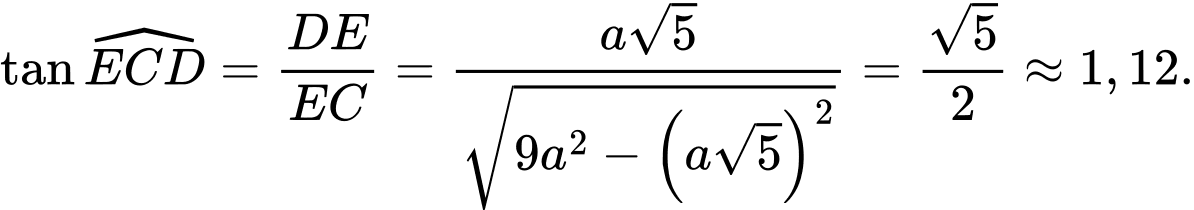
Câu 18 [696499]: Một nhà khoa học có 7 chai thuốc, trong đó có đúng 1 chai thuốc độc. Chất độc sẽ giết chết bất kỳ sinh vật nào uống phải trong vòng 1 giờ. Cần tối thiểu bao nhiêu con chuột thí nghiệm để nhà khoa học tìm ra chai thuốc độc trong đúng 1 giờ (thời gian cho con chuột thí nghiệm thử thuốc là không đáng kể)?
Điền đáp án: 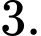
Minh họa:
0: không cho uống. 1: cho uống.
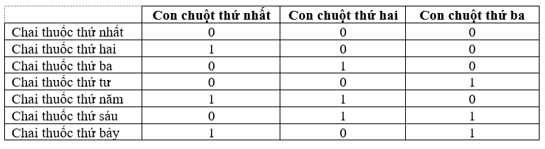
Không có con chuột nào chết Chai thứ nhất có độc.
Chai thứ nhất có độc.
Chỉ có con chuột thứ nhất chết Chai thứ hai có độc.
Chai thứ hai có độc.
Chỉ có con chuột thứ hai chết Chai thứ ba có độc.
Chai thứ ba có độc.
Chỉ có con chuột thứ ba chết Chai thứ tư có độc.
Chai thứ tư có độc.
Con chuột thứ nhất và thứ hai chết Chai thứ năm có độc.
Chai thứ năm có độc.
Con chuột thứ hai và thứ ba chết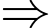 Chai thứ sáu có độc.
Chai thứ sáu có độc.
Con chuột thứ nhất và thứ ba chết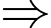 Chai thứ bảy có độc.
Chai thứ bảy có độc.
Thậm chí: 3 con chuột có thể thử được 8 chai thuốc (chai thuốc thứ tám cho 3 con chuột thử, nếu cả 3 con đều chết thì chai thuốc thứ tám có độc).
Vậy, chỉ cần 3 con chuột ta có thể thử 7 chai thuốc.
Bằng cách này, ta có công thức sau: với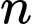 con chuột, chúng ta có thể thử
con chuột, chúng ta có thể thử 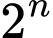 chai rượu.
chai rượu.
Áp dụng với bài toán trên ta có:
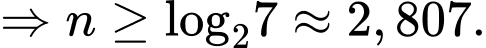
Vì nên giá trị nhỏ nhất của
nên giá trị nhỏ nhất của 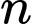 là 3.
là 3.
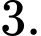
Minh họa:
0: không cho uống. 1: cho uống.

Không có con chuột nào chết
 Chai thứ nhất có độc.
Chai thứ nhất có độc. Chỉ có con chuột thứ nhất chết
 Chai thứ hai có độc.
Chai thứ hai có độc. Chỉ có con chuột thứ hai chết
 Chai thứ ba có độc.
Chai thứ ba có độc. Chỉ có con chuột thứ ba chết
 Chai thứ tư có độc.
Chai thứ tư có độc. Con chuột thứ nhất và thứ hai chết
 Chai thứ năm có độc.
Chai thứ năm có độc. Con chuột thứ hai và thứ ba chết
 Chai thứ sáu có độc.
Chai thứ sáu có độc. Con chuột thứ nhất và thứ ba chết
 Chai thứ bảy có độc.
Chai thứ bảy có độc. Thậm chí: 3 con chuột có thể thử được 8 chai thuốc (chai thuốc thứ tám cho 3 con chuột thử, nếu cả 3 con đều chết thì chai thuốc thứ tám có độc).
Vậy, chỉ cần 3 con chuột ta có thể thử 7 chai thuốc.
Bằng cách này, ta có công thức sau: với
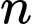 con chuột, chúng ta có thể thử
con chuột, chúng ta có thể thử 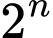 chai rượu.
chai rượu. Áp dụng với bài toán trên ta có:

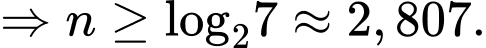
Vì
 nên giá trị nhỏ nhất của
nên giá trị nhỏ nhất của 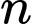 là 3.
là 3.
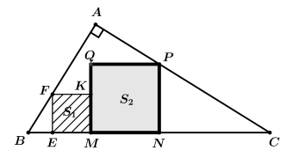
Câu 19 [693542]: Từ một miếng vật liệu hình tam giác 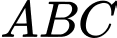 vuông tại
vuông tại 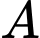 có
có 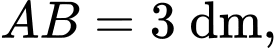
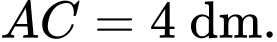 Người ta muốn cắt từ đó ra 2 miếng hình vuông, mà mỗi hình vuông này đều có 2 đỉnh nằm trên cạnh huyền của tam giác
Người ta muốn cắt từ đó ra 2 miếng hình vuông, mà mỗi hình vuông này đều có 2 đỉnh nằm trên cạnh huyền của tam giác 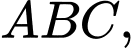 còn đỉnh thứ 3 của mỗi hình nằm trên một cạnh khác của tam giác (như hình vẽ). Gọi diện tích các hình này là
còn đỉnh thứ 3 của mỗi hình nằm trên một cạnh khác của tam giác (như hình vẽ). Gọi diện tích các hình này là 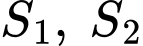 (đơn vị deximét vuông). Hãy tính giá trị nhỏ nhất của tổng diện tích vật liệu được cắt ra. (kết quả làm tròn đến hàng phần mười).
(đơn vị deximét vuông). Hãy tính giá trị nhỏ nhất của tổng diện tích vật liệu được cắt ra. (kết quả làm tròn đến hàng phần mười).
 vuông tại
vuông tại  có
có 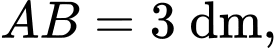
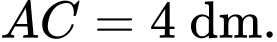 Người ta muốn cắt từ đó ra 2 miếng hình vuông, mà mỗi hình vuông này đều có 2 đỉnh nằm trên cạnh huyền của tam giác
Người ta muốn cắt từ đó ra 2 miếng hình vuông, mà mỗi hình vuông này đều có 2 đỉnh nằm trên cạnh huyền của tam giác 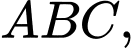 còn đỉnh thứ 3 của mỗi hình nằm trên một cạnh khác của tam giác (như hình vẽ). Gọi diện tích các hình này là
còn đỉnh thứ 3 của mỗi hình nằm trên một cạnh khác của tam giác (như hình vẽ). Gọi diện tích các hình này là 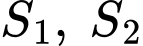 (đơn vị deximét vuông). Hãy tính giá trị nhỏ nhất của tổng diện tích vật liệu được cắt ra. (kết quả làm tròn đến hàng phần mười).
(đơn vị deximét vuông). Hãy tính giá trị nhỏ nhất của tổng diện tích vật liệu được cắt ra. (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 2,9.
Đặt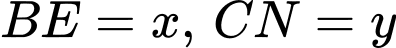
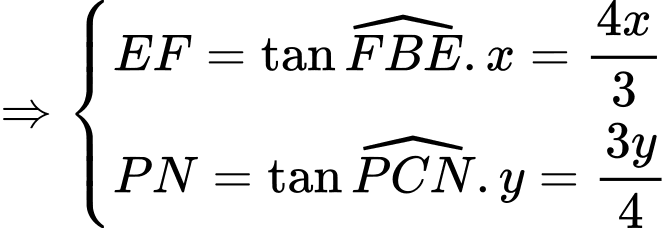
Ta có: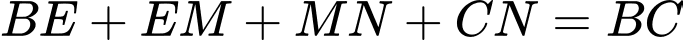
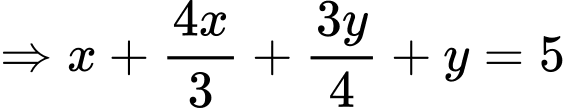
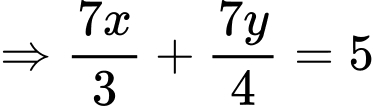
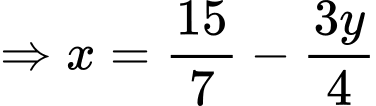
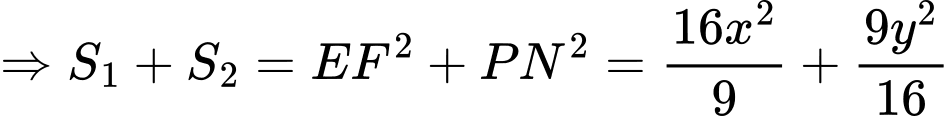
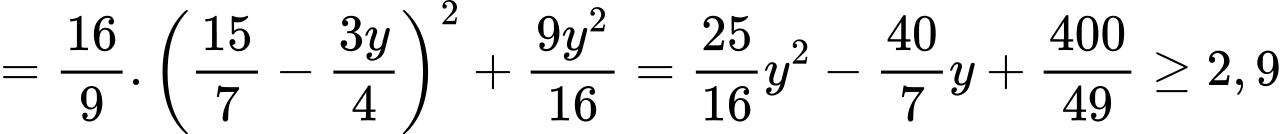
Đặt
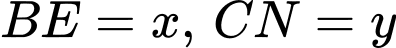
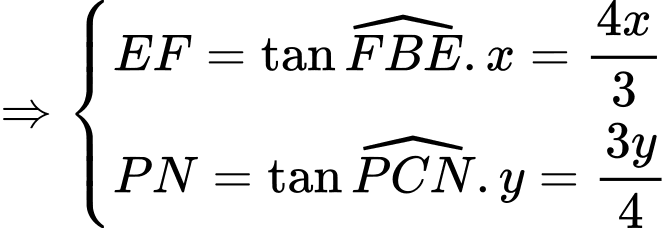
Ta có:
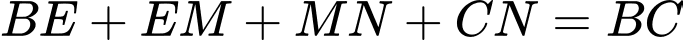
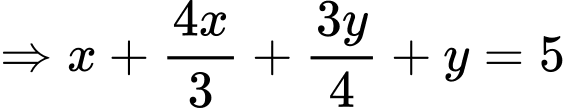
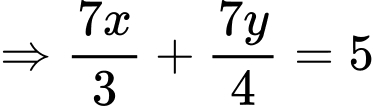
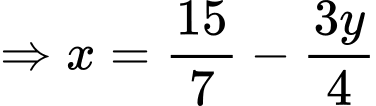
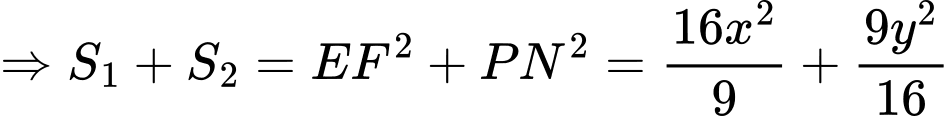
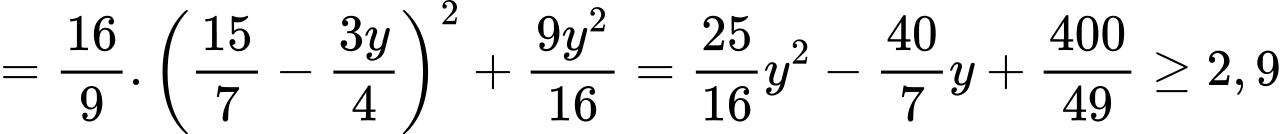
Câu 20 [703161]: Trong không gian với hệ trục toạ độ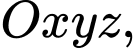 cho hai mặt cầu
cho hai mặt cầu 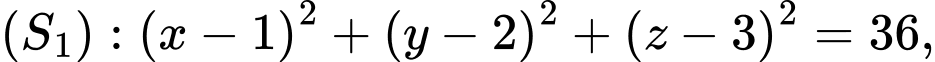
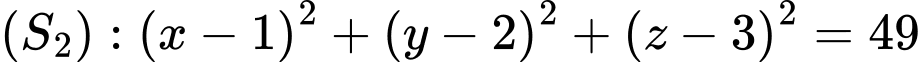 và điểm
và điểm 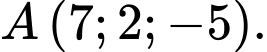 Xét đường thẳng
Xét đường thẳng  di động luôn tiếp xúc với
di động luôn tiếp xúc với 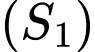 đồng thời cắt
đồng thời cắt 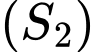 tại hai điểm
tại hai điểm 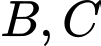 phân biệt. Diện tích lớn nhất của tam giác
phân biệt. Diện tích lớn nhất của tam giác 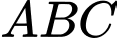 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
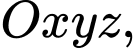 cho hai mặt cầu
cho hai mặt cầu 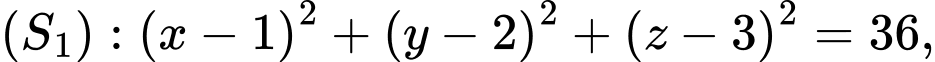
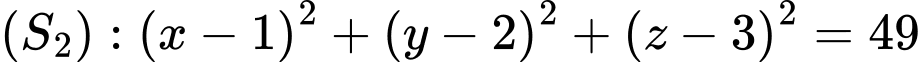 và điểm
và điểm 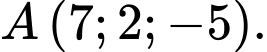 Xét đường thẳng
Xét đường thẳng  di động luôn tiếp xúc với
di động luôn tiếp xúc với 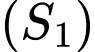 đồng thời cắt
đồng thời cắt 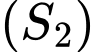 tại hai điểm
tại hai điểm 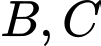 phân biệt. Diện tích lớn nhất của tam giác
phân biệt. Diện tích lớn nhất của tam giác 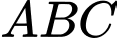 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 57,7.
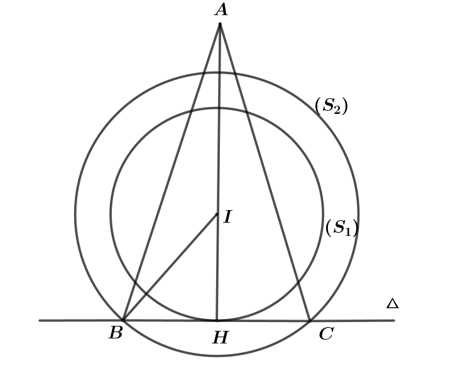
Mặt cầu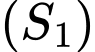 có tâm
có tâm 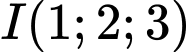 ,
, 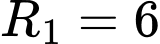 .
.
Mặt cầu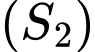 có tâm
có tâm 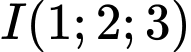 ,
, 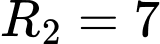 .
.
Ta có: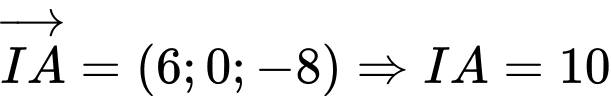 .
.
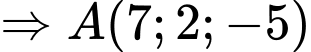 nằm ngoài
nằm ngoài 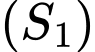 và
và 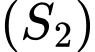 .
.
Gọi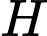 là giao điểm của đường thẳng
là giao điểm của đường thẳng 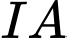 với mặt cầu
với mặt cầu 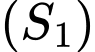 .
.
Diện tích tam giác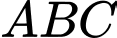 lớn nhất khi
lớn nhất khi  tiếp xúc với
tiếp xúc với 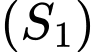 tại tiếp điểm
tại tiếp điểm 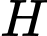 .
.
Phương trình đường thẳng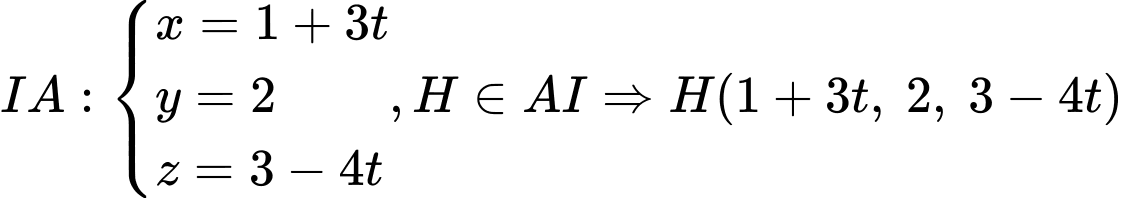 .
.
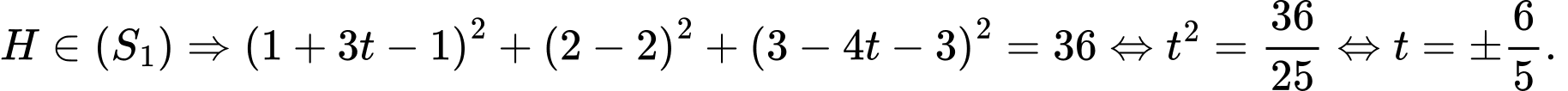
Với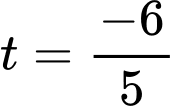
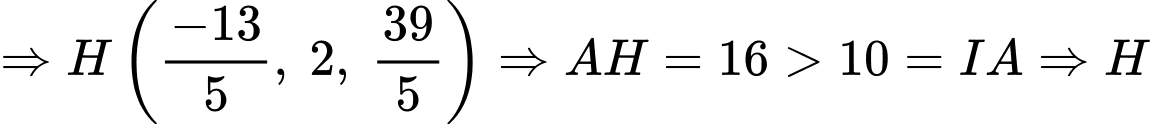 là điểm cần tìm.
là điểm cần tìm.
Trong tam giác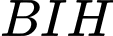 vuông tại
vuông tại 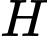 có:
có:  .
.
Diện tích lớn nhất của tam giác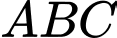 là
là 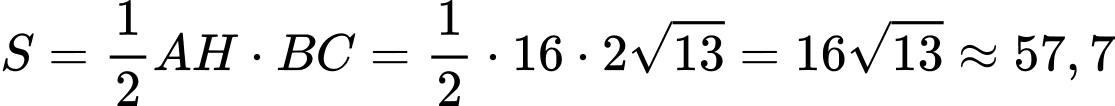 .
.

Mặt cầu
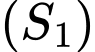 có tâm
có tâm 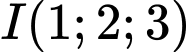 ,
, 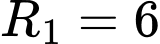 .
.Mặt cầu
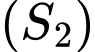 có tâm
có tâm 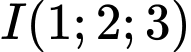 ,
, 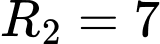 .
.Ta có:
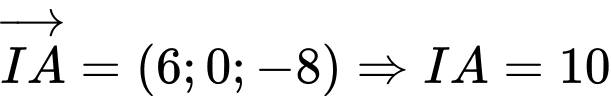 .
.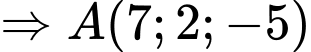 nằm ngoài
nằm ngoài 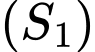 và
và 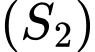 .
.Gọi
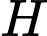 là giao điểm của đường thẳng
là giao điểm của đường thẳng 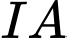 với mặt cầu
với mặt cầu 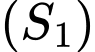 .
.Diện tích tam giác
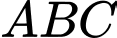 lớn nhất khi
lớn nhất khi  tiếp xúc với
tiếp xúc với 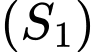 tại tiếp điểm
tại tiếp điểm 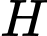 .
.Phương trình đường thẳng
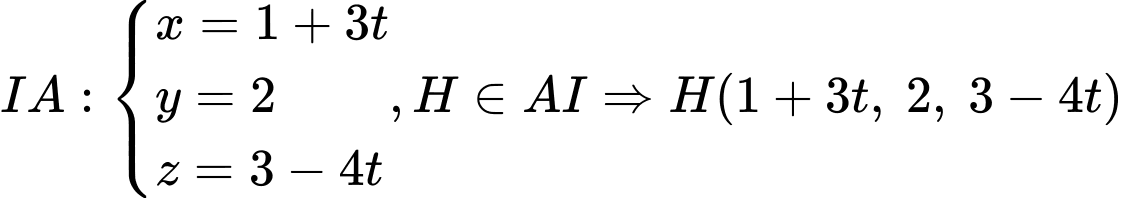 .
.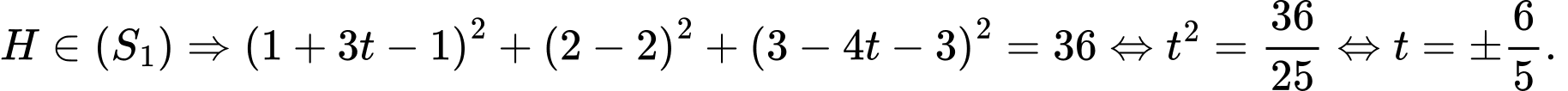
Với
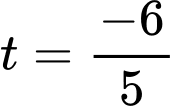
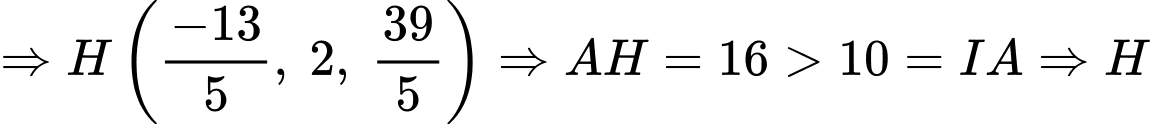 là điểm cần tìm.
là điểm cần tìm.Trong tam giác
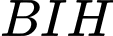 vuông tại
vuông tại 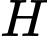 có:
có:  .
.Diện tích lớn nhất của tam giác
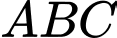 là
là 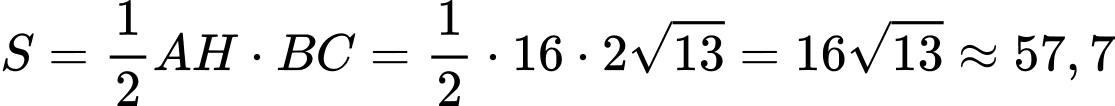 .
.
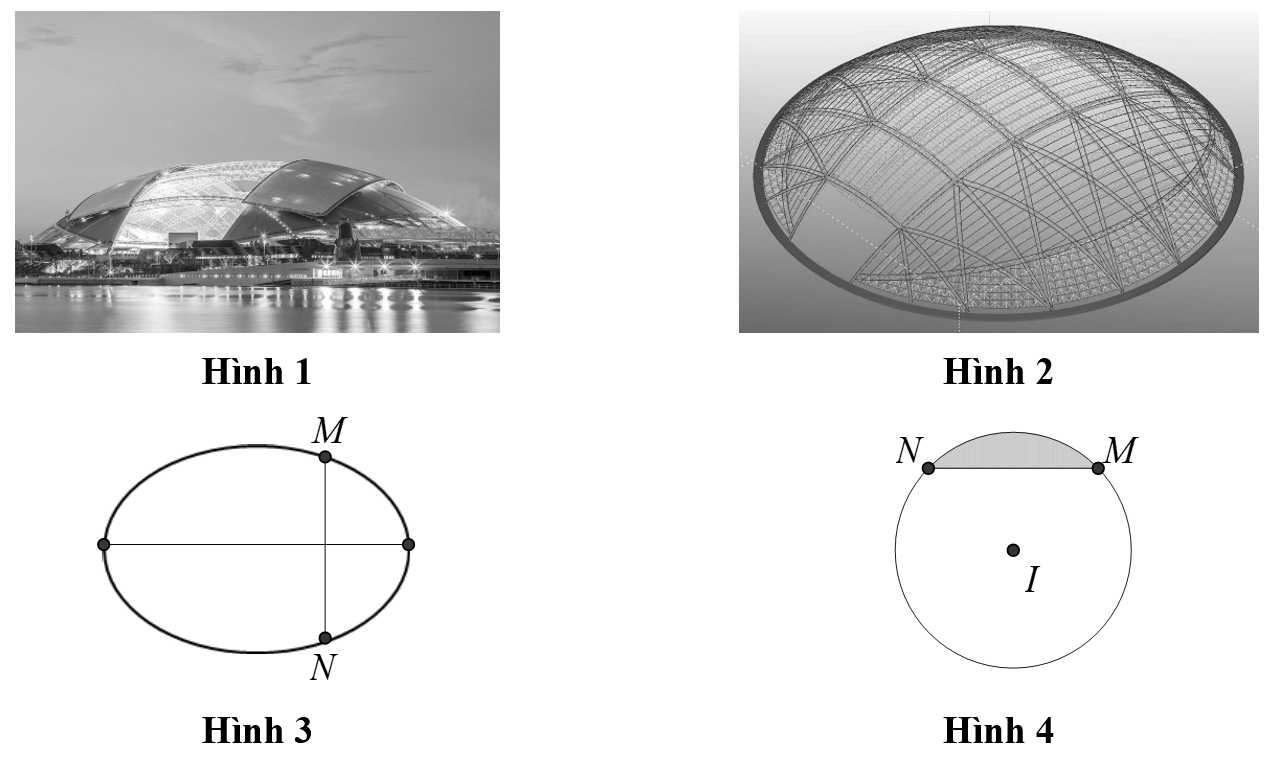
Câu 21 [696500]: Sân vận động Sport Hub (Singapore) là sân có mái vòm kỳ vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm 2015. Nền sân là một elip  có trục lớn dài 150 m, trục bé dài 90 m (hình vẽ). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của
có trục lớn dài 150 m, trục bé dài 90 m (hình vẽ). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của  và cắt elip ở
và cắt elip ở 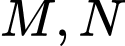 (hình vẽ) thì ta được thiết diện luôn là một phần của hình tròn có tâm
(hình vẽ) thì ta được thiết diện luôn là một phần của hình tròn có tâm 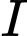 (phần tô đậm trong hình 4) với
(phần tô đậm trong hình 4) với 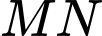 là một dây cung và góc
là một dây cung và góc 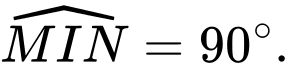 Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích phần không gian đó bằng bao nhiêu nghìn mét khối? (làm tròn kết quả đến hàng đơn vị).
Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích phần không gian đó bằng bao nhiêu nghìn mét khối? (làm tròn kết quả đến hàng đơn vị).
 có trục lớn dài 150 m, trục bé dài 90 m (hình vẽ). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của
có trục lớn dài 150 m, trục bé dài 90 m (hình vẽ). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của  và cắt elip ở
và cắt elip ở 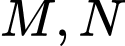 (hình vẽ) thì ta được thiết diện luôn là một phần của hình tròn có tâm
(hình vẽ) thì ta được thiết diện luôn là một phần của hình tròn có tâm 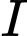 (phần tô đậm trong hình 4) với
(phần tô đậm trong hình 4) với 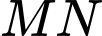 là một dây cung và góc
là một dây cung và góc 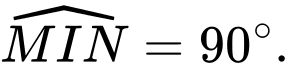 Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích phần không gian đó bằng bao nhiêu nghìn mét khối? (làm tròn kết quả đến hàng đơn vị).
Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích phần không gian đó bằng bao nhiêu nghìn mét khối? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 116.
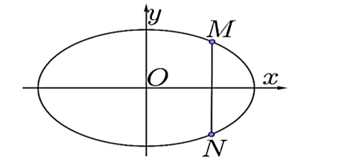
Chọn hệ trục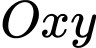 như hình vẽ.
như hình vẽ.
Phương trình chính tắc của E-líp đáy là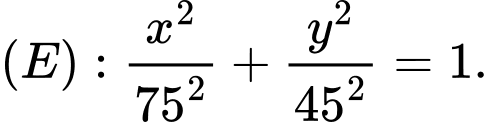
Gọi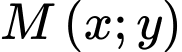
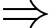
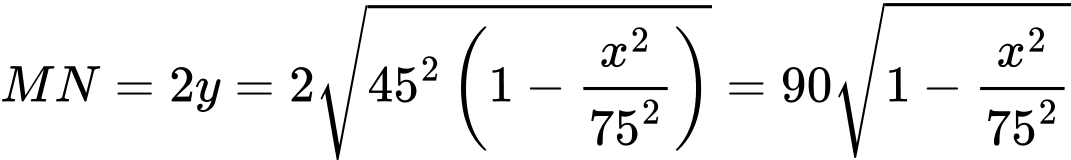
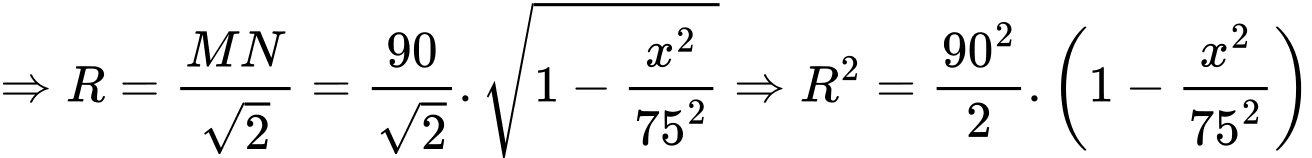 .
.
Ta có công thức diện tích hình quạt:
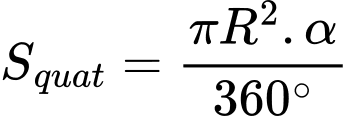 với
với 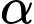 (theo đơn vị độ) là số đo góc ở tâm chắn cung tương ứng.
(theo đơn vị độ) là số đo góc ở tâm chắn cung tương ứng.
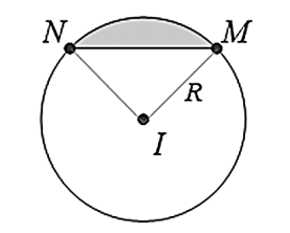
Gọi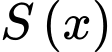 là diện tích thiết diện, ta có:
là diện tích thiết diện, ta có:
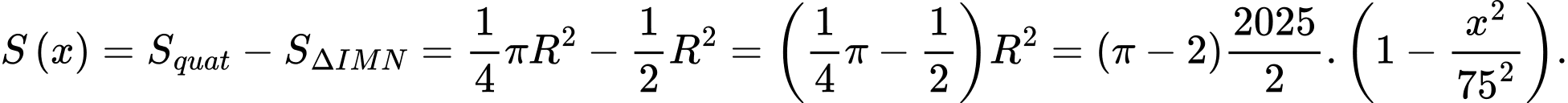
Thể tích khoảng không gian sân vận động là
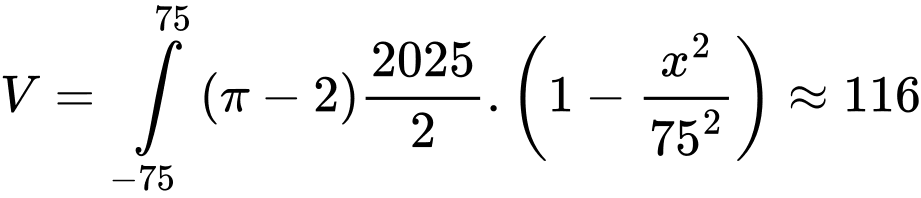 nghìn mét khối.
nghìn mét khối.

Chọn hệ trục
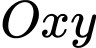 như hình vẽ.
như hình vẽ.Phương trình chính tắc của E-líp đáy là
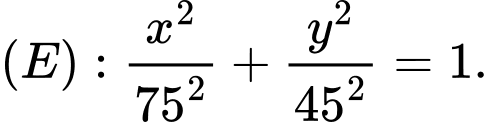
Gọi
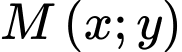
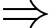
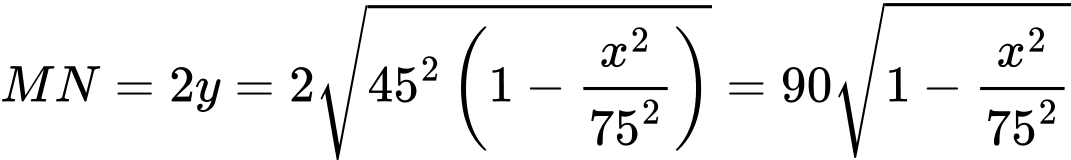
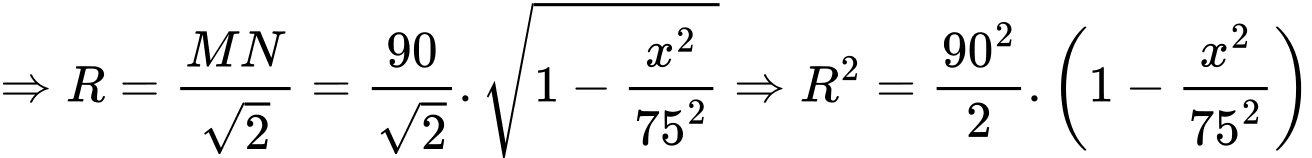 .
.Ta có công thức diện tích hình quạt:
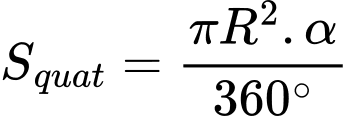 với
với 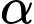 (theo đơn vị độ) là số đo góc ở tâm chắn cung tương ứng.
(theo đơn vị độ) là số đo góc ở tâm chắn cung tương ứng.
Gọi
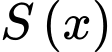 là diện tích thiết diện, ta có:
là diện tích thiết diện, ta có: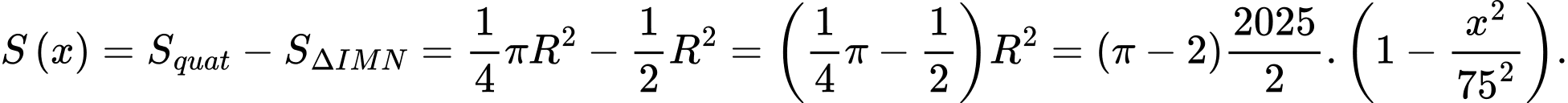
Thể tích khoảng không gian sân vận động là
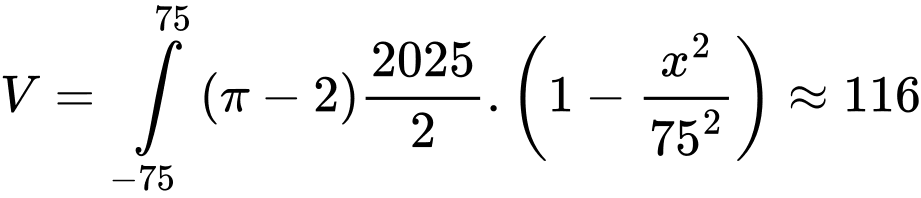 nghìn mét khối.
nghìn mét khối.
Câu 22 [703162]: Một sân chơi hình vuông 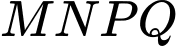 có 64 ô vuông
có 64 ô vuông  hai nửa đường tròn đường kính
hai nửa đường tròn đường kính 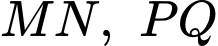 chia sân chơi thành 4 khu
chia sân chơi thành 4 khu 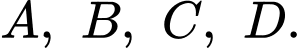 Một trò chơi được diễn ra, người chơi đứng kín ở đỉnh các hình vuông
Một trò chơi được diễn ra, người chơi đứng kín ở đỉnh các hình vuông  nhưng không được đứng ở vị trí
nhưng không được đứng ở vị trí 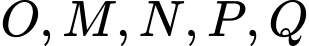 (như hình vẽ bên dưới).
(như hình vẽ bên dưới).
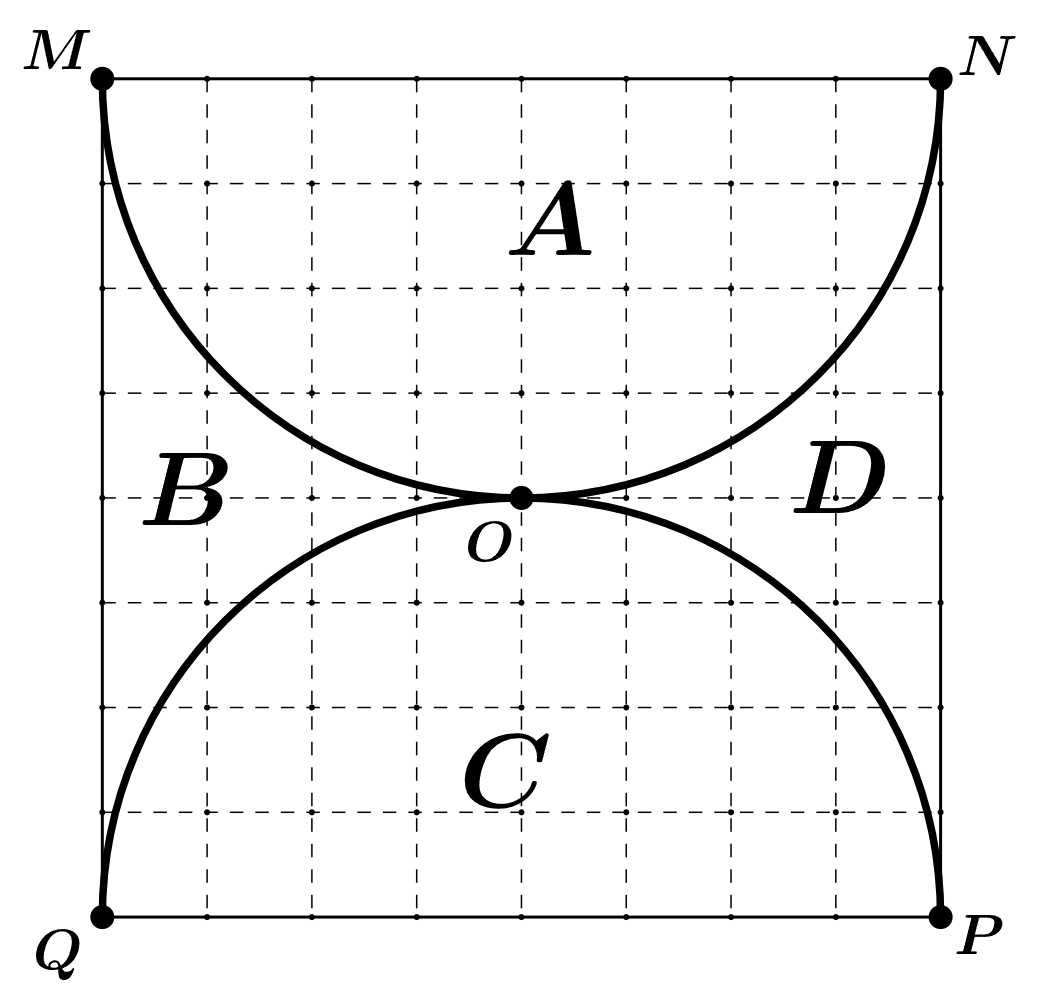
Ban đầu mỗi khu đều có số nam bằng số nữ. Quản trò đưa 2 người ở khu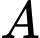 (trong đó có ít nhất một nam) sang khu
(trong đó có ít nhất một nam) sang khu 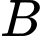 sau đó chuyển lại 2 người bất kì ở khu
sau đó chuyển lại 2 người bất kì ở khu 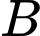 sang khu
sang khu 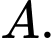 Tính xác suất để khu
Tính xác suất để khu 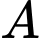 chuyển đi 2 nam biết rằng ở khu
chuyển đi 2 nam biết rằng ở khu 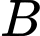 có số nam nhiều hơn số nữ. (số người đã chuyển đi có thể chuyển về).
có số nam nhiều hơn số nữ. (số người đã chuyển đi có thể chuyển về).
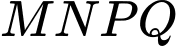 có 64 ô vuông
có 64 ô vuông  hai nửa đường tròn đường kính
hai nửa đường tròn đường kính 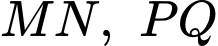 chia sân chơi thành 4 khu
chia sân chơi thành 4 khu 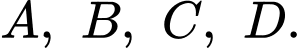 Một trò chơi được diễn ra, người chơi đứng kín ở đỉnh các hình vuông
Một trò chơi được diễn ra, người chơi đứng kín ở đỉnh các hình vuông  nhưng không được đứng ở vị trí
nhưng không được đứng ở vị trí 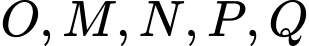 (như hình vẽ bên dưới).
(như hình vẽ bên dưới).
Ban đầu mỗi khu đều có số nam bằng số nữ. Quản trò đưa 2 người ở khu
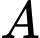 (trong đó có ít nhất một nam) sang khu
(trong đó có ít nhất một nam) sang khu 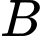 sau đó chuyển lại 2 người bất kì ở khu
sau đó chuyển lại 2 người bất kì ở khu 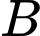 sang khu
sang khu 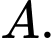 Tính xác suất để khu
Tính xác suất để khu  chuyển đi 2 nam biết rằng ở khu
chuyển đi 2 nam biết rằng ở khu  có số nam nhiều hơn số nữ. (số người đã chuyển đi có thể chuyển về).
có số nam nhiều hơn số nữ. (số người đã chuyển đi có thể chuyển về).
Điền đáp án: 0,58
Gọi là biến cố “Khu
là biến cố “Khu  chuyển đi 2 nam” ,
chuyển đi 2 nam” , 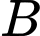 là biến cố “ Khu
là biến cố “ Khu 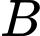 có số nam nhiều hơn số nữ”
có số nam nhiều hơn số nữ”
Khu vực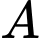 có
có 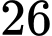 người trong đó 13 nam và 13 nữ.
người trong đó 13 nam và 13 nữ.
Khu vực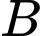 có
có  người trong đó có 6 nam và 6 nữ.
người trong đó có 6 nam và 6 nữ.
Vì ta chuyển đi khu vực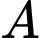 ít nhất 1 nam nên có 2 trường hợp:
ít nhất 1 nam nên có 2 trường hợp:
+) Chuyển đi khu vực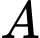 đi 2 nam :
đi 2 nam :  cách .
cách .
+) Chuyển đi khu vực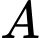 đi 1 nam, 1 nữ:
đi 1 nam, 1 nữ: 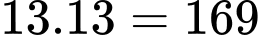 cách.
cách.
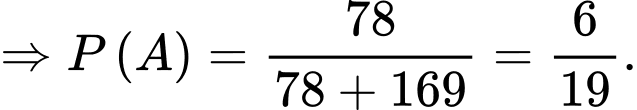
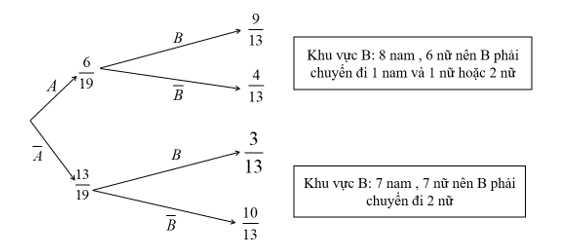
Ta có sơ đồ hình cây như sau:
Theo đề bài ta có:
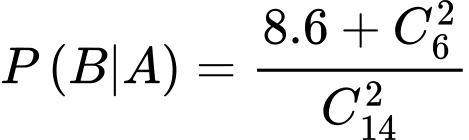
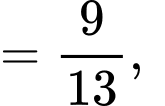
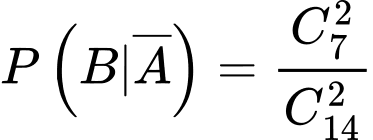
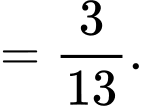
Theo công thức xác suất toàn phần ta có:
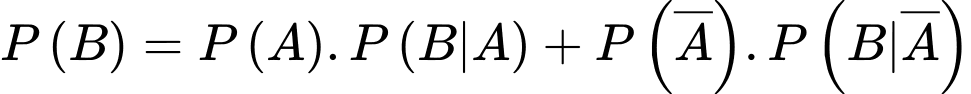
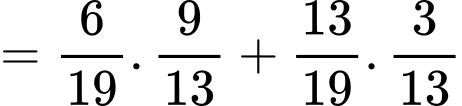
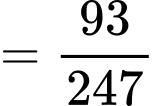 .
.
Theo công thức Bayes ta có:
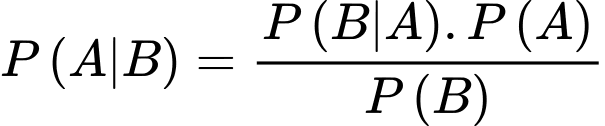
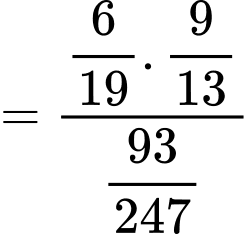
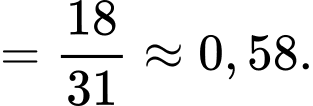
Gọi
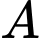 là biến cố “Khu
là biến cố “Khu 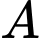 chuyển đi 2 nam” ,
chuyển đi 2 nam” , 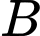 là biến cố “ Khu
là biến cố “ Khu 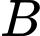 có số nam nhiều hơn số nữ”
có số nam nhiều hơn số nữ”Khu vực
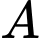 có
có 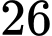 người trong đó 13 nam và 13 nữ.
người trong đó 13 nam và 13 nữ.Khu vực
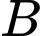 có
có  người trong đó có 6 nam và 6 nữ.
người trong đó có 6 nam và 6 nữ.Vì ta chuyển đi khu vực
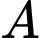 ít nhất 1 nam nên có 2 trường hợp:
ít nhất 1 nam nên có 2 trường hợp: +) Chuyển đi khu vực
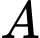 đi 2 nam :
đi 2 nam :  cách .
cách .+) Chuyển đi khu vực
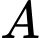 đi 1 nam, 1 nữ:
đi 1 nam, 1 nữ: 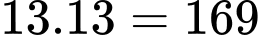 cách.
cách.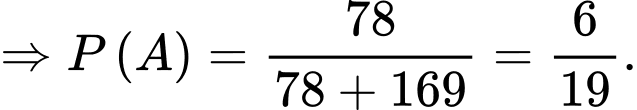
Ta có sơ đồ hình cây như sau:

Theo đề bài ta có:
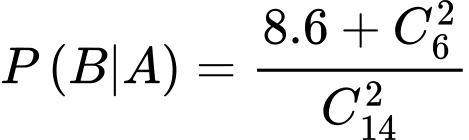
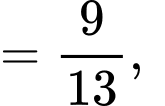
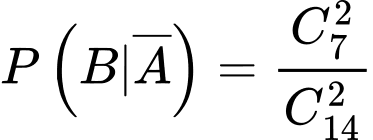
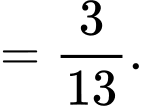
Theo công thức xác suất toàn phần ta có:
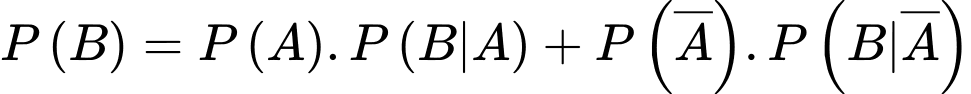
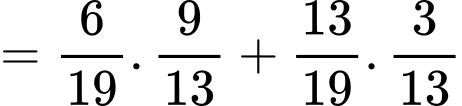
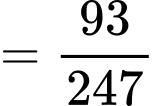 .
.Theo công thức Bayes ta có: