PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [315665]: Trong không gian 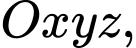 cho mặt phẳng
cho mặt phẳng 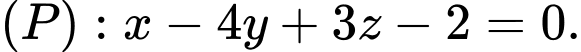 Vectơ nào dưới đây là một vectơ pháp tuyến của
Vectơ nào dưới đây là một vectơ pháp tuyến của 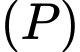 ?
?
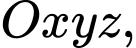 cho mặt phẳng
cho mặt phẳng 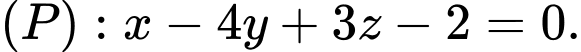 Vectơ nào dưới đây là một vectơ pháp tuyến của
Vectơ nào dưới đây là một vectơ pháp tuyến của 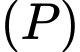 ?
? A, 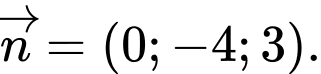
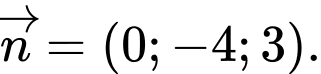
B, 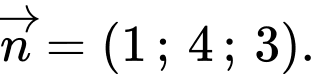
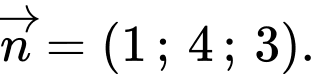
C, 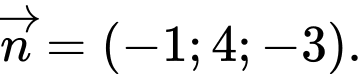
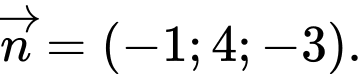
D, 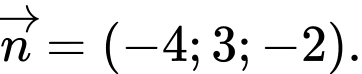
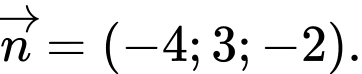
Chọn đáp án C.
Mặt phẳng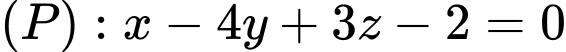 có một VTPT là
có một VTPT là 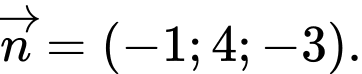 Đáp án: C
Đáp án: C
Mặt phẳng
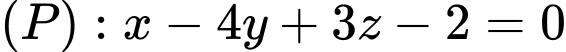 có một VTPT là
có một VTPT là 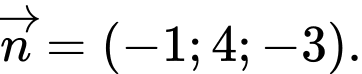 Đáp án: C
Đáp án: C
Câu 2 [605008]: Cho hàm số 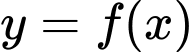 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ.
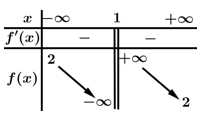
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
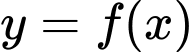 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ.
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
A, 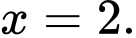
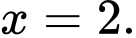
B, 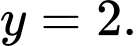
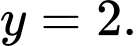
C, 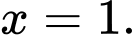
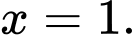
D, 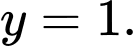
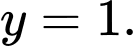
Chọn đáp án C
Dựa vào bảng biến thiên ta có đường tiệm cận đứng của đồ thị hàm số là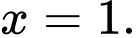 Đáp án: C
Đáp án: C
Dựa vào bảng biến thiên ta có đường tiệm cận đứng của đồ thị hàm số là
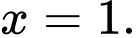 Đáp án: C
Đáp án: C
Câu 3 [518257]: Cho các hàm số 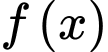 và
và 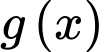 liên tục trên tập xác định. Mệnh đề nào sau đây sai?
liên tục trên tập xác định. Mệnh đề nào sau đây sai?
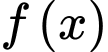 và
và 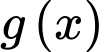 liên tục trên tập xác định. Mệnh đề nào sau đây sai?
liên tục trên tập xác định. Mệnh đề nào sau đây sai? A, 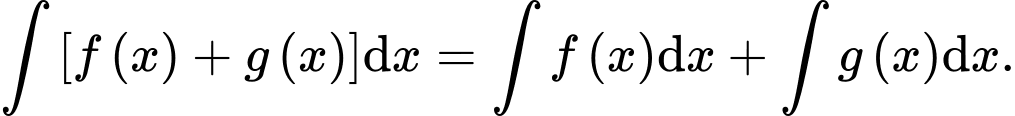
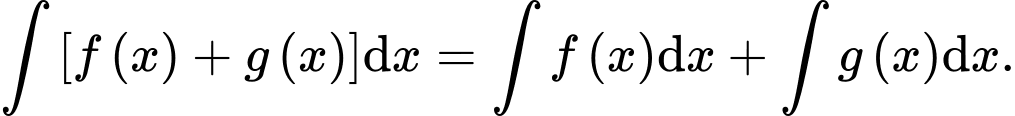
B, 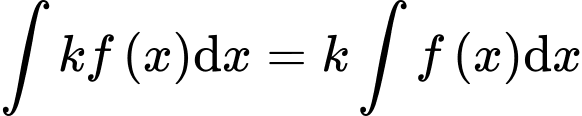 (số thực
(số thực 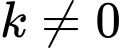 ).
).
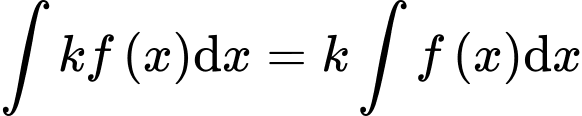 (số thực
(số thực 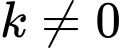 ).
).C, 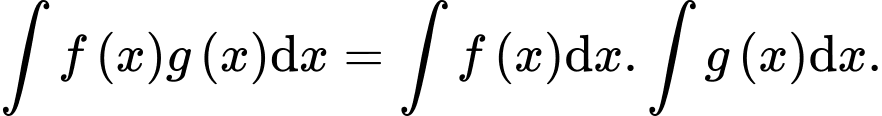
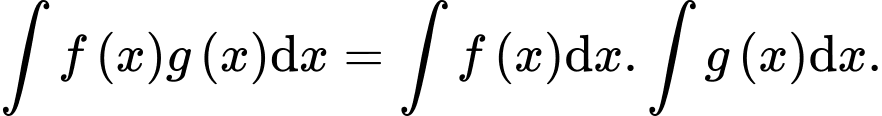
D, 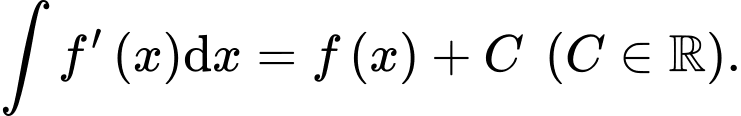
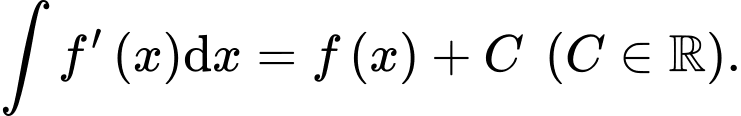
Chọn đáp án C
Theo lý thuyết:
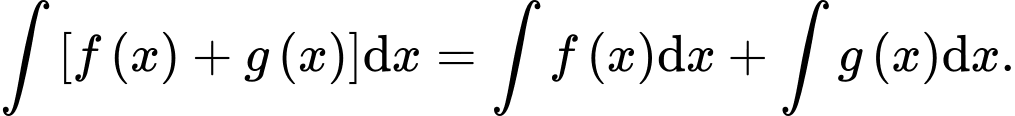
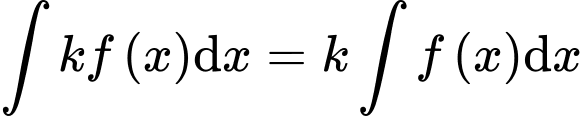 (số thực
(số thực 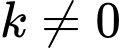 ).
).
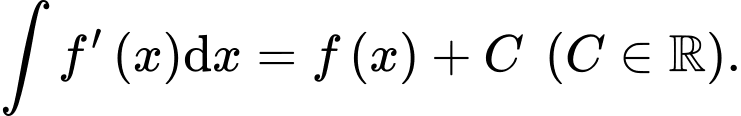 Đáp án: C
Đáp án: C
Theo lý thuyết:
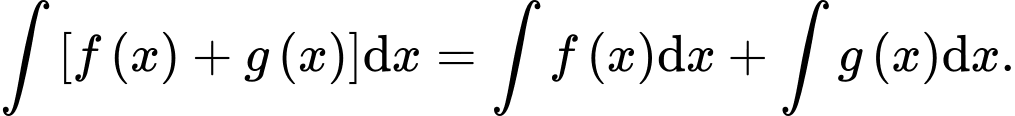
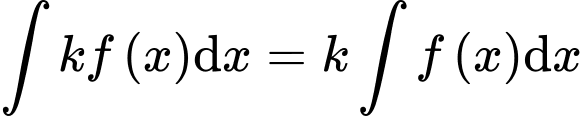 (số thực
(số thực 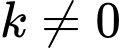 ).
).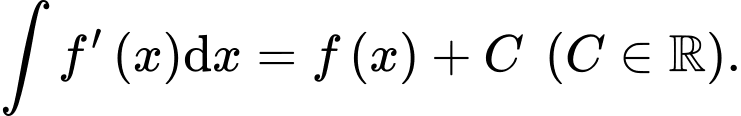 Đáp án: C
Đáp án: C
Câu 4 [16424]: Với 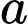 là số thực dương tùy ý,
là số thực dương tùy ý, 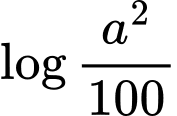 bằng
bằng
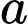 là số thực dương tùy ý,
là số thực dương tùy ý, 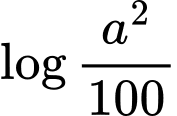 bằng
bằng A, 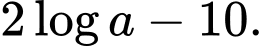
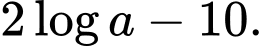
B, 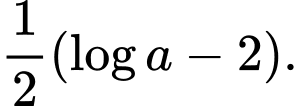
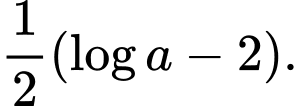
C, 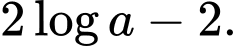
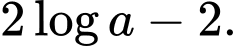
D, 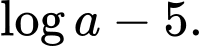
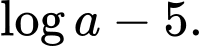
Chọn đáp án C
Ta có: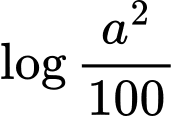
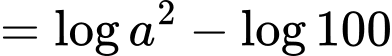
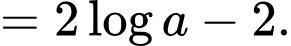 Đáp án: C
Đáp án: C
Ta có:
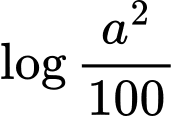
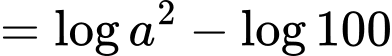
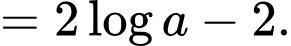 Đáp án: C
Đáp án: C Sử dụng thông tin dưới đây để trả lời câu 5 và câu 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA=a√3, đường thẳng SA vuông góc với mặt phẳng (ABCD) (tham khảo hình vẽ).
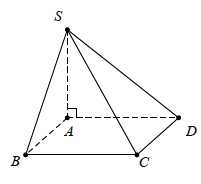

Câu 5 [697652]: Góc giữa đường thẳng 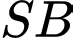 và mặt phẳng
và mặt phẳng 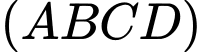 là
là
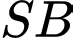 và mặt phẳng
và mặt phẳng 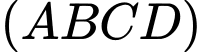 là
là A, 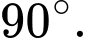
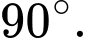
B, 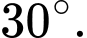
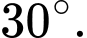
C, 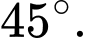
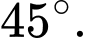
D, 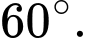
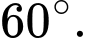
Chọn đáp án D.
Ta có:
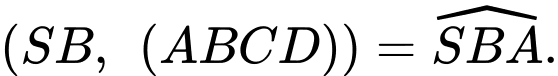
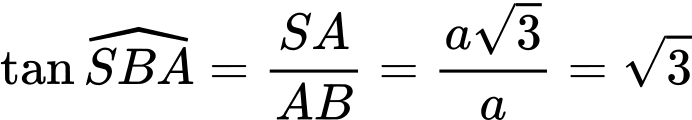

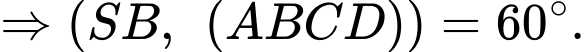
Vậy góc giữa đường thẳng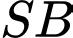 và mặt phẳng
và mặt phẳng 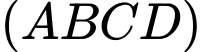 là
là 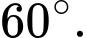 Đáp án: D
Đáp án: D
Ta có:
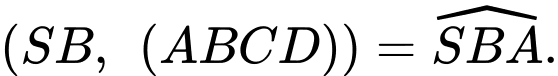
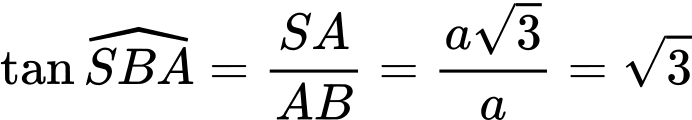

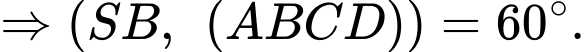
Vậy góc giữa đường thẳng
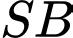 và mặt phẳng
và mặt phẳng 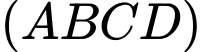 là
là 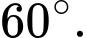 Đáp án: D
Đáp án: D
Câu 6 [697653]: Tổng 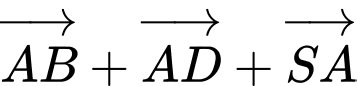 bằng:
bằng:
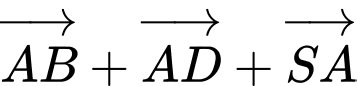 bằng:
bằng: A, 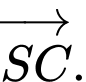
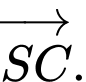
B, 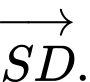
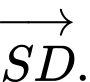
C, 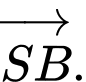
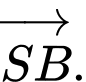
D, 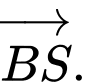
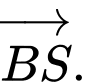
Chọn đáp án A.
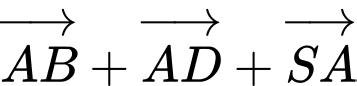
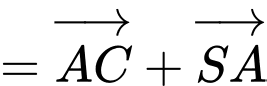
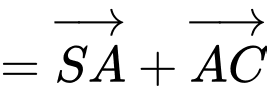
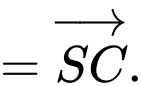 Đáp án: A
Đáp án: A
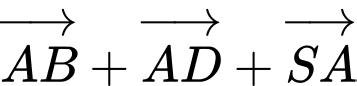
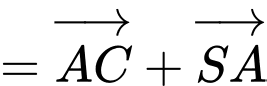
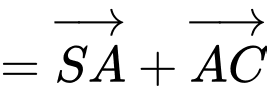
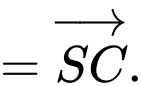 Đáp án: A
Đáp án: A
Câu 7 [135926]: Gọi 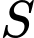 là diện tích của hình phẳng giới hạn bởi các đường
là diện tích của hình phẳng giới hạn bởi các đường 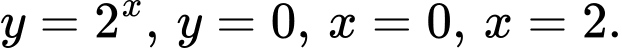 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
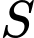 là diện tích của hình phẳng giới hạn bởi các đường
là diện tích của hình phẳng giới hạn bởi các đường 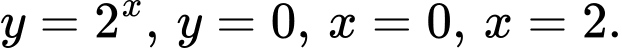 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng? A, 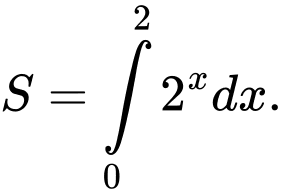
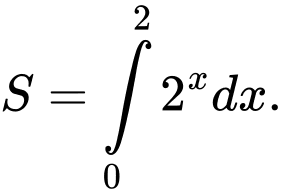
B, 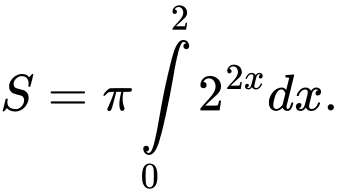
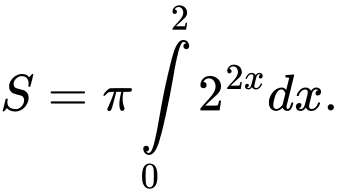
C, 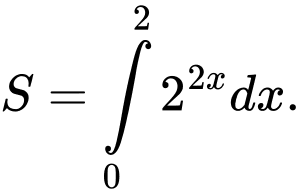
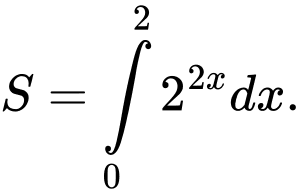
D, 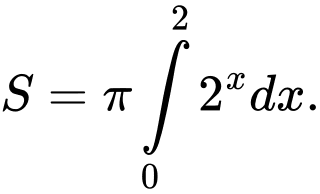
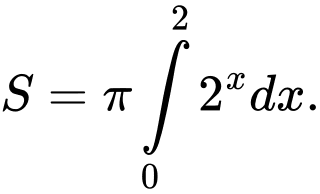
Chọn đáp án A.
Diện tích của hình phẳng giới hạn bởi các đường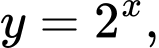
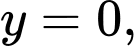
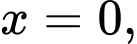
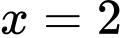 là
là 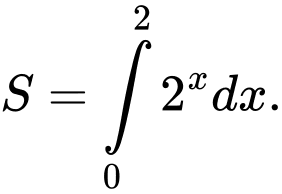 Đáp án: A
Đáp án: A
Diện tích của hình phẳng giới hạn bởi các đường
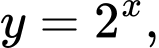
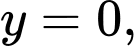
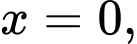
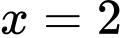 là
là 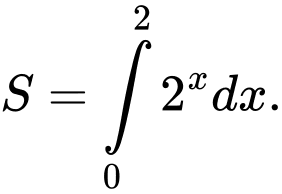 Đáp án: A
Đáp án: A
Câu 8 [317412]: Cho cấp số nhân 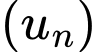 với
với 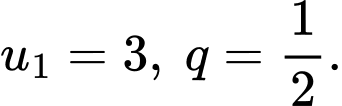 Số
Số 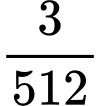 là số hạng thứ mấy?
là số hạng thứ mấy?
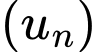 với
với 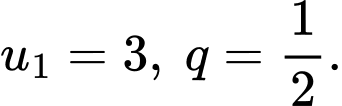 Số
Số 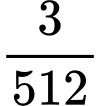 là số hạng thứ mấy?
là số hạng thứ mấy? A, 11.
B, 9.
C, 10.
D, 12.
Chọn đáp án C.
Ta có:
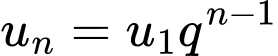
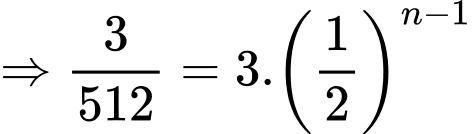
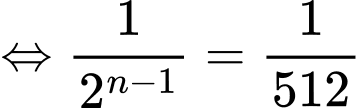
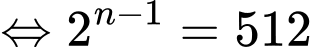
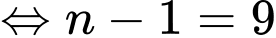
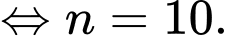 Đáp án: C
Đáp án: C
Ta có:
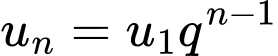
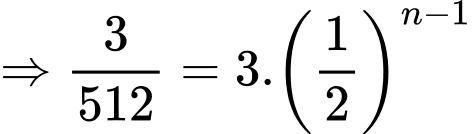
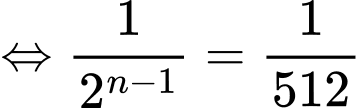
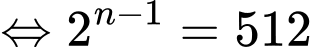
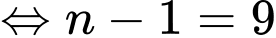
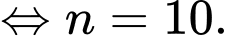 Đáp án: C
Đáp án: C
Câu 9 [687392]: Nhiệt độ trong 55 ngày của một địa phương được cho trong bảng ghép lớp sau:

Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất nằm trong khoảng

Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất nằm trong khoảng
A, 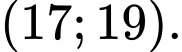
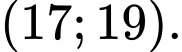
B, 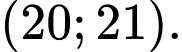
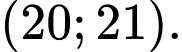
C, 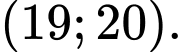
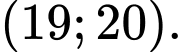
D, 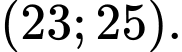
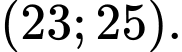
Chọn đáp án C.
Nhiệt độ trung bình trong một ngày là:
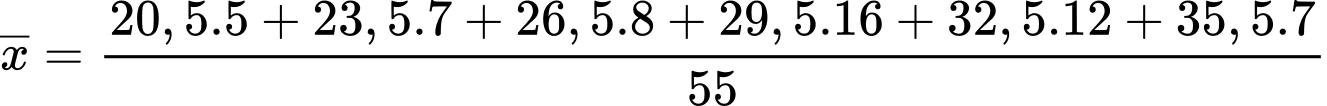
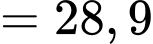
Phương sai của mẫu số liệu là:
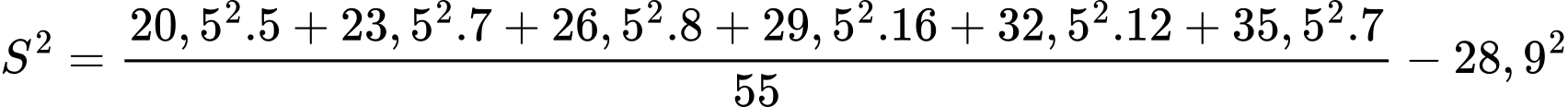
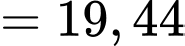
Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất là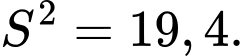 Đáp án: C
Đáp án: C
Nhiệt độ trung bình trong một ngày là:
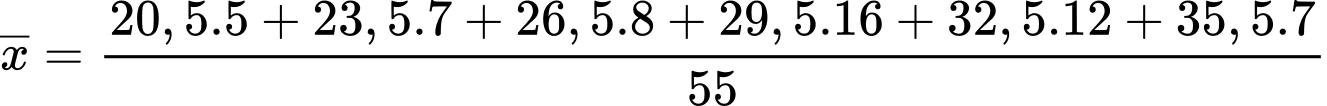
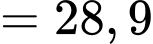
Phương sai của mẫu số liệu là:
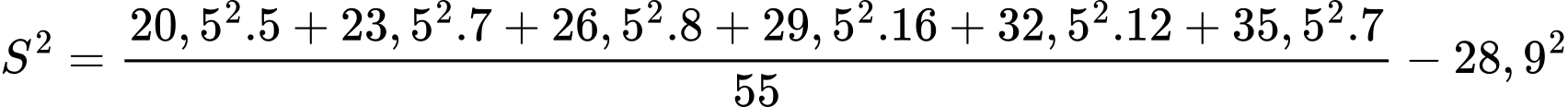
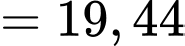
Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất là
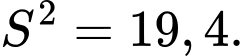 Đáp án: C
Đáp án: C
Câu 10 [809006]: Tìm tập nghiệm của bất phương trình 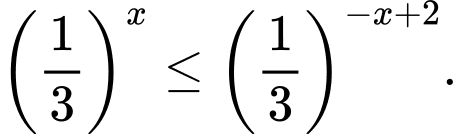
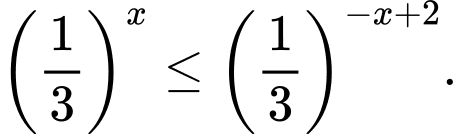
A, 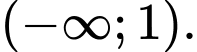
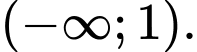
B, 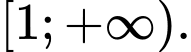
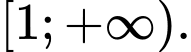
C, 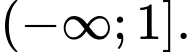
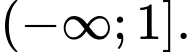
D, 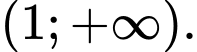
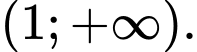
Chọn đáp án B.
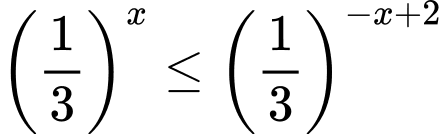
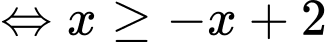
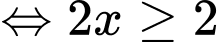
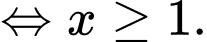
Vậy tập nghiệm của bất phương trình là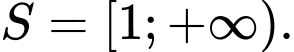 Đáp án: B
Đáp án: B
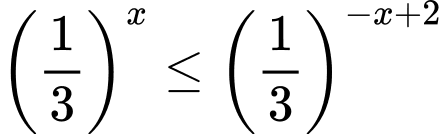
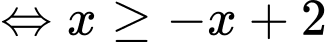
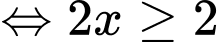
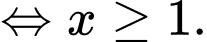
Vậy tập nghiệm của bất phương trình là
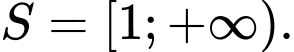 Đáp án: B
Đáp án: B
Câu 11 [383010]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
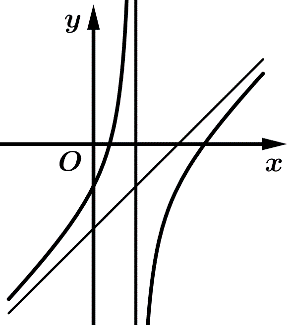

A, 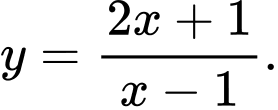
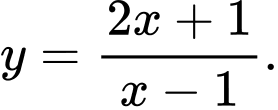
B, 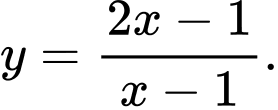
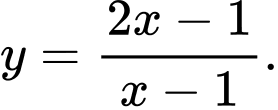
C, 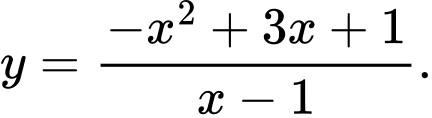
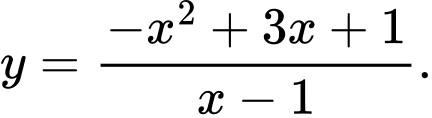
D, 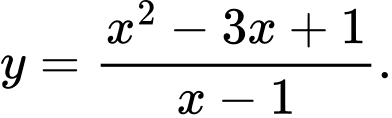
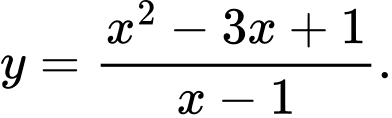
Chọn đáp án D.
Dựa vào hình dạng đồ thị ta thấy hàm số đã cho là hàm số bậc hai trên bậc nhất. Do đó, loại A, B.
Hàm số đã cho không có cực trị và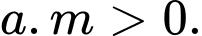 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
Dựa vào hình dạng đồ thị ta thấy hàm số đã cho là hàm số bậc hai trên bậc nhất. Do đó, loại A, B.
Hàm số đã cho không có cực trị và
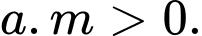 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
Câu 12 [16456]: Trong không gian, cho điểm 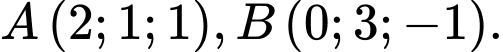 Mặt cầu đường kính
Mặt cầu đường kính  có phương trình là
có phương trình là
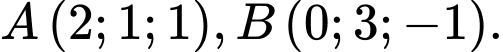 Mặt cầu đường kính
Mặt cầu đường kính  có phương trình là
có phương trình là A, 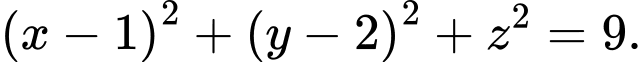
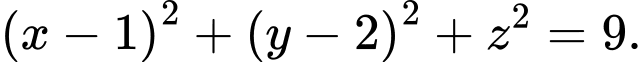
B, 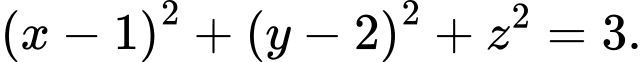
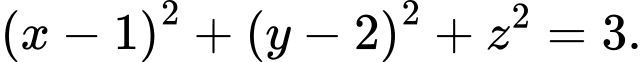
C, 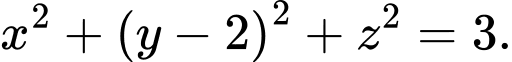
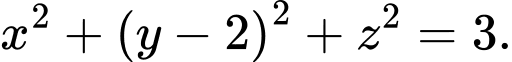
D, 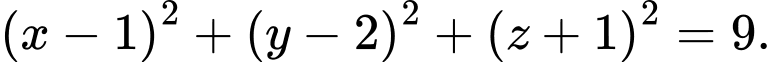
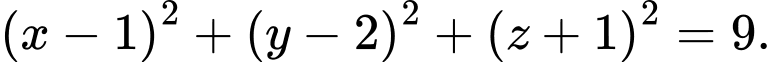
Chọn đáp án B.
+ Gọi là trung điểm của
là trung điểm của 
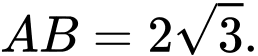
+ Ta có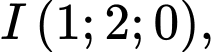
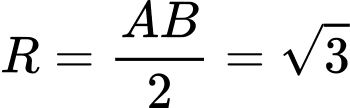 là tâm và bán kính mặt cầu đường kính
là tâm và bán kính mặt cầu đường kính 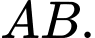
+ Mặt cầu đường kính có phương trình là
có phương trình là 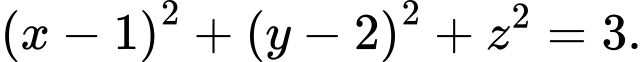 Đáp án: B
Đáp án: B
+ Gọi
 là trung điểm của
là trung điểm của 
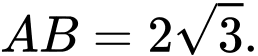
+ Ta có
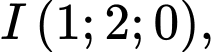
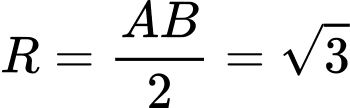 là tâm và bán kính mặt cầu đường kính
là tâm và bán kính mặt cầu đường kính 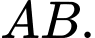
+ Mặt cầu đường kính
 có phương trình là
có phương trình là 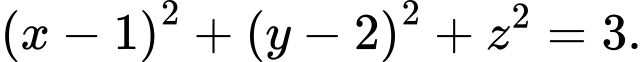 Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [697654]: Cho hình phẳng  giới hạn bởi các đồ thị hàm số
giới hạn bởi các đồ thị hàm số 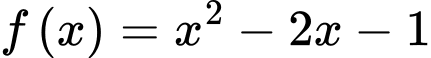 và
và 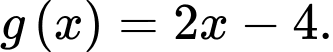 Xét hàm số
Xét hàm số 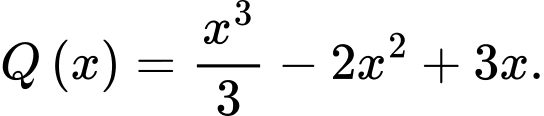
 giới hạn bởi các đồ thị hàm số
giới hạn bởi các đồ thị hàm số 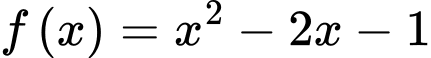 và
và 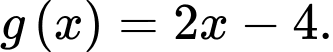 Xét hàm số
Xét hàm số 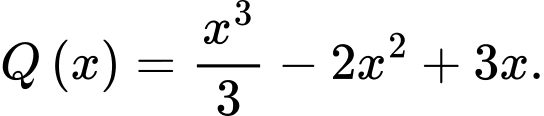
a) Đúng.
Ta có: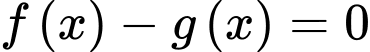
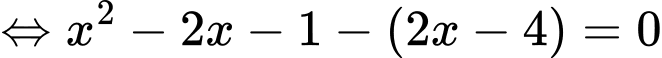
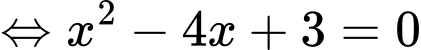
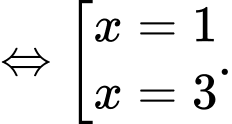
Vậy phương trình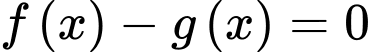 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
b) Sai.
Vì phương trình có 2 nghiệm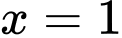 và
và 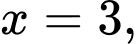 nên ta có trục xét dấu của
nên ta có trục xét dấu của  như sau:
như sau:
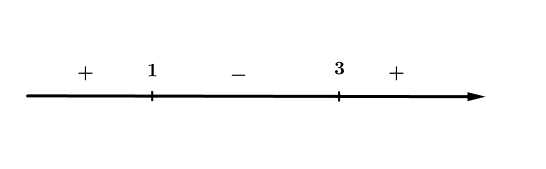
Suy ra hiệu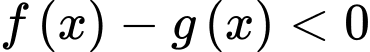 với mọi
với mọi 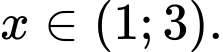
c) Đúng.
Để kiểm tra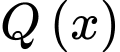 có là một nguyên hàm của hàm số
có là một nguyên hàm của hàm số  hay không. Ta có thể kiểm tra bằng cách tính đạo hàm của
hay không. Ta có thể kiểm tra bằng cách tính đạo hàm của 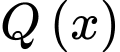 và so sánh xem kết quả có đúng bằng
và so sánh xem kết quả có đúng bằng  hay không.
hay không.
Ta có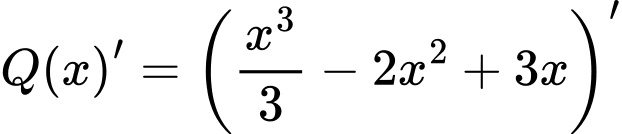
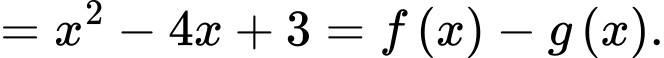
Suy ra hàm số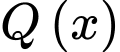 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 
d) Đúng.
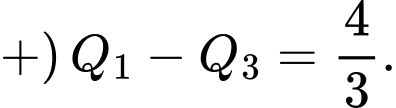
+) Hình phẳng được giới hạn bởi các đồ thị hàm số
được giới hạn bởi các đồ thị hàm số 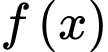 và
và 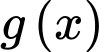 và các đường
và các đường 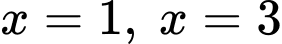 sẽ có diện tích là:
sẽ có diện tích là:
Cách 1:
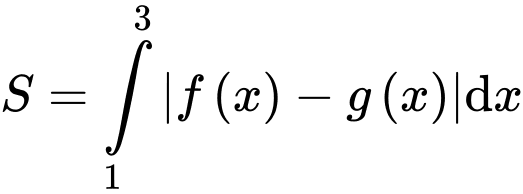
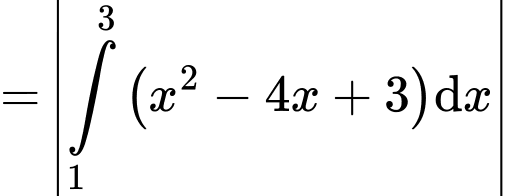
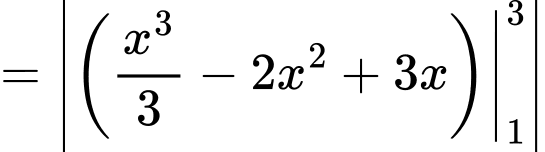
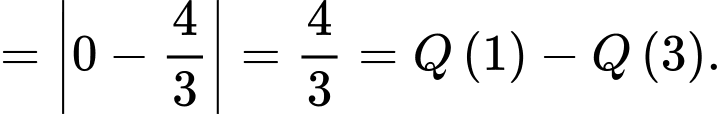
Cách 2:
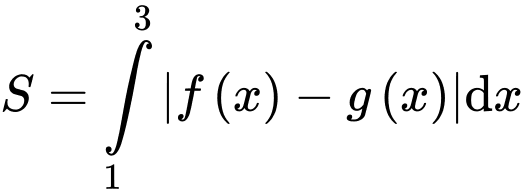
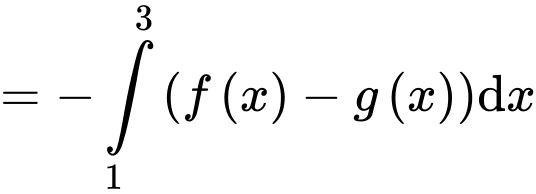 (Vì
(Vì 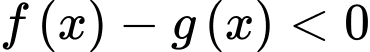 với mọi
với mọi 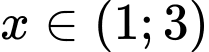 )
)
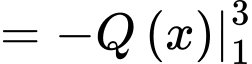
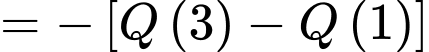

Ta có:
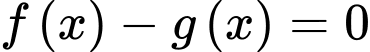
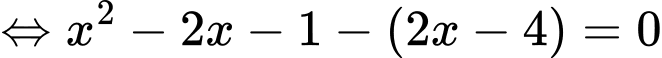
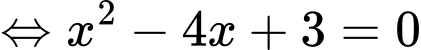
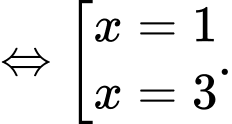
Vậy phương trình
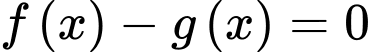 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.b) Sai.
Vì phương trình có 2 nghiệm
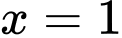 và
và 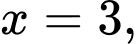 nên ta có trục xét dấu của
nên ta có trục xét dấu của  như sau:
như sau:
Suy ra hiệu
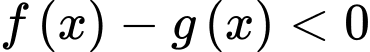 với mọi
với mọi 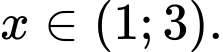
c) Đúng.
Để kiểm tra
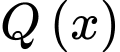 có là một nguyên hàm của hàm số
có là một nguyên hàm của hàm số  hay không. Ta có thể kiểm tra bằng cách tính đạo hàm của
hay không. Ta có thể kiểm tra bằng cách tính đạo hàm của 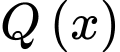 và so sánh xem kết quả có đúng bằng
và so sánh xem kết quả có đúng bằng  hay không.
hay không.Ta có
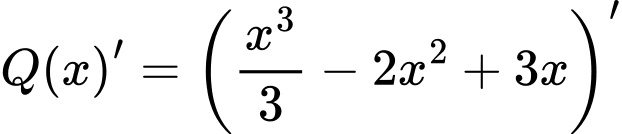
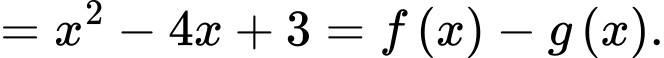
Suy ra hàm số
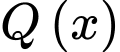 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 
d) Đúng.
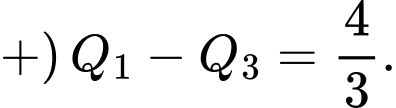
+) Hình phẳng
 được giới hạn bởi các đồ thị hàm số
được giới hạn bởi các đồ thị hàm số 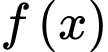 và
và 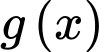 và các đường
và các đường 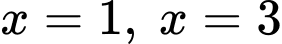 sẽ có diện tích là:
sẽ có diện tích là:Cách 1:
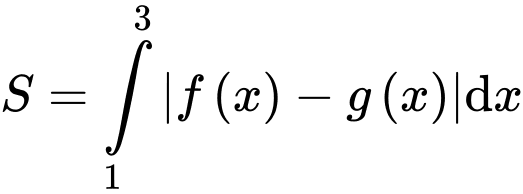
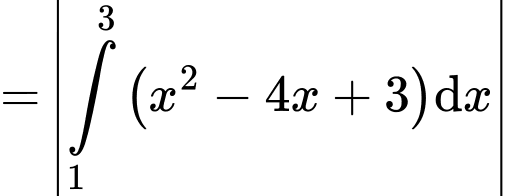
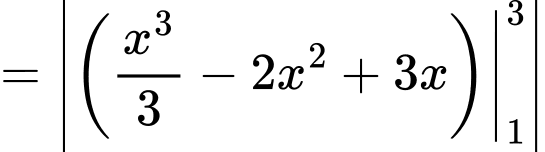
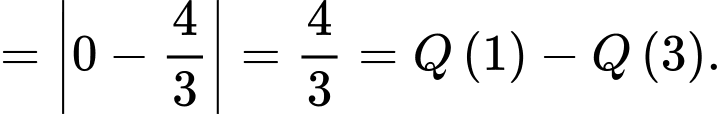
Cách 2:
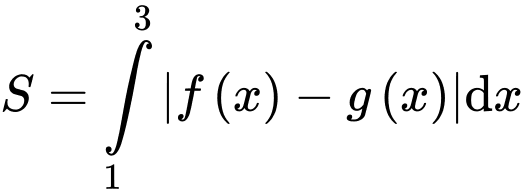
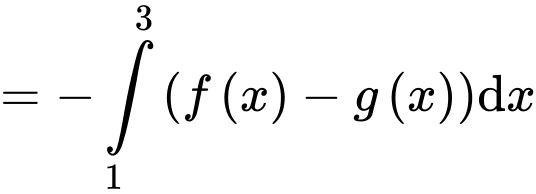 (Vì
(Vì 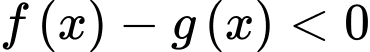 với mọi
với mọi 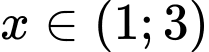 )
)
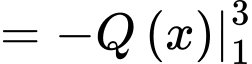
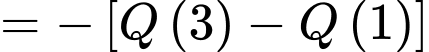

Câu 14 [700496]: Khi thả một quả bóng từ đỉnh một toà tháp xuống, nó chạm đất sau 3 giây. Sau đó, quả bóng nảy lên trước khi chạm đất lần nữa 4 giây sau đó. Chiều cao tính bằng mét của quả bóng so với mặt đất sau 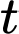 giây tuân theo một hàm số liên tục trên
giây tuân theo một hàm số liên tục trên 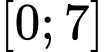 như sau:
như sau: 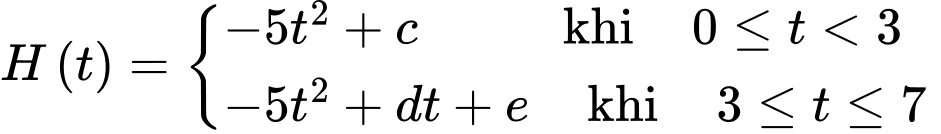
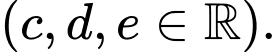
 giây tuân theo một hàm số liên tục trên
giây tuân theo một hàm số liên tục trên 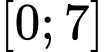 như sau:
như sau: 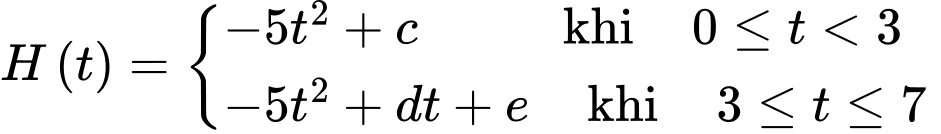
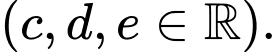

a) Đúng.
Dựa vào hình vẽ ta thấy
b) Sai.
Quả bóng được thả tại thời điểm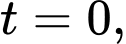 nên để tìm độ cao quả bóng ta cần đi tìm
nên để tìm độ cao quả bóng ta cần đi tìm 
Vì hàm số liên tục tại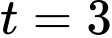 nên
nên 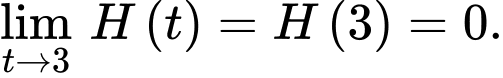
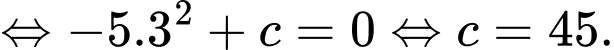
Vậy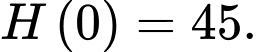 Do đó, quả bóng được thả từ độ cao 45 m.
Do đó, quả bóng được thả từ độ cao 45 m.
c) Sai.
Ta có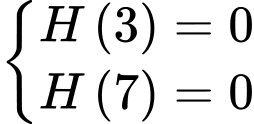
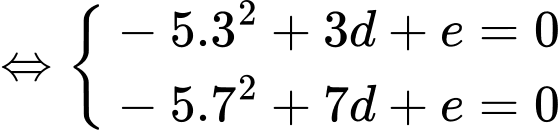
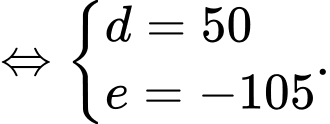
Vậy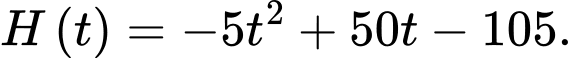
d) Đúng.
Độ cao của quả bóng sau lần nảy đầu tiên trong khoảng thời gian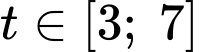 nên sẽ được mô tả bởi
nên sẽ được mô tả bởi 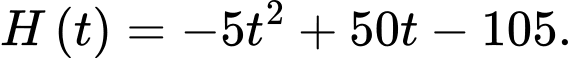
Khảo sát hàm số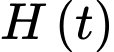 trên đoạn
trên đoạn 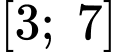
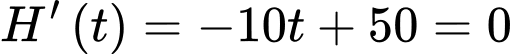
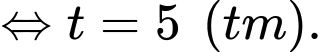
Ta có
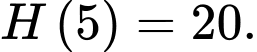
Vậy độ cao lớn nhất mà quả bóng đạt được sau lần nảy đầu tiên là 20 m.
Dựa vào hình vẽ ta thấy

b) Sai.
Quả bóng được thả tại thời điểm
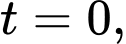 nên để tìm độ cao quả bóng ta cần đi tìm
nên để tìm độ cao quả bóng ta cần đi tìm 
Vì hàm số liên tục tại
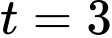 nên
nên 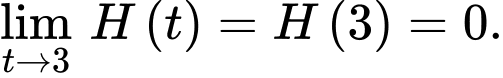
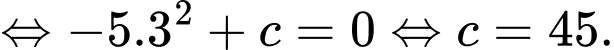
Vậy
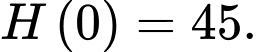 Do đó, quả bóng được thả từ độ cao 45 m.
Do đó, quả bóng được thả từ độ cao 45 m.
c) Sai.
Ta có
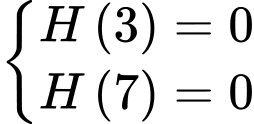
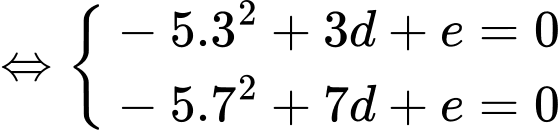
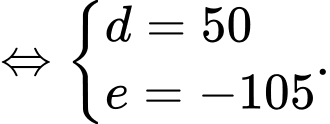
Vậy
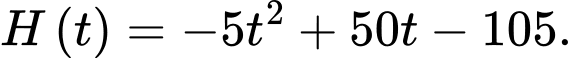
d) Đúng.
Độ cao của quả bóng sau lần nảy đầu tiên trong khoảng thời gian
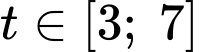 nên sẽ được mô tả bởi
nên sẽ được mô tả bởi 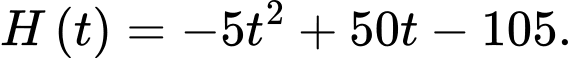
Khảo sát hàm số
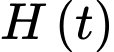 trên đoạn
trên đoạn 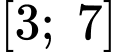
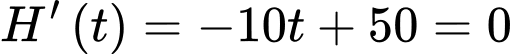
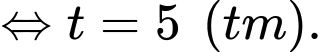
Ta có

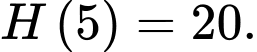
Vậy độ cao lớn nhất mà quả bóng đạt được sau lần nảy đầu tiên là 20 m.
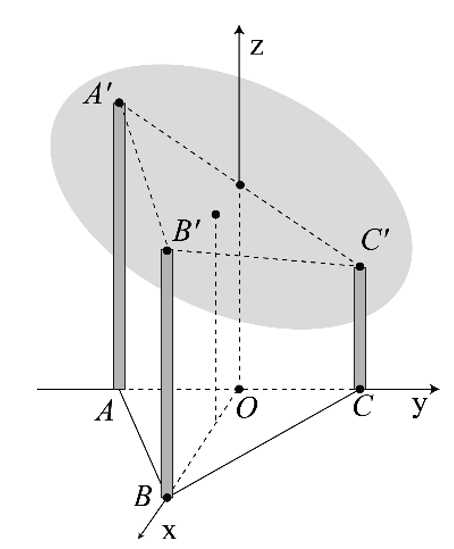
Câu 15 [694447]: Một mái nhà hình tròn được đặt trên ba cây cột trụ. Các cây cộc trụ vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 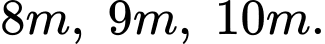 Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài
Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 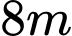 . Chọn hệ trục toạ độ như hình vẽ, với
. Chọn hệ trục toạ độ như hình vẽ, với 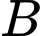 thuộc tia
thuộc tia 
 thuộc tia
thuộc tia 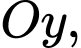 tia
tia  cùng hướng với vectơ
cùng hướng với vectơ 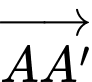 gốc toạ độ
gốc toạ độ  trùng với trung điểm của
trùng với trung điểm của 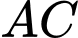 và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
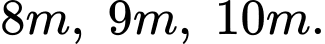 Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài
Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 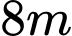 . Chọn hệ trục toạ độ như hình vẽ, với
. Chọn hệ trục toạ độ như hình vẽ, với 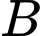 thuộc tia
thuộc tia 
 thuộc tia
thuộc tia 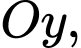 tia
tia  cùng hướng với vectơ
cùng hướng với vectơ 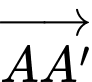 gốc toạ độ
gốc toạ độ  trùng với trung điểm của
trùng với trung điểm của 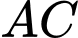 và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).
a) Đúng.
Ta có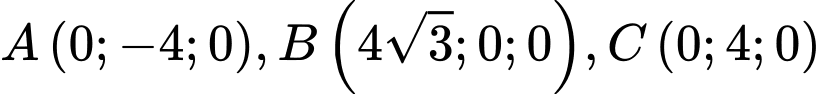 .
. 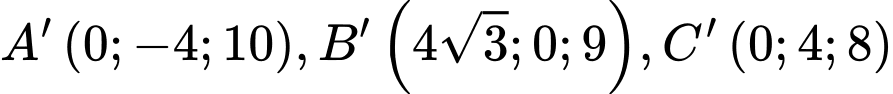 .
.
b) Đúng.
Ta có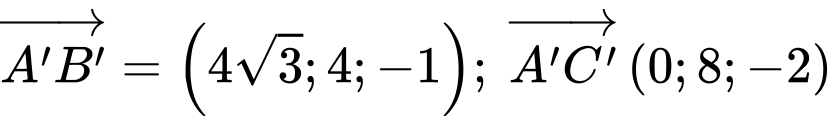 <.
<.
Vectơ pháp tuyến của mặt phẳng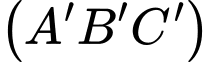 là:
là: 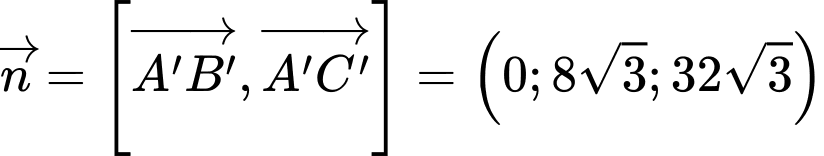
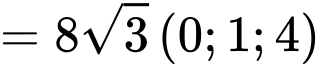 suy ra phương trình mặt phẳng
suy ra phương trình mặt phẳng 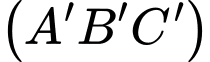 là:
là: 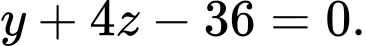
c) Sai.
Vectơ pháp tuyến của mặt phẳng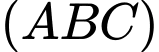 là
là 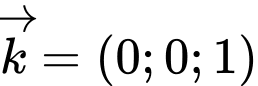
Khi đó: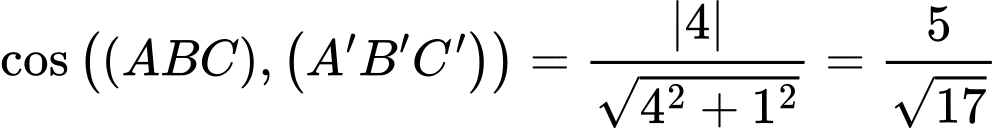
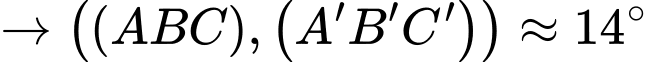
Vậy độ dốc của mái khoảng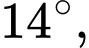 mái nhà trên không ở mức tiêu chuẩn
mái nhà trên không ở mức tiêu chuẩn
d) Đúng.
Gọi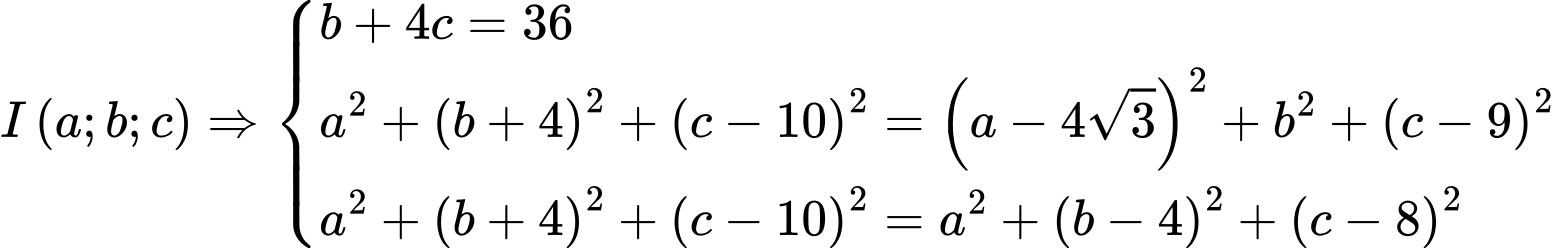
Suy ra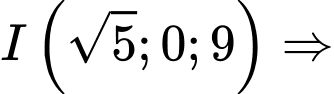 điểm I cách mặt sàn một khoảng là 9 mét.
điểm I cách mặt sàn một khoảng là 9 mét.
Ta có
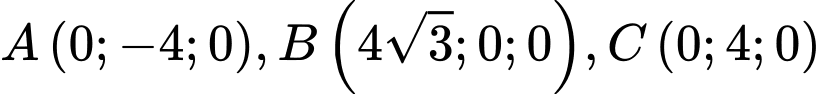 .
. 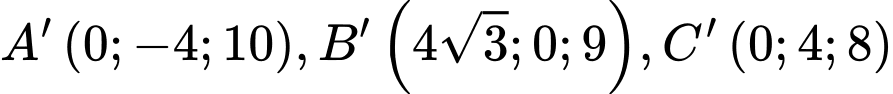 .
.b) Đúng.
Ta có
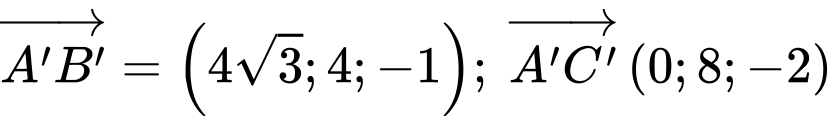 <.
<.Vectơ pháp tuyến của mặt phẳng
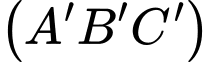 là:
là: 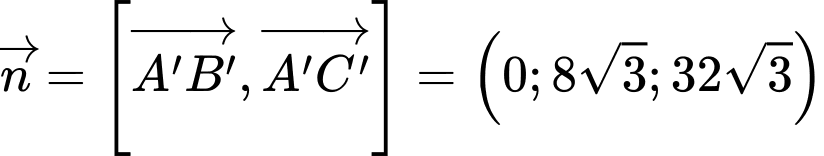
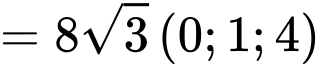 suy ra phương trình mặt phẳng
suy ra phương trình mặt phẳng 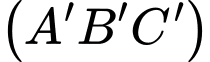 là:
là: 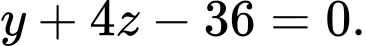
c) Sai.
Vectơ pháp tuyến của mặt phẳng
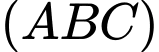 là
là 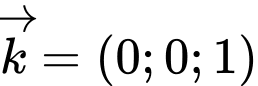
Khi đó:
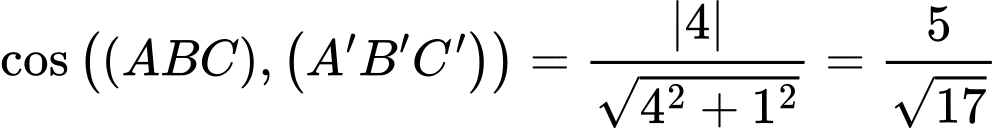
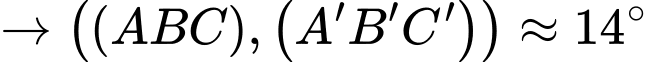
Vậy độ dốc của mái khoảng
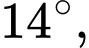 mái nhà trên không ở mức tiêu chuẩn
mái nhà trên không ở mức tiêu chuẩnd) Đúng.
Gọi
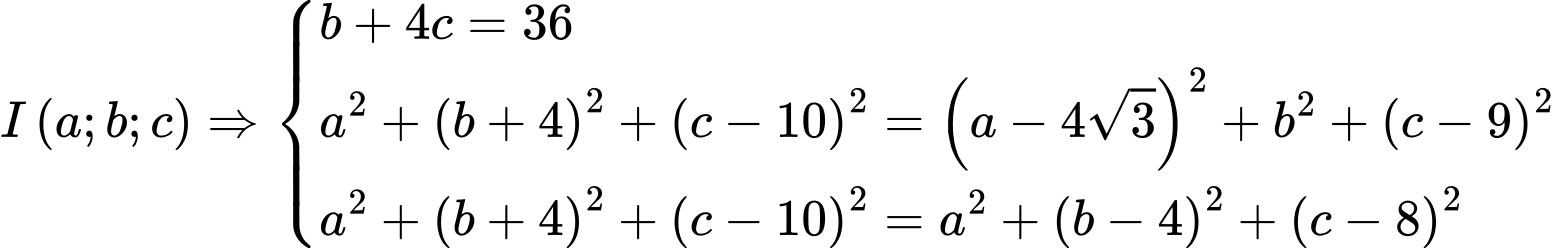
Suy ra
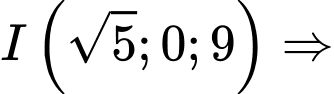 điểm I cách mặt sàn một khoảng là 9 mét.
điểm I cách mặt sàn một khoảng là 9 mét.
Câu 16 [694448]: Nobita và Shizuka chuẩn bị đi tham quan hòn đảo Honshu trong hai ngày thứ Bảy và Chủ nhật tuần này. Ở hòn đảo Honshu này, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy tuần này là 0,7. Gọi A là biến cố “Ngày thứ Bảy tuần này trời nắng” và B là biến cố “Ngày Chủ nhật tuần này trời mưa”.
a) Đúng.
Ta có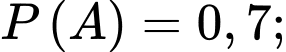

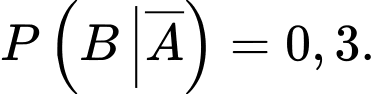
b) Sai.
Do đó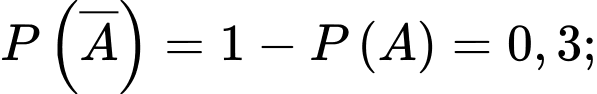
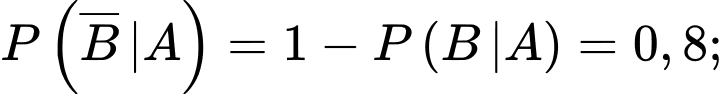
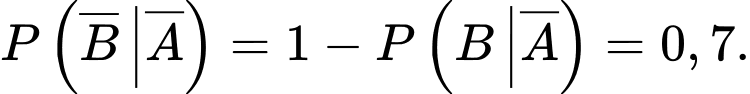
Áp dụng công thức nhân xác suất, ta có xác suất trời nắng vào thứ Bảy và trời mưa vào Chủ nhật là
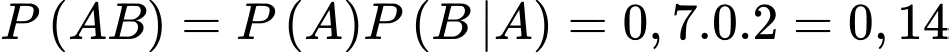
Tương tự, ta có



Ta có thể biểu diễn các kết quả trên theo sơ đồ cây như sau:
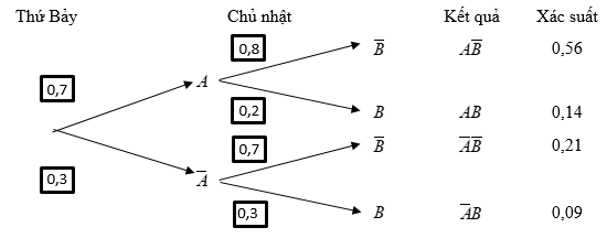
c) Sai.
Xác xuất ngày chủ nhật nắng là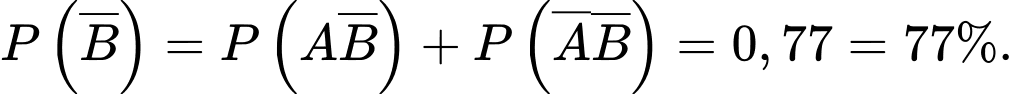
d) Sai.
Xác xuất chủ nhật trời mưa là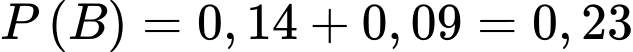
Ta có: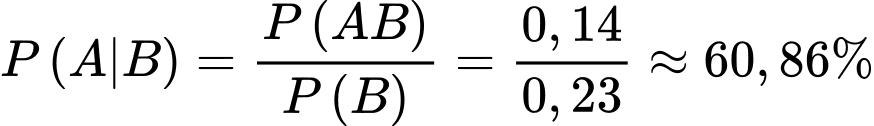
Ta có
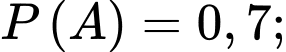

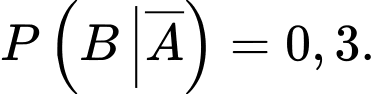
b) Sai.
Do đó
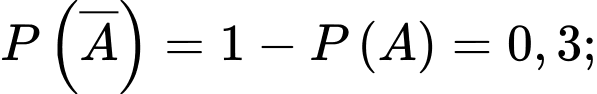
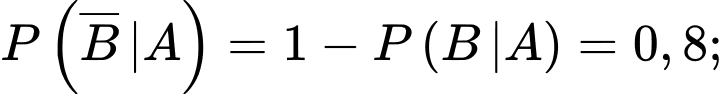
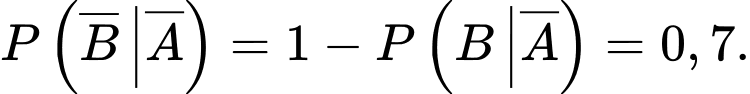
Áp dụng công thức nhân xác suất, ta có xác suất trời nắng vào thứ Bảy và trời mưa vào Chủ nhật là
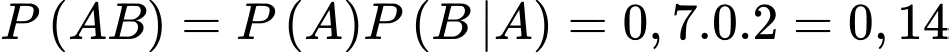
Tương tự, ta có



Ta có thể biểu diễn các kết quả trên theo sơ đồ cây như sau:

c) Sai.
Xác xuất ngày chủ nhật nắng là
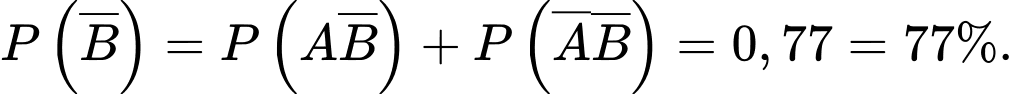
d) Sai.
Xác xuất chủ nhật trời mưa là
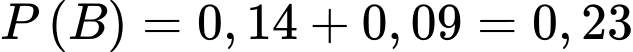
Ta có:
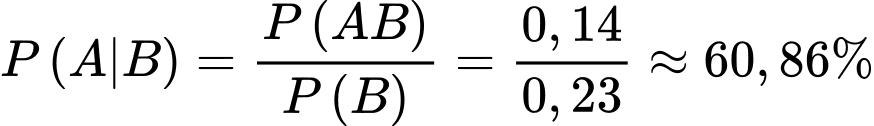
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [687490]: Cho hình lăng trụ đứng  có đáy
có đáy 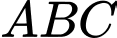 là tam giác đều cạnh
là tam giác đều cạnh 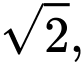
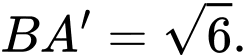 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 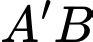 và
và 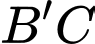 là bao nhiêu? (làm tròn đến hàng phần trăm)
là bao nhiêu? (làm tròn đến hàng phần trăm)
 có đáy
có đáy 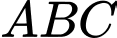 là tam giác đều cạnh
là tam giác đều cạnh 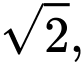
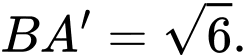 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 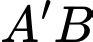 và
và 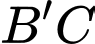 là bao nhiêu? (làm tròn đến hàng phần trăm)
là bao nhiêu? (làm tròn đến hàng phần trăm)
Điền đáp án: 0,67.
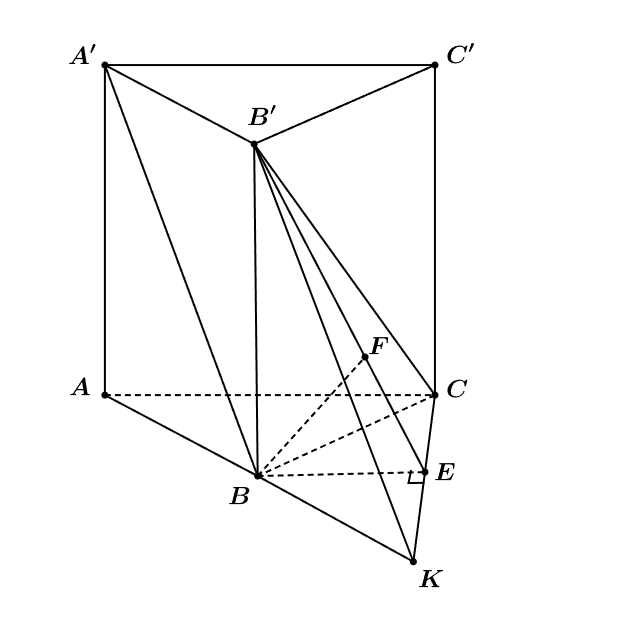
Kẻ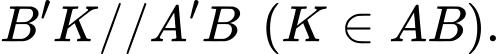
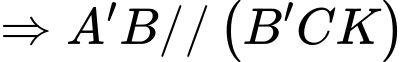
Suy ra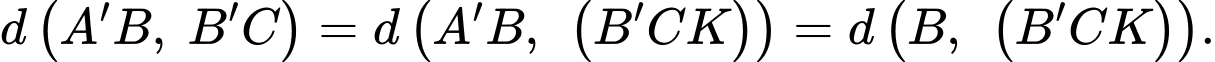
Kẻ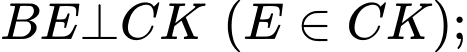

Ta có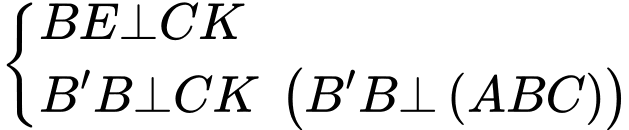
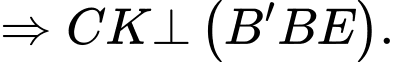
Suy ra
Ta có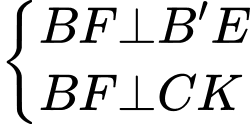
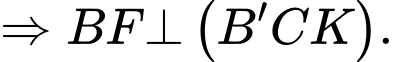
Vậy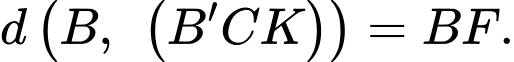
+) Trong tam giác vuông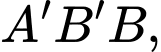 ta có:
ta có: 
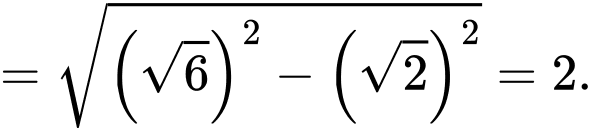
+)
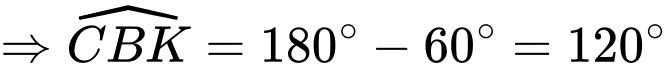
Vì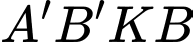 là hình bình hành nên ta có
là hình bình hành nên ta có 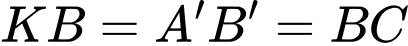
Suy ra tam giác cân tại
cân tại 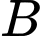
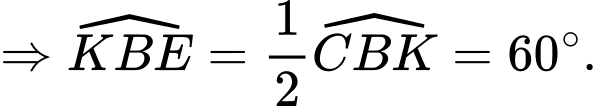
Xét tam giác vuông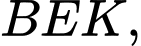 ta có
ta có 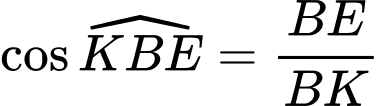
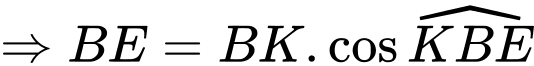

Áp dụng hệ thức lượng trong tam giác vuông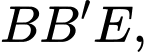 ta có
ta có 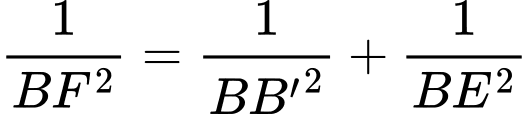
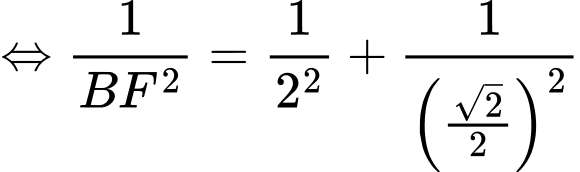
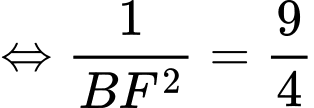
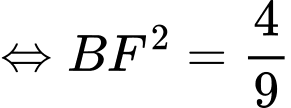
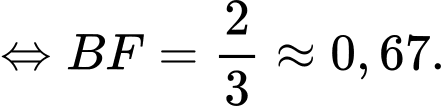

Kẻ
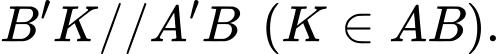
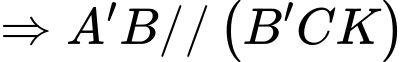
Suy ra
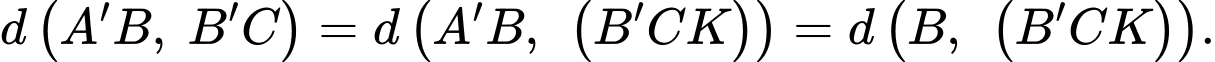
Kẻ
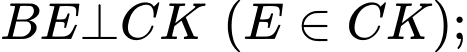

Ta có
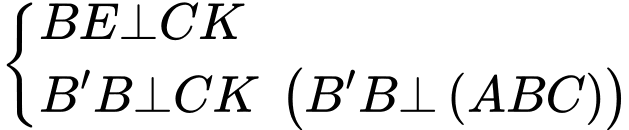
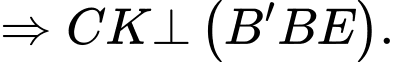
Suy ra

Ta có
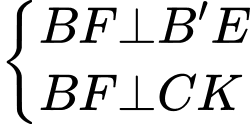
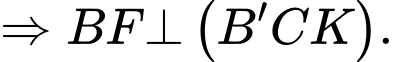
Vậy
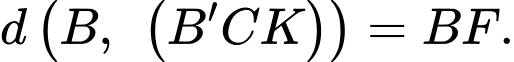
+) Trong tam giác vuông
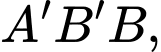 ta có:
ta có: 
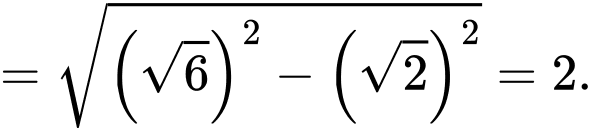
+)

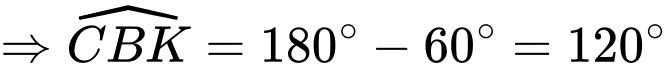
Vì
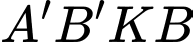 là hình bình hành nên ta có
là hình bình hành nên ta có 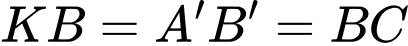
Suy ra tam giác
 cân tại
cân tại 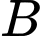
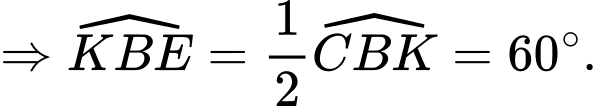
Xét tam giác vuông
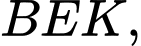 ta có
ta có 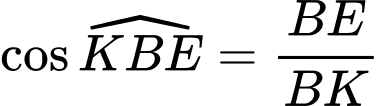
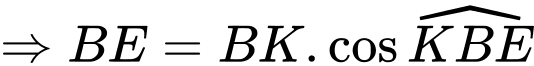

Áp dụng hệ thức lượng trong tam giác vuông
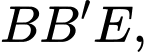 ta có
ta có 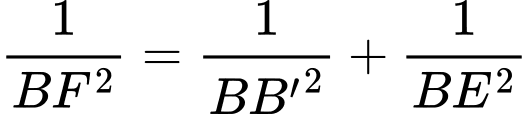
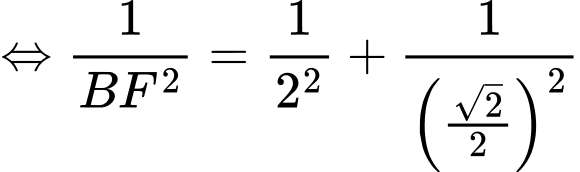
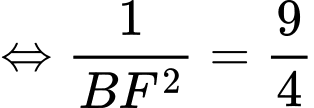
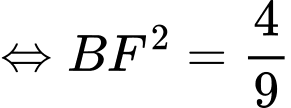
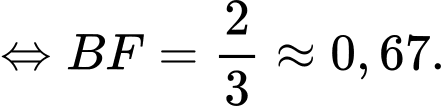
Câu 18 [694449]: Trong một giải đấu bóng đá, đội bóng của Hưng thi đấu 30 trận với đúng hai chiến thuật tấn công hoặc phòng ngự, xuyên suốt cả trận đấu. Biết rằng, số trận thi đấu theo chiến thuật tấn công gấp đôi số trận thi đấu theo chiến thuật phòng ngự. Khi chơi theo chiến thuật tấn công, họ thắng 30% số trận và thua 20% số trận. Khi họ chơi theo chiến thuật phòng ngự, họ thắng 20% số trận và thua 40% số trận. Mỗi trận thắng đội được cộng 3 điểm, mỗi trận hoà đội được cộng 1 điểm và không cộng điểm cho trận thua. Tổng số điểm đội bóng đạt được trong giải là bao nhiêu điểm?
Điền đáp án: 
Gọi số trận thi đấu theo chiến thuật tấn công, phòng ngự lần lượt là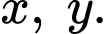
Ta có hệ phương trình: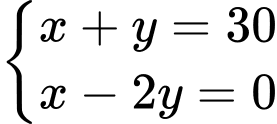
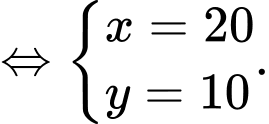
Số điểm mà đội bóng đạt được khi chơi theo chiến thuật tấn công là:
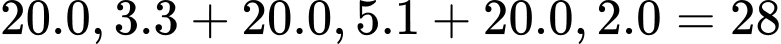 ( điểm).
( điểm).
Số điểm mà đội bóng đạt được khi chơi theo chiến thuật phòng ngự là:
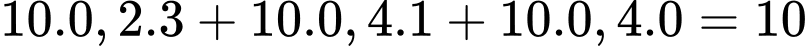 ( điểm).
( điểm).
Vậy tổng số điểm mà đội bóng đạt được trong giải là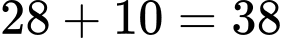 điểm.
điểm.
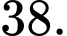
Gọi số trận thi đấu theo chiến thuật tấn công, phòng ngự lần lượt là
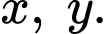
Ta có hệ phương trình:
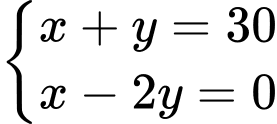
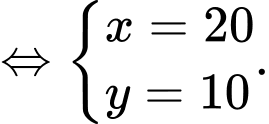
Số điểm mà đội bóng đạt được khi chơi theo chiến thuật tấn công là:
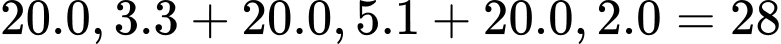 ( điểm).
( điểm).Số điểm mà đội bóng đạt được khi chơi theo chiến thuật phòng ngự là:
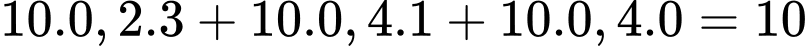 ( điểm).
( điểm).Vậy tổng số điểm mà đội bóng đạt được trong giải là
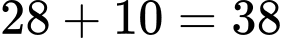 điểm.
điểm.
Câu 19 [694450]: Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline (là đường thẳng) từ vị trí 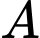 cao
cao  m của tháp một này sang vị trí
m của tháp một này sang vị trí 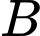 cao
cao  m của tháp hai trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ
m của tháp hai trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ 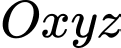 cho trước (đơn vị: mét), toạ độ của
cho trước (đơn vị: mét), toạ độ của 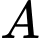 và
và 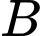 lần lượt là
lần lượt là 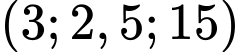 và
và 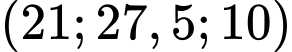 . Bạn Tuấn đang đứng ở mặt đất vị trí có toạ độ
. Bạn Tuấn đang đứng ở mặt đất vị trí có toạ độ 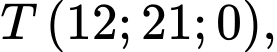 hỏi khi du khách ở độ cao bao nhiêu mét trên cáp treo sẽ cách bạn Tuấn một khoảng nhỏ nhất (làm tròn kết quả đến hàng phần mười).
hỏi khi du khách ở độ cao bao nhiêu mét trên cáp treo sẽ cách bạn Tuấn một khoảng nhỏ nhất (làm tròn kết quả đến hàng phần mười).

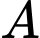 cao
cao  m của tháp một này sang vị trí
m của tháp một này sang vị trí 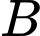 cao
cao  m của tháp hai trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ
m của tháp hai trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ 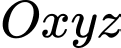 cho trước (đơn vị: mét), toạ độ của
cho trước (đơn vị: mét), toạ độ của 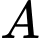 và
và 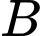 lần lượt là
lần lượt là 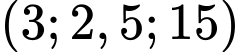 và
và 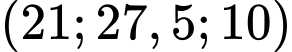 . Bạn Tuấn đang đứng ở mặt đất vị trí có toạ độ
. Bạn Tuấn đang đứng ở mặt đất vị trí có toạ độ 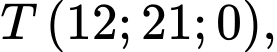 hỏi khi du khách ở độ cao bao nhiêu mét trên cáp treo sẽ cách bạn Tuấn một khoảng nhỏ nhất (làm tròn kết quả đến hàng phần mười).
hỏi khi du khách ở độ cao bao nhiêu mét trên cáp treo sẽ cách bạn Tuấn một khoảng nhỏ nhất (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 11,4.
Giả sử bạn Tuấn đang đứng ở vị trí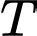 và
và 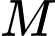 là vị trí của du khách.
là vị trí của du khách.
Khi đó du khách gần bạn Tuấn nhất khi
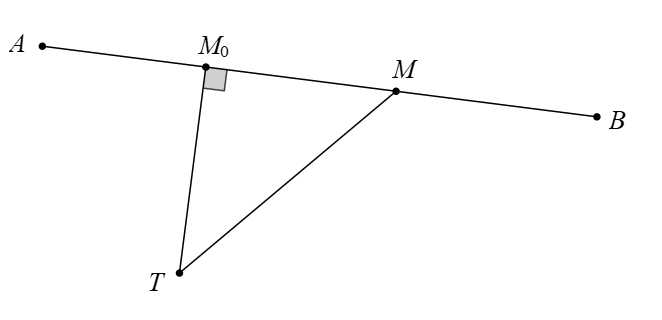
Ta có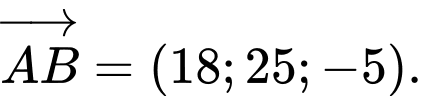
Phương trình tham số chứa đường zipline là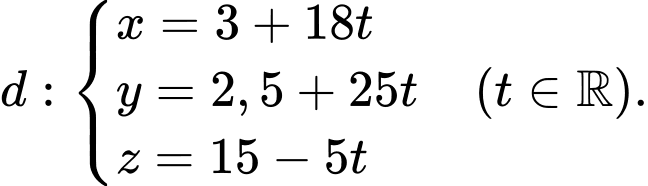
Gọi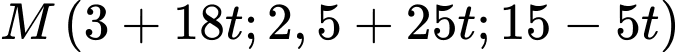 ta có:
ta có: 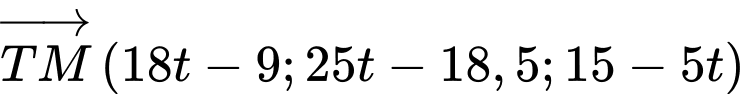
Khi đó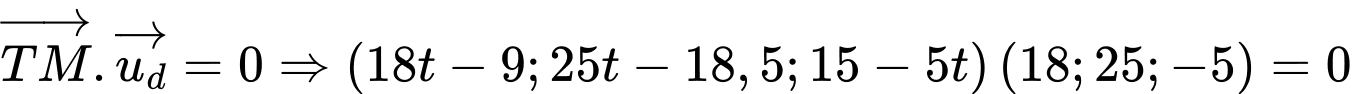
Suy ra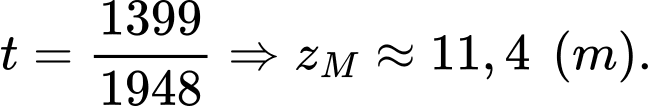
Giả sử bạn Tuấn đang đứng ở vị trí
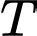 và
và 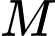 là vị trí của du khách.
là vị trí của du khách.
Khi đó du khách gần bạn Tuấn nhất khi


Ta có
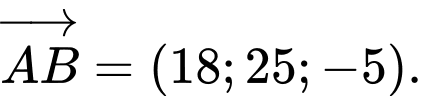
Phương trình tham số chứa đường zipline là
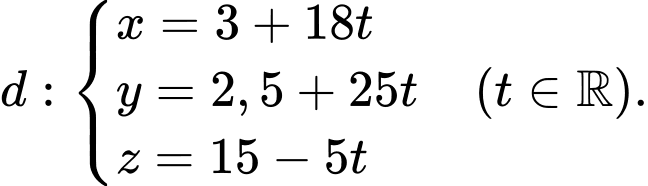
Gọi
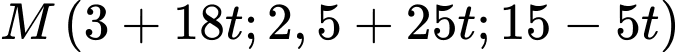 ta có:
ta có: 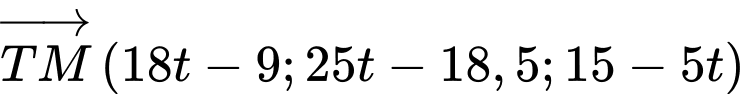
Khi đó
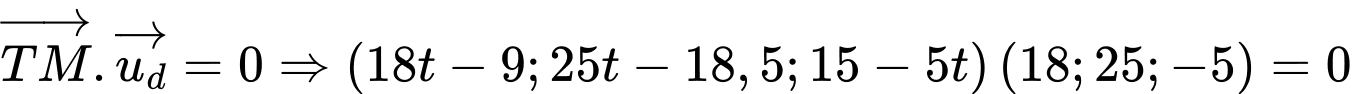
Suy ra
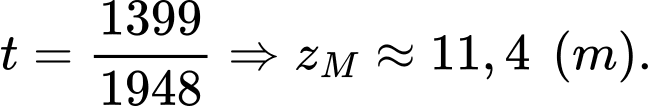
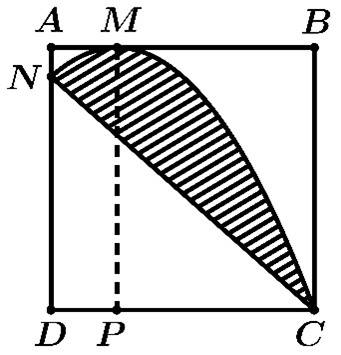
Câu 20 [694451]: Ông Duy có một mảnh vườn hình vuông cạnh bằng 8 m. Ông dự định xây một cái bể bơi đặc biệt (phần kẻ sọc trong hình vẽ bên). Biết 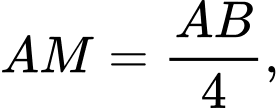 phần đường cong đi qua các điểm
phần đường cong đi qua các điểm 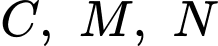 là một phần của đường Parabol có trục đối xứng là
là một phần của đường Parabol có trục đối xứng là 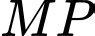 và chi phí để làm bể bơi là 5 triệu đồng/1
và chi phí để làm bể bơi là 5 triệu đồng/1 Số tiền ông Duy phải trả để xây cái bể bơi đó là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).
Số tiền ông Duy phải trả để xây cái bể bơi đó là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).
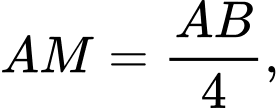 phần đường cong đi qua các điểm
phần đường cong đi qua các điểm 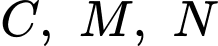 là một phần của đường Parabol có trục đối xứng là
là một phần của đường Parabol có trục đối xứng là 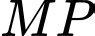 và chi phí để làm bể bơi là 5 triệu đồng/1
và chi phí để làm bể bơi là 5 triệu đồng/1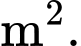 Số tiền ông Duy phải trả để xây cái bể bơi đó là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).
Số tiền ông Duy phải trả để xây cái bể bơi đó là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 95.
Gắn trục toạ độ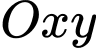 như hình vẽ.
như hình vẽ.
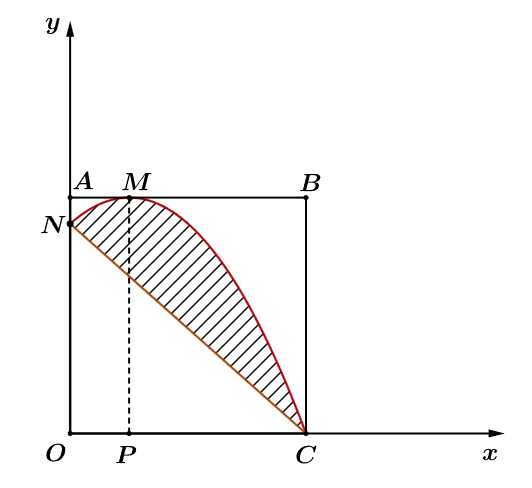
Gọi phương trình parabol đi qua 3 điểm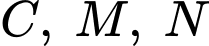 là
là 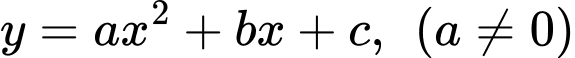
Trục đối xứng của parabol là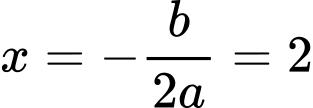
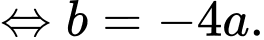
Ta có parabol đi qua các điểm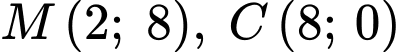 nên ta có hệ phương trình
nên ta có hệ phương trình
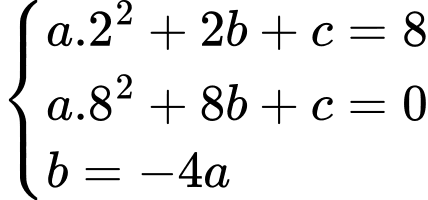
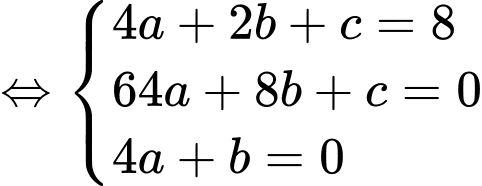
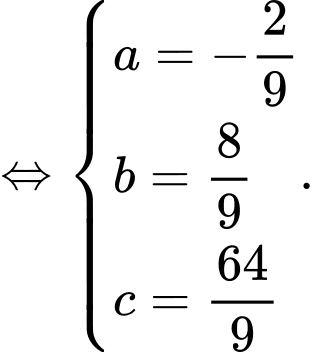
 Phương trình của parabol là
Phương trình của parabol là 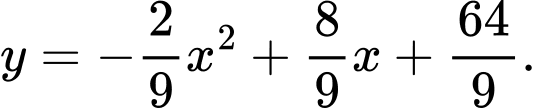
Ta có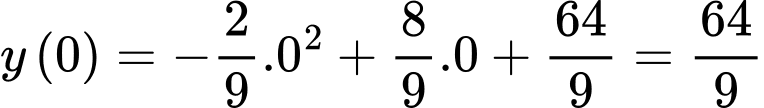
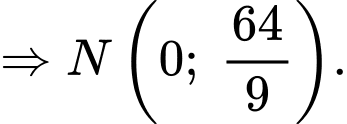
Phương trình đường thẳng đi qua điểm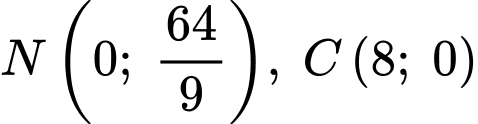 là
là 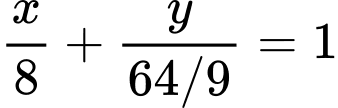
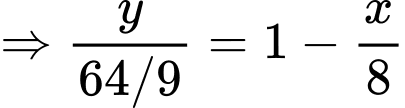
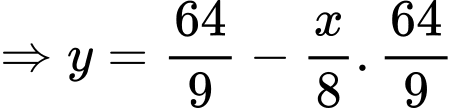
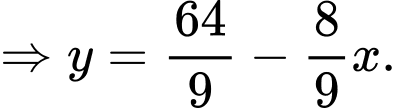
Suy ra diện tích bể bơi bằng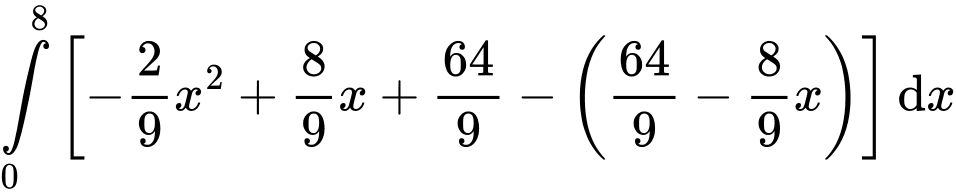
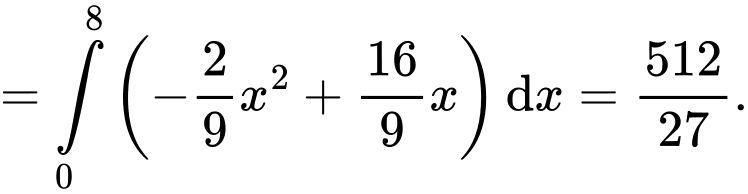
Vậy số tiền cần trả để xây bể bơi là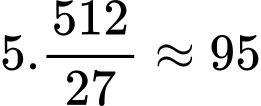 triệu đồng.
triệu đồng.
Gắn trục toạ độ
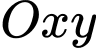 như hình vẽ.
như hình vẽ.
Gọi phương trình parabol đi qua 3 điểm
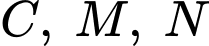 là
là 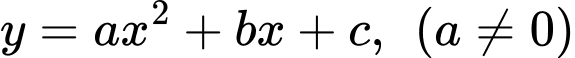
Trục đối xứng của parabol là
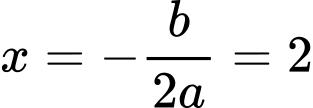
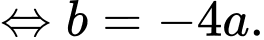
Ta có parabol đi qua các điểm
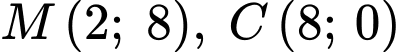 nên ta có hệ phương trình
nên ta có hệ phương trình 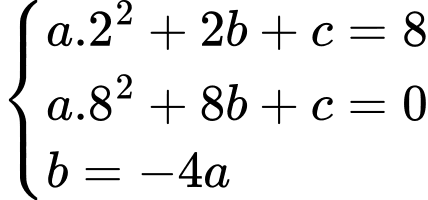
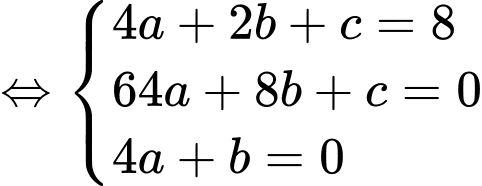
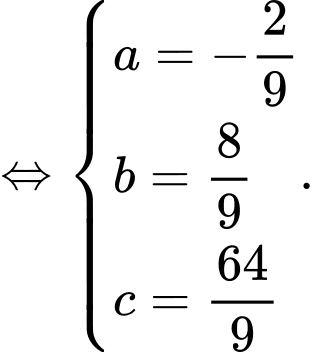
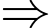 Phương trình của parabol là
Phương trình của parabol là 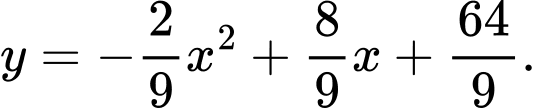
Ta có
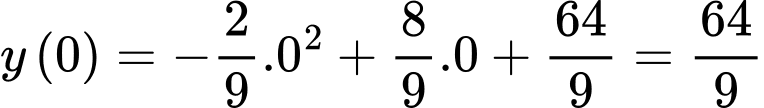
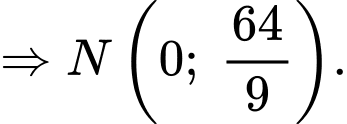
Phương trình đường thẳng đi qua điểm
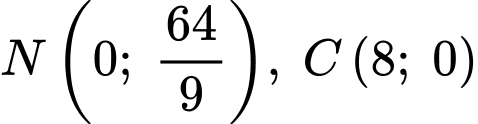 là
là 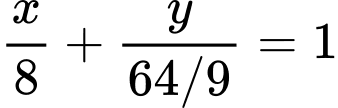
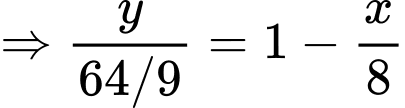
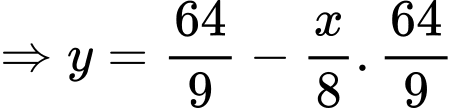
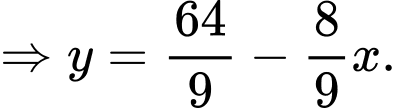
Suy ra diện tích bể bơi bằng
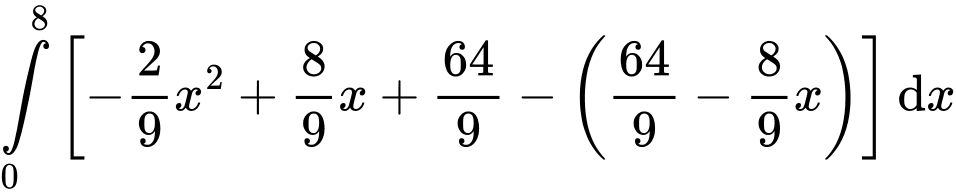
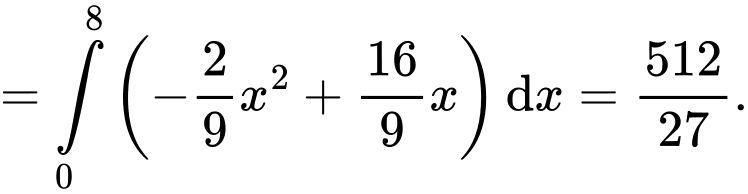
Vậy số tiền cần trả để xây bể bơi là
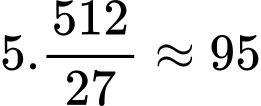 triệu đồng.
triệu đồng.
Câu 21 [694452]: Có một kho chứa bia kém chất lượng chứa các thùng giống nhau (24 lon/thùng) gồm 2 loại: loại I để lẫn mỗi thùng 5 lon quá hạn sử dụng, loại II để lẫn mỗi thùng 3 lon quá hạn. Biết số lượng thùng loại I gấp 2 lần số lượng thùng loại II. Chọn ngẫu nhiên 1 thùng từ trong kho, từ thùng đó chọn ngẫu nhiên 10 lon thì thấy trong 10 lon đó có hai lon quá hạn sử dụng. Tính xác suất 10 lon được lấy là bia loại I (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,71.
Gọi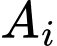 là biến cố chọn được thùng loại
là biến cố chọn được thùng loại 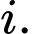
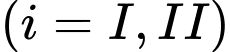
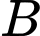 là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
Từ đó, ta có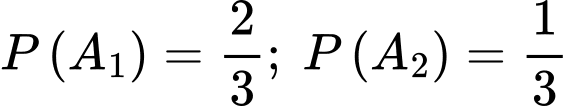
Áp dụng công thức xác suất có điều kiện, ta có: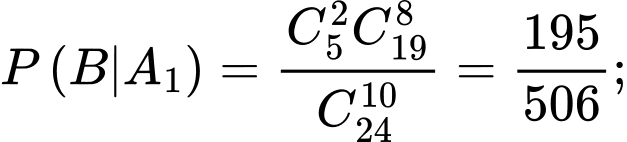
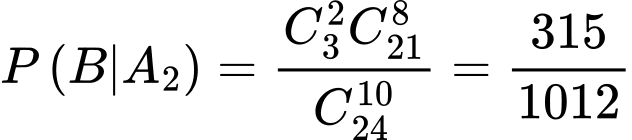
Ta có sơ đồ cây sau:
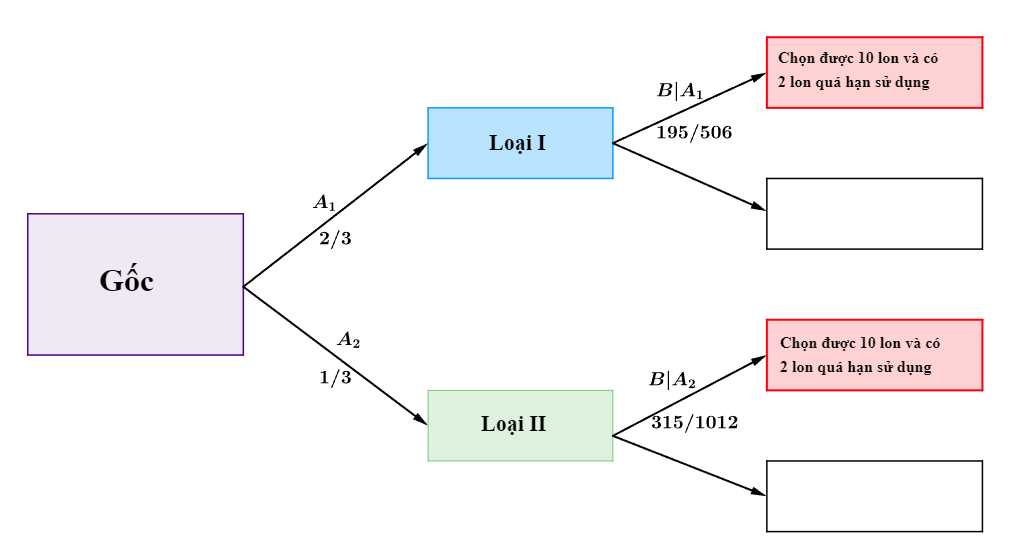
Xác suất để chọn được 2 lon quá hạn là:

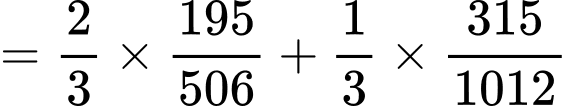
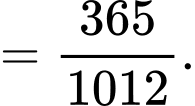
Suy ra xác suất bia được lấy thuộc loại I là: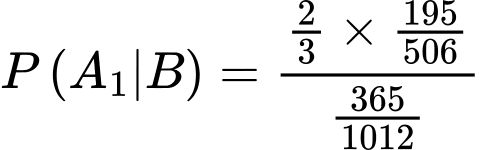
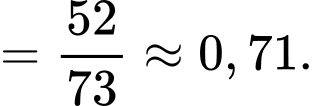
Gọi
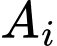 là biến cố chọn được thùng loại
là biến cố chọn được thùng loại 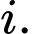
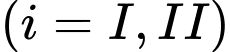
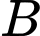 là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.Từ đó, ta có
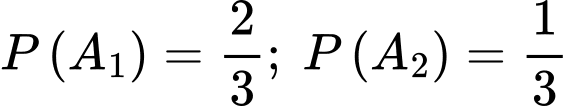
Áp dụng công thức xác suất có điều kiện, ta có:
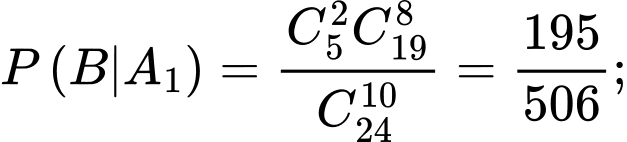
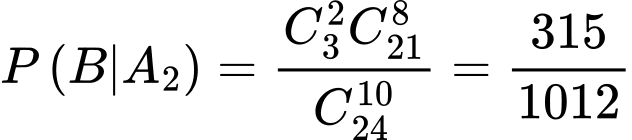
Ta có sơ đồ cây sau:

Xác suất để chọn được 2 lon quá hạn là:

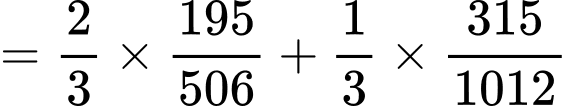
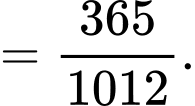
Suy ra xác suất bia được lấy thuộc loại I là:
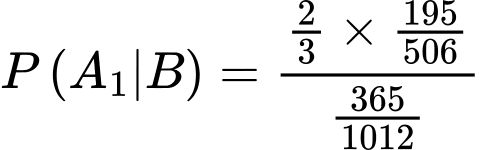
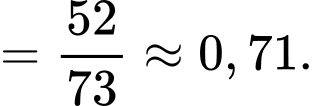
Câu 22 [697655]: Một hồ nước ở Bắc Ontario đã phục hồi sau một vụ tràn axit khiến tất cả cá hồi ở đó chết. Một chương trình tái thả cá đã thả 800 con cá hồi vào hồ. Ba năm sau, số lượng được ước tính là 6000 con. Sức chứa của hồ được cho là 8000 con. Để đánh giá khả năng tăng trưởng, người ta mô phỏng số lượng cá trong hồ qua từng năm thông qua hàm số 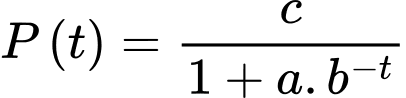 (
(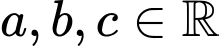 ) có đồ thị như hình vẽ bên (trong đó tính theo năm kể từ lúc bắt đầu thả cá vào hồ). Sử dụng mô hình trên, hãy tính tốc độ tăng trưởng tối đa (đơn vị con/năm) của đàn cá (kết quả làm tròn đến hàng đơn vị).
) có đồ thị như hình vẽ bên (trong đó tính theo năm kể từ lúc bắt đầu thả cá vào hồ). Sử dụng mô hình trên, hãy tính tốc độ tăng trưởng tối đa (đơn vị con/năm) của đàn cá (kết quả làm tròn đến hàng đơn vị).
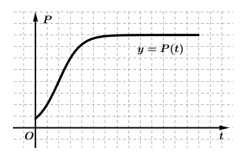
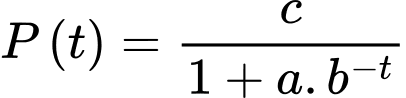 (
(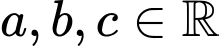 ) có đồ thị như hình vẽ bên (trong đó tính theo năm kể từ lúc bắt đầu thả cá vào hồ). Sử dụng mô hình trên, hãy tính tốc độ tăng trưởng tối đa (đơn vị con/năm) của đàn cá (kết quả làm tròn đến hàng đơn vị).
) có đồ thị như hình vẽ bên (trong đó tính theo năm kể từ lúc bắt đầu thả cá vào hồ). Sử dụng mô hình trên, hãy tính tốc độ tăng trưởng tối đa (đơn vị con/năm) của đàn cá (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 2197.
Dựa vào dữ kiện đề bài, ta có:
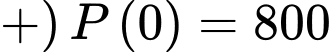
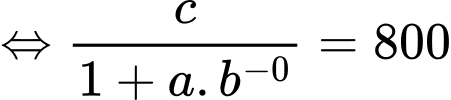
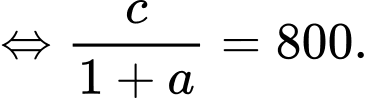
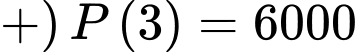
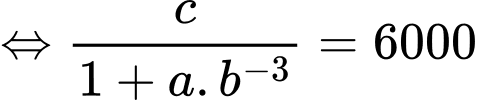
+) Sức chứa của hồ là 8000 con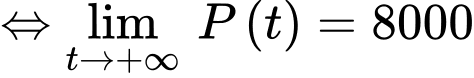
Khi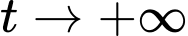
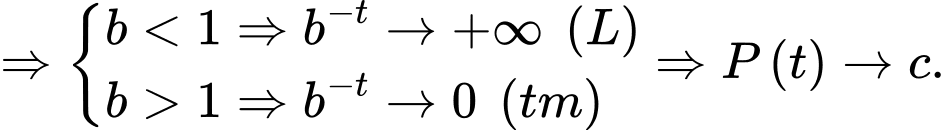
Khi đó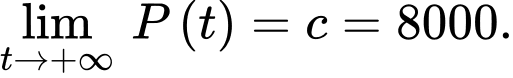
Mà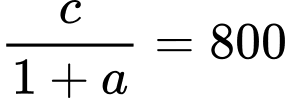
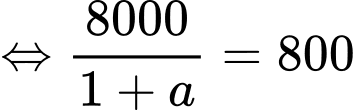
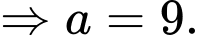
Thay vào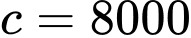 và
và 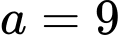 phương trình
phương trình 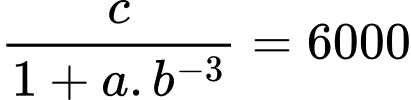 ta được
ta được
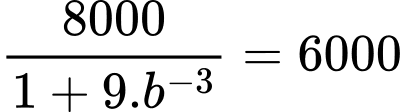
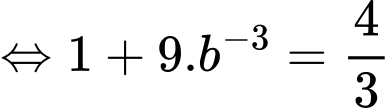
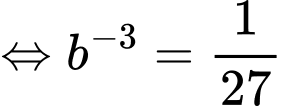
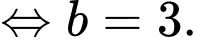
Suy ra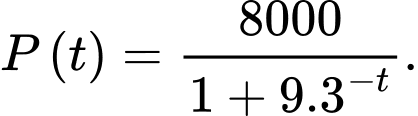
Hàm số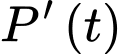 là tốc độ tăng trưởng của đàn cá.
là tốc độ tăng trưởng của đàn cá.
Suy ra tốc độ tăng trưởng tối đa của đàn cá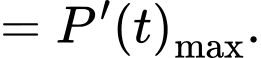
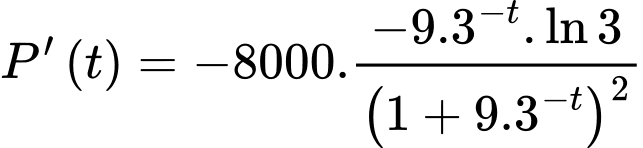

Để tìm max của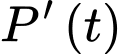 ta có 3 cách sau:
ta có 3 cách sau:
+) Cách 1: Thực hiện như video thầy Tiến giải.
+) Cách 2: Côsi:
Ta tìm max của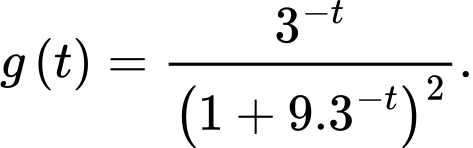
Đặt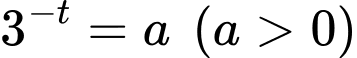
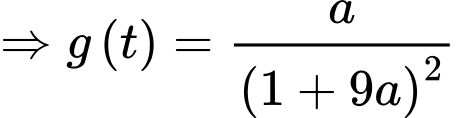
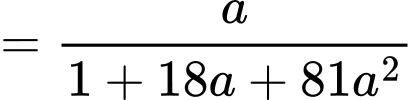
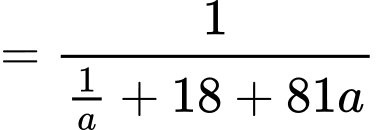
Nhận xét: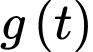 max khi
max khi 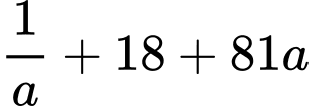 min.
min.
Áp dụng cosi cho 2 số dương và
và 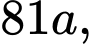 ta có:
ta có: 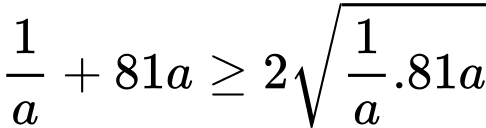
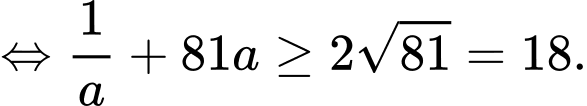
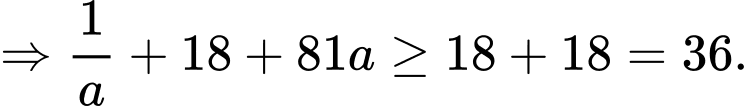
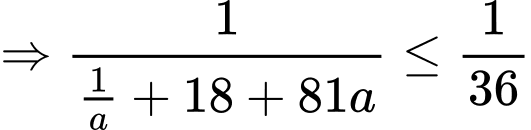
Dấu “=” xảy ra khi và chỉ khi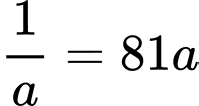
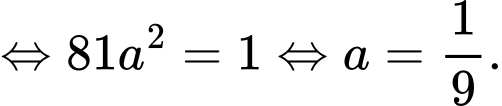
Khi đó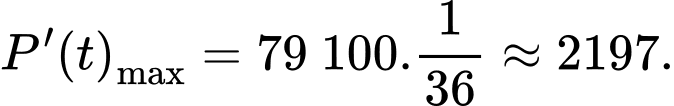
+) Cách 3: Lập bảng biến thiên.
Dựa vào dữ kiện đề bài, ta có:
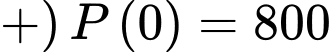
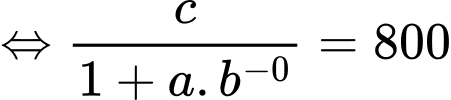
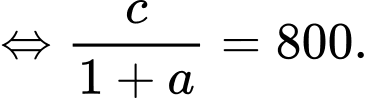
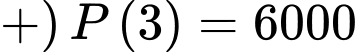
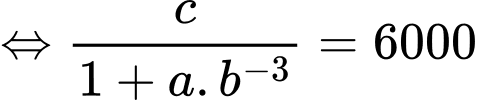
+) Sức chứa của hồ là 8000 con
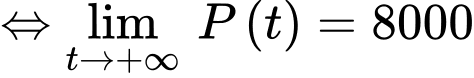
Khi
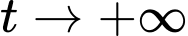
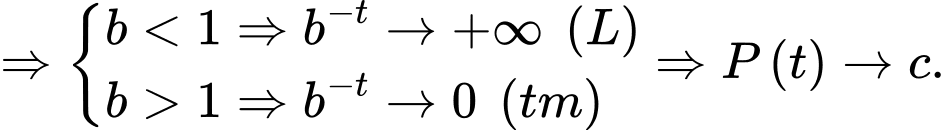
Khi đó
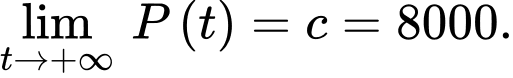
Mà
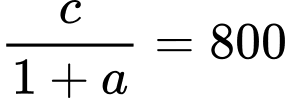
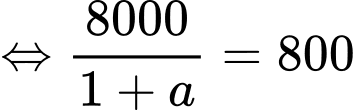
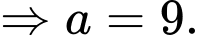
Thay vào
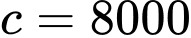 và
và 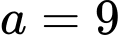 phương trình
phương trình 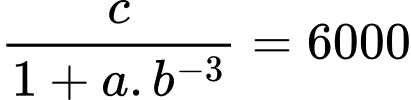 ta được
ta được
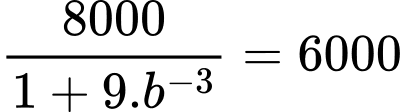
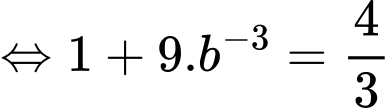
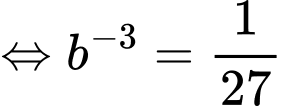
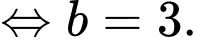
Suy ra
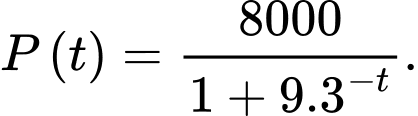
Hàm số
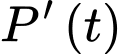 là tốc độ tăng trưởng của đàn cá.
là tốc độ tăng trưởng của đàn cá.
Suy ra tốc độ tăng trưởng tối đa của đàn cá
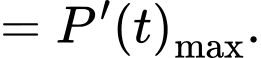
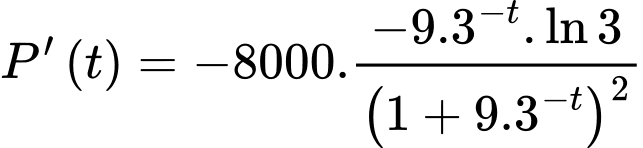

Để tìm max của
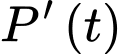 ta có 3 cách sau:
ta có 3 cách sau:
+) Cách 1: Thực hiện như video thầy Tiến giải.
+) Cách 2: Côsi:
Ta tìm max của
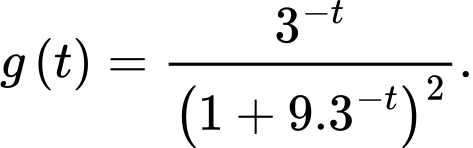
Đặt
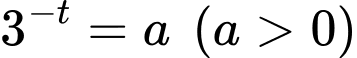
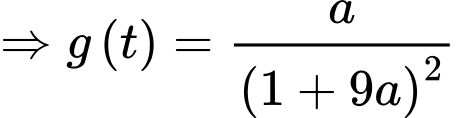
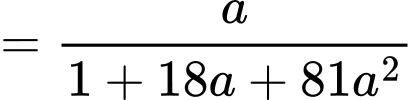
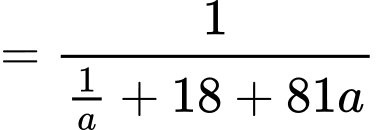
Nhận xét:
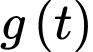 max khi
max khi 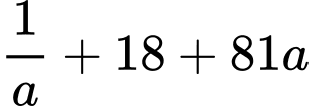 min.
min.
Áp dụng cosi cho 2 số dương
 và
và 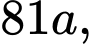 ta có:
ta có: 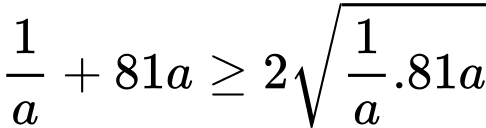
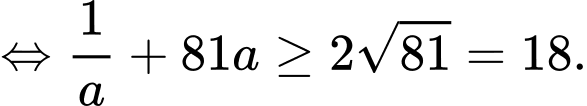
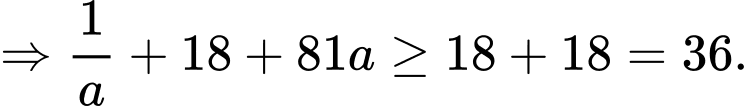
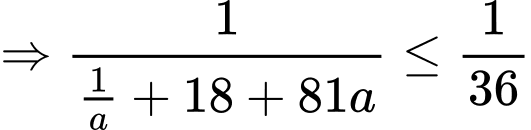
Dấu “=” xảy ra khi và chỉ khi
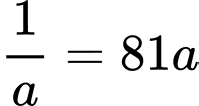
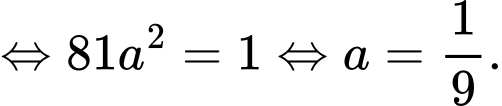
Khi đó
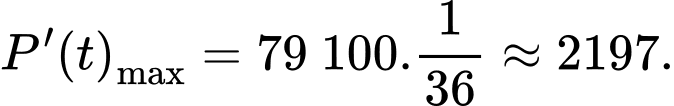
+) Cách 3: Lập bảng biến thiên.