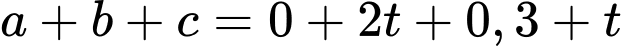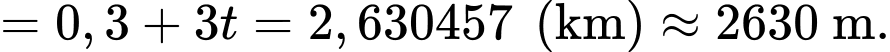PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [255997]: Cho hàm số 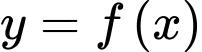 có bảng biến thiên như hình sau:
có bảng biến thiên như hình sau:

Giá trị cực đại của hàm số đã cho bằng
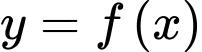 có bảng biến thiên như hình sau:
có bảng biến thiên như hình sau: 
Giá trị cực đại của hàm số đã cho bằng
A, 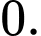
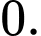
B, 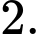
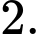
C, 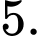
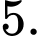
D, 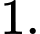
Chọn đáp án C.
Từ bảng biến thiên, hàm số có giá trị cực đại là: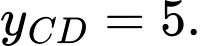 Đáp án: C
Đáp án: C
Từ bảng biến thiên, hàm số có giá trị cực đại là:
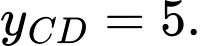 Đáp án: C
Đáp án: C
Câu 2 [693196]: Trong không gian 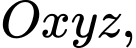 cho mặt cầu
cho mặt cầu 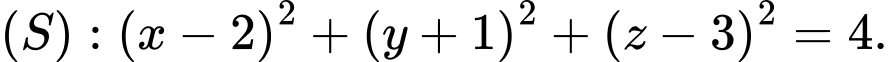 Tâm của
Tâm của 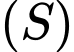 có toạ độ là
có toạ độ là
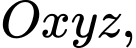 cho mặt cầu
cho mặt cầu 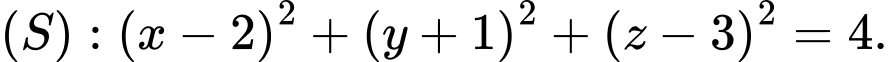 Tâm của
Tâm của 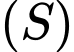 có toạ độ là
có toạ độ là A, 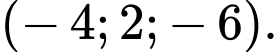
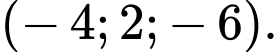
B, 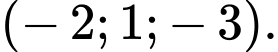
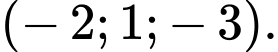
C, 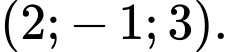
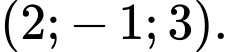
D, 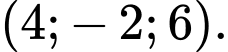
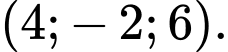
Chọn đáp án C.
Từ phương trình mặt cầu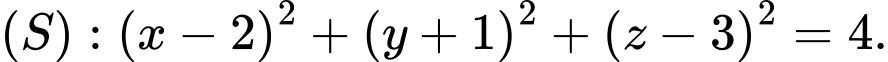
Suy ra tâm của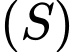 có toạ độ là:
có toạ độ là: 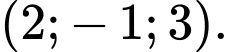 Đáp án: C
Đáp án: C
Từ phương trình mặt cầu
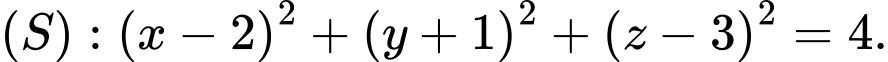
Suy ra tâm của
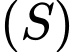 có toạ độ là:
có toạ độ là: 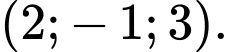 Đáp án: C
Đáp án: C
Câu 3 [697752]: Nếu 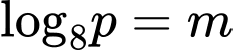 thì
thì 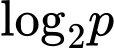 bằng
bằng
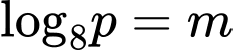 thì
thì 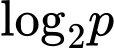 bằng
bằng A, 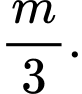
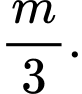
B, 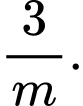
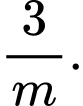
C, 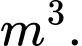
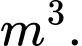
D, 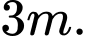
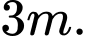
Chọn đáp án D.
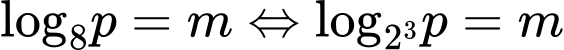

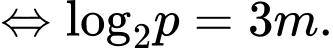 Đáp án: D
Đáp án: D
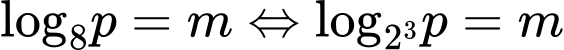

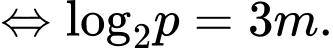 Đáp án: D
Đáp án: D
Câu 4 [693198]: Cho hình hộp chữ nhật 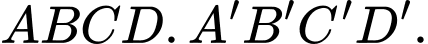 Hai đường thẳng nào sau đây vuông góc với nhau?
Hai đường thẳng nào sau đây vuông góc với nhau?
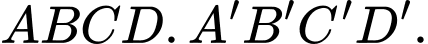 Hai đường thẳng nào sau đây vuông góc với nhau?
Hai đường thẳng nào sau đây vuông góc với nhau? A, 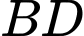 và
và 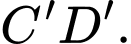
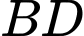 và
và 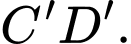
B, 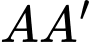 và
và 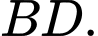
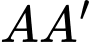 và
và 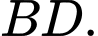
C, 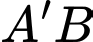 và
và 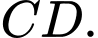
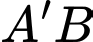 và
và 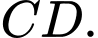
D, 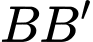 và
và 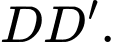
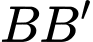 và
và 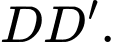
Chọn đáp án B.
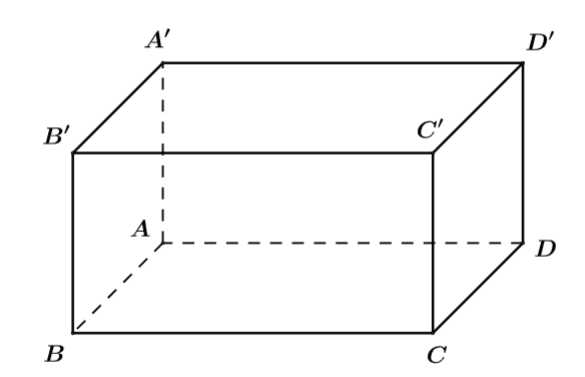
Từ hình vẽ ta suy ra: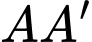 và
và 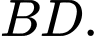 vuông góc với nhau. Đáp án: B
vuông góc với nhau. Đáp án: B

Từ hình vẽ ta suy ra:
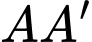 và
và 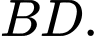 vuông góc với nhau. Đáp án: B
vuông góc với nhau. Đáp án: B
Câu 5 [693199]: Hàm số 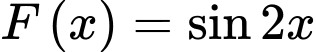 là một nguyên hàm của hàm số nào sau đây?
là một nguyên hàm của hàm số nào sau đây?
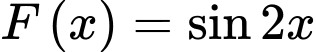 là một nguyên hàm của hàm số nào sau đây?
là một nguyên hàm của hàm số nào sau đây? A, 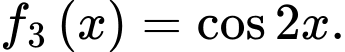
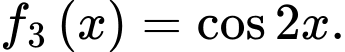
B, 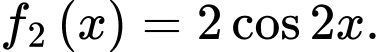
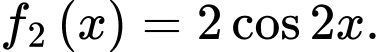
C, 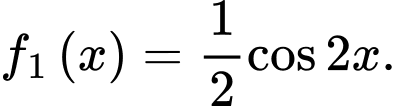
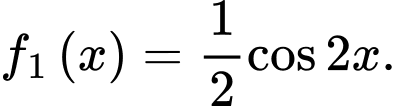
D, 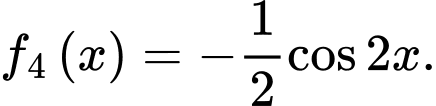
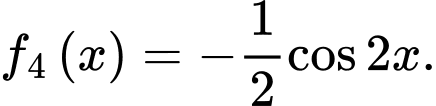
Chọn đáp án B.
Theo bài cho ta có: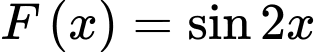 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 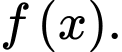
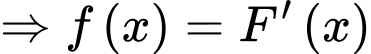
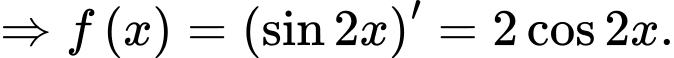 Đáp án: B
Đáp án: B
Theo bài cho ta có:
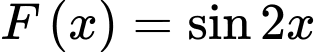 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 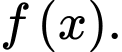
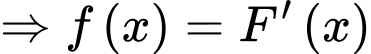
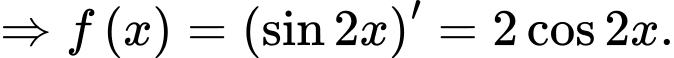 Đáp án: B
Đáp án: B
Câu 6 [693200]: Hàm số 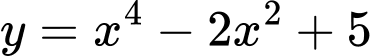 đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây?
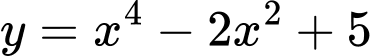 đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây? A, 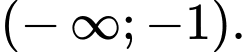
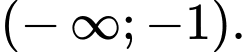
B, 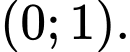
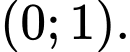
C, 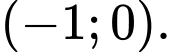
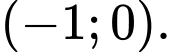
D, 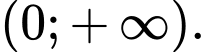
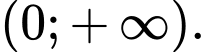
Chọn đáp án C.
Xét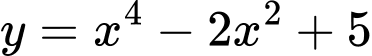 có:
có:
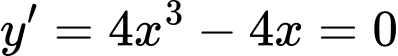
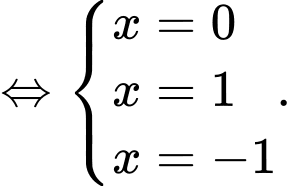
Ta có trục xét dấu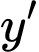 như sau:
như sau:

Từ trục xét dấu ta suy ta ra hàm số đồng biến trên khoảng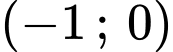 và
và  Đáp án: C
Đáp án: C
Xét
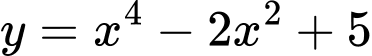 có:
có: 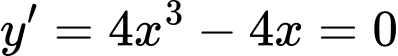
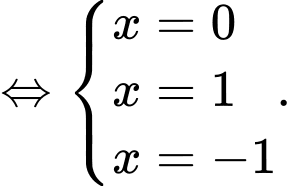
Ta có trục xét dấu
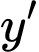 như sau:
như sau:
Từ trục xét dấu ta suy ta ra hàm số đồng biến trên khoảng
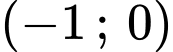 và
và  Đáp án: C
Đáp án: C
Câu 7 [693201]: Cho hình chóp 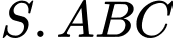 có đáy
có đáy 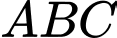 là tam giác đều,
là tam giác đều, 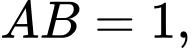 cạnh bên
cạnh bên 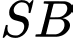 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 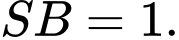 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ  và
và 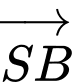 bằng
bằng
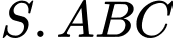 có đáy
có đáy 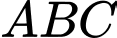 là tam giác đều,
là tam giác đều, 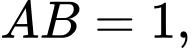 cạnh bên
cạnh bên 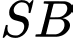 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 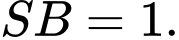 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ  và
và 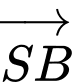 bằng
bằng A, 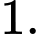
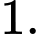
B, 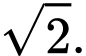
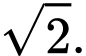
C, 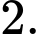
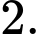
D, 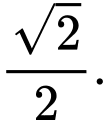
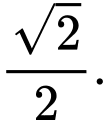
Chọn đáp án A.
Xét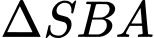 có
có  và
và 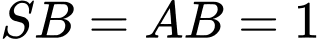
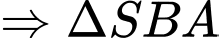 vuông cân tại
vuông cân tại 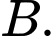
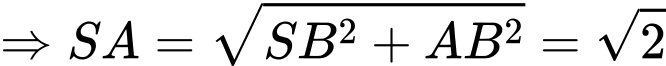 và
và 
Ta có: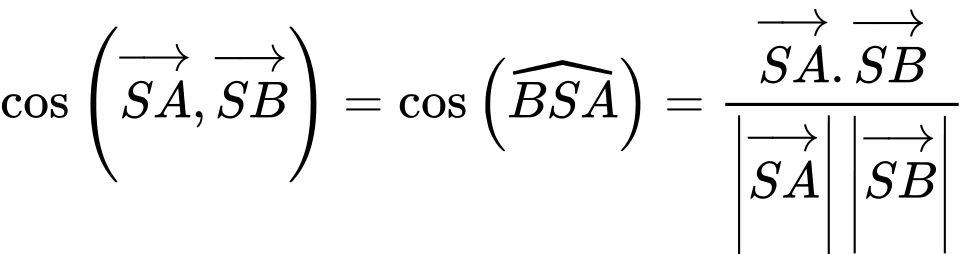
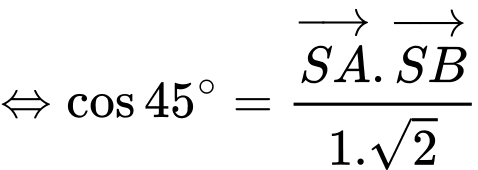
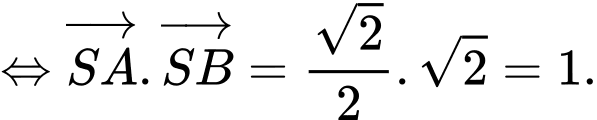 Đáp án: A
Đáp án: A
Xét
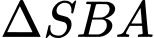 có
có  và
và 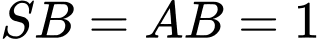
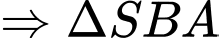 vuông cân tại
vuông cân tại 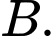
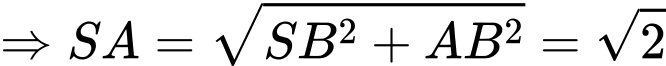 và
và 
Ta có:
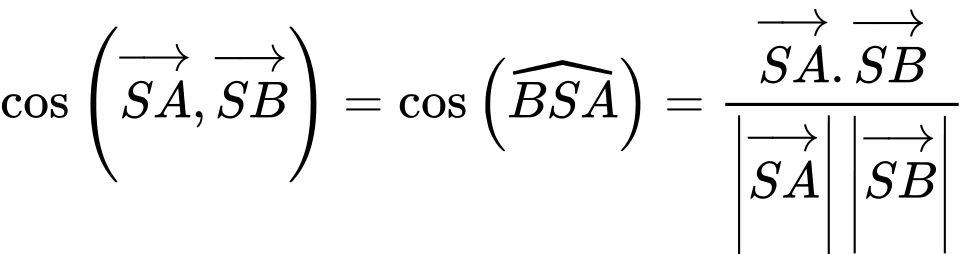
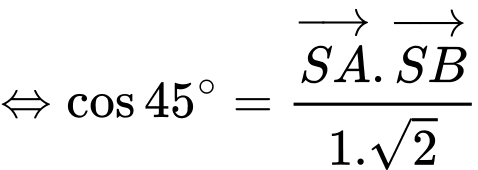
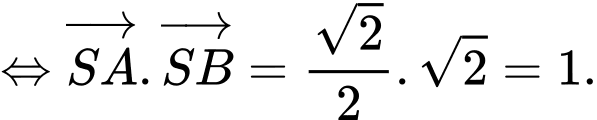 Đáp án: A
Đáp án: A
Câu 8 [693202]: Cho cấp số cộng 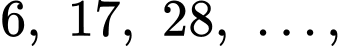 số hạng thứ 10 của cấp số cộng đã cho bằng
số hạng thứ 10 của cấp số cộng đã cho bằng
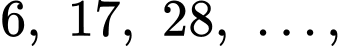 số hạng thứ 10 của cấp số cộng đã cho bằng
số hạng thứ 10 của cấp số cộng đã cho bằng A, 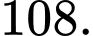
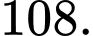
B, 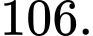
C, 
D, 

Chọn đáp án D.
Theo bài cho: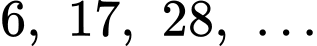 là dãy cấp số cộng nên ta có:
là dãy cấp số cộng nên ta có:
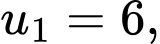
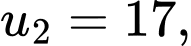
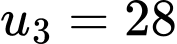
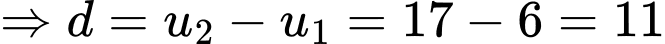 là công sai của cấp số cộng.
là công sai của cấp số cộng.
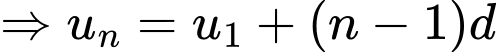

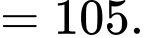 Đáp án: D
Đáp án: D
Theo bài cho:
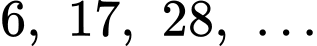 là dãy cấp số cộng nên ta có:
là dãy cấp số cộng nên ta có: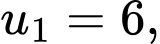
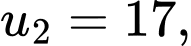
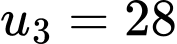
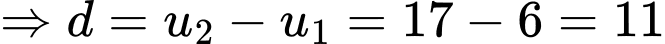 là công sai của cấp số cộng.
là công sai của cấp số cộng.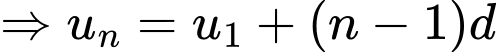

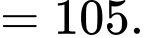 Đáp án: D
Đáp án: D
Câu 9 [693203]: Nếu 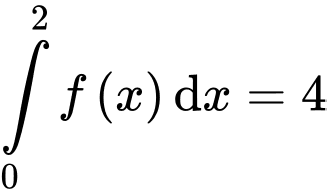 thì
thì 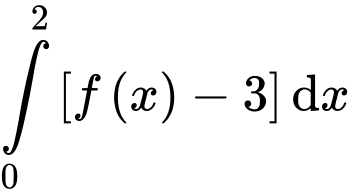 bằng
bằng
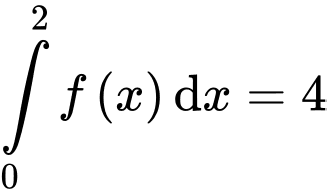 thì
thì 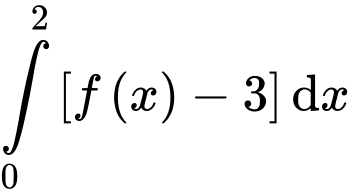 bằng
bằng A, 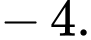
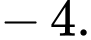
B, 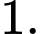
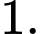
C, 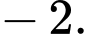
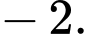
D, 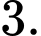
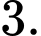
Chọn đáp án C.
Ta có: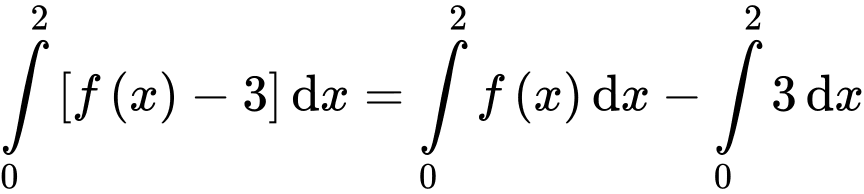
Mà theo bài ra ta có: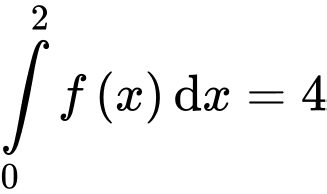
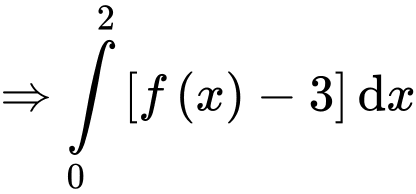
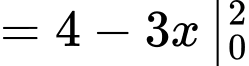
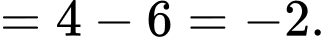 Đáp án: C
Đáp án: C
Ta có:
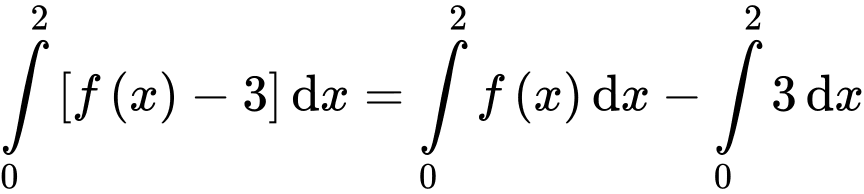
Mà theo bài ra ta có:
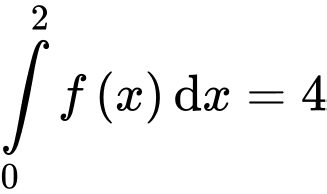
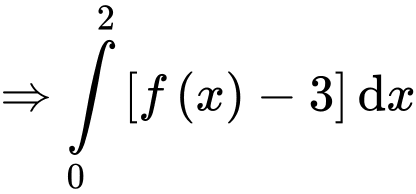
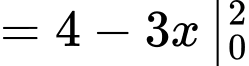
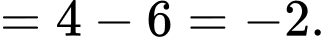 Đáp án: C
Đáp án: C
Câu 10 [693204]: Cân nặng của một số quả mít trong khu vườn được thống kê ở bảng sau:

Số quả mít có cân nặng ít hơn 10 kg trong bảng trên là

Số quả mít có cân nặng ít hơn 10 kg trong bảng trên là
A, 
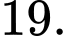
B, 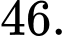
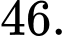
C, 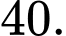
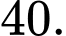
D, 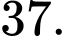
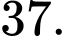
Chọn đáp án D.
Số quả mít có cân nặng ít hơn 10 kg trong bảng trên là: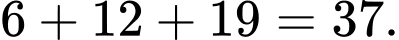 Đáp án: D
Đáp án: D
Số quả mít có cân nặng ít hơn 10 kg trong bảng trên là:
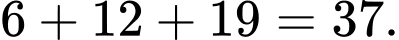 Đáp án: D
Đáp án: D
Câu 11 [693206]: Trong không gian 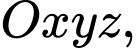 cho điểm
cho điểm 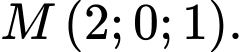 Gọi
Gọi 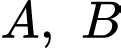 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 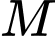 trên trục
trên trục 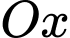 và trên mặt phẳng
và trên mặt phẳng  Đường thẳng
Đường thẳng  có một vectơ chỉ phương là vectơ nào sau đây?
có một vectơ chỉ phương là vectơ nào sau đây?
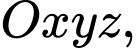 cho điểm
cho điểm 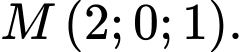 Gọi
Gọi 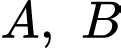 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 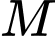 trên trục
trên trục 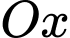 và trên mặt phẳng
và trên mặt phẳng  Đường thẳng
Đường thẳng  có một vectơ chỉ phương là vectơ nào sau đây?
có một vectơ chỉ phương là vectơ nào sau đây? A, 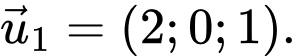
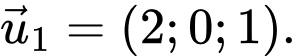
B, 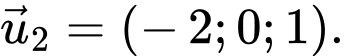
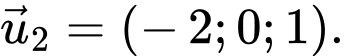
C, 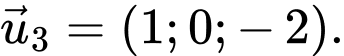
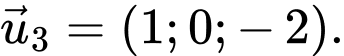
D, 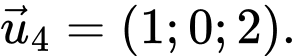
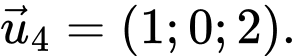
Chọn đáp án B.
Ta có: Hình chiếu của điểm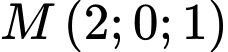 trên trục
trên trục 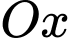 là
là 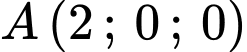 và hình chiếu của điểm
và hình chiếu của điểm 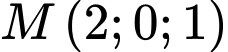 trên mặt phằng
trên mặt phằng 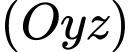 là điểm
là điểm 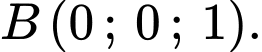
Suy ra vecto chỉ phương của đường thẳng là
là 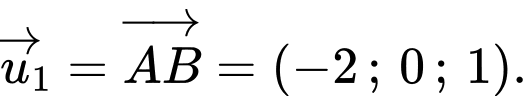 Đáp án: B
Đáp án: B
Ta có: Hình chiếu của điểm
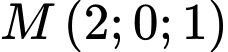 trên trục
trên trục 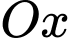 là
là 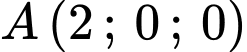 và hình chiếu của điểm
và hình chiếu của điểm 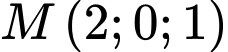 trên mặt phằng
trên mặt phằng 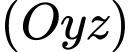 là điểm
là điểm 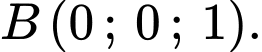
Suy ra vecto chỉ phương của đường thẳng
 là
là 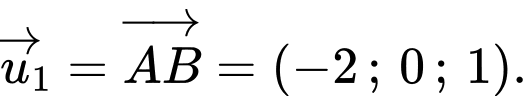 Đáp án: B
Đáp án: B
Câu 12 [693205]: Tập nghiệm của bất phương trình 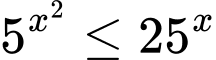 chứa bao nhiêu số nguyên?
chứa bao nhiêu số nguyên?
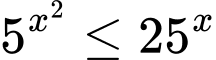 chứa bao nhiêu số nguyên?
chứa bao nhiêu số nguyên? A, 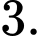
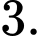
B, 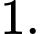
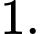
C, 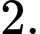
D, 
Chọn đáp án A.
Ta có: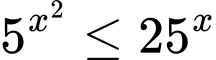
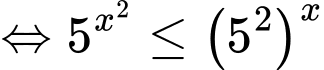
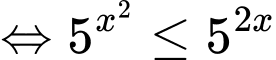
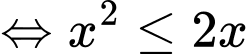
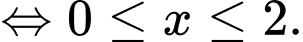
Vậy tập nghiệm của bất phương trình chứa 3 số nguyên. Đáp án: A
Ta có:
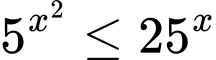
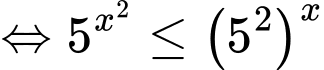
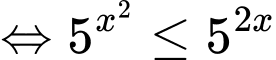
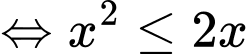
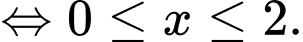
Vậy tập nghiệm của bất phương trình chứa 3 số nguyên. Đáp án: A
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693207]: Cho hàm số 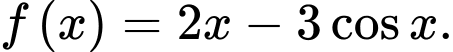 Gọi
Gọi 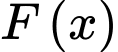 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 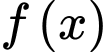 thoả mãn điều kiện
thoả mãn điều kiện 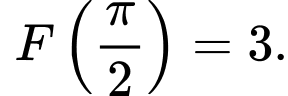
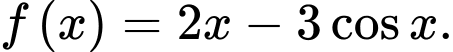 Gọi
Gọi 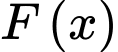 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 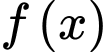 thoả mãn điều kiện
thoả mãn điều kiện 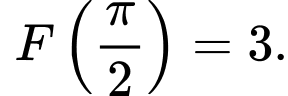
a) Đúng.
Ta có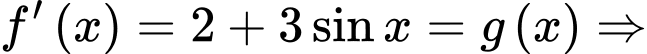
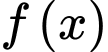 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 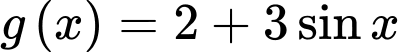
b) Sai.
Ta có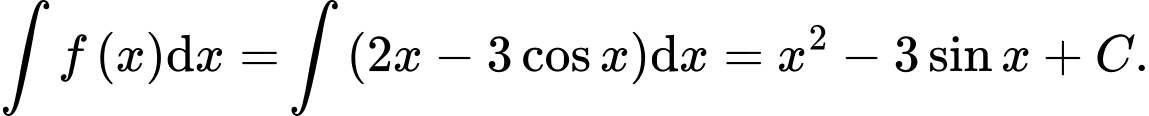
c) Đúng.
Dựa vào ý b) ta có: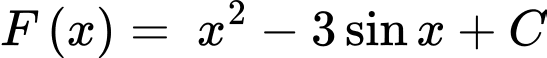
Khi đó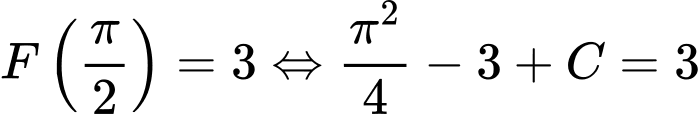
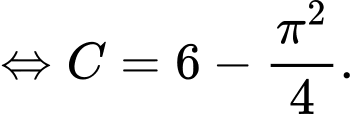
Vậy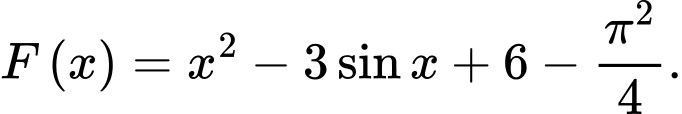
d) Sai.
Dựa vào ý c) ta có: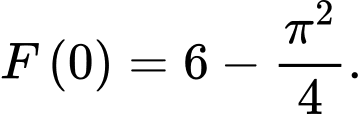
Ta có
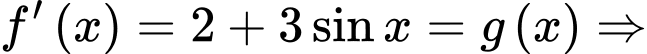
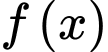 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 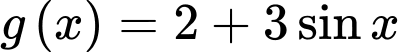
b) Sai.
Ta có
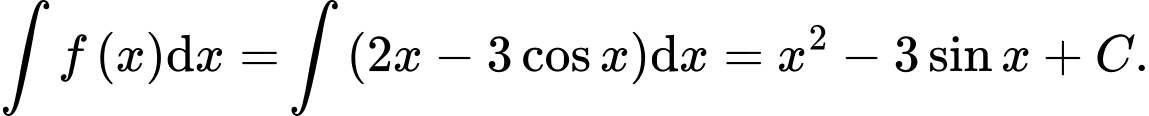
c) Đúng.
Dựa vào ý b) ta có:
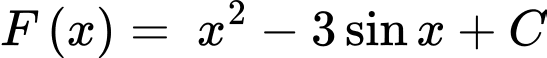
Khi đó
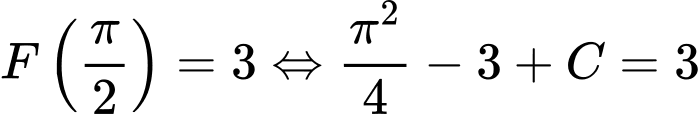
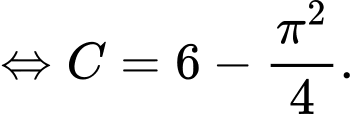
Vậy
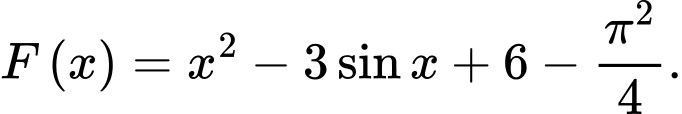
d) Sai.
Dựa vào ý c) ta có:
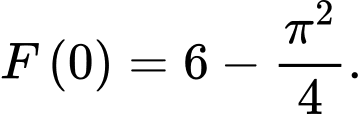
Câu 14 [696340]: Vào lúc 12 giờ trưa, tàu 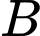 đang nằm ở vị trí
đang nằm ở vị trí  tàu
tàu 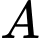 cách tàu
cách tàu 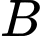 12 km. Tàu A đang di chuyển về phía
12 km. Tàu A đang di chuyển về phía  với vận tốc 12 km/h và tiếp tục di chuyển như vậy cả ngày. Tàu B có vận tốc 8 km/h đang di chuyển theo hướng vuông góc với hướng đi của tàu
với vận tốc 12 km/h và tiếp tục di chuyển như vậy cả ngày. Tàu B có vận tốc 8 km/h đang di chuyển theo hướng vuông góc với hướng đi của tàu 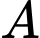 và tiếp tục di chuyển như vậy cả ngày. Quãng đường tàu A và tàu B di chuyển được sau
và tiếp tục di chuyển như vậy cả ngày. Quãng đường tàu A và tàu B di chuyển được sau 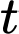 (giờ) (tính từ lúc 12 giờ trưa) lần lượt là
(giờ) (tính từ lúc 12 giờ trưa) lần lượt là 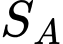 và
và 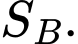
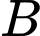 đang nằm ở vị trí
đang nằm ở vị trí  tàu
tàu 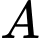 cách tàu
cách tàu 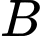 12 km. Tàu A đang di chuyển về phía
12 km. Tàu A đang di chuyển về phía  với vận tốc 12 km/h và tiếp tục di chuyển như vậy cả ngày. Tàu B có vận tốc 8 km/h đang di chuyển theo hướng vuông góc với hướng đi của tàu
với vận tốc 12 km/h và tiếp tục di chuyển như vậy cả ngày. Tàu B có vận tốc 8 km/h đang di chuyển theo hướng vuông góc với hướng đi của tàu 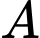 và tiếp tục di chuyển như vậy cả ngày. Quãng đường tàu A và tàu B di chuyển được sau
và tiếp tục di chuyển như vậy cả ngày. Quãng đường tàu A và tàu B di chuyển được sau 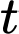 (giờ) (tính từ lúc 12 giờ trưa) lần lượt là
(giờ) (tính từ lúc 12 giờ trưa) lần lượt là 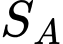 và
và 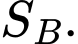
a) Đúng.
Vì vận tốc của tàu A là 12 km/h, nên quãng đường tàu A di chuyển được sau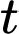 giờ là
giờ là 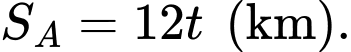 Tương tự, ta có quãng đường tàu A di chuyển được sau
Tương tự, ta có quãng đường tàu A di chuyển được sau 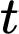 giờ là
giờ là 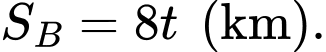
b) Sai.
Gọi điểm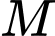 là vị trí ban đầu của tàu
là vị trí ban đầu của tàu 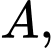 sau
sau 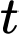 giờ tàu A đến được vị trí
giờ tàu A đến được vị trí 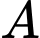 mới và đi được quãng đường
mới và đi được quãng đường 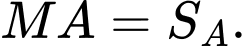 Tương tự với tàu B, ta được hình vẽ như sau.
Tương tự với tàu B, ta được hình vẽ như sau.
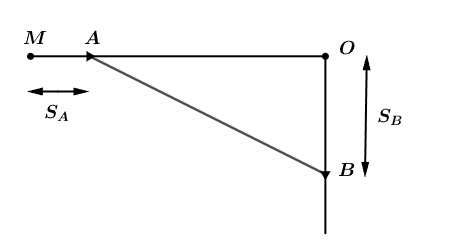
Dựa vào hình vẽ, ta có khoảng cách giữa 2 tàu là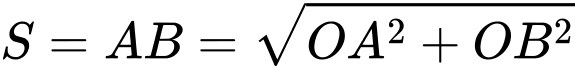
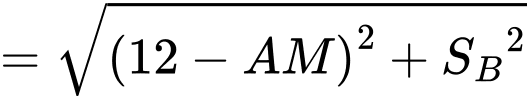
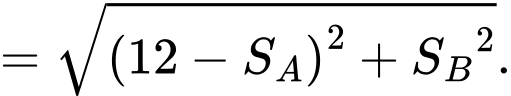
c) Sai.
Lúc 13 giờ, ta có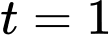 (vì ta so với gốc là 12 giờ trưa) suy ra khoảng cách giữa 2 tàu bằng
(vì ta so với gốc là 12 giờ trưa) suy ra khoảng cách giữa 2 tàu bằng  (với
(với 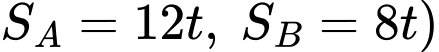
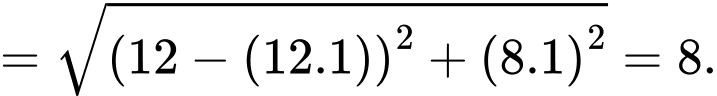
d) Sai.
Tốc độ thay đổi khoảng cách sẽ là đạo hàm của hàm khoảng cách, nên lúc 13 giờ, tốc độ thay đổi khoảng cách giữa 2 tàu là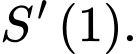
Để tính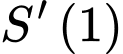 ta có thể thực hiện bấm máy như trong video thầy Tiến giải hoặc thực hiện đạo hàm như sau:
ta có thể thực hiện bấm máy như trong video thầy Tiến giải hoặc thực hiện đạo hàm như sau:
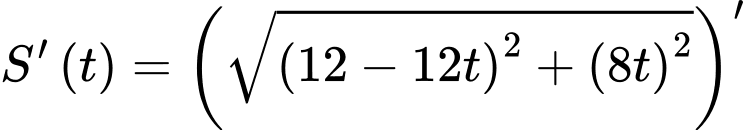
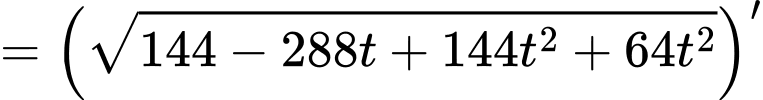
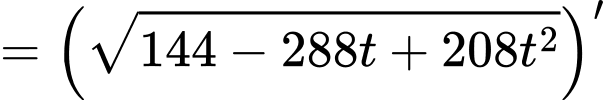
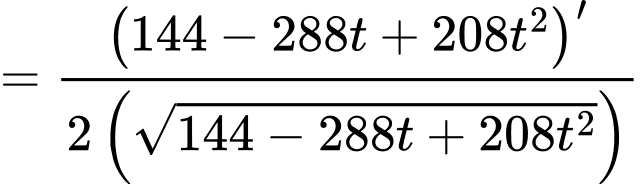
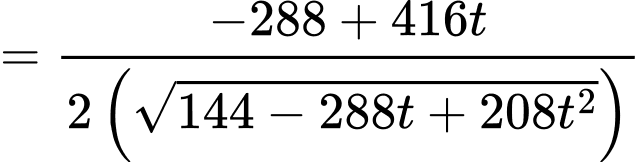
Suy ra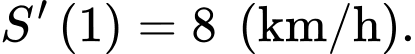
Vì vận tốc của tàu A là 12 km/h, nên quãng đường tàu A di chuyển được sau
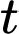 giờ là
giờ là 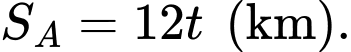 Tương tự, ta có quãng đường tàu A di chuyển được sau
Tương tự, ta có quãng đường tàu A di chuyển được sau 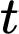 giờ là
giờ là 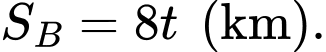
b) Sai.
Gọi điểm
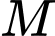 là vị trí ban đầu của tàu
là vị trí ban đầu của tàu 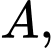 sau
sau 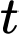 giờ tàu A đến được vị trí
giờ tàu A đến được vị trí 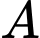 mới và đi được quãng đường
mới và đi được quãng đường 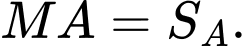 Tương tự với tàu B, ta được hình vẽ như sau.
Tương tự với tàu B, ta được hình vẽ như sau.
Dựa vào hình vẽ, ta có khoảng cách giữa 2 tàu là
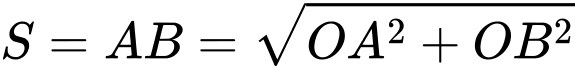
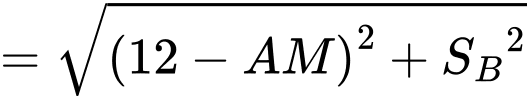
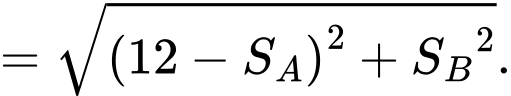
c) Sai.
Lúc 13 giờ, ta có
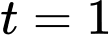 (vì ta so với gốc là 12 giờ trưa) suy ra khoảng cách giữa 2 tàu bằng
(vì ta so với gốc là 12 giờ trưa) suy ra khoảng cách giữa 2 tàu bằng  (với
(với 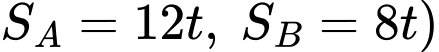
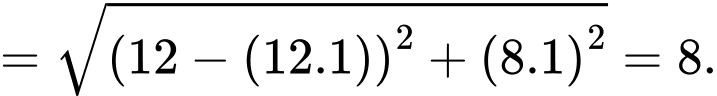
d) Sai.
Tốc độ thay đổi khoảng cách sẽ là đạo hàm của hàm khoảng cách, nên lúc 13 giờ, tốc độ thay đổi khoảng cách giữa 2 tàu là
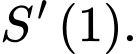
Để tính
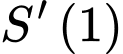 ta có thể thực hiện bấm máy như trong video thầy Tiến giải hoặc thực hiện đạo hàm như sau:
ta có thể thực hiện bấm máy như trong video thầy Tiến giải hoặc thực hiện đạo hàm như sau: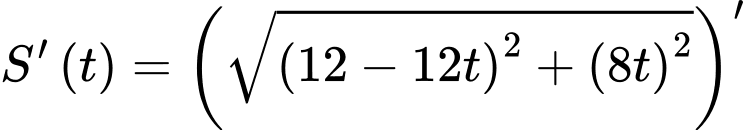
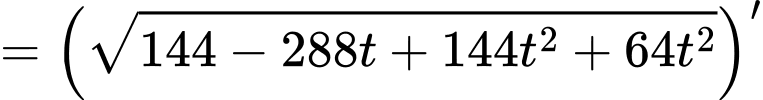
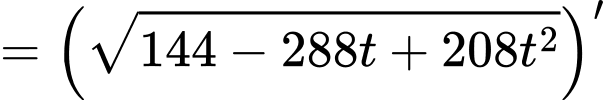
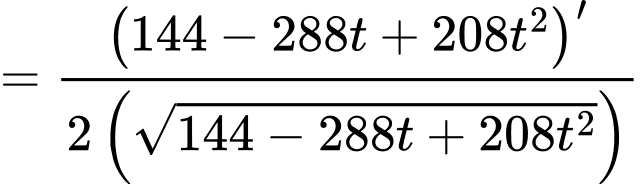
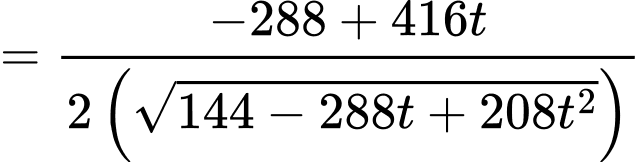
Suy ra
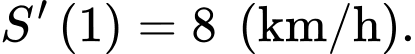
Câu 15 [693209]: Một tờ tiền giả lần lượt bị hai người A và B kiểm tra. Xác suất để người A phát hiện ra tờ này giả là 0,7. Nếu người A cho rằng tờ này tiền giả, thì xác suất để người B cũng nhận định như thể là 0,8. Ngược lại, nếu người A cho rằng tờ này là tiền thật thì xác suất để người B cũng nhận định như thể là 0,4.
Gọi 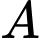 là biến cố: “Người A phát hiện ra tờ này là tiền giả”.
là biến cố: “Người A phát hiện ra tờ này là tiền giả”.
Gọi B là biến cố: “Người B phát hiện ra tờ tiền này là giả”.
Khi đó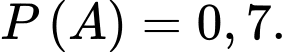
a) Sai.
Xác suất để A không phát hiện ra tờ tiền đó giả là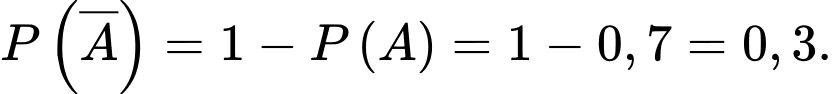
b) Đúng.
Xác suất để hai người này đều nhận định đây là tờ tiền thật là

c) Đúng.
Dựa vào ý b) ta có: Xác suất để ít nhất một trong hai người này phát hiện ra tờ tiền đó là giả là: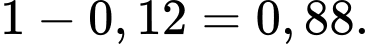
d) Đúng.
Biết tờ tiền đó đã bị ít nhất một trong hai người này phát hiện là giả, xác suất để A phát hiện ra nó giả là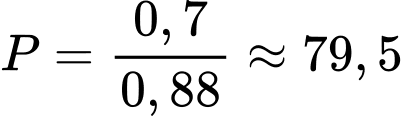
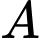 là biến cố: “Người A phát hiện ra tờ này là tiền giả”.
là biến cố: “Người A phát hiện ra tờ này là tiền giả”.Gọi B là biến cố: “Người B phát hiện ra tờ tiền này là giả”.
Khi đó
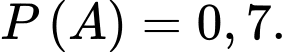
a) Sai.
Xác suất để A không phát hiện ra tờ tiền đó giả là
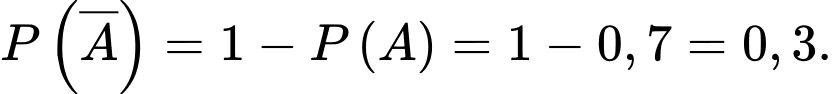
b) Đúng.
Xác suất để hai người này đều nhận định đây là tờ tiền thật là

c) Đúng.
Dựa vào ý b) ta có: Xác suất để ít nhất một trong hai người này phát hiện ra tờ tiền đó là giả là:
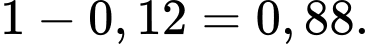
d) Đúng.
Biết tờ tiền đó đã bị ít nhất một trong hai người này phát hiện là giả, xác suất để A phát hiện ra nó giả là
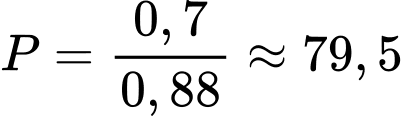
Câu 16 [693210]: Một tháp kiểm soát không lưu ở sân bay cao 109 m đặt một đài kiểm soát không lưu ở độ cao 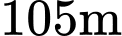 . Máy bay trong phạm vi cách đài kiểm soát
. Máy bay trong phạm vi cách đài kiểm soát  sẽ hiển thị trên màn hình ra đa. Chọn hệ trục toạ độ
sẽ hiển thị trên màn hình ra đa. Chọn hệ trục toạ độ 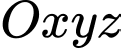 có gốc
có gốc  trùng với vị trí chân tháp, mặt phẳng
trùng với vị trí chân tháp, mặt phẳng 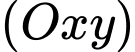 trùng với mặt đất sao cho trục
trùng với mặt đất sao cho trục 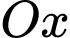 là hướng tây, trục
là hướng tây, trục 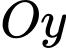 là hướng nam và trục
là hướng nam và trục  là trục thẳng đứng (Hình vẽ), đơn vị trên mỗi trục là kilômét. Một máy bay đang ở vị trí
là trục thẳng đứng (Hình vẽ), đơn vị trên mỗi trục là kilômét. Một máy bay đang ở vị trí 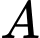 cách mặt đất
cách mặt đất 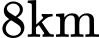 , cách
, cách  về phía đông,
về phía đông, 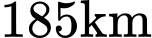 về phía nam so với tháp kiểm soát không lưu và đang chuyển động theo đường thẳng
về phía nam so với tháp kiểm soát không lưu và đang chuyển động theo đường thẳng 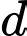 có vectơ chỉ phương là
có vectơ chỉ phương là 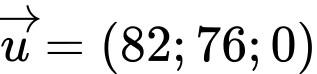 hướng về đài kiểm soát không lưu.
hướng về đài kiểm soát không lưu.
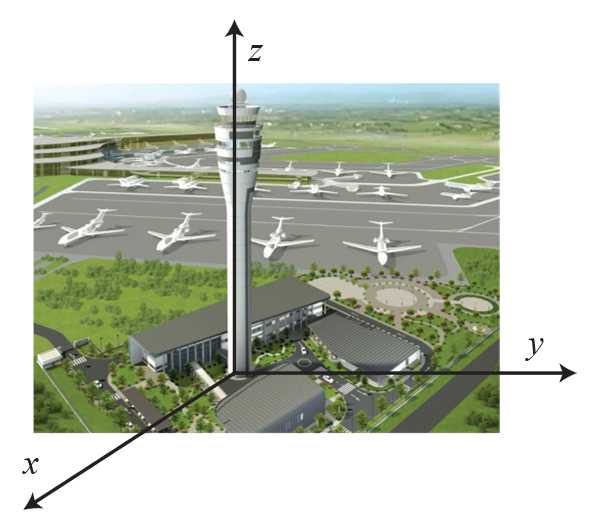
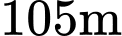 . Máy bay trong phạm vi cách đài kiểm soát
. Máy bay trong phạm vi cách đài kiểm soát  sẽ hiển thị trên màn hình ra đa. Chọn hệ trục toạ độ
sẽ hiển thị trên màn hình ra đa. Chọn hệ trục toạ độ 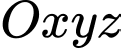 có gốc
có gốc  trùng với vị trí chân tháp, mặt phẳng
trùng với vị trí chân tháp, mặt phẳng 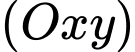 trùng với mặt đất sao cho trục
trùng với mặt đất sao cho trục 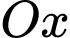 là hướng tây, trục
là hướng tây, trục 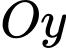 là hướng nam và trục
là hướng nam và trục  là trục thẳng đứng (Hình vẽ), đơn vị trên mỗi trục là kilômét. Một máy bay đang ở vị trí
là trục thẳng đứng (Hình vẽ), đơn vị trên mỗi trục là kilômét. Một máy bay đang ở vị trí 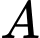 cách mặt đất
cách mặt đất 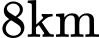 , cách
, cách  về phía đông,
về phía đông, 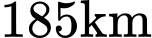 về phía nam so với tháp kiểm soát không lưu và đang chuyển động theo đường thẳng
về phía nam so với tháp kiểm soát không lưu và đang chuyển động theo đường thẳng 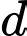 có vectơ chỉ phương là
có vectơ chỉ phương là 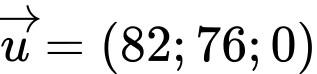 hướng về đài kiểm soát không lưu.
hướng về đài kiểm soát không lưu.
a) Sai.
Gốc trùng với vị trí chân tháp và đài kiểm soát không lưu được đặt ở độ cao
trùng với vị trí chân tháp và đài kiểm soát không lưu được đặt ở độ cao 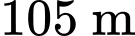 nên có toạ độ là
nên có toạ độ là 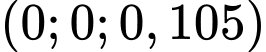
Hệ trục toạ độ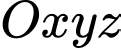 có trục
có trục 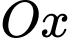 là hướng tây, trục
là hướng tây, trục 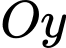 là hướng nam và trục
là hướng nam và trục  là trục thẳng đứng và vị trí
là trục thẳng đứng và vị trí 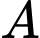 cách mặt đất
cách mặt đất 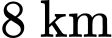 , cách
, cách  về phía đông,
về phía đông,  về phía nam nên có toạ độ là
về phía nam nên có toạ độ là 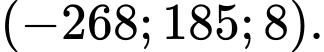
b) Đúng.
Khoảng cách từ máy bay đến đài kiểm soát không lưu là:
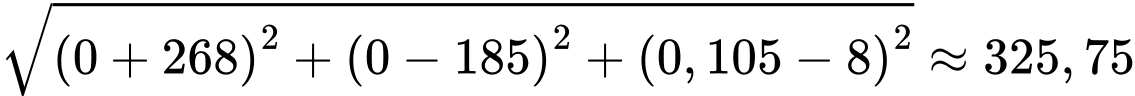 (km).
(km).
Vì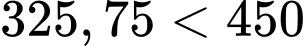 nên đài kiểm soát không lưu có phát hiện được máy bay tại vị trí
nên đài kiểm soát không lưu có phát hiện được máy bay tại vị trí 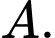
c) Đúng.
Gọi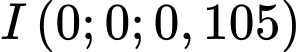 là vị trí đài kiểm soát không lưu.
là vị trí đài kiểm soát không lưu.
Phương trình tham số của đường thẳng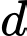 là:
là: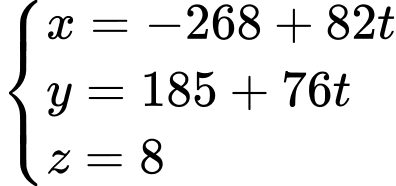 (
(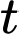 là tham số).
là tham số).
d) Sai.
Gọi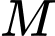 là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất khi đó:
là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất khi đó:
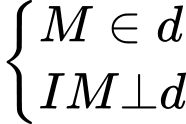 hay
hay 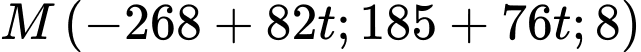 và
và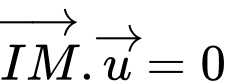
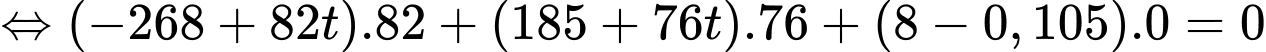
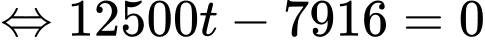
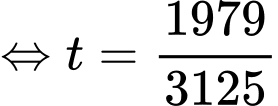
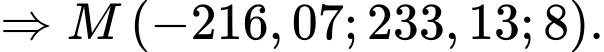
Khoảng cách gần nhất giữa máy bay và đài kiểm soát không lưu là:
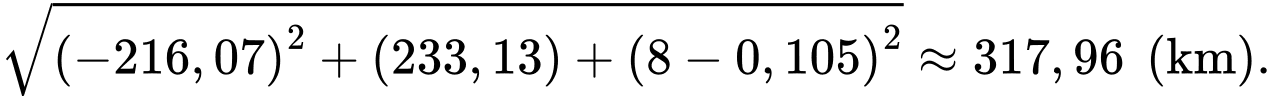
Gốc
 trùng với vị trí chân tháp và đài kiểm soát không lưu được đặt ở độ cao
trùng với vị trí chân tháp và đài kiểm soát không lưu được đặt ở độ cao 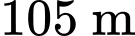 nên có toạ độ là
nên có toạ độ là 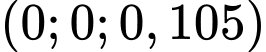
Hệ trục toạ độ
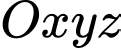 có trục
có trục 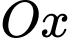 là hướng tây, trục
là hướng tây, trục 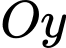 là hướng nam và trục
là hướng nam và trục  là trục thẳng đứng và vị trí
là trục thẳng đứng và vị trí 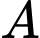 cách mặt đất
cách mặt đất 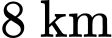 , cách
, cách  về phía đông,
về phía đông,  về phía nam nên có toạ độ là
về phía nam nên có toạ độ là 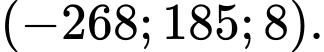
b) Đúng.
Khoảng cách từ máy bay đến đài kiểm soát không lưu là:
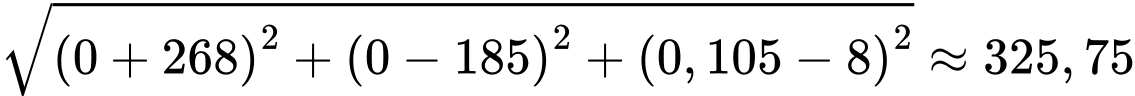 (km).
(km).Vì
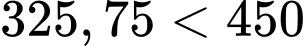 nên đài kiểm soát không lưu có phát hiện được máy bay tại vị trí
nên đài kiểm soát không lưu có phát hiện được máy bay tại vị trí 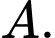
c) Đúng.
Gọi
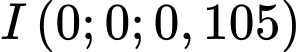 là vị trí đài kiểm soát không lưu.
là vị trí đài kiểm soát không lưu.Phương trình tham số của đường thẳng
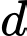 là:
là: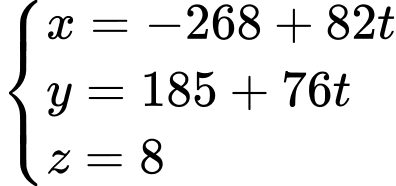 (
(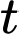 là tham số).
là tham số).d) Sai.
Gọi
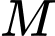 là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất khi đó:
là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất khi đó: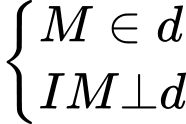 hay
hay 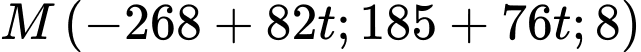 và
và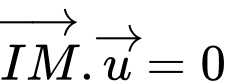
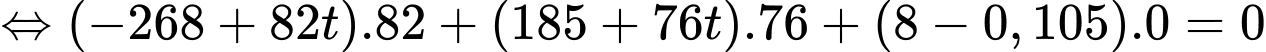
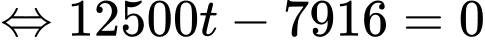
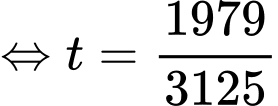
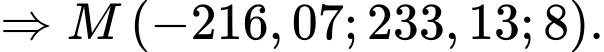
Khoảng cách gần nhất giữa máy bay và đài kiểm soát không lưu là:
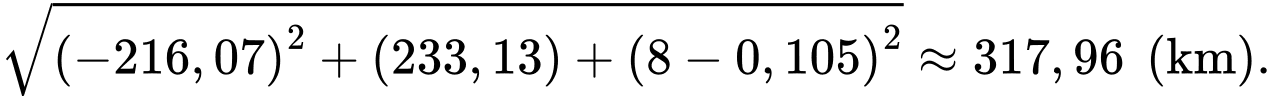
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693211]: Cho hình chóp 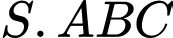 có
có 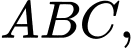
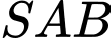 là các tam giác đều và mặt bên
là các tam giác đều và mặt bên 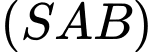 vuông góc với mặt đáy. Gọi
vuông góc với mặt đáy. Gọi 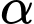 là góc phẳng nhị diện
là góc phẳng nhị diện 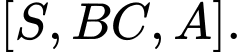 Tính
Tính 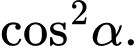
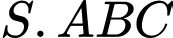 có
có 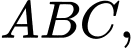
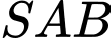 là các tam giác đều và mặt bên
là các tam giác đều và mặt bên 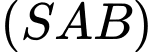 vuông góc với mặt đáy. Gọi
vuông góc với mặt đáy. Gọi 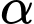 là góc phẳng nhị diện
là góc phẳng nhị diện 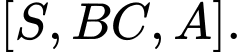 Tính
Tính 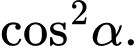
Điền đáp án: 0,2.
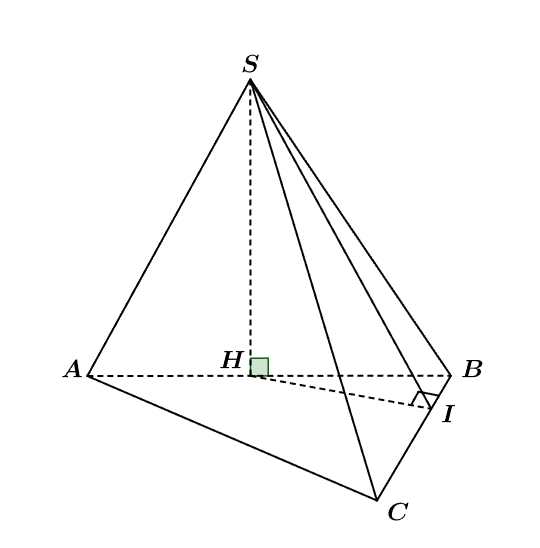
Gọi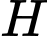 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 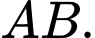
Mà tam giác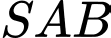 đều nên suy ra
đều nên suy ra 
Ta có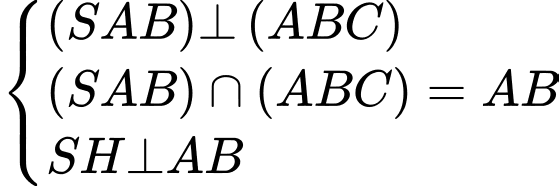
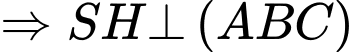
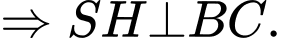
Kẻ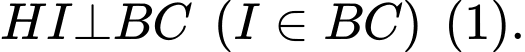
Mà suy ra
suy ra 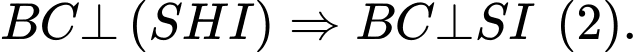
Từ (1) và (2) suy ra góc phẳng nhị diện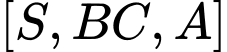 là góc
là góc 
Vì tam giác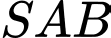 đều nên
đều nên 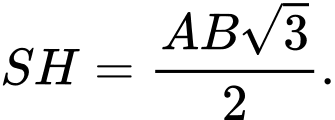
Đặt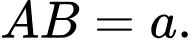
Trong tam giác vuông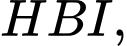 ta có
ta có 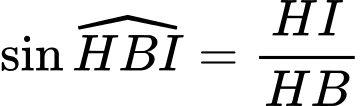

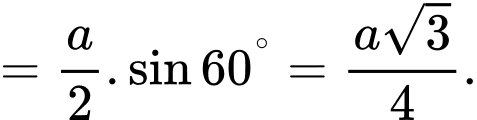
Xét tam giác vuông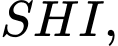 ta có
ta có 
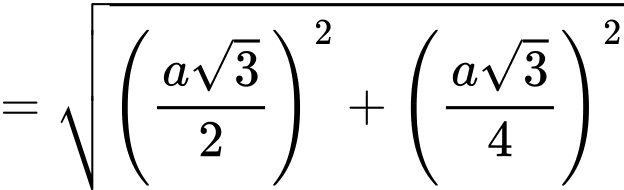
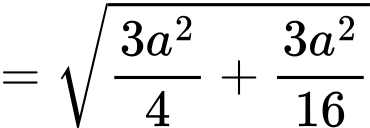
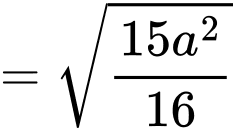
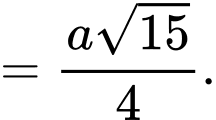
Trong tam giác vuông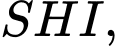 ta có
ta có 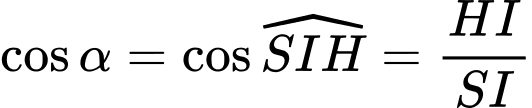
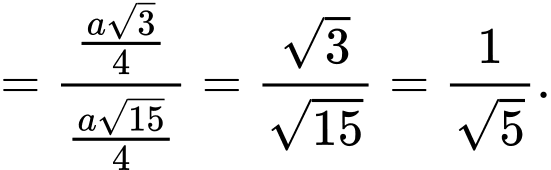
Suy ra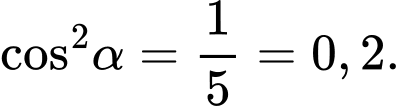

Gọi
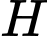 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 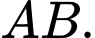
Mà tam giác
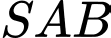 đều nên suy ra
đều nên suy ra 
Ta có
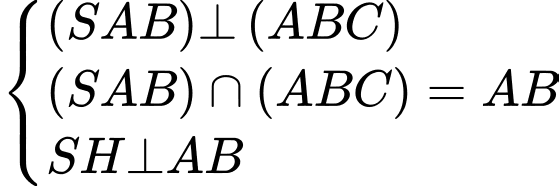
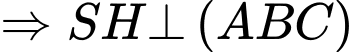
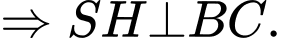
Kẻ
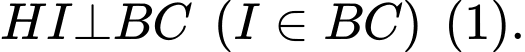
Mà
 suy ra
suy ra 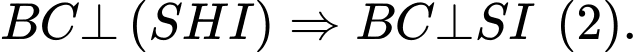
Từ (1) và (2) suy ra góc phẳng nhị diện
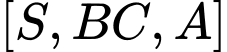 là góc
là góc 
Vì tam giác
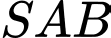 đều nên
đều nên 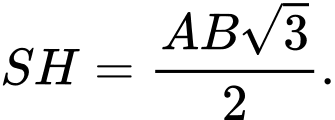
Đặt
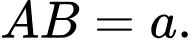
Trong tam giác vuông
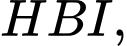 ta có
ta có 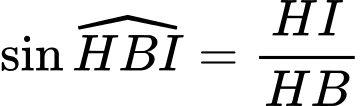

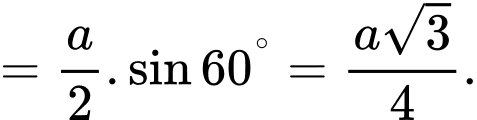
Xét tam giác vuông
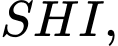 ta có
ta có 
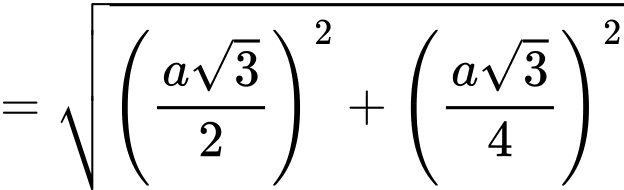
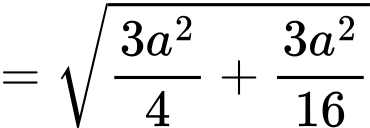
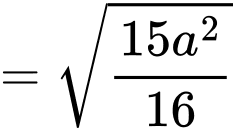
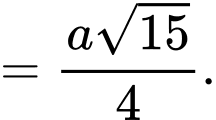
Trong tam giác vuông
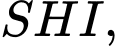 ta có
ta có 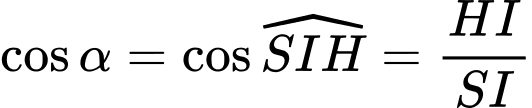
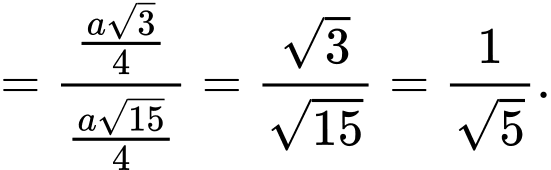
Suy ra
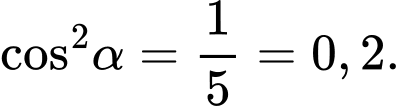
Câu 18 [693213]: Một người bình thường với chiều cao 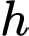 cm, nặng
cm, nặng 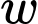 kilogram có diện tích bề mặt cơ thể
kilogram có diện tích bề mặt cơ thể 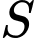 được mô hình hoá bởi công thức
được mô hình hoá bởi công thức 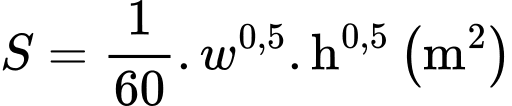 (công thức Mosteller). Một đối tượng có chiều cao bằng
(công thức Mosteller). Một đối tượng có chiều cao bằng 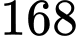 cm, nặng
cm, nặng 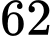 kg tham gia một cuộc nghiên cứu về sức khỏe trong 5 năm. Người ta nhận thấy cân nặng của đối tượng quan sát thay đổi với tốc độ
kg tham gia một cuộc nghiên cứu về sức khỏe trong 5 năm. Người ta nhận thấy cân nặng của đối tượng quan sát thay đổi với tốc độ 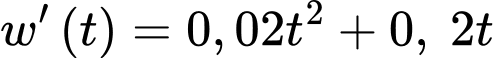 kg/năm
kg/năm 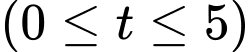 và chiều cao tăng đều mỗi năm
và chiều cao tăng đều mỗi năm 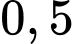 cm. Sau 5 năm quan sát, diện tích bề mặt cơ thể của đối tượng trên tăng thêm bao nhiêu centimet vuông so với ban đầu? (làm tròn kết quả đến hàng đơn vị).
cm. Sau 5 năm quan sát, diện tích bề mặt cơ thể của đối tượng trên tăng thêm bao nhiêu centimet vuông so với ban đầu? (làm tròn kết quả đến hàng đơn vị).
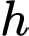 cm, nặng
cm, nặng 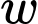 kilogram có diện tích bề mặt cơ thể
kilogram có diện tích bề mặt cơ thể 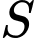 được mô hình hoá bởi công thức
được mô hình hoá bởi công thức 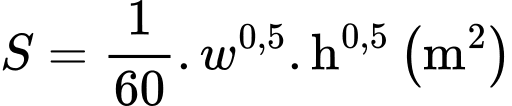 (công thức Mosteller). Một đối tượng có chiều cao bằng
(công thức Mosteller). Một đối tượng có chiều cao bằng 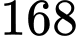 cm, nặng
cm, nặng 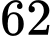 kg tham gia một cuộc nghiên cứu về sức khỏe trong 5 năm. Người ta nhận thấy cân nặng của đối tượng quan sát thay đổi với tốc độ
kg tham gia một cuộc nghiên cứu về sức khỏe trong 5 năm. Người ta nhận thấy cân nặng của đối tượng quan sát thay đổi với tốc độ 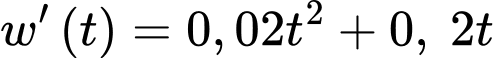 kg/năm
kg/năm 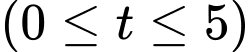 và chiều cao tăng đều mỗi năm
và chiều cao tăng đều mỗi năm 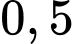 cm. Sau 5 năm quan sát, diện tích bề mặt cơ thể của đối tượng trên tăng thêm bao nhiêu centimet vuông so với ban đầu? (làm tròn kết quả đến hàng đơn vị).
cm. Sau 5 năm quan sát, diện tích bề mặt cơ thể của đối tượng trên tăng thêm bao nhiêu centimet vuông so với ban đầu? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 581.
Ta có chiều cao và cân nặng ban đầu của người đó lần lượt là 168 cm, 62 kg, nên diện tích bề mặt cơ thể ban đầu của người đó là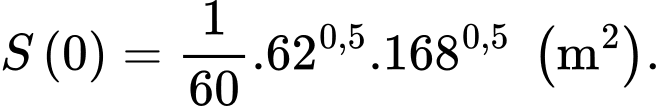
Việc còn lại là tính diện tích bề mặt cơ thể của đối tượng sau 5 năm. Để tính được diện tích bề mặt cơ thể ta cần biết cân nặng và chiều cao của đối tượng sau 5 năm.
+) Vì chiều cao của người đó tăng đều mỗi năm 0,5 cm, nên sau 5 năm người đó tăng thêm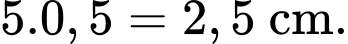
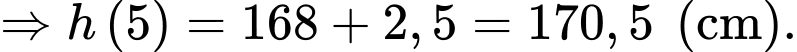
+) Ta có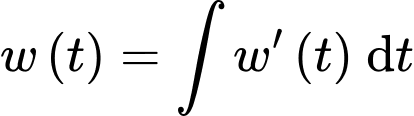
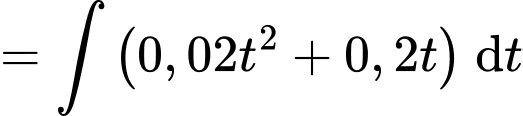
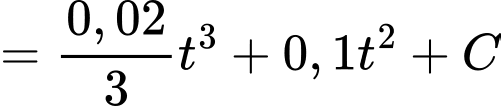
Dựa vào dữ kiện, ta có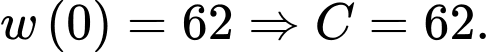
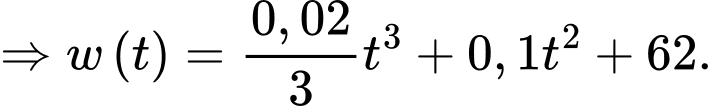
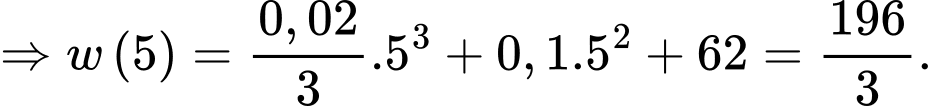
Suy ra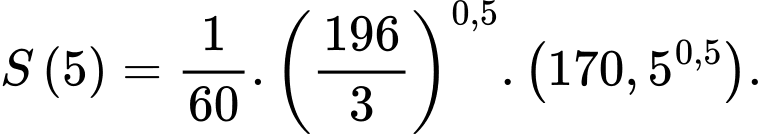
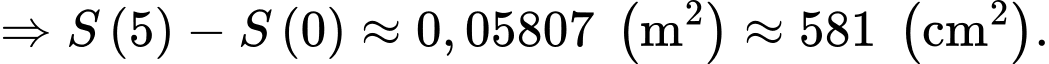
Ta có chiều cao và cân nặng ban đầu của người đó lần lượt là 168 cm, 62 kg, nên diện tích bề mặt cơ thể ban đầu của người đó là
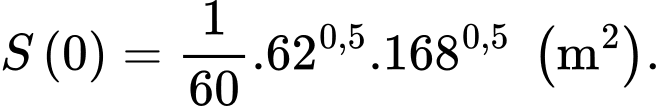
Việc còn lại là tính diện tích bề mặt cơ thể của đối tượng sau 5 năm. Để tính được diện tích bề mặt cơ thể ta cần biết cân nặng và chiều cao của đối tượng sau 5 năm.
+) Vì chiều cao của người đó tăng đều mỗi năm 0,5 cm, nên sau 5 năm người đó tăng thêm
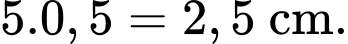
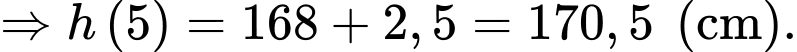
+) Ta có
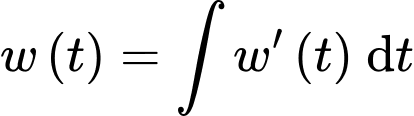
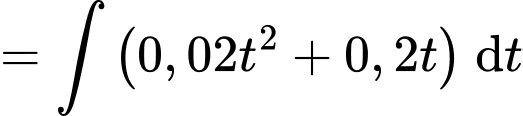
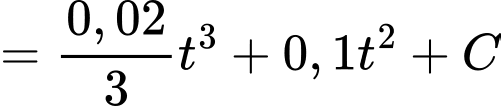
Dựa vào dữ kiện, ta có
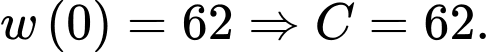
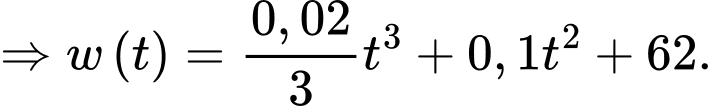
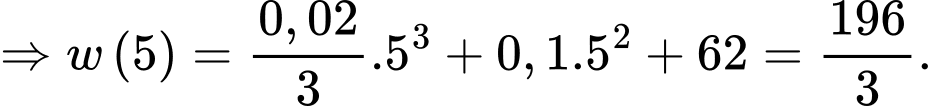
Suy ra
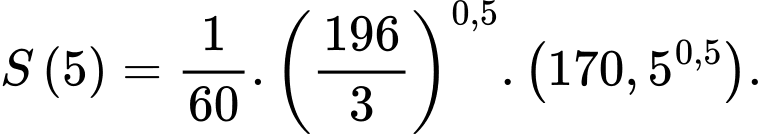
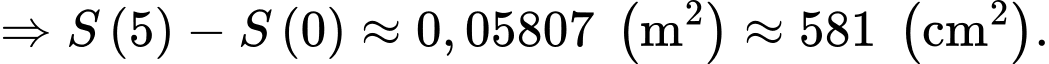
Câu 19 [693212]: Một lớp học hè có 15 học sinh. Biết rằng mỗi ngày 3 học sinh trong lớp có nhiệm vụ trực nhật sau giờ học. Sau khi kết thúc khoá học hè, người ta thấy rằng hai học sinh bất kỳ trực nhật cùng nhau đúng một ngày. Hỏi lớp học hè kéo dài trong bao nhiêu ngày?
Điền đáp án: 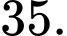
Cách giải 1:
Số cặp học sinh trực nhật bất kỳ trong 15 học sinh là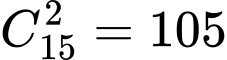 (cặp)
(cặp)
Vì mỗi nhóm 3 học sinh sẽ có 3 cặp học sinh nên số nhóm gồm 3 học sinh là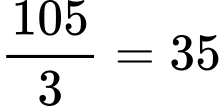 (nhóm)
(nhóm)
Mỗi nhóm học sinh chỉ trực nhật 1 ngày duy nhất nên số ngày lớp học kéo dài là 35 ngày.
Cách giải 2:
Giả sử lớp học hè kéo dài trong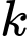 ngày
ngày 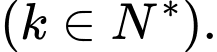
Ta xét ma trận mỗi hàng ứng với một học sinh và mỗi cột ứng với một ngày học.
mỗi hàng ứng với một học sinh và mỗi cột ứng với một ngày học.
Phần tử tương ứng của ma trận nhận giá trị 1 nếu học sinh ứng với hàng chứa nó trực nhật vào ngày tương ứng cột của nó, nhận giá trị 0 trong trường hợp còn lại.
Vì mỗi ngày có 3 học sinh trực nhật nên mỗi cột có đúng ba số 1.
Hai học sinh bất kỳ trực nhật cùng nhau đúng một buổi nên hai hàng bất kỳ có đúng một số cặp số 1 trên cùng một cột.
Bây giờ ta đi đếm số lượng các cặp số 1 trên cùng một cột theo hai cách.
Theo cột: Do mỗi cột có đúng ba số 1 nên mỗi cột có đúng 3 cặp số 1. Như vậy tổng số cặp số 1 trên cùng một cột của ma trận là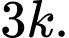
Theo hàng: Do hai hàng bất kỳ có đúng một cặp số 1 trên cùng một cột nên cả ma trận có đúng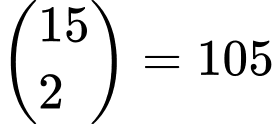 cặp số 1 trên cùng một cột.
cặp số 1 trên cùng một cột.
Từ đây ta có đẳng thức: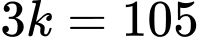
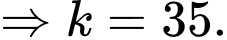
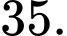
Cách giải 1:
Số cặp học sinh trực nhật bất kỳ trong 15 học sinh là
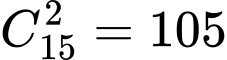 (cặp)
(cặp)Vì mỗi nhóm 3 học sinh sẽ có 3 cặp học sinh nên số nhóm gồm 3 học sinh là
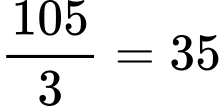 (nhóm)
(nhóm)Mỗi nhóm học sinh chỉ trực nhật 1 ngày duy nhất nên số ngày lớp học kéo dài là 35 ngày.
Cách giải 2:
Giả sử lớp học hè kéo dài trong
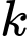 ngày
ngày 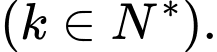
Ta xét ma trận
 mỗi hàng ứng với một học sinh và mỗi cột ứng với một ngày học.
mỗi hàng ứng với một học sinh và mỗi cột ứng với một ngày học. Phần tử tương ứng của ma trận nhận giá trị 1 nếu học sinh ứng với hàng chứa nó trực nhật vào ngày tương ứng cột của nó, nhận giá trị 0 trong trường hợp còn lại.
Vì mỗi ngày có 3 học sinh trực nhật nên mỗi cột có đúng ba số 1.
Hai học sinh bất kỳ trực nhật cùng nhau đúng một buổi nên hai hàng bất kỳ có đúng một số cặp số 1 trên cùng một cột.
Bây giờ ta đi đếm số lượng các cặp số 1 trên cùng một cột theo hai cách.
Theo cột: Do mỗi cột có đúng ba số 1 nên mỗi cột có đúng 3 cặp số 1. Như vậy tổng số cặp số 1 trên cùng một cột của ma trận là
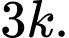
Theo hàng: Do hai hàng bất kỳ có đúng một cặp số 1 trên cùng một cột nên cả ma trận có đúng
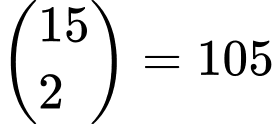 cặp số 1 trên cùng một cột.
cặp số 1 trên cùng một cột.Từ đây ta có đẳng thức:
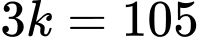
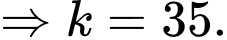
Câu 20 [700891]: Giả sử cường độ ánh sáng của một nguồn điểm tỉ lệ thuận với cường độ của nguồn sáng đó và tỉ lệ nghịch với bình phương khoảng cách từ nguồn sáng. Hai nguồn điểm có cường độ lần lượt là 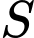 và
và 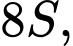 cách nhau 90 cm. Xét một điểm
cách nhau 90 cm. Xét một điểm 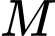 nằm trên đoạn thẳng nối hai nguồn, cường độ ánh sáng tại điểm đó nhỏ nhất thì điểm đó cách nguồn có cường độ
nằm trên đoạn thẳng nối hai nguồn, cường độ ánh sáng tại điểm đó nhỏ nhất thì điểm đó cách nguồn có cường độ 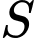 bằng bao nhiêu centimet ( cho biết cường độ sáng tại điểm
bằng bao nhiêu centimet ( cho biết cường độ sáng tại điểm 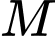 bằng tổng cường độ sáng mỗi nguồn tại điểm đó)?
bằng tổng cường độ sáng mỗi nguồn tại điểm đó)?

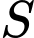 và
và 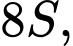 cách nhau 90 cm. Xét một điểm
cách nhau 90 cm. Xét một điểm 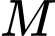 nằm trên đoạn thẳng nối hai nguồn, cường độ ánh sáng tại điểm đó nhỏ nhất thì điểm đó cách nguồn có cường độ
nằm trên đoạn thẳng nối hai nguồn, cường độ ánh sáng tại điểm đó nhỏ nhất thì điểm đó cách nguồn có cường độ 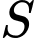 bằng bao nhiêu centimet ( cho biết cường độ sáng tại điểm
bằng bao nhiêu centimet ( cho biết cường độ sáng tại điểm 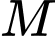 bằng tổng cường độ sáng mỗi nguồn tại điểm đó)?
bằng tổng cường độ sáng mỗi nguồn tại điểm đó)?
Điền đáp án: 30.
Ta có công thức tính cường độ ánh sáng của một nguồn điểm là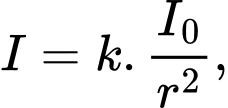 trong đó:
trong đó: 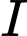 là cường độ ánh sáng của một nguồn điểm,
là cường độ ánh sáng của một nguồn điểm, 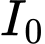 là cường độ của nguồn sáng,
là cường độ của nguồn sáng, 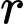 là khoảng cách của điểm đó đến nguồn sáng.
là khoảng cách của điểm đó đến nguồn sáng.
Gọi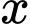 là khoảng cách từ
là khoảng cách từ 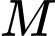 đến nguồn có cường độ là
đến nguồn có cường độ là 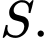
Vì cường độ sáng tại điểm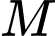 bằng tổng cường độ sáng mỗi nguồn tại điểm đó nên suy ra
cường độ sáng tại điểm
bằng tổng cường độ sáng mỗi nguồn tại điểm đó nên suy ra
cường độ sáng tại điểm 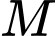 là
là 
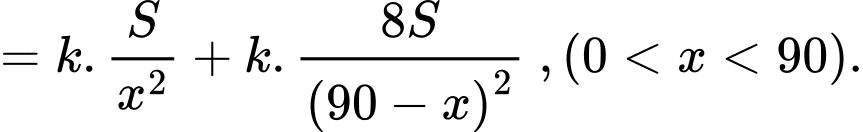
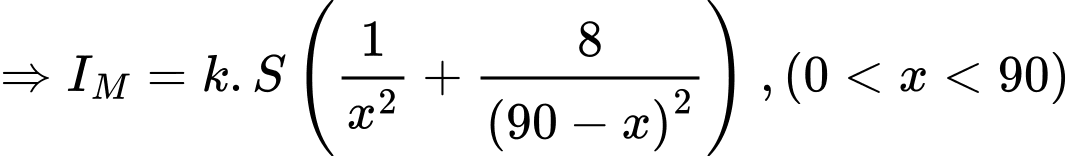
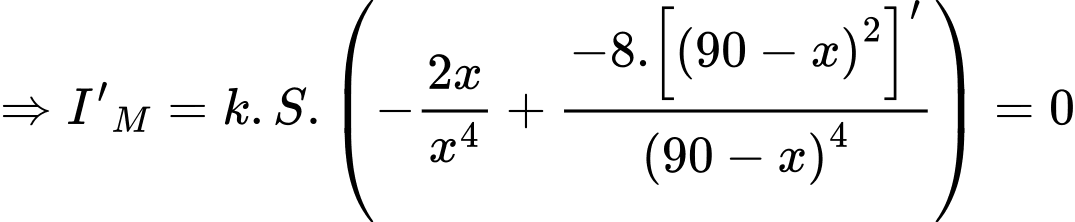
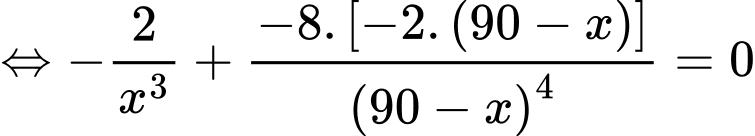
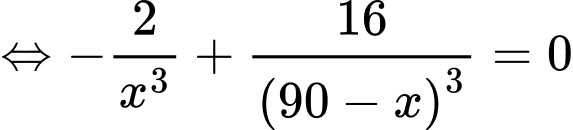
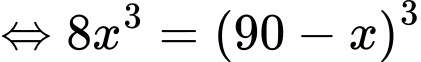
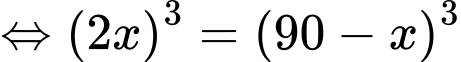
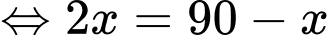
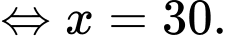
Bảng biến thiên
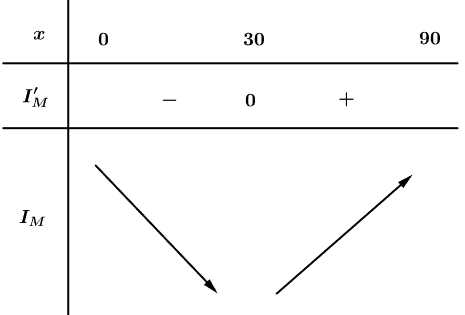
Vậy cường độ ánh sáng tại điểm đó nhỏ nhất khi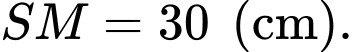
Ta có công thức tính cường độ ánh sáng của một nguồn điểm là
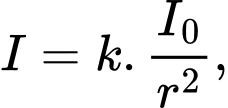 trong đó:
trong đó: 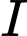 là cường độ ánh sáng của một nguồn điểm,
là cường độ ánh sáng của một nguồn điểm, 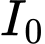 là cường độ của nguồn sáng,
là cường độ của nguồn sáng, 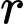 là khoảng cách của điểm đó đến nguồn sáng.
là khoảng cách của điểm đó đến nguồn sáng.
Gọi
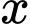 là khoảng cách từ
là khoảng cách từ 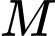 đến nguồn có cường độ là
đến nguồn có cường độ là 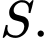
Vì cường độ sáng tại điểm
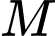 bằng tổng cường độ sáng mỗi nguồn tại điểm đó nên suy ra
cường độ sáng tại điểm
bằng tổng cường độ sáng mỗi nguồn tại điểm đó nên suy ra
cường độ sáng tại điểm 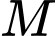 là
là 
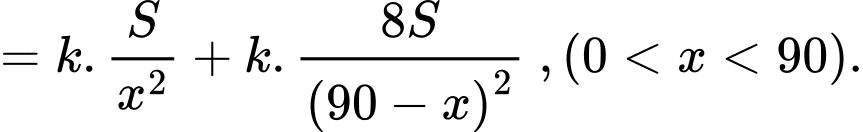
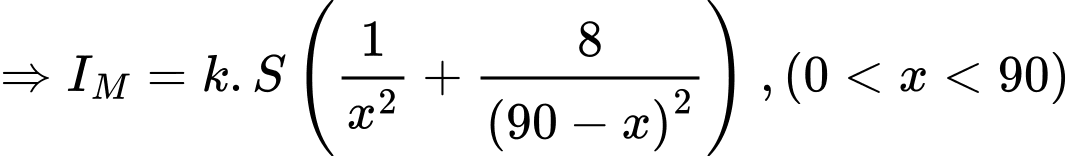
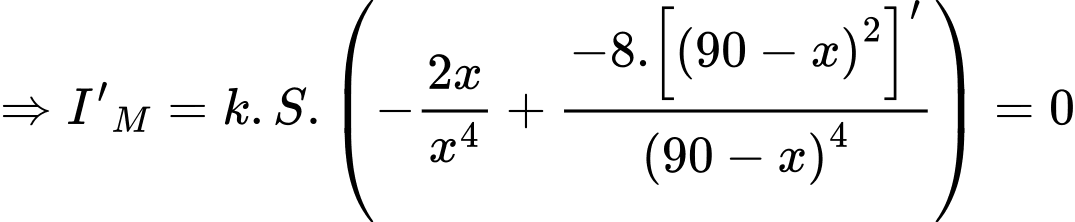
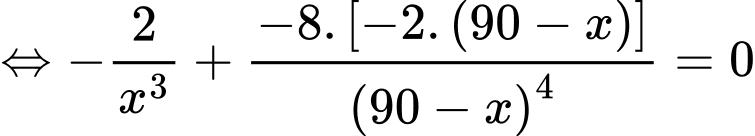
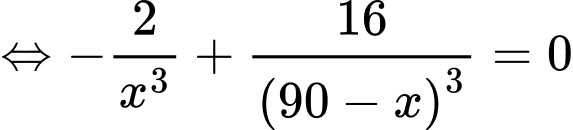
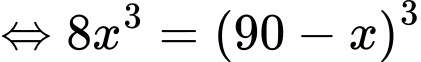
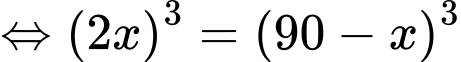
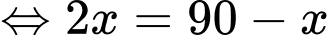
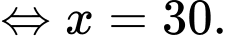
Bảng biến thiên

Vậy cường độ ánh sáng tại điểm đó nhỏ nhất khi
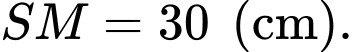
Câu 21 [697793]: Ở vùng A có hai nhóm, nhóm 1 là nhóm người có thu nhập tốt (trên 15 triệu đồng/tháng) và nhóm 2 là nhóm có thu nhập không tốt. Ở vùng A có 40% người có thu nhập tốt và 58% người không gửi tiết kiệm. Khảo sát độc lập những người thuộc nhóm 1 và nhóm 2 và tính tỉ lệ phần trăm số người gửi tiết kiệm của từng nhóm thì thấy rằng: Tỷ lệ người gửi tiết kiệm của nhóm 1 gấp đôi tỉ lệ người tiết kiệm của nhóm 2. Giả sử một người ở vùng A không gửi tiết kiệm. Xác suất để người ấy có thu nhập tốt là bao nhiêu % (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 40.
Gọi xác suất người gửi tiết kiệm ở nhóm 2 là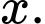
Suy ra số người không gửi tiết kiệm ở nhóm 2 bằng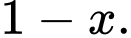
Vì tỷ lệ người gửi tiết kiệm của nhóm 1 gấp đôi người gửi tiết kiệm của nhóm 2, nên ta có xác suất người gửi tiết kiệm ở nhóm 1 là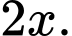 Do đó, số người không gửi tiết kiệm ở nhóm 1 bằng
Do đó, số người không gửi tiết kiệm ở nhóm 1 bằng 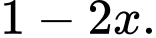
Từ đó, ta có sơ đồ cây như sau:
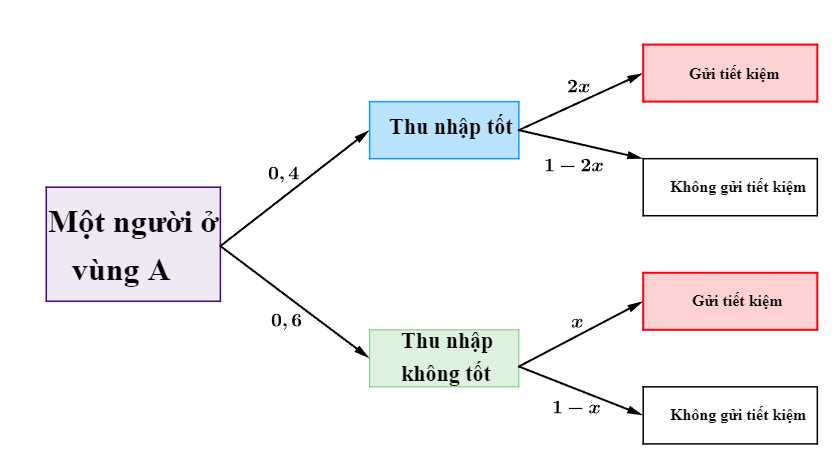
Từ sơ đồ cây, ta có xác suất người không gửi tiết kiệm ở vùng A là P(không gửi tiết kiệm)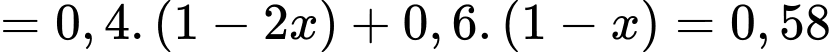 (Vì giả thiết cho biết 58% người không gửi tiết kiệm)
(Vì giả thiết cho biết 58% người không gửi tiết kiệm)
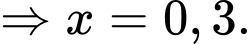
Ta có xác suất người có thu nhập tốt khi biết người đó không gửi tiết kiệm là
P(thu nhập tốt | không gửi tiết kiệm) = P(người có thu nhập tốt và không gửi tiết kiệm)/ P(không gửi tiết kiệm)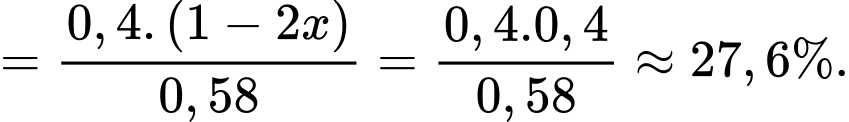
Gọi xác suất người gửi tiết kiệm ở nhóm 2 là
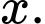
Suy ra số người không gửi tiết kiệm ở nhóm 2 bằng
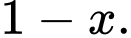
Vì tỷ lệ người gửi tiết kiệm của nhóm 1 gấp đôi người gửi tiết kiệm của nhóm 2, nên ta có xác suất người gửi tiết kiệm ở nhóm 1 là
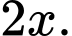 Do đó, số người không gửi tiết kiệm ở nhóm 1 bằng
Do đó, số người không gửi tiết kiệm ở nhóm 1 bằng 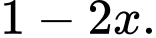
Từ đó, ta có sơ đồ cây như sau:

Từ sơ đồ cây, ta có xác suất người không gửi tiết kiệm ở vùng A là P(không gửi tiết kiệm)
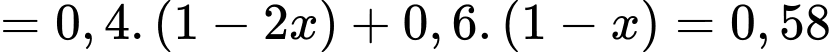 (Vì giả thiết cho biết 58% người không gửi tiết kiệm)
(Vì giả thiết cho biết 58% người không gửi tiết kiệm)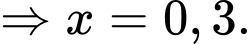
Ta có xác suất người có thu nhập tốt khi biết người đó không gửi tiết kiệm là
P(thu nhập tốt | không gửi tiết kiệm) = P(người có thu nhập tốt và không gửi tiết kiệm)/ P(không gửi tiết kiệm)
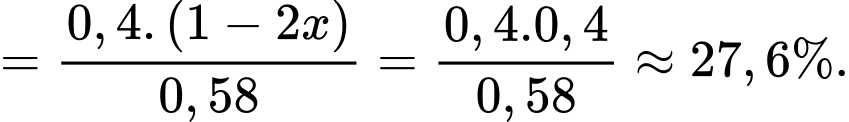
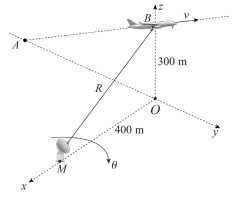
Câu 22 [693216]: Một radar có thể quay 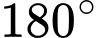 để quan sát máy bay quanh vùng phủ sóng của nó. Một máy bay cất cánh từ điểm
để quan sát máy bay quanh vùng phủ sóng của nó. Một máy bay cất cánh từ điểm 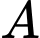 nằm trên mặt đất theo chiều cùng chiều với vectơ
nằm trên mặt đất theo chiều cùng chiều với vectơ 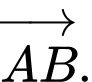 Trong hệ tọa độ
Trong hệ tọa độ 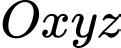 mặt đất là mặt phẳng
mặt đất là mặt phẳng 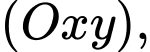 trục
trục  hướng lên trời, điểm
hướng lên trời, điểm 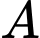 nằm trên trục
nằm trên trục 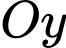 cách gốc tọa độ
cách gốc tọa độ 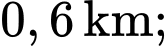 điểm
điểm 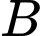 nằm trên trục
nằm trên trục  có cao độ bằng
có cao độ bằng 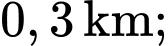 radar đang nằm trên trục
radar đang nằm trên trục 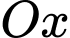 có hoành độ bằng
có hoành độ bằng 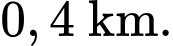 Máy bay đang ở điểm
Máy bay đang ở điểm 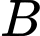 bay theo hướng bay như cũ đến điểm
bay theo hướng bay như cũ đến điểm 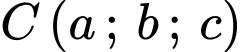 thì radar quay một góc bằng
thì radar quay một góc bằng 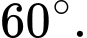 Tính
Tính 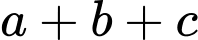 theo đơn vị mét (làm tròn đến hàng đơn vị).
theo đơn vị mét (làm tròn đến hàng đơn vị).
 để quan sát máy bay quanh vùng phủ sóng của nó. Một máy bay cất cánh từ điểm
để quan sát máy bay quanh vùng phủ sóng của nó. Một máy bay cất cánh từ điểm  nằm trên mặt đất theo chiều cùng chiều với vectơ
nằm trên mặt đất theo chiều cùng chiều với vectơ 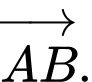 Trong hệ tọa độ
Trong hệ tọa độ 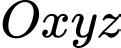 mặt đất là mặt phẳng
mặt đất là mặt phẳng 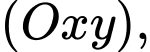 trục
trục  hướng lên trời, điểm
hướng lên trời, điểm 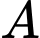 nằm trên trục
nằm trên trục 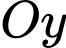 cách gốc tọa độ
cách gốc tọa độ 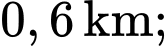 điểm
điểm 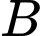 nằm trên trục
nằm trên trục  có cao độ bằng
có cao độ bằng 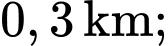 radar đang nằm trên trục
radar đang nằm trên trục 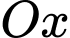 có hoành độ bằng
có hoành độ bằng 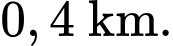 Máy bay đang ở điểm
Máy bay đang ở điểm 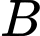 bay theo hướng bay như cũ đến điểm
bay theo hướng bay như cũ đến điểm 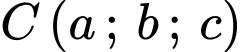 thì radar quay một góc bằng
thì radar quay một góc bằng 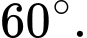 Tính
Tính 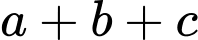 theo đơn vị mét (làm tròn đến hàng đơn vị).
theo đơn vị mét (làm tròn đến hàng đơn vị).
Điền đáp án: 2630.
Vì máy bay bay theo hướng cũ (cùng chiều với vectơ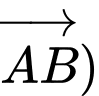 đến điểm
đến điểm  nên suy ra
nên suy ra 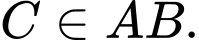 (xem hình vẽ dưới).
(xem hình vẽ dưới).
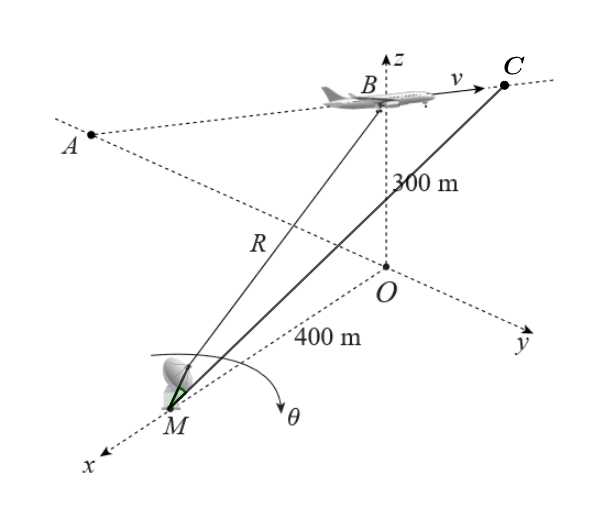
Dựa vào dữ kiện bài toán, ta có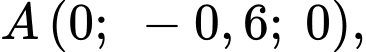
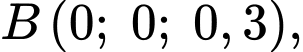
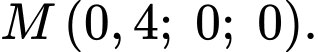
+) Viết phương trình đường thẳng để tham số toạ độ điểm
để tham số toạ độ điểm 
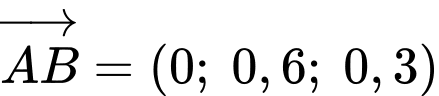
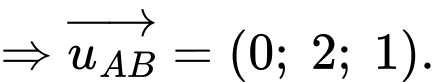
Suy ra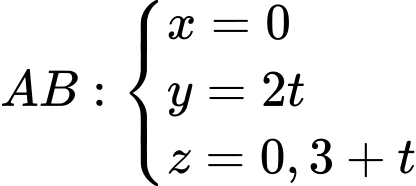
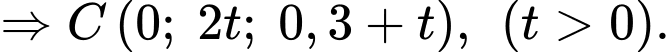
(Vì máy bay càng bay sẽ càng cao, nên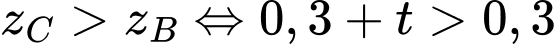
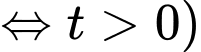
+) Ta có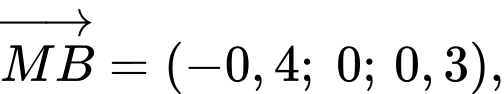
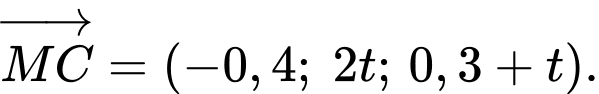
Vì radar quay từ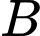 đến
đến  một góc bằng
một góc bằng 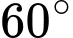 nên
nên 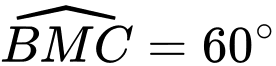 hay
hay 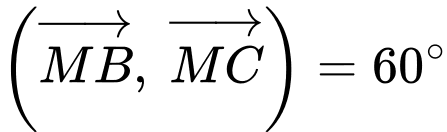
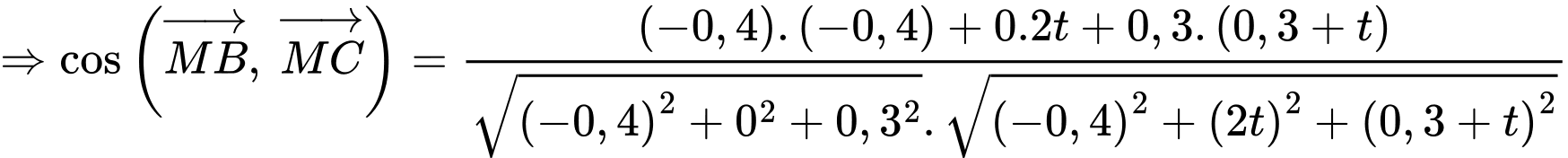
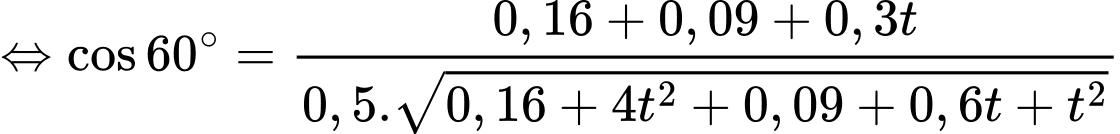
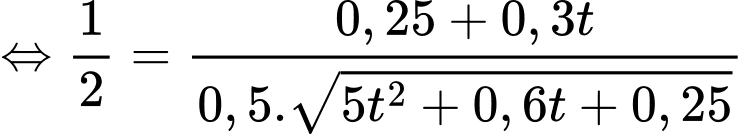
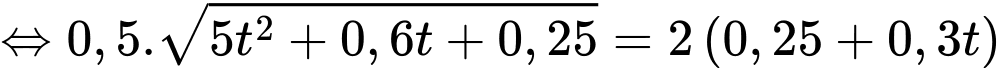
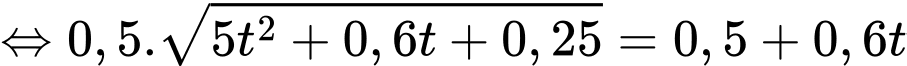
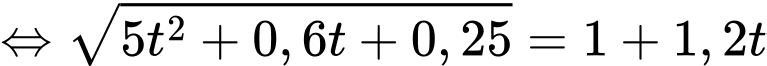
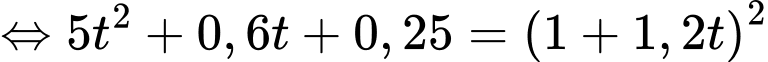
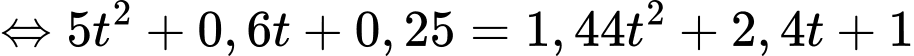
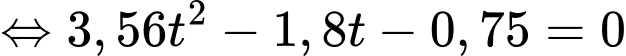
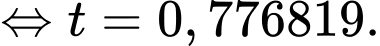
Vậy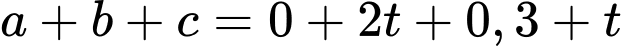
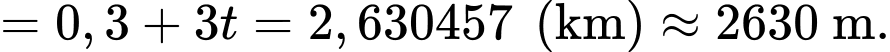
Vì máy bay bay theo hướng cũ (cùng chiều với vectơ
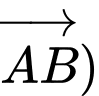 đến điểm
đến điểm  nên suy ra
nên suy ra 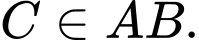 (xem hình vẽ dưới).
(xem hình vẽ dưới).
Dựa vào dữ kiện bài toán, ta có
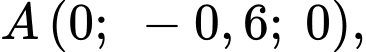
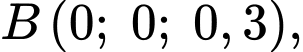
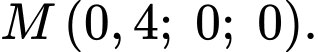
+) Viết phương trình đường thẳng
 để tham số toạ độ điểm
để tham số toạ độ điểm 
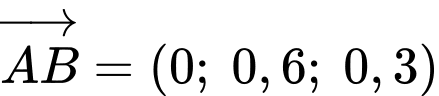
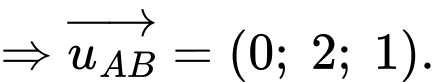
Suy ra
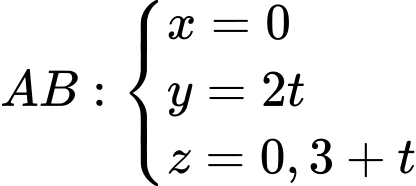
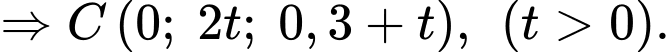
(Vì máy bay càng bay sẽ càng cao, nên
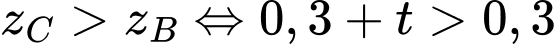
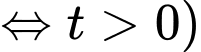
+) Ta có
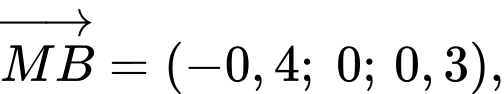
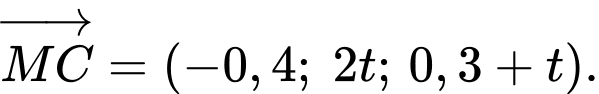
Vì radar quay từ
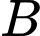 đến
đến  một góc bằng
một góc bằng 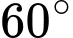 nên
nên 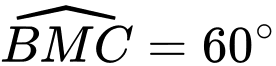 hay
hay 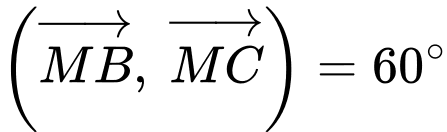
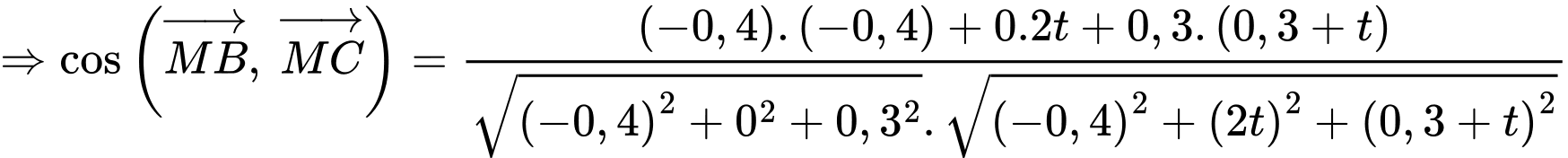
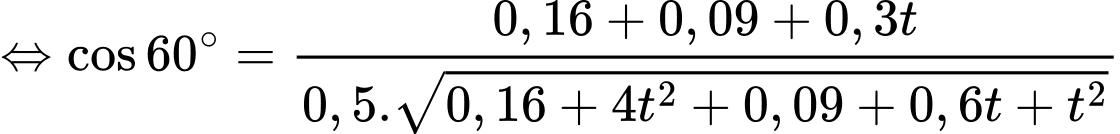
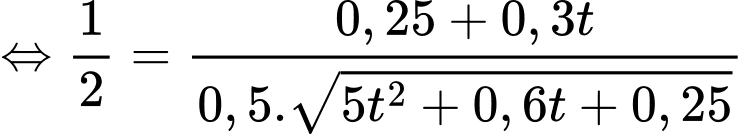
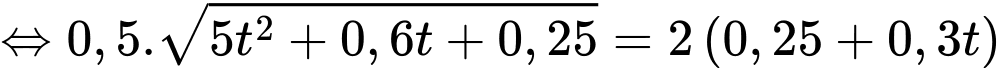
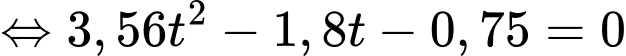
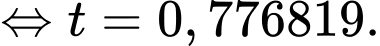
Vậy