PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [333921]: Nghiệm của phương trình 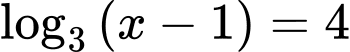 là
là
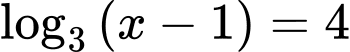 là
là A, 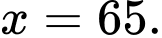
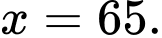
B, 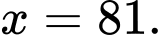
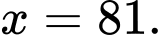
C, 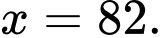
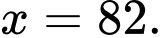
D, 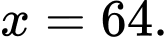
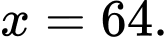
Chọn đáp án C
Ta có: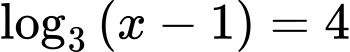
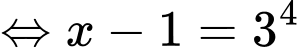
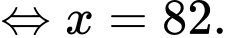 Đáp án: C
Đáp án: C
Ta có:
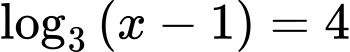
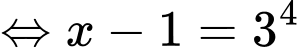
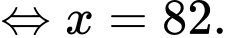 Đáp án: C
Đáp án: C
Câu 2 [694760]: Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A, 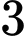
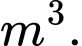
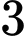
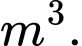
B, 
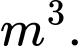

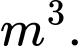
C, 
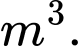

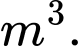
D, 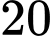
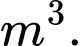
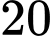
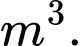
Chọn đáp án B.
Khoảng biến thiên của mẫu số liệu ghép nhóm là: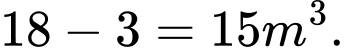 Đáp án: B
Đáp án: B
Khoảng biến thiên của mẫu số liệu ghép nhóm là:
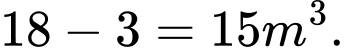 Đáp án: B
Đáp án: B
Câu 3 [529647]: Cho cấp số nhân 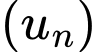 với
với 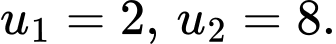 Công bội của cấp số nhân đã cho bằng
Công bội của cấp số nhân đã cho bằng
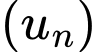 với
với 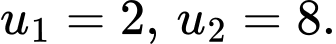 Công bội của cấp số nhân đã cho bằng
Công bội của cấp số nhân đã cho bằng A, 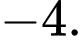
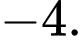
B, 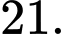
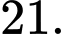
C, 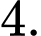
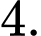
D, 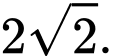
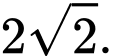
Chọn đáp án C.
Gọi công bội của cấp số nhân là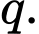
Ta có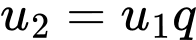 suy ra
suy ra 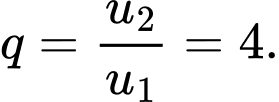 Đáp án: C
Đáp án: C
Gọi công bội của cấp số nhân là
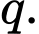
Ta có
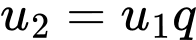 suy ra
suy ra 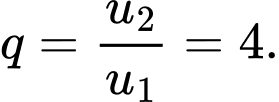 Đáp án: C
Đáp án: C
Câu 4 [333938]: Trong không gian 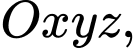 cho đường thẳng
cho đường thẳng 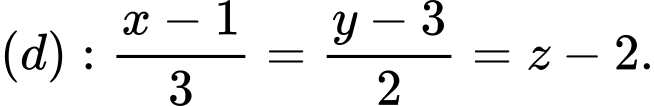 Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng  ?
?
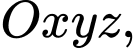 cho đường thẳng
cho đường thẳng 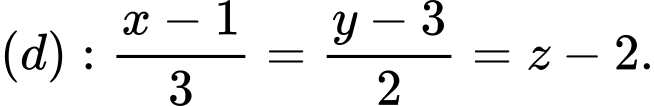 Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng  ?
? A, 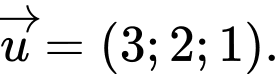
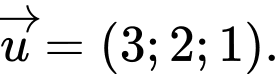
B, 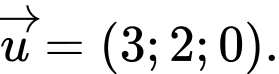
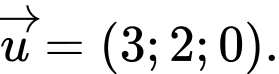
C, 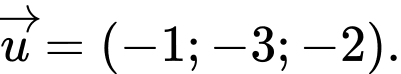
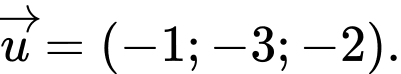
D, 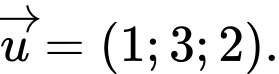
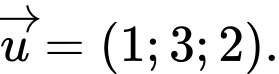
Chọn đáp án A.
Phương trình đường thẳng được viết lại dưới dạng
được viết lại dưới dạng 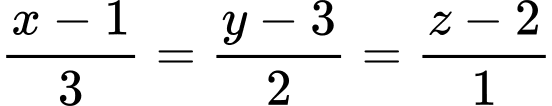 nên có một vectơ chỉ phương là
nên có một vectơ chỉ phương là 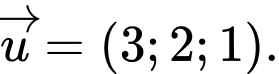 Đáp án: A
Đáp án: A
Phương trình đường thẳng
 được viết lại dưới dạng
được viết lại dưới dạng 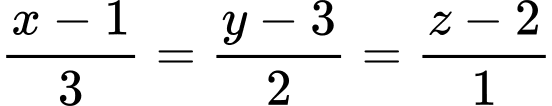 nên có một vectơ chỉ phương là
nên có một vectơ chỉ phương là 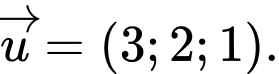 Đáp án: A
Đáp án: A Sử dụng thông tin dưới đây để trả lời câu 5 và câu 6
Cho hàm số F(x)=4x3+1 là một nguyên hàm của hàm số f(x) trên tập số thực R.
Câu 5 [698834]: Với  là hằng số. Khẳng định nào dưới đây là đúng.
là hằng số. Khẳng định nào dưới đây là đúng.
 là hằng số. Khẳng định nào dưới đây là đúng.
là hằng số. Khẳng định nào dưới đây là đúng. A, 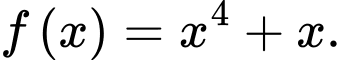
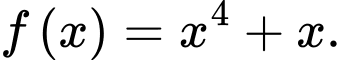
B, 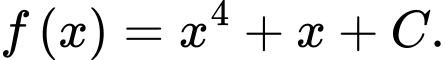
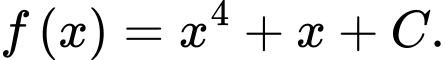
C, 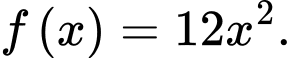
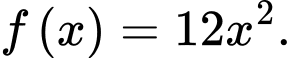
D, 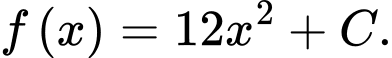
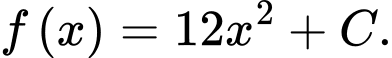
Chọn đáp án C.
Ta có: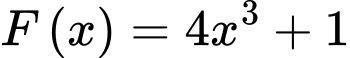 là một nguyên hàm của
là một nguyên hàm của 
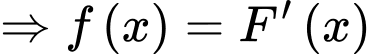
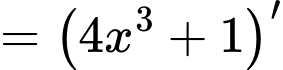
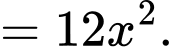 Đáp án: C
Đáp án: C
Ta có:
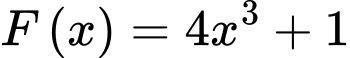 là một nguyên hàm của
là một nguyên hàm của 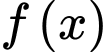
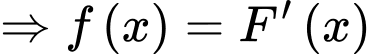
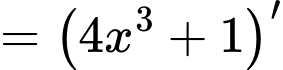
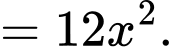 Đáp án: C
Đáp án: C
Câu 6 [698835]: Diện tích hình thang cong giới hạn bởi đồ thị hàm số 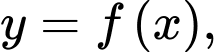 trục
trục 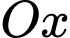 và hai đường thẳng
và hai đường thẳng 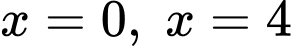 bằng:
bằng:
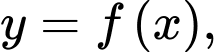 trục
trục 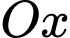 và hai đường thẳng
và hai đường thẳng 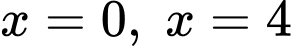 bằng:
bằng: A, 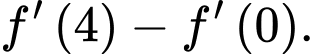
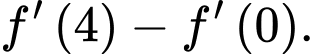
B, 

C, 

D, 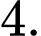
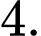
Chọn đáp án C.
Diện tích hình thang cong giới hạn bởi đồ thị hàm số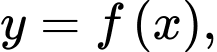 trục
trục 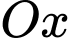 và hai đường thẳng
và hai đường thẳng 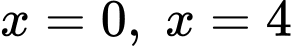 bằng:
bằng:
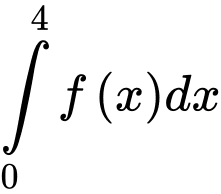
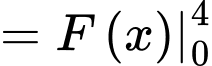
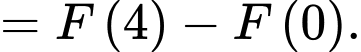 Đáp án: C
Đáp án: C
Diện tích hình thang cong giới hạn bởi đồ thị hàm số
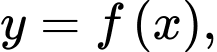 trục
trục 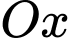 và hai đường thẳng
và hai đường thẳng 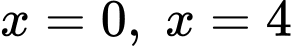 bằng:
bằng: 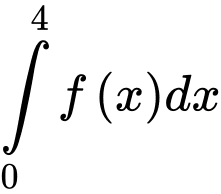
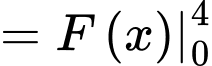
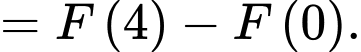 Đáp án: C
Đáp án: C
Câu 7 [529339]: Cho khối chóp có đáy là hình vuông cạnh bằng 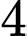 và chiều cao bằng 3. Tính thể tích
và chiều cao bằng 3. Tính thể tích  của khối chóp đã cho.
của khối chóp đã cho.
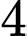 và chiều cao bằng 3. Tính thể tích
và chiều cao bằng 3. Tính thể tích  của khối chóp đã cho.
của khối chóp đã cho. A, 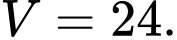
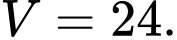
B, 

C, 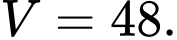
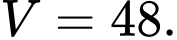
D, 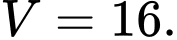
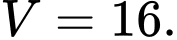
Chọn đáp án D.
Thể tích của khối chóp có đáy là hình vuông cạnh bằng
của khối chóp có đáy là hình vuông cạnh bằng 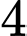 và chiều cao bằng
và chiều cao bằng 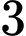 là
là 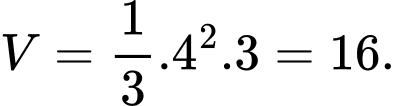 Đáp án: D
Đáp án: D
Thể tích
 của khối chóp có đáy là hình vuông cạnh bằng
của khối chóp có đáy là hình vuông cạnh bằng 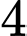 và chiều cao bằng
và chiều cao bằng 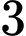 là
là 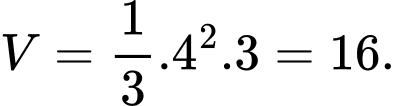 Đáp án: D
Đáp án: D
Câu 8 [681566]: Đường tiệm cận ngang của đồ thị hàm số 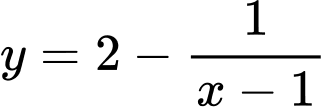 có phương trình là
có phương trình là
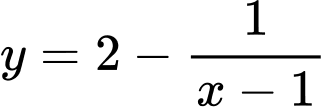 có phương trình là
có phương trình là A, 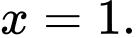
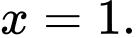
B, 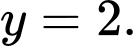
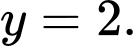
C, 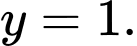
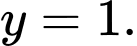
D, 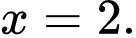
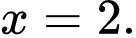
Chọn đáp án B.
Ta có: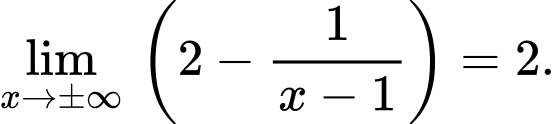
Tiệm cận ngang là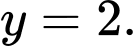 Đáp án: B
Đáp án: B
Ta có:
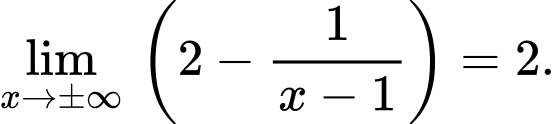
Tiệm cận ngang là
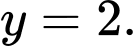 Đáp án: B
Đáp án: B
Câu 9 [975693]: Tập xác định của hàm số 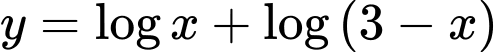 là
là
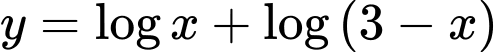 là
là A, 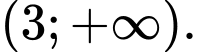
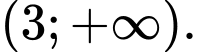
B, 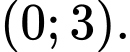
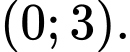
C, 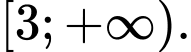
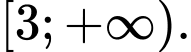
D, 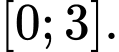
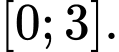
Chọn đáp án B.
Hàm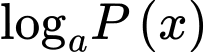 xác định khi
xác định khi 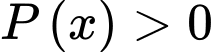 (với
(với 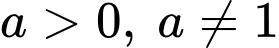 ).
).
Điều kiện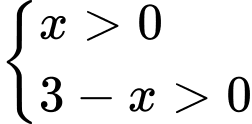
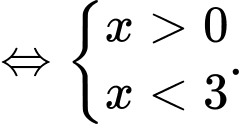
Vậy tập xác định của hàm số là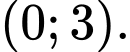 Đáp án: B
Đáp án: B
Hàm
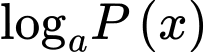 xác định khi
xác định khi 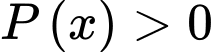 (với
(với 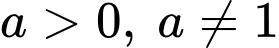 ).
).Điều kiện
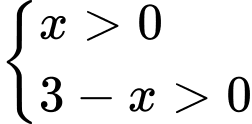
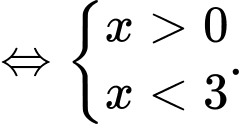
Vậy tập xác định của hàm số là
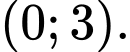 Đáp án: B
Đáp án: B
Câu 10 [681583]: Đồ thị hàm số 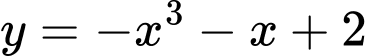 là đường cong nào trong bốn đường cong sau?
là đường cong nào trong bốn đường cong sau?
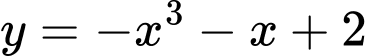 là đường cong nào trong bốn đường cong sau?
là đường cong nào trong bốn đường cong sau? A, 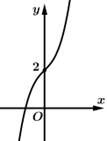

B, 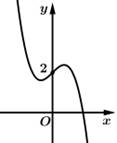

C, 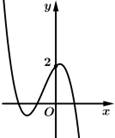

D, 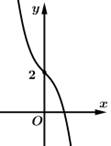

Chọn đáp án D.
Xét hàm số: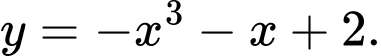
Tập xác định của hàm số là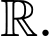
Ta có: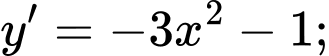
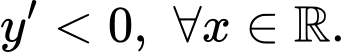
Do đó, hàm số đã cho nghịch biến trên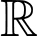 nên đồ thị hàm số này đi xuống từ trái qua phải, vậy đường cong ở phương án D thỏa mãn. Đáp án: D
nên đồ thị hàm số này đi xuống từ trái qua phải, vậy đường cong ở phương án D thỏa mãn. Đáp án: D
Xét hàm số:
Tập xác định của hàm số là
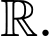
Ta có:
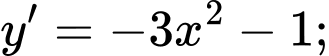
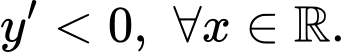
Do đó, hàm số đã cho nghịch biến trên
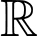 nên đồ thị hàm số này đi xuống từ trái qua phải, vậy đường cong ở phương án D thỏa mãn. Đáp án: D
nên đồ thị hàm số này đi xuống từ trái qua phải, vậy đường cong ở phương án D thỏa mãn. Đáp án: D
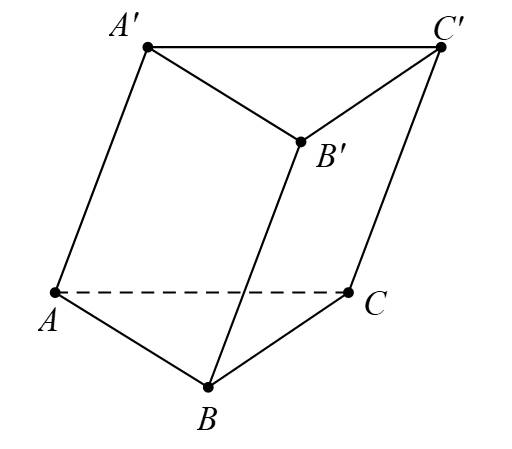
Câu 11 [684120]: Cho hình lăng trụ  có hai đáy là các tam giác đều như hình vẽ. Góc giữa hai vectơ
có hai đáy là các tam giác đều như hình vẽ. Góc giữa hai vectơ 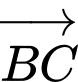 và
và  bằng
bằng
 có hai đáy là các tam giác đều như hình vẽ. Góc giữa hai vectơ
có hai đáy là các tam giác đều như hình vẽ. Góc giữa hai vectơ  và
và  bằng
bằng
A, 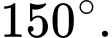
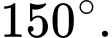
B, 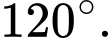
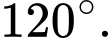
C, 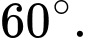
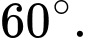
D, 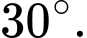
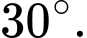
Chọn đáp án C.
Vì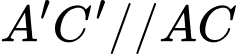
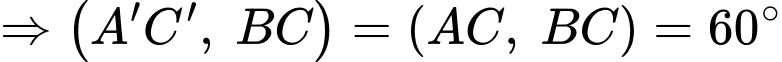
(Vì tam giác đều).
Đáp án: C
đều).
Đáp án: C
Vì
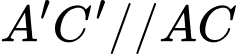
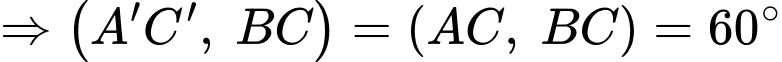
(Vì tam giác
 đều).
Đáp án: C
đều).
Đáp án: C
Câu 12 [310234]: Phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm 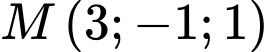 và vuông góc với đường thẳng
và vuông góc với đường thẳng 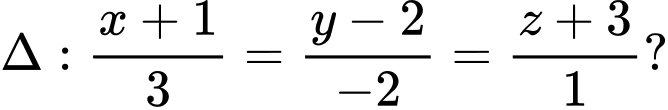
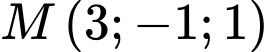 và vuông góc với đường thẳng
và vuông góc với đường thẳng 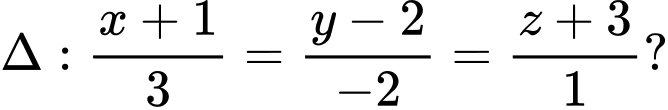
A, 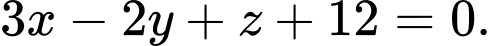
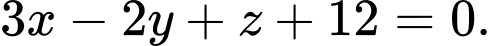
B, 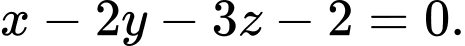
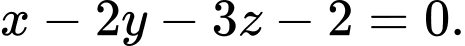
C, 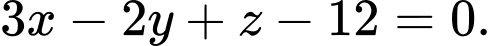
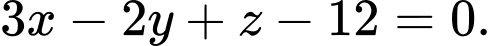
D, 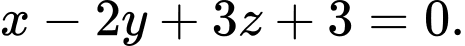
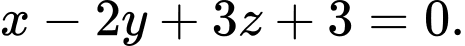
Chọn đáp án C.
Mặt phẳng cần tìm có một VTPT là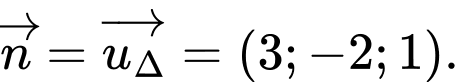
Phương trình mặt phẳng cần tìm là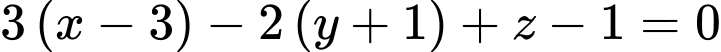 hay
hay 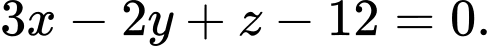 Đáp án: C
Đáp án: C
Mặt phẳng cần tìm có một VTPT là
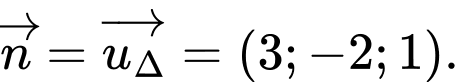
Phương trình mặt phẳng cần tìm là
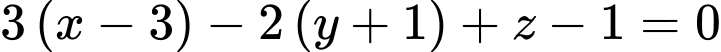 hay
hay 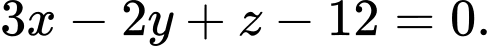 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [694761]: Cho hàm số 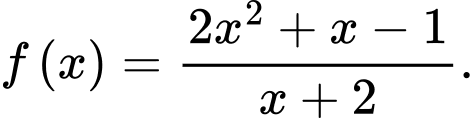
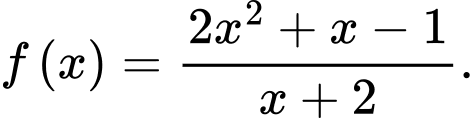
a) Đúng.
Ta có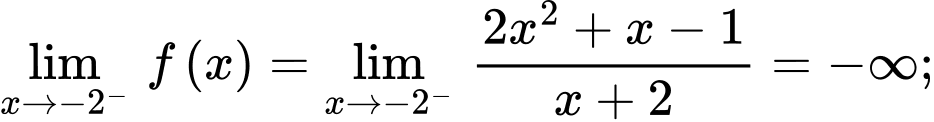
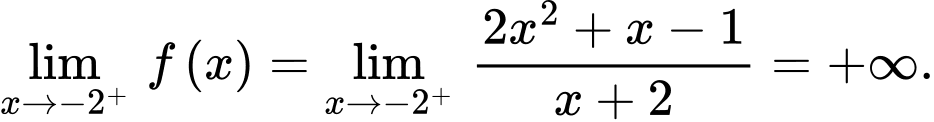
Vậy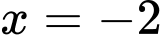 là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số 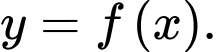
b) Sai.
Ta có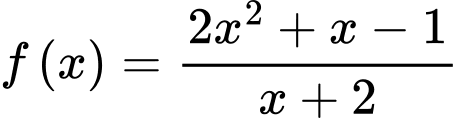
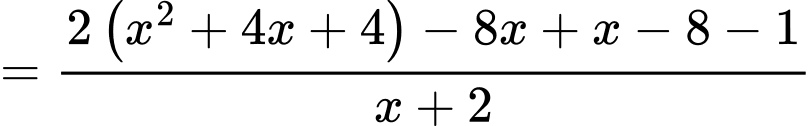
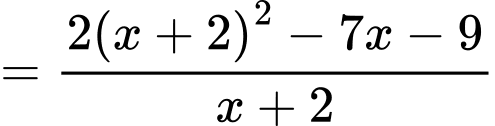
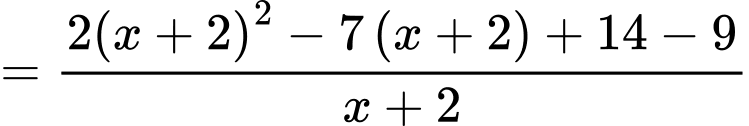
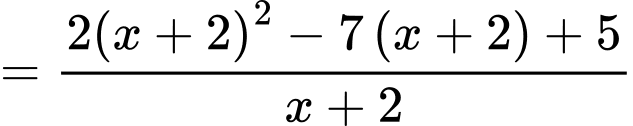
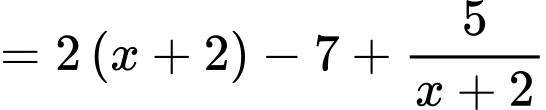
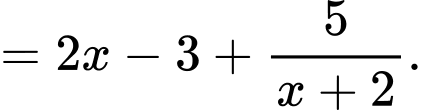
Suy ra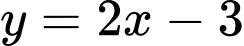 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
c) Sai.
Vì đồ thị hàm số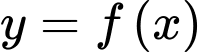 có 1 đường tiệm cận đứng và 1 đường tiệm cận xiên nên tâm đối xứng của đồ thị hàm số là giao của 2 đường tiệm cận đó.
có 1 đường tiệm cận đứng và 1 đường tiệm cận xiên nên tâm đối xứng của đồ thị hàm số là giao của 2 đường tiệm cận đó.
Suy ra tâm đối xứng của đồ thị là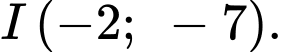
d) Sai.
Vì toạ độ của tâm đối xứng là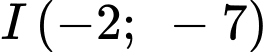 nên ta có
nên ta có 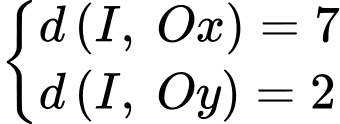
Suy ra tổng khoảng cách từ tâm đối xứng đến 2 trục toạ độ bằng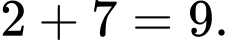
Ta có
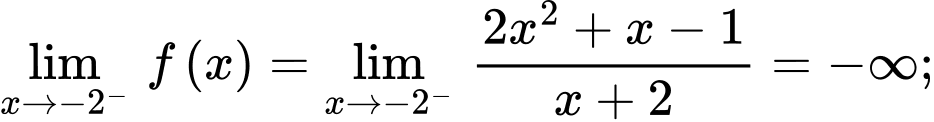
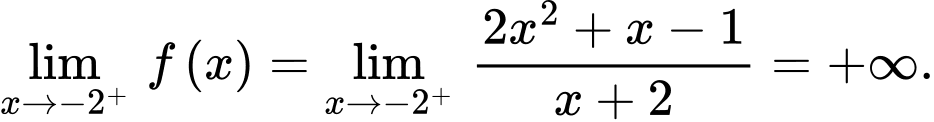
Vậy
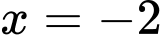 là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số 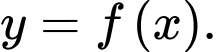
b) Sai.
Ta có
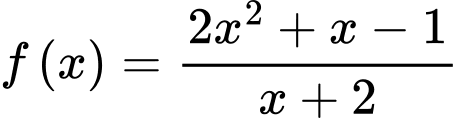
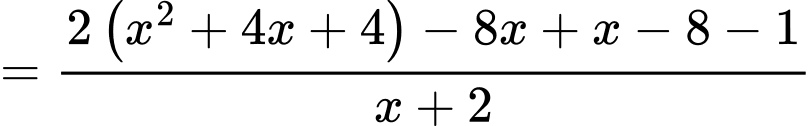
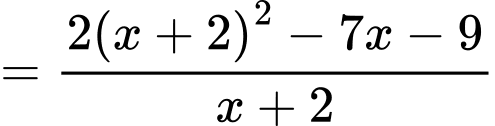
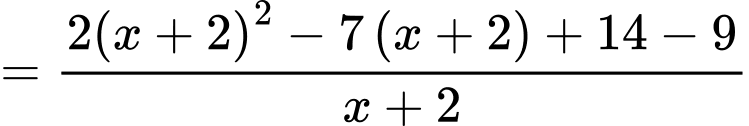
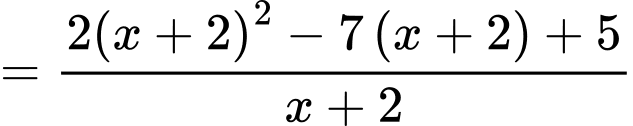
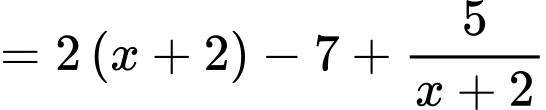
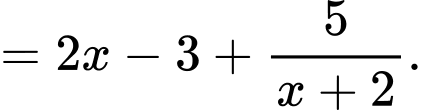
Suy ra
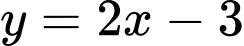 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
c) Sai.
Vì đồ thị hàm số
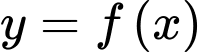 có 1 đường tiệm cận đứng và 1 đường tiệm cận xiên nên tâm đối xứng của đồ thị hàm số là giao của 2 đường tiệm cận đó.
có 1 đường tiệm cận đứng và 1 đường tiệm cận xiên nên tâm đối xứng của đồ thị hàm số là giao của 2 đường tiệm cận đó.
Suy ra tâm đối xứng của đồ thị là
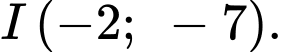
d) Sai.
Vì toạ độ của tâm đối xứng là
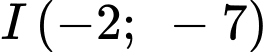 nên ta có
nên ta có 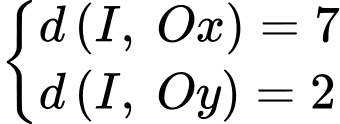
Suy ra tổng khoảng cách từ tâm đối xứng đến 2 trục toạ độ bằng
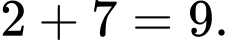
Câu 14 [698836]: Trong không gian với hệ toạ độ 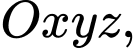 một cabin cáp treo xuất phát từ điểm
một cabin cáp treo xuất phát từ điểm 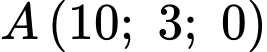 và chuyển động thẳng đều theo đường cáp có vectơ chỉ phương là
và chuyển động thẳng đều theo đường cáp có vectơ chỉ phương là 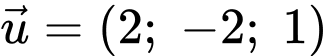 với tốc độ là
với tốc độ là 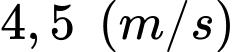 (đơn vị trên mỗi trục toạ độ là mét, hướng chuyển động cùng chiều với hướng vectơ
(đơn vị trên mỗi trục toạ độ là mét, hướng chuyển động cùng chiều với hướng vectơ 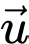 ).
).

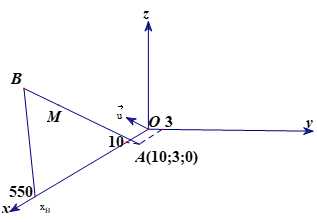
 một cabin cáp treo xuất phát từ điểm
một cabin cáp treo xuất phát từ điểm 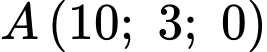 và chuyển động thẳng đều theo đường cáp có vectơ chỉ phương là
và chuyển động thẳng đều theo đường cáp có vectơ chỉ phương là 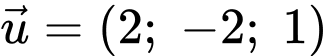 với tốc độ là
với tốc độ là 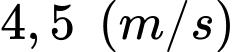 (đơn vị trên mỗi trục toạ độ là mét, hướng chuyển động cùng chiều với hướng vectơ
(đơn vị trên mỗi trục toạ độ là mét, hướng chuyển động cùng chiều với hướng vectơ 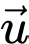 ).
).

a) Sai.
Đường cáp đi qua điểm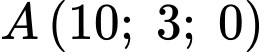 và có vectơ chỉ phương
và có vectơ chỉ phương 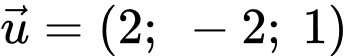 có phương trình chính tắc là:
có phương trình chính tắc là: 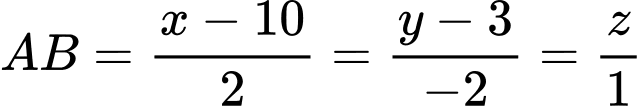
b) Đúng.
Do tốc độ chuyển động của cabin là 4,5 m/s nên quãng đường cabin chuyển động sau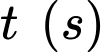 bằng
bằng 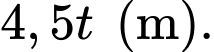
c) Sai.
Vì cabin chuyển động trên đường cáp nên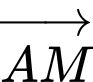 cùng hướng với vectơ
cùng hướng với vectơ 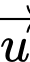 nên ta có
nên ta có 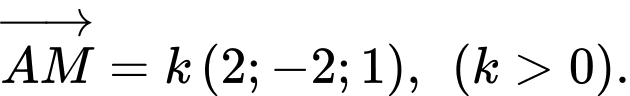
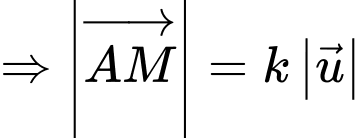
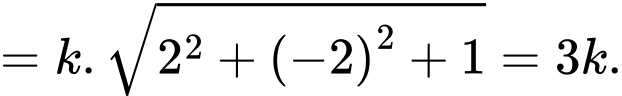
Do đó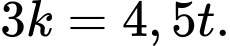 Suy ra
Suy ra 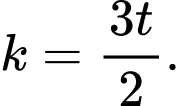
Vì thế, ta có: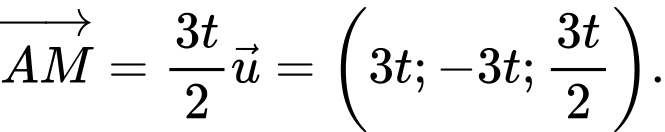
Gọi toạ độ của điểm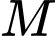 là
là 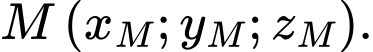
Do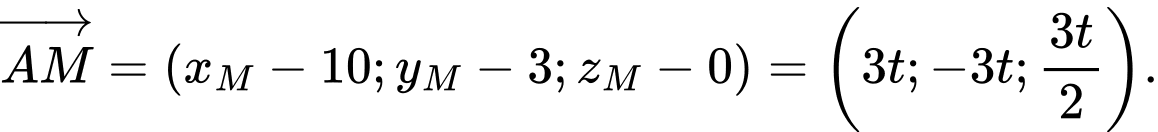
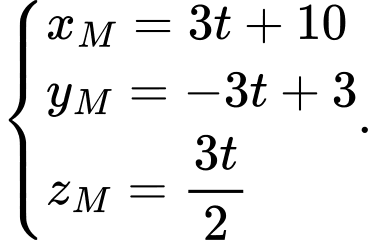
Vậy điểm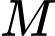 có toạ độ là
có toạ độ là 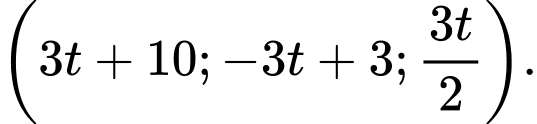
d) Đúng.
Do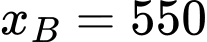 nên
nên 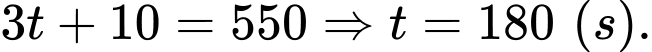
Do đó, ta có điểm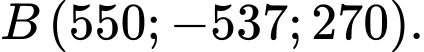
Vậy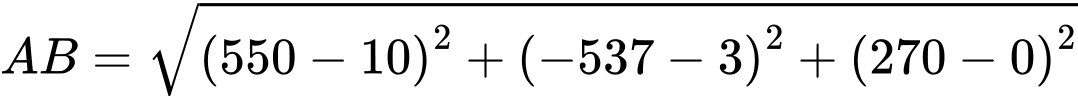

Đường cáp đi qua điểm
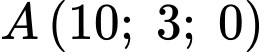 và có vectơ chỉ phương
và có vectơ chỉ phương 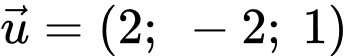 có phương trình chính tắc là:
có phương trình chính tắc là: 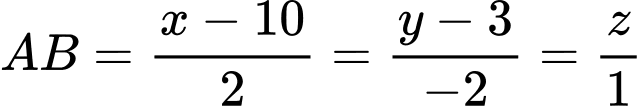
b) Đúng.
Do tốc độ chuyển động của cabin là 4,5 m/s nên quãng đường cabin chuyển động sau
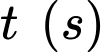 bằng
bằng 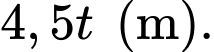
c) Sai.
Vì cabin chuyển động trên đường cáp nên
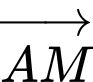 cùng hướng với vectơ
cùng hướng với vectơ 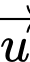 nên ta có
nên ta có 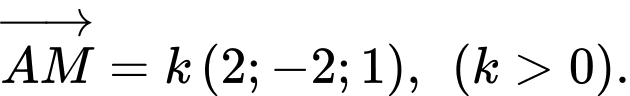
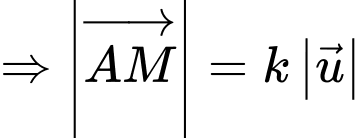
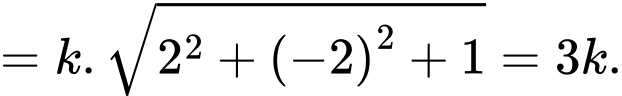
Do đó
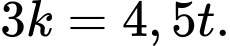 Suy ra
Suy ra 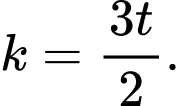
Vì thế, ta có:
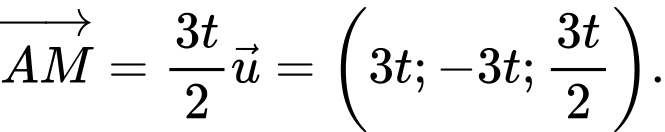
Gọi toạ độ của điểm
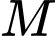 là
là 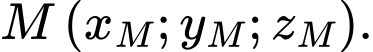
Do
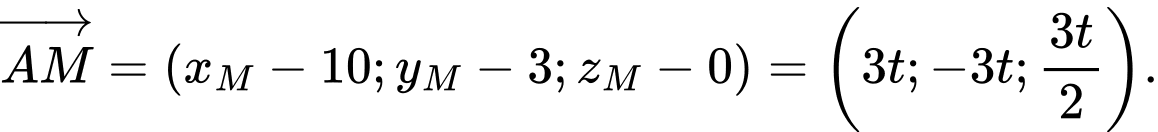
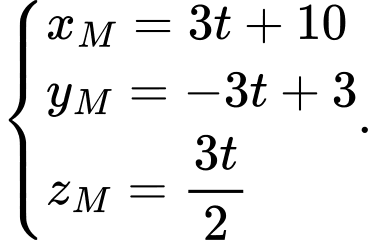
Vậy điểm
 có toạ độ là
có toạ độ là 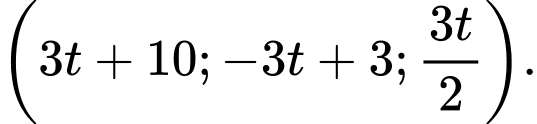
d) Đúng.
Do
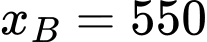 nên
nên 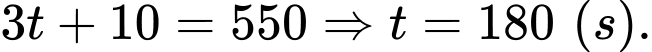
Do đó, ta có điểm
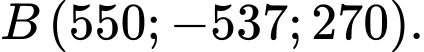
Vậy
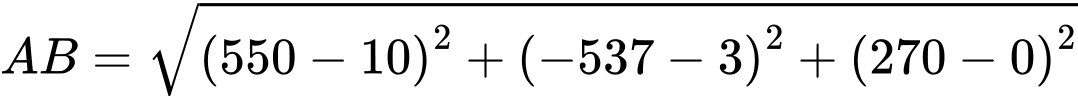

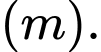
Câu 15 [703068]: Một lô hàng có 6 sản phẩm tốt, 4 sản phẩm xấu. Lấy ngẫu nhiên không hoàn lại từng sản phẩm cho đến khi lấy được 2 sản phẩm tốt thì dừng lại.
+ Gọi A là biến cố: “lần thứ nhất lấy được sản phẩm tốt”.
+ Gọi B là biến cố: “Dừng lại ở lần lấy thứ 4”.
+ Gọi A là biến cố: “lần thứ nhất lấy được sản phẩm tốt”.
+ Gọi B là biến cố: “Dừng lại ở lần lấy thứ 4”.
a) Sai.
Xác suất lần thứ nhất lấy được sản phẩm tốt là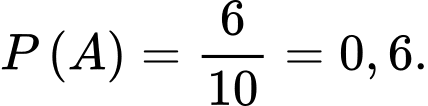
b) Sai.
Xác suất lần đầu lấy được sản phẩm xấu là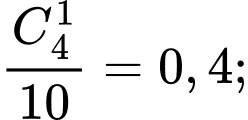
Xác suất lần thứ hai lấy được sản phẩm xấu là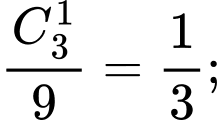 (vì khi thực hiện lấy không hoàn lại, thì ở lần lấy thứ 2 sẽ còn lại 9 sản phẩm trong đó có 3 sản phẩm xấu)
(vì khi thực hiện lấy không hoàn lại, thì ở lần lấy thứ 2 sẽ còn lại 9 sản phẩm trong đó có 3 sản phẩm xấu)
Tương tự, (sau 2 lần lấy đầu tiên thì còn lại 8 sản phẩm trong đó có 2 sản phẩm xấu và 6 sản phẩm tốt) ta có xác suất lần thứ 3 và lần thứ 4 lấy được sản phẩm tốt lần lượt là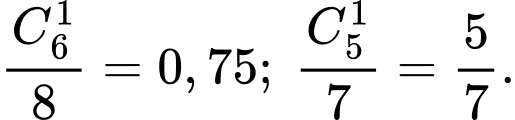
Vậy xác suất hai lần đầu lấy được sản phẩm xấu, hai lần sau đó lấy được sản phẩm tốt bằng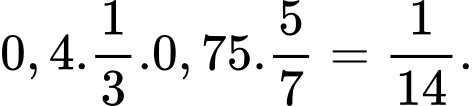
c) Đúng.
Sẽ có 3 trường hợp để lấy được 2 sản phẩm tốt và dừng lại ở lần lấy thứ 4 là: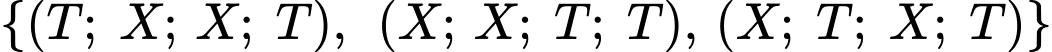
Thực hiện cách tính như ở phần b) ta được kết quả như sau:
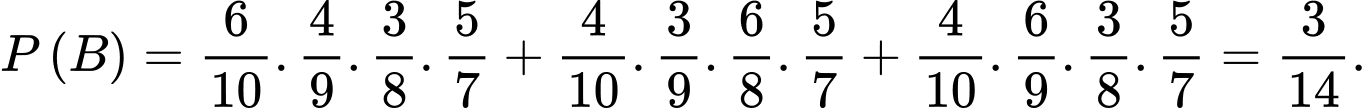
d) Sai.
Ta có: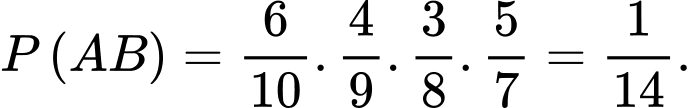
Do đó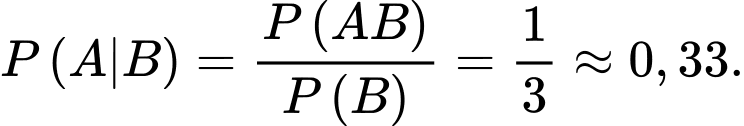
Xác suất lần thứ nhất lấy được sản phẩm tốt là
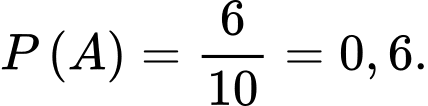
b) Sai.
Xác suất lần đầu lấy được sản phẩm xấu là
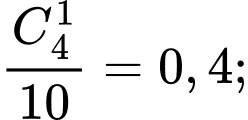
Xác suất lần thứ hai lấy được sản phẩm xấu là
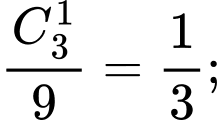 (vì khi thực hiện lấy không hoàn lại, thì ở lần lấy thứ 2 sẽ còn lại 9 sản phẩm trong đó có 3 sản phẩm xấu)
(vì khi thực hiện lấy không hoàn lại, thì ở lần lấy thứ 2 sẽ còn lại 9 sản phẩm trong đó có 3 sản phẩm xấu)
Tương tự, (sau 2 lần lấy đầu tiên thì còn lại 8 sản phẩm trong đó có 2 sản phẩm xấu và 6 sản phẩm tốt) ta có xác suất lần thứ 3 và lần thứ 4 lấy được sản phẩm tốt lần lượt là
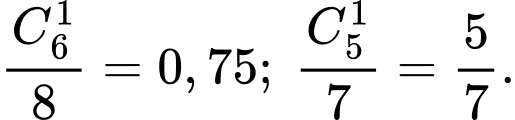
Vậy xác suất hai lần đầu lấy được sản phẩm xấu, hai lần sau đó lấy được sản phẩm tốt bằng
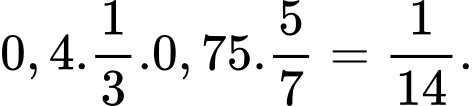
c) Đúng.
Sẽ có 3 trường hợp để lấy được 2 sản phẩm tốt và dừng lại ở lần lấy thứ 4 là:
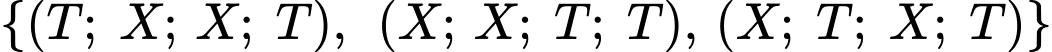
Thực hiện cách tính như ở phần b) ta được kết quả như sau:
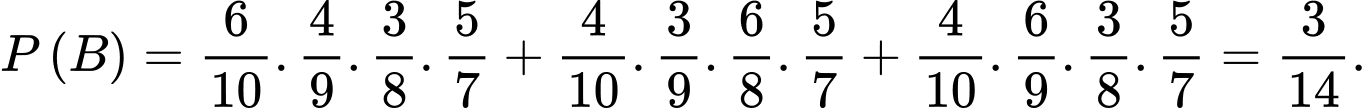
d) Sai.
Ta có:
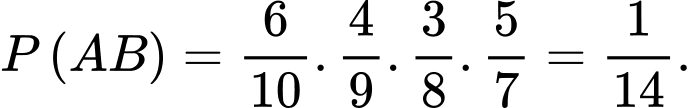
Do đó
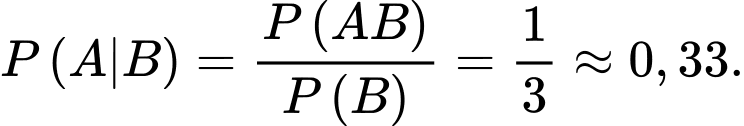
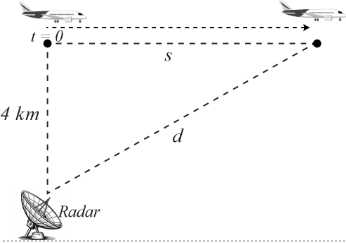
Câu 16 [694762]: Một máy bay bay thẳng qua một trạm radar tại thời điểm  . Máy bay duy trì độ cao
. Máy bay duy trì độ cao 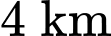 và bay với tốc độ thay đổi theo thời gian được mô phỏng qua hàm số
và bay với tốc độ thay đổi theo thời gian được mô phỏng qua hàm số 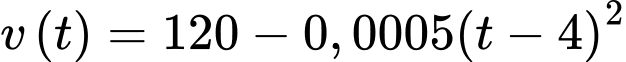 m/s
m/s 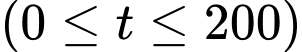 . Gọi
. Gọi 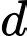 là khoảng cách từ trạm radar đến máy bay và
là khoảng cách từ trạm radar đến máy bay và 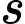 là khoảng cách theo phương ngang mà máy bay đã bay kể từ khi nó bay qua trạm radar (tham khảo hình vẽ).
là khoảng cách theo phương ngang mà máy bay đã bay kể từ khi nó bay qua trạm radar (tham khảo hình vẽ).
 . Máy bay duy trì độ cao
. Máy bay duy trì độ cao  và bay với tốc độ thay đổi theo thời gian được mô phỏng qua hàm số
và bay với tốc độ thay đổi theo thời gian được mô phỏng qua hàm số 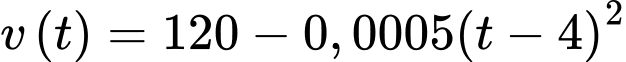 m/s
m/s 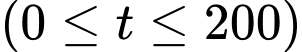 . Gọi
. Gọi 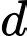 là khoảng cách từ trạm radar đến máy bay và
là khoảng cách từ trạm radar đến máy bay và 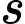 là khoảng cách theo phương ngang mà máy bay đã bay kể từ khi nó bay qua trạm radar (tham khảo hình vẽ).
là khoảng cách theo phương ngang mà máy bay đã bay kể từ khi nó bay qua trạm radar (tham khảo hình vẽ).
a) Sai.
Vận tốc của máy bay tại thời điểm bắt đầu quan sát là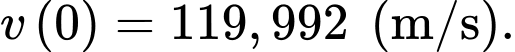
b) Sai.
Ta có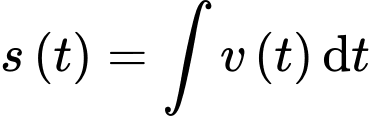
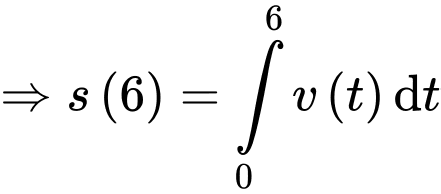
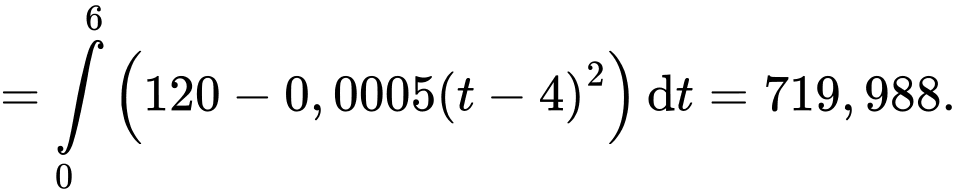
c) Sai.
Nhìn hình vẽ, nhận thấy khoảng cách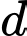 là cạnh huyền của tam giác vuông với 2 cạnh góc vuông lần lượt bằng
là cạnh huyền của tam giác vuông với 2 cạnh góc vuông lần lượt bằng 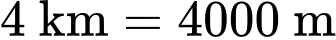 và bằng
và bằng 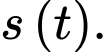
Theo định lý Pythagore, ta có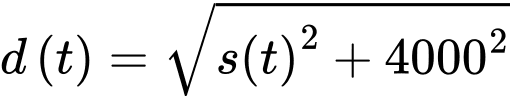
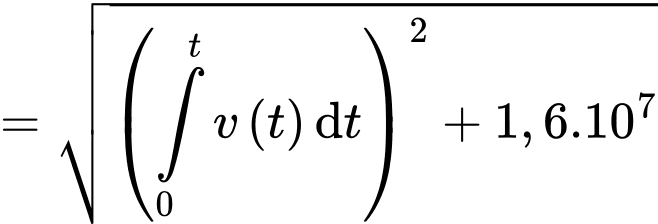
(Vì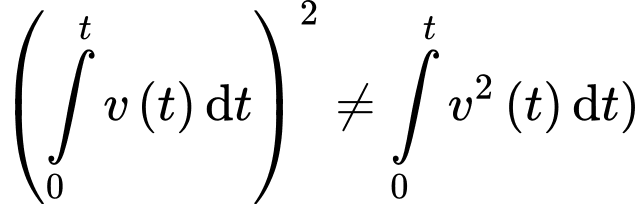
d) Đúng.
Dựa vào kết quả vừa tìm được ở phần c) ta có khoảng cách khi máy bay bay qua trạm Radar 3 phút = 180 giây là
khi máy bay bay qua trạm Radar 3 phút = 180 giây là 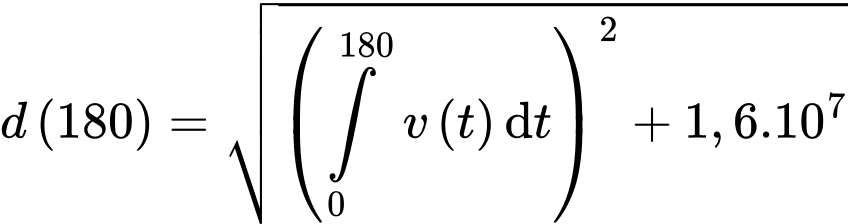

Vậy máy bay đã nằm ngoài vùng quan sát của radar.
Vận tốc của máy bay tại thời điểm bắt đầu quan sát là
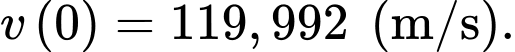
b) Sai.
Ta có
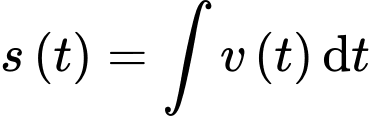
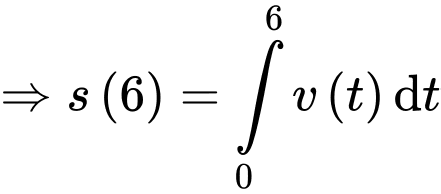
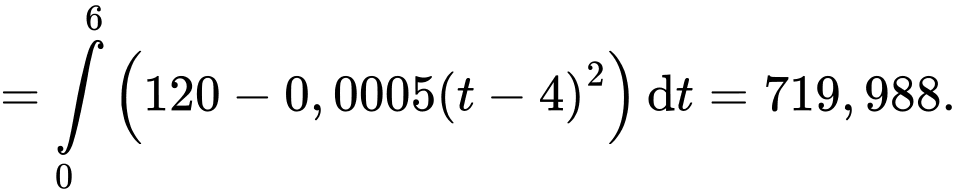
c) Sai.
Nhìn hình vẽ, nhận thấy khoảng cách
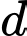 là cạnh huyền của tam giác vuông với 2 cạnh góc vuông lần lượt bằng
là cạnh huyền của tam giác vuông với 2 cạnh góc vuông lần lượt bằng 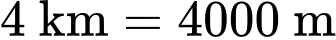 và bằng
và bằng 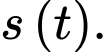
Theo định lý Pythagore, ta có
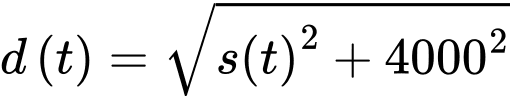
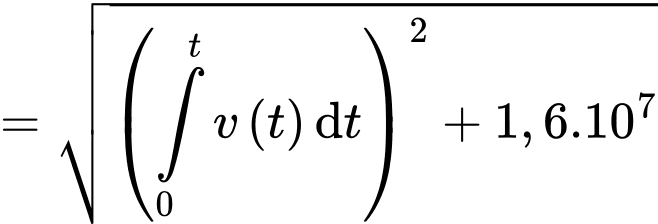
(Vì
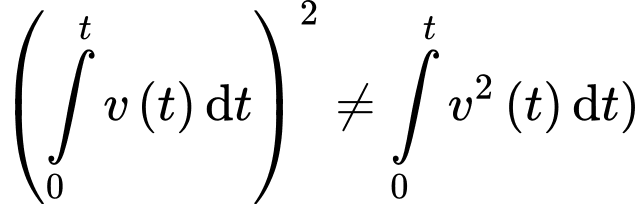
d) Đúng.
Dựa vào kết quả vừa tìm được ở phần c) ta có khoảng cách
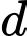 khi máy bay bay qua trạm Radar 3 phút = 180 giây là
khi máy bay bay qua trạm Radar 3 phút = 180 giây là 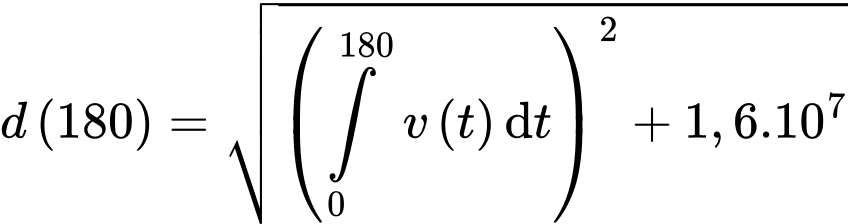

Vậy máy bay đã nằm ngoài vùng quan sát của radar.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [694763]: Cho hình lăng trụ đứng  có đáy
có đáy 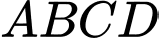 là hình thoi,
là hình thoi, 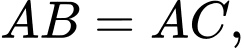
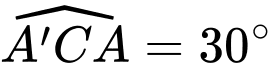 và
và 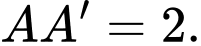 Khoảng cách từ điểm
Khoảng cách từ điểm 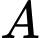 đến mặt phẳng
đến mặt phẳng 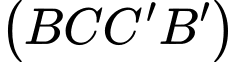 bằng bao nhiêu?
bằng bao nhiêu?
 có đáy
có đáy 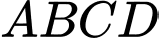 là hình thoi,
là hình thoi, 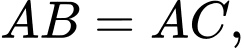
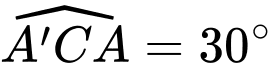 và
và 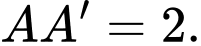 Khoảng cách từ điểm
Khoảng cách từ điểm 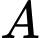 đến mặt phẳng
đến mặt phẳng 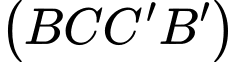 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 3.
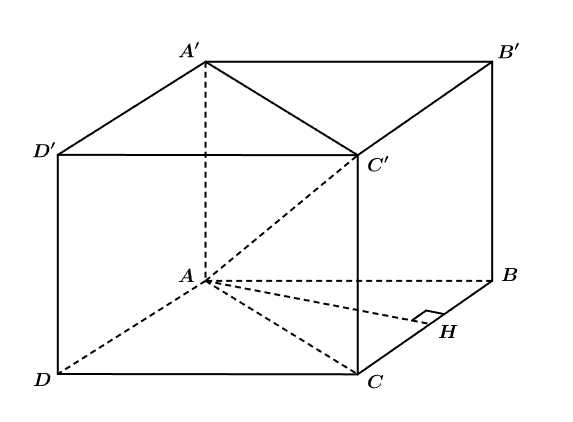
Kẻ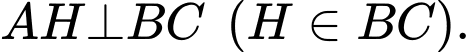
Suy ra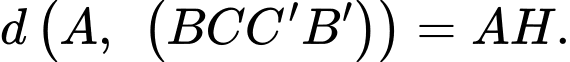
Xét tam giác vuông ta có
ta có 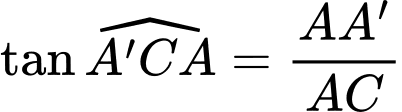
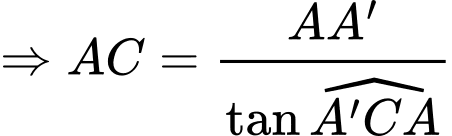
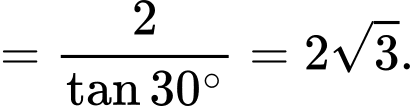
Vì là hình thoi nên ta có
là hình thoi nên ta có 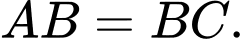
Mà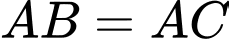
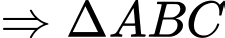 đều.
đều.
Suy ra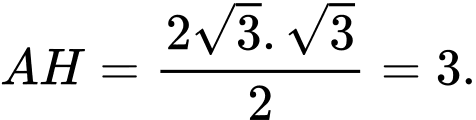
(Áp dụng công thức tính nhanh độ dài đường cao trong tam giác đều)

Kẻ
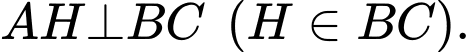
Suy ra
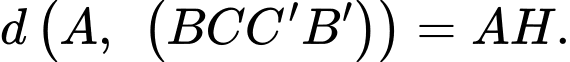
Xét tam giác vuông
 ta có
ta có 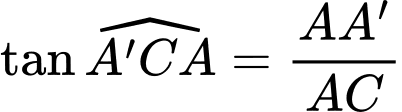
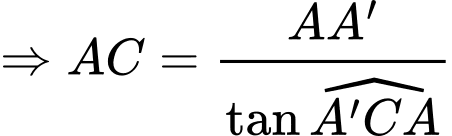
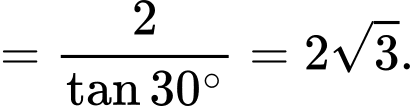
Vì
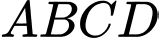 là hình thoi nên ta có
là hình thoi nên ta có 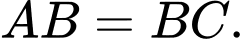
Mà
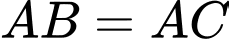
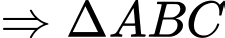 đều.
đều.Suy ra
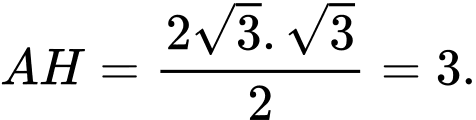
(Áp dụng công thức tính nhanh độ dài đường cao trong tam giác đều)
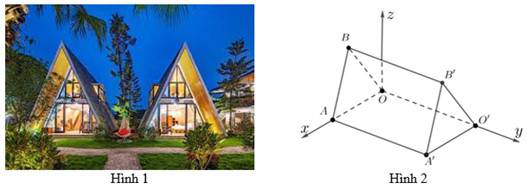
Câu 18 [694766]: Những căn lều gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác 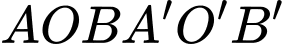 như trong Hình 2. Với hệ trục toạ độ
như trong Hình 2. Với hệ trục toạ độ 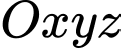 thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm
thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm 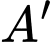 và
và 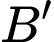 có tọa độ lần lượt là
có tọa độ lần lượt là 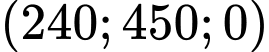 và
và 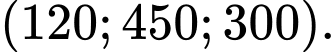 Mỗi căn nhà gỗ có chiều dài là
Mỗi căn nhà gỗ có chiều dài là 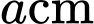 , chiều rộng là
, chiều rộng là 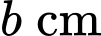 , mỗi cạnh bên của mặt tiền có độ dài là
, mỗi cạnh bên của mặt tiền có độ dài là 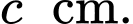 Tính
Tính 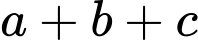 (Làm tròn đến hàng đơn vị).
(Làm tròn đến hàng đơn vị).
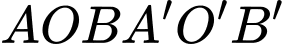 như trong Hình 2. Với hệ trục toạ độ
như trong Hình 2. Với hệ trục toạ độ 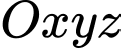 thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm
thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm 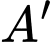 và
và 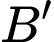 có tọa độ lần lượt là
có tọa độ lần lượt là 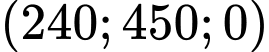 và
và 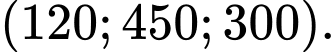 Mỗi căn nhà gỗ có chiều dài là
Mỗi căn nhà gỗ có chiều dài là 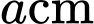 , chiều rộng là
, chiều rộng là 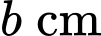 , mỗi cạnh bên của mặt tiền có độ dài là
, mỗi cạnh bên của mặt tiền có độ dài là 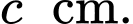 Tính
Tính 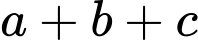 (Làm tròn đến hàng đơn vị).
(Làm tròn đến hàng đơn vị).
Điền đáp án: 1013.
Vì điểm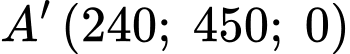 nên suy ra
nên suy ra 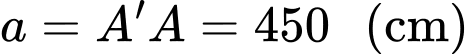 và
và 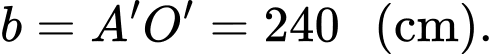 Ta có
Ta có 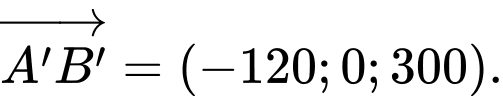
Do đó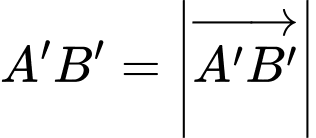
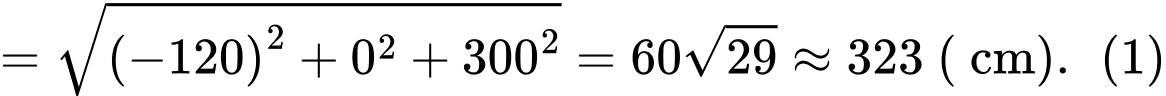
Vì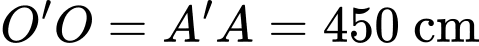 và
và  nằm trên trục
nằm trên trục 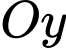 nên toạ độ của điểm
nên toạ độ của điểm  là
là 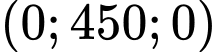 .
.
Do đó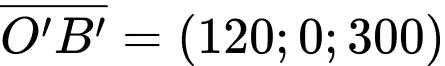 và
và 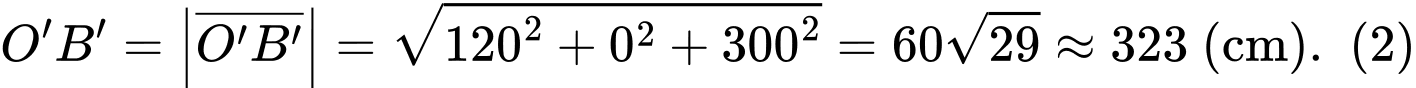
Từ (1) và (2), ta thấy mỗi cạnh bên của mặt tiền có độ dài bằng nhau và bằng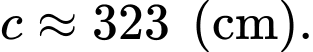
Vậy mỗi căn lều gỗ có chiều dài là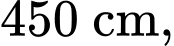 chiều rộng là
chiều rộng là 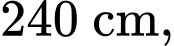 mỗi cạnh bên của mặt tiền có độ dài là 323 cm
mỗi cạnh bên của mặt tiền có độ dài là 323 cm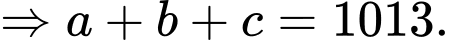
Vì điểm
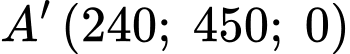 nên suy ra
nên suy ra 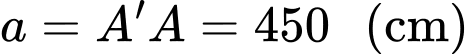 và
và 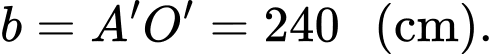 Ta có
Ta có 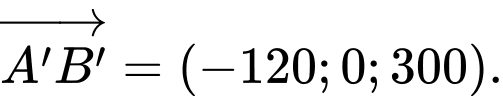
Do đó
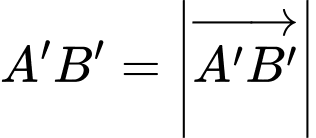
Vì
 và
và  nằm trên trục
nằm trên trục 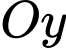 nên toạ độ của điểm
nên toạ độ của điểm  là
là 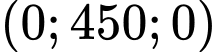 .
.Do đó
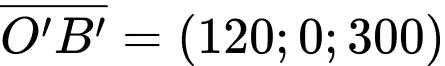 và
và 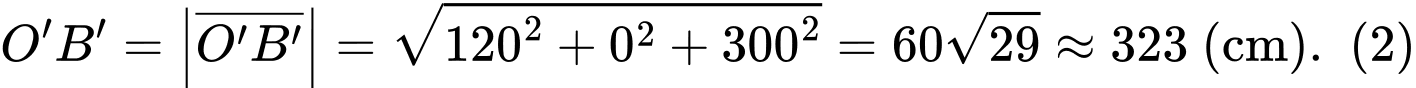
Từ (1) và (2), ta thấy mỗi cạnh bên của mặt tiền có độ dài bằng nhau và bằng
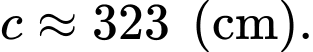
Vậy mỗi căn lều gỗ có chiều dài là
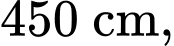 chiều rộng là
chiều rộng là 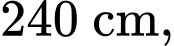 mỗi cạnh bên của mặt tiền có độ dài là 323 cm
mỗi cạnh bên của mặt tiền có độ dài là 323 cm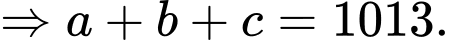
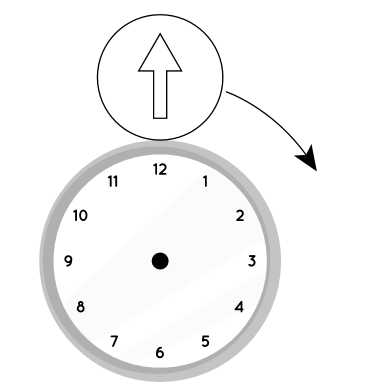
Câu 19 [696434]: Hình minh họa bên cạnh cho biết mặt đồng hồ hình tròn có bán kính 20 cm và một đĩa tròn có bán kính 10 cm tiếp xúc ngoài với mặt đồng hồ tại vị trí 12 giờ. Trên đĩa có vẽ một mũi tên, ban đầu chỉ theo hướng thẳng đứng hướng lên. Đĩa bắt đầu lăn theo chiều kim đồng hồ xung quanh mặt đồng hồ. Khi mũi tên lần tiếp theo chỉ theo hướng thẳng đứng hướng lên thì đĩa sẽ tiếp xúc với mặt đồng hồ tại thời điểm mấy giờ?

Điền đáp án: 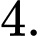
Dựa vào dữ kiện: “đĩa tiếp xúc ngoài với mặt đồng hồ tại vị trí 12 giờ. Trên đĩa có vẽ một mũi tên, ban đầu chỉ theo hướng thẳng đứng hướng lên”.
Kết hợp với yêu cầu bài toán: “Khi mũi tên lần tiếp theo chỉ theo hướng thẳng đứng hướng lên thì đĩa sẽ tiếp xúc với mặt đồng hồ tại thời điểm mấy giờ”.
 Cần tìm thời điểm đĩa tiếp xúc với mặt đồng hồ khi quay hết 1 vòng.
Cần tìm thời điểm đĩa tiếp xúc với mặt đồng hồ khi quay hết 1 vòng.
Vì đây là chuyển động cong nên quãng đường đĩa đi được bằng khoảng cách di chuyển của tâm đĩa.
Quãng đường đĩa đi được khi quay xung quanh mặt đồng hồ và quay lại điểm xuất phát là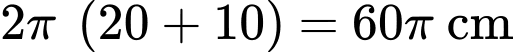 và cũng bằng số vòng quay
và cũng bằng số vòng quay  khoảng cách đi được của mỗi vòng quay =
khoảng cách đi được của mỗi vòng quay = 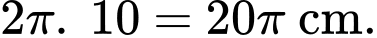
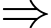 Số vòng quay để đĩa quay xung quanh mặt đồng hồ và quay lại điểm xuất phát là
Số vòng quay để đĩa quay xung quanh mặt đồng hồ và quay lại điểm xuất phát là 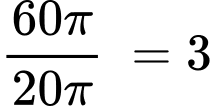 vòng.
vòng.
Vì đồng hồ có 12 giờ nên để đĩa quay hết 1 vòng xung quanh mặt đồng hồ thì đĩa sẽ tiếp xúc với mặt đồng hồ tại vị trí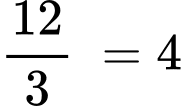 giờ.
giờ.
Dựa vào dữ kiện: “đĩa tiếp xúc ngoài với mặt đồng hồ tại vị trí 12 giờ. Trên đĩa có vẽ một mũi tên, ban đầu chỉ theo hướng thẳng đứng hướng lên”.
Kết hợp với yêu cầu bài toán: “Khi mũi tên lần tiếp theo chỉ theo hướng thẳng đứng hướng lên thì đĩa sẽ tiếp xúc với mặt đồng hồ tại thời điểm mấy giờ”.
 Cần tìm thời điểm đĩa tiếp xúc với mặt đồng hồ khi quay hết 1 vòng.
Cần tìm thời điểm đĩa tiếp xúc với mặt đồng hồ khi quay hết 1 vòng.
Vì đây là chuyển động cong nên quãng đường đĩa đi được bằng khoảng cách di chuyển của tâm đĩa.
Quãng đường đĩa đi được khi quay xung quanh mặt đồng hồ và quay lại điểm xuất phát là
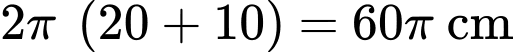 và cũng bằng số vòng quay
và cũng bằng số vòng quay  khoảng cách đi được của mỗi vòng quay =
khoảng cách đi được của mỗi vòng quay = 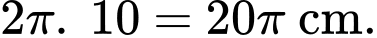
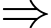 Số vòng quay để đĩa quay xung quanh mặt đồng hồ và quay lại điểm xuất phát là
Số vòng quay để đĩa quay xung quanh mặt đồng hồ và quay lại điểm xuất phát là 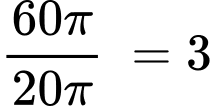 vòng.
vòng.
Vì đồng hồ có 12 giờ nên để đĩa quay hết 1 vòng xung quanh mặt đồng hồ thì đĩa sẽ tiếp xúc với mặt đồng hồ tại vị trí
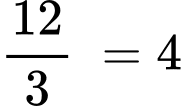 giờ.
giờ.
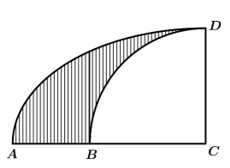
Câu 20 [698837]: Một vật trang trí có dạng khối tròn xoay được tạo thành khi quay miền  (Phần gạch sọc trong hình vẽ bên) quanh trục
(Phần gạch sọc trong hình vẽ bên) quanh trục 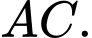 Biết rằng
Biết rằng 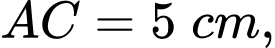
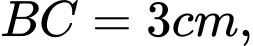 miền
miền  được giới hạn bởi đoạn thẳng
được giới hạn bởi đoạn thẳng  cung tròn
cung tròn 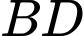 có tâm
có tâm 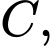 đường cong elip
đường cong elip 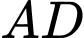 có trục
có trục 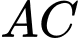 và
và 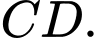 Thể tích của vật trang trí bằng bao nhiêu centimet khối (kết quả làm tròn đến hàng phần mười).
Thể tích của vật trang trí bằng bao nhiêu centimet khối (kết quả làm tròn đến hàng phần mười).
 (Phần gạch sọc trong hình vẽ bên) quanh trục
(Phần gạch sọc trong hình vẽ bên) quanh trục 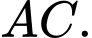 Biết rằng
Biết rằng 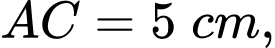
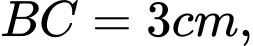 miền
miền  được giới hạn bởi đoạn thẳng
được giới hạn bởi đoạn thẳng  cung tròn
cung tròn 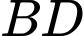 có tâm
có tâm 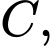 đường cong elip
đường cong elip 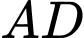 có trục
có trục 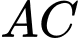 và
và 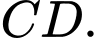 Thể tích của vật trang trí bằng bao nhiêu centimet khối (kết quả làm tròn đến hàng phần mười).
Thể tích của vật trang trí bằng bao nhiêu centimet khối (kết quả làm tròn đến hàng phần mười).
Điền đáp án: 37,7.
Gọi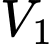 là thể tích khối tròn xoay khi ta quay
là thể tích khối tròn xoay khi ta quay 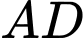 quanh trục
quanh trục 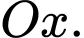
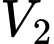 là thể tích khối tròn xoay khi ta quay
là thể tích khối tròn xoay khi ta quay 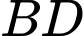 quanh trục
quanh trục 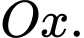
Khi đó, thể tích của khối là
là 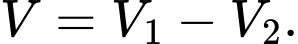
+) Tính thể tích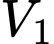
Cách 1: Dùng công thức thể tích khối elip:
Ta có công thức tính thể tích khối tròn xoay tạo thành khi quay hình elip là
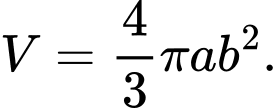
(trong đó,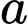 bằng một nửa độ dài trục lớn,
bằng một nửa độ dài trục lớn, 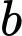 bằng một nửa độ dài trục nhỏ)
bằng một nửa độ dài trục nhỏ)
Khi đó, thể tích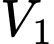 bằng 1/2 thể tích của khối tròn xoay tạo bởi hình elip.
bằng 1/2 thể tích của khối tròn xoay tạo bởi hình elip.
Vì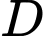 thuộc vào đường tròn
thuộc vào đường tròn  nên ta có
nên ta có 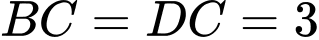

Suy ra thể tích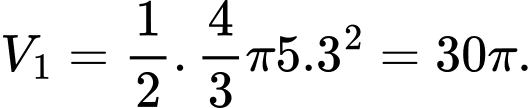
Cách 2: Viết phương trình elip và dùng tích phân tính thể tích như video thầy Tiến giảng.
+) Tính thể tích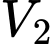
Ta có khi quay cung tròn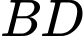 quanh trục
quanh trục  ta sẽ được 1/2 thể tích của khối cầu, do đó thể tích
ta sẽ được 1/2 thể tích của khối cầu, do đó thể tích 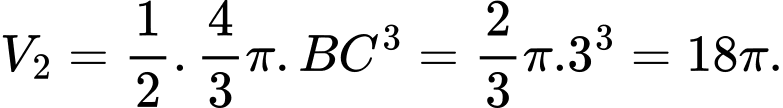
(công thức tính thể tích khối cầu là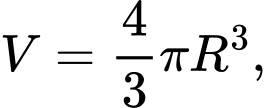 với
với 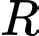 là bán kính của khối cầu)
là bán kính của khối cầu)
Vậy thể tích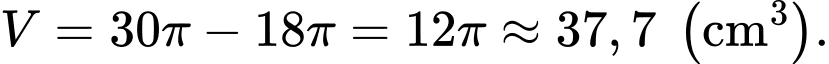
Gọi
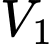 là thể tích khối tròn xoay khi ta quay
là thể tích khối tròn xoay khi ta quay 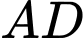 quanh trục
quanh trục 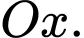
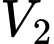 là thể tích khối tròn xoay khi ta quay
là thể tích khối tròn xoay khi ta quay 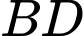 quanh trục
quanh trục 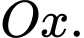
Khi đó, thể tích của khối
 là
là 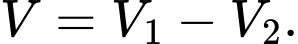
+) Tính thể tích
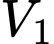
Cách 1: Dùng công thức thể tích khối elip:
Ta có công thức tính thể tích khối tròn xoay tạo thành khi quay hình elip là
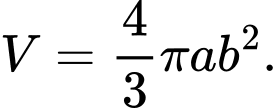
(trong đó,
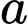 bằng một nửa độ dài trục lớn,
bằng một nửa độ dài trục lớn, 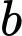 bằng một nửa độ dài trục nhỏ)
bằng một nửa độ dài trục nhỏ)Khi đó, thể tích
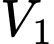 bằng 1/2 thể tích của khối tròn xoay tạo bởi hình elip.
bằng 1/2 thể tích của khối tròn xoay tạo bởi hình elip.Vì
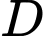 thuộc vào đường tròn
thuộc vào đường tròn  nên ta có
nên ta có 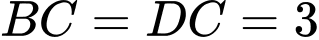

Suy ra thể tích
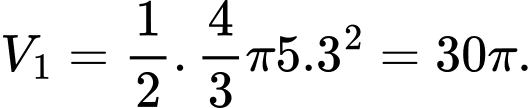
Cách 2: Viết phương trình elip và dùng tích phân tính thể tích như video thầy Tiến giảng.
+) Tính thể tích
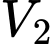
Ta có khi quay cung tròn
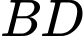 quanh trục
quanh trục  ta sẽ được 1/2 thể tích của khối cầu, do đó thể tích
ta sẽ được 1/2 thể tích của khối cầu, do đó thể tích 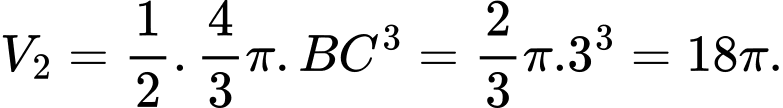
(công thức tính thể tích khối cầu là
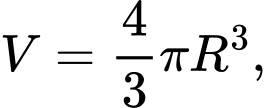 với
với 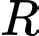 là bán kính của khối cầu)
là bán kính của khối cầu)Vậy thể tích
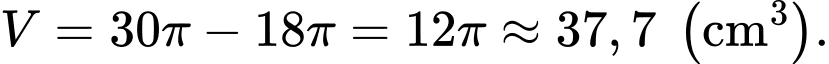
Câu 21 [694767]: Có hai hộp bóng bàn, các quả bóng bàn có kích thước và hình dạng như nhau. Hộp thứ nhất có 3 quả bóng bàn màu trắng và 2 quả bóng bàn màu vàng. Hộp thứ hai có 8 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Lần thứ nhất: Lấy ngẫu nhiên 4 quả bóng bàn ở hộp thứ nhất bỏ vào hộp thứ hai, lần thứ hai: lấy ngẫu nhiên 1 quả bóng bàn ở hộp thứ hai. Biết rằng lấy được quả bóng bàn màu vàng ở lần thứ hai, tính xác suất ở lần thứ nhất lấy được số quả bóng bàn màu trắng và màu vàng bằng nhau (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,63.
Trong lần lấy thứ nhất, vì hộp thứ nhất có 3 quả bóng bàn màu trắng và 2 quả bóng bàn màu vàng nên khi lấy ngẫu nhiên 4 quả bóng bàn ở hộp thứ nhất thì chỉ có 2 khả năng có thể xảy ra là :
+) Lấy được 1 quả bóng bàn màu vàng và 3 quả bóng bàn màu trắng;
+) Lấy được 2 quả bóng bàn màu vàng và 2 quả bóng bàn màu trắng.
Xét các biến cố:
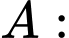 “Lấy được quả bóng bàn màu vàng từ hộp thứ hai”;
“Lấy được quả bóng bàn màu vàng từ hộp thứ hai”;
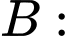 “Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 1 quả bóng bàn màu vàng”;
“Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 1 quả bóng bàn màu vàng”;
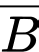 “Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 2 quả bóng bàn màu vàng”.
“Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 2 quả bóng bàn màu vàng”.
Ta có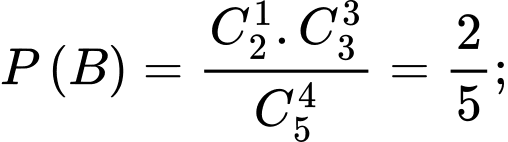
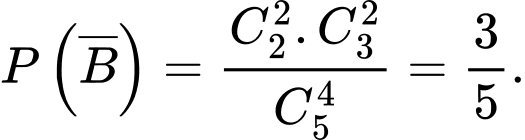
Và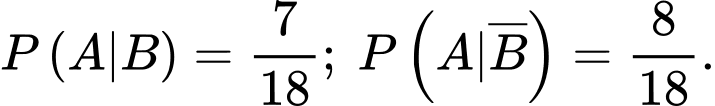
Ta có sơ đồ cây sau:
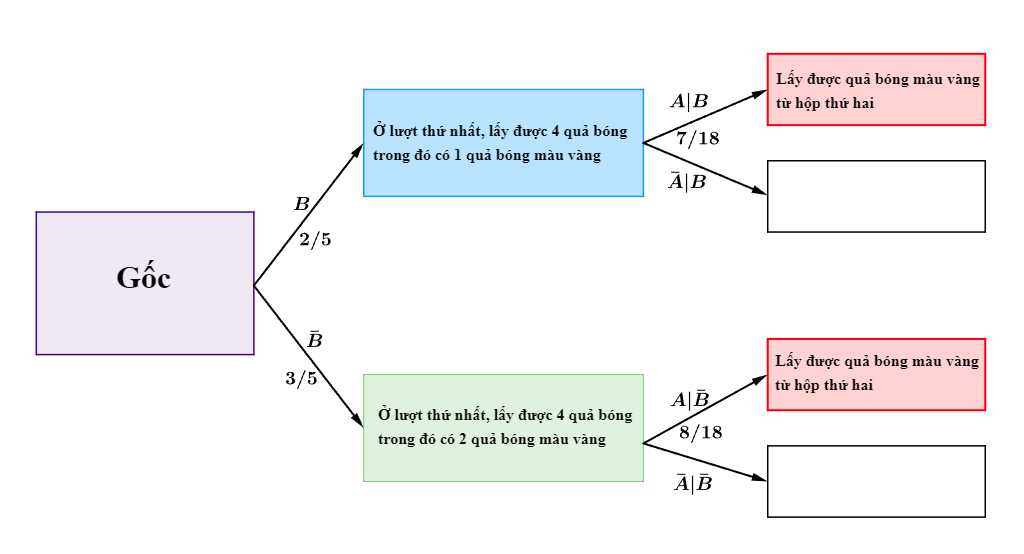
Áp dụng công thức xác suất toàn phần ta có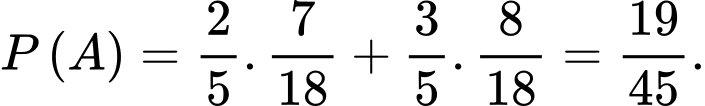
Áp dụng công thức Bayes, ta có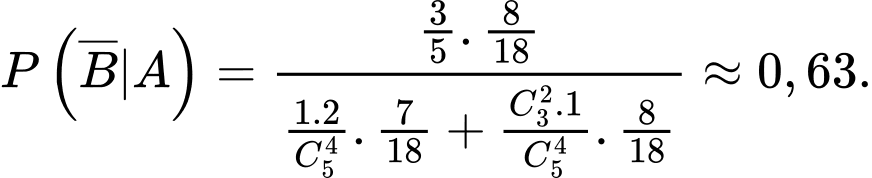
Trong lần lấy thứ nhất, vì hộp thứ nhất có 3 quả bóng bàn màu trắng và 2 quả bóng bàn màu vàng nên khi lấy ngẫu nhiên 4 quả bóng bàn ở hộp thứ nhất thì chỉ có 2 khả năng có thể xảy ra là :
+) Lấy được 1 quả bóng bàn màu vàng và 3 quả bóng bàn màu trắng;
+) Lấy được 2 quả bóng bàn màu vàng và 2 quả bóng bàn màu trắng.
Xét các biến cố:
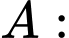 “Lấy được quả bóng bàn màu vàng từ hộp thứ hai”;
“Lấy được quả bóng bàn màu vàng từ hộp thứ hai”; “Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 1 quả bóng bàn màu vàng”;
“Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 1 quả bóng bàn màu vàng”; “Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 2 quả bóng bàn màu vàng”.
“Lấy được 4 quả bóng bàn ở hộp thứ nhất, trong đó có 2 quả bóng bàn màu vàng”.Ta có
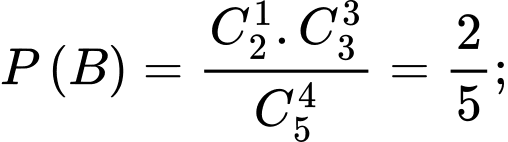
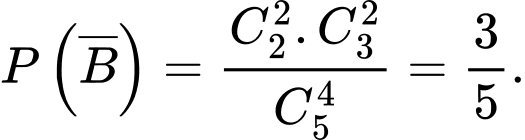
Và
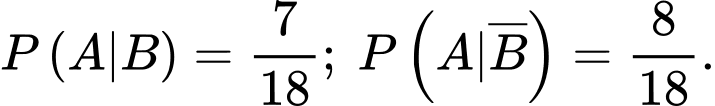
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần ta có
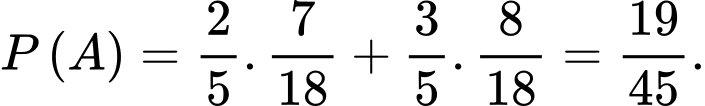
Áp dụng công thức Bayes, ta có
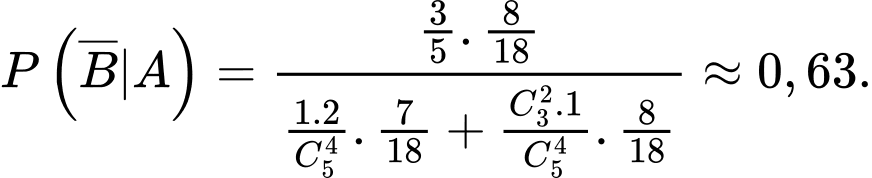
Câu 22 [695203]: Một vườn hoa có chiều dài 15 mét được xây dựng giữa 2 tòa nhà ở 2 hướng Đông và Tây. Biết rằng 2 tòa nhà cách nhau 150 mét và độ cao của tòa nhà hướng Đông là 105 mét, độ cao của tòa nhà hướng Tây là 60 mét. Người ta tìm địa điểm trồng hoa cách tòa nhà ở hướng Tây x (mét) để thời gian chiếu sáng vào vườn hoa là lớn nhất. Giá trị của x bằng bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị). Biết thời gian ánh sáng mặt trời chiếu vào vườn hoa đạt lớn nhất khi góc  lớn nhất (như hình vẽ).
lớn nhất (như hình vẽ).
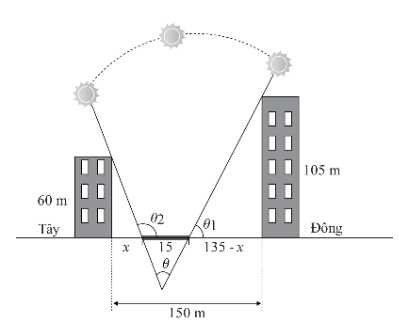
 lớn nhất (như hình vẽ).
lớn nhất (như hình vẽ). 
Điền đáp án: 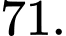
Ta có: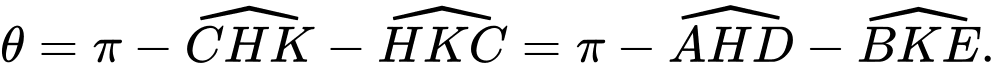
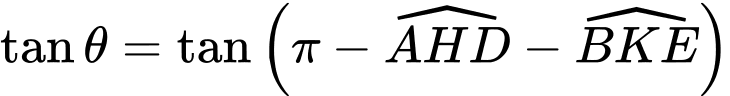


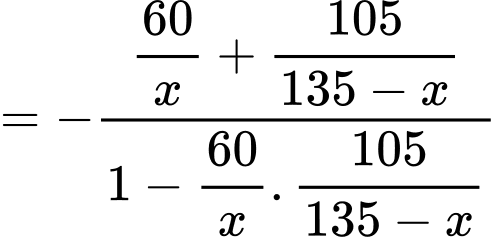
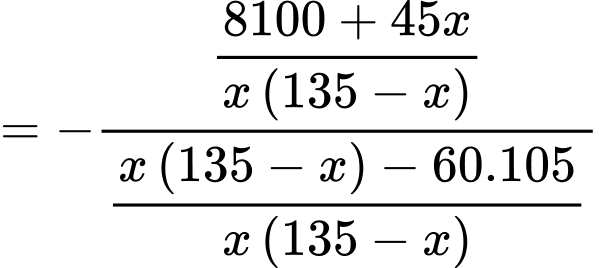
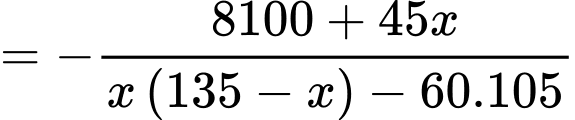
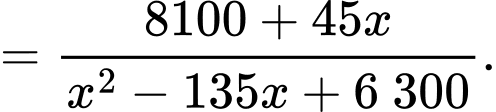
Xét hàm số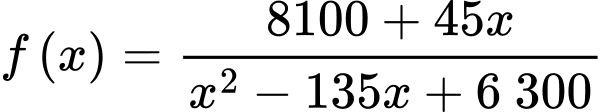 với
với 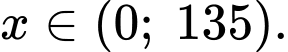
Ta có: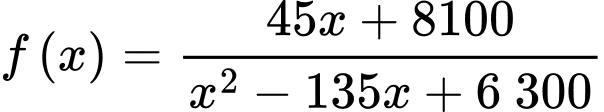
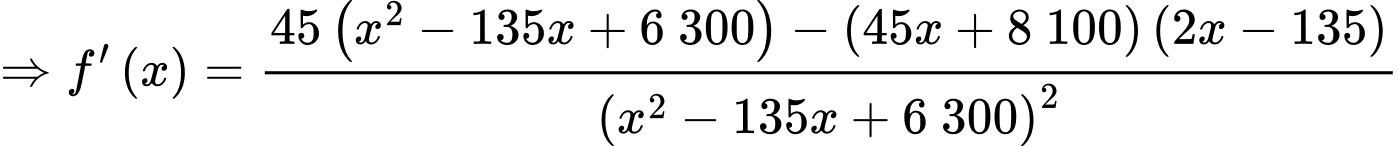
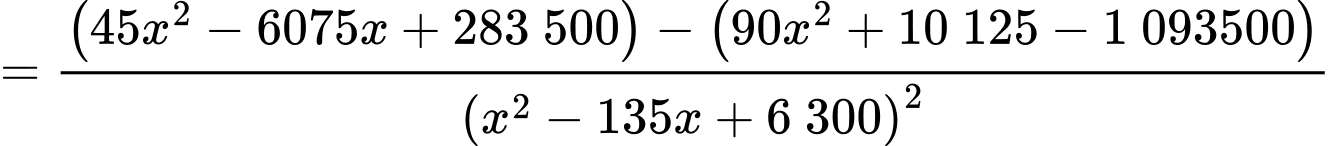
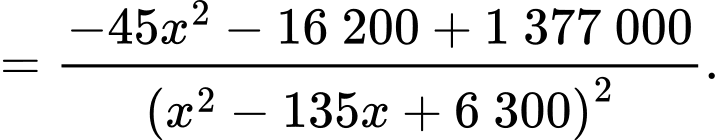
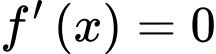
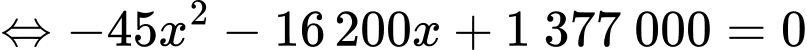
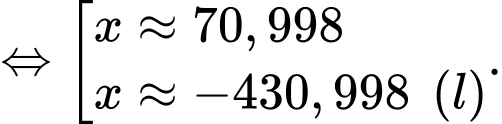
Bảng biến thiên:
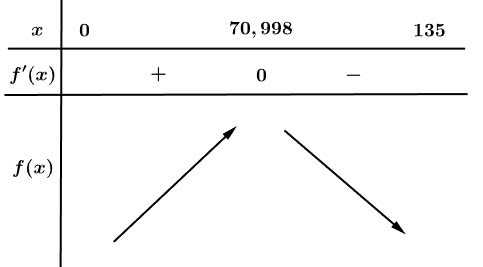
Vậy giá trị của là
là 
Ta có:
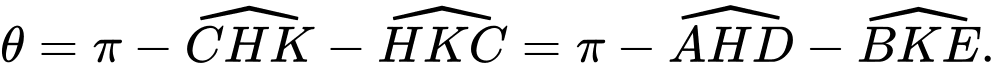
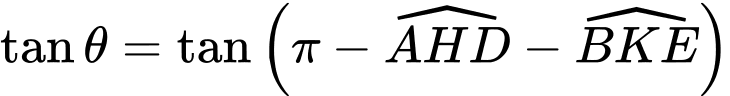


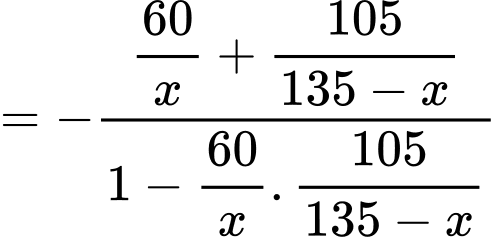
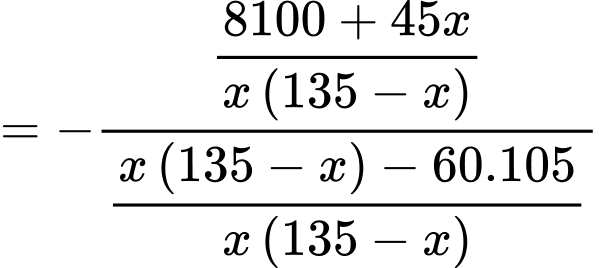
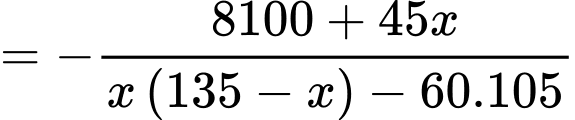
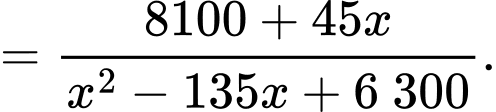
Xét hàm số
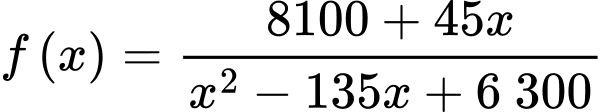 với
với 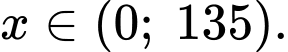
Ta có:
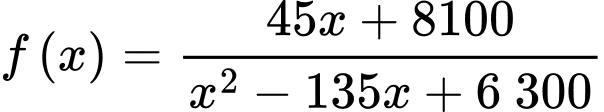
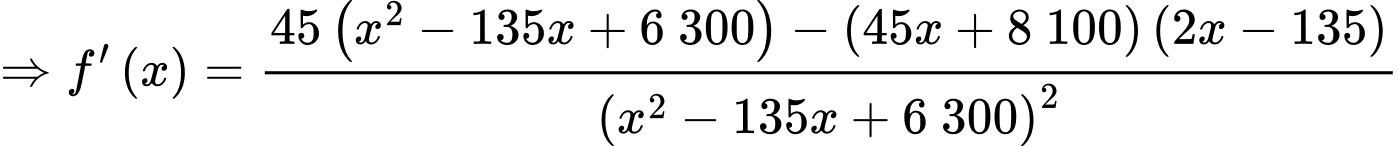
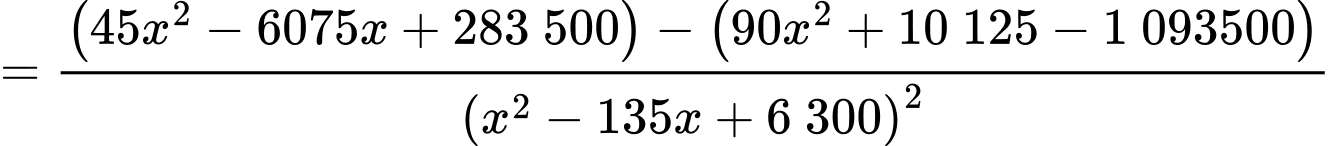
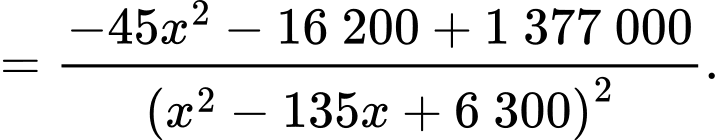
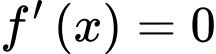
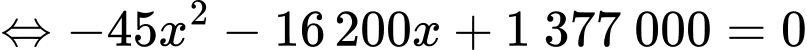
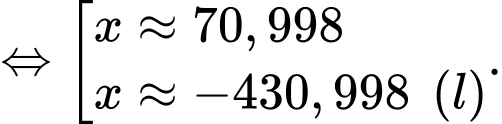
Bảng biến thiên:

Vậy giá trị của
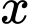 là
là