PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [695063]: Hàm số nào dưới đây đồng biến trên  ?
?
 ?
? A, 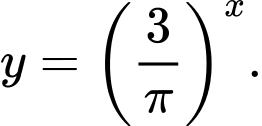
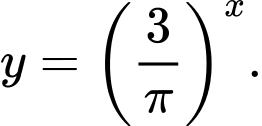
B, 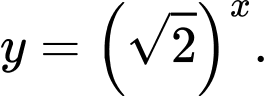
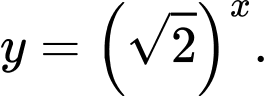
C, 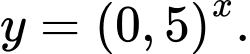
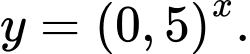
D, 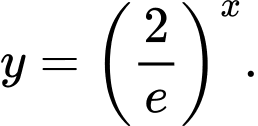
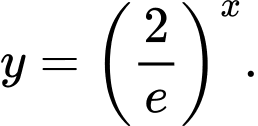
Chọn đáp án B.
Theo tính chất chiều biến thiên của hàm mũ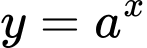 với:
với:
 : Hàm số luôn đồng biến;
: Hàm số luôn đồng biến;
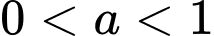 : hàm số luôn nghịch biến.
: hàm số luôn nghịch biến.
Nên ta có:
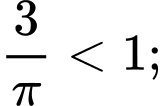
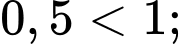
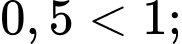
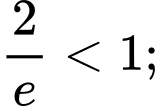
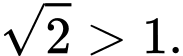
Vậy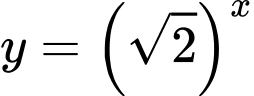 là hàm số đồng biến trên
là hàm số đồng biến trên 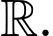 Đáp án: B
Đáp án: B
Theo tính chất chiều biến thiên của hàm mũ
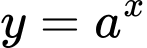 với:
với: : Hàm số luôn đồng biến;
: Hàm số luôn đồng biến;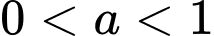 : hàm số luôn nghịch biến.
: hàm số luôn nghịch biến. Nên ta có:
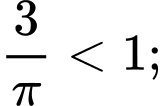
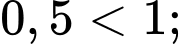
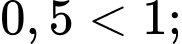
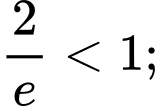
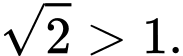
Vậy
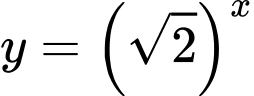 là hàm số đồng biến trên
là hàm số đồng biến trên 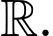 Đáp án: B
Đáp án: B
Câu 2 [695064]: Trong không gian 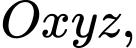 viết phương trình đường thẳng
viết phương trình đường thẳng  đi qua điểm
đi qua điểm 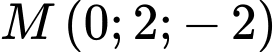 và song song với đường thẳng
và song song với đường thẳng 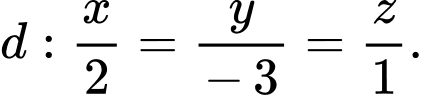
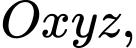 viết phương trình đường thẳng
viết phương trình đường thẳng  đi qua điểm
đi qua điểm 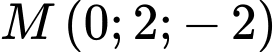 và song song với đường thẳng
và song song với đường thẳng 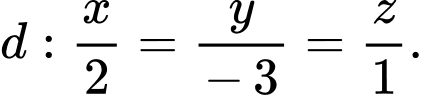
A, 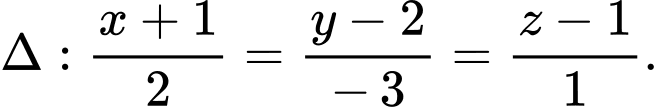
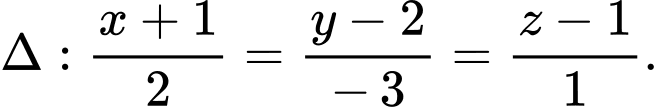
B, 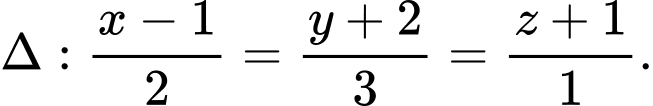
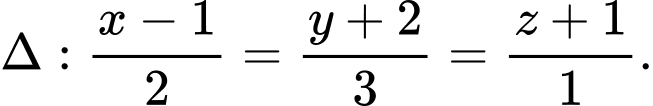
C, 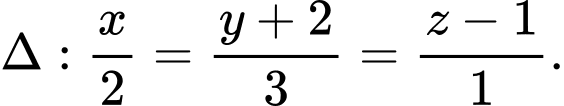
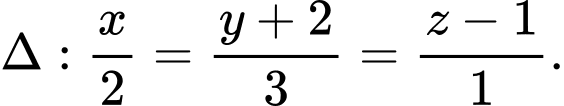
D, 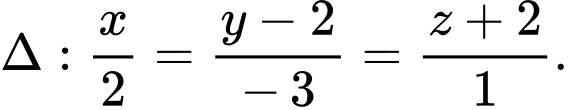
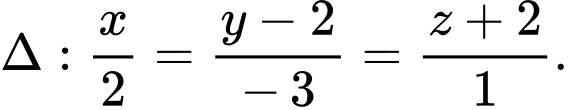
Chọn đáp án D.
Ta có: đường thẳng song song với đường thẳng
song song với đường thẳng 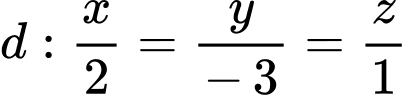
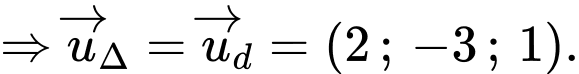
Đường thẳng đi qua điểm
đi qua điểm 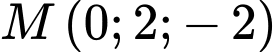 và có vtcp là
và có vtcp là 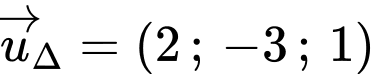 ta có phương trình tham số:
ta có phương trình tham số:
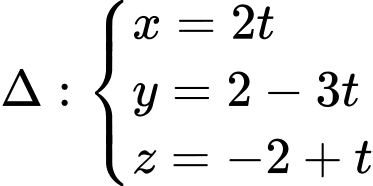
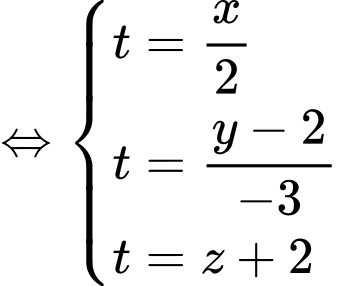
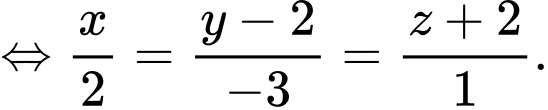 Đáp án: D
Đáp án: D
Ta có: đường thẳng
 song song với đường thẳng
song song với đường thẳng 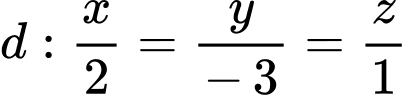
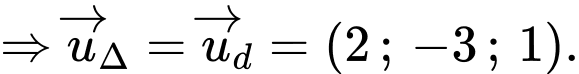
Đường thẳng
 đi qua điểm
đi qua điểm 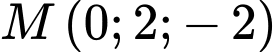 và có vtcp là
và có vtcp là 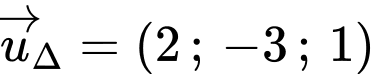 ta có phương trình tham số:
ta có phương trình tham số: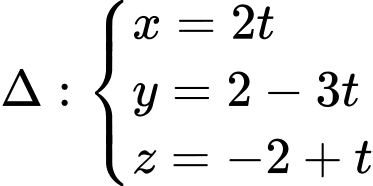
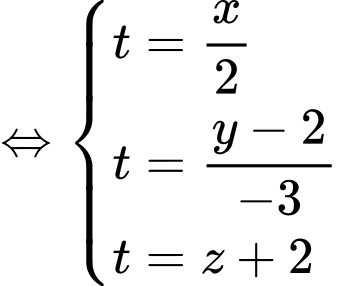
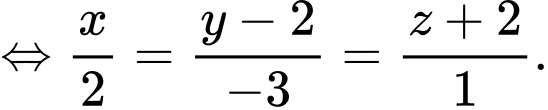 Đáp án: D
Đáp án: D
Câu 3 [687336]: Cho hàm số 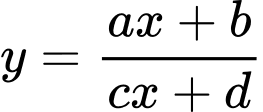 có đồ thị là đường cong như hình sau:
có đồ thị là đường cong như hình sau:
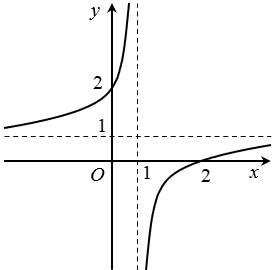
Toạ độ giao điểm của đồ thị hàm số với trục hoành là
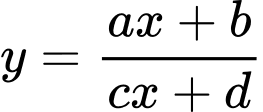 có đồ thị là đường cong như hình sau:
có đồ thị là đường cong như hình sau: 
Toạ độ giao điểm của đồ thị hàm số với trục hoành là
A, 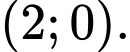
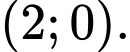
B, 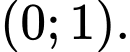
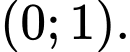
C, 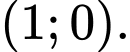
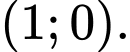
D, 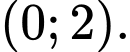
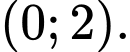
Chọn đáp án A.
Từ đồ thị hình vẽ ta thấy toạ độ giao điểm của đồ thị hàm số với trục hoành là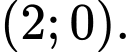 Đáp án: A
Đáp án: A
Từ đồ thị hình vẽ ta thấy toạ độ giao điểm của đồ thị hàm số với trục hoành là
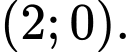 Đáp án: A
Đáp án: A
Câu 4 [256185]: Tìm công bội 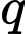 của cấp số nhân
của cấp số nhân 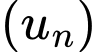 biết
biết 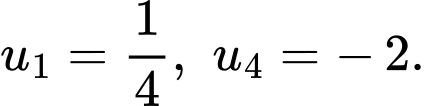
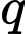 của cấp số nhân
của cấp số nhân 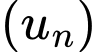 biết
biết 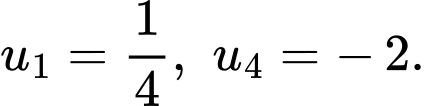
A, 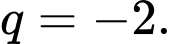
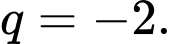
B, 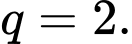
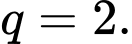
C, 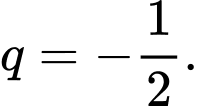
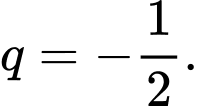
D, 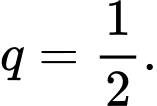
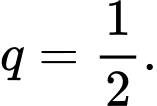
Chọn đáp án A.
Cấp số nhân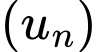 biết
biết 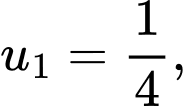
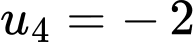
Nên ta có: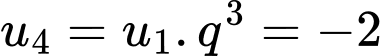
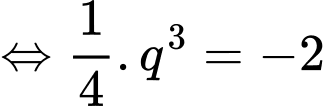
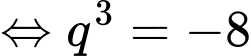
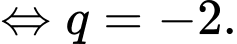 Đáp án: A
Đáp án: A
Cấp số nhân
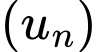 biết
biết 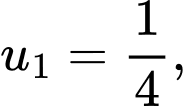
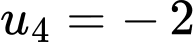
Nên ta có:
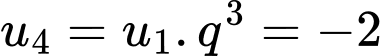
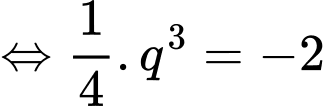
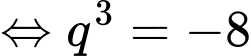
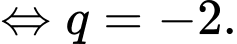 Đáp án: A
Đáp án: A
Câu 5 [695065]: Khẳng định nào dưới đây đúng?
A, 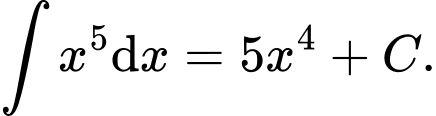
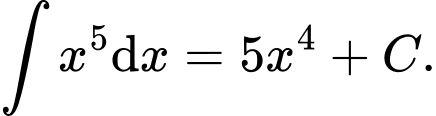
B, 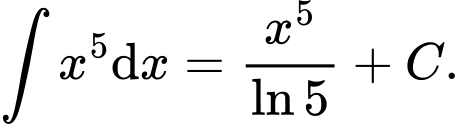
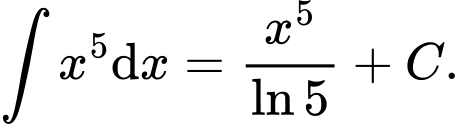
C, 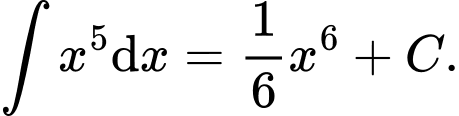
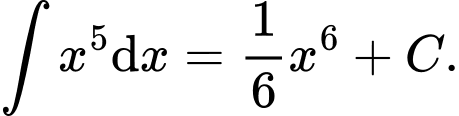
D, 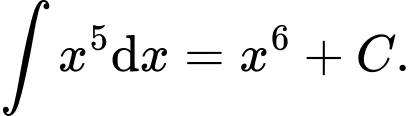
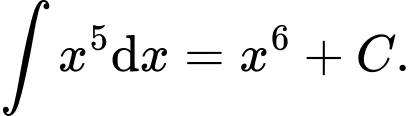
Chọn đáp án C.
Ta có: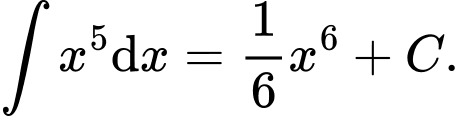 Đáp án: C
Đáp án: C
Ta có:
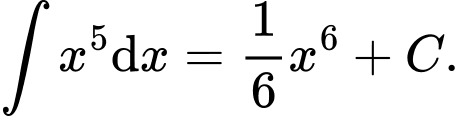 Đáp án: C
Đáp án: C
Câu 6 [256197]: Cho hình lập phương 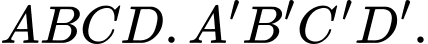 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng  và
và 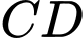 bằng
bằng
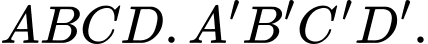 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng  và
và 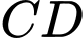 bằng
bằng A, 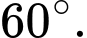
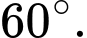
B, 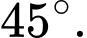
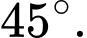
C, 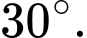
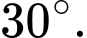
D, 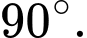
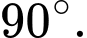
Chọn đáp án B.
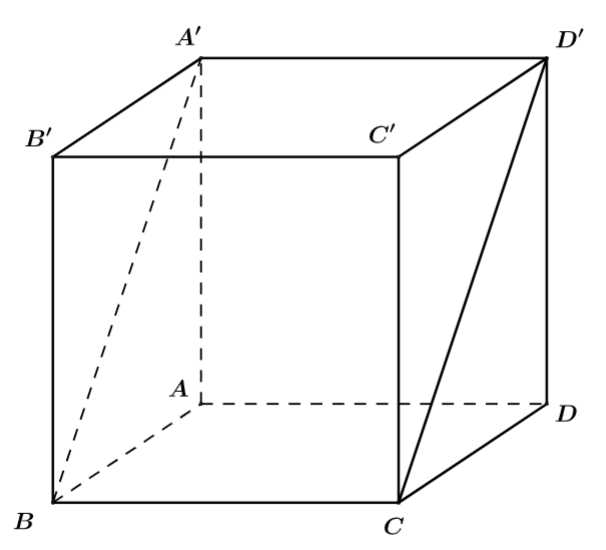
Dựa vào hình vẽ ta có góc giữa hai đường thẳng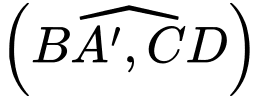
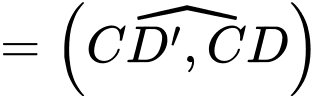
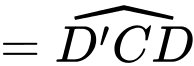
Xét tam giác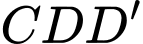 vuông tại
vuông tại 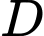 và
và 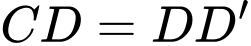
 vuông cân tại
vuông cân tại 
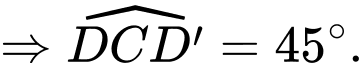
Vậy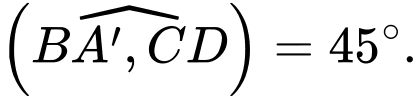 Đáp án: B
Đáp án: B

Dựa vào hình vẽ ta có góc giữa hai đường thẳng
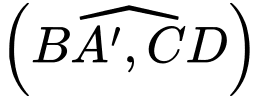
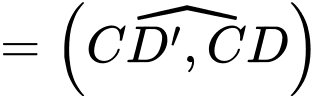
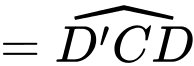
Xét tam giác
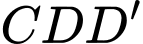 vuông tại
vuông tại 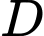 và
và 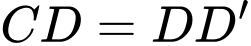
 vuông cân tại
vuông cân tại 
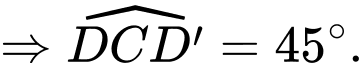
Vậy
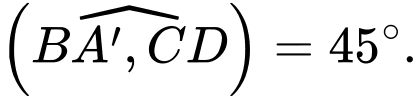 Đáp án: B
Đáp án: B
Câu 7 [695066]: Số nghiệm nguyên của bất phương trình  là
là
 là
là A, 
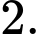
B, 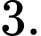
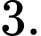
C, 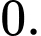
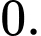
D, 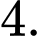
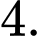
Chọn đáp án B.

ĐKXĐ: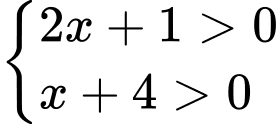
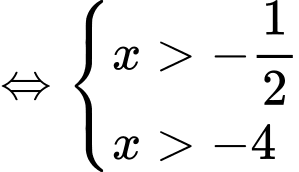
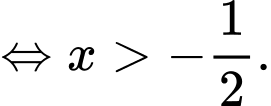

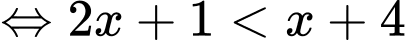
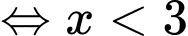
Kết hợp điều kiện ta có tập nghiệm của bất phương trình là: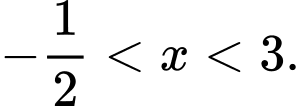
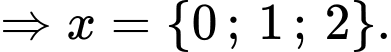 > Đáp án: B
> Đáp án: B

ĐKXĐ:
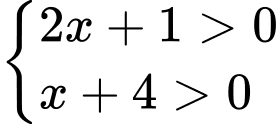
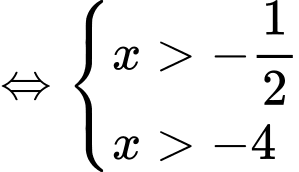
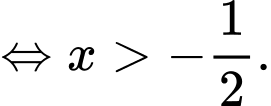

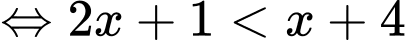
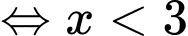
Kết hợp điều kiện ta có tập nghiệm của bất phương trình là:
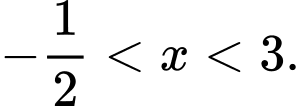
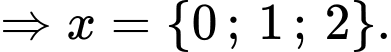 > Đáp án: B
> Đáp án: B
Câu 8 [687337]: Cho hàm số 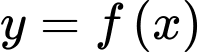 xác định trên
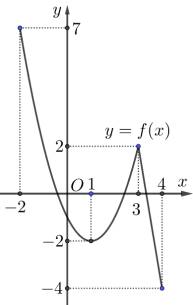
xác định trên 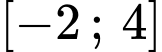 có đồ thị như hình vẽ bên. Giá trị lớn nhất hàm số
có đồ thị như hình vẽ bên. Giá trị lớn nhất hàm số 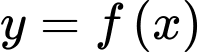 trên đoạn
trên đoạn 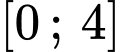 là
là
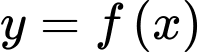 xác định trên
xác định trên 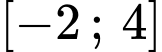 có đồ thị như hình vẽ bên. Giá trị lớn nhất hàm số
có đồ thị như hình vẽ bên. Giá trị lớn nhất hàm số 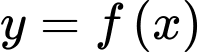 trên đoạn
trên đoạn 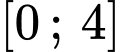 là
là
A, 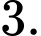
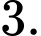
B, 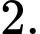
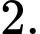
C, 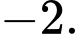
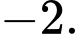
D, 
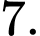
Chọn đáp án B.
Từ đồ thị như hình vẽ trên ta có: Giá trị lớn nhất của hàm số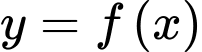 trên đoạn
trên đoạn 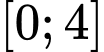 là
là  Đáp án: B
Đáp án: B
Từ đồ thị như hình vẽ trên ta có: Giá trị lớn nhất của hàm số
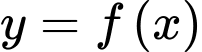 trên đoạn
trên đoạn 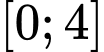 là
là  Đáp án: B
Đáp án: B
Câu 9 [698918]: Cho hàm số 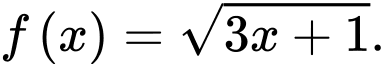 Tính
Tính 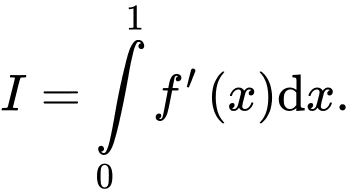
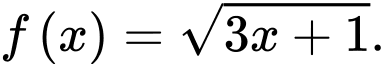 Tính
Tính 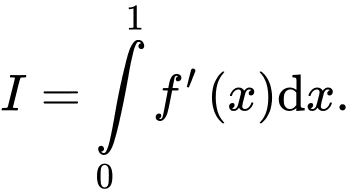
A, 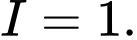
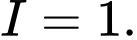
B, 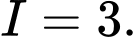
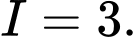
C, 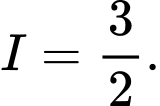
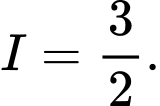
D, 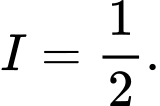
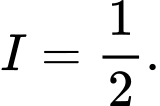
Chọn đáp án A.
Ta có: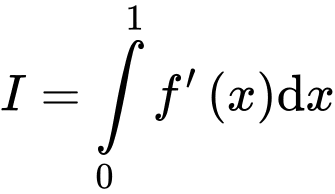
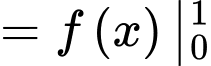
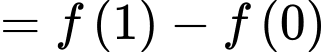
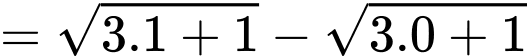
 Đáp án: A
Đáp án: A
Ta có:
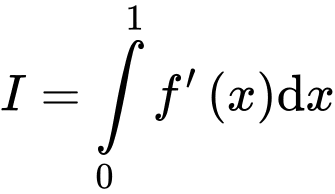
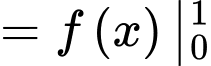
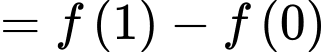
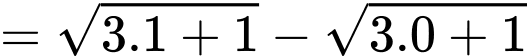
 Đáp án: A
Đáp án: A
Câu 10 [349054]: Trong không gian 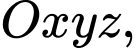 cho hai điểm
cho hai điểm 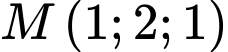 và
và 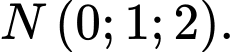 Tìm điểm
Tìm điểm 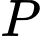 thuộc mặt phẳng
thuộc mặt phẳng 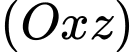 sao cho ba điểm
sao cho ba điểm 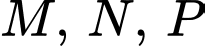 thẳng hàng.
thẳng hàng.
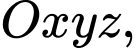 cho hai điểm
cho hai điểm 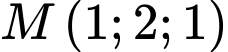 và
và 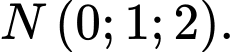 Tìm điểm
Tìm điểm 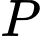 thuộc mặt phẳng
thuộc mặt phẳng 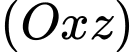 sao cho ba điểm
sao cho ba điểm 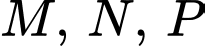 thẳng hàng.
thẳng hàng. A, 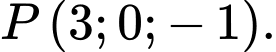
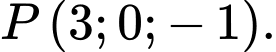
B, 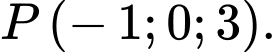
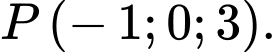
C, 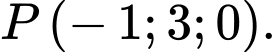
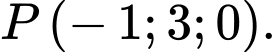
D, 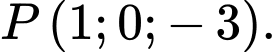
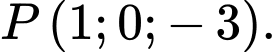
Chọn đáp án B.
Theo bài ra ta có, điểm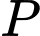 thuộc mặt phẳng
thuộc mặt phẳng 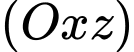 nên ta có tọa độ điểm
nên ta có tọa độ điểm 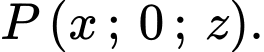
Ta có: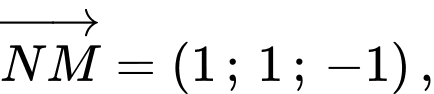
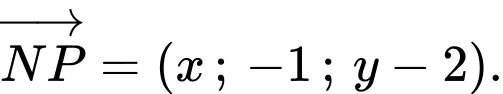
Do ba điểm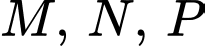 thẳng hàng.
thẳng hàng.
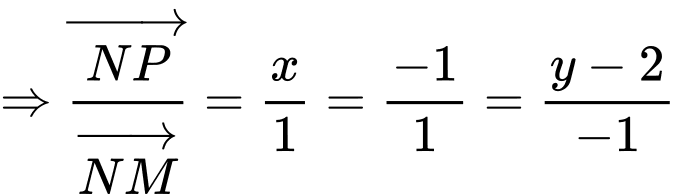
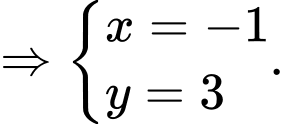
Suy ra tọa độ điểm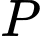 là
là 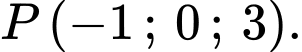 Đáp án: B
Đáp án: B
Theo bài ra ta có, điểm
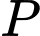 thuộc mặt phẳng
thuộc mặt phẳng 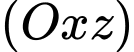 nên ta có tọa độ điểm
nên ta có tọa độ điểm 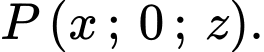
Ta có:
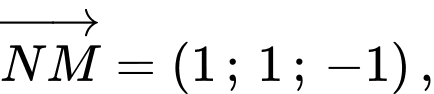
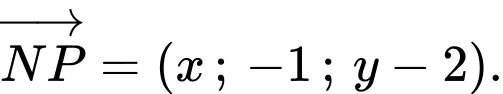
Do ba điểm
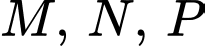 thẳng hàng.
thẳng hàng.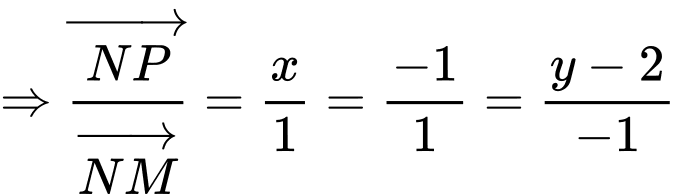
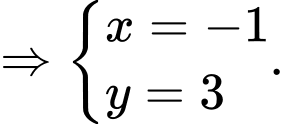
Suy ra tọa độ điểm
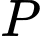 là
là 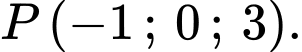 Đáp án: B
Đáp án: B
Câu 11 [687484]: Thống kê điểm trung bình môn Toán của một số học sinh lớp 12 được mẫu số liệu như sau

Phương sai của mẫu số liệu về điểm trung bình môn Toán của các học sinh đó là

Phương sai của mẫu số liệu về điểm trung bình môn Toán của các học sinh đó là
A, 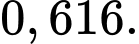
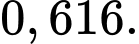
B, 

C, 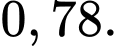
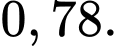
D, 
Chọn đáp án D.
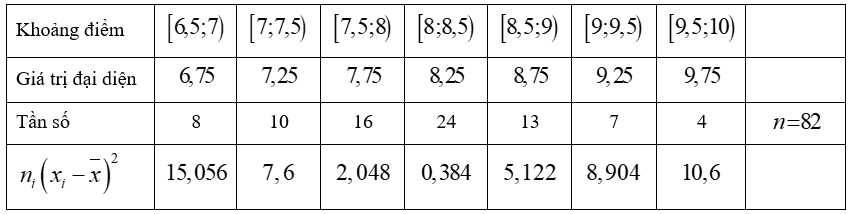
Cỡ mẫu là
Số trung bình của mẫu số liệu ghép nhóm là:
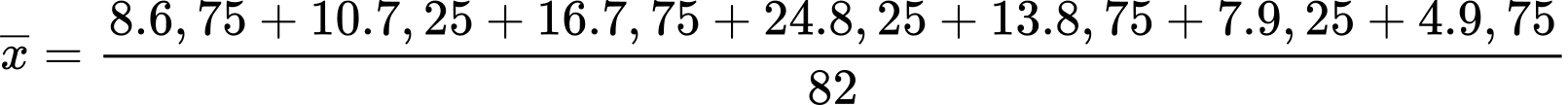
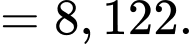
Phương sai của mẫu số liệu về điểm trung bình môn Toán của các học sinh đó là:
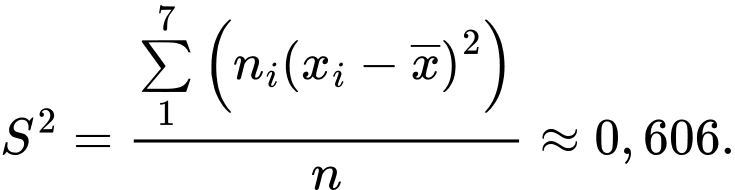 Đáp án: D
Đáp án: D

Cỡ mẫu là

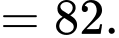
Số trung bình của mẫu số liệu ghép nhóm là:
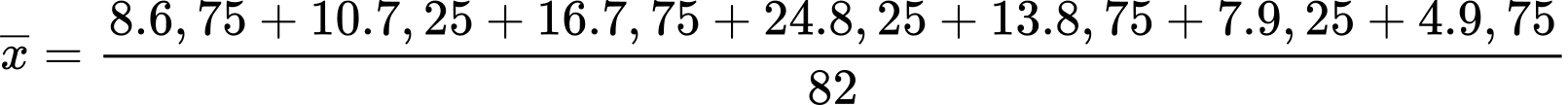
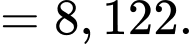
Phương sai của mẫu số liệu về điểm trung bình môn Toán của các học sinh đó là:
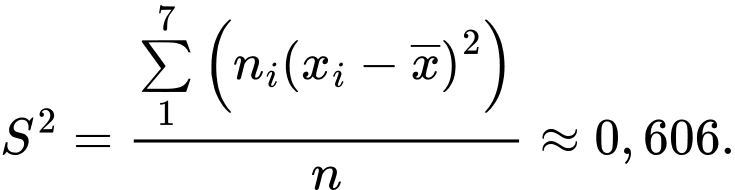 Đáp án: D
Đáp án: D
Câu 12 [687485]: Cho tứ diện 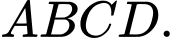 Gọi
Gọi 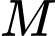 và
và 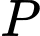 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh  và
và 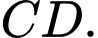 Đặt
Đặt 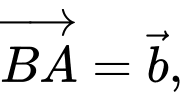
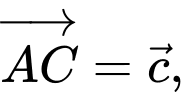
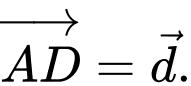 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng?
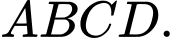 Gọi
Gọi 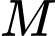 và
và 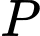 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh  và
và 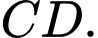 Đặt
Đặt 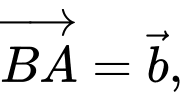
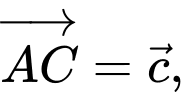
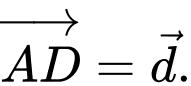 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng? A, 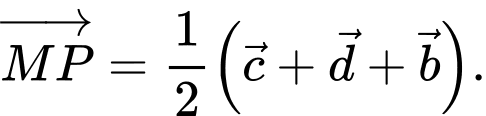
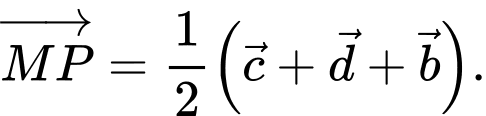
B, 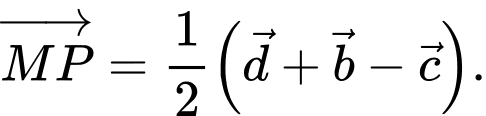
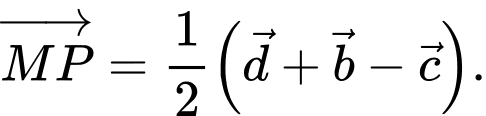
C, 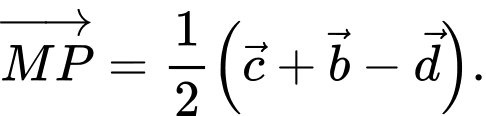
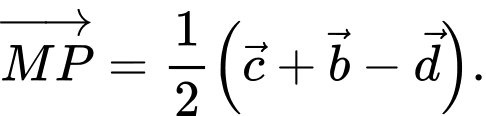
D, 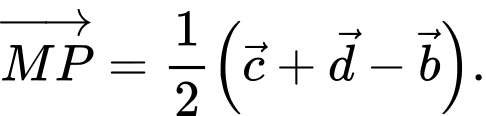
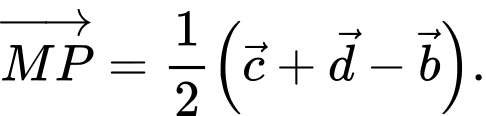
Chọn đáp án A.
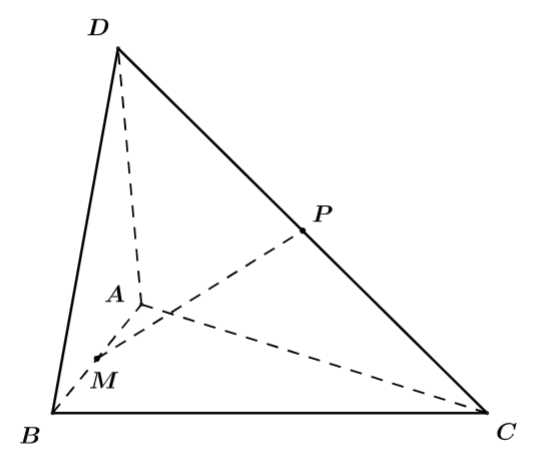
Ta có: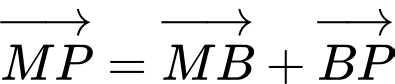
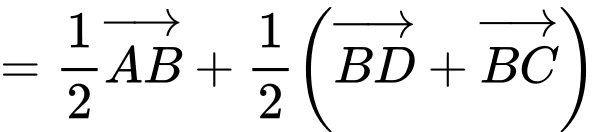
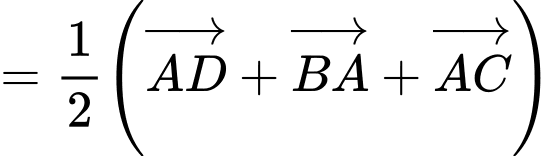
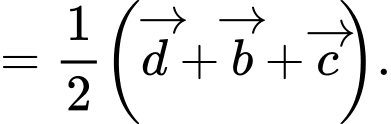 Đáp án: A
Đáp án: A

Ta có:
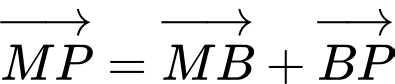
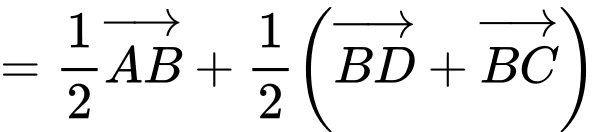
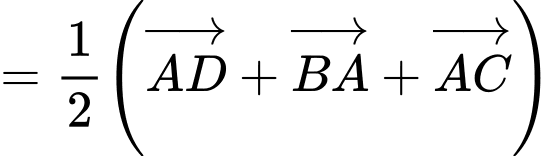
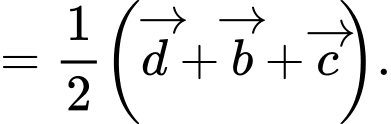 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [698919]: Trong không gian với hệ tọa độ 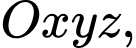 gọi
gọi 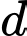 là giao tuyến của mặt phẳng
là giao tuyến của mặt phẳng 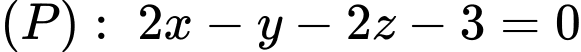 và mặt phẳng
và mặt phẳng 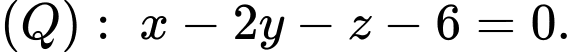
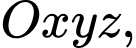 gọi
gọi 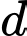 là giao tuyến của mặt phẳng
là giao tuyến của mặt phẳng 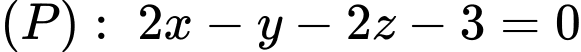 và mặt phẳng
và mặt phẳng 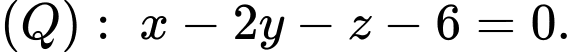
a) Sai.
Một vectơ pháp tuyến của mặt phẳng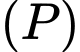 là
là 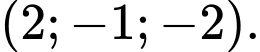
b) Đúng.
Vì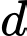 là giao tuyến của 2 mặt phẳng
là giao tuyến của 2 mặt phẳng 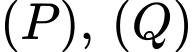 nên đường thẳng
nên đường thẳng 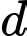 có 2 vectơ pháp tuyến là
có 2 vectơ pháp tuyến là 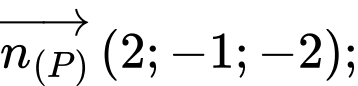
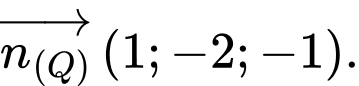
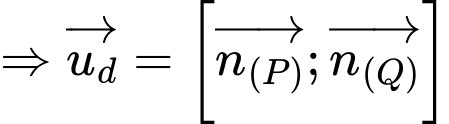
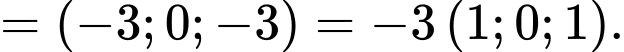
Suy ra đường thẳng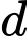 có 1 vectơ chỉ phương là
có 1 vectơ chỉ phương là 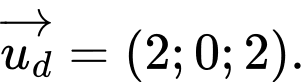
c) Đúng.
Nếu
Cho ta xét hệ phương trình
ta xét hệ phương trình 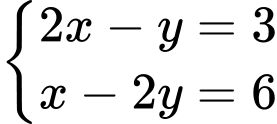
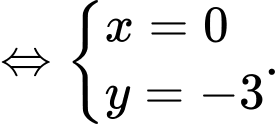
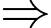 Điểm
Điểm 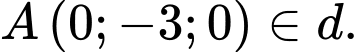
d) Đúng.
Đường thẳng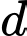 đi qua điểm
đi qua điểm 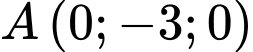 và có vectơ chỉ phương
và có vectơ chỉ phương 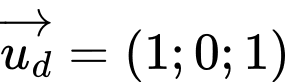 có phương trình là
có phương trình là 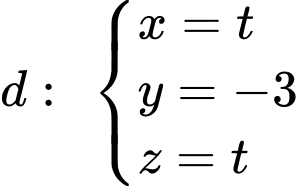
Khi đó, đường thẳng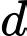 đi qua điểm
đi qua điểm 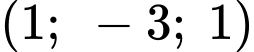 và có vectơ chỉ phương
và có vectơ chỉ phương 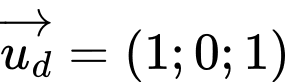 nên ta có
nên ta có 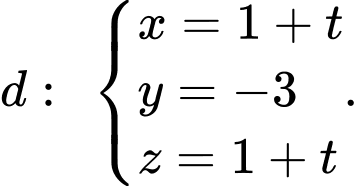
Một vectơ pháp tuyến của mặt phẳng
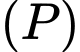 là
là 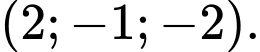
b) Đúng.
Vì
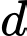 là giao tuyến của 2 mặt phẳng
là giao tuyến của 2 mặt phẳng 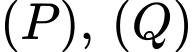 nên đường thẳng
nên đường thẳng 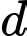 có 2 vectơ pháp tuyến là
có 2 vectơ pháp tuyến là 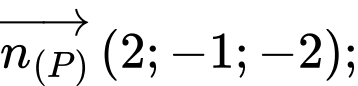
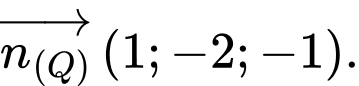
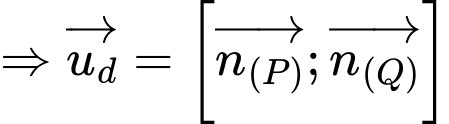
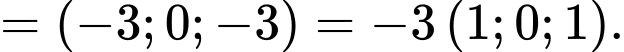
Suy ra đường thẳng
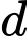 có 1 vectơ chỉ phương là
có 1 vectơ chỉ phương là 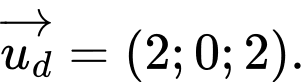
c) Đúng.
Nếu

Cho
 ta xét hệ phương trình
ta xét hệ phương trình 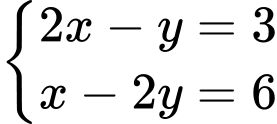
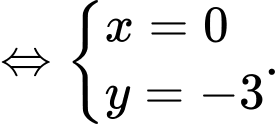
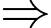 Điểm
Điểm 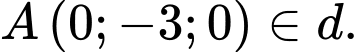
d) Đúng.
Đường thẳng
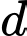 đi qua điểm
đi qua điểm 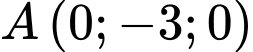 và có vectơ chỉ phương
và có vectơ chỉ phương 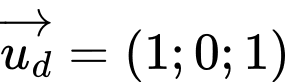 có phương trình là
có phương trình là 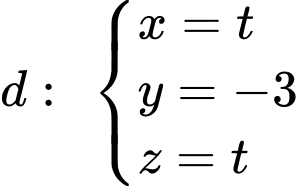
Khi đó, đường thẳng
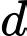 đi qua điểm
đi qua điểm 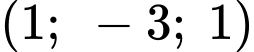 và có vectơ chỉ phương
và có vectơ chỉ phương 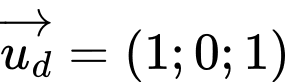 nên ta có
nên ta có 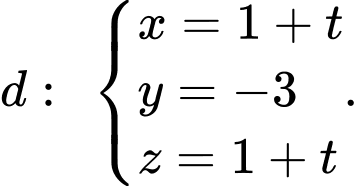
Câu 14 [700890]: Một viên muối hình cầu có đường kính 8cm đang tan trong nước với tốc độ giảm thể tích tại bất kỳ thời điểm nào tỷ lệ thuận với diện tích bề mặt quả cầu tại thời điểm đó. Sau 30 giây thì viên muối tan được một nửa. Gọi 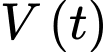 và
và 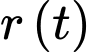 lần là thể tích và bán kính của viên muối sau
lần là thể tích và bán kính của viên muối sau 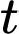 phút
phút
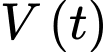 và
và 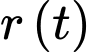 lần là thể tích và bán kính của viên muối sau
lần là thể tích và bán kính của viên muối sau 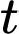 phút
phút
a) Đúng.
Thể tích của viên muối sau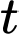 phút là
phút là 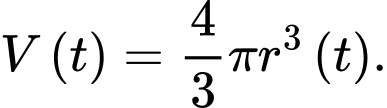
b) Đúng.
Ta có:
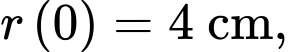
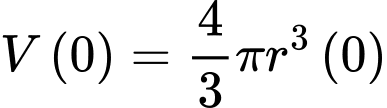
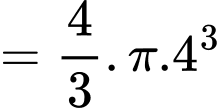
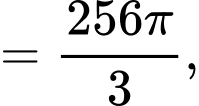
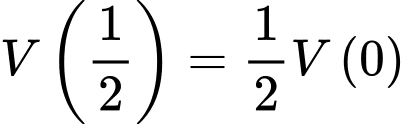
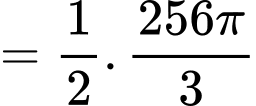
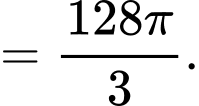
Diện tích quả cầu tại thời điểm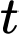 phút là
phút là
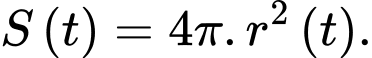
Khi đó: Tốc độ giảm thể tích tại thời điểm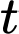 phút là
phút là
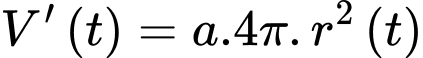
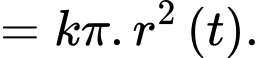
c) Sai.
Ta có: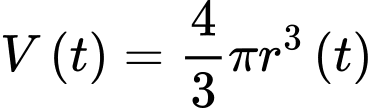
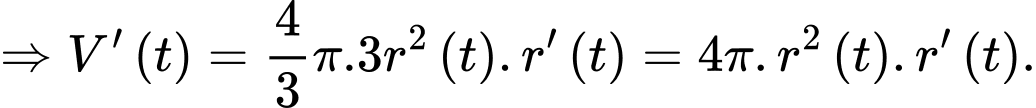
Theo câu b) ta có: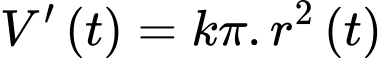
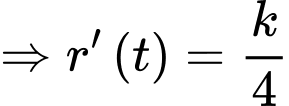
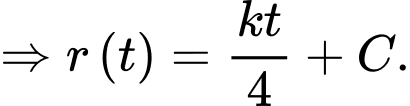
Mặt khác,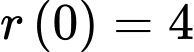
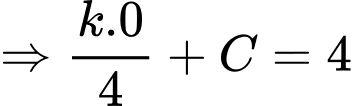
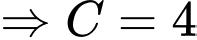
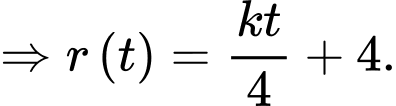
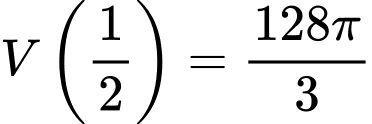
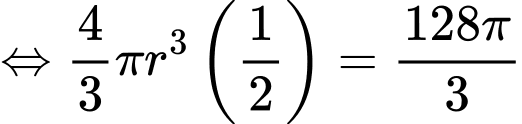
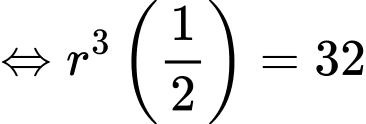
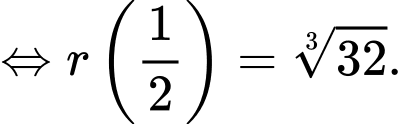
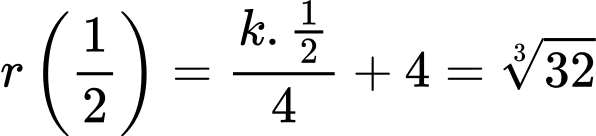
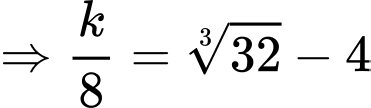
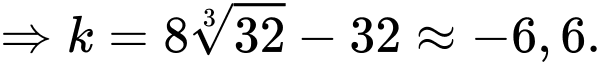
d) Sai.
Ta có:
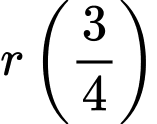
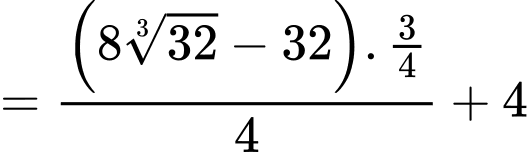
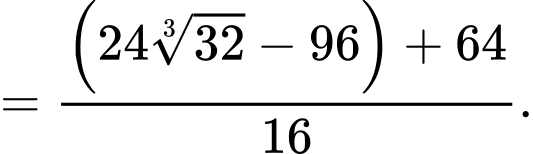
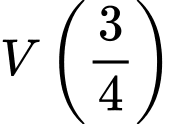
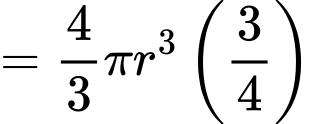
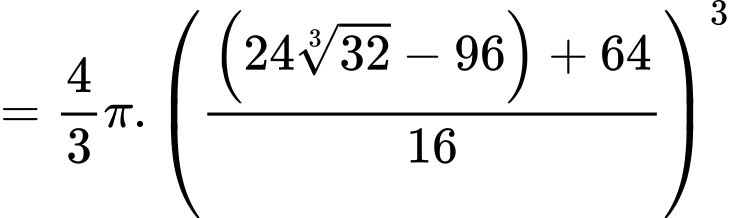
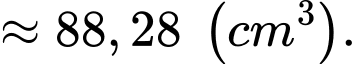
Thể tích của viên muối sau
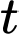 phút là
phút là 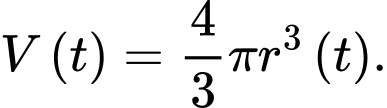
b) Đúng.
Ta có:
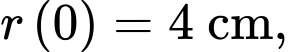
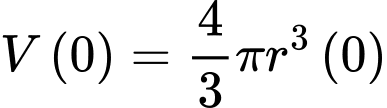
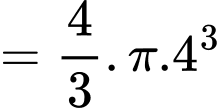
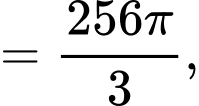
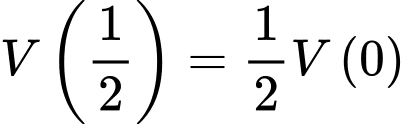
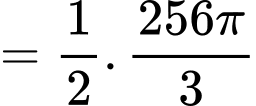
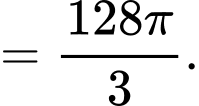
Diện tích quả cầu tại thời điểm
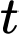 phút là
phút là 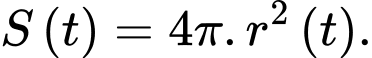
Khi đó: Tốc độ giảm thể tích tại thời điểm
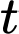 phút là
phút là 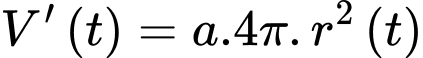
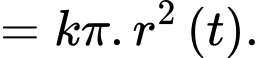
c) Sai.
Ta có:
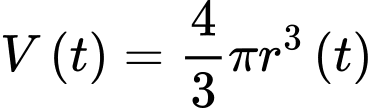
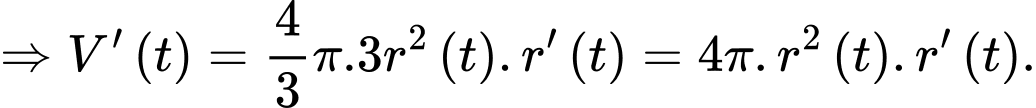
Theo câu b) ta có:
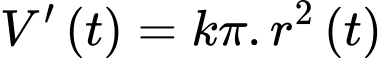
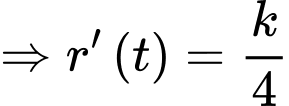
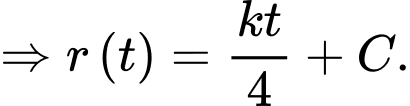
Mặt khác,
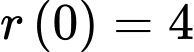
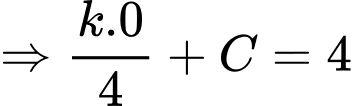
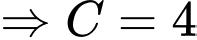
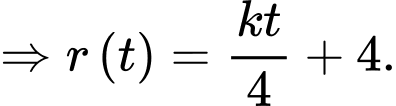
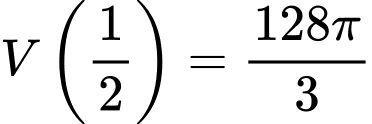
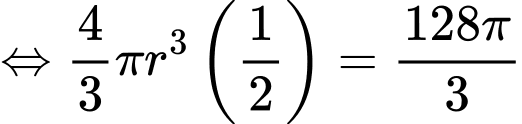
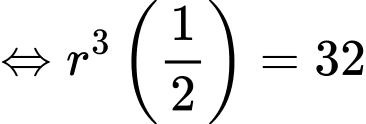
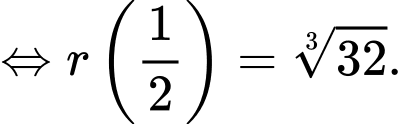
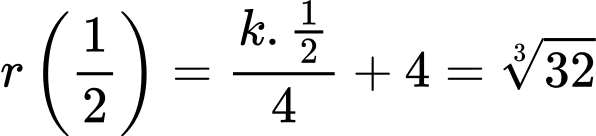
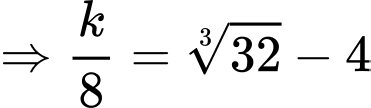
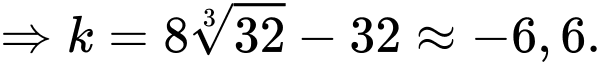
d) Sai.
Ta có:
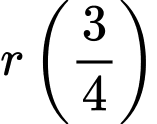
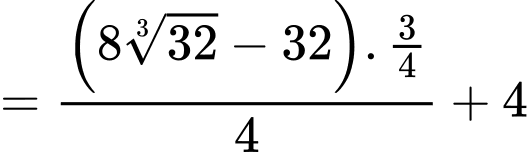
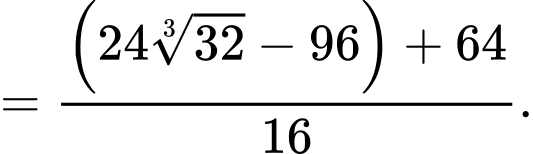
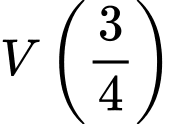
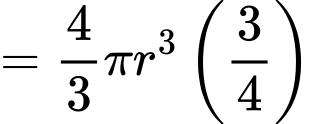
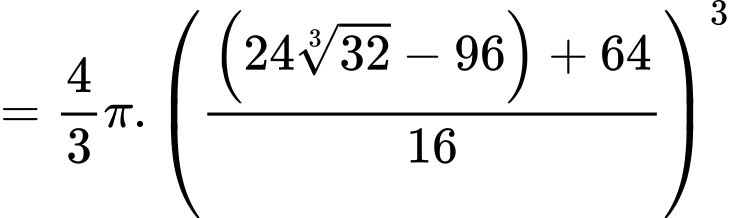
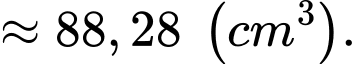
Câu 15 [695069]: Một công ty đấu thầu hai dự án. Khả năng thắng thầu các dự án lần lượt là 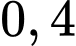 và
và 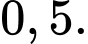 Khả năng thắng thầu cả hai dự án là
Khả năng thắng thầu cả hai dự án là 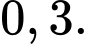 Gọi
Gọi 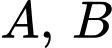 lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
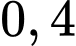 và
và 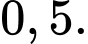 Khả năng thắng thầu cả hai dự án là
Khả năng thắng thầu cả hai dự án là 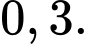 Gọi
Gọi 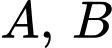 lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) Sai.
Nhắc lại kiến thức: Hai biến cố A, B độc lập khi và chỉ khi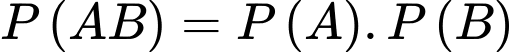
Ta có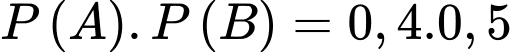
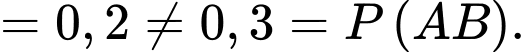
b) Đúng.
Xác suất để công ty thắng thầu dự án 2 khi đã biết thắng dự án 1 là
Ta có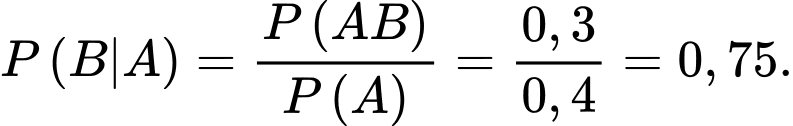
c) Sai.
Xác suất để công ty thắng thầu dự án 2 khi đã biết điều kiện không thắng dự án 1 là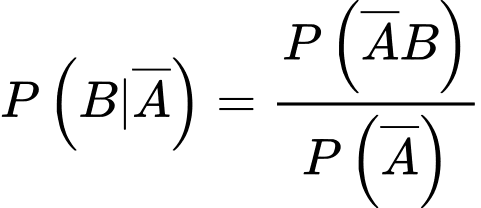
Vì hai biến cố và
và  xung khắc nhau và
xung khắc nhau và  nên theo tính chất của xác suất ta có
nên theo tính chất của xác suất ta có 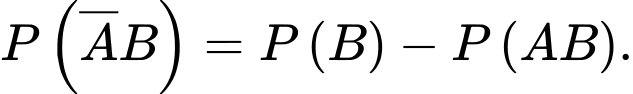
Suy ra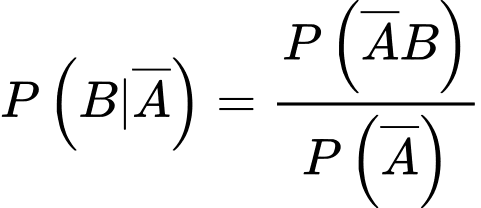
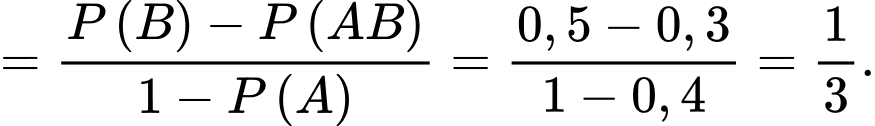
d) Đúng.
Xác suất để công ty thắng thầu đúng 1 dự án là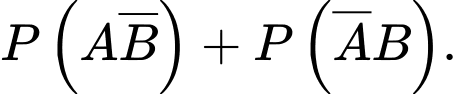
Vì hai biến cố và
và  xung khắc nhau và
xung khắc nhau và  nên theo tính chất của xác suất ta có
nên theo tính chất của xác suất ta có 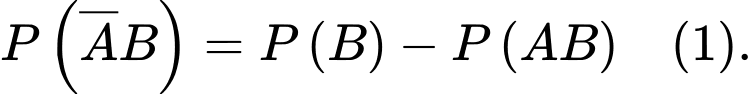
Vì hai biến cố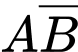 và
và  xung khắc nhau và
xung khắc nhau và  nên theo tính chất của xác suất ta có:
nên theo tính chất của xác suất ta có: 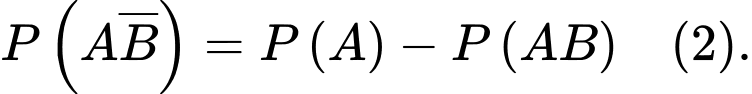
Từ và
và  ta được như sau:
ta được như sau:
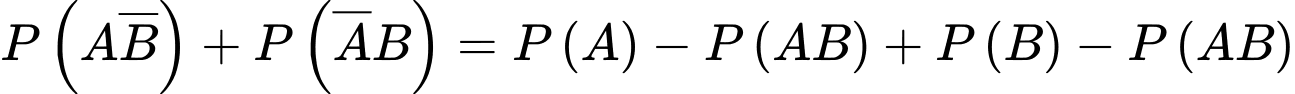
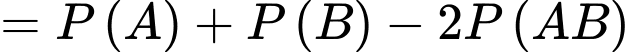
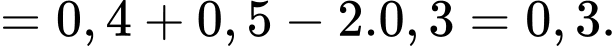
Nhắc lại kiến thức: Hai biến cố A, B độc lập khi và chỉ khi
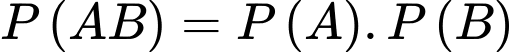
Ta có
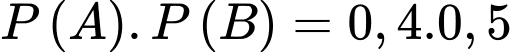
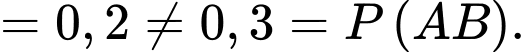
b) Đúng.
Xác suất để công ty thắng thầu dự án 2 khi đã biết thắng dự án 1 là

Ta có
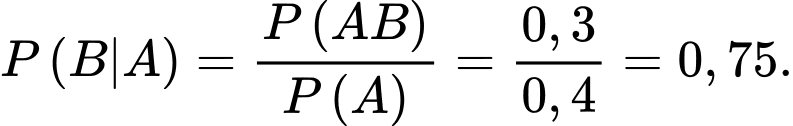
c) Sai.
Xác suất để công ty thắng thầu dự án 2 khi đã biết điều kiện không thắng dự án 1 là
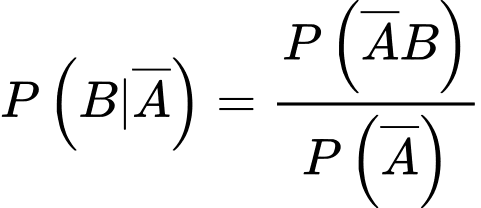
Vì hai biến cố
 và
và  xung khắc nhau và
xung khắc nhau và  nên theo tính chất của xác suất ta có
nên theo tính chất của xác suất ta có 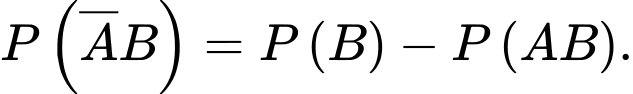
Suy ra
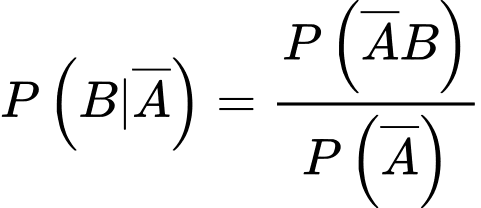
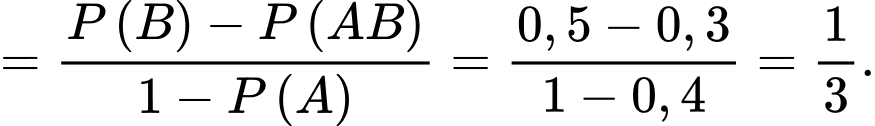
d) Đúng.
Xác suất để công ty thắng thầu đúng 1 dự án là
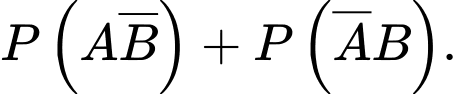
Vì hai biến cố
 và
và  xung khắc nhau và
xung khắc nhau và  nên theo tính chất của xác suất ta có
nên theo tính chất của xác suất ta có 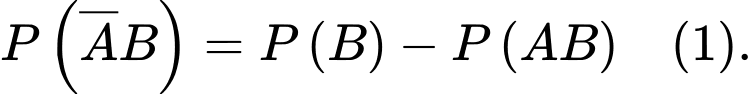
Vì hai biến cố
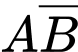 và
và  xung khắc nhau và
xung khắc nhau và  nên theo tính chất của xác suất ta có:
nên theo tính chất của xác suất ta có: 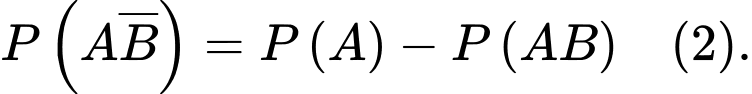
Từ
 và
và  ta được như sau:
ta được như sau:
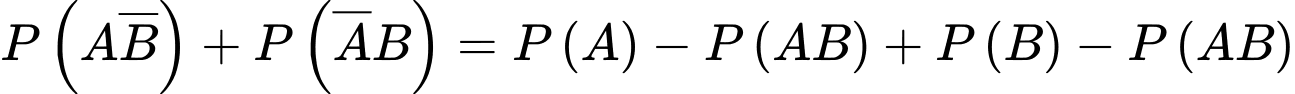
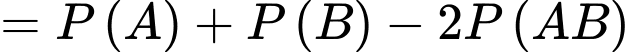
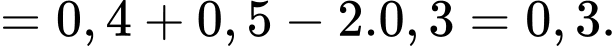
Câu 16 [695070]: Một miếng thịt sống được lấy ra khỏi ngăn đá của tủ lạnh và để trên bàn để rã đông. Nhiệt độ của miếng thịt khi nó được lấy ra khỏi ngăn đá là 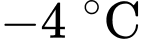 và sau
và sau 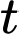 giờ nhiệt độ của miếng thịt tăng với tốc độ
giờ nhiệt độ của miếng thịt tăng với tốc độ 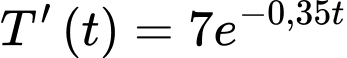 °C/giờ. Miếng thịt này được rã đông khi nhiệt độ của nó đạt đến 10°C.
°C/giờ. Miếng thịt này được rã đông khi nhiệt độ của nó đạt đến 10°C.
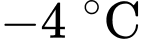 và sau
và sau 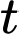 giờ nhiệt độ của miếng thịt tăng với tốc độ
giờ nhiệt độ của miếng thịt tăng với tốc độ 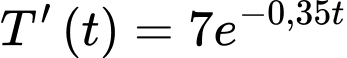 °C/giờ. Miếng thịt này được rã đông khi nhiệt độ của nó đạt đến 10°C.
°C/giờ. Miếng thịt này được rã đông khi nhiệt độ của nó đạt đến 10°C.
a) Đúng.
Tốc độ thay đổi nhiệt độ của miếng thịt sau 2 giờ là:
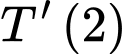
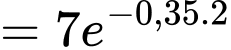
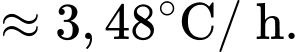
b) Sai.
Nhiệt độ của miếng thịt sau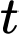 giờ là:
giờ là:
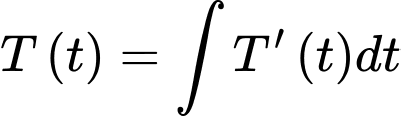
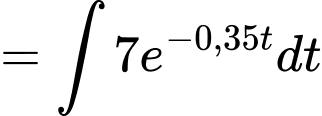
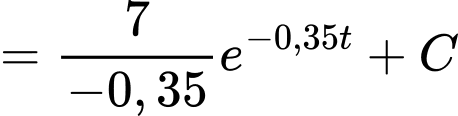
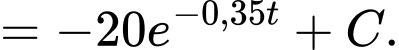
Nhiệt độ của miếng thịt khi nó được lấy ra khỏi ngăn đá là
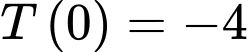
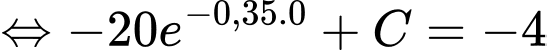

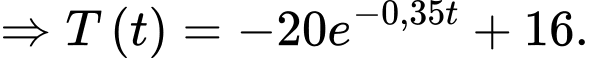
Ta có:
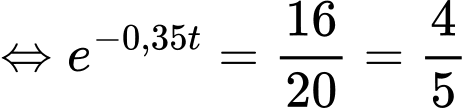
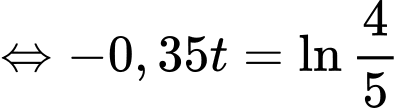
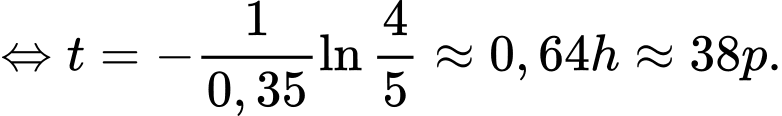
Vậy nhiệt độ của miếng thịt bằng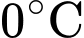 sau 38 phút.
sau 38 phút.
c) Sai.
Ta có:
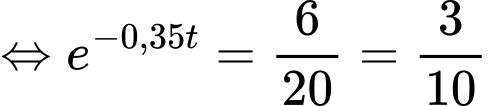
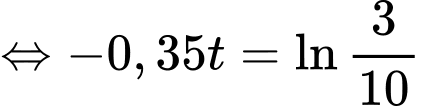
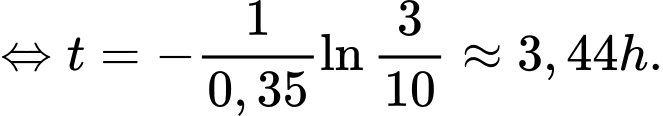
Vậy cần mất 3,44 giờ để miếng thịt nướng được rã đông.
d) Sai.
Nhiệt độ của miếng thịt sau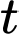 giờ đưa vào lò vi sóng là
giờ đưa vào lò vi sóng là
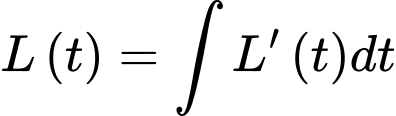
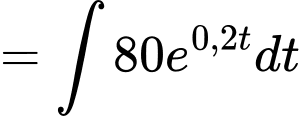
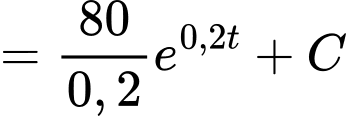
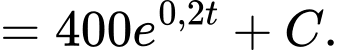
Thời điểm miếng thịt được đưa vào lò vi sóng là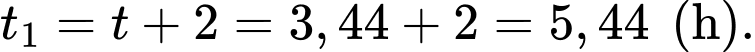
Nhiệt độ của miếng thịt lúc đưa vào lò vi sóng là
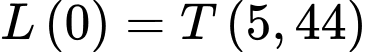
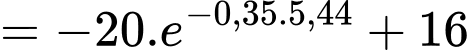
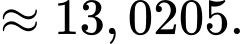
Ta có: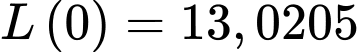
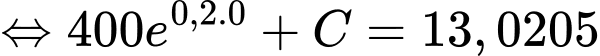
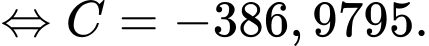
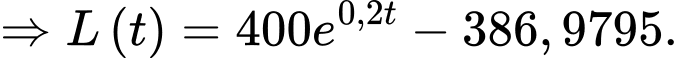
Ta có: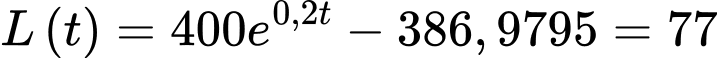
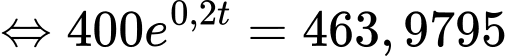
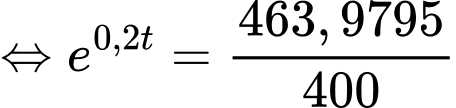
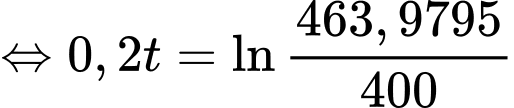
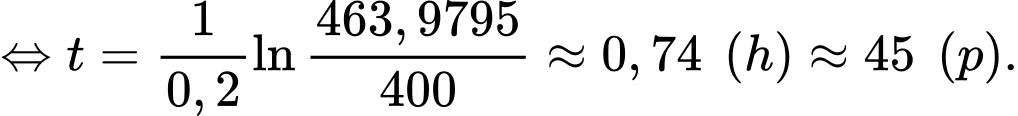
Tốc độ thay đổi nhiệt độ của miếng thịt sau 2 giờ là:
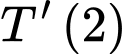
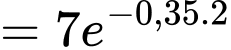
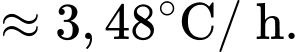
b) Sai.
Nhiệt độ của miếng thịt sau
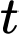 giờ là:
giờ là: 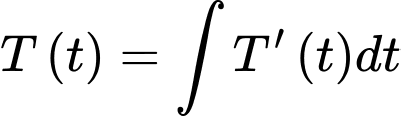
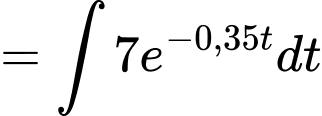
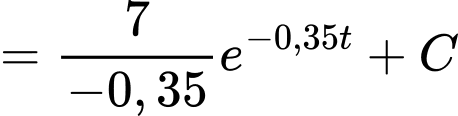
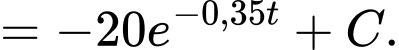
Nhiệt độ của miếng thịt khi nó được lấy ra khỏi ngăn đá là
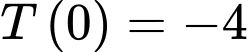
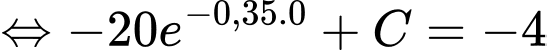

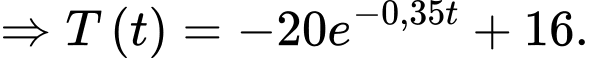
Ta có:

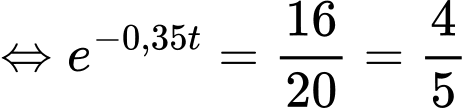
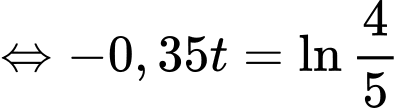
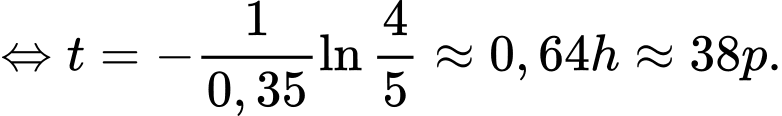
Vậy nhiệt độ của miếng thịt bằng
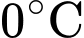 sau 38 phút.
sau 38 phút.c) Sai.
Ta có:

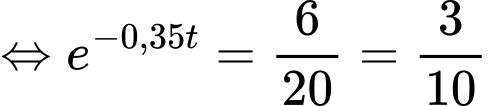
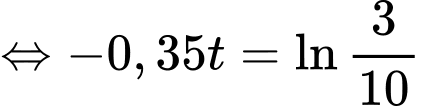
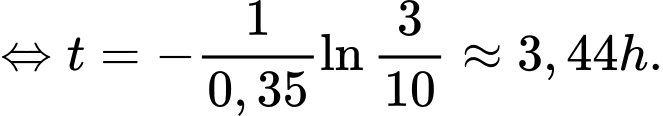
Vậy cần mất 3,44 giờ để miếng thịt nướng được rã đông.
d) Sai.
Nhiệt độ của miếng thịt sau
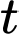 giờ đưa vào lò vi sóng là
giờ đưa vào lò vi sóng là 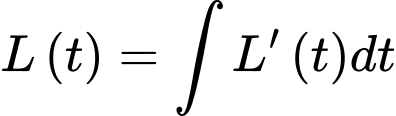
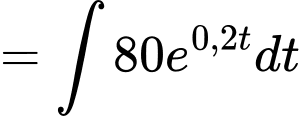
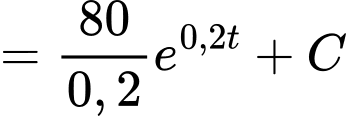
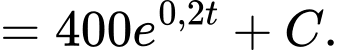
Thời điểm miếng thịt được đưa vào lò vi sóng là
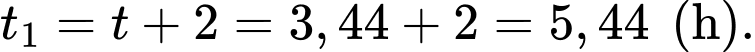
Nhiệt độ của miếng thịt lúc đưa vào lò vi sóng là
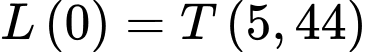
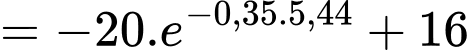
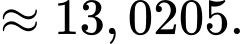
Ta có:
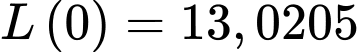
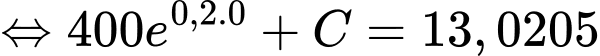
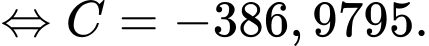
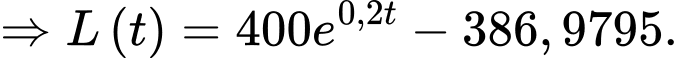
Ta có:
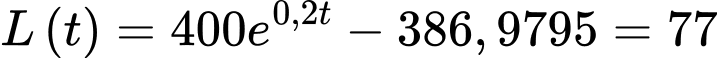
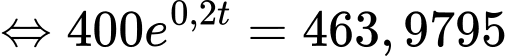
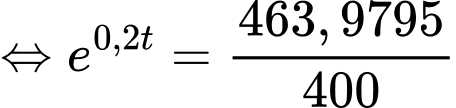
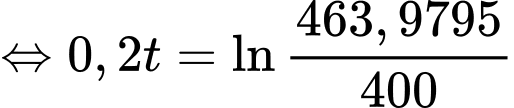
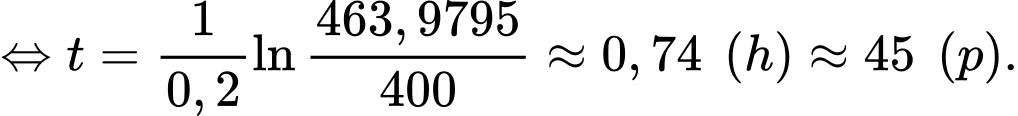
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
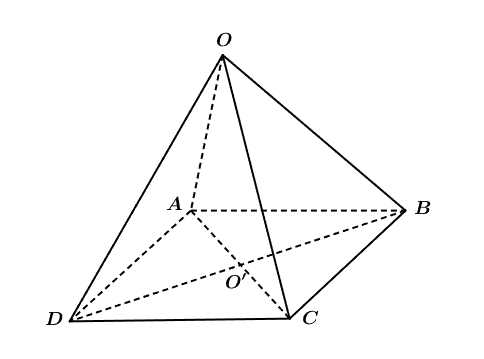
Câu 17 [695071]: Cho khối trụ có trục 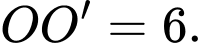 Một khối chóp đều
Một khối chóp đều 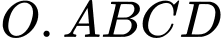 có thể tích bằng
có thể tích bằng 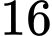 và đáy
và đáy 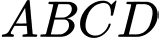 nội tiếp đường tròn
nội tiếp đường tròn  là đường tròn đáy khối trụ. Thể tích của khối trụ đã cho là
là đường tròn đáy khối trụ. Thể tích của khối trụ đã cho là 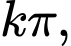 giá trị của
giá trị của 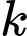 bằng bao nhiêu?
bằng bao nhiêu?
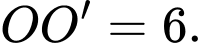 Một khối chóp đều
Một khối chóp đều 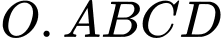 có thể tích bằng
có thể tích bằng 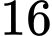 và đáy
và đáy 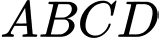 nội tiếp đường tròn
nội tiếp đường tròn  là đường tròn đáy khối trụ. Thể tích của khối trụ đã cho là
là đường tròn đáy khối trụ. Thể tích của khối trụ đã cho là 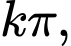 giá trị của
giá trị của 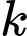 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 24.
Ta có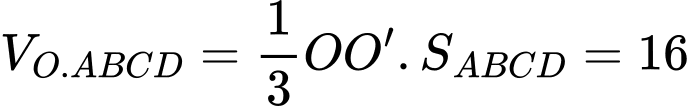
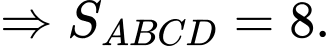
Suy ra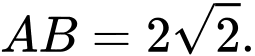
Ta có khối trụ có bán kính đáy bằng bán kính đường tròn và bằng
và bằng 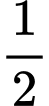 độ dài đường chéo của hình vuông
độ dài đường chéo của hình vuông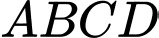 và bằng 2.
và bằng 2.
Suy ra thể tích của khối trụ bằng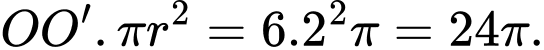
Vậy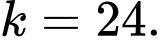

Ta có
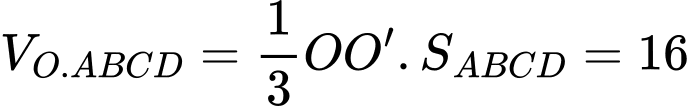
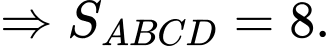
Suy ra
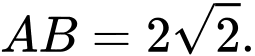
Ta có khối trụ có bán kính đáy bằng bán kính đường tròn
 và bằng
và bằng 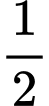 độ dài đường chéo của hình vuông
độ dài đường chéo của hình vuông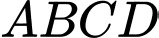 và bằng 2.
và bằng 2.
Suy ra thể tích của khối trụ bằng
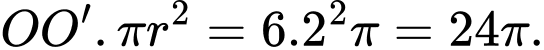
Vậy
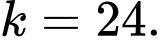
Câu 18 [695072]: An đã tạo ra một cầu thang 3 bậc bằng 18 que tăm như hình minh họa. Vậy An cần thêm bao nhiêu que tăm để hoàn thành một cầu thang 5 bậc?
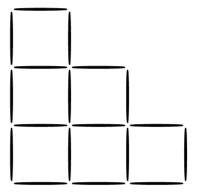

Điền đáp án: 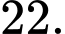
Cách 1:
Chúng ta có thể thấy rằng cầu thang 1 bậc cần 4 tăm và cầu thang 2 bậc cần 10 tăm.
Do đó, để đi từ cầu thang 1 bậc đến 2 bậc cần thêm 6 tăm và để đi từ cầu thang 2 bậc đến 3 bậc cần thêm 8 tăm.
Áp dụng mô hình này, để đi từ cầu thang 3 bậc đến 4 bậc cần thêm 10 tăm và để đi từ cầu thang 4 bậc đến 5 bậc cần thêm 12 tăm.
Vậy bạn An cần thêm là tăm.
tăm.
Cách 2:
Ngoài ra, chúng ta có thể thấy với cầu thang 3 bậc có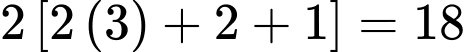 tăm.
tăm.
Tổng quát, chúng ta thấy rẳng cầu thang có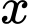 bậc có
bậc có 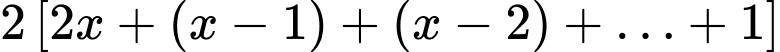 tăm.
tăm.
Vì vậy, đối với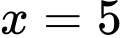 bậc, chúng ta có
bậc, chúng ta có 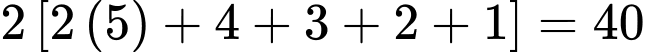 tăm.
tăm.
Vậy bạn An cần thêm là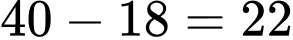 tăm.
tăm.
Cách 3:
Nếu quá lười để đưa ra công thức tính số lượng que cần thiết cho một số bước nhất định, ta có thể thấy rằng để đến được 4 các bước, ta thêm hai khối có ba que (phía trên và bên phải) và hai khối nữa có hai khối để tạo thành các bước. Điều này sẽ thêm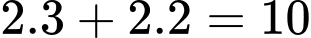 que.
que.
Sau đó, để đến được 5 các bước, ta thêm hai khối cạnh nữa có 3 que và 3 nhiều khối nữa có hai que. Ta thêm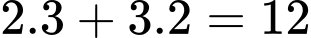 nhiều hơn nữa để tăng tổng cộng
nhiều hơn nữa để tăng tổng cộng  .
.
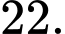
Cách 1:
Chúng ta có thể thấy rằng cầu thang 1 bậc cần 4 tăm và cầu thang 2 bậc cần 10 tăm.
Do đó, để đi từ cầu thang 1 bậc đến 2 bậc cần thêm 6 tăm và để đi từ cầu thang 2 bậc đến 3 bậc cần thêm 8 tăm.
Áp dụng mô hình này, để đi từ cầu thang 3 bậc đến 4 bậc cần thêm 10 tăm và để đi từ cầu thang 4 bậc đến 5 bậc cần thêm 12 tăm.
Vậy bạn An cần thêm là
 tăm.
tăm.
Cách 2:
Ngoài ra, chúng ta có thể thấy với cầu thang 3 bậc có
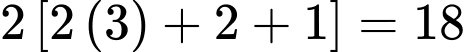 tăm.
tăm. Tổng quát, chúng ta thấy rẳng cầu thang có
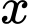 bậc có
bậc có 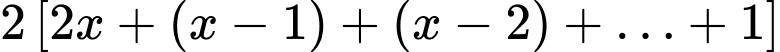 tăm.
tăm. Vì vậy, đối với
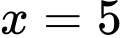 bậc, chúng ta có
bậc, chúng ta có 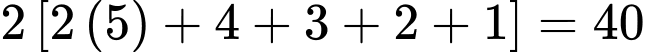 tăm.
tăm. Vậy bạn An cần thêm là
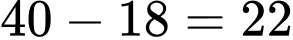 tăm.
tăm.
Cách 3:
Nếu quá lười để đưa ra công thức tính số lượng que cần thiết cho một số bước nhất định, ta có thể thấy rằng để đến được 4 các bước, ta thêm hai khối có ba que (phía trên và bên phải) và hai khối nữa có hai khối để tạo thành các bước. Điều này sẽ thêm
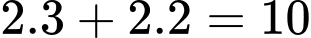 que.
que. Sau đó, để đến được 5 các bước, ta thêm hai khối cạnh nữa có 3 que và 3 nhiều khối nữa có hai que. Ta thêm
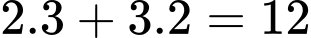 nhiều hơn nữa để tăng tổng cộng
nhiều hơn nữa để tăng tổng cộng  .
.
Câu 19 [694839]: Trong quang học, chúng ta đã biết đến định luật quang học về độ chiếu sáng. Nó được phát biểu như sau: Độ chiếu sáng từ một nguồn sáng 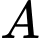 đến một điểm
đến một điểm 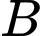 cho bởi công thức
cho bởi công thức 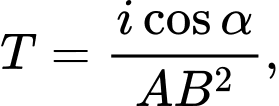 trong đó
trong đó 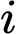 là độ phát sáng của nguồn
là độ phát sáng của nguồn 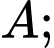
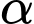 là góc phản xạ của ánh sáng lên người quan sát (coi rằng người quan sát nhìn thẳng xuống mặt bàn, xem hình vẽ).
là góc phản xạ của ánh sáng lên người quan sát (coi rằng người quan sát nhìn thẳng xuống mặt bàn, xem hình vẽ).
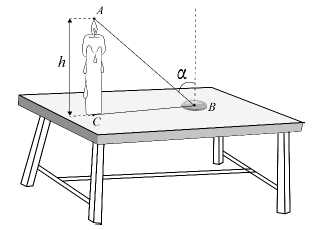
Một đồng xu được đặt cách ngọn nến một khoảng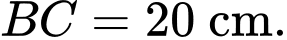 Hỏi ngọn lửa của cây nến nên đặt ở độ cao
Hỏi ngọn lửa của cây nến nên đặt ở độ cao 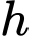 bằngbao nhiêu cm để chiếu sáng rõ nhất đồng tiền xu nằm trên bàn (kết quả làm tròn đến hàng phần chục).
bằngbao nhiêu cm để chiếu sáng rõ nhất đồng tiền xu nằm trên bàn (kết quả làm tròn đến hàng phần chục).
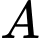 đến một điểm
đến một điểm 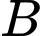 cho bởi công thức
cho bởi công thức 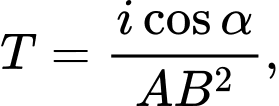 trong đó
trong đó 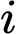 là độ phát sáng của nguồn
là độ phát sáng của nguồn 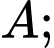
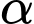 là góc phản xạ của ánh sáng lên người quan sát (coi rằng người quan sát nhìn thẳng xuống mặt bàn, xem hình vẽ).
là góc phản xạ của ánh sáng lên người quan sát (coi rằng người quan sát nhìn thẳng xuống mặt bàn, xem hình vẽ).
Một đồng xu được đặt cách ngọn nến một khoảng
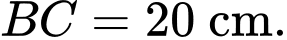 Hỏi ngọn lửa của cây nến nên đặt ở độ cao
Hỏi ngọn lửa của cây nến nên đặt ở độ cao 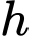 bằngbao nhiêu cm để chiếu sáng rõ nhất đồng tiền xu nằm trên bàn (kết quả làm tròn đến hàng phần chục).
bằngbao nhiêu cm để chiếu sáng rõ nhất đồng tiền xu nằm trên bàn (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 14,1.
+) Trong trường hợp này, chúng ta có thể thay đổi chiều cao của cây nến bằng cách tăng chiều cao của đế nên đặt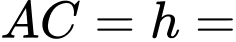 khoảng cách từ chỗ nến cháy xuống mặt bàn.
khoảng cách từ chỗ nến cháy xuống mặt bàn.
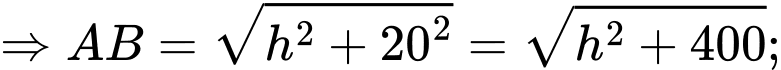
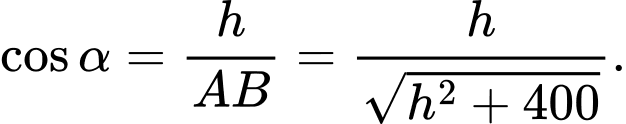
Khi đó độ chiếu sáng: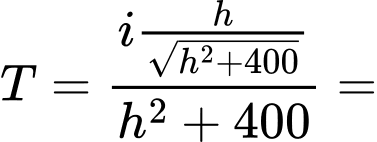
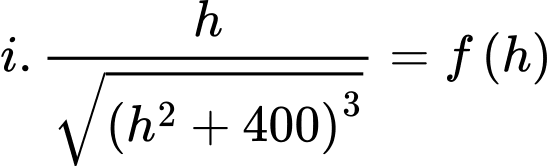
Cách 1: Khảo sát hàm số
Khảo sát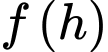 trong khoảng
trong khoảng 
Ta có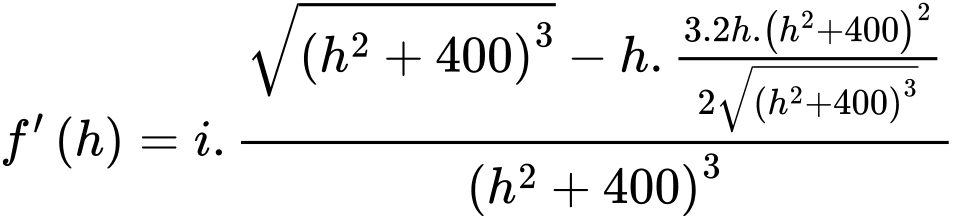
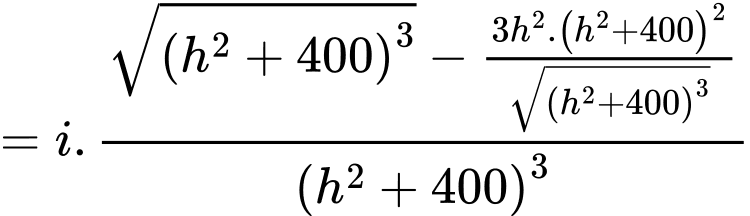
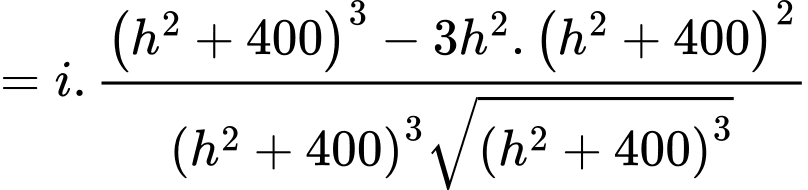
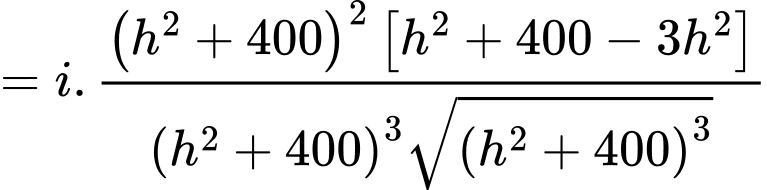
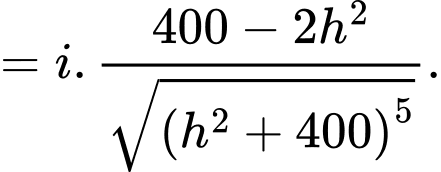
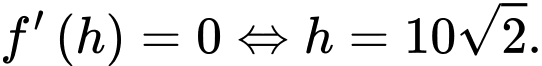
Bảng biến thiên
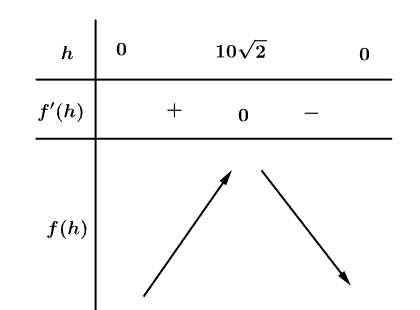
Từ bảng biến thiên suy ra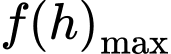 khi
khi 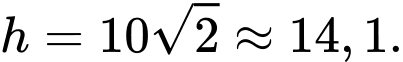
Cách 2: Dùng Cosi:
Ta có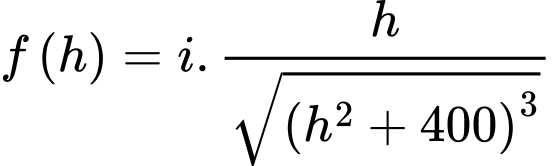
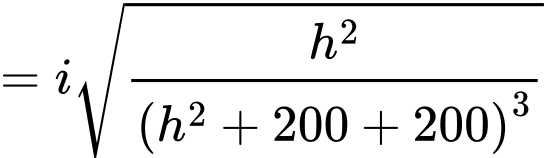
Áp dụng bất đẳng thức Côsi cho 3 số dương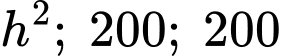 ta có
ta có
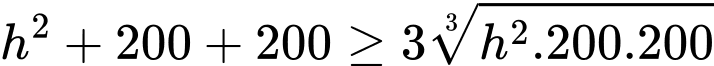
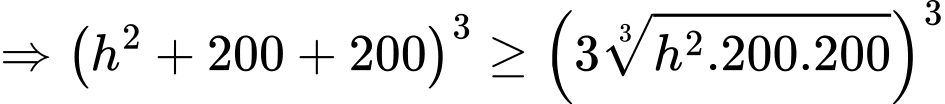
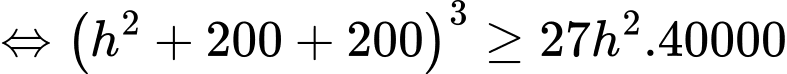
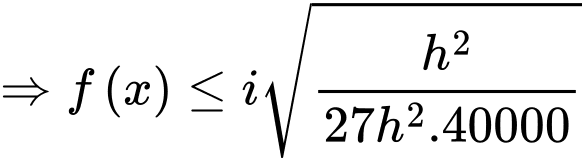
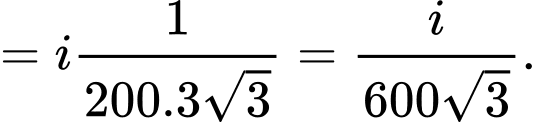
Dấu “=” xảy ra khi và chỉ khi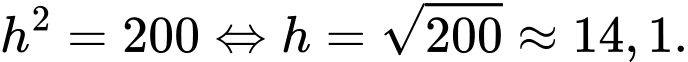
+) Trong trường hợp này, chúng ta có thể thay đổi chiều cao của cây nến bằng cách tăng chiều cao của đế nên đặt
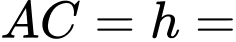 khoảng cách từ chỗ nến cháy xuống mặt bàn.
khoảng cách từ chỗ nến cháy xuống mặt bàn.
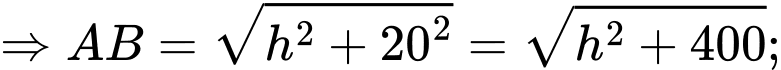
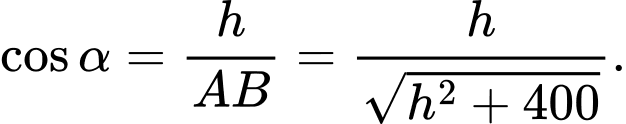
Khi đó độ chiếu sáng:
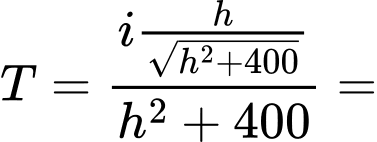
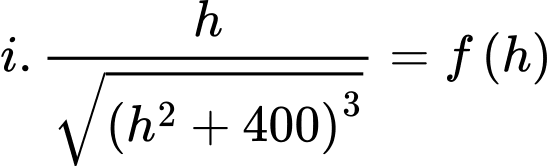
Cách 1: Khảo sát hàm số
Khảo sát
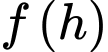 trong khoảng
trong khoảng 
Ta có
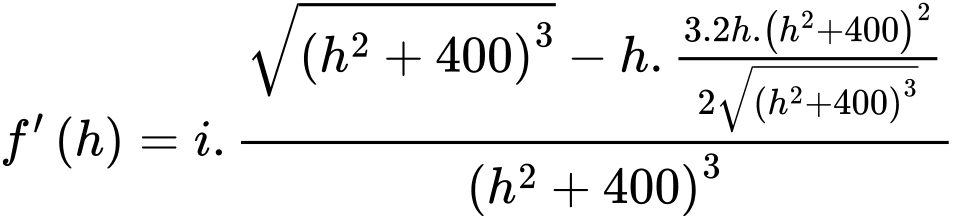
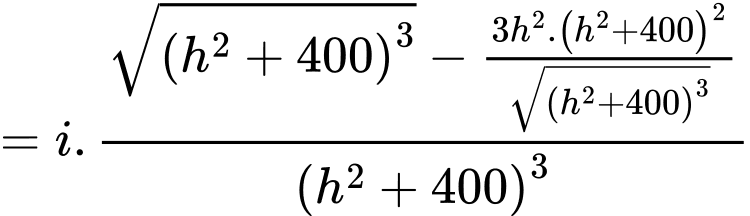
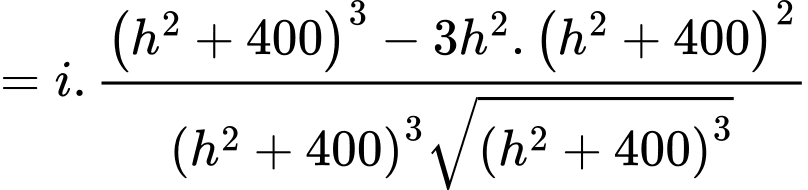
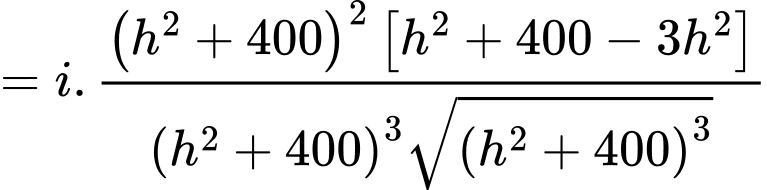
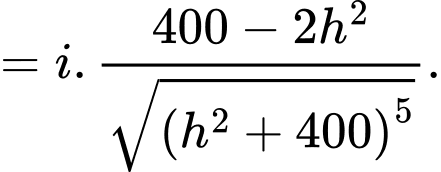
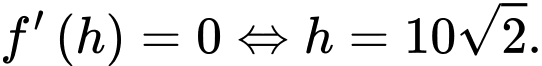
Bảng biến thiên

Từ bảng biến thiên suy ra
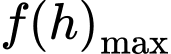 khi
khi 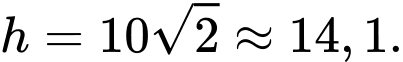
Cách 2: Dùng Cosi:
Ta có
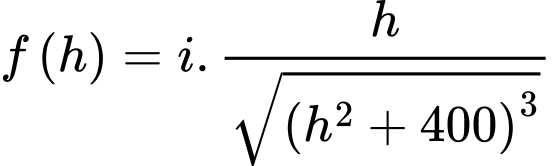
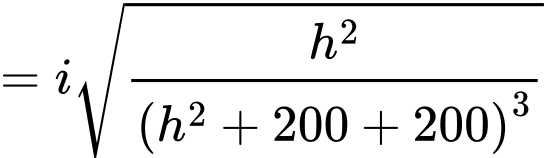
Áp dụng bất đẳng thức Côsi cho 3 số dương
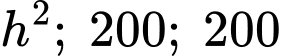 ta có
ta có
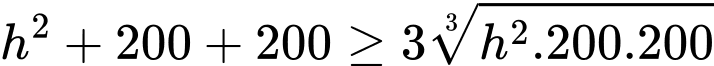
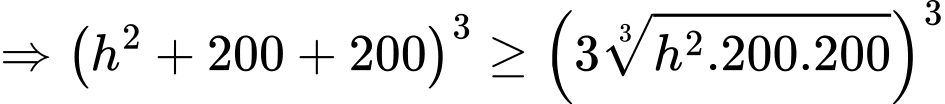
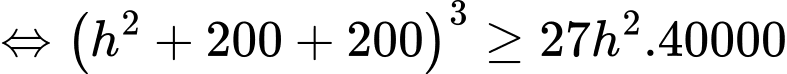
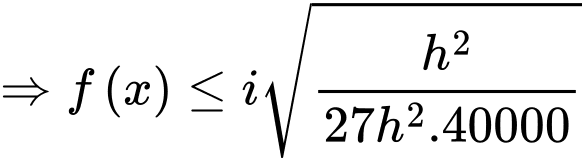
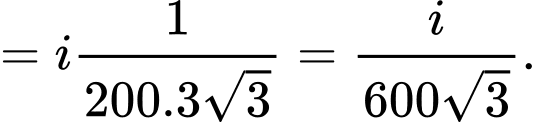
Dấu “=” xảy ra khi và chỉ khi
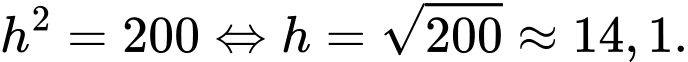
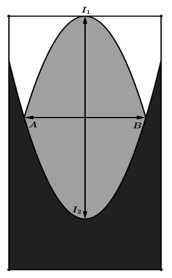
Câu 20 [695073]: Một nhà sản xuất dự kiến xây dựng sân khấu cho một concept âm nhạc trên một mảnh đất hình chữ nhật có kích thước là 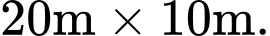 Nhà sản xuất mô phỏng sân khấu thông qua bản vẽ trên hệ trục
Nhà sản xuất mô phỏng sân khấu thông qua bản vẽ trên hệ trục 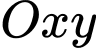 như sau: vẽ hai parabol có đỉnh
như sau: vẽ hai parabol có đỉnh 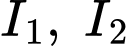 có cùng hoành độ, trong đó parabol đỉnh
có cùng hoành độ, trong đó parabol đỉnh 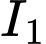 tiếp xúc với cạnh ngắn của hình chữ nhật. Vị trí giao nhau của hai parabol là
tiếp xúc với cạnh ngắn của hình chữ nhật. Vị trí giao nhau của hai parabol là 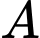 và
và 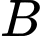 cùng với hai đỉnh
cùng với hai đỉnh 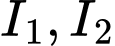 tạo thành hình thoi có độ dài hai đường chéo là
tạo thành hình thoi có độ dài hai đường chéo là 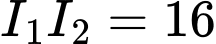 (m) và
(m) và 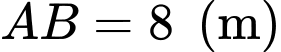 (tham khảo hình vẽ). Trên thực tế, khu vực màu đen là khu vực thiết kế dành cho khán giả, màu xám là khu vực sân khấu và màu trắng là khu vực hậu trường. Chi phí để xây dựng khu vực sân khấu, hậu trường, khán đài lần lượt là
(tham khảo hình vẽ). Trên thực tế, khu vực màu đen là khu vực thiết kế dành cho khán giả, màu xám là khu vực sân khấu và màu trắng là khu vực hậu trường. Chi phí để xây dựng khu vực sân khấu, hậu trường, khán đài lần lượt là 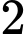 triệu đồng,
triệu đồng, 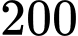 nghìn đồng và
nghìn đồng và 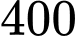 nghìn đồng mỗi mét vuông. Tổng chi phí xây dựng bằng bao nhiêu triệu đồng? Làm tròn đến hàng đơn vị.
nghìn đồng mỗi mét vuông. Tổng chi phí xây dựng bằng bao nhiêu triệu đồng? Làm tròn đến hàng đơn vị.
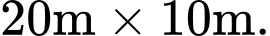 Nhà sản xuất mô phỏng sân khấu thông qua bản vẽ trên hệ trục
Nhà sản xuất mô phỏng sân khấu thông qua bản vẽ trên hệ trục 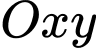 như sau: vẽ hai parabol có đỉnh
như sau: vẽ hai parabol có đỉnh 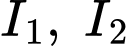 có cùng hoành độ, trong đó parabol đỉnh
có cùng hoành độ, trong đó parabol đỉnh 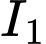 tiếp xúc với cạnh ngắn của hình chữ nhật. Vị trí giao nhau của hai parabol là
tiếp xúc với cạnh ngắn của hình chữ nhật. Vị trí giao nhau của hai parabol là 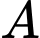 và
và 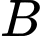 cùng với hai đỉnh
cùng với hai đỉnh 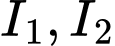 tạo thành hình thoi có độ dài hai đường chéo là
tạo thành hình thoi có độ dài hai đường chéo là 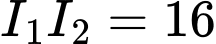 (m) và
(m) và 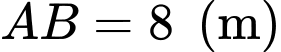 (tham khảo hình vẽ). Trên thực tế, khu vực màu đen là khu vực thiết kế dành cho khán giả, màu xám là khu vực sân khấu và màu trắng là khu vực hậu trường. Chi phí để xây dựng khu vực sân khấu, hậu trường, khán đài lần lượt là
(tham khảo hình vẽ). Trên thực tế, khu vực màu đen là khu vực thiết kế dành cho khán giả, màu xám là khu vực sân khấu và màu trắng là khu vực hậu trường. Chi phí để xây dựng khu vực sân khấu, hậu trường, khán đài lần lượt là 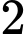 triệu đồng,
triệu đồng, 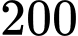 nghìn đồng và
nghìn đồng và 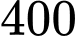 nghìn đồng mỗi mét vuông. Tổng chi phí xây dựng bằng bao nhiêu triệu đồng? Làm tròn đến hàng đơn vị.
nghìn đồng mỗi mét vuông. Tổng chi phí xây dựng bằng bao nhiêu triệu đồng? Làm tròn đến hàng đơn vị.
Điền đáp án: 
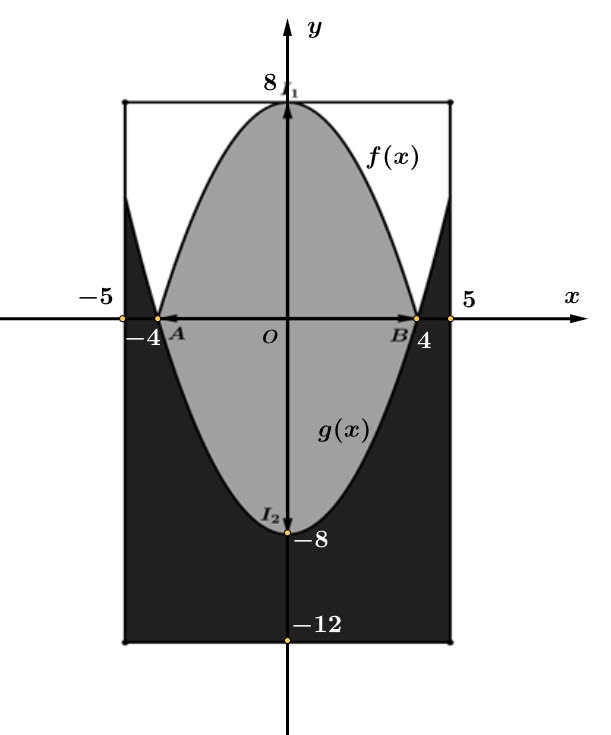
Gắn hệ trục toạ độ như hình vẽ.
Gọi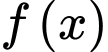 là hàm số của parabol phía trên khi đó:
là hàm số của parabol phía trên khi đó: 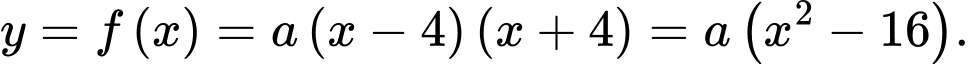
Parabol phía trên đi qua điêm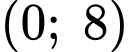 nên
nên 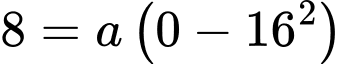
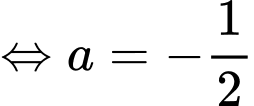
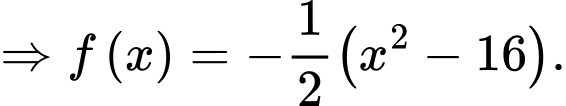
Gọi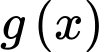 là hàm số của parabol phía dưới khi đó:
là hàm số của parabol phía dưới khi đó: 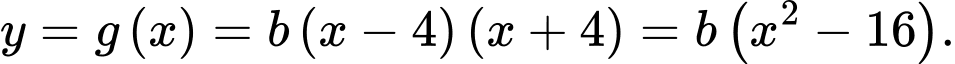
Parabol phía dưới đi qua điêm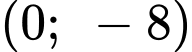 nên
nên 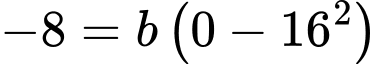
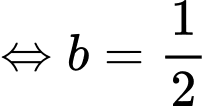
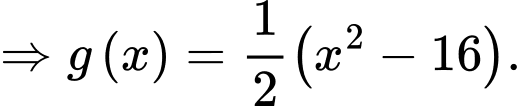
Diện tích sân khấu là:
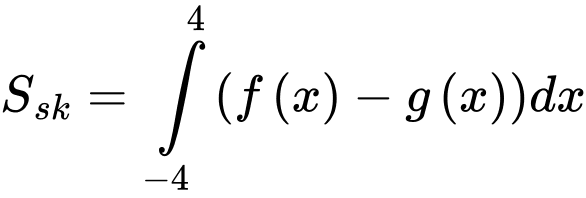
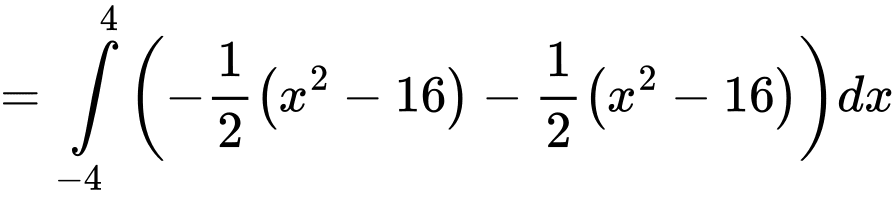
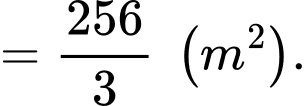
Diện tích khán đài là:
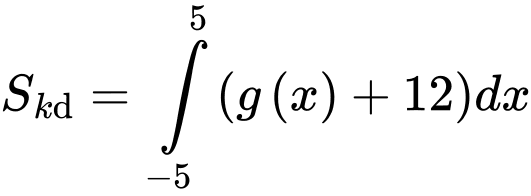
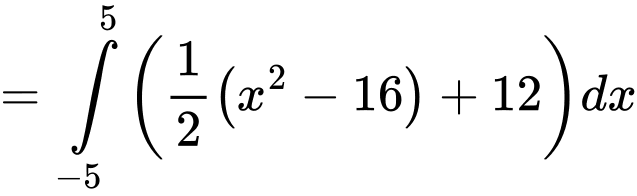
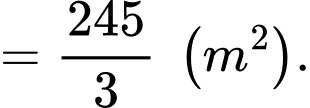
Diện tích hậu trường là:
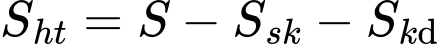
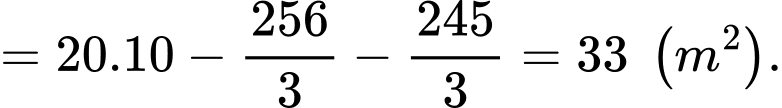
Tổng chi phí xây dựng bằng:
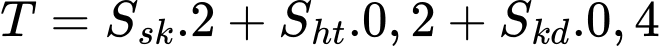
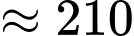 (triệu đồng)
(triệu đồng)

Gắn hệ trục toạ độ như hình vẽ.
Gọi
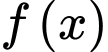 là hàm số của parabol phía trên khi đó:
là hàm số của parabol phía trên khi đó: 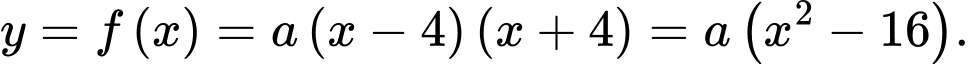
Parabol phía trên đi qua điêm
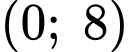 nên
nên 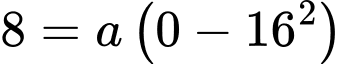
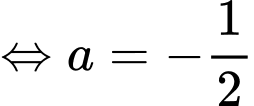
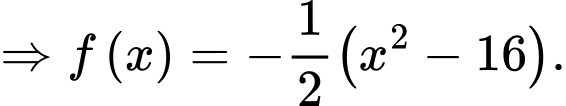
Gọi
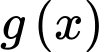 là hàm số của parabol phía dưới khi đó:
là hàm số của parabol phía dưới khi đó: 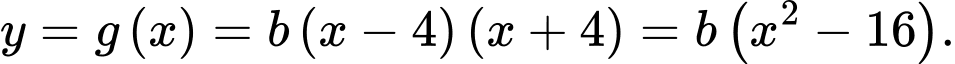
Parabol phía dưới đi qua điêm
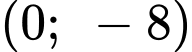 nên
nên 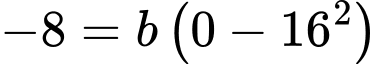
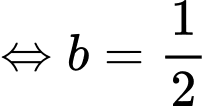
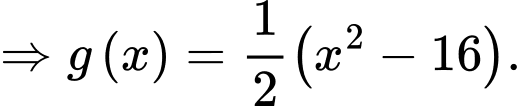
Diện tích sân khấu là:
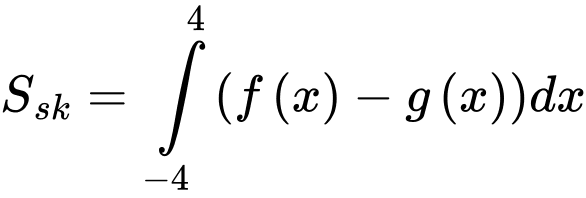
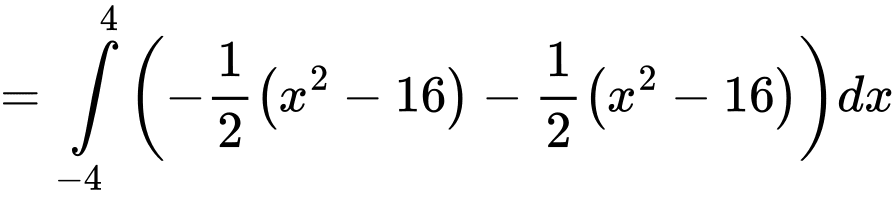
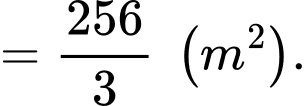
Diện tích khán đài là:
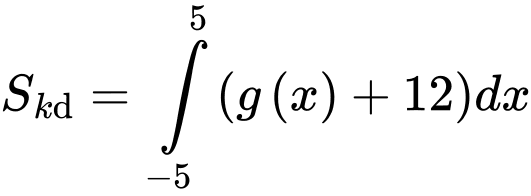
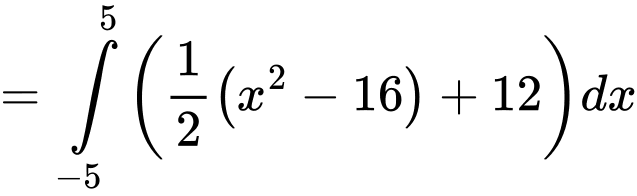
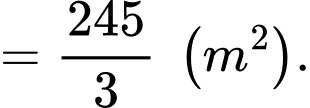
Diện tích hậu trường là:
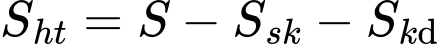
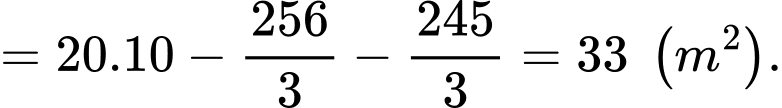
Tổng chi phí xây dựng bằng:
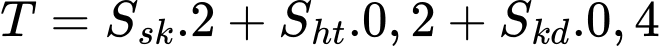
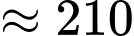 (triệu đồng)
(triệu đồng)
Câu 21 [698960]: Một công nhân đi làm ở thành phố khi trở về nhà chỉ có 2 cách: hoặc đi theo đường ngầm hoặc đi qua cầu. Nếu đi lối đường ngầm 75% trường hợp ông ta về đến nhà trước 6 giờ tối; còn nếu đi lối cầu chỉ có 70% trường hợp (nhưng đi lối cầu thích hơn). Vợ ông ta nhận thấy rằng: Bình quân cứ 100 lần về nhà thì 71 lần ông ta về nhà trước 6 giờ tối. Tìm xác suất để công nhân đó đã đi lối cầu biết rằng ông ta về đến nhà sau 6 giờ tối (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,83.
Gọi xác suất người đó đi theo đường ngầm là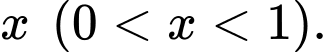
Từ dữ kiện bài cho, ta có sơ đồ cây sau:
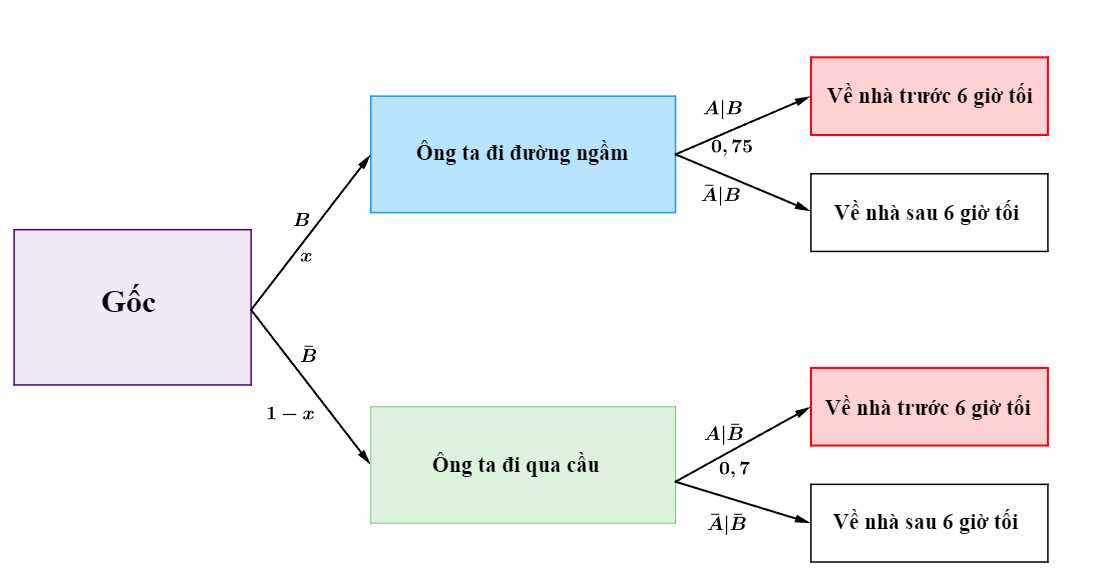
Gọi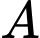 là biến cố “Ông ta về đến nhà trước 6 giờ tối”
là biến cố “Ông ta về đến nhà trước 6 giờ tối”
Suy ra là biến cố “Ông ta về đến nhà sau 6 giờ tối”
là biến cố “Ông ta về đến nhà sau 6 giờ tối”
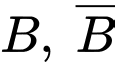 lần lượt là biến cố : “Ông ta đi đường ngầm” và “Ông ta đi lối cầu”.
lần lượt là biến cố : “Ông ta đi đường ngầm” và “Ông ta đi lối cầu”.
Ta có dữ kiện: Bình quân cứ 100 lần về nhà thì 71 lần ông ta về nhà trước 6 giờ tối nên suy ra xác suất ông ta về nhà trước 6 giờ tối là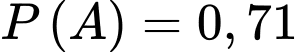
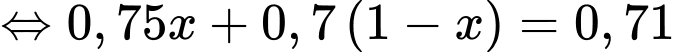
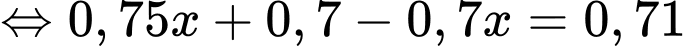
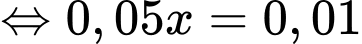
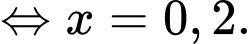 Suy ra
Suy ra 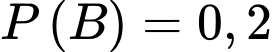
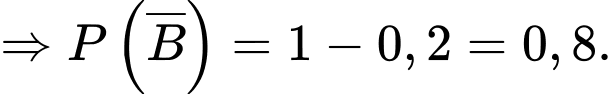
Áp dụng công thức Bayes, ta có xác suất để công nhân đó đã đi lối cầu biết rằng ông ta về đến nhà sau 6 giờ tối là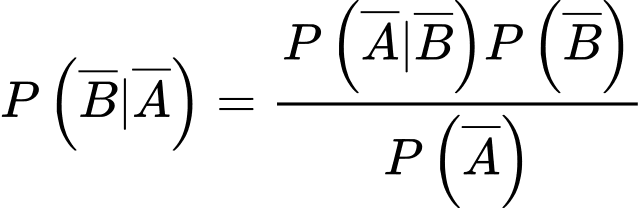
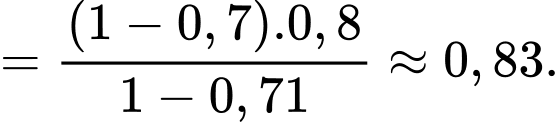
Gọi xác suất người đó đi theo đường ngầm là
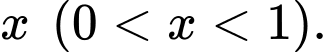
Từ dữ kiện bài cho, ta có sơ đồ cây sau:

Gọi
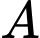 là biến cố “Ông ta về đến nhà trước 6 giờ tối”
là biến cố “Ông ta về đến nhà trước 6 giờ tối”Suy ra
 là biến cố “Ông ta về đến nhà sau 6 giờ tối”
là biến cố “Ông ta về đến nhà sau 6 giờ tối”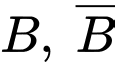 lần lượt là biến cố : “Ông ta đi đường ngầm” và “Ông ta đi lối cầu”.
lần lượt là biến cố : “Ông ta đi đường ngầm” và “Ông ta đi lối cầu”.Ta có dữ kiện: Bình quân cứ 100 lần về nhà thì 71 lần ông ta về nhà trước 6 giờ tối nên suy ra xác suất ông ta về nhà trước 6 giờ tối là
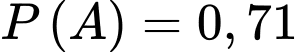
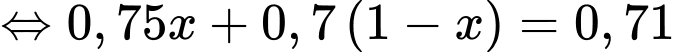
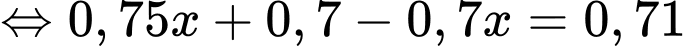
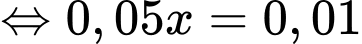
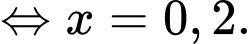 Suy ra
Suy ra 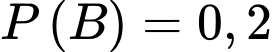
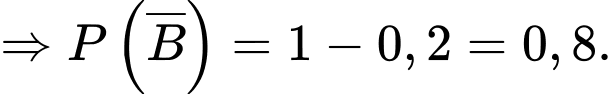
Áp dụng công thức Bayes, ta có xác suất để công nhân đó đã đi lối cầu biết rằng ông ta về đến nhà sau 6 giờ tối là
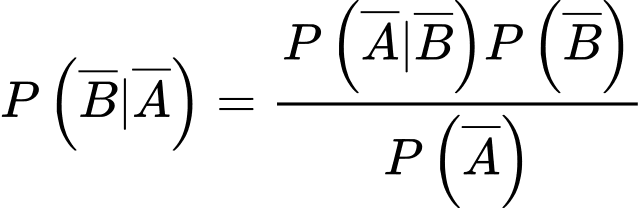
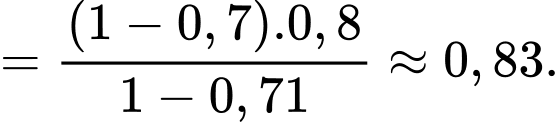
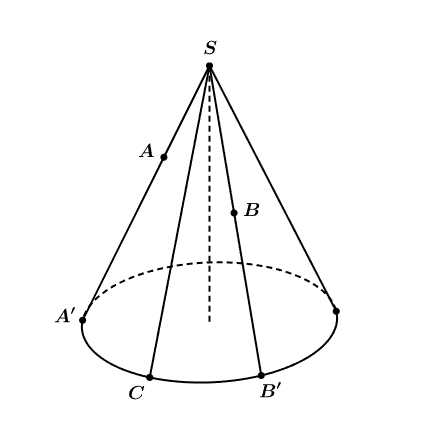
Câu 22 [696475]: Chiếc nón lá có dạng hình nón 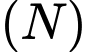 được đặt trong không gian với hệ trục toạ độ
được đặt trong không gian với hệ trục toạ độ 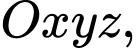 biết đỉnh của chiếc nón là điểm
biết đỉnh của chiếc nón là điểm 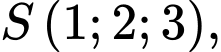
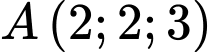 và
và 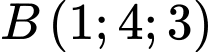 là các điểm nằm trên mặt xung quanh của chiếc nón, điểm
là các điểm nằm trên mặt xung quanh của chiếc nón, điểm 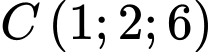 nằm trên đường tròn đáy. Diện tích xung quanh của chiếc nón bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
nằm trên đường tròn đáy. Diện tích xung quanh của chiếc nón bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
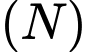 được đặt trong không gian với hệ trục toạ độ
được đặt trong không gian với hệ trục toạ độ 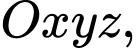 biết đỉnh của chiếc nón là điểm
biết đỉnh của chiếc nón là điểm 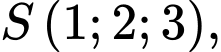
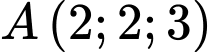 và
và 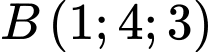 là các điểm nằm trên mặt xung quanh của chiếc nón, điểm
là các điểm nằm trên mặt xung quanh của chiếc nón, điểm 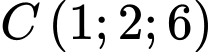 nằm trên đường tròn đáy. Diện tích xung quanh của chiếc nón bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
nằm trên đường tròn đáy. Diện tích xung quanh của chiếc nón bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án : 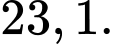
Ta có:
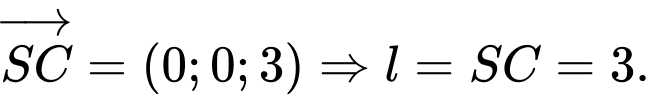
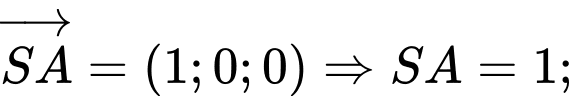
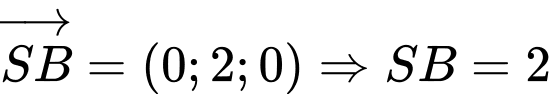 .
.
Dễ thấy đôi một vuông góc tại
đôi một vuông góc tại 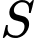 .
.
Lấy điểm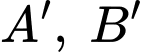 thỏa
thỏa 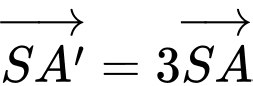 và
và 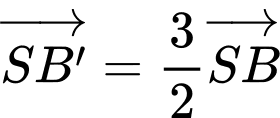 , suy ra
, suy ra 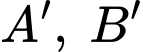 nằm trên đường tròn đáy hình nón.
nằm trên đường tròn đáy hình nón.
Vậy đáy hình nón là đường tròn ngoại tiếp tam giác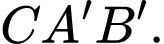
Các tam giác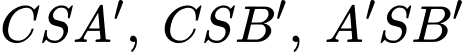 là các tam giác bằng nhau và đều vuông cân tại đỉnh
là các tam giác bằng nhau và đều vuông cân tại đỉnh 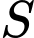 nên tam giác
nên tam giác 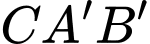 là tam giác đều cạnh bằng
là tam giác đều cạnh bằng 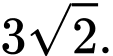
Từ đó ta tính được bán kính đường tròn ngoại tiếp tam giác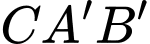 bằng
bằng
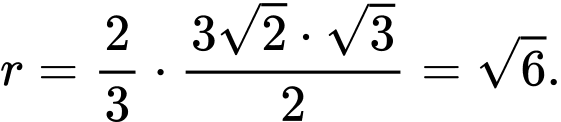
Diện tích xung quanh của hình nón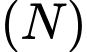 là
là
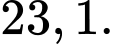

Ta có:
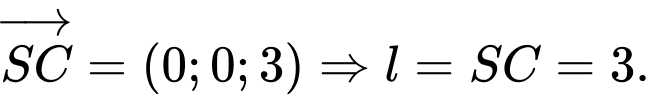
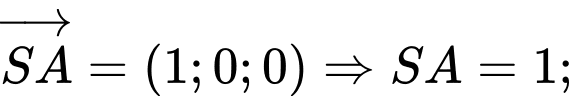
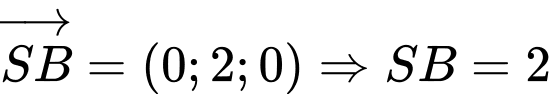 .
.Dễ thấy
 đôi một vuông góc tại
đôi một vuông góc tại 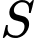 .
.Lấy điểm
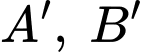 thỏa
thỏa 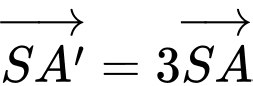 và
và 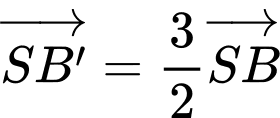 , suy ra
, suy ra 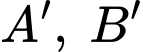 nằm trên đường tròn đáy hình nón.
nằm trên đường tròn đáy hình nón.Vậy đáy hình nón là đường tròn ngoại tiếp tam giác
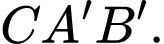
Các tam giác
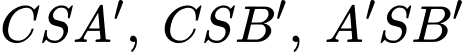 là các tam giác bằng nhau và đều vuông cân tại đỉnh
là các tam giác bằng nhau và đều vuông cân tại đỉnh 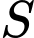 nên tam giác
nên tam giác 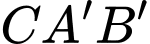 là tam giác đều cạnh bằng
là tam giác đều cạnh bằng 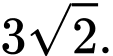
Từ đó ta tính được bán kính đường tròn ngoại tiếp tam giác
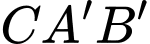 bằng
bằng 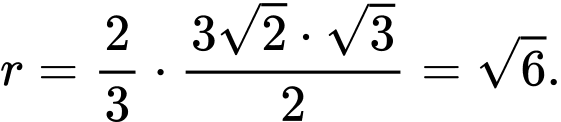
Diện tích xung quanh của hình nón
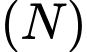 là
là