Đáp án Bài tập tự luyện số 1
Câu 1 [808933]: Cho hàm số 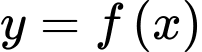 xác định trên tập
xác định trên tập 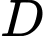 . Số
. Số 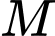 được gọi là giá trị lớn nhất của hàm số
được gọi là giá trị lớn nhất của hàm số 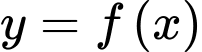 trên
trên 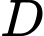 nếu
nếu
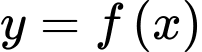 xác định trên tập
xác định trên tập 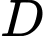 . Số
. Số 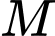 được gọi là giá trị lớn nhất của hàm số
được gọi là giá trị lớn nhất của hàm số 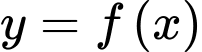 trên
trên 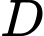 nếu
nếu A, 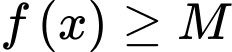 với mọi
với mọi 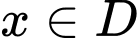 .
.
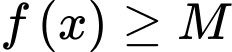 với mọi
với mọi 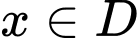 .
.B, 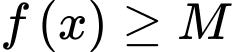 với mọi
với mọi 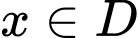 và tồn tại
và tồn tại  sao cho
sao cho 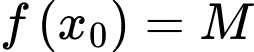 .
.
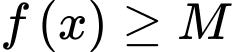 với mọi
với mọi 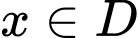 và tồn tại
và tồn tại  sao cho
sao cho 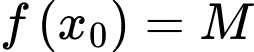 .
.C, 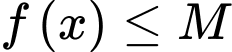 với mọi
với mọi 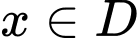 .
.
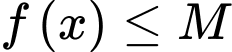 với mọi
với mọi 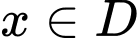 .
.D, 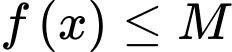 với mọi
với mọi 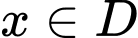 và tồn tại
và tồn tại  sao cho
sao cho 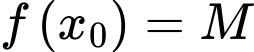 .
.
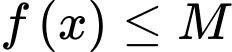 với mọi
với mọi 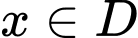 và tồn tại
và tồn tại  sao cho
sao cho 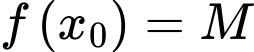 .
.
Chọn D
Theo định nghĩa giá trị lớn nhất của hàm số trên một khoảng. Đáp án: D
Theo định nghĩa giá trị lớn nhất của hàm số trên một khoảng. Đáp án: D
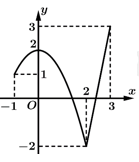
Câu 2 [508878]: Cho hàm số 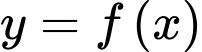 liên tục trên đoạn
liên tục trên đoạn 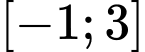 và có đồ thị như hình vẽ bên. Gọi
và có đồ thị như hình vẽ bên. Gọi 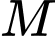 và
và 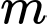 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn 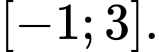 Giá trị của
Giá trị của 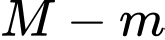 bằng
bằng
 liên tục trên đoạn
liên tục trên đoạn 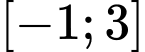 và có đồ thị như hình vẽ bên. Gọi
và có đồ thị như hình vẽ bên. Gọi 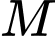 và
và 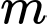 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn 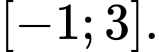 Giá trị của
Giá trị của 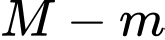 bằng
bằng
A, 0.
B, 1.
C, 4.
D, 5.
Từ đồ thị ta có 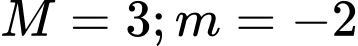 . Giá trị là
. Giá trị là 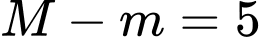 Đáp án: D
Đáp án: D
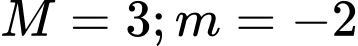 . Giá trị là
. Giá trị là 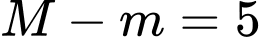 Đáp án: D
Đáp án: D
Câu 3 [33133]: Cho hàm số 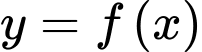 liên tục trên đoạn
liên tục trên đoạn 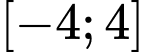 và có đồ thị như hình vẽ bên dưới. Gọi
và có đồ thị như hình vẽ bên dưới. Gọi 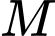 và
và 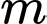 lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 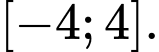 Giá trị của
Giá trị của 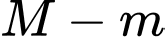 bằng
bằng
=kphan2de1/7.kslan6.png)
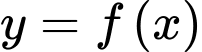 liên tục trên đoạn
liên tục trên đoạn 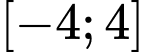 và có đồ thị như hình vẽ bên dưới. Gọi
và có đồ thị như hình vẽ bên dưới. Gọi 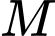 và
và 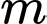 lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 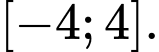 Giá trị của
Giá trị của 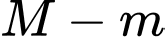 bằng
bằng=kphan2de1/7.kslan6.png)
A, 4.
B, 6.
C, 8
D, 1.
Đáp án B. 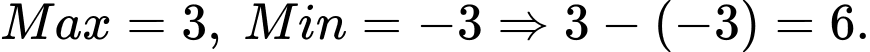 Đáp án: B
Đáp án: B
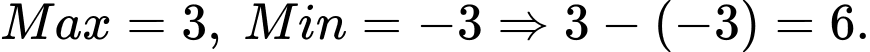 Đáp án: B
Đáp án: B
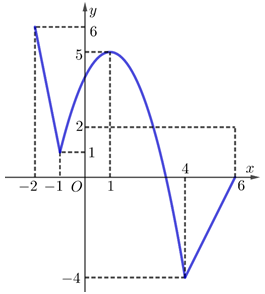
Câu 4 [33134]: Cho hàm số 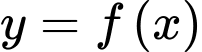 liên tục trên đoạn
liên tục trên đoạn 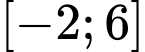 , có đồ thị như hình vẽ. Gọi
, có đồ thị như hình vẽ. Gọi 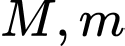 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của 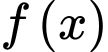 trên miền
trên miền 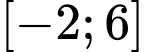 . Tính giá trị của biểu thức
. Tính giá trị của biểu thức 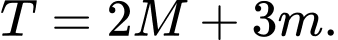
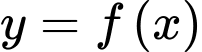 liên tục trên đoạn
liên tục trên đoạn 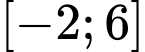 , có đồ thị như hình vẽ. Gọi
, có đồ thị như hình vẽ. Gọi 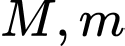 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của 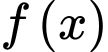 trên miền
trên miền 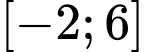 . Tính giá trị của biểu thức
. Tính giá trị của biểu thức 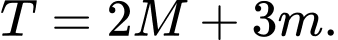

A, 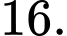
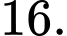
B, 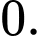
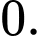
C, 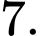
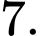
D, 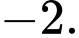
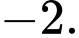
Dựa vào đồ thị trong đoạn 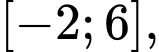 ta thấy:
ta thấy:
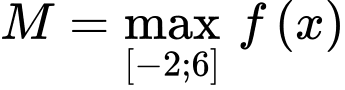
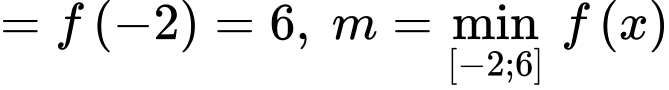
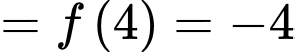
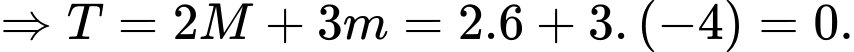
Chọn B. Đáp án: B
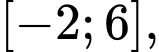 ta thấy:
ta thấy: 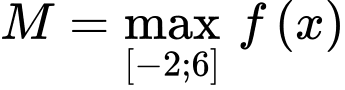
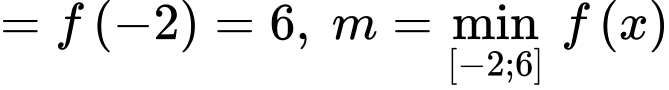
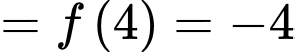
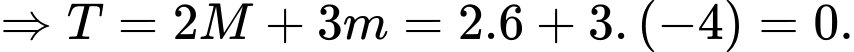
Chọn B. Đáp án: B
Câu 5 [307454]: Cho hàm số 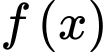 có bảng biến thiên như hình vẽ .
có bảng biến thiên như hình vẽ .

Giá trị nhỏ nhất của hàm số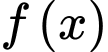 trên đoạn
trên đoạn 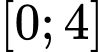 là
là
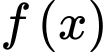 có bảng biến thiên như hình vẽ .
có bảng biến thiên như hình vẽ . 
Giá trị nhỏ nhất của hàm số
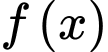 trên đoạn
trên đoạn 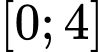 là
là A, 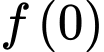 .
.
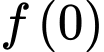 .
.B, 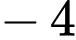 .
.
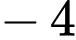 .
.C, 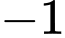 .
.
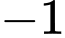 .
.D, 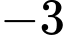 .
.
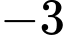 .
.
Chọn D.
Vì hàm số nghịch biến trên khoảng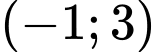 và
và  nên
nên 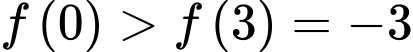 .
.
Vì hàm số đồng biến trên khoảng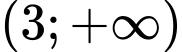 và
và 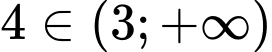 nên
nên 
Vậy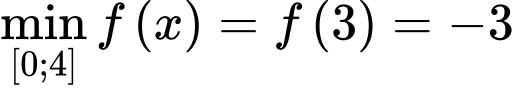 . Đáp án: D
. Đáp án: D
Vì hàm số nghịch biến trên khoảng
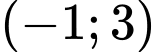 và
và  nên
nên 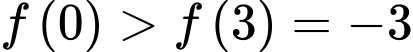 .
.
Vì hàm số đồng biến trên khoảng
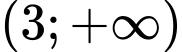 và
và 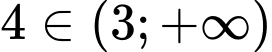 nên
nên 
Vậy
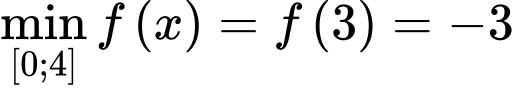 . Đáp án: D
. Đáp án: D
Câu 6 [327460]: Cho hàm số 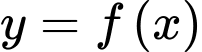 có bảng biến thiên như sau:
có bảng biến thiên như sau: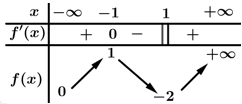
Khẳng định nào sau đây đúng?
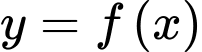 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A, Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
B, Hàm số có giá trị lớn nhất bằng 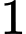 và có giá trị nhỏ nhất bằng
và có giá trị nhỏ nhất bằng  .
.
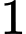 và có giá trị nhỏ nhất bằng
và có giá trị nhỏ nhất bằng  .
.C, Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng 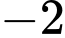 .
.
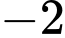 .
.D, Hàm số có giá trị lớn nhất bằng 1 và có giá trị nhỏ nhất bằng 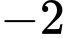 .
.
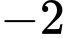 .
.
Chọn C
Từ bảng biến thiên suy ra hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng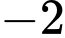 khi
khi 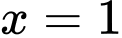 . Đáp án: C
. Đáp án: C
Từ bảng biến thiên suy ra hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng
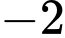 khi
khi 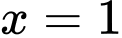 . Đáp án: C
. Đáp án: C
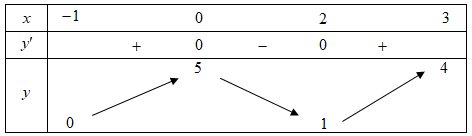
Câu 7 [32853]: Cho hàm số 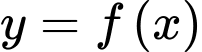 liên tục và có bảng biến thiên trên đoạn
liên tục và có bảng biến thiên trên đoạn 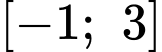 (hình vẽ). Gọi
(hình vẽ). Gọi  là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 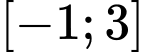 . Tìm
. Tìm 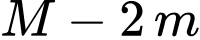 .
.
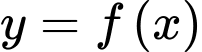 liên tục và có bảng biến thiên trên đoạn
liên tục và có bảng biến thiên trên đoạn 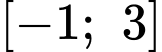 (hình vẽ). Gọi
(hình vẽ). Gọi  là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 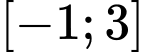 . Tìm
. Tìm 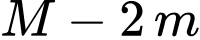 .
.
A, 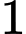 .
.
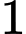 .
.B, 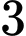 .
.
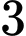 .
.C, 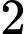 .
.
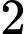 .
.D, 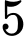 .
.
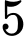 .
.
Ta có: 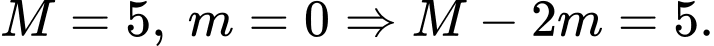 Đáp án: D
Đáp án: D
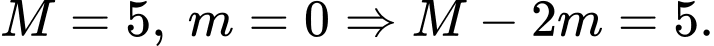 Đáp án: D
Đáp án: D
Câu 8 [399672]: Hàm số 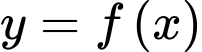 liên tục trên
liên tục trên 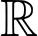 và có bảng biến thiên như hình bên dưới
và có bảng biến thiên như hình bên dưới
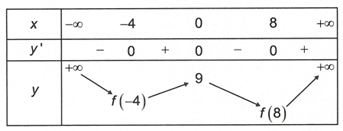
Biết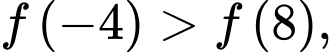 khi đó giá trị nhỏ nhất của hàm số đã cho trên
khi đó giá trị nhỏ nhất của hàm số đã cho trên 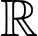 bằng
bằng
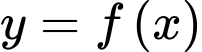 liên tục trên
liên tục trên 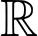 và có bảng biến thiên như hình bên dưới
và có bảng biến thiên như hình bên dưới

Biết
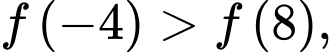 khi đó giá trị nhỏ nhất của hàm số đã cho trên
khi đó giá trị nhỏ nhất của hàm số đã cho trên 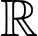 bằng
bằng A, 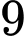
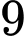
B, 

C, 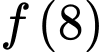
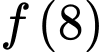
D, 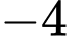
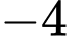
Từ bảng biến thiên ta có 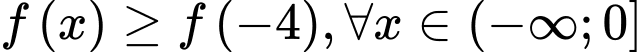 và
và 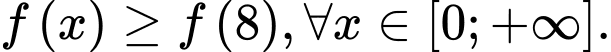
Mặt khác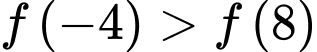 suy ra
suy ra 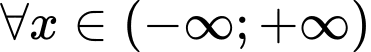 thì
thì 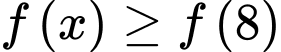
Vậy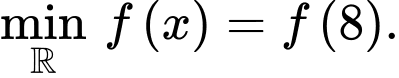 Đáp án: C
Đáp án: C
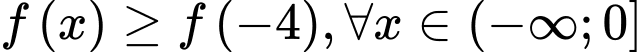 và
và 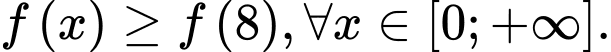
Mặt khác
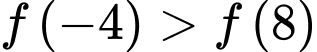 suy ra
suy ra 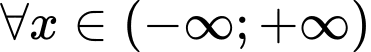 thì
thì 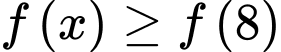
Vậy
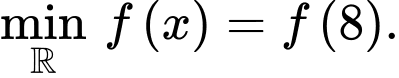 Đáp án: C
Đáp án: C
Câu 9 [399932]: Cho hàm số 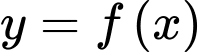 có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau:

Biết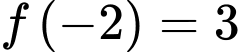 ,
, 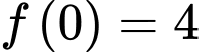 . Giá trị lớn nhất của hàm số
. Giá trị lớn nhất của hàm số 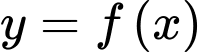 trên đoạn
trên đoạn 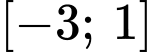 bằng
bằng
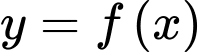 có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau:
Biết
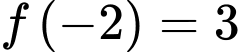 ,
, 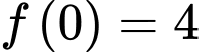 . Giá trị lớn nhất của hàm số
. Giá trị lớn nhất của hàm số 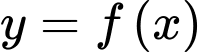 trên đoạn
trên đoạn 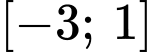 bằng
bằng A, 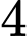 .
.
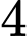 .
.B, 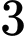 .
.
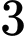 .
.C, 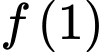 .
.
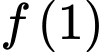 .
.D,  .
.
 .
.
Ta có bảng biến thiên của hàm số 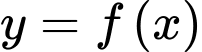 như sau:
như sau:
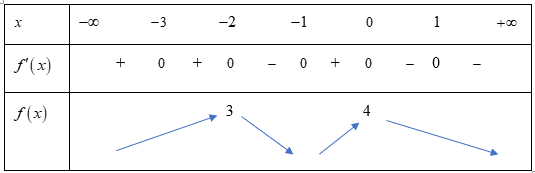
Từ bảng biến thiên ta có: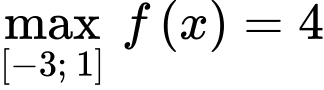 tại
tại 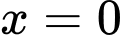 . Đáp án: A
. Đáp án: A
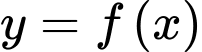 như sau:
như sau:
Từ bảng biến thiên ta có:
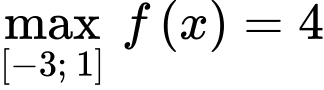 tại
tại 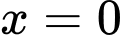 . Đáp án: A
. Đáp án: A
Câu 10 [378924]: Cho hàm số 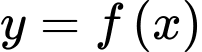 liên tục trên đoạn
liên tục trên đoạn 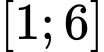 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau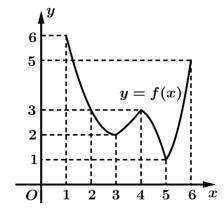
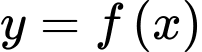 liên tục trên đoạn
liên tục trên đoạn 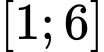 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
A, a) Giá trị lớn nhất của hàm số trên đoạn 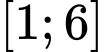 bằng
bằng 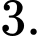
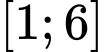 bằng
bằng 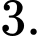
B, b) Giá trị lớn nhất của hàm số trên đoạn 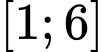 bằng
bằng 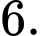
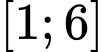 bằng
bằng 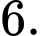
C, c) Giá trị nhỏ nhất của hàm số trên đoạn 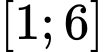 bằng
bằng 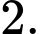
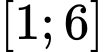 bằng
bằng 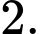
D, d) Trên đoạn 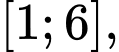 hàm số đạt giá trị nhỏ nhất tại điểm
hàm số đạt giá trị nhỏ nhất tại điểm 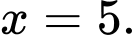
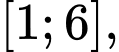 hàm số đạt giá trị nhỏ nhất tại điểm
hàm số đạt giá trị nhỏ nhất tại điểm 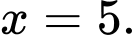
a, Sai. Giá trị lớn nhất của hàm số trên đoạn 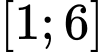 bằng
bằng 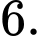
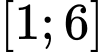 bằng
bằng 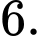
b, Đúng
c, Sai. Giá trị nhỏ nhất của hàm số trên đoạn 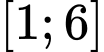 bằng
bằng 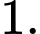
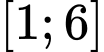 bằng
bằng 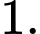
d, Đúng
Câu 11 [378925]: Cho hàm số 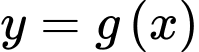 liên tục trên đoạn
liên tục trên đoạn 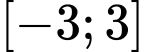 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau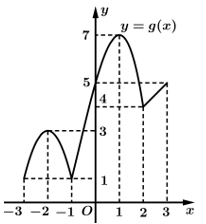
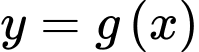 liên tục trên đoạn
liên tục trên đoạn 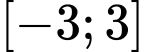 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
A, a) Giá trị lớn nhất của hàm số trên đoạn 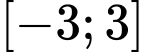 bằng
bằng 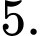
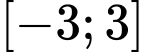 bằng
bằng 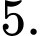
B, b) Trên đoạn 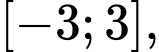 hàm số đạt giá trị lớn nhất tại điểm
hàm số đạt giá trị lớn nhất tại điểm 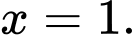
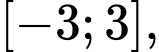 hàm số đạt giá trị lớn nhất tại điểm
hàm số đạt giá trị lớn nhất tại điểm 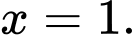
C, c) Giá trị nhỏ nhất của hàm số trên đoạn 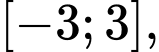 bằng
bằng 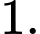
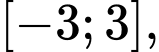 bằng
bằng 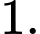
D, d) Trên đoạn 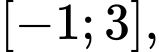 hàm số đạt giá trị nhỏ nhất tại điểm
hàm số đạt giá trị nhỏ nhất tại điểm 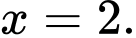
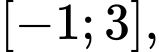 hàm số đạt giá trị nhỏ nhất tại điểm
hàm số đạt giá trị nhỏ nhất tại điểm 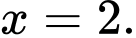
a, Sai. Giá trị lớn nhất của hàm số trên đoạn 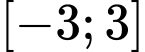 bằng
bằng 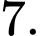
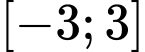 bằng
bằng 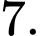
b, Đúng..
c, Đúng
d, Sai.Trên đoạn 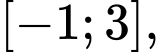 hàm số đạt giá trị nhỏ nhất tại điểm
hàm số đạt giá trị nhỏ nhất tại điểm 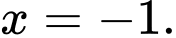
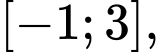 hàm số đạt giá trị nhỏ nhất tại điểm
hàm số đạt giá trị nhỏ nhất tại điểm 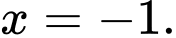
Câu 12 [377583]: Cho hàm số 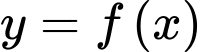 liên tục trên đoạn
liên tục trên đoạn 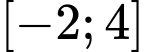 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau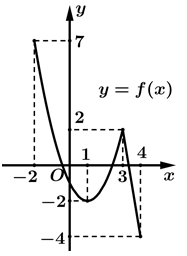
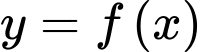 liên tục trên đoạn
liên tục trên đoạn 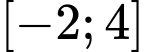 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau
A, a) Giá trị lớn nhất của hàm số trên đoạn 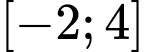 bằng
bằng 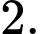
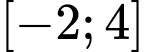 bằng
bằng 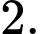
B, b) Giá trị lớn nhất của hàm số trên đoạn 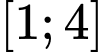 bằng
bằng 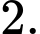
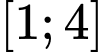 bằng
bằng 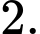
C, c) Giá trị nhỏ nhất của hàm số trên đoạn 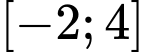 bằng
bằng 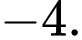
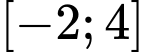 bằng
bằng 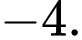
D, d) Hàm số đạt giá trị nhỏ nhất trên đoạn 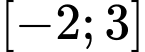 tại điểm
tại điểm 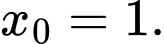
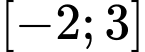 tại điểm
tại điểm 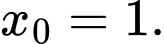
a) Sai. Giá trị lớn nhất của hàm số trên đoạn 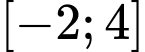 bằng
bằng 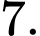
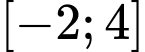 bằng
bằng 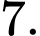
b) Đúng. Giá trị lớn nhất của hàm số trên đoạn 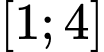 bằng
bằng 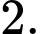
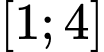 bằng
bằng 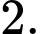
c) Đúng. Giá trị nhỏ nhất của hàm số trên đoạn 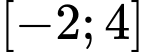 bằng
bằng 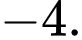
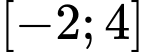 bằng
bằng 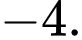
d) Đúng. Hàm số đạt giá trị nhỏ nhất trên đoạn 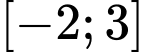 tại điểm
tại điểm 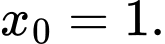
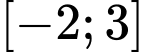 tại điểm
tại điểm 
Câu 13 [377584]: Cho hàm số 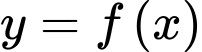 có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau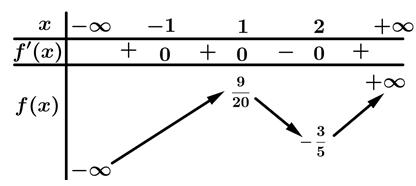
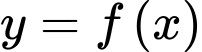 có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
A, a) Hàm số đồng biến trên khoảng 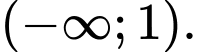
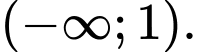
B, b) Hàm số đạt cực đại tại 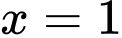 và đạt cực tiểu tại
và đạt cực tiểu tại 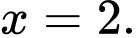
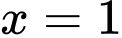 và đạt cực tiểu tại
và đạt cực tiểu tại 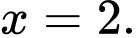
C, c) Hàm số có 3 cực trị.
D, d) Hàm số có giá trị lớn nhất bằng 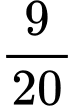 và giá trị nhỏ nhất bằng
và giá trị nhỏ nhất bằng 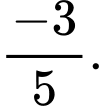
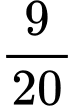 và giá trị nhỏ nhất bằng
và giá trị nhỏ nhất bằng 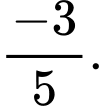
a) Đúng. Hàm số đồng biến trên khoảng 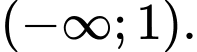
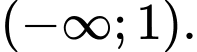
b) Đúng. Hàm số đạt cực đại tại 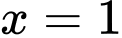 và đạt cực tiểu tại
và đạt cực tiểu tại 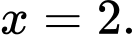
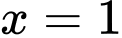 và đạt cực tiểu tại
và đạt cực tiểu tại 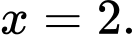
c) Sai. Hàm số có 2 cực trị.
d) Sai. Hàm số không có giá tri lớn nhất và giá trị nhỏ nhất.
Câu 14 [377585]: Cho hàm số 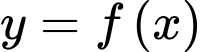 có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau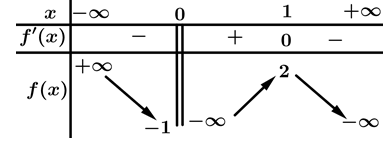
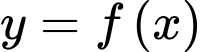 có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
A, a) Hàm số đã cho có hai điểm cực trị.
B, b) 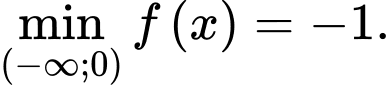
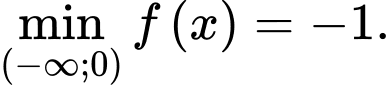
C, c) 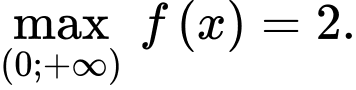
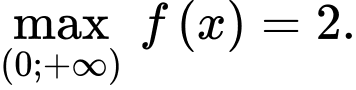
D, d) 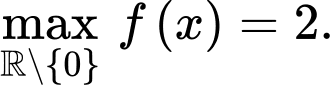
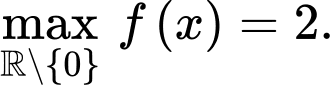
a) Sai. Hàm số đã cho có 1 điểm cực trị.&
b) Sai. Hàm số không có giá trị nhỏ nhất trên khoảng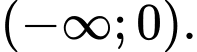
c) Đúng.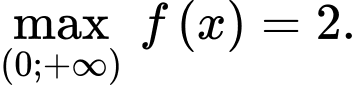
d) Sai. Hàm số không có giá trị lớn nhất trên tập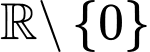
b) Sai. Hàm số không có giá trị nhỏ nhất trên khoảng
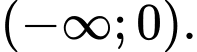
c) Đúng.
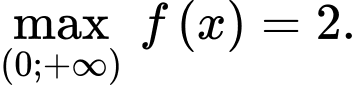
d) Sai. Hàm số không có giá trị lớn nhất trên tập
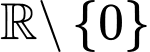
Câu 15 [377586]: Cho hàm số 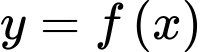 xác định, liên tục trên
xác định, liên tục trên 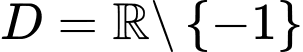 và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau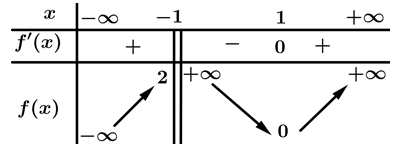
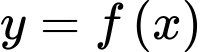 xác định, liên tục trên
xác định, liên tục trên 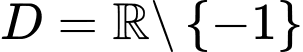 và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các mệnh đề sau
A, a) Hàm số đã cho đạt cực tiểu tại 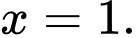
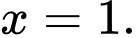
B, b) Hàm số đã cho đạt cực đại tại điểm 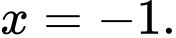
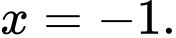
C, c) 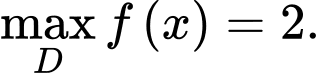
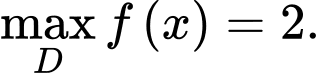
D, d) 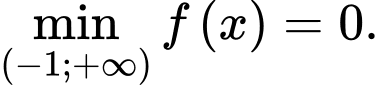
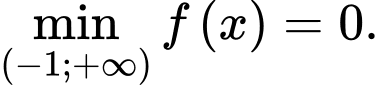
a) Đúng. Hàm số đã cho đạt cực tiểu tại 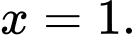
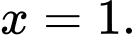
b) Sai. Hàm số không xác định tại 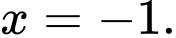
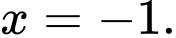
c) Sai. Hàm số không có giá trị lớn nhất.
d) Đúng. 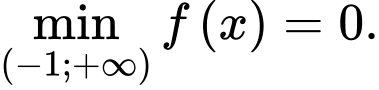
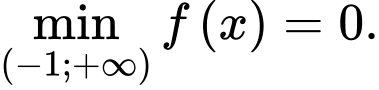
Câu 16 [135942]: Giá trị nhỏ nhất của hàm số $y = {x^3} + 2{x^2} - 7x$ trên đoạn $\left[ {0;4} \right]$ bằng
Ta có: $y={{x}^{3}}+2{{x}^{2}}-7x=0$
${y}'=3{{x}^{2}}+4x-7$
${y}'=3{{x}^{2}}+4x-7$
$\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=\frac{-7}{3} (L) \\ \end{align} \right.$
Lại có: $f\left( 0 \right)=0$; $f\left( 4 \right)=68$;$f\left( 1 \right)=-4$
$\underset{x\in [0;4]}{\mathop{Max}}\,y=68$; $\underset{x\in \left[ 0;4 \right]}{\mathop{Min}}\,y=-4$
Đáp án: D
Câu 17 [322505]: Giá trị lớn nhất của hàm số $y={{x}^{4}}-4{{x}^{2}}+5$ trên đoạn $\left[ -2;3 \right]$ bằng
Ta có $y' = 4{x^3} - 8x,\,y' = 0$$ \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \pm \sqrt 2
\end{array} \right..$
Mặt khác $f\left( 0 \right) = 5;\,f\left( {\sqrt 2 } \right) = 1\,;$$f\left( { - \sqrt 2 } \right) = 1;\,f\left( { - 2} \right) = 5;\,f\left( 3 \right) = 50$
Do đó giá trị lớn nhất của hàm số là $50$ khi $x = 3.$ Chọn A.
Đáp án: A
x = 0\\
x = \pm \sqrt 2
\end{array} \right..$
Mặt khác $f\left( 0 \right) = 5;\,f\left( {\sqrt 2 } \right) = 1\,;$$f\left( { - \sqrt 2 } \right) = 1;\,f\left( { - 2} \right) = 5;\,f\left( 3 \right) = 50$
Do đó giá trị lớn nhất của hàm số là $50$ khi $x = 3.$ Chọn A.
Đáp án: A
Câu 18 [395583]: Giá trị lớn nhất của hàm số $ f\left( x \right) = - {x^4} + 6{x^2} - 4$ bằng
$ f\left( x \right) = - {x^4} + 6{x^2} - 4$
TXĐ: $ D=\mathbb{R}.$
$ f'\left( x \right) = - 4{x^3} + 12{x} = 0$ $ \Leftrightarrow \left[ \begin{array}{l} x = \pm \sqrt 3; x = 0 \end{array} \right..$
Bảng biến thiên:
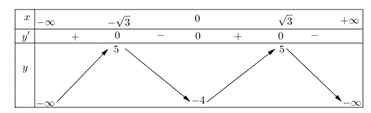
Từ bảng biến thiên suy ra: Giá trị lớn nhất của hàm số $ f\left( x \right)$ bằng $ 5.$
Đáp án: C $ f'\left( x \right) = - 4{x^3} + 12{x} = 0$ $ \Leftrightarrow \left[ \begin{array}{l} x = \pm \sqrt 3; x = 0 \end{array} \right..$
Bảng biến thiên:

Từ bảng biến thiên suy ra: Giá trị lớn nhất của hàm số $ f\left( x \right)$ bằng $ 5.$