Đáp án Bài tập tự luyện số 3
Câu 1 [33123]: Giá trị lớn nhất của hàm số 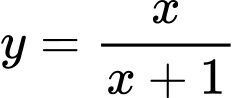 trên đoạn
trên đoạn 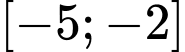 là
là
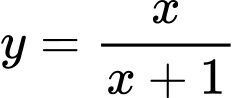 trên đoạn
trên đoạn 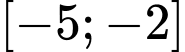 là
là A, 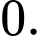
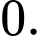
B, 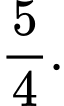
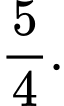
C, 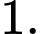
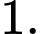
D, 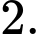
Ta có: 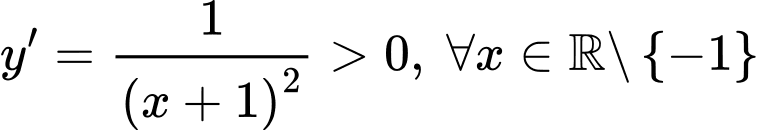
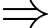 Hàm số đồng biến trên đoạn
Hàm số đồng biến trên đoạn 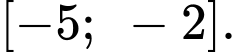 Đáp án: D
Đáp án: D
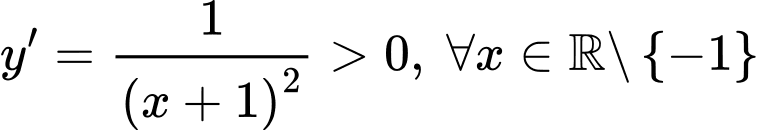
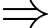 Hàm số đồng biến trên đoạn
Hàm số đồng biến trên đoạn 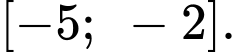
Suy ra 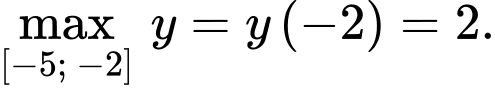
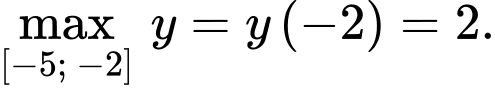
Chọn D.
Câu 2 [29324]: Cho hàm số 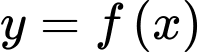 có đạo hàm
có đạo hàm 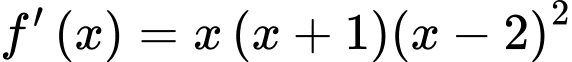 với mọi
với mọi 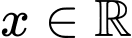 . Giá trị nhỏ nhất của hàm số
. Giá trị nhỏ nhất của hàm số 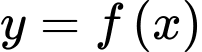 trên đoạn
trên đoạn 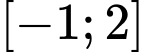 là
là
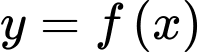 có đạo hàm
có đạo hàm 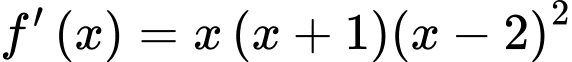 với mọi
với mọi 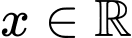 . Giá trị nhỏ nhất của hàm số
. Giá trị nhỏ nhất của hàm số 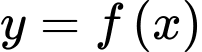 trên đoạn
trên đoạn 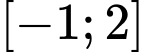 là
là A, 

B, 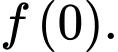
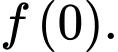
C, 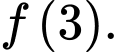
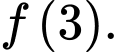
D, 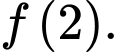
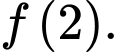
Ta có: 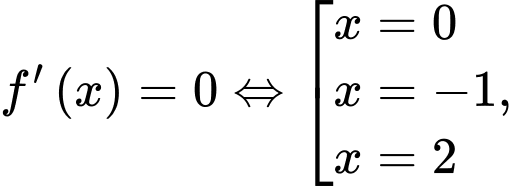 chú ý
chú ý 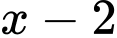 là nghiệm kép của
là nghiệm kép của 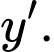
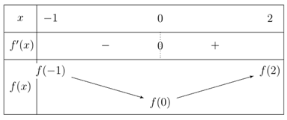
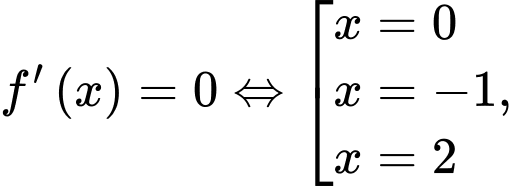 chú ý
chú ý 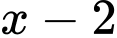 là nghiệm kép của
là nghiệm kép của 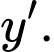
Ta có bảng biến thiên của hàm số trên đoạn 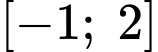
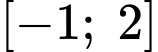

Suy ra 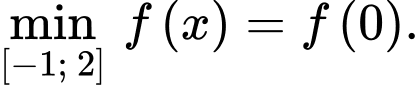
Đáp án: B 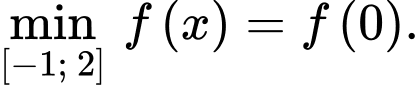
Câu 3 [310357]: Giá trị nhỏ nhất của hàm số 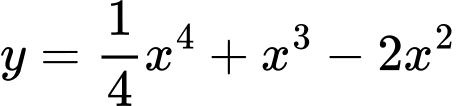 trên đoạn
trên đoạn 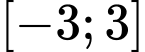 bằng
bằng
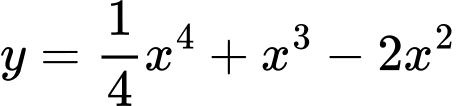 trên đoạn
trên đoạn 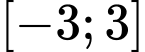 bằng
bằng A, 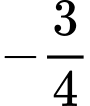 .
.
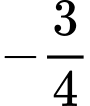 .
.B, 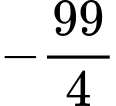 .
.
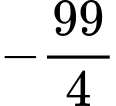 .
.C, 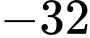 .
.
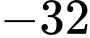 .
.D, 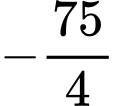 .
.
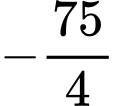 .
.
Đáp án B. 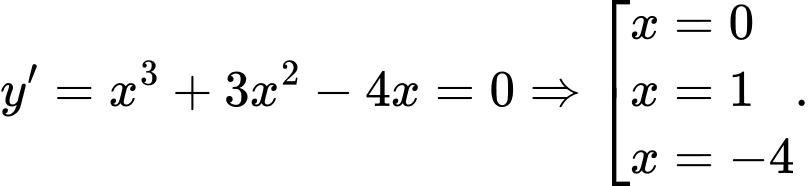
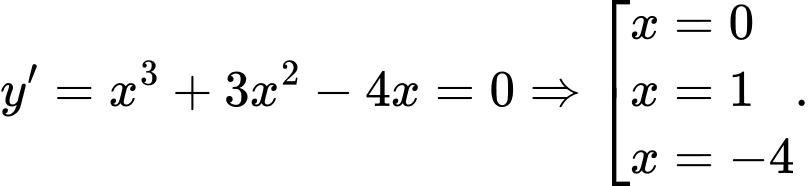
So sánh 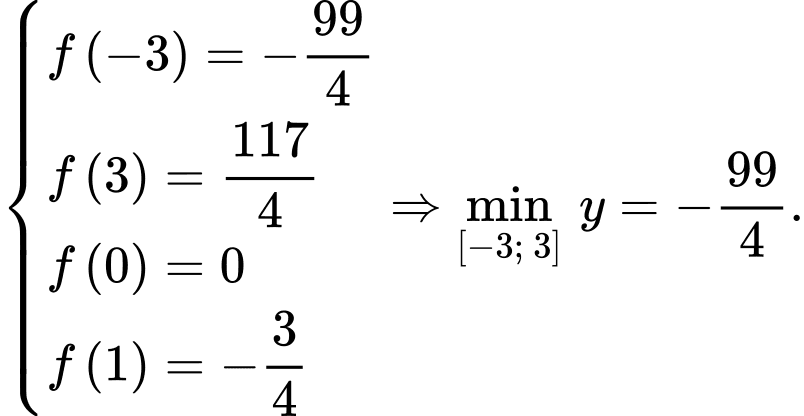
Đáp án: B 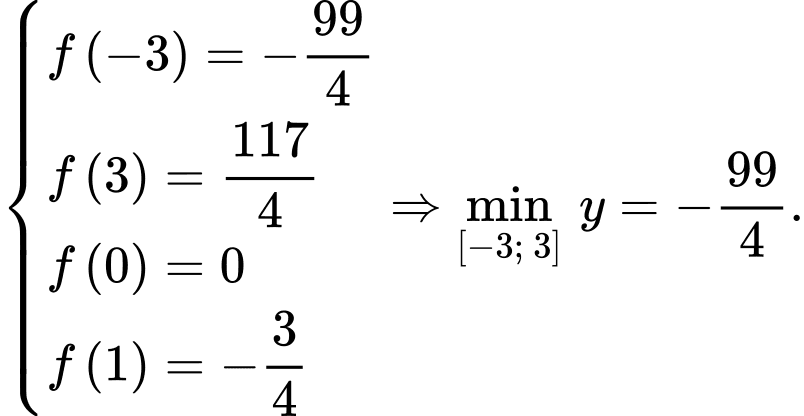
Câu 4 [33143]: Giá trị lớn nhất của hàm số 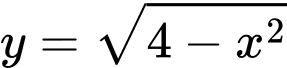 là
là
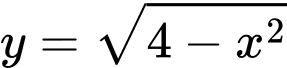 là
là A, 2.
B, 3.
C, 4.
D, 5.
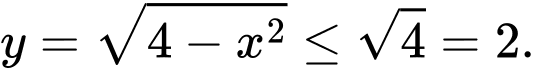 Chọn A Đáp án: A
Chọn A Đáp án: A
Câu 5 [33137]: Cho hàm số 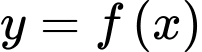 xác định và liên tục trên
xác định và liên tục trên 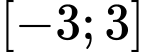 . Đồ thị hàm số
. Đồ thị hàm số 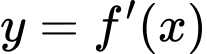 như hình vẽ.
như hình vẽ.
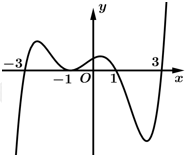
Hỏi hàm số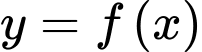 đạt giá trị lớn nhất trên đoạn
đạt giá trị lớn nhất trên đoạn 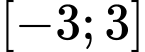 tại điểm
tại điểm 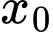 nào dưới đây?
nào dưới đây?
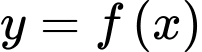 xác định và liên tục trên
xác định và liên tục trên 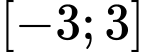 . Đồ thị hàm số
. Đồ thị hàm số 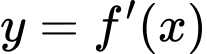 như hình vẽ.
như hình vẽ.
Hỏi hàm số
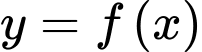 đạt giá trị lớn nhất trên đoạn
đạt giá trị lớn nhất trên đoạn 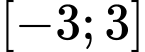 tại điểm
tại điểm 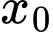 nào dưới đây?
nào dưới đây? A, 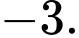
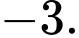
B, 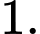
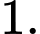
C, 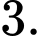
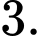
D, 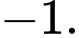
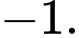
Đáp án B. 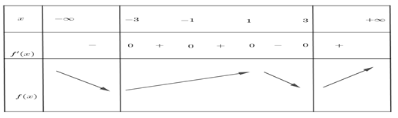
Từ đồ thị của hàm số 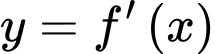 ta suy ra được bảng biến thiên của hàm số
ta suy ra được bảng biến thiên của hàm số 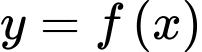
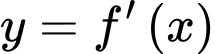 ta suy ra được bảng biến thiên của hàm số
ta suy ra được bảng biến thiên của hàm số 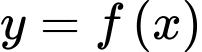

Dựa vào bảng biến thiên ta nhận thây hàm số 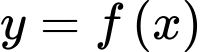 đạt giá trị lớn nhất trên đoạn
đạt giá trị lớn nhất trên đoạn 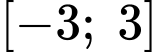 tại
tại 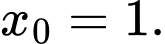
Đáp án: B 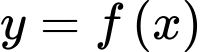 đạt giá trị lớn nhất trên đoạn
đạt giá trị lớn nhất trên đoạn 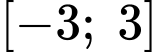 tại
tại 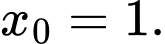
Câu 6 [31723]: Cho hàm số 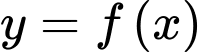 liên tục trên đoạn
liên tục trên đoạn 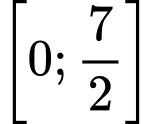 có đồ thị hàm số
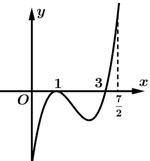
có đồ thị hàm số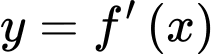 như hình vẽ bên dưới. Hàm số
như hình vẽ bên dưới. Hàm số 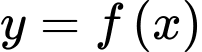 đạt giá trị nhỏ nhất trên đoạn
đạt giá trị nhỏ nhất trên đoạn 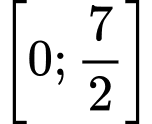 tại điểm
tại điểm 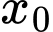 nào dưới đây?
nào dưới đây?
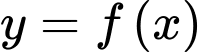 liên tục trên đoạn
liên tục trên đoạn 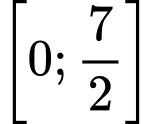 có đồ thị hàm số
có đồ thị hàm số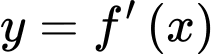 như hình vẽ bên dưới. Hàm số
như hình vẽ bên dưới. Hàm số 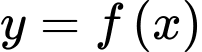 đạt giá trị nhỏ nhất trên đoạn
đạt giá trị nhỏ nhất trên đoạn 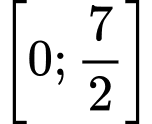 tại điểm
tại điểm 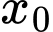 nào dưới đây?
nào dưới đây?
A, 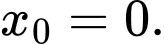
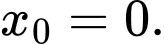
B, 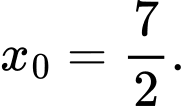
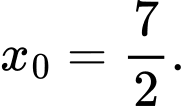
C, 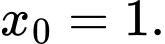
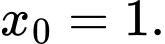
D, 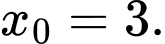
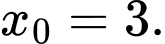
Đáp án D
Dựa vào BBT ta có: và
và 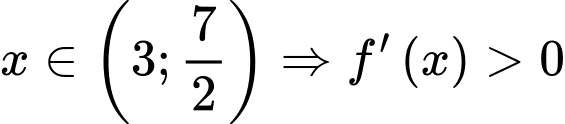
Ta có BBT sau:
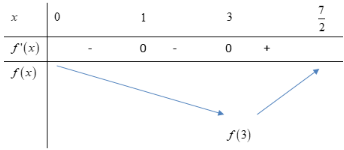
Vậy hàm số đạt giá trị nhỏ nhất là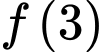 tại điểm
tại điểm 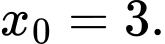 Đáp án: D
Đáp án: D
Dựa vào BBT ta có:
 và
và 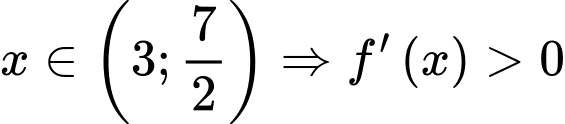
Ta có BBT sau:

Vậy hàm số đạt giá trị nhỏ nhất là
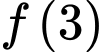 tại điểm
tại điểm 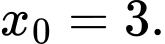 Đáp án: D
Đáp án: D
Câu 7 [503737]: Gọi 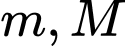 lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 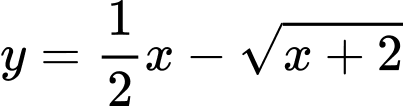 trên đoạn
trên đoạn 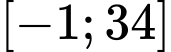 . Tính tổng
. Tính tổng 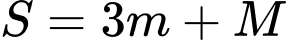
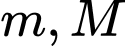 lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 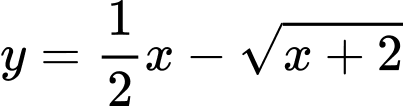 trên đoạn
trên đoạn 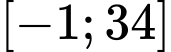 . Tính tổng
. Tính tổng 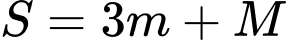
A, 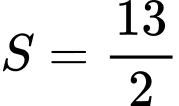 .
.
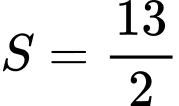 .
.B, 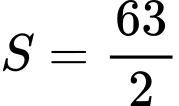 .
.
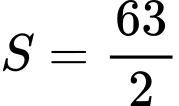 .
.C, 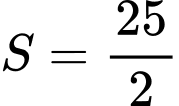 .
.
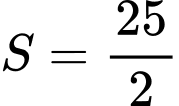 .
.D, 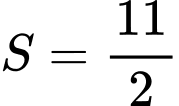 .
.
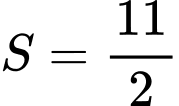 .
.
Chọn A
Ta có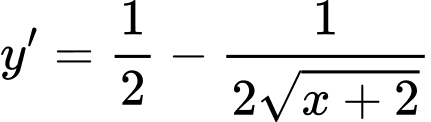
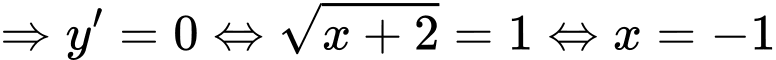
Khi đó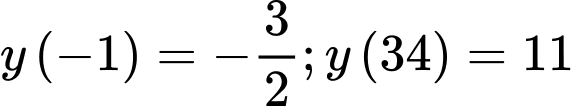
Vậy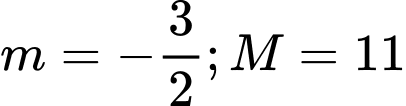 , khi đó
, khi đó 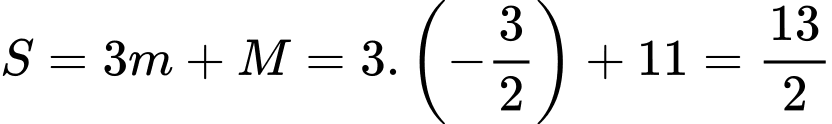 . Đáp án: A
. Đáp án: A
Ta có
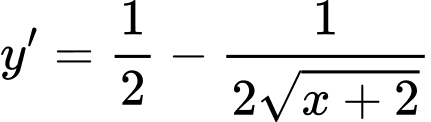
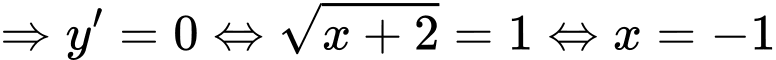
Khi đó
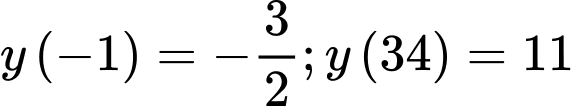
Vậy
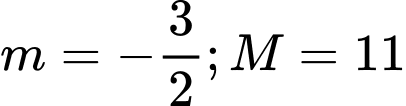 , khi đó
, khi đó 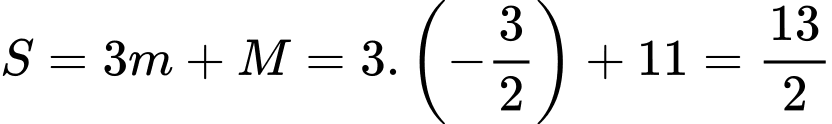 . Đáp án: A
. Đáp án: A
Câu 8 [306867]: Gọi 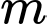 ,
, 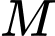 lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 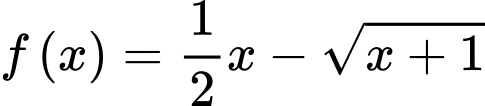 trên đoạn
trên đoạn 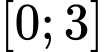 . Tính tổng
. Tính tổng 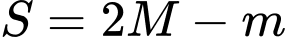 .
.
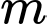 ,
, 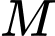 lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 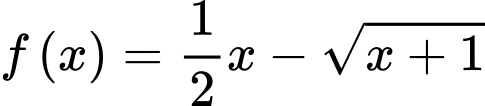 trên đoạn
trên đoạn 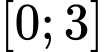 . Tính tổng
. Tính tổng 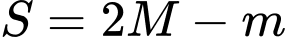 .
. A, 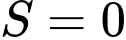 .
.
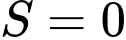 .
.B, 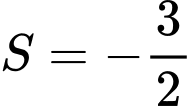 .
.
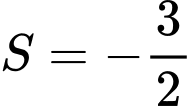 .
.C, 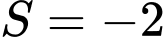 .
.
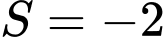 .
.D, 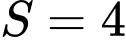 .
.
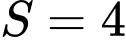 .
.
Ta có: 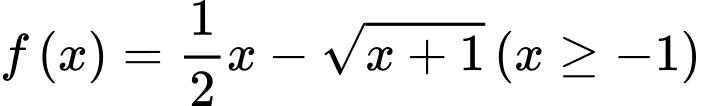
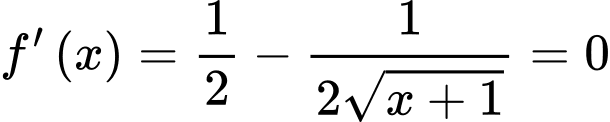
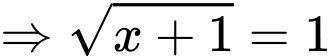
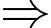
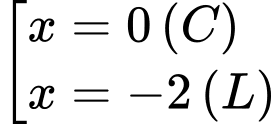
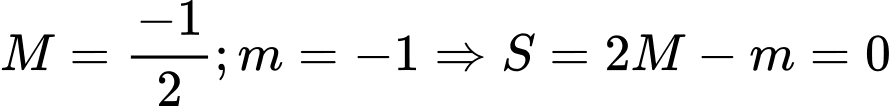 Đáp án: A
Đáp án: A
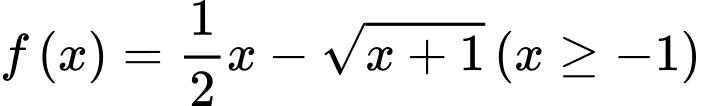
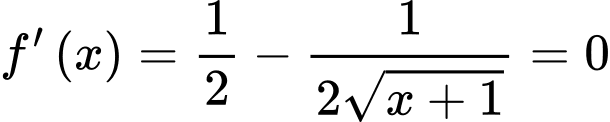
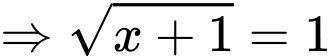
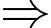
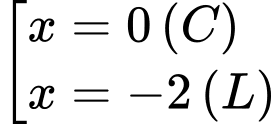
Lại có: 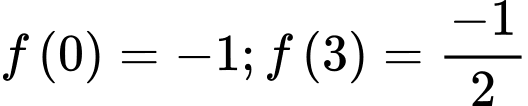
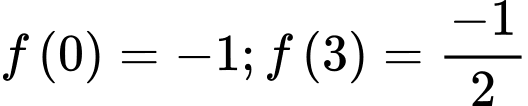
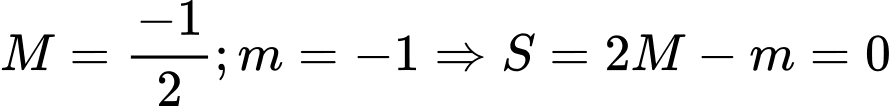
Câu 9 [32864]: Giá trị lớn nhất của hàm số 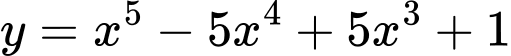 trên đoạn
trên đoạn 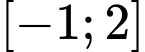 bằng
bằng
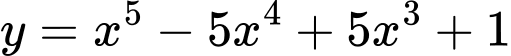 trên đoạn
trên đoạn 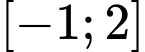 bằng
bằng A, 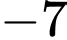 .
.
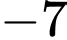 .
.B, 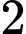 .
.
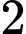 .
.C, 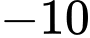 .
.
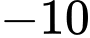 .
.D, 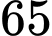 .
.
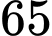 .
.
Đáp án B. 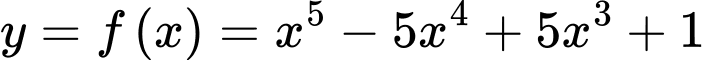 suy ra
suy ra 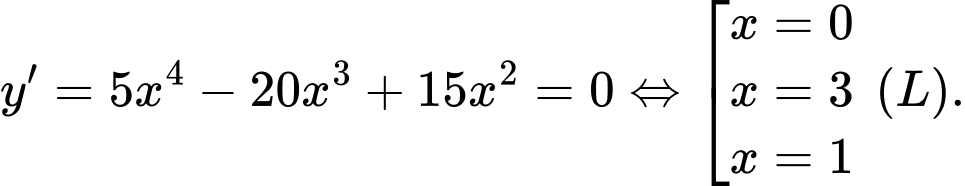
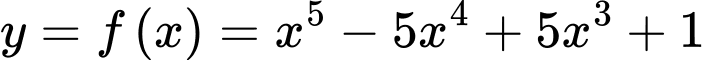 suy ra
suy ra 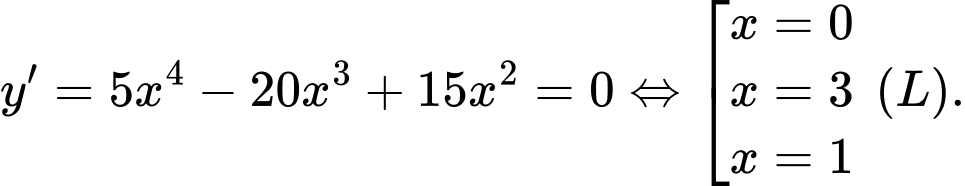
So sánh 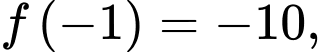
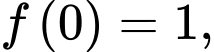
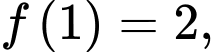
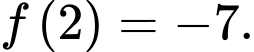 Vậy
Vậy 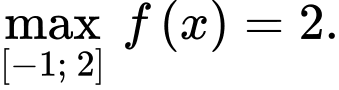
Đáp án: B 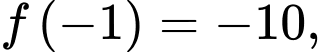
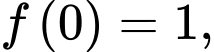
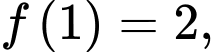
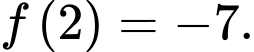 Vậy
Vậy 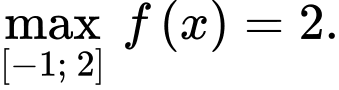
Câu 10 [33108]: Giá trị nhỏ nhất của hàm số 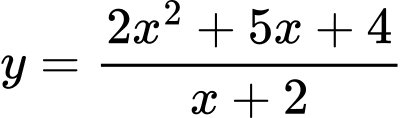 trên đoạn
trên đoạn 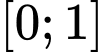 là
là
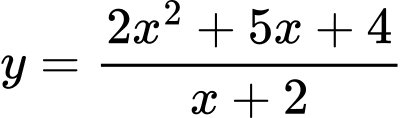 trên đoạn
trên đoạn 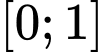 là
là A, 2.
B, 3.
C, 4.
D, 5.
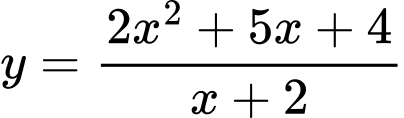
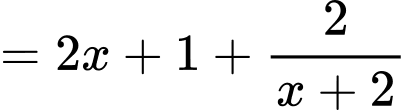
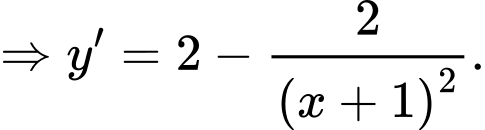
rên
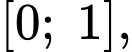 hàm số đồng biến nên min là
hàm số đồng biến nên min là 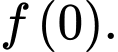
Chọn A. Đáp án: A
Câu 11 [338464]: Giá trị lớn nhất của hàm số 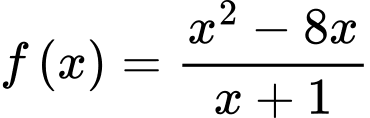 trên đoạn
trên đoạn 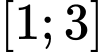 bằng
bằng
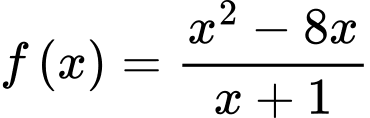 trên đoạn
trên đoạn 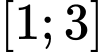 bằng
bằng A, 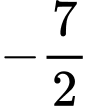 .
.
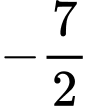 .
.B, 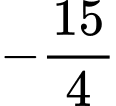 .
.
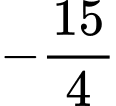 .
.C, 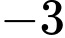 .
.
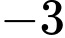 .
.D, 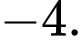
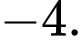
Chọn A
+)Ta có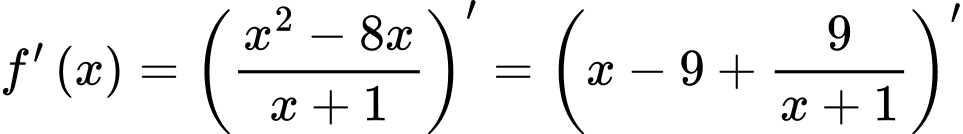
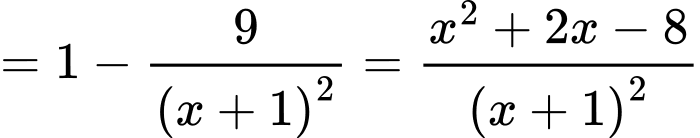 .
.
+)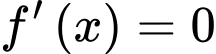
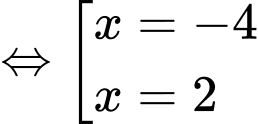 , xét trên đoạn
, xét trên đoạn 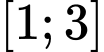 ta chọn
ta chọn 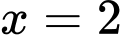 .
.
+)Ta có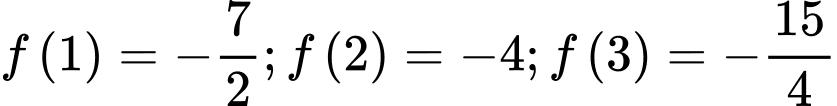 . Suy ra giá trị lớn nhất của hàm số bằng
. Suy ra giá trị lớn nhất của hàm số bằng 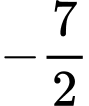 . Đáp án: A
. Đáp án: A
+)Ta có
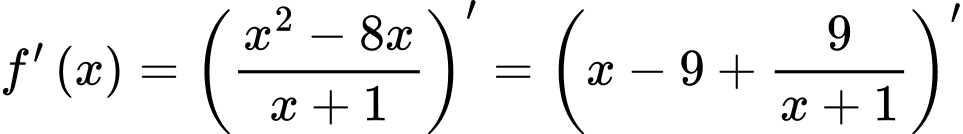
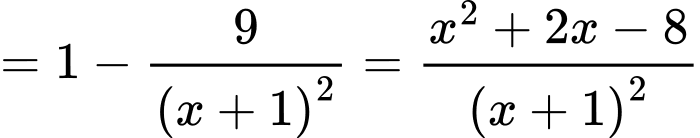 .
.+)
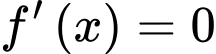
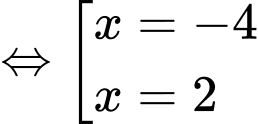 , xét trên đoạn
, xét trên đoạn 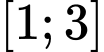 ta chọn
ta chọn 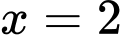 .
.+)Ta có
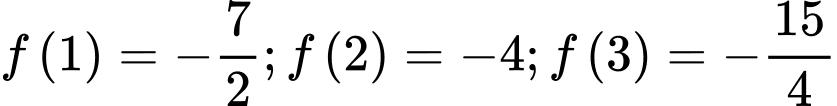 . Suy ra giá trị lớn nhất của hàm số bằng
. Suy ra giá trị lớn nhất của hàm số bằng 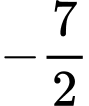 . Đáp án: A
. Đáp án: A
Câu 12 [33115]: Giá trị nhỏ nhất của hàm số 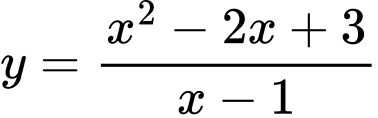 với
với 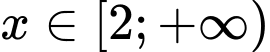 là
là
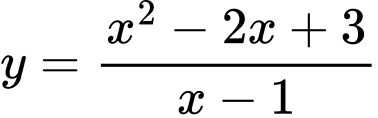 với
với 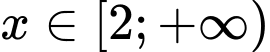 là
là A, 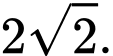
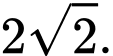
B, 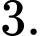
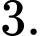
C, 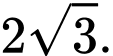
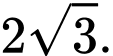
D, 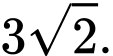
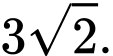
Có: 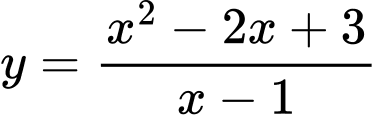
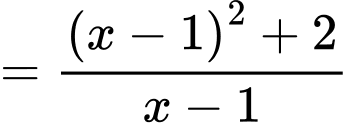
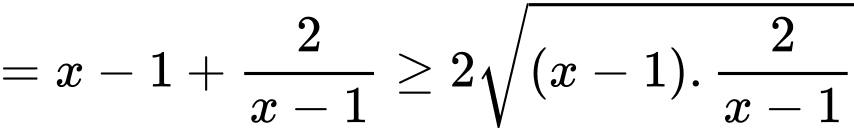
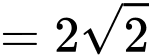
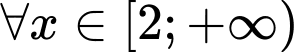
Vậy giá trị nhỏ nhất của hàm số đã cho là: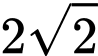 khi
khi 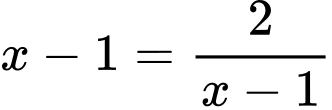
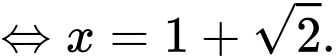 Đáp án: A
Đáp án: A
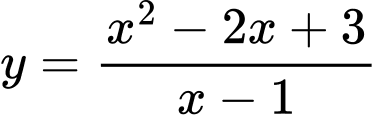
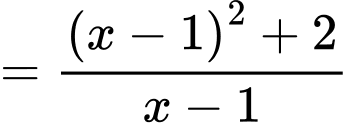
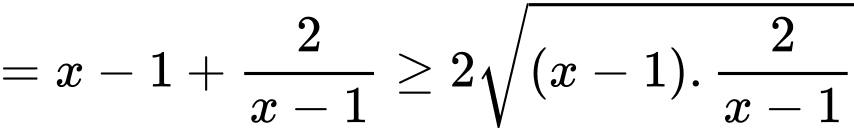
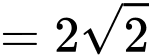
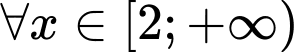
Vậy giá trị nhỏ nhất của hàm số đã cho là:
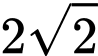 khi
khi 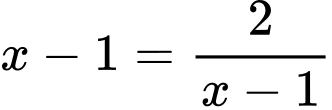
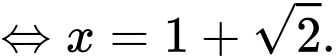 Đáp án: A
Đáp án: A
Câu 13 [28160]: Gọi 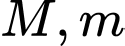 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 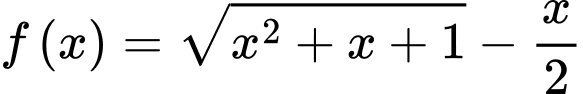 trên đoạn
trên đoạn 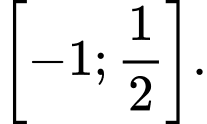 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
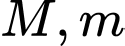 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 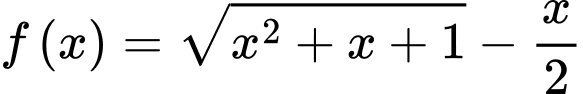 trên đoạn
trên đoạn 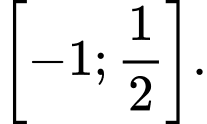 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai? A, 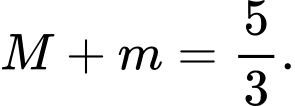
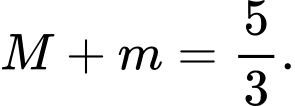
B, 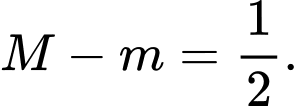
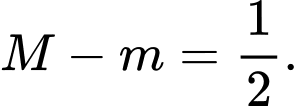
C, 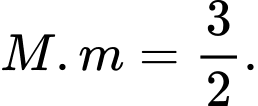
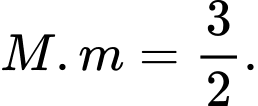
D, 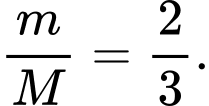
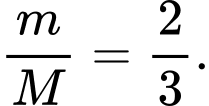
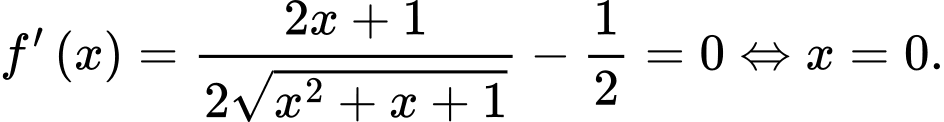
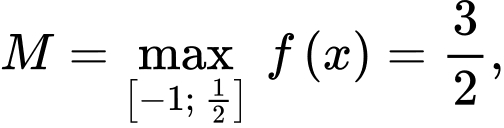
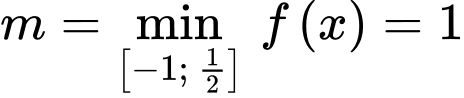
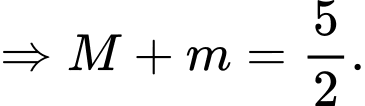
Chọn A.
Đáp án: A
Câu 14 [31631]: Cho hàm số 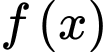 có đạo hàm là
có đạo hàm là 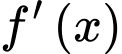 . Đồ thị của hàm số
. Đồ thị của hàm số 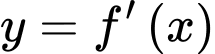 được cho như hình vẽ bên. Biết rằng
được cho như hình vẽ bên. Biết rằng 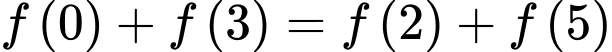 . Giá trị nhỏ nhất và giá trị lớn nhất của
. Giá trị nhỏ nhất và giá trị lớn nhất của 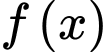 trên đoạn
trên đoạn 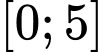 lần lượt là
lần lượt là
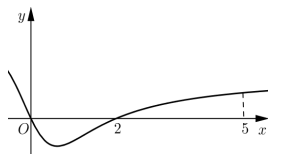
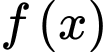 có đạo hàm là
có đạo hàm là 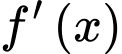 . Đồ thị của hàm số
. Đồ thị của hàm số 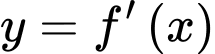 được cho như hình vẽ bên. Biết rằng
được cho như hình vẽ bên. Biết rằng 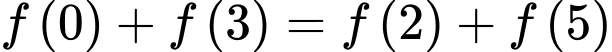 . Giá trị nhỏ nhất và giá trị lớn nhất của
. Giá trị nhỏ nhất và giá trị lớn nhất của 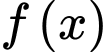 trên đoạn
trên đoạn 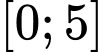 lần lượt là
lần lượt là
A, 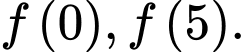
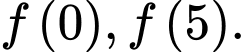
B, 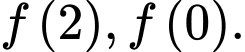
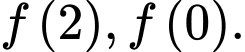
C, 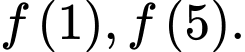
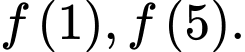
D, 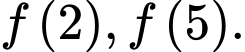
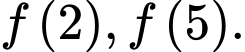
Từ đồ thị 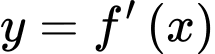 trên đoạn
trên đoạn 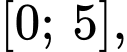 ta có bảng biến thiên của hàm số
ta có bảng biến thiên của hàm số 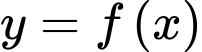 như hình vẽ sau.
như hình vẽ sau. 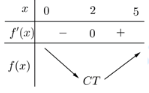
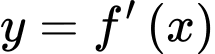 trên đoạn
trên đoạn 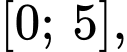 ta có bảng biến thiên của hàm số
ta có bảng biến thiên của hàm số 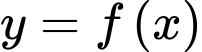 như hình vẽ sau.
như hình vẽ sau. 
Suy ra 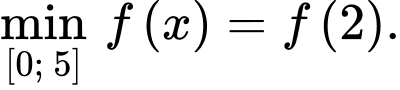
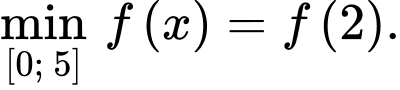
Từ giả thiết, ta có 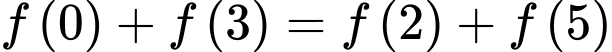
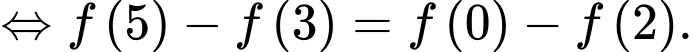
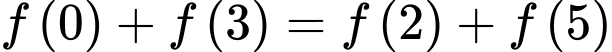
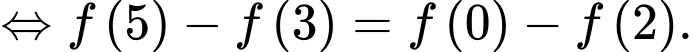
Hàm số 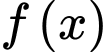 đồng biến trên
đồng biến trên 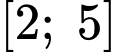
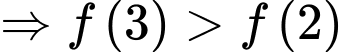
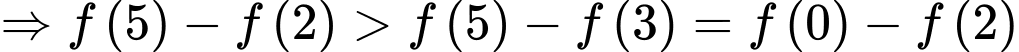

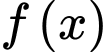 đồng biến trên
đồng biến trên 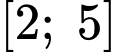
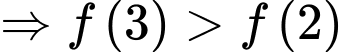
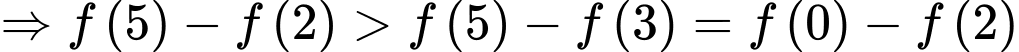

Suy ra 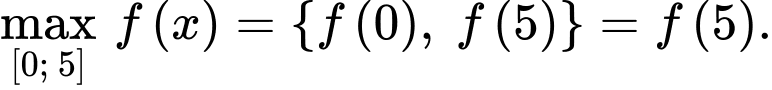
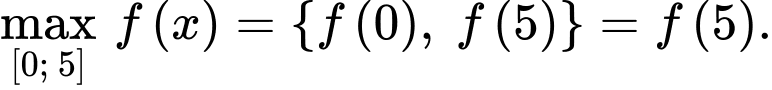
Chọn D
Đáp án: D
Câu 15 [377589]: Cho hàm số 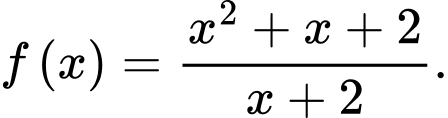 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
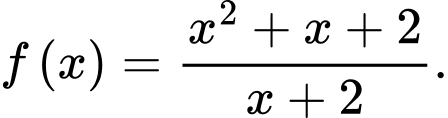 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) Hàm số 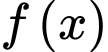 đồng biến trên mỗi khoảng xác định.
đồng biến trên mỗi khoảng xác định.
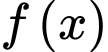 đồng biến trên mỗi khoảng xác định.
đồng biến trên mỗi khoảng xác định.B, b) Hàm số 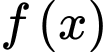 có hai điểm cực trị.
có hai điểm cực trị.
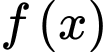 có hai điểm cực trị.
có hai điểm cực trị.C, c) Giá trị lớn nhất của hàm số bằng 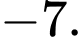
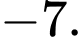
D, d) Hàm số 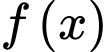 không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
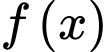 không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
Ta có:
TXĐ: 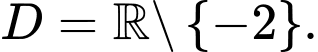
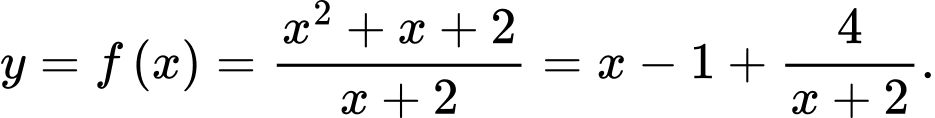
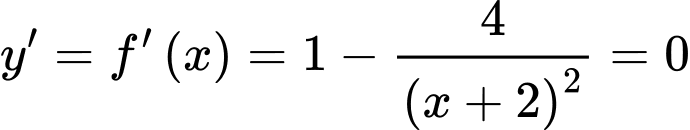

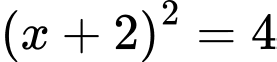

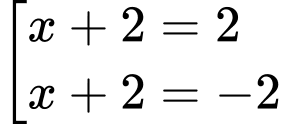

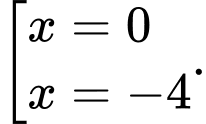
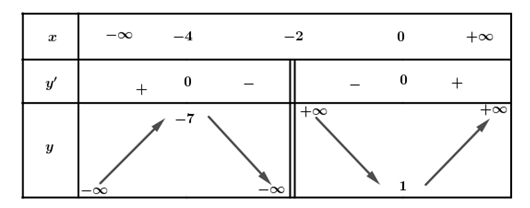
a) Sai. Hàm số 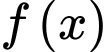 đồng biến trên
đồng biến trên 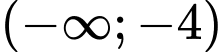 và
và 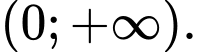
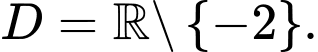
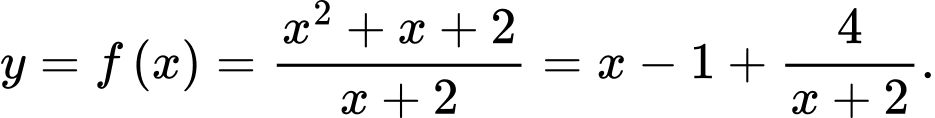
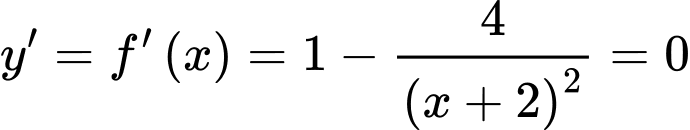

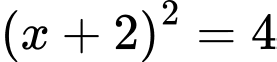

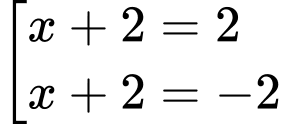

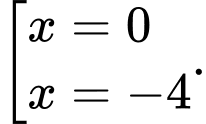
Bảng biến thiên:

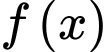 đồng biến trên
đồng biến trên 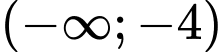 và
và 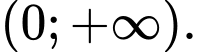
b) Đúng. Hàm số 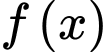 có hai điểm cực trị
có hai điểm cực trị 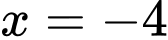 và
và 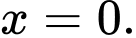
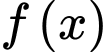 có hai điểm cực trị
có hai điểm cực trị 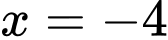 và
và 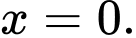
c) Sai. Hàm số không có giá trị lớn nhất.
d) Đúng. Hàm số 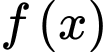 không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
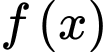 không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
không có giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
Câu 16 [377590]: Cho hàm số 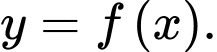 Đồ thị hàm số
Đồ thị hàm số 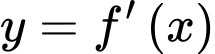 trên đoạn
trên đoạn 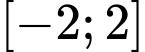 là đường cong trong hình vẽ. Biết rằng
là đường cong trong hình vẽ. Biết rằng 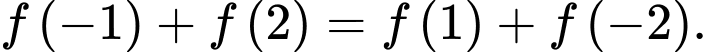 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau: 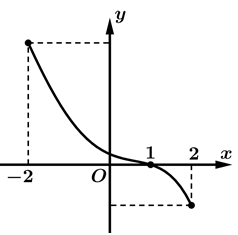
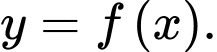 Đồ thị hàm số
Đồ thị hàm số 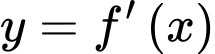 trên đoạn
trên đoạn 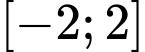 là đường cong trong hình vẽ. Biết rằng
là đường cong trong hình vẽ. Biết rằng 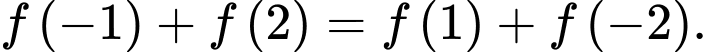 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau: 
A, a) 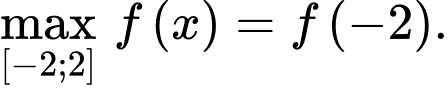
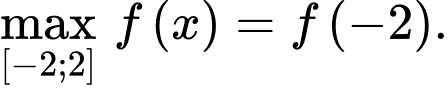
B, b) 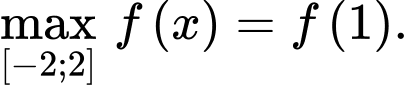
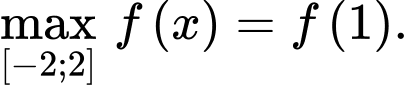
C, c) 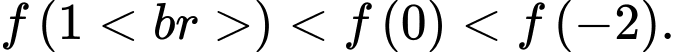
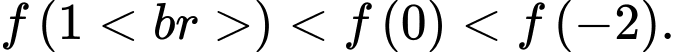
D, d) 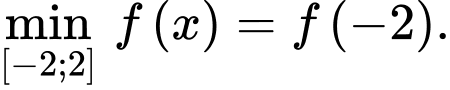
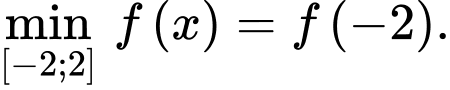
a, Sai b, Đúng c, Sai d, Đúng
Từ đồ thị ta có bảng biến thiên
Từ đồ thị ta có bảng biến thiên
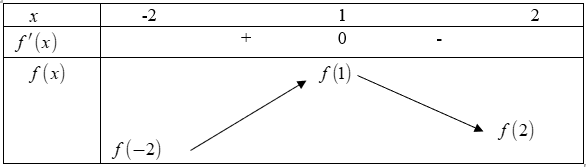
Từ bảng biến thiên có
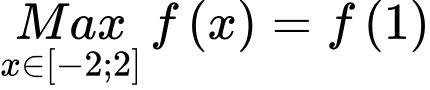
Hàm số đồng biến trên đoạn 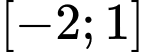 nên
nên 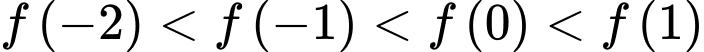 .
.
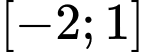 nên
nên 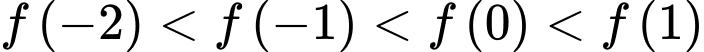 .
. Suy ra 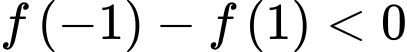
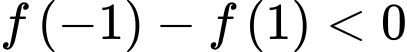
Lại có:
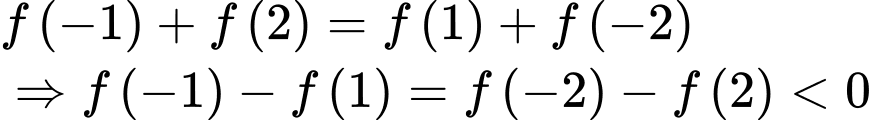
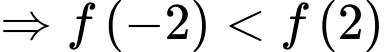
Suy ra 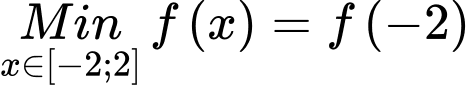
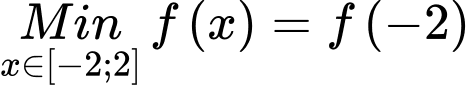
Câu 17 [378926]: Cho hàm số 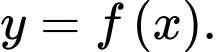 Đồ thị hàm số
Đồ thị hàm số 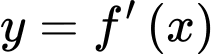 trên đoạn
trên đoạn 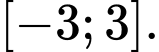 là đường cong trong hình vẽ.Biết rằng
là đường cong trong hình vẽ.Biết rằng 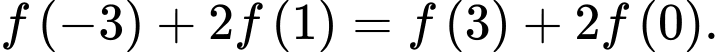 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau: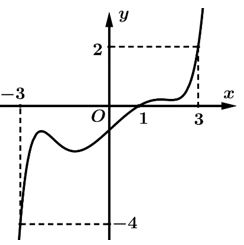
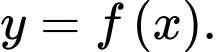 Đồ thị hàm số
Đồ thị hàm số 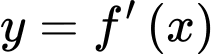 trên đoạn
trên đoạn 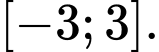 là đường cong trong hình vẽ.Biết rằng
là đường cong trong hình vẽ.Biết rằng 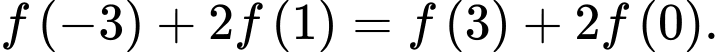 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau:
A, a) 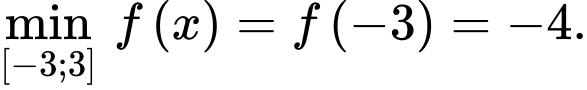
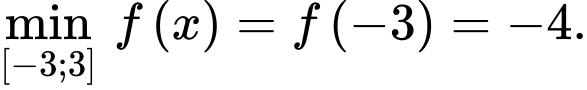
B, b) 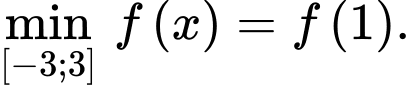
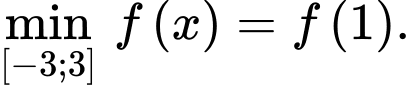
C, c) 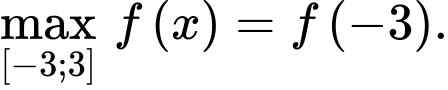
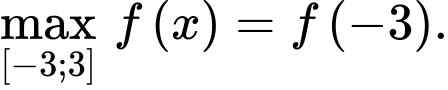
D, d) 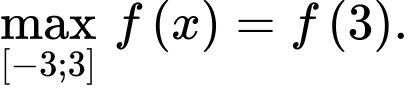
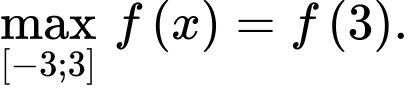
a) Sai, b) Đúng, C) Đúng, d) Sai
Từ đồ thị ta có bảng biến thiên
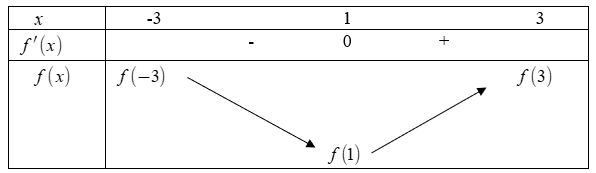
Từ bảng biến thiên có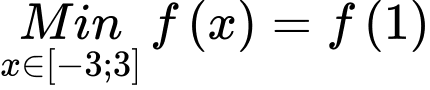
Từ đồ thị ta có bảng biến thiên

Từ bảng biến thiên có
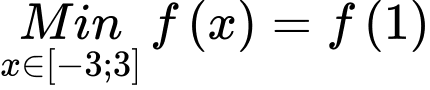
Hàm số đồng biến trên đoạn 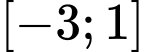 nên
nên 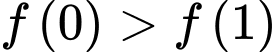 .
.
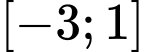 nên
nên 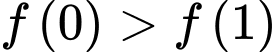 .
. Suy ra 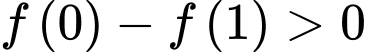
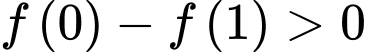
Lại có:
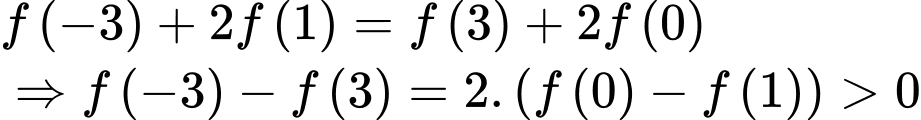
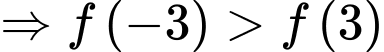
Suy ra
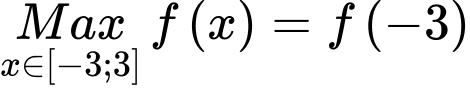
Câu 18 [28153]: Gọi $M$ là giá trị lớn nhất và $m$ là giá trị nhỏ nhất của hàm số $y = x\sqrt {1 - {x^2}} .$ Khi đó $M + m$ bằng
HD: TXĐ: $D=\left[ -1;1 \right].$
Ta có: ${y}'=\sqrt{1-{{x}^{2}}}-\dfrac{{{x}^{2}}}{\sqrt{1-{{x}^{2}}}}=0$$\Leftrightarrow \dfrac{1-2{{x}^{2}}}{\sqrt{1-{{x}^{2}}}}=0$$\Leftrightarrow x=\pm \frac{1}{\sqrt{2}}.$
Lại có: $y\left( -1 \right)=y\left( 1 \right)=0;\,\,y\left( -\dfrac{1}{\sqrt{2}} \right)$$=-\dfrac{1}{2};\,\,y\left( \dfrac{1}{\sqrt{2}} \right)$$=\dfrac{1}{2}$$\Rightarrow M+m=-\dfrac{1}{2}+\dfrac{1}{2}=0.$ Đáp án: A
Ta có: ${y}'=\sqrt{1-{{x}^{2}}}-\dfrac{{{x}^{2}}}{\sqrt{1-{{x}^{2}}}}=0$$\Leftrightarrow \dfrac{1-2{{x}^{2}}}{\sqrt{1-{{x}^{2}}}}=0$$\Leftrightarrow x=\pm \frac{1}{\sqrt{2}}.$
Lại có: $y\left( -1 \right)=y\left( 1 \right)=0;\,\,y\left( -\dfrac{1}{\sqrt{2}} \right)$$=-\dfrac{1}{2};\,\,y\left( \dfrac{1}{\sqrt{2}} \right)$$=\dfrac{1}{2}$$\Rightarrow M+m=-\dfrac{1}{2}+\dfrac{1}{2}=0.$ Đáp án: A
Câu 19 [33113]: Tìm giá trị nhỏ nhất của hàm số $y={{x}^{2}}-4x+\frac{54}{x-2}$ trên khoảng $\left( 2;+\infty \right).$
Ta có: ${y}'=2x-4-\frac{54}{{{\left( x-2 \right)}^{2}}}=0\Leftrightarrow {{\left( x-2 \right)}^{3}}=27\Leftrightarrow x=5.$
Đáp án: C
Mặt khác, $\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,y=+\infty ,$ $y\left( 3 \right)=23,$ $\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty .$ Do đó, $\underset{\left[ 2;\ +\infty \right)}{\mathop{\min }}\,y=23.$
Câu 20 [28162]: Gọi 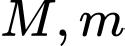 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 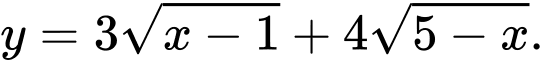 Tính
Tính 
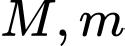 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 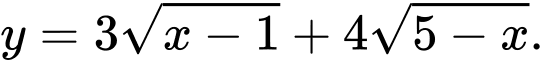 Tính
Tính 
A, 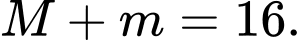
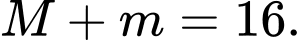
B, 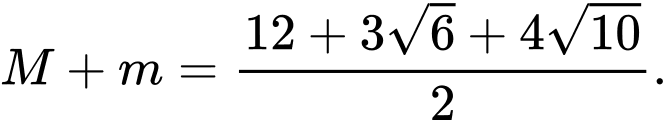
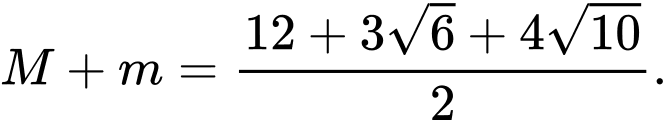
C, 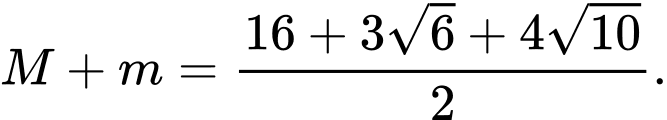
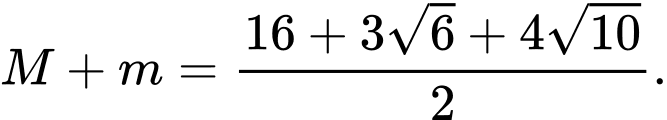
D, 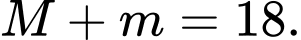
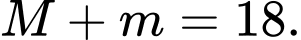
Cách 1:
Hàm số xác định khi và chỉ khi 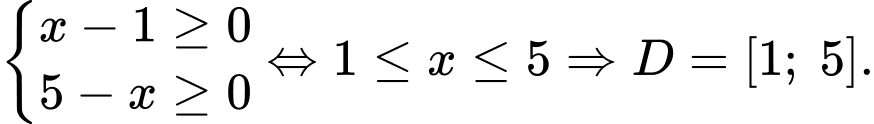
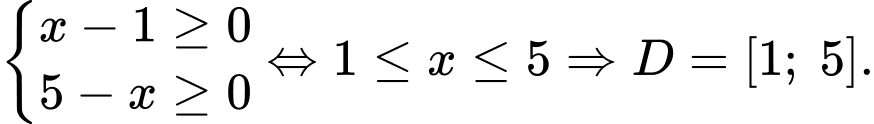
Khi đó, 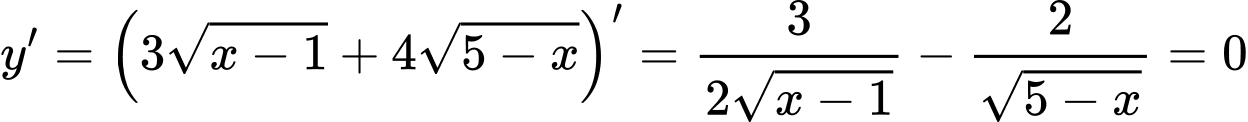
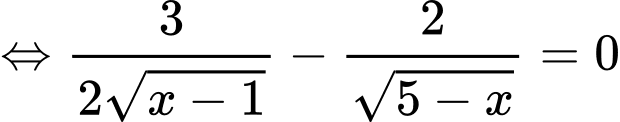
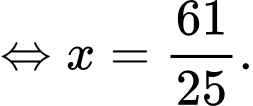
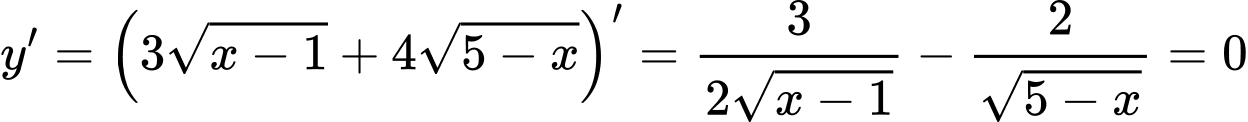
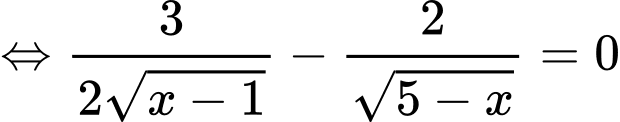
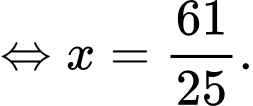
Suy ra, 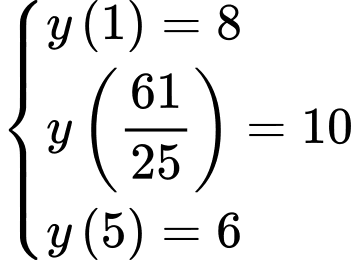
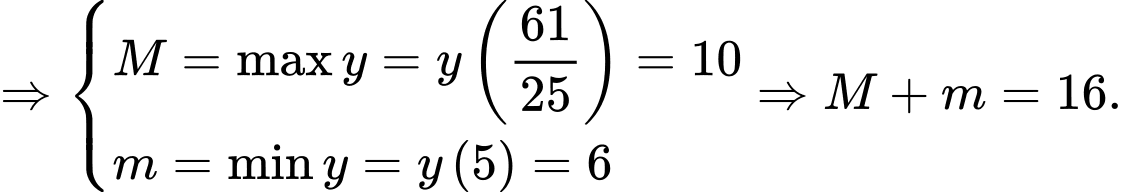 Chọn A.
Chọn A.
Cách 2: Ta có: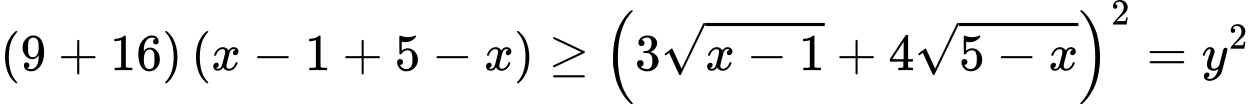 (BĐT Cauchy- Swart)
(BĐT Cauchy- Swart)
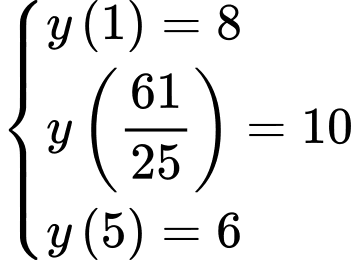
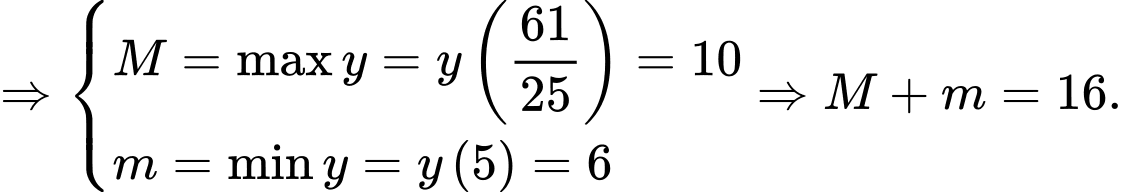 Chọn A.
Chọn A. Cách 2: Ta có:
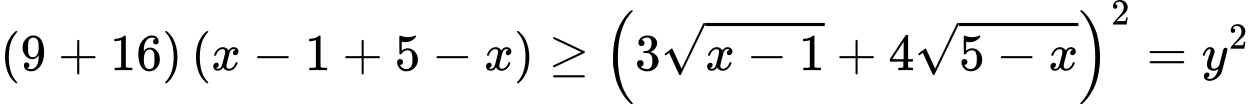 (BĐT Cauchy- Swart)
(BĐT Cauchy- Swart) Do đó, 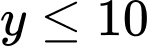 do đó
do đó 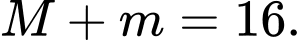 Dấu bằng xảy ra khi
Dấu bằng xảy ra khi 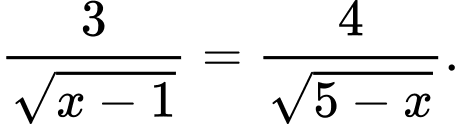
Đáp án: A 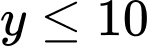 do đó
do đó 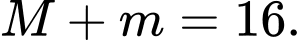 Dấu bằng xảy ra khi
Dấu bằng xảy ra khi