Đáp án Bài tập tự luyện số 2
Câu 1 [185161]: Tiệm cận đứng của đồ thị hàm số 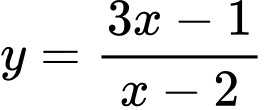 có phương trình là
có phương trình là
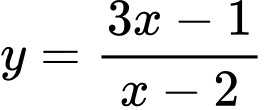 có phương trình là
có phương trình là A, 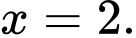
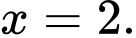
B, 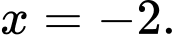
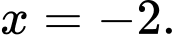
C, 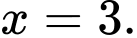
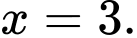
D, 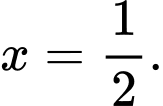
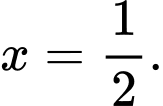
Ta có 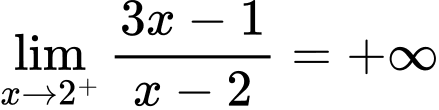 và
và 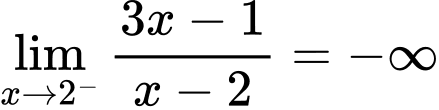 nên tiệm cận đứng của đồ thị hàm số
nên tiệm cận đứng của đồ thị hàm số 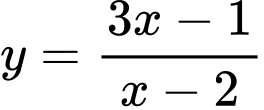 có phương trình là
có phương trình là 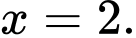 Đáp án: A
Đáp án: A
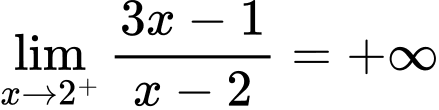 và
và 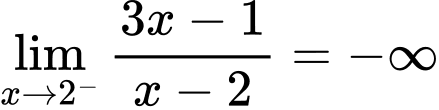 nên tiệm cận đứng của đồ thị hàm số
nên tiệm cận đứng của đồ thị hàm số 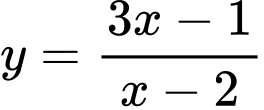 có phương trình là
có phương trình là 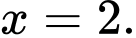 Đáp án: A
Đáp án: A
Câu 2 [975578]: Phương trình đường tiệm cận ngang của đồ thị hàm số 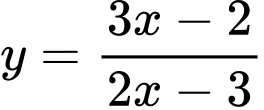 là
là
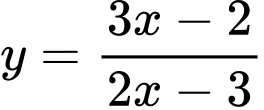 là
là A, 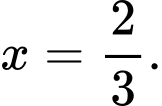
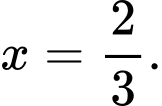
B, 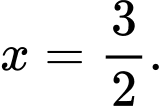
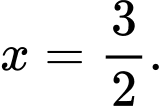
C, 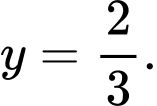
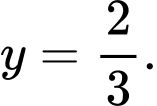
D, 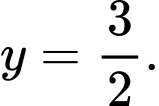
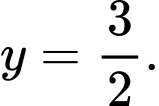
HD: Đồ thị hàm số 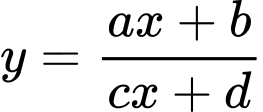 có tiệm cận ngang là
có tiệm cận ngang là 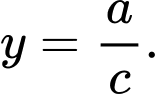 Chọn D. Đáp án: D
Chọn D. Đáp án: D
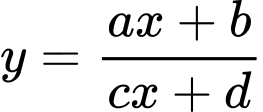 có tiệm cận ngang là
có tiệm cận ngang là 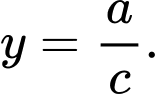 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 3 [513360]: Đồ thị hàm số 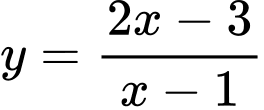 có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
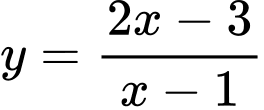 có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là A, 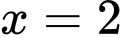 và
và 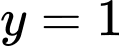 .
.
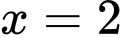 và
và 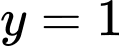 .
.B, 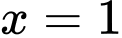 và
và 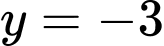 .
.
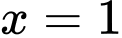 và
và 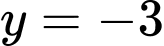 .
.C, 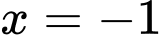 và
và 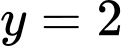 .
.
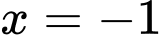 và
và 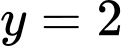 .
.D, 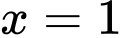 và
và 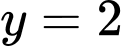 .
.
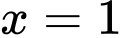 và
và 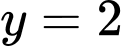 .
.
Chọn D
Ta có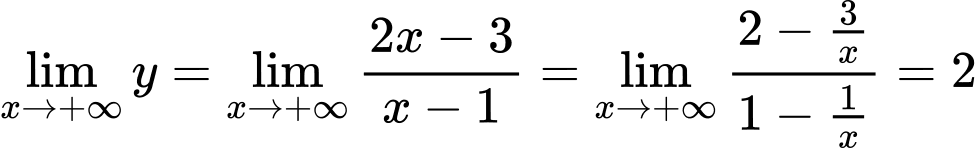 ,
, 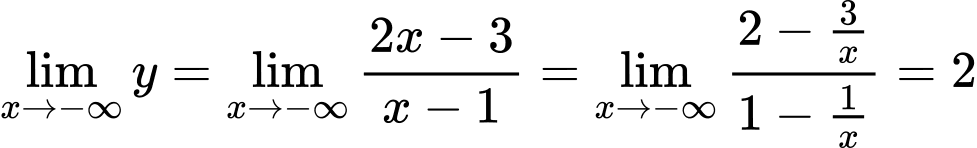 .
.
Do đó đường tiệm cận ngang của đồ thị hàm số là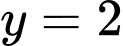 .
.
Và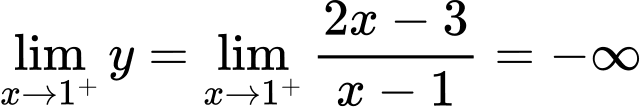 ,
, 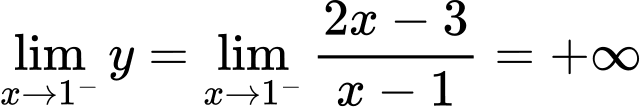 .
.
Do đó đường tiệm cận đứng của đồ thị hàm số là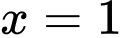 . Đáp án: D
. Đáp án: D
Ta có
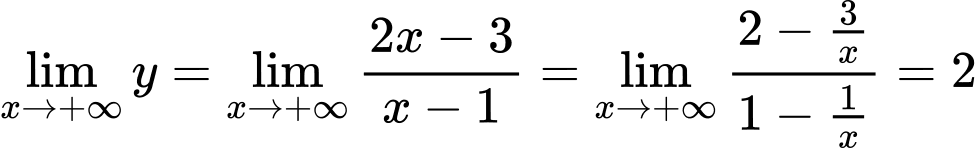 ,
, 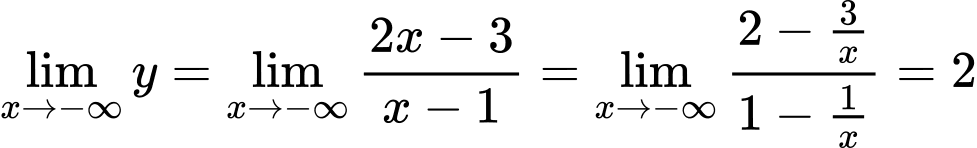 .
.Do đó đường tiệm cận ngang của đồ thị hàm số là
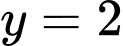 .
.Và
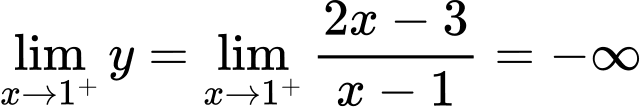 ,
, 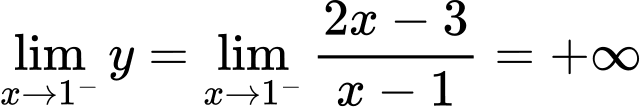 .
.Do đó đường tiệm cận đứng của đồ thị hàm số là
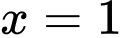 . Đáp án: D
. Đáp án: D
Câu 4 [529665]: Tiệm cận ngang của đồ thị hàm số 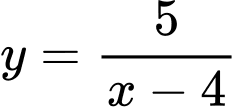 là
là
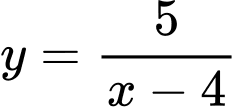 là
là A, 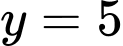 .
.
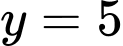 .
.B, 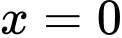 .
.
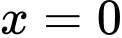 .
.C,  .
.
 .
.D, 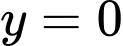 .
.
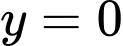 .
.
Chọn D
Ta có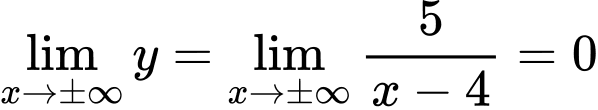 nên đồ thị có tiệm cận ngang
nên đồ thị có tiệm cận ngang 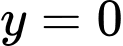 . Đáp án: D
. Đáp án: D
Ta có
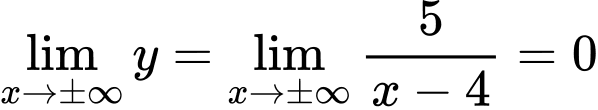 nên đồ thị có tiệm cận ngang
nên đồ thị có tiệm cận ngang 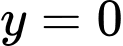 . Đáp án: D
. Đáp án: D
Câu 5 [801837]: Tiệm cận ngang của đồ thị hàm số 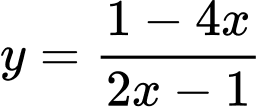 .
.
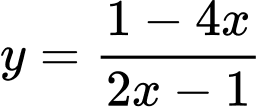 .
. A, 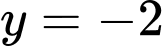 .
.
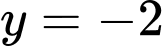 .
.B, 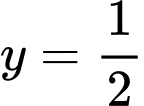 .
.
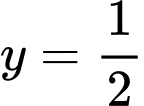 .
.C, 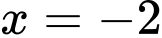 .
.
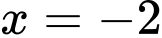 .
.D, 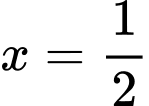 .
.
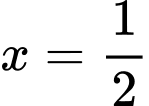 .
.
Chọn A
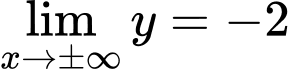
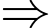 ĐTHS có TCN:
ĐTHS có TCN: 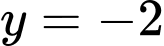 Đáp án: A
Đáp án: A
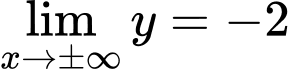
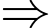 ĐTHS có TCN:
ĐTHS có TCN: 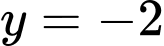 Đáp án: A
Đáp án: A
Câu 6 [382470]: Nếu trong một ngày, một xưởng sản xuất được 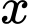 kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức:
kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: 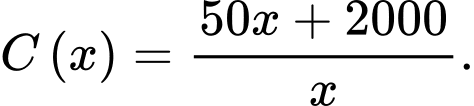 Tiệm cận ngang của đồ thị hàm số
Tiệm cận ngang của đồ thị hàm số  là:
là:
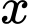 kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức:
kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: 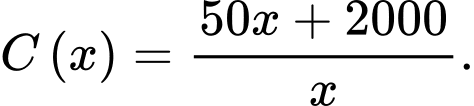 Tiệm cận ngang của đồ thị hàm số
Tiệm cận ngang của đồ thị hàm số  là:
là: A, 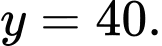
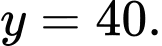
B, 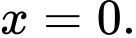
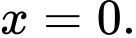
C, 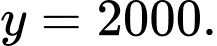
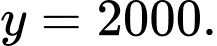
D, 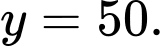
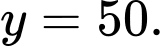
Ta có: 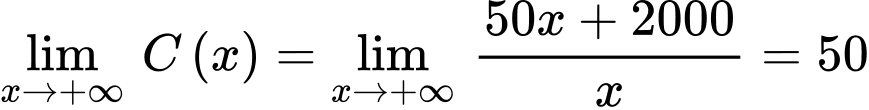
Vậy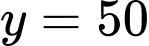 là tiệm cận ngang của đồ thị hàm số. Đáp án: D
là tiệm cận ngang của đồ thị hàm số. Đáp án: D
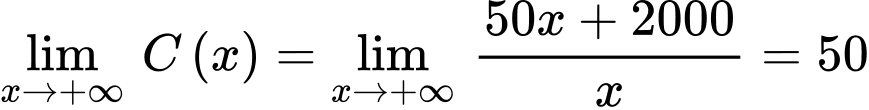
Vậy
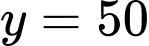 là tiệm cận ngang của đồ thị hàm số. Đáp án: D
là tiệm cận ngang của đồ thị hàm số. Đáp án: D
Câu 7 [31230]: Tìm giao điểm hai đường tiệm cận của đồ thị hàm số 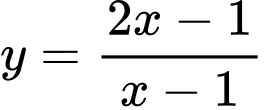 .
.
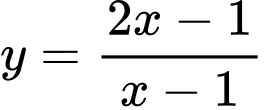 .
. A, 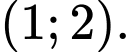
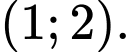
B, 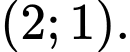
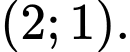
C, 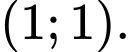
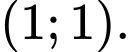
D, 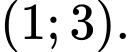
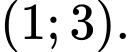
HD: ĐTHS có tiệm cận đứng 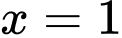 và tiệm cận ngang
và tiệm cận ngang 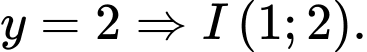 Chọn A Đáp án: A
Chọn A Đáp án: A
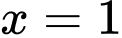 và tiệm cận ngang
và tiệm cận ngang 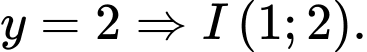 Chọn A Đáp án: A
Chọn A Đáp án: A
Câu 8 [382471]: Số lượng sản phẩm bán được của một công ty trong 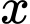 (tháng) được tính theo công thức
(tháng) được tính theo công thức 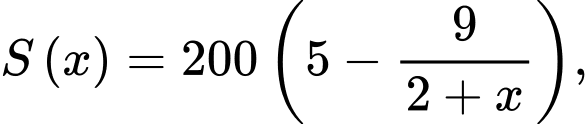 trong đó
trong đó 
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014)
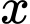 (tháng) được tính theo công thức
(tháng) được tính theo công thức 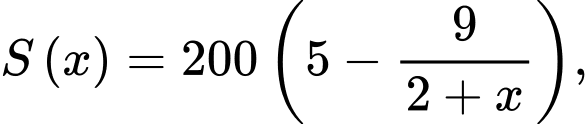 trong đó
trong đó 
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014)
Xem 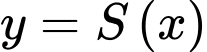 là một số hàm số xác định trên nửa khoảng
là một số hàm số xác định trên nửa khoảng 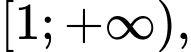 tiệm cận ngang của đồ thị của hàm số đó là
tiệm cận ngang của đồ thị của hàm số đó là
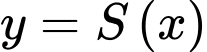 là một số hàm số xác định trên nửa khoảng
là một số hàm số xác định trên nửa khoảng 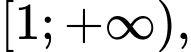 tiệm cận ngang của đồ thị của hàm số đó là
tiệm cận ngang của đồ thị của hàm số đó làA, 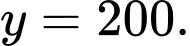
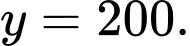
B, 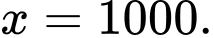
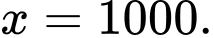
C, 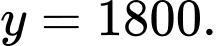
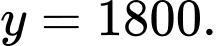
D, 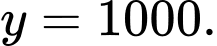
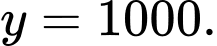
Ta có: 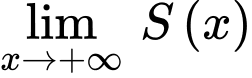
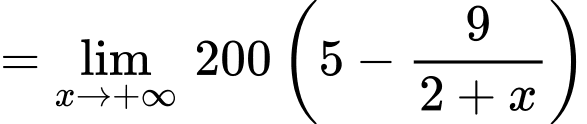
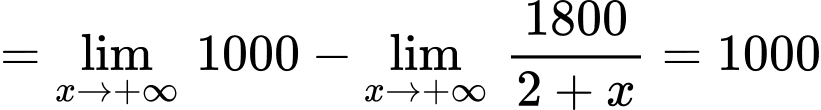
Vậy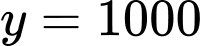 là tiệm cận ngang của đồ thị hàm số . Đáp án: D
là tiệm cận ngang của đồ thị hàm số . Đáp án: D
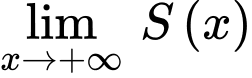
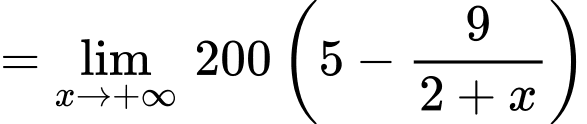
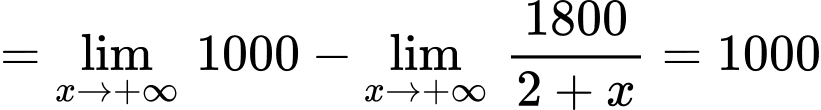
Vậy
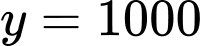 là tiệm cận ngang của đồ thị hàm số . Đáp án: D
là tiệm cận ngang của đồ thị hàm số . Đáp án: D
Câu 9 [306980]: Đường thẳng 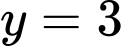 là tiệm cận ngang của đồ thị hàm số nào sau đây?
là tiệm cận ngang của đồ thị hàm số nào sau đây?
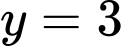 là tiệm cận ngang của đồ thị hàm số nào sau đây?
là tiệm cận ngang của đồ thị hàm số nào sau đây? A, 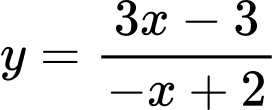 .
.
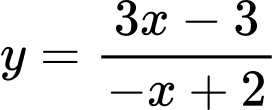 .
.B, 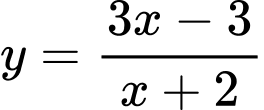 .
.
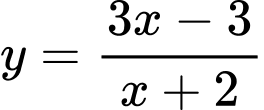 .
.C, 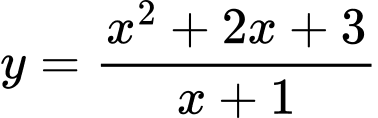 .
.
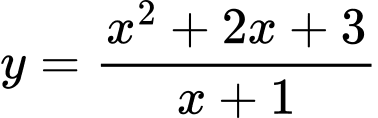 .
.D, 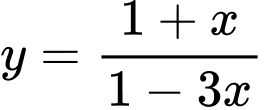 .
.
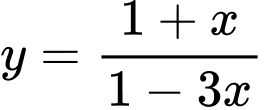 .
.
Chọn B
Ta có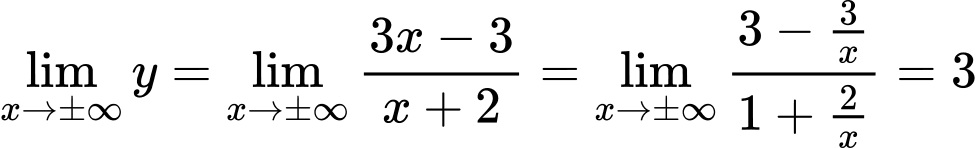 suy ra đường thẳng
suy ra đường thẳng 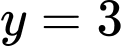 là tiệm cận ngang của đồ thị hàm số
là tiệm cận ngang của đồ thị hàm số 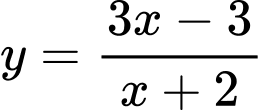 . Đáp án: B
. Đáp án: B
Ta có
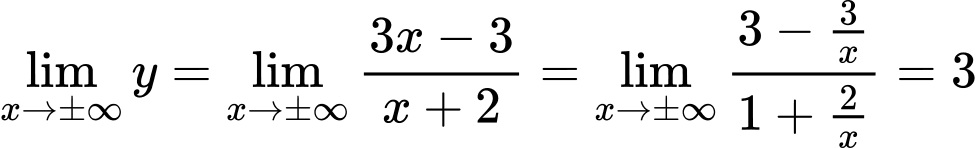 suy ra đường thẳng
suy ra đường thẳng 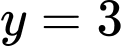 là tiệm cận ngang của đồ thị hàm số
là tiệm cận ngang của đồ thị hàm số 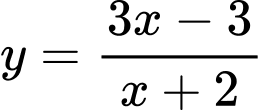 . Đáp án: B
. Đáp án: B
Câu 10 [382472]: Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất 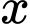 đơn vị sản phẩm là
đơn vị sản phẩm là 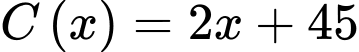 (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là
(triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là 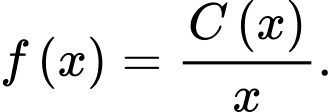 Nhận xét nào sau đây là đúng?
Nhận xét nào sau đây là đúng?
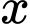 đơn vị sản phẩm là
đơn vị sản phẩm là 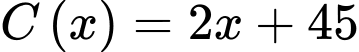 (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là
(triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là 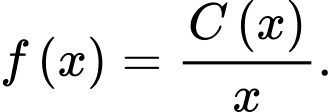 Nhận xét nào sau đây là đúng?
Nhận xét nào sau đây là đúng? A, Chi phí trung bình luôn tăng khi 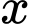 tăng dần.
tăng dần.
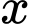 tăng dần.
tăng dần.B, Chi phí trung bình luôn giảm khi 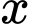 tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.
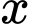 tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.C, Chi phí trung bình luôn giảm khi 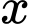 tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.
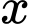 tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.D, Chi phí trung bình luôn giảm khi 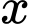 tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
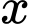 tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
Ta có: 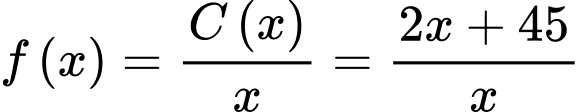
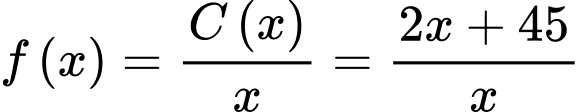
Có 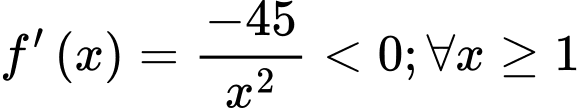 nên hàm số
nên hàm số 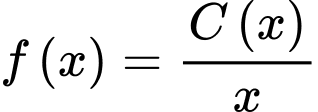 là hàm số giảm.
là hàm số giảm.
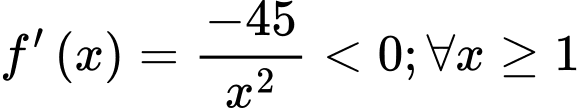 nên hàm số
nên hàm số 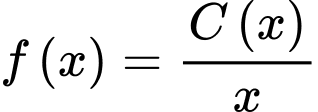 là hàm số giảm.
là hàm số giảm. Có 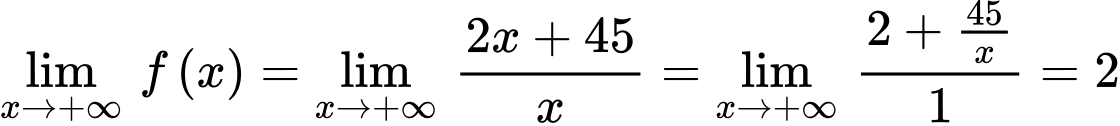
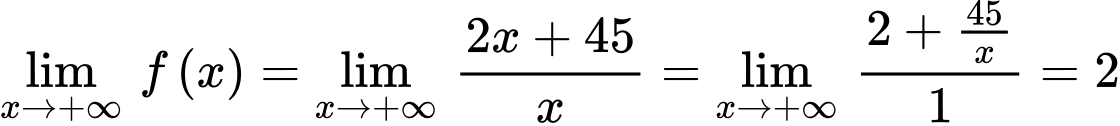
Do đó chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm.
Đáp án: B
Câu 11 [31234]: Đồ thị hàm số 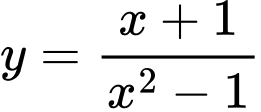 có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận?
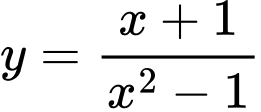 có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận? A, 0.
B, 1.
C, 2.
D, 3.
Ta có: 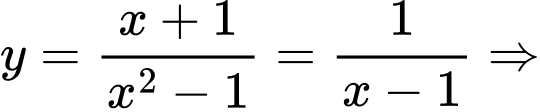 TCĐ
TCĐ 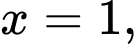 TCN
TCN 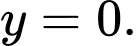
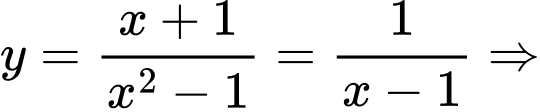 TCĐ
TCĐ 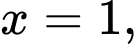 TCN
TCN 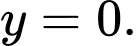
Chọn C.
Đáp án: C
Câu 12 [382473]: Nồng độ Oxygen trong hồ theo thời gian 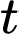 được cho bởi công thức
được cho bởi công thức 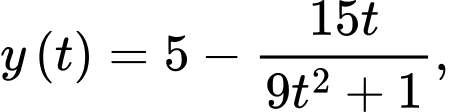 với
với 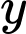 được tính theo
được tính theo 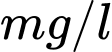 và
và 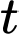 được tính theo giờ,
được tính theo giờ,  Đồ thị hàm số
Đồ thị hàm số 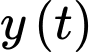 có bao nhiêu đường tiệm cận.
có bao nhiêu đường tiệm cận.
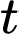 được cho bởi công thức
được cho bởi công thức 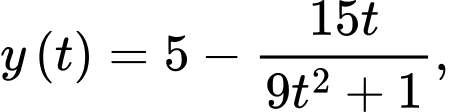 với
với 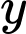 được tính theo
được tính theo 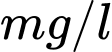 và
và 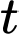 được tính theo giờ,
được tính theo giờ,  Đồ thị hàm số
Đồ thị hàm số 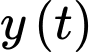 có bao nhiêu đường tiệm cận.
có bao nhiêu đường tiệm cận. A, 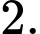
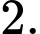
B, 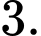
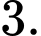
C, 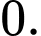
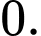
D, 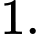
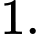
Ta có: 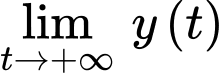
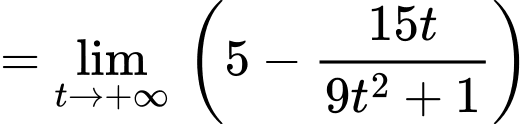
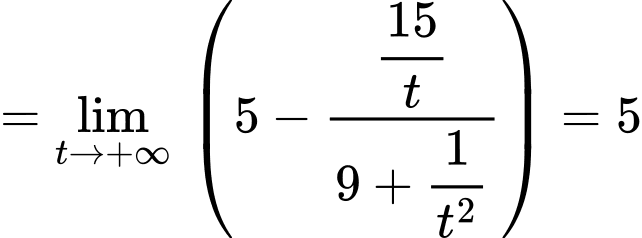
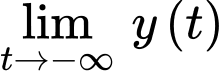
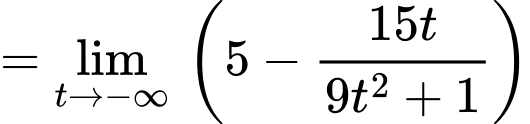
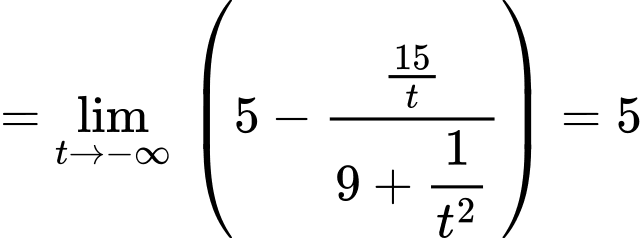
Do đó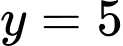 là tiệm cận ngang của đồ thị hàm số và hàm số không có tiệm cận đứng và tiệm cận xiên. Đáp án: D
là tiệm cận ngang của đồ thị hàm số và hàm số không có tiệm cận đứng và tiệm cận xiên. Đáp án: D
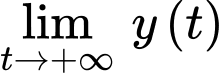
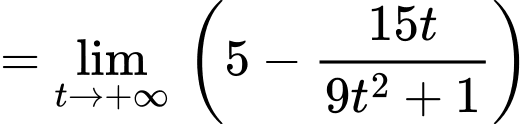
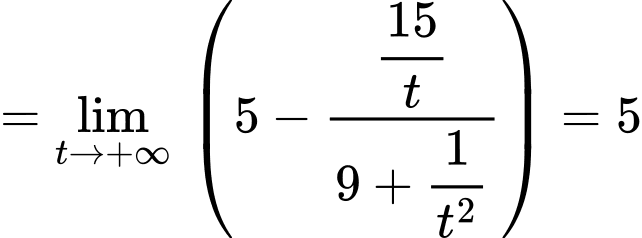
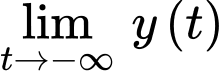
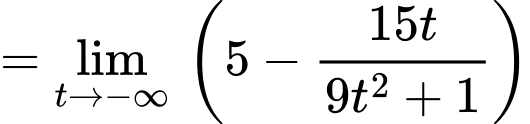
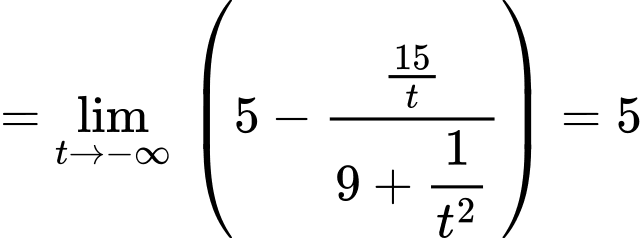
Do đó
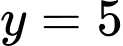 là tiệm cận ngang của đồ thị hàm số và hàm số không có tiệm cận đứng và tiệm cận xiên. Đáp án: D
là tiệm cận ngang của đồ thị hàm số và hàm số không có tiệm cận đứng và tiệm cận xiên. Đáp án: D
Câu 13 [522404]: Tìm số tiệm cận đứng của đồ thị hàm số 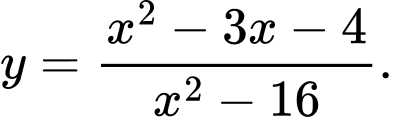
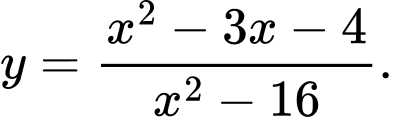
A, 2.
B, 3.
C, 0.
D, 1.
Lời giải: TXĐ: 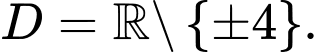 Khi đó:
Khi đó: 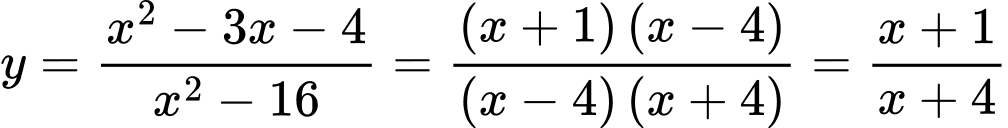
Suy ra đồ thị hàm số có một đường tiệm cận đứng là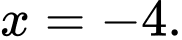 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
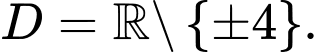 Khi đó:
Khi đó: 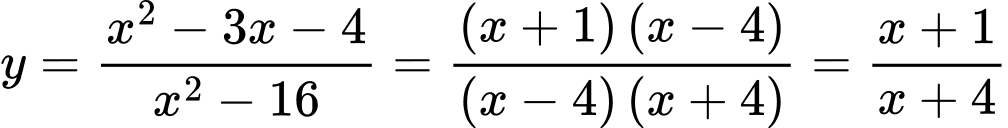
Suy ra đồ thị hàm số có một đường tiệm cận đứng là
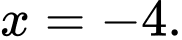 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 14 [31231]: Đồ thị hàm số 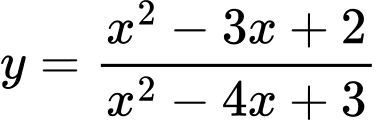 có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận?
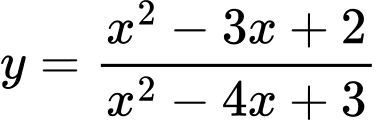 có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận? A, 0.
B, 1.
C, 2.
D, 3.
Ta có: 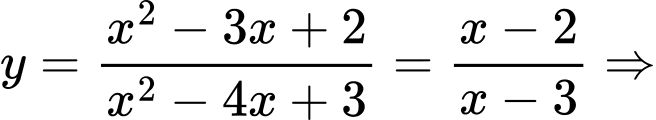 TCĐ
TCĐ 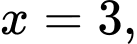 TCN
TCN 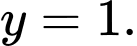 Chọn C. Đáp án: C
Chọn C. Đáp án: C
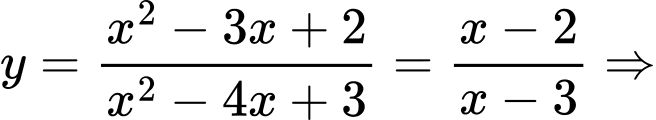 TCĐ
TCĐ 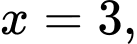 TCN
TCN 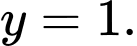 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 15 [31226]: Đồ thị hàm số 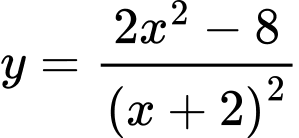 có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận?
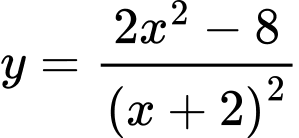 có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận? A, 0.
B, 1.
C, 2.
D, 3.
TXĐ: 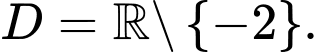
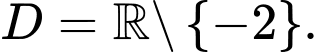
Ta có: 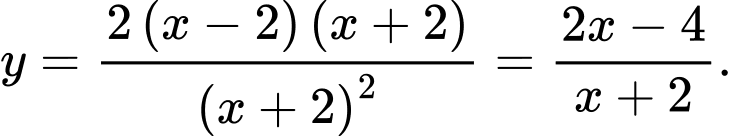
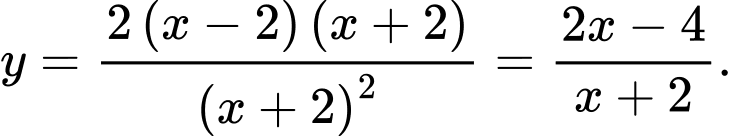
Dễ thấy đồ thị hàm số có TCĐ là 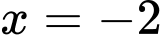 và TCN là
và TCN là 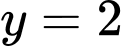 nên đồ thị hàm số có hai đường tiệm cận.
nên đồ thị hàm số có hai đường tiệm cận.
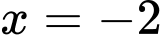 và TCN là
và TCN là 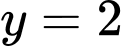 nên đồ thị hàm số có hai đường tiệm cận.
nên đồ thị hàm số có hai đường tiệm cận.
Chọn C.
Đáp án: C
Câu 16 [358933]: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 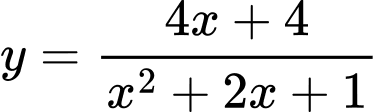 là:
là:
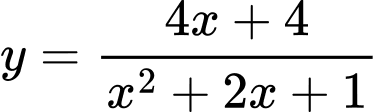 là:
là: A, 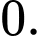
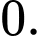
B, 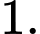
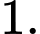
C, 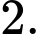
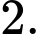
D, 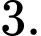
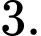
Ta có: 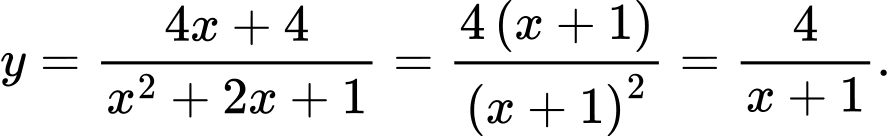
ĐKXĐ: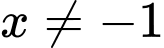
Do đó đồ thị hàm số có đường tiệm cận đứng là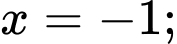 đường tiệm cận ngang là
đường tiệm cận ngang là 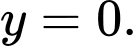
Vậy đồ thị hàm số đã cho có hai đường tiệm cận. Đáp án: C
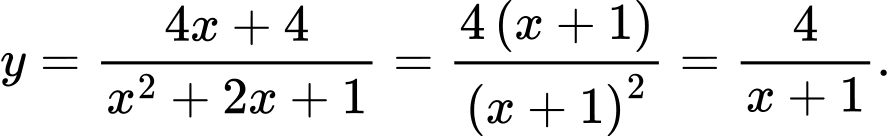
ĐKXĐ:
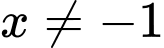
Do đó đồ thị hàm số có đường tiệm cận đứng là
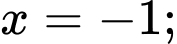 đường tiệm cận ngang là
đường tiệm cận ngang là 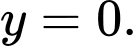
Vậy đồ thị hàm số đã cho có hai đường tiệm cận. Đáp án: C
Câu 17 [382474]: [Nguồn SGK Cùng Khám Phá] Tại một công ty sản xuất đồ chơi A, công ty phải chi 50 000 USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi A, công ty phải trả 5 USD cho nguyên liệu thô và nhân công. Gọi 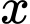 là số đồ chơi A mà công ty đã sản xuất và
là số đồ chơi A mà công ty đã sản xuất và 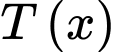 (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là
(đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là 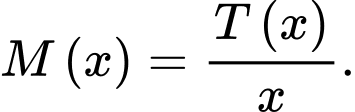 Xem
Xem 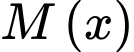 là hàm số theo
là hàm số theo 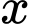 xác định trên nửa khoảng
xác định trên nửa khoảng 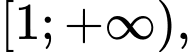 tiệm cận ngang của đồ thị hàm số này là:
tiệm cận ngang của đồ thị hàm số này là:
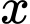 là số đồ chơi A mà công ty đã sản xuất và
là số đồ chơi A mà công ty đã sản xuất và 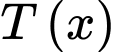 (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là
(đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là 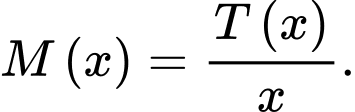 Xem
Xem 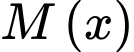 là hàm số theo
là hàm số theo 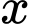 xác định trên nửa khoảng
xác định trên nửa khoảng 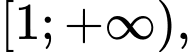 tiệm cận ngang của đồ thị hàm số này là:
tiệm cận ngang của đồ thị hàm số này là: A, 

B, 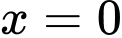
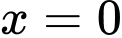
C, 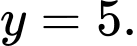
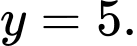
D, 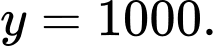
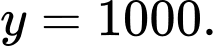
Ta có: 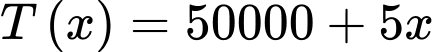 .
.
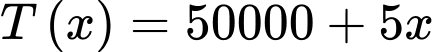 .
. Suy ra 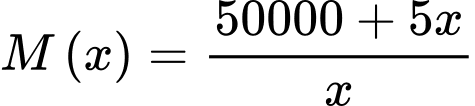 .
.
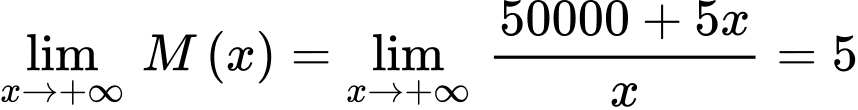
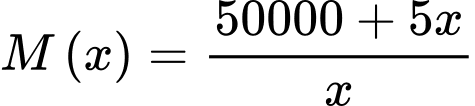 .
.
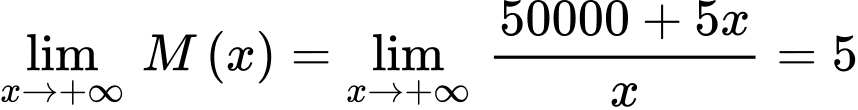
Vậy 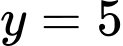 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Đáp án: C 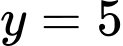 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Câu 18 [522407]: Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A, 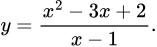
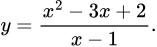
B, 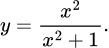
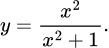
C, 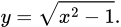
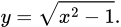
D, 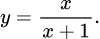
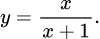
Lời giải: Phân tích các đáp án:
Đáp án A. Ta có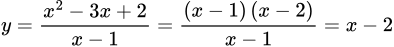 nên hàm số không có tiệm cận đứng
nên hàm số không có tiệm cận đứng
Đáp án B. Phương trình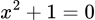 vô nghiệm nên hàm số không có tiệm cận đứng
vô nghiệm nên hàm số không có tiệm cận đứng
Đáp án C. Đồ thị hàm số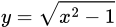 không có tiệm cận đứng
không có tiệm cận đứng
Đáp án D. Đồ thị hàm số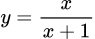 có tiệm cận đứng là
có tiệm cận đứng là 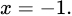 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Đáp án A. Ta có
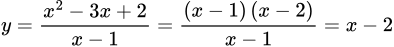 nên hàm số không có tiệm cận đứng
nên hàm số không có tiệm cận đứngĐáp án B. Phương trình
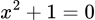 vô nghiệm nên hàm số không có tiệm cận đứng
vô nghiệm nên hàm số không có tiệm cận đứngĐáp án C. Đồ thị hàm số
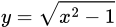 không có tiệm cận đứng
không có tiệm cận đứngĐáp án D. Đồ thị hàm số
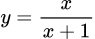 có tiệm cận đứng là
có tiệm cận đứng là 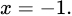 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 19 [132931]: Số tiệm cận đứng của đồ thị hàm số 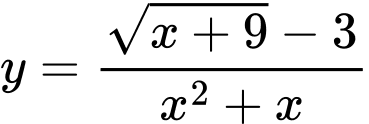 là
là
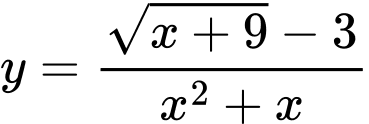 là
là A, 3.
B, 2.
C, 0.
D, 1.
Ta có 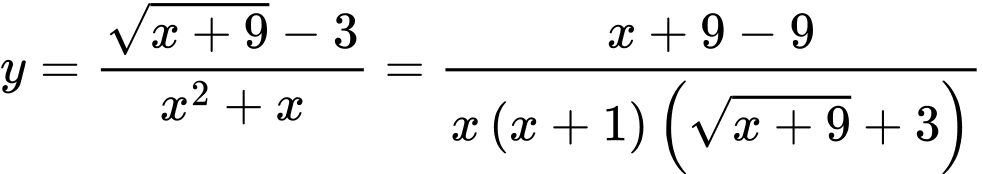
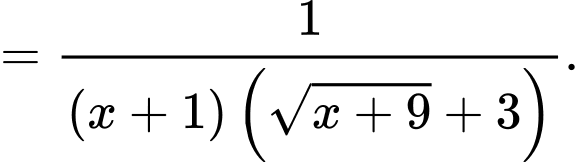
Đồ thị hàm số có đúng 1 tiệm cận đứng là đường thẳng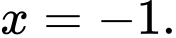 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
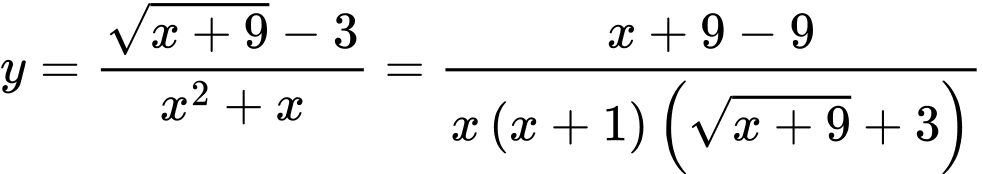
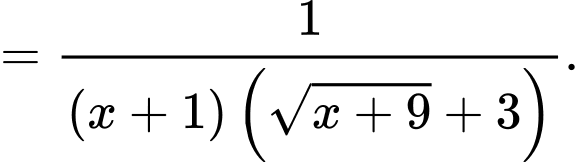
Đồ thị hàm số có đúng 1 tiệm cận đứng là đường thẳng
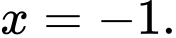 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 20 [135946]: Số tiệm cận đứng của đồ thị hàm số 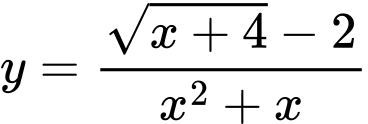 là
là
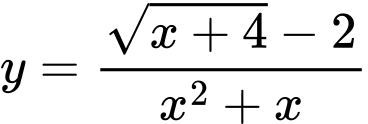 là
là A, 3.
B, 0.
C, 2.
D, 1.
Tập xác định: 
Tại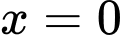 ta có:
ta có:
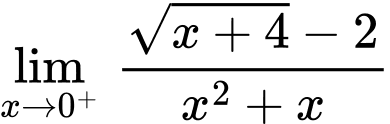
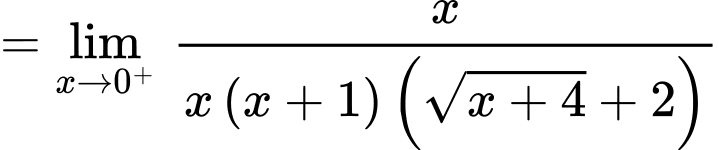
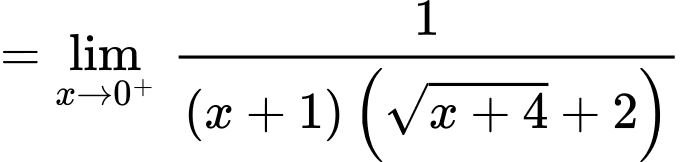
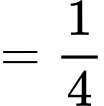
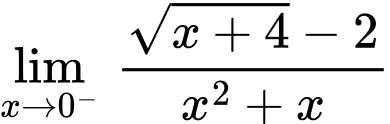
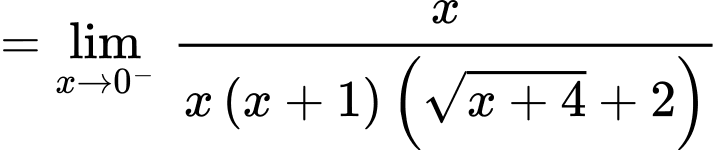
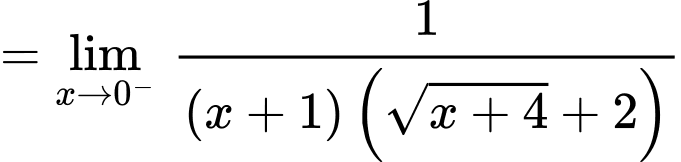
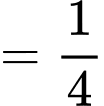
Suy ra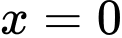 không phải là đường tiệm cận đứng của đồ thị hàm số.
không phải là đường tiệm cận đứng của đồ thị hàm số.
Tại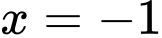 ; ta có:
; ta có: 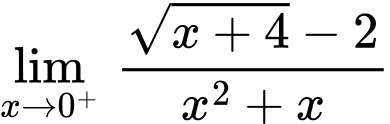

Suy ra đường thẳng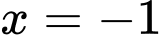 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D

Tại
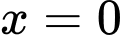 ta có:
ta có: 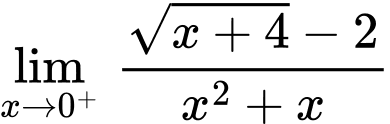
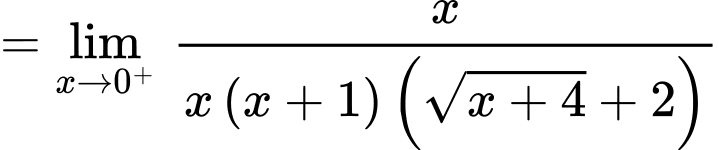
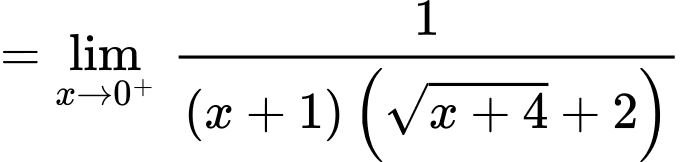
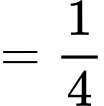
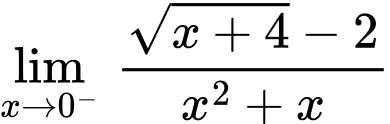
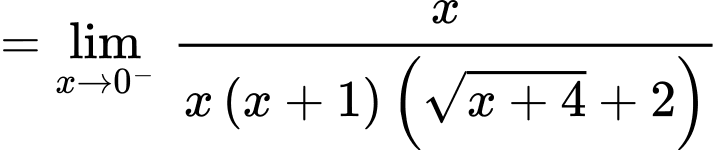
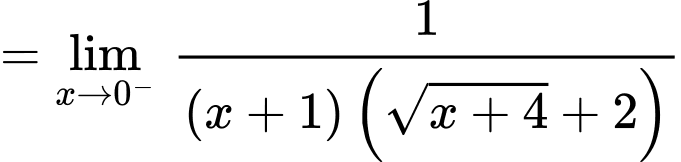
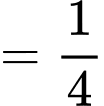
Suy ra
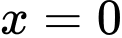 không phải là đường tiệm cận đứng của đồ thị hàm số.
không phải là đường tiệm cận đứng của đồ thị hàm số. Tại
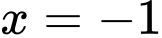 ; ta có:
; ta có: 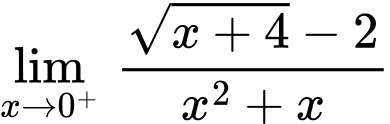

Suy ra đường thẳng
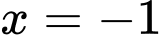 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
Câu 21 [31166]: Tìm số đường tiệm cận đứng của đồ thị hàm 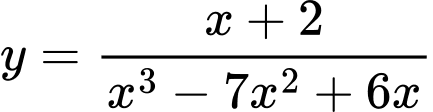 .
.
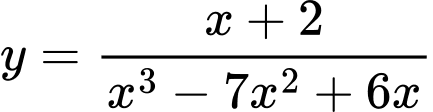 .
. A, 
B, 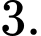
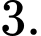
C, 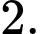
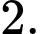
D, 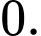
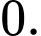
Ta có: 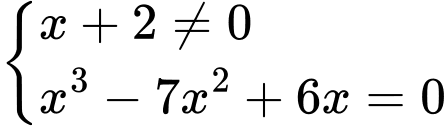
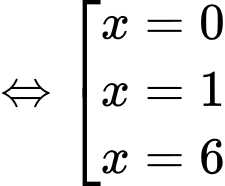
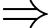 Đồ thị hàm số
Đồ thị hàm số 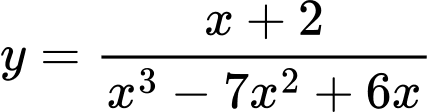 có 3 TCĐ. Chọn B.
có 3 TCĐ. Chọn B.
Đáp án: B
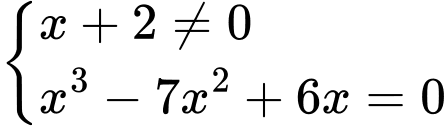
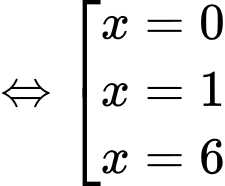
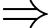 Đồ thị hàm số
Đồ thị hàm số 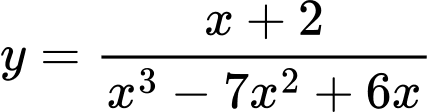 có 3 TCĐ. Chọn B.
có 3 TCĐ. Chọn B.Đáp án: B
Câu 22 [31172]: Số các đường tiệm cận đứng của đồ thị hàm số 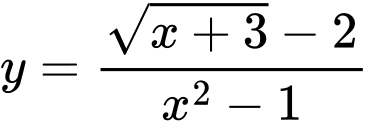 là
là
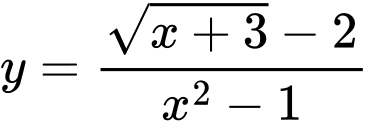 là
là A, 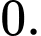
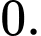
B, 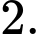
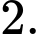
C, 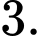
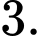
D, 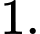
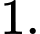
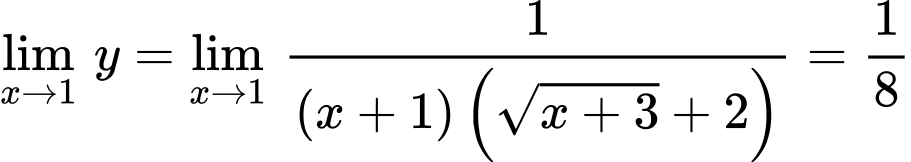 nên đường thẳng
nên đường thẳng 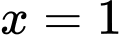 không phải là TCĐ. Do đó, đồ thị hàm số có 1 TCĐ
không phải là TCĐ. Do đó, đồ thị hàm số có 1 TCĐ 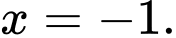 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 23 [522408]: Tìm tất cả các tiệm cận đứng của đồ thị hàm số 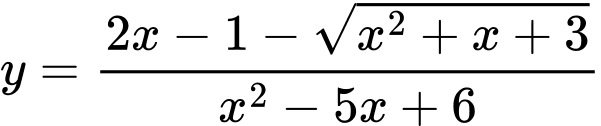 .
.
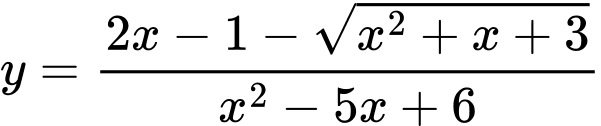 .
. A, 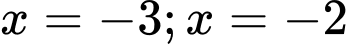 .
.
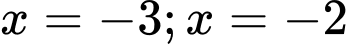 .
.B, 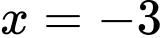 .
.
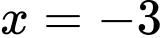 .
.C, 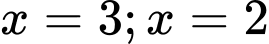 .
.
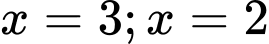 .
.D, 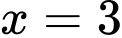 .
.
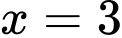 .
.
Lời giải: Hàm số có tập xác định 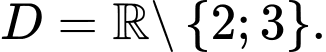
Ta có: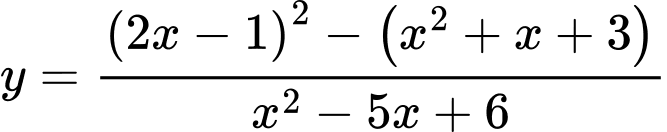
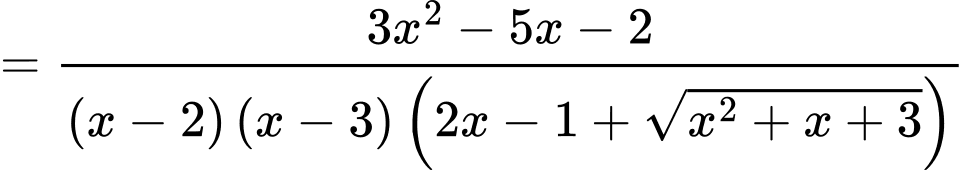
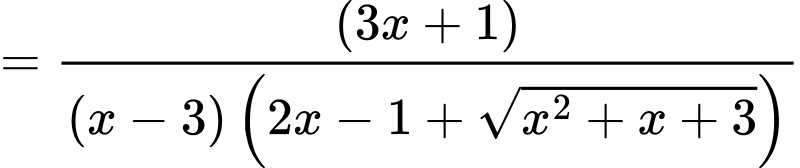
Do vậy chỉ có đường thẳng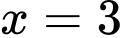 là tiệm cận đứng của đồ thị hàm số đã cho. Chọn D.
Đáp án: D
là tiệm cận đứng của đồ thị hàm số đã cho. Chọn D.
Đáp án: D
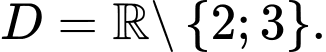
Ta có:
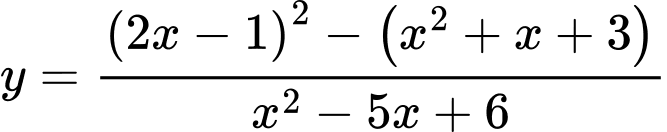
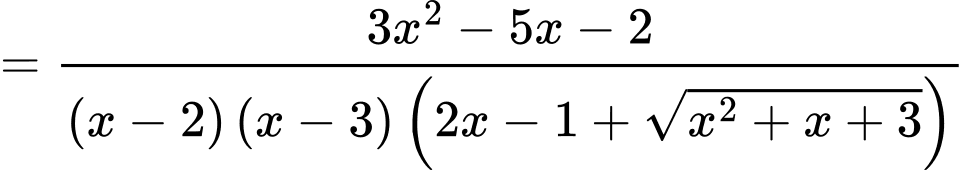
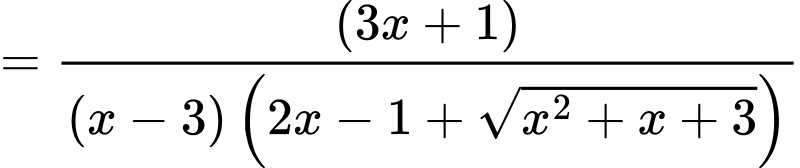
Do vậy chỉ có đường thẳng
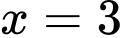 là tiệm cận đứng của đồ thị hàm số đã cho. Chọn D.
Đáp án: D
là tiệm cận đứng của đồ thị hàm số đã cho. Chọn D.
Đáp án: D
Câu 24 [31248]: Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số 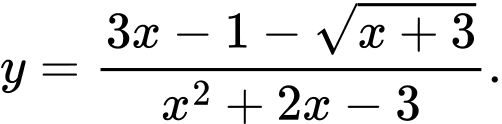
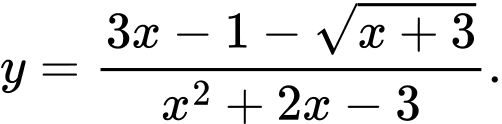
A, 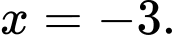
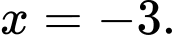
B, 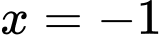 và
và 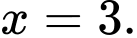
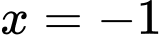 và
và 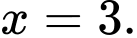
C, 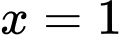 và
và 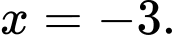
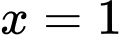 và
và 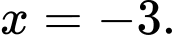
D, 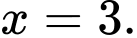
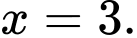
Hàm số có tập xác định 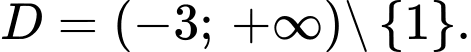
Khi đó,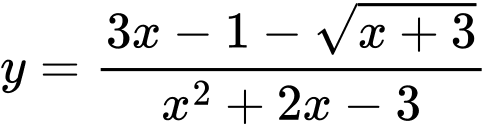
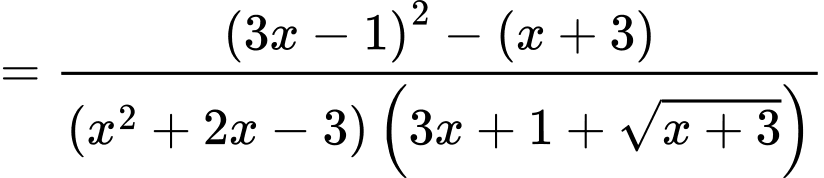
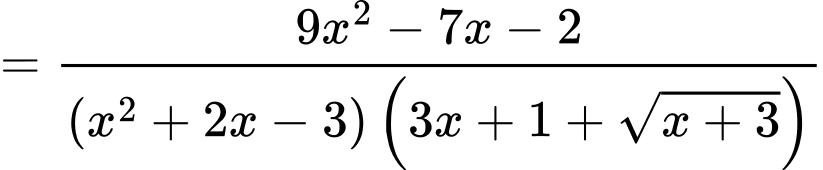
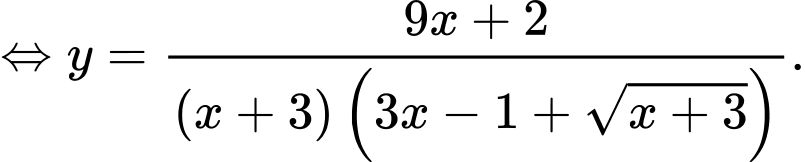
Suy ra,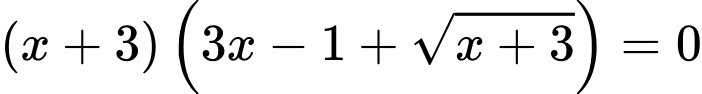
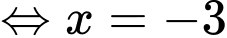
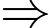 Đồ thị có TCĐ
Đồ thị có TCĐ 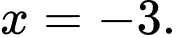
Chọn A. Đáp án: A
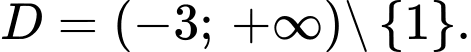
Khi đó,
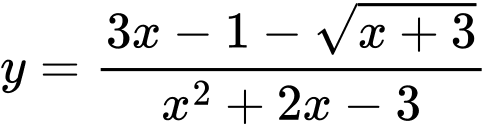
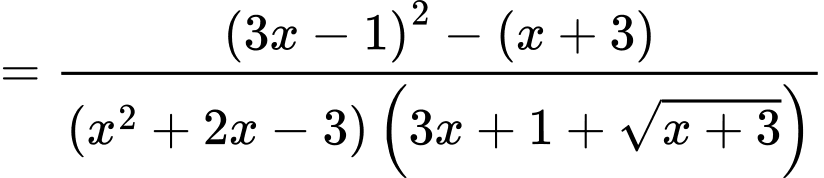
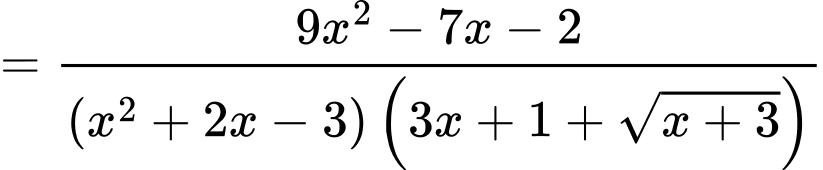
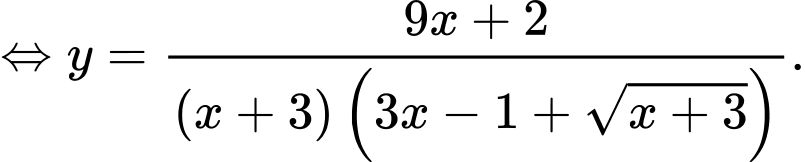
Suy ra,
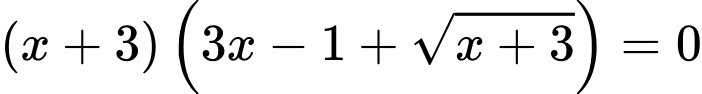
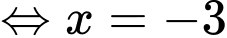
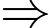 Đồ thị có TCĐ
Đồ thị có TCĐ 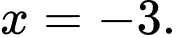
Chọn A. Đáp án: A
Câu 25 [377595]: Cho hàm số 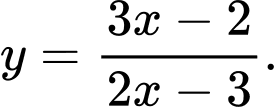 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
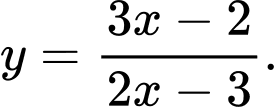 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) Hàm số đã cho đồng biến trên mỗi khoảng xác định.
B, b) Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng 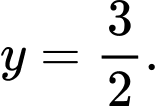
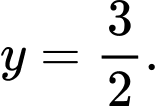
C, c) Hàm số đã cho có một điểm cực trị.
D, d) Tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng 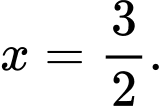
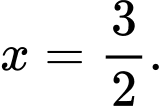
TXĐ:  Ta có:
Ta có:
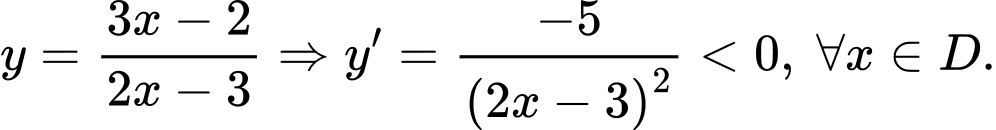 Bảng biến thiên:
Bảng biến thiên:
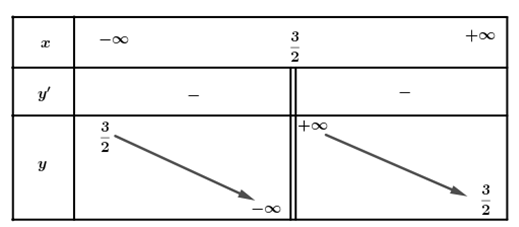
a) Sai. Hàm số đã cho nghịch biến trên mỗi khoảng xác định.
 Ta có:
Ta có:
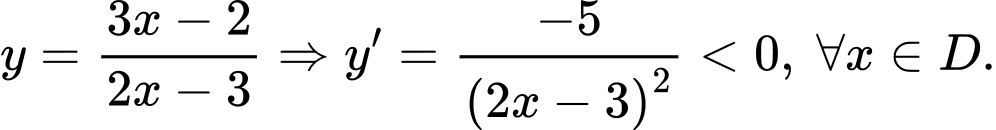 Bảng biến thiên:
Bảng biến thiên:

b) Sai. Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng 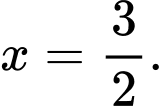
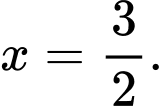
c) Sai. Hàm số đã cho không có điểm cực trị.
d) Sai. Tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng 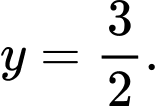
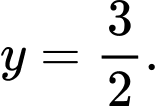
Câu 26 [377596]: Cho hàm số 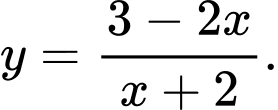 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
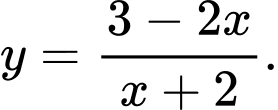 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
TXĐ: 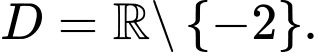
Ta có:
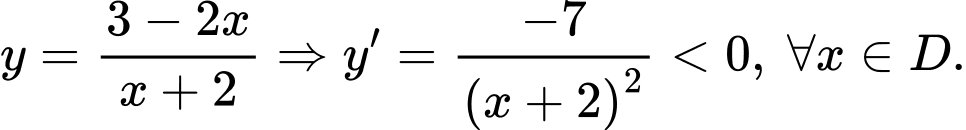
Bảng biến thiên:
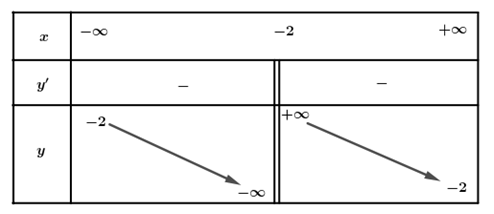
a) Đúng. Hàm số đã cho nghịch biến trên mỗi khoảng xác định.
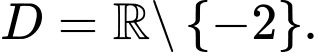
Ta có:
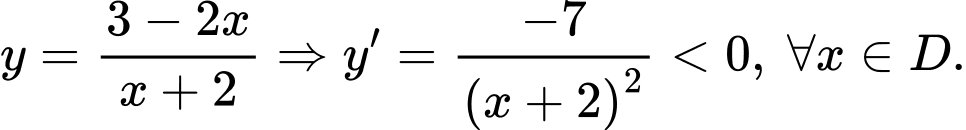
Bảng biến thiên:

b) Đúng. Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng 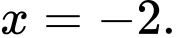
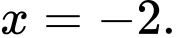
c) Đúng. Tâm đối xứng của đồ thị hàm số là điểm 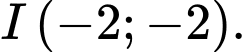
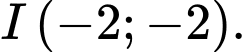
d) Sai. Tiệm cận ngang của đồ thị hàm số đã cho đường thẳng 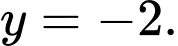
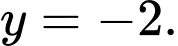
Câu 27 [380964]: [Trích SGK Kết Nối Tri Thức]: Giả sử số dân của một thị trấn sau 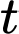 năm kể từ năm 2000 được mô tả bởi hàm số :
năm kể từ năm 2000 được mô tả bởi hàm số : 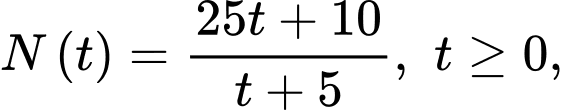 trong đó
trong đó 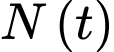 được tính bằng nghìn người. Xét tính đúng sai của mệnh đề sau
được tính bằng nghìn người. Xét tính đúng sai của mệnh đề sau
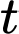 năm kể từ năm 2000 được mô tả bởi hàm số :
năm kể từ năm 2000 được mô tả bởi hàm số : 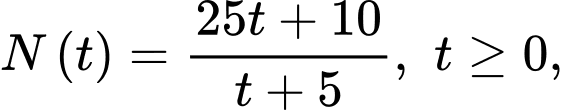 trong đó
trong đó 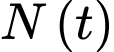 được tính bằng nghìn người. Xét tính đúng sai của mệnh đề sau
được tính bằng nghìn người. Xét tính đúng sai của mệnh đề sau A, a) Dân số của thị trấn đó năm 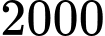 là
là 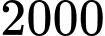 người.
người.
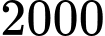 là
là 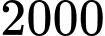 người.
người.B, b) Dân số của thị trấn đó năm  là
là 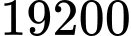 người.
người.
 là
là 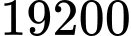 người.
người.C, c) Hàm số 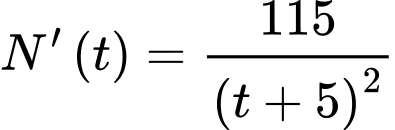
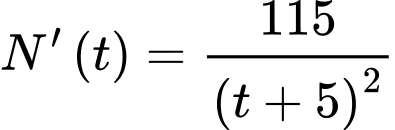
D, d) Dân số của thị trấn đó luôn tăng nhưng sẽ không vượt quá 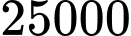 người.
người.
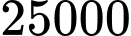 người.
người.
a) Đúng. Dân số của thị trấn đó năm 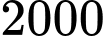 là
là 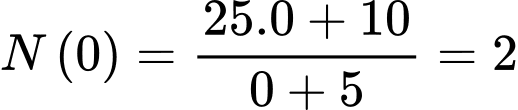 nghìn người.
nghìn người.
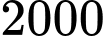 là
là 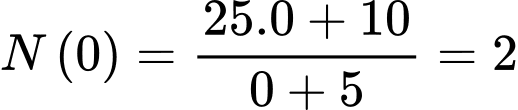 nghìn người.
nghìn người. b) Sai. Dân số của thị trấn đó năm  là
là 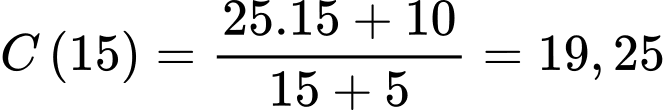 nghìn người.
nghìn người.
 là
là 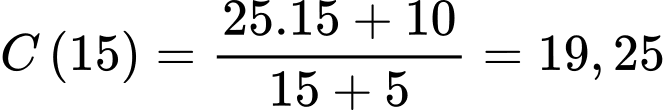 nghìn người.
nghìn người. c) Đúng. Hàm số 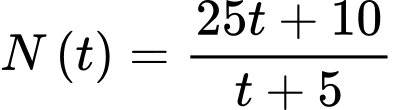
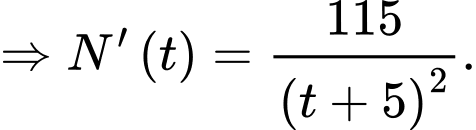
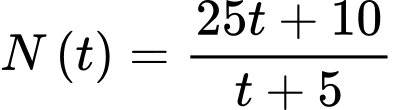
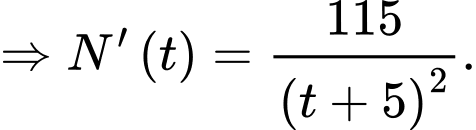
d) Đúng. Dân số của thị trấn đó luôn tăng nhưng sẽ không vượt quá 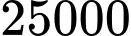 người.
.
người.
.
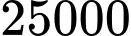 người.
.
người.
.
Câu 28 [383417]: [Nguồn SGK Kết Nối Tri Thức]: Để loại bỏ 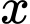 chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là:
chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là: 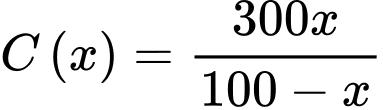 (triệu đồng)
(triệu đồng)  Xét tính đúng sai của mệnh đề sau:
Xét tính đúng sai của mệnh đề sau:
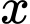 chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là:
chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là: 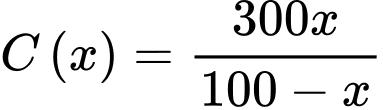 (triệu đồng)
(triệu đồng)  Xét tính đúng sai của mệnh đề sau:
Xét tính đúng sai của mệnh đề sau: A, a) 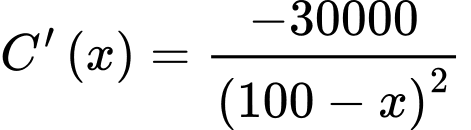 với mọi
với mọi 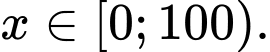
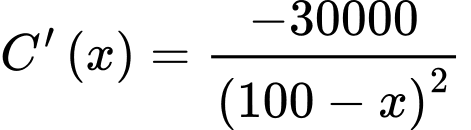 với mọi
với mọi 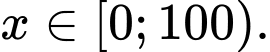
B, b) Để loại bỏ được 50% chất gây ô nhiễm cần 300 triệu đồng.
C, c) Chi phí bỏ ra luôn tăng khi 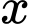 tăng.
tăng.
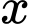 tăng.
tăng.D, d) Không thể loại bỏ 100% chất gây ô nhiễm dù bỏ ra chi phí là bao nhiêu đi chăng nữa
a) Sai. 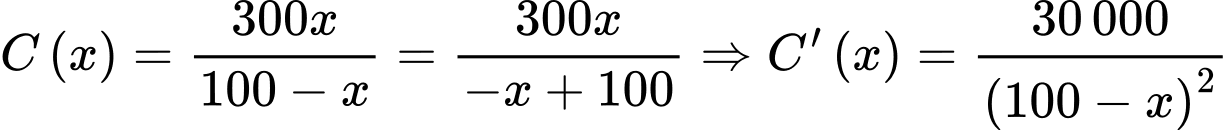 với mọi
với mọi 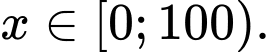
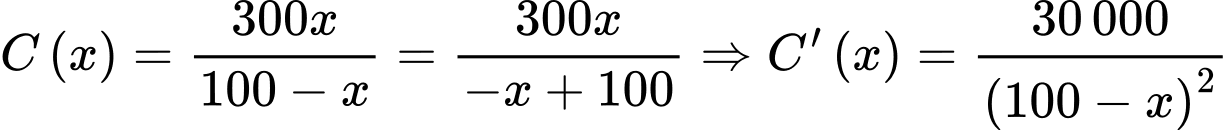 với mọi
với mọi 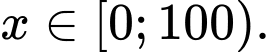
b) Đúng. Để loại bỏ được 50% chất gây ô nhiễm cần 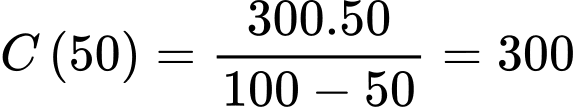 triệu đồng.
triệu đồng.
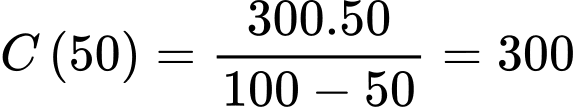 triệu đồng.
triệu đồng. c) Đúng. Ta có: 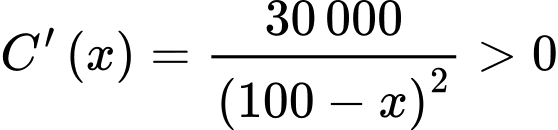 với mọi
với mọi 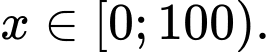 Do đó, chi phí bỏ ra luôn tăng khi
Do đó, chi phí bỏ ra luôn tăng khi 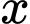 tăng.
tăng.
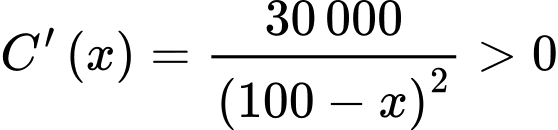 với mọi
với mọi 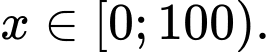 Do đó, chi phí bỏ ra luôn tăng khi
Do đó, chi phí bỏ ra luôn tăng khi 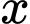 tăng.
tăng. d) Đúng. Không thể loại bỏ 100% chất gây ô nhiễm dù bỏ ra chi phí là bao nhiêu đi chăng nữa
Câu 29 [377597]: Cho hàm số 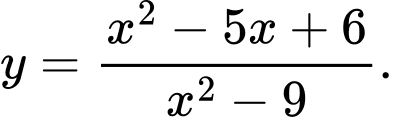 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
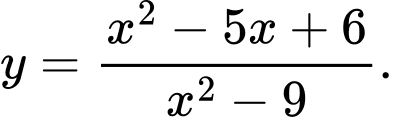 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) Đồ thị hàm số đã cho có hai đường tiệm cận đứng.
B, b) Đồ thị hàm số đã cho có hai đường tiệm cận.
C, c) Đồ thị hàm số đã cho có một đường tiệm cận ngang.
D, d) Hàm số đã cho đồng biến trên mỗi khoảng xác định của nó.
TXĐ: 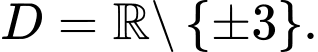
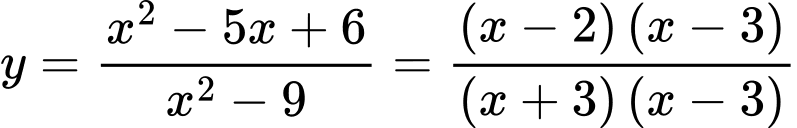
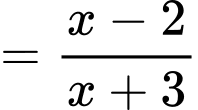
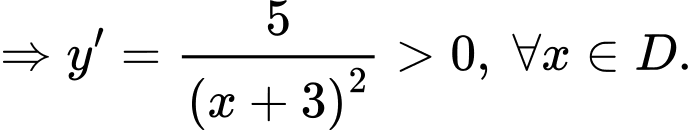
a) Sai. Đồ thị hàm số đã cho có một đường tiệm cận đứng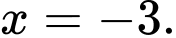
b) Đúng. Đồ thị hàm số đã cho có hai đường tiệm cận: 1 TCĐ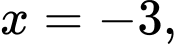 1 TCN
1 TCN 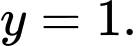
c) Đúng. Đồ thị hàm số đã cho có một đường tiệm cận ngang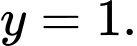
d) Đúng. Hàm số đã cho đồng biến trên mỗi khoảng xác định của nó.
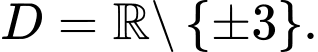
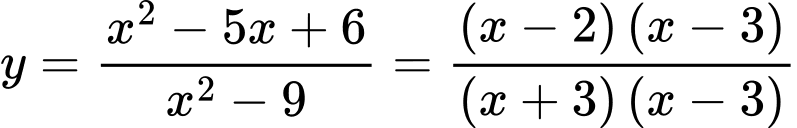
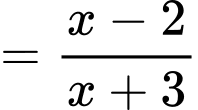
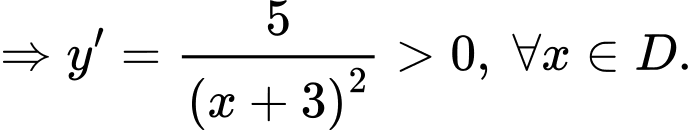
a) Sai. Đồ thị hàm số đã cho có một đường tiệm cận đứng
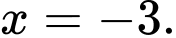
b) Đúng. Đồ thị hàm số đã cho có hai đường tiệm cận: 1 TCĐ
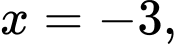 1 TCN
1 TCN 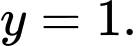
c) Đúng. Đồ thị hàm số đã cho có một đường tiệm cận ngang
d) Đúng. Hàm số đã cho đồng biến trên mỗi khoảng xác định của nó.
Câu 30 [382475]: Theo thuyết tương đối hẹp, khối lượng 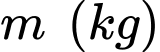 của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức
của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức 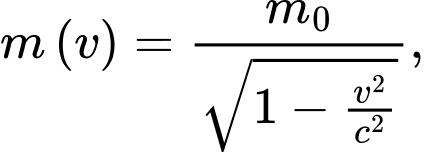 trong đó
trong đó 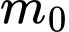 là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng. Trọng hệ toạ độ
là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng. Trọng hệ toạ độ 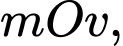 xét tính đúng sai của các mệnh đề sau:
xét tính đúng sai của các mệnh đề sau:
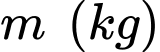 của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức
của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức 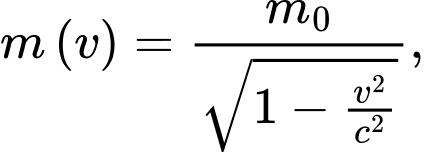 trong đó
trong đó 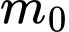 là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng. Trọng hệ toạ độ
là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng. Trọng hệ toạ độ 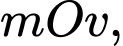 xét tính đúng sai của các mệnh đề sau:
xét tính đúng sai của các mệnh đề sau: A, a) Khi 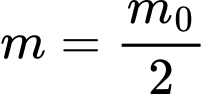 thì
thì 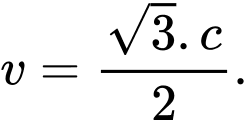
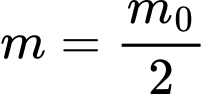 thì
thì 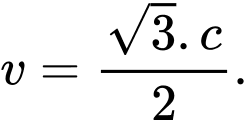
B, b) Một đường tiệm cận đứng của đồ thị hàm số 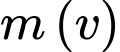 là
là 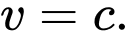
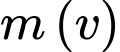 là
là 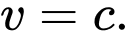
C, c) Đường tiệm cận ngang của đồ thị hàm số 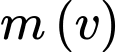 là
là 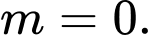
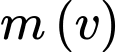 là
là 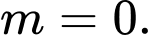
D, d) Khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt gần bằng 0.
a, Sai
b, Đúng
c, Sai
d, Sai
Xét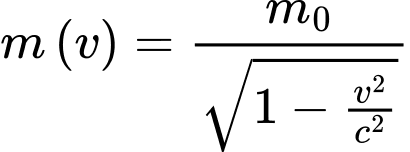 .
.
Tập xác định
Ta có: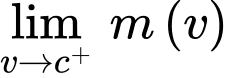
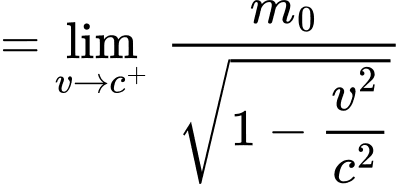
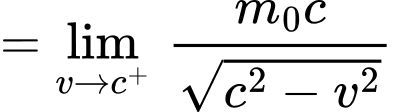
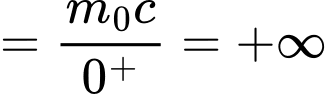
Vậy đường thẳng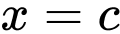 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Đồ thị hàm số không có tiệm cận ngang vì không tồn tại giới hạn khi v tiến đến vô cung
Dựa vào đồ thị ta có:
Khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt tiến gần tới vô cùng.
Trên hình điều này được thể hiện đường cong biểu diễn m(v) sẽ tiến dần đến vô cùng khi v → c. Điều này cho thấy rằng khối lượng của hạt sẽ tăng tới vô cùng khi tốc độ di chuyển của nó tiến gần tốc độ ánh sáng.
b, Đúng
c, Sai
d, Sai
Xét
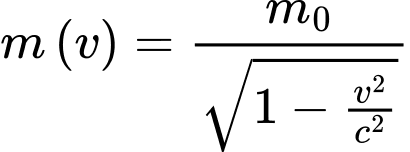 .
.Tập xác định

Ta có:
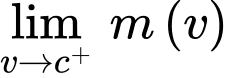
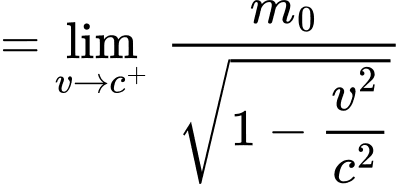
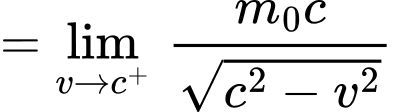
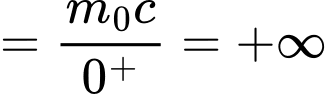
Vậy đường thẳng
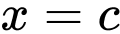 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.Đồ thị hàm số không có tiệm cận ngang vì không tồn tại giới hạn khi v tiến đến vô cung
Dựa vào đồ thị ta có:
Khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt tiến gần tới vô cùng.
Trên hình điều này được thể hiện đường cong biểu diễn m(v) sẽ tiến dần đến vô cùng khi v → c. Điều này cho thấy rằng khối lượng của hạt sẽ tăng tới vô cùng khi tốc độ di chuyển của nó tiến gần tốc độ ánh sáng.
Câu 31 [383418]: [Nguồn SGK Kết Nối Tri Thức]: Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số 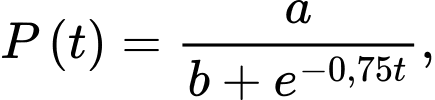 trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Xét tính đúng sai của mệnh đề sau
trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Xét tính đúng sai của mệnh đề sau
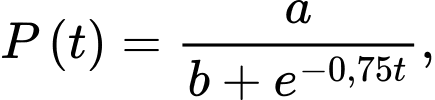 trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Xét tính đúng sai của mệnh đề sau
trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Xét tính đúng sai của mệnh đề sau A, a) 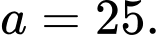
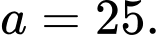
B, b) 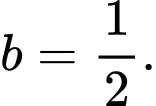
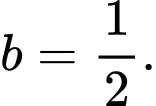
C, c) Số lượng quần thể nấm men luôn tăng.
D, d) Số lượng quần thể nấm men luôn tăng nhưng không vượt quá 50 tế bào.
Có 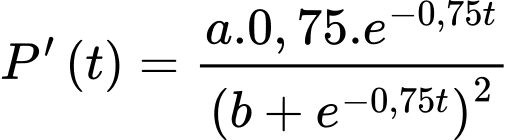 là hàm số thể hiện tốc độ tăng số lượng của quần thể nấm men.
là hàm số thể hiện tốc độ tăng số lượng của quần thể nấm men. 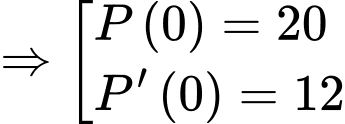
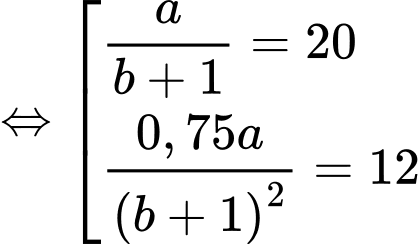
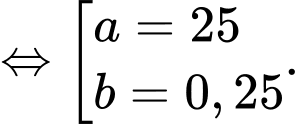
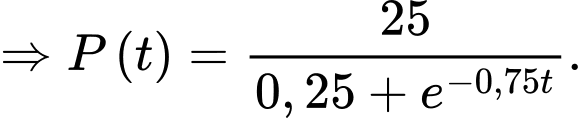
Có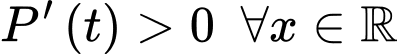
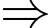 Số lượng quần thể nấm men luôn tăng.
Số lượng quần thể nấm men luôn tăng.
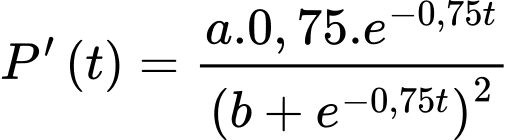 là hàm số thể hiện tốc độ tăng số lượng của quần thể nấm men.
là hàm số thể hiện tốc độ tăng số lượng của quần thể nấm men. Tại thời điểm ban đầu t = 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ.
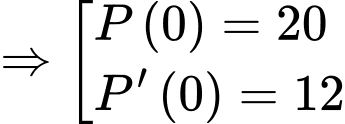
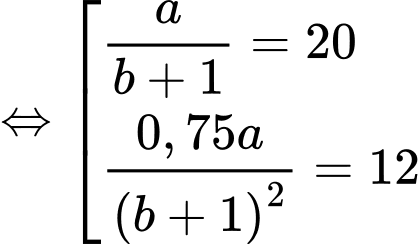
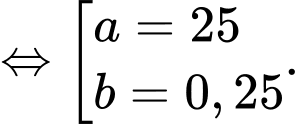
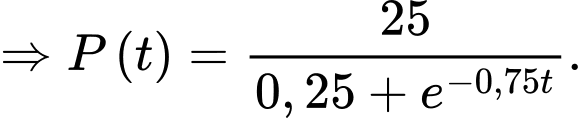
Có
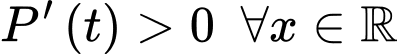
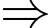 Số lượng quần thể nấm men luôn tăng.
Số lượng quần thể nấm men luôn tăng. Nhận xét:  Số lượng quần thể nấm men luôn tăng nhưng không vượt quá 100 tế bào.
Số lượng quần thể nấm men luôn tăng nhưng không vượt quá 100 tế bào.
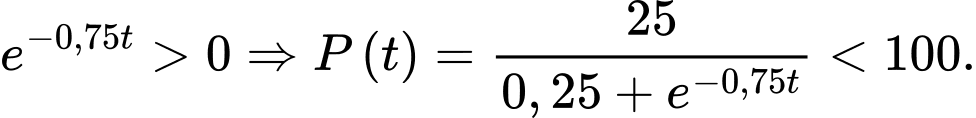 Số lượng quần thể nấm men luôn tăng nhưng không vượt quá 100 tế bào.
Số lượng quần thể nấm men luôn tăng nhưng không vượt quá 100 tế bào. Vậy các mệnh đề a, c là mệnh đề đúng.
Câu 32 [380965]: sử một loại virus  truyền nhiễm gây bệnh cho người. Số người viên bị nhiễm sau
truyền nhiễm gây bệnh cho người. Số người viên bị nhiễm sau 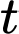 ngày được cho bởi công thức
ngày được cho bởi công thức 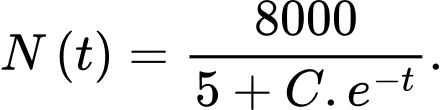 Ban đầu người ta phát hiện có 4 người nhiễm bệnh. Xét tính đúng sai của mệnh đề sau
Ban đầu người ta phát hiện có 4 người nhiễm bệnh. Xét tính đúng sai của mệnh đề sau
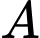 truyền nhiễm gây bệnh cho người. Số người viên bị nhiễm sau
truyền nhiễm gây bệnh cho người. Số người viên bị nhiễm sau 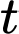 ngày được cho bởi công thức
ngày được cho bởi công thức 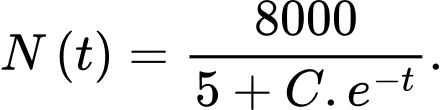 Ban đầu người ta phát hiện có 4 người nhiễm bệnh. Xét tính đúng sai của mệnh đề sau
Ban đầu người ta phát hiện có 4 người nhiễm bệnh. Xét tính đúng sai của mệnh đề sau A, a) 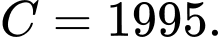
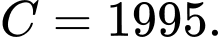
B, b) Sau 3 ngày sẽ có khoảng  người nhiễm bệnh.
người nhiễm bệnh.
 người nhiễm bệnh.
người nhiễm bệnh.C, c) Kể từ ngày thứ 40 trở đi thì số lượng người nhiễm bệnh sẽ giảm dần.
D, d) Số người nhiễm bệnh luôn tăng nhưng không vượt quá 1600 người.
a) Đúng. 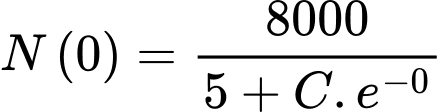
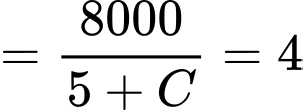
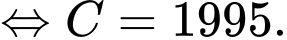
b) Đúng. Sau 3 ngày sẽ có khoảng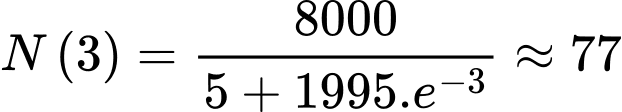 người nhiễm bệnh.
người nhiễm bệnh.
c) Sai. Ta có: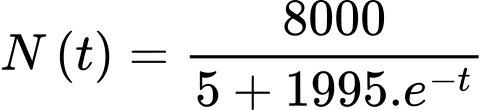
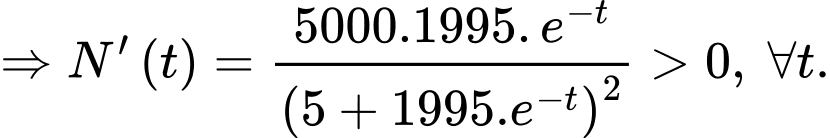 Do đó, số lượng người nhiễm bệnh luôn tăng dần.
Do đó, số lượng người nhiễm bệnh luôn tăng dần.
d) Đúng. Số người nhiễm bệnh luôn tăng nhưng không vượt quá 1600 người.
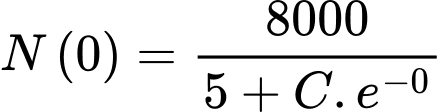
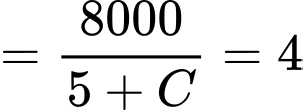
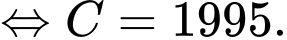
b) Đúng. Sau 3 ngày sẽ có khoảng
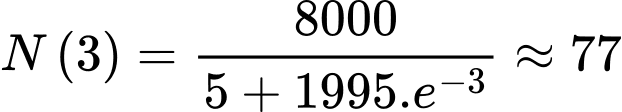 người nhiễm bệnh.
người nhiễm bệnh. c) Sai. Ta có:
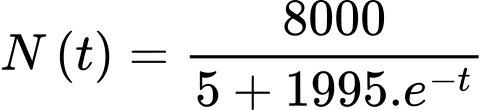
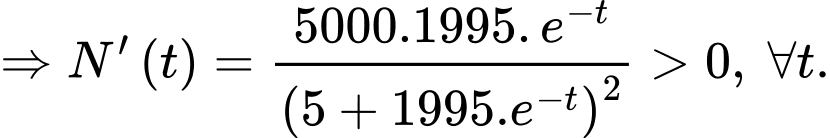 Do đó, số lượng người nhiễm bệnh luôn tăng dần.
Do đó, số lượng người nhiễm bệnh luôn tăng dần.d) Đúng. Số người nhiễm bệnh luôn tăng nhưng không vượt quá 1600 người.
Câu 33 [522405]: Tìm số tiệm cận (đứng và ngang) của đồ thị hàm số 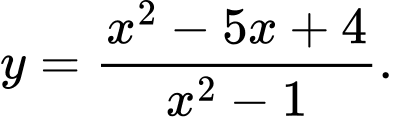
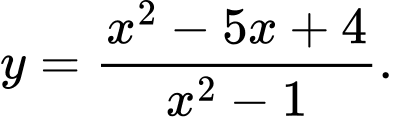
A,
B,
C,
D,
Ta có: 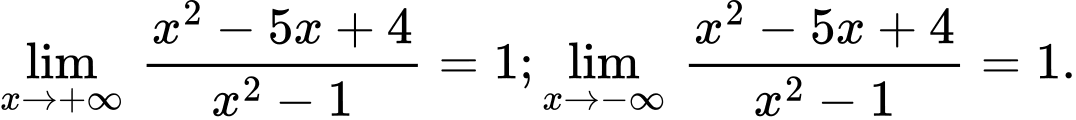
Vậy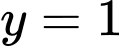 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
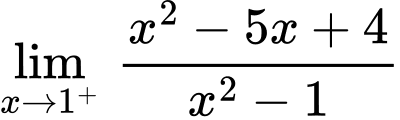
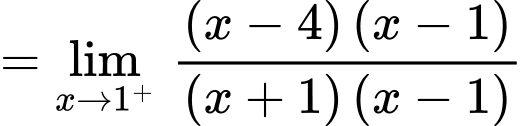
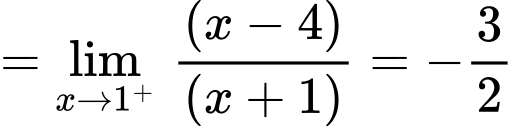
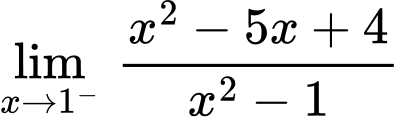
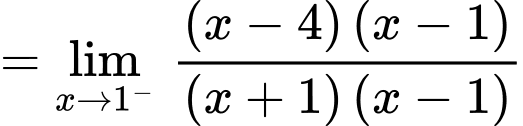
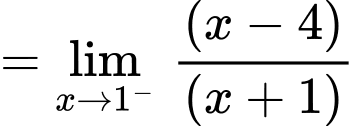
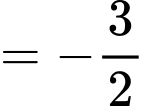
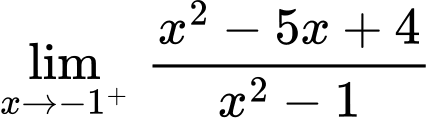
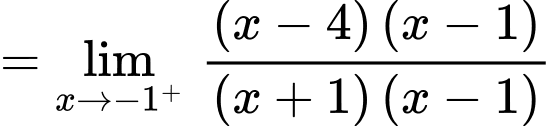
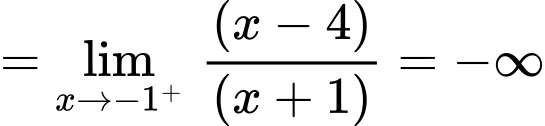
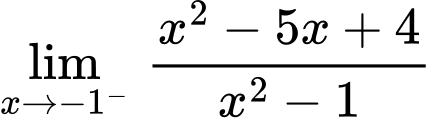
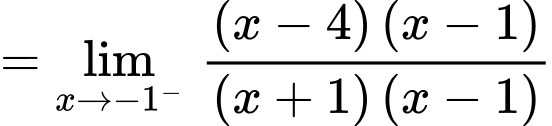
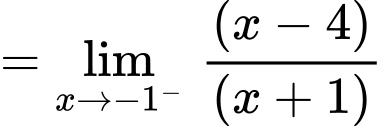

Vậy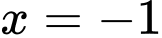 là tiệm cận đứng của đồ thị hàm số. Đáp án: A
là tiệm cận đứng của đồ thị hàm số. Đáp án: A
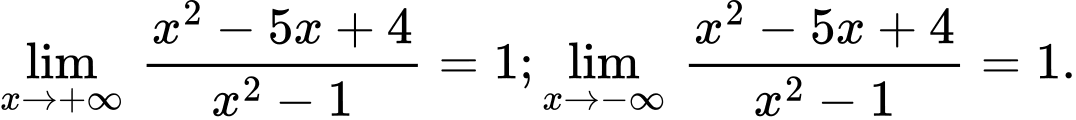
Vậy
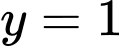 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.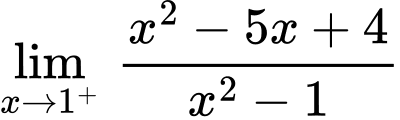
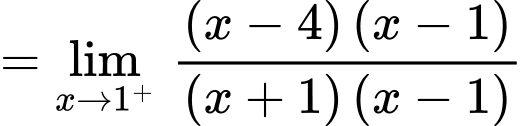
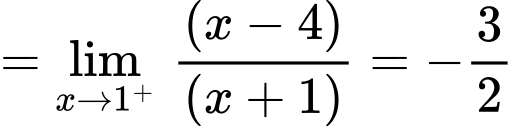
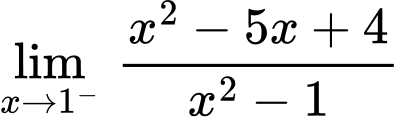
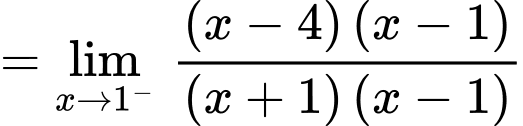
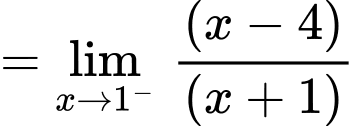
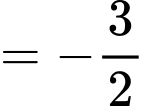
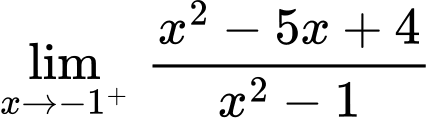
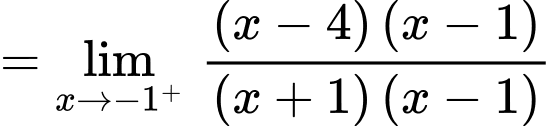
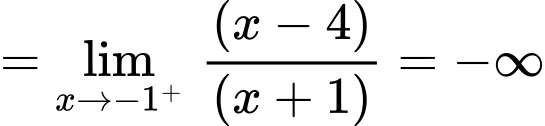
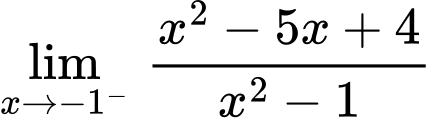
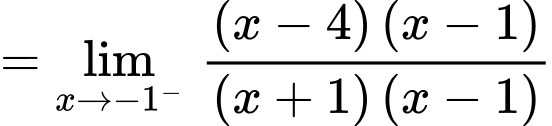
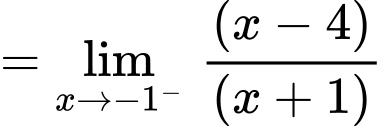

Vậy
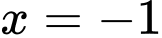 là tiệm cận đứng của đồ thị hàm số. Đáp án: A
là tiệm cận đứng của đồ thị hàm số. Đáp án: A
Câu 34 [309644]: Số đường tiệm cận của đồ thị hàm số 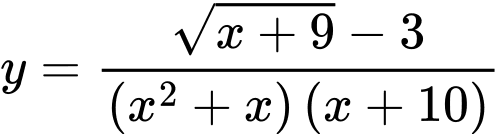 là
là
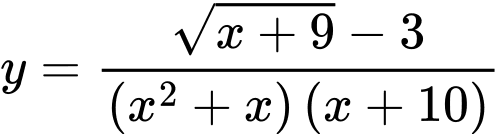 là
là A,
B,
C,
D,
Điều kiện:
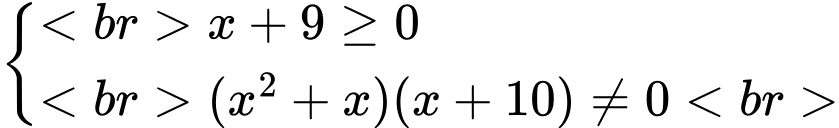
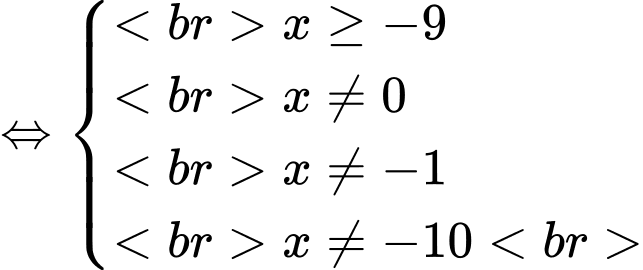
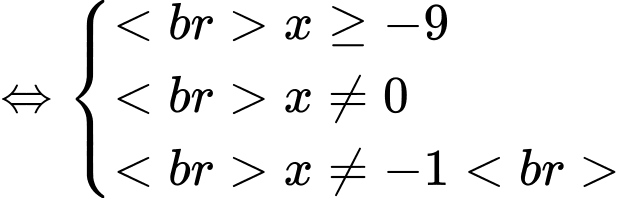
Do
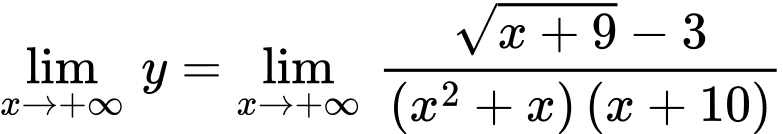
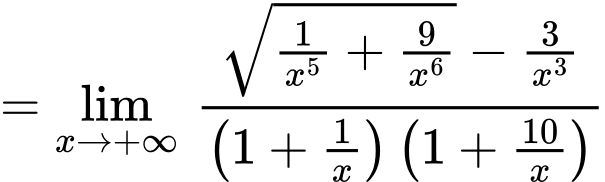
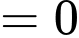 nên đường thẳng
nên đường thẳng 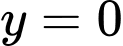 là tiệm cận ngang
là tiệm cận ngang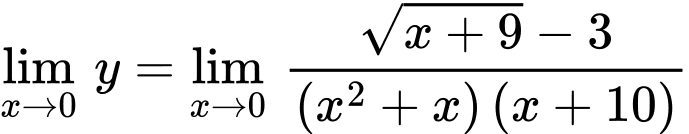
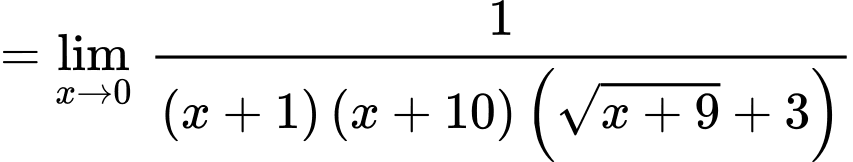
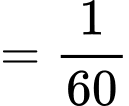 và nên đường thẳng
và nên đường thẳng 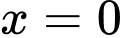 không là tiệm cận đứng.
không là tiệm cận đứng.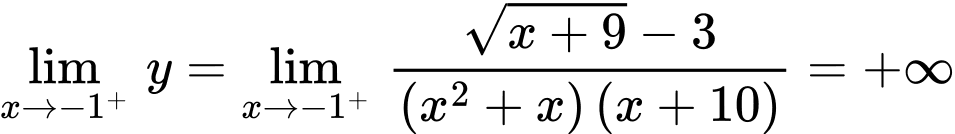 và
và 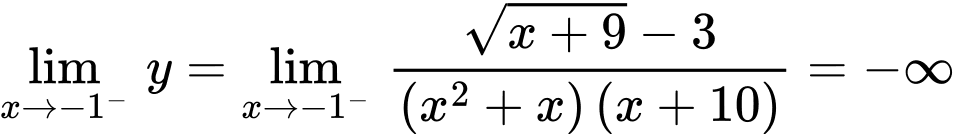 nên đường thẳng
nên đường thẳng 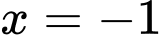 là tiệm cận đứng. Đáp án: B
là tiệm cận đứng. Đáp án: B
Câu 35 [31174]: Cho hàm số $y = \frac{{\sqrt {{x^2} - 4} }}{{x - 1}}.$ Đồ thị hàm số có mấy đường tiệm cận?
A,
B,
C,
D,
Tập xác định của hàm số là $D=\left( -\infty ;-2 \right]\cup \left[ 2;+\infty \right).$
Ta thấy rằng $x=1\notin D\Rightarrow $ Đồ thi hàm số không có tiệm cận đứng.
Và $\underset{x\to \infty }{\mathop{\lim }}\,y=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{\sqrt{{{x}^{2}}-4}}{x-1}$$=\underset{x\to \infty }{\mathop{\lim }}\,\frac{\left| x \right|.\sqrt{1-\dfrac{4}{{{x}^{2}}}}}{x.\left( 1-\dfrac{1}{x} \right)}$$=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{\left| x \right|}{x}$ $\Rightarrow \left\{ \begin{align} & \underset{x\to +\infty }{\mathop{\lim }}\,y=1 \\ & \underset{x\to -\infty }{\mathop{\lim }}\,y=-1 \\ \end{align} \right.$ $\Rightarrow y=1,$ $y=-1$ $\Rightarrow $ Đồ thị hàm số có hai tiệm cận ngang.
Đáp án: C
Ta thấy rằng $x=1\notin D\Rightarrow $ Đồ thi hàm số không có tiệm cận đứng.
Và $\underset{x\to \infty }{\mathop{\lim }}\,y=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{\sqrt{{{x}^{2}}-4}}{x-1}$$=\underset{x\to \infty }{\mathop{\lim }}\,\frac{\left| x \right|.\sqrt{1-\dfrac{4}{{{x}^{2}}}}}{x.\left( 1-\dfrac{1}{x} \right)}$$=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{\left| x \right|}{x}$ $\Rightarrow \left\{ \begin{align} & \underset{x\to +\infty }{\mathop{\lim }}\,y=1 \\ & \underset{x\to -\infty }{\mathop{\lim }}\,y=-1 \\ \end{align} \right.$ $\Rightarrow y=1,$ $y=-1$ $\Rightarrow $ Đồ thị hàm số có hai tiệm cận ngang.
Đáp án: C
Câu 36 [31203]: Số đường tiệm cận của đồ thị hàm số 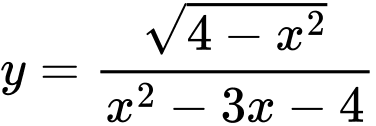 là
là
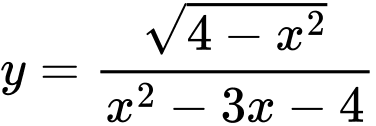 là
là A, 1.
B, 0.
C, 2.
D, 3.
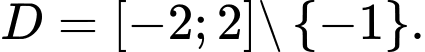
Đồ thị hàm số không có TCN. Lại có 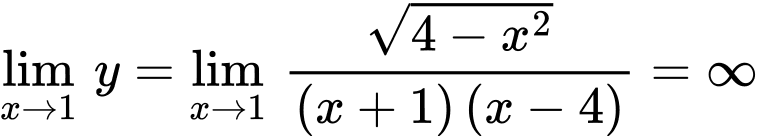 nên
nên 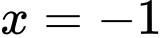 là TCĐ.
là TCĐ.
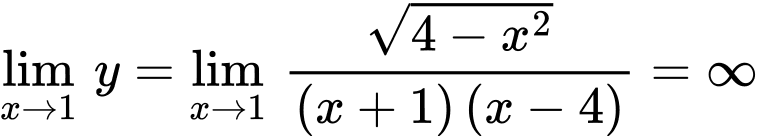 nên
nên 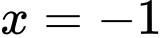 là TCĐ.
là TCĐ. Do đó đồ thị hàm số có 1 tiệm cận.
Chọn A.
Đáp án: A
Câu 37 [399668]: Biết đồ thị hàm số 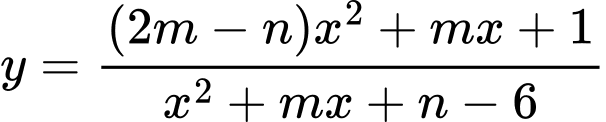 nhận trục hoành và trục tung làm hai đường tiệm cận. Tính
nhận trục hoành và trục tung làm hai đường tiệm cận. Tính 
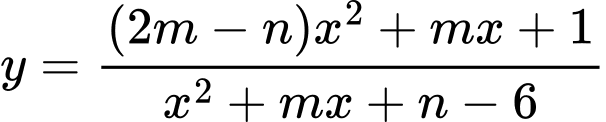 nhận trục hoành và trục tung làm hai đường tiệm cận. Tính
nhận trục hoành và trục tung làm hai đường tiệm cận. Tính 
Đặt 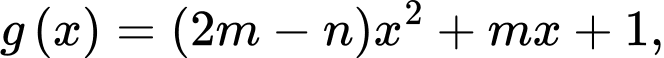
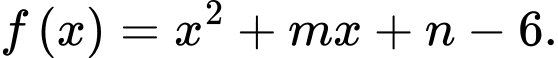
Ta có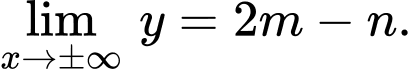 Suy ra tiệm cận ngang là
Suy ra tiệm cận ngang là 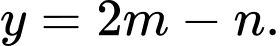
Theo giả thiết ta có tiệm cận ngang là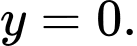 Do đó ta có
Do đó ta có 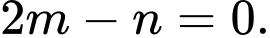 (1).
(1).
Mặt khác, tiệm cận đứng của đồ thị là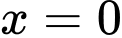 suy ra
suy ra 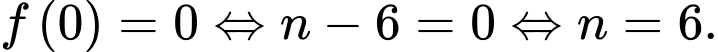
Khi đó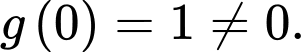
Từ (1) và (2) suy ra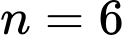 và
và 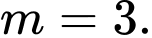
Vậy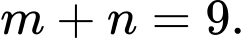
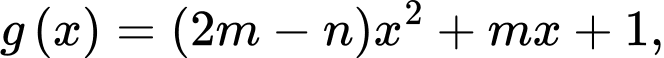
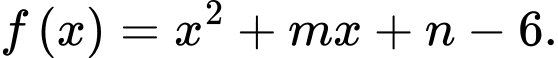
Ta có
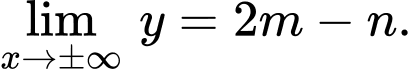 Suy ra tiệm cận ngang là
Suy ra tiệm cận ngang là 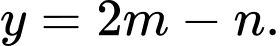
Theo giả thiết ta có tiệm cận ngang là
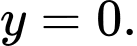 Do đó ta có
Do đó ta có 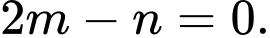 (1).
(1).
Mặt khác, tiệm cận đứng của đồ thị là
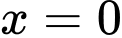 suy ra
suy ra 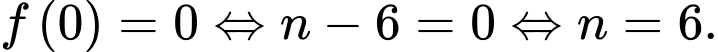
Khi đó
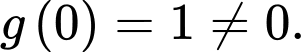
Từ (1) và (2) suy ra
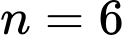 và
và 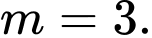
Vậy
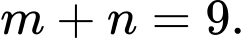
Câu 38 [31268]: Biết đồ thị hàm số $y = \frac{{\left( {4a - b} \right){x^2} + ax + 1}}{{{x^2} + ax + b - 12}}$ nhận trục hoành và trục tung làm hai tiệm cận thì giá trị $a + b$ bằng
A,
B,
C,
D,
Do đồ thị nhận trục hoành làm tiệm cận ngang mà $\underset{x\to +\infty }{\mathop{\lim }}\,y=4a-b=0\Rightarrow b=4a.$
Đáp án: D
Do đồ thị nhận trục tung làm tiệm cận đứng $\Rightarrow $ Biểu thức ${{x}^{2}}+ax+b-12$ nhận $x=0$ làm nghiệm $\Rightarrow b=12$ $\Rightarrow a=3$ $\Rightarrow a+b=15.$
Câu 39 [31259]: Biết đồ thị $y = \frac{(a - 2b)x^2 + bx + 1}{x^2 + x - b}$ có đường tiệm cận đứng là $x = 1$ và đường tiệm cận ngang là $y = 0.$ Tính $a + 2b.$
A,
B,
C,
D,
Ta thấy:
Đáp án: C
Đồ thị hàm số có tiệm cận đứng $x=1\Rightarrow $ phương trình ${{x}^{2}}+x-b=0$ có nghiệm $x=1$ và $\left( a-2b \right){{x}^{2}}+bx+1=0$ không có nghiệm $x=1$ $\Rightarrow \left\{ \begin{align}
& 1+1-b=0 \\
& a-2b+b+1\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& b=2 \\
& a\ne 1 \\
\end{align} \right..$
& 1+1-b=0 \\
& a-2b+b+1\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& b=2 \\
& a\ne 1 \\
\end{align} \right..$
Hàm số có dạng $y=\frac{\left( a-4 \right){{x}^{2}}+2x+1}{{{x}^{2}}+x-2}.$
Hàm số có tiệm cận ngang $y=0$ $\Leftrightarrow \underset{x\to +\infty }{\mathop{\lim }}\,y=0$ $\Leftrightarrow \underset{x\to +\infty }{\mathop{\lim }}\,\frac{\left( a-4 \right){{x}^{2}}+2x+1}{{{x}^{2}}+x-2}=0$ $\Leftrightarrow \underset{x\to +\infty }{\mathop{\lim }}\,\frac{\left( a-4 \right)+\frac{2}{x}+\frac{1}{{{x}^{2}}}}{1+\frac{1}{x}-\frac{2}{{{x}^{2}}}}$ $=\Leftrightarrow \underset{x\to +\infty }{\mathop{\lim }}\,\frac{a-4}{1}=0$ $\Leftrightarrow a-4=0\Leftrightarrow a=4\Rightarrow a+2b=8.$