Đáp án Bài tập tự luyện số 3
Câu 1 [357814]: Tiệm cận xiên của đồ thị hàm số 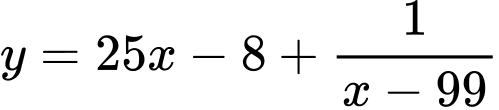 là:
là:
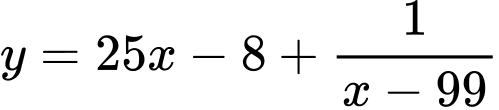 là:
là: A, 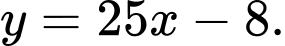
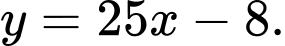
B, 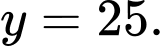
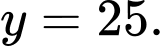
C, 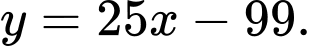
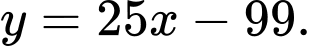
D, 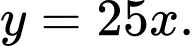
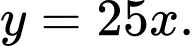

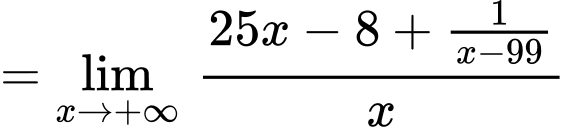
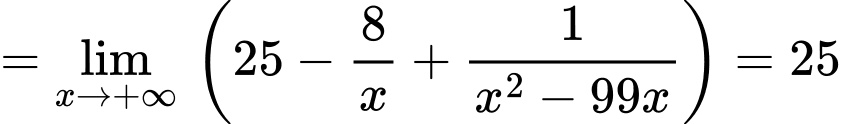
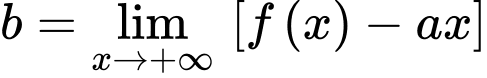
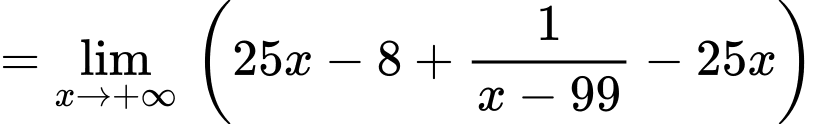
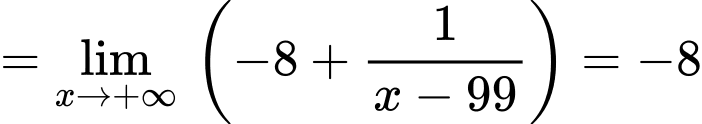
Tương tự,
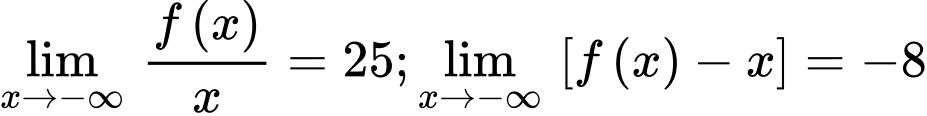
Vậy đường thẳng
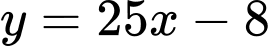 là tiệm cận xiên của đồ thị hàm số. Đáp án: A
là tiệm cận xiên của đồ thị hàm số. Đáp án: A
Câu 2 [46678]: Tìm số đường tiệm cận của đồ thị hàm số 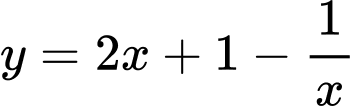 .
.
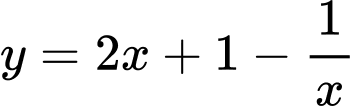 .
. A, 2.
B, 1.
C, 3.
D, 0.
TXĐ: 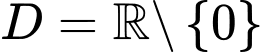
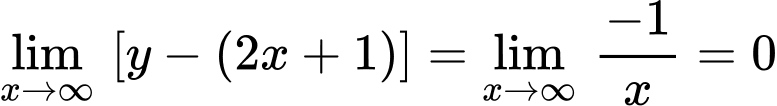
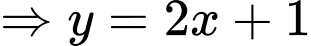 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số. 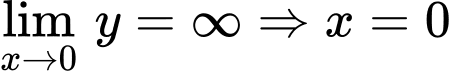 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
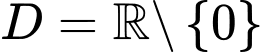
Ta có:
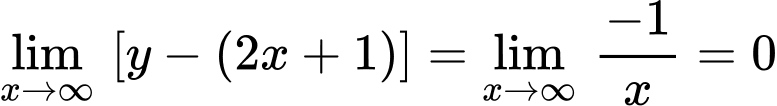
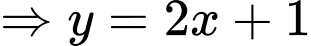 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số. 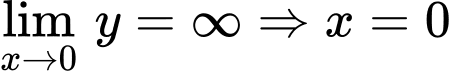 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số. Vậy đồ thị có 2 đường tiệm cận. Chọn A.
Đáp án: A
Câu 3 [382476]: Đồ thị hàm số nào dưới đây có đường tiệm cận xiên:
A, 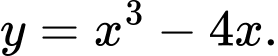
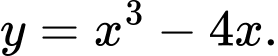
B, 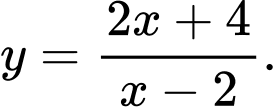
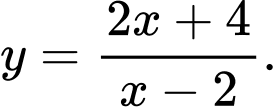
C, 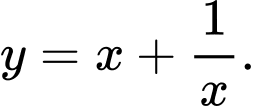
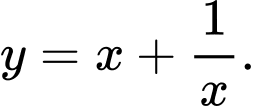
D, 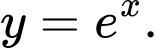
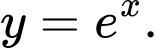
ĐKXĐ: 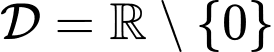 .
.
Ta có: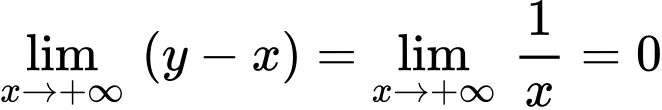
Suy ra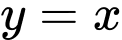 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
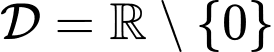 .
.
Ta có:
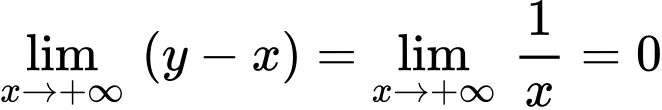
Suy ra
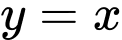 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
Câu 4 [358921]: Tiệm cận xiên của đồ thị hàm số 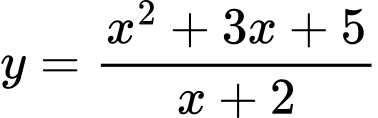 là
là
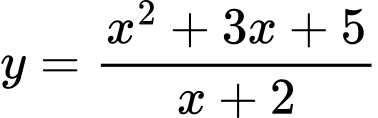 là
là A, 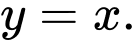
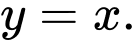
B, 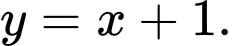
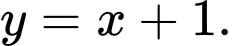
C, 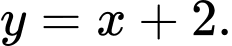
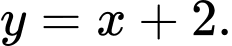
D, 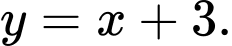
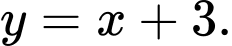
Tiệm cận xiên của hàm số có dạng 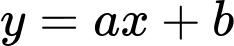
Ta có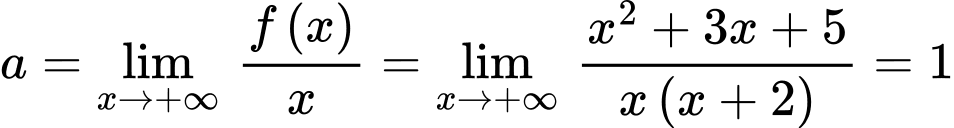 và
và 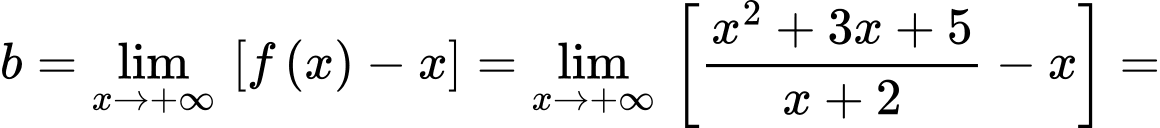
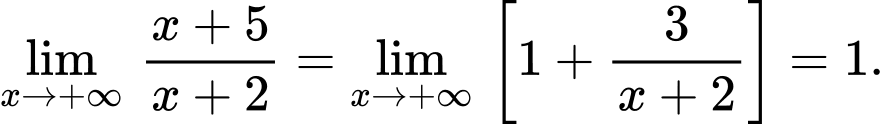
Vậy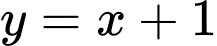 là tiệm cận xiên của hàm số đã cho (khi
là tiệm cận xiên của hàm số đã cho (khi 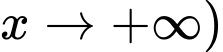
Tương tự, ta có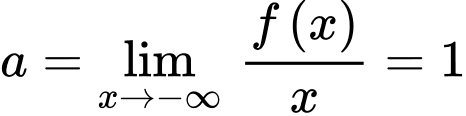 và
và 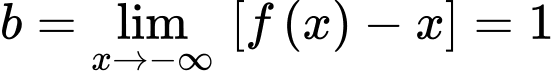 suy ra
suy ra 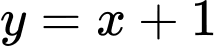 cũng là tiệm cận xiên của hàm số đã cho (khi
cũng là tiệm cận xiên của hàm số đã cho (khi 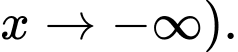 Đáp án: B
Đáp án: B
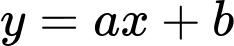
Ta có
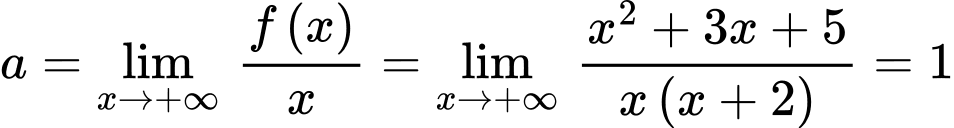 và
và 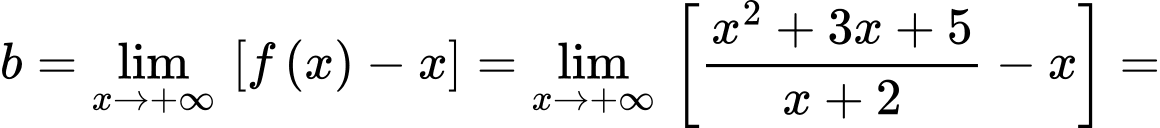
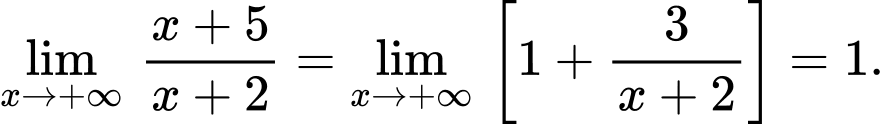
Vậy
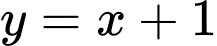 là tiệm cận xiên của hàm số đã cho (khi
là tiệm cận xiên của hàm số đã cho (khi 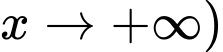
Tương tự, ta có
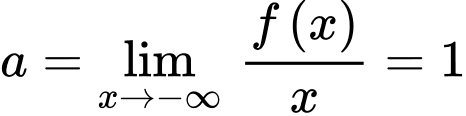 và
và 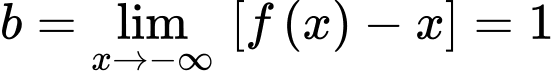 suy ra
suy ra 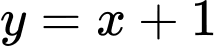 cũng là tiệm cận xiên của hàm số đã cho (khi
cũng là tiệm cận xiên của hàm số đã cho (khi 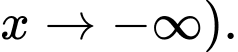 Đáp án: B
Đáp án: B
Câu 5 [358587]: Phương trình đường tiệm cận xiên của đồ thị hàm số 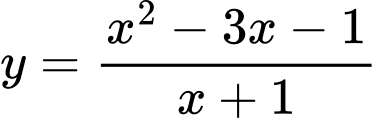 là
là
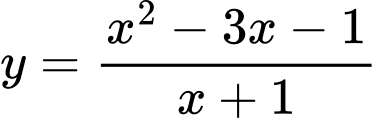 là
là A, 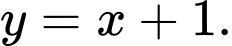
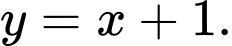
B, 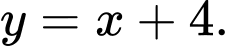
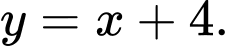
C, 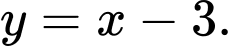
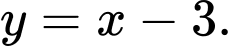
D, 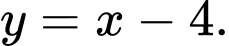
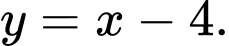
HD: Phương trình tiệm cận xiên của ĐTHS là: 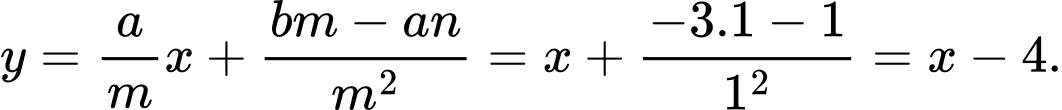 Chọn D. Đáp án: D
Chọn D. Đáp án: D
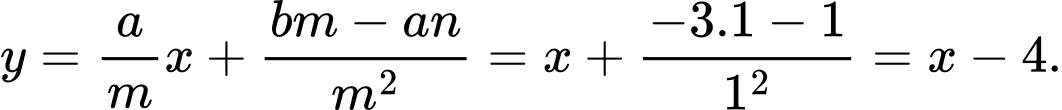 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 6 [46679]: Tìm đường tiệm cận xiên của đồ thị hàm số 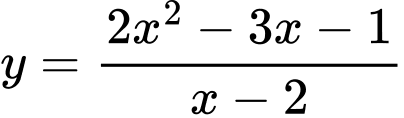 .
.
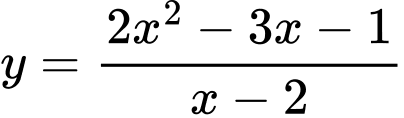 .
. A, 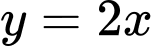
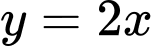
B, 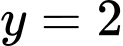
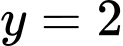
C, 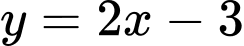
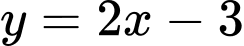
D, 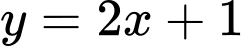
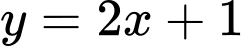
Ta có 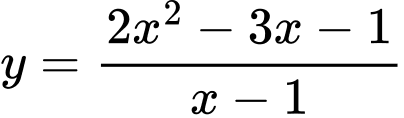
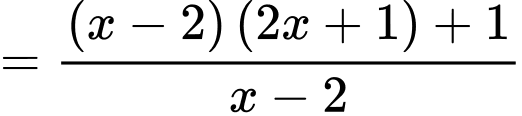
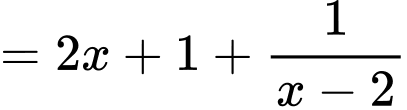
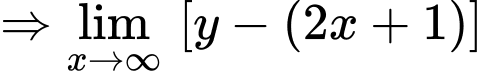
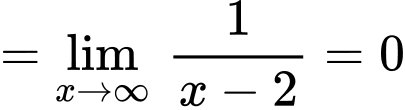
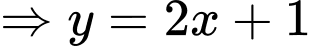 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
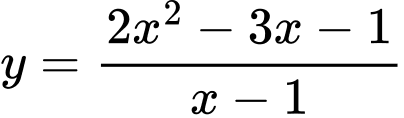
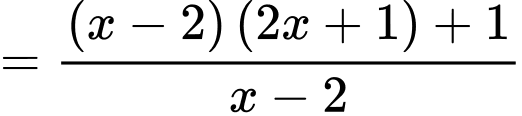
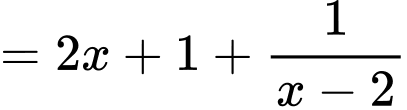
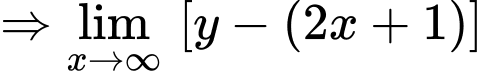
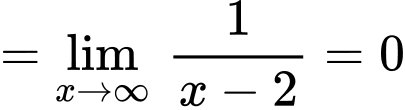
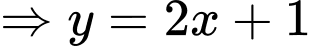 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số. Chọn đáp án D.
Đáp án: D
Đáp án: D
Câu 7 [371923]: Tiệm cận xiên của đồ thị hàm số 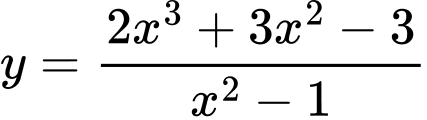 là đường thẳng có phương trình
là đường thẳng có phương trình
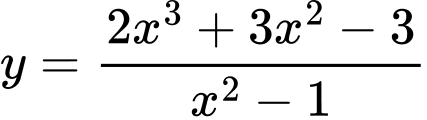 là đường thẳng có phương trình
là đường thẳng có phương trình A, 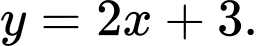
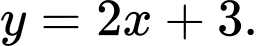
B, 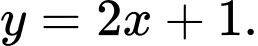
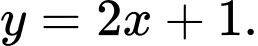
C, 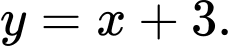
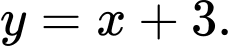
D, 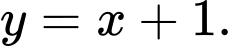
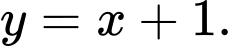
ĐKXĐ: 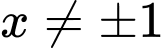
Ta có: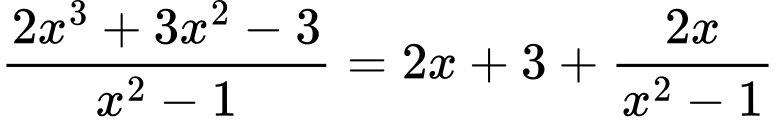
Suy ra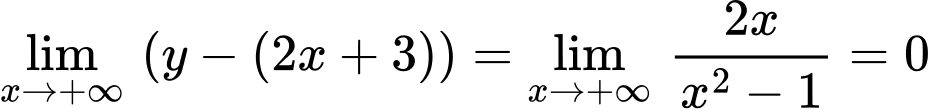
Vậy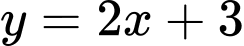 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: A
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: A
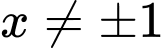
Ta có:
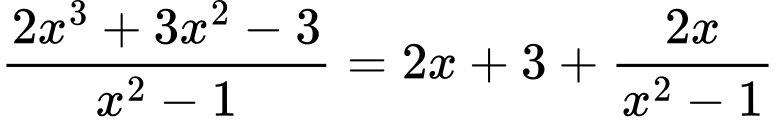
Suy ra
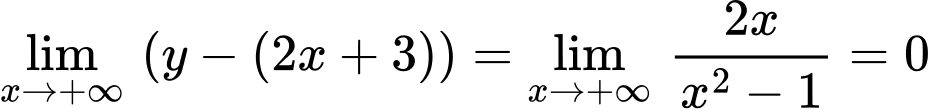
Vậy
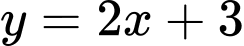 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: A
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: A
Câu 8 [358588]: Đồ thị hàm số nào dưới đây có đường tiệm cận xiên
A, 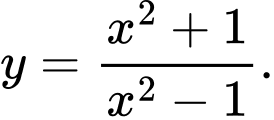
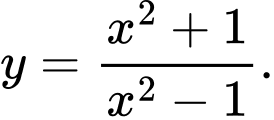
B, 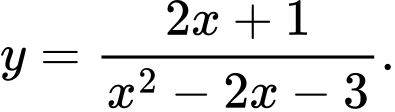
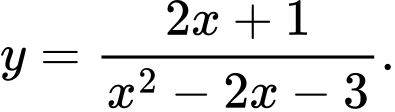
C, 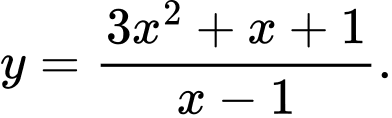
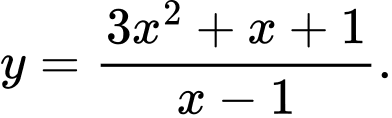
D, 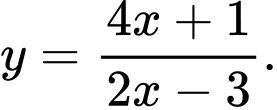
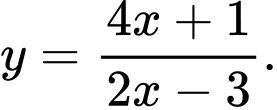
ĐKXĐ: 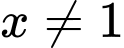
Ta có: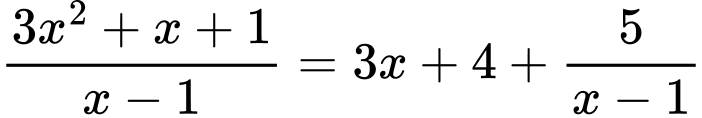
Suy ra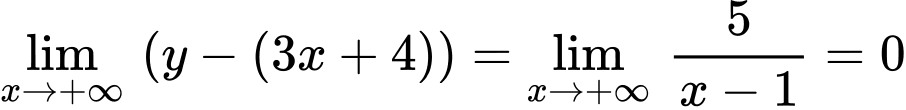
Vậy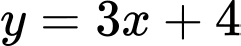 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
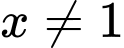
Ta có:
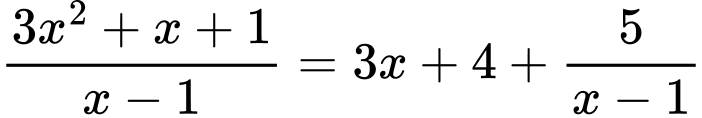
Suy ra
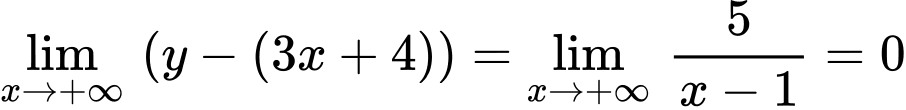
Vậy
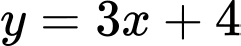 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: C
Câu 9 [357815]: Tiệm cận xiên của đồ thị hàm số 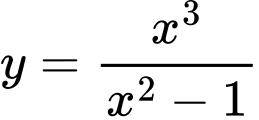 là:
là:
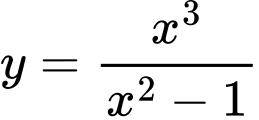 là:
là: A, 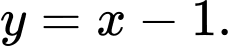
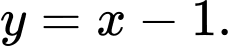
B, 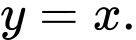
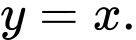
C, 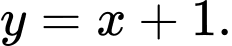
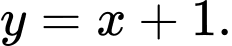
D, 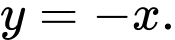
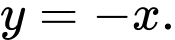
ĐKXĐ: 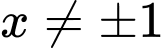
Ta có: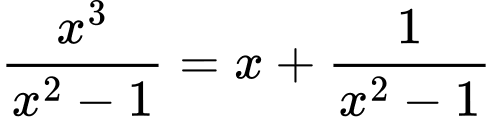
Suy ra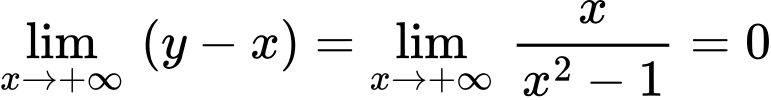
Vậy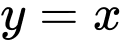 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
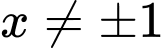
Ta có:
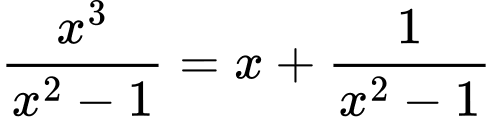
Suy ra
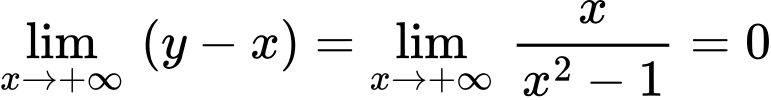
Vậy
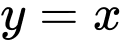 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
Câu 10 [382477]: Đồ thị hàm số nào dưới đây có đường tiệm cận xiên:
A, 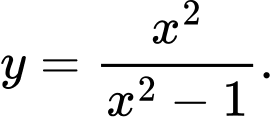
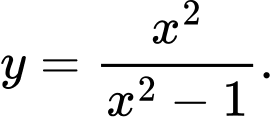
B, 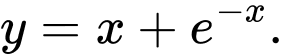
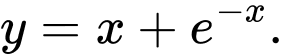
C, 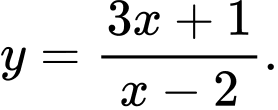
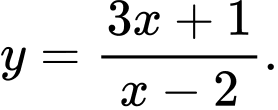
D, 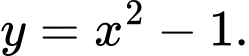
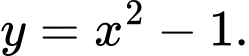
Ta có:
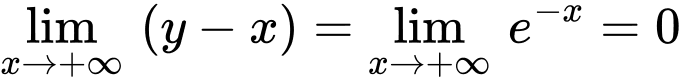
Vậy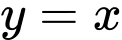 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
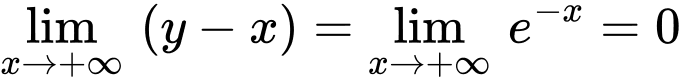
Vậy
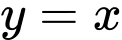 là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
là đường tiệm cận xiên của đồ thị hàm số.
Đáp án: B
Câu 11 [382478]: Đồ thị hàm số nào dưới đây không có đường tiệm cận xiên:
A, 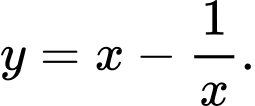
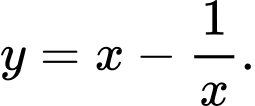
B, 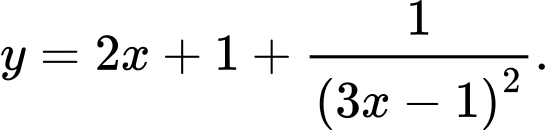
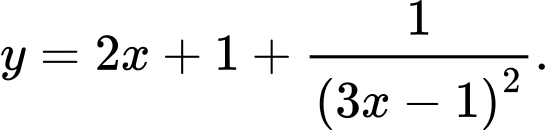
C, 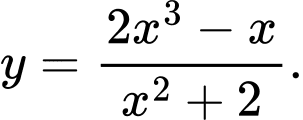
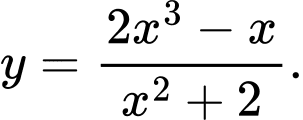
D, 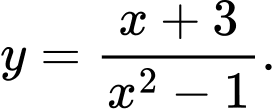
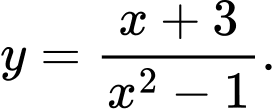
Chọn đáp án D Đáp án: D
Câu 12 [382479]: Đường tiệm cận xiên của đồ thị hàm số 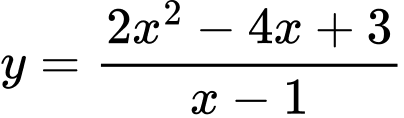 có dạng
có dạng 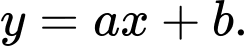 Khi đó
Khi đó 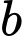 bằng
bằng
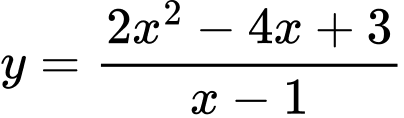 có dạng
có dạng 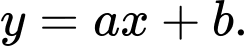 Khi đó
Khi đó 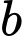 bằng
bằng A, 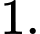
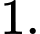
B, 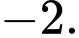
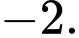
C, 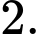
D, 
ĐKXĐ: 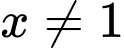
Ta có: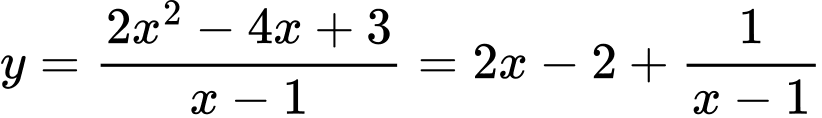
Suy ra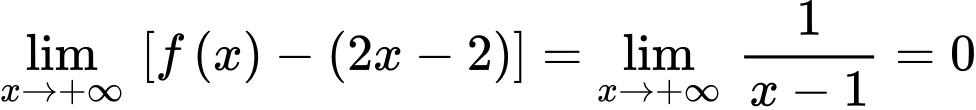
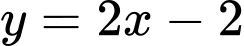 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Vậy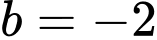 Đáp án: B
Đáp án: B
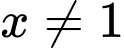
Ta có:
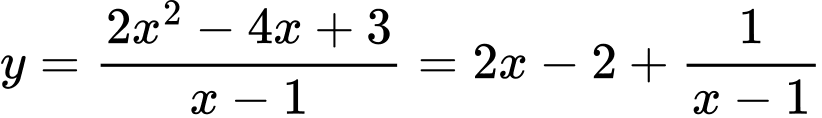
Suy ra
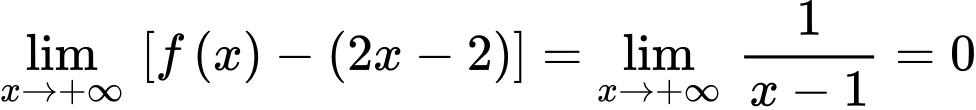
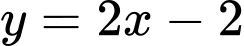 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Vậy
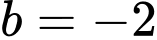 Đáp án: B
Đáp án: B
Câu 13 [46680]: Tìm giao điểm của trục tung với tiệm cận xiên của đường cong 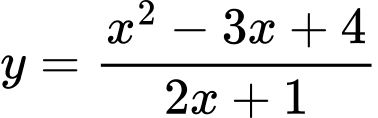 .
.
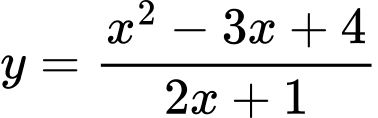 .
. A, 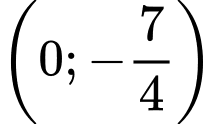
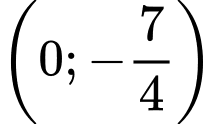
B, (0;4)
C, (0;– 2)
D, 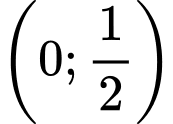
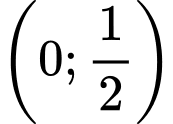
Ta có 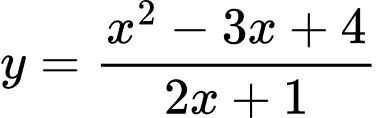
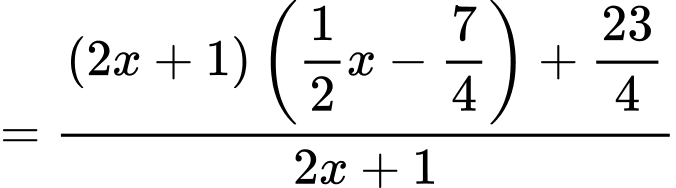
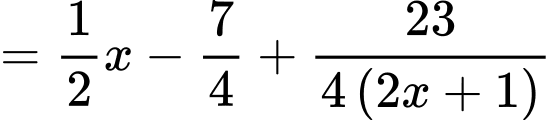
Do đó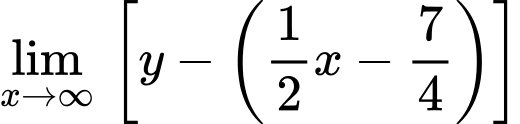
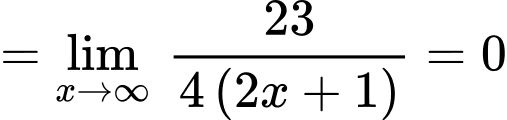
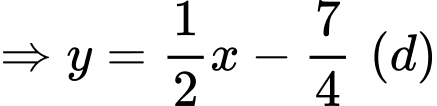 là tiệm cận xiên của đường cong
là tiệm cận xiên của đường cong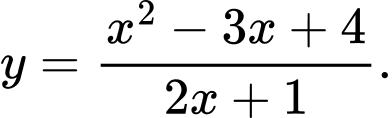
Khi đó
Chọn đáp án A. Đáp án: A
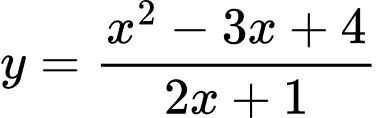
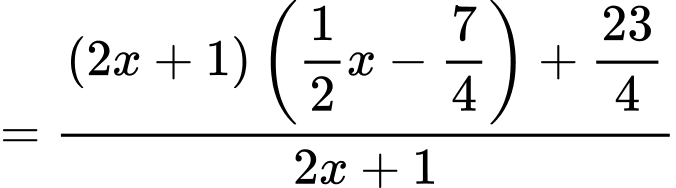
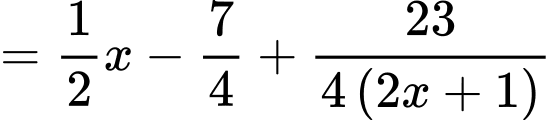
Do đó
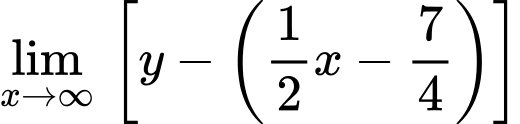
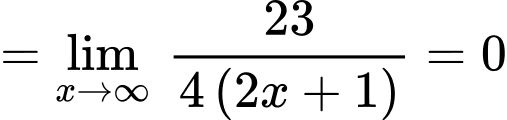
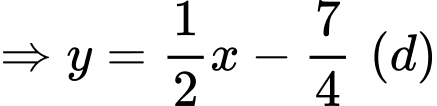 là tiệm cận xiên của đường cong
là tiệm cận xiên của đường cong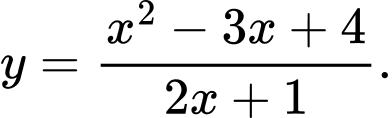
Khi đó

Chọn đáp án A. Đáp án: A
Câu 14 [382480]: Khoảng cách từ gốc toạ độ  đến tiệm cận xiên của đồ thị hàm số
đến tiệm cận xiên của đồ thị hàm số 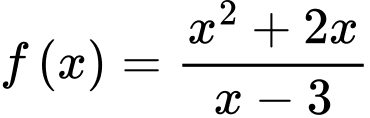 bằng
bằng
 đến tiệm cận xiên của đồ thị hàm số
đến tiệm cận xiên của đồ thị hàm số 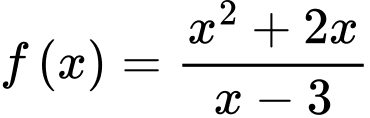 bằng
bằng A, 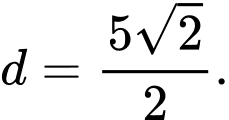
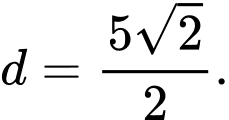
B, 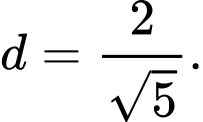
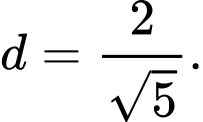
C, 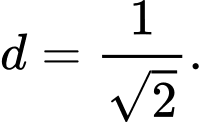
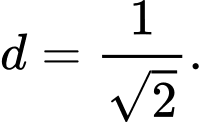
D, 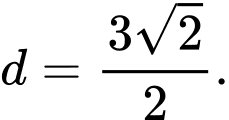
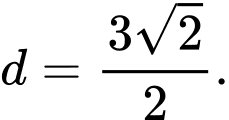
ĐKXĐ: 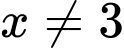
Ta có: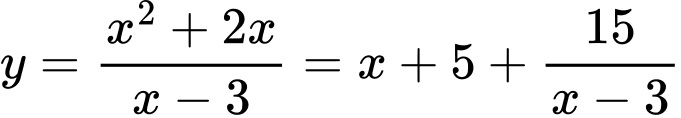
Suy ra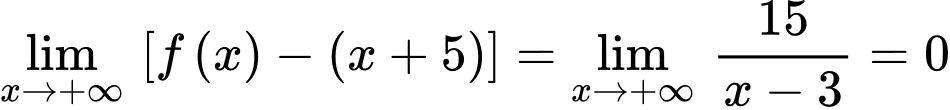
Nên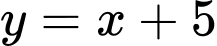 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Vậy khoảng cách từ gốc tọa độ đến tiệm cận xiên của đồ thị hàm số là
đến tiệm cận xiên của đồ thị hàm số là 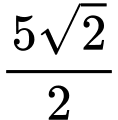 .
Đáp án: A
.
Đáp án: A
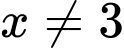
Ta có:
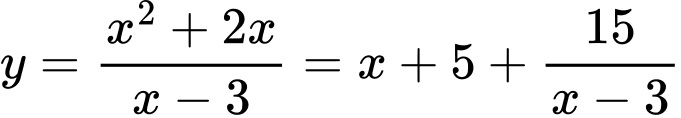
Suy ra
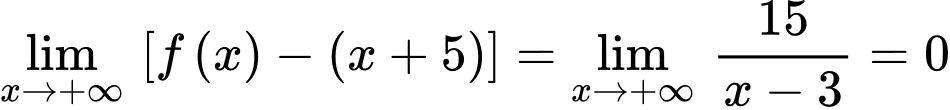
Nên
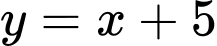 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Vậy khoảng cách từ gốc tọa độ
 đến tiệm cận xiên của đồ thị hàm số là
đến tiệm cận xiên của đồ thị hàm số là 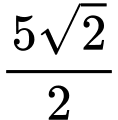 .
Đáp án: A
.
Đáp án: A
Câu 15 [382481]: Một mảnh vườn hình chữ nhật có diện tích bằng 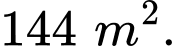 Biết độ dài một cạnh của mảnh vườn là
Biết độ dài một cạnh của mảnh vườn là 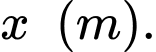 Gọi
Gọi 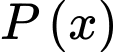 (mét) là biểu thức tính chu vi của mảnh vườn. Xét hàm số
(mét) là biểu thức tính chu vi của mảnh vườn. Xét hàm số 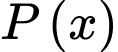 trên khoảng
trên khoảng 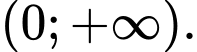 Tiệm cận xiên của đồ thị hàm số
Tiệm cận xiên của đồ thị hàm số 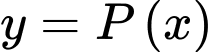 là
là
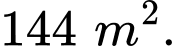 Biết độ dài một cạnh của mảnh vườn là
Biết độ dài một cạnh của mảnh vườn là 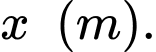 Gọi
Gọi 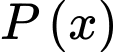 (mét) là biểu thức tính chu vi của mảnh vườn. Xét hàm số
(mét) là biểu thức tính chu vi của mảnh vườn. Xét hàm số 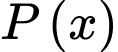 trên khoảng
trên khoảng 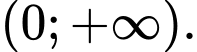 Tiệm cận xiên của đồ thị hàm số
Tiệm cận xiên của đồ thị hàm số 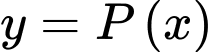 là
là A, 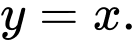
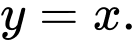
B, 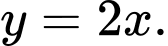
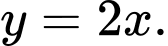
C, 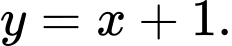
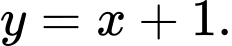
D, 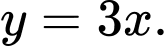
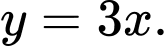
Độ dài cạnh còn lại của mảnh vườn là 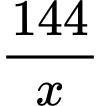
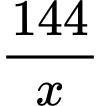
Chu vi của mảnh vườn là: 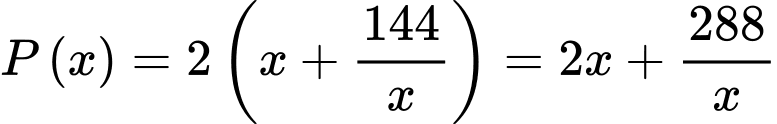
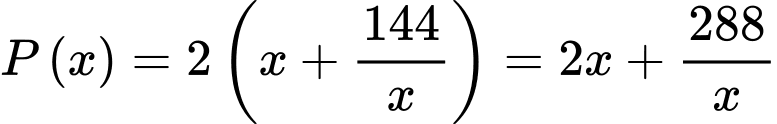
Suy ra tiệm cận xiên của đồ thị hàm số 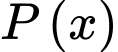 là
là 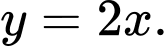
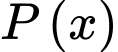 là
là 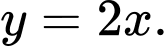
Chọn B.
Đáp án: B
Câu 16 [358589]: Đường tiệm cận xiên của đồ thị hàm số 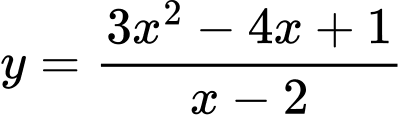 tạo với các trục toạ độ một tam giác có diện tích
tạo với các trục toạ độ một tam giác có diện tích 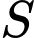 bằng
bằng
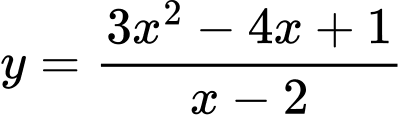 tạo với các trục toạ độ một tam giác có diện tích
tạo với các trục toạ độ một tam giác có diện tích 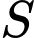 bằng
bằng A, 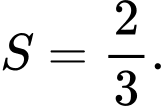
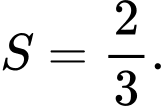
B, 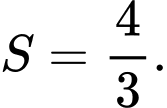
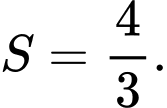
C, 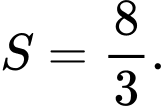
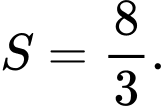
D, 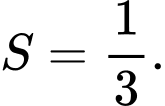
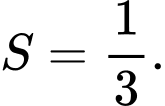
HD: PT đường tiệm cận xiên của đồ thị hàm số là: 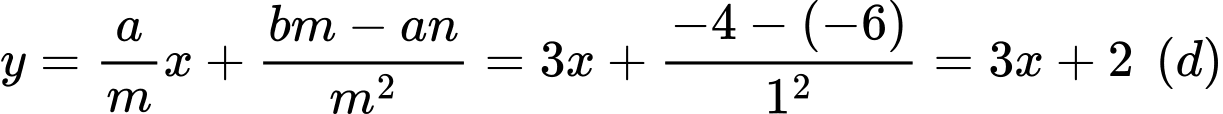
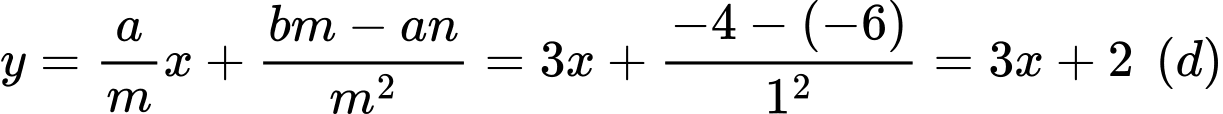
Khi đó giao điểm của đường thẳng 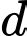 với các trục toạ độ là
với các trục toạ độ là 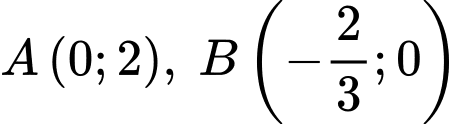
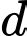 với các trục toạ độ là
với các trục toạ độ là 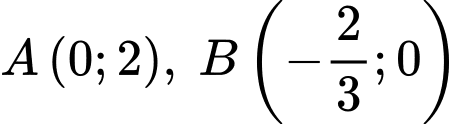
Suy ra 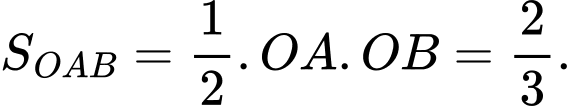
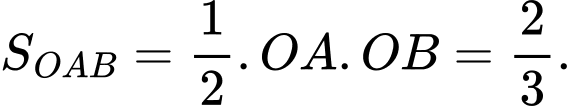
Chọn A.
Đáp án: A
Câu 17 [358590]: Đường tiệm cận xiên của đồ thị hàm số 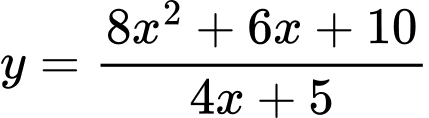 đi qua điểm nào trong các điểm sau đây:
đi qua điểm nào trong các điểm sau đây:
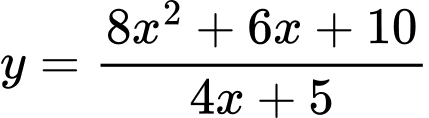 đi qua điểm nào trong các điểm sau đây:
đi qua điểm nào trong các điểm sau đây: A, 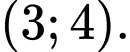
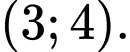
B, 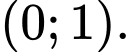
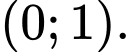
C, 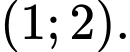
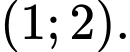
D, 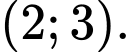
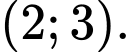
HD: PT đường tiệm cận xiên của đồ thị hàm số là: 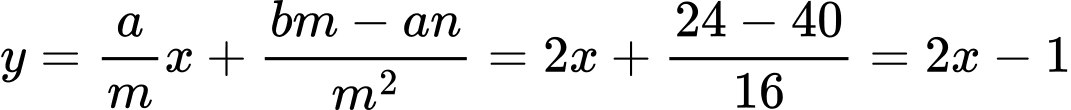 Do đó đường tiệm cận xiên của đồ thị hàm số đi qua điểm
Do đó đường tiệm cận xiên của đồ thị hàm số đi qua điểm 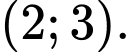 Chọn D. Đáp án: D
Chọn D. Đáp án: D
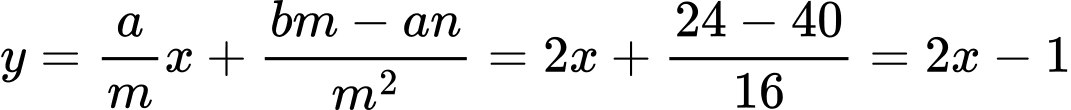 Do đó đường tiệm cận xiên của đồ thị hàm số đi qua điểm
Do đó đường tiệm cận xiên của đồ thị hàm số đi qua điểm 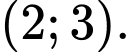 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 18 [46681]: Tìm đường tiệm cận xiên của đồ thị hàm số 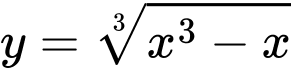 .
.
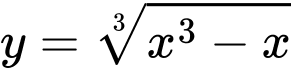 .
. A, 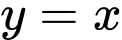
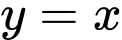
B, 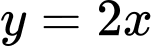
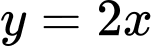
C, 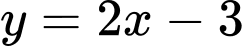
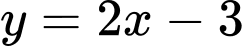
D, 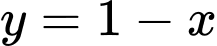
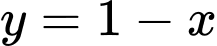
Ta có 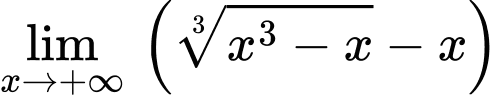
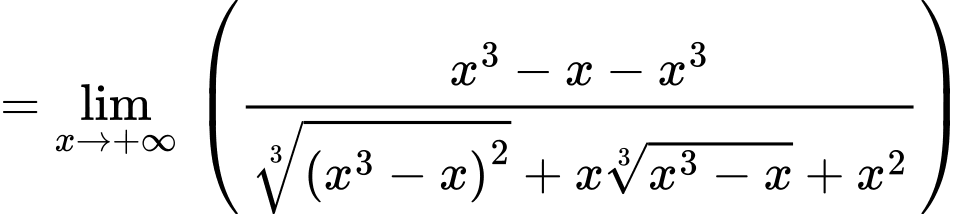
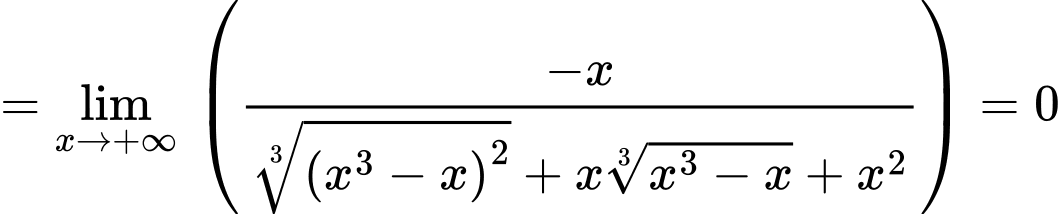
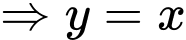 là đường tiệm cận xiên của đồ thị hàm số
là đường tiệm cận xiên của đồ thị hàm số 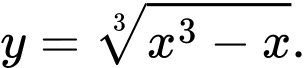
Chọn đáp án A. Đáp án: A
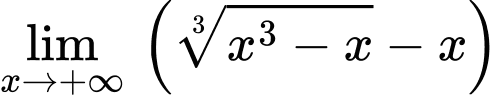
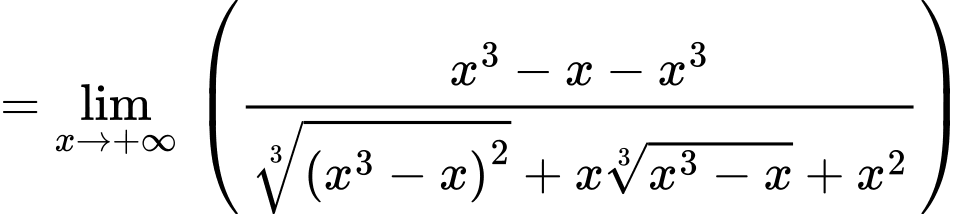
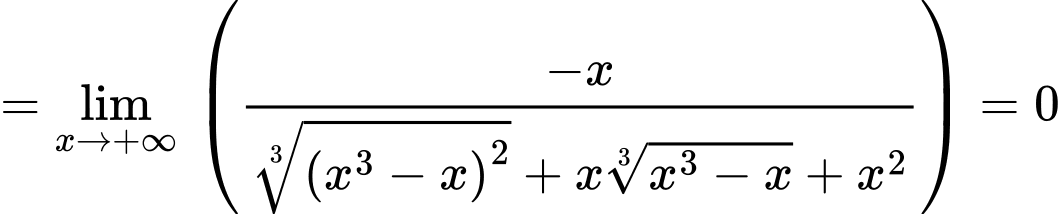
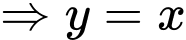 là đường tiệm cận xiên của đồ thị hàm số
là đường tiệm cận xiên của đồ thị hàm số 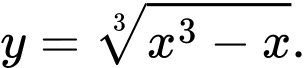
Chọn đáp án A. Đáp án: A
Câu 19 [382482]: Biết đồ thị hàm số 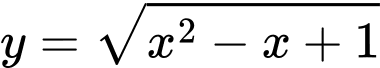 có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu
có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu
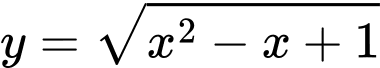 có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu
có hai đường tiệm cận xiên. Hỏi chúng cắt nhau tại điểm có hoành độ bằng bao nhiêu A, 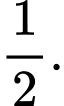
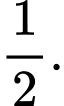
B, 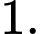
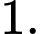
C, 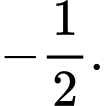
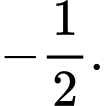
D, 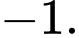
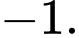
Ta có:
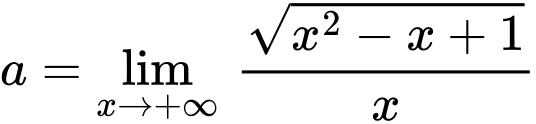
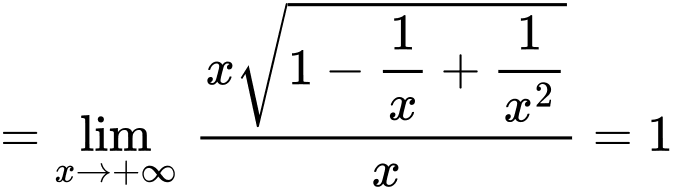
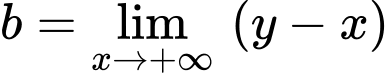
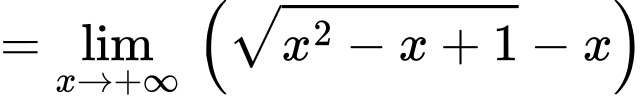
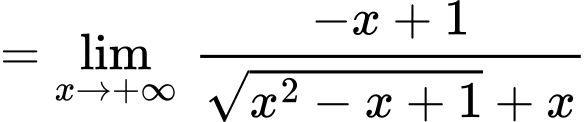
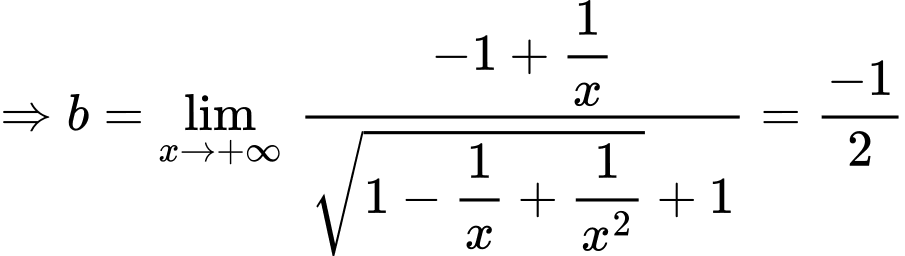
Suy ra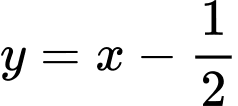 là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng
Lại có: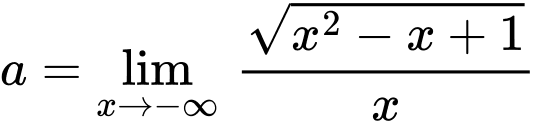
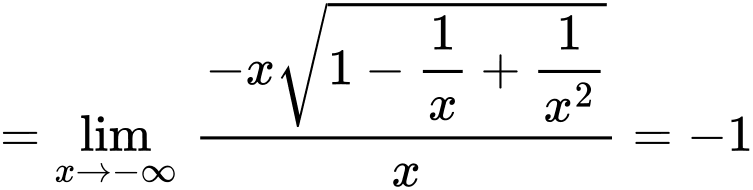
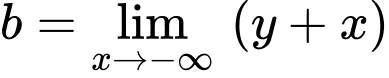
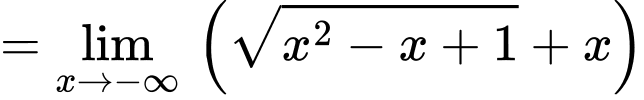
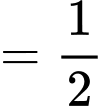 Suy ra
Suy ra 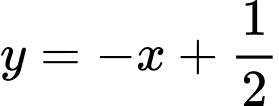 là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng
Vậy 2 đường tiệm cận xiên cắt nhau tại điểm của có hoành độ là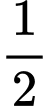 Đáp án: A
Đáp án: A
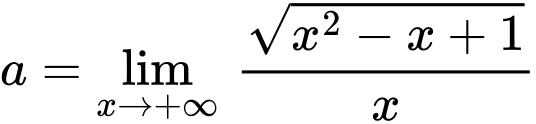
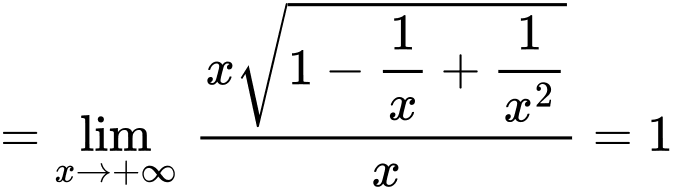
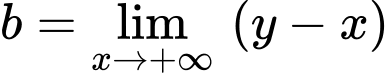
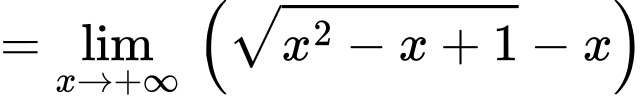
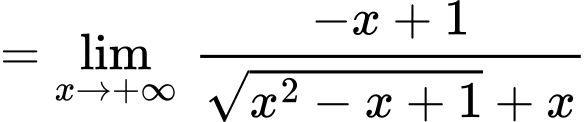
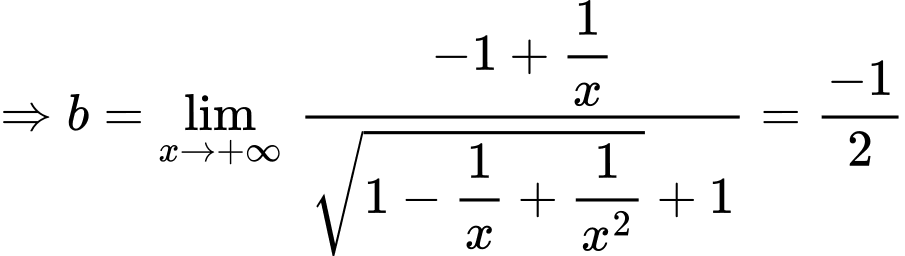
Suy ra
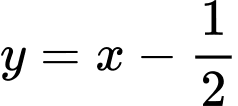 là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về dương vô cùng Lại có:
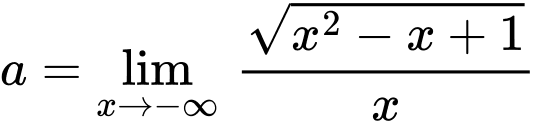
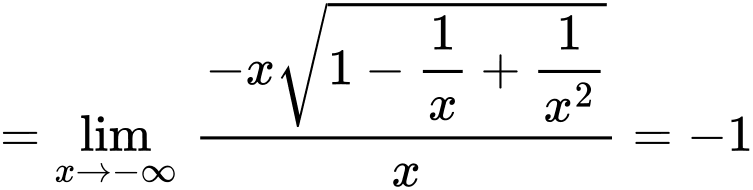
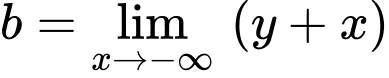
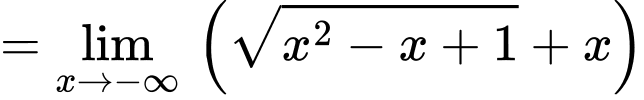
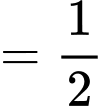 Suy ra
Suy ra 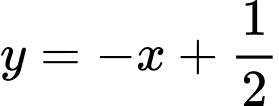 là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng
là tiệm cận xiên của đồ thị hàm số khi x tiến về âm vô cùng Vậy 2 đường tiệm cận xiên cắt nhau tại điểm của có hoành độ là
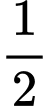 Đáp án: A
Đáp án: A
Câu 20 [382483]: Đồ thị hàm số 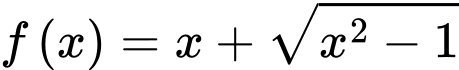 có bao nhiêu đường tiệm cận xiên
có bao nhiêu đường tiệm cận xiên
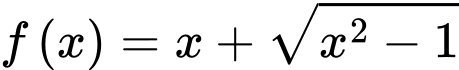 có bao nhiêu đường tiệm cận xiên
có bao nhiêu đường tiệm cận xiên A, 2.
B, 1.
C, 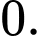
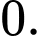
D, 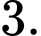
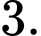
Ta có:
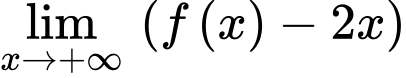
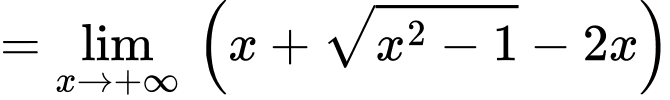
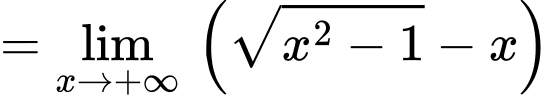
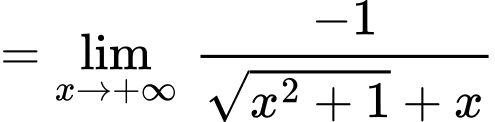
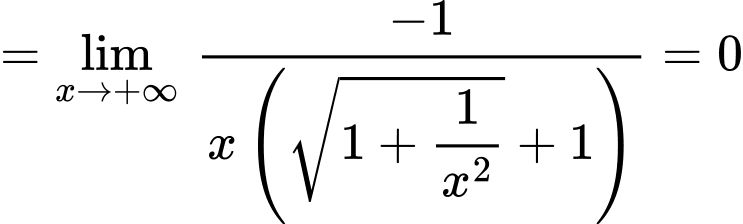
Vậy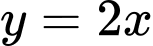 là đường tiệm cận xiên của đồ thị hàm số. Đáp án: B
là đường tiệm cận xiên của đồ thị hàm số. Đáp án: B
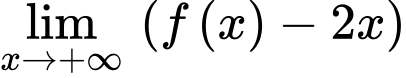
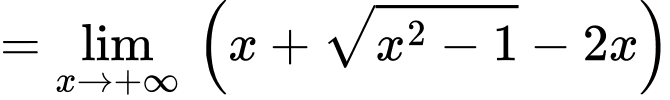
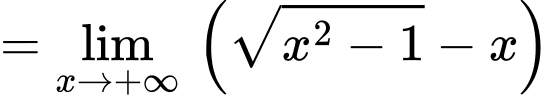
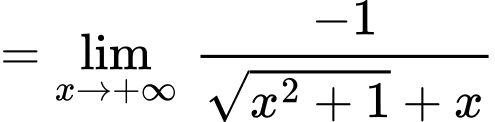
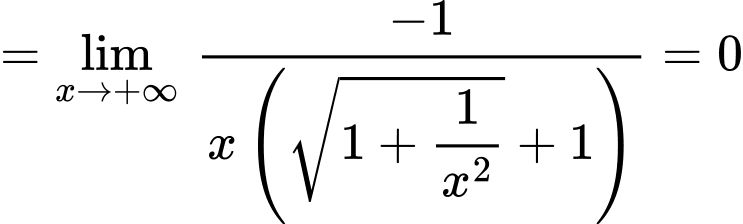
Vậy
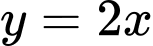 là đường tiệm cận xiên của đồ thị hàm số. Đáp án: B
là đường tiệm cận xiên của đồ thị hàm số. Đáp án: B
Câu 21 [382484]: Đồ thị hàm số 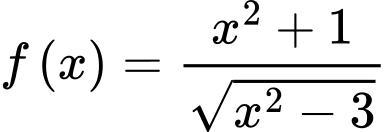 có tất cả bao nhiêu đường tiệm cận
có tất cả bao nhiêu đường tiệm cận
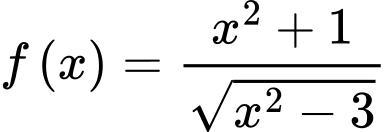 có tất cả bao nhiêu đường tiệm cận
có tất cả bao nhiêu đường tiệm cận A, 4.
B, 3.
C, 1.
D, 2.
Ta có:
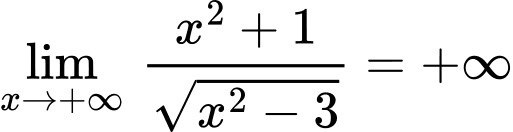 ;
;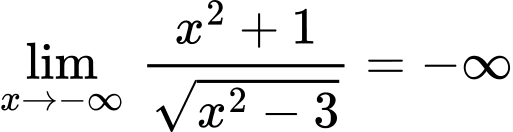 .
.
Nên đồ thị hàm số không có tiệm cận ngang.
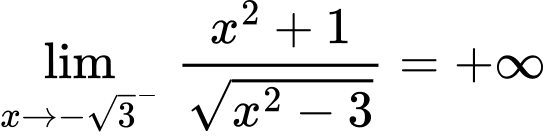 ;
;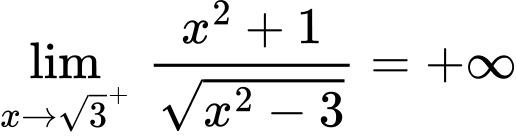
Nên đồ thị hàm số có 2 tiệm cận đứng là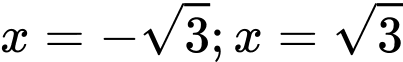 .
.
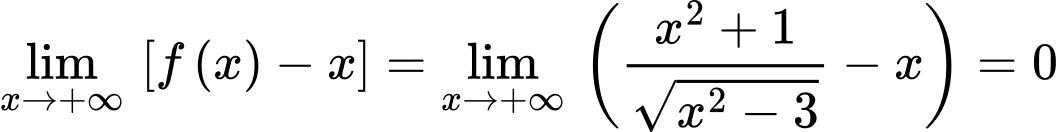
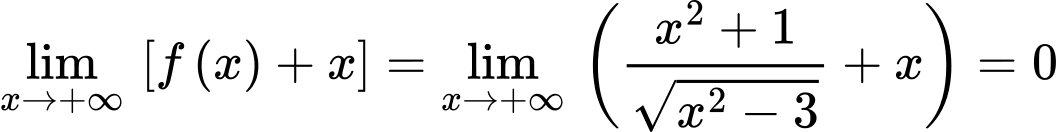
Nên đồ thị hàm số có 2 tiệm cận xiên là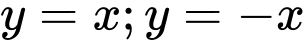 .
.
Đáp án: A
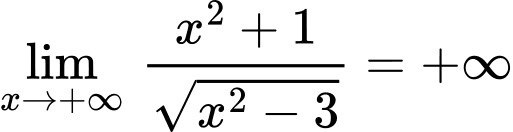 ;
;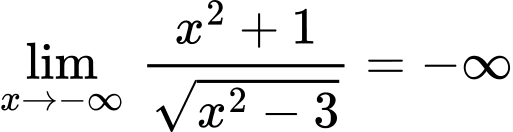 .
.Nên đồ thị hàm số không có tiệm cận ngang.
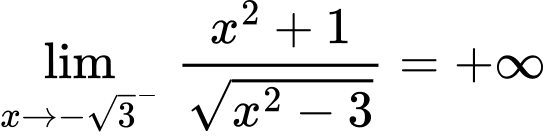 ;
;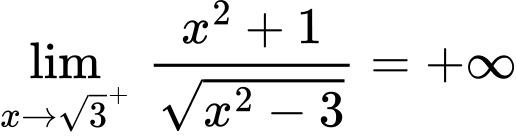
Nên đồ thị hàm số có 2 tiệm cận đứng là
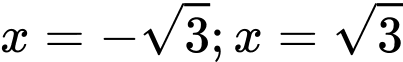 .
.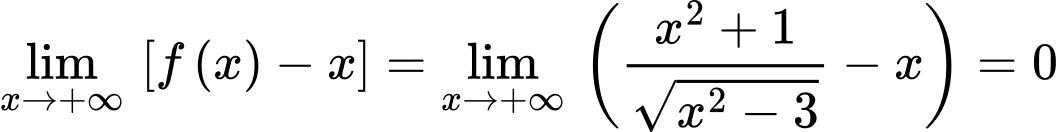
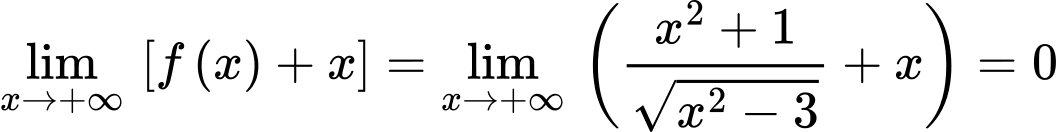
Nên đồ thị hàm số có 2 tiệm cận xiên là
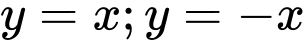 .
.Đáp án: A
Câu 22 [399671]: Cho hàm số 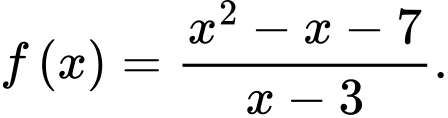
a)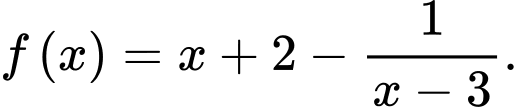
b)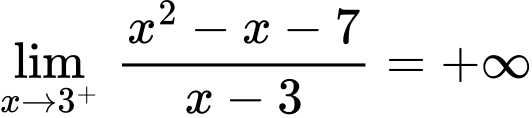
c)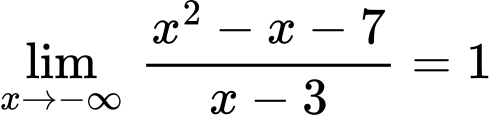
d) Đồ thị hàm số có 1 tiệm cận đứng, 1 tiệm cận ngang và 1 tiệm cận xiên.
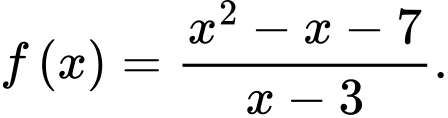
a)
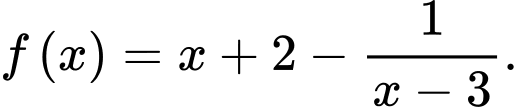
b)
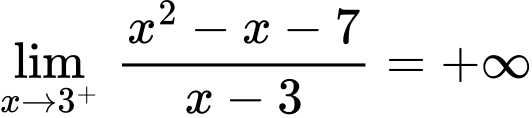
c)
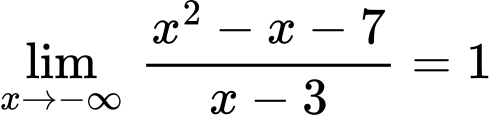
d) Đồ thị hàm số có 1 tiệm cận đứng, 1 tiệm cận ngang và 1 tiệm cận xiên.
a) Đúng, thực hiện chia đa thức.
b) Sai,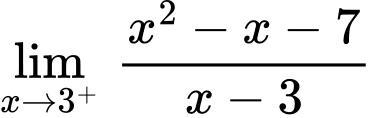
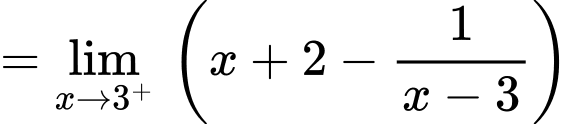
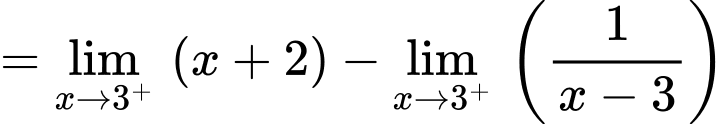
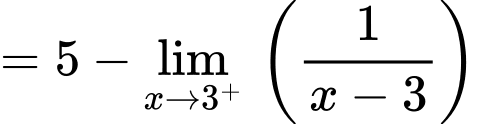

Có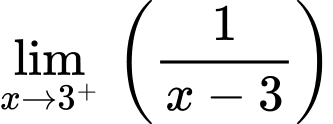
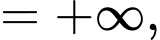 vì
vì 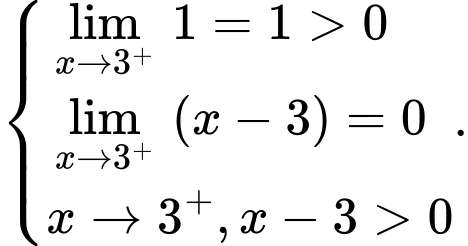
c) Sai,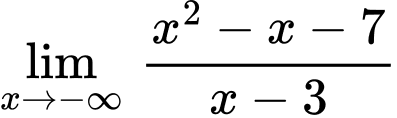
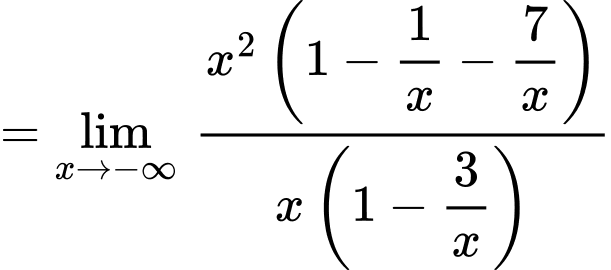
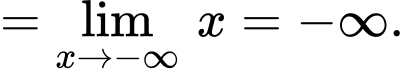
d) Sai, Ta có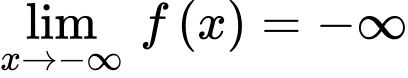 nên đồ thị hàm số không có tiệm cận ngang.
nên đồ thị hàm số không có tiệm cận ngang.
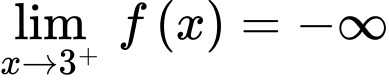 nên
nên 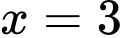 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
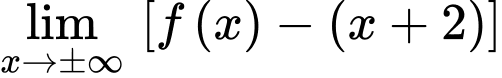
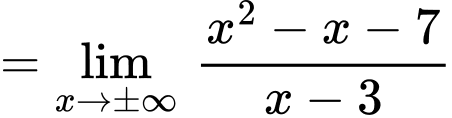
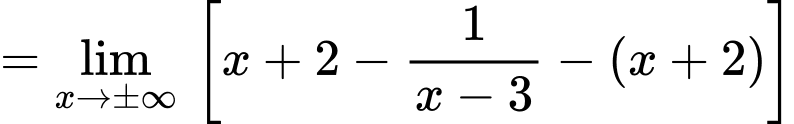
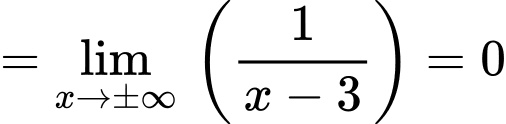 nên
nên 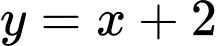 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
b) Sai,
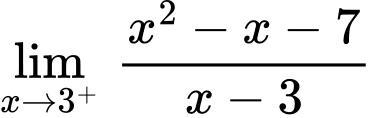
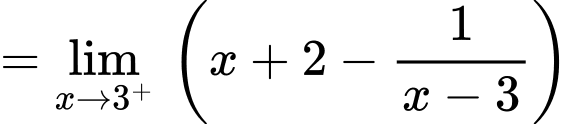
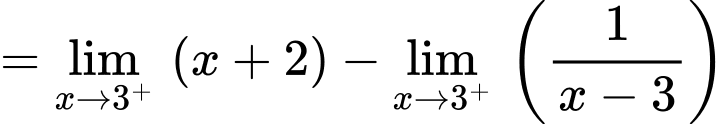
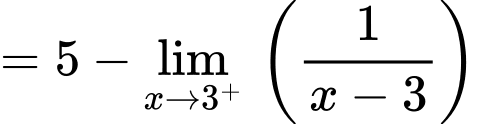

Có
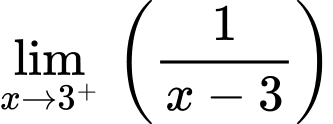
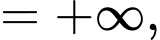 vì
vì 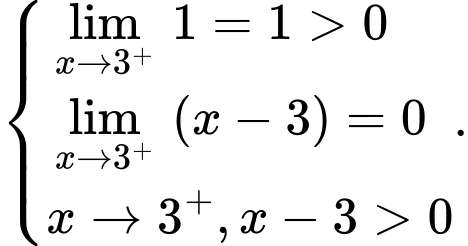
c) Sai,
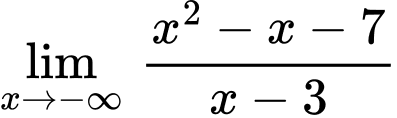
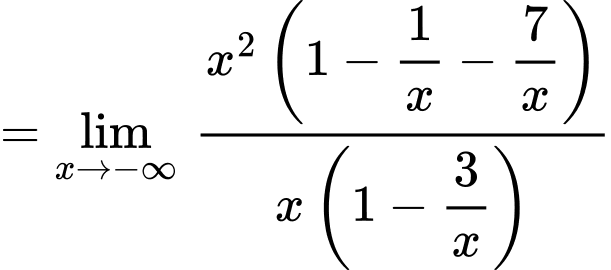
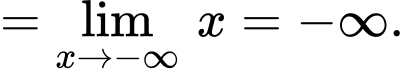
d) Sai, Ta có
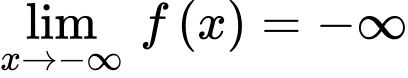 nên đồ thị hàm số không có tiệm cận ngang.
nên đồ thị hàm số không có tiệm cận ngang.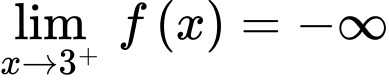 nên
nên 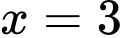 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.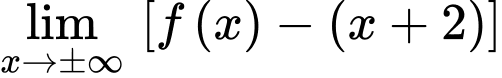
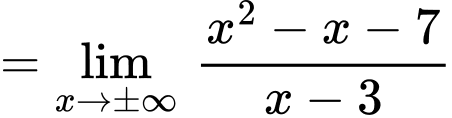
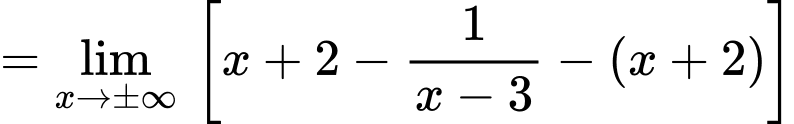
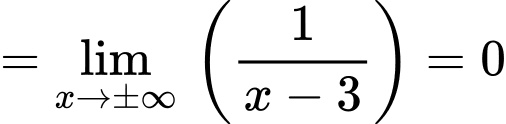 nên
nên 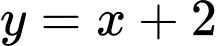 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
Câu 23 [399669]: Cho hàm số 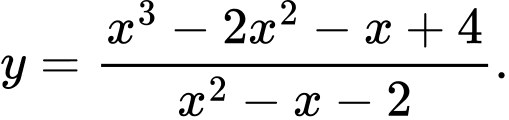 Số tiệm cận của đồ thị hàm số bằng
Số tiệm cận của đồ thị hàm số bằng
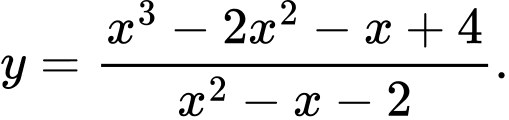 Số tiệm cận của đồ thị hàm số bằng
Số tiệm cận của đồ thị hàm số bằng
Tập xác định 
Viết lại hàm số dưới dạng:
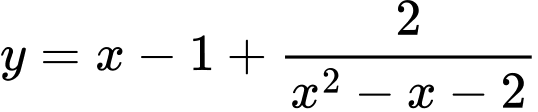
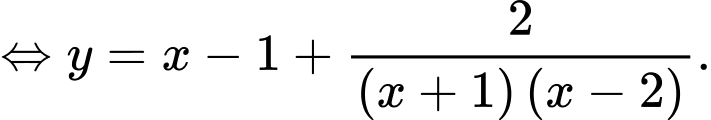
Từ đó, ta nhận được kết luận:
Đường thẳng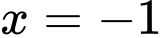 là tiệm cận đứng vì
là tiệm cận đứng vì 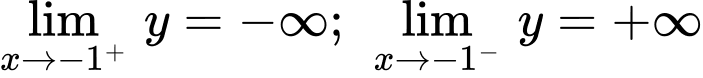
Đường thẳng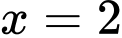 là tiệm cận đứng vì
là tiệm cận đứng vì 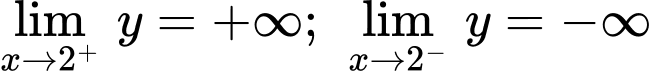
Đường thẳng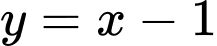 là tiệm cận xiên vì
là tiệm cận xiên vì 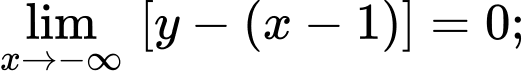
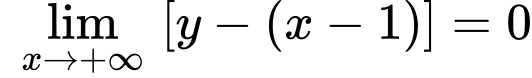
Vậy đồ thị hàm số có ba đường tiệm cận.

Viết lại hàm số dưới dạng:
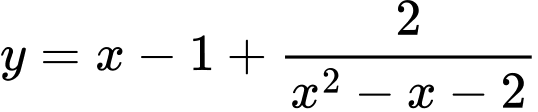
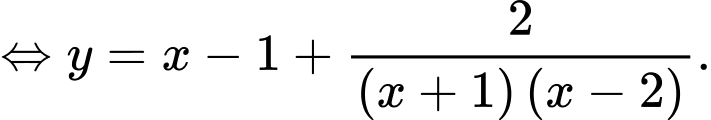
Từ đó, ta nhận được kết luận:
Đường thẳng
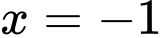 là tiệm cận đứng vì
là tiệm cận đứng vì 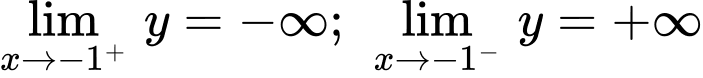
Đường thẳng
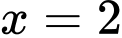 là tiệm cận đứng vì
là tiệm cận đứng vì 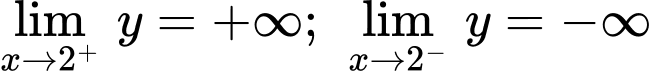
Đường thẳng
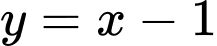 là tiệm cận xiên vì
là tiệm cận xiên vì 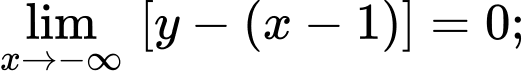
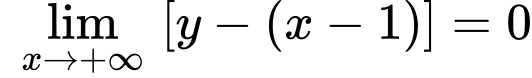
Vậy đồ thị hàm số có ba đường tiệm cận.
Câu 24 [382485]: Đường tiệm cận xiên của đồ thị hàm số 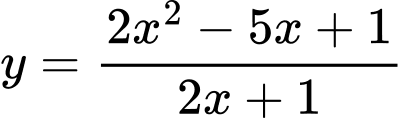 cắt các trục toạ độ tại hai điểm
cắt các trục toạ độ tại hai điểm 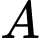 và
và 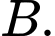 Diện tích của tam giác
Diện tích của tam giác 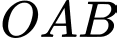 bằng
bằng
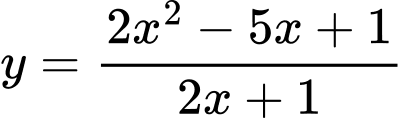 cắt các trục toạ độ tại hai điểm
cắt các trục toạ độ tại hai điểm 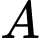 và
và 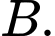 Diện tích của tam giác
Diện tích của tam giác 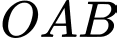 bằng
bằng
Ta có: 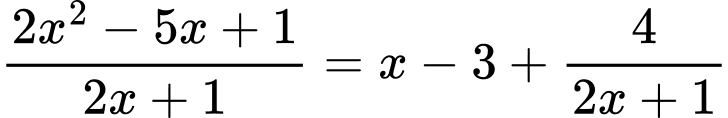
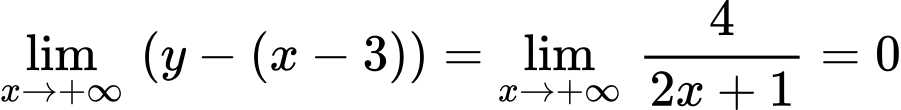
Nên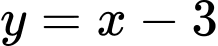 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Vì đường tiệm cận xiên cắt các trục tọa độ tại hai điểm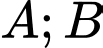 . Suy ra
. Suy ra 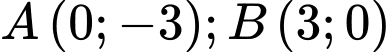 .
.
Vì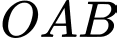 là tam giác vuông tại
là tam giác vuông tại  nên
nên 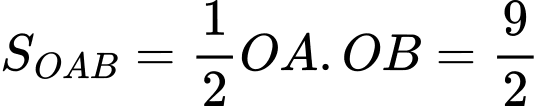
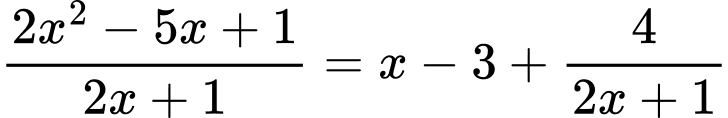
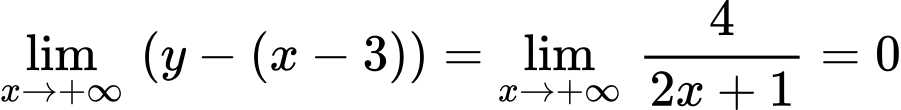
Nên
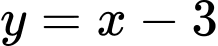 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.Vì đường tiệm cận xiên cắt các trục tọa độ tại hai điểm
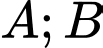 . Suy ra
. Suy ra 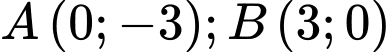 .
.Vì
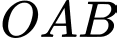 là tam giác vuông tại
là tam giác vuông tại  nên
nên 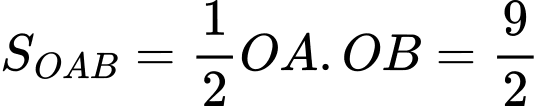
Câu 25 [382487]: Khoảng cách từ gốc toạ độ  đến tiệm cận xiên của đồ thị hàm số
đến tiệm cận xiên của đồ thị hàm số 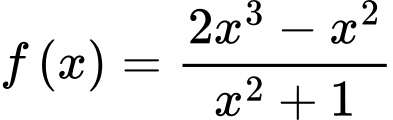 bằng
bằng 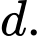 Tính
Tính 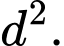
 đến tiệm cận xiên của đồ thị hàm số
đến tiệm cận xiên của đồ thị hàm số 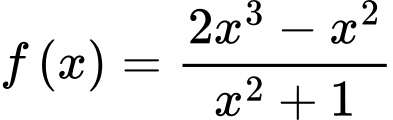 bằng
bằng 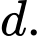 Tính
Tính 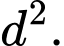
Ta có: 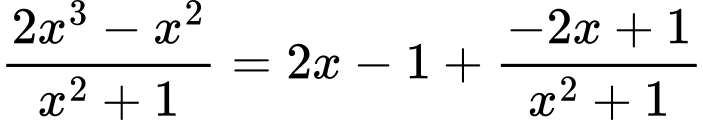
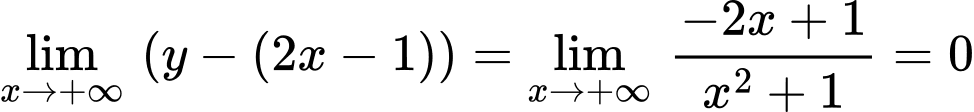
Nên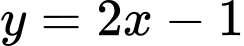 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Khoảng cách từ gốc tọa độ O đến tiệm cận xiên của đồ thị hàm số là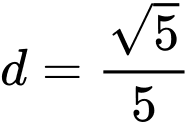
Vậy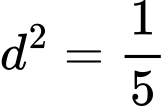
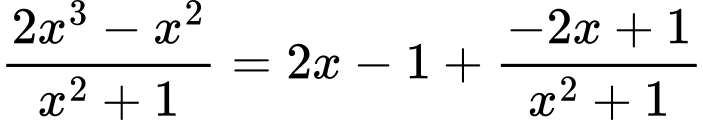
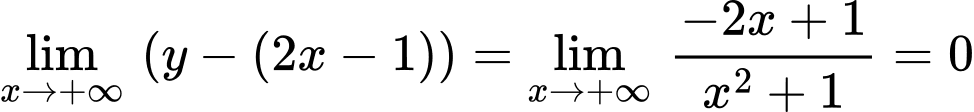
Nên
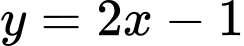 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Khoảng cách từ gốc tọa độ O đến tiệm cận xiên của đồ thị hàm số là
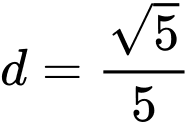
Vậy
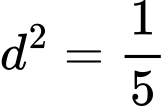
Câu 26 [382488]: Đường tiệm đứng và tiệm cận xiên của đồ thị hàm số 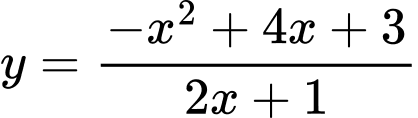 tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
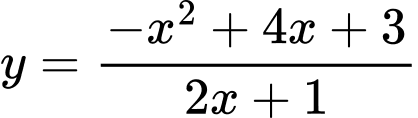 tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
tạo với nhau một góc bao nhiêu độ (làm tròn đến hàng đơn vị của độ)?
Ta có:
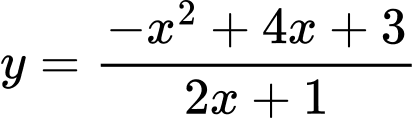
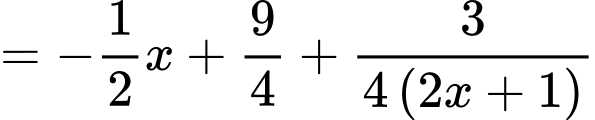
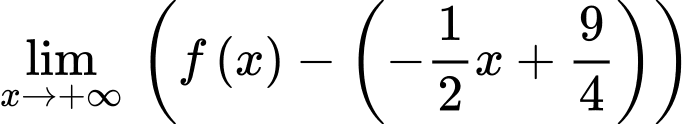
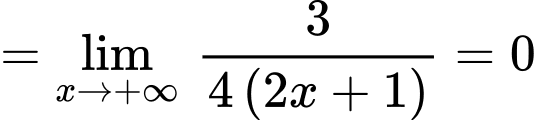
Suy ra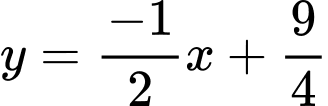 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.
Lại có: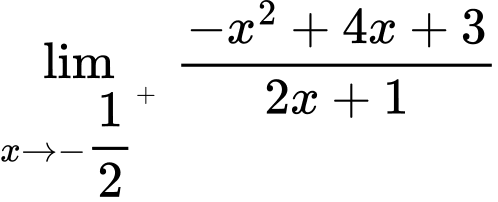
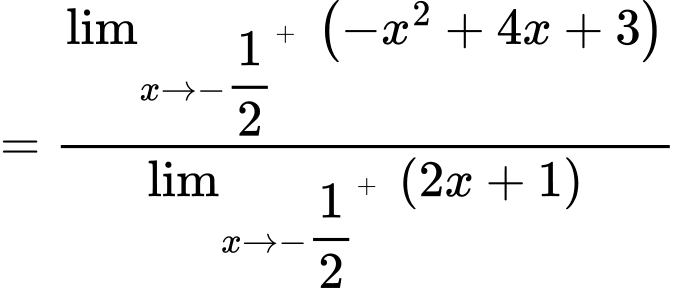

Suy ra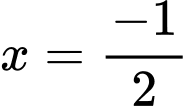 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Vậy tiệm cận đứng và tiệm cận xiên của đồ thị tạo với nhau 1 góc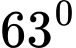
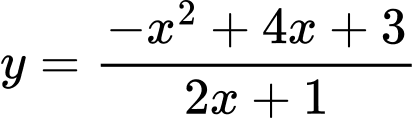
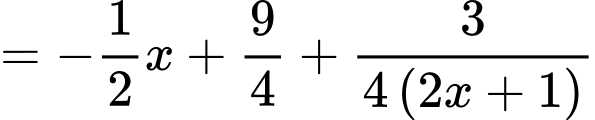
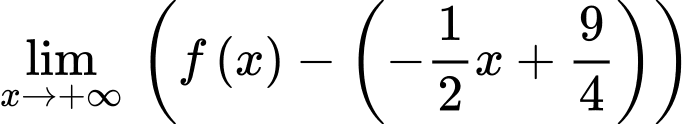
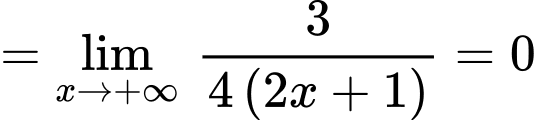
Suy ra
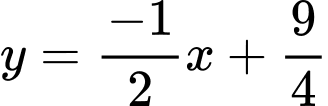 là đường tiệm cận xiên của đồ thị hàm số.
là đường tiệm cận xiên của đồ thị hàm số.Lại có:
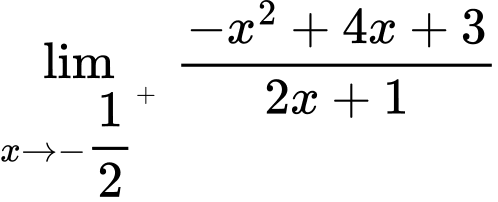
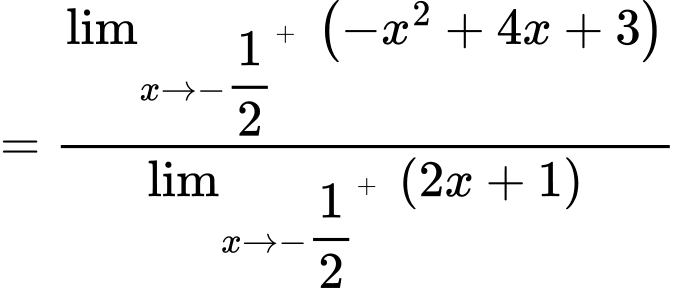

Suy ra
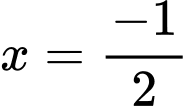 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.Vậy tiệm cận đứng và tiệm cận xiên của đồ thị tạo với nhau 1 góc
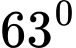
Câu 27 [31293]: Tìm giá trị thực của tham số 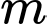 sao cho đồ thị của hàm số
sao cho đồ thị của hàm số 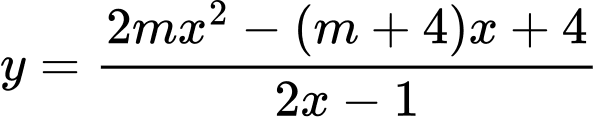 có tiệm cận xiên đi qua điểm
có tiệm cận xiên đi qua điểm 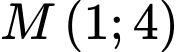 .
.
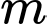 sao cho đồ thị của hàm số
sao cho đồ thị của hàm số 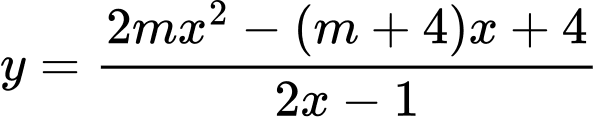 có tiệm cận xiên đi qua điểm
có tiệm cận xiên đi qua điểm 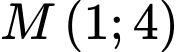 .
. A, 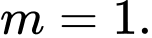
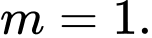
B, 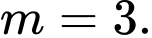
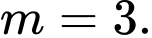
C, 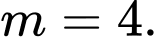
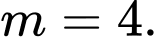
D, 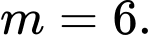
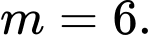
Ta có 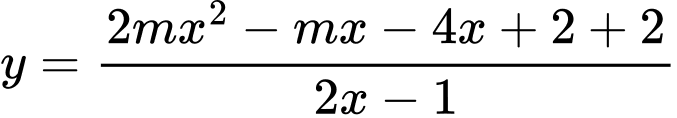
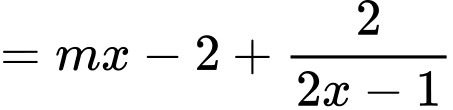
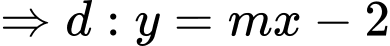 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Mà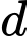 qua
qua 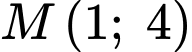
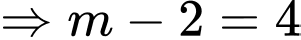
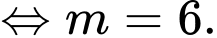
Chọn đáp án D. Đáp án: D
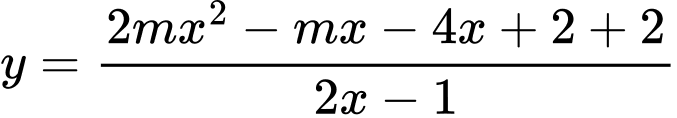
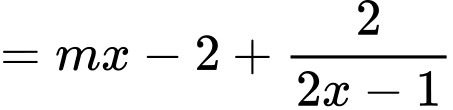
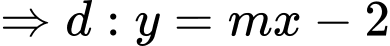 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số. Mà
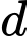 qua
qua 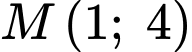
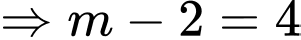
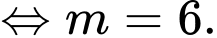
Chọn đáp án D. Đáp án: D
Câu 28 [382489]: Cho hàm số 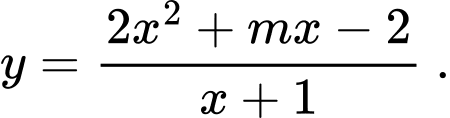 Gọi
Gọi 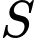 là tập hợp các giá trị của
là tập hợp các giá trị của 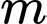 để đồ thị hàm số có tiệm cận xiên tạo với hai trục tọa độ một tam giác có diện tích bằng
để đồ thị hàm số có tiệm cận xiên tạo với hai trục tọa độ một tam giác có diện tích bằng 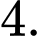 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 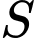 bằng
bằng
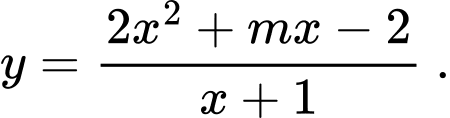 Gọi
Gọi 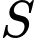 là tập hợp các giá trị của
là tập hợp các giá trị của 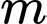 để đồ thị hàm số có tiệm cận xiên tạo với hai trục tọa độ một tam giác có diện tích bằng
để đồ thị hàm số có tiệm cận xiên tạo với hai trục tọa độ một tam giác có diện tích bằng 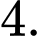 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 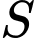 bằng
bằng
Ta có: 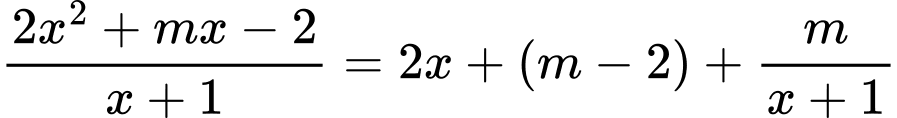
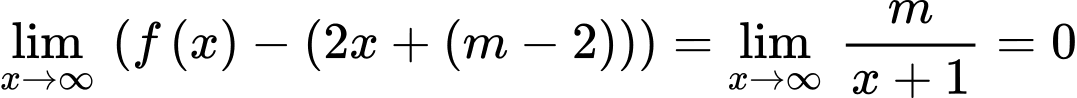
Suy ra là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
Tiệm cận xiên cắt 2 trục tọa độ tại 2 điểm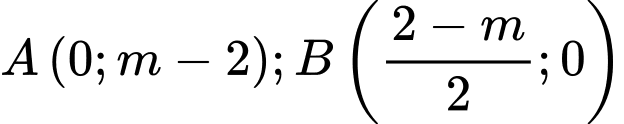
Vì tam giác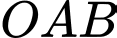 vuông tại O nên
vuông tại O nên 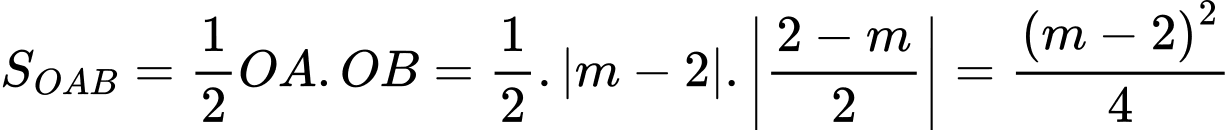
Để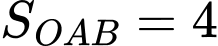 thì
thì 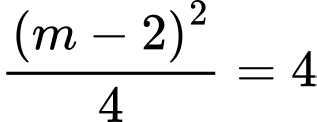
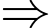
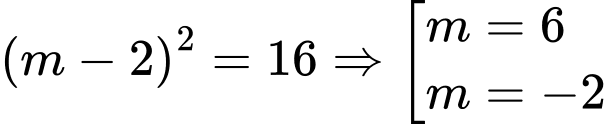
Suy ra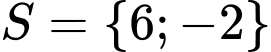
Vậy tổng các phần tử của tập hợp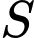 là 4
là 4
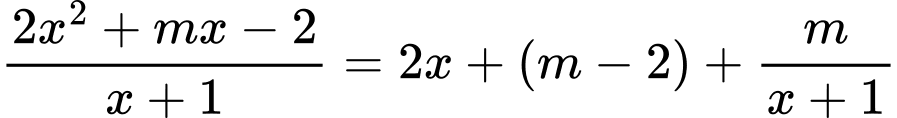
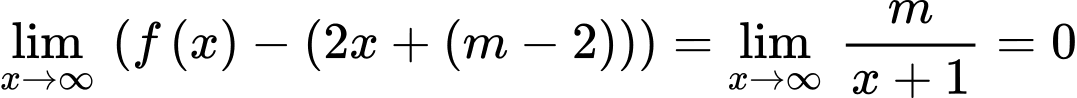
Suy ra
 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
Tiệm cận xiên cắt 2 trục tọa độ tại 2 điểm
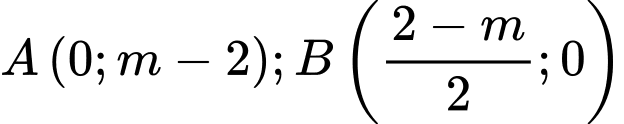
Vì tam giác
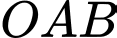 vuông tại O nên
vuông tại O nên 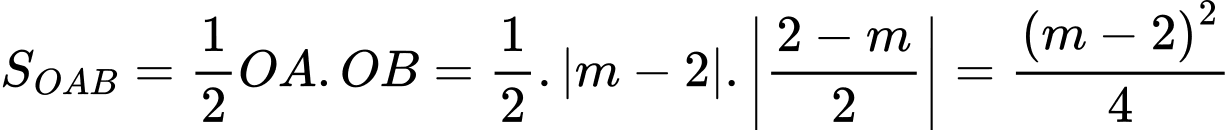
Để
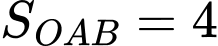 thì
thì 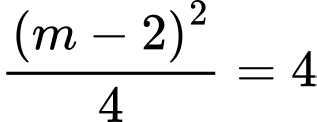
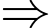
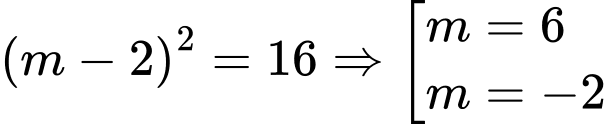
Suy ra
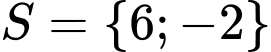
Vậy tổng các phần tử của tập hợp
 là 4
là 4