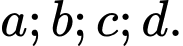Đáp án Bài tập tự luyện số 2
Câu 1 [27362]: Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 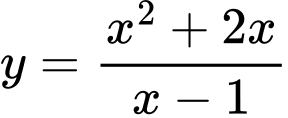 là
là
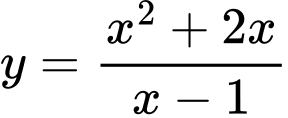 là
là A, 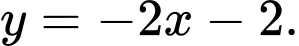
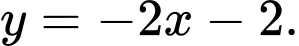
B, 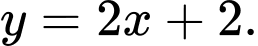
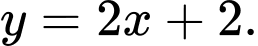
C, 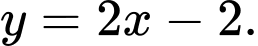
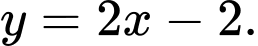
D, 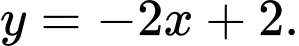
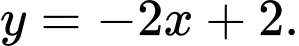
Bài toán tổng quát: Cho hàm số 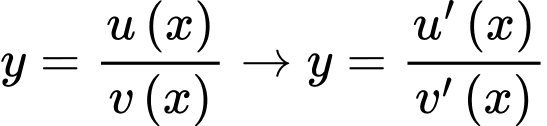 là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số với
là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số với 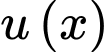 bậc 2 và
bậc 2 và  bậc 1.
bậc 1.
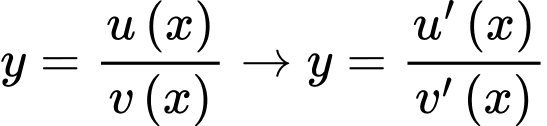 là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số với
là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số với 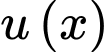 bậc 2 và
bậc 2 và  bậc 1.
bậc 1. Vậy với hàm số 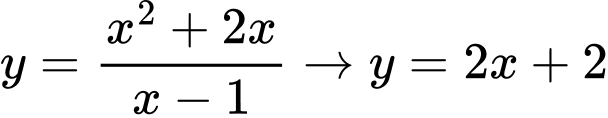 là đường thẳng cần tìm. Chọn B.
là đường thẳng cần tìm. Chọn B.
Đáp án: B 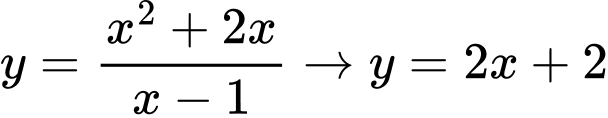 là đường thẳng cần tìm. Chọn B.
là đường thẳng cần tìm. Chọn B.
Câu 2 [802067]: Đường thẳng qua  điểm cực trị của đồ thị hàm số
điểm cực trị của đồ thị hàm số 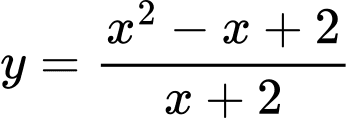 có phương trình là
có phương trình là
 điểm cực trị của đồ thị hàm số
điểm cực trị của đồ thị hàm số 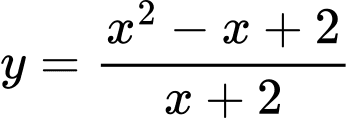 có phương trình là
có phương trình là A, 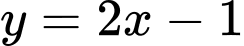 .
.
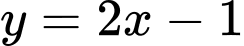 .
.B, 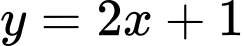 .
.
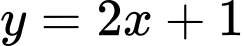 .
.C, 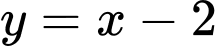 .
.
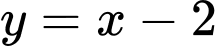 .
.D, 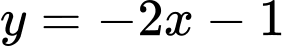 .
.
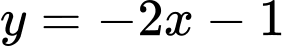 .
.
Chọn A
Áp dụng công thức phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số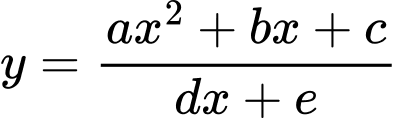 là
là 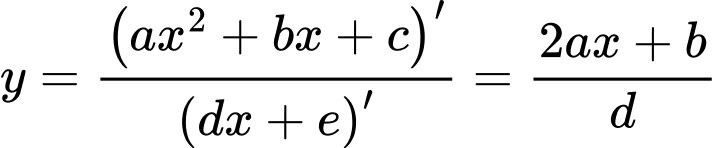 .
.
Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị đã cho là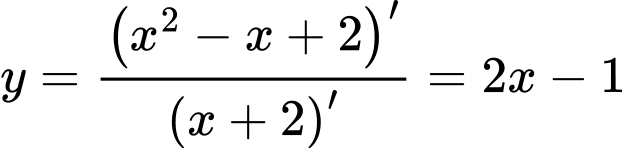 . Đáp án: A
. Đáp án: A
Áp dụng công thức phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
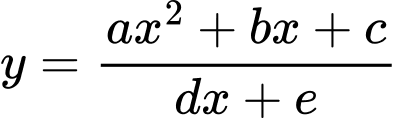 là
là 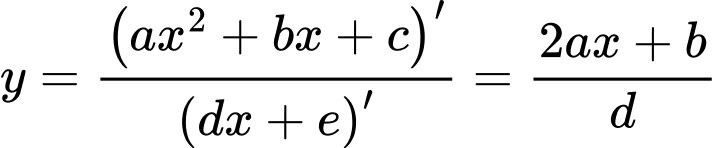 .
.Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị đã cho là
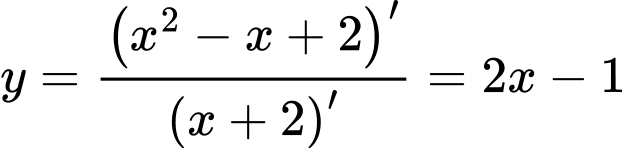 . Đáp án: A
. Đáp án: A
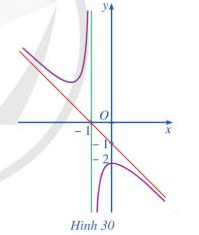
Câu 3 [360115]: Đường cong ở Hình 30 là đồ thị của hàm số:

A, 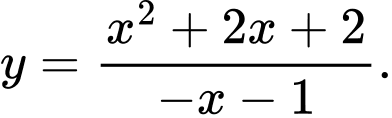
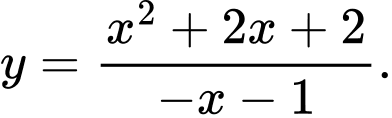
B, 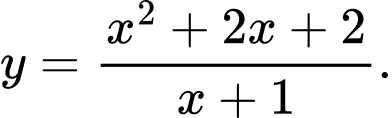
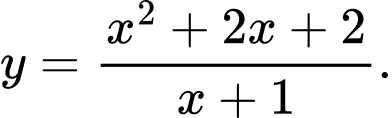
C, 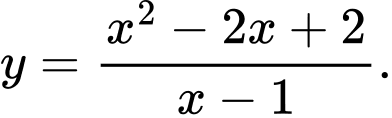
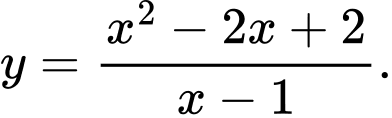
D, 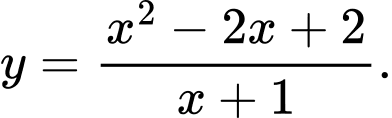
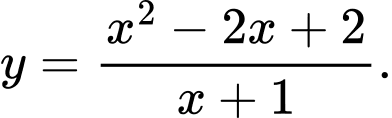
Dựa vào hình dạng đồ thị ta thấy hàm số đã có có 2 cực trị và 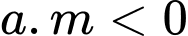 .
.
Chọn đáp án A. Đáp án: A
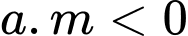 .
.
Chọn đáp án A. Đáp án: A
Câu 4 [383010]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
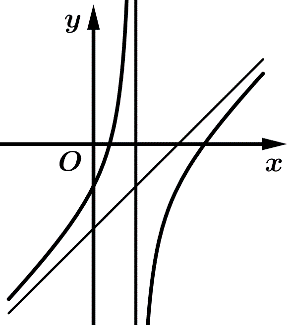

A, 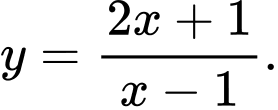
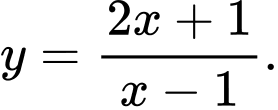
B, 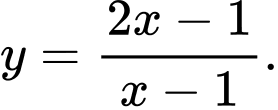
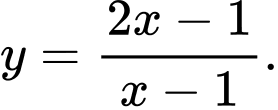
C, 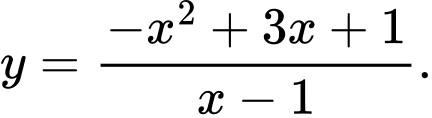
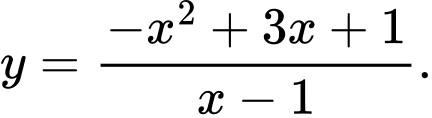
D, 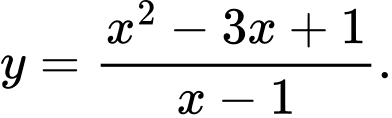
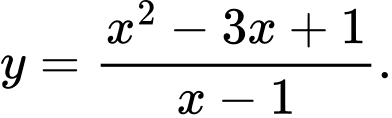
Chọn đáp án D.
Dựa vào hình dạng đồ thị ta thấy hàm số đã cho là hàm số bậc hai trên bậc nhất. Do đó, loại A, B.
Hàm số đã cho không có cực trị và Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
Dựa vào hình dạng đồ thị ta thấy hàm số đã cho là hàm số bậc hai trên bậc nhất. Do đó, loại A, B.
Hàm số đã cho không có cực trị và
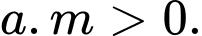 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
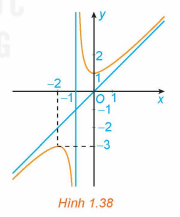
Câu 5 [382883]: Đồ thị trong Hình 1.38 là đồ thị của hàm số:

A, 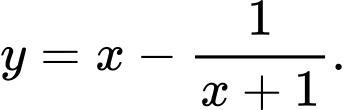
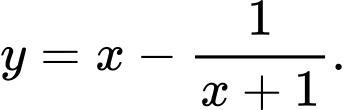
B, 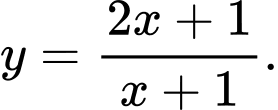
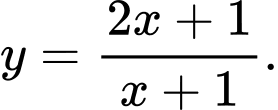
C, 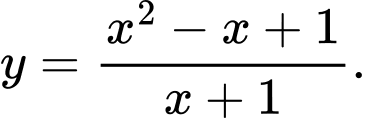
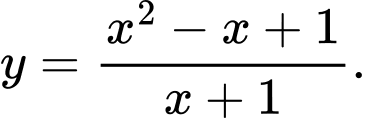
D, 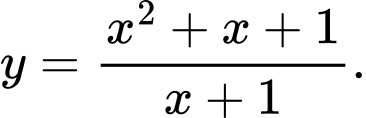
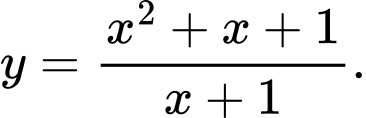
Ta có: 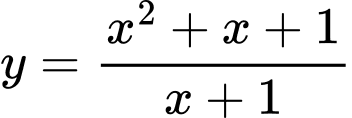
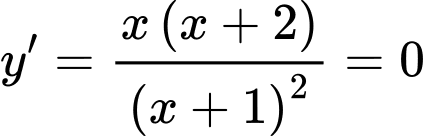
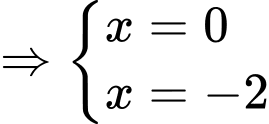
Bảng biến thiên
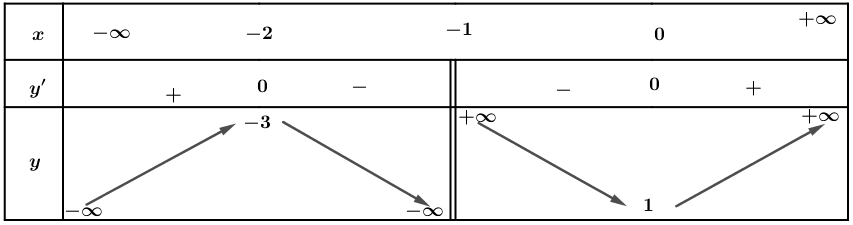
Chọn đáp án D Đáp án: D
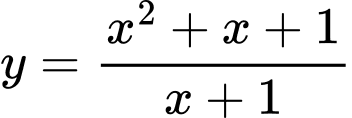
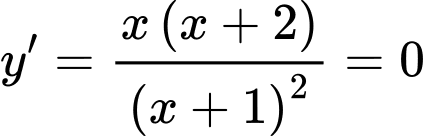
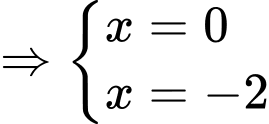
Bảng biến thiên

Chọn đáp án D Đáp án: D
Câu 6 [383011]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây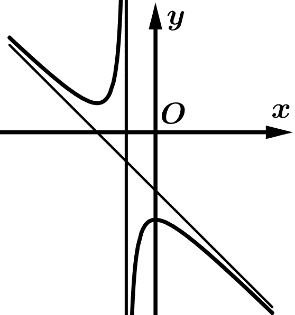

A, 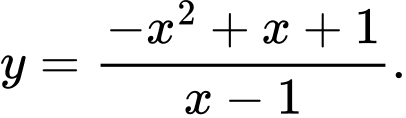
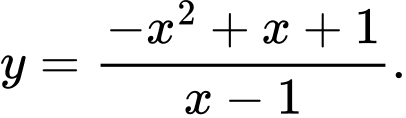
B, 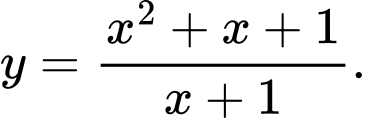
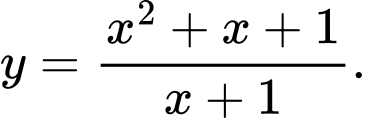
C, 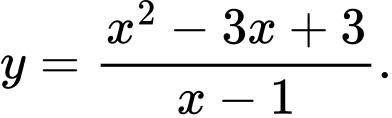
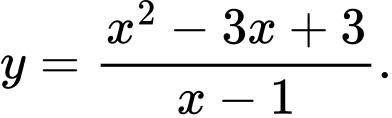
D, 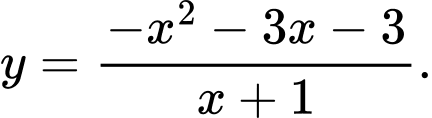
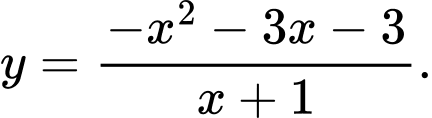
Từ đồ thị ta thấy hàm số đã cho 2 cực trị và 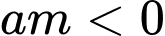 .
.
Xét các đáp án A, B, C, D suy ra loại B, C
Dựa vào đồ thị hàm số ta có hàm số có tiệm cận đứng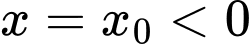 .
.
Suy ra loại đáp án A
Vậy đáp án đúng là D Đáp án: D
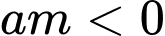 .
.
Xét các đáp án A, B, C, D suy ra loại B, C
Dựa vào đồ thị hàm số ta có hàm số có tiệm cận đứng
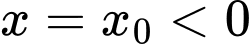 .
.
Suy ra loại đáp án A
Vậy đáp án đúng là D Đáp án: D
Câu 7 [383012]: Đường cong ở hình vẽ bên là đồ thị của hàm số 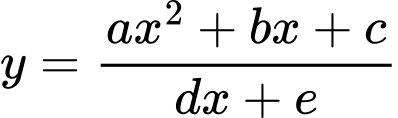 với
với 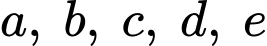 là các số thực. Mệnh đề nào dưới đây đúng?
là các số thực. Mệnh đề nào dưới đây đúng?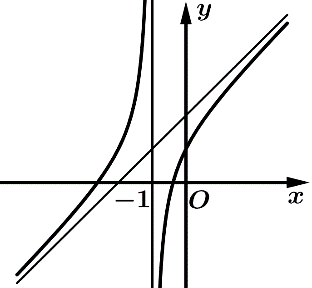
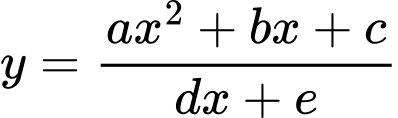 với
với 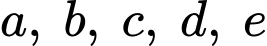 là các số thực. Mệnh đề nào dưới đây đúng?
là các số thực. Mệnh đề nào dưới đây đúng?
A, 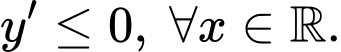
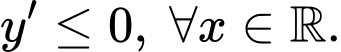
B, 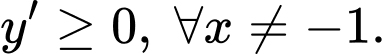
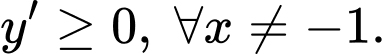
C, 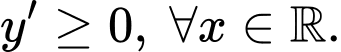
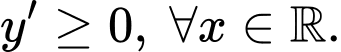
D, 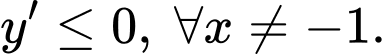
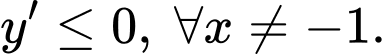
Dựa vào đồ thị hàm số dễ thấy hàm số đồng biến trên khoảng xác định
Chọn đáp án B Đáp án: B
Chọn đáp án B Đáp án: B
Câu 8 [383013]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây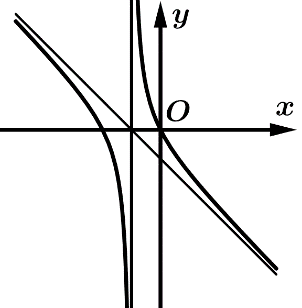

A, 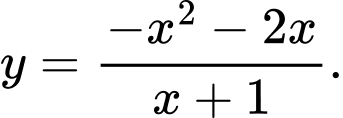
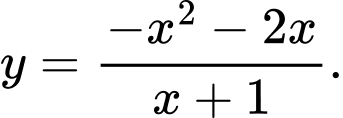
B, 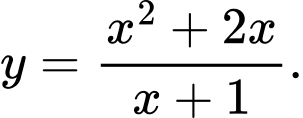
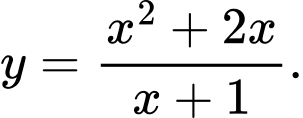
C, 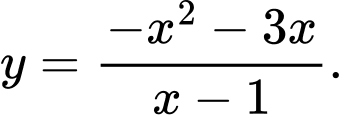
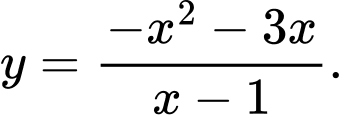
D, 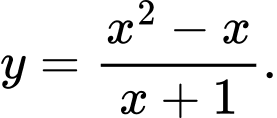
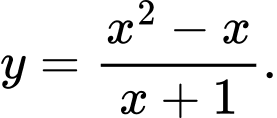
Dựa vào đồ thị ta thấy
Hàm số nghịch biến trên khoảng xác định. Suy ra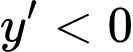 .
.
Suy ra loại đáp án B, D
Đồ thị hàm số có tiệm cận đứng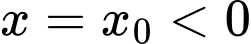 . Suy ra loại đáp án C
. Suy ra loại đáp án C
Vậy đáp án đúng là A Đáp án: A
Hàm số nghịch biến trên khoảng xác định. Suy ra
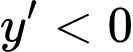 .
.
Suy ra loại đáp án B, D
Đồ thị hàm số có tiệm cận đứng
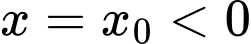 . Suy ra loại đáp án C
. Suy ra loại đáp án C
Vậy đáp án đúng là A Đáp án: A
Câu 9 [383014]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau: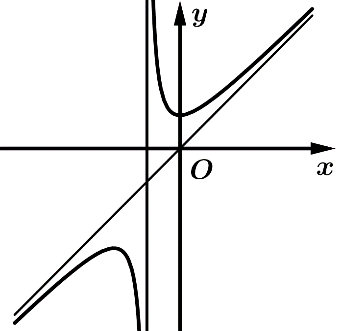

A, 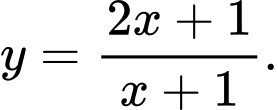
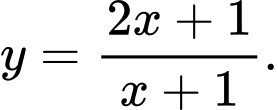
B, 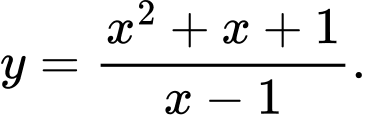
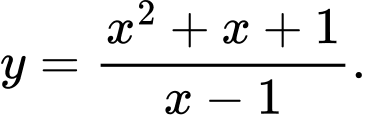
C, 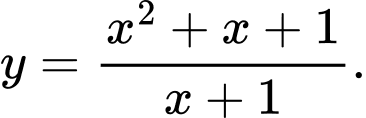
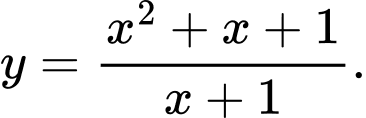
D, 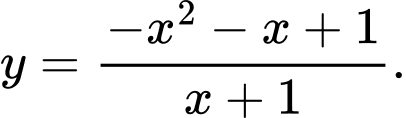
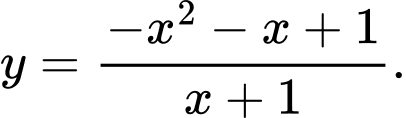
Dựa vào đồ thị ta thấy
Hàm số có dạng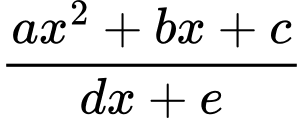 nên loại đáp án A.
nên loại đáp án A.
Hàm số có 2 điểm cực trị và . Loại đáp án D.
. Loại đáp án D.
Đồ thị hàm số có tiệm cận đứng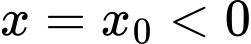 . Suy ra loại đáp án B
. Suy ra loại đáp án B
Vậy đáp án đúng là C Đáp án: C
Hàm số có dạng
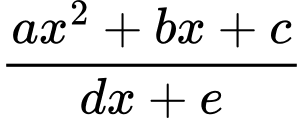 nên loại đáp án A.
nên loại đáp án A.Hàm số có 2 điểm cực trị và
 . Loại đáp án D.
. Loại đáp án D.Đồ thị hàm số có tiệm cận đứng
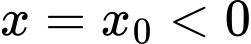 . Suy ra loại đáp án B
. Suy ra loại đáp án BVậy đáp án đúng là C Đáp án: C
Câu 10 [383015]: Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau: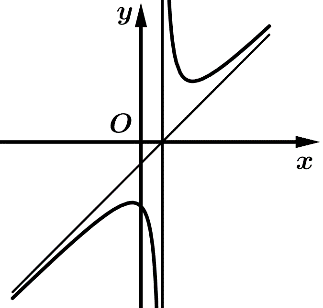

A, 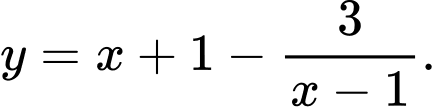
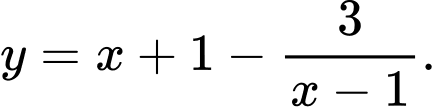
B, 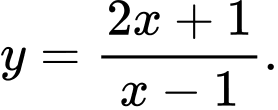
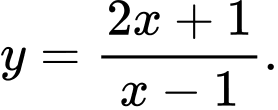
C, 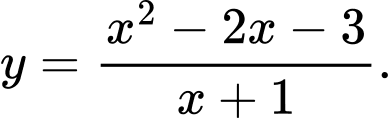
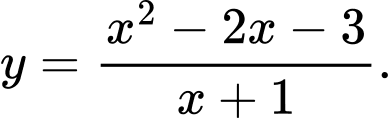
D, 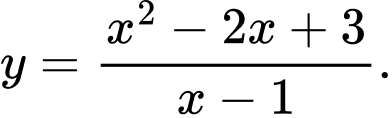
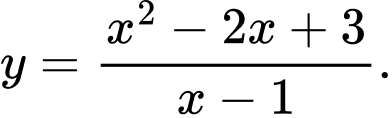
Dựa vào đồ thị ta thấy
Hàm số có dạng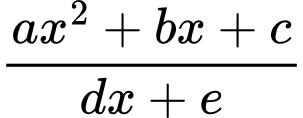 nên loại đáp án B.
nên loại đáp án B.
Đồ thị hàm số có tiệm cận đứng . Suy ra loại đáp án C
. Suy ra loại đáp án C
Hàm số có 2 điểm cực trị nên ta loại đáp án A.
Vậy đáp án đúng là A. Đáp án: D
Hàm số có dạng
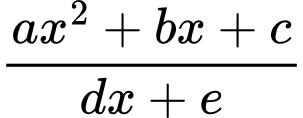 nên loại đáp án B.
nên loại đáp án B.Đồ thị hàm số có tiệm cận đứng
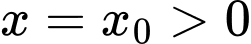 . Suy ra loại đáp án C
. Suy ra loại đáp án CHàm số có 2 điểm cực trị nên ta loại đáp án A.
Vậy đáp án đúng là A. Đáp án: D
Câu 11 [382822]: Tâm đối xứng của đồ thị hàm số 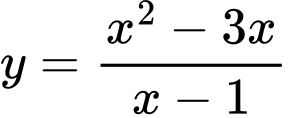 có toạ độ là
có toạ độ là
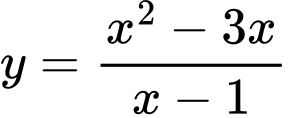 có toạ độ là
có toạ độ là A, 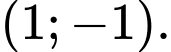
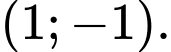
B, 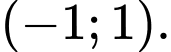
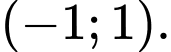
C, 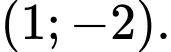
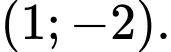
D, 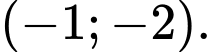
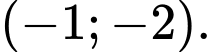
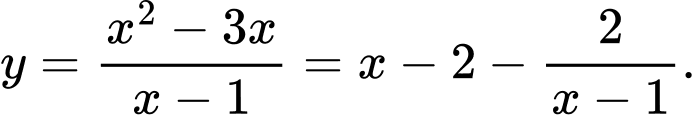
Đồ thị hàm số
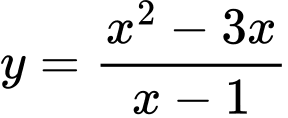 có TCĐ
có TCĐ 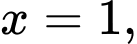 TCX
TCX 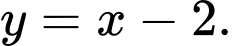
Vậy tâm đối xứng của đồ thị hàm số
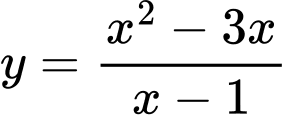 có toạ độ là
có toạ độ là 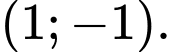 Đáp án: A
Đáp án: A
Câu 12 [382511]: (Chuyên Lê Hồng Phong – Nam Định – 2020) Biết rằng đồ thị 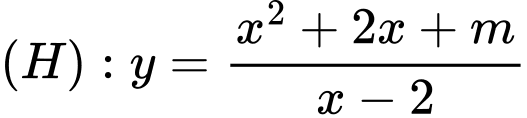 (với
(với 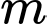 là tham số thực) có hai điểm cực trị là
là tham số thực) có hai điểm cực trị là 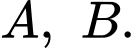 Hãy tính khoảng cách từ gốc toạ độ
Hãy tính khoảng cách từ gốc toạ độ  đến đường thẳng
đến đường thẳng 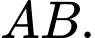
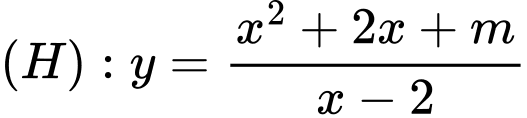 (với
(với 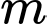 là tham số thực) có hai điểm cực trị là
là tham số thực) có hai điểm cực trị là 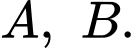 Hãy tính khoảng cách từ gốc toạ độ
Hãy tính khoảng cách từ gốc toạ độ  đến đường thẳng
đến đường thẳng 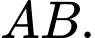
A, 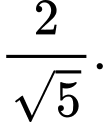
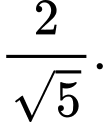
B, 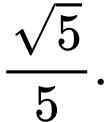
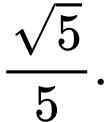
C, 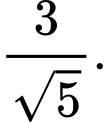
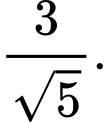
D, 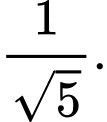
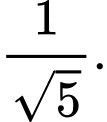
TXĐ: 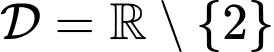
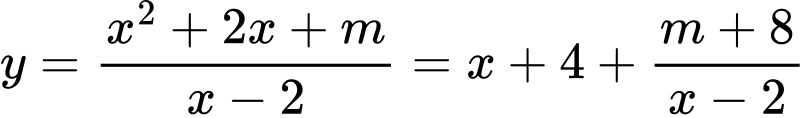
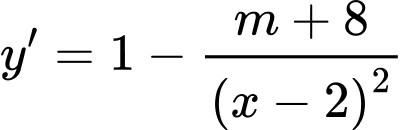
Khi đó: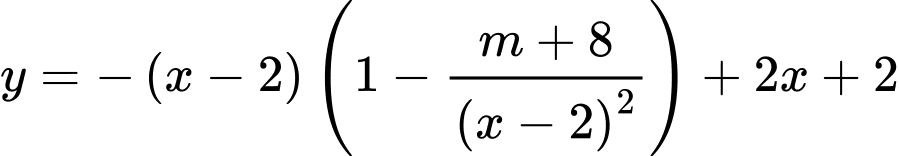
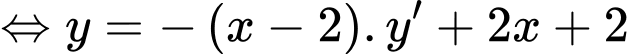
Giả sử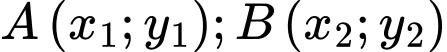 là hai điểm cực trị của đồ thị hàm số
là hai điểm cực trị của đồ thị hàm số
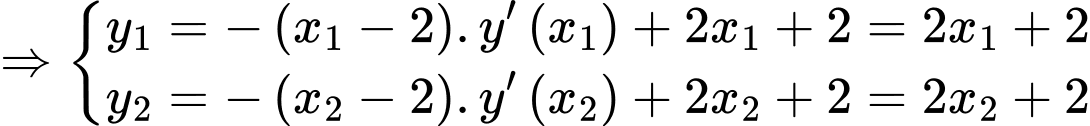
Suy ra phương trình đường thẳng đi qua hai điểm cực trị trên là:
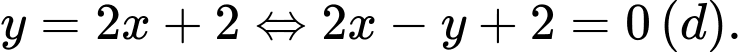
Vậy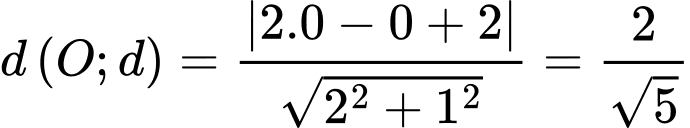
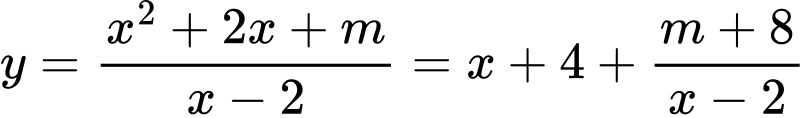
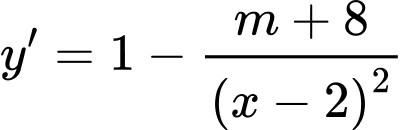
Khi đó:
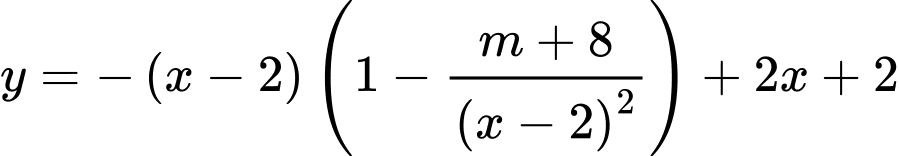
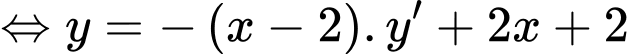
Giả sử
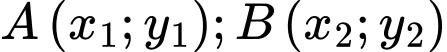 là hai điểm cực trị của đồ thị hàm số
là hai điểm cực trị của đồ thị hàm số
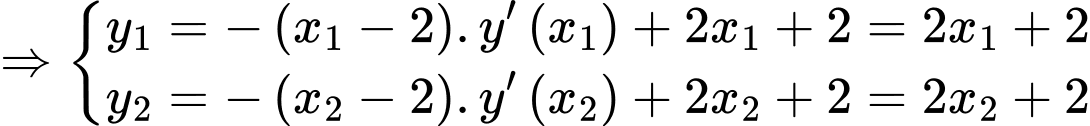
Suy ra phương trình đường thẳng đi qua hai điểm cực trị trên là:
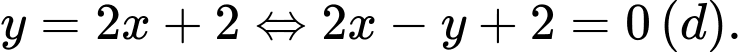
Vậy
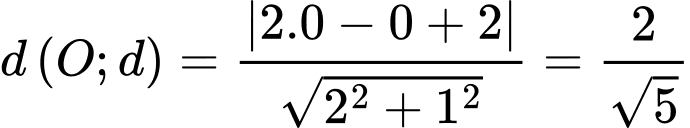
Câu 13 [377598]: Cho hàm số 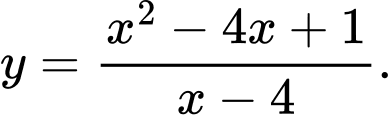 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
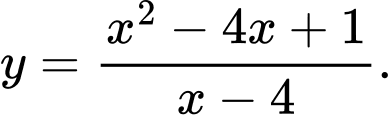 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng 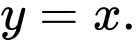
B, b) Hàm số đã cho có hai điểm cực trị.
C, c) Đồ thị hàm số đã cho nhận điểm 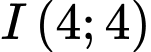 là tâm đối xứng.
là tâm đối xứng.
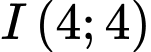 là tâm đối xứng.
là tâm đối xứng.D, d) Đồ thị hàm số đã cho không có tiệm cận ngang.
TXĐ: 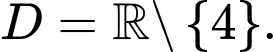
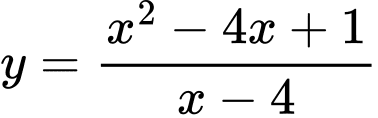
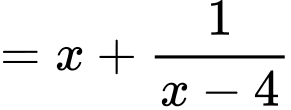
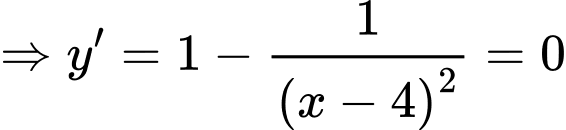
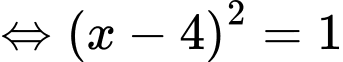

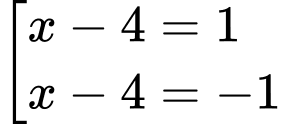

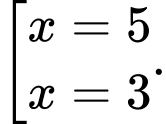
Bảng biến thiên:
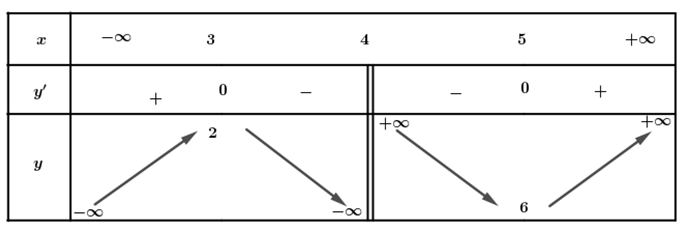
a) Đúng. Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng vì:
vì:
+)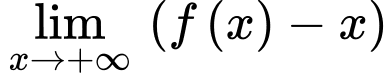
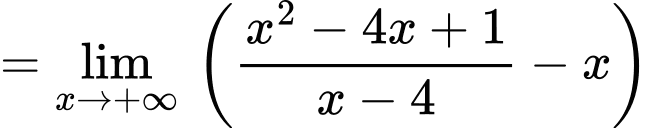
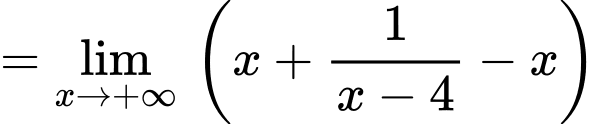
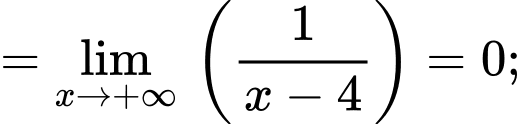
+)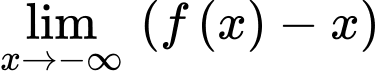
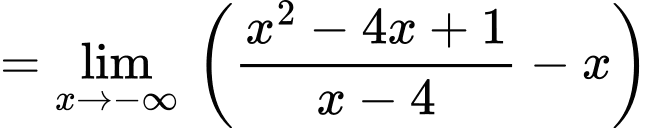
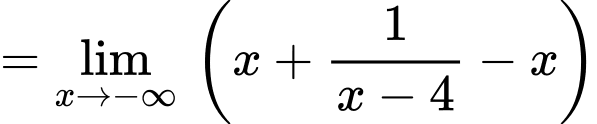
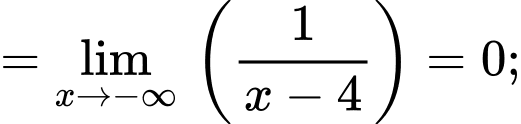
b) Đúng. Hàm số đã cho có hai điểm cực trị.
c) Đúng. Đồ thị hàm số đã cho nhận điểm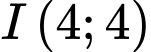 là tâm đối xứng.
là tâm đối xứng.
d) Đúng. Đồ thị hàm số đã cho không có tiệm cận ngang.
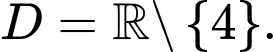
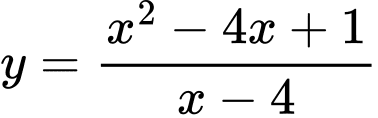
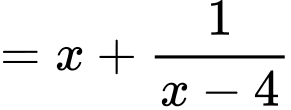
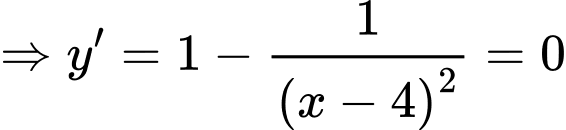
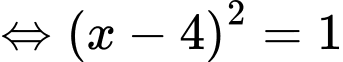

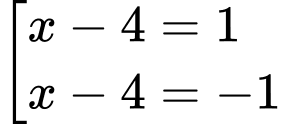

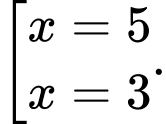
Bảng biến thiên:

a) Đúng. Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng
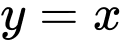 vì:
vì: +)
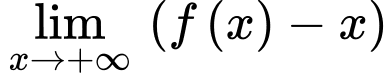
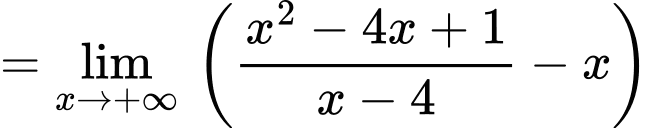
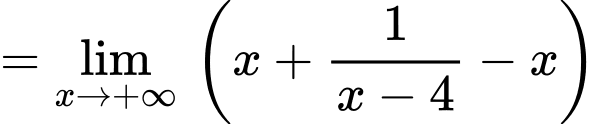
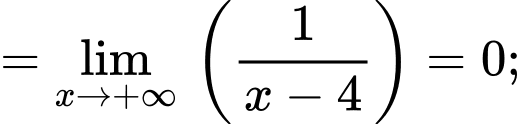
+)
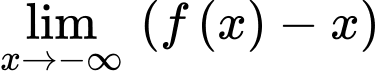
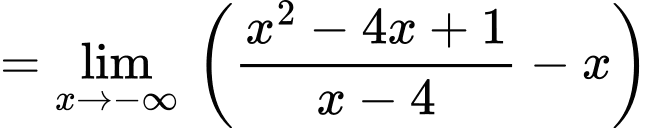
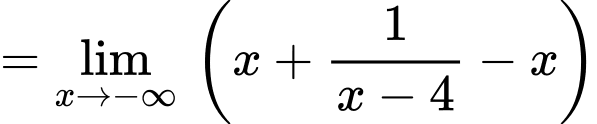
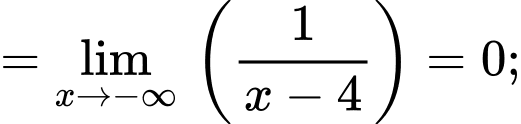
b) Đúng. Hàm số đã cho có hai điểm cực trị.
c) Đúng. Đồ thị hàm số đã cho nhận điểm
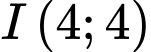 là tâm đối xứng.
là tâm đối xứng.d) Đúng. Đồ thị hàm số đã cho không có tiệm cận ngang.
Câu 14 [399639]: Cho hàm số 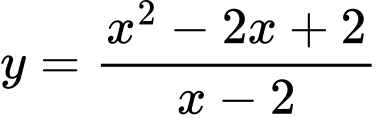 . Mỗi khẳng định sau đúng hay sai?
. Mỗi khẳng định sau đúng hay sai?
a) Đồ thị hàm số đã cho có một đường tiệm cận đứng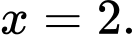
b) Đồ thị hàm số đã cho có một đường tiệm cận xiên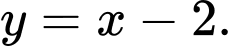
c) Đồ thị hàm số đã cho không có tiệm cận ngang.
d) Đồ thị hàm số có ba đường tiệm cận.
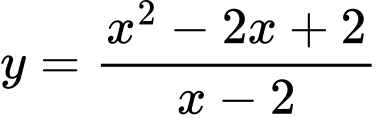 . Mỗi khẳng định sau đúng hay sai?
. Mỗi khẳng định sau đúng hay sai?
a) Đồ thị hàm số đã cho có một đường tiệm cận đứng
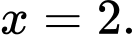
b) Đồ thị hàm số đã cho có một đường tiệm cận xiên
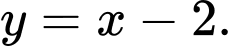
c) Đồ thị hàm số đã cho không có tiệm cận ngang.
d) Đồ thị hàm số có ba đường tiệm cận.
a) Ta có: 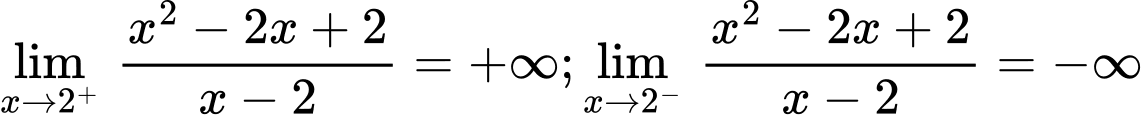
Đồ thị hàm số đã cho có một đường tiệm cận đứng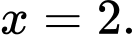
b) Ta có: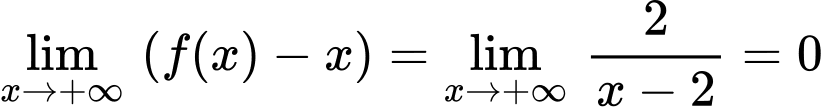 ;
; 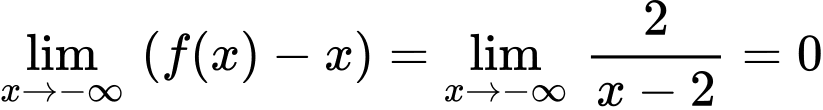
Đồ thị hàm số đã cho có một đường tiệm cận xiên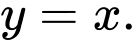
c) Ta có: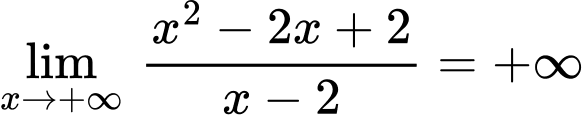 ;
; 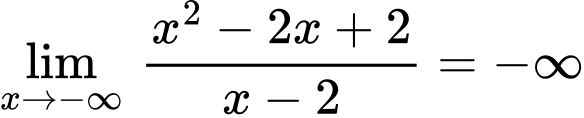
Đồ thị hàm số đã cho không có tiệm cận ngang.
d) Đồ thị hàm số đã cho có hai đường tiệm cận.
a) Đúng b) Sai c) Đúng d) Sai
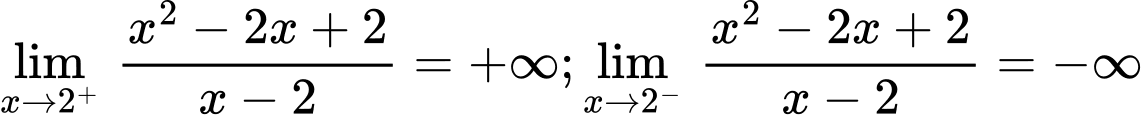
Đồ thị hàm số đã cho có một đường tiệm cận đứng
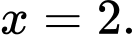
b) Ta có:
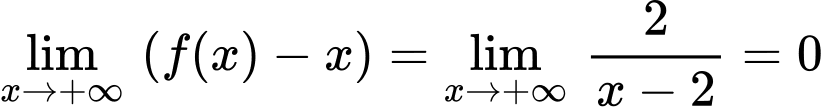 ;
; 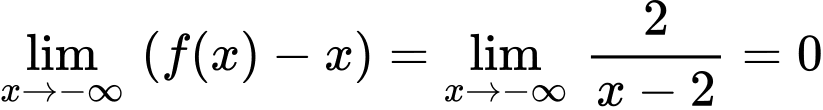
Đồ thị hàm số đã cho có một đường tiệm cận xiên
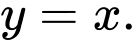
c) Ta có:
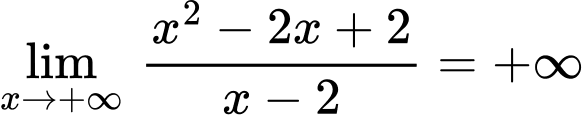 ;
; 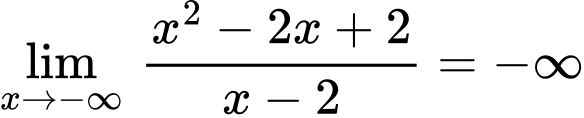
Đồ thị hàm số đã cho không có tiệm cận ngang.
d) Đồ thị hàm số đã cho có hai đường tiệm cận.
a) Đúng b) Sai c) Đúng d) Sai
Câu 15 [399640]: Cho hàm số 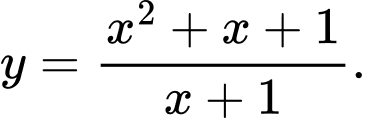 Mỗi khẳng định sau đúng hay sai?
Mỗi khẳng định sau đúng hay sai?
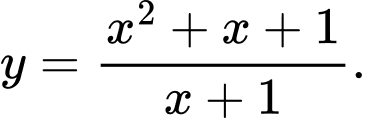 Mỗi khẳng định sau đúng hay sai?
Mỗi khẳng định sau đúng hay sai?
a) Ta có: 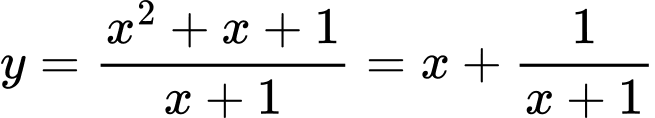
Tập xác định:
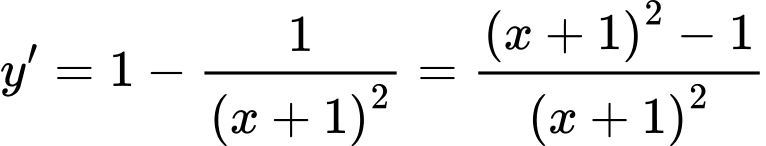
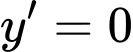

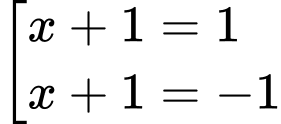

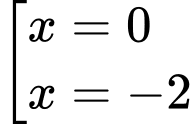
Trên các khoảng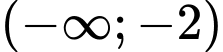 và
và 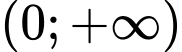 ta có
ta có 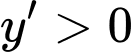 nên hàm số đồng biến trên các khoảng này.
nên hàm số đồng biến trên các khoảng này.
b) Hàm số đạt cực đại tại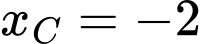 và
và 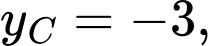 hàm số đạt cực tiểu tại
hàm số đạt cực tiểu tại 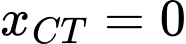 và
và 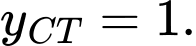
c) Ta có: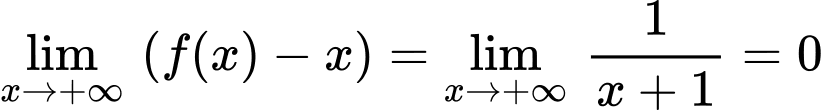 ;
; 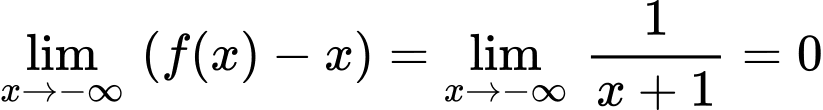
Đồ thị hàm số đã cho có một đường tiệm cận xiên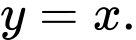
d) Đồ thị hàm số có tâm đối xứng là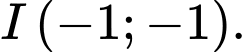
a) Đúng b) Sai c) Đúng d) Đúng
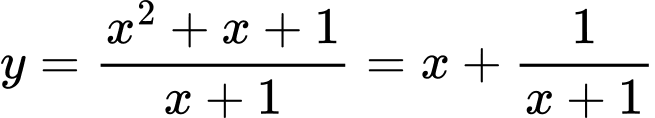
Tập xác định:

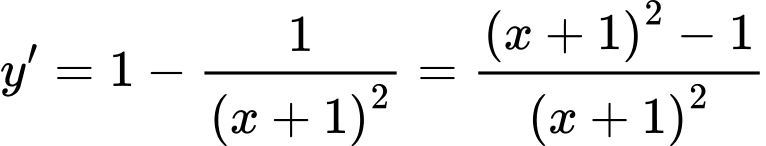
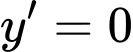

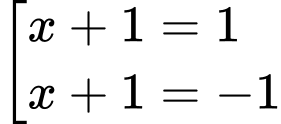

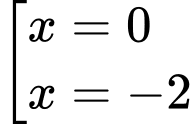
Trên các khoảng
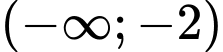 và
và 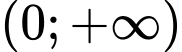 ta có
ta có 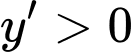 nên hàm số đồng biến trên các khoảng này.
nên hàm số đồng biến trên các khoảng này. b) Hàm số đạt cực đại tại
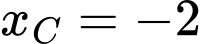 và
và 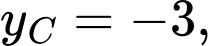 hàm số đạt cực tiểu tại
hàm số đạt cực tiểu tại 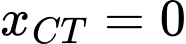 và
và 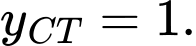
c) Ta có:
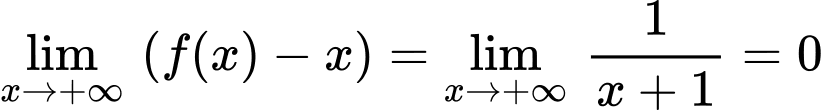 ;
; 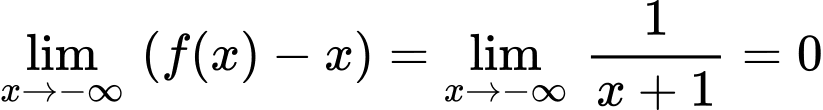
Đồ thị hàm số đã cho có một đường tiệm cận xiên
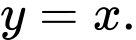
d) Đồ thị hàm số có tâm đối xứng là
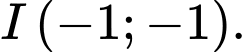
a) Đúng b) Sai c) Đúng d) Đúng
Câu 16 [383016]: Cho hàm số 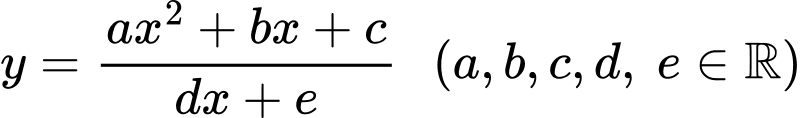 có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau
có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau 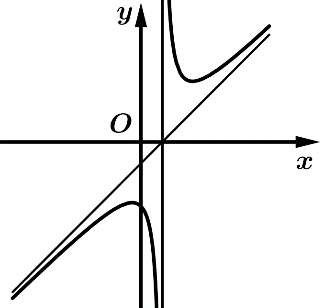
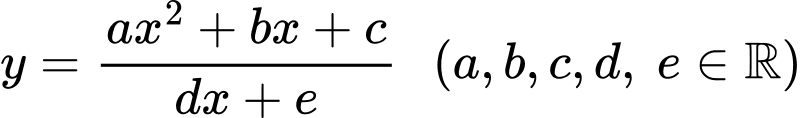 có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau
có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau 
A, a) 

B, b) 

C, c) 

D, d) 

a, Đúng. Vì dựa vào hình dáng đồ thị.
b, Sai. Vì đồ thị có tiệm đường tiệm cận đứng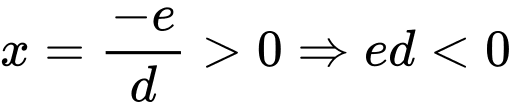 .
.
c, Đúng. Vì hàm số cắt trục tung tại điểm có tung độ âm nên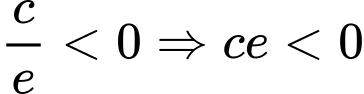
d, Sai. Vì đường thẳng đi qua 2 điểm cực trị của hàm số đã cho là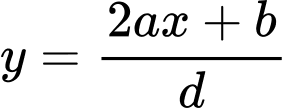 .
.
Mà đường thẳng cắt trục tung tại điểm có tung độ âm nên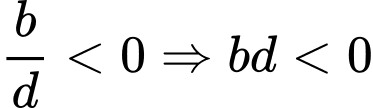 .
.
b, Sai. Vì đồ thị có tiệm đường tiệm cận đứng
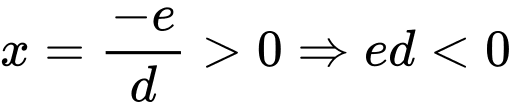 .
.
c, Đúng. Vì hàm số cắt trục tung tại điểm có tung độ âm nên
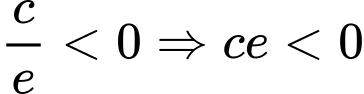
d, Sai. Vì đường thẳng đi qua 2 điểm cực trị của hàm số đã cho là
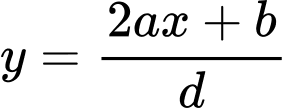 .
.
Mà đường thẳng cắt trục tung tại điểm có tung độ âm nên
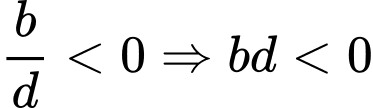 .
.
Câu 17 [383017]: Cho hàm số 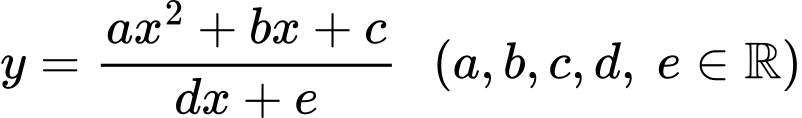 có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau
có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau 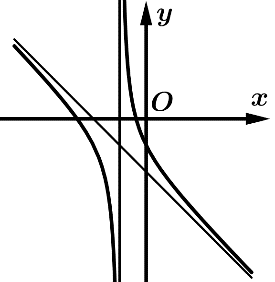
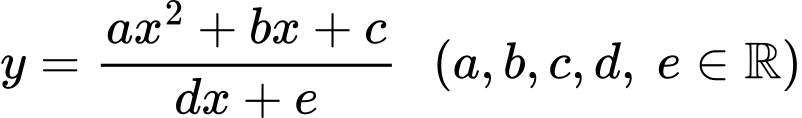 có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau
có đồ thị như hình vẽ bên. Xét tính đúng sai của các mệnh đề sau 
A, a) 

B, b) 

C, c) 

D, d) 

a, Sai. Dựa vào hình dạng đồ thị hàm số.
b, Sai. Vì đồ thị hàm số có đường tiệm cận đứng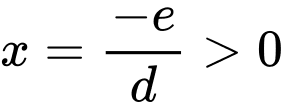 . Nên
. Nên  .
.
c, Đúng. Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ âm.
Nên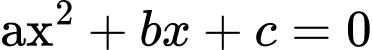 có 2 nghiệm phân biệt âm.
có 2 nghiệm phân biệt âm.
Suy ra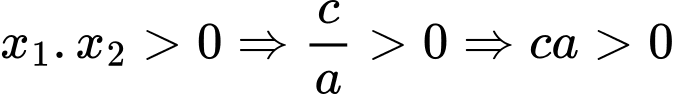
d, Sai. Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ âm (nhìn đồ thị) Suy ra phương trình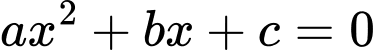 có hai nghiệm âm phân biệt
có hai nghiệm âm phân biệt
Do đó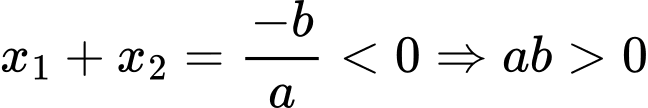 , mà
, mà  (vì nét cuối đi xuống)
Suy ra
(vì nét cuối đi xuống)
Suy ra 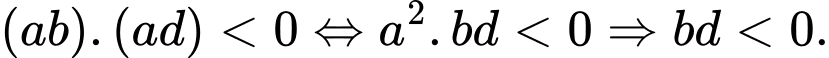
b, Sai. Vì đồ thị hàm số có đường tiệm cận đứng
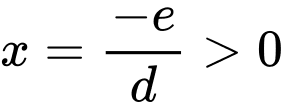 . Nên
. Nên  .
.c, Đúng. Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ âm.
Nên
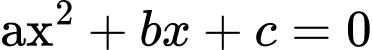 có 2 nghiệm phân biệt âm.
có 2 nghiệm phân biệt âm. Suy ra
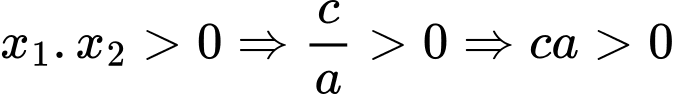
d, Sai. Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ âm (nhìn đồ thị) Suy ra phương trình
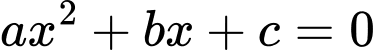 có hai nghiệm âm phân biệt
có hai nghiệm âm phân biệt
Do đó
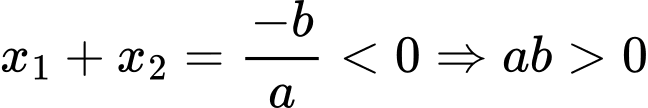 , mà
, mà  (vì nét cuối đi xuống)
Suy ra
(vì nét cuối đi xuống)
Suy ra 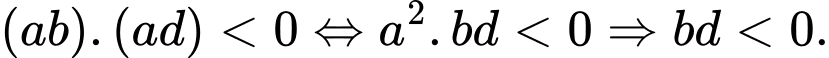
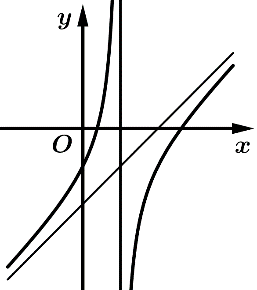
Câu 18 [383018]: Đồ thị trong hình vẽ là đồ thị của hàm số 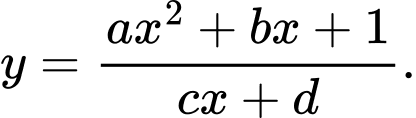 Hỏi có bao nhiêu số dương trong các số
Hỏi có bao nhiêu số dương trong các số 
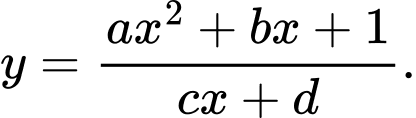 Hỏi có bao nhiêu số dương trong các số
Hỏi có bao nhiêu số dương trong các số 

Đáp số: 2
Từ đồ thị hàm số đã cho ta thấy
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên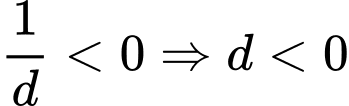 .
.
Đồ thị hàm số có 1 đường tiệm cận đứng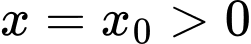 . Suy ra
. Suy ra 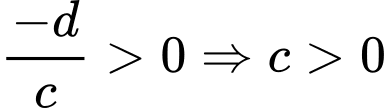 .
.
Dựa vào hình dạng đồ thị hàm số dễ thấy hàm số không có cực trị và . Suy ra
. Suy ra  .
.
Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ dương.
Nên phương trình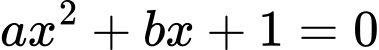 có hai nghiệm phân biệt dương.
có hai nghiệm phân biệt dương.
Suy ra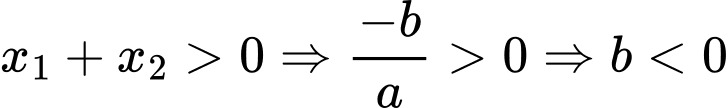 .
.
Vậy có 2 số dương trong các số .
.
Từ đồ thị hàm số đã cho ta thấy
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên
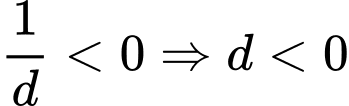 .
.
Đồ thị hàm số có 1 đường tiệm cận đứng
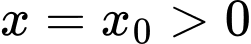 . Suy ra
. Suy ra 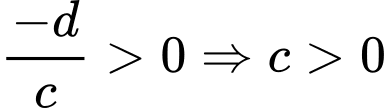 .
.
Dựa vào hình dạng đồ thị hàm số dễ thấy hàm số không có cực trị và
 . Suy ra
. Suy ra  .
.
Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ dương.
Nên phương trình
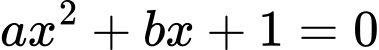 có hai nghiệm phân biệt dương.
có hai nghiệm phân biệt dương.
Suy ra
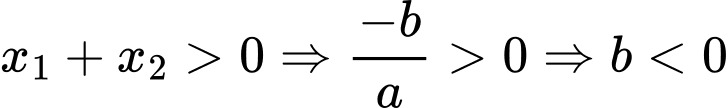 .
.
Vậy có 2 số dương trong các số
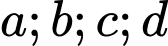 .
.
Câu 19 [383019]: Cho hàm số 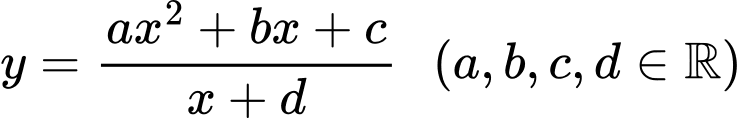 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 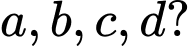
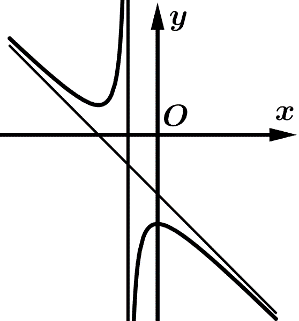
 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 

Đáp số: 1
Từ đồ thị hàm số đã cho ta có
Đồ thị hàm số có 1 đường tiệm cận đứng .
.
Suy ra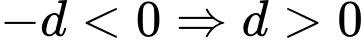 .
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Nên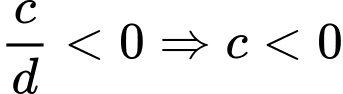 .
.
Dựa vào hình dạng đồ thị dễ thấy hàm số đã cho có 2 cực trị và .
.
Đồ thị hàm số có đường thẳng đi qua 2 điểm cực trị có dạng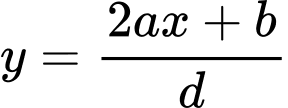 .
.
Mà đường thẳng cắt trục tung tại điểm có tung độ âm nên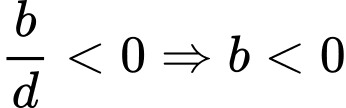 .
.
Vậy có 1 số dương trong các số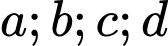 .
.
Từ đồ thị hàm số đã cho ta có
Đồ thị hàm số có 1 đường tiệm cận đứng
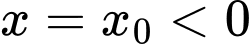 .
.
Suy ra
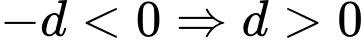 .
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Nên
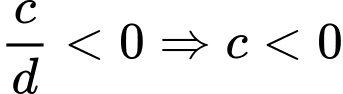 .
.
Dựa vào hình dạng đồ thị dễ thấy hàm số đã cho có 2 cực trị và
 .
.
Đồ thị hàm số có đường thẳng đi qua 2 điểm cực trị có dạng
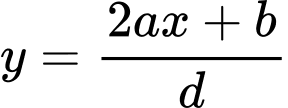 .
.
Mà đường thẳng cắt trục tung tại điểm có tung độ âm nên
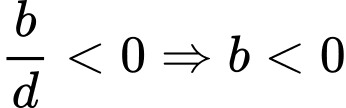 .
.
Vậy có 1 số dương trong các số
 .
.
Câu 20 [383020]: Cho hàm số 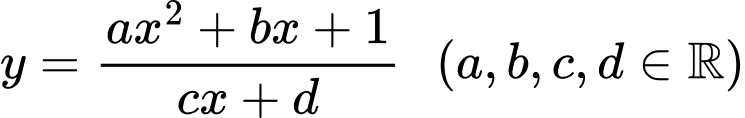 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 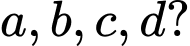
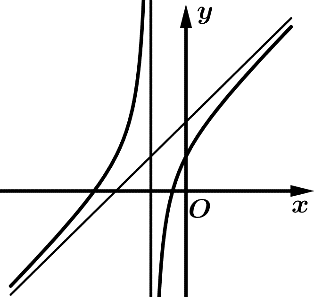
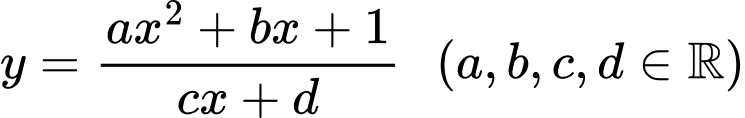 có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số
có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số 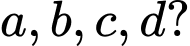

Đáp số: 4
Từ đồ thị hàm số đã cho ta thấy
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên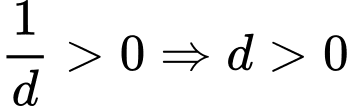 .
.
Đồ thị hàm số có 1 đường tiệm cận đứng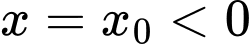 . Suy ra
. Suy ra 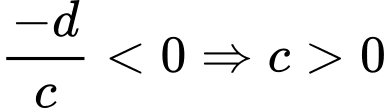 .
.
Dựa vào hình dạng đồ thị hàm số dễ thấy hàm số không có cực trị và . Suy ra
. Suy ra  .
.
Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ âm.
Nên phương trình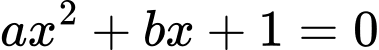 có hai nghiệm phân biệt âm.
có hai nghiệm phân biệt âm.
Suy ra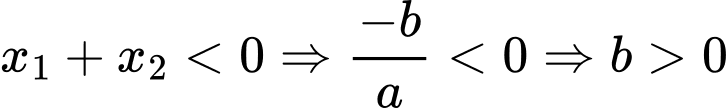 .
.
Vậy có 4 số dương trong các số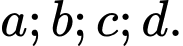
Từ đồ thị hàm số đã cho ta thấy
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
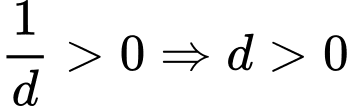 .
.Đồ thị hàm số có 1 đường tiệm cận đứng
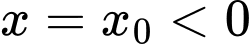 . Suy ra
. Suy ra 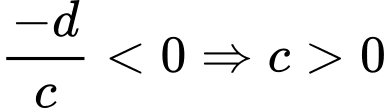 .
.Dựa vào hình dạng đồ thị hàm số dễ thấy hàm số không có cực trị và
 . Suy ra
. Suy ra  .
.Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ âm.
Nên phương trình
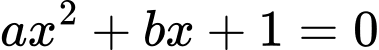 có hai nghiệm phân biệt âm.
có hai nghiệm phân biệt âm.Suy ra
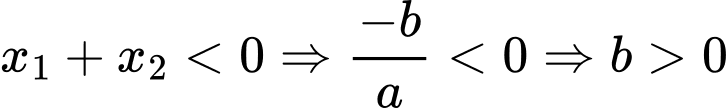 .
.Vậy có 4 số dương trong các số