Đáp án Bài tập tự luyện số 1
Câu 1 [31109]: Trong tất cả các hình chữ nhật có chu vi bằng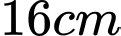 
thì hình chữ nhật có diện tích lớn nhất bằng
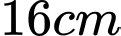thì hình chữ nhật có diện tích lớn nhất bằng A, 
B, 
C, 
D, 
Giả sử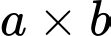 
là kích thước của hình chữ nhật có chu vi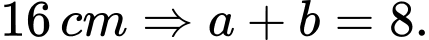 
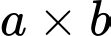là kích thước của hình chữ nhật có chu vi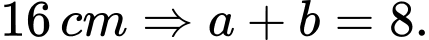 Diện tích hình chữ nhật là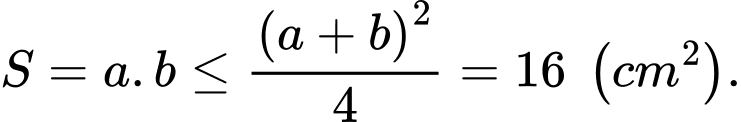 
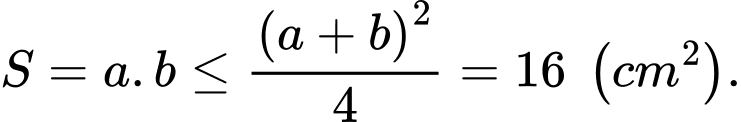
Dấu bằng xảy ra khi 
Chọn C.
Đáp án: C Chọn C.
Câu 2 [31038]: Trong tất cả các hình chữ nhật có cùng diện tích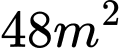 
, hình chữ nhật có chu vi nhỏ nhất là
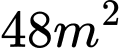, hình chữ nhật có chu vi nhỏ nhất là A,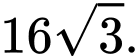 
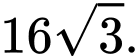
B,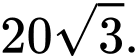 
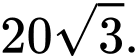
C, 
D, 
Đáp án A.
Gọi hai cạnh của hình chữ nhật lần lượt là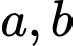 
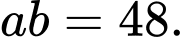
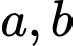với 
với 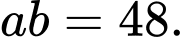Khi đó, chu vi hình chữ nhật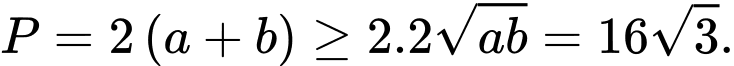 
Đáp án: A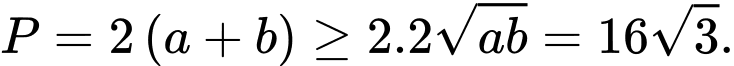
Câu 3 [384767]: Trong hệ trục toạ độ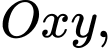 
cho đồ thị hàm số 
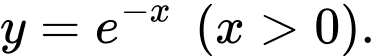Trên đồ thị, ta lấy điểm 
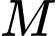và dựng hình chữ nhật 
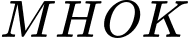(xem hình vẽ bên). Diện tích lớn nhất của hình chữ nhật 
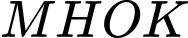bằng bao nhiêu?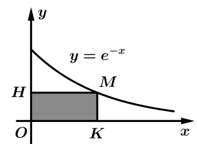
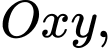cho đồ thị hàm số 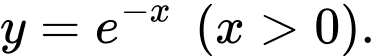Trên đồ thị, ta lấy điểm 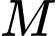và dựng hình chữ nhật 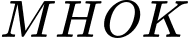(xem hình vẽ bên). Diện tích lớn nhất của hình chữ nhật 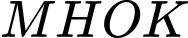bằng bao nhiêu?A,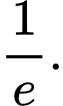 
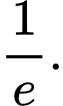
B,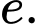 
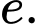
C,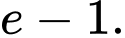 
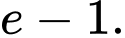
D,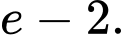 
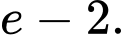
Chọn đáp án A.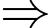 
Hình chữ nhật 
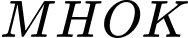có diện tích là: 
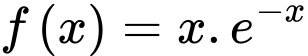với 
Ta có: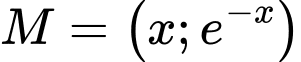 
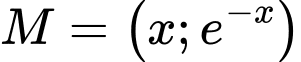
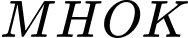Hình chữ nhật có diện tích là: 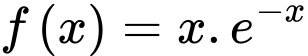với Có: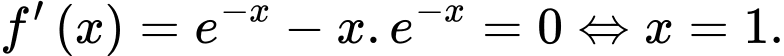 
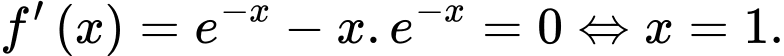
Ta có bảng biến thiên:
Vậy diện tích lớn nhất của hình chữ nhật 
bằng 
khi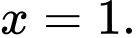 
Đáp án: A 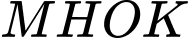bằng khi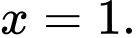
Câu 4 [31039]: Cho một tấm nhôm hình vuông cạnh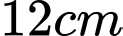 
. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 
, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm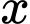 
để hộp nhận được có thể tích lớn nhất.
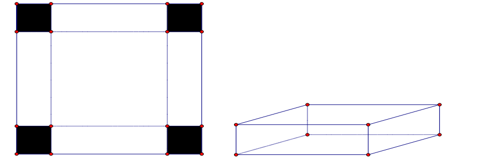
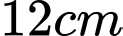. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng , rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm 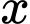để hộp nhận được có thể tích lớn nhất.A,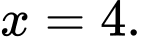 
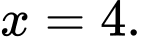
B,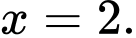 
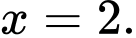
C,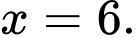 
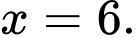
D,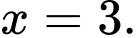 
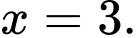
Diện tích mặt đáy của hộp là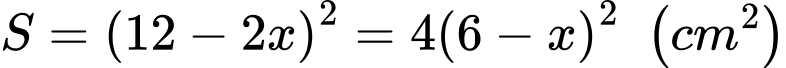 
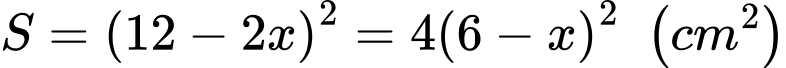
Chiều cao của hộp là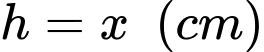 
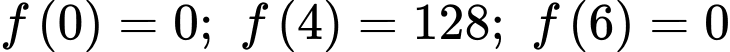
Đáp án: B 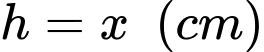Thể tích của hộp là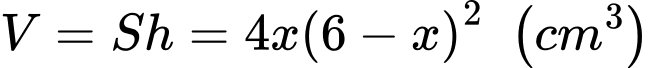 
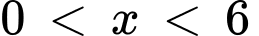
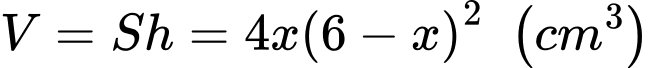với 
với 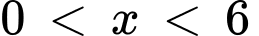Đặt 
Ta được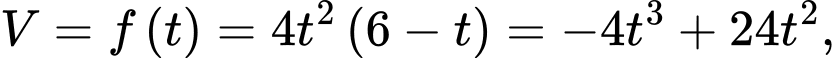 
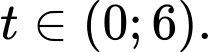
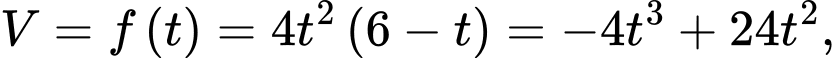với 
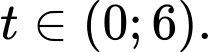
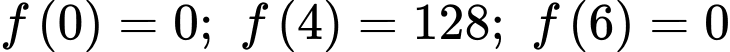
với Vậy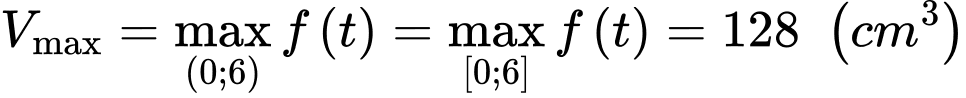 
khi 
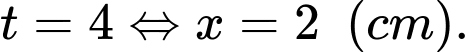
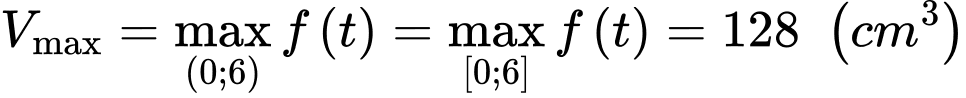khi 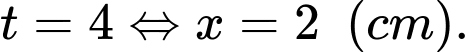Chọn đáp án B.
Câu 5 [6341]: Một công ty muốn thiết kế một loại hộp có dạng hình chữ nhật có đáy là hình vuông sao cho thể tích của khối hộp được tạo thành là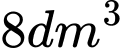 
và diện tích toàn phần đạt giá trị nhỏ nhất. Độ dài cạnh đáy của mỗi hộp muốn thiết kế là
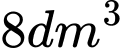và diện tích toàn phần đạt giá trị nhỏ nhất. Độ dài cạnh đáy của mỗi hộp muốn thiết kế là A,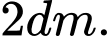 
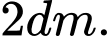
B,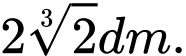 
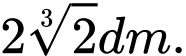
C,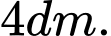 
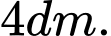
D,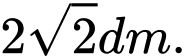 
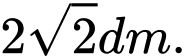
Đáp án A.
Gọi cạnh đáy hình vuông là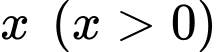
thì chiều cao của khối hộp là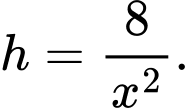 
Ta có diện tích toàn phần của khối hộp là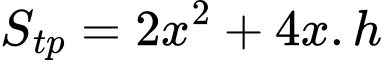
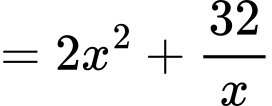
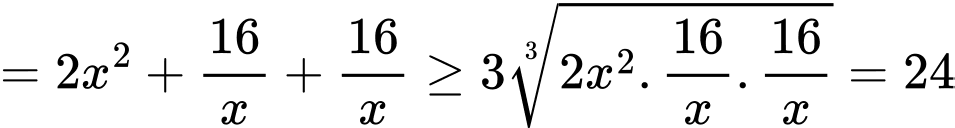
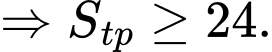
Dấu bằng xảy ra khi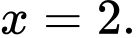
Vậy độ dài cạnh đáy của mỗi hộp muốn thiết kế là 2dm. Đáp án: A
Gọi cạnh đáy hình vuông là
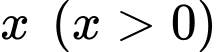thì chiều cao của khối hộp là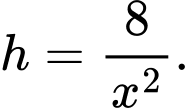 Ta có diện tích toàn phần của khối hộp là
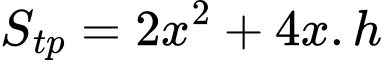
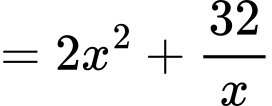
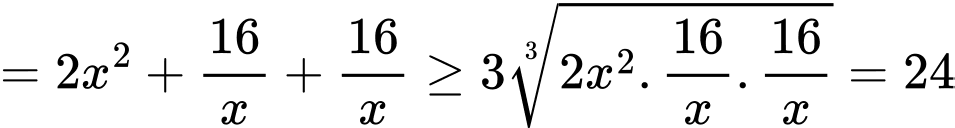
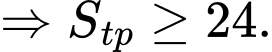
Dấu bằng xảy ra khi
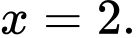
Vậy độ dài cạnh đáy của mỗi hộp muốn thiết kế là 2dm. Đáp án: A
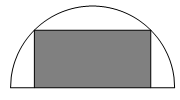
Câu 6 [31023]: Tính diện tích lớn nhất 
của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính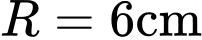 
nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp.
của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính 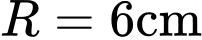nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp. A,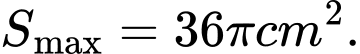 
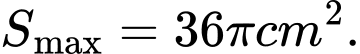
B,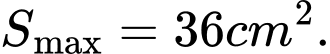 
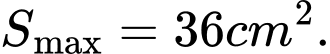
C,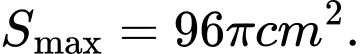 
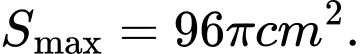
D,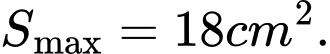 
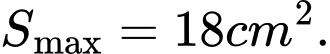
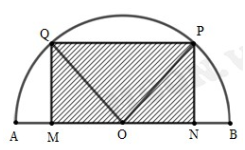
Khi đó,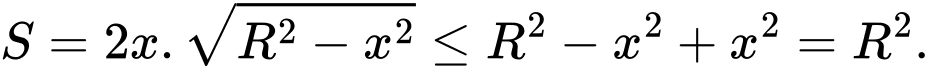 
Vậy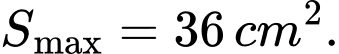 
Chọn B.
Đáp án: B 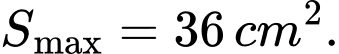Chọn B.
Câu 7 [5884]: Người ta muốn mạ vàng cho bề mặt phía ngoài của một cái hộp dạng hộp đứng không nắp (nắp trên), có đáy là một hình vuông. Tìm chiều cao của hộp để lượng vàng phải dùng để mạ là ít nhất, biết lớp mạ ở mọi nơi như nhau, giao giữa các mặt là không đáng kể và thể tích của hộp là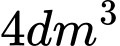 
.
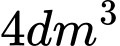. A,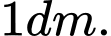 
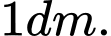
B,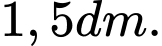 
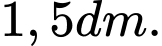
C,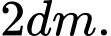 
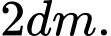
D,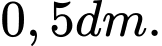 
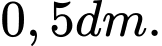
Gọi cạnh đáy là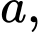 
chiều cao là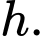 
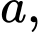chiều cao là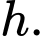 Diện tích đáy là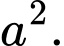 
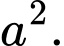
Diện tích xung quanh là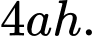 
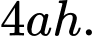
Ta có: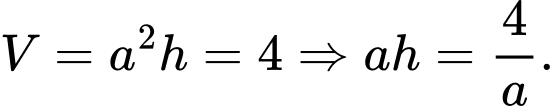 
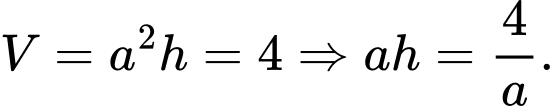
Lượng vàng cần phải dùng là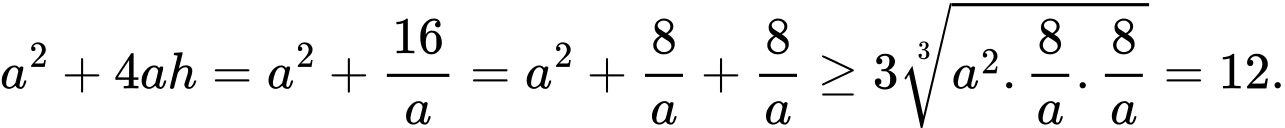 
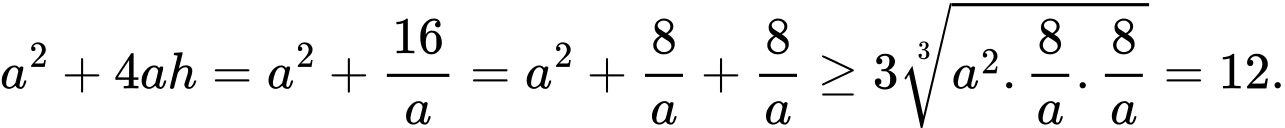
Dấu bằng xảy ra khi và chỉ khi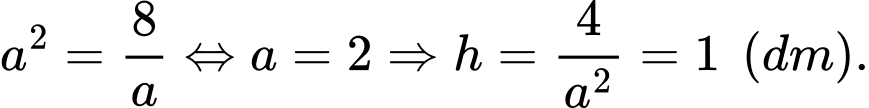 
Chọn A.
Đáp án: A 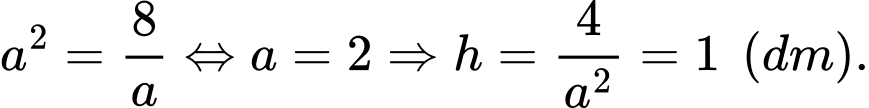Chọn A.
Câu 8 [28857]: Một chú cá hồi bơi ngược dòng để vượt một khoảng cách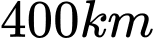 
. Vận tốc dòng nước là 
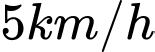. Nếu vận tốc bơi của con cá khi nước đứng yên là 
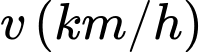thì năng lượng tiêu hao của cá trong 
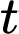giờ được cho bởi công thức 
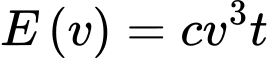, trong đó c là một hằng số, 
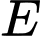được tính bằng jun. Giả sử 
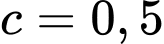, hãy tính năng lượng tiêu hao tối thiểu của chú cá hồi.
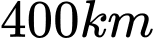. Vận tốc dòng nước là 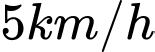. Nếu vận tốc bơi của con cá khi nước đứng yên là 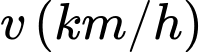thì năng lượng tiêu hao của cá trong 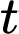giờ được cho bởi công thức 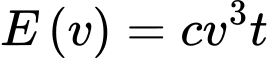, trong đó c là một hằng số, 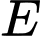được tính bằng jun. Giả sử 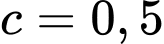, hãy tính năng lượng tiêu hao tối thiểu của chú cá hồi. A, 40250 jun.
B, 33750 jun.
C, 25960 jun.
D, 36450 jun.
Vận tốc khi cá bơi ngược dòng là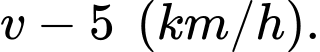 
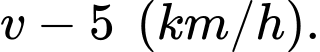
Thời gian để cá bới vượt khoảng cách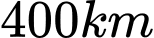 
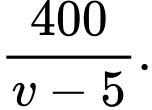
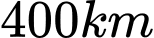là 
là 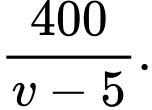Năng lượng tiêu hao của cá khi ngược dòng là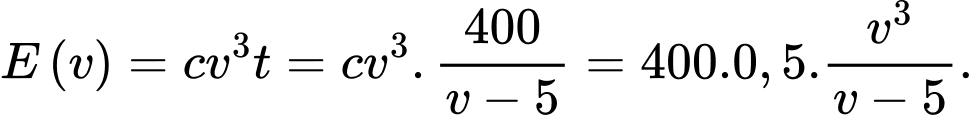 
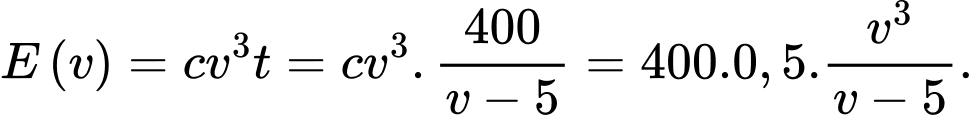
Khảo sát hàm số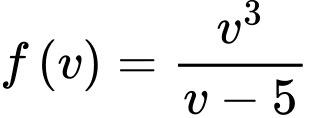 
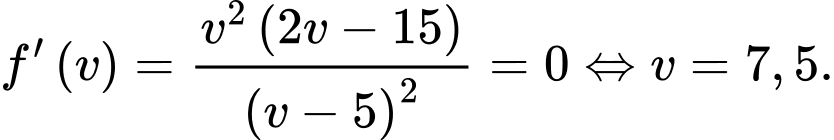
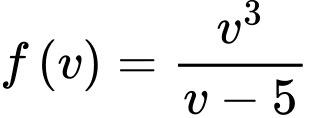thì 
thì 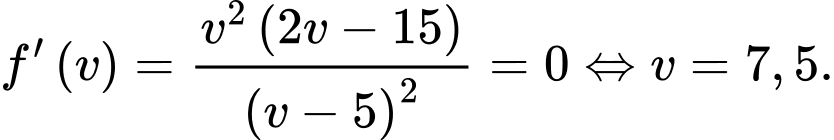Khi đó, năng lượng tiêu hao đạt giá trị nhỏ nhất là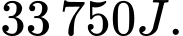 
Đáp án: B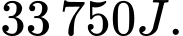
Câu 9 [31026]: Cho hình thang cân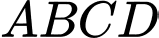 
có đáy nhỏ 
và hai cạnh bên đều có độ dài bằng 
. Tìm diện tích lớn nhất 
của hình thang.
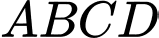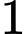có đáy nhỏ và hai cạnh bên đều có độ dài bằng . Tìm diện tích lớn nhất của hình thang. A,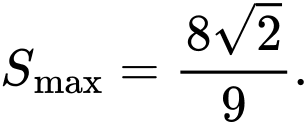 
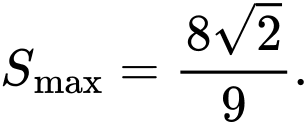
B,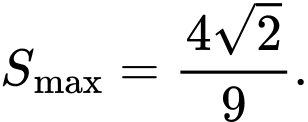 
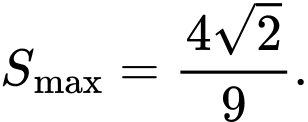
C,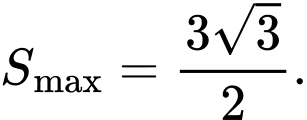 
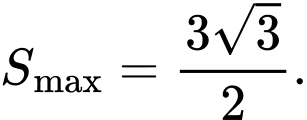
D,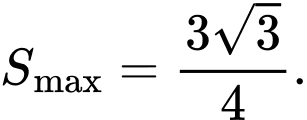 
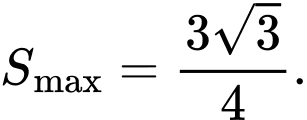
Đặt
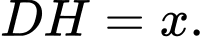Ta có: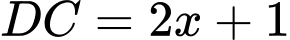 
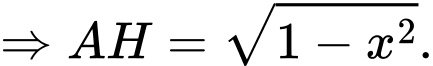
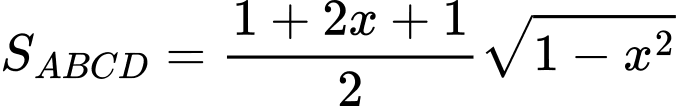
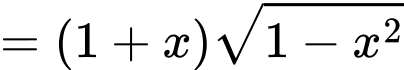
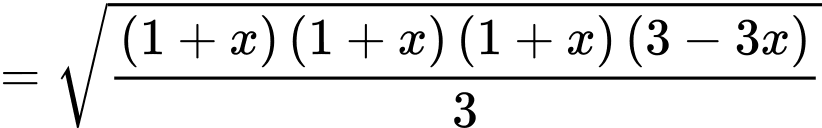
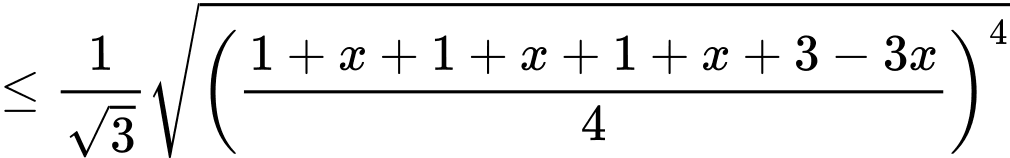
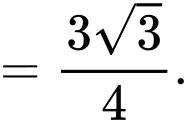
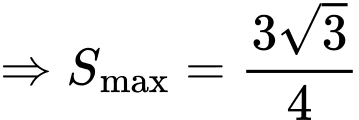
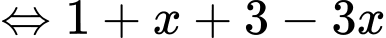
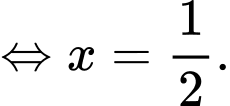
Chọn D. Đáp án: D
Câu 10 [327627]: Cho một tấm nhôm hình vuông cạnh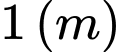 
như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng 
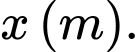Tìm giá trị của 
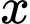để khối chóp nhận được có thể tích lớn nhất.
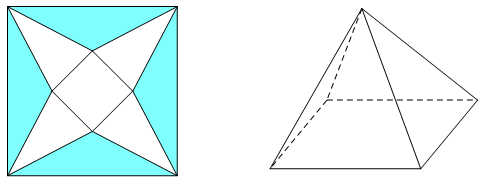
như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng 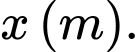Tìm giá trị của 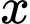để khối chóp nhận được có thể tích lớn nhất. A,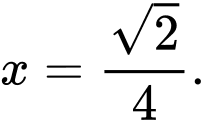 
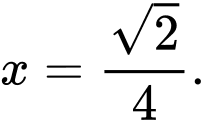
B,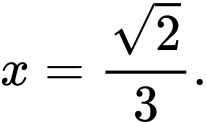 
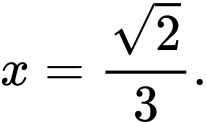
C,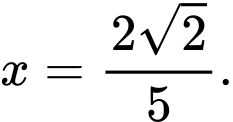 
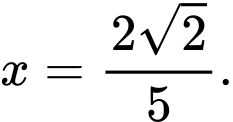
D,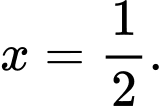 
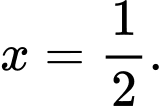
Đặt cạnh bên là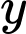 
và cạnh đáy của chóp đều là 
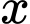ta đi tìm mối quan hệ giữa 
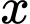và 
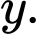
Độ dài đường cao của một mặt bên là: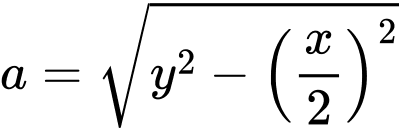
Khi đó theo hình 1 ta được: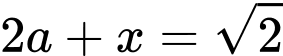
(bằng nhau và bằng đường chéo hình vuông)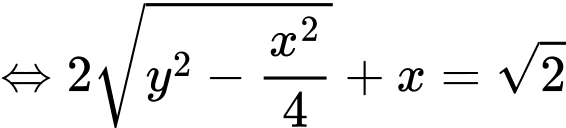 
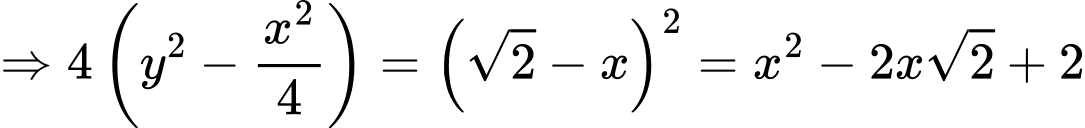
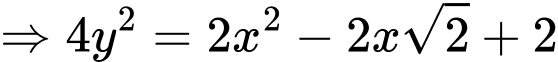
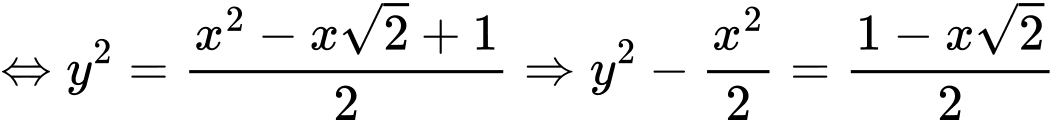
Lại có: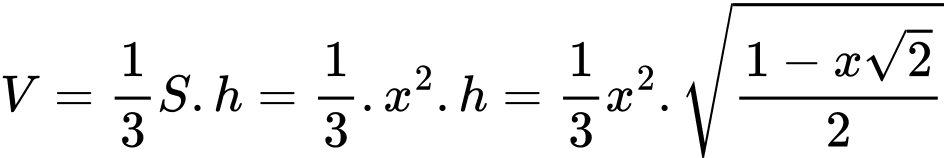
Suy ra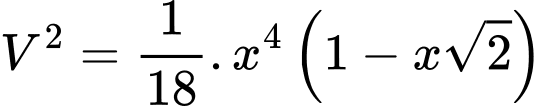
Xét hàm số: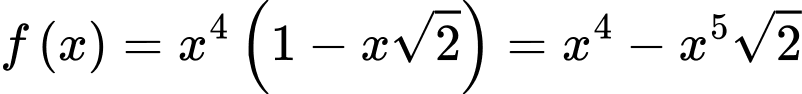
trên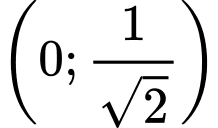 
ta có: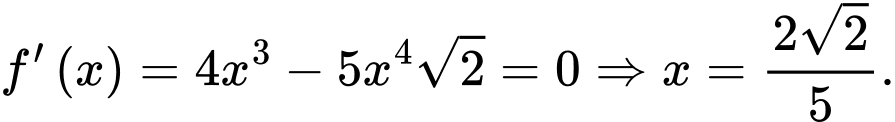 
Từ đó suy ra
đạt được khi 
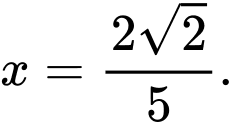Chọn C.
Đáp án: C
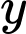và cạnh đáy của chóp đều là 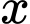ta đi tìm mối quan hệ giữa 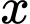và
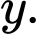
Độ dài đường cao của một mặt bên là:
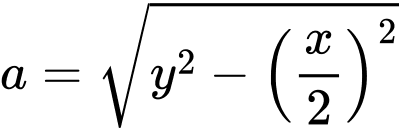
Khi đó theo hình 1 ta được:
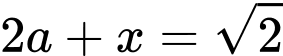(bằng nhau và bằng đường chéo hình vuông)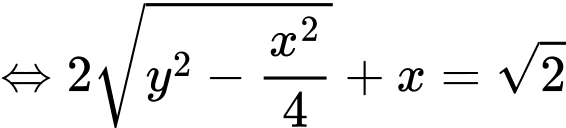
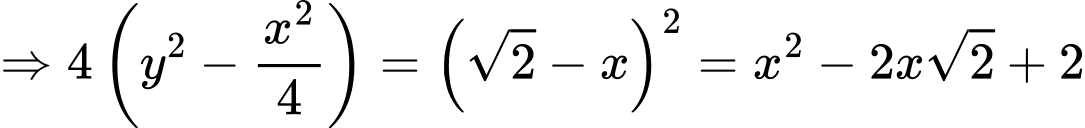
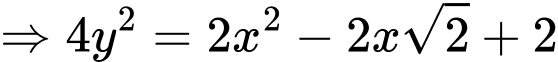
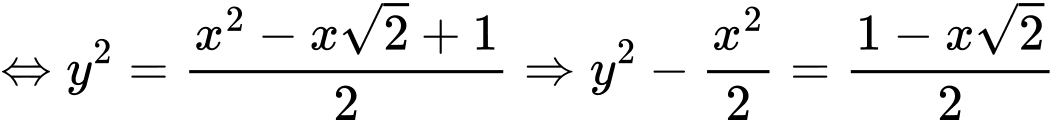
Lại có:
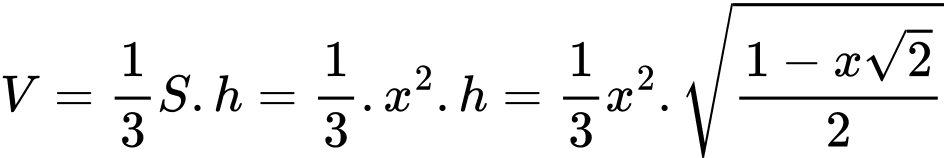
Suy ra
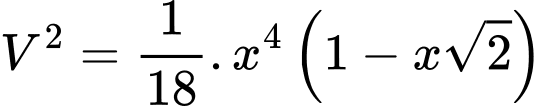
Xét hàm số:
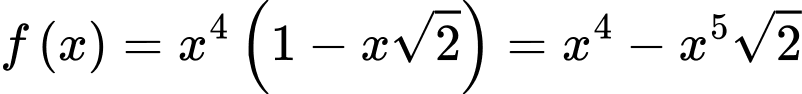trên 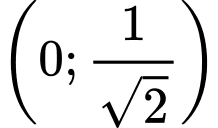ta có: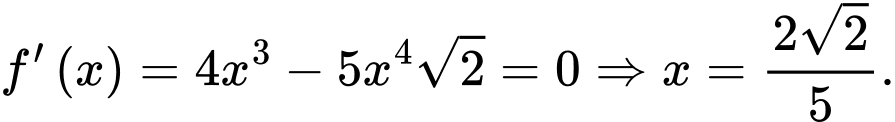
Từ đó suy ra
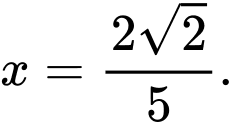đạt được khi Chọn C.
Đáp án: C
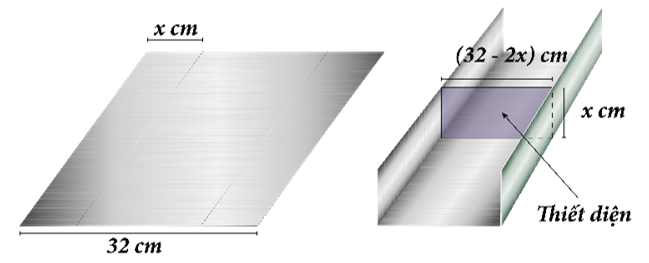
Câu 11 [383946]: Một miếng nhôm có bề ngang
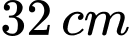được uốn cong tạo thành rãnh dẫn nước bằng cách chia tấm nhôm thành 3 phần rồi gấp 2 bên lại theo một góc vuông. Người ta cần nghiên cứu cách để tạo ra đường rãnh có diện tích mặt ngang 
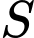lớn nhất để có thể cho nước đi qua nhiều nhất. Diện tích lớn nhất của thiết diện (tính theo đơn vị 
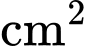) là
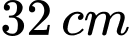được uốn cong tạo thành rãnh dẫn nước bằng cách chia tấm nhôm thành 3 phần rồi gấp 2 bên lại theo một góc vuông. Người ta cần nghiên cứu cách để tạo ra đường rãnh có diện tích mặt ngang 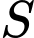lớn nhất để có thể cho nước đi qua nhiều nhất. Diện tích lớn nhất của thiết diện (tính theo đơn vị 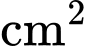) là
Gọi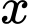 
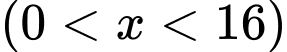là độ rộng phần được gấp lại mỗi bên của miếng nhôm.
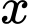
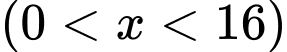là độ rộng phần được gấp lại mỗi bên của miếng nhôm. Khi đó, ta có
diện tích của thiết diện cần tính là: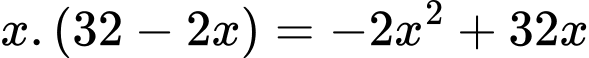 
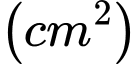
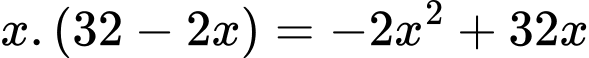
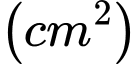
Bài toán trở
thành tính giá trị lớn nhất của hàm số: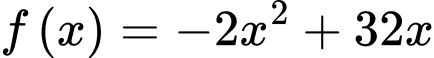 
với
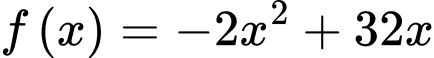với
Ta có: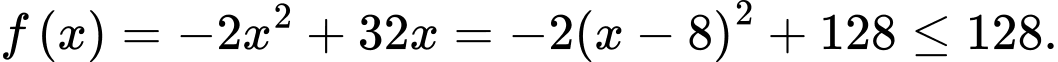 
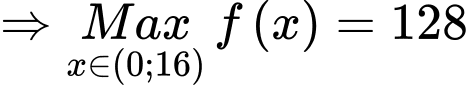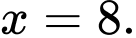
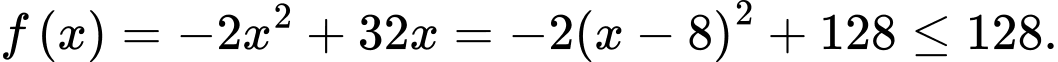
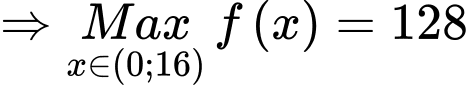khi 
khi 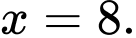Vậy diện tích lớn
nhất của thiết diện là: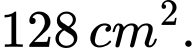 
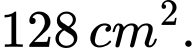
Câu 12 [31022]: Một ông nông dân có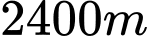 
hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu?
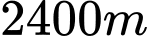hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu? A,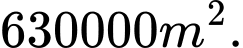 
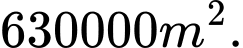
B,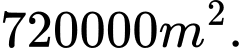 
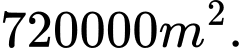
C,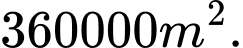 
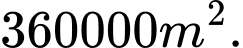
D,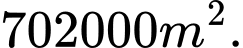 
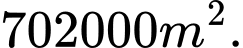
Giả sử chiều dài của hình chữ nhật giáp với bờ sông.
Gọi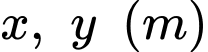
lần lượt là chiều rộng, chiều dài của hình chữ nhật.
Theo giả thiết, ta có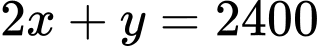
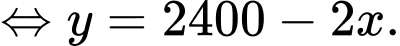
Suy ra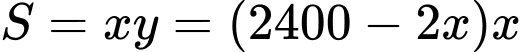
Dấu “=” xảy ra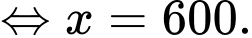
Vậy diện tích lớn nhất là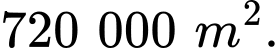
Chọn đáp án B. Đáp án: B
Gọi
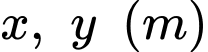lần lượt là chiều rộng, chiều dài của hình chữ nhật. Theo giả thiết, ta có
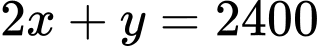
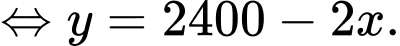
Suy ra
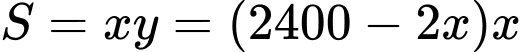
Dấu “=” xảy ra
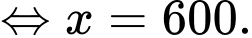
Vậy diện tích lớn nhất là
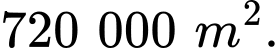
Chọn đáp án B. Đáp án: B
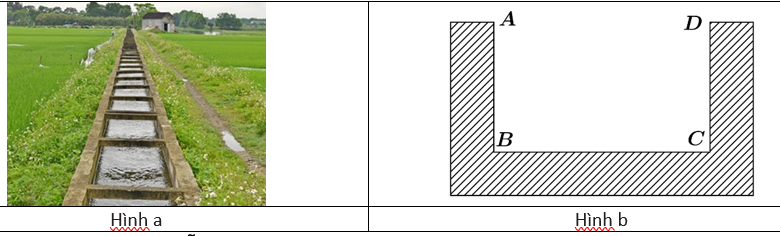
Câu 13 [383950]: Hình vẽ a bên dưới là một mương dẫn nước thuỷ lợi tại một địa phương. Phần không gian trong mương để nước chảy có mặt cắt ngang là một hình chữ nhật ABCD (Hình b). Với điều kiện lưu lượng nước qua mương cho phép ở đây thì diện tích mặt cắt ABCD là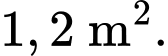 
Để đảm bảo yêu cầu kĩ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài 
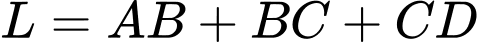là ngắn nhất, biết rằng theo quy định thì đoạn BC (chiều rộng đáy mương) phải dưới 10 m. Tính 
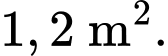Để đảm bảo yêu cầu kĩ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài 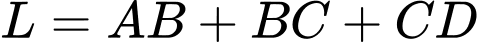là ngắn nhất, biết rằng theo quy định thì đoạn BC (chiều rộng đáy mương) phải dưới 10 m. Tính
Đặt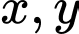 
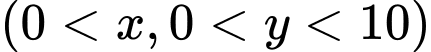lần lượt là độ dài của 
và 
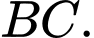
Diện tích mặt cắt ABCD là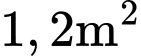
Bài toán trở thành tìm giá trị nhỏ nhất của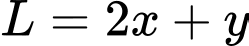
với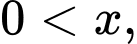 
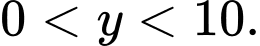
Ta có: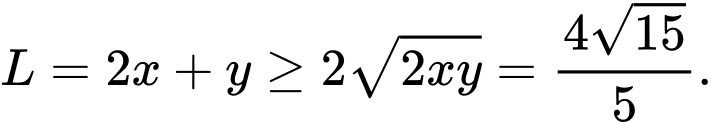
Dấu “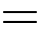
” xảy ra khi và chỉ khi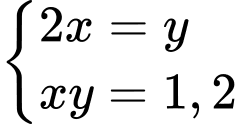 
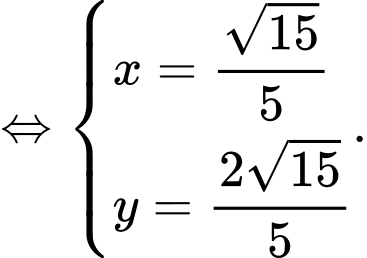
Vậy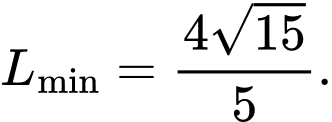
Điền đáp án 3,10
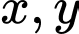
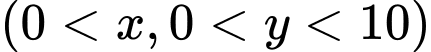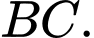
lần lượt là độ dài của và Diện tích mặt cắt ABCD là
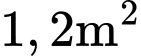
Bài toán trở thành tìm giá trị nhỏ nhất của
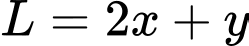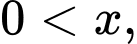
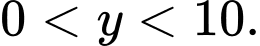
với Ta có:
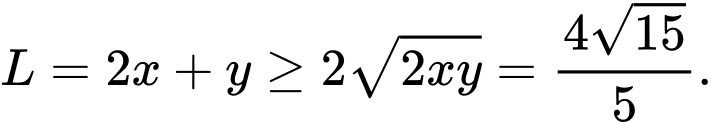
Dấu “
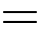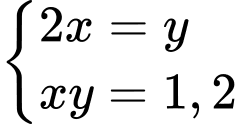
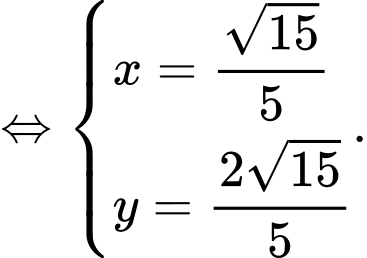
” xảy ra khi và chỉ khi Vậy
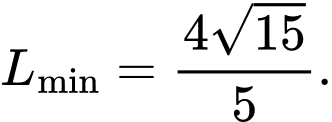
Điền đáp án 3,10
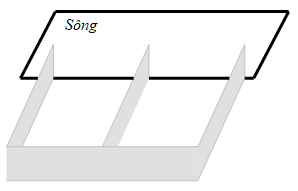
Câu 14 [383948]: Người ta cần rào một mảnh đất hình chữ nhật ABCD có diện tích là 
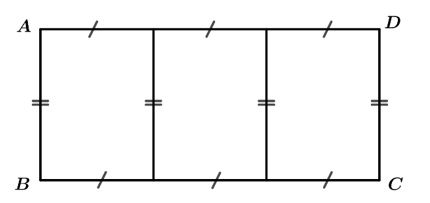
Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình vẽ). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60 000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm) 
Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình vẽ). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60 000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm)
Gọi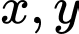 
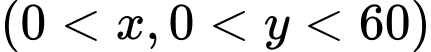lần lượt là độ dài của 
và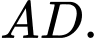 
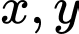
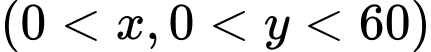lần lượt là độ dài của và 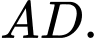Mảnh đất hình chữ nhật ABCD có diện
tích là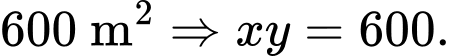 
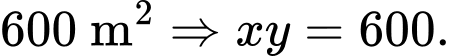
Khi đó, kích thước của hàng rào
là: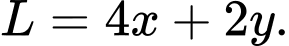 
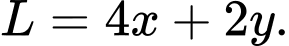
Ta có: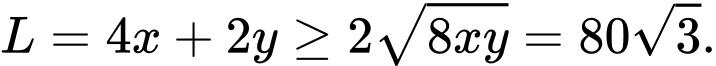 
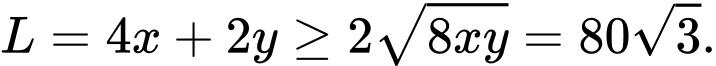
Dấu “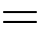
” xảy ra khi và chỉ khi: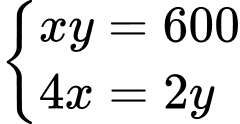 
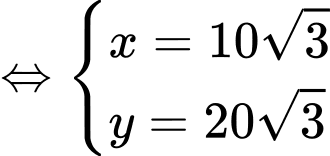
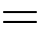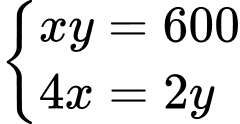
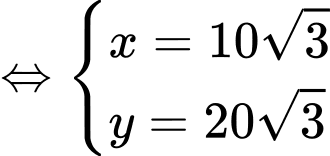
” xảy ra khi và chỉ khi: Vậy để chi phí xây dựng hàng rào
là thấp nhất thì chiều dài của hình chữ nhật ABCD là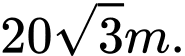 
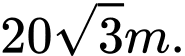
Câu 15 [31060]: Một người nông dân có 
đồng để làm một cái hàng rào hình chữ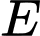 
dọc theo một con sông (như hình vẽ) để ngăn khu đất thành hai hình chữ nhật bằng nhau với mục đích trồng rau. Đối với mặt hàng rào song song với bờ sông, chi phí nguyên vật liệu 
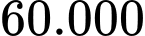đồng/mét. Còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 
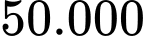đồng/mét. Tìm diện tích lớn nhất của đất rào thu được.
đồng để làm một cái hàng rào hình chữ 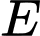dọc theo một con sông (như hình vẽ) để ngăn khu đất thành hai hình chữ nhật bằng nhau với mục đích trồng rau. Đối với mặt hàng rào song song với bờ sông, chi phí nguyên vật liệu 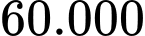đồng/mét. Còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 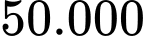đồng/mét. Tìm diện tích lớn nhất của đất rào thu được. A,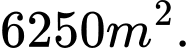 
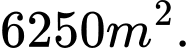
B,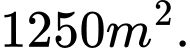 
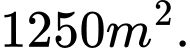
C,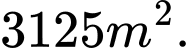 
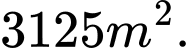
D,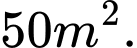 
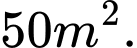
Gọi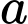 
là chiều dài hàng rào song song bờ sông, 
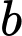là chiều dài mặt hàng rào vuông góc bờ sông.
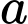là chiều dài hàng rào song song bờ sông, 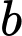là chiều dài mặt hàng rào vuông góc bờ sông. Suy ra diện tích đất rào là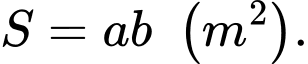 
Đáp án: A 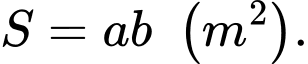Chi phí xây dựng vậy liệu được tính là
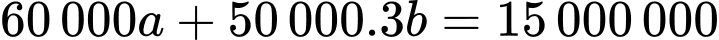
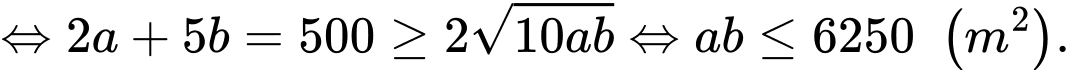
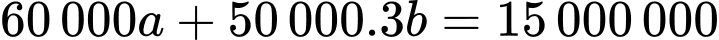
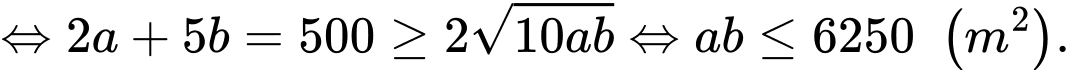
Vậy diện tích lớn nhất của đất rào là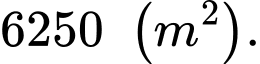 
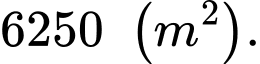
Câu 16 [390557]: Một cửa sổ có dạng phía dưới là hình chữ nhật, phía trên là nửa hình tròn có đường kính bằng chiều rộng của hình chữ nhật (như hình vẽ). Biết rằng tổng độ dài phần mép ngoài của cửa (gồm phần dưới và nửa đường tròn phía trên) là 10 m. Cửa sổ có diện tích lớn nhất là bao nhiêu 
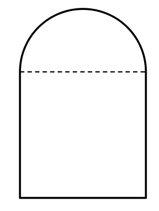
Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục. Đáp số:…………………..
Gọi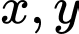 
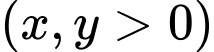lần lượt là chiều rộng và chiều dài của hình nhữ nhật.
Khi đó, bán kính của nửa hình tròn là: 
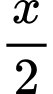(m).
Tổng độ dài phần mép ngoài của cửa là 10 m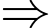 
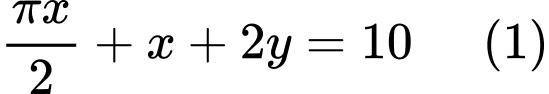Diện tích của cửa sổ là: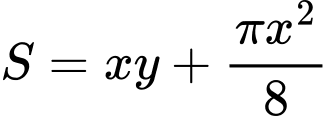 
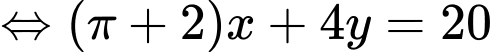
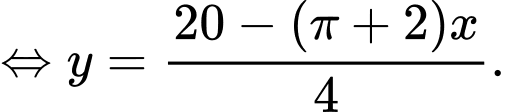
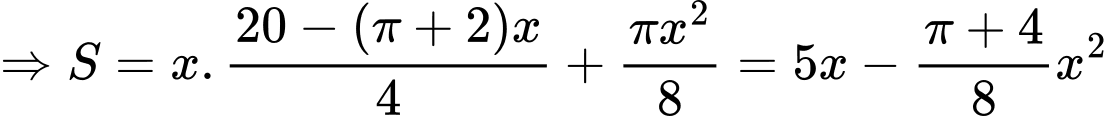Vậy diện tích lớn nhất của cửa sổ là: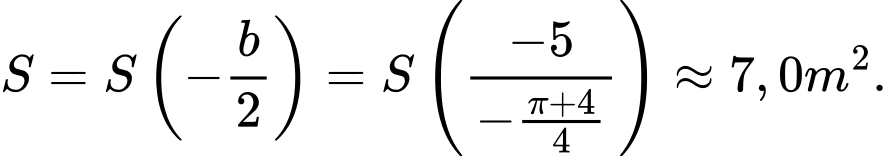 
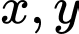
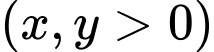lần lượt là chiều rộng và chiều dài của hình nhữ nhật.
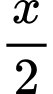Khi đó, bán kính của nửa hình tròn là: (m).
Tổng độ dài phần mép ngoài của cửa là 10 m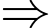
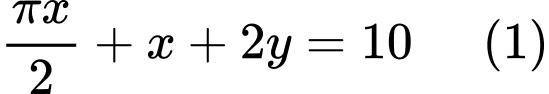Diện tích của cửa sổ là: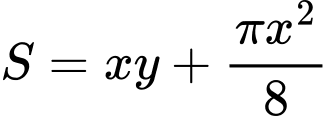
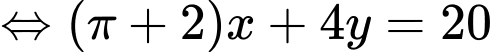
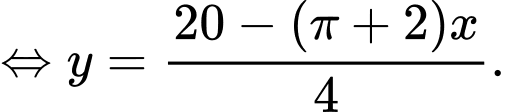
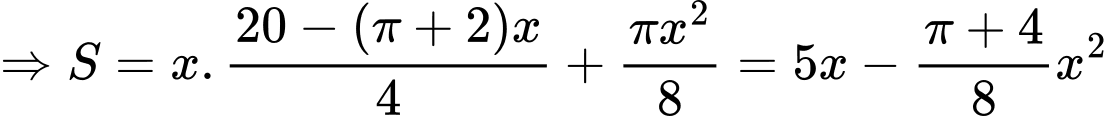Vậy diện tích lớn nhất của cửa sổ là: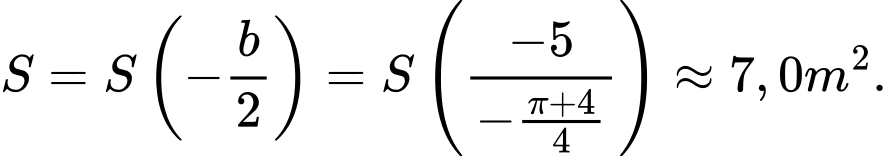
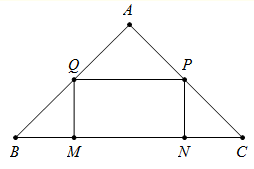
Câu 17 [31085]: Một miếng bìa hình tam giác đều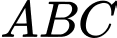 
, cạnh bằng 16. Học sinh Trang cắt một hình chữ nhật 
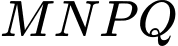từ miếng bìa trên để làm biển trông xe cho lớp trong buổi ngoại khóa (với 
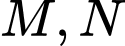thuộc cạnh 
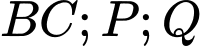lần lượt thuộc cạnh 
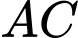và 
). Diện tich hình chữ nhật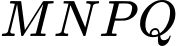 
lớn nhất bằng bao nhiêu?
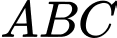, cạnh bằng 16. Học sinh Trang cắt một hình chữ nhật 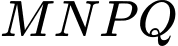từ miếng bìa trên để làm biển trông xe cho lớp trong buổi ngoại khóa (với 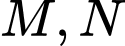thuộc cạnh 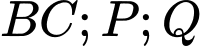lần lượt thuộc cạnh 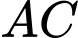và ). Diện tich hình chữ nhật 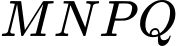lớn nhất bằng bao nhiêu? A,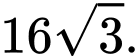 
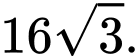
B,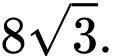 
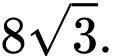
C,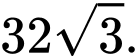 
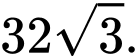
D,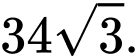 
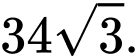
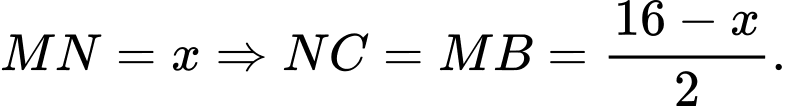
Xét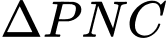 
vuông tại 
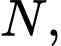có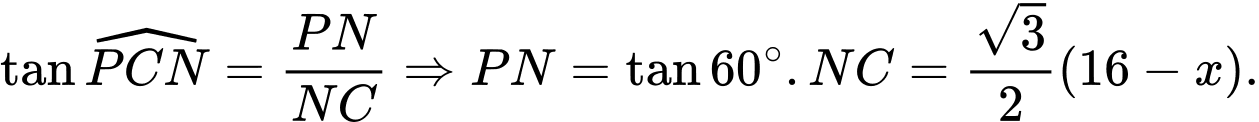 
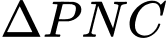vuông tại 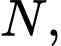có 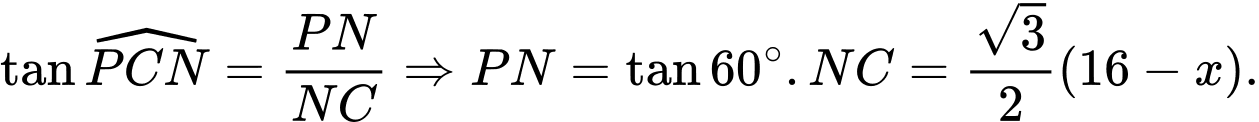Diện tích hình chữ nhật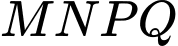 
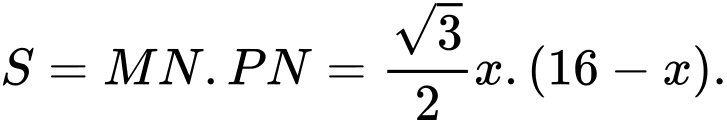
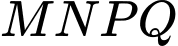là 
là 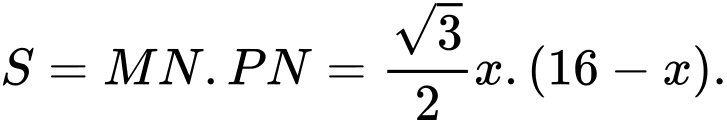Ta có: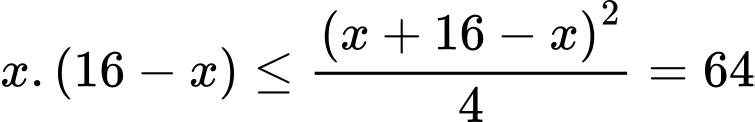 
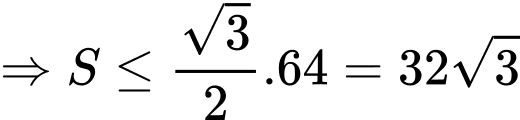khi 
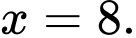Chọn C.
Đáp án: C 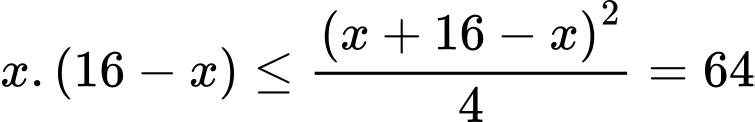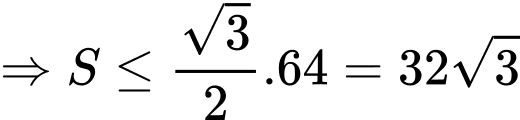khi 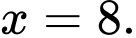Chọn C.
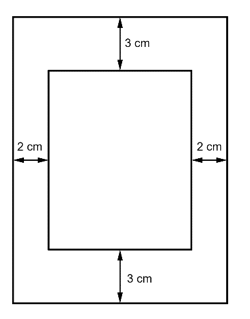
Câu 18 [383947]: Một trang sách có dạng hình chữ nhật với diện tích là 
Sau khi để lề trên và lề dưới đều là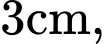 
để lề trái và lề phải đều là 
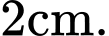Phần còn lại của trang sách được in chữ. Phần in chữ trên trang sách có diện tích lớn nhất bằng bao nhiêu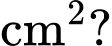 
Đáp số:…………………..
Sau khi để lề trên và lề dưới đều là 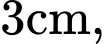để lề trái và lề phải đều là 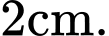Phần còn lại của trang sách được in chữ. Phần in chữ trên trang sách có diện tích lớn nhất bằng bao nhiêu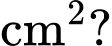 Đáp số:…………………..
Gọi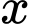 
(cm) là chiều rộng của trang sách.Khi đó, chiều dài của trang sách là 
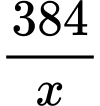(cm).
Sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là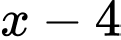
(cm) và chiều dài là 
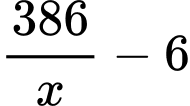(cm).
Rõ ràng,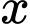
phải thỏa mãn điều kiện
Diện tích phần in nghiêng trên trang sách là:
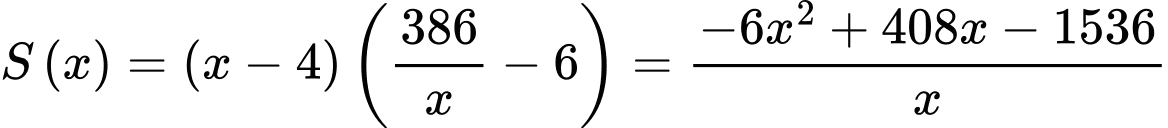
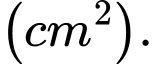
Xét hàm số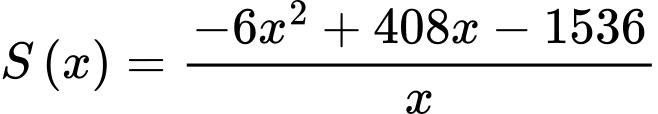
với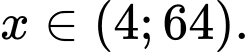 
Ta có: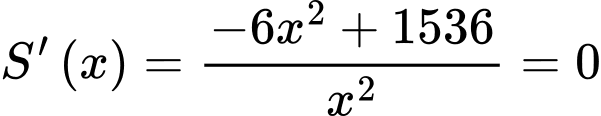
Bảng biến thiên:
>
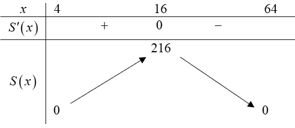
Căn cứ vào bảng biến thiên, hàm số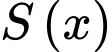
đạt giá trị lớn nhất bằng 
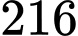tại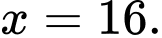 
Khi đó, chiều dài trang sách là: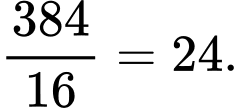
Vậy sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là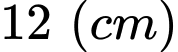
và chiều dài là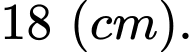 
Vậy phần in chữ trên trang sách có diện tích lớn nhất bằng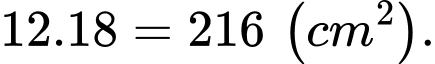
Đáp án: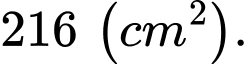
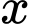(cm) là chiều rộng của trang sách.Khi đó, chiều dài của trang sách là 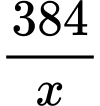(cm).
Sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là
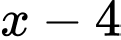(cm) và chiều dài là 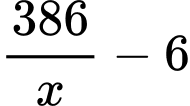(cm).
Rõ ràng,
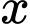phải thỏa mãn điều kiện
Diện tích phần in nghiêng trên trang sách là:
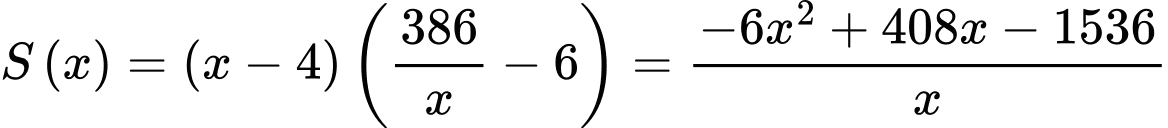
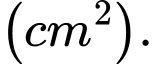
Xét hàm số
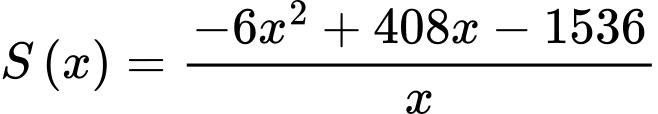với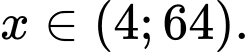
Ta có:
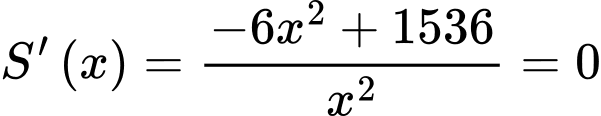
Bảng biến thiên:
>
Căn cứ vào bảng biến thiên, hàm số
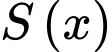đạt giá trị lớn nhất bằng 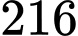tại 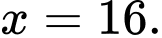Khi đó, chiều dài trang sách là:
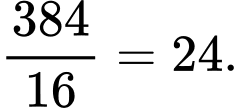
Vậy sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là
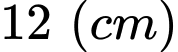và chiều dài là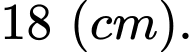
Vậy phần in chữ trên trang sách có diện tích lớn nhất bằng
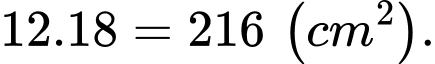
Đáp án:
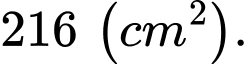
Câu 19 [31071]: Người ta dùng một tấm sắt tây hình chữ nhật có kích thước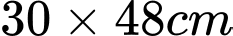 
để làm một cái hộp không nắp bằng cách cắt bỏ đi bốn hình vuông bằng nhau ở bốn góc rồi gấp lên. Thể tích lớn nhất của hộp là
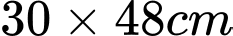để làm một cái hộp không nắp bằng cách cắt bỏ đi bốn hình vuông bằng nhau ở bốn góc rồi gấp lên. Thể tích lớn nhất của hộp là A,
B,
C,
D,
Gọi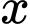 
là độ dài cạnh hình vuông bị cắt. Khi đó, thể tíchkhối hộp là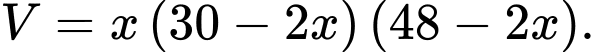 
Xét hàm số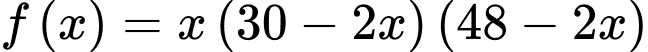
với 
Ta có: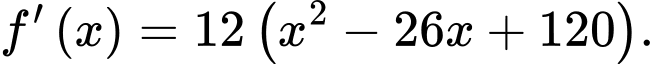
Phương trình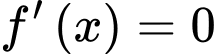
"
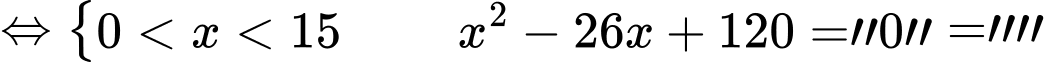
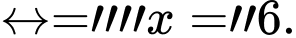Dựa vào bảng biến thiên, suy ra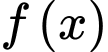
đạt giá trị lớn nhấtbằng 
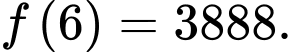Đáp án: D
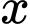là độ dài cạnh hình vuông bị cắt. Khi đó, thể tíchkhối hộp là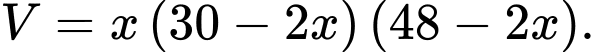 Xét hàm số
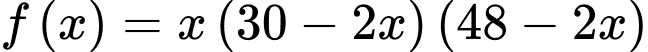với Ta có:
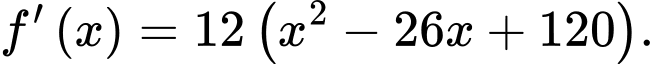
Phương trình
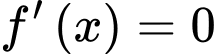
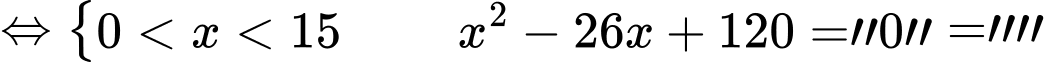
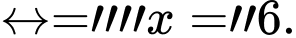" Dựa vào bảng biến thiên, suy ra
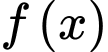đạt giá trị lớn nhấtbằng 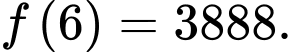Đáp án: D
Câu 20 [372695]: Từ một tấm bìa hình chữ nhật có chiều rộng 30 cm và chiều dài 80 cm (Hình 4a), người ta cắt ở bốn góc bốn hình vuông có cạnh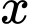 
(cm) với 
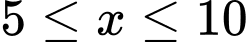và gấp lại để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp như Hình 4b. Tìm 
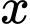để thể tích chiếc hộp là lớn nhất (kết quả làm tròn đến hàng phần trăm).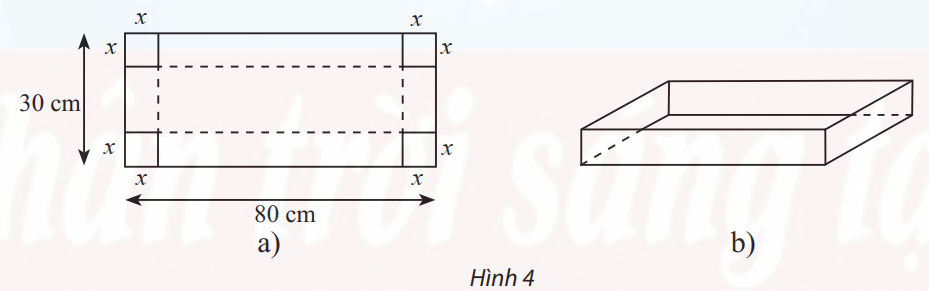
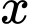(cm) với 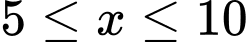và gấp lại để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp như Hình 4b. Tìm 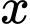để thể tích chiếc hộp là lớn nhất (kết quả làm tròn đến hàng phần trăm).
Chiều dài của hình hộp là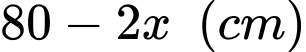 
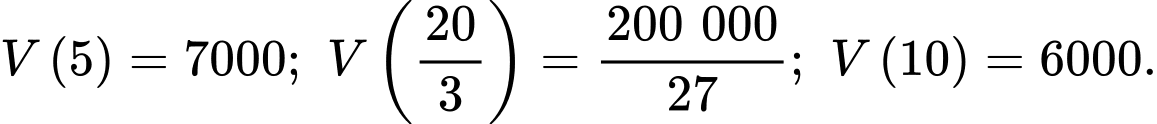
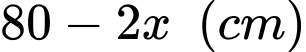
Chiều rộng của chiếc hộp là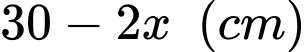 
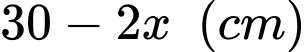
Chiều cao của chiếc hộp là 
Suy ra thể tích của chiếc hộp là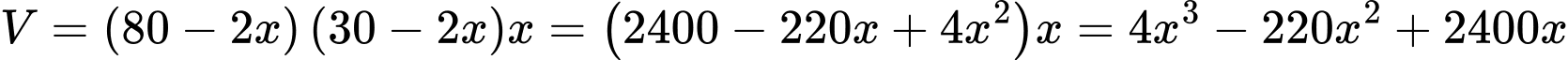 
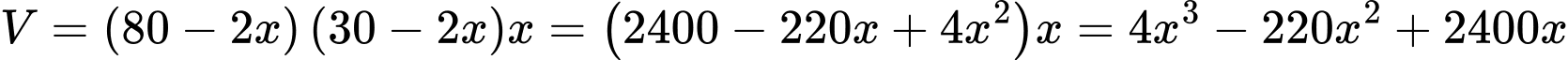
Xét hàm số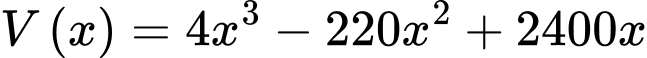 
trên đoạn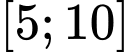 
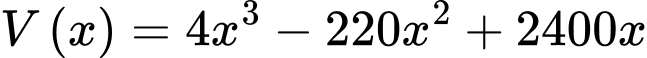trên đoạn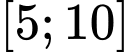 Ta có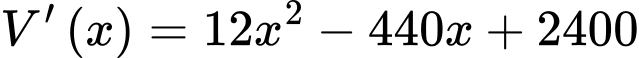 
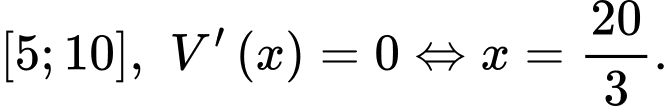
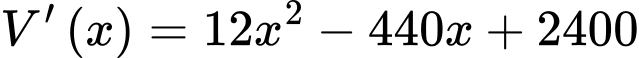
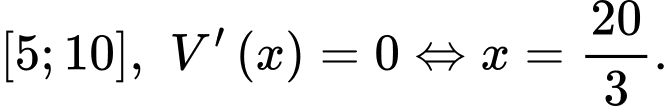
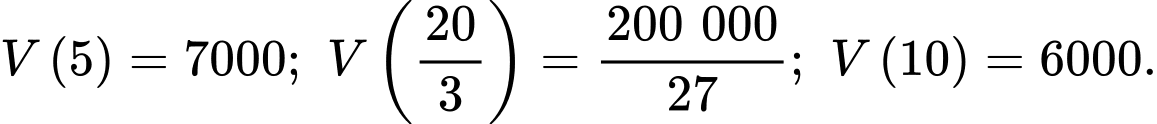
Suy ra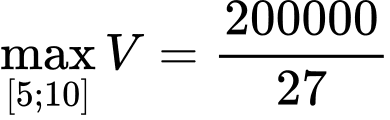 
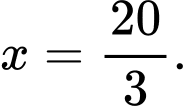
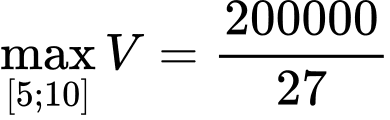tại 
tại 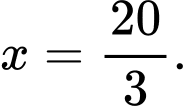Vậy để thể tích chiếc hộp là lớn nhất khi 