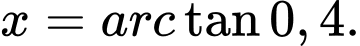Đáp án Bài tập tự luyện số 2
Câu 1 [399674]: Người ta xây một bể chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng 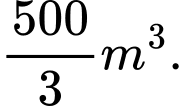 Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là
Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là  đồng /
đồng /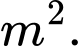 Giả sử
Giả sử 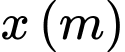 là chiều rộng của đáy bể. Khi đó
là chiều rộng của đáy bể. Khi đó
a) Thể tích của bể biểu diễn theo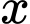 là
là 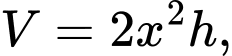 trong đó
trong đó 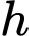 là chiều cao của bể.
là chiều cao của bể.
b) Diện tích bể cần xây là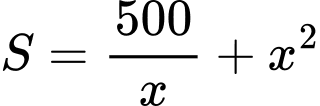
c) Nếu chiều rộng của bể là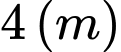 thì chi phí thuê nhân công thấp nhất.
thì chi phí thuê nhân công thấp nhất.
d) Chi phí thuê nhân công thấp nhất là 30 triệu đồng.
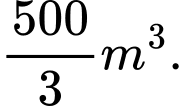 Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là
Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là  đồng /
đồng /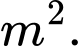 Giả sử
Giả sử 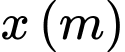 là chiều rộng của đáy bể. Khi đó
là chiều rộng của đáy bể. Khi đó a) Thể tích của bể biểu diễn theo
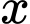 là
là 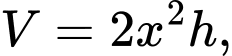 trong đó
trong đó 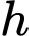 là chiều cao của bể.
là chiều cao của bể. b) Diện tích bể cần xây là
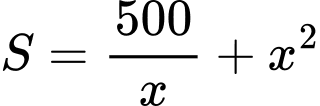
c) Nếu chiều rộng của bể là
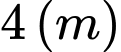 thì chi phí thuê nhân công thấp nhất.
thì chi phí thuê nhân công thấp nhất. d) Chi phí thuê nhân công thấp nhất là 30 triệu đồng.
a) Gọi 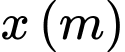 là chiều rộng của đáy bể, khi đó chiều dài của đáy bể là
là chiều rộng của đáy bể, khi đó chiều dài của đáy bể là 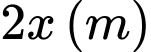 và
và 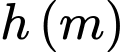 là chiều cao bể
là chiều cao bể
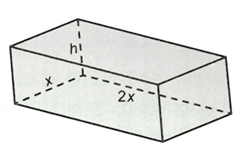
Thể tích của bể là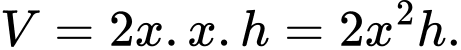 Vậy a – Đúng.
Vậy a – Đúng.
b) Bể có thể tích bằng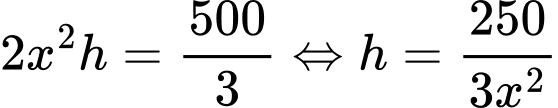
Diện tích cần xây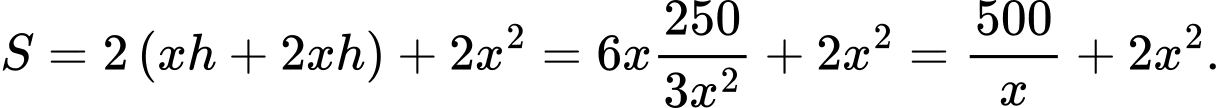 Vậy b – Sai.
Vậy b – Sai.
c) Xét hàm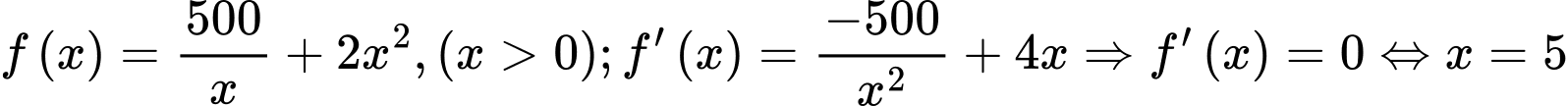
Bảng biến thiên
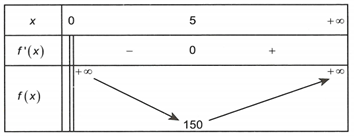
Do đó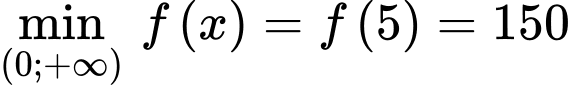 .
.
Chi phí thuê nhân công thấp nhất khi diện tích xây dựng là nhỏ nhất và bằng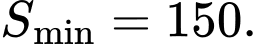
Khi đó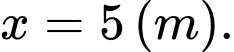 Vậy c – Sai.
Vậy c – Sai.
d) Chi phí thuê nhân công thấp nhất khi diện tích xây dựng là nhỏ nhất và bằng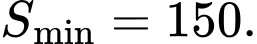
Khi đó chi phí thuê nhân công thấp nhất là 150 x 200000 = 30.000.000 đồng. Vậy d – Đúng.
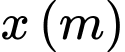 là chiều rộng của đáy bể, khi đó chiều dài của đáy bể là
là chiều rộng của đáy bể, khi đó chiều dài của đáy bể là 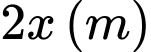 và
và 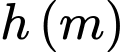 là chiều cao bể
là chiều cao bể
Thể tích của bể là
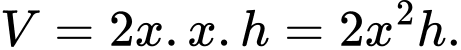 Vậy a – Đúng.
Vậy a – Đúng.b) Bể có thể tích bằng
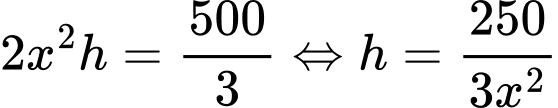
Diện tích cần xây
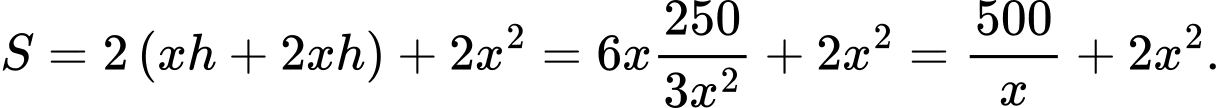 Vậy b – Sai.
Vậy b – Sai.c) Xét hàm
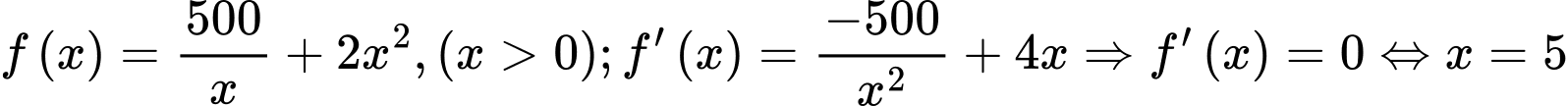
Bảng biến thiên

Do đó
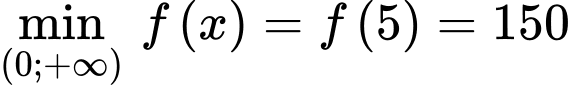 .
. Chi phí thuê nhân công thấp nhất khi diện tích xây dựng là nhỏ nhất và bằng
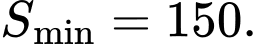
Khi đó
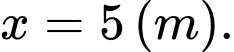 Vậy c – Sai.
Vậy c – Sai.d) Chi phí thuê nhân công thấp nhất khi diện tích xây dựng là nhỏ nhất và bằng
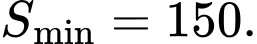
Khi đó chi phí thuê nhân công thấp nhất là 150 x 200000 = 30.000.000 đồng. Vậy d – Đúng.
Câu 2 [6167]: Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước 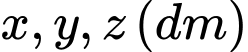 . Biết tỉ số hai cạnh đáy là
. Biết tỉ số hai cạnh đáy là 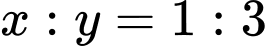 và thể tích của hộp bằng
và thể tích của hộp bằng 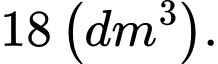 Để tốn ít vật liệu nhất thì tổng
Để tốn ít vật liệu nhất thì tổng 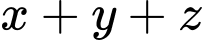 bằng
bằng
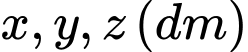 . Biết tỉ số hai cạnh đáy là
. Biết tỉ số hai cạnh đáy là 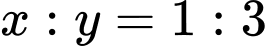 và thể tích của hộp bằng
và thể tích của hộp bằng 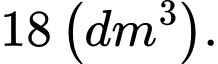 Để tốn ít vật liệu nhất thì tổng
Để tốn ít vật liệu nhất thì tổng 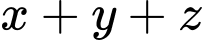 bằng
bằng A,
B,
C,
D,
Đáp án C.
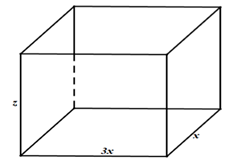
Đáy có kích thước là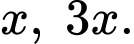 Chiều cao là
Chiều cao là 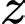 nên thể tích thùng là
nên thể tích thùng là 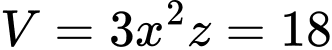
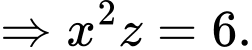
Để tốn ít vật liệu nhất thì diện tích sản xuất phải nhỏ nhất.
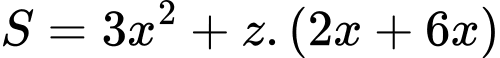
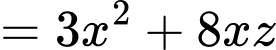
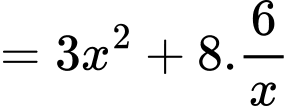
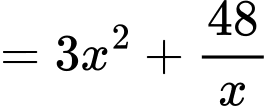
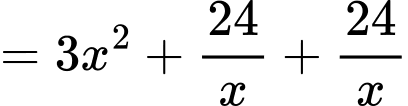
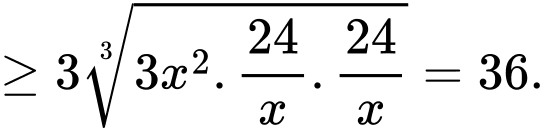
Dấu bằng xảy ra khi và chỉ khi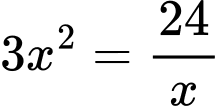
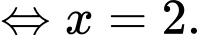
Khi đó,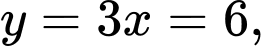
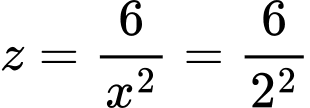
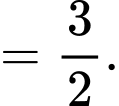
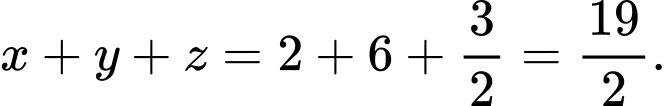 Đáp án: C
Đáp án: C

Đáy có kích thước là
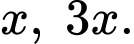 Chiều cao là
Chiều cao là 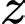 nên thể tích thùng là
nên thể tích thùng là 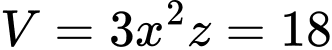
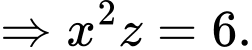
Để tốn ít vật liệu nhất thì diện tích sản xuất phải nhỏ nhất.
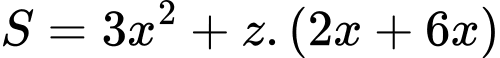
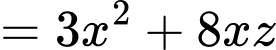
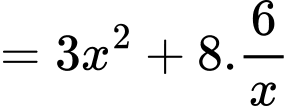
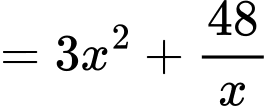
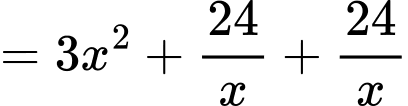
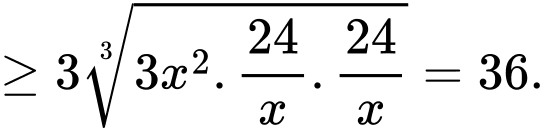
Dấu bằng xảy ra khi và chỉ khi
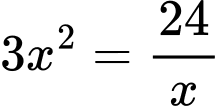
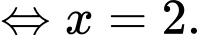
Khi đó,
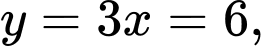
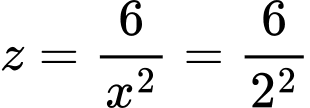
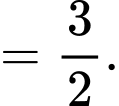
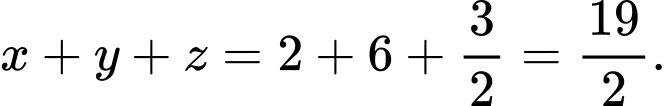 Đáp án: C
Đáp án: C
Câu 3 [327615]: [Đề thi THPT QG năm 2018] Ông 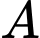 dự định sử dụng hết
dự định sử dụng hết 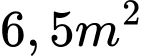 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
 dự định sử dụng hết
dự định sử dụng hết 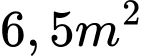 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A, 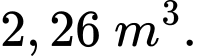
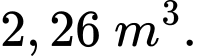
B, 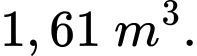
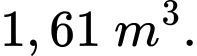
C, 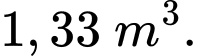
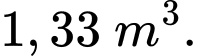
D, 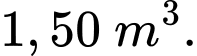
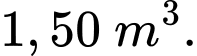
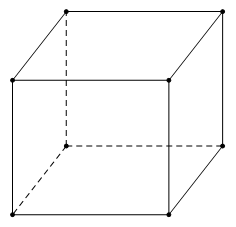
Vì chiều dài bể cá gấp đôi chiều rộng nên ta gọi chiều rộng, chiều dài, chiều cao của bể cá lần lượt là
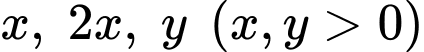
Thể tích của bể cá là:
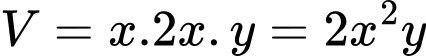
Ta sẽ tìm mối quan hệ giữa
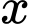 và
và 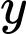 dựa vào diện tích phần lắp kính:
dựa vào diện tích phần lắp kính: 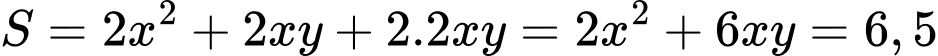
Rút
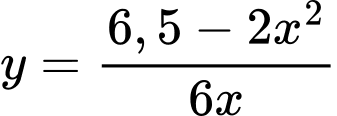 (với
(với 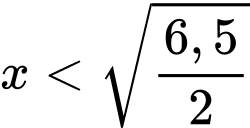 ) ta có:
) ta có: 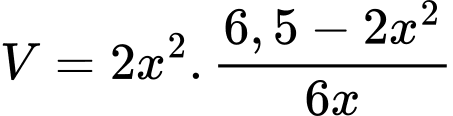
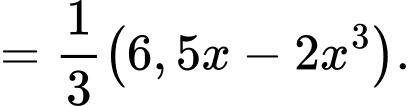
Xét hàm số
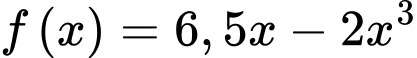 với
với 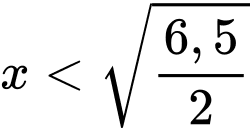 ta có:
ta có: 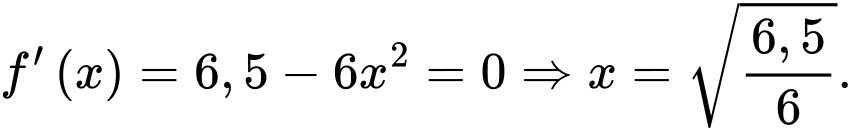
Lập BBT suy ra
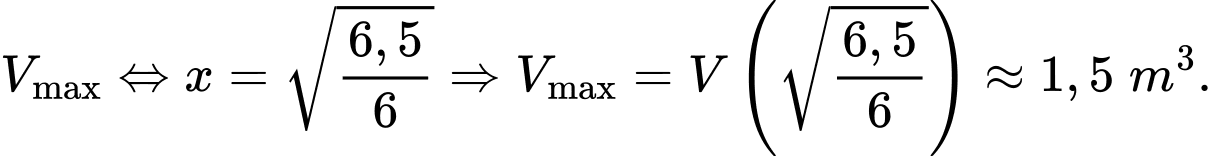 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 4 [5934]: Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng 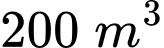 đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là
đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 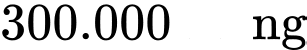 /
/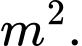 Chi phí thuê nhân công thấp nhất là
Chi phí thuê nhân công thấp nhất là
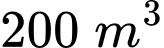 đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là
đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 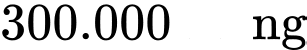 /
/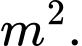 Chi phí thuê nhân công thấp nhất là
Chi phí thuê nhân công thấp nhất là A, 75 triệu đồng.
B, 51 triệu đồng.
C, 36 triệu đồng.
D, 46 triệu đồng.
Gọi chiều rộng của hình chữ nhật đáy bể là 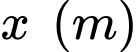 suy ra chiều dài của hình chữ nhật là
suy ra chiều dài của hình chữ nhật là 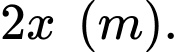
Gọi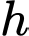 là chiều cao của bể nên ta có
là chiều cao của bể nên ta có 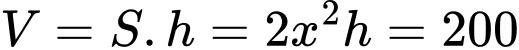
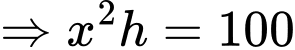
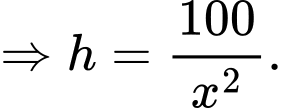
Diện tích của bể là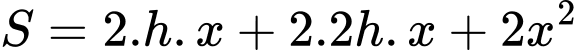
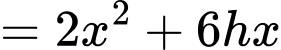
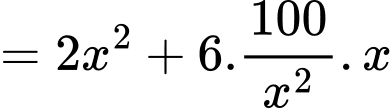
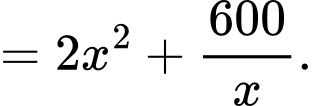
Áp dụng bất đẳng thức AM – GM, ta có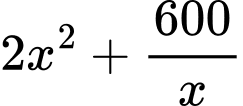
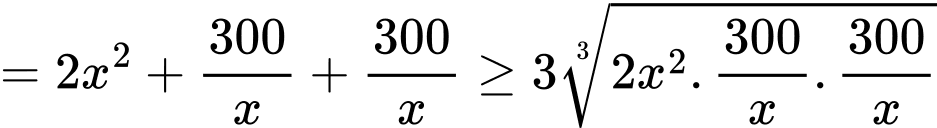
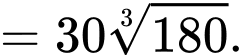
Dấu bằng xảy ra khi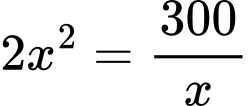
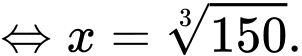
Chi phí thấp nhất thuê nhân công là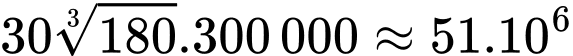 đồng = 51 triệu đồng. Chọn B. Đáp án: B
đồng = 51 triệu đồng. Chọn B. Đáp án: B
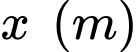 suy ra chiều dài của hình chữ nhật là
suy ra chiều dài của hình chữ nhật là 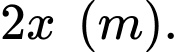
Gọi
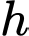 là chiều cao của bể nên ta có
là chiều cao của bể nên ta có 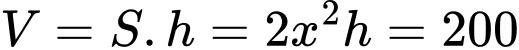
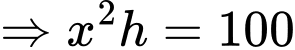
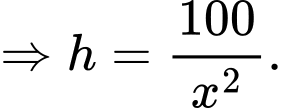
Diện tích của bể là
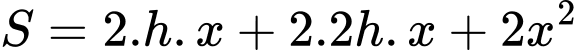
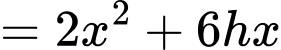
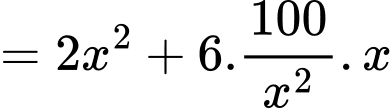
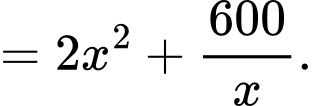
Áp dụng bất đẳng thức AM – GM, ta có
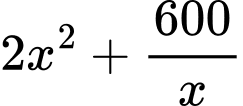
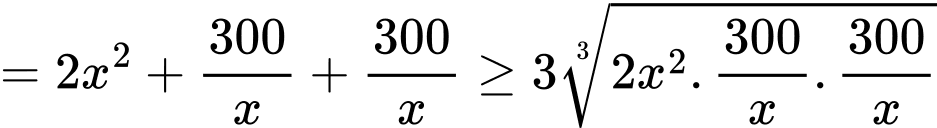
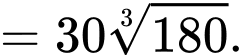
Dấu bằng xảy ra khi
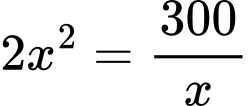
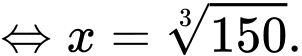
Chi phí thấp nhất thuê nhân công là
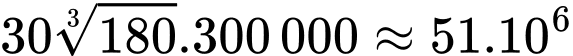 đồng = 51 triệu đồng. Chọn B. Đáp án: B
đồng = 51 triệu đồng. Chọn B. Đáp án: B
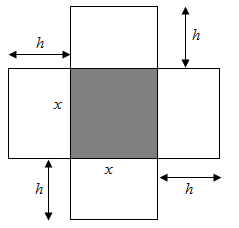
Câu 5 [327622]: Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh  chiều cao
chiều cao  và thể tích
và thể tích 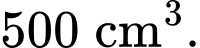 Tính độ dài cạnh hình vuông
Tính độ dài cạnh hình vuông 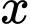 sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
 chiều cao
chiều cao  và thể tích
và thể tích 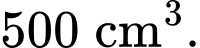 Tính độ dài cạnh hình vuông
Tính độ dài cạnh hình vuông 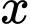 sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
sao cho chiếc hộp làm ra tốn ít bìa cát tông nhất.
A, 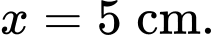
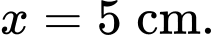
B, 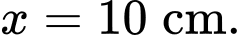
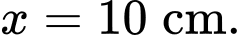
C, 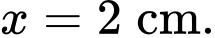
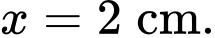
D, 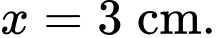
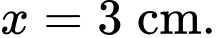
Theo giả thiết ta có thể tích chiếc hộp là 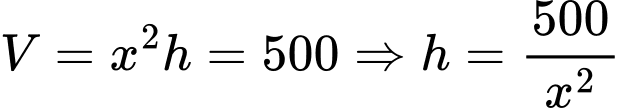
Diện tích các mạnh cát tông là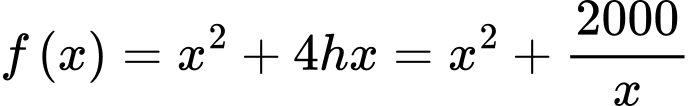
Xét hàm số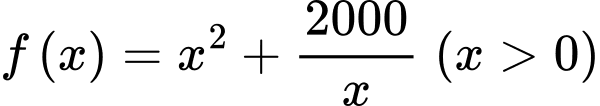 ta có:
ta có: 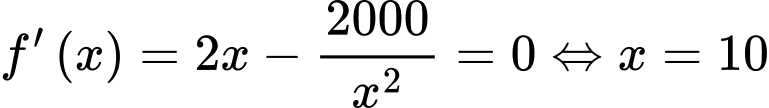
Lập bảng biến thiên ta có: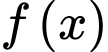 nhỏ nhất khi
nhỏ nhất khi 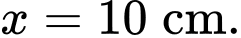 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
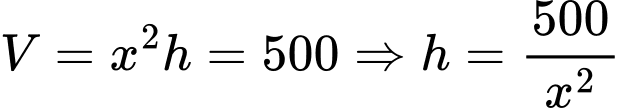
Diện tích các mạnh cát tông là
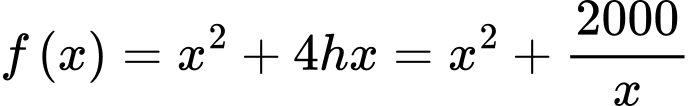
Xét hàm số
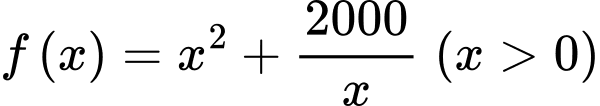 ta có:
ta có: 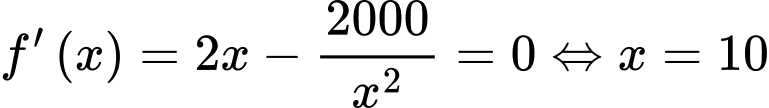
Lập bảng biến thiên ta có:
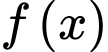 nhỏ nhất khi
nhỏ nhất khi 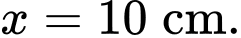 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 6 [383949]: Từ một miếng bìa hình chữ nhật với kích thước 20 cm × 10 cm, bạn Lan cắt bỏ hai hình vuông có cạnh là x (cm) và hai hình chữ nhật (phần gạch sọc như hình vẽ) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp có dạng hình hộp chữ nhật. Thể tích lớn nhất của chiếc hộp có thể đạt được là bao nhiêu (làm tròn kết quả đến hàng phần chục)?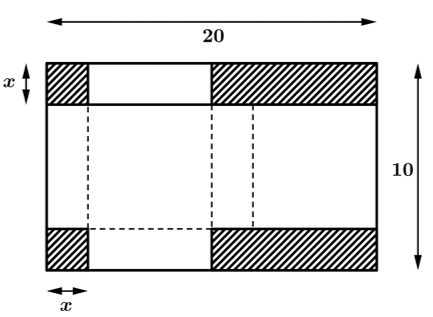

Dựa vào hình minh họa đã cho, ta có kích thước đáy của hộp có dạng hình hộp chữ nhật lần lượt là 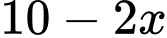 và
và 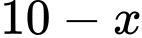 (cm) với
(cm) với 
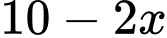 và
và 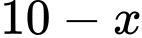 (cm) với
(cm) với 
Hộp có chiều cao là: 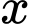 (cm).
(cm).
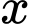 (cm).
(cm). Thể tích của chiếc hộp là: 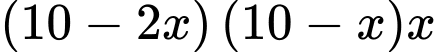 (
(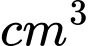 )
)
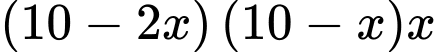 (
(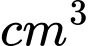 )
) Bài toán trở thành tìm giá trị lớn nhất của hàm số: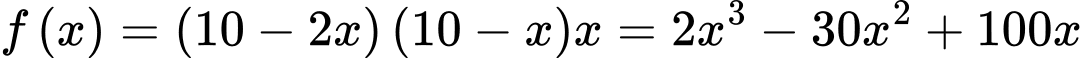 với
với 
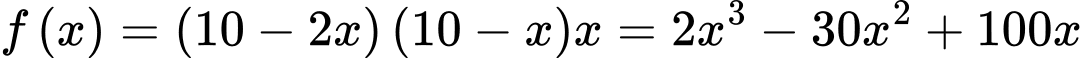 với
với 
Có: 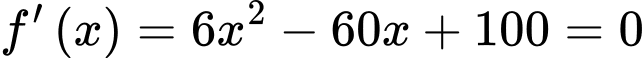
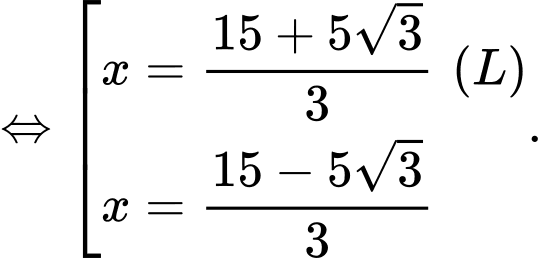
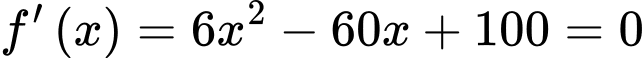
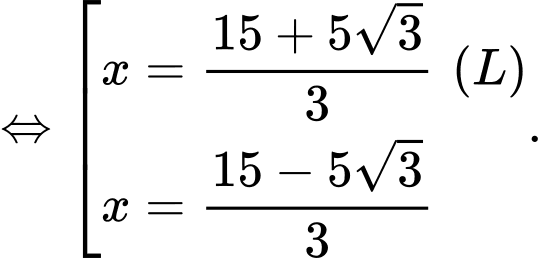
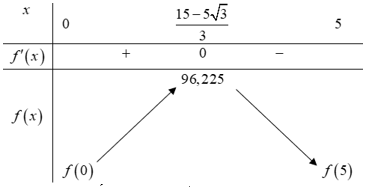
Bảng biến thiên:

Dựa vào bảng biến thiên, ta có: 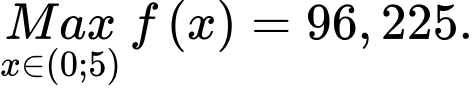
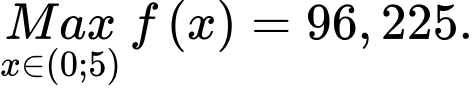
Suy ra thể tích lớn nhất của chiếc hộp có thể đạt được là: 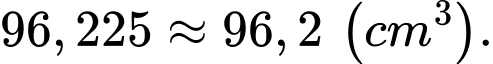
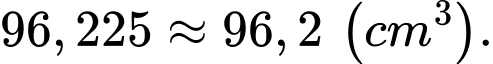
Câu 7 [5879]: Cho một tấm bìa hình chữ nhật chiều dài 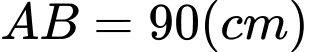 , chiều rộng
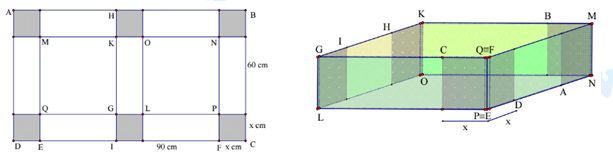
, chiều rộng 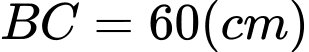 . Người ta cắt 6 hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng
. Người ta cắt 6 hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng 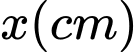 , rồi gập tấm bìa lại như hình vẽ dưới đây để được một hộp quà có nắp. Tìm
, rồi gập tấm bìa lại như hình vẽ dưới đây để được một hộp quà có nắp. Tìm 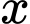 để hộp nhận được có thể tích lớn nhất.
để hộp nhận được có thể tích lớn nhất.
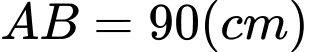 , chiều rộng
, chiều rộng 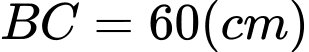 . Người ta cắt 6 hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng
. Người ta cắt 6 hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng 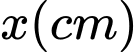 , rồi gập tấm bìa lại như hình vẽ dưới đây để được một hộp quà có nắp. Tìm
, rồi gập tấm bìa lại như hình vẽ dưới đây để được một hộp quà có nắp. Tìm 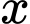 để hộp nhận được có thể tích lớn nhất.
để hộp nhận được có thể tích lớn nhất.
A,
B,
C,
D,
Hộp quà là hình hộp chữ nhật có chiều cao là 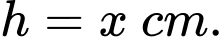
Đáy là hình chữ nhật với hai kích thước lần lượt là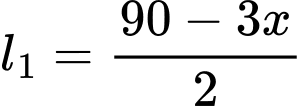 và
và 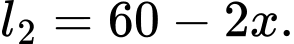
Vậy thể tích của hộp quà là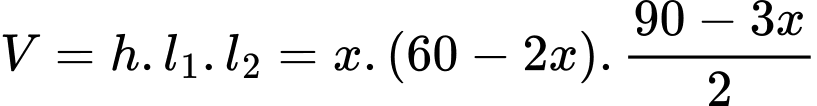
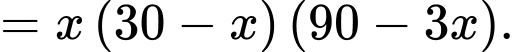
Ta có: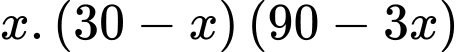
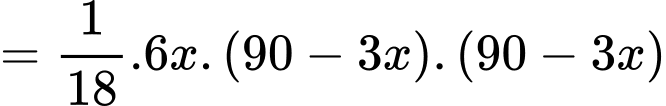
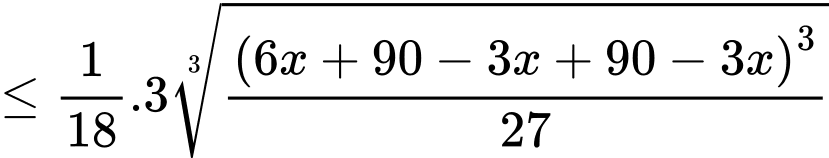
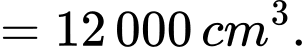
Dấu bằng xảy ra khi và chỉ khi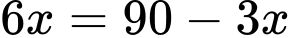
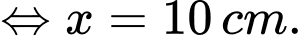 Chọn A. Đáp án: A
Chọn A. Đáp án: A
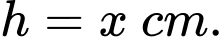
Đáy là hình chữ nhật với hai kích thước lần lượt là
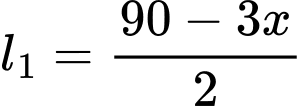 và
và 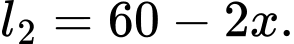
Vậy thể tích của hộp quà là
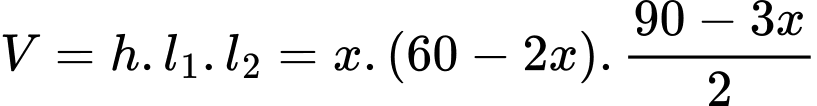
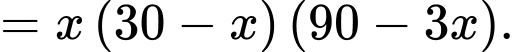
Ta có:
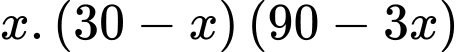
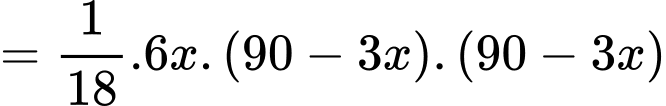
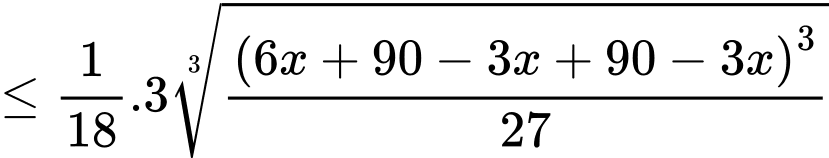
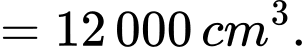
Dấu bằng xảy ra khi và chỉ khi
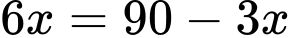
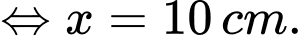 Chọn A. Đáp án: A
Chọn A. Đáp án: A
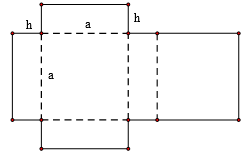
Câu 8 [6085]: Một bạn đã cắt tấm bìa carton phẳng và cứng có kích thước như hình vẽ. Sau đó bạn ấy gấp theo đường nét đứt thành một hình chữ nhật. Hình hộp có đáy là hình vuông cạnh  , chiều cao là
, chiều cao là 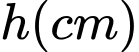 và diện tích tấm bìa là
và diện tích tấm bìa là 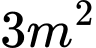 . Tổng
. Tổng  bằng bao nhiêu để thể tích hộp là lớn nhất.
bằng bao nhiêu để thể tích hộp là lớn nhất.
 , chiều cao là
, chiều cao là 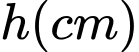 và diện tích tấm bìa là
và diện tích tấm bìa là 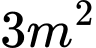 . Tổng
. Tổng  bằng bao nhiêu để thể tích hộp là lớn nhất.
bằng bao nhiêu để thể tích hộp là lớn nhất.
Thể tích của khối hộp là 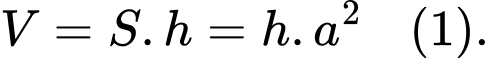
Diện tích của tấm bìa là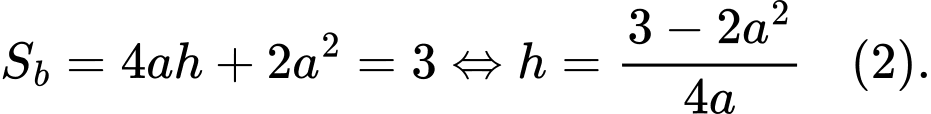
Từ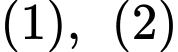 suy ra
suy ra 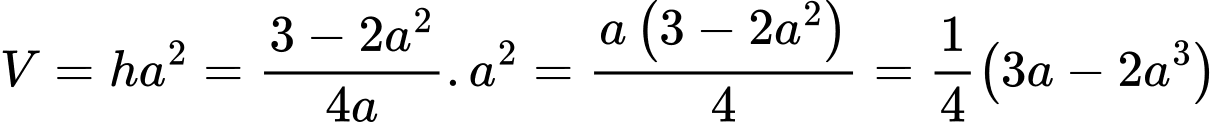
Suy ra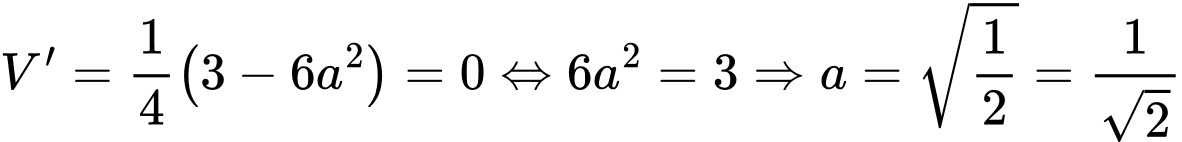
Mặt khác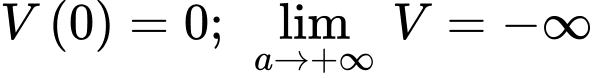 nên
nên 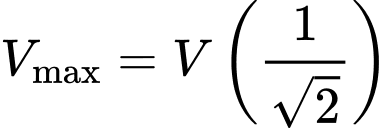 xảy ra khi và chỉ khi
xảy ra khi và chỉ khi 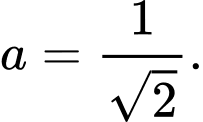
Thế vào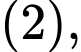 ta được
ta được 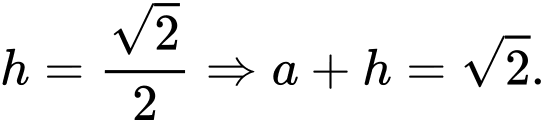 Chọn D.
Điền đáp số: 1,41
Đáp án: D
Chọn D.
Điền đáp số: 1,41
Đáp án: D
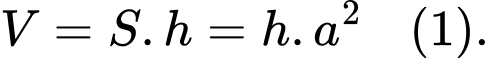
Diện tích của tấm bìa là
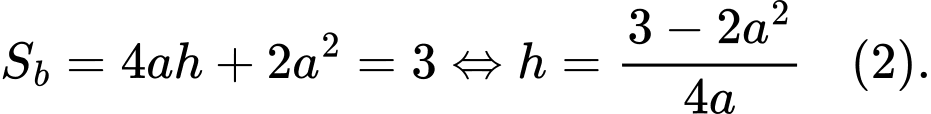
Từ
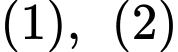 suy ra
suy ra 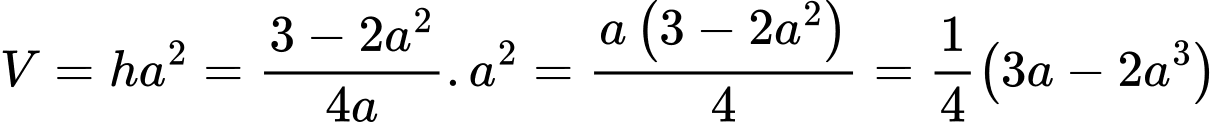
Suy ra
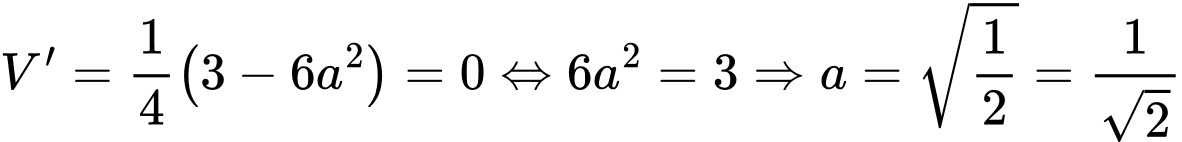
Mặt khác
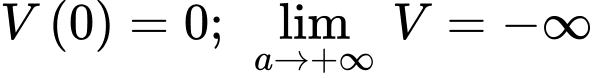 nên
nên 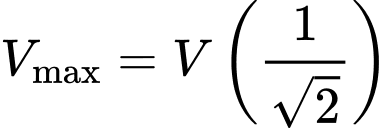 xảy ra khi và chỉ khi
xảy ra khi và chỉ khi 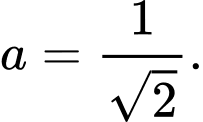
Thế vào
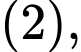 ta được
ta được 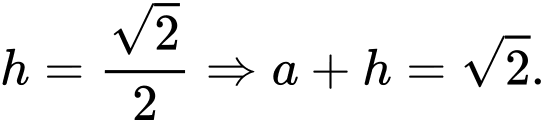 Chọn D.
Điền đáp số: 1,41
Đáp án: D
Chọn D.
Điền đáp số: 1,41
Đáp án: D
Câu 9 [383951]: [Trích Đề thi mẫu ĐGTD ĐH Bách Khoa HN]: Một người thợ nhôm kính nhận đơn đặt hàng làm một bể cá cảnh bằng kính dạng hình hộp chữ nhật không có nắp với thể tích bằng 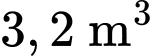 và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).
và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).
Đáp số:…………………..
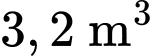 và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).
và chiều cao của bể gấp 2 lần chiều rộng của đáy. Biết giá một mét vuông kính để làm bể cá là 1 triệu đồng. Để mua đủ mét vuông kính làm bể cá theo yêu cầu thì người thợ cần tối thiểu số tiền bằng ... triệu đồng. (Coi độ dày của kính là không đáng kể so với kích thước của bể).Đáp số:…………………..
Gọi 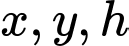
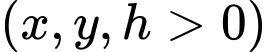 lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể.
lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể.
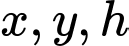
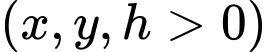 lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể.
lần lượt là chiều rộng của đáy, chiều dài của đáy và chiều cao của bể. Từ dữ kiện bài cho, ta có:
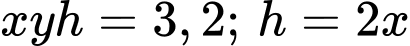
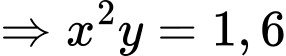
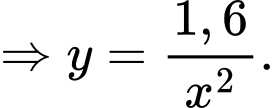
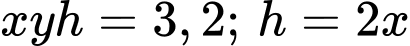
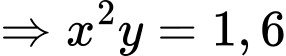
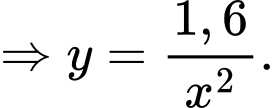
Tổng diện tích 5 mặt của bể cá là:
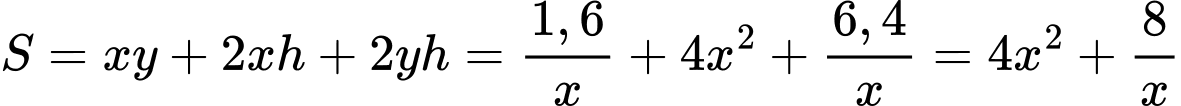
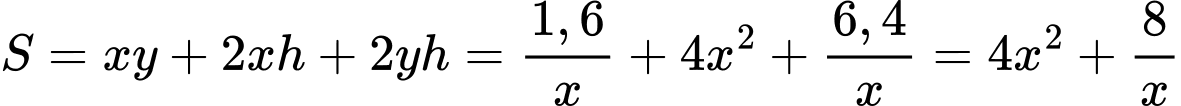
Sử dụng bất đẳng thức Cauchy 3 số dương ta có:
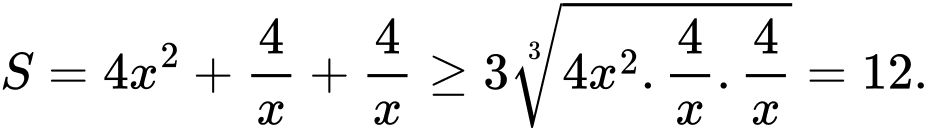
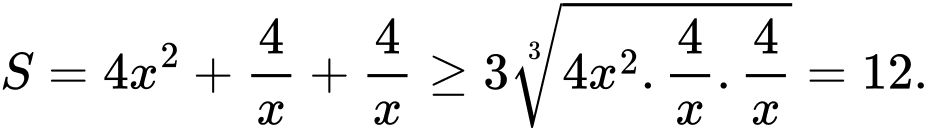
Dấu “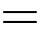 ” xảy ra khi và chỉ khi
” xảy ra khi và chỉ khi 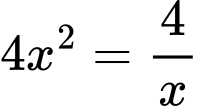
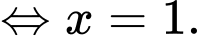
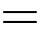 ” xảy ra khi và chỉ khi
” xảy ra khi và chỉ khi 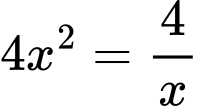
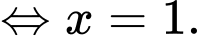
Lúc này chi phí tối thiểu để mua nguyên liệu là: 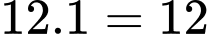 triệu.
triệu.
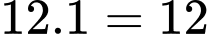 triệu.
triệu.
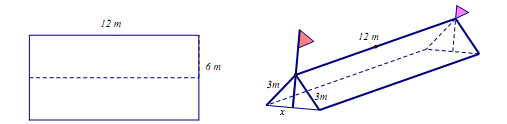
Câu 10 [382885]: Trong một đợt tổ chức cho học sinh tham gia dã ngoại ngoài trời. Để có thể có chỗ nghỉ ngơi trong quá trình tham quan dã ngoại, các bạn học sinh đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ một tấm bạt hình chữ nhật có chiều dài là 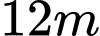 và chiều rộng là
và chiều rộng là 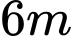 bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau
bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau 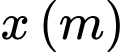 (xem hình vẽ). Khoảng không gian phía trong có thể tích lớn nhất bằng bao nhiêu?
(xem hình vẽ). Khoảng không gian phía trong có thể tích lớn nhất bằng bao nhiêu?
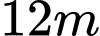 và chiều rộng là
và chiều rộng là 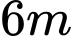 bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau
bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau 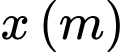 (xem hình vẽ). Khoảng không gian phía trong có thể tích lớn nhất bằng bao nhiêu?
(xem hình vẽ). Khoảng không gian phía trong có thể tích lớn nhất bằng bao nhiêu?
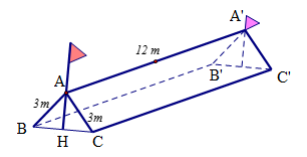
Gọi tên như hình vẽ với 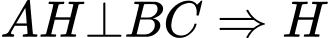 là trung điểm của
là trung điểm của 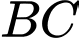
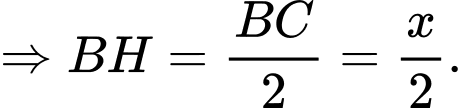
Xét tam giác 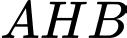 vuông tại
vuông tại 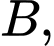 theo định lý
theo định lý
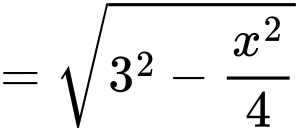
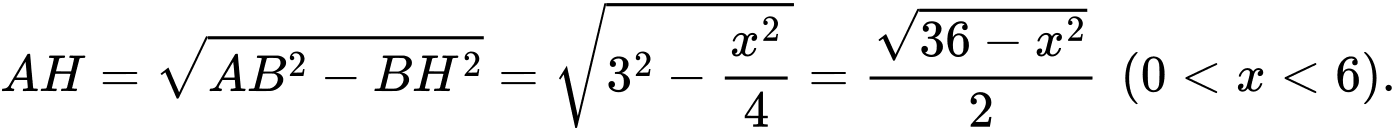
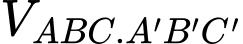
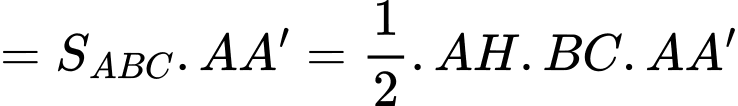
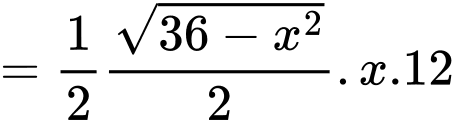
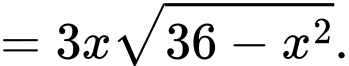
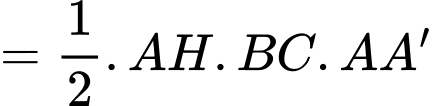
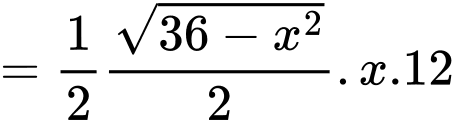
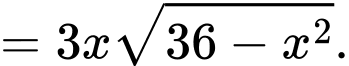
Áp dụng bất đẳng thức, 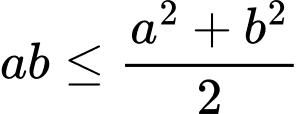
ta có: 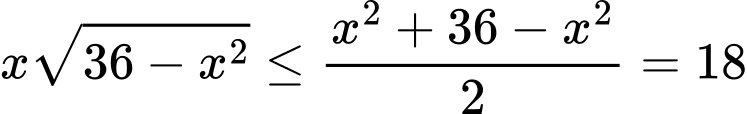
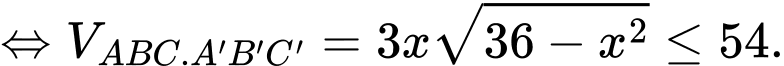
Dấu bằng xảy ra khi 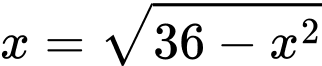
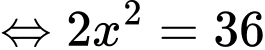
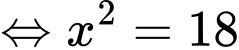
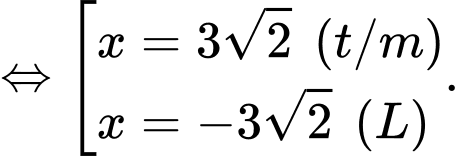
Vậy 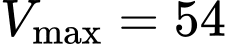 khi
khi 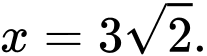
Câu 11 [5938]: Gia đình Toán xây một bể nước dạng hình hộp chữ nhật có nắp dung tích 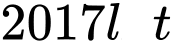 . Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng được làm bằng bê tông có giá
. Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng được làm bằng bê tông có giá  đồng/
đồng/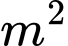 , thân bể được xây bằng gạch có giá
, thân bể được xây bằng gạch có giá  đồng/
đồng/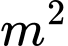 và nắp bể được làm bằng tôn có giá
và nắp bể được làm bằng tôn có giá  đồng/
đồng/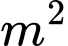 . Hỏi chi phí thấp nhất gia đình Toán cần bỏ ra để xây bể nước là bao nhiêu nghìn đồng (làm tròn kết quả đến hàng đơn vị)
?
. Hỏi chi phí thấp nhất gia đình Toán cần bỏ ra để xây bể nước là bao nhiêu nghìn đồng (làm tròn kết quả đến hàng đơn vị)
?
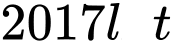 . Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng được làm bằng bê tông có giá
. Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng được làm bằng bê tông có giá  đồng/
đồng/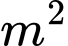 , thân bể được xây bằng gạch có giá
, thân bể được xây bằng gạch có giá  đồng/
đồng/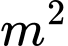 và nắp bể được làm bằng tôn có giá
và nắp bể được làm bằng tôn có giá  đồng/
đồng/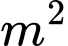 . Hỏi chi phí thấp nhất gia đình Toán cần bỏ ra để xây bể nước là bao nhiêu nghìn đồng (làm tròn kết quả đến hàng đơn vị)
?
. Hỏi chi phí thấp nhất gia đình Toán cần bỏ ra để xây bể nước là bao nhiêu nghìn đồng (làm tròn kết quả đến hàng đơn vị)
?
Đổi 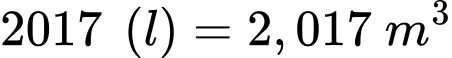
Gọi chiều dài và chiều rộng đáy bể lần lượt là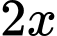 và
và 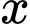
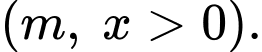
Diện tích đáy là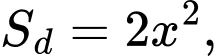 diện tích xung quanh là
diện tích xung quanh là 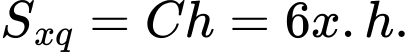
Thể tích bể nước: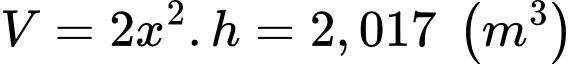
Ta có: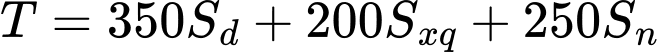 (nghìn đồng)
(nghìn đồng)
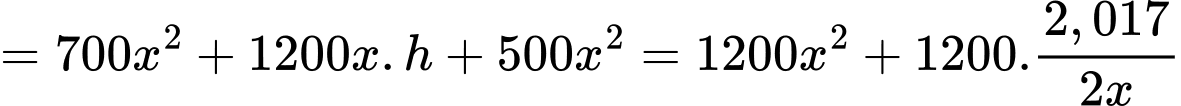
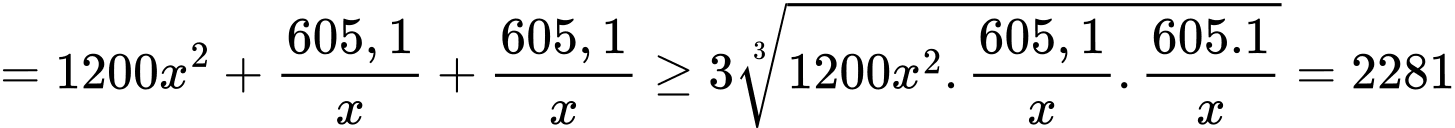
Vậy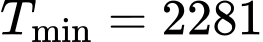 nghìn đồng.
nghìn đồng.
Điền đáp số: 2281 nghìn đồng Đáp án: A
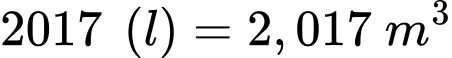
Gọi chiều dài và chiều rộng đáy bể lần lượt là
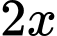 và
và 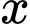
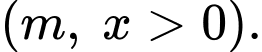
Diện tích đáy là
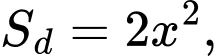 diện tích xung quanh là
diện tích xung quanh là 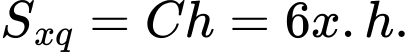
Thể tích bể nước:
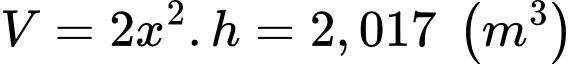
Ta có:
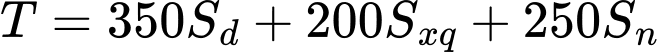 (nghìn đồng)
(nghìn đồng)
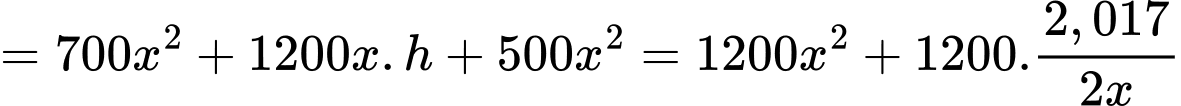
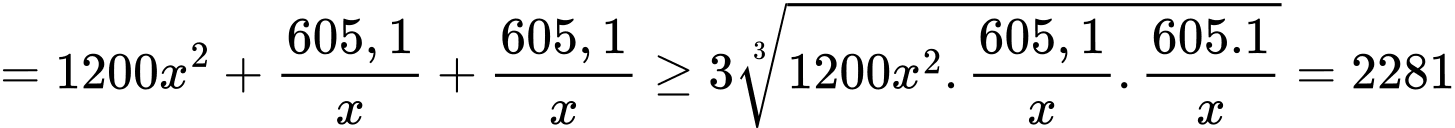
Vậy
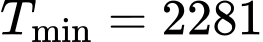 nghìn đồng.
nghìn đồng.
Điền đáp số: 2281 nghìn đồng Đáp án: A
Câu 12 [390558]: Cần phải đặt một ngọn đèn điện ở phía trên và chính giữa một cái bàn hình tròn có bán kính 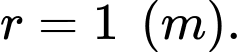 Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức
Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức 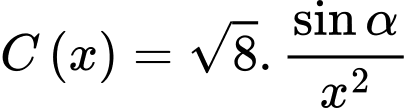 ( là góc nghiêng giữa tia sáng và mép bà và
( là góc nghiêng giữa tia sáng và mép bà và 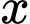 là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.
là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.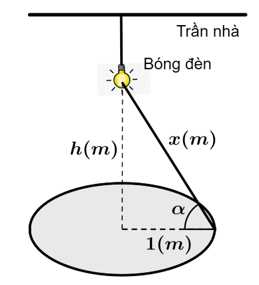
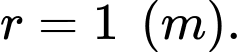 Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức
Hỏi phải treo ở độ cao h bằng bao nhiêu mét để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được biểu thị bởi công thức 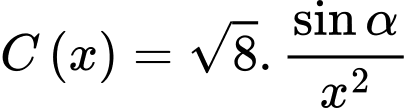 ( là góc nghiêng giữa tia sáng và mép bà và
( là góc nghiêng giữa tia sáng và mép bà và 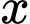 là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.
là khoảng cách từ bóng đèn đến mép bàn). Viết kết quả làm tròn đến hàng phần trăm.
Đáp số:………………………………
Dựa vào hình ảnh minh họa, ta có: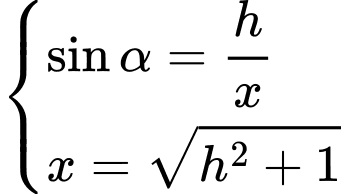
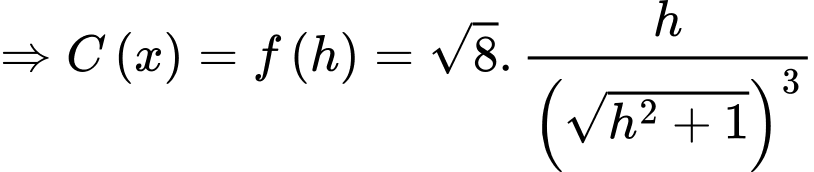
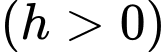
Đặt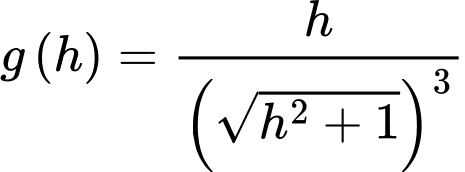
Có: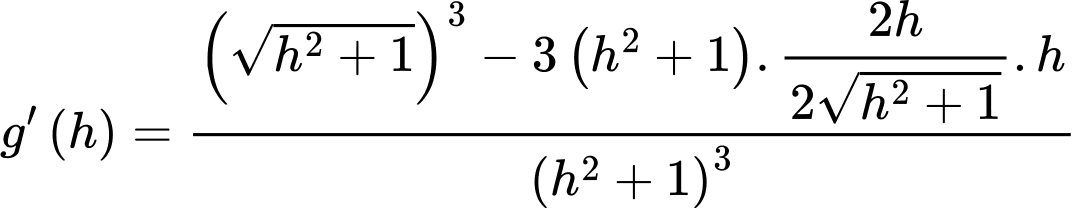
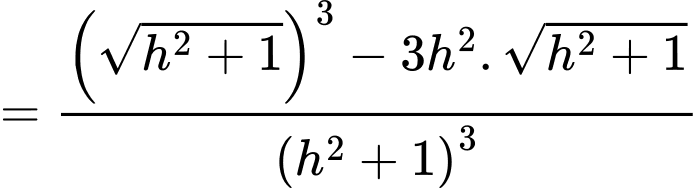
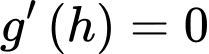
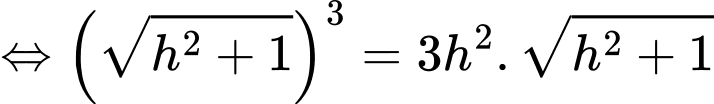
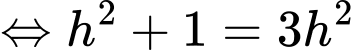
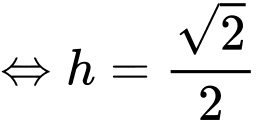
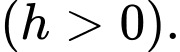
Bảng biến thiên:
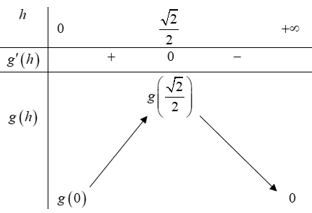
Dựa vào bảng biến thiên, để mép bàn được nhiều ánh sáng nhất thì giá trị của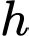 là:
là: 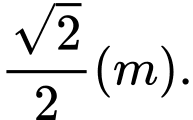
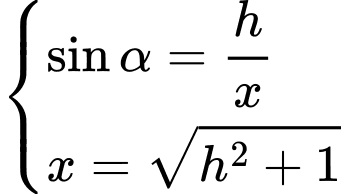
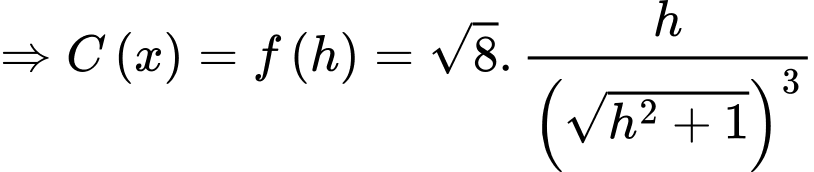
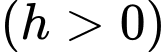
Đặt
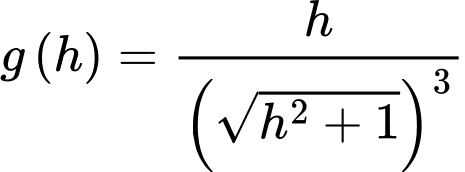
Có:
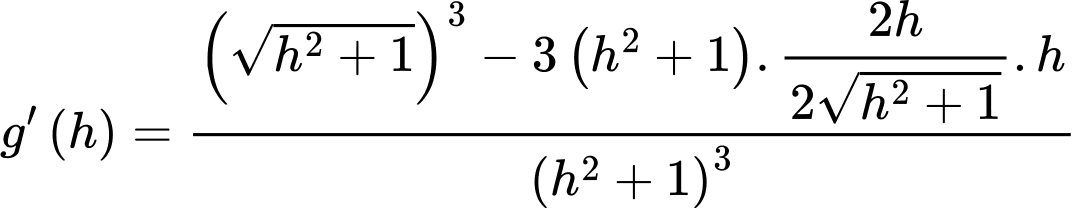
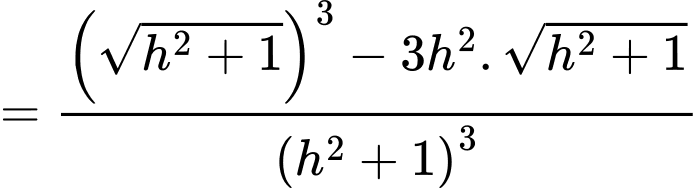
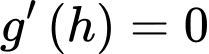
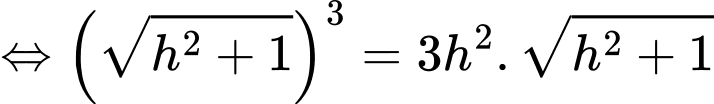
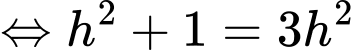
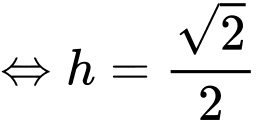
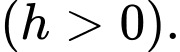
Bảng biến thiên:

Dựa vào bảng biến thiên, để mép bàn được nhiều ánh sáng nhất thì giá trị của
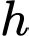 là:
là: 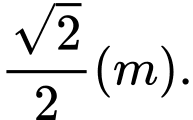
Câu 13 [384768]: Hai con tàu A và B đang ở cùng một vĩ
tuyến và cách nhau 5 hải lý. Đồng thời cả hai tàu cùng khởi hành, tàu A chạy về hướng Nam với 6 hải lý/giờ, còn tàu B chạy về vị trí hiện tại của tàu A với vận tốc 7 hải lý/giờ. Hãy tính khoảng cách giữa lớn nhất giữa hai con tàu trong khoảng thời gian tính từ lúc hai tàu xuất phát đến khi tàu B đến vị trí ban đầu của tàu A (đơn vị hải lý, làm tròn đến hàng phần trăm)?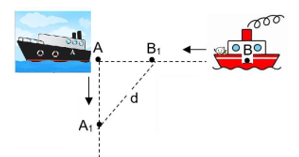
tuyến và cách nhau 5 hải lý. Đồng thời cả hai tàu cùng khởi hành, tàu A chạy về hướng Nam với 6 hải lý/giờ, còn tàu B chạy về vị trí hiện tại của tàu A với vận tốc 7 hải lý/giờ. Hãy tính khoảng cách giữa lớn nhất giữa hai con tàu trong khoảng thời gian tính từ lúc hai tàu xuất phát đến khi tàu B đến vị trí ban đầu của tàu A (đơn vị hải lý, làm tròn đến hàng phần trăm)?

Đáp số:………………………………
Gọi 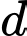 là khoảng cách của hai tàu sau khi xuất phát
là khoảng cách của hai tàu sau khi xuất phát 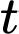 (giờ),
(giờ), 
Ta có: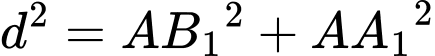
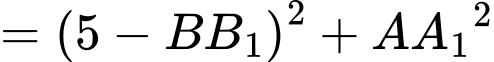
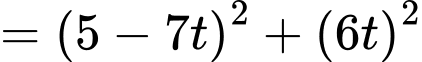
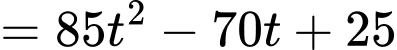
Đặt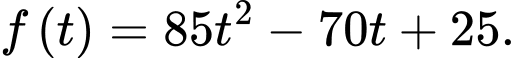
Để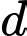 lớn nhất thì
lớn nhất thì 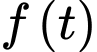 phải lớn nhất.
phải lớn nhất.
Nhận xét: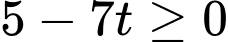
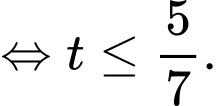
Có:
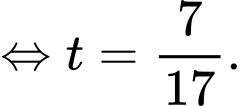
Bảng biến thiên:
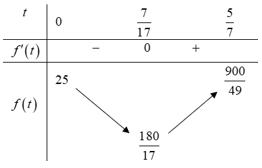
Dựa vào bảng biến thiên, suy ra hai con tàu có khoảng cách lớn nhất là khi hai tàu chưa di chuyển,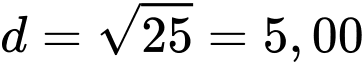 (hải lý).
(hải lý).
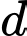 là khoảng cách của hai tàu sau khi xuất phát
là khoảng cách của hai tàu sau khi xuất phát 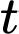 (giờ),
(giờ), 
Ta có:
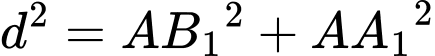
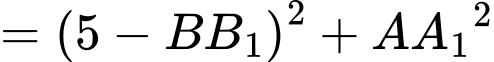
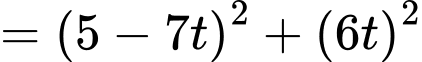
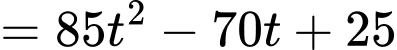
Đặt
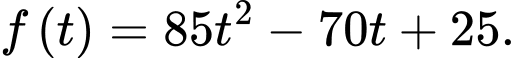
Để
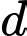 lớn nhất thì
lớn nhất thì 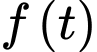 phải lớn nhất.
phải lớn nhất.Nhận xét:
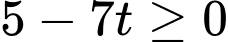
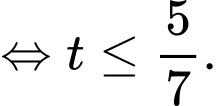
Có:

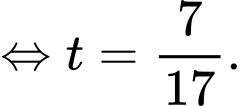
Bảng biến thiên:

Dựa vào bảng biến thiên, suy ra hai con tàu có khoảng cách lớn nhất là khi hai tàu chưa di chuyển,
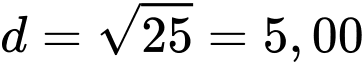 (hải lý).
(hải lý).
Câu 14 [383952]: [Trích Đề thi mẫu ĐGNL ĐHQG Hà Nội]: Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng  Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu
Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu 
(Kết quả làm tròn đến hàng đơn vị)
Đáp số:…………………………………….
 Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu
Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu 
(Kết quả làm tròn đến hàng đơn vị)
Đáp số:…………………………………….
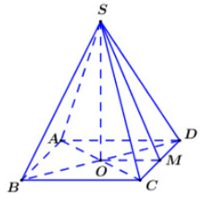
Giả sử chóp tứ giác đều là
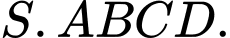 Gọi
Gọi 
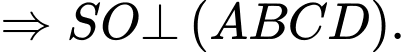
Đặt
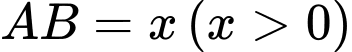 ta có
ta có 
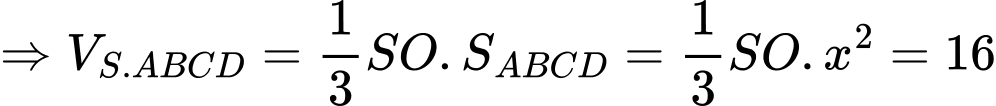
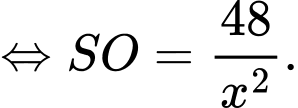
Gọi M là trung điểm của CD ta có:
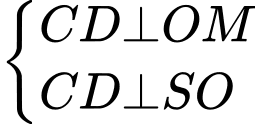
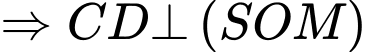
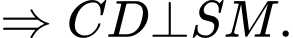
Ta có:
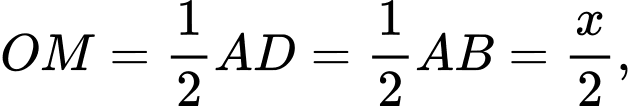 áp dụng định lí Pytago ta có:
áp dụng định lí Pytago ta có: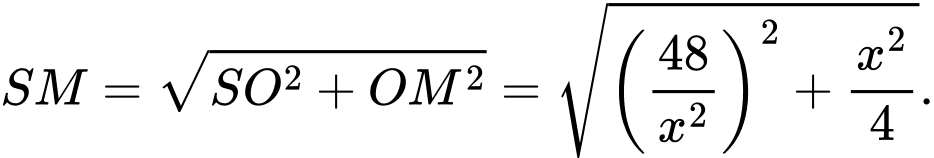
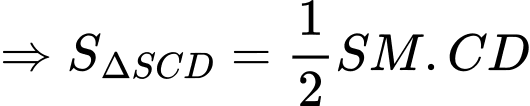
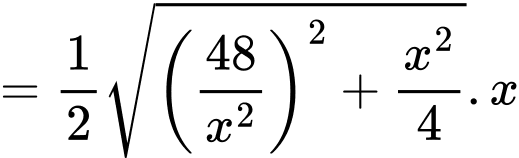
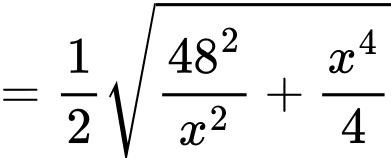
Để diện tích mạ vàng nhỏ nhất thì
 nhỏ nhất
nhỏ nhất 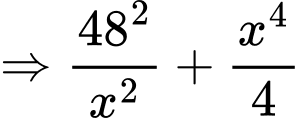 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. Ta có:
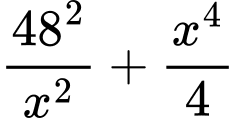
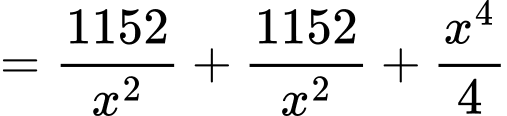
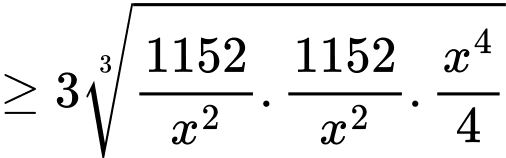
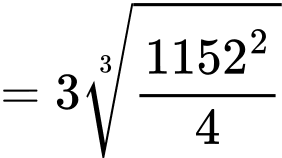 (BĐT Cauchy).
(BĐT Cauchy). Vậy diện tích mạ vàng nhỏ nhất là:
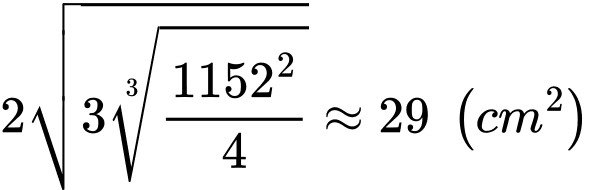
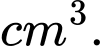
Câu 15 [390559]: Một người thợ thủ công muốn làm một con diều bằng giấy có kích thước 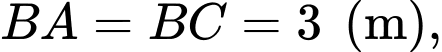
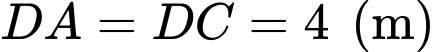 như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo
như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo 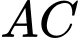 theo đơn vị mét.
theo đơn vị mét. 
Đáp số:…………………….
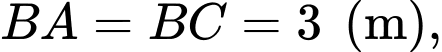
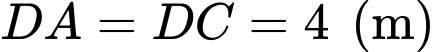 như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo
như hình vẽ bên. Khi diện tích con diều lớn nhất, em hãy tính độ dài đường chéo 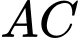 theo đơn vị mét.
theo đơn vị mét. 
Đáp số:…………………….
Cách 1: Xem video bài giảng (cách này sẽ ngắn hơn)
Cách 2: Sử dụng phương pháp hàm số.
Gọi là giao điểm của
là giao điểm của 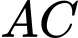 và
và 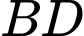 .
.
Gọi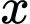 là độ dài của
là độ dài của 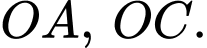

Diện tích của con diều là: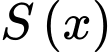 =
= 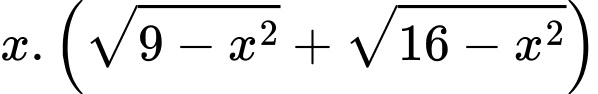 với
với 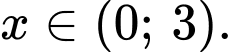
Lại có: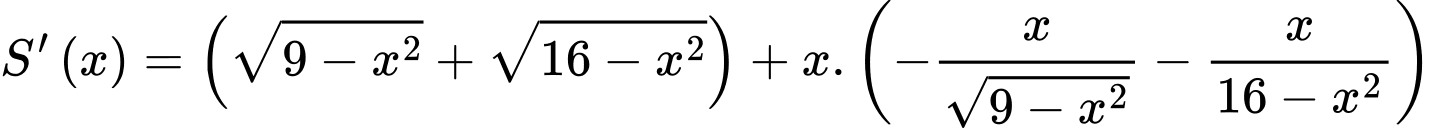
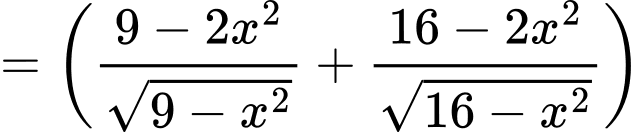
Do vậy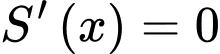
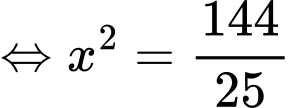
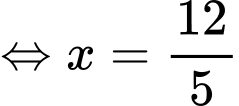
Bảng biến thiên:
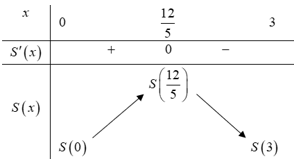 Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo
Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo 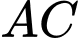 là:
là: 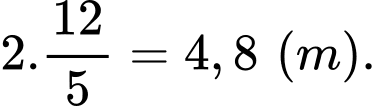
Cách 2: Sử dụng phương pháp hàm số.
Gọi
 là giao điểm của
là giao điểm của 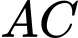 và
và 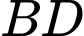 .
.Gọi
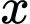 là độ dài của
là độ dài của 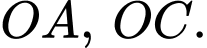

Diện tích của con diều là:
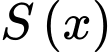 =
= 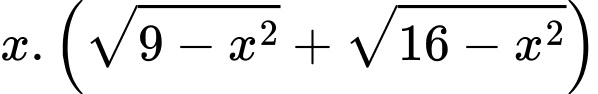 với
với 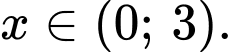
Lại có:
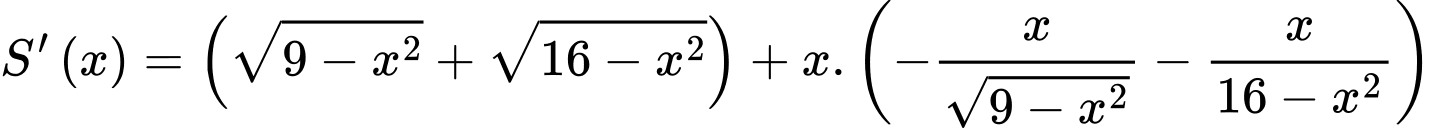
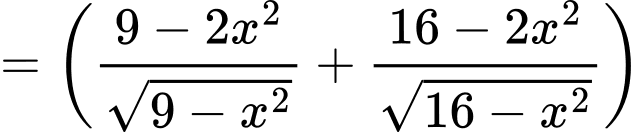
Do vậy
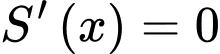
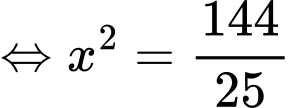
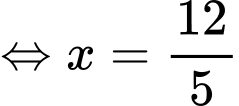
Bảng biến thiên:
 Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo
Dựa vào bảng biến thiên, suy ra khi diện tích con diều lớn nhất thì độ dài đường chéo 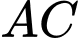 là:
là: 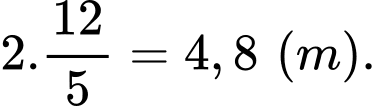
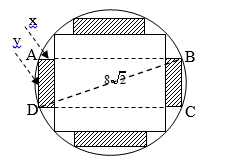
Câu 16 [31068]: Từ một khúc gôc tròn hình trụ, đường kính bằng 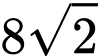 cần xẻ thành một chiếu xà có tiết diện ngang là hình vuông và 4 miếng phụ kích thước
cần xẻ thành một chiếu xà có tiết diện ngang là hình vuông và 4 miếng phụ kích thước 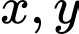 như hình vẽ. Hãy xác định
như hình vẽ. Hãy xác định 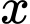 để diện tích sử dụng theo tiết diện ngang là lớn nhất.
để diện tích sử dụng theo tiết diện ngang là lớn nhất.
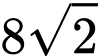 cần xẻ thành một chiếu xà có tiết diện ngang là hình vuông và 4 miếng phụ kích thước
cần xẻ thành một chiếu xà có tiết diện ngang là hình vuông và 4 miếng phụ kích thước 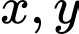 như hình vẽ. Hãy xác định
như hình vẽ. Hãy xác định 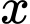 để diện tích sử dụng theo tiết diện ngang là lớn nhất.
để diện tích sử dụng theo tiết diện ngang là lớn nhất.
A, 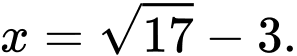
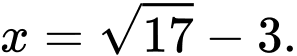
B, 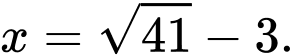
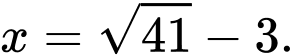
C, 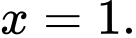
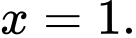
D, 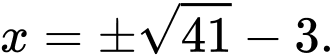
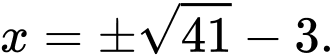
Ta có: 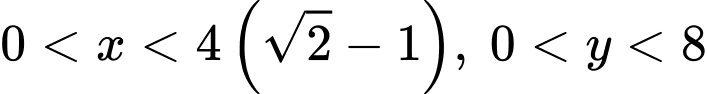
Theo Pitago ta có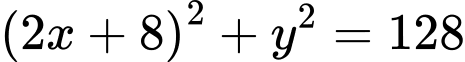
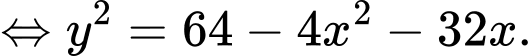
Diện tích sử dụng theo tiết diện ngang lớn nhất khi diện tích miếng phụ là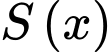 lớn nhất.
lớn nhất.
Ta có: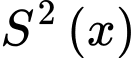
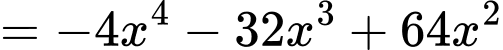
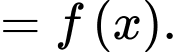 Hàm số
Hàm số 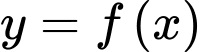 có BBT
có BBT
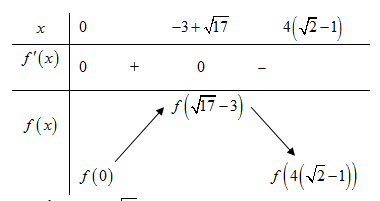
Suy ra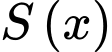 lớn nhất khi
lớn nhất khi 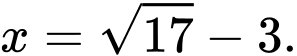
Chọn A. Đáp án: A
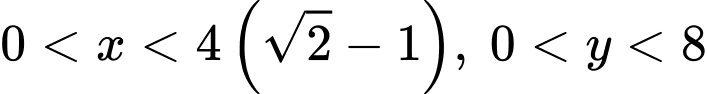
Theo Pitago ta có
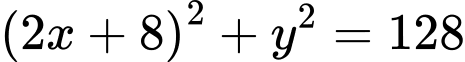
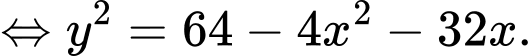
Diện tích sử dụng theo tiết diện ngang lớn nhất khi diện tích miếng phụ là
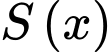 lớn nhất.
lớn nhất. Ta có:
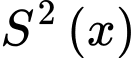
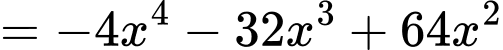
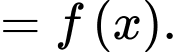 Hàm số
Hàm số 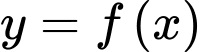 có BBT
có BBT 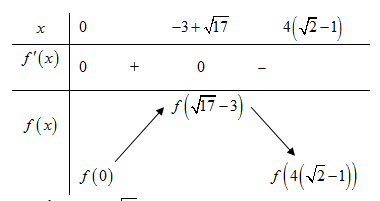
Suy ra
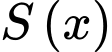 lớn nhất khi
lớn nhất khi 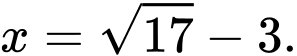
Chọn A. Đáp án: A
Câu 17 [390560]: Một vật nặng có khối lượng 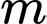 được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc
được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc 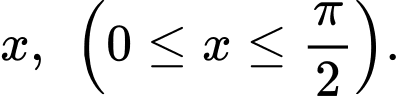 Trong Vật lí, ta biết rằng lực kéo
Trong Vật lí, ta biết rằng lực kéo  cần thiết để di chuyển vật được cho bởi công thức:
cần thiết để di chuyển vật được cho bởi công thức: 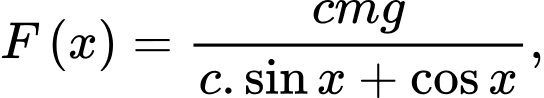 trong đó
trong đó 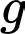 là gia tốc trọng trường và
là gia tốc trọng trường và  là hệ số ma sát của bề mặt
(Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014).
Với
là hệ số ma sát của bề mặt
(Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014).
Với 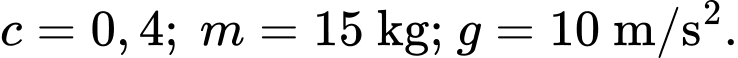 Tìm giá trị nhỏ nhất của lực kéo
Tìm giá trị nhỏ nhất của lực kéo 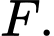 Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục.
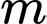 được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc
được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc 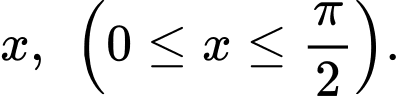 Trong Vật lí, ta biết rằng lực kéo
Trong Vật lí, ta biết rằng lực kéo  cần thiết để di chuyển vật được cho bởi công thức:
cần thiết để di chuyển vật được cho bởi công thức: 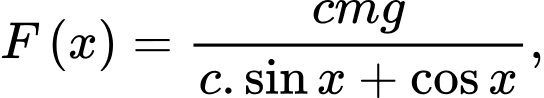 trong đó
trong đó 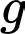 là gia tốc trọng trường và
là gia tốc trọng trường và  là hệ số ma sát của bề mặt
(Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014).
Với
là hệ số ma sát của bề mặt
(Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014).
Với 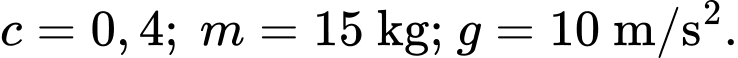 Tìm giá trị nhỏ nhất của lực kéo
Tìm giá trị nhỏ nhất của lực kéo 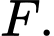 Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục. Đáp số:………………………………
Ta có: 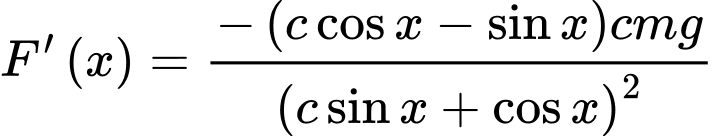
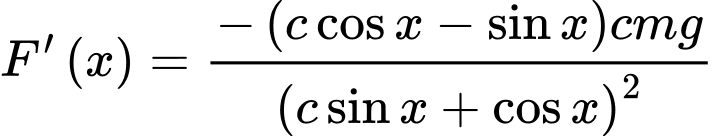
Cho 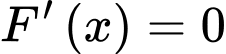
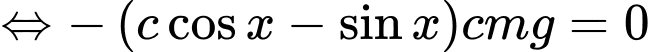
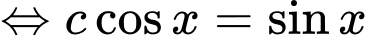
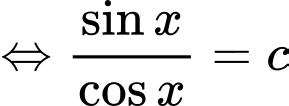
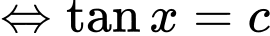
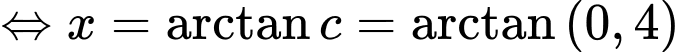
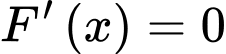
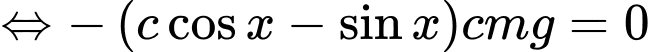
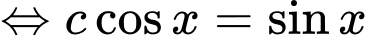
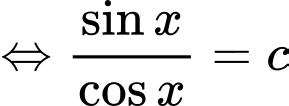
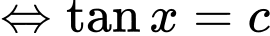
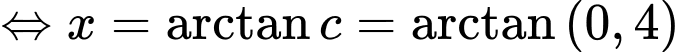
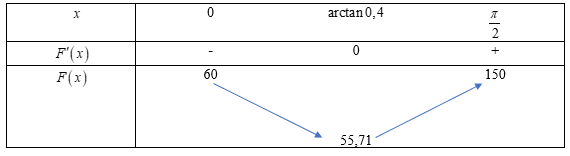
Bảng biến thiên:

Dựa vào bảng biến thiên, ta thấy giá trị nhỏ nhất của lực kéo 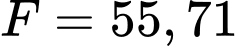 , đạt tại khi
, đạt tại khi 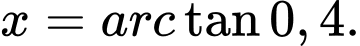
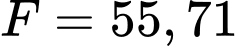 , đạt tại khi
, đạt tại khi