Đáp án Bài tập tự luyện số 1
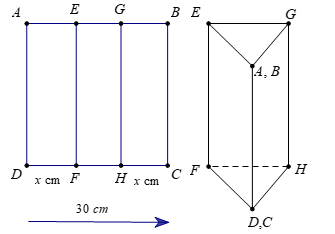
Câu 1 [5873]: Một tấm kẽm hình vuông 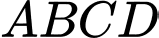 có cạnh bằng
có cạnh bằng 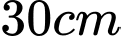 . Người ta gập tấm kẽm theo hai cạnh
. Người ta gập tấm kẽm theo hai cạnh 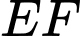 và
và 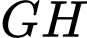 cho đến khi
cho đến khi 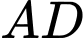 và
và 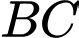 trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của
trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của 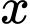 để thể tích khối lăng trụ lớn nhất là
để thể tích khối lăng trụ lớn nhất là
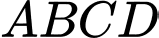 có cạnh bằng
có cạnh bằng 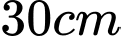 . Người ta gập tấm kẽm theo hai cạnh
. Người ta gập tấm kẽm theo hai cạnh 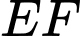 và
và 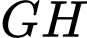 cho đến khi
cho đến khi 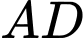 và
và 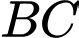 trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của
trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của 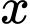 để thể tích khối lăng trụ lớn nhất là
để thể tích khối lăng trụ lớn nhất là
A, 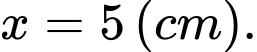
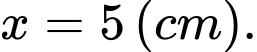
B, 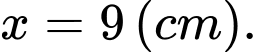
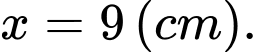
C, 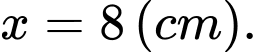
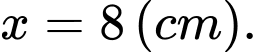
D, 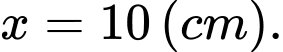
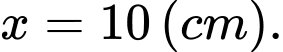
HD: Thể tích khối lăng trụ được tạo thành là 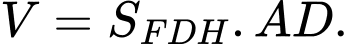
Thể tích đạt GTLN khi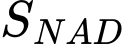 lớn nhất.
lớn nhất.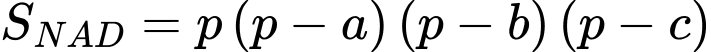
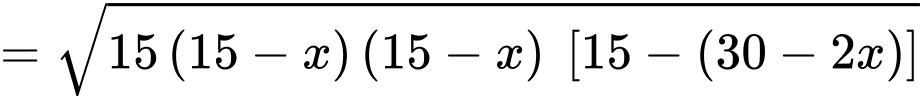
Hay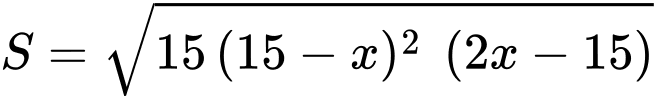
Xét hàm số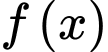
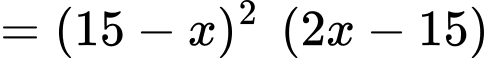
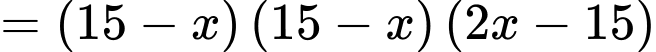
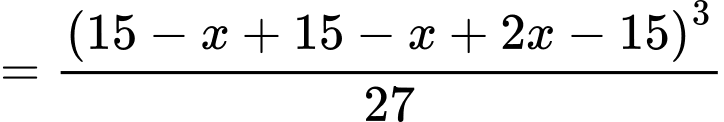 (Áp dụng BĐT
(Áp dụng BĐT 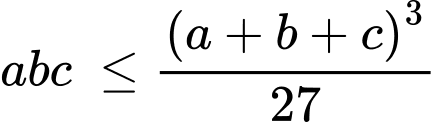
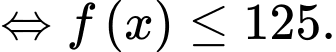
Dấu bằng xảy ra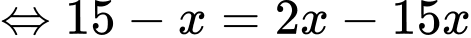
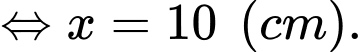
Chọn D. Đáp án: D
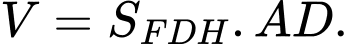
Thể tích đạt GTLN khi
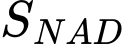 lớn nhất.
lớn nhất.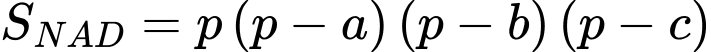
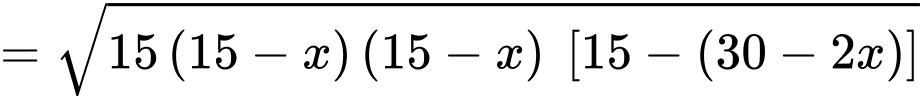
Hay
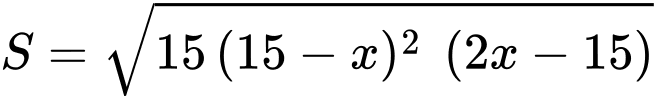
Xét hàm số
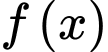
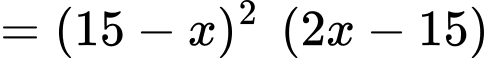
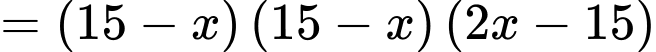
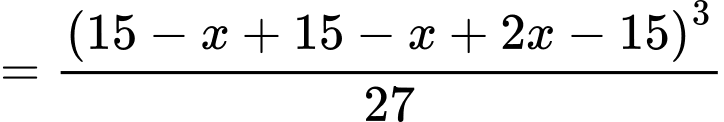 (Áp dụng BĐT
(Áp dụng BĐT 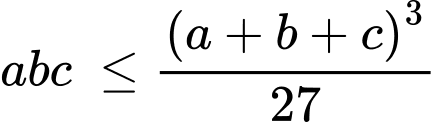
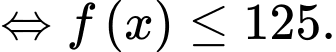
Dấu bằng xảy ra
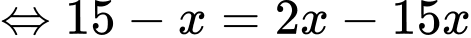
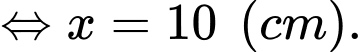
Chọn D. Đáp án: D
Câu 2 [382886]: Từ một tấm bìa hình vuông 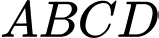 có cạnh bằng
có cạnh bằng 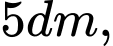 người ta cắt bỏ bốn tam giác bằng nhau là
người ta cắt bỏ bốn tam giác bằng nhau là 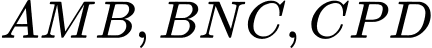 và
và 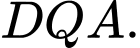 Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi thể tích khối chóp lớn nhất bằng bao nhiêu dm^3 (Viết kết quả làm tròn
Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi thể tích khối chóp lớn nhất bằng bao nhiêu dm^3 (Viết kết quả làm tròn
đến hàng phần mười)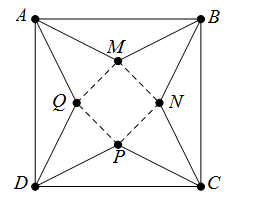
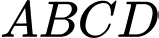 có cạnh bằng
có cạnh bằng 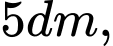 người ta cắt bỏ bốn tam giác bằng nhau là
người ta cắt bỏ bốn tam giác bằng nhau là 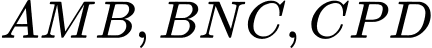 và
và 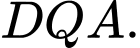 Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi thể tích khối chóp lớn nhất bằng bao nhiêu dm^3 (Viết kết quả làm tròn
Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi thể tích khối chóp lớn nhất bằng bao nhiêu dm^3 (Viết kết quả làm trònđến hàng phần mười)

Giả sử 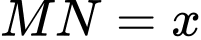
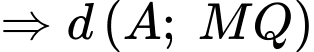
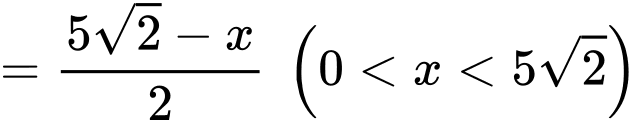
Chiều cao hình chóp là:
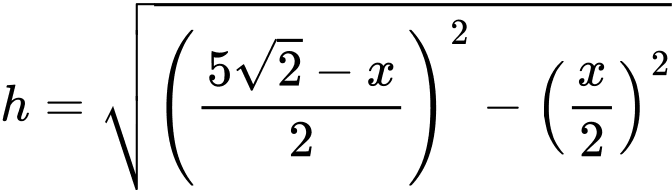
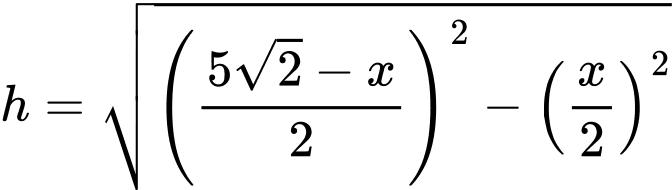
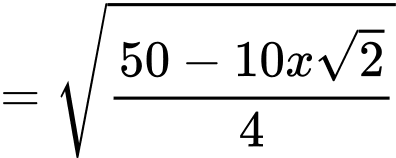
Ta có:
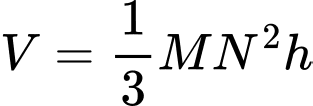
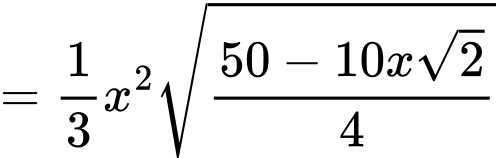
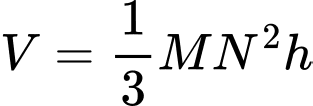
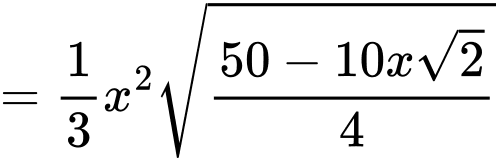
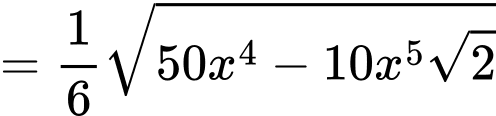
Đặt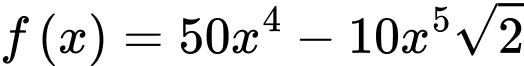
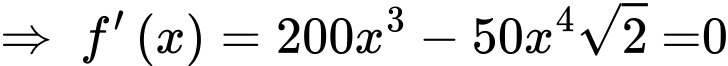
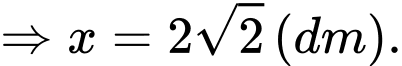
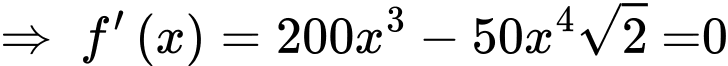
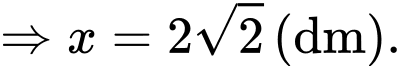
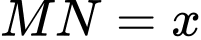
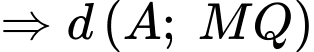
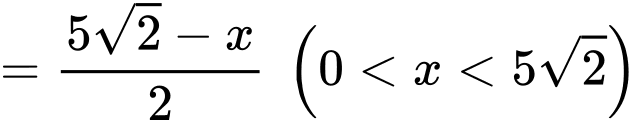
Chiều cao hình chóp là:
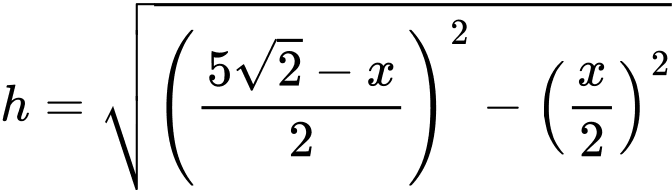
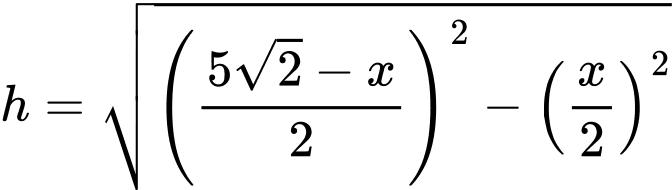
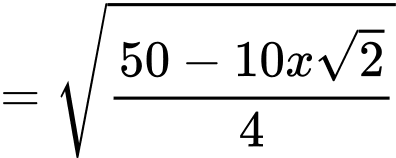
Ta có:
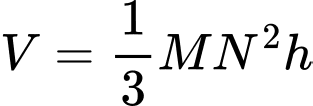
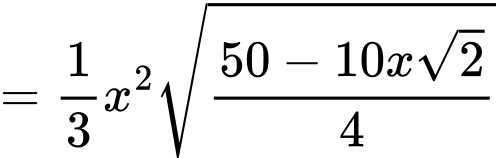
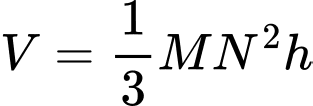
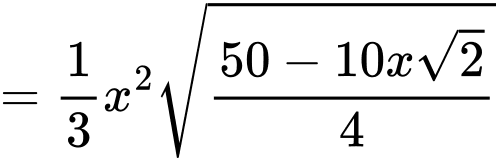
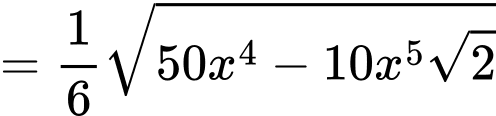
Đặt
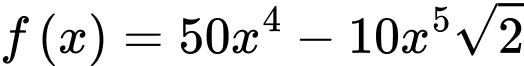
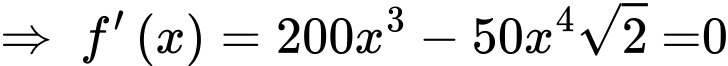
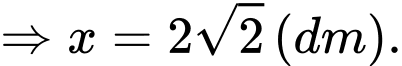
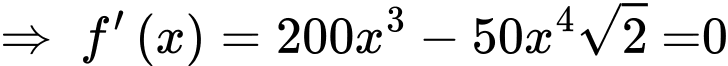
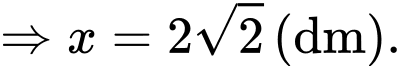
Câu 3 [31003]: Một ngọn hải đăng đặt tại vị trí 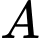 có khoảng cách đến bờ biển
có khoảng cách đến bờ biển 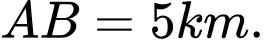 Trên bờ biển có một cái kho ở vị trí
Trên bờ biển có một cái kho ở vị trí  cách
cách 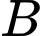 một khoảng
một khoảng 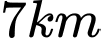 . Người canh hải đăng có thể chèo đò từ
. Người canh hải đăng có thể chèo đò từ 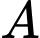 đến
đến 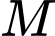 trên bờ biển với vận tốc
trên bờ biển với vận tốc 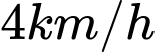 rồi đi bộ đến
rồi đi bộ đến  với vận tốc
với vận tốc 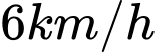 . Vị trí của điểm
. Vị trí của điểm 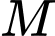 cách
cách 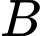 một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
 có khoảng cách đến bờ biển
có khoảng cách đến bờ biển 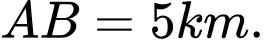 Trên bờ biển có một cái kho ở vị trí
Trên bờ biển có một cái kho ở vị trí  cách
cách  một khoảng
một khoảng 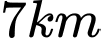 . Người canh hải đăng có thể chèo đò từ
. Người canh hải đăng có thể chèo đò từ 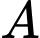 đến
đến 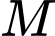 trên bờ biển với vận tốc
trên bờ biển với vận tốc 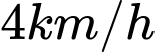 rồi đi bộ đến
rồi đi bộ đến  với vận tốc
với vận tốc 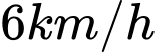 . Vị trí của điểm
. Vị trí của điểm 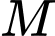 cách
cách 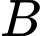 một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
A, 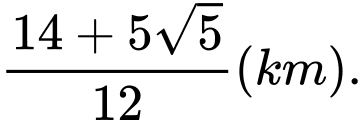
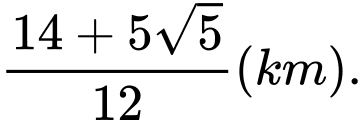
B, 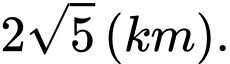
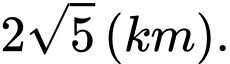
C, 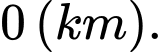
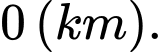
D, 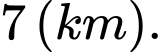
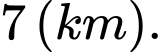
HD: Đặt 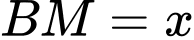
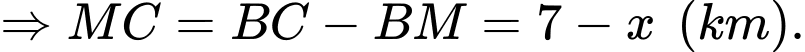
Tam giác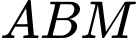 vuông tại
vuông tại 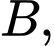 có
có 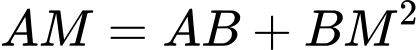
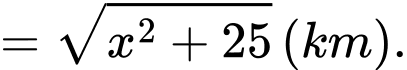
Thời gian đi từ là
là 
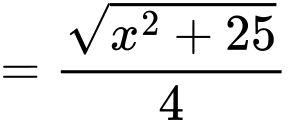
Thời gian đi từ là
là 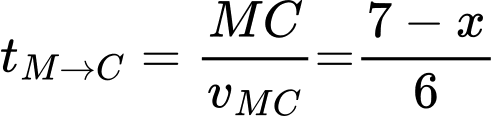
Tổng thời gia thời gian đi từ là
là 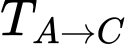
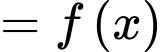
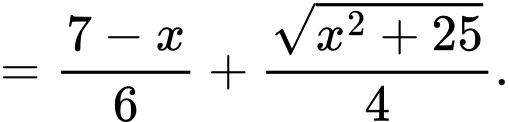
Xét hàm số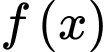
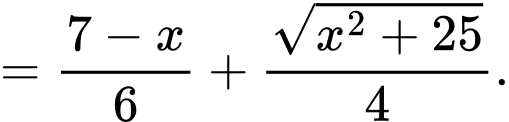 trên khoảng
trên khoảng 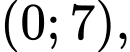 có
có 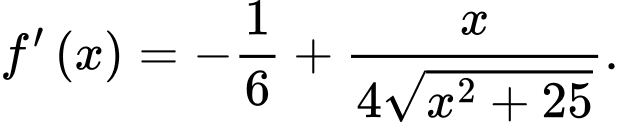
Phương trình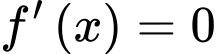
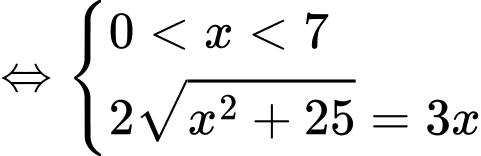
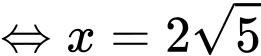
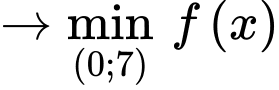
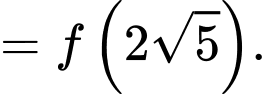
Vậy để đi từ nhanh nhất khi
nhanh nhất khi 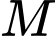 cách
cách  một khoảng
một khoảng 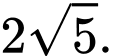 Chọn B. Đáp án: B
Chọn B. Đáp án: B
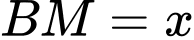
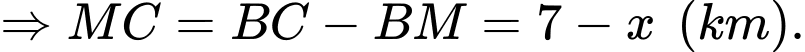
Tam giác
 vuông tại
vuông tại  có
có 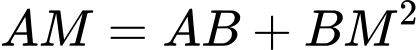
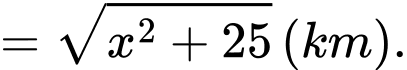
Thời gian đi từ
 là
là 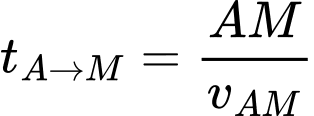
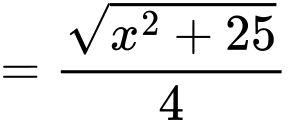
Thời gian đi từ
 là
là 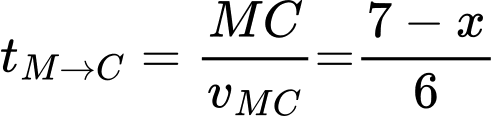
Tổng thời gia thời gian đi từ
 là
là 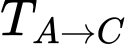
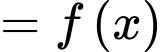
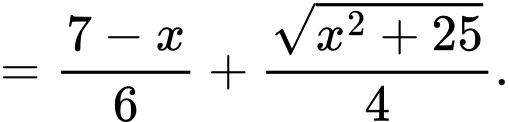
Xét hàm số
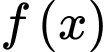
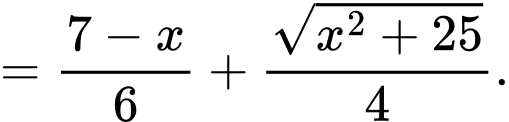 trên khoảng
trên khoảng  có
có 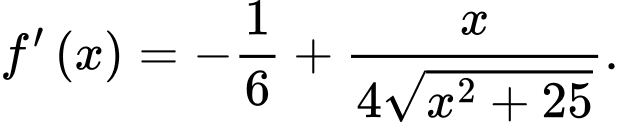
Phương trình
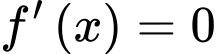
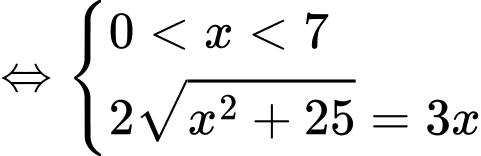
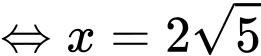
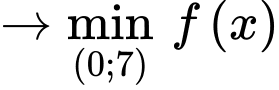
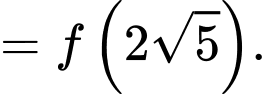
Vậy để đi từ
 nhanh nhất khi
nhanh nhất khi 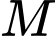 cách
cách  một khoảng
một khoảng 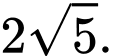 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 4 [31024]: Một người cần đi từ khách sạn  bên bờ biển đến hòn đảo
bên bờ biển đến hòn đảo  Biết rằng khoảng cách từ đảo
Biết rằng khoảng cách từ đảo  đến bờ biển là
đến bờ biển là 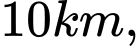 khoảng cách từ khách sạn
khoảng cách từ khách sạn 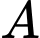 đến điểm
đến điểm 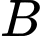 trên bờ gần đảo
trên bờ gần đảo  nhất là
nhất là 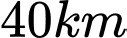 . Người đó có thể di đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là
. Người đó có thể di đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là 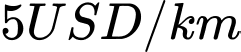 , đi đường bộ là
, đi đường bộ là 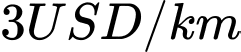 . Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất (
. Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất (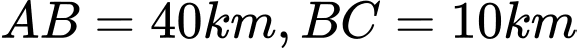 )?
)?
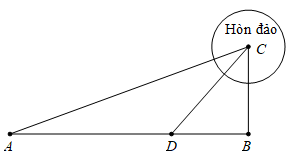
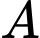 bên bờ biển đến hòn đảo
bên bờ biển đến hòn đảo  Biết rằng khoảng cách từ đảo
Biết rằng khoảng cách từ đảo  đến bờ biển là
đến bờ biển là 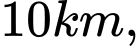 khoảng cách từ khách sạn
khoảng cách từ khách sạn 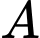 đến điểm
đến điểm 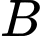 trên bờ gần đảo
trên bờ gần đảo  nhất là
nhất là 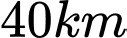 . Người đó có thể di đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là
. Người đó có thể di đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là 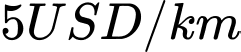 , đi đường bộ là
, đi đường bộ là 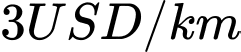 . Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất (
. Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất (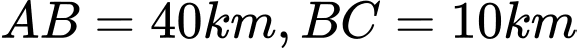 )?
)?
A, 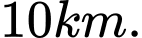
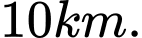
B, 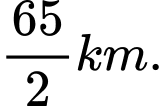
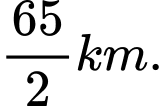
C, 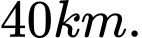
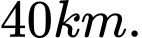
D, 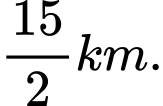
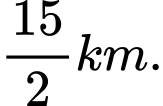
HD: Đặt 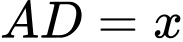
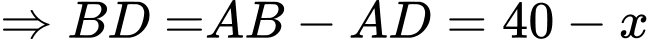
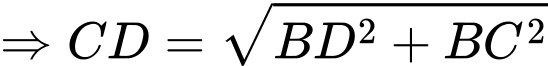
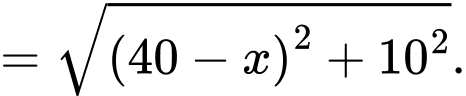
Suy ra kinh phí người đó phải bỏ là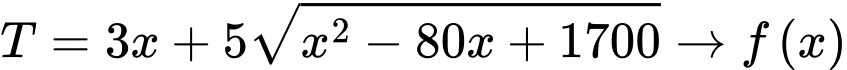
Khảo sát hàm số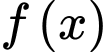 trên
trên 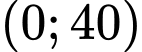 ta được:
ta được: 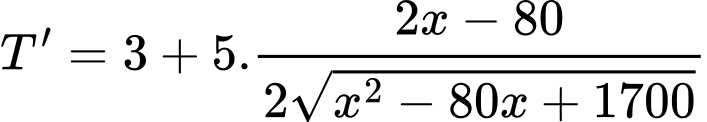
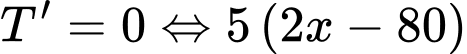
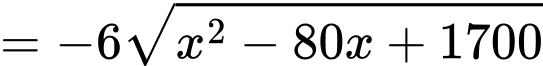
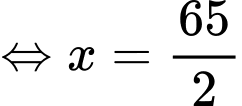
Suy ra
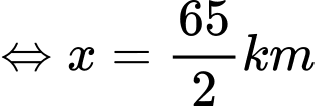
Vậy chi phí nhỏ nhất cần phải bỏ khi người đó đi bộ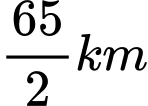 và chi phí thấp nhất là 160 USD.
và chi phí thấp nhất là 160 USD.
Chọn B. Đáp án: B
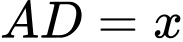
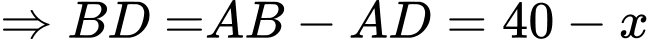
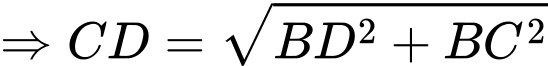
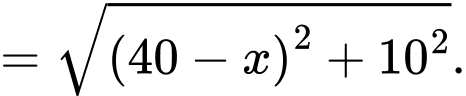
Suy ra kinh phí người đó phải bỏ là
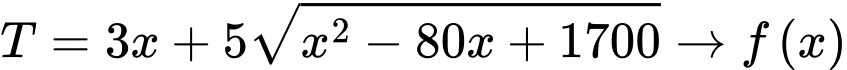
Khảo sát hàm số
 trên
trên  ta được:
ta được: 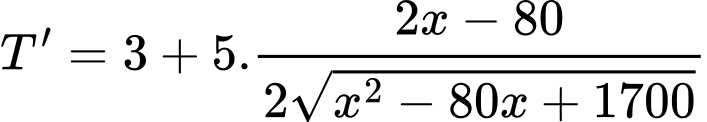
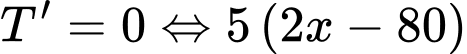
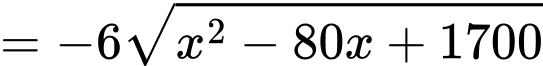
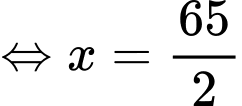
Suy ra

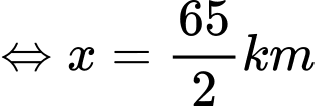
Vậy chi phí nhỏ nhất cần phải bỏ khi người đó đi bộ
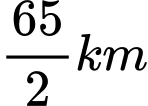 và chi phí thấp nhất là 160 USD.
và chi phí thấp nhất là 160 USD. Chọn B. Đáp án: B
Câu 5 [307636]: Đường dây điện 110KV kéo từ trạm phát trong đất liền (điểm  ) ra đảo (điểm
) ra đảo (điểm  ). Biết khoảng cách ngắn nhất từ
). Biết khoảng cách ngắn nhất từ  đến
đến  là 60 km, khoảng cách từ
là 60 km, khoảng cách từ 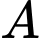 đến
đến 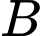 là 100 km, mỗi km dây điện dưới nước chi phí là 100 triệu đồng, chi phí mỗi km dây điện trên bờ là 60 triệu đồng. Hỏi điểm
là 100 km, mỗi km dây điện dưới nước chi phí là 100 triệu đồng, chi phí mỗi km dây điện trên bờ là 60 triệu đồng. Hỏi điểm  cách
cách 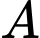 bao nhiêu km để mắc dây điện từ
bao nhiêu km để mắc dây điện từ 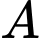 đến
đến  rồi từ
rồi từ  đến
đến  chi phí thấp nhất? (Đoạn
chi phí thấp nhất? (Đoạn  trên bờ, đoạn
trên bờ, đoạn 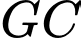 dưới nước )
dưới nước )
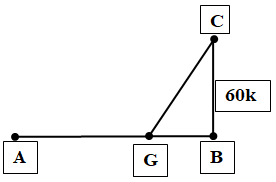
 ) ra đảo (điểm
) ra đảo (điểm  ). Biết khoảng cách ngắn nhất từ
). Biết khoảng cách ngắn nhất từ  đến
đến  là 60 km, khoảng cách từ
là 60 km, khoảng cách từ 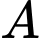 đến
đến 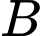 là 100 km, mỗi km dây điện dưới nước chi phí là 100 triệu đồng, chi phí mỗi km dây điện trên bờ là 60 triệu đồng. Hỏi điểm
là 100 km, mỗi km dây điện dưới nước chi phí là 100 triệu đồng, chi phí mỗi km dây điện trên bờ là 60 triệu đồng. Hỏi điểm  cách
cách 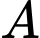 bao nhiêu km để mắc dây điện từ
bao nhiêu km để mắc dây điện từ 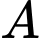 đến
đến  rồi từ
rồi từ  đến
đến  chi phí thấp nhất? (Đoạn
chi phí thấp nhất? (Đoạn  trên bờ, đoạn
trên bờ, đoạn 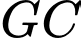 dưới nước )
dưới nước ) 
A,  .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn D
Ta gọi khoảng cách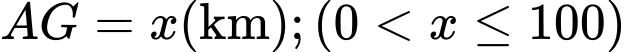 .
.
Tính được khoảng cách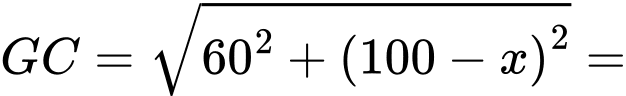
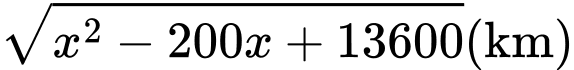 .
.
Suy ra hàm số tính chi phí dây điện từ A đến G rồi G đến C là
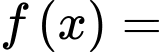

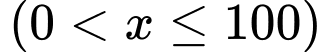
Tính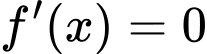 ra nghiệm
ra nghiệm 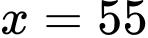 , ta lập BBT như sau
, ta lập BBT như sau
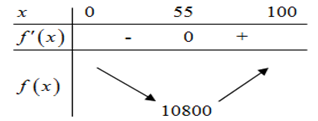
Vậy chi phí thấp nhất khi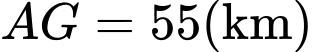 . Đáp án: D
. Đáp án: D
Ta gọi khoảng cách
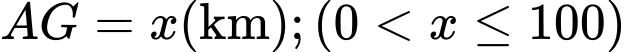 .
.
Tính được khoảng cách
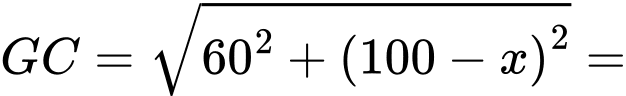
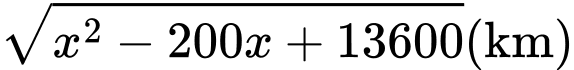 .
.
Suy ra hàm số tính chi phí dây điện từ A đến G rồi G đến C là
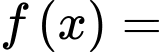

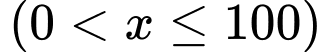
Tính
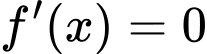 ra nghiệm
ra nghiệm 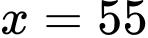 , ta lập BBT như sau
, ta lập BBT như sau
Vậy chi phí thấp nhất khi
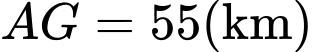 . Đáp án: D
. Đáp án: D
Câu 6 [384769]: Trong nội dung thi điền kinh và bơi lội phối hợp được diễn ra tại một hồ bơi có chiều rộng 50 m và chiều dài 200 m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả hai) khi phải thực hiện lộ trình xuất phát từ A đến B như hình vẽ. Hỏi rằng sau khi chạy được bao xa (quãng đường x) thì vận động viên nên nhảy xuống để tiếp tục bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ và khi bơi lần lượt là 4,5 m/s và 1,5 m/s. 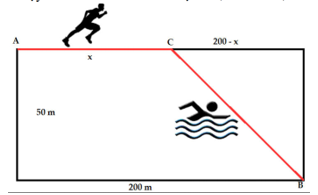

Đáp số:……………………………
Gọi quãng đường vận động viên chạy trên bờ là: 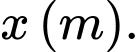
Khi đó quãng đường vận động viên bơi dưới nước sẽ là: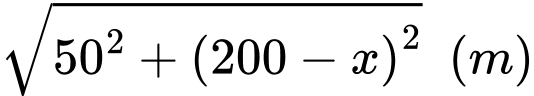
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là:
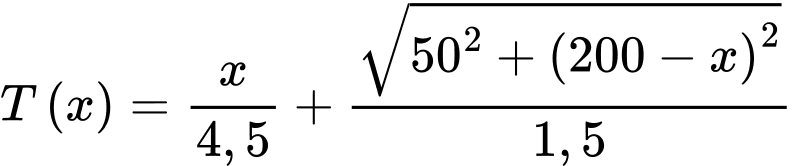

Yêu cầu bài toán tương đương với: Tìm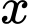 để
để 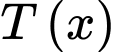 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Có:
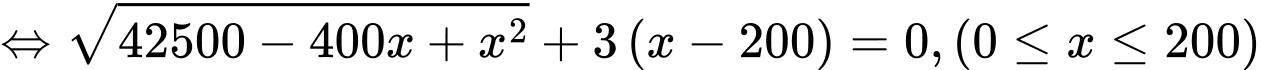
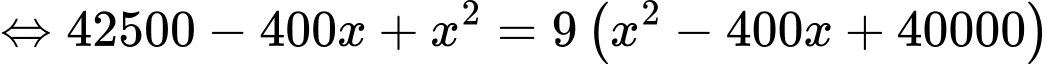
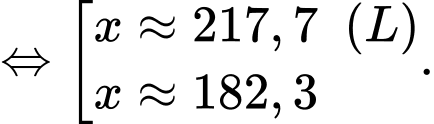
Bảng biến thiên:
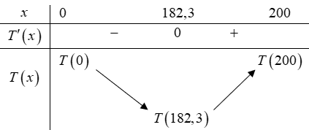
Dựa vào bảng biến thiên, suy ra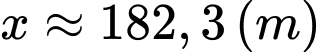 thì
thì 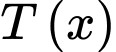 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
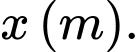
Khi đó quãng đường vận động viên bơi dưới nước sẽ là:
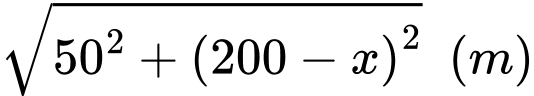
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là:
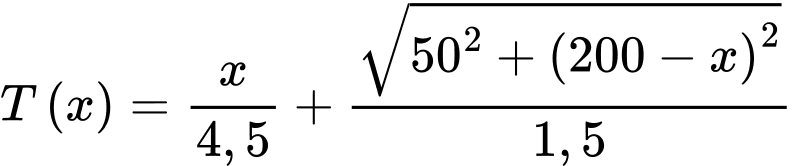

Yêu cầu bài toán tương đương với: Tìm
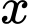 để
để 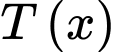 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. Có:

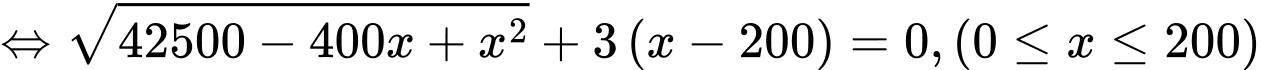
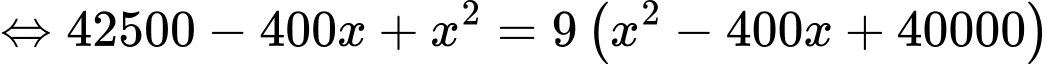
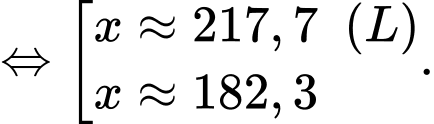
Bảng biến thiên:

Dựa vào bảng biến thiên, suy ra
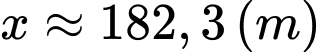 thì
thì 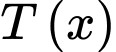 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
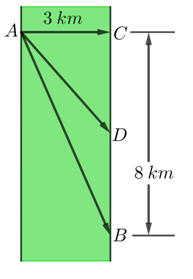
Câu 7 [31013]: Một người đàn ông muốn chèo thuyền ở vị trí 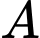 tới điểm
tới điểm 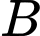 về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng
về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 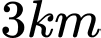 (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến
(như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến  và sau đó chạy đến
và sau đó chạy đến 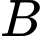 , hay có thể chèo trực tiếp đến
, hay có thể chèo trực tiếp đến 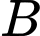 , hoặc anh ta có thể chèo thuyền đến một điểm
, hoặc anh ta có thể chèo thuyền đến một điểm 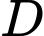 giữa
giữa  và
và 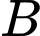 và sau đó chạy đến
và sau đó chạy đến 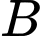 . Biết anh ấy có thể chèo thuyền
. Biết anh ấy có thể chèo thuyền 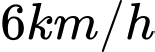 , chạy
, chạy 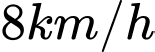 và quãng đường
và quãng đường 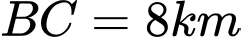 . Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến
. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến 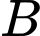 .
.
 tới điểm
tới điểm  về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng
về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng  (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến
(như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến  và sau đó chạy đến
và sau đó chạy đến 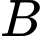 , hay có thể chèo trực tiếp đến
, hay có thể chèo trực tiếp đến 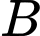 , hoặc anh ta có thể chèo thuyền đến một điểm
, hoặc anh ta có thể chèo thuyền đến một điểm 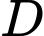 giữa
giữa  và
và 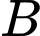 và sau đó chạy đến
và sau đó chạy đến 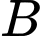 . Biết anh ấy có thể chèo thuyền
. Biết anh ấy có thể chèo thuyền 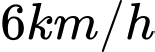 , chạy
, chạy 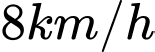 và quãng đường
và quãng đường 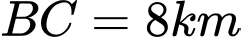 . Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến
. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến 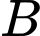 .
.
A, 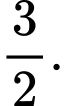
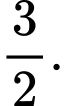
B, 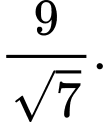
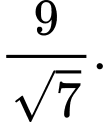
C, 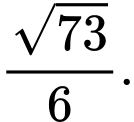
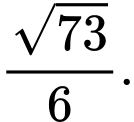
D, 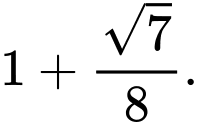
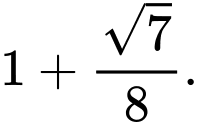
HD: Thời gian đi từ  đến
đến  là
là 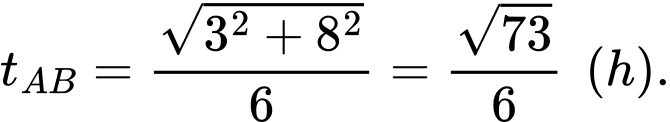
 đến
đến  là
là 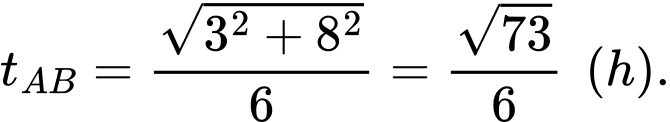
Thời gian đi từ  đến
đến  rồi đến
rồi đến  là
là 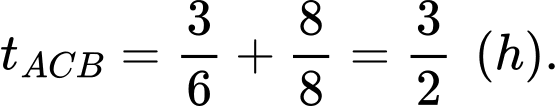
 đến
đến  rồi đến
rồi đến  là
là 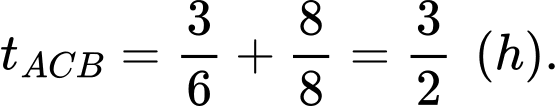
Goi 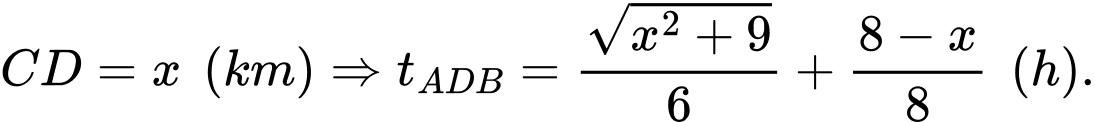
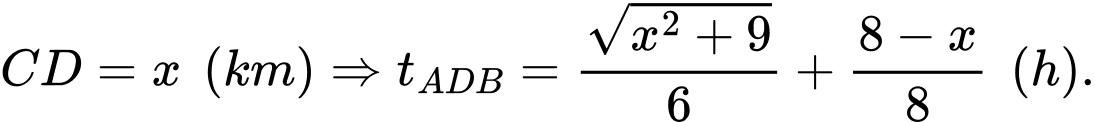
Xét hàm số 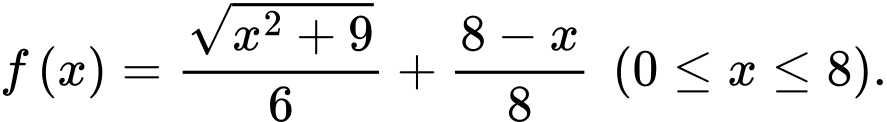
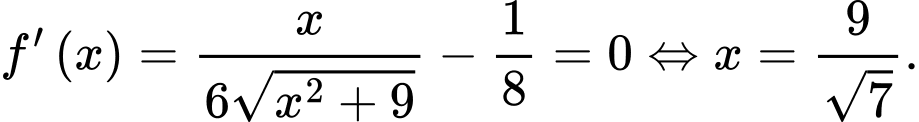
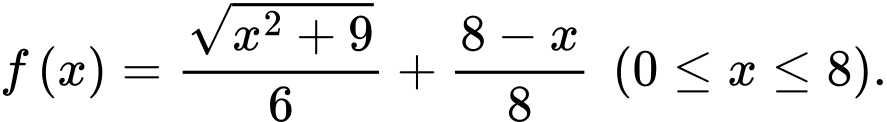
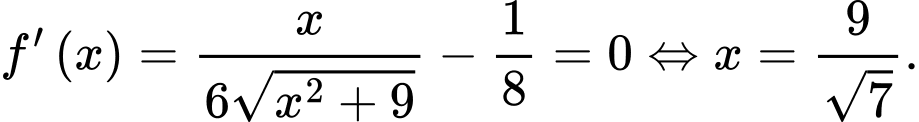
Suy ra 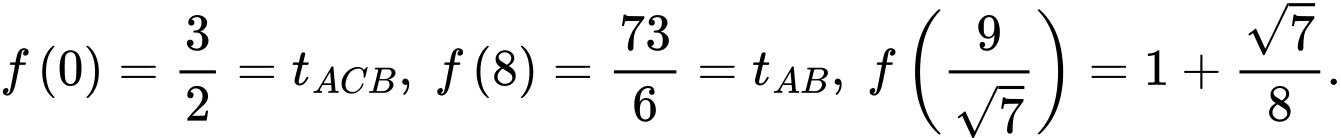
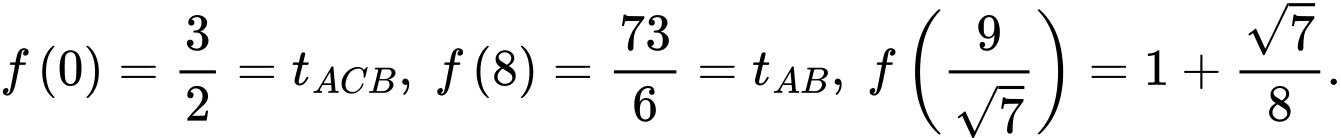
Suy ra thời gian ngắn nhất bằng 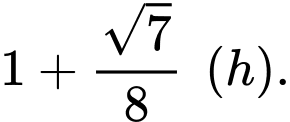 Chọn D.
Chọn D.
Đáp án: D 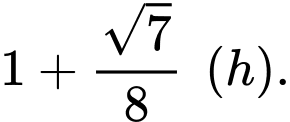 Chọn D.
Chọn D.
Câu 8 [358939]: Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài 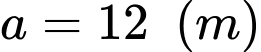 và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân 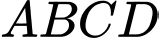 như Hình 36 (bờ sông là đường thẳng
như Hình 36 (bờ sông là đường thẳng 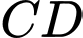 không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?
không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?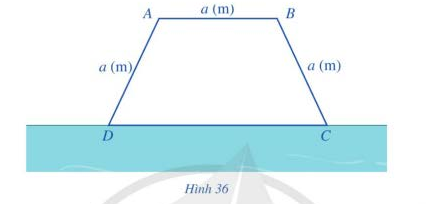
Viết kết quả làm tròn kết quả đến hang đơn vị.
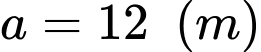 và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân 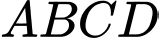 như Hình 36 (bờ sông là đường thẳng
như Hình 36 (bờ sông là đường thẳng 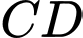 không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?
không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?
Viết kết quả làm tròn kết quả đến hang đơn vị.
Gọi 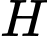 là hình chiếu vuông góc của
là hình chiếu vuông góc của 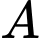 trên
trên 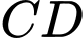 và đặt
và đặt 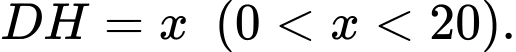
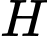 là hình chiếu vuông góc của
là hình chiếu vuông góc của 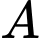 trên
trên 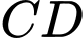 và đặt
và đặt 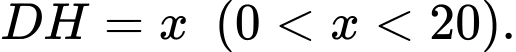
Có: 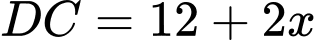 và
và 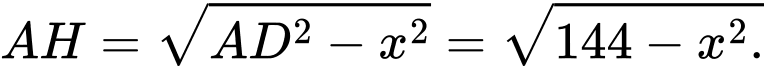
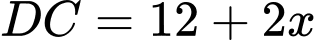 và
và 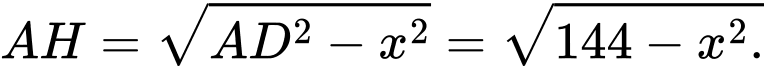
Diện tích hình thang  là:
là: 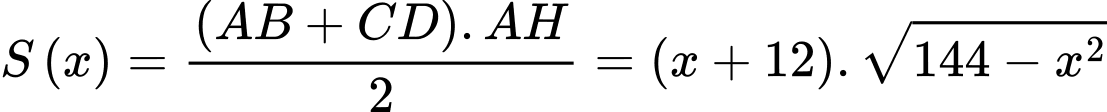
 là:
là: 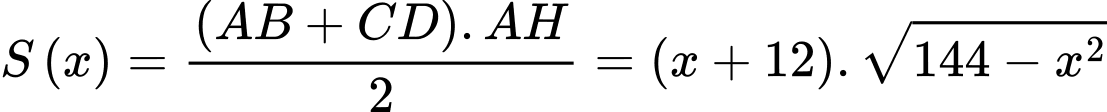
Có: 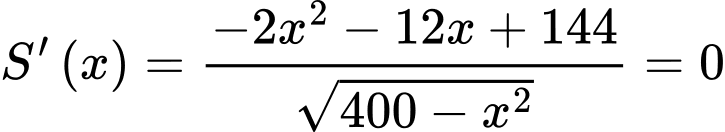
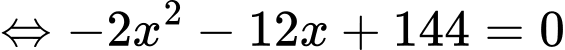
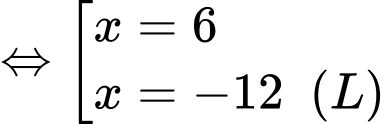
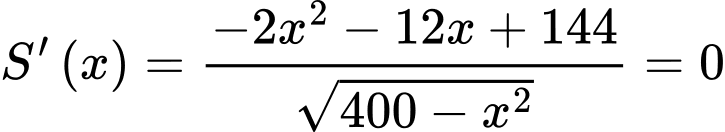
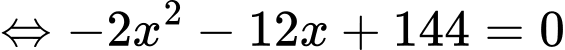
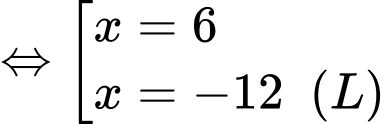
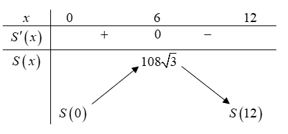
Bảng biến thiên:

Dựa vào bảng biến thiên, suy ra bác đó có thể rào được
mảnh vườn có diện tích lớn nhất là 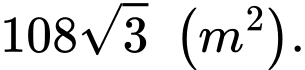
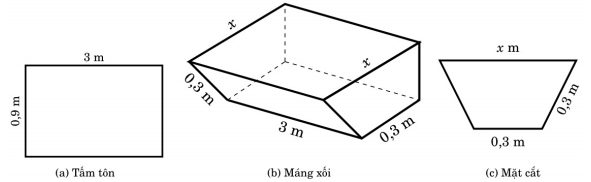
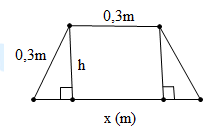
Câu 9 [5882]: Để làm một máng xối nước, từ một tấm tôn kích thước 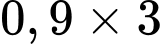 người ta gấp tấm tôn đó như hình vẽ dưới, biết mặt cắt của máng xối (bởi mặt phẳng song song với hai mặt đáy) là một hình thang cân và máng xối là một hình lăng trụ, có chiều cao bằng chiều dài của tấm tôn. Hỏi
người ta gấp tấm tôn đó như hình vẽ dưới, biết mặt cắt của máng xối (bởi mặt phẳng song song với hai mặt đáy) là một hình thang cân và máng xối là một hình lăng trụ, có chiều cao bằng chiều dài của tấm tôn. Hỏi 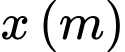 bằng bao nhiêu thì thể tích máng xối lớn nhất?
bằng bao nhiêu thì thể tích máng xối lớn nhất?
 người ta gấp tấm tôn đó như hình vẽ dưới, biết mặt cắt của máng xối (bởi mặt phẳng song song với hai mặt đáy) là một hình thang cân và máng xối là một hình lăng trụ, có chiều cao bằng chiều dài của tấm tôn. Hỏi
người ta gấp tấm tôn đó như hình vẽ dưới, biết mặt cắt của máng xối (bởi mặt phẳng song song với hai mặt đáy) là một hình thang cân và máng xối là một hình lăng trụ, có chiều cao bằng chiều dài của tấm tôn. Hỏi 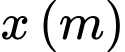 bằng bao nhiêu thì thể tích máng xối lớn nhất?
bằng bao nhiêu thì thể tích máng xối lớn nhất?
A,
B,
C,
D,
HD: Mặt đáy của máng xối nước thang cân có đáy lớn là 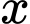 đáy bé là
đáy bé là 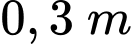
Cạnh bên của hình thang là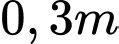 suy ra chiều cao của hình thang là
suy ra chiều cao của hình thang là 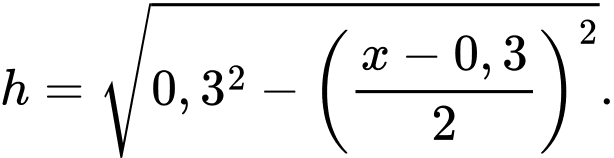
Khi đó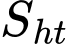
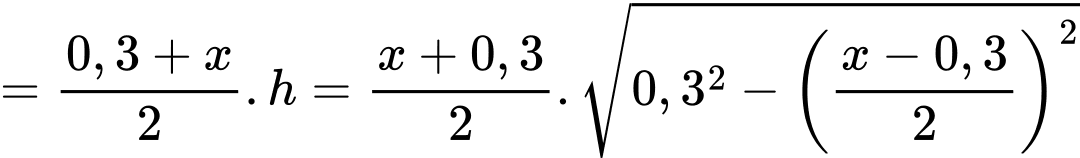
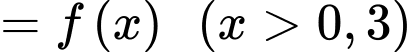
Đến đây chúng ta có thể xét hàm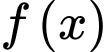 hoặc sử dụng CASIO, CALC các giá trị
hoặc sử dụng CASIO, CALC các giá trị 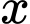 để bài đã cho ta được
để bài đã cho ta được 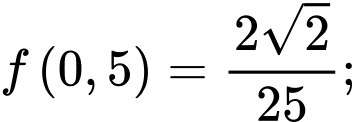
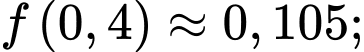
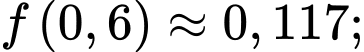
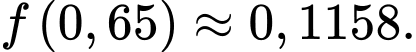
Do đó ta thấy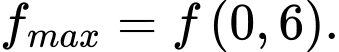
Đáp án: C
 đáy bé là
đáy bé là 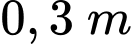
Cạnh bên của hình thang là
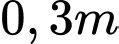 suy ra chiều cao của hình thang là
suy ra chiều cao của hình thang là 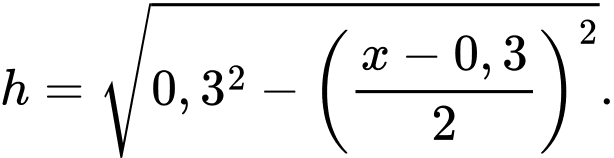

Khi đó
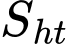
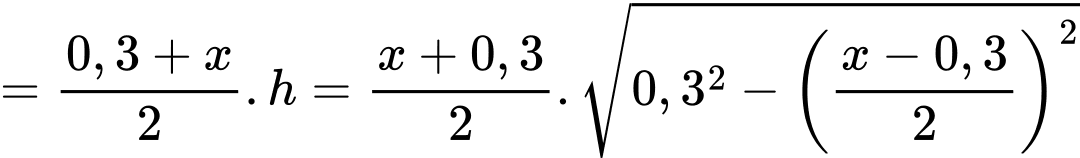
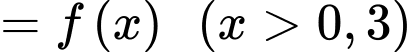
Đến đây chúng ta có thể xét hàm
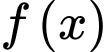 hoặc sử dụng CASIO, CALC các giá trị
hoặc sử dụng CASIO, CALC các giá trị 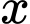 để bài đã cho ta được
để bài đã cho ta được 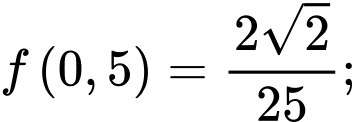
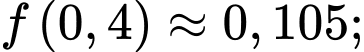
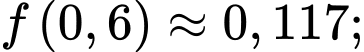
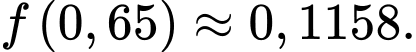
Do đó ta thấy
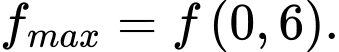
Đáp án: C
Câu 10 [31001]: Một sợi dây có chiều dài là 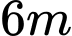 , được chia thành 2 phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai uốn thành tam giác đều. Hỏi độ dài của cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 2 hình thu được là nhỏ nhất?
, được chia thành 2 phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai uốn thành tam giác đều. Hỏi độ dài của cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 2 hình thu được là nhỏ nhất?
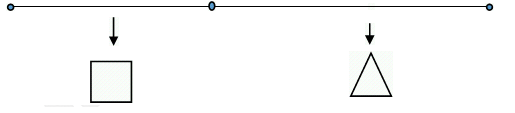
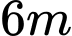 , được chia thành 2 phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai uốn thành tam giác đều. Hỏi độ dài của cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 2 hình thu được là nhỏ nhất?
, được chia thành 2 phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai uốn thành tam giác đều. Hỏi độ dài của cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 2 hình thu được là nhỏ nhất?
A, 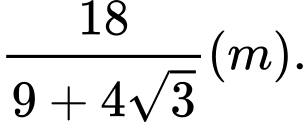
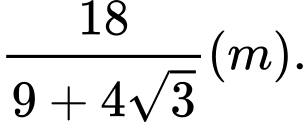
B, 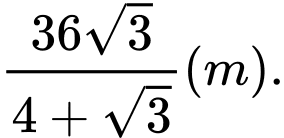
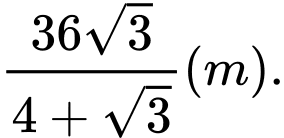
C, 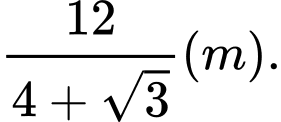
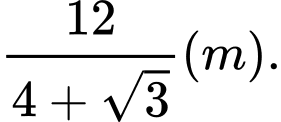
D, 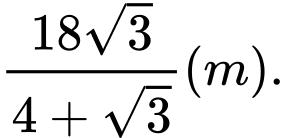
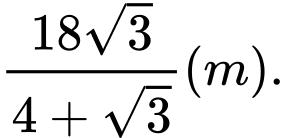
HD:Gọi độ dài hai phần lần lượt là 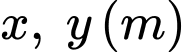
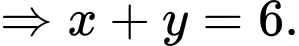
Suy ra độ dài cạnh hình vuông và độ dài tam giác sẽ bằng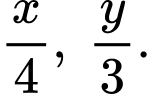
Suy ra diện tích hai hình sẽ bằng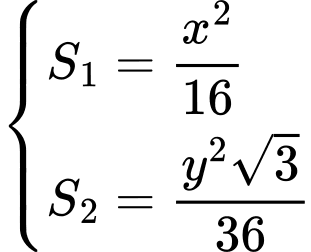
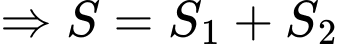
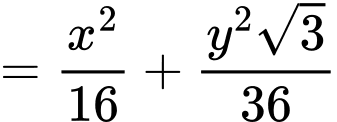
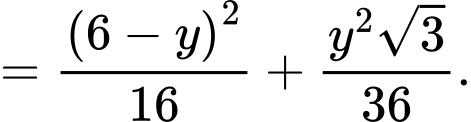
Ta có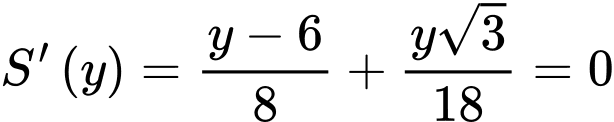
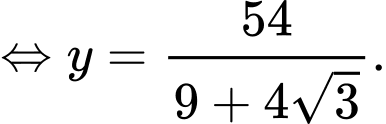
Lập bảng biến thiện hàm số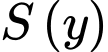 trên đoạn
trên đoạn 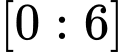 ta thấy
ta thấy 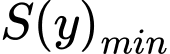
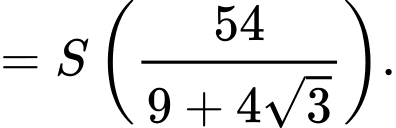
Suy ra độ dài cạnh tam giác sẽ bằng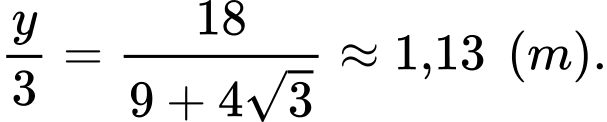 Chọn A. Điền đáp số 1,13
Đáp án: A
Chọn A. Điền đáp số 1,13
Đáp án: A
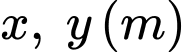
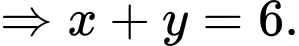
Suy ra độ dài cạnh hình vuông và độ dài tam giác sẽ bằng
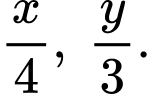
Suy ra diện tích hai hình sẽ bằng
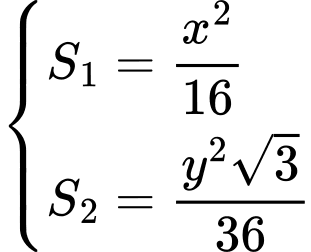
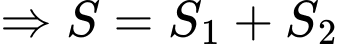
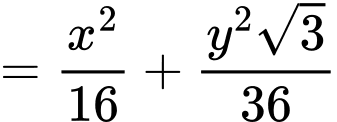
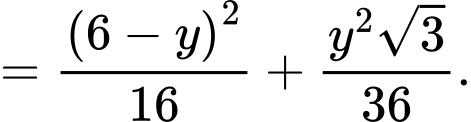
Ta có
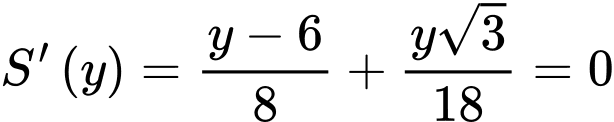
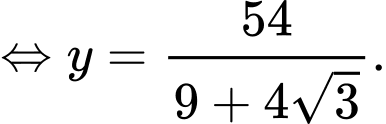
Lập bảng biến thiện hàm số
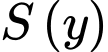 trên đoạn
trên đoạn 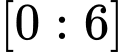 ta thấy
ta thấy 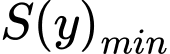
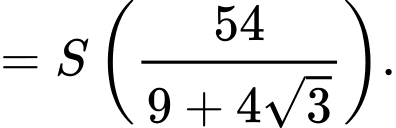
Suy ra độ dài cạnh tam giác sẽ bằng
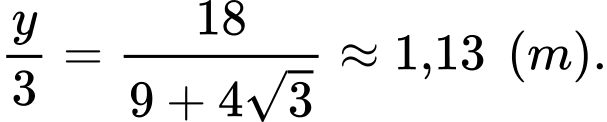 Chọn A. Điền đáp số 1,13
Đáp án: A
Chọn A. Điền đáp số 1,13
Đáp án: A
Câu 11 [31097]: Một sợi dây kim loại dài 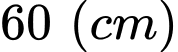 được cắt ra thành hai đoạn. Đoạn dây thứ nhất có độ dài
được cắt ra thành hai đoạn. Đoạn dây thứ nhất có độ dài 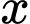 được uốn thành một hình vuông. Đoạn dây còn lại được uốn thành một vòng tròn. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì giá trị của
được uốn thành một hình vuông. Đoạn dây còn lại được uốn thành một vòng tròn. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì giá trị của 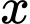 xấp xỉ bao nhiêu
xấp xỉ bao nhiêu 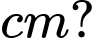
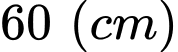 được cắt ra thành hai đoạn. Đoạn dây thứ nhất có độ dài
được cắt ra thành hai đoạn. Đoạn dây thứ nhất có độ dài 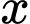 được uốn thành một hình vuông. Đoạn dây còn lại được uốn thành một vòng tròn. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì giá trị của
được uốn thành một hình vuông. Đoạn dây còn lại được uốn thành một vòng tròn. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì giá trị của 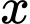 xấp xỉ bao nhiêu
xấp xỉ bao nhiêu 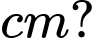
A, 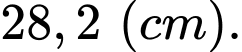
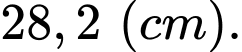
B, 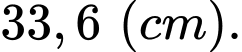
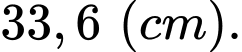
C, 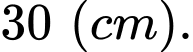
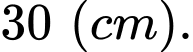
D, 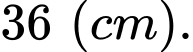
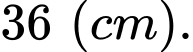
+Độ dài cạnh hình vuông là 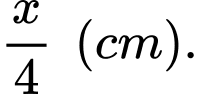
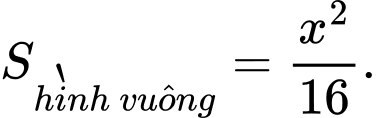
Chu vi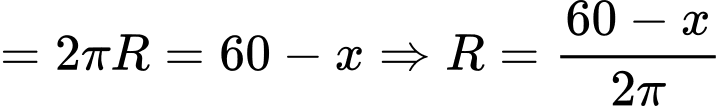
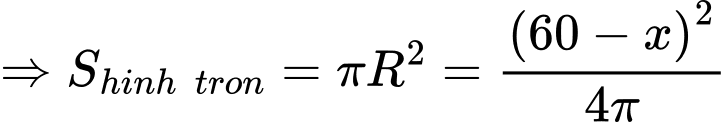
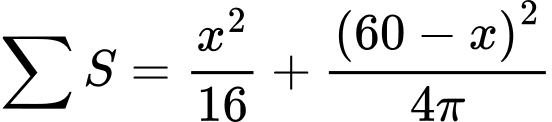
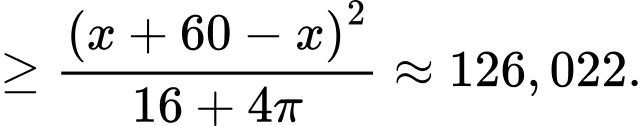
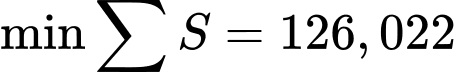
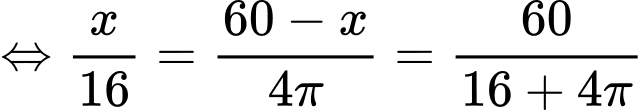
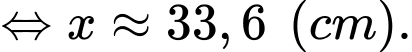 Đáp án: B
Đáp án: B
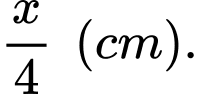
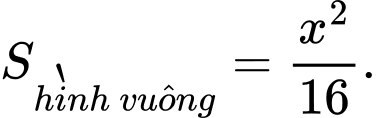
Chu vi
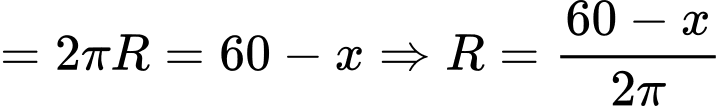
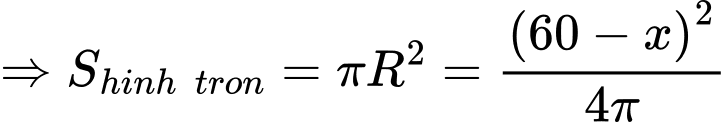
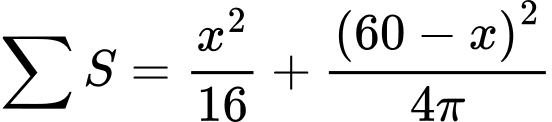
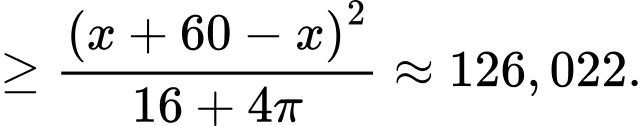
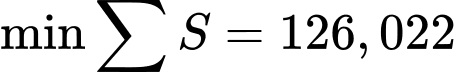
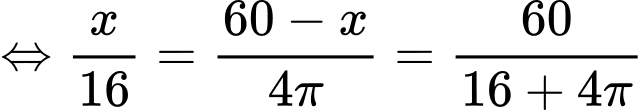
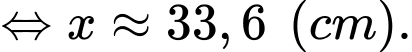 Đáp án: B
Đáp án: B
Câu 12 [31014]: Có một tấm gỗ hình vuông cạnh 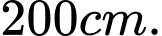 Cắt một tấm gỗ có hình tam giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số
Cắt một tấm gỗ có hình tam giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số 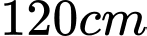 từ tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
từ tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
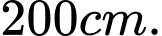 Cắt một tấm gỗ có hình tam giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số
Cắt một tấm gỗ có hình tam giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số 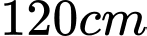 từ tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
từ tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu? A, 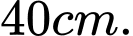
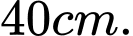
B, 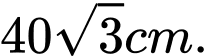
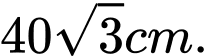
C, 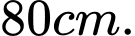
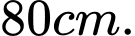
D, 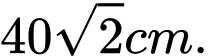
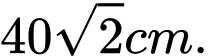
Gọi kích thước 2 cạnh góc vuông tam giác vuông là 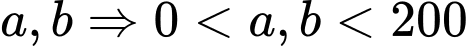
Độ dài cạnh huyển là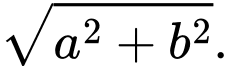 Không mất tính tổng quát, giả sử
Không mất tính tổng quát, giả sử 
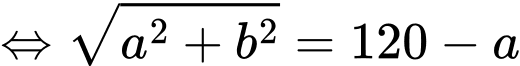
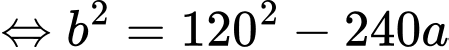
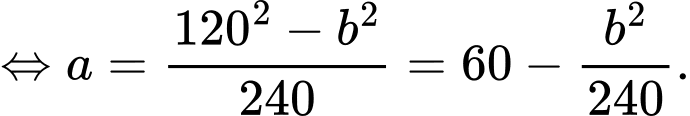
Diện tích tấm gỗ tam giác vuông là:
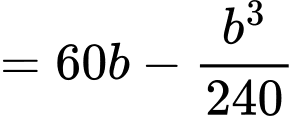
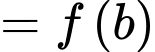
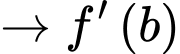
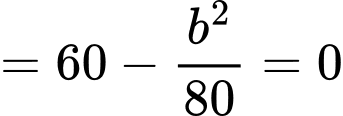
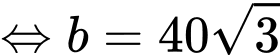
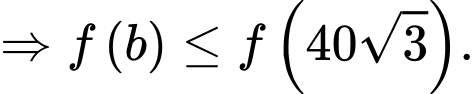
Dấu bằng khi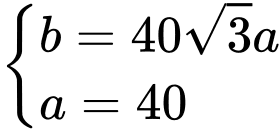
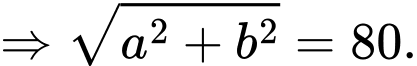 Chọn C. Đáp án: C
Chọn C. Đáp án: C
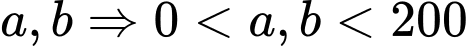
Độ dài cạnh huyển là
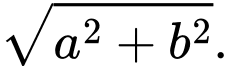 Không mất tính tổng quát, giả sử
Không mất tính tổng quát, giả sử 
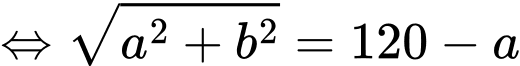
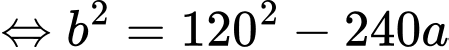
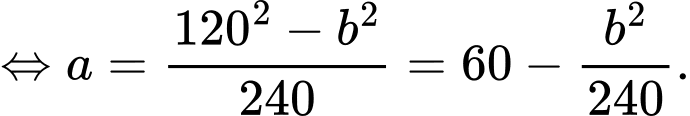
Diện tích tấm gỗ tam giác vuông là:

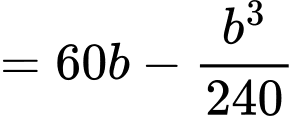
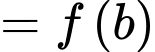
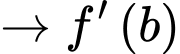
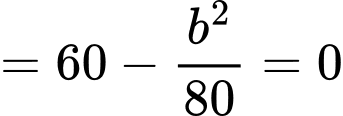
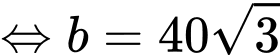
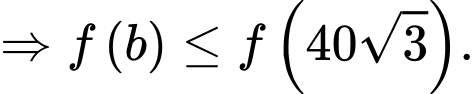
Dấu bằng khi
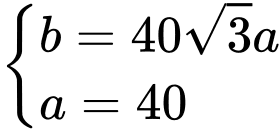
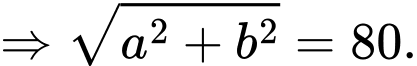 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 13 [384770]: Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ bên, nó được giới hạn bởi các trục toạ độ và đồ thị của hàm số 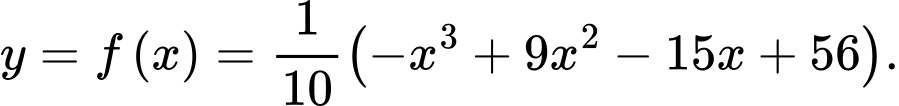 Đơn vị đo độ dài trên mỗi trục toạ độ là
Đơn vị đo độ dài trên mỗi trục toạ độ là 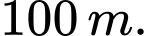 Trong công viên có một con đường chạy dọc theo đồ thị hàm số
Trong công viên có một con đường chạy dọc theo đồ thị hàm số 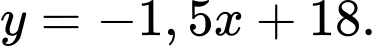 Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?
Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?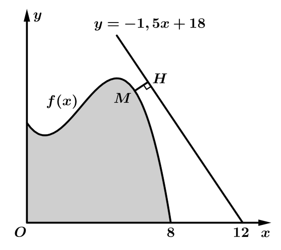
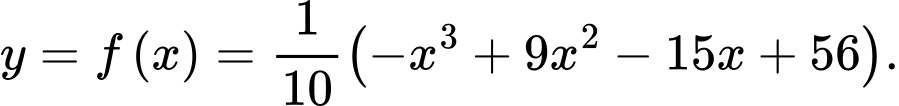 Đơn vị đo độ dài trên mỗi trục toạ độ là
Đơn vị đo độ dài trên mỗi trục toạ độ là 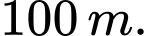 Trong công viên có một con đường chạy dọc theo đồ thị hàm số
Trong công viên có một con đường chạy dọc theo đồ thị hàm số 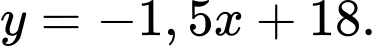 Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?
Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước Khoảng cách từ bến thuyền đến con đường này là ngắn nhất la bao nhiêu mét?Viết kết quả làm tròn đến hàng phần chục?
Gọi 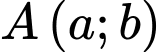
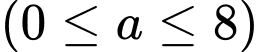 là điểm tượng trưng cho bến thuyền trên bờ hồ.
là điểm tượng trưng cho bến thuyền trên bờ hồ.
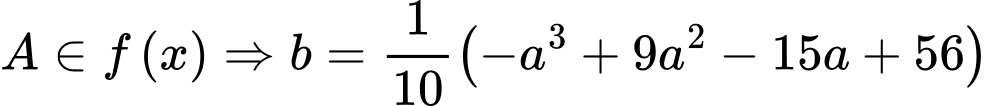 (1)
(1)
Khoảng cách từ bến thuyền đến con đường là: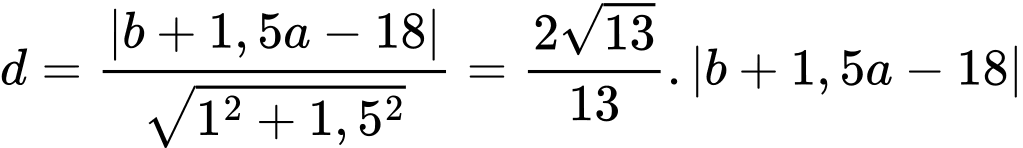 (2)
(2)
Từ (1) và (2), ta có: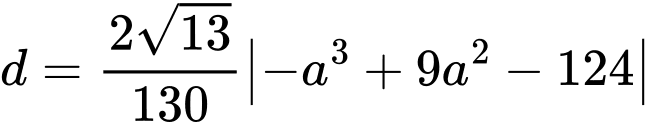
Đặt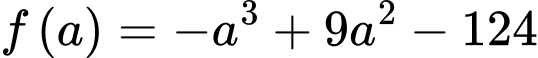 với
với 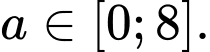
Có: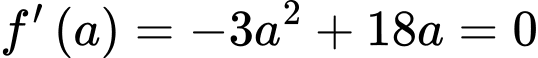
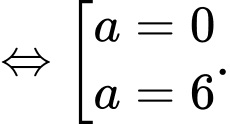
Bảng biến thiên:
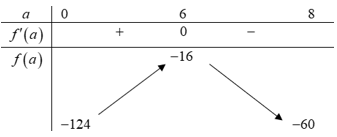
Để ngắn nhất
ngắn nhất  Hàm số
Hàm số 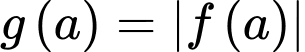 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Dựa vào bảng biến thiên, suy ra giá trị nhỏ nhất của là 16 khi
là 16 khi 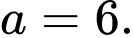
Vậy khoảng cách ngắn nhất từ bến thuyền đến con đường là: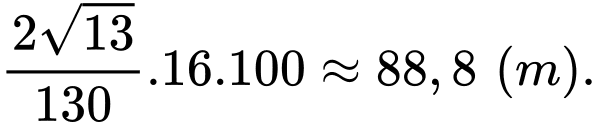
 là điểm tượng trưng cho bến thuyền trên bờ hồ.
là điểm tượng trưng cho bến thuyền trên bờ hồ.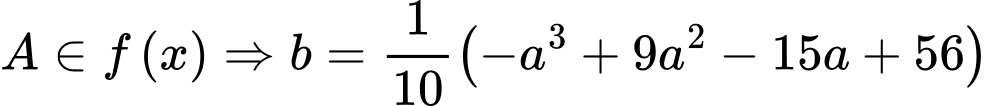 (1)
(1)Khoảng cách từ bến thuyền đến con đường là:
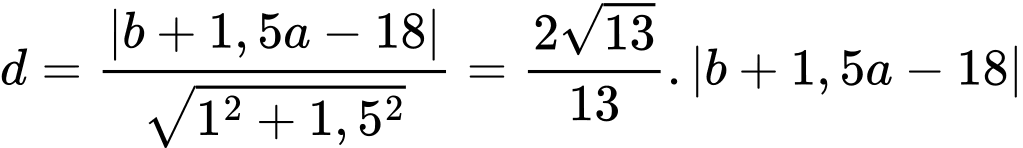 (2)
(2)Từ (1) và (2), ta có:
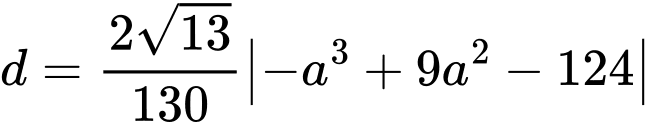
Đặt
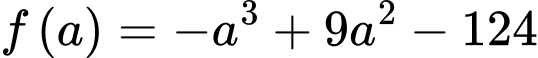 với
với 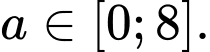
Có:
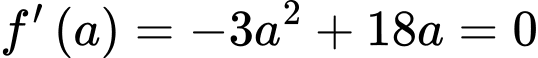
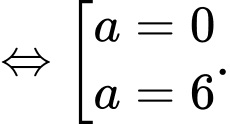
Bảng biến thiên:

Để
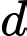 ngắn nhất
ngắn nhất 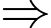 Hàm số
Hàm số 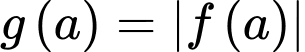 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.Dựa vào bảng biến thiên, suy ra giá trị nhỏ nhất của
 là 16 khi
là 16 khi 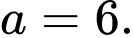
Vậy khoảng cách ngắn nhất từ bến thuyền đến con đường là:
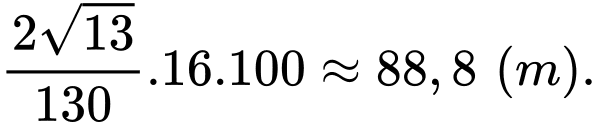
Câu 14 [390553]: Có ba khu dân cư 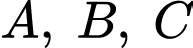 tạo thành một tam giác. Trên đoạn đường
tạo thành một tam giác. Trên đoạn đường 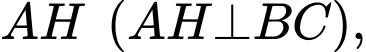 người ta xây dựng một cây xăng tại
người ta xây dựng một cây xăng tại 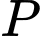 sao cho tổng khoảng cách
sao cho tổng khoảng cách 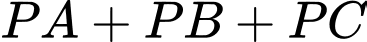 là ngắn nhất. Biết rằng
là ngắn nhất. Biết rằng 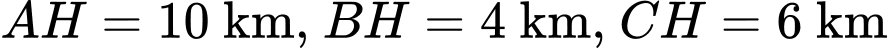 (như hình vẽ), tính độ dài
(như hình vẽ), tính độ dài 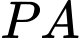 để xác định vị trí xây dựng cây xăng. Viết kết quả làm tròn đến một chữ số thập phân theo đơn vị km.
để xác định vị trí xây dựng cây xăng. Viết kết quả làm tròn đến một chữ số thập phân theo đơn vị km. 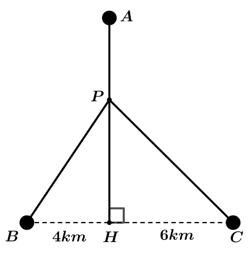
 tạo thành một tam giác. Trên đoạn đường
tạo thành một tam giác. Trên đoạn đường 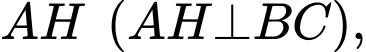 người ta xây dựng một cây xăng tại
người ta xây dựng một cây xăng tại 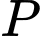 sao cho tổng khoảng cách
sao cho tổng khoảng cách 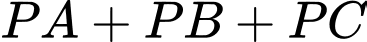 là ngắn nhất. Biết rằng
là ngắn nhất. Biết rằng 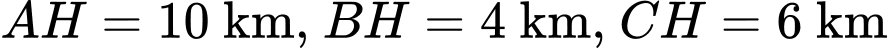 (như hình vẽ), tính độ dài
(như hình vẽ), tính độ dài 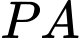 để xác định vị trí xây dựng cây xăng. Viết kết quả làm tròn đến một chữ số thập phân theo đơn vị km.
để xác định vị trí xây dựng cây xăng. Viết kết quả làm tròn đến một chữ số thập phân theo đơn vị km. 
Đáp số:………………………………
HD: Đặt 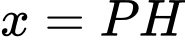
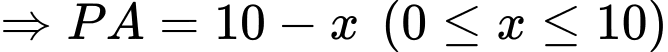
Khi đó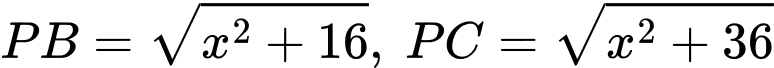
Suy ra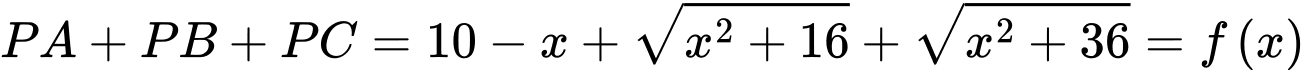
Ta có: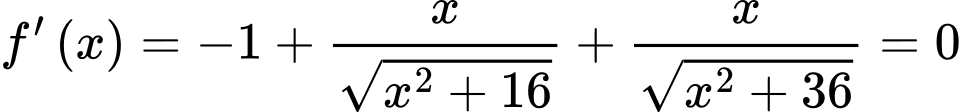
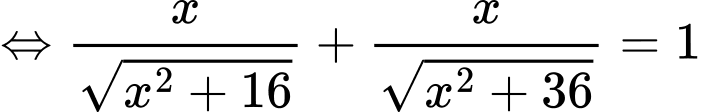
Sử dụng chức năng SHIFT-CALC ta tìm được nghiệm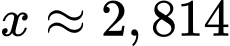 Lại có
Lại có 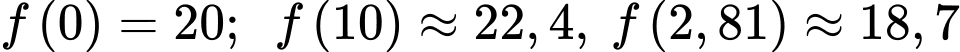
Khi đó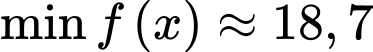 khi
khi 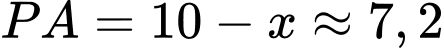
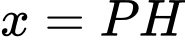
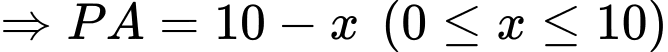
Khi đó
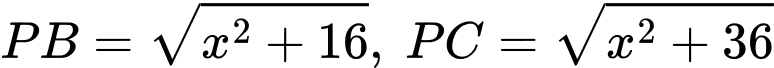
Suy ra
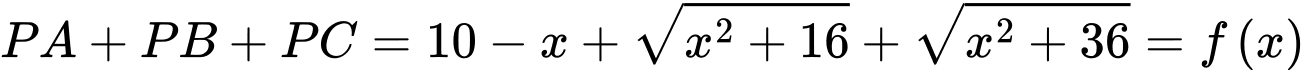
Ta có:
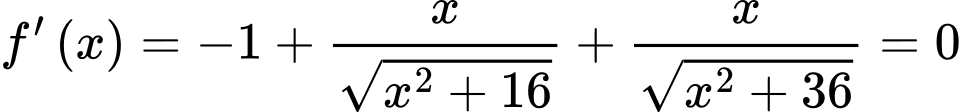
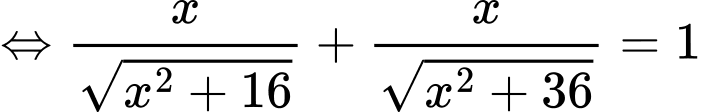

Sử dụng chức năng SHIFT-CALC ta tìm được nghiệm
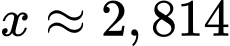 Lại có
Lại có 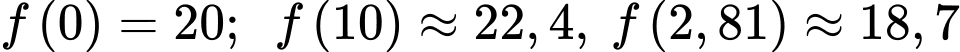
Khi đó
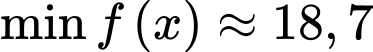 khi
khi 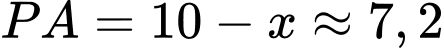
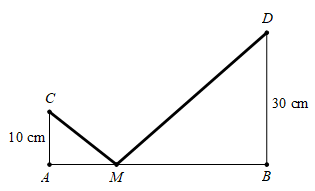
Câu 15 [31034]: Có hai chiếc cọc cao 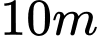 và
và 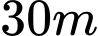 lần lượt đặt hai vị trí
lần lượt đặt hai vị trí 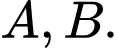 Biết khoảng cách giữa hai cọc bằng
Biết khoảng cách giữa hai cọc bằng 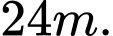 Người ta chọn một cái chốt ở vị trí
Người ta chọn một cái chốt ở vị trí 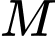 trên mặt đất nằm giữa hai chân cột để giăng giăng giây nối đến hai đỉnh
trên mặt đất nằm giữa hai chân cột để giăng giăng giây nối đến hai đỉnh  và
và 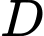 của cọc như hình vẽ. Hỏi ta phải đặt chốt ở vị trí nào để tổng độ dài của hai sợi dây đó là ngắn nhất?
của cọc như hình vẽ. Hỏi ta phải đặt chốt ở vị trí nào để tổng độ dài của hai sợi dây đó là ngắn nhất?
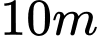 và
và 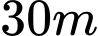 lần lượt đặt hai vị trí
lần lượt đặt hai vị trí 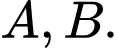 Biết khoảng cách giữa hai cọc bằng
Biết khoảng cách giữa hai cọc bằng 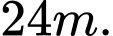 Người ta chọn một cái chốt ở vị trí
Người ta chọn một cái chốt ở vị trí 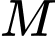 trên mặt đất nằm giữa hai chân cột để giăng giăng giây nối đến hai đỉnh
trên mặt đất nằm giữa hai chân cột để giăng giăng giây nối đến hai đỉnh  và
và 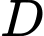 của cọc như hình vẽ. Hỏi ta phải đặt chốt ở vị trí nào để tổng độ dài của hai sợi dây đó là ngắn nhất?
của cọc như hình vẽ. Hỏi ta phải đặt chốt ở vị trí nào để tổng độ dài của hai sợi dây đó là ngắn nhất?
A, 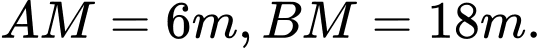
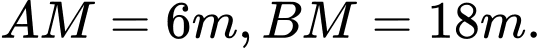
B, 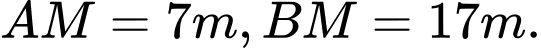
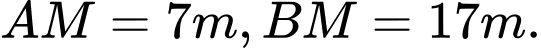
C, 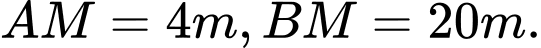
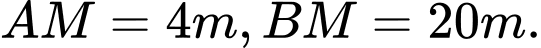
D, 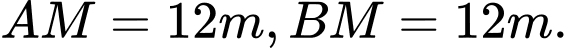
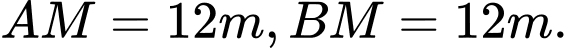
HD: Đặt 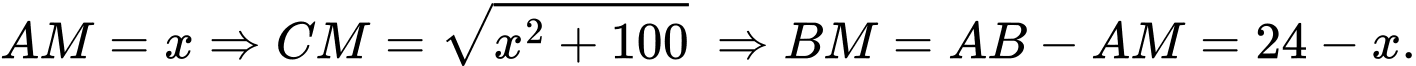
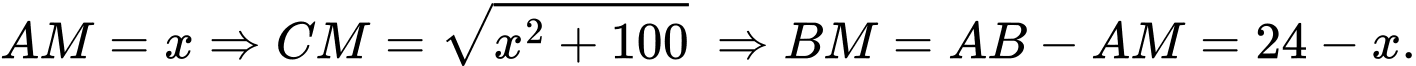
Tam giác 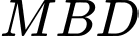 vuông tại
vuông tại 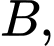 có
có 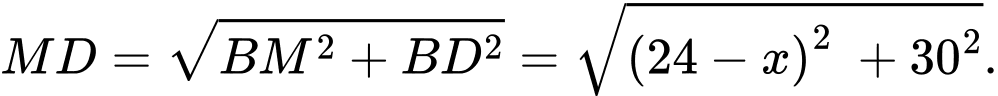
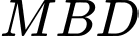 vuông tại
vuông tại  có
có 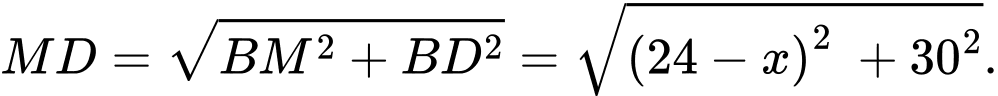
Khi đó 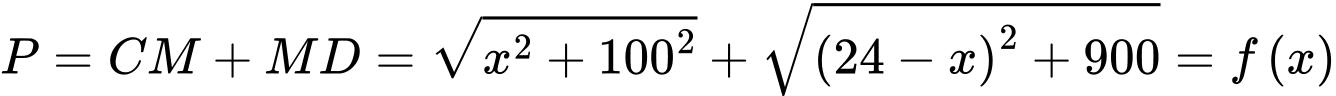
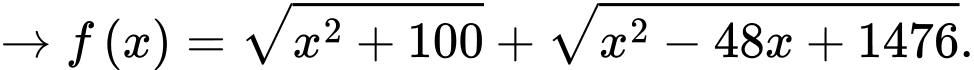
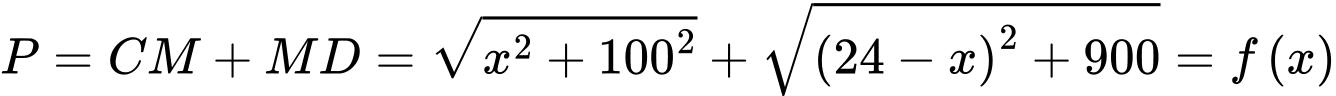
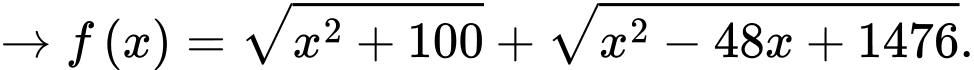
Xét hàm số 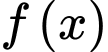 với
với 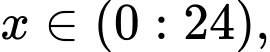 ta có
ta có 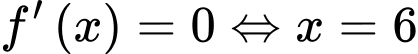 (thỏa mãn điều kiện )
(thỏa mãn điều kiện )
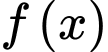 với
với 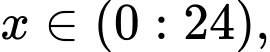 ta có
ta có 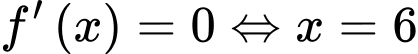 (thỏa mãn điều kiện )
(thỏa mãn điều kiện ) Dựa vào BBT, suy ra 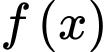 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất 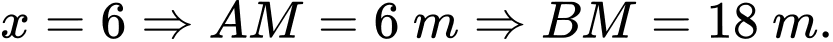 Chọn A.
Chọn A.
Đáp án: A 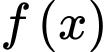 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất 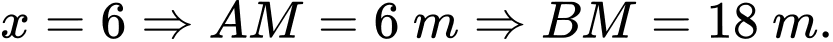 Chọn A.
Chọn A.