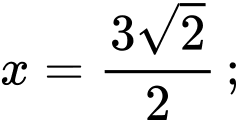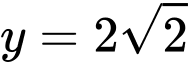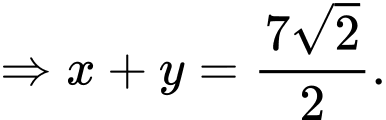Đáp án Bài tập tự luyện số 2
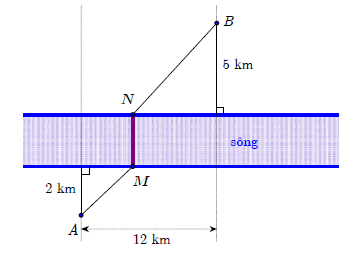
Câu 1 [31009]: Hai thành phố  và
và 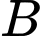 ngăn cách nhau bởi một con sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố
ngăn cách nhau bởi một con sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố 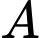 cách bờ sông
cách bờ sông 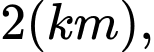 thành phố
thành phố 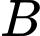 cách bờ sông
cách bờ sông 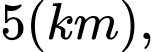 khoảng cách giữ đường thẳng đi qua
khoảng cách giữ đường thẳng đi qua 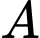 và đường thẳng đi qua
và đường thẳng đi qua 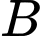 cùng vuông góc với bờ sông là
cùng vuông góc với bờ sông là 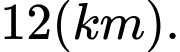 Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố
Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố 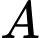 đến thành phố
đến thành phố 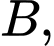 người ta xây cây cầu ở vị trí
người ta xây cây cầu ở vị trí 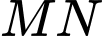 để quãng đường đi từ thành phố
để quãng đường đi từ thành phố 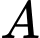 đến thành phố
đến thành phố  là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn
là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn  bằng
bằng
 và
và  ngăn cách nhau bởi một con sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố
ngăn cách nhau bởi một con sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố 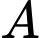 cách bờ sông
cách bờ sông 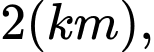 thành phố
thành phố 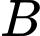 cách bờ sông
cách bờ sông 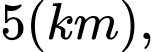 khoảng cách giữ đường thẳng đi qua
khoảng cách giữ đường thẳng đi qua 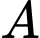 và đường thẳng đi qua
và đường thẳng đi qua 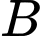 cùng vuông góc với bờ sông là
cùng vuông góc với bờ sông là 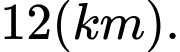 Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố
Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố  đến thành phố
đến thành phố  người ta xây cây cầu ở vị trí
người ta xây cây cầu ở vị trí  để quãng đường đi từ thành phố
để quãng đường đi từ thành phố  đến thành phố
đến thành phố  là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn
là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn  bằng
bằng 
A, 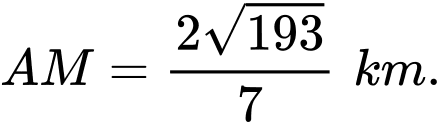
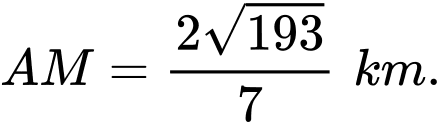
B, 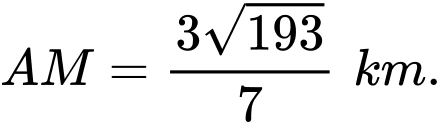
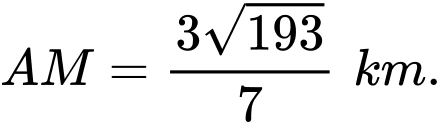
C, 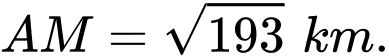
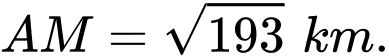
D, 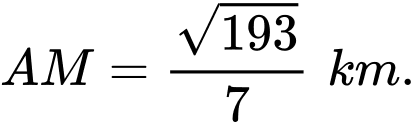
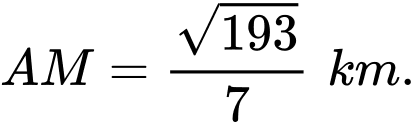
HD:
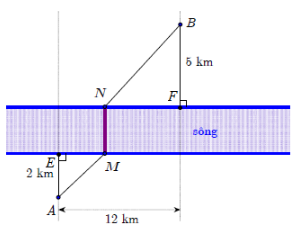
Với hình vẽ trên giả sử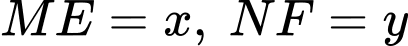 khi đó
khi đó 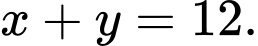
Khi đó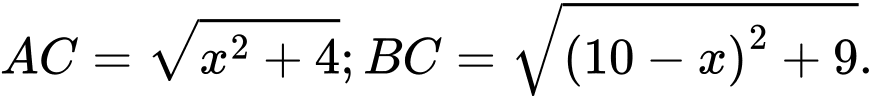
Quảng đường là:
là: 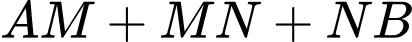 ngắn nhất khi
ngắn nhất khi  nhỏ nhất.
nhỏ nhất.
Ta có: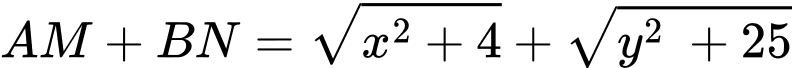
Đặt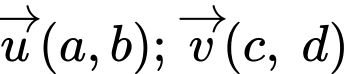 thì ta có
thì ta có 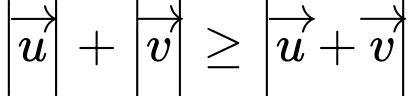
Do đó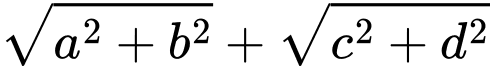
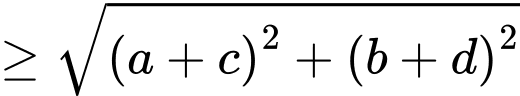 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi 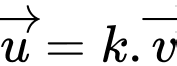
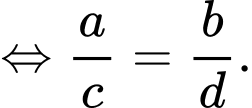
Áp dụng ta có: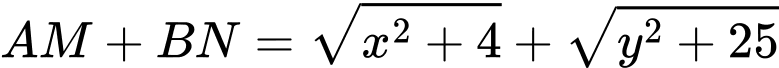
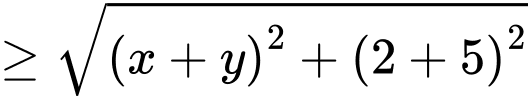
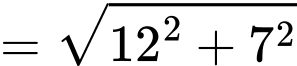
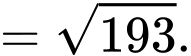
Dấu bằng xảy ra khi: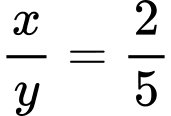
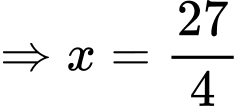
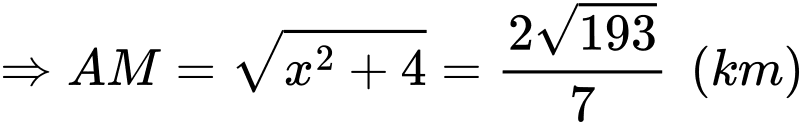 Đáp án: A
Đáp án: A

Với hình vẽ trên giả sử
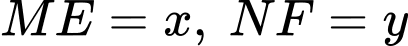 khi đó
khi đó 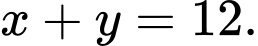
Khi đó
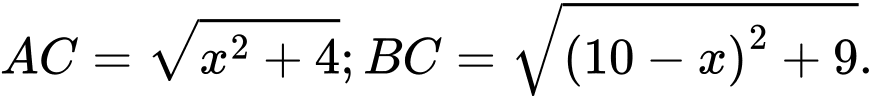
Quảng đường
 là:
là: 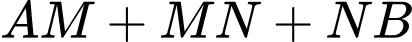 ngắn nhất khi
ngắn nhất khi  nhỏ nhất.
nhỏ nhất. Ta có:
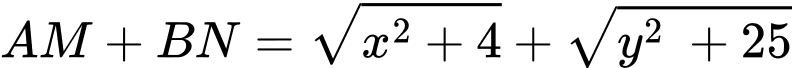
Đặt
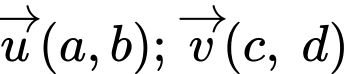 thì ta có
thì ta có 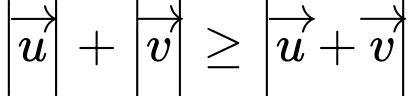
Do đó
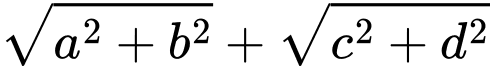
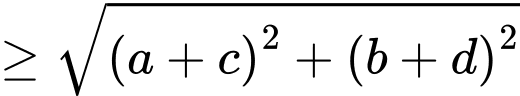 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi 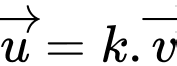
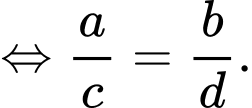
Áp dụng ta có:
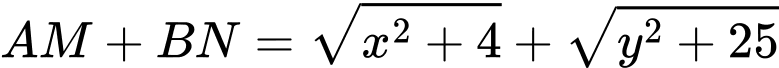
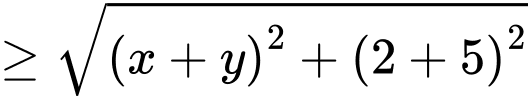
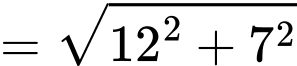
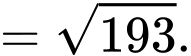
Dấu bằng xảy ra khi:
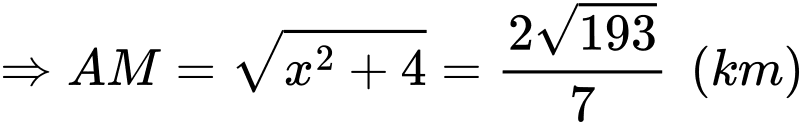 Đáp án: A
Đáp án: A
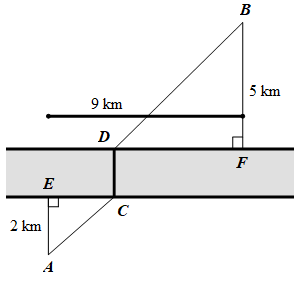
Câu 2 [31058]: Một người muốn kéo đường dây đi từ vị trí  đến vị trí
đến vị trí  nằm ở hai bên bờ sông bằng cách kéo từ
nằm ở hai bên bờ sông bằng cách kéo từ  đến
đến  , rồi từ
, rồi từ  kéo đến vị trí
kéo đến vị trí 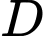 , sau đó từ
, sau đó từ 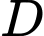 kéo đến
kéo đến 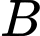 theo đường gấp khúc
theo đường gấp khúc 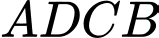 (các số liệu như hình vẽ). Biết rằng chi phí lắp đặt cho mỗi
(các số liệu như hình vẽ). Biết rằng chi phí lắp đặt cho mỗi 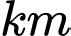 dây kéo từ
dây kéo từ 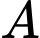 đến
đến  là
là 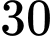 triệu đồng, từ
triệu đồng, từ 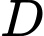 đến
đến 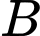 là
là 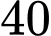 triệu đồng và chi phí lắp đặt cho mỗi dây kéo từ
triệu đồng và chi phí lắp đặt cho mỗi dây kéo từ  đến
đến 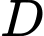 tại địa điểm nào cũng như nhau. Hỏi vị trí điểm
tại địa điểm nào cũng như nhau. Hỏi vị trí điểm  phải cách
phải cách 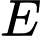 một khoảng là bao nhiêu để tổng chi phí lắp đặt là ít nhất. (Kết quả làm tròn đến hàng phần trăm).
một khoảng là bao nhiêu để tổng chi phí lắp đặt là ít nhất. (Kết quả làm tròn đến hàng phần trăm).
 đến vị trí
đến vị trí  nằm ở hai bên bờ sông bằng cách kéo từ
nằm ở hai bên bờ sông bằng cách kéo từ  đến
đến  , rồi từ
, rồi từ  kéo đến vị trí
kéo đến vị trí 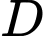 , sau đó từ
, sau đó từ 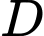 kéo đến
kéo đến 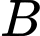 theo đường gấp khúc
theo đường gấp khúc 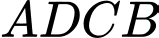 (các số liệu như hình vẽ). Biết rằng chi phí lắp đặt cho mỗi
(các số liệu như hình vẽ). Biết rằng chi phí lắp đặt cho mỗi 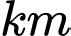 dây kéo từ
dây kéo từ 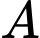 đến
đến  là
là 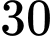 triệu đồng, từ
triệu đồng, từ 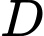 đến
đến 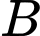 là
là 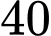 triệu đồng và chi phí lắp đặt cho mỗi dây kéo từ
triệu đồng và chi phí lắp đặt cho mỗi dây kéo từ  đến
đến 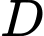 tại địa điểm nào cũng như nhau. Hỏi vị trí điểm
tại địa điểm nào cũng như nhau. Hỏi vị trí điểm  phải cách
phải cách 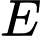 một khoảng là bao nhiêu để tổng chi phí lắp đặt là ít nhất. (Kết quả làm tròn đến hàng phần trăm).
một khoảng là bao nhiêu để tổng chi phí lắp đặt là ít nhất. (Kết quả làm tròn đến hàng phần trăm). 
A, 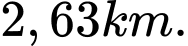
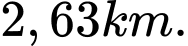
B, 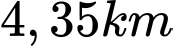 .
.
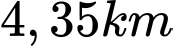 .
.C, 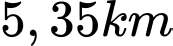 .
.
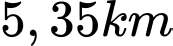 .
.D, 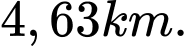
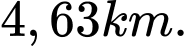
Đặt 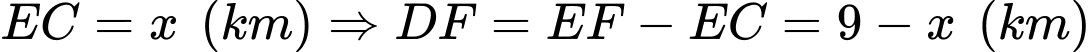
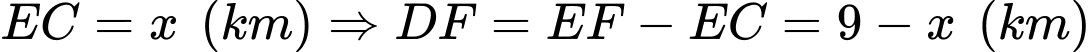
Tam giác 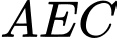 vuông tại
vuông tại 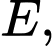 có
có 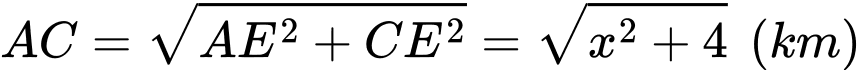
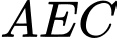 vuông tại
vuông tại 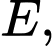 có
có 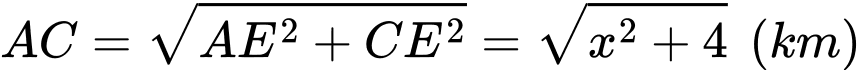
Tam giác  vuông tại
vuông tại  có
có 
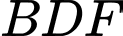 vuông tại
vuông tại 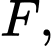 có
có 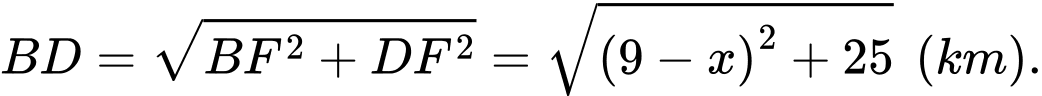
Vậy tổng chi phí để lắp đặt quãng đường từ  và
và 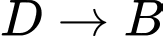 là
là 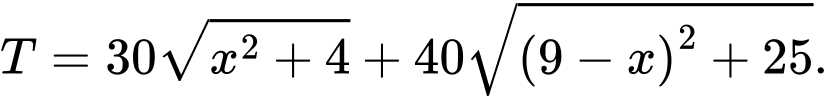
 và
và  là
là 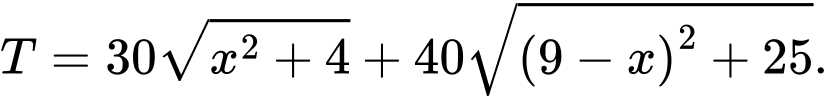
Xét hàm số 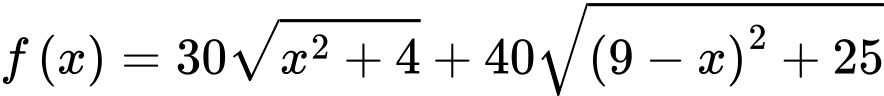 với
với  có
có 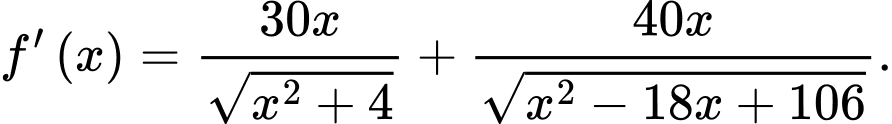
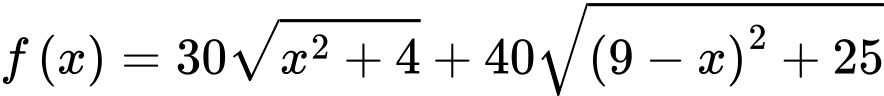 với
với  có
có 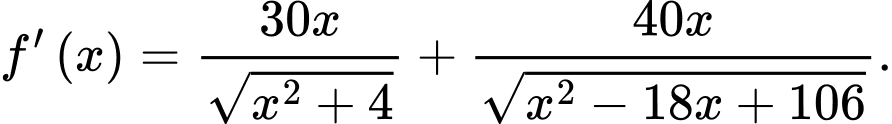
Phương trình 
Vậy hàm số đạt giá trị nhỏ nhất khi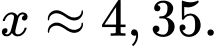 Chọn B.
Chọn B.
Đáp án: B 
Vậy hàm số đạt giá trị nhỏ nhất khi
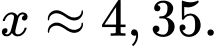 Chọn B.
Chọn B.
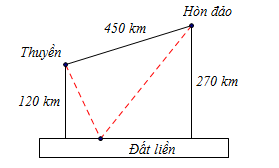
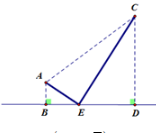
Câu 3 [31087]: Một con thuyền đang ở ngoài khơi cách đất liền 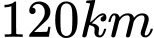 và cách hòn đảo
và cách hòn đảo 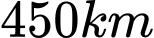 . Hòn đảo cách đất liền
. Hòn đảo cách đất liền 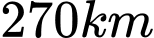 . Con thuyền cần cập bến để tiếp nhiên liệu rồi mang quà Tết ra đảo. Quãng đường ngắn nhất mà con thuyền đó đi là (làm tròn đến hàng đơn vị)
. Con thuyền cần cập bến để tiếp nhiên liệu rồi mang quà Tết ra đảo. Quãng đường ngắn nhất mà con thuyền đó đi là (làm tròn đến hàng đơn vị)
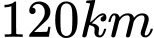 và cách hòn đảo
và cách hòn đảo 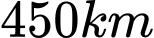 . Hòn đảo cách đất liền
. Hòn đảo cách đất liền 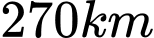 . Con thuyền cần cập bến để tiếp nhiên liệu rồi mang quà Tết ra đảo. Quãng đường ngắn nhất mà con thuyền đó đi là (làm tròn đến hàng đơn vị)
. Con thuyền cần cập bến để tiếp nhiên liệu rồi mang quà Tết ra đảo. Quãng đường ngắn nhất mà con thuyền đó đi là (làm tròn đến hàng đơn vị)
A, 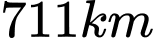 .
.
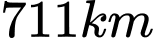 .
.B, 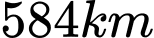 .
.
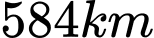 .
.C, 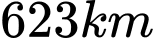 .
.
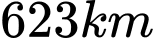 .
.D, 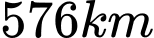 .
.
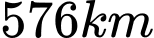 .
.
Thuyền ở vị trí  sẽ đi đến
sẽ đi đến 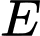 (đất liền) và đi ra đảo
(đất liền) và đi ra đảo 
Bài toán yêu cầu tìm GTNN của quãng đường
Chuẩn hoá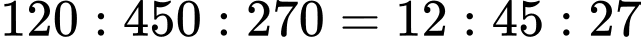
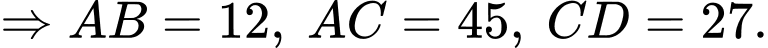
Cách 1: Đặt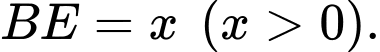 Ta có:
Ta có: 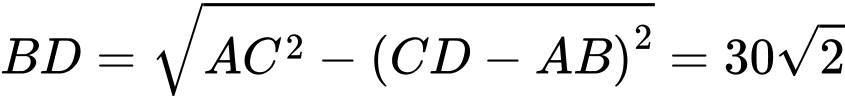
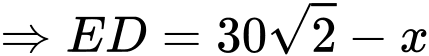
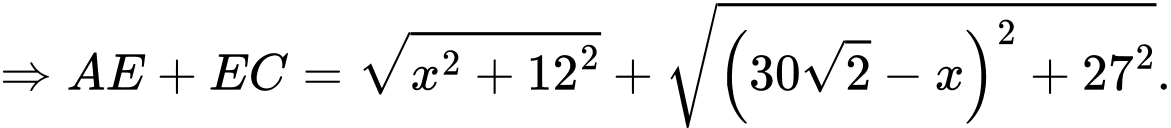
Đặt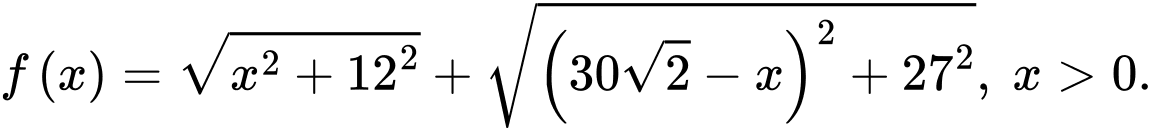
Khảo sát hàm số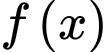 trên khoảng
trên khoảng 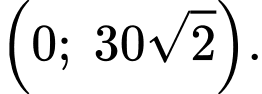
Cách 2: Gọi là điểm đối xứng với
là điểm đối xứng với 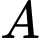 qua
qua 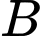 và
và 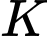 là điểm đối xứng với
là điểm đối xứng với  qua
qua  Vì
Vì 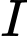 là hình chiếu của
là hình chiếu của 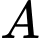 lên
lên 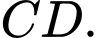
Khi đó,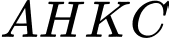 là hình thang cân và
là hình thang cân và  Ta thấy
Ta thấy  nên
nên 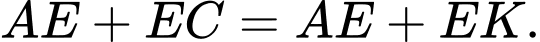
Để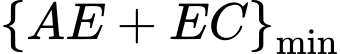
 và điều đó có nghĩa là
và điều đó có nghĩa là 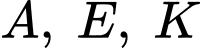 thẳng hàng.
thẳng hàng.
Vì thế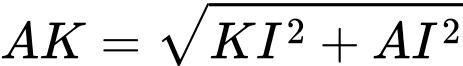
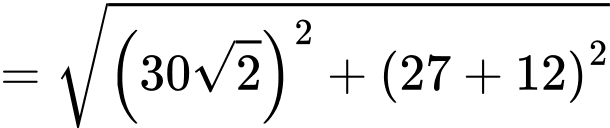

Hay quãng đường ngắn nhất cần tính là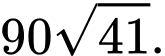 Chọn D Đáp án: D
Chọn D Đáp án: D
 sẽ đi đến
sẽ đi đến  (đất liền) và đi ra đảo
(đất liền) và đi ra đảo 
Bài toán yêu cầu tìm GTNN của quãng đường

Chuẩn hoá
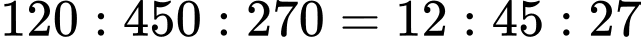
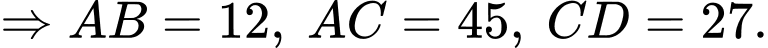

Cách 1: Đặt
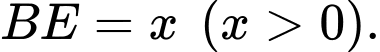 Ta có:
Ta có: 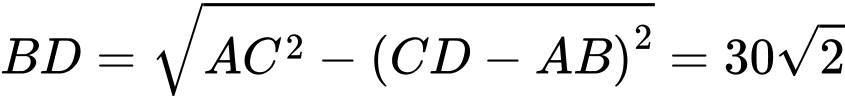
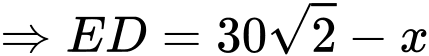
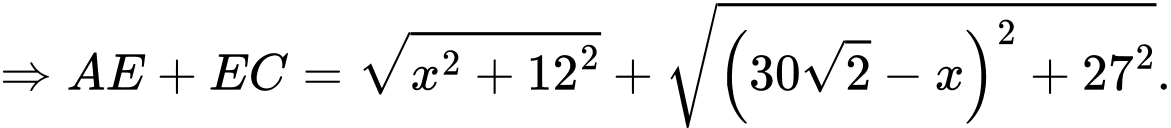
Đặt
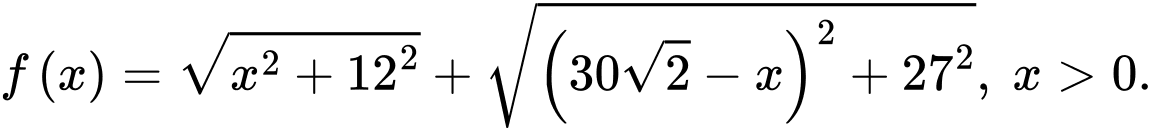
Khảo sát hàm số
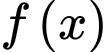 trên khoảng
trên khoảng 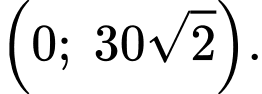
Cách 2: Gọi
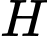 là điểm đối xứng với
là điểm đối xứng với 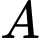 qua
qua 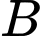 và
và 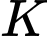 là điểm đối xứng với
là điểm đối xứng với  qua
qua  Vì
Vì 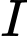 là hình chiếu của
là hình chiếu của 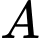 lên
lên 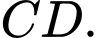
Khi đó,
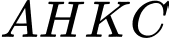 là hình thang cân và
là hình thang cân và  Ta thấy
Ta thấy  nên
nên 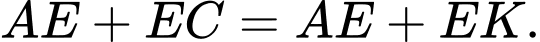
Để
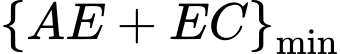
 và điều đó có nghĩa là
và điều đó có nghĩa là 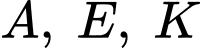 thẳng hàng.
thẳng hàng. Vì thế
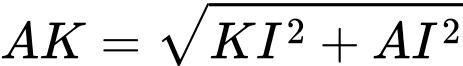
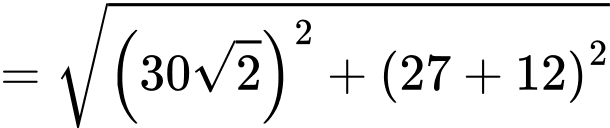

Hay quãng đường ngắn nhất cần tính là
 Chọn D Đáp án: D
Chọn D Đáp án: D
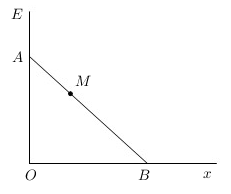
Câu 4 [358940]: Có hai xã  cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là
cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là 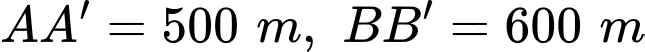 và người ta đo được
và người ta đo được 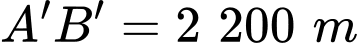 (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí
(Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí 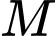 của trạm cung cấp nước sạch đó trên đoạn
của trạm cung cấp nước sạch đó trên đoạn 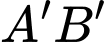 sao cho tổng khoảng cách từ hai xã đến vị trí
sao cho tổng khoảng cách từ hai xã đến vị trí 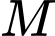 là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).
là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).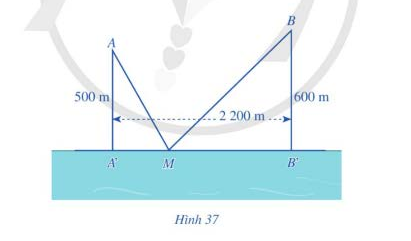
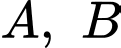 cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là
cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là 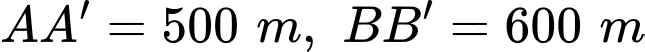 và người ta đo được
và người ta đo được 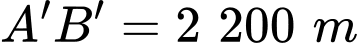 (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí
(Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí 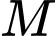 của trạm cung cấp nước sạch đó trên đoạn
của trạm cung cấp nước sạch đó trên đoạn 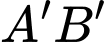 sao cho tổng khoảng cách từ hai xã đến vị trí
sao cho tổng khoảng cách từ hai xã đến vị trí 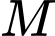 là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).
là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó (làm tròn kết quả đến hàng đơn vị của mét).
Điền đáp án: 2460.
Đặt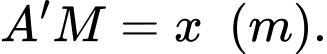
Suy ra: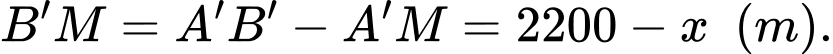
Rõ ràng,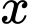 phảithỏa mãn điều kiện
phảithỏa mãn điều kiện 
Áp dụng định lí Pythagore ta tính được: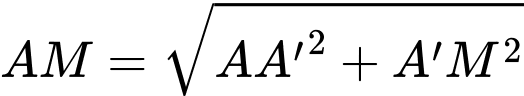
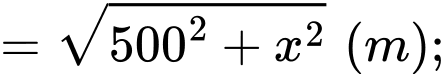
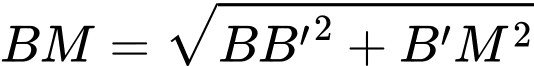
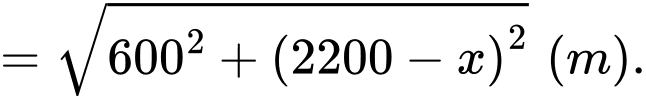
Tổng khoảng cách từ hai vị trí đến vị trí
đến vị trí  là:
là: 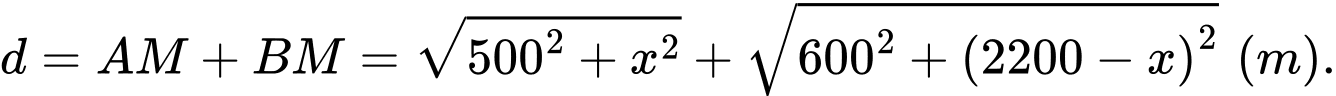
Xét hàm số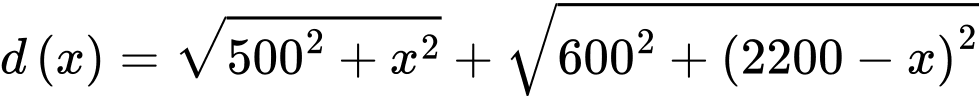 với
với 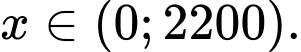
Ta có: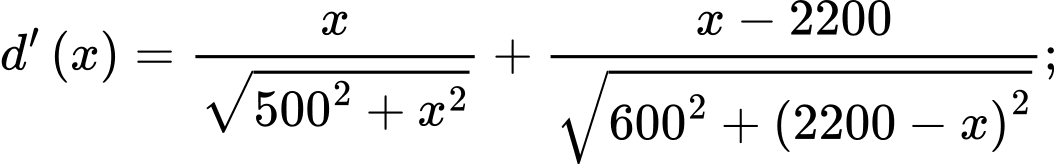 Trên khoảng
Trên khoảng 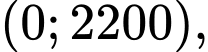 ta thấy
ta thấy 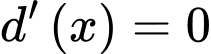 khi
khi 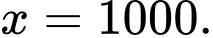
Bảng biến thiên:
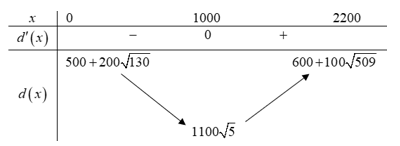
Dựa vào bảng biếnthiên, ta thấy hàm số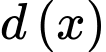 đạt giá trị nhỏ nhất bằng
đạt giá trị nhỏ nhất bằng 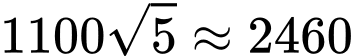 khi
khi 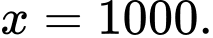
Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là 2460 m.
Đặt
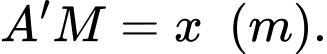
Suy ra:
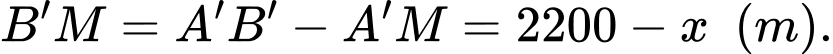
Rõ ràng,
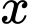 phảithỏa mãn điều kiện
phảithỏa mãn điều kiện 
Áp dụng định lí Pythagore ta tính được:
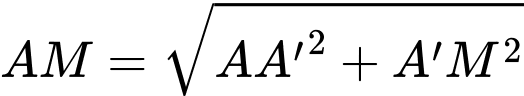
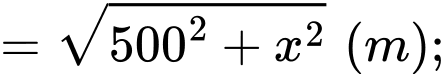
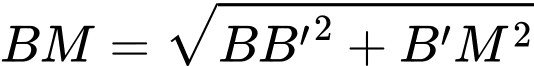
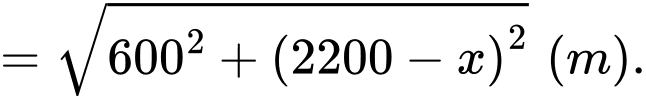
Tổng khoảng cách từ hai vị trí
 đến vị trí
đến vị trí  là:
là: 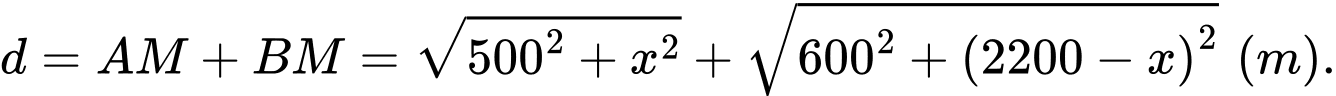
Xét hàm số
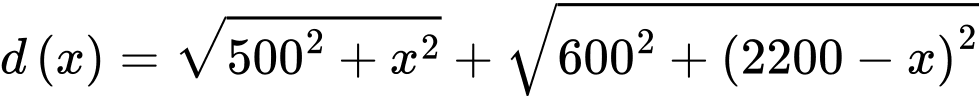 với
với 
Ta có:
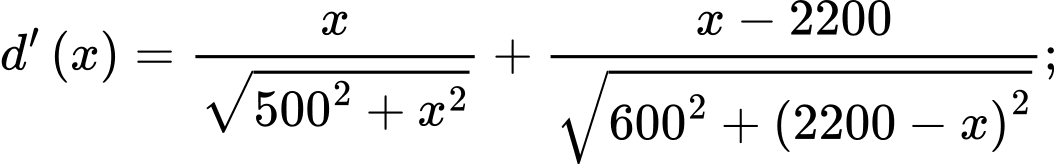 Trên khoảng
Trên khoảng 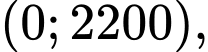 ta thấy
ta thấy 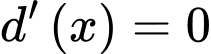 khi
khi 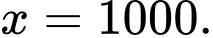
Bảng biến thiên:

Dựa vào bảng biếnthiên, ta thấy hàm số
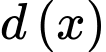 đạt giá trị nhỏ nhất bằng
đạt giá trị nhỏ nhất bằng 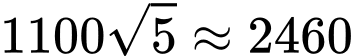 khi
khi 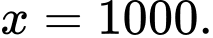
Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là 2460 m.
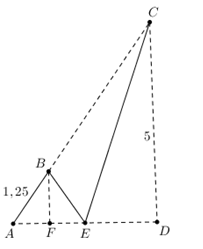
Câu 5 [31062]: Một người lính đặc công thực hiện bơi luyện tập từ vị trí 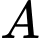 trên bờ biển đến một cái thuyền đang neo đậu ở vị trí
trên bờ biển đến một cái thuyền đang neo đậu ở vị trí  trên biển. Sau khi bơi được
trên biển. Sau khi bơi được 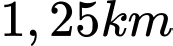 do khác nước người này đã bơi vào vị trí
do khác nước người này đã bơi vào vị trí 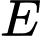 trên bờ để uống nước rồi mới từ
trên bờ để uống nước rồi mới từ 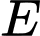 bơi đến
bơi đến  . Hãy tính xem người lính này phải bơi ít nhất bao nhiêu
. Hãy tính xem người lính này phải bơi ít nhất bao nhiêu 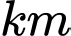 . Biết rằng khoảng cách từ
. Biết rằng khoảng cách từ 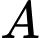 đến
đến  là
là 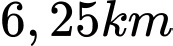 và khoảng cách ngắn nhất từ
và khoảng cách ngắn nhất từ  vào bờ là
vào bờ là 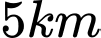 .
.
 trên bờ biển đến một cái thuyền đang neo đậu ở vị trí
trên bờ biển đến một cái thuyền đang neo đậu ở vị trí  trên biển. Sau khi bơi được
trên biển. Sau khi bơi được 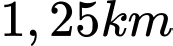 do khác nước người này đã bơi vào vị trí
do khác nước người này đã bơi vào vị trí 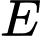 trên bờ để uống nước rồi mới từ
trên bờ để uống nước rồi mới từ 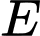 bơi đến
bơi đến  . Hãy tính xem người lính này phải bơi ít nhất bao nhiêu
. Hãy tính xem người lính này phải bơi ít nhất bao nhiêu 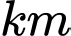 . Biết rằng khoảng cách từ
. Biết rằng khoảng cách từ 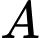 đến
đến  là
là 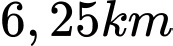 và khoảng cách ngắn nhất từ
và khoảng cách ngắn nhất từ  vào bờ là
vào bờ là 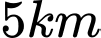 .
.
A, 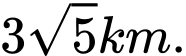
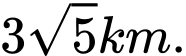
B, 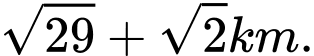
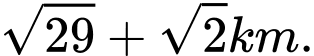
C, 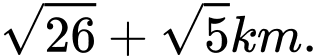
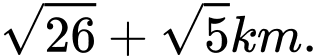
D, 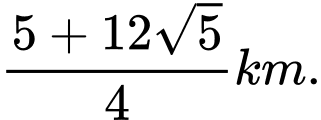
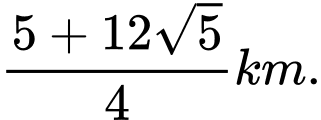
Tam giác  vuông có
vuông có  và
và 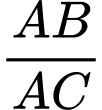
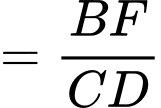
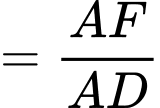
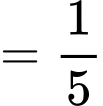
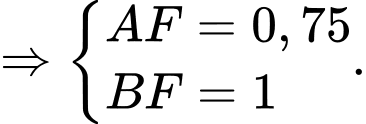
Đặt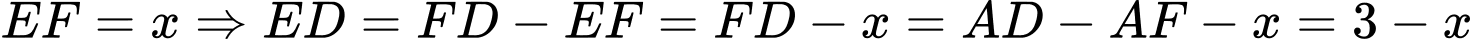
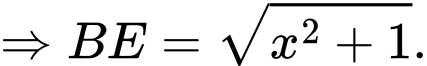
Tam giác vuông tại
vuông tại  có
có 
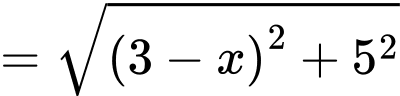

Khi đó,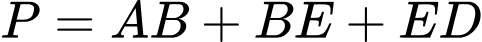
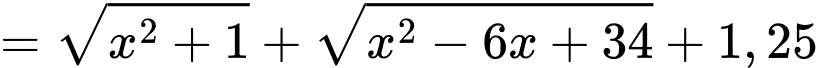
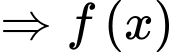
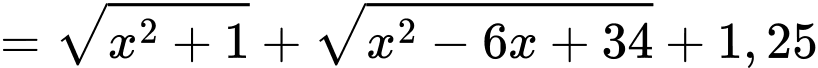
Xét hàm số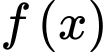 với
với 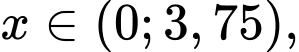 ta có
ta có 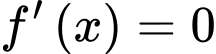
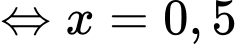 (thoả mãn điều kiện).
(thoả mãn điều kiện).
Dựa vào BBT, suy ra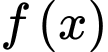 đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là 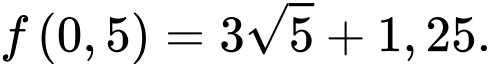 Chọn D Đáp án: D
Chọn D Đáp án: D
 vuông có
vuông có  và
và 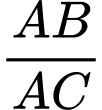
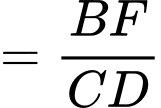
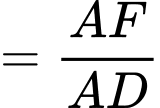
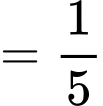
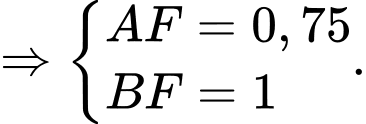
Đặt
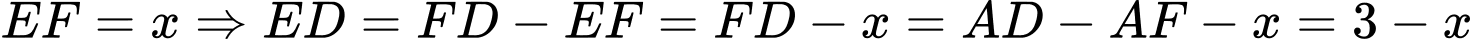
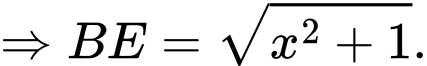
Tam giác
 vuông tại
vuông tại 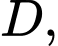 có
có 
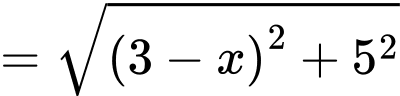

Khi đó,
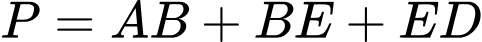
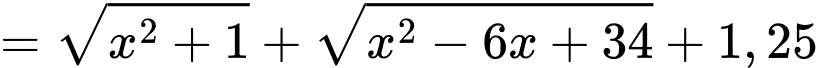
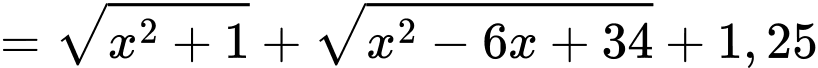
Xét hàm số
 với
với 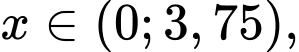 ta có
ta có 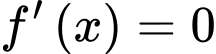
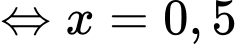 (thoả mãn điều kiện).
(thoả mãn điều kiện). Dựa vào BBT, suy ra
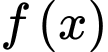 đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là 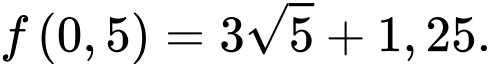 Chọn D Đáp án: D
Chọn D Đáp án: D
Câu 6 [31043]: Trên sân bay có một máy bay cất cánh trên đường băng 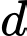 (từ trái sang phải) và bắt đầu rời mặt đất tại điểm
(từ trái sang phải) và bắt đầu rời mặt đất tại điểm  . Gọi
. Gọi 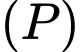 là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là đường băng
là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là đường băng 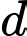 của máy bay. Dọc theo đường băng
của máy bay. Dọc theo đường băng 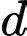 cách vị trị máy bay cất cánh
cách vị trị máy bay cất cánh  một khoảng
một khoảng 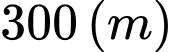 về phía bên phải có 1 người quan sát
về phía bên phải có 1 người quan sát 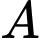 . Biết máy bay chuyển động trong mặt phẳng
. Biết máy bay chuyển động trong mặt phẳng 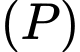 và độ cao y của máy bay xác định bởi phương trình
và độ cao y của máy bay xác định bởi phương trình 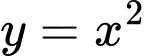 (với
(với 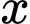 là độ dời của máy bay dọc theo đường thẳng
là độ dời của máy bay dọc theo đường thẳng 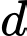 và tính từ
và tính từ  ). Khoảng cách ngắn nhất từ người
). Khoảng cách ngắn nhất từ người 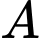 (đứng cố định) đến máy bay là
(đứng cố định) đến máy bay là
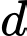 (từ trái sang phải) và bắt đầu rời mặt đất tại điểm
(từ trái sang phải) và bắt đầu rời mặt đất tại điểm  . Gọi
. Gọi 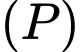 là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là đường băng
là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là đường băng 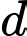 của máy bay. Dọc theo đường băng
của máy bay. Dọc theo đường băng 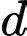 cách vị trị máy bay cất cánh
cách vị trị máy bay cất cánh  một khoảng
một khoảng 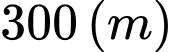 về phía bên phải có 1 người quan sát
về phía bên phải có 1 người quan sát 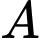 . Biết máy bay chuyển động trong mặt phẳng
. Biết máy bay chuyển động trong mặt phẳng 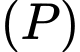 và độ cao y của máy bay xác định bởi phương trình
và độ cao y của máy bay xác định bởi phương trình 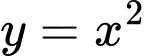 (với
(với 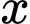 là độ dời của máy bay dọc theo đường thẳng
là độ dời của máy bay dọc theo đường thẳng 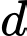 và tính từ
và tính từ  ). Khoảng cách ngắn nhất từ người
). Khoảng cách ngắn nhất từ người 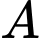 (đứng cố định) đến máy bay là
(đứng cố định) đến máy bay là A, 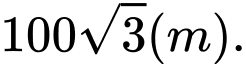
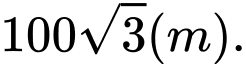
B, 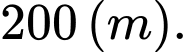
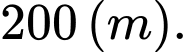
C, 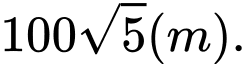
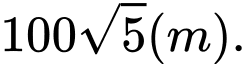
D, 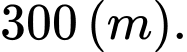
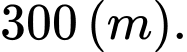
Lấy 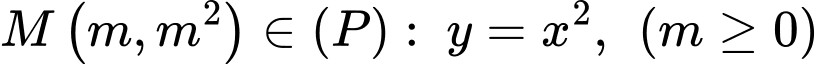
Ta có: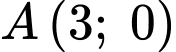
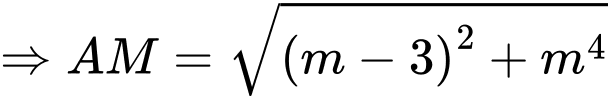
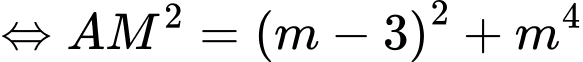
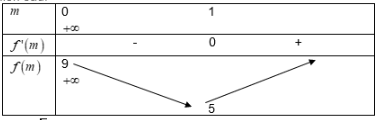
Xét hàm số: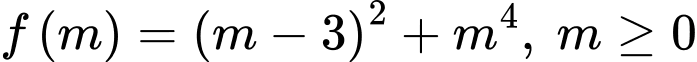
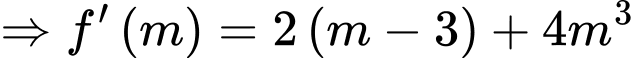

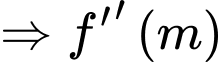
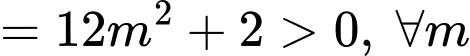
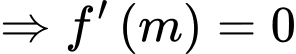 có nghiệm duy nhất
có nghiệm duy nhất 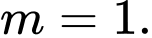
Ta có bảng biến thiên sau
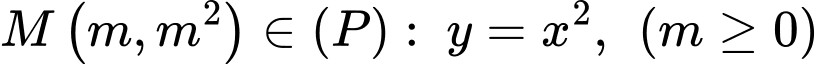
Ta có:
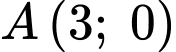
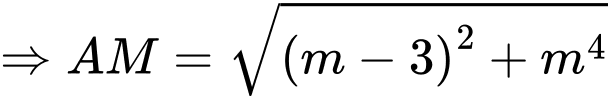
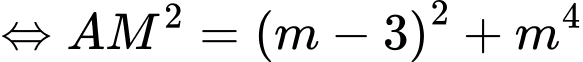
Xét hàm số:
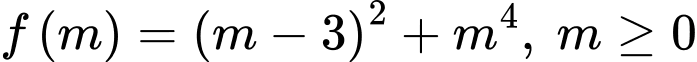
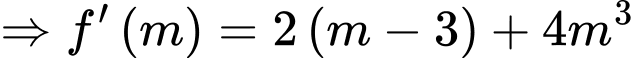

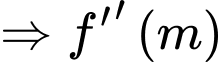
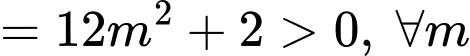
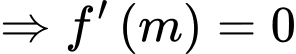 có nghiệm duy nhất
có nghiệm duy nhất 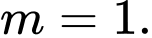
Ta có bảng biến thiên sau

 Đáp án: C
Đáp án: C
Câu 7 [31012]: Một màn ảnh hình chữ nhật cao 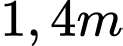 được đặt ở độ cao
được đặt ở độ cao 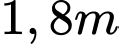 so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác đinh khoảng cách đó.
so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác đinh khoảng cách đó.
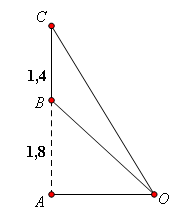
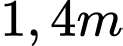 được đặt ở độ cao
được đặt ở độ cao 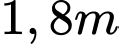 so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác đinh khoảng cách đó.
so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác đinh khoảng cách đó.
A, 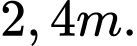
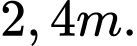
B, 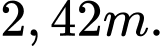
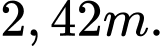
C, 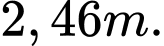
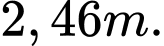
D, 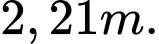
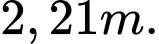
Với bài toán này, ta cần xác định 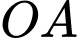 để góc
để góc  lớn nhất. Điều này xảy ra
lớn nhất. Điều này xảy ra  lớn nhất.
lớn nhất.
Đặt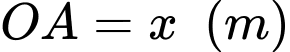 với
với 
Ta có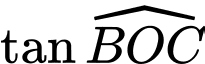
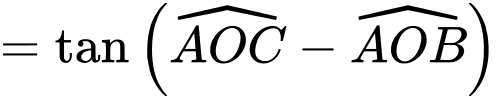
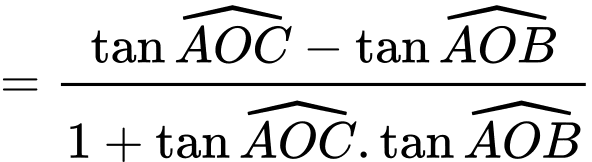
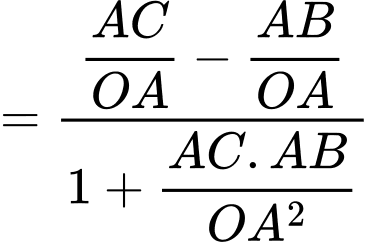
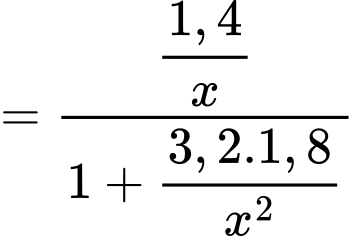
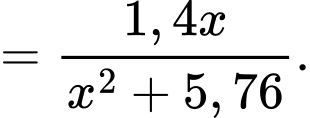
Xét hàm số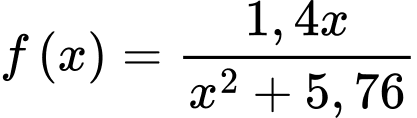 trên khoảng
trên khoảng 
Ta có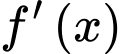
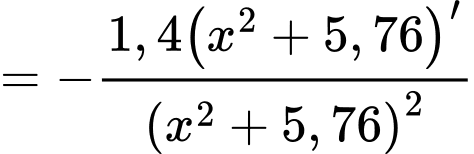
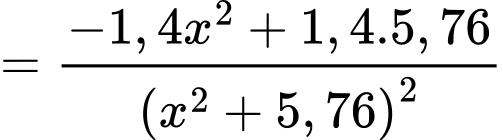
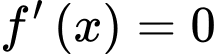
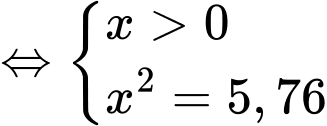
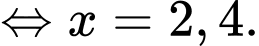
Tính các giá trị tại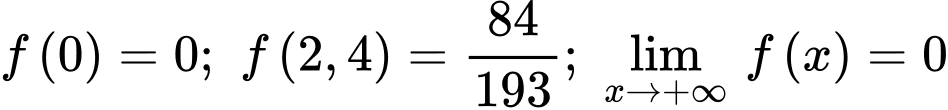
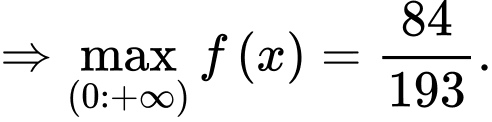
Vậy khoảng cách cần tìm là
cần tìm là 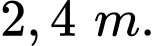 Đáp án: A
Đáp án: A
 để góc
để góc  lớn nhất. Điều này xảy ra
lớn nhất. Điều này xảy ra  lớn nhất.
lớn nhất. Đặt
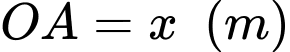 với
với 
Ta có
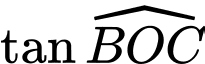
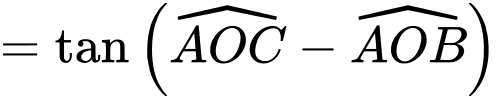
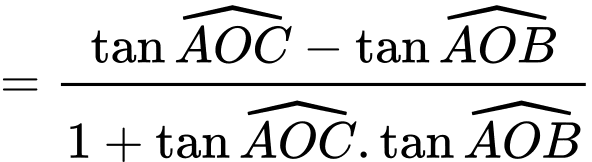
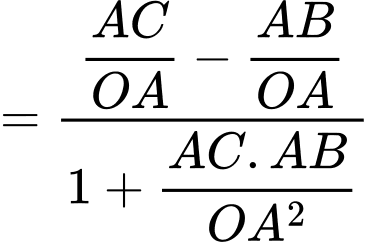
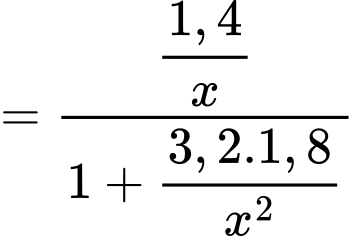
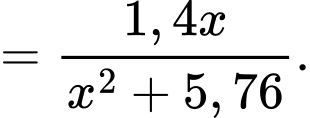
Xét hàm số
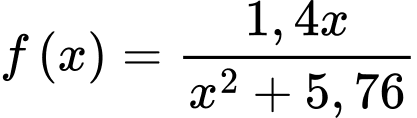 trên khoảng
trên khoảng 
Ta có
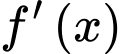
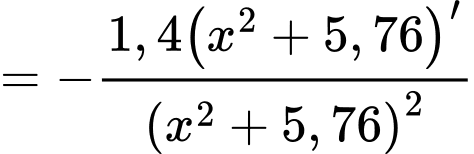
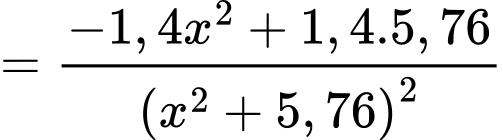
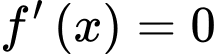
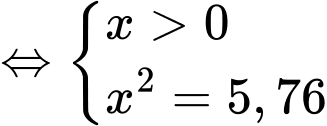
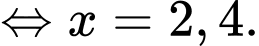
Tính các giá trị tại
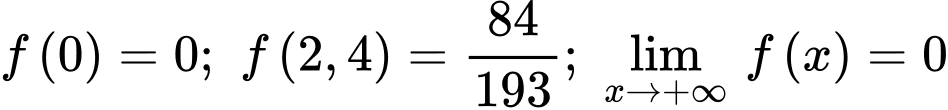
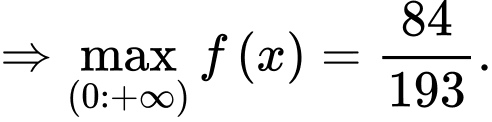
Vậy khoảng cách
 cần tìm là
cần tìm là 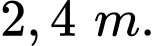 Đáp án: A
Đáp án: A
Câu 8 [390554]: Một người quan sát đang đứng ở điểm 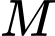 cách con đường một khoảng
cách con đường một khoảng 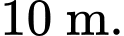 Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn
Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn 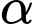 của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ.
của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ. 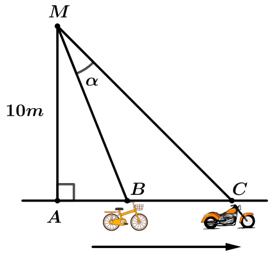
 cách con đường một khoảng
cách con đường một khoảng 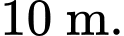 Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn
Tại một thời điểm nào đó, có một chiếc xe đạp và xe máy cùng xuất phát tại điểm A và chạy về cùng một hướng (xem hình vẽ bên), biết rằng vận tốc của xe máy gấp bốn lần vận tốc xe đạp. Tìm giá trị lớn nhất của góc nhìn 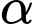 của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ.
của người quan sát với hai chiếc xe đó. Viết kết quả làm tròn đến hàng đơn vị theo đơn vị độ. 
Đáp số:……………………..
Đặt 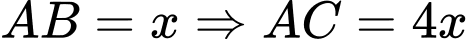 (vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)
(vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)
Ta có: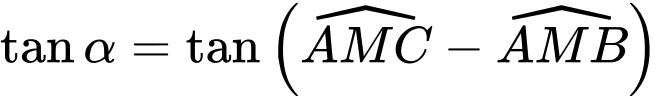
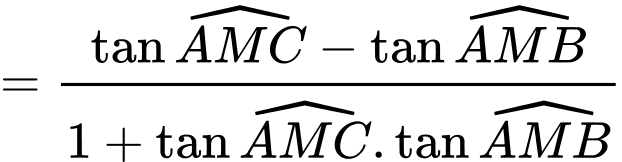
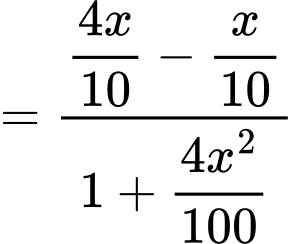
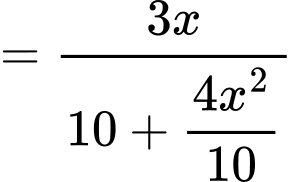
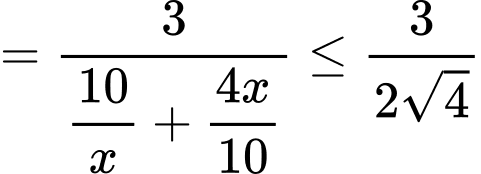
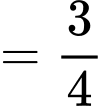
Do đó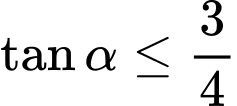

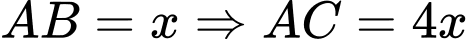 (vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)
(vì vận tốc của xe máy gấp 4 lần vân tốc xe đạp)Ta có:
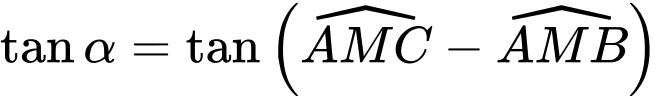
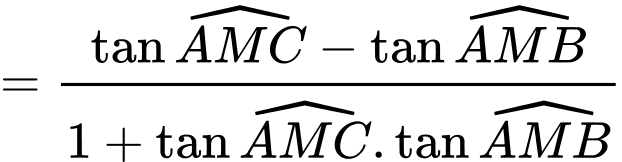
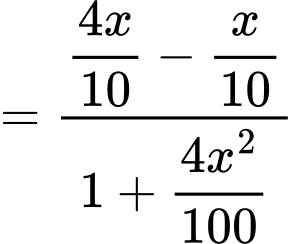
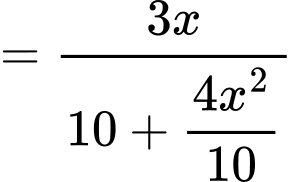
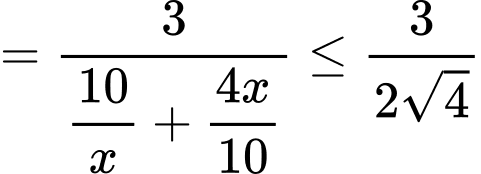
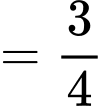
Do đó
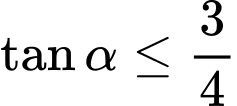

Câu 9 [390555]: Bạn Nam có thể chèo thuyền với vận tốc  và có thể đi bộ với vận tốc
và có thể đi bộ với vận tốc  Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị.
Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị. 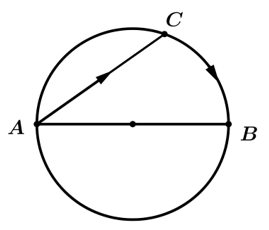
 và có thể đi bộ với vận tốc
và có thể đi bộ với vận tốc  Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị.
Hiện tại Nam đang ở vị trí A trên bờ hồ bán kính 2 km. Nam sẽ chèo thuyền đến điểm C, sau đó đi bộ quanh bờ đến điểm B đối diện với A (như hình vẽ). Thời gian dài nhất bạn Nam đi từ A đến C rồi đến B là bao nhiều phút?. Viết kết quả làm tròn đến hàng đơn vị. 
Đáp số:……………………………
Quãng đường Nam đi là: 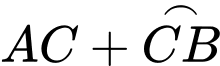
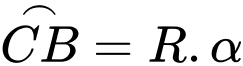
Gọi tâm hồ là
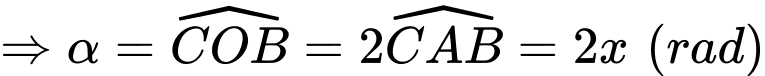
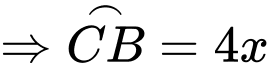
Ta có: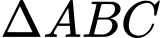 có
có  là đường kính của đường tròn ngoại tiếp tam giác
là đường kính của đường tròn ngoại tiếp tam giác
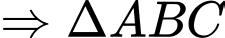 vuông tại
vuông tại 
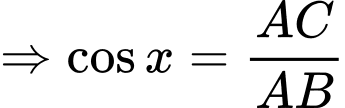

Tổng thời gian Nam đi là: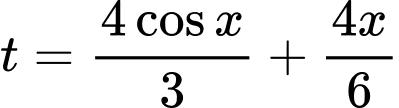 (giờ)
(giờ)
Xét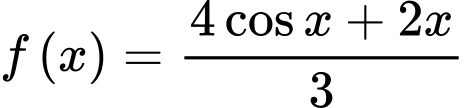 với
với 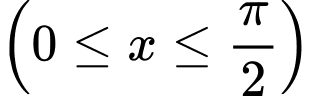
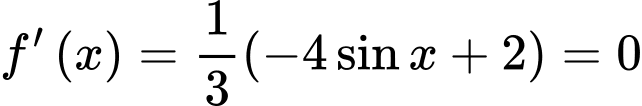
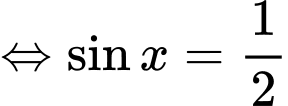
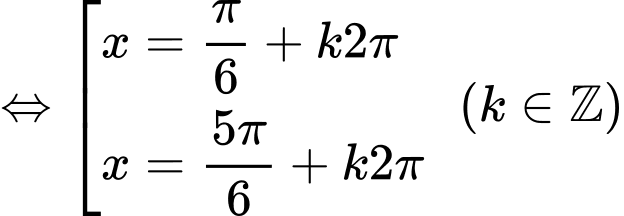
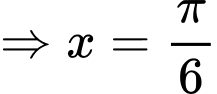
Ta bấm máy, nhận thấy bạn Nam đi từ A đến B với khoảng thời gian lớn nhất tại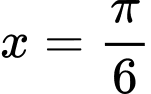 và
và 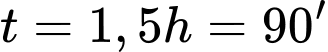
Đáp án: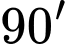
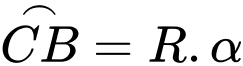
Gọi tâm hồ là

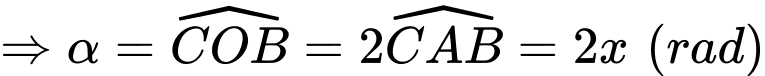
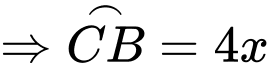
Ta có:
 có
có  là đường kính của đường tròn ngoại tiếp tam giác
là đường kính của đường tròn ngoại tiếp tam giác  vuông tại
vuông tại 
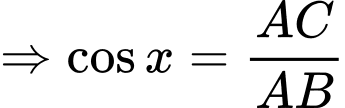

Tổng thời gian Nam đi là:
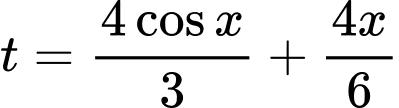 (giờ)
(giờ)Xét
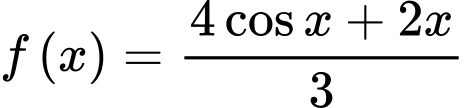 với
với 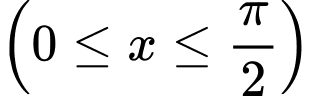
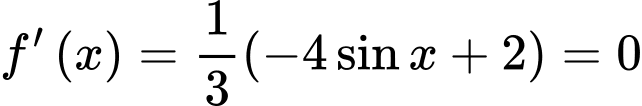
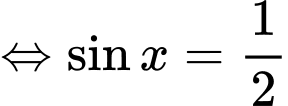
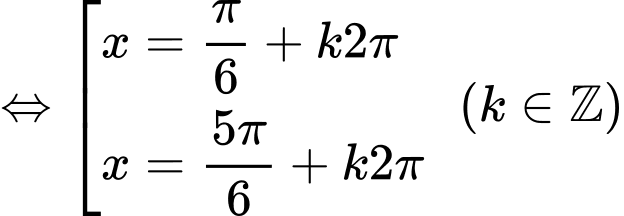
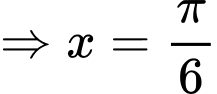
Ta bấm máy, nhận thấy bạn Nam đi từ A đến B với khoảng thời gian lớn nhất tại
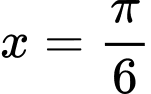 và
và 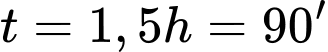
Đáp án:
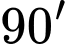
Câu 10 [390556]: Trên con đường 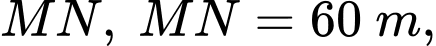 người ta muốn xây dựng một trạm quan sát
người ta muốn xây dựng một trạm quan sát 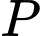 để theo dõi hai vị trí
để theo dõi hai vị trí 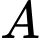 và
và 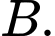 Biết rằng hai vị trí
Biết rằng hai vị trí 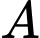 và
và 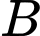 này cách con đường
này cách con đường 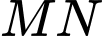 một khoảng lần lượt là
một khoảng lần lượt là  và
và 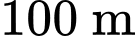 (như hình vẽ). Hãy tính độ dài
(như hình vẽ). Hãy tính độ dài 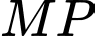 khi góc quan sát
khi góc quan sát 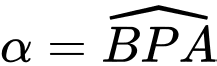 đạt giá trị lớn nhất. Viết kết quả làm tròn đến hàng đơn vị của mét.
đạt giá trị lớn nhất. Viết kết quả làm tròn đến hàng đơn vị của mét. 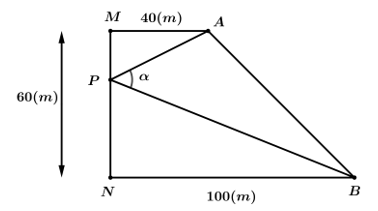
 người ta muốn xây dựng một trạm quan sát
người ta muốn xây dựng một trạm quan sát  để theo dõi hai vị trí
để theo dõi hai vị trí 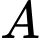 và
và 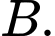 Biết rằng hai vị trí
Biết rằng hai vị trí 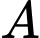 và
và 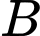 này cách con đường
này cách con đường 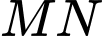 một khoảng lần lượt là
một khoảng lần lượt là  và
và 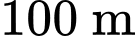 (như hình vẽ). Hãy tính độ dài
(như hình vẽ). Hãy tính độ dài 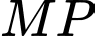 khi góc quan sát
khi góc quan sát 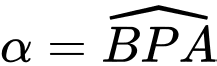 đạt giá trị lớn nhất. Viết kết quả làm tròn đến hàng đơn vị của mét.
đạt giá trị lớn nhất. Viết kết quả làm tròn đến hàng đơn vị của mét. 
Đáp số:……………………..
Đặt 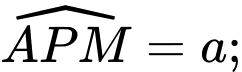
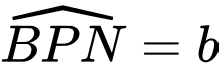 thì
thì 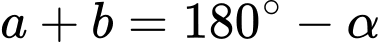
Khi đó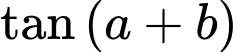
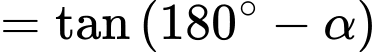
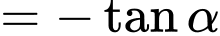 (1)
(1) 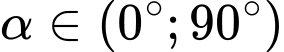
Ta đặt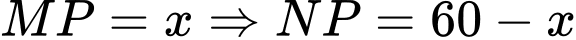 Mặt khác
Mặt khác 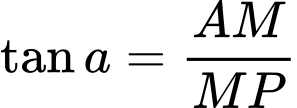
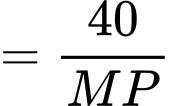
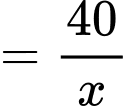 và
và 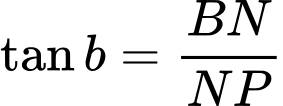
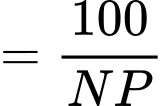
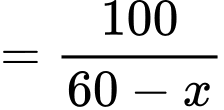
Thay vào (1) ta được:
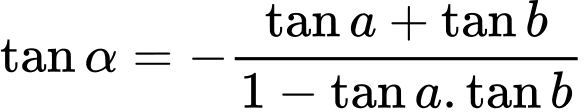
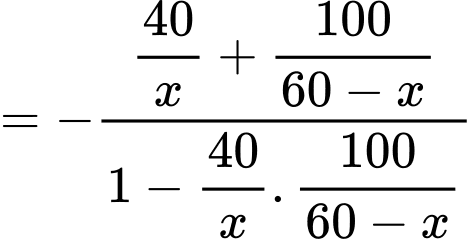
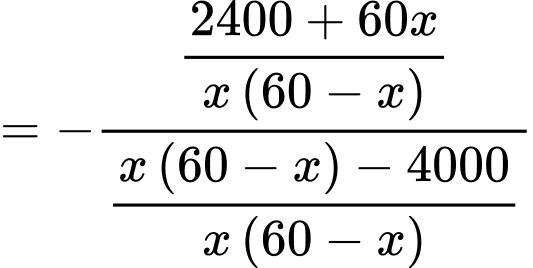
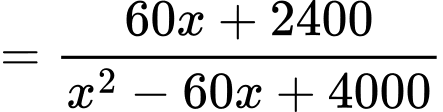
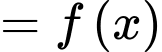
Để thì
thì 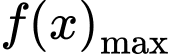
Giải phương trình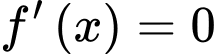
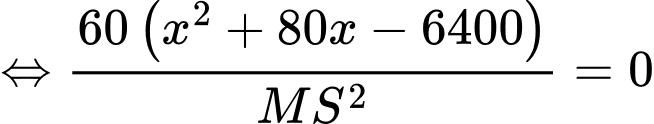 Suy ra
Suy ra 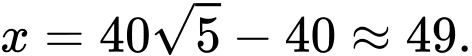
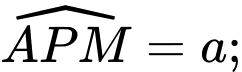
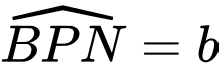 thì
thì 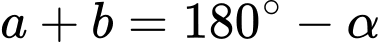
Khi đó
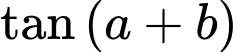
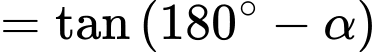
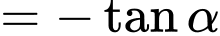 (1)
(1) 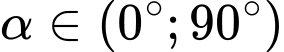
Ta đặt
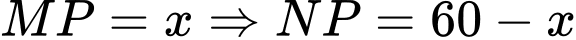 Mặt khác
Mặt khác 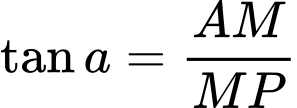
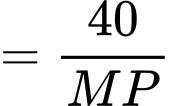
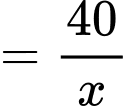 và
và 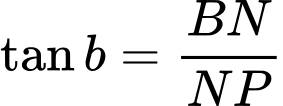
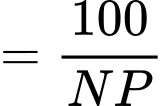
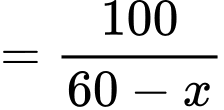
Thay vào (1) ta được:
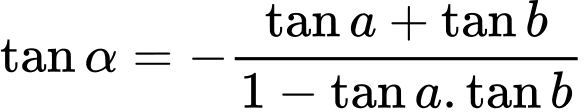
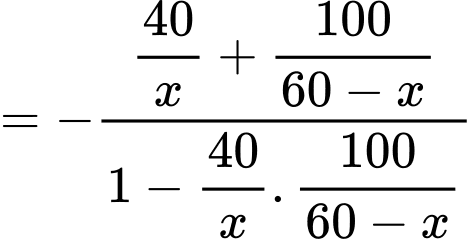
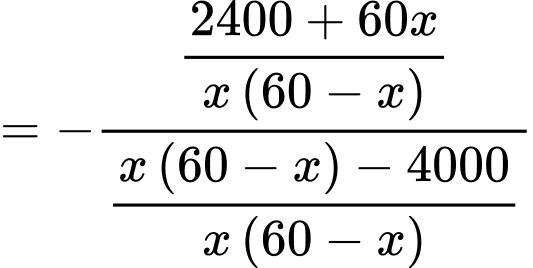
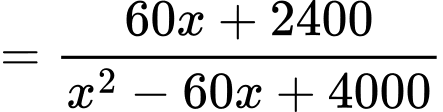
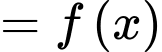
Để
 thì
thì 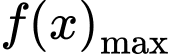
Giải phương trình
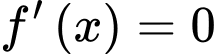
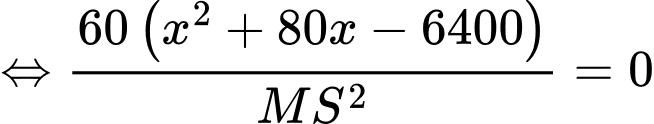 Suy ra
Suy ra 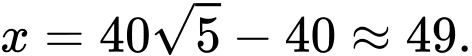
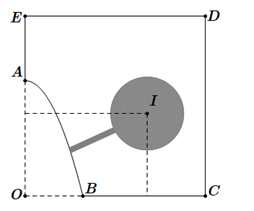
Câu 11 [31027]: Một cái ao có hình  (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính
(như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 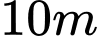 , người ta muốn bắc một cây cầu từ bờ
, người ta muốn bắc một cây cầu từ bờ  của ao đến vườn. Tính gần đúng độ dài tối thiểu
của ao đến vườn. Tính gần đúng độ dài tối thiểu 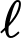 cây cầu biết:
cây cầu biết:
- Hai bờ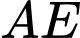 và
và 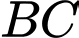 nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại
nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại  .
.
- Bờ là một phần của một parabol có đỉnh là điểm
là một phần của một parabol có đỉnh là điểm 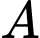 và có trục đối xứng là đoạn thẳng
và có trục đối xứng là đoạn thẳng 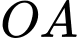 .
.
- Độ dài đoạn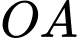 và
và 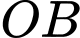 lần lượt là
lần lượt là 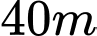 và
và 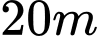 .
.
- Tâm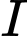 của mảnh vườn cách đường thẳng
của mảnh vườn cách đường thẳng 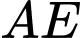 và
và 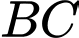 lần lượt là
lần lượt là 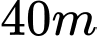 và
và 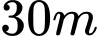 .
.
 (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính
(như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 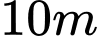 , người ta muốn bắc một cây cầu từ bờ
, người ta muốn bắc một cây cầu từ bờ  của ao đến vườn. Tính gần đúng độ dài tối thiểu
của ao đến vườn. Tính gần đúng độ dài tối thiểu 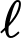 cây cầu biết:
cây cầu biết:- Hai bờ
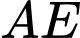 và
và 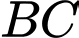 nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại
nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại  .
.- Bờ
 là một phần của một parabol có đỉnh là điểm
là một phần của một parabol có đỉnh là điểm 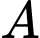 và có trục đối xứng là đoạn thẳng
và có trục đối xứng là đoạn thẳng 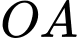 .
.- Độ dài đoạn
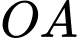 và
và 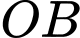 lần lượt là
lần lượt là 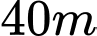 và
và 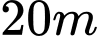 .
.- Tâm
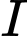 của mảnh vườn cách đường thẳng
của mảnh vườn cách đường thẳng 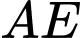 và
và 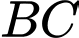 lần lượt là
lần lượt là 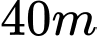 và
và 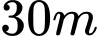 .
.
A, 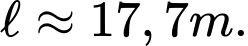
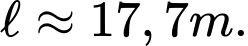
B, 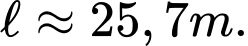
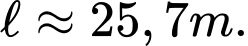
C, 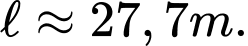
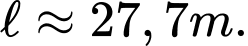
D, 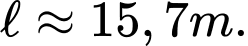
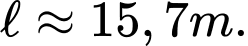
Gắn hệ trục toạ độ 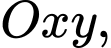 với
với 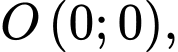
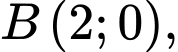

 Toạ độ tâm
Toạ độ tâm 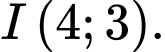
 với
với 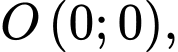
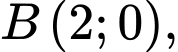

 Toạ độ tâm
Toạ độ tâm 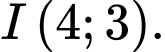
Phương trình parabol có đỉnh là điểm 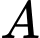 đi qua
đi qua  là
là 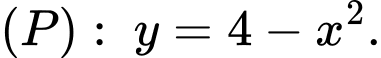
 đi qua
đi qua  là
là 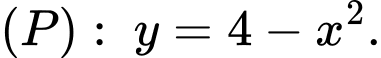
Điểm 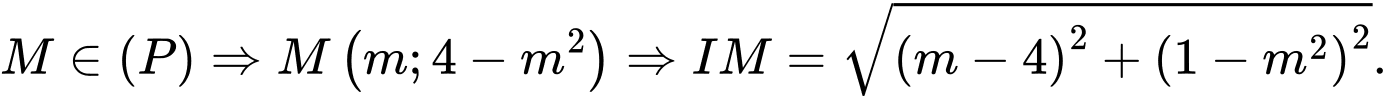
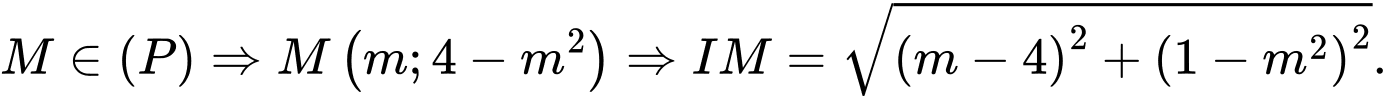
Độ dài cây cầu ngắn nhất 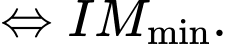
Xét hàm số 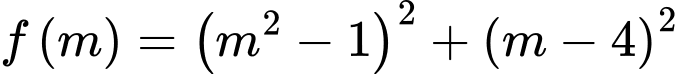 trên
trên  suy ra
suy ra 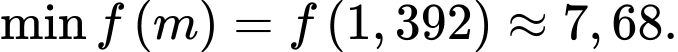
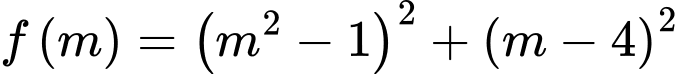 trên
trên 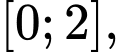 suy ra
suy ra 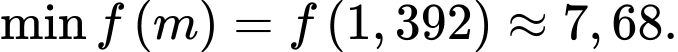
Vậy 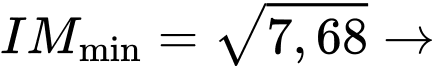 Độ dài cây cầu cần tính là
Độ dài cây cầu cần tính là 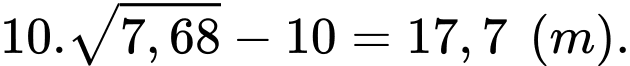 Chọn A
Chọn A
Đáp án: A 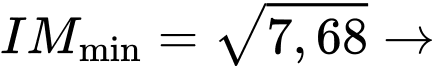 Độ dài cây cầu cần tính là
Độ dài cây cầu cần tính là 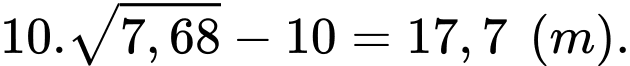 Chọn A
Chọn A
Câu 12 [30959]: Lúc 10 giờ sáng trên sa mạc, một nhà địa chất đang ở tại vị trí 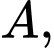 anh ta muốn đến vị trí
anh ta muốn đến vị trí 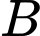 (bằng ôtô) trước 12 giờ trưa, với
(bằng ôtô) trước 12 giờ trưa, với 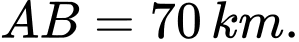 Nhưng trong xa mạc thì xe chỉ có thể di chuyển với vận tốc
Nhưng trong xa mạc thì xe chỉ có thể di chuyển với vận tốc 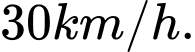 Cách vị trí
Cách vị trí 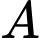 một đoạn
một đoạn 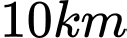 có một con đường nhựa chạy song song với đường thẳng nối từ
có một con đường nhựa chạy song song với đường thẳng nối từ 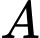 đến
đến 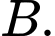 Trên đường nhwuaj thì xe có thể di chuyển với vận tốc
Trên đường nhwuaj thì xe có thể di chuyển với vận tốc 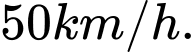 Tìm thời gian ít nhất để nhà địa chất đến
Tìm thời gian ít nhất để nhà địa chất đến 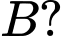
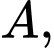 anh ta muốn đến vị trí
anh ta muốn đến vị trí 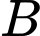 (bằng ôtô) trước 12 giờ trưa, với
(bằng ôtô) trước 12 giờ trưa, với 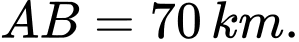 Nhưng trong xa mạc thì xe chỉ có thể di chuyển với vận tốc
Nhưng trong xa mạc thì xe chỉ có thể di chuyển với vận tốc 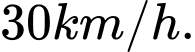 Cách vị trí
Cách vị trí 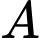 một đoạn
một đoạn 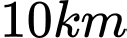 có một con đường nhựa chạy song song với đường thẳng nối từ
có một con đường nhựa chạy song song với đường thẳng nối từ 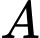 đến
đến 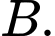 Trên đường nhwuaj thì xe có thể di chuyển với vận tốc
Trên đường nhwuaj thì xe có thể di chuyển với vận tốc 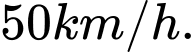 Tìm thời gian ít nhất để nhà địa chất đến
Tìm thời gian ít nhất để nhà địa chất đến 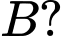
A, 1 giờ 52 phút.
B, 1 giờ 56 phút.
C, 1 giờ 54 phút.
D, 1 giờ 58 phút.
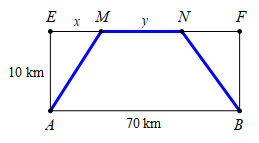
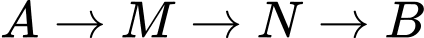 như hình vẽ.
như hình vẽ. Đặt
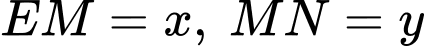
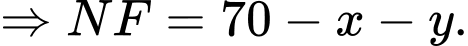
Khi đó, tổng thời gian ô tô đi từ
 là
là 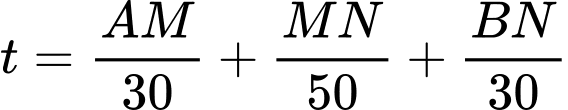
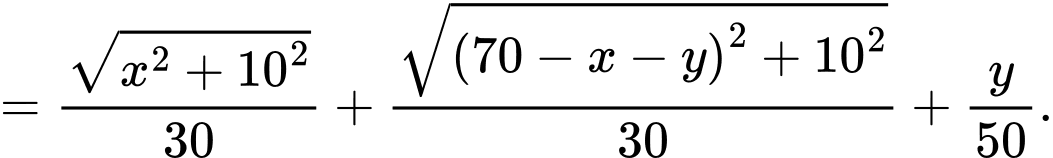
Ta có:
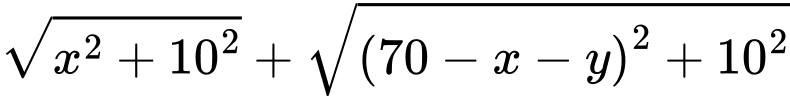
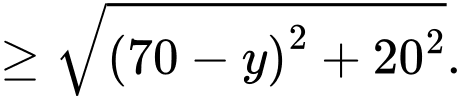
Suy ra
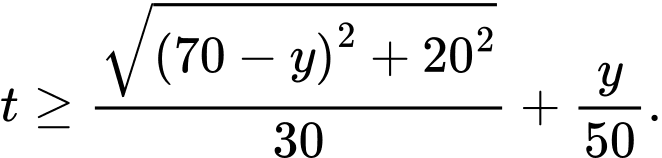
Xét hàm số
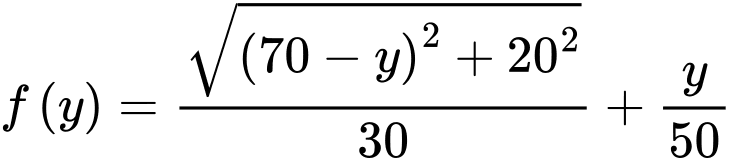
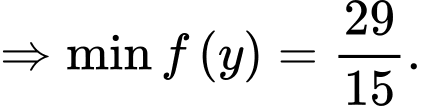
Vậy thời gian nhỏ nhất đi từ
 là 1 giờ 56 phút. Chọn B Đáp án: B
là 1 giờ 56 phút. Chọn B Đáp án: B
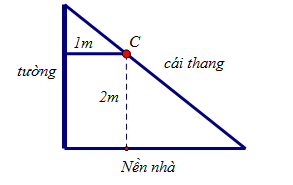
Câu 13 [31072]: Ông An cần sản xuất một cái thang để trèo qua một bức tường nhà. Ông muốn một cái thang luôn được đặt đi qua vị trí  biết rằng điểm
biết rằng điểm  cao
cao 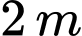 so với nền nhà và điểm
so với nền nhà và điểm  cách tường nhà
cách tường nhà 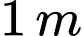 (như hình vẽ). Giả sử kinh phí để sản xuất thang là 400.000 đồng/1 mét dài. Hỏi ông An cần ít nhất bao nhiêu tiền để sản xuất 1 cái thang? (kết quả làm tròn đến hàng nghìn đồng)
(như hình vẽ). Giả sử kinh phí để sản xuất thang là 400.000 đồng/1 mét dài. Hỏi ông An cần ít nhất bao nhiêu tiền để sản xuất 1 cái thang? (kết quả làm tròn đến hàng nghìn đồng)
 biết rằng điểm
biết rằng điểm  cao
cao 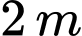 so với nền nhà và điểm
so với nền nhà và điểm  cách tường nhà
cách tường nhà 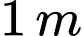 (như hình vẽ). Giả sử kinh phí để sản xuất thang là 400.000 đồng/1 mét dài. Hỏi ông An cần ít nhất bao nhiêu tiền để sản xuất 1 cái thang? (kết quả làm tròn đến hàng nghìn đồng)
(như hình vẽ). Giả sử kinh phí để sản xuất thang là 400.000 đồng/1 mét dài. Hỏi ông An cần ít nhất bao nhiêu tiền để sản xuất 1 cái thang? (kết quả làm tròn đến hàng nghìn đồng)
A, 1.400.000 đồng.
B, 800.000 đồng.
C, 2.160.000 đồng.
D, 1.665.000 đồng.
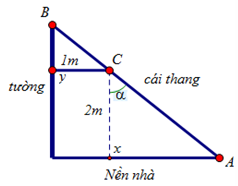
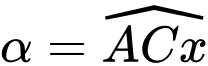 khi đó
khi đó 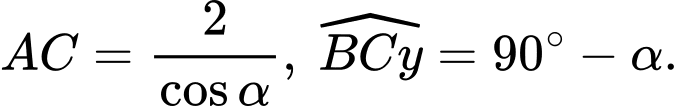
Do đó, 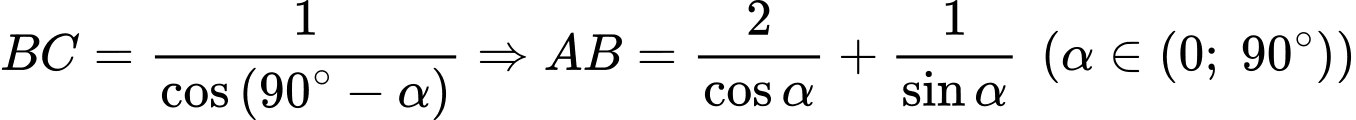
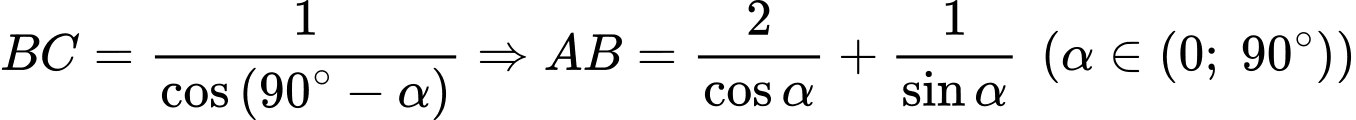
Ta có: 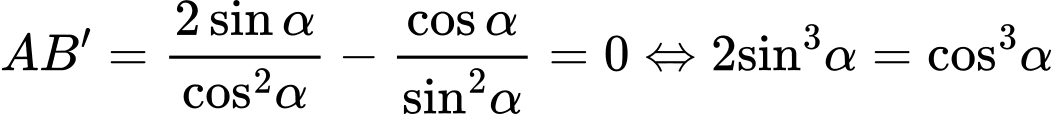
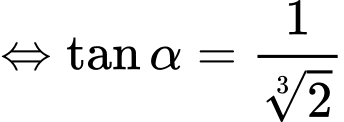
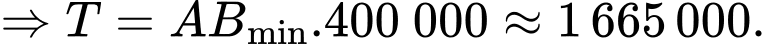 Chọn D
Chọn D
Đáp án: D 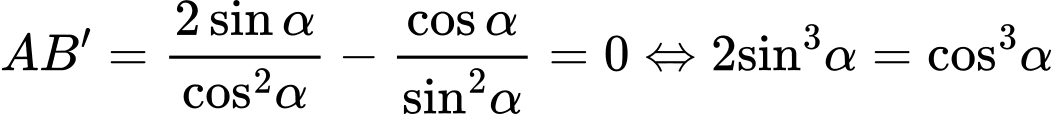
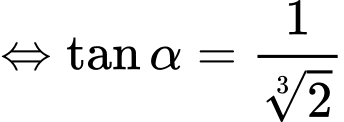
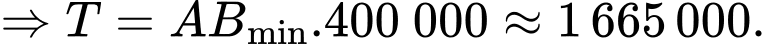 Chọn D
Chọn D
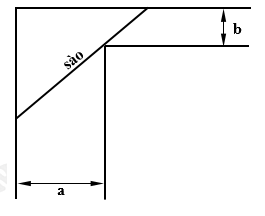
Câu 14 [31098]: Để chặn đường hành lang hình chữ  người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng
người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng 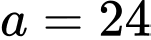 và
và 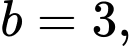 hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?
hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?
 người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng
người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng 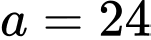 và
và 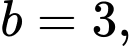 hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?
hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?
A, 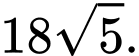
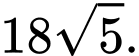
B, 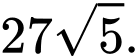
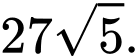
C, 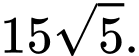
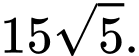
D, 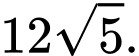
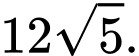
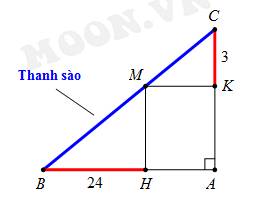
Theo bài ra, thanh sào sẽ đi qua các điểm
 (như hình vẽ trên).
(như hình vẽ trên).Suy ra độ dài thanh sào là
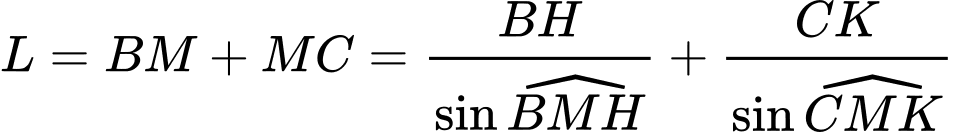
Đặt
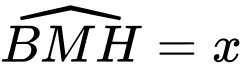
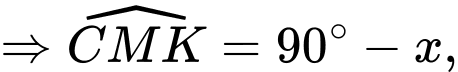 do đó
do đó 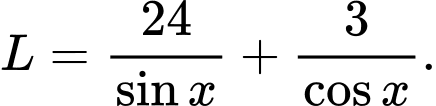
Yêu cầu bài toán
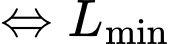
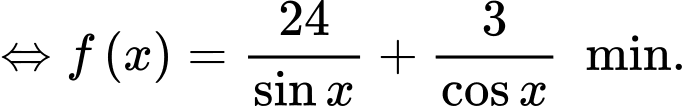
Ta có
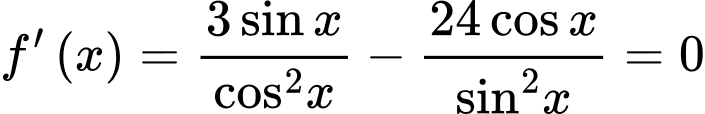
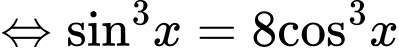
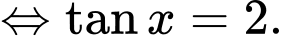
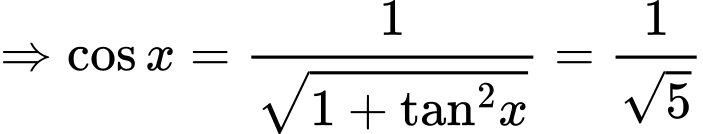
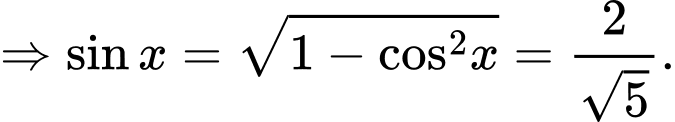
Suy ra
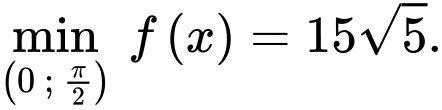
Vậy độ dài tối thiểu của thanh sào là
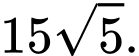 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 15 [31094]: Trên một đoạn đường giao thông có hai con đường vuông góc với nhau như hình vẽ. Một địa danh lịch sử có vị trí đặt tại 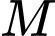 , vị trí
, vị trí 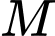 cách đường
cách đường 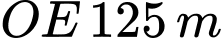 và cách đường
và cách đường 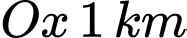 . Vì lý do thực tiễn người ta muốn làm một đoạn đường
. Vì lý do thực tiễn người ta muốn làm một đoạn đường  đi qua vị trí
đi qua vị trí 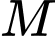 , biết rằng để làm
, biết rằng để làm 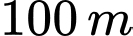 đường là 150 triệu đồng. Chọn vị trí của
đường là 150 triệu đồng. Chọn vị trí của 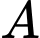 và
và  để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
 , vị trí
, vị trí  cách đường
cách đường 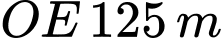 và cách đường
và cách đường 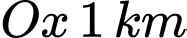 . Vì lý do thực tiễn người ta muốn làm một đoạn đường
. Vì lý do thực tiễn người ta muốn làm một đoạn đường  đi qua vị trí
đi qua vị trí 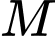 , biết rằng để làm
, biết rằng để làm 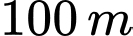 đường là 150 triệu đồng. Chọn vị trí của
đường là 150 triệu đồng. Chọn vị trí của 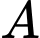 và
và 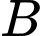 để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
A, 1,9063 tỷ đồng.
B, 2,3965 tỷ đồng.
C, 2,0963 tỷ đồng.
D, 3 tỷ đồng.
Chọn hệ trục toạ độ với 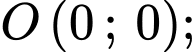
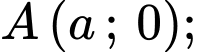
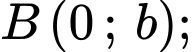
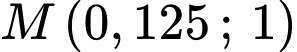
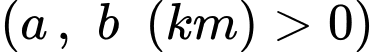
Khi đó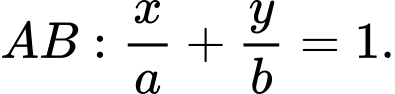 Do
Do  luôn đi qua
luôn đi qua 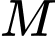 nên ta có
nên ta có 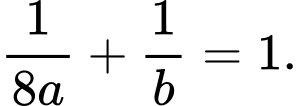
Ta có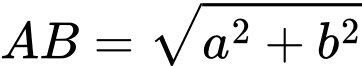
 Chi phí làm đường là
Chi phí làm đường là 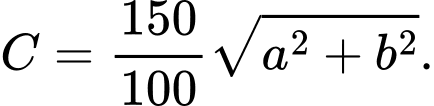
Chi phí nhỏ nhất
Ta có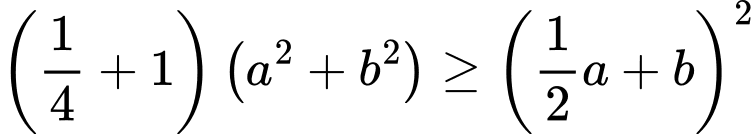 (BĐT Cauchy Schwarz)
(BĐT Cauchy Schwarz)
Mặt khác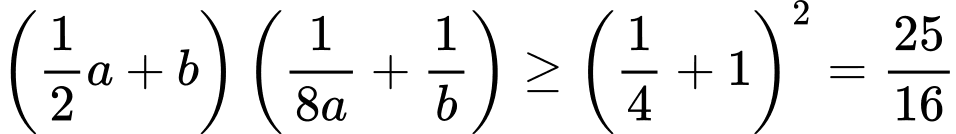
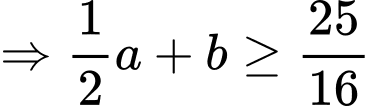
Khi đó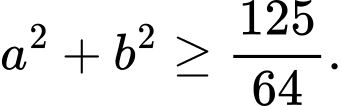 Dấu “=” xảy ra
Dấu “=” xảy ra 
Suy ra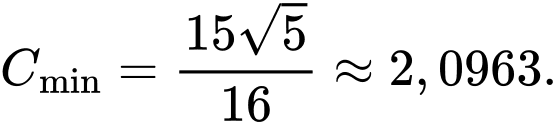 Chọn C. Đáp án: C
Chọn C. Đáp án: C
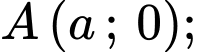
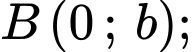
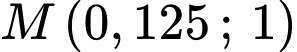
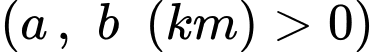
Khi đó
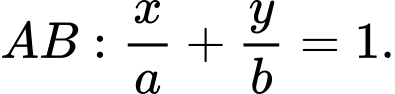 Do
Do  luôn đi qua
luôn đi qua  nên ta có
nên ta có 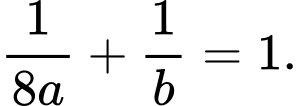
Ta có
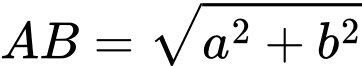
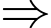 Chi phí làm đường là
Chi phí làm đường là 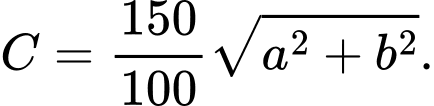
Chi phí nhỏ nhất
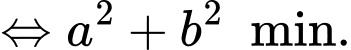
Ta có
 (BĐT Cauchy Schwarz)
(BĐT Cauchy Schwarz)Mặt khác
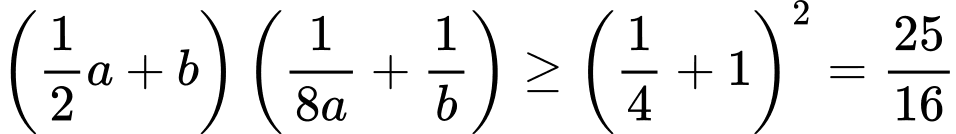
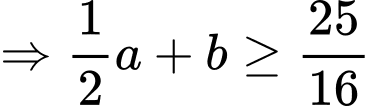
Khi đó
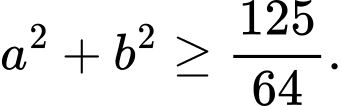 Dấu “=” xảy ra
Dấu “=” xảy ra 
Suy ra
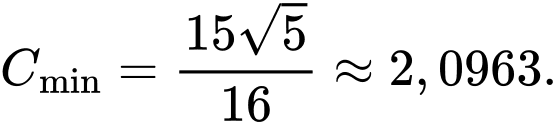 Chọn C. Đáp án: C
Chọn C. Đáp án: C
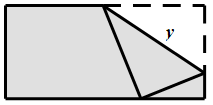
Câu 16 [31020]: Cho một tờ giấy hình chữ nhật có chiều dài 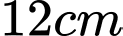 , chiều rộng
, chiều rộng 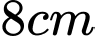 . Gấp góc bên phải của tờ giấy sao cho khi gấp, đỉnh của góc đó chạm với đáy dưới (như hình vẽ). Gọi độ dài nếp gấp là
. Gấp góc bên phải của tờ giấy sao cho khi gấp, đỉnh của góc đó chạm với đáy dưới (như hình vẽ). Gọi độ dài nếp gấp là 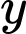 thì giá trị nhỏ nhất của
thì giá trị nhỏ nhất của 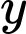 là bao nhiêu?
là bao nhiêu?
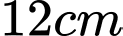 , chiều rộng
, chiều rộng 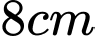 . Gấp góc bên phải của tờ giấy sao cho khi gấp, đỉnh của góc đó chạm với đáy dưới (như hình vẽ). Gọi độ dài nếp gấp là
. Gấp góc bên phải của tờ giấy sao cho khi gấp, đỉnh của góc đó chạm với đáy dưới (như hình vẽ). Gọi độ dài nếp gấp là 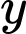 thì giá trị nhỏ nhất của
thì giá trị nhỏ nhất của 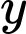 là bao nhiêu?
là bao nhiêu?
A, 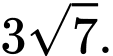
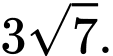
B, 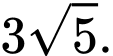
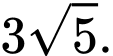
C, 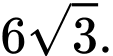
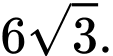
D, 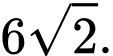
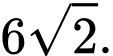
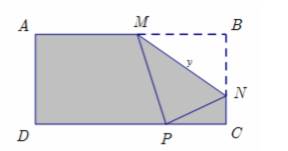
Ta kí hiệu như hình.
Ta có

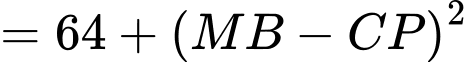
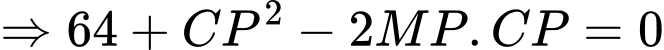
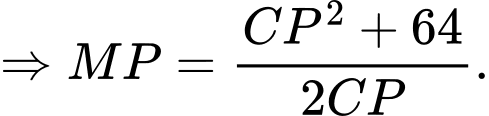
Lại có
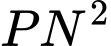
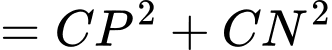
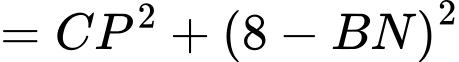
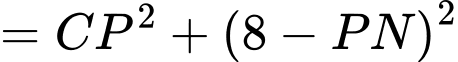
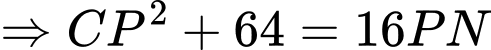

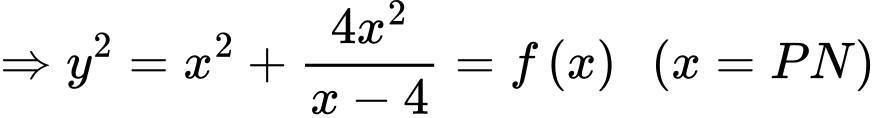
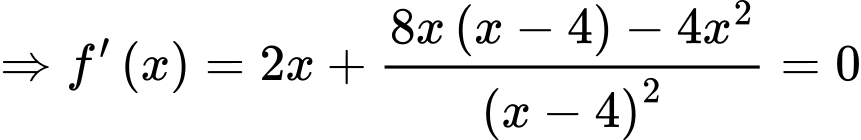
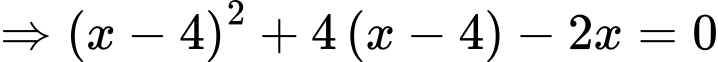
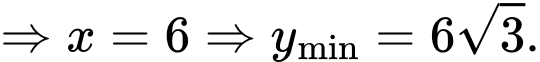
Chọn C. Đáp án: C
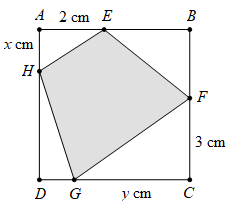
Câu 17 [31077]: Cho một tấm nhôm hình vuông cạnh 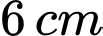 . Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng
. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng  để diện tích hình thang
để diện tích hình thang  đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
 . Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng
. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng  để diện tích hình thang
để diện tích hình thang  đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
đạt giá trị nhỏ nhất (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 4,95.
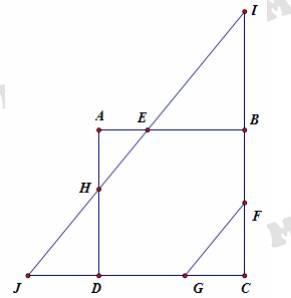
Đường thẳng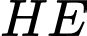 cắt
cắt 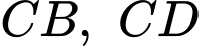 lần lượt tại
lần lượt tại 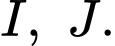
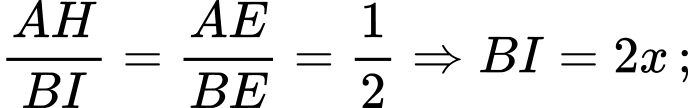
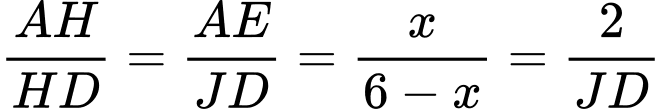
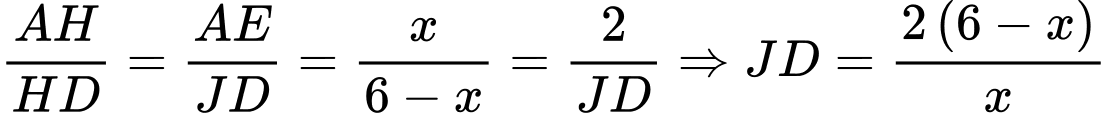
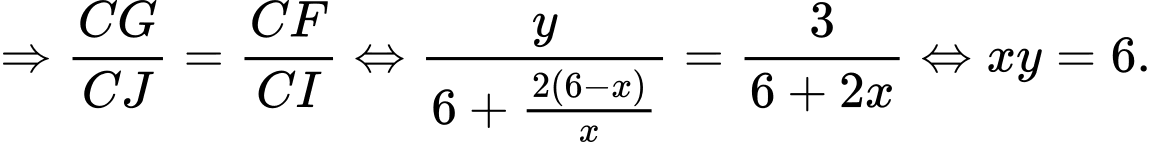
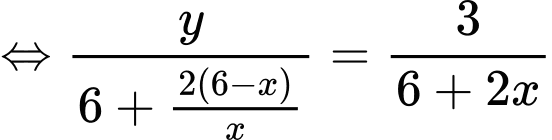
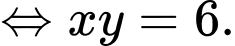

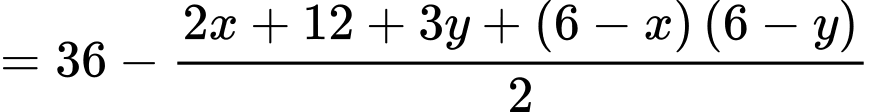
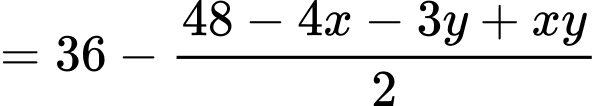
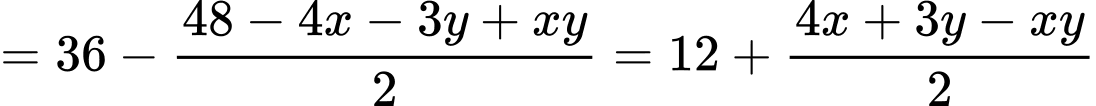
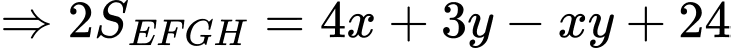
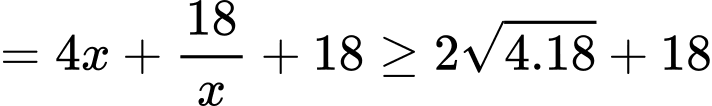
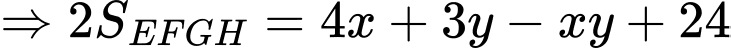
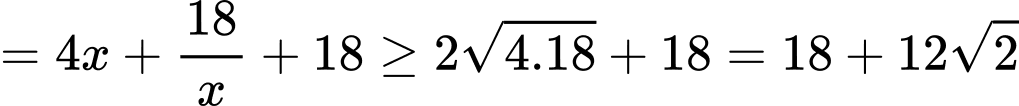
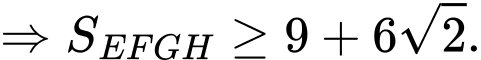
Dấu “=” xảy ra khi và chỉ khi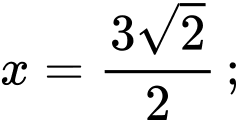
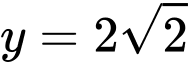
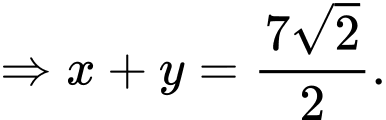

Đường thẳng
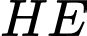 cắt
cắt 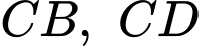 lần lượt tại
lần lượt tại 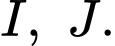
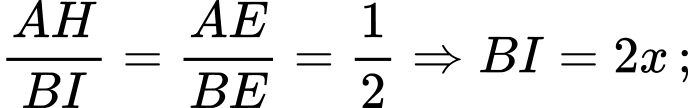
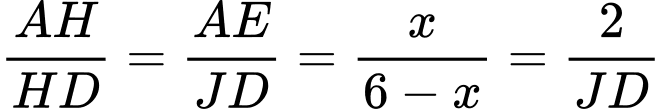
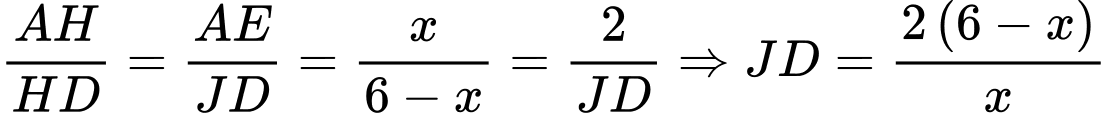
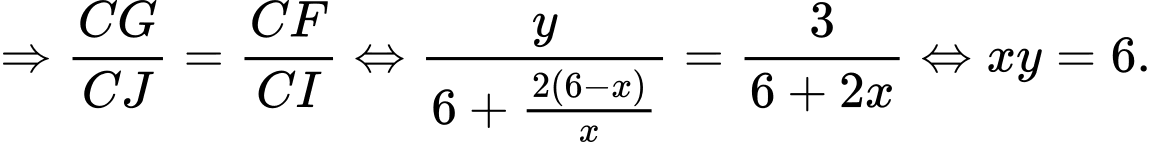
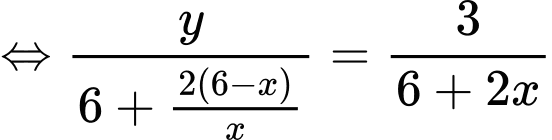
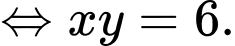

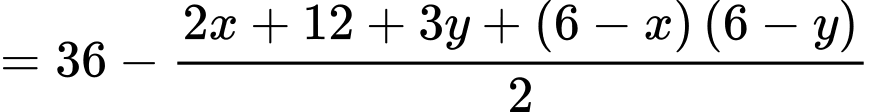
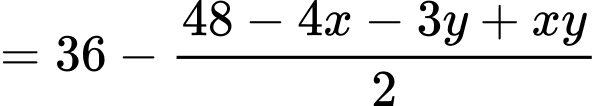
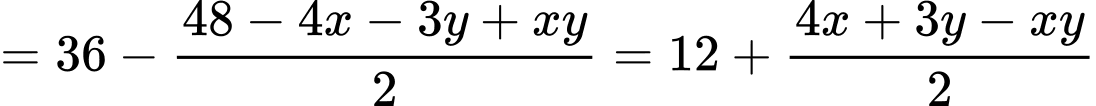
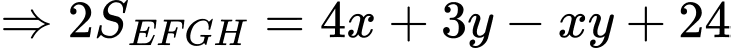
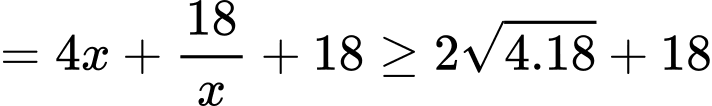
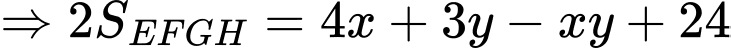
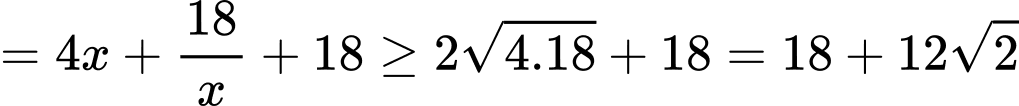
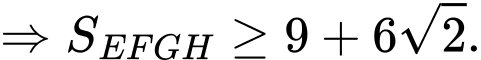
Dấu “=” xảy ra khi và chỉ khi