Đáp án Bài tập tự luyện số 2
Câu 1 [402714]: Cho khối cầu tâm  bán kính
bán kính 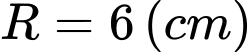 mặt phẳng
mặt phẳng 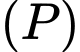 cách
cách  một khoảng bằng
một khoảng bằng 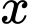 cắt khối cầu theo một hình tròn
cắt khối cầu theo một hình tròn  . Một khối nón có đỉnh thuộc mặt cầu và đáy là hình tròn
. Một khối nón có đỉnh thuộc mặt cầu và đáy là hình tròn  . Biết khối nón có thể tích lớn nhất, giá trị của
. Biết khối nón có thể tích lớn nhất, giá trị của 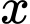 bằng bao nhiêu cm?
bằng bao nhiêu cm?
 bán kính
bán kính 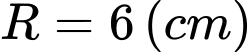 mặt phẳng
mặt phẳng 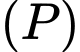 cách
cách  một khoảng bằng
một khoảng bằng 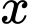 cắt khối cầu theo một hình tròn
cắt khối cầu theo một hình tròn  . Một khối nón có đỉnh thuộc mặt cầu và đáy là hình tròn
. Một khối nón có đỉnh thuộc mặt cầu và đáy là hình tròn  . Biết khối nón có thể tích lớn nhất, giá trị của
. Biết khối nón có thể tích lớn nhất, giá trị của 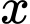 bằng bao nhiêu cm?
bằng bao nhiêu cm?
Gọi 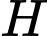 là tâm của
là tâm của  ,
, 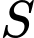 là đỉnh của hình nón,
là đỉnh của hình nón, 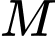 là điểm trên đường tròn
là điểm trên đường tròn 
Ta có ,
, 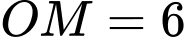 vậy
vậy  .
.
Thể tích khối nón là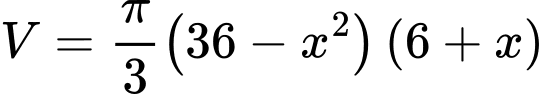
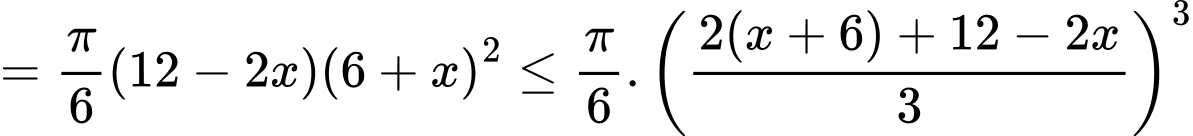
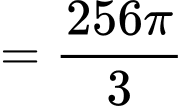 .
.
Dấu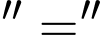 xảy ra khi
xảy ra khi 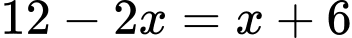
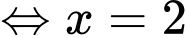 .
.
 là tâm của
là tâm của  ,
,  là đỉnh của hình nón,
là đỉnh của hình nón, 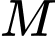 là điểm trên đường tròn
là điểm trên đường tròn 
Ta có
 ,
, 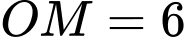 vậy
vậy  .
. Thể tích khối nón là
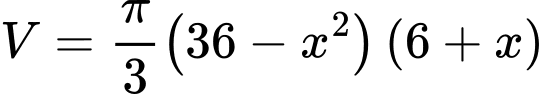
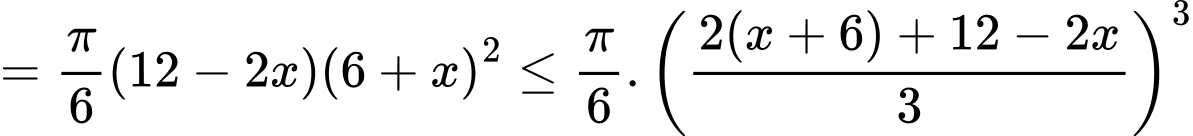
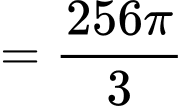 .
. Dấu
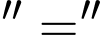 xảy ra khi
xảy ra khi 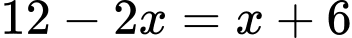
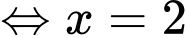 .
.
Câu 2 [5940]: Gia đình an xây bể hình trụ có thể tích 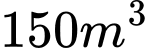 . Đáy bể bằng bê tông giá
. Đáy bể bằng bê tông giá 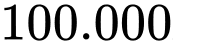 /
/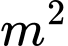 . Phần thân làm bằng tôn giá
. Phần thân làm bằng tôn giá 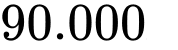 /
/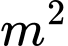 , nắp bằng nhôm giá
, nắp bằng nhôm giá 
 /
/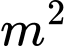 . Hỏi khi chi phí sản xuất bể đạt mức thấp nhất thì tỉ số giữa chiều cao bể và bán kính đáy là bao nhiêu?
. Hỏi khi chi phí sản xuất bể đạt mức thấp nhất thì tỉ số giữa chiều cao bể và bán kính đáy là bao nhiêu?
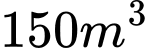 . Đáy bể bằng bê tông giá
. Đáy bể bằng bê tông giá 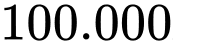 /
/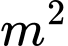 . Phần thân làm bằng tôn giá
. Phần thân làm bằng tôn giá 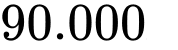 /
/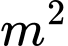 , nắp bằng nhôm giá
, nắp bằng nhôm giá 
 /
/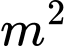 . Hỏi khi chi phí sản xuất bể đạt mức thấp nhất thì tỉ số giữa chiều cao bể và bán kính đáy là bao nhiêu?
. Hỏi khi chi phí sản xuất bể đạt mức thấp nhất thì tỉ số giữa chiều cao bể và bán kính đáy là bao nhiêu? A, 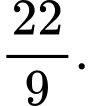
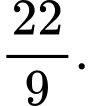
B, 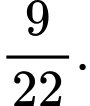
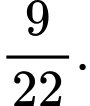
C, 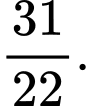
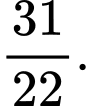
D, 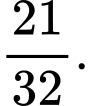
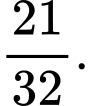
Gọi bán kính đáy của bể là 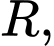 chiều cao là
chiều cao là 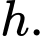
Ta có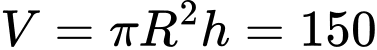
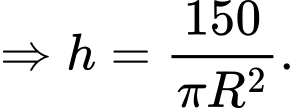
Diện tích đáy là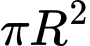
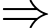 Chi phí làm đáy là
Chi phí làm đáy là 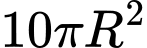 (chục nghìn đồng)
(chục nghìn đồng)
Diện tích thân là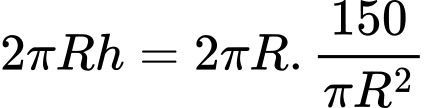
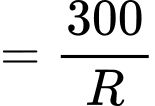
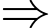 Chi phí làm thân là
Chi phí làm thân là 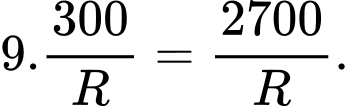
Diện tích nắp là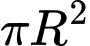
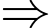 Chi phí làm nắp là
Chi phí làm nắp là 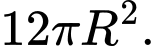
Chi phí sản xuất bể là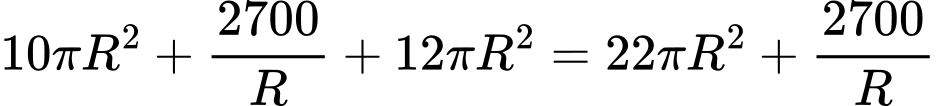 (đồng)
(đồng)
Ta có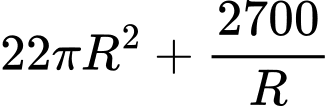
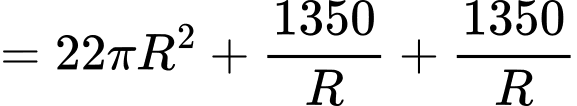
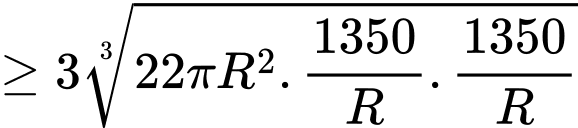
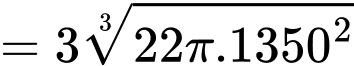
Dấu “=” xảy ra khi và chỉ khi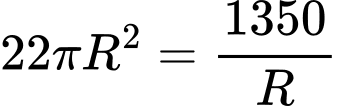
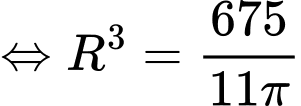
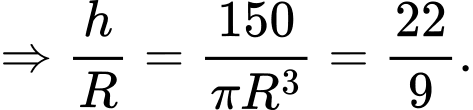
Chọn A. Đáp án: A
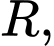 chiều cao là
chiều cao là 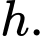
Ta có
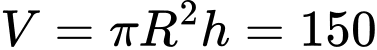
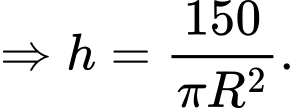
Diện tích đáy là
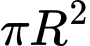
 Chi phí làm đáy là
Chi phí làm đáy là 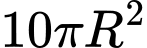 (chục nghìn đồng)
(chục nghìn đồng)Diện tích thân là
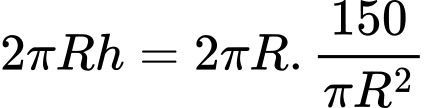
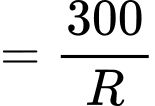
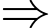 Chi phí làm thân là
Chi phí làm thân là 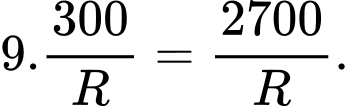
Diện tích nắp là
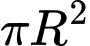
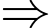 Chi phí làm nắp là
Chi phí làm nắp là 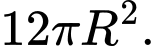
Chi phí sản xuất bể là
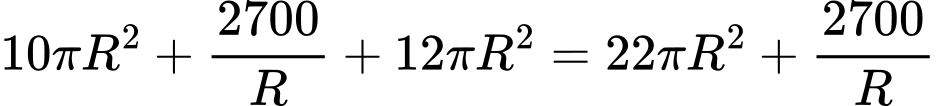 (đồng)
(đồng)Ta có
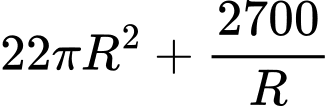
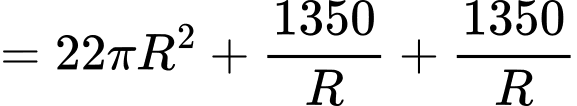
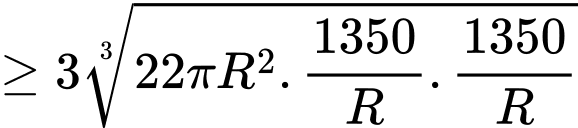
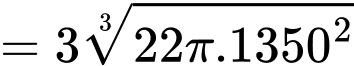
Dấu “=” xảy ra khi và chỉ khi
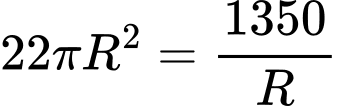
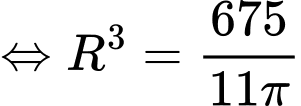
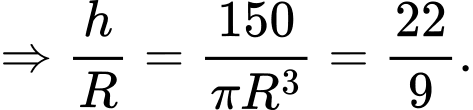
Chọn A. Đáp án: A
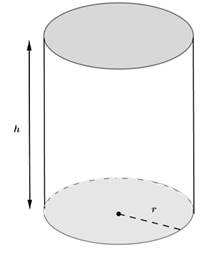
Câu 3 [5923]: Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích  nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (cho phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là
nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (cho phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là 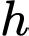 và bán kính đáy là
và bán kính đáy là  Tính tỉ số
Tính tỉ số 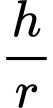 sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?
sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?
 nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (cho phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là
nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (cho phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là 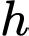 và bán kính đáy là
và bán kính đáy là  Tính tỉ số
Tính tỉ số 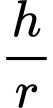 sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?
sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?
A, 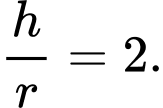
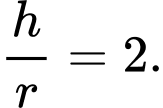
B, 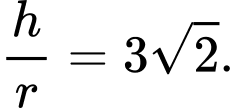
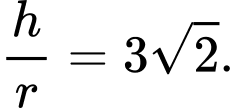
C, 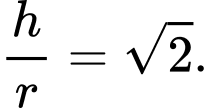
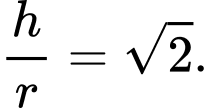
D, 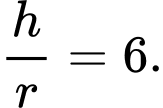
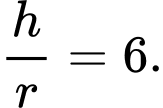
Ta có 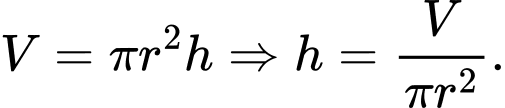
Ta có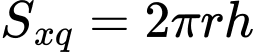
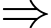 Chi phí sản xuất mặt xung quanh của thùng là
Chi phí sản xuất mặt xung quanh của thùng là 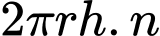 (đồng)
(đồng)
Tổng diện tích đáy và nắp là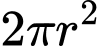
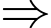 Chi phí sản xuất đáy và nắp là
Chi phí sản xuất đáy và nắp là 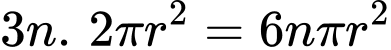 (đồng)
(đồng)
Suy ra chi phí để sản xuất thùng là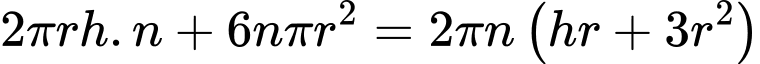
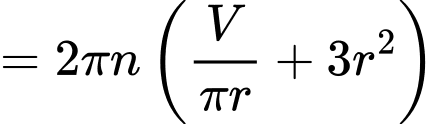
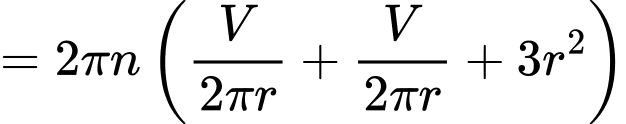
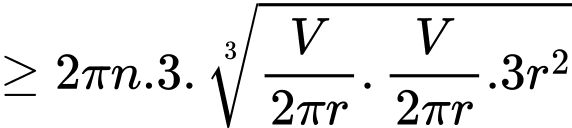
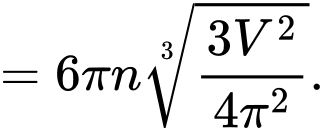
Chi phí thấp nhất khi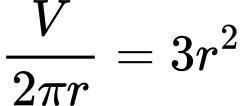
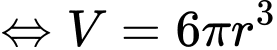
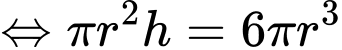
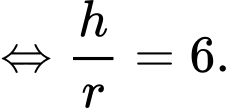
Chọn D. Đáp án: D
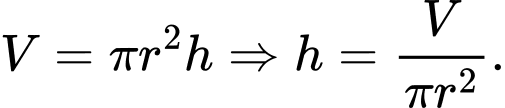
Ta có
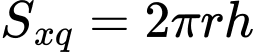
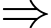 Chi phí sản xuất mặt xung quanh của thùng là
Chi phí sản xuất mặt xung quanh của thùng là 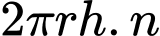 (đồng)
(đồng)Tổng diện tích đáy và nắp là
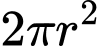
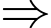 Chi phí sản xuất đáy và nắp là
Chi phí sản xuất đáy và nắp là 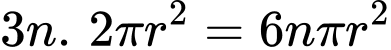 (đồng)
(đồng)Suy ra chi phí để sản xuất thùng là
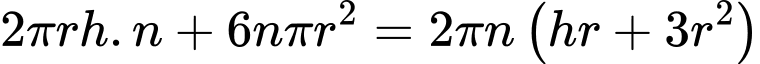
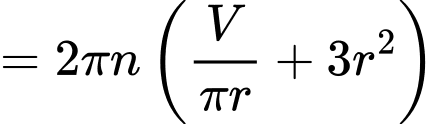
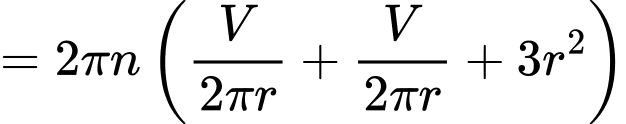
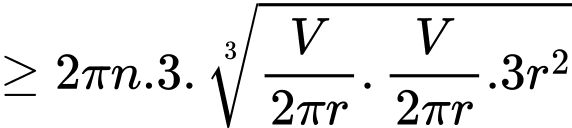
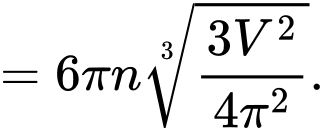
Chi phí thấp nhất khi
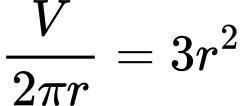
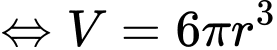
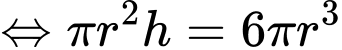
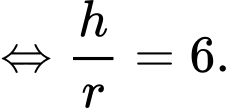
Chọn D. Đáp án: D
Câu 4 [390980]: Một chiếc cốc uống nước bằng giấy có dạng hình nón được làm để đựng được 27 cm³ nước. Tìm chiều cao của cốc để sử dụng lượng giấy là nhỏ nhất. Viết kết quả làm tròn đến hàng phần trăm theo đơn vị cm.
Ta có: 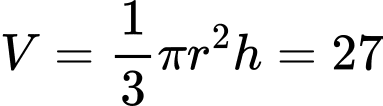
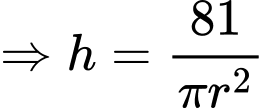
Cốc sử dụng lượng giấy nhỏ nhất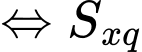 nhỏ nhất
nhỏ nhất
Ta có: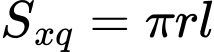
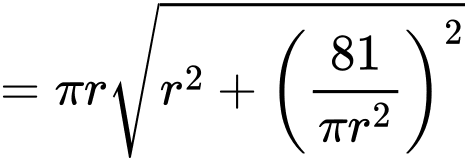
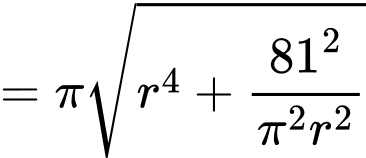
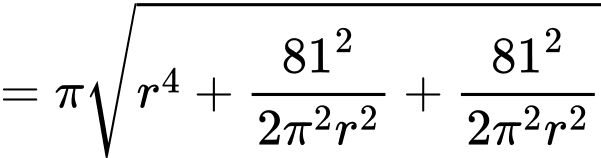
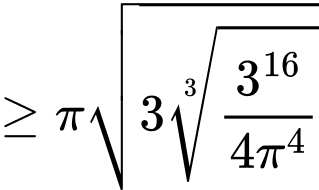
Dấu “ = ” xảy ra khi và chỉ khi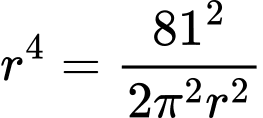
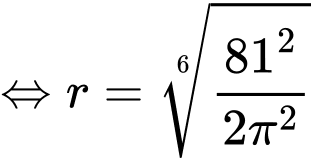
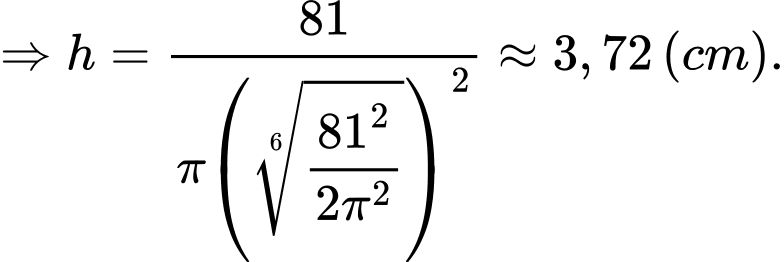
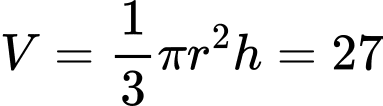
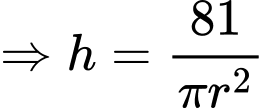
Cốc sử dụng lượng giấy nhỏ nhất
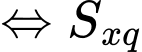 nhỏ nhất
nhỏ nhất Ta có:
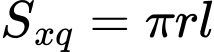
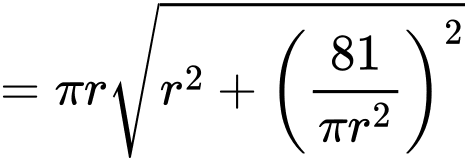
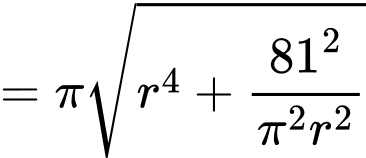
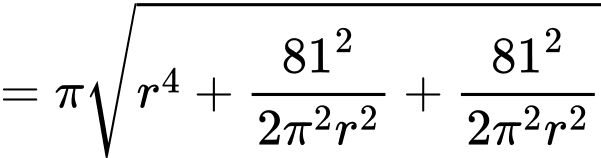
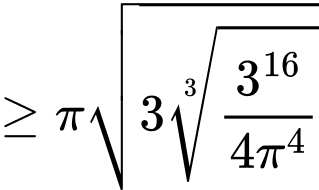
Dấu “ = ” xảy ra khi và chỉ khi
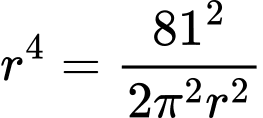
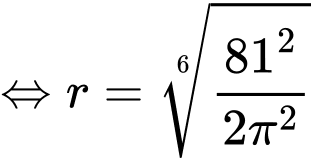
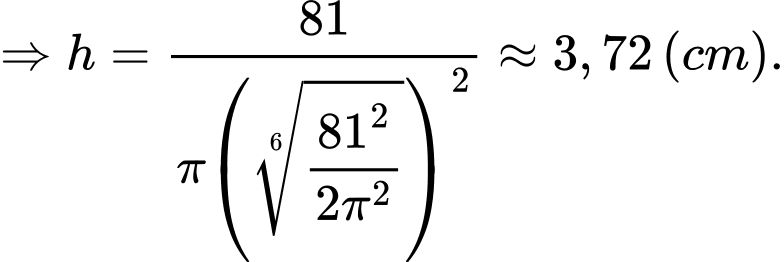
Câu 5 [327636]: Với một miếng tôn hình tròn có bán kính đáy 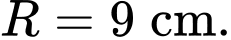 Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Muốn được cái phễu có thể tích lớn nhất thì hình quạt cần phải làm phễu có độ dài cung bằng bao nhiêu
Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Muốn được cái phễu có thể tích lớn nhất thì hình quạt cần phải làm phễu có độ dài cung bằng bao nhiêu
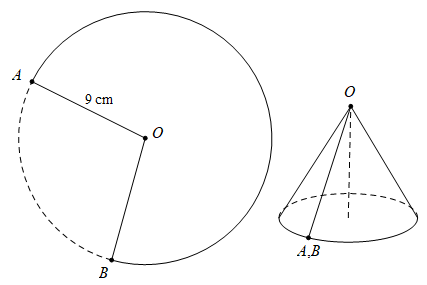
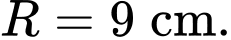 Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Muốn được cái phễu có thể tích lớn nhất thì hình quạt cần phải làm phễu có độ dài cung bằng bao nhiêu
Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Muốn được cái phễu có thể tích lớn nhất thì hình quạt cần phải làm phễu có độ dài cung bằng bao nhiêu 
A, 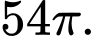
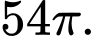
B, 

C, 

D, 

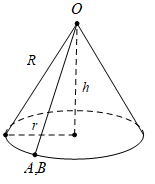
Bán kính đáy của hình quạt chính là đường sinh của khối nón.
Gọi
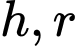 lần lượt là chiều cao và bán kính đáy của hình nón
lần lượt là chiều cao và bán kính đáy của hình nón Thể tích khối nón là:
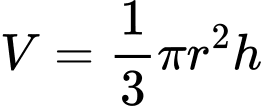 , trong đó
, trong đó 
Thế vào thể tích ta có:
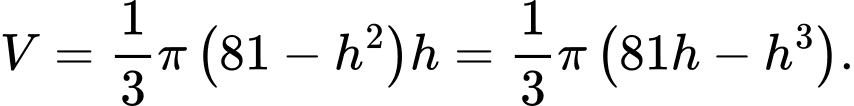
Xét hàm số
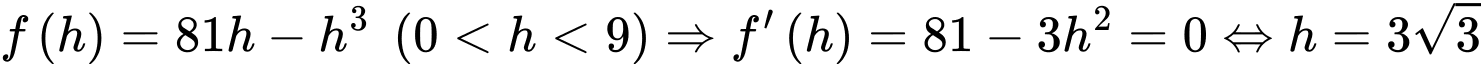
Từ đó suy ra
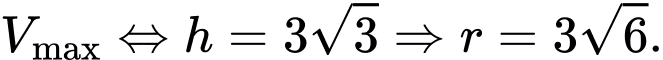
Độ dài cung của hình quạt chính là chu vi đáy của hình nón suy ra
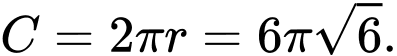 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 6 [399940]: Cho miếng tôn có diện tích 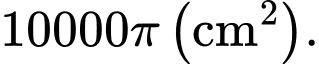 Người ta dùng miếng tôn hình tròn để tạo thành hình nón có diện tích toàn phần đúng bằng diện tích miếng tôn. Khi đó khối nón có thể tích lớn nhất được tạo thành sẽ có bán kính hình tròn đáy bằng bao nhiêu cm?
Người ta dùng miếng tôn hình tròn để tạo thành hình nón có diện tích toàn phần đúng bằng diện tích miếng tôn. Khi đó khối nón có thể tích lớn nhất được tạo thành sẽ có bán kính hình tròn đáy bằng bao nhiêu cm?
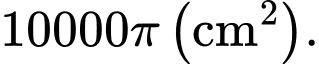 Người ta dùng miếng tôn hình tròn để tạo thành hình nón có diện tích toàn phần đúng bằng diện tích miếng tôn. Khi đó khối nón có thể tích lớn nhất được tạo thành sẽ có bán kính hình tròn đáy bằng bao nhiêu cm?
Người ta dùng miếng tôn hình tròn để tạo thành hình nón có diện tích toàn phần đúng bằng diện tích miếng tôn. Khi đó khối nón có thể tích lớn nhất được tạo thành sẽ có bán kính hình tròn đáy bằng bao nhiêu cm? A, 

B, 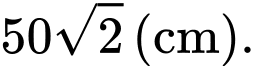
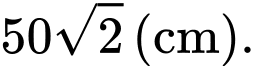
C, 

D, 

Phương pháp:
Từ diện tích toàn phần bằng diện tích miếng tôn tính 1 theo
Từ đó tình thể tích theo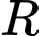 , khảo sát hàm số và tìm GTLN của thể tích theo
, khảo sát hàm số và tìm GTLN của thể tích theo 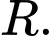
Cách giải:
Ta có diện tích miếng tôn là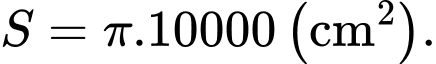
Diện tích toàn phần của hình nón là: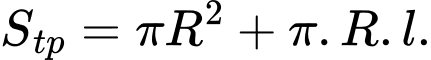
Thỏa mãn yêu cầu bài toán ta có: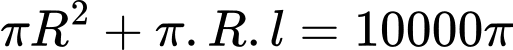
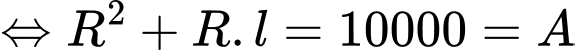
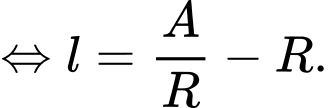
Thể tích khối nón là:
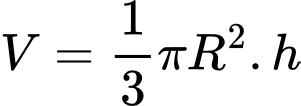
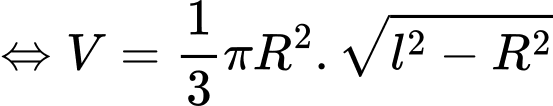
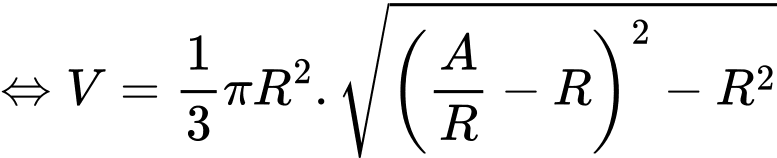
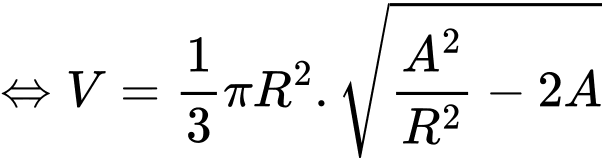
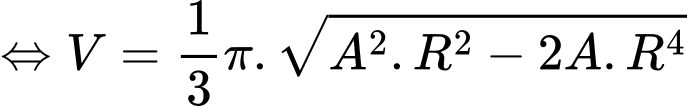
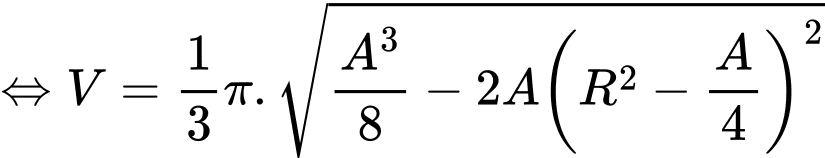
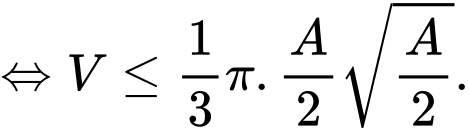
Dấu bằng xảy ra khi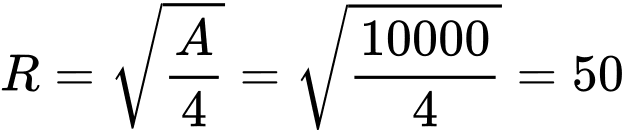 , vậy
, vậy  đạt GTLN khi
đạt GTLN khi 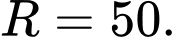
Chọn D. Đáp án: D
Từ diện tích toàn phần bằng diện tích miếng tôn tính 1 theo

Từ đó tình thể tích theo
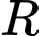 , khảo sát hàm số và tìm GTLN của thể tích theo
, khảo sát hàm số và tìm GTLN của thể tích theo 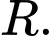
Cách giải:
Ta có diện tích miếng tôn là
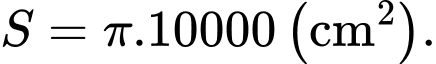
Diện tích toàn phần của hình nón là:
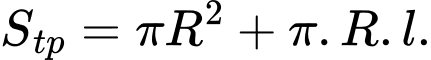
Thỏa mãn yêu cầu bài toán ta có:
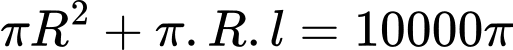
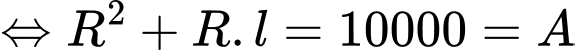
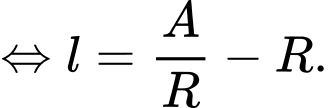
Thể tích khối nón là:
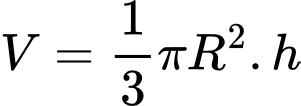
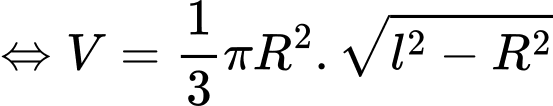
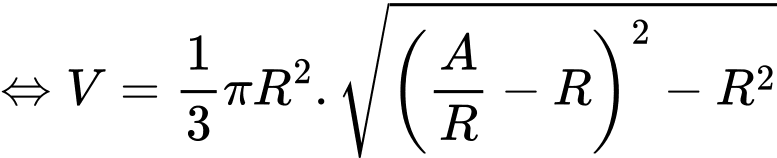
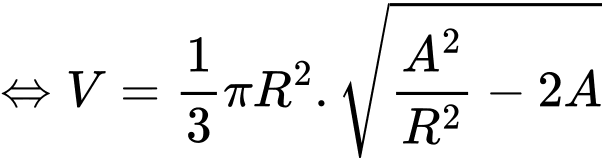
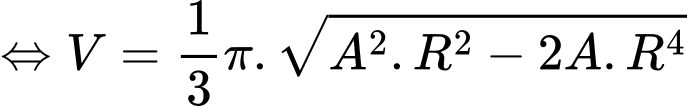
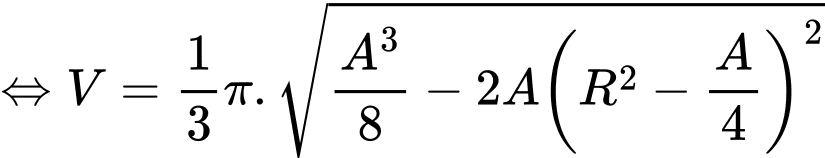
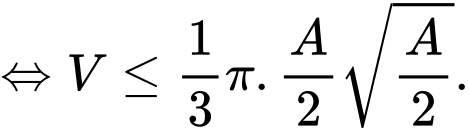
Dấu bằng xảy ra khi
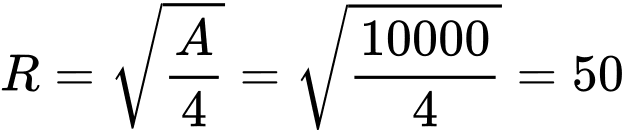 , vậy
, vậy  đạt GTLN khi
đạt GTLN khi 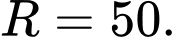
Chọn D. Đáp án: D
Câu 7 [5978]: Bạn A có một tấm bìa hình tròn (như hình vẽ), bạn ấy muốn dùng tấm bìa đó tạo thành một cái phễu hình nón, vì vậy bạn phải cắt bỏ phần quạt tròn  rồi dán hai bán kính
rồi dán hai bán kính 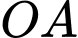 và
và 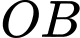 lại với nhau. Gọi
lại với nhau. Gọi 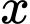 là góc ở tâm của hình quạt tròn dùng làm phễu. Giá trị của
là góc ở tâm của hình quạt tròn dùng làm phễu. Giá trị của 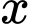 để thể tích phễu lớn nhất là
để thể tích phễu lớn nhất là
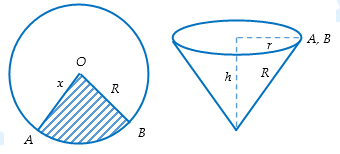
 rồi dán hai bán kính
rồi dán hai bán kính 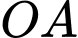 và
và 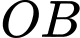 lại với nhau. Gọi
lại với nhau. Gọi 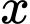 là góc ở tâm của hình quạt tròn dùng làm phễu. Giá trị của
là góc ở tâm của hình quạt tròn dùng làm phễu. Giá trị của 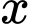 để thể tích phễu lớn nhất là
để thể tích phễu lớn nhất là
A, 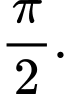
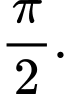
B, 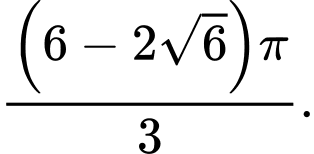
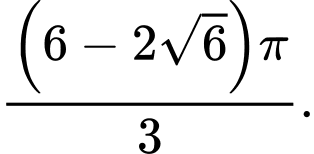
C, 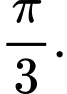
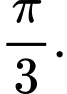
D, 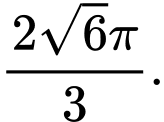
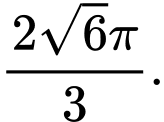
Phễu chính là khối nón có độ dài đường sinh 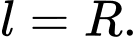 Chuẩn hoá
Chuẩn hoá 
Gọi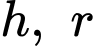 lần lượt là chiều cao và bán kính đáy của khối nón.
lần lượt là chiều cao và bán kính đáy của khối nón.
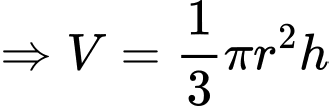
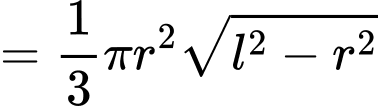
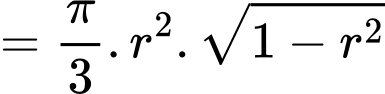
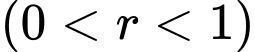
Ta có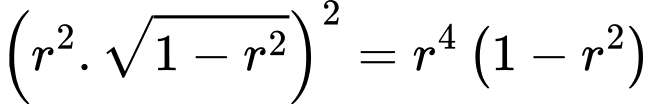
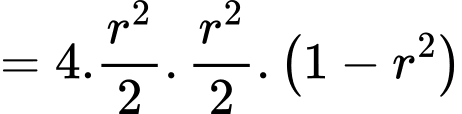
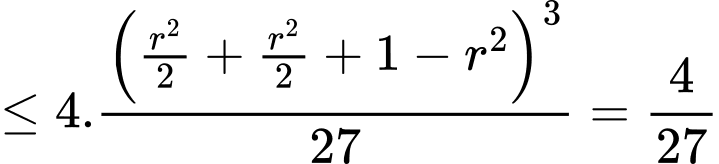
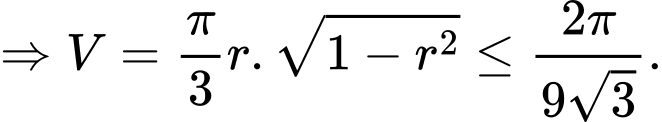
Dấu “=” xảy ra khi và chỉ khi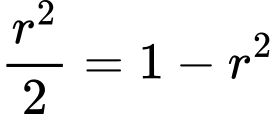
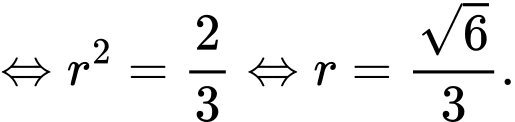
Độ dài cung tròn là
là 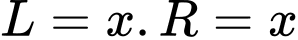 chính bằng chu vi đường tròn đáy của khối nón.
chính bằng chu vi đường tròn đáy của khối nón.
Khi đó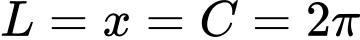
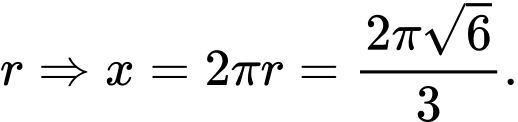 Chọn D. Đáp án: D
Chọn D. Đáp án: D
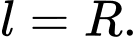 Chuẩn hoá
Chuẩn hoá 
Gọi
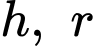 lần lượt là chiều cao và bán kính đáy của khối nón.
lần lượt là chiều cao và bán kính đáy của khối nón.
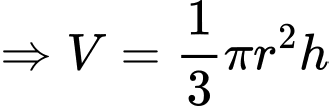
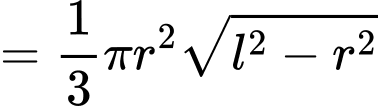
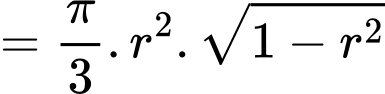
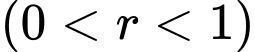
Ta có
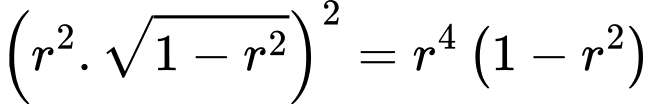
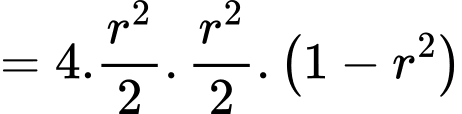
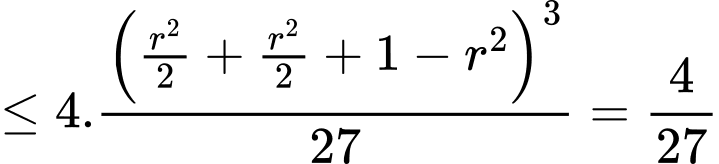
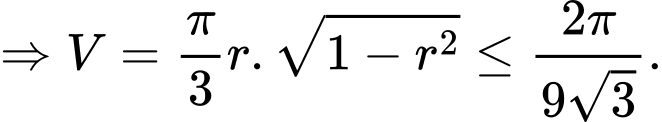
Dấu “=” xảy ra khi và chỉ khi
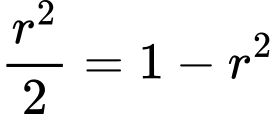
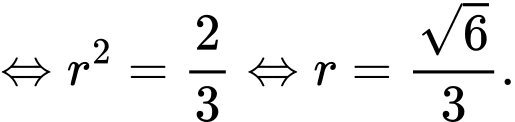
Độ dài cung tròn
 là
là 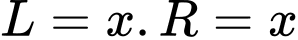 chính bằng chu vi đường tròn đáy của khối nón.
chính bằng chu vi đường tròn đáy của khối nón.
Khi đó
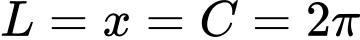
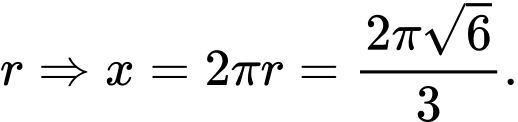 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 8 [6394]: Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều 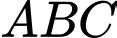 có cạnh bằng
có cạnh bằng  Bạn muốn cắt mảnh tôn hình chữ nhật
Bạn muốn cắt mảnh tôn hình chữ nhật 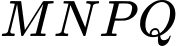 từ mảnh tôn nguyên liệu (với
từ mảnh tôn nguyên liệu (với  thuộc cạnh
thuộc cạnh 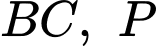 và
và  tương ứng thuộc cạnh
tương ứng thuộc cạnh 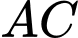 và
và  ) để tạo thành hình trụ có chiều cao bằng
) để tạo thành hình trụ có chiều cao bằng 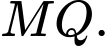 Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là bao nhiêu
Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là bao nhiêu 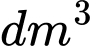 . Viết kết quả làm tròn đến hàng phần trăm?
. Viết kết quả làm tròn đến hàng phần trăm? 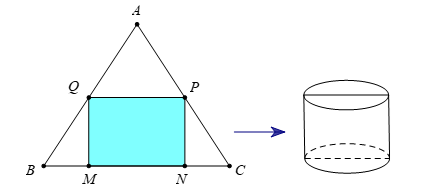
 có cạnh bằng
có cạnh bằng  Bạn muốn cắt mảnh tôn hình chữ nhật
Bạn muốn cắt mảnh tôn hình chữ nhật 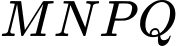 từ mảnh tôn nguyên liệu (với
từ mảnh tôn nguyên liệu (với  thuộc cạnh
thuộc cạnh 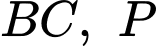 và
và  tương ứng thuộc cạnh
tương ứng thuộc cạnh 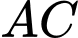 và
và  ) để tạo thành hình trụ có chiều cao bằng
) để tạo thành hình trụ có chiều cao bằng 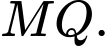 Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là bao nhiêu
Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là bao nhiêu 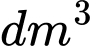 . Viết kết quả làm tròn đến hàng phần trăm?
. Viết kết quả làm tròn đến hàng phần trăm? 
Gọi 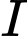 là trung điểm của
là trung điểm của 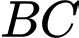 dễ dàng suy ra
dễ dàng suy ra 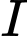 là trung điểm của
là trung điểm của 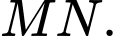
Khi đó đặt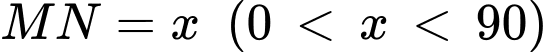
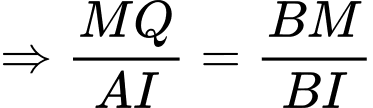
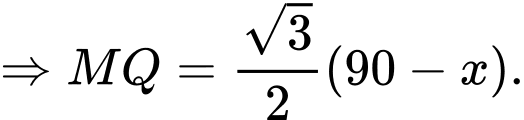
Gọi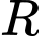 là bán kính hình trụ
là bán kính hình trụ 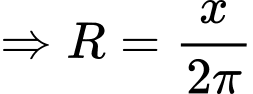
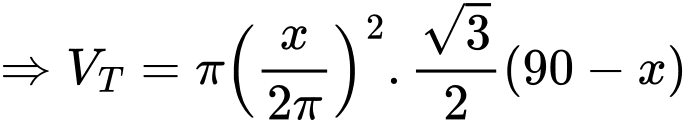
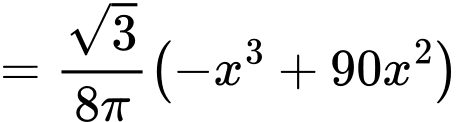
Xét hàm số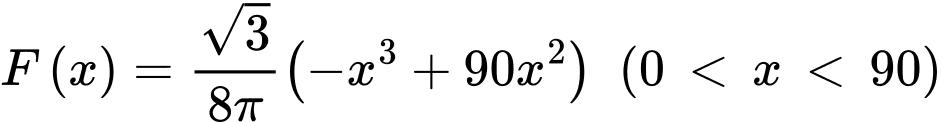
Khi đó ta tìm được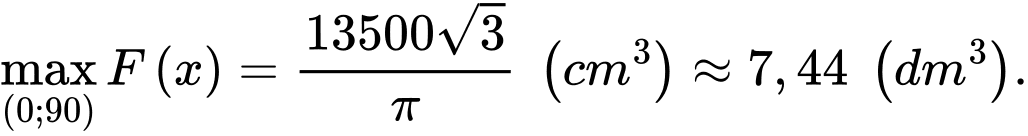 Đáp án: D
Đáp án: D
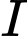 là trung điểm của
là trung điểm của 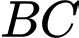 dễ dàng suy ra
dễ dàng suy ra 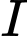 là trung điểm của
là trung điểm của 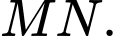
Khi đó đặt
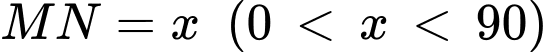
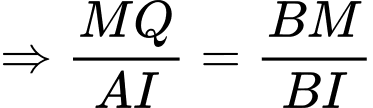
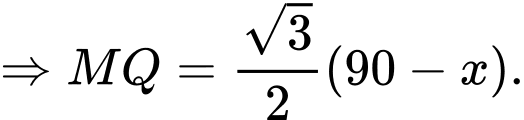
Gọi
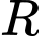 là bán kính hình trụ
là bán kính hình trụ 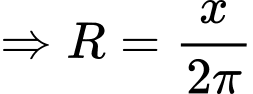
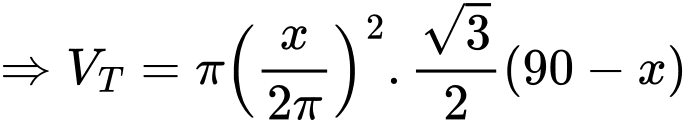
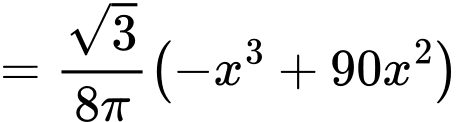
Xét hàm số
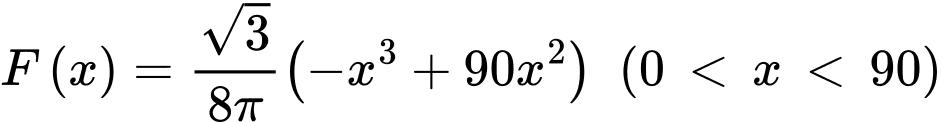
Khi đó ta tìm được
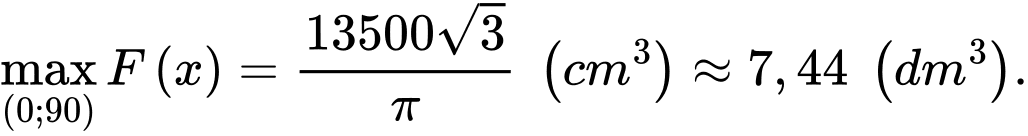 Đáp án: D
Đáp án: D
Câu 9 [6402]: Cho hình chóp 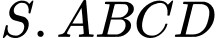 có
có 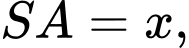 các cạnh còn lại đều bằng 18. Tìm giá trị lớn nhất của thể tích khối chóp
các cạnh còn lại đều bằng 18. Tìm giá trị lớn nhất của thể tích khối chóp 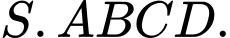
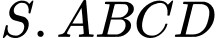 có
có 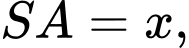 các cạnh còn lại đều bằng 18. Tìm giá trị lớn nhất của thể tích khối chóp
các cạnh còn lại đều bằng 18. Tìm giá trị lớn nhất của thể tích khối chóp 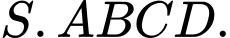
A, 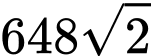 (đvdt).
(đvdt).
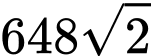 (đvdt).
(đvdt).B, 1458 (đvdt).
C, 8748 (đvdt).
D, 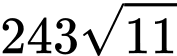 (đvdt).
(đvdt).
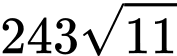 (đvdt).
(đvdt).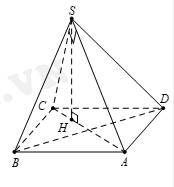
Vì
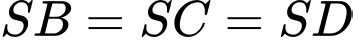 suy ra hình chiếu vuông góc
suy ra hình chiếu vuông góc 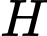 của
của 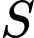 trên mặt phẳng
trên mặt phẳng 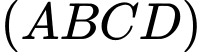 là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác 
Tam giác
 cân tại
cân tại  nên tâm
nên tâm 
Ta có
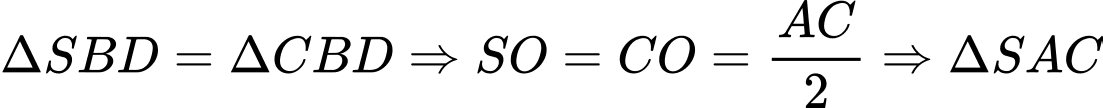 vuông tại
vuông tại 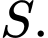
Suy ra

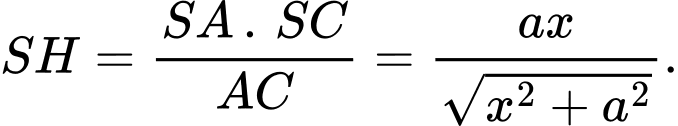
Và
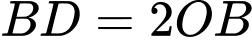
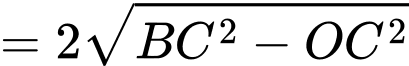
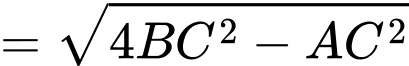
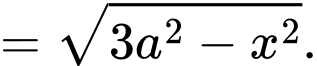
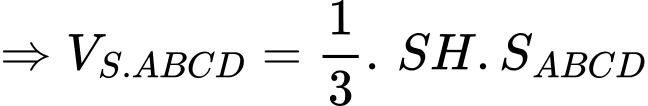
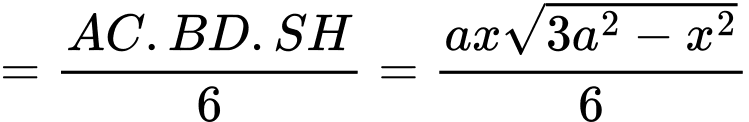
Áp dụng BĐT AM-GM, ta có
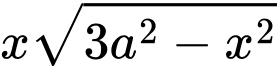
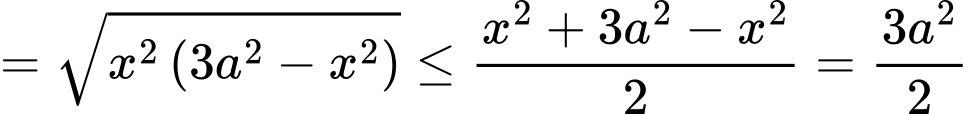
Suy ra
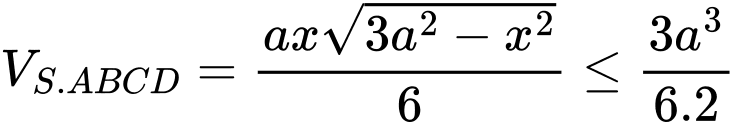
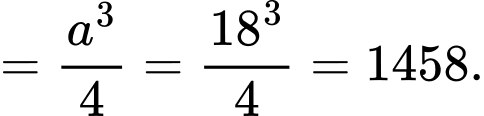
Chọn B. Đáp án: B
Câu 10 [5906]: Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng 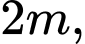 chiều cao
chiều cao 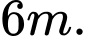 Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình trụ như hình vẽ. Gọi
Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình trụ như hình vẽ. Gọi  là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính
là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính  .
.
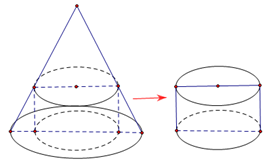
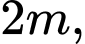 chiều cao
chiều cao 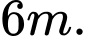 Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình trụ như hình vẽ. Gọi
Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình trụ như hình vẽ. Gọi  là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính
là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính  .
.
A, 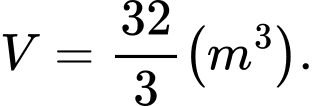
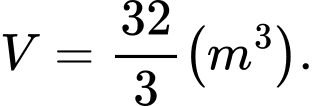
B, 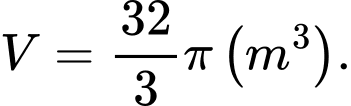
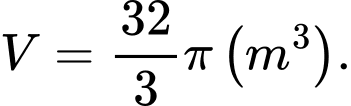
C, 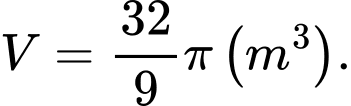
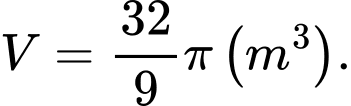
D, 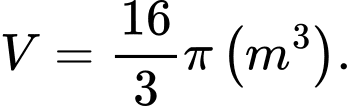
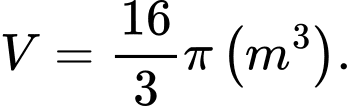
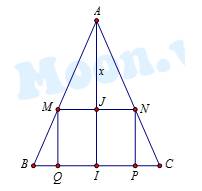
Đặt
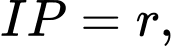
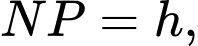
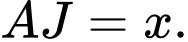
Ta có
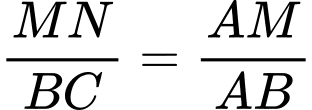
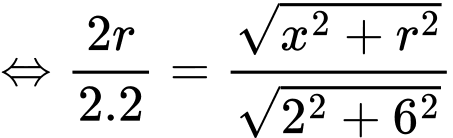
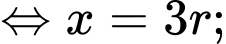
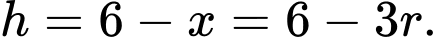
Thể tích khúc gỗ hình trụ là
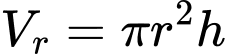
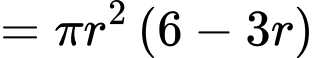
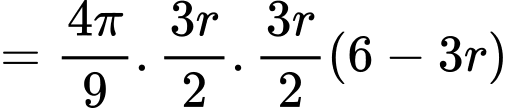
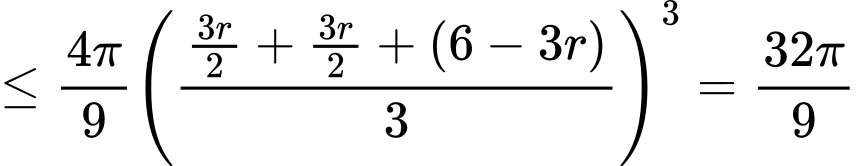
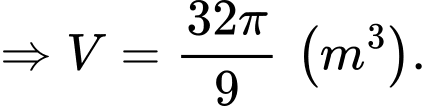
Chọn C. Đáp án: C
Câu 11 [6340]: Cho hình chóp tứ giác đều 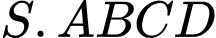 mà khoảng cách từ
mà khoảng cách từ 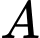 đến mặt phẳng
đến mặt phẳng 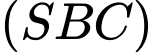 bằng
bằng 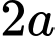 . Gọi
. Gọi 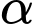 là góc giữa mặt bên và mặt đáy của hình chóp. Khối chóp có thể tích nhỏ nhất khi
là góc giữa mặt bên và mặt đáy của hình chóp. Khối chóp có thể tích nhỏ nhất khi 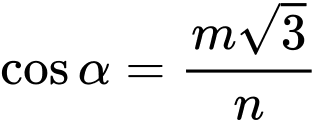 (
(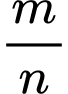 là phân số tối giản). Tính
là phân số tối giản). Tính 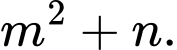
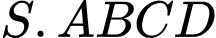 mà khoảng cách từ
mà khoảng cách từ 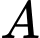 đến mặt phẳng
đến mặt phẳng 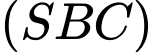 bằng
bằng 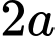 . Gọi
. Gọi 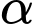 là góc giữa mặt bên và mặt đáy của hình chóp. Khối chóp có thể tích nhỏ nhất khi
là góc giữa mặt bên và mặt đáy của hình chóp. Khối chóp có thể tích nhỏ nhất khi 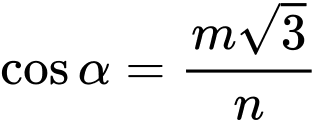 (
(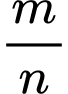 là phân số tối giản). Tính
là phân số tối giản). Tính 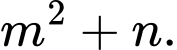
A, 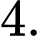
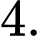
B, 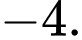
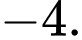
C, 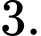
D, 
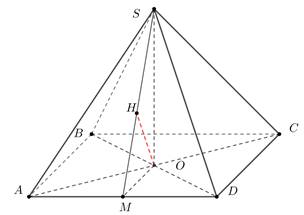
Gọi
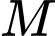 là trung điểm của
là trung điểm của 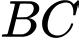 ta có
ta có 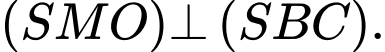
Kẻ
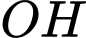 vuông góc với
vuông góc với 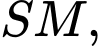 ta có
ta có 
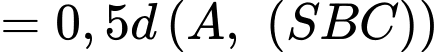
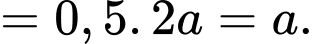
Khi đó trong tam giác vuông
 đặt
đặt 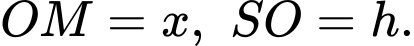
Theo hệ thức lượng trong tam giác vuông
 , ta có
, ta có 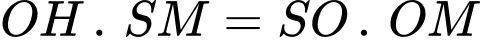
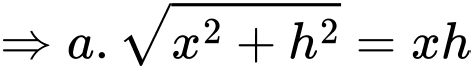
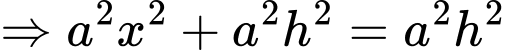
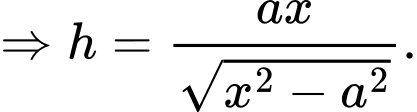
Thể tích khối chóp
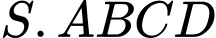 là
là 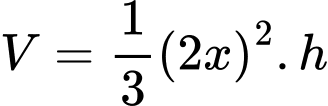
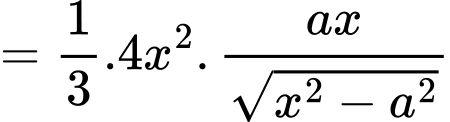
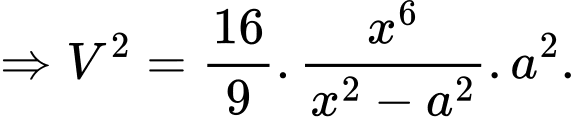
Khảo sát hàm số
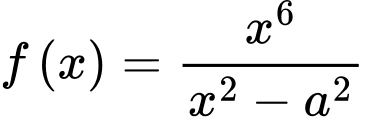
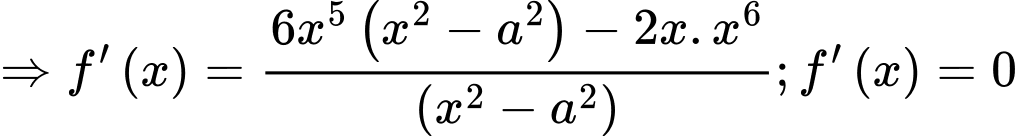
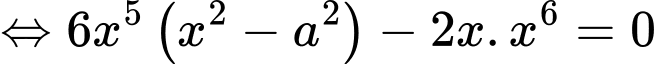
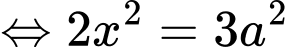
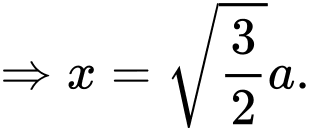
Trong tam giác vuông
 ta có
ta có 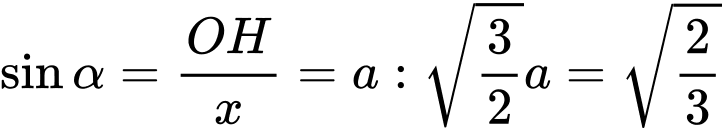
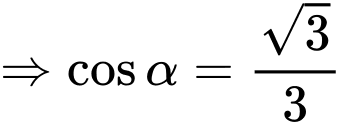
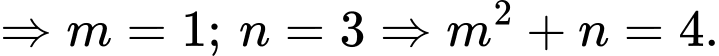
Chọn A. Đáp án: A
Câu 12 [327620]: [Đề thi THPT QG năm 2017-Mã 104] Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 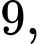 tính thể tích
tính thể tích  của khối chóp có thể tích lớn nhất.
của khối chóp có thể tích lớn nhất.
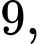 tính thể tích
tính thể tích  của khối chóp có thể tích lớn nhất.
của khối chóp có thể tích lớn nhất. A, 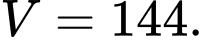
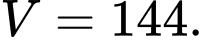
B, 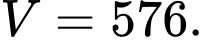
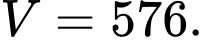
C, 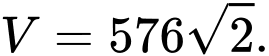
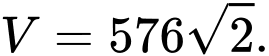
D, 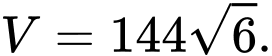
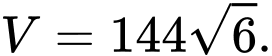
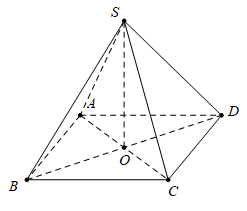
Xét mặt cầu
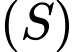 ngoại tiếp hình chóp
ngoại tiếp hình chóp 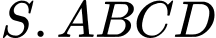
Gọi
 là tâm hình vuông
là tâm hình vuông 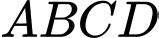
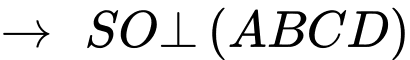
Ta đặt
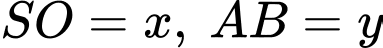 suy ra
suy ra 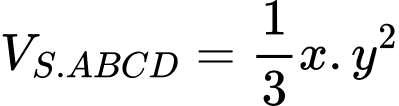
Hình chóp
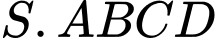 đều nên bán kính mặt cầu
đều nên bán kính mặt cầu 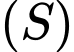 là
là 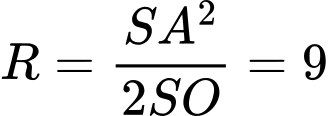
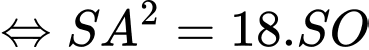
Ta sẽ tìm mối quan hệ giữa
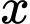 và
và 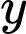 , ta có:
, ta có: 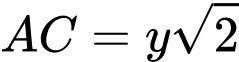
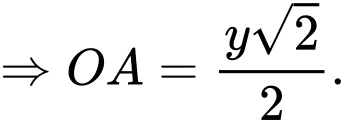
Do đó
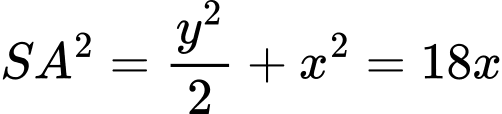
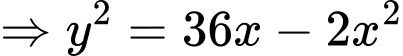
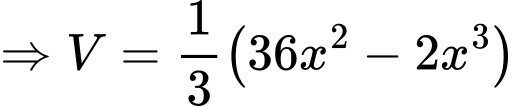 với
với 
Ta có:
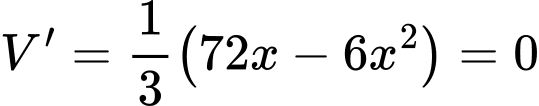
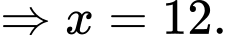 Lập BBT suy ra
Lập BBT suy ra 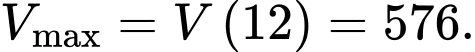 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 13 [791425]: Một loại kẹo có hình dạng là khối cầu với bán kính bằng 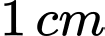 được đặt trong vỏ kẹo có hình dạng là hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể tích bé nhất, tính tổng diện tích tất cả các mặt xung quanh của vỏ kẹo
được đặt trong vỏ kẹo có hình dạng là hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể tích bé nhất, tính tổng diện tích tất cả các mặt xung quanh của vỏ kẹo
 được đặt trong vỏ kẹo có hình dạng là hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể tích bé nhất, tính tổng diện tích tất cả các mặt xung quanh của vỏ kẹo
được đặt trong vỏ kẹo có hình dạng là hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể tích bé nhất, tính tổng diện tích tất cả các mặt xung quanh của vỏ kẹo A,
B,
C,
D,
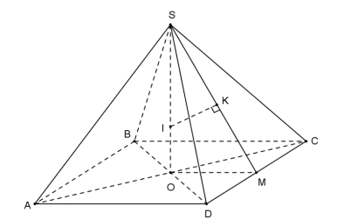
Giả sử vỏ kẹo có hình dạng là hình chóp tứ giác đều
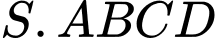 có đáy
có đáy 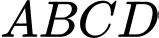 là hình vuông tâm
là hình vuông tâm  , cạnh
, cạnh 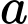 , đường cao
, đường cao 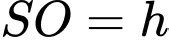 . Loại kẹo có hình dạng là khối cầu có tâm
. Loại kẹo có hình dạng là khối cầu có tâm 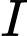 .
.Gọi
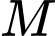 là trung điểm cạnh
là trung điểm cạnh 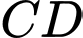 .
.Gọi
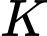 là hình chiếu của
là hình chiếu của 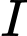 trên
trên 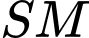
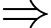
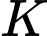 là hình chiếu của
là hình chiếu của 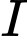 trên mặt phẳng
trên mặt phẳng  .
.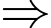
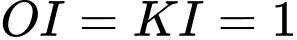
Dễ thấy
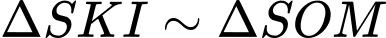
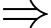
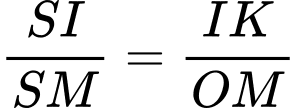
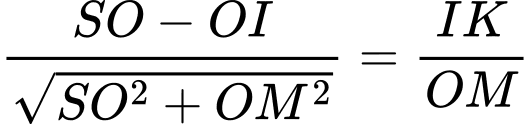
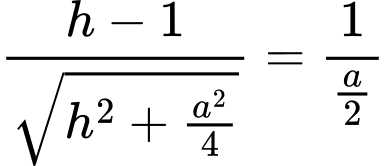
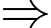
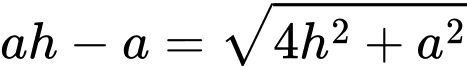
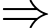
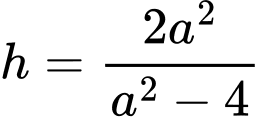
Thể tích khối chóp
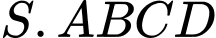 là:
là: 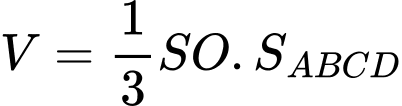
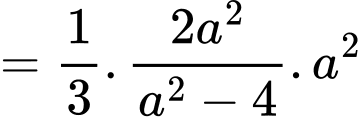
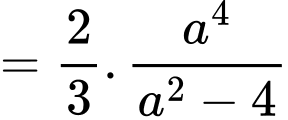
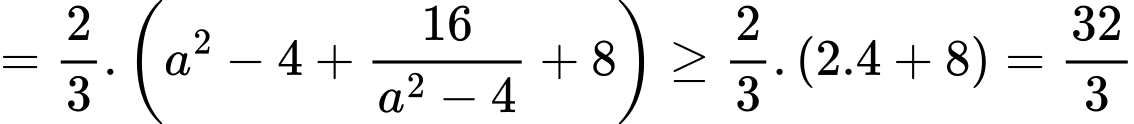
Dấu bằng xảy ra

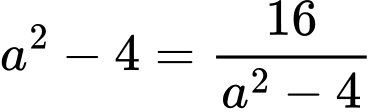

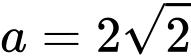
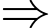

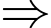
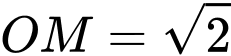 ;
; 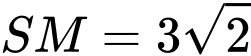
Vậy tổng diện tích tất cả các mặt xung quanh của vỏ kẹo là:
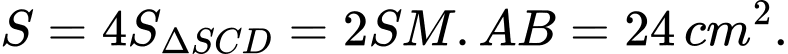 Đáp án: D
Đáp án: D
Câu 14 [26515]: Sử dụng mảnh inox hình chữ nhật 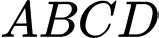 có diện tích bằng
có diện tích bằng 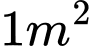 và cạnh
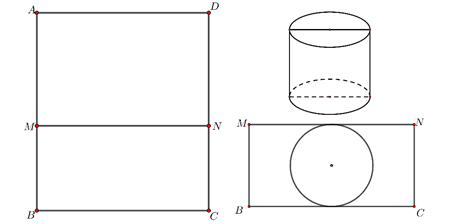
và cạnh 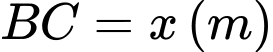 để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật
để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật 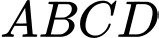 thành
thành 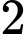 hình chữ nhật
hình chữ nhật 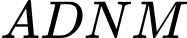 và
và 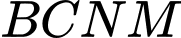 , trong đó phần hình chữ nhật
, trong đó phần hình chữ nhật 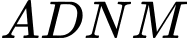 được gò thành phần xung quanh hình trụ có chiều cao bằng
được gò thành phần xung quanh hình trụ có chiều cao bằng  ; phần hình chữ nhật
; phần hình chữ nhật 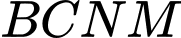 được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi). Tính gần đúng giá trị
được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi). Tính gần đúng giá trị 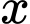 để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
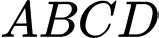 có diện tích bằng
có diện tích bằng 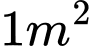 và cạnh
và cạnh 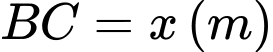 để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật
để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật 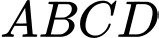 thành
thành 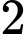 hình chữ nhật
hình chữ nhật 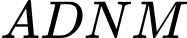 và
và 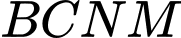 , trong đó phần hình chữ nhật
, trong đó phần hình chữ nhật 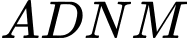 được gò thành phần xung quanh hình trụ có chiều cao bằng
được gò thành phần xung quanh hình trụ có chiều cao bằng  ; phần hình chữ nhật
; phần hình chữ nhật 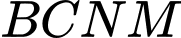 được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi). Tính gần đúng giá trị
được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi). Tính gần đúng giá trị 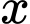 để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
A, 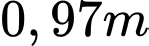 .
.
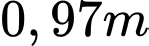 .
.B, 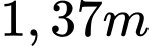 .
.
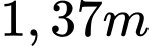 .
.C, 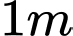 .
.
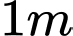 .
.D, 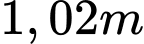 .
.
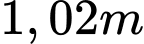 .
.
Ta có 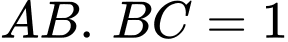
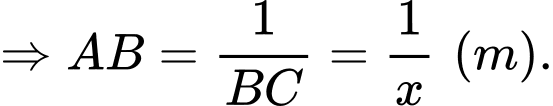
Gọi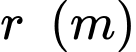 là bán kính đáy hình trụ inox gò được.
là bán kính đáy hình trụ inox gò được.
Ta có chu vi hình tròn đáy bằng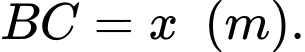
Do đó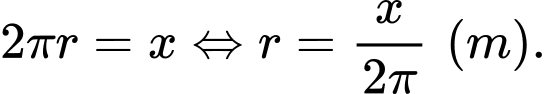
Như vậy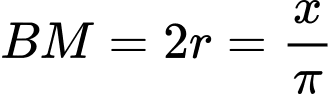
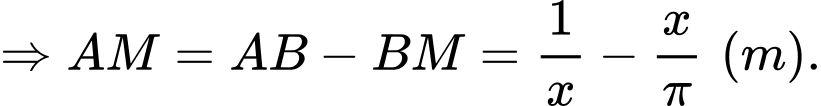
Thể tích khối trụ inox gò được là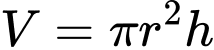
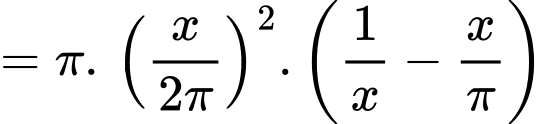
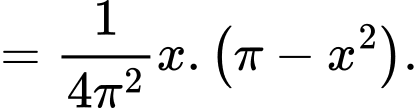
Để thể tích khối trụ là lớn nhất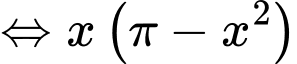 lớn nhất.
lớn nhất.
Xét hàm số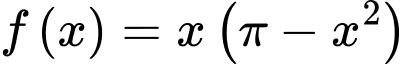 với
với 
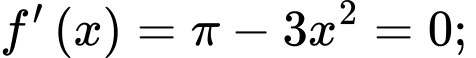
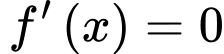
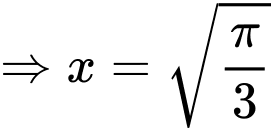
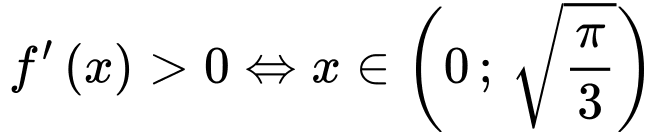 và
và 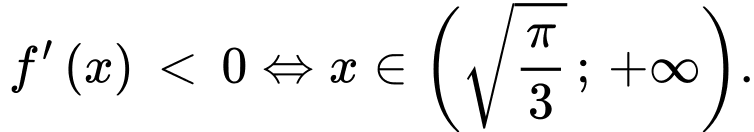
Bởi vậy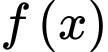 đồng biến trên khoảng
đồng biến trên khoảng 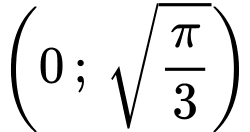 và nghịch biến trên khoảng
và nghịch biến trên khoảng 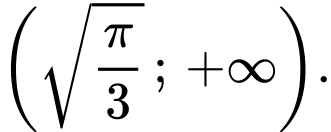
Suy ra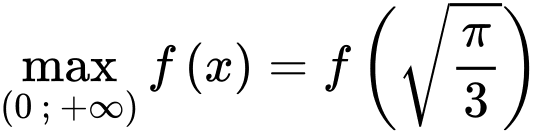
Vậy thể tích lớn nhất tại
lớn nhất tại 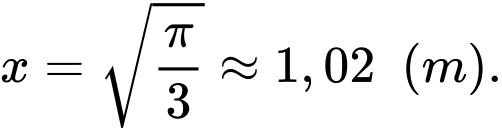 Chọn D. Đáp án: D
Chọn D. Đáp án: D
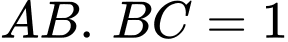
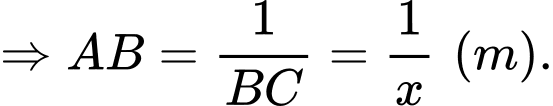
Gọi
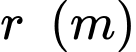 là bán kính đáy hình trụ inox gò được.
là bán kính đáy hình trụ inox gò được.
Ta có chu vi hình tròn đáy bằng
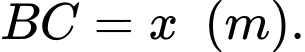
Do đó
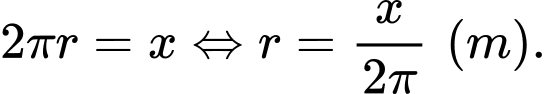
Như vậy
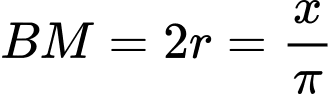
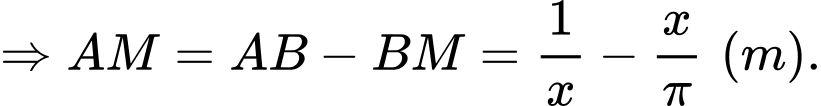
Thể tích khối trụ inox gò được là
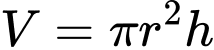
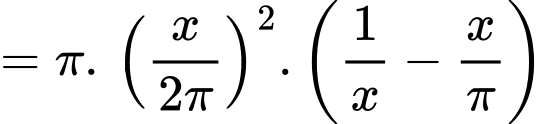
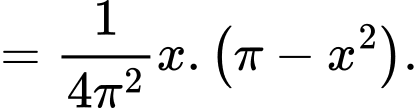
Để thể tích khối trụ là lớn nhất
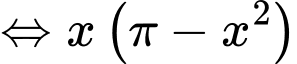 lớn nhất.
lớn nhất.
Xét hàm số
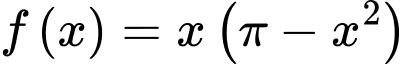 với
với 
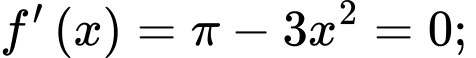
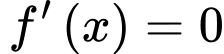
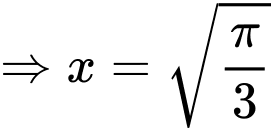
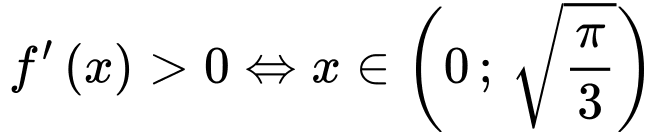 và
và 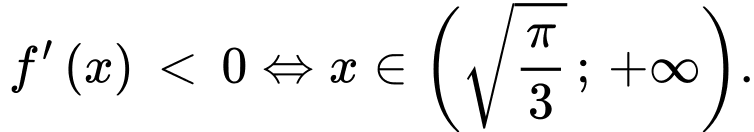
Bởi vậy
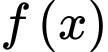 đồng biến trên khoảng
đồng biến trên khoảng 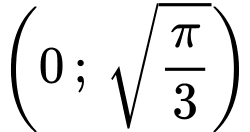 và nghịch biến trên khoảng
và nghịch biến trên khoảng 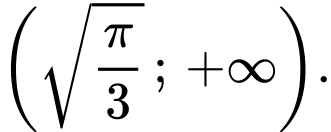
Suy ra
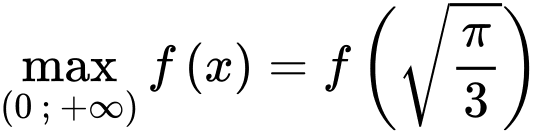
Vậy thể tích
 lớn nhất tại
lớn nhất tại 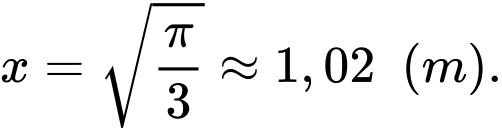 Chọn D. Đáp án: D
Chọn D. Đáp án: D