Đáp án Bài tập tự luyện số 1
Câu 1 [25490]: Đường thẳng 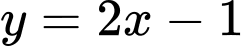 có bao nhiêu điểm chung với đồ thị hàm số
có bao nhiêu điểm chung với đồ thị hàm số 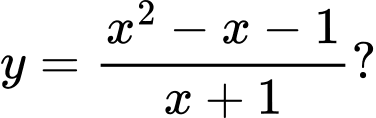
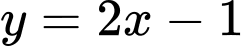 có bao nhiêu điểm chung với đồ thị hàm số
có bao nhiêu điểm chung với đồ thị hàm số 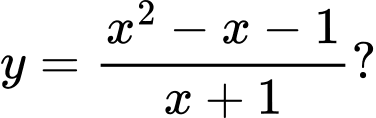
A, 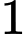 .
.
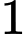 .
.B, 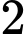 .
.
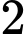 .
.C,  .
.
 .
.D,  .
.
 .
.
Đáp án B
Phương trình hoành độ giao điểm hai đồ thị là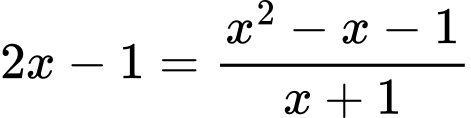
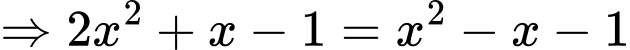
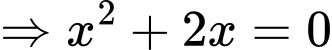
Kết quả thu được 2 giao điểm. Đáp án: B
Phương trình hoành độ giao điểm hai đồ thị là
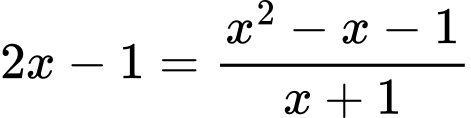
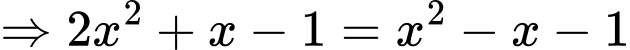
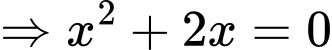
Kết quả thu được 2 giao điểm. Đáp án: B
Câu 2 [25529]: Biết đường thẳng 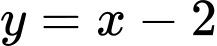 cắt đồ thị hàm số
cắt đồ thị hàm số 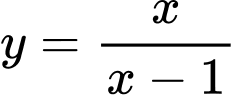 tại
tại 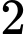 điểm phân biệt
điểm phân biệt 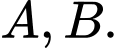 Tìm hoành độ trọng tâm tam giác
Tìm hoành độ trọng tâm tam giác 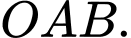
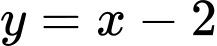 cắt đồ thị hàm số
cắt đồ thị hàm số 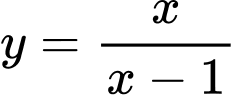 tại
tại 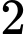 điểm phân biệt
điểm phân biệt 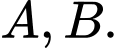 Tìm hoành độ trọng tâm tam giác
Tìm hoành độ trọng tâm tam giác 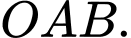
A, 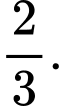
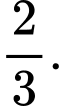
B, 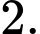
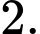
C, 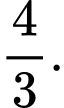
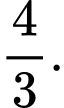
D, 
Phương trình hoành độ giao điểm là: 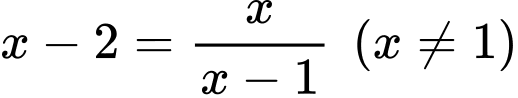
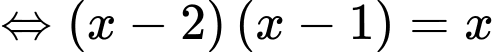
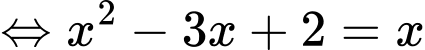
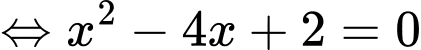
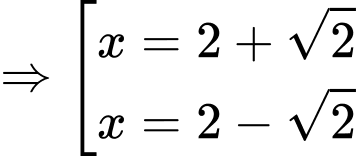
Gọi là trọng tâm tam giác
là trọng tâm tam giác 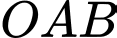 thì
thì 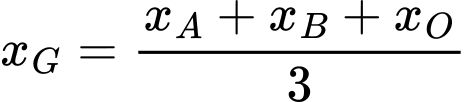
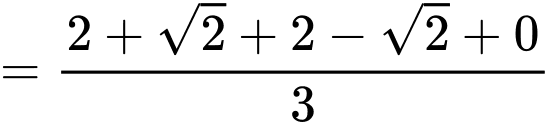
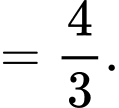
Chọn C. Đáp án: C
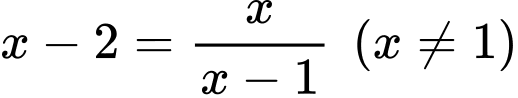
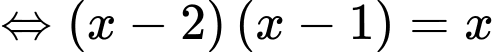
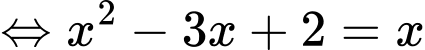
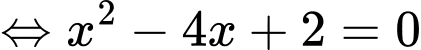
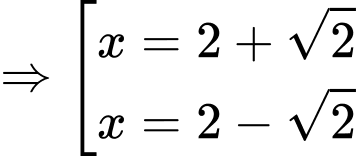
Gọi
 là trọng tâm tam giác
là trọng tâm tam giác 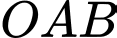 thì
thì 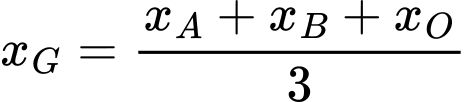
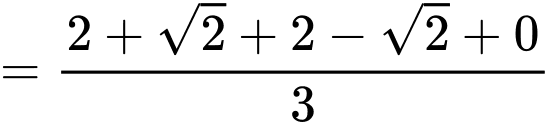
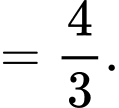
Chọn C. Đáp án: C
Câu 3 [25554]: Cho hàm số 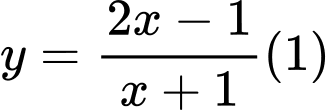 . Đường thẳng
. Đường thẳng 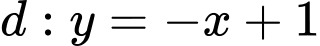 cắt đồ thị hàm số
cắt đồ thị hàm số  tại hai điểm phân biệt
tại hai điểm phân biệt 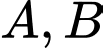 . Tính diện tích của tam giác
. Tính diện tích của tam giác 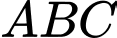 với
với 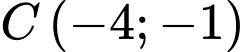 .
.
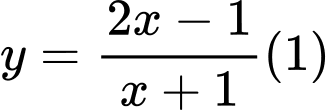 . Đường thẳng
. Đường thẳng 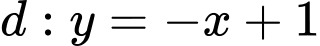 cắt đồ thị hàm số
cắt đồ thị hàm số  tại hai điểm phân biệt
tại hai điểm phân biệt 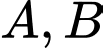 . Tính diện tích của tam giác
. Tính diện tích của tam giác 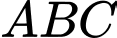 với
với 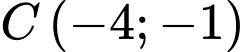 .
. A, 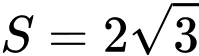 .
.
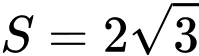 .
.B, 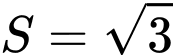 .
.
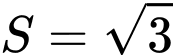 .
.C, 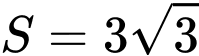 .
.
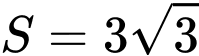 .
.D, 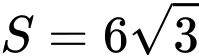 .
.
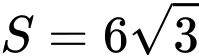 .
.
Phương trình hoành độ giao điểm 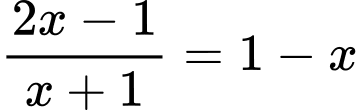
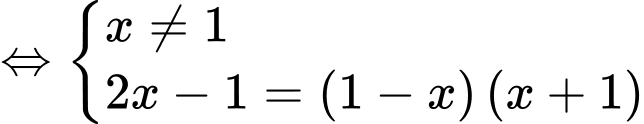
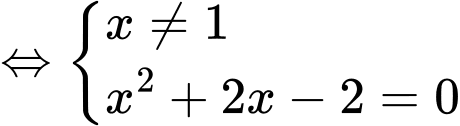
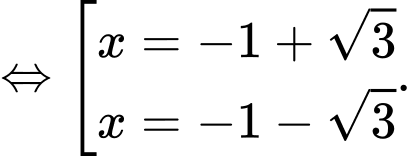
Suy ra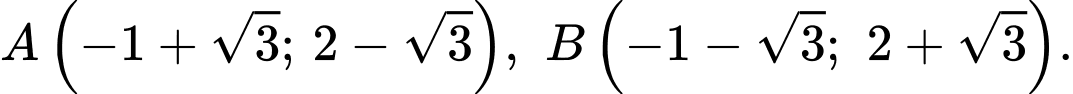
Ta có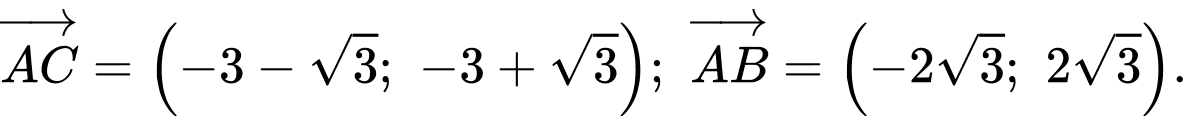
Suy ra diện tích tam giác là
là 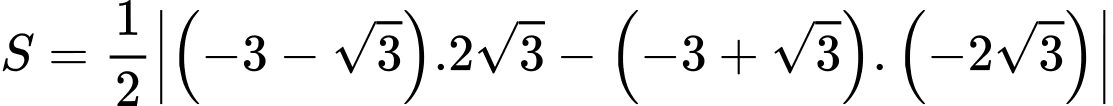
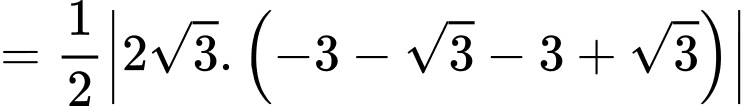
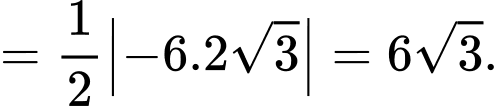
Chọn D. Đáp án: D
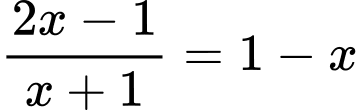
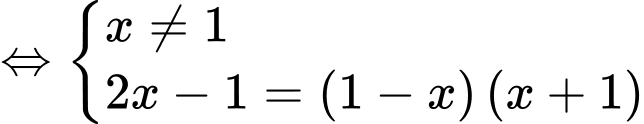
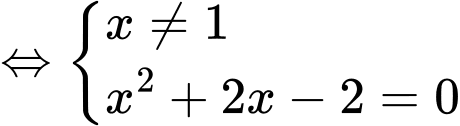
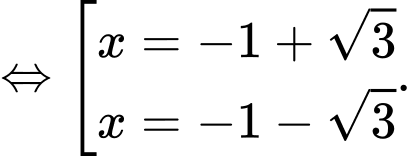
Suy ra
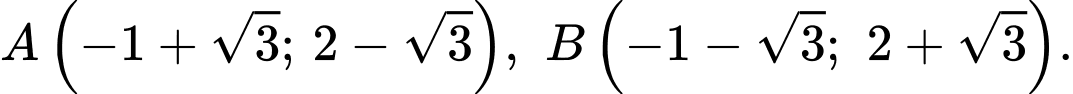
Ta có
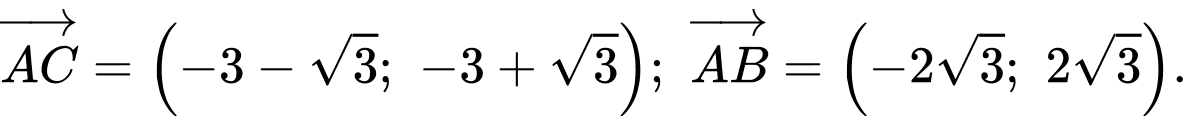
Suy ra diện tích tam giác
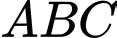 là
là 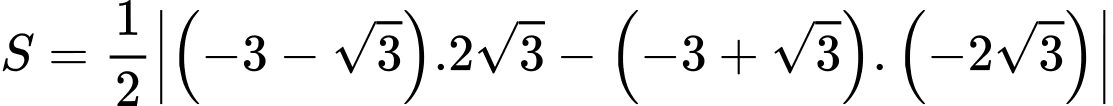
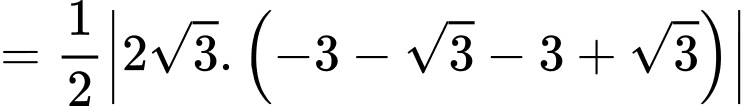
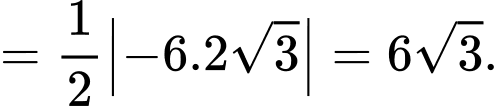
Chọn D. Đáp án: D
Câu 4 [19101]: Tìm điều kiện của 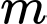 để đường thẳng
để đường thẳng 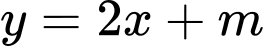 cắt đường cong
cắt đường cong 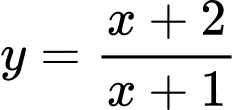 tại hai điểm phân biệt.
tại hai điểm phân biệt.
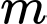 để đường thẳng
để đường thẳng 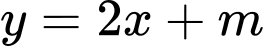 cắt đường cong
cắt đường cong 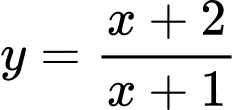 tại hai điểm phân biệt.
tại hai điểm phân biệt. A, 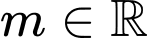 .
.
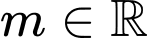 .
.B, 

C, 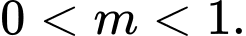
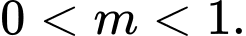
D, 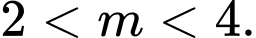
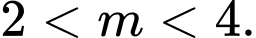
Phương trình hoành độ giao điểm của hai đồ thị là 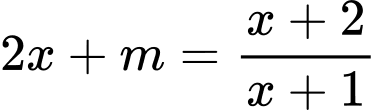
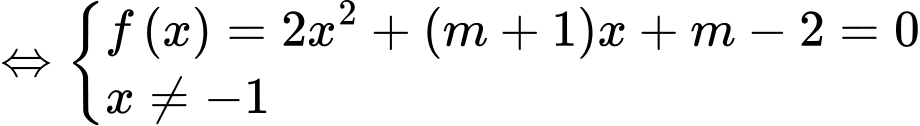
Phương trình luôn có nghiệm khác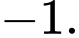 Tồn tại hai giao điểm khi phương trình có hai nghiệm phân biệt.
Tồn tại hai giao điểm khi phương trình có hai nghiệm phân biệt.
Khi đó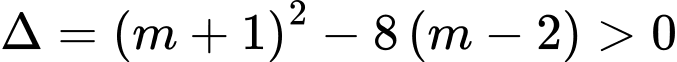
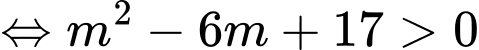 (luôn đúng).
(luôn đúng).
Chọn đáp án A. Đáp án: A
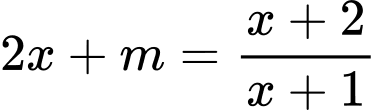
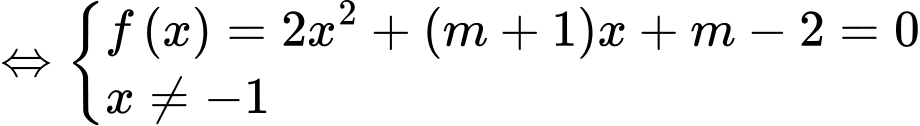
Phương trình luôn có nghiệm khác
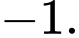 Tồn tại hai giao điểm khi phương trình có hai nghiệm phân biệt.
Tồn tại hai giao điểm khi phương trình có hai nghiệm phân biệt. Khi đó
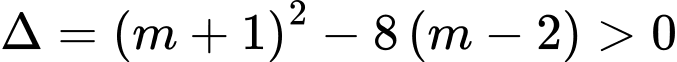
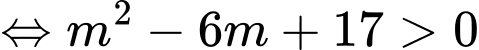 (luôn đúng).
(luôn đúng). Chọn đáp án A. Đáp án: A
Câu 5 [25566]: Cho hàm số 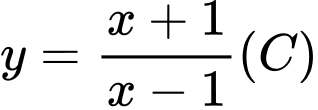 và đường thẳng
và đường thẳng 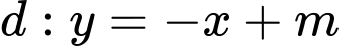 . Giá trị của
. Giá trị của 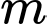 để
để 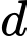 cắt
cắt  tại 2 điểm phân biệt
tại 2 điểm phân biệt 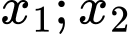 biệt thỏa mãn
biệt thỏa mãn 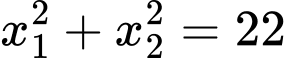 là
là
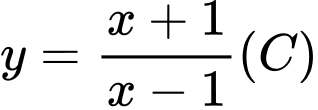 và đường thẳng
và đường thẳng 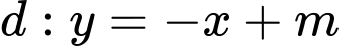 . Giá trị của
. Giá trị của 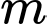 để
để 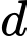 cắt
cắt  tại 2 điểm phân biệt
tại 2 điểm phân biệt 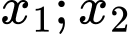 biệt thỏa mãn
biệt thỏa mãn 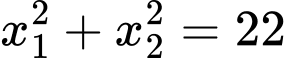 là
là A, 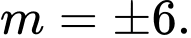
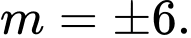
B, 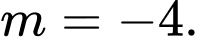
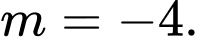
C, 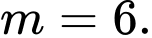
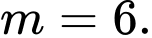
D, cả B và C.
Phương trình hoành độ giao điểm của hai đường:
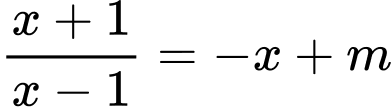
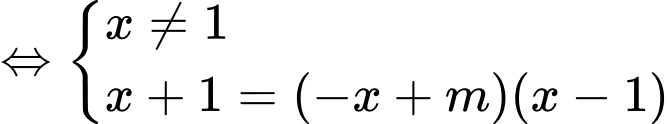
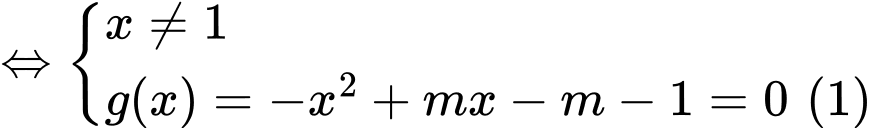
Phương trình (1) có 2 nghiệm phân biệt khác 1 thỏa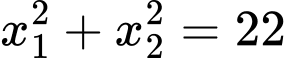
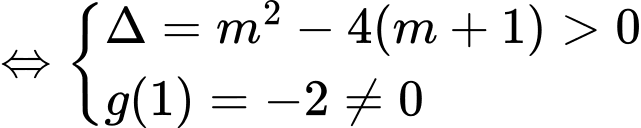
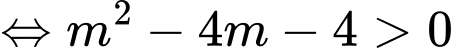
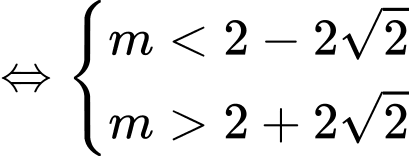
Theo định lý vi-ét ta có: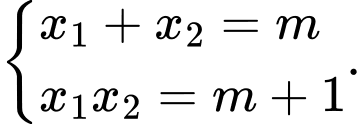
Yêu cầu bài toán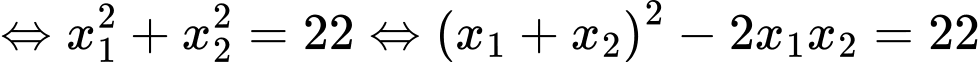
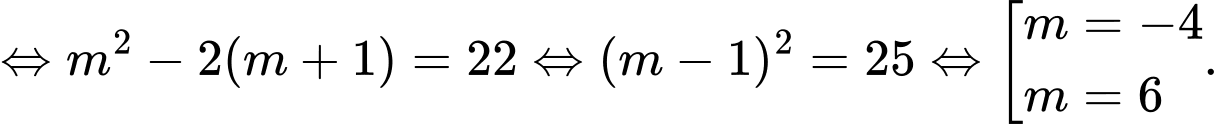 Chọn D. Đáp án: D
Chọn D. Đáp án: D
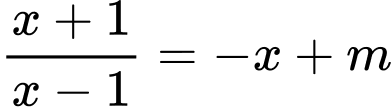
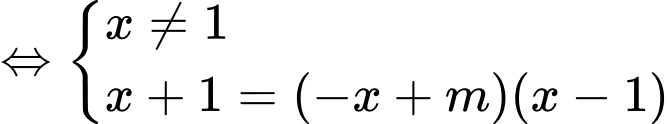
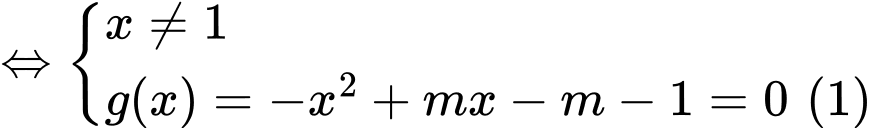
Phương trình (1) có 2 nghiệm phân biệt khác 1 thỏa
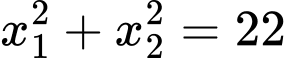
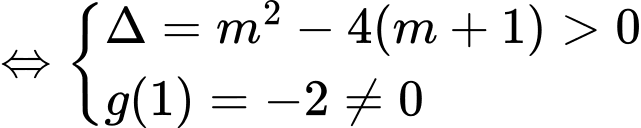
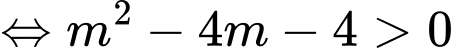
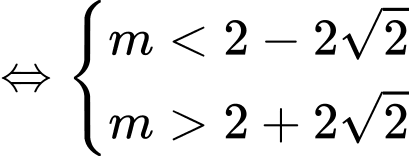
Theo định lý vi-ét ta có:
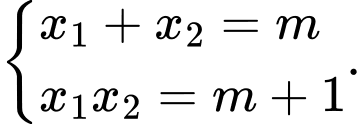
Yêu cầu bài toán
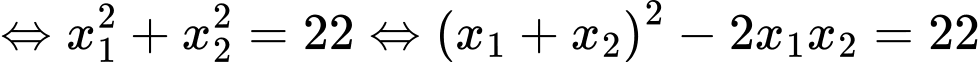
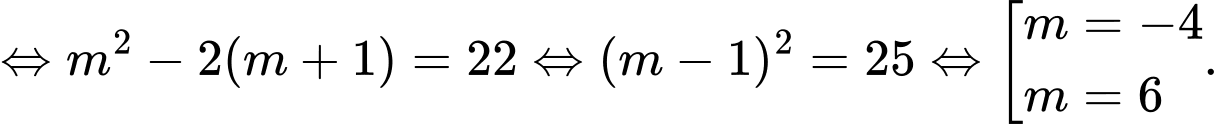 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 6 [25502]: Cho hàm số 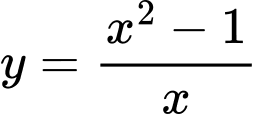 có đồ thị
có đồ thị  Giá trị của
Giá trị của 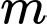 để đường thẳng
để đường thẳng 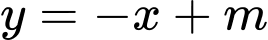 cắt
cắt  tại hai điểm
tại hai điểm 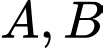 sao cho
sao cho 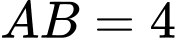 là
là
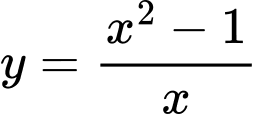 có đồ thị
có đồ thị  Giá trị của
Giá trị của 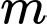 để đường thẳng
để đường thẳng 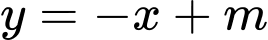 cắt
cắt  tại hai điểm
tại hai điểm 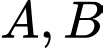 sao cho
sao cho 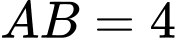 là
là A, 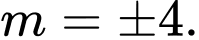
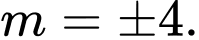
B, 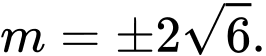
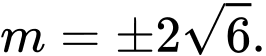
C, 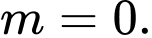
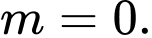
D, 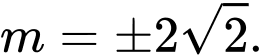
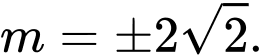
Phương trình hoành độ giao điểm là 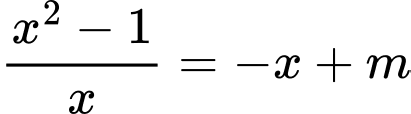
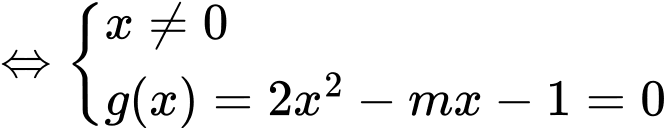
Để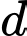 cắt
cắt  tại 2 điểm phân biệt thì
tại 2 điểm phân biệt thì 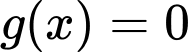 có 2 nghiệm phân biệt khác 0
có 2 nghiệm phân biệt khác 0
Khi đó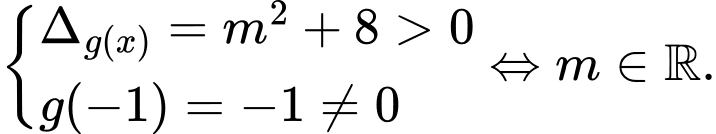
Gọi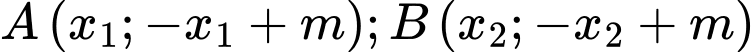
Theo Viet ta có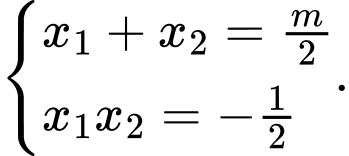
Ta có: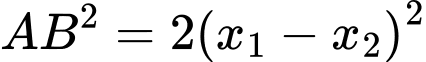
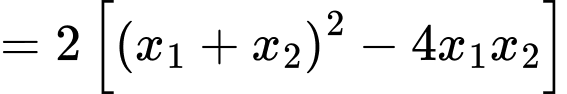
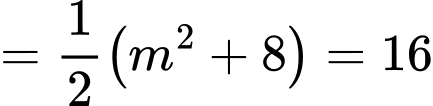
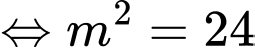
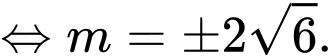
Chọn B. Đáp án: B
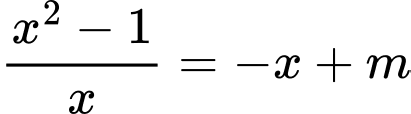
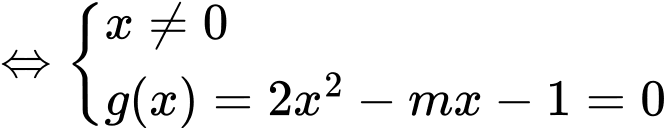
Để
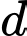 cắt
cắt  tại 2 điểm phân biệt thì
tại 2 điểm phân biệt thì 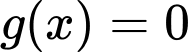 có 2 nghiệm phân biệt khác 0
có 2 nghiệm phân biệt khác 0
Khi đó
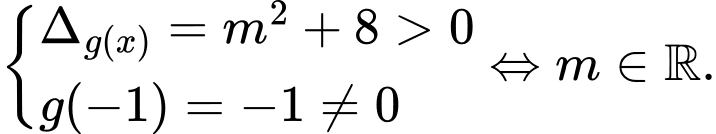
Gọi
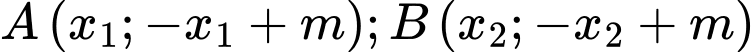
Theo Viet ta có
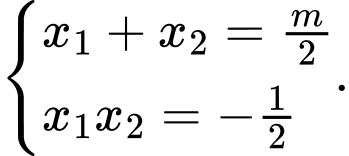
Ta có:
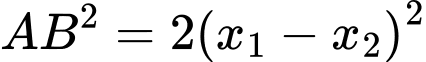
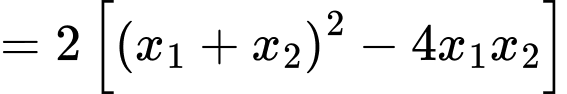
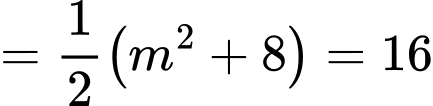
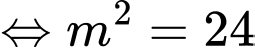
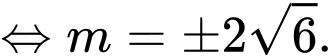
Chọn B. Đáp án: B
Câu 7 [25506]: Cho hàm số 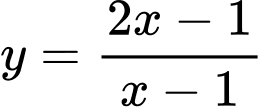 có đồ thị
có đồ thị  Tìm tất cảc các giá trị thực của tham số
Tìm tất cảc các giá trị thực của tham số 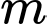 để đường thẳng
để đường thẳng 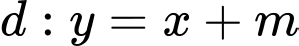 và cắt
và cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 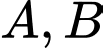 sao cho
sao cho 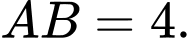
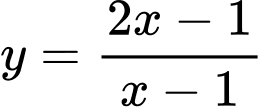 có đồ thị
có đồ thị  Tìm tất cảc các giá trị thực của tham số
Tìm tất cảc các giá trị thực của tham số 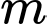 để đường thẳng
để đường thẳng 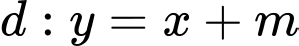 và cắt
và cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 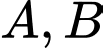 sao cho
sao cho 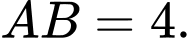
A, 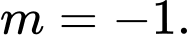
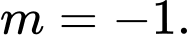
B, 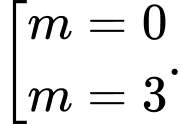
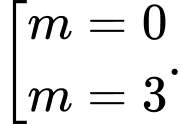
C, 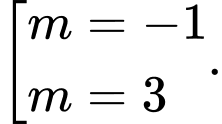
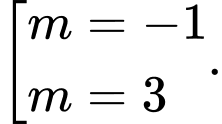
D, 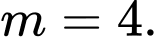
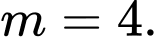
Phương trình hoành độ giao điểm là 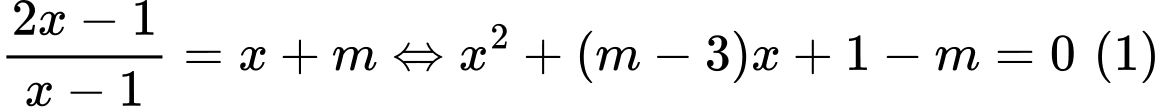
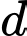 cắt
cắt  tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt khác
tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt khác 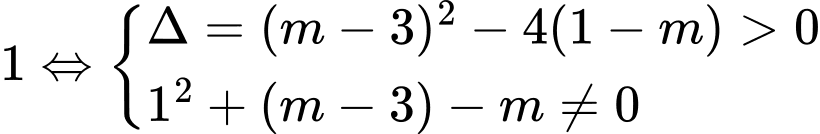
Suy ra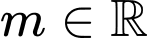
Khi đó: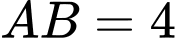
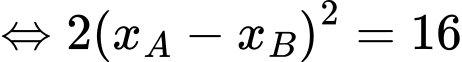
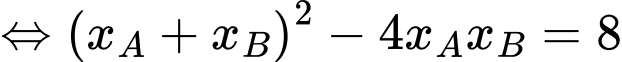
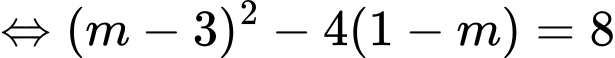
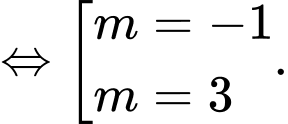
Chọn C. Đáp án: C
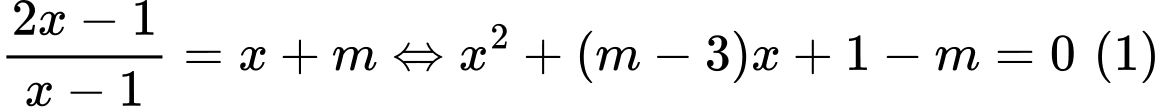
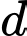 cắt
cắt  tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt khác
tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt khác 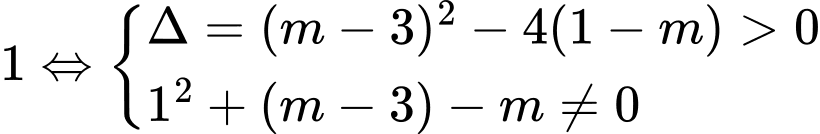
Suy ra
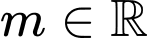
Khi đó:
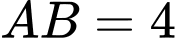
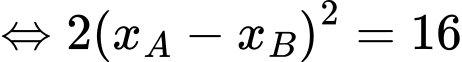
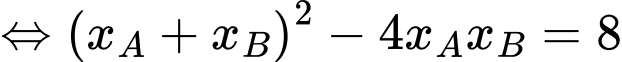
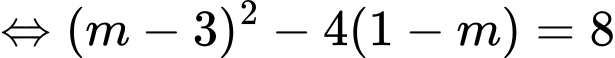
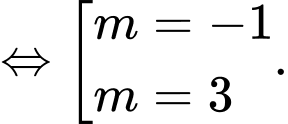
Chọn C. Đáp án: C
Câu 8 [324360]: Giá trị của 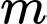 đề đường thẳng
đề đường thẳng 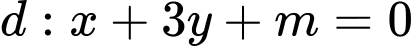 cắt đồ thị hàm số
cắt đồ thị hàm số 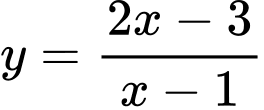 tại hai điểm
tại hai điểm 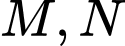 sao cho tam giác
sao cho tam giác 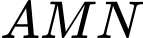 vuông tại điểm
vuông tại điểm 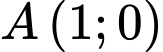 là
là
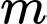 đề đường thẳng
đề đường thẳng 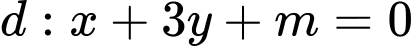 cắt đồ thị hàm số
cắt đồ thị hàm số 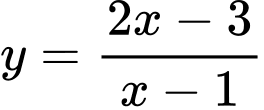 tại hai điểm
tại hai điểm 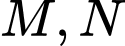 sao cho tam giác
sao cho tam giác 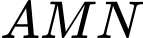 vuông tại điểm
vuông tại điểm 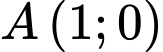 là
là A, 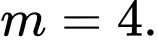
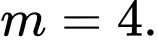
B, 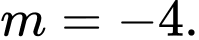
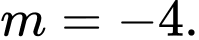
C, 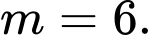
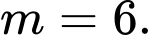
D, 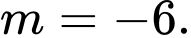
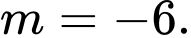
Đáp án D
Phương trình hoành độ giao điểm hai đồ thị là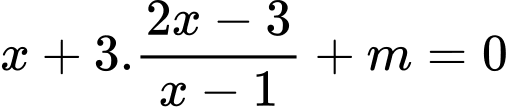
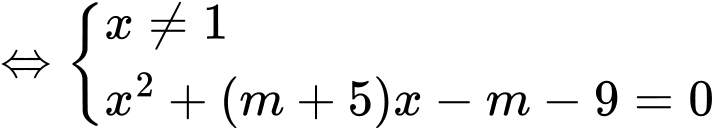
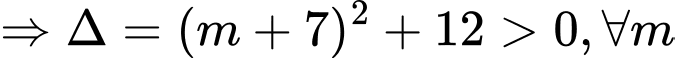
Vậy hai đồ thị luôn có 2 giao điểm phân biệt với mọi m.
Ta có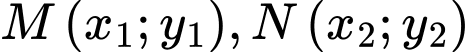
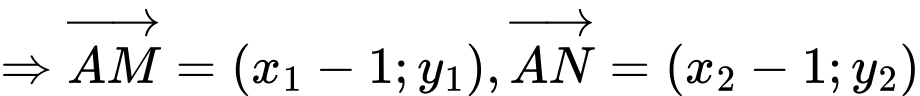 .
.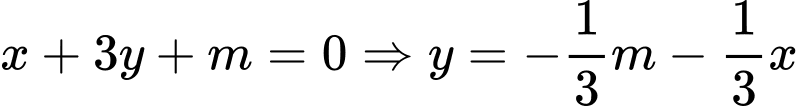
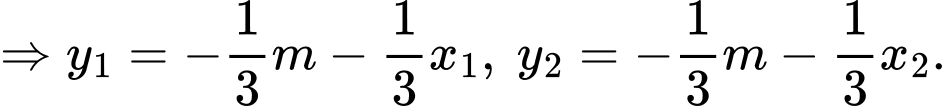
Khi đó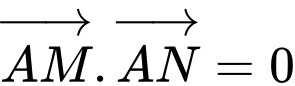
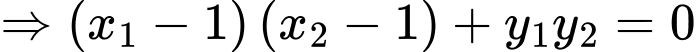
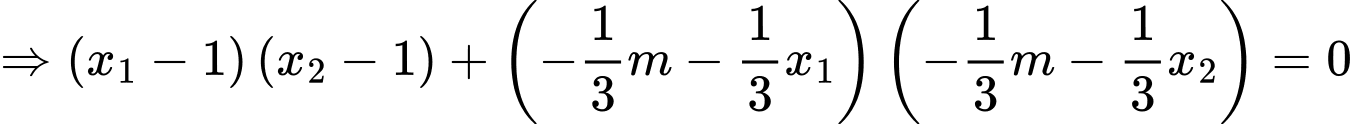
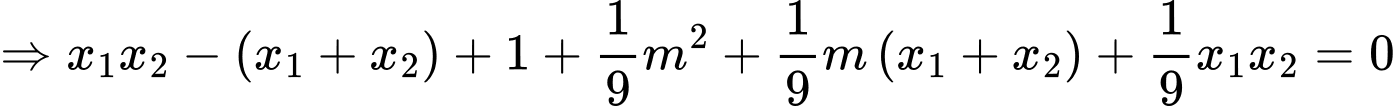
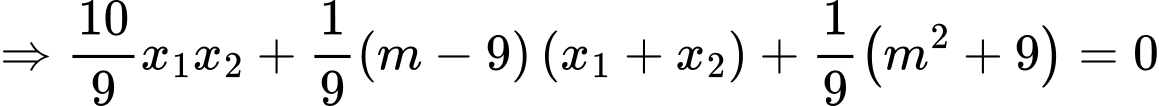
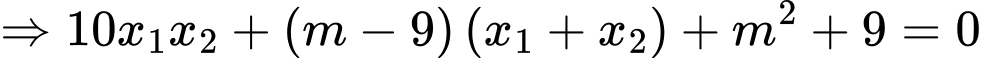
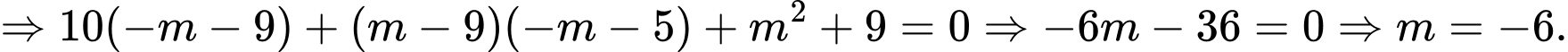 Đáp án: D
Đáp án: D
Phương trình hoành độ giao điểm hai đồ thị là
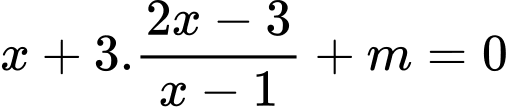
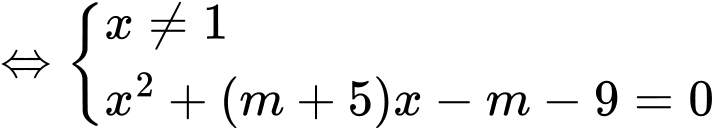
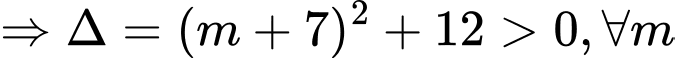
Vậy hai đồ thị luôn có 2 giao điểm phân biệt với mọi m.
Ta có
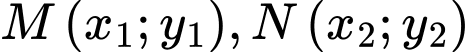
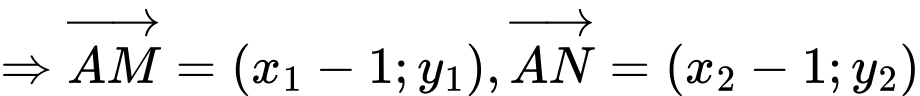 .
.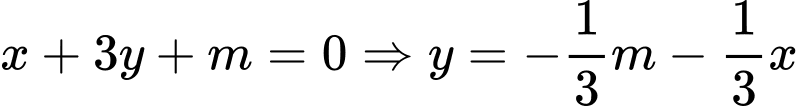
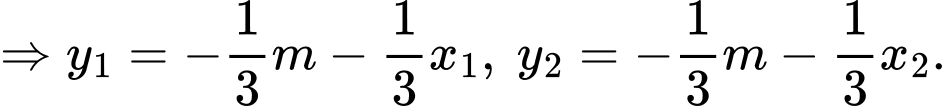
Khi đó
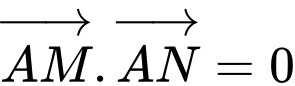
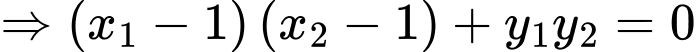
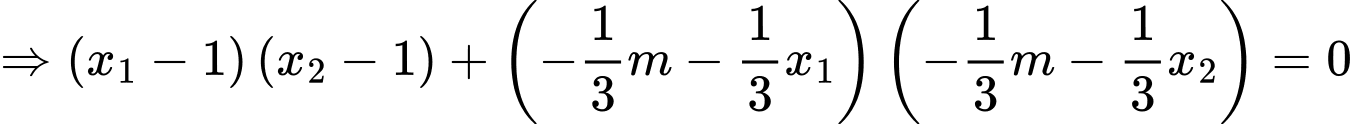
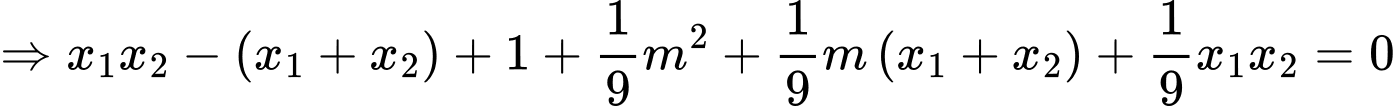
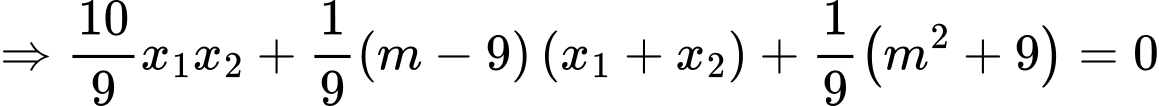
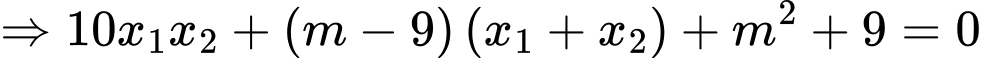
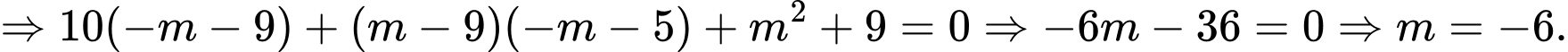 Đáp án: D
Đáp án: D
Câu 9 [25531]: Gọi 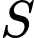 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số 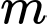 để đồ thị hàm số
để đồ thị hàm số 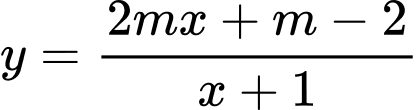 cắt đường thẳng
cắt đường thẳng 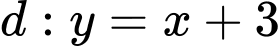 tại hai điểm phân biệt
tại hai điểm phân biệt 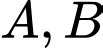 sao cho tam giác
sao cho tam giác 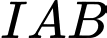 có diện tích bằng 3, với
có diện tích bằng 3, với 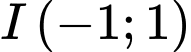 . Tính tổng tất cả các phần tử của
. Tính tổng tất cả các phần tử của 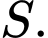
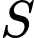 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số 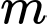 để đồ thị hàm số
để đồ thị hàm số 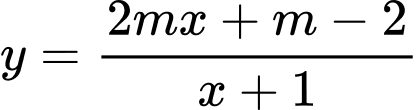 cắt đường thẳng
cắt đường thẳng 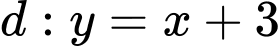 tại hai điểm phân biệt
tại hai điểm phân biệt 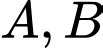 sao cho tam giác
sao cho tam giác 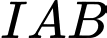 có diện tích bằng 3, với
có diện tích bằng 3, với 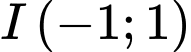 . Tính tổng tất cả các phần tử của
. Tính tổng tất cả các phần tử của 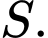
A, 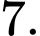
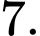
B, 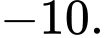
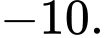
C, 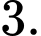
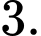
D, 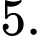
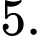
PT hoành độ giao điểm là 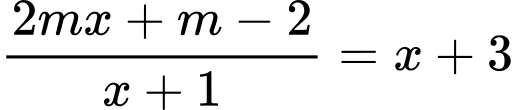
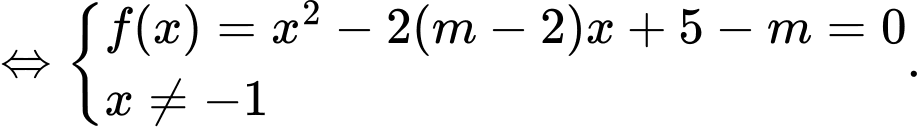
Hai đồ thị có hai giao điểm khi và chỉ khi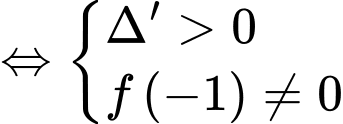
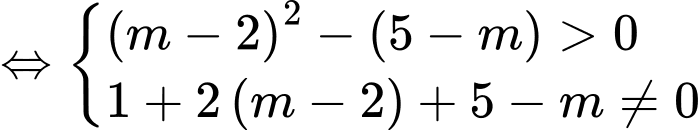
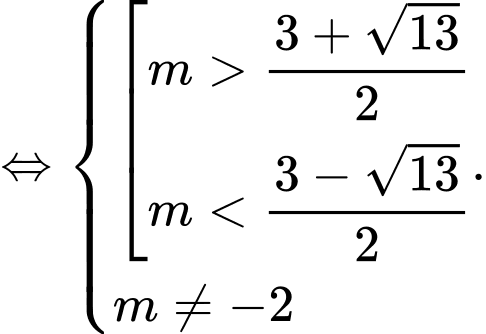
Khi đó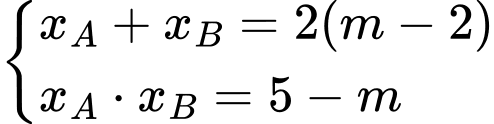
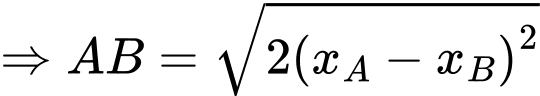
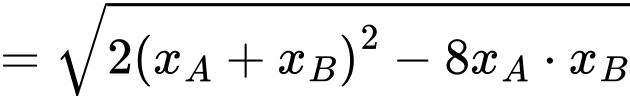
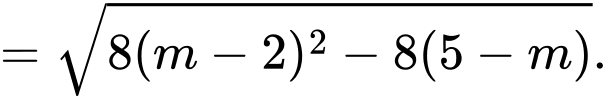
Mặt khác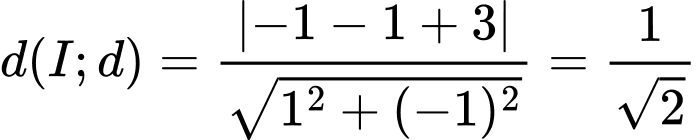
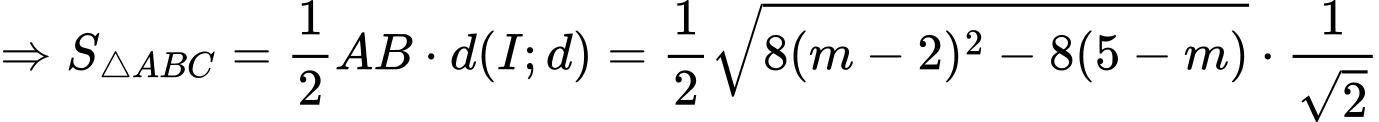
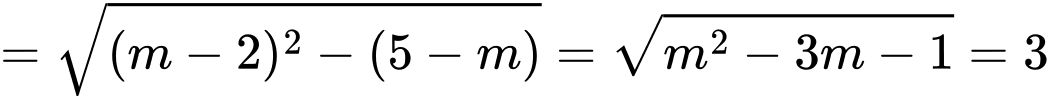
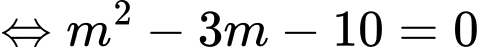
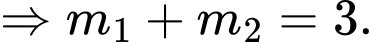 Chọn C. Đáp án: C
Chọn C. Đáp án: C
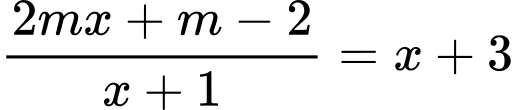
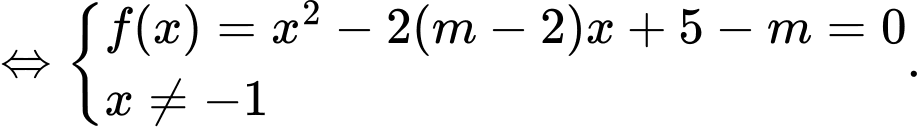
Hai đồ thị có hai giao điểm khi và chỉ khi
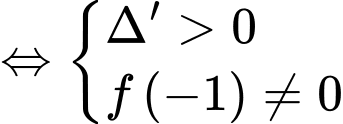
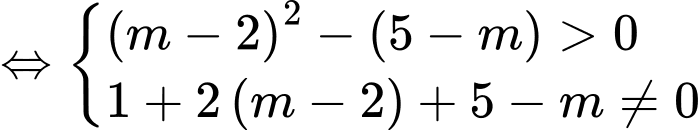
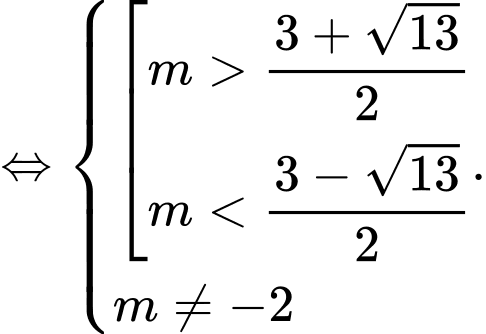
Khi đó
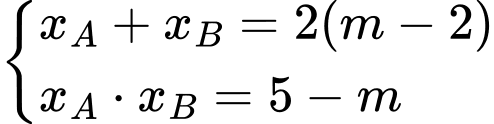
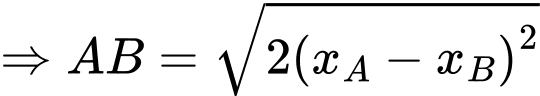
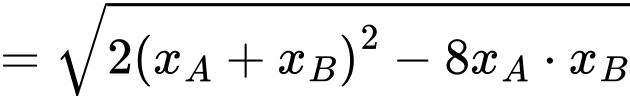
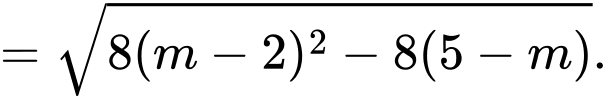
Mặt khác
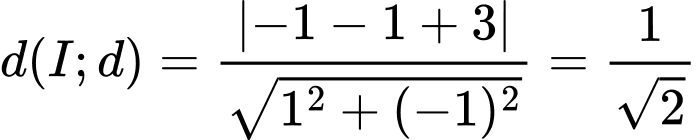
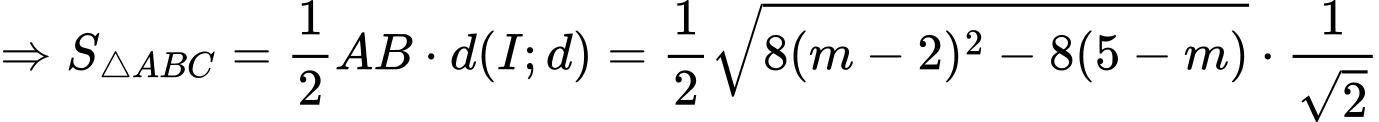
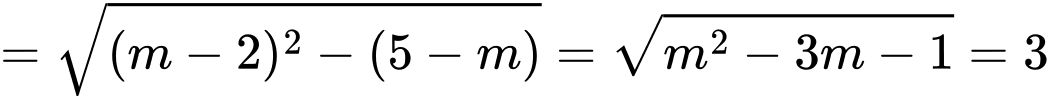
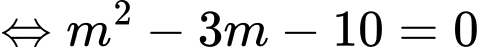
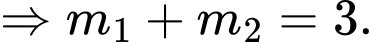 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 10 [25552]: Cho hàm số 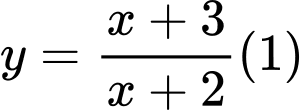 . Gọi
. Gọi 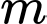 là giá trị để đường thẳng
là giá trị để đường thẳng 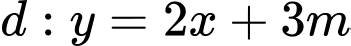 cắt đồ thị hàm số
cắt đồ thị hàm số  tại hai điểm phân biệt
tại hai điểm phân biệt 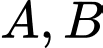 thỏa mãn
thỏa mãn 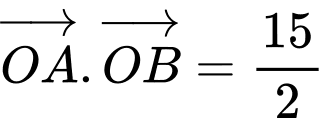 với
với  là gốc tọa độ. Giá trị của
là gốc tọa độ. Giá trị của 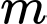 bằng
bằng
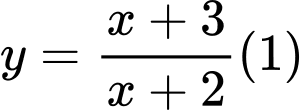 . Gọi
. Gọi 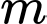 là giá trị để đường thẳng
là giá trị để đường thẳng 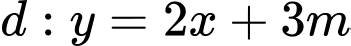 cắt đồ thị hàm số
cắt đồ thị hàm số  tại hai điểm phân biệt
tại hai điểm phân biệt 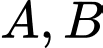 thỏa mãn
thỏa mãn 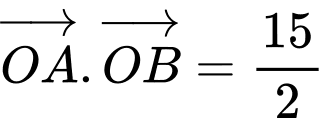 với
với  là gốc tọa độ. Giá trị của
là gốc tọa độ. Giá trị của 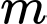 bằng
bằng A, 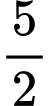 .
.
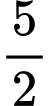 .
.B, 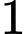 .
.
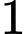 .
.C, 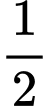 .
.
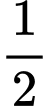 .
.D, 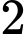 .
.
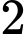 .
.
Phương trình hoành độ giao điểm 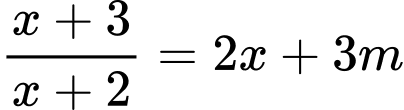
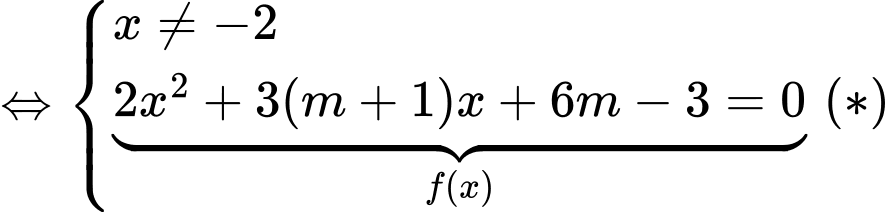
 cắt
cắt 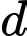 tại hai điểm phân biệt khi
tại hai điểm phân biệt khi 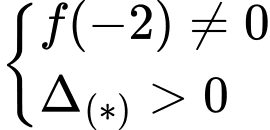
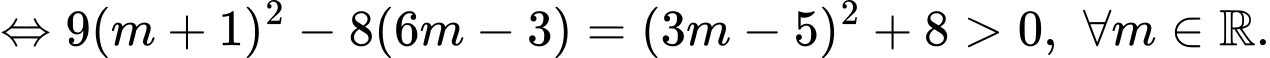
Gọi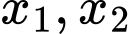 là hai nghiệm của phương trình
là hai nghiệm của phương trình  ta có
ta có 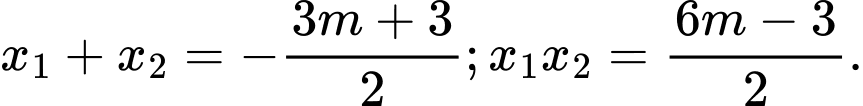
Và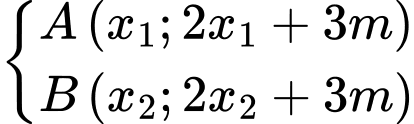
Ta có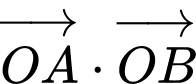
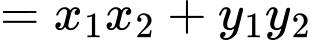
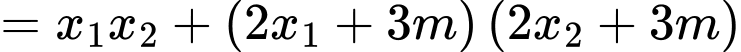
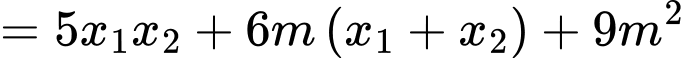
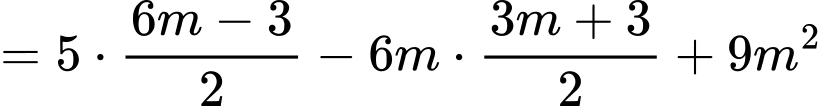
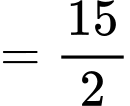
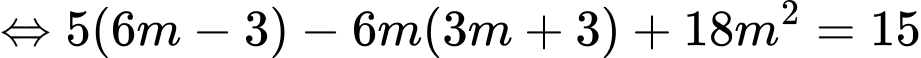
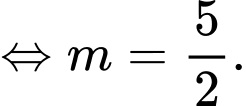 Chọn A. Đáp án: A
Chọn A. Đáp án: A
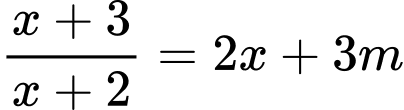
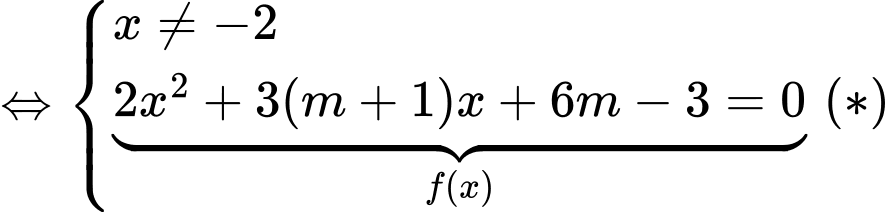
 cắt
cắt 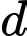 tại hai điểm phân biệt khi
tại hai điểm phân biệt khi 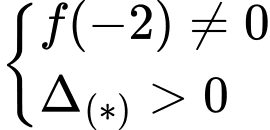
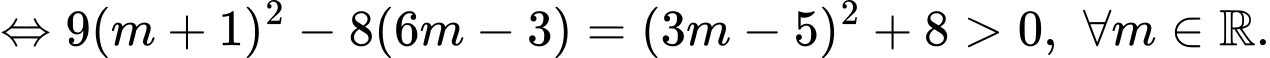
Gọi
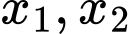 là hai nghiệm của phương trình
là hai nghiệm của phương trình  ta có
ta có 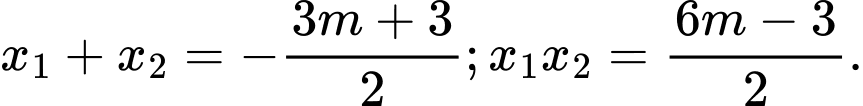
Và
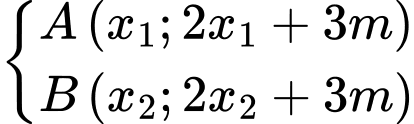
Ta có
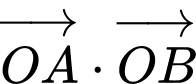
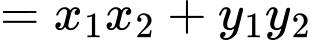
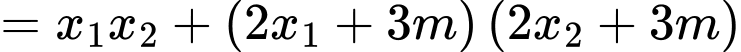
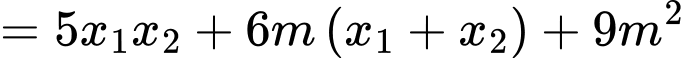
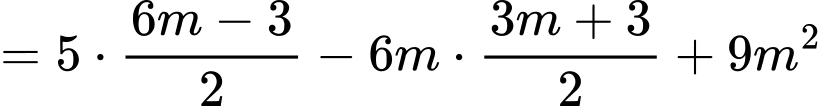
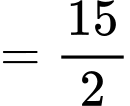
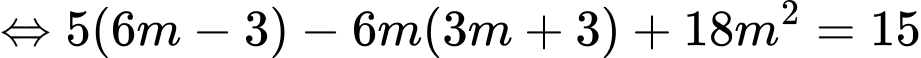
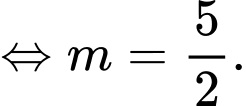 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 11 [25569]: Cho hàm số 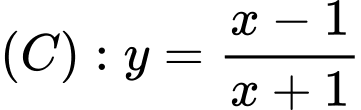 và đường thẳng
và đường thẳng 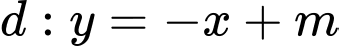 . Với giá trị nào của
. Với giá trị nào của 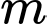 thì đường thẳng
thì đường thẳng 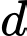 cắt đồ thị
cắt đồ thị  tại hai điểm phân biệt
tại hai điểm phân biệt 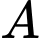 và
và 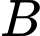 thỏa mãn tiếp tuyến tại
thỏa mãn tiếp tuyến tại 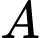 và
và 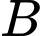 song song với nhau
song song với nhau
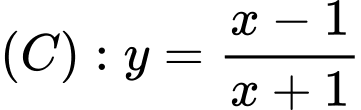 và đường thẳng
và đường thẳng 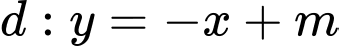 . Với giá trị nào của
. Với giá trị nào của 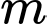 thì đường thẳng
thì đường thẳng 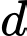 cắt đồ thị
cắt đồ thị  tại hai điểm phân biệt
tại hai điểm phân biệt 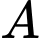 và
và 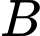 thỏa mãn tiếp tuyến tại
thỏa mãn tiếp tuyến tại 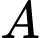 và
và 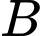 song song với nhau
song song với nhau A, 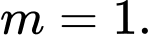
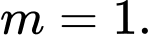
B, 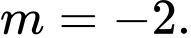
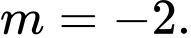
C, 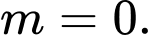
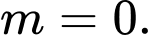
D, 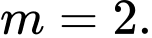
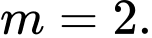
PT hoành độ giao điểm 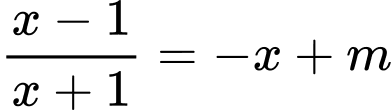
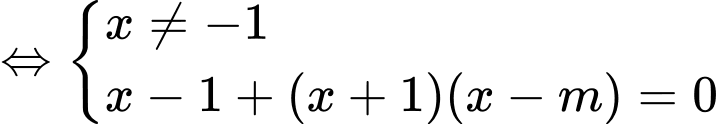
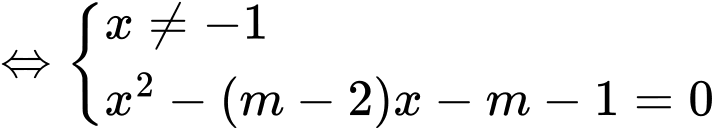
Cần có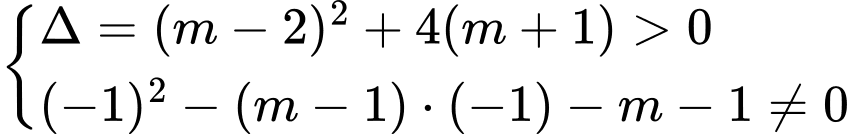
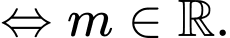
Gọi
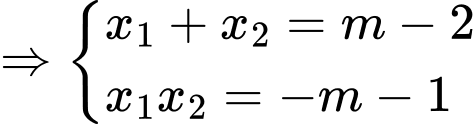
Ta có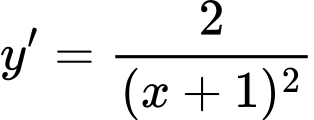
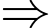 ép cho
ép cho 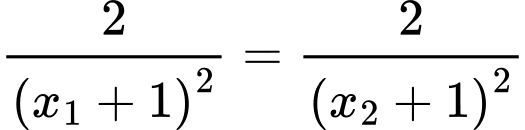
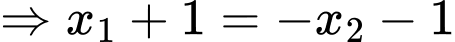
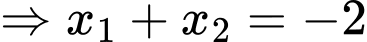
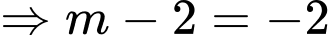
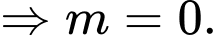
Thử lại ta thấy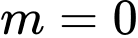 thỏa mãn. Chọn C. Đáp án: C
thỏa mãn. Chọn C. Đáp án: C
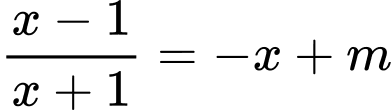
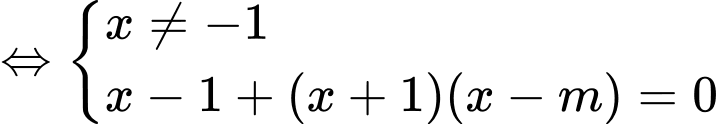
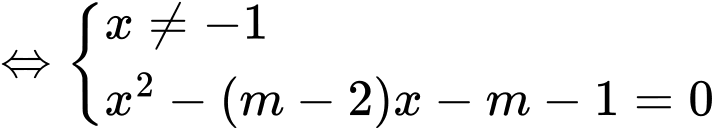
Cần có
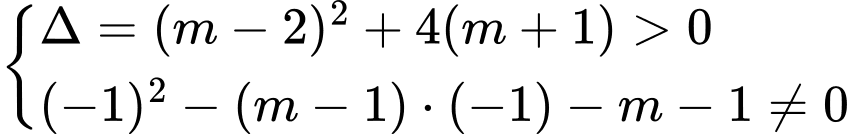
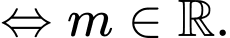
Gọi

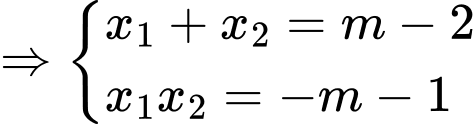
Ta có
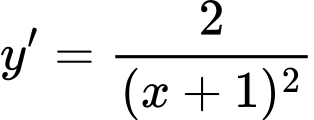
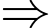 ép cho
ép cho 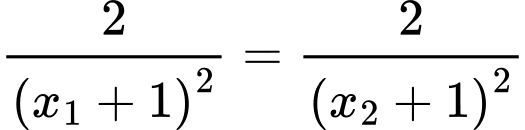
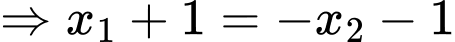
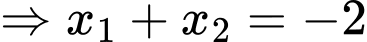
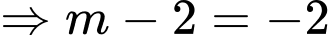
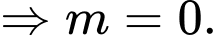
Thử lại ta thấy
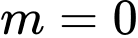 thỏa mãn. Chọn C. Đáp án: C
thỏa mãn. Chọn C. Đáp án: C
Câu 12 [19261]: Đường cong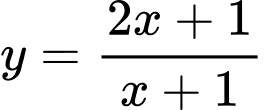 cắt đường thẳng
cắt đường thẳng 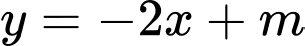 tại hai điểm phân biệt
tại hai điểm phân biệt 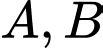 sao cho tam giác
sao cho tam giác  có diện tích bằng
có diện tích bằng 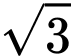 , với
, với  là gốc tọa độ. Tính tổng
là gốc tọa độ. Tính tổng 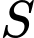 bao gồm tất cả các giá trị
bao gồm tất cả các giá trị 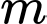 có thể xảy ra.
có thể xảy ra.
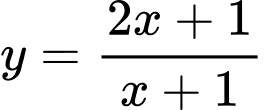 cắt đường thẳng
cắt đường thẳng 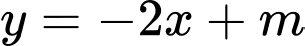 tại hai điểm phân biệt
tại hai điểm phân biệt 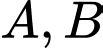 sao cho tam giác
sao cho tam giác  có diện tích bằng
có diện tích bằng 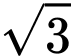 , với
, với  là gốc tọa độ. Tính tổng
là gốc tọa độ. Tính tổng 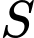 bao gồm tất cả các giá trị
bao gồm tất cả các giá trị 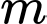 có thể xảy ra.
có thể xảy ra. A, 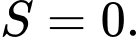
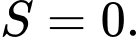
B, 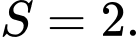
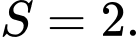
C, 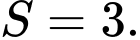
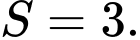
D, 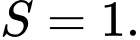
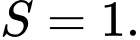
Phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng là
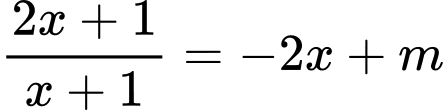
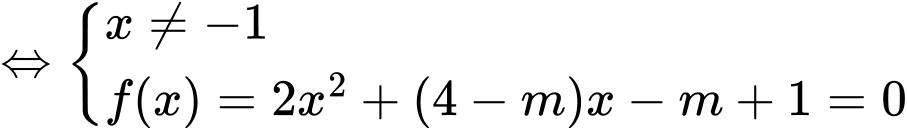
Điều kiện có hai nghiệm phân biệt là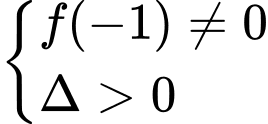
Kẻ OH vuông góc với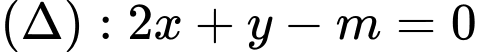
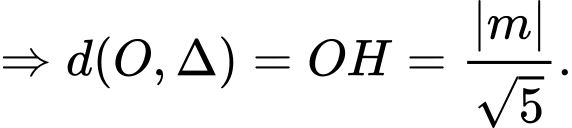
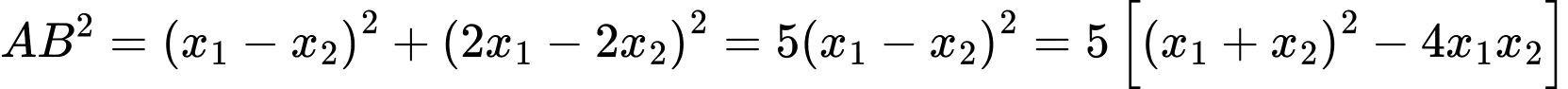
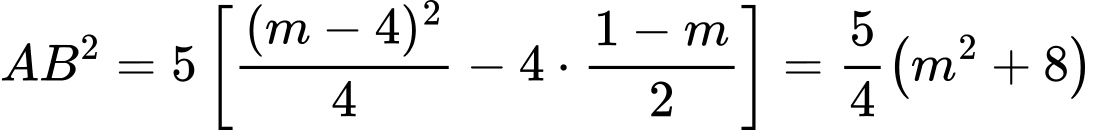
Diện tích tam giác là
là

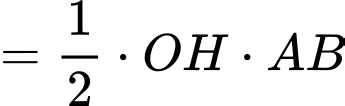
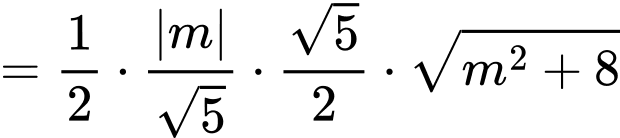
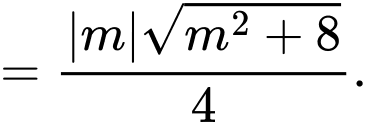
Theo bài ra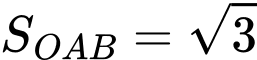
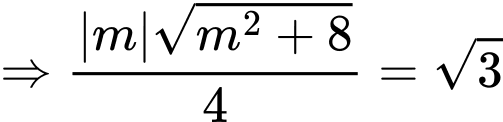
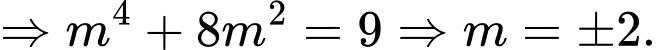
Ngoài ra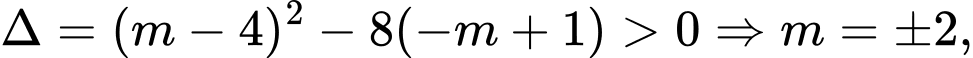 tổng giá trị m bằng 0 . Đáp án: A
tổng giá trị m bằng 0 . Đáp án: A
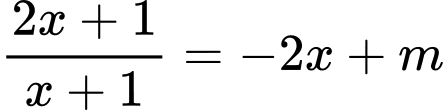
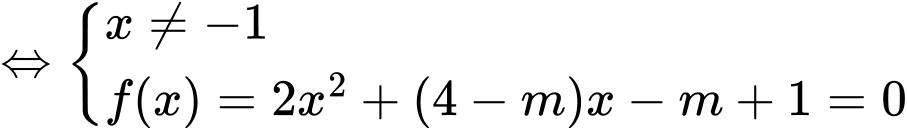
Điều kiện có hai nghiệm phân biệt là
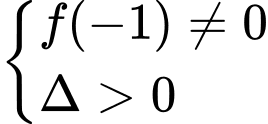
Kẻ OH vuông góc với
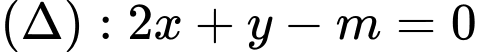
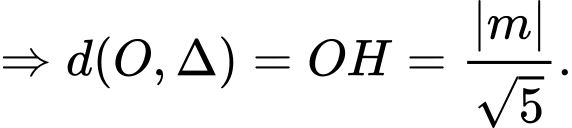
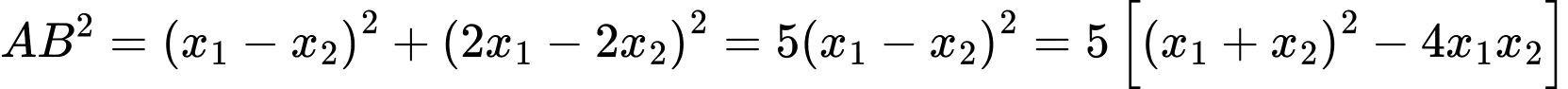
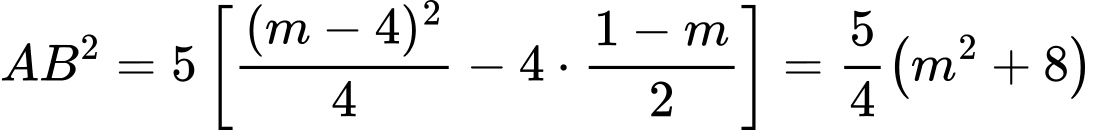
Diện tích tam giác
 là
là 
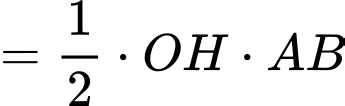
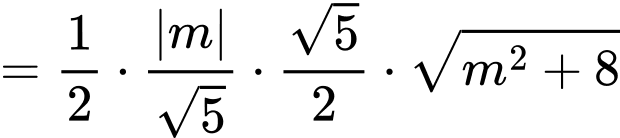
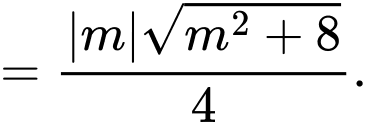
Theo bài ra
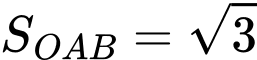
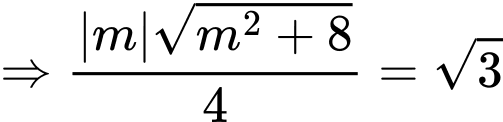
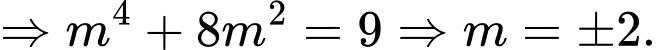
Ngoài ra
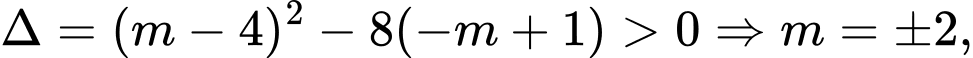 tổng giá trị m bằng 0 . Đáp án: A
tổng giá trị m bằng 0 . Đáp án: A
Câu 13 [803773]: Cho đồ thị 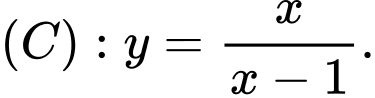 Đường thẳng
Đường thẳng 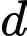 đi qua điểm
đi qua điểm 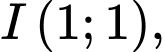 cắt
cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 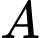 và
và 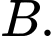 Khi diện tích tam giác
Khi diện tích tam giác  với
với  đạt giá trị nhỏ nhất thì độ dài đoạn
đạt giá trị nhỏ nhất thì độ dài đoạn  bằng
bằng
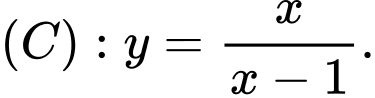 Đường thẳng
Đường thẳng 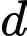 đi qua điểm
đi qua điểm 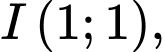 cắt
cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 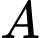 và
và 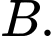 Khi diện tích tam giác
Khi diện tích tam giác  với
với  đạt giá trị nhỏ nhất thì độ dài đoạn
đạt giá trị nhỏ nhất thì độ dài đoạn  bằng
bằng A, 

B, 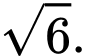
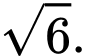
C, 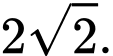
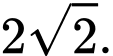
D, 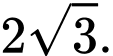
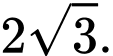
Gọi 
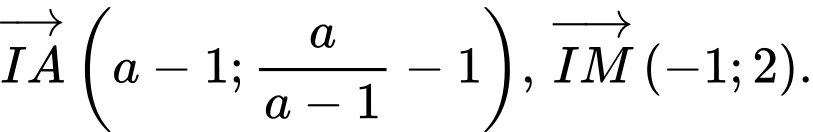
Diện tích tam giác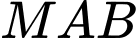 đạt GTNN khi và chỉ khi diện tích tam giác
đạt GTNN khi và chỉ khi diện tích tam giác 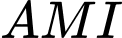 đạt GTNN.
đạt GTNN.
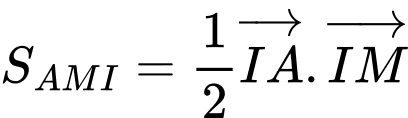
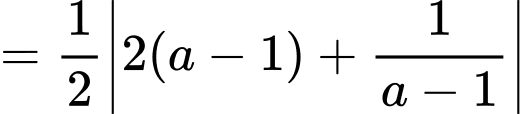
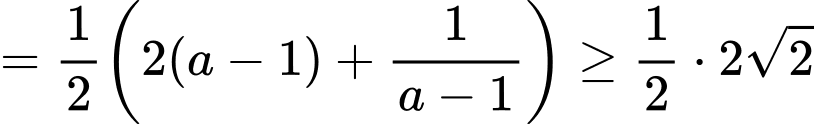

Dấu bằng xảy ra khi: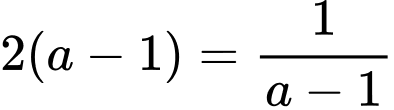
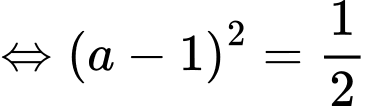
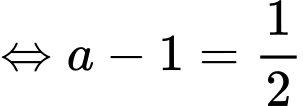
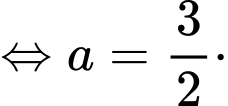
Khi đó: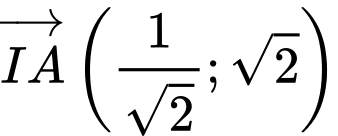
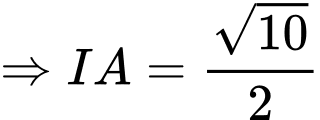
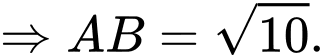
Chọn đáp án A. Đáp án: A

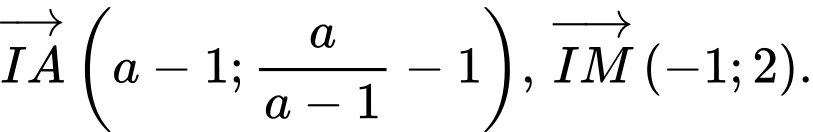
Diện tích tam giác
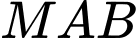 đạt GTNN khi và chỉ khi diện tích tam giác
đạt GTNN khi và chỉ khi diện tích tam giác 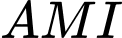 đạt GTNN.
đạt GTNN. 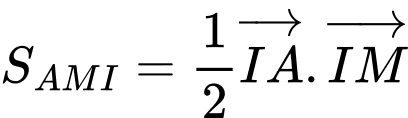
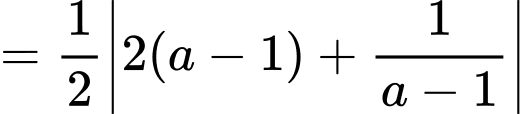
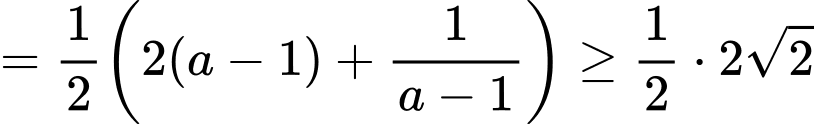

Dấu bằng xảy ra khi:
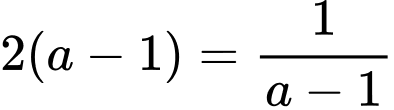
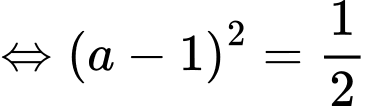
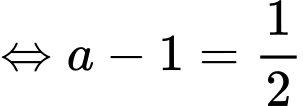
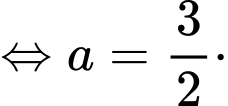
Khi đó:
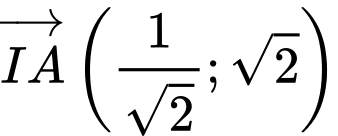
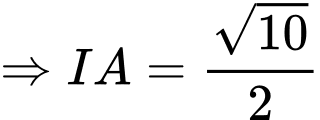
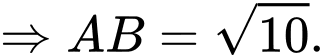
Chọn đáp án A. Đáp án: A