Đáp án Bài tập tự luyện số 2
Câu 1 [28596]: Tìm tất cả các giá trị thực của tham số 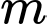 để đường thẳng
để đường thẳng 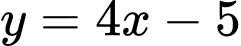 cắt đồ thị của hàm số
cắt đồ thị của hàm số 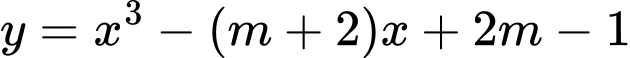 tại ba điểm phân biệt.
tại ba điểm phân biệt.
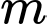 để đường thẳng
để đường thẳng 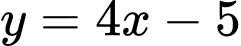 cắt đồ thị của hàm số
cắt đồ thị của hàm số 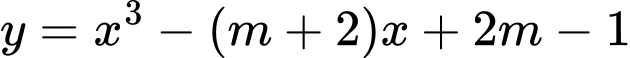 tại ba điểm phân biệt.
tại ba điểm phân biệt. A, 

B, 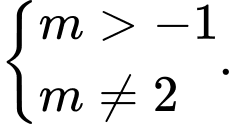
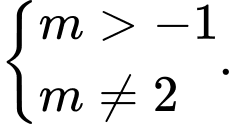
C, 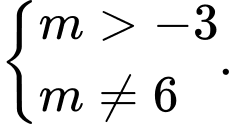
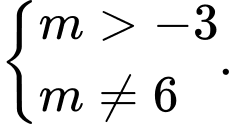
D, 

Phương trình hoành độ giao điểm 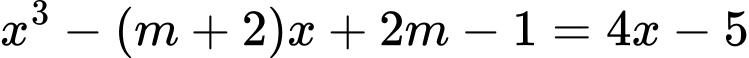
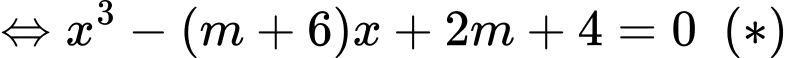
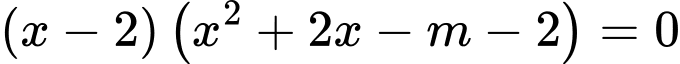
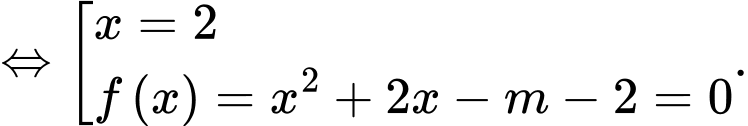
Hai đồ thị có ba giao điểm khi và chỉ khi có ba nghiệm phân biệt, khi đó
có ba nghiệm phân biệt, khi đó 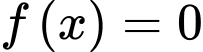 có hai nghiệm phân biệt khác 2
có hai nghiệm phân biệt khác 2
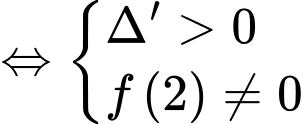
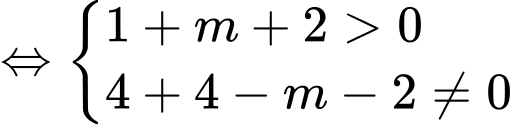
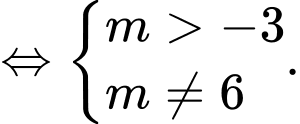
Chọn đáp án C. Đáp án: C
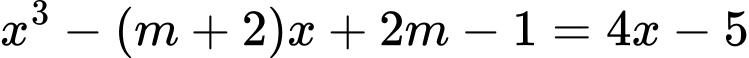
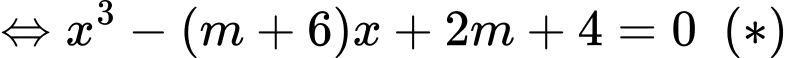
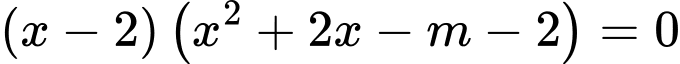
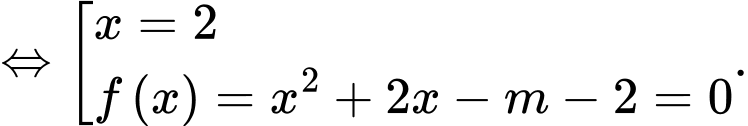
Hai đồ thị có ba giao điểm khi và chỉ khi
 có ba nghiệm phân biệt, khi đó
có ba nghiệm phân biệt, khi đó 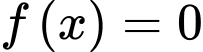 có hai nghiệm phân biệt khác 2
có hai nghiệm phân biệt khác 2 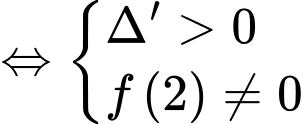
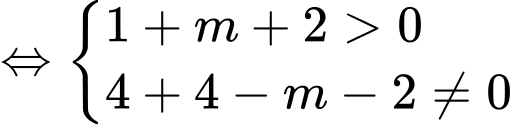
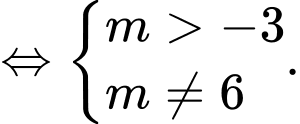
Chọn đáp án C. Đáp án: C
Câu 2 [28587]: Cho đồ thị 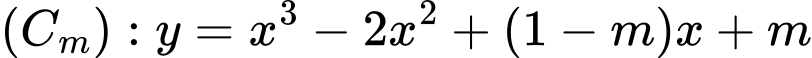 . Tất cả giá trị của tham số
. Tất cả giá trị của tham số 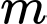 để
để 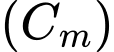 cắt trục hoành tại ba điểm phân biệt có hoành độ
cắt trục hoành tại ba điểm phân biệt có hoành độ 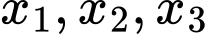 thỏa
thỏa 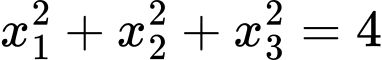 là
là
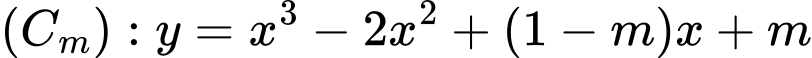 . Tất cả giá trị của tham số
. Tất cả giá trị của tham số 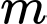 để
để 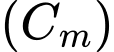 cắt trục hoành tại ba điểm phân biệt có hoành độ
cắt trục hoành tại ba điểm phân biệt có hoành độ 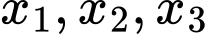 thỏa
thỏa 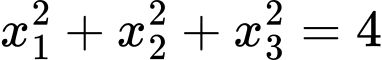 là
là A, 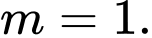
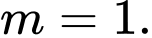
B, 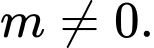
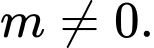
C, 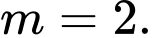
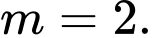
D, 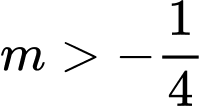 và
và 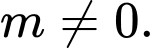
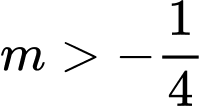 và
và 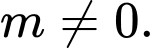
Phương trình hoành độ giao điểm của 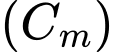 và trục hoành là
và trục hoành là
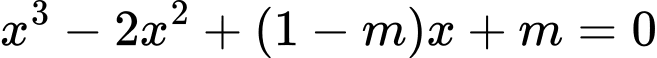
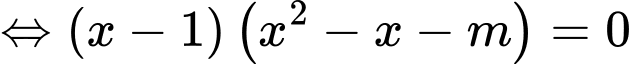
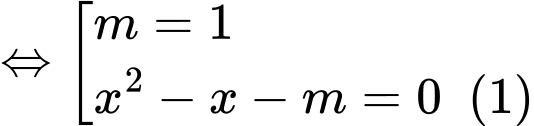
 cắt trục hoành tại ba điểm phân biệt khi và chỉ khi
cắt trục hoành tại ba điểm phân biệt khi và chỉ khi  có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 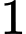
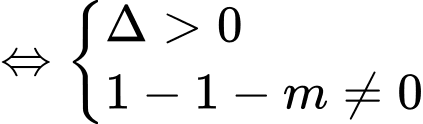
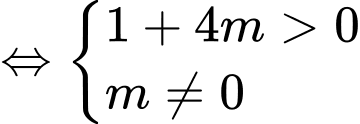
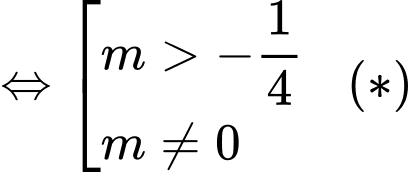
Gọi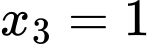 và
và 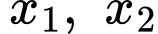 là nghiệm của phương trình
là nghiệm của phương trình  nên theo Vi-et ta có
nên theo Vi-et ta có 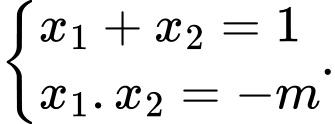
Vậy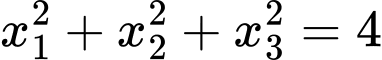
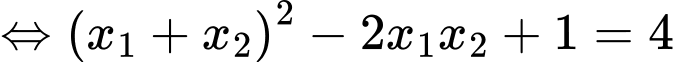
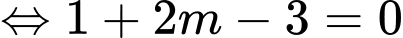
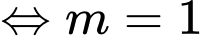 (thoả mãn điều kiện (*).
(thoả mãn điều kiện (*).
Vậy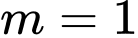 thoả mãn ycbt.
thoả mãn ycbt.
Chọn đáp án A. Đáp án: A
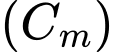 và trục hoành là
và trục hoành là 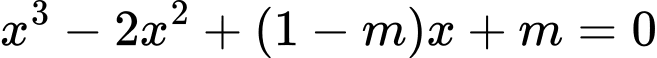
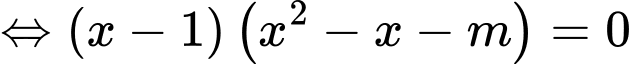
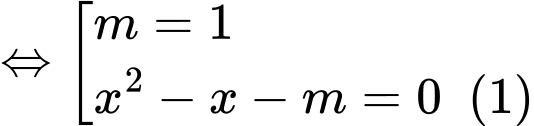
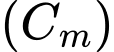 cắt trục hoành tại ba điểm phân biệt khi và chỉ khi
cắt trục hoành tại ba điểm phân biệt khi và chỉ khi  có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 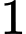
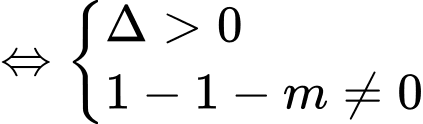
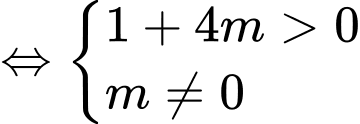
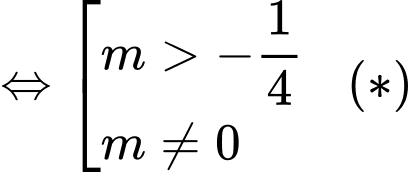
Gọi
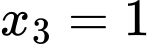 và
và 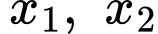 là nghiệm của phương trình
là nghiệm của phương trình  nên theo Vi-et ta có
nên theo Vi-et ta có 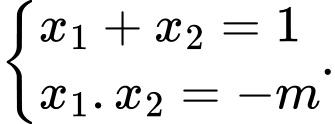
Vậy
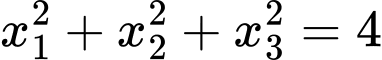
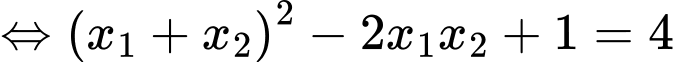
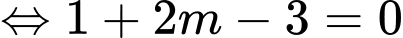
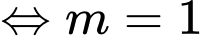 (thoả mãn điều kiện (*).
(thoả mãn điều kiện (*). Vậy
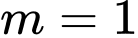 thoả mãn ycbt.
thoả mãn ycbt. Chọn đáp án A. Đáp án: A
Câu 3 [28603]: Cho hàm số 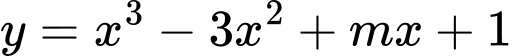 và
và 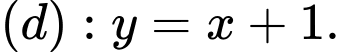 Tìm tất cả các giá trị của tham số
Tìm tất cả các giá trị của tham số 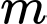 để đồ thị hàm số cắt
để đồ thị hàm số cắt  tại ba điểm phân biệt có hoành độ
tại ba điểm phân biệt có hoành độ 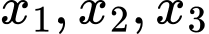 thỏa mãn
thỏa mãn 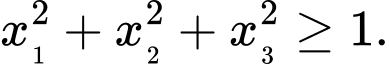
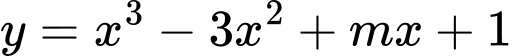 và
và 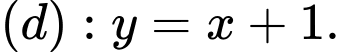 Tìm tất cả các giá trị của tham số
Tìm tất cả các giá trị của tham số 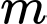 để đồ thị hàm số cắt
để đồ thị hàm số cắt  tại ba điểm phân biệt có hoành độ
tại ba điểm phân biệt có hoành độ 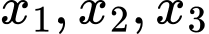 thỏa mãn
thỏa mãn 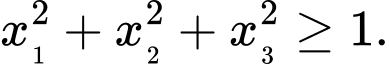
A, 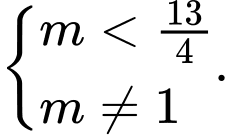
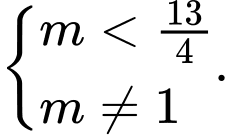
B, 

C, 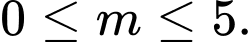
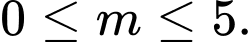
D, 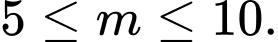
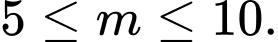
Phương trình hoành độ giao điểm 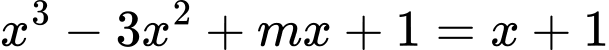
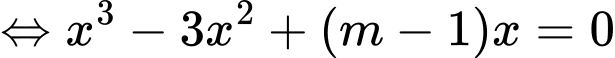
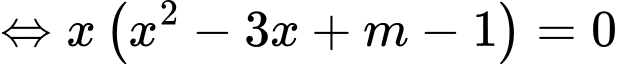
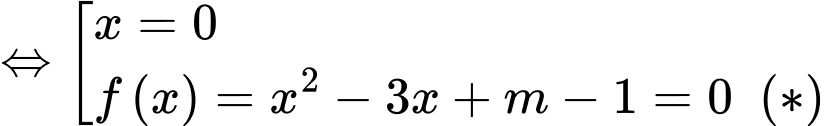
Để đồ thị hàm số cắt tại 3 điểm phân biệt thì
tại 3 điểm phân biệt thì  có 2 nghiệm phân biệt khác
có 2 nghiệm phân biệt khác 
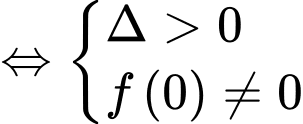
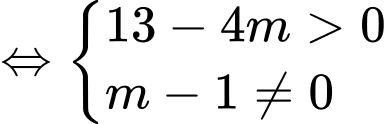
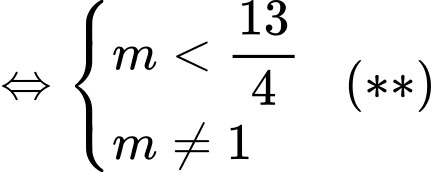
Giả sử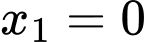
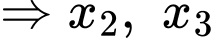 là nghiệm của phương trình
là nghiệm của phương trình 
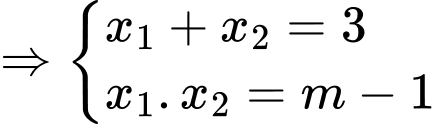
Ta có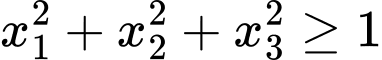
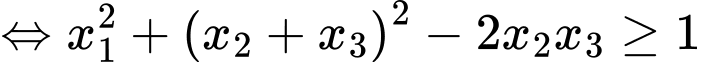
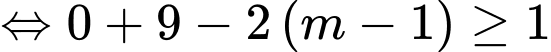
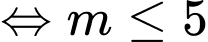
Kết hợp với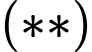 ta suy ra
ta suy ra 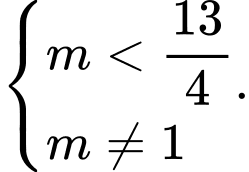
Chọn đáp án A. Đáp án: A
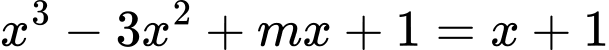
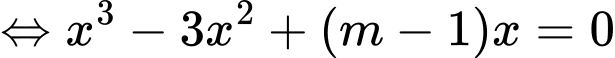
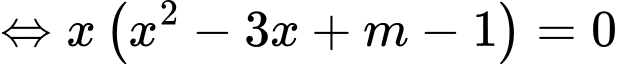
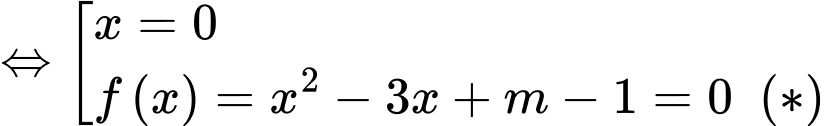
Để đồ thị hàm số cắt
 tại 3 điểm phân biệt thì
tại 3 điểm phân biệt thì  có 2 nghiệm phân biệt khác
có 2 nghiệm phân biệt khác 
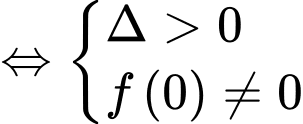
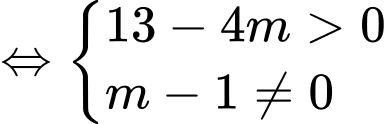
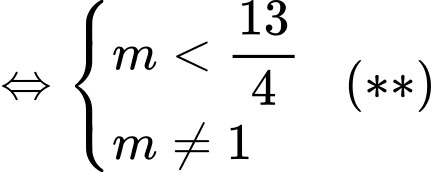
Giả sử
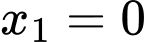
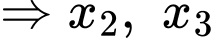 là nghiệm của phương trình
là nghiệm của phương trình 
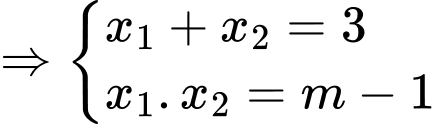
Ta có
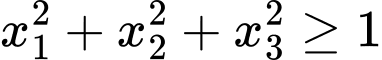
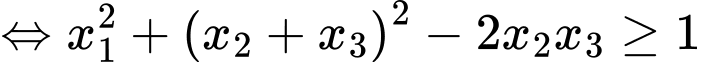
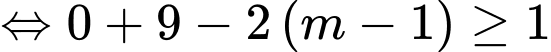
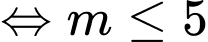
Kết hợp với
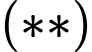 ta suy ra
ta suy ra 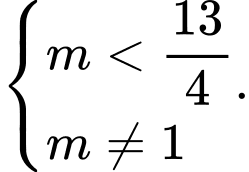
Chọn đáp án A. Đáp án: A
Câu 4 [28611]: Tìm tất cả các giá trị của tham số 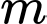 để đường cong
để đường cong 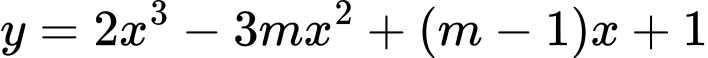 cắt đường thẳng
cắt đường thẳng 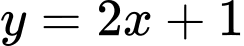 tại ba điểm phân biệt
tại ba điểm phân biệt 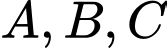 thỏa mãn điểm
thỏa mãn điểm  nằm giữa
nằm giữa 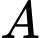 và
và 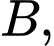 đồng thời đoạn thẳng
đồng thời đoạn thẳng  có độ dài
có độ dài 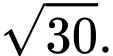
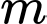 để đường cong
để đường cong 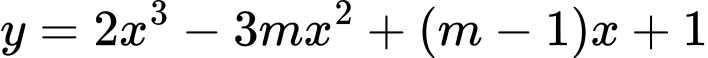 cắt đường thẳng
cắt đường thẳng 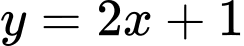 tại ba điểm phân biệt
tại ba điểm phân biệt 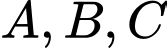 thỏa mãn điểm
thỏa mãn điểm  nằm giữa
nằm giữa 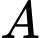 và
và 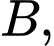 đồng thời đoạn thẳng
đồng thời đoạn thẳng  có độ dài
có độ dài 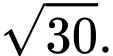
A, 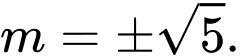
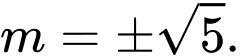
B, 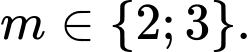
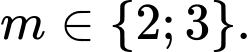
C, 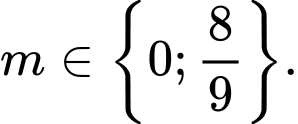
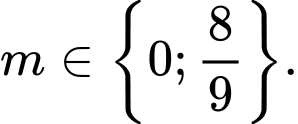
D, 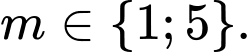
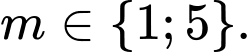
Ta có 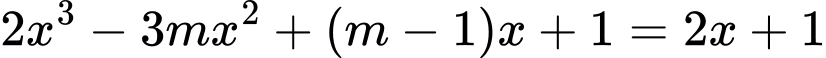
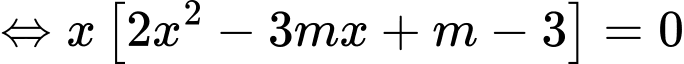
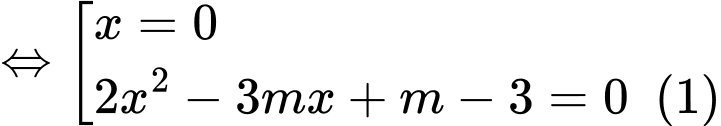
Để đường cong cắt đường thẳng đã cho tại ba điểm phân biệt thì phương trình phải có hai nghiệm phân biệt khác 0
phải có hai nghiệm phân biệt khác 0
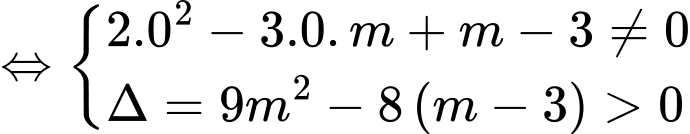
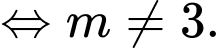
Gọi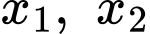 là hai nghiệm của phương trình
là hai nghiệm của phương trình 
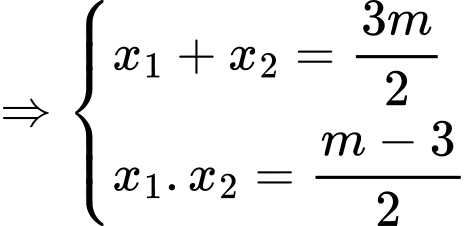
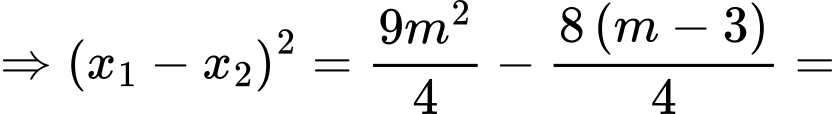
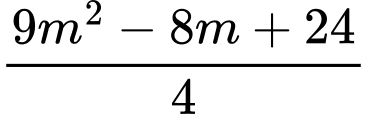 và
và
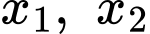 cũng là hoành độ của hai điểm
cũng là hoành độ của hai điểm 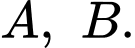 Vì
Vì 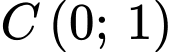 nằm giữa
nằm giữa 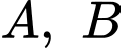 nên
nên 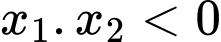
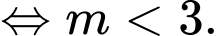
Ta có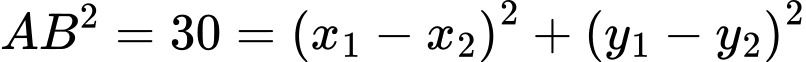
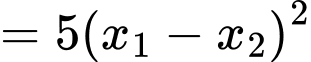
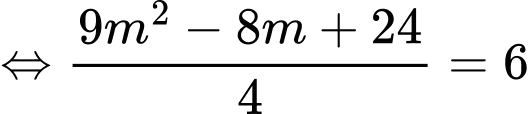
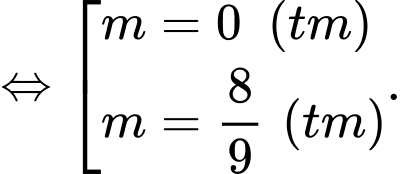
Chọn đáp án C. Đáp án: C
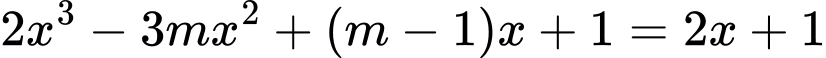
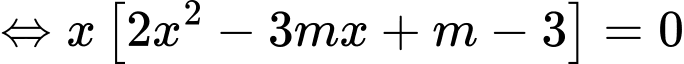
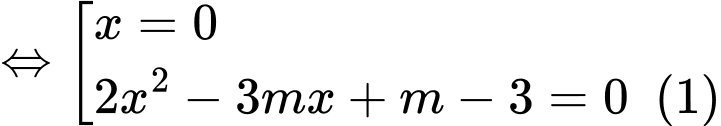
Để đường cong cắt đường thẳng đã cho tại ba điểm phân biệt thì phương trình
 phải có hai nghiệm phân biệt khác 0
phải có hai nghiệm phân biệt khác 0 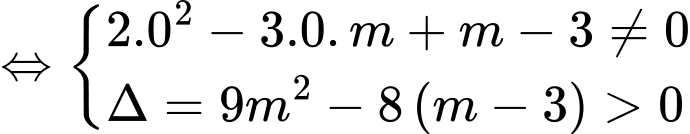
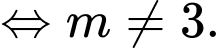
Gọi
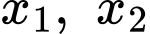 là hai nghiệm của phương trình
là hai nghiệm của phương trình 
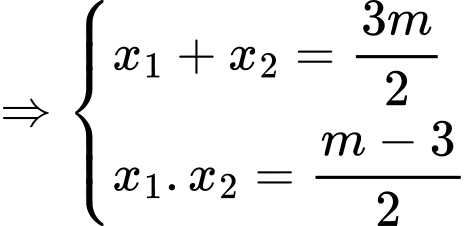
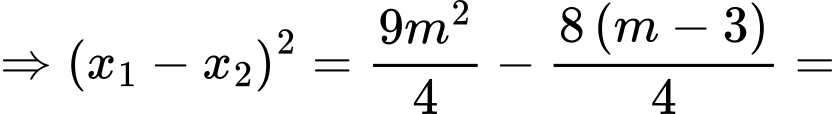
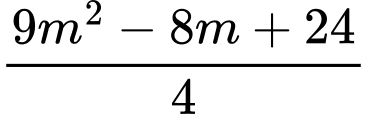 và
và 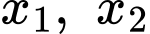 cũng là hoành độ của hai điểm
cũng là hoành độ của hai điểm 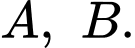 Vì
Vì 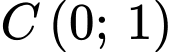 nằm giữa
nằm giữa 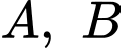 nên
nên 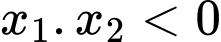
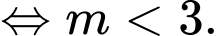
Ta có
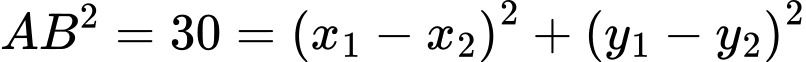
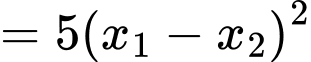
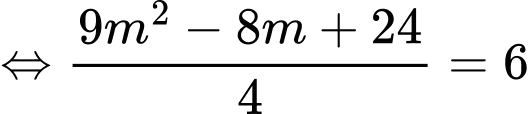
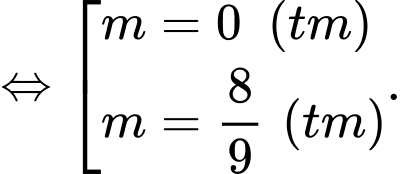
Chọn đáp án C. Đáp án: C
Câu 5 [28643]: Đường thẳng 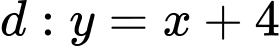 cắt đồ thị hàm số
cắt đồ thị hàm số 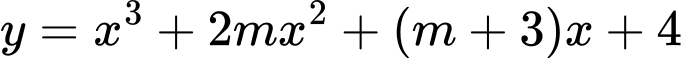 tại 3 điểm phân biệt
tại 3 điểm phân biệt 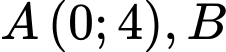 và
và  sao cho diện tích tam giác
sao cho diện tích tam giác 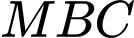 bằng 4, với
bằng 4, với 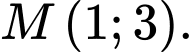 Tìm tất cả các giá trị của
Tìm tất cả các giá trị của 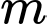 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
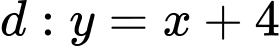 cắt đồ thị hàm số
cắt đồ thị hàm số 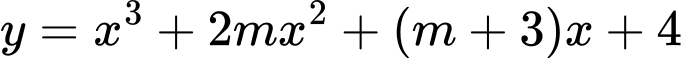 tại 3 điểm phân biệt
tại 3 điểm phân biệt 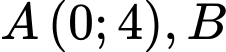 và
và  sao cho diện tích tam giác
sao cho diện tích tam giác 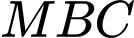 bằng 4, với
bằng 4, với 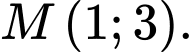 Tìm tất cả các giá trị của
Tìm tất cả các giá trị của 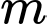 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán. A, 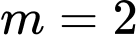 hoặc
hoặc 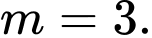
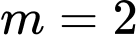 hoặc
hoặc 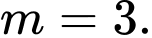
B, 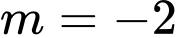 hoặc
hoặc 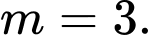
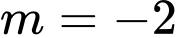 hoặc
hoặc 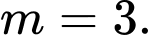
C, 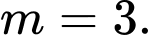
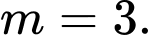
D, 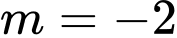 hoặc
hoặc 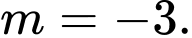
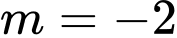 hoặc
hoặc 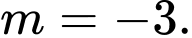
Phương trình hoành độ giao điểm 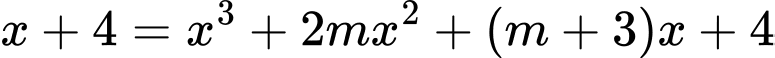

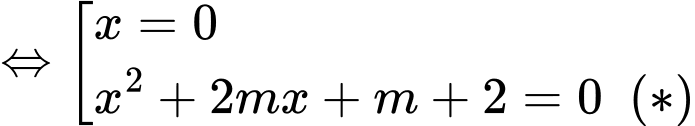
Để đường thẳng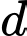 cắt đồ thị hàm số tại 3 điểm phân biệt thì phương trình
cắt đồ thị hàm số tại 3 điểm phân biệt thì phương trình 
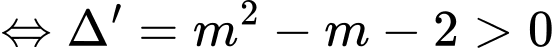
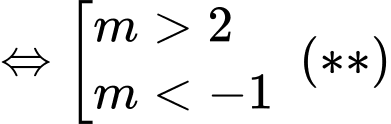
Gọi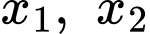 lần lượt là hoành độ điểm
lần lượt là hoành độ điểm 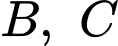 thoả mãn phương trình
thoả mãn phương trình 
Theo định lý Vi-ét ta có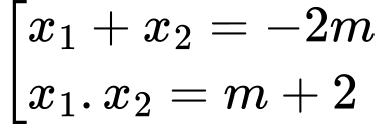
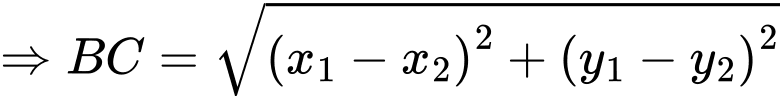
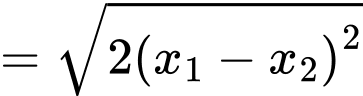
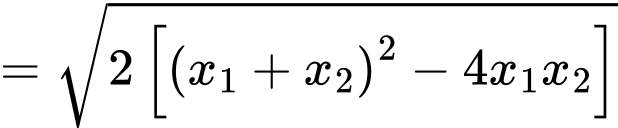
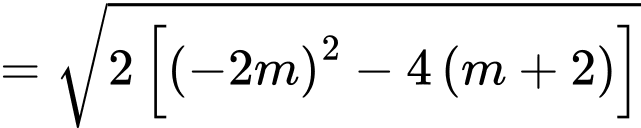

Ta có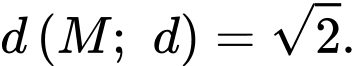 Suy ra
Suy ra 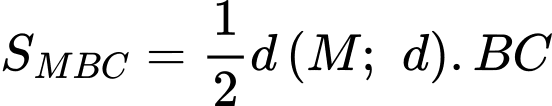
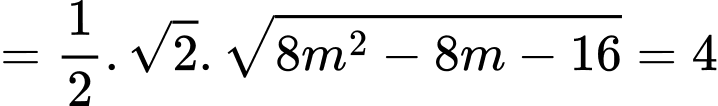
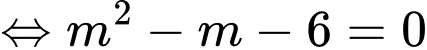
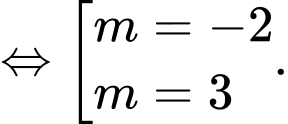
Kết hợp với điều kiện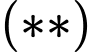 suy ra
suy ra 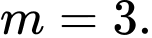
Chọn đáp án C. Đáp án: C
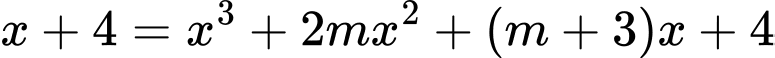

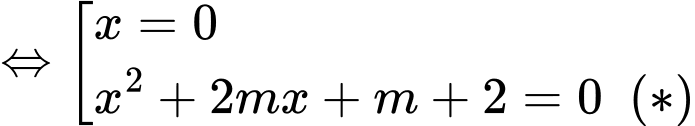
Để đường thẳng
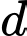 cắt đồ thị hàm số tại 3 điểm phân biệt thì phương trình
cắt đồ thị hàm số tại 3 điểm phân biệt thì phương trình 
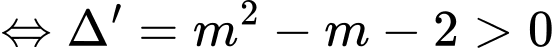
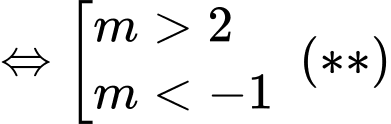
Gọi
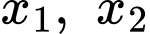 lần lượt là hoành độ điểm
lần lượt là hoành độ điểm 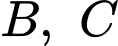 thoả mãn phương trình
thoả mãn phương trình 
Theo định lý Vi-ét ta có
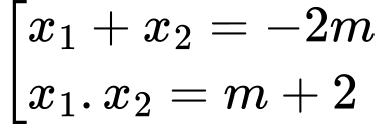
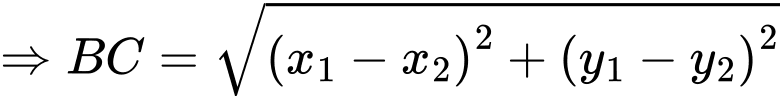
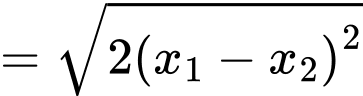
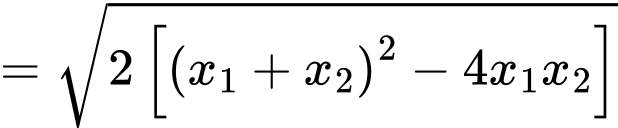
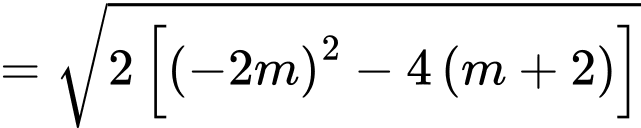

Ta có
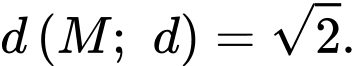 Suy ra
Suy ra 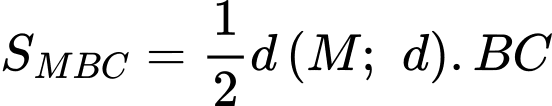
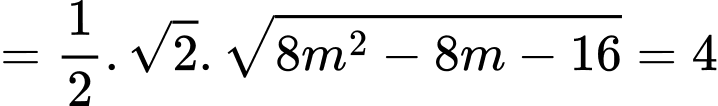
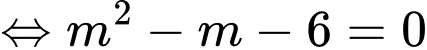
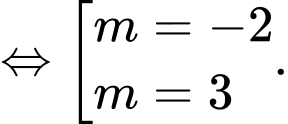
Kết hợp với điều kiện
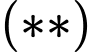 suy ra
suy ra 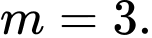
Chọn đáp án C. Đáp án: C
Câu 6 [28655]: Cho hàm số 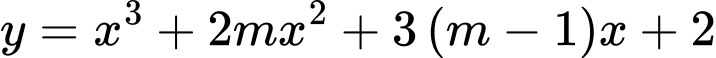 có đồ thị là
có đồ thị là  . Cho điểm
. Cho điểm 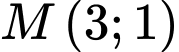 và đường thẳng
và đường thẳng 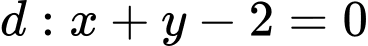 . Tìm các giá trị của
. Tìm các giá trị của 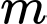 để đường thẳng
để đường thẳng  cắt đồ thị
cắt đồ thị  tại 3 điểm
tại 3 điểm 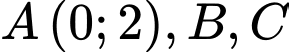 sao cho tam giác
sao cho tam giác 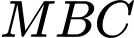 có diện tích bằng
có diện tích bằng 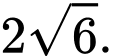
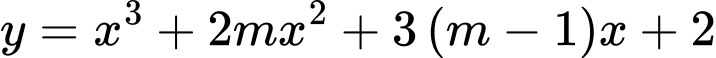 có đồ thị là
có đồ thị là  . Cho điểm
. Cho điểm 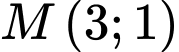 và đường thẳng
và đường thẳng 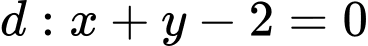 . Tìm các giá trị của
. Tìm các giá trị của 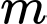 để đường thẳng
để đường thẳng  cắt đồ thị
cắt đồ thị  tại 3 điểm
tại 3 điểm 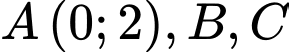 sao cho tam giác
sao cho tam giác 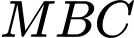 có diện tích bằng
có diện tích bằng 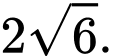
A, 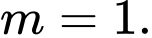
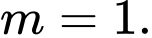
B, 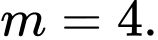
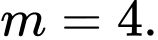
C, 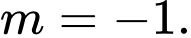
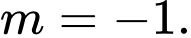
D, 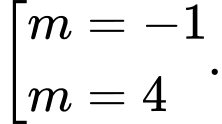
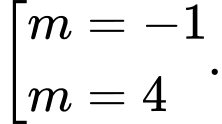
Ta có 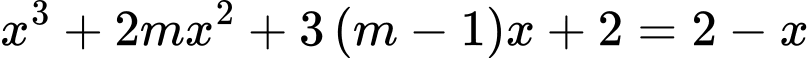
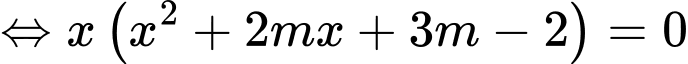
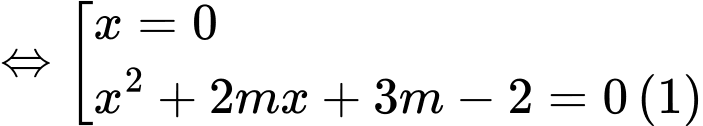
Để cắt
cắt 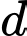 tại ba điểm phân biệt thì phương trình
tại ba điểm phân biệt thì phương trình  phải có hai nghiệm phân biệt khác
phải có hai nghiệm phân biệt khác 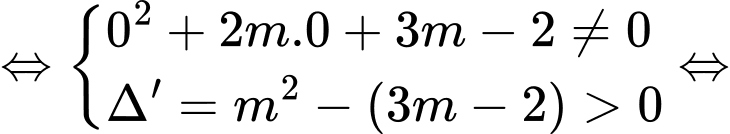
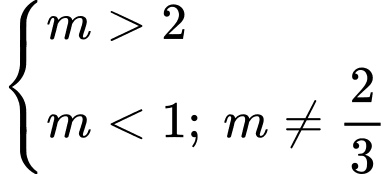
Khi đó ta có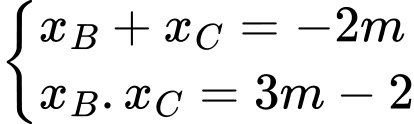
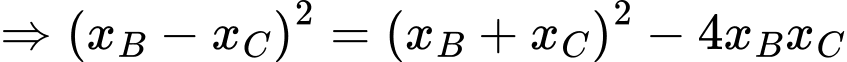
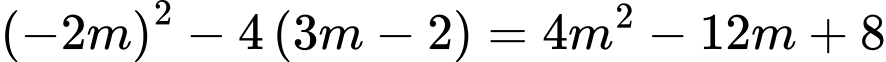
Suy ra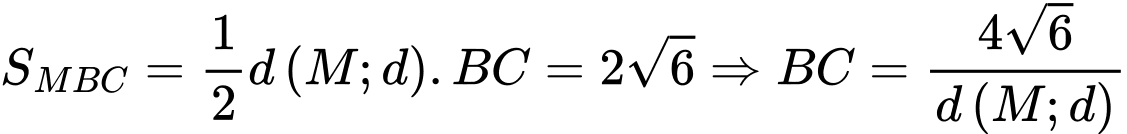 (với
(với 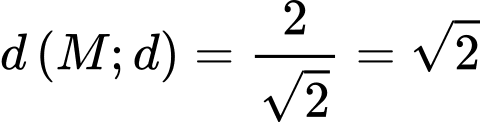 )
)
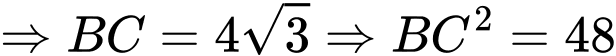
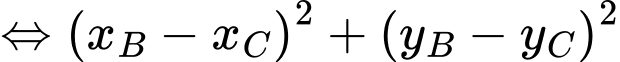
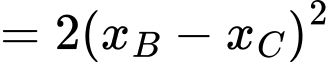
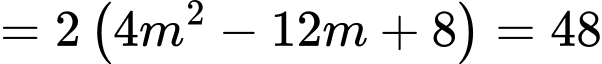
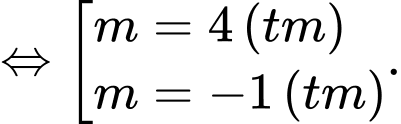 Chọn đáp án D. Đáp án: D
Chọn đáp án D. Đáp án: D
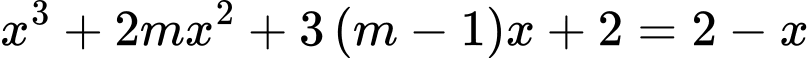
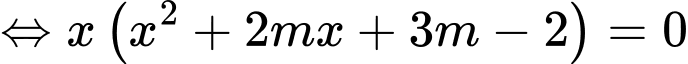
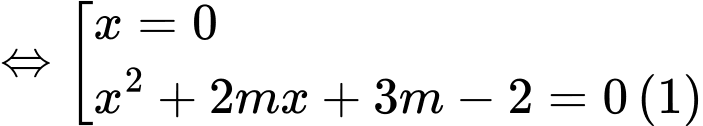
Để
 cắt
cắt 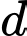 tại ba điểm phân biệt thì phương trình
tại ba điểm phân biệt thì phương trình  phải có hai nghiệm phân biệt khác
phải có hai nghiệm phân biệt khác 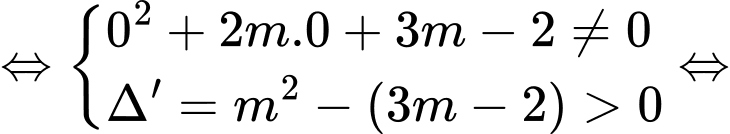
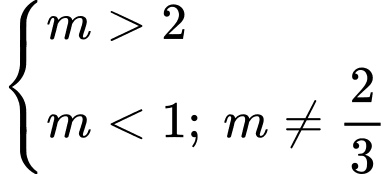
Khi đó ta có
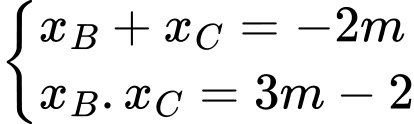
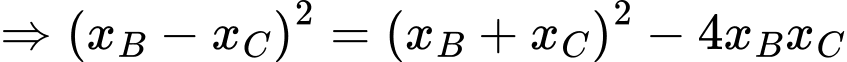
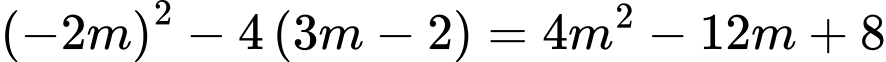
Suy ra
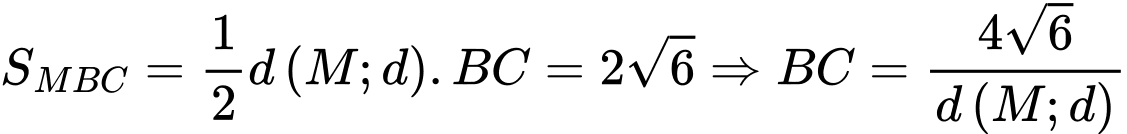 (với
(với 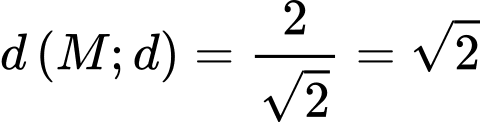 )
)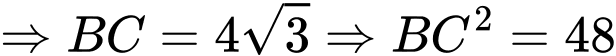
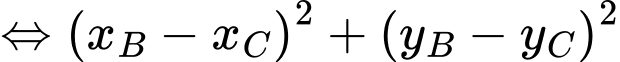
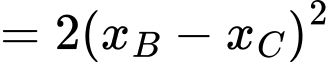
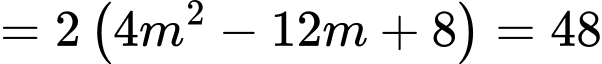
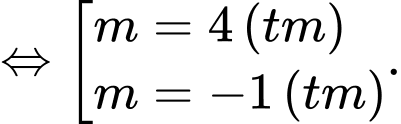 Chọn đáp án D. Đáp án: D
Chọn đáp án D. Đáp án: D
Câu 7 [28590]: Tìm tất cả các giá trị thực của tham số 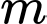 để đường thẳng
để đường thẳng 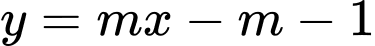 cắt đồ thị của hàm số
cắt đồ thị của hàm số 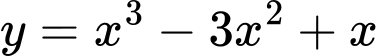 tại ba điểm
tại ba điểm 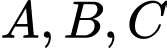 phân biệt sao cho
phân biệt sao cho 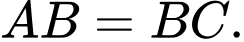
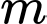 để đường thẳng
để đường thẳng 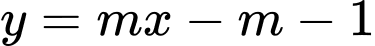 cắt đồ thị của hàm số
cắt đồ thị của hàm số 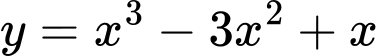 tại ba điểm
tại ba điểm 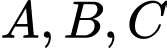 phân biệt sao cho
phân biệt sao cho 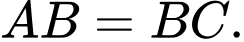
A, 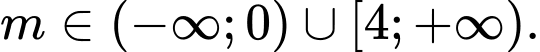
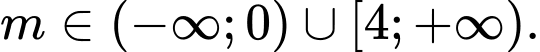
B, 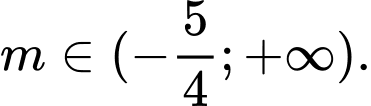
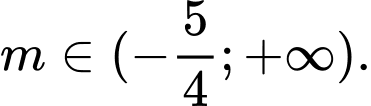
C, 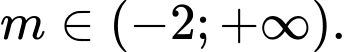
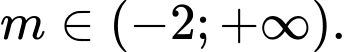
D, m 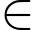
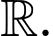
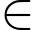
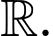
Phương trình hoành độ giao điểm 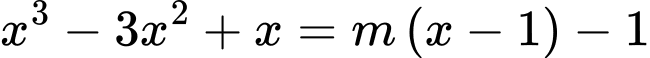
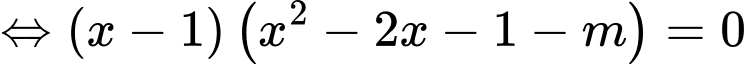
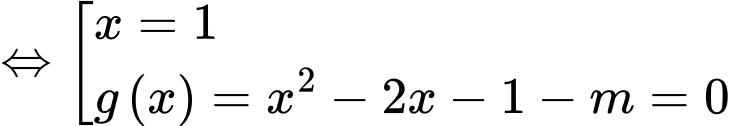
Giả thiết bài toán: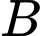 là trung điểm của
là trung điểm của 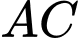 hay
hay 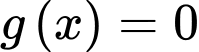 có hai nghiệm phân biệt
có hai nghiệm phân biệt 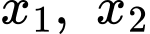 khác 1 thoả mãn
khác 1 thoả mãn
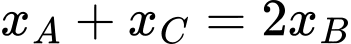
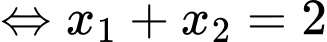
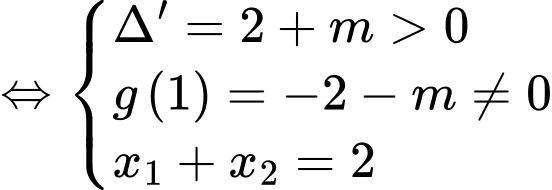
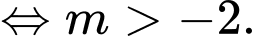
Chọn đáp án C. Đáp án: C
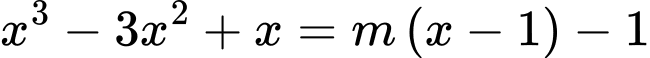
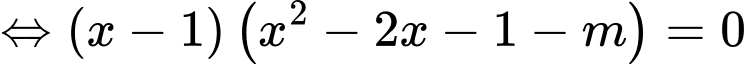
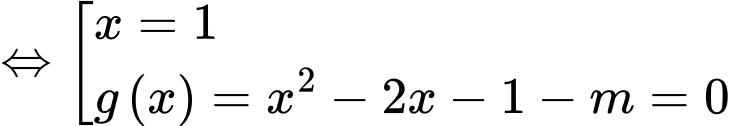
Giả thiết bài toán:
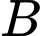 là trung điểm của
là trung điểm của 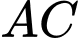 hay
hay 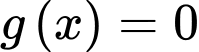 có hai nghiệm phân biệt
có hai nghiệm phân biệt 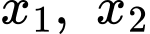 khác 1 thoả mãn
khác 1 thoả mãn 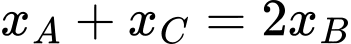
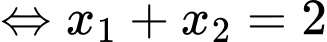
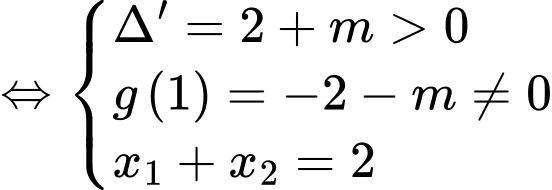
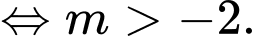
Chọn đáp án C. Đáp án: C
Câu 8 [30825]: Tìm giá trị của 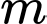 để đường cong
để đường cong 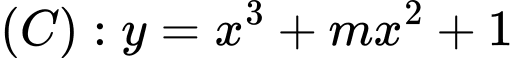 cắt đường thẳng
cắt đường thẳng 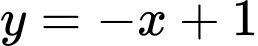 tại ba điểm phân biệt
tại ba điểm phân biệt 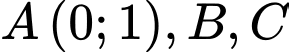 sao cho các tiếp tuyến của
sao cho các tiếp tuyến của  tại
tại 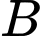 và
và  của đường cong vuông góc với nhau.
của đường cong vuông góc với nhau.
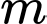 để đường cong
để đường cong 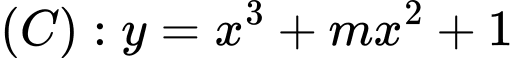 cắt đường thẳng
cắt đường thẳng 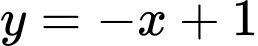 tại ba điểm phân biệt
tại ba điểm phân biệt 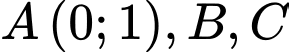 sao cho các tiếp tuyến của
sao cho các tiếp tuyến của  tại
tại 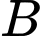 và
và  của đường cong vuông góc với nhau.
của đường cong vuông góc với nhau. A, 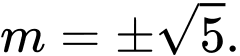
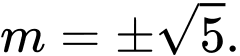
B, 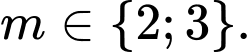
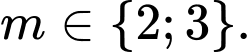
C, 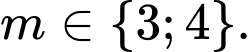
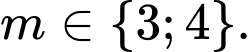
D, 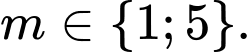
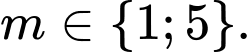
Đặt 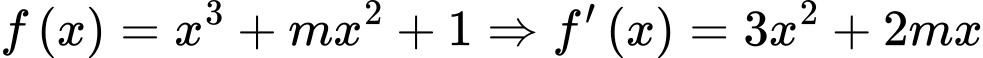
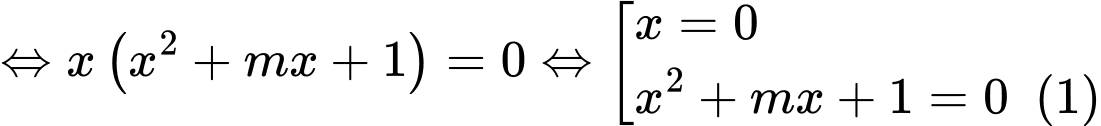
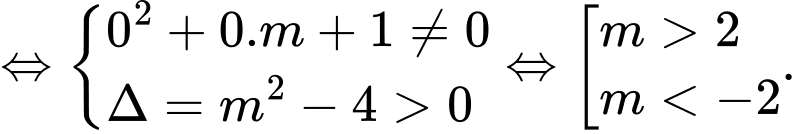 Đáp án: A
Đáp án: A
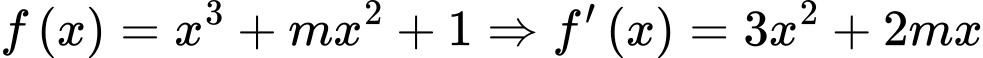
Phương trình hoành độ giao điểm 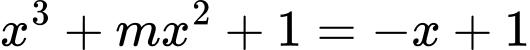
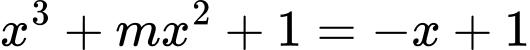
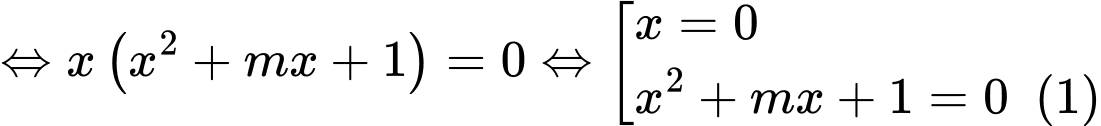
Để đường cong cắt đường thẳng đã cho tại 3 điểm phân biệt thì  phải có hai nghiệm phân biệt đều khác 0
phải có hai nghiệm phân biệt đều khác 0
 phải có hai nghiệm phân biệt đều khác 0
phải có hai nghiệm phân biệt đều khác 0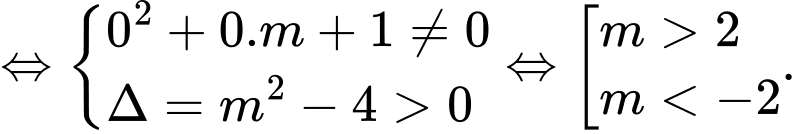
Gọi 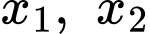 là 2 nghiệm của phương trình
là 2 nghiệm của phương trình 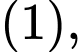 theo Vi-ét ta có
theo Vi-ét ta có 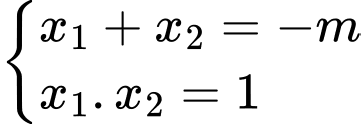 và đây cũng là hoành độ của
và đây cũng là hoành độ của 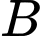 và
và 
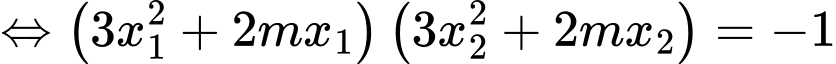
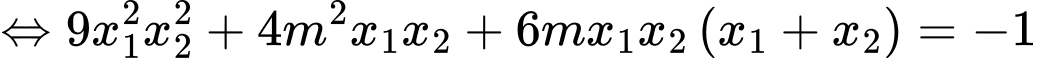
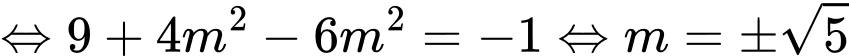 (thoả mãn)
(thoả mãn)
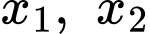 là 2 nghiệm của phương trình
là 2 nghiệm của phương trình 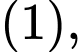 theo Vi-ét ta có
theo Vi-ét ta có 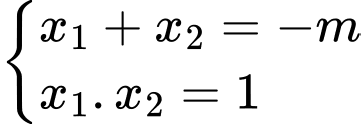 và đây cũng là hoành độ của
và đây cũng là hoành độ của 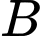 và
và 
Để tiếp tuyến tại 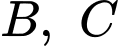 vuông góc với nhau, thì cần có
vuông góc với nhau, thì cần có 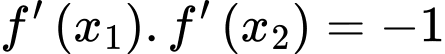
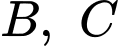 vuông góc với nhau, thì cần có
vuông góc với nhau, thì cần có 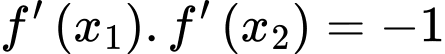
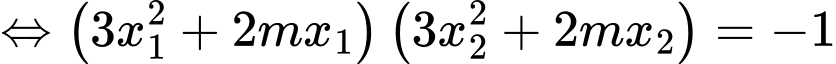
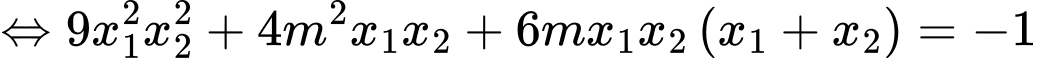
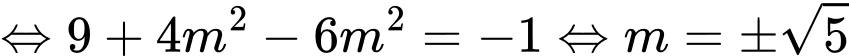 (thoả mãn)
(thoả mãn) Chọn đáp án A.
Câu 9 [399937]: Cho hàm số 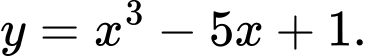 Có bao nhiêu giá trị nguyên dương của tham số
Có bao nhiêu giá trị nguyên dương của tham số 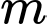 để đường thẳng
để đường thẳng 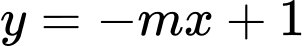 cắt đồ thị tại ba điểm phân biệt ?
cắt đồ thị tại ba điểm phân biệt ?
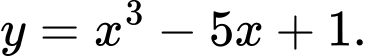 Có bao nhiêu giá trị nguyên dương của tham số
Có bao nhiêu giá trị nguyên dương của tham số 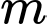 để đường thẳng
để đường thẳng 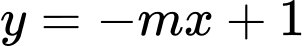 cắt đồ thị tại ba điểm phân biệt ?
cắt đồ thị tại ba điểm phân biệt ? A, 3.
B, 5.
C, 4.
D, 0.
Xét phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho:
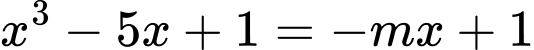
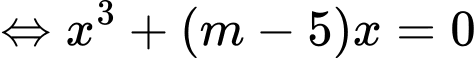
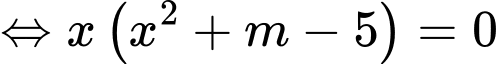
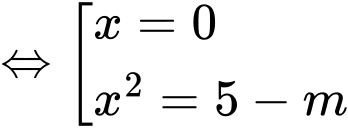
Để thoả đề thì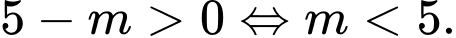
Kết hợp với điều kiện ta được: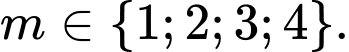 Đáp án: C
Đáp án: C
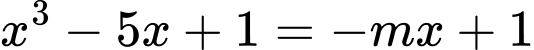
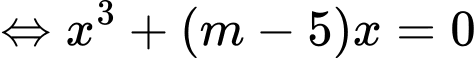
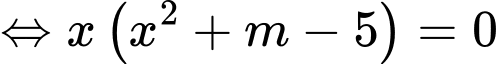
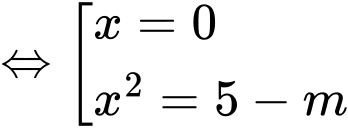
Để thoả đề thì
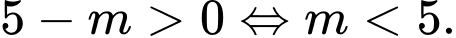
Kết hợp với điều kiện ta được:
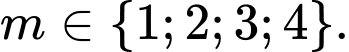 Đáp án: C
Đáp án: C
Câu 10 [399914]: Có bao nhiêu giá trị nguyên dương của tham số 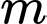 để đồ thị của hàm số
để đồ thị của hàm số 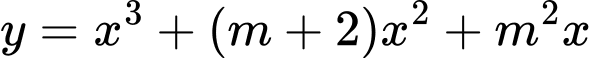 cắt đường thẳng
cắt đường thẳng 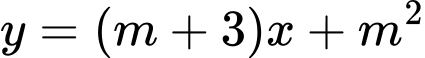 tại ba điểm phân biệt?
tại ba điểm phân biệt?
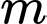 để đồ thị của hàm số
để đồ thị của hàm số 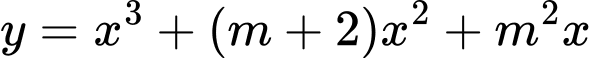 cắt đường thẳng
cắt đường thẳng 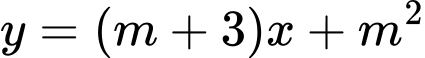 tại ba điểm phân biệt?
tại ba điểm phân biệt? A, 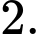
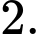
B, 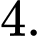
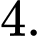
C, 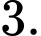
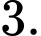
D, 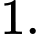
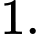
Chọn A
Phương trình hoành độ giao điểm là: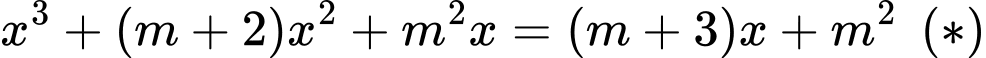
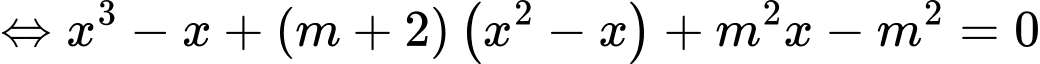
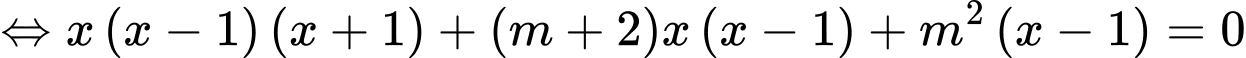
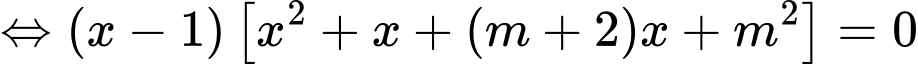
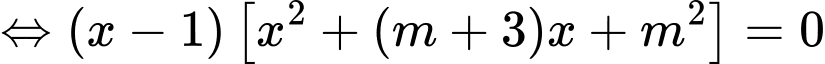
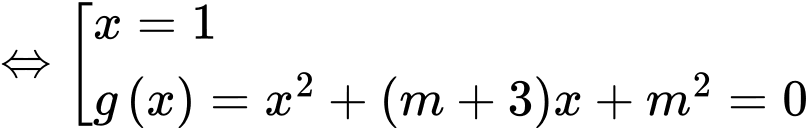
Để hai đồ thị cắt nhau tại 3 điểm phân biệt thì (*) có 3 nghiệm phân biệt
 có hai nghiệm phân biệt khác 1
có hai nghiệm phân biệt khác 1
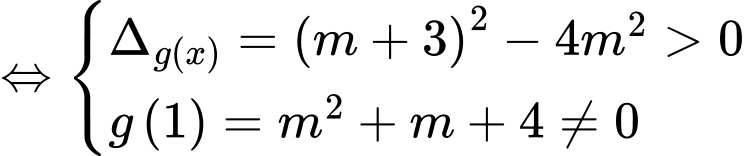
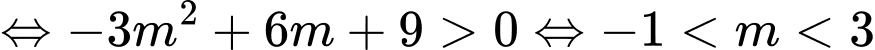
Kết hợp với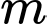 là số nguyên dương ta được
là số nguyên dương ta được 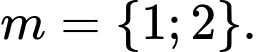 Đáp án: A
Đáp án: A
Phương trình hoành độ giao điểm là:
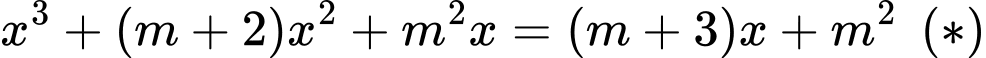
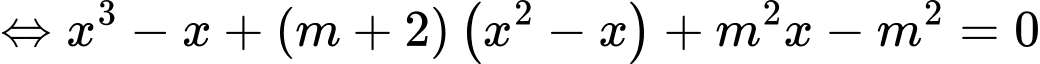
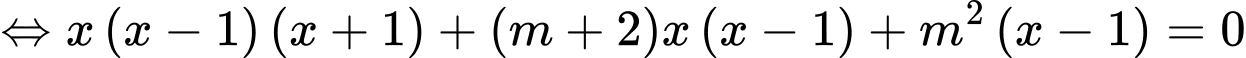
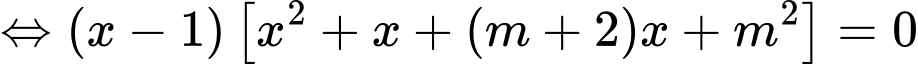
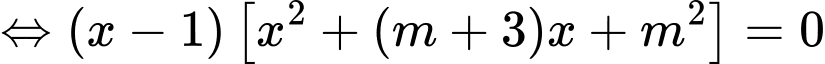
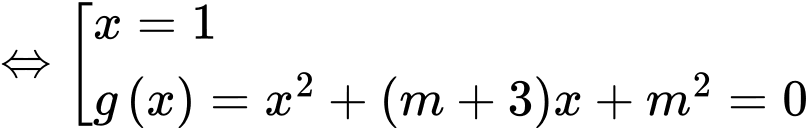
Để hai đồ thị cắt nhau tại 3 điểm phân biệt thì (*) có 3 nghiệm phân biệt
 có hai nghiệm phân biệt khác 1
có hai nghiệm phân biệt khác 1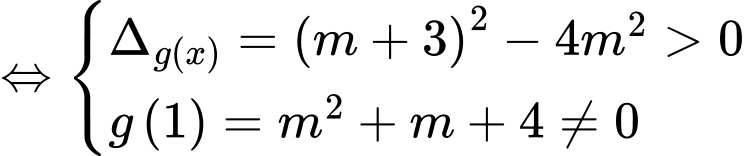
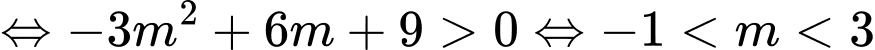
Kết hợp với
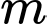 là số nguyên dương ta được
là số nguyên dương ta được 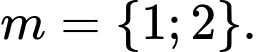 Đáp án: A
Đáp án: A
Câu 11 [28697]: Cho hàm số 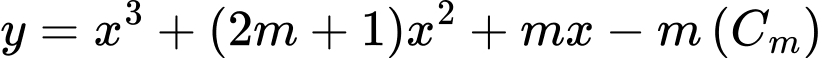 . Có tất cả bao nhiêu giá trị nguyên của m để đường thẳng
. Có tất cả bao nhiêu giá trị nguyên của m để đường thẳng 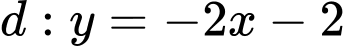 cắt đồ thị hàm số
cắt đồ thị hàm số 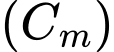 tại ba điểm phân biệt có hoành độ lần lượt là
tại ba điểm phân biệt có hoành độ lần lượt là 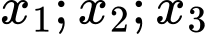 thỏa mãn điều kiện
thỏa mãn điều kiện 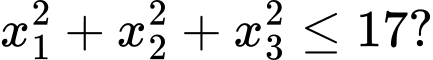
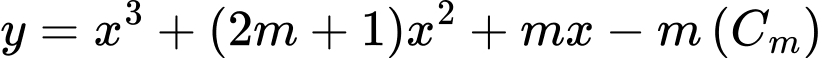 . Có tất cả bao nhiêu giá trị nguyên của m để đường thẳng
. Có tất cả bao nhiêu giá trị nguyên của m để đường thẳng 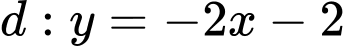 cắt đồ thị hàm số
cắt đồ thị hàm số 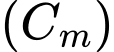 tại ba điểm phân biệt có hoành độ lần lượt là
tại ba điểm phân biệt có hoành độ lần lượt là 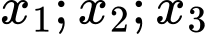 thỏa mãn điều kiện
thỏa mãn điều kiện 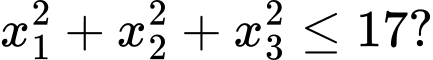
A, 1.
B, 5.
C, 3.
D, 4.
Phương trình hoành độ giao điểm 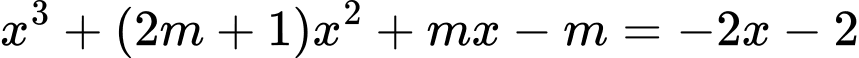
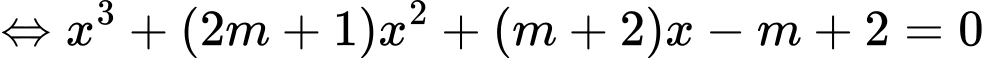
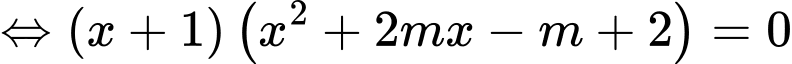
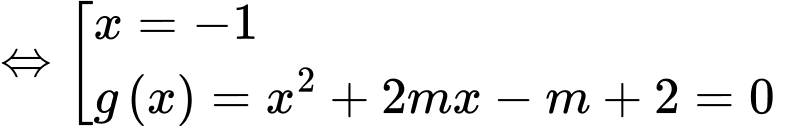
Để đồ thị hàm số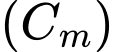 cắt
cắt 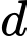 tại ba điểm phân biệt thì
tại ba điểm phân biệt thì 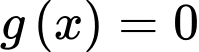 có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 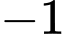
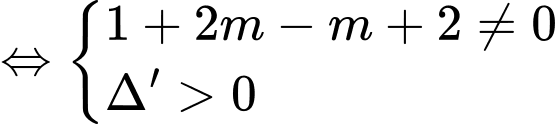
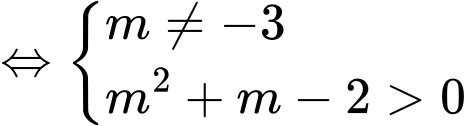

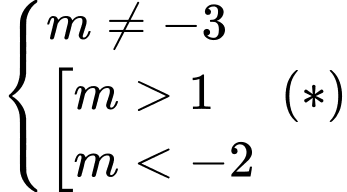
Giả sử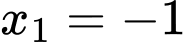 và
và 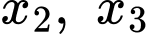 là nghiệm của phương trình
là nghiệm của phương trình 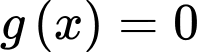
Theo Vi-ét ta có: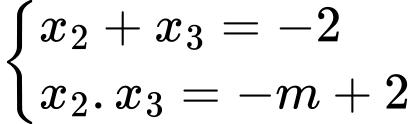
Ta có
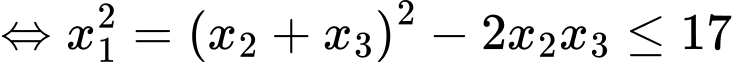
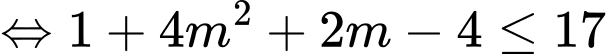
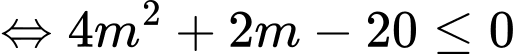
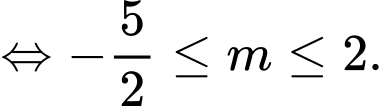
Kết hợp với điều kiện suy ra
suy ra 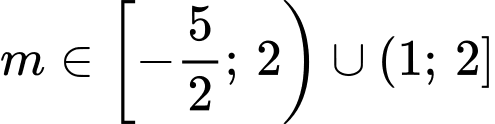 nên chỉ có một giá trị nguyên
nên chỉ có một giá trị nguyên 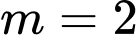 thoả mãn ycbt.
thoả mãn ycbt.
Chọn đáp án A. Đáp án: A
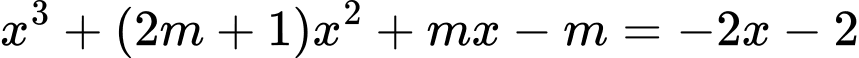
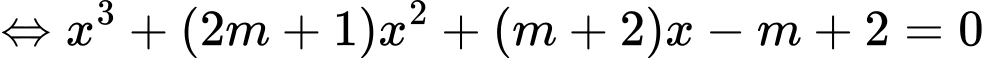
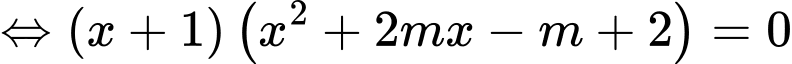
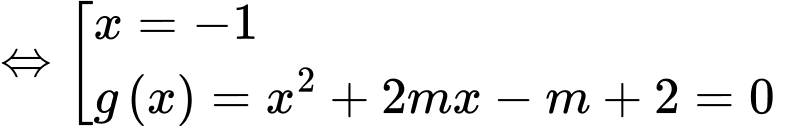
Để đồ thị hàm số
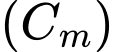 cắt
cắt 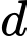 tại ba điểm phân biệt thì
tại ba điểm phân biệt thì 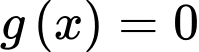 có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 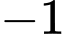
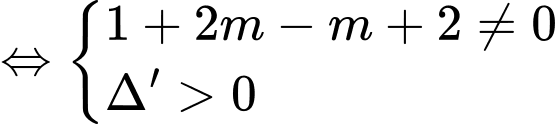
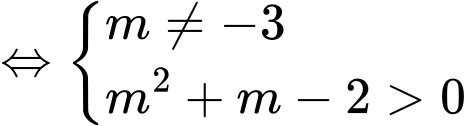

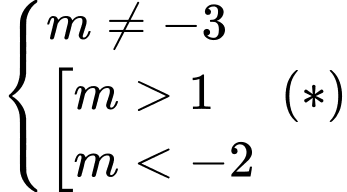
Giả sử
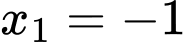 và
và 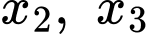 là nghiệm của phương trình
là nghiệm của phương trình 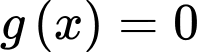
Theo Vi-ét ta có:
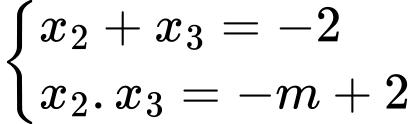
Ta có

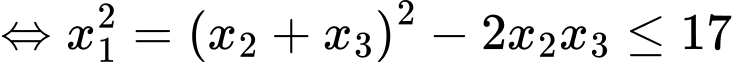
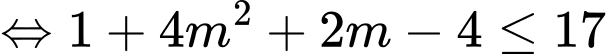
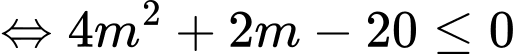
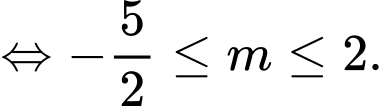
Kết hợp với điều kiện
 suy ra
suy ra 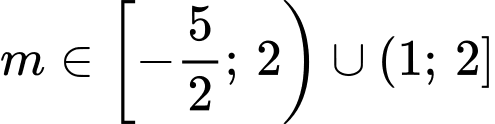 nên chỉ có một giá trị nguyên
nên chỉ có một giá trị nguyên 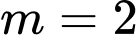 thoả mãn ycbt.
thoả mãn ycbt. Chọn đáp án A. Đáp án: A
Câu 12 [330117]: Có tất cả bao nhiêu giá trị thực của tham số 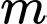 để đường thẳng
để đường thẳng 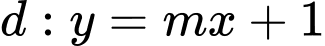 cắt đồ thị
cắt đồ thị 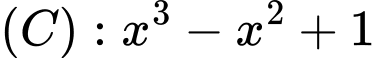 tại ba điểm
tại ba điểm 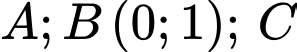 phân biệt sao cho tam giác
phân biệt sao cho tam giác  vuông tại
vuông tại 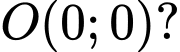
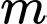 để đường thẳng
để đường thẳng 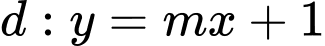 cắt đồ thị
cắt đồ thị 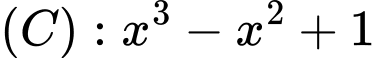 tại ba điểm
tại ba điểm 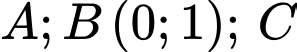 phân biệt sao cho tam giác
phân biệt sao cho tam giác  vuông tại
vuông tại 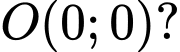
A, 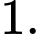
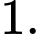
B, 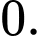
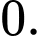
C, 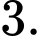
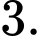
D, 
Phương trình hoành độ giao điểm 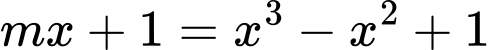
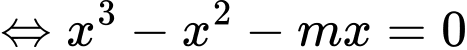
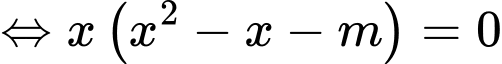
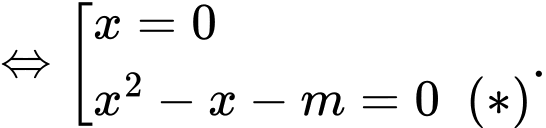
Để đường thẳng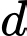 cắt
cắt  tại 3 điểm phân biệt
tại 3 điểm phân biệt 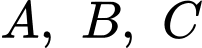
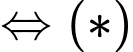 có 2 nghiệm phân biệt khác 0.
có 2 nghiệm phân biệt khác 0.
Giả sử phương trình có 2 nghiệm phân biệt là
có 2 nghiệm phân biệt là 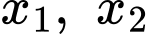
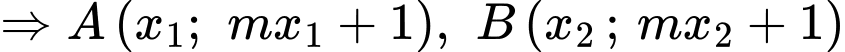
Theo định lý Viet ta có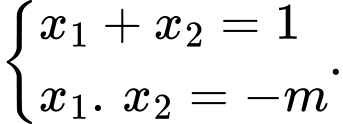
Theo giả thiết, ta có tam giác vuông tại
vuông tại  nên ta có
nên ta có 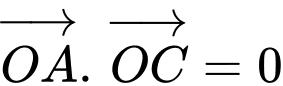

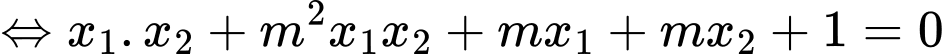
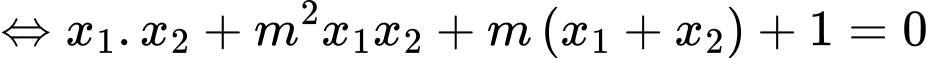
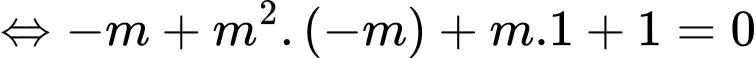
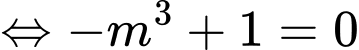
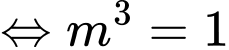
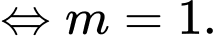
Vậy có 1 giá trị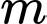 thoả mãn ycbt. Chọn A. Đáp án: A
thoả mãn ycbt. Chọn A. Đáp án: A
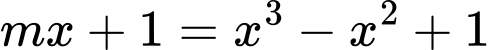
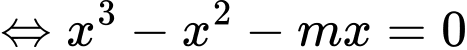
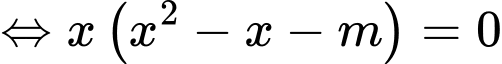
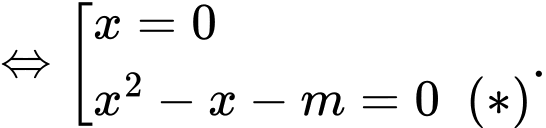
Để đường thẳng
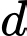 cắt
cắt  tại 3 điểm phân biệt
tại 3 điểm phân biệt 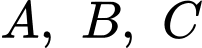
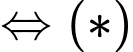 có 2 nghiệm phân biệt khác 0.
có 2 nghiệm phân biệt khác 0.Giả sử phương trình
 có 2 nghiệm phân biệt là
có 2 nghiệm phân biệt là 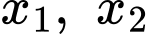
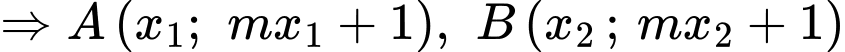
Theo định lý Viet ta có
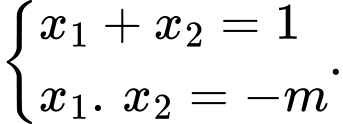
Theo giả thiết, ta có tam giác
 vuông tại
vuông tại  nên ta có
nên ta có 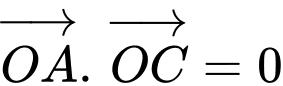

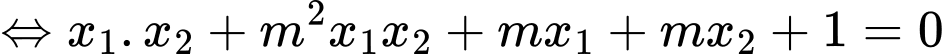
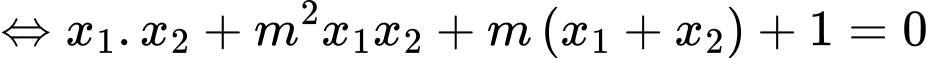
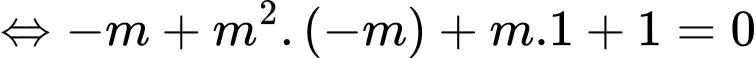
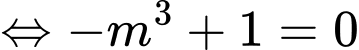
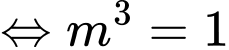
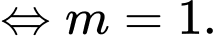
Vậy có 1 giá trị
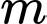 thoả mãn ycbt. Chọn A. Đáp án: A
thoả mãn ycbt. Chọn A. Đáp án: A
Câu 13 [28629]: Tìm giá trị của tham số 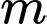 để đồ thị
để đồ thị  của hàm số
của hàm số 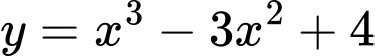 và đường thẳng
và đường thẳng 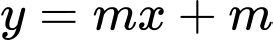 cắt nhau tại 3 điểm phân biệt
cắt nhau tại 3 điểm phân biệt 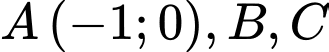 sao cho
sao cho 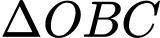 có diện tích bằng 8.
có diện tích bằng 8.
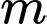 để đồ thị
để đồ thị  của hàm số
của hàm số 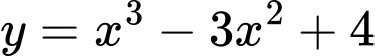 và đường thẳng
và đường thẳng 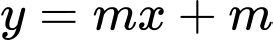 cắt nhau tại 3 điểm phân biệt
cắt nhau tại 3 điểm phân biệt 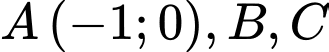 sao cho
sao cho 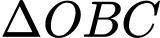 có diện tích bằng 8.
có diện tích bằng 8. A, 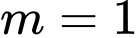 .
.
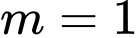 .
.B, 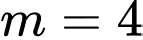 .
.
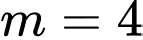 .
.C, 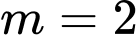 .
.
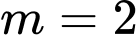 .
.D, 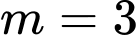 .
.
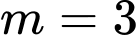 .
.
Phương trình hoành độ giao điểm 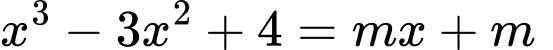
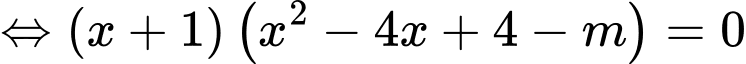
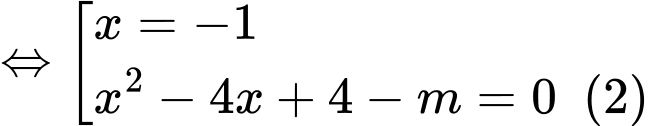
Đồ thị cắt đường thẳng
cắt đường thẳng 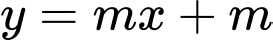 cắt nhau tại ba điểm phân biệt khi và chỉ khi phương trình
cắt nhau tại ba điểm phân biệt khi và chỉ khi phương trình  có hai nghiệm phân biệt đều khác
có hai nghiệm phân biệt đều khác 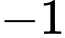
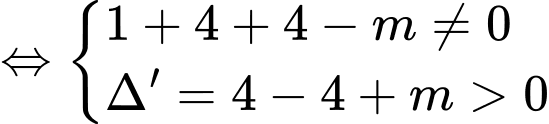
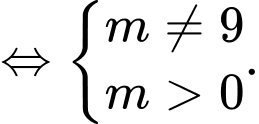
Khi đó, ta có hoành độ của điểm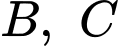 là nghiệm của phương trình
là nghiệm của phương trình 
Theo Vi-ét, ta có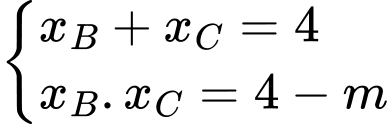
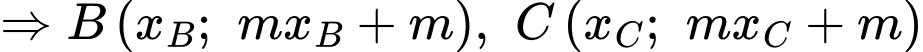
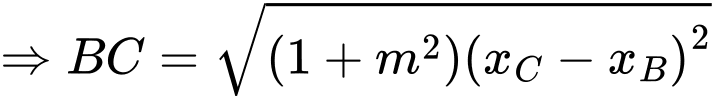
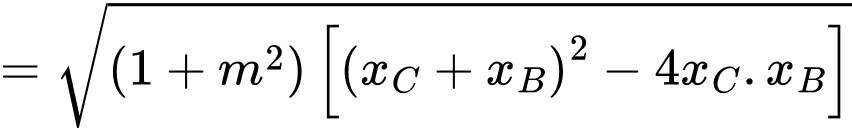
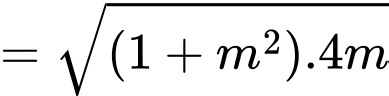
Ta có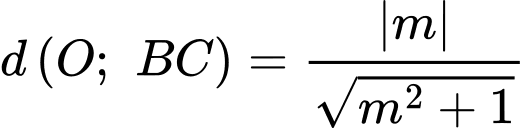
Suy ra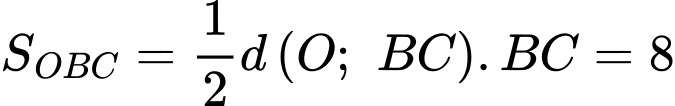
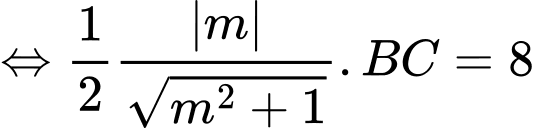
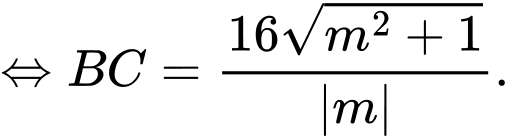
Suy ra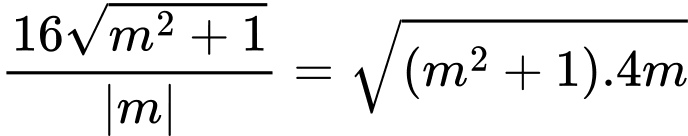
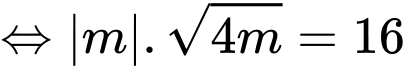
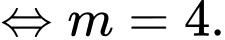
Chọn đáp án B. Đáp án: B
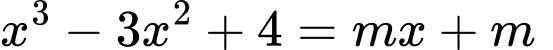
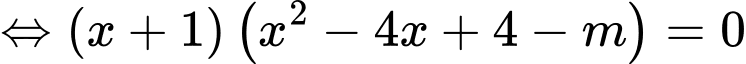
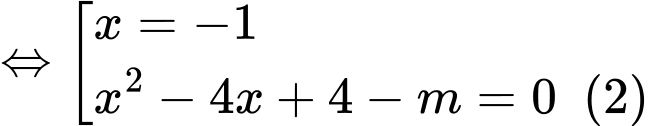
Đồ thị
 cắt đường thẳng
cắt đường thẳng 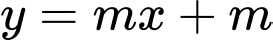 cắt nhau tại ba điểm phân biệt khi và chỉ khi phương trình
cắt nhau tại ba điểm phân biệt khi và chỉ khi phương trình  có hai nghiệm phân biệt đều khác
có hai nghiệm phân biệt đều khác 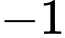
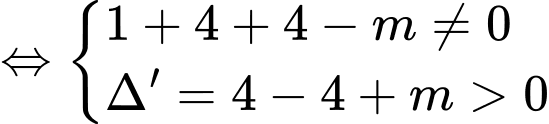
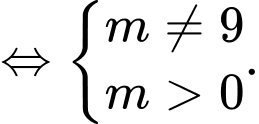
Khi đó, ta có hoành độ của điểm
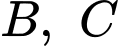 là nghiệm của phương trình
là nghiệm của phương trình 
Theo Vi-ét, ta có
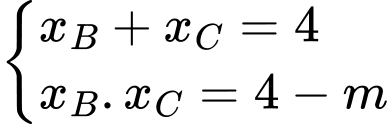
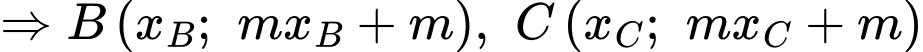
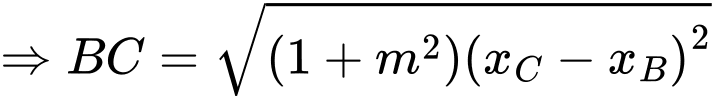
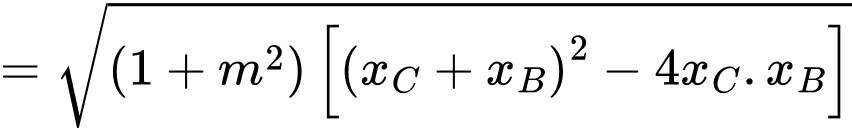
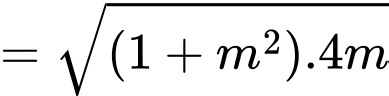
Ta có
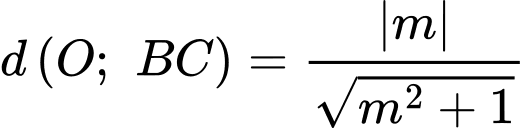
Suy ra
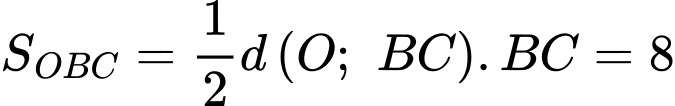
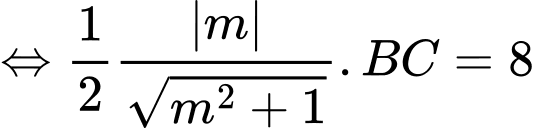
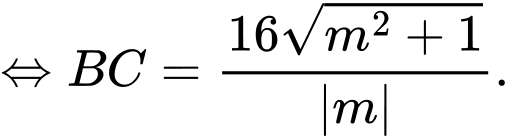
Suy ra
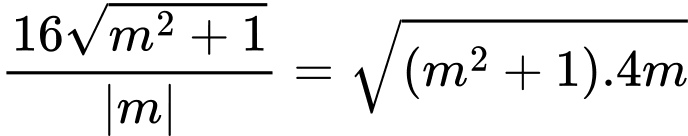
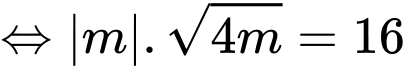
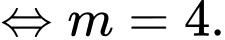
Chọn đáp án B. Đáp án: B
Câu 14 [28635]: Tính tổng tất cả các giá trị của 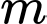 biết đồ thị hàm số
biết đồ thị hàm số 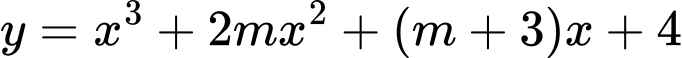 và đường thẳng
và đường thẳng 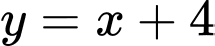 cắt nhau tại 3 điểm phân biệt
cắt nhau tại 3 điểm phân biệt 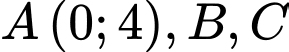 sao cho
sao cho 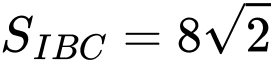 với
với 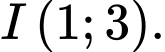
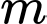 biết đồ thị hàm số
biết đồ thị hàm số 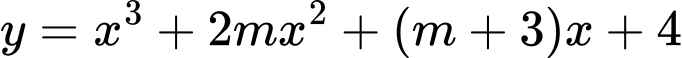 và đường thẳng
và đường thẳng 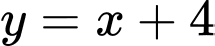 cắt nhau tại 3 điểm phân biệt
cắt nhau tại 3 điểm phân biệt 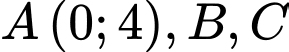 sao cho
sao cho 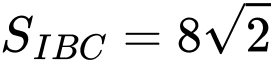 với
với 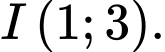
A, 3.
B, 8.
C, 1.
D, 5.
Phương trình hoành độ giao điểm 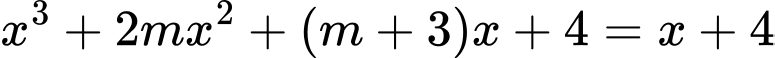
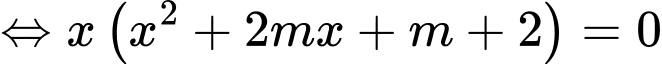
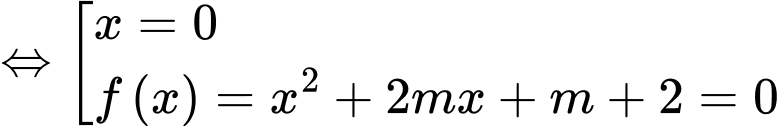
Yêu cầu bài toán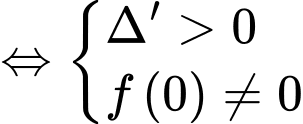
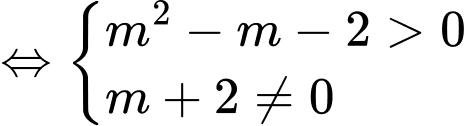
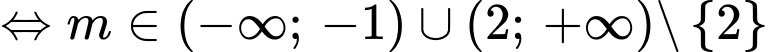
Khi đó 3 giao điểm phân biệt là
Theo Vi-ét, ta có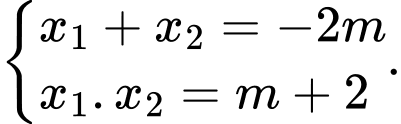
Ta có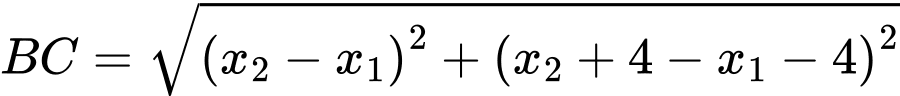
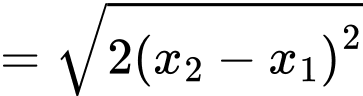
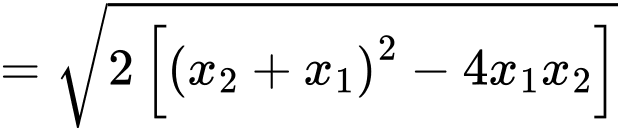
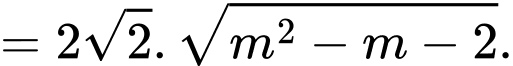
Ta có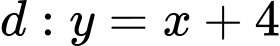
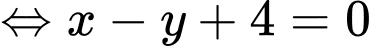
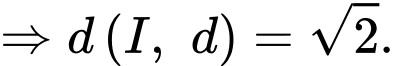
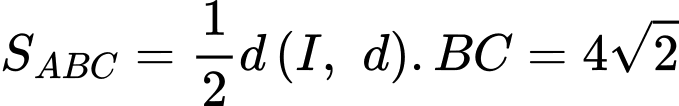
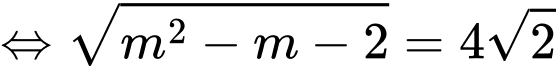
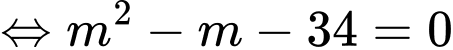 &
&
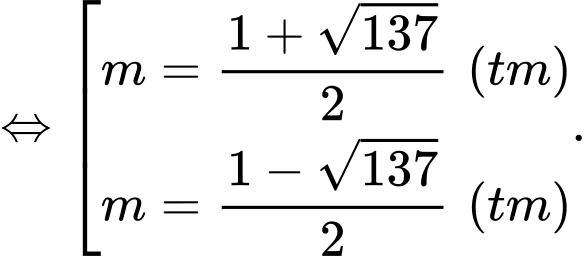
Vậy tổng tất cả các giá trị của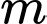 là
là 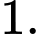
Chọn đáp án C. Đáp án: C
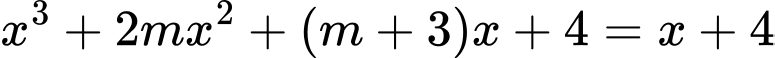
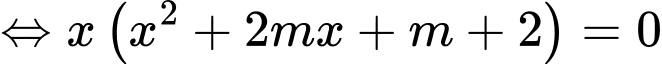
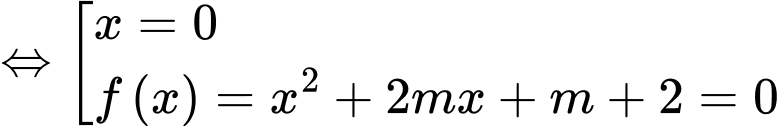
Yêu cầu bài toán
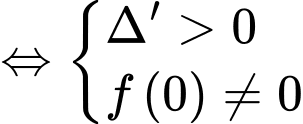
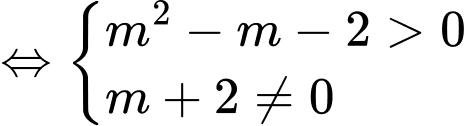
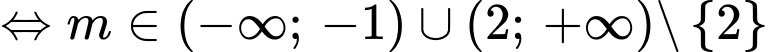
Khi đó 3 giao điểm phân biệt là

Theo Vi-ét, ta có
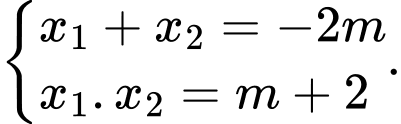
Ta có
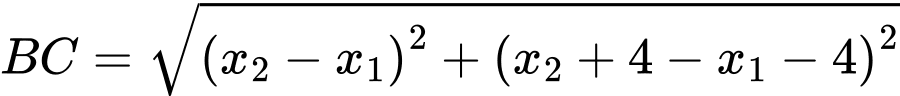
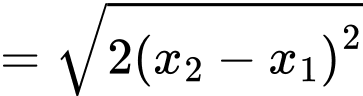
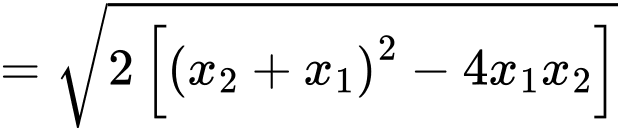
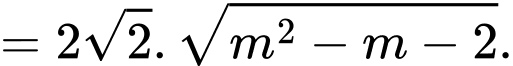
Ta có
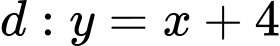
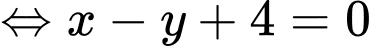
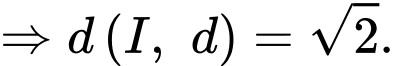
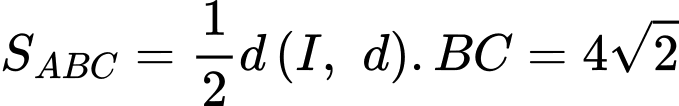
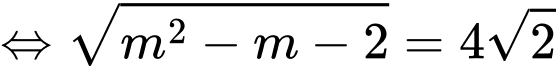
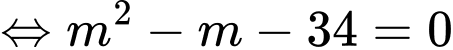 &
& 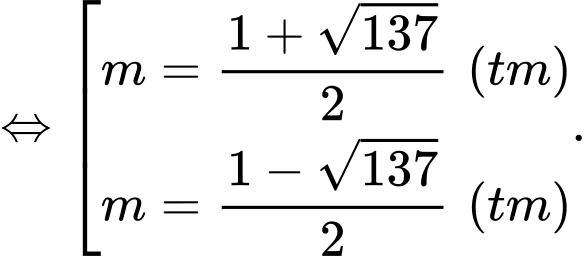
Vậy tổng tất cả các giá trị của
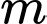 là
là 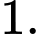
Chọn đáp án C. Đáp án: C
Câu 15 [28665]: Gọi 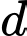 là đường thẳng đi qua
là đường thẳng đi qua 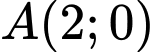 có hệ số góc
có hệ số góc 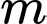 cắt đồ thị
cắt đồ thị 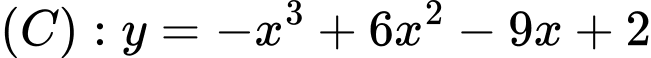 tại ba điểm phân biệt
tại ba điểm phân biệt 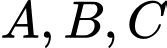 . Gọi
. Gọi 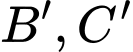 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 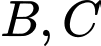 lên trục tung. Tìm giá trị dương của
lên trục tung. Tìm giá trị dương của 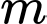 để hình thang
để hình thang 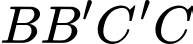 có diện tích bằng 8.
có diện tích bằng 8.
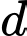 là đường thẳng đi qua
là đường thẳng đi qua 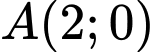 có hệ số góc
có hệ số góc 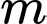 cắt đồ thị
cắt đồ thị 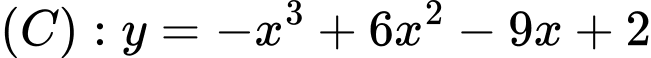 tại ba điểm phân biệt
tại ba điểm phân biệt 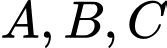 . Gọi
. Gọi 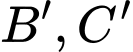 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 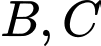 lên trục tung. Tìm giá trị dương của
lên trục tung. Tìm giá trị dương của 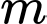 để hình thang
để hình thang 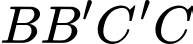 có diện tích bằng 8.
có diện tích bằng 8. A, 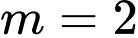 .
.
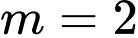 .
.B, 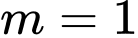 .
.
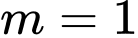 .
.C, 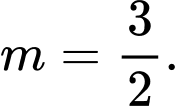
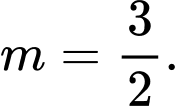
D, 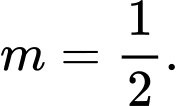
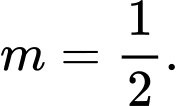
Phương trình đường thẳng 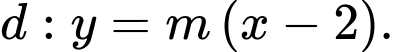
Phương trình hoành độ giao điểm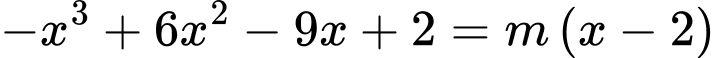
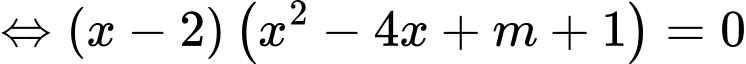
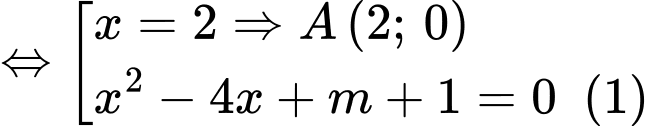
Để cắt
cắt 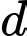 tại 3 điểm phân biệt thì phương trình
tại 3 điểm phân biệt thì phương trình  có 2 nghiệm phân biệt khác 2
có 2 nghiệm phân biệt khác 2
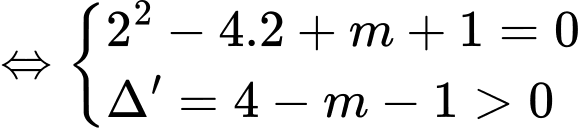
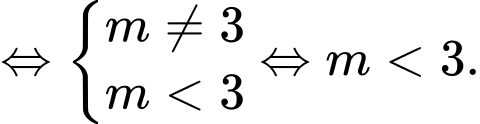
Giả sử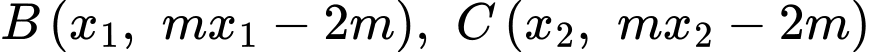 với
với 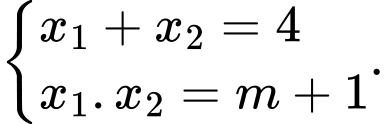
Ta có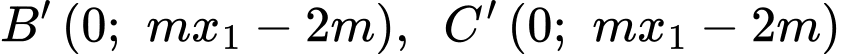
Ta có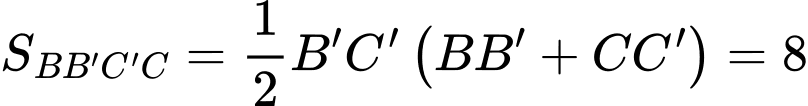
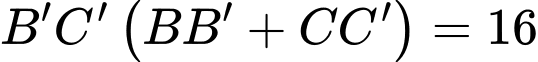
Mà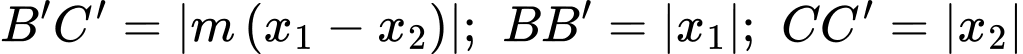
Do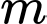 dương nên
dương nên 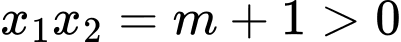 mà
mà 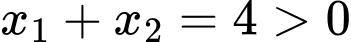
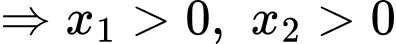
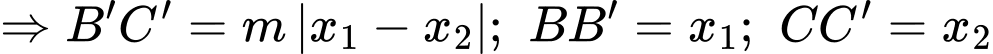

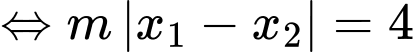
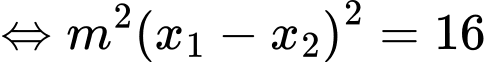
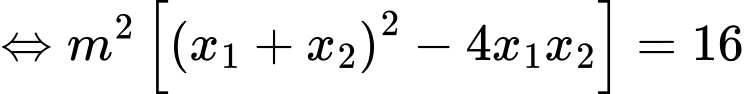
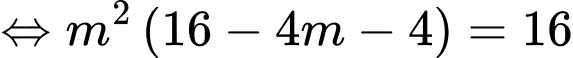
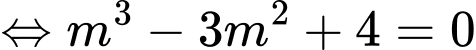
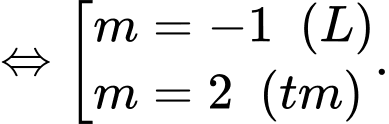
Chọn đáp án A. Đáp án: A
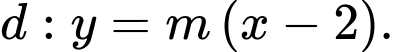
Phương trình hoành độ giao điểm
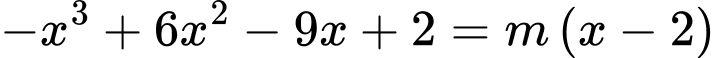
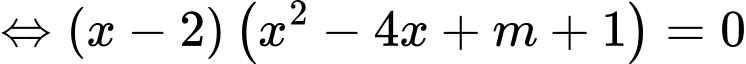
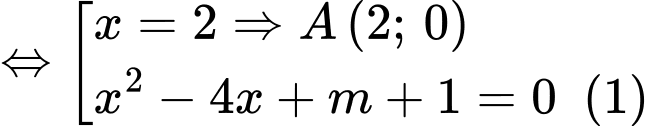
Để
 cắt
cắt 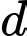 tại 3 điểm phân biệt thì phương trình
tại 3 điểm phân biệt thì phương trình  có 2 nghiệm phân biệt khác 2
có 2 nghiệm phân biệt khác 2 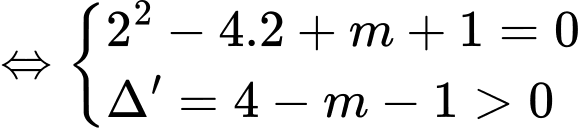
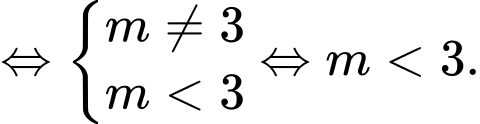
Giả sử
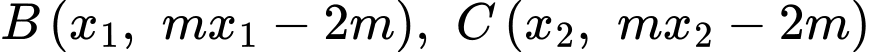 với
với 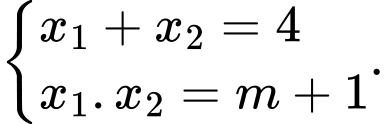
Ta có
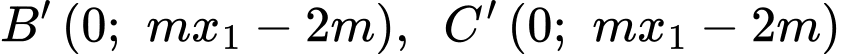
Ta có
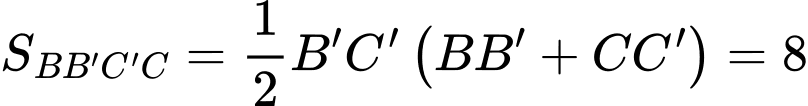
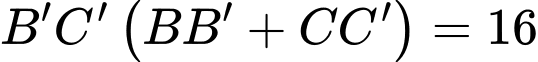
Mà
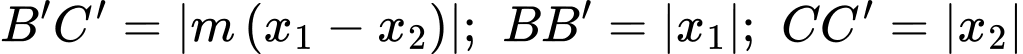
Do
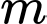 dương nên
dương nên 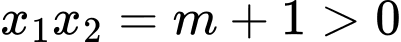 mà
mà 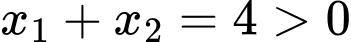
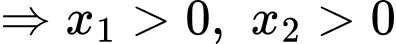
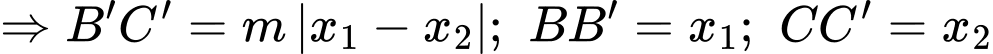

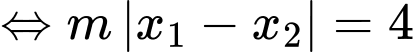
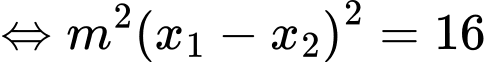
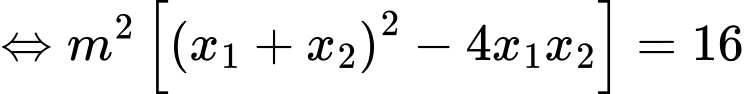
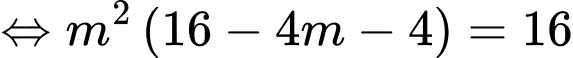
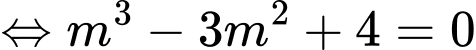
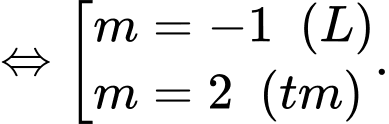
Chọn đáp án A. Đáp án: A
Câu 16 [28669]: Cho hàm số 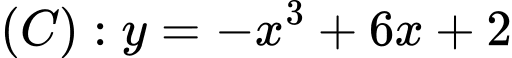 và đường thẳng
và đường thẳng 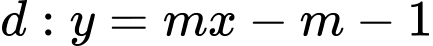 . Với giá trị nào của
. Với giá trị nào của 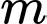 thì đường thẳng
thì đường thẳng 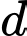 cắt đồ thị
cắt đồ thị  tại ba điểm phân biệt
tại ba điểm phân biệt 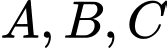 sao cho tổng hệ số góc các tiếp tuyến với
sao cho tổng hệ số góc các tiếp tuyến với  tại
tại 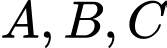 bằng
bằng 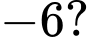
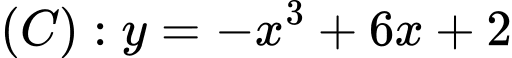 và đường thẳng
và đường thẳng 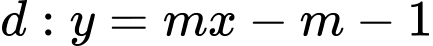 . Với giá trị nào của
. Với giá trị nào của 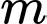 thì đường thẳng
thì đường thẳng 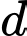 cắt đồ thị
cắt đồ thị  tại ba điểm phân biệt
tại ba điểm phân biệt 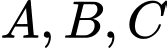 sao cho tổng hệ số góc các tiếp tuyến với
sao cho tổng hệ số góc các tiếp tuyến với  tại
tại 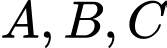 bằng
bằng 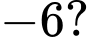
A, 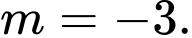
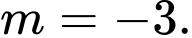
B, 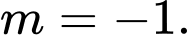
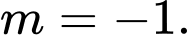
C, 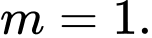
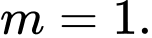
D, 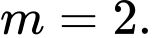
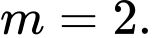
Phương trình hoành độ giao điểm 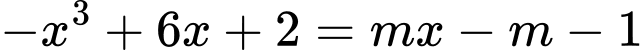
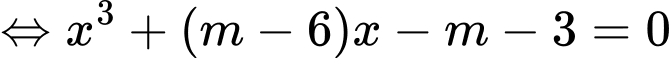
Ta có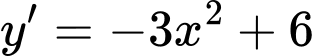
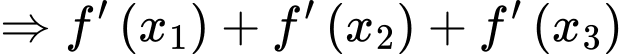
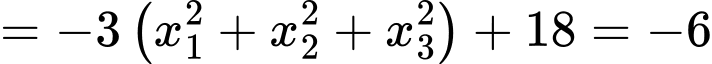
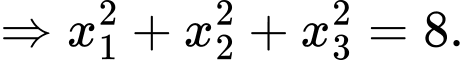
Ép cho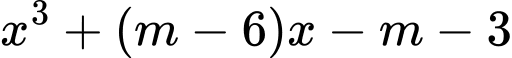
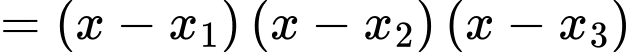
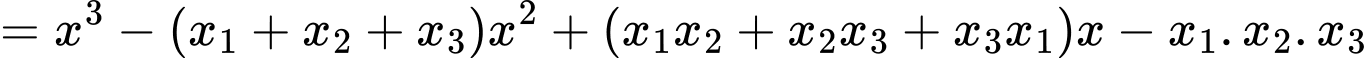
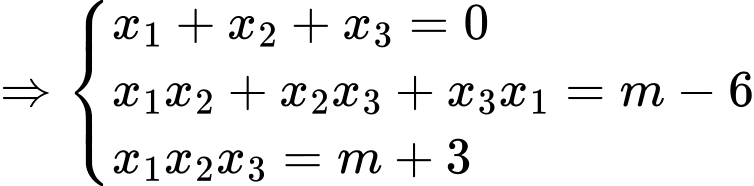
Lại có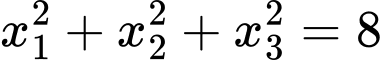
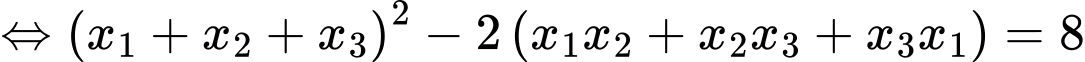
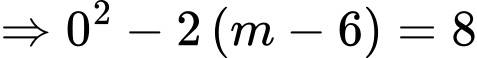
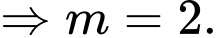
Thử lại thấy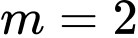 thoả mãn. Chọn đáp án D. Đáp án: D
thoả mãn. Chọn đáp án D. Đáp án: D
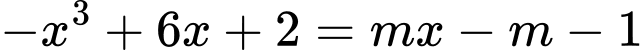
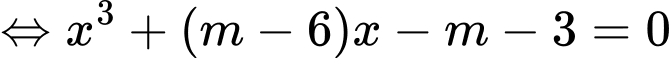
Ta có
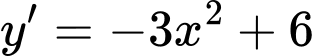
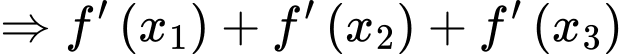
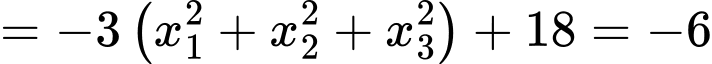
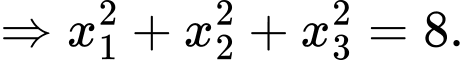
Ép cho
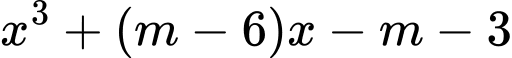
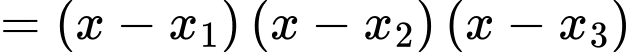
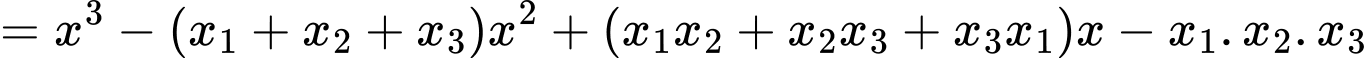
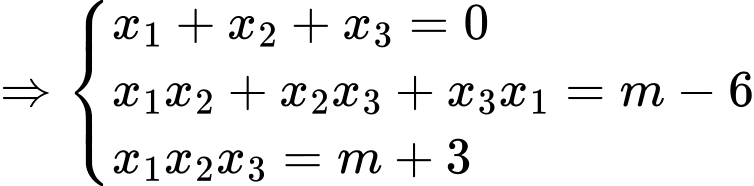
Lại có
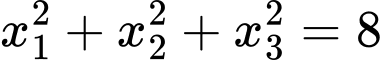
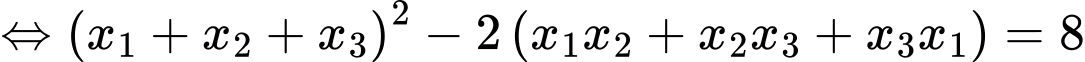
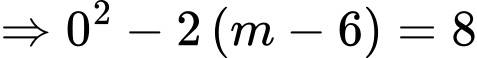
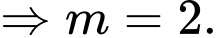
Thử lại thấy
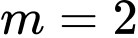 thoả mãn. Chọn đáp án D. Đáp án: D
thoả mãn. Chọn đáp án D. Đáp án: D