Đáp án Bài tập tự luyện số 2
Câu 1 [15701]: Tìm tham số 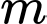 để hàm số
để hàm số 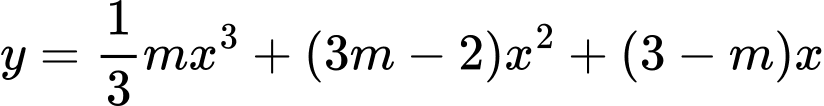 đạt cực đại tại
đạt cực đại tại 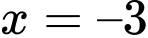 .
.
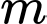 để hàm số
để hàm số 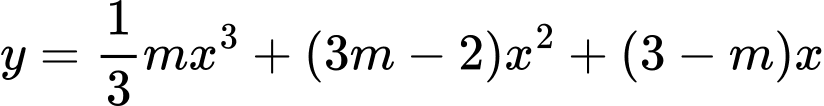 đạt cực đại tại
đạt cực đại tại 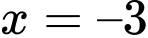 .
. A, 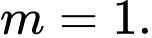
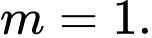
B, 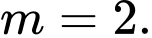
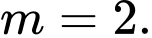
C, 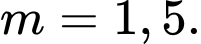
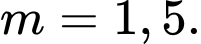
D, 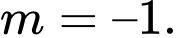
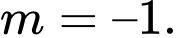
Thầy Tuấn-Xinlỗi các em về lỗi đề (sách 3000 bài tập nên không thể tránh khỏi trong lần đầuxuất bản) - Các em sửa lại đề theo đề Web nhé!. Cảm ơn các em nhiều!
Ta có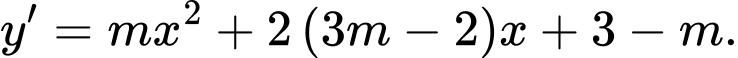
Hàm số đạt cực đại tại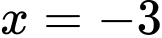 khi
khi 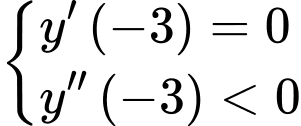
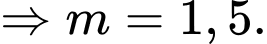
Chọn đáp án C. Đáp án: C
Ta có
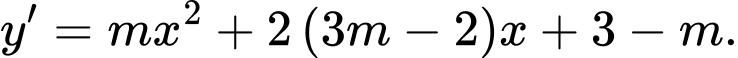
Hàm số đạt cực đại tại
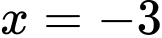 khi
khi 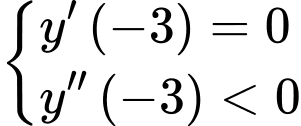
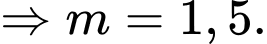
Chọn đáp án C. Đáp án: C
Câu 2 [15699]: Tìm tham số 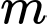 để hàm số
để hàm số 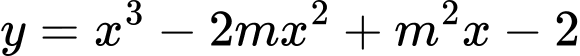 đạt cực tiểu tại
đạt cực tiểu tại 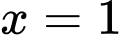 .
.
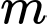 để hàm số
để hàm số 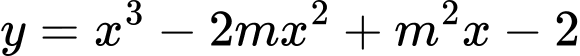 đạt cực tiểu tại
đạt cực tiểu tại 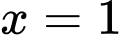 .
. A, 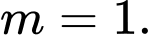
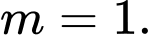
B, 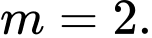
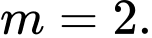
C, 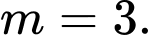
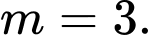
D, 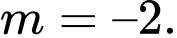
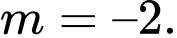
Ta có 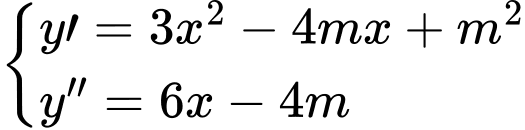
Hàm số đạt cực tiểu tại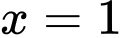
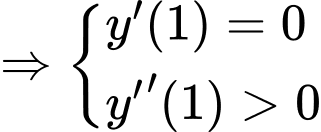
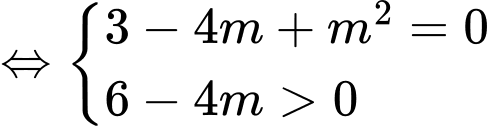
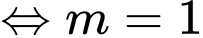 Đáp án: A
Đáp án: A
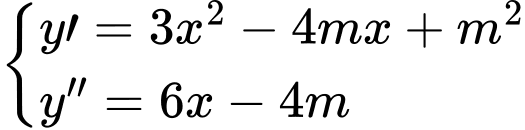
Hàm số đạt cực tiểu tại
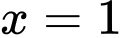
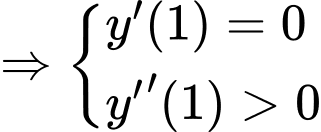
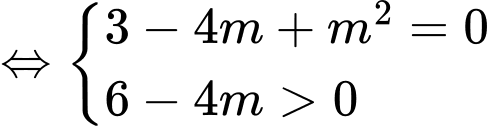
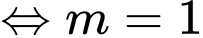 Đáp án: A
Đáp án: A
Câu 3 [791716]: Cho hàm số 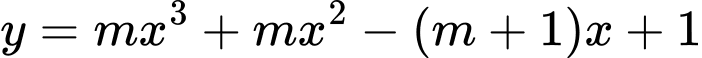 . Tìm tất cả các giá trị của
. Tìm tất cả các giá trị của 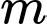 để hàm số nghịch biến trên
để hàm số nghịch biến trên 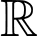 .
.
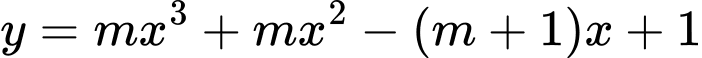 . Tìm tất cả các giá trị của
. Tìm tất cả các giá trị của 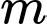 để hàm số nghịch biến trên
để hàm số nghịch biến trên 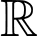 .
. A, 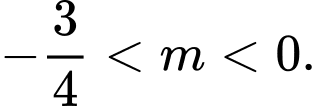
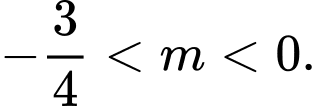
B, 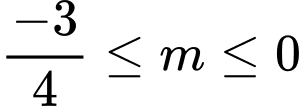 .
.
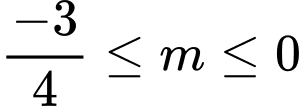 .
.C,  .
.
 .
.D, 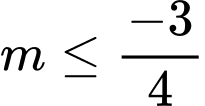 .
.
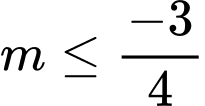 .
.
Chọn B.
Tập xác định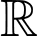 .
.
Ta có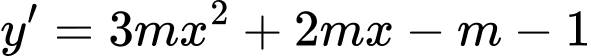 .
.
Để hàm số nghịch biến trên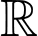
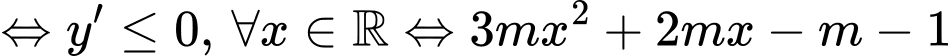
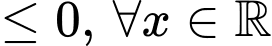 (1).
(1).
TH1: . Với
. Với 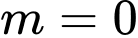 , hàm số nghịch biến trên
, hàm số nghịch biến trên 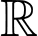 .
.
TH2: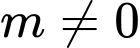 .
.
BPT (1)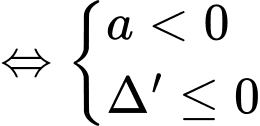
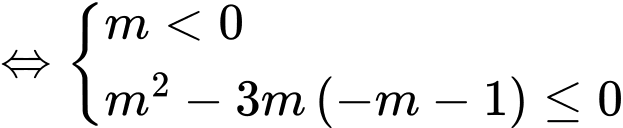
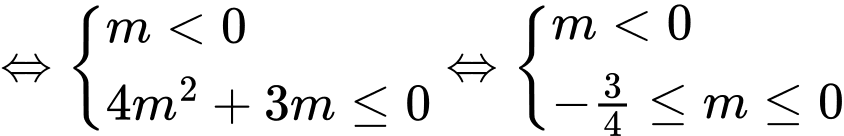
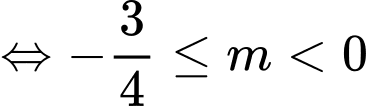 . Vậy
. Vậy 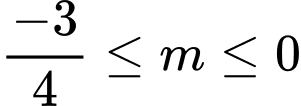 . Đáp án: B
. Đáp án: B
Tập xác định
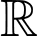 .
.Ta có
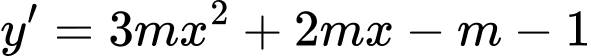 .
.Để hàm số nghịch biến trên
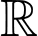
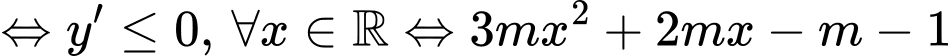
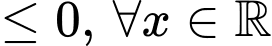 (1).
(1). TH1:
 . Với
. Với 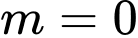 , hàm số nghịch biến trên
, hàm số nghịch biến trên 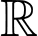 .
.TH2:
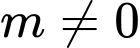 .
.BPT (1)
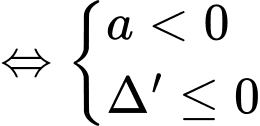
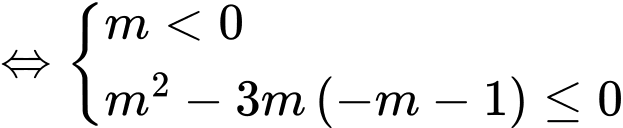
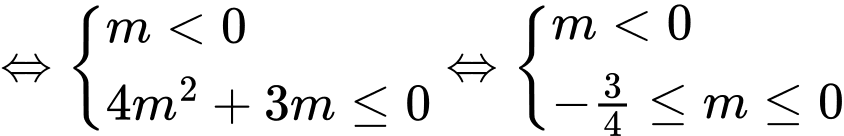
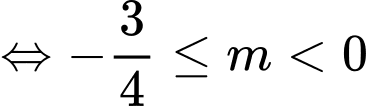 . Vậy
. Vậy 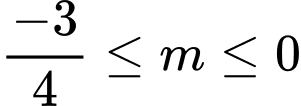 . Đáp án: B
. Đáp án: B
Câu 4 [15705]: Tìm tham số 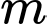 để hàm số
để hàm số 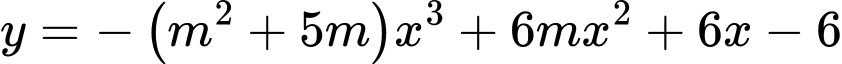 đạt cực đại tại
đạt cực đại tại 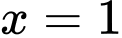 .
.
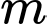 để hàm số
để hàm số 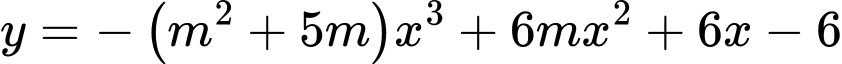 đạt cực đại tại
đạt cực đại tại 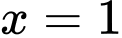 .
. A, 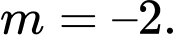
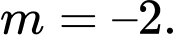
B, 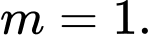
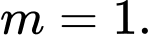
C, 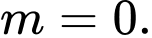
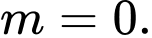
D, 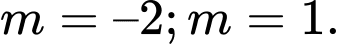
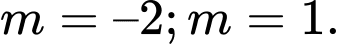
Ta có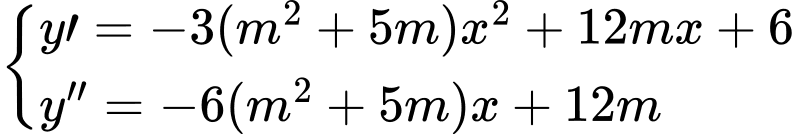
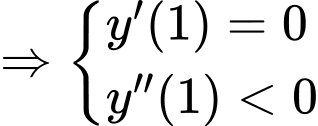
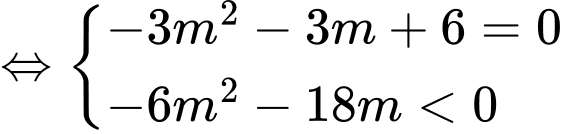
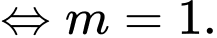 Chọn B. Đáp án: B
Chọn B. Đáp án: B
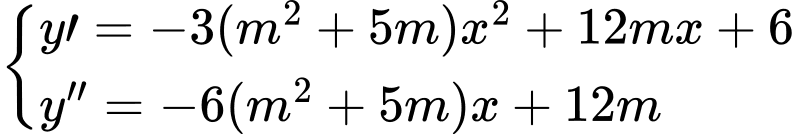
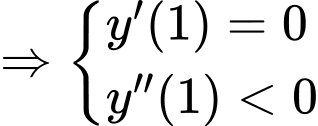
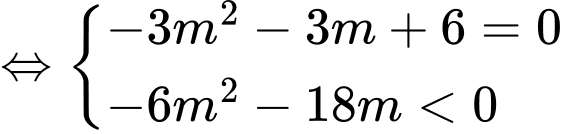
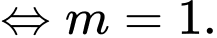 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 5 [509246]: Hỏi có bao nhiêu số nguyên m để hàm số 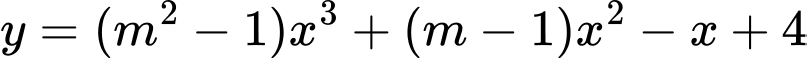 nghịch biến trên khoảng
nghịch biến trên khoảng 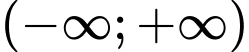 ?
?
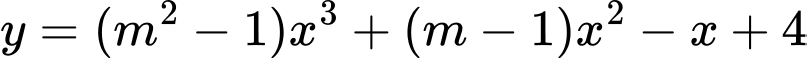 nghịch biến trên khoảng
nghịch biến trên khoảng 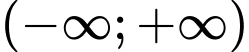 ?
? A, 2.
B, 1.
C, 0.
D, 3.
Với 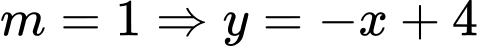 hàm số nghịch biến trên
hàm số nghịch biến trên 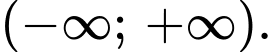
Với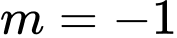
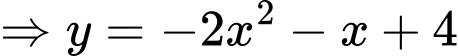 không thỏa mãn nghịch biến trên
không thỏa mãn nghịch biến trên 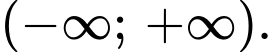
Với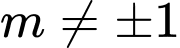
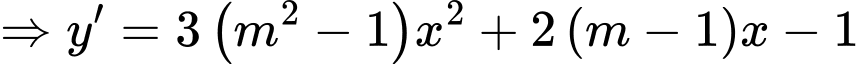 nghịch biến trên
nghịch biến trên 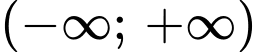
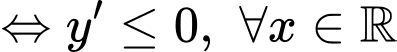
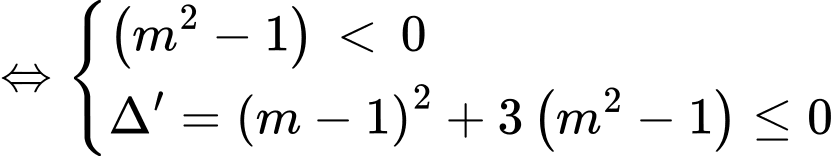
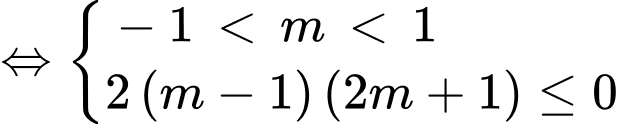
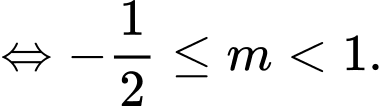
Kết hợp YCBT suy ra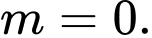
Chọn đáp án A. Đáp án: A
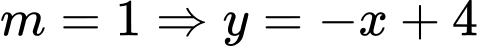 hàm số nghịch biến trên
hàm số nghịch biến trên 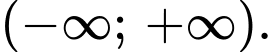
Với
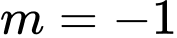
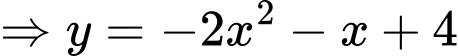 không thỏa mãn nghịch biến trên
không thỏa mãn nghịch biến trên 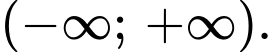
Với
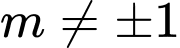
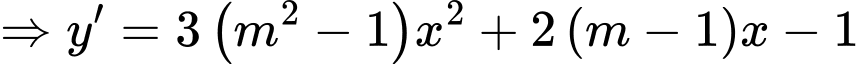 nghịch biến trên
nghịch biến trên 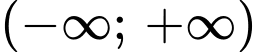
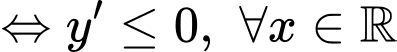
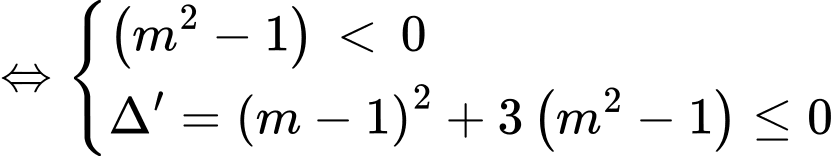
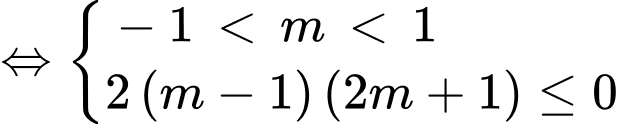
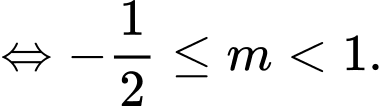
Kết hợp YCBT suy ra
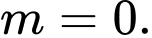
Chọn đáp án A. Đáp án: A
Câu 6 [2674]: Cho hàm số 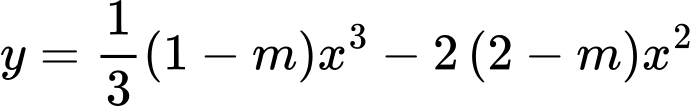
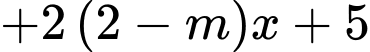 .
.
Giá trị nào của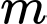 thì hàm số đã cho luôn nghịch biến trên
thì hàm số đã cho luôn nghịch biến trên 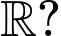
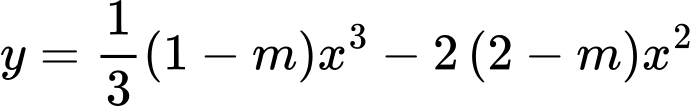
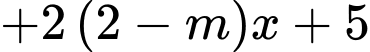 .
.Giá trị nào của
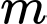 thì hàm số đã cho luôn nghịch biến trên
thì hàm số đã cho luôn nghịch biến trên 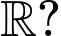
A, 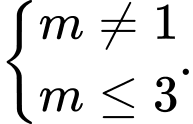
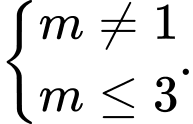
B, 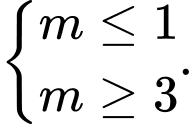
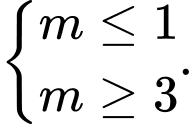
C, 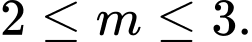
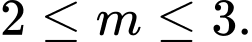
D, 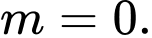
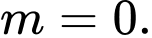
Ta có 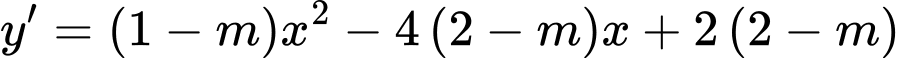
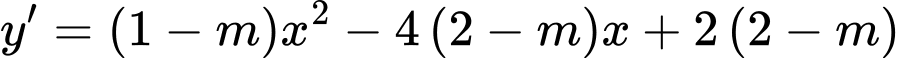
Để hàm số nghịch biến trên 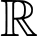 thì
thì 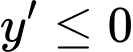 với mọi
với mọi 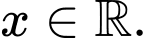
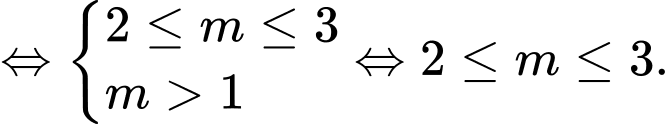
Đáp án: C 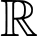 thì
thì 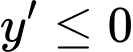 với mọi
với mọi 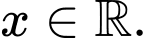
TH1: 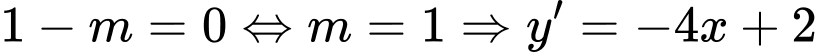 (loại)
(loại)
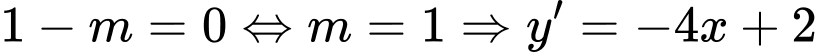 (loại)
(loại) TH2: 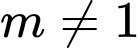
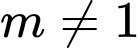
ĐK tương đương với 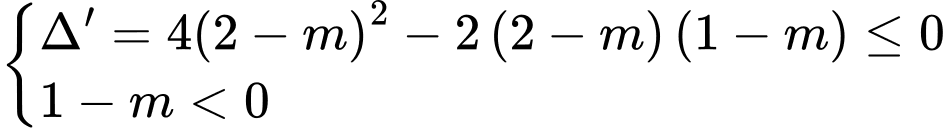
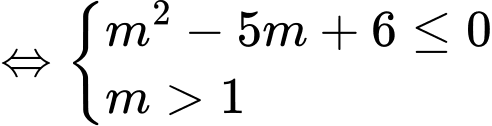
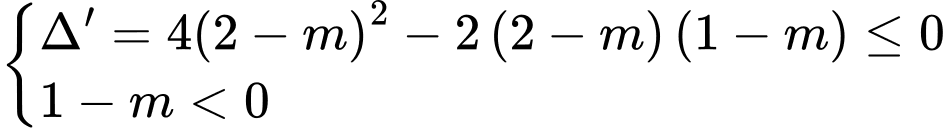
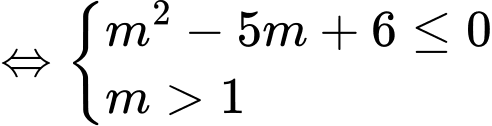
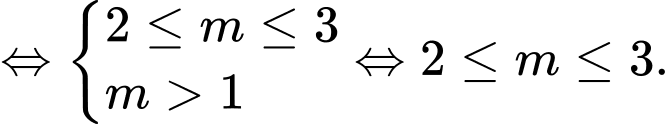
Chọn đáp án C.
Câu 7 [382498]: Cho hàm số 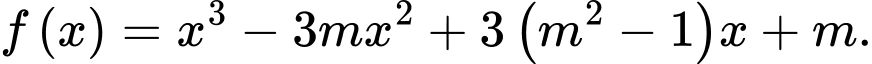 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau:
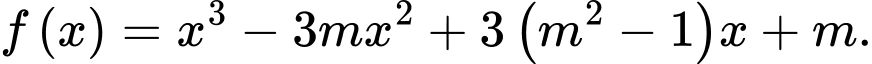 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau: A, a) 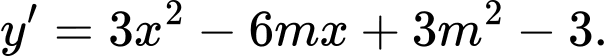
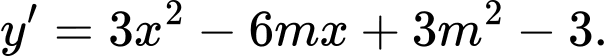
B, b) Hàm số đã cho luôn đồng biến trên tập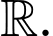
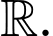
C, c) Có hai giá trị của 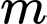 để hàm số đạt cực trị tại điểm
để hàm số đạt cực trị tại điểm 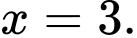
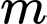 để hàm số đạt cực trị tại điểm
để hàm số đạt cực trị tại điểm 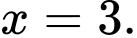
D, d) Có một giá trị của 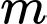 để hàm số đạt cực đại tại điểm
để hàm số đạt cực đại tại điểm 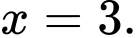
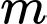 để hàm số đạt cực đại tại điểm
để hàm số đạt cực đại tại điểm 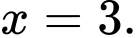
Ta có: 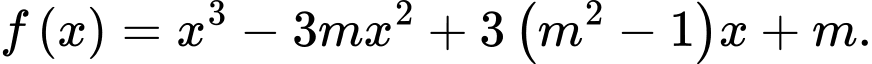
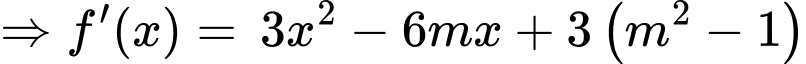
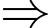 Đáp án A đúng.
Đáp án A đúng.
Để hàm số đã cho luôn đồng biến trên tập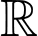 khi và chỉ khi
khi và chỉ khi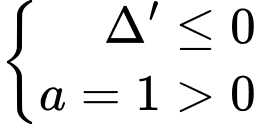
Lại có: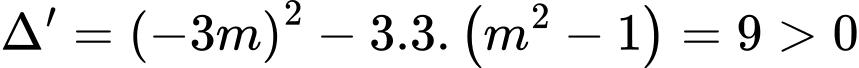
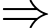 Đáp án B sai.
Đáp án B sai.
Hàm số đạt cực trị tại điểm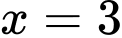
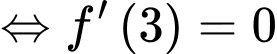
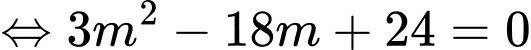
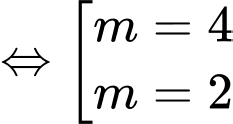
Thử lại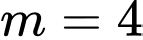
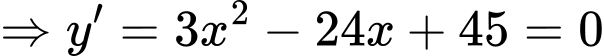 có 2 nghiệm phân biệt và
có 2 nghiệm phân biệt và 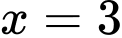 là điểm cực đại
là điểm cực đại
Thử lại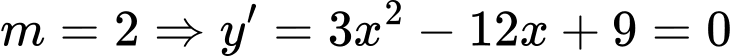 có 2 nghiệm phân biệt và
có 2 nghiệm phân biệt và 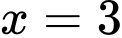 là điểm cực tiểu.
là điểm cực tiểu.
Vậy có 2 giá trị của m để hàm số đã cho đạt cực trị tại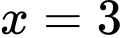 .
.
 Đán án C đúng, đáp án D đúng.
Đán án C đúng, đáp án D đúng.
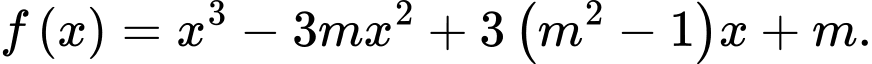
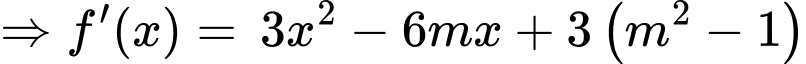
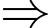 Đáp án A đúng.
Đáp án A đúng. Để hàm số đã cho luôn đồng biến trên tập
 khi và chỉ khi
khi và chỉ khi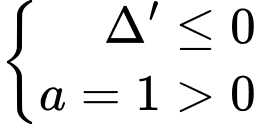
Lại có:
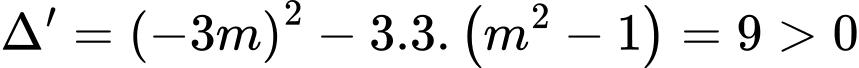
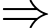 Đáp án B sai.
Đáp án B sai. Hàm số đạt cực trị tại điểm
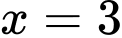
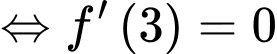
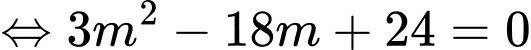
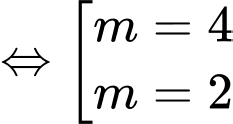
Thử lại
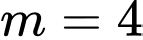
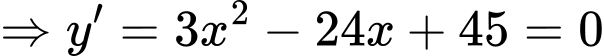 có 2 nghiệm phân biệt và
có 2 nghiệm phân biệt và 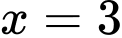 là điểm cực đại
là điểm cực đạiThử lại
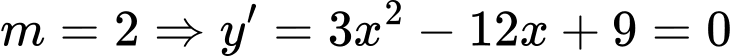 có 2 nghiệm phân biệt và
có 2 nghiệm phân biệt và 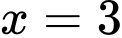 là điểm cực tiểu.
là điểm cực tiểu.Vậy có 2 giá trị của m để hàm số đã cho đạt cực trị tại
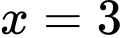 .
.  Đán án C đúng, đáp án D đúng.
Đán án C đúng, đáp án D đúng.
Câu 8 [382499]: Cho hàm số 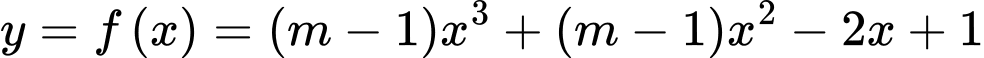 với
với 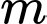 là tham số. Xét tính đúng sai của các mệnh đề sau:
là tham số. Xét tính đúng sai của các mệnh đề sau:
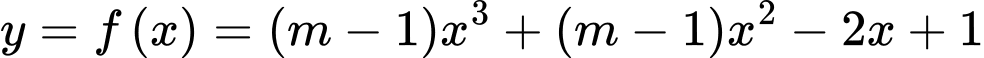 với
với 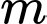 là tham số. Xét tính đúng sai của các mệnh đề sau:
là tham số. Xét tính đúng sai của các mệnh đề sau: A, a) 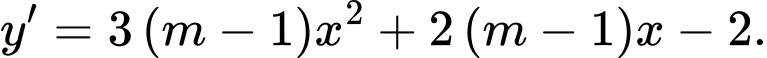
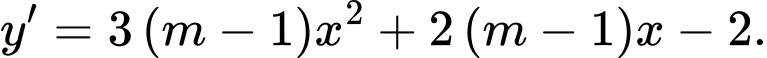
B, b) Có 6 giá trị nguyên của 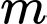 để hàm số nghịch biến trên tập
để hàm số nghịch biến trên tập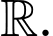
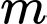 để hàm số nghịch biến trên tập
để hàm số nghịch biến trên tập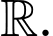
C, c) Có một giá trị của 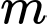 để hàm số đạt cực trị tại điểm
để hàm số đạt cực trị tại điểm 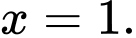
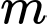 để hàm số đạt cực trị tại điểm
để hàm số đạt cực trị tại điểm 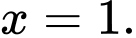
D, d) Có một giá trị của 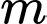 để hàm số đạt cực đại tại điểm
để hàm số đạt cực đại tại điểm 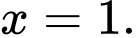
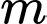 để hàm số đạt cực đại tại điểm
để hàm số đạt cực đại tại điểm 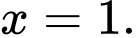
Trường hợp 1: 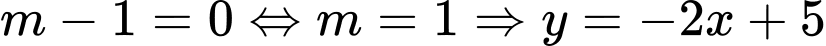 hàm số nghịch biến trên
hàm số nghịch biến trên 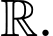
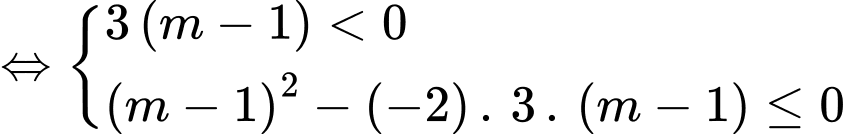
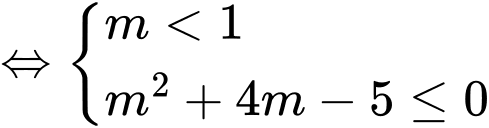
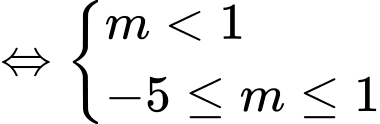

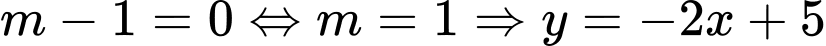 hàm số nghịch biến trên
hàm số nghịch biến trên 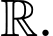
Do đó 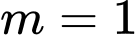 (nhận)
(nhận)
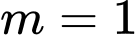 (nhận)
(nhận) Trường hợp 2: 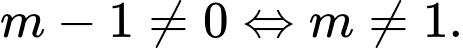
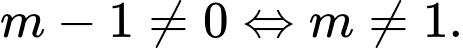
Ta có 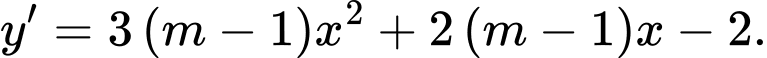
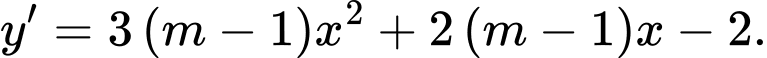
Hàm số nghịch biến trên khoảng 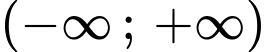
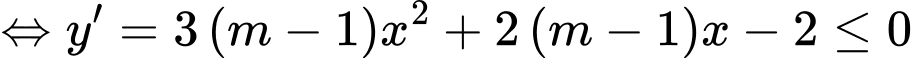
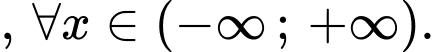
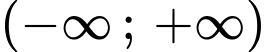
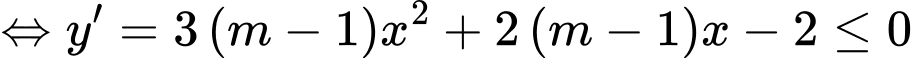
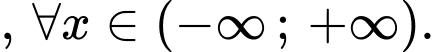
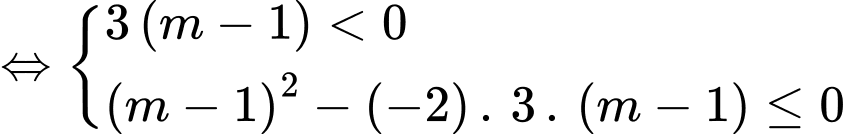
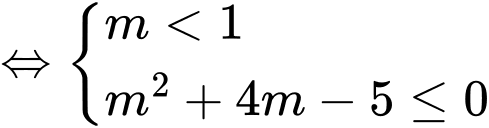
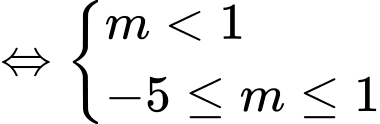

Do 

Vậy có 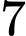 giá trị nguyên của
giá trị nguyên của 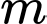 để hàm số nghịch biến trên
để hàm số nghịch biến trên 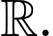
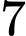 giá trị nguyên của
giá trị nguyên của 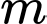 để hàm số nghịch biến trên
để hàm số nghịch biến trên 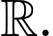
Mặt khác 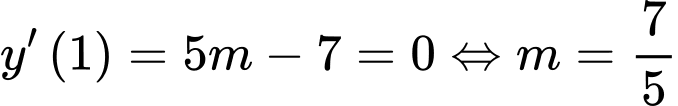
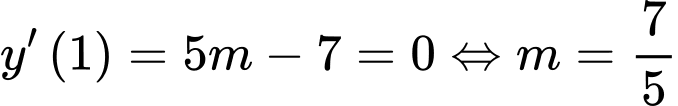
Thử lại với 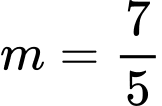 thì hàm số đạt cực tiểu tại điểm
thì hàm số đạt cực tiểu tại điểm 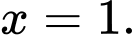
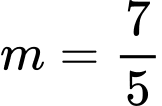 thì hàm số đạt cực tiểu tại điểm
thì hàm số đạt cực tiểu tại điểm 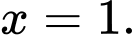
a) Đúng b) Sai c) Đúng d) Sai
Câu 9 [382500]: Cho hàm số 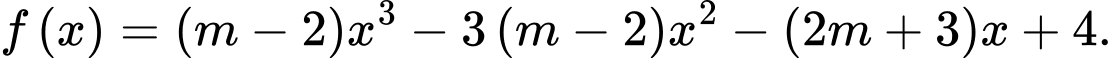 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau:
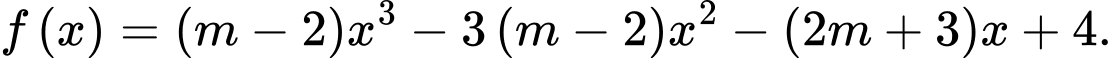 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau: A, a) Với 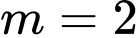 thì hàm số nghịch biến trên
thì hàm số nghịch biến trên 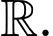
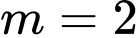 thì hàm số nghịch biến trên
thì hàm số nghịch biến trên 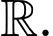
B, b) Có một giá trị của 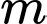 để hàm số đạt cực đại tại điểm
để hàm số đạt cực đại tại điểm 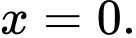
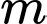 để hàm số đạt cực đại tại điểm
để hàm số đạt cực đại tại điểm 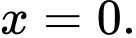
C, c) Có 3 giá trị nguyên của 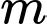 để hàm số nghịch biến trên
để hàm số nghịch biến trên 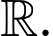
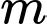 để hàm số nghịch biến trên
để hàm số nghịch biến trên 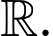
D, d) Không có giá trị nào của 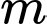 để hàm số đồng biến trên
để hàm số đồng biến trên 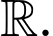
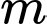 để hàm số đồng biến trên
để hàm số đồng biến trên 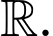
Ta có: 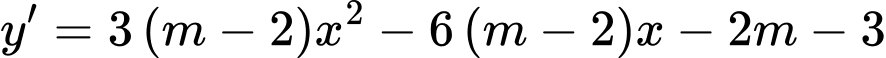
Khi đó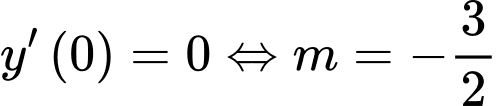
Với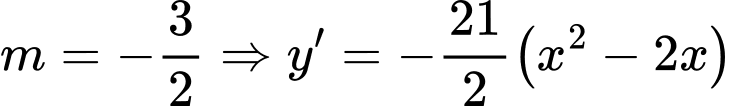 suy ra hàm số đạt cực tiểu tại điểm
suy ra hàm số đạt cực tiểu tại điểm 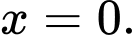
Để hàm số nghịch biến trên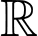

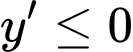 ,
, , ta xét hai trường hợp.
, ta xét hai trường hợp.
Trường hợp 1: Xét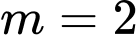 ,
, 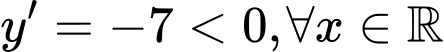 .
.
Trường hợp 2: Xét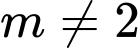 ,
, 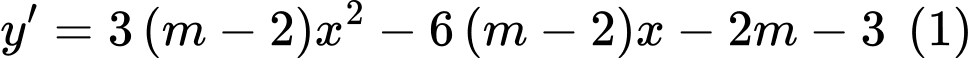 .
.
Để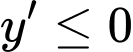 ,
,
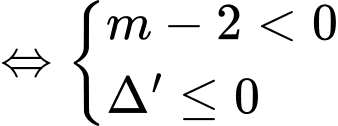
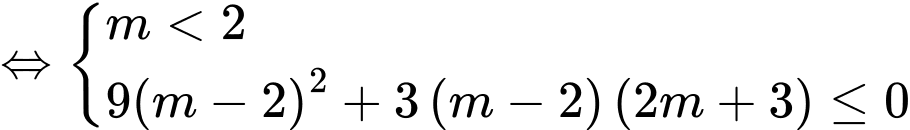
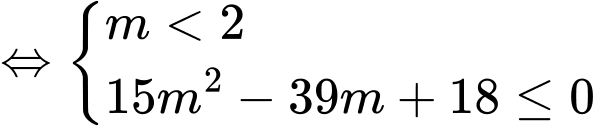
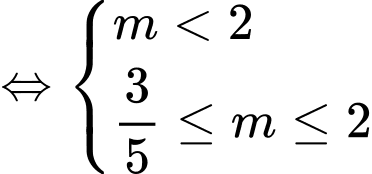
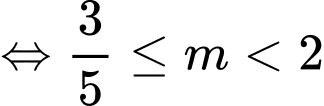
Kết hợp TH1 ta được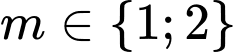 thì hàm số nghịch biến trên
thì hàm số nghịch biến trên 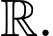
Không có giá trị nào của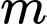 để hàm số đồng biến trên
để hàm số đồng biến trên 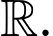
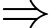 Đáp án D đúng.
Đáp án D đúng.
a) Đúng b) Sai c) Sai d) Đúng
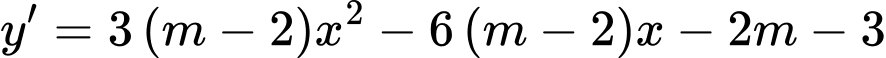
Khi đó
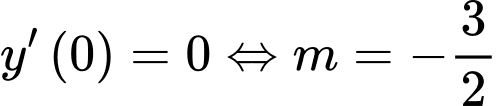
Với
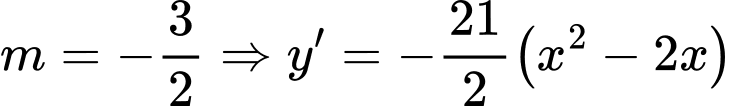 suy ra hàm số đạt cực tiểu tại điểm
suy ra hàm số đạt cực tiểu tại điểm 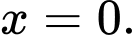
Để hàm số nghịch biến trên
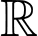

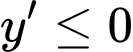 ,
, , ta xét hai trường hợp.
, ta xét hai trường hợp. Trường hợp 1: Xét
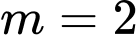 ,
, 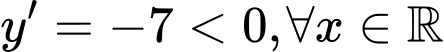 .
. Trường hợp 2: Xét
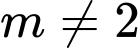 ,
, 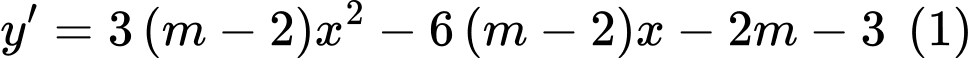 .
. Để
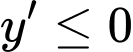 ,
,
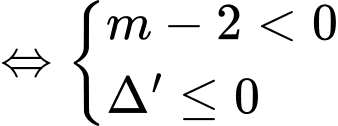
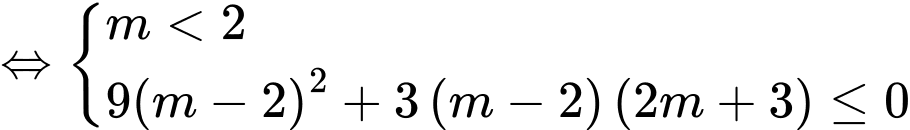
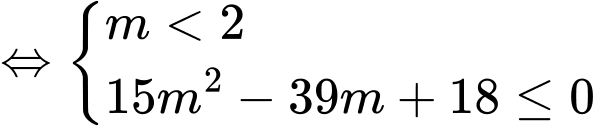
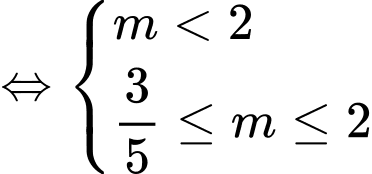
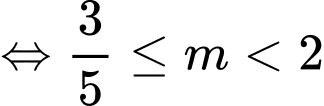
Kết hợp TH1 ta được
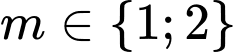 thì hàm số nghịch biến trên
thì hàm số nghịch biến trên 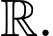
Không có giá trị nào của
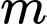 để hàm số đồng biến trên
để hàm số đồng biến trên 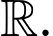
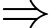 Đáp án D đúng.
Đáp án D đúng. a) Đúng b) Sai c) Sai d) Đúng
Câu 10 [399924]: Có bao nhiêu giá trị nguyên của tham số 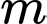 sao cho hàm số
sao cho hàm số 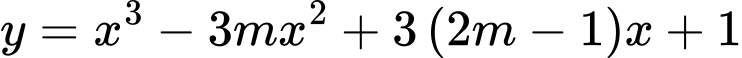 đồng biến trên khoảng
đồng biến trên khoảng 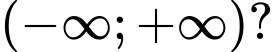
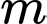 sao cho hàm số
sao cho hàm số 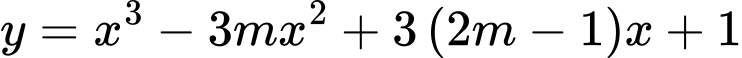 đồng biến trên khoảng
đồng biến trên khoảng 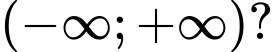
A, 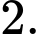
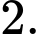
B, 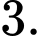
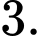
C, 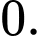
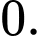
D, 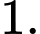
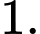
Chọn D
Tập xác định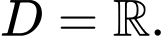
Ta có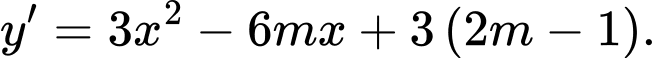
Hàm số đã cho đồng biến trên khoảng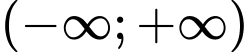
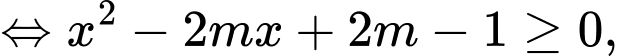

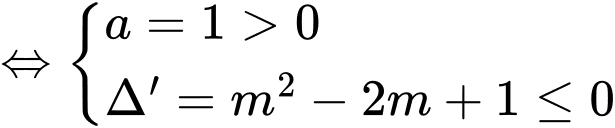
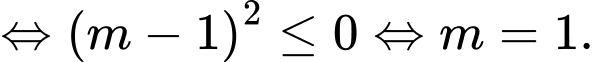 Đáp án: D
Đáp án: D
Tập xác định
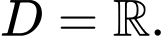
Ta có
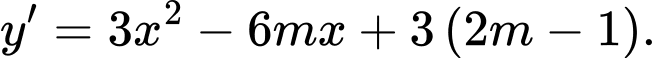
Hàm số đã cho đồng biến trên khoảng
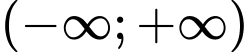
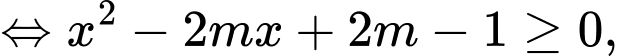

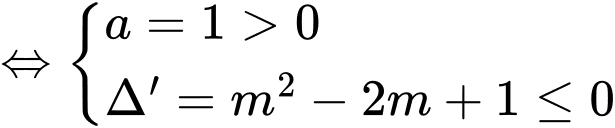
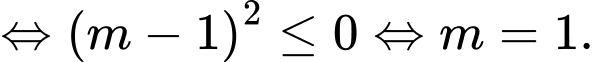 Đáp án: D
Đáp án: D
Câu 11 [298791]: [MĐ2] Đồ thị hàm số 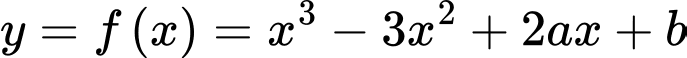 có điểm cực tiểu là
có điểm cực tiểu là 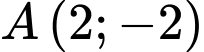 . Tính
. Tính  .
.
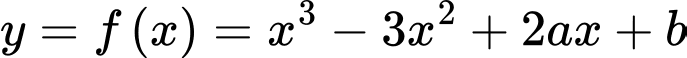 có điểm cực tiểu là
có điểm cực tiểu là 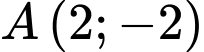 . Tính
. Tính  .
. A, 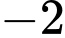 .
.
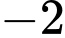 .
.B, 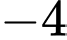 .
.
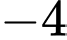 .
.C, 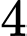 .
.
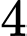 .
.D, 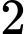 .
.
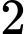 .
.
Ta có 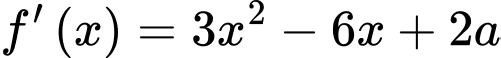 ,
, 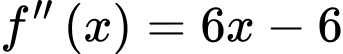
Đồ thị hàm số có điểm cực tiểu là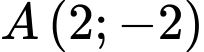
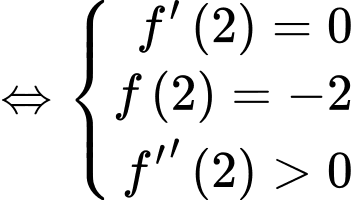
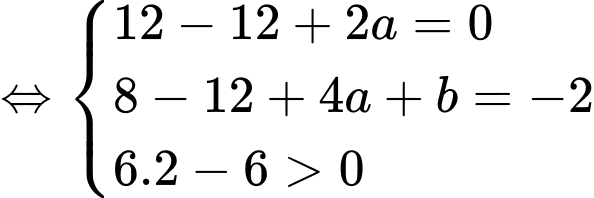
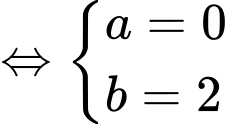
Vậy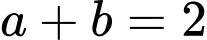 . Đáp án: D
. Đáp án: D
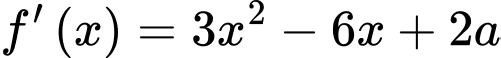 ,
, 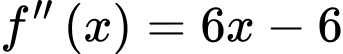
Đồ thị hàm số có điểm cực tiểu là
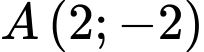
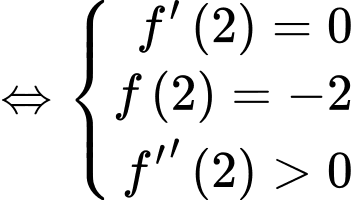
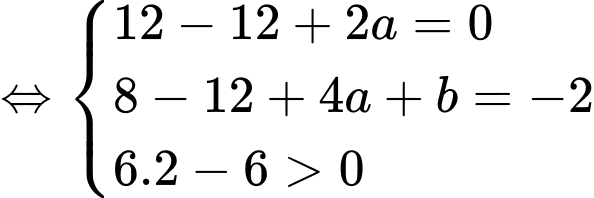
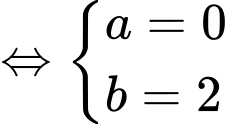
Vậy
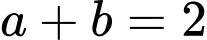 . Đáp án: D
. Đáp án: D
Câu 12 [377892]: Cho hàm số 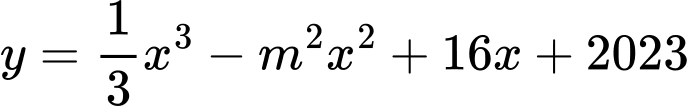 (với
(với 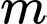 là tham số). Số giá trị nguyên của tham số
là tham số). Số giá trị nguyên của tham số 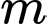 để hàm số đã cho đồng biến trên
để hàm số đã cho đồng biến trên 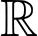 là
là
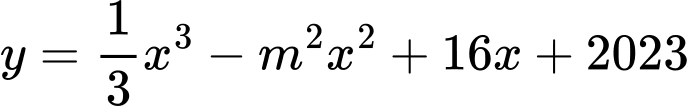 (với
(với 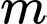 là tham số). Số giá trị nguyên của tham số
là tham số). Số giá trị nguyên của tham số 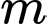 để hàm số đã cho đồng biến trên
để hàm số đã cho đồng biến trên 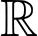 là
là A, 5.
B, 4.
C, 9.
D, 8.
Phương pháp:
Hàm số đồng biến trên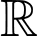 khi
khi 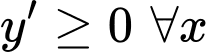
Cách giải:
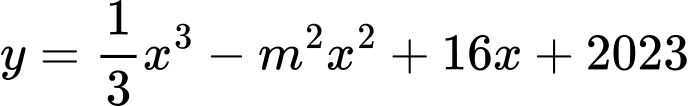
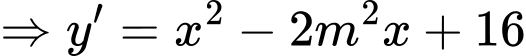

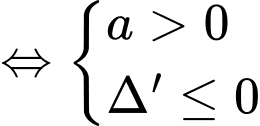
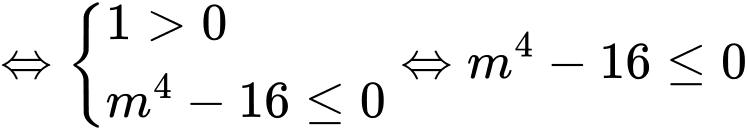
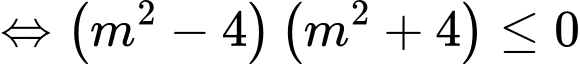
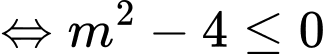
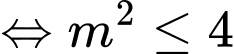

Mà m nguyên nên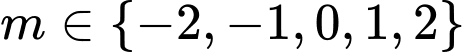
Chọn A Đáp án: A
Hàm số đồng biến trên
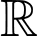 khi
khi 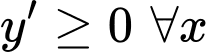
Cách giải:
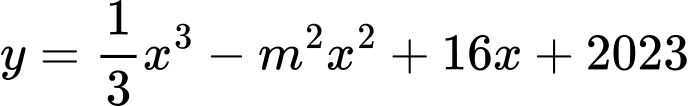
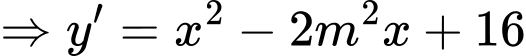

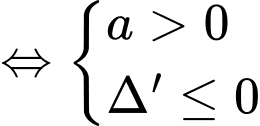
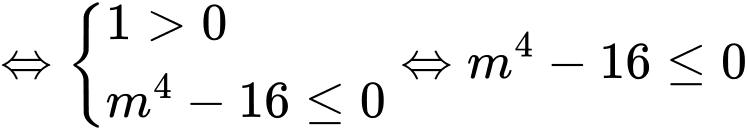
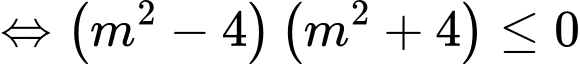
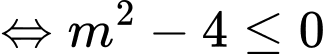
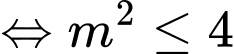

Mà m nguyên nên
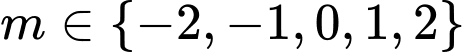
Chọn A Đáp án: A
Câu 13 [316196]: Cho hàm số 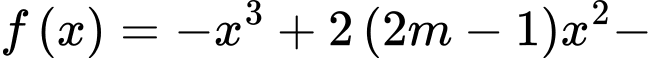
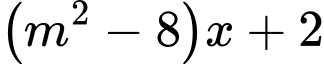 . Tìm giá trị thực của tham số
. Tìm giá trị thực của tham số 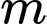 để hàm số đạt giá trị cực tiểu tại điểm
để hàm số đạt giá trị cực tiểu tại điểm 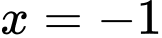 .
.
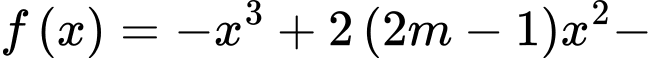
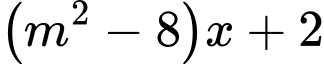 . Tìm giá trị thực của tham số
. Tìm giá trị thực của tham số 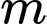 để hàm số đạt giá trị cực tiểu tại điểm
để hàm số đạt giá trị cực tiểu tại điểm 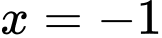 .
. A, 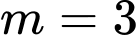 .
.
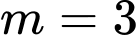 .
.B, 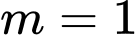 .
.
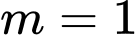 .
.C, 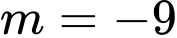 .
.
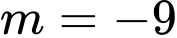 .
.D, 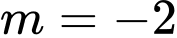 .
.
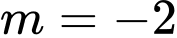 .
.
Chọn B
Tập xác định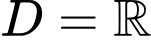 .
.
Có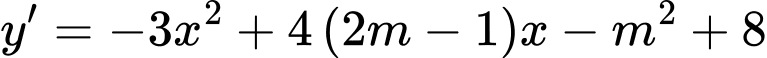 ;
; 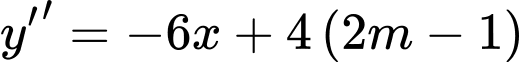 .
.
Hàm số đạt cực đại tại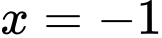
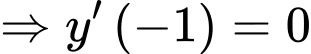 .
.
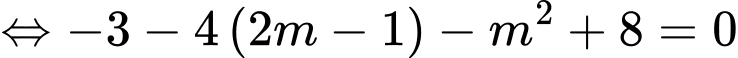
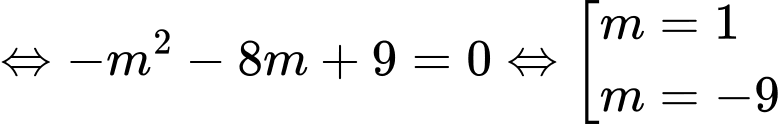
Khi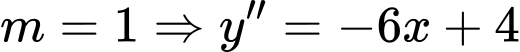
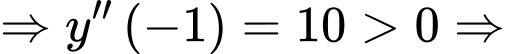 tại
tại 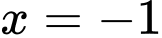 hàm số đạt cực tiểu.
hàm số đạt cực tiểu.
Khi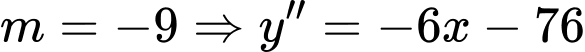
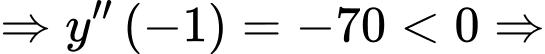 tại
tại 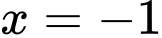 hàm số đạt cực đại.
hàm số đạt cực đại.
Vậy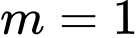 . Đáp án: B
. Đáp án: B
Tập xác định
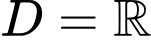 .
.Có
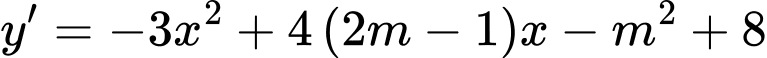 ;
; 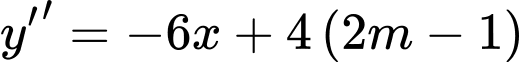 .
.Hàm số đạt cực đại tại
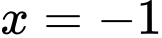
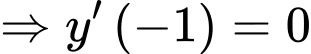 .
.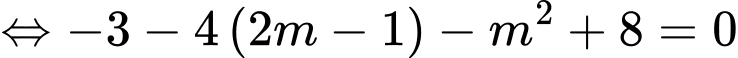
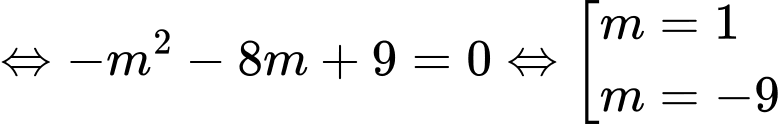
Khi
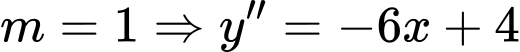
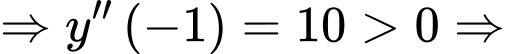 tại
tại 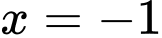 hàm số đạt cực tiểu.
hàm số đạt cực tiểu.Khi
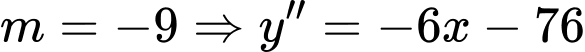
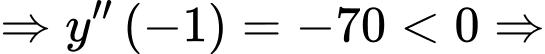 tại
tại 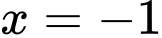 hàm số đạt cực đại.
hàm số đạt cực đại.Vậy
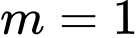 . Đáp án: B
. Đáp án: B
Câu 14 [503740]: Có bao nhiêu giá trị nguyên của 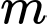 để hàm số sau đồng biến trên tập số thực
để hàm số sau đồng biến trên tập số thực 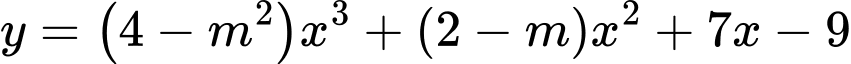 ?
?
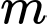 để hàm số sau đồng biến trên tập số thực
để hàm số sau đồng biến trên tập số thực 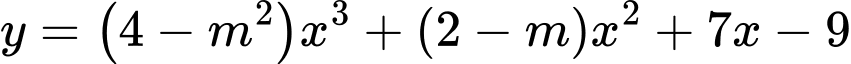 ?
? A, 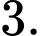
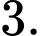
B, 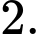
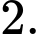
C, 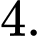
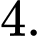
D, 
Chọn C
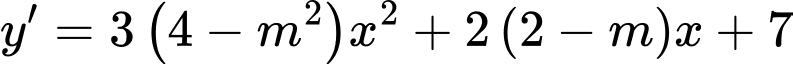 .
.
+ Nếu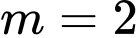 , ta có:
, ta có: 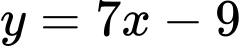 là hàm số đồng biến trên nên
là hàm số đồng biến trên nên 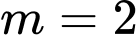 thỏa mãn yêu cầu bài toán
thỏa mãn yêu cầu bài toán  .
.
+ Nếu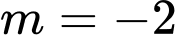 , ta có:
, ta có: 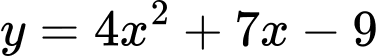 , hàm số đồng biến trên khoảng
, hàm số đồng biến trên khoảng 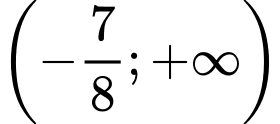 nên
nên 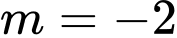 không thỏa mãn yêu cầu bài toán.
không thỏa mãn yêu cầu bài toán.
+ Nếu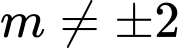 thì hàm số
thì hàm số 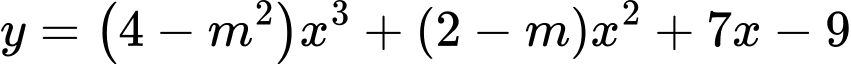 đồng biến trên
đồng biến trên
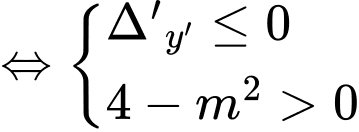
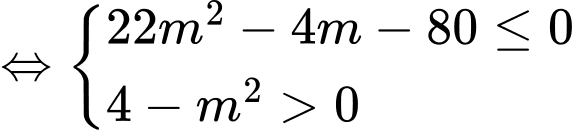
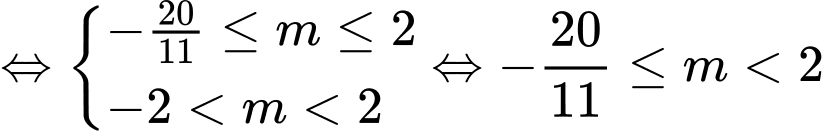 .
.
Mà nên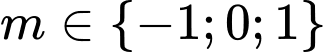
 .
.
Từ ,
,  suy ra có 4 giá trị nguyên của
suy ra có 4 giá trị nguyên của 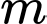 thỏa mãn yêu cầu đề bài. Đáp án: C
thỏa mãn yêu cầu đề bài. Đáp án: C
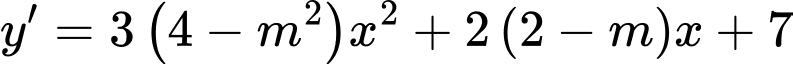 .
. + Nếu
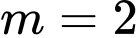 , ta có:
, ta có: 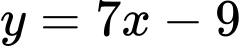 là hàm số đồng biến trên nên
là hàm số đồng biến trên nên 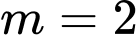 thỏa mãn yêu cầu bài toán
thỏa mãn yêu cầu bài toán  .
.+ Nếu
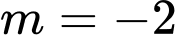 , ta có:
, ta có: 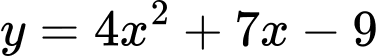 , hàm số đồng biến trên khoảng
, hàm số đồng biến trên khoảng 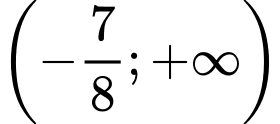 nên
nên 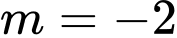 không thỏa mãn yêu cầu bài toán.
không thỏa mãn yêu cầu bài toán.+ Nếu
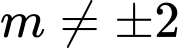 thì hàm số
thì hàm số 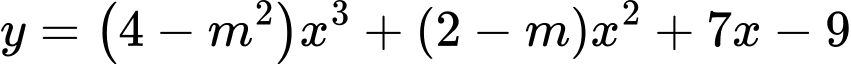 đồng biến trên
đồng biến trên 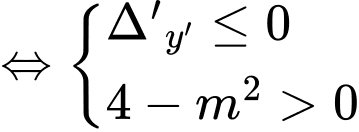
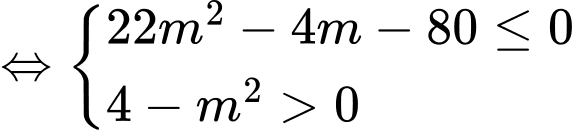
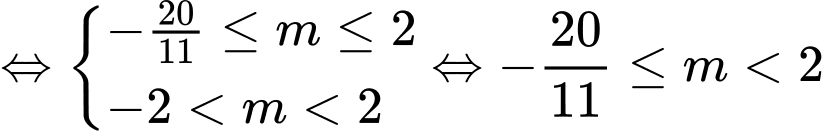 .
.Mà nên
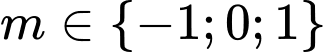
 .
.Từ
 ,
,  suy ra có 4 giá trị nguyên của
suy ra có 4 giá trị nguyên của 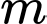 thỏa mãn yêu cầu đề bài. Đáp án: C
thỏa mãn yêu cầu đề bài. Đáp án: C
Câu 15 [2761]: Tìm hệ số 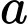 của hàm số
của hàm số 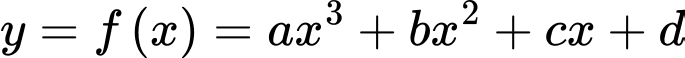 sao cho hàm số
sao cho hàm số 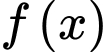 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 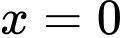 , đạt cực đại tại điểm
, đạt cực đại tại điểm 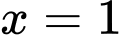 và
và 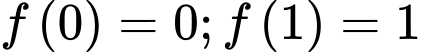 .
.
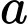 của hàm số
của hàm số 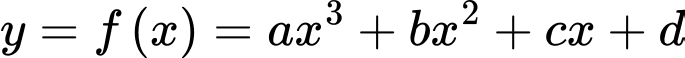 sao cho hàm số
sao cho hàm số 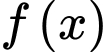 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 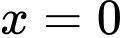 , đạt cực đại tại điểm
, đạt cực đại tại điểm 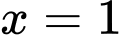 và
và 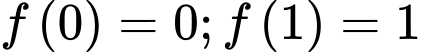 .
. A, 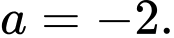
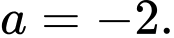
B, 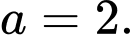
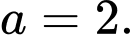
C, 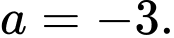
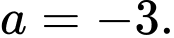
D, 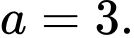
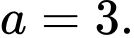
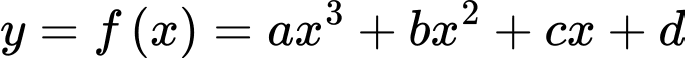
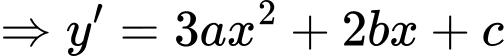
Ta có
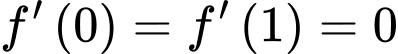 và
và 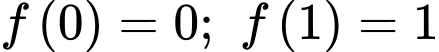 nên ta có hệ sau
nên ta có hệ sau 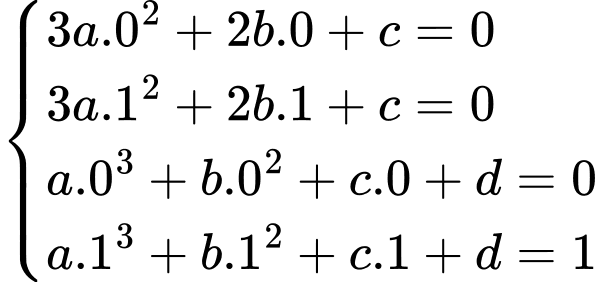
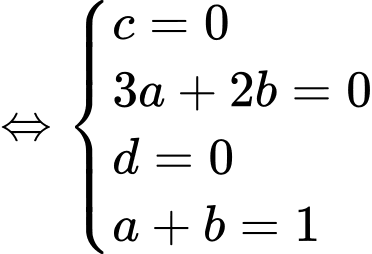
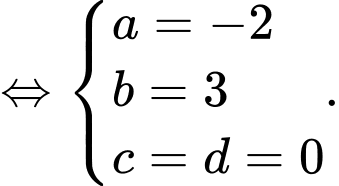
Chọn đáp án A. Đáp án: A
Câu 16 [15762]: Biết rằng hàm số 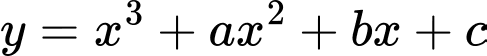 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 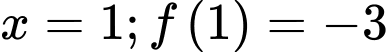 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính
và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính  .
.
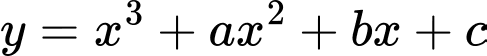 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 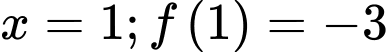 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính
và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính  .
. A, 24.
B, 4.
C, 2.
D, 16.
HD: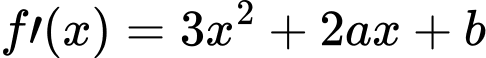
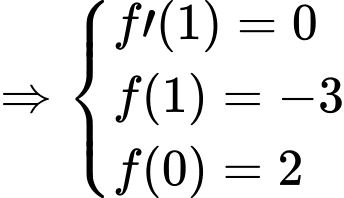
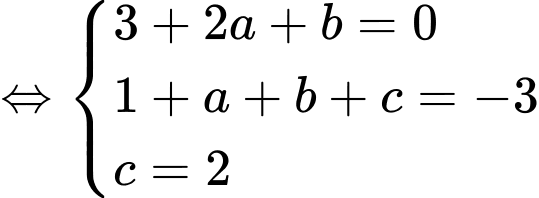
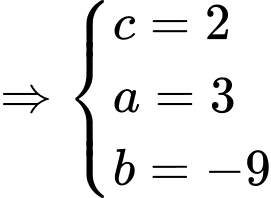
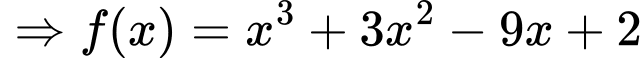
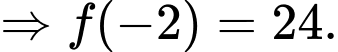 Đáp án: A
Đáp án: A
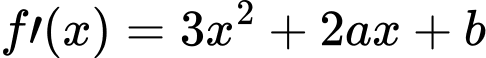
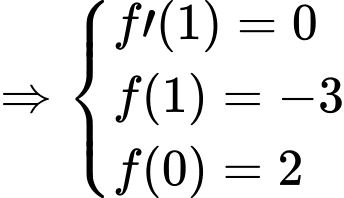
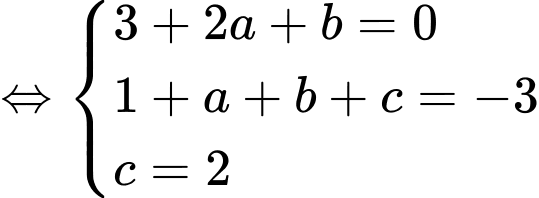
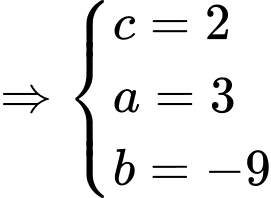
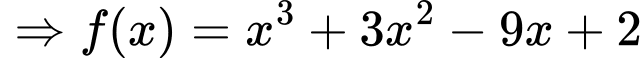
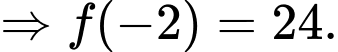 Đáp án: A
Đáp án: A
Câu 17 [399919]: Có bao nhiêu giá trị thực của tham số 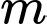 để điểm cực trị của đồ thị hàm số
để điểm cực trị của đồ thị hàm số 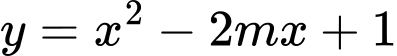 cũng là điểm cực trị của đồ thị hàm số
cũng là điểm cực trị của đồ thị hàm số 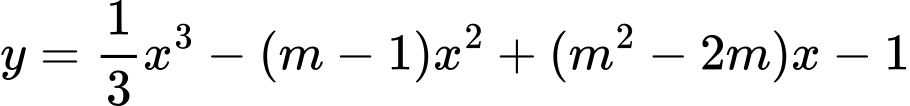 ?
?
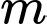 để điểm cực trị của đồ thị hàm số
để điểm cực trị của đồ thị hàm số 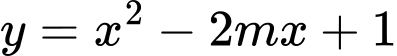 cũng là điểm cực trị của đồ thị hàm số
cũng là điểm cực trị của đồ thị hàm số 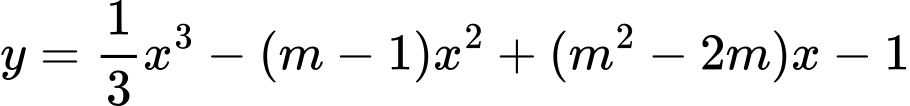 ?
? A, 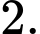
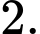
B, 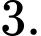
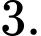
C, 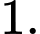
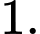
D, 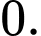
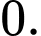
Nhận thấy đồ thị hàm số 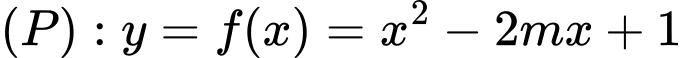 có tọa độ điểm cực tiểu là
có tọa độ điểm cực tiểu là 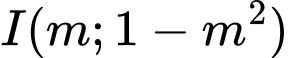
Xét hàm số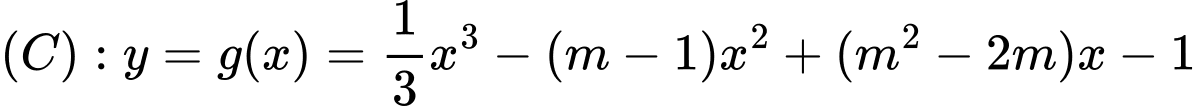
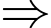
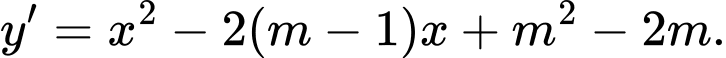
Cho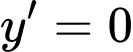
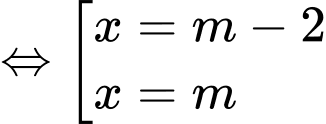
Ycbt
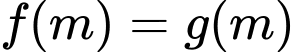

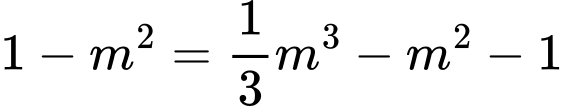

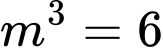

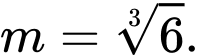 Đáp án: C
Đáp án: C
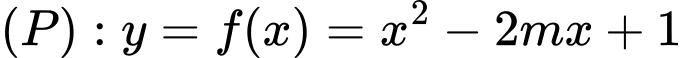 có tọa độ điểm cực tiểu là
có tọa độ điểm cực tiểu là 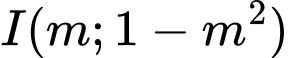
Xét hàm số
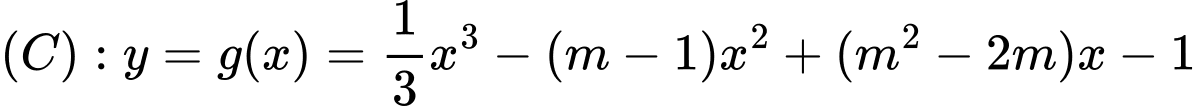
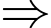
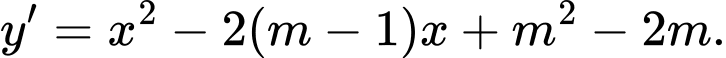
Cho
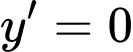
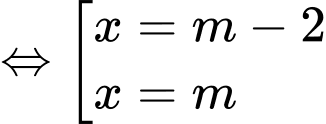
Ycbt

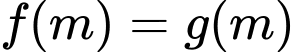

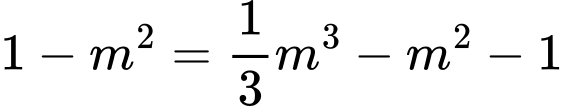

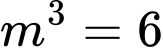

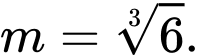 Đáp án: C
Đáp án: C
Câu 18 [399675]: Hàm số  đồng biến trên khoảng
đồng biến trên khoảng 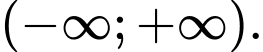 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 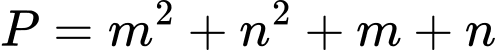 bằng
bằng
 đồng biến trên khoảng
đồng biến trên khoảng 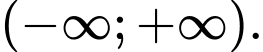 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 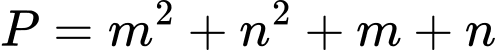 bằng
bằng
Đáp số: 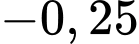
Ta có điều kiện :
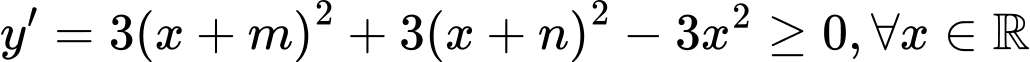
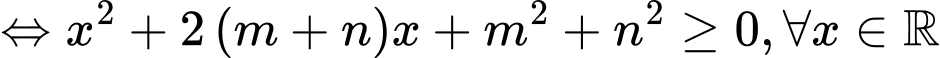
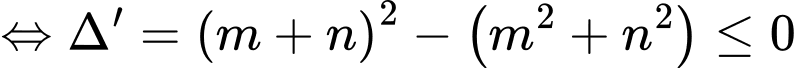
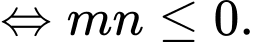
Khi đó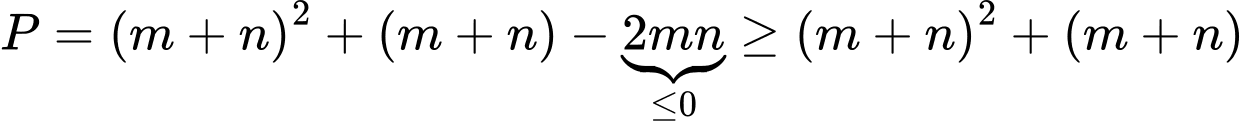
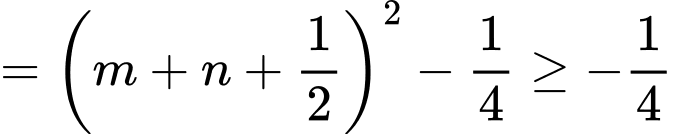 .
.
Dấu bằng đạt tại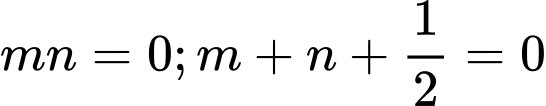
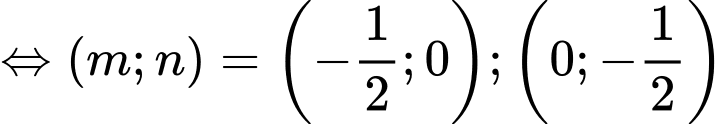 .
.
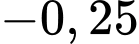
Ta có điều kiện :
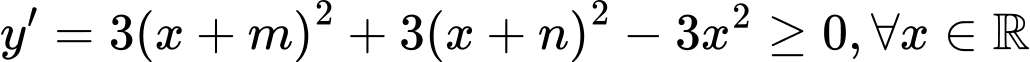
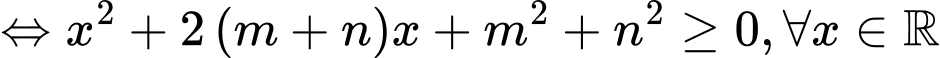
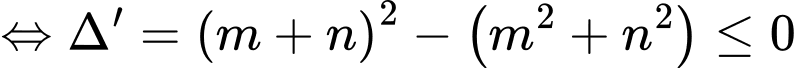
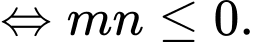
Khi đó
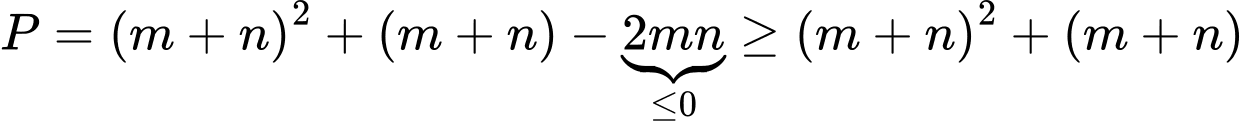
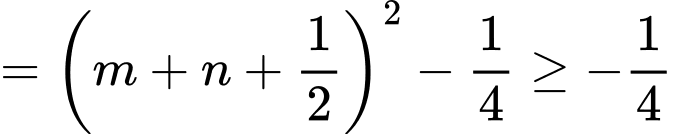 .
.Dấu bằng đạt tại
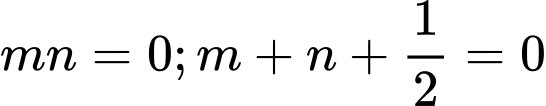
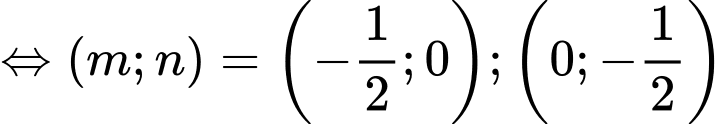 .
.
Câu 19 [399931]: Cho hàm số 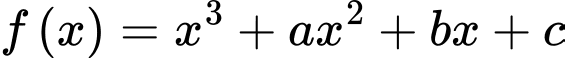 có
có 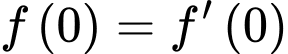 và
và 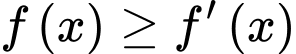 với mọi
với mọi 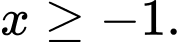 Có bao nhiêu giá trị nguyên của
Có bao nhiêu giá trị nguyên của 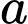 để hàm số đã cho đồng biển trên khoảng
để hàm số đã cho đồng biển trên khoảng 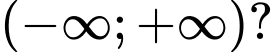
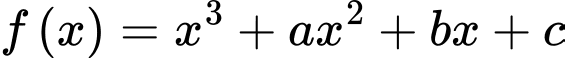 có
có 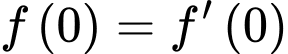 và
và 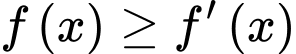 với mọi
với mọi 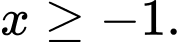 Có bao nhiêu giá trị nguyên của
Có bao nhiêu giá trị nguyên của 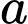 để hàm số đã cho đồng biển trên khoảng
để hàm số đã cho đồng biển trên khoảng 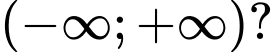
A, 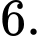
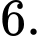
B, 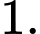
C, 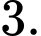
D, Vô số.
Chọn C
Ta có: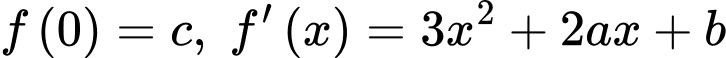
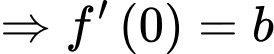
Vì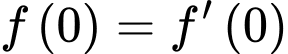
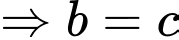
Khi đó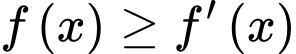
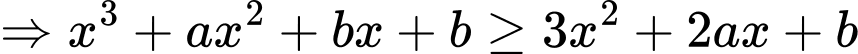
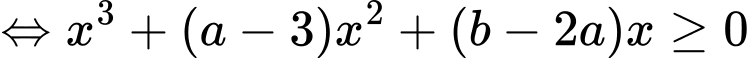
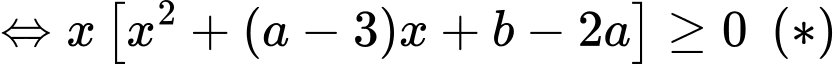
 đúng với mọi
đúng với mọi  suy ra phương trình
suy ra phương trình 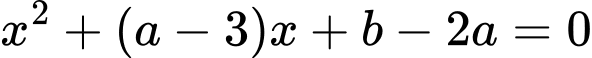 có một nghiệm
có một nghiệm 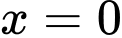
Khi đó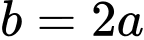 và
và 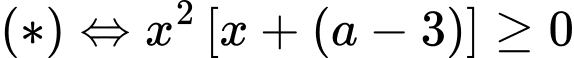
Ta có: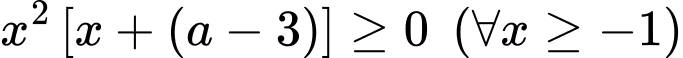
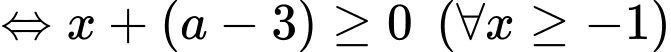
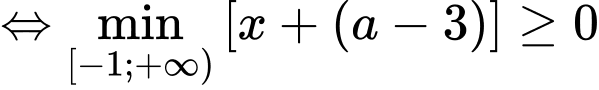
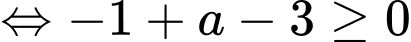
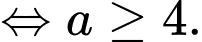
Mặt khác hàm số đã cho đồng biến trên khoảng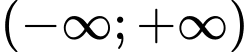
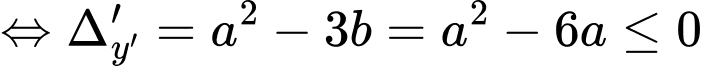
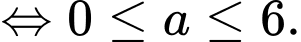
Vậy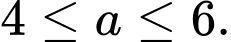 Đáp án: C
Đáp án: C
Ta có:
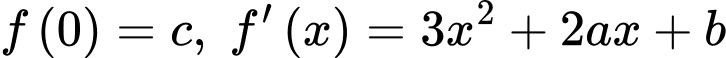
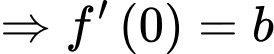
Vì
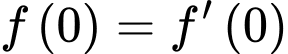
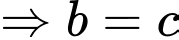
Khi đó
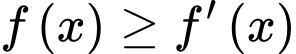
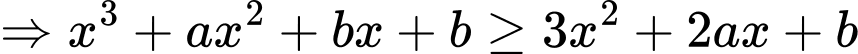
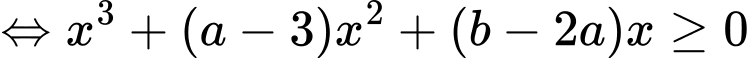
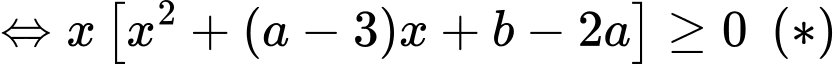
 đúng với mọi
đúng với mọi  suy ra phương trình
suy ra phương trình 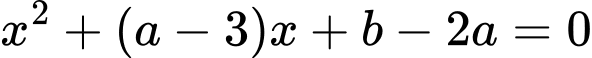 có một nghiệm
có một nghiệm 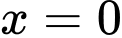
Khi đó
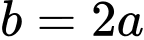 và
và 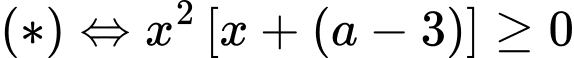
Ta có:
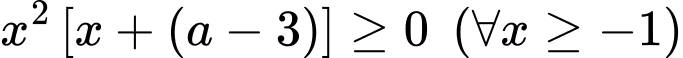
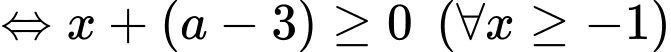
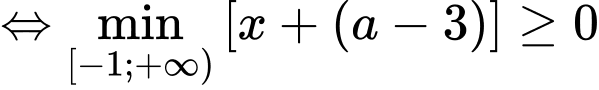
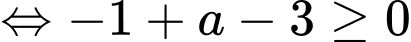
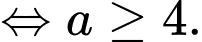
Mặt khác hàm số đã cho đồng biến trên khoảng
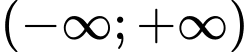
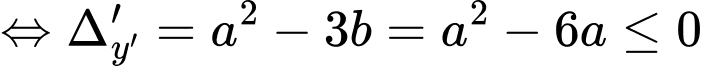
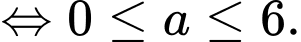
Vậy
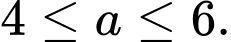 Đáp án: C
Đáp án: C