Đáp án Bài tập tự luyện số 2
Câu 1 [2569]: Tìm tất cả các giá trị thực của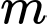 
để hàm số 
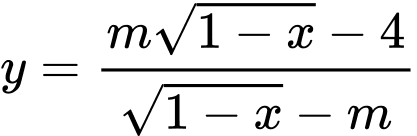đồng biến trên khoảng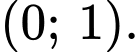 
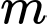để hàm số 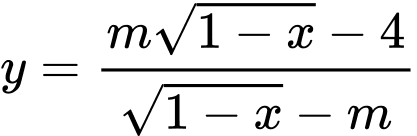đồng biến trên khoảng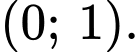 A,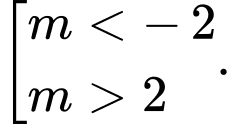 
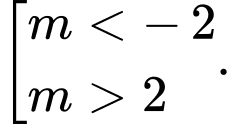
B,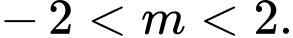 
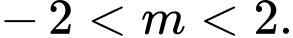
C,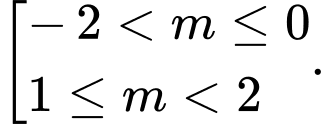 
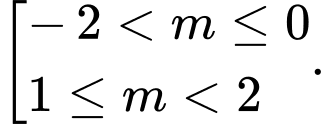
D,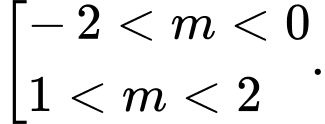 
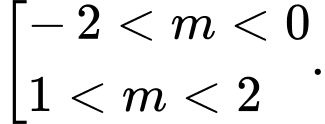
Đặt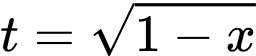 
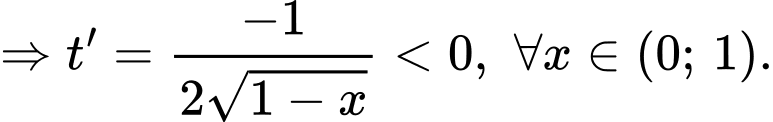
Với
Khi đó bài toán trở thành tìm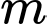
để hàm số 
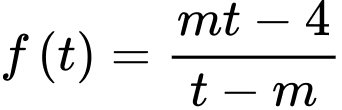nghịch biến trên khoảng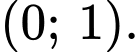 
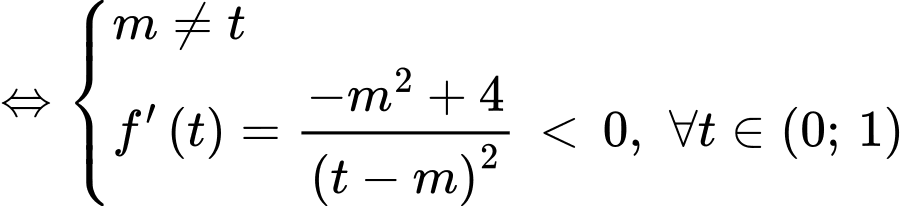
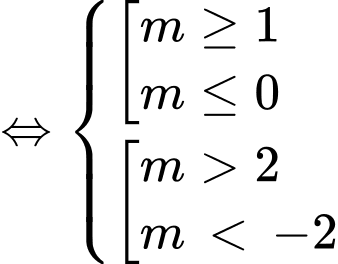
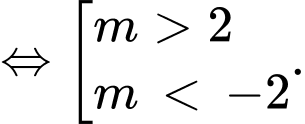
Chọn đáp án A. Đáp án: A
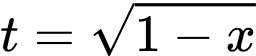
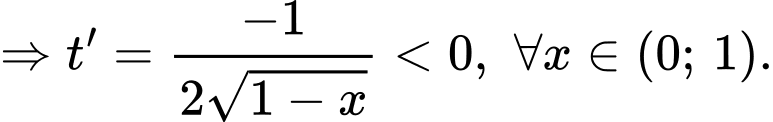
Với
Khi đó bài toán trở thành tìm
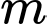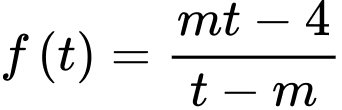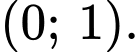
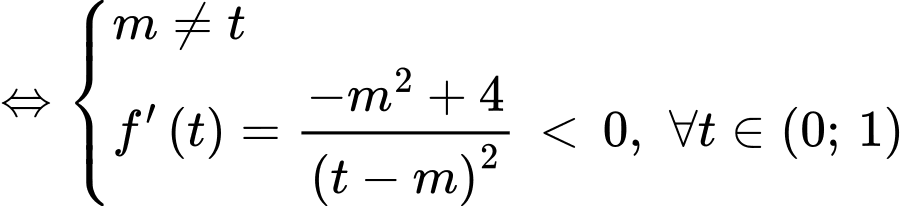
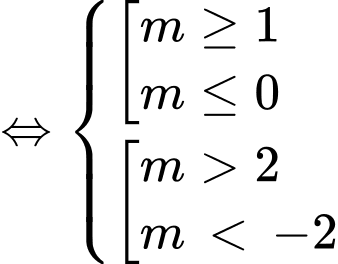
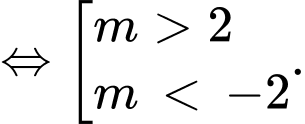
để hàm số nghịch biến trên khoảng Chọn đáp án A. Đáp án: A
Câu 2 [2582]: Tìm tất cả các giá trị thực của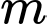 
để hàm số 
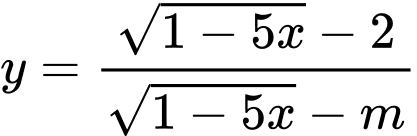nghịch biến trên khoảng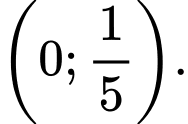 
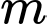để hàm số 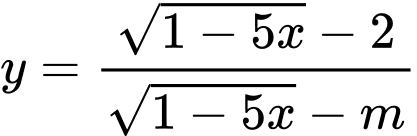nghịch biến trên khoảng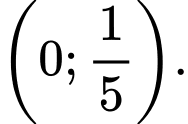 A,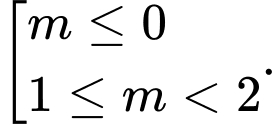 
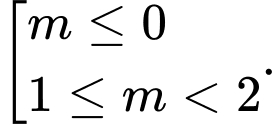
B, 
C,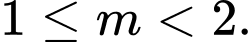 
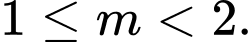
D, 
Đặt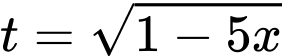 
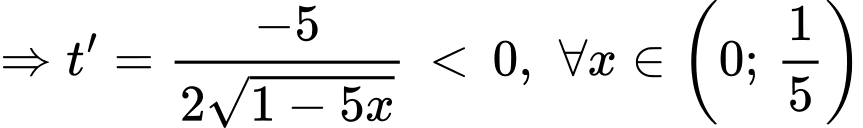
Với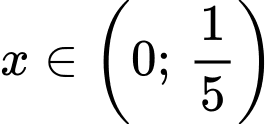
Khi đó bài toán trở thành tìm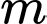
để hàm số 
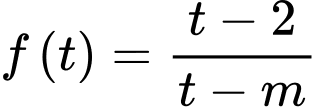đồng biến trên khoảng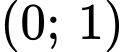 
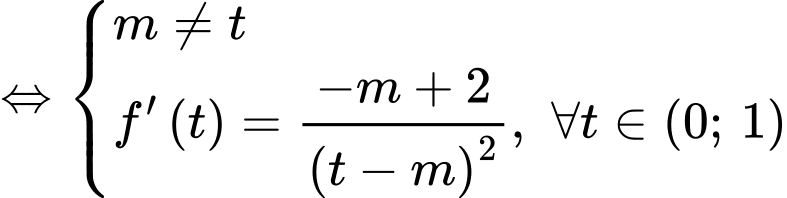
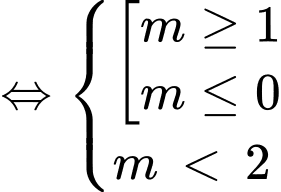
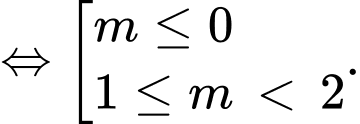
Chọn đáp án A. Đáp án: A
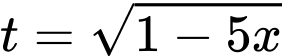
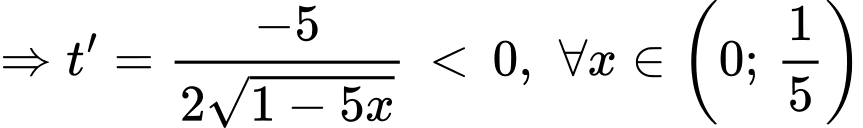
Với
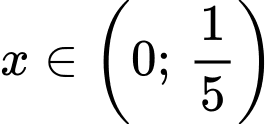
Khi đó bài toán trở thành tìm
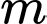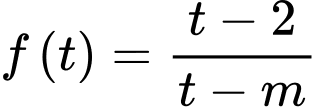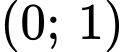
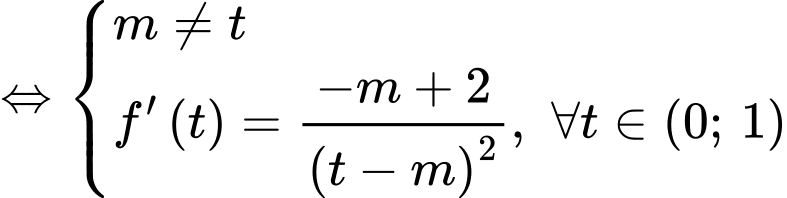
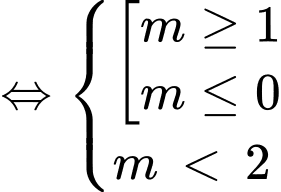
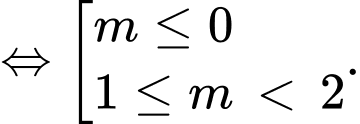
để hàm số đồng biến trên khoảng Chọn đáp án A. Đáp án: A
Câu 3 [2579]: Tìm tất cả các giá trị thực của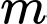 
để hàm số 
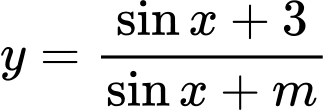nghịch biến trên khoảng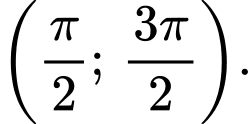 
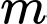để hàm số 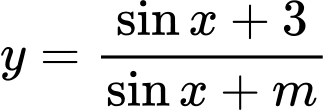nghịch biến trên khoảng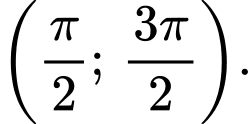 A,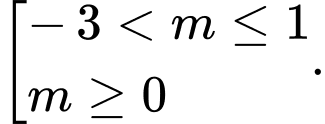 
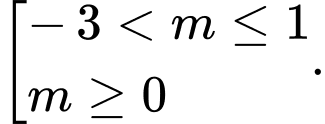
B, 
C, 
D, 
Điều kiện: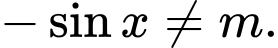 
Ta có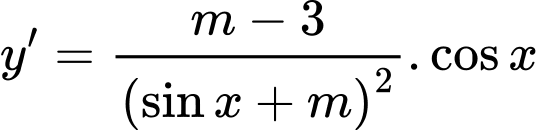
Hàm số nghịch biến trên khoảng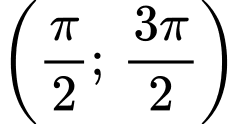
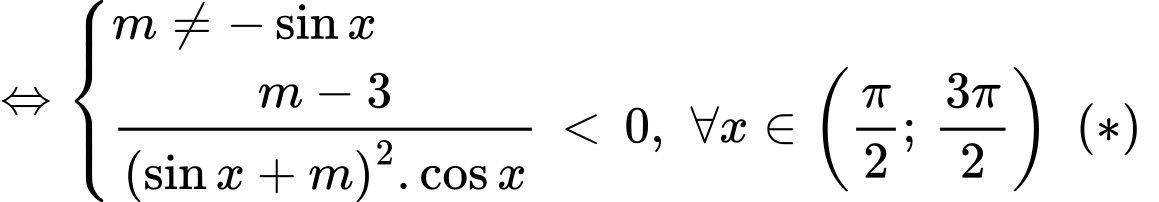
Với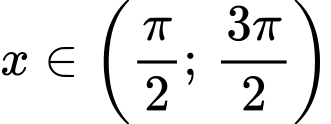
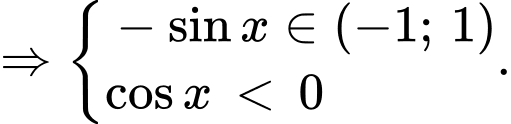
Do đó
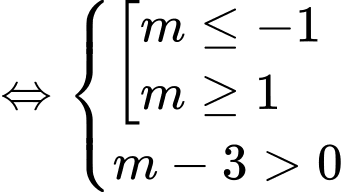
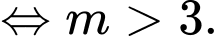
Chọn đáp án B. Đáp án: B
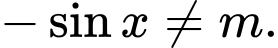
Ta có
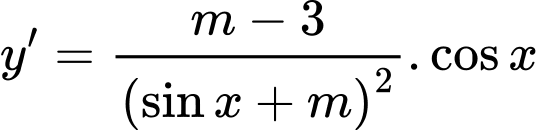
Hàm số nghịch biến trên khoảng
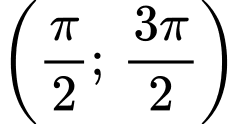
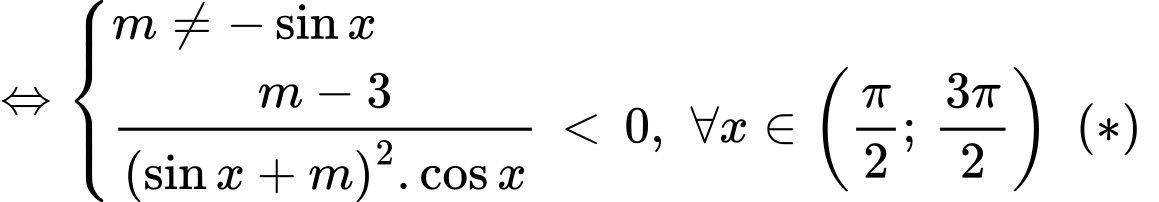
Với
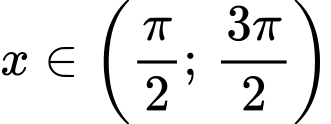
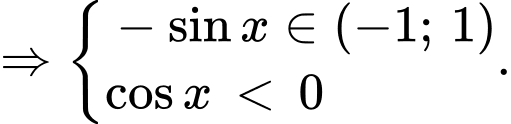
Do đó
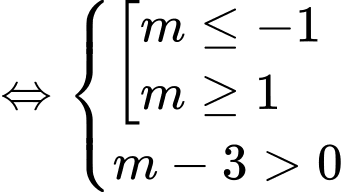
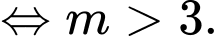
Chọn đáp án B. Đáp án: B
Câu 4 [23101]: Tìm tất cả các giá trị thực của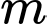 
để hàm số 
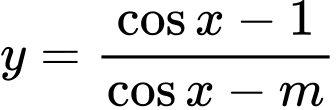đồng biến trên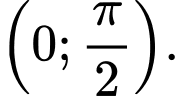 
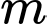để hàm số 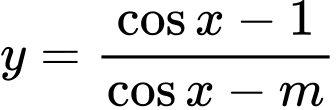đồng biến trên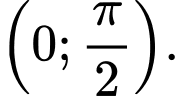 A, 
B, 
C,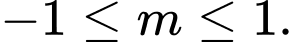 
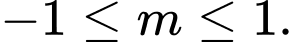
D, 
Ta có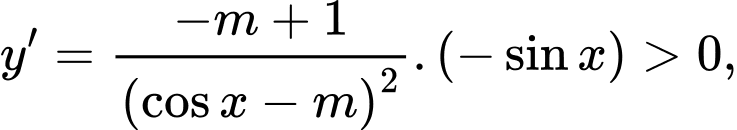 
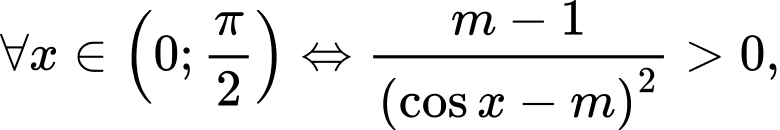
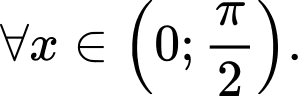
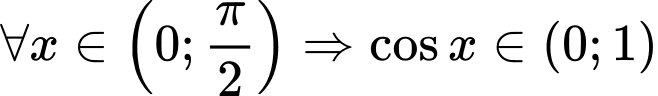
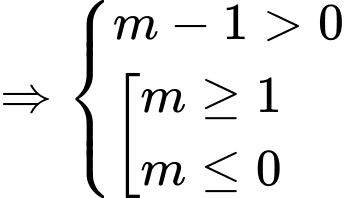
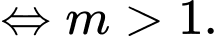Chọn B Đáp án: B
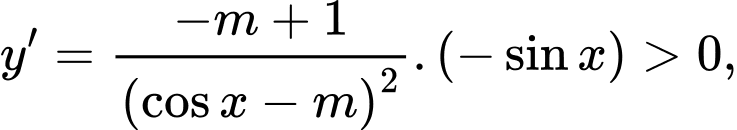
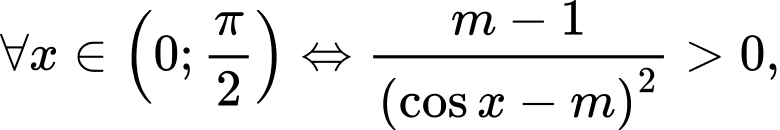
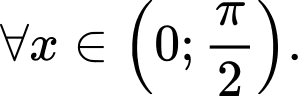
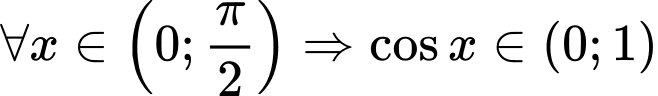
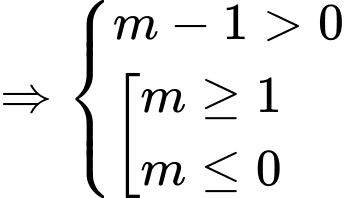
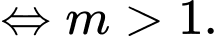Chọn B Đáp án: B
Câu 5 [23100]: Tìm tất cả các giá trị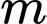 
để hàm số 
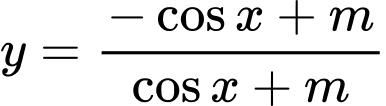đồng biến trên khoảng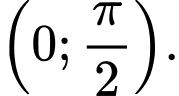 
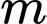để hàm số 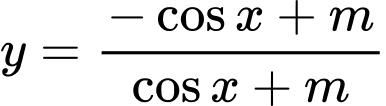đồng biến trên khoảng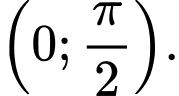 A,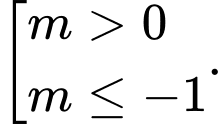 
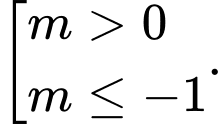
B, 
C, 
D, 
Ta có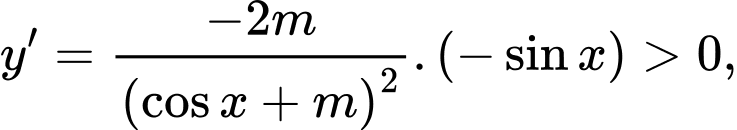 
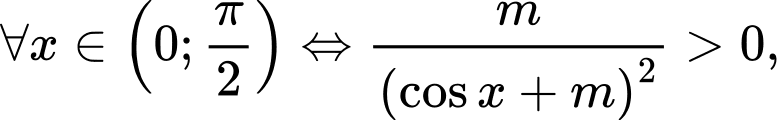
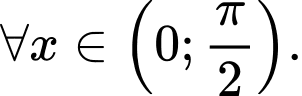
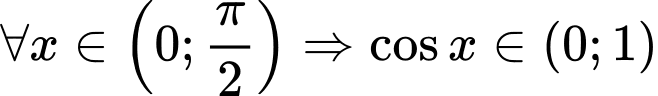
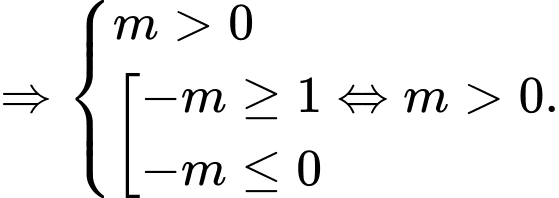Chọn B Đáp án: B
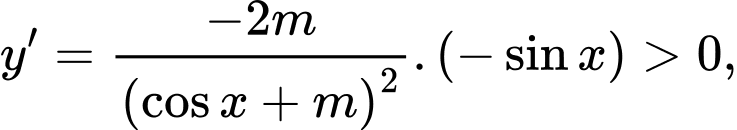
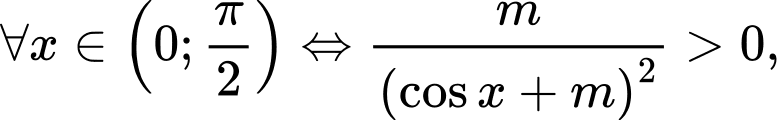
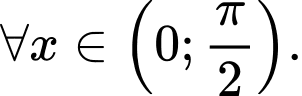
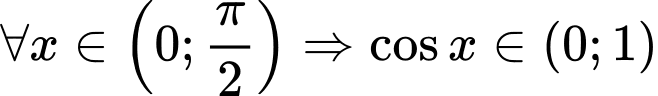
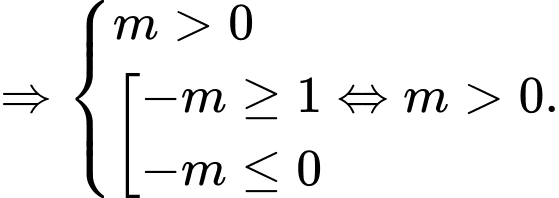Chọn B Đáp án: B
Câu 6 [23072]: Tìm tất cả các giá trị tham số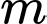 
để hàm số 
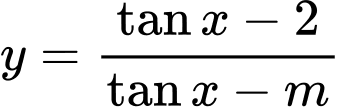đồng biến trên khoảng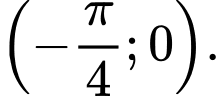 
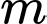để hàm số 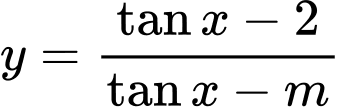đồng biến trên khoảng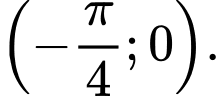 A,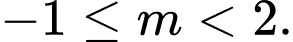 
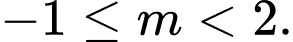
B, 
C, 
D,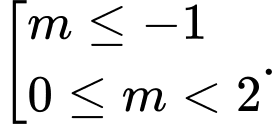 
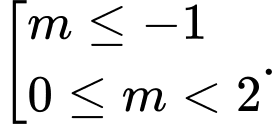
Ta có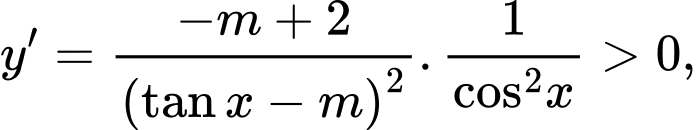 
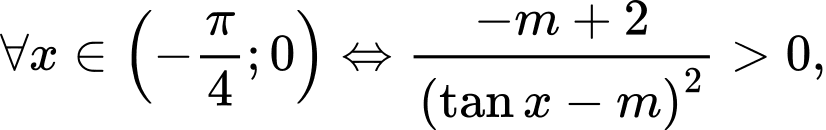
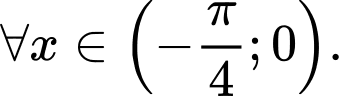
Với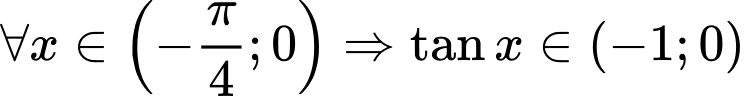
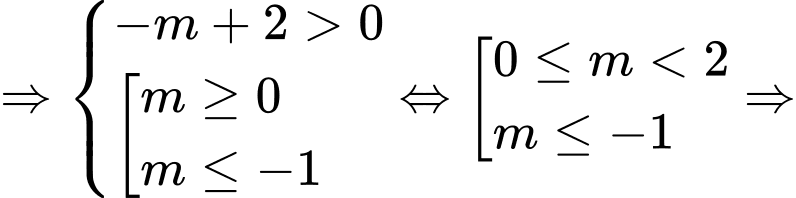Chọn D Đáp án: D
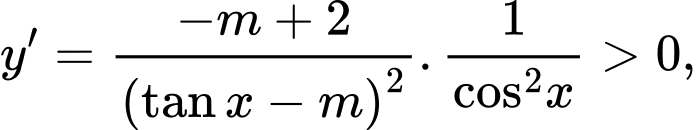
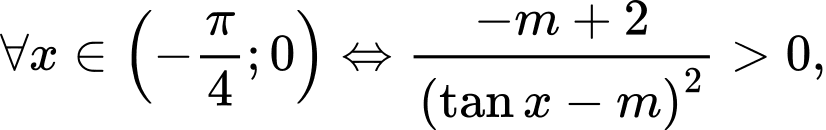
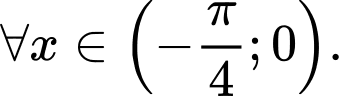
Với
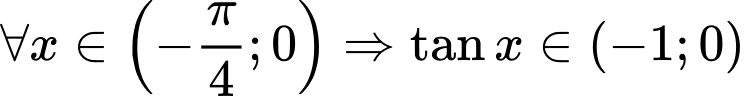
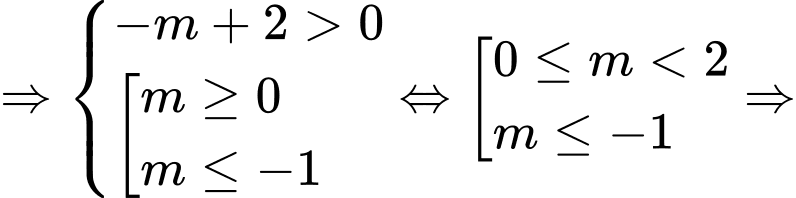Chọn D Đáp án: D
Câu 7 [23078]: Tìm tất cả các giá trị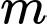 
để hàm số 
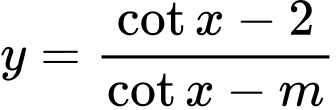nghịch biến trên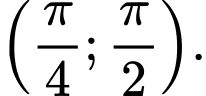 
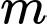để hàm số 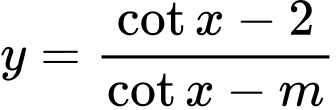nghịch biến trên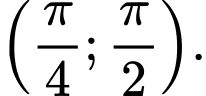 A, 
B,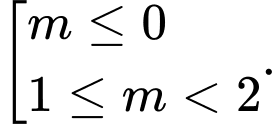 
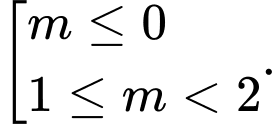
C,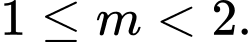 
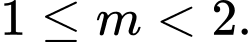
D, 
Xét hàm số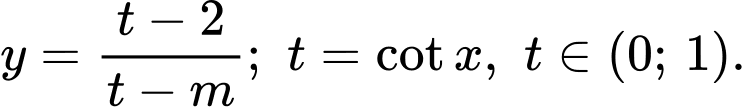 
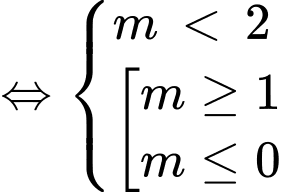
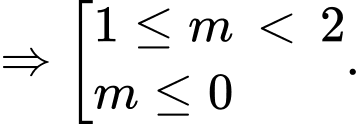
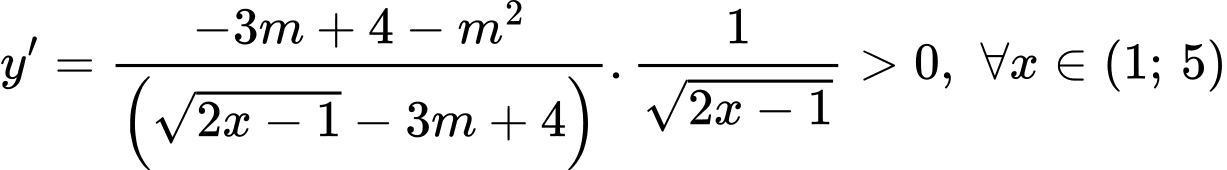
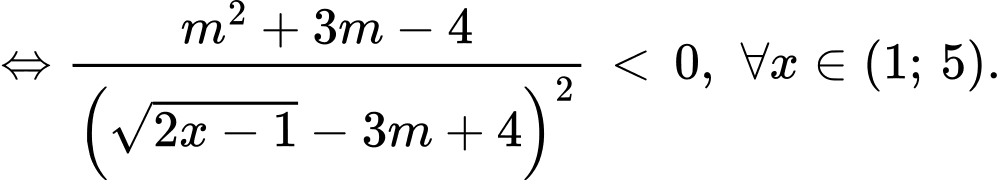
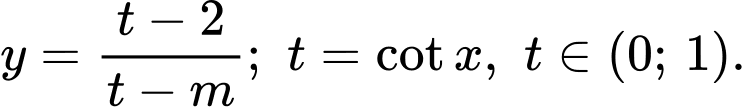
Khi đó hàm số nghịch biến trên miền đã cho khi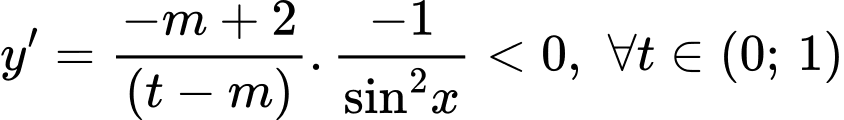 
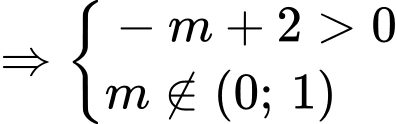
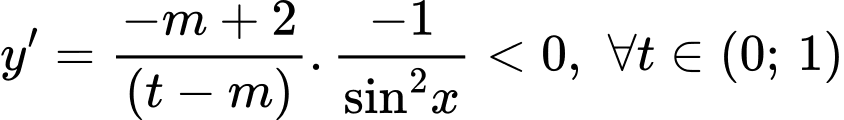
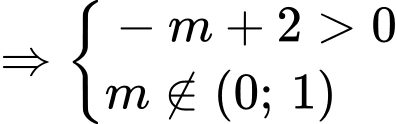
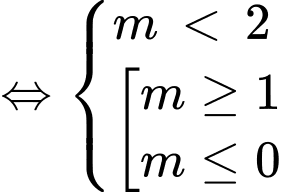
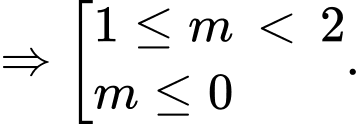
Chọn đáp án B. Đáp án: B
Câu 8 [520255]: Có tất cả bao nhiêu giá trị nguyên của tham số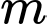 
để hàm số 
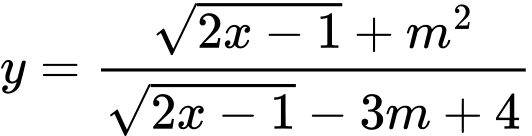đồng biến trên khoảng 
?
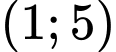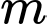để hàm số 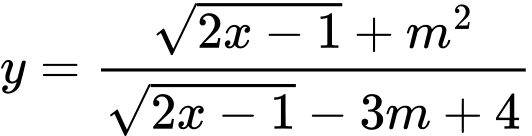đồng biến trên khoảng 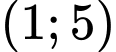? A, 6.
B, 4.
C, 5.
D, 3.
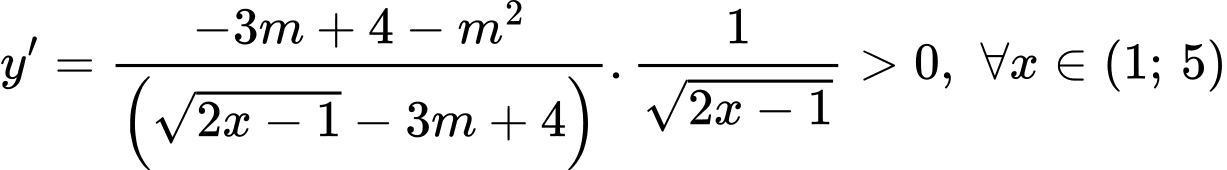
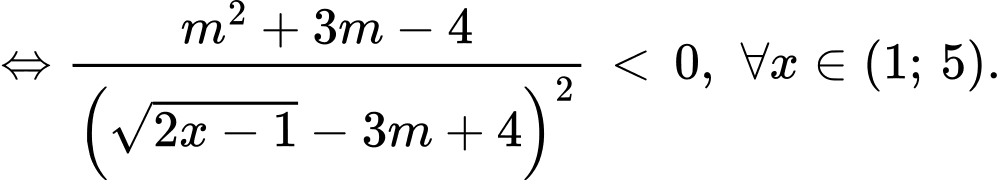
Với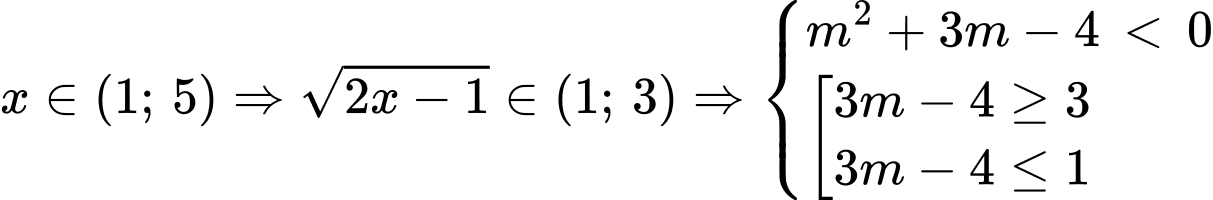 
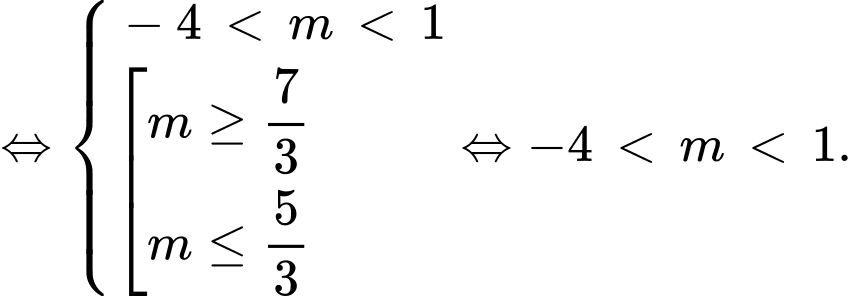
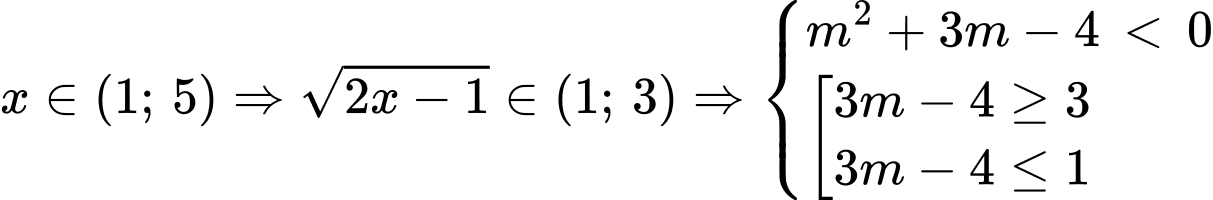
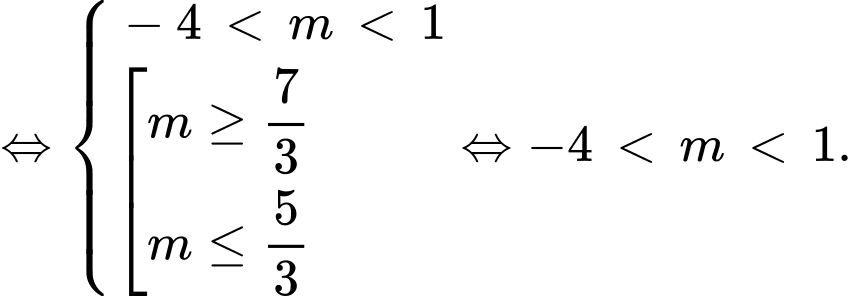
Đáp án: B Chọn đáp án B.
Câu 9 [998547]: Cho hàm số bậc ba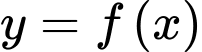 
có đồ thị là đường cong như hình bên dưới. Có tất cả bao nhiêu giá trị nguyên của tham số 
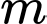để hàm số 
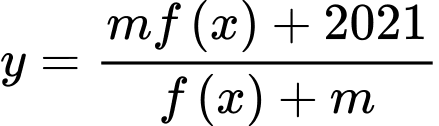nghịch biến trên khoảng 
?
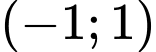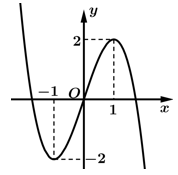
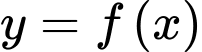có đồ thị là đường cong như hình bên dưới. Có tất cả bao nhiêu giá trị nguyên của tham số 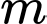để hàm số 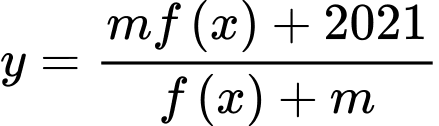nghịch biến trên khoảng 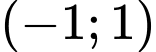? A,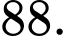 
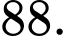
B,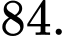 
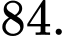
C,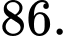 
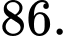
D,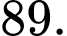 
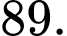
Chọn C.
Đặt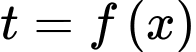
. Nhận thấy hàm số 
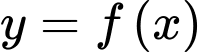đồng biến trên khoảng 
và 
.
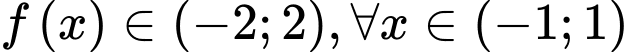Do đó yêu cầu bài toán dẫn đến bài toán tìm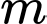
để hàm số 
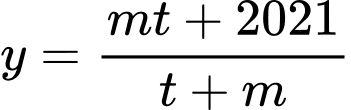nghịch biến trên 
.
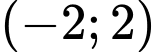ĐK: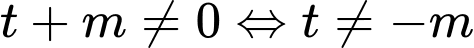
.
Ta có: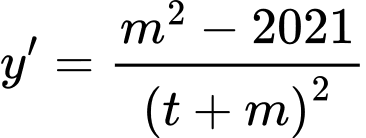
ycbt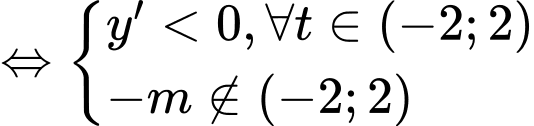
.
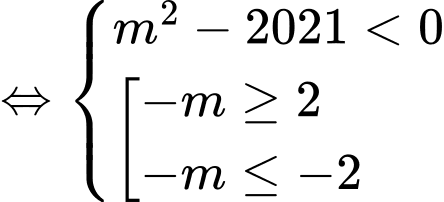
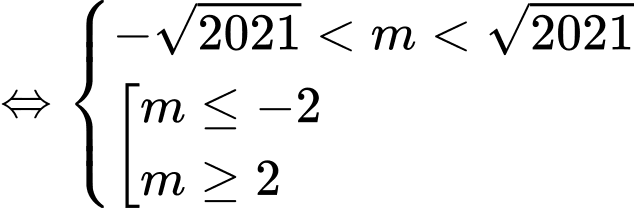
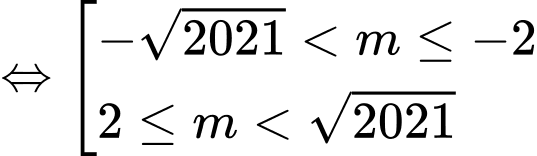Và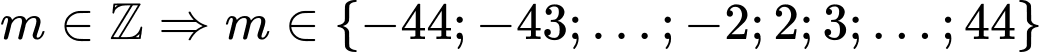
. Vậy có 86 giá trị nguyên của tham số 
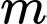thỏa ycbt.
Đáp án: C
Đặt
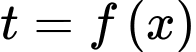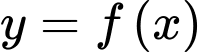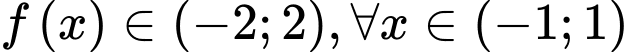. Nhận thấy hàm số đồng biến trên khoảng và .Do đó yêu cầu bài toán dẫn đến bài toán tìm
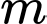để hàm số 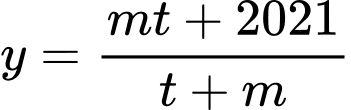nghịch biến trên 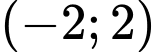.ĐK:
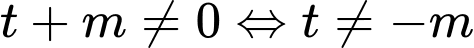.Ta có:
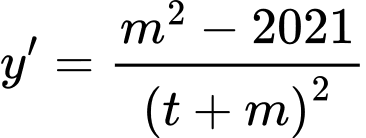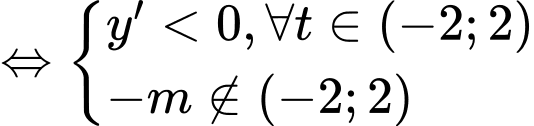
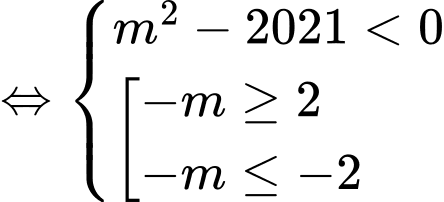
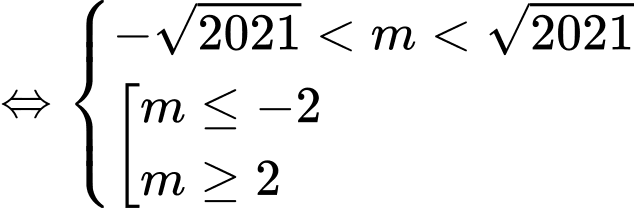
ycbt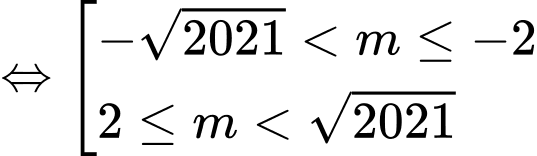.Và
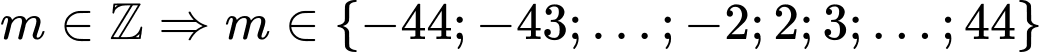. Vậy có 86 giá trị nguyên của tham số 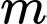thỏa ycbt.
Đáp án: C
Câu 10 [520256]: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn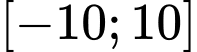 
để hàm 
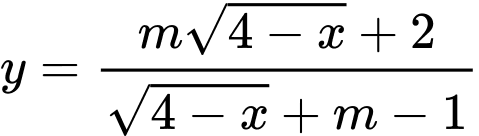đồng biến trên khoảng 
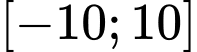để hàm 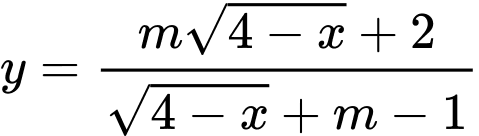đồng biến trên khoảng A, 8.
B, 1.
C, 9.
D, 2.
Đặt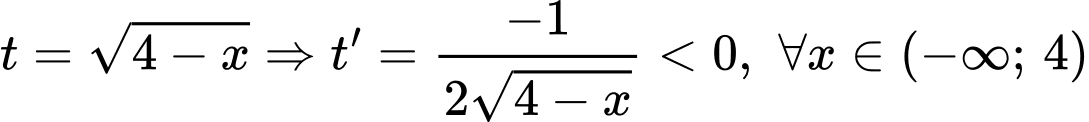 
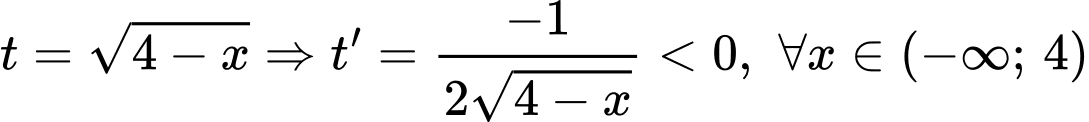
Với 
Đáp án: B Khi đó bài toán trở thành tìm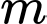 
để hàm số 
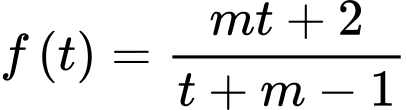nghịch biến trên khoảng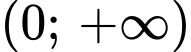 
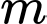để hàm số 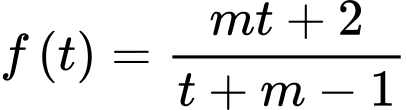nghịch biến trên khoảng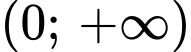 Ta có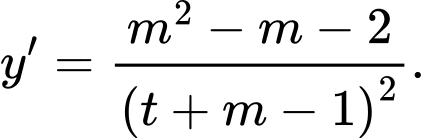 
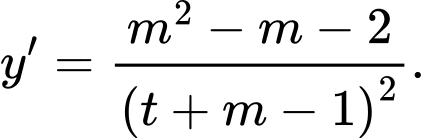
Hàm số nghịch biến trên khoảng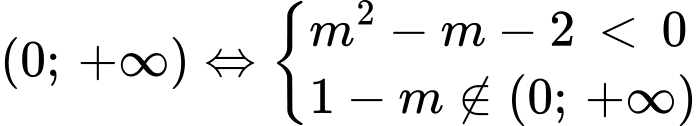 
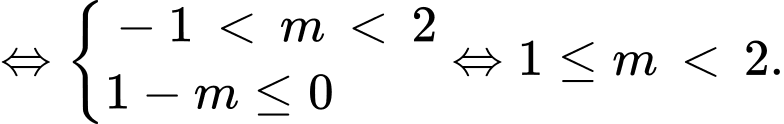
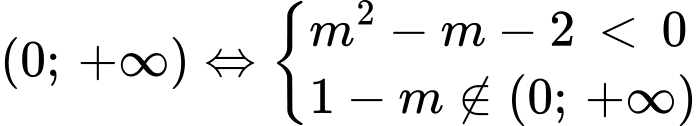
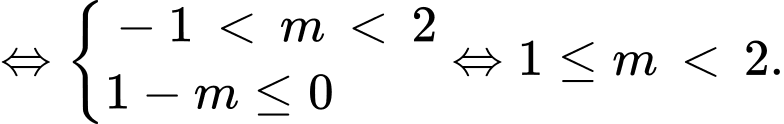
Vì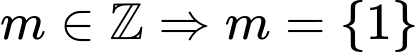 
suy ra có 1 giá trị thỏa mãn ycbt.
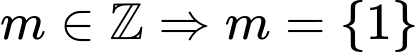suy ra có 1 giá trị thỏa mãn ycbt. Chọn đáp án B.
Câu 11 [23087]: Có bao nhiêu số nguyên dương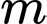 
để hàm số 
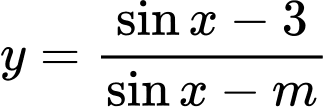đồng biến trên khoảng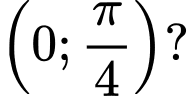 
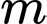để hàm số 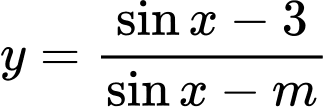đồng biến trên khoảng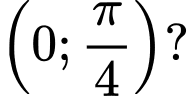 A, 2.
B, 3.
C, Vô số.
D, 1.
Ta có 
thì 
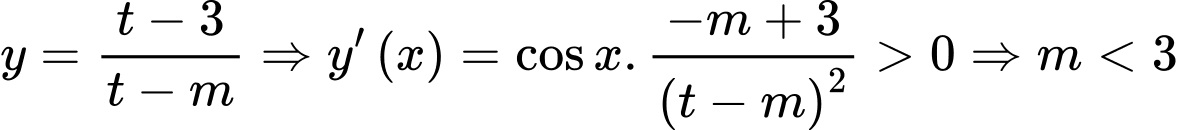(do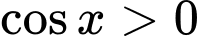 
)
Để hàm số đã cho liên tục thì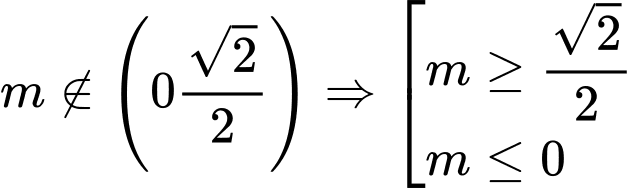
Do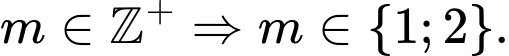
Vậy có 2 giá trị nguyên dương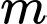
thoả mãn ycbt.
Chọn đáp án A. Đáp án: A
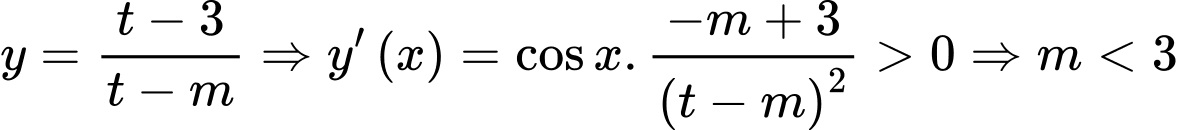thì (do )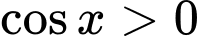
Để hàm số đã cho liên tục thì
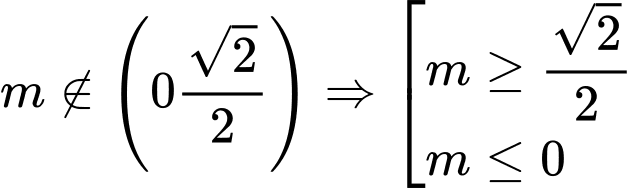
Do
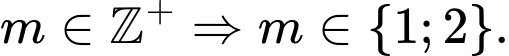
Vậy có 2 giá trị nguyên dương
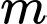thoả mãn ycbt.
Chọn đáp án A. Đáp án: A