Đáp án Bài tập tự luyện số 3
Câu 1 [51360]: Trong không gian 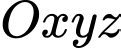 , cho ba điểm
, cho ba điểm 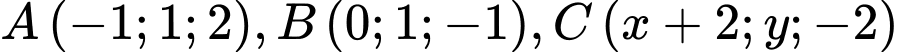 thẳng hàng. Tổng
thẳng hàng. Tổng  bằng
bằng
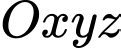 , cho ba điểm
, cho ba điểm 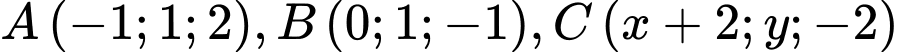 thẳng hàng. Tổng
thẳng hàng. Tổng  bằng
bằng A, 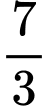 .
.
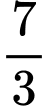 .
.B, 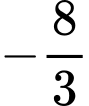 .
.
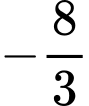 .
.C, 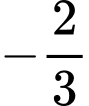 .
.
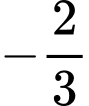 .
.D, 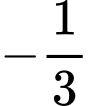 .
.
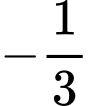 .
.
Chọn C.
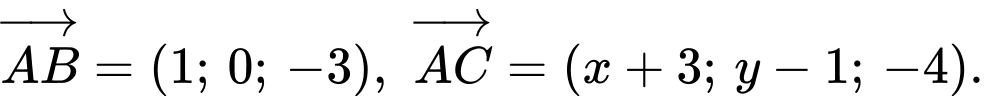
Điều kiện thẳng hàng là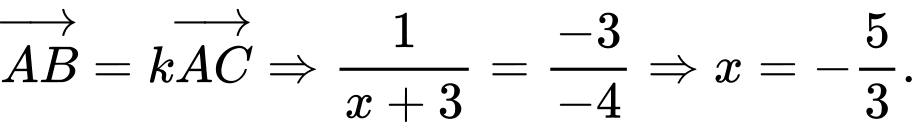
Ngoài ra tất yếu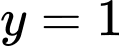 do
do 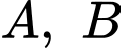 cùng tung độ
cùng tung độ 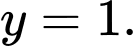
Vậy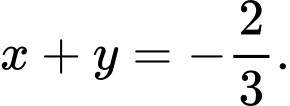 Đáp án: C
Đáp án: C
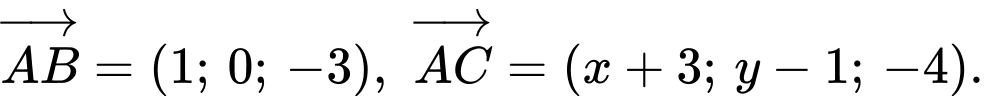
Điều kiện thẳng hàng là
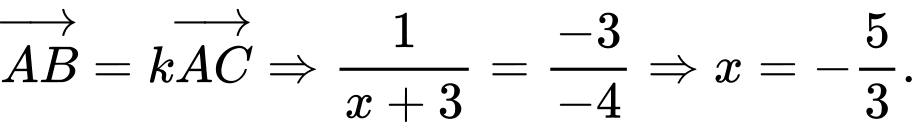
Ngoài ra tất yếu
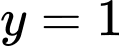 do
do 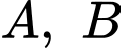 cùng tung độ
cùng tung độ 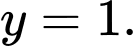
Vậy
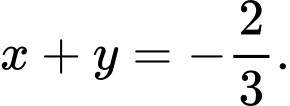 Đáp án: C
Đáp án: C
Câu 2 [51033]: Trong không gian với hệ tọa độ 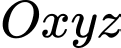 cho
cho 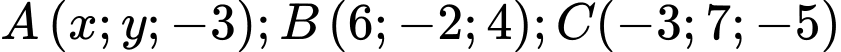 . Giá trị
. Giá trị 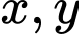 để
để 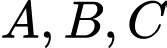 thẳng hàng là
thẳng hàng là
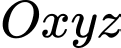 cho
cho 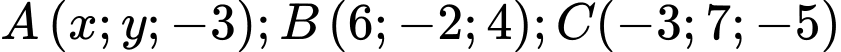 . Giá trị
. Giá trị 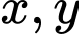 để
để 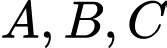 thẳng hàng là
thẳng hàng là A, 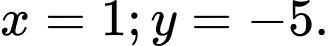
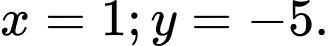
B, 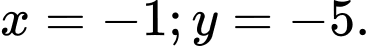
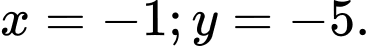
C, 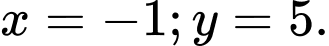
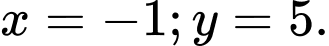
D, 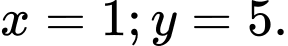
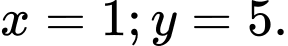
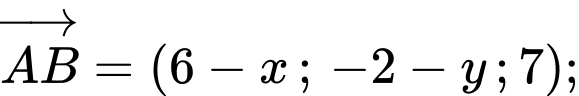
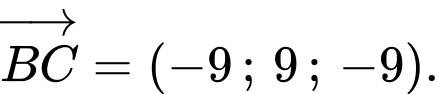
Để
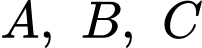 thẳng hàng
thẳng hàng 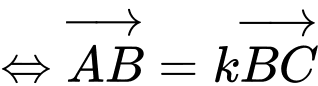
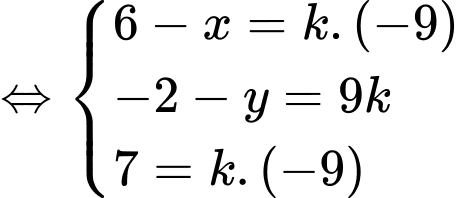
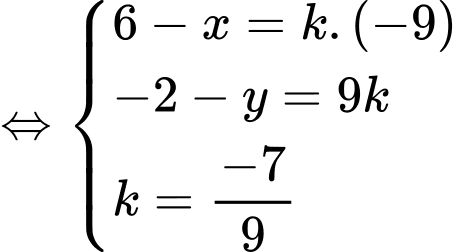
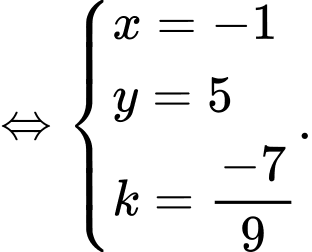
Chọn C. Đáp án: C
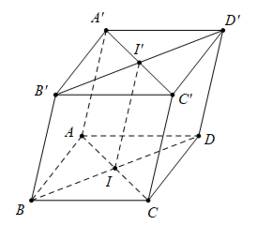
Câu 3 [380269]: Cho hình lập phương  có cạnh bằng
có cạnh bằng 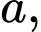 gọi
gọi 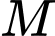 là trung điểm của cạnh
là trung điểm của cạnh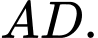 Tính
Tính 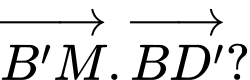
 có cạnh bằng
có cạnh bằng 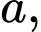 gọi
gọi 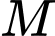 là trung điểm của cạnh
là trung điểm của cạnh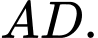 Tính
Tính 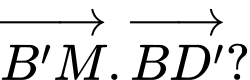
A, 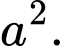
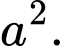
B, 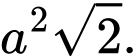
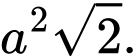
C, 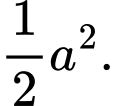
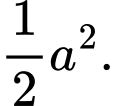
D, 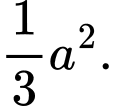
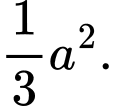

Ta có:
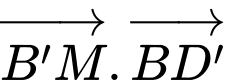
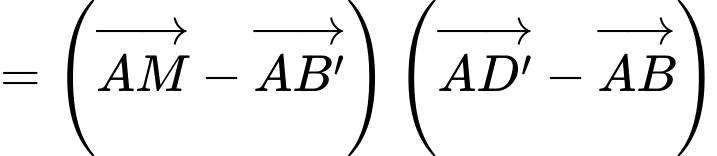
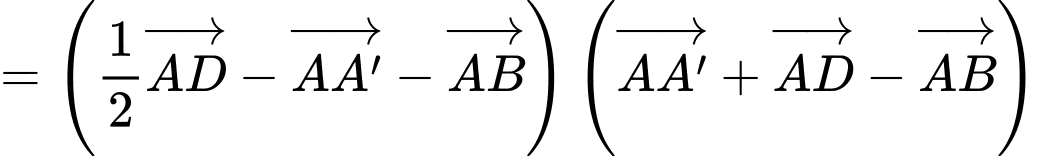
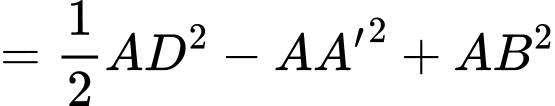
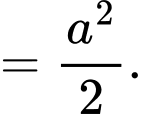 Đáp án: C
Đáp án: C
Câu 4 [379542]: Cho hình lập phương  có cạnh bằng
có cạnh bằng 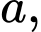 gọi
gọi 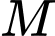 là trung điểm của cạnh
là trung điểm của cạnh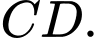 Tính
Tính 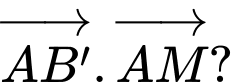
 có cạnh bằng
có cạnh bằng 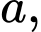 gọi
gọi 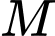 là trung điểm của cạnh
là trung điểm của cạnh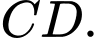 Tính
Tính 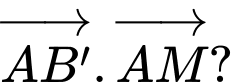
A, 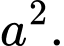
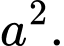
B, 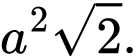
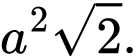
C, 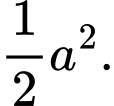
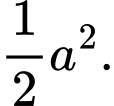
D, 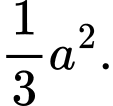
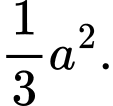
HD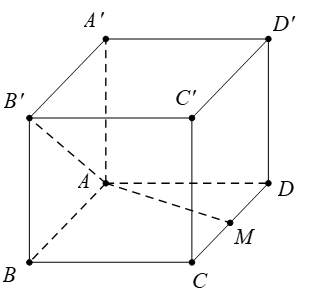
Ta có:  Chọn C. Đáp án: C
Chọn C. Đáp án: C

 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 5 [380270]: Cho hình lập phương  có cạnh bằng
có cạnh bằng 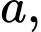 gọi
gọi 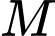 là trung điểm của cạnh
là trung điểm của cạnh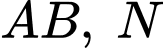 là điểm trên cạnh
là điểm trên cạnh 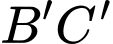 sao cho
sao cho 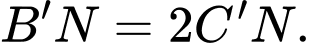 Tính
Tính 
 có cạnh bằng
có cạnh bằng 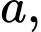 gọi
gọi 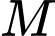 là trung điểm của cạnh
là trung điểm của cạnh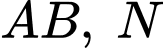 là điểm trên cạnh
là điểm trên cạnh 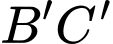 sao cho
sao cho 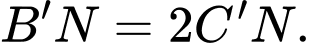 Tính
Tính 
A, 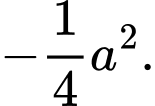
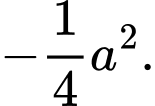
B, 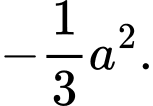
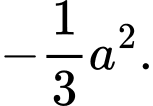
C, 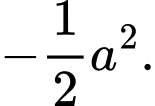
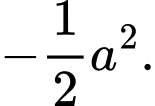
D, 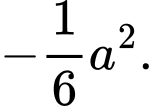
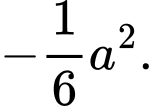
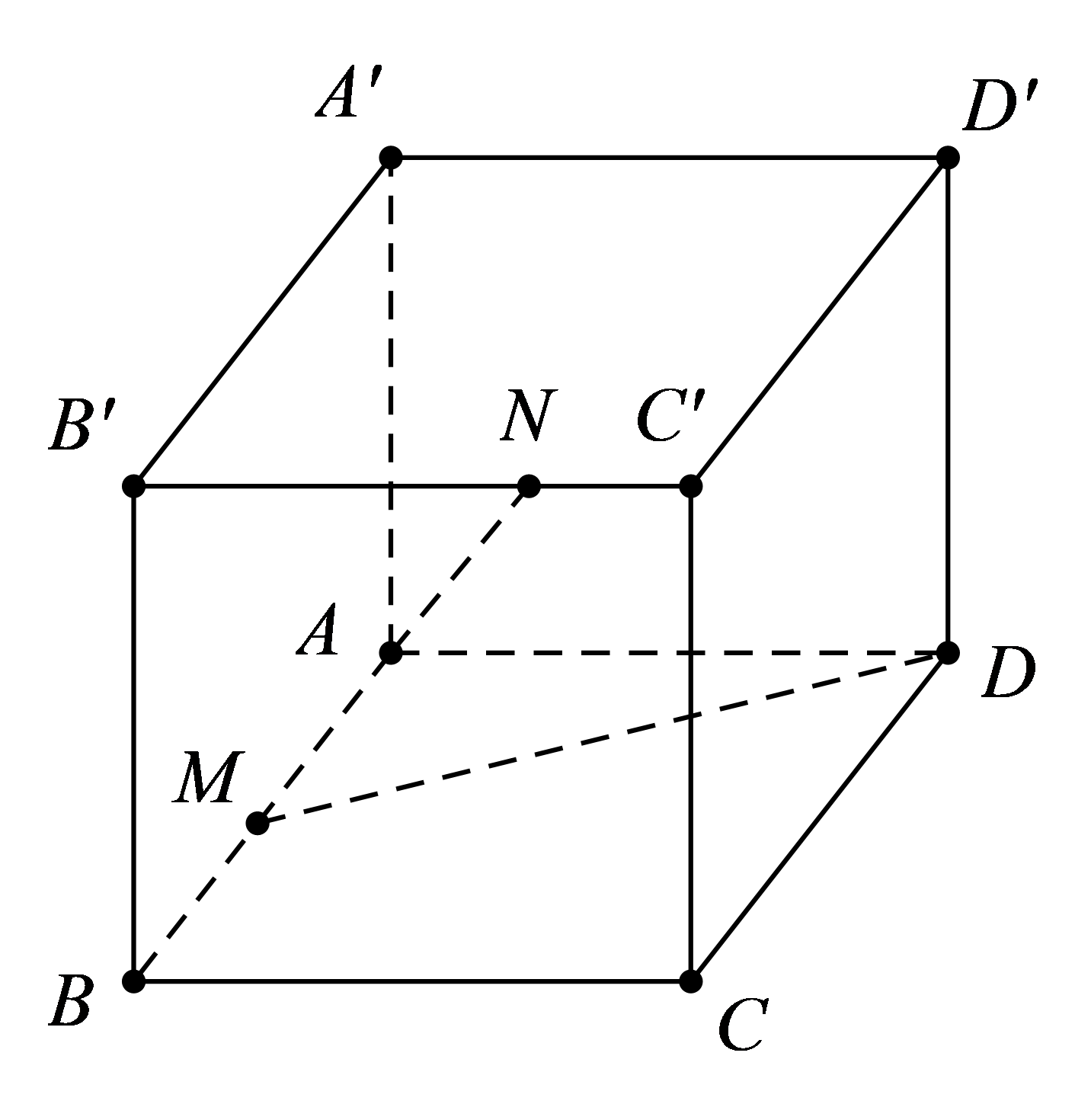
Ta có:
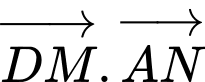
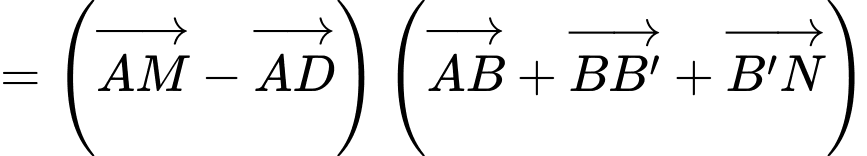
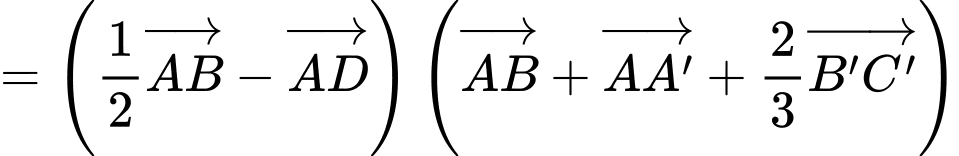
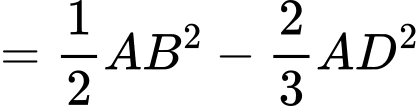
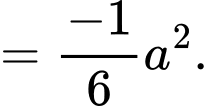 Chọn D.Đáp án: D
Chọn D.Đáp án: D
Câu 6 [51386]: Trong không gian với hệ tọa độ 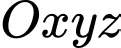 , cho các điểm
, cho các điểm 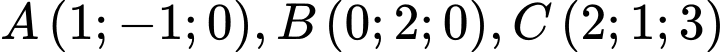 . Tọa độ điểm
. Tọa độ điểm 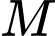 thỏa mãn
thỏa mãn 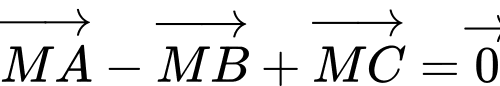 là
là
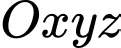 , cho các điểm
, cho các điểm 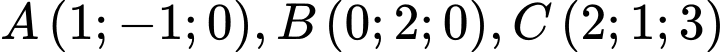 . Tọa độ điểm
. Tọa độ điểm 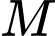 thỏa mãn
thỏa mãn 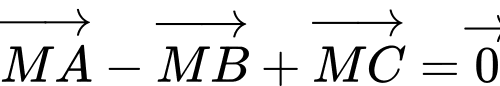 là
là A, 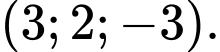
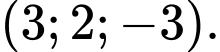
B, 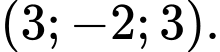
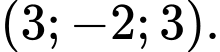
C, 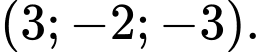
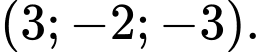
D, 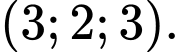
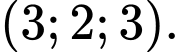
Gọi 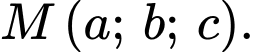
Ta có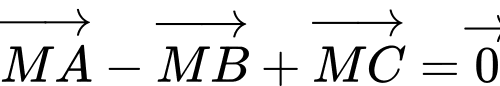
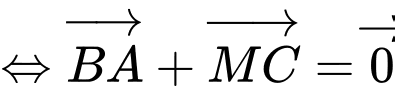
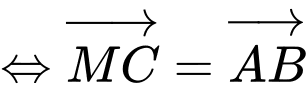
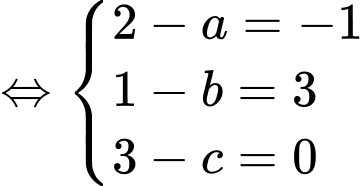
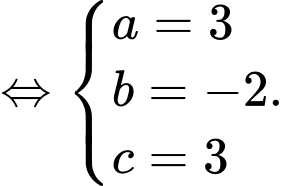 Suy ra
Suy ra 
Chọn B. Đáp án: B
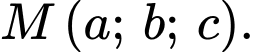
Ta có
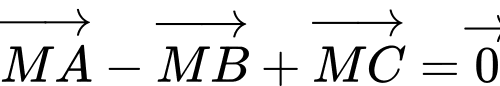
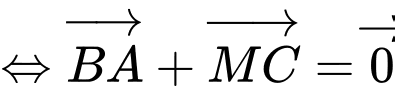
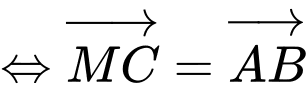
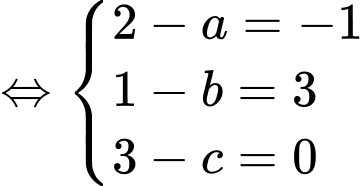
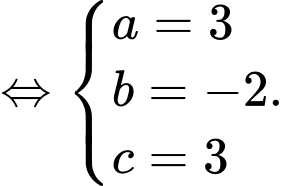 Suy ra
Suy ra 
Chọn B. Đáp án: B
Câu 7 [51361]: Trong không gian 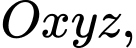 cho hai điểm
cho hai điểm 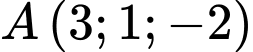 ,
, 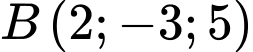 . Điểm
. Điểm 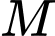 thuộc đoạn
thuộc đoạn  sao cho
sao cho 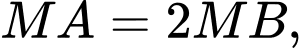 tọa độ điểm
tọa độ điểm 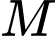 là
là
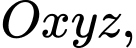 cho hai điểm
cho hai điểm 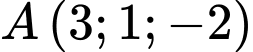 ,
, 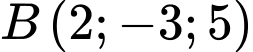 . Điểm
. Điểm 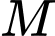 thuộc đoạn
thuộc đoạn  sao cho
sao cho 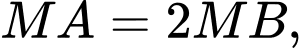 tọa độ điểm
tọa độ điểm 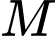 là
là A, 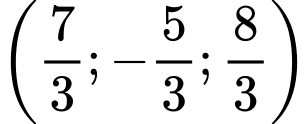 .
.
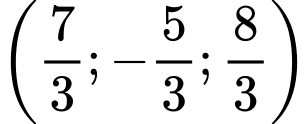 .
.B, 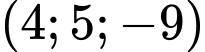 .
.
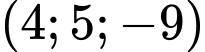 .
.C, 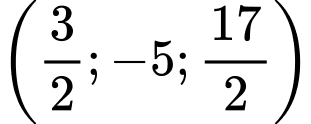 .
.
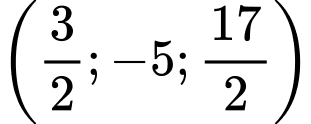 .
.D, 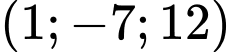 .
.
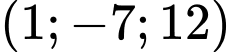 .
.
Phương trình đường thẳng 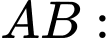
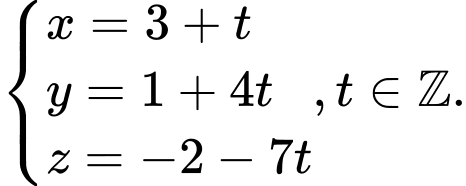
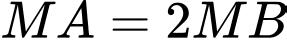
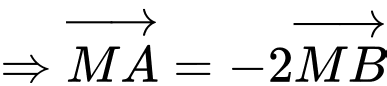
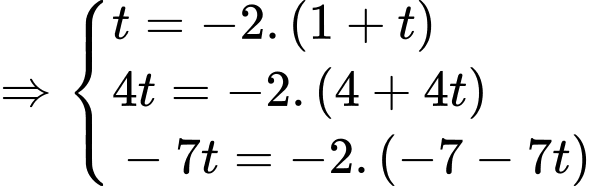
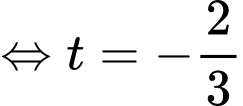
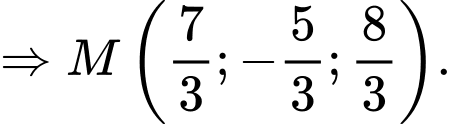 Đáp án: A
Đáp án: A
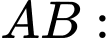
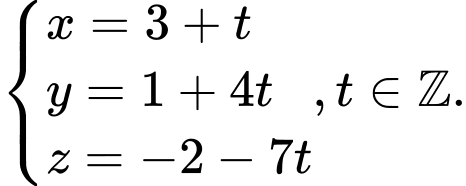
Gọi 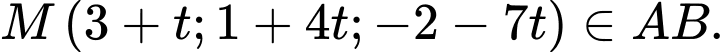
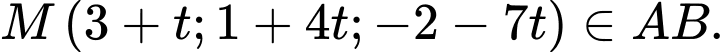
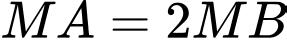
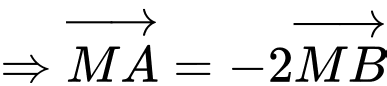
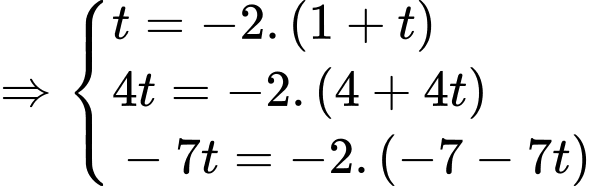
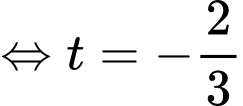
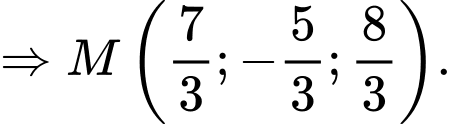 Đáp án: A
Đáp án: A
Câu 8 [51136]: Trong không gian với hệ tọa độ 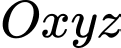 cho
cho 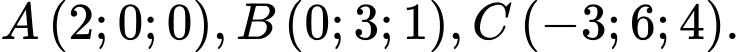 Gọi
Gọi 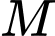 là điểm nằm trên cạnh
là điểm nằm trên cạnh 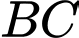 sao cho
sao cho 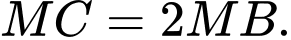 Độ dài đoạn
Độ dài đoạn  là
là
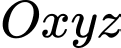 cho
cho 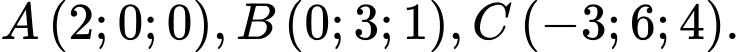 Gọi
Gọi 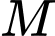 là điểm nằm trên cạnh
là điểm nằm trên cạnh 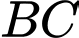 sao cho
sao cho 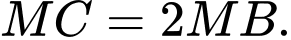 Độ dài đoạn
Độ dài đoạn  là
là A, 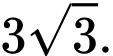
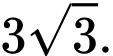
B, 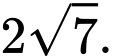
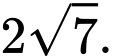
C, 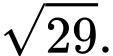
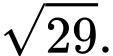
D, 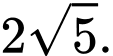
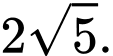
Gọi 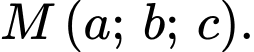
Ta có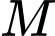 nằm trên đoạn
nằm trên đoạn 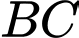 và
và 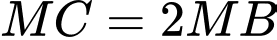
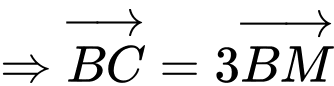
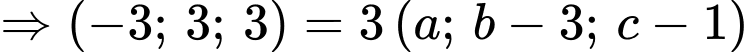
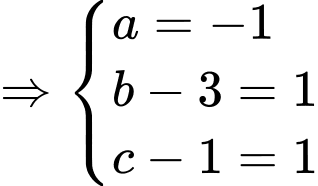
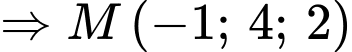
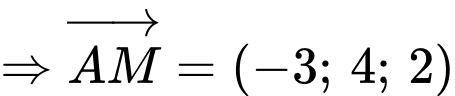
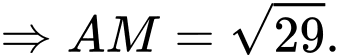
Chọn C. Đáp án: C
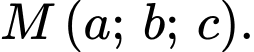
Ta có
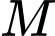 nằm trên đoạn
nằm trên đoạn 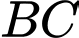 và
và 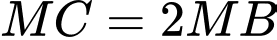
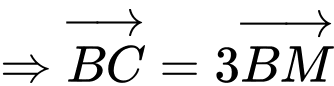
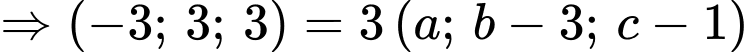
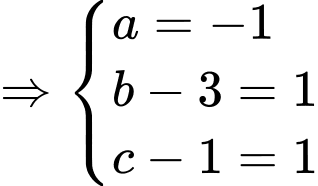
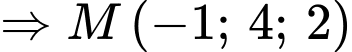
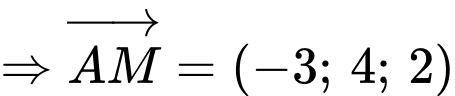
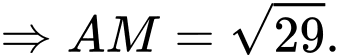
Chọn C. Đáp án: C
Câu 9 [380276]: Cho hình lập phương  có cạnh bằng
có cạnh bằng 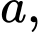 gọi
gọi 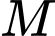 là trung điểm của cạnh
là trung điểm của cạnh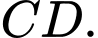 Tính cosin góc giữa hai vectơ
Tính cosin góc giữa hai vectơ 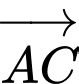 và
và 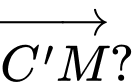
 có cạnh bằng
có cạnh bằng 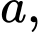 gọi
gọi 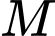 là trung điểm của cạnh
là trung điểm của cạnh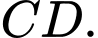 Tính cosin góc giữa hai vectơ
Tính cosin góc giữa hai vectơ 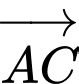 và
và 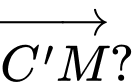
A, 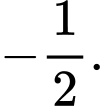
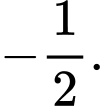
B, 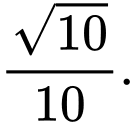
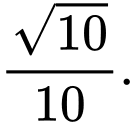
C, 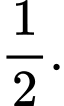
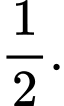
D, 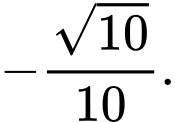
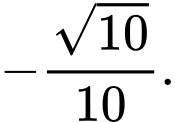
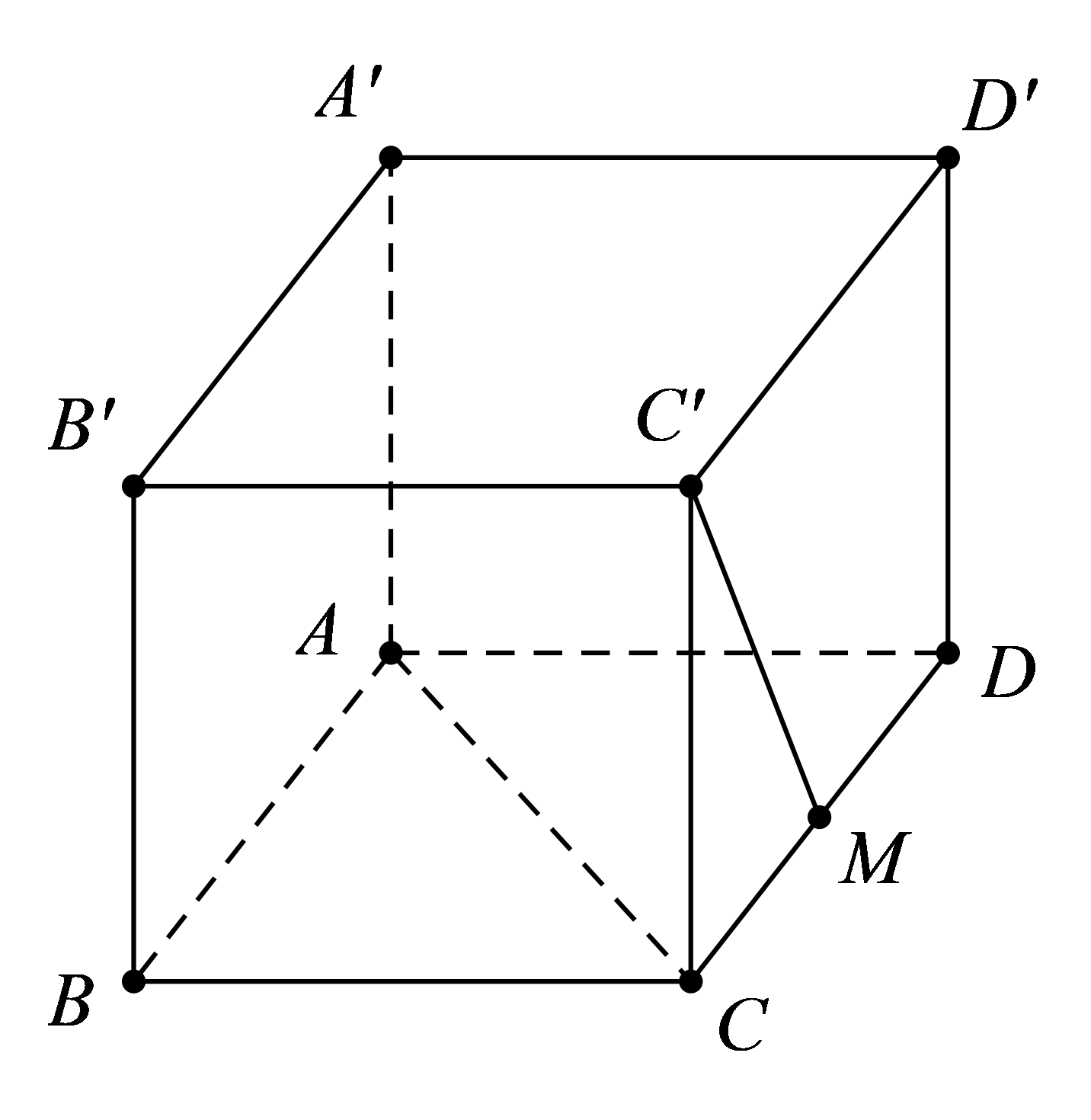
Ta có:
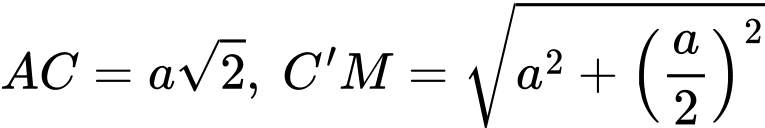
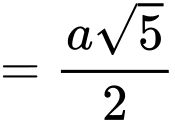
Lại có:
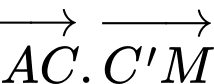
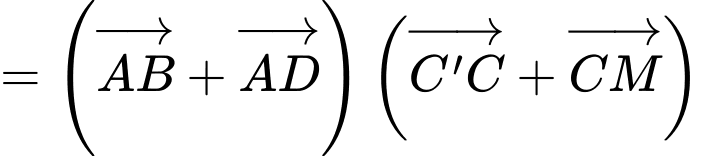
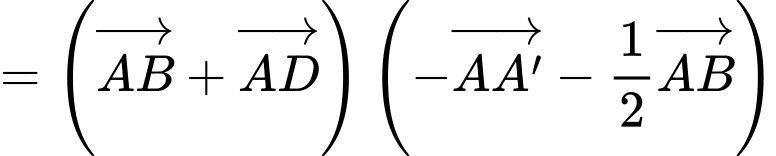
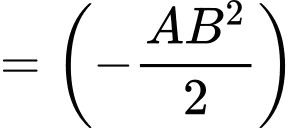
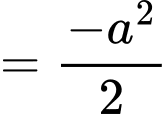
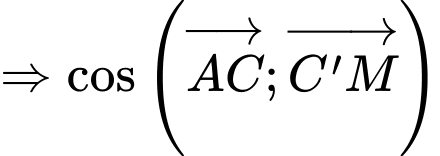
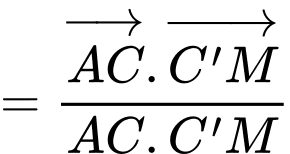
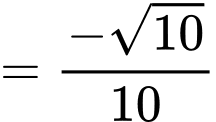 Đáp án: D
Đáp án: D
Câu 10 [380277]: Cho hình chóp 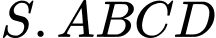 có đáy
có đáy 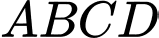 là hình vuông cạnh
là hình vuông cạnh 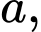 hai mặt phẳng
hai mặt phẳng 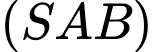 và
và 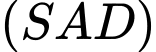 cùng vuông góc với đáy. Biết rằng
cùng vuông góc với đáy. Biết rằng 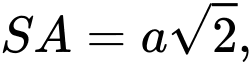 tính cosin góc tạo bởi hai vectơ
tính cosin góc tạo bởi hai vectơ 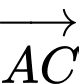 và
và 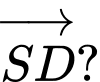
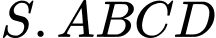 có đáy
có đáy 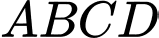 là hình vuông cạnh
là hình vuông cạnh 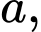 hai mặt phẳng
hai mặt phẳng 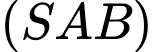 và
và 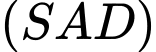 cùng vuông góc với đáy. Biết rằng
cùng vuông góc với đáy. Biết rằng 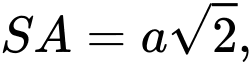 tính cosin góc tạo bởi hai vectơ
tính cosin góc tạo bởi hai vectơ 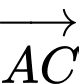 và
và 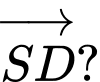
A, 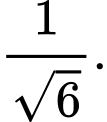
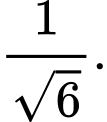
B, 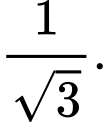
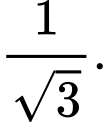
C, 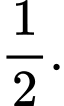
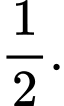
D, 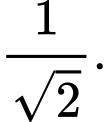
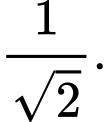

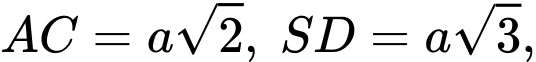

Suy ra 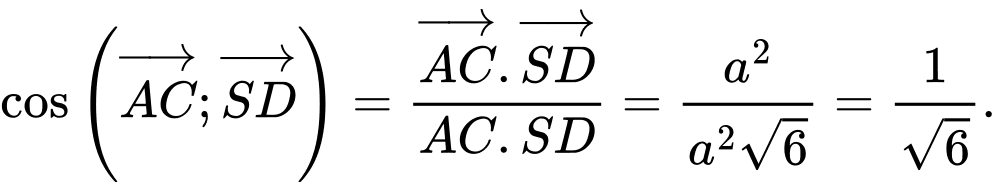
Đáp án: A 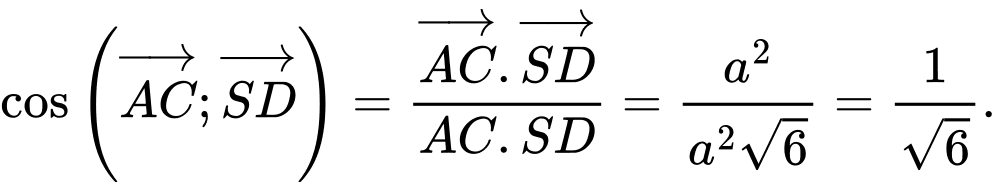
Câu 11 [51383]: Trong không gian với hệ tọa độ 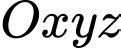 , cho khối lập phương
, cho khối lập phương  có
có 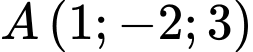 và
và 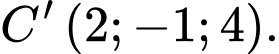 Tính thể tích
Tính thể tích  của khối lập phương đã cho.
của khối lập phương đã cho.
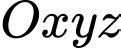 , cho khối lập phương
, cho khối lập phương  có
có 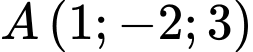 và
và 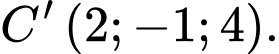 Tính thể tích
Tính thể tích  của khối lập phương đã cho.
của khối lập phương đã cho. A, 

B, 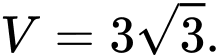
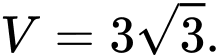
C, 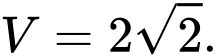
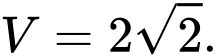
D, 

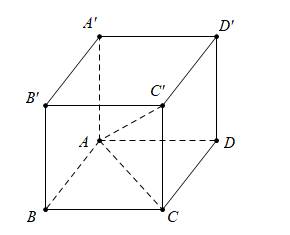
Gọi cạnh của hình lập phương là
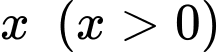
Ta có
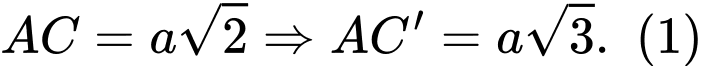
Mà
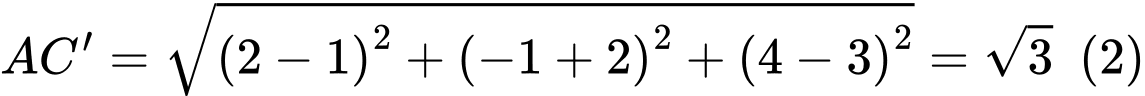
Từ
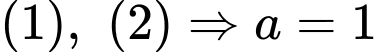
Vậy thể tích của khối lập phương là

Chọn A. Đáp án: A
Câu 12 [103906]: Trong không gian với hệ trục tọa độ 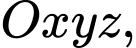 cho hình hộp
cho hình hộp 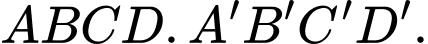 Biết
Biết 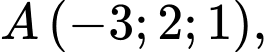
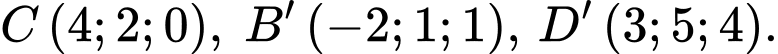 Tìm tọa độ
Tìm tọa độ 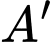 của hình hộp
của hình hộp 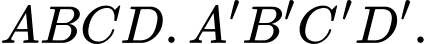
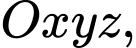 cho hình hộp
cho hình hộp 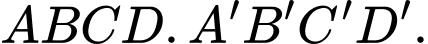 Biết
Biết 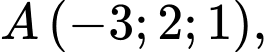
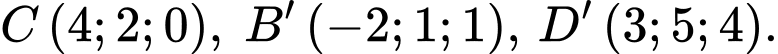 Tìm tọa độ
Tìm tọa độ 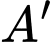 của hình hộp
của hình hộp 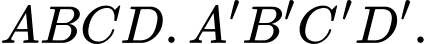
A, 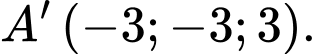
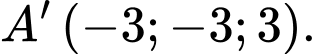
B, 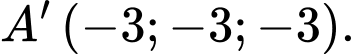
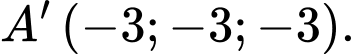
C, 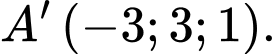
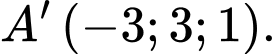
D, 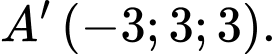
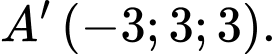
Trung điểm của
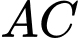 là
là 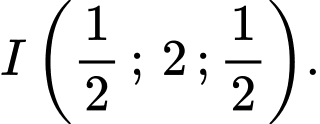
Trung điểm của
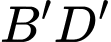 là
là 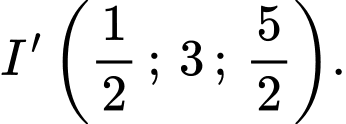
Do
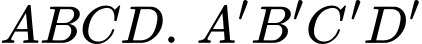 là hình hộp nên
là hình hộp nên 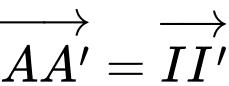
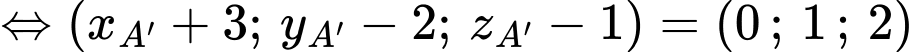
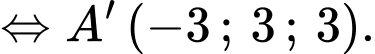 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 13 [380499]: Cho hình hộp chữ nhật  có
có 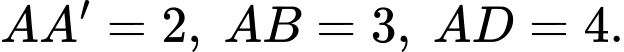 Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các mệnh đề sau
Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các mệnh đề sau 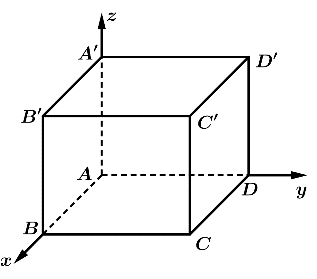
 có
có 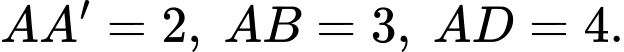 Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các mệnh đề sau
Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các mệnh đề sau 
A, a) 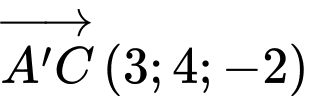
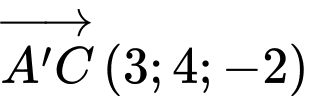
B, b) Trọng tâm tam giác 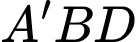 là điểm
là điểm 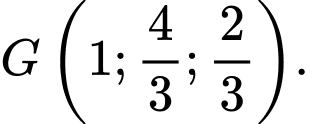
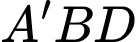 là điểm
là điểm 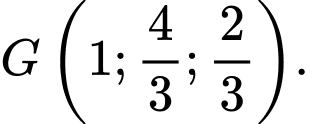
C, c) 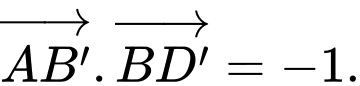
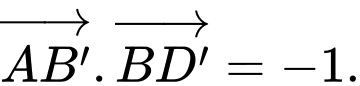
D, d) Góc 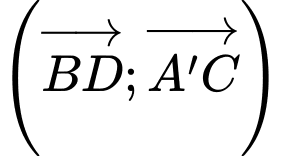 (làm tròn đến hàng phần mười) bằng
(làm tròn đến hàng phần mười) bằng 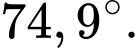
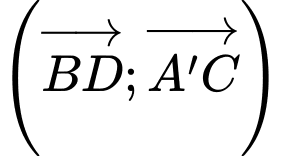 (làm tròn đến hàng phần mười) bằng
(làm tròn đến hàng phần mười) bằng 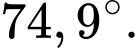
Ta có: 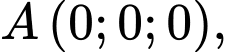
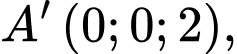
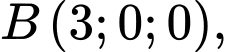
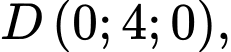
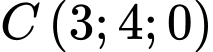
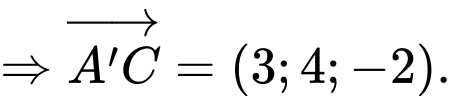
Trọng tâm tam giác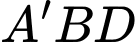 là điểm
là điểm 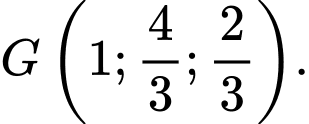
Điểm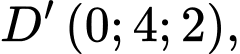
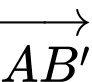
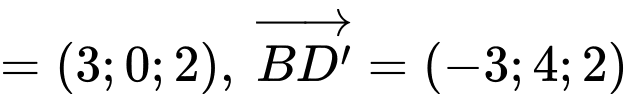
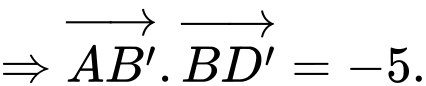
Lại có: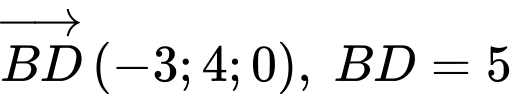 suy ra
suy ra 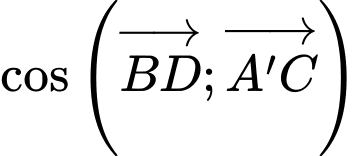
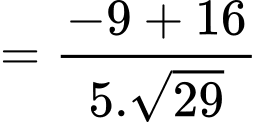
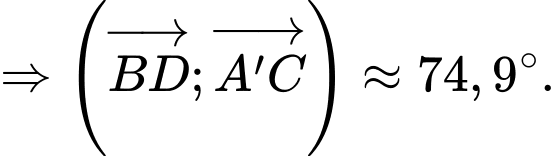
a) Đúng
b) Đúng
c) Sai
d) Đúng.
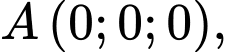
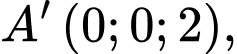
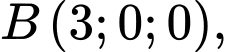
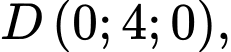
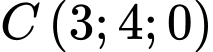
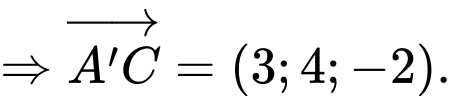
Trọng tâm tam giác
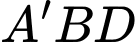 là điểm
là điểm 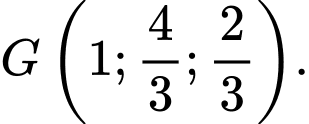
Điểm
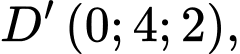
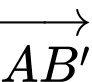
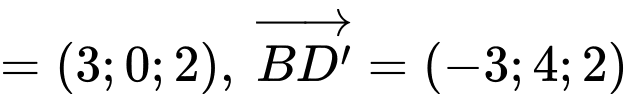
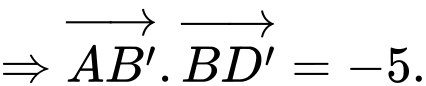
Lại có:
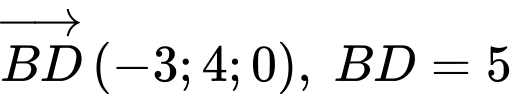 suy ra
suy ra 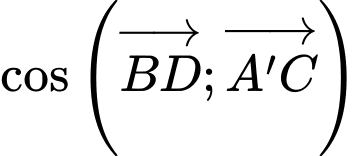
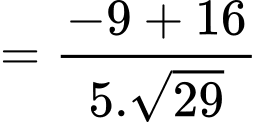
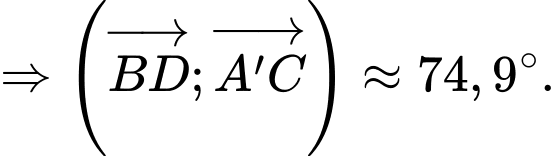
a) Đúng
b) Đúng
c) Sai
d) Đúng.
Câu 14 [380500]: Cho hình lăng trụ tam giác đều  có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 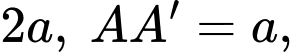 gọi
gọi  là trung điểm của
là trung điểm của 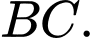 Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các khẳng định sau
Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các khẳng định sau 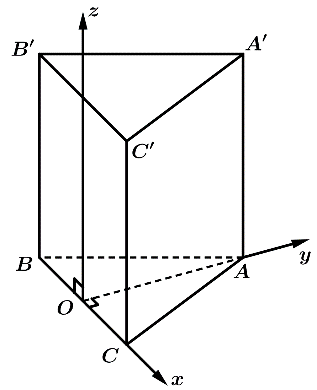
 có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh 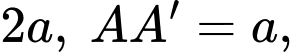 gọi
gọi  là trung điểm của
là trung điểm của 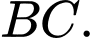 Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các khẳng định sau
Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy xét tính đúng sai của các khẳng định sau 
A, a) Trọng tâm của tam giác 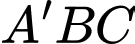 là điểm
là điểm 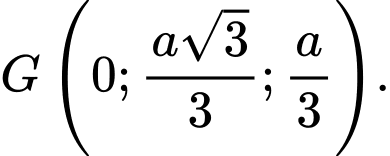
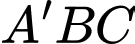 là điểm
là điểm 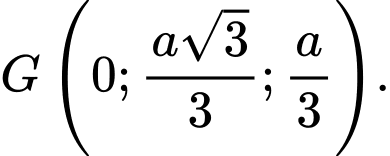
B, b) 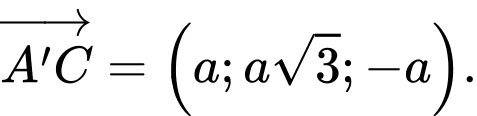
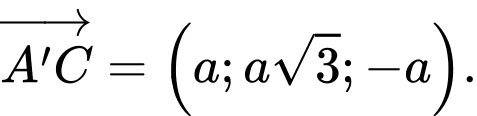
C, c) 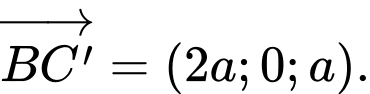
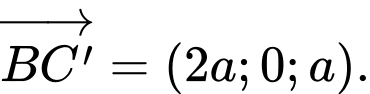
D, Góc 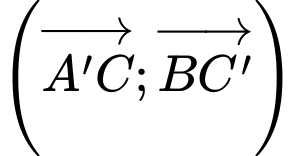 (làm tròn đến hàng phần trăm) bằng
(làm tròn đến hàng phần trăm) bằng 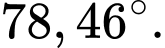
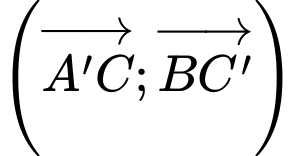 (làm tròn đến hàng phần trăm) bằng
(làm tròn đến hàng phần trăm) bằng 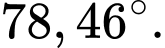
Ta có: 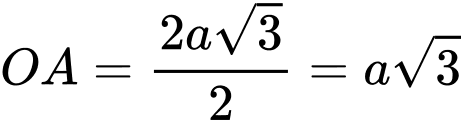
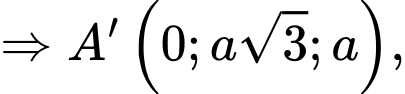
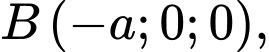
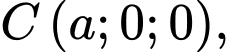
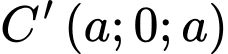
Trọng tâm của tam giác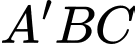 là điểm
là điểm 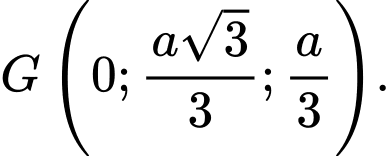
Lại có: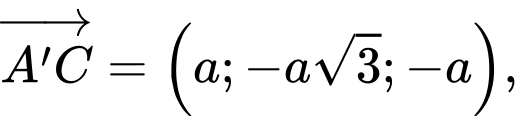
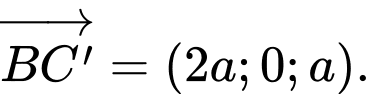
Do đó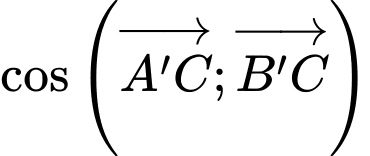
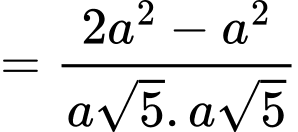
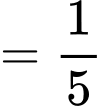
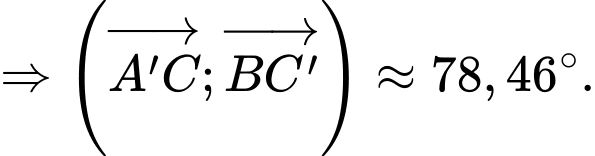
a) Đúng
b) Sai
c) Đúng
d) Đúng
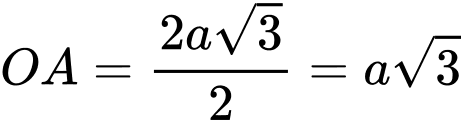
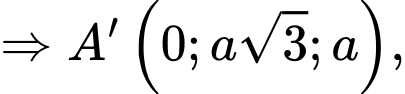
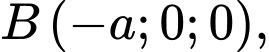
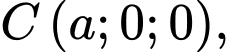
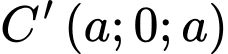
Trọng tâm của tam giác
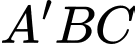 là điểm
là điểm 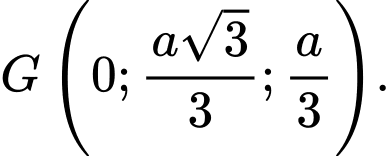
Lại có:
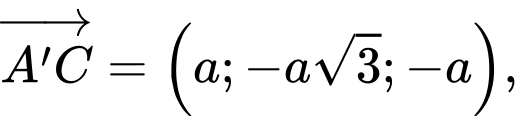
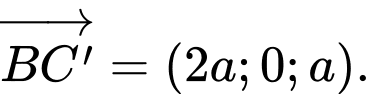
Do đó
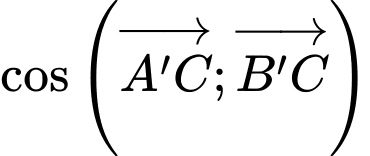
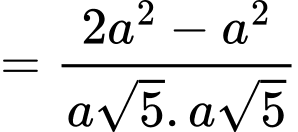
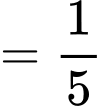
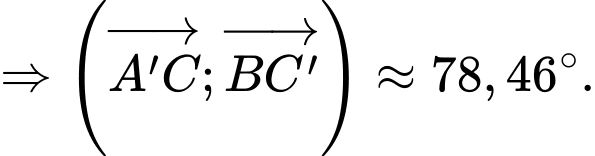
a) Đúng
b) Sai
c) Đúng
d) Đúng
Câu 15 [380590]: Trong không gian với hệ trục tọa độ 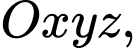 cho hình hộp
cho hình hộp 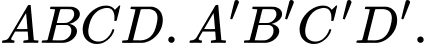 Biết
Biết 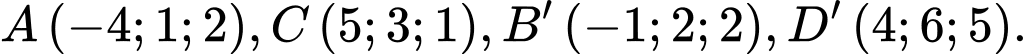 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
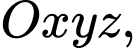 cho hình hộp
cho hình hộp 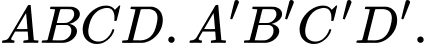 Biết
Biết 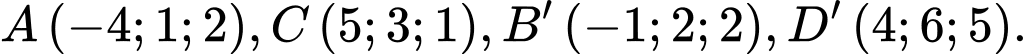 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) 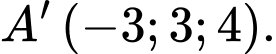
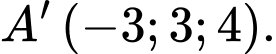
B, b) 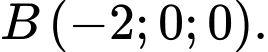
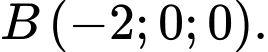
C, c) 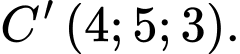
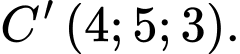
D, d)  là góc tù.
là góc tù.
 là góc tù.
là góc tù.
HD: Trung điểm của 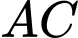 là điểm
là điểm 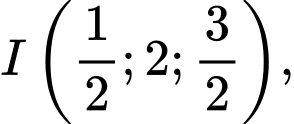 trung điểm của
trung điểm của 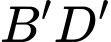 là
là 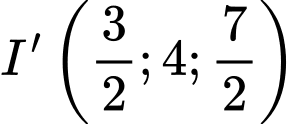
Ta có: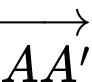

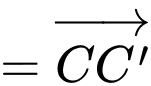
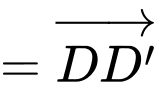
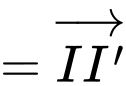
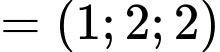
Suy ra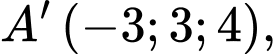
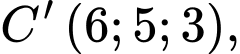
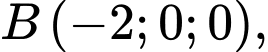
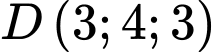
Ta có: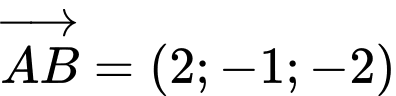 và
và 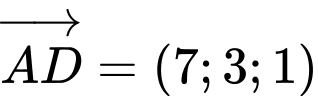 nên
nên 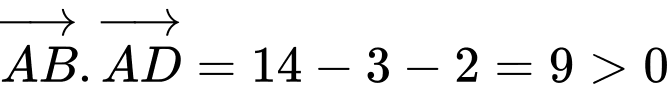 suy ra
suy ra  là góc nhọn.
là góc nhọn.
a) Đúng
b) Đúng
c) Sai
d) Sai
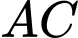 là điểm
là điểm 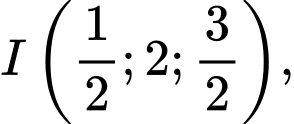 trung điểm của
trung điểm của 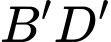 là
là 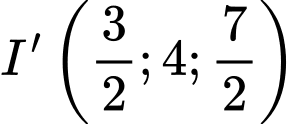
Ta có:
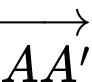

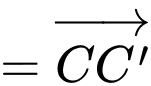
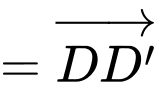
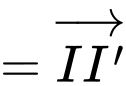
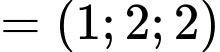
Suy ra
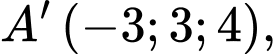
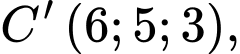
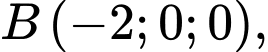
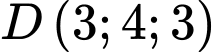
Ta có:
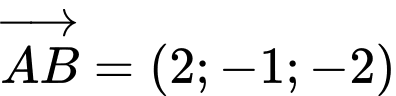 và
và 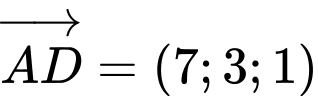 nên
nên 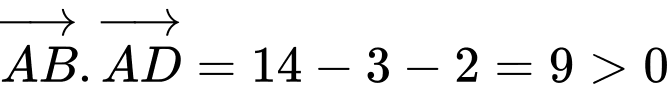 suy ra
suy ra  là góc nhọn.
là góc nhọn. a) Đúng
b) Đúng
c) Sai
d) Sai
Câu 16 [383112]: Trong không gian 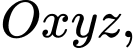 cho hai điểm
cho hai điểm 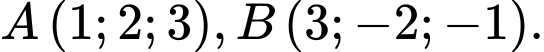 Đường thẳng
Đường thẳng  cắt mặt phẳng tọa độ
cắt mặt phẳng tọa độ 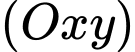 tại điểm
tại điểm 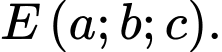 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
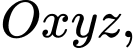 cho hai điểm
cho hai điểm 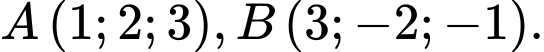 Đường thẳng
Đường thẳng  cắt mặt phẳng tọa độ
cắt mặt phẳng tọa độ 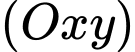 tại điểm
tại điểm 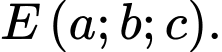 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
A, 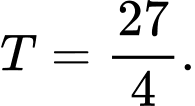
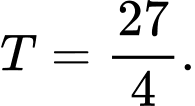
B, 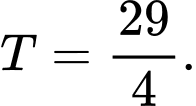
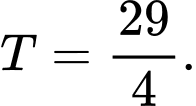
C, 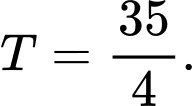
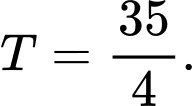
D, 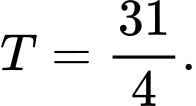
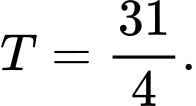
Đường thẳng  cắt mặt phẳng tọa độ
cắt mặt phẳng tọa độ 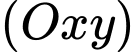 tại điểm
tại điểm 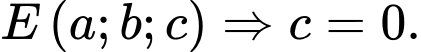
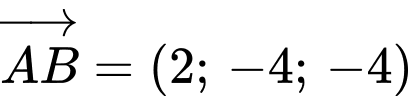 ,
, 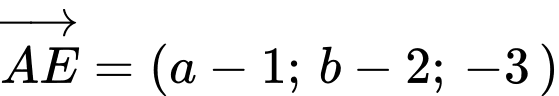
Ba điểm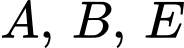 thẳng hàng
thẳng hàng 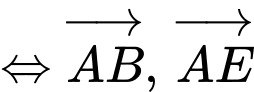 cùng phương.
cùng phương.
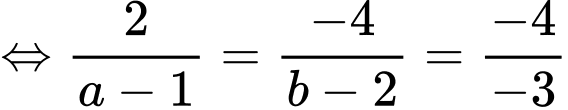
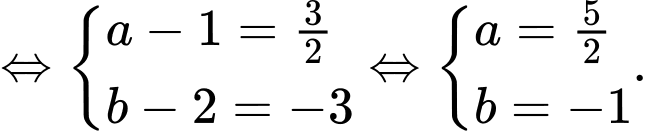
Vậy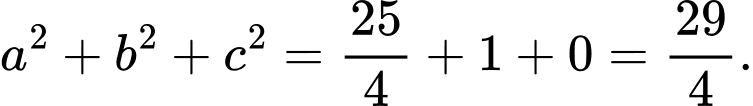 Đáp án: B
Đáp án: B
 cắt mặt phẳng tọa độ
cắt mặt phẳng tọa độ 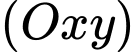 tại điểm
tại điểm 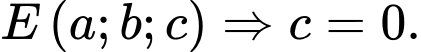
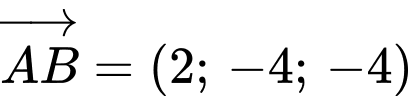 ,
, 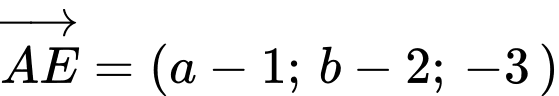
Ba điểm
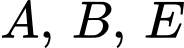 thẳng hàng
thẳng hàng 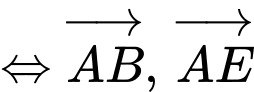 cùng phương.
cùng phương.
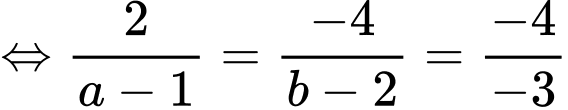
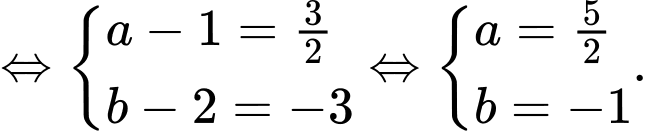
Vậy
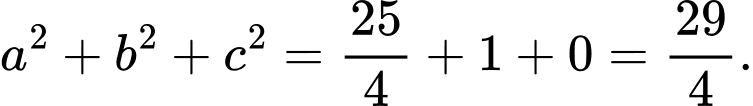 Đáp án: B
Đáp án: B
Câu 17 [103908]: Trong không gian với hệ tọa độ 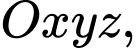 cho hình hộp
cho hình hộp 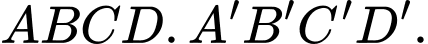 Biết
Biết 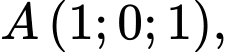
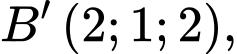
 Gọi tọa độ của đỉnh
Gọi tọa độ của đỉnh 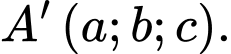 Khi đó
Khi đó 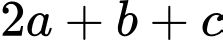 bằng?
bằng?
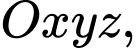 cho hình hộp
cho hình hộp 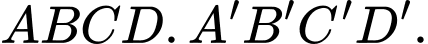 Biết
Biết 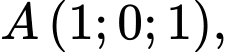
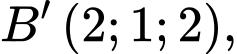
 Gọi tọa độ của đỉnh
Gọi tọa độ của đỉnh 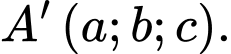 Khi đó
Khi đó 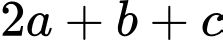 bằng?
bằng? A, 7.
B, 2.
C, 8.
D, 3.
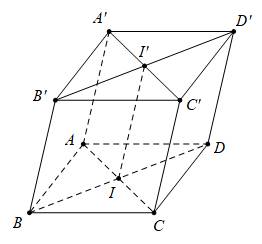
Trung điểm của
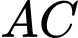 là
là 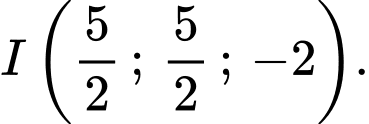
Trung điểm của
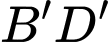 là
là 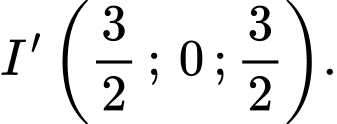
Do
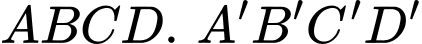 là hình hộp nên
là hình hộp nên 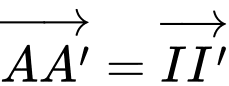
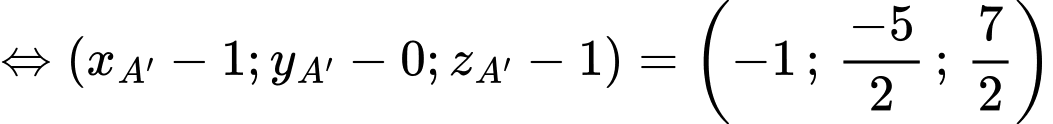
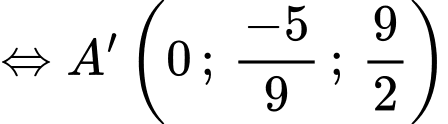
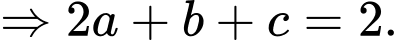
Chọn B. Đáp án: B
Câu 18 [380502]: Trong không gian 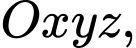 cho ba điểm
cho ba điểm 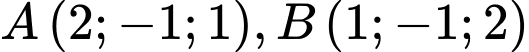 và
và 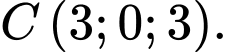 Biết điểm
Biết điểm 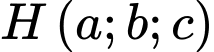 là toạ độ chân đường cao hạ từ
là toạ độ chân đường cao hạ từ 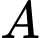 của tam giác
của tam giác 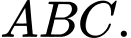 Tính
Tính 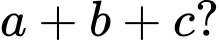
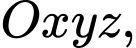 cho ba điểm
cho ba điểm 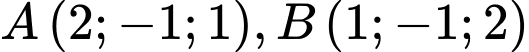 và
và 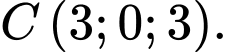 Biết điểm
Biết điểm 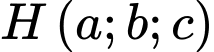 là toạ độ chân đường cao hạ từ
là toạ độ chân đường cao hạ từ 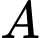 của tam giác
của tam giác 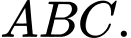 Tính
Tính 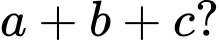
Ta có: 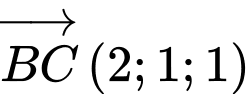 , gọi
, gọi 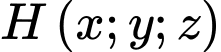 là chân đường cao của tam giác
là chân đường cao của tam giác 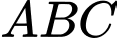 kẻ từ
kẻ từ 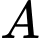 Suy ra
Suy ra 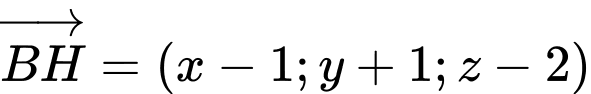 cùng phương với vectơ
cùng phương với vectơ 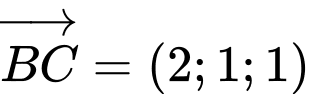 nên
nên
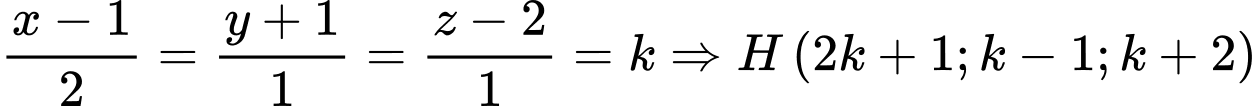 Khi đó
Khi đó 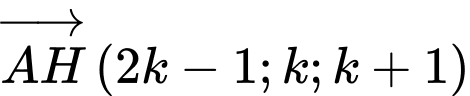 vuông góc với
vuông góc với 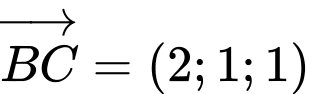 nên
nên 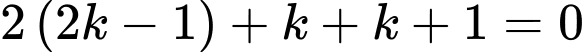
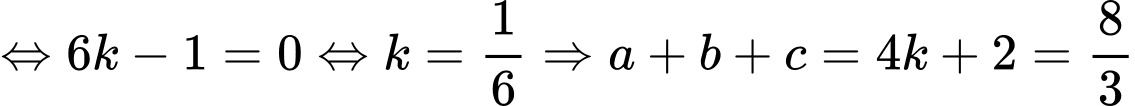
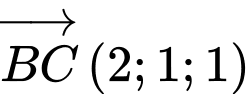 , gọi
, gọi 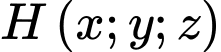 là chân đường cao của tam giác
là chân đường cao của tam giác 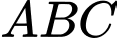 kẻ từ
kẻ từ 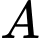 Suy ra
Suy ra 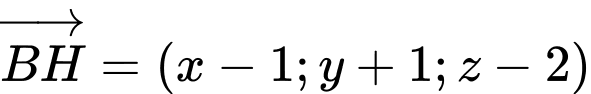 cùng phương với vectơ
cùng phương với vectơ 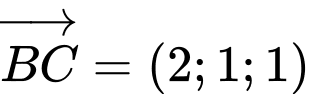 nên
nên
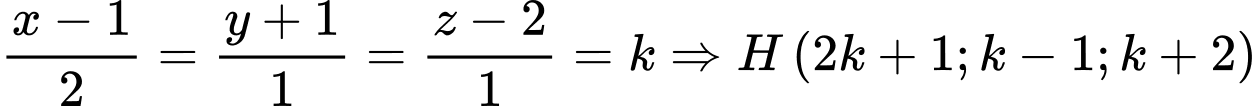 Khi đó
Khi đó 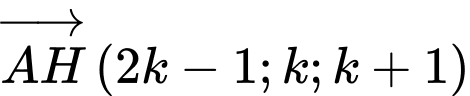 vuông góc với
vuông góc với 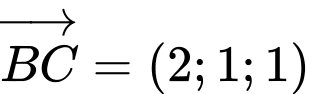 nên
nên 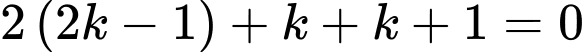
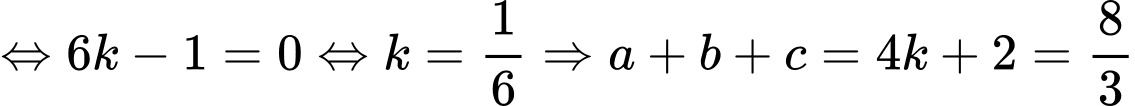
Câu 19 [380503]: Cho hình chóp 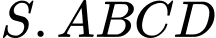 có đáy là hình vuông có cạnh bằng
có đáy là hình vuông có cạnh bằng 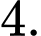 Gọi
Gọi 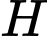 là điểm thuộc cạnh
là điểm thuộc cạnh  sao cho
sao cho 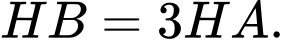 Biết
Biết 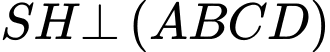 và
và  Gọi
Gọi 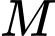 và
và 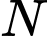 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 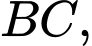 bằng cách dựng hệ trục toạ độ như hình vẽ bên, hãy tính góc giữa hai vectơ
bằng cách dựng hệ trục toạ độ như hình vẽ bên, hãy tính góc giữa hai vectơ 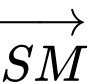 và
và  (làm tròn đến hàng đơn vị của độ).
(làm tròn đến hàng đơn vị của độ).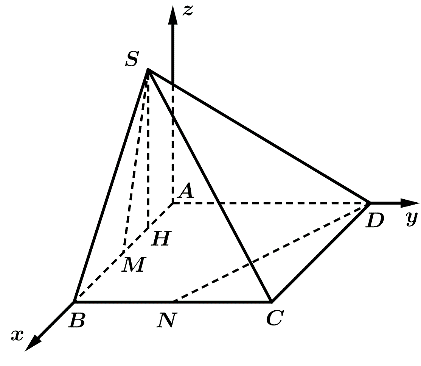
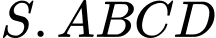 có đáy là hình vuông có cạnh bằng
có đáy là hình vuông có cạnh bằng 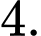 Gọi
Gọi 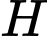 là điểm thuộc cạnh
là điểm thuộc cạnh  sao cho
sao cho 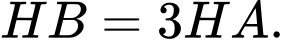 Biết
Biết 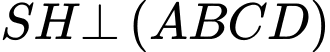 và
và  Gọi
Gọi 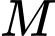 và
và 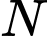 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 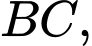 bằng cách dựng hệ trục toạ độ như hình vẽ bên, hãy tính góc giữa hai vectơ
bằng cách dựng hệ trục toạ độ như hình vẽ bên, hãy tính góc giữa hai vectơ 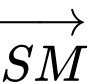 và
và  (làm tròn đến hàng đơn vị của độ).
(làm tròn đến hàng đơn vị của độ).
Ta có: 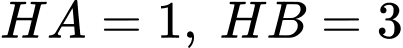
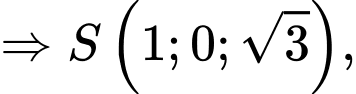
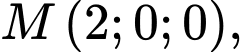
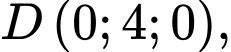
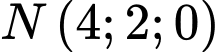
Suy ra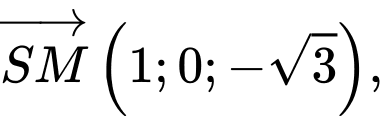
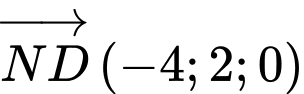 suy ra
suy ra 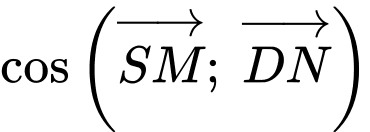
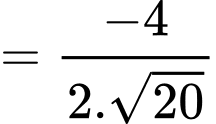
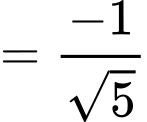
Do đó
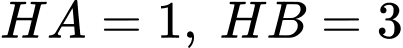
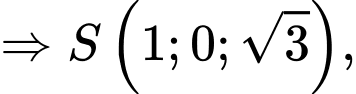
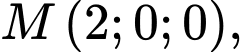
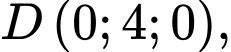
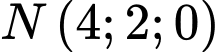
Suy ra
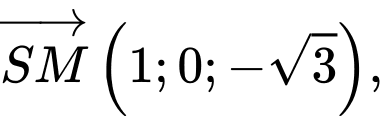
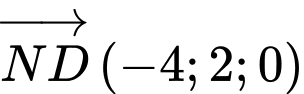 suy ra
suy ra 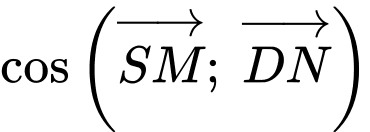
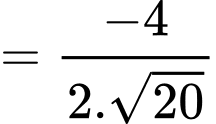
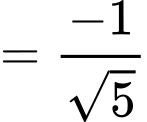
Do đó

Câu 20 [383111]: Trong không gian 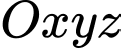 , cho tam giác
, cho tam giác 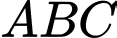 có
có 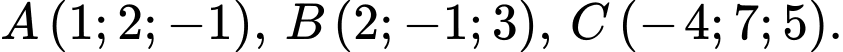 Trong tam giác
Trong tam giác 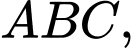 gọi
gọi 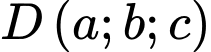 là chân đường phân giác trong góc
là chân đường phân giác trong góc 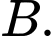 Giá trị của
Giá trị của 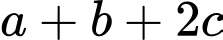 bằng
bằng
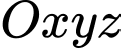 , cho tam giác
, cho tam giác 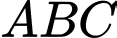 có
có 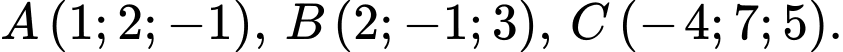 Trong tam giác
Trong tam giác 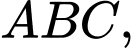 gọi
gọi 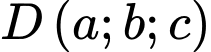 là chân đường phân giác trong góc
là chân đường phân giác trong góc 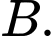 Giá trị của
Giá trị của 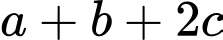 bằng
bằng A, 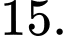
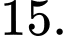
B, 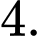
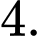
C, 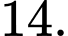
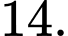
D, 
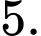
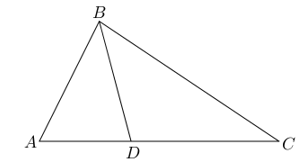
Ta có
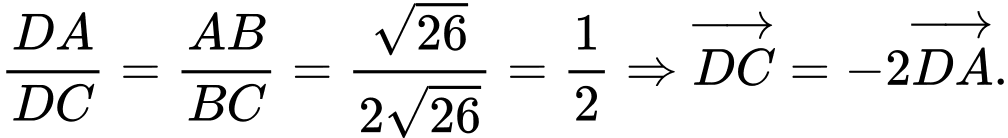
Khi đó
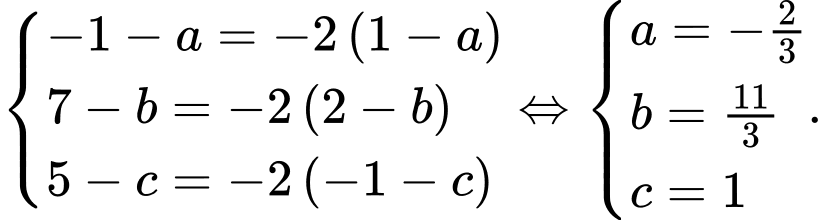
Vậy
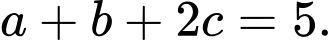 Đáp án: D
Đáp án: D
Câu 21 [380218]: Trong không gian với hệ tọa độ 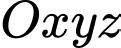 , cho hai điểm
, cho hai điểm 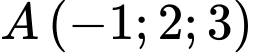 và
và 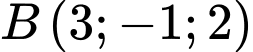 . Điểm
. Điểm 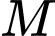 thỏa mãn
thỏa mãn 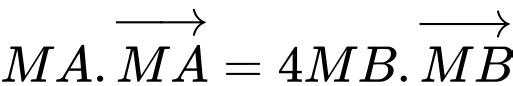 tính độ dài đoạn thẳng
tính độ dài đoạn thẳng 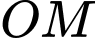 (làm tròn đến một chữ số thập phân)
(làm tròn đến một chữ số thập phân)
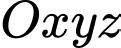 , cho hai điểm
, cho hai điểm 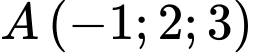 và
và 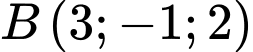 . Điểm
. Điểm 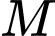 thỏa mãn
thỏa mãn 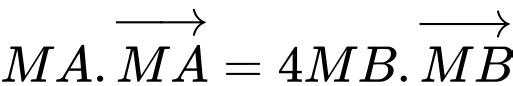 tính độ dài đoạn thẳng
tính độ dài đoạn thẳng 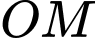 (làm tròn đến một chữ số thập phân)
(làm tròn đến một chữ số thập phân)
Gọi 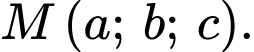
Ta có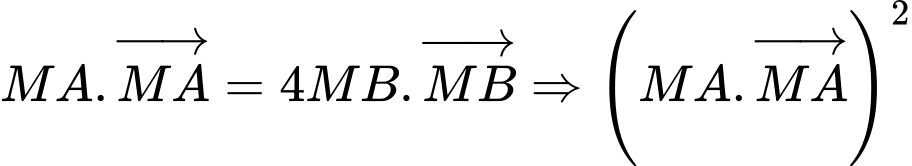
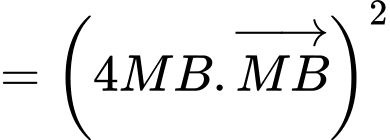
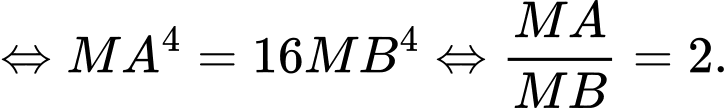
Với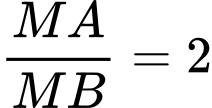 khi đó
khi đó 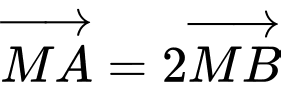
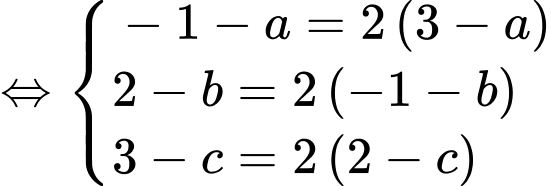
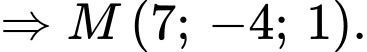
Suy ra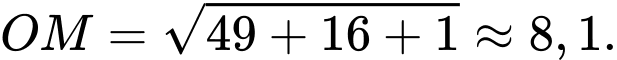
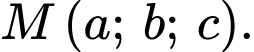
Ta có
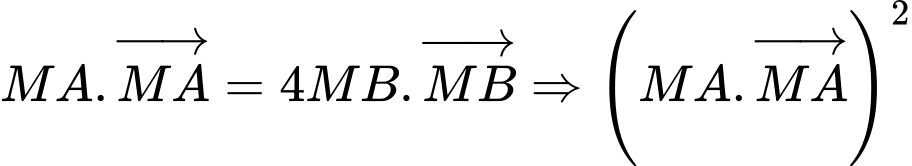
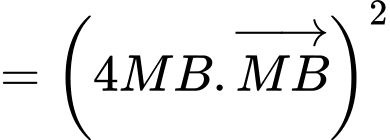
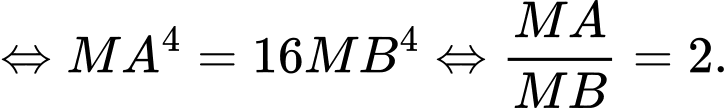
Với
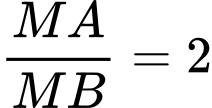 khi đó
khi đó 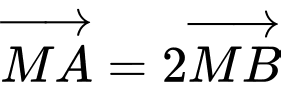
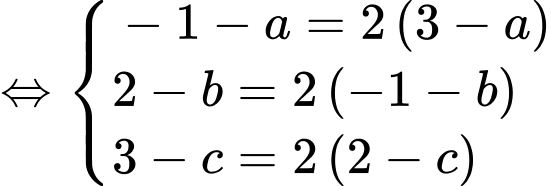
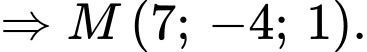
Suy ra
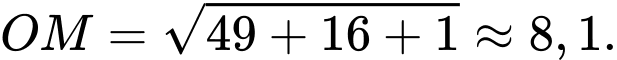
Câu 22 [216405]: Trong không gian tọa độ 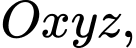 cho điểm
cho điểm 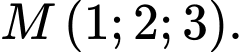 Đường thẳng
Đường thẳng 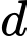 đi qua điểm
đi qua điểm 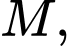 cắt tia
cắt tia 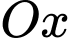 tại
tại 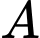 và cắt mặt phẳng
và cắt mặt phẳng 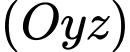 tại
tại 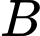 sao cho
sao cho 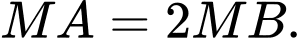 Độ dài đoạn thẳng
Độ dài đoạn thẳng  bằng
bằng
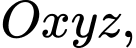 cho điểm
cho điểm 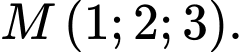 Đường thẳng
Đường thẳng 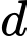 đi qua điểm
đi qua điểm 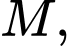 cắt tia
cắt tia 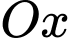 tại
tại 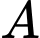 và cắt mặt phẳng
và cắt mặt phẳng 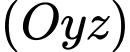 tại
tại 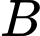 sao cho
sao cho 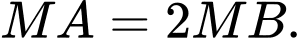 Độ dài đoạn thẳng
Độ dài đoạn thẳng  bằng
bằng A, 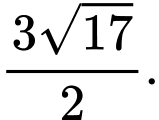
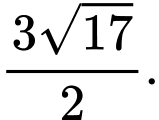
B, 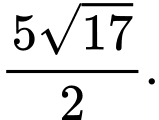
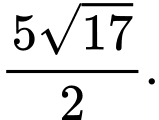
C, 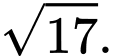
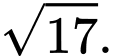
D, 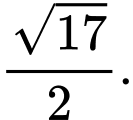
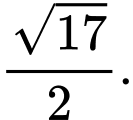
Gọi 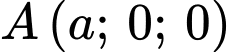 là giao điểm của
là giao điểm của 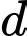 và
và 
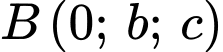 là giao điểm của
là giao điểm của 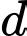 và
và 
Ta có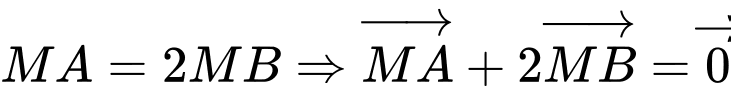
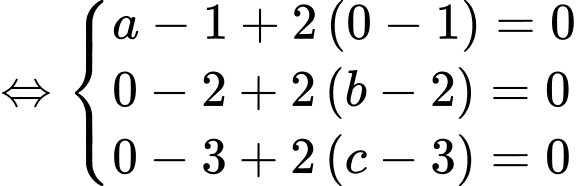
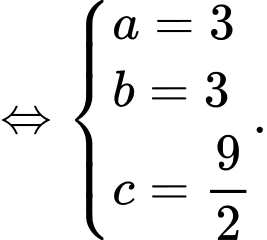
Khi đó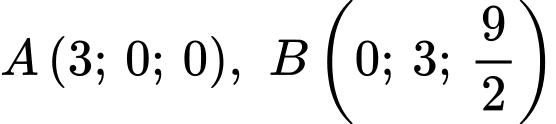 và
và 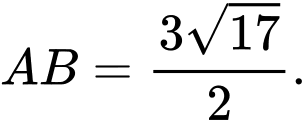
Chọn A. Đáp án: A
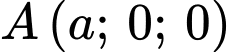 là giao điểm của
là giao điểm của 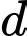 và
và 
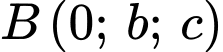 là giao điểm của
là giao điểm của 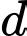 và
và 
Ta có
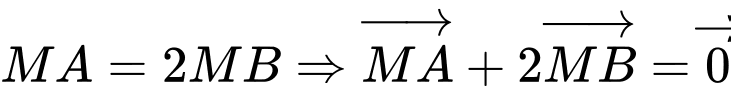
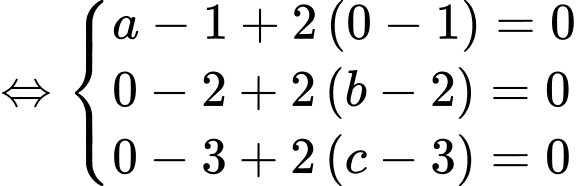
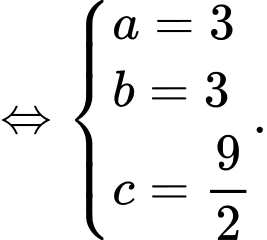
Khi đó
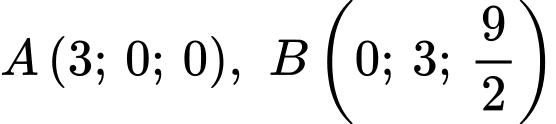 và
và 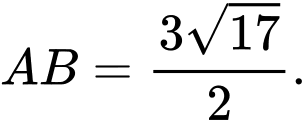
Chọn A. Đáp án: A
Câu 23 [399641]: Trong không gian với hệ trục tọa độ 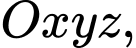 cho
cho 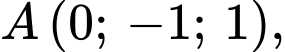
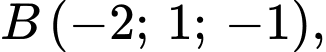
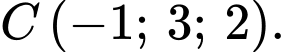
Điểm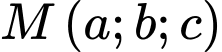 để biểu thức
để biểu thức 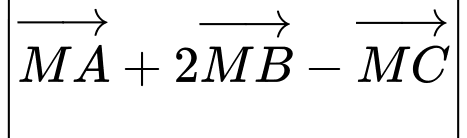 đạt giá trị nhỏ nhất, tổng
đạt giá trị nhỏ nhất, tổng 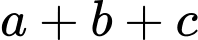 bằng
bằng
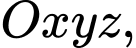 cho
cho 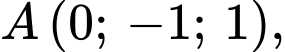
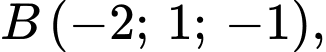
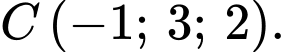
Điểm
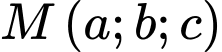 để biểu thức
để biểu thức 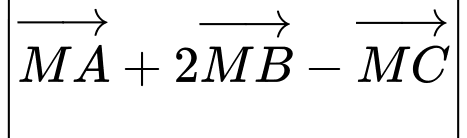 đạt giá trị nhỏ nhất, tổng
đạt giá trị nhỏ nhất, tổng 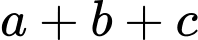 bằng
bằng
Đáp số: 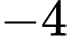
Gọi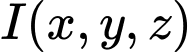 là điểm thỏa mãn
là điểm thỏa mãn
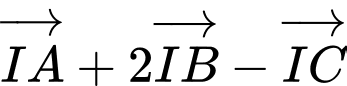
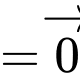 thì tọa độ điểm
thì tọa độ điểm 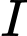 thỏa mãn
thỏa mãn
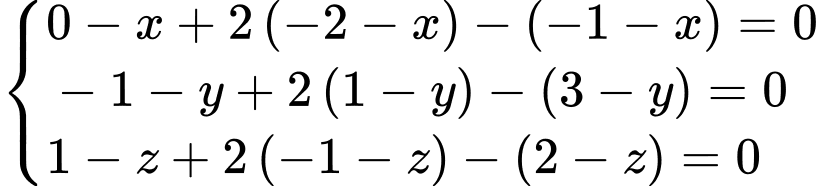

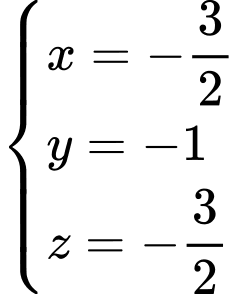
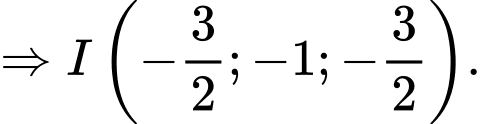
Khi đó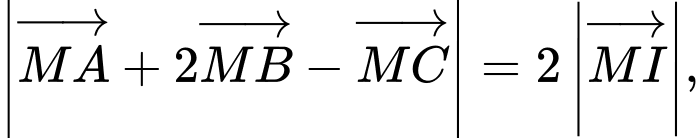 nên
nên
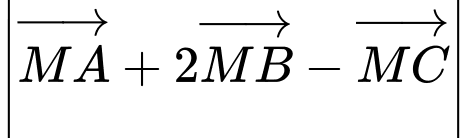 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi
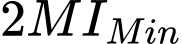
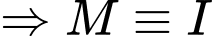
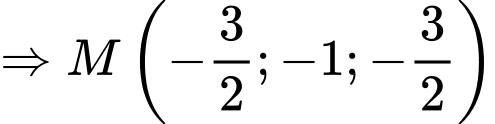
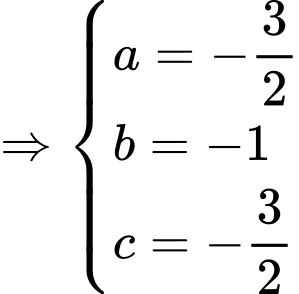

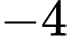
Gọi
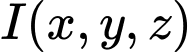 là điểm thỏa mãn
là điểm thỏa mãn 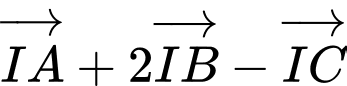
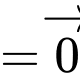 thì tọa độ điểm
thì tọa độ điểm 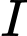 thỏa mãn
thỏa mãn 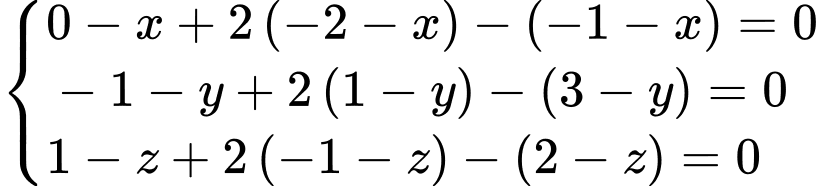

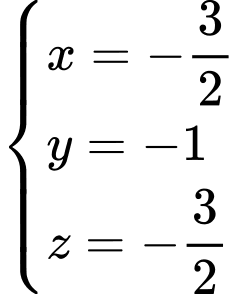
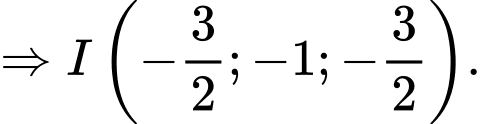
Khi đó
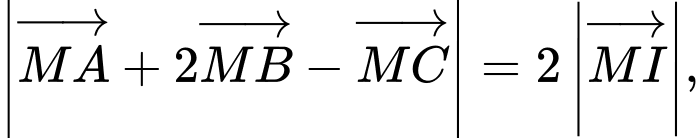 nên
nên 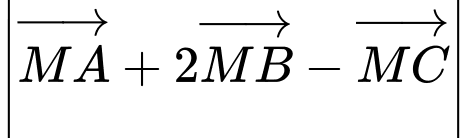 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi 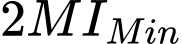
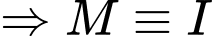
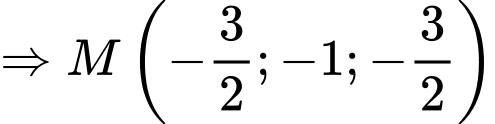
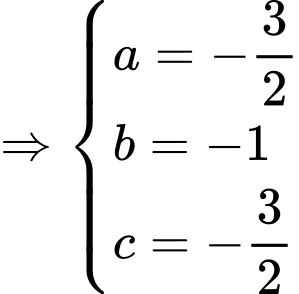

Câu 24 [398657]: Trong không gian 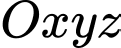 , cho hai điểm
, cho hai điểm 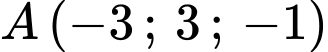 ,
, 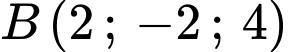 . Xét điểm
. Xét điểm 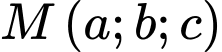 thuộc mặt phẳng
thuộc mặt phẳng 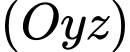 sao cho biểu thức
sao cho biểu thức 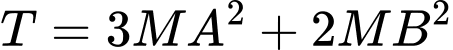 đạt giá trị nhỏ nhất. Khi đó
đạt giá trị nhỏ nhất. Khi đó 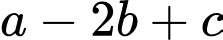 .
.
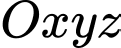 , cho hai điểm
, cho hai điểm 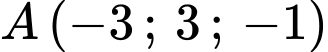 ,
, 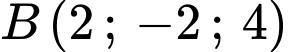 . Xét điểm
. Xét điểm 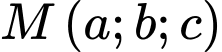 thuộc mặt phẳng
thuộc mặt phẳng 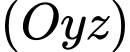 sao cho biểu thức
sao cho biểu thức 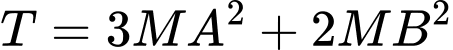 đạt giá trị nhỏ nhất. Khi đó
đạt giá trị nhỏ nhất. Khi đó 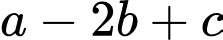 .
. A,  .
.
 .
.B, 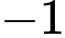 .
.
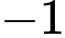 .
.C, 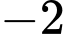 .
.
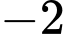 .
.D, 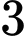 .
.
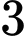 .
.
Chọn B
Xét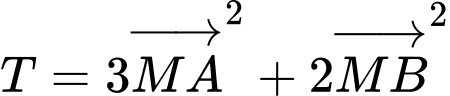
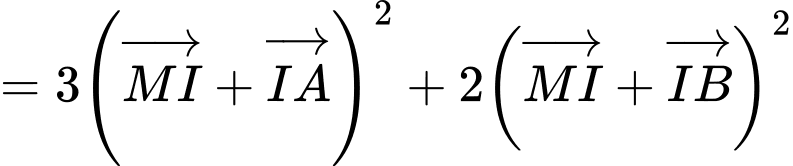
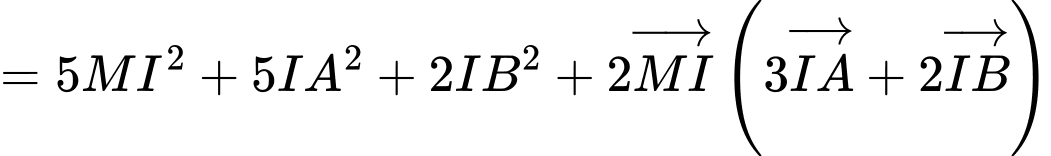
Gọi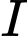 là điểm thỏa mãn
là điểm thỏa mãn 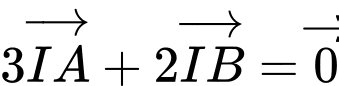
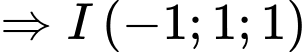
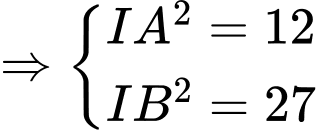
Khi đó: . Do đó
. Do đó 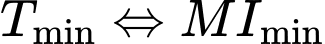 .
.
Gọi là hình chiếu vuông góc của
là hình chiếu vuông góc của  lên mặt phẳng
lên mặt phẳng 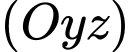
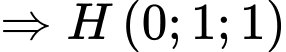
Dễ thấy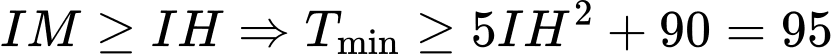
Dấu “=” xảy ra
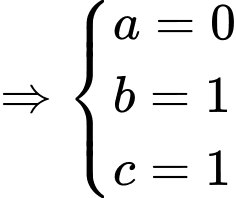
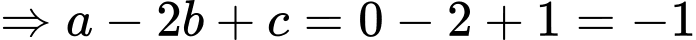 Đáp án: B
Đáp án: B
Xét
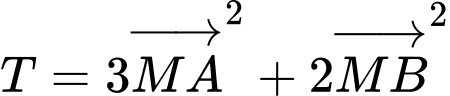
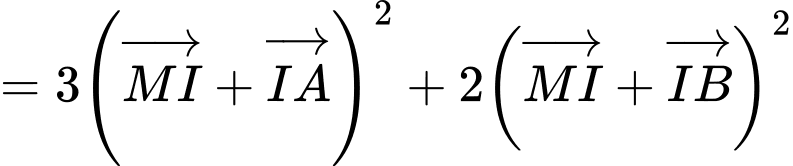
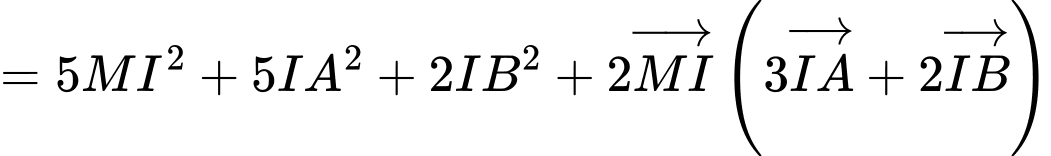
Gọi
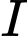 là điểm thỏa mãn
là điểm thỏa mãn 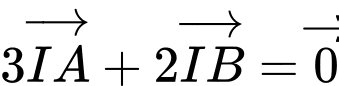
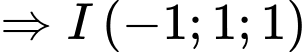
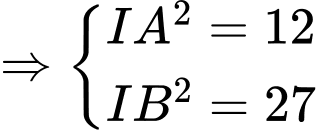
Khi đó:
 . Do đó
. Do đó 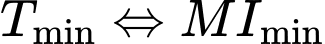 .
.Gọi
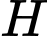 là hình chiếu vuông góc của
là hình chiếu vuông góc của 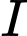 lên mặt phẳng
lên mặt phẳng 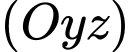
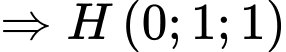
Dễ thấy
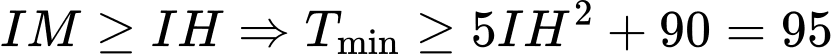
Dấu “=” xảy ra

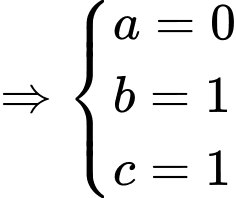
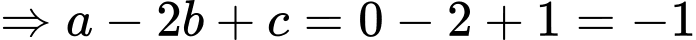 Đáp án: B
Đáp án: B
Câu 25 [399652]: Cho 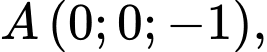
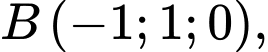
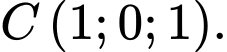 Điểm
Điểm 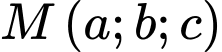 thoả
thoả 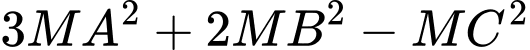 đạt giá trị nhỏ nhất. Tính
đạt giá trị nhỏ nhất. Tính 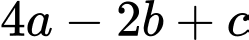
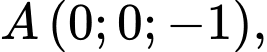
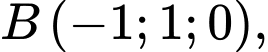
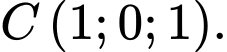 Điểm
Điểm 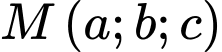 thoả
thoả 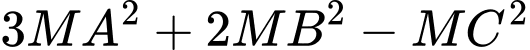 đạt giá trị nhỏ nhất. Tính
đạt giá trị nhỏ nhất. Tính 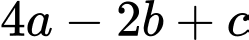
Đáp số: 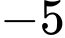
Ta có: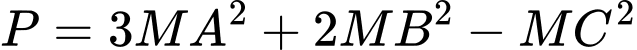
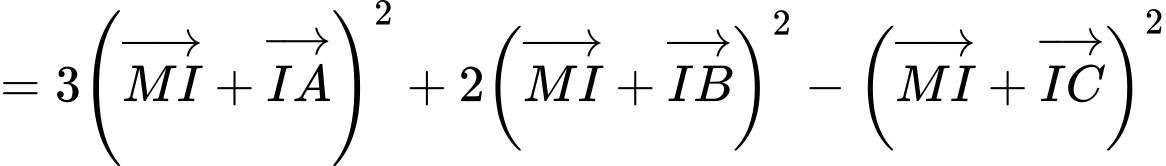
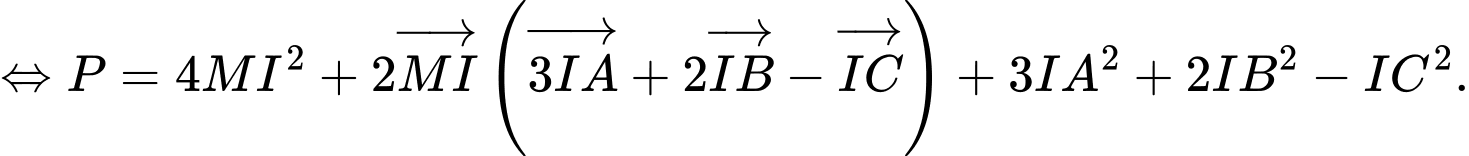
Chọn điểm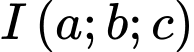 thoả
thoả 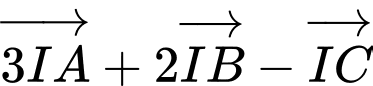
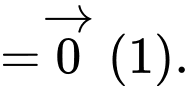
Khi đó

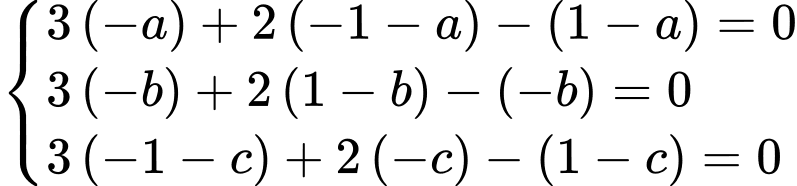

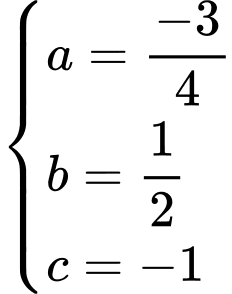
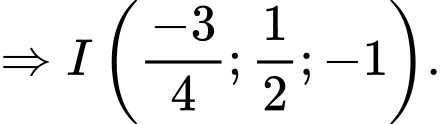
Do tổng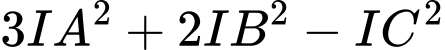 không đổi nên
không đổi nên 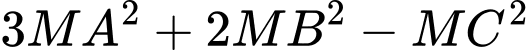 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi 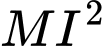 nhỏ nhất.
nhỏ nhất.
Vậy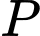 nhỏ nhất thì
nhỏ nhất thì 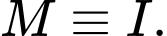 Vậy
Vậy 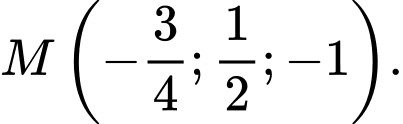
Suy ra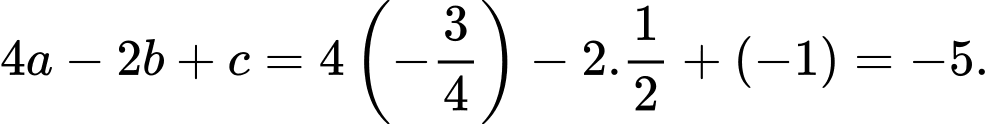
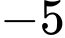
Ta có:
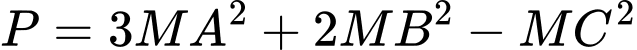
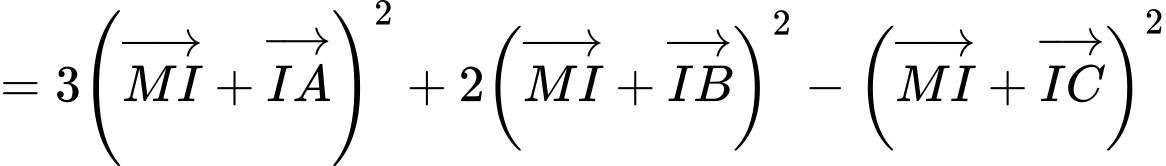
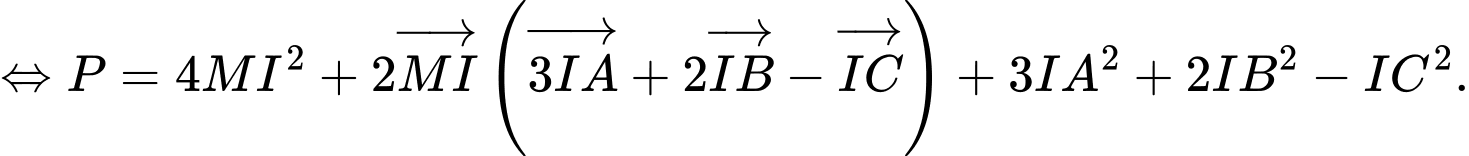
Chọn điểm
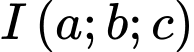 thoả
thoả 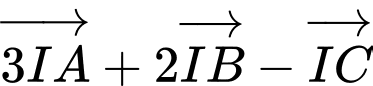
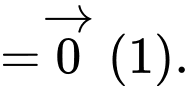
Khi đó


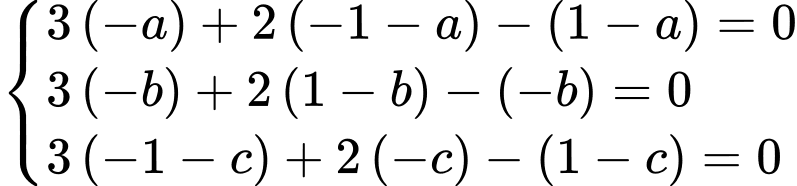

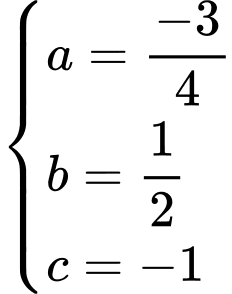
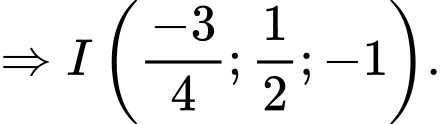
Do tổng
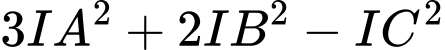 không đổi nên
không đổi nên 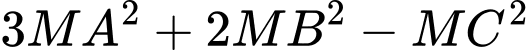 đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi 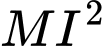 nhỏ nhất.
nhỏ nhất. Vậy
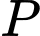 nhỏ nhất thì
nhỏ nhất thì 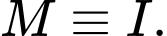 Vậy
Vậy 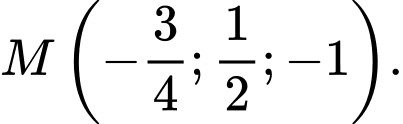
Suy ra
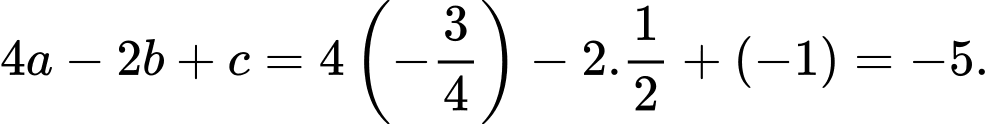
Câu 26 [384968]: Trong không gian 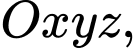 cho hai điểm
cho hai điểm 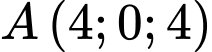 và
và 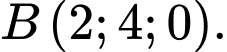 Điểm
Điểm 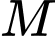 di động trên tia
di động trên tia 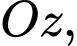 điểm
điểm 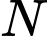 di động trên tia
di động trên tia 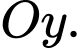 Đường gấp khúc
Đường gấp khúc 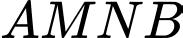 có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
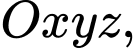 cho hai điểm
cho hai điểm 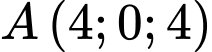 và
và 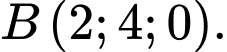 Điểm
Điểm 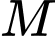 di động trên tia
di động trên tia 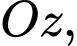 điểm
điểm 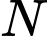 di động trên tia
di động trên tia 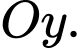 Đường gấp khúc
Đường gấp khúc 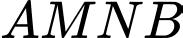 có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục). Đáp số:……………………………..
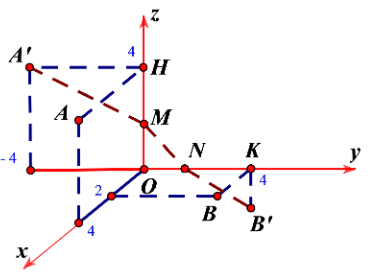
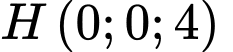 và
và 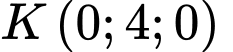 là hình chiếu của
là hình chiếu của 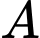 trên
trên  và
và 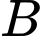 trên
trên 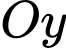
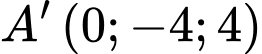 ;
; 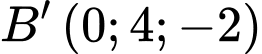
Xét hai tam giác vuông 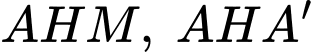 có chung
có chung
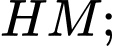
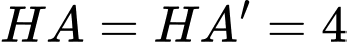
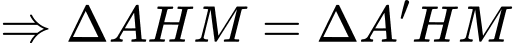 (2 cạnh góc vuông)
(2 cạnh góc vuông)
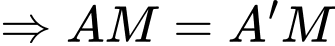
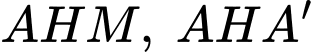 có chung
có chung
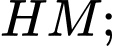
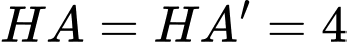
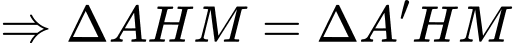 (2 cạnh góc vuông)
(2 cạnh góc vuông)
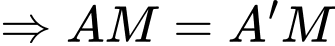
Chứng minh tương tự ta có 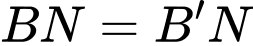
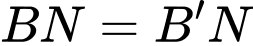
Độ dài đường gấp khúc 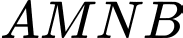 là
là

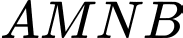 là
là

Vậy đường gấp khúc 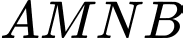 có độ dài nhỏ nhất bằng 10
có độ dài nhỏ nhất bằng 10
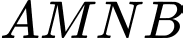 có độ dài nhỏ nhất bằng 10
có độ dài nhỏ nhất bằng 10