Đáp án Bài tập tự luyện số 2
Câu 1 [79878]: Cho hai số thực dương 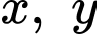 thỏa mãn
thỏa mãn 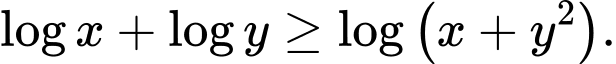 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 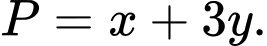
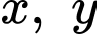 thỏa mãn
thỏa mãn 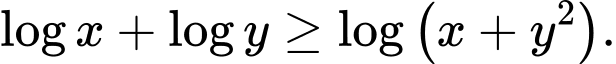 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 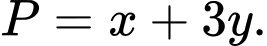
A, 1.
B, 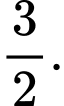
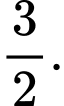
C, 9.
D, 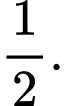
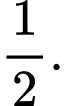
Ta có 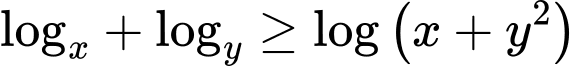
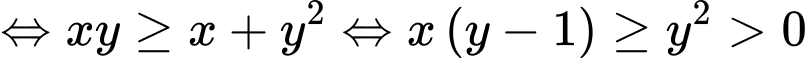
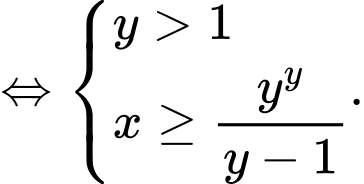
Khi đó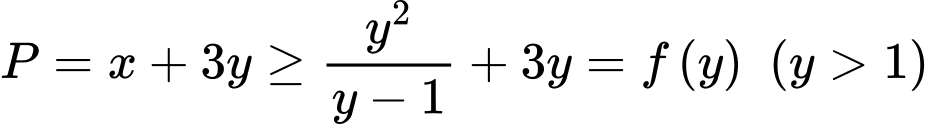
Ta có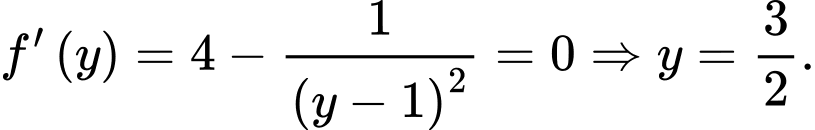
Lại có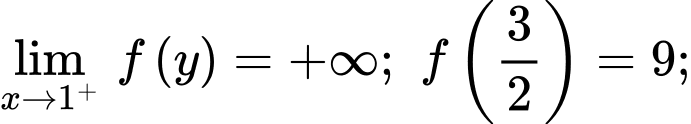
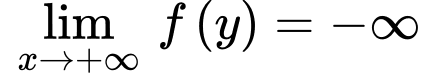
Suy ra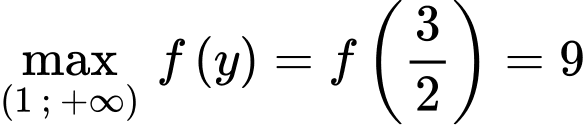
Suy ra
Chọn đáp án C. Đáp án: C
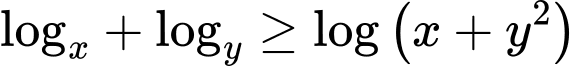
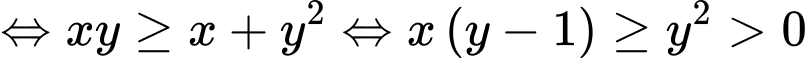
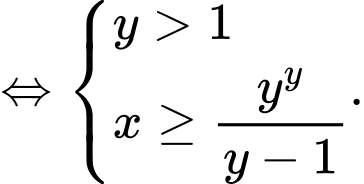
Khi đó
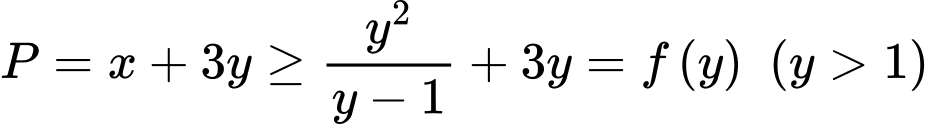
Ta có
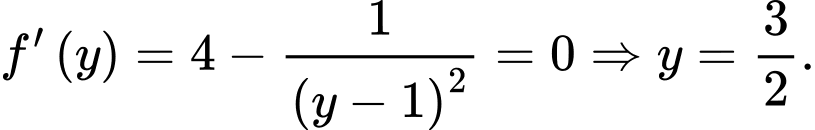
Lại có
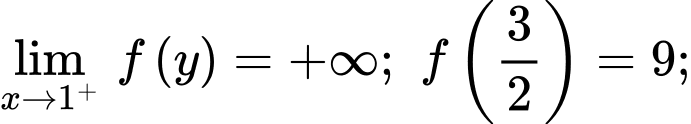
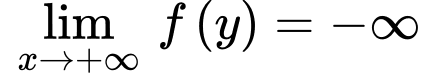
Suy ra
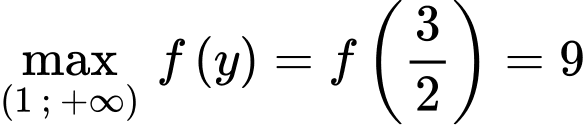
Suy ra

Chọn đáp án C. Đáp án: C
Câu 2 [511326]: Xét các số thực dương 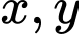 thỏa mãn
thỏa mãn 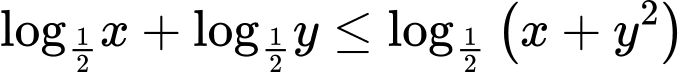 . Tìm giá trị nhỏ nhất
. Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 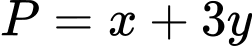 .
.
 thỏa mãn
thỏa mãn 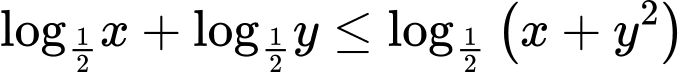 . Tìm giá trị nhỏ nhất
. Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 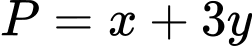 .
. A, 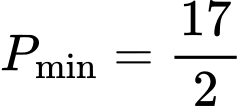
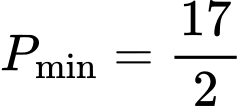
B, 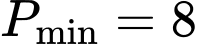 .
.
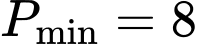 .
.C, 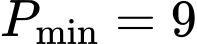 .
.
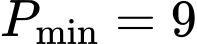 .
.D, 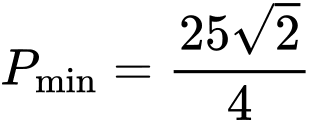 .
.
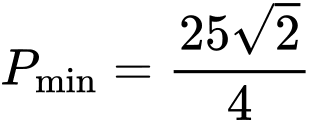 .
.
Chọn C
Với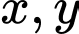 dương, ta có:
dương, ta có:
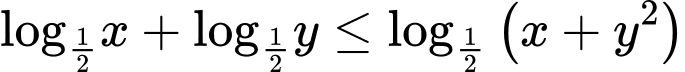
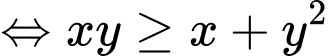
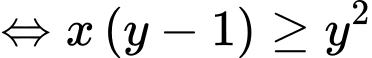
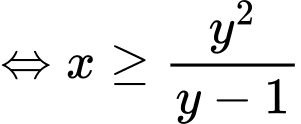 (vì
(vì 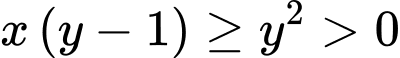 nên
nên 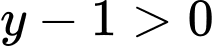 ).
).
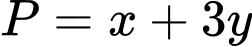
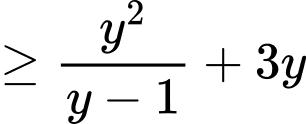
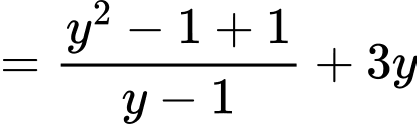
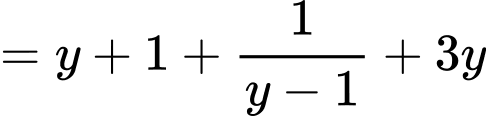
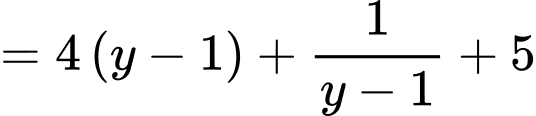
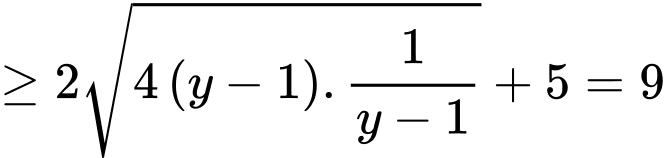 .
.
Đẳng thức xảy ra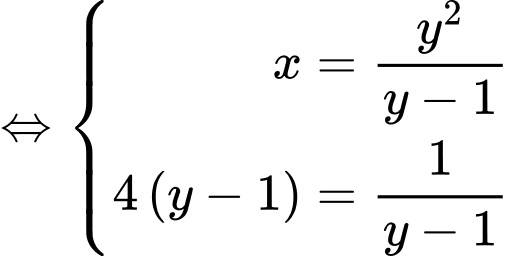
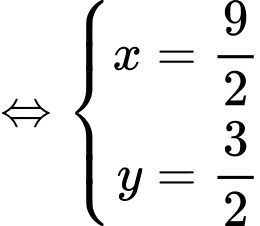 .
.
Vậy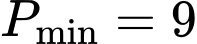 khi
khi 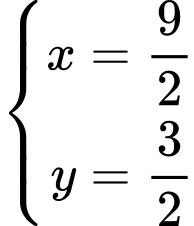 . Đáp án: C
. Đáp án: C
Với
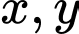 dương, ta có:
dương, ta có: 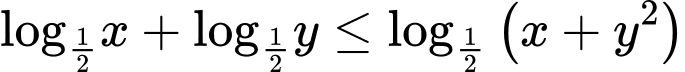
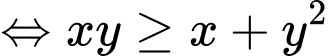
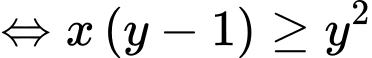
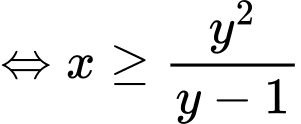 (vì
(vì 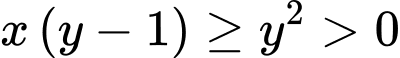 nên
nên 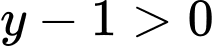 ).
).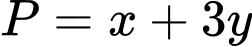
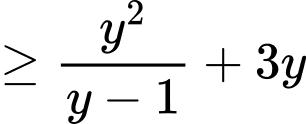
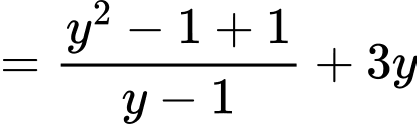
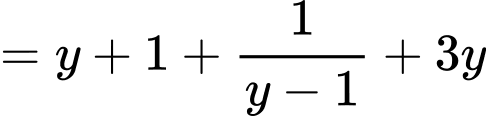
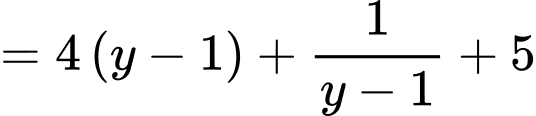
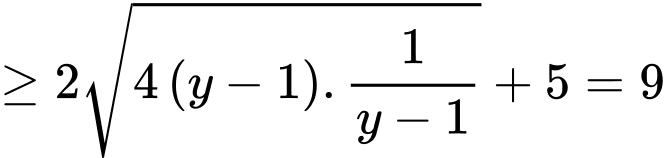 .
.Đẳng thức xảy ra
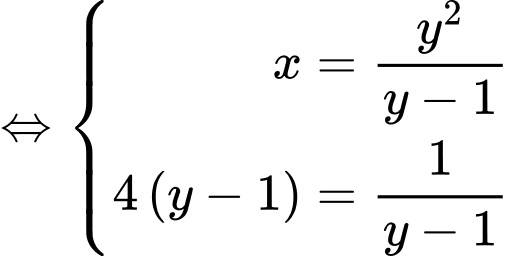
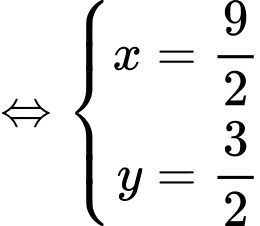 .
.Vậy
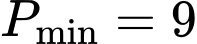 khi
khi 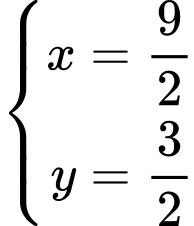 . Đáp án: C
. Đáp án: C
Câu 3 [510423]: [Học kỳ 2-Chuyên LHP-Nam Định] Xét các số thực 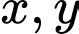 thỏa mãn
thỏa mãn 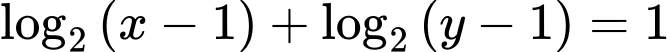 . Khi biểu thức
. Khi biểu thức 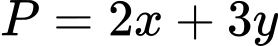 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 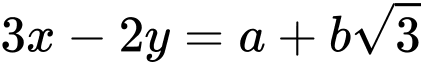 với
với 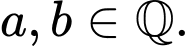 Tính
Tính 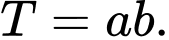
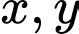 thỏa mãn
thỏa mãn 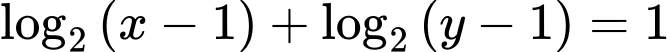 . Khi biểu thức
. Khi biểu thức 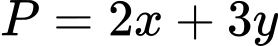 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 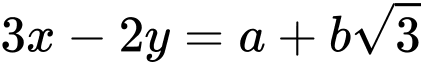 với
với 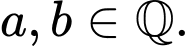 Tính
Tính 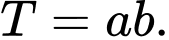
A, 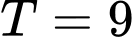 .
.
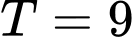 .
.B, 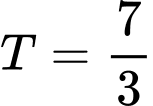 .
.
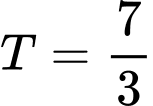 .
.C, 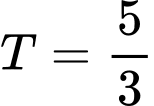 .
.
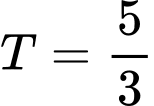 .
.D, 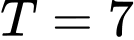 .
.
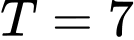 .
.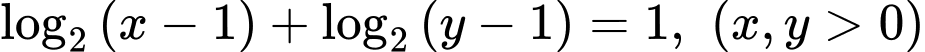
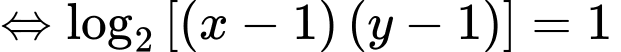
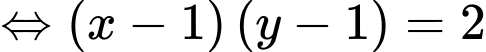
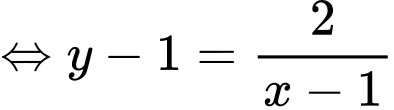
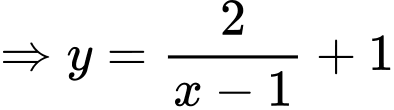
Có:
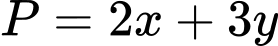
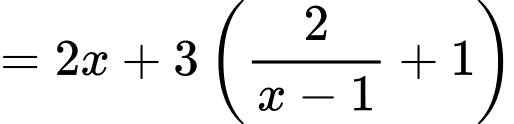
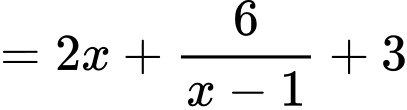
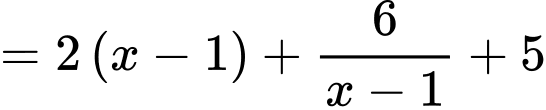
Áp dụng bất đẳng thức Co-si, ta có:
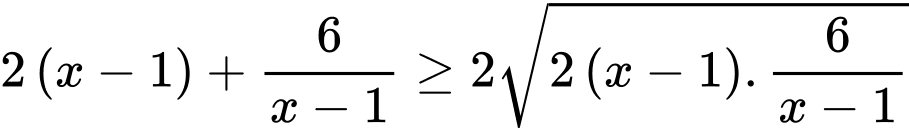
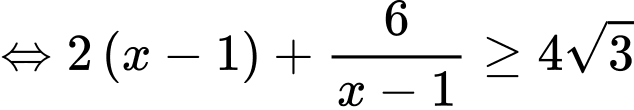
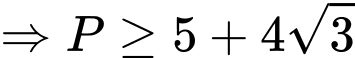
Dấu ‘’=’’ xảy ra khi và chỉ khi:
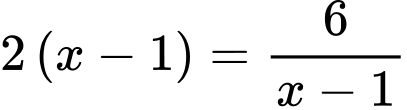
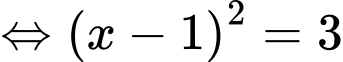
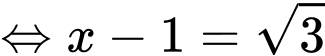
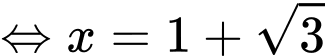
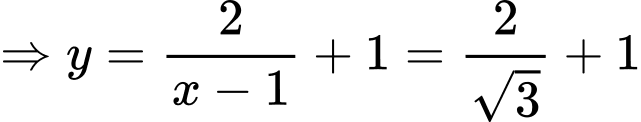
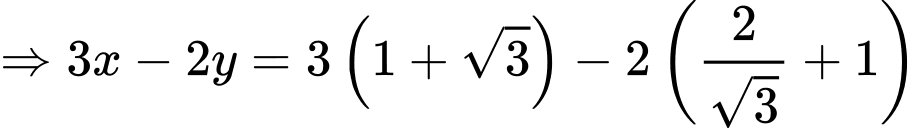
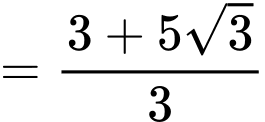
Đáp án: C. Đáp án: C
Câu 4 [29507]: Xét các số thực 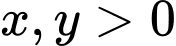 :
: 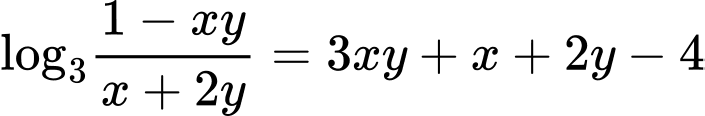 . Tìm giá trị nhỏ nhất của
. Tìm giá trị nhỏ nhất của 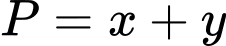
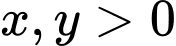 :
: 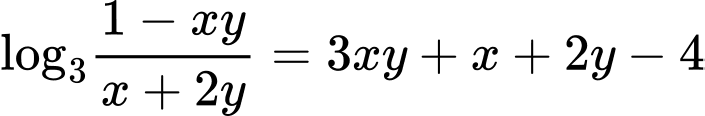 . Tìm giá trị nhỏ nhất của
. Tìm giá trị nhỏ nhất của 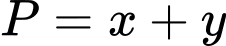
A, 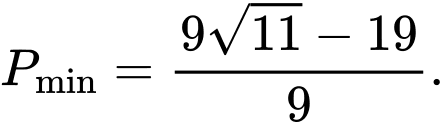
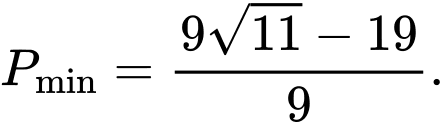
B, 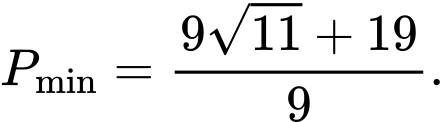
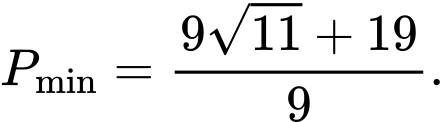
C, 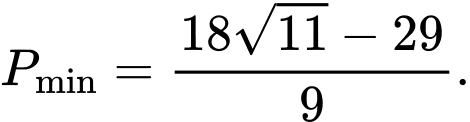
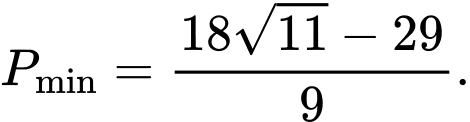
D, 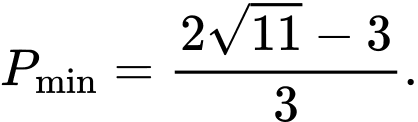
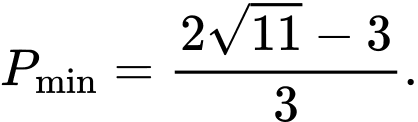
Ta có 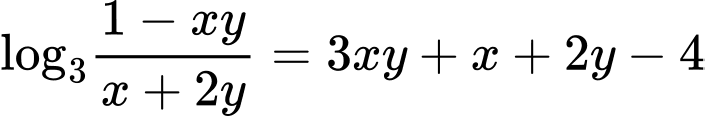
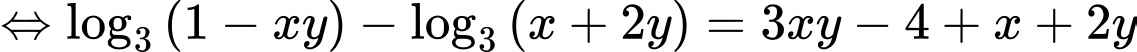
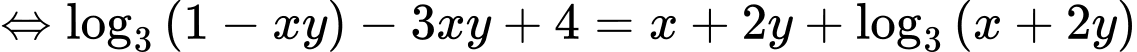


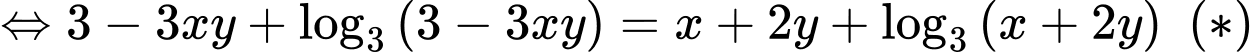
Xét hàm số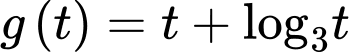 trên khoảng
trên khoảng 
Ta có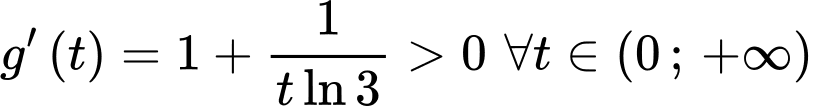
Suy ra hàm số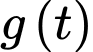 đồng biến trên khoảng
đồng biến trên khoảng 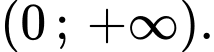
Khi đó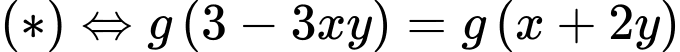
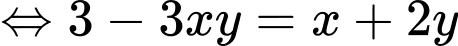
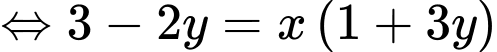
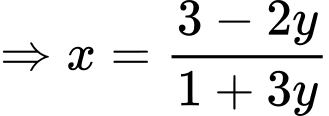
Vì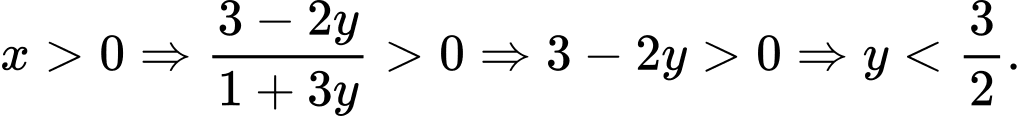
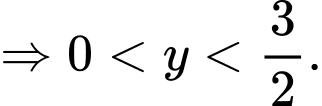
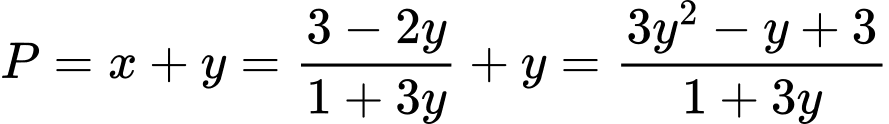
Khảo sát hàm số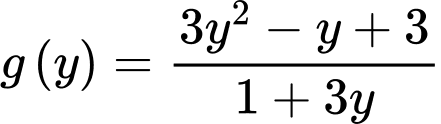 trên khoảng
trên khoảng 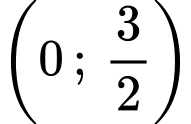
Ta có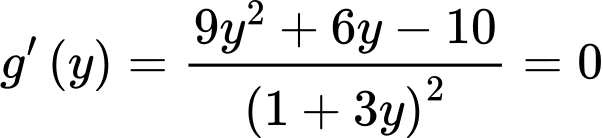
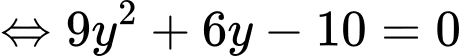
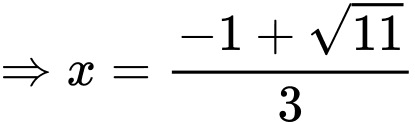
Lại có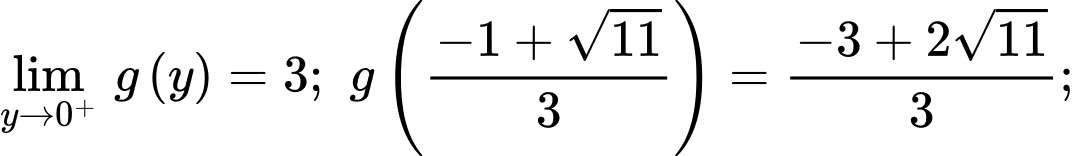
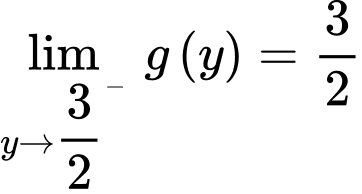
Suy ra giá trị nhỏ nhất của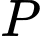 bằng
bằng 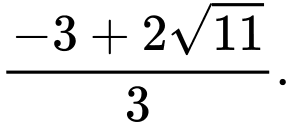
Chọn D.Đáp án: D
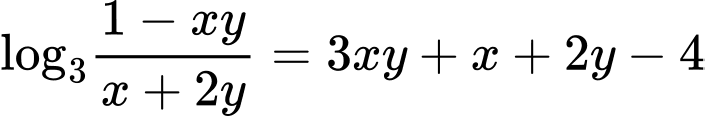
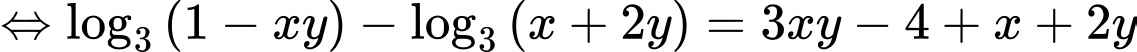
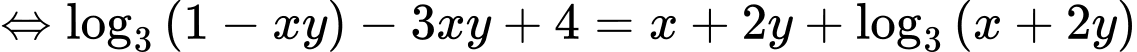


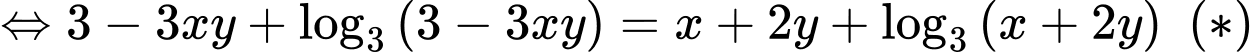
Xét hàm số
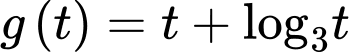 trên khoảng
trên khoảng 
Ta có
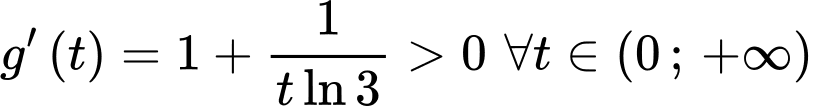
Suy ra hàm số
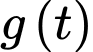 đồng biến trên khoảng
đồng biến trên khoảng 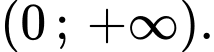
Khi đó
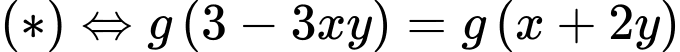
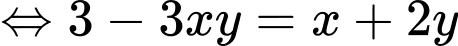
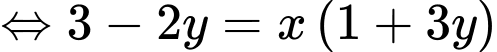
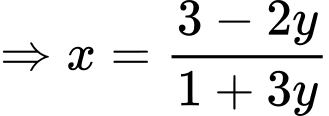
Vì
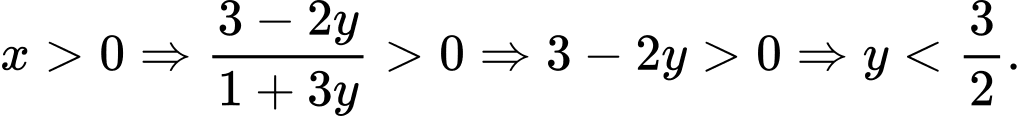
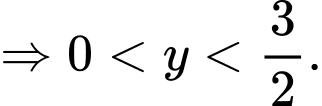
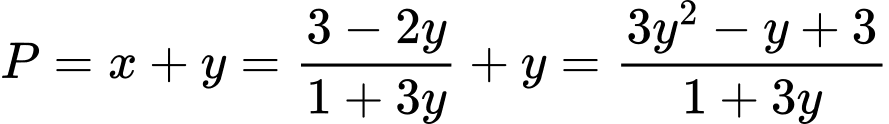
Khảo sát hàm số
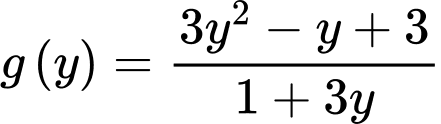 trên khoảng
trên khoảng 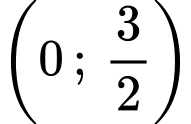
Ta có
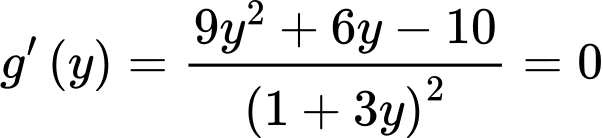
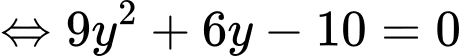
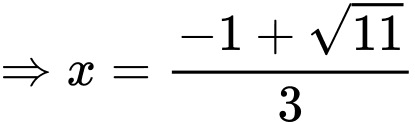
Lại có
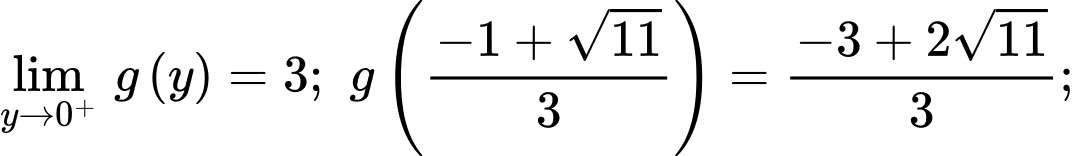
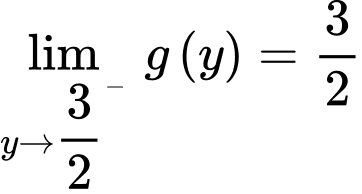
Suy ra giá trị nhỏ nhất của
 bằng
bằng 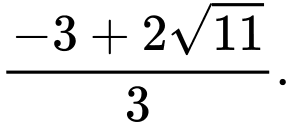
Chọn D.Đáp án: D
Câu 5 [25941]: Cho 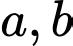 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 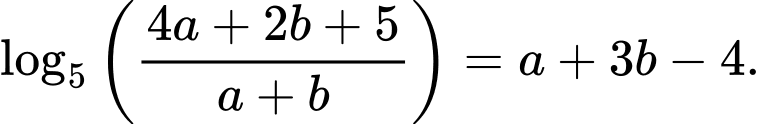 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 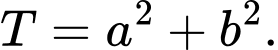
 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 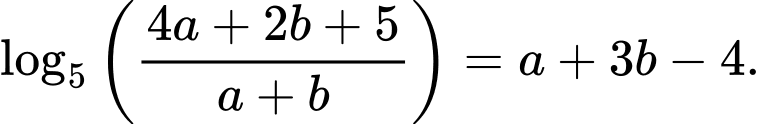 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 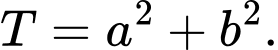
A, 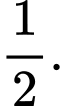
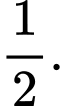
B, 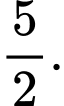
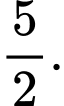
C, 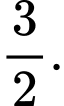
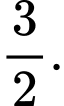
D, 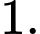
Ta có 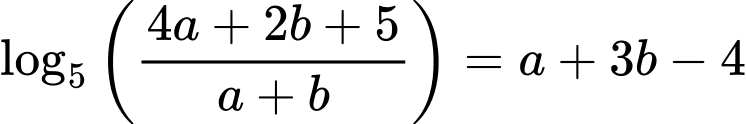

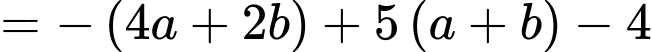

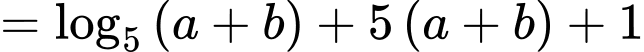

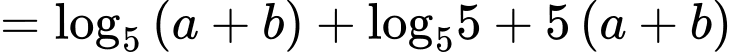

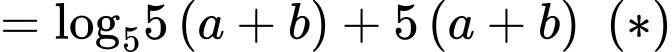
Xét hàm đặc trưng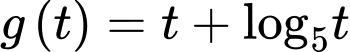 trên khoảng
trên khoảng 
Ta có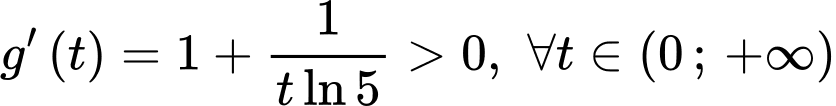
Suy ra hàm số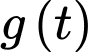 đồng biến trên
đồng biến trên 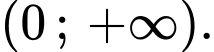
Khi đó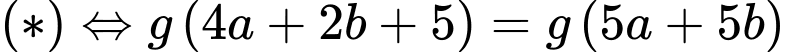
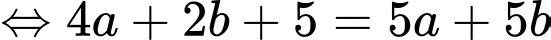
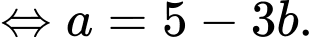
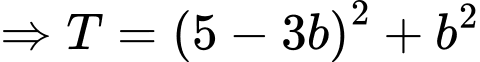
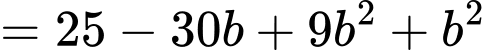
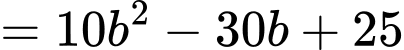
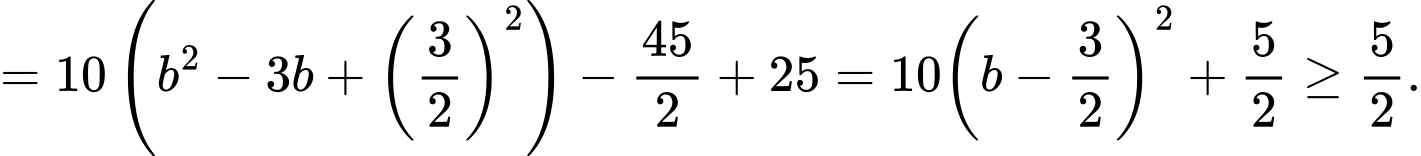
Vậy giá trị nhỏ nhất của biểu thức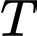 là
là 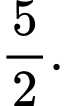 Đáp án: B
Đáp án: B
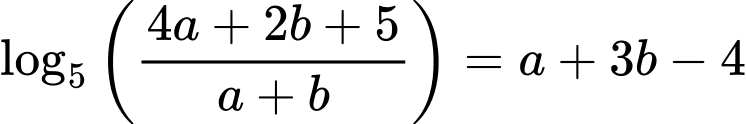

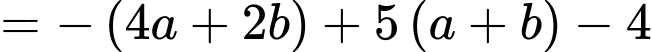

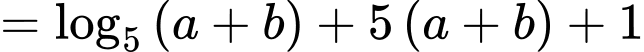

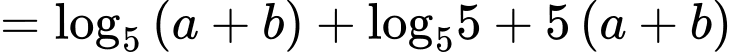

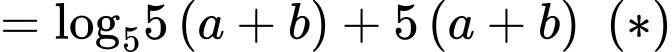
Xét hàm đặc trưng
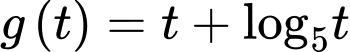 trên khoảng
trên khoảng 
Ta có
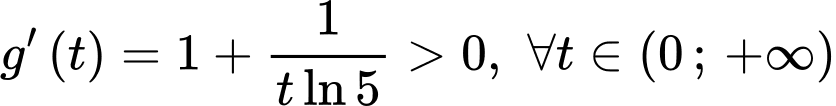
Suy ra hàm số
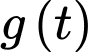 đồng biến trên
đồng biến trên 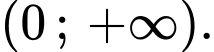
Khi đó
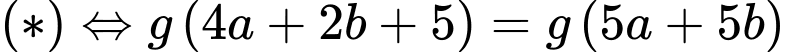
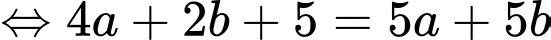
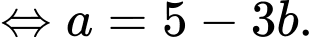
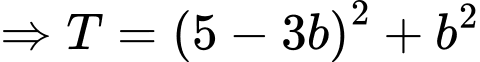
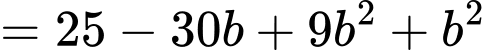
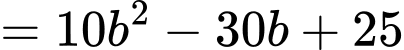
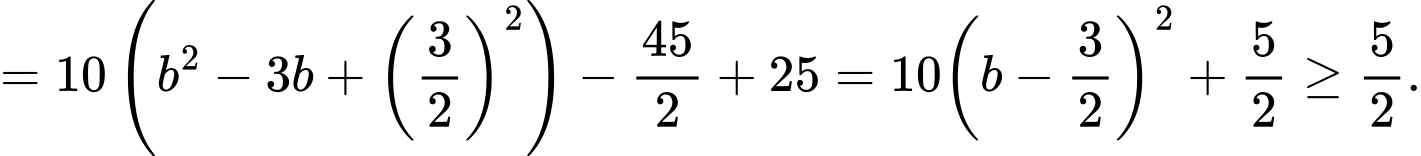
Vậy giá trị nhỏ nhất của biểu thức
 là
là 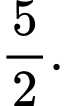 Đáp án: B
Đáp án: B
Câu 6 [79780]: [Đề thi THPTQG năm 2017] Xét các số thực dương 𝑎, 𝑏 thỏa mãn 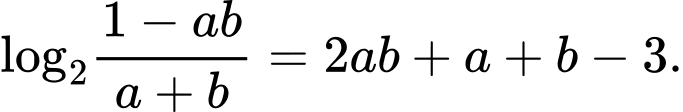 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của
của 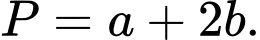
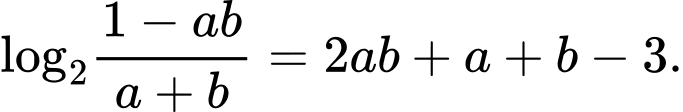 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của
của 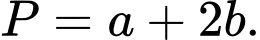
A, 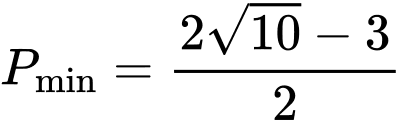 .
.
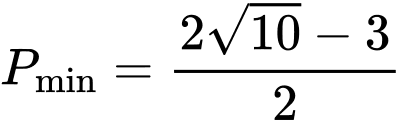 .
.B, 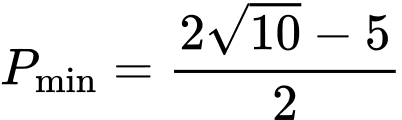 .
.
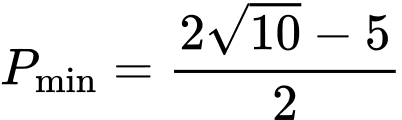 .
.C, 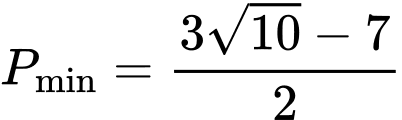 .
.
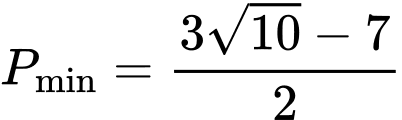 .
.D, 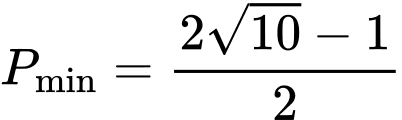 .
.
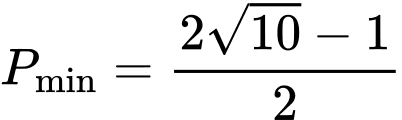 .
.
Ta có 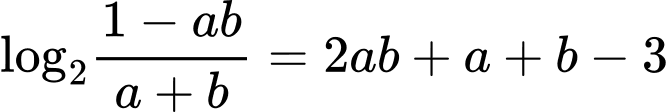
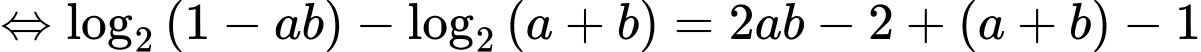
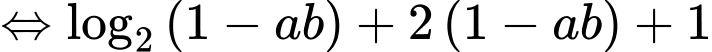
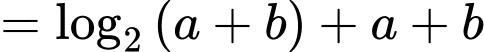
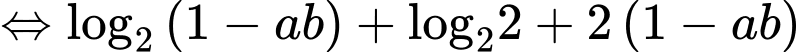
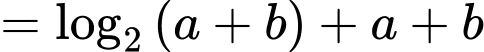
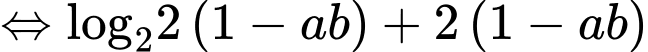
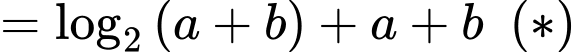
Xét hàm đặc trưng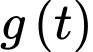
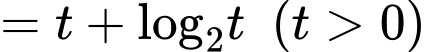
Ta có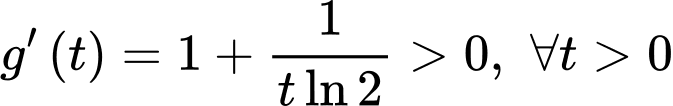
Suy ra hàm số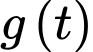 đồng biến trên
đồng biến trên 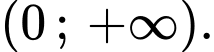
Khi đó
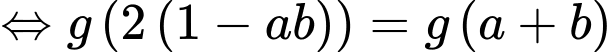
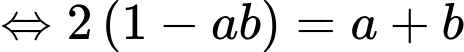
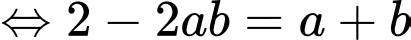
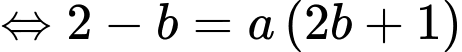
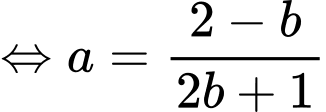
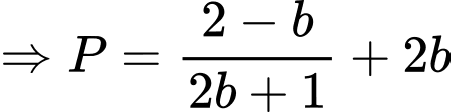
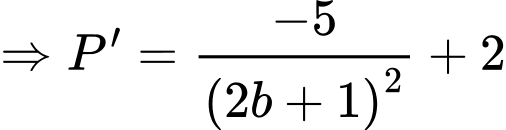
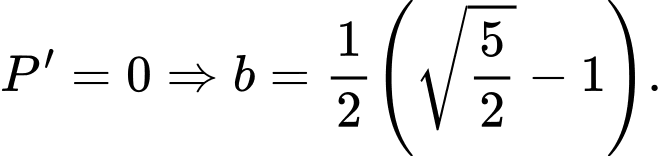
Lại có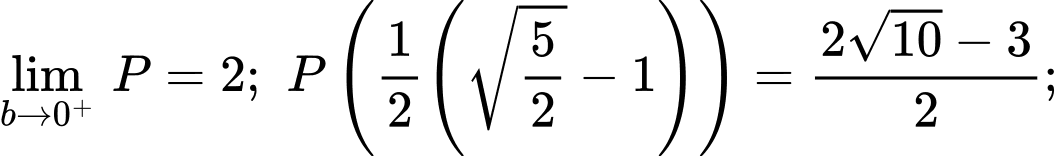
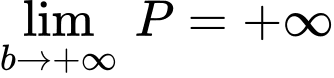
Suy ra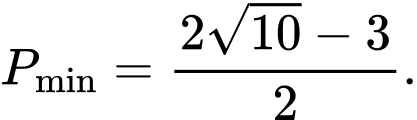 Chọn A. Đáp án: A
Chọn A. Đáp án: A
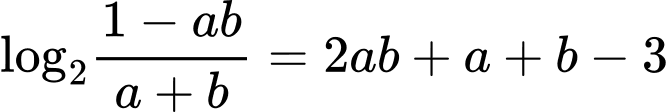
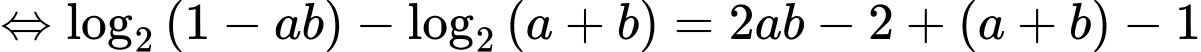
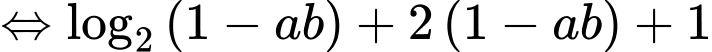
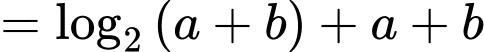
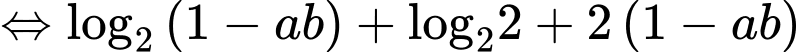
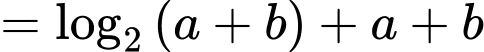
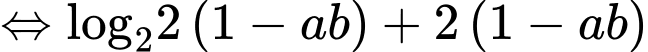
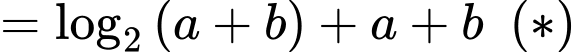
Xét hàm đặc trưng
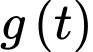
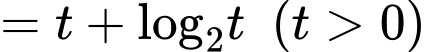
Ta có
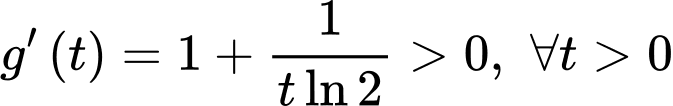
Suy ra hàm số
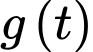 đồng biến trên
đồng biến trên 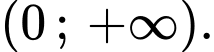
Khi đó

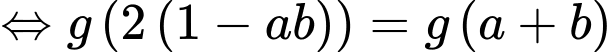
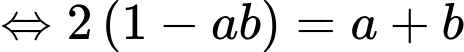
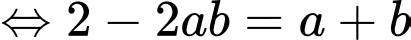
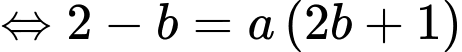
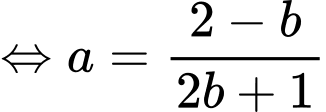
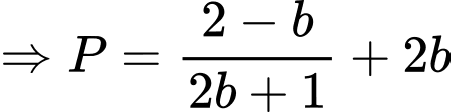
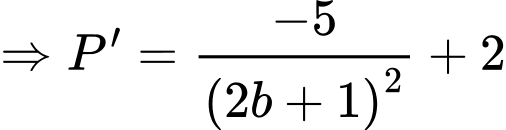
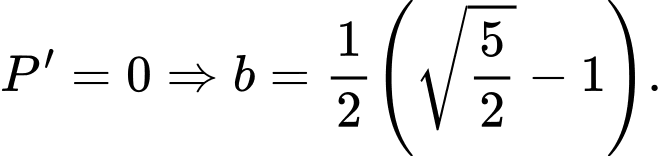
Lại có
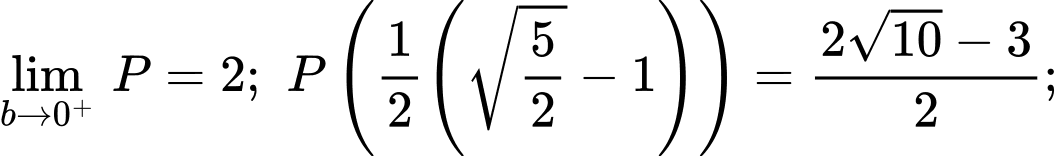
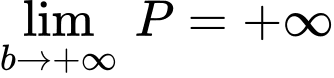
Suy ra
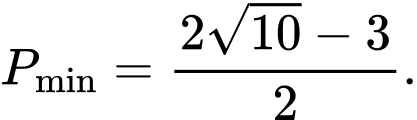 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 7 [29495]: Cho hai số thực dương 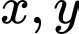 thay đổi thỏa mãn hệ thức
thay đổi thỏa mãn hệ thức 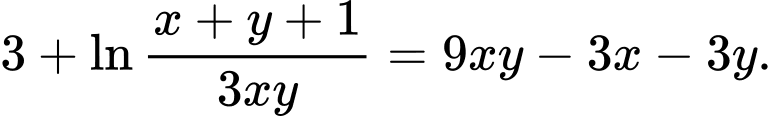 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất 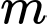 của biểu thức
của biểu thức 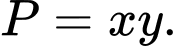
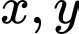 thay đổi thỏa mãn hệ thức
thay đổi thỏa mãn hệ thức 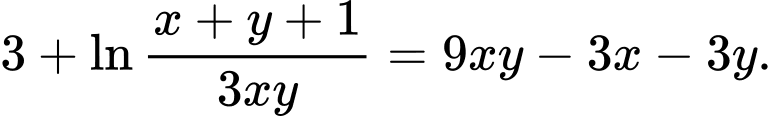 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 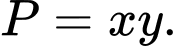
A, 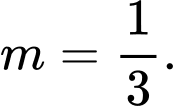
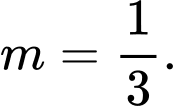
B, 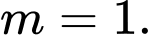
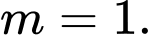
C, 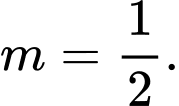
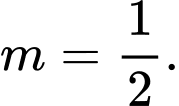
D, 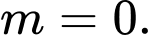
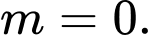
Ta có 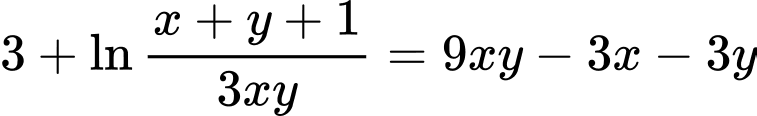
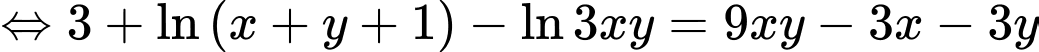
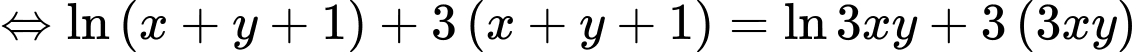
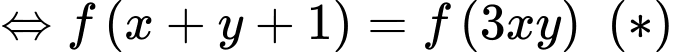
Xét hàm đặc trưng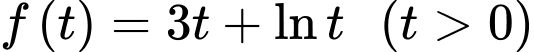
Ta có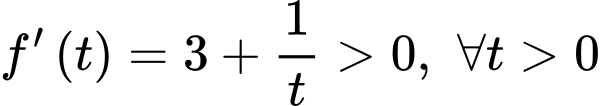
Suy ra hàm số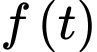 đồng biến.
đồng biến.
Khi đó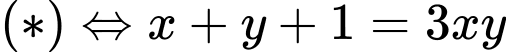
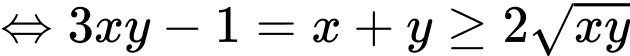 (theo BĐT AM – GM)
(theo BĐT AM – GM)
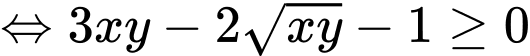
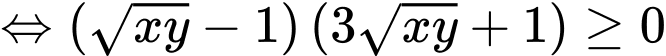
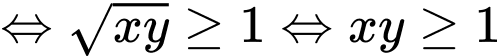
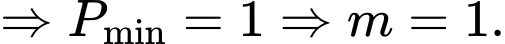
Chọn B. Đáp án: B
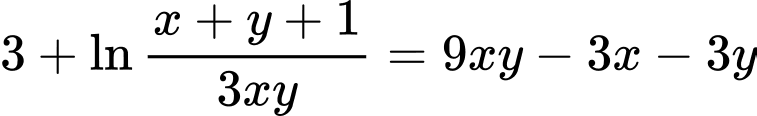
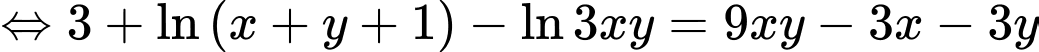
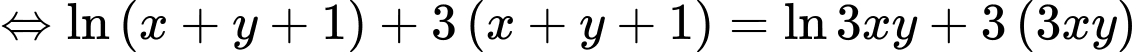
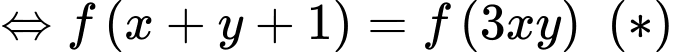
Xét hàm đặc trưng
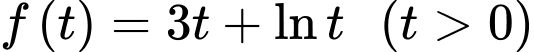
Ta có
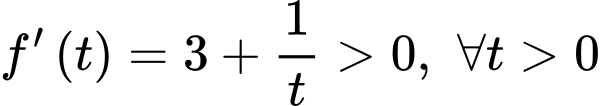
Suy ra hàm số
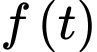 đồng biến.
đồng biến.
Khi đó
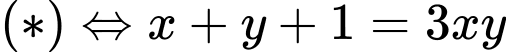
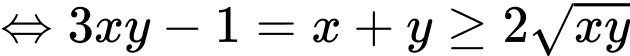 (theo BĐT AM – GM)
(theo BĐT AM – GM)
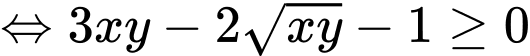
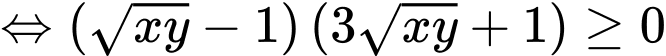
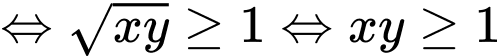
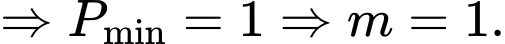
Chọn B. Đáp án: B
Câu 8 [789066]: (SỞ GD&ĐT TIỀN GIANG NĂM 2019-2020) Xét các số thực dương 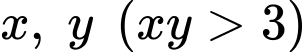 thỏa mãn
thỏa mãn 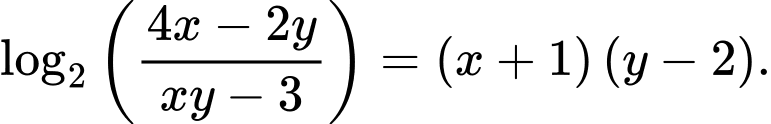 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 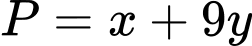 bằng
bằng
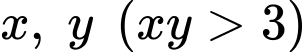 thỏa mãn
thỏa mãn 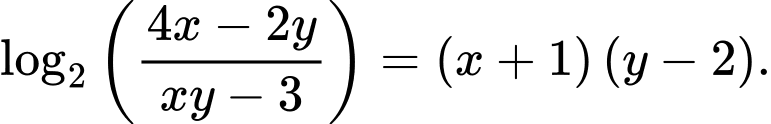 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 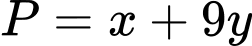 bằng
bằng A, 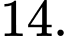
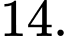
B, 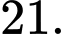
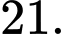
C, 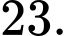
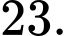
D, 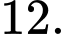
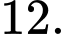
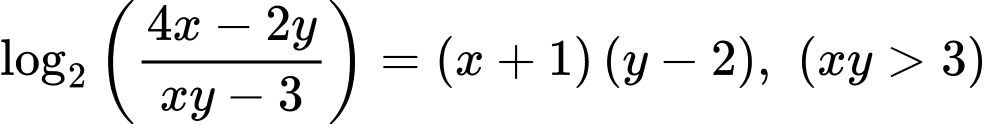
Giả sử:
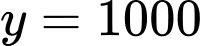 ta bấm máy tính được
ta bấm máy tính được 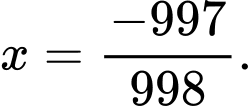
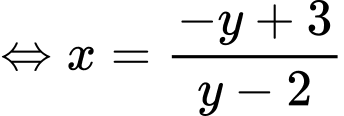
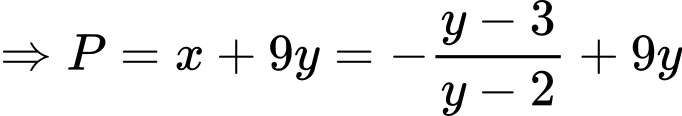
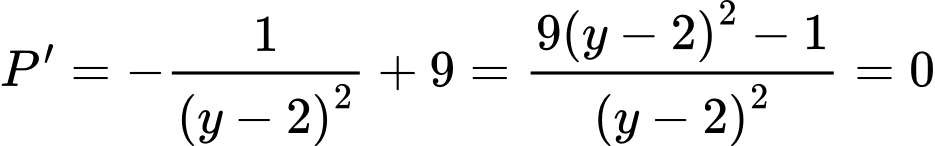
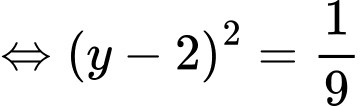
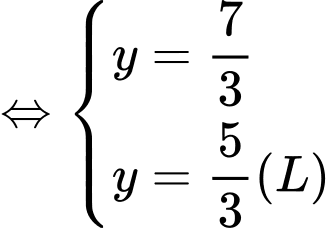 vì
vì 
 tại
tại 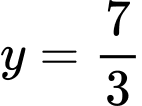
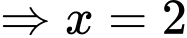
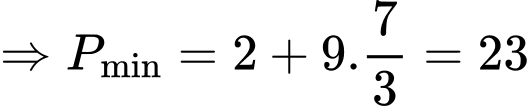
Đáp án: C. Đáp án: C
Câu 9 [79784]: Cho hai số thực dương 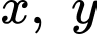 thỏa mãn
thỏa mãn 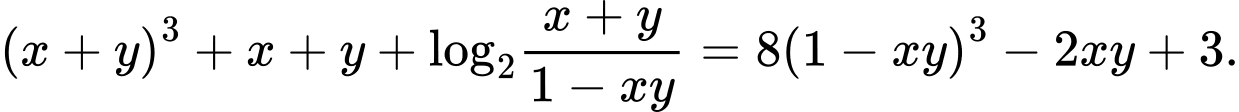 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 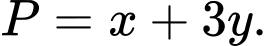
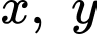 thỏa mãn
thỏa mãn 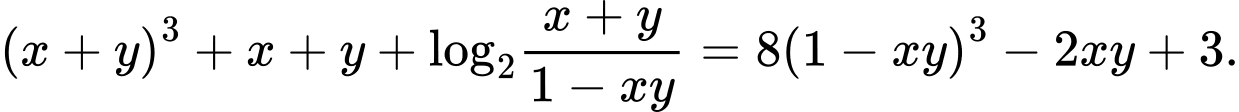 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 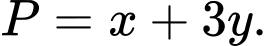
A, 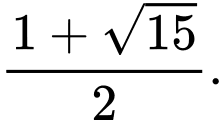
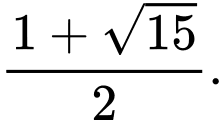
B, 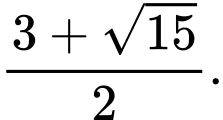
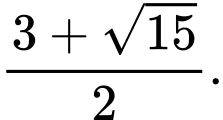
C, 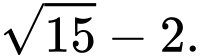
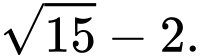
D, 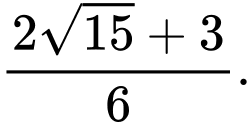
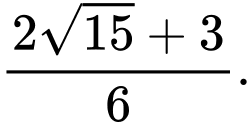
Ta có 
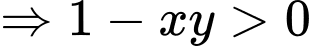
Khi đó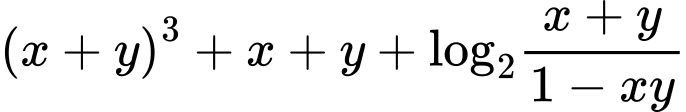
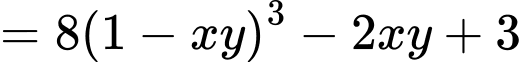
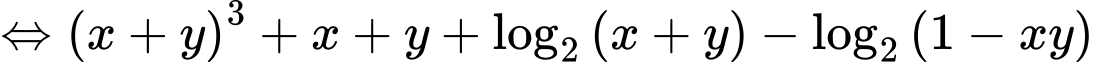
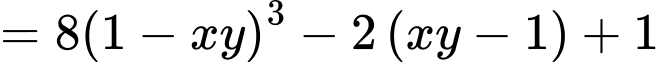
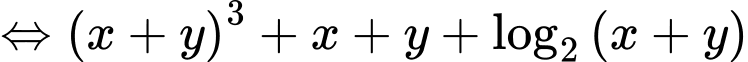
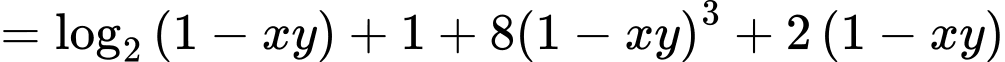
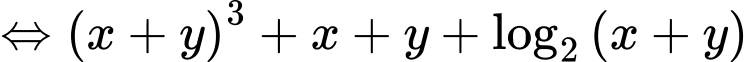
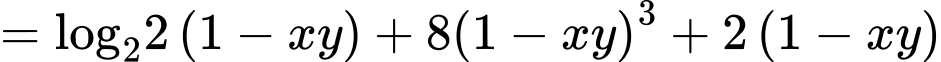
Xét hàm số
Ta có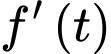
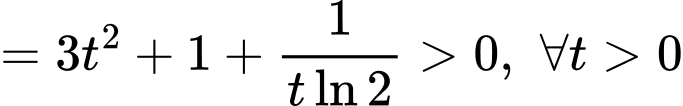
Do đó hàm số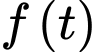 đồng biến trên khoảng
đồng biến trên khoảng 
Khi đó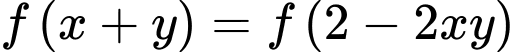
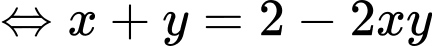
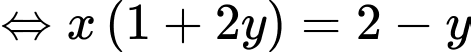
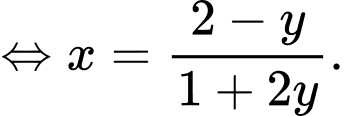
Khi đó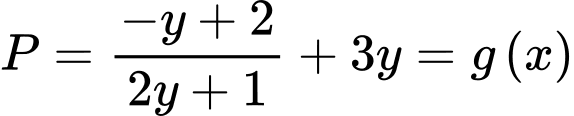
Ta có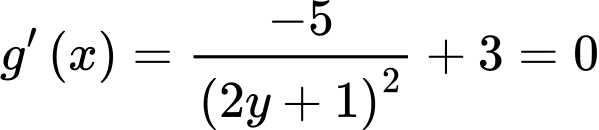
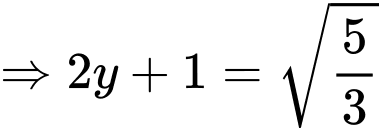
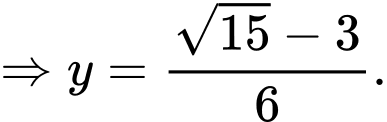
Suy ra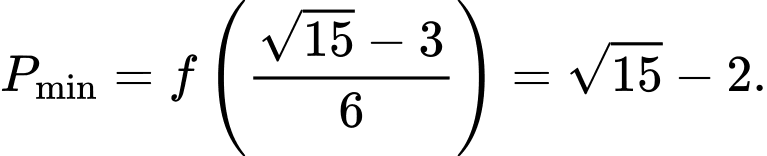
Chọn C. Đáp án: C
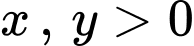
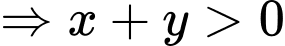
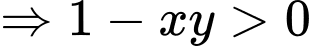
Khi đó
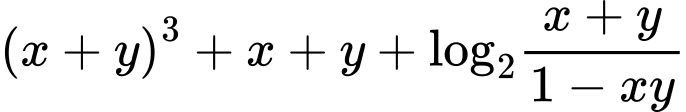
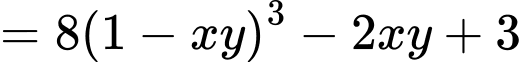
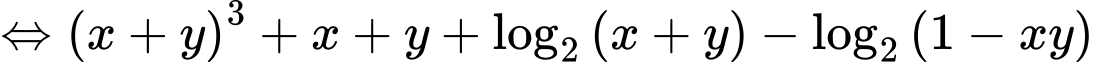
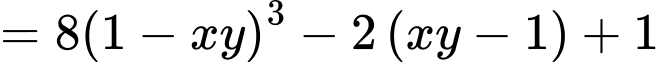
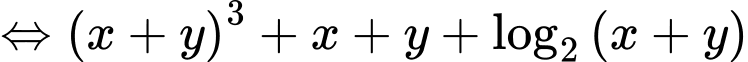
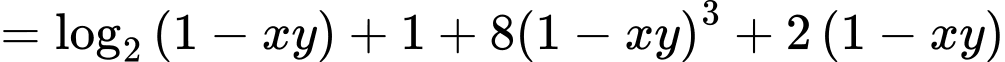
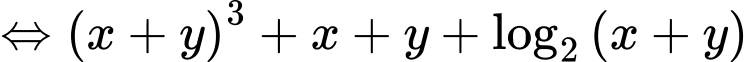
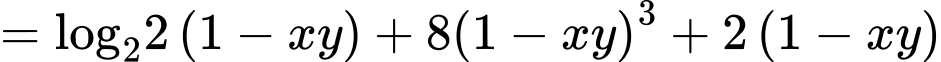
Xét hàm số

Ta có
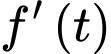
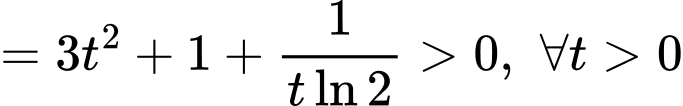
Do đó hàm số
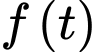 đồng biến trên khoảng
đồng biến trên khoảng 
Khi đó
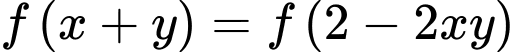
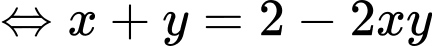
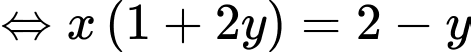
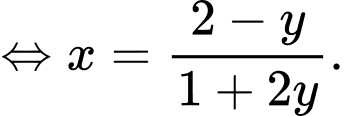
Khi đó
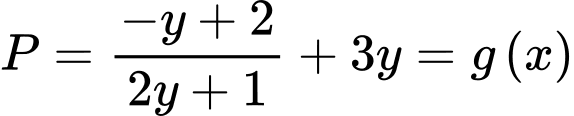
Ta có
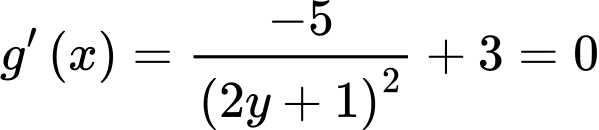
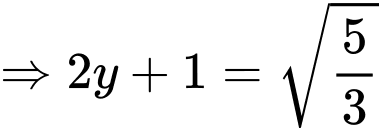
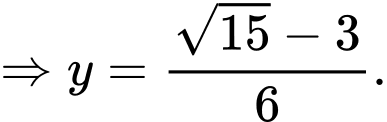
Suy ra
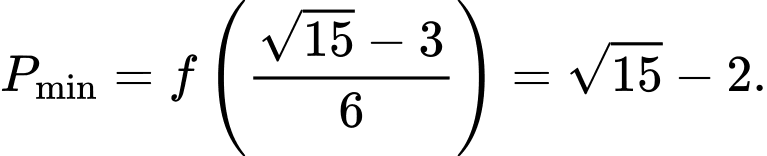
Chọn C. Đáp án: C
Câu 10 [79824]: Cho hai số 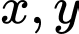 dương thỏa mãn
dương thỏa mãn 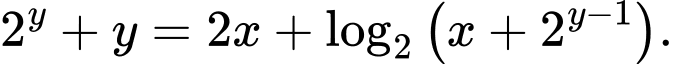 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 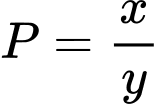 bằng
bằng
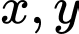 dương thỏa mãn
dương thỏa mãn 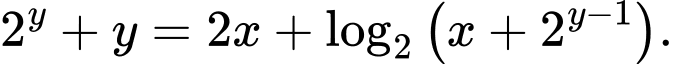 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 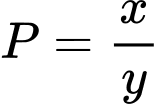 bằng
bằng A, 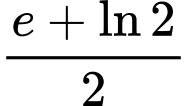 .
.
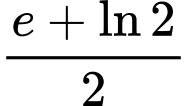 .
.B, 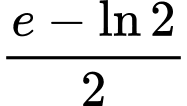 .
.
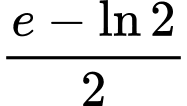 .
.C, 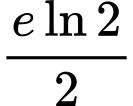 .
.
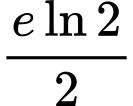 .
.D, 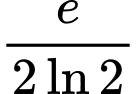 .
.
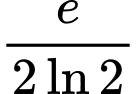 .
.
Gọi 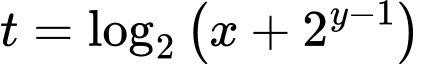
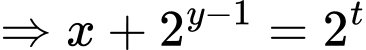
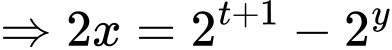
Ta có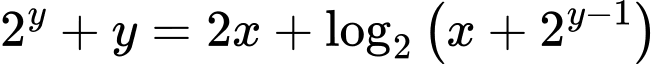
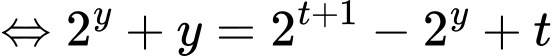
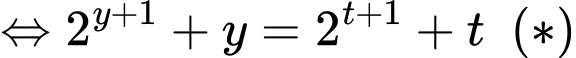
Xét hàm số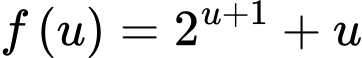 trên
trên 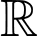
Ta có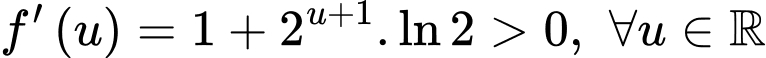
Suy ra hàm số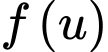 đồng biến trên
đồng biến trên 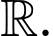
Khi đó
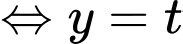
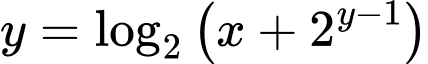
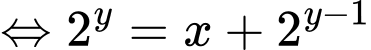
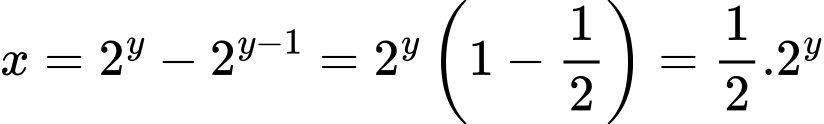
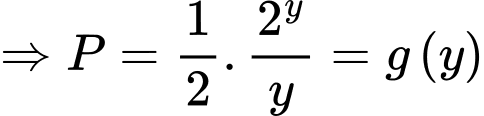
Xét hàm số ta có
ta có 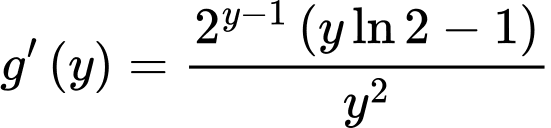
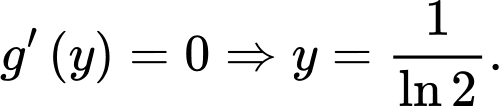
Bảng biến thiên
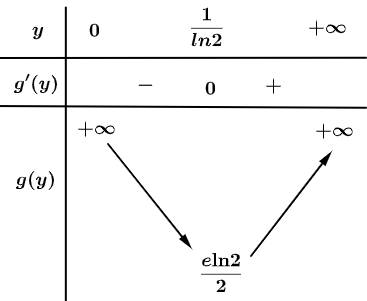
Vậy giá trị nhỏ nhất của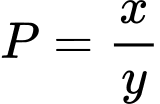 là
là 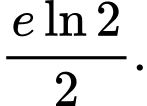
Chọn C. Đáp án: C
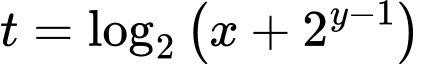
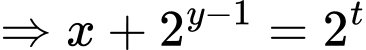
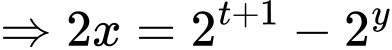
Ta có
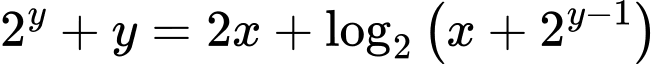
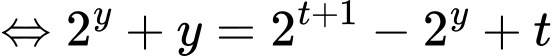
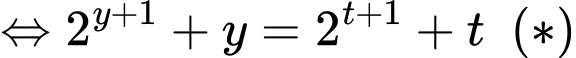
Xét hàm số
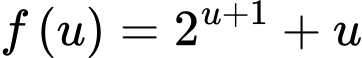 trên
trên 
Ta có
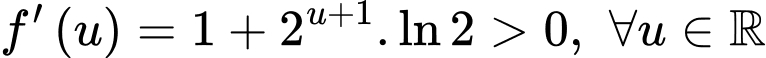
Suy ra hàm số
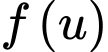 đồng biến trên
đồng biến trên 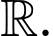
Khi đó

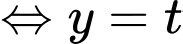
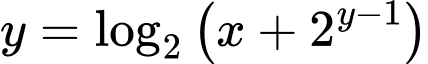
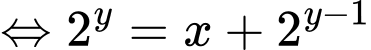
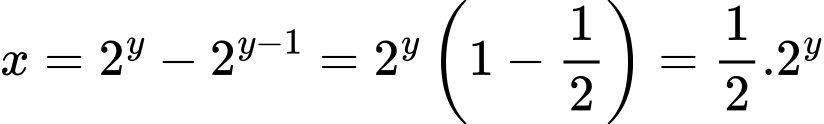
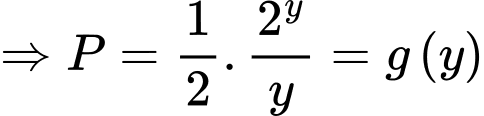
Xét hàm số
 ta có
ta có 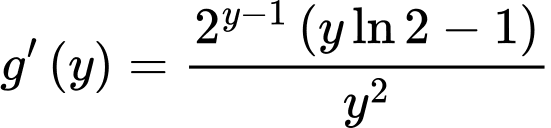
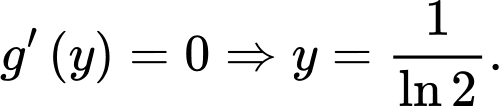
Bảng biến thiên

Vậy giá trị nhỏ nhất của
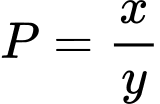 là
là 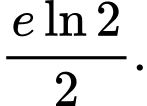
Chọn C. Đáp án: C
Câu 11 [789067]: Cho hai số thực dương 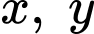 thỏa mãn
thỏa mãn 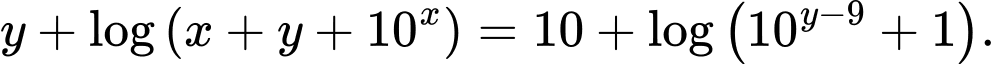 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức  bằng
bằng
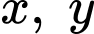 thỏa mãn
thỏa mãn 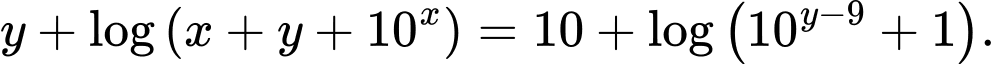 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức  bằng
bằng A, 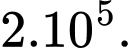
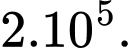
B, 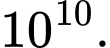
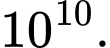
C, 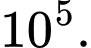
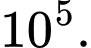
D, 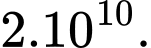
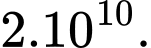
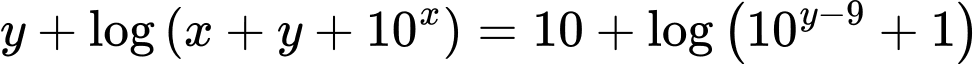
Ta loga 2 vế được:
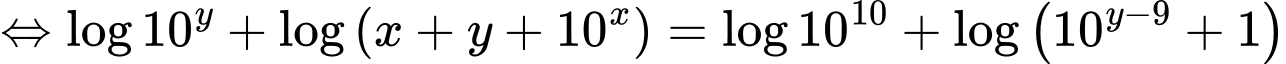
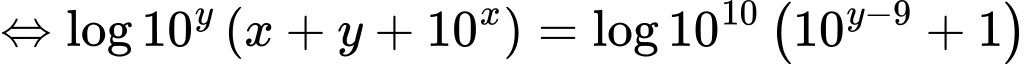
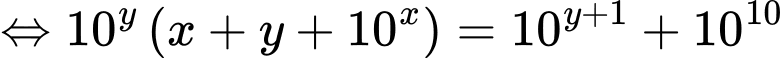
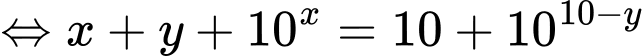
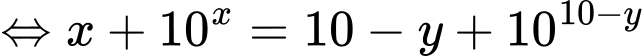
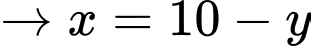
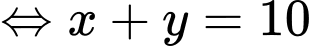
Áp dụng bất đẳng thức Co-si ta có:
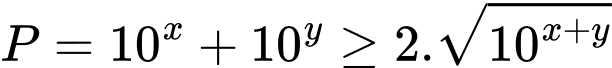

Đáp án: A. Đáp án: A
Câu 12 [510426]: [Chuyên Đại học Vinh 2020] Xét các số thực dương 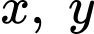 thỏa mãn
thỏa mãn 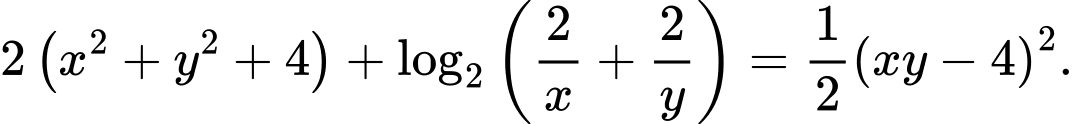 Khi
Khi 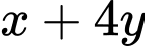 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 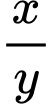 bằng
bằng
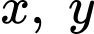 thỏa mãn
thỏa mãn 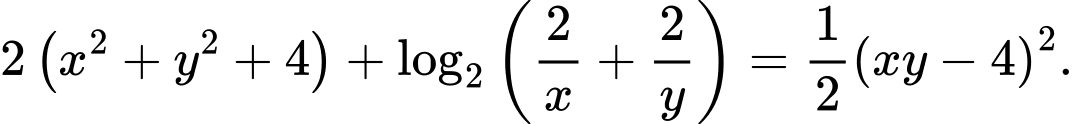 Khi
Khi 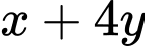 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 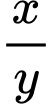 bằng
bằng A, 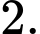
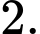
B, 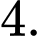
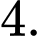
C, 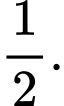
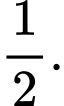
D, 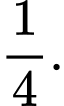
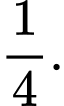
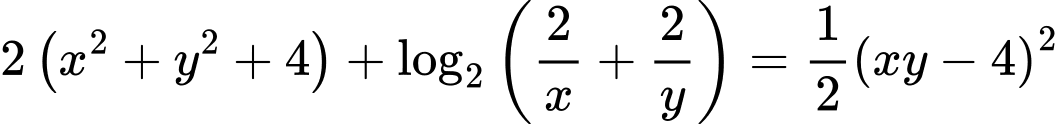
ĐKXĐ:
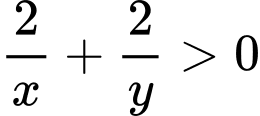
Giả sử:
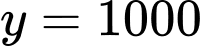 ta bấm máy tính được
ta bấm máy tính được 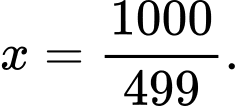
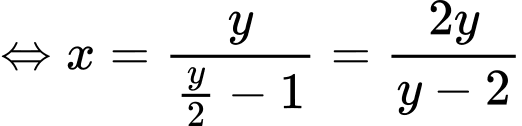
Xét:
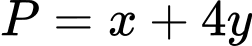
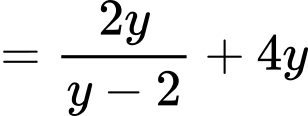
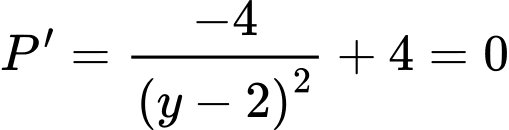
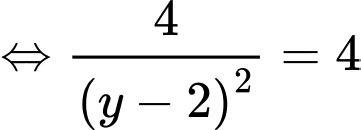
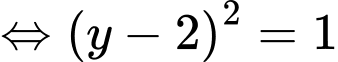
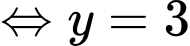
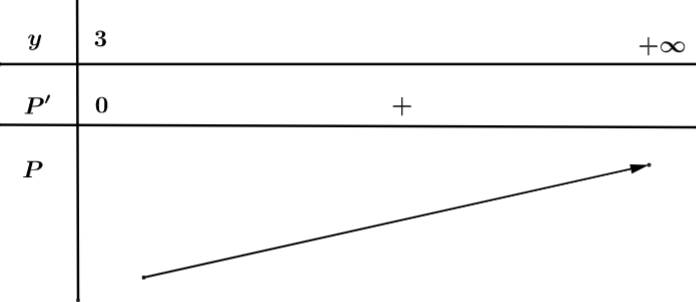
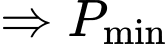 tại
tại 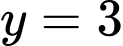
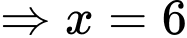
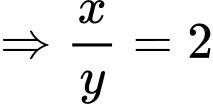
Đáp án: A. Đáp án: A
Câu 13 [803781]: Xét tất cả các số thực dương 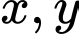 thỏa mãn
thỏa mãn 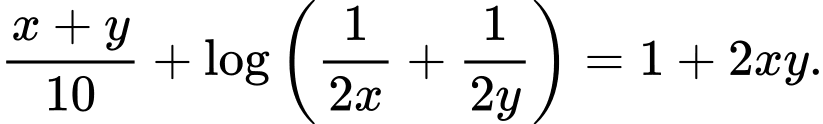 Khi biểu thức
Khi biểu thức 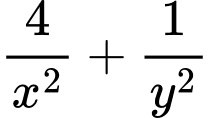 đạt giá trị nhỏ nhất, tích
đạt giá trị nhỏ nhất, tích 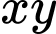 bằng
bằng
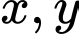 thỏa mãn
thỏa mãn 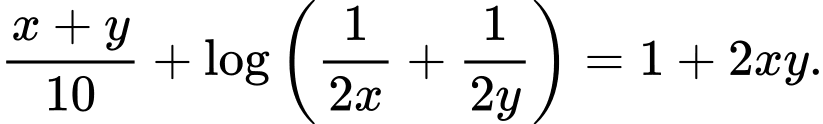 Khi biểu thức
Khi biểu thức 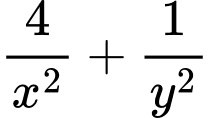 đạt giá trị nhỏ nhất, tích
đạt giá trị nhỏ nhất, tích 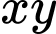 bằng
bằng A, 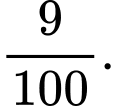
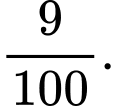
B, 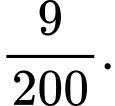
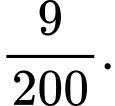
C, 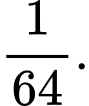
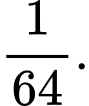
D, 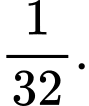
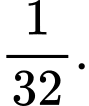
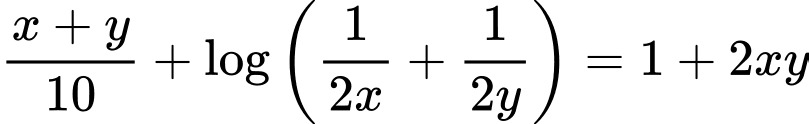
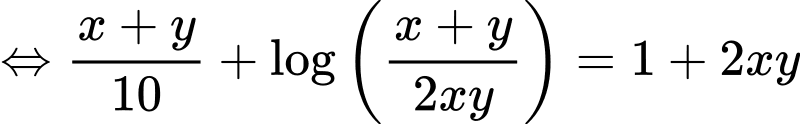
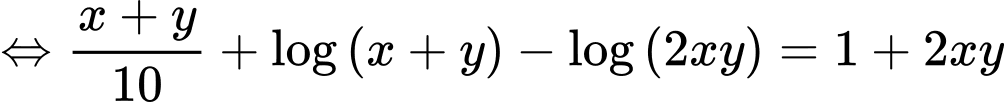
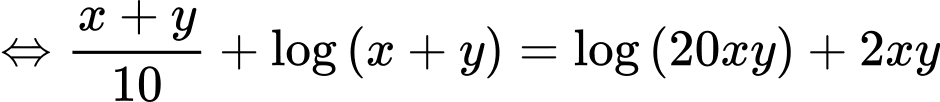
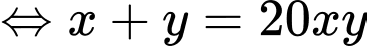
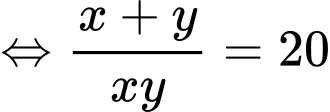
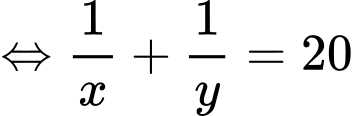
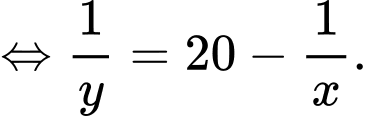
Khi đó:
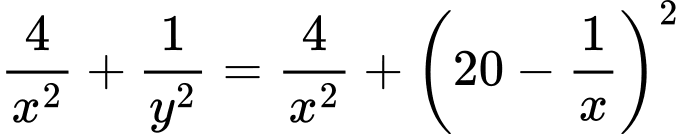
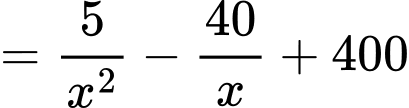
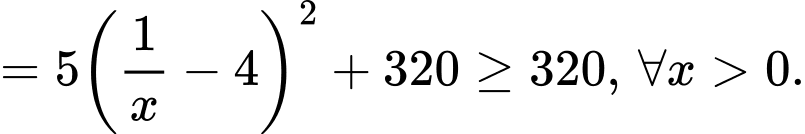
Dấu bằng xảy ra khi:
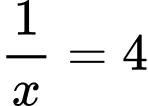
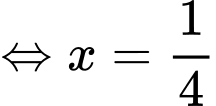
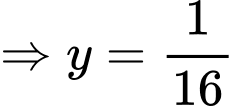
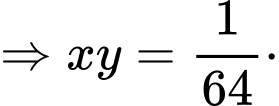
Chọn đáp án C. Đáp án: C
Câu 14 [789070]: Cho  thỏa mãn
thỏa mãn 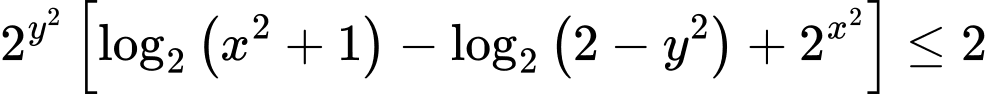 . Giá trị lớn nhất của biểu thức
. Giá trị lớn nhất của biểu thức 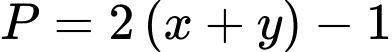 bằng
bằng
 thỏa mãn
thỏa mãn 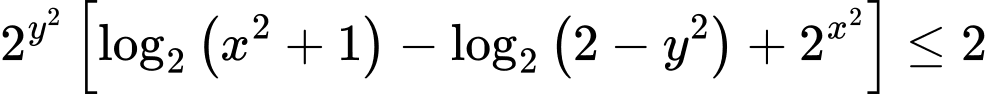 . Giá trị lớn nhất của biểu thức
. Giá trị lớn nhất của biểu thức 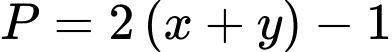 bằng
bằng A, 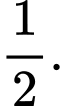
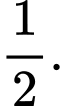
B, 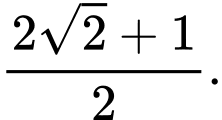
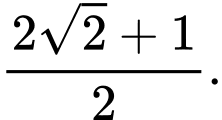
C, 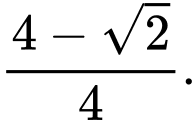
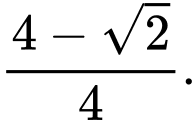
D, 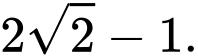
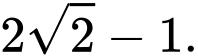
Ta có 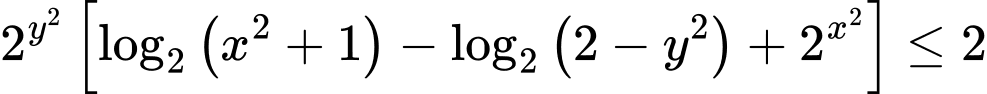
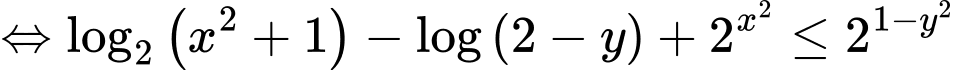
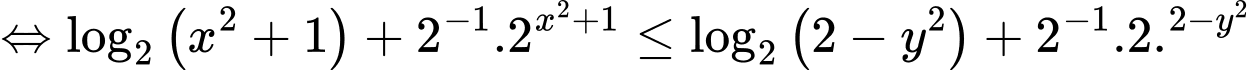
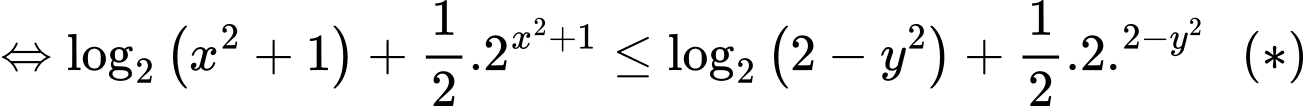
Xét hàm số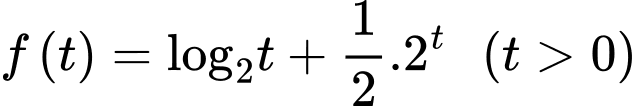
Ta có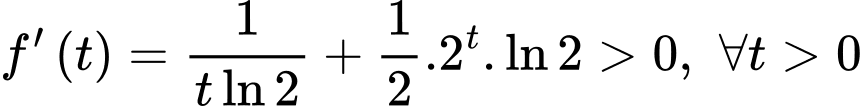
 Hàm số
Hàm số 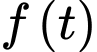 đồng biến trên
đồng biến trên 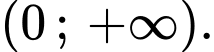
Khi đó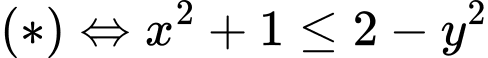
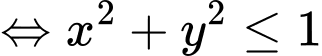
Áp dụng bất đẳng thức Bunhia – Côpxki: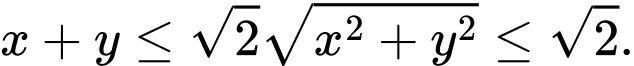
Dấu “=” xảy ra khi và chỉ khi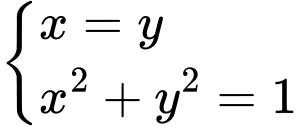
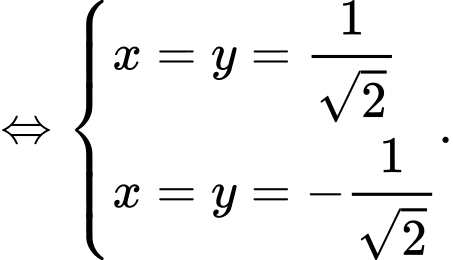
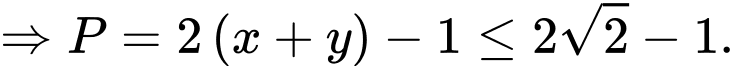
Vậy giá trị lớn nhất của biểu thức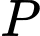 bằng
bằng 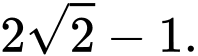
Chọn D. Đáp án: D
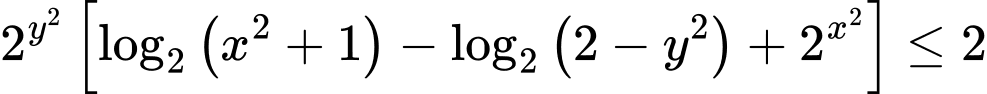
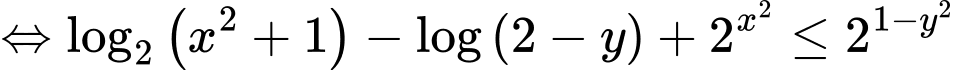
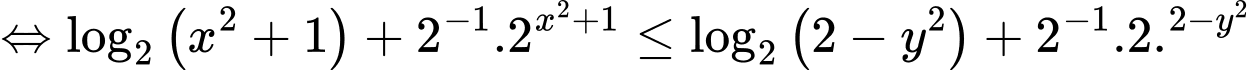
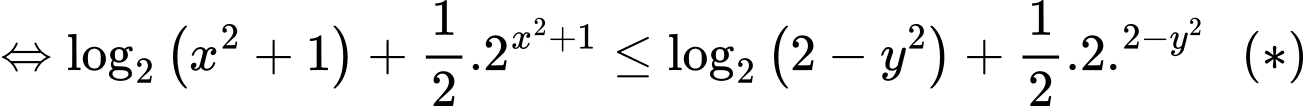
Xét hàm số
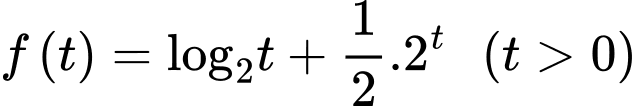
Ta có
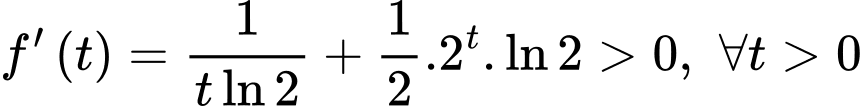
 Hàm số
Hàm số 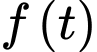 đồng biến trên
đồng biến trên 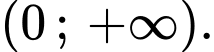
Khi đó
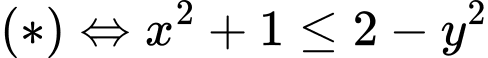
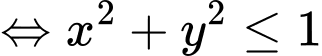
Áp dụng bất đẳng thức Bunhia – Côpxki:
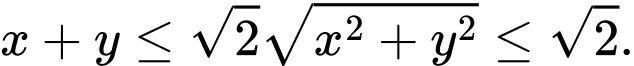
Dấu “=” xảy ra khi và chỉ khi
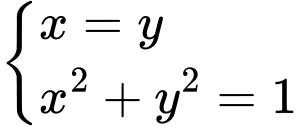
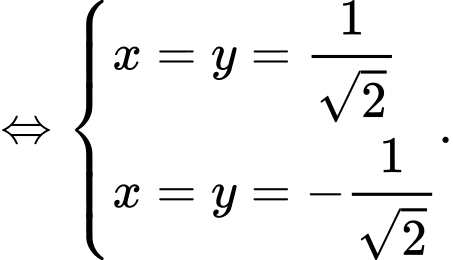
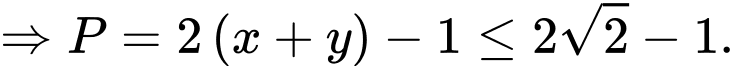
Vậy giá trị lớn nhất của biểu thức
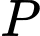 bằng
bằng 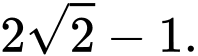
Chọn D. Đáp án: D
Câu 15 [510427]: [Chuyên Biên Hòa-Hà Nam 2020] Cho 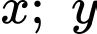 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 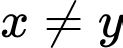 và
và 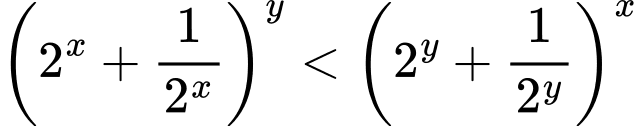 . Tìm giá trị nhỏ nhất của biểu thức
. Tìm giá trị nhỏ nhất của biểu thức 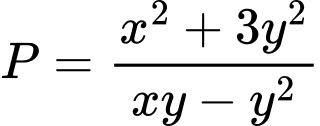 .
.
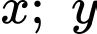 là hai số thực dương thỏa mãn
là hai số thực dương thỏa mãn 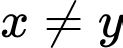 và
và 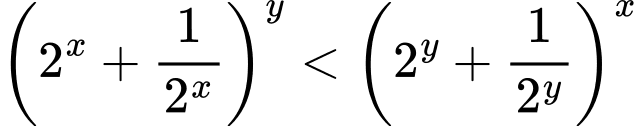 . Tìm giá trị nhỏ nhất của biểu thức
. Tìm giá trị nhỏ nhất của biểu thức 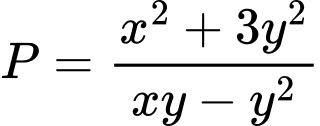 .
. A, 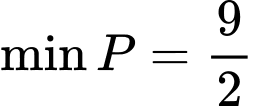 .
.
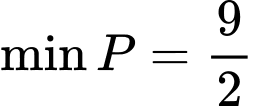 .
.B, 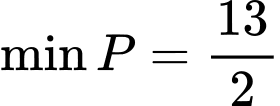 .
.
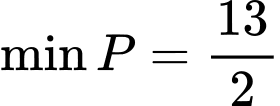 .
.C, 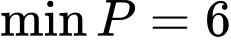 .
.
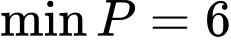 .
.D, 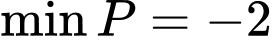 .
.
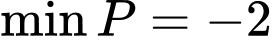 .
.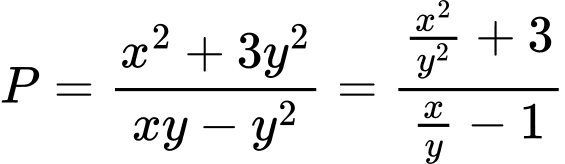
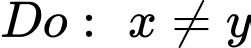
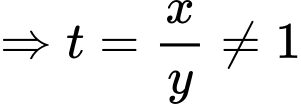
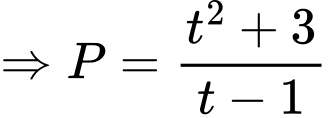
Có:
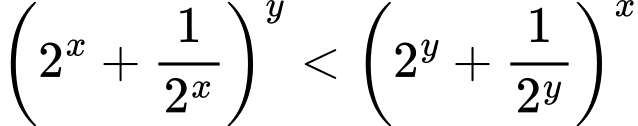
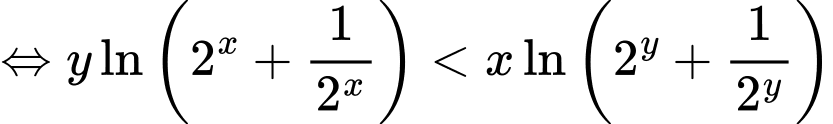
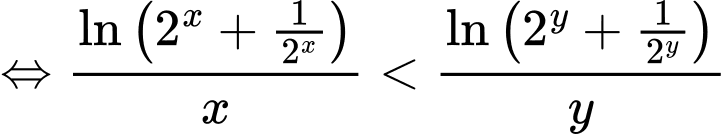
Hàm
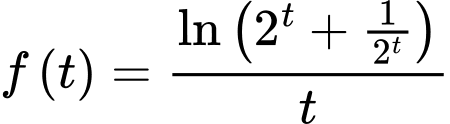 là hàm nghịch biến.
là hàm nghịch biến.
Theo hàm đặc trưng, suy ra:

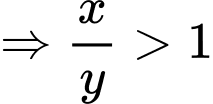
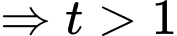
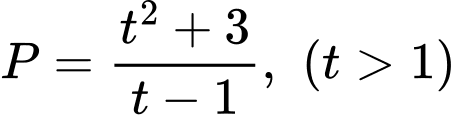
Ta sử dụng Table của máy tính để xác định giá trị:
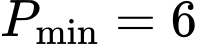
Đáp án: C Đáp án: C
Câu 16 [510428]: Cho các số thực  dương và thỏa mãn
dương và thỏa mãn 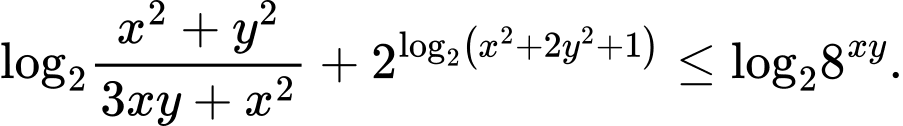 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 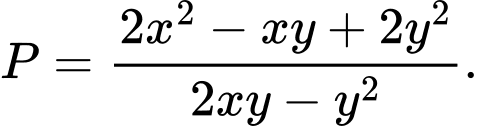
 dương và thỏa mãn
dương và thỏa mãn 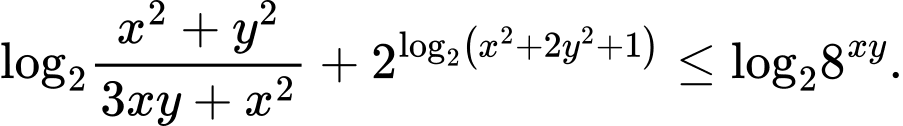 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 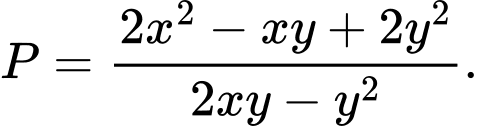
A, 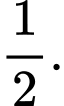
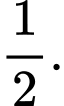
B, 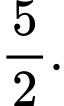
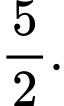
C, 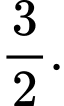
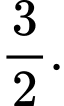
D, 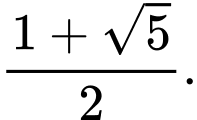
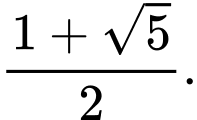
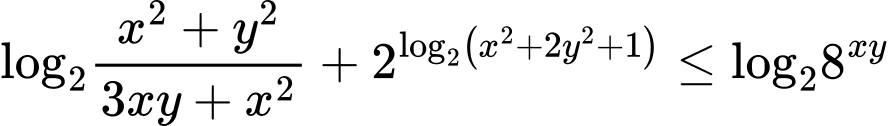
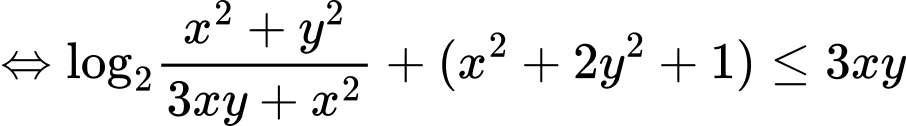
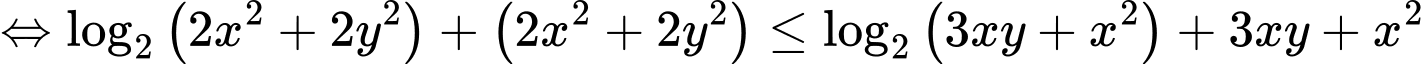
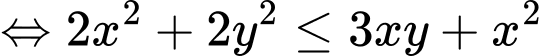
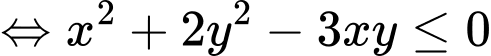
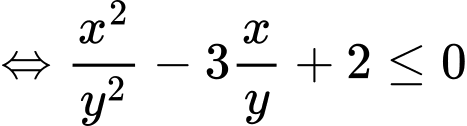
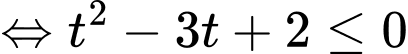
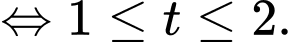
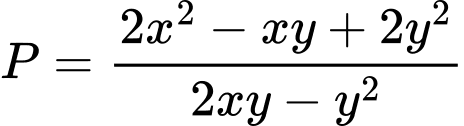
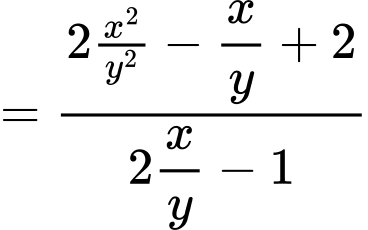
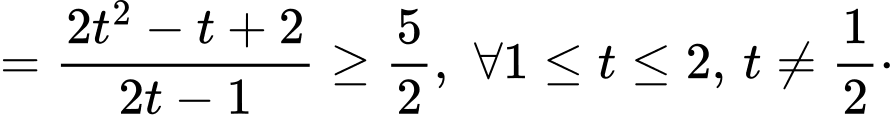
Chọn đáp án B. Đáp án: B
Câu 17 [510435]: Cho các số thực 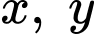 dương và thỏa mãn
dương và thỏa mãn 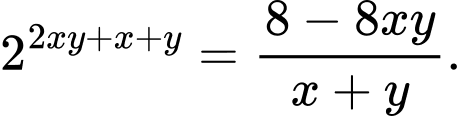 Khi
Khi 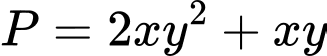 đạt giá trị lớn nhất, giá trị của biểu thức
đạt giá trị lớn nhất, giá trị của biểu thức  bằng
bằng
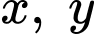 dương và thỏa mãn
dương và thỏa mãn 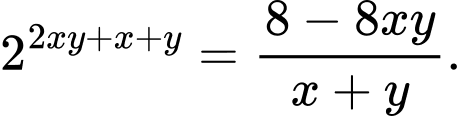 Khi
Khi 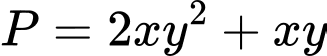 đạt giá trị lớn nhất, giá trị của biểu thức
đạt giá trị lớn nhất, giá trị của biểu thức  bằng
bằng A, 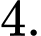
B, 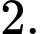
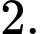
C, 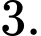
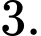
D, 
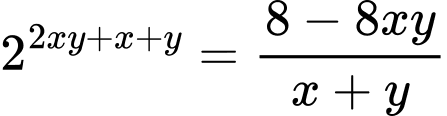
Đặt
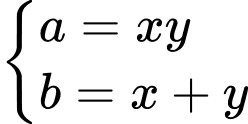
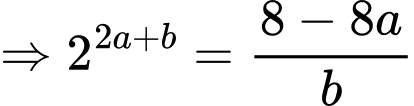
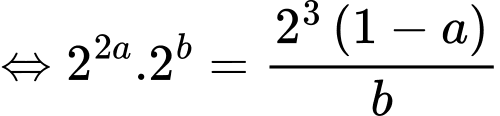
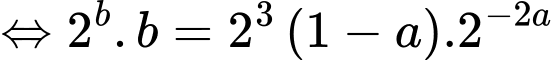
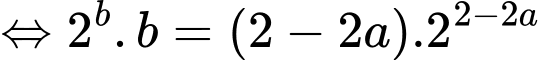
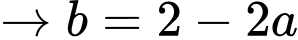

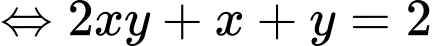
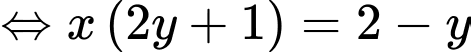
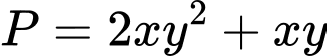
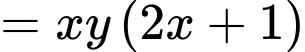
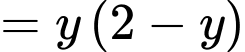
Ta có: đồ thị hàm số
 là hình parabol có bề lõm hướng xuống
là hình parabol có bề lõm hướng xuống tại
tại 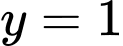
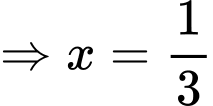
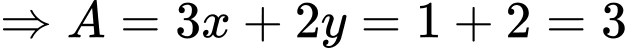
Đáp án: C. Đáp án: C
Câu 18 [377855]: Cho các số thực dương 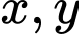 thỏa mãn
thỏa mãn 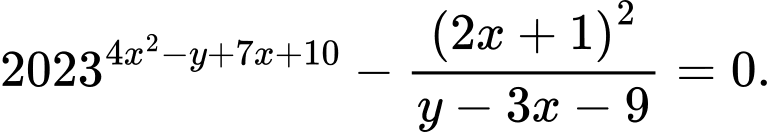 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 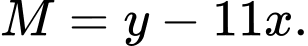
 thỏa mãn
thỏa mãn 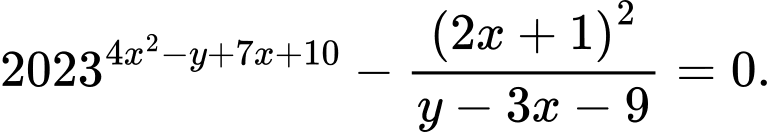 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 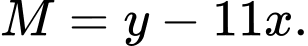
A, 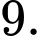
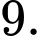
B, 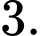
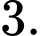
C, 

D, 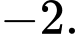
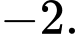
Chọn A
Do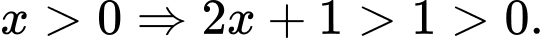
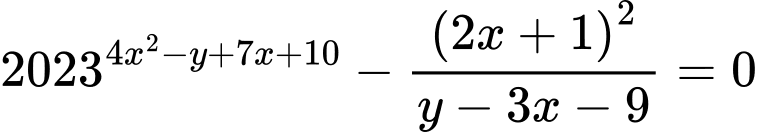
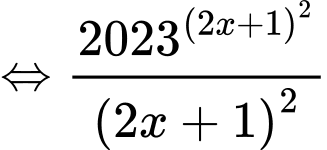
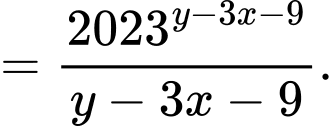
Đặt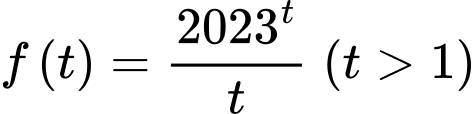
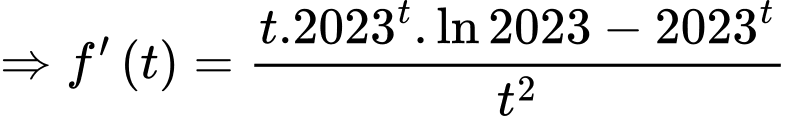
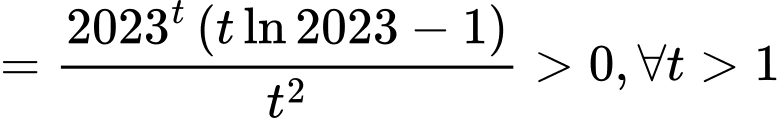
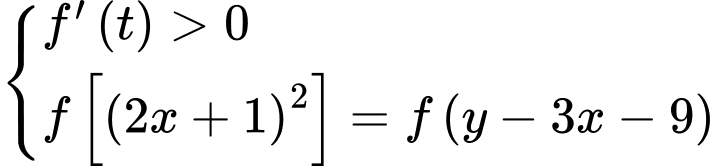
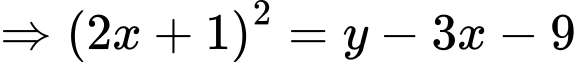
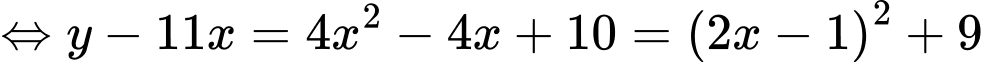
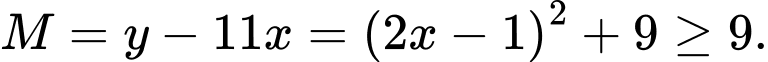
Giá trị nhỏ nhất của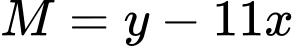 là
là 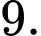 Đáp án: A
Đáp án: A
Do
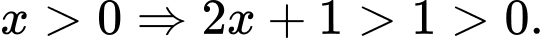
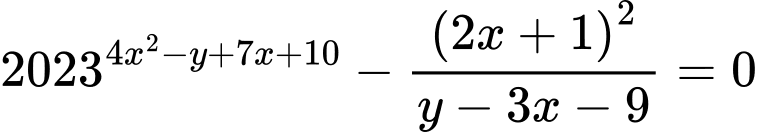
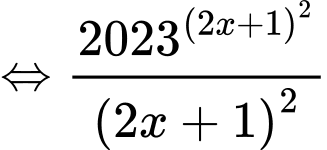
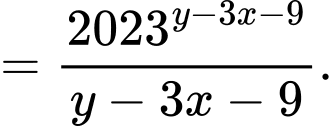
Đặt
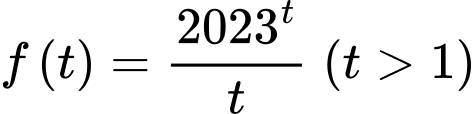
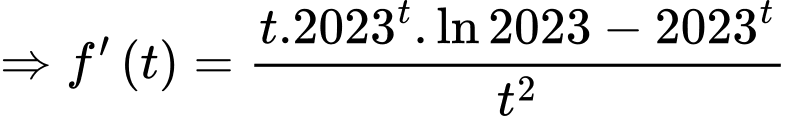
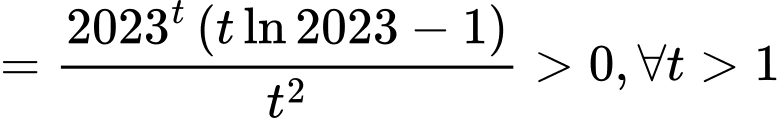
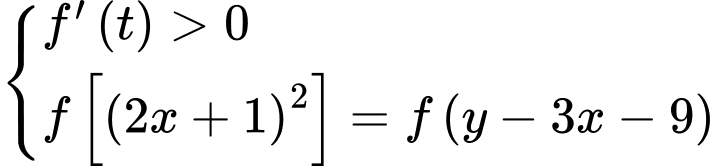
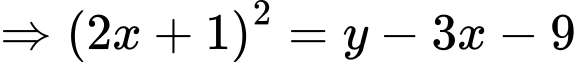
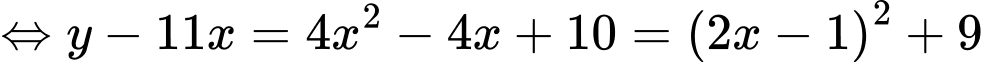
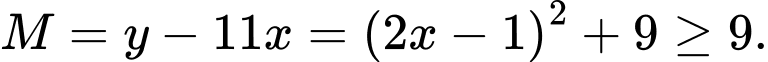
Giá trị nhỏ nhất của
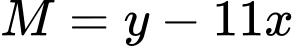 là
là 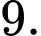 Đáp án: A
Đáp án: A
Câu 19 [399933]: Xét các số thực 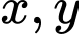 thỏa mãn
thỏa mãn 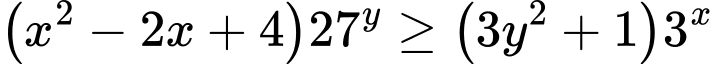 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức 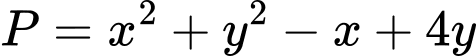 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
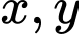 thỏa mãn
thỏa mãn 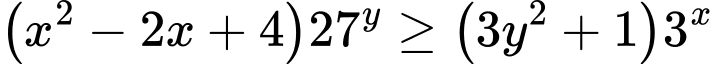 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức 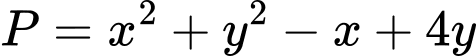 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? A, 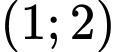 .
.
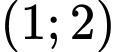 .
.B, 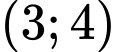 .
.
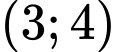 .
. C, 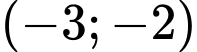 .
.
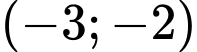 .
.D, 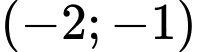 .
.
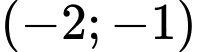 .
.
Ta có: 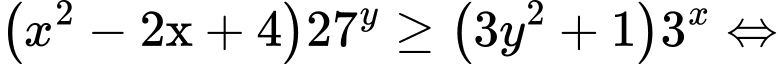
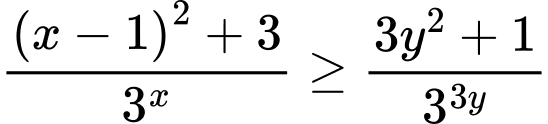
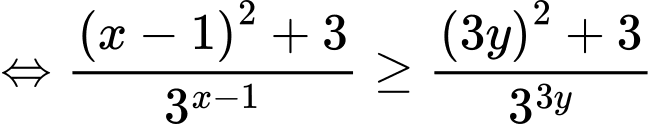
 Xét hàm đặc trưng
Xét hàm đặc trưng 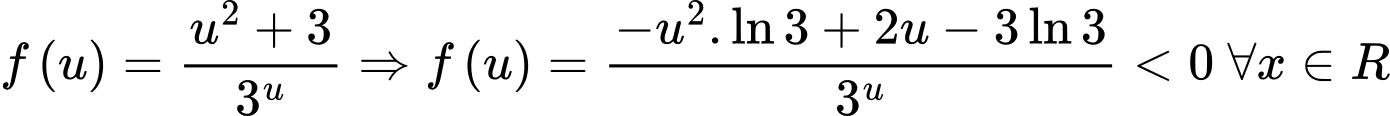
 Hàm số
Hàm số 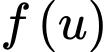 nghịch biến trên
nghịch biến trên 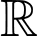
Khi đó,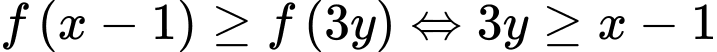
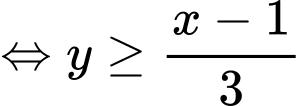 .
.
Xét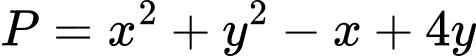

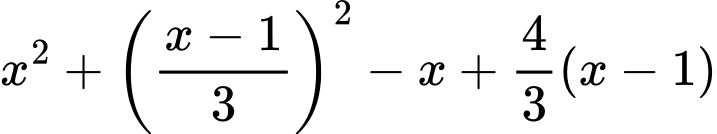 x
x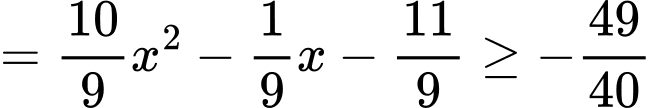
Vậy giá trị nhỏ nhất của biểu thức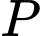 là
là 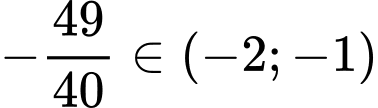 .
Đáp án: D
.
Đáp án: D
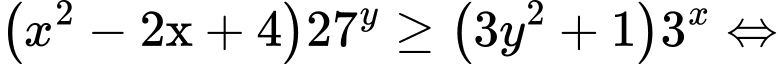
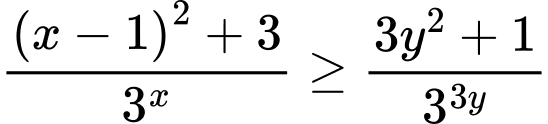
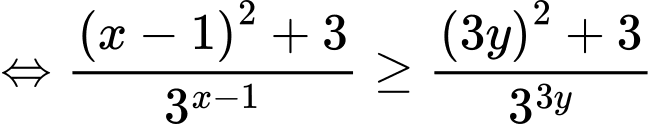
 Xét hàm đặc trưng
Xét hàm đặc trưng 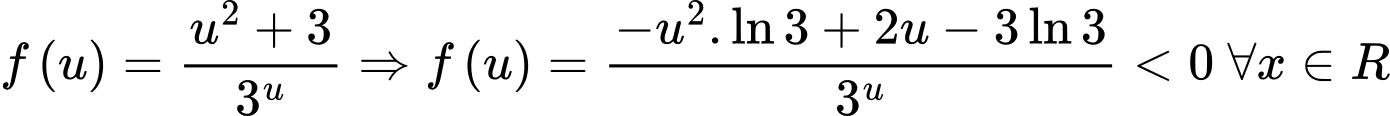
 Hàm số
Hàm số 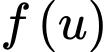 nghịch biến trên
nghịch biến trên 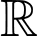
Khi đó,
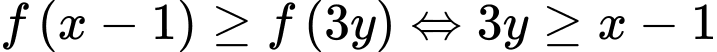
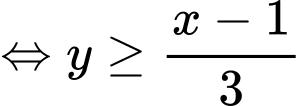 .
.
Xét
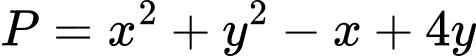

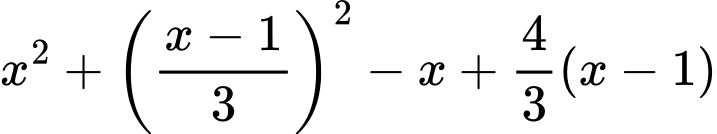 x
x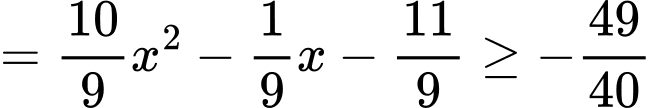
Vậy giá trị nhỏ nhất của biểu thức
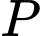 là
là 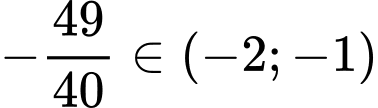 .
Đáp án: D
.
Đáp án: D
Câu 20 [678150]: [ĐỀ BGD-2020-L1-MĐ 104] Xét các số thực không âm 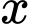 và
và 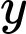 thỏa mãn
thỏa mãn 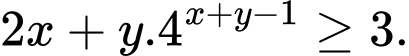 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 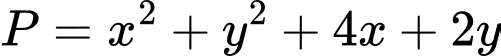 bằng
bằng
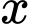 và
và 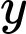 thỏa mãn
thỏa mãn 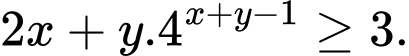 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 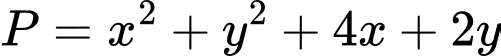 bằng
bằng A, 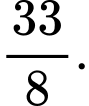
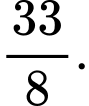
B, 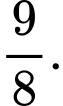
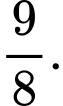
C, 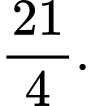
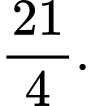
D, 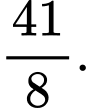
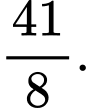
Ta có 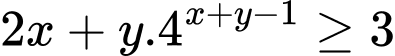
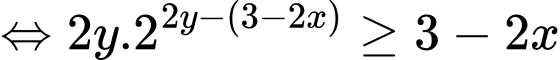
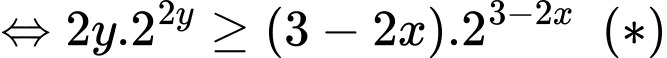
Xét hàm số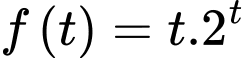 có
có 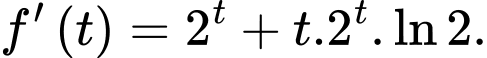
TH1: Với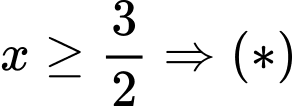 luôn đúng
luôn đúng 
Ta có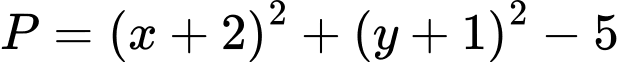
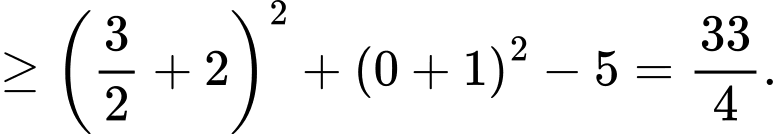 Dấu “=” xảy ra
Dấu “=” xảy ra 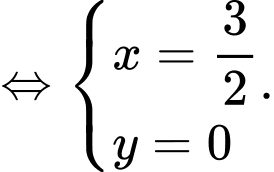
TH2: Với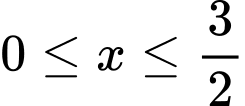 suy ra
suy ra 
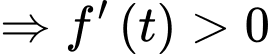 hay hàm số
hay hàm số 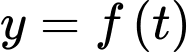 luôn đồng biến nên
luôn đồng biến nên 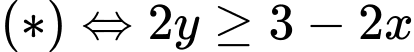
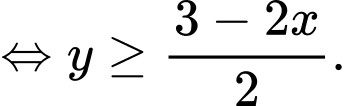
Ta có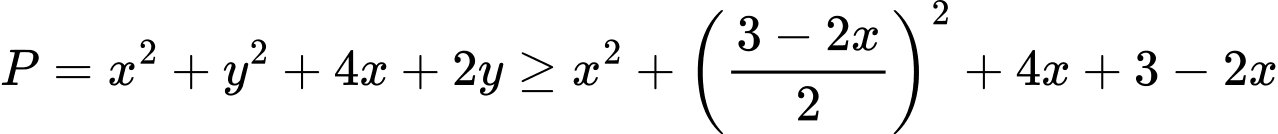
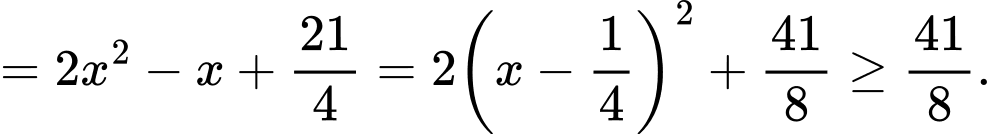
Dấu “=” xảy ra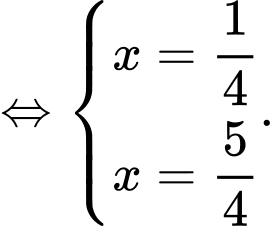
Vậy giá trị nhỏ nhất của biểu thức là
là 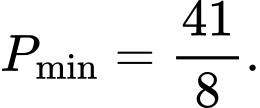
Chọn D. Đáp án: D
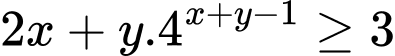
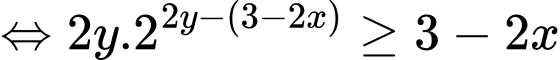
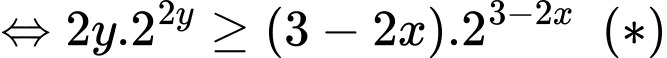
Xét hàm số
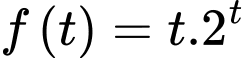 có
có 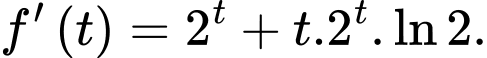
TH1: Với
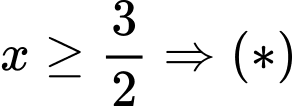 luôn đúng
luôn đúng 
Ta có
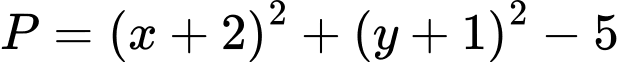
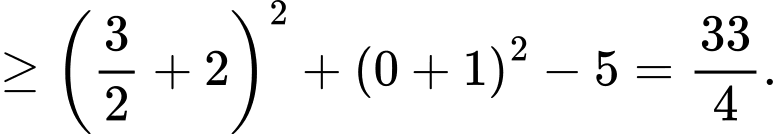 Dấu “=” xảy ra
Dấu “=” xảy ra 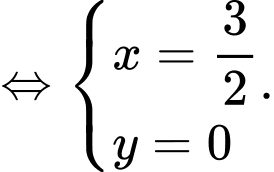
TH2: Với
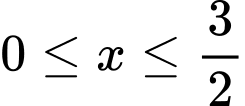 suy ra
suy ra 
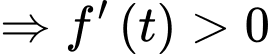 hay hàm số
hay hàm số 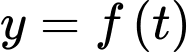 luôn đồng biến nên
luôn đồng biến nên 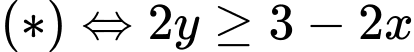
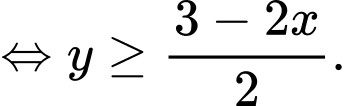
Ta có
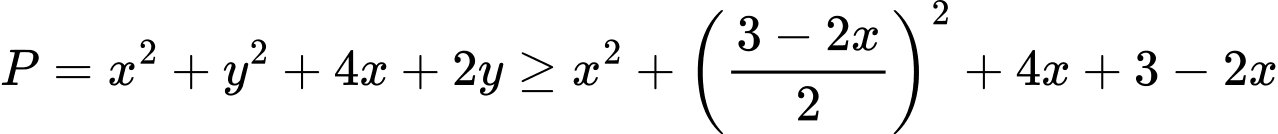
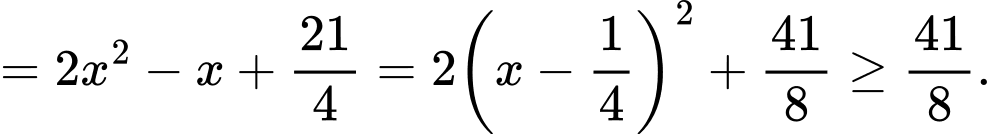
Dấu “=” xảy ra
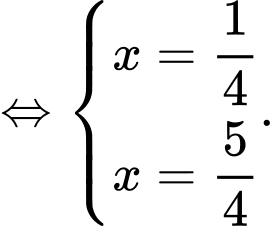
Vậy giá trị nhỏ nhất của biểu thức
 là
là 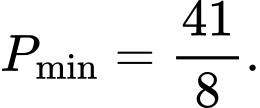
Chọn D. Đáp án: D