Đáp án Bài tập tự luyện số 1
Câu 1 [677073]: Cho hai số thực 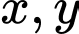 thỏa mãn
thỏa mãn 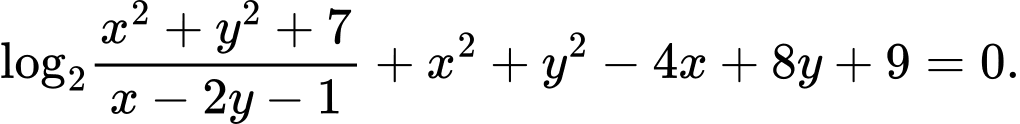 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 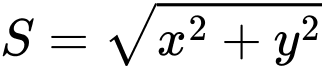 có dạng
có dạng 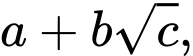 trong đó
trong đó 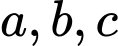 nguyên và
nguyên và  là số nguyên tố. Hỏi
là số nguyên tố. Hỏi 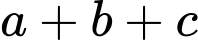 bằng
bằng
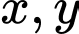 thỏa mãn
thỏa mãn 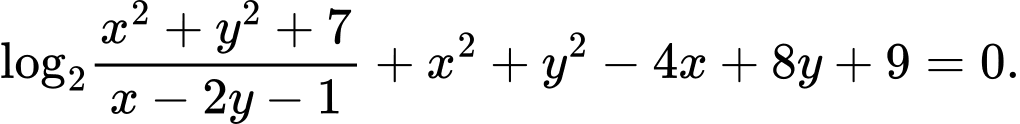 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 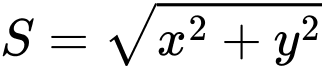 có dạng
có dạng 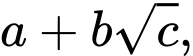 trong đó
trong đó 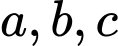 nguyên và
nguyên và  là số nguyên tố. Hỏi
là số nguyên tố. Hỏi 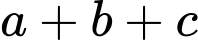 bằng
bằng A, 10.
B, 13.
C, 11.
D, 14.
Đặt 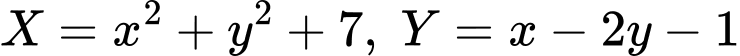
Ta có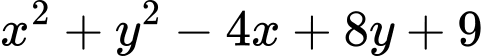
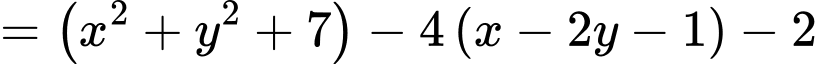
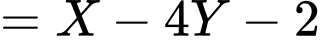
Khi đó ta có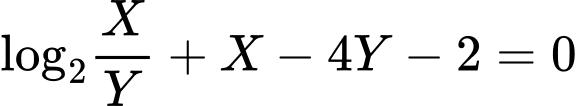
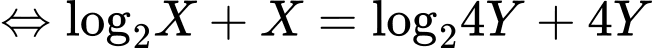

Suy ra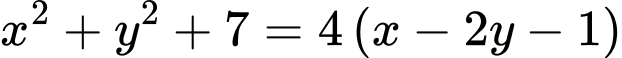
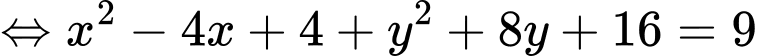
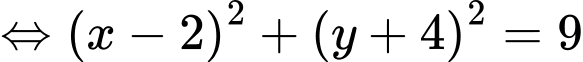
Đặt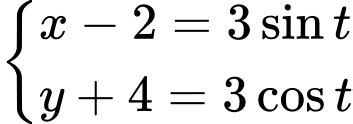
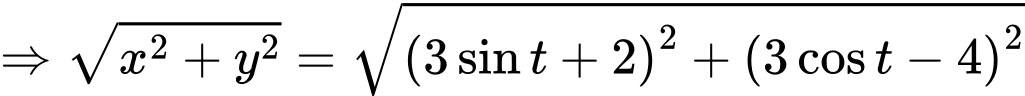
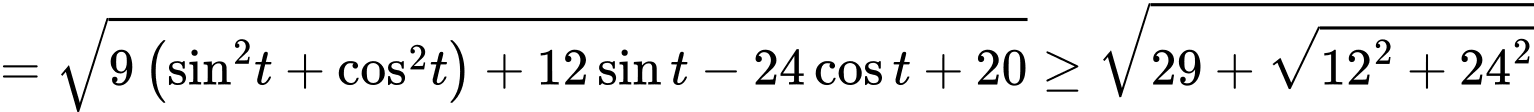
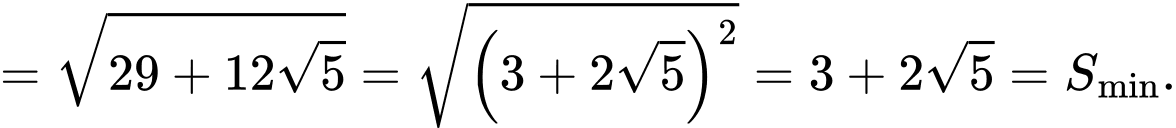 Vậy
Vậy 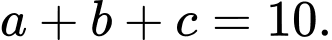 Chọn A. Đáp án: A
Chọn A. Đáp án: A
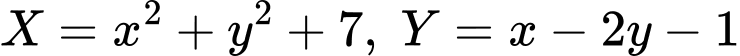
Ta có
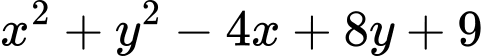
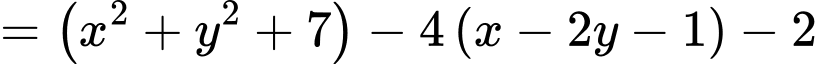
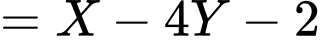
Khi đó ta có
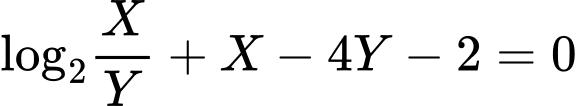
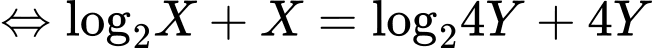

Suy ra
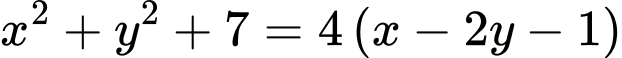
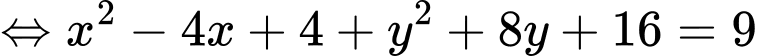
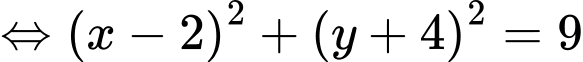
Đặt
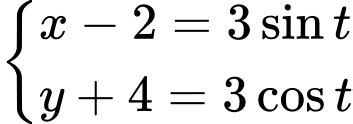
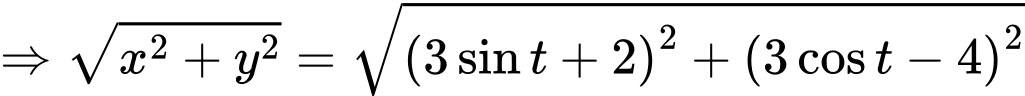
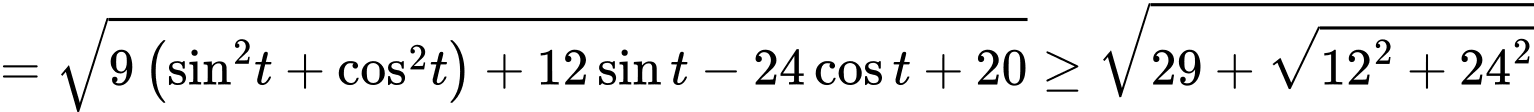
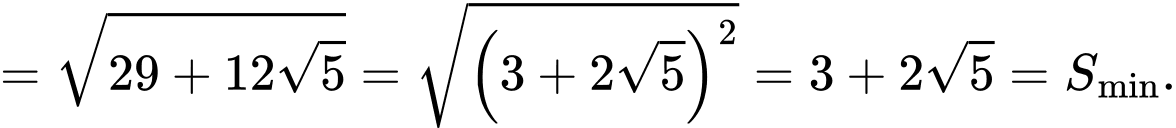 Vậy
Vậy 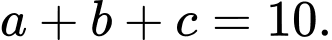 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 2 [791671]: Cho hai số thực 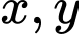 thỏa mãn
thỏa mãn 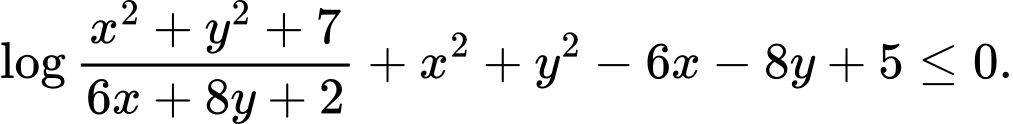 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 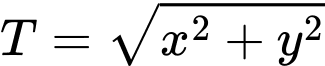 là
là
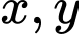 thỏa mãn
thỏa mãn 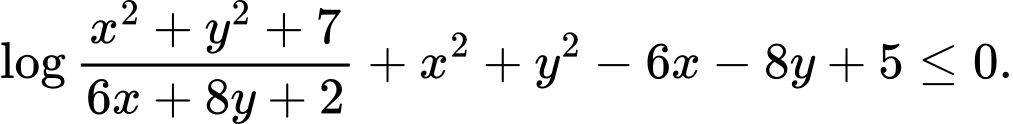 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 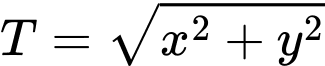 là
là A, 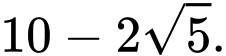
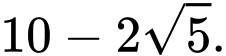
B, 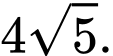
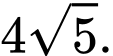
C, 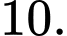
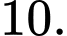
D, 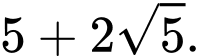
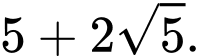
BPT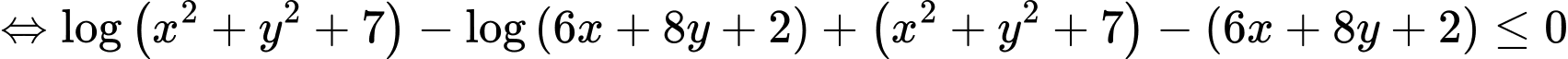
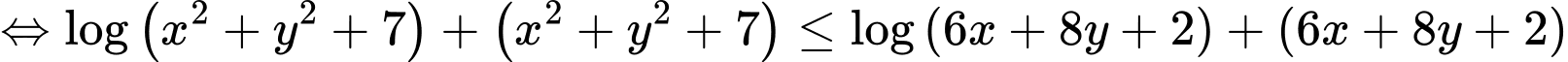
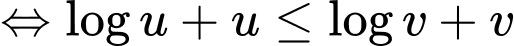
Xét hàm số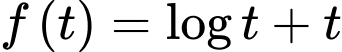 trên khoảng
trên khoảng 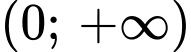
Ta có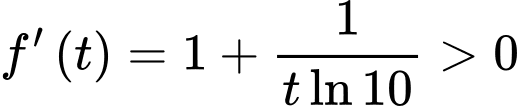
Suy ra hàm số đồng biến
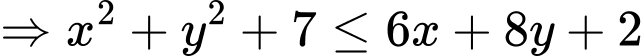
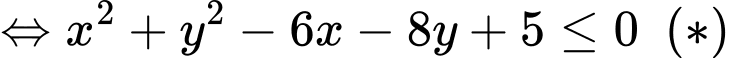
Ta thấy PT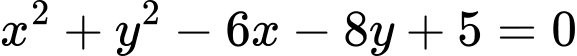 là một phương trình đường tròn nên tập hợp các điểm
là một phương trình đường tròn nên tập hợp các điểm 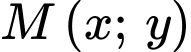 thoả mãn bất phương trình
thoả mãn bất phương trình  là các điểm nằm trên hoặc bên trong đường tròn.
là các điểm nằm trên hoặc bên trong đường tròn.
Đường tròn có tâm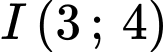 và có bán kính là
và có bán kính là 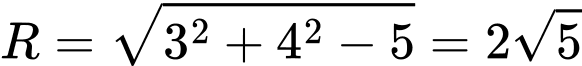
Ta có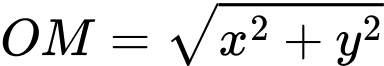
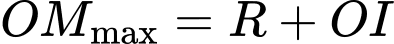
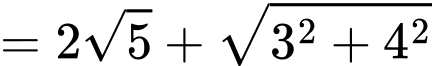
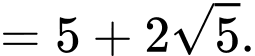
Chọn D. Đáp án: D
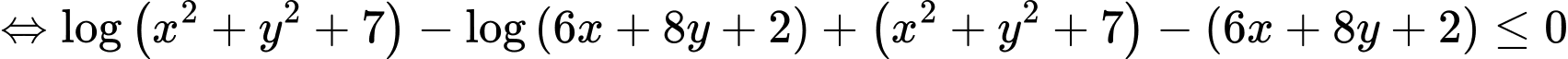
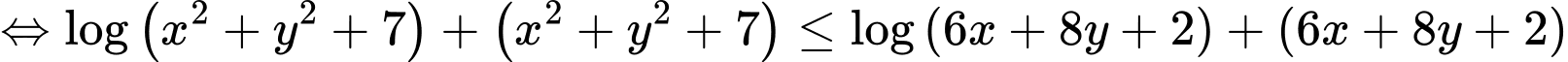
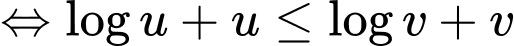
Xét hàm số
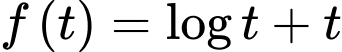 trên khoảng
trên khoảng 
Ta có
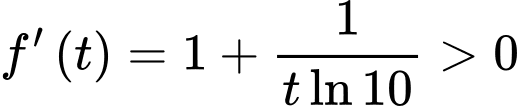
Suy ra hàm số đồng biến
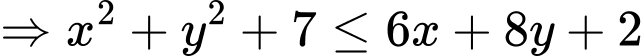
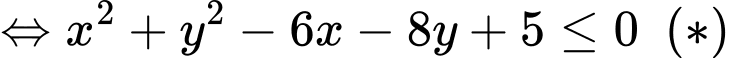
Ta thấy PT
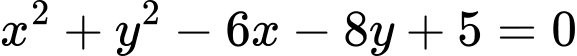 là một phương trình đường tròn nên tập hợp các điểm
là một phương trình đường tròn nên tập hợp các điểm 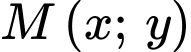 thoả mãn bất phương trình
thoả mãn bất phương trình  là các điểm nằm trên hoặc bên trong đường tròn.
là các điểm nằm trên hoặc bên trong đường tròn. Đường tròn có tâm
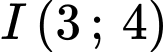 và có bán kính là
và có bán kính là 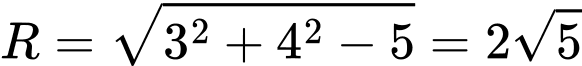
Ta có
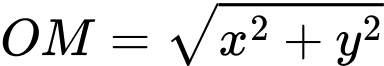
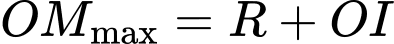
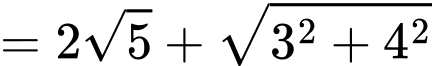
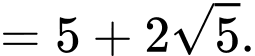
Chọn D. Đáp án: D
Câu 3 [791672]: Cho 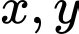 là hai số thực không âm thỏa mãn đẳng thức
là hai số thực không âm thỏa mãn đẳng thức 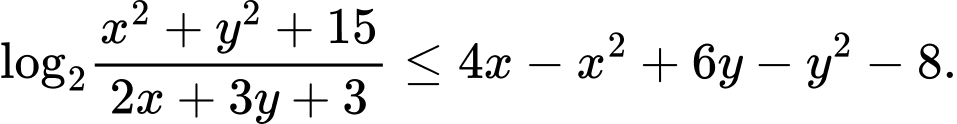 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức  là
là
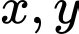 là hai số thực không âm thỏa mãn đẳng thức
là hai số thực không âm thỏa mãn đẳng thức 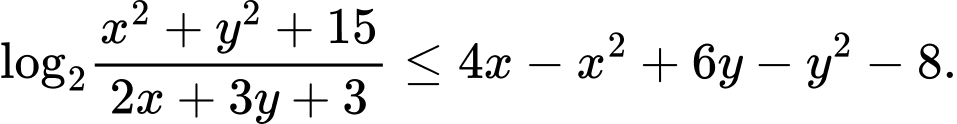 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức  là
là A, 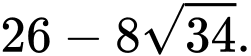
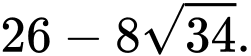
B, 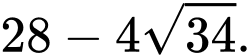
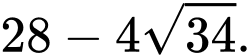
C, 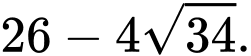
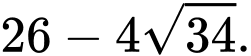
D, 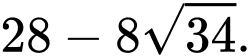
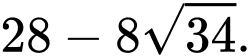
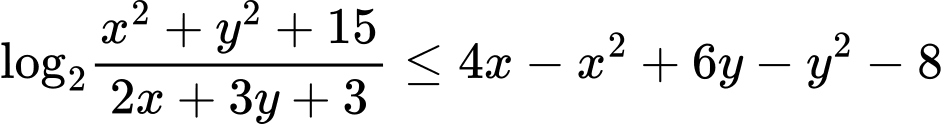
Xét:
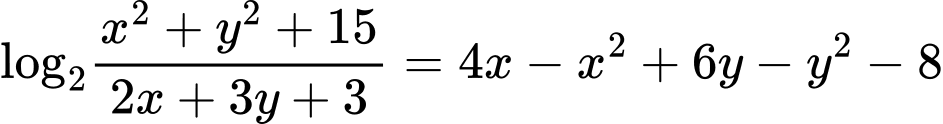
Đặt:

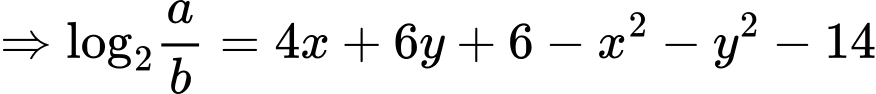
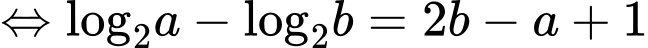
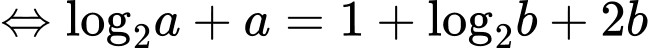
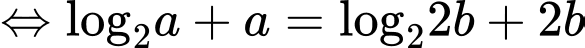
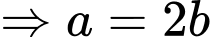
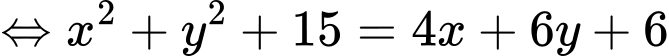
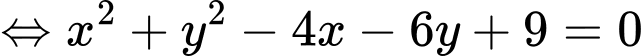
Ta được phương trình đường tròn tâm
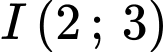 và bán kính
và bán kính 
Điểm
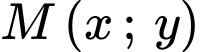 thuộc đường tròn tâm
thuộc đường tròn tâm 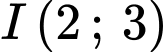 và bán kính
và bán kính 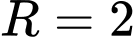
Có:

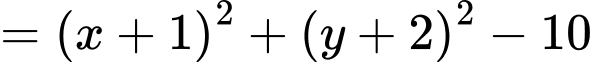
Lấy điểm
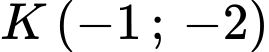

Ta thấy tìm giá trị nhỏ nhất của
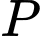 là tìm min của
là tìm min của  hay
hay  nhỏ nhất.
nhỏ nhất.
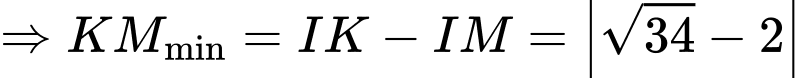
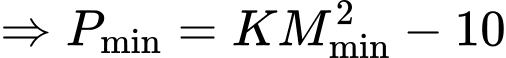
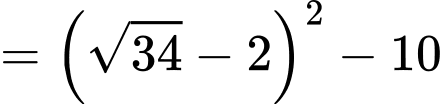
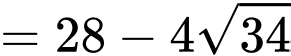
Đáp án: B. Đáp án: B
Câu 4 [234120]: [Đề thi TN THPT 2022]: Xét các số thực 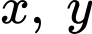 sao cho
sao cho 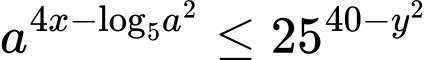 với mọi số thực dương
với mọi số thực dương 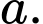 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 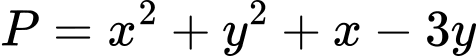 bằng
bằng
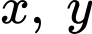 sao cho
sao cho 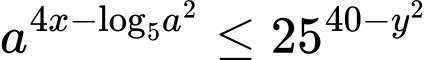 với mọi số thực dương
với mọi số thực dương 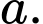 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 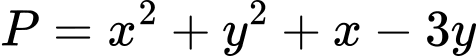 bằng
bằng A, 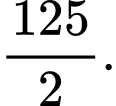
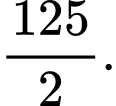
B, 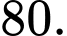
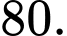
C, 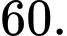
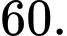
D, 
HD: Ta có: 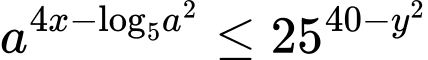
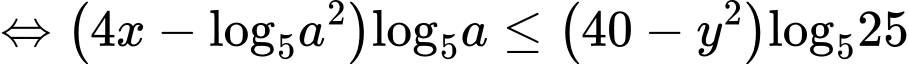 (lấy logarit cơ số 5 cả 2 vế)
(lấy logarit cơ số 5 cả 2 vế)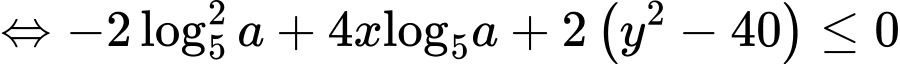
Bất phương trình đúng với mọi khi
khi 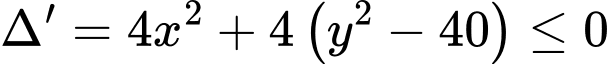
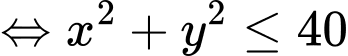
Lại có: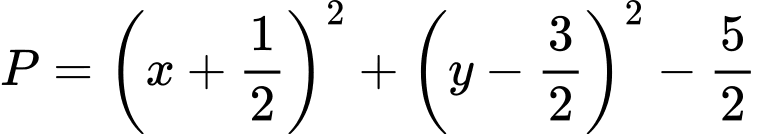
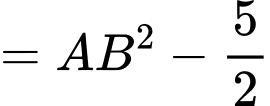
Trong đó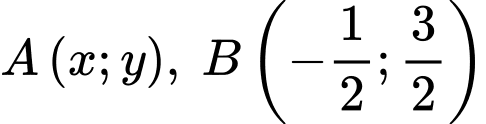 và điểm
và điểm 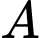 nằm ở miền trong đường tròn
nằm ở miền trong đường tròn 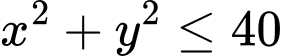 (đường tròn tâm
(đường tròn tâm 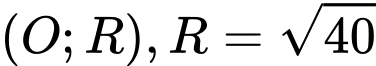 )
)
Lại có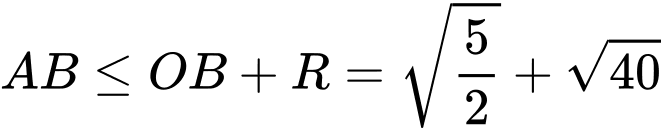
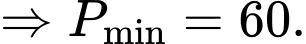
Chọn C. Đáp án: C
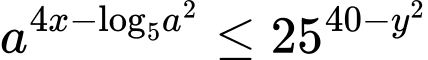
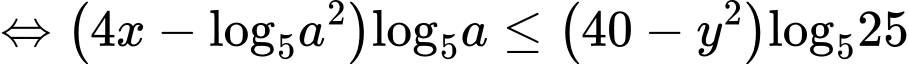 (lấy logarit cơ số 5 cả 2 vế)
(lấy logarit cơ số 5 cả 2 vế)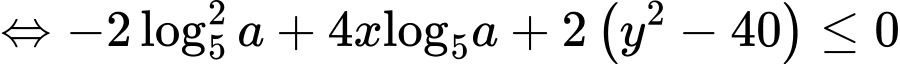
Bất phương trình đúng với mọi
 khi
khi 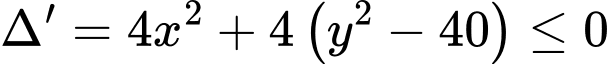
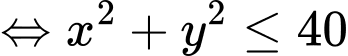
Lại có:
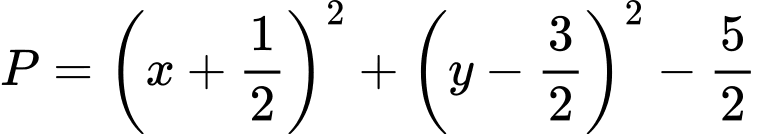
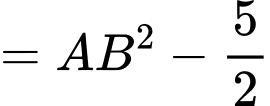
Trong đó
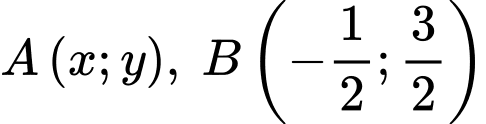 và điểm
và điểm 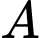 nằm ở miền trong đường tròn
nằm ở miền trong đường tròn 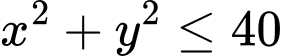 (đường tròn tâm
(đường tròn tâm 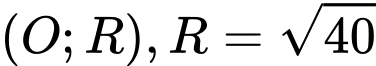 )
) Lại có
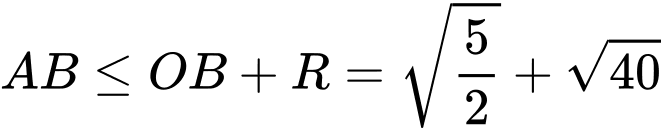
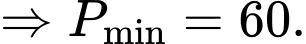
Chọn C. Đáp án: C
Câu 5 [234121]: Xét các số thực 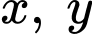 sao cho
sao cho 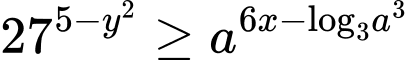 với mọi số thực dương
với mọi số thực dương 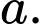 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 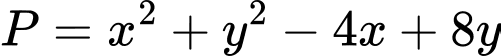 bằng
bằng
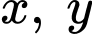 sao cho
sao cho 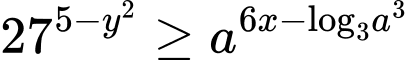 với mọi số thực dương
với mọi số thực dương 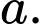 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 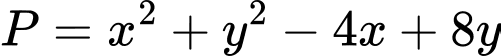 bằng
bằng A, 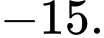
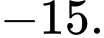
B, 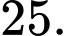
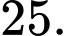
C, 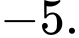
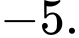
D, 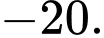
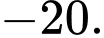
Giả sử 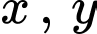 thoả mãn với mọi số dương
thoả mãn với mọi số dương 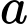
Ta có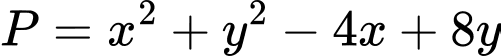
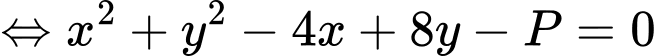
Suy ra điểm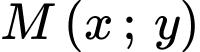 thuộc đường tròn tâm
thuộc đường tròn tâm 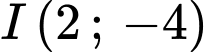 và bán kính
và bán kính 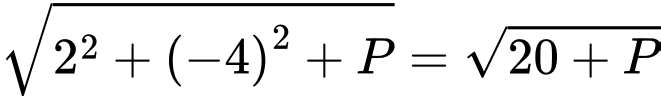
Ta có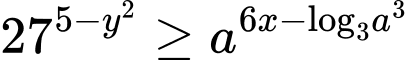
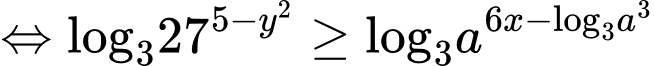
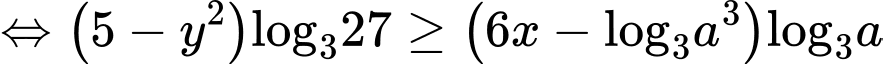
Đặt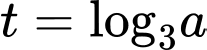
PT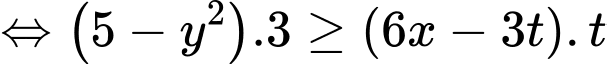
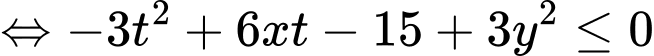
Theo đề bài, bất phương trình trên đúng với mọi số thực dương nên
nên 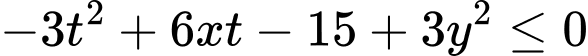 đúng với mọi
đúng với mọi 
Do đó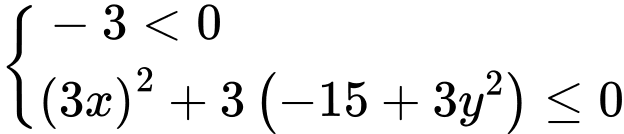
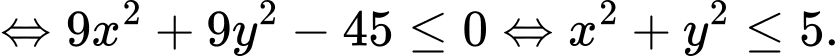
Suy ra tập hợp các điểm là hình tròn tâm
là hình tròn tâm 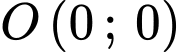 và bán kính
và bán kính 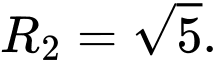
Vậy để tồn tại cặp thì đường tròn
thì đường tròn 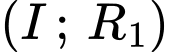 và hình tròn
và hình tròn 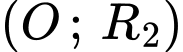 phải có điểm chung.
phải có điểm chung.
Do đó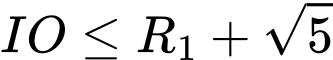
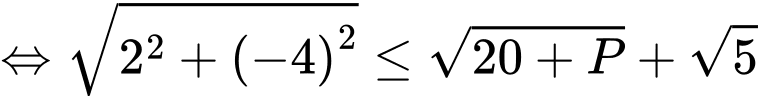
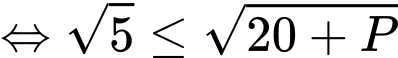

Vậy giá trị nhỏ nhất của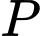 là
là 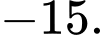
Chọn A. Đáp án: A
 thoả mãn với mọi số dương
thoả mãn với mọi số dương 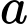
Ta có
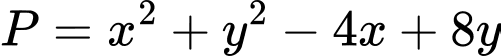
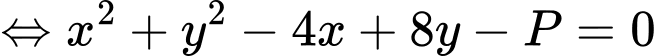
Suy ra điểm
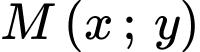 thuộc đường tròn tâm
thuộc đường tròn tâm 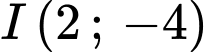 và bán kính
và bán kính 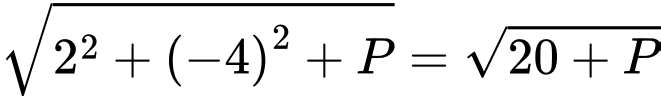
Ta có
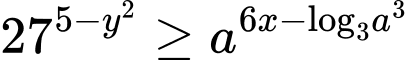
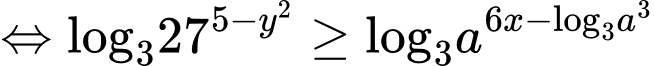
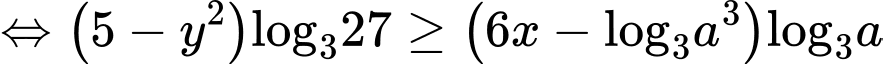
Đặt
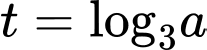
PT
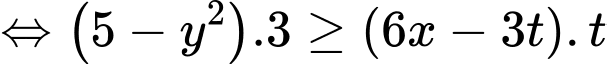
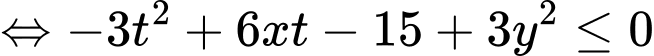
Theo đề bài, bất phương trình trên đúng với mọi số thực dương
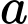 nên
nên 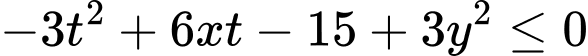 đúng với mọi
đúng với mọi 
Do đó
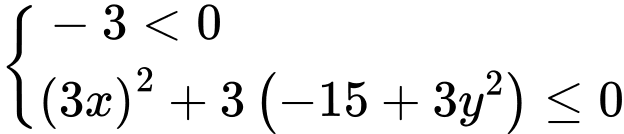
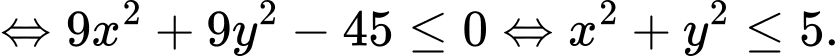
Suy ra tập hợp các điểm
 là hình tròn tâm
là hình tròn tâm 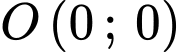 và bán kính
và bán kính 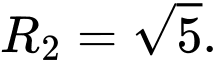
Vậy để tồn tại cặp
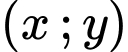 thì đường tròn
thì đường tròn 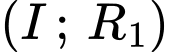 và hình tròn
và hình tròn 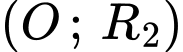 phải có điểm chung.
phải có điểm chung.Do đó
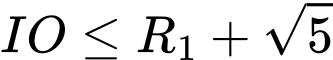
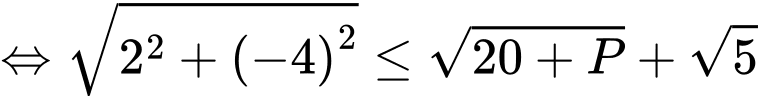
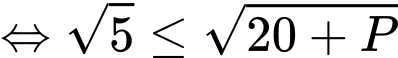

Vậy giá trị nhỏ nhất của
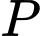 là
là 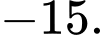
Chọn A. Đáp án: A
Câu 6 [804427]: Xét các số thực không âm 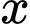 và
và 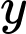 thỏa mãn
thỏa mãn 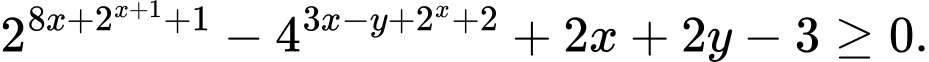 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 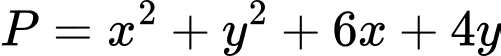 gần nhất với số nào dưới đây?
gần nhất với số nào dưới đây?
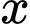 và
và 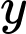 thỏa mãn
thỏa mãn 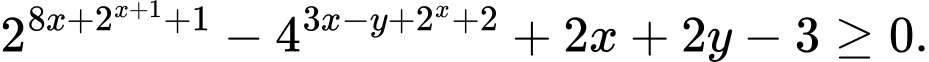 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 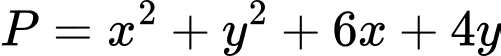 gần nhất với số nào dưới đây?
gần nhất với số nào dưới đây? A, 6.
B, 7.
C, 9.
D, 8.
Ta có: 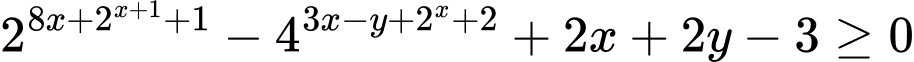
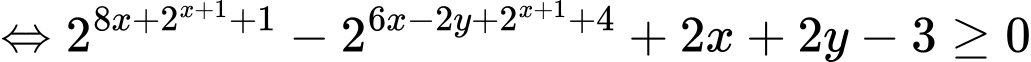
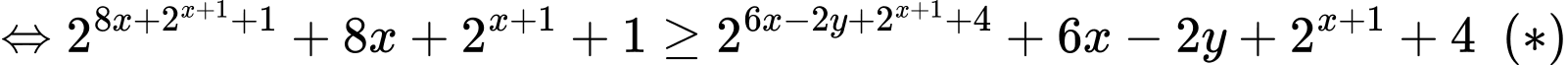
Xét hàm số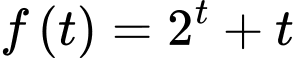
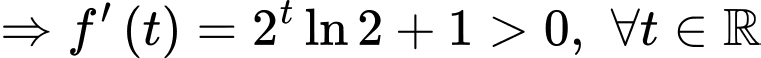
Suy ra hàm số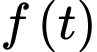 đồng biến trên
đồng biến trên 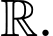
Do đó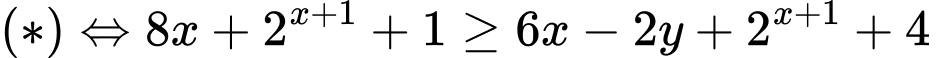
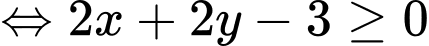
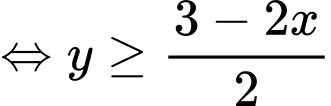
Khi đó ta có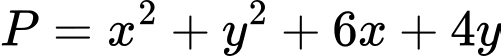
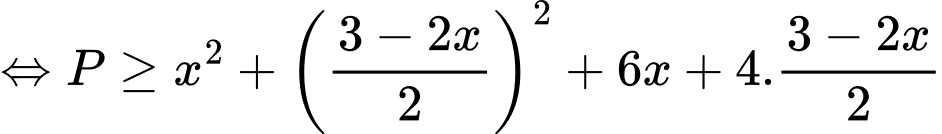
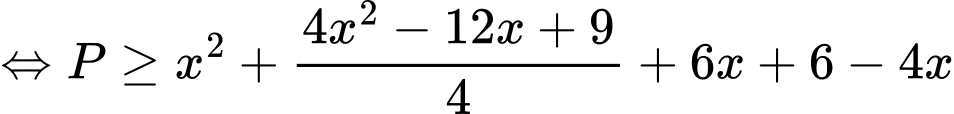
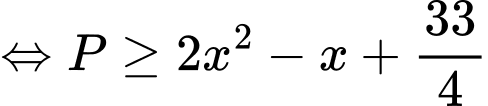
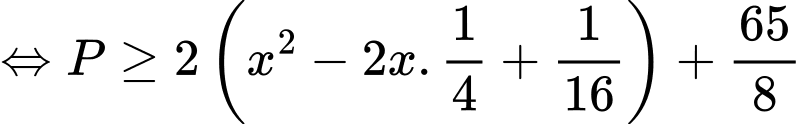
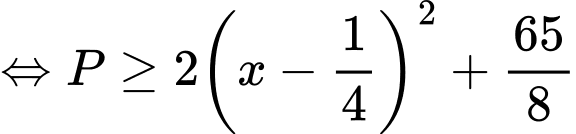
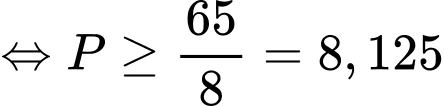
Vậy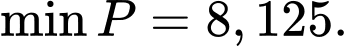
Chọn đáp án D. Đáp án: D
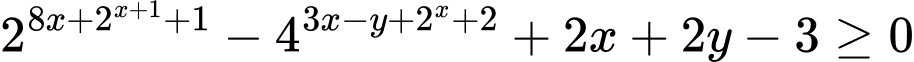
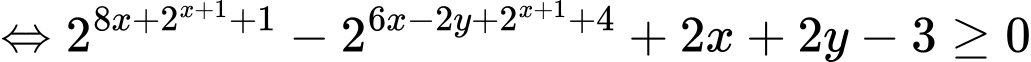
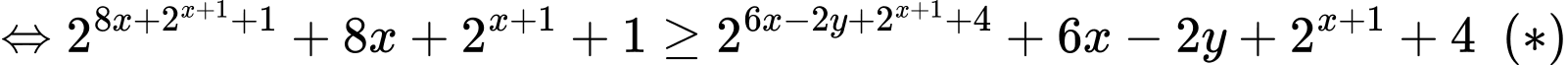
Xét hàm số
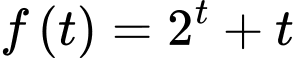
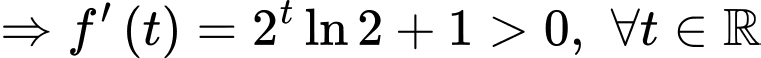
Suy ra hàm số
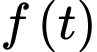 đồng biến trên
đồng biến trên 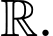
Do đó
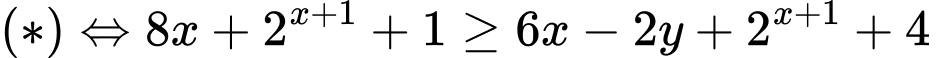
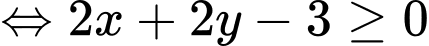
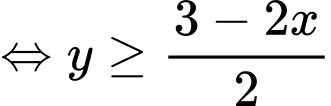
Khi đó ta có
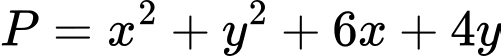
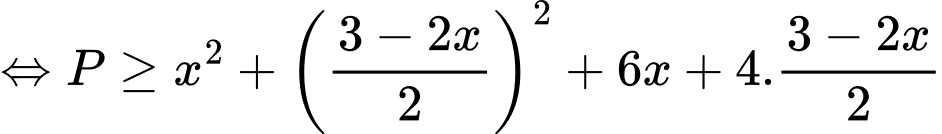
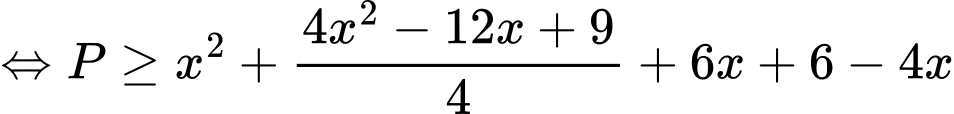
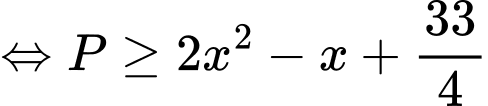
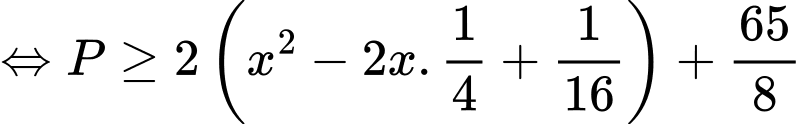
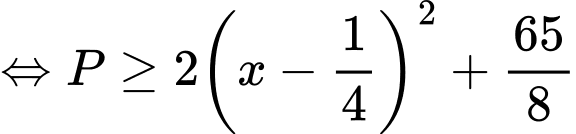
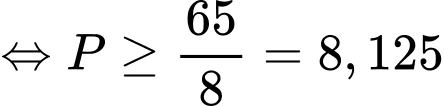
Vậy
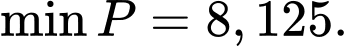
Chọn đáp án D. Đáp án: D
Câu 7 [678152]: Xét các số thực thỏa mãn 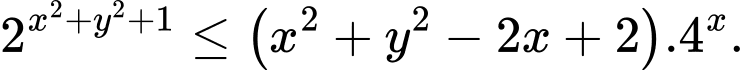 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 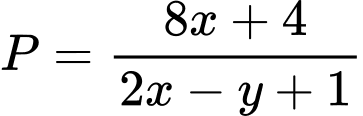 gần nhất với số nào dưới đây?
gần nhất với số nào dưới đây?
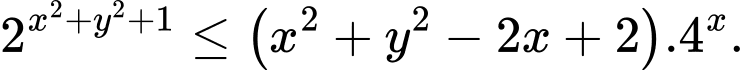 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 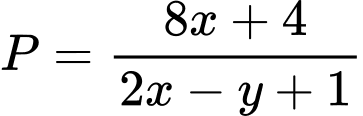 gần nhất với số nào dưới đây?
gần nhất với số nào dưới đây? A, 
B, 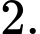
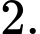
C, 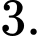
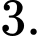
D, 
Nhận xét 
Bất phương trình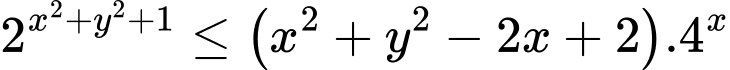
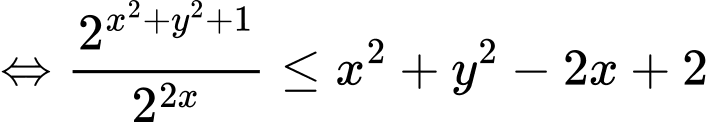
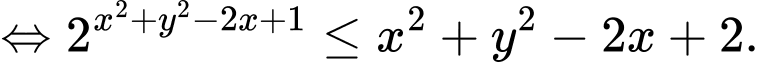
Đặt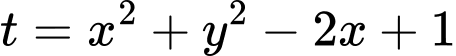
BPT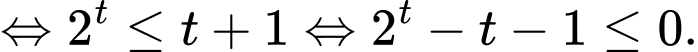
Xét hàm số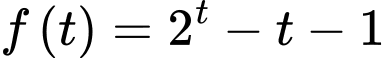 trên
trên 
Ta thấy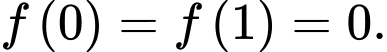
Ta có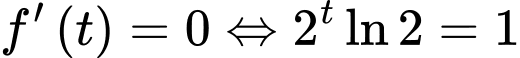
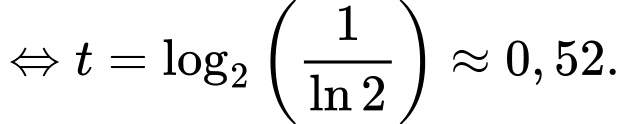
Bảng biến thiên
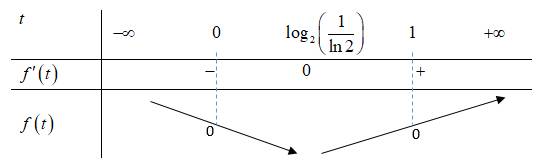
Quan sát bảng biến thiên ta thấy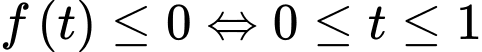
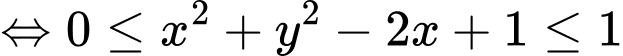
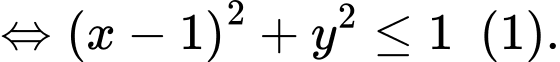
Xét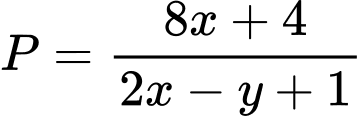
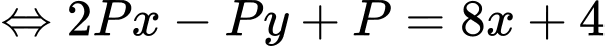
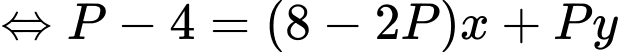
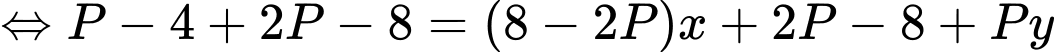
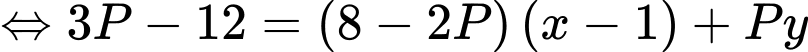
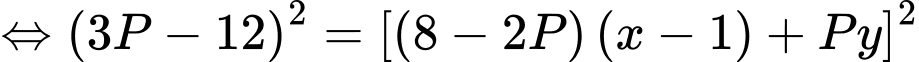
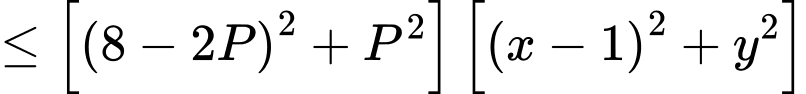
Thế vào ta được
vào ta được 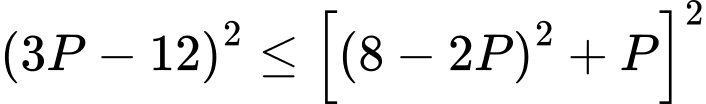
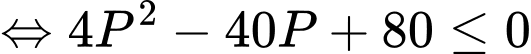
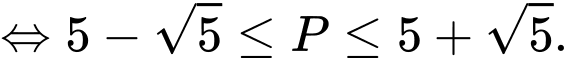
Dấu “=” xảy ra khi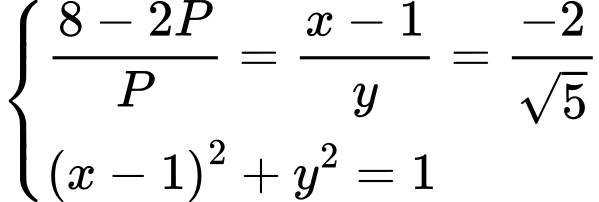
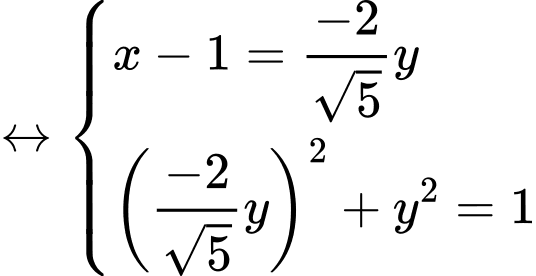
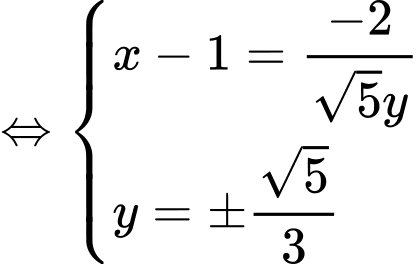
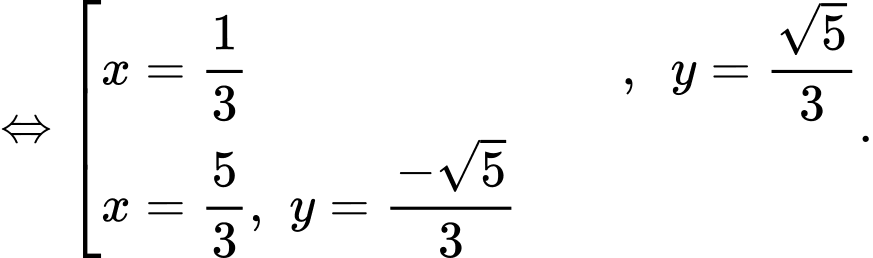
Vậy giá trị nhỏ nhất của là
là 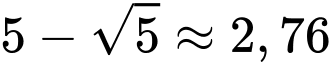 gần giá trị 3 nhất.
gần giá trị 3 nhất.
Chọn C. Đáp án: C

Bất phương trình
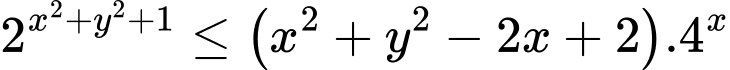
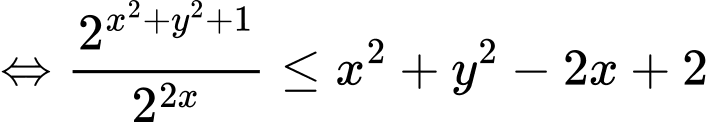
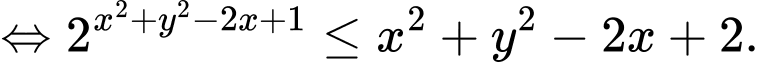
Đặt
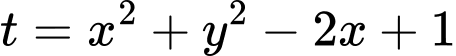
BPT
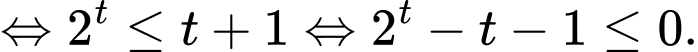
Xét hàm số
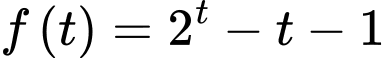 trên
trên 
Ta thấy
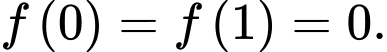
Ta có
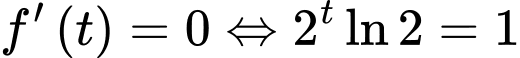
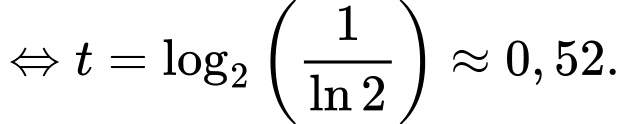
Bảng biến thiên

Quan sát bảng biến thiên ta thấy
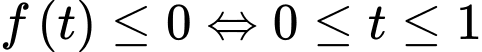
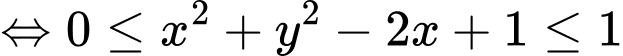
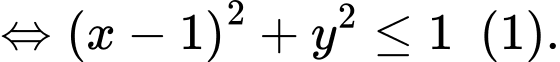
Xét
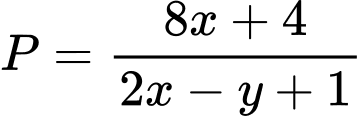
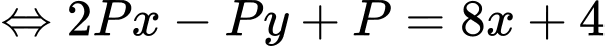
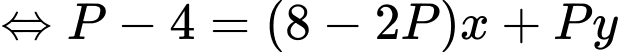
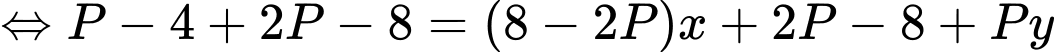
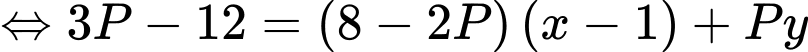
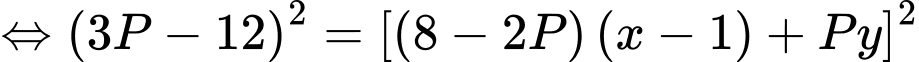
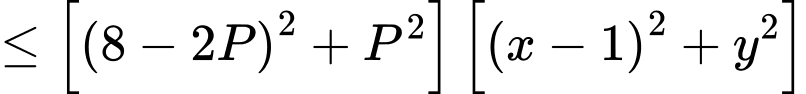
Thế
 vào ta được
vào ta được 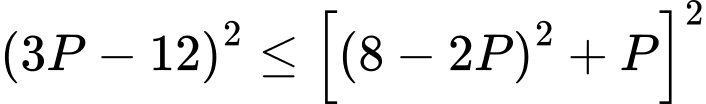
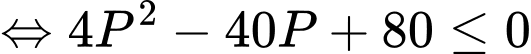
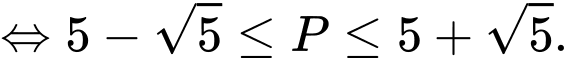
Dấu “=” xảy ra khi
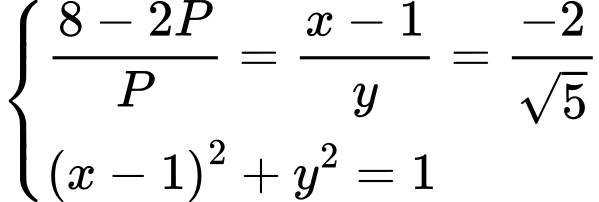
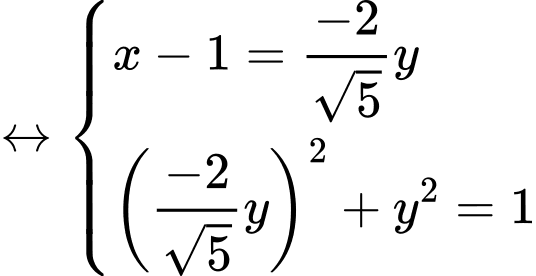
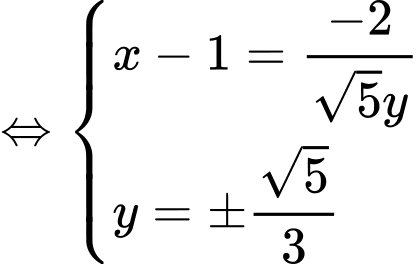
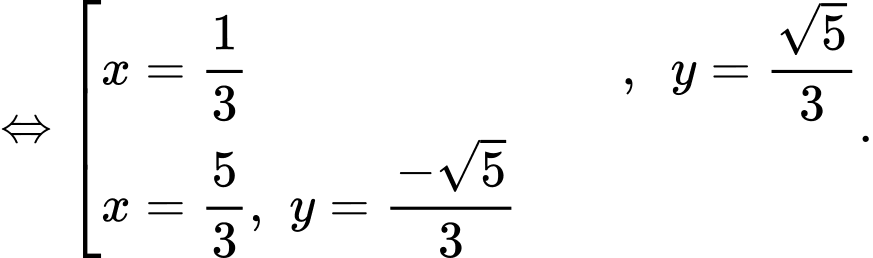
Vậy giá trị nhỏ nhất của
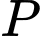 là
là 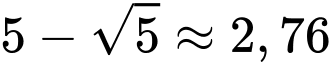 gần giá trị 3 nhất.
gần giá trị 3 nhất.
Chọn C. Đáp án: C
Câu 8 [677072]: Cho các số thực 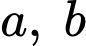 thỏa mãn
thỏa mãn 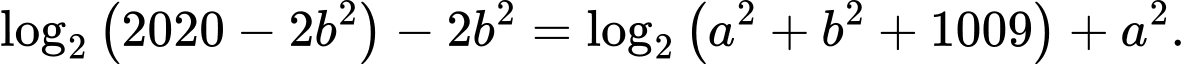 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 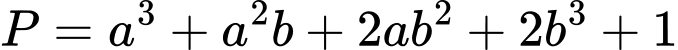 thuộc khoảng nào trong các khoảng sau đây?
thuộc khoảng nào trong các khoảng sau đây?
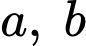 thỏa mãn
thỏa mãn 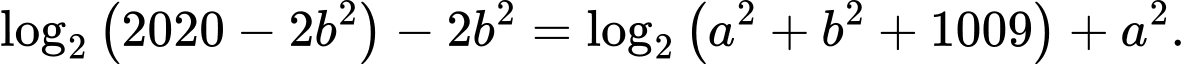 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 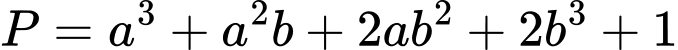 thuộc khoảng nào trong các khoảng sau đây?
thuộc khoảng nào trong các khoảng sau đây? A, 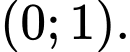
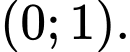
B, 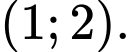
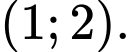
C, 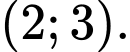
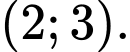
D, 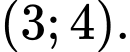
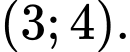
Ta có: 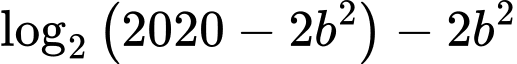
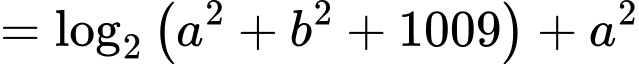
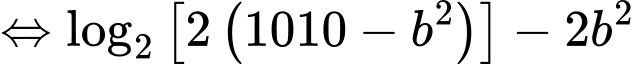
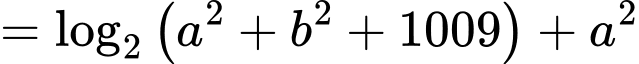
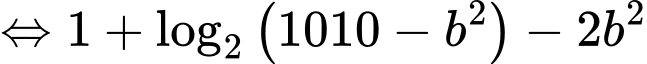
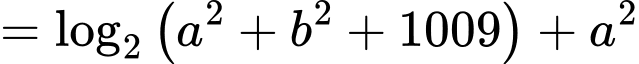
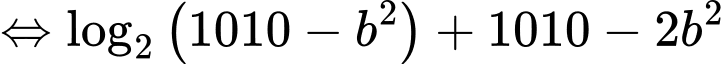
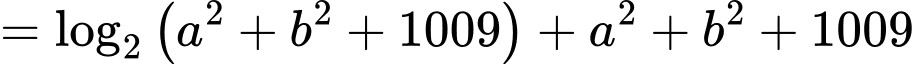
Sử dụng phương pháp hàm đặc trưng suy ra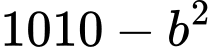
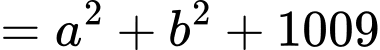
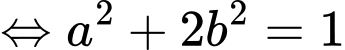
Khi đó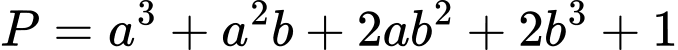
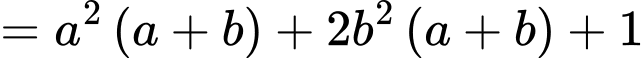
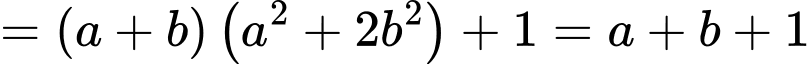
Do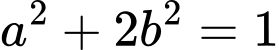
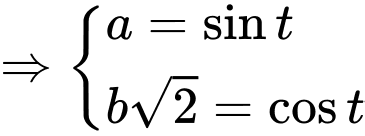
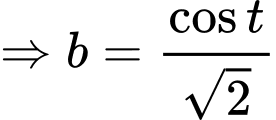
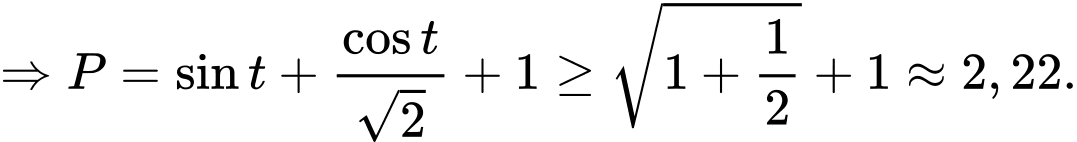
Chọn C. Đáp án: C
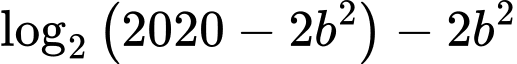
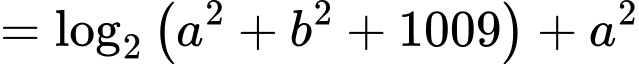
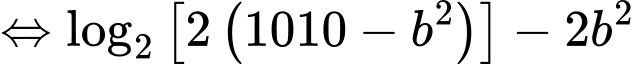
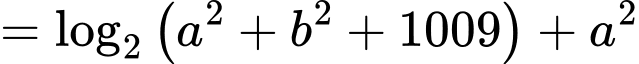
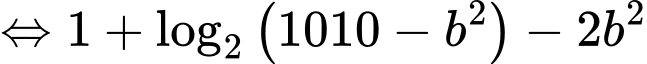
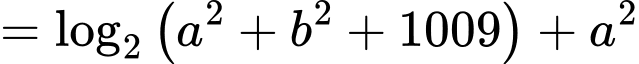
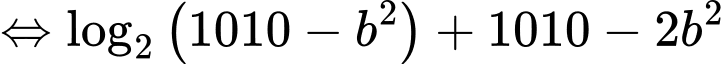
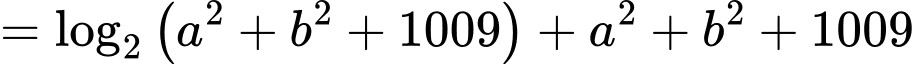
Sử dụng phương pháp hàm đặc trưng suy ra
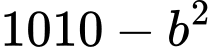
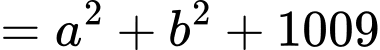
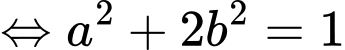
Khi đó
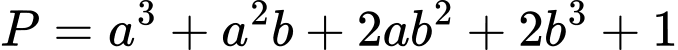
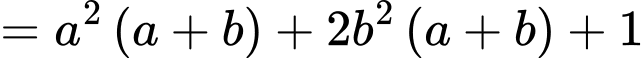
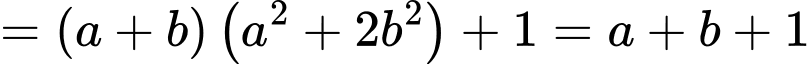
Do
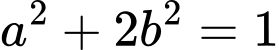
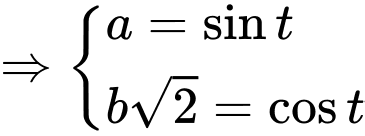
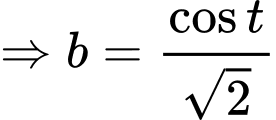
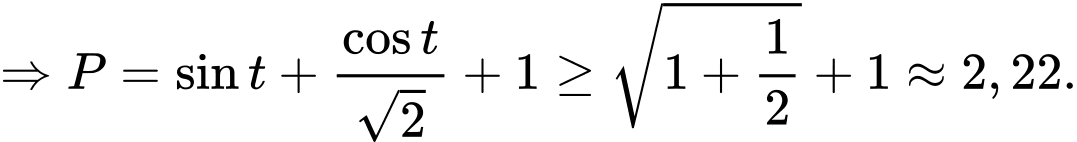
Chọn C. Đáp án: C
Câu 9 [677074]: Cho 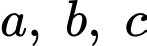 là các số thực thỏa mãn
là các số thực thỏa mãn 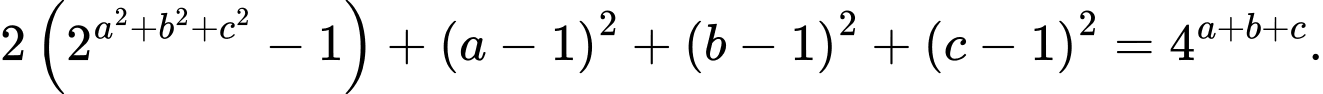 Đặt
Đặt 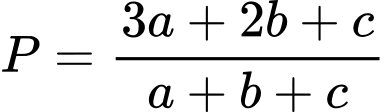 và gọi
và gọi  là tập hợp những giá trị nguyên của
là tập hợp những giá trị nguyên của 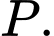 Tổng tất cả các phần tử của tập hợp
Tổng tất cả các phần tử của tập hợp 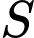 là
là
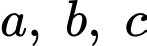 là các số thực thỏa mãn
là các số thực thỏa mãn 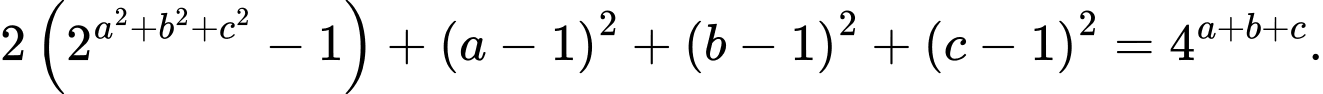 Đặt
Đặt 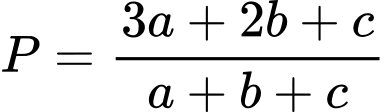 và gọi
và gọi 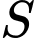 là tập hợp những giá trị nguyên của
là tập hợp những giá trị nguyên của 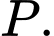 Tổng tất cả các phần tử của tập hợp
Tổng tất cả các phần tử của tập hợp 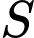 là
là A, 4.
B, 6.
C, 0.
D, 5.
Biến đổi giả thiết ta có: 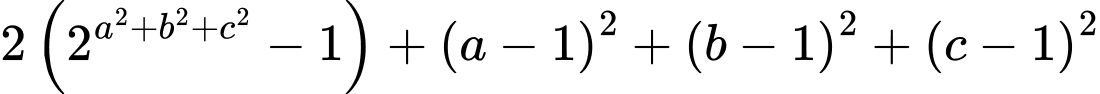
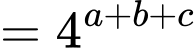
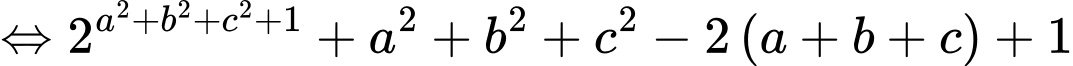
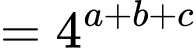
Đặt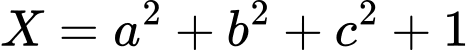 và
và 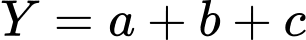 ta có:
ta có: 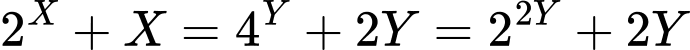
Sử dụng phương pháp hàm số đặc trưng suy ra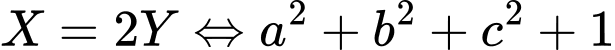

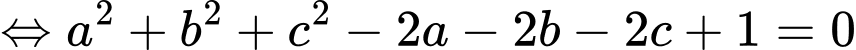

Ta coi là phương trình mặt cầu có tâm
là phương trình mặt cầu có tâm 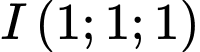 bán kính
bán kính 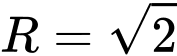
Mặt khác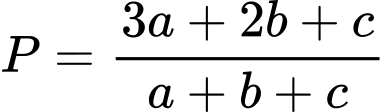
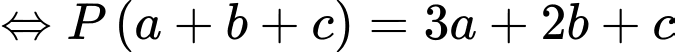
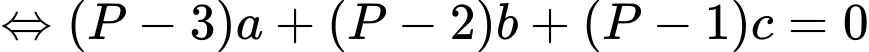
Ta coi đây là phương trình mặt phẳng
Để tồn tại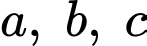 thì
thì 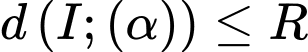
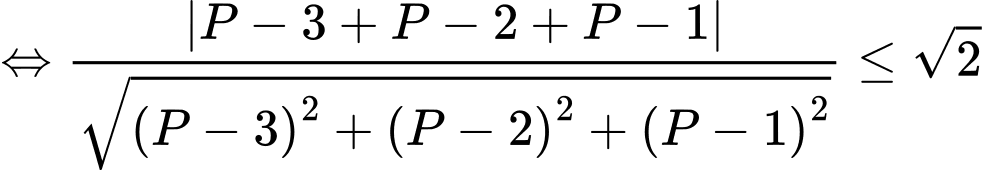
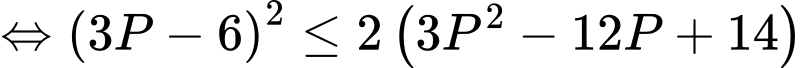
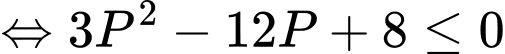

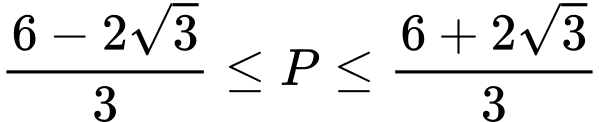
Kết hợp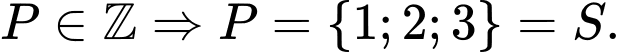 Tổng tất cả các phần tử của tập hợp
Tổng tất cả các phần tử của tập hợp 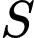 là
là  Chọn B. Đáp án: B
Chọn B. Đáp án: B
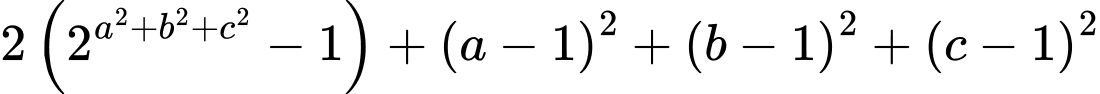
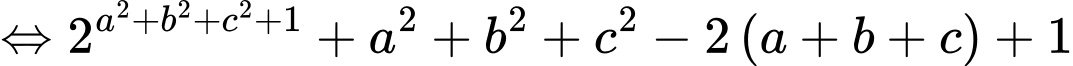
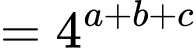
Đặt
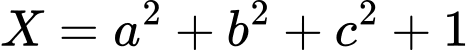 và
và 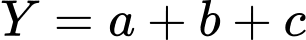 ta có:
ta có: 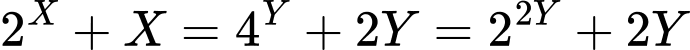
Sử dụng phương pháp hàm số đặc trưng suy ra
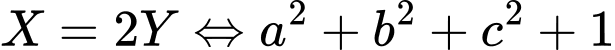

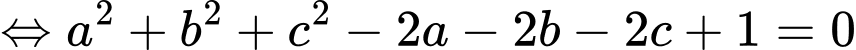

Ta coi
 là phương trình mặt cầu có tâm
là phương trình mặt cầu có tâm 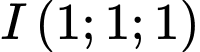 bán kính
bán kính 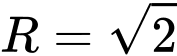
Mặt khác
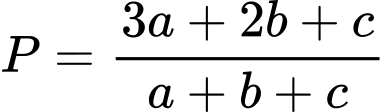
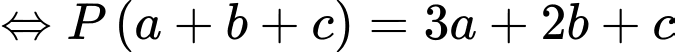
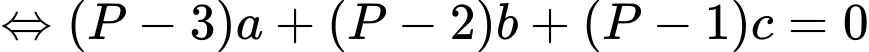
Ta coi đây là phương trình mặt phẳng
Để tồn tại
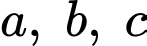 thì
thì 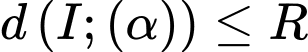
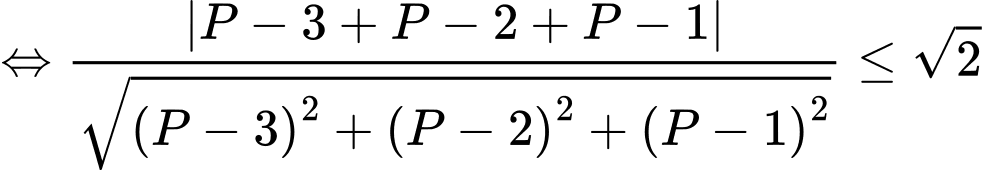
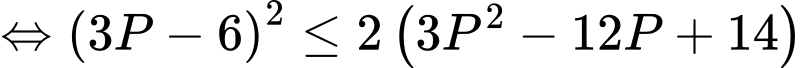
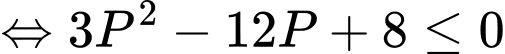

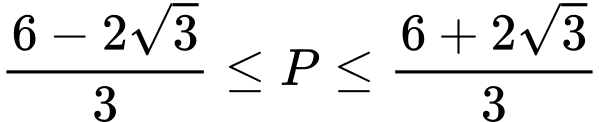
Kết hợp
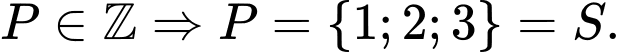 Tổng tất cả các phần tử của tập hợp
Tổng tất cả các phần tử của tập hợp 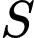 là
là 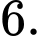 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 10 [29472]: Cho các số thực 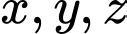 thỏa mãn
thỏa mãn 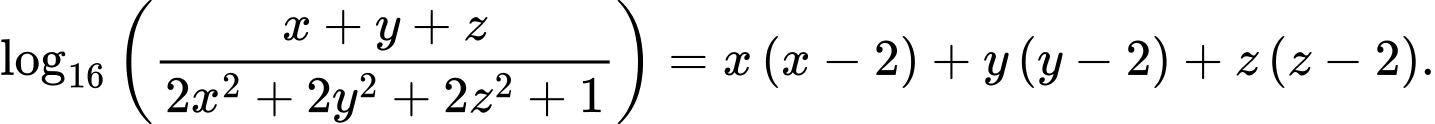 Tổng giá trị lớn nhất và nhỏ nhất của biểu thức
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức 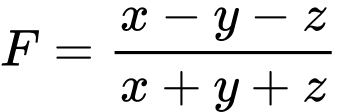 bằng
bằng
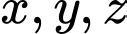 thỏa mãn
thỏa mãn 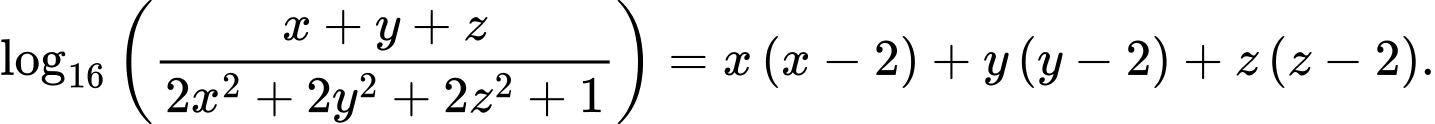 Tổng giá trị lớn nhất và nhỏ nhất của biểu thức
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức 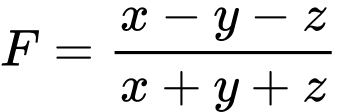 bằng
bằng A, 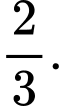
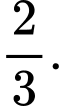
B, 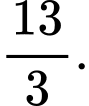
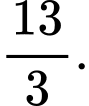
C, 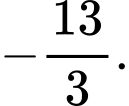
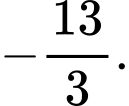
D, 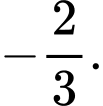
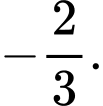
Điều kiện 
Ta có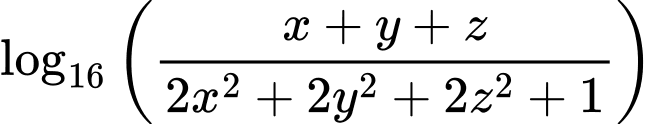
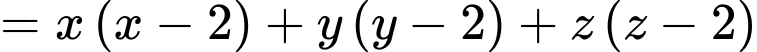

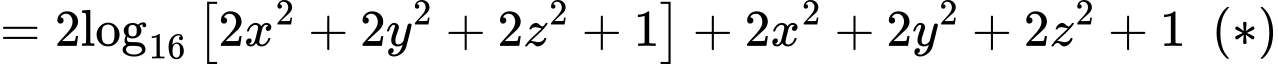
Xét hàm số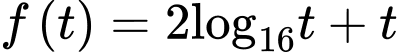 trên khoảng
trên khoảng 
Ta có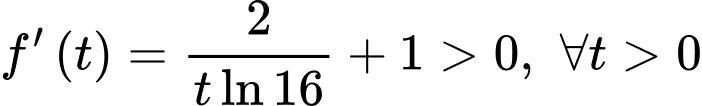
Do đó hàm số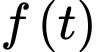 đồng biến.
đồng biến.
Khi đó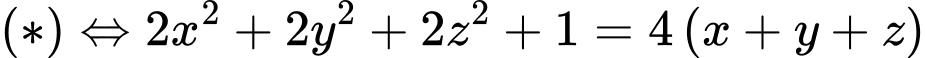
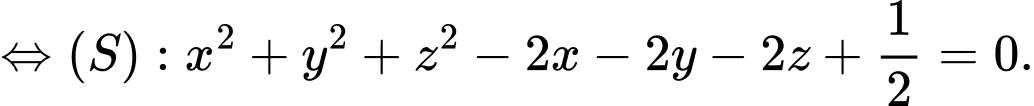
Ta có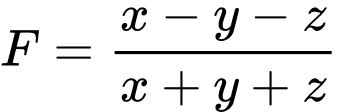
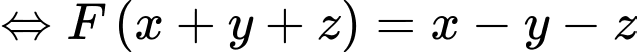
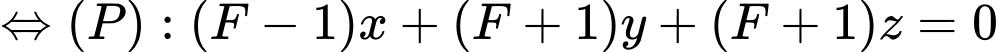
Mặt phẳng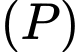 có điểm chung với mặt cầu
có điểm chung với mặt cầu 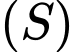 nên ta có
nên ta có 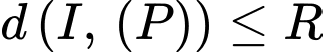
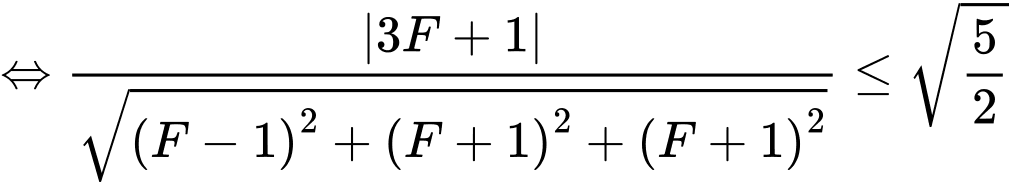
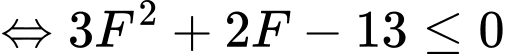
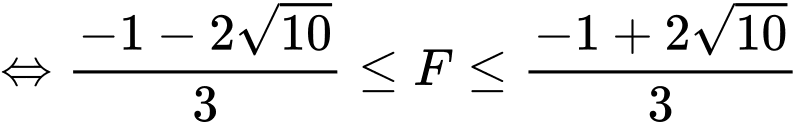
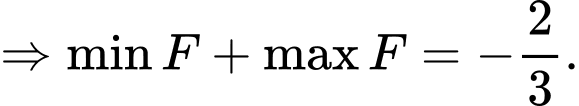
Chọn D. Đáp án: D

Ta có
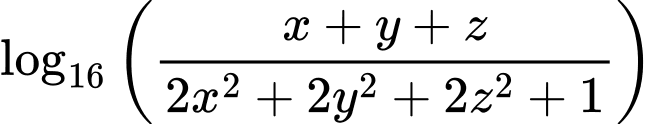
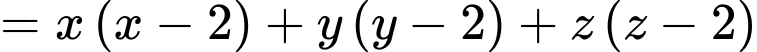

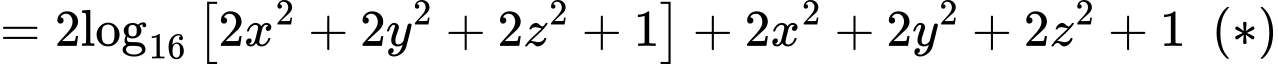
Xét hàm số
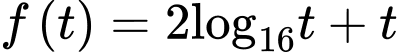 trên khoảng
trên khoảng 
Ta có
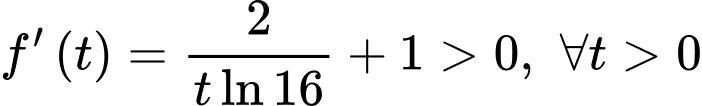
Do đó hàm số
 đồng biến.
đồng biến.Khi đó
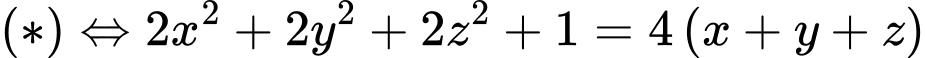
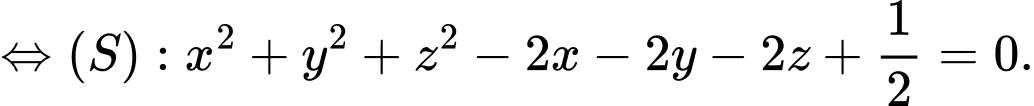
Ta có
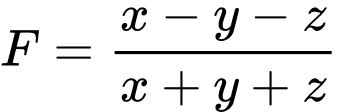
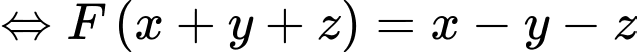
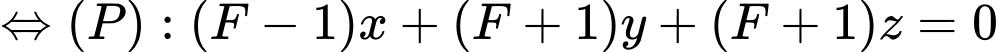
Mặt phẳng
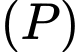 có điểm chung với mặt cầu
có điểm chung với mặt cầu 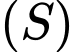 nên ta có
nên ta có 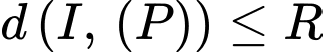
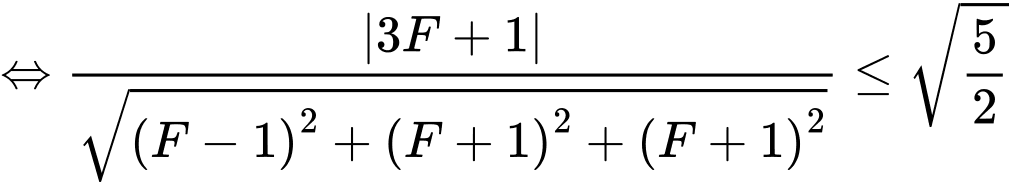
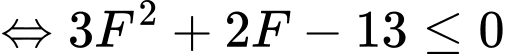
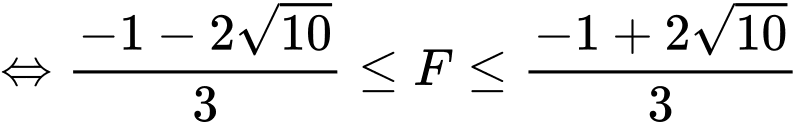
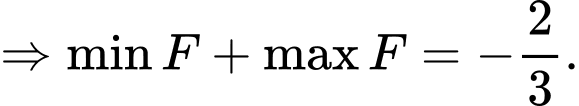
Chọn D. Đáp án: D
Câu 11 [520179]: Cho các số thực  thỏa mãn
thỏa mãn 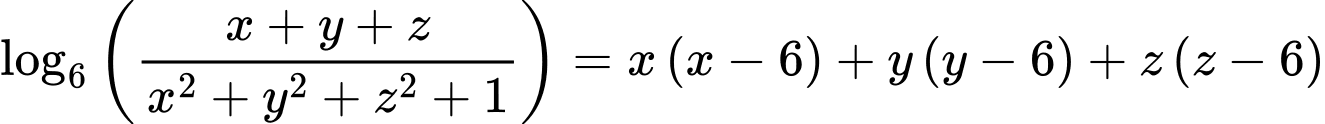 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức 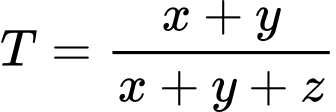 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
 thỏa mãn
thỏa mãn 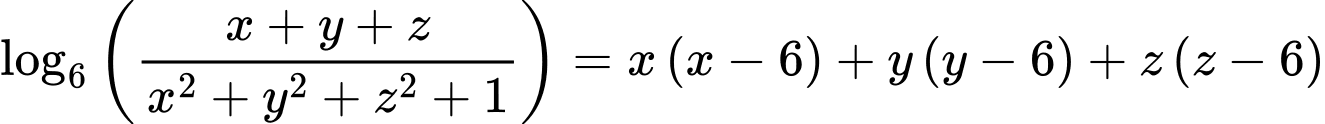 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức 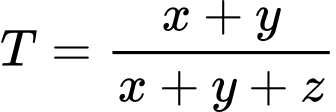 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? A, 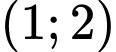 .
.
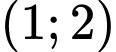 .
.B, 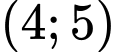 .
.
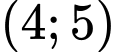 .
.C, 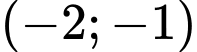 .
.
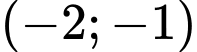 .
.D, 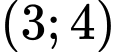 .
.
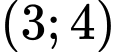 .
.
Chọn C
Điều kiện .
.
Ta có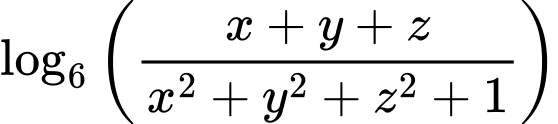
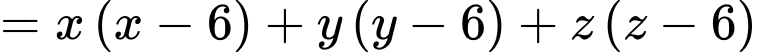
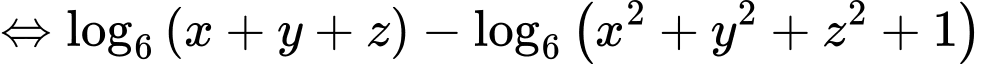
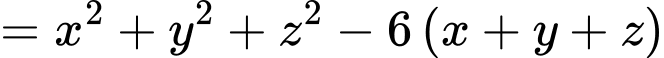
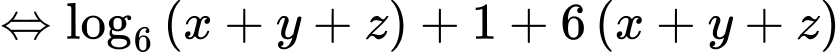
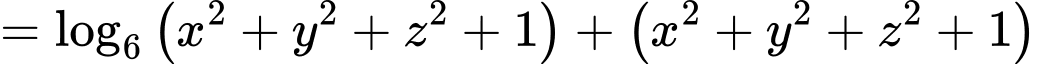
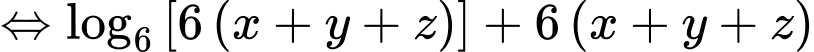
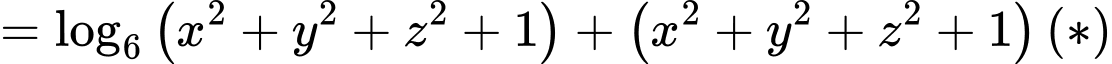
Xét hàm số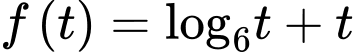 với
với 
Ta có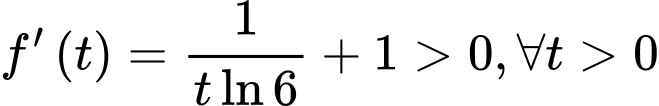 nên
nên 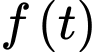 đồng biến trên
đồng biến trên 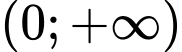 .
.
Do đó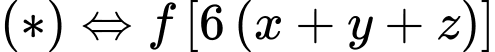
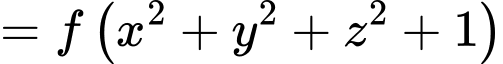
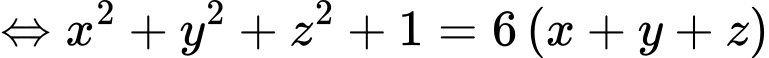
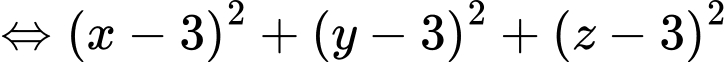
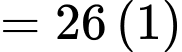
Ta thấy phương trình có dạng phương trình mặt cầu
có dạng phương trình mặt cầu 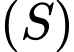 tâm
tâm 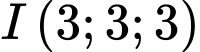 , bán kính
, bán kính 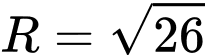 .
.
Xét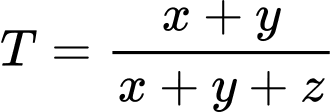
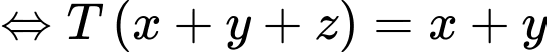

Ta thấy phương trình có dạng phương trình mặt phẳng
có dạng phương trình mặt phẳng 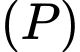 .
.
Yêu cầu đề bài phương trình
phương trình  và
và  có nghiệm chung hay mặt cầu
có nghiệm chung hay mặt cầu 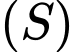 giao với mặt phẳng
giao với mặt phẳng 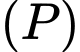 .
.
Khi đó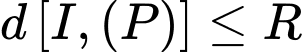
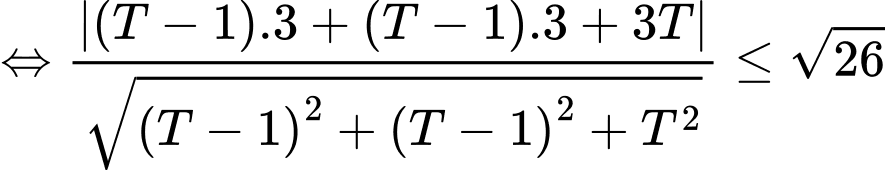
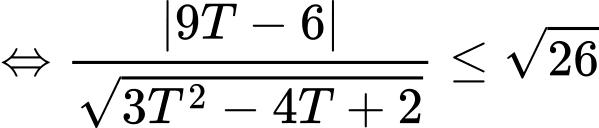
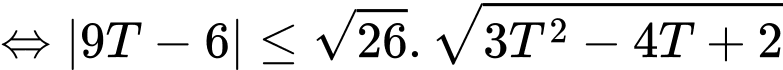
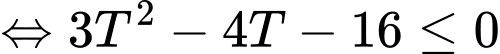
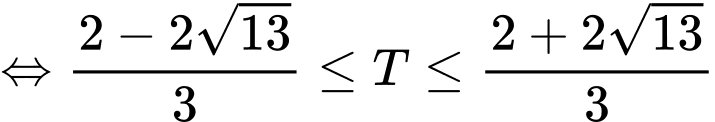 .
.
Giá trị nhỏ nhất của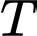 là
là 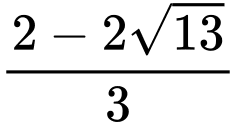 . Đáp án: C
. Đáp án: C
Điều kiện
 .
. Ta có
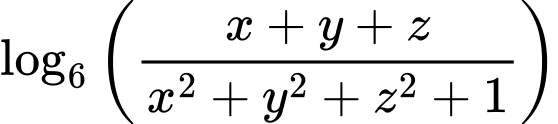
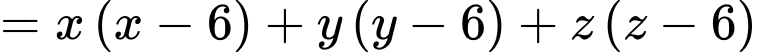
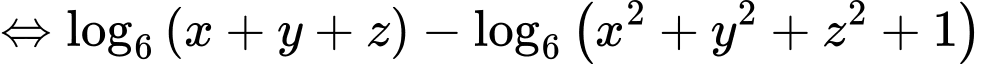
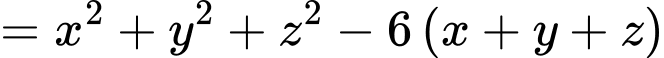
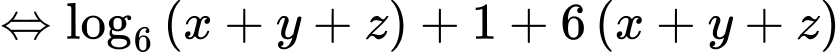
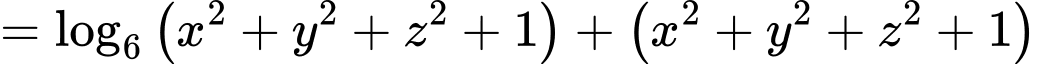
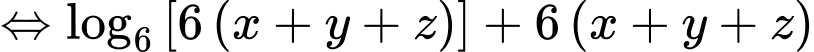
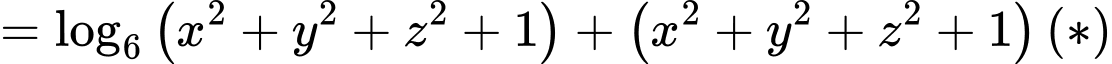
Xét hàm số
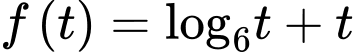 với
với 
Ta có
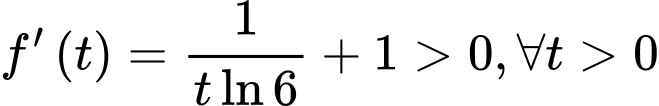 nên
nên 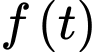 đồng biến trên
đồng biến trên 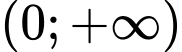 .
. Do đó
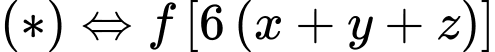
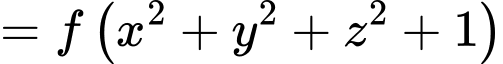
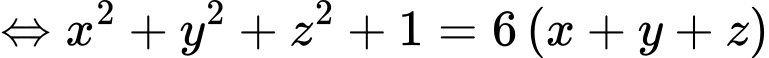
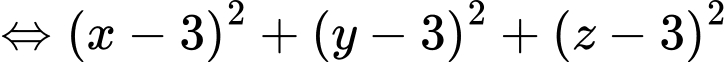
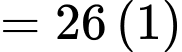
Ta thấy phương trình
 có dạng phương trình mặt cầu
có dạng phương trình mặt cầu 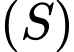 tâm
tâm 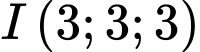 , bán kính
, bán kính 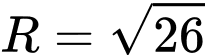 .
. Xét
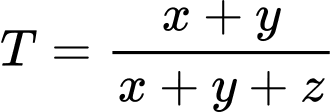
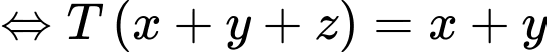

Ta thấy phương trình
 có dạng phương trình mặt phẳng
có dạng phương trình mặt phẳng 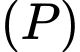 .
. Yêu cầu đề bài
 phương trình
phương trình  và
và  có nghiệm chung hay mặt cầu
có nghiệm chung hay mặt cầu 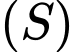 giao với mặt phẳng
giao với mặt phẳng 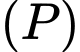 .
. Khi đó
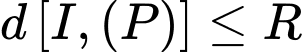
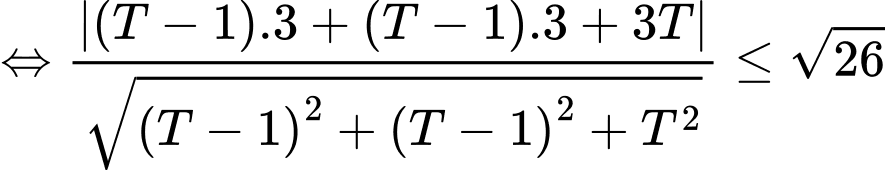
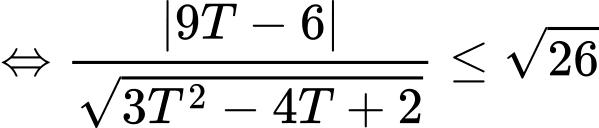
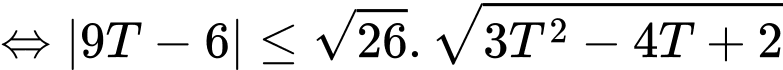
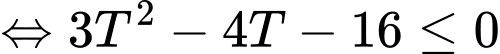
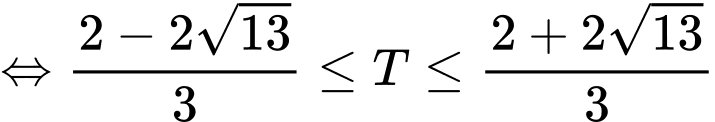 .
. Giá trị nhỏ nhất của
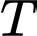 là
là 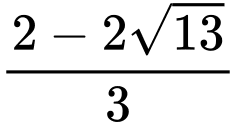 . Đáp án: C
. Đáp án: C
Câu 12 [29471]: Cho 3 số thực 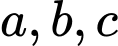 thỏa mãn
thỏa mãn 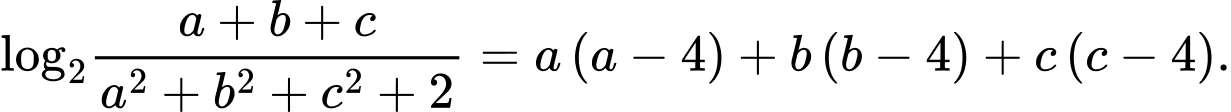 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 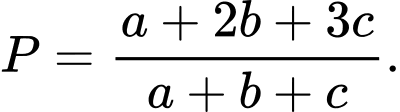
 thỏa mãn
thỏa mãn 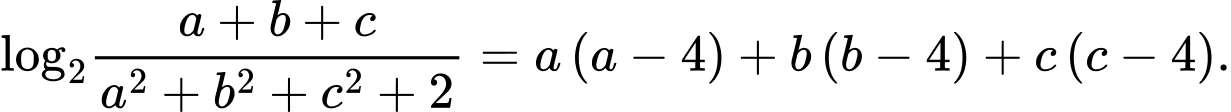 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 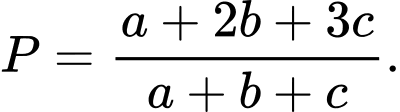
A, 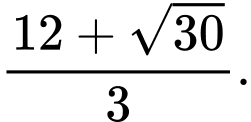
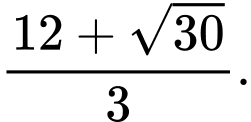
B, 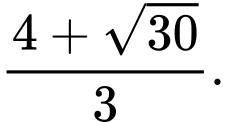
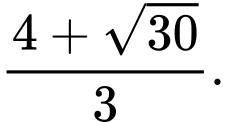
C, 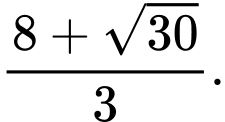
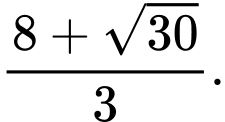
D, 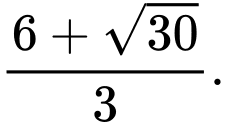
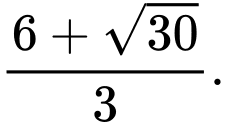
Ta có 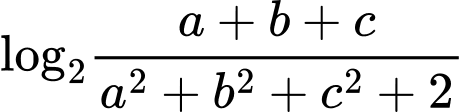
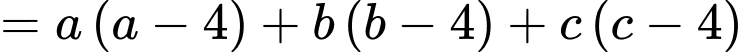
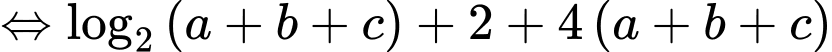
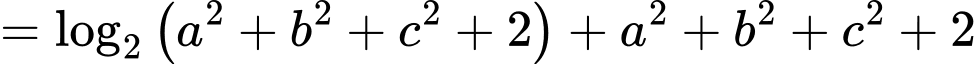
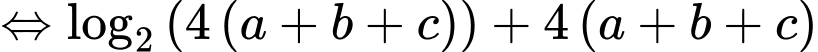
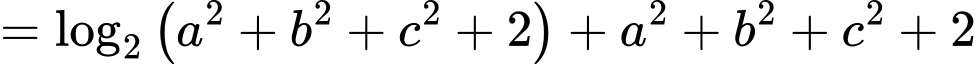
Xét hàm số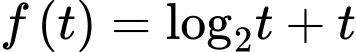 trên khoảng
trên khoảng 
Ta có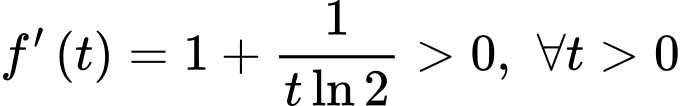
Suy ra hàm số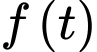 đồng biến trên
đồng biến trên 
Khi đó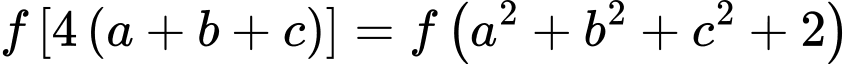
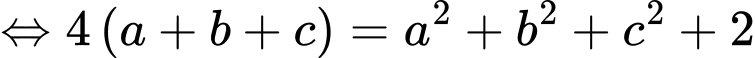
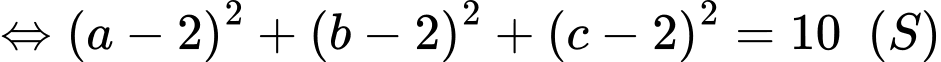
Giả sử điểm thuộc mặt cầu
thuộc mặt cầu 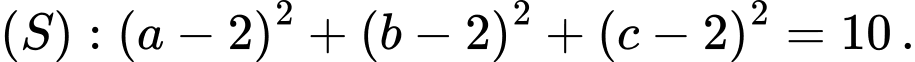
Mặt khác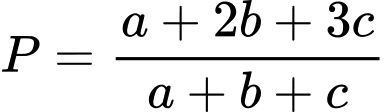
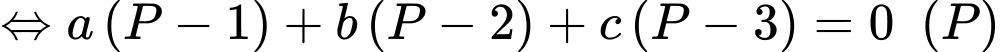
Điều kiện để và
và  có giao điểm là
có giao điểm là
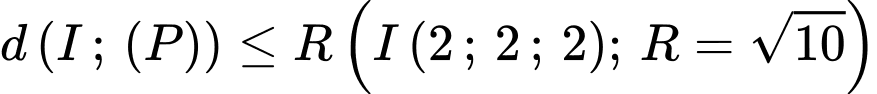
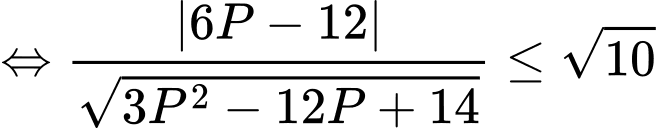
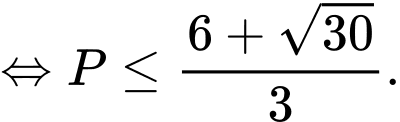 Chọn D. Đáp án: D
Chọn D. Đáp án: D
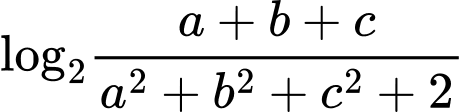
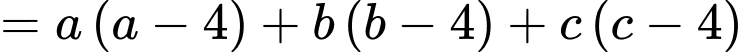
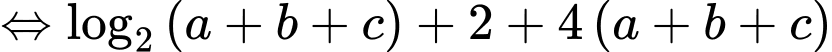
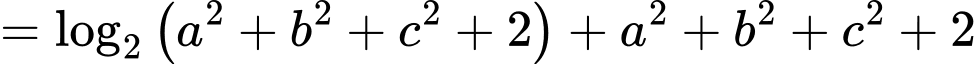
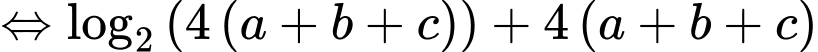
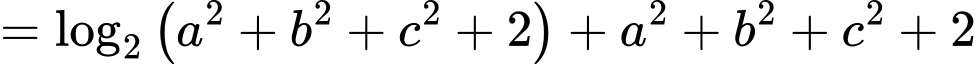
Xét hàm số
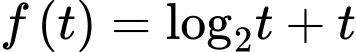 trên khoảng
trên khoảng 
Ta có
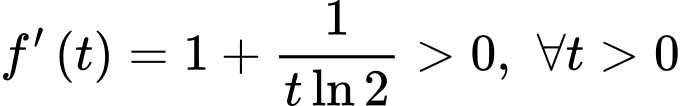
Suy ra hàm số
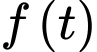 đồng biến trên
đồng biến trên 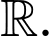
Khi đó
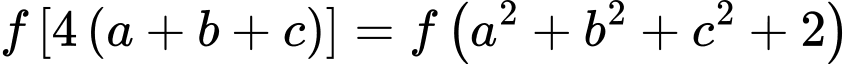
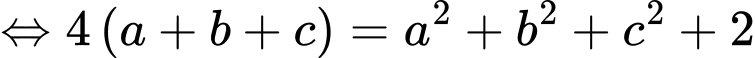
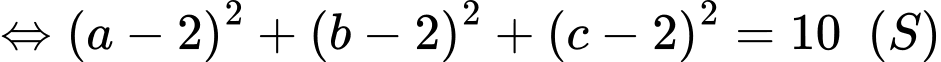
Giả sử điểm
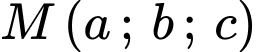 thuộc mặt cầu
thuộc mặt cầu 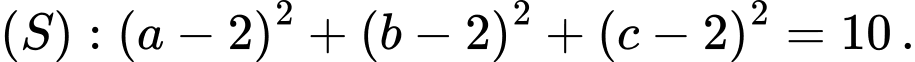
Mặt khác
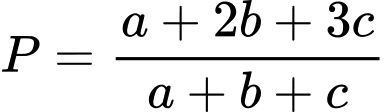
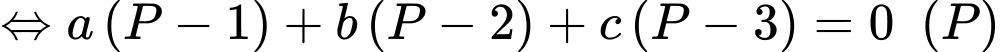
Điều kiện để
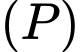 và
và 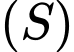 có giao điểm là
có giao điểm là 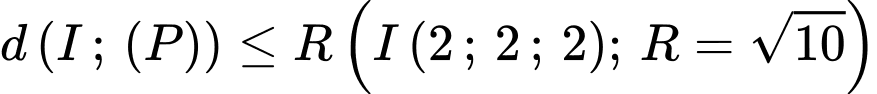
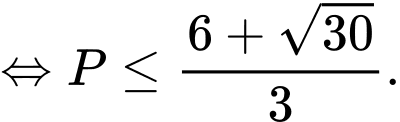 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 13 [512044]: Cho các số thực 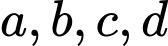 thỏa mãn
thỏa mãn 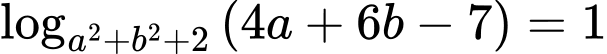 và
và 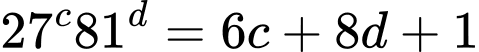 . Tìm giá trị nhỏ nhất của biểu thức
. Tìm giá trị nhỏ nhất của biểu thức 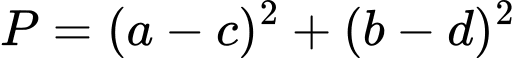 .
.
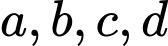 thỏa mãn
thỏa mãn 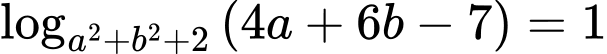 và
và 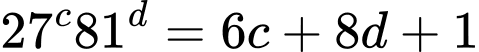 . Tìm giá trị nhỏ nhất của biểu thức
. Tìm giá trị nhỏ nhất của biểu thức 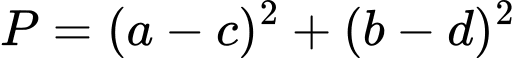 .
. A, 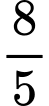 .
.
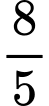 .
.B, 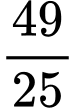 .
.
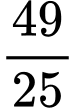 .
.C, 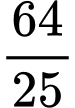 .
.
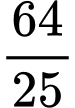 .
.D, 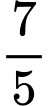
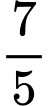
Ta có: 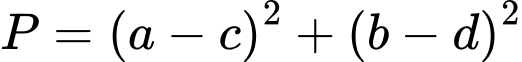
Giả sử, cho tọa độ 2 điểm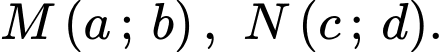
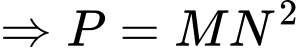
Theo giả thiết, ta có: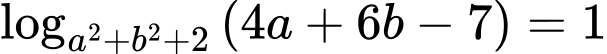
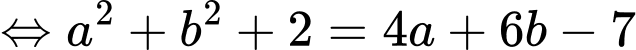
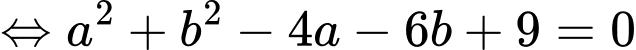
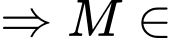 đường tròn tâm
đường tròn tâm 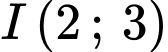 bán kính
bán kính 
Lại có: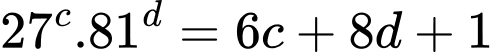
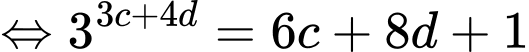
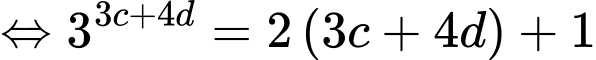
Đặt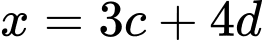
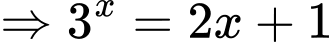

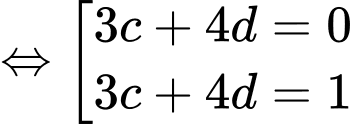
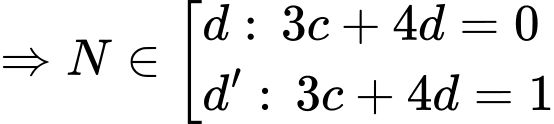
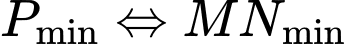
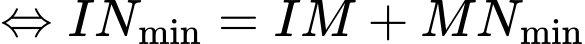
Có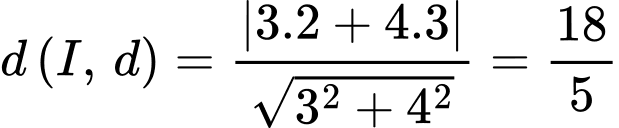
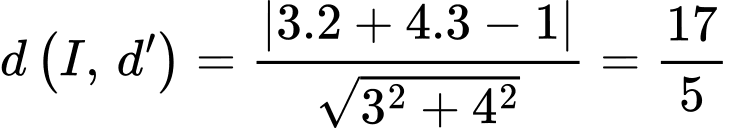
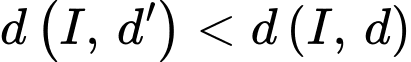
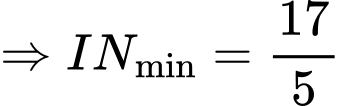
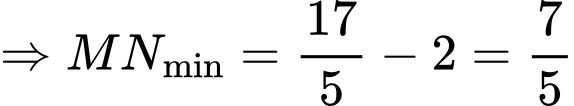
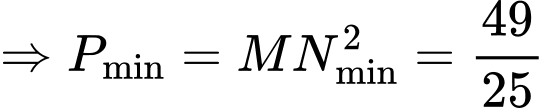
Đáp án: B. Đáp án: B
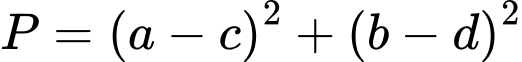
Giả sử, cho tọa độ 2 điểm
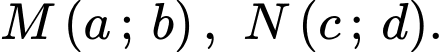
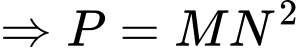
Theo giả thiết, ta có:
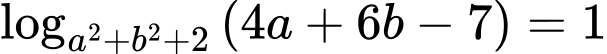
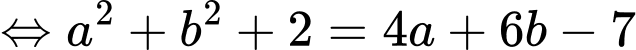
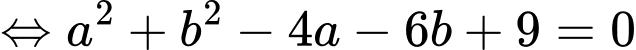
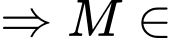 đường tròn tâm
đường tròn tâm 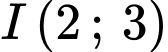 bán kính
bán kính 
Lại có:
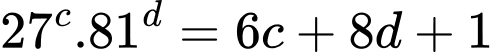
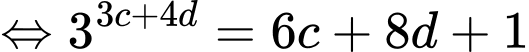
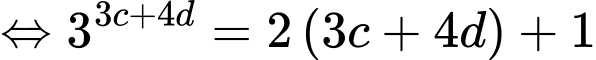
Đặt
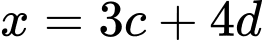
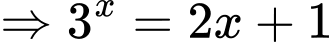

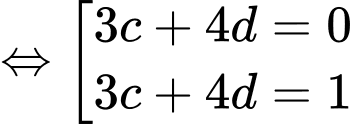
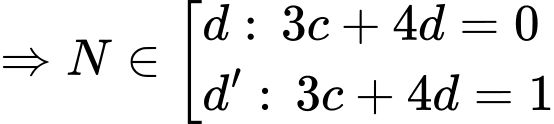
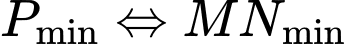
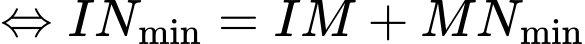
Có
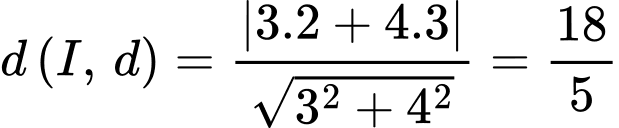
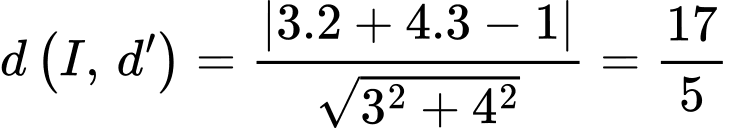
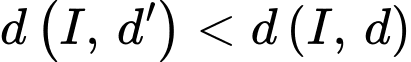
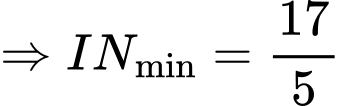
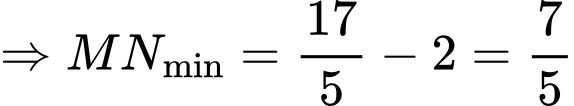
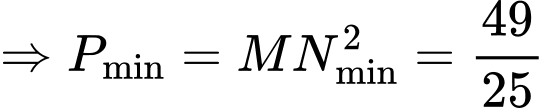
Đáp án: B. Đáp án: B
Câu 14 [383281]: Xét các số thực không âm 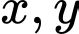 thỏa mãn
thỏa mãn 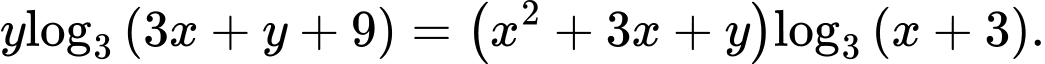 Khi biểu thức
Khi biểu thức 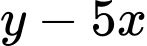 đạt giá trị nhỏ nhất, giá trị của biểu thức
đạt giá trị nhỏ nhất, giá trị của biểu thức 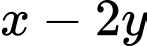 bằng
bằng
 thỏa mãn
thỏa mãn 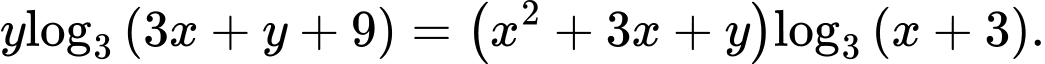 Khi biểu thức
Khi biểu thức 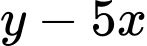 đạt giá trị nhỏ nhất, giá trị của biểu thức
đạt giá trị nhỏ nhất, giá trị của biểu thức 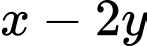 bằng
bằng A, 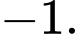
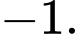
B, 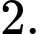
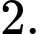
C, 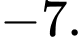
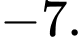
D, 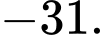
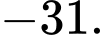
PT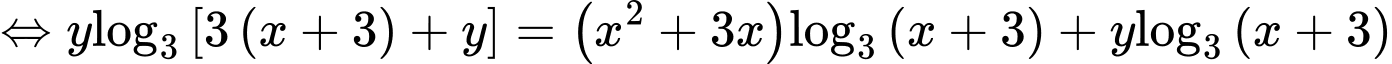
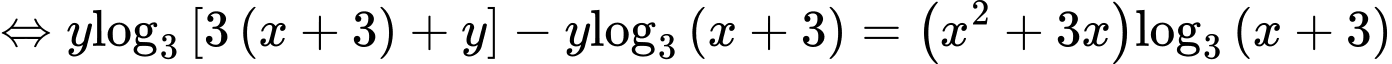
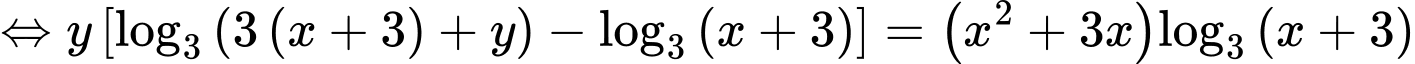
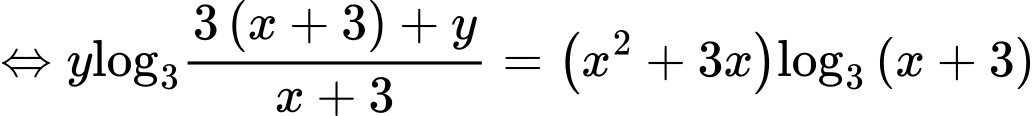
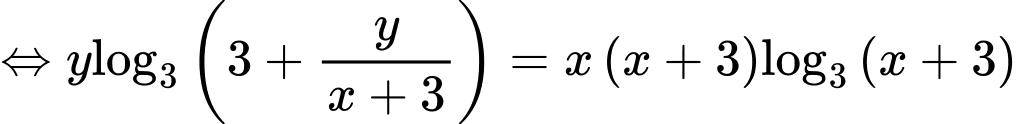
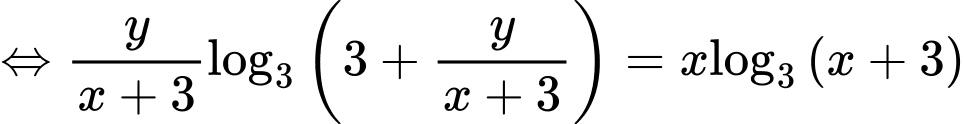
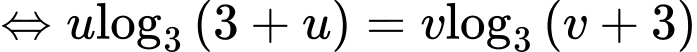
Xét hàm số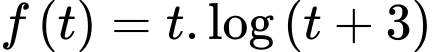 trên khoảng
trên khoảng 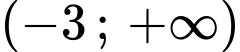
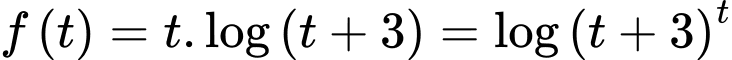
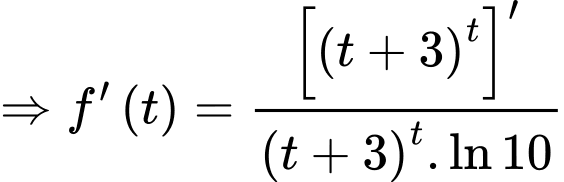
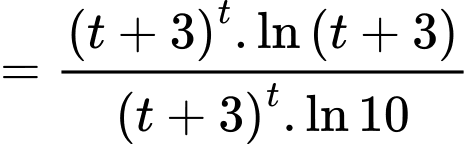
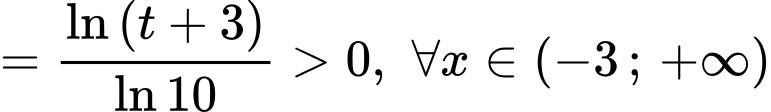
Suy ra hàm số đồng biến.
Suy ra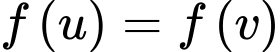
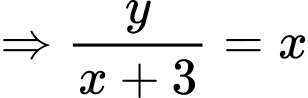
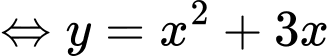
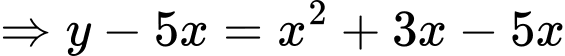
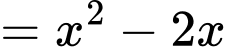
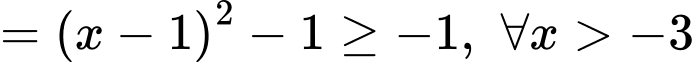
Dấu “=” xảy ra tại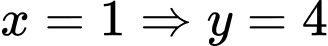
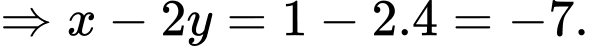
Chọn C.
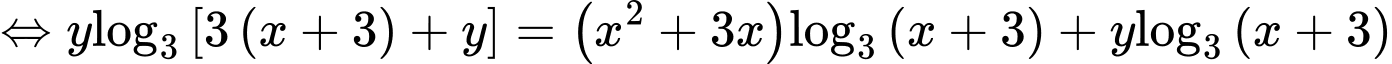
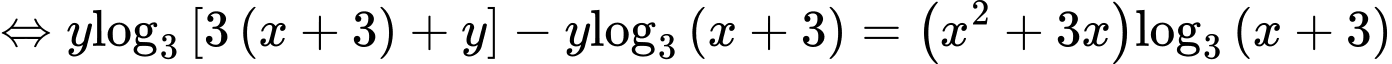
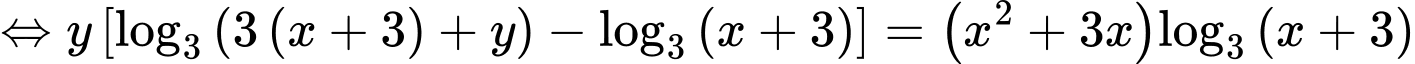
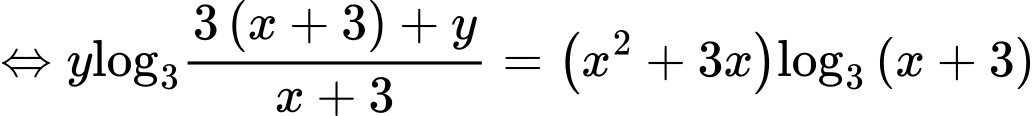
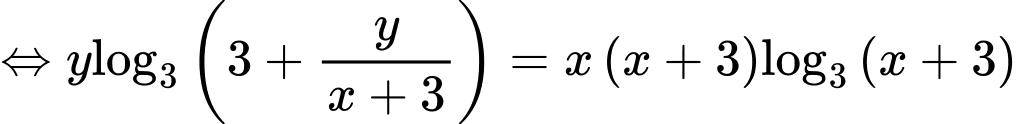
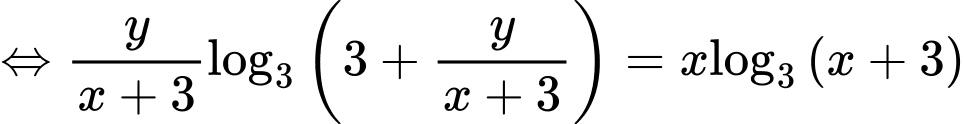
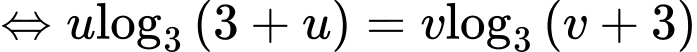
Xét hàm số
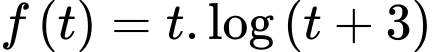 trên khoảng
trên khoảng 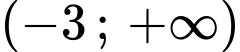
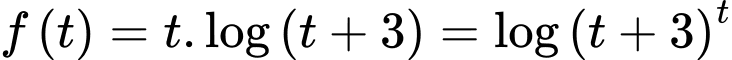
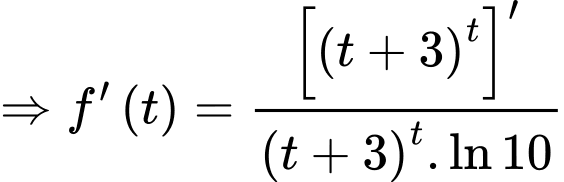
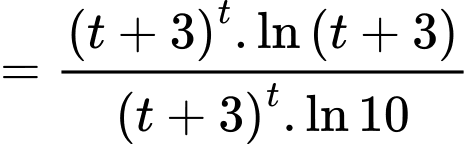
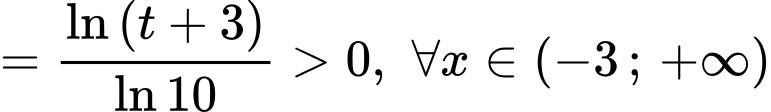
Suy ra hàm số đồng biến.
Suy ra
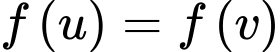
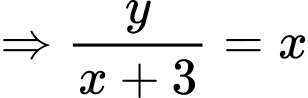
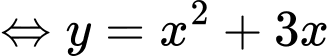
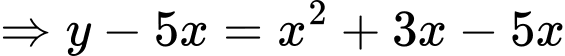
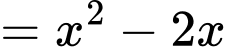
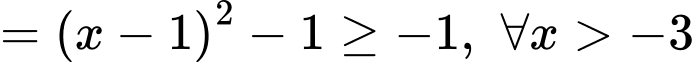
Dấu “=” xảy ra tại
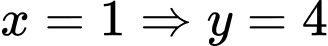
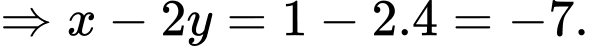
Chọn C.