Đáp án Bài tập tự luyện số 2
Câu 1 [791683]: Có bao nhiêu cặp số nguyên 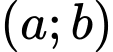 thỏa mãn đồng thời các điều kiện sau
thỏa mãn đồng thời các điều kiện sau 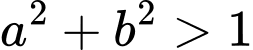 và
và 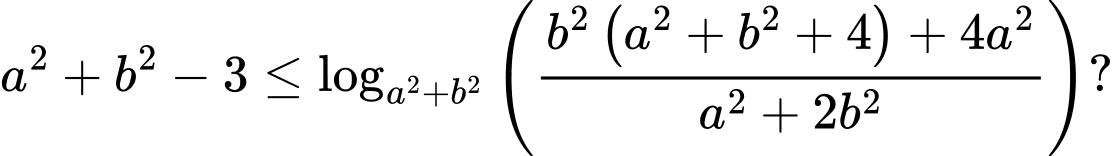
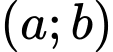 thỏa mãn đồng thời các điều kiện sau
thỏa mãn đồng thời các điều kiện sau 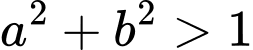 và
và 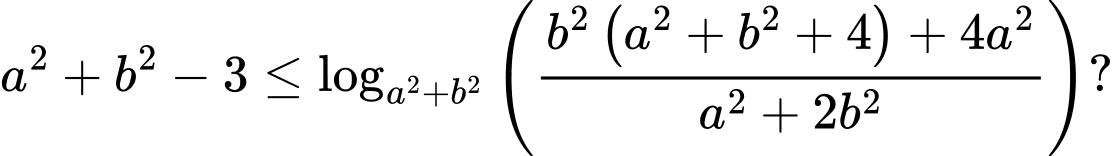
A, 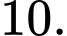
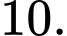
B, 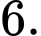
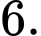
C, 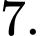
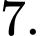
D, 
Tính: 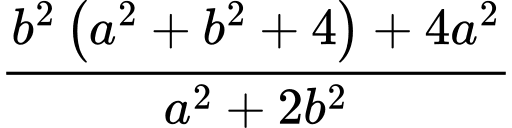
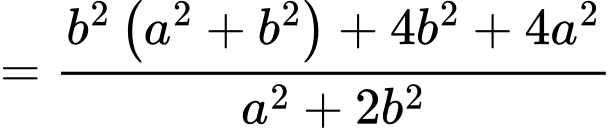
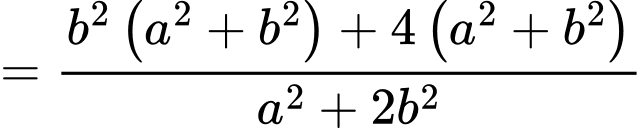
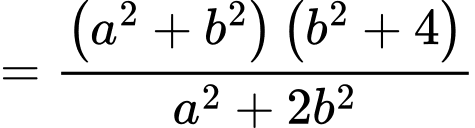
Theo bài ra, ta có: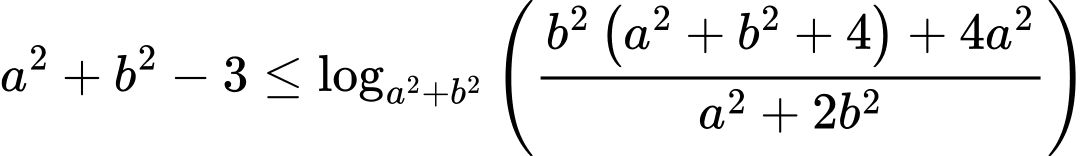
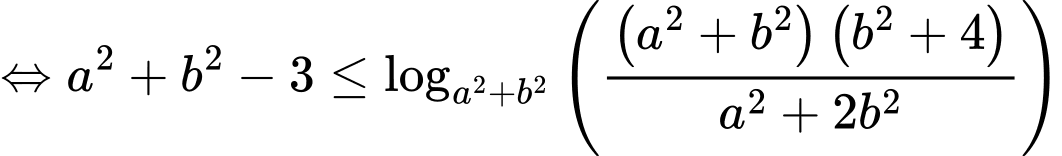
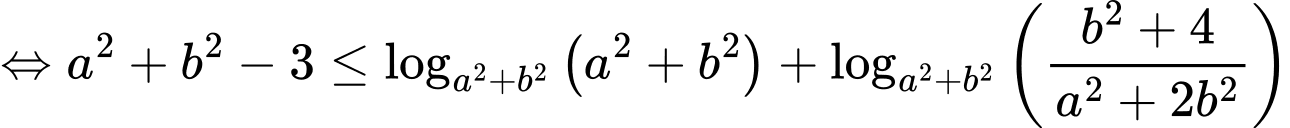
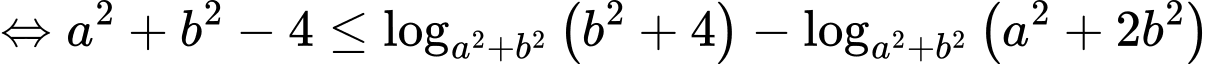
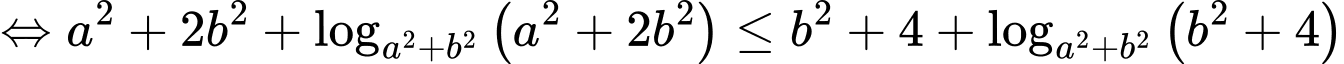
Ta có: là hàm số đồng biến, áp dụng tính chất hàm số đặc trưng ta có:
là hàm số đồng biến, áp dụng tính chất hàm số đặc trưng ta có:
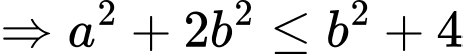
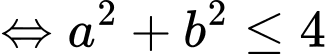
Theo giả thiết, ta suy ra: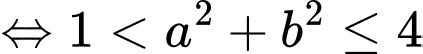
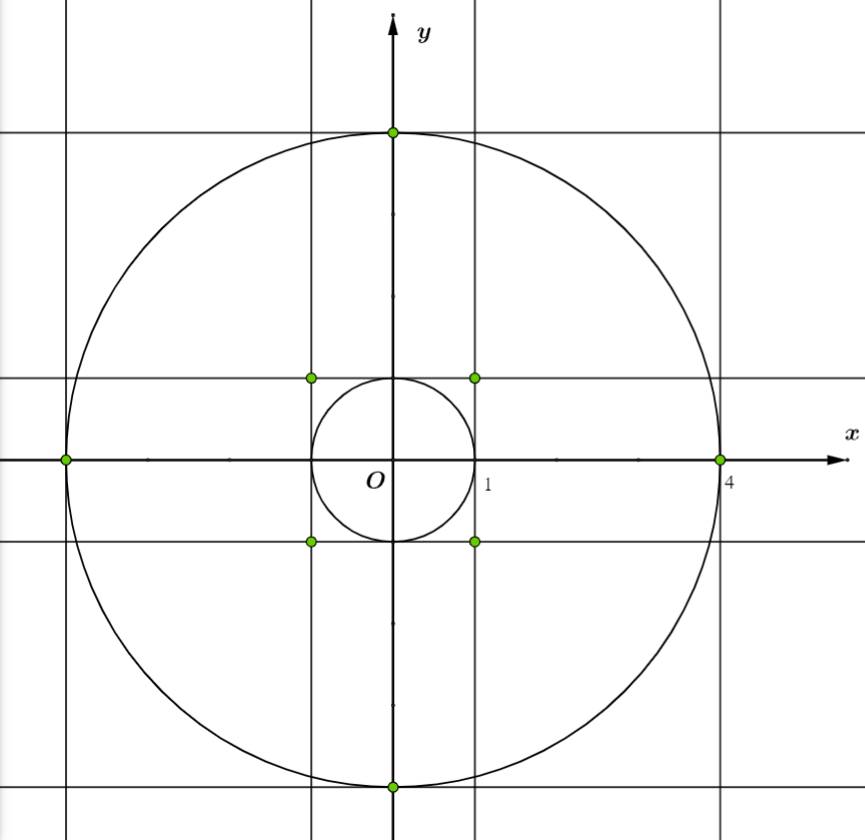
Theo đồ thị hình vẽ, ta được 8 cắp số nguyên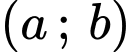 thỏa mãn điều kiện.
thỏa mãn điều kiện.
Đáp án: D. Đáp án: D
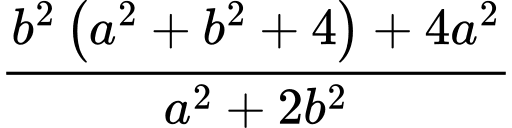
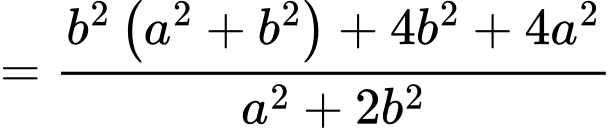
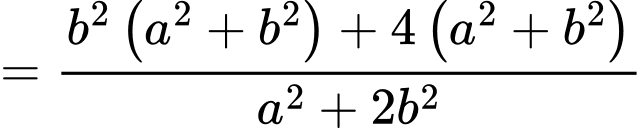
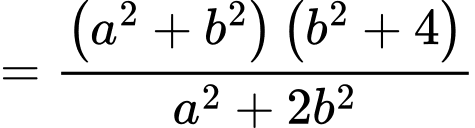
Theo bài ra, ta có:
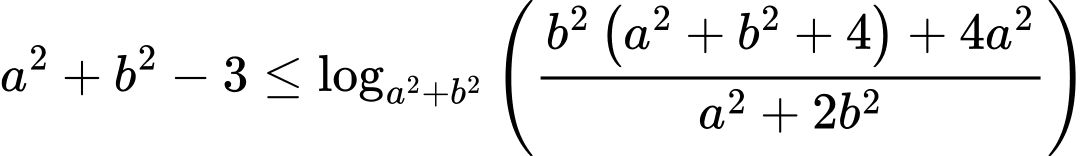
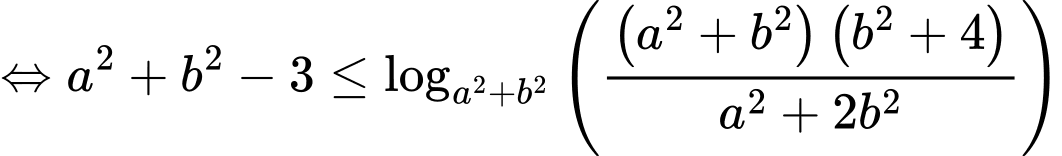
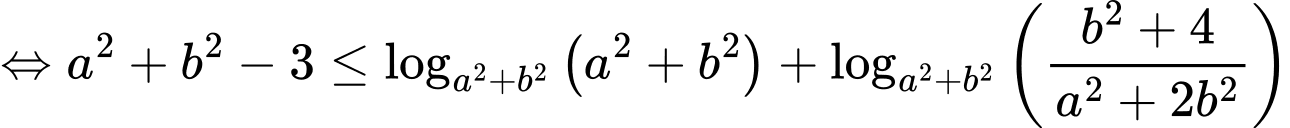
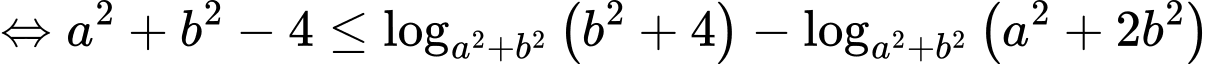
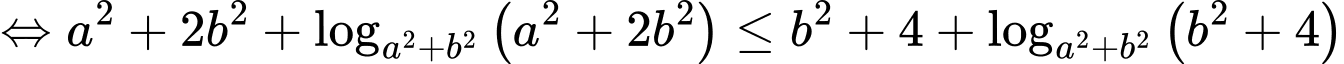
Ta có:
 là hàm số đồng biến, áp dụng tính chất hàm số đặc trưng ta có:
là hàm số đồng biến, áp dụng tính chất hàm số đặc trưng ta có: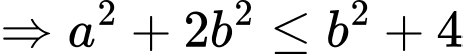
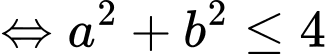
Theo giả thiết, ta suy ra:
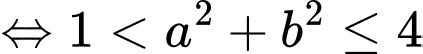

Theo đồ thị hình vẽ, ta được 8 cắp số nguyên
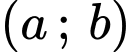 thỏa mãn điều kiện.
thỏa mãn điều kiện.Đáp án: D. Đáp án: D
Câu 2 [512020]: [Đề thi sở Hà Tĩnh 2020]: Cho ba số thực dương 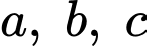 thỏa mãn
thỏa mãn 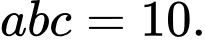 Biết giá trị lớn nhất của biểu thức
Biết giá trị lớn nhất của biểu thức 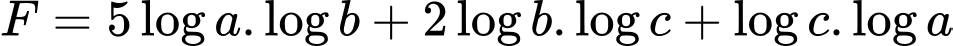 bằng
bằng 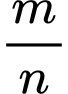 với
với 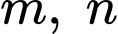 nguyên dương và
nguyên dương và 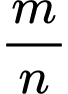 tối giản. Tính tổng
tối giản. Tính tổng  bằng
bằng
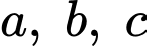 thỏa mãn
thỏa mãn 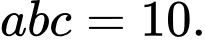 Biết giá trị lớn nhất của biểu thức
Biết giá trị lớn nhất của biểu thức 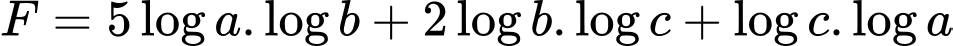 bằng
bằng 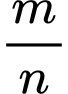 với
với 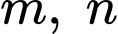 nguyên dương và
nguyên dương và 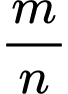 tối giản. Tính tổng
tối giản. Tính tổng  bằng
bằng A, 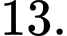
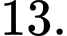
B, 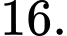
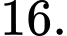
C, 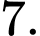
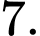
D, 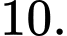
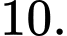
Chọn đáp án C.
Theo bài ta có: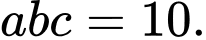
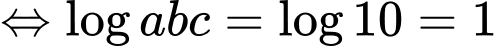
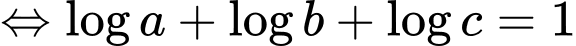
Ta đặt: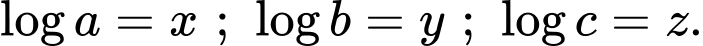
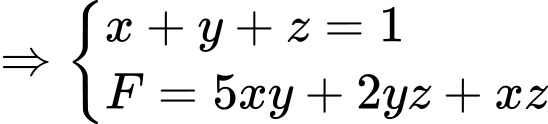
Có:
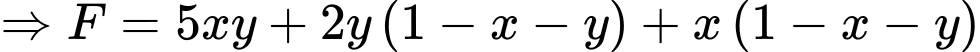
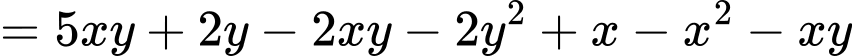
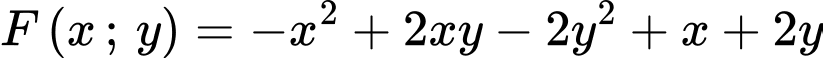
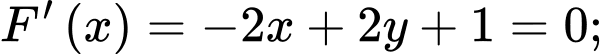
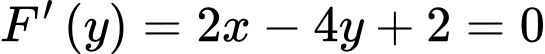
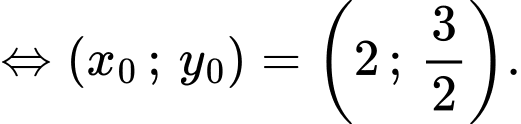
Vậy giá trị lớn nhất của biểu thức sẽ đạt tại điểm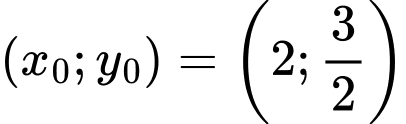
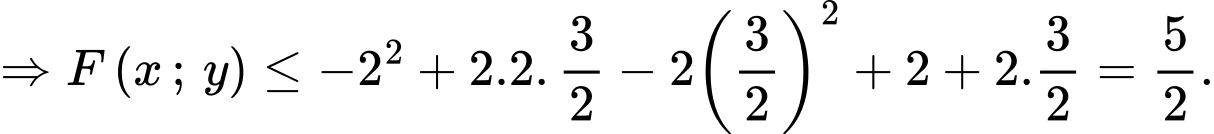
Vậy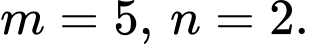 Đáp án: C
Đáp án: C
Theo bài ta có:
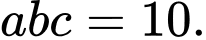
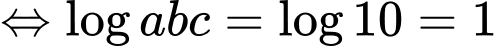
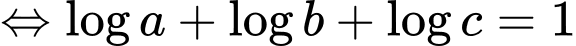
Ta đặt:
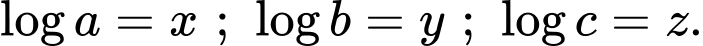
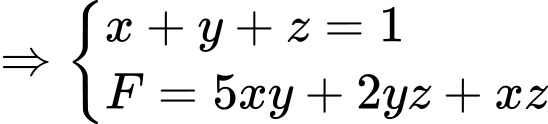
Có:

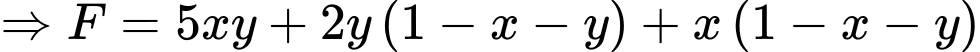
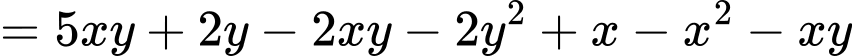
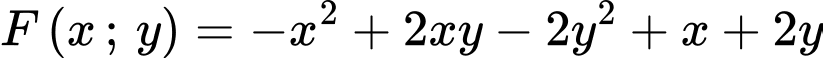
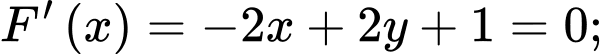
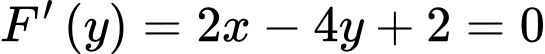
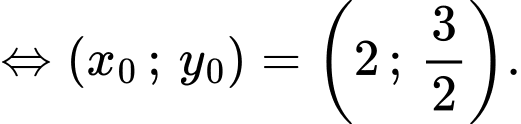
Vậy giá trị lớn nhất của biểu thức sẽ đạt tại điểm
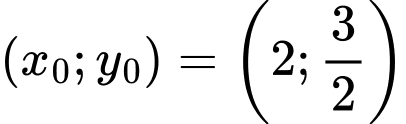
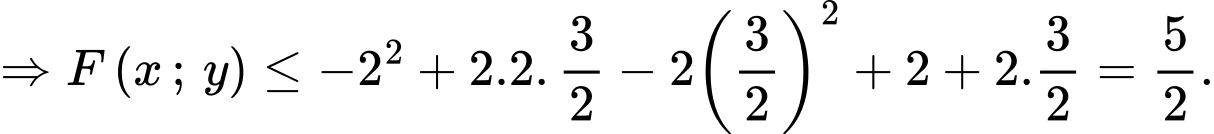
Vậy
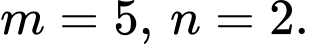 Đáp án: C
Đáp án: C
Câu 3 [512450]: Xét các số thực dương 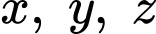 thay đổi sao cho tồn tại các số thực
thay đổi sao cho tồn tại các số thực 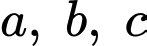 lớn hơn 1 và thỏa mãn
lớn hơn 1 và thỏa mãn 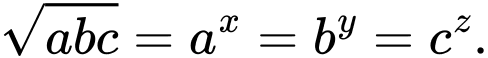 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 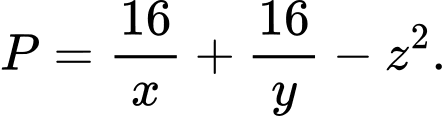
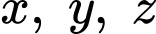 thay đổi sao cho tồn tại các số thực
thay đổi sao cho tồn tại các số thực 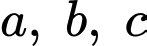 lớn hơn 1 và thỏa mãn
lớn hơn 1 và thỏa mãn 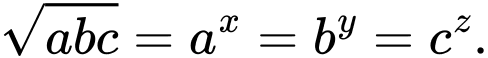 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 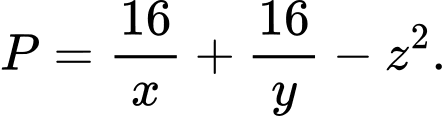
A, 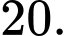
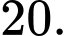
B, 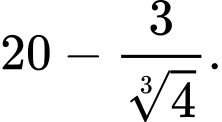
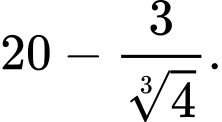
C, 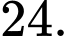
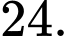
D, 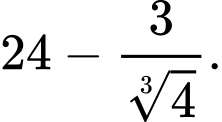
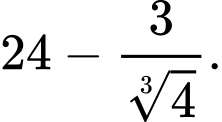
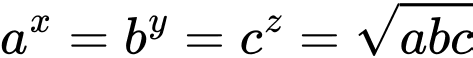
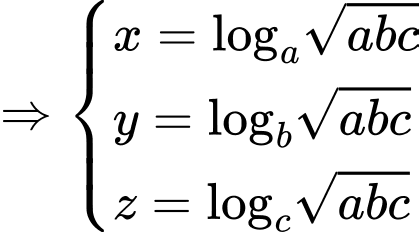
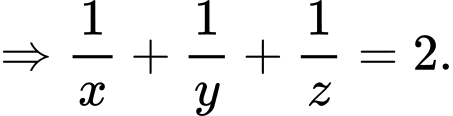
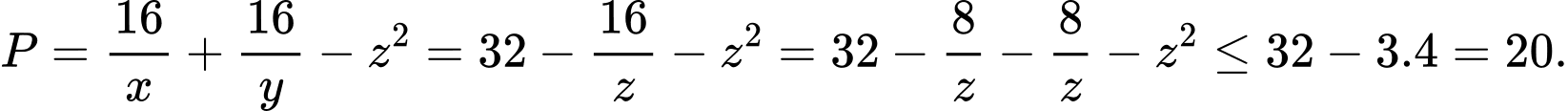
Dấu bằng xảy ra khi:
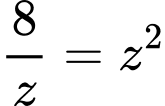
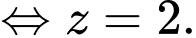
Chọn đáp án A. Đáp án: A
Câu 4 [512456]: Cho 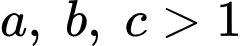 và các số
và các số 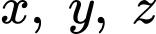 thỏa mãn
thỏa mãn 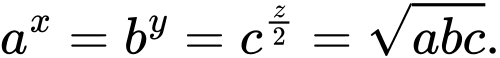 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 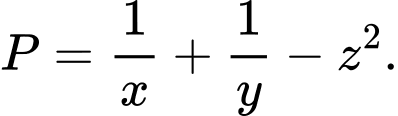
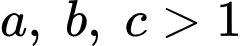 và các số
và các số 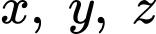 thỏa mãn
thỏa mãn 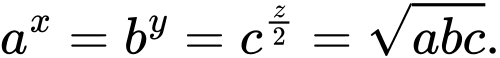 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 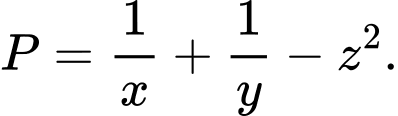
A, 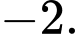
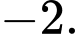
B, 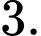
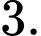
C, 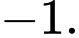
D, 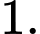
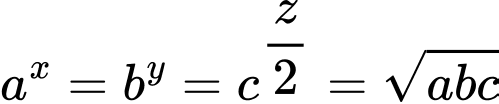
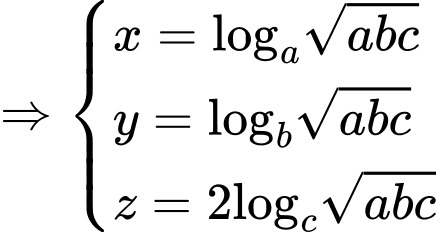
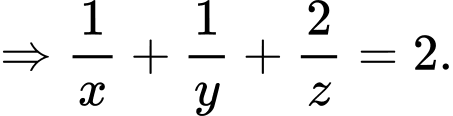
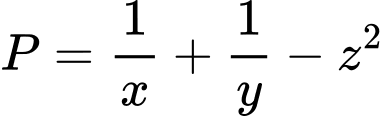
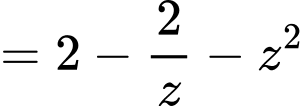
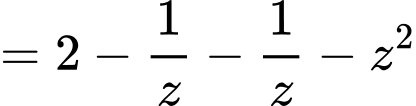
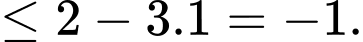
Dấu bằng xảy ra khi:
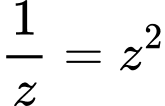
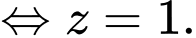
Chọn đáp án C. Đáp án: C
Câu 5 [512453]: [Sở Thái Nguyên 2020] Cho 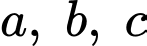 là các số thực lớn hơn 1 và
là các số thực lớn hơn 1 và 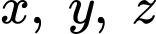 là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 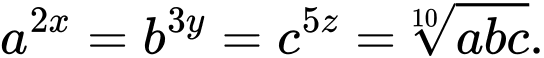 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 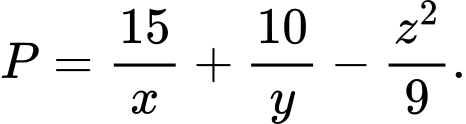
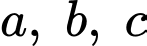 là các số thực lớn hơn 1 và
là các số thực lớn hơn 1 và 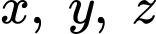 là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 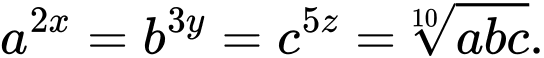 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 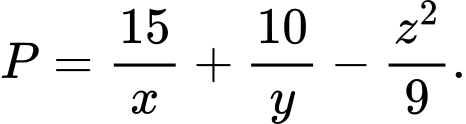
A, 
B, 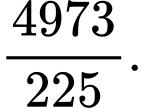
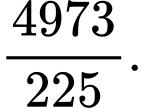
C, 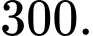
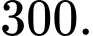
D, 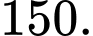
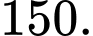
Ta có: 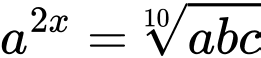
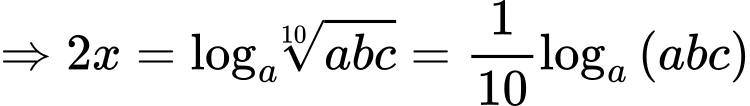
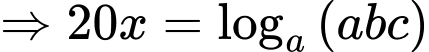
Tương tự ta có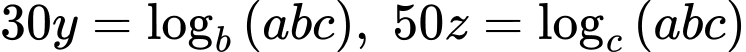 do đó
do đó 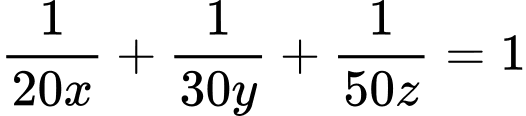
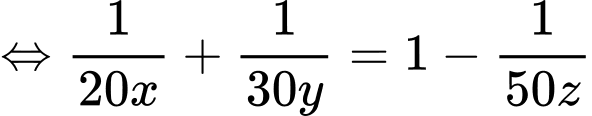
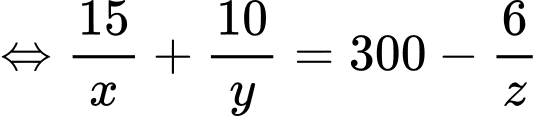
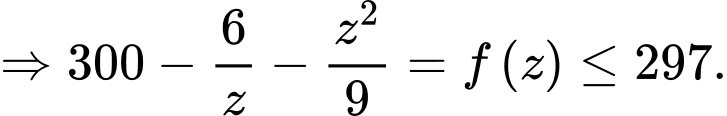
Đoạn cuối các bạn có thể xét hàm hoặc dùng bất đẳng thức Cosi:
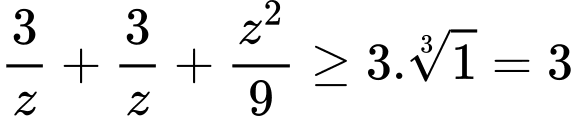
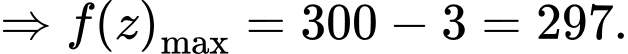 Chọn A. Đáp án: A
Chọn A. Đáp án: A
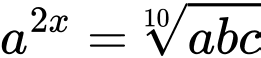
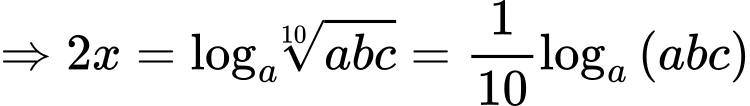
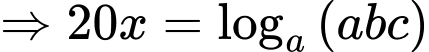
Tương tự ta có
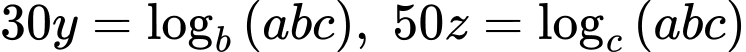 do đó
do đó 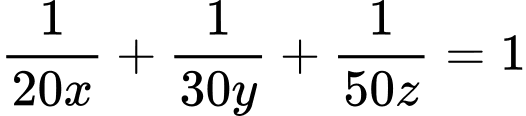
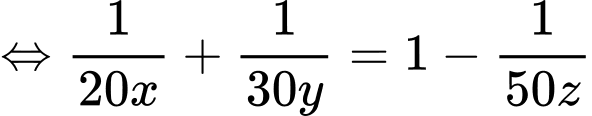
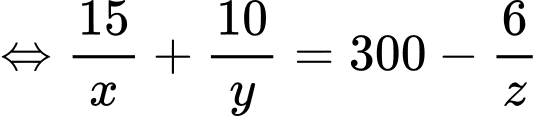
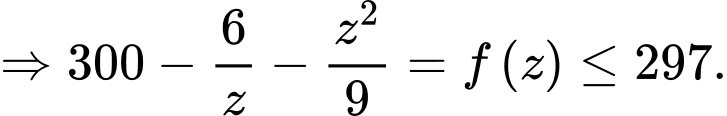
Đoạn cuối các bạn có thể xét hàm hoặc dùng bất đẳng thức Cosi:
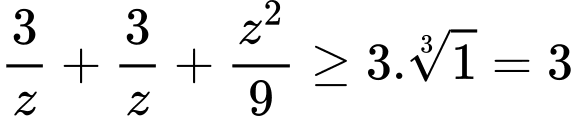
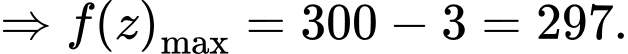 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 6 [512452]: Xét 2 số thực dương 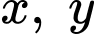 thỏa mãn
thỏa mãn  và
và 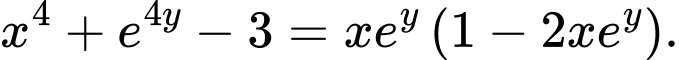 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 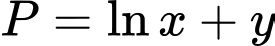 thuộc tập nào dưới đây
thuộc tập nào dưới đây
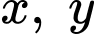 thỏa mãn
thỏa mãn  và
và 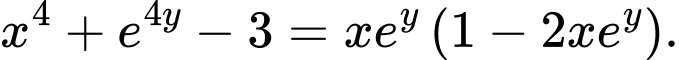 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 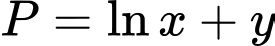 thuộc tập nào dưới đây
thuộc tập nào dưới đây A, 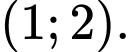
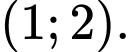
B, 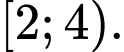
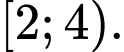
C, 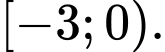
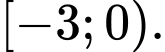
D, 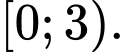
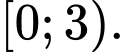
Đặt 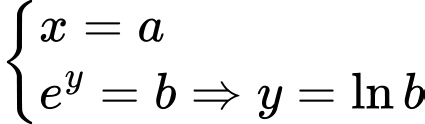
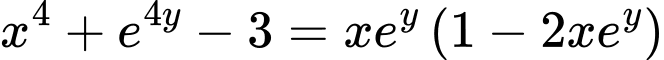
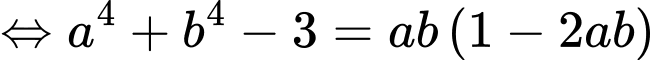
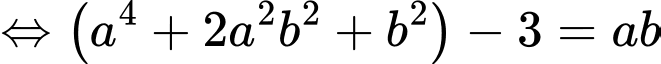
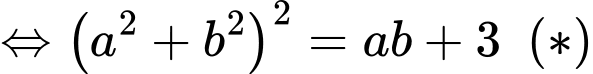
Ta có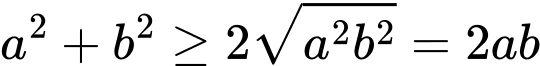
Suy ra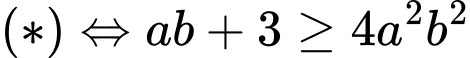
Đặt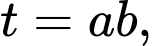 BPT
BPT 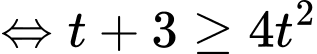
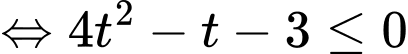
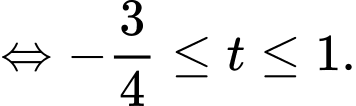
Ta có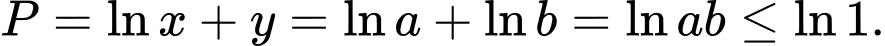
Vậy giá trị lớn nhất của biểu thức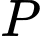 là
là 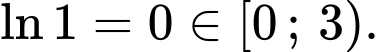
Chọn D. Đáp án: D
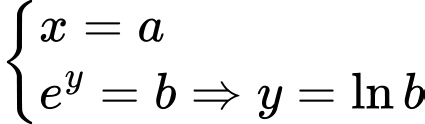
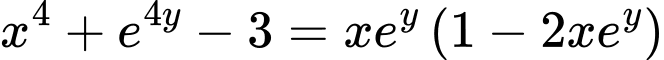
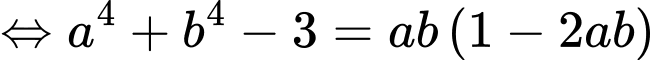
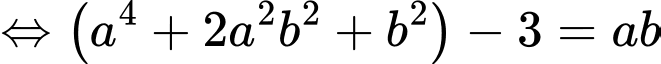
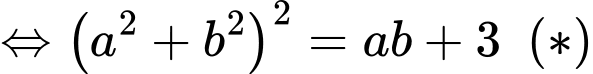
Ta có
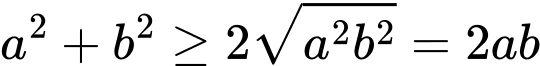
Suy ra
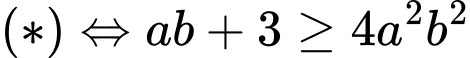
Đặt
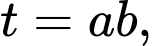 BPT
BPT 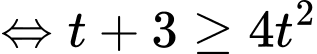
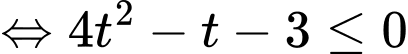
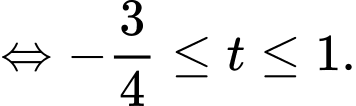
Ta có
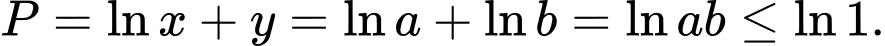
Vậy giá trị lớn nhất của biểu thức
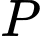 là
là 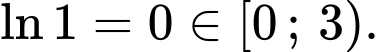
Chọn D. Đáp án: D
Câu 7 [512507]: Xét 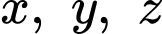 là các số thực lớn hơn 1 thỏa mãn điều kiện
là các số thực lớn hơn 1 thỏa mãn điều kiện 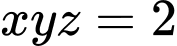 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức
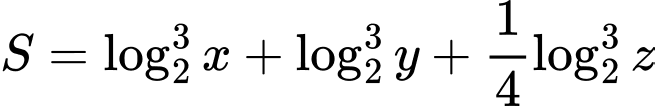 bằng
bằng
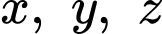 là các số thực lớn hơn 1 thỏa mãn điều kiện
là các số thực lớn hơn 1 thỏa mãn điều kiện 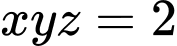 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức 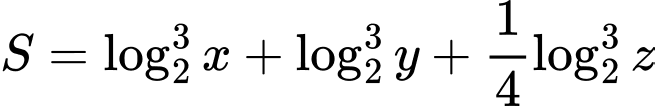 bằng
bằng A, 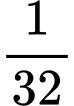 .
.
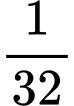 .
.B, 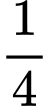 .
.
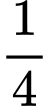 .
.C, 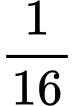 .
.
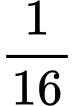 .
.D, 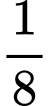 .
.
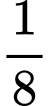 .
.
Chọn C
Ta có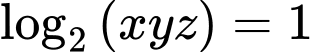
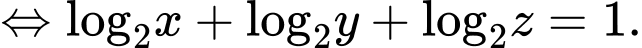 Đặt
Đặt 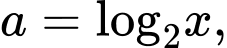
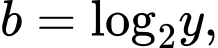
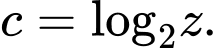
Khi đó ta có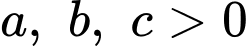 và
và 
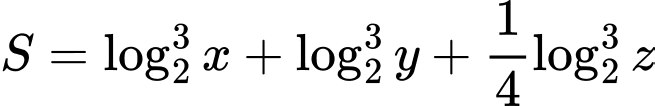
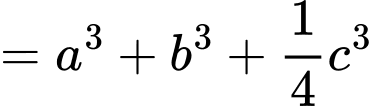
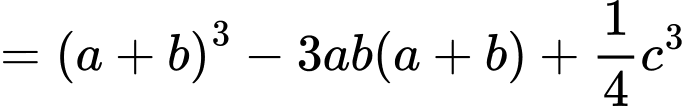
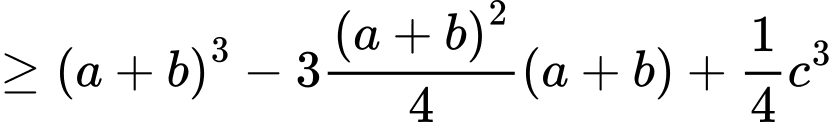
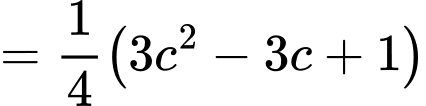 với
với 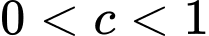 .
.
Đặt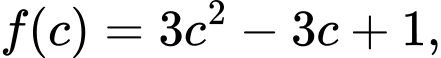
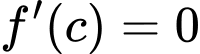
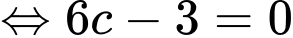
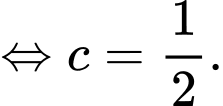
Ta có bảng biến thiên
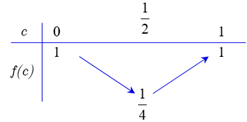
Từ đây ta suy ra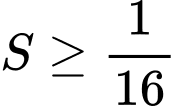 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi 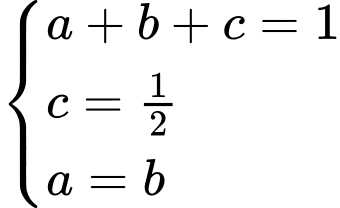
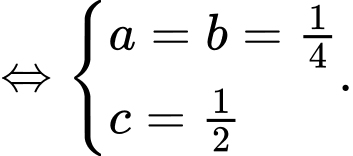
Khi đó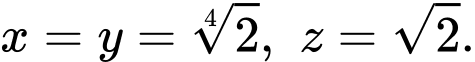 Đáp án: C
Đáp án: C
Ta có
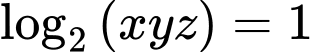
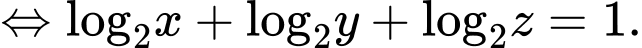 Đặt
Đặt 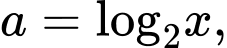
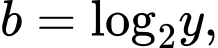
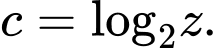
Khi đó ta có
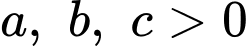 và
và 
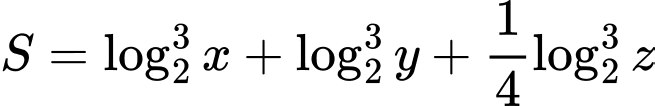
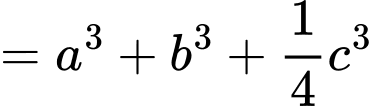
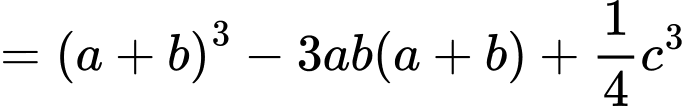
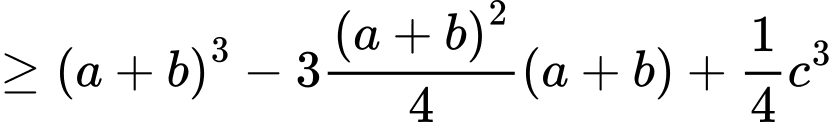
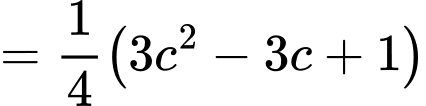 với
với 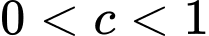 .
.Đặt
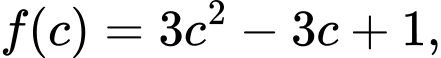
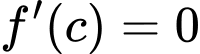
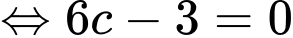
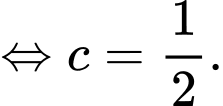
Ta có bảng biến thiên

Từ đây ta suy ra
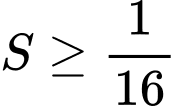 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi 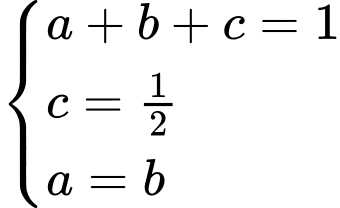
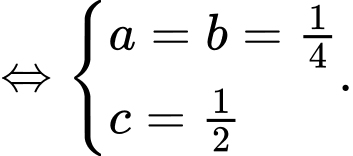
Khi đó
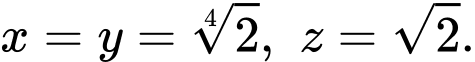 Đáp án: C
Đáp án: C
Câu 8 [791679]: Cho các số thực 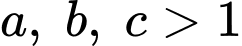 và các số thực
và các số thực 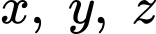 thỏa mãn
thỏa mãn 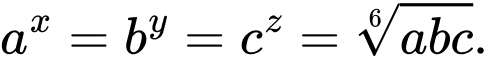 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 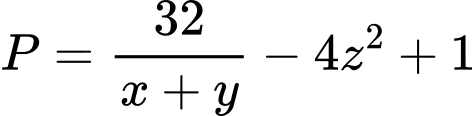 thuộc tập nào dưới đây?
thuộc tập nào dưới đây?
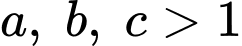 và các số thực
và các số thực 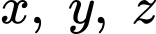 thỏa mãn
thỏa mãn 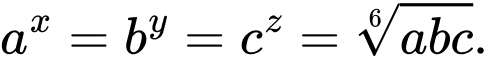 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 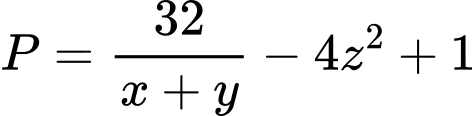 thuộc tập nào dưới đây?
thuộc tập nào dưới đây? A, 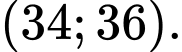
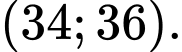
B, 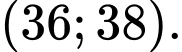
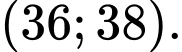
C, 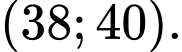
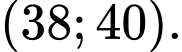
D, 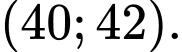
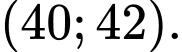
Ta có: 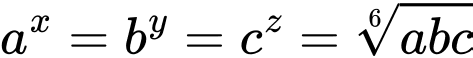
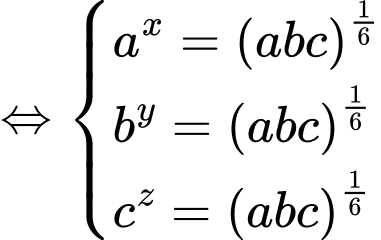
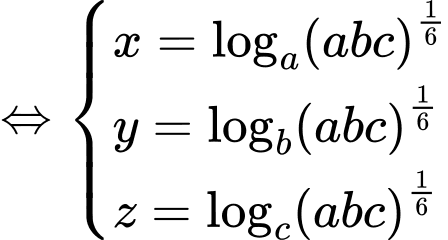
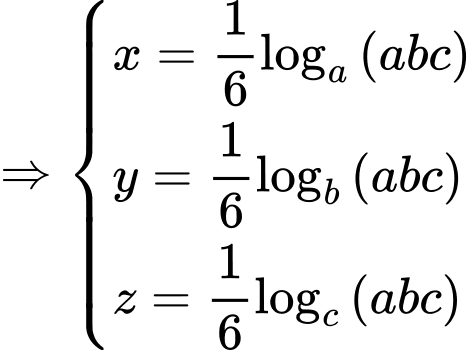
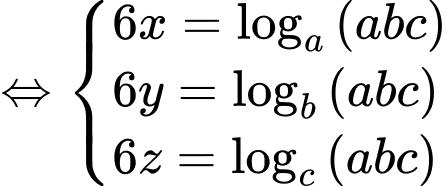
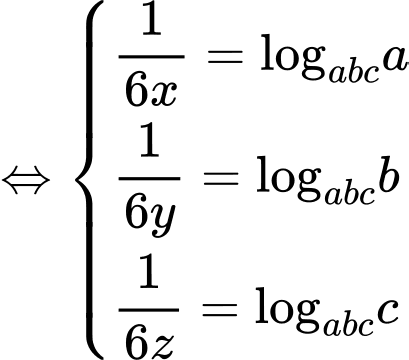
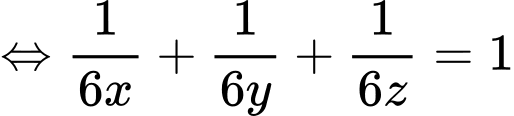
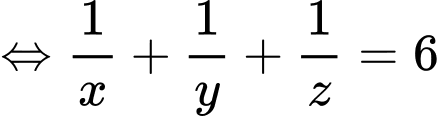
Áp dụng bất đẳng thức Cosi với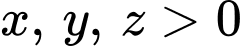 ta có:
ta có:
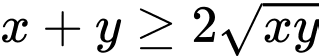
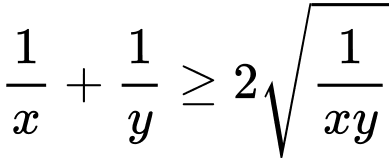
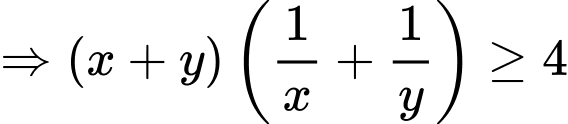
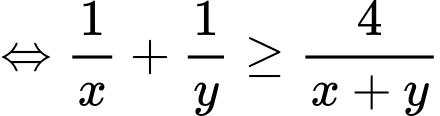
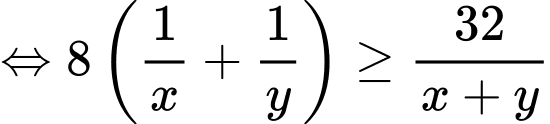
Có: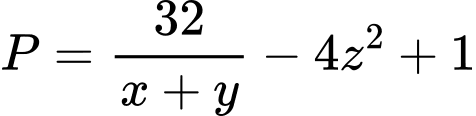
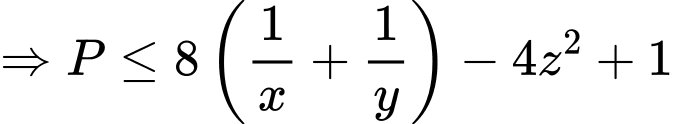
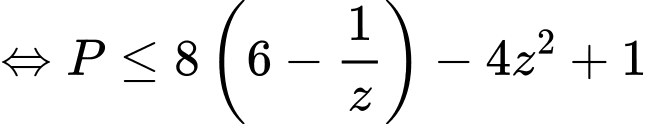
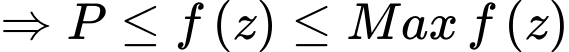
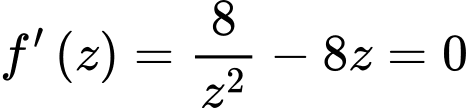
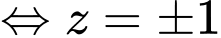
Có: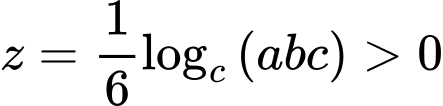
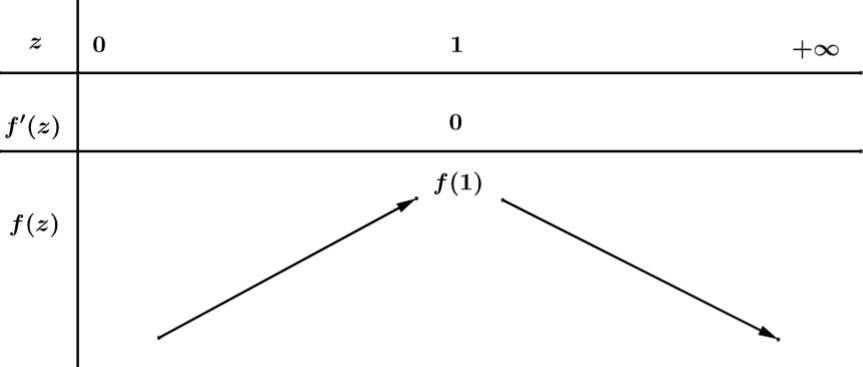
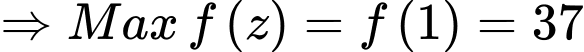

Đáp án: B. Đáp án: B
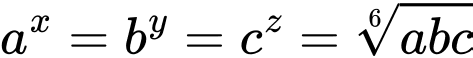
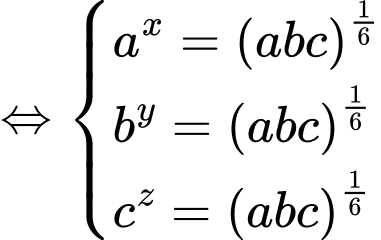
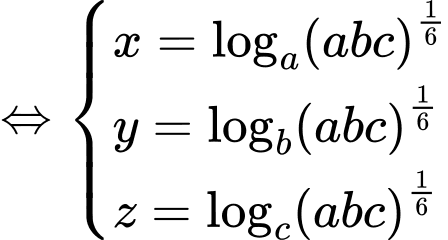
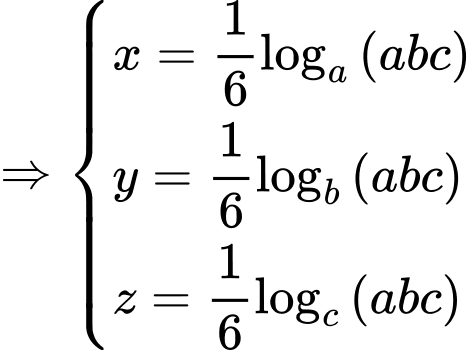
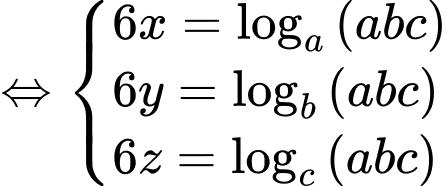
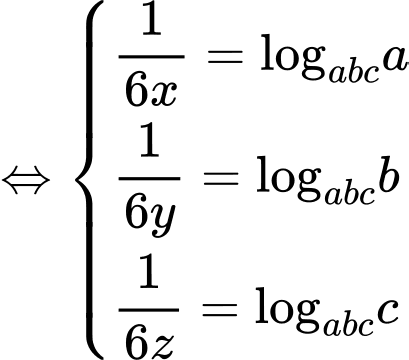
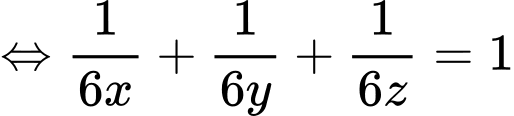
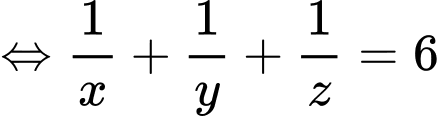
Áp dụng bất đẳng thức Cosi với
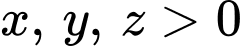 ta có:
ta có: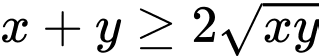
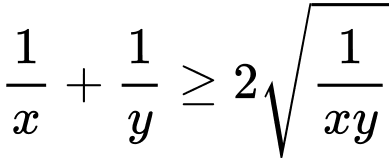
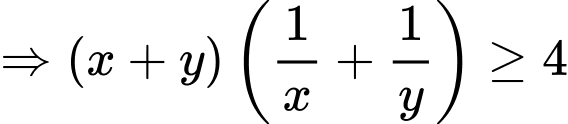
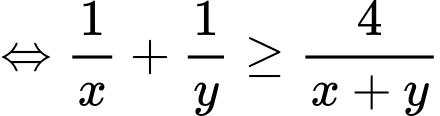
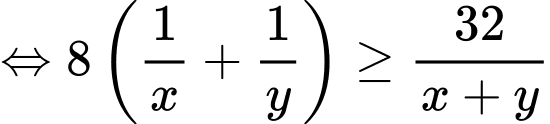
Có:
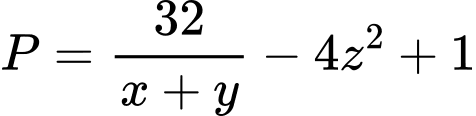
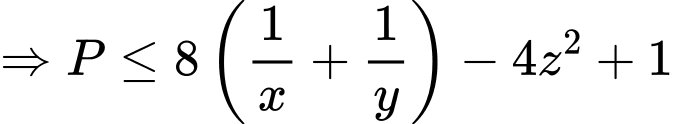
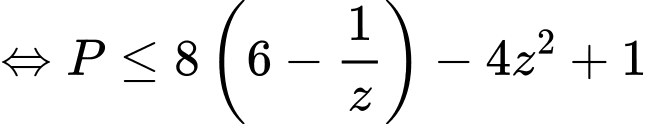
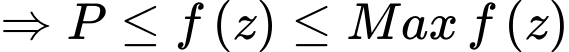
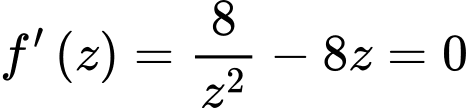
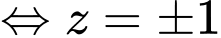
Có:
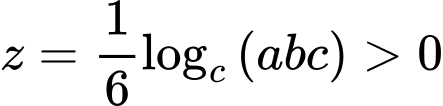

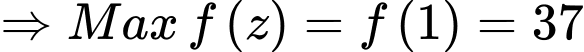

Đáp án: B. Đáp án: B
Câu 9 [791680]: Cho các số 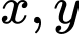 thỏa mãn đồng thời
thỏa mãn đồng thời 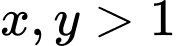 và
và 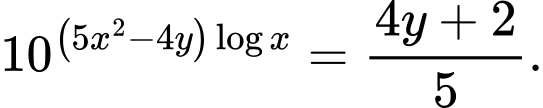 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 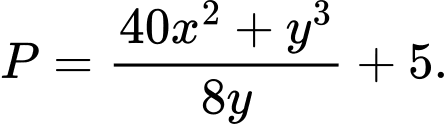
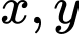 thỏa mãn đồng thời
thỏa mãn đồng thời 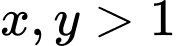 và
và 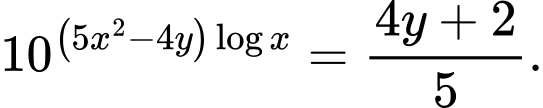 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 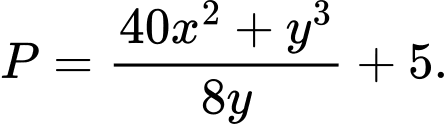
A, 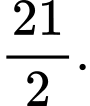
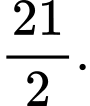
B, 

C, 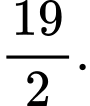
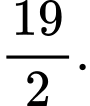
D, 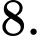
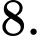
Theo giả thiết, ta có: 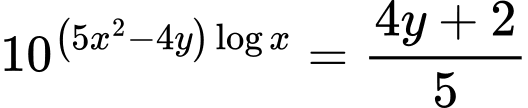
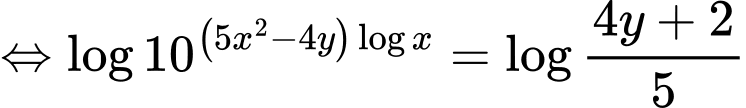
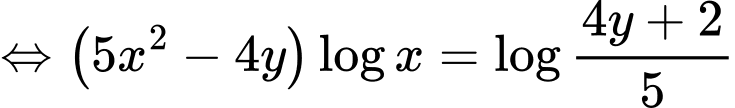
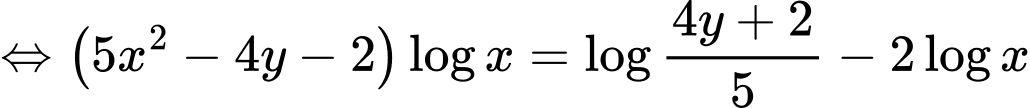
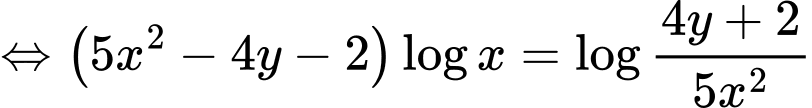
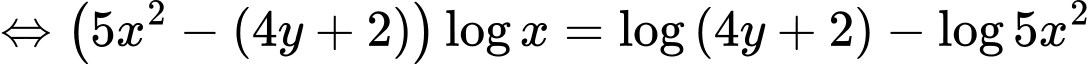
Đặt: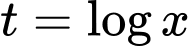
PT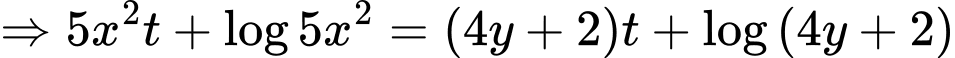
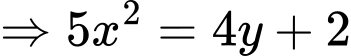
Ta có: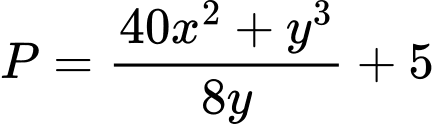
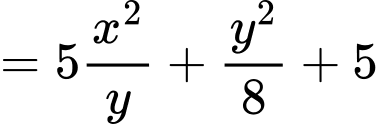
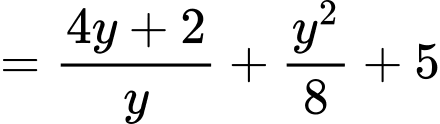
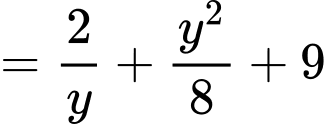
Áp dụng BĐT Co-si, ta có:
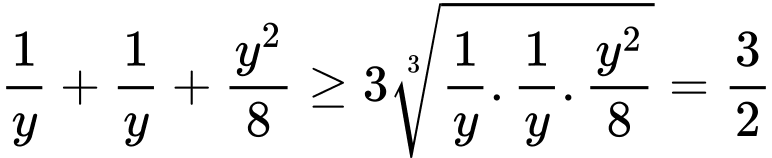
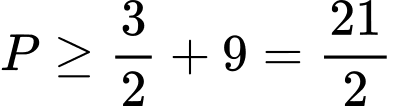
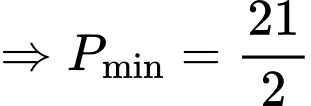
Đáp án: A. Đáp án: A
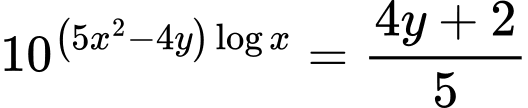
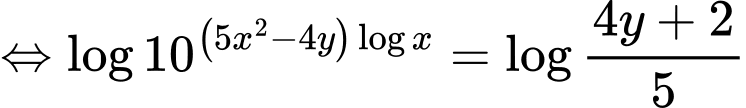
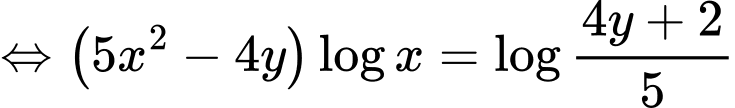
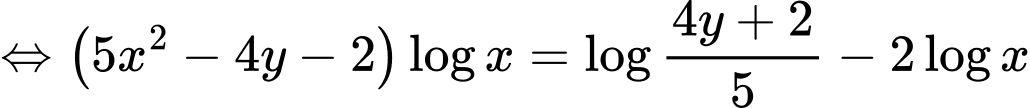
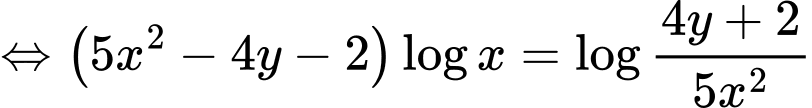
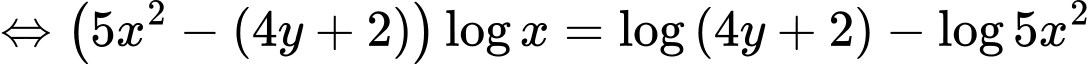
Đặt:
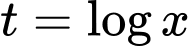
PT
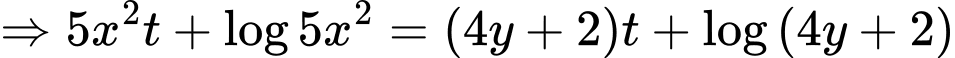
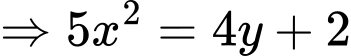
Ta có:
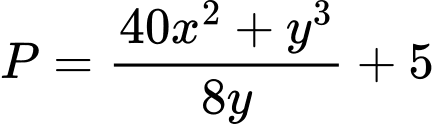
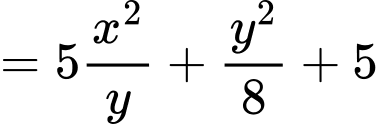
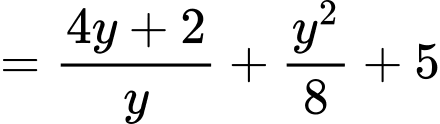
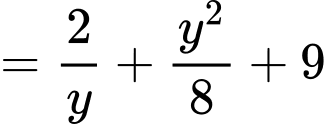
Áp dụng BĐT Co-si, ta có:
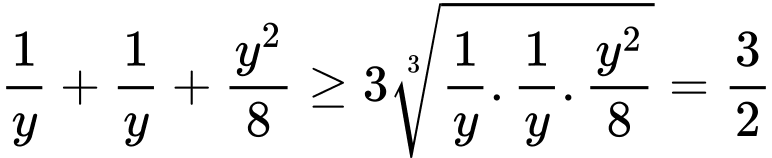
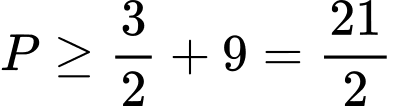
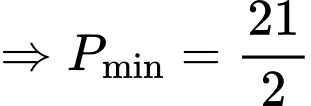
Đáp án: A. Đáp án: A
Câu 10 [791682]: Cho các số thực 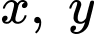 thỏa mãn đồng thời
thỏa mãn đồng thời 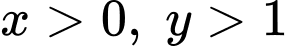 và
và 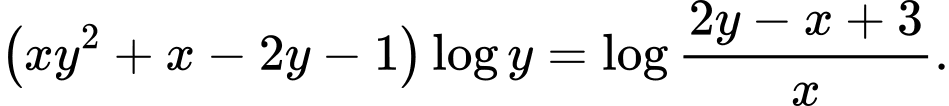 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 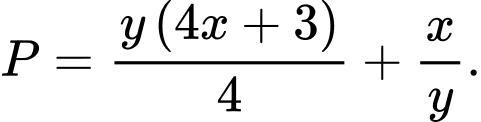
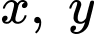 thỏa mãn đồng thời
thỏa mãn đồng thời 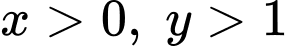 và
và 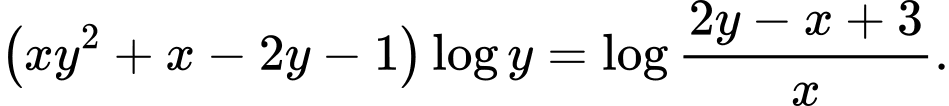 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 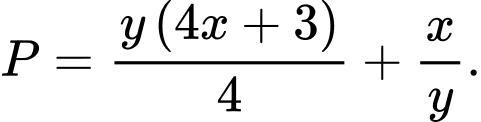
A, 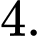
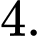
B, 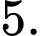
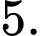
C, 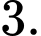
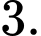
D, 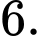
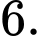
Xét: 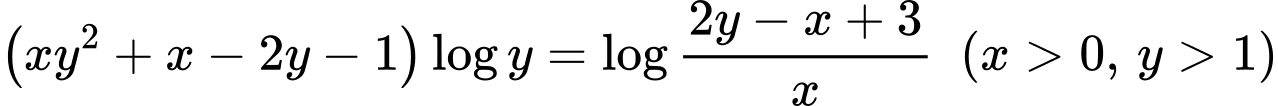
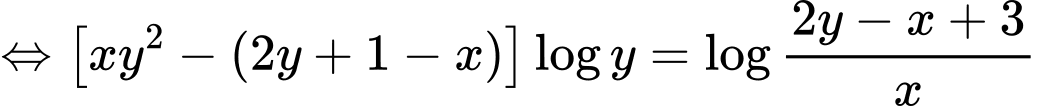
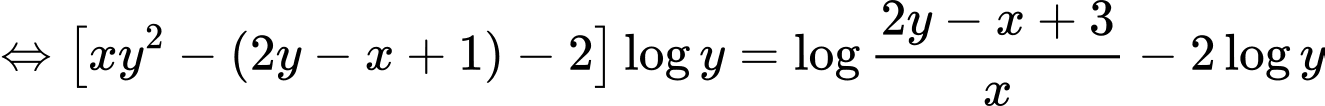
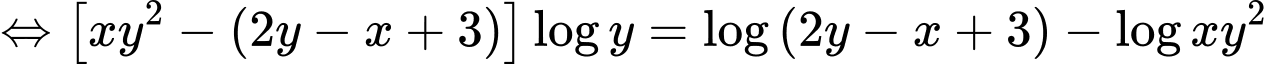
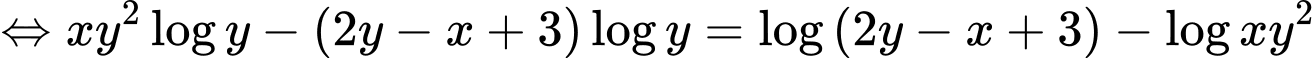
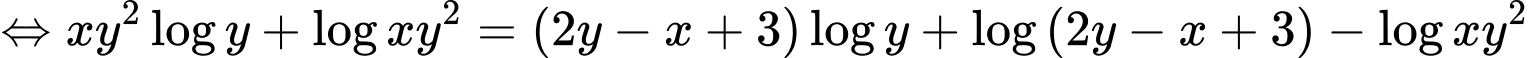
Áp dụng tính chất hàm đặc trưng, ta có:
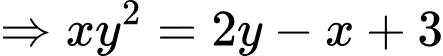
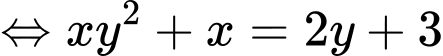
Ta có: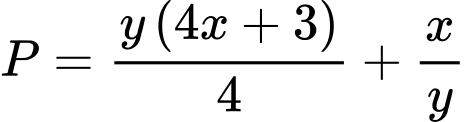
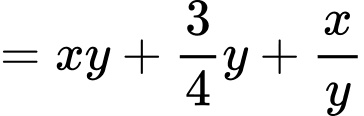
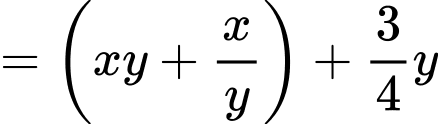
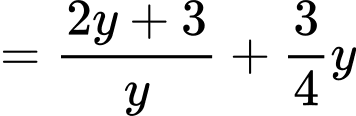
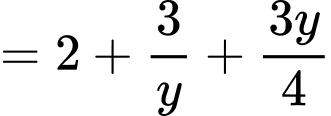
Với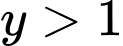 áp dụng bất đắng thức Co-si ta có:
áp dụng bất đắng thức Co-si ta có:
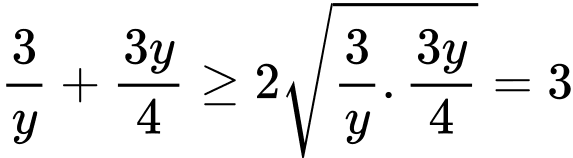
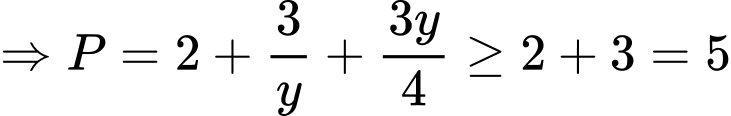

Đáp án: B. Đáp án: B
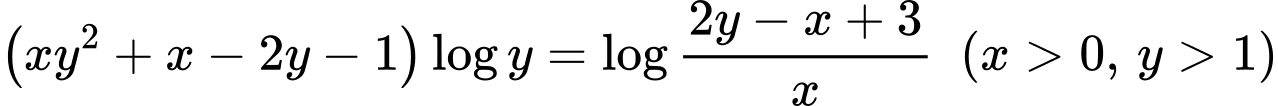
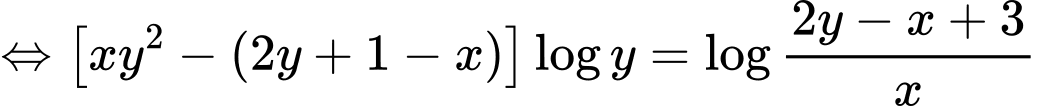
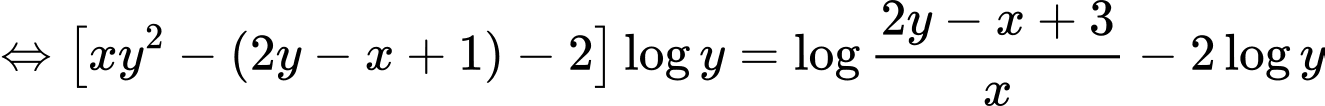
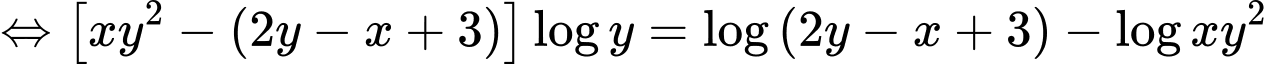
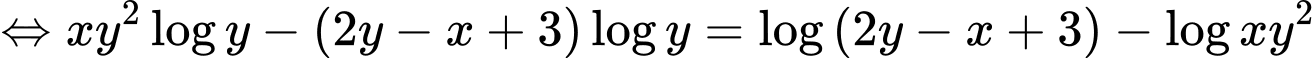
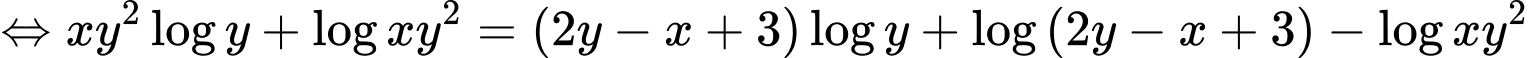
Áp dụng tính chất hàm đặc trưng, ta có:
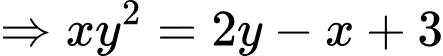
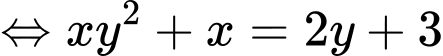
Ta có:
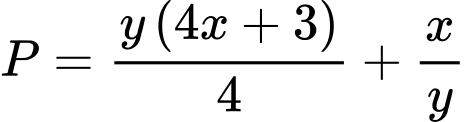
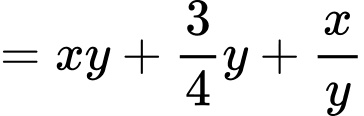
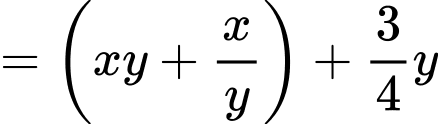
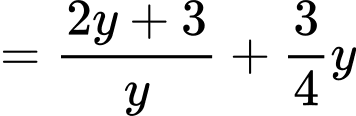
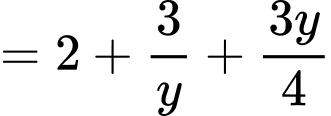
Với
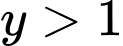 áp dụng bất đắng thức Co-si ta có:
áp dụng bất đắng thức Co-si ta có:
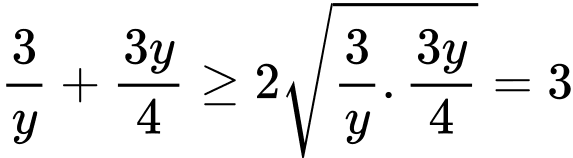
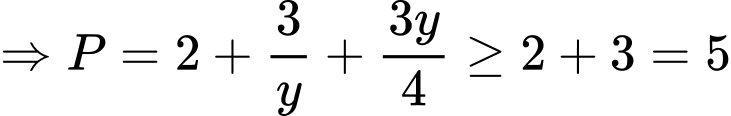

Đáp án: B. Đáp án: B
Câu 11 [791678]: Cho 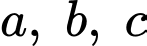 là các số thực dương khác 1 thỏa mãn
là các số thực dương khác 1 thỏa mãn 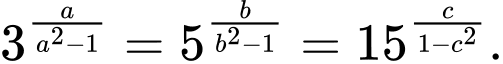 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 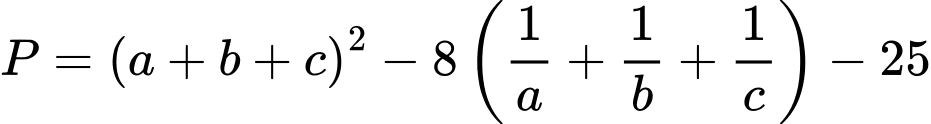 thuộc khoảng nào dưới đây
thuộc khoảng nào dưới đây
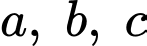 là các số thực dương khác 1 thỏa mãn
là các số thực dương khác 1 thỏa mãn 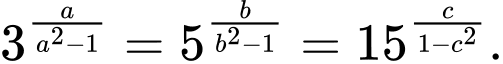 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 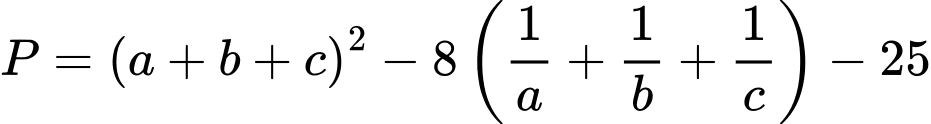 thuộc khoảng nào dưới đây
thuộc khoảng nào dưới đây A, 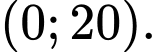
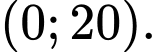
B, 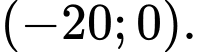
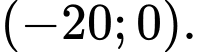
C, 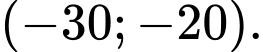
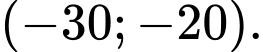
D, 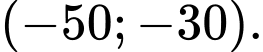
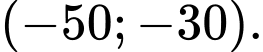
Theo giả thiết: 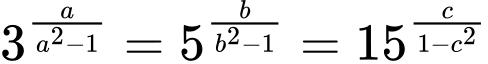
Đặt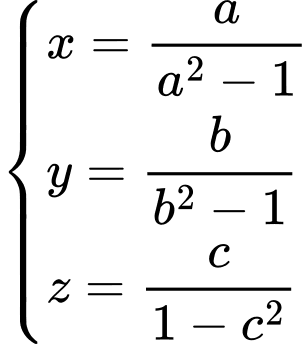
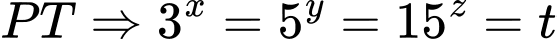
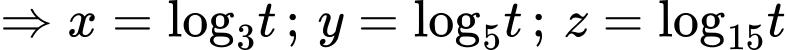
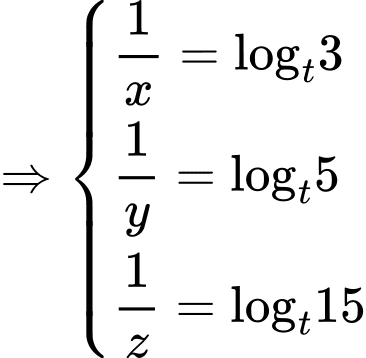
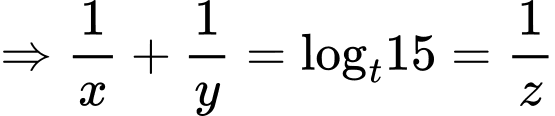
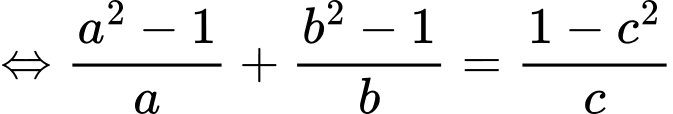
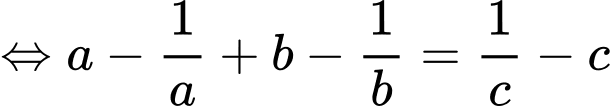
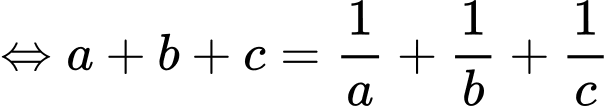
Ta có: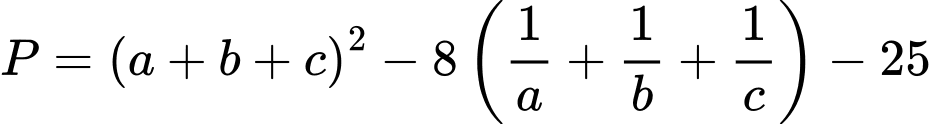
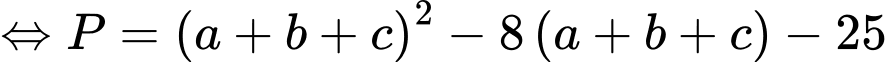
Ta đặt:
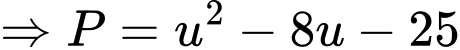
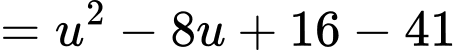
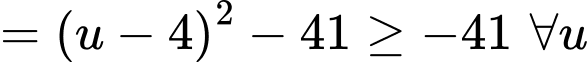
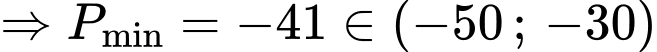
Đáp án: D. Đáp án: D
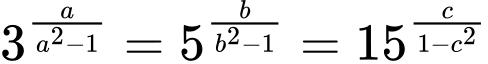
Đặt
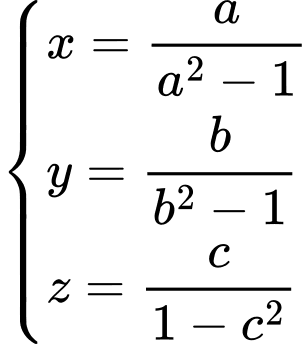
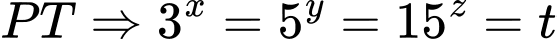
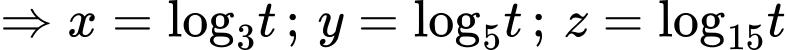
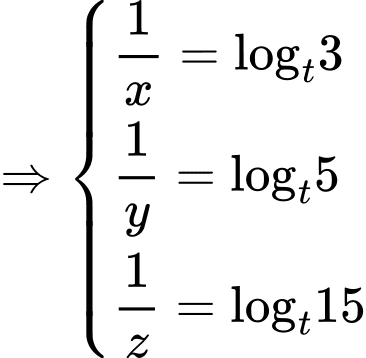
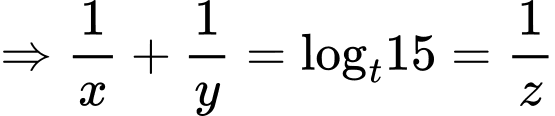
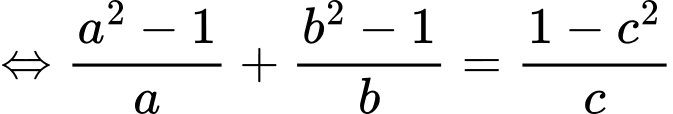
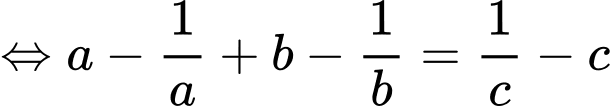
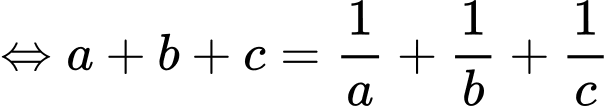
Ta có:
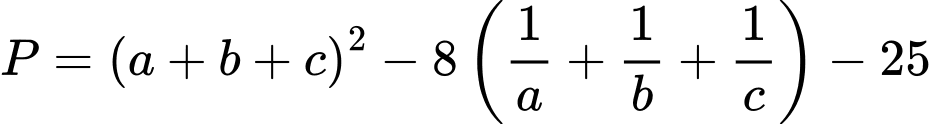
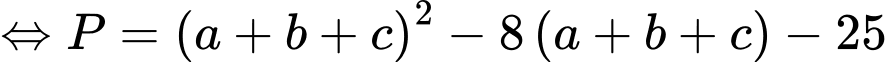
Ta đặt:

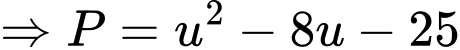
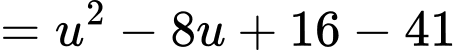
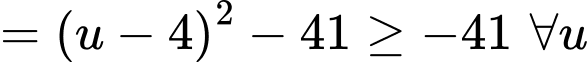
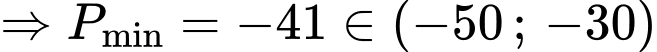
Đáp án: D. Đáp án: D
Câu 12 [511514]: Cho hàm số 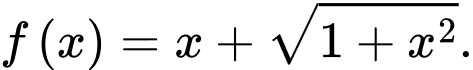 Tìm các giá trị của
Tìm các giá trị của 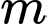 để bất phương trình
để bất phương trình 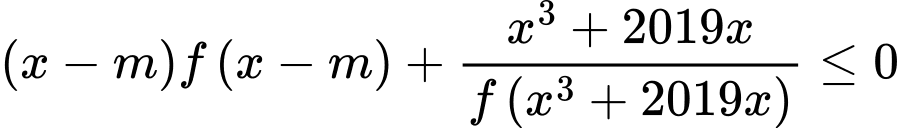 nghiệm đúng với mọi
nghiệm đúng với mọi 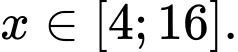
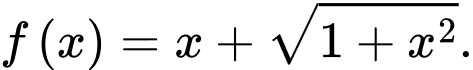 Tìm các giá trị của
Tìm các giá trị của 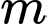 để bất phương trình
để bất phương trình 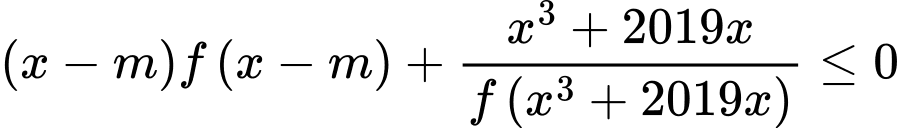 nghiệm đúng với mọi
nghiệm đúng với mọi 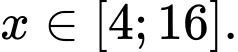
A, 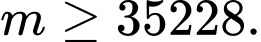
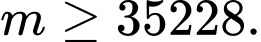
B, 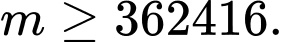
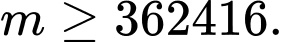
C, 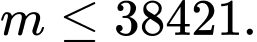
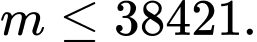
D, 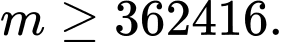
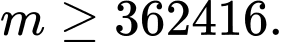
Đáp án: B
Câu 13 [511517]: Cho hàm số 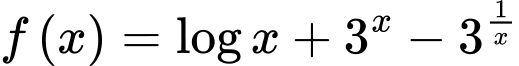 . Tổng bình phương các giá trị của tham số
. Tổng bình phương các giá trị của tham số 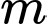 để phương trình
để phương trình 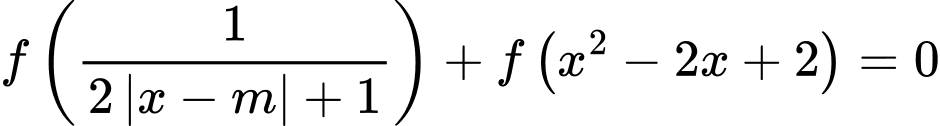 có đúng 3 nghiệm phân biệt bằng
có đúng 3 nghiệm phân biệt bằng
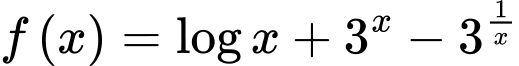 . Tổng bình phương các giá trị của tham số
. Tổng bình phương các giá trị của tham số 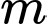 để phương trình
để phương trình 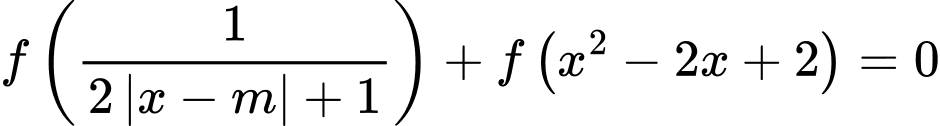 có đúng 3 nghiệm phân biệt bằng
có đúng 3 nghiệm phân biệt bằng A, 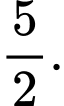
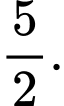
B, 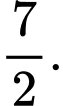
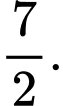
C, 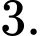
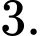
D, 
Đáp án: B
Câu 14 [511518]: Cho hàm số 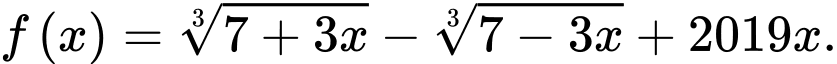 Gọi
Gọi 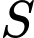 là tập hợp các giá trị nguyên của
là tập hợp các giá trị nguyên của 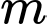 thỏa mãn điều kiện
thỏa mãn điều kiện 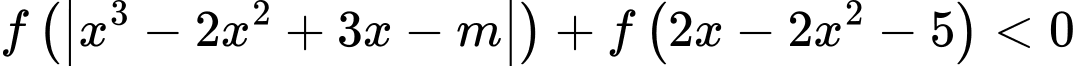 với mọi
với mọi  Số phần tử của tập S là
Số phần tử của tập S là
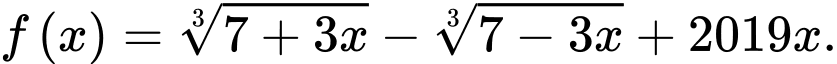 Gọi
Gọi 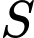 là tập hợp các giá trị nguyên của
là tập hợp các giá trị nguyên của 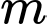 thỏa mãn điều kiện
thỏa mãn điều kiện 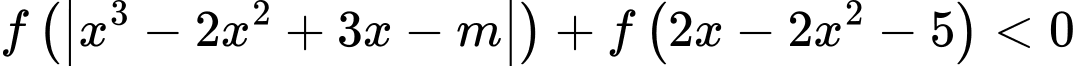 với mọi
với mọi  Số phần tử của tập S là
Số phần tử của tập S là A, 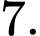
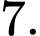
B, 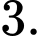
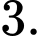
C, 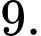
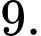
D, 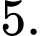
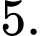
Có: 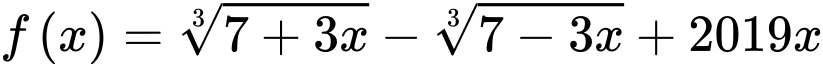
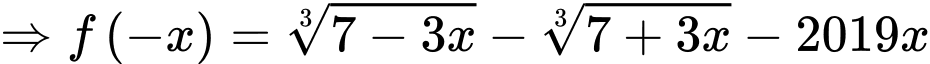
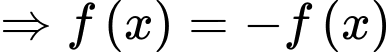
Xét bất phương trình: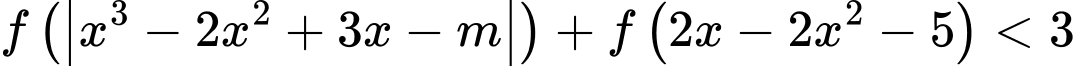

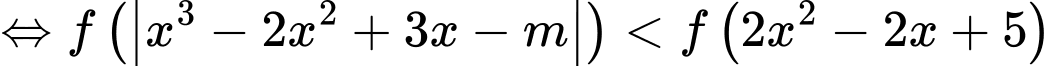
Ta có: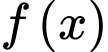 là hàm đồng biến trên khoảng
là hàm đồng biến trên khoảng 
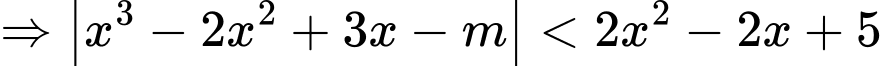
Vì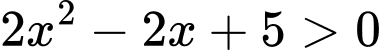 với
với 
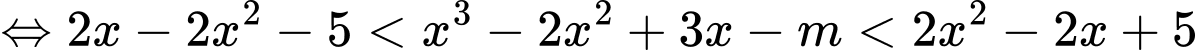
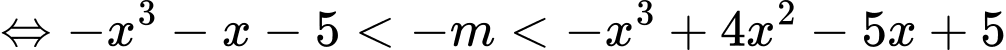
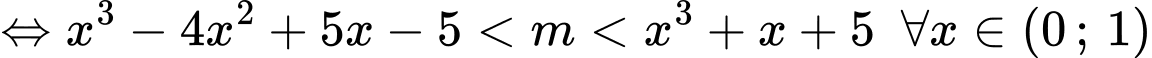
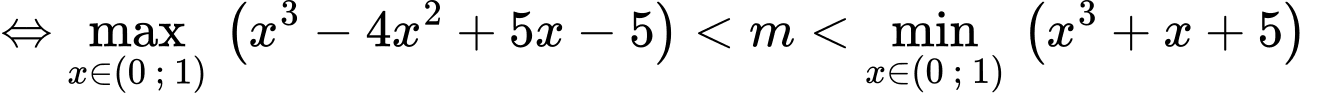
 Suy ra: 9 giá trị.
Suy ra: 9 giá trị.
Đáp án: C. Đáp án: C
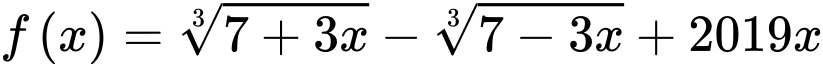
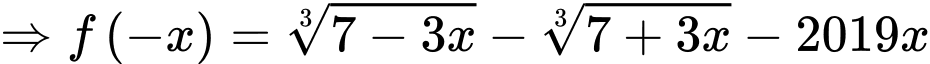
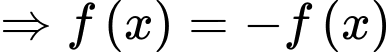
Xét bất phương trình:
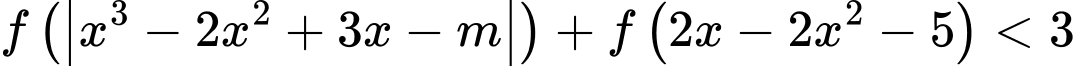

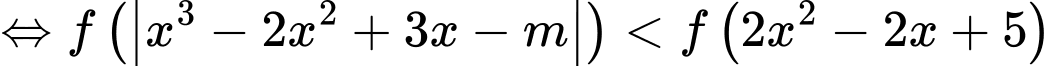
Ta có:
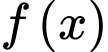 là hàm đồng biến trên khoảng
là hàm đồng biến trên khoảng 
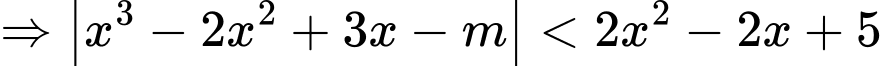
Vì
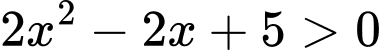 với
với 
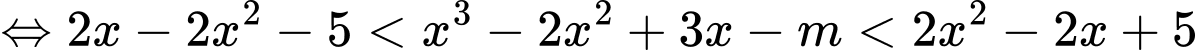
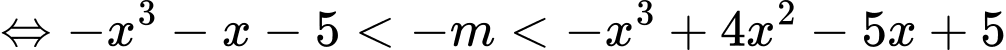
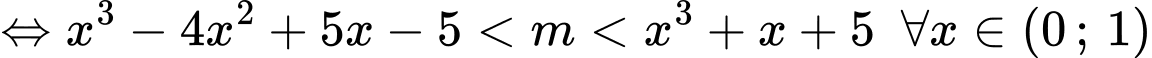
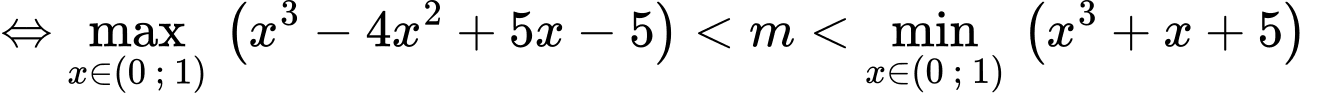
 Suy ra: 9 giá trị.
Suy ra: 9 giá trị.
Đáp án: C. Đáp án: C