Đáp án Bài tập tự luyện số 2 - Phương trình mũ chứa tham số
Câu 1 [508859]: Cho phương trình 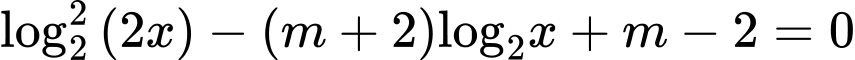 (với
(với 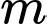 là tham số thực). Tập hợp các giá trị của tham số
là tham số thực). Tập hợp các giá trị của tham số 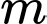 để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 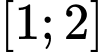 là
là
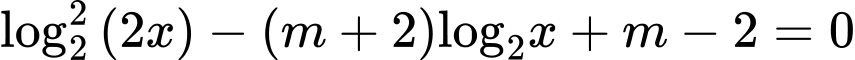 (với
(với 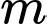 là tham số thực). Tập hợp các giá trị của tham số
là tham số thực). Tập hợp các giá trị của tham số 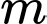 để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 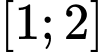 là
là A, 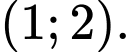
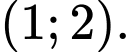
B, 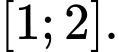
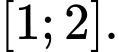
C, 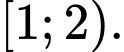
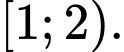
D, 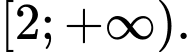
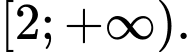
Ta có:
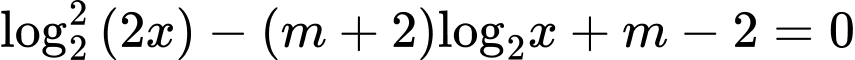
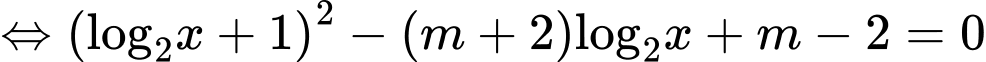

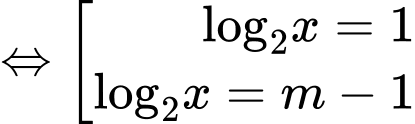
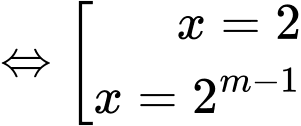
Để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn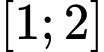 thì:
thì:

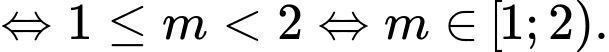
Chọn đáp án C. Đáp án: C
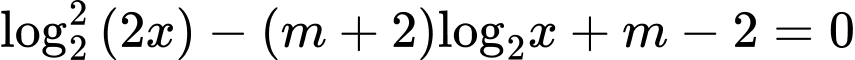
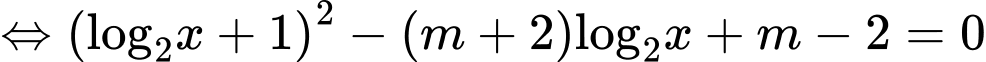

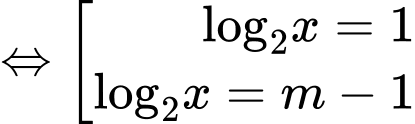
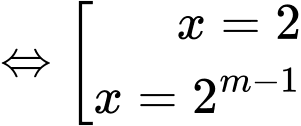
Để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
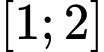 thì:
thì:
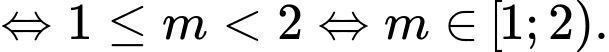
Chọn đáp án C. Đáp án: C
Câu 2 [79223]: Tìm tập hợp tất cả các giá trị thực của tham số 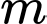 để phương trình
để phương trình 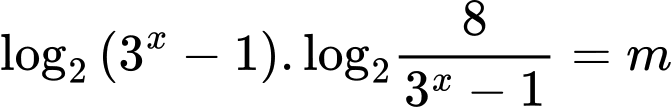 có nghiệm thuộc khoảng
có nghiệm thuộc khoảng 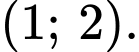
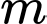 để phương trình
để phương trình 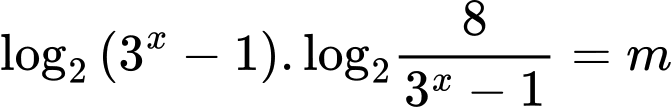 có nghiệm thuộc khoảng
có nghiệm thuộc khoảng 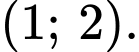
A, 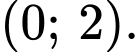
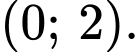
B, 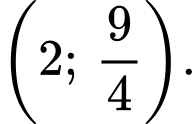
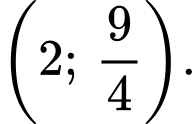
C, 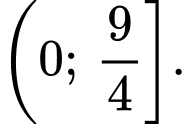
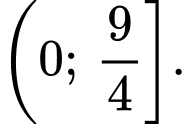
D, 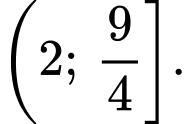
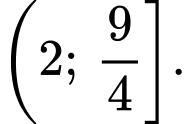
PT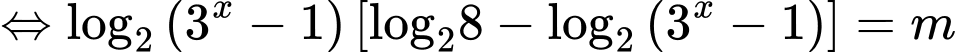
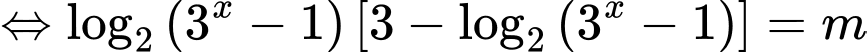
Đặt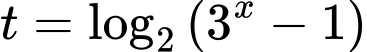 với
với 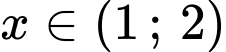

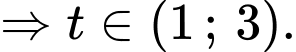
Khi đó phương trình trở thành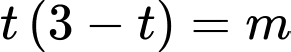
Xét hàm số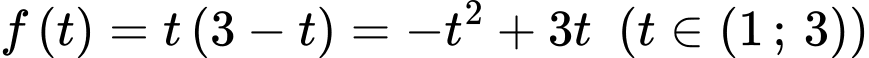
Ta có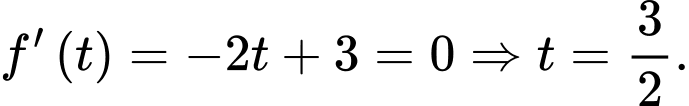
Bảng biến thiên
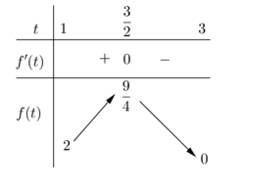
Suy ra phương trình đã cho có nghiệm thuộc khoảng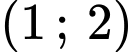 khi
khi 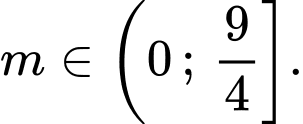
Chọn C. Đáp án: C
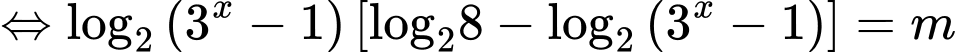
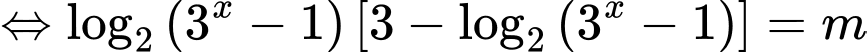
Đặt
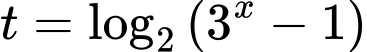 với
với 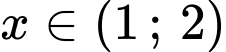

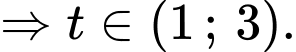
Khi đó phương trình trở thành
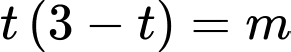
Xét hàm số
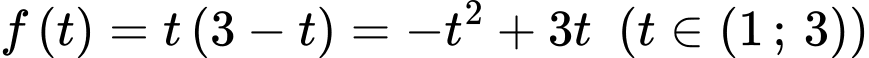
Ta có
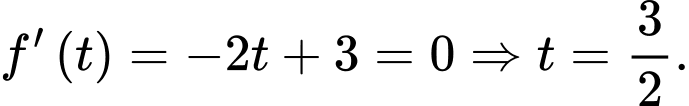
Bảng biến thiên

Suy ra phương trình đã cho có nghiệm thuộc khoảng
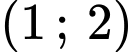 khi
khi 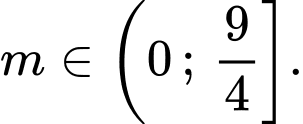
Chọn C. Đáp án: C
Câu 3 [508863]: Tìm điều kiện của tham số 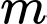 để phương trình
để phương trình 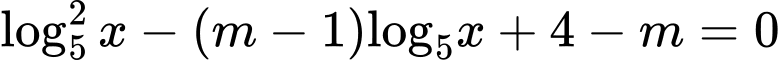 có hai nghiệm phân biệt thuộc
có hai nghiệm phân biệt thuộc 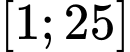
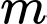 để phương trình
để phương trình 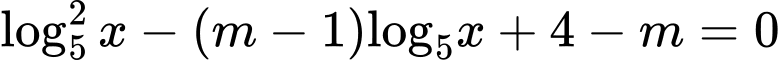 có hai nghiệm phân biệt thuộc
có hai nghiệm phân biệt thuộc 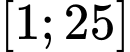
A, 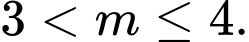
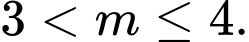
B, 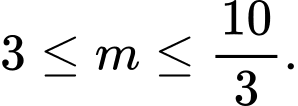
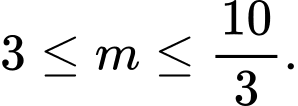
C, 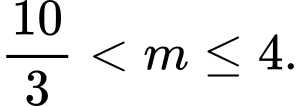
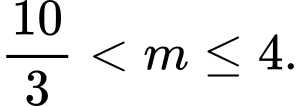
D, 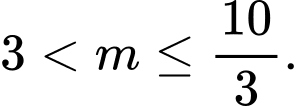
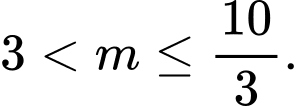
Đặt 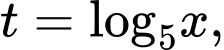
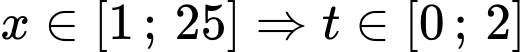
PT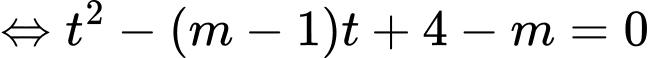
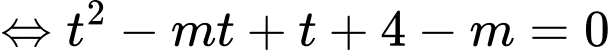
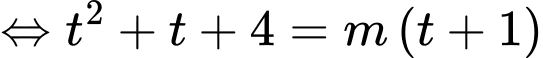
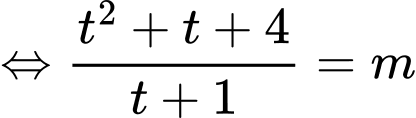
Xét hàm số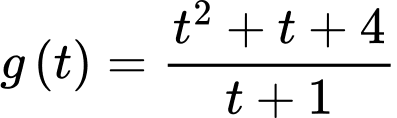 trên đoạn
trên đoạn
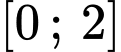
Ta có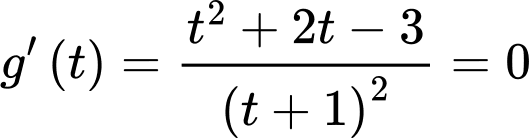
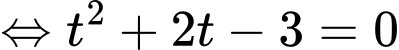
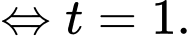
Bảng biến thiên
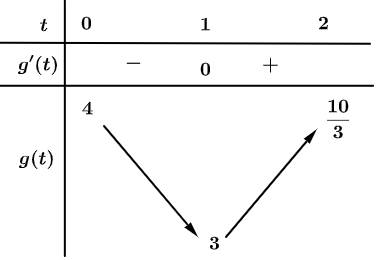
Vậy để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn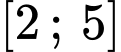 thì
thì 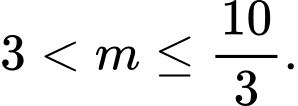
Chọn D. Đáp án: D
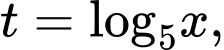
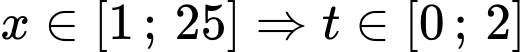
PT
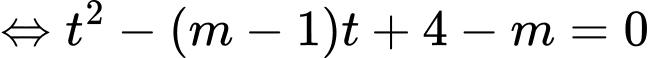
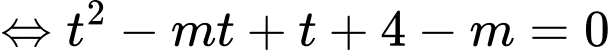
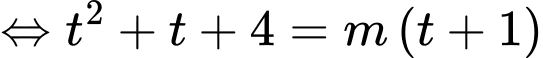
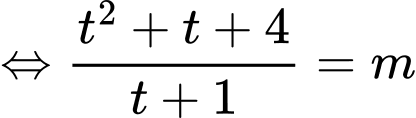
Xét hàm số
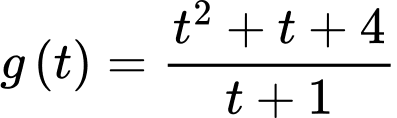 trên đoạn
trên đoạn 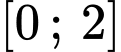
Ta có
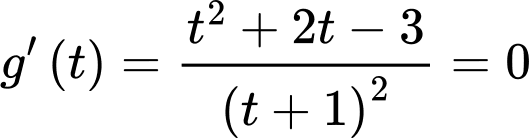
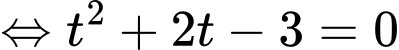
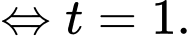
Bảng biến thiên

Vậy để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
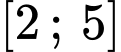 thì
thì 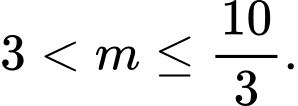
Chọn D. Đáp án: D
Câu 4 [79228]: Gọi 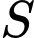 là tập hợp các giá trị nguyên của tham số
là tập hợp các giá trị nguyên của tham số 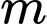 để phương trình
để phương trình 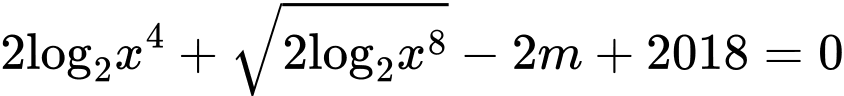 có ít nhất một nghiệm thuộc đoạn
có ít nhất một nghiệm thuộc đoạn 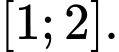 Số phần tử của tập hợp
Số phần tử của tập hợp 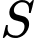 là
là
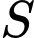 là tập hợp các giá trị nguyên của tham số
là tập hợp các giá trị nguyên của tham số 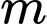 để phương trình
để phương trình 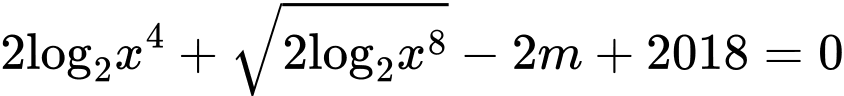 có ít nhất một nghiệm thuộc đoạn
có ít nhất một nghiệm thuộc đoạn 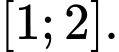 Số phần tử của tập hợp
Số phần tử của tập hợp  là
là A, 7.
B, 9.
C, 8.
D, 6.
PT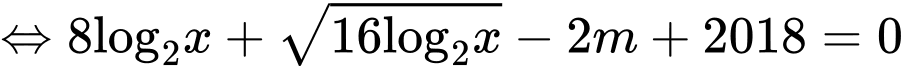
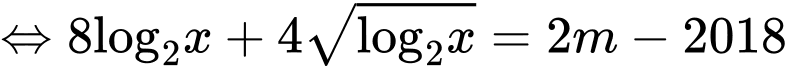
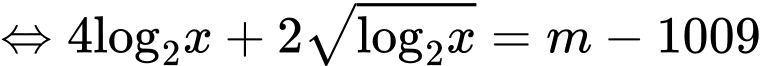
Đặt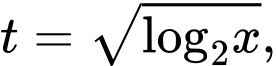 với
với 
Khi đó phương trình trở thành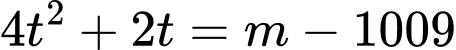
Xét hàm số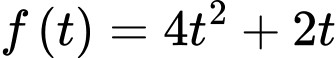 với
với 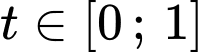
Ta có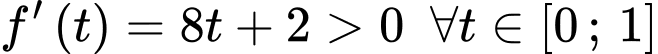
Suy ra hàm số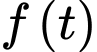 đồng biến trên
đồng biến trên 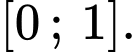
Mặt khác,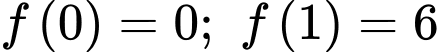 suy ra phương trình
suy ra phương trình 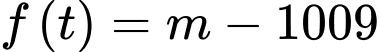
có nghiệm khi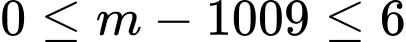
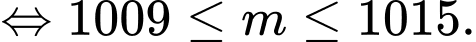
Kết hợp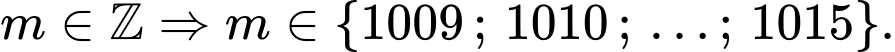
Vậy có 7 giá trị nguyên của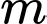 thoả mãn ycbt.
thoả mãn ycbt.
Chọn A. Đáp án: A
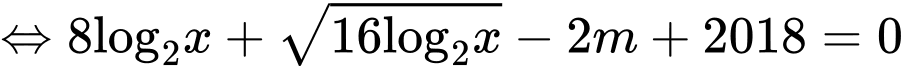
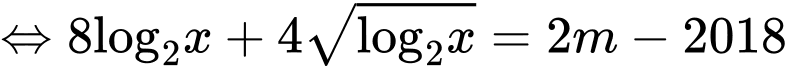
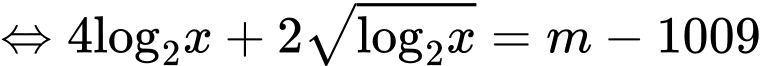
Đặt
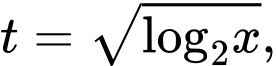 với
với 
Khi đó phương trình trở thành
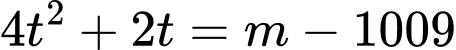
Xét hàm số
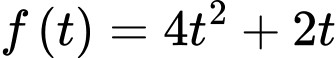 với
với 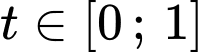
Ta có
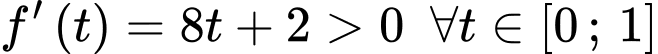
Suy ra hàm số
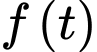 đồng biến trên
đồng biến trên 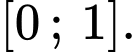
Mặt khác,
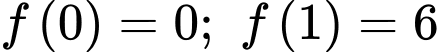 suy ra phương trình
suy ra phương trình 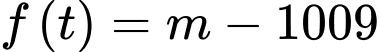
có nghiệm khi
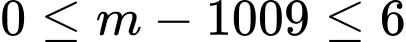
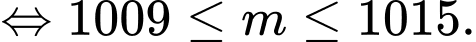
Kết hợp
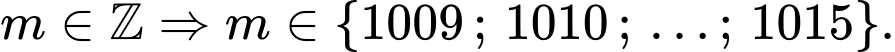
Vậy có 7 giá trị nguyên của
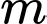 thoả mãn ycbt.
thoả mãn ycbt.
Chọn A. Đáp án: A
Câu 5 [508861]: Cho phương trình 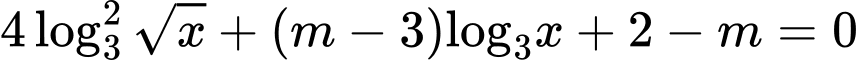 (với
(với 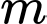 là tham số thực). Số giá trị nguyên của tham số
là tham số thực). Số giá trị nguyên của tham số 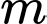 để phương trình đã cho có hai nghiệm phân biệt thuộc
để phương trình đã cho có hai nghiệm phân biệt thuộc 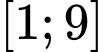 là
là
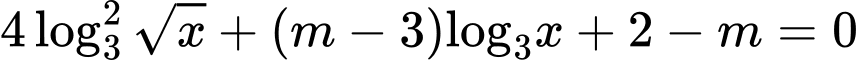 (với
(với 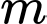 là tham số thực). Số giá trị nguyên của tham số
là tham số thực). Số giá trị nguyên của tham số 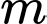 để phương trình đã cho có hai nghiệm phân biệt thuộc
để phương trình đã cho có hai nghiệm phân biệt thuộc 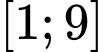 là
là A, 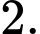
B, 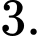
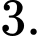
C, 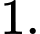
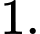
D, 
Xét 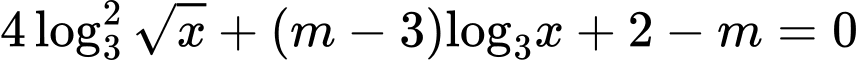
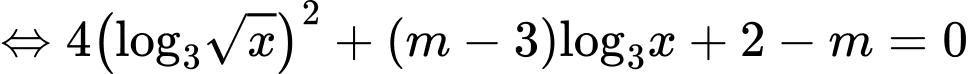
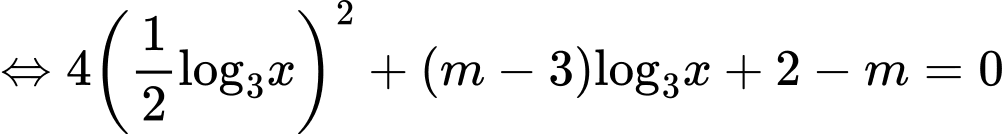
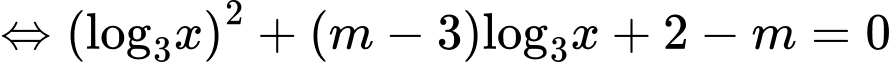
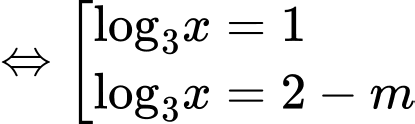
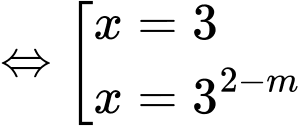
Để phương trình đã cho có hai nghiệm nguyên phân biệt thuộc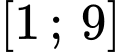
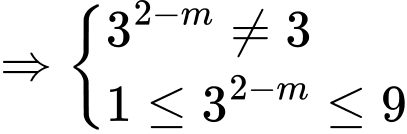
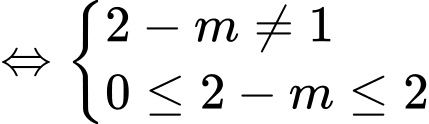
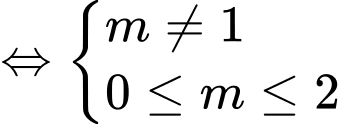
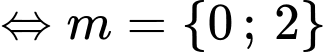
Đáp án: A Đáp án: A
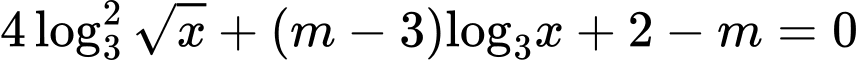
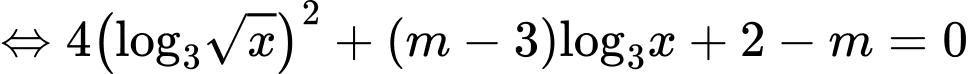
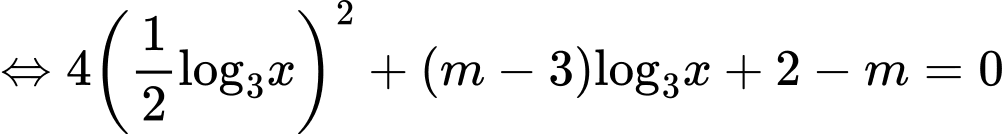
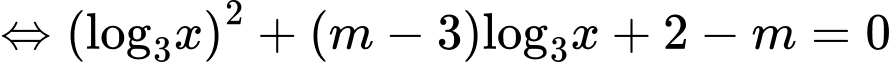
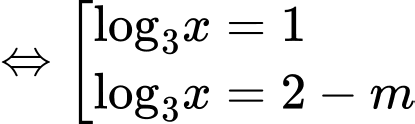
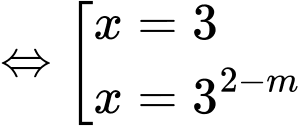
Để phương trình đã cho có hai nghiệm nguyên phân biệt thuộc
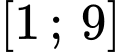
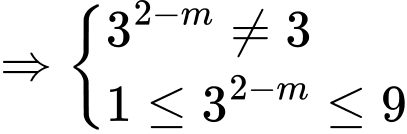
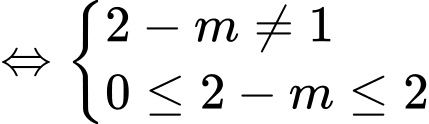
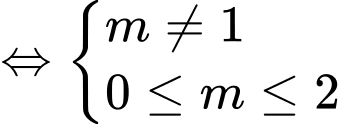
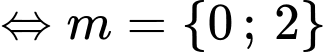
Đáp án: A Đáp án: A
Câu 6 [508862]: Có bao nhiêu giá trị nguyên của tham số 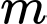 để phương trình
để phương trình  (với
(với 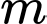 là tham số thực để phương trình đã cho có 4 nghiệm phân biệt
là tham số thực để phương trình đã cho có 4 nghiệm phân biệt
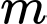 để phương trình
để phương trình  (với
(với 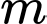 là tham số thực để phương trình đã cho có 4 nghiệm phân biệt
là tham số thực để phương trình đã cho có 4 nghiệm phân biệt A, 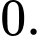
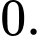
B, 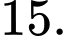
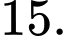
C, 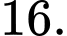
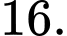
D, 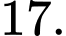
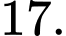
Ta có 
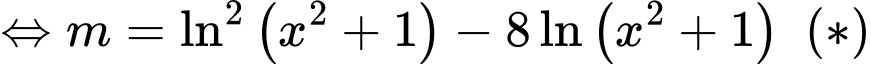
Đặt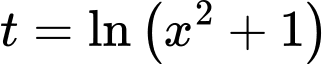
Ta có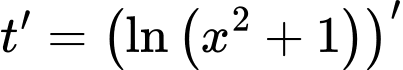
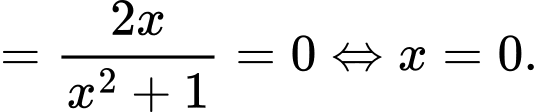
Bảng biến thiên của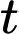
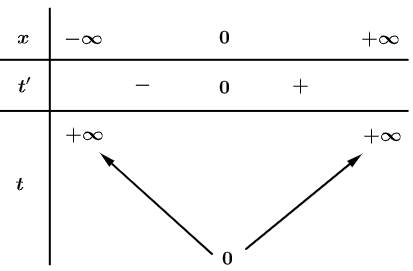
Suy ra
Nhận xét: Tại sẽ cho ra duy nhất 1 nghiệm
sẽ cho ra duy nhất 1 nghiệm 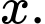 Với mỗi nghiệm
Với mỗi nghiệm 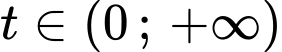 sẽ cho ra đúng 2 nghiệm
sẽ cho ra đúng 2 nghiệm 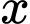 phân biệt.
phân biệt.
Khi đó PT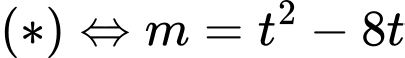
Xét hàm số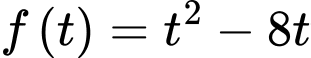 trên khoảng
trên khoảng 
Ta có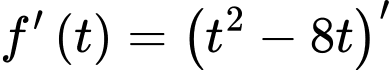
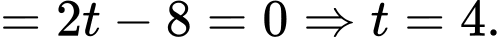
Bảng biến thiên của hàm số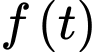
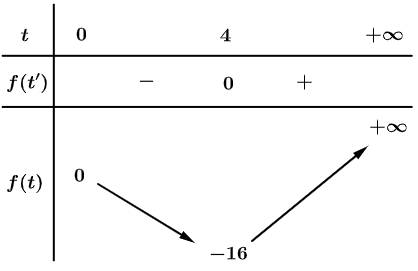
Dựa vào bảng biến thiên, suy ra phương trình có 4 nghiệm phân biệt khi và chỉ khi
có 4 nghiệm phân biệt khi và chỉ khi 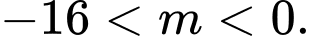
Kết hợp với 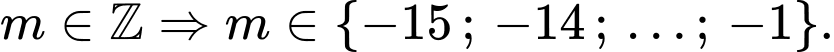 Vậy có 15 giá trị của nguyên của
Vậy có 15 giá trị của nguyên của 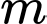 thoả mãn ycbt.
thoả mãn ycbt.
Chọn B. Đáp án: B

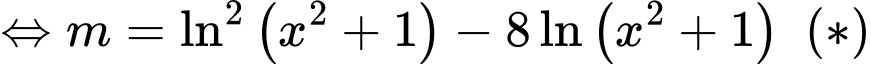
Đặt
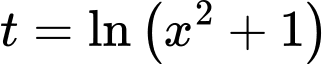
Ta có
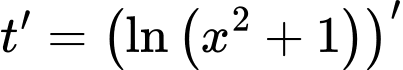
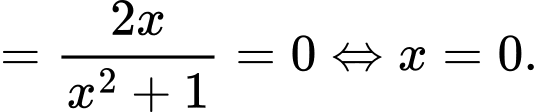
Bảng biến thiên của
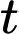

Suy ra
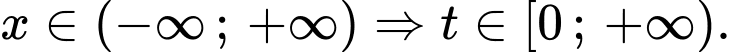
Nhận xét: Tại
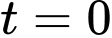 sẽ cho ra duy nhất 1 nghiệm
sẽ cho ra duy nhất 1 nghiệm 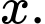 Với mỗi nghiệm
Với mỗi nghiệm 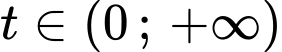 sẽ cho ra đúng 2 nghiệm
sẽ cho ra đúng 2 nghiệm 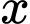 phân biệt.
phân biệt.
Khi đó PT
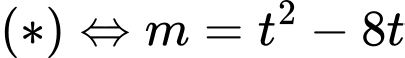
Xét hàm số
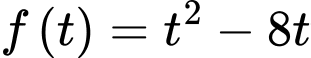 trên khoảng
trên khoảng 
Ta có
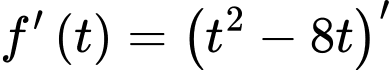
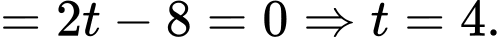
Bảng biến thiên của hàm số
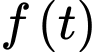

Dựa vào bảng biến thiên, suy ra phương trình
 có 4 nghiệm phân biệt khi và chỉ khi
có 4 nghiệm phân biệt khi và chỉ khi 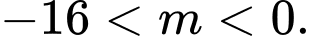
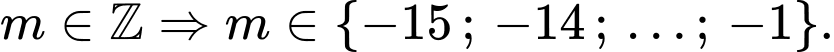 Vậy có 15 giá trị của nguyên của
Vậy có 15 giá trị của nguyên của 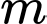 thoả mãn ycbt.
thoả mãn ycbt.
Chọn B. Đáp án: B
Câu 7 [508828]: Cho phương trình 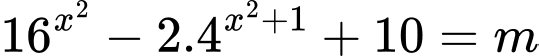 (với
(với 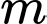 là tham số). Số giá trị nguyên của
là tham số). Số giá trị nguyên của 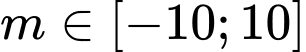 để phương trình đã cho có đúng 2 nghiệm thực phân biệt là
để phương trình đã cho có đúng 2 nghiệm thực phân biệt là
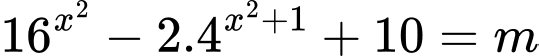 (với
(với 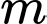 là tham số). Số giá trị nguyên của
là tham số). Số giá trị nguyên của 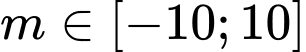 để phương trình đã cho có đúng 2 nghiệm thực phân biệt là
để phương trình đã cho có đúng 2 nghiệm thực phân biệt là A, 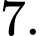
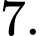
B, 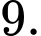
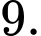
C, 
D, 
Ta có 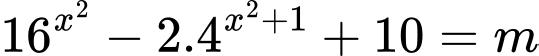
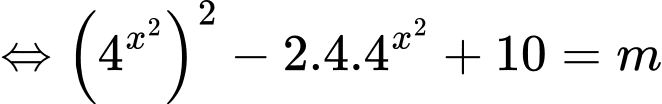
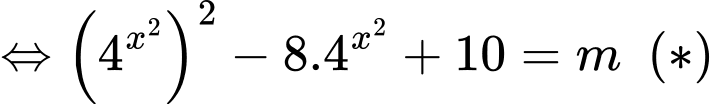
Đặt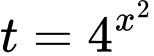
Ta có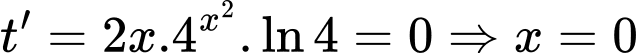
Bảng biến thiên của
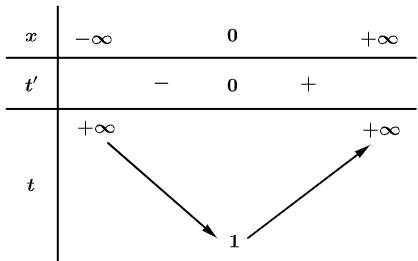
Nhận xét:
+)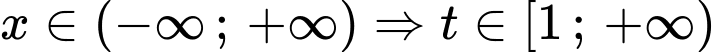
+) Tại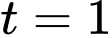 sẽ cho ra duy nhất 1 nghiệm
sẽ cho ra duy nhất 1 nghiệm 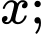 Với
Với 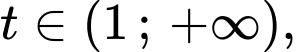 mỗi nghiệm
mỗi nghiệm 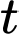 tìm được sẽ cho ra 2 nghiệm
tìm được sẽ cho ra 2 nghiệm 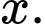
Với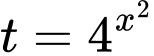 phương trình
phương trình 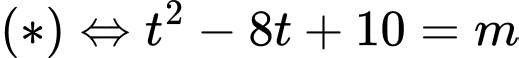
Xét hàm số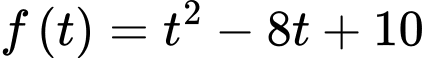 trên khoảng
trên khoảng 
Ta có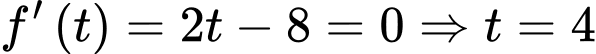
Bảng biến thiên của hàm số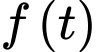
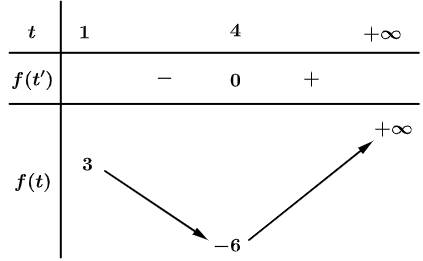
Dựa vào bảng biến thiên, suy ra để phương trình đã cho có đúng 2 nghiệm thực phân biệt khi và chỉ khi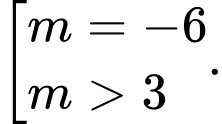
Kết hợp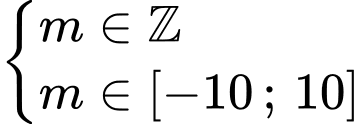
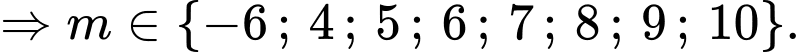
Vậy có 8 giá trị nguyên của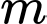 thoả mãn ycbt.
thoả mãn ycbt.
Chọn C. Đáp án: C
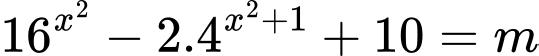
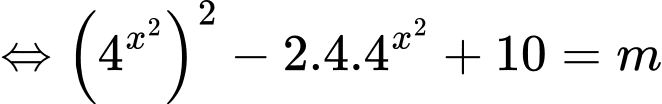
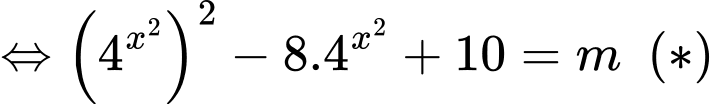
Đặt
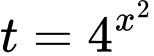
Ta có
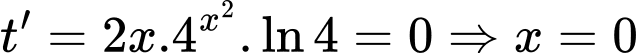
Bảng biến thiên của
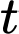

Nhận xét:
+)
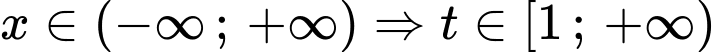
+) Tại
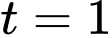 sẽ cho ra duy nhất 1 nghiệm
sẽ cho ra duy nhất 1 nghiệm 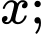 Với
Với 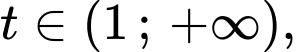 mỗi nghiệm
mỗi nghiệm 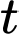 tìm được sẽ cho ra 2 nghiệm
tìm được sẽ cho ra 2 nghiệm 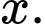
Với
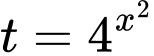 phương trình
phương trình 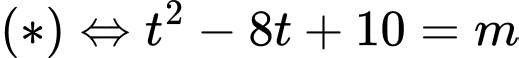
Xét hàm số
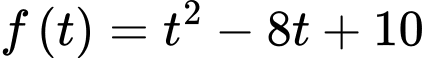 trên khoảng
trên khoảng 
Ta có
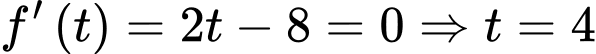
Bảng biến thiên của hàm số
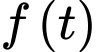

Dựa vào bảng biến thiên, suy ra để phương trình đã cho có đúng 2 nghiệm thực phân biệt khi và chỉ khi
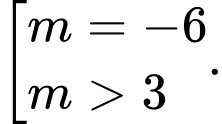
Kết hợp
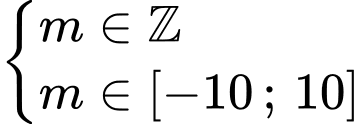
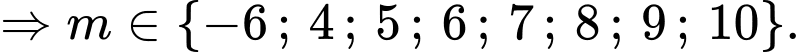
Vậy có 8 giá trị nguyên của
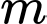 thoả mãn ycbt.
thoả mãn ycbt.
Chọn C. Đáp án: C
Câu 8 [508829]: Có bao nhiêu giá trị nguyên của tham số 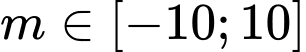 để phương trình
để phương trình 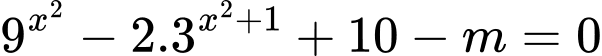 có đúng 2 nghiệm phân biệt
có đúng 2 nghiệm phân biệt
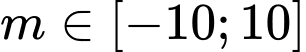 để phương trình
để phương trình 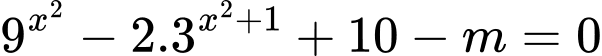 có đúng 2 nghiệm phân biệt
có đúng 2 nghiệm phân biệt A, 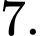
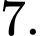
B, 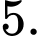
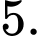
C, 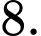
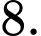
D, 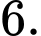
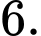
Đặt 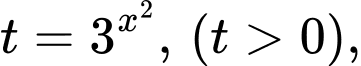 khi đó phương trình trở thành:
khi đó phương trình trở thành: 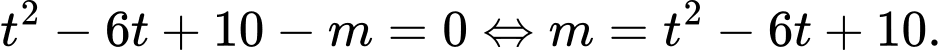
ta có: phương trình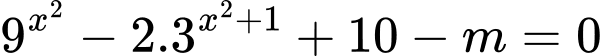 có đúng 2 nghiệm phân biệt khi
có đúng 2 nghiệm phân biệt khi
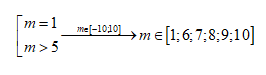
Vậy có 6 giá trị của x thỏa mãn đề bài.
Chọn đáp án D. Đáp án: D
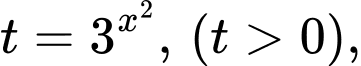 khi đó phương trình trở thành:
khi đó phương trình trở thành: 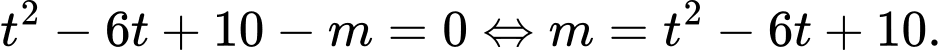
ta có: phương trình
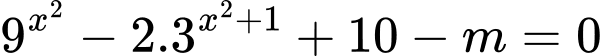 có đúng 2 nghiệm phân biệt khi
có đúng 2 nghiệm phân biệt khi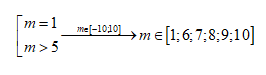
Vậy có 6 giá trị của x thỏa mãn đề bài.
Chọn đáp án D. Đáp án: D
Câu 9 [512505]: Có bao nhiêu số nguyên 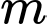 thuộc
thuộc 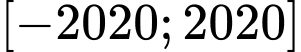 sao cho phương trình
sao cho phương trình 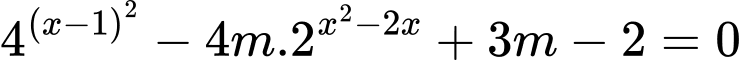 có bốn nghiệm phân biệt?
có bốn nghiệm phân biệt?
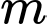 thuộc
thuộc 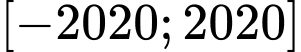 sao cho phương trình
sao cho phương trình 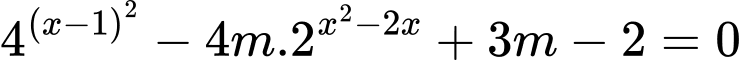 có bốn nghiệm phân biệt?
có bốn nghiệm phân biệt? A,  .
.
 .
.B, 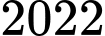 .
.
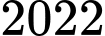 .
.C, 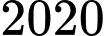 .
.
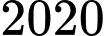 .
.D,  .
.
 .
.
Chọn A
Ta có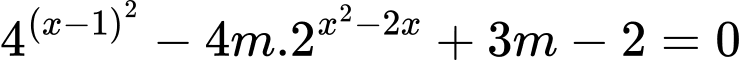
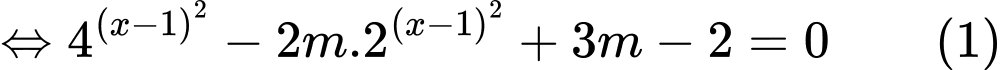
Đặt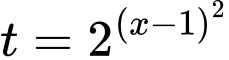
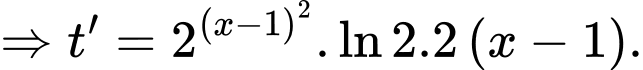
Khi đó
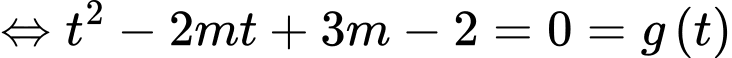
Để phương trình đã cho có bốn nghiệm phân biệt thì phương trình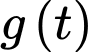 phải có hai nghiệm phân biệt lớn hơn
phải có hai nghiệm phân biệt lớn hơn 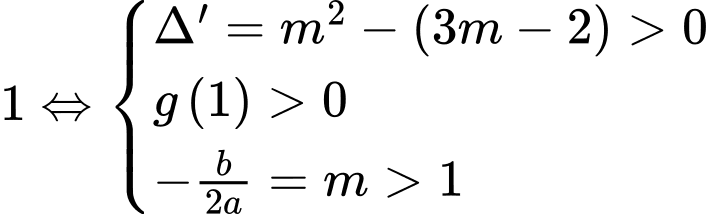
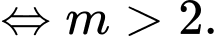
Kết hợp điều kiện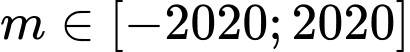
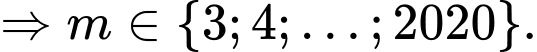
Vậy có giá trị của
giá trị của 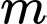 thỏa mãn. Đáp án: A
thỏa mãn. Đáp án: A
Ta có
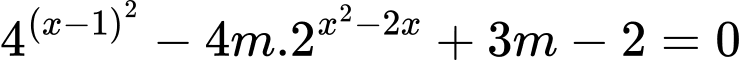
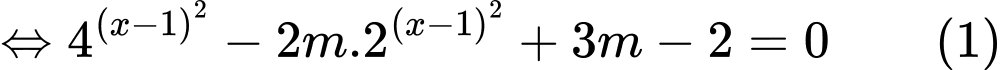
Đặt
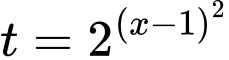
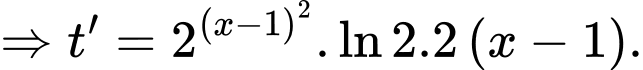
Khi đó

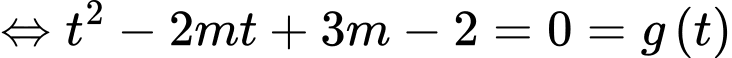
Để phương trình đã cho có bốn nghiệm phân biệt thì phương trình
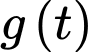 phải có hai nghiệm phân biệt lớn hơn
phải có hai nghiệm phân biệt lớn hơn 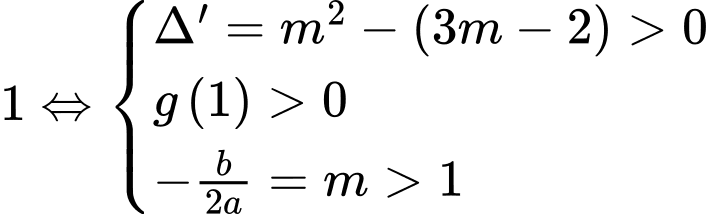
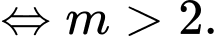
Kết hợp điều kiện
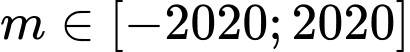
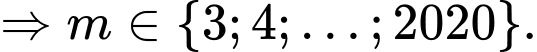
Vậy có
 giá trị của
giá trị của 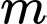 thỏa mãn. Đáp án: A
thỏa mãn. Đáp án: A
Câu 10 [10461]: Tìm số giá trị nguyên của tham số 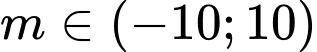 để phương trình
để phương trình 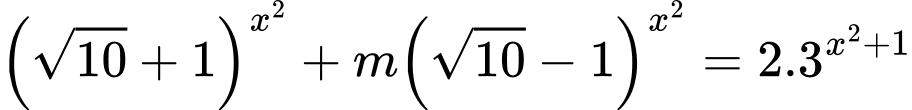 có đúng hai nghiệm phân biệt.
có đúng hai nghiệm phân biệt.
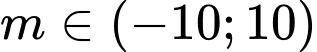 để phương trình
để phương trình 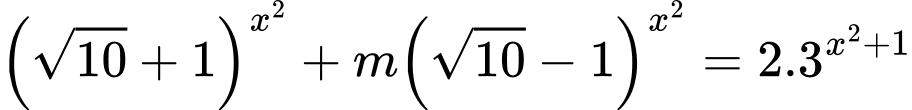 có đúng hai nghiệm phân biệt.
có đúng hai nghiệm phân biệt. A, 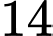 .
.
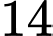 .
.B,  .
.
 .
.C,  .
.
 .
.D, 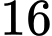 .
.
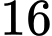 .
.
Ta có 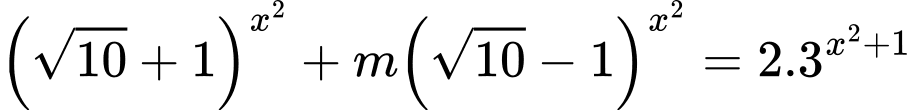
Chia cả hai vế cho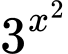 ta được
ta được
PT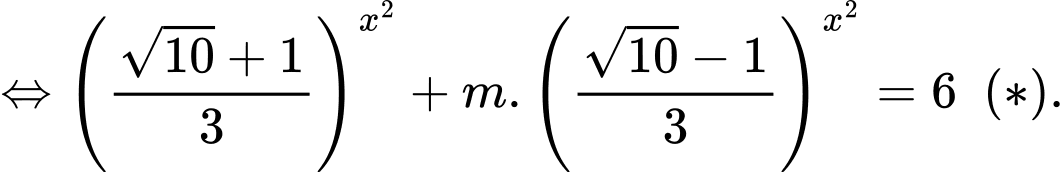
Đặt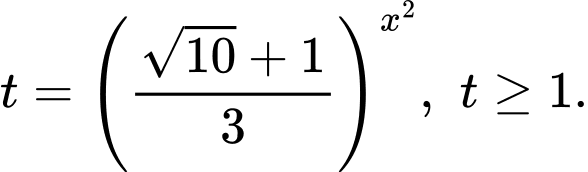
Phương trình trở thành
trở thành 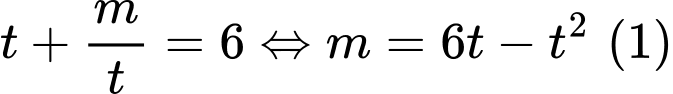
Xét hàm số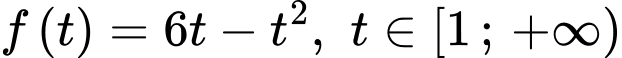
Ta có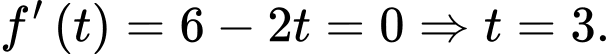
Bảng biến thiên
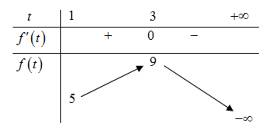
Phương trình đã cho có 2 nghiệm phân biệt khi phương trình có một nghiệm duy nhất
có một nghiệm duy nhất 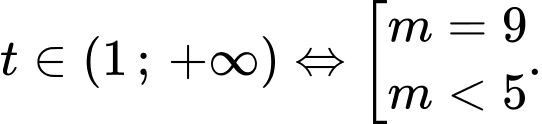
Kết hợp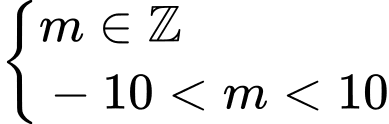
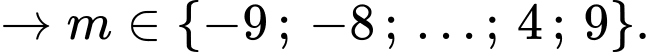
Vậy có 15 giá trị nguyên của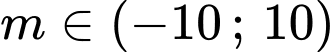 thoả mãn ycbt.
thoả mãn ycbt.
Chọn B. Đáp án: B
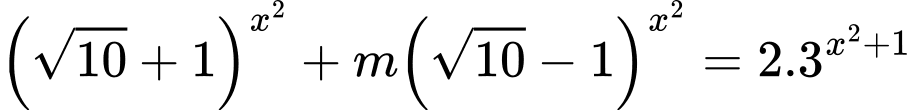
Chia cả hai vế cho
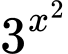 ta được
ta được
PT
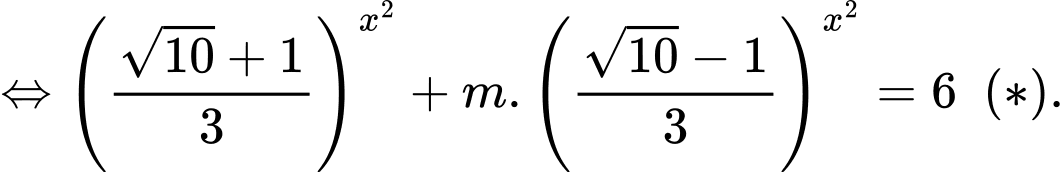
Đặt
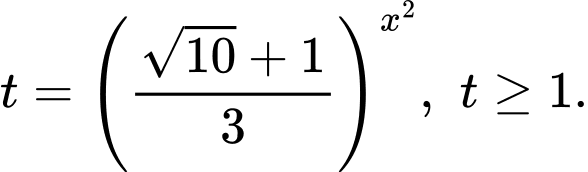
Phương trình
 trở thành
trở thành 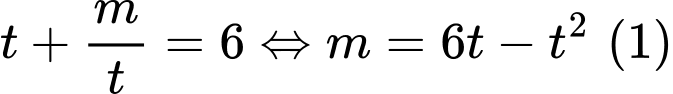
Xét hàm số
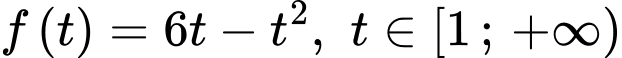
Ta có
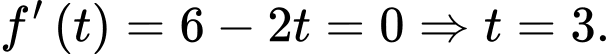
Bảng biến thiên

Phương trình đã cho có 2 nghiệm phân biệt khi phương trình
 có một nghiệm duy nhất
có một nghiệm duy nhất 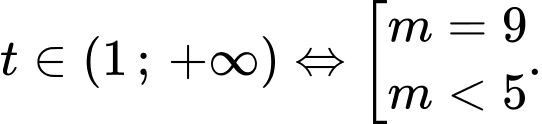
Kết hợp
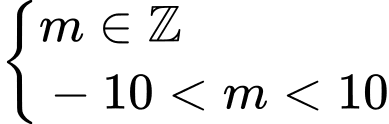
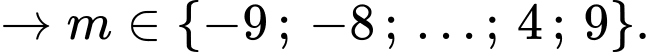
Vậy có 15 giá trị nguyên của
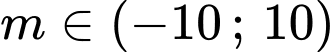 thoả mãn ycbt.
thoả mãn ycbt.
Chọn B. Đáp án: B
Câu 11 [79224]: Biết rằng để phương trình 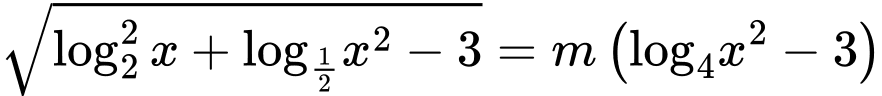 có nghiệm thuộc nửa khoảng
có nghiệm thuộc nửa khoảng 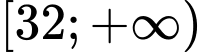 thì
thì 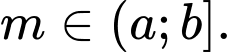 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
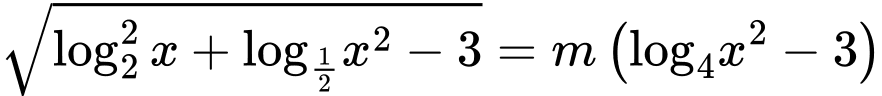 có nghiệm thuộc nửa khoảng
có nghiệm thuộc nửa khoảng 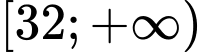 thì
thì 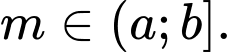 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
A, 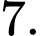
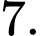
B, 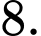
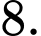
C, 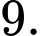
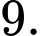
D, 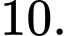
PT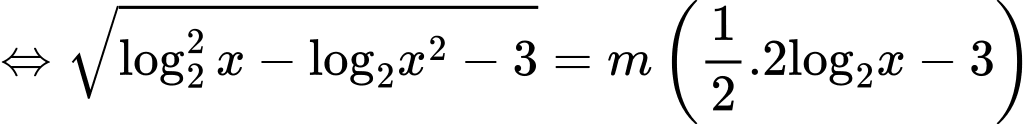
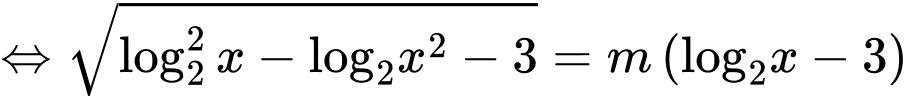
Đặt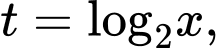 với
với 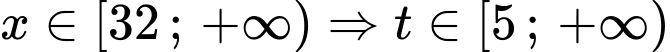
Phương trình đã cho trở thành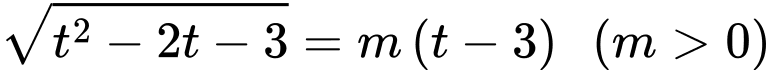
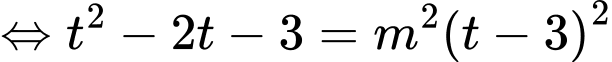
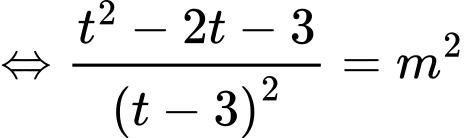
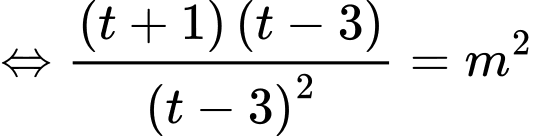
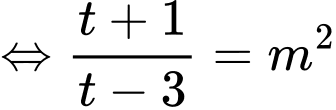
Xét hàm số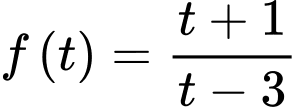 với
với 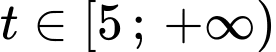
Ta có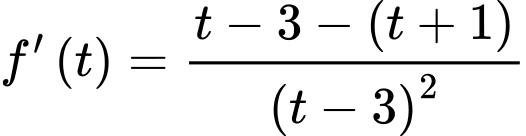
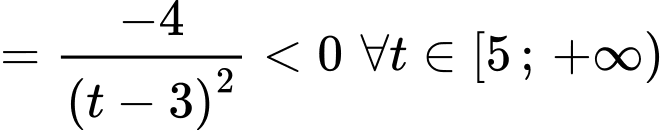
Do đó hàm số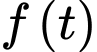 nghịch biến trên
nghịch biến trên 
Mặt khác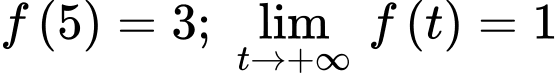 suy ra phương trình
suy ra phương trình 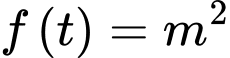 có nghiệm
có nghiệm 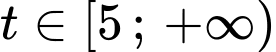 khi
khi 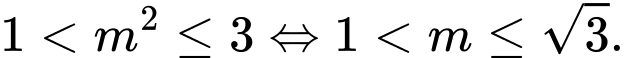 =""
="" Kết hợp 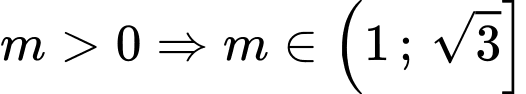
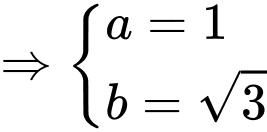
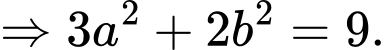 Chọn C. Đáp án: C
Chọn C. Đáp án: C
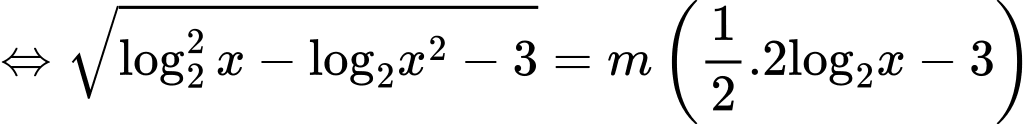
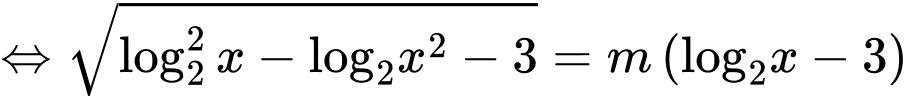
Đặt
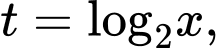 với
với 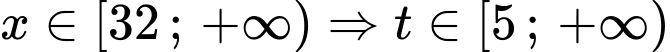
Phương trình đã cho trở thành
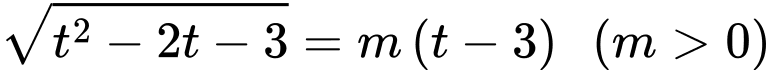
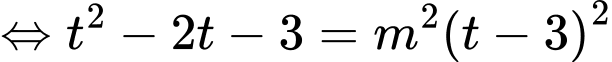
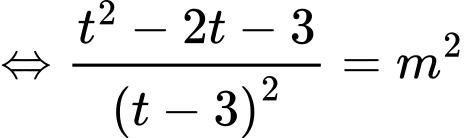
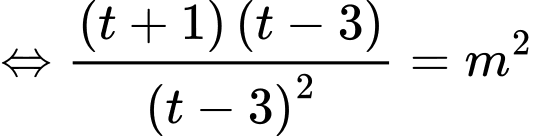
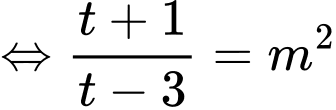
Xét hàm số
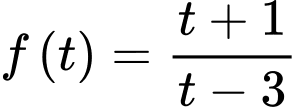 với
với 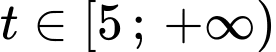
Ta có
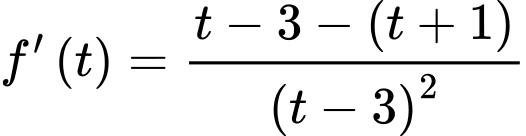
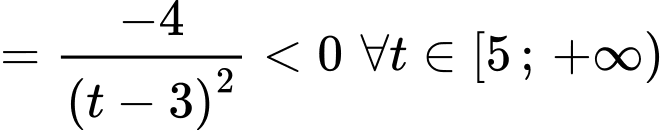
Do đó hàm số
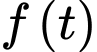 nghịch biến trên
nghịch biến trên 
Mặt khác
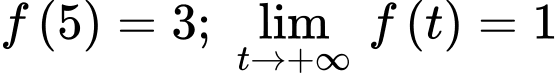 suy ra phương trình
suy ra phương trình 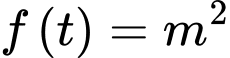 có nghiệm
có nghiệm 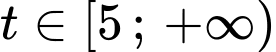 khi
khi 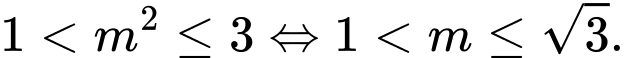 =""
="" 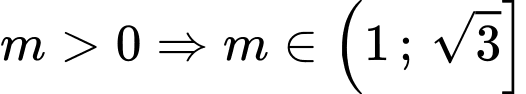
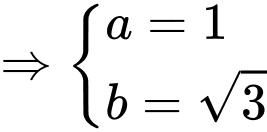
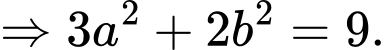 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 12 [789420]: Cho hàm số 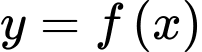 liên tục trên
liên tục trên  có
có 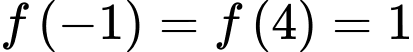 . Hàm số
. Hàm số 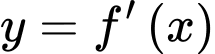 có bảng xét dấu
có bảng xét dấu
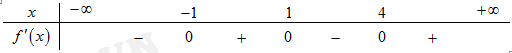
Có bao nhiêu giá trị nguyên của tham số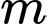 thuộc đoạn
thuộc đoạn 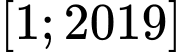 để phương trình
để phương trình 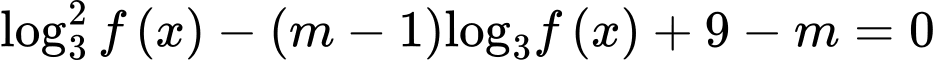 có nghiệm?
có nghiệm?
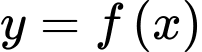 liên tục trên
liên tục trên  có
có 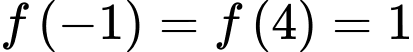 . Hàm số
. Hàm số  có bảng xét dấu
có bảng xét dấu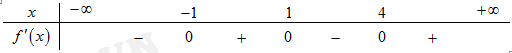
Có bao nhiêu giá trị nguyên của tham số
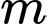 thuộc đoạn
thuộc đoạn 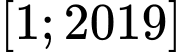 để phương trình
để phương trình 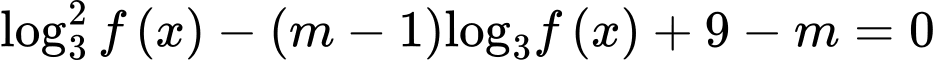 có nghiệm?
có nghiệm? A,  .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D, 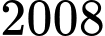 .
.
 .
.
Chọn B
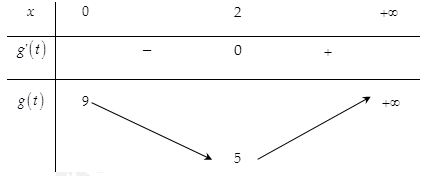
Ta có bảng biến thiên của hàm số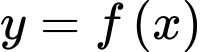 như sau:
như sau:
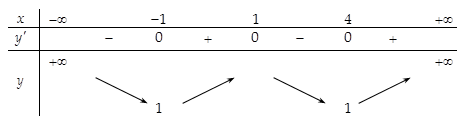
Từ bảng biến thiên suy ra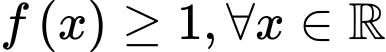 .
.
Đặt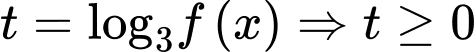 .
.
Phương trình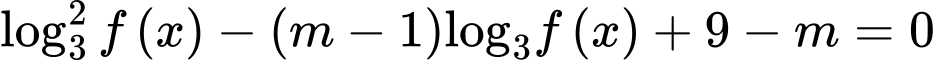 trở thành:
trở thành:
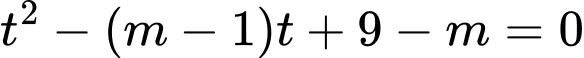
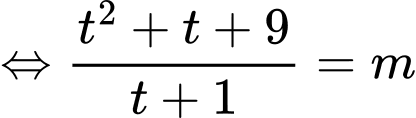 (1)
(1)
Xét hàm số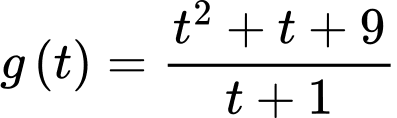 với
với  .
.
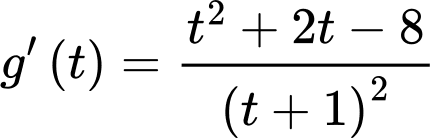 ;
; 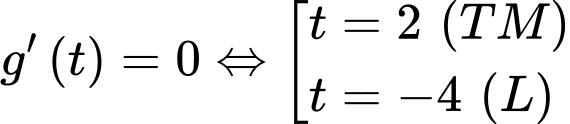
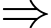 Phương trình
Phương trình  có nghiệm
có nghiệm 
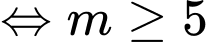 . Mà
. Mà 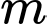 là số nguyên thuộc đoạn
là số nguyên thuộc đoạn 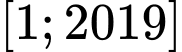 nên có 2015 số
nên có 2015 số 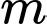 thỏa mãn. Đáp án: B
thỏa mãn. Đáp án: B
Ta có bảng biến thiên của hàm số
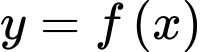 như sau:
như sau: 
Từ bảng biến thiên suy ra
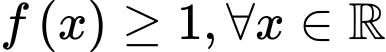 .
. Đặt
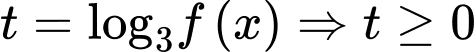 .
. Phương trình
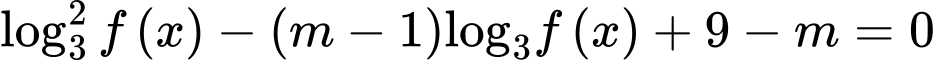 trở thành:
trở thành: 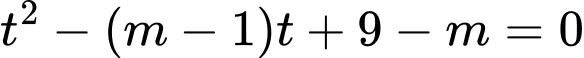
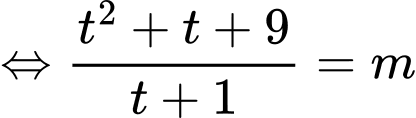 (1)
(1) Xét hàm số
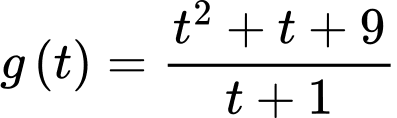 với
với  .
.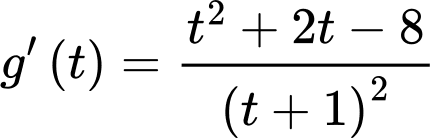 ;
; 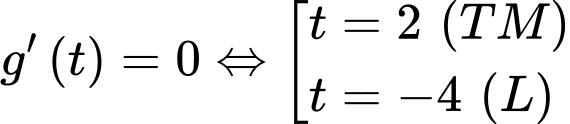

 Phương trình
Phương trình  có nghiệm
có nghiệm 
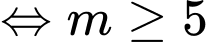 . Mà
. Mà 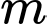 là số nguyên thuộc đoạn
là số nguyên thuộc đoạn 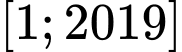 nên có 2015 số
nên có 2015 số 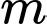 thỏa mãn. Đáp án: B
thỏa mãn. Đáp án: B