Đáp án Bài tập luyện tập số 1 - Tư duy hàm đặc trưng phần 2
Câu 1 [79369]: [Đề thi THPT QG năm 2018] Cho phương trình 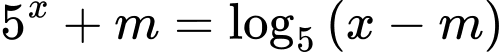 với
với 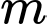 là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 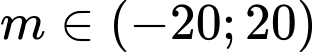 để phương trình đã cho có nghiệm?
để phương trình đã cho có nghiệm?
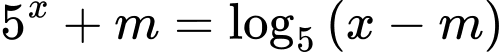 với
với 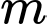 là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 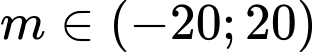 để phương trình đã cho có nghiệm?
để phương trình đã cho có nghiệm? A, 20.
B, 19.
C, 9.
D, 21.
Đặt 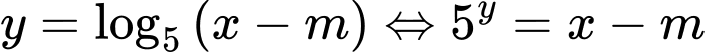
Khi đó ta có hệ phương trình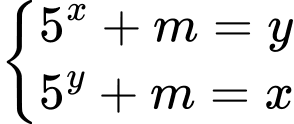
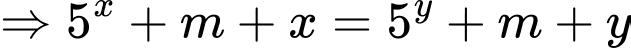
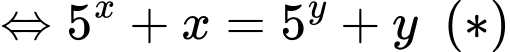
Xét hàm số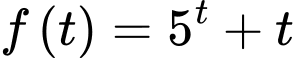 với
với 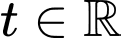
Ta có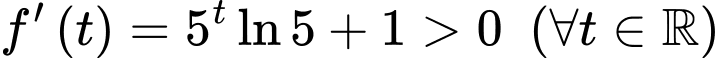
Do đó hàm số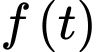 đồng biến trên
đồng biến trên 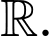
Phương trình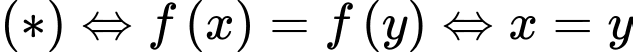
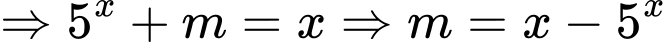
Xét hàm số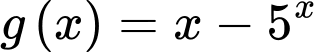 với
với 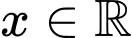
Ta có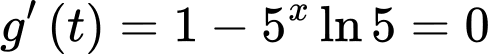
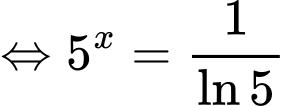
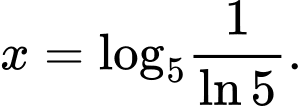
Ta có bảng biến thiên
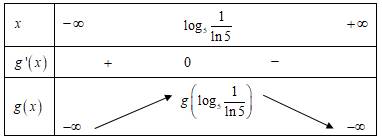
Dựa vào bảng biến thiên suy ra phương trình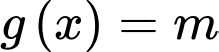 có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi 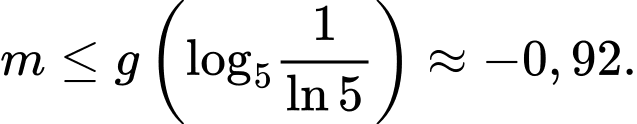
Kết hợp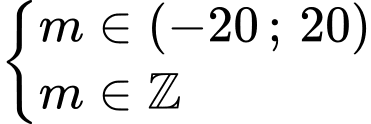
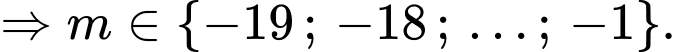
Vậy có 19 giá trị của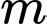 thoả mãn ycbt. Chọn B. Đáp án: B
thoả mãn ycbt. Chọn B. Đáp án: B
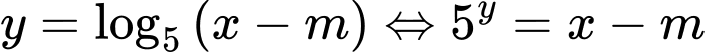
Khi đó ta có hệ phương trình
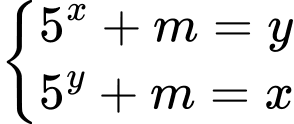
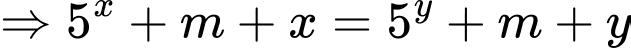
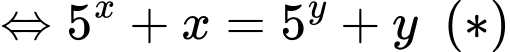
Xét hàm số
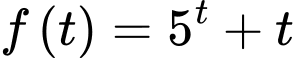 với
với 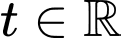
Ta có
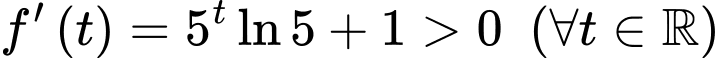
Do đó hàm số
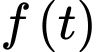 đồng biến trên
đồng biến trên 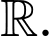
Phương trình
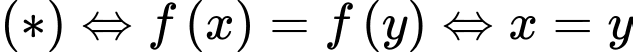
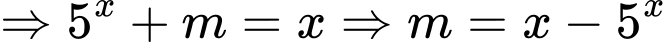
Xét hàm số
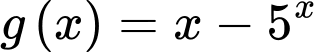 với
với 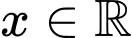
Ta có
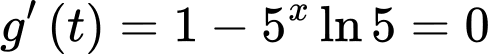
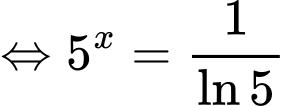
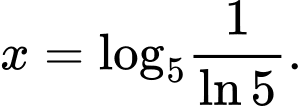
Ta có bảng biến thiên

Dựa vào bảng biến thiên suy ra phương trình
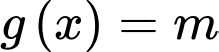 có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi 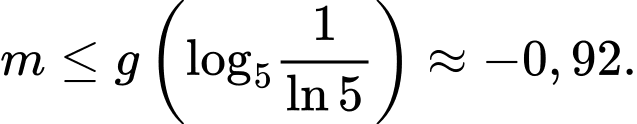
Kết hợp
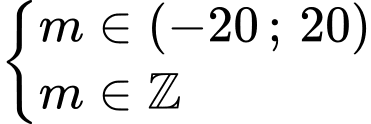
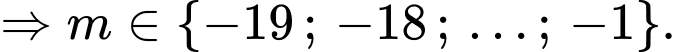
Vậy có 19 giá trị của
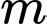 thoả mãn ycbt. Chọn B. Đáp án: B
thoả mãn ycbt. Chọn B. Đáp án: B
Câu 2 [508799]: Có bao nhiêu giá trị nguyên của tham số 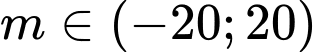 để phương trình
để phương trình 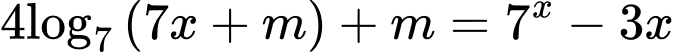 có nghiệm
có nghiệm
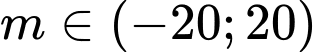 để phương trình
để phương trình 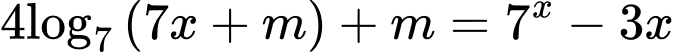 có nghiệm
có nghiệm A, 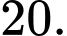
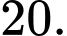
B, 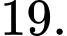
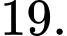
C, 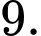
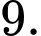
D, 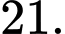
Xét 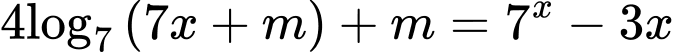
Đặt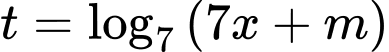
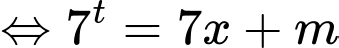
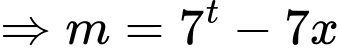
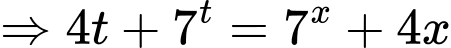
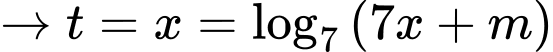
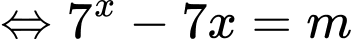
Đặt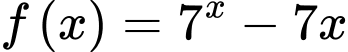
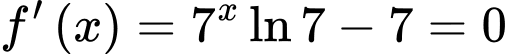
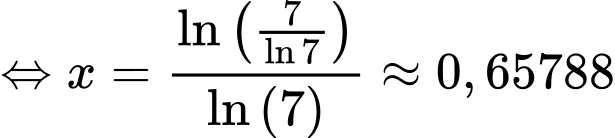
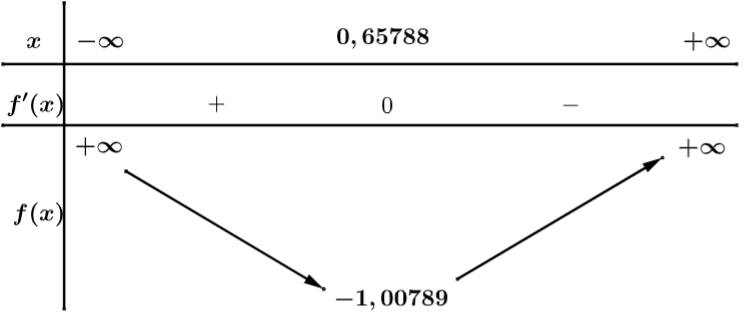
Để phương trình có nghiệm đường thẳng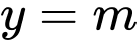 cắt
cắt 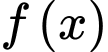
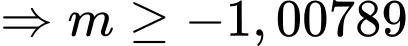
Mà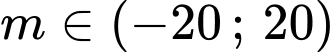
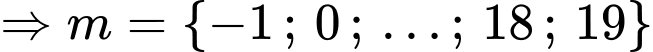
Đáp án: C Đáp án: D
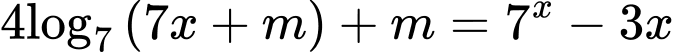
Đặt
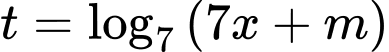
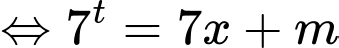
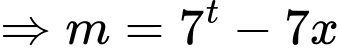
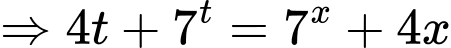
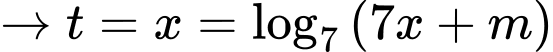
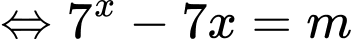
Đặt
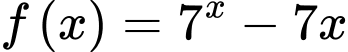
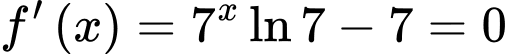
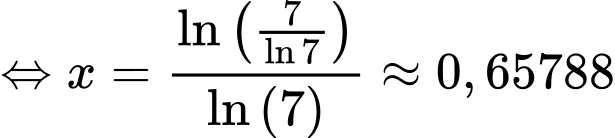

Để phương trình có nghiệm đường thẳng
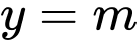 cắt
cắt 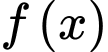
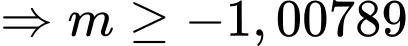
Mà
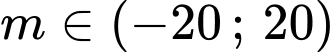
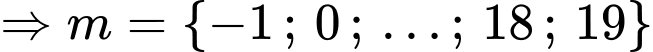
Đáp án: C Đáp án: D
Câu 3 [377856]: Có bao nhiêu giá trị nguyên của tham số 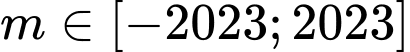 để phương trình
để phương trình 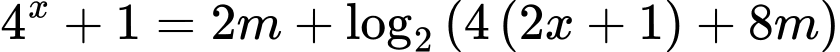 có nghiệm?
có nghiệm?
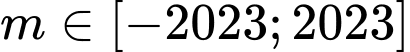 để phương trình
để phương trình 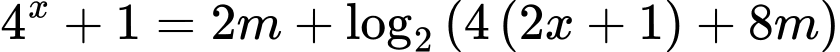 có nghiệm?
có nghiệm? A, 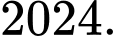
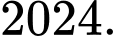
B, 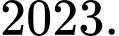
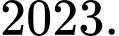
C, 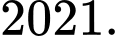
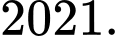
D, 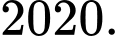
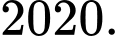
Chọn A
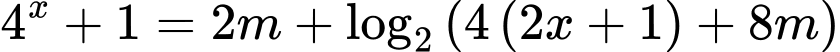
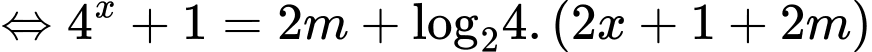
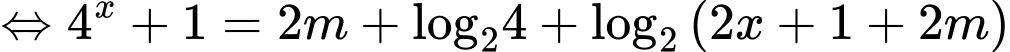
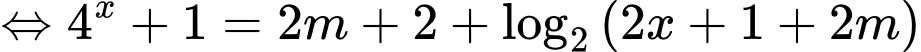
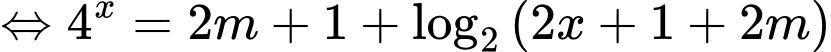
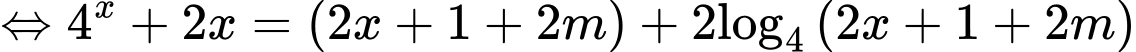
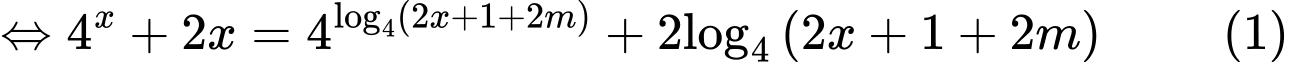
Xét hàm số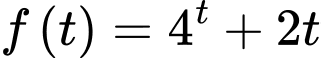 , ta có
, ta có
Nên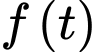 đồng biến trên
đồng biến trên 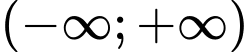 , khi đó:
, khi đó:
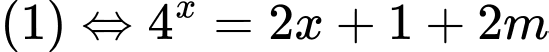
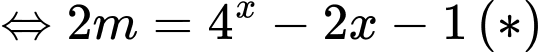
Để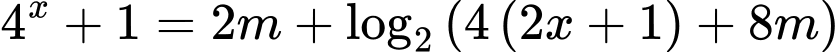 có nghiệm
có nghiệm 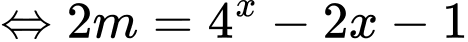 có nghiệm.
có nghiệm.
Xét hàm số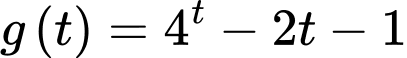
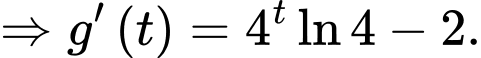 Ta có
Ta có 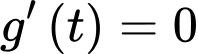
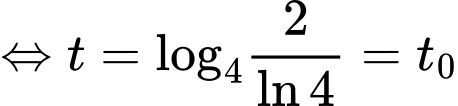
Bảng biến thiên
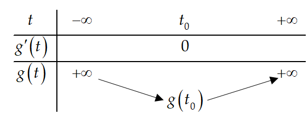
Để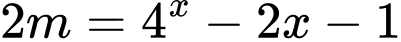
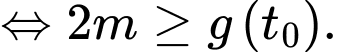 Mà
Mà 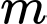 là số nguyên và
là số nguyên và 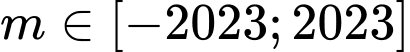 nên
nên 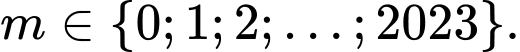 Đáp án: A
Đáp án: A
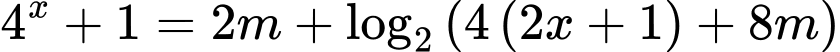
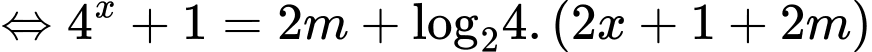
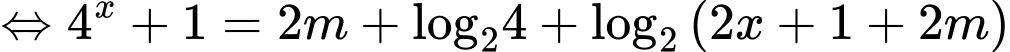
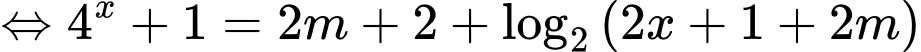
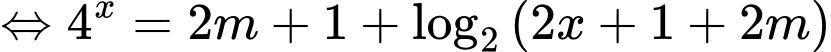
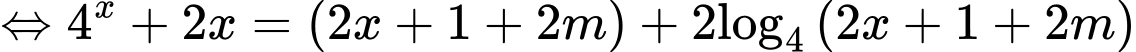
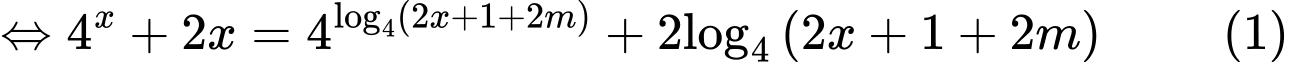
Xét hàm số
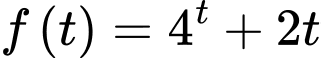 , ta có
, ta cóNên
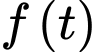 đồng biến trên
đồng biến trên 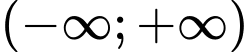 , khi đó:
, khi đó: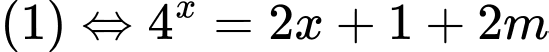
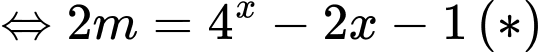
Để
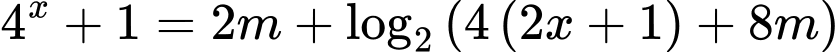 có nghiệm
có nghiệm 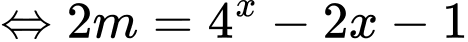 có nghiệm.
có nghiệm.Xét hàm số
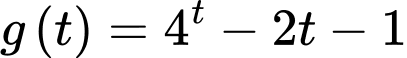
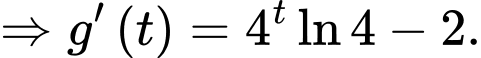 Ta có
Ta có 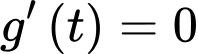
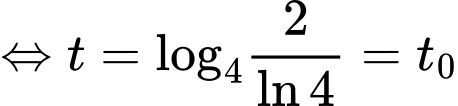
Bảng biến thiên

Để
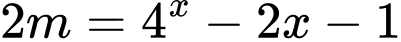
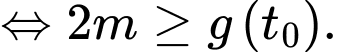 Mà
Mà 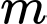 là số nguyên và
là số nguyên và 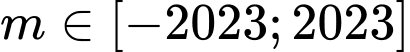 nên
nên 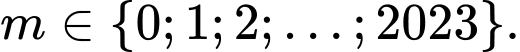 Đáp án: A
Đáp án: A
Câu 4 [508802]: Cho phương trình 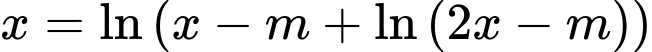 với
với 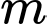 là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 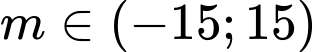 để phương trình đã cho có nghiệm?
để phương trình đã cho có nghiệm?
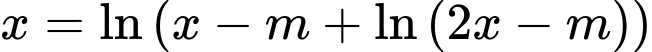 với
với 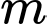 là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 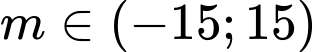 để phương trình đã cho có nghiệm?
để phương trình đã cho có nghiệm? A, 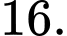
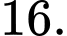
B, 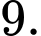
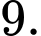
C, 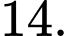
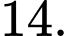
D, 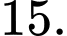
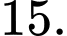
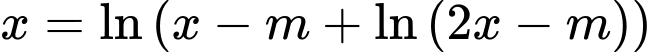
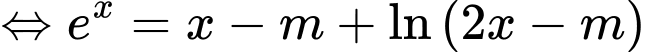
Đặt
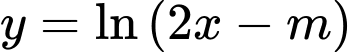
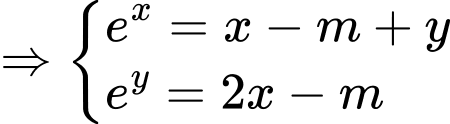
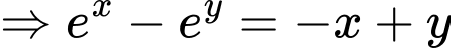
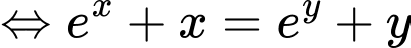
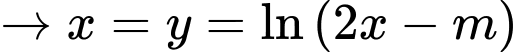
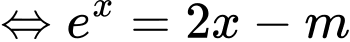

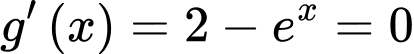
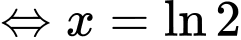
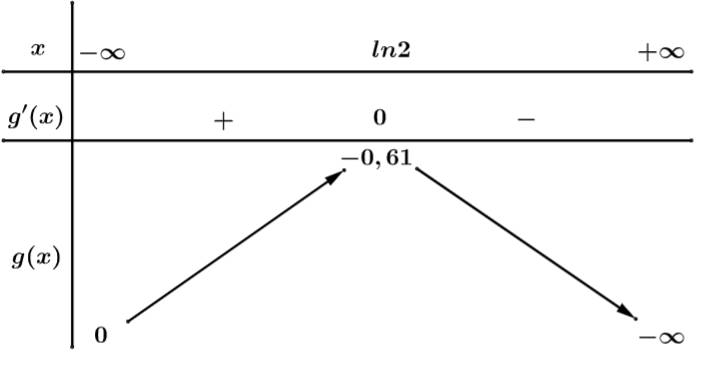
Phương trình có nghiệm khi và chỉ khi
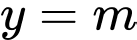 cắt đồ thị hàm số
cắt đồ thị hàm số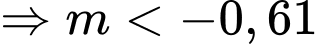
Lại có
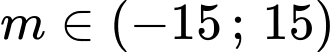
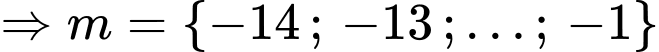
Đáp án: C. Đáp án: C
Câu 5 [972529]: Có bao nhiêu số nguyên dương 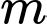 nhỏ hơn 20 thỏa mãn phương trình
nhỏ hơn 20 thỏa mãn phương trình 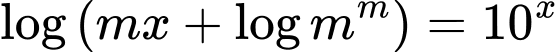 có đủ hai nghiệm thực
có đủ hai nghiệm thực 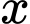 phân biệt
phân biệt
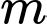 nhỏ hơn 20 thỏa mãn phương trình
nhỏ hơn 20 thỏa mãn phương trình 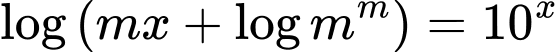 có đủ hai nghiệm thực
có đủ hai nghiệm thực 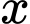 phân biệt
phân biệt A, 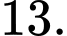
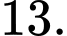
B, 
C, 
D, 

PT: 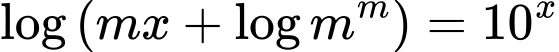
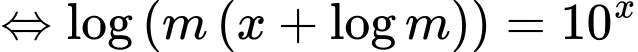

Đặt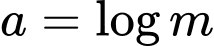

Đặt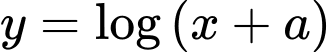
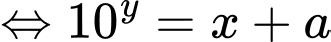
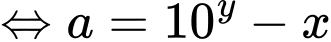
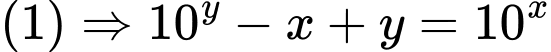
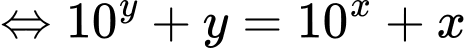
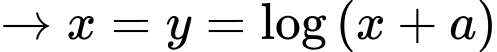
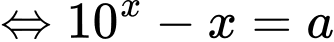
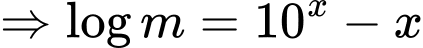
Đặt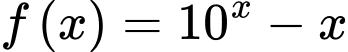
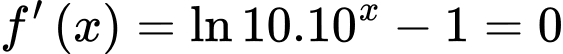
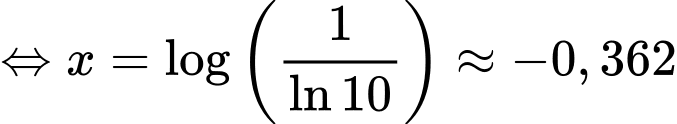
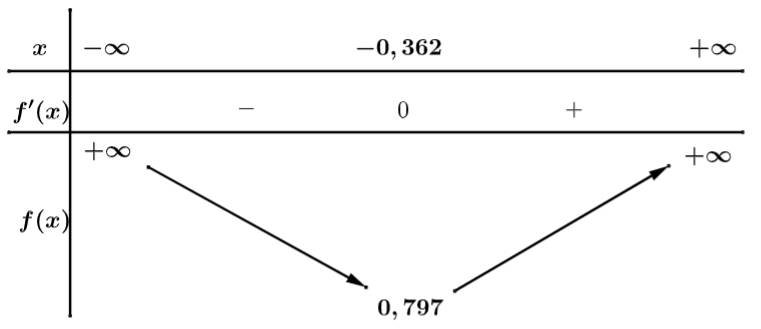
Phương trình có đủ hai nghiệm thực khi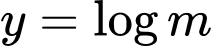 cắt
cắt 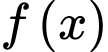 tại 2 điểm phân biệt
tại 2 điểm phân biệt
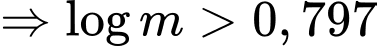

Mặt khác, theo đề bài ta có:
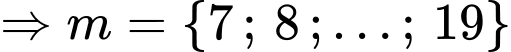
Đáp án: A Đáp án: A
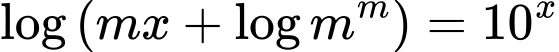
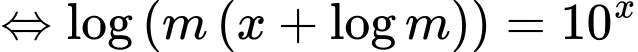

Đặt
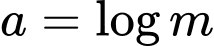

Đặt
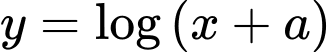
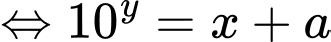
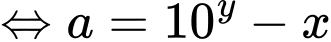
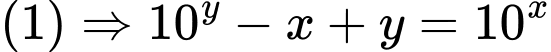
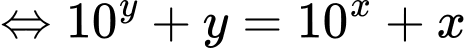
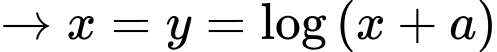
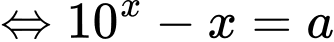
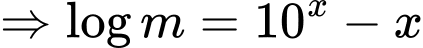
Đặt
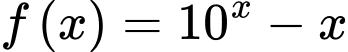
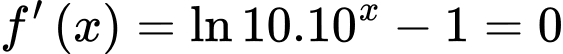
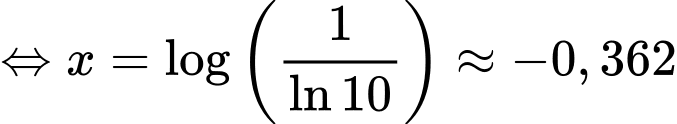

Phương trình có đủ hai nghiệm thực khi
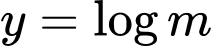 cắt
cắt 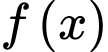 tại 2 điểm phân biệt
tại 2 điểm phân biệt
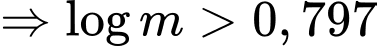

Mặt khác, theo đề bài ta có:

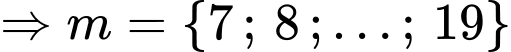
Đáp án: A Đáp án: A
Câu 6 [677066]: Có bao nhiêu giá trị nguyên của tham số 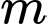 để phương trình
để phương trình 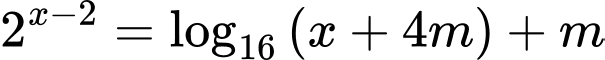 có nghiệm
có nghiệm 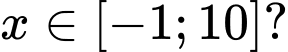
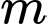 để phương trình
để phương trình 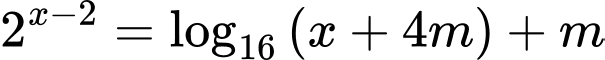 có nghiệm
có nghiệm 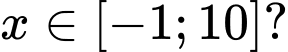
A, 252.
B, 253.
C, 1014.
D, 1013.
Điều kiện 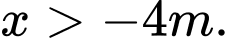
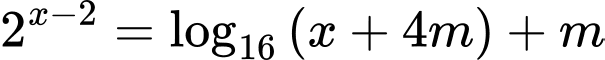
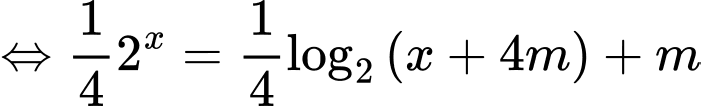
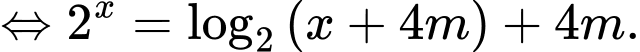
Đặt Khi đó ta có phương trình đã cho tương đương với hệ phương trình sau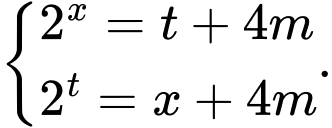
Cộng chéo ta có: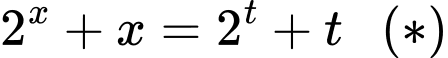
Rõ ràng hàm số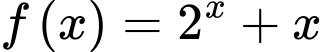 đồng biến trên
đồng biến trên 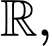 nên từ
nên từ  ta có
ta có
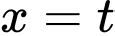
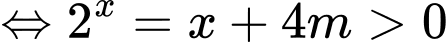
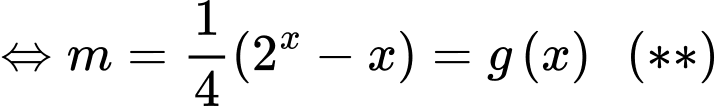
Ta có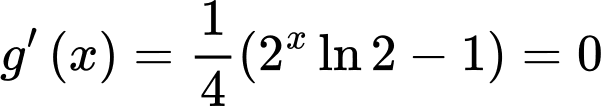
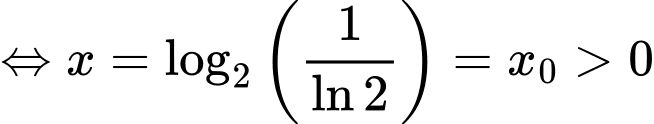 và
và 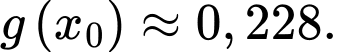
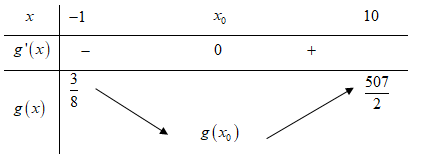
Như vậy, phương trình (*) có nghiệm phương trình (**) có nghiệm
phương trình (**) có nghiệm 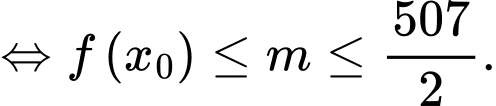 Mà
Mà  nên
nên 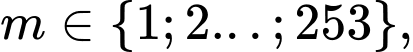 tức là có 253 giá trị
tức là có 253 giá trị 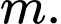 Chọn B. Đáp án: B
Chọn B. Đáp án: B
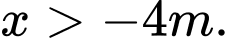
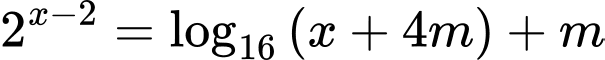
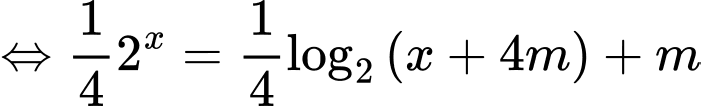
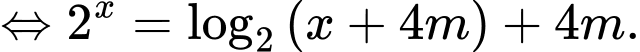
Đặt Khi đó ta có phương trình đã cho tương đương với hệ phương trình sau
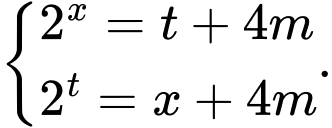
Cộng chéo ta có:
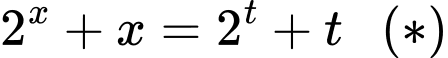
Rõ ràng hàm số
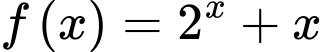 đồng biến trên
đồng biến trên 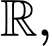 nên từ
nên từ  ta có
ta có 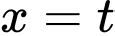
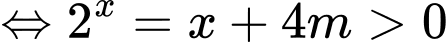
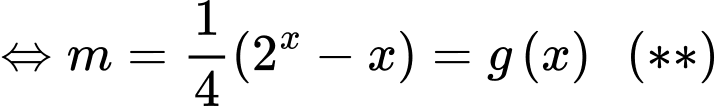
Ta có
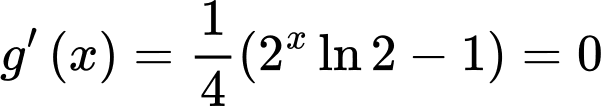
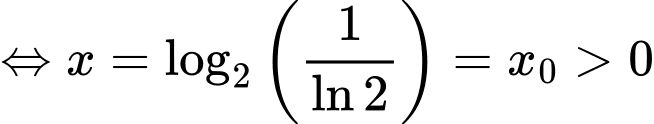 và
và 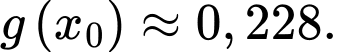

Như vậy, phương trình (*) có nghiệm
 phương trình (**) có nghiệm
phương trình (**) có nghiệm 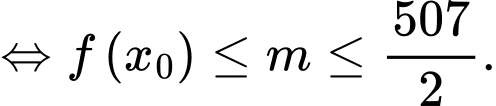 Mà
Mà  nên
nên 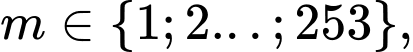 tức là có 253 giá trị
tức là có 253 giá trị 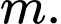 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 7 [663558]: Có tất cả bao nhiêu giá trị nguyên của tham số 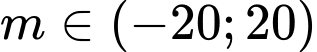 để phương trình
để phương trình 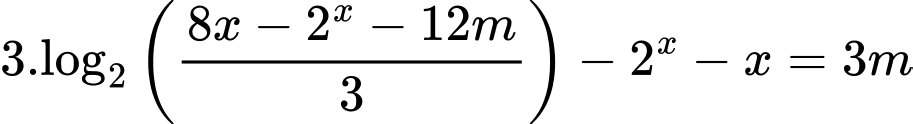 có đúng hai nghiệm thực phân biệt?
có đúng hai nghiệm thực phân biệt?
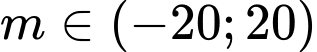 để phương trình
để phương trình 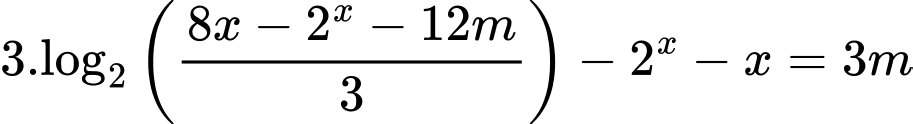 có đúng hai nghiệm thực phân biệt?
có đúng hai nghiệm thực phân biệt? A, 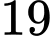 .
.
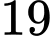 .
.B,  .
.
 .
.C, 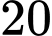 .
.
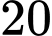 .
.D, 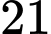 .
.
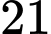 .
.
Chọn C
Đặt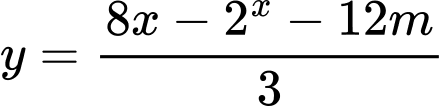
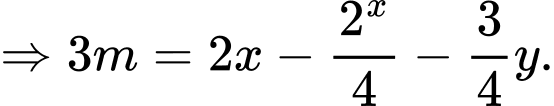
Ta được phương trình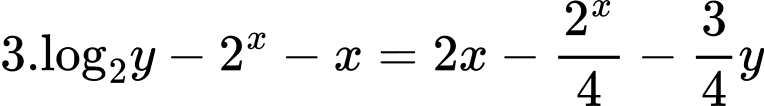
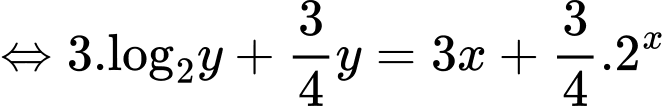
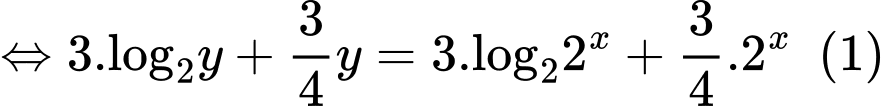
Xét hàm số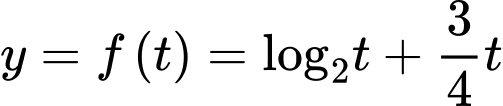 với
với 
Ta có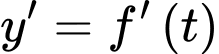
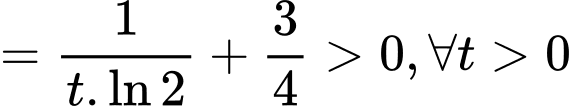 , suy ra hàm số
, suy ra hàm số 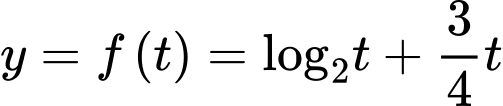 đồng biến trên khoảng
đồng biến trên khoảng 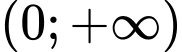 .
.
Do đó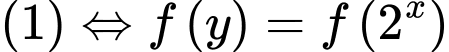
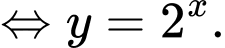
Suy ra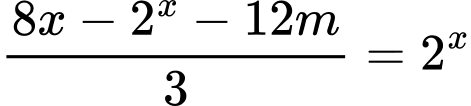
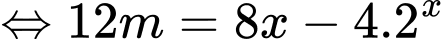
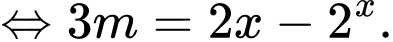
Xét hàm số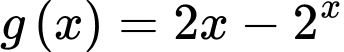
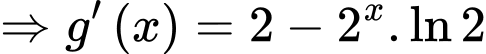
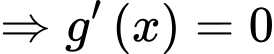
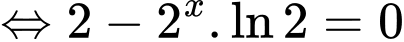
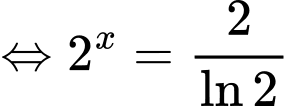
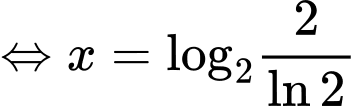 ;
;  .
.
Bảng biến thiên
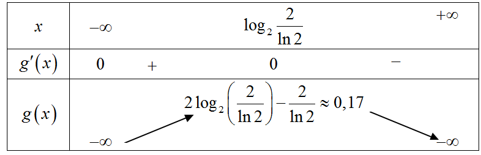
Từ bảng biến thiên suy ra phương trình có đúng hai nghiệm thực phân biệt
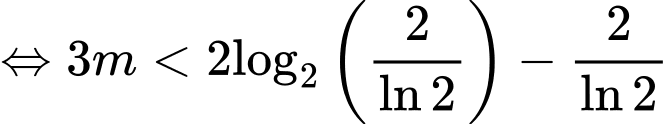
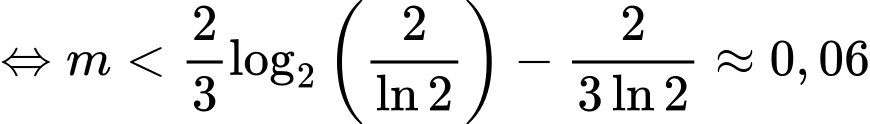
Mặt khác ta có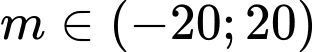 và
và 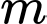 nguyên nên
nguyên nên 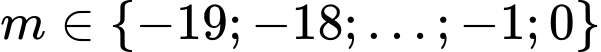 .
.
Vậy có 20 giá trị nguyên của tham số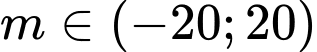 để phương trình
để phương trình 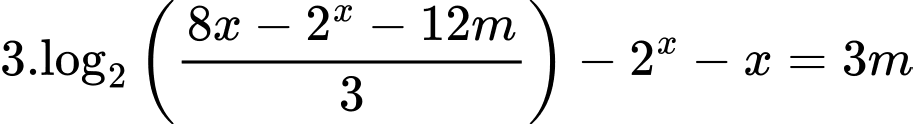 có đúng hai nghiệm thực phân biệt. Đáp án: C
có đúng hai nghiệm thực phân biệt. Đáp án: C
Đặt
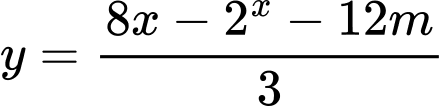
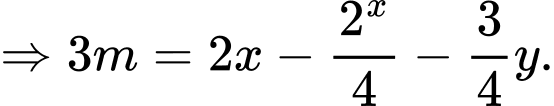
Ta được phương trình
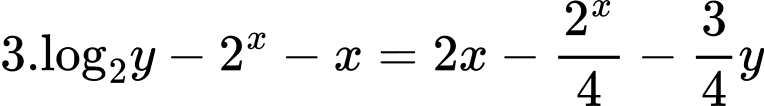
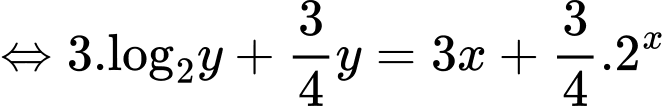
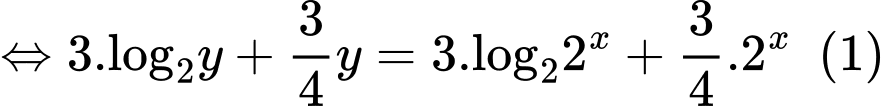
Xét hàm số
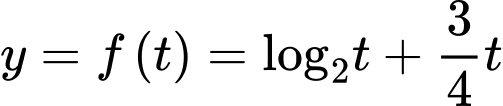 với
với 
Ta có
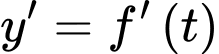
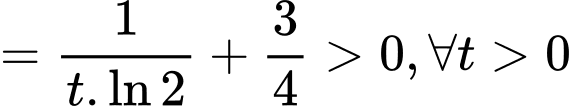 , suy ra hàm số
, suy ra hàm số 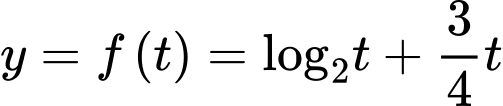 đồng biến trên khoảng
đồng biến trên khoảng 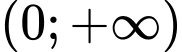 .
. Do đó
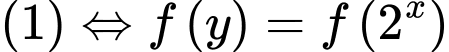
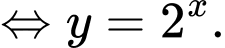
Suy ra
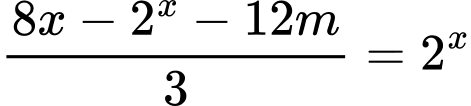
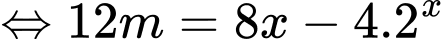
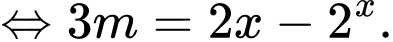
Xét hàm số
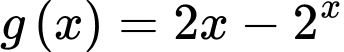
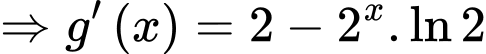
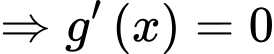
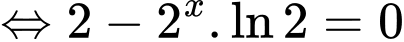
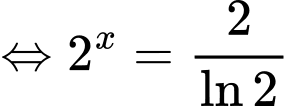
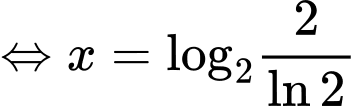 ;
;  .
.Bảng biến thiên

Từ bảng biến thiên suy ra phương trình có đúng hai nghiệm thực phân biệt
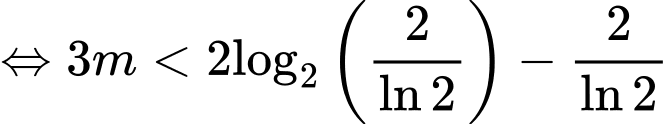
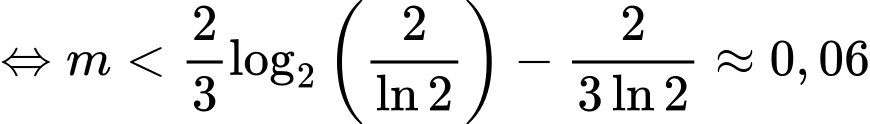
Mặt khác ta có
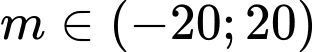 và
và 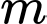 nguyên nên
nguyên nên 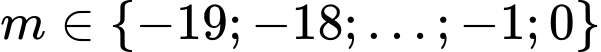 .
.Vậy có 20 giá trị nguyên của tham số
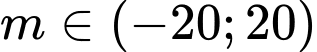 để phương trình
để phương trình 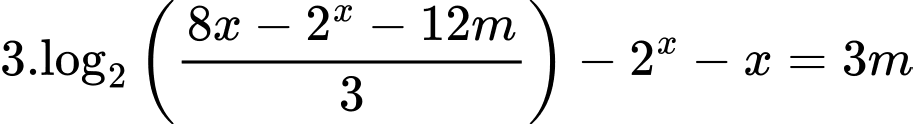 có đúng hai nghiệm thực phân biệt. Đáp án: C
có đúng hai nghiệm thực phân biệt. Đáp án: C
Câu 8 [384333]: Có bao nhiêu giá trị nguyên của tham số 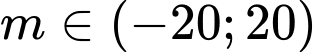 để phương trình
để phương trình 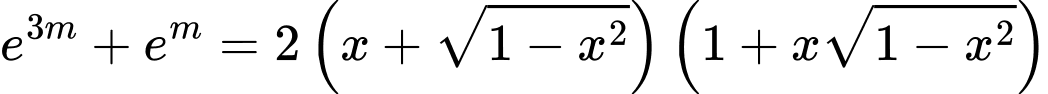 có nghiệm.
có nghiệm.
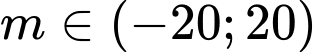 để phương trình
để phương trình 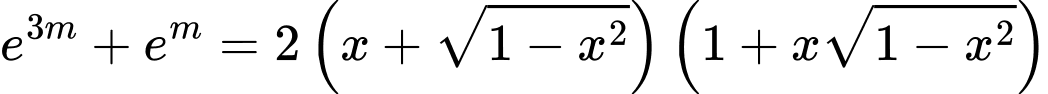 có nghiệm.
có nghiệm.
Nhận thấy 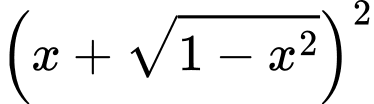
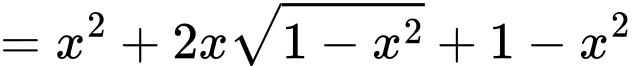
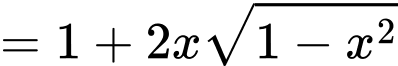
Đặt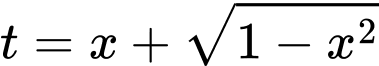
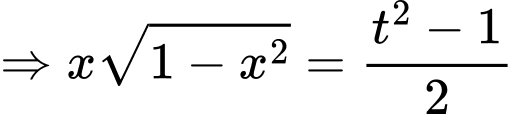
Do đó phương trình trở thành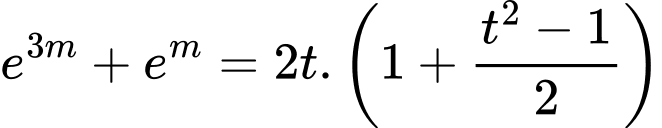
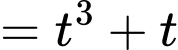
Xét hàm số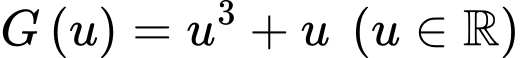 ta có
ta có 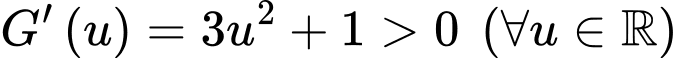 nên hàm số
nên hàm số 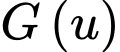 là hàm số đồng biến trên
là hàm số đồng biến trên 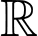 do đó
do đó 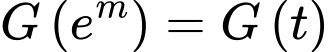
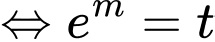
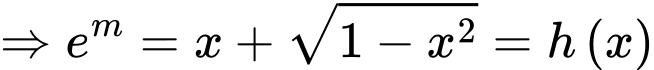
Mặt khác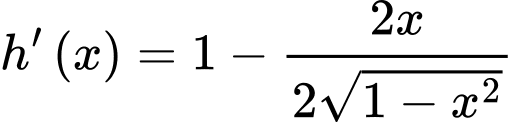
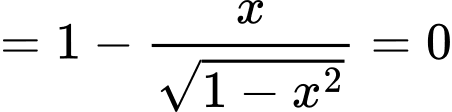

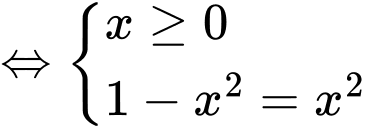
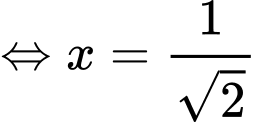
Ta có bảng biến thiên của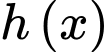 như sau:
như sau:
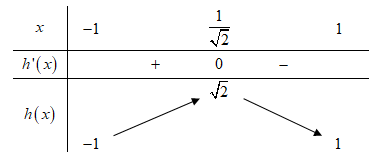
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi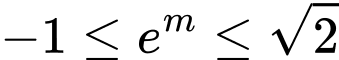
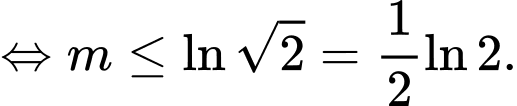 Vậy có 20 giá trị nguyên của m thoả mãn ycbt.
Vậy có 20 giá trị nguyên của m thoả mãn ycbt.
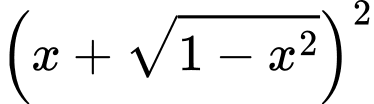
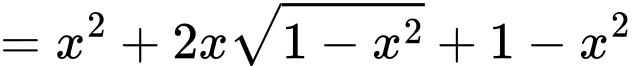
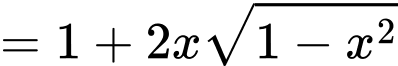
Đặt
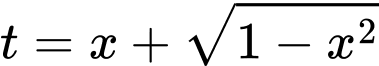
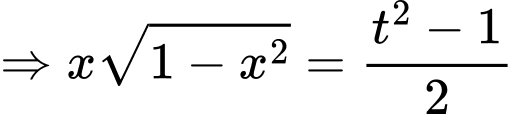
Do đó phương trình trở thành
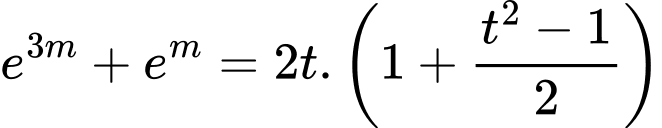
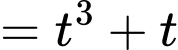
Xét hàm số
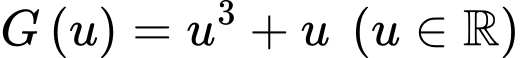 ta có
ta có 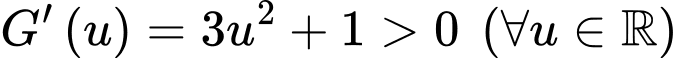 nên hàm số
nên hàm số 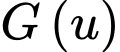 là hàm số đồng biến trên
là hàm số đồng biến trên 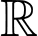 do đó
do đó 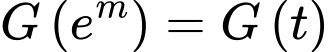
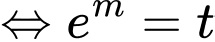
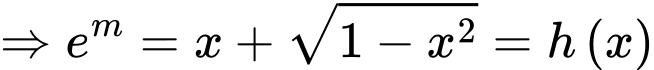
Mặt khác
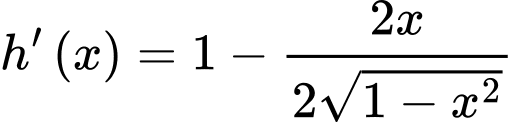
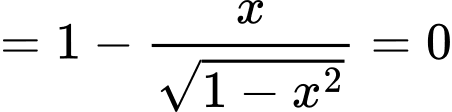

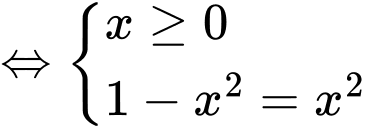
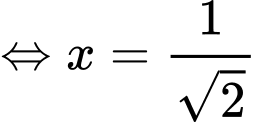
Ta có bảng biến thiên của
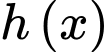 như sau:
như sau:
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi
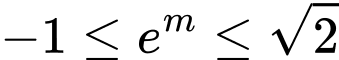
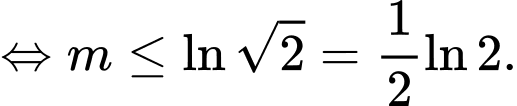 Vậy có 20 giá trị nguyên của m thoả mãn ycbt.
Vậy có 20 giá trị nguyên của m thoả mãn ycbt.
Câu 9 [677079]: Có bao nhiêu giá trị nguyên của tham số 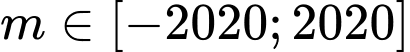 để phương trình
để phương trình 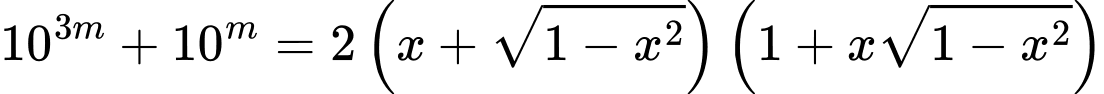 có nghiệm?
có nghiệm?
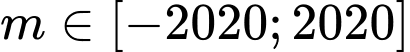 để phương trình
để phương trình 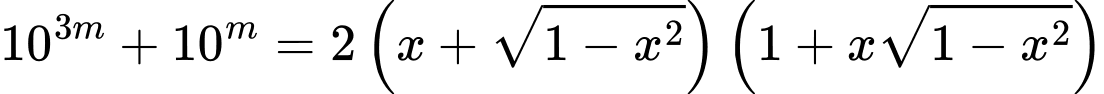 có nghiệm?
có nghiệm? A, 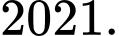
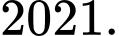
B, 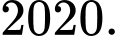
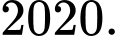
C, 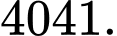
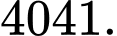
D, 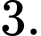
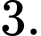
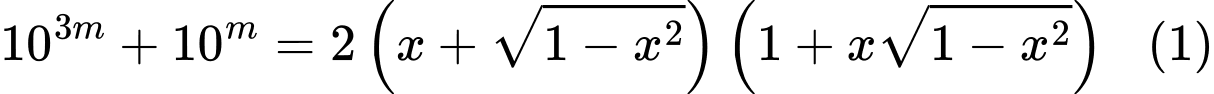
ĐK:

Đặt
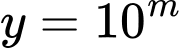
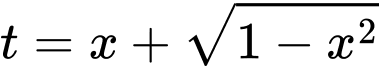
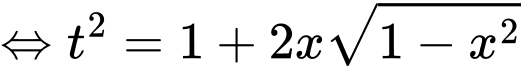
Phương trình
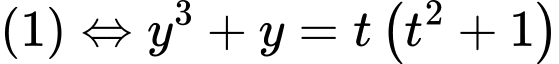
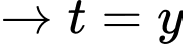
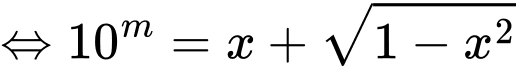
Đặt
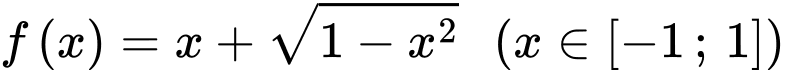
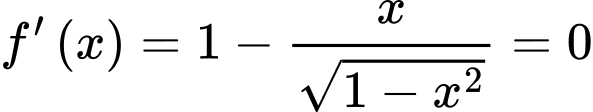
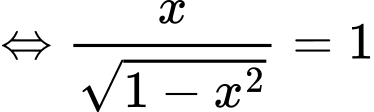
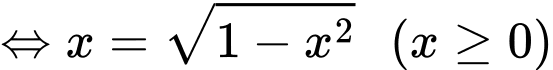
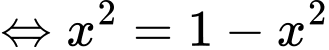
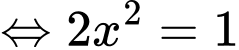
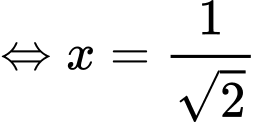
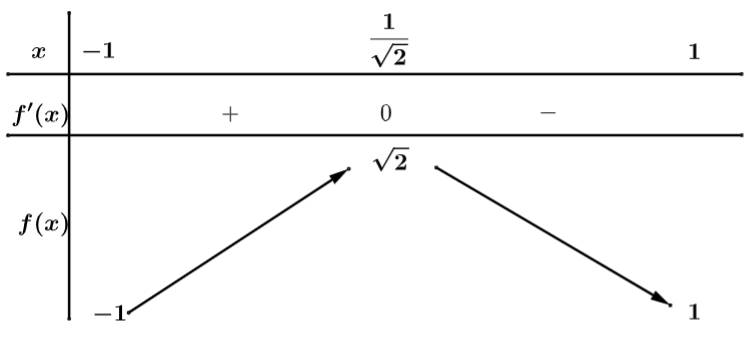
Để phương phình (1) có nghiệm thì
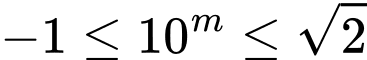
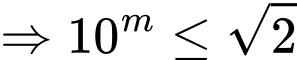
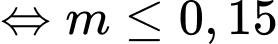
Mặt khác:
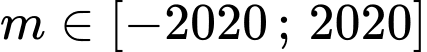
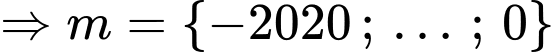
Đáp án: A. Đáp án: A
Câu 10 [508813]: Có bao nhiêu giá trị nguyên của tham số 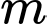 để phương trình
để phương trình 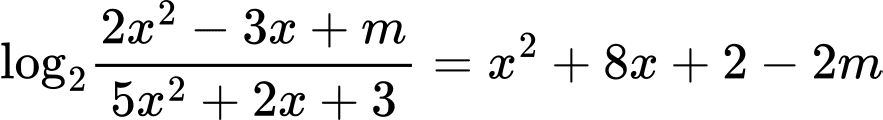 có nghiệm
có nghiệm 
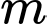 để phương trình
để phương trình 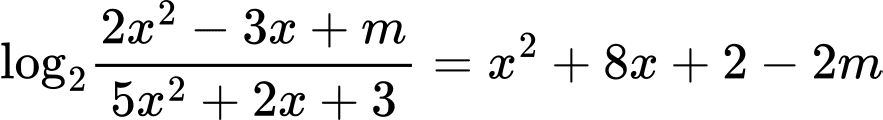 có nghiệm
có nghiệm 
A, 

B, 
C, 
D, 
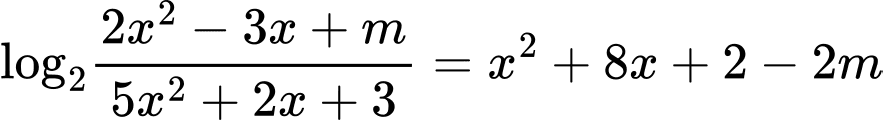
Đk:
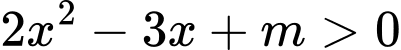
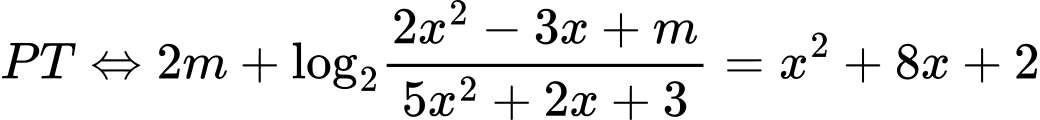
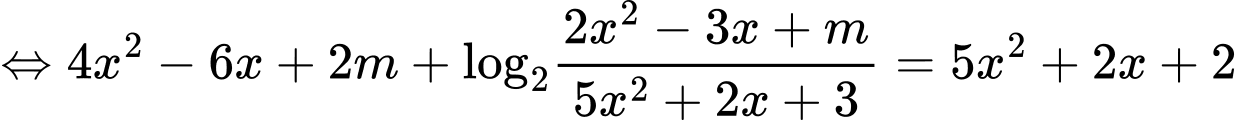
Đặt:
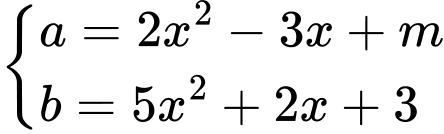
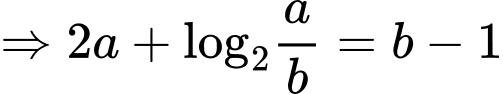

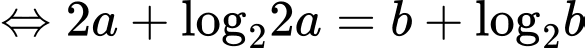
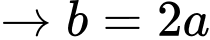
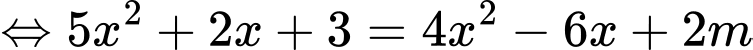
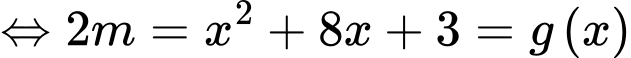
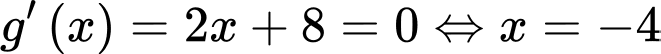
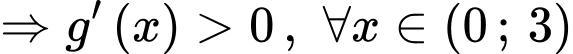
Với
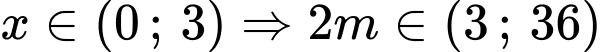
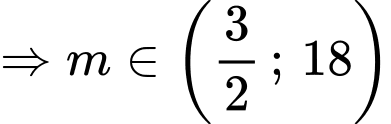
Đáp án: C. Đáp án: C
Câu 11 [671168]: Có bao nhiêu số nguyên 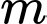 để phương trình
để phương trình 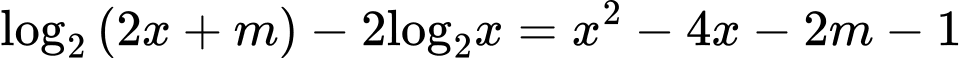 có hai nghiệm thực phân biệt?
có hai nghiệm thực phân biệt?
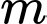 để phương trình
để phương trình 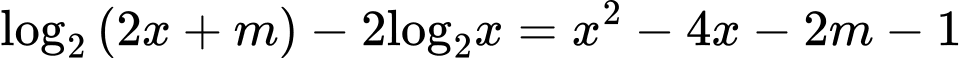 có hai nghiệm thực phân biệt?
có hai nghiệm thực phân biệt? A, 2.
B, 3.
C, 1.
D, 4.
Điều kiện 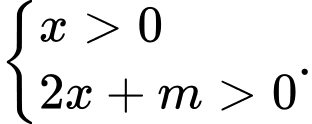
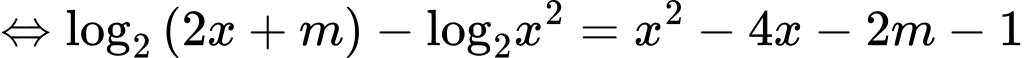
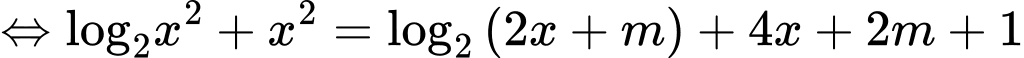
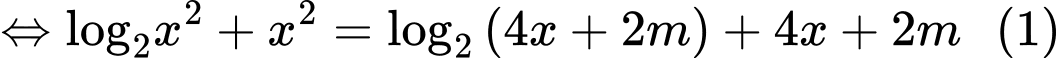
Xét hàm số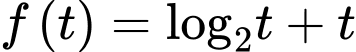 trên
trên 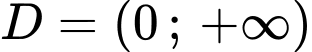
Ta có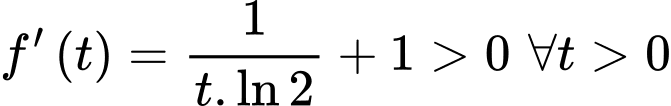 nên hàm số
nên hàm số 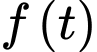 luôn đồng biến trên
luôn đồng biến trên 
Khi đó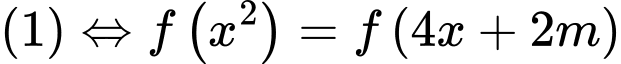
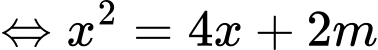
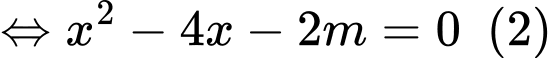
Yêu cầu bài toán tương đương với phương trình có 2 nghiệm dương phân biệt
có 2 nghiệm dương phân biệt
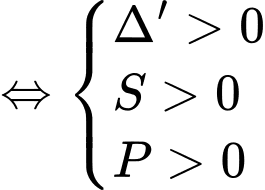
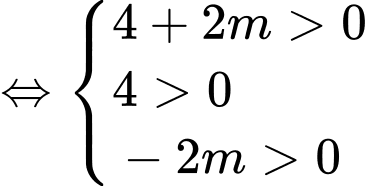
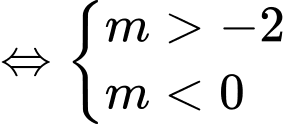

Kết hợp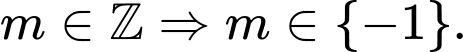
Vậy có duy nhất một số nguyên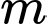 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
Chọn C. Đáp án: C
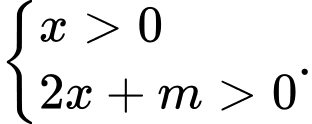
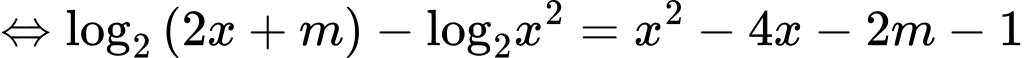
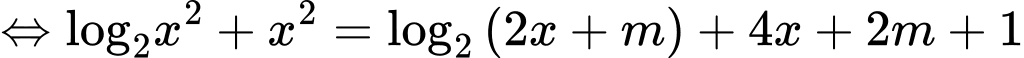
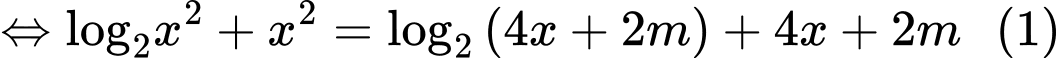
Xét hàm số
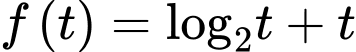 trên
trên 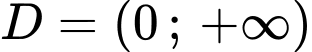
Ta có
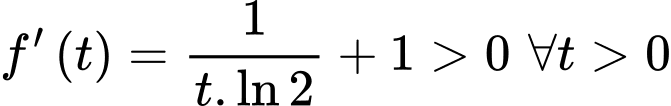 nên hàm số
nên hàm số 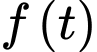 luôn đồng biến trên
luôn đồng biến trên 
Khi đó
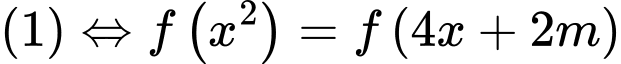
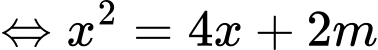
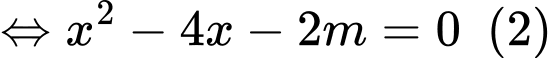
Yêu cầu bài toán tương đương với phương trình
 có 2 nghiệm dương phân biệt
có 2 nghiệm dương phân biệt
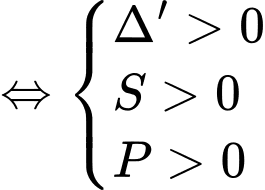
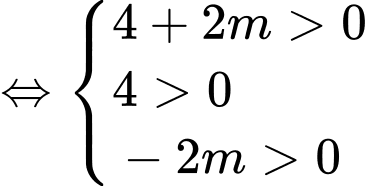
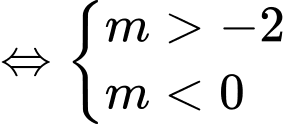

Kết hợp
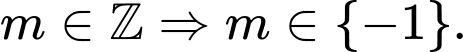
Vậy có duy nhất một số nguyên
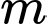 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
Chọn C. Đáp án: C
Câu 12 [671169]: Có bao nhiêu số nguyên dương của tham số 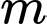 để phương trình
để phương trình 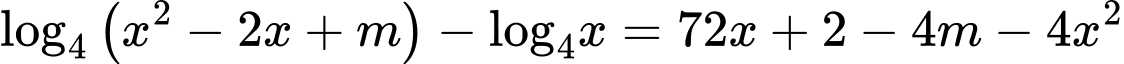 có nghiệm?
có nghiệm?
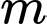 để phương trình
để phương trình 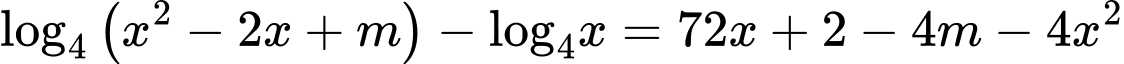 có nghiệm?
có nghiệm? A, 80.
B, 82.
C, 81.
D, 83.
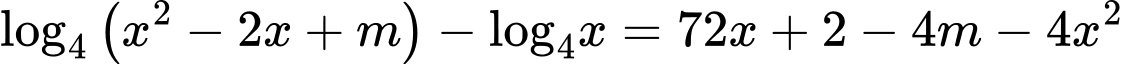
ĐK:
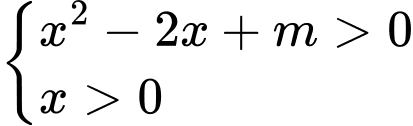
Đặt
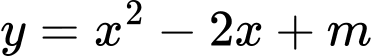
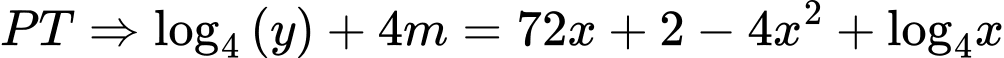
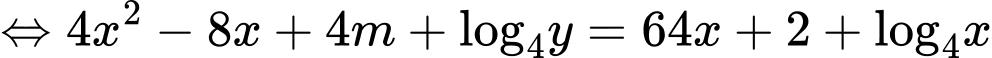
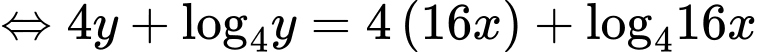
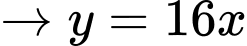
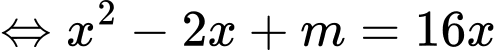
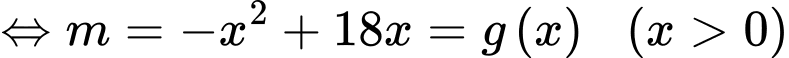
BBT:
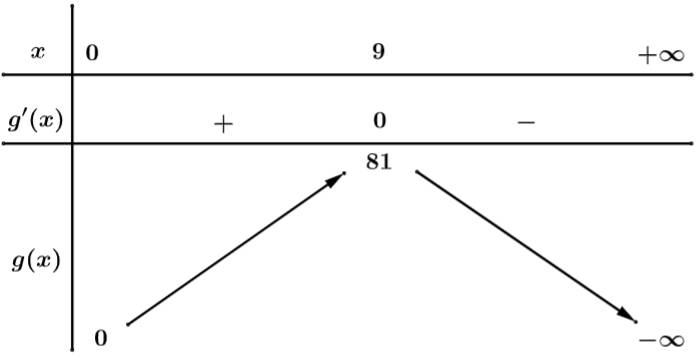
Để phương trình có nghiệm thì
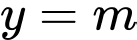 phải cắt đồ thị hàm số.
phải cắt đồ thị hàm số.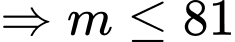 (
(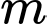 là số nguyên dương)
là số nguyên dương)Suy ra, có 81 giá trị của
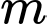 thỏa mãn.
thỏa mãn.Đáp án: C Đáp án: C
Câu 13 [384334]: Cho phương trình 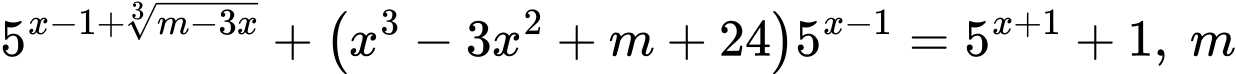 là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 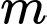 để phương trình có 3 nghiệm phân biệt?
để phương trình có 3 nghiệm phân biệt?
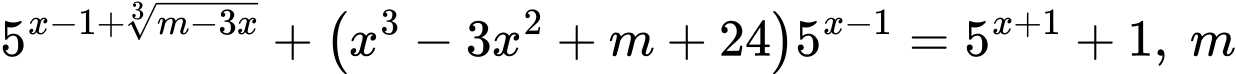 là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 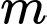 để phương trình có 3 nghiệm phân biệt?
để phương trình có 3 nghiệm phân biệt?
Ta có: 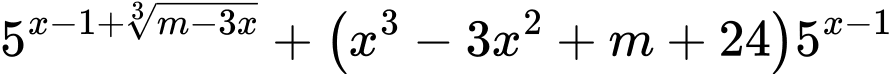
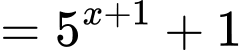
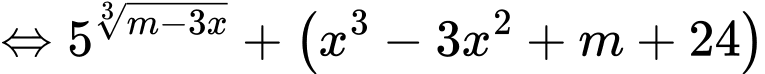
 (chia cả 2 vế cho
(chia cả 2 vế cho 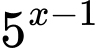 )
)
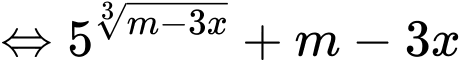
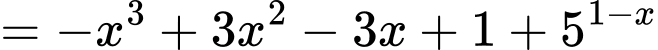
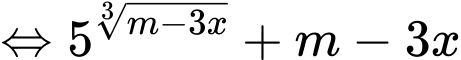
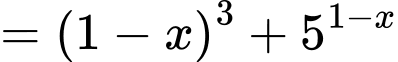

Xét hàm số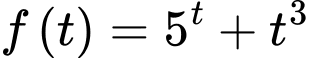 trên tập
trên tập  ta có:
ta có: 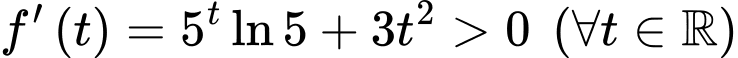 nên hàm số
nên hàm số 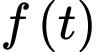 đồng biến trên
đồng biến trên  .
.
Khi đó
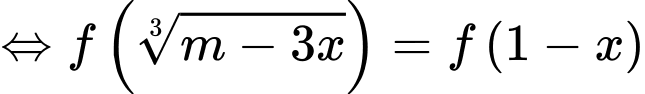
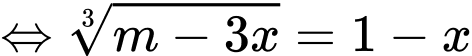
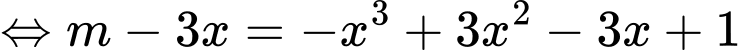
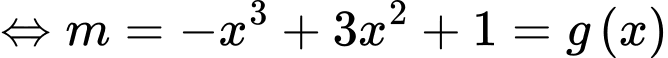
Xét hàm số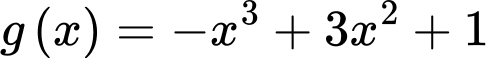 trên
trên 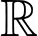 có
có 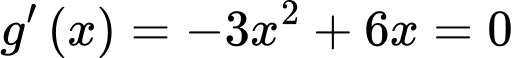
 .
.
Suy ra hai giá trị cực trị của hàm số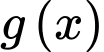 là
là 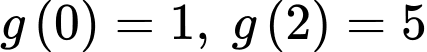 .
.
Từ đó suy ra phương trình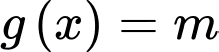 có ba nghiệm phân biệt
có ba nghiệm phân biệt 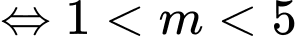
Kết hợp
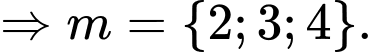
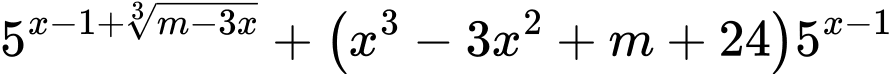
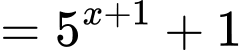
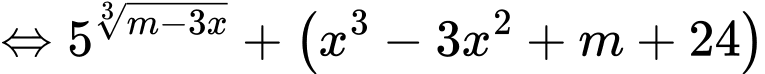
 (chia cả 2 vế cho
(chia cả 2 vế cho 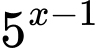 )
)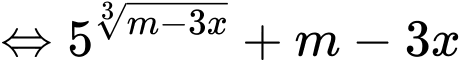
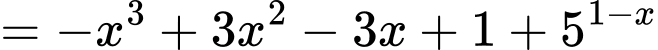
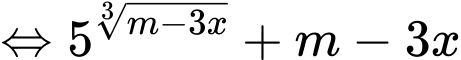
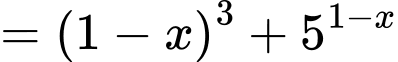

Xét hàm số
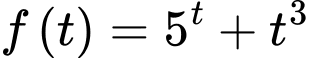 trên tập
trên tập 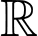 ta có:
ta có: 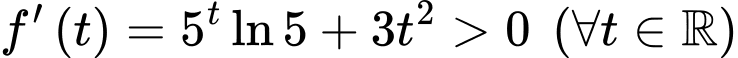 nên hàm số
nên hàm số 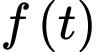 đồng biến trên
đồng biến trên 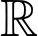 .
.Khi đó

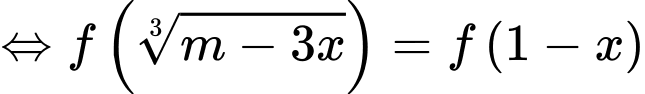
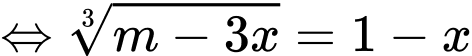
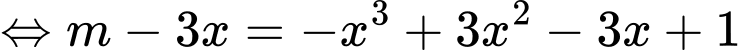
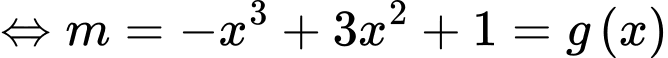
Xét hàm số
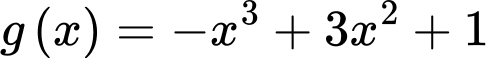 trên
trên 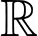 có
có 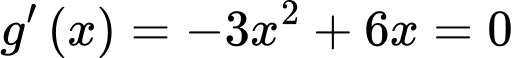
 .
.Suy ra hai giá trị cực trị của hàm số
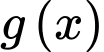 là
là 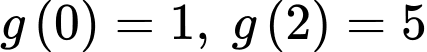 .
.Từ đó suy ra phương trình
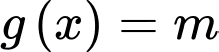 có ba nghiệm phân biệt
có ba nghiệm phân biệt 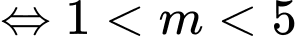
Kết hợp

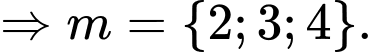
Câu 14 [512871]: Cho phương trình 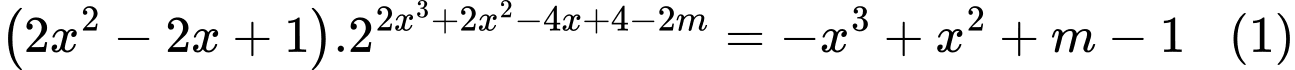 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số 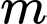 để phương trình
để phương trình  có nghiệm
có nghiệm 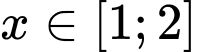 ?
?
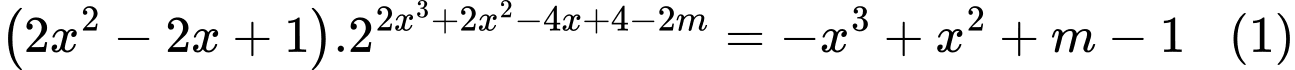 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số 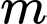 để phương trình
để phương trình  có nghiệm
có nghiệm 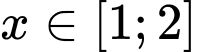 ?
? A, 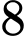 .
.
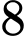 .
.B,  .
.
 .
.C, 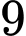 .
.
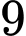 .
.D, 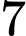 .
.
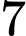 .
.
Chọn C
Có: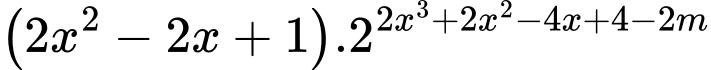
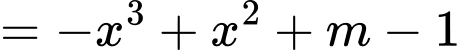

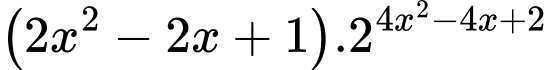
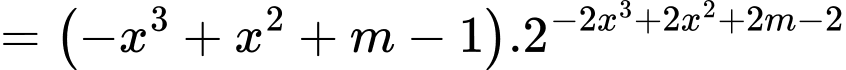
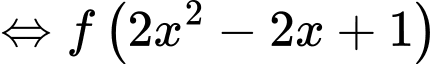
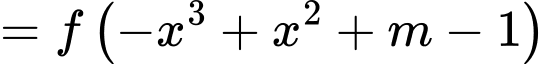 với
với 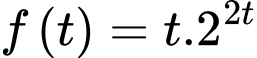 .
.
Với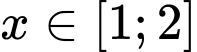
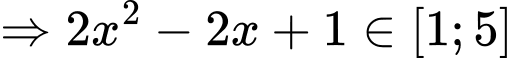 .
.
Lại có: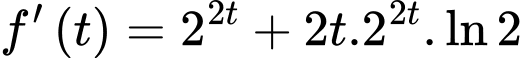
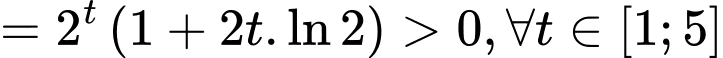 hay
hay 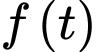 đồng biến trên đoạn
đồng biến trên đoạn 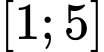 .
.
Khi đó: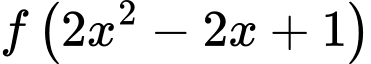
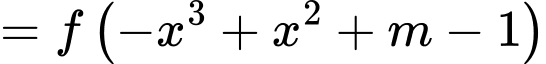
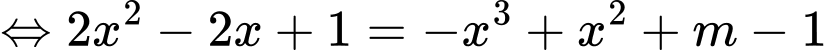
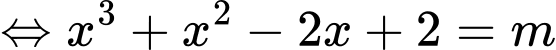
 .
.
Phương trình có nghiệm
có nghiệm 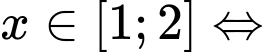 phương trình
phương trình  có nghiệm
có nghiệm 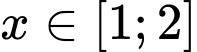
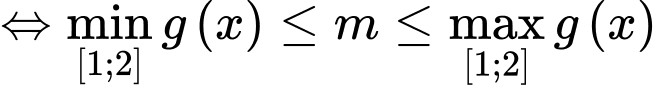 với
với 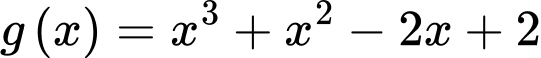 .
.
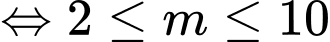 hay
hay 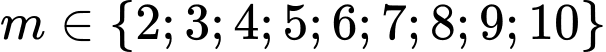 .
.
Vậy có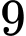 giá trị nguyên của
giá trị nguyên của 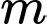 thỏa mãn yêu cầu bài toán. Đáp án: C
thỏa mãn yêu cầu bài toán. Đáp án: C
Có:
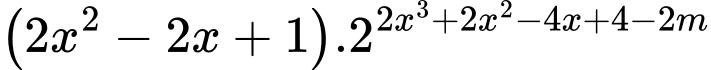
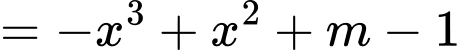

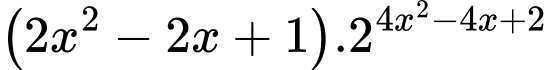
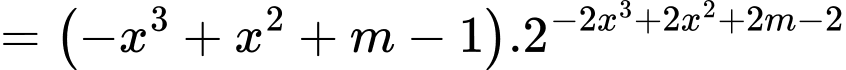
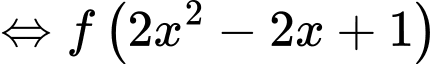
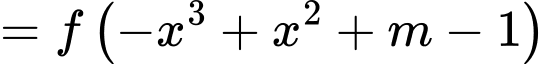 với
với 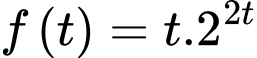 .
.Với
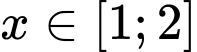
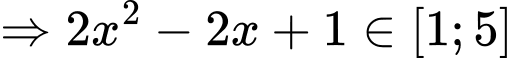 .
.Lại có:
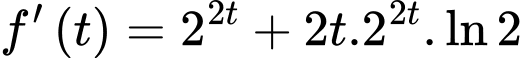
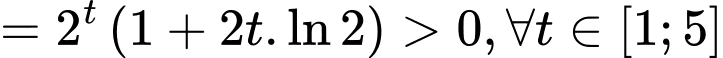 hay
hay 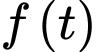 đồng biến trên đoạn
đồng biến trên đoạn 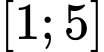 .
.Khi đó:
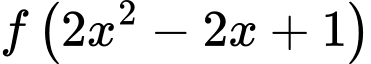
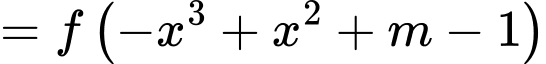
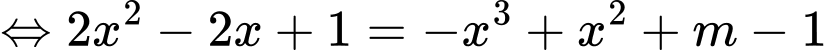
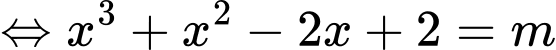
 .
.Phương trình
 có nghiệm
có nghiệm 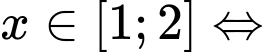 phương trình
phương trình  có nghiệm
có nghiệm 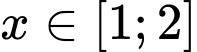
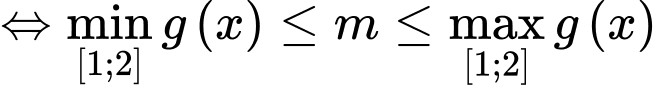 với
với 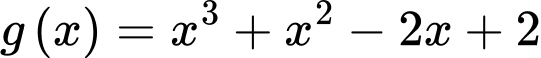 .
.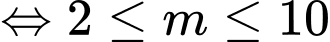 hay
hay 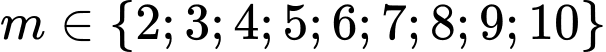 .
.Vậy có
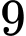 giá trị nguyên của
giá trị nguyên của 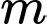 thỏa mãn yêu cầu bài toán. Đáp án: C
thỏa mãn yêu cầu bài toán. Đáp án: C
Câu 15 [521615]: Có bao nhiêu giá trị nguyên của tham số 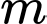 để phương trình
để phương trình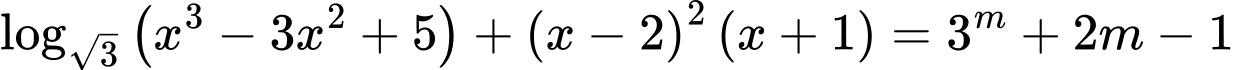 có nghiệm duy nhất trên
có nghiệm duy nhất trên 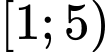 ?
?
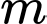 để phương trình
để phương trình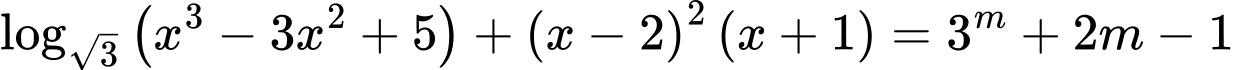 có nghiệm duy nhất trên
có nghiệm duy nhất trên 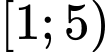 ?
? A, 4.
B, 0.
C, 3.
D, 2.
Chọn C
Đặt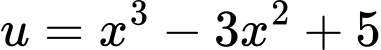 , với
, với 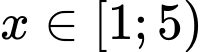 ta có bảng biến thiên:
ta có bảng biến thiên:
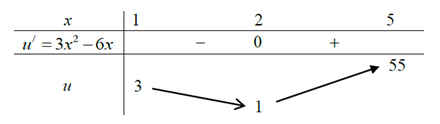
Xét với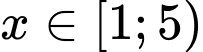 ta có biến đổi:
ta có biến đổi:
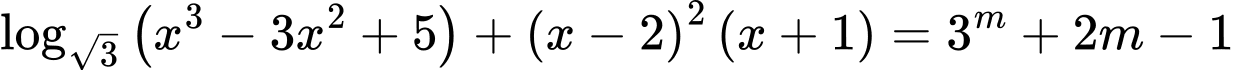
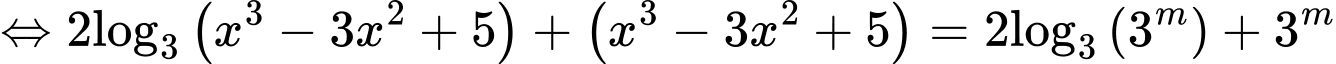
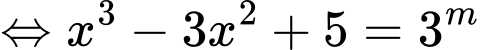 (do hàm
(do hàm 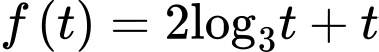 đồng biến trên
đồng biến trên 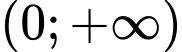 )
)
Từ đó dẫn đến điều kiện của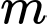 là
là 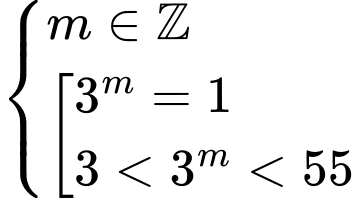
 . Đáp án: C
. Đáp án: C
Đặt
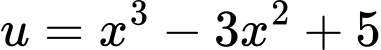 , với
, với 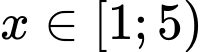 ta có bảng biến thiên:
ta có bảng biến thiên: 
Xét với
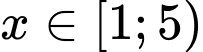 ta có biến đổi:
ta có biến đổi: 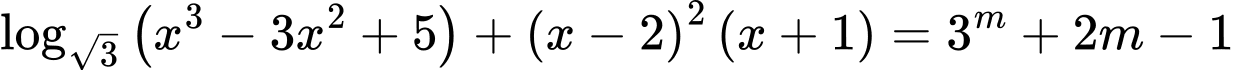
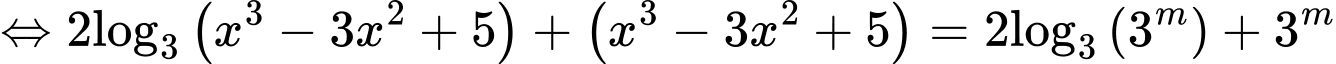
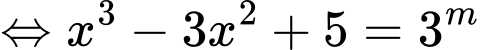 (do hàm
(do hàm 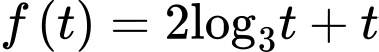 đồng biến trên
đồng biến trên 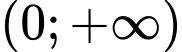 )
) Từ đó dẫn đến điều kiện của
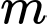 là
là 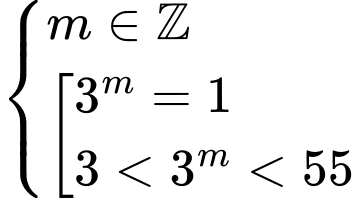
 . Đáp án: C
. Đáp án: C
Câu 16 [319718]: Số giá trị 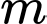 nguyên thuộc khoảng
nguyên thuộc khoảng 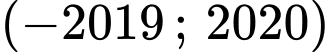 để phương trình
để phương trình 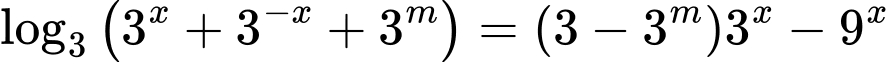 có đúng hai nghiệm là
có đúng hai nghiệm là
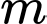 nguyên thuộc khoảng
nguyên thuộc khoảng 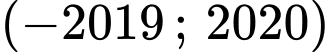 để phương trình
để phương trình 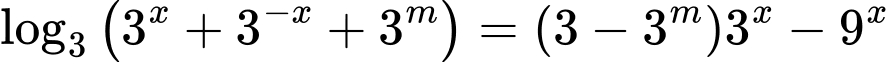 có đúng hai nghiệm là
có đúng hai nghiệm là A,  .
.
 .
.B, 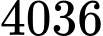 .
.
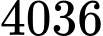 .
.C,  .
.
 .
.D, 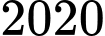 .
.
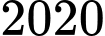 .
.
Chọn A
Ta có:
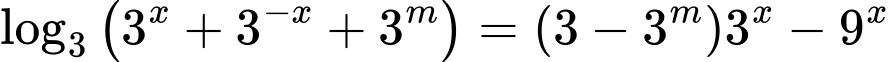
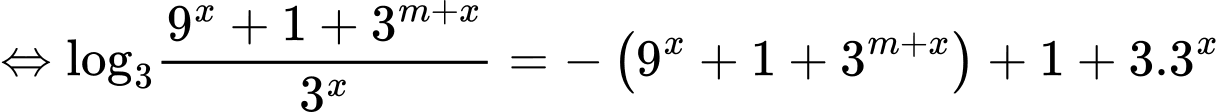
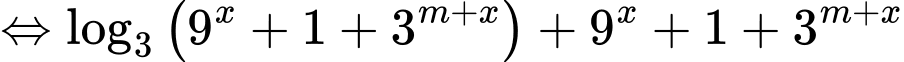
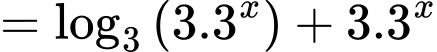 .(*)
.(*)
Xét hàm số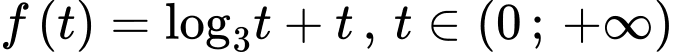 .
.
Ta có :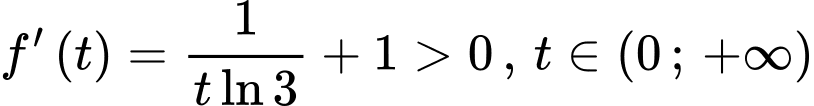
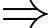 Hàm số
Hàm số 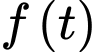 đồng biến trên
đồng biến trên 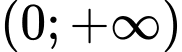 .
.
Do đó :
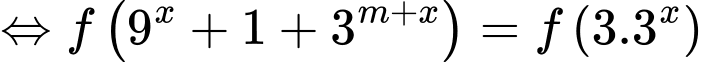
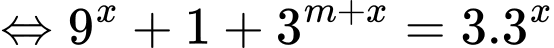
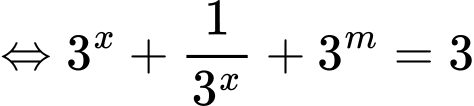
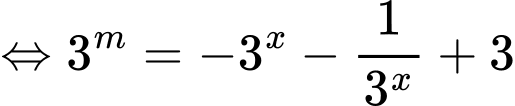 .(1)
.(1)
Đặt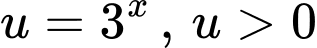 . Phương trình (1) trở thành :
. Phương trình (1) trở thành : 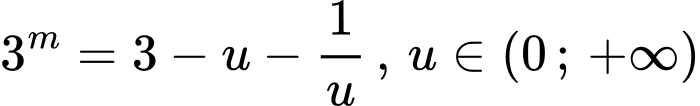
Xét hàm số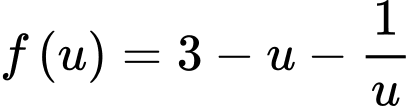 trên
trên  , ta có :
, ta có :
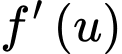
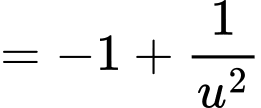
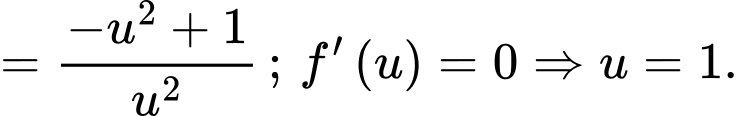
Bảng biến thiên:
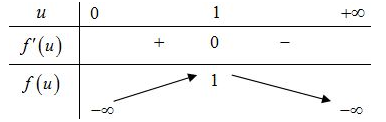 Đáp án: A
Đáp án: A
Ta có:
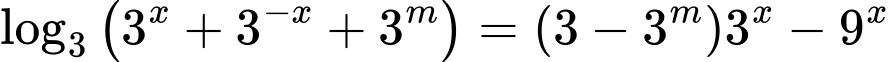
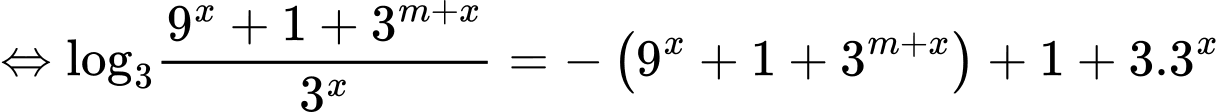
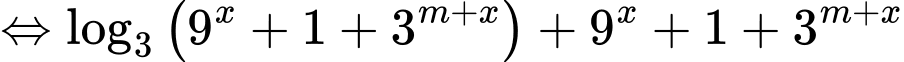
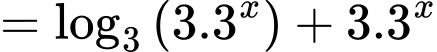 .(*)
.(*)Xét hàm số
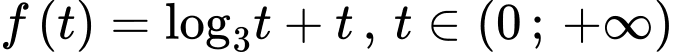 .
.Ta có :
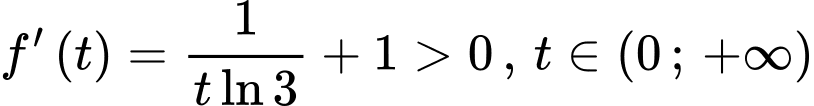
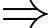 Hàm số
Hàm số 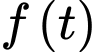 đồng biến trên
đồng biến trên 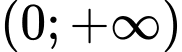 .
.Do đó :

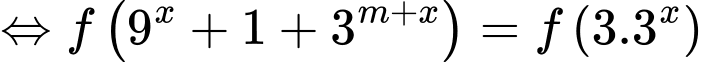
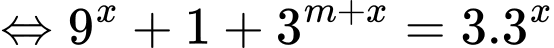
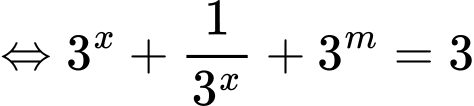
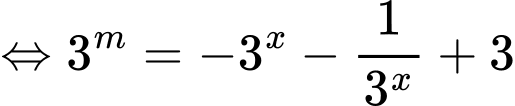 .(1)
.(1)Đặt
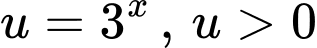 . Phương trình (1) trở thành :
. Phương trình (1) trở thành : 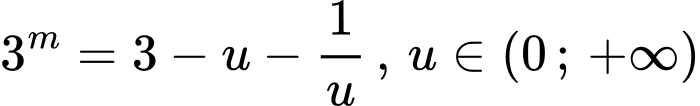
Xét hàm số
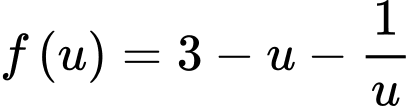 trên
trên  , ta có :
, ta có : 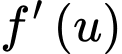
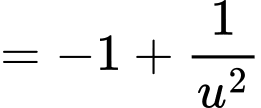
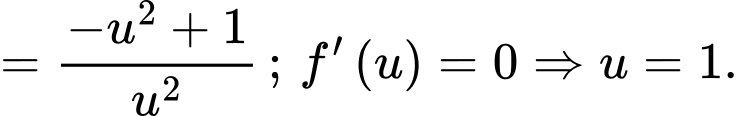
Bảng biến thiên:
 Đáp án: A
Đáp án: A