Đáp án Bài tập tự luyện số 2
Câu 1 [677030]: Cho hàm số 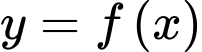 liên tục trên
liên tục trên 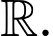 Hàm số
Hàm số 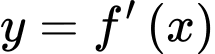 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
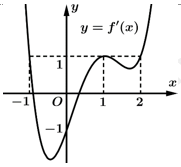
Hàm số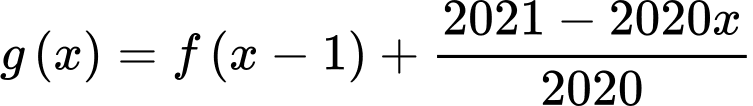 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
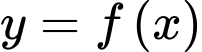 liên tục trên
liên tục trên 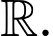 Hàm số
Hàm số 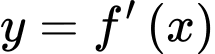 có đồ thị như hình vẽ.
có đồ thị như hình vẽ. 
Hàm số
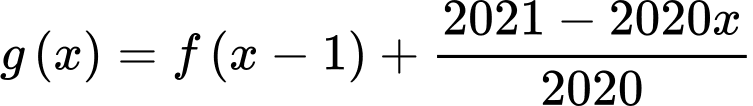 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 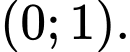
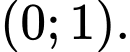
B, 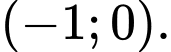
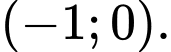
C, 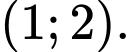
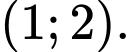
D, 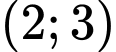
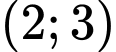
Ta có: 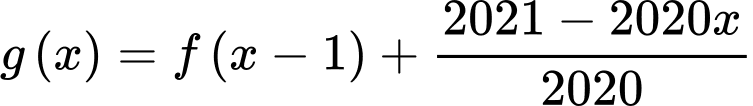
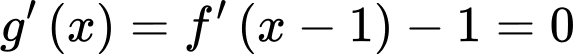
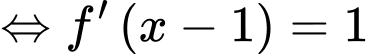
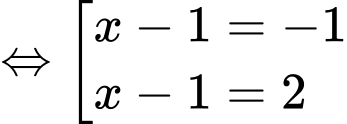

Ta có, trục xét dấu của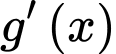 như sau:
như sau:
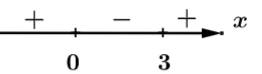
Suy ra hàm số đồng biến trên khoảng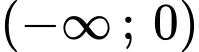 và
và 
Đáp án: B. Đáp án: B
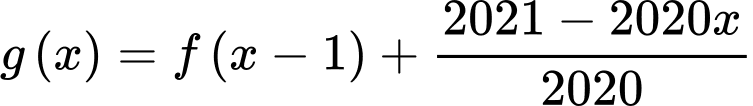
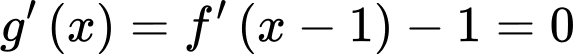
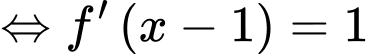
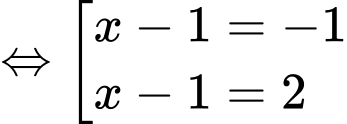

Ta có, trục xét dấu của
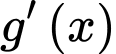 như sau:
như sau:
Suy ra hàm số đồng biến trên khoảng
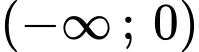 và
và 
Đáp án: B. Đáp án: B
Câu 2 [319698]: Cho hàm số 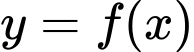 liên tục trên
liên tục trên 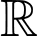 và đồ thị bên dưới là của hàm số
và đồ thị bên dưới là của hàm số 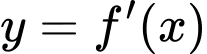 .
.
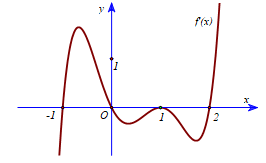
Hỏi hàm số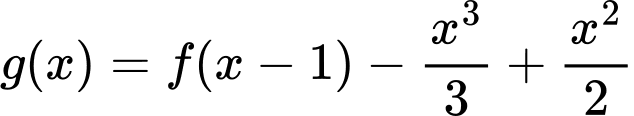 đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây?
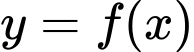 liên tục trên
liên tục trên 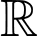 và đồ thị bên dưới là của hàm số
và đồ thị bên dưới là của hàm số 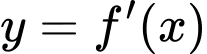 .
.
Hỏi hàm số
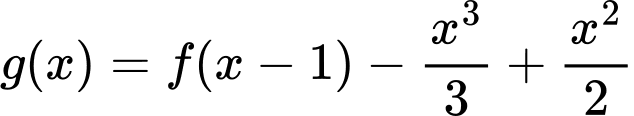 đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây? A, 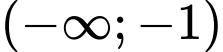 .
.
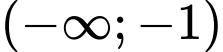 .
.B, 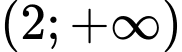 .
.
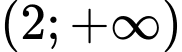 .
.C, 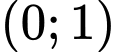 .
.
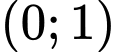 .
.D, 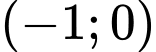 .
.
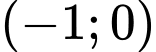 .
.
Chọn C
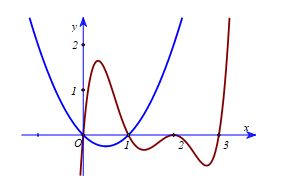
Ta có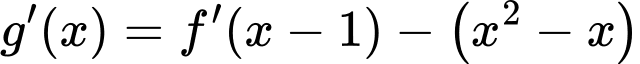 .
.
Xét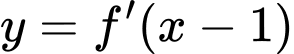 có đồ thị như hình vẽ bằng cách tịnh tiến đồ thị
có đồ thị như hình vẽ bằng cách tịnh tiến đồ thị 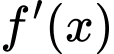 sang phải 1 đơn vị.
sang phải 1 đơn vị.
Xét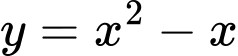 là một Parabol có trục đối xứng là
là một Parabol có trục đối xứng là 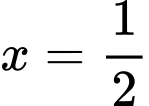 , tọa độ đỉnh
, tọa độ đỉnh 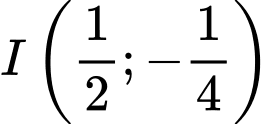 đi qua các điểm
đi qua các điểm 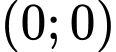 và
và 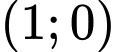 .
.
Ta vẽ hai đồ thị trên cùng một hệ trục tọa độ (như hình vẽ trên)
Trong khoảng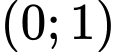 đồ thị hàm số
đồ thị hàm số 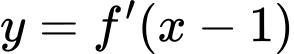 nằm trên đồ thị
nằm trên đồ thị 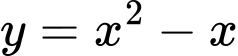 nên
nên 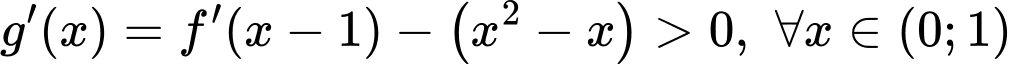 nên hàm số
nên hàm số 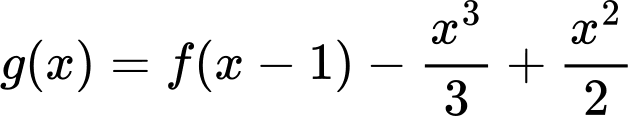 đồng biến trên
đồng biến trên 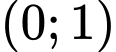 . Đáp án: C
. Đáp án: C

Ta có
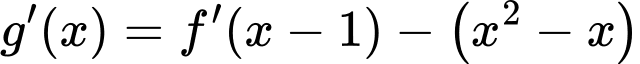 .
.Xét
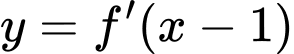 có đồ thị như hình vẽ bằng cách tịnh tiến đồ thị
có đồ thị như hình vẽ bằng cách tịnh tiến đồ thị 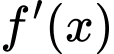 sang phải 1 đơn vị.
sang phải 1 đơn vị.Xét
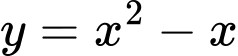 là một Parabol có trục đối xứng là
là một Parabol có trục đối xứng là 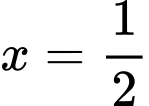 , tọa độ đỉnh
, tọa độ đỉnh 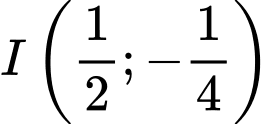 đi qua các điểm
đi qua các điểm 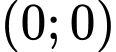 và
và 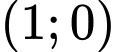 .
.Ta vẽ hai đồ thị trên cùng một hệ trục tọa độ (như hình vẽ trên)
Trong khoảng
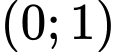 đồ thị hàm số
đồ thị hàm số 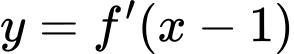 nằm trên đồ thị
nằm trên đồ thị 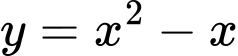 nên
nên 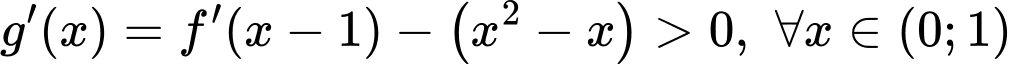 nên hàm số
nên hàm số 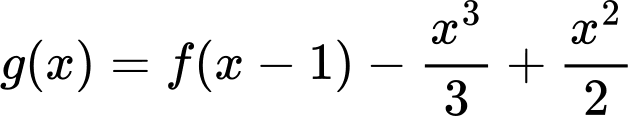 đồng biến trên
đồng biến trên 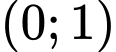 . Đáp án: C
. Đáp án: C
Câu 3 [678707]: Cho hàm số 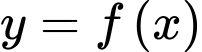 có đồ thị hàm số
có đồ thị hàm số 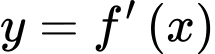 như hình vẽ
như hình vẽ
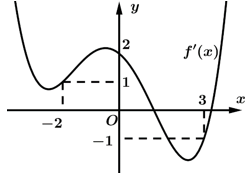
Hàm số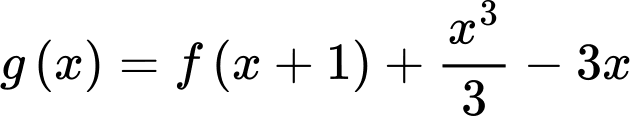 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
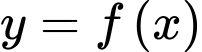 có đồ thị hàm số
có đồ thị hàm số 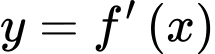 như hình vẽ
như hình vẽ
Hàm số
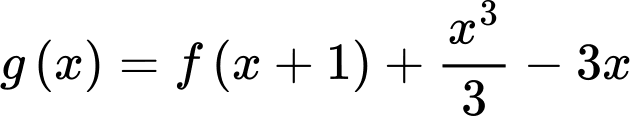 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 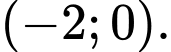
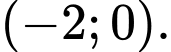
B, 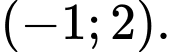
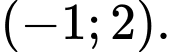
C, 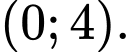
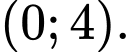
D, 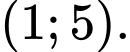
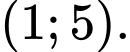
Ta có: 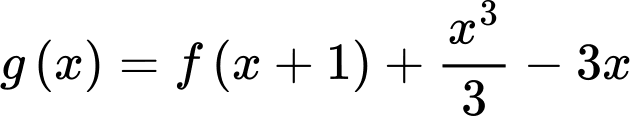
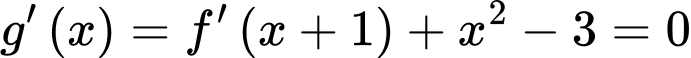
Đặt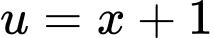

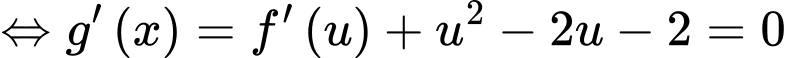
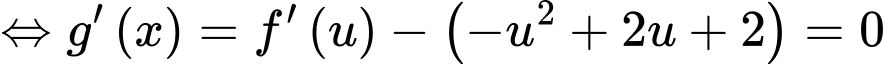
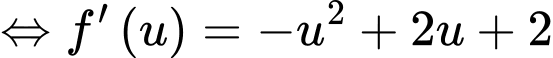
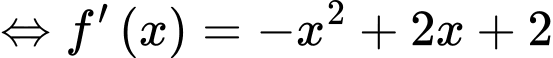
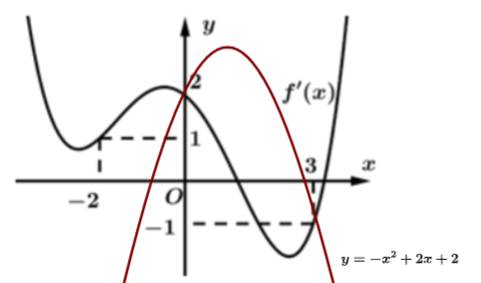

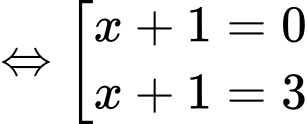
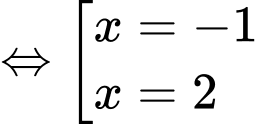
Ta có, trục xét dấu của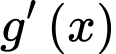 như sau:
như sau:
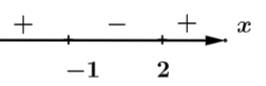
Suy ra hàm số nghịch biến trên khoảng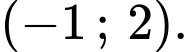
Đáp án: B. Đáp án: B
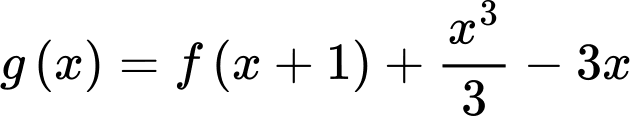
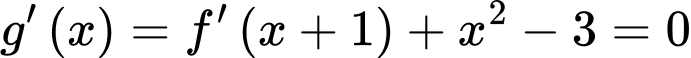
Đặt
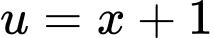

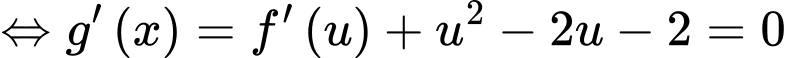
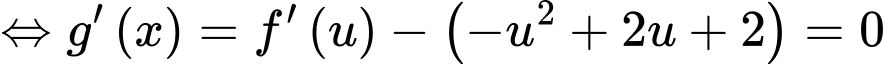
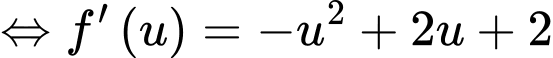
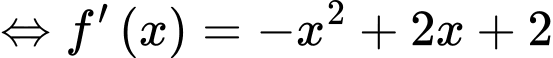


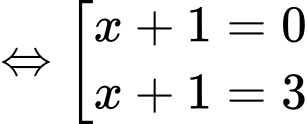
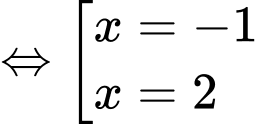
Ta có, trục xét dấu của
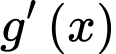 như sau:
như sau:
Suy ra hàm số nghịch biến trên khoảng
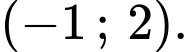
Đáp án: B. Đáp án: B
Câu 4 [520108]: Cho hàm số 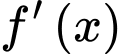 có đồ thị như hình bên. Hàm số
có đồ thị như hình bên. Hàm số 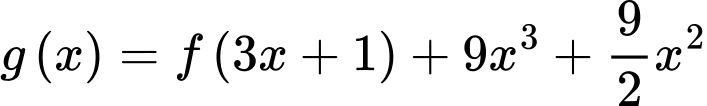 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
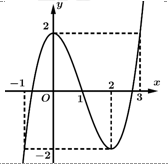
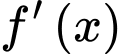 có đồ thị như hình bên. Hàm số
có đồ thị như hình bên. Hàm số 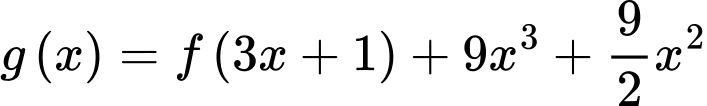 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
A, 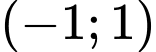 .
.
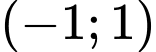 .
.B, 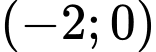 .
.
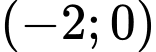 .
.C,  .
.
 .
.D, 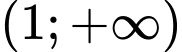 .
.
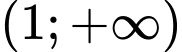 .
.
Chọn D
Xét hàm số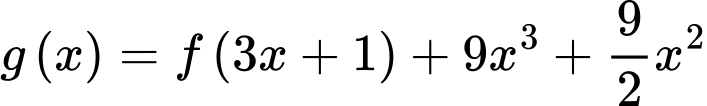
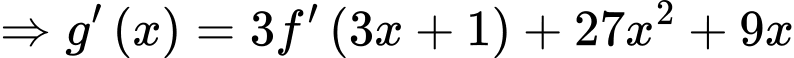
Hàm số đồng biến tương đương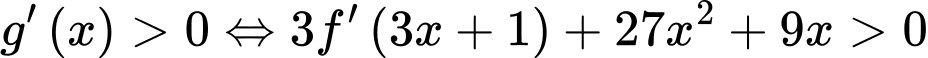
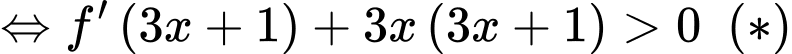 .
.
Đặt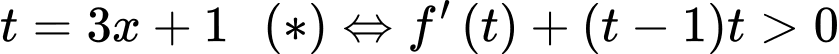
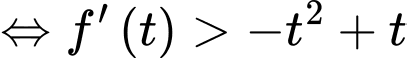
Vẽ parabol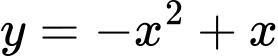 và đồ thị hàm số
và đồ thị hàm số 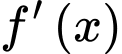 trên cùng một hệ trục
trên cùng một hệ trục
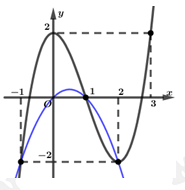
Dựa vào đồ thị ta thấy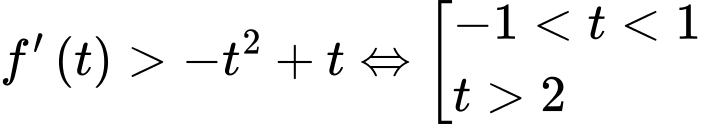
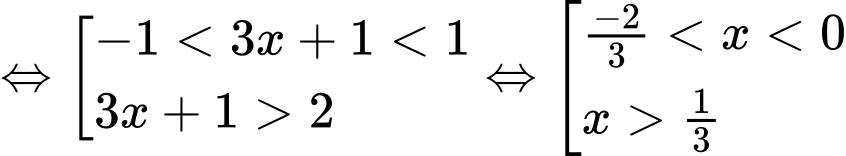 . Đáp án: D
. Đáp án: D
Xét hàm số
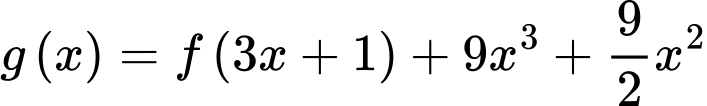
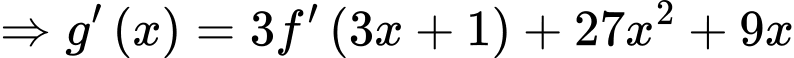
Hàm số đồng biến tương đương
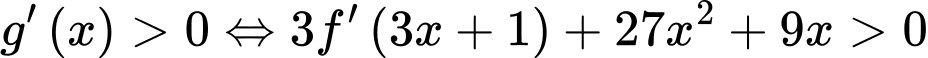
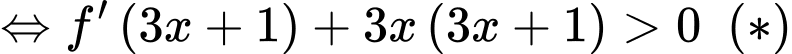 .
.Đặt
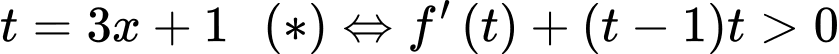
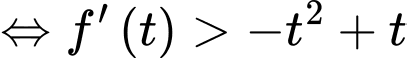
Vẽ parabol
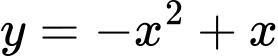 và đồ thị hàm số
và đồ thị hàm số 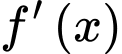 trên cùng một hệ trục
trên cùng một hệ trục
Dựa vào đồ thị ta thấy
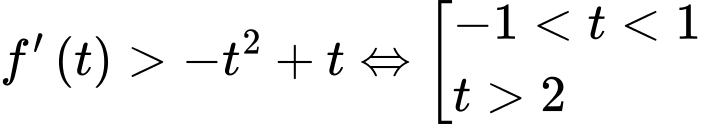
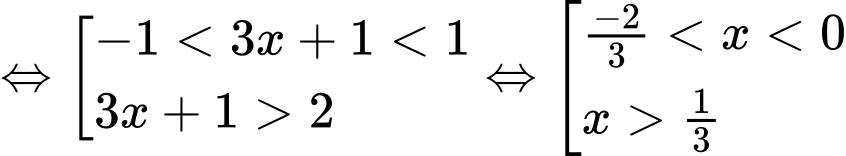 . Đáp án: D
. Đáp án: D
Câu 5 [927131]: Cho hàm số đa thức bậc năm 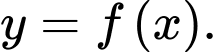 Đồ thị của hàm số
Đồ thị của hàm số 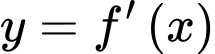 như hình vẽ bên, biết rằng
như hình vẽ bên, biết rằng 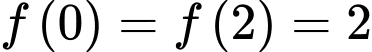 hỏi hàm số
hỏi hàm số 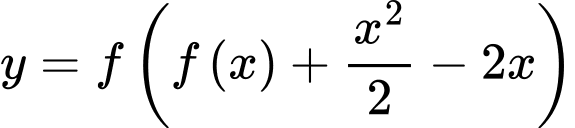 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
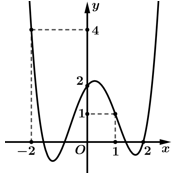
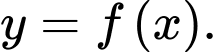 Đồ thị của hàm số
Đồ thị của hàm số 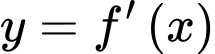 như hình vẽ bên, biết rằng
như hình vẽ bên, biết rằng 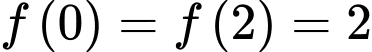 hỏi hàm số
hỏi hàm số 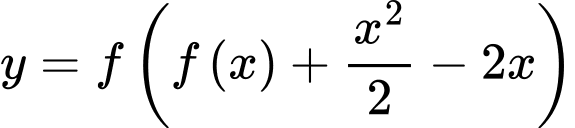 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
A, 9.
B, 10.
C, 12.
D, 11.
Ta có: 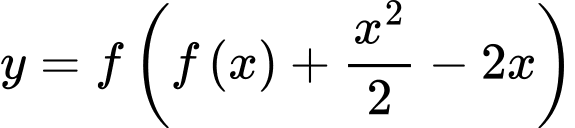
Đặt: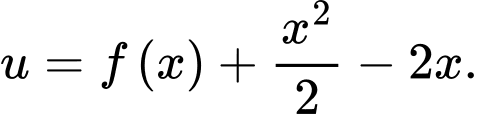
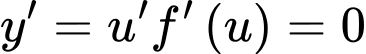
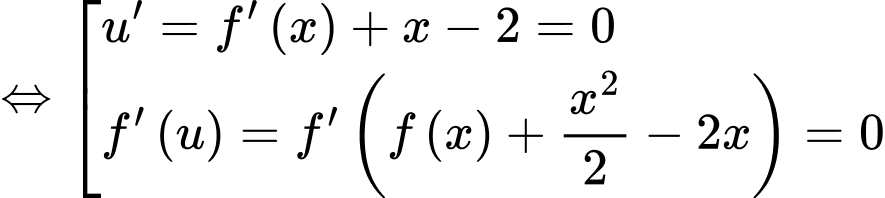
Xét: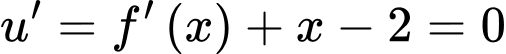
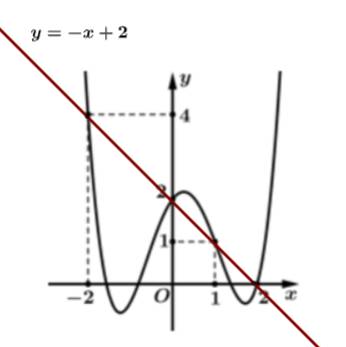
Suy ra ta có: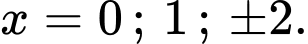
Xét: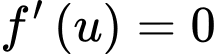
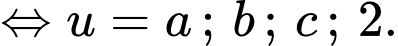
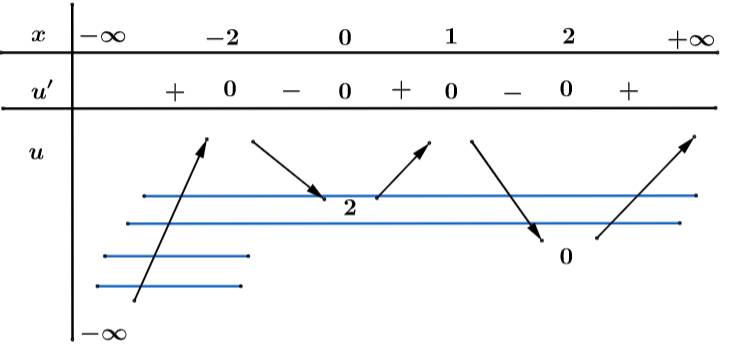
Suy ra: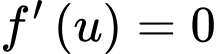 có 8 nghiệm phân biệt bội lẻ.
có 8 nghiệm phân biệt bội lẻ.
Suy ra: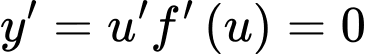 có tổng 12 nghiệm phân biệt bội lẻ.
có tổng 12 nghiệm phân biệt bội lẻ.
Suy ra hàm số có 12 diểm cực trị.
Đáp án: C. Đáp án: C
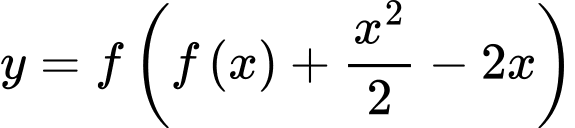
Đặt:
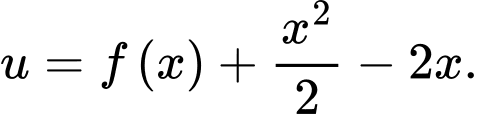
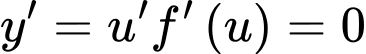
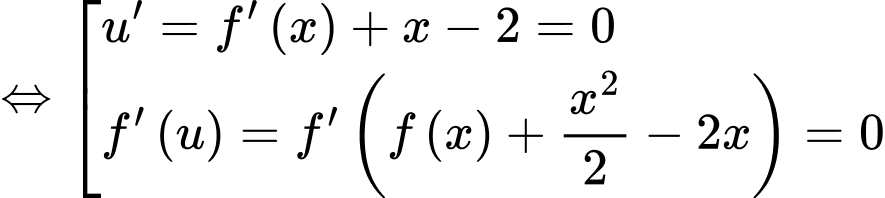
Xét:
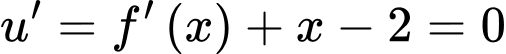

Suy ra ta có:
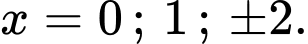
Xét:
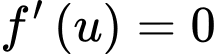
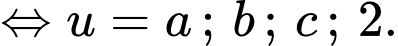

Suy ra:
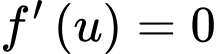 có 8 nghiệm phân biệt bội lẻ.
có 8 nghiệm phân biệt bội lẻ.
Suy ra:
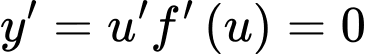 có tổng 12 nghiệm phân biệt bội lẻ.
có tổng 12 nghiệm phân biệt bội lẻ.
Suy ra hàm số có 12 diểm cực trị.
Đáp án: C. Đáp án: C
Câu 6 [922353]: Cho hàm số đa thức bậc sáu có đồ thị của đạo hàm 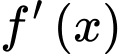 như hình vẽ bên. Biết rằng
như hình vẽ bên. Biết rằng 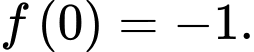 Số điểm cực trị của hàm số
Số điểm cực trị của hàm số 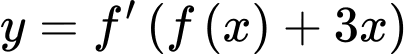 bằng
bằng
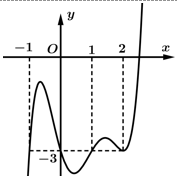
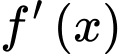 như hình vẽ bên. Biết rằng
như hình vẽ bên. Biết rằng 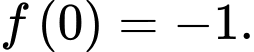 Số điểm cực trị của hàm số
Số điểm cực trị của hàm số 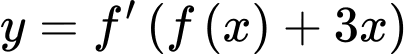 bằng
bằng
A, 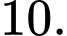
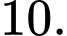
B, 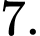
C, 

D, 
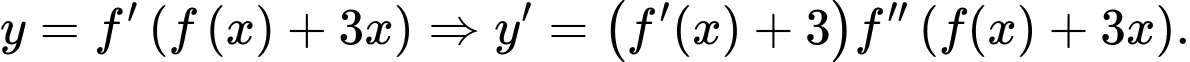
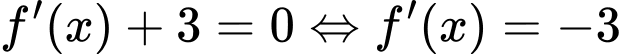
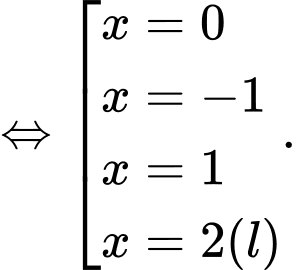
BBT:
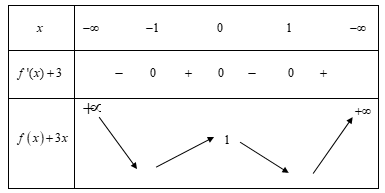
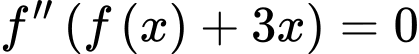
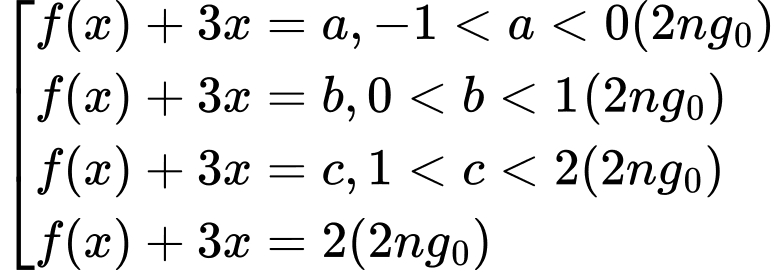
Vậy hàm số có 11 điểm cực trị. Chọn đáp án C. Đáp án: C
Câu 7 [31489]: Cho hàm số 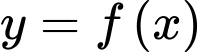 có đạo hàm liên tục trên
có đạo hàm liên tục trên 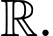 Bảng biến thiên của hàm số
Bảng biến thiên của hàm số 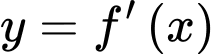 được cho như hình vẽ.
được cho như hình vẽ.
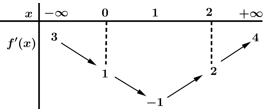
Hàm số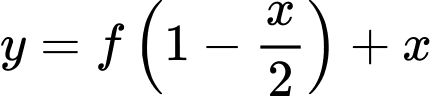 nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào?
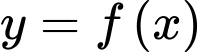 có đạo hàm liên tục trên
có đạo hàm liên tục trên 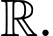 Bảng biến thiên của hàm số
Bảng biến thiên của hàm số 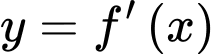 được cho như hình vẽ.
được cho như hình vẽ. 
Hàm số
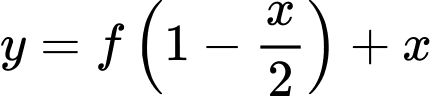 nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào? A, 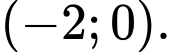
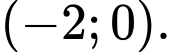
B, 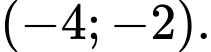
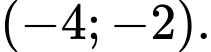
C, 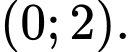
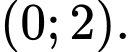
D, 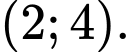
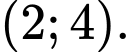
Ta có: 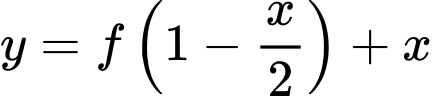 nghịch biến
nghịch biến
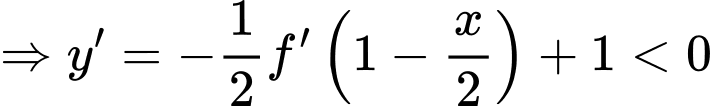
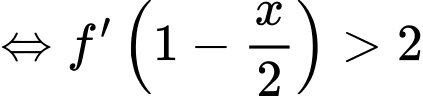
Đặt: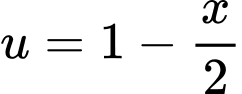
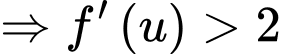
Từ bảng biến thiên bài cho ta có:
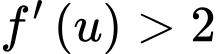
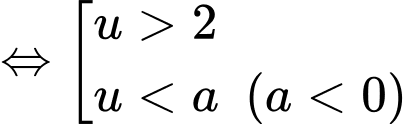
Xét:
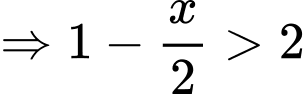

Xét:
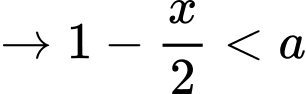
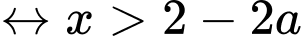
Đáp án: B. Đáp án: B
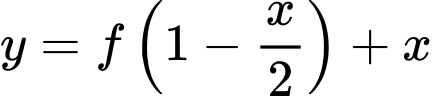 nghịch biến
nghịch biến 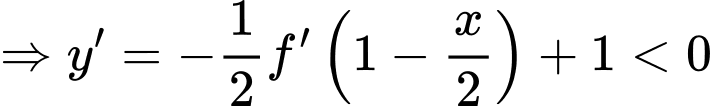
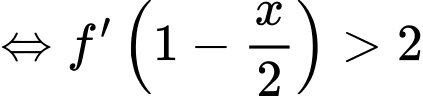
Đặt:
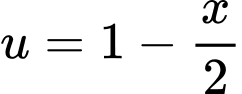
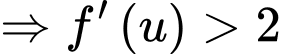
Từ bảng biến thiên bài cho ta có:
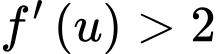
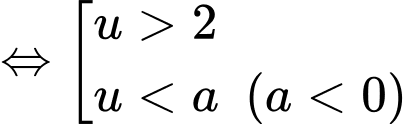
Xét:

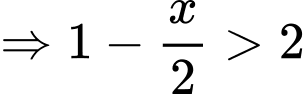

Xét:

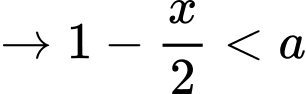
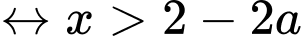
Đáp án: B. Đáp án: B
Câu 8 [528661]: Cho hàm số 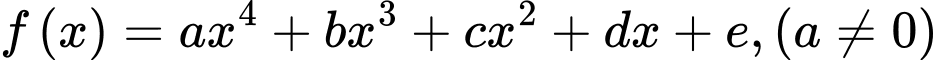 có đồ thị của đạo hàm
có đồ thị của đạo hàm 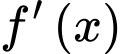 như hình vẽ. Biết rằng
như hình vẽ. Biết rằng 
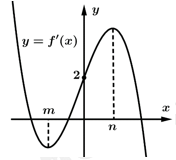
Số điểm cực trị của hàm số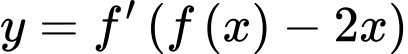 bằng
bằng
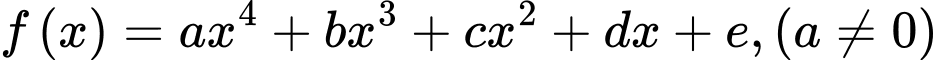 có đồ thị của đạo hàm
có đồ thị của đạo hàm 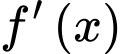 như hình vẽ. Biết rằng
như hình vẽ. Biết rằng 

Số điểm cực trị của hàm số
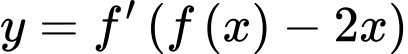 bằng
bằng A, 6.
B, 7.
C, 10.
D, 14.
Chọn B
Đặt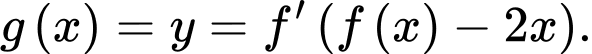
Ta có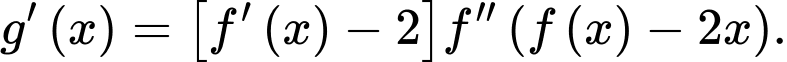
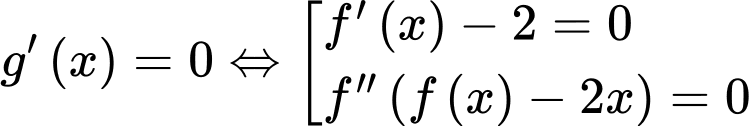
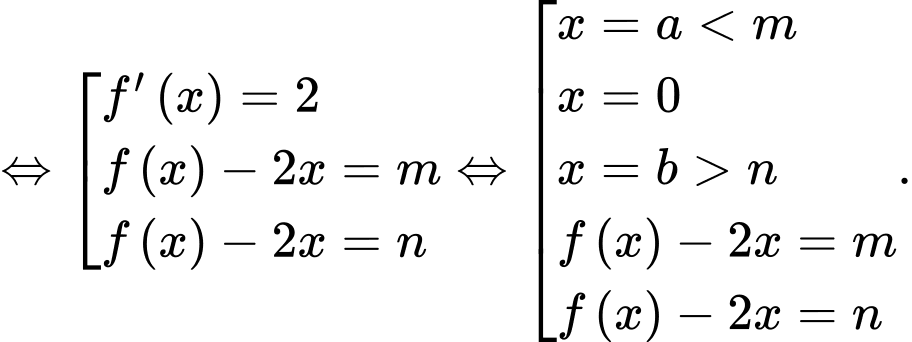
Từ đồ thị hàm số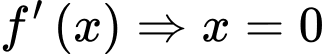 thì
thì 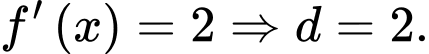
Xét hàm số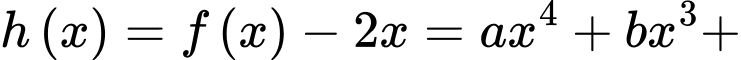
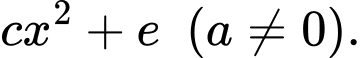
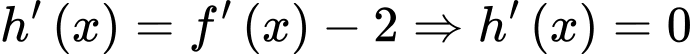
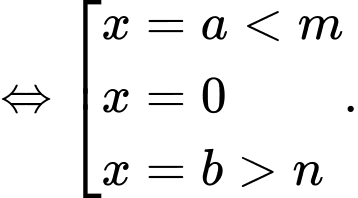
Bảng biến thiên của hàm số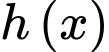
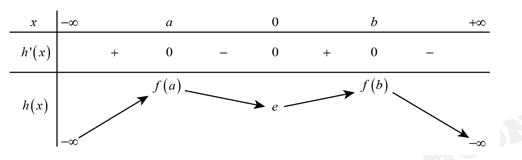
Từ bảng biến thiên của hàm số và điều kiện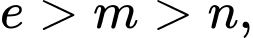 suy ra phương trình
suy ra phương trình 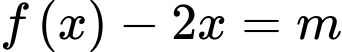 và
và 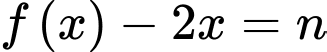 mỗi phương trình có hai nghiệm phân biệt khác nhau và khác
mỗi phương trình có hai nghiệm phân biệt khác nhau và khác 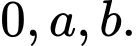
Suy ra phương trình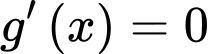 có
có 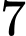 nghiệm phân biệt và là nghiệm bội lẻ. Chọn B.
nghiệm phân biệt và là nghiệm bội lẻ. Chọn B.
Do đó hàm số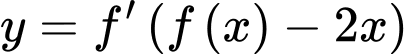 có
có 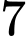 điểm cực trị. Đáp án: B
điểm cực trị. Đáp án: B
Đặt
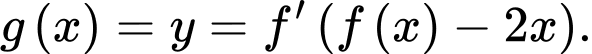
Ta có
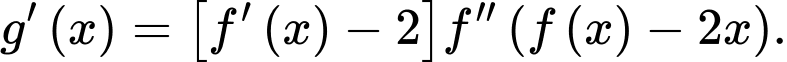
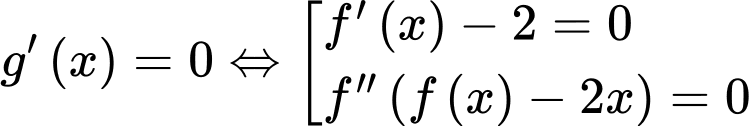
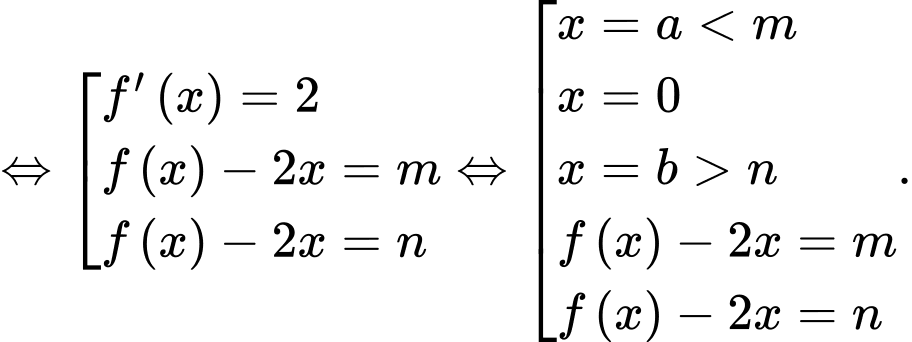
Từ đồ thị hàm số
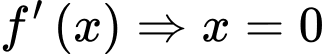 thì
thì 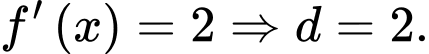
Xét hàm số
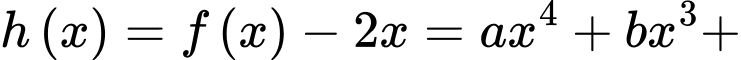
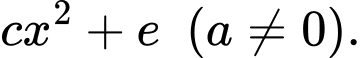
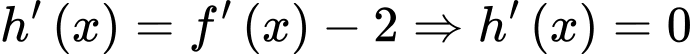
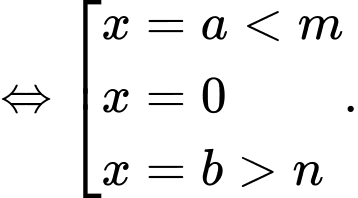
Bảng biến thiên của hàm số
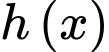

Từ bảng biến thiên của hàm số và điều kiện
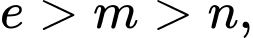 suy ra phương trình
suy ra phương trình 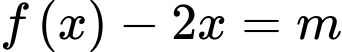 và
và 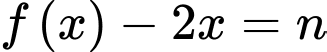 mỗi phương trình có hai nghiệm phân biệt khác nhau và khác
mỗi phương trình có hai nghiệm phân biệt khác nhau và khác 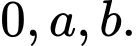
Suy ra phương trình
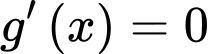 có
có 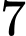 nghiệm phân biệt và là nghiệm bội lẻ. Chọn B.
nghiệm phân biệt và là nghiệm bội lẻ. Chọn B. Do đó hàm số
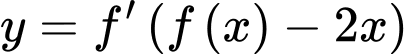 có
có 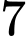 điểm cực trị. Đáp án: B
điểm cực trị. Đáp án: B
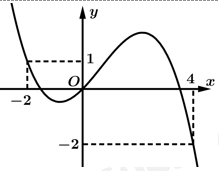
Câu 9 [521856]: Cho hàm số bậc bốn 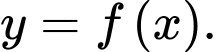 Đồ thị của hàm số
Đồ thị của hàm số 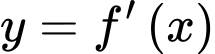 như hình vẽ bên, biết
như hình vẽ bên, biết 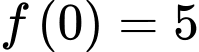 hỏi hàm số
hỏi hàm số 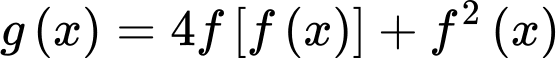 có bao nhiêu điểm cực tiểu?
có bao nhiêu điểm cực tiểu?
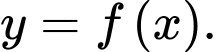 Đồ thị của hàm số
Đồ thị của hàm số 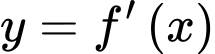 như hình vẽ bên, biết
như hình vẽ bên, biết 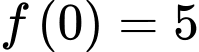 hỏi hàm số
hỏi hàm số 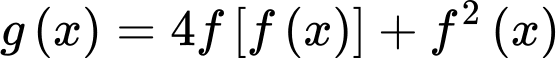 có bao nhiêu điểm cực tiểu?
có bao nhiêu điểm cực tiểu?
A, 9.
B, 4.
C, 7.
D, 5.
Ta có: 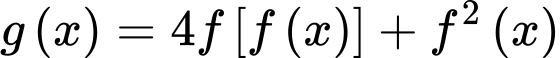
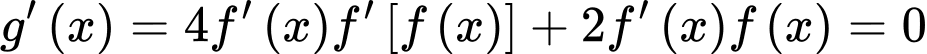
Đặt: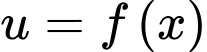
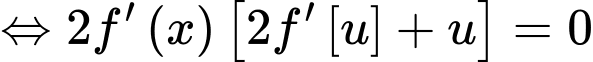
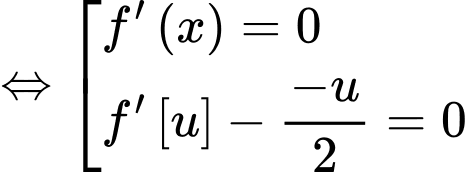
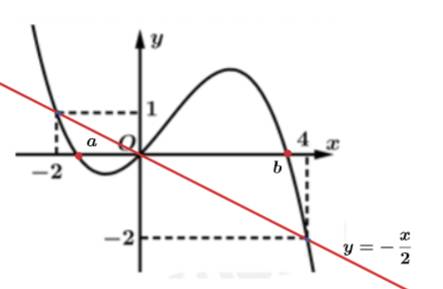
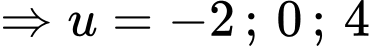
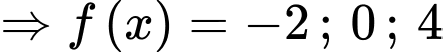
Ta có bảng biến thiên:
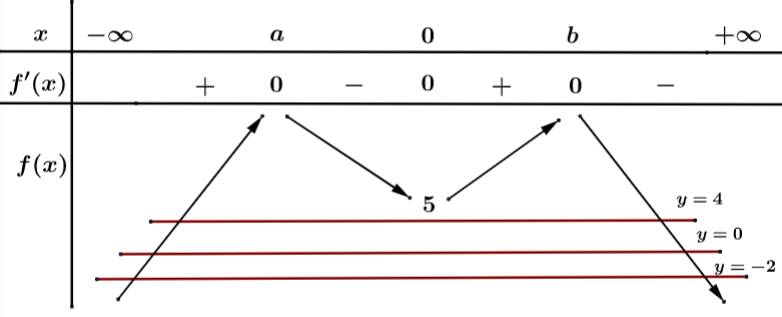
Vậy PT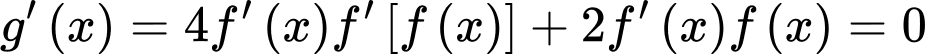 có 9 nghiệm phân biệt bội lẻ.
có 9 nghiệm phân biệt bội lẻ.

Mỗi lần đổi dấu từ âm sang dương ta có một điểm cực tiểu. Vậy từ trục xét dấu trên, ta suy ra PT có 4 cực tiểu.
Đáp án: B. Đáp án: B
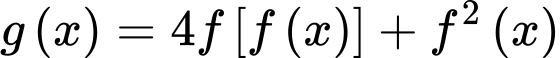
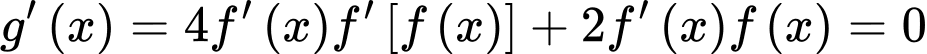
Đặt:
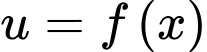
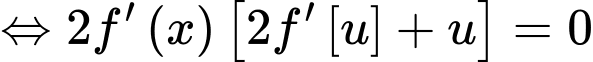
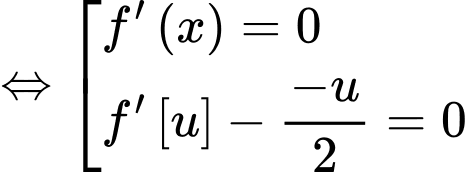

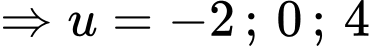
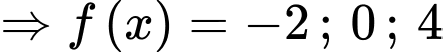
Ta có bảng biến thiên:

Vậy PT
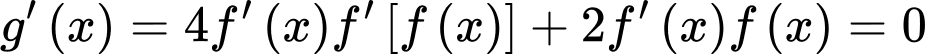 có 9 nghiệm phân biệt bội lẻ.
có 9 nghiệm phân biệt bội lẻ.
Mỗi lần đổi dấu từ âm sang dương ta có một điểm cực tiểu. Vậy từ trục xét dấu trên, ta suy ra PT có 4 cực tiểu.
Đáp án: B. Đáp án: B
Câu 10 [521863]: Cho hàm số 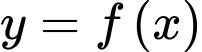 là hàm đa thức bậc 4 có đồ thị hàm số
là hàm đa thức bậc 4 có đồ thị hàm số  như hình vẽ. Hàm số
như hình vẽ. Hàm số 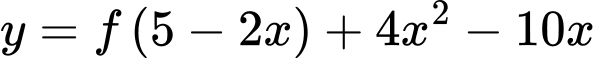 đồng biến trong khoảng nào dưới đây?
đồng biến trong khoảng nào dưới đây?
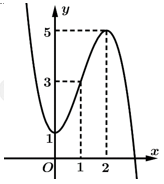
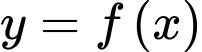 là hàm đa thức bậc 4 có đồ thị hàm số
là hàm đa thức bậc 4 có đồ thị hàm số  như hình vẽ. Hàm số
như hình vẽ. Hàm số 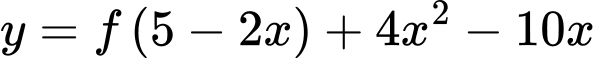 đồng biến trong khoảng nào dưới đây?
đồng biến trong khoảng nào dưới đây?
A, 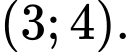
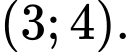
B, 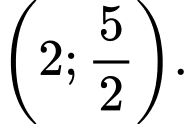
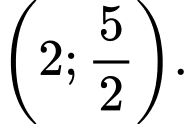
C, 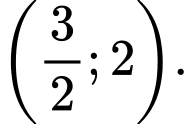
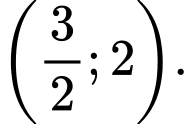
D, 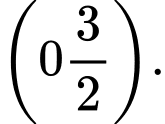
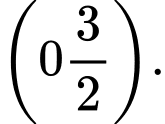
Ta có: 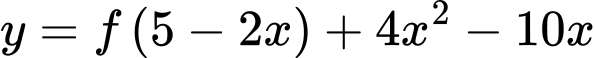
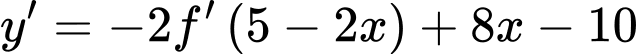
Đặt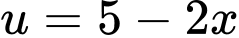
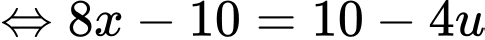
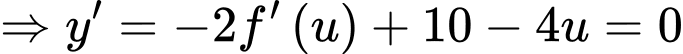
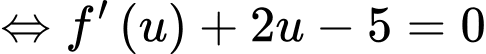
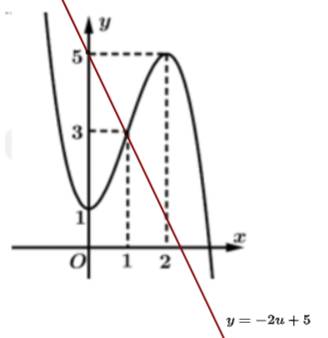
Hàm số đồng biến trong khoảng khi và chỉ khi
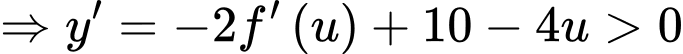
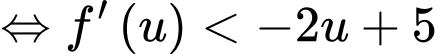
Thấy trên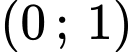 thì
thì 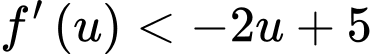
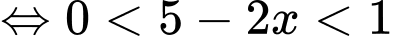
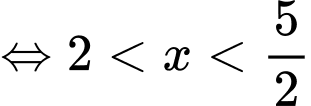
Đáp án: B. Đáp án: B
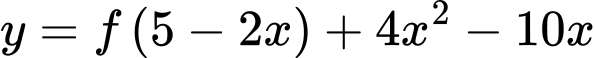
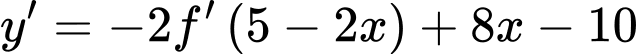
Đặt
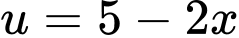
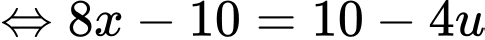
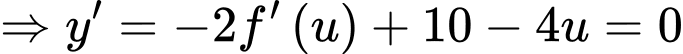
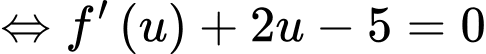

Hàm số đồng biến trong khoảng khi và chỉ khi
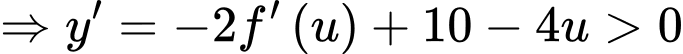
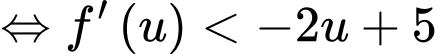
Thấy trên
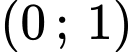 thì
thì 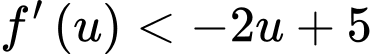
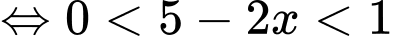
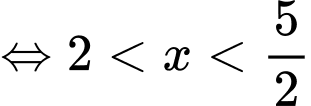
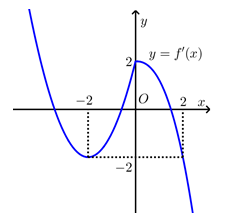
Câu 11 [322484]: Cho 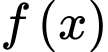 mà đồ thị hàm số
mà đồ thị hàm số 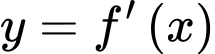 như hình bên. Hàm số
như hình bên. Hàm số 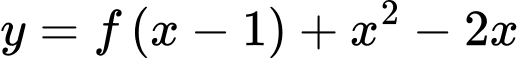 đồng biến trên khoảng
đồng biến trên khoảng
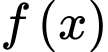 mà đồ thị hàm số
mà đồ thị hàm số 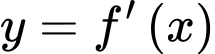 như hình bên. Hàm số
như hình bên. Hàm số 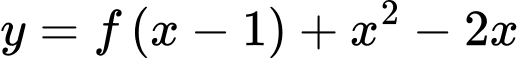 đồng biến trên khoảng
đồng biến trên khoảng
A, 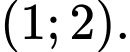
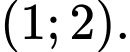
B, 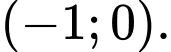
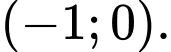
C, 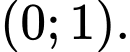
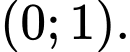
D, 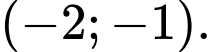
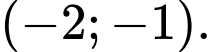
Đáp án A
Ta có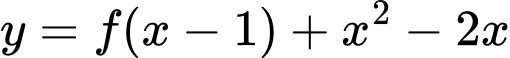
Khi đó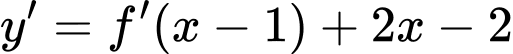 . Hàm số đồng biến khi
. Hàm số đồng biến khi 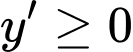
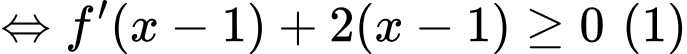
Đặt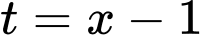 thì (1) trở thành:
thì (1) trở thành: 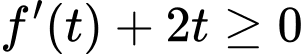
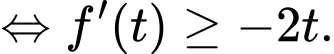
Quan sát đồ thị hàm số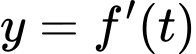 và
và 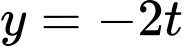 trên cùng một hệ trục tọa độ như hình vẽ.
trên cùng một hệ trục tọa độ như hình vẽ.
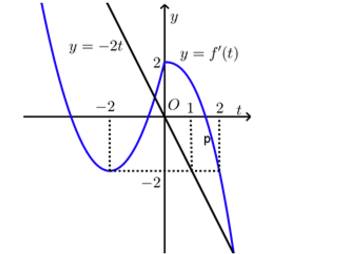
Khi đó ta thấy với thì đồ thị hàm số
thì đồ thị hàm số 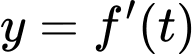 luôn nằm trên đường thảng
luôn nằm trên đường thảng 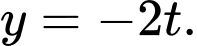
Suy ra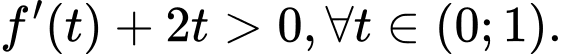 Do đó
Do đó  thì hàm số
thì hàm số 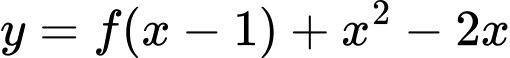 đồng biến. Đáp án: A
đồng biến. Đáp án: A
Ta có
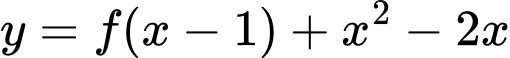
Khi đó
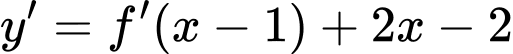 . Hàm số đồng biến khi
. Hàm số đồng biến khi 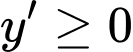
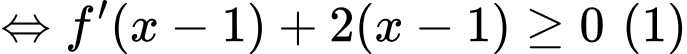
Đặt
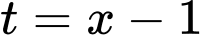 thì (1) trở thành:
thì (1) trở thành: 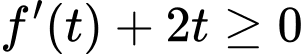
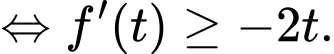
Quan sát đồ thị hàm số
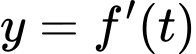 và
và 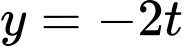 trên cùng một hệ trục tọa độ như hình vẽ.
trên cùng một hệ trục tọa độ như hình vẽ.
Khi đó ta thấy với
 thì đồ thị hàm số
thì đồ thị hàm số 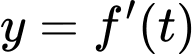 luôn nằm trên đường thảng
luôn nằm trên đường thảng 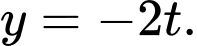
Suy ra
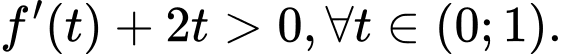 Do đó
Do đó  thì hàm số
thì hàm số 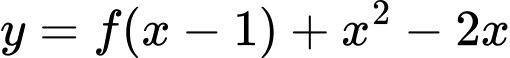 đồng biến. Đáp án: A
đồng biến. Đáp án: A
Câu 12 [899383]: [Đề Chuyên Lê Quý Đôn-Bình Định 2021]: Cho hàm số đa thức bậc năm 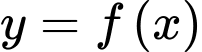 có đồ thị hàm số
có đồ thị hàm số 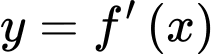 như hình vẽ sau
như hình vẽ sau
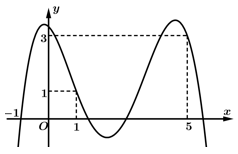
Số điểm cực trị của hàm số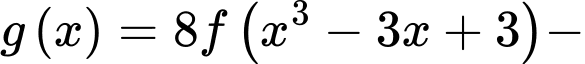
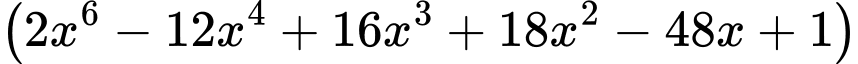 là
là
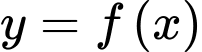 có đồ thị hàm số
có đồ thị hàm số 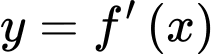 như hình vẽ sau
như hình vẽ sau
Số điểm cực trị của hàm số
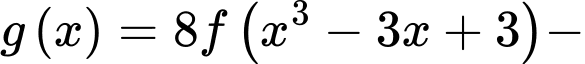
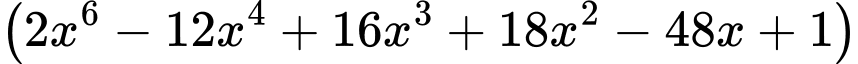 là
là A, 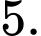
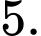
B, 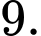
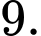
C, 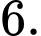
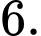
D, 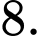
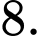
Ta có: 
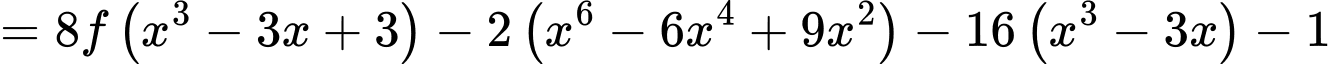
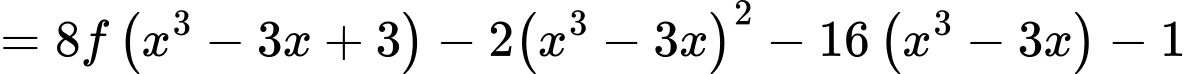
Xét: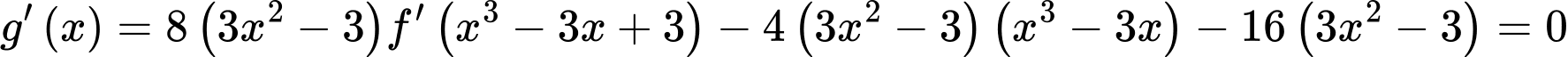
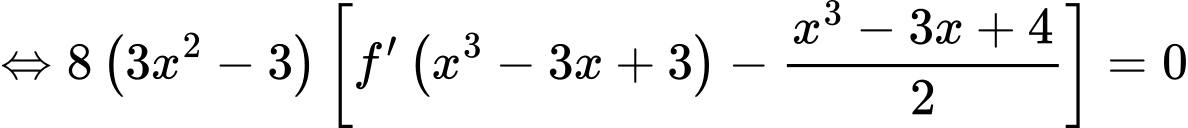
Đặt:
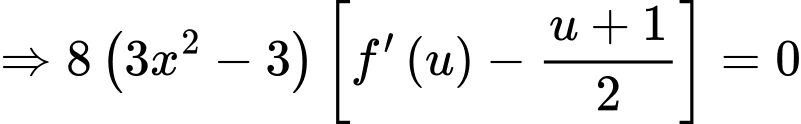
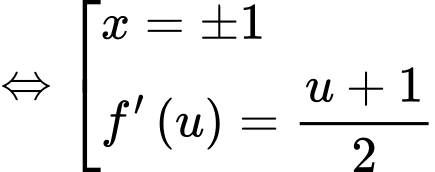
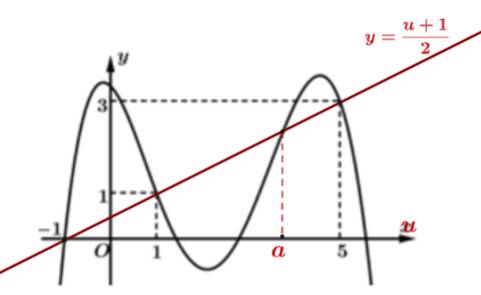
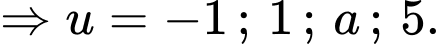
Ta xét: có:
có:
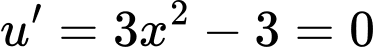
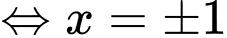
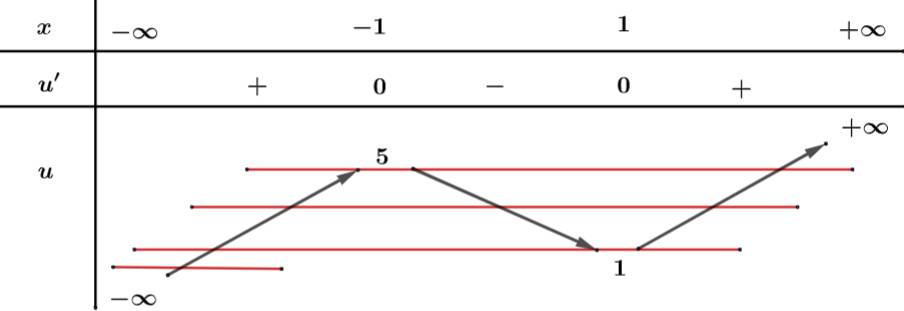
Từ bảng biến thiên ta suy ra PT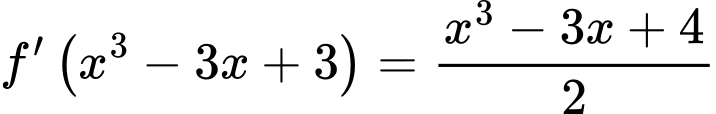 có 6 nghiệm bội lẻ phân biệt.
có 6 nghiệm bội lẻ phân biệt.
Vậy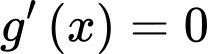 có tổng 8 nghiệm phân biệt bội lẻ.
có tổng 8 nghiệm phân biệt bội lẻ.
Suy ra, hàm số bài cho có 8 điểm cực trị.
Đáp án: D. Đáp án: D

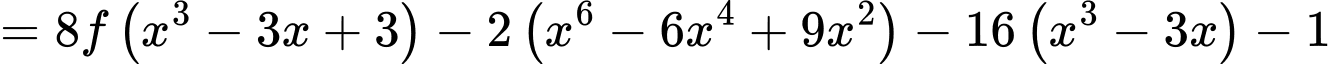
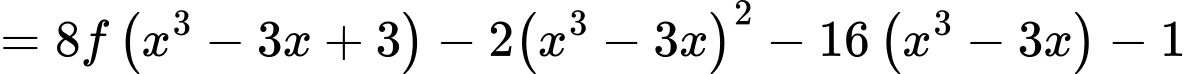
Xét:
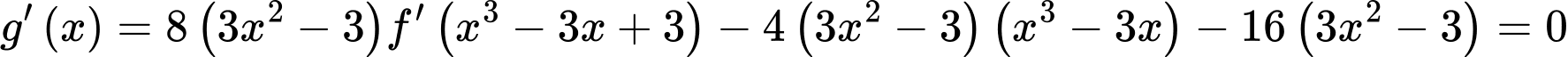
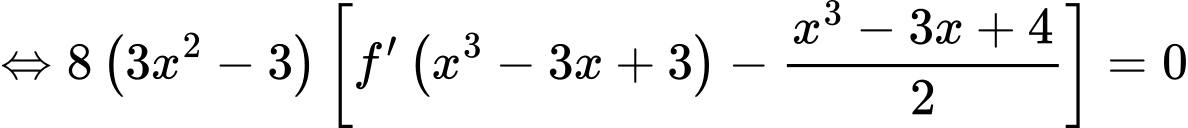
Đặt:

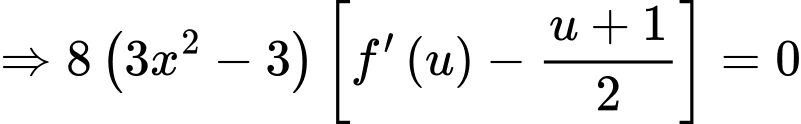
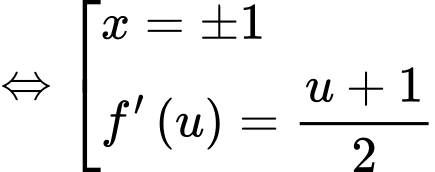

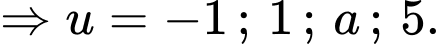
Ta xét:
 có:
có:
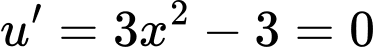
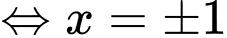

Từ bảng biến thiên ta suy ra PT
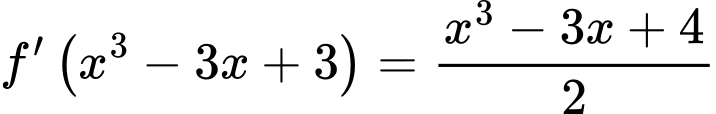 có 6 nghiệm bội lẻ phân biệt.
có 6 nghiệm bội lẻ phân biệt.
Vậy
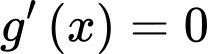 có tổng 8 nghiệm phân biệt bội lẻ.
có tổng 8 nghiệm phân biệt bội lẻ.
Suy ra, hàm số bài cho có 8 điểm cực trị.
Đáp án: D. Đáp án: D
Câu 13 [677035]: Cho hàm số bậc ba 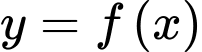 có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình 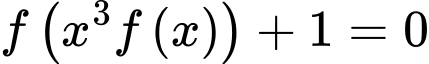 là
là
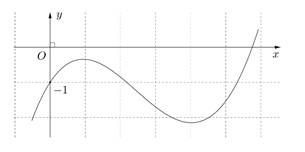
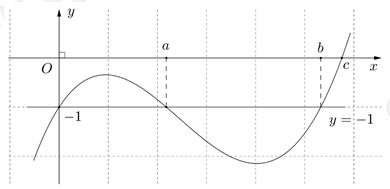
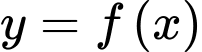 có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình 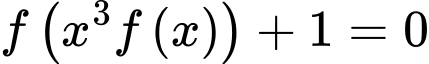 là
là 
A, 8.
B, 5.
C, 6.
D, 4.
Ta có 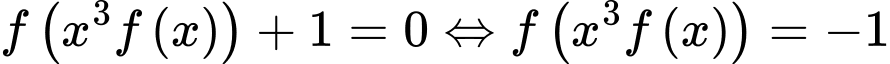
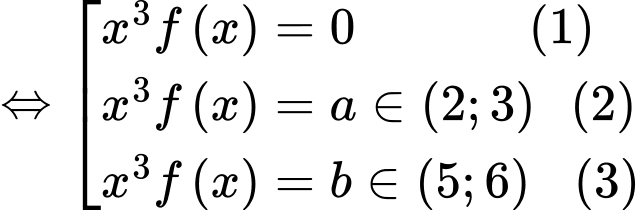
Ta có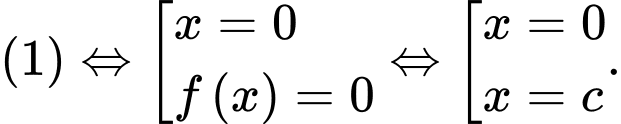
Xét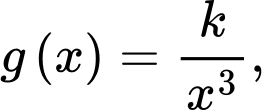 với
với  Ta có
Ta có 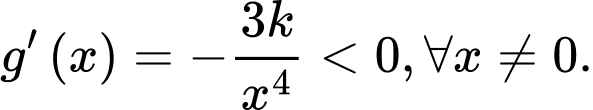
Bảng biến thiên
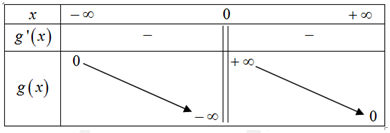
Với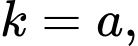 dựa vào đồ thị suy ra phương trình (2) có hai nghiệm phân biệt khác 0 và
dựa vào đồ thị suy ra phương trình (2) có hai nghiệm phân biệt khác 0 và 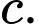
Với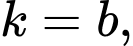 dựa vào đồ thị suy ra phương trình (3) có hai nghiệm phân biệt khác
dựa vào đồ thị suy ra phương trình (3) có hai nghiệm phân biệt khác 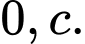 và khác hai nghiệm của phương trình (2).
và khác hai nghiệm của phương trình (2).
Vậy phương trình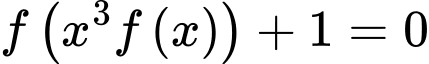 có 6 nghiệm phân biệt. Đáp án: C
có 6 nghiệm phân biệt. Đáp án: C
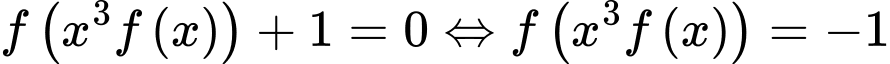
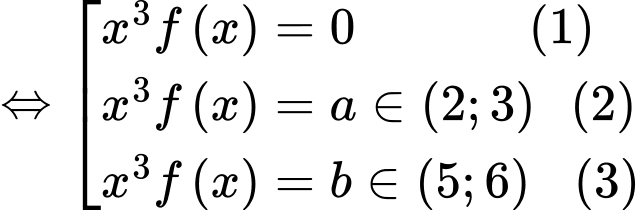

Ta có
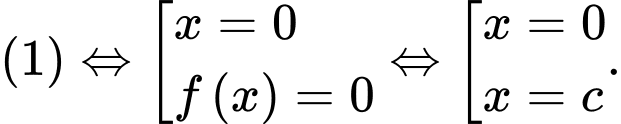
Xét
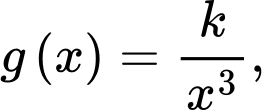 với
với  Ta có
Ta có 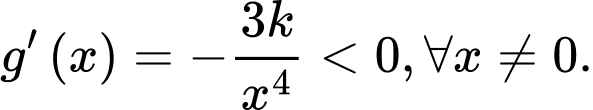
Bảng biến thiên

Với
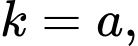 dựa vào đồ thị suy ra phương trình (2) có hai nghiệm phân biệt khác 0 và
dựa vào đồ thị suy ra phương trình (2) có hai nghiệm phân biệt khác 0 và 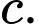
Với
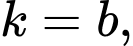 dựa vào đồ thị suy ra phương trình (3) có hai nghiệm phân biệt khác
dựa vào đồ thị suy ra phương trình (3) có hai nghiệm phân biệt khác 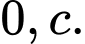 và khác hai nghiệm của phương trình (2).
và khác hai nghiệm của phương trình (2).
Vậy phương trình
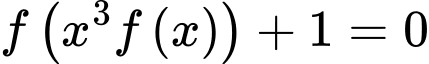 có 6 nghiệm phân biệt. Đáp án: C
có 6 nghiệm phân biệt. Đáp án: C
Câu 14 [677037]: Cho hàm số bậc bốn 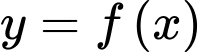 có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình 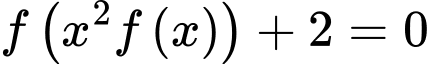 là
là
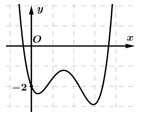
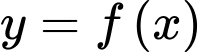 có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình 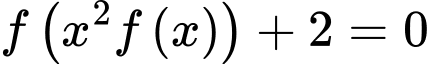 là
là 
A, 8.
B, 12.
C, 6.
D, 9.
Cách 1:
Ta có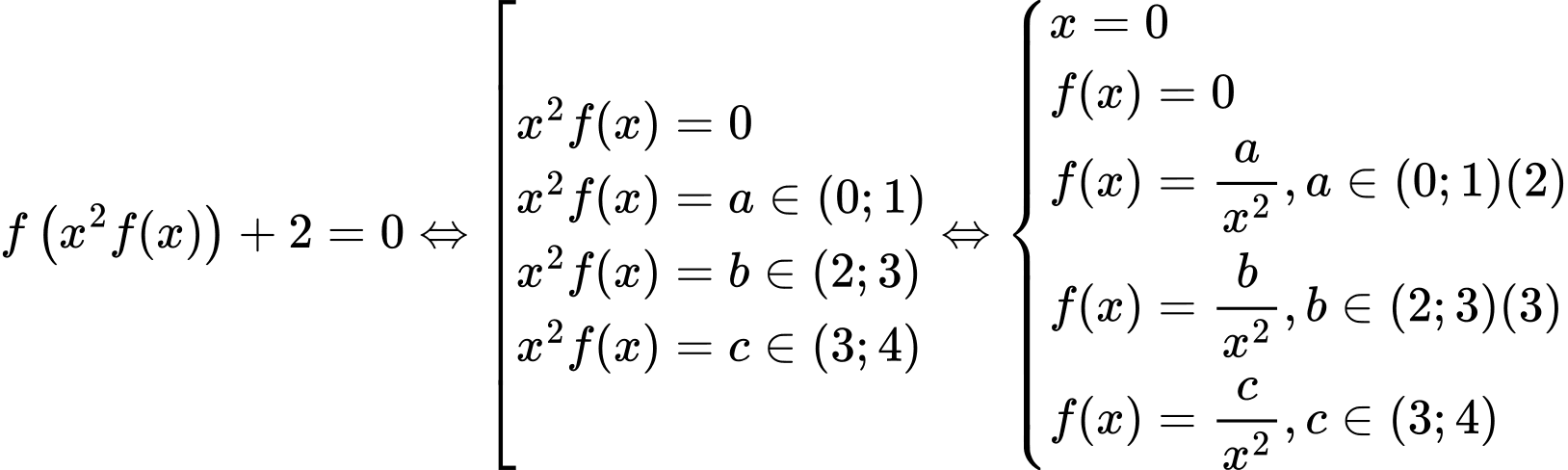
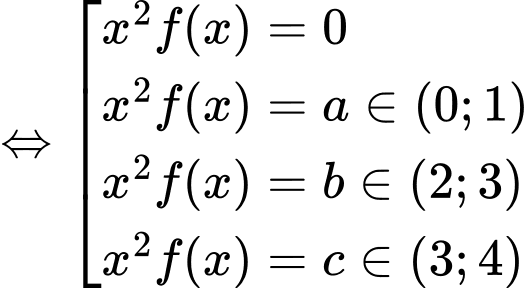
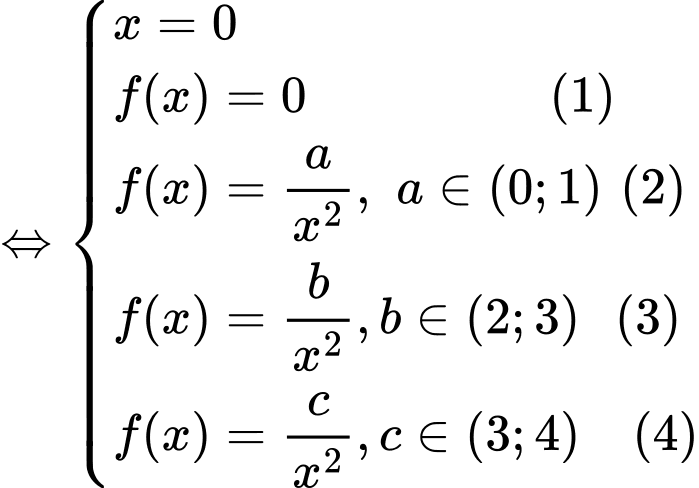
Xét hàm số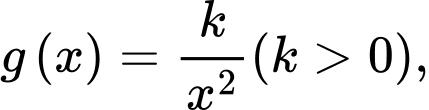 ta có
ta có 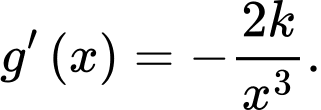
Bảng biến thiên
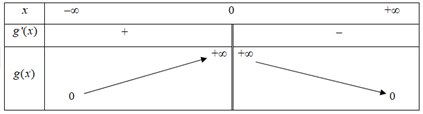
Đồ thị của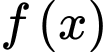 và
và 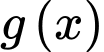 được mô tả như sau:
được mô tả như sau:
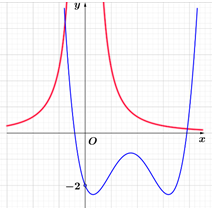
Do đó ta có: (1), (2), (3) và (4) mỗi phương trình có 2 nghiệm phân biệt.
Suy ra phương trình đã cho có 9 nghiệm. Đáp án: D
Ta có
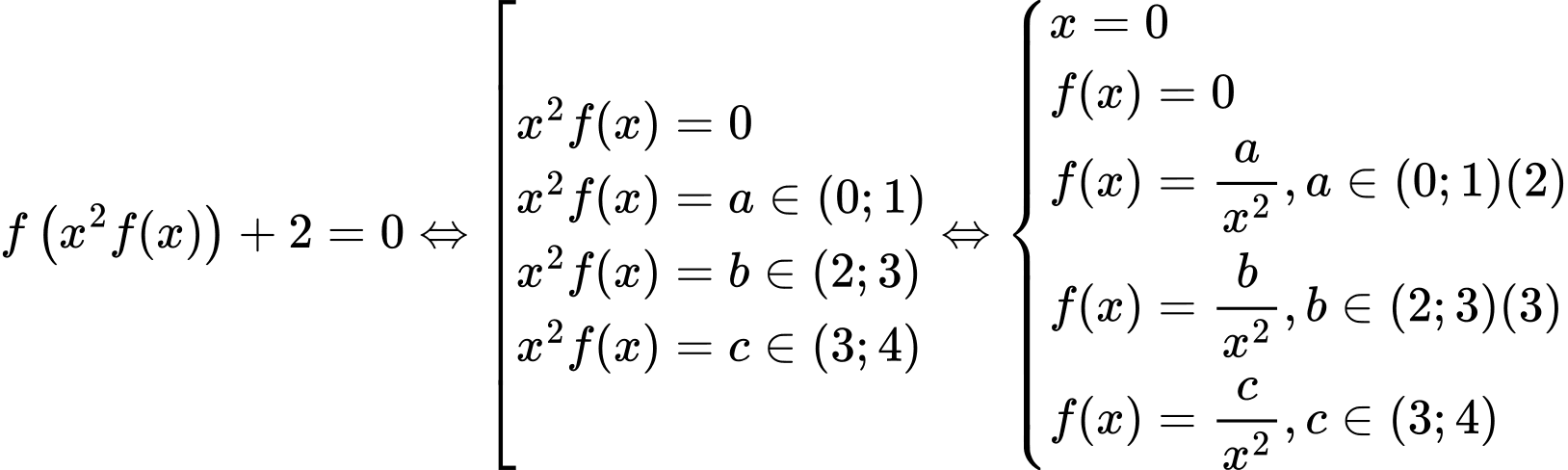
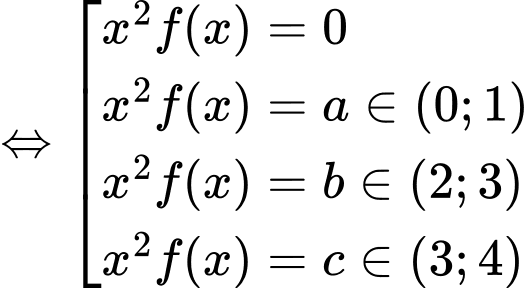
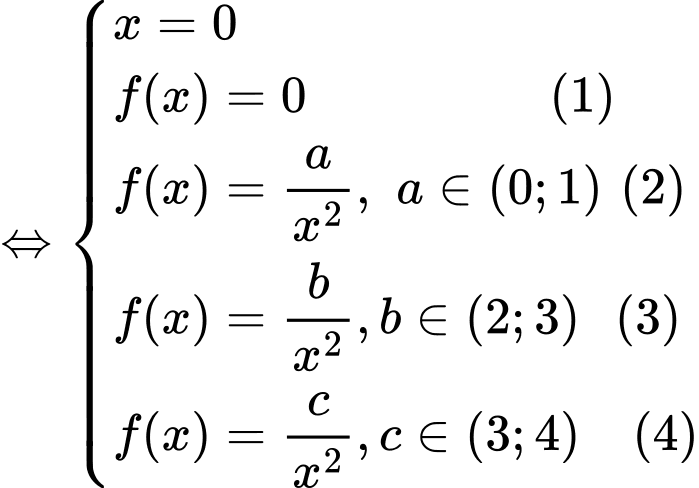
Xét hàm số
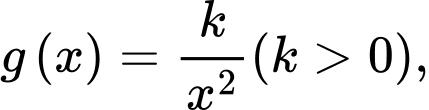 ta có
ta có 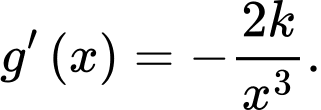
Bảng biến thiên

Đồ thị của
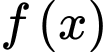 và
và 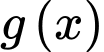 được mô tả như sau:
được mô tả như sau: 
Do đó ta có: (1), (2), (3) và (4) mỗi phương trình có 2 nghiệm phân biệt.
Suy ra phương trình đã cho có 9 nghiệm. Đáp án: D
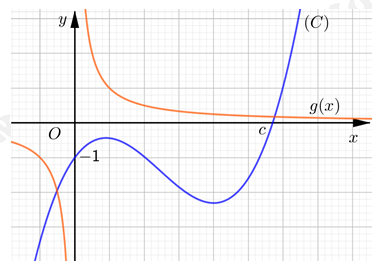
Câu 15 [398651]: Cho hàm số bậc ba 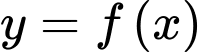 có đồ thị như hình vẽ. Phương trình
có đồ thị như hình vẽ. Phương trình 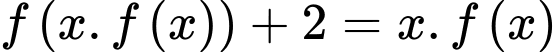 có bao nhiêu nghiệm thực phân biệt?
có bao nhiêu nghiệm thực phân biệt?
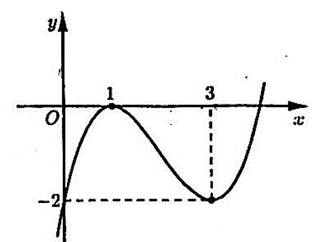
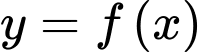 có đồ thị như hình vẽ. Phương trình
có đồ thị như hình vẽ. Phương trình 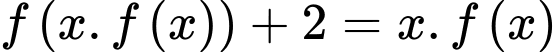 có bao nhiêu nghiệm thực phân biệt?
có bao nhiêu nghiệm thực phân biệt?

A, 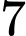 .
.
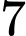 .
. B, 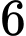 .
.
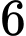 .
.C, 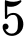 .
.
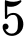 .
.D, 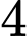 .
.
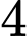 .
.
Gọi 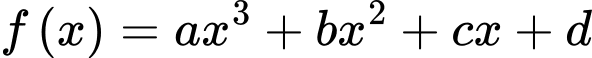 . Từ đồ thị hàm số ta suy ra:
. Từ đồ thị hàm số ta suy ra: 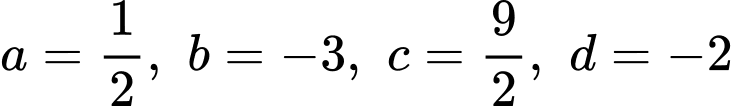 nên
nên 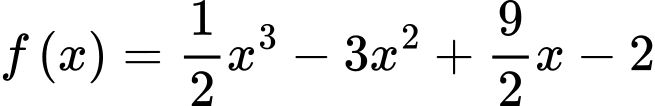 .
Đặt
.
Đặt 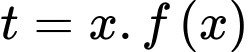 thì phương trình trở thành
thì phương trình trở thành 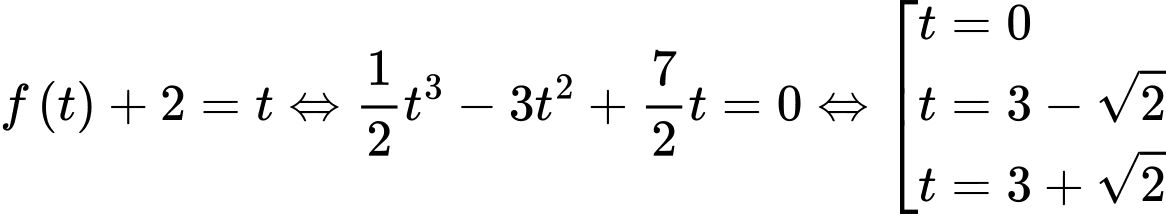 .
Với
.
Với 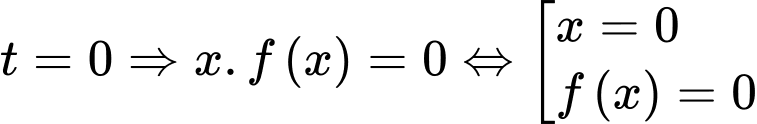 có
có 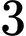 nghiệm phân biệt.
Với
nghiệm phân biệt.
Với 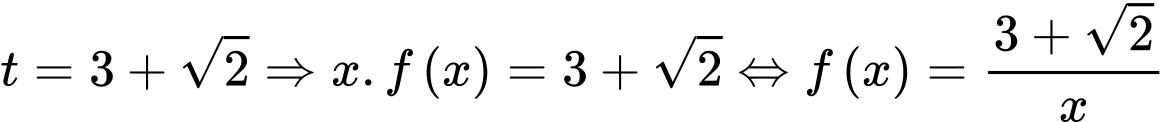 có
có 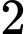 nghiệm phân biệt.
Với
nghiệm phân biệt.
Với 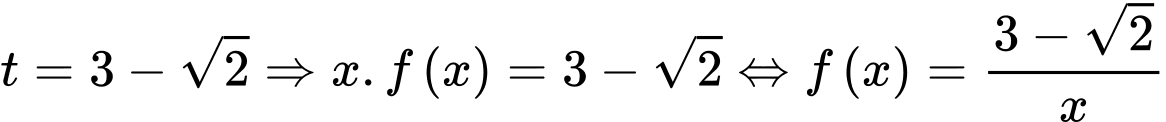 có
có 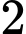 nghiệm phân biệt.
Vậy phương trình
nghiệm phân biệt.
Vậy phương trình 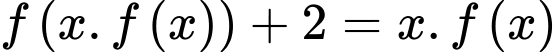 có
có 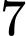 nghiệm phân biệt. Đáp án: A
nghiệm phân biệt. Đáp án: A
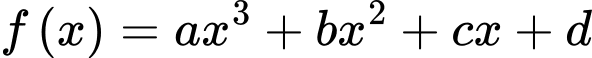 . Từ đồ thị hàm số ta suy ra:
. Từ đồ thị hàm số ta suy ra: 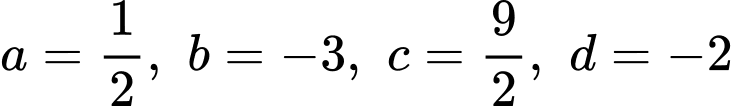 nên
nên 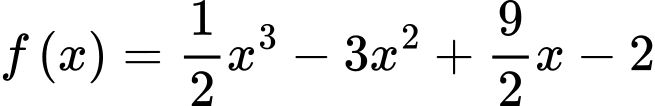 .
Đặt
.
Đặt 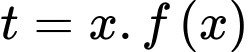 thì phương trình trở thành
thì phương trình trở thành 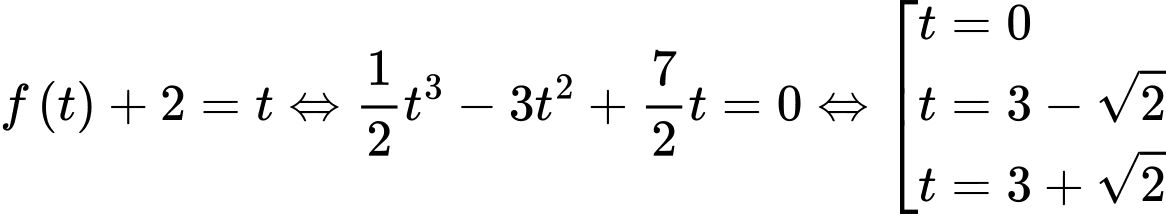 .
Với
.
Với 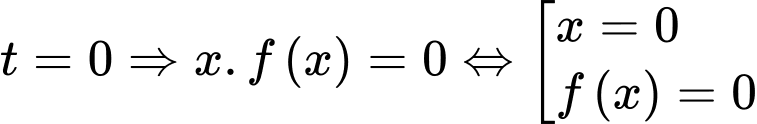 có
có 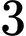 nghiệm phân biệt.
Với
nghiệm phân biệt.
Với 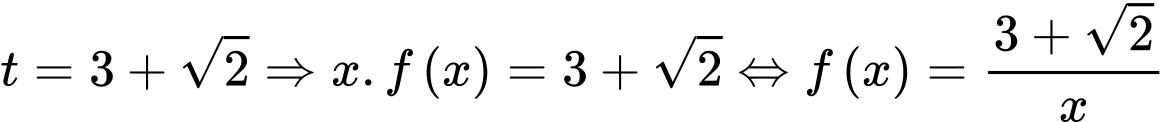 có
có 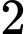 nghiệm phân biệt.
Với
nghiệm phân biệt.
Với 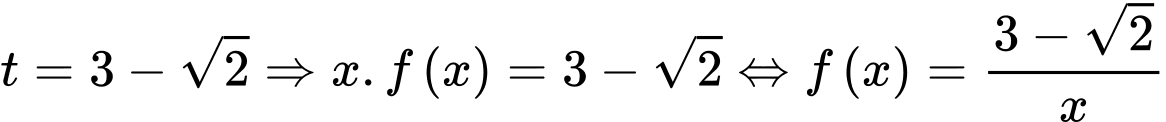 có
có 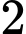 nghiệm phân biệt.
Vậy phương trình
nghiệm phân biệt.
Vậy phương trình 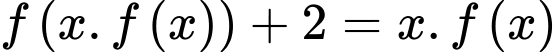 có
có 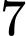 nghiệm phân biệt. Đáp án: A
nghiệm phân biệt. Đáp án: A
Câu 16 [31460]: Cho hàm số 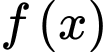 có đồ thị hàm số
có đồ thị hàm số 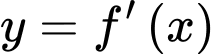 được cho như hình vẽ bên. Hàm số
được cho như hình vẽ bên. Hàm số 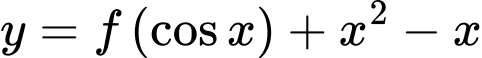 đồng biến trên khoảng
đồng biến trên khoảng
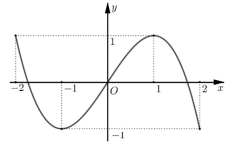
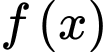 có đồ thị hàm số
có đồ thị hàm số 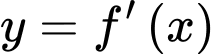 được cho như hình vẽ bên. Hàm số
được cho như hình vẽ bên. Hàm số 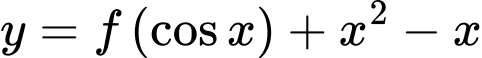 đồng biến trên khoảng
đồng biến trên khoảng
A, 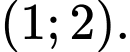
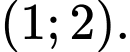
B, 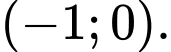
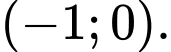
C, 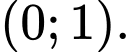
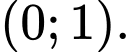
D, 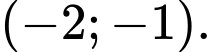
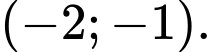
Đáp án A
Dựa theo đồ thị và kết hợp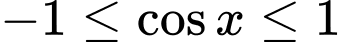
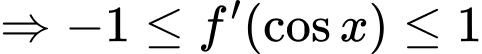
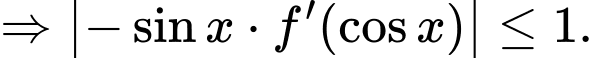
Khi đó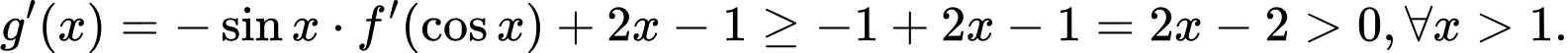
Vậy hàm số đồng biến trên (1;2). Đáp án: A
Dựa theo đồ thị và kết hợp
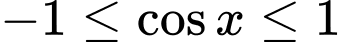
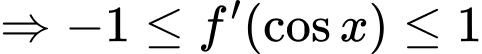
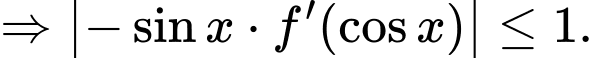
Khi đó
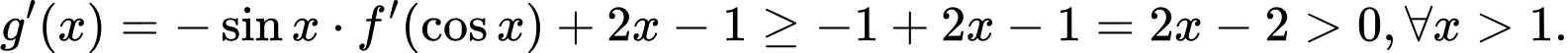
Vậy hàm số đồng biến trên (1;2). Đáp án: A
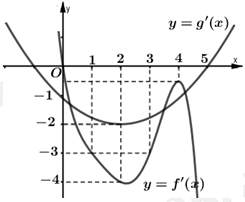
Câu 17 [789327]: Cho hàm số 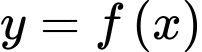 có đạo hàm trên
có đạo hàm trên  . Đường cong trong hình vẽ dưới đây là đồ thị của hàm số
. Đường cong trong hình vẽ dưới đây là đồ thị của hàm số 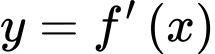 và
và 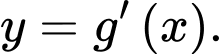 Hàm số
Hàm số 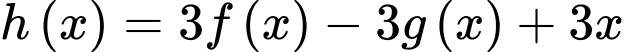 nghịch biến trên khoảng nào sau đây?
nghịch biến trên khoảng nào sau đây?
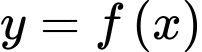 có đạo hàm trên
có đạo hàm trên 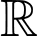 . Đường cong trong hình vẽ dưới đây là đồ thị của hàm số
. Đường cong trong hình vẽ dưới đây là đồ thị của hàm số 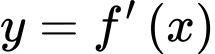 và
và 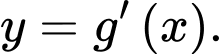 Hàm số
Hàm số 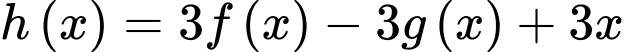 nghịch biến trên khoảng nào sau đây?
nghịch biến trên khoảng nào sau đây? 
A, 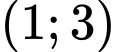 .
.
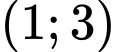 .
.B, 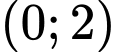 .
.
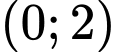 .
.C, 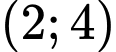 .
.
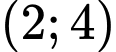 .
.D, 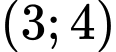 .
.
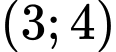 .
.
Chọn A
Có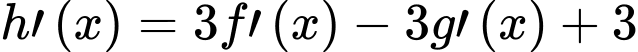
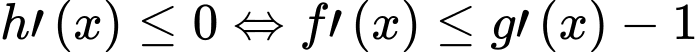
Tịnh tiến đồ thị hàm số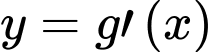 theo vectơ
theo vectơ 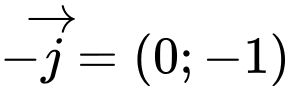 được đồ thị hàm số
được đồ thị hàm số 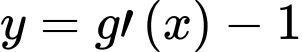 (như hình vẽ).
(như hình vẽ).
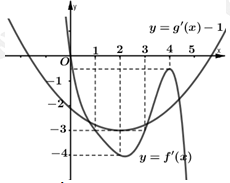
Dựa vào vị trí tương đối giữa 2 đồ thị hàm số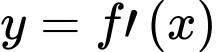 và
và 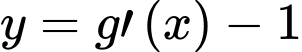 , ta có:
, ta có:
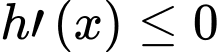 khi
khi  hoặc
hoặc 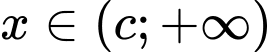 với
với 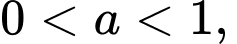
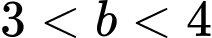 và
và 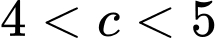 .
.
Có nên hàm số
nên hàm số 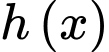 nghịch biến trên khoảng
nghịch biến trên khoảng 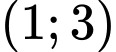 . Đáp án: A
. Đáp án: A
Có
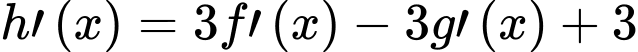
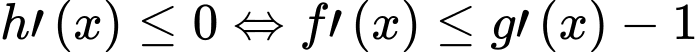
Tịnh tiến đồ thị hàm số
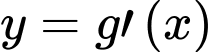 theo vectơ
theo vectơ 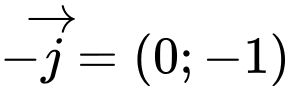 được đồ thị hàm số
được đồ thị hàm số 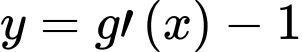 (như hình vẽ).
(như hình vẽ). 
Dựa vào vị trí tương đối giữa 2 đồ thị hàm số
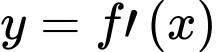 và
và 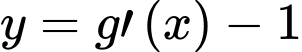 , ta có:
, ta có: 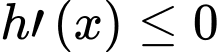 khi
khi  hoặc
hoặc 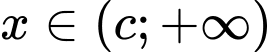 với
với 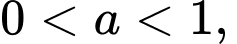
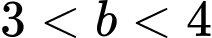 và
và 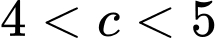 .
.Có
 nên hàm số
nên hàm số 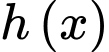 nghịch biến trên khoảng
nghịch biến trên khoảng 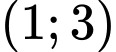 . Đáp án: A
. Đáp án: A