Đáp án Bài tập tự luyện
Câu 1 [518092]: Cho hàm số 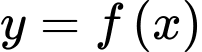 có bảng xét dấu của đạo hàm như sau.
có bảng xét dấu của đạo hàm như sau.

Hàm số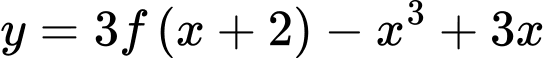 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
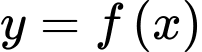 có bảng xét dấu của đạo hàm như sau.
có bảng xét dấu của đạo hàm như sau.
Hàm số
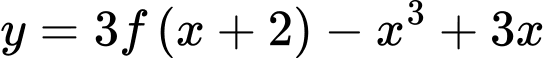 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 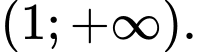
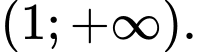
B, 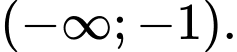
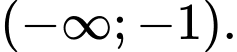
C, 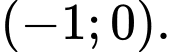
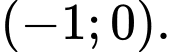
D, 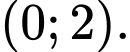
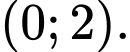
Ta có: 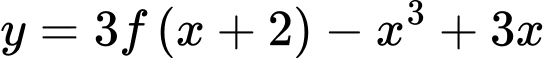
Đặt: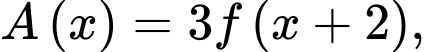
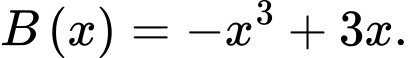
Ta xét: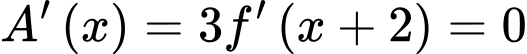
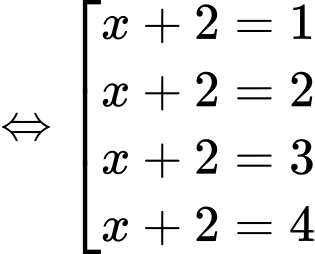
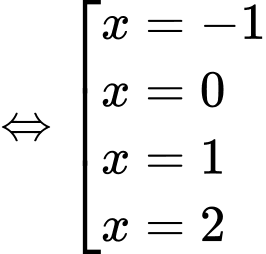
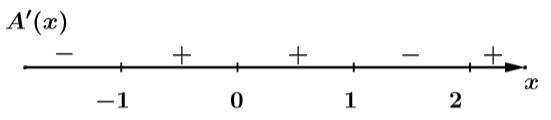
Xét: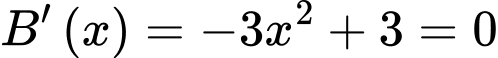
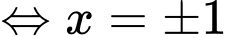
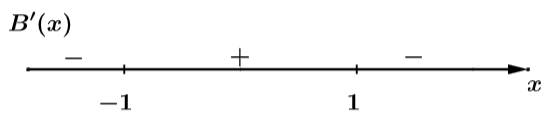
Có: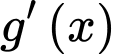
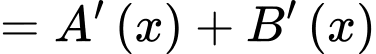
Dễ dàng thấy: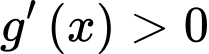 với mọi
với mọi 
Đáp án: C. Đáp án: C
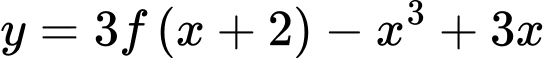
Đặt:
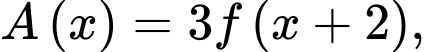
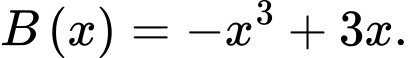
Ta xét:
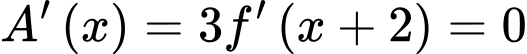
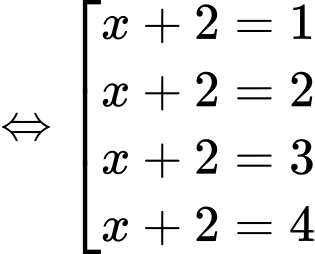
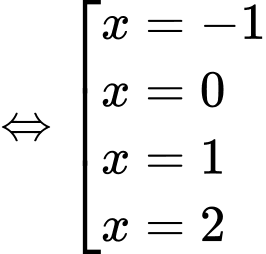
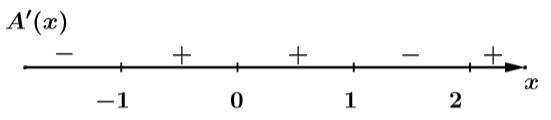
Xét:
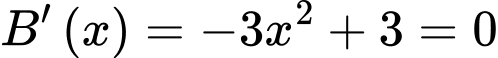
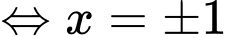

Có:
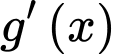
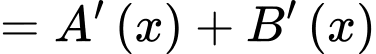
Dễ dàng thấy:
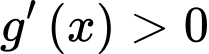 với mọi
với mọi 
Đáp án: C. Đáp án: C
Câu 2 [31790]: Cho hàm số 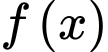 có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau:
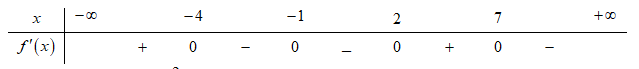
Hàm số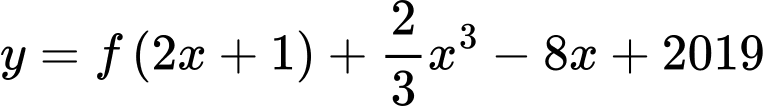 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
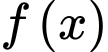 có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau: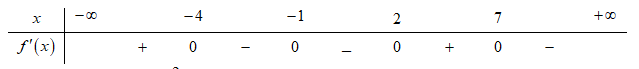
Hàm số
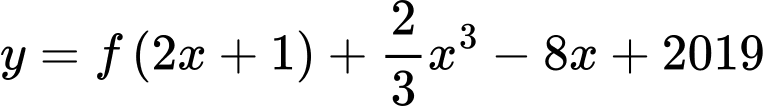 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 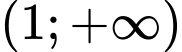 .
.
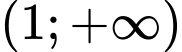 .
.B, 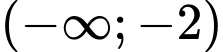 .
.
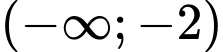 .
.C, 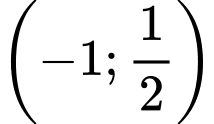 .
.
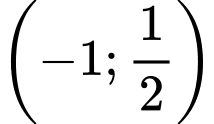 .
.D, 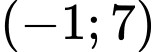 .
.
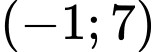 .
.
Đáp án C
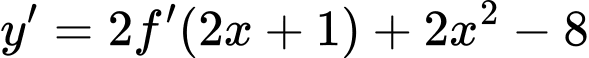
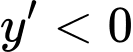
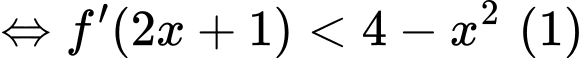
Đặt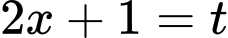
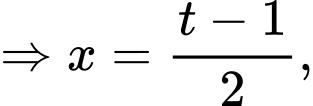 ta có:
ta có: 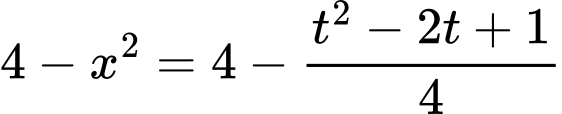
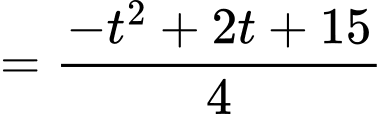
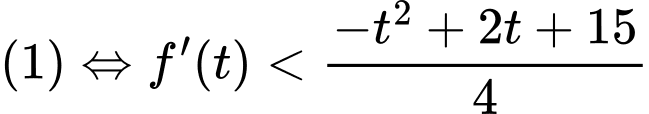
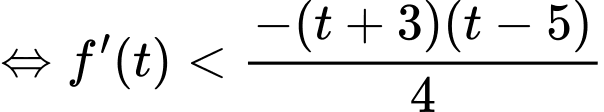
Khi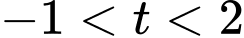 thì
thì 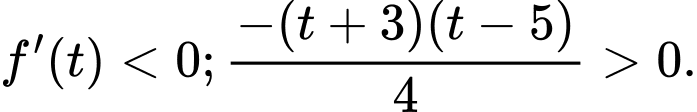 Khi đó
Khi đó 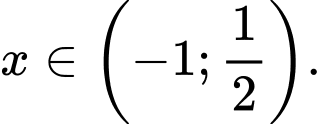 Đáp án: C
Đáp án: C
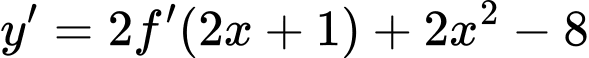
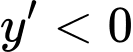
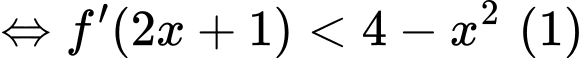
Đặt
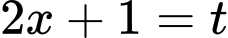
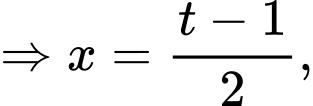 ta có:
ta có: 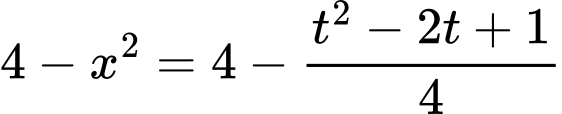
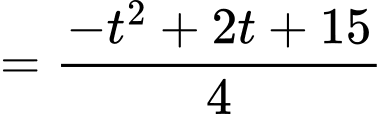
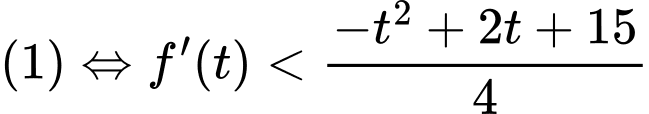
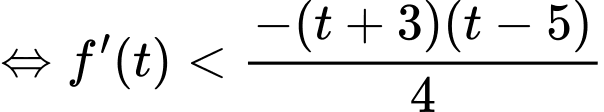
Khi
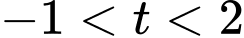 thì
thì 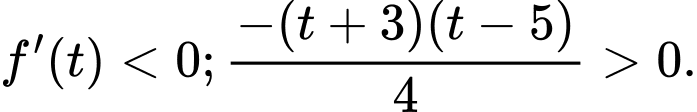 Khi đó
Khi đó 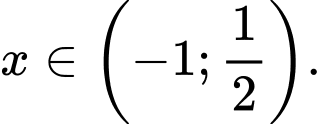 Đáp án: C
Đáp án: C
Câu 3 [521834]: Cho hàm số 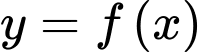 xác định trên
xác định trên 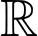 và có bảng xét dấu đạo hàm
và có bảng xét dấu đạo hàm 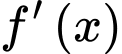 như hình vẽ.
như hình vẽ.
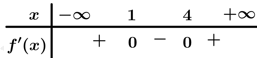
Hàm số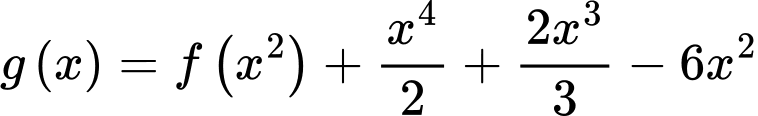 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
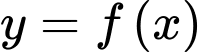 xác định trên
xác định trên 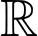 và có bảng xét dấu đạo hàm
và có bảng xét dấu đạo hàm 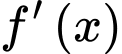 như hình vẽ.
như hình vẽ.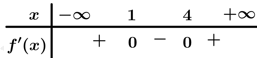
Hàm số
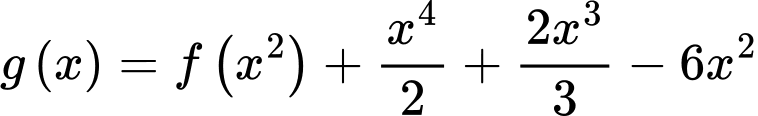 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 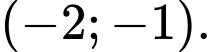
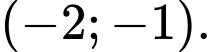
B, 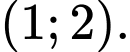
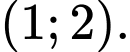
C, 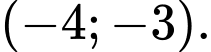
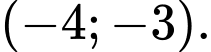
D, 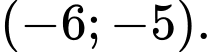
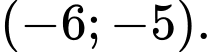
Ta có: 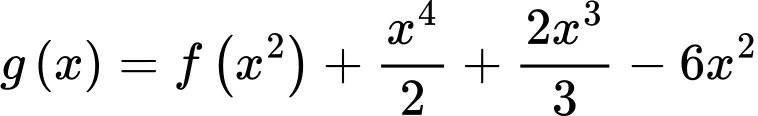
Đặt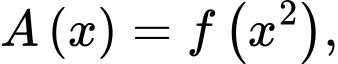
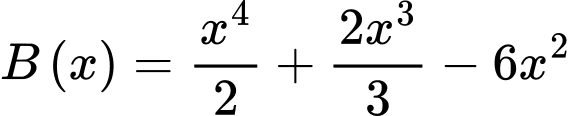
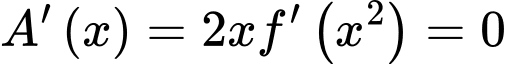
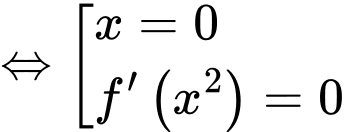
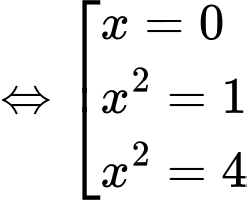
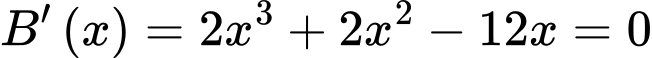
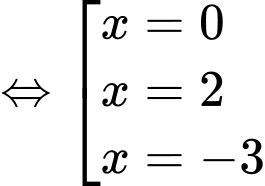
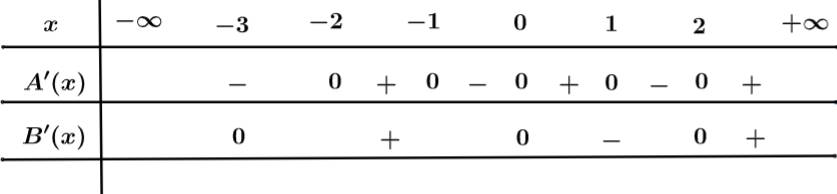
Từ bảng trên luôn lớn hơn 0 trên khoảng
luôn lớn hơn 0 trên khoảng 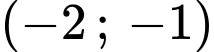 và
và 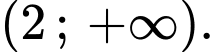
Vậy hàm số trên đồng biên trên khoảng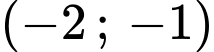 và
và 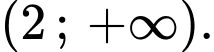
Đáp án: A. Đáp án: A
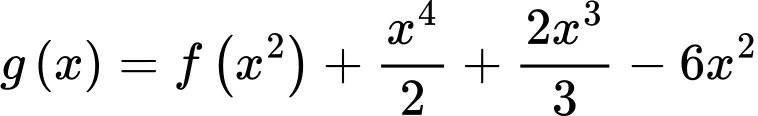
Đặt
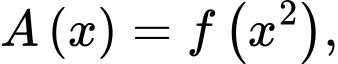
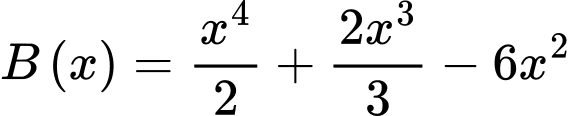
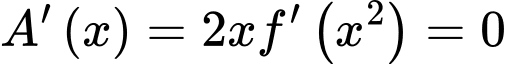
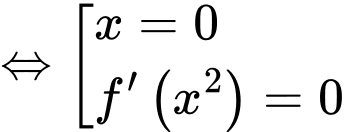
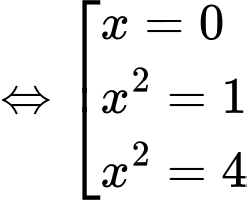
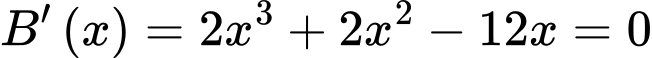
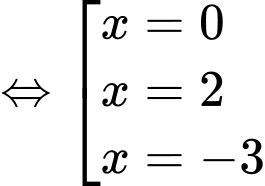

Từ bảng trên
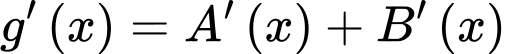 luôn lớn hơn 0 trên khoảng
luôn lớn hơn 0 trên khoảng 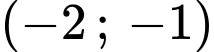 và
và 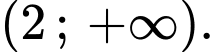
Vậy hàm số trên đồng biên trên khoảng
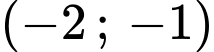 và
và 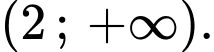
Đáp án: A. Đáp án: A
Câu 4 [31767]: Cho hàm số 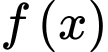 có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau:
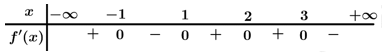
Hàm số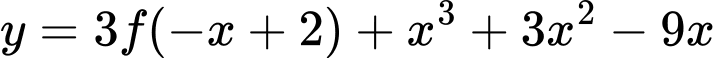 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
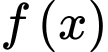 có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau: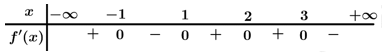
Hàm số
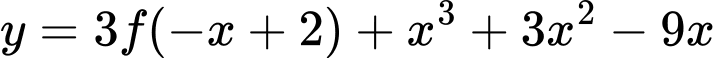 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 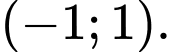
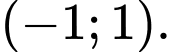
B, 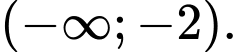
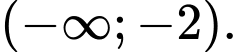
C, 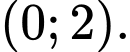
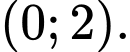
D, 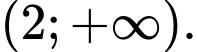
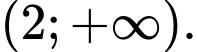
Ta có: 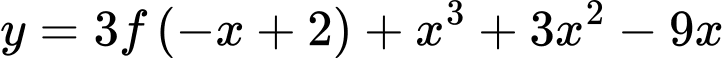
Đặt: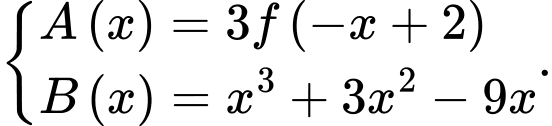
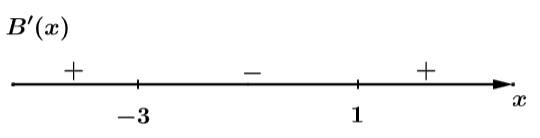
Ta xét: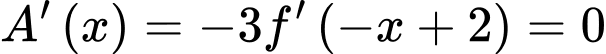
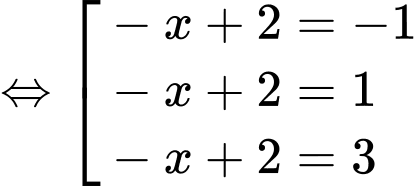
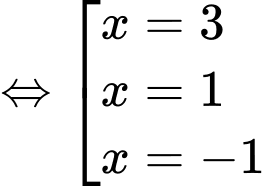
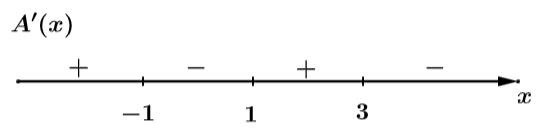
Ta xét: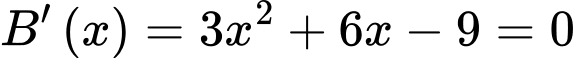
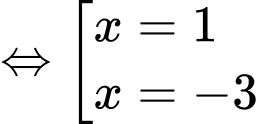
Có: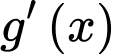
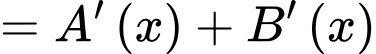
Dễ dàng thấy: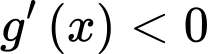 với mọi
với mọi 
Đáp án: A. Đáp án: A
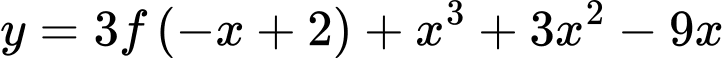
Đặt:
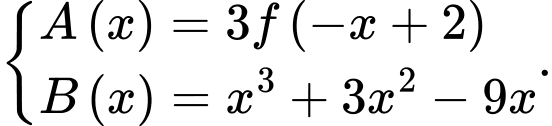
Ta xét:
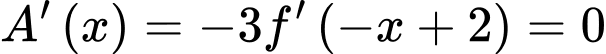
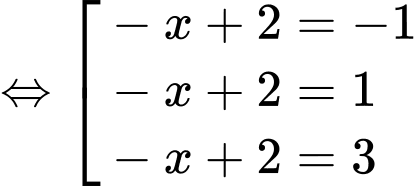
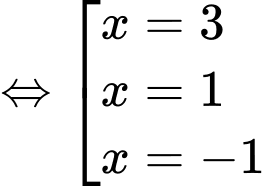

Ta xét:
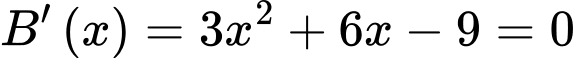
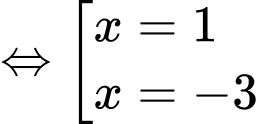

Có:
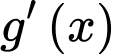
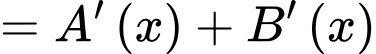
Dễ dàng thấy:
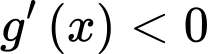 với mọi
với mọi 
Đáp án: A. Đáp án: A
Câu 5 [31783]: Cho hàm số 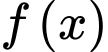 có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau:
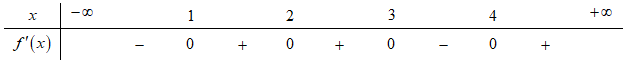
Hàm số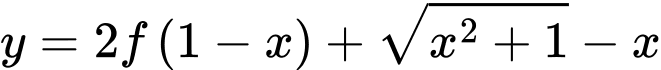 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
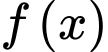 có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau: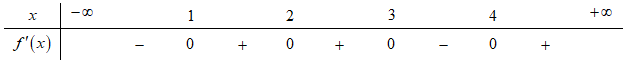
Hàm số
 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A,  .
.
 .
.B,  .
.
 .
.C, 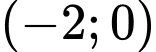 .
.
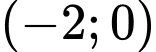 .
.D, 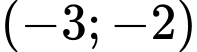 .
.
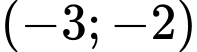 .
.
Đáp án C
Ta có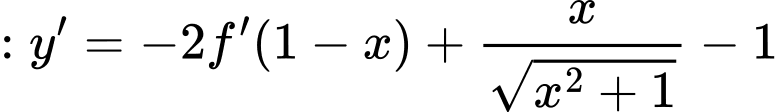
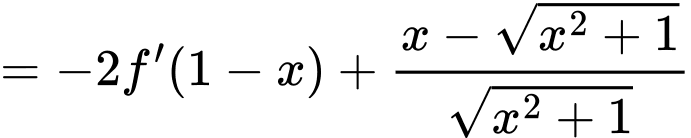
Chú ý :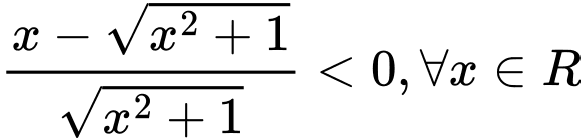
+) Với
 (loại vì không thể kết luận được)
(loại vì không thể kết luận được)
+) Với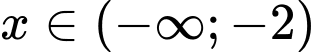
 (loại vì không thể kết luận được)
(loại vì không thể kết luận được)
+) Với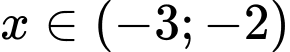
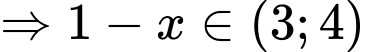 (loại vì không thể kết luận được)
(loại vì không thể kết luận được)
+) Với
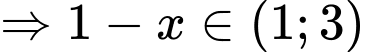
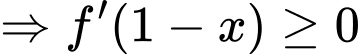
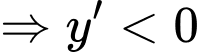 (thỏa mãn). Đáp án: C
(thỏa mãn). Đáp án: C
Ta có
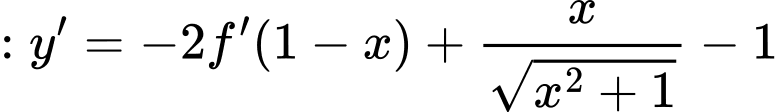
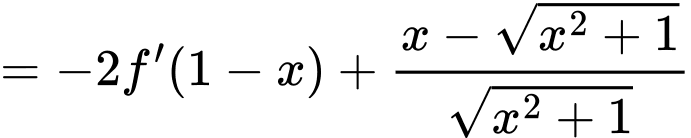
Chú ý :
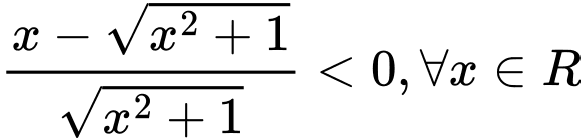
+) Với

 (loại vì không thể kết luận được)
(loại vì không thể kết luận được)
+) Với
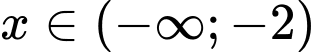
 (loại vì không thể kết luận được)
(loại vì không thể kết luận được)
+) Với
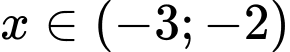
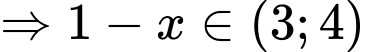 (loại vì không thể kết luận được)
(loại vì không thể kết luận được)
+) Với

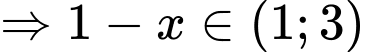
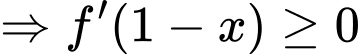
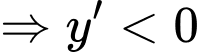 (thỏa mãn). Đáp án: C
(thỏa mãn). Đáp án: C
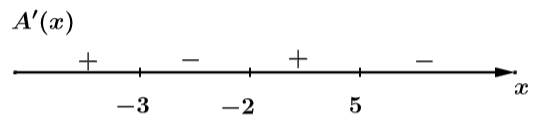
Câu 6 [518097]: Cho hàm số 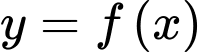 có bảng xét dấu của đạo hàm như hình vẽ.
có bảng xét dấu của đạo hàm như hình vẽ.
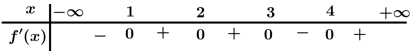
Biết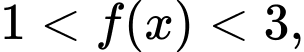 với mọi
với mọi 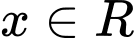 . Hàm số
. Hàm số 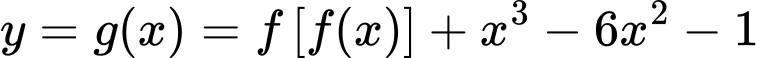 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
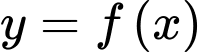 có bảng xét dấu của đạo hàm như hình vẽ.
có bảng xét dấu của đạo hàm như hình vẽ.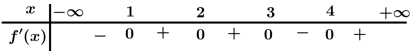
Biết
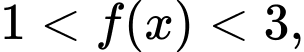 với mọi
với mọi 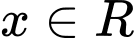 . Hàm số
. Hàm số 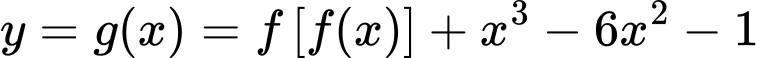 nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây? A, 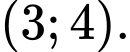
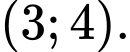
B, 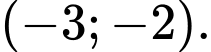
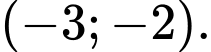
C, 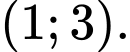
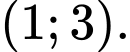
D, 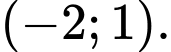
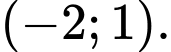
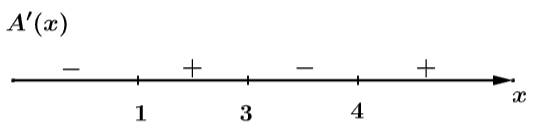
Ta có: 
Đặt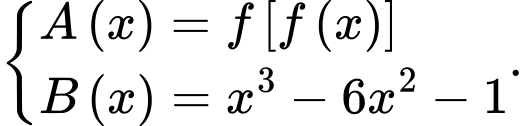
Xét: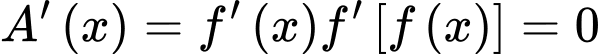
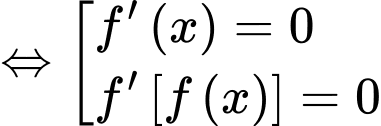
Dựa vào bảng biến thiên bài cho ta có:
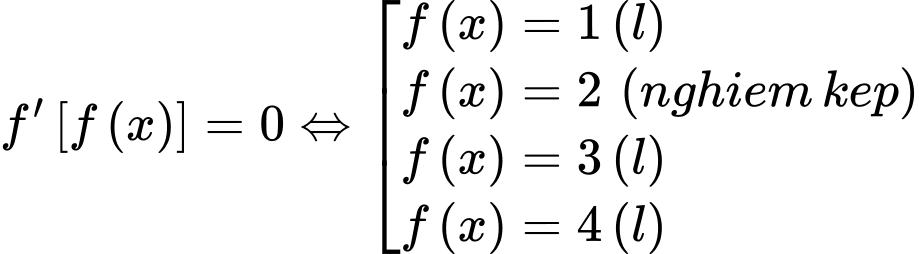
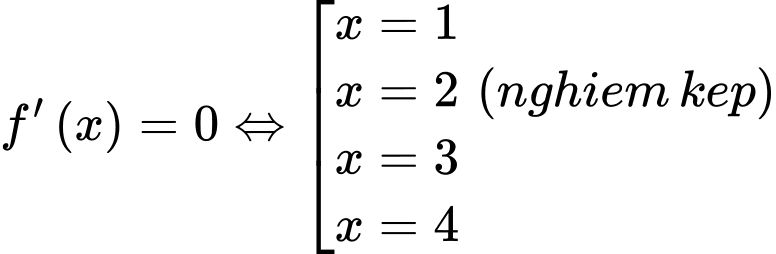
Xét: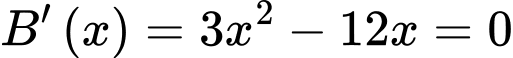


Có: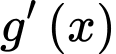
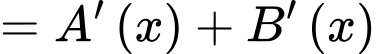
Dễ dàng thấy: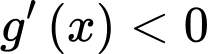 với mọi
với mọi 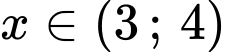
Đáp án: A. Đáp án: A

Đặt
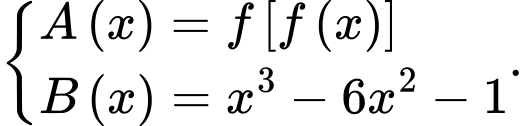
Xét:
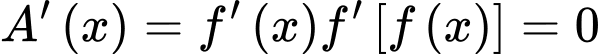
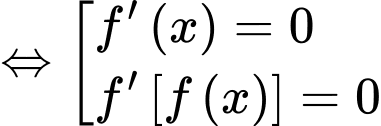
Dựa vào bảng biến thiên bài cho ta có:
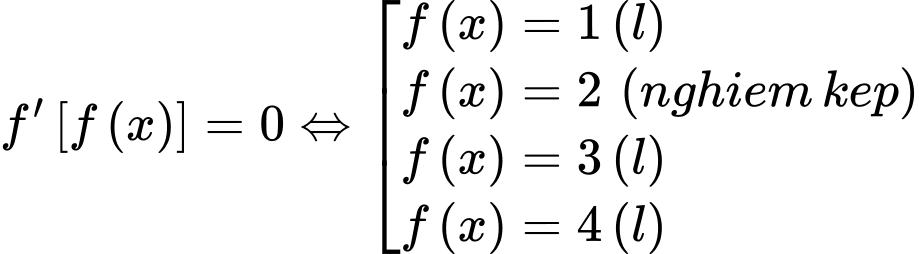
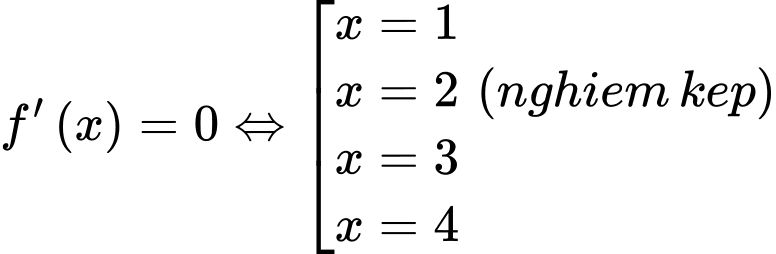

Xét:
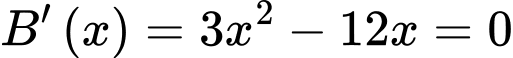


Có:
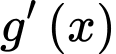
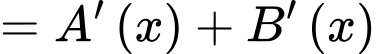
Dễ dàng thấy:
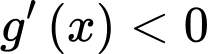 với mọi
với mọi 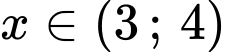
Đáp án: A. Đáp án: A
Câu 7 [518098]: Cho hàm số  và có bảng xét dấu đạo hàm như sau:
và có bảng xét dấu đạo hàm như sau:
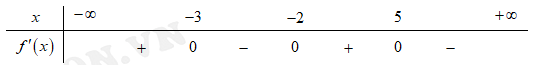
Hàm số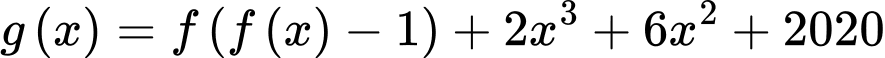 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
 và có bảng xét dấu đạo hàm như sau:
và có bảng xét dấu đạo hàm như sau: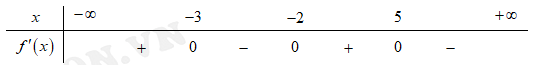
Hàm số
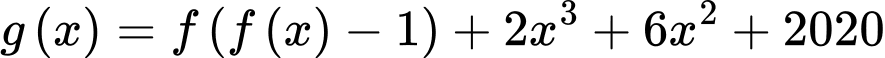 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 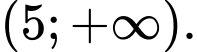
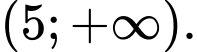
B, 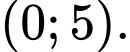
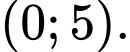
C, 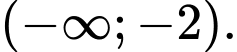
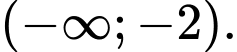
D, 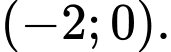
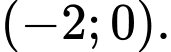
Ta có: 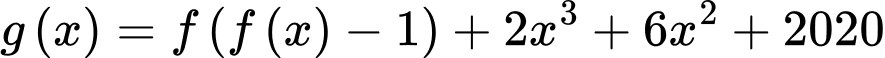
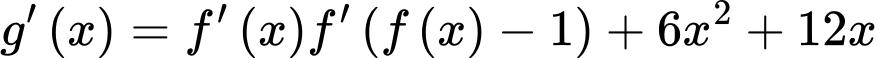
Đặt: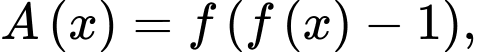
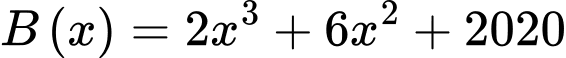
Xét: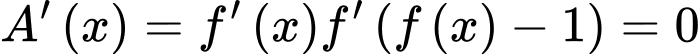
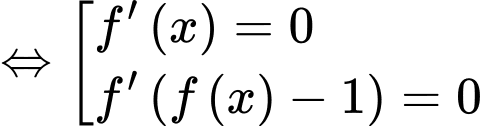
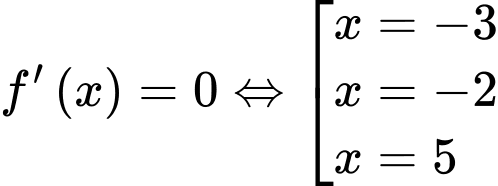
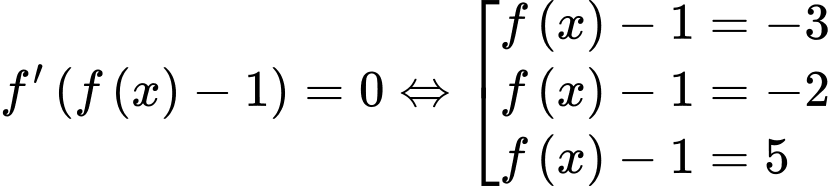
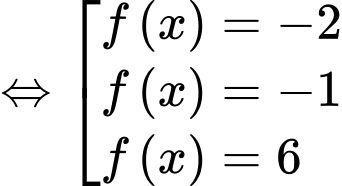 (loại vì
(loại vì 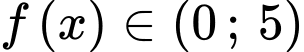 )
)
Ta có: luôn dương vì
luôn dương vì 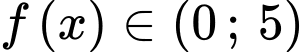
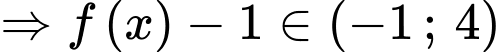
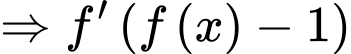 mang dấu dương.
mang dấu dương.
Xét: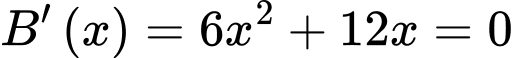
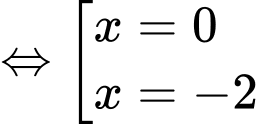
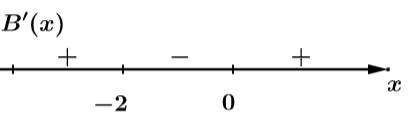
Có: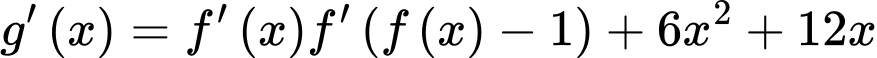
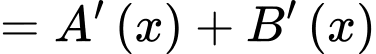
Dễ dàng thấy: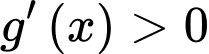 với mọi
với mọi 
Đáp án: B. Đáp án: B
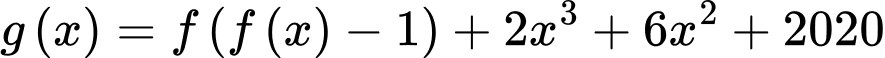
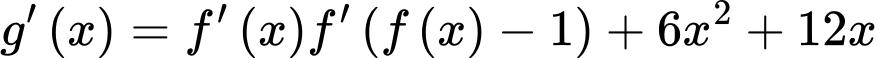
Đặt:
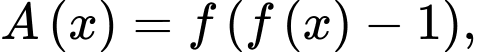
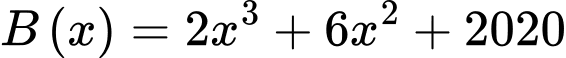
Xét:
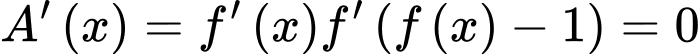
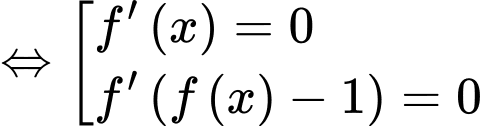
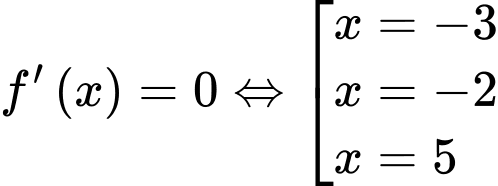
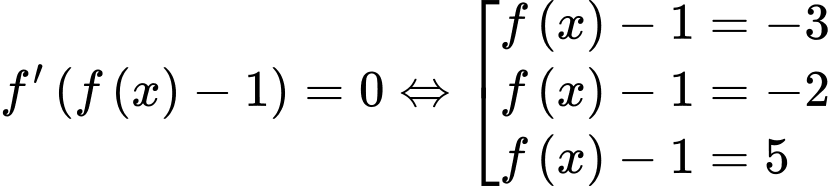
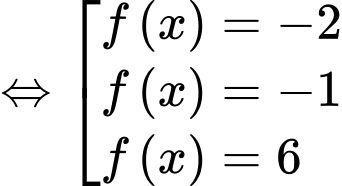 (loại vì
(loại vì 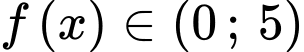 )
)
Ta có:
 luôn dương vì
luôn dương vì 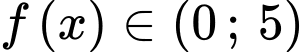
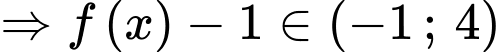
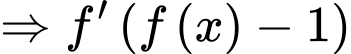 mang dấu dương.
mang dấu dương.
Xét:
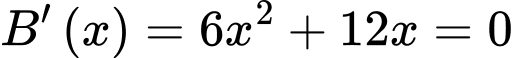
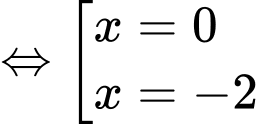

Có:
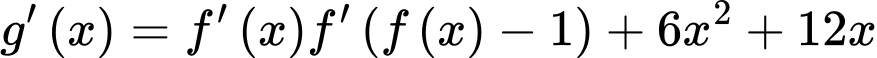
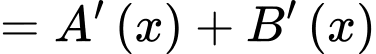
Dễ dàng thấy:
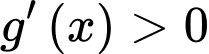 với mọi
với mọi 
Đáp án: B. Đáp án: B
Câu 8 [791660]: (Chuyên Hưng Yên - 2020) Cho hàm số 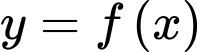 có đạo hàm đến cấp hai trên
có đạo hàm đến cấp hai trên  và có bảng xét dấu của hàm số
và có bảng xét dấu của hàm số 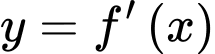 như hình sau
như hình sau
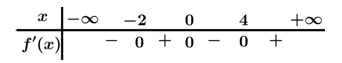
Hỏi hàm số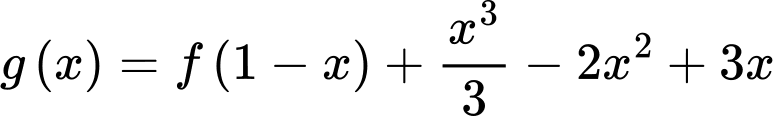 đạt cực tiểu tại điểm nào trong các điểm sau?
đạt cực tiểu tại điểm nào trong các điểm sau?
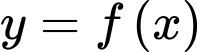 có đạo hàm đến cấp hai trên
có đạo hàm đến cấp hai trên 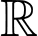 và có bảng xét dấu của hàm số
và có bảng xét dấu của hàm số 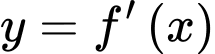 như hình sau
như hình sau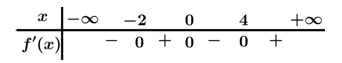
Hỏi hàm số
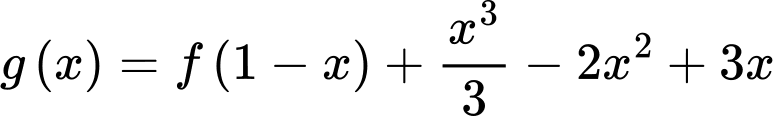 đạt cực tiểu tại điểm nào trong các điểm sau?
đạt cực tiểu tại điểm nào trong các điểm sau? A, 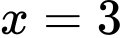 .
.
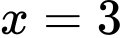 .
.B, 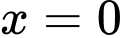 .
.
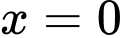 .
.C, 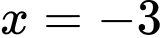 .
.
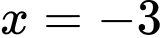 .
.D, 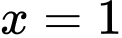 .
.
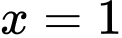 .
.
Chọn A
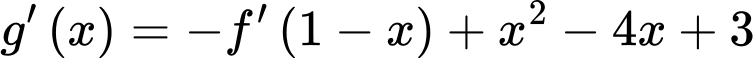 .
.
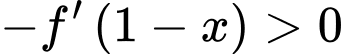
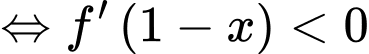
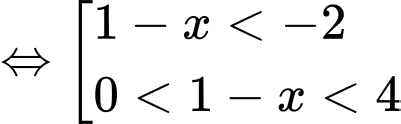
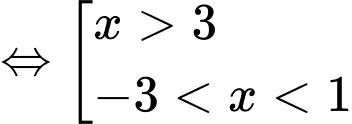
Bảng xét dấu :
:
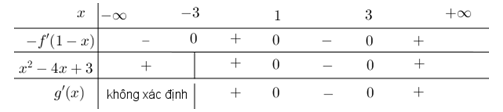
Từ bảng xét dấu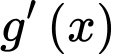 ta suy ra hàm số đạt cực tiểu tại
ta suy ra hàm số đạt cực tiểu tại 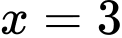 . Đáp án: A
. Đáp án: A
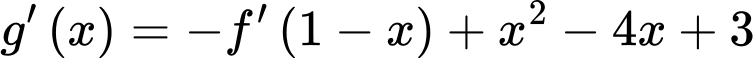 .
.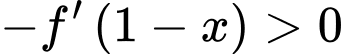
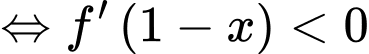
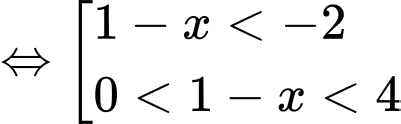
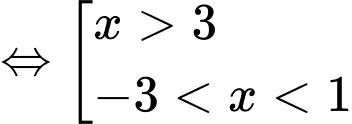
Bảng xét dấu
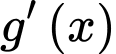 :
:
Từ bảng xét dấu
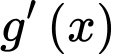 ta suy ra hàm số đạt cực tiểu tại
ta suy ra hàm số đạt cực tiểu tại 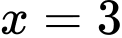 . Đáp án: A
. Đáp án: A
Câu 9 [521838]: Cho hàm số 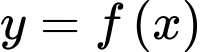 có đạo hàm liên tục trên
có đạo hàm liên tục trên 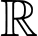 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
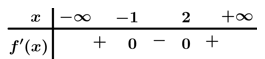
Hàm số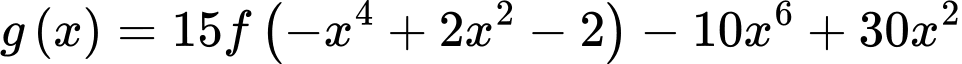 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
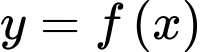 có đạo hàm liên tục trên
có đạo hàm liên tục trên 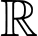 và có bảng biến thiên như sau:
và có bảng biến thiên như sau: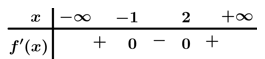
Hàm số
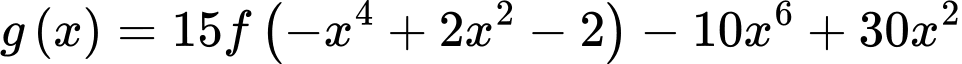 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 2.
B, 3.
C, 7.
D, 5.
Ta có: 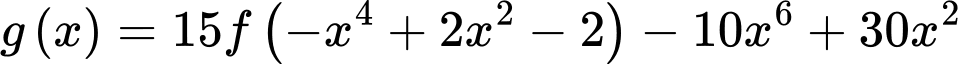
Đặt: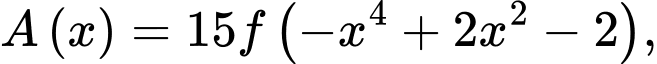
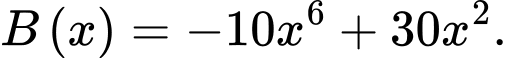
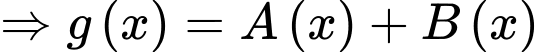
Xét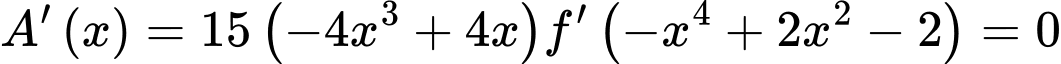
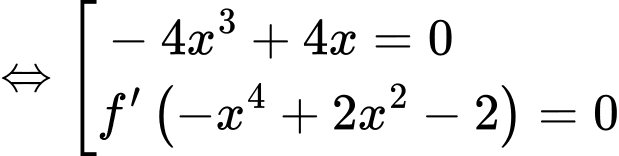
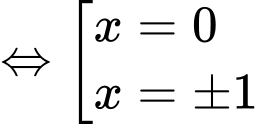
Xét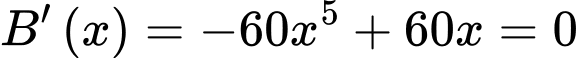
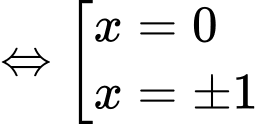
Ta có BBT:
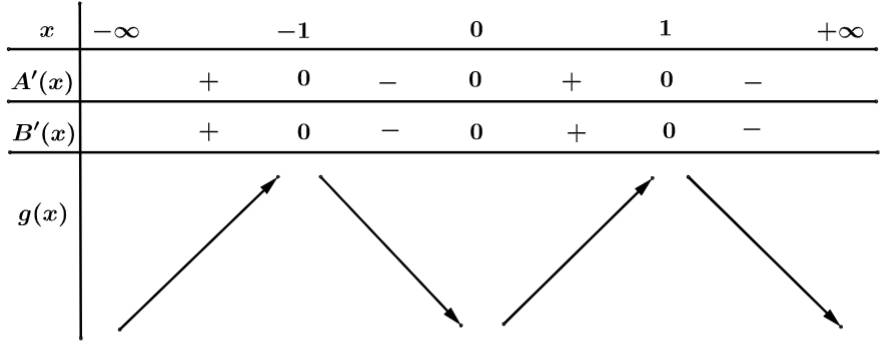
Từ bảng biến thiên, suy ra pt có 3 điểm cực trị.
Đáp án: B. Đáp án: B
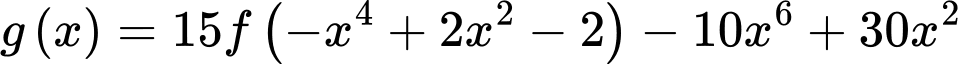
Đặt:
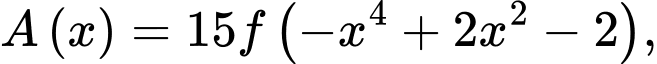
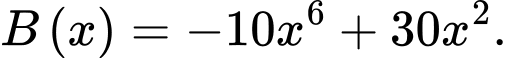
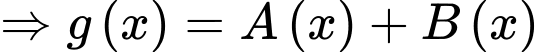
Xét
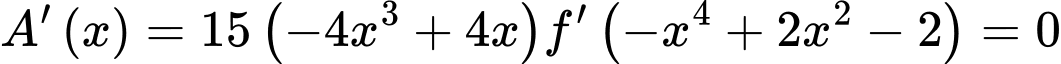
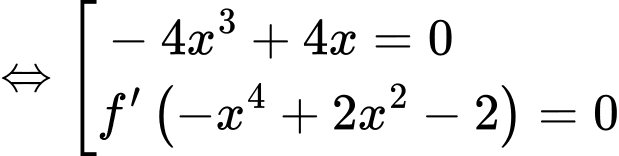
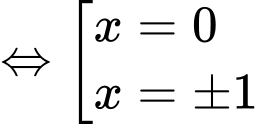
Xét
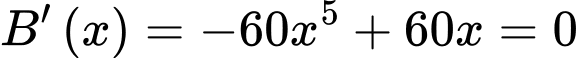
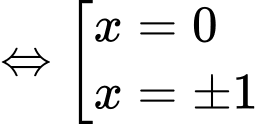
Ta có BBT:

Từ bảng biến thiên, suy ra pt có 3 điểm cực trị.
Đáp án: B. Đáp án: B
Câu 10 [521839]: Cho hàm số 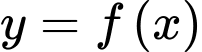 có đạo hàm liên tục trên
có đạo hàm liên tục trên 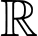 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
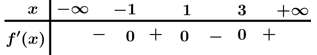
Hàm số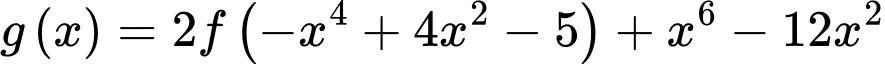 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
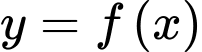 có đạo hàm liên tục trên
có đạo hàm liên tục trên 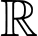 và có bảng biến thiên như sau:
và có bảng biến thiên như sau: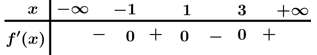
Hàm số
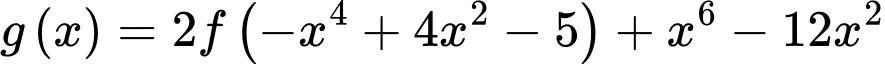 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 2.
B, 3.
C, 7.
D, 5.
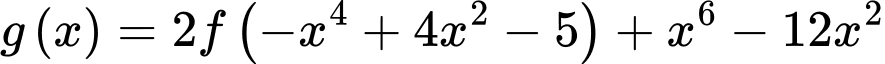
Đặt:
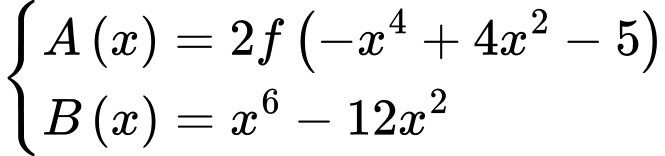
Xét
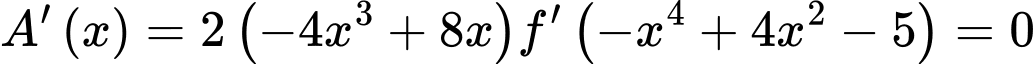
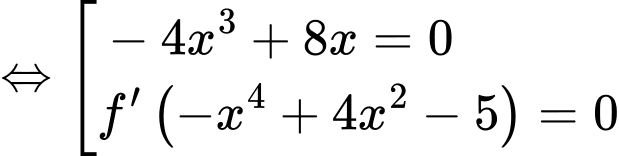
+)
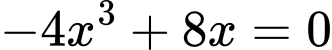
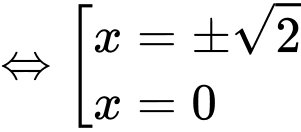
+)
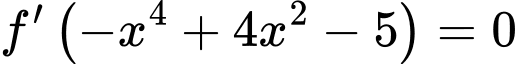
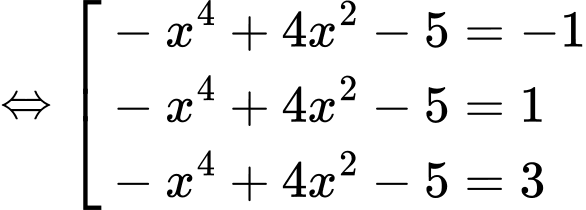
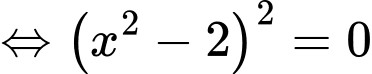
Xét
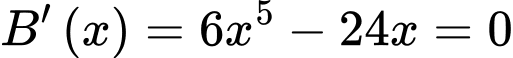
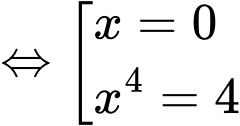
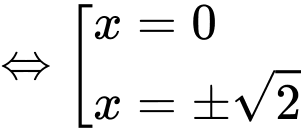
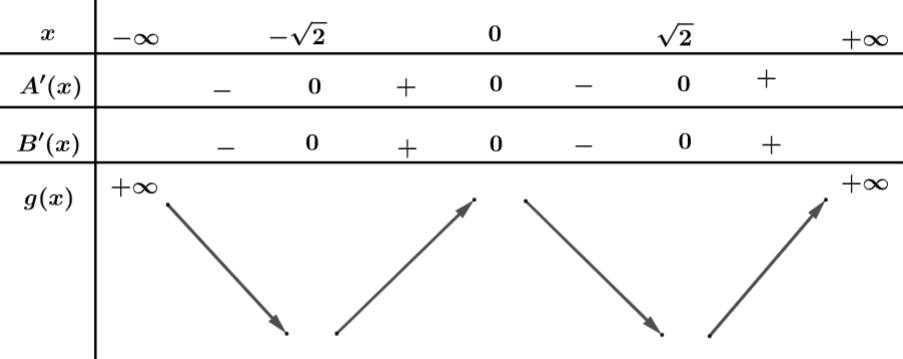
Vậy hàm có 3 cực trị.
Đáp án: B. Đáp án: B
Câu 11 [33130]: Cho hàm số 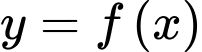 có bảng biến thiên như sau
có bảng biến thiên như sau
Tìm giá trị lớn nhất của hàm số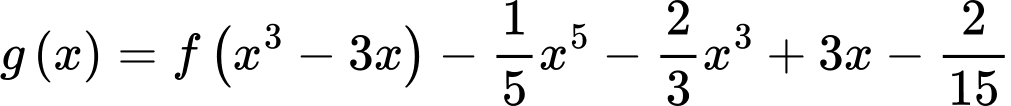 trên đoạn
trên đoạn 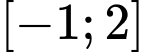 .
.
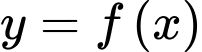 có bảng biến thiên như sau
có bảng biến thiên như sau
Tìm giá trị lớn nhất của hàm số
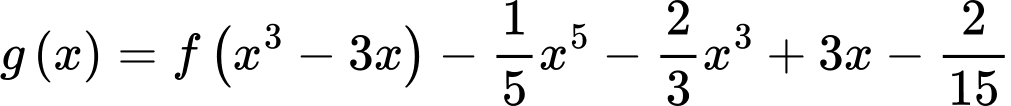 trên đoạn
trên đoạn 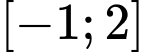 .
. A, 2022.
B, 2019.
C, 2020.
D, 2021.
Đáp án D
Ta có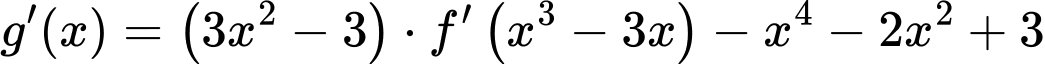
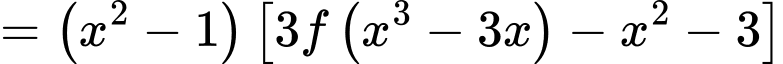
Với ta có
ta có 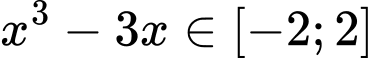 v
v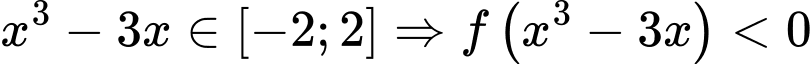
Suy ra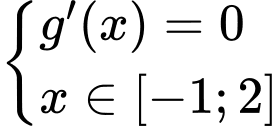
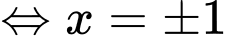
Suy ra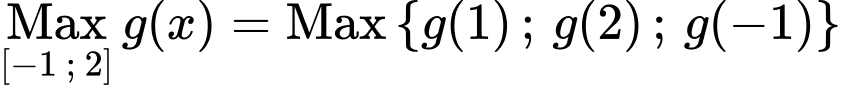
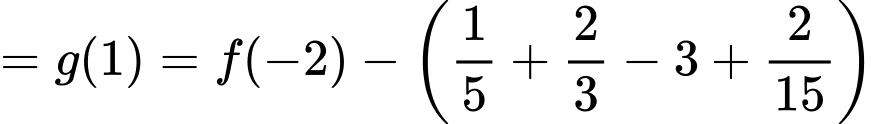 Đáp án: D
Đáp án: D
Ta có
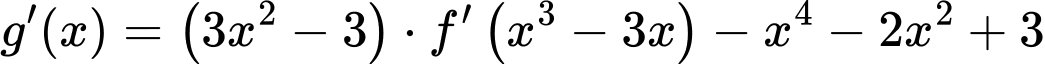
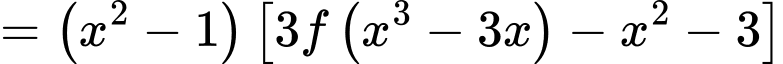
Với
 ta có
ta có 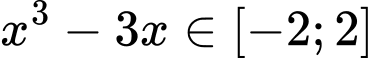 v
v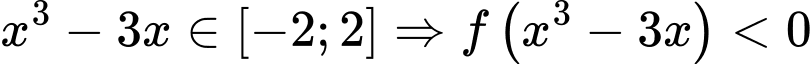
Suy ra
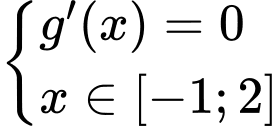
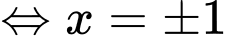
Suy ra
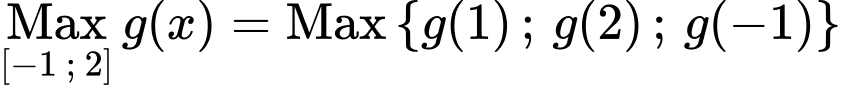
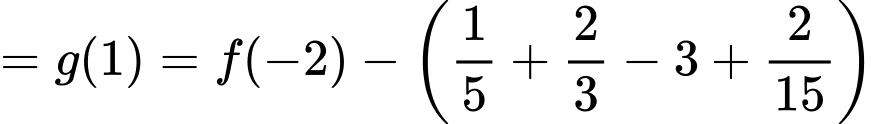 Đáp án: D
Đáp án: D
Câu 12 [636797]: Cho hàm số 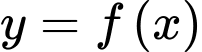 có bảng biến thiên như hình vẽ. Tìm giá trị lớn nhất của hàm số
có bảng biến thiên như hình vẽ. Tìm giá trị lớn nhất của hàm số 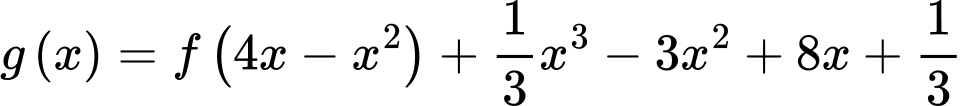 trên đoạn
trên đoạn 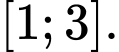
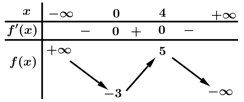
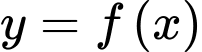 có bảng biến thiên như hình vẽ. Tìm giá trị lớn nhất của hàm số
có bảng biến thiên như hình vẽ. Tìm giá trị lớn nhất của hàm số 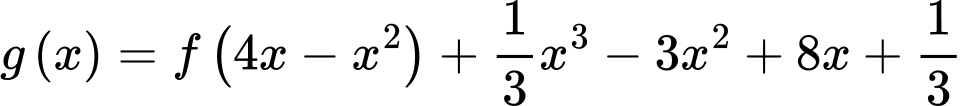 trên đoạn
trên đoạn 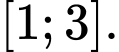

A, 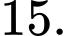
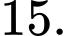
B, 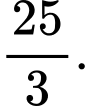
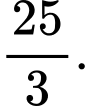
C, 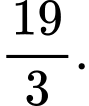
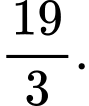
D, 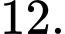
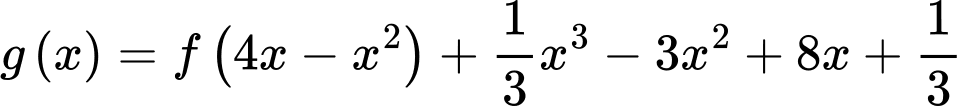
Đặt:
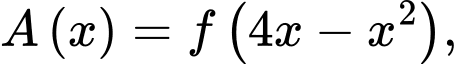
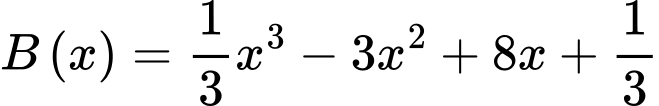
Xét
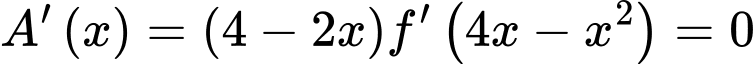
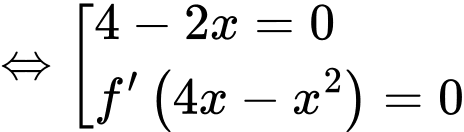
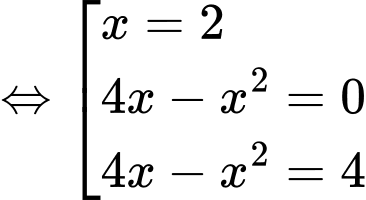
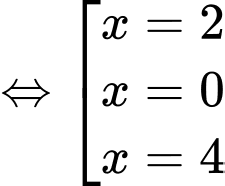
Xét
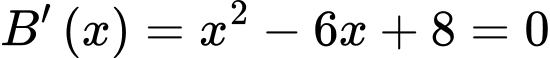

Ta có bảng biến thiên:
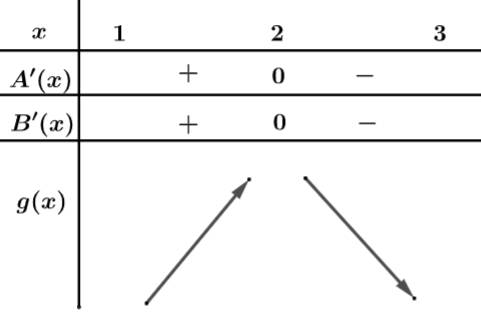
Dựa vào bảng biến thiên ta có trên đoạn
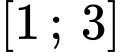 có:
có: 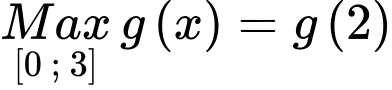
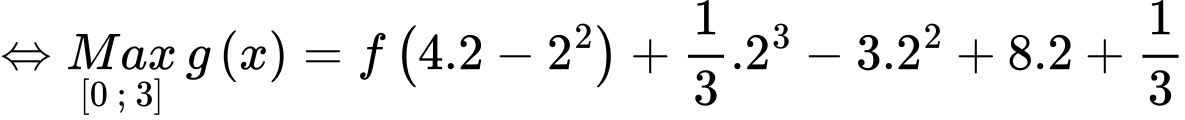
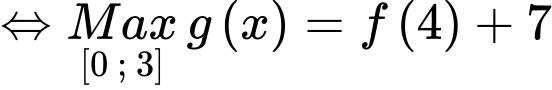
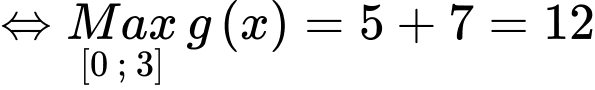
Đáp án: D. Đáp án: D
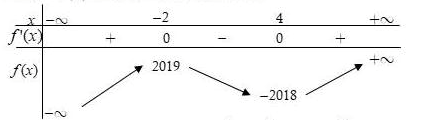
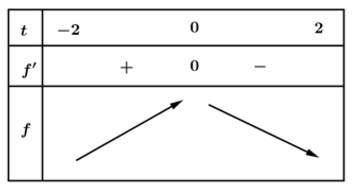
Câu 13 [31705]: Cho hàm số 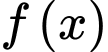 . Hàm số
. Hàm số 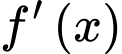 có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số
có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số 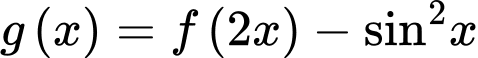 trên đoạn
trên đoạn 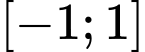 là
là
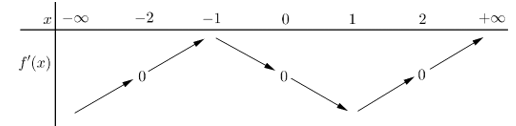
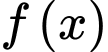 . Hàm số
. Hàm số 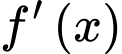 có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số
có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số 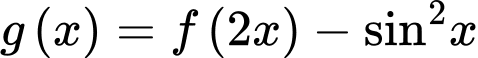 trên đoạn
trên đoạn 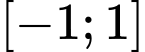 là
là
A, 

B, 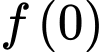 .
.
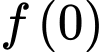 .
.C, 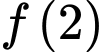 .
.
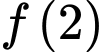 .
.D, 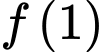 .
.
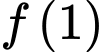 .
.
Chọn B
Ta có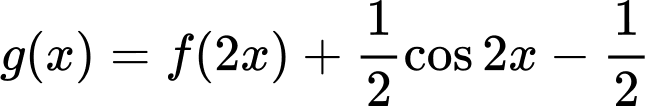
Đặt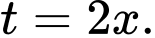 Với
Với  thì
thì 
Khi đó ta có: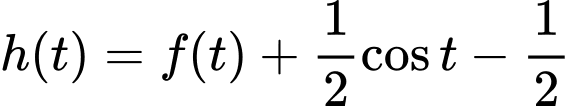
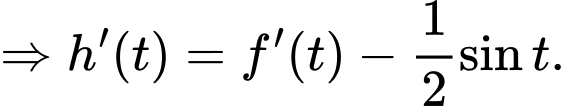
Từ bảng biến thiên ta thấy:
+) Với thì
thì 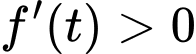 và
và 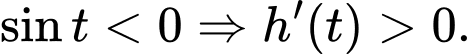
+) Với thì
thì 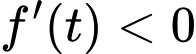 và
và 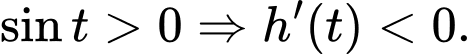
+) Với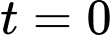 thì
thì 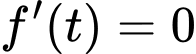
Từ đó ta có BBT sau:
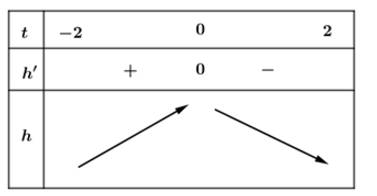
Vậy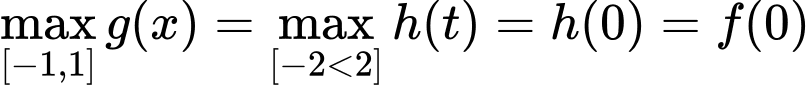 .
.
Cách 2:
Ta có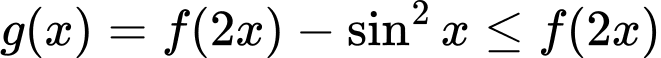 với
với 
Đặt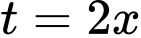 . Với
. Với  thì
thì 
Xét hàm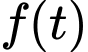 với
với 
Ta có BBT

Lại có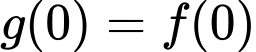 nên
nên 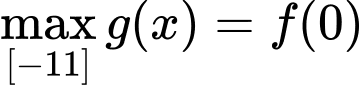 .
.
Nhận xét: Với lời giải như cách 2 ta thấy bài toán có thể tổng quát hoá bằng cách thay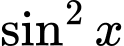 bởi
bởi 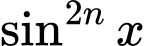 thì kết quả không thay đổi. Đáp án: B
thì kết quả không thay đổi. Đáp án: B
Ta có
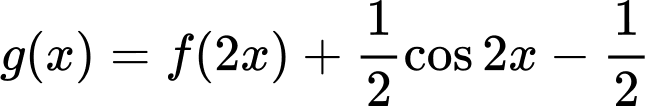
Đặt
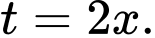 Với
Với  thì
thì 
Khi đó ta có:
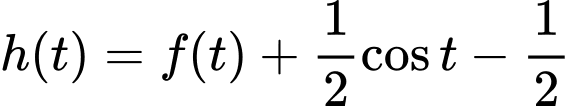
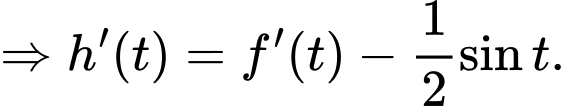
Từ bảng biến thiên ta thấy:
+) Với
 thì
thì 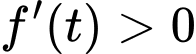 và
và 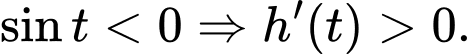
+) Với
 thì
thì 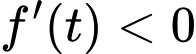 và
và 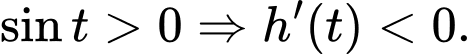
+) Với
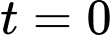 thì
thì 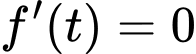
Từ đó ta có BBT sau:

Vậy
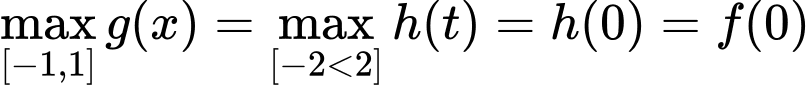 .
.Cách 2:
Ta có
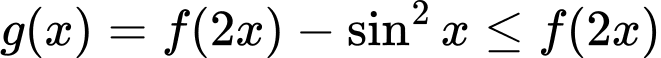 với
với 
Đặt
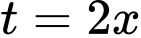 . Với
. Với  thì
thì 
Xét hàm
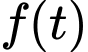 với
với 
Ta có BBT


Lại có
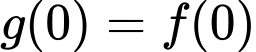 nên
nên 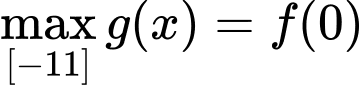 .
.Nhận xét: Với lời giải như cách 2 ta thấy bài toán có thể tổng quát hoá bằng cách thay
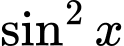 bởi
bởi 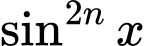 thì kết quả không thay đổi. Đáp án: B
thì kết quả không thay đổi. Đáp án: B
Câu 14 [636801]: Cho hàm số 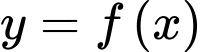 liên tục, có đạo hàm trên
liên tục, có đạo hàm trên 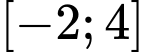 và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ
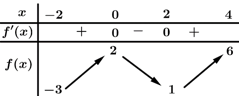
Có bao nhiêu giá trị nguyên của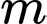 để phương trình
để phương trình 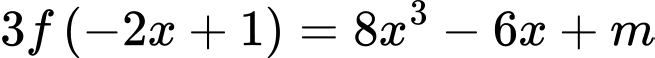 có đúng ba nghiệm thuộc đoạn
có đúng ba nghiệm thuộc đoạn 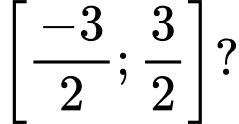
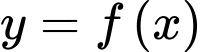 liên tục, có đạo hàm trên
liên tục, có đạo hàm trên 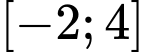 và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên của
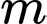 để phương trình
để phương trình 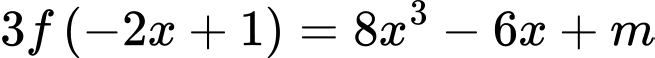 có đúng ba nghiệm thuộc đoạn
có đúng ba nghiệm thuộc đoạn 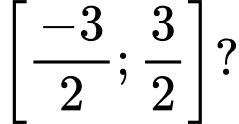
A, 7.
B, 4.
C, 6.
D, 5.
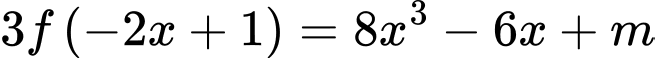

Đặt:
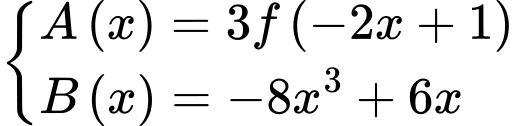
Xét:
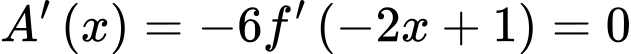
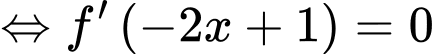
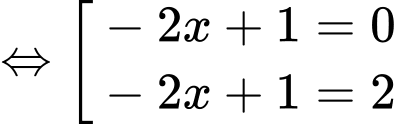
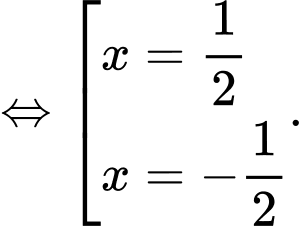
Xét:
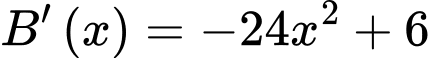
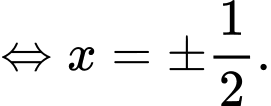
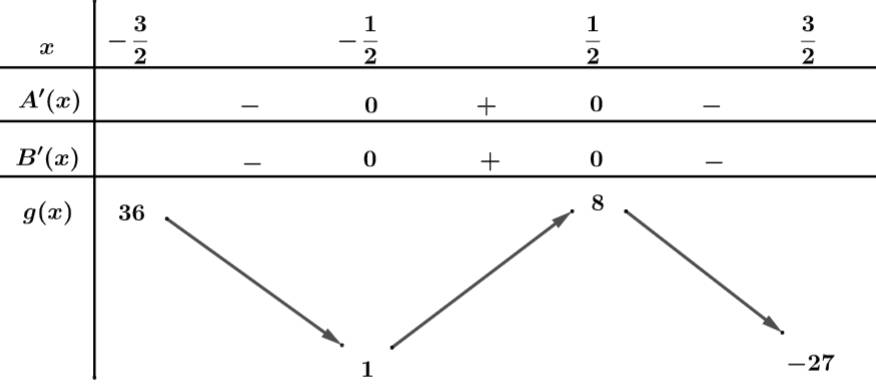
PT
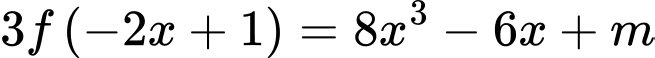 có đúng 3 nghiệm khi và chỉ khi
có đúng 3 nghiệm khi và chỉ khi 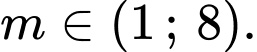
Suy ra có 6 giá trị nguyên của m thỏa mãn điều kiện.
Đáp án: C. Đáp án: C
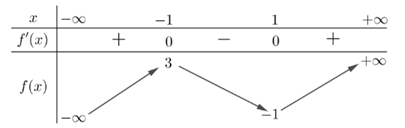
Câu 15 [636802]: Cho hàm số 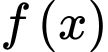 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số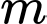 để phương trình
để phương trình 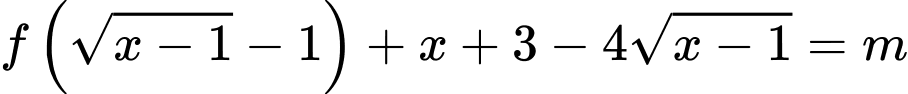 có hai nghiệm phân biêt?
có hai nghiệm phân biêt?
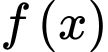 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
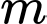 để phương trình
để phương trình 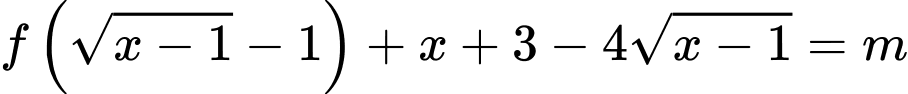 có hai nghiệm phân biêt?
có hai nghiệm phân biêt? A, 7.
B, 8.
C, 0.
D, 4.
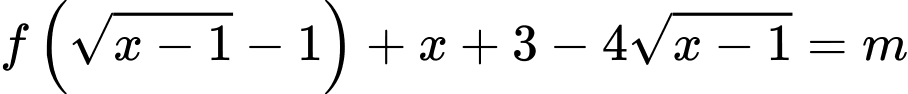
Đặt:

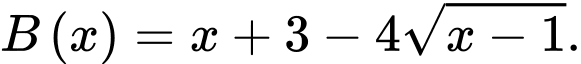
Xét
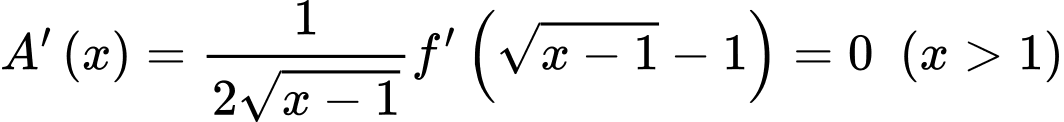
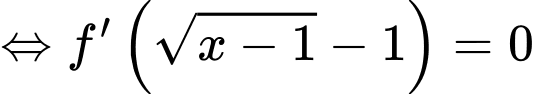
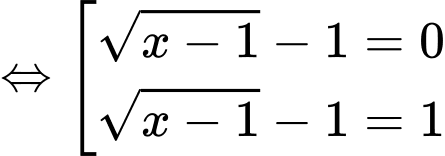

Xét
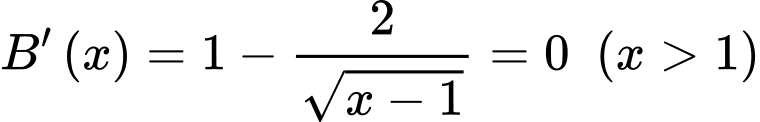
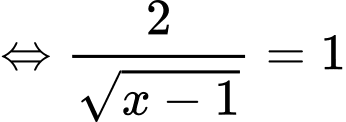

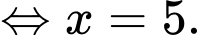
Ta có bảng biến thiên:
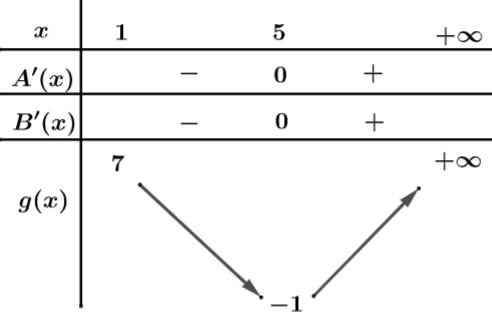
Phương trình có 2 nghiệm phân biệt khi và chỉ khi:

Suy ra, ta có:
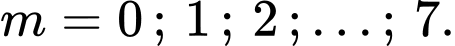
Đáp án: B. Đáp án: B
Câu 16 [636815]: Cho hàm số 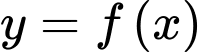 liên tục trên
liên tục trên 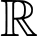 và thỏa mãn
và thỏa mãn 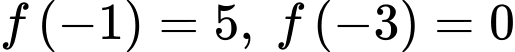 và có bảng xét dấu đạo hàm như sau:
và có bảng xét dấu đạo hàm như sau:
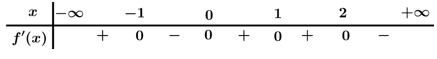
Số giá trị nguyên dương của tham số để phương trình
để phương trình 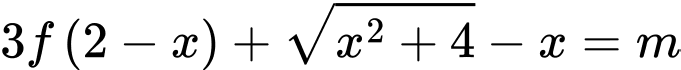 có nghiệm trong khoảng
có nghiệm trong khoảng 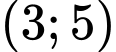 là
là
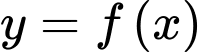 liên tục trên
liên tục trên 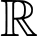 và thỏa mãn
và thỏa mãn 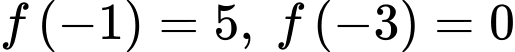 và có bảng xét dấu đạo hàm như sau:
và có bảng xét dấu đạo hàm như sau: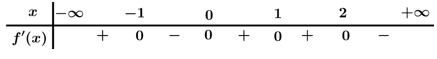
Số giá trị nguyên dương của tham số
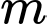 để phương trình
để phương trình 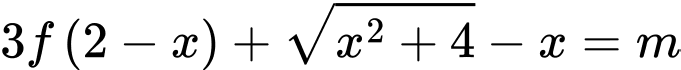 có nghiệm trong khoảng
có nghiệm trong khoảng 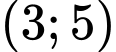 là
là A, 16.
B, 17.
C, 0.
D, 15.
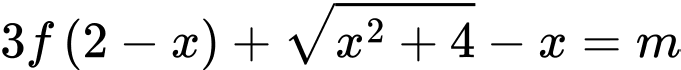
Đặt
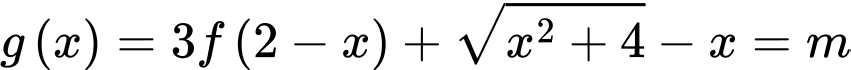
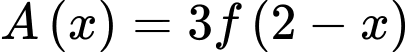
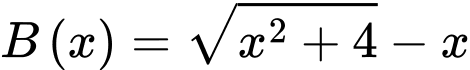
Xét
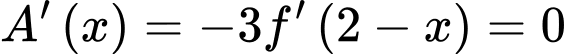
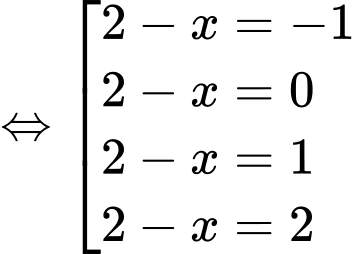
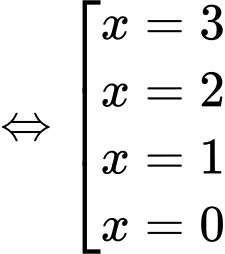
Xét
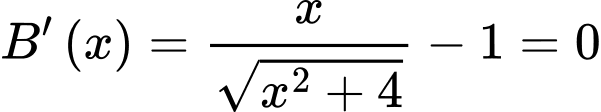
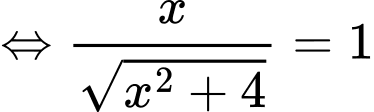
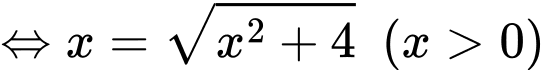
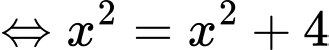 (vô nghiệm)
(vô nghiệm)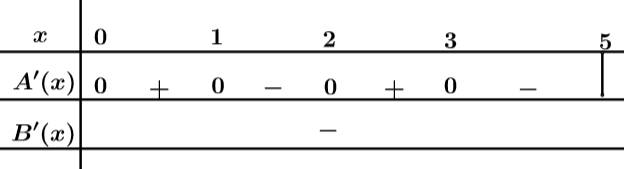
Từ Bảng xét dấu, suy ra
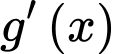 âm trên đoạn
âm trên đoạn 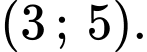
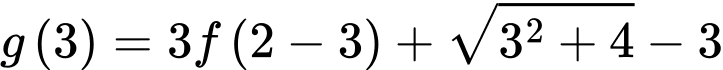
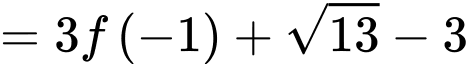
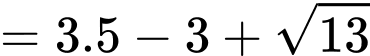
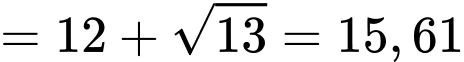
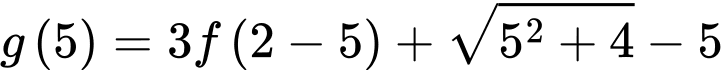
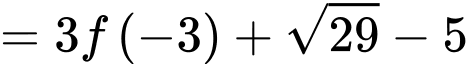
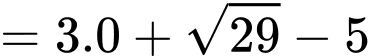
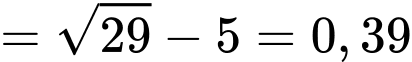
Để phương trình
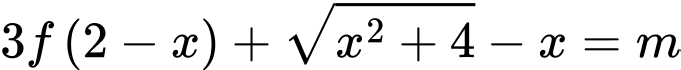 có nghiệm trong khoảng
có nghiệm trong khoảng 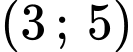 thì
thì 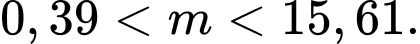
Suy ra có 15 giá trị nguyên của
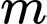 thỏa mãn điều kiện phương trình.
thỏa mãn điều kiện phương trình.Đáp án: D. Đáp án: D
Câu 17 [636800]: Cho hàm số 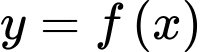 liên tục trên
liên tục trên 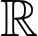 sao cho
sao cho 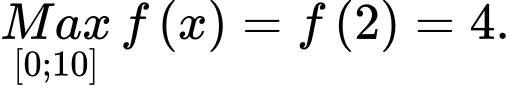 Xét hàm số
Xét hàm số 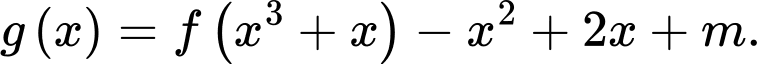 Giá trị của tham số
Giá trị của tham số 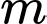 để
để 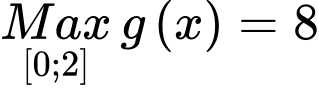 là
là
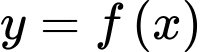 liên tục trên
liên tục trên 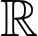 sao cho
sao cho 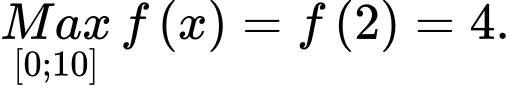 Xét hàm số
Xét hàm số 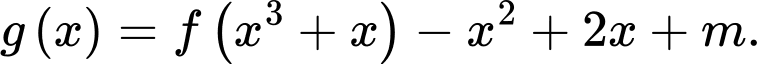 Giá trị của tham số
Giá trị của tham số 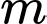 để
để 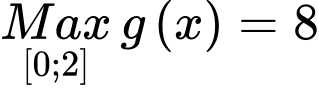 là
là A, 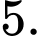
B, 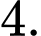
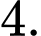
C, 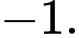
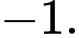
D, 
Có: 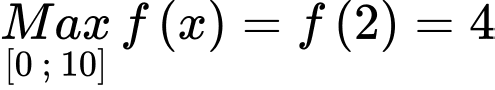
Ta có bảng biến thiên:
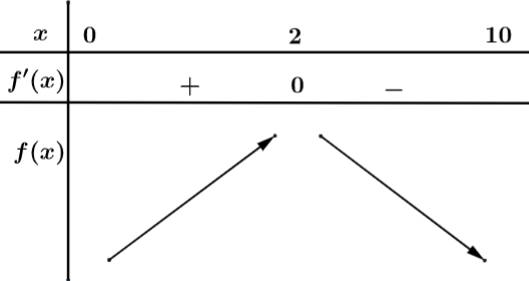
Có: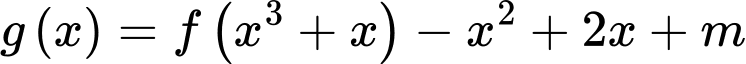
Ta đặt: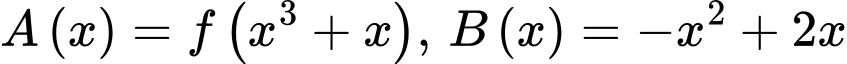
Xét: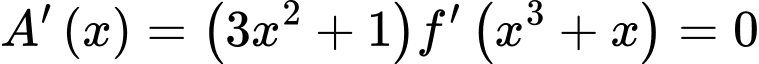
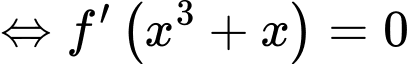

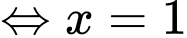
Xét: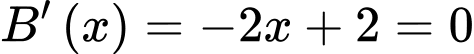
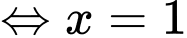
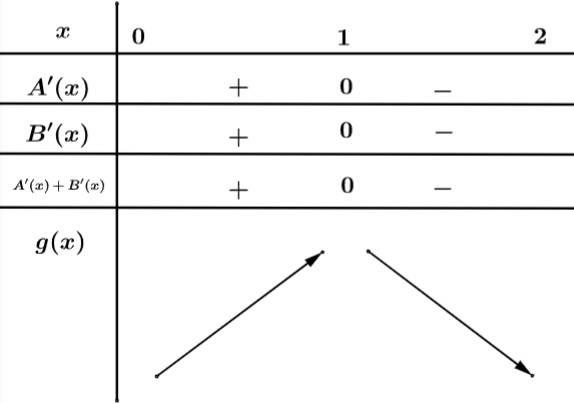
Từ bảng biến thiên ta có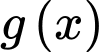 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 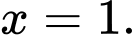
Suy ra, ta có: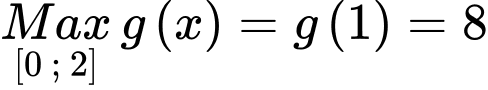
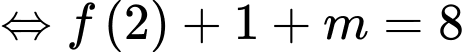
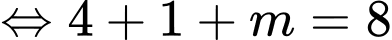
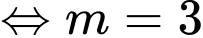
Đáp án: D. Đáp án: D
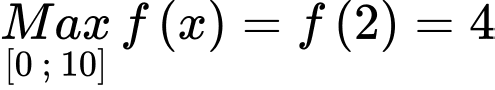
Ta có bảng biến thiên:

Có:
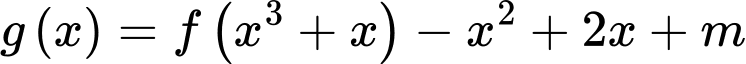
Ta đặt:
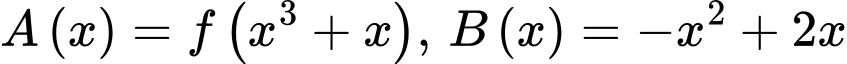
Xét:
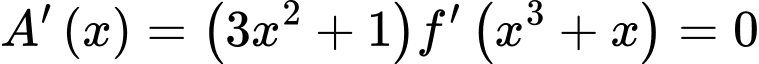
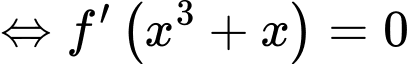

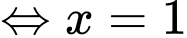
Xét:
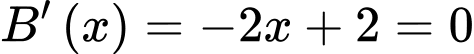
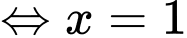

Từ bảng biến thiên ta có
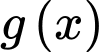 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 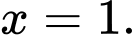
Suy ra, ta có:
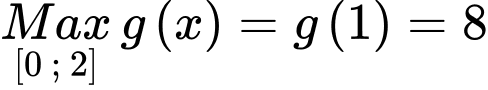
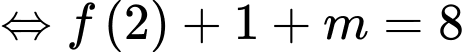
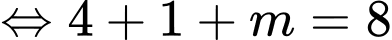
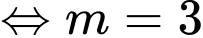
Đáp án: D. Đáp án: D