Đáp án Bài tập tự luyện số 1
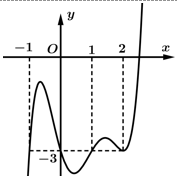
Câu 1 [45868]: Cho hàm số bậc ba 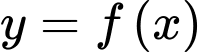 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 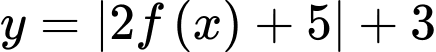 là
là
=kphan2de1/8.cuctrituyetdoide1.png)
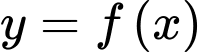 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 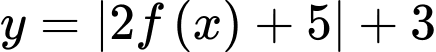 là
là=kphan2de1/8.cuctrituyetdoide1.png)
A, 2.
B, 5.
C, 3.
D, 7.
Đáp án C
Tịnh tiến đồ thị hàm số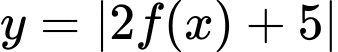 theo phương song song trục tung lên trên 3 đơn vị ta được đồ thị hàm số
theo phương song song trục tung lên trên 3 đơn vị ta được đồ thị hàm số 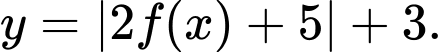 Do đó, hàm số
Do đó, hàm số 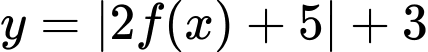 và hàm số
và hàm số 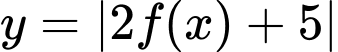 có cùng số điểm cực trị.
có cùng số điểm cực trị.
Xét hàm số với
với 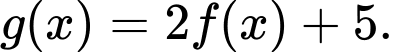
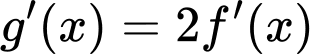


Đồ thị hàm số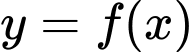 cắt đường thẳng
cắt đường thẳng 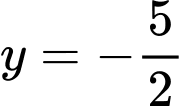 tại ba điểm phân biệt có hoành độ
tại ba điểm phân biệt có hoành độ 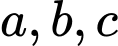 sao cho
sao cho 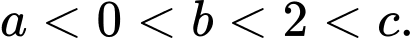 Suy ra phương trình
Suy ra phương trình 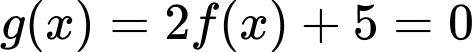 có ba nghiệm phân biệt
có ba nghiệm phân biệt 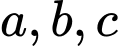 sao cho
sao cho 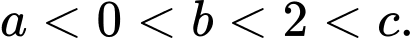
Ta có bảng biến thiên:
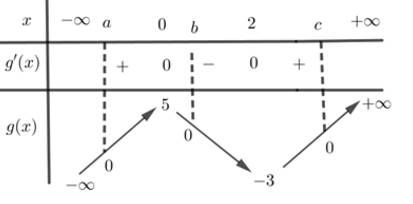
Từ bảng biến thiên suy ra đồ thị hàm số có 5 điểm cực trị. Đáp án: B
có 5 điểm cực trị. Đáp án: B
Tịnh tiến đồ thị hàm số
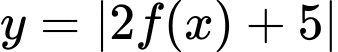 theo phương song song trục tung lên trên 3 đơn vị ta được đồ thị hàm số
theo phương song song trục tung lên trên 3 đơn vị ta được đồ thị hàm số 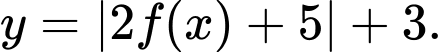 Do đó, hàm số
Do đó, hàm số 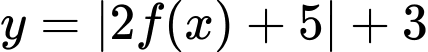 và hàm số
và hàm số 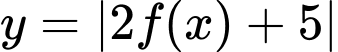 có cùng số điểm cực trị.
có cùng số điểm cực trị.Xét hàm số
 với
với 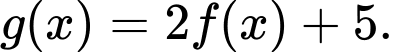
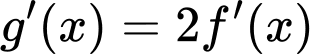


Đồ thị hàm số
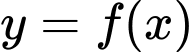 cắt đường thẳng
cắt đường thẳng 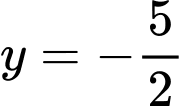 tại ba điểm phân biệt có hoành độ
tại ba điểm phân biệt có hoành độ 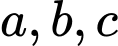 sao cho
sao cho 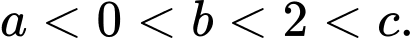 Suy ra phương trình
Suy ra phương trình 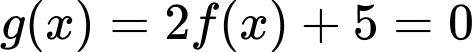 có ba nghiệm phân biệt
có ba nghiệm phân biệt 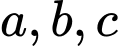 sao cho
sao cho 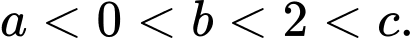
Ta có bảng biến thiên:

Từ bảng biến thiên suy ra đồ thị hàm số
 có 5 điểm cực trị. Đáp án: B
có 5 điểm cực trị. Đáp án: B
Câu 2 [528642]: Cho hàm số 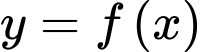 liên tục trên
liên tục trên  và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ
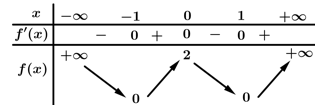
Tìm số điểm cực trị của hàm số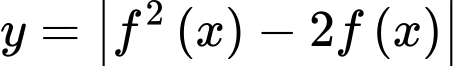
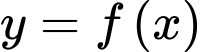 liên tục trên
liên tục trên  và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ 
Tìm số điểm cực trị của hàm số
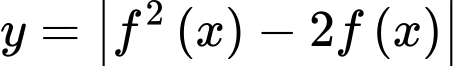
A, 7.
B, 9.
C, 11.
D, 10.
Số điểm cực trị hàm số 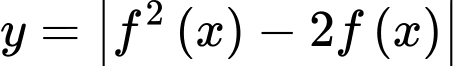 bằng số nghiệm của
bằng số nghiệm của 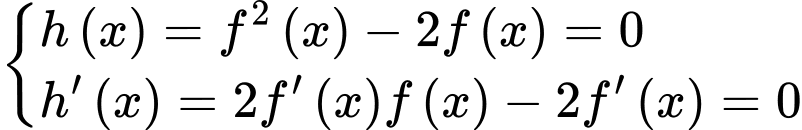
Xét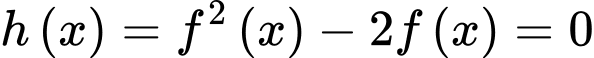
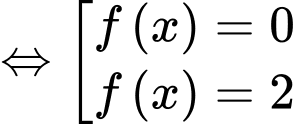
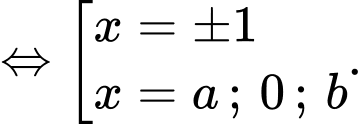
Xét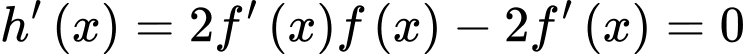
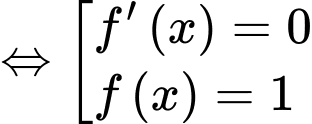
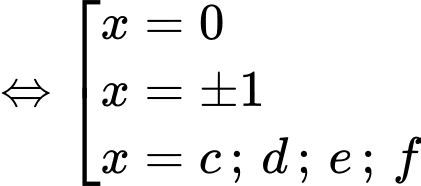
Ta thấy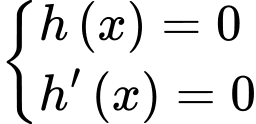 tổng 9 nghiệm phân biệt, suy ra hàm số có 9 điểm cực trị.
tổng 9 nghiệm phân biệt, suy ra hàm số có 9 điểm cực trị.
Đáp án: B. Đáp án: B
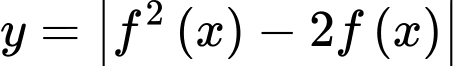 bằng số nghiệm của
bằng số nghiệm của 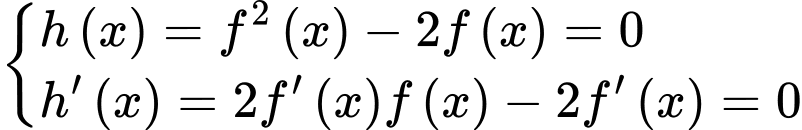
Xét
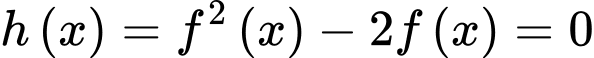
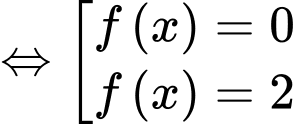
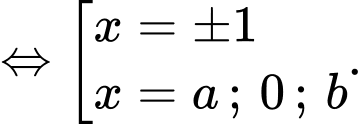
Xét
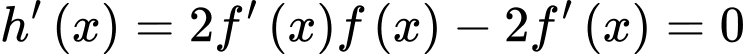
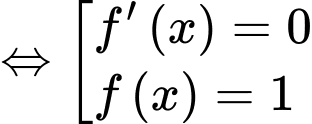
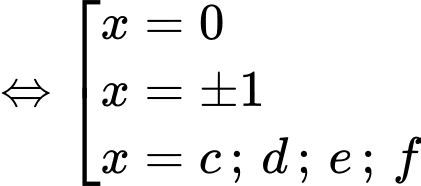
Ta thấy
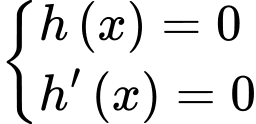 tổng 9 nghiệm phân biệt, suy ra hàm số có 9 điểm cực trị.
tổng 9 nghiệm phân biệt, suy ra hàm số có 9 điểm cực trị.
Đáp án: B. Đáp án: B
Câu 3 [791661]: Cho hàm số 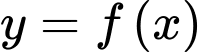 có đạo hàm trên
có đạo hàm trên 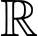 , đồ thị hàm số
, đồ thị hàm số 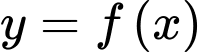 là đường cong ở hình vẽ. Hỏi hàm số
là đường cong ở hình vẽ. Hỏi hàm số 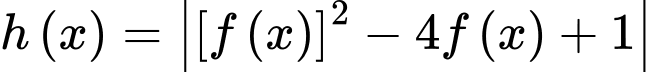 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
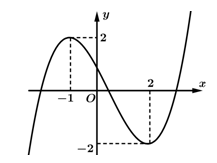
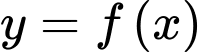 có đạo hàm trên
có đạo hàm trên 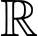 , đồ thị hàm số
, đồ thị hàm số 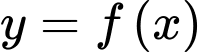 là đường cong ở hình vẽ. Hỏi hàm số
là đường cong ở hình vẽ. Hỏi hàm số 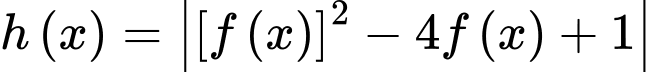 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? 
A, 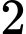 .
.
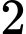 .
.B, 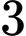 .
.
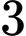 .
.C, 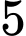 .
.
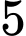 .
.D, 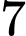 .
.
 .
.
Chọn D
Đặt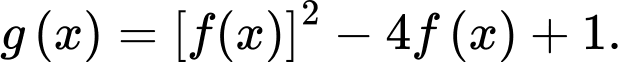
Khi đó,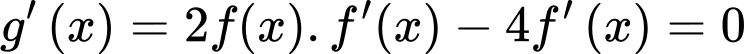
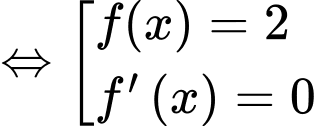
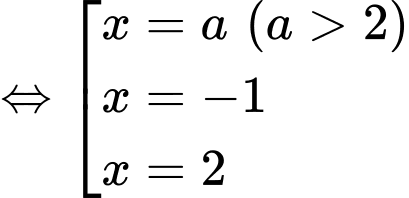
Do đó, ta có bảng biến thiên:
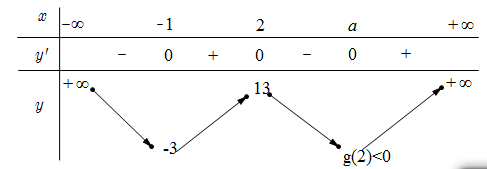
Suy ra đồ thị hàm số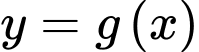 có ba điểm cực không nằm trên trục hoành và bốn giao điểm với
có ba điểm cực không nằm trên trục hoành và bốn giao điểm với 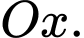
Vậy đồ thị hàm số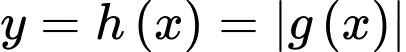 có số cực trị là
có số cực trị là 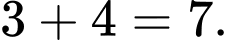 Đáp án: D
Đáp án: D
Đặt
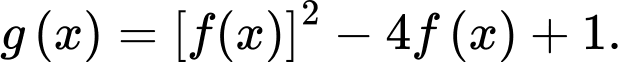
Khi đó,
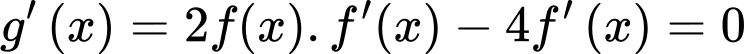
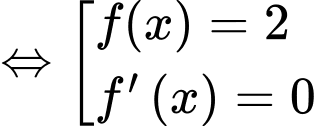
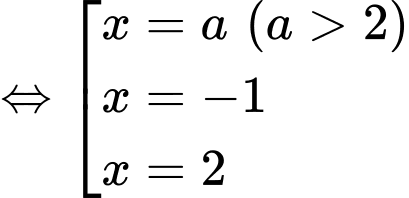
Do đó, ta có bảng biến thiên:

Suy ra đồ thị hàm số
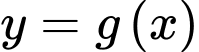 có ba điểm cực không nằm trên trục hoành và bốn giao điểm với
có ba điểm cực không nằm trên trục hoành và bốn giao điểm với 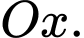
Vậy đồ thị hàm số
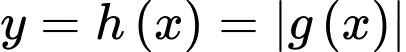 có số cực trị là
có số cực trị là 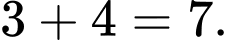 Đáp án: D
Đáp án: D
Câu 4 [528644]: Cho hàm số 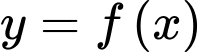 liên tục trên
liên tục trên 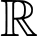 và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ
=kphan2de1/12.cuctritrituyetdoide1.png)
Số điểm cực trị của hàm số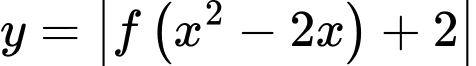 là
là
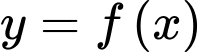 liên tục trên
liên tục trên 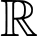 và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ =kphan2de1/12.cuctritrituyetdoide1.png)
Số điểm cực trị của hàm số
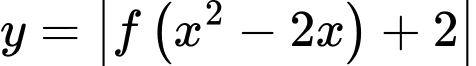 là
là A, 12.
B, 13.
C, 11.
D, 10.
Ta có: 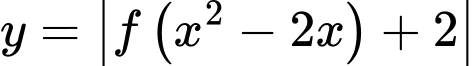 có số điểm cực trị bằng số nghiệm của
có số điểm cực trị bằng số nghiệm của 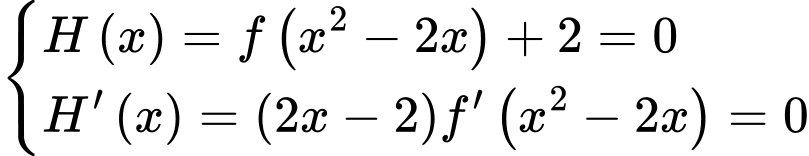
Xét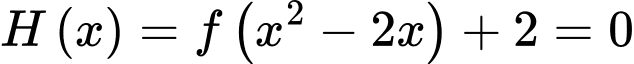
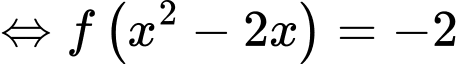
Đặt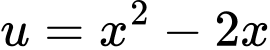
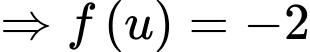
Dựa vào BBT ta có: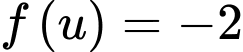
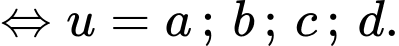
Ta xét: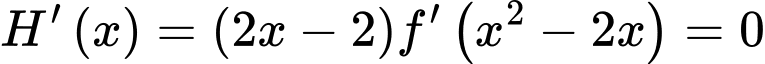
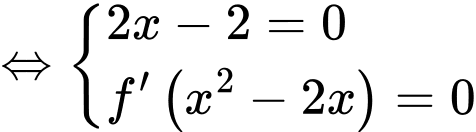
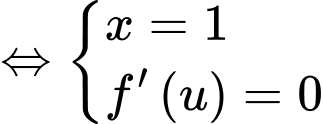
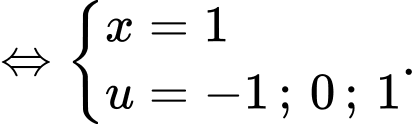
Ta xét: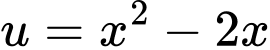
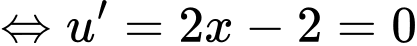
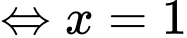
Ta có BBT như sau:
Từ BBT ta thấy có 11 giao điểm, Suy ra hàm số đã cho có 11 điểm cực trị.
Đáp án: C. Đáp án: C
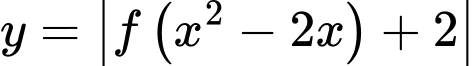 có số điểm cực trị bằng số nghiệm của
có số điểm cực trị bằng số nghiệm của 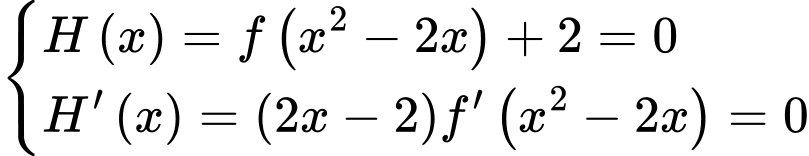
Xét
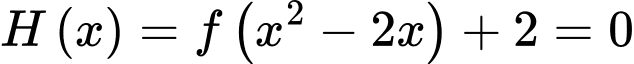
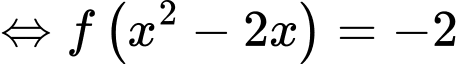
Đặt
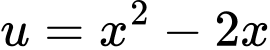
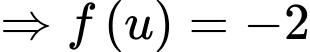
Dựa vào BBT ta có:
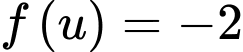
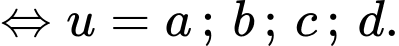
Ta xét:
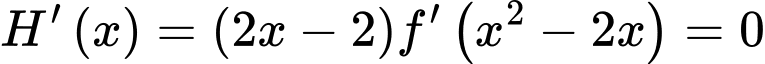
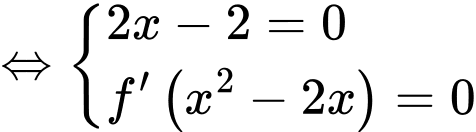
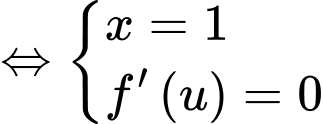
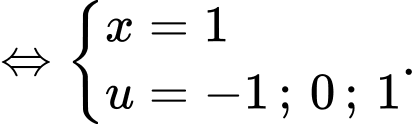
Ta xét:
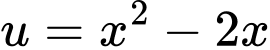
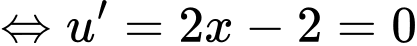
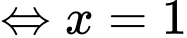
Ta có BBT như sau:

Từ BBT ta thấy có 11 giao điểm, Suy ra hàm số đã cho có 11 điểm cực trị.
Đáp án: C. Đáp án: C
Câu 5 [528645]: Cho hàm số 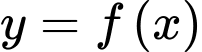 liên tục trên
liên tục trên 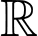 và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ
=kphan2de1/13.cuctritrituyetdoidw1.png)
Số điểm cực trị của hàm số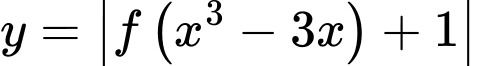 là
là
 liên tục trên
liên tục trên 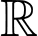 và có bảng biến thiên như hình vẽ
và có bảng biến thiên như hình vẽ =kphan2de1/13.cuctritrituyetdoidw1.png)
Số điểm cực trị của hàm số
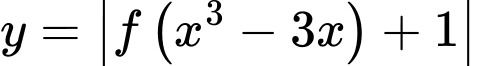 là
là A, 12.
B, 15.
C, 13.
D, 17.
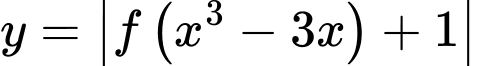 có số điểm cực trị bằng tổng nghiệm của
có số điểm cực trị bằng tổng nghiệm của
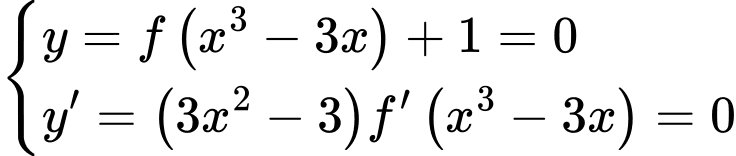
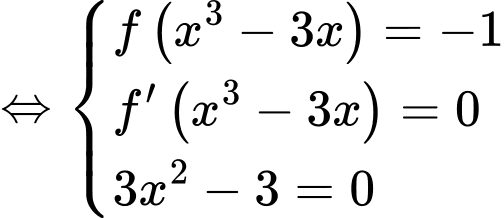
Đặt
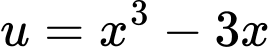
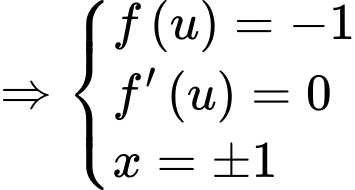
Dựa vào bảng biến thiên bài cho
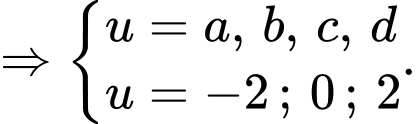
Ta xét:
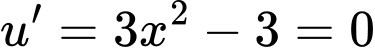
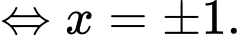
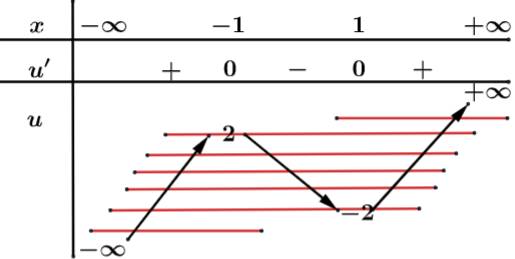
Từ bảng biến thiên ta suy ra:
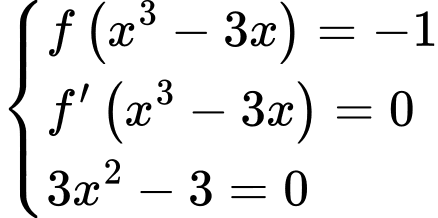 có tổng 15 nghiệm.
có tổng 15 nghiệm.
Suy ra Hàm số bài cho có 15 điểm cực trị.
Đáp án: B. Đáp án: B
Câu 6 [528648]: Cho hàm số bậc ba 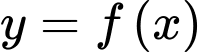 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 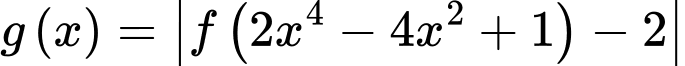 là
là
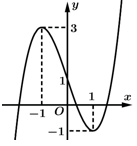
 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 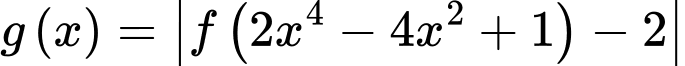 là
là
A, 8.
B, 9.
C, 7.
D, 11.
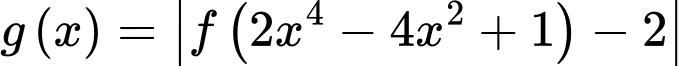
Đặt:
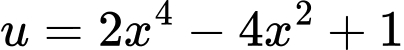
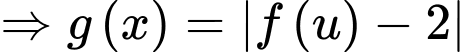
Xét:
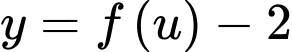
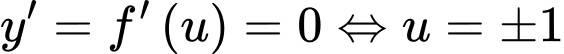
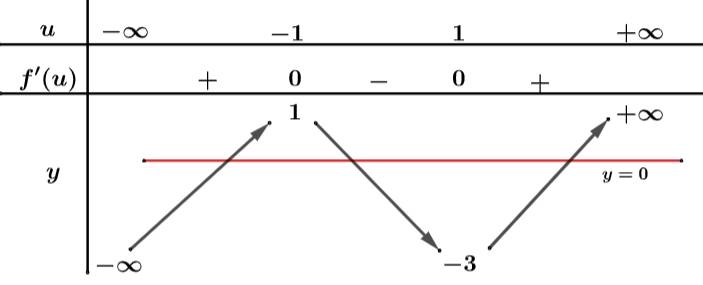
Suy ra ta có bảng của
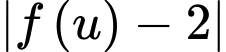 như sau:
như sau: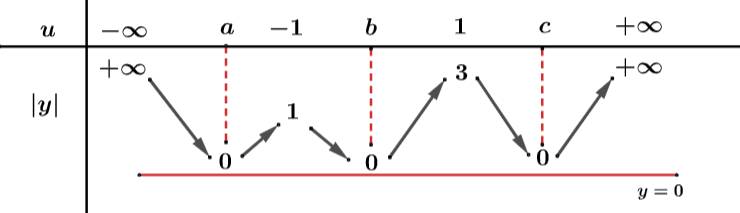
Ta xét
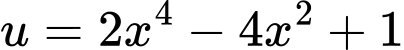 ta có:
ta có: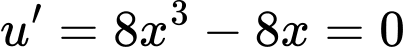
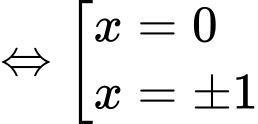
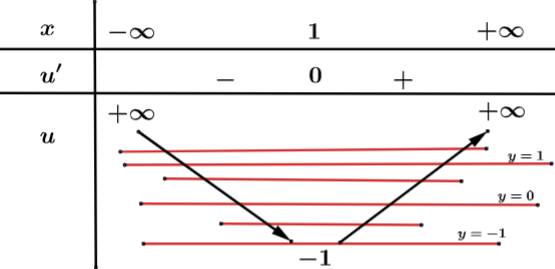
Ta có bảng biến thiên của u:
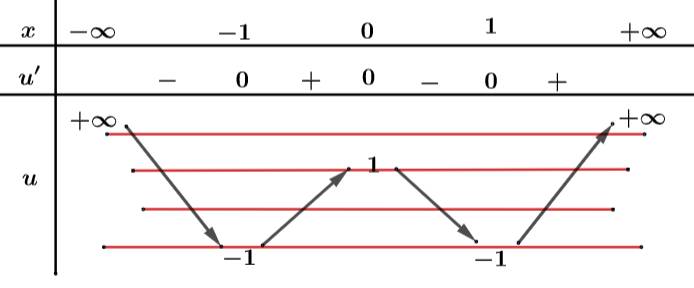
Từ bảng biến thiên trên ta suy ra PT có 11 nghiệm phân biệt.
Vậy
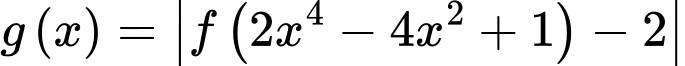 có 11 điểm cực trị
có 11 điểm cực trị Đáp án: D. Đáp án: D
Câu 7 [528651]: Cho hàm số 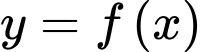 có bảng biến thiên như hình vẽ
có bảng biến thiên như hình vẽ
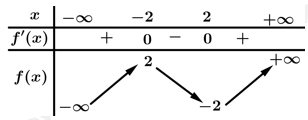
Số điểm cực trị của hàm số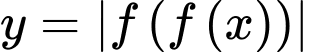 là
là
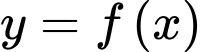 có bảng biến thiên như hình vẽ
có bảng biến thiên như hình vẽ 
Số điểm cực trị của hàm số
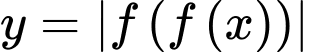 là
là A, 7.
B, 6.
C, 9.
D, 8.
Ta có: Số điểm cực trị của 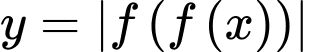 bẳng tổng số nghiệm bội lẻ của
bẳng tổng số nghiệm bội lẻ của 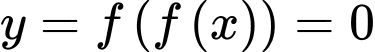 và
và 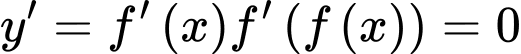
Xét: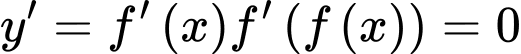
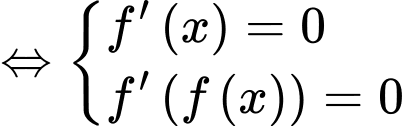
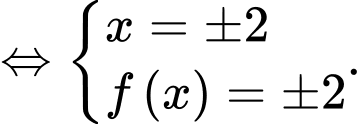
Xét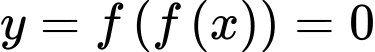 dựa vào BBT bài cho, ta suy ra:
dựa vào BBT bài cho, ta suy ra:
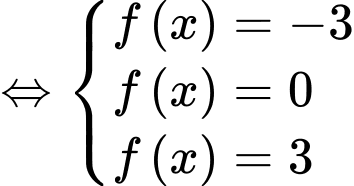
Ta có BBT:
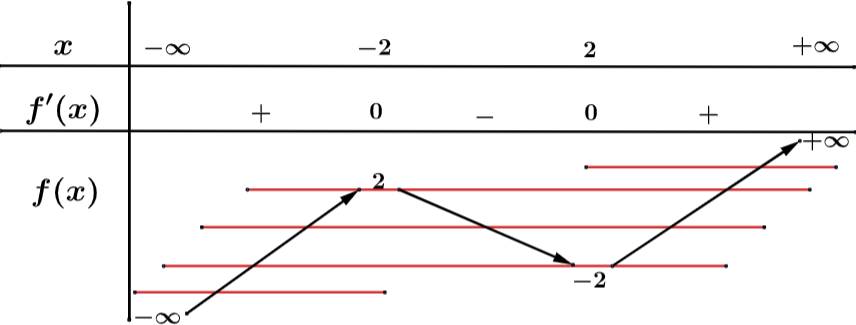
Suy ra, tổng số nghiệm bội lẻ của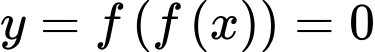 và
và 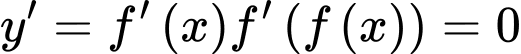 là 9 nghiệm.
là 9 nghiệm.
Vậy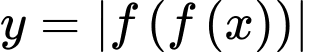 có 9 điểm cực trị.
có 9 điểm cực trị.
Đáp án: C. Đáp án: C
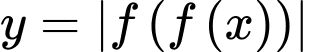 bẳng tổng số nghiệm bội lẻ của
bẳng tổng số nghiệm bội lẻ của 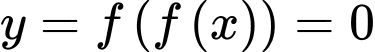 và
và 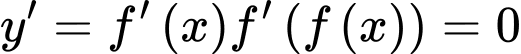
Xét:
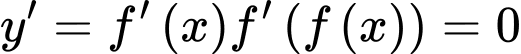
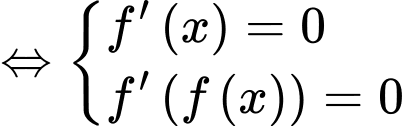
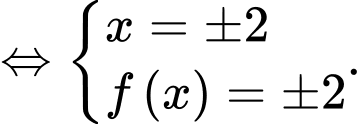
Xét
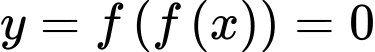 dựa vào BBT bài cho, ta suy ra:
dựa vào BBT bài cho, ta suy ra:
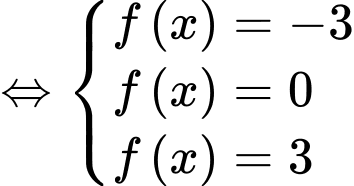
Ta có BBT:

Suy ra, tổng số nghiệm bội lẻ của
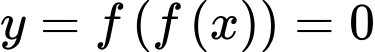 và
và 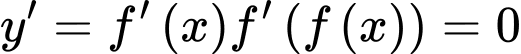 là 9 nghiệm.
là 9 nghiệm.
Vậy
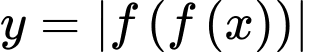 có 9 điểm cực trị.
có 9 điểm cực trị.
Đáp án: C. Đáp án: C
Câu 8 [528652]: Cho hàm số 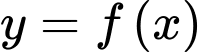 có đạo hàm
có đạo hàm 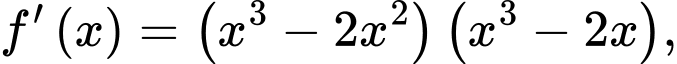 với mọi
với mọi 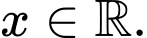 Hàm số
Hàm số 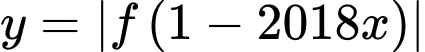 có nhiều nhất bao nhiêu điểm cực trị?
có nhiều nhất bao nhiêu điểm cực trị?
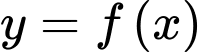 có đạo hàm
có đạo hàm 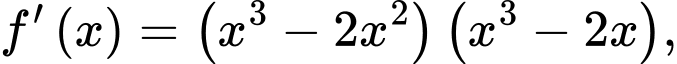 với mọi
với mọi 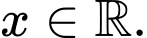 Hàm số
Hàm số 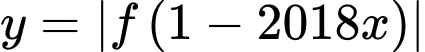 có nhiều nhất bao nhiêu điểm cực trị?
có nhiều nhất bao nhiêu điểm cực trị? A, 9.
B, 2018.
C, 2022.
D, 11.
Số cực trị của hàm số 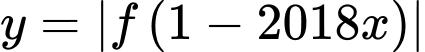 bằng số nghiệm của phương trình
bằng số nghiệm của phương trình 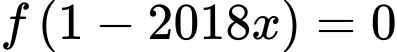 và
và 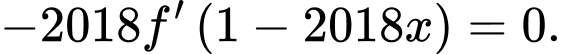
Đặt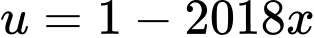
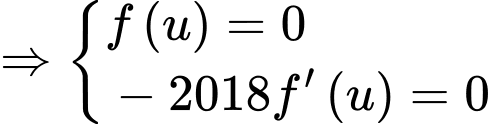
Xét: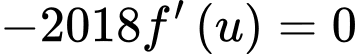
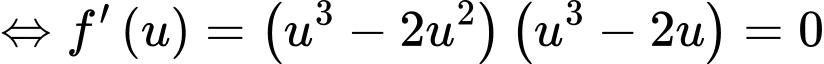
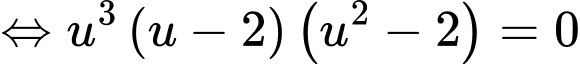
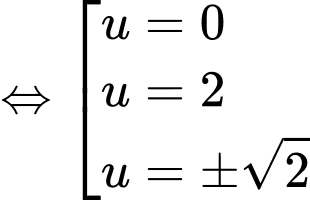
Để hàm số có nhiều cực trị nhất thì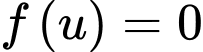 phải có nhiều cực trị nhất.
phải có nhiều cực trị nhất.
Ta có BBT:
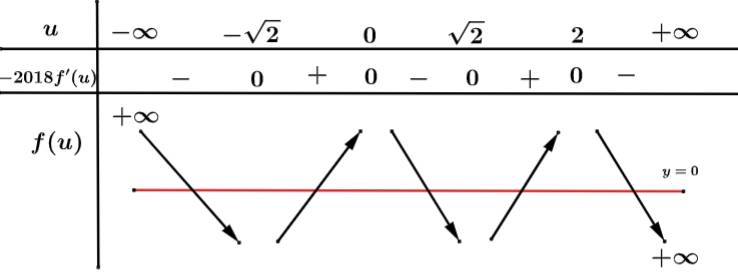
-Từ bảng biến thiên ta thấy phương trình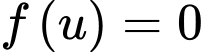 có nhiều nhất 5 nghiệm.
có nhiều nhất 5 nghiệm.
Suy ra hàm số có nhiều nhất 9 điểm cực trị.
Đáp án: A. Đáp án: A
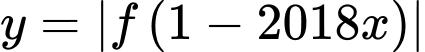 bằng số nghiệm của phương trình
bằng số nghiệm của phương trình 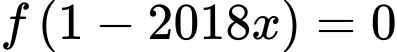 và
và 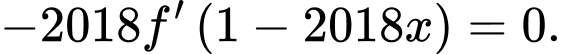
Đặt
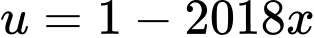
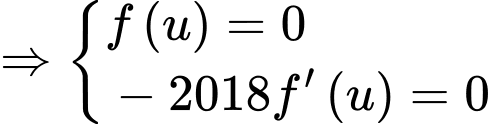
Xét:
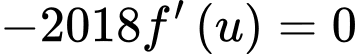
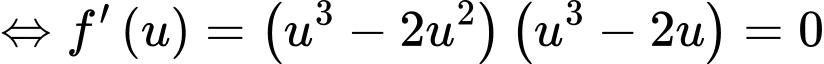
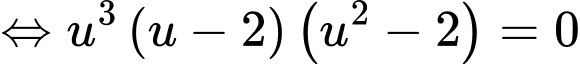
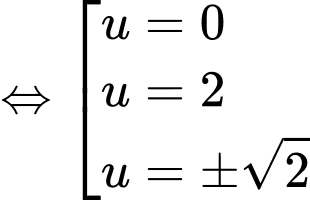
Để hàm số có nhiều cực trị nhất thì
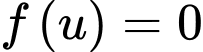 phải có nhiều cực trị nhất.
phải có nhiều cực trị nhất.
Ta có BBT:

-Từ bảng biến thiên ta thấy phương trình
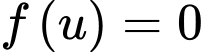 có nhiều nhất 5 nghiệm.
có nhiều nhất 5 nghiệm.
Suy ra hàm số có nhiều nhất 9 điểm cực trị.
Đáp án: A. Đáp án: A
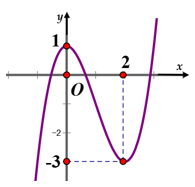
Câu 9 [732423]: [MĐ3] Cho hàm số 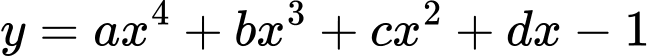 có đồ thị hàm số
có đồ thị hàm số 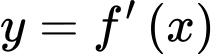 như hình vẽ bên dưới. Số điểm cực trị của hàm số
như hình vẽ bên dưới. Số điểm cực trị của hàm số 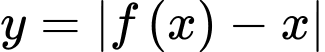 là
là
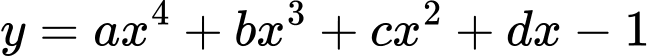 có đồ thị hàm số
có đồ thị hàm số 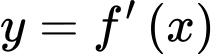 như hình vẽ bên dưới. Số điểm cực trị của hàm số
như hình vẽ bên dưới. Số điểm cực trị của hàm số 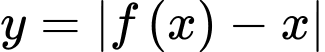 là
là
A, 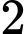 .
.
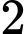 .
.B, 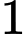 .
.
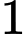 .
.C, 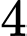 .
.
 .
.D, 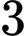 .
.
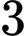 .
.
•Dựa vào đồ thị hàm số đã cho ta có 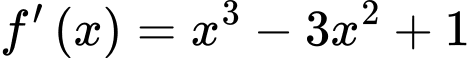
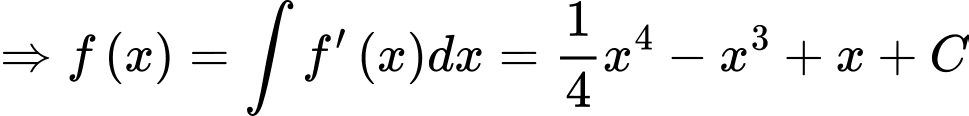 .
.
Mà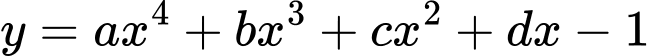
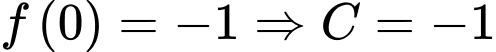 .
.
Khi đó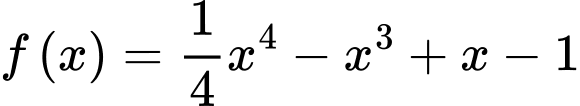 .
.
Để xét số điểm cực trị của hàm số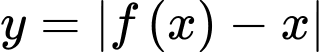 , ta xét hàm số
, ta xét hàm số 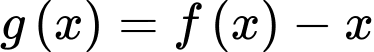 .
.
• Số điểm cực trị của hàm số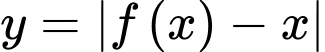 bằng số điểm cực trị của hàm số
bằng số điểm cực trị của hàm số 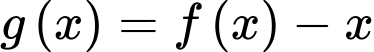 cộng số nghiệm bội lẻ của phương trình
cộng số nghiệm bội lẻ của phương trình 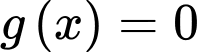 .
.
• Ta có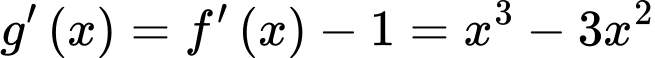 ,
, 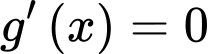
 , trong đó
, trong đó 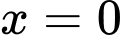 là nghiệm bội chẵn.
là nghiệm bội chẵn.
Do đó hàm số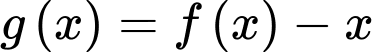 có
có 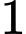 điểm cực trị.
điểm cực trị.
•Xét phương trình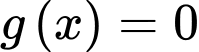
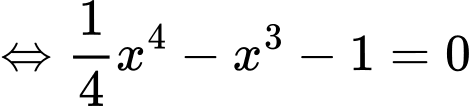
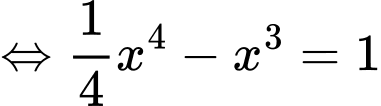 .
.
Xét hàm số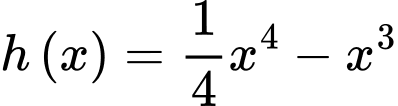
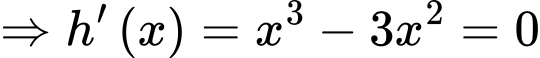
 (
(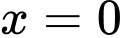 là nghiệm bội chẵn).
là nghiệm bội chẵn).
Ta có bảng biến thiên
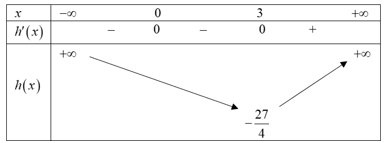
Dựa vào bảng biến thiên, phương trình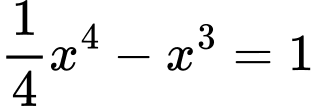 có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
• Vậy Số điểm cực trị của hàm số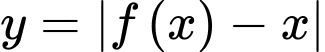 là
là 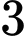 . Đáp án: D
. Đáp án: D
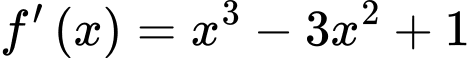
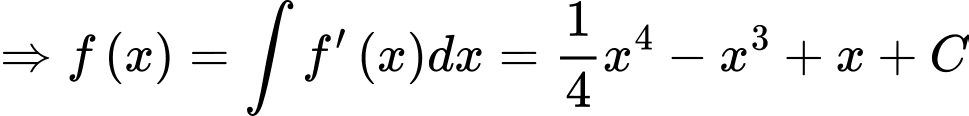 .
.
Mà
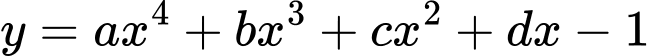
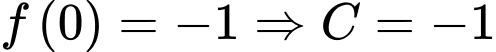 .
.
Khi đó
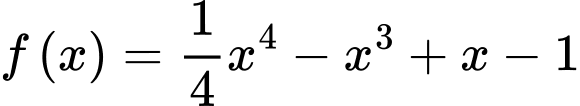 .
.
Để xét số điểm cực trị của hàm số
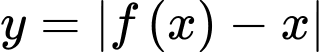 , ta xét hàm số
, ta xét hàm số 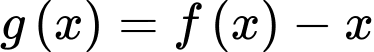 .
.
• Số điểm cực trị của hàm số
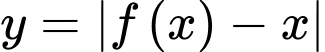 bằng số điểm cực trị của hàm số
bằng số điểm cực trị của hàm số 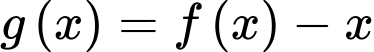 cộng số nghiệm bội lẻ của phương trình
cộng số nghiệm bội lẻ của phương trình 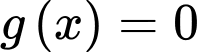 .
.
• Ta có
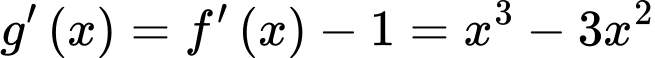 ,
, 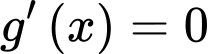
 , trong đó
, trong đó 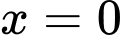 là nghiệm bội chẵn.
là nghiệm bội chẵn.
Do đó hàm số
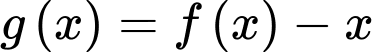 có
có 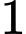 điểm cực trị.
điểm cực trị.
•Xét phương trình
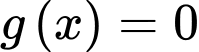
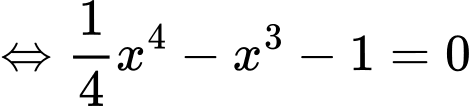
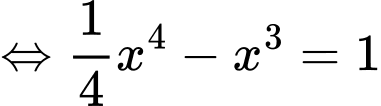 .
.
Xét hàm số
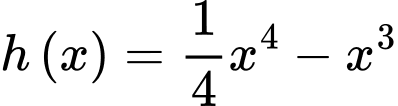
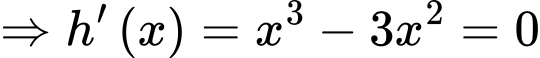
 (
(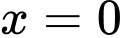 là nghiệm bội chẵn).
là nghiệm bội chẵn).
Ta có bảng biến thiên

Dựa vào bảng biến thiên, phương trình
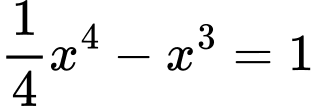 có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
• Vậy Số điểm cực trị của hàm số
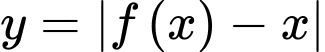 là
là 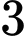 . Đáp án: D
. Đáp án: D
Câu 10 [789315]: Cho hàm số đa thức 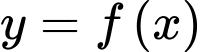 có đạo hàm trên
có đạo hàm trên 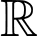 ,
, 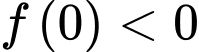 và đồ thị hình bên dưới là đồ thị của đạo hàm
và đồ thị hình bên dưới là đồ thị của đạo hàm 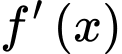 . Hỏi hàm số
. Hỏi hàm số 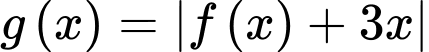 có bao nhiêu cực trị?
có bao nhiêu cực trị?
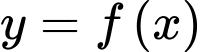 có đạo hàm trên
có đạo hàm trên 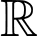 ,
, 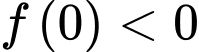 và đồ thị hình bên dưới là đồ thị của đạo hàm
và đồ thị hình bên dưới là đồ thị của đạo hàm 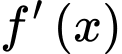 . Hỏi hàm số
. Hỏi hàm số 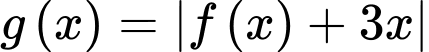 có bao nhiêu cực trị?
có bao nhiêu cực trị? 
A, 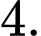
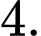
B, 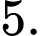
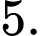
C, 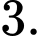
D, 
Chọn B
Đặt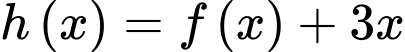
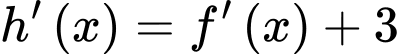
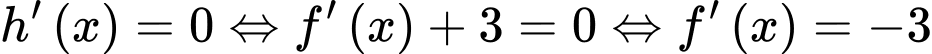
Theo đồ thị của hàm số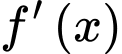 thì phương trình
thì phương trình 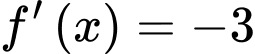 có
có 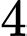 nghiệm
nghiệm 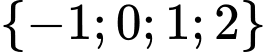
Ta có bảng biến thiên
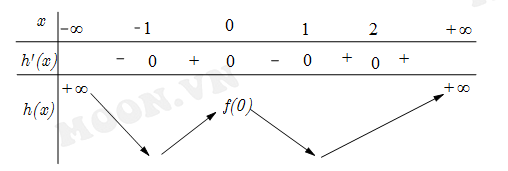
Theo bảng biến thiên ta có phương trình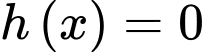 có hai nghiệm
có hai nghiệm 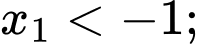 và
và  (do có
(do có 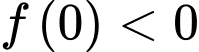 )
)
Khi đó ta có
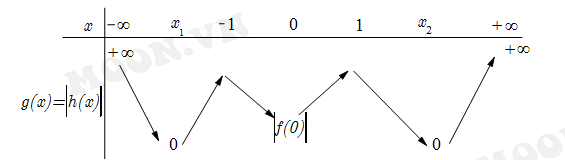
Vậy hàm số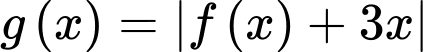 có
có  cực trị. Đáp án: B
cực trị. Đáp án: B
Đặt
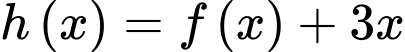
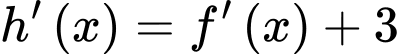
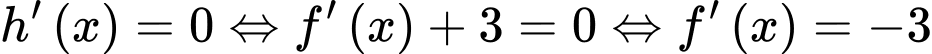
Theo đồ thị của hàm số
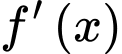 thì phương trình
thì phương trình 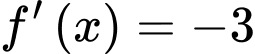 có
có 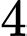 nghiệm
nghiệm 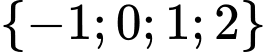
Ta có bảng biến thiên

Theo bảng biến thiên ta có phương trình
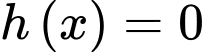 có hai nghiệm
có hai nghiệm 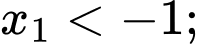 và
và  (do có
(do có 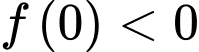 )
)Khi đó ta có

Vậy hàm số
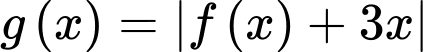 có
có 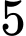 cực trị. Đáp án: B
cực trị. Đáp án: B
Câu 11 [528653]: Cho hàm số đa thức 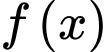 có đạo hàm trên
có đạo hàm trên 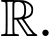 Biết
Biết 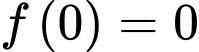 và đồ thị hàm số
và đồ thị hàm số 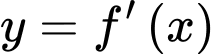 như hình sau:
như hình sau:
=kphan2de1/19.cuctritrituyetdoide1.png)
Hàm số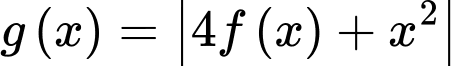 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
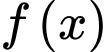 có đạo hàm trên
có đạo hàm trên 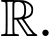 Biết
Biết 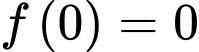 và đồ thị hàm số
và đồ thị hàm số 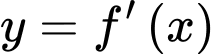 như hình sau:
như hình sau: =kphan2de1/19.cuctritrituyetdoide1.png)
Hàm số
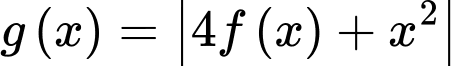 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 6.
B, 2.
C, 5.
D, 3.
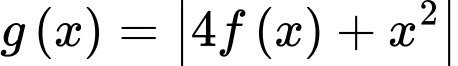
Xét
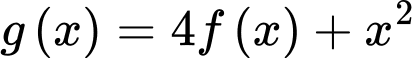
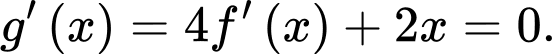
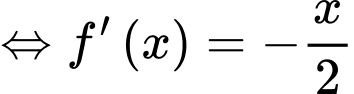
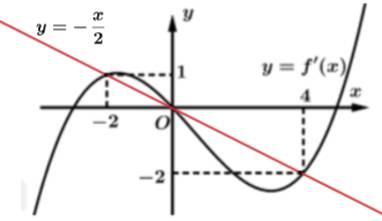
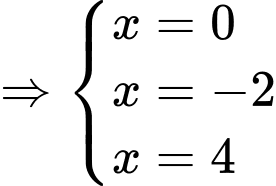
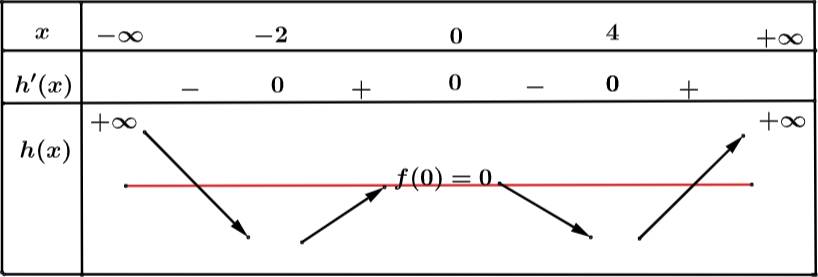
Suy ra
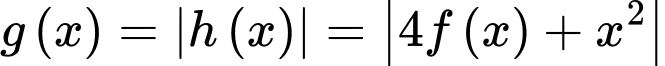 có 5 điểm cực trị.
có 5 điểm cực trị.
Đáp án: C. Đáp án: C
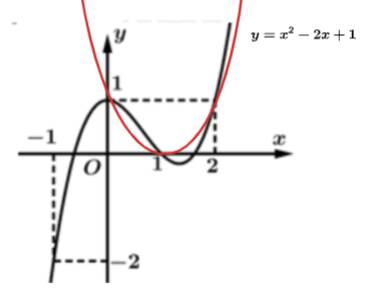
Câu 12 [677694]: Cho hàm số 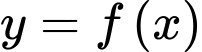 có đạo hàm trên
có đạo hàm trên 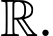 Đồ thị hàm số
Đồ thị hàm số 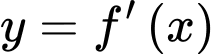 như hình vẽ dưới.
như hình vẽ dưới.
=kphan2de1/17.cuctrijtrituyetdoide1.png)
Xét hàm số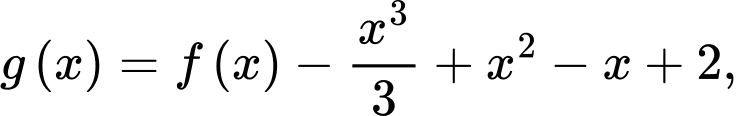 biết
biết 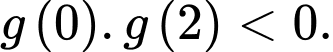 Khi đó số điểm cực trị của hàm số
Khi đó số điểm cực trị của hàm số 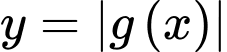 là
là
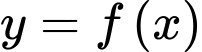 có đạo hàm trên
có đạo hàm trên 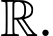 Đồ thị hàm số
Đồ thị hàm số 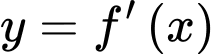 như hình vẽ dưới.
như hình vẽ dưới. =kphan2de1/17.cuctrijtrituyetdoide1.png)
Xét hàm số
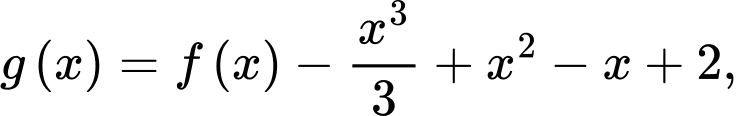 biết
biết 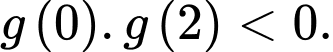 Khi đó số điểm cực trị của hàm số
Khi đó số điểm cực trị của hàm số 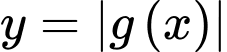 là
là A, 6.
B, 3.
C, 4.
D, 5.
Ta có: 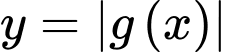 có số cực trị bằng số nghiệm của
có số cực trị bằng số nghiệm của 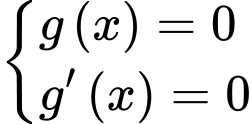
Xét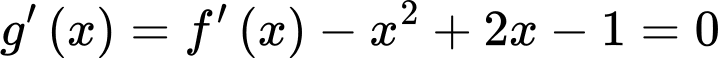
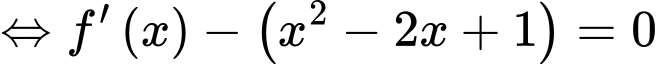
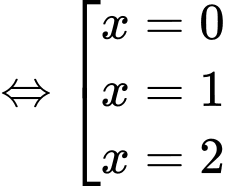
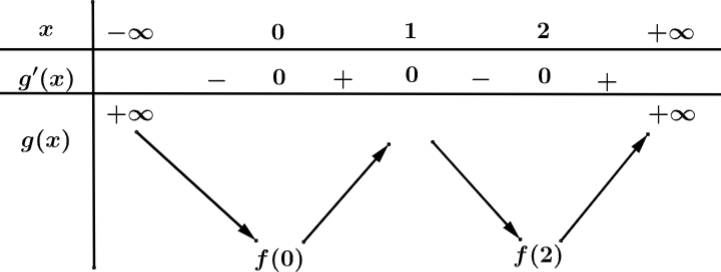
Ta có bảng biến thiên:
Theo giả thiết, lại có: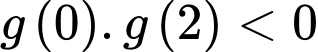
Suy ra, kết hợp cùng bảng biến thiên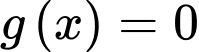 luôn có 2 nghiệm.
luôn có 2 nghiệm.
Suy ra: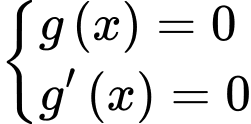 có tổng 5 nghiệm, suy ra hàm số có 5 điểm cực trị.
có tổng 5 nghiệm, suy ra hàm số có 5 điểm cực trị.
Đáp án: D. Đáp án: D
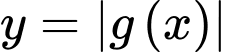 có số cực trị bằng số nghiệm của
có số cực trị bằng số nghiệm của 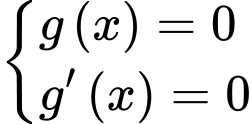
Xét
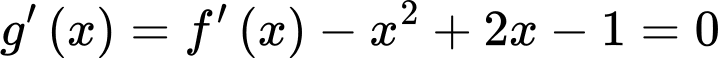
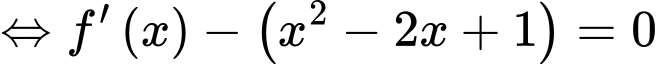

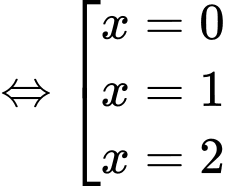
Ta có bảng biến thiên:

Theo giả thiết, lại có:
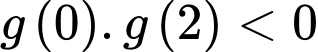
Suy ra, kết hợp cùng bảng biến thiên
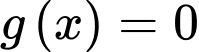 luôn có 2 nghiệm.
luôn có 2 nghiệm.Suy ra:
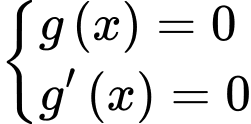 có tổng 5 nghiệm, suy ra hàm số có 5 điểm cực trị.
có tổng 5 nghiệm, suy ra hàm số có 5 điểm cực trị.Đáp án: D. Đáp án: D