Đáp án Bài tập tự luyện số 1
Câu 1 [531021]: Cho hàm số 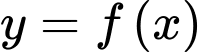 có đạo hàm
có đạo hàm 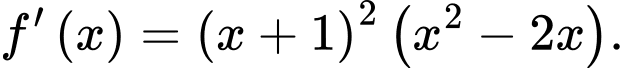 Có bao nhiêu giá trị nguyên dương của m để hàm số
Có bao nhiêu giá trị nguyên dương của m để hàm số 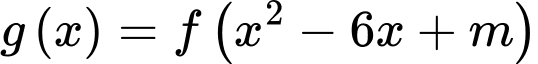 có năm điểm cực trị?
có năm điểm cực trị?
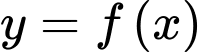 có đạo hàm
có đạo hàm 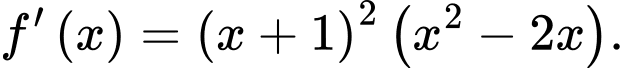 Có bao nhiêu giá trị nguyên dương của m để hàm số
Có bao nhiêu giá trị nguyên dương của m để hàm số 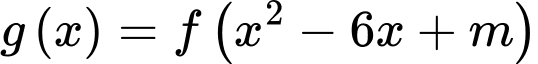 có năm điểm cực trị?
có năm điểm cực trị? A, 7
B, 8.
C, 10.
D, 11.
Chọn B
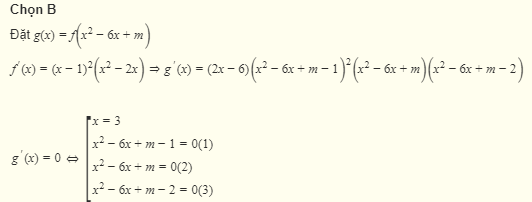
Các phương trình không có nghiệm chung từng đôi một và
không có nghiệm chung từng đôi một và 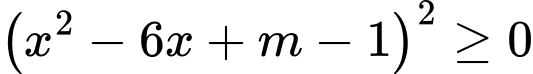 với
với 
Suy ra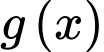 có 5 cực trị khi và chỉ
có 5 cực trị khi và chỉ  và
và  có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 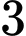 .
.
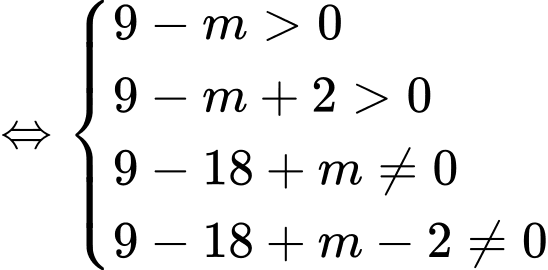
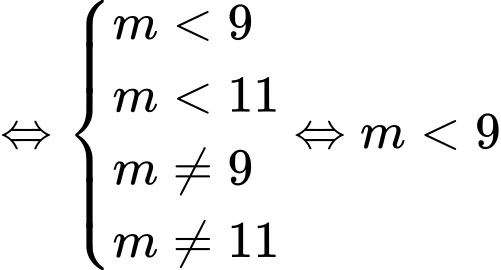
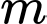 nguyên dương và
nguyên dương và  nên có
nên có 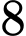 giá trị
giá trị 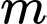 cần tìm. Đáp án: B
cần tìm. Đáp án: B
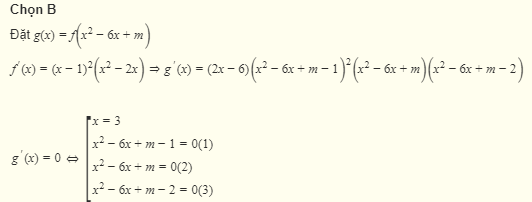
Các phương trình
 không có nghiệm chung từng đôi một và
không có nghiệm chung từng đôi một và 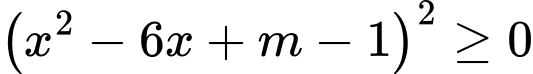 với
với 
Suy ra
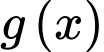 có 5 cực trị khi và chỉ
có 5 cực trị khi và chỉ  và
và  có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác 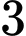 .
.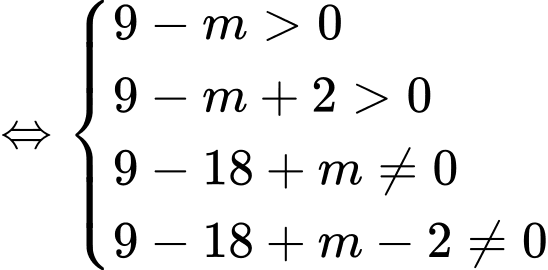
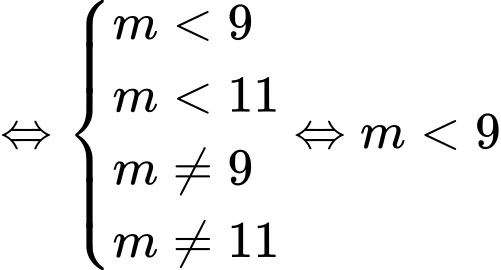
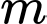 nguyên dương và
nguyên dương và  nên có
nên có 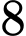 giá trị
giá trị 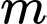 cần tìm. Đáp án: B
cần tìm. Đáp án: B
Câu 2 [31385]: Cho hàm số 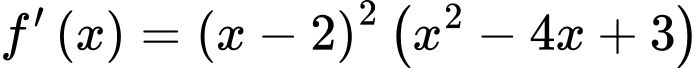 với mọi
với mọi 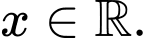 Có bao nhiêu giá trị nguyên dương của tham số
Có bao nhiêu giá trị nguyên dương của tham số 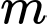 để hàm số
để hàm số 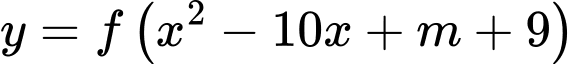 có 5 điểm cực trị?
có 5 điểm cực trị?
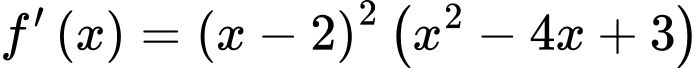 với mọi
với mọi 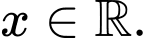 Có bao nhiêu giá trị nguyên dương của tham số
Có bao nhiêu giá trị nguyên dương của tham số 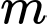 để hàm số
để hàm số 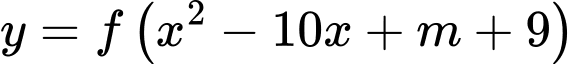 có 5 điểm cực trị?
có 5 điểm cực trị? A, 18.
B, 17.
C, 16.
D, 15.
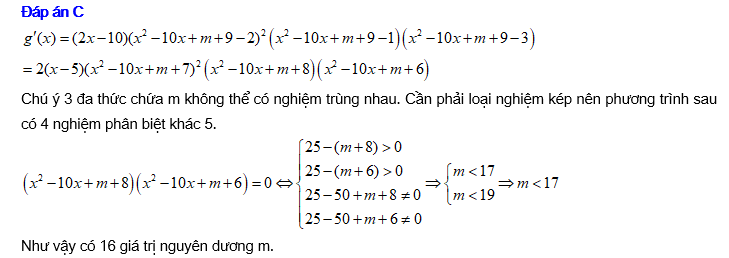 Đáp án: C
Đáp án: C
Câu 3 [806550]: Cho hàm số 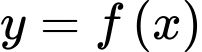 có đạo hàm là
có đạo hàm là 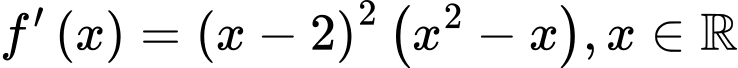 . Gói S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số
. Gói S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 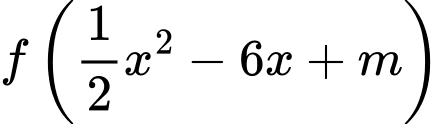 có 5 điểm cực trị. Tính tổng tất cả các phần tử của S.
có 5 điểm cực trị. Tính tổng tất cả các phần tử của S.
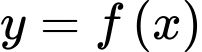 có đạo hàm là
có đạo hàm là 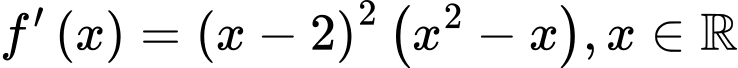 . Gói S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số
. Gói S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 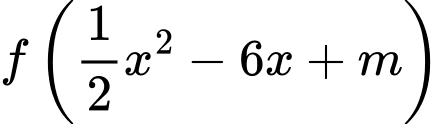 có 5 điểm cực trị. Tính tổng tất cả các phần tử của S.
có 5 điểm cực trị. Tính tổng tất cả các phần tử của S. A, 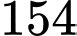 .
.
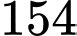 .
.B, 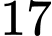 .
.
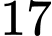 .
.C, 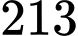 .
.
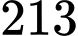 .
.D, 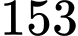 .
.
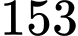 .
. Đáp án: D
Đáp án: D
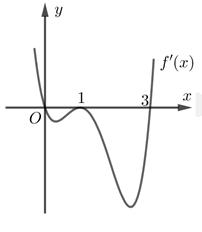
Câu 4 [531024]: Cho hàm số 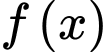 có đạo hàm liên tục trên
có đạo hàm liên tục trên 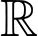 và có đồ thị hàm số
và có đồ thị hàm số 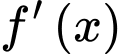 như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
như hình vẽ. Có bao nhiêu giá trị nguyên của tham số 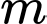 để hàm số
để hàm số 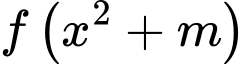 có đúng 3 điểm cực trị?
có đúng 3 điểm cực trị?
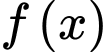 có đạo hàm liên tục trên
có đạo hàm liên tục trên 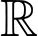 và có đồ thị hàm số
và có đồ thị hàm số 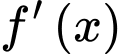 như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
như hình vẽ. Có bao nhiêu giá trị nguyên của tham số 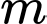 để hàm số
để hàm số 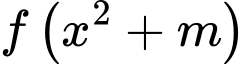 có đúng 3 điểm cực trị?
có đúng 3 điểm cực trị?
A, Vô số.
B, 4.
C, 3.
D, 2.
Đáp án: C
Câu 5 [930975]: Cho hàm số 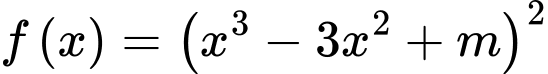 với
với  là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 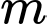 để hàm số có đúng ba điểm cực trị?
để hàm số có đúng ba điểm cực trị?
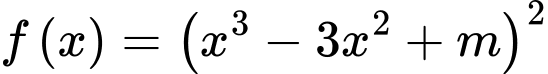 với
với  là tham số. Có bao nhiêu giá trị nguyên của
là tham số. Có bao nhiêu giá trị nguyên của 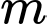 để hàm số có đúng ba điểm cực trị?
để hàm số có đúng ba điểm cực trị? A, 8.
B, 13.
C, 10.
D, 12.
Đáp án: C
Câu 6 [531040]: Có bao nhiêu giá trị nguyên của tham số 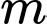 để hàm số
để hàm số 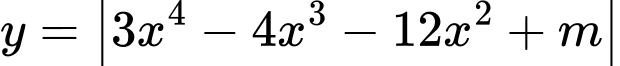 có 7 điểm cực trị?
có 7 điểm cực trị?
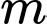 để hàm số
để hàm số 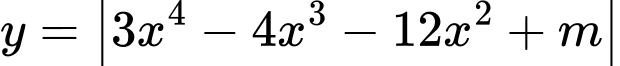 có 7 điểm cực trị?
có 7 điểm cực trị? A, 3.
B, 5.
C, 6.
D, 4.
Đáp án: D
Câu 7 [789331]: Tập tất các giá trị của tham số 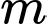 để hàm số
để hàm số 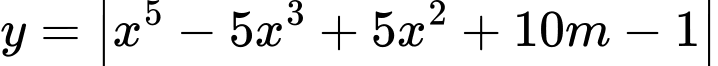 có 5 điểm cực trị là khoảng
có 5 điểm cực trị là khoảng 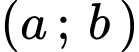 .Tính tổng
.Tính tổng  .
.
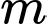 để hàm số
để hàm số 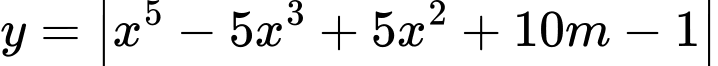 có 5 điểm cực trị là khoảng
có 5 điểm cực trị là khoảng 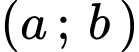 .Tính tổng
.Tính tổng  .
. A, 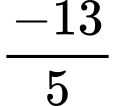 .
.
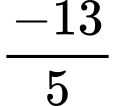 .
.B, 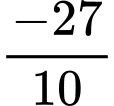 .
.
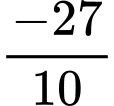 .
.C, 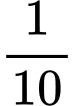 .
.
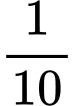 .
.D, 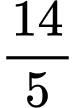 .
.
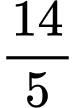 .
.
Chọn A
Xét hàm số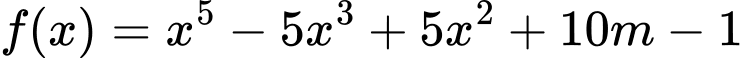 .
.
Ta có: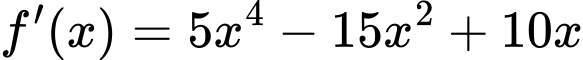 .
.
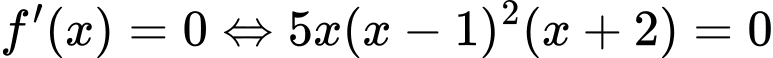
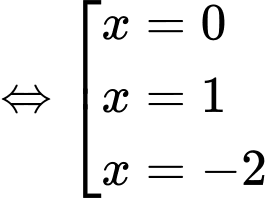 .
.
Bảng biến thiên:
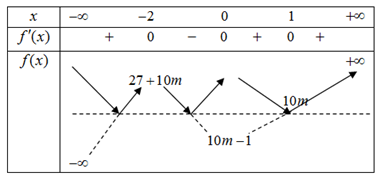
Để hàm số đã cho có 5 điểm cực trị thì
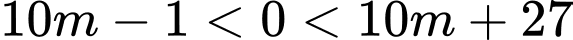
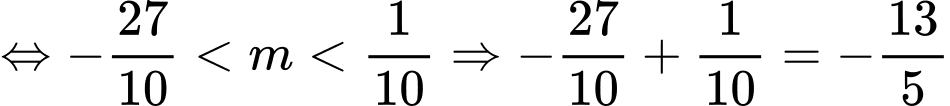 . Đáp án: A
. Đáp án: A
Xét hàm số
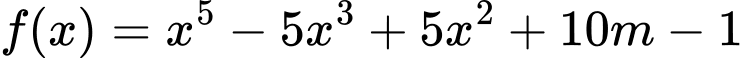 .
.Ta có:
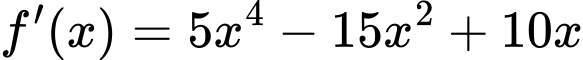 .
.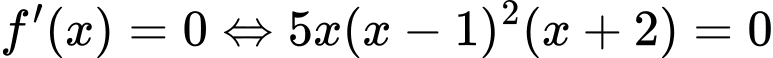
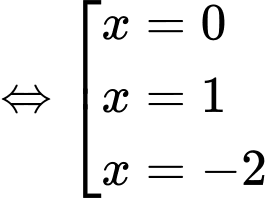 .
.Bảng biến thiên:

Để hàm số đã cho có 5 điểm cực trị thì
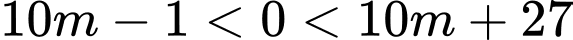
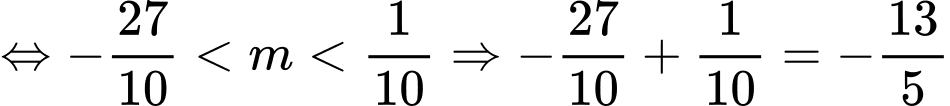 . Đáp án: A
. Đáp án: A
Câu 8 [679681]: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 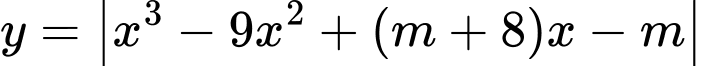 có năm điểm cực trị?
có năm điểm cực trị?
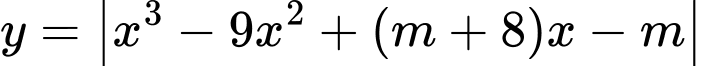 có năm điểm cực trị?
có năm điểm cực trị? A, 
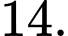
B, 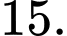
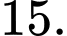
C, vô số.
D, 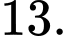
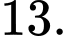
HD: Xét 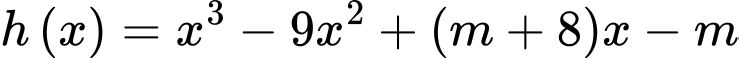
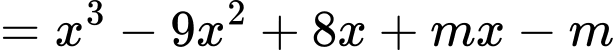

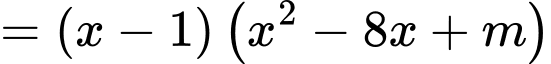
Để hàm số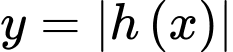 có 5 điểm cực trị khi và chỉ khi đồ thị hàm số
có 5 điểm cực trị khi và chỉ khi đồ thị hàm số 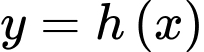 cắt trục hoành tại 3 điểm phân biệt
cắt trục hoành tại 3 điểm phân biệt
Khi đó phương trình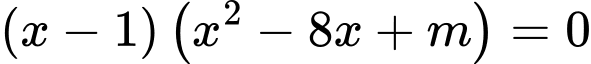 có 3 nghiệm phân biệt
có 3 nghiệm phân biệt 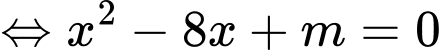 có 2 nghiệm phân biệt khác 1
có 2 nghiệm phân biệt khác 1
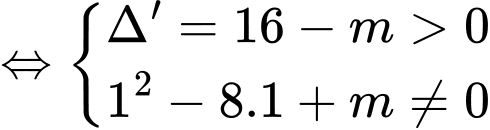
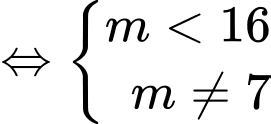
Kết hợp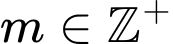
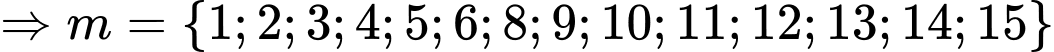 nên có 14 giá trị của m. Đáp án: A
nên có 14 giá trị của m. Đáp án: A
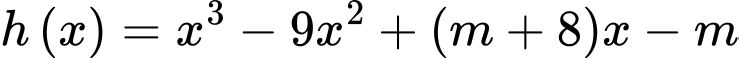
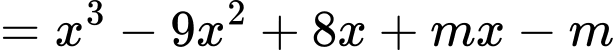

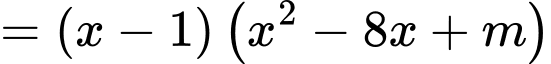
Để hàm số
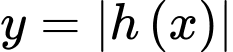 có 5 điểm cực trị khi và chỉ khi đồ thị hàm số
có 5 điểm cực trị khi và chỉ khi đồ thị hàm số 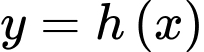 cắt trục hoành tại 3 điểm phân biệt
cắt trục hoành tại 3 điểm phân biệt Khi đó phương trình
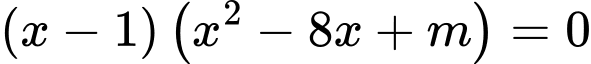 có 3 nghiệm phân biệt
có 3 nghiệm phân biệt 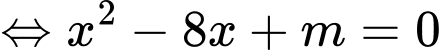 có 2 nghiệm phân biệt khác 1
có 2 nghiệm phân biệt khác 1 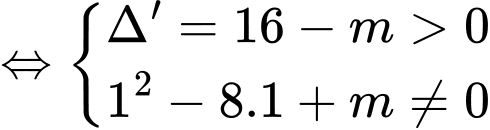
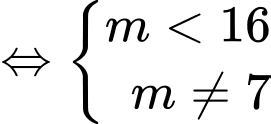
Kết hợp
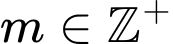
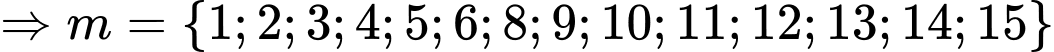 nên có 14 giá trị của m. Đáp án: A
nên có 14 giá trị của m. Đáp án: A
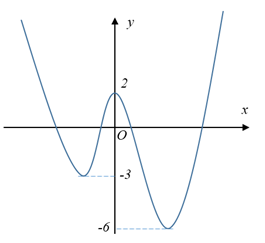
Câu 9 [531052]: Cho 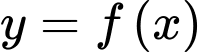 là hàm số đa thức bậc bốn và có đồ thị như hình vẽ.
là hàm số đa thức bậc bốn và có đồ thị như hình vẽ.
Có bao nhiêu giá trị của tham số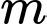 thuộc đoạn
thuộc đoạn 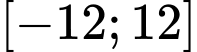 để hàm số
để hàm số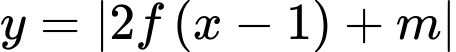 có 5 điểm cực trị?
có 5 điểm cực trị?
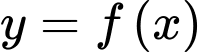 là hàm số đa thức bậc bốn và có đồ thị như hình vẽ.
là hàm số đa thức bậc bốn và có đồ thị như hình vẽ.
Có bao nhiêu giá trị của tham số
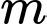 thuộc đoạn
thuộc đoạn 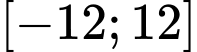 để hàm số
để hàm số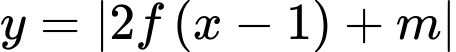 có 5 điểm cực trị?
có 5 điểm cực trị? A, 13.
B, 14.
C, 15.
D, 12.
Từ đồ thị hàm số 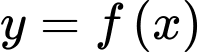 suy ra
suy ra 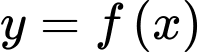 có 3 điểm cực trị nên hàm số
có 3 điểm cực trị nên hàm số 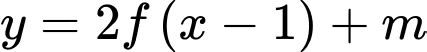 có 3 điểm cực trị.
có 3 điểm cực trị.
Do đó đồ thị hàm số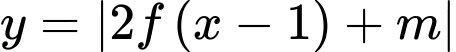 có 5 điểm cực trị khi và chỉ khi đồ thị hàm số
có 5 điểm cực trị khi và chỉ khi đồ thị hàm số 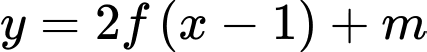 cắt trục hoành tại hai điểm phân biệt hoặc phương trình
cắt trục hoành tại hai điểm phân biệt hoặc phương trình 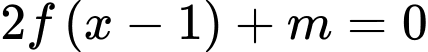 có 3 nghiệm phân biệt trong đó có 1 nghiệm kép
có 3 nghiệm phân biệt trong đó có 1 nghiệm kép 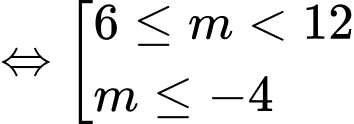
Suy ra có 15 giá trị của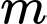 thuộc đoạn
thuộc đoạn 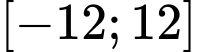 thỏa mãn. Chọn C.
Đáp án: C
thỏa mãn. Chọn C.
Đáp án: C
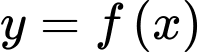 suy ra
suy ra 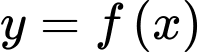 có 3 điểm cực trị nên hàm số
có 3 điểm cực trị nên hàm số 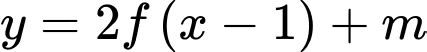 có 3 điểm cực trị.
có 3 điểm cực trị.Do đó đồ thị hàm số
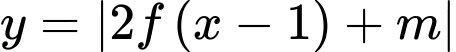 có 5 điểm cực trị khi và chỉ khi đồ thị hàm số
có 5 điểm cực trị khi và chỉ khi đồ thị hàm số 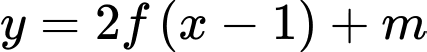 cắt trục hoành tại hai điểm phân biệt hoặc phương trình
cắt trục hoành tại hai điểm phân biệt hoặc phương trình 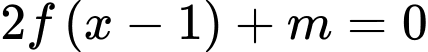 có 3 nghiệm phân biệt trong đó có 1 nghiệm kép
có 3 nghiệm phân biệt trong đó có 1 nghiệm kép 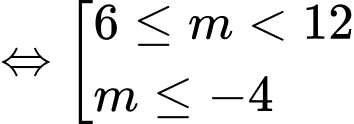
Suy ra có 15 giá trị của
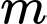 thuộc đoạn
thuộc đoạn 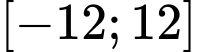 thỏa mãn. Chọn C.
Đáp án: C
thỏa mãn. Chọn C.
Đáp án: C
Câu 10 [971331]: Cho hàm số 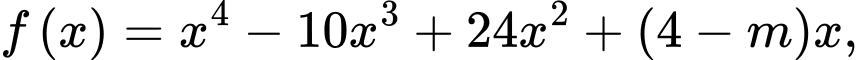 với
với 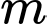 là tham số thực.Có bao nhiêu giá trị nguyên của tham số
là tham số thực.Có bao nhiêu giá trị nguyên của tham số 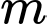 để hàm số
để hàm số 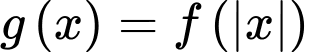 có đúng 7 điểm cực trị?
có đúng 7 điểm cực trị?
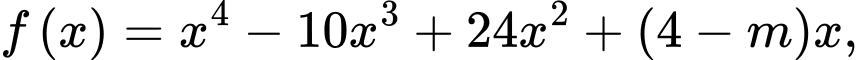 với
với 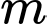 là tham số thực.Có bao nhiêu giá trị nguyên của tham số
là tham số thực.Có bao nhiêu giá trị nguyên của tham số 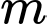 để hàm số
để hàm số 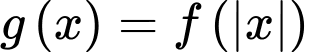 có đúng 7 điểm cực trị?
có đúng 7 điểm cực trị? A, 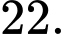
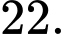
B, 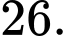
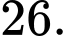
C, 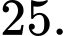
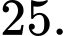
D, 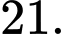
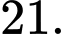
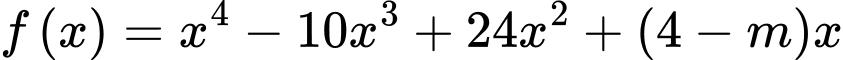
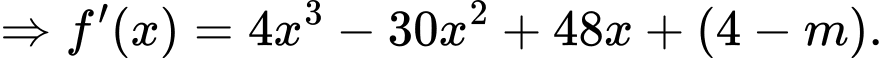
Để hàm số 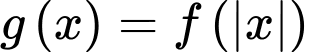 có đúng 7 điểm cực trị thì hàm số
có đúng 7 điểm cực trị thì hàm số 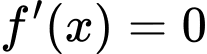 có 3 nghiệm bội lẻ dương.
có 3 nghiệm bội lẻ dương.
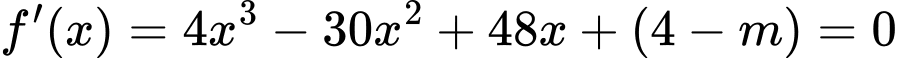
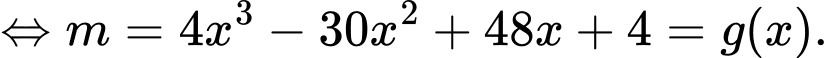
BBT:
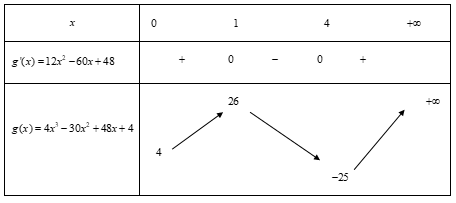
Vậy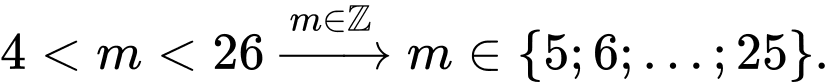
Chọn đáp án D. Đáp án: D
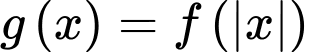 có đúng 7 điểm cực trị thì hàm số
có đúng 7 điểm cực trị thì hàm số 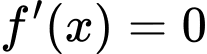 có 3 nghiệm bội lẻ dương.
có 3 nghiệm bội lẻ dương.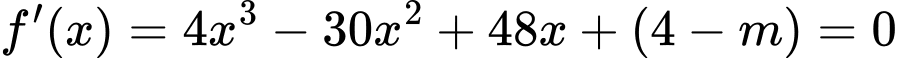
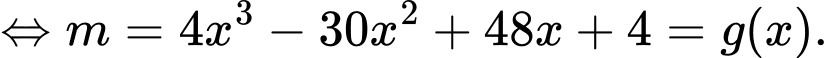
BBT:

Vậy
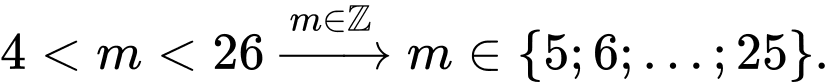
Chọn đáp án D. Đáp án: D
Câu 11 [971332]: Cho hàm số 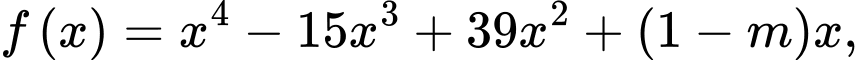 với
với 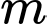 là tham số thực.Có bao nhiêu giá trị nguyên của tham số
là tham số thực.Có bao nhiêu giá trị nguyên của tham số 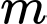 để hàm số
để hàm số 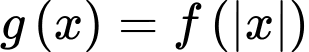 có đúng 7 điểm cực trị?
có đúng 7 điểm cực trị?
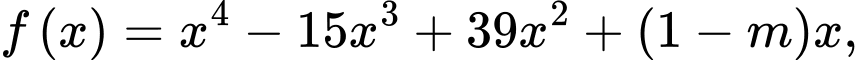 với
với 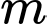 là tham số thực.Có bao nhiêu giá trị nguyên của tham số
là tham số thực.Có bao nhiêu giá trị nguyên của tham số 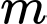 để hàm số
để hàm số 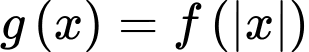 có đúng 7 điểm cực trị?
có đúng 7 điểm cực trị? A, 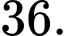
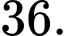
B, 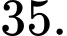
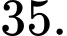
C, 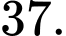
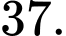
D, 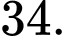
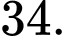
Đáp án: A
Câu 12 [212401]: Cho hàm số 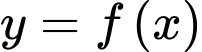 có đạo hàm là
có đạo hàm là 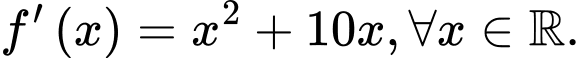 Có bao nhiêu giá trị nguyên của tham số
Có bao nhiêu giá trị nguyên của tham số 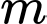 để hàm số
để hàm số 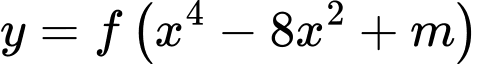 có đúng 9 điểm cực trị?
có đúng 9 điểm cực trị?
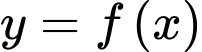 có đạo hàm là
có đạo hàm là 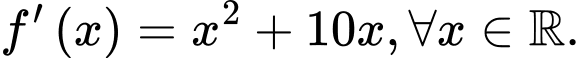 Có bao nhiêu giá trị nguyên của tham số
Có bao nhiêu giá trị nguyên của tham số 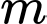 để hàm số
để hàm số 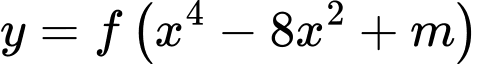 có đúng 9 điểm cực trị?
có đúng 9 điểm cực trị? A, 16.
B, 9.
C, 15.
D, 10.
Chọn D
Ta có 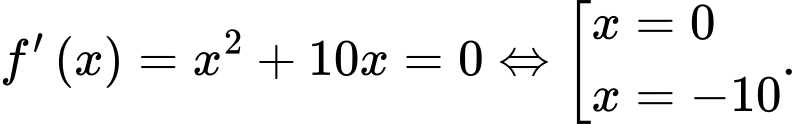 Khi đó
Khi đó 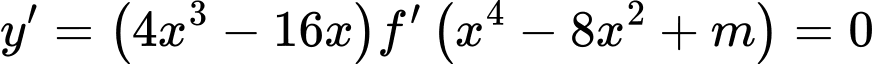
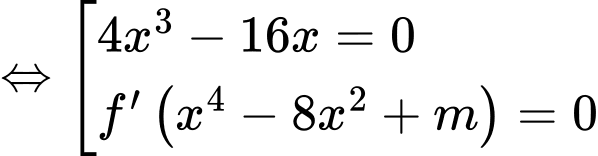
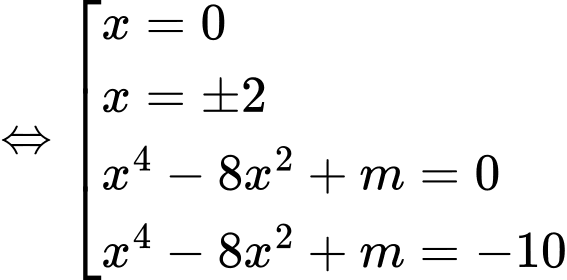
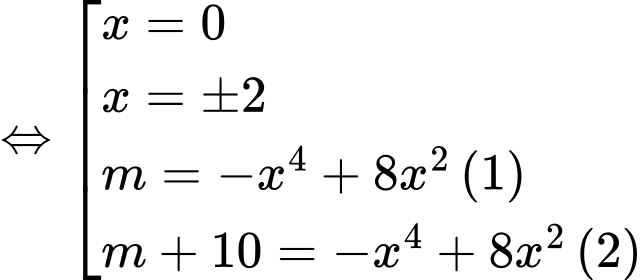 Xét hàm số
Xét hàm số 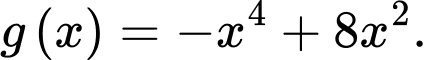 Ta có
Ta có 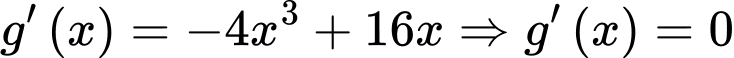
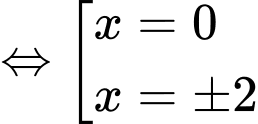 Bảng biến thiên:
Hàm số
Bảng biến thiên:
Hàm số 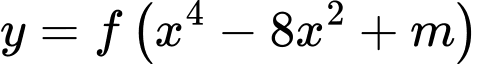 có đúng
có đúng 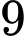 điểm cực trị khi
điểm cực trị khi  có hai nghiệm hoặc ba nghiệm trong đó có
có hai nghiệm hoặc ba nghiệm trong đó có 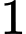 nghiệm bằng
nghiệm bằng  và
và  có
có 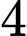 nghiệm phân biệt. Do đó dựa vào bảng biến thiên của hàm số
nghiệm phân biệt. Do đó dựa vào bảng biến thiên của hàm số 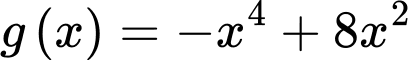 ta có
ta có

 Vì
Vì  nên
nên 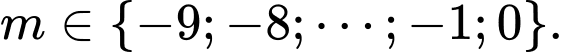 Vậy có
Vậy có  giá trị nguyên
giá trị nguyên 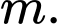 Đáp án: D
Đáp án: D
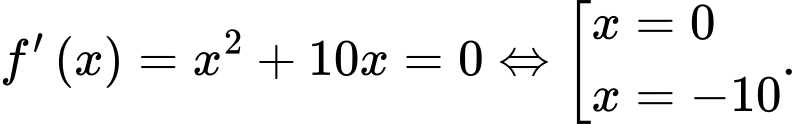 Khi đó
Khi đó 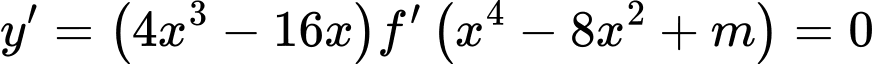
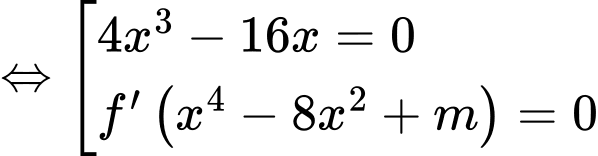
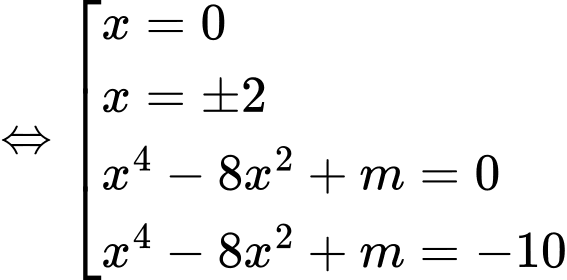
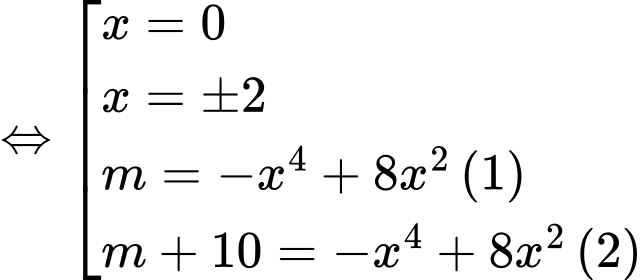 Xét hàm số
Xét hàm số 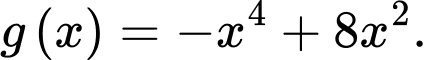 Ta có
Ta có 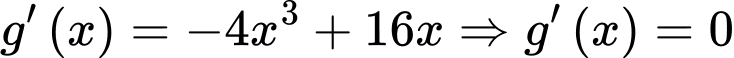
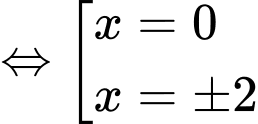 Bảng biến thiên:
Hàm số
Bảng biến thiên:
Hàm số 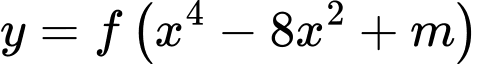 có đúng
có đúng 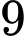 điểm cực trị khi
điểm cực trị khi  có hai nghiệm hoặc ba nghiệm trong đó có
có hai nghiệm hoặc ba nghiệm trong đó có 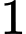 nghiệm bằng
nghiệm bằng  và
và  có
có 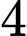 nghiệm phân biệt. Do đó dựa vào bảng biến thiên của hàm số
nghiệm phân biệt. Do đó dựa vào bảng biến thiên của hàm số 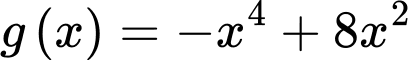 ta có
ta có

 Vì
Vì  nên
nên 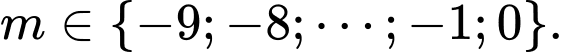 Vậy có
Vậy có  giá trị nguyên
giá trị nguyên 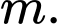 Đáp án: D
Đáp án: D
Câu 13 [222184]: Cho hàm số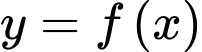 có đạo hàm là
có đạo hàm là 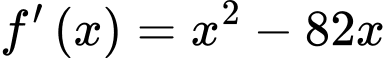 . Có bao nhiêu giá trị nguyên dương của tham số
. Có bao nhiêu giá trị nguyên dương của tham số 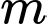 để hàm số
để hàm số 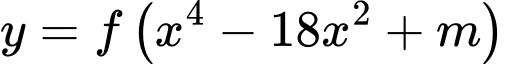 có đúng
có đúng 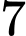 cực trị?
cực trị?
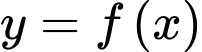 có đạo hàm là
có đạo hàm là 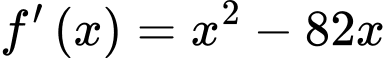 . Có bao nhiêu giá trị nguyên dương của tham số
. Có bao nhiêu giá trị nguyên dương của tham số 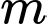 để hàm số
để hàm số 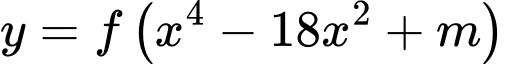 có đúng
có đúng 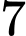 cực trị?
cực trị? A, 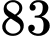 .
.
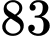 .
.B, Vô số.
C, 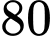 .
.
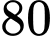 .
.D, 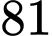 .
.
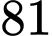 .
.
Chọn C
Ta có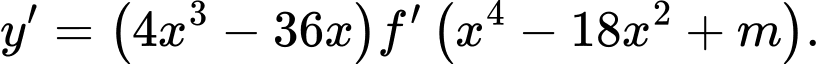
Cho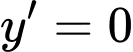
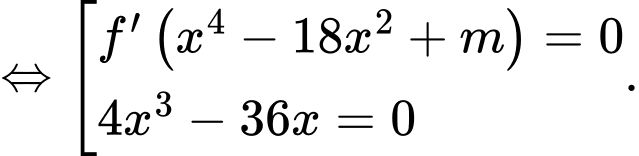
*) Với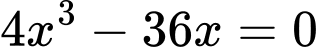
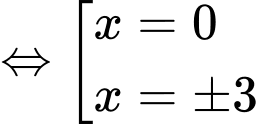 có 3 nghiệm đơn.
có 3 nghiệm đơn.
*) Với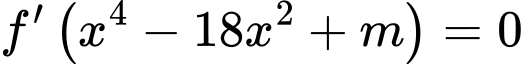
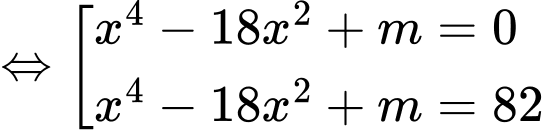
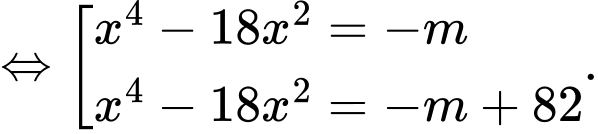
Xét hàm số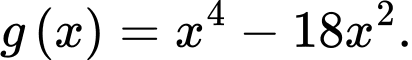
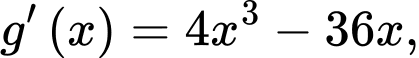
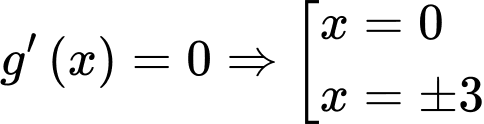
Ta có bảng biến thiên của hàm số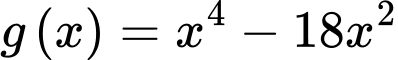 .
.
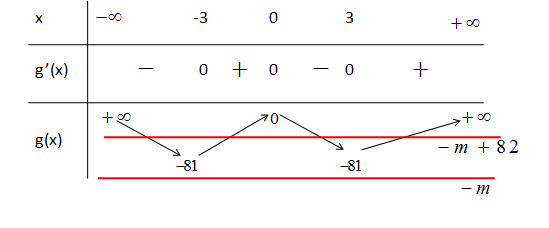
Để hàm số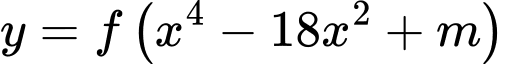 có đúng
có đúng 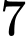 cực trị thì
cực trị thì 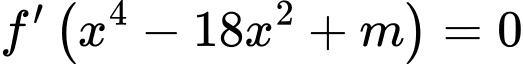 phải có 4 nghiệm đơn khác
phải có 4 nghiệm đơn khác 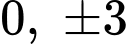 . Do đó dựa vào bảng biến thiên ta có
. Do đó dựa vào bảng biến thiên ta có 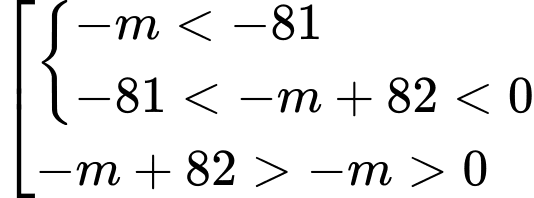
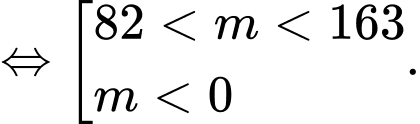
Mà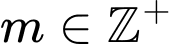 nên
nên 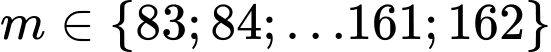 nên có 80 giá trị. Đáp án: C
nên có 80 giá trị. Đáp án: C
Ta có
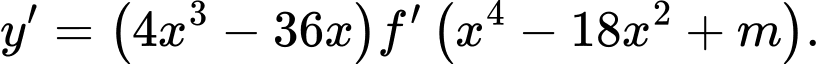
Cho
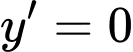
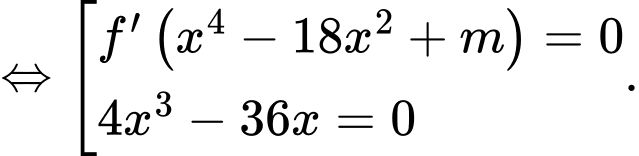
*) Với
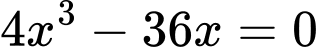
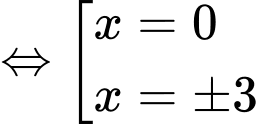 có 3 nghiệm đơn.
có 3 nghiệm đơn.*) Với
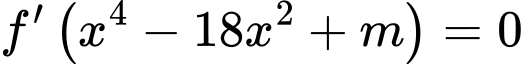
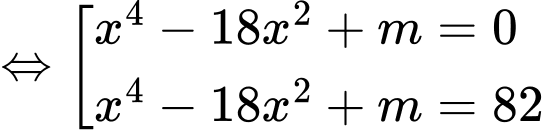
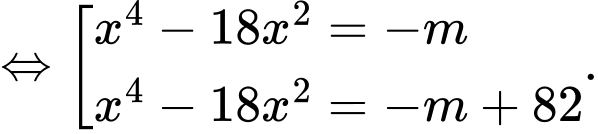
Xét hàm số
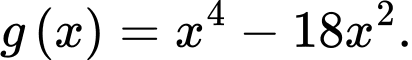
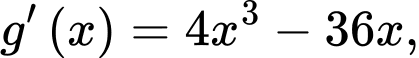
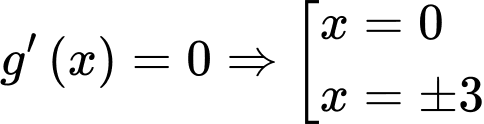
Ta có bảng biến thiên của hàm số
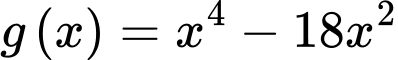 .
.
Để hàm số
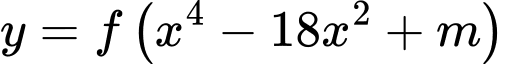 có đúng
có đúng 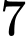 cực trị thì
cực trị thì 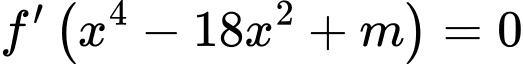 phải có 4 nghiệm đơn khác
phải có 4 nghiệm đơn khác 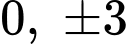 . Do đó dựa vào bảng biến thiên ta có
. Do đó dựa vào bảng biến thiên ta có 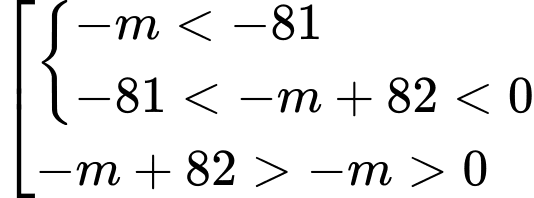
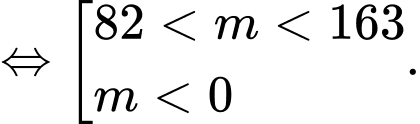
Mà
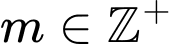 nên
nên 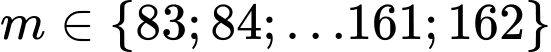 nên có 80 giá trị. Đáp án: C
nên có 80 giá trị. Đáp án: C
Câu 14 [225108]: Cho hàm số 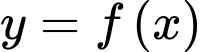 có đạo hàm
có đạo hàm 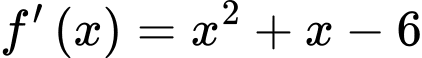 . Có bao nhiêu giá trị nguyên của
. Có bao nhiêu giá trị nguyên của 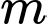 để hàm số
để hàm số 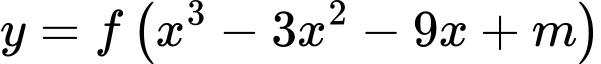 có đúng 6 điểm cực trị?
có đúng 6 điểm cực trị?
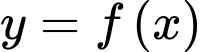 có đạo hàm
có đạo hàm 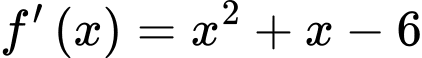 . Có bao nhiêu giá trị nguyên của
. Có bao nhiêu giá trị nguyên của 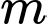 để hàm số
để hàm số 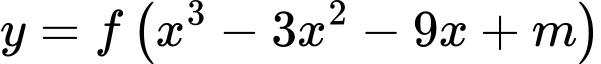 có đúng 6 điểm cực trị?
có đúng 6 điểm cực trị? A, 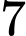 .
.
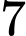 .
.B, 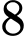 .
.
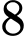 .
.C, 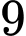 .
.
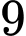 .
.D,  .
.
 .
.
Chọn D
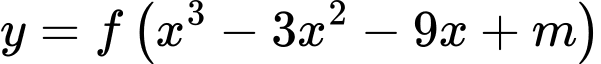
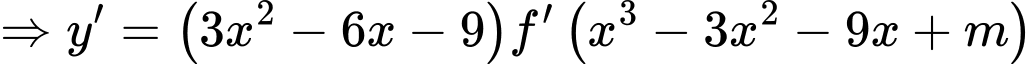
Ta có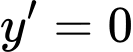
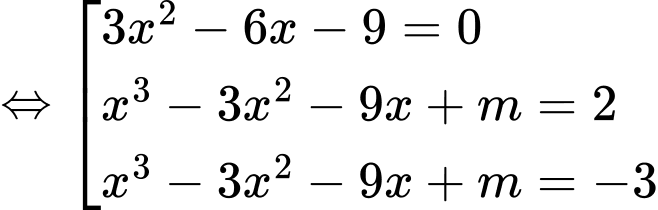
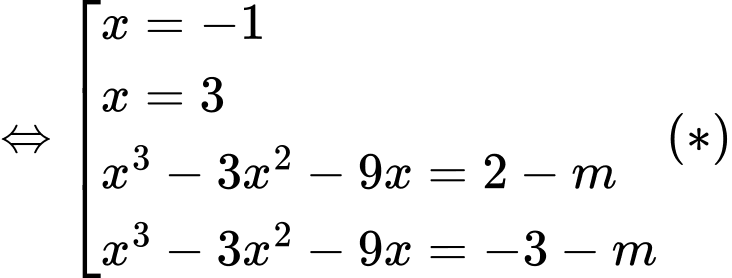
Xét hàm số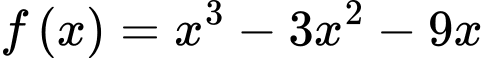
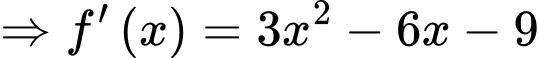
Ta có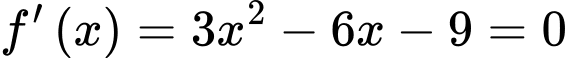
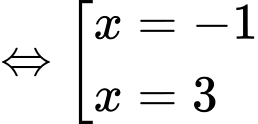
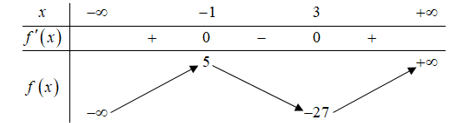
Bảng biến thiên:
Để có 6 nghiệm phân biệt
có 6 nghiệm phân biệt 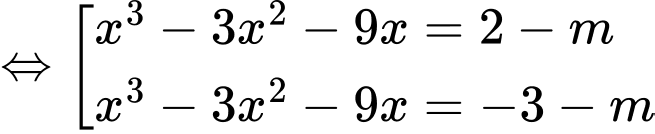 có 4 nghiệm phân biệt
có 4 nghiệm phân biệt 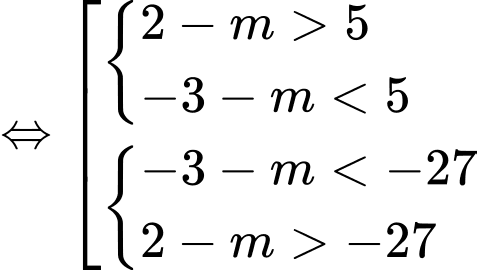
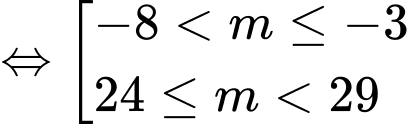 . Đáp án: D
. Đáp án: D
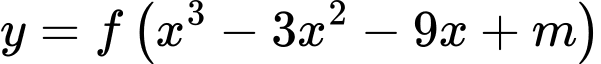
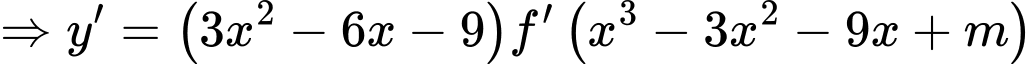
Ta có
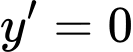
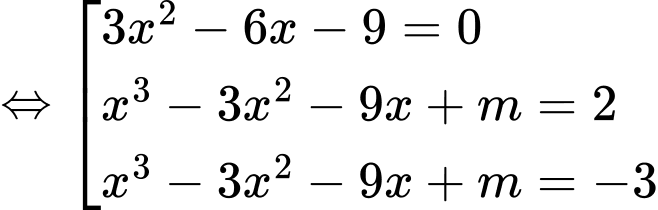
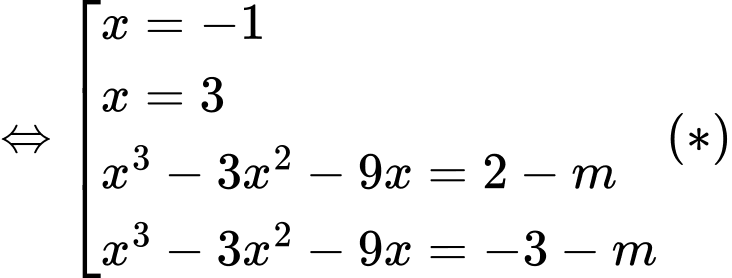
Xét hàm số
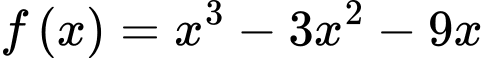
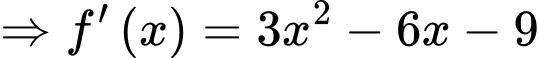
Ta có
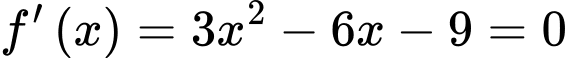
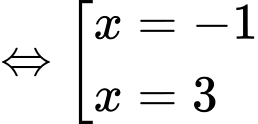
Bảng biến thiên:

Để
 có 6 nghiệm phân biệt
có 6 nghiệm phân biệt 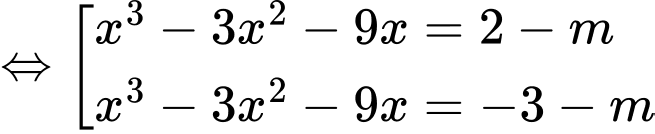 có 4 nghiệm phân biệt
có 4 nghiệm phân biệt 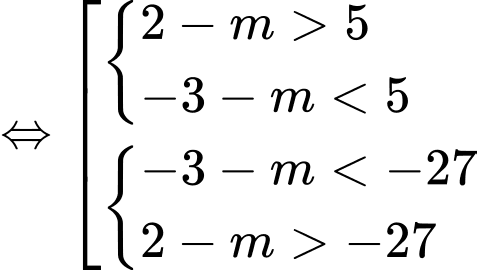
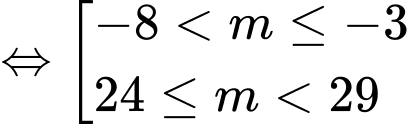 . Đáp án: D
. Đáp án: D
Câu 15 [282752]: Cho hai hàm số 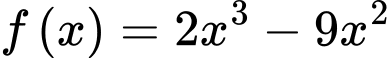 và
và 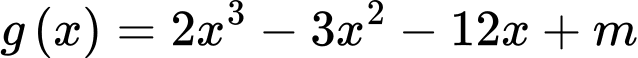 (
(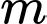 là tham số). Có bao nhiêu số nguyên
là tham số). Có bao nhiêu số nguyên 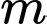 để hàm số
để hàm số 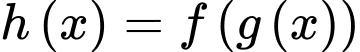 có đúng 6 điểm cực trị?
có đúng 6 điểm cực trị?
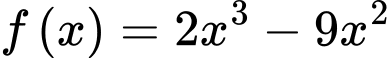 và
và 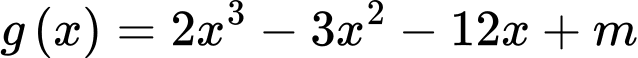 (
(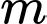 là tham số). Có bao nhiêu số nguyên
là tham số). Có bao nhiêu số nguyên 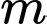 để hàm số
để hàm số 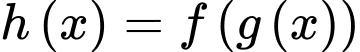 có đúng 6 điểm cực trị?
có đúng 6 điểm cực trị? A, 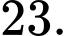
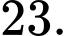
B, 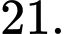
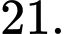
C, 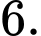
D, 
a Đáp án: C
Đáp án: C
 Đáp án: C
Đáp án: C