Đáp án Bài tập tự luyện-Đơn điệu của hàm trị tuyệt đối chứa m
Câu 1 [677050]: Có bao nhiêu giá trị nguyên dương của tham số 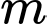 để hàm số
để hàm số  đồng biến trên khoảng
đồng biến trên khoảng 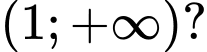
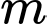 để hàm số
để hàm số  đồng biến trên khoảng
đồng biến trên khoảng 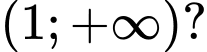
A, 2.
B, 6.
C, 3.
D, 4.
Đáp án: C
Câu 2 [328060]: Tìm số giá trị nguyên của 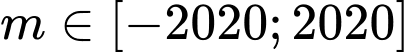 để hàm số
để hàm số 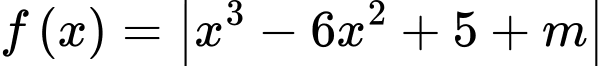 đồng biến trên
đồng biến trên 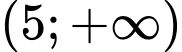 .
.
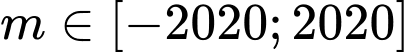 để hàm số
để hàm số 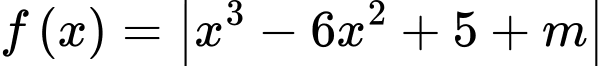 đồng biến trên
đồng biến trên 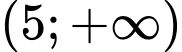 .
. A,  .
.
 .
.B, 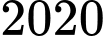 .
.
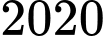 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn C
Xét với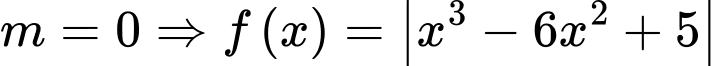 .
.
Gọi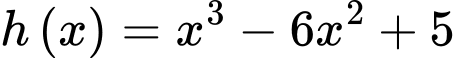
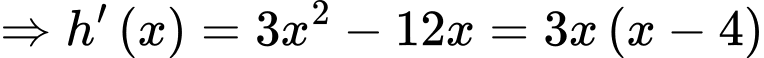 .
.
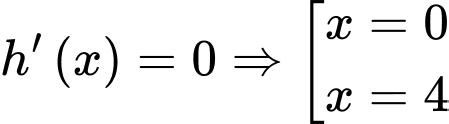
Gọi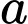 là số thực sao cho
là số thực sao cho  và
và 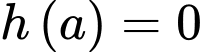 .
.
Ta có bảng biến thiên sau:
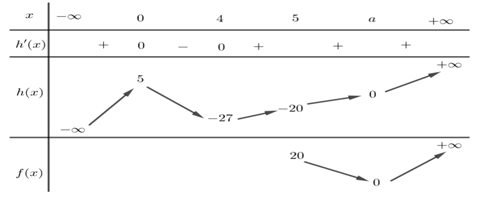
Nhìn vào bảng biến thiên muốn để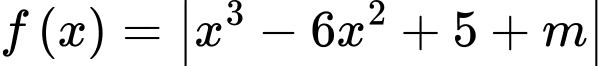 đồng biến trên
đồng biến trên 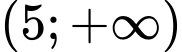 thì
thì
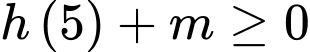
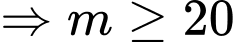 . Do
. Do 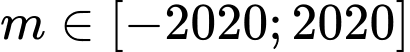 nên có
nên có 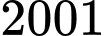 giá trị thỏa mãn. Đáp án: C
giá trị thỏa mãn. Đáp án: C
Xét với
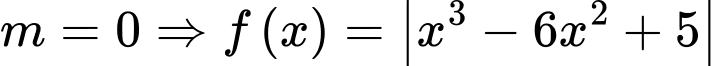 .
.Gọi
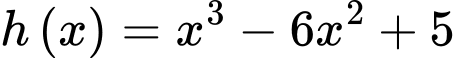
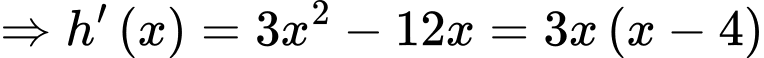 .
.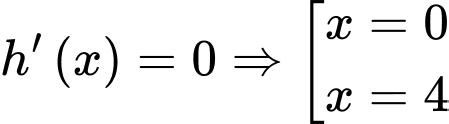
Gọi
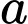 là số thực sao cho
là số thực sao cho  và
và 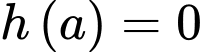 .
.Ta có bảng biến thiên sau:

Nhìn vào bảng biến thiên muốn để
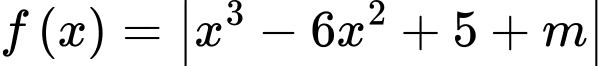 đồng biến trên
đồng biến trên 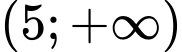 thì
thì
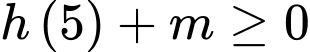
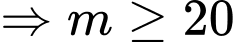 . Do
. Do 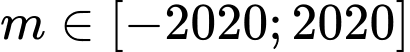 nên có
nên có 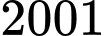 giá trị thỏa mãn. Đáp án: C
giá trị thỏa mãn. Đáp án: C
Câu 3 [677051]: Có bao nhiêu gía trị nguyên của tham số 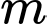 nhỏ hơn
nhỏ hơn  để hàm số
để hàm số 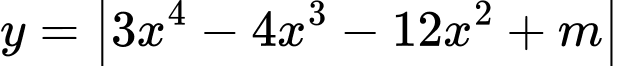 nghịch biến trên khoảng
nghịch biến trên khoảng 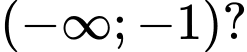
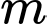 nhỏ hơn
nhỏ hơn  để hàm số
để hàm số 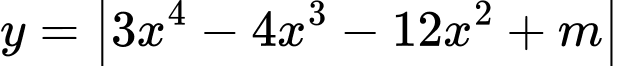 nghịch biến trên khoảng
nghịch biến trên khoảng 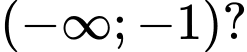
A, 6.
B, 4.
C, 3.
D, 5.
Đáp án: D
Câu 4 [280815]: Có bao nhiêu giá trị nguyên của tham số 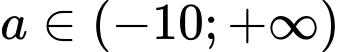 để hàm số
để hàm số 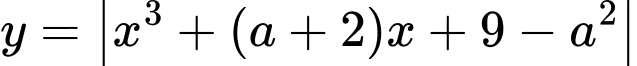 đồng biến trên khoảng
đồng biến trên khoảng 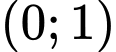 ?
?
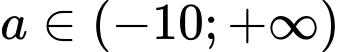 để hàm số
để hàm số 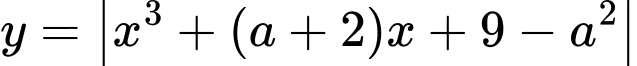 đồng biến trên khoảng
đồng biến trên khoảng 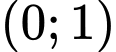 ?
? A, 12.
B, 11.
C, 6.
D, 5.
Chọn B
Xét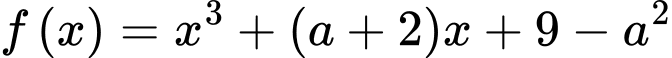
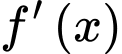

Để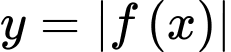 đồng biến trên khoảng
đồng biến trên khoảng 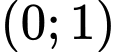
TH1: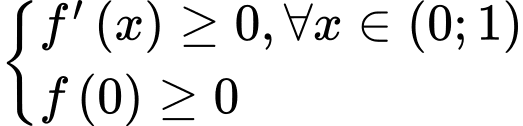
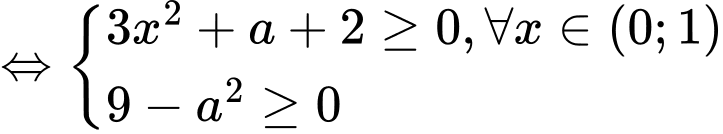
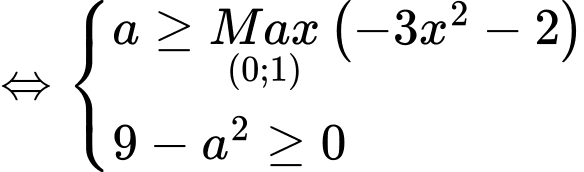
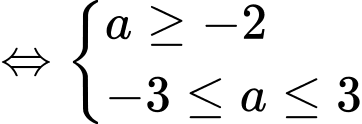

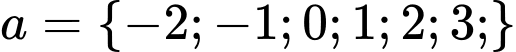 → 6 giá trị
→ 6 giá trị
TH2: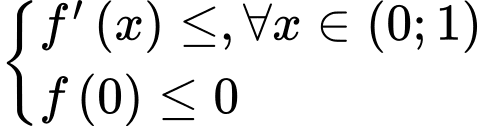
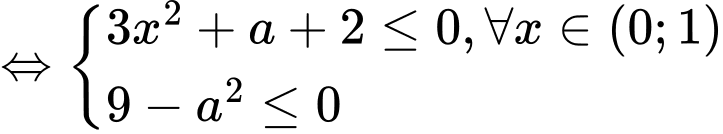
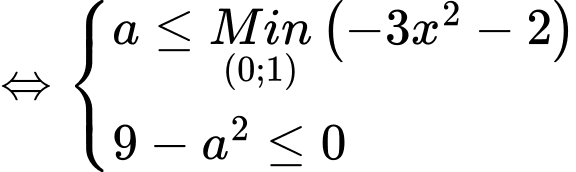
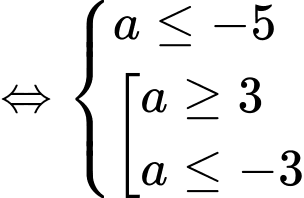

Kết hợp với điều kiện bài toán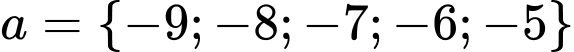 → 5 giá trị
→ 5 giá trị
Vậy có 11 giá trị thoả mãn Đáp án: B
Xét
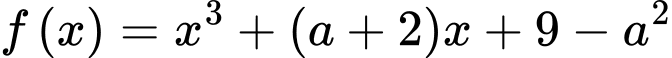
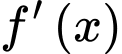

Để
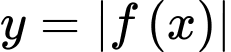 đồng biến trên khoảng
đồng biến trên khoảng 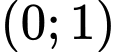
TH1:
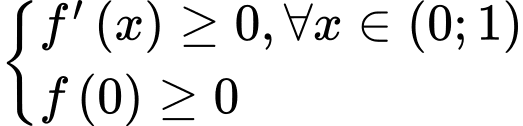
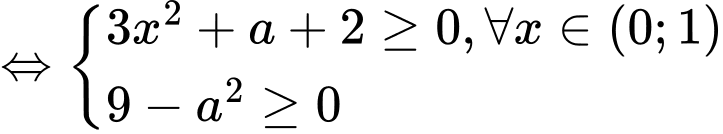
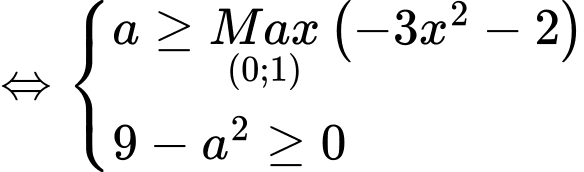
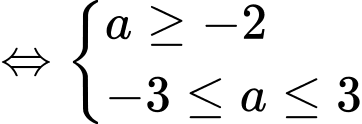

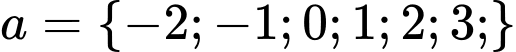 → 6 giá trị
→ 6 giá trịTH2:
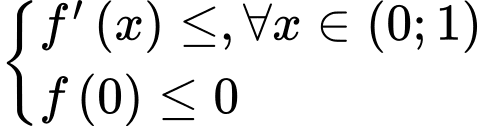
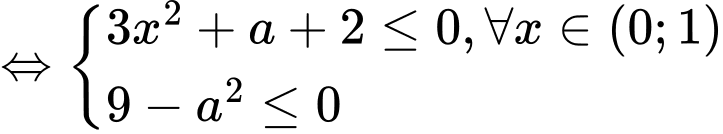
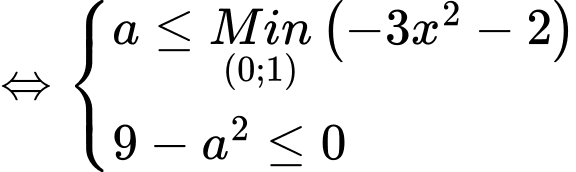
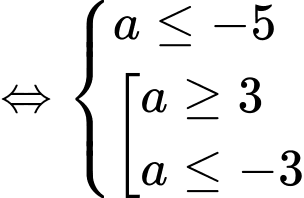

Kết hợp với điều kiện bài toán
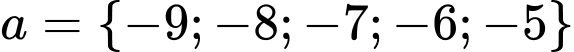 → 5 giá trị
→ 5 giá trịVậy có 11 giá trị thoả mãn Đáp án: B
Câu 5 [738464]: Có bao nhiêu giá trị nguyên của tham số 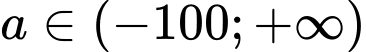 để hàm số
để hàm số 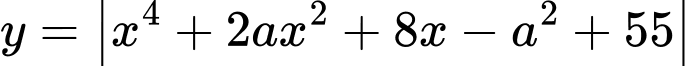 nghịch biến trên khoảng
nghịch biến trên khoảng 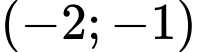 ?
?
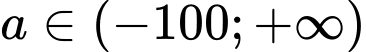 để hàm số
để hàm số 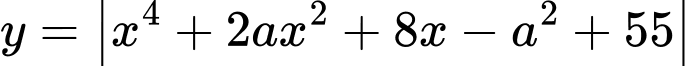 nghịch biến trên khoảng
nghịch biến trên khoảng 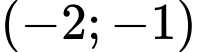 ?
? A, 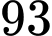 .
.
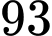 .
.B, 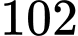 .
.
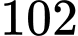 .
.C, 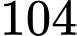 .
.
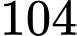 .
.D, 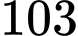 .
.
 .
.
Chọn B
Xét hàm số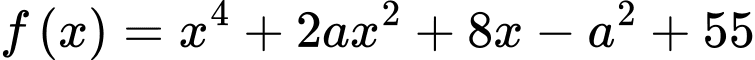
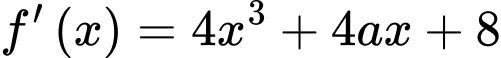
Để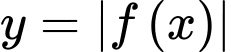 nghịch biến trên khoảng
nghịch biến trên khoảng 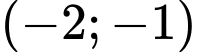
TH1: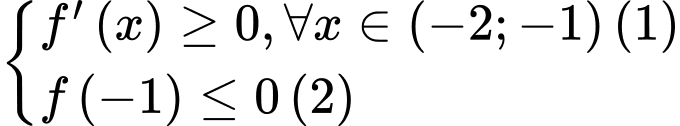
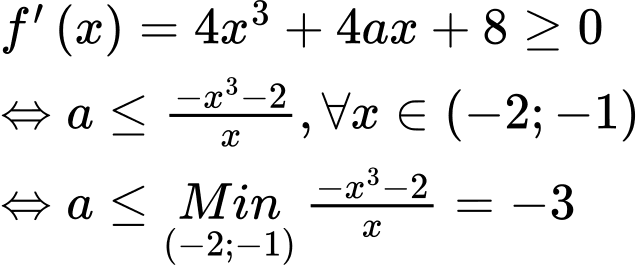
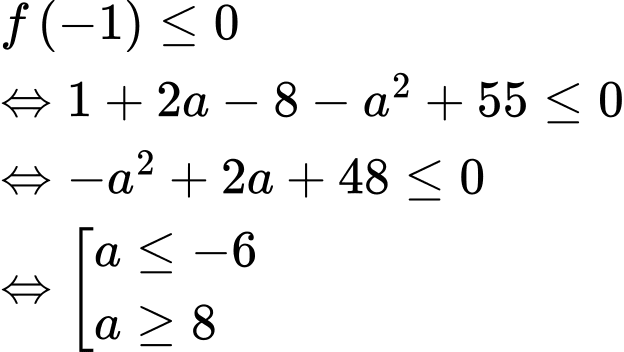
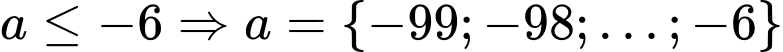 có 94 giá trị
có 94 giá trị
TH2: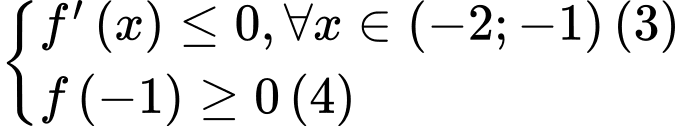
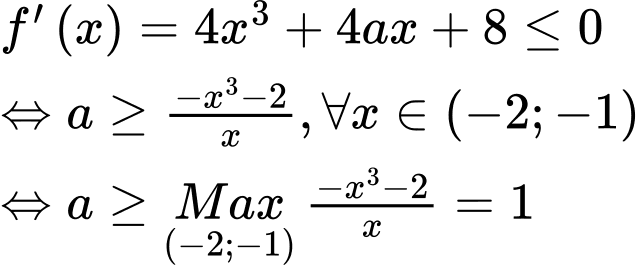
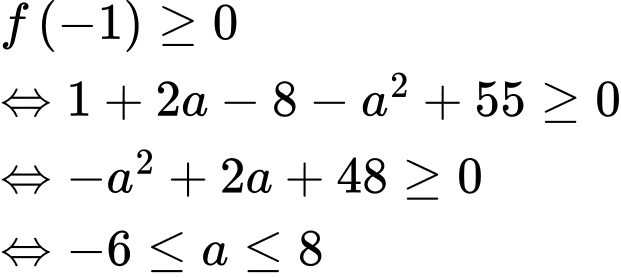
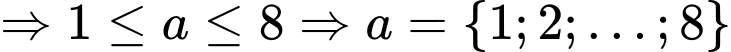 có 8 giá trị
có 8 giá trị
Vậy có 102 giá trị thoả mãn Đáp án: B
Xét hàm số
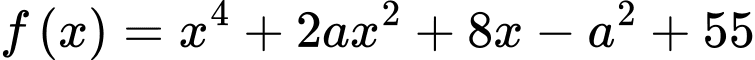
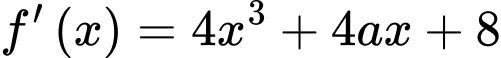
Để
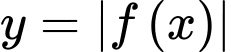 nghịch biến trên khoảng
nghịch biến trên khoảng 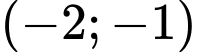
TH1:
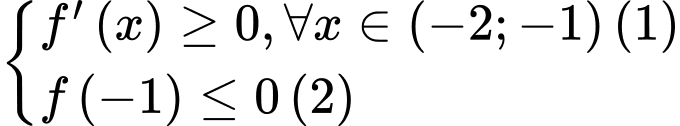
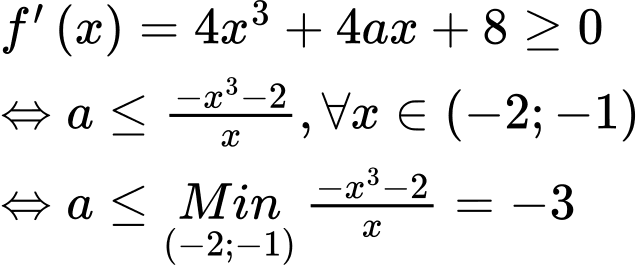
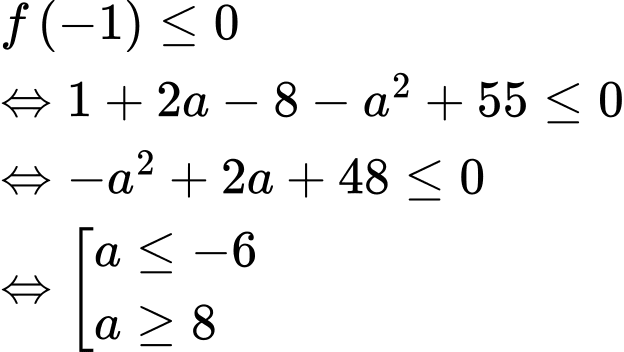
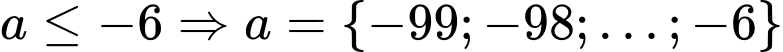 có 94 giá trị
có 94 giá trị
TH2:
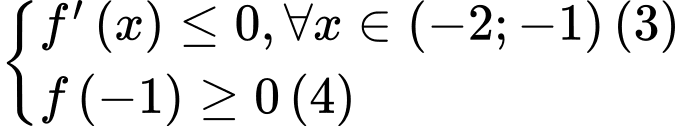
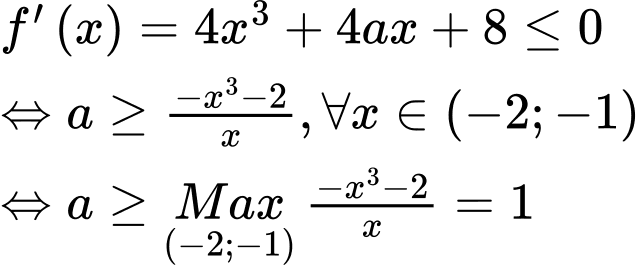
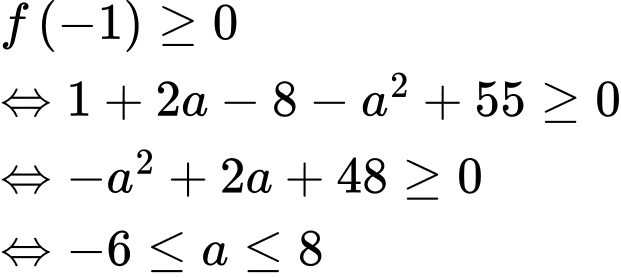
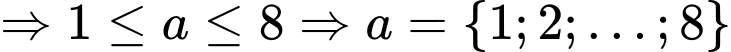 có 8 giá trị
có 8 giá trị
Vậy có 102 giá trị thoả mãn Đáp án: B
Câu 6 [677053]: Có bao nhiêu giá trị nguyên của tham số 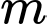 để hàm số
để hàm số 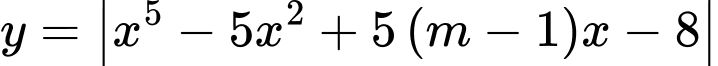 nghịch biến trên khoảng
nghịch biến trên khoảng 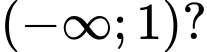
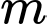 để hàm số
để hàm số 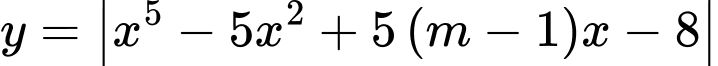 nghịch biến trên khoảng
nghịch biến trên khoảng 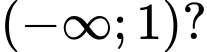
A, 2.
B, 0.
C, 4.
D, 1.
Đáp án: D
Câu 7 [677055]: Tập hợp tất cả các giá trị của tham số 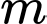 để hàm số
để hàm số 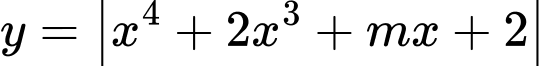 đồng biến trên khoảng
đồng biến trên khoảng 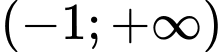 là
là
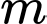 để hàm số
để hàm số 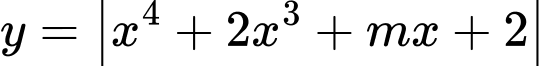 đồng biến trên khoảng
đồng biến trên khoảng 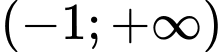 là
là A, 

B, 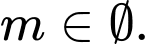
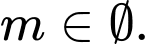
C, 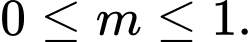
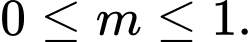
D, 

Đáp án: C
Câu 8 [677056]: Có bao nhiêu gía trị nguyên của tham số 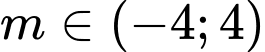 để hàm số
để hàm số 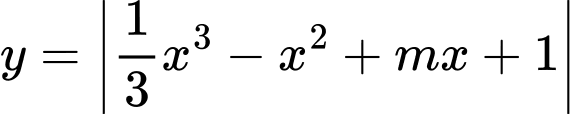 đồng biến trên khoảng
đồng biến trên khoảng 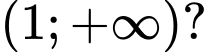
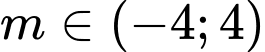 để hàm số
để hàm số 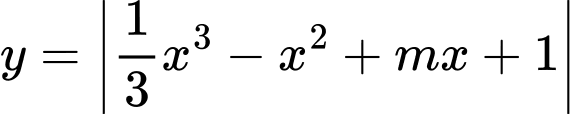 đồng biến trên khoảng
đồng biến trên khoảng 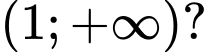
A, 5.
B, 4.
C, 3.
D, 6.
Đáp án: C
Câu 9 [677058]: Có bao nhiêu số nguyên dương 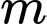 để hàm số
để hàm số 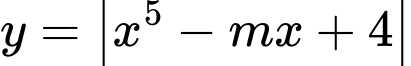 đồng biến trên khoảng
đồng biến trên khoảng 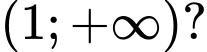
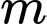 để hàm số
để hàm số 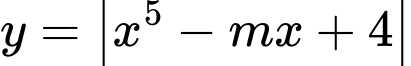 đồng biến trên khoảng
đồng biến trên khoảng 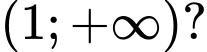
A, 4.
B, 5.
C, 6.
D, 7.
Đáp án: B
Câu 10 [677059]: Có bao nhiêu số nguyên của 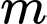 thuộc khoảng
thuộc khoảng 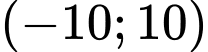 để hàm số
để hàm số 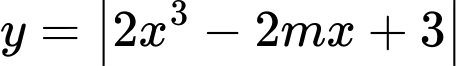 đồng biến trên khoảng
đồng biến trên khoảng 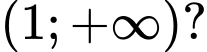
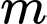 thuộc khoảng
thuộc khoảng 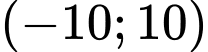 để hàm số
để hàm số 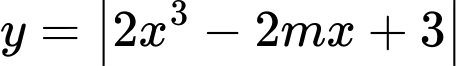 đồng biến trên khoảng
đồng biến trên khoảng 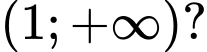
A, 12.
B, 8.
C, 11.
D, 7.
Đáp án: A
Câu 11 [677060]: Có tất cả bao nhiêu giá trị nguyên của 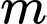 để hàm số
để hàm số 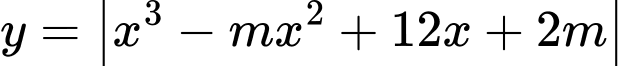 luôn đồng biến trên khoảng
luôn đồng biến trên khoảng 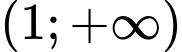 ?
?
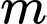 để hàm số
để hàm số 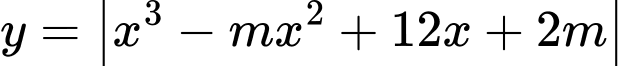 luôn đồng biến trên khoảng
luôn đồng biến trên khoảng 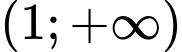 ?
? A, 18.
B, 19.
C, 21.
D, 20.
Chọn D
Xét hàm số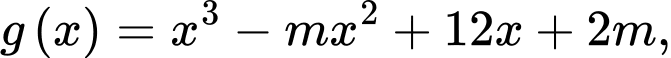 ta có
ta có 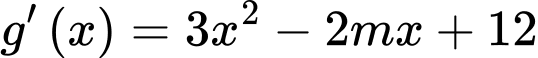
YCBT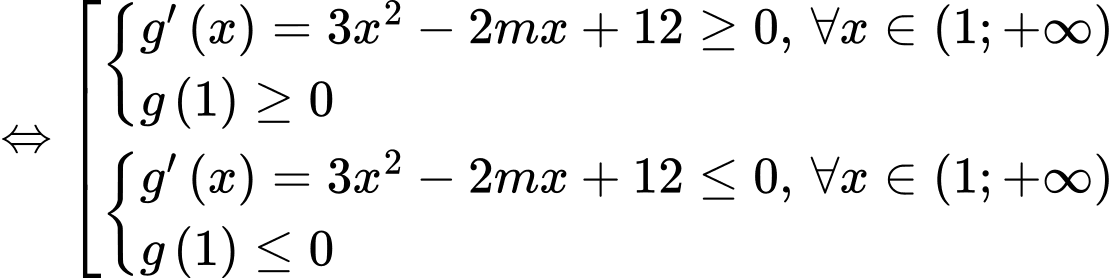
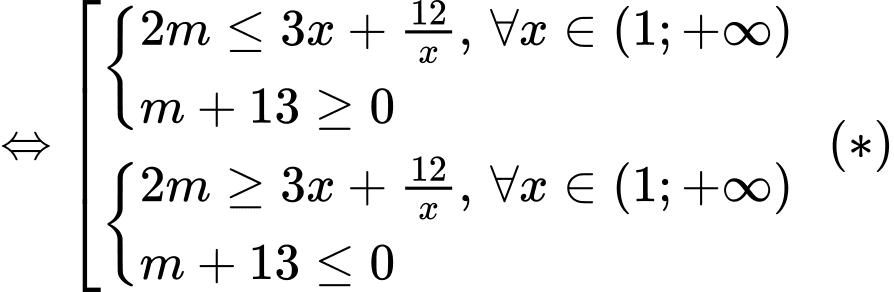
Xét hàm số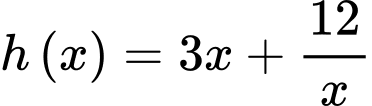 trên
trên 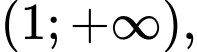 ta có:
ta có:
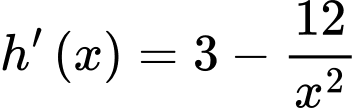
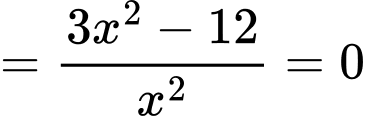

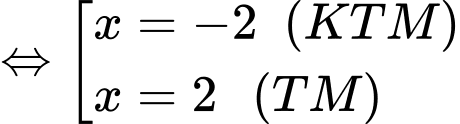
Bảng biến thiên của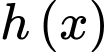 trên
trên 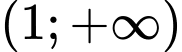
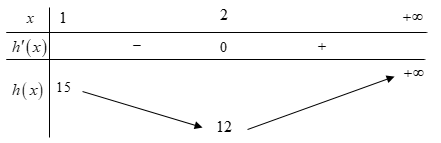
Từ bảng biến thiên, ta có:
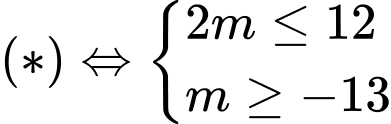
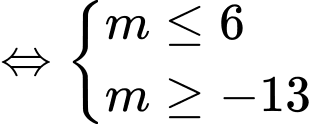

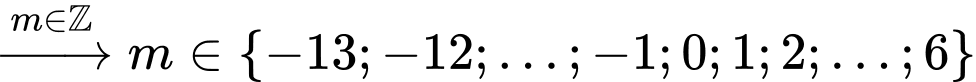
Vậy có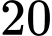 giá trị nguyên của
giá trị nguyên của 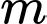 thỏa mãn đề bài. Đáp án: D
thỏa mãn đề bài. Đáp án: D
Xét hàm số
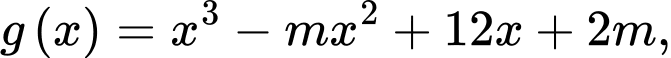 ta có
ta có 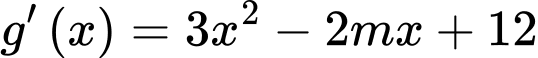
YCBT
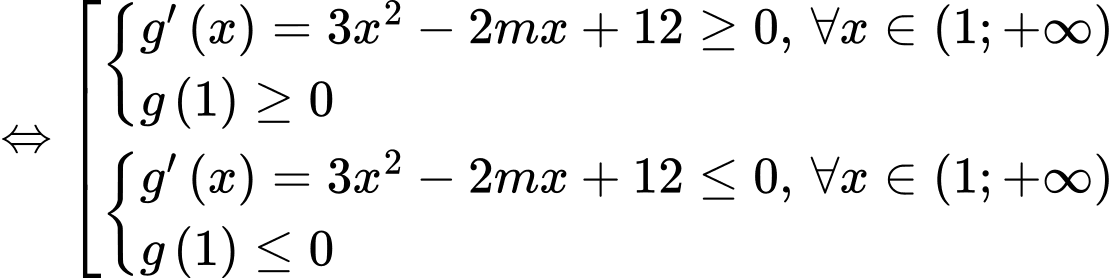
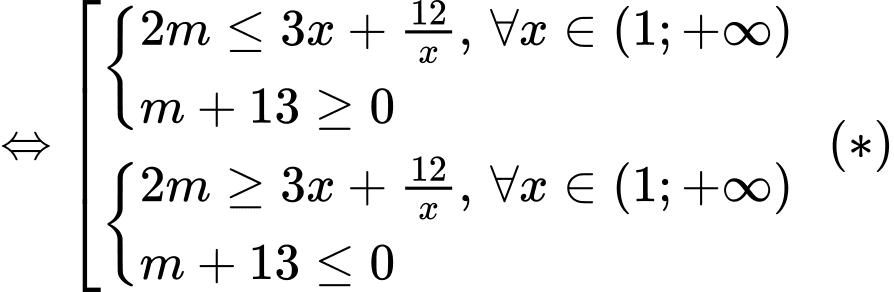
Xét hàm số
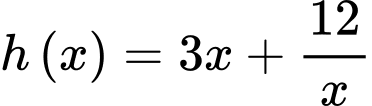 trên
trên 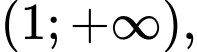 ta có:
ta có: 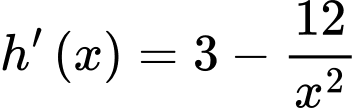
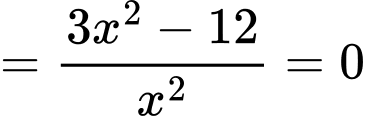

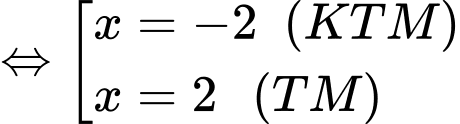
Bảng biến thiên của
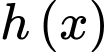 trên
trên 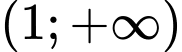

Từ bảng biến thiên, ta có:
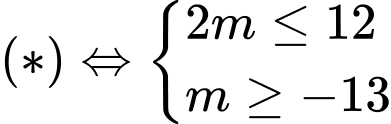
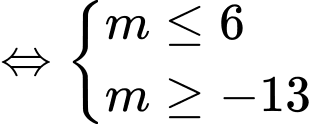

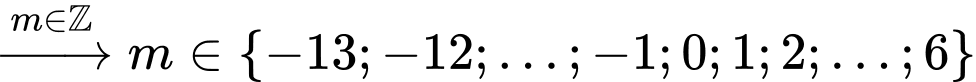
Vậy có
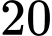 giá trị nguyên của
giá trị nguyên của 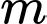 thỏa mãn đề bài. Đáp án: D
thỏa mãn đề bài. Đáp án: D
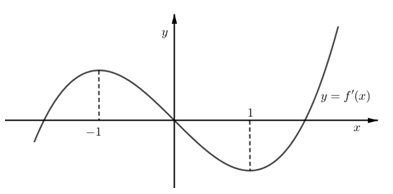
Câu 12 [677062]: Cho hàm số 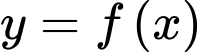 có đạo hàm trên
có đạo hàm trên 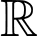 và
và 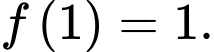 Đồ thị hàm số
Đồ thị hàm số 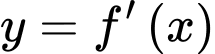 như hình bên.
như hình bên.
Có bao nhiêu số nguyên dương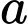 để hàm số
để hàm số 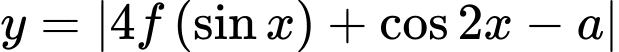 nghịch biến trên
nghịch biến trên 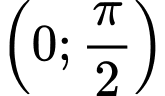 ?
?
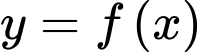 có đạo hàm trên
có đạo hàm trên 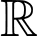 và
và 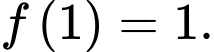 Đồ thị hàm số
Đồ thị hàm số 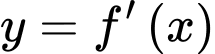 như hình bên.
như hình bên. 
Có bao nhiêu số nguyên dương
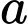 để hàm số
để hàm số 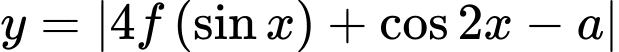 nghịch biến trên
nghịch biến trên 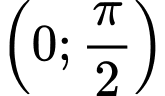 ?
? A, 2.
B, 3.
C, Vô số.
D, 5.
Chọn B
Xét hàm số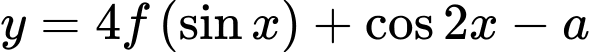

Ta thấy,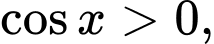
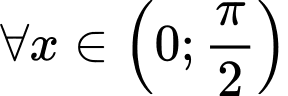
Đồ thị của hàm số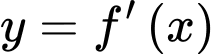 và
và 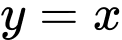 vẽ trên cùng hệ trục tọa độ như sau:
vẽ trên cùng hệ trục tọa độ như sau:
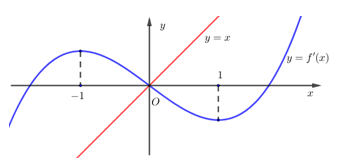
Từ đồ thị ta có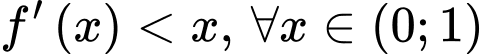
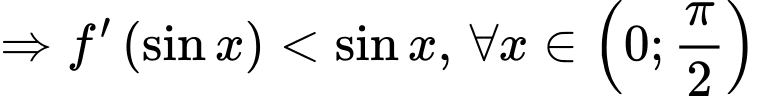
Suy ra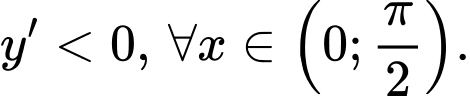
Ta có bảng biến thiên
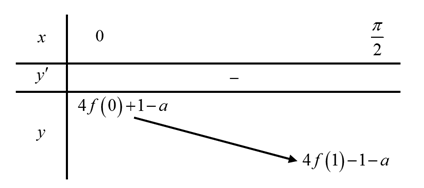
Dựa vào bảng biến thiên thì ycbt
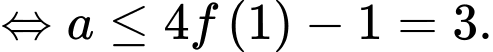
Vì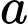 là số nguyên dương nên
là số nguyên dương nên 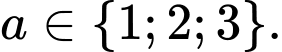 Đáp án: B
Đáp án: B
Xét hàm số
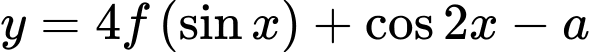

Ta thấy,
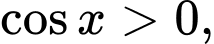
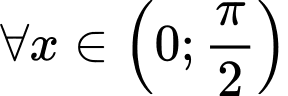
Đồ thị của hàm số
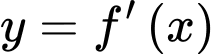 và
và 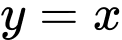 vẽ trên cùng hệ trục tọa độ như sau:
vẽ trên cùng hệ trục tọa độ như sau: 
Từ đồ thị ta có
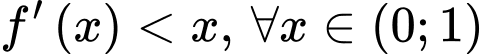
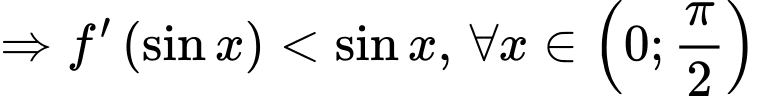
Suy ra
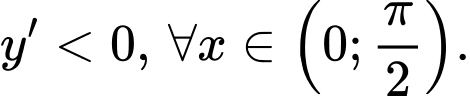
Ta có bảng biến thiên

Dựa vào bảng biến thiên thì ycbt

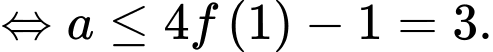
Vì
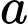 là số nguyên dương nên
là số nguyên dương nên 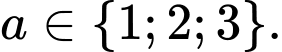 Đáp án: B
Đáp án: B