Đáp án Bài tập tự luyện số 2
Câu 1 [789074]: [Sở Ninh Bình 2021]: Cho hàm số 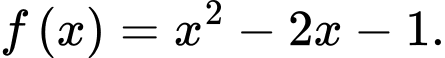 Có bao nhiêu giá trị nguyên của tham số
Có bao nhiêu giá trị nguyên của tham số 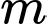 để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số 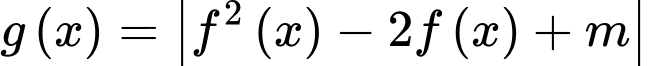 trên đoạn
trên đoạn 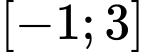 bằng 8.
bằng 8.
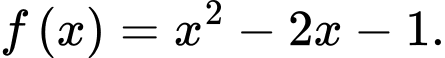 Có bao nhiêu giá trị nguyên của tham số
Có bao nhiêu giá trị nguyên của tham số 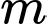 để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số 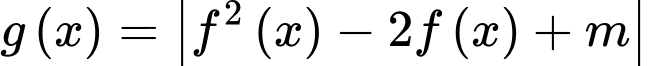 trên đoạn
trên đoạn 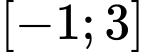 bằng 8.
bằng 8. A, 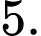
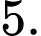
B, 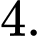
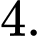
C, 
D, 
Xét hàm số 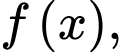 ta có bảng biến thiên
ta có bảng biến thiên

Đặt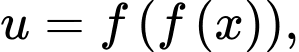 từ bảng biến thiên ta thấy
từ bảng biến thiên ta thấy 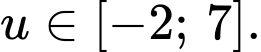 Suy ra
Suy ra 
Do đó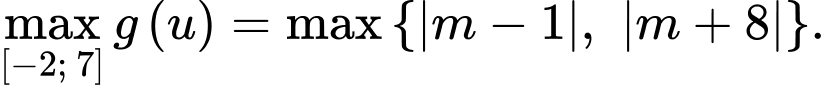
TH1: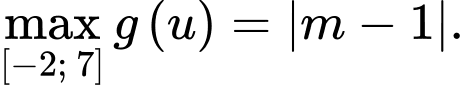
Suy ra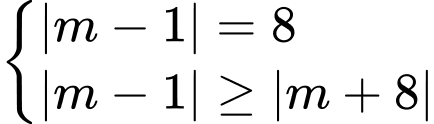
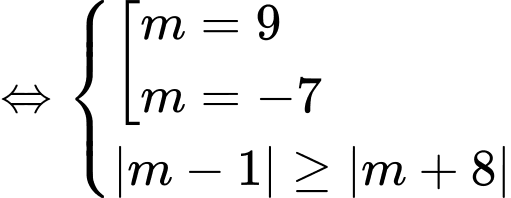
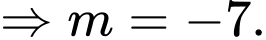
TH2: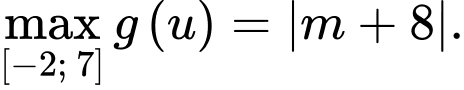
Suy ra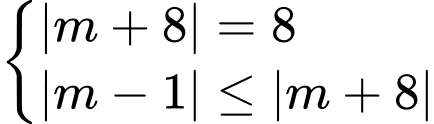
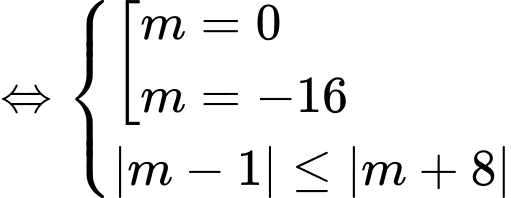
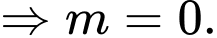
Vậy có 2 giá trị nguyên của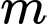 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
Chọn D. Đáp án: D
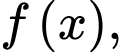 ta có bảng biến thiên
ta có bảng biến thiên

Đặt
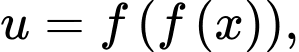 từ bảng biến thiên ta thấy
từ bảng biến thiên ta thấy 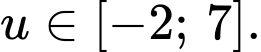 Suy ra
Suy ra 
Do đó
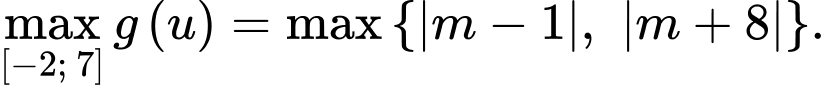
TH1:
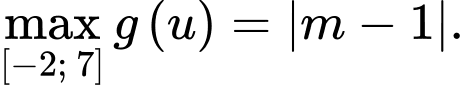
Suy ra
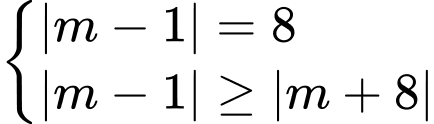
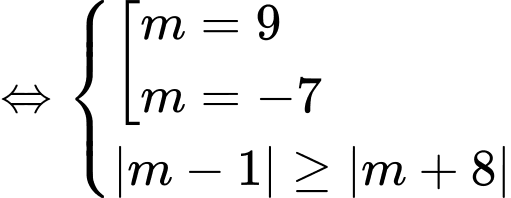
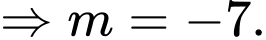
TH2:
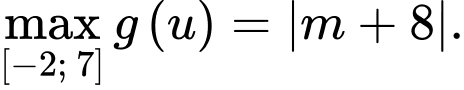
Suy ra
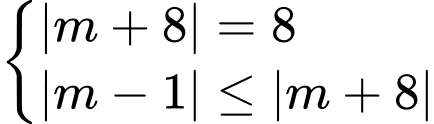
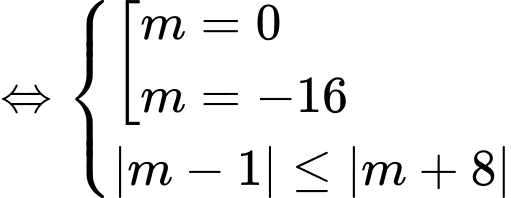
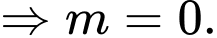
Vậy có 2 giá trị nguyên của
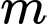 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.Chọn D. Đáp án: D
Câu 2 [635526]: Cho hàm số 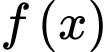 liên tục trên đoạn
liên tục trên đoạn 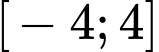 và có bảng biến thiên như hình vẽ bên dưới
và có bảng biến thiên như hình vẽ bên dưới
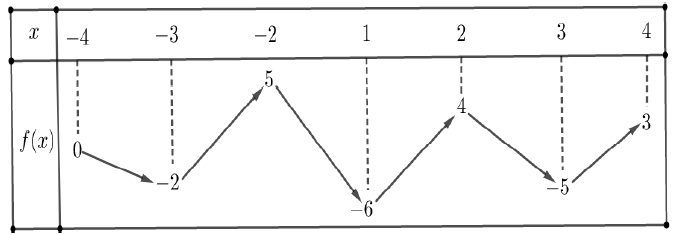
Có tất cả bao nhiêu giá trị thực của để hàm số
để hàm số 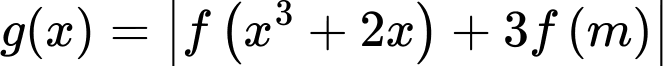 có giá trị lớn nhất trên đoạn
có giá trị lớn nhất trên đoạn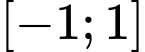 bằng
bằng 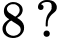
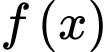 liên tục trên đoạn
liên tục trên đoạn 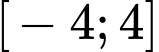 và có bảng biến thiên như hình vẽ bên dưới
và có bảng biến thiên như hình vẽ bên dưới 
Có tất cả bao nhiêu giá trị thực của
 để hàm số
để hàm số 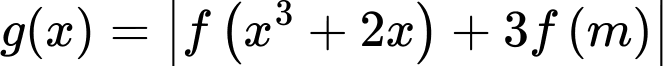 có giá trị lớn nhất trên đoạn
có giá trị lớn nhất trên đoạn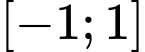 bằng
bằng 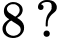
A, 12.
B, 11.
C, 9.
D, 10.
Đáp án: B
Câu 3 [635529]: Gọi 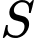 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số 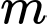 sao cho giá trị nhỏ nhất của hàm số
sao cho giá trị nhỏ nhất của hàm số 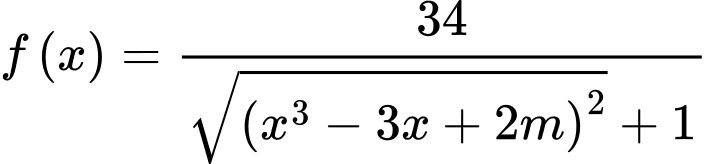 trên đoạn
trên đoạn 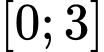 bằng 2. Tổng tất cả các phần tử của
bằng 2. Tổng tất cả các phần tử của 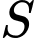 bằng
bằng
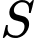 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số 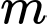 sao cho giá trị nhỏ nhất của hàm số
sao cho giá trị nhỏ nhất của hàm số 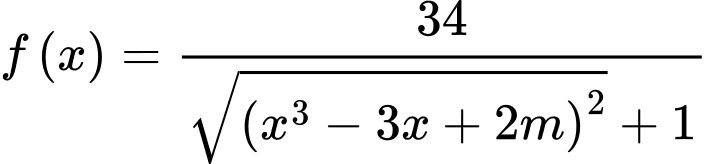 trên đoạn
trên đoạn 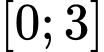 bằng 2. Tổng tất cả các phần tử của
bằng 2. Tổng tất cả các phần tử của 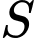 bằng
bằng A, 
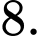
B, 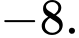
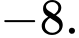
C, 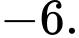
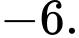
D, 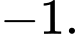
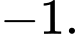
Đáp án: B
Câu 4 [635532]: Có bao nhiêu giá trị nguyên của tham số 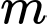 để hàm số
để hàm số 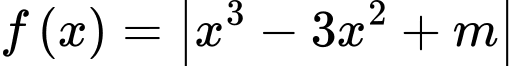 có giá trị nhỏ nhất trên đoạn
có giá trị nhỏ nhất trên đoạn 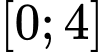 đạt giá trị nhỏ nhất?
đạt giá trị nhỏ nhất?
 để hàm số
để hàm số 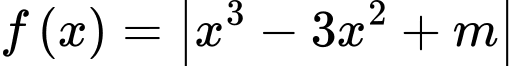 có giá trị nhỏ nhất trên đoạn
có giá trị nhỏ nhất trên đoạn 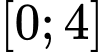 đạt giá trị nhỏ nhất?
đạt giá trị nhỏ nhất? A, 20.
B, 21.
C, 22.
D, 23.
Đáp án: B
Câu 5 [635535]: Gọi 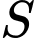 là tập hợp các giá trị của tham số
là tập hợp các giá trị của tham số 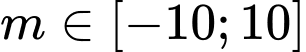 để hàm số
để hàm số 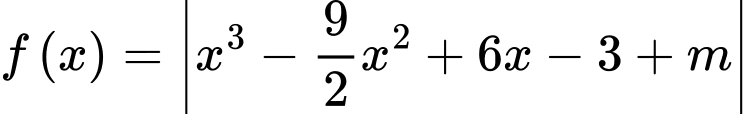 có giá trị nhỏ nhất trên đoạn
có giá trị nhỏ nhất trên đoạn 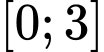 lớn hơn 5. Số phần tử của tập
lớn hơn 5. Số phần tử của tập 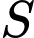 là
là
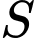 là tập hợp các giá trị của tham số
là tập hợp các giá trị của tham số 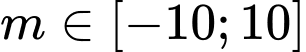 để hàm số
để hàm số 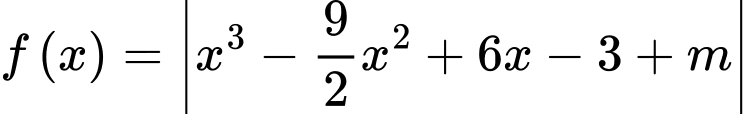 có giá trị nhỏ nhất trên đoạn
có giá trị nhỏ nhất trên đoạn 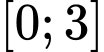 lớn hơn 5. Số phần tử của tập
lớn hơn 5. Số phần tử của tập 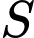 là
là A, 6.
B, 7.
C, 8.
D, 9.
Đặt 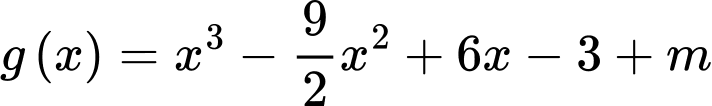
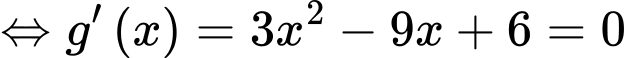
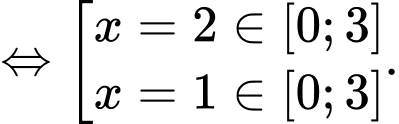
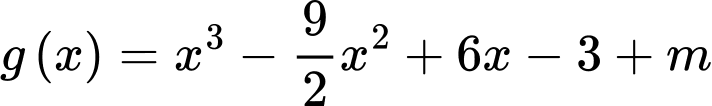
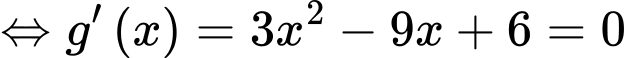
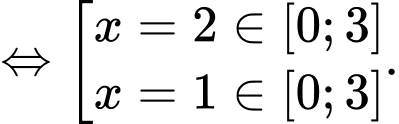
Ta có: 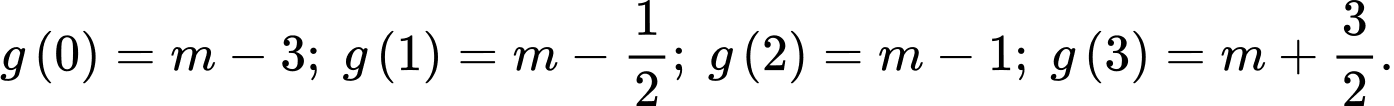
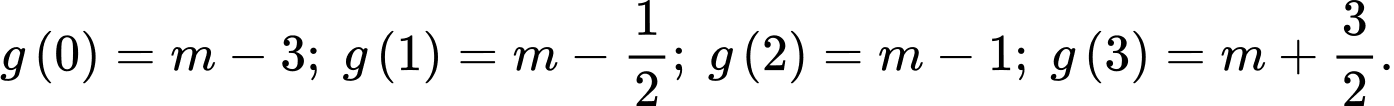
Để hàm số 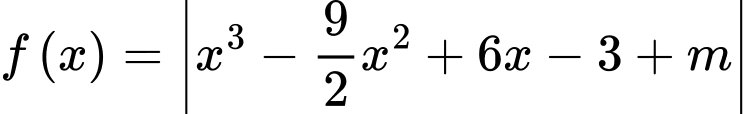 có giá trị nhỏ nhất trên đoạn
có giá trị nhỏ nhất trên đoạn 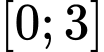 lớn hơn 5 thì:
lớn hơn 5 thì: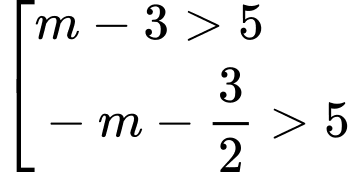
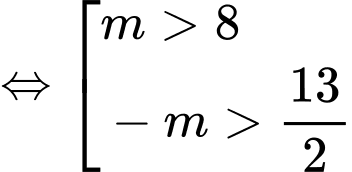
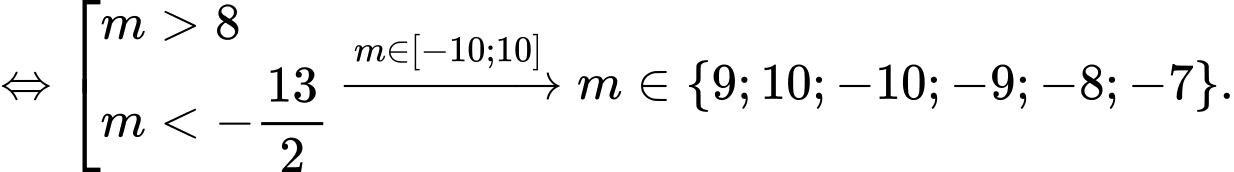
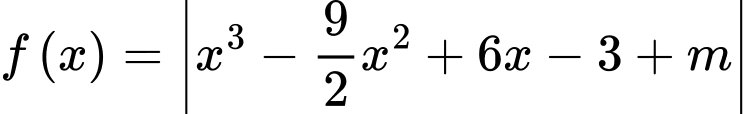 có giá trị nhỏ nhất trên đoạn
có giá trị nhỏ nhất trên đoạn 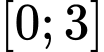 lớn hơn 5 thì:
lớn hơn 5 thì: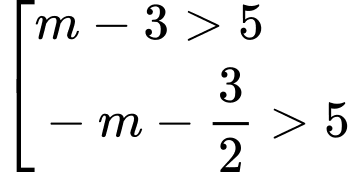
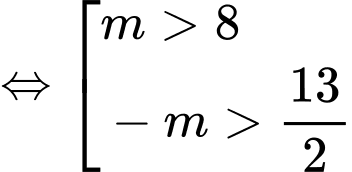
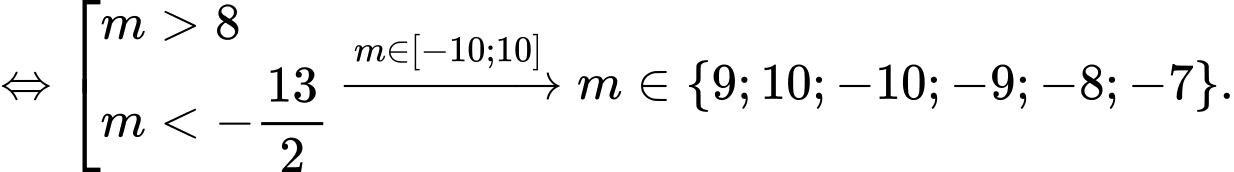
Vậy số phần tử của  là 6.
là 6.
Đáp án: A  là 6.
là 6.
Câu 6 [789342]: Cho hàm số 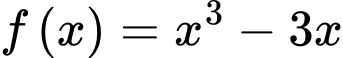 . Gọi
. Gọi 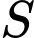 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số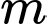 sao cho giá trị nhỏ nhất của hàm số
sao cho giá trị nhỏ nhất của hàm số 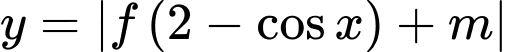 bằng 2. Tổng tất cả các phần tử của
bằng 2. Tổng tất cả các phần tử của 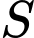 bằng
bằng
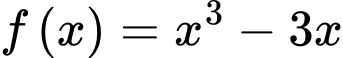 . Gọi
. Gọi 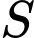 là tập hợp tất cả các giá trị thực của tham số
là tập hợp tất cả các giá trị thực của tham số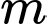 sao cho giá trị nhỏ nhất của hàm số
sao cho giá trị nhỏ nhất của hàm số 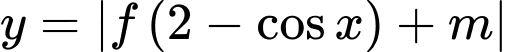 bằng 2. Tổng tất cả các phần tử của
bằng 2. Tổng tất cả các phần tử của 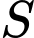 bằng
bằng A, 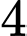 .
.
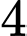 .
.B, 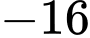 .
.
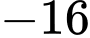 .
.C, 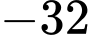 .
.
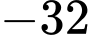 .
.D, 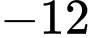 .
.
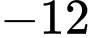 .
.
Chọn B
Đặt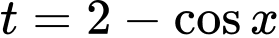 ta có
ta có 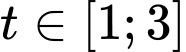 . Khi đó bài toán trở thành tìm m để hàm số
. Khi đó bài toán trở thành tìm m để hàm số 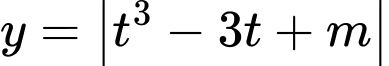 với
với  đạt giá trị nhỏ nhất bằng 2.
đạt giá trị nhỏ nhất bằng 2.
Xét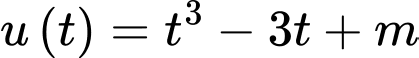 trên đoạn
trên đoạn 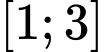 . Ta có hàm số
. Ta có hàm số 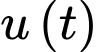 liên tục trên đoạn
liên tục trên đoạn 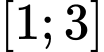 .
.
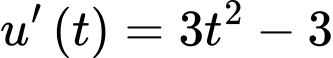 ;
;  .
.
Khi đó: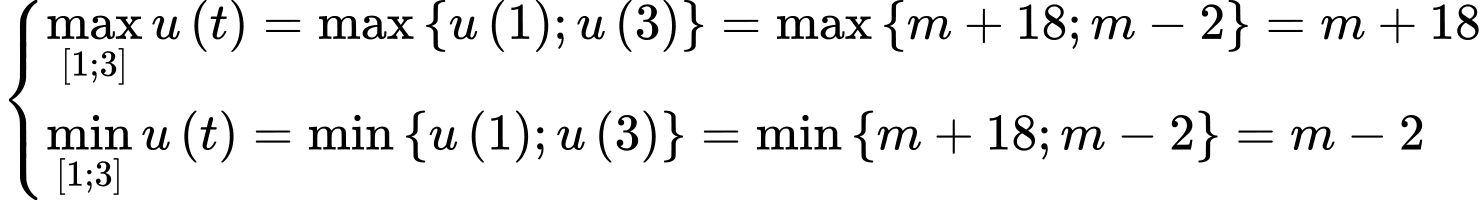 .
.
Yêu cầu bài tập: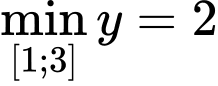 .
.
Trường hợp 1: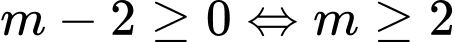
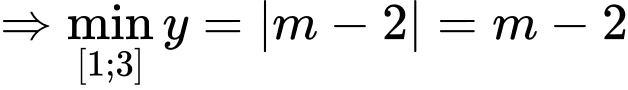 ;
; 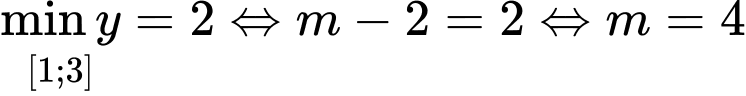 (thỏa mãn)
(thỏa mãn)
Trường hợp 2: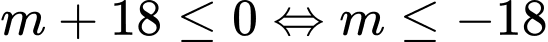
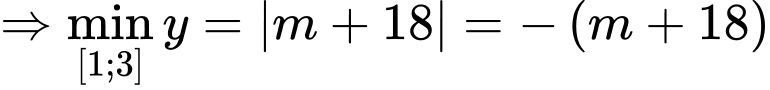 ;
; 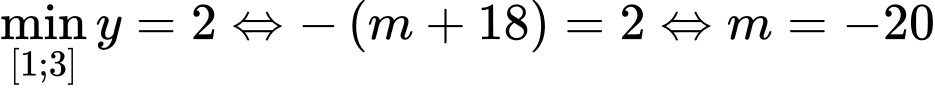 (thỏa mãn)
(thỏa mãn)
Trường hợp 3: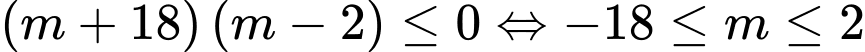
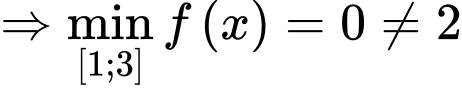 (loại)
(loại)
Vậy tổng tất cả các phần tử của bằng
bằng 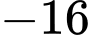 . Chọn phương án
. Chọn phương án 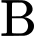 . Đáp án: B
. Đáp án: B
Đặt
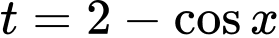 ta có
ta có 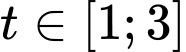 . Khi đó bài toán trở thành tìm m để hàm số
. Khi đó bài toán trở thành tìm m để hàm số 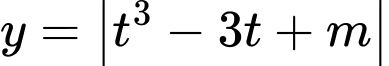 với
với  đạt giá trị nhỏ nhất bằng 2.
đạt giá trị nhỏ nhất bằng 2. Xét
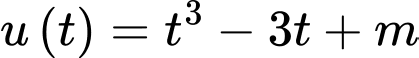 trên đoạn
trên đoạn 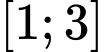 . Ta có hàm số
. Ta có hàm số 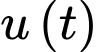 liên tục trên đoạn
liên tục trên đoạn 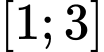 .
.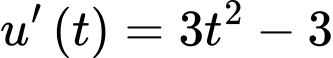 ;
;  .
.Khi đó:
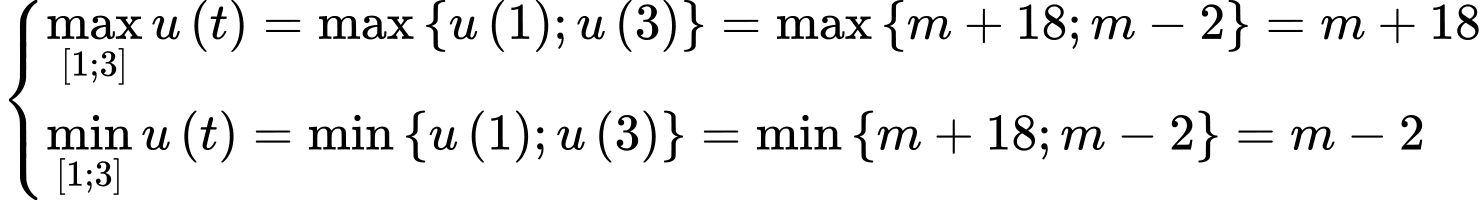 .
.Yêu cầu bài tập:
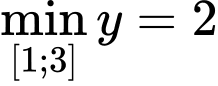 .
.Trường hợp 1:
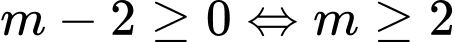
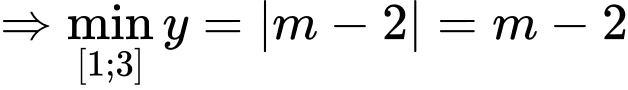 ;
; 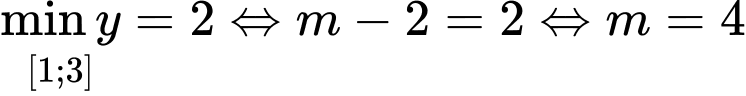 (thỏa mãn)
(thỏa mãn) Trường hợp 2:
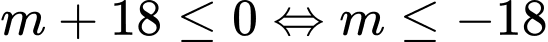
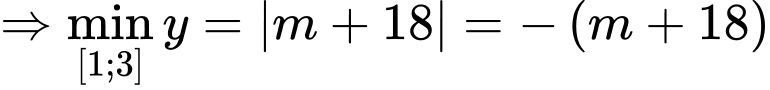 ;
; 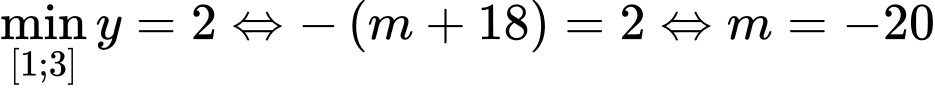 (thỏa mãn)
(thỏa mãn) Trường hợp 3:
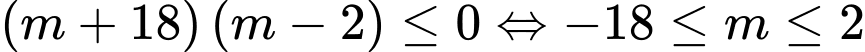
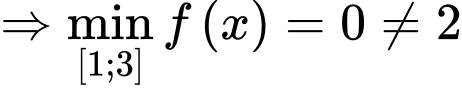 (loại)
(loại) Vậy tổng tất cả các phần tử của
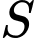 bằng
bằng 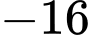 . Chọn phương án
. Chọn phương án 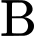 . Đáp án: B
. Đáp án: B
Câu 7 [518137]: Cho hàm số 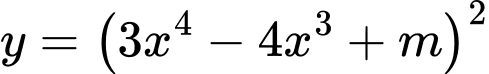 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số 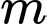 để giá trị nhỏ nhất của hàm số trên
để giá trị nhỏ nhất của hàm số trên 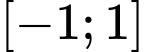 luôn bằng
luôn bằng  ?
?
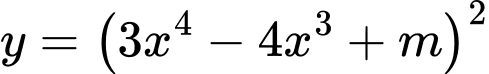 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số 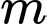 để giá trị nhỏ nhất của hàm số trên
để giá trị nhỏ nhất của hàm số trên 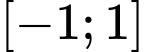 luôn bằng
luôn bằng  ?
? A, 0.
B, 7.
C, 3.
D, 9.
Chọn D
Xét hàm số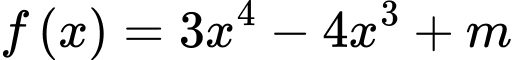
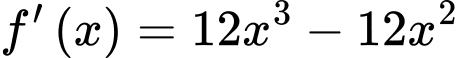
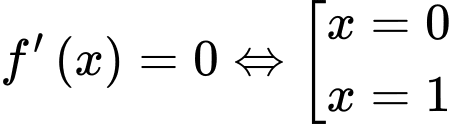
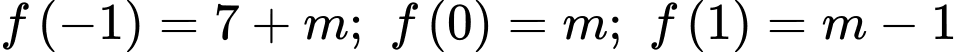
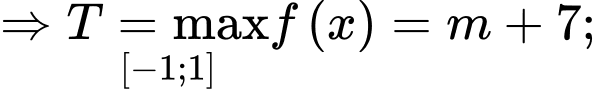
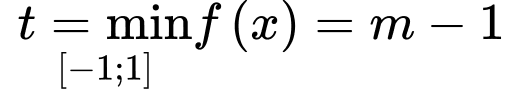 .
.
Trường hợp 1: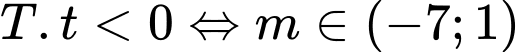 .
.
Khi đó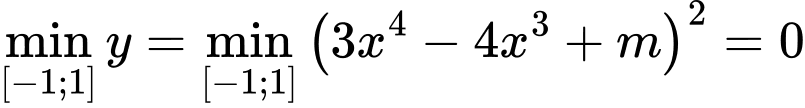 ( thỏa mãn yêu cầu bài toán)
( thỏa mãn yêu cầu bài toán)
Trường hợp 2: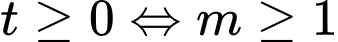
Khi đó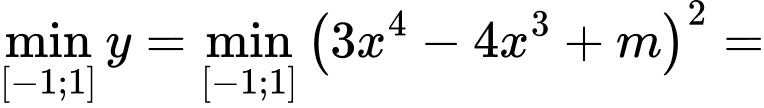
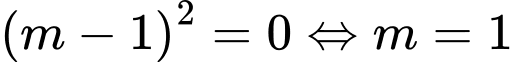 (thỏa mãn).
(thỏa mãn).
Trường hợp 3: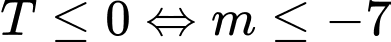
Khi đó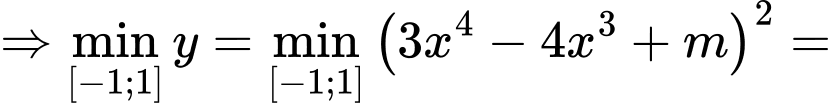
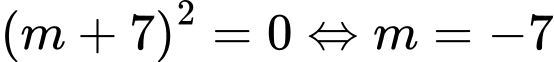 (thỏa mãn).
(thỏa mãn).
Vậy các giá trị nguyên của m là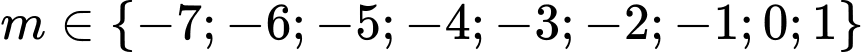
 có
có 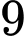 giá trị
giá trị 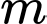 thỏa mãn yêu cầu bài toán. Đáp án: D
thỏa mãn yêu cầu bài toán. Đáp án: D
Xét hàm số
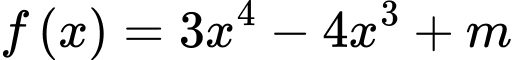
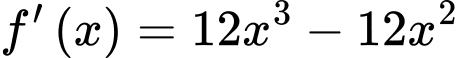
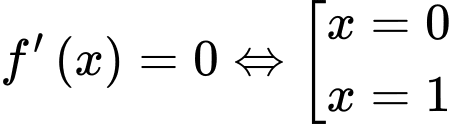
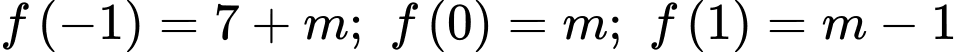
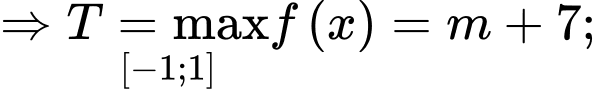
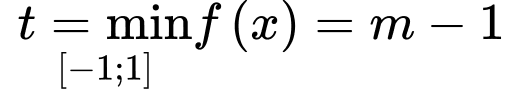 .
. Trường hợp 1:
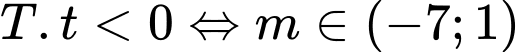 .
. Khi đó
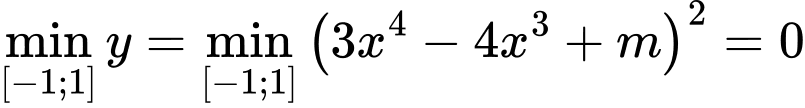 ( thỏa mãn yêu cầu bài toán)
( thỏa mãn yêu cầu bài toán) Trường hợp 2:
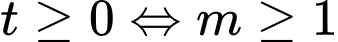
Khi đó
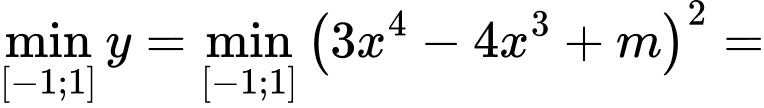
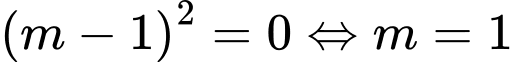 (thỏa mãn).
(thỏa mãn). Trường hợp 3:
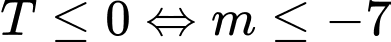
Khi đó
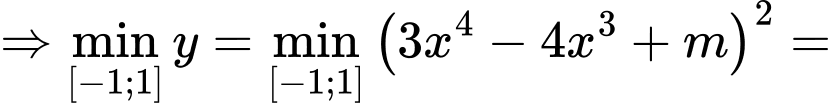
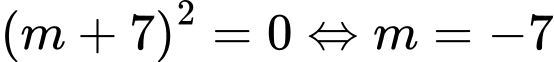 (thỏa mãn).
(thỏa mãn). Vậy các giá trị nguyên của m là
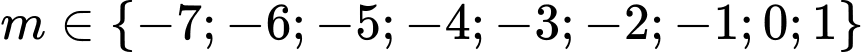
 có
có 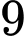 giá trị
giá trị 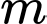 thỏa mãn yêu cầu bài toán. Đáp án: D
thỏa mãn yêu cầu bài toán. Đáp án: D
Câu 8 [399939]: Cho hàm số 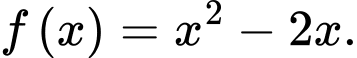 Gọi
Gọi 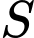 là tập các giá trị
là tập các giá trị 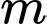 để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số 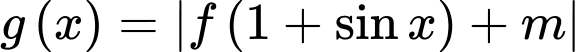 bằng
bằng 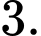 Tích các phần tử của S bằng
Tích các phần tử của S bằng
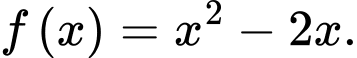 Gọi
Gọi 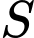 là tập các giá trị
là tập các giá trị 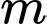 để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số 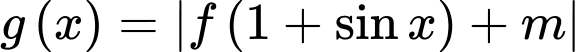 bằng
bằng 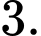 Tích các phần tử của S bằng
Tích các phần tử của S bằng A, 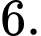
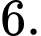
B, 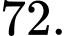
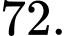
C, 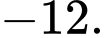
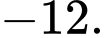
D, 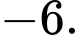
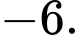
Chọn D
Xét hàm số
Đặt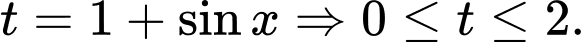
Khi đó bài toán trở thành tìm các giá trị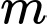 để
để 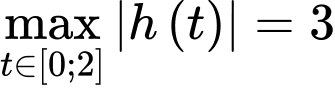 với
với 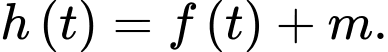
Ta có bảng biến thiên của hàm số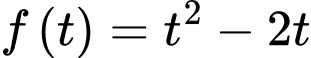 :
:
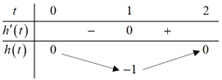
Ta có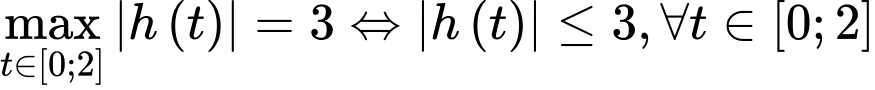
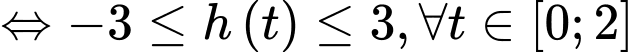
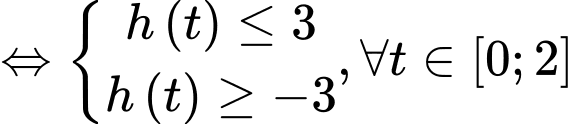
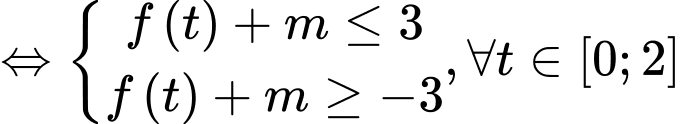
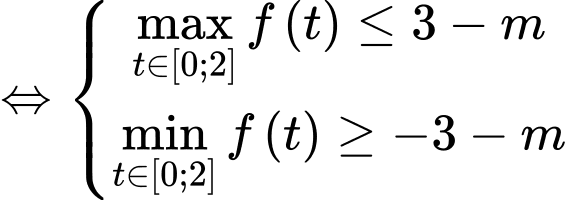
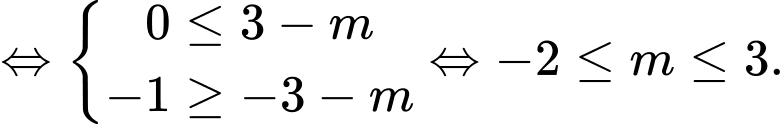
Đẳng thức xảy ra khi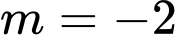 hay
hay 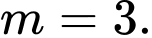 Khi đó
Khi đó  Đáp án: D
Đáp án: D
Xét hàm số

Đặt
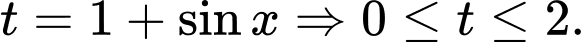
Khi đó bài toán trở thành tìm các giá trị
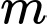 để
để 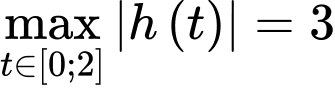 với
với 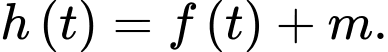
Ta có bảng biến thiên của hàm số
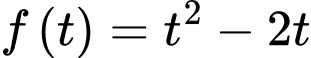 :
:
Ta có
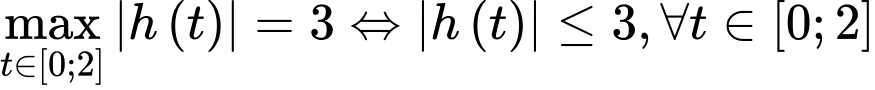
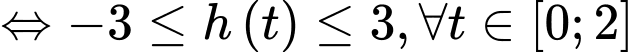
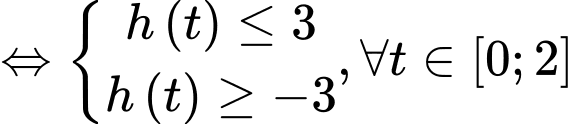
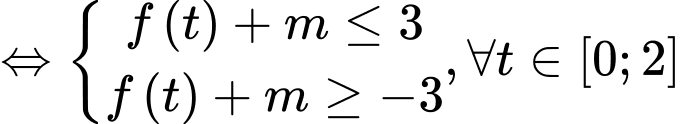
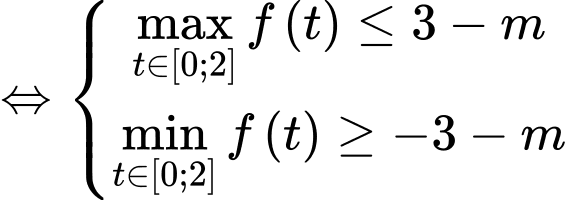
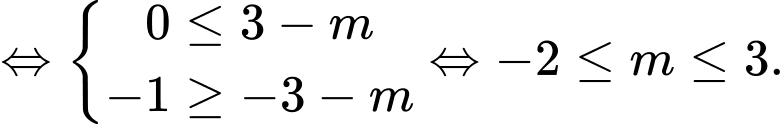
Đẳng thức xảy ra khi
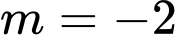 hay
hay 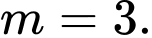 Khi đó
Khi đó  Đáp án: D
Đáp án: D
Câu 9 [509044]: Cho hàm số 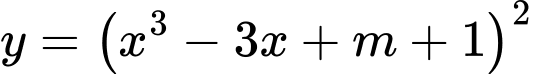 . Tổng tất cả các giá trị của tham số
. Tổng tất cả các giá trị của tham số 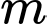 sao cho giá trị nhỏ nhất của hàm số trên đoạn
sao cho giá trị nhỏ nhất của hàm số trên đoạn 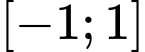 bằng
bằng 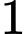 là
là
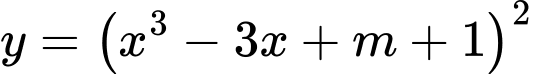 . Tổng tất cả các giá trị của tham số
. Tổng tất cả các giá trị của tham số 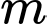 sao cho giá trị nhỏ nhất của hàm số trên đoạn
sao cho giá trị nhỏ nhất của hàm số trên đoạn 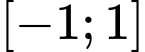 bằng
bằng 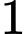 là
là A, 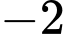 .
.
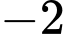 .
.B, 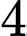 .
.
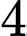 .
.C, 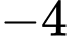 .
.
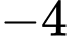 .
.D,  .
.
 .
.
Chọn A
Xét hàm số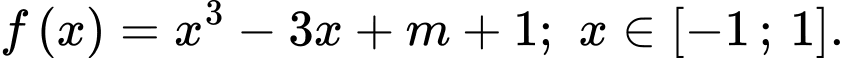
Có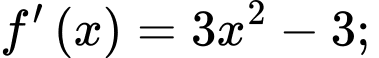
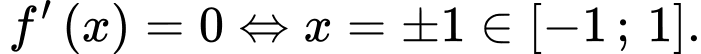
Đặt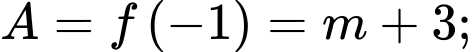
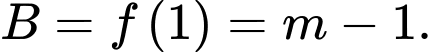
TH1: Nếu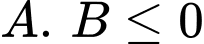
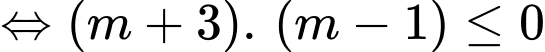
 thì
thì 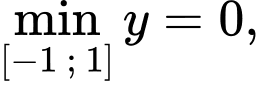 bài toán không thoả mãn.
bài toán không thoả mãn.
TH2: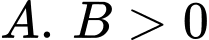
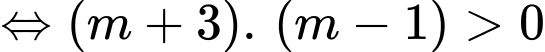
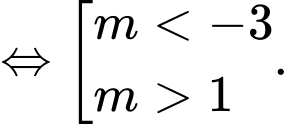 Khi đó
Khi đó 
TH2.1: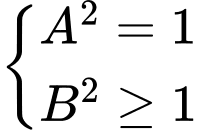
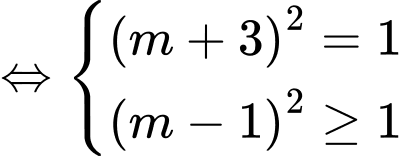
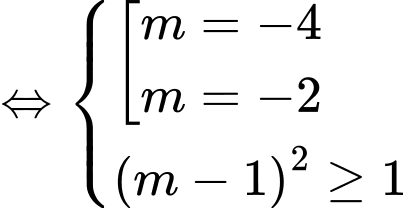
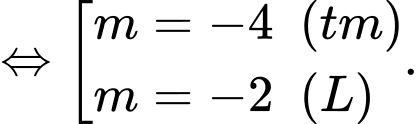
TH2.2: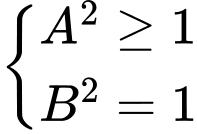
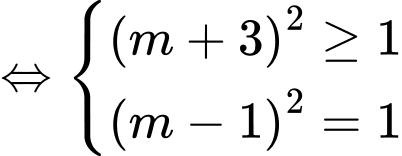
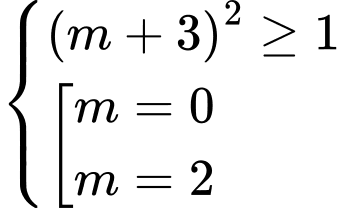
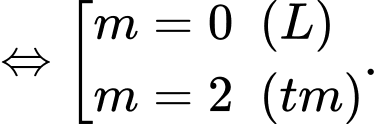
Vậy suy ra tổng các giá trị của
suy ra tổng các giá trị của 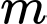 bằng -2. Đáp án: A
bằng -2. Đáp án: A
Xét hàm số
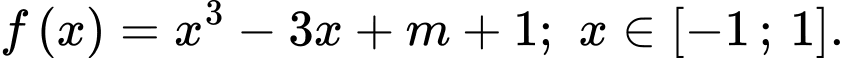
Có
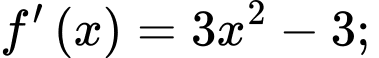
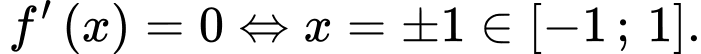
Đặt
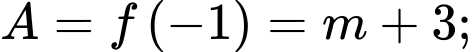
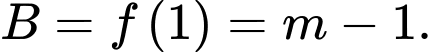
TH1: Nếu
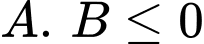
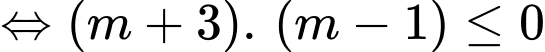
 thì
thì 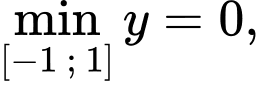 bài toán không thoả mãn.
bài toán không thoả mãn.
TH2:
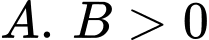
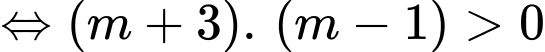
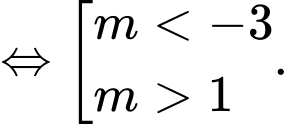 Khi đó
Khi đó 
TH2.1:
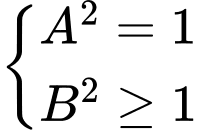
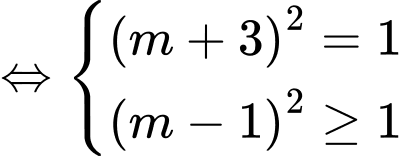
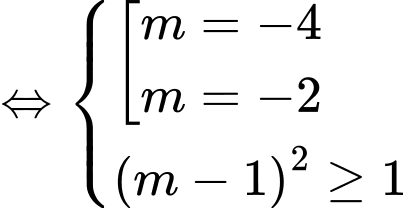
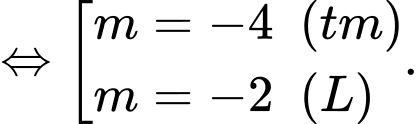
TH2.2:
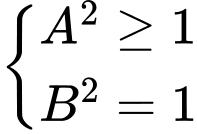
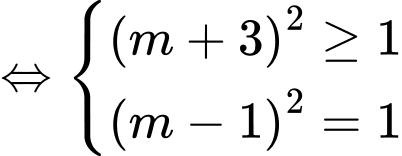
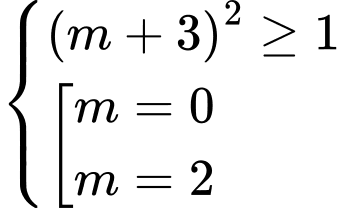
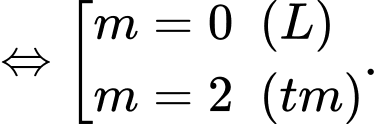
Vậy
 suy ra tổng các giá trị của
suy ra tổng các giá trị của 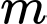 bằng -2. Đáp án: A
bằng -2. Đáp án: A
Câu 10 [520598]: Cho hàm số 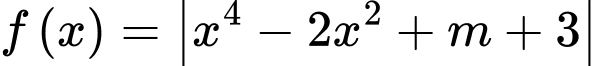 (
(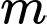 là tham số thực ). Gọi
là tham số thực ). Gọi 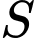 là tập hợp tất cả giá trị của
là tập hợp tất cả giá trị của 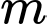 sao cho
sao cho 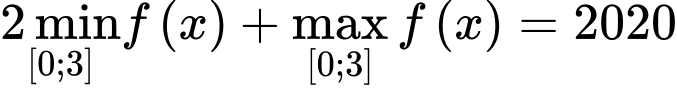 . Tổng giá trị tất cả các phần tử của
. Tổng giá trị tất cả các phần tử của 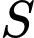 bằng
bằng
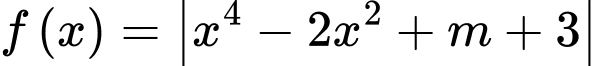 (
(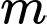 là tham số thực ). Gọi
là tham số thực ). Gọi 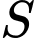 là tập hợp tất cả giá trị của
là tập hợp tất cả giá trị của 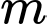 sao cho
sao cho 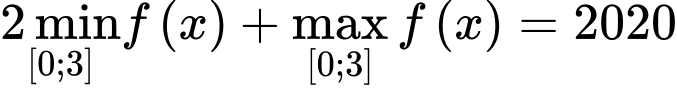 . Tổng giá trị tất cả các phần tử của
. Tổng giá trị tất cả các phần tử của 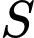 bằng
bằng A, 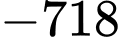 .
.
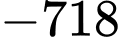 .
.B, 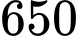 .
.
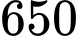 .
.C, 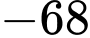 .
.
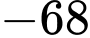 .
.D, 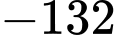 .
.
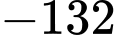 .
.
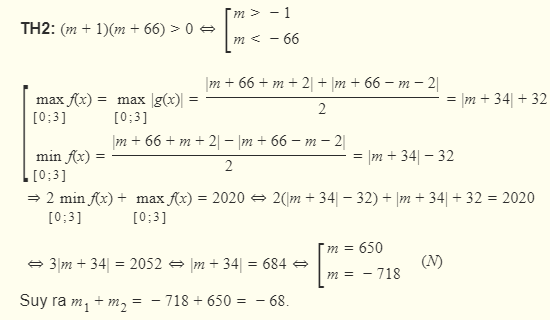 Đáp án: C
Đáp án: C
Câu 11 [512737]: Biết giá trị lớn nhất của hàm số 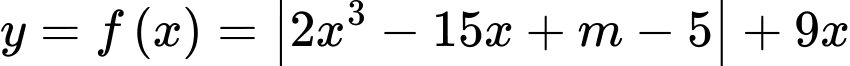 trên
trên 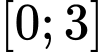 bằng
bằng 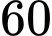 . Tính tổng tất cả các giá trị của tham số thực
. Tính tổng tất cả các giá trị của tham số thực 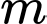 .
.
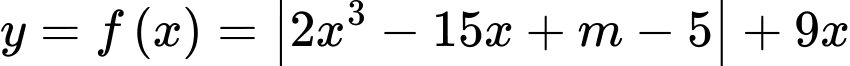 trên
trên 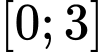 bằng
bằng 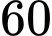 . Tính tổng tất cả các giá trị của tham số thực
. Tính tổng tất cả các giá trị của tham số thực 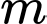 .
. A, 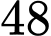 .
.
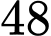 .
.B, 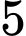 .
.
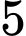 .
.C, 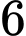 .
.
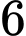 .
.D, 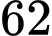 .
.
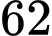 .
.
Chọn C
Có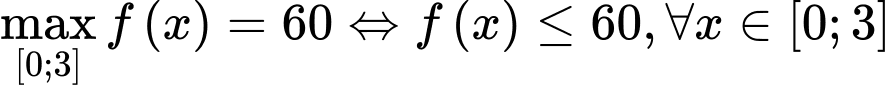 và
và  sao cho
sao cho 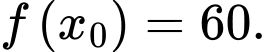
Có
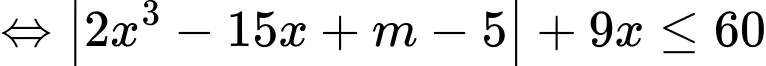
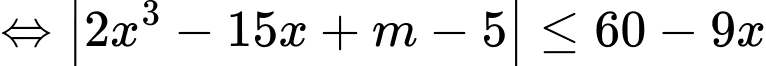
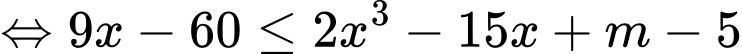
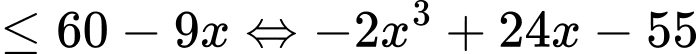
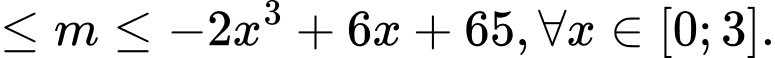
Có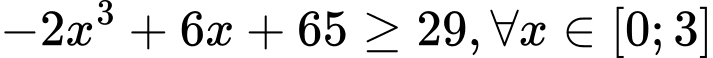 nên
nên 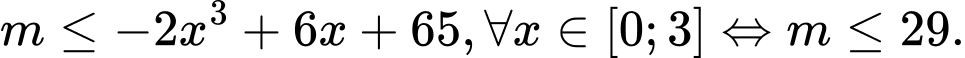
Tương tự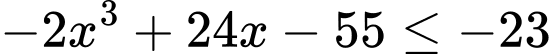 nên
nên 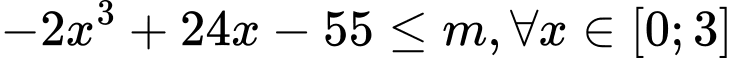

Vậy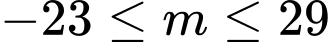 thì
thì 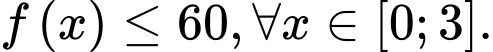
Để sao cho
sao cho 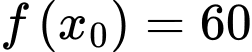 thì
thì 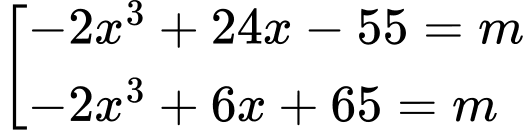 có nghiệm trên
có nghiệm trên 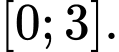
Hay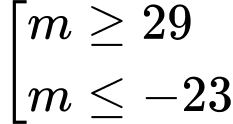 Vậy
Vậy 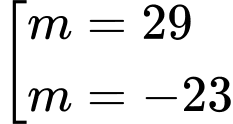 thì
thì 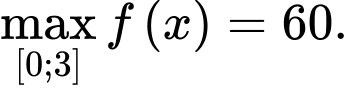
Khi đó tổng các giá trị của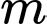 là
là 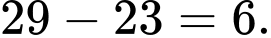 Đáp án: C
Đáp án: C
Có
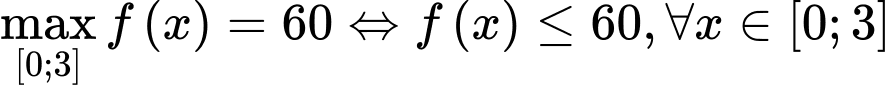 và
và  sao cho
sao cho 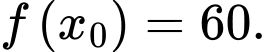
Có

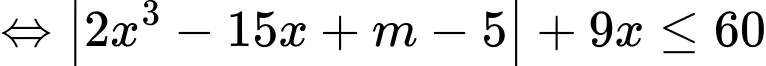
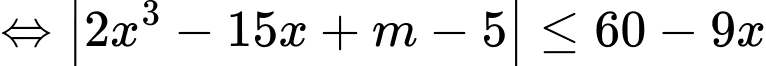
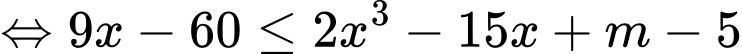
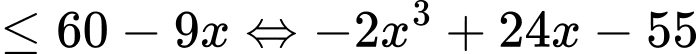
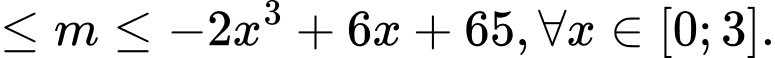
Có
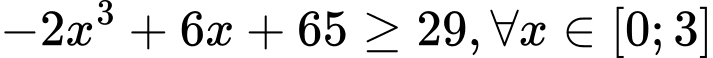 nên
nên 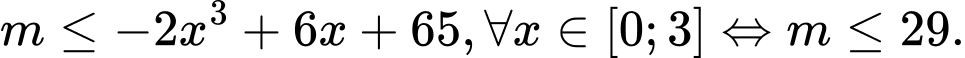
Tương tự
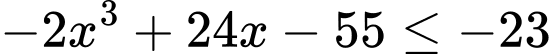 nên
nên 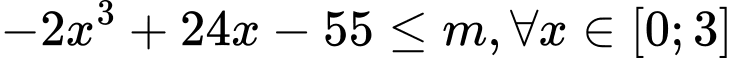

Vậy
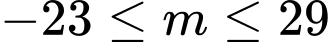 thì
thì 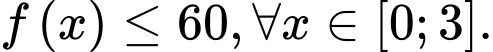
Để
 sao cho
sao cho 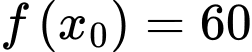 thì
thì 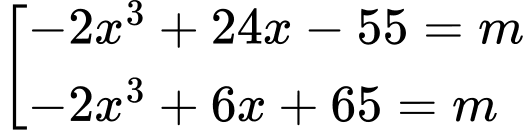 có nghiệm trên
có nghiệm trên 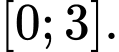
Hay
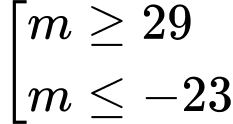 Vậy
Vậy 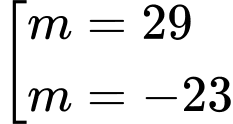 thì
thì 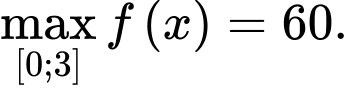
Khi đó tổng các giá trị của
 là
là 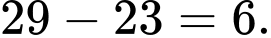 Đáp án: C
Đáp án: C
Câu 12 [31477]: Cho hàm số 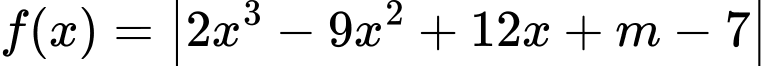 . Có bao nhiêu giá trị nguyên của
. Có bao nhiêu giá trị nguyên của 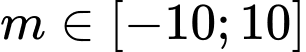 sao cho với mọi số thực
sao cho với mọi số thực 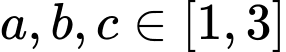 thì
thì 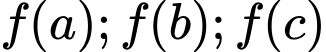 là độ dài ba cạnh của một tam giác?
là độ dài ba cạnh của một tam giác?
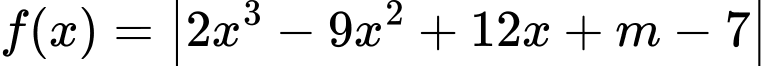 . Có bao nhiêu giá trị nguyên của
. Có bao nhiêu giá trị nguyên của 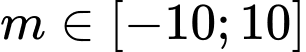 sao cho với mọi số thực
sao cho với mọi số thực 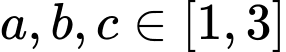 thì
thì 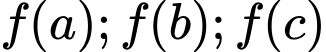 là độ dài ba cạnh của một tam giác?
là độ dài ba cạnh của một tam giác? A, 8.
B, 6.
C, 5.
D, 4.
 Đáp án: C
Đáp án: C