Đáp án Bài tập tự luyện số 2
Câu 1 [31430]: Cho hàm số 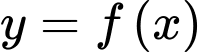 có đồ thị của hàm số
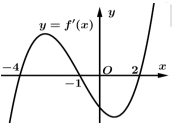
có đồ thị của hàm số 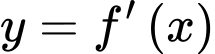 như hình vẽ. Hàm số
như hình vẽ. Hàm số 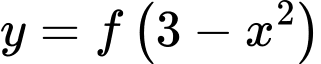 đồng biến trên khoảng
đồng biến trên khoảng
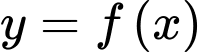 có đồ thị của hàm số
có đồ thị của hàm số 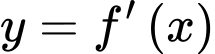 như hình vẽ. Hàm số
như hình vẽ. Hàm số 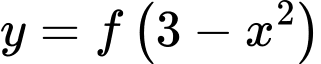 đồng biến trên khoảng
đồng biến trên khoảng
A, 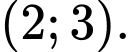
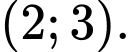
B, 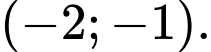
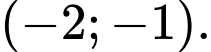
C, 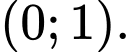
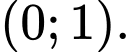
D, 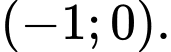
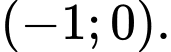
 Đáp án: D
Đáp án: D
Câu 2 [31732]: Cho hàm số 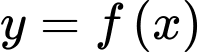 được xác định trên
được xác định trên 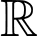 và hàm số
và hàm số 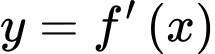 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
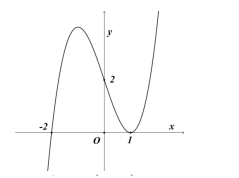
Tìm khoảng nghịch biến của hàm số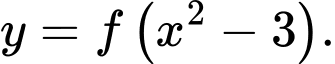
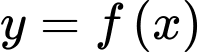 được xác định trên
được xác định trên 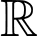 và hàm số
và hàm số 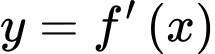 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Tìm khoảng nghịch biến của hàm số
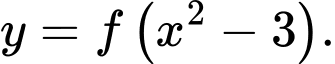
A, 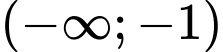 và
và 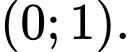
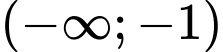 và
và 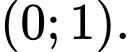
B, . 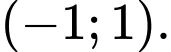
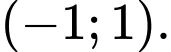
C, 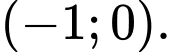
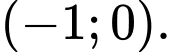
D, 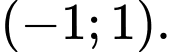
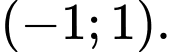
Đáp án A.
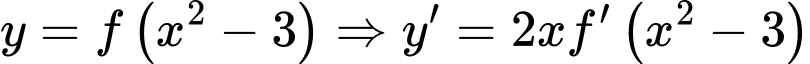
Nếu ta có
ta có 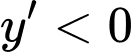
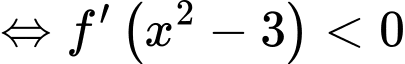
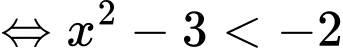
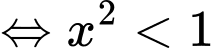
 Hàm số nghịch biến trên
Hàm số nghịch biến trên 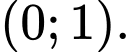
Nếu ta có
ta có 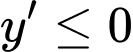
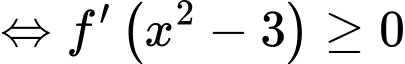
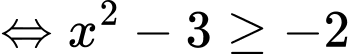
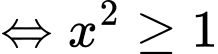
 Hàm số nghịch biến trên
Hàm số nghịch biến trên 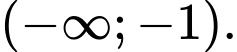 Đáp án: A
Đáp án: A
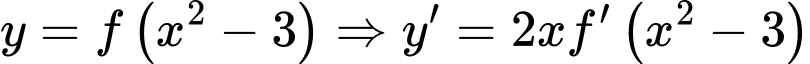
Nếu
 ta có
ta có 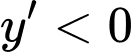
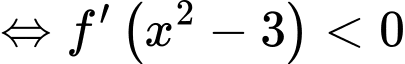
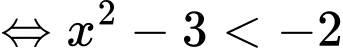
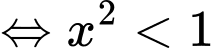
 Hàm số nghịch biến trên
Hàm số nghịch biến trên 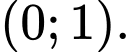
Nếu
 ta có
ta có 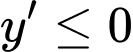
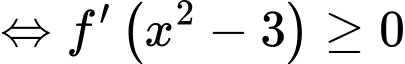
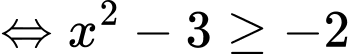
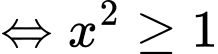
 Hàm số nghịch biến trên
Hàm số nghịch biến trên 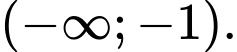 Đáp án: A
Đáp án: A
Câu 3 [31683]: Cho hàm số 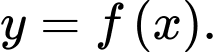 Đồ thị hàm số
Đồ thị hàm số 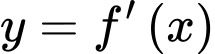 được cho như hình vẽ bên. Hàm số
được cho như hình vẽ bên. Hàm số 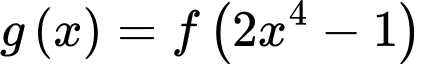 đồng biến trên khoảng nào dưới đây ?
đồng biến trên khoảng nào dưới đây ?
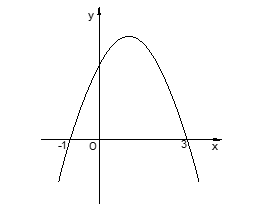
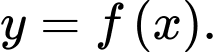 Đồ thị hàm số
Đồ thị hàm số 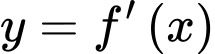 được cho như hình vẽ bên. Hàm số
được cho như hình vẽ bên. Hàm số 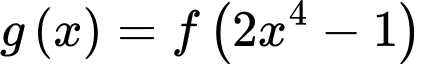 đồng biến trên khoảng nào dưới đây ?
đồng biến trên khoảng nào dưới đây ?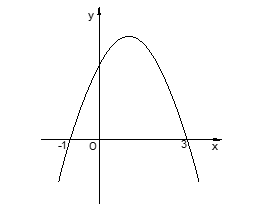
A, 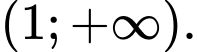
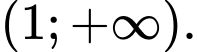
B, 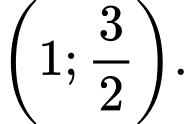
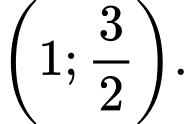
C, 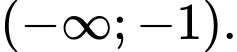
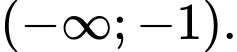
D, 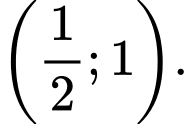
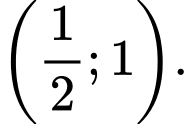
Đáp án D
Ta có: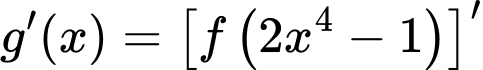
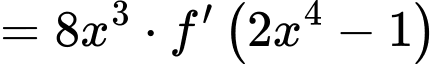
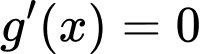
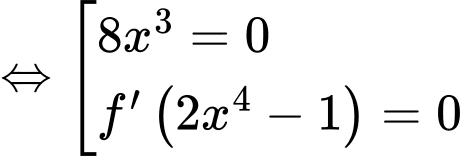
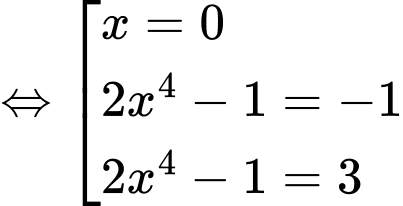
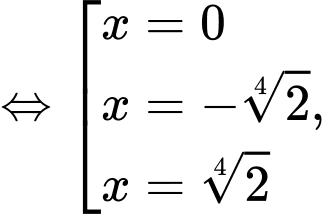 với
với 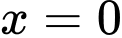 là nghiệm bội lẻ
là nghiệm bội lẻ
Ta có bảng biến thiên của hàm số: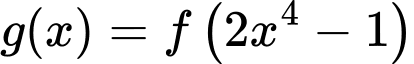
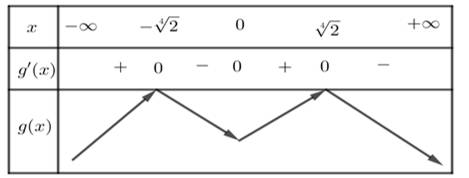
Nhìn vào bảng biến thiên ta nhận thấy hàm số đồng biến trong khoảng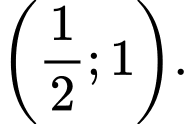 Đáp án: D
Đáp án: D
Ta có:
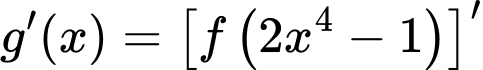
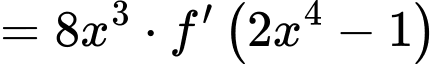
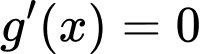
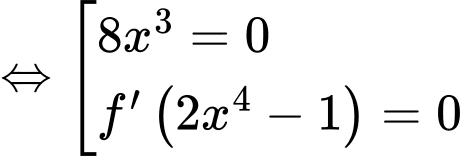
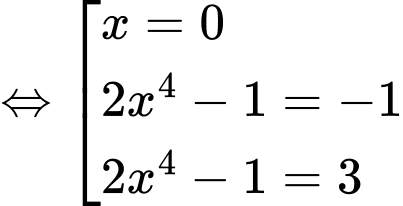
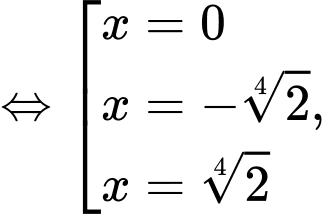 với
với 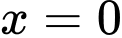 là nghiệm bội lẻ
là nghiệm bội lẻ
Ta có bảng biến thiên của hàm số:
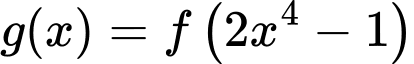

Nhìn vào bảng biến thiên ta nhận thấy hàm số đồng biến trong khoảng
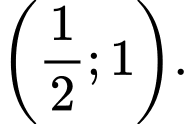 Đáp án: D
Đáp án: D
Câu 4 [6245]: Cho hàm số 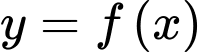 có đạo hàm
có đạo hàm 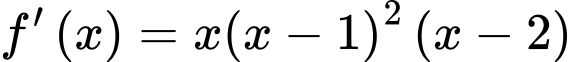 với mọi
với mọi 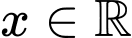 . Hàm số
. Hàm số 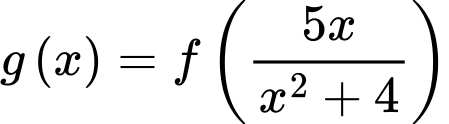 đồng biến trên khoảng nào trong các khoảng sau?
đồng biến trên khoảng nào trong các khoảng sau?
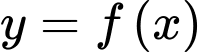 có đạo hàm
có đạo hàm 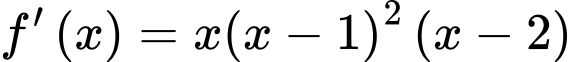 với mọi
với mọi 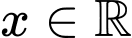 . Hàm số
. Hàm số 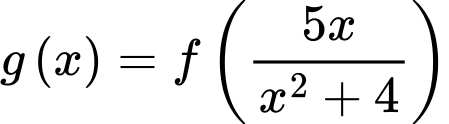 đồng biến trên khoảng nào trong các khoảng sau?
đồng biến trên khoảng nào trong các khoảng sau? A, 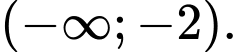
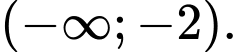
B, 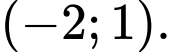
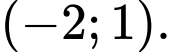
C, 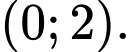
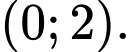
D, 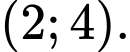
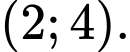
Ta có 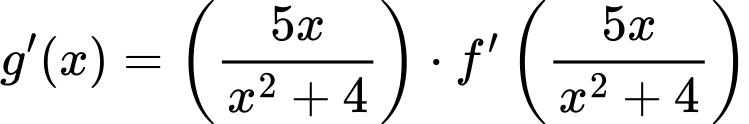
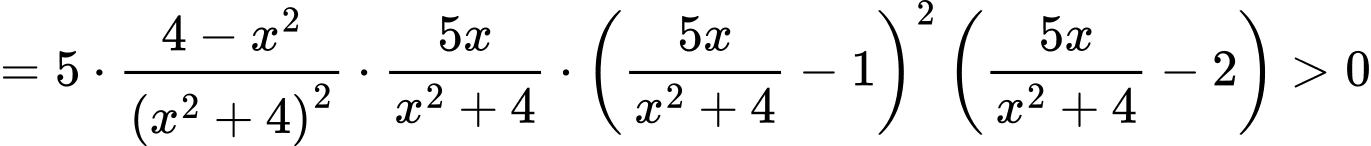
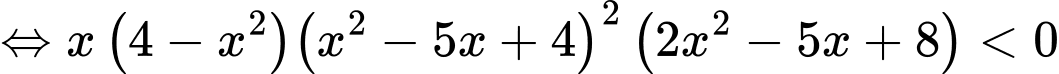
Mà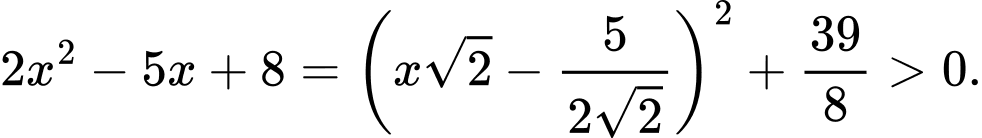
Nên
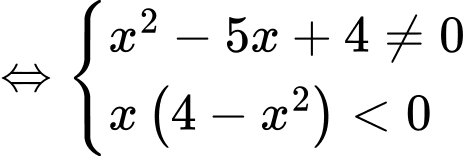
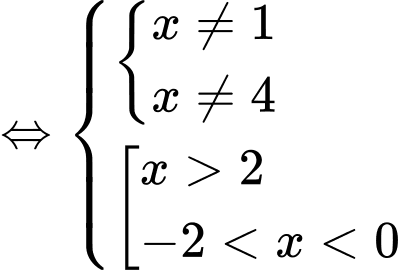
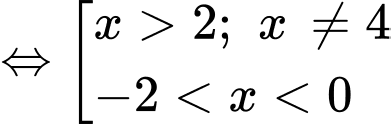
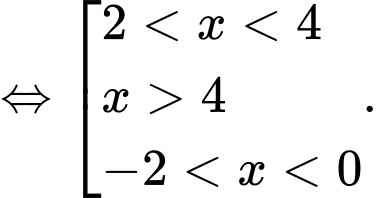
Hàm số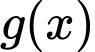 đồng biến trên khoàng
đồng biến trên khoàng 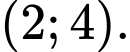 Chọn D Đáp án: D
Chọn D Đáp án: D
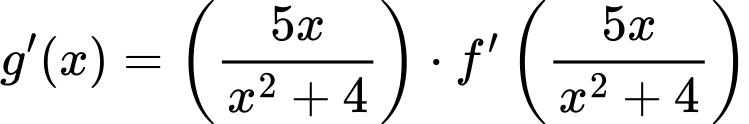
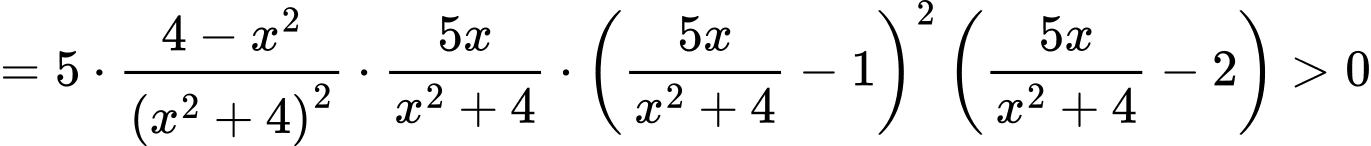
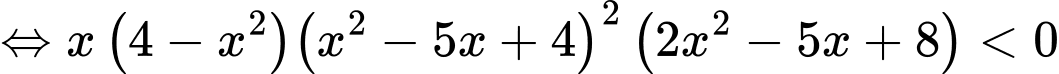
Mà
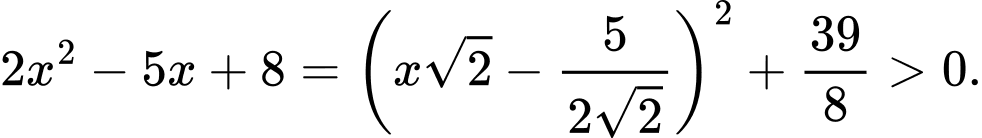
Nên

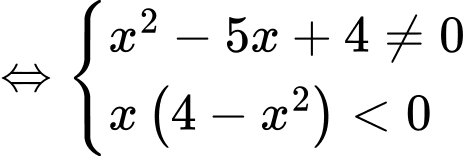
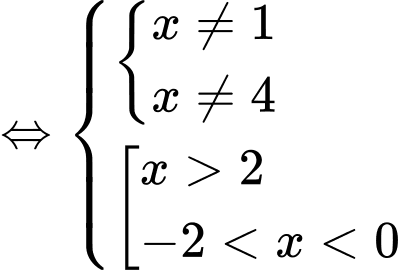
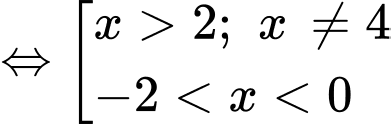
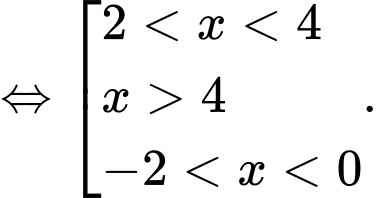
Hàm số
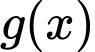 đồng biến trên khoàng
đồng biến trên khoàng 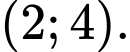 Chọn D Đáp án: D
Chọn D Đáp án: D
Câu 5 [45931]: Cho hàm số 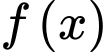 , bảng biến thiên của hàm số
, bảng biến thiên của hàm số 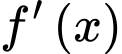 như sau:
như sau:
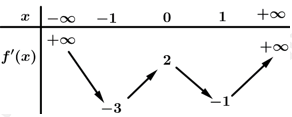
Số điểm cực trị của hàm số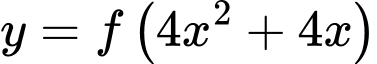 là
là
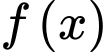 , bảng biến thiên của hàm số
, bảng biến thiên của hàm số 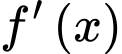 như sau:
như sau:
Số điểm cực trị của hàm số
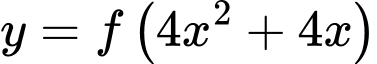 là
là A, 5.
B, 9.
C, 7.
D, 3.
Ta có: 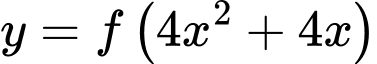
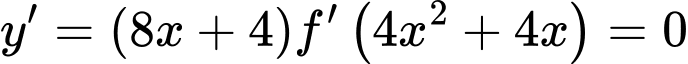
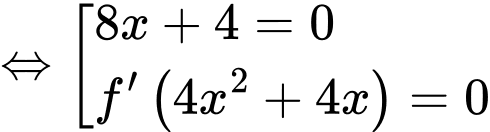
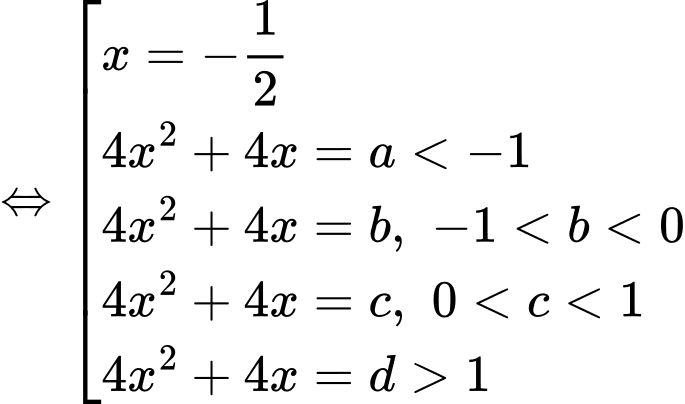
Đặt: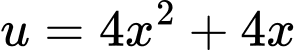
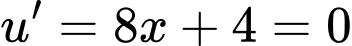
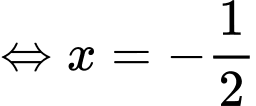
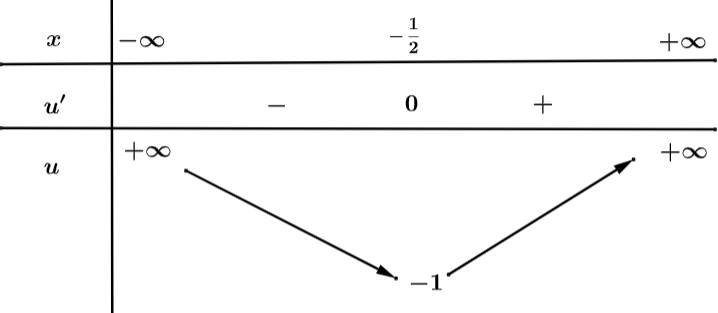
Từ bảng biến thiên suy ra phương trình có 7 nghiệm.
Đáp án: C. Đáp án: C
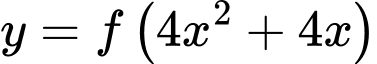
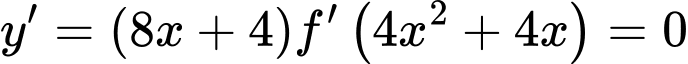
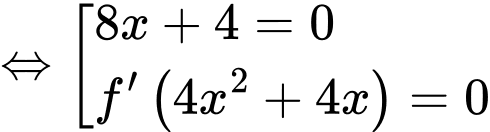
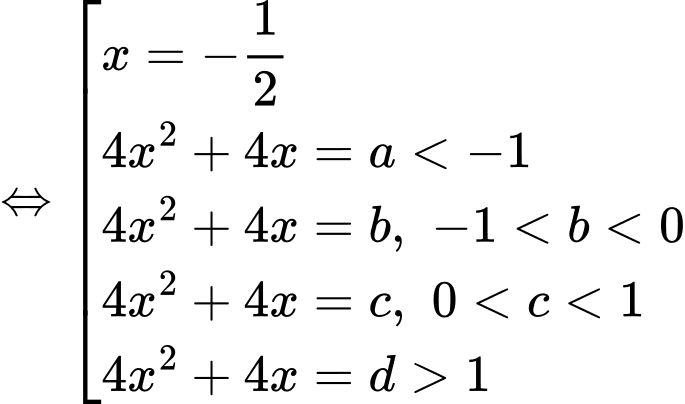
Đặt:
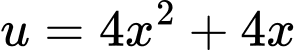
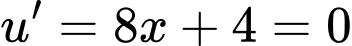
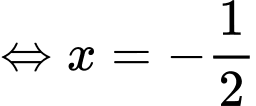

Từ bảng biến thiên suy ra phương trình có 7 nghiệm.
Đáp án: C. Đáp án: C
Câu 6 [526230]: Cho hàm số bậc bốn 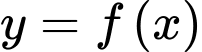 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 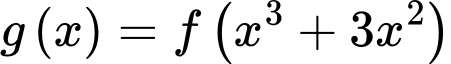 là
là
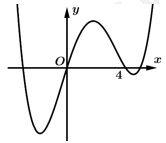
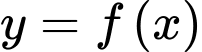 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 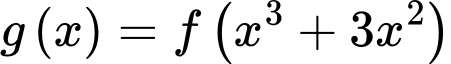 là
là
A, 5.
B, 3.
C, 7.
D, 11.
Ta có: 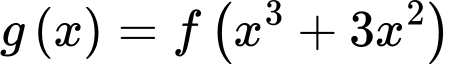
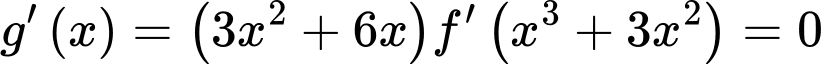
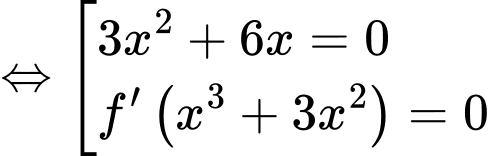
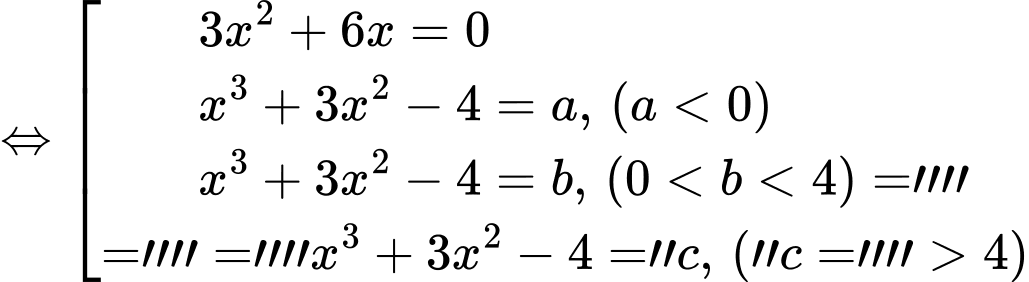
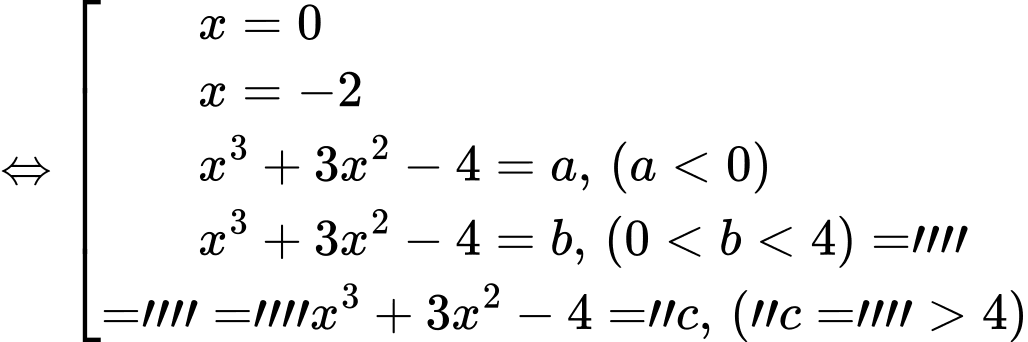
Đặt:
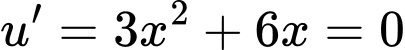
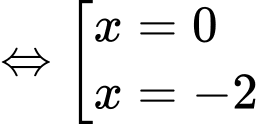
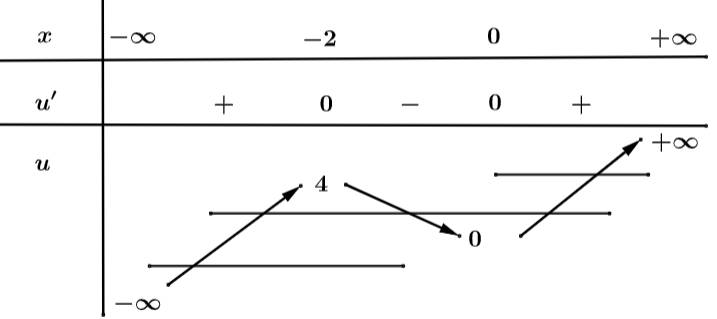
Suy ra phương trình: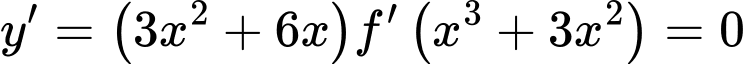 có tổng 7 nghiệm.
có tổng 7 nghiệm.
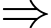 Phương trình có 7 cực trị.
Phương trình có 7 cực trị.
Đáp án: C.
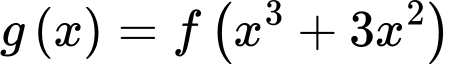
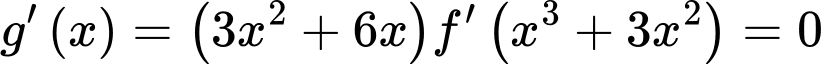
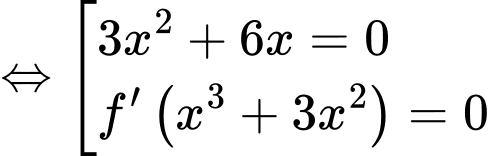
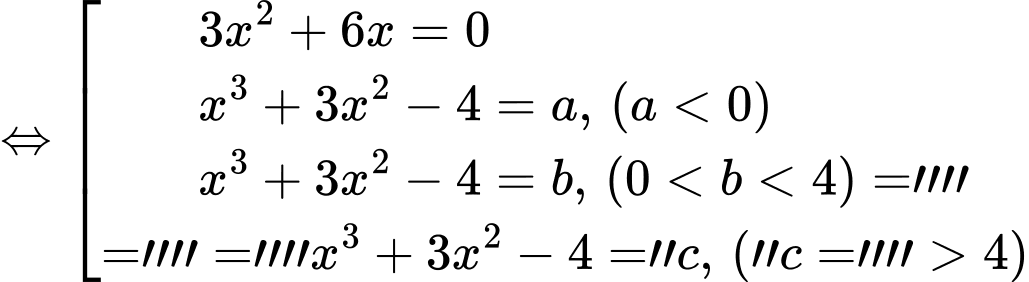
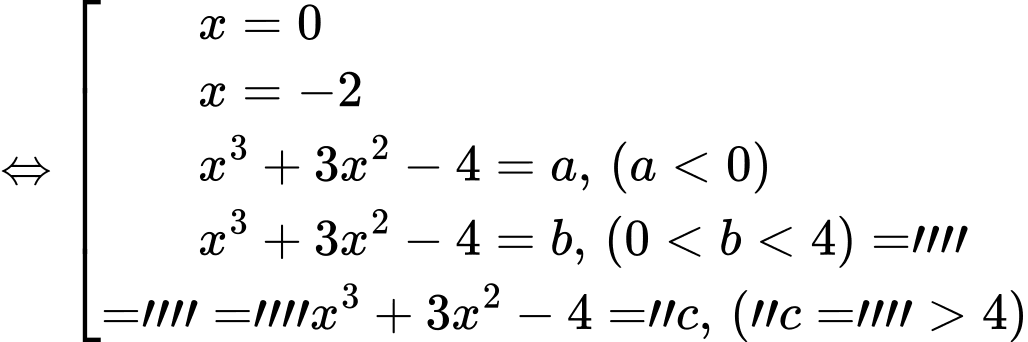
Đặt:

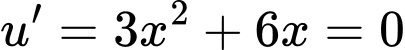
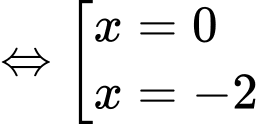

Suy ra phương trình:
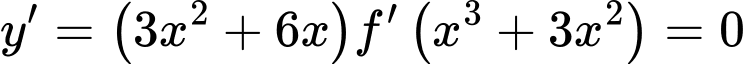 có tổng 7 nghiệm.
có tổng 7 nghiệm.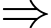 Phương trình có 7 cực trị.
Phương trình có 7 cực trị.Đáp án: C.
Câu 7 [526231]: Cho hàm số bậc bốn 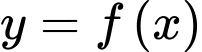 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 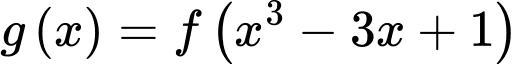 là
là
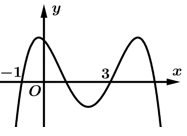
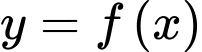 có đồ thị như hình vẽ. Số điểm cực trị của hàm số
có đồ thị như hình vẽ. Số điểm cực trị của hàm số 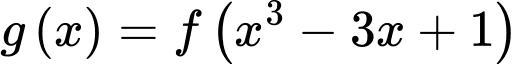 là
là
A, 7.
B, 9.
C, 10.
D, 8.
Ta có: 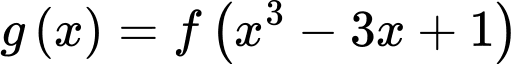
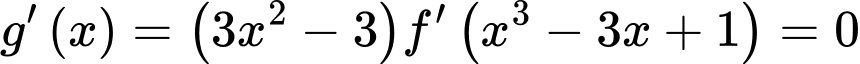
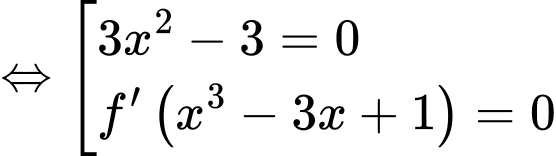
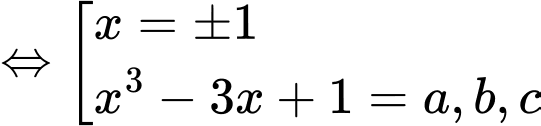
Đặt:
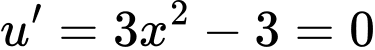
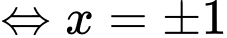
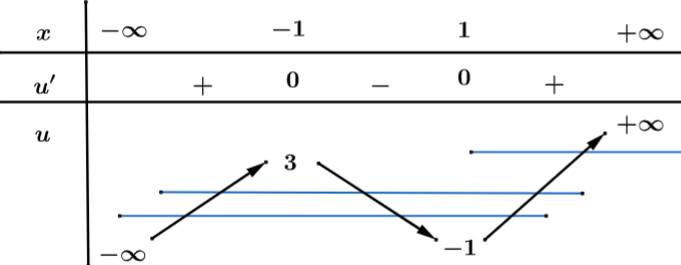
Suy ra phương trình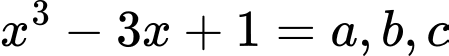 có tổng 7 nghiệm.
có tổng 7 nghiệm.
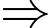 Phương trình
Phương trình 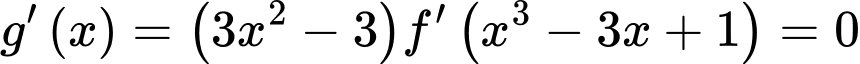 có tổng 9 nghiệm phân biệt.
có tổng 9 nghiệm phân biệt.
Vậy phương trình có 9 cực trị.
Đáp án: B. Đáp án: B
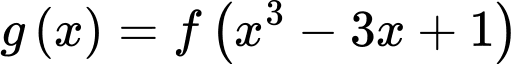
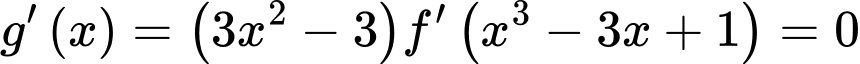
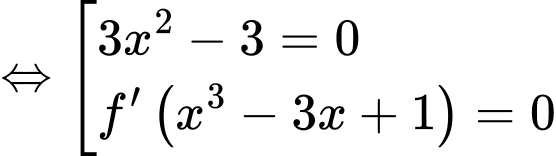
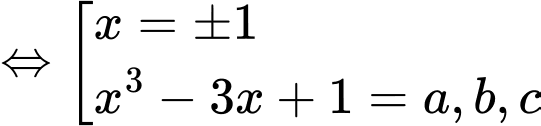
Đặt:

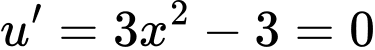
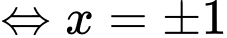

Suy ra phương trình
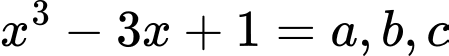 có tổng 7 nghiệm.
có tổng 7 nghiệm.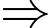 Phương trình
Phương trình 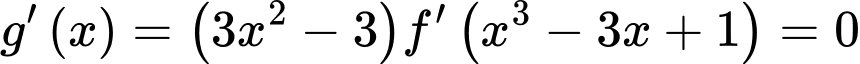 có tổng 9 nghiệm phân biệt.
có tổng 9 nghiệm phân biệt.Vậy phương trình có 9 cực trị.
Đáp án: B. Đáp án: B
Câu 8 [526243]: Cho hàm số 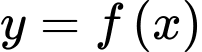 có đạo hàm trên
có đạo hàm trên 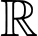 và có bảng biến thiên như hình vẽ dưới đây.
và có bảng biến thiên như hình vẽ dưới đây.
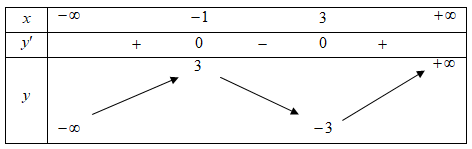
Số điểm cực trị của hàm số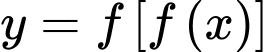 là
là
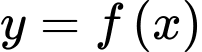 có đạo hàm trên
có đạo hàm trên 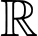 và có bảng biến thiên như hình vẽ dưới đây.
và có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số
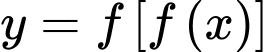 là
là A, 8.
B, 7.
C, 6.
D, 5.
Ta có: 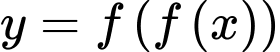
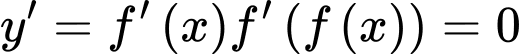
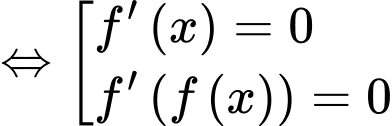
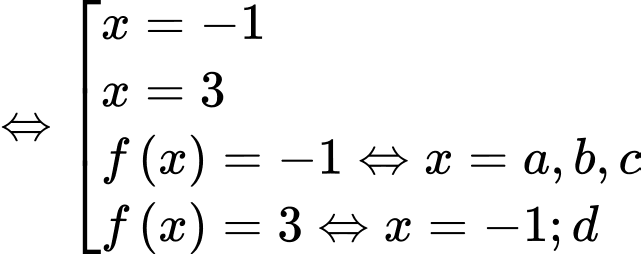
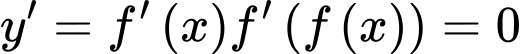 có 6 nghiệm bội lẻ.
có 6 nghiệm bội lẻ.
Vậy phương trình có 6 điểm cực trị.
Đáp án: C. Đáp án: C
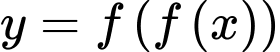
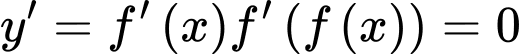
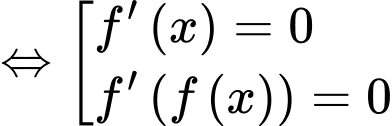
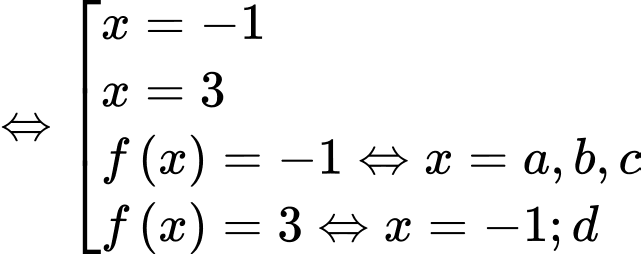
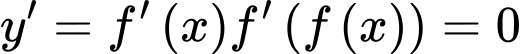 có 6 nghiệm bội lẻ.
có 6 nghiệm bội lẻ.Vậy phương trình có 6 điểm cực trị.
Đáp án: C. Đáp án: C
Câu 9 [526247]: Cho hàm số 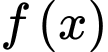 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.

Đặt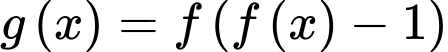 . Số nghiệm của phương trình
. Số nghiệm của phương trình 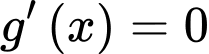 là
là
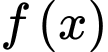 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Đặt
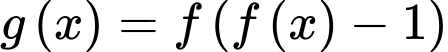 . Số nghiệm của phương trình
. Số nghiệm của phương trình 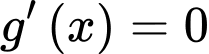 là
là A, 6.
B, 10.
C, 9.
D, 8.
Chọn C. Ta có 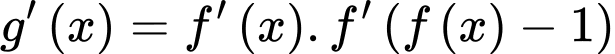 .
.
Suy ra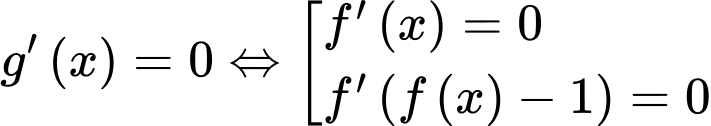 .
.
+) Với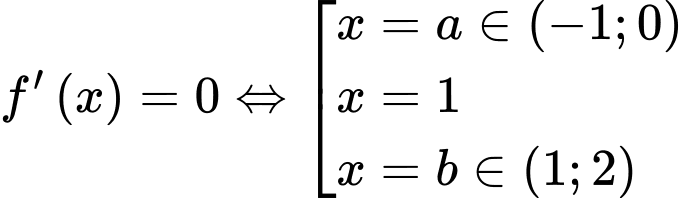
+) Với
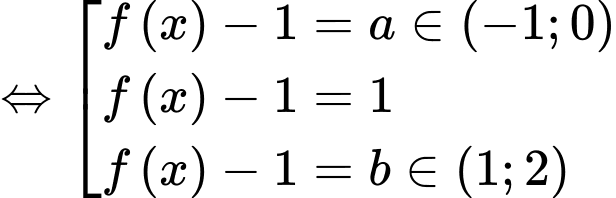
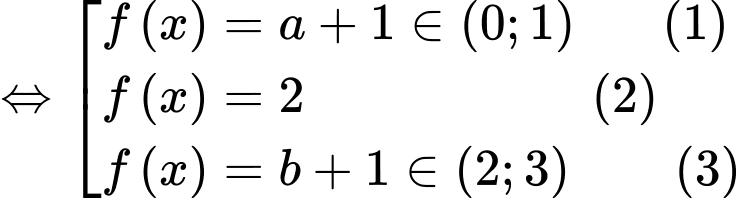
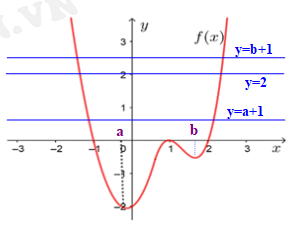
Từ đồ thị hàm số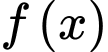 suy ra:
suy ra:
Phương trình (1) có 2 nghiệm.
Phương trình (2) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1).
Phương trình (3) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1) và 2 nghiệm của phương trình (2).
Vậy phương trình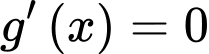 có tất cả 9 nghiệm. Đáp án: C
có tất cả 9 nghiệm. Đáp án: C
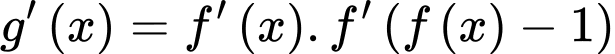 .
.Suy ra
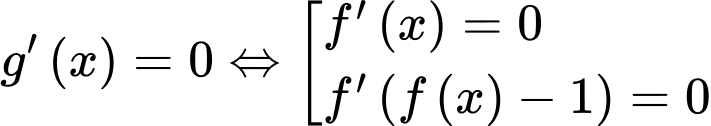 .
.+) Với
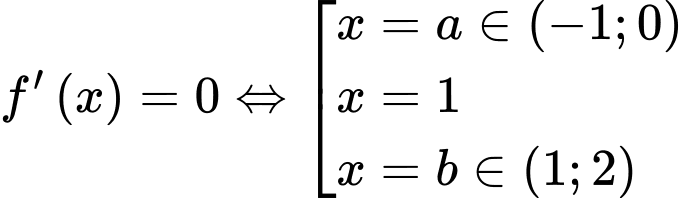
+) Với

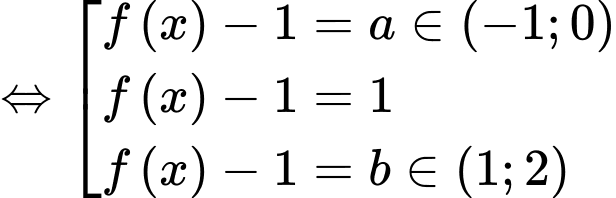
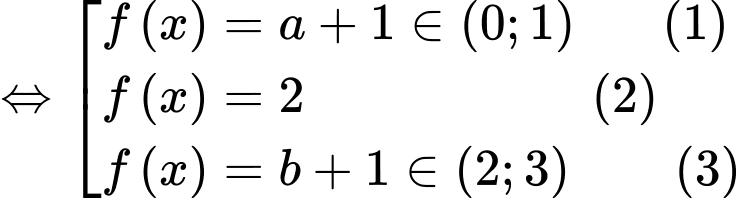

Từ đồ thị hàm số
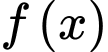 suy ra:
suy ra:Phương trình (1) có 2 nghiệm.
Phương trình (2) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1).
Phương trình (3) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1) và 2 nghiệm của phương trình (2).
Vậy phương trình
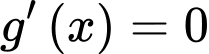 có tất cả 9 nghiệm. Đáp án: C
có tất cả 9 nghiệm. Đáp án: C
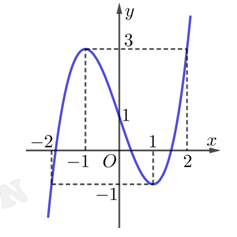
Câu 10 [678397]: Cho hàm số bậc ba 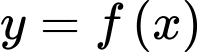 có đồ thị như sau:
có đồ thị như sau:
Hỏi hàm số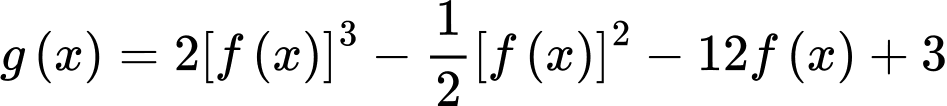 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
 có đồ thị như sau:
có đồ thị như sau: 
Hỏi hàm số
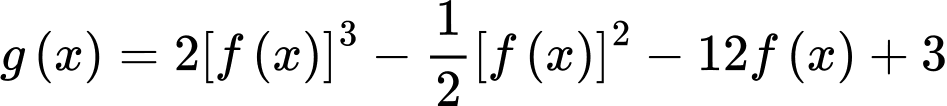 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 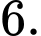
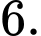
B, 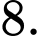
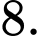
C, 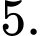
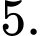
D, 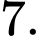
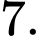
Ta có 
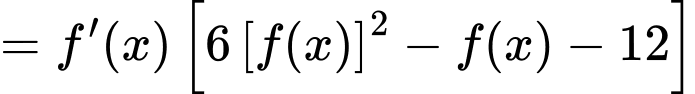
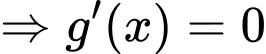
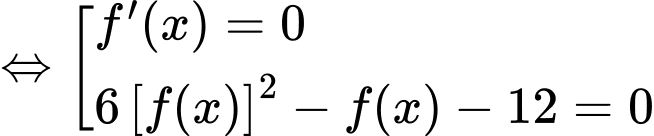
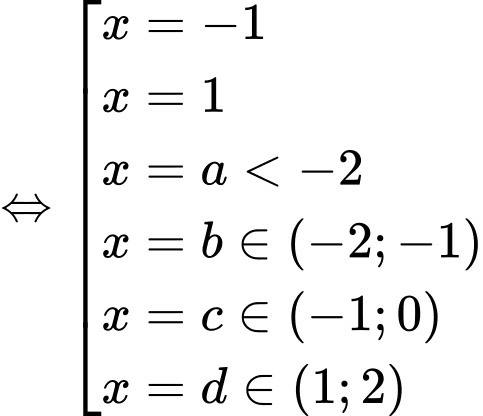
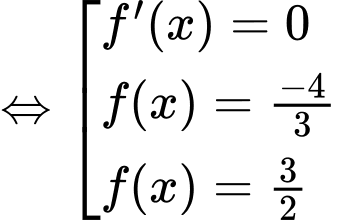
Vậy hàm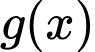 có 6 điểm cực trị. Đáp án: A
có 6 điểm cực trị. Đáp án: A

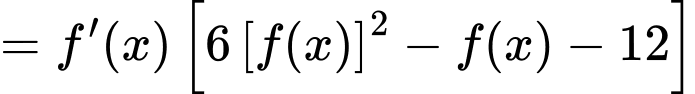
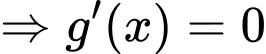
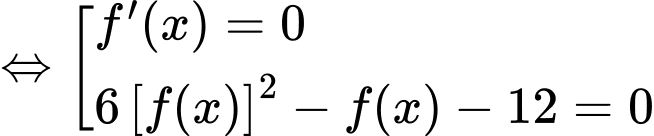
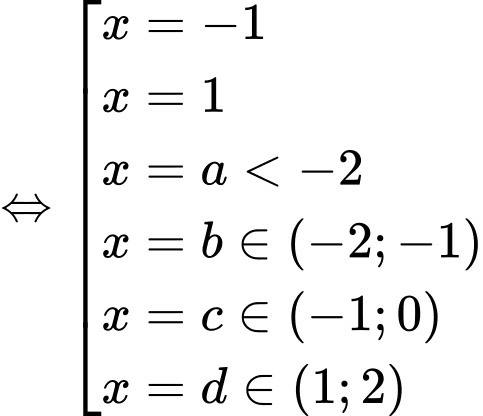
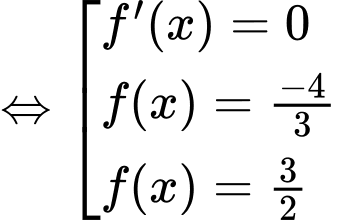
Vậy hàm
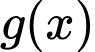 có 6 điểm cực trị. Đáp án: A
có 6 điểm cực trị. Đáp án: A
Câu 11 [947123]: Cho hàm số 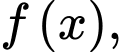 bảng biến thiên của hàm số
bảng biến thiên của hàm số 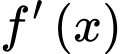 như sau. Số điểm cực trị của hàm số
như sau. Số điểm cực trị của hàm số 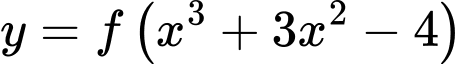 là
là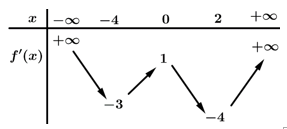
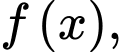 bảng biến thiên của hàm số
bảng biến thiên của hàm số 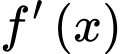 như sau. Số điểm cực trị của hàm số
như sau. Số điểm cực trị của hàm số 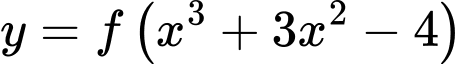 là
là
A, 7.
B, 8.
C, 9.
D, 10.
Ta có: 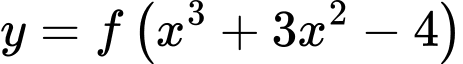
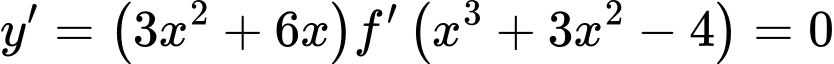
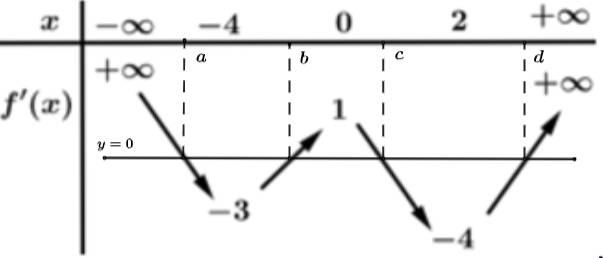
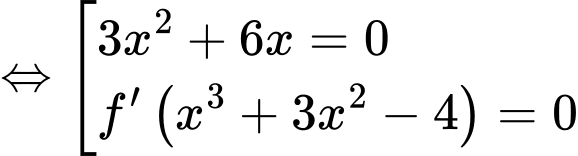
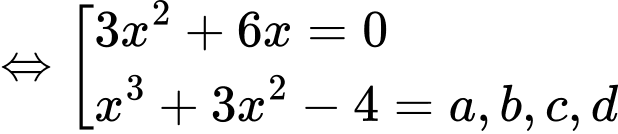
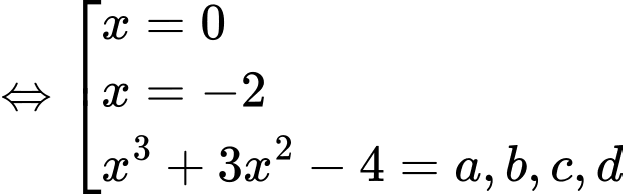
Xét
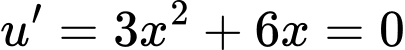
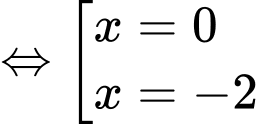
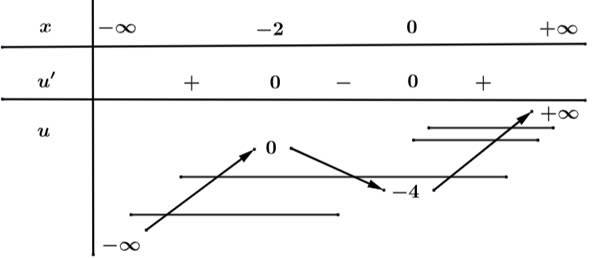
Suy ra phương trình: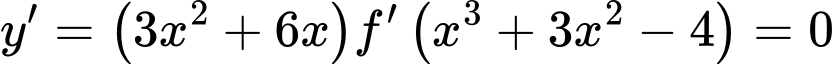 có tổng 8 nghiệm.
có tổng 8 nghiệm.
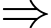 Phương trình có 8 cực trị.
Phương trình có 8 cực trị.
Đáp án: B. Đáp án: B
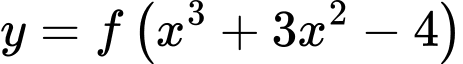
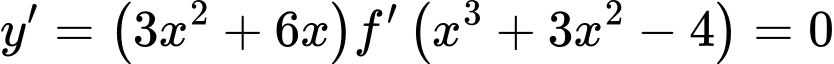

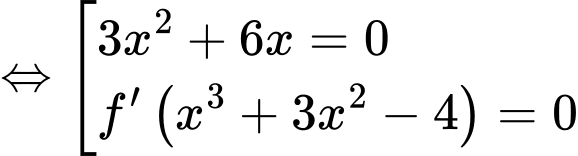
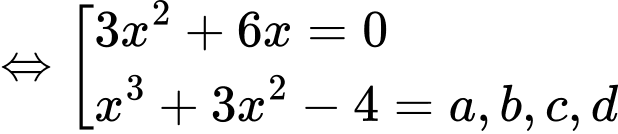
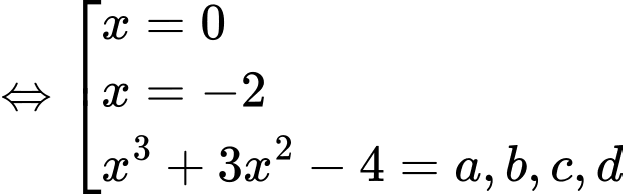
Xét

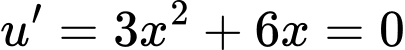
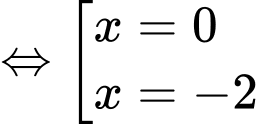

Suy ra phương trình:
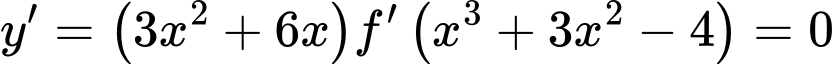 có tổng 8 nghiệm.
có tổng 8 nghiệm.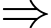 Phương trình có 8 cực trị.
Phương trình có 8 cực trị.Đáp án: B. Đáp án: B
Câu 12 [526235]: Cho hàm số 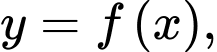 bảng biến thiên của hàm số
bảng biến thiên của hàm số 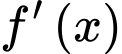 như sau
như sau
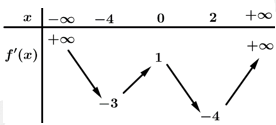
Hàm số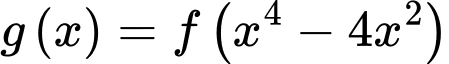 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
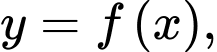 bảng biến thiên của hàm số
bảng biến thiên của hàm số 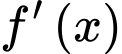 như sau
như sau
Hàm số
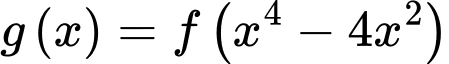 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 11.
B, 8.
C, 9.
D, 10.
Ta có: 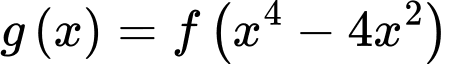
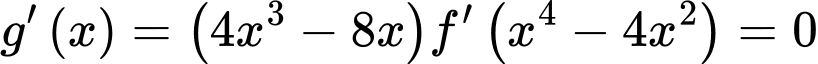
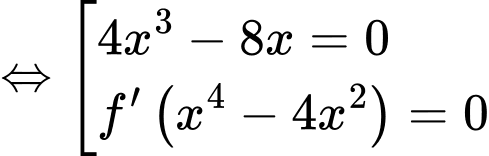
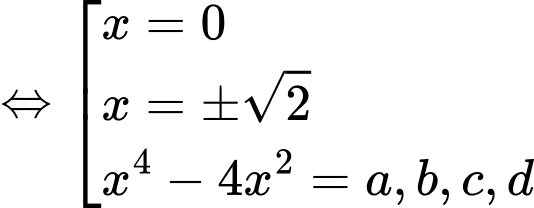
Đặt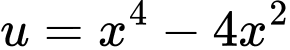
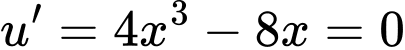
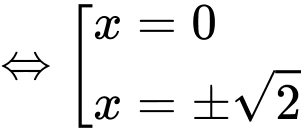
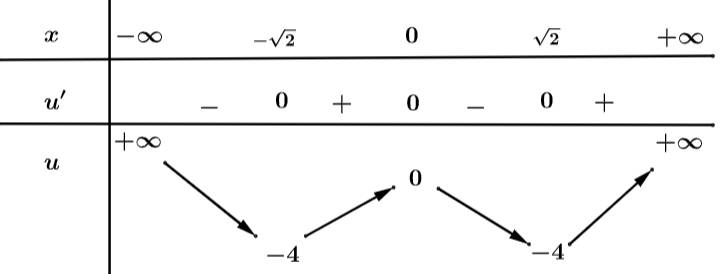
Từ bbt ta thấy được PT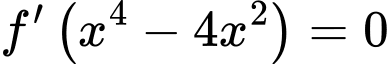 có 8 nghiệm.
có 8 nghiệm.
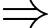 Phương trình
Phương trình 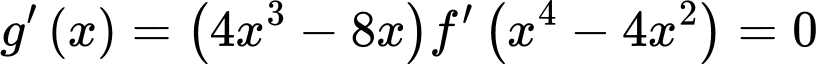 có tổng 11 nghiệm phân biệt.
có tổng 11 nghiệm phân biệt.
Suy ra phương trình có 11 điểm cực trị.
Đáp án: A. Đáp án: A
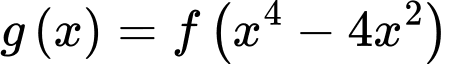
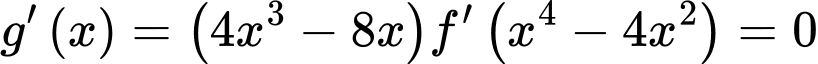
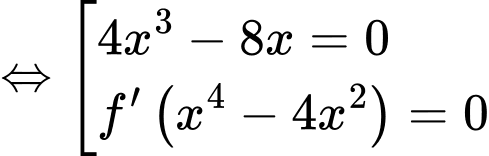
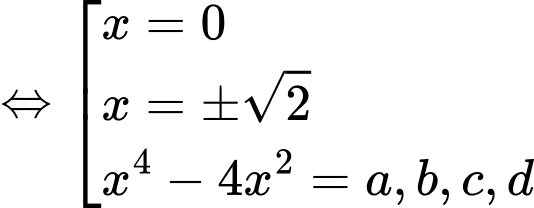
Đặt
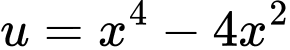
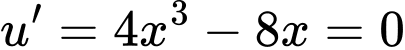
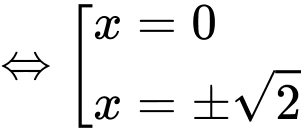

Từ bbt ta thấy được PT
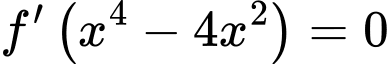 có 8 nghiệm.
có 8 nghiệm.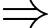 Phương trình
Phương trình 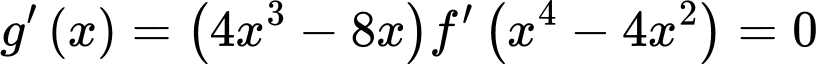 có tổng 11 nghiệm phân biệt.
có tổng 11 nghiệm phân biệt.Suy ra phương trình có 11 điểm cực trị.
Đáp án: A. Đáp án: A
Câu 13 [392801]: [Đề mẫu ĐGNL ĐHQG HN]: Hàm số 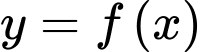 có đạo hàm
có đạo hàm 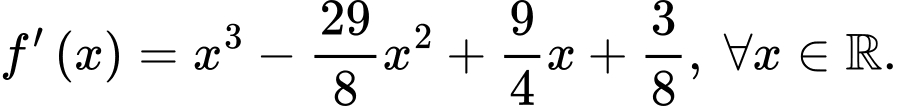 Gọi
Gọi 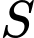 là tập hợp các điểm cực tiểu của hàm số
là tập hợp các điểm cực tiểu của hàm số 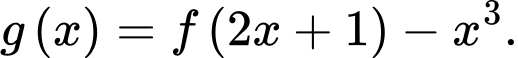 Tổng giá trị các phần tử của
Tổng giá trị các phần tử của 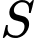 bằng
bằng
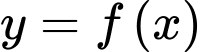 có đạo hàm
có đạo hàm 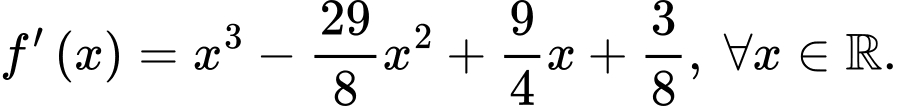 Gọi
Gọi 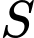 là tập hợp các điểm cực tiểu của hàm số
là tập hợp các điểm cực tiểu của hàm số 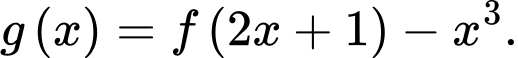 Tổng giá trị các phần tử của
Tổng giá trị các phần tử của 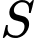 bằng
bằng Đáp số:…………………
Ta có 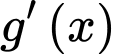
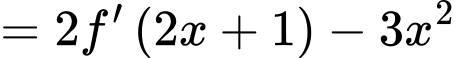
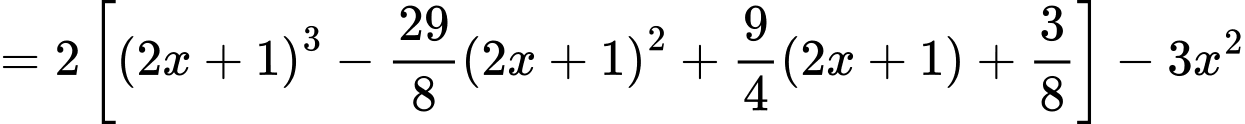
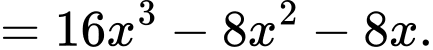
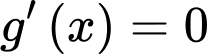
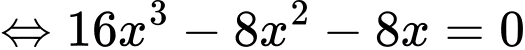
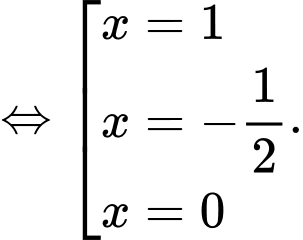
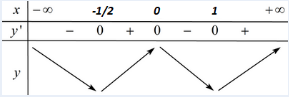
Vậy hàm số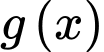 có hai điểm cực tiểu tại điểm
có hai điểm cực tiểu tại điểm 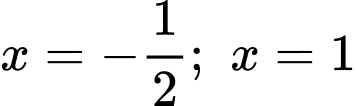
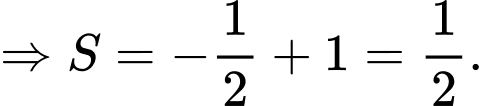
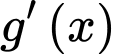
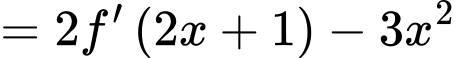
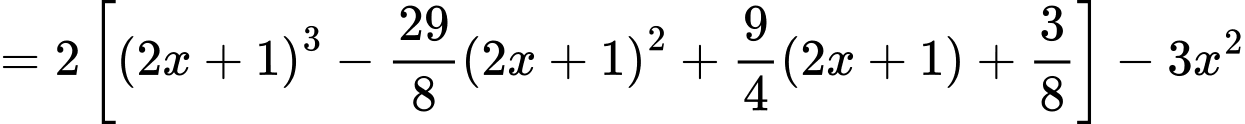
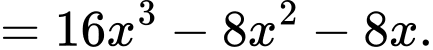
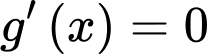
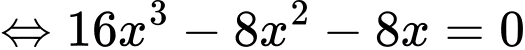
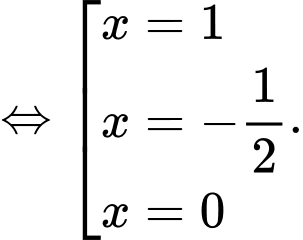
Bảng biến thiên

Vậy hàm số
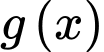 có hai điểm cực tiểu tại điểm
có hai điểm cực tiểu tại điểm 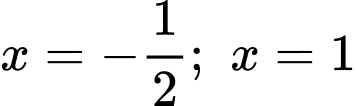
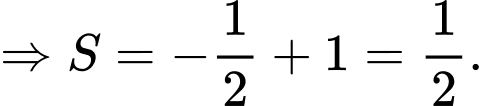
Câu 14 [526225]: Cho hàm số bậc ba 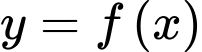 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
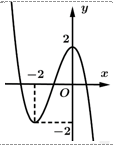
Số điểm cực tiểu của hàm số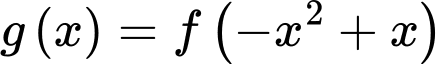 bằng
bằng
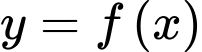 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Số điểm cực tiểu của hàm số
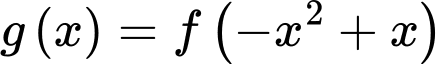 bằng
bằng A, 1.
B, 5.
C, 2.
D, 3.
Ta có: 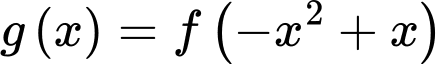
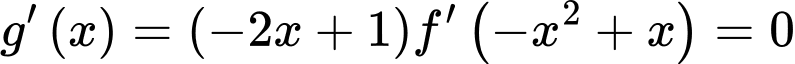
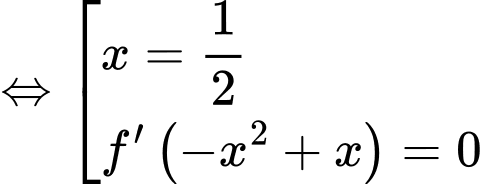
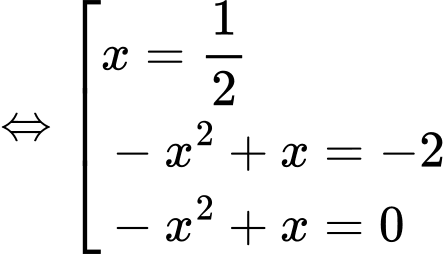
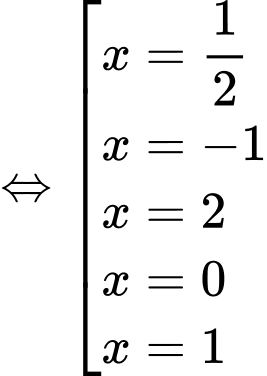

Hàm số có 3 cực tiểu.
Đáp án: D. Đáp án: D
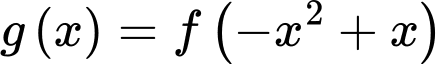
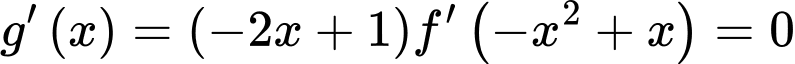
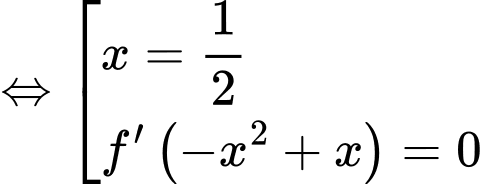
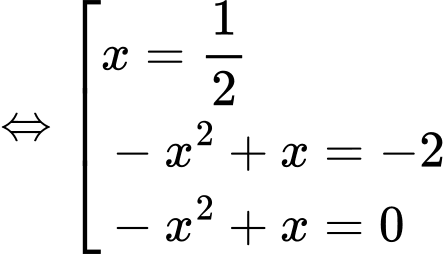
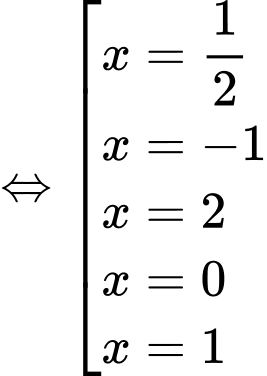

Hàm số có 3 cực tiểu.
Đáp án: D. Đáp án: D
Câu 15 [789416]: Cho hàm số 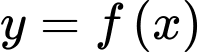 có bảng biến thiên như sau
có bảng biến thiên như sau

Số điểm cực tiểu của hàm số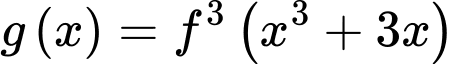 là
là
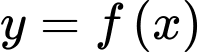 có bảng biến thiên như sau
có bảng biến thiên như sau
Số điểm cực tiểu của hàm số
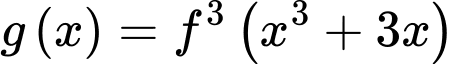 là
là A, 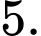
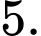
B, 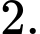
C, 
D, 
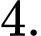
Chọn B
Ta có: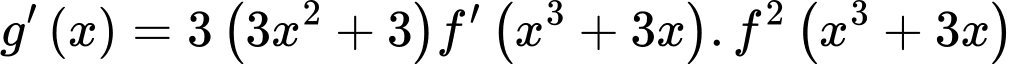 .
.
Ta thấy và
và 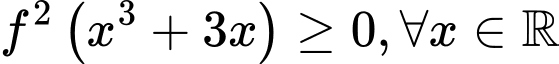 nên dấu của
nên dấu của 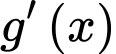 chính là dấu của
chính là dấu của 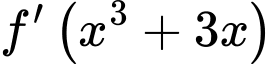
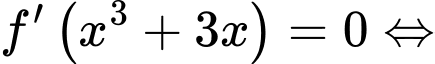
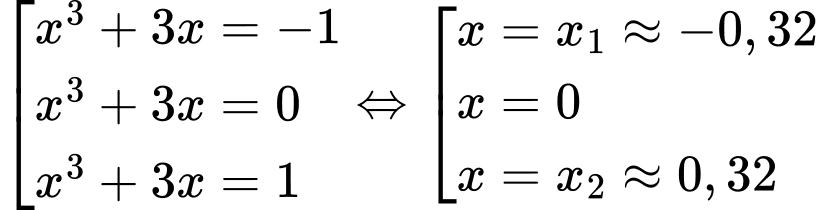
Từ bảng biến thiên của hàm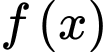 ta có
ta có 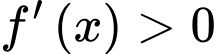
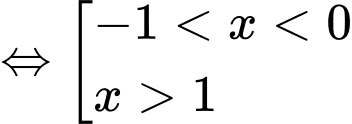
Do đó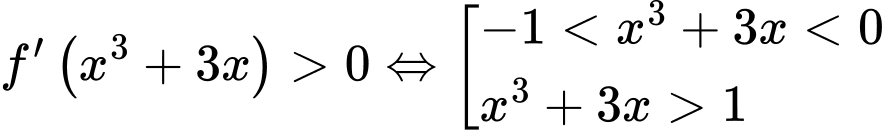
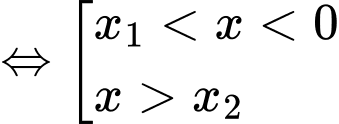
Ta có bảng biến thiên của hàm số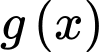
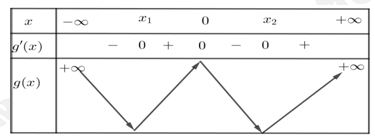
Vậy hàm số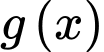 có 2 điểm cực tiểu. Đáp án: B
có 2 điểm cực tiểu. Đáp án: B
Ta có:
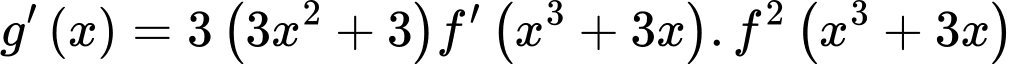 .
.Ta thấy
 và
và 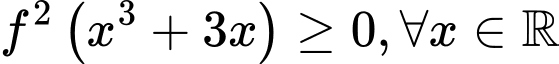 nên dấu của
nên dấu của 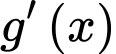 chính là dấu của
chính là dấu của 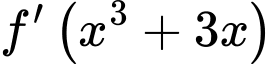
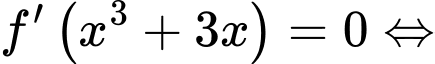
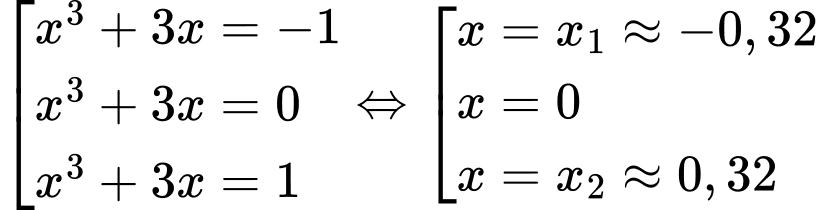
Từ bảng biến thiên của hàm
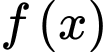 ta có
ta có 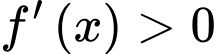
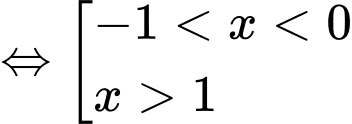
Do đó
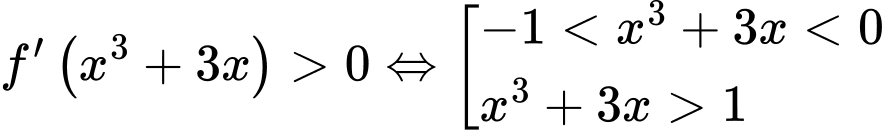
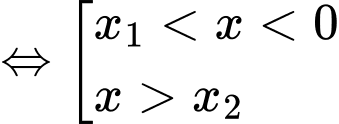
Ta có bảng biến thiên của hàm số
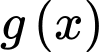

Vậy hàm số
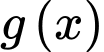 có 2 điểm cực tiểu. Đáp án: B
có 2 điểm cực tiểu. Đáp án: B
Câu 16 [789314]: Cho hàm số 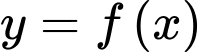 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
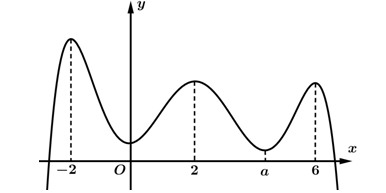
Biết tất cả các điểm cực trị của hàm số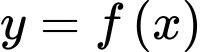 là
là 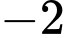 ;
;  ;
; 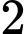 ;
; 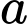 ;
; 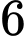 với
với 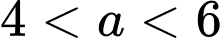 . Số điểm cực trị của hàm số
. Số điểm cực trị của hàm số 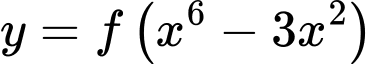 là
là
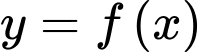 có đồ thị như hình vẽ.
có đồ thị như hình vẽ. 
Biết tất cả các điểm cực trị của hàm số
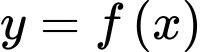 là
là 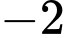 ;
;  ;
; 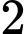 ;
; 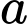 ;
; 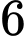 với
với 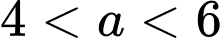 . Số điểm cực trị của hàm số
. Số điểm cực trị của hàm số 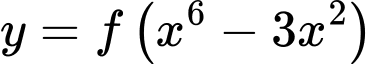 là
là A, 
B, 

C, 
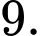
D, 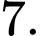
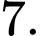
Chọn B
Từ đồ thị ta có -2; 0; 2;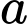 ; 6 là tất cả các nghiệm của
; 6 là tất cả các nghiệm của 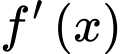 .
.
Ta có: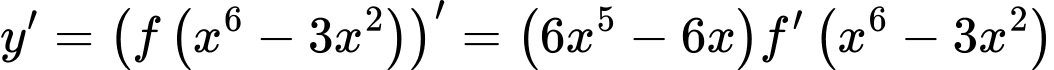
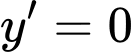
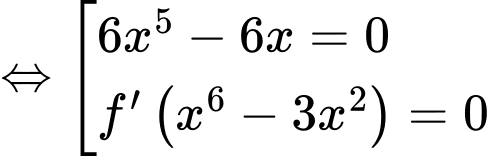
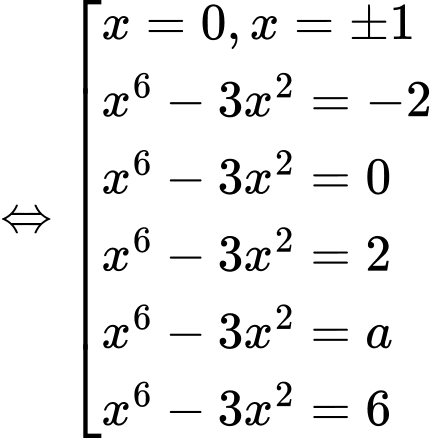
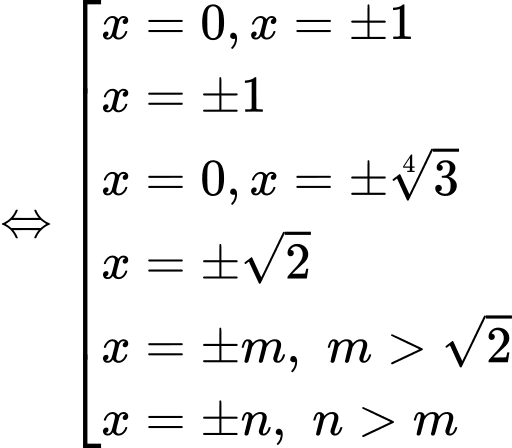
Dựa vào bảng biến thiên của hàm số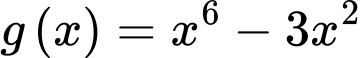 , ta suy ra
, ta suy ra  là nghiệm kép của phương trình
là nghiệm kép của phương trình 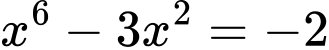 và
và  là nghiệm kép của phương trình
là nghiệm kép của phương trình 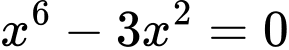 . Do đó
. Do đó  và
và  là nghiệm kép của
là nghiệm kép của 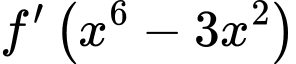 . Do vậy
. Do vậy  và
và  là nghiệm bội ba của
là nghiệm bội ba của 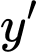 .
.
Các nghiệm khác và
và  của
của 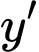 đều là nghiệm đơn.
đều là nghiệm đơn.
Vậy hàm số đã cho có 11 cực trị. Đáp án: B
Từ đồ thị ta có -2; 0; 2;
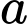 ; 6 là tất cả các nghiệm của
; 6 là tất cả các nghiệm của 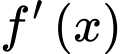 .
.Ta có:
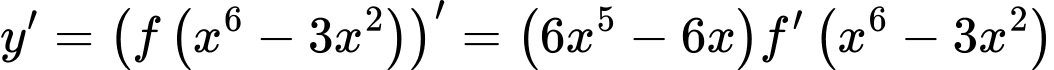
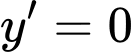
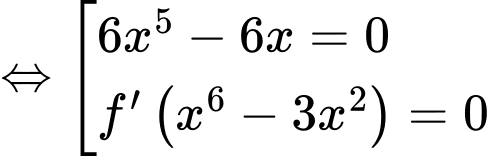
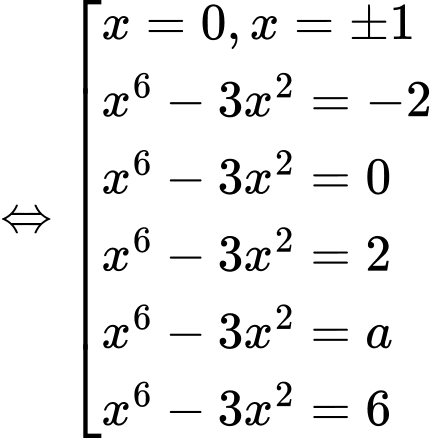
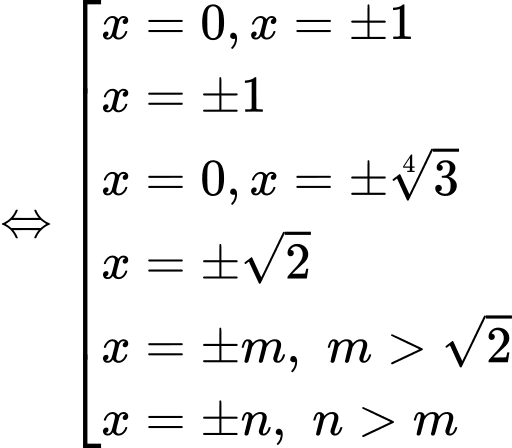
Dựa vào bảng biến thiên của hàm số
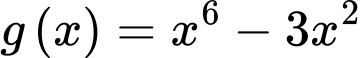 , ta suy ra
, ta suy ra  là nghiệm kép của phương trình
là nghiệm kép của phương trình 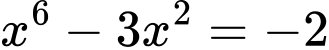 và
và  là nghiệm kép của phương trình
là nghiệm kép của phương trình 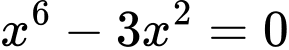 . Do đó
. Do đó  và
và  là nghiệm kép của
là nghiệm kép của 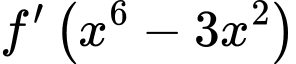 . Do vậy
. Do vậy  và
và  là nghiệm bội ba của
là nghiệm bội ba của 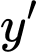 .
.Các nghiệm khác
 và
và  của
của 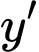 đều là nghiệm đơn.
đều là nghiệm đơn. Vậy hàm số đã cho có 11 cực trị. Đáp án: B
Câu 17 [31451]: Cho hàm số 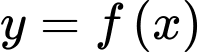 liên tục trên
liên tục trên 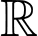 và có đồ thị là đường cong trơn (không bị gãy khúc), hình vẽ bên. Gọi hàm
và có đồ thị là đường cong trơn (không bị gãy khúc), hình vẽ bên. Gọi hàm 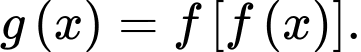 Hỏi phương trình
Hỏi phương trình 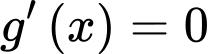 có bao nhiêu nghiệm phân biệt?
có bao nhiêu nghiệm phân biệt?

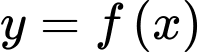 liên tục trên
liên tục trên 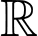 và có đồ thị là đường cong trơn (không bị gãy khúc), hình vẽ bên. Gọi hàm
và có đồ thị là đường cong trơn (không bị gãy khúc), hình vẽ bên. Gọi hàm 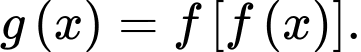 Hỏi phương trình
Hỏi phương trình 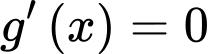 có bao nhiêu nghiệm phân biệt?
có bao nhiêu nghiệm phân biệt?
A, 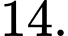
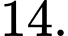
B, 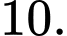
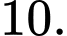
C, 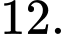
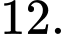
D, 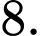
Đáp án C
Ta có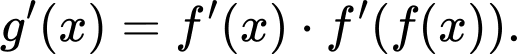
Xét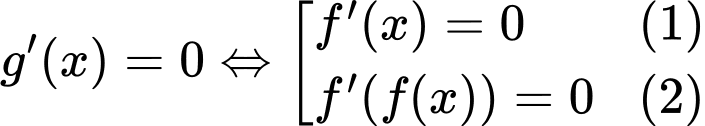
Với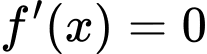
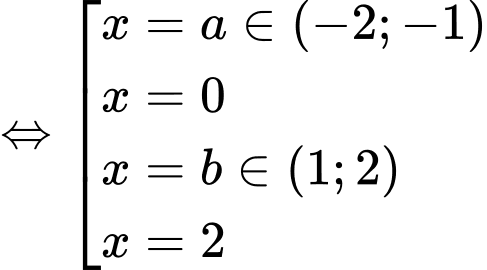
Với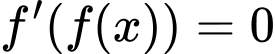
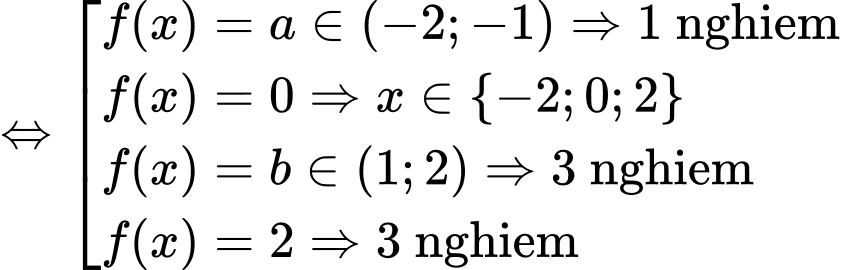
Như vậy ta có tổng cộng 12 nghiệm phân biệt (đã trừ đi 2 nghiệm trùng là 0 và 2). Đáp án: C
Ta có
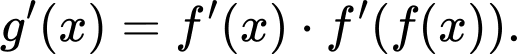
Xét
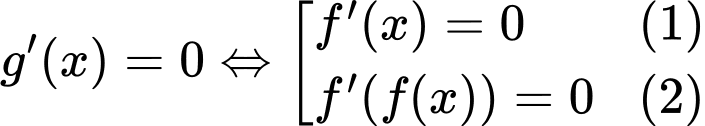
Với
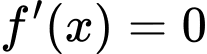
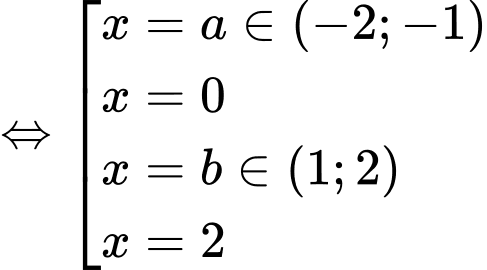
Với
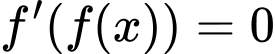
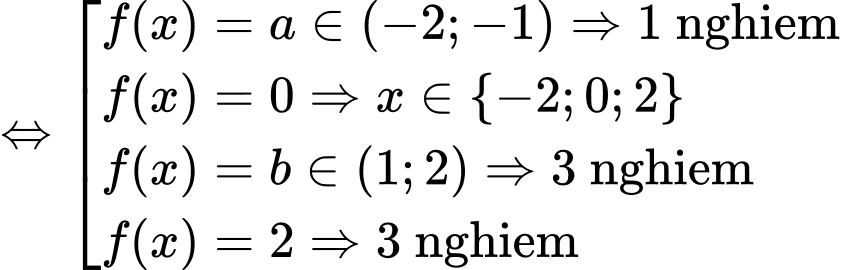
Như vậy ta có tổng cộng 12 nghiệm phân biệt (đã trừ đi 2 nghiệm trùng là 0 và 2). Đáp án: C