Đáp án Bài tập tự luyện số 1
Câu 1 [80815]: Cho hai số thực 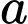 ,
, 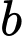 tùy ý,
tùy ý, 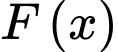 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 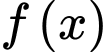 trên tập
trên tập 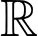 . Mệnh đề nào dưới đây là đúng?
. Mệnh đề nào dưới đây là đúng?
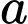 ,
, 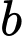 tùy ý,
tùy ý, 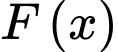 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 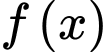 trên tập
trên tập 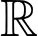 . Mệnh đề nào dưới đây là đúng?
. Mệnh đề nào dưới đây là đúng? A, 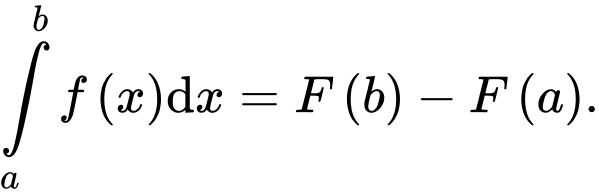
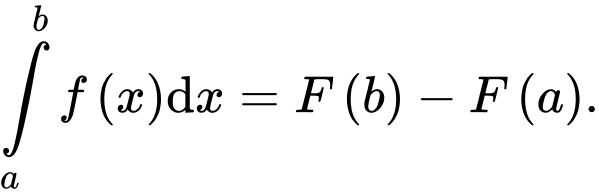
B, 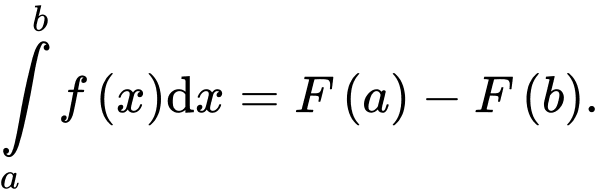
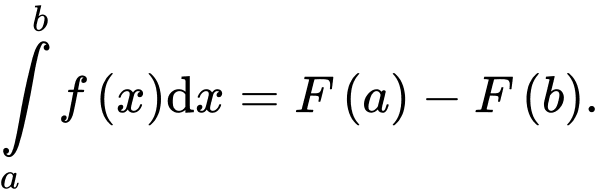
C, 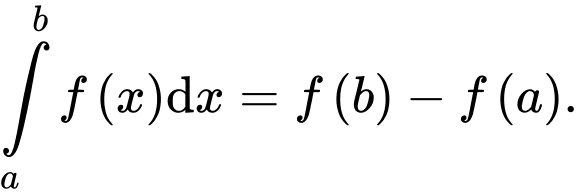
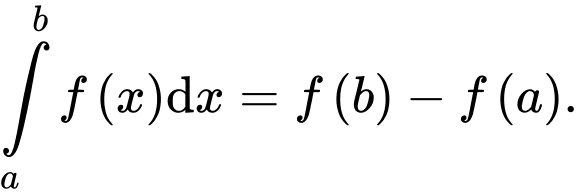
D, 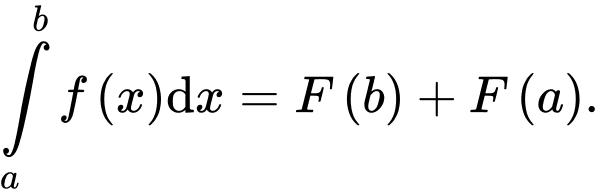
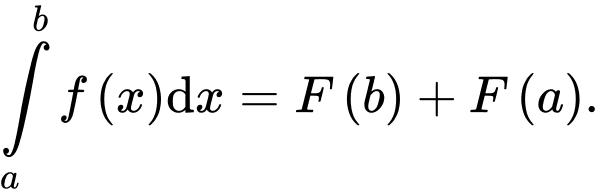
Chọn đáp án A.
Theo định nghĩa tích phân, ta có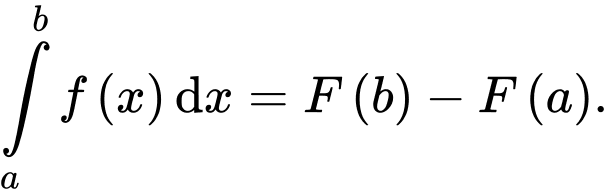 Đáp án: A
Đáp án: A
Theo định nghĩa tích phân, ta có
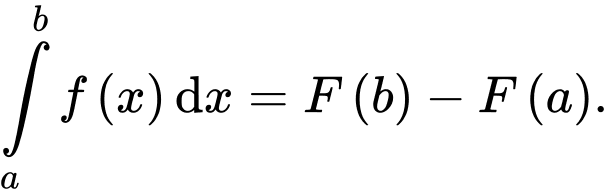 Đáp án: A
Đáp án: A
Câu 2 [389951]: Diện tích hình thang cong được tô đậm ở hình bên bằng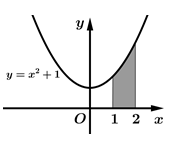

A, 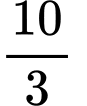 (đvdt).
(đvdt).
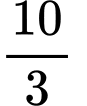 (đvdt).
(đvdt).B, 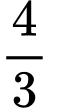 (đvdt).
(đvdt).
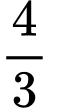 (đvdt).
(đvdt).C, 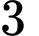 (đvdt).
(đvdt).
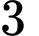 (đvdt).
(đvdt).D, 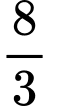 (đvdt).
(đvdt).
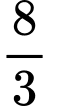 (đvdt).
(đvdt).
Diện tích hình thang là 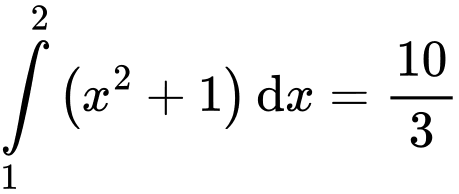 (đvdt) Đáp án: A
(đvdt) Đáp án: A
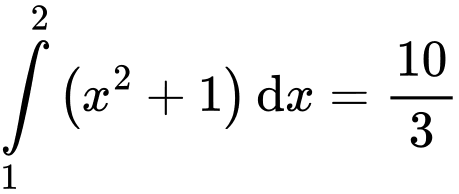 (đvdt) Đáp án: A
(đvdt) Đáp án: A
Câu 3 [149131]: Cho các số thực 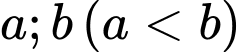 . Nếu hàm số
. Nếu hàm số 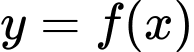 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 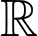 thì
thì
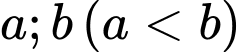 . Nếu hàm số
. Nếu hàm số 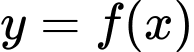 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 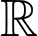 thì
thì A, 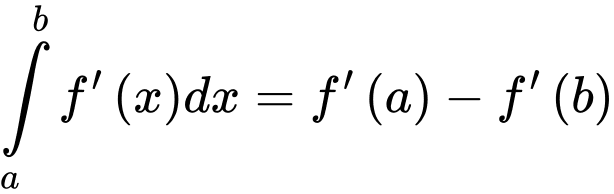 .
.
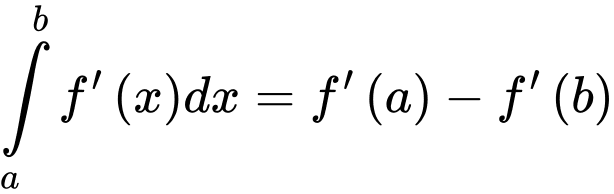 .
.B, 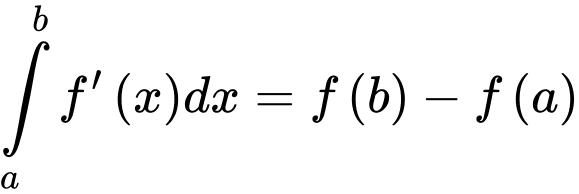 .
.
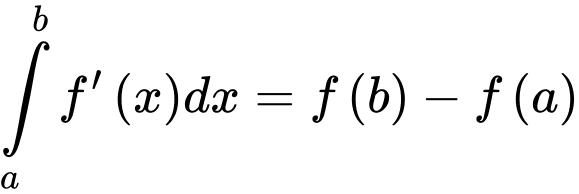 .
.C, 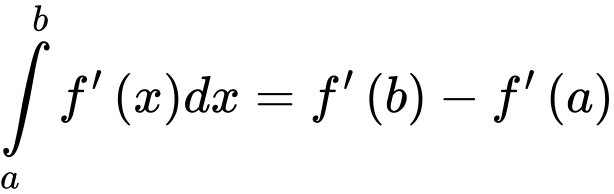 .
.
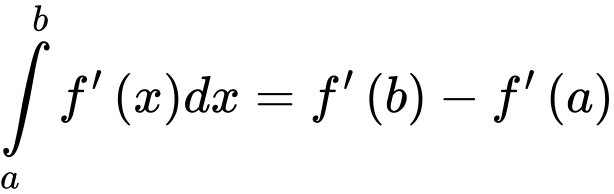 .
.D, 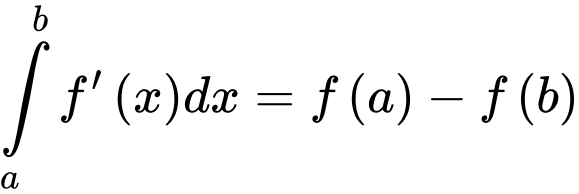 .
.
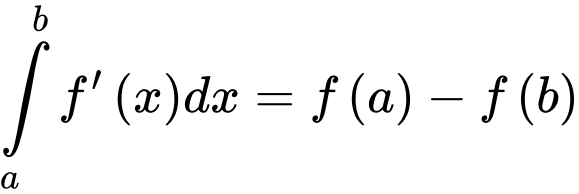 .
. Đáp án: B
Đáp án: B
Câu 4 [389952]: Diện tích hình thang cong được tô đậm trong hình vẽ bên bằng: 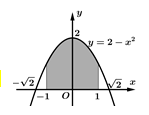

A, 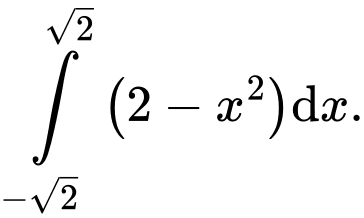
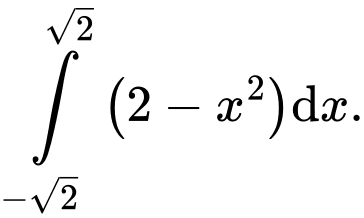
B, 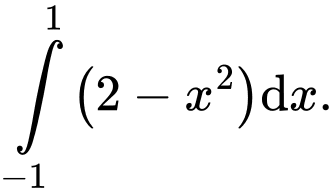
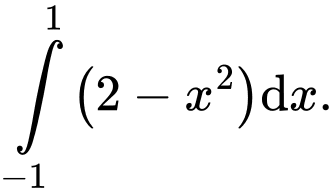
C, 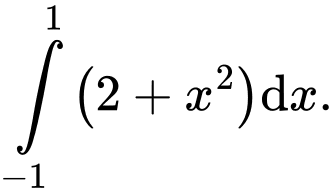
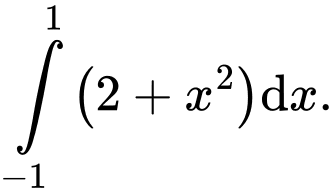
D, 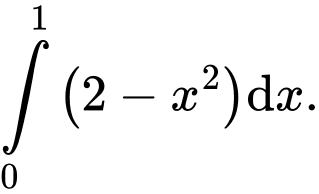
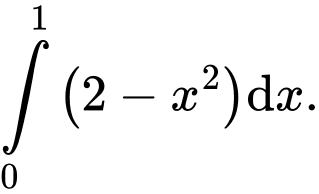
Chọn đáp án B. Đáp án: B
Câu 5 [389953]: Cho hai số thực tùy ý và hàm số 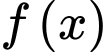 liên tục trên
liên tục trên 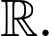 Mệnh đề nào dưới đây là sai?
Mệnh đề nào dưới đây là sai?
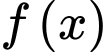 liên tục trên
liên tục trên 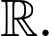 Mệnh đề nào dưới đây là sai?
Mệnh đề nào dưới đây là sai? A, 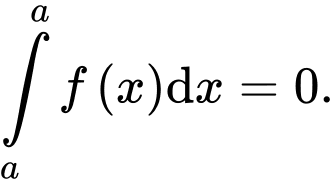
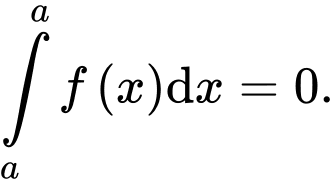
B, 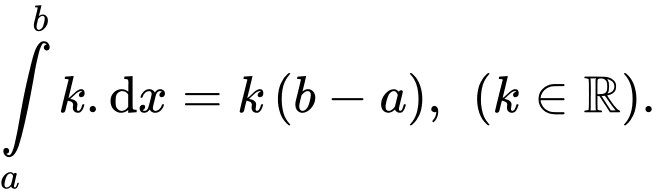
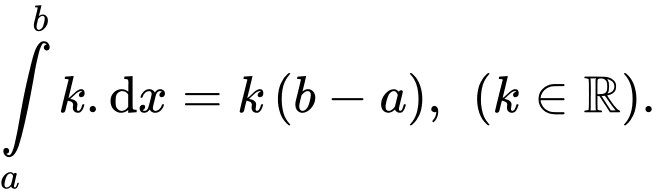
C, 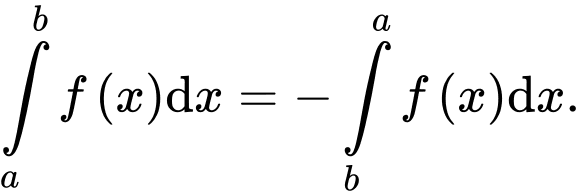
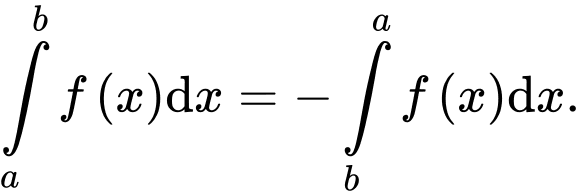
D, 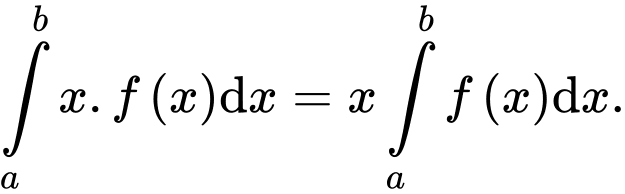
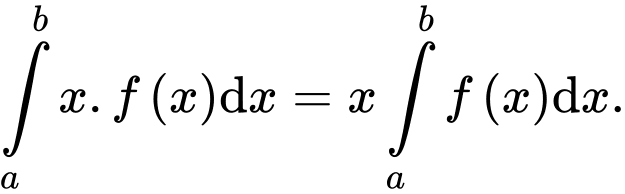
Đáp án A, C đúng theo kiến thức sách giáo khoa.
B.
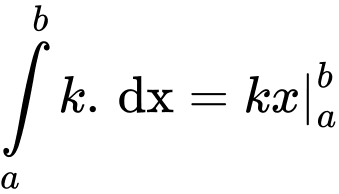
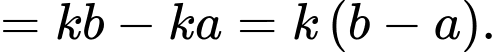
Do đó B đúng.
Suy ra đáp án D sai. Chọn D. Đáp án: D
Câu 6 [378613]: Cho hàm số 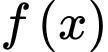 có đạo hàm
có đạo hàm 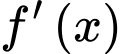 liên tục trên
liên tục trên 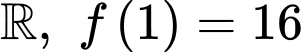 và
và 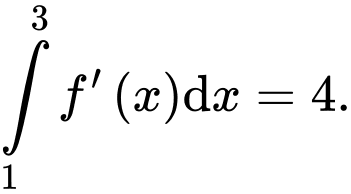 Khi đó giá trị của
Khi đó giá trị của 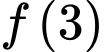 bằng
bằng
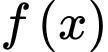 có đạo hàm
có đạo hàm 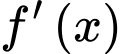 liên tục trên
liên tục trên 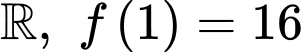 và
và 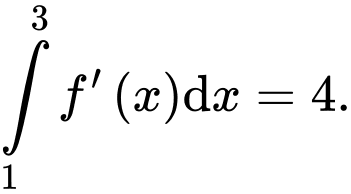 Khi đó giá trị của
Khi đó giá trị của 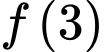 bằng
bằng A, 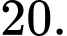
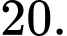
B, 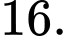
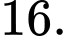
C, 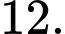
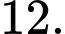
D, 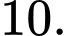
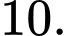
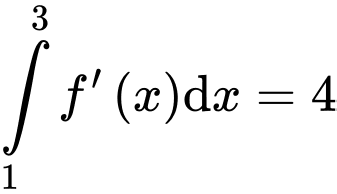
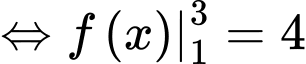
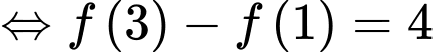
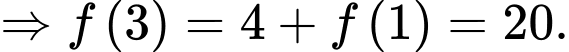
Chọn A. Đáp án: A
Câu 7 [360303]: Biết 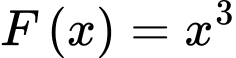 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 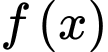 trên
trên 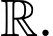 Giá trị của
Giá trị của 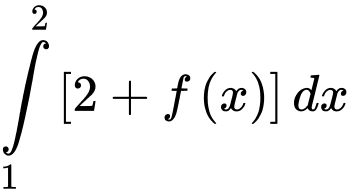 bằng:
bằng:
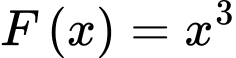 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 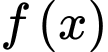 trên
trên 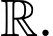 Giá trị của
Giá trị của 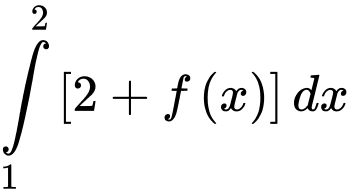 bằng:
bằng: A, 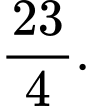
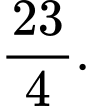
B, 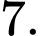
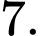
C, 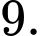
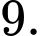
D, 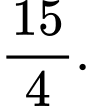
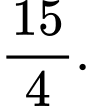
Chọn đáp án C.
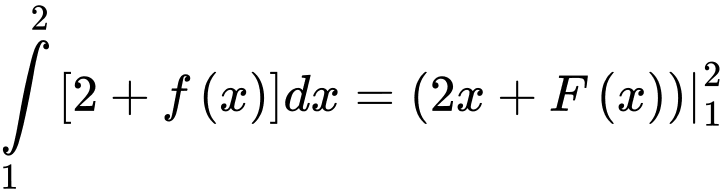
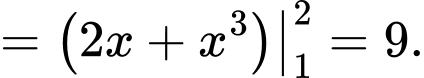
Đáp án: C
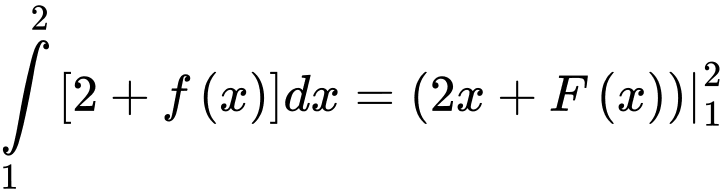
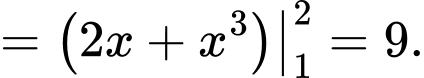
Đáp án: C
Câu 8 [360304]: Biết 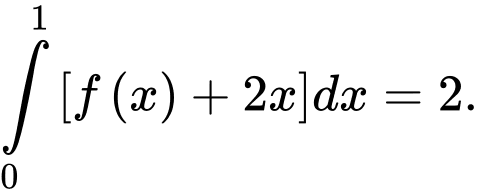 Khi đó,
Khi đó, 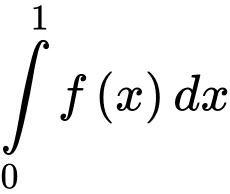 bằng:
bằng:
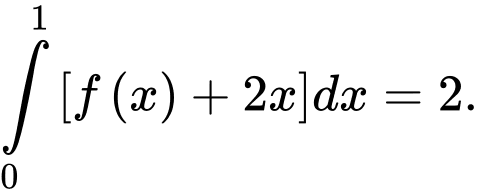 Khi đó,
Khi đó, 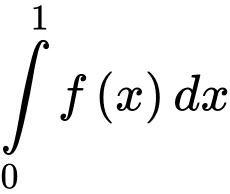 bằng:
bằng: A, 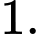
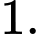
B, 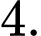
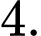
C, 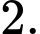
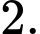
D, 
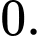
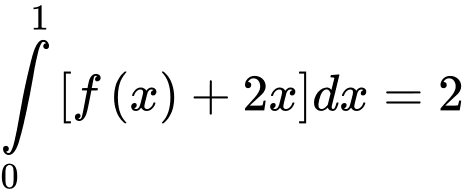
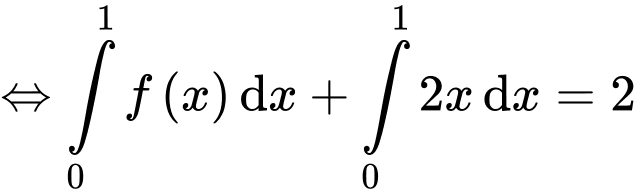
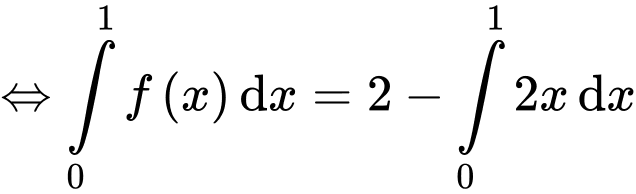
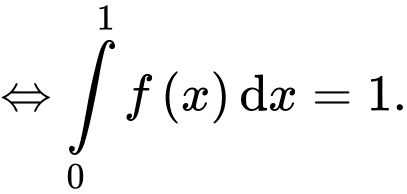
Chọn A. Đáp án: A
Câu 9 [149134]: Cho hàm số 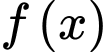 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên  . Tính
. Tính 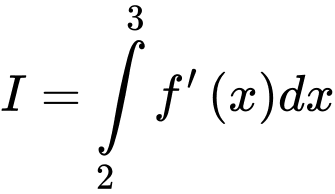 .
.
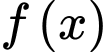 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên  . Tính
. Tính 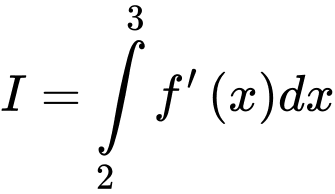 .
. A, 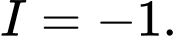
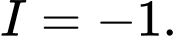
B, 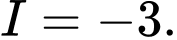
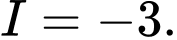
C, 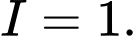
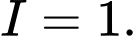
D, 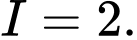
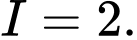
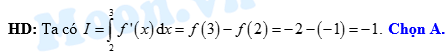 Đáp án: A
Đáp án: A
Câu 10 [185163]: Cho hàm số 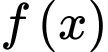 liên tục trên
liên tục trên 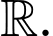 Biết hàm số
Biết hàm số 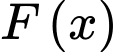 là một nguyên hàm của
là một nguyên hàm của 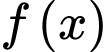 trên và
trên và 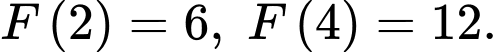 Tích phân
Tích phân 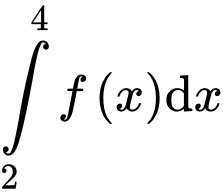 bằng
bằng
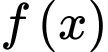 liên tục trên
liên tục trên 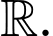 Biết hàm số
Biết hàm số 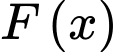 là một nguyên hàm của
là một nguyên hàm của 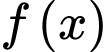 trên và
trên và 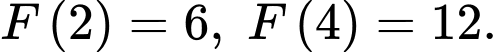 Tích phân
Tích phân 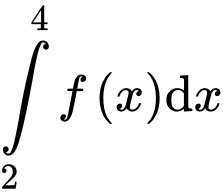 bằng
bằng A, 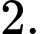
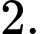
B, 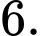
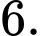
C, 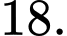
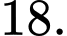
D, 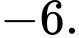
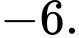
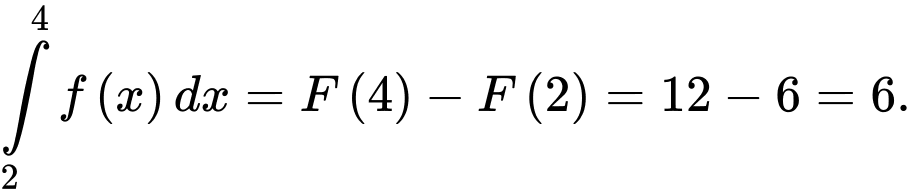 Đáp án: B
Đáp án: B
Câu 11 [149138]: Biết 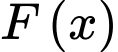 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 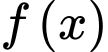 trên
trên 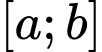 và
và 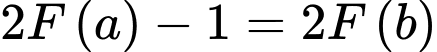 . Tính
. Tính 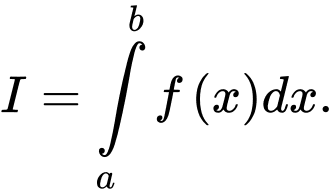
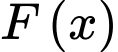 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 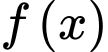 trên
trên 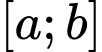 và
và 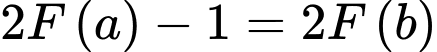 . Tính
. Tính 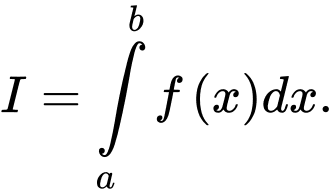
A, 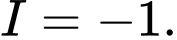
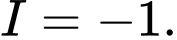
B, 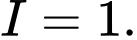
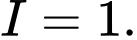
C, 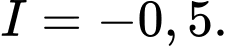
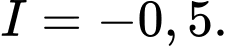
D, 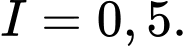
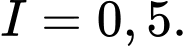
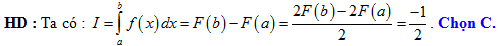 Đáp án: C
Đáp án: C
Câu 12 [142524]: Cho 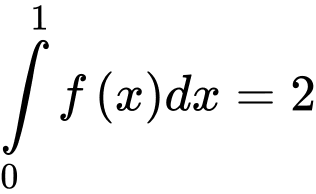 và
và 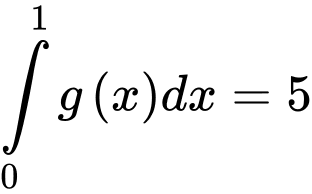 , khi đó
, khi đó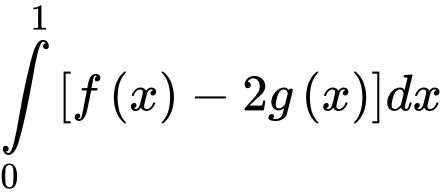 bằng
bằng
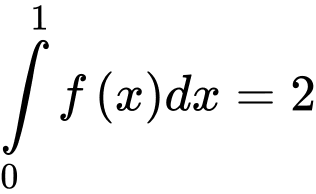 và
và 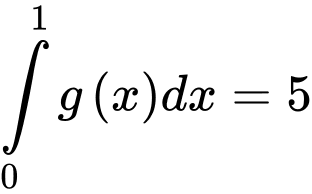 , khi đó
, khi đó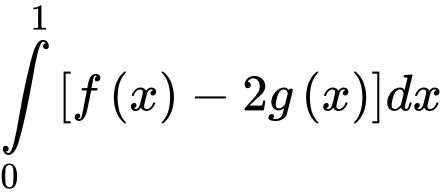 bằng
bằng A, 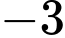
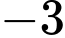
B, 

C, 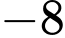
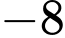
D, 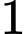
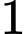
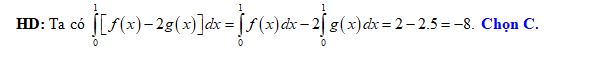 Đáp án: C
Đáp án: C
Câu 13 [146606]: Cho 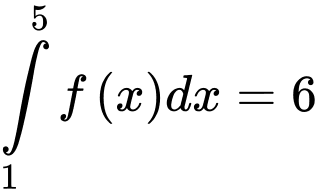 và
và 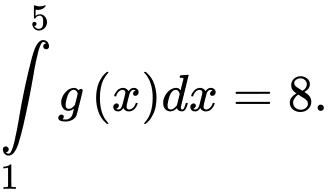 Giá trị của
Giá trị của 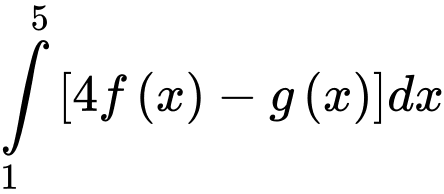 bằng
bằng
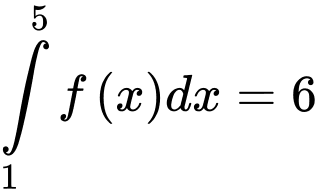 và
và 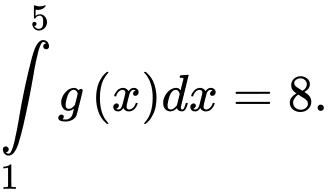 Giá trị của
Giá trị của 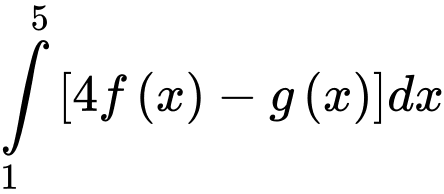 bằng
bằng A, 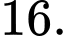
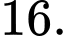
B, 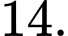
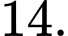
C, 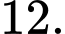
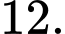
D, 
Chọn đáp án A.
Ta có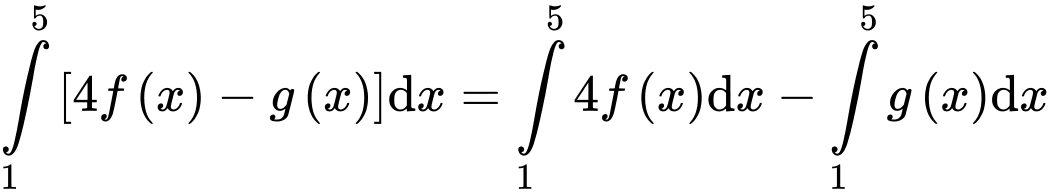 (tính chất của tích phân)
(tính chất của tích phân)
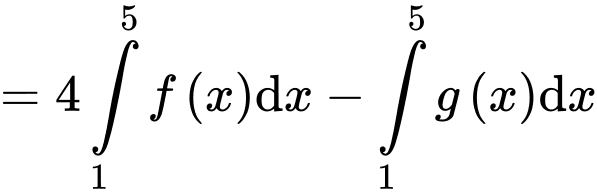
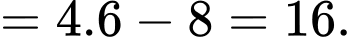 Đáp án: A
Đáp án: A
Ta có
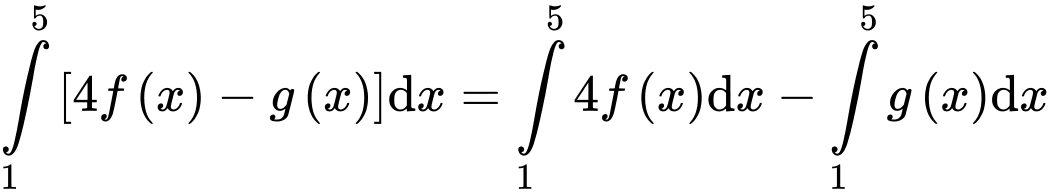 (tính chất của tích phân)
(tính chất của tích phân)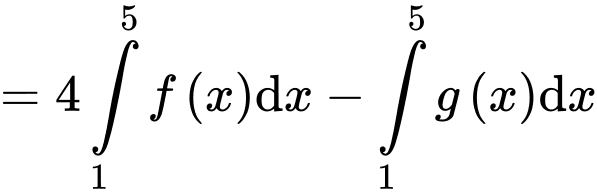
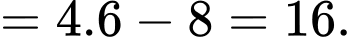 Đáp án: A
Đáp án: A
Câu 14 [42038]: Cho 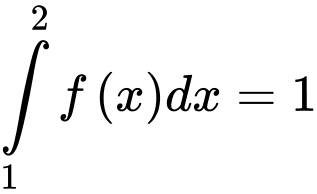 và
và 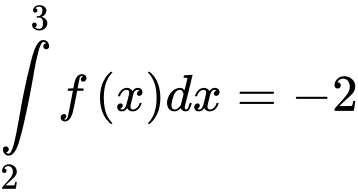 . Giá trị của
. Giá trị của 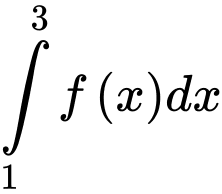 bằng
bằng
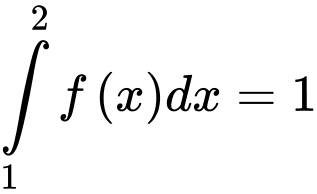 và
và 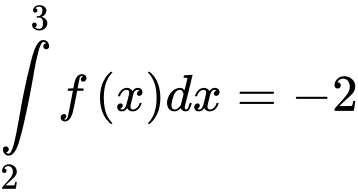 . Giá trị của
. Giá trị của 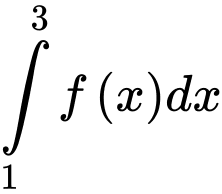 bằng
bằng A, 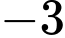 .
.
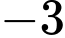 .
.B, 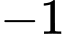 .
.
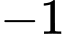 .
.C, 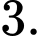
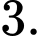
D, 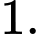
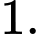
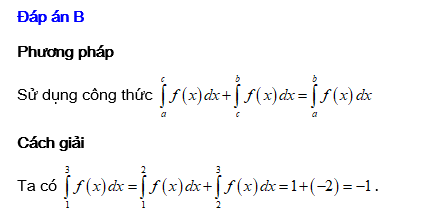 Đáp án: B
Đáp án: B
Câu 15 [389954]: Diện tích hình thang cong được tô đậm trong hình vẽ bên bằng: 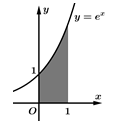

A, 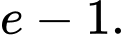
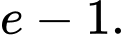
B, 

C, 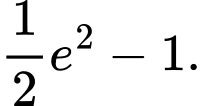
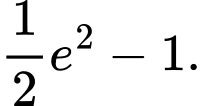
D, 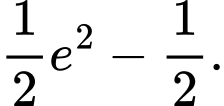
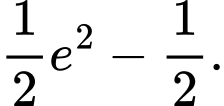
Chọn đáp án A.
Diện tích hình tô đậm là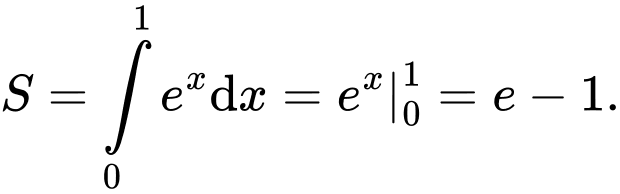
Đáp án: A
Diện tích hình tô đậm là
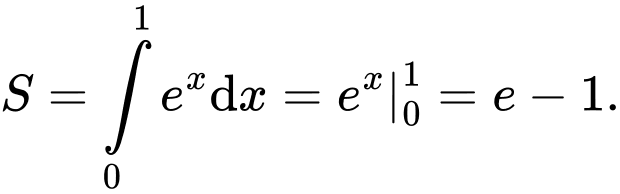
Đáp án: A
Câu 16 [149181]: Cho hàm số 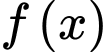 liên tục trên đoạn
liên tục trên đoạn 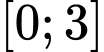 và
và 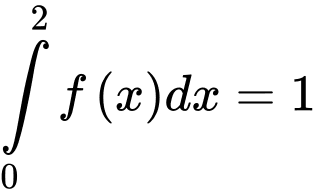 ,
, 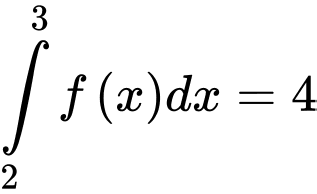 . Tính
. Tính 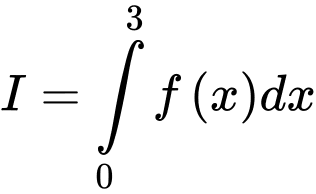 .
.
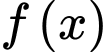 liên tục trên đoạn
liên tục trên đoạn 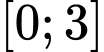 và
và 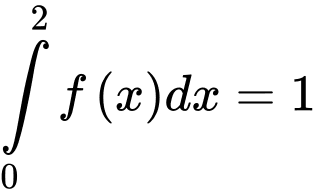 ,
, 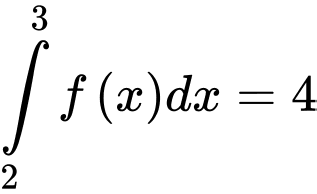 . Tính
. Tính 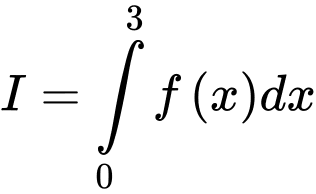 .
. A,  .
.
 .
.B, 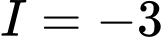 .
.
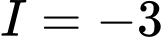 .
.C,  .
.
 .
.D,  .
.
 .
.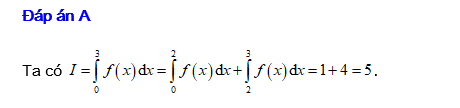 Đáp án: A
Đáp án: A
Câu 17 [149173]: Cho hàm số 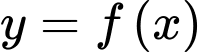 liên tục trên khoảng
liên tục trên khoảng 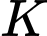 và
và 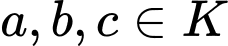 . Mệnh đề nào sau đây sai?
. Mệnh đề nào sau đây sai?
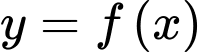 liên tục trên khoảng
liên tục trên khoảng 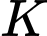 và
và 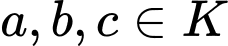 . Mệnh đề nào sau đây sai?
. Mệnh đề nào sau đây sai? A, 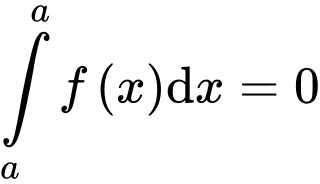 .
.
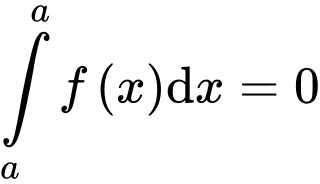 .
.B, 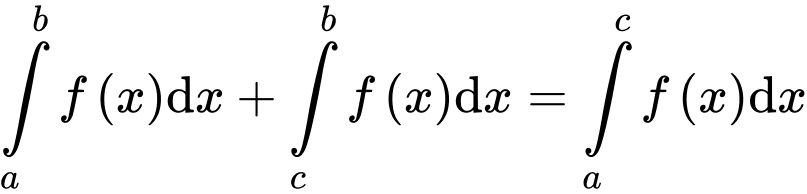 .
.
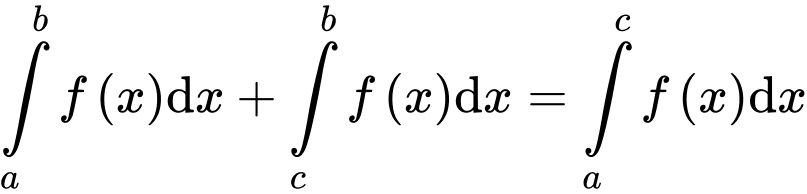 .
.C, 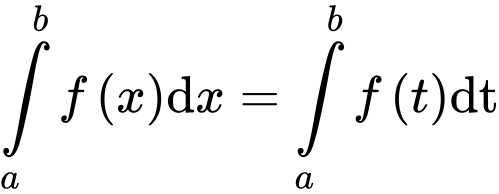 .
.
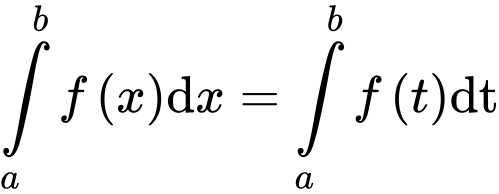 .
.D, 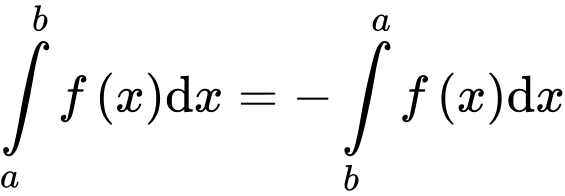 .
.
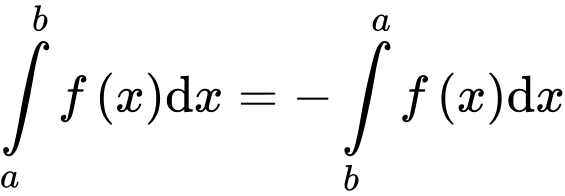 .
.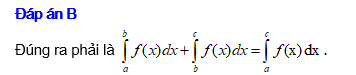 Đáp án: B
Đáp án: B
Câu 18 [389955]: Diện tích phần tô đậm trong hình vẽ bên bằng.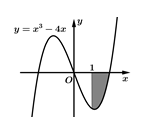

A, 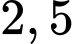 (đvdt).
(đvdt).
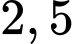 (đvdt).
(đvdt).B, 4 (đvdt).
C, 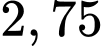 (đvdt).
(đvdt).
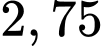 (đvdt).
(đvdt).D, 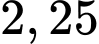 (đvdt).
(đvdt).
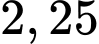 (đvdt).
(đvdt).
Phương trình hoành độ giao điểm của đồ thị hàm số 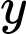 với trục hoành là
với trục hoành là
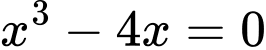
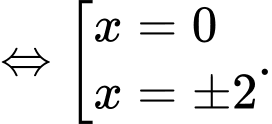
Suy ra diện tích phần tô đậm bằng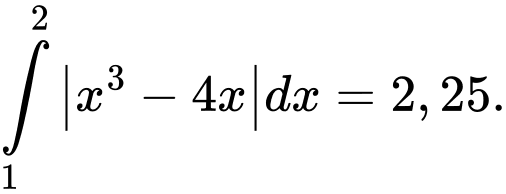
Chọn D. Đáp án: D
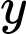 với trục hoành là
với trục hoành là
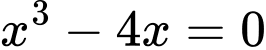
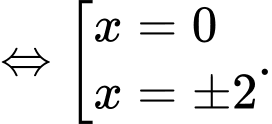
Suy ra diện tích phần tô đậm bằng
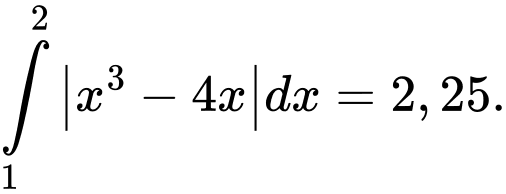
Chọn D. Đáp án: D
Câu 19 [140472]: Cho hàm số 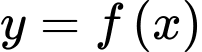 có đạo hàm trên đoạn
có đạo hàm trên đoạn 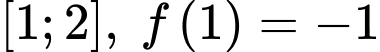 và
và 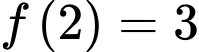 . Tính tích phân
. Tính tích phân 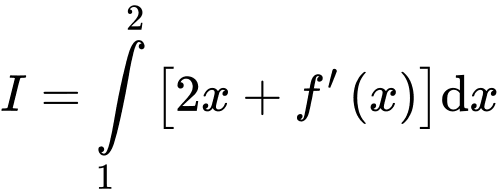 .
.
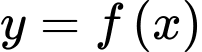 có đạo hàm trên đoạn
có đạo hàm trên đoạn 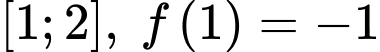 và
và 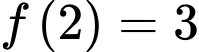 . Tính tích phân
. Tính tích phân 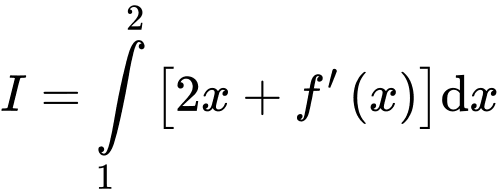 .
. A, 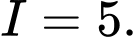
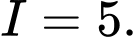
B, 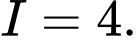
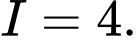
C, 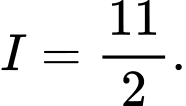
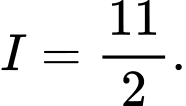
D, 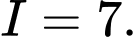
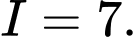
Lời giải: Ta có: 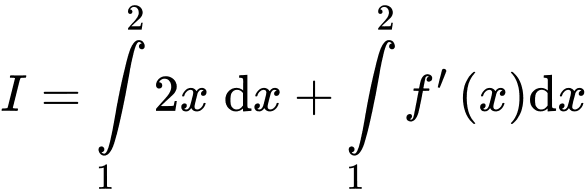
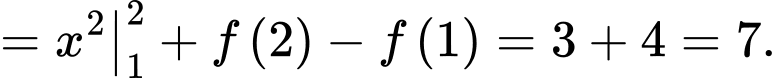 Chọn D. Đáp án: D
Chọn D. Đáp án: D
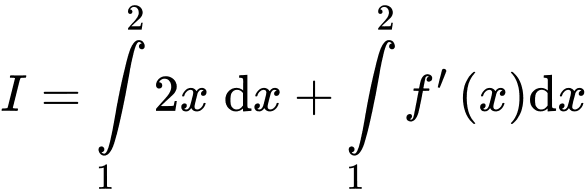
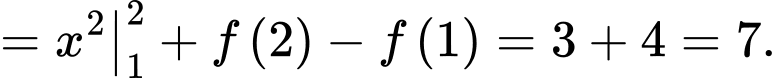 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 20 [389956]: Diện tích phần tô đậm trong hình vẽ bên bằng.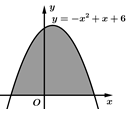

A, 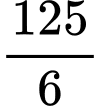 (đvdt).
(đvdt).
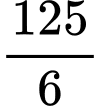 (đvdt).
(đvdt).B, 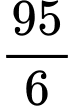 (đvdt).
(đvdt).
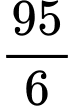 (đvdt).
(đvdt).C,  (đvdt).
(đvdt).
 (đvdt).
(đvdt).D, 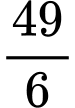 (đvdt).
(đvdt).
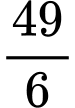 (đvdt).
(đvdt).Phương trình hoành độ giao điểm của đồ thị hàm số
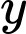 với trục hoành là
với trục hoành là
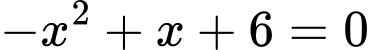
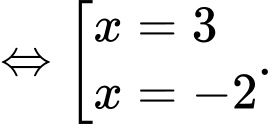
Suy ra diện tích phần tô đậm là
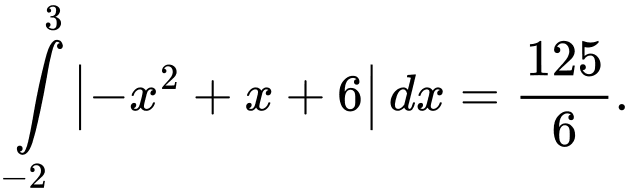
Chọn A. Đáp án: A
Câu 21 [389957]: Cho hàm số 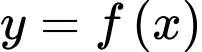 có đồ thị như hình vẽ, tính
có đồ thị như hình vẽ, tính 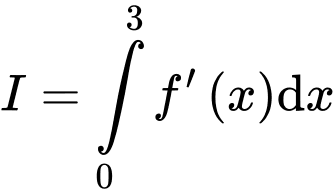
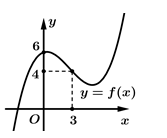
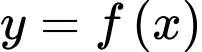 có đồ thị như hình vẽ, tính
có đồ thị như hình vẽ, tính 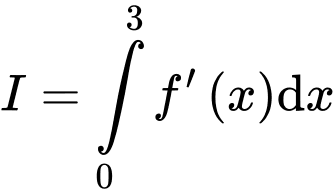

A, 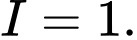
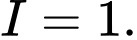
B, 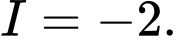
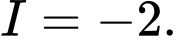
C, 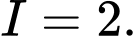
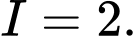
D, 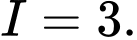
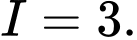
Chọn đáp án B.
Ta có:
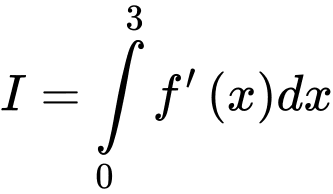
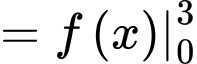
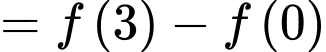
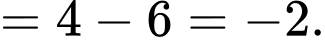 Đáp án: B
Đáp án: B
Ta có:
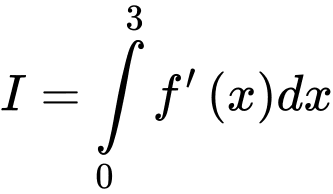
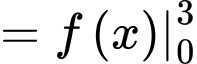
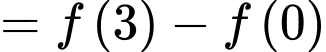
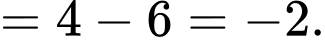 Đáp án: B
Đáp án: B
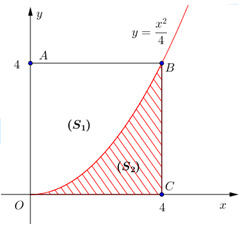
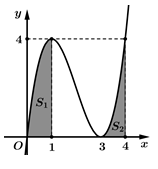
Câu 22 [151274]: Hình vuông 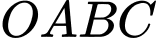 có cạnh bằng 4 được chia thành hai phần bởi đường cong
có cạnh bằng 4 được chia thành hai phần bởi đường cong  có phương trình
có phương trình 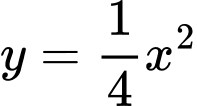 . Gọi
. Gọi 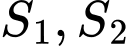 là diện tích phần không bị gạch và phần bị gạch (như hình vẽ). Tính tỉ số
là diện tích phần không bị gạch và phần bị gạch (như hình vẽ). Tính tỉ số 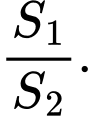
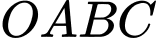 có cạnh bằng 4 được chia thành hai phần bởi đường cong
có cạnh bằng 4 được chia thành hai phần bởi đường cong  có phương trình
có phương trình 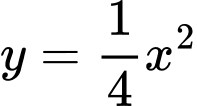 . Gọi
. Gọi 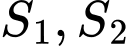 là diện tích phần không bị gạch và phần bị gạch (như hình vẽ). Tính tỉ số
là diện tích phần không bị gạch và phần bị gạch (như hình vẽ). Tính tỉ số 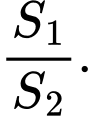

A, 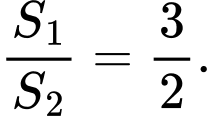
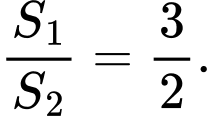
B, 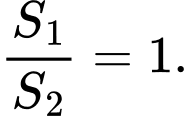
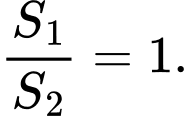
C, 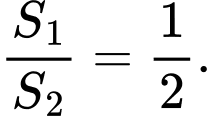
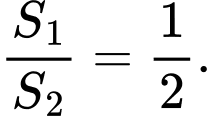
D, 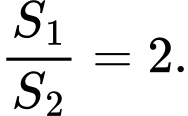
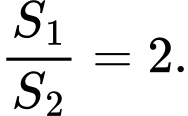
Ta có 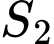 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 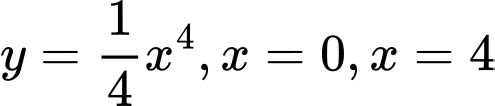 và trục hoành. Suy ra
và trục hoành. Suy ra 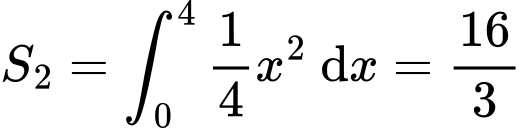 . Mặt khác
. Mặt khác 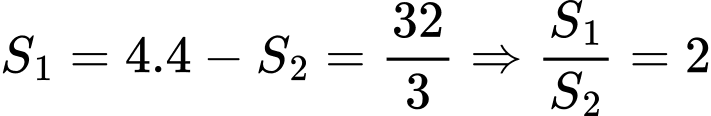
Chọn D. Đáp án: D
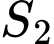 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 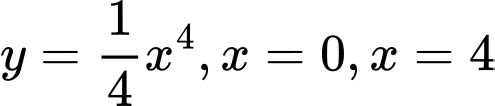 và trục hoành. Suy ra
và trục hoành. Suy ra 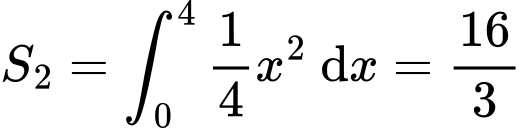 . Mặt khác
. Mặt khác 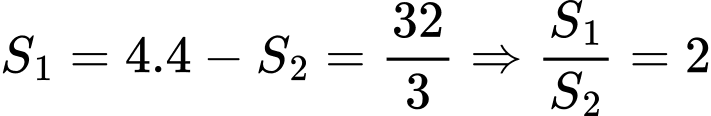
Chọn D. Đáp án: D
Câu 23 [389958]: Cho hàm số 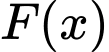 là một nguyên hàm của hàm số trên
là một nguyên hàm của hàm số trên 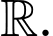 Biết đồ thị hàm số
Biết đồ thị hàm số 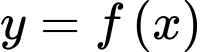 như hình vẽ và diện tích phần tô đậm
như hình vẽ và diện tích phần tô đậm 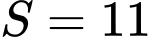 và
và 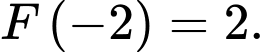 Tính
Tính 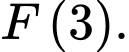
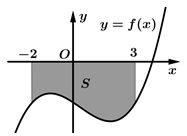
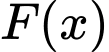 là một nguyên hàm của hàm số trên
là một nguyên hàm của hàm số trên 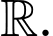 Biết đồ thị hàm số
Biết đồ thị hàm số 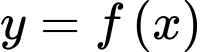 như hình vẽ và diện tích phần tô đậm
như hình vẽ và diện tích phần tô đậm 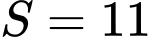 và
và 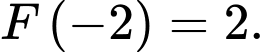 Tính
Tính 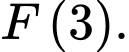

A, 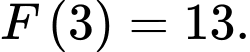
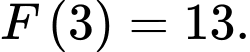
B, 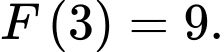
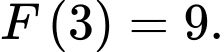
C, 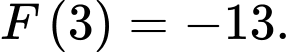
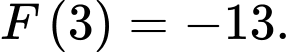
D, 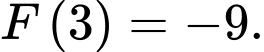
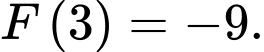
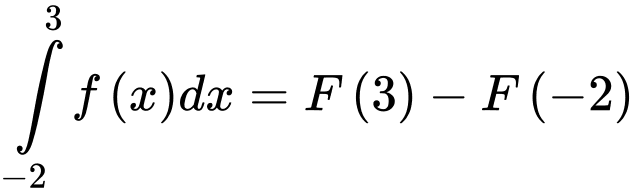
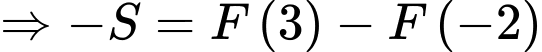
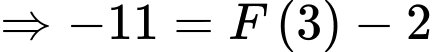
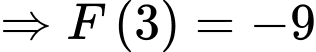
Chọn đáp án D. Đáp án: D
Câu 24 [408527]: Đường gấp khúc trong hình vẽ bên là đồ thị hàm số 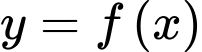 trên đoạn
trên đoạn 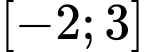 . Tích phân
. Tích phân 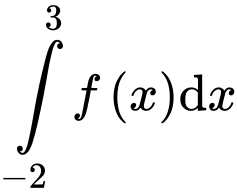 bằng
bằng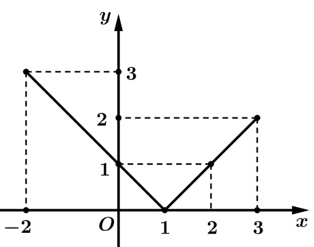
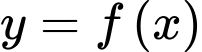 trên đoạn
trên đoạn 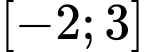 . Tích phân
. Tích phân 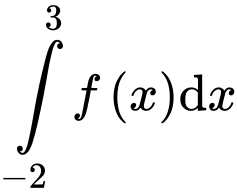 bằng
bằng
A, 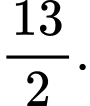
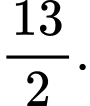
B, 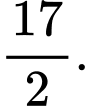
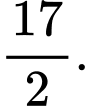
C, 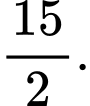
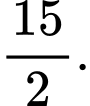
D, 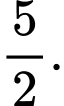
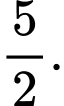
Trên đoạn 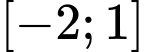 , đồ thị hàm số
, đồ thị hàm số 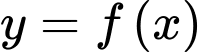 là đường thẳng
là đường thẳng 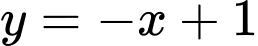 ; trên đoạn
; trên đoạn 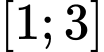 , đồ thị hàm số
, đồ thị hàm số 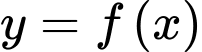 là đường thẳng
là đường thẳng 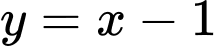 .
.
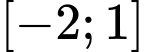 , đồ thị hàm số
, đồ thị hàm số 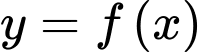 là đường thẳng
là đường thẳng 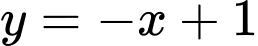 ; trên đoạn
; trên đoạn 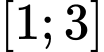 , đồ thị hàm số
, đồ thị hàm số 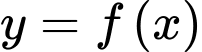 là đường thẳng
là đường thẳng 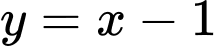 .
. Do đó 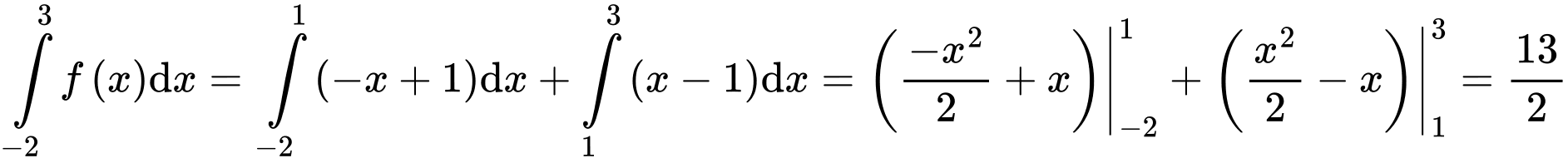 .
.
Đáp án: A 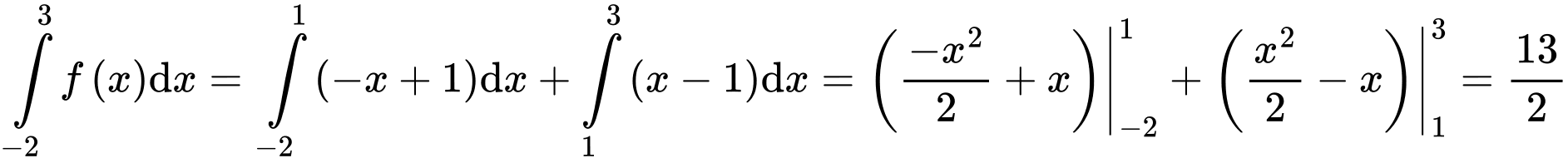 .
.
Câu 25 [408528]: Cho hai hàm số 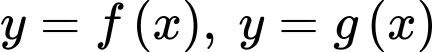 liên tục trên
liên tục trên 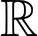 và các số thực
và các số thực 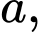
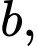

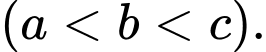 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
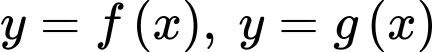 liên tục trên
liên tục trên 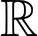 và các số thực
và các số thực 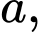
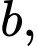

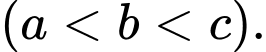 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai? A, 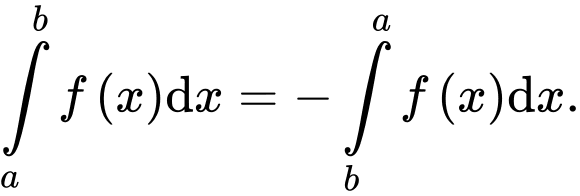
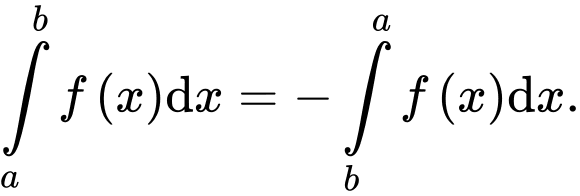
B, 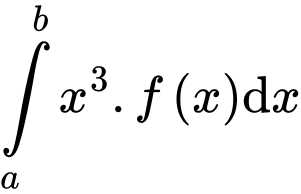
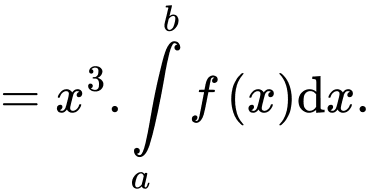
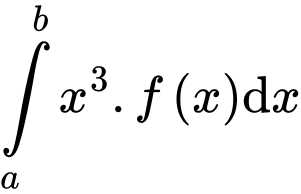
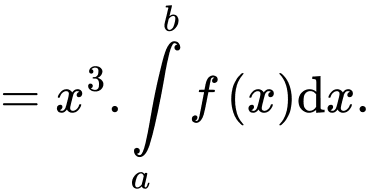
C, 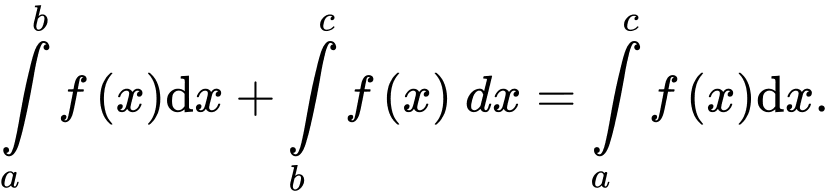
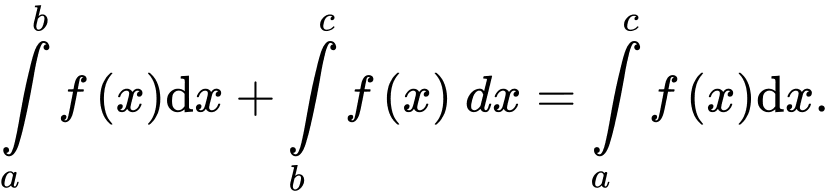
D, Nếu 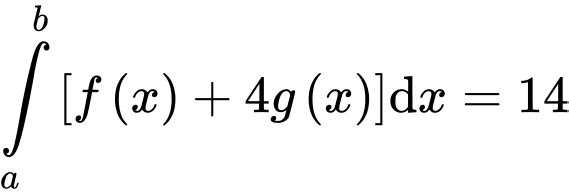 và
và 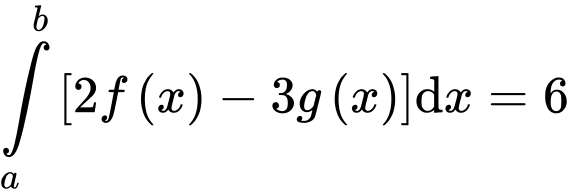 thì
thì 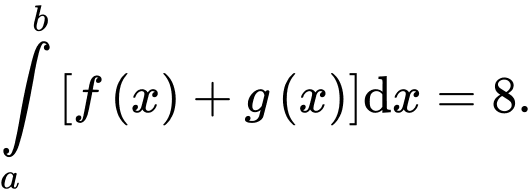
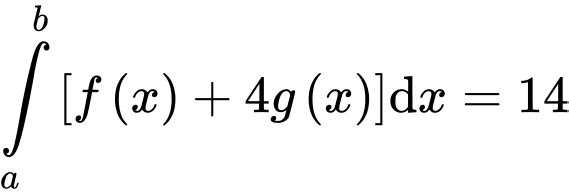 và
và 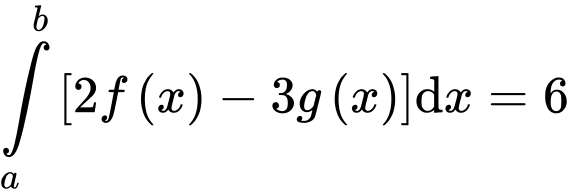 thì
thì 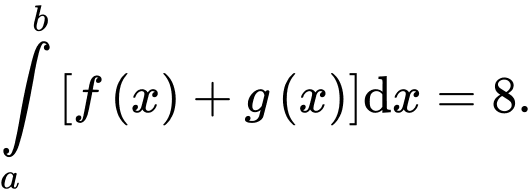
a) Mệnh đề a) đúng. Dựa vào phân tích chất. b) Mệnh đề b) sai. Vì 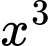 không phải hằng số.
không phải hằng số.
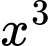 không phải hằng số.
không phải hằng số. c) Mệnh đề
c) đúng. Dựa vào tính chất của phân tích.
d) Mệnh đề d) đúng. Ta có: 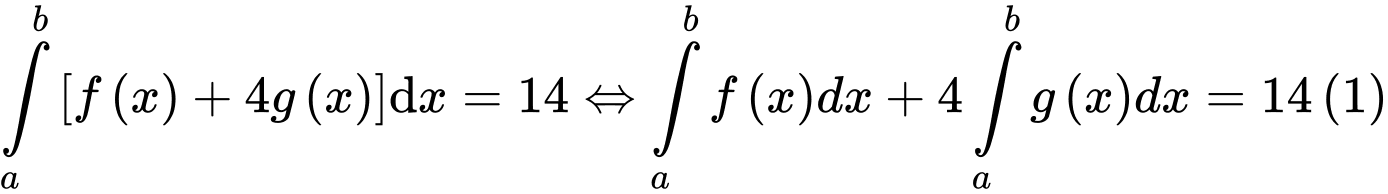
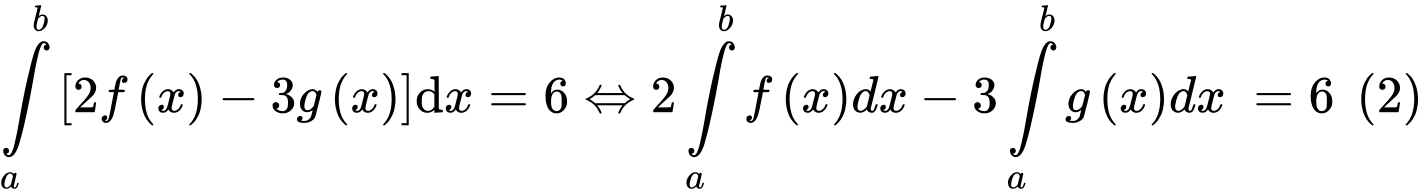 Từ
Từ 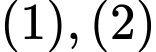 suy ra
suy ra 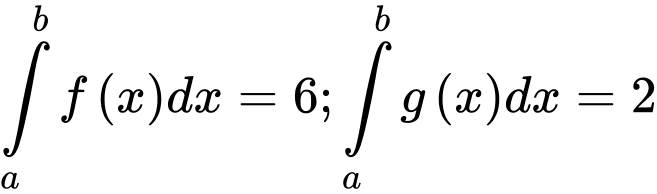 Nên
Nên 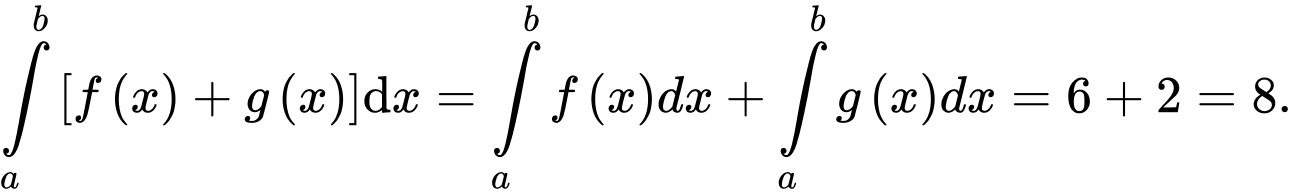
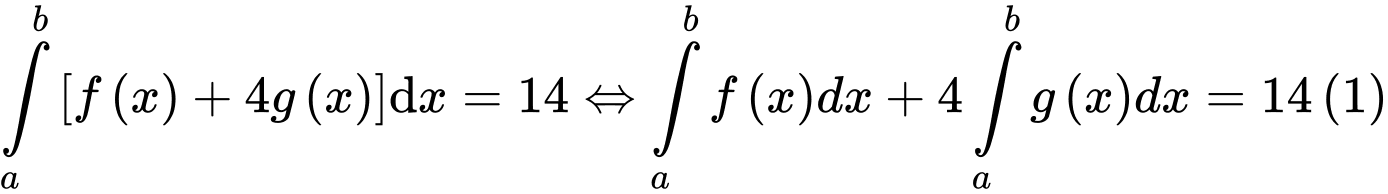
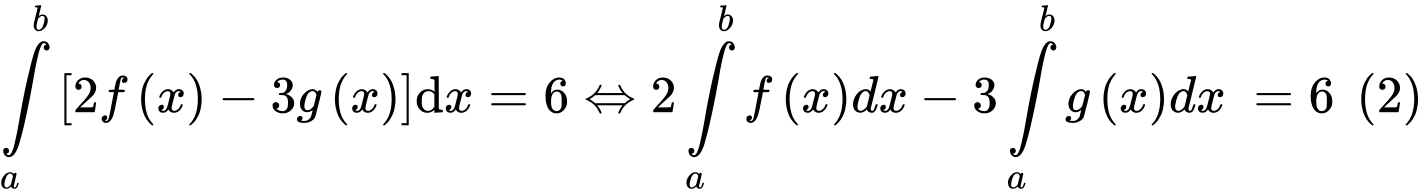 Từ
Từ 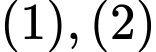 suy ra
suy ra 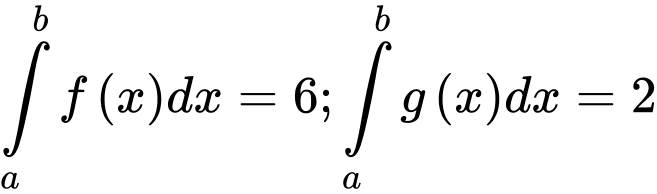 Nên
Nên 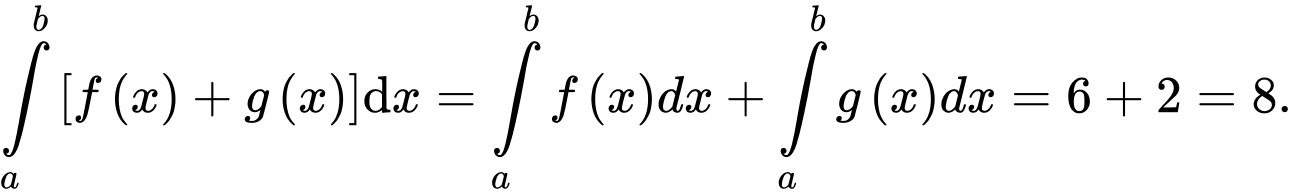
Câu 26 [389960]: Cho hàm số 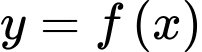 có đồ thị trên đoạn
có đồ thị trên đoạn 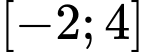 như hình vẽ. Biết rằng
như hình vẽ. Biết rằng 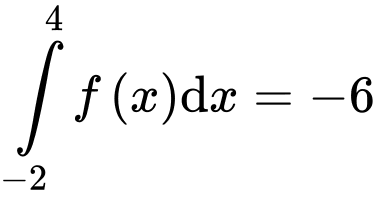 và
và 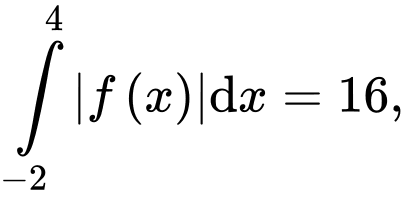 các vùng
các vùng 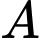 và
và 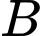 lần lượt có diện tích là
lần lượt có diện tích là 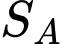 và
và 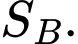 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.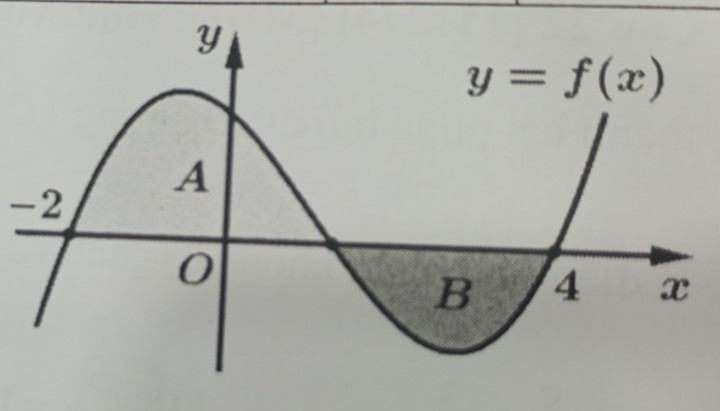
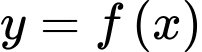 có đồ thị trên đoạn
có đồ thị trên đoạn 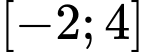 như hình vẽ. Biết rằng
như hình vẽ. Biết rằng 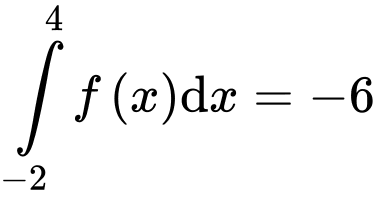 và
và 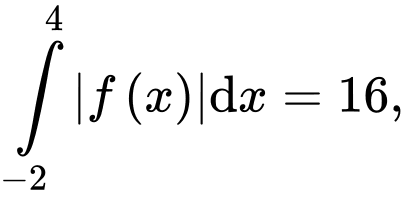 các vùng
các vùng 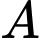 và
và 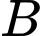 lần lượt có diện tích là
lần lượt có diện tích là 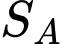 và
và 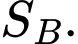 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
A, a) 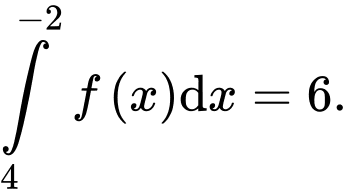
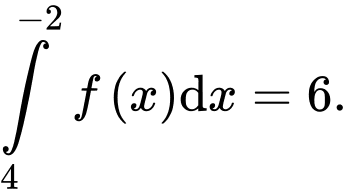
B, b) 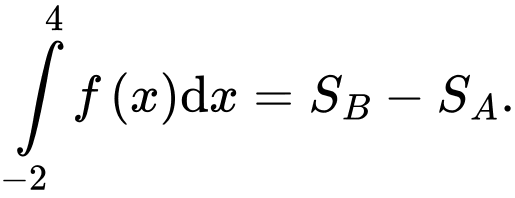
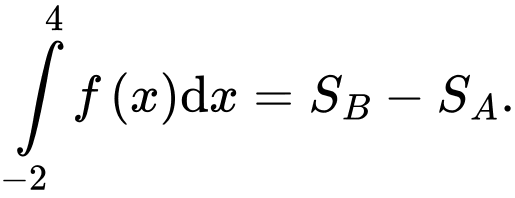
C, c) 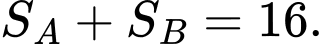
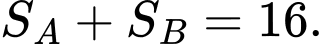
D, d) 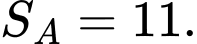
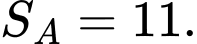
Có 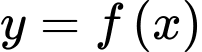
Theo gt có: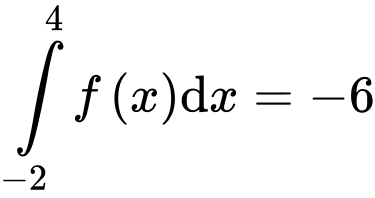
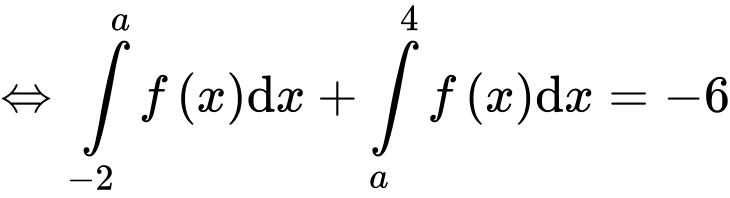
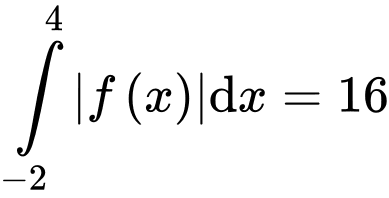
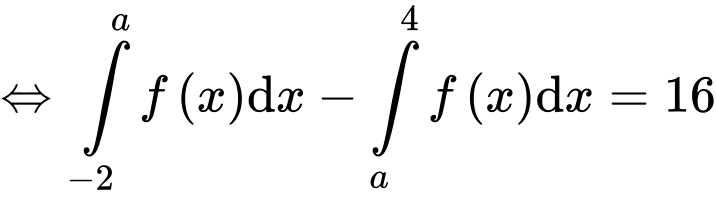
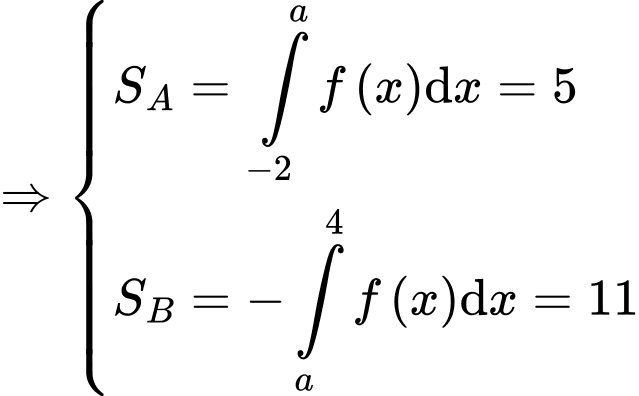
Vậy a),c) đúng; b),d) sai.
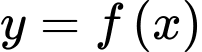
Theo gt có:
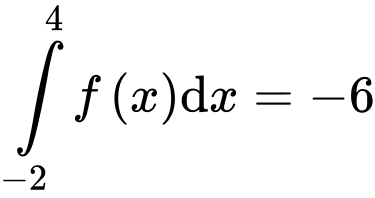
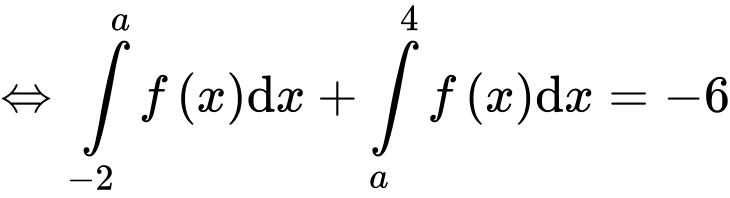
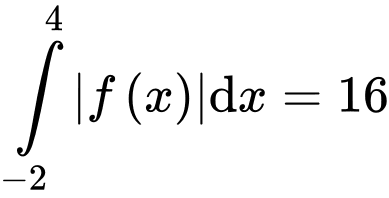
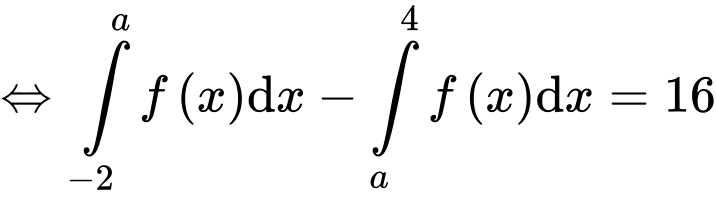
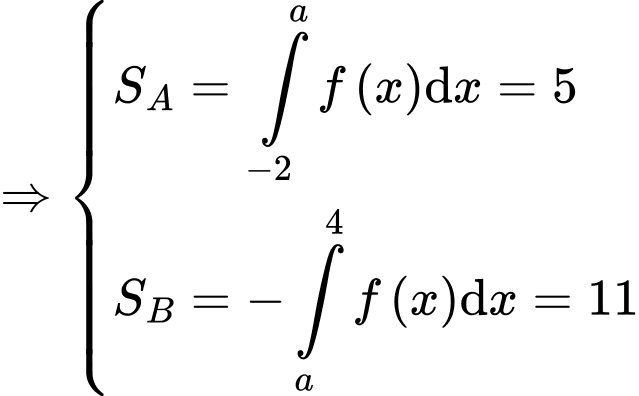
Vậy a),c) đúng; b),d) sai.
Câu 27 [149202]: Cho hàm số 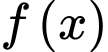 liên tục trên đoạn
liên tục trên đoạn 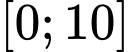 và thỏa mãn
và thỏa mãn 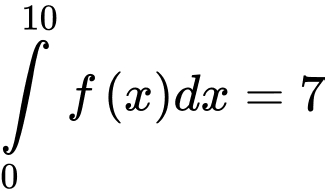 và
và 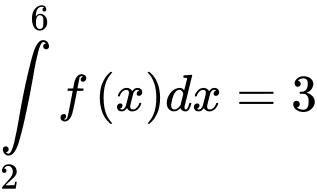 . Tính
. Tính 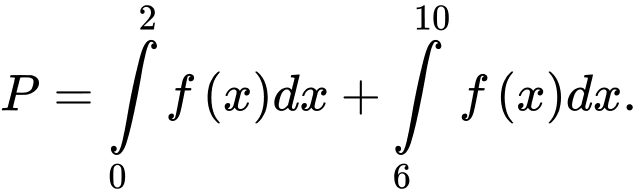
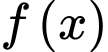 liên tục trên đoạn
liên tục trên đoạn 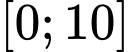 và thỏa mãn
và thỏa mãn 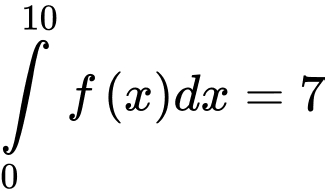 và
và 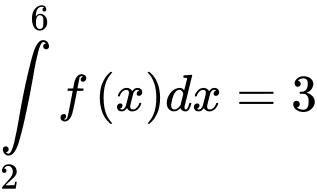 . Tính
. Tính 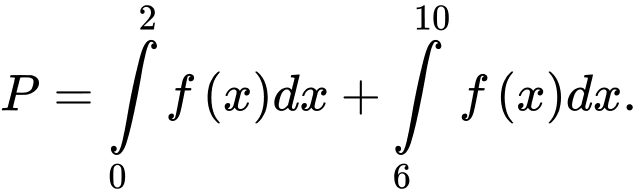
A, 

B, 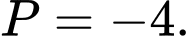
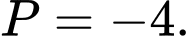
C, 

D, 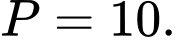
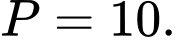
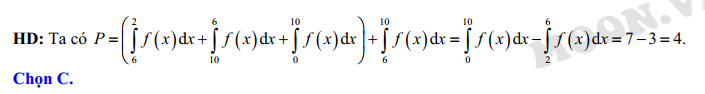 Đáp án: C
Đáp án: C
Câu 28 [389961]: Cho hàm số 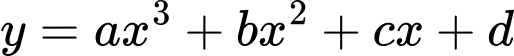 với
với 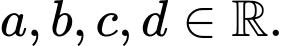 Gọi
Gọi 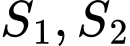 lần lượt là diện tích các phần tô đậm như hình bên. Tính
lần lượt là diện tích các phần tô đậm như hình bên. Tính 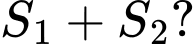
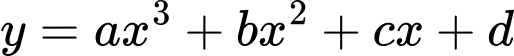 với
với 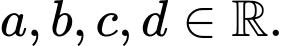 Gọi
Gọi 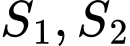 lần lượt là diện tích các phần tô đậm như hình bên. Tính
lần lượt là diện tích các phần tô đậm như hình bên. Tính 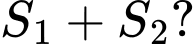

Dựa vào đồ thị ta thấy, đồ thị hàm số đi qua điểm  và tiếp xúc với trục hoành tại điểm
và tiếp xúc với trục hoành tại điểm 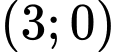 suy ra
suy ra 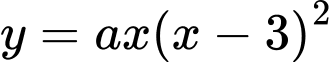
Mặt khác đồ thị hàm số đi qua điểm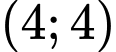 nên
nên 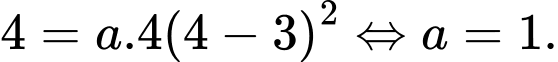
Vậy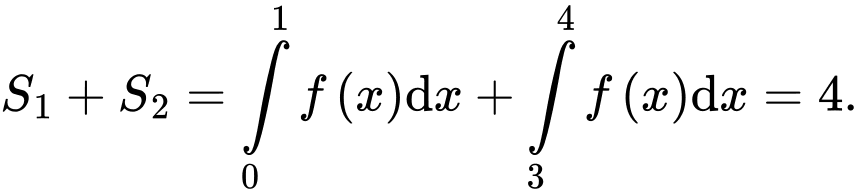
 và tiếp xúc với trục hoành tại điểm
và tiếp xúc với trục hoành tại điểm 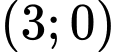 suy ra
suy ra 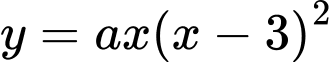
Mặt khác đồ thị hàm số đi qua điểm
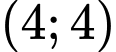 nên
nên 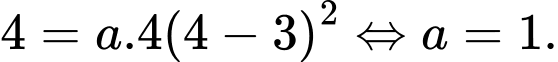
Vậy
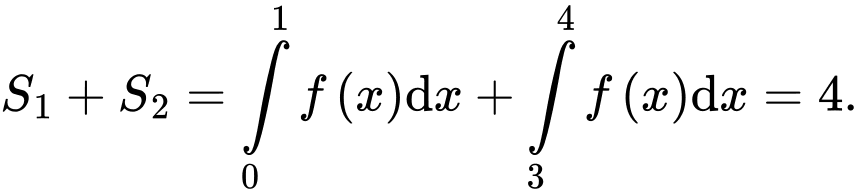
Câu 29 [151379]: Cho hàm số 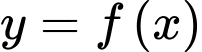 có đồ thị trên đoạn
có đồ thị trên đoạn 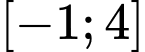 như hình vẽ bên. Tính tích phân
như hình vẽ bên. Tính tích phân 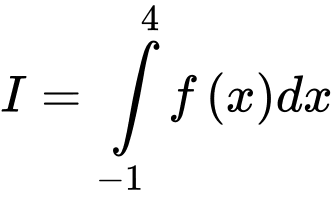 .
.
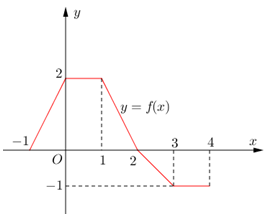
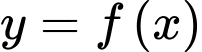 có đồ thị trên đoạn
có đồ thị trên đoạn 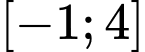 như hình vẽ bên. Tính tích phân
như hình vẽ bên. Tính tích phân 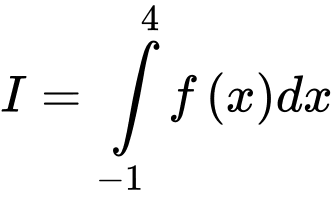 .
.
A, 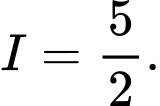
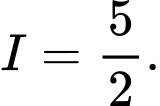
B, 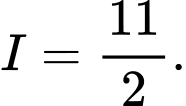
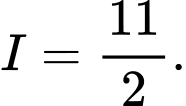
C, 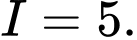
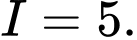
D, 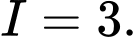
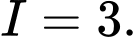
 Đáp án: A
Đáp án: A
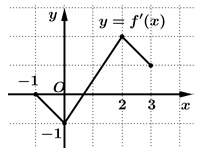
Câu 30 [389962]: Cho hàm số 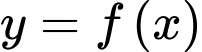 có đạo hàm trên đoạn
có đạo hàm trên đoạn 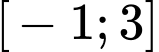 . Đồ thị của hàm số
. Đồ thị của hàm số 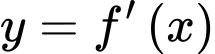 được cho như hình vẽ. Biết
được cho như hình vẽ. Biết 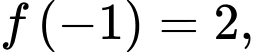 tính
tính 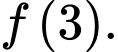
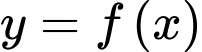 có đạo hàm trên đoạn
có đạo hàm trên đoạn 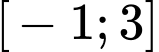 . Đồ thị của hàm số
. Đồ thị của hàm số 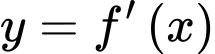 được cho như hình vẽ. Biết
được cho như hình vẽ. Biết 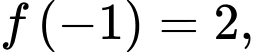 tính
tính 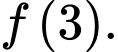

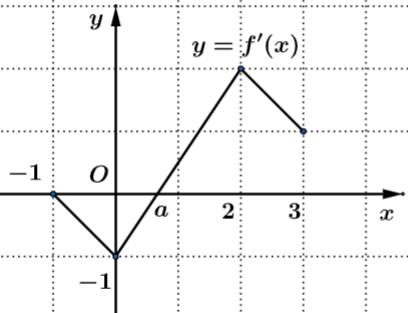
Từ đồ thị hình vẽ, ta có:
Trên đoạn
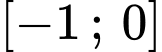 :
: 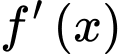 đi qua điểm
đi qua điểm 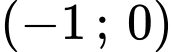 và
và 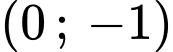 nên ta có:
nên ta có: 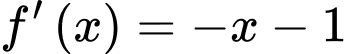
Trên đoạn
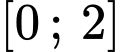 :
: 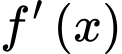 đi qua điểm
đi qua điểm 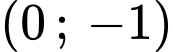 và
và 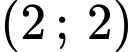 nên ta có:
nên ta có: 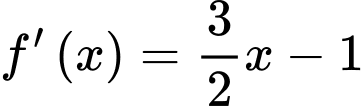
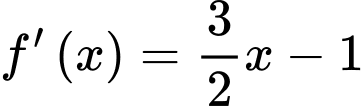 cắt trục hoành tại điểm có tọa độ
cắt trục hoành tại điểm có tọa độ 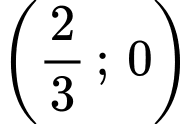
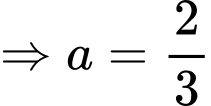
Trên đoạn
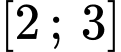 :
: 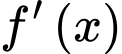 đi qua điểm
đi qua điểm 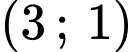 và
và 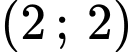 nên ta có:
nên ta có: 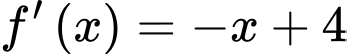
Suy ra
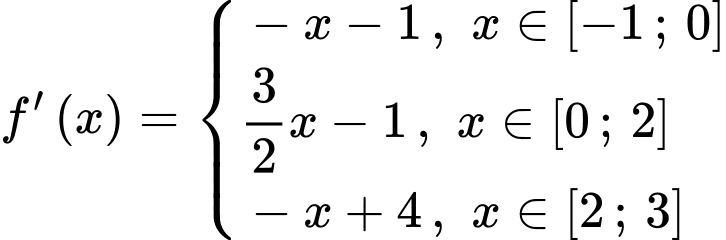
Ta có:
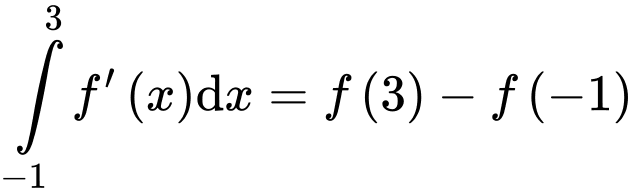

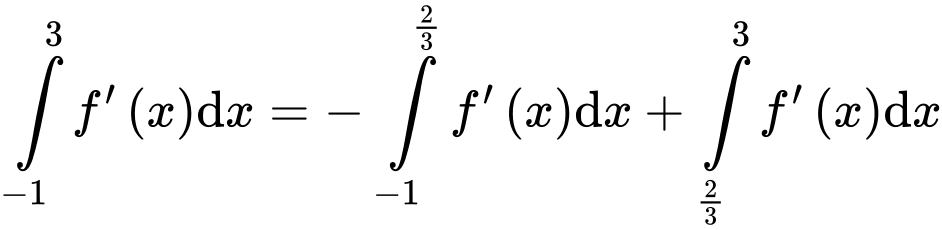
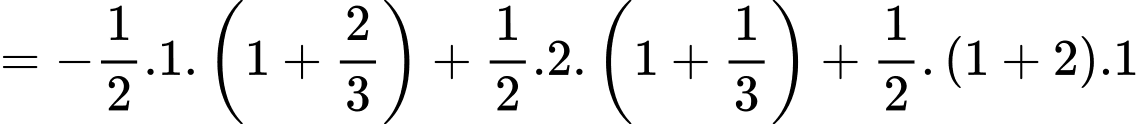
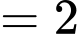
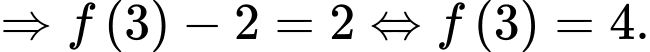
Đáp án:
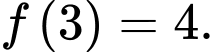
Câu 31 [151370]: Cho hàm số 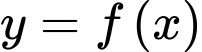 có đồ thị như hình bên.Tìm
có đồ thị như hình bên.Tìm 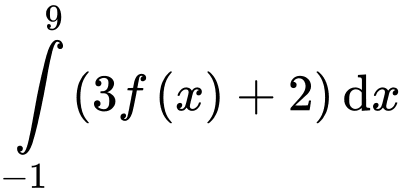 .
.
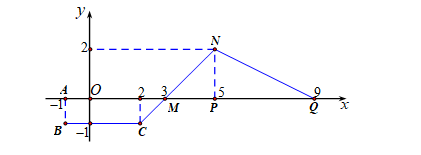
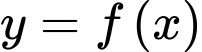 có đồ thị như hình bên.Tìm
có đồ thị như hình bên.Tìm 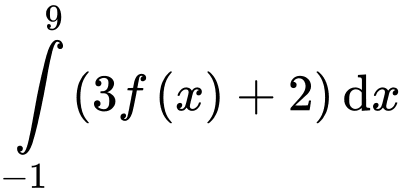 .
.
A, 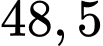 .
.
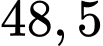 .
.B, 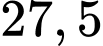 .
.
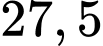 .
.C, 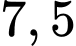 .
.
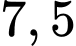 .
.D, 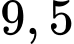 .
.
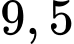 .
.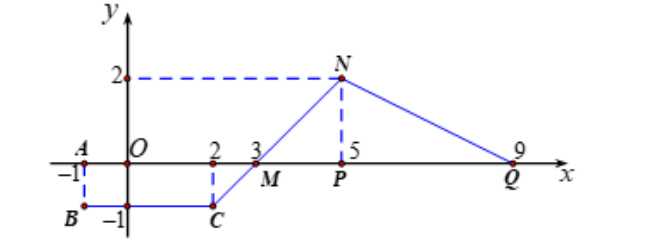
Ta có:
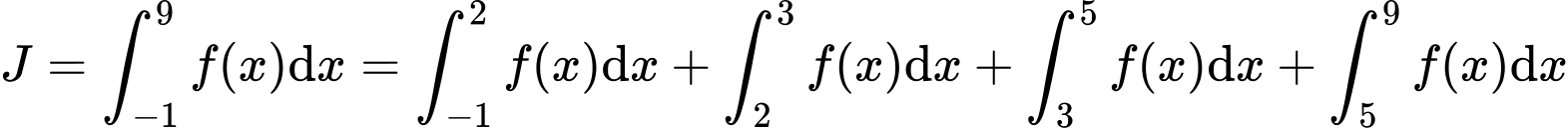
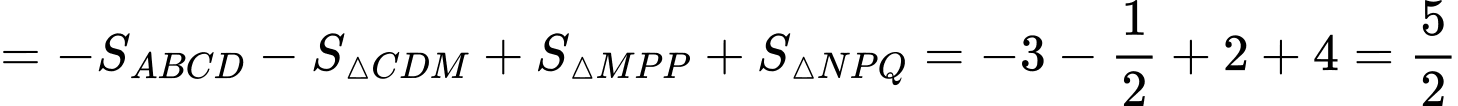
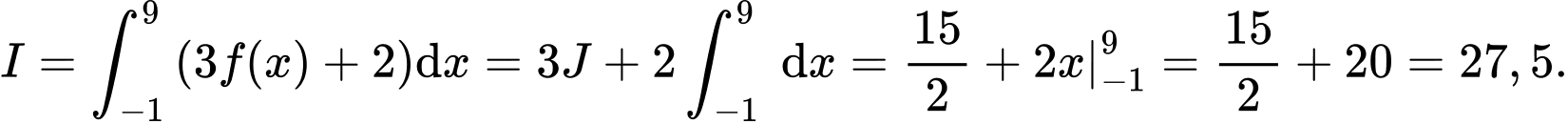 Đáp án: B
Đáp án: B
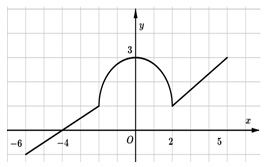
Câu 32 [151380]: Cho hàm số 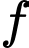 liên tục trên đoạn
liên tục trên đoạn 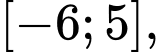 có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ. Tính giá trị
có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ. Tính giá trị 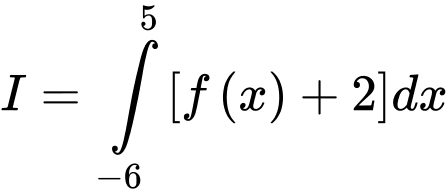 .
.
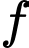 liên tục trên đoạn
liên tục trên đoạn 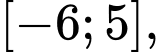 có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ. Tính giá trị
có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ. Tính giá trị 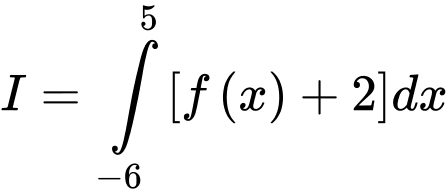 .
.
A, 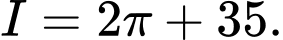
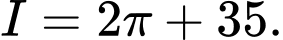
B, 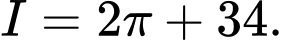
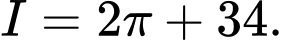
C, 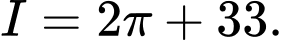
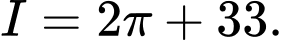
D, 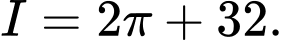
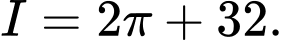
Dựa vào hình vẽ, ta thấy 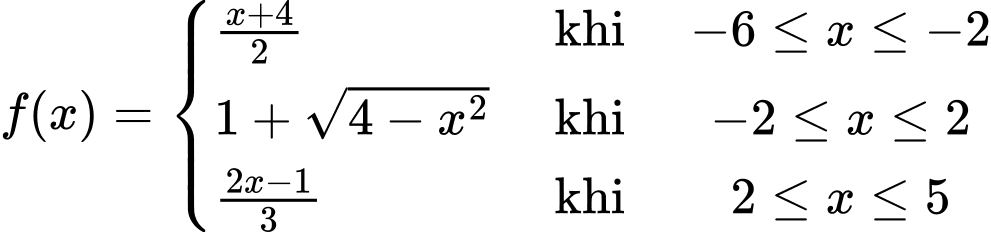
Vậy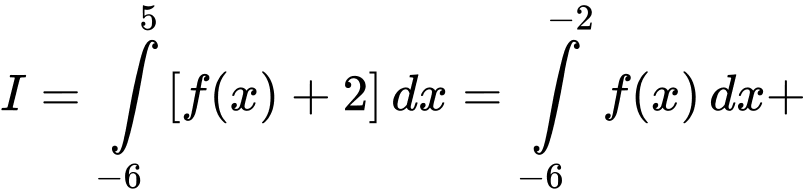
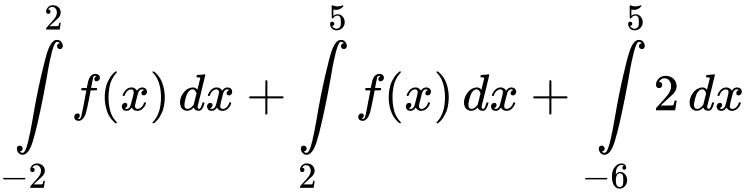
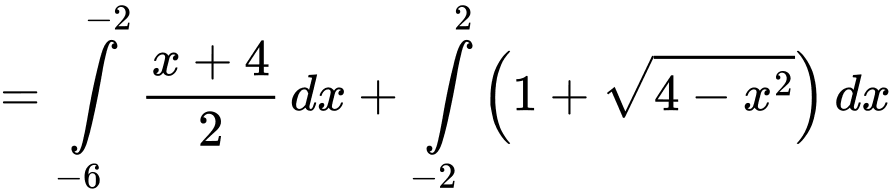
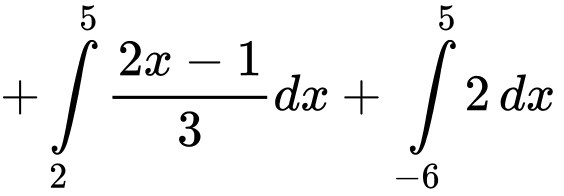
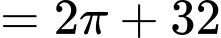
Chọn D. Đáp án: D
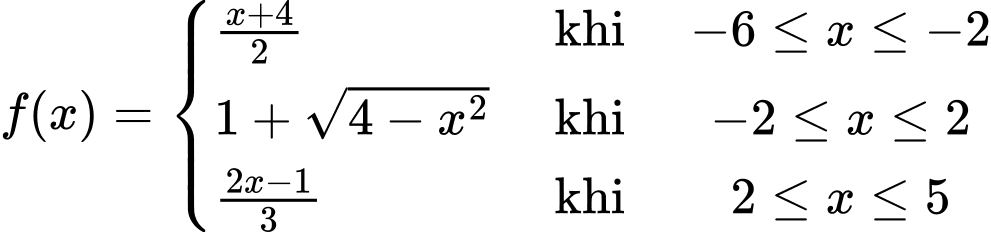
Vậy
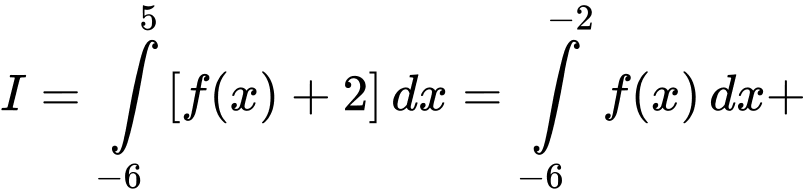
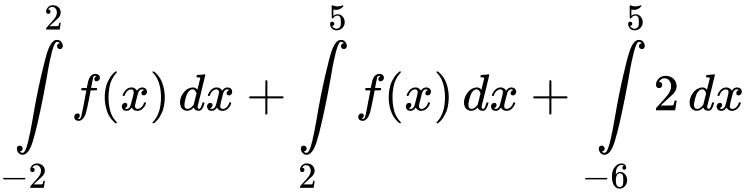
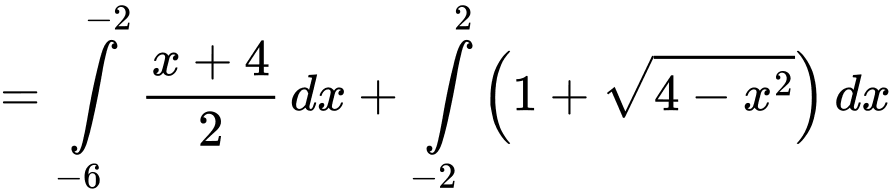
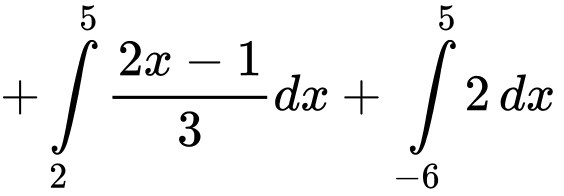
Chọn D. Đáp án: D