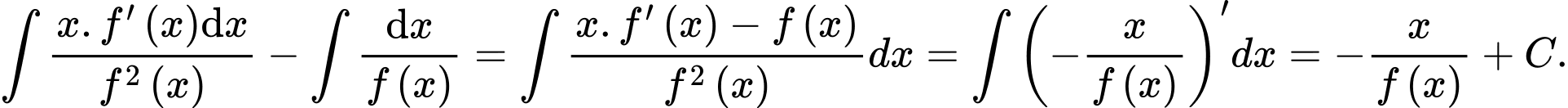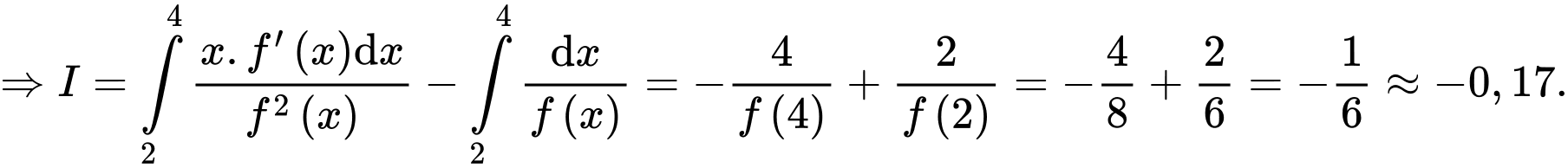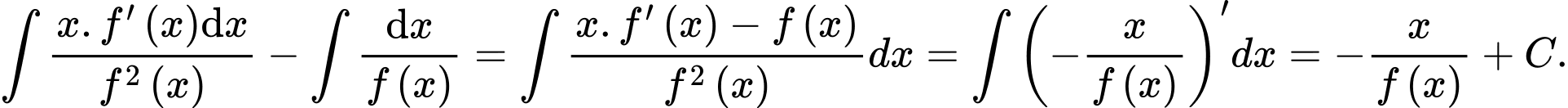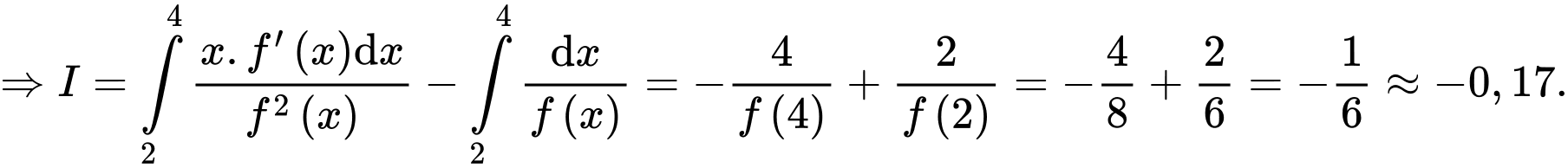Đáp án Bài tập tự luyện số 3
Câu 1 [389959]: Cho hàm số 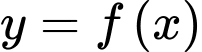 có đồ thị trên đoạn
có đồ thị trên đoạn 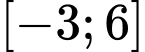 như hình vẽ, biết rằng diện tích
như hình vẽ, biết rằng diện tích 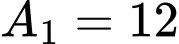 (đvdt),
(đvdt), 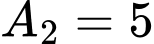 (đvdt). Tính
(đvdt). Tính 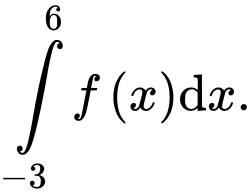
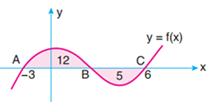
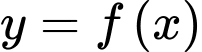 có đồ thị trên đoạn
có đồ thị trên đoạn 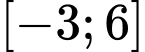 như hình vẽ, biết rằng diện tích
như hình vẽ, biết rằng diện tích 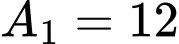 (đvdt),
(đvdt), 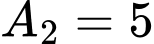 (đvdt). Tính
(đvdt). Tính 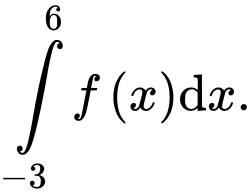

A, 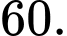
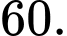
B, 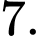
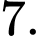
C, 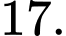
D, 
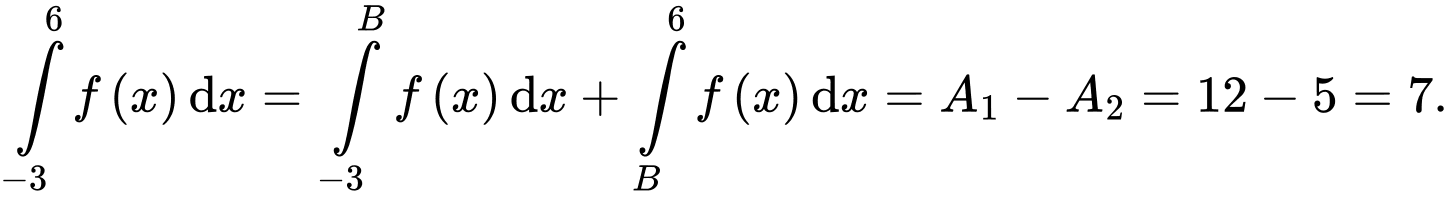
Chọn đáp án B.
Câu 2 [149172]: Giả sử 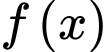 là hàm liên tục trên
là hàm liên tục trên 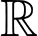 và các số thực
và các số thực 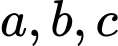 thoả mãn
thoả mãn 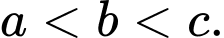 Mệnh đề nào sau đây sai?
Mệnh đề nào sau đây sai?
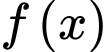 là hàm liên tục trên
là hàm liên tục trên 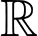 và các số thực
và các số thực 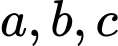 thoả mãn
thoả mãn 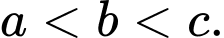 Mệnh đề nào sau đây sai?
Mệnh đề nào sau đây sai? A, 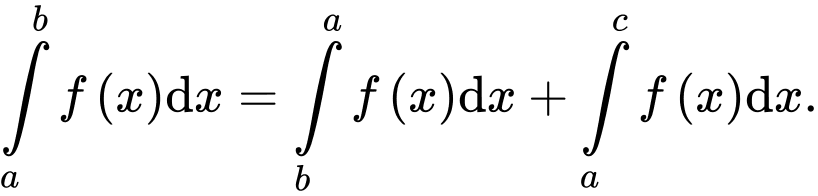
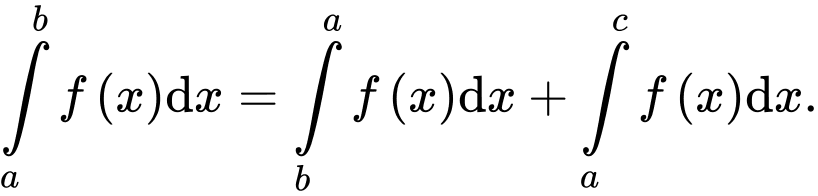
B, 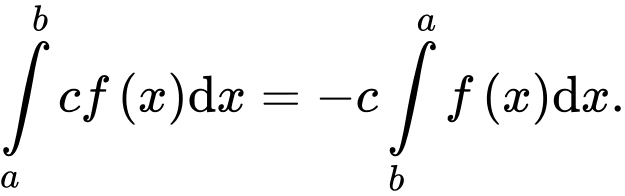
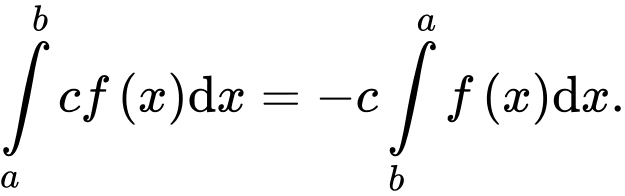
C, 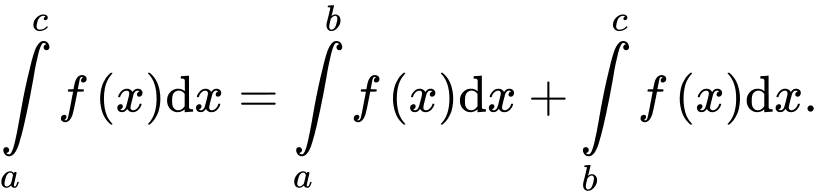
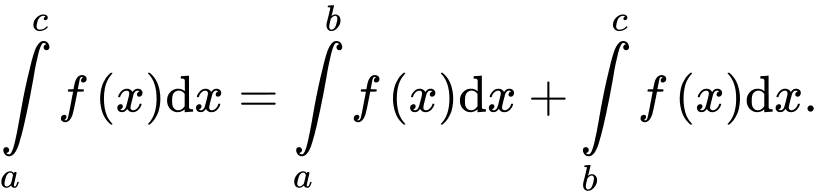
D, 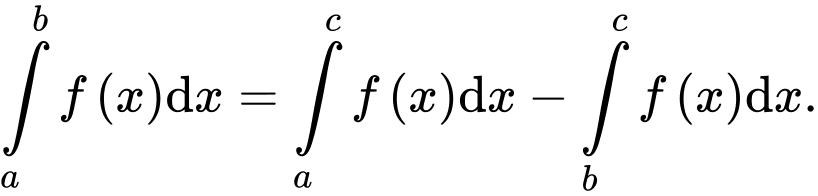
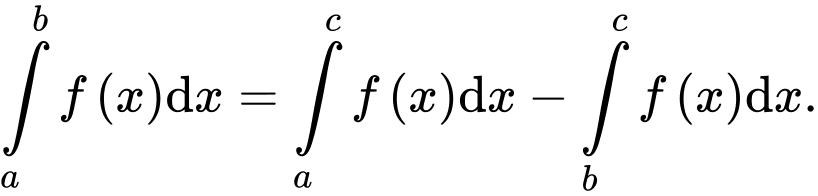
Chọn đáp án A.
Dựa vào tính chất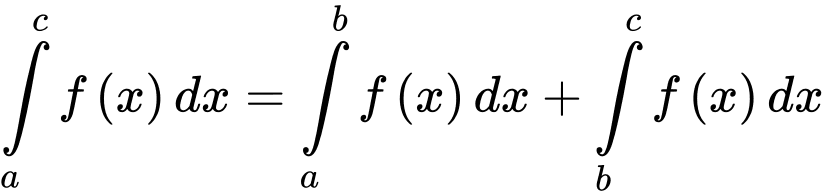 và
và 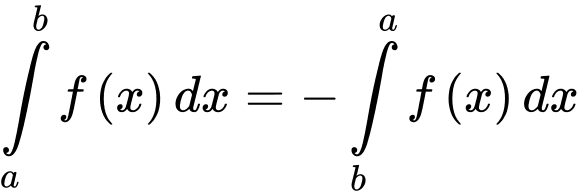
Suy ra đáp án A sai. Đáp án: A
Dựa vào tính chất
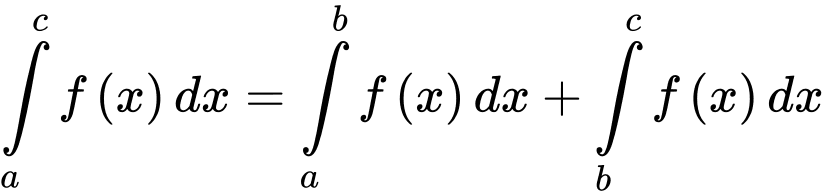 và
và 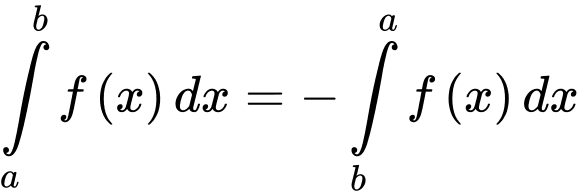
Suy ra đáp án A sai. Đáp án: A
Câu 3 [149174]: Cho 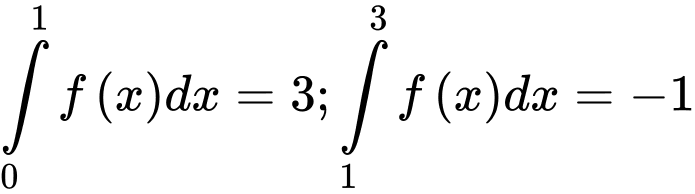 . Tính tích phân
. Tính tích phân 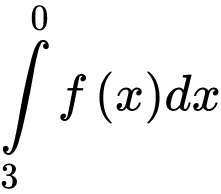 .
.
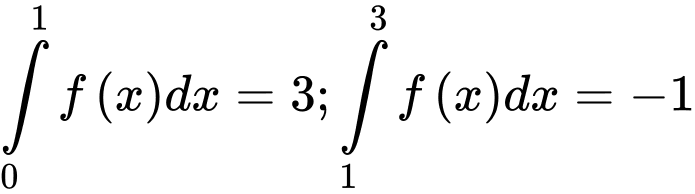 . Tính tích phân
. Tính tích phân 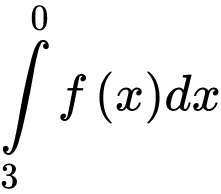 .
. A, 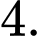
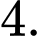
B, 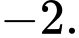
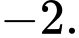
C, 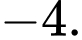
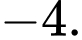
D, 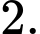
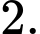
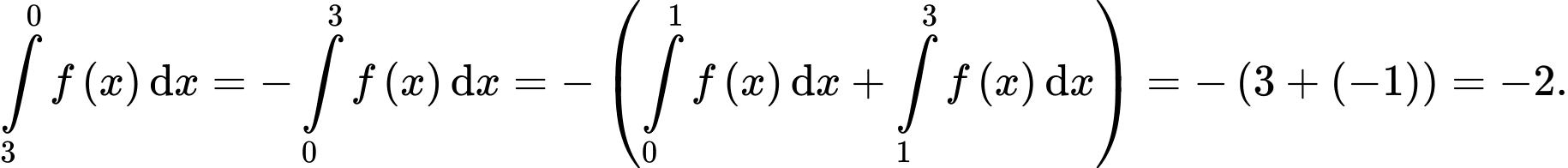
Chọn đáp án B.
Đáp án: B
Câu 4 [151265]: Cho đồ thị hàm số 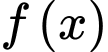 trên đoạn
trên đoạn 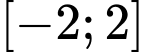 như hình vẽ ở bên và có diện tích
như hình vẽ ở bên và có diện tích 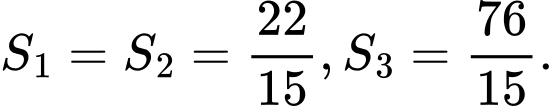 Tính tích phân
Tính tích phân 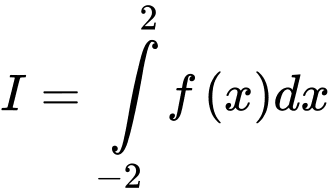 .
.
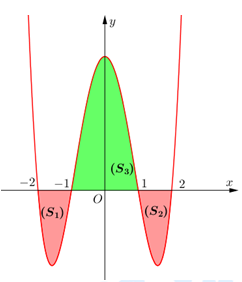
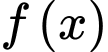 trên đoạn
trên đoạn 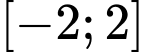 như hình vẽ ở bên và có diện tích
như hình vẽ ở bên và có diện tích 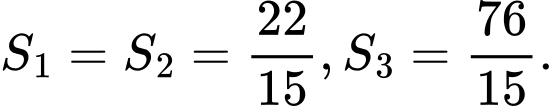 Tính tích phân
Tính tích phân 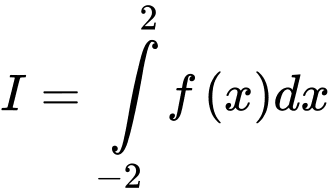 .
.
A, 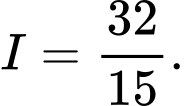
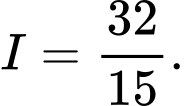
B, 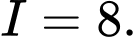
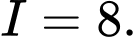
C, 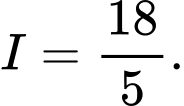
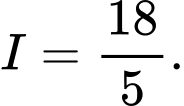
D, 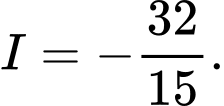
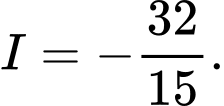
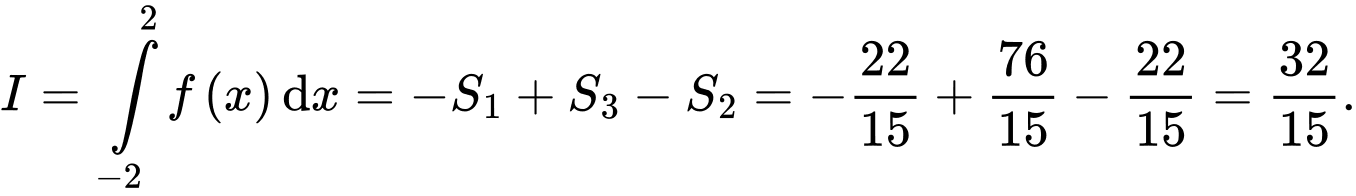
Chọn đáp án A.
Đáp án: A
Câu 5 [149176]: Cho hàm số 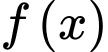 liên tục trên
liên tục trên  và
và 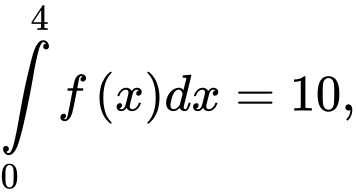
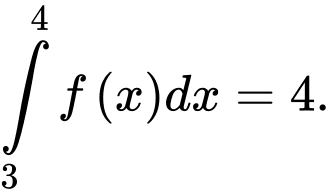 Tích phân
Tích phân 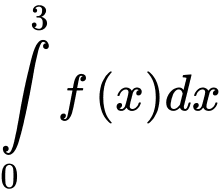 bằng
bằng
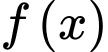 liên tục trên
liên tục trên 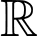 và
và 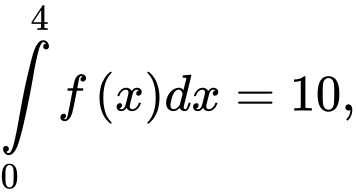
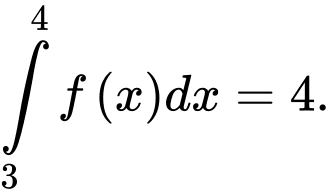 Tích phân
Tích phân 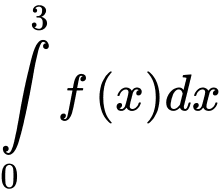 bằng
bằng A, 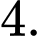
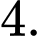
B, 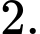
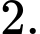
C, 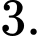
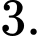
D, 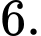
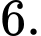
Ta có 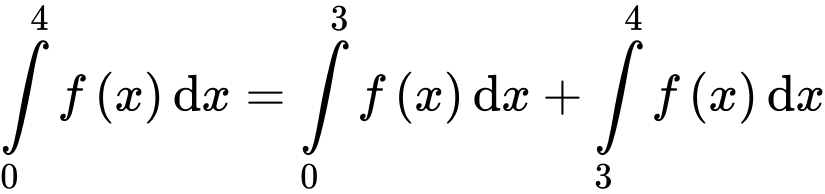

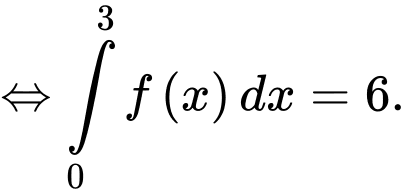
Chọn đáp án D. Đáp án: D
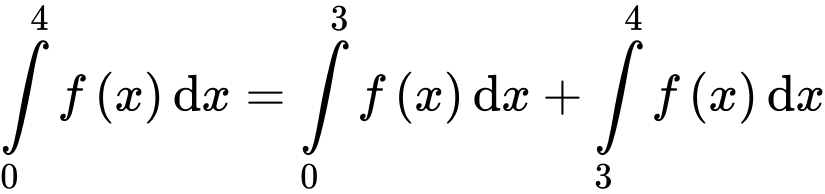

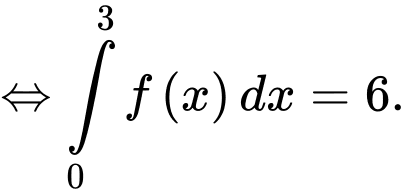
Chọn đáp án D. Đáp án: D
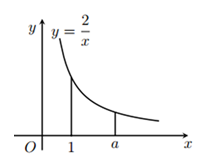
Câu 6 [142495]: Tìm 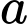 để diện tích hình phẳng được giới hạn bởi các đường
để diện tích hình phẳng được giới hạn bởi các đường 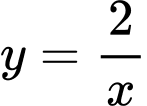 ; trục
; trục 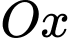 ;
;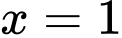 ;
;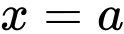
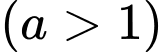 bằng 2.
bằng 2.
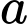 để diện tích hình phẳng được giới hạn bởi các đường
để diện tích hình phẳng được giới hạn bởi các đường 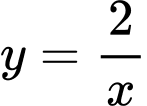 ; trục
; trục 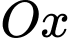 ;
;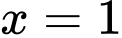 ;
;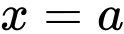
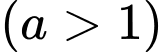 bằng 2.
bằng 2.
A, 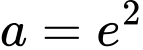 .
.
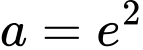 .
.B, 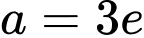 .
.
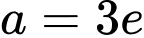 .
.C, 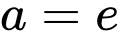 .
.
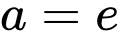 .
.D, 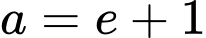 .
.
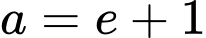 .
.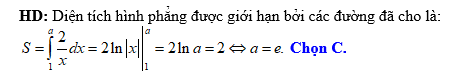 Đáp án: C
Đáp án: C
Câu 7 [149177]: Cho hàm số 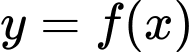 thoả mãn
thoả mãn 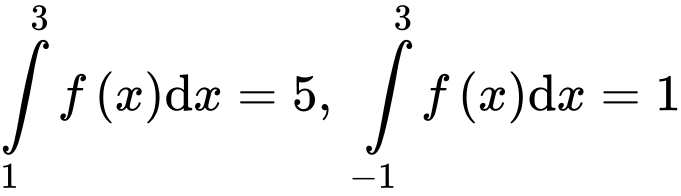 . Tính tích phân
. Tính tích phân 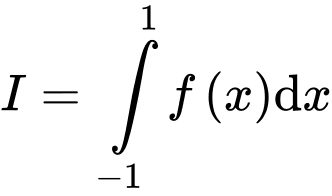 .
.
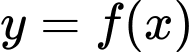 thoả mãn
thoả mãn 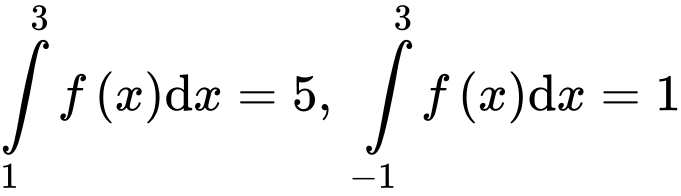 . Tính tích phân
. Tính tích phân 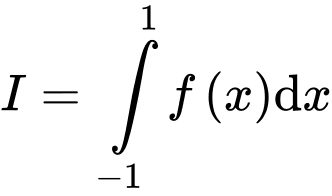 .
. A, 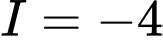 .
.
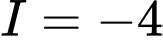 .
.B, 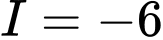 .
.
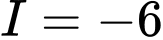 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn đáp án A.
 Đáp án: A
Đáp án: A
 Đáp án: A
Đáp án: A
Câu 8 [389974]: Cho hàm số bậc nhất 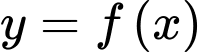 có đồ thị như hình vẽ bên. Biết rằng
có đồ thị như hình vẽ bên. Biết rằng 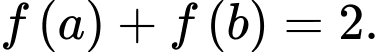 Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau:
Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau: 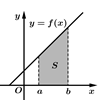
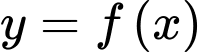 có đồ thị như hình vẽ bên. Biết rằng
có đồ thị như hình vẽ bên. Biết rằng 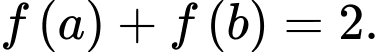 Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau:
Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau: 
A, 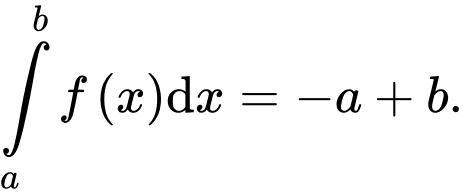
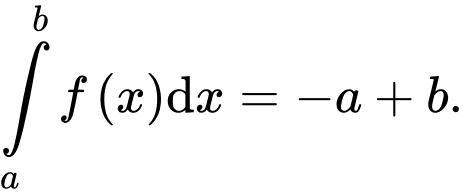
B, 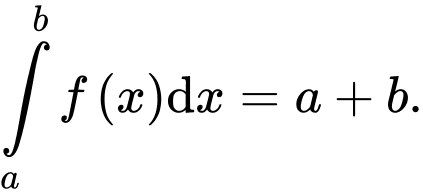
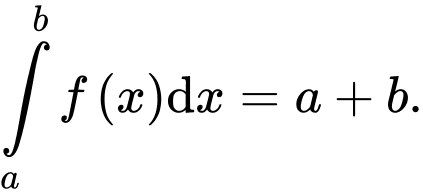
C, 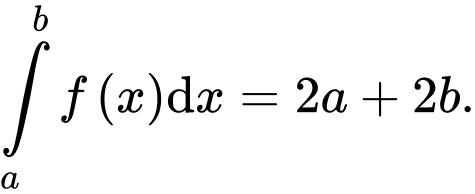
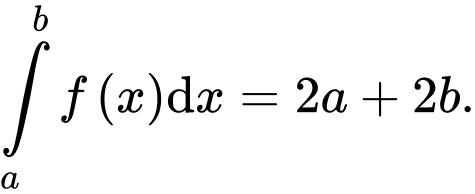
D, 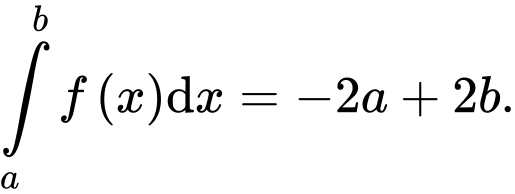
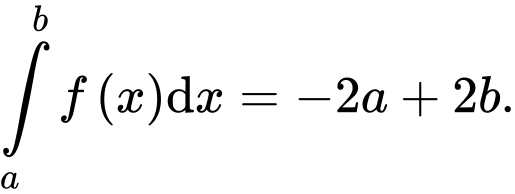
Theo hình vẽ, ta thấy 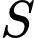 phần cần tính có dạng hình thang có chiều cao là
phần cần tính có dạng hình thang có chiều cao là 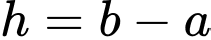 đáy lớn, đáy nhỏ lần lượt là
đáy lớn, đáy nhỏ lần lượt là 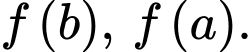
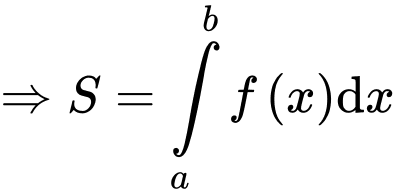
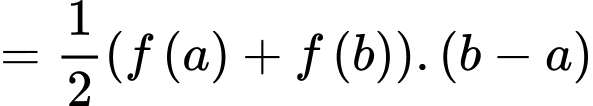
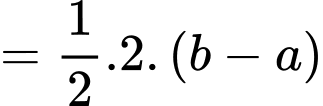
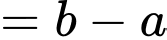
Đáp án: A. Đáp án: A
 phần cần tính có dạng hình thang có chiều cao là
phần cần tính có dạng hình thang có chiều cao là 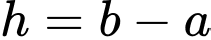 đáy lớn, đáy nhỏ lần lượt là
đáy lớn, đáy nhỏ lần lượt là 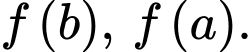
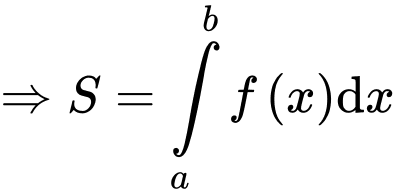
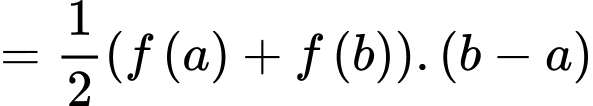
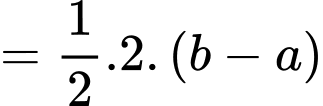
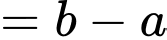
Đáp án: A. Đáp án: A
Câu 9 [147737]: Cho 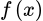 là hàm số chẵn và
là hàm số chẵn và 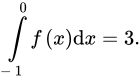 Tính
Tính 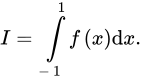
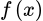 là hàm số chẵn và
là hàm số chẵn và 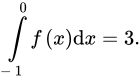 Tính
Tính 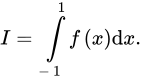
A, 

B, 

C, 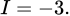
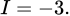
D, 

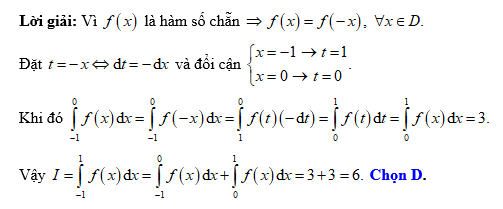 Đáp án: D
Đáp án: D
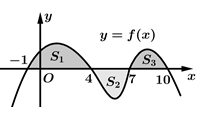
Câu 10 [389975]: Cho hàm số 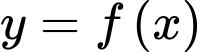 có đồ thị như hình vẽ, biết rằng diện tích
có đồ thị như hình vẽ, biết rằng diện tích 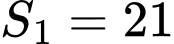 (đvdt),
(đvdt), 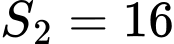 (đvdt) và
(đvdt) và 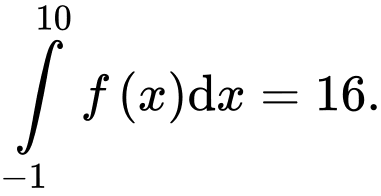 Tính
Tính 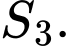
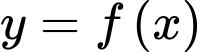 có đồ thị như hình vẽ, biết rằng diện tích
có đồ thị như hình vẽ, biết rằng diện tích 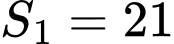 (đvdt),
(đvdt), 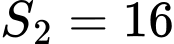 (đvdt) và
(đvdt) và 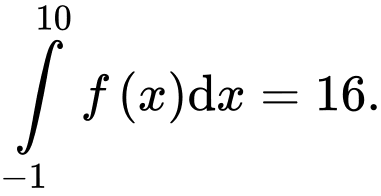 Tính
Tính 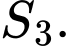

A, 

B, 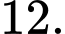
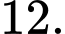
C, 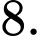
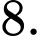
D, 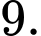
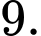
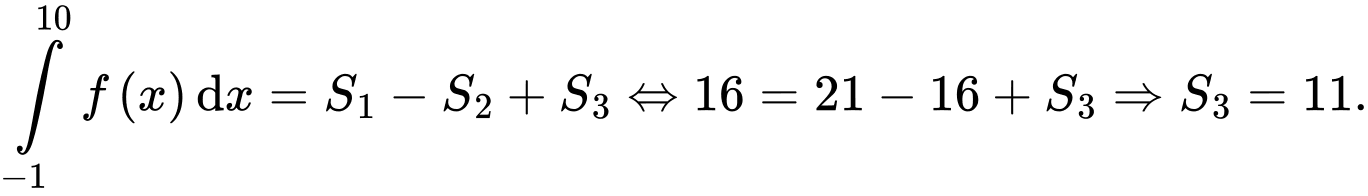
Chọn đáp án A.
Câu 11 [149151]: Cho 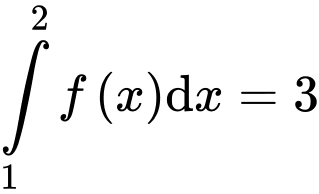 và
và 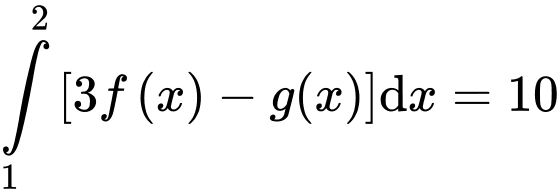 . Khi đó
. Khi đó 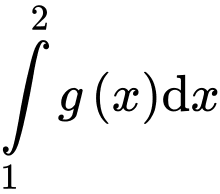 bằng
bằng
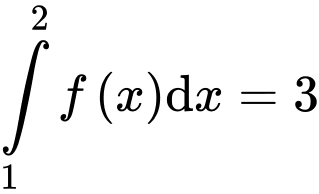 và
và 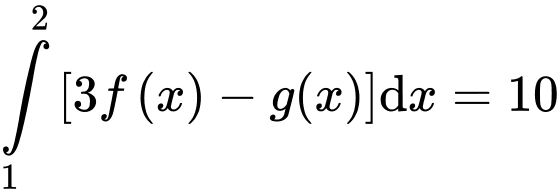 . Khi đó
. Khi đó 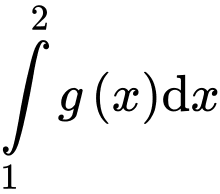 bằng
bằng A, 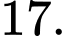
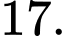
B, 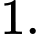
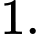
C, 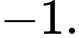
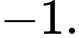
D, 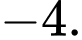
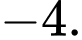
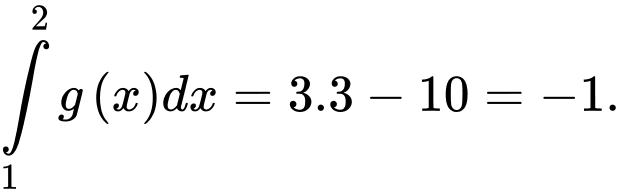 Chọn C. Đáp án: C
Chọn C. Đáp án: C
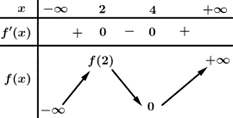
Câu 12 [161571]: Cho hàm số 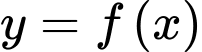 có bảng biến thiên như hình vẽ, biết
có bảng biến thiên như hình vẽ, biết 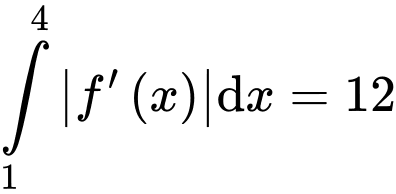 và
và 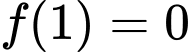 . Tính
. Tính 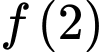 .
.
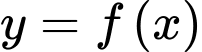 có bảng biến thiên như hình vẽ, biết
có bảng biến thiên như hình vẽ, biết 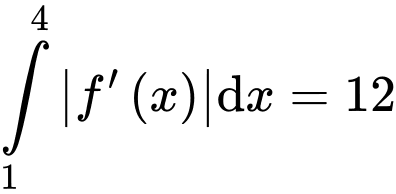 và
và 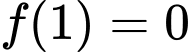 . Tính
. Tính 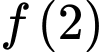 .
.
A, 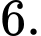
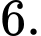
B, 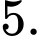
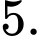
C, 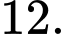
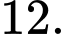
D, 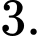
Chọn A
Quan sát đồ thị ta thấy hàm số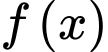 đồng biến trên
đồng biến trên
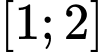 và nghịch biến trên
và nghịch biến trên 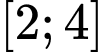 .
.
Ta có: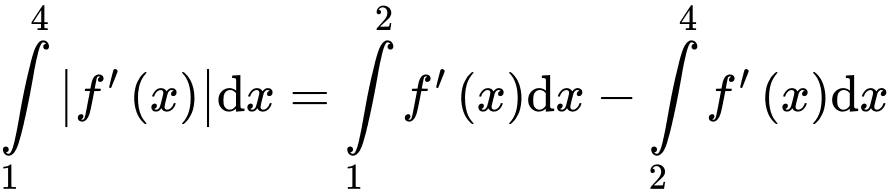 .
.
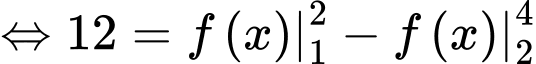
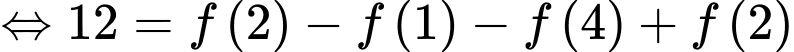
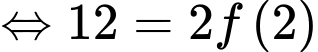
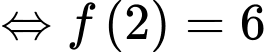 . Đáp án: A
. Đáp án: A
Quan sát đồ thị ta thấy hàm số
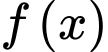 đồng biến trên
đồng biến trên 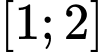 và nghịch biến trên
và nghịch biến trên 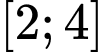 .
.
Ta có:
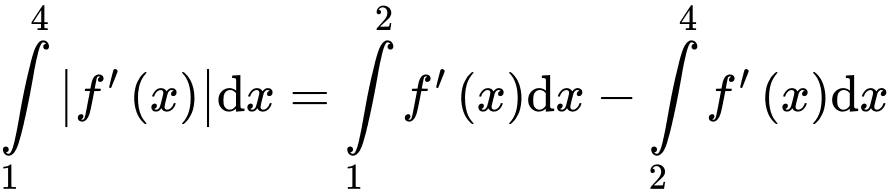 .
.
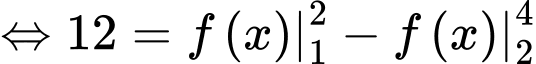
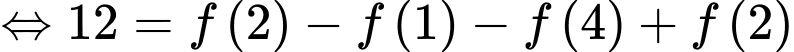
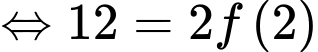
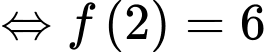 . Đáp án: A
. Đáp án: A
Câu 13 [389976]: Biết diện tích hai hình thang cong 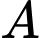 và
và 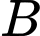 bằng nhau, tìm
bằng nhau, tìm 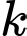
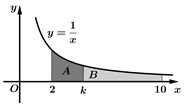
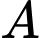 và
và 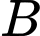 bằng nhau, tìm
bằng nhau, tìm 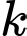

A, 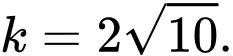
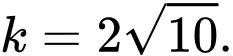
B, 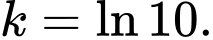
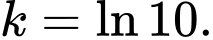
C, 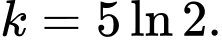
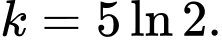
D, 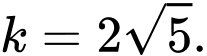
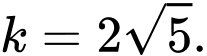
Diện tích hình cong 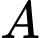 là
là 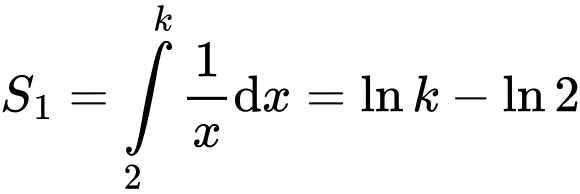
Diện tích hình cong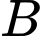 là
là 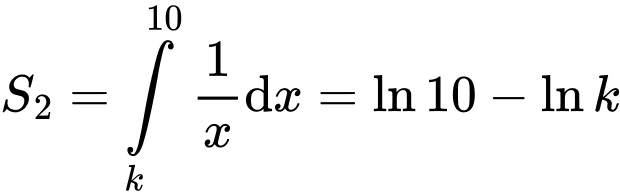
Vì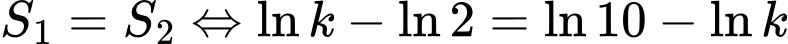
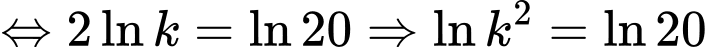
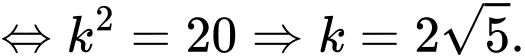
Chọn đáp án D. Đáp án: D
 là
là 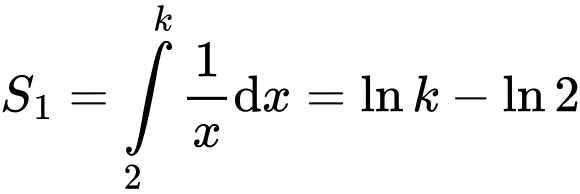
Diện tích hình cong
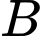 là
là 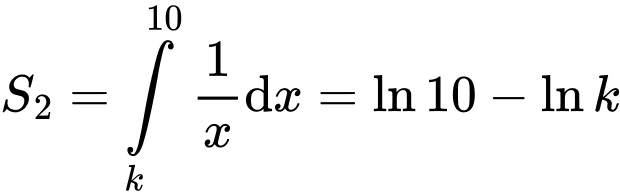
Vì
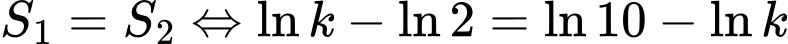
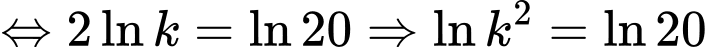
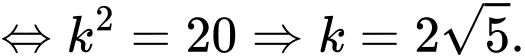
Chọn đáp án D. Đáp án: D
Câu 14 [149165]: Cho hàm số 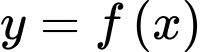 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 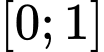 và
và 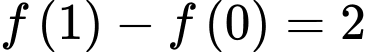 . Tính
. Tính 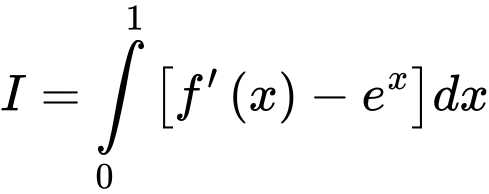 .
.
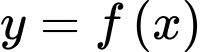 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 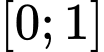 và
và 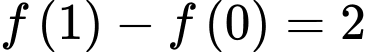 . Tính
. Tính 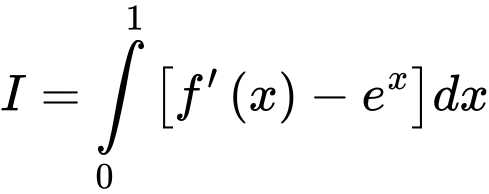 .
. A, 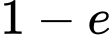 .
.
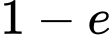 .
.B,  .
.
 .
.C, 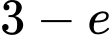 .
.
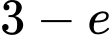 .
.D,  .
.
 .
.
Chọn đáp án C.
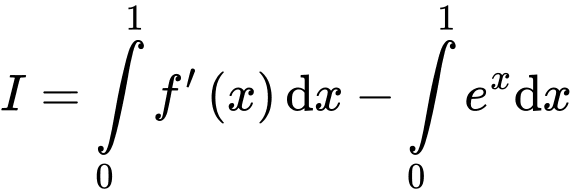
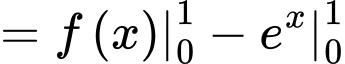
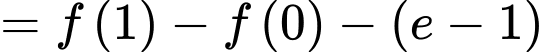

Đáp án: C
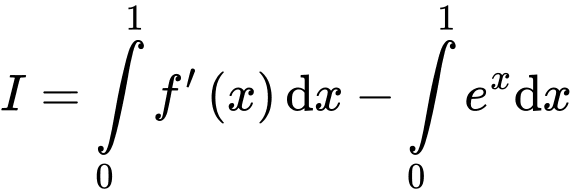
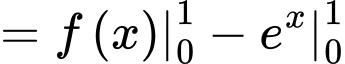
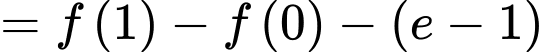

Đáp án: C
Câu 15 [389977]: Biết diện tích phần tô đậm bằng 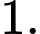 Tìm giá trị của
Tìm giá trị của 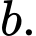
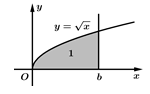
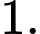 Tìm giá trị của
Tìm giá trị của 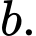

A, 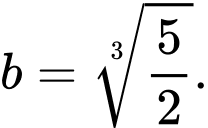
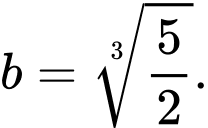
B, 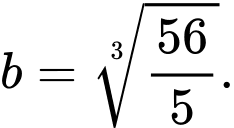
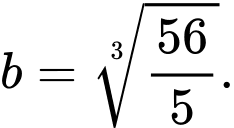
C, 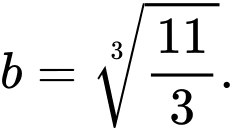
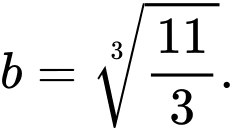
D, 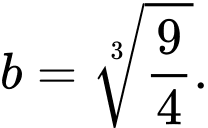
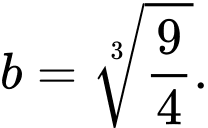
Diện tích phần tô đậm là 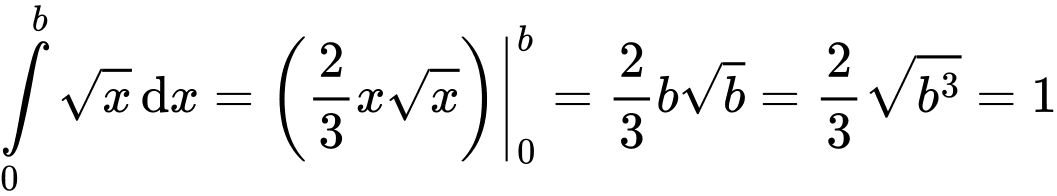
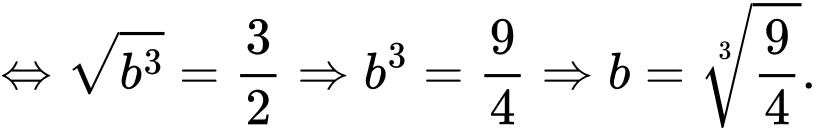
Chọn đáp án D. Đáp án: D
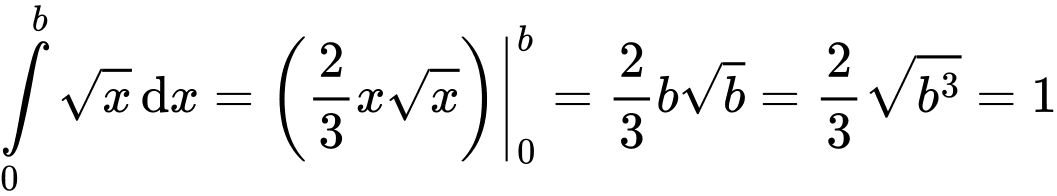
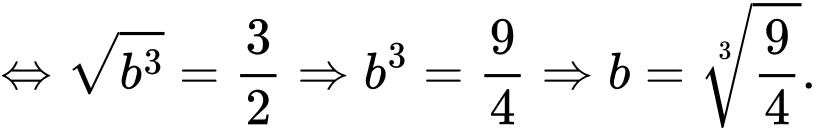
Chọn đáp án D. Đáp án: D
Câu 16 [149168]: Cho biết 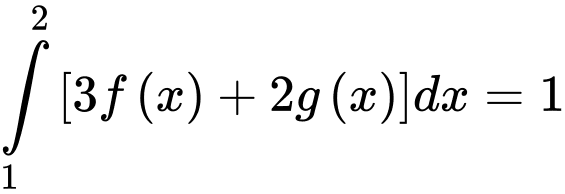 và
và 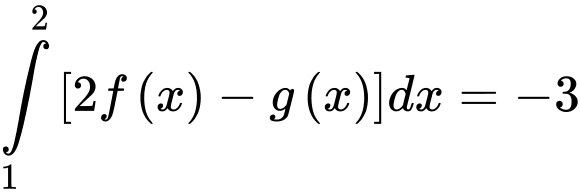 . Tính giá trị của
. Tính giá trị của 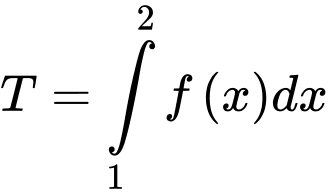 .
.
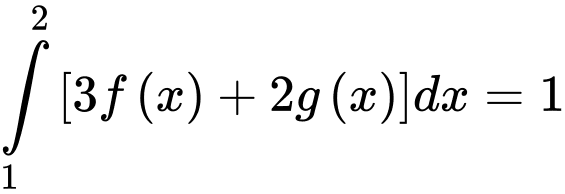 và
và 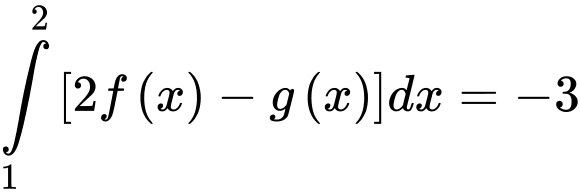 . Tính giá trị của
. Tính giá trị của 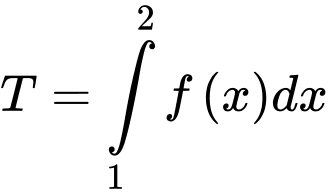 .
. A, 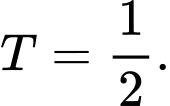
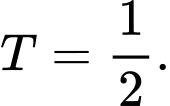
B, 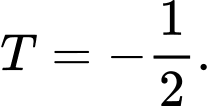
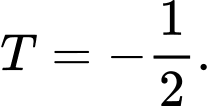
C, 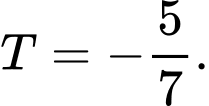
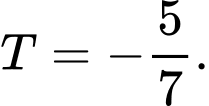
D, 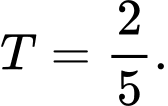
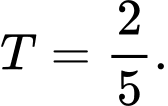

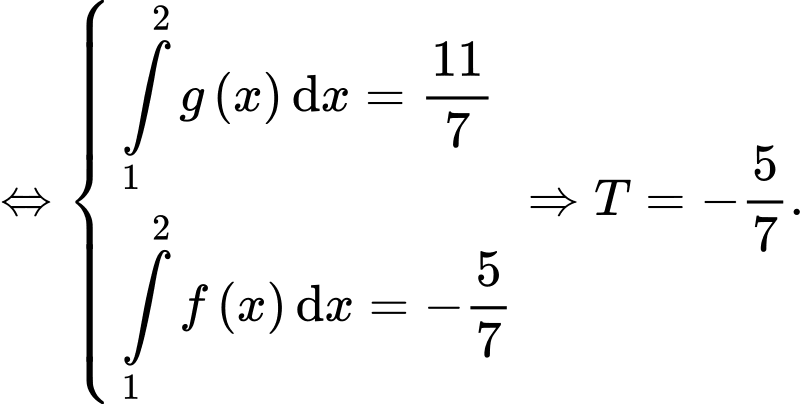
Chọn đáp án C.
Đáp án: C
Câu 17 [389978]: Cho hàm số 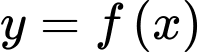 có đồ thị như hình vẽ, biết rằng các diện tích
có đồ thị như hình vẽ, biết rằng các diện tích 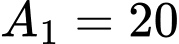 (đvdt),
(đvdt), 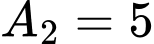 (đvdt). Tính
(đvdt). Tính 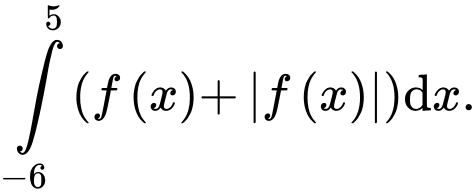
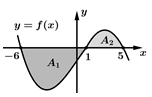
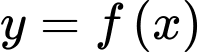 có đồ thị như hình vẽ, biết rằng các diện tích
có đồ thị như hình vẽ, biết rằng các diện tích 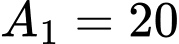 (đvdt),
(đvdt), 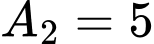 (đvdt). Tính
(đvdt). Tính 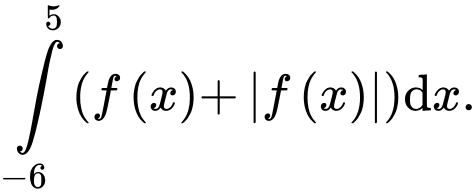

A, 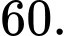
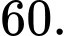
B, 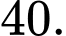
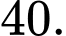
C, 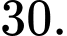
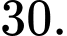
D, 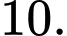
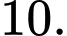
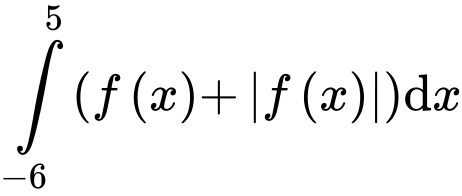
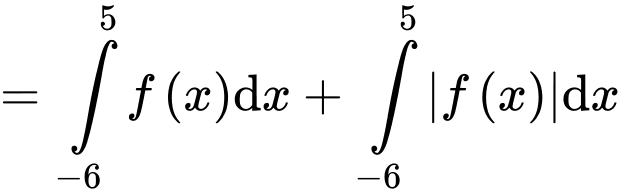
+)
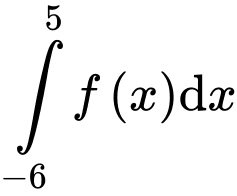
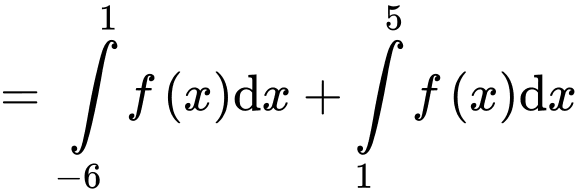
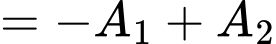
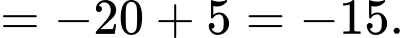
+)
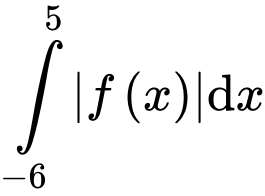
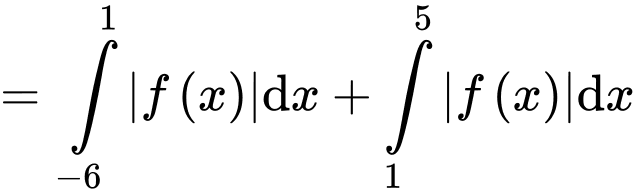
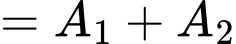
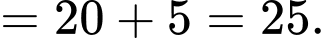
Vậy
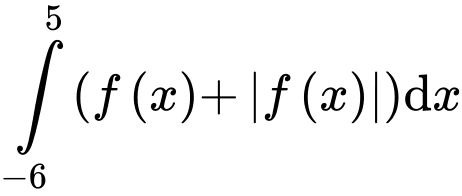
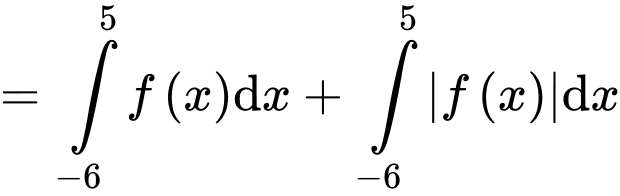
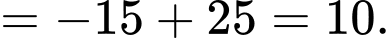
Chọn đáp án D. Đáp án: D
Câu 18 [147736]: Cho 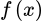 là hàm số lẻ và
là hàm số lẻ và 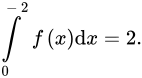 Tính
Tính 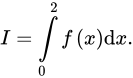
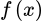 là hàm số lẻ và
là hàm số lẻ và 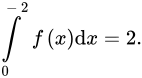 Tính
Tính 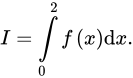
A, 

B, 

C, 

D, 

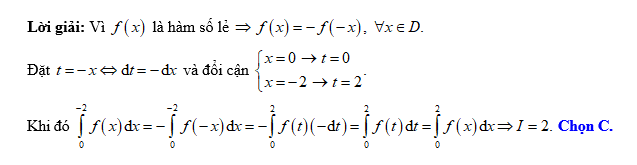 Đáp án: C
Đáp án: C
Câu 19 [140073]: Cho 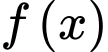 là hàm số lẻ liên tục trên đoạn
là hàm số lẻ liên tục trên đoạn 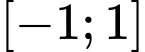 và
và 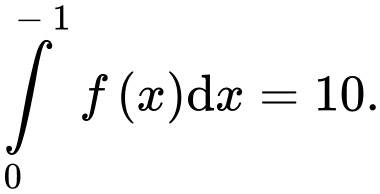 Tính
Tính 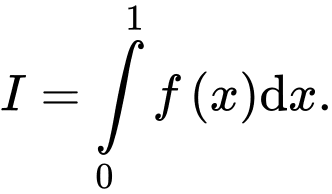
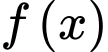 là hàm số lẻ liên tục trên đoạn
là hàm số lẻ liên tục trên đoạn 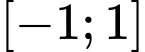 và
và 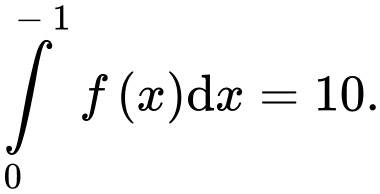 Tính
Tính 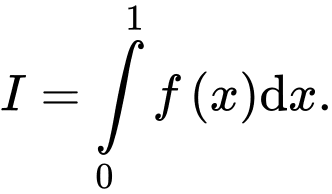
A, 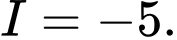
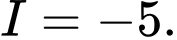
B, 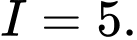
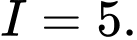
C, 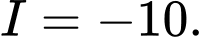
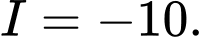
D, 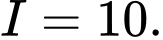
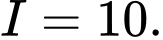
Do 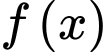 là hàm số lẻ nên
là hàm số lẻ nên 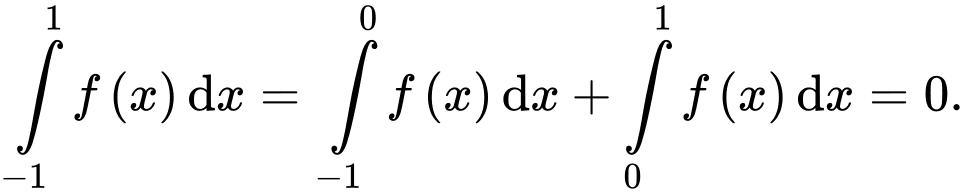
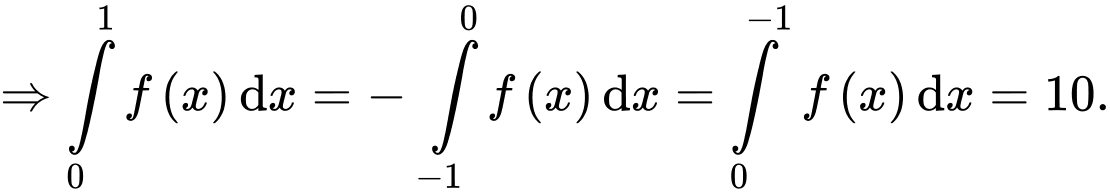
Chọn đáp án D.
Đáp án: D
Câu 20 [149527]: Cho 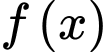 là hàm số chẵn và
là hàm số chẵn và 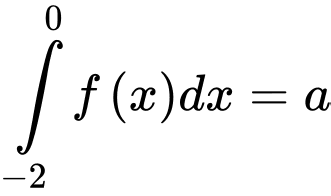 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
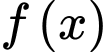 là hàm số chẵn và
là hàm số chẵn và 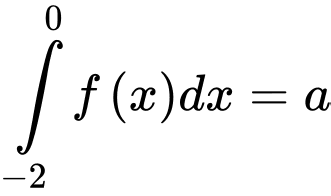 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng? A, 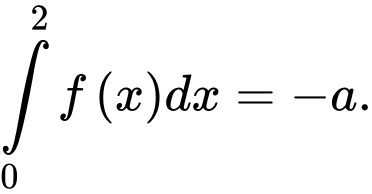
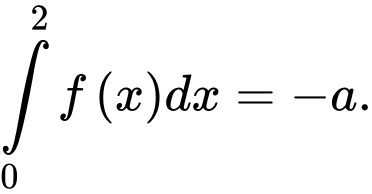
B, 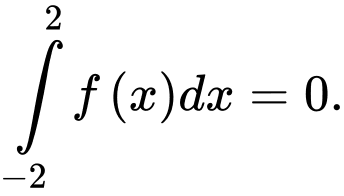
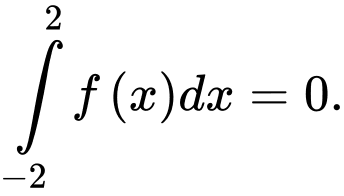
C, 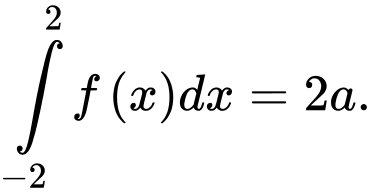
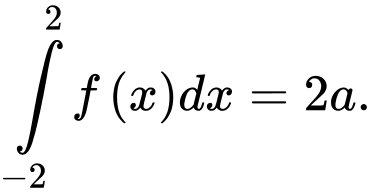
D, 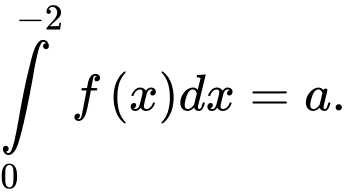
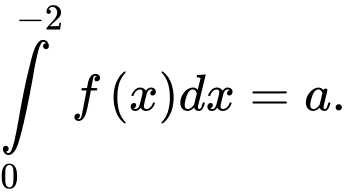
Đặt 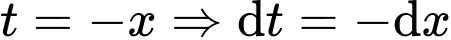
Đổi cận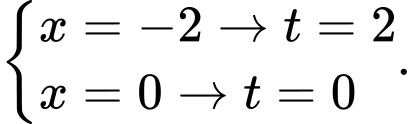
Khi đó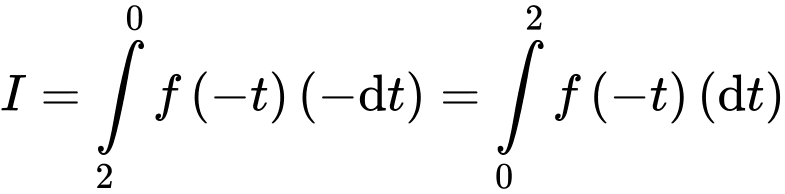
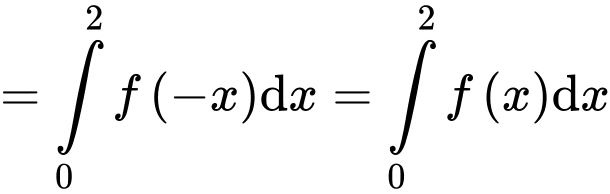 (Do hàm
(Do hàm 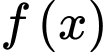 chẵn nên
chẵn nên 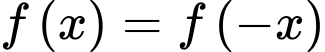 )
)
Khi đó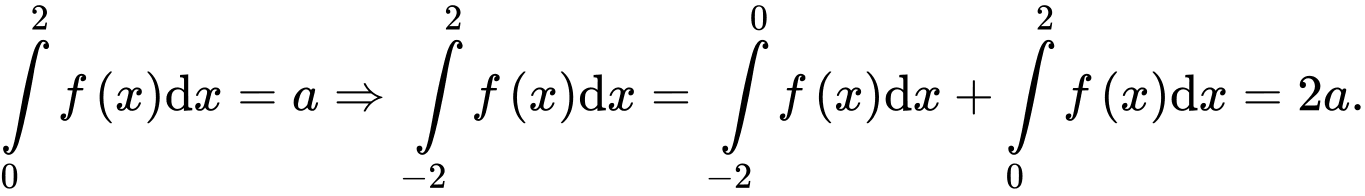
Chọn đáp án C. Đáp án: C
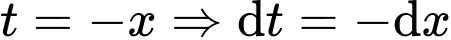
Đổi cận
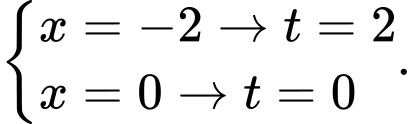
Khi đó
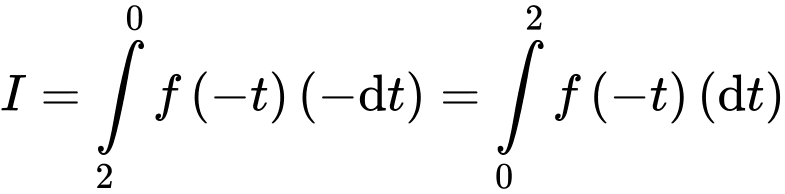
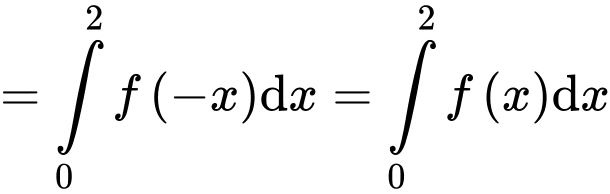 (Do hàm
(Do hàm 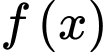 chẵn nên
chẵn nên 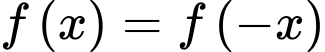 )
)
Khi đó
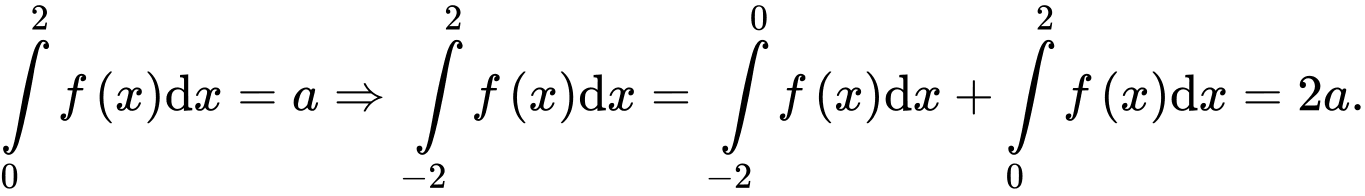
Chọn đáp án C. Đáp án: C
Câu 21 [389979]: Biết rằng 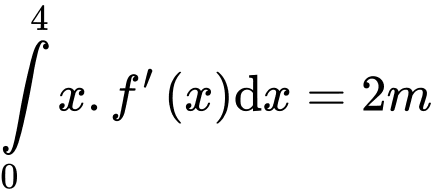 và
và 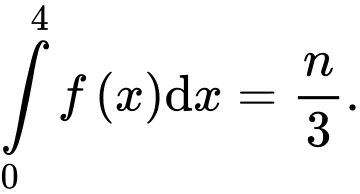 Tính giá trị của
Tính giá trị của 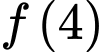 theo
theo 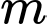 và
và 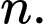
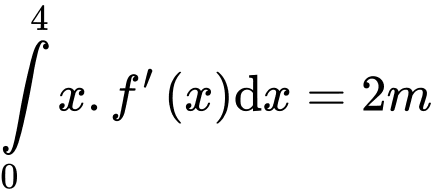 và
và 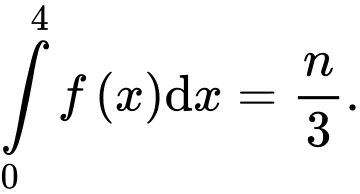 Tính giá trị của
Tính giá trị của 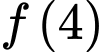 theo
theo 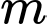 và
và 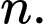
A, 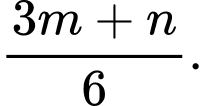
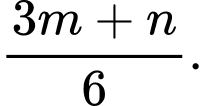
B, 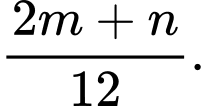
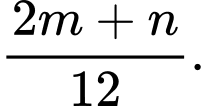
C, 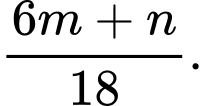
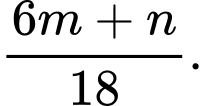
D, 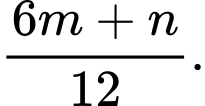
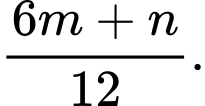
Ta có 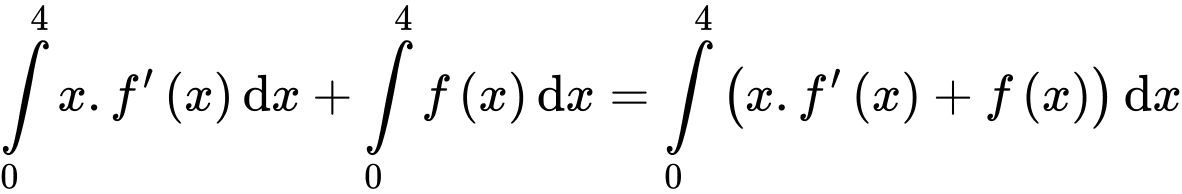
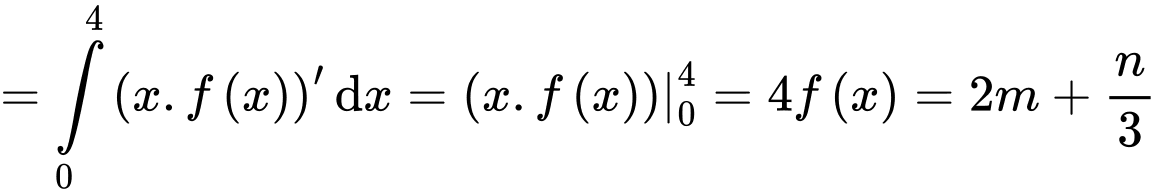
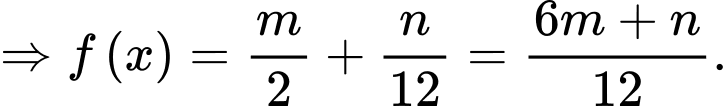
Chọn đáp án D. Đáp án: D
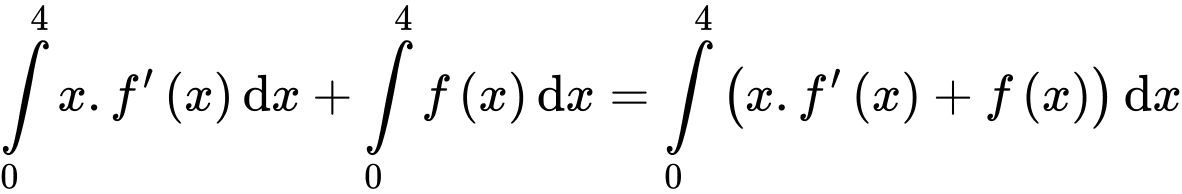
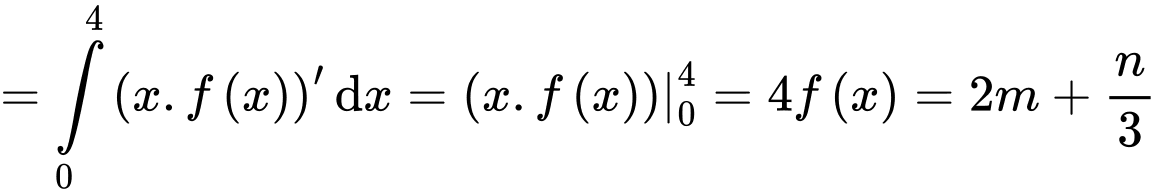
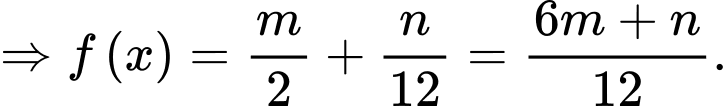
Chọn đáp án D. Đáp án: D
Câu 22 [161572]: Cho hàm số 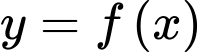 có bảng biến thiên:
có bảng biến thiên:
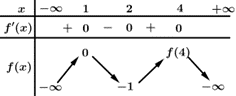
Các mệnh đề sau đúng hay sai?
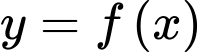 có bảng biến thiên:
có bảng biến thiên: 
Các mệnh đề sau đúng hay sai?
A, a) 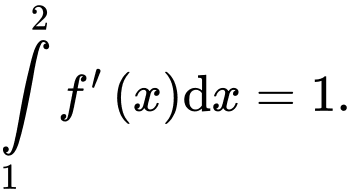
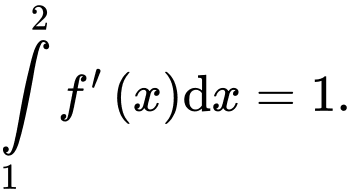
B, b) 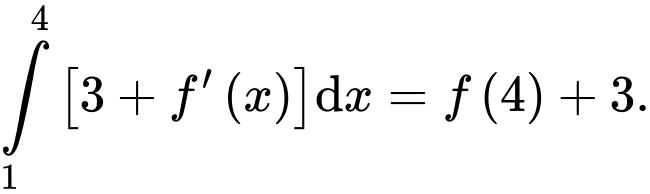
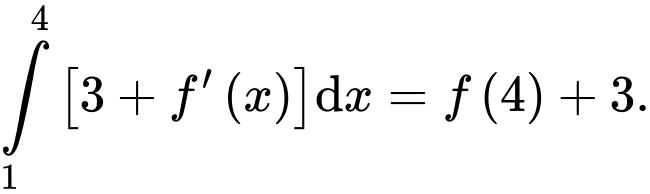
C, c) 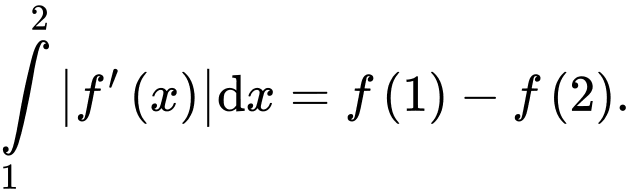
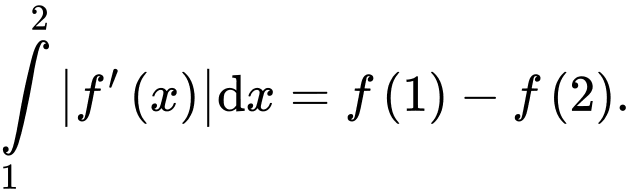
D, d) Nếu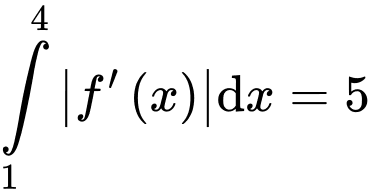 thì
thì 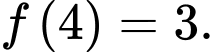
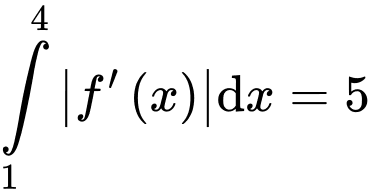 thì
thì 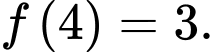
a) Sai. 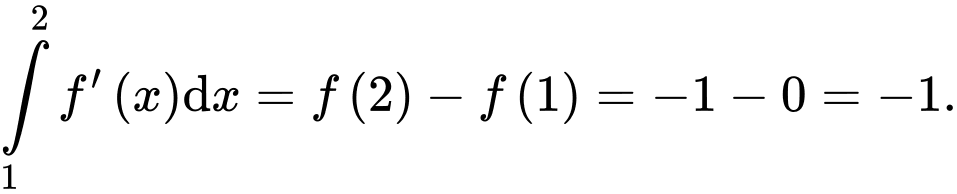
b) Sai.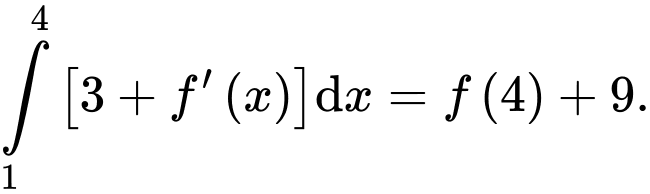
c) Đúng.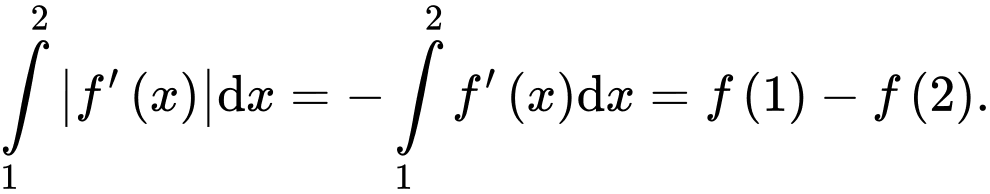
d) Đúng. Từ đồ thị, ta có bảng xét dấu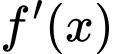 như sau:
như sau:
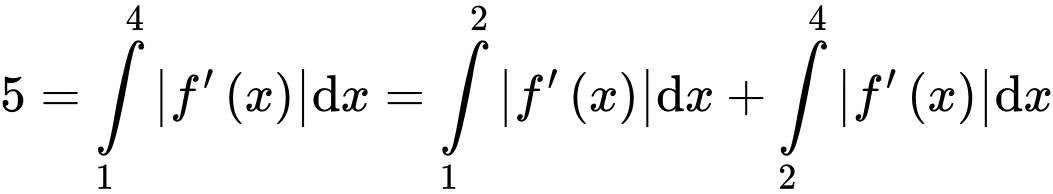
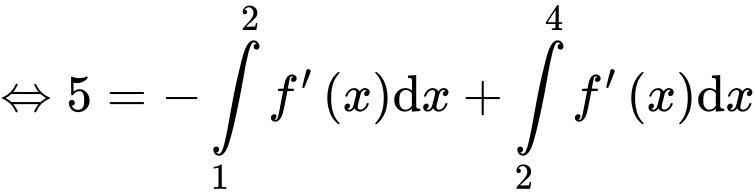
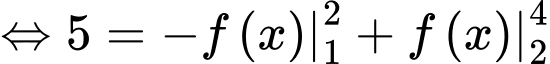
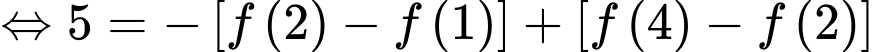
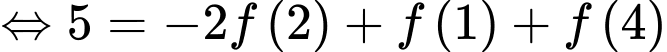
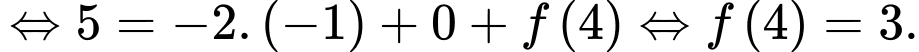
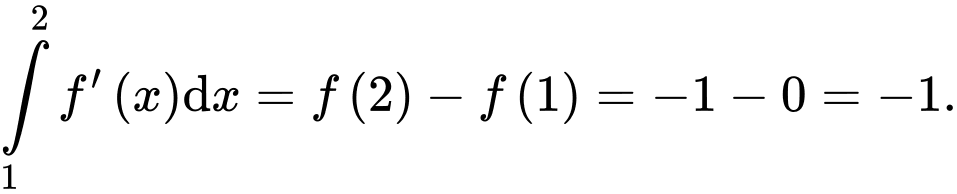
b) Sai.
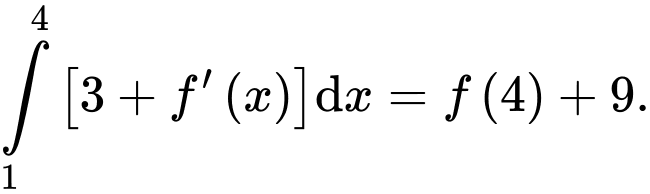
c) Đúng.
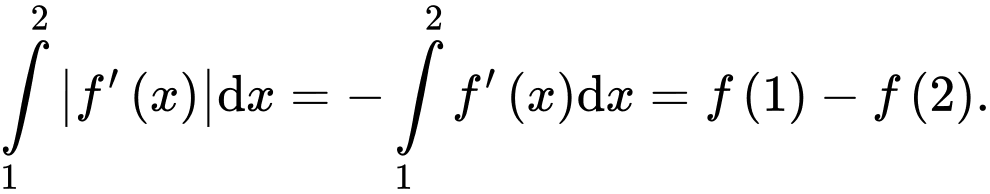
d) Đúng. Từ đồ thị, ta có bảng xét dấu
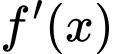 như sau:
như sau: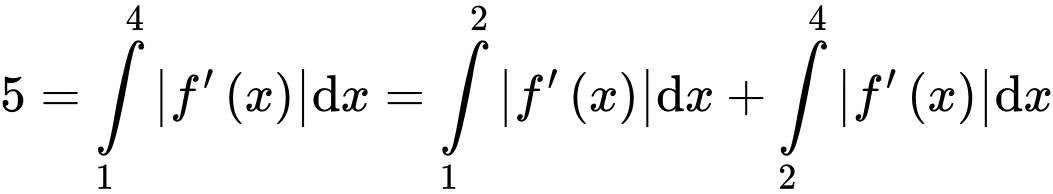
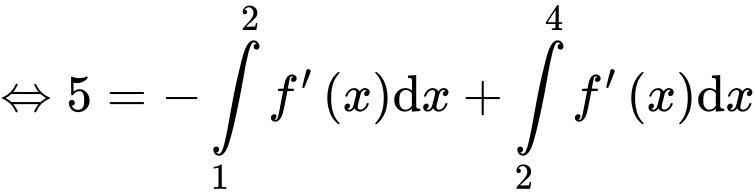
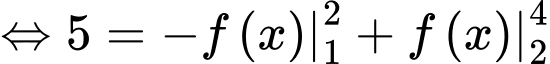
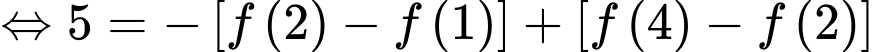
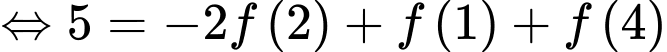
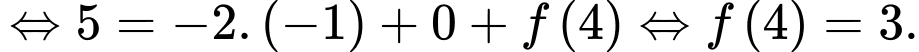
Câu 23 [151372]: Cho hình thang  giới hạn bởi các đường
giới hạn bởi các đường 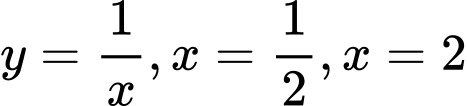 và trục hoành. Đường thẳng
và trục hoành. Đường thẳng 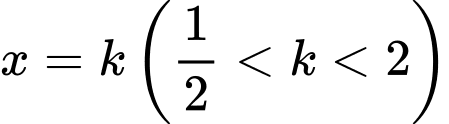 chia
chia  thành hai phần có diện tích là
thành hai phần có diện tích là 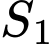 và
và 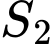 như hình vẽ dưới đây. Tìm tất cả giá trị thực của
như hình vẽ dưới đây. Tìm tất cả giá trị thực của 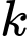 để
để 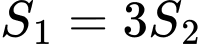 .
.
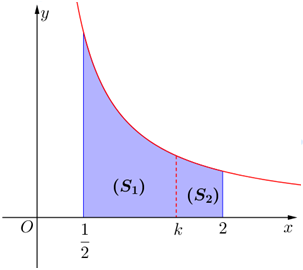
 giới hạn bởi các đường
giới hạn bởi các đường 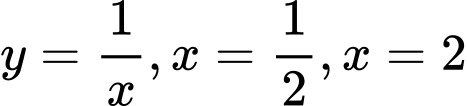 và trục hoành. Đường thẳng
và trục hoành. Đường thẳng 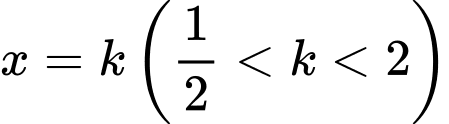 chia
chia  thành hai phần có diện tích là
thành hai phần có diện tích là 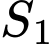 và
và 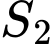 như hình vẽ dưới đây. Tìm tất cả giá trị thực của
như hình vẽ dưới đây. Tìm tất cả giá trị thực của 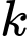 để
để 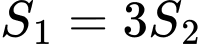 .
.
A, 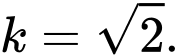
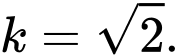
B, 

C, 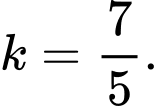
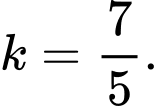
D, 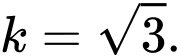
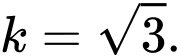
Gọi 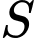 là diện tích hình
là diện tích hình 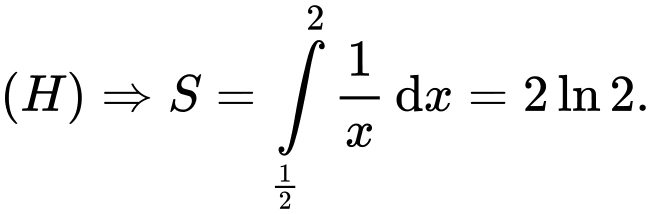
Lại có 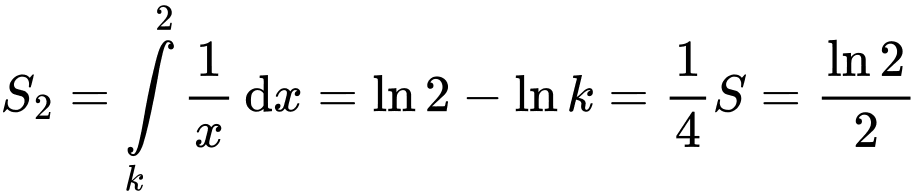
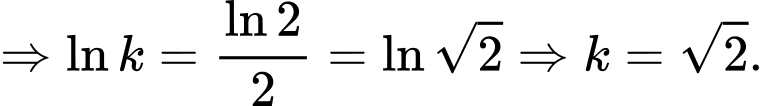
Chọn đáp án A.
Đáp án: A
Câu 24 [396641]: [Trích SGK Cùng Khám Phá]: Trọng lực của Trái Đất tác dụng lên một vệ tinh trong quá trình vệ tinh này được phóng lên từ mặt đất tới vị trí cách tâm Trái Đất r (m) xác định bởi công thức 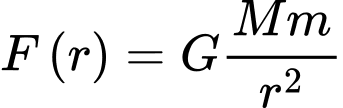 trong đó
trong đó 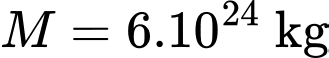 là khối lượng Trái Đất, m (kg) là khối lượng vệ tinh và
là khối lượng Trái Đất, m (kg) là khối lượng vệ tinh và 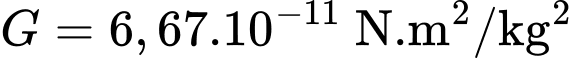 là hằng số hấp dẫn. Trọng lực này sinh công
là hằng số hấp dẫn. Trọng lực này sinh công 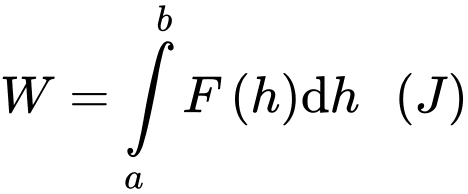 khi vệ tinh thay đổi từ vị trí cách tâm Trái Đất a (m) lên vị trí cách tâm Trái Đất b (m) (nguồn: http://hyperphysics.phy-astr.gsu.edu/hbase/wint.html). Công tối thiểu để phóng một vệ tinh nặng m = 1000 kg từ mặt đất lên độ cao 35780 km so với mặt đất là
khi vệ tinh thay đổi từ vị trí cách tâm Trái Đất a (m) lên vị trí cách tâm Trái Đất b (m) (nguồn: http://hyperphysics.phy-astr.gsu.edu/hbase/wint.html). Công tối thiểu để phóng một vệ tinh nặng m = 1000 kg từ mặt đất lên độ cao 35780 km so với mặt đất là 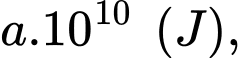 biết bán kính Trái Đất là 6370 km. Giá trị của
biết bán kính Trái Đất là 6370 km. Giá trị của 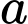 làm tròn đến hàng đơn vị là
làm tròn đến hàng đơn vị là
Đáp số:……………………………
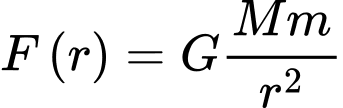 trong đó
trong đó 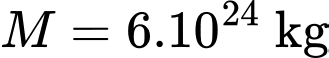 là khối lượng Trái Đất, m (kg) là khối lượng vệ tinh và
là khối lượng Trái Đất, m (kg) là khối lượng vệ tinh và 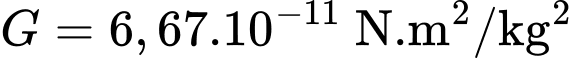 là hằng số hấp dẫn. Trọng lực này sinh công
là hằng số hấp dẫn. Trọng lực này sinh công 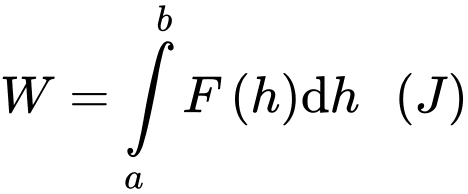 khi vệ tinh thay đổi từ vị trí cách tâm Trái Đất a (m) lên vị trí cách tâm Trái Đất b (m) (nguồn: http://hyperphysics.phy-astr.gsu.edu/hbase/wint.html). Công tối thiểu để phóng một vệ tinh nặng m = 1000 kg từ mặt đất lên độ cao 35780 km so với mặt đất là
khi vệ tinh thay đổi từ vị trí cách tâm Trái Đất a (m) lên vị trí cách tâm Trái Đất b (m) (nguồn: http://hyperphysics.phy-astr.gsu.edu/hbase/wint.html). Công tối thiểu để phóng một vệ tinh nặng m = 1000 kg từ mặt đất lên độ cao 35780 km so với mặt đất là 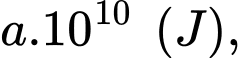 biết bán kính Trái Đất là 6370 km. Giá trị của
biết bán kính Trái Đất là 6370 km. Giá trị của 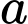 làm tròn đến hàng đơn vị là
làm tròn đến hàng đơn vị làĐáp số:……………………………
Vì công thức tính lực sinh công 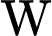 sẽ được tính khi vệ tinh thay đổi từ vị trí cách tâm trái đất
sẽ được tính khi vệ tinh thay đổi từ vị trí cách tâm trái đất 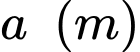 lên vị trí cách tâm trái đất
lên vị trí cách tâm trái đất 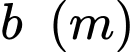 nên để phóng 1 vệ tinh lên độ cao
nên để phóng 1 vệ tinh lên độ cao 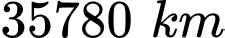 so với mặt đất thì
so với mặt đất thì 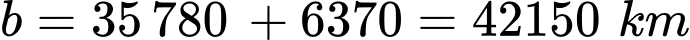
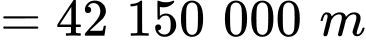 và
và 
Ta có
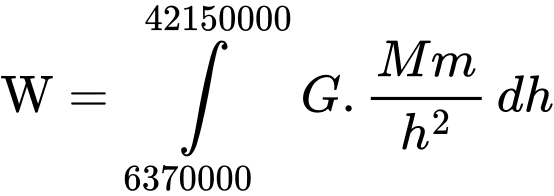
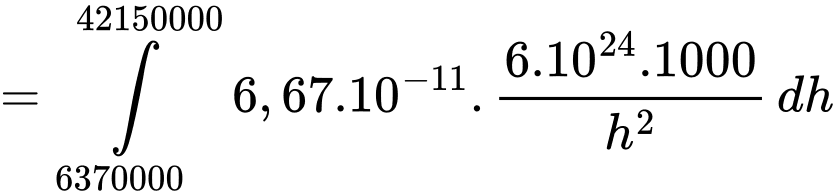
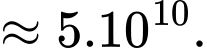
Vì công tối thiểu để phóng vệ tinh bằng công của trọng lực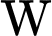 và bằng
và bằng 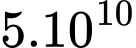
Suy ra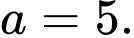
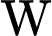 sẽ được tính khi vệ tinh thay đổi từ vị trí cách tâm trái đất
sẽ được tính khi vệ tinh thay đổi từ vị trí cách tâm trái đất 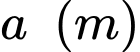 lên vị trí cách tâm trái đất
lên vị trí cách tâm trái đất 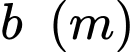 nên để phóng 1 vệ tinh lên độ cao
nên để phóng 1 vệ tinh lên độ cao 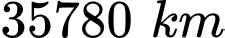 so với mặt đất thì
so với mặt đất thì 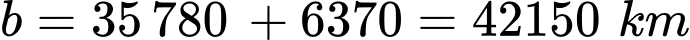
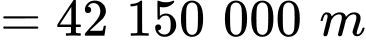 và
và 
Ta có
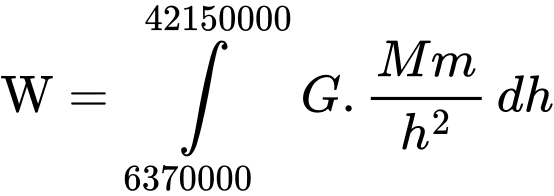
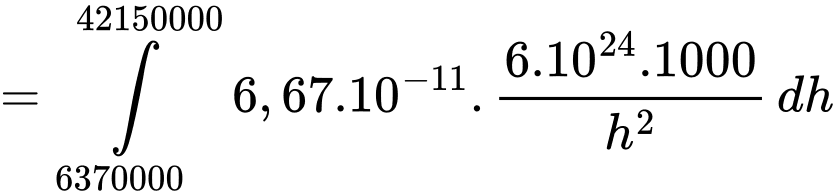
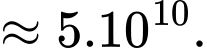
Vì công tối thiểu để phóng vệ tinh bằng công của trọng lực
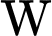 và bằng
và bằng 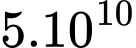
Suy ra
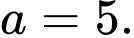
Câu 25 [151368]: Trong mặt phẳng tọa độ, cho hình chữ nhật  có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là
có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là 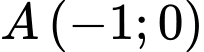 và
và 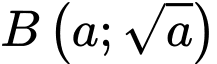 , với
, với  . Biết rằng đồ thị hàm số
. Biết rằng đồ thị hàm số 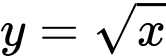 chia hình
chia hình  thành hai phần có diện tích bằng nhau, tìm
thành hai phần có diện tích bằng nhau, tìm 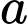 .
.
 có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là
có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là 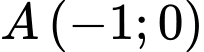 và
và 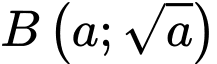 , với
, với  . Biết rằng đồ thị hàm số
. Biết rằng đồ thị hàm số 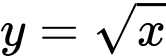 chia hình
chia hình  thành hai phần có diện tích bằng nhau, tìm
thành hai phần có diện tích bằng nhau, tìm 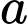 .
. A, 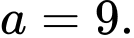
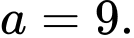
B, 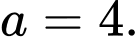
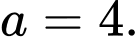
C, 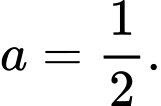
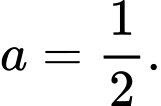
D, 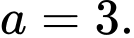
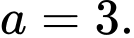
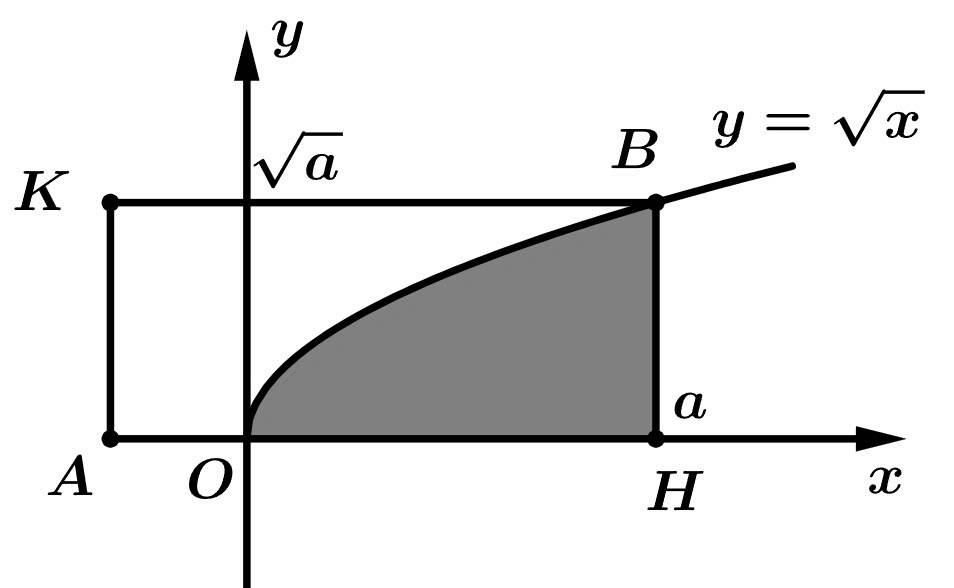
Từ hình vẽ, suy ra
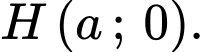
Hình chữ nhật
 có
có 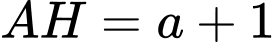 và
và 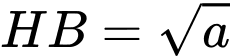 nên có diện tích là
nên có diện tích là 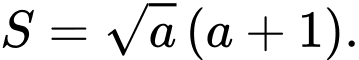
Ta có diện tích miền tô đậm là
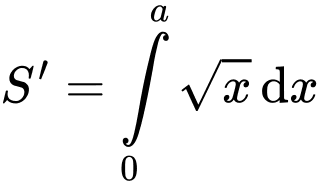

Theo giả thiết, ta có
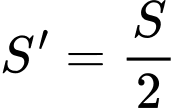
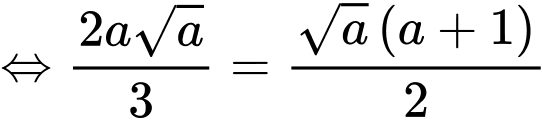
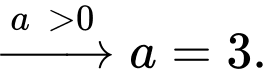
Chọn D. Đáp án: D
Câu 26 [151373]: Cho hình thang cong  giới hạn bởi các đường
giới hạn bởi các đường 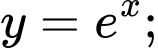
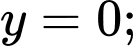
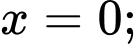
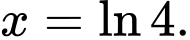 Đường thẳng
Đường thẳng 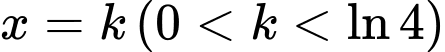 chia
chia  thành hai phân có diện tích
thành hai phân có diện tích 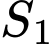 và
và 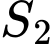 như hình bên. Tìm
như hình bên. Tìm 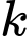 để
để 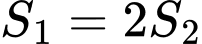 .
.
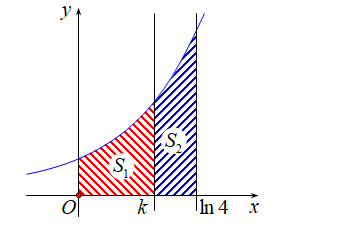
 giới hạn bởi các đường
giới hạn bởi các đường 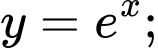
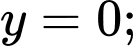
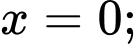
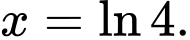 Đường thẳng
Đường thẳng 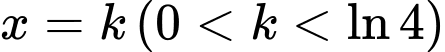 chia
chia  thành hai phân có diện tích
thành hai phân có diện tích 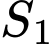 và
và 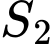 như hình bên. Tìm
như hình bên. Tìm 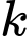 để
để 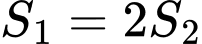 .
.
A, 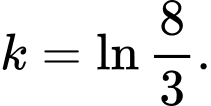
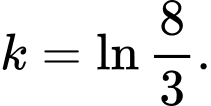
B, 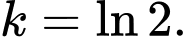
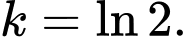
C, 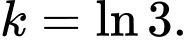
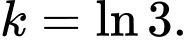
D, 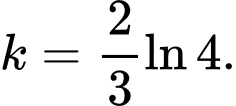
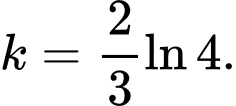
Giả sử 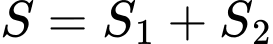 nên
nên 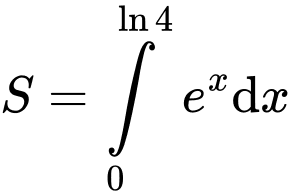
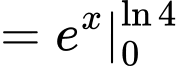
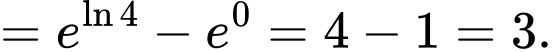
Mà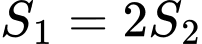
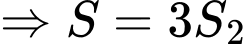
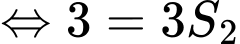
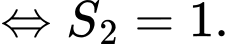
Do đó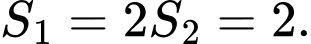
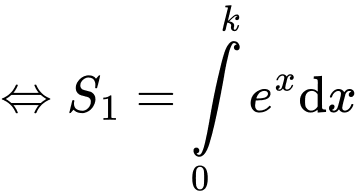
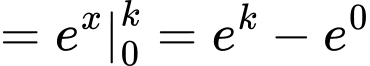
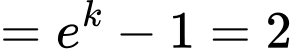
 Đáp án: C
Đáp án: C
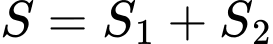 nên
nên 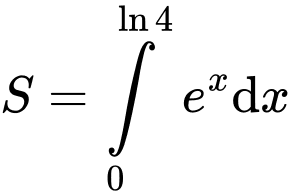
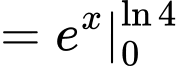
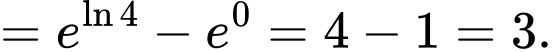
Mà
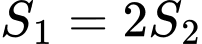
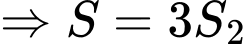
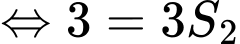
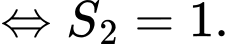
Do đó
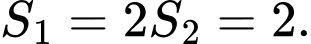
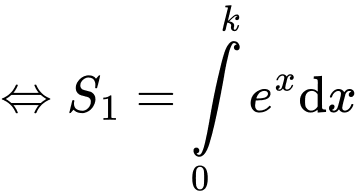
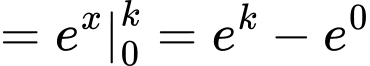
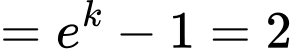
 Đáp án: C
Đáp án: C
Câu 27 [809358]: Cho hình thang cong  giới hạn bởi các đường
giới hạn bởi các đường 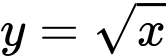 ,
, 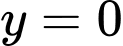 ,
, 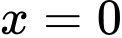 ,
,  . Đường thẳng
. Đường thẳng 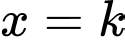
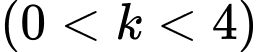 chia
chia  thành hai phần có diện tích
thành hai phần có diện tích 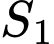 và
và 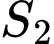 như hình vẽ.
như hình vẽ.
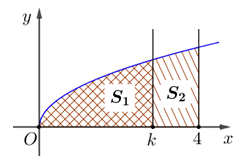
Để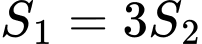 thì giá trị
thì giá trị 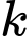 thuộc khoảng nào sau đây?
thuộc khoảng nào sau đây?
 giới hạn bởi các đường
giới hạn bởi các đường 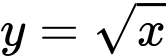 ,
, 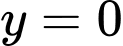 ,
, 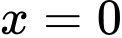 ,
,  . Đường thẳng
. Đường thẳng 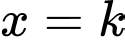
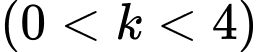 chia
chia  thành hai phần có diện tích
thành hai phần có diện tích 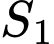 và
và 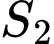 như hình vẽ.
như hình vẽ. 
Để
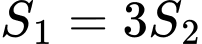 thì giá trị
thì giá trị 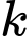 thuộc khoảng nào sau đây?
thuộc khoảng nào sau đây? A, 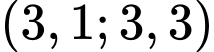 .
.
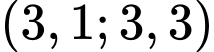 .
.B, 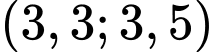 .
.
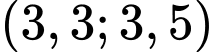 .
.C, 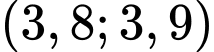 .
.
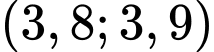 .
.D, 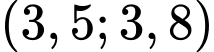 .
.
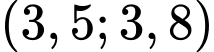 .
.
Chọn B
Diện tích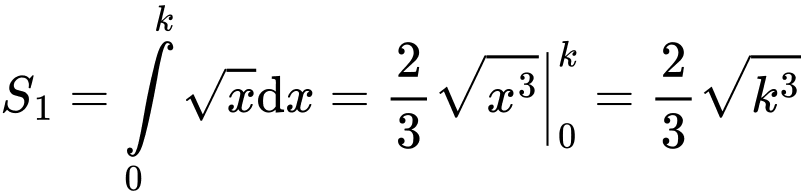 .
.
Diện tích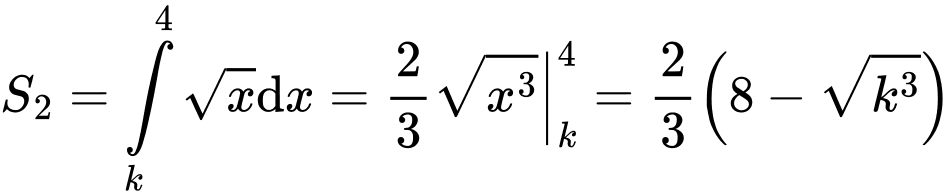 .
.
Suy ra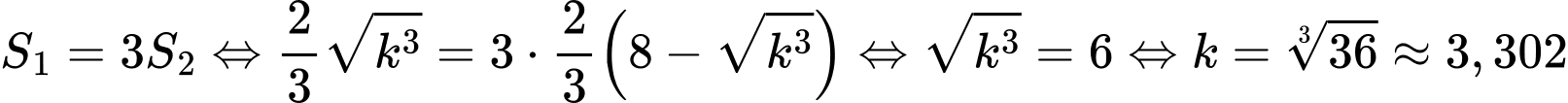 . Đáp án: B
. Đáp án: B
Diện tích
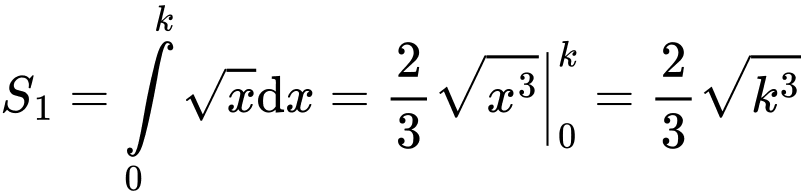 .
.Diện tích
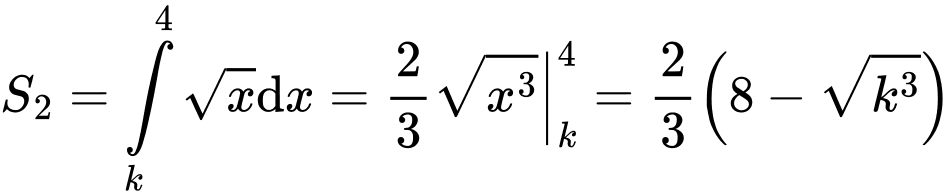 .
.Suy ra
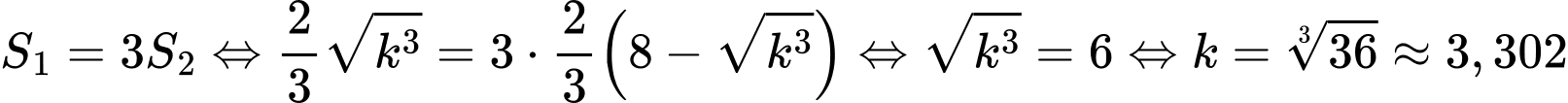 . Đáp án: B
. Đáp án: B
Câu 28 [389973]: Cho hàm số 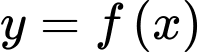 có đồ thị là đường gấp khúc như hình vẽ. Tính
có đồ thị là đường gấp khúc như hình vẽ. Tính 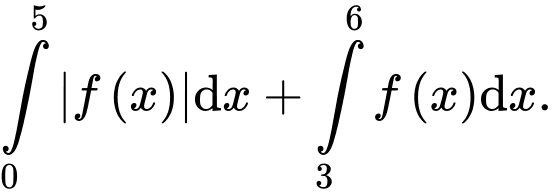
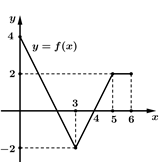
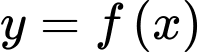 có đồ thị là đường gấp khúc như hình vẽ. Tính
có đồ thị là đường gấp khúc như hình vẽ. Tính 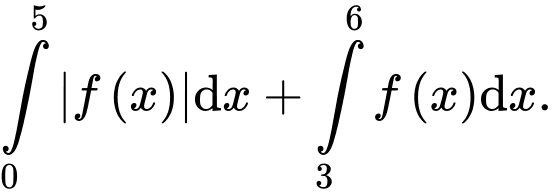

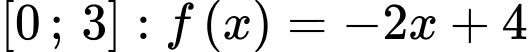

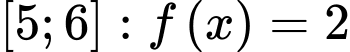
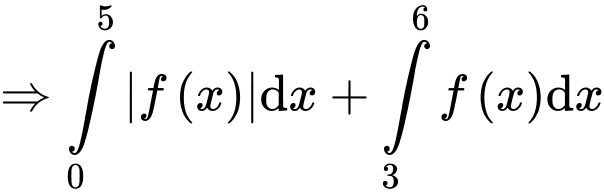
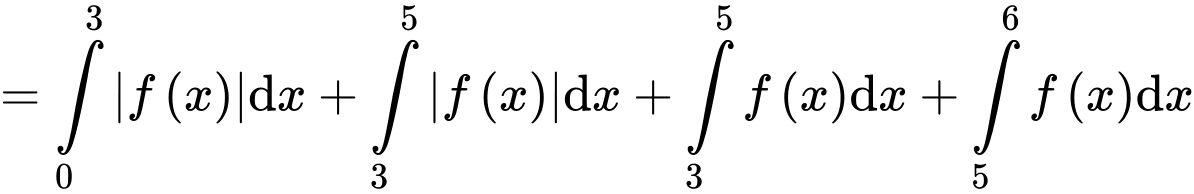
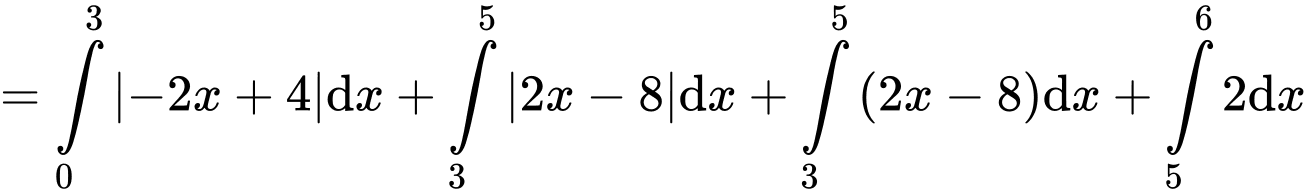
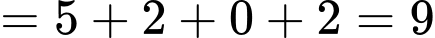
Đáp án: 9.
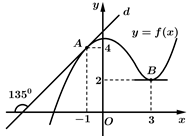
Câu 29 [389980]: Cho hàm số 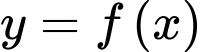 có đồ thị như hình vẽ bên. Đường thẳng
có đồ thị như hình vẽ bên. Đường thẳng 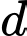 là tiếp tuyến của đồ thị hàm số tại điểm
là tiếp tuyến của đồ thị hàm số tại điểm 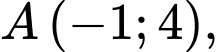 điểm
điểm 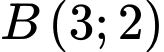 là điểm cực tiểu của đồ thị hàm số. Tính
là điểm cực tiểu của đồ thị hàm số. Tính 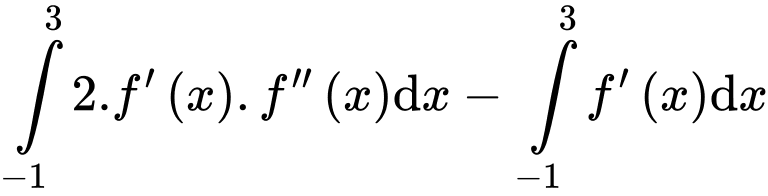
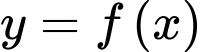 có đồ thị như hình vẽ bên. Đường thẳng
có đồ thị như hình vẽ bên. Đường thẳng 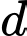 là tiếp tuyến của đồ thị hàm số tại điểm
là tiếp tuyến của đồ thị hàm số tại điểm 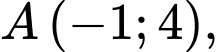 điểm
điểm 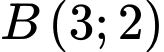 là điểm cực tiểu của đồ thị hàm số. Tính
là điểm cực tiểu của đồ thị hàm số. Tính 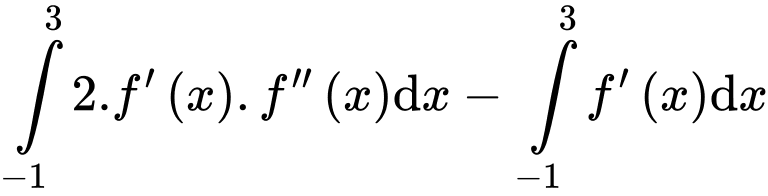

Ta có 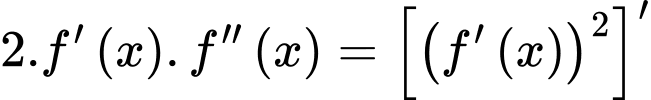
Suy ra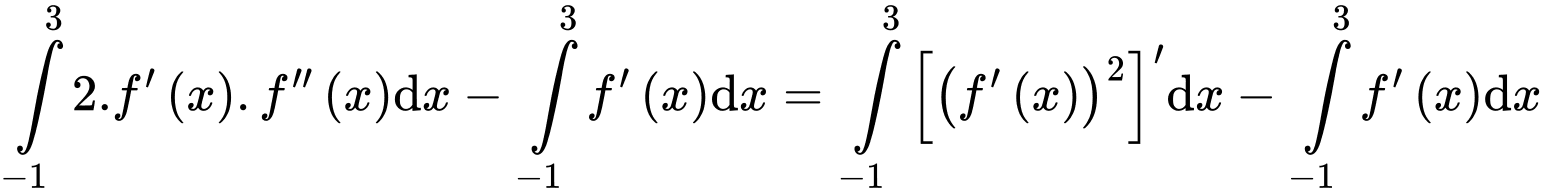
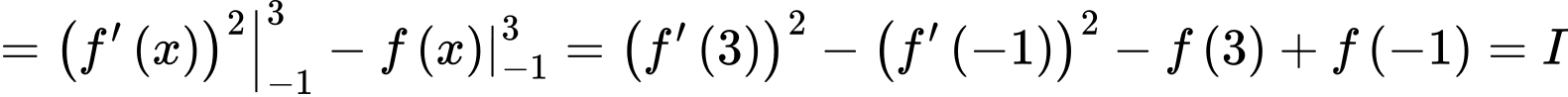
Có:
+) Quan sát đồ thị, ta thấy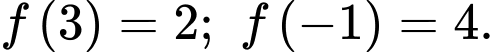
+)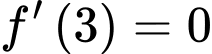 (Do
(Do 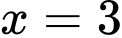 là điểm cực tiểu của hàm số).
là điểm cực tiểu của hàm số).
+) Hệ số góc tiếp tuyến tại điểm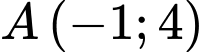 là
là 
Suy ra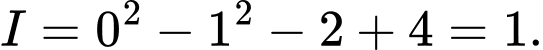
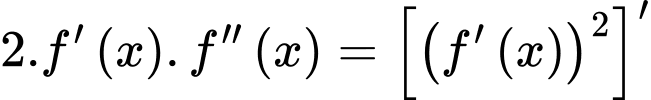
Suy ra
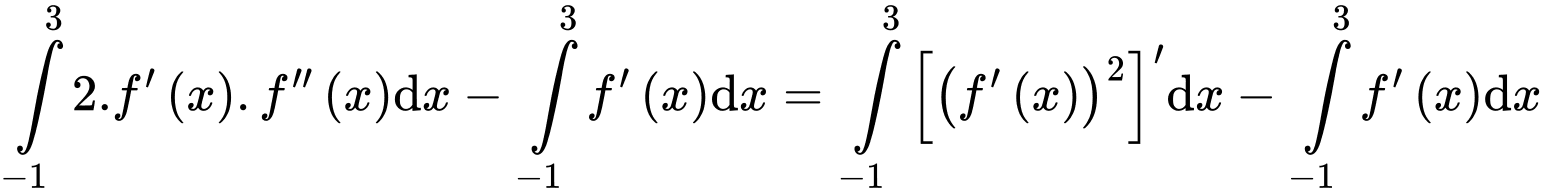
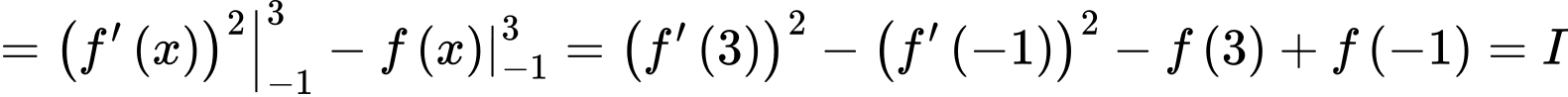
Có:
+) Quan sát đồ thị, ta thấy
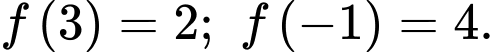
+)
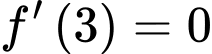 (Do
(Do 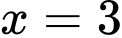 là điểm cực tiểu của hàm số).
là điểm cực tiểu của hàm số).+) Hệ số góc tiếp tuyến tại điểm
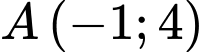 là
là 
Suy ra
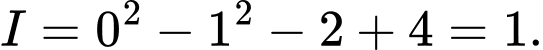
Câu 30 [389981]: Cho hàm số 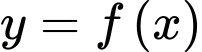 liên tục và luôn dương trên
liên tục và luôn dương trên 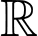 có đồ thị đi qua các điểm
có đồ thị đi qua các điểm 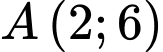 và
và 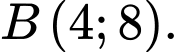 Tính
Tính 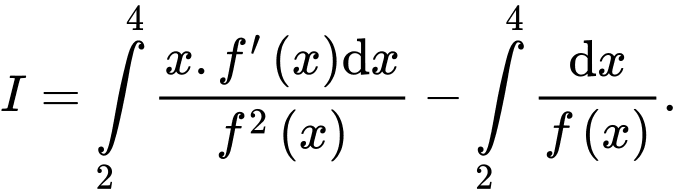 Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả làm tròn đến hàng phần trăm.
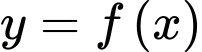 liên tục và luôn dương trên
liên tục và luôn dương trên 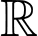 có đồ thị đi qua các điểm
có đồ thị đi qua các điểm 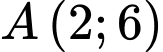 và
và 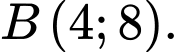 Tính
Tính 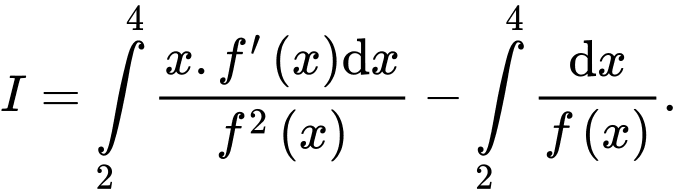 Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả làm tròn đến hàng phần trăm.
Ta có: